Representing Experimental
Procedures through Diagrams
at CERN’s Large Hadron
Collider: The Communicatory
Value of Diagrammatic
Representations in
Collaborative Research

Koray Karaca
University of Twente

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

The aim of this paper is to elucidate the use and role of diagrams in the design
of present-day high energy physics experiments. To this end, drawing upon a
prominent account of diagrammatic representations advanced by the cognitive
scientists Jill Larkin and Herbert Simon, I provide an analysis of the dia-
grammatic representations of the data selection and acquisition procedures pre-
sented in the Technical Design Report of the ATLAS experiment at CERN’s
Large Hadron Collider, where the Higgs particle was discovered in 2012.
Based upon this analysis, I argue that diagrams are more useful than texts
in organizing and communicating the procedural information concerning the
design of the aforementioned experimental procedures in the ATLAS experi-
ment. De plus, I point out that by virtue of their representational features,
diagrams have a particular communicatory value in the collaborative work of
designing the data acquisition system of the ATLAS experiment.

Introduction

1.
In relatively recent years, quite a number of diverse case studies concerning
the use of visual displays—such as graphs, diagrams, tables, pictures,
drawings, etc.—in both the physical and biological sciences have been
offered in the literature of the history and philosophy of science (HPS)—see,

I thank Christian Zeitnitz, Martina Merz, Efe Yazgan and an anonymous referee of this
journal for helpful discussions and comments on earlier versions of this paper. This research
is funded by the German Research Foundation (DFG) under project reference: Epistemologie des
LHC (PAK 428) – GZ: STE 717/3-1.

Perspectives on Science 2017, vol. 25, Non. 2
©2017 by The Massachusetts Institute of Technology

est ce que je:10.1162/POSC_a_00240

177

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

178

Representing Procedures through Diagrams at LHC

par exemple., Miller 1984; Lynch and Woolgar 1990; Baigrie 1996; Pauwels 2006.
These case studies have shown that visual representations fulfill important
functions in both the theoretical and experimental practices of science, thereby
emphasizing the non-verbal dimension of scientific inquiry that had been ne-
glected by the traditional language-based conception of science, which takes
the production, justification and dissemination of scientific knowledge to be
essentially linguistic processes expressed in the form of scientific theories and
hypotheses.1

The notion of diagrammatic representation has been long studied by
cognitive scientists in relation to the issue of problem solving and thinking
with diagrams, as well as in relation to the analysis of cognitive processes
involved in diagram interpretation and understanding (voir, par exemple., Cheng
et autres. 2001). Cependant, even though historians and philosophers of science
have drawn upon the resources of cognitive science to account for the cog-
nitive aspects of scientific inquiry (voir, par exemple., Giere 1992), the HPS literature
concerning the use of diagrams in scientific practice has not sufficiently
benefited from the literature of cognitive science on reasoning with dia-
grams. The present paper is an attempt to make use of the resources of
cognitive science to understand the role of diagrammatic representations in
the current practice of experimental high energy physics (HEP).

Using diagrams to describe experimental procedures is an established
practice in experimental HEP. Par exemple, block diagrams2 and flowcharts3
were used in the technical design reports of the HEP experiments performed
in the 1980s and 1990s, such as Large Electron-Positron Collider (LEP) ex-
periments at CERN (see LEP Collaboration 1984) and the Collider De-
tector II (CDF II) experiment at Fermilab (see CDF II Collaboration
1996). In this paper, as a case study, I will examine the use of diagrams
in the design of the data acquisition system of the ATLAS (A Toroidal
Large Hadron Collider Apparatus) experiment that has been running at
CERN’s Large Hadron Collider (LHC) in Geneva since September 2008 (voir
ATLAS Collaboration 2008). The ATLAS experiment is a multi-purpose
experiment aimed to test the prediction of the Higgs boson by the Standard

1. This conception dates back to the writings of the logical positivists who characterized
scientific discourse in terms of the logical and linguistic structures of scientific theories.
Karl Popper, who was the earliest critic of logical positivism, as well as the philosophers
of the post-positivist era in the philosophy of science—such as Norwood Russell Hanson,
Thomas Kuhn and Imre Lakatos—also saw scientific inquiry mainly as a linguistic process
driven by scientific theories and hypotheses.

2. A block diagram is a type of diagram that represents the main parts of a system as blocks

connected through lines that show the relationships between different parts of the system.

3. A flowchart is a type of diagram that represents the different steps of a process by

connecting them through arrows.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Perspectives on Science

179

Model (SM) of elementary particle physics4 as well as the predictions of a
wide range of theoretical models—often referred to as the models beyond the
SM (BSM models)—which have been offered as possible extensions of the
SM in the literature of HEP (voir, par exemple., Élise 2012). Dans 2012, the long-sought
Higgs boson was discovered in the ATLAS experiment (ATLAS Collaboration
2012) as well as in the CMS experiment (CMS Collaboration 2012), which is the
other multi-purpose experiment currently running at the LHC. As I shall show
in this paper, different types of diagrams borrowed from the literature of System
and Software Engineering (SSE)5 are used in the ATLAS Technical Design
Report (ATDR),6 which is a technical document that contains the design in-
formation concerning the principal components and functions of the ATLAS
data acquisition system (ATLAS Collaboration 2003). It is to be noted that the
diagrams of SSE I will analyze in this paper are much more complex than block
diagrams and flow charts used in the technical design reports of the LEP and
CDF II experiments. Before I start discussing the use of diagrams in the case
of the ATLAS experiment, in the next section I will offer a brief overview
of the HPS literature on the role of non-verbal reasoning in scientific practice.

2. HPS Perspectives on Non-Verbal Reasoning in Scientific Practice
In the HPS literature, the role of non-verbal reasoning in scientific practice has
been most prominently studied by David Gooding in the context of scientific
experimentation. Gooding has pointed out that even though “human agency
is essential to both exploratory observation and experimental testing” (Gooding
1990un, p. 10) it has not been addressed by the standard philosophy of science

4. The SM of elementary particle physics consists of two gauge theories; namely, le
unified theory of the weak and electromagnetic interactions, and the theory of quantum
chromo-dynamics that describes strong interactions.

5. SSE is a discipline concerned with the diagrammatic modeling of information sys-
tems for design and analysis purposes (see Booch et al. 2007; Hoffer et al. 2008). For a
philosophical discussion concerning diagrammatic modeling in SSE, see Karaca 2012.

6. The ATDR for data acquisition was reviewed by the Large Hadron Collider Experiments
Committee (LHCC). The LHCC reviews the technical design reports of the experiments planned
to run at the LHC, and makes recommendations to the CERN Research Board that takes final
decisions regarding experimental proposals. The approved proposals become part of the CERN
experimental program. It is stated in the minutes of the LHCC’s 67th meeting held on 26–27
Novembre 2003 that the LHCC recommended general approval of the ATDR to the CERN
Research Board. It is also stated in the minutes of the 167th meeting of the Research Board held
sur 26 Février 2004 that the ATDR was approved by the CERN Research Board. The minutes
of the meetings of the LHCC and those of the CERN research board, as well as the information
regarding these experimental committees, can be accessed at the URL: http://committees.web.
cern.ch/Committees. I am grateful to Peter Jenni, former spokesperson of the ATLAS exper-
iment, for clarifying the review process of the ATDR, as well as for drawing my attention to the
aforementioned minutes of the LHCC (personal communication, Juillet 22, 2014).

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

180

Representing Procedures through Diagrams at LHC

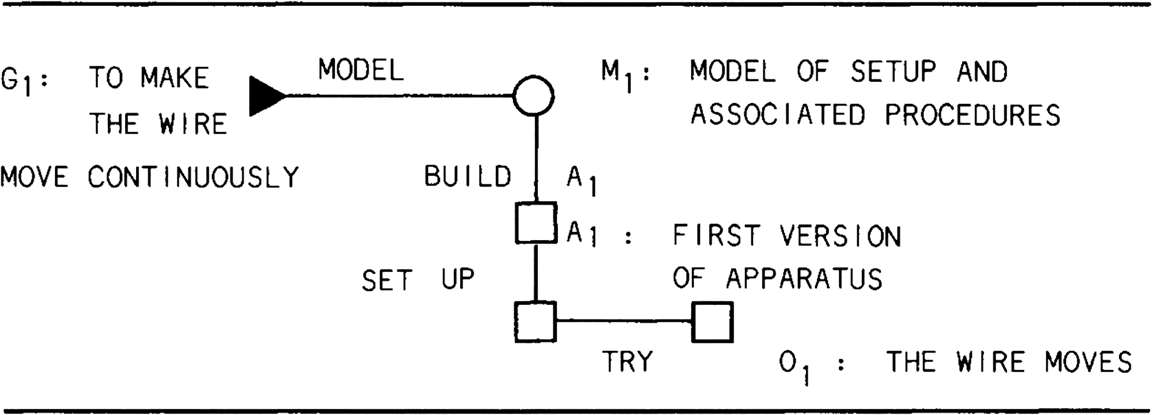
Chiffre 1. A Gooding map (Gooding 1990b, p. 180) that represents “Faraday’s
decision to build a setup, experiment with it, and represent and record outcomes”
(1990b, p. 179). In this map, a “square denotes the outcome of manipulations in the
matériel, phenomenal world (such as noticing, seeing, recording); and a circle denotes the
outcome of mental operations (such as imagining, visualizing, describing, inferring,
comparing) […] a solid triangle indicates a change of a major goal or method (par exemple.,
from seeking evidence for one hypothesis to proving the methods
used to obtain that evidence)» (1990b, p. 177–178).

that “has sought to reduce the interaction of theory and experiment to a
logical relationship, c'est, a relationship between propositions” (Gooding
1992, p. 65). In Gooding’s view, cependant, this is an untenably simple view
of the relationship between theory and experiment, as “[m]uch of what
experimenters do involves nonverbal doing” (Gooding 1992, p. 66). Good-
ing’s proposed solution to remedy this shortcoming is to elucidate what he
calls the “procedural knowledge” of experiment that is manifest in the im-
plementation of experimental procedures (Gooding 1990b, p.177).7 To this
end, Gooding has introduced a diagrammatic notation8 for mapping exper-
imental procedures and applied it to the case of Michael Faraday’s electro-
magnetic induction experiments in order to characterize the human agency
involved in performing these experiments in terms of Faraday’s “conceptual
and material manipulations” (Gooding 1990a,b). Using his diagrammatic
notation and Faraday’s laboratory notes, Gooding has provided, what he
calls, the “experimental maps” of Faraday’s manipulations during the
course of his experiments—as shown in Figure 1. In Gooding’s view, ces

7. Ici, Gooding draws upon a standard distinction in epistemology—originally due to
Gilbert Ryle (1945)—between two types of knowledge, namely, declarative knowledge
(“knowing-that”) and procedural knowledge (“knowing-how”), which are respectively defined
to be the knowledge of facts, things, or concepts, and the knowledge of performing actions.
8. Gooding’s notation is an elaboration of an earlier notation introduced by Ryan Tweney

(1989) to map the procedures of Faraday’s electromagnetic induction experiments.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Perspectives on Science

181

maps make visible the human agency that is essential to perform Faraday’s
experiments.

De plus, Gooding has argued that the visual imagery that consists of
lines of force and magnetic curves, and which Faraday created and used in his
experiments, was essential to the latter’s theorizing of the law of electromag-
netic induction. In Gooding’s view, through this visual imagery and
the physical concepts it implied, Faraday was able to make the phenomenon
of electromagnetic induction accessible to visual perception and eventually to
verbal expression in the form of a law of nature.

Unlike Gooding, Nancy Nersessian has examined the role of internal
representations associated with mental processes taking place during
scientific reasoning, rather than external representations provided by visual
displays. Nersessian has long advocated an approach, which she calls
“cognitive-historical method,” to analyze the problem solving practices of
scientists (Nersessian 1992). This method is based on the idea that the
resources of cognitive science can be used to elucidate some historical cases
of scientific reasoning (Nersessian 2008, chap. 1). In accordance with her
cognitive-historical method, Nersessian (2008, sect. 4.1) has adopted the
“mental models framework,” which emerged in the literature of cognitive
science in the 1980s following the seminal work of the cognitive psychologist
Philip Johnson-Laird (1980, 1983).9 Instead of subscribing to an already
existing account of mental models, Nersessian has advanced her own account,
which she calls the “minimalist mental modeling hypothesis” (2008, p. 128).
According to this account, in certain problem solving tasks, human reasoning
is carried out by means of the construction, implementation and manipu-
lation of a mental model, which Nersessian defines as “an organized unit
of knowledge that embodies representations of spatiotemporal relations, rep-
resentations of situations, entities, and processes, as well as representations of
other pertinent information, such as causal structure” (2008, p. 128).

Nersessian’s main purpose in drawing upon the mental models frame-
work is to understand how human reasoning is modeled during scientific
inquiry. Nersessian has applied her account of mental modeling to James
Clark Maxwell’s work on electromagnetism. She has argued that Maxwell’s
train of thought leading to his derivation of the electromagnetic field equa-
tions can be seen as reasoning through a mental model (2008, chap. 5).
Nersessian has noted that various diagrams, such as the vortex-idle wheel
diagram introduced by Maxwell, assisted him in his reasoning with the
mental model he worked with. This last point concerns the issue of how

9. For an overview of different accounts proposed in the mental models framework, voir

Nersessian 2008, sect. 4.1.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

182

Representing Procedures through Diagrams at LHC

mental models interact with external representations such as diagrams.10
Nersessian has argued that there exist

correspondences between elements of mental models and elements
represented in diagrams, [in the sense that] manipulating the
components of a diagrammatic representation as one perceives it or
acts on it can lead to corresponding transformations of the mental
model. (2008, p. 161)

In this way, according to Nersessian, diagrams have the potential to facili-
tate the human reasoning process through interplay with mental models
(Nersessian 2008).

In this paper, I will not address the issue of how scientists reason through
mental models during scientific inquiry. Plutôt, in line with Nersessian’s
cognitive-historical method, I will elucidate the role of diagrammatic
representations in the design of experimental procedures in the context
of the ATLAS experiment. To this end, I will draw upon a prominent
account of diagrammatic representations advanced by the cognitive sci-
entists Jill Larkin and Herbert Simon (hereafter L&S) (1987). In passing,
let me note that Nersessian has also drawn upon L&S’s account to argue
in what respects diagrammatic and propositional (sentential) represen-
tations differ from each other (Nersessian 2008, chaps. 4 et 5). Mais, elle
has not applied L&S’s account to a case study to examine the role of
diagrammatic representations in scientific practice.

3. L&S on Differences between Diagrammatic and Propositional
Representations
In a seminal paper, entitled “Why a diagram is (sometimes) worth ten
thousand words,” L&S (1987) have contrasted diagrammatic representa-
tions with propositional representations in order to characterize how these
two types of knowledge representation differ from one another, specifically
with respect to reasoning involved in problem solving in domains such as
physics and geometry. In L&S’s account, a propositional representation is a
“data structure in which elements appear in a single sequence,” whereas a
diagrammatic representation is a “data structure in which information is
indexed by two-dimensional location” (L&S 1987, p. 68). Based on these

10. The same issue has been also addressed in the literature of cognitive science; voir,

par exemple., Scaife and Rogers 1996; Hegarty 2004; Liu and Stasko 2010.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Perspectives on Science

183

definitions, L&S suggest that the “fundamental difference between our di-
agrammatic and sentential representations is that the diagrammatic repre-
sentation preserves explicitly the information about the topological and
geometric relations among the components of the problem, while the sen-
tential representation does not” (L&S 1987, p. 66). Donc, the distinc-
tion L&S draws between diagrammatic and propositional representations
indicates that, unlike propositional representations, “[d]iagrams are a kind
of analogical (or direct) knowledge representation mechanism that is charac-
terized by a parallel (though not necessarily isomorphic) correspondence
between the structure of the representation and the structure of the repre-
sented” (Kulpa 1994, p. 77).

L&S offer two main reasons “why a diagram can be superior to a verbal
description for solving problems” (1987, p. 98). The first reason concerns
what they call the “localization of information” (1987, p. 98), namely, le
spatial groupings of information that is necessary to solve a problem.
According to L&S’s account, in diagrammatic representations, since “infor-
mation is indexed by location in a plane, many elements may share the
same location, and each element may be ‘adjacent’ to any number of other
elements” (1987, p. 98). Diagrams thereby “can group together all infor-
mation that is used together” (L&S 1987, p. 98), and their use in domains
of problem solving (such as geometry and physics) substantially reduces
the need to search for the pieces of information relevant to make a problem
solving inference. Unlike in diagrammatic representations, in proposi-
tional representations, since “the data structure is indexed by position in
a list […] each element [lies] ‘adjacent’ only to the next element in the
list” (L&S 1987, p. 98). Par conséquent, the related pieces of represented in-
formation get increasingly separated from each other in propositional rep-
resentations as the amount of information increases, thus working against
the spatial localization of information (L&S 1987, p. 69). This in turn
makes propositional representations less efficient than diagrammatic repre-
sentations to solve problems in domains such as physics and geometry.

The second main reason L&S offer concerns the perceptual ease pro-
vided by diagrams in problem solving. Since there exists a structural
correspondence (not necessarily one-to-one), in terms of spatial relations
contained, between the information and its diagrammatic representation,
the latter has the ability to “automatically support a large number of
perceptual inferences, which are extremely easy for humans” (L&S
1987, p. 98). Par exemple, “when we draw a rectangle and its two diag-
onals, the existence of the point of intersection of the diagonals is inferred
automatically—the point is created on the paper, accessible to perception”
(L&S 1987, p. 98). Cependant, since no structural correspondence exists be-
tween spatial relations and their corresponding propositional representations,

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

184

Representing Procedures through Diagrams at LHC

information regarding spatial relations is not readily available to visual per-
ception when represented by texts and needs to be inferred from the syntactic
and semantic structures of sentences; thus making texts less efficient than
diagrams in terms of the representation of spatial relations. In L&S’s
account:

Two representations are informationally equivalent if all of the
information in the one is also inferable from the other, and vice
versa […] Two representations are computationally equivalent if
they are informationally equivalent and, in addition, any inference
that can be drawn easily and quickly from the information given
explicitly in the one can also be drawn easily and quickly from
the information given explicitly in the other, and vice versa.
(L&S 1987, p. 67)

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

In L&S’s account, diagrammatic and propositional representations are
not computationally equivalent, in that by virtue of spatial localization of
information and perceptual ease provided by diagrams, the ease and rapid-
ity of making a problem-solving inference through diagrammatic repre-
sentations are considerably greater than through propositional representations.
It is important to note that, in L&S’s account, as the title of their 1987
paper also indicates, the above-mentioned virtues of diagrams should not be
taken to imply that they are always superior to propositional representations
for problem solving. Plutôt, in order for a diagram to be useful in the problem-
solving process, it must be constructed in such a way to take advantage of
the above-mentioned virtues of diagrammatic representations (L&S 1987,
pp. 98–99).

The above overview suggests that L&S provide a ground not only to
account for the use and function of diagrammatic representations in experi-
mentation, but also to compare the diagrammatic and propositional rep-
resentations of experimental procedures to assess their relative effectiveness.
In this paper, I shall make use of L&S’s account to examine the diagram-
matic representations of data selection and acquisition procedures presented
in the ATDR, as well as to compare them with the corresponding textual
descriptions. It is worth noting that typically relatively simple examples of
diagrams, such as those used in physics and geometry textbooks, have been
examined in the literature of cognitive science. In this sense, the diagrams of
SSE used in the ATDR present a novel case in which to analyze the differences
between diagrammatic and propositional representations, in that the fore-
going diagrams are far more complex and standardized than those diagrams
previously considered in cognitive science studies.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Perspectives on Science

185

4. Description of the ATLAS Data Acquisition System through Diagrams
In order for a HEP experiment to achieve its intended objectives, what
are often called interesting events11 need to be acquired during the process
of data acquisition. Interesting events are those collision events that are
considered to have the potential to serve the objectives of the experiment.
Given that in HEP experiments, new particles are detected through their
signatures, c'est à dire., stable decay products, the collision events that contain the
signatures of novel particles are considered to be interesting in the afore-
mentioned sense. In the case of the ATLAS experiment, interesting colli-
sion events refer to those collision events that contain the signatures of the
Higgs boson predicted by the SM and those of the novel particles pre-
dicted by the BSM models, such as superpartner particles predicted by
supersymmetric models. The foregoing signatures include particles,
namely, photons and leptons12 with transverse momentum ( pT)13 at or
above O (10) GeV, and jets with pT at or above O (100) GeV, ainsi que
missing or total transverse energy (ET) at or above O (10) GeV.14

The process of data acquisition in the ATLAS experiment is carried out
in three stages by using trigger systems that perform an online selection
(c'est à dire., while proton beams are colliding inside the LHC) of interesting
events according to a set of pre-determined selection criteria called a
trigger menu.15 The selection criteria are given in terms of the afore-
mentioned signatures. Tableau 1 illustrates a sample trigger menu that consists
of some of the major data selection criteria used in the ATLAS experiment.
Each selection signature (or criterion) given in the left column of Table 1 est
denoted as “NoXXi.” Here, “N” denotes the minimum number of signatures
required for a particular selection, and “o” denotes the type of the selected
signature; par exemple., “e” for electron; “γ” for photon; “μ” for muon; “xE” for
missing ET; “E” for total ET; and “jE” for total ET associated with jet(s).
The label “XX” denotes a lowest ET (in units of GeV) for the signature under

11. In the terminology of experimental HEP, a collision event is defined to be a set of
particle interactions that occur as a result of one bunch crossing, which takes place when
two beams of particles collide with each other inside the particle collider.

12. A lepton is a spin ½ particle that interacts through electromagnetic and weak
interactions, but not through strong interactions. In the SM, leptons are: electron, muon,
tau, and their respective neutrinos.

13. Transverse momentum ( pT) is the component of the momentum of a particle that is
transverse to the proton-proton collision axis inside the ATLAS detector, and transverse
energy (ET) is the energy due to transverse momentum.

14. For a thorough discussion of interesting events in the case of the ATLAS experi-

ment, see ATLAS Collaboration 2003, sect. 4.

15. For the details of how selection criteria are determined, see ATLAS Collaboration

2003, chap. 4. For a philosophical discussion, see Karaca (2017).

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

186

Representing Procedures through Diagrams at LHC

Tableau 1. Major selection criteria used in the ATLAS experiment. (Source:
ATLAS Collaboration 2003, p. 38)

Selection signature

Examples of physics coverage

e25i

2e15i
μ20i

2μ10
γ60i
2γ20i

j400

2j350

3j165

4j110
τ60i
μ10 + e15i
τ35i + xE45

j70 + xE70

xE200

E1000

0

0
, Z

W → eν, Z → ee, top production, H → WW(*)/ZZ(*),
W
Z → ee, H → WW(*)/ZZ(*)
W → μν, Z → μμ, top production, H → WW(*)/ZZ(*),
W0, Z0
Z → μμ, H → WW(*)/ZZ(*)
direct photon production, H → γγ
H → γγ

QCD, SUSY, new resonances

QCD, SUSY, new resonances

QCD, SUSY

QCD, SUSY

charged Higgs
H → WW(*)/ZZ(*), SUSY
qqH(ττ), W → τν, Z → ττ, SUSY at large tan β

SUSY

new phenomena

new phenomena

jE1000
2μ6 + μ+μ−

+ mass cuts

new phenomena
rare b-hadron decays (B → μμX) and B → J/ψ (ψ0

)X

consideration, and “i” denotes an isolation requirement for the given signa-
ture. Par exemple, the selection criterion “e25i” in Table 1 amounts to the
requirement of at least one isolated electron with an ET at or above
25 GeV. The right column of Table 1 shows the physics processes predicted
by the SM and the BSM models to which the selection signatures in the left
column of the same table are relevant (for details, see ATLAS Collaboration
2003, sect. 4.4.1).

The first stage of the data acquisition process is carried out by the level-1
trigger system that performs a crude selection of potentially interesting
events from the collision events detected by the calorimeter and muon detec-
tors, which are the components of the ATLAS detector system. The level-1

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Perspectives on Science

187

trigger system produces a trigger decision within 2.5 microseconds and
thereby reduces the LHC event rate of 40 MHz down to the range of
75–100 kHz. For future reference, note that the regions in the ATLAS
detector that contain signals for interesting events are called “regions of
interest” (RoIs) and that the RoIs and the energy information associated
with the signals detected inside the RoIs are together referred to as the
“RoI data.”

In addition to the calorimeter and muon detectors, the tracking detectors
are also used in the ATLAS experiment.16 Since the event rate is so high and
thus the trigger decision time is so short, it is technologically impossible for
the tracking detectors to determine particle tracks quickly enough for the
level-1 event selection. Only the hit points produced by particles inside the
tracking detectors could be recorded. Software algorithms later assemble
these space points in order to determine particle tracks. Par conséquent, the data
from the tracking detectors are not used directly by the level-1 trigger sys-
tem for event selection. De plus, even though the hit points are recorded,
they are not completely read out from the tracking detectors during the
level-1 selection due to the shortness of the level-1 trigger-decision time.
This means that the information (c'est à dire., in terms of location in the detector,
and pT or ET for each particle or jet contained, or associated missing ET)
necessary to fully specify a selected event is fragmented across the individual
detectors of the ATLAS detector system, and all pieces of this fragmented
information are not assembled yet so as to fully describe a selected event.
Donc, the full description of the event is not yet known, and as a
result, the level-1 event selection is performed without full granularity,
c'est à dire., without the availability of data from all the channels of the individual
detectors.

The level-2 and level-3 trigger systems, which are jointly called the High
Level Trigger (HLT) système, have longer trigger decision times and thus can
provide much finer selections of interesting events than the level-1 trigger
système. The event accept rates of these trigger systems are respectively
autour 2 kHz et 200 Hz.17 Unlike the level-1 trigger system that is
hardware-based, the HLT system is software-based, meaning that event
selections are performed directly by specialized software algorithms. In the
diagram shown in Figure 2, which illustrates what is called a communication

16. In HEP experiments, the tracking detectors are used to determine particle tracks as
well as to measure the momenta of electrically charged particles by means of the curvatures
of their tracks in a magnetic field.

17. These and previous event accept rates are valid for early data taking at the LHC, comme

they have later changed significantly.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

188

Representing Procedures through Diagrams at LHC

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

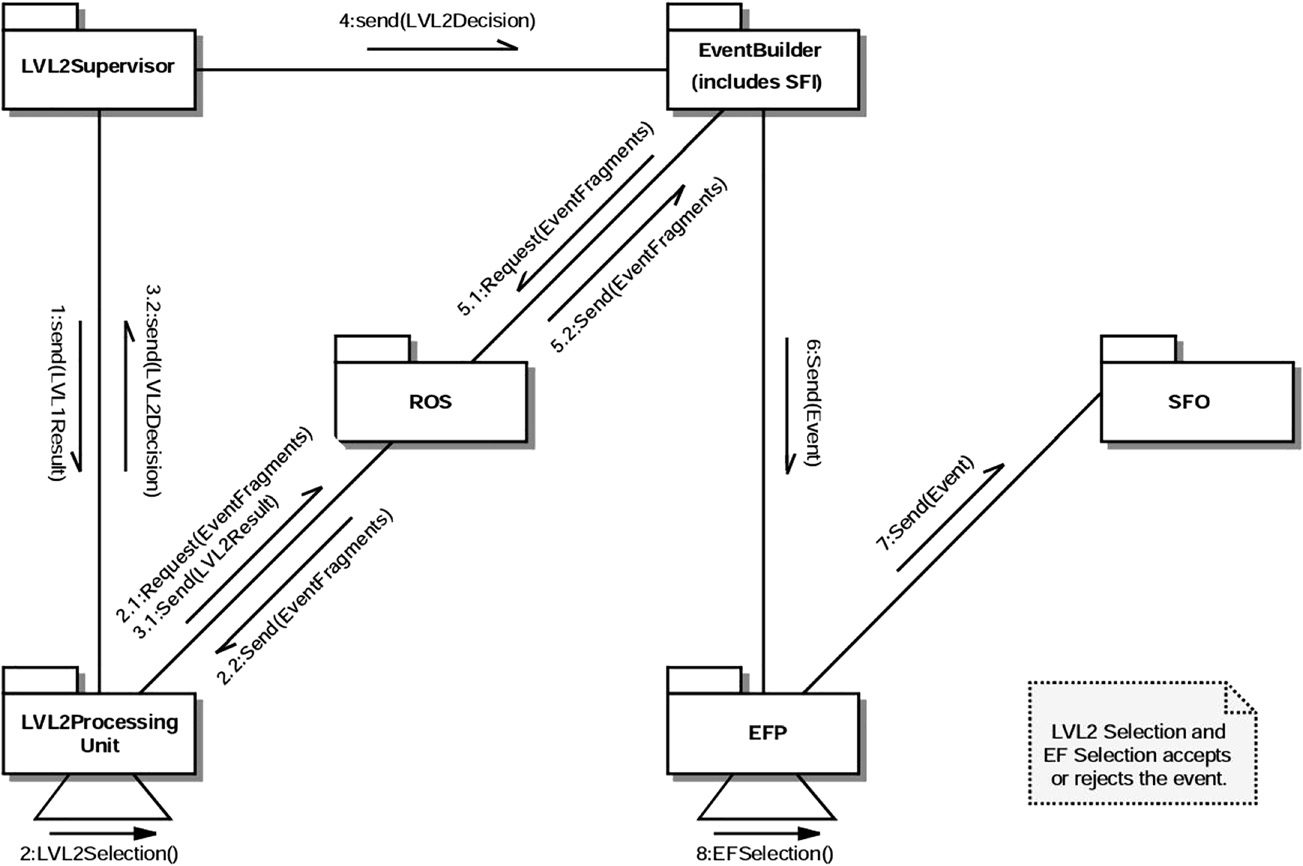
Chiffre 2. The communication diagram for the implementation of the HLT system
in the ATLAS experiment. (Source: ATLAS Collaboration 2003, p. 126, Chiffre 9-2)

diagram18 in SSE, the sub-units of the HLT system are represented as objects,
and the messages exchanged among them are represented by text-labeled
solid arrows. As shown in this communication diagram, the level-2 event
selection begins when the sub-unit called “level-2 supervisor” (denoted as
“LVL2Supervisor”) sends the results of the level-1 selection to the sub-unit
called “level-2 processing” (denoted as “LVL2Processing Unit”). Unlike the
level-1 trigger system, the level-2 trigger system uses the RoI data processed
by the sub-unit called “Read-out System” (ROS) from all the sub-detectors of
the ATLAS detector with full granularity. The communication between the

18. In SSE, a communication diagram (also called a collaboration diagram) provides a
diagrammatic representation of the ways in which a particular set of objects exchange in-
formation with each other during a certain period of time in order to achieve a common
but (voir, par exemple., Booch et al. 2007, sect. 5.14). The term object is used in SSE to denote
entities that perform specific tasks whenever they are called upon by messages. Each rect-
angular box in the communication diagram shows a particular object, the name of which
appears in the same box. A communication diagram does not include a time axis, because it
does not specifically focus on the temporal order of messaging among objects. In a com-
munication diagram, messages exchanged among objects are shown by number-tags and
text-labeled arrows. The temporal order of messages is indicated by the increasing order
of number-tags. If a message prompted other messages in a system, the prompted messages
are nested inside the prompting one.

Perspectives on Science

189

LVL2Supervisor and the LVL2Processing is shown by the message labeled “1”
in Figure 2.

The event fragments, which are temporarily stored in the ROS, sont
accepted to the level-2 selection in small amounts. This way of performing
event selection is called the seeding mechanism in the ATDR (ATLAS
Collaboration 2003, sect. 9.5.3.1). Note that if event fragments were
accepted at once, this would considerably diminish the level-2 trigger
decision time and thus render the selection process ineffective. The seeding
mechanism is initiated by the transmission of the message labeled “2.1” by
the LVL2Processing unit to the ROS. Upon the reception of this message,
the ROS sends to the Level2Processing Unit a subset of the event-
fragments data, namely, the information regarding the locations (dans le
detector), momenta, and energies of the events selected at the level-1 selec-
tion. This communication between the Level2Processing Unit and the ROS
is represented by the message labeled “2.2” in the communication diagram.
The LVL2Processing unit sends the information regarding the events
accepted by the level-2 trigger system back to the ROS. The LVL2Processing
unit also sends the same information to the LVL2Supervisor. The foregoing
communications are shown respectively by the messages labeled “3.1” and
“3.2” in the communication diagram. The LVL2Supervisor forwards the
same information, indicated by the message labeled “4”, to the sub-unit
called “Event Builder,” which, as shown by the message labeled “5.1”,
requests from the ROS the event-fragments data for the events selected by
the LVL2Processsing unit. Upon this message, as shown by the message
labeled “5.2”, the ROS sends the event fragments to the Event Builder.
The component called “Sub-Farm Input” (SFI) of the Event Builder assem-
bles the event fragments associated with each selected event into a single
record. Donc, at this stage, the full description of each selected event
is available. As shown by the message labeled “6”, the events that have been
built are then passed to the sub-unit called “Event Filter Processor” (EFP),
through which the level-3 event selection, which is also called “event filter”
(EF) selection, is carried out by specialized software algorithms. As shown by
the message labeled “7”, the events that have passed the level-3 selection are
then sent to the sub-unit called “Sub-Farm Output” (SFO) for permanent
storage and offline data analysis.19

Note that the details of the level-2 and level-3 selection processes are
not shown in the communication diagram in Figure 2. These selection
processes are carried out by the Event Selection Software (ESS) système,
which is a software component of the HLT system (ATLAS Collaboration

19. Note that in the communication diagram shown in Figure 2, the correct number-
tags for the messages “EFSelection” and “SendEvent” should be “7” and “8” respectively.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

190

Representing Procedures through Diagrams at LHC

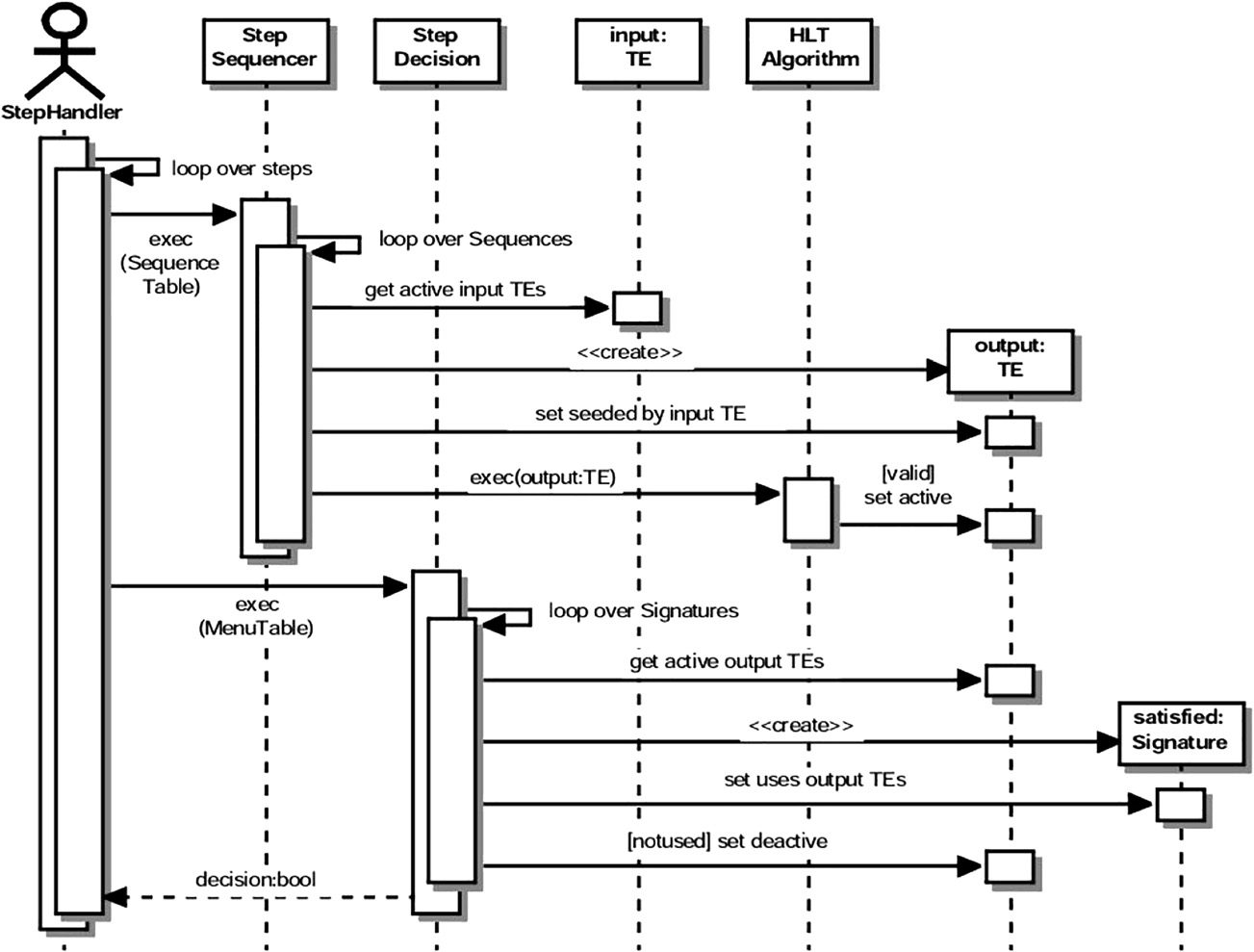
2003, sect. 9).20 The details of the level-2 selection process are shown in
the diagram in Figure 3, which illustrates what is called a sequence dia-
gram21 in SSE. As shown in this sequence diagram, the level-2 selection
of an event is carried out in a series of steps each of which consists of
two stages. In the first stage, the event is partially reconstructed, meaning
that the trigger elements (TEs)22 associated with the event are refined and
reconstructed by the reconstruction algorithms according to what is called
the sequence table of the step. Each sequence in this table consists of an
input TE and a reconstruction algorithm that is to be executed to refine
and reconstruct an input TE into an output TE.23 In the second stage, le
event partially reconstructed undergoes a selection process based on what is
called the menu table of the step that contains a list of the selection sig-
natures required for this step.

As shown in the sequence diagram in Figure 3, the Step Handler initi-
ates the first stage of the level-2 selection by executing the Step Sequencer
to access the list of the active input TEs associated with an event selected by
the level-1 trigger system. The Step Sequencer next compares the list of the
active TEs with the required TEs given in the sequence table of the step. Pour
all matching TEs, the Step Sequencer executes the reconstruction algo-
rithms to refine and reconstruct the input TEs into the output TEs accord-
ing to the sequence table of the step. The Step Sequencer also creates the list
of the output TEs for the implementation of the seeding mechanism
discussed earlier. The Step Sequencer also marks each output TE as “seeded

20. For future reference, note that the following units to be mentioned in what follows,
namely, Step Handler, Step Sequencer, Step Decision, Step Controller and Result Builder,
are the software components of the ESS system that steers the HLT selection process.

21. Note that the communication and sequence diagrams for the same system contain
the same information. Cependant, unlike a communication diagram, a sequence diagram fo-
cuses on the temporal order of messages exchanged among objects in a system (voir, par exemple.,
Hoffer et al. 2008, pp. 268–75). In a sequence diagram, time increases down the vertical
axis. Each object in the system is shown by a rectangular box lying along the horizontal axis
at the top of the diagram. What is called the “lifeline” of an object is denoted by either a
dashed or solid line emanating from that object and lying along the vertical axis. Each thin
rectangular box emanating from an object and superimposed on the lifeline of the same
object represents the time period during which an object performs a task. Message scripts
are generally put just above the message arrows, and return messages are typically not
shown, as they unnecessarily complicate sequence diagrams.

22. A TE denotes one specific signature identified by the level-1 trigger system, par exemple.,
“e25i”. A TE is said to be active if it has previously satisfied a selection signature at the
level-1 selection, or at the previous step of the level-2 selection, if the step under consid-
eration is not the first step of the level-2 selection.

23. Reconstruction algorithms are a class of HLT algorithms that act on the RoI data
with full granularity from all sub-detectors to find new features associated with input TEs,
such as a track or an isolation requirement.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Perspectives on Science

191

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

Chiffre 3. The sequence diagram for the implementation of the ESS system for the
level-2 event selection in the ATLAS experiment. (Source: ATLAS Collaboration
2003, p. 150, Chiffre 9.21)

by input TE” depending on from which input TE it has been previously
created. Alors, it passes each output TE to the relevant hypothesis
algorithms—another class of HLT algorithms—that decide whether the
TE is valid, depending on whether its reconstructed features are consistent
with its physics interpretation. Par exemple, if a track or an isolation
requirement associated with a TE is found by a reconstruction algorithm,
then the relevant hypothesis algorithm determines whether this track or
isolation requirement matches the physics interpretation of the TE. Le
hypothesis algorithms activate the validated TEs and discard the invali-
dated TEs by deactivating them.

As shown in the sequence diagram in Figure 3, the Step Handler ini-
tiates the second stage of the level-2 selection by calling the Step Decision
to access the list of the active output TEs, c'est à dire., the TEs validated by the
hypothesis algorithms in the first stage of the level-1 selection. The Step
Decision compares the list of the active output TEs with the required
selection signatures given in the menu table of the step. For the TE combi-
nations that match the selection signatures in the menu table, the Step

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

192

Representing Procedures through Diagrams at LHC

Decision creates a list of the satisfied signatures that consist of those matching
TE combinations. The Step Decision accepts the event for the next step if
the TE combinations it contains satisfy at least one signature given in the
menu table of the step; otherwise it is rejected and thus not considered for
the level-3 selection. In the next step, only those TEs that have been used to
satisfy at least one signature in the previous step are considered, et le
others are discarded from further processing. The Step Decision sends the in-
formation regarding the decision about the event to the Step Handler that
will initiate the next step configured with a different sequence table and a
menu table. The level-2 selection of an event ends at the step where it is re-
jected, or it continues until all required steps are completed, indicating that
the event is finally accepted for the level-3 selection.

If an event is accepted at the level-2 selection, the Step Controller ex-
ecutes the Result Builder to provide the information necessary to seed the
level-3 selection. This includes all satisfied signatures and the associated
TE combinations as well as the level-1 RoI data. The Result Builder as-
sembles all these data-fragments, and the results are subsequently used for
the seeding of the level-3 selection. The level-3 selection is implemented
and coordinated by the Step Handler in the similar way as the level-2 se-
lection is carried out, as shown in the sequence diagram in Figure 3. Mais
the level-3 selection differs from the level-2 selection in that the TEs are
now the active TEs of the level-2 selection, and that more sophisticated
HLT algorithms are used to achieve a much finer event selection. As has
been mentioned previously, the events that have passed the level-3 selec-
tion are stored in the SFO for data analysis.

The above overview indicates that the process of data acquisition in the
ATLAS experiment is essentially a selection process through which inter-
esting collision events are selected in three stages by the ATLAS trigger
systèmes. This selection process consists of various experimental procedures
that are represented in the ATDR through communication and sequence
diagrams borrowed from the literature of SSE.24 As shown in Table 2, le
communication and sequence diagrams shown in Figures 2 et 3 represent

24. The ATDR also uses other types of SSE diagrams. The procedures concerning the flow of
various types of data between the HLT system and the level-1 trigger system as well as between
the HLT system and the external systems, including the LHC machine, the ATLAS detector
system and the data storage unit, are represented by what is called a context diagram in SSE
(see ATLAS Collaboration 2003, Chiffre 5-1, p. 48; for details about a context diagram in
SSE, see Hoffer et al. 2008, chap. 7). De plus, the procedures concerning how the HLT algo-
rithms relate to and depend on each other are represented by what is called a class diagram
(see ATLAS Collaboration 2003, Chiffre 9.18, p. 147; for details about a class diagram in
SSE, see Booch et al. 2007, chap. 3 and sect. 5.7). I shall not discuss the use of the foregoing
types of diagrams in the ATDR, as they are not necessary for the argument of the present paper.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

s

w
o
fl

un
t
un
d

F
o

s
n
o
je
t
c
e
r
je
d

s
e
g
un
s
s
e
m

F
o

d
n
un

s

w
o
fl

s
n
o
je
t
c
e
r
je
d

:
s

w
o
r
r
un

d
je
je
o
S

F
o

s
t
n
e
t
n
o
c

:
s
je
e
b
un
je

t
X
e
T

je
un
c
je
t
r
e
v

:
s
n
o
je
t
un
je
e
r

je
un
je
t
un
p
S

je
un
r
o
p
m
e
t

:
s
n
o
je
t
un
je
e
r

je
un
r
o
p
m
e
T

e
t
o
n
e
d

s

w
o
r
r
un

d
je
je
o
s

F
o

un
t
un
d

F
o

d
n
un

s
e
g
un
s
s
e

m

d
e
je
e
b
un
je
–
t
X
e
t

F
o

r
e
d
r
o

je
un
je
t
un
p
s

F
o
d
n
un

s

w
o
fl

un
t
un
d
F
o

r
e
d
r
o

c
je
t
un
m
m
un
r
g
un
je
d

c
je
je
o
b
m
oui
S

d
e
t
un
je
c
o
s
s
un
d
n
un

s
t
n
e
m
e
je
e

c
je
t
un

m
m

un
r
g
un
je
d

c
je
t
s
je
toi
g
n
je
L

d
e
t
un
je
c
o
s
s
un

d
n
un

s
t
n
e

m

e
je
e

s
n
o
je
t
n
e
v
n
o
c

s
n
o
je
t
n
e
v
n
o
c

s
n
o
je
t
c
e
r
je
d
:
s

w
o
r
r
un
d
je
je
o
S

F
o

s
t
n
e
t
n
o
c

:
s
je
e
b
un
je

t
X
e
T

e
t
o
n
e
d

s

w
o
r
r
un
d
je
je
o
s

F
o

un
t
un
d

F
o

d
n
un

s
e
g
un
s
s
e

m

s

w
o
fl

un
t
un
d

F
o

s
n
o
je
t
c
e
r
je
d

s
e
g
un
s
s
e
m

F
o
d
n
un

s

w
o
fl

:
s
g
un
t
–
r
e
b
m
toi
n

e
g
un
s
s
e

M.

s
g
un
t
–
r
e
b
m
toi
n

e
g
un
s
s
e

m

r
e
d
r
o

e
m

je
t

s
e
t
o
n
e
d

F
o

r
e
d
r
o

je
un
c
je
r
e
m
toi
n

s
e
g
un
s
s
e
m

F
o

F
o

s
t
n
e
t
n
o
c

:
s
je
e
b
un
je

t
X
e
T

un
t
un
d

F
o

d
n
un

s
e
g
un
s
s
e

m

s

w
o
fl

s
n
o
je
t
c
e
r
je
d

:
s

w
o
r
r
un

d
je
je
o
S

F
o

s
t
n
e
t
n
o
c

:
s
je
e
b
un
je

t
X
e
T

e
t
o
n
e
d

s

w
o
r
r
un

d
je
je
o
s

F
o

un
t
un
d

F
o

d
n
un

s
e
g
un
s
s
e

m

s

w
o
fl

un
t
un
d

F
o

s
n
o
je
t
c
e
r
je
d

s
e
g
un
s
s
e
m

F
o

d
n
un

s

w
o
fl

g
n
je
t
n
e
s
e
r
p
e
r

g
n
je
d
n
o
p
s
e
r
r
o
C

s
n
o
je
t
un
je
e
r

je
un
r
toi
d
e
c
o
r
P.

d
n
un
n
o
je
t
c
e
je
e
s

un
t
un
d
S
UN
L
T
UN

s
n
o
je
t
c
e
r
je
d

:
s
n
o
je
t
un
je
e
r

je
un
je
t
un
p
S

s

w
o
r
r
un

d
je
je
o
s

d
e
je
e
b
un
je
–
t
X
e
t

F
o

s
t
je
n
toi
m

un
r
g
un
je
d

g
n
o
m

un

e
g
un
s
s
e

m

F
o

r
e
d
r
o

je
un
c
je
r
e

m
toi
n

:
s
n
o
je
t
un
je
e
r

je
un
c
je
r
e

m
toi
N

s
g
un
t
–
r
e
b
m
toi
n

s
n
o
je
t
c
e
r
je
d
:
s
n
o
je
t
un
je
e
r

je
un
je
t
un
p
S

s

w
o
r
r
un
d
je
je
o
s

d
e
je
e
b
un
je
–
t
X
e
t

F
o

s
t
je
n
toi
m

un
r
g
un
je
d
g
n
o
m

un

s
n
o
je
t
c
e
r
je
d

:
s
n
o
je
t
un
je
e
r

F
o

d
n
un

s

w
o
fl

je
un
je
t
un
p
S

un
t
un
d

F
o

g
n
o
m
un
d
e
g
n
un
h
c
X
e

s
e
g
un
s
s
e
m

m

e
t
s
oui
s
T
L
H
e
h
t

F
o

s
t
je
n
toi

e
h
t

s

w
o
fl

un
t
un
d

F
o

r
e
d
r
o

je
un
r
o
p
m
e
t

:
s
n
o
je
t
un
je
e
r

je
un
r
o
p
m
e
T

T
L
H
e
h
t

F
o

s
t
je
n
toi

e
h
t
g
n
o
m
un

d
e
g
n
un
h
c
X
e

s
e
g
un
s
s
e
m

F
o
d
n
un

s
e
g
un
s
s
e

m

F
o
d
n
un

s

w
o
fl

s
n
o
je
t
c
e
r
je
d

:
s
n
o
je
t
un
je
e
r

m
e
t
s
oui
s

je
un
je
t
un
p
S

un
t
un
d

F
o

s
t
je
n
toi

e
h
t
g
n
o
m
un
d
e
g
n
un
h
c
X
e

m
e
t
s
oui
s

S
S
E
e
h
t

F
o

s

m

un
r
g
un
je
d

n
je

s
n
o
je
t
un
je
e
r

s

m
un
r
g
un
je
d

oui
b

d
e
t
n
e
s
e
r
p
e
r

s
e
r
toi
d
e
c
o
r
p

n
o
je
t
je
s
je
toi
q
c
un

g
n
je
d
n
o
p
s
e
r
r
o
c
d
n
un

c
je
t
un
m
m
un
r
g
un
je
d

s
n
o
je
t
un
t
n
e
s
e
r
p
e
r

e
h
t

F
o
n
o
je
t
un
t
n
e
m
e
je
p
m

je

:

m
e
t
s
oui
s
T
L
H

m
un
r
g
un
je
d
n
o
je
t
un
c
je
n
toi
m
m
o
c

e
h
t

F
o

n
o
je
t
un
t
n
e
m
e
je
p
m

je

e
c
n
e
toi
q
e
s

:

m
e
t
s
oui
s

S
S
E

m
un
r
g
un
je
d

c
je
t
un
m
m
un
r
g
un
je
d

g
n
je
d
n
o
p
s
e
r
r
o
c

r
je
e
h
t

d
n
un

m

e
t
s
oui
s

n
o
je
t
je
s
je
toi
q
c
un

un
t
un
d

S
UN
L
T
UN

e
h
t

n
je

s
n
o
je
t
un
je
e
r

je
un
r
toi
d
e
c
o
r
P.

.

2

e
je
b
un
T

.
s
t
n
e

m

e
je
e

c
je
t
un

m
m

un
r
g
un
je
d

c
je
je
o
b
m
oui
s

d
n
un

c
je
t
s
je
toi
g
n
je
je

r
je
e
h
t

h
t
je

w

r
e
h
t
e
g
o
t

s
n
o
je
t
un
t
n
e
s
e
r
p
e
r

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

s

w
o
r
r
un
d
je
je
o
s

g
n
o
m
un
d
e
g
n
un
h
c
X
e

s
e
g
un
s
s
e
m

m

e
t
s
oui
s

S
S
E
e
h
t

F
o

s
t
je
n
toi

e
h
t

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

194

Representing Procedures through Diagrams at LHC

the procedural information regarding the implementation of the HLT and
ESS systems, respectivement. This procedural information includes both
spatial relations, namely, directions of data flows and those of messages
exchanged as well as temporal relations, namely, temporal order of data
flows and that of messages exchanged. In both of the aforementioned di-
agrams the directions of data flows and those of messages exchanged are
represented as spatial relations, namely, text-labeled solid arrows. In the
communication diagram, the temporal order of data flows and that of mes-
sages exchanged are represented by the numerical order of the message
number-tags. In the sequence diagram, the temporal order of data flows
and that of messages exchanged are represented by the vertical spatial order
of text-labeled solid arrows.

Since the foregoing spatial relations existing among the sub-units of the
HLT and ESS systems are represented as spatial relations by the commu-
nication and sequence diagrams in Figures 2 et 3 respectivement, là
exists a structural correspondence, in terms of spatial relations contained,
between the communication diagram in Figure 2 and the HLT system as
well as between the sequence diagram in Figure 3 and the ESS system. Comme
shown in Table 2, the communication and sequence diagrams maintain the
foregoing structural similarities through the use of both symbolic (c'est à dire.,
consisting of a diagrammatic symbol) and linguistic (c'est à dire., involving both
syntactic and semantic structures) diagrammatic elements. These diagrams
also make use of certain symbolic and linguistic elements for the represen-
tation of temporal relations.

It is to be noted that by virtue of the aforementioned structural corre-
spondence, the spatial and numerical relationships contained in the afore-
mentioned communication and sequence diagrams enable one to draw
inferences about the spatial and temporal relationships found in the
HLT and ESS systems of the ATLAS experiment. Par exemple, the tempo-
ral order of the messages exchanged during the implementation of the
HLT system can be inferred by examining the numerical order of the mes-
sage number-tags in the communication diagram in Figure 2. Incidentally,
this last point indicates a similarity between the aforementioned diagrams
and mental models, in that the latter, in Nersessian’s account, also “em-
body and comply with the constraints of the phenomena being reasoned
à propos, and thus enable inferences about these phenomena” (Nersessian
2008, p. 129).

5. Advantages of Diagrams over Texts for the Representation of Data
Selection and Acquisition Procedures in the ATLAS Experiment
The use of communication and sequence diagrams in the ATDR is essential
to presenting the data selection and acquisition procedures implemented

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Perspectives on Science

195

in the ATLAS experiment. Both the communication diagram shown in
Chiffre 2 and the sequence diagram shown in Figure 3 are presented in
the main text of the ATDR, rather than in an appendix, to introduce, concernant-
spectively, the procedures concerning the implementation of the HLT and
ESS systems.25 In the main text of the ATDR, each of the foregoing dia-
grams is immediately followed by its corresponding textual description
(voir, ATLAS Collaboration 2003, pp. 126, 150–51, respectivement). These
textual descriptions are provided in the ATDR in a very similar manner
as presented in Section 4 of the present paper. A comparison of the commu-
nication and sequence diagrams with their corresponding textual descrip-
tions indicates that all the procedural information (regarding the
implementation of the HLT and ESS systems) that can be inferred from
the communication and sequence diagrams can also be inferred from their
corresponding textual descriptions, and vice versa. This suggests that the
foregoing diagrammatic and propositional representations of the data
acquisition and selection procedures implemented in the ATLAS experi-
ment are, to use L&S’s terminology, informationally equivalent.

It is also worth noting that unlike the communication and sequence
diagrams in Figures 2 et 3, the corresponding textual descriptions, dans
addition, include some short explanations concerning the details of the
HLT and ESS systems. These explanations are intended to provide the users
of the ATDR with the information regarding certain key considerations
underlying the design of the HLT and ESS systems, rather than regarding
their implementation in the ATLAS experiment. In this sense, they are not
essential to the (textual) descriptions of the implementation of the forego-
ing systems. Par exemple, the textual description concerning the imple-
mentation of the HLT system (following the communication diagram in
Chiffre 2) includes an explanation, which is similar to the explanation
given in Section 4 of the present paper, as to why the seeding mechanism
underlying the level-2 event selection is necessary for the HLT process (voir
ATLAS Collaboration 2003, p. 126). Note that this explanation does not
include any description at all as to how the seeding mechanism is imple-
mented in the HLT system. Plutôt, it involves the primary consideration
as to why the seeding mechanism in the level-2 selection is necessary. Pour
that reason, the foregoing explanation about the seeding mechanism is not
essential to the textual description concerning the implementation of the
HLT system.

25. This is also true for the context and class diagrams used in the ATDR.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

196

Representing Procedures through Diagrams at LHC

The fact that the communication and sequence diagrams and their cor-
responding textual representations are informationally equivalent does not
mean that they are also computationally equivalent—in the sense of L&S’s
account. In what follows, I shall argue that the diagrammatic representa-
tions of the data selection and acquisition procedures implemented in the
ATLAS experiment are computationally more efficient than the textual de-
scriptions of the same procedures. To this end, I shall first note that, comme
indicated by Table 2, the spatial and temporal procedural relations that
exist in the HLT and ESS systems are represented as spatial and numerical
relations by the communication and sequence diagrams in Figures 2 et 3.
The foregoing spatial and temporal procedural relations thereby become
directly accessible to visual perception. Cependant, the same spatial and
temporal procedural relations must be inferred from the linguistic (c'est à dire.,
syntactic and semantic) structures involved in propositional representations
when they are textually described. As indicated by Table 2, the size of the
set comprising the linguistic and symbolic diagrammatic elements and
their associated conventions, used by the communication and sequence di-
agrams in Figures 2 et 3 to represent spatial and temporal procedural
relations within the HLT and ESS systems, is far smaller and less detailed
than the size of the set comprising the linguistic elements (such as words,
verbs and propositions) and their associated rules and conventions used by
texts to represent the same procedural relations. Donc, it requires more
cognitive effort to infer the foregoing relations from the textual descrip-
tions than the communication and sequence diagrams. The above consid-
erations regarding the differences between the diagrammatic and
propositional representations of data selection and acquisition procedures
in the ATLAS experiment illustrate the perceptual ease of inferring infor-
mation from diagrams, as suggested by L&S’s account.

Another advantage of diagrammatic representations over propositional
representations as suggested by L&S’s account is their ability to spatially
localize the represented information. In order to see whether and how this
feature of diagrammatic representations plays a role in the case of the com-
munication and sequence diagrams in Figures 2 et 3, I shall first note
that the various procedural relations represented by these diagrams can
be regarded as related pieces of information about the data selection and
acquisition procedures implemented in the ATLAS experiment. Deuxième, dans
the textual descriptions of these experimental procedures presented in the
ATDR, as the number of pieces of information to be represented increases,
the number of sentences needed to represent these relations also increases.
This in turn results in a gradual separation of the representing relations,
and thus of the related pieces of information, from each other in the textual
descriptions. In the remainder of this section, I shall argue that this is an

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Perspectives on Science

197

unsuitable separation of the related pieces of the relevant procedural infor-
mation in the sense that it makes the textual descriptions less efficient than
the corresponding diagrammatic representations.

To this end, first, remember that, as pointed out by L&S, diagrams pre-
serve spatial relations to the extent that they transform them into other
spatial relations. As a direct result of this feature, in the communication
and sequence diagrams in Figures 2 et 3, the incoming and outgoing
messages associated with a particular unit in the HLT and ESS systems
lie adjacent to each other and in the proximity of this unit. This illustrates
spatial localization of information by diagrammatic representation—in the
sense of L&S’s account. Donc, in order to extract the information re-
garding the incoming and outgoing messages associated with a particular
object from the communication and sequence diagrams, it is sufficient to
check only the proximity of the object about which the foregoing informa-
tion is sought, because all the messages relevant to the required informa-
tion are grouped in the proximity of this particular object. This in turn
means that, in both the communication and sequence diagrams shown in
Figures 2 et 3, the information regarding the incoming and outgoing
messages associated with a particular unit within the HLT and ESS systems
can be obtained directly by checking the contents of the text labels for the
message arrows coming in and out of the object representing this particular
unit. Par exemple, in order to extract the information regarding the com-
munication between the ROS unit and the LVL2Processing and Event-
Builder units from the communication diagram shown in Figure 2, it is
sufficient to check the contents of the message-texts associated with the
ROS, c'est à dire., the incoming message-texts labeled “2.1”, “3.1” and “5.1”,
and the outgoing message-texts labeled “2.2” and “5.2”.

In contrast, in the textual descriptions of the HLT and ESS systems, le
sentences representing the incoming and outgoing messages associated
with the individual units in these systems are spread throughout the tex-
tual descriptions, rather than grouped together, because unlike diagram-
matic representations, propositional representations do not preserve spatial
relations. Par conséquent, in the foregoing textual descriptions, the sentences
relevant to the messaging information associated with an individual unit
do not necessarily succeed one another without intervening sentences
whose contents are not relevant to the messaging information. This means
that in order to extract the messaging information of interest from the cor-
responding textual description, it is necessary to check also the content of
each of these intervening sentences. Par exemple, the message texts labeled
“3.2” and “4” shown in the communication diagram in Figure 2 are neither
incoming nor outgoing messages for the ROS. Donc, it is not necessary to
take them into account in extracting the messaging information associated

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

198

Representing Procedures through Diagrams at LHC

with the ROS from the communication diagram. Cependant, in extracting the
same messaging information from the corresponding textual description, it is
necessary to check the contents of the sentences representing the foregoing
messages, as they lie among the sentences representing the message texts
labeled “2.1”, “2.2”, “3.1”, “5.1”, “5.2”, which are relevant to the messaging
information of interest. The same is true in the case of the messaging infor-
mation associated with the LVL2Supervisor unit, Pour qui, as shown in the
communication diagram in Figure 2, the message-text labeled “3.2” is the
incoming message, and the message-texts labeled “1” and “4” are the out-
going messages. Only the foregoing message-texts need to be considered
in order to extract the messaging information of interest from the communi-
cation diagrams. Cependant, in order to extract the same messaging informa-
tion from the corresponding textual description, the contents of the sentences
representing the message-texts labeled “2”, “2.1”, “2.2” and “3.1”, which are
not relevant to the messaging information of interest, also need to be taken
into account, as they lie between the sentences representing the message-texts
labeled “3.2” and “4”.

The sequence diagram in Figure 3 also illustrates spatial localization of
information by diagrammatic representation. This diagram represents the
procedural information as to how the first and second stages of the level-2
event selection are carried out by the aforementioned components of the
ESS system. The related pieces of this procedural information for each stage
of the level-2 selection can be found in the same proximity in the sequence
diagram, in that the message-texts relevant to the above information for
each of the relevant components of the ESS system lie in the proximity
of the thin rectangular box representing the time period during which
the component of interest operates. Donc, in the case of the sequence
diagram, the inference leading to the above procedural information is
direct, in the sense that the related pieces of this information can be
perceived at once by checking the dashed lines that represent the time
lines for the relevant components of the ESS system. The above procedural
information can also be inferred from the corresponding textual description
in the ATDR. Cependant, in this case, the inference leading to the informa-
tion of interest is indirect, in that it cannot be drawn until the contents
of all the sentences in the textual description are checked and the relevant
messaging information for each of the components of the ESS system is
identified.

The above discussion illustrates the spatial localization feature of dia-
grammatic representations in the cases of the communication and sequence
diagrams used in the ATDR. In both of these diagrams, the message-texts
used together to infer a conclusion regarding the communication among
the different units in the HLT and ESS systems are found in close proximity

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Perspectives on Science

199

to each other and also to the units under consideration. The advantage
offered by this localization feature is that it substantially facilitates the cog-
nitive process of inferring the information regarding the messaging among
the units of the HLT and ESS systems. In contrast, in the textual descrip-
tions of these systems presented in the ATDR, the sentences used together
to infer the same messaging information are separated from each other in
ways that substantially complicate the inference process.

The discussion in this section suggests that by virtue of their represen-
tational features, namely, perceptual ease and spatial localization, the com-
munication and sequence diagrams used in the ATDR are better suited for
the representation of the HLT and ESS related procedures than their cor-
responding textual descriptions, even though diagrammatic and textual
descriptions are informationally equivalent in this case. It is to be noted
that the aforementioned advantages of the SSE diagrams only apply if
all the rules and conventions of these diagrams are known to the users
of the ATDR. Incidentally, this last point relates to the notion of visual
literacy, which Daniel Rothbart has illustrated in the context of the design
of experimental instruments. Rothbart has remarked that “[e]xperiments
in contemporary research are often depicted through visual language,
based on schematic drawings associated with an instrument’s design”
and that this requires visual literacy about diagrams, namely, that one
must know what the individual symbols stand for in a given diagram in
order to extract the relevant information from this diagram (Rothbart
2003, p. 239). In a similar way, the present case study suggests that ex-
tracting the procedural information concerning the ATLAS data acquisi-
tion system from the diagrams presented in the ATDR requires visual
literacy about these diagrams. This point is especially important for the
training of newcomers (especially young experimenters) to the ATLAS
Collaboration, as these diagrams are also used to train them about the
essential features of the ATLAS data acquisition system.

6. Conclusion
In this paper, I have shown that the procedural information represented by
the communication and sequence diagrams in the ATDR illustrates how
the data selection and acquisition procedures are carried out by means of
software and hardware based automated devices in a large-scale HEP ex-
periment. Since the foregoing diagrams of SSE are used in the ATDR to
represent experimental procedures, in terms of the content of diagrammatic
representations, the present case study differs from much of the recent
philosophical studies that have examined various types of diagrams used to
represent scientific claims about natural phenomena such as hypotheses,
models and mechanisms. The general line of argument in these studies

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

200

Representing Procedures through Diagrams at LHC

is that in scientific practice there are cases in which diagrammatic rep-
resentations are more appropriate for scientific explanation and model
construction than propositional representations (voir, par exemple., Perini 2005;
Goodwin 2010; Barberousse 2013; Sheredos et al. 2013). Some of these
recent studies have explicitly drawn upon the localization feature of
diagrammatic representations, as suggested by L&S’s account (voir, par exemple.,
Bechtel and Abrahamsen 2005; Jones and Wolkenhauer 2012). Unlike
the foregoing studies that are concerned with the epistemic value of using
diagrams in representing scientific claims, the present case study suggests
that diagrams are more appropriate than texts to represent the procedural
information necessary to perform a large-scale HEP experiment, tel que
the ATLAS and CMS experiments at CERN’s LHC.

An important implication of the above conclusion concerns the practical
value of using diagrams in the ATDR for the collaborative work of design-
ing the ATLAS data acquisition system. The procedures of this system are
carried out jointly by internal and external research groups (for details, voir
ATLAS Collaboration 2003, sect. 17), as the system consists of three dif-
ferent trigger systems that are connected to the external systems such as
the ATLAS detector system and the CERN data management system. Ce
suggests that the collaborative work of designing the ATLAS data acqui-
sition system had both internal stakeholders, such as trigger groups, et
external stakeholders, such as detector operation and data analysis groups.
Given that the procedural information represented by both texts and the
diagrams of SSE in the ATDR involves the design requirements for the
data selection and acquisition procedures in the ATLAS experiment, an ef-
ficient communication of the foregoing procedural information among the
stakeholders was necessary in order for the collaborative design work to
achieve its intended objectives. The analysis offered in the previous section
shows that by virtue of their representational features, namely, perceptual
ease and spatial localization of information, the cognitive process of infer-
ring the procedural information regarding the data selection and acquisi-
tion procedures in the ATLAS experiment from the diagrams of SSE is
substantially less complex than the cognitive process of inferring the same
procedural information from their corresponding textual descriptions.
Donc, the present case study suggests that the diagrams of SSE used
in the ATDR were better suited than their corresponding textual descrip-
tions to provide a medium for efficient communication of the relevant pro-
cedural information among the stakeholders of the collaborative work of
designing the ATLAS data acquisition system.

The above considerations indicate an important difference between the
diagrams of SSE examined in this paper and Gooding’s maps, despite the
fact that they both represent experimental procedures. It is to be noted that

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Perspectives on Science

201

Gooding’s maps are aimed at a diagrammatic reconstruction of the proce-
dures of Faraday’s experiments that eventually led him to theorize the law
of electromagnetic induction. In this sense, Gooding’s maps are part of a
retrospective analysis of Faraday’s experiments on electromagnetic induction,
rather than being an essential part of these experiments. Unlike Gooding’s
maps, the foregoing diagrams of SSE have been an essential part of the
instrumentation needed to carry out the ATLAS experiment, in that they
have been used as visual tools in the collaborative work of designing the
data acquisition system of this experiment. De plus, as I have argued
au-dessus de, by virtue of their representational features, these diagrams have
served an important communicatory function in the aforementioned col-
laborative design work.26 Therefore, the conclusions of the present paper
go beyond illustrating Gooding’s idea that the procedural aspects of an
experiment can be elucidated through diagrammatic representations of
experimental procedures. They also show that these representations have
a particular communicatory value in the practice of experimental HEP.

Les références
ATLAS Collaboration. 2003. “ATLAS Technical Design Report: High
Level Trigger, Data Acquisition and Controls.” ATLAS-TDR-16;
CERN-LHCC-2003-022: http://cdsweb.cern.ch/record/616089

ATLAS Collaboration. 2008. “The ATLAS Experiment at the CERN Large

Hadron Collider.” Journal of Instrumentation 3: S08003.

ATLAS Collaboration. 2012. “Observation of a New Particle in the Search
for the Standard Model Higgs Boson with the ATLAS Detector at the
LHC.” Physics Letters B 716: 1–29.

Baigrie, Brian S. (éd.). 1996. Picturing Knowledge: Historical and Philosoph-
ical Problems Concerning the Use of Art in Science. Toronto: Université de
Toronto Press.

Barberousse, Anouk. 2013. “What Is the Use of Diagrams in Theoretical

Modeling?” Science in Context 26: 345–362.

Bechtel, William and Adele Abrahamsen. 2005. “Explanation: A Mecha-
nist Alternative.” Studies in History and Philosophy of Biological & Biomed-
ical Sciences 36: 421–441.

Booch, Grady, et autres. 2007. Object-Oriented Analysis and Design with Applica-

tion. Upper Saddle River, New Jersey: Addison-Wesley.

CDF II Collaboration. 1996. “The CDF II Detector Technical Design
Report.” FERMILAB-Pub-96/390-E. http://www-cdf.fnal.gov/upgrades/
tdr/tdr.html

26. Note that the diagrams of SSE used in the ATDR can also be used retrospectively to

optimize the ATLAS data acquisition system.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

202

Representing Procedures through Diagrams at LHC

Cheng, Pierre, Ric Lowe, and Mike Scaife. 2001. “Cognitive Science
Approaches to Diagrammatic Representations.” Artificial Intelligence
Review 15 (1–2): 79–94.

CMS Collaboration. 2012. “Observation of a New Boson at a Mass of
125 GeV with the CMS Experiment at the LHC.” Physics Letters B
716: 30–61.

Élise, John. 2012. “Outstanding Questions: Physics Beyond the Standard
Model.” Philosophical Transactions of the Royal Society A 370: 818–830.
Giere, Ronald N. (éd.). 1992. Cognitive Models of Science. Minnesota Studies in
the Philosophy of Science, Vol. 15. Minneapolis: University of Minnesota
Presse.

Gooding, David C. 1990un. Experiment and the Making of Meaning: Human

Agency in Scientific Observation and Experiment. Dordrecht: Kluwer.

Gooding, David C. 1990b. “Mapping Experiment as a Learning Process:
How the First Electromagnetic Motor Was Invented.” Science, Technologie
and Human Values 15: 165–201.

Gooding, David C. 1992. “Putting Agency Back into Experiment.”
Pp. 65–112 in Science as Practice and Culture. Edited by Andrew Pickering.
Chicago: The University of Chicago Press.

Goodwin, William. 2010. “How Do Structural Formulas Embody the
Theory of Organic Chemistry?” The British Journal for the Philosophy of
Science 61: 621–33.

Hegarty, Mary. 2004. “Diagrams in the Mind and in the World: Relations
between Internal and External Visualizations.” Pp. 1–17 in Diagram-
matic Representation and Inference. Edited by Alan Blackwell, Kim Mariott
and Shimojima Atsushi. Berlin: Springer.

Hoffer, Jeffrey, Joey George, and Joseph Valacich. 2008. Modern Systems
Analysis and Design (5th edn.). Upper Saddle River, New Jersey: Pearson Educa-
tion, Inc.

Johnson-Laird, Philip. 1980. “Mental Models in Cognitive Science.” Cognitive

Science 4: 71–115.

Johnson-Laird, Philip. 1983. Mental Models. Cambridge, MA: AVEC Presse.
Jones, Nicholaos, and Olaf Wolkenhauer. 2012. “Diagrams as Locality
Aids for Model Construction and Explanation in Cell Biology.” Biology
and Philosophy 27: 705–21.

Karaca, Koray. 2012. “Philosophical Reflections on Diagram Models and
Diagrammatic Representations.” Journal of Experimental & Theoretical
Artificial Intelligence 24: 365–84.

Karaca, Koray. 2017. “A Case Study in Experimental Exploration: Exploratory
Data Selection at the Large Hadron Collider.” Synthese 194: 333–354.
Kulpa, Zenon. 1994. “Diagrammatic Representation and Reasoning.”

Machine Graphics and Vision 3: 7–103.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Perspectives on Science

203

Larkin, Jill H., and Herbert A. Simon. 1987. “Why a Diagram Is (Some-
times) Worth Ten Thousand Words.” Cognitive Science 11: 65–100.
LEP Collaboration. 1984. LEP Design Report. CERN-LEP-84-01. https://

cds.cern.ch/record/102083?ln=en

Liu, Zhicheng, and John T. Stasko. 2010. “Mental Models, Visual Reasoning
and Interaction in Information Visualization: A Top-down Perspective.”
IEEE Transactions on Visualization and Computer Graphics 16: 999–1008.
Lynch, Michael, and Steve Woolgar (éd.). 1990. Representation in Scientific

Practice. Cambridge, MA: AVEC Presse.

Miller, Arthur I. 1984. Imagery in Scientific Thought: Creating 20th-century

Physics. Boston: Birkhauser.

Nersessian, Nancy J. 1992. “How Do Scientists Think? Capturing the
Dynamics of Conceptual Change in Science.” Pp. 3–44 in Cognitive Models
of Science. Edited by Ronald N. Giere. Minneapolis, MN: Université de
Minnesota Press.

Nersessian, Nancy J. 2008. Creating Scientific Concepts. Cambridge, MA:

AVEC Presse.

Pauwels, Luc (éd.). 2006. Visual Cultures of Science: Rethinking Representational
practices in Knowledge Building and Science Communication. Hanover,
New Hampshire: University Press of New England.

Perini, Laura. 2005. “Explanation in Two Dimensions: Diagrams and

Biological Explanation.” Biology and Philosophy 20: 257–269.

Rothbart, Daniel. 2003. “Designing Instruments and the Design of
Nature.” Pp. 236–254 in Scientific Experimentation and Its Philosophical
Significance. Edited by Hans Radder. Pittsburgh, Pennsylvanie: Université de
Pittsburgh Press.

Ryle, Gilbert. 1945. “Knowing How and Knowing That.” Proceedings of the

Aristotelian Society 46: 1–16.

Scaife, Mike, and Yvonne Rogers. 1996. “External Cognition: How Do
Graphical Representations Work?” International Journal of Human-Computer
Études 45: 185–213.

Sheredos, Benjamin, Daniel C. Burnston, Adele Abrahamsen, and William
Bechtel. 2013. “Why Do Biologists Use So Many Diagrams?” Philosophy
of Science 80: 931–44.

Tweney, Ryan D. 1989. “A Framework for the Cognitive Psychology of
Science.” Pp. 342–366 in Psychology of Science: Contributions to Metascience.
Edited by Barry Gholson et al. (éd.). New York, New York: Cambridge
Presse universitaire.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
p
o
s
c
/
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

2
5
2
1
7
7
1
7
9
0
2
9
9
p
o
s
c
_
un
_
0
0
2
4
0
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Télécharger le PDF