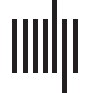REPORT - Recherche en IA spécialisée au MIT

REPORT

Neural Networks Track the Logical Complexity
of Boolean Concepts

Fausto Carcassi1

and Jakub Szymanik2

1Seminar für Sprachwissenschaft, Tübingen, Allemagne
2Institute for Logic, Language, and Computation, Universiteit van Amsterdam, Amsterdam, Netherlands

Mots clés: artificial neural networks, Boolean complexity, category acquisition

un accès ouvert

journal

ABSTRAIT

The language of thought hypothesis and connectionism provide two main accounts of
category acquisition in the cognitive sciences. Cependant, it is unclear to what extent their
predictions agree. In this article, we tackle this problem by comparing the two accounts with
respect to a common set of predictions about the effort required to acquire categories. We find
that the two accounts produce similar predictions in the domain of Boolean categorization,
cependant, with substantial variation depending on the operators in the language of thought.

INTRODUCTION

Category acquisition is one of the most important topics in cognitive science. Various accounts
of category acquisition have been proposed, among which are the language of thought
hypothèse (LOTH) and connectionism. The LOTH claims that human thinking consists of
manipulation of symbols in a language (Fodor, 1975). Connectionism is a program attempting
to explain various aspects of cognition using artificial neural networks (ANNs) (see Sutton,
1995, for a discussion of levels of description and explanation in connectionism). The relations
between these two accounts have been the subject of extensive philosophical debate, mais
there is little empirical data directly comparing the two approaches.1

In this article, we explore the relation between these two accounts of cognition with respect
to categorization. En particulier, the two accounts can be compared with respect to their empir-
ical predictions, leading to the following question:

Question. Do connectionism and the LOTH have similar empirical import in the domain of
category acquisition?

Category acquisition is a complex phenomenon with various empirically interesting fea-
photos. The first step in answering this question is then finding an aspect of category acquisition
for which both accounts make predictions.

Connectionism makes predictions for various aspects of category acquisition. Parmi
others, ANNs have been used to predict and explain base-rate neglect (Estes et al., 1989;

1 Voir, Par exemple, Davies (1991) and Fodor and Pylyshyn (1988) for classical discussions and Rescorla (2019)
for an overview of the debate. See Gallistel and King (2009) for discussion of empirical case studies in support of
LOTH and against connectionism.

Citation: Carcassi, F., & Szymanik, J..
(2022). Neural Networks Track the
Logical Complexity of Boolean
Concepts. Open Mind: Discoveries in
Sciences cognitives, 6, 132–146. https://
doi.org/10.1162/opmi_a_00059

EST CE QUE JE:
https://doi.org/10.1162/opmi_a_00059

Supplemental Materials:
https://doi.org/10.1162/opmi_a_00059;
https://github.com/thelogicalgrammar
/ANN; https://osf.io/gfsdq/

Reçu: 3 Décembre 2021
Accepté: 22 Juin 2022

Intérêts concurrents: The authors
declare no conflict of interest.

Auteur correspondant:
Fausto Carcassi
fausto.carcassi@gmail.com

droits d'auteur: © 2022
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence

La presse du MIT

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neural Networks and Logical Complexity

Carcassi and Szymanik

Gluck & Bower, 1988), stages of learning (Rumelhart & McClelland, 1987), et, in more
recent work patterns, in categorization of individuals with autism spectrum disorder (Dovgopoly
& Mercado, 2013). Recent work on deep learning, involving ANNs with many layers, shows that
there are interesting connections between cognitive processing and the representations
formed at various depth in ANNs (Guest & Love, 2019). Most importantly for the present
purposes, connectionism predicts a correlation between the effort required to learn a cate-
gory by ANNs and by humans (Bartos, 2002; Kruschke, 1991).

The LOTH also makes empirical predictions about various aspects of category acquisition.
Par exemple, it predicts which inductive generalizations will be made at each stage of learning
(Kemp et al., 2008). Much of the previous literature has focused on predictions concerning the
effort required to learn each category. Spécifiquement, categories encoded by longer formulas in
the language of thought (LOT) will take longer to learn. Previous work has verified this experi-
mentally by comparing the learning efforts predicted by the model with those in human partic-
ipants. A foundational paper in this approach is Feldman (2000), which considers the minimal
formulas required to encode a set of Boolean functions in a specific LOT.2 Goodman et al. (2008)
develops similar ideas in a Bayesian model. While both papers are relevant to the model we
present here, they only consider one specific shape for the formulas (namely, disjunctive normal
formulaire), rather than exploring the possible LOTs.3

In sum, given some natural assumptions we discuss below, both LOTH and connectionism
make predictions about the effort required to acquire categories, which offers a natural set of
empirical predictions to consider. In order to answer the question above, we therefore com-
pare for each category in the conceptual domain the learning efforts predicted by the two
accounts. We find a much better fit between the learning effort of simple ANNs and Boolean
logical complexity than would be expected by chance. At a minimum, this result constitutes
evidence that these accounts are compatible with each other. De plus, if alternative combi-
nations of accounts show worse fit than the one we observed, our results constitute evidence
that connectionism and the language of thought hypothesis are particularly compatible:
evidence in favor of one will also make the other more plausible.

MODELING CATEGORY ACQUISITION

Our aim is to compare connectionism and LOTH in the domain of category acquisition. We do
this by finding the predictions of the two accounts separately via computational models and
then comparing them. D'abord, we discuss the model of categories, present a model of category
acquisition in the two accounts, and derive the behavioral predictions with respect to which
the accounts can be compared. Alors, we present our method for comparing the predictions
made by the two accounts.

Categorization in our model relies on identifying which properties define a category and in
which combination. Donc, we start with a set of binary properties, Par exemple, “small” or
“square.” An object can be thought of as a set of properties.4 For instance, an object might be

2 Though see Vigo (2006) for a discussion of a technical problem in the original paper.
3 Classical studies in a similar paradigm include Shepard et al. (1961), which studies the generalization errors
of different Boolean categories, and Bruner et al. (2017) in the constructivist program. In contrast to more recent
travail, this work does not explicitly model the learning process in terms of an LOT, making a direct comparison
difficult.
4 Alternativement, we can think of an object as an equivalence class of entities that are indistinguishable with
respect to the chosen properties. If we consider all properties humans can represent, by definition entities within
these equivalence classes must be treated equivalently by the LOT.

OPEN MIND: Discoveries in Cognitive Science

133

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neural Networks and Logical Complexity

Carcassi and Szymanik

Example of the setup with two properties: square and red (top left). For simplicity, we represent nonsquareness as circle and
Chiffre 1.
nonredness as white. An object is defined as a set of properties or their negation (bottom left). Since we have two properties, four possible
objects can be distinguished. A category is then defined as a set of objects (droite). With four objects, 16 categories can be defined. Par exemple,
catégorie 1 is the empty category, containing no objects. Category 7 contains any object that is a circle, regardless of its being red. Category 12
contains all objects that are either red or a circle.

identified by being small and square. Two objects are then only distinguishable via a differ-
ence in which properties they have. Donc, given n properties 2n possible objects can be
constructed. Enfin, we define a category as a set of objects, namely, those objects that belong
to the category. Donc, there will be one category for each possible set of objects. With n
properties, there are 2(2n) possible categories. In the models below, we will include four prop-
erties, which can construct 16 possible objects and 65,536 possible categories.5

Chiffre 1 gives an example of the setup for two properties. The example shows two prop-
erties p (being-square) and q (being-red). Four objects can be defined with these two proper-
liens: {p, q}, {p, ¬q}, {¬p, q}, et {¬p, ¬q}. Any set of these four objects is a category, and there
sont 16 possible categories. Par exemple, one category does not contain any of the objects
(catégorie 1 in Figure 1), and one category contains only the red objects (catégorie 6).

Boolean Fragment of the Language of Thought

The case of Boolean conceptual domain has received particular attention starting from Boole
(1854), because of its tractability and importance in thinking. The LOTH offers a natural
approach to modeling categorization in the Boolean conceptual domain. In practice, notre
aim is to construct an LOT whose expressions encode Boolean functions: functions from truth
valeurs (specifying for each property whether the object has it) to a truth value (specifying
whether the object belongs to the category). Each expression in the LOT then encodes a cat-
egory, namely, the set of those objects that verify the corresponding Boolean function.6 To see
how this works in practice, consider the example of the Boolean LOT with the two properties
pictured in Figure 1 and the operators ¬, ∧, and ∨. Category 13 ({{¬p, q}, {p, q}, {p, ¬q}}) peut,
Par exemple, be expressed in this LOT simply as p ∨ q.

Previous work has analysed the complexity of Boolean formulas in specific LOTs. Pour
instance, Feldman (2003un) categorizes Boolean functions up to four inputs in an LOT with
negation, conjunction, and disjunction, as well as their formulation in disjunctive normal form
(DNF). Feldman (2003b) shows that in humans Boolean complexity, calculated with a specific

5 Note that there is a correspondence between the set of categories and the set of functions from objects to a
Boolean.
6 To be more precise, if “LOT” is taken to refer to the whole language underlying human thinking, it is more
appropriate here to talk of the Boolean fragment of the LOT. In the following we just talk of “Boolean LOT” for
simplicity.

OPEN MIND: Discoveries in Cognitive Science

134

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neural Networks and Logical Complexity

Carcassi and Szymanik

LOT, correlates with learning effort. Feldman (2006) deepens these results by defining a dif-
ferent coding pattern for these formulas. Cependant, previous literature has not systematically
explored the set of possible LOTs.

Since the same category is encoded by formulas with possibly different lengths in LOTs with
different operators, and therefore different LOTs make different empirical predictions for cat-
egory acquisition, we must define the space of possible LOTs to be considered in the model
below. Different LOTs are distinguished in our model by different syntactic primitives. Le
primitives include literals referring to the properties and the Boolean operators to encode func-
tions of the properties. In the following we assume a set of four properties, which are identical
across LOTs, and we let the operators vary across LOTs. To reduce the space of LOTs to a
manageable size, we only consider binary and unary operators.

In order to produce behavioral predictions about category learning from this picture, nous
rely on the natural assumption that categories that are expressed by more complex formulas
in the LOT are harder to learn. Donc, while each category can be expressed by multiple
(and possibly infinitely many) formulas in a given LOT, here we will assume that the relevant
formula is the shortest among the formulas that encode the category, following among others
(Feldman, 2000). This is also in line with previous work emphasizing the importance of com-
plexity in cognition (Chater & Vitányi, 2003; Grünwald, 2007). This assumption implies that
LOTs that produce the same minimal formula length across all categories are equivalent for
our purposes.7

Given these restrictions, we can immediately exclude some operators, on three grounds.
D'abord, some operators would not appear in any minimal formula even in LOTs that contain
eux, because any formula that contains them is equivalent to a shorter formula without them.
These operators are (1) affirmation, the unary operator that simply return the truth value of its
argument and can therefore be substituted by the argument alone, (2) left-affirmation, le
binary operator that returns the truth value of its left argument and can therefore be substituted
by the left argument alone, et (3) right-affirmation, which is similar to left-affirmation for right
argument. Deuxième, some operators produce the same minimal formula lengths as an LOT with
just negation instead. These operators are (1) the binary left-negation, which can be substituted
by the negation of the left argument and (2) the binary right-negation, which can be substituted
by the negation of the right argument. Troisième, any LOT with ← produces the same minimal
formula lengths as an LOT that is the same up to substitution of ← for →, and similarly for
↚ and ↛. Donc, we exclude ← and ↚ and only keep → and ↛ (see Table 1 for the mean-
ing of the symbols).

As mentioned above, we assume that all LOTs can express the same set of properties. While
this modeling choice might seem arbitrary, it is in fact required for our model. LOTs expressing
different sets of properties would be incapable of describing the same sets of objects and cat-
egories, and therefore the complexity of the corresponding expressions could not be compared
with each other.

These restrictions leave us with nine out of the 16 possible operators, listed in Table 1. Le
set of LOTs is then the powerset of the set of these nine operators, c'est, any set constructed
with zero or more of these nine operators. En principe, 29 = 512 LOTs can be constructed from

7 A large literature in computer science concerns itself with the similar problem of finding the smallest circuit
for computing Boolean functions, Par exemple, Wegener (1987). This literature is mostly focused on finding
efficient algorithms for minimization with specific operators or showing general results on bounds of circuit
complexity. Donc, it will mostly not be relevant for the present purposes.

OPEN MIND: Discoveries in Cognitive Science

135

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neural Networks and Logical Complexity

Carcassi and Szymanik

Tableau 1.
LOTs

The Nine Operators That Appear in at Least One Minimal Formula in Some Boolean

Nom
conjunction (et)

disjunction (ou)

conditional

negated conditional

biconditional

negated biconditional

negated conjunction

negated disjunction

negation

Symbol
∧

∨

→

↛

↔

↮

∧
/
/∨

these nine operators. We reduce the number of LOTs further by assuming that the LOTs are
Boolean bases, c'est, that every category can be expressed with them.8 This leaves 468 LOTs.
Enfin, we exclude LOTs that in practice produce the same minimal formula length for all
catégories, leaving a total of 358 LOTs with unique complexity profiles.

We assume that the learning effort predicted by the LOTH given a specific LOT is a mono-
tonically increasing function of these minimal formula lengths in that LOT (see Table 2 pour
some examples of minimal formulas). Since we do not know which function this is, we only
interpret the length-ranks of these minimal formulas as the predicted complexity ranks: le
categories with the shortest minimal formulas will be easiest, the categories with the second
shortest minimal formulas will be the second easiest, et ainsi de suite. Donc, we take the LOTH
with a specific LOT to predict the rank of acquisition complexity.

Connectionism

Category acquisition has been a historically crucial case in the study of ANNs, specifically in
the case of the parity function, expressed in the binary case by the negated biconditional ↮.9
One n-bits parity function f : (cid:1)n
{0, 1} → {0, 1} is defined as:
i¼1

ð
f x1; …; xn

Þ ¼

(cid:2)

1
0

P.
n
i¼1 xi

si
else:

is even:

and the other parity function is its negation f 0(x1, …, xn) = 1 − f (x1, …, xn). The parity problem in
the context of ANNs is the problem of constructing an ANN that implements a parity function.
An early version of ANNs, the Perceptron ( Blanc & Rosenblatt, 1963), was shown by Minsky
and Papert (1972) incapable of solving the parity problem. Plus tard, Rumelhart et al. (1986)

8 Such sets of operators can also be described as functionally complete. The sets of operators usually consid-
ered are bases. To get a sense of a functionally incomplete sets, consider the LOT {p, q, ou}. With such an LOT, it
is not possible to define the category consisting of only the object that is neither p nor q. To get the set of bases,
we calculated the powerset of the set of nine operators described above, and then filtered the supersets of the
known list of minimal bases, as described, Par exemple, in Wernick (1942).
9 This is often also called XOR (exclusive OR) in the literature.

OPEN MIND: Discoveries in Cognitive Science

136

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neural Networks and Logical Complexity

Carcassi and Szymanik

Tableau 2. Minimal Formulas for All Categories Definable With Two Properties (p and q), for Three Language of Thoughts (LOTs): A Minimal
LOT Containing Only the Operator “nand,” an English-like LOT with “not,” “and,” “or,” and “nor,” and an LOT With a Parity Operator
(Negated Biconditional)*

Categories
1100

1010

0011

0111

0101

1111

1011

1101

1110

1000

1001

0000

0100

0010

0110

0001

∧
/

¬, ∧, ∨, /∨

¬, ∨, ↮

∧ ( p, q))

∧ ( p, p))

∧ ( p, p)
/
∧ ( p, q)
/
∧ (q, q)
/
∧ ( p, /
/
∧ ( p, /
/
∧ (q, /
/
∧ (/
/
∧ (/
/
∧ (/
/
∧ (/
/
∧ (/
/
∧ (/
/
∧ (/
/
∧ (/
/

∧ ( p, p), /
∧ ( p, q), /
∧ ( p, q), /
∧ ( p, /
∧ ( p, /
∧ ( p, /
∧ ( p, /
∧ ( p, /

∧ (q, q))

∧ ( p, q))

∧ (q, q)))

∧ ( p, p)))

∧ ( p, q)))

∧ ( p, p)))

∧ (/
∧ ( p, p)), /
∧ ( p, p)), /
∧ ( p, p)), /
∧ ( p, q)), /
∧ ( p, p)), /

∧ ( p, p), /
∧ ( p, /
∧ ( p, /
∧ (q, /
∧ (q, /
∧ (/

∧ ( p, p), /

∧ (q, q)))

¬( p)

¬(∧( p, q))

¬(q)

∨( p, ¬( p))

∨(q, ¬( p))

∨( p, ¬(q))

∨( p, q)

∧( p, q)

∨(∧( p, q), /∨ ( p, q))
∧( p, ¬( p))

∧( p, ¬(q))

∧(q, ¬( p))

/∨ (∧( p, q), /∨ ( p, q))
/∨ ( p, q)

¬( p)

∨(¬( p), ¬(q))

¬(q)

¬(↮ ( p, p))

∨(q, ¬( p))

∨( p, ¬(q))

∨( p, q)

¬(∨(¬( p), ¬(q)))

¬(↮ ( p, q))

↮ ( p, p)

¬(∨(q, ¬( p)))

¬(∨( p, ¬(q)))

↮ ( p, q)

¬(∨( p, q))

* Each row corresponds to one possible category, conveyed by the first column as a Boolean vector over the truth table for p and q (in left-to-
right order: p and q, p and not q, not q and p, not q and not p). It is instructive to compare the behavior of the three LOTs for the different
catégories. D'abord, since all LOTs have lexical means to refer to the properties directly, the two categories that refer to all and only the objects
having one of the properties have the same minimal formula in all languages. Deuxième, the longest formulas for an LOT with fewer operators
(first columns) are longer than for an LOT with more operators (second columns). Troisième, some categories which are among the simplest in one
LOT [par exemple., “and(p, q)»] can be among the most complex for another [par exemple., “not(ou(pas(p), pas(q)))»].

showed that backpropagation and nonlinear activation functions allow an ANN to solve the
parity problem.10

More recent work has produced more insights into Boolean learning by ANNs.11
Sprinkhuizen-Kuyper and Boers (1996) shows that some simple ANN architecture, across all
possible inputs, encode the trivial functions (always output 0 or always output 1) very often
and the parity functions very rarely. Mingard et al. (2020) also study the inductive biases of
simple ANN, by studying the distribution of Boolean functions obtained with randomly initial-
ized weights. They find a bias for Boolean functions with low entropy, c'est, functions that are

10 De plus, Mhaskar et al. (2016) shows that depth also has an impact on how efficiently the functions can be
représentée. See Anthony (2010) for a more detailed discussion of the representation power of various types of
ANN.
11 See Penny and Stonham (1992) for a discussion of Boolean function learning with probabilistic logic nodes
(PLN), which can be implemented directly in RAM. De plus, see Deolalikar (2001) for an analysis of Boolean
category acquisition in ANNs comprising only neurons with zero thresholds and binary weights.

OPEN MIND: Discoveries in Cognitive Science

137

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neural Networks and Logical Complexity

Carcassi and Szymanik

verified by few or many inputs. De plus, they find that given some specific entropy levels,
ANNs have a prior bias for Boolean functions with low Lempel-Ziv complexity.

Rather than focusing on the distribution of Boolean functions for random initializations, nous
look at the effort required to acquire different categories. Donc, we train ANNs on each
possible Boolean function (A slight complication arises with respect to the interpretation of the
input and output of the ANNs, which we describe in the Appendix.). Each network has four
input neurons, one for each property, and one output neuron, which encodes the network’s
confidence that the object described by the input belongs to the category. Each network has
two hidden layers of 16 neurons each and ReLU (rectified linear unit) activation functions,
except on the last layer, where a sigmoid function is applied to squeeze the output in the
(0, 1) interval. We used binary cross entropy to measure the difference between the network’s
output and the true output as determined by the category. To train the network, we use the Adam
optimizer, a popular algorithm for gradient-descent (Kingma & Ba, 2015). We made these design
choices so that the networks had enough expressive power to represent every category. Future
work will analyze the effect of architecture choices on the results presented below.

For each of these categories, we train 25 ANNs. Each training has batch sizes of eight and
400 epochs. We measure the effort needed by an ANN to learn a specific category by taking
the average loss across epochs and batches.12 Therefore, for each category we have 25 sam-
ples of our measure of complexity of ANN learning effort for the category.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

COMPARING THE TWO ACCOUNTS’ PREDICTIONS

Dans la section précédente, we have discussed how to model category acquisition within a con-
nectionist account and an LOT account. De plus, we have extracted for both of these
accounts empirical predictions of the effort of acquiring each category. Recall that in our sim-
ulations we considered all categories definable with the set of objects that can be constructed
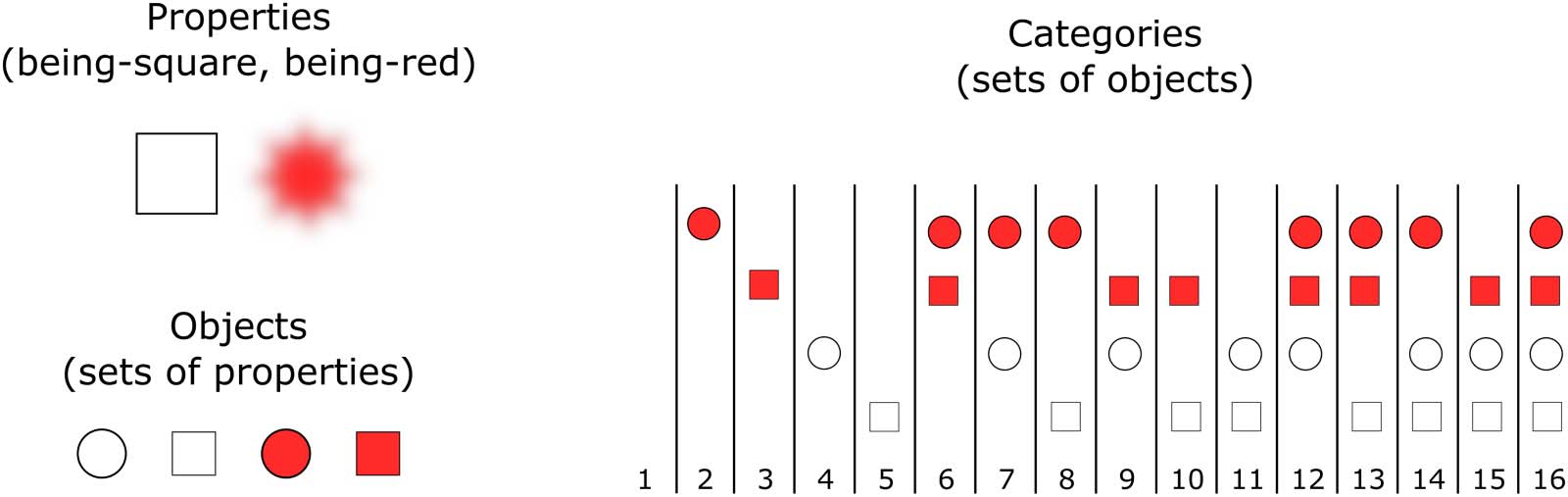
with four features or, equivalently, the set of possible functions f : Bool4 → Bool. Chiffre 2
shows examples of the relation between the length of the minimal formulas in four LOTs
and the ANN learning efforts for the corresponding categories. Since the ANN learning efforts
are the same for all LOTs, each plot shows a reordering of the learning efforts that depends on
the minimal formula lengths in the LOT. While all four displayed LOTs show an increasing
trend, there are also substantial differences between them. This is because different sets of
operators produce different formulas (and therefore different formula lengths) for different cat-
egories, so that the same category might be expressible compactly in one LOT but require a
long formula for another LOT. This raises the question of whether there is across LOTs an over-
all correlation between minimal formula length and ANN learning effort.

We hypothesize an overall monotonically increasing relation between ANN learning effort
and logical complexity. Since this hypothesis does not imply or assume a functional relation
between the two, a parametric measure such as Pearson’s correlation coefficient r would be
inappropriate. Plutôt, we use a nonparametric measure, c'est, Spearman’s rank correlation
coefficient ρ, which is the Pearson’s correlation between the ranks of the two variables. The ρ
quantifies how well the relation between the two variables can be encoded by a monotonic
fonction. When ρ = 1, the two samples can be perfectly described by a monotonically increas-
ing function, while when ρ = −1, a monotonically decreasing function. Our hypothesis can

12 See Mazzoni and Wagstaff (2004), Pérez and Rendell (1995), and Settles and Craven (2008) for other exam-
ples of area under the curve being used as measure of learning. See Settles and Craven (2008) for a more general
discussion of learning curves of ANNs.

OPEN MIND: Discoveries in Cognitive Science

138

Neural Networks and Logical Complexity

Carcassi and Szymanik

Chiffre 2. Artificial neural network (ANN) learning effort as a function of minimal formula length for all categories, for four language of
thoughts (LOTs). The title of each subplot indicates the operators in the displayed LOT. Par exemple, the LOT displayed in top left plot only
contains negated conjunction, while the bottom right LOT contains negated biconditional, negated conjunction, and negated conditional. Le
plot displays some differences in the way different LOTs encode formulas. D'abord, LOTs with more operators generally have a smaller range of
minimal formula lengths, since even the most complex categories for that LOT can be described with shorter formulas. Par exemple, the length
of minimal formulas for the LOT with just negated conjunction (top left) go up to 26, while for an LOT with four operators they only go up to 15
(top right). Deuxième, while all LOTs show a positive rank correlation between the two variables, there is considerable variation in the strength of
this correlation. Namely, LOTs with the parity operators (bottom subplots) have a weaker rank correlation than LOTs without them.

then be operationalized as the claim that there is a positive rank correlation between the ANN
learning effort and the logical complexity of categories.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

A welcome side effect of using rank correlations is that the results, since they depend only
on complexity ranks, are not sensitive to any monotonic transformation of the involved vari-
ables. Donc, while the particular measures of learning effort we chose (average loss across
epochs and batches, see footnote 12 for discussion) is not uniquely identified by theoretical
considerations, our results are not sensitive to other choices, as long as they preserve the com-
plexity ranks. Donc, the results are robust to different accounts of how simplicity affects
learning—for example, Bayesian learning (Piantadosi et al., 2016) or minimum description
length (Grünwald, 2007)—as long as simpler categories are easier to learn.

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

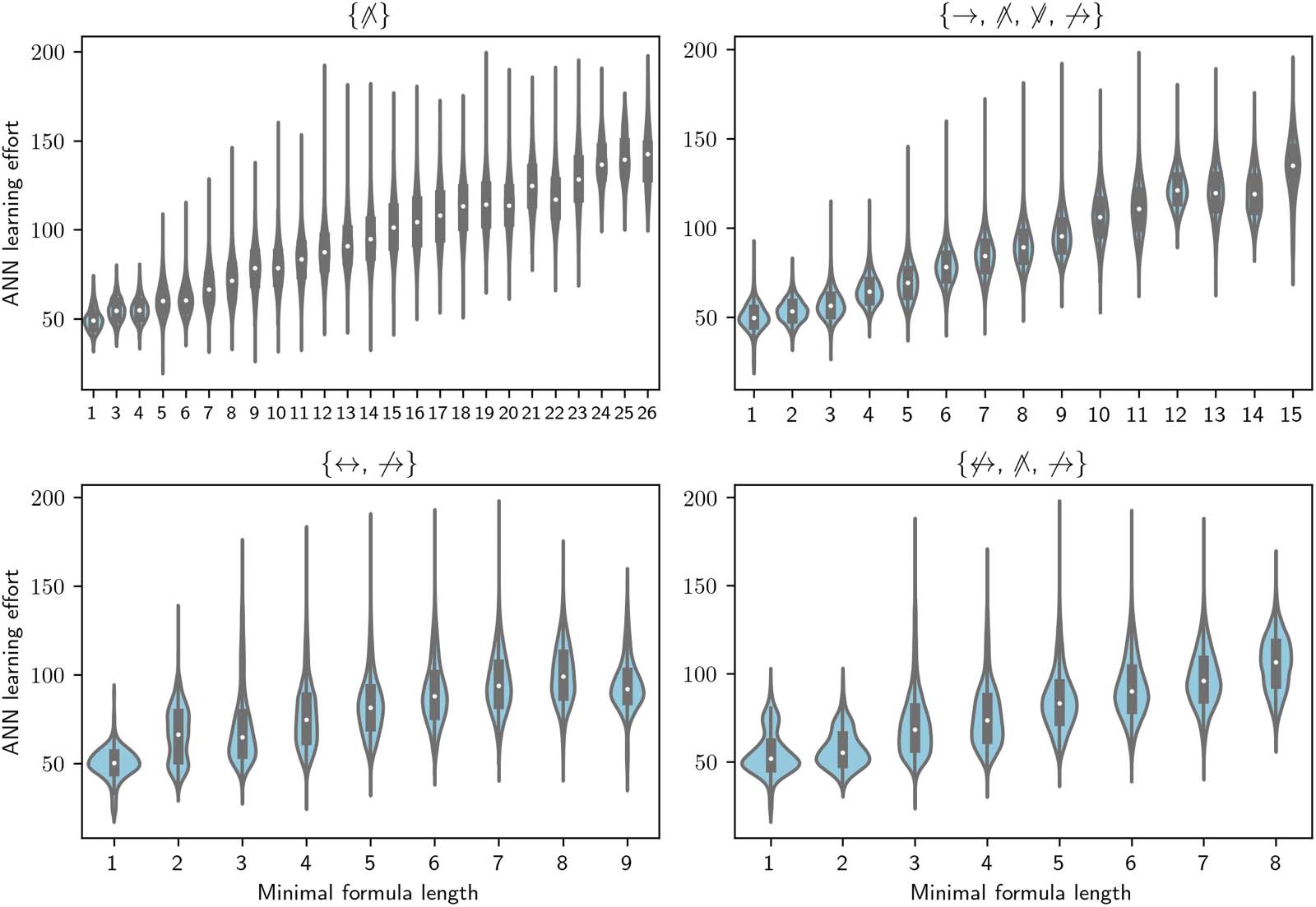
The main question is answered in the positive, as displayed in the top plot of Figure 3.13
The main result when considering rank correlation across all LOTs is therefore that there is an
overall positive rank correlation between logical complexity and ANN learning effort. Ce
means that categories that are simpler in a logical sense can be learned faster by the ANNs.

Chiffre 3 also informs us as to which LOTs best correlate with the ANN learning efforts. Comme
the top plot shows, depending on the specific LOT, the rank correlation goes from weak (0.22)

1 3 Readers interested in replicating the results can find the needed code at https://github.com
/thelogicalgrammar/ANN_complexity. The data reported in the article can be found at https://osf.io/gfsdq/.

OPEN MIND: Discoveries in Cognitive Science

139

Neural Networks and Logical Complexity

Carcassi and Szymanik

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 3. The model’s aim is to measure the extent to which artificial neural network (ANN) learning effort and logical complexity (given a
language of thought [LOT]) agree across categories. In order to quantify the level of agreement between them, we use the rank correlation ρ,
which is the linear correlation between the category-wise complexity ranks in the two measures, and is robust to monotonic transformation of
the complexity measures. The top left plot shows ρ between learning efforts and minimal formula length for all LOTs, where LOTs are ordered
by decreasing rank correlation (as can be seen by the strictly decreasing value of ρ). Two things ought to be noticed about this subplot. D'abord, ρ is
always positive: across all LOTs there is a positive rank correlation between logical complexity and ANN learning effort. Deuxième, autour 200
there is a stark decrease in ρ. The reason for this stark decrease can be seen in the bottom left subplot, which shows the cumulative number of
occurrences of each of the nine operators from Table 1 (c'est à dire., the total number of time each operator appeared in the LOTs with at least that level
of ρ). Par exemple, the line for A when x = 3 shows the number of times A occurs in the three LOTs with the highest correlation to ANN learning
efforts. The bottom left plot then shows that the introduction of parity operators causes the stark reduction in correlation: the stark decrease can
be seen to correspond to the appearance of parity operators. The right plots restrict the corresponding left plots to LOTs up to the first occur-
rence of the parity operators. This allows a closer analysis of the occurrences of each operator for the LOTs with the highest correlation with
ANN learning effort. The shape of the curves shows where each operator occurs most often. Par exemple, a straight curve means that the
operator appears with a constant frequency, as is the case with negation. On the other hand, a convex curve means that the operator appears
more frequently among the LOTs with stronger ρ. This is the case for all operators, reflecting the fact that LOTs with more operators in general,
rather than with specific operators, tend to have stronger ρ (this point is explored more in detail in Figure 4).

to strong (0.77). This shows that there is interesting and substantial variation in how well ANN
learning effort correlates with different LOTs. We find two main characteristics of LOT that
account for the correlation, namely, whether the LOT has parity operators and how many
operators are in the LOT.14

D'abord, as the bottom plot in Figure 3 shows, much of the variation in rank-correlation is
explained by the presence or absence of the parity operators in the LOT. The categories’ log-
ical complexity in LOTs without parity operators rank correlates well with ANNs’ learning
effort, with a stark decrease for LOTs with a parity operator. This result is consistent with
the previous work discussed above showing that nonlinearly separable categories are

14 Interested readers can find a plot of the by-category average minimal formula length vs. ANN learning effort
at https://thelogicalgrammar.github.io/ANN_complexity/ hover_cat.

OPEN MIND: Discoveries in Cognitive Science

140

Neural Networks and Logical Complexity

Carcassi and Szymanik

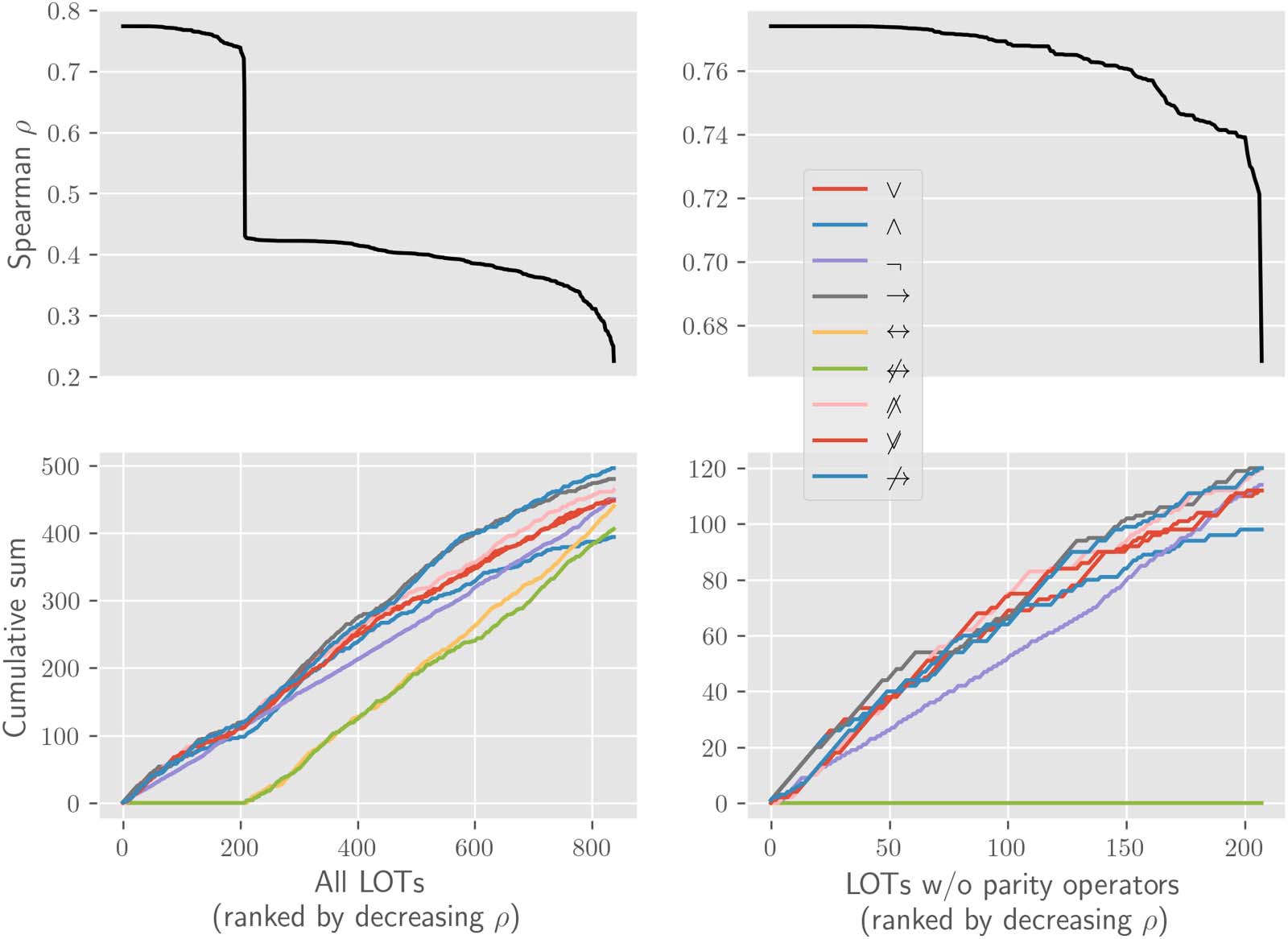
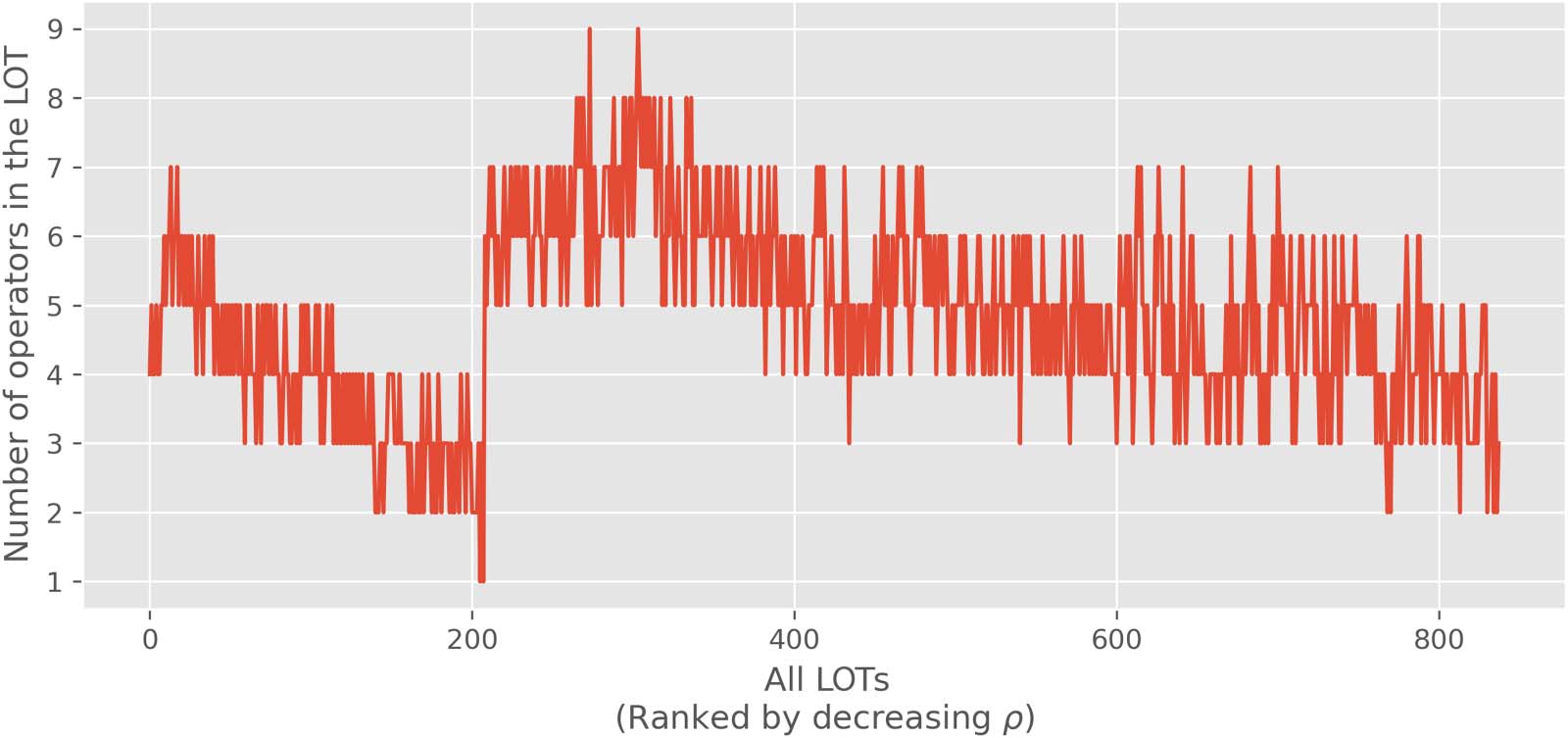
Chiffre 4. Number of operators in each language of thought (LOT). On the x-axis, LOTs are ordered in decreasing rank correlation with
artificial neural network (ANN) learning effort. Par exemple, the LOT displayed at x = 0 has the highest rank correlation with ANNs, et le
rank correlation becomes lower and lower for successive LOTs. The plot shows that both for LOTs with and without the parity operator, having
more operators generally increases the rank correlation. As shown in the plot, the maximum number of operators without parity operators
(before the transition at ≈ 200) is seven, which increases to nine if the parity operators are included (after the transition at ≈ 200).

particularly hard for ANNs to acquire, since nonlinearly separable categories are those that
receive short descriptions in LOTs with parity operators.

The correlation data also shows a second pattern. Among LOTs without a parity operator
(and also among the LOTs with a parity operator) there are differences in rank correlation to
ANN learning efforts. Namely, LOTs with more operators have higher rank correlations, Un scanner
be seen in Figure 4. While the reason for this is not transparent, the explanation might have to
do with the fact that LOTs with more operators have more ties in their ranks, since they have a
smaller range of minimal formula lengths needed to express all categories. This is a conse-
quence of the fact that the minimal formula length for a category in an LOT is upperbounded
by the minimal formula length for that category in any LOT with a subset of its operators.

The interpretation of these results depends on whether one sees connectionism and LOT
models as being competing accounts or as belonging to different levels of description (com-
putational for the LOT model, implementational for the ANN model). If so, our article can be
seen as a contribution to the project of understanding the relation between different levels of
explanation of cognition. En général, accounts of cognition at different levels of analysis can
inform each other. Sometimes, they do so by ruling out possible accounts. Par exemple, con-
siderations of computational complexity can restrict the class of possible algorithms a brain
might be implementing ( Van Rooij, 2008). Dans d'autres cas, support is more graded, with one
account increasing another account’s plausibility. Cependant, establishing the degree of com-
patibility between two accounts at different levels of abstraction is not trivial in practice. In the
ideal scenario, an explicit characterization is given of the way that higher levels reduce to
lower ones. Connectionism and LOT are, cependant, too complex to directly establish whether
the reduction can be done.

Plutôt, we take the natural approach of comparing the behavioral predictions of the two
accounts in the rich domain of category acquisition. If the predictions of the two accounts
strongly diverged, this would constitute evidence against the possibility of a reduction. Sur
the other hand, if they are in agreement, this is prima facie evidence for their compatibility,
and the two accounts stand or fall together vis-à-vis experimental data from that behavioral

OPEN MIND: Discoveries in Cognitive Science

141

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neural Networks and Logical Complexity

Carcassi and Szymanik

domain.15 Our article shows that there is considerable agreement between a simple connec-
tionist model and some but not all specifications of the LOT, in terms of their predictions for
complexity of category acquisition. We believe therefore that a main contribution of this article
is to pave the way to a disentanglement and comparison of the predictions made by connec-
tionism and the LOT hypothesis.

Dans cette lumière, the two results presented above are significant as they suggest possible avenues
for empirical investigation. The first result shows that if independent evidence were to support
an LOT model of human cognition, the extent to which such a model would also support a
connectionist account would depend on which LOT the data supports. Spécifiquement, our model
shows that learning data supporting an LOT model with parity operators would not support a
connectionist account, while evidence in favor of an LOT without parity operators would
mostly also support a connectionist account. The second result, though to a lesser extent,
has similar implications for the number of operators in the LOT.

Bien sûr, one could also see the ANN and the LOT models are competing models. Dans ce
perspective, our model shows that depending on the operators in the human LOT, learning
data will be more or less capable of providing evidence that disambiguates between the
two models. If the human LOT has parity operators or contains fewer operators, data from
category learning experiments will be more capable of uniquely supporting one of the two
models.

CONCLUSIONS

Much work has been devoted to the problem of Boolean category learning both in the tradi-
tion of LOTH and in connectionism. Both of these traditions have pointed to learning effort as
a crucial empirical prediction made by the models. Cependant, the relation between the pre-
dictions made by the two accounts with respect to learning effort has not been investigated. Dans
the model above, we have presented an initial investigation of this relation. We first formulated
predicted learning efforts for the LOTH and for a simple connectionist model in the case of
Boolean categories. A comparison between them shows that they are correlated. This indicates
that the empirical content of the two accounts is similar for the case of Boolean categorization.

Arguably, one limitation of our results is that we only consider categories definable with up
to four properties. By the invariance theorem, the differences in the logical complexity of a
given category across LOTs only differ up to an additive constant, which becomes small in
the limit of complex enough categories (Li & Vitányi, 1990). A first barrier to increasing the
number of properties is computational. Since the complexity of finding the minimal formula
increases exponentially with the number of properties, running full simulations with more
properties would be impractical. One option would be to only calculate the minimal formulas
for some of the categories definable with more operators. Cependant, we believe that beyond
the computational limits, the results for few number of properties are in fact the most important
in the context of cognitive science. Precisely because of the exponential complexity, we know
that either humans are using categories that only depend on a few properties, or they are using
heuristics instead of the most compact encoding of the category. Since we do not have any
account of what such heuristics could be, the most useful approach at the moment is to con-
sider a set of categories small enough that minimal formulas can be found exactly. This has a

15 De plus, if their predictions agree more than any other combination of plausible accounts, this lends evi-
dence to the idea that the higher level one indeed reduces to the lower level one. In our case, we have not
compared our computational-level account (the LOT) with other alternatives, and therefore cannot yet assess
this situation.

OPEN MIND: Discoveries in Cognitive Science

142

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neural Networks and Logical Complexity

Carcassi and Szymanik

better change of being close to the way humans are in fact encoding these categories, should
the LOTH be correct.16

While we used a general purpose ANN architecture to make our results as general as pos-
sible, the results can be extended in various directions. From the connectionist side, our anal-
ysis focuses on one specific choice of ANN architecture, model parameters, and training
regime. Future work can explore to what extent the results presented above are robust with
respect to other choices. A particularly natural extension is not to consider just feedforward
ANNs, but rather previous connectionist models of Boolean category acquisition.

Different choices can also be made from the LOT side. In the model we discussed, different
LOTs are distinguished by their syntactic primitives. Cependant, Boolean LOTs can also vary with
respect to the set of rules that construct formulas from the syntactic primitives. Popular options
for the shape of formulas are DNFs (disjunction of conjunctions of literals and their negations),
conjunctive normal forms (conjunction of disjunctions of literals and their negations), Blake
canonical form, and algebraic normal form. In the model above we did not restrict the shape
of the formulas at all, and considered all well-formed formulas in the usual grammar for prop-
ositional logic with the LOT’s operators. Cependant, such restrictions might make a difference.
Consider again the example of the Boolean LOT with the two properties pictured in Figure 1
above and the operators ¬, ∧, and ∨. Cependant, assume now that every formula is in DNF.
Category 13 can be then encoded as ( p ∧ q) ∨ ( p ∧ ¬q) ∨ (¬p ∧ q). This example shows that
restricting sentence form, Par exemple, to DNF, can lengthen the shortest formula: without this
restriction category 13 could be expressed simply as p ∨ q. Previous work has looked at some
ways to constrain the shape of formulas in the context of Boolean LOTs (Piantadosi et al., 2016).
Cependant, systematically exploring the space of Boolean grammars is a much harder task than
exploring the set of primitives, and therefore we leave the task to future work.

A limitation of the article is its focus on the Boolean domain. There is extensive literature
showing how LOT models, enriched with probabilistic tools, show learning behavior resem-
bling that of humans. Par exemple, this has been shown in domains such as taxonomies
(Tenenbaum et al., 2006), handwritten symbols (Lake et al., 2015), kinship terms (Mollica &
Piantadosi, 2022), and numerical concepts (Piantadosi et al., 2012). Bien sûr, analyzing
these domains would go beyond the scope of this article. Néanmoins, they suggest further
ways of comparing learning patterns of ANNs and LOT models.

Connections to other previous work can also be analyzed more in depth. One particularly
relevant paper is Griffiths et al. (2012), which compares the inductive biases of ANNs and a
Bayesian learner. Our article differs from Griffiths et al. (2012) in at least three important ways.
D'abord, Griffiths et al. (2012) uses linear activations functions, restricting the expressive power of
the ANNs compared to the ones usually used in the literature. Deuxième, they do not use a gen-
eratively structured hypothesis space, but rather directly infer a matrix. Troisième, they only con-
sider a restricted set of possible bases for the Bayesian inference, rather than systematically
exploring a set of possible LOTs.

Despite its limitations, this article has shown that connectionism and many LOTs have sim-
ilar empirical import in the case of learning effort for Boolean categorization. One suggestive
explanation for this is that they both approximately track the underlying complexity of the
functions characterizing each category. While complexity cannot be computed exactly, là
are methods to approximate it. Showing a correlation between the measures presented in this

16 For a thorough discussion of the role that considerations of computational complexity can play in theory
building in the cognitive sciences, see Van Rooij (2008).

OPEN MIND: Discoveries in Cognitive Science

143

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neural Networks and Logical Complexity

Carcassi and Szymanik

article and approximated complexity would therefore provide evidence for a unified account
based on complexity. We leave these possible developments to future work.

REMERCIEMENTS

The research leading to these results has received funding from the European Research Coun-
cil under the European Union’s Seventh Framework Programme (FP/2007-2013) / ERC Grant
Agreement n. STG 716230 CoSaQ. We thank Steven Piantadosi and Shane Steinert Threlkeld
for the interesting discussion that was inspiring for this project.

INFORMATIONS SUR LE FINANCEMENT

JS, Seventh Framework Programme (https://dx.doi.org/10.13039/100011102), Award ID:
STG716230.

CONTRIBUTIONS DES AUTEURS

FC: Conceptualisation: Equal; Analyse formelle: Lead; Méthodologie: Lead; Visualisation: Lead;
En écrivant – brouillon original: Lead; En écrivant – revoir & édition: Equal. JS: Conceptualisation: Equal;
Analyse formelle: Equal; Visualisation: Equal; En écrivant – brouillon original: Equal; En écrivant – revoir &
édition: Equal.

RÉFÉRENCES

Antoine, M.. (2010). Neural networks and Boolean functions. Dans
P.. L. Hammer & Oui. Crama (Éd.), Boolean models and methods in
mathematics, computer science, and engineering (pp. 554–576).
C a m b r i d g e U n i v e r s i t y P r e s s . h t t p s : / / d o i . o rg / 1 0 . 1 0 1 7
/CBO9780511780448.016

Bartos, P.. D. (2002). Connectionist modelling of category learning

(Unpublished doctoral dissertation). The Open University.

Boole, G. (1854). An investigation of the laws of thought: On which
are founded the mathematical theories of logic and probabilities.
Walton & Maberly. https://doi.org/10.5962/bhl.title.29413

Bruner, J.. S., Goodnow, J.. J., & Austin, G. UN. (2017). A study of thinking
(2nd ed.). Routledge. https://doi.org/10.4324/9781315083223
Chater, N., & Vitányi, P.. (2003). Simplicity: A unifying principle in cog-
nitive science? Tendances des sciences cognitives, 7(1), 19–22. https://est ce que je
.org/10.1016/S1364-6613(02)00005-0, PubMed: 12517354

Davies, M.. (1991). Concepts, connectionism, and the language of
thought. In W. Ramsey, S. P.. Stich, & D. Rumelhart (Éd.), Philos-
ophy and connectionist theory (pp. 485–503). Lawrence Erlbaum
Associates.

Deolalikar, V. (2001). Mapping Boolean functions with neural net-
works having binary weights and zero thresholds. IEEE Transac-
tions on Neural Networks, 12(3), 639–642. https://est ce que je.org/10
.1109/72.925568, PubMed: 18249898

Dovgopoly, UN., & Mercado, E. (2013). A connectionist model of
category learning by individuals with high-functioning autism
spectrum disorder. Cognitive, Affective & Behavioral Neuroscience,
13(2), 371–389. https://doi.org/10.3758/s13415-012-0148-0,
PubMed: 23299250

Estes, W. K., Campbell, J.. UN., Hatsopoulos, N., & Hurwitz, J.. B.
(1989). Base-rate effects in category learning: A comparison of
parallel network and memory storage-retrieval models. Journal
of Experimental Psychology: Apprentissage, Mémoire, et cognitif,
15(4), 556–571. https://doi.org/10.1037/0278-7393.15.4.556,
PubMed: 2526853

Feldman, J.. (2000). Minimization of Boolean complexity in human
concept learning. Nature, 407(6804), 630–633. https://est ce que je.org/10
.1038/35036586, PubMed: 11034211

Feldman, J.. (2003un). A catalog of Boolean concepts. Journal de
Mathematical Psychology, 47(1), 75–89. https://est ce que je.org/10.1016
/S0022-2496(02)00025-1

Feldman, J.. (2003b). The simplicity principle in human concept
learning. Current Directions in Psychological Science, 12(6),
227–232. https://doi.org/10.1046/j.0963-7214.2003.01267.X
Feldman, J.. (2006). An algebra of human concept learning. Journal
of Mathematical Psychology, 50(4), 339–368. https://est ce que je.org/10
.1016/j.jmp.2006.03.002

Fodor, J.. UN. (1975). The language of thought. Presse universitaire de Harvard.
Fodor, J.. UN., & Pylyshyn, Z. W. (1988). Connectionism and cognitive
architecture: A critical analysis. Cognition, 28(1–2), 3–71. https://
doi.org/10.1016/0010-0277(88)90031-5, PubMed: 2450716
Gallistel, C. R., & King, UN. P.. (2009). Memory and the computa-
tional brain: Why cognitive science will transform neuroscience.
Wiley-Blackwell. https://doi.org/10.1002/9781444310498

Gluck, M.. UN., & Bower, G. H. (1988). From conditioning to cate-
gory learning: An adaptive network model. Journal of Experimen-
tal Psychology: General, 117(3), 227–247. https://est ce que je.org/10
.1037/0096-3445.117.3.227, PubMed: 2971760

Homme bon, N. D., Tenenbaum, J.. B., Feldman, J., & Griffiths, T. L.
(2008). A rational analysis of rule-based concept learning. Cog-
nitive Science, 32(1), 108–154. https://est ce que je.org/10.1080
/03640210701802071, PubMed: 21635333

Griffiths, T. L., Austerweil, J.. L., & Berthiaume, V. G. (2012). Compar-
ing the inductive biases of simple neural networks and Bayesian
models. In Proceedings of the 34th Annual Meeting of the Cognitive
Science Society (pp. 402–407). Cognitive Science Society.

Grünwald, P.. D. (2007). The minimum description length principle.

AVEC Presse. https://doi.org/10.7551/mitpress/4643.001.0001

Guest, O., & Love, B. C. (2019). Levels of representation in a deep
learning model of categorization. bioRxiv. https://est ce que je.org/10
.1101/626374

Kemp, C., Homme bon, N. D., & Tenenbaum, J.. B. (2008). Theory
acquisition and the language of thought. In Proceedings of
the 30th Annual Conference of the Cognitive Science Society
(pp. 1606–1611). Cognitive Science Society.

OPEN MIND: Discoveries in Cognitive Science

144

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neural Networks and Logical Complexity

Carcassi and Szymanik

Kingma, D. P., & Ba, J.. (2015). Adam: A method for stochastic opti-
mization. In International Conference of Learning Representa-
tion (ICLR). ArXiv.

Kruschke, J.. (1991). ALCOVE: A connectionist model of human cat-
egory learning. In R. P.. Lippmann, J.. E. Moody, & D. S. Touretzky
(Éd.), Advances in Neural Information Processing Systems (Vol. 3,
pp. 649–655). Morgan-Kaufmann.

Lake, B. M., Salakhutdinov, R., & Tenenbaum, J.. B. (2015). Human-
level concept learning through probabilistic program induction.
Science, 350(6266), 1332–1338. https://doi.org/10.1126/science
.aab3050, PubMed: 26659050

Li, M., & Vitányi, P.. M.. (1990). Kolmogorov complexity and its
applications. In Algorithms and complexity (pp. 187–254). Else-
vier. https://doi.org/10.1016/B978-0-444-88071-0.50009-6

Mazzoni, D., & Wagstaff, K. (2004). Active learning in the presence
of unlabelable examples. In J.-F. Boulicaut, F. Esposito, F. Giannotti,
& D. Pedreschi (Éd.), European Conference on Machine Learning.
Springer.

Mhaskar, H., Liao, Q., & Poggio, T. (2016). Learning real and Bool-
ean functions: When is deep better than shallow (Technique
report). Center for Brains, Minds, and Machines.

Mingard, C., Skalse, J., Valle-Pérez, G., Martínez-Rubio, D., Mikulik,
V., & Louis, UN. UN. (2020). Neural networks are a priori biased
towards Boolean functions with low entropy. ArXiv.

Minsky, M., & Papert, S. UN. (1972). Perceptrons: An introduction to

computational geometry (2nd ed.). AVEC Presse.

Mollica, F., & Piantadosi, S. T. (2022). Logical word learning: The case
of kinship. Psychonomic Bulletin & Review, 29(3), 766–799. https://
doi.org/10.3758/s13423-021-02017-5, PubMed: 34918269

Penny, W., & Stonham, T. (1992). On the generalisation ability and
storage capacity of logical neural networks. In Proceedings of the
IJCNN International Joint Conference on Neural Networks (Vol. 3,
pp. 845–850). IEEE. https://doi.org/10.1109/IJCNN.1992.227047
Pérez, E., & Rendell, L. UN. (1995). Using multidimensional projection
to find relations. In A. Prieditis & S. Russell (Éd.), Proceedings of
the Twelfth International Conference on International Conference
on Machine Learning (pp. 447–455). Morgan Kaufmann Pub-
lishers. https://doi.org/10.1016/B978-1-55860-377-6.50062-1
Piantadosi, S. T., Tenenbaum, J.. B., & Homme bon, N. D. (2012).
Bootstrapping in a language of thought: A formal model of
numerical concept learning. Cognition, 123(2), 199–217. https://
doi.org/10.1016/j.cognition.2011.11.005, PubMed: 22284806
Piantadosi, S. T., Tenenbaum, J.. B., & Homme bon, N. D. (2016). Le
logical primitives of thought: Empirical foundations for composi-
tional cognitive models. Psychological Review, 123(4), 392–424.
https://doi.org/10.1037/a0039980, PubMed: 27077241

Rescorla, M.. (2019). The language of thought hypothesis. In E. N.
Zalta (Ed.), The stanford encyclopedia of philosophy (Été
éd.). Metaphysics Research Lab, Université de Stanford.

Rumelhart, D. E., Hinton, G. E., & Williams, R.. J.. (1986). Apprentissage
representations by back-propagating errors. Nature, 323(6088),
533–536. https://doi.org/10.1038/323533a0

Rumelhart, D. E., & McClelland, J.. L. (1987). Learning the past
tenses of English verbs: Implicit rules or parallel distributed pro-
cessation? In B. MacWhinney (Ed.), Mechanisms of language aqui-
sition (pp. 195–248). Lawrence Erlbaum Associates.

Settles, B., & Craven, M.. (2008). An analysis of active learning
strategies for sequence labeling tasks. En M. Lapata & H. T.
Ng (Éd.), Proceedings of the Conference on Empirical Methods
in Natural Language Processing (pp. 1070–1079). Association
for Computational Linguistics. https://doi.org/10.3115/1613715
.1613855

Shepard, R.. N., Hovland, C. JE., & Jenkins, H. M.. (1961). Apprentissage
and memorization of classifications. Psychological Monographs:
General and Applied, 75(13), 1–42. https://doi.org/10.1037
/h0093825

Sprinkhuizen-Kuyper, je. G., & Boers, E. J.. W. (1996). Probabilities
and entropy of some small neural networks for Boolean functions
(Technical report No. 96-30). Leiden University.

Sutton, J.. (1995). Reduction and levels of explanation in connec-
tionism. In P. Slezak, T. Caelli, & R.. Clark (Éd.), Perspectives
on cognitive science: Theories, experiments, and foundations
(pp. 347–368). Ablex.

Tenenbaum, J.. B., Griffiths, T. L., & Kemp, C. (2006). Theory-based
Bayesian models of inductive learning and reasoning. Trends in
Sciences cognitives, 10(7), 309–318. https://doi.org/10.1016/j.tics
.2006.05.009, PubMed: 16797219

Van Rooij, je. (2008). The tractable cognition thesis. Sciences cognitives,
32(6), 939–984. https://doi.org/10.1080/03640210801897856,
PubMed: 21585437

Vigo, R.. (2006). A note on the complexity of Boolean concepts.
Journal of Mathematical Psychology, 50(5), 501–510. https://est ce que je
.org/10.1016/j.jmp.2006.05.007

Wegener, je. (1987). The complexity of Boolean functions. Wiley-

Teubner. https://doi.org/10.1007/3-540-18170-9_185

Wernick, W. (1942). Complete sets of logical functions. Transac-
tions of the American Mathematical Society, 51, 117–132.
https://doi.org/10.1090/S0002-9947-1942-0005281-2

Blanc, B. W., & Rosenblatt, F. (1963). Principles of neurodynamics:
Perceptrons and the theory of brain mechanisms. The American
Journal of Psychology, 76(4), 705–707. https://doi.org/10.2307
/1419730

APPENDIX
INTERPRETING ANN INPUT/OUTPUT

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
5
9
2
0
4
1
6
8
8
o
p
m
_
un
_
0
0
0
5
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

The situation is complicated somewhat by the fact that each input/output relation can be inter-
preted by the artificial neural network (ANN) as different categories depending on whether 0 et
1 are interpreted as meaning True or False (the interpretation of binary values is given indepen-
dently for input and output). Par exemple, consider the following possible input/output relation
for an ANN (with only two objects instead of four for ease of visualization):

8
>>< >>:

0; 0ð
0; 1ð
1; 0ð
1; 1ð

Þ ⇒ 1
Þ ⇒ 0
Þ ⇒ 0
Þ ⇒ 0

9
>>=
>>;

OPEN MIND: Discoveries in Cognitive Science

145

Neural Networks and Logical Complexity

Carcassi and Szymanik

This can be interpreted as encoding different categories as follows (where each cell gives the
category as a set of sets of properties):

1 in output as True

1 in input as True
{¬p, ¬q}

1 in input as False
{p, q}

1 in output as False

{¬p, q}, {p, ¬q}, {p, q}

{p, ¬q}, {¬p, q}, {¬p, ¬q}

From a total of 65,536 possible categories (with four objects), we train the ANNs on 32,768
input/output relations, and interpret the learning efforts as representative of both
interpretations of the input binary values.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
o
p
m

je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/