REPORT
Numeral Systems Across Languages
Support Efficient Communication: Depuis
Approximate Numerosity to Recursion
Yang Xu 1∗, Emmy Liu2∗, and Terry Regier3
1Department of Computer Science, Cognitive Science Program, University of Toronto
2Computer Science and Cognitive Science Programs, University of Toronto
3Department of Linguistics, Cognitive Science Program, Université de Californie, Berkeley
un accès ouvert
journal
*These authors contributed equally to the work.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
.
/
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
.
/
je
Mots clés: number, semantic typology, efficient communication, functionalism, recursion
ABSTRAIT
Languages differ qualitatively in their numeral systems. At one extreme, some languages have
a small set of number terms, which denote approximate or inexact numerosities; at the other
extrême, many languages have forms for exact numerosities over a very large range, through
a recursively defined counting system. Why do numeral systems vary as they do? Ici, nous
use computational analyses to explore the numeral systems of 30 languages that span this
spectrum. We find that these numeral systems all reflect a functional need for efficient
communication, mirroring existing arguments in other semantic domains such as color,
kinship, and space. Our findings suggest that cross-language variation in numeral systems
may be understood in terms of a shared functional need to communicate precisely while
using minimal cognitive resources.
NUMERAL SYSTEMS
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A central question in cognitive science is why languages partition human experience into
categories in the ways they do (Berlin & Kay, 1969; Levinson & Meira, 2003). Ici, we ex-
plore this question in the domain of number.
Number is a core element of human knowledge (par exemple., Jeux & Kinzler, 2007) and lan-
guages vary widely in their numeral systems (Beller & Cintreuse, 2008; Cintreuse & Beller, 2014;
Comrie, 2013; Greenberg, 1978; Hammarström, 2010). De plus, there are qualitatively dis-
tinct classes of such numeral systems. Some languages have numeral systems that express only
approximate or inexact numerosity; other languages have systems that express exact numeros-
ity but only over a restricted range of relatively small numbers; while yet other languages have
fully recursive counting systems that express exact numerosity over a very large range. These
different numeral systems are likely to be grounded in different cognitive capacities for judging
numerosity. Par exemple, approximate numeral systems may be grounded directly in the non-
linguistic approximate number system, a cognitive capacity for approximate numerosity that
humans share with nonhuman animals (Dehaene, 2011). At the other extreme, the ability to
judge exact high numerosity is not universal but appears instead to rely on the existence of a
linguistic counting system that singles out such exact high numerosities (Gordon, 2004; Pica,
Lemer, Izard, & Dehaene, 2004).
Citation: Xu, Y., Liu, E., & Regier, T.
(2020). Numeral Systems Across
Languages Support Efficient
Communication: From Approximate
Numerosity to Recursion. Open Mind:
Discoveries in Cognitive Science, 4,
57–70 https://doi.org/10.1162/opmi_a_
00034
EST CE QUE JE:
https://doi.org/10.1162/opmi_a_00034
Supplemental Materials:
https://www.mitpressjournals.org/doi/
suppl/10.1162/opmi_a_00034
Reçu: 24 Novembre 2019
Accepté: 28 May 2020
Intérêts concurrents: The authors
declare no conflict of interest.
Corresponding Authors:
Yang Xu
yangxu@cs.toronto.edu
Emmy Liu
me.liu@utoronto.ca
droits d'auteur: © 2020
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
Numeral Systems and Efficient Communication Xu et al.
We seek to understand why certain numeral systems are attested in the world’s languages
while other logically possible systems are not. We also seek to understand why the qualitative
classes of such systems—from approximate counting, to exact counting over a restricted range,
to fully recursive counting—appear as they do.
EFFICIENT COMMUNICATION
An existing proposal has the potential to answer these questions. It has long been argued
(par exemple., von der Gabelentz, 1901; Zipf, 1949) that languages are shaped by functional pressure
for efficient communication—that is, pressure to communicate precisely yet with minimal
cognitive effort—and this idea has attracted increasing attention recently (par exemple., Fedzechkina,
Jaeger, & Newport, 2012; Gibson et al., 2019; Haspelmath, 1999; Hopper & Traugott, 2003;
Kanwal, Forgeron, Culbertson, & Kirby, 2017; Piantadosi, Tily, & Gibson, 2011; Forgeron, Tamariz,
& Kirby, 2013). Of direct relevance to numeral systems, it has been argued in particular that
systems of word meanings across languages reflect such a need for efficient communication
(Kemp, Xu, & Regier, 2018). On this account, for any given semantic domain, the different
categorical partitionings of that domain observed in the world’s languages represent different
means to the same functional end of efficiency. This idea has been supported by cross-language
computational analyses in the domains of color (Regier, Kemp, & Kay, 2015; Zaslavsky, Kemp,
Regier, & Tishby, 2018), kinship (Kemp & Regier, 2012), spatial relations (Khetarpal, Neveu,
Majid, Michael, & Regier, 2013), names for containers (Xu, Regier, & Malt, 2016; Zaslavsky,
Regier, Tishby, & Kemp, 2019), and names for seasons (Kemp, Gaby, & Regier, 2019). We ask
whether the same idea explains why numeral systems appear as they do, from approximate to
fully recursive form.
The idea of efficient communication involves a tradeoff between two competing forces:
informativeness and simplicity. An informative system is one that supports precise communica-
tion; a simple system is one with a compact cognitive representation. A maximally informative
system would have a separate word for each object in a given semantic domain—which would
be complex, not simple. In contrast, a maximally simple system would have just one word for
all objects in a given semantic domain—which would not support precise communication.
The proposal is that attested semantic systems are those that achieve a near-optimal tradeoff
between these two competing forces, and thus achieve communicative efficiency.
Chiffre 1 illustrates these ideas. Ici, a speaker has a particular number in mind (4,
mentally represented as an exact point on a number line), and wishes to convey that number
to a listener. The speaker has expressed that number using the English approximate term “a
few,” rather than the exact term “four” that is also available in English. On the basis of this
utterance, the listener mentally reconstructs the number that the listener believes the speaker
intended. Because the term “a few” is inexact, the listener’s reconstruction of the intended
number is also inexact, and is shown as a probability distribution centered near 4 ou 5 et
extending to neighboring numbers as well. Par conséquent, the listener’s mental reconstruction does
not match the speaker’s intention perfectly. Cependant, if the speaker had instead used the exact
term “four,” that term would have allowed the listener to reconstruct the speaker’s intended
meaning perfectly. We take the informativeness of communication to be the extent to which
the listener’s mental reconstruction matches the speaker’s representation. Communication is
not perfectly informative in the illustrated case of “a few” but would be perfectly informative
in the case of “four.”
Clairement, an exact numeral system that picks out specific integers is more informative
than an approximate system—but it is less simple. A system of approximate numerals can
OPEN MIND: Discoveries in Cognitive Science
58
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
.
/
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
.
/
je
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Numeral Systems and Efficient Communication Xu et al.
Chiffre 1. Scenario for communicating a number.
span a given range of the number line using very few terms, whereas many exact integer
terms would be needed to span the same range. Ainsi, the high informativeness of an exact
numeral system comes at a high cognitive cost. Surtout, cependant, a recursive exact system
would be specifiable using a relatively small number of generative rules, rather than separate
lexical entries for each exact numeral. Ainsi, recursive numeral systems may be a cognitive tool
(Frank, Everett, Fedorenko, & Gibson, 2008) that enables highly informative communication
about number at the price of only modest cognitive complexity (par exemple., Piantadosi, Tenenbaum,
& Homme bon, 2012).
We wish to know whether these ideas can account for which numeral systems, et
which classes of such systems, are attested across languages. To this end, we require: (1) un
cross-language data set of numeral systems that captures the distinctions between classes of
such systems, (2) a formal specification of our theory, et (3) a test of the theory against the
data. We specify each of these in turn below, and then present our results. To preview our
résultats, we find that numeral systems across languages tend to support near-optimally efficient
communication, and that the drive for efficient communication also helps to explain why the
different classes of numeral systems appear as they do. Our results suggest that the different
types of numeral system found across languages all support the same functional goal of efficient
communication, in different ways.
CROSS-LINGUISTIC DATA
We considered the numeral systems of 30 languages, listed in Table 1, which span the spec-
trum from approximate to exact restricted to recursive numeral systems. We have used these
class designations somewhat loosely up until now, and define them more precisely in the
Supplemental Materials. The majority of the languages in this data set were drawn from
Comrie’s chapter on numeral bases in the World Atlas of Language Structures (WALS) (Comrie,
2013). That chapter includes references to grammars for individual languages, each of which
describes that language’s numeral system. We also considered the numeral systems of French
and Spanish, and three languages (Chiquitano, Fuyuge, Krenák) from Hammarström’s (2010)
OPEN MIND: Discoveries in Cognitive Science
59
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
/
.
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
/
.
je
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Numeral Systems and Efficient Communication Xu et al.
Tableau 1. Le 30 languages in the data set, grouped by type of numeral system.
Approximate systems (6 languages):
Chiquitano, Fuyuge, Gooniyandi, Mundurukú, Pirahã, Wari’
Exact restricted systems (18 languages):
Achagua, Araona, Awa Pit, Barasano, Baré, Hixkaryana, Hup, Imonda, Kayardild, Krenák,
Mangarrayi, Martuthunira, Pitjantjatjara, Rama, Waskia, Wichí, Yidiny, !Xóõ
Recursive systems (6 languages):
English, Mandarin, and Spanish (base 10), Ainu (base 20), French and Georgian (base 10
et 20)
survey of rare numeral systems. These numeral systems were supplemented by a description
of the Mundurukú numeral system (Pica et al., 2004).
FORMAL PRESENTATION OF THEORY
We have seen that the notion of efficient communication involves a tradeoff between the com-
peting forces of simplicity and informativeness. We first formalize each of these two forces
à son tour, and then the tradeoff between them (Kemp & Regier, 2012; Regier et al., 2015).
Throughout this article, we restrict our attention to numerals over the range 1–100.
Simplicity
Simplicity is the opposite of complexity, and we define the complexity of a numeral system
to be the number of symbols needed to specify it. This notion of complexity is grounded in
standard ideas from algorithmic information theory (par exemple., Kolmogorov, 1963; Li & Vitányi,
2013). We specify numeral systems as grammars, expressed in a language of thought (Fodor,
1975; Piantadosi et al., 2012), and based on the primitive components listed in Table 2 et
explained in the Supplemental Materials. The complexity of each system is thus given by the
number of symbols in the corresponding grammar.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
.
/
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
/
.
je
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Tableau 2. Grammatical components for representing numeral systems.
Component
Description
c
˜x
m(w)
s(w, v)
h(w)
+
–
×
÷
p(X, n)
d
=
∈
≡
Primitive concept c = 1, 2 ou 3
Gaussian with approximate mean ˜x
Meaning of form w
Successor of w with interval v; s(w)=s(w,1)
Higher than w
Addition
Subtraction
Multiplication
Division
x to the nth power
Form definition
Set definition
Equivalence
OPEN MIND: Discoveries in Cognitive Science
60
Numeral Systems and Efficient Communication Xu et al.
Tableau 3. Grammar for Piraha (approximate) numeral system for the range 1–100.
Nombre
1
∼2–4
∼5–100
Rule
‘hoi1’
‘hoi2’
‘aibaagi’
d
= ˜1
d
= ˜3
d
= e52
Complexity
3
3
3
Σ = 9
Note. Each rule is composed of symbols, and each symbol adds a unit complexity
de 1. We do not use subitizing because work by Gordon (2004) suggests that the
numeral for 1 is inexact in Piraha.
Tableau 4. Grammar for Kayardild (exact restricted) numeral system for the range 1–100.
Nombre
Rule
Complexity
1
2
3
4
5–100
‘warngiida’
‘kiyarrngka’
d
= 1
d
= 2
d
= 3
‘burldamurra’
d
= s(‘burldamurra’)
‘mirndinda’
d
= h(‘mirndinda’)
‘muthaa’
3
3
3
4
4
Σ = 17
Note. Each rule is composed of symbols, and each symbol adds a unit complexity of 1.
Tables 3, 4, et 5 present grammars for the numeral systems of three languages, un
from each of the three classes we consider here, and indicate the complexity of each grammar.
Different authors sometimes hold different views on the grammar of a given numeral system,
and here we chose to work with grammars from representative sources, while acknowledging
that such disagreement exists.1
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
.
/
/
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
.
/
je
Informativeness
Informativeness of communication was illustrated in the communicative scenario of Figure 1.
Returning to that scenario, we may represent the speaker’s intended meaning as a probability
distribution S(je) over numbers i, and analogously represent the listener’s mental reconstruction
of that meaning as a distribution Lw(je) over numbers i, based on the word w uttered by the
conférencier. We assume that the speaker is certain of the target number: S(t) = 1 for the intended
target number t, et S(je) = 0 for all other numbers i 6= t (Regier et al., 2015; cf. Zaslavsky et al.,
2018). We assume that the listener distribution Lw(je) depends on the number word w produced
by the speaker, which may be grounded in primitives drawn from the subitizing number system,
the approximate number system, or exact numerosity, as specified in the Supplemental
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1 Par exemple, different accounts of the Pirahã numeral system were presented by Gordon (2004) and by Frank
(2008), in large part because the two studies explored different numerical tasks. Specifically, Frank et al.
et autres.
(2008) examined both counting upward from a small number, and counting downward from a large number,
whereas Gordon (2004) examined numeral use in a variety of contexts that did not include counting downward.
We have chosen to use Gordon’s (2004) analysis in our cross-language study because downward counting has
not been widely investigated across languages. We leave as an open question whether the principles we explore
here will generalize to both forward and backward counting, across languages.
OPEN MIND: Discoveries in Cognitive Science
61
Numeral Systems and Efficient Communication Xu et al.
Tableau 5. Grammar for English (recursive) numeral system for the range 1–100.
Nombre
Rule
Complexity
1
2
3
4
5
6
7
8
9
10
11
12
13…19
20…90
21…99
100
‘one’
‘two’
‘three’
‘four’
‘five’
‘six’
d
= 1
d
= 2
d
= 3
d
= s(‘three’)
d
= s(‘four’)
d
= s(‘five’)
‘eight’
‘seven’
d
= s(‘six’)
d
= s(‘seven’)
d
= s(‘eight’)
‘nine’
d
= s(‘nine’)
‘ten’
‘eleven’
‘twelve’
d
= s(‘ten’)
d
= s(‘eleven’)
d
= m(toi)+m(‘ten’)
u‘teen’
d
= m(toi)×m(‘ten’)
u‘ty’
u‘ty’-v
d
= m(toi)×m(‘ten’)+m(v)
d
= p(m(‘ten’),m(‘two’))
‘hundred’
u ∈ { ‘twen’,‘thir’,…,‘eigh’,‘nine’ }
v ∈ { ‘one’,‘two’,…,‘eight’,‘nine’ }
‘twen’ ≡ ‘two’
‘thir’ ≡ ‘three’
‘for’ ≡ ‘four’
‘fif’ ≡ ‘five’
‘eigh’ ≡ ‘eight’
3
3
3
4
4
4
4
4
4
4
4
4
8
8
13
7
10
11
3
3
3
3
3
Σ = 117
Note. Each rule is composed of symbols, and each symbol adds a unit complexity
de 1.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
/
.
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
.
/
je
Materials. We do not model pragmatic reasoning in which the listener and speaker reason
recursively about each other (Brooks, Audet, & Barner, 2013; Frank & Homme bon, 2012).
Given specifications of the speaker (S) and listener (Lw) distributions, we define the com-
municative cost C(t) of communicating a target number t under a given numeral system to
be the information lost in communication—that is, the information lost in the listener’s recon-
struction Lw when compared to the speaker’s distribution S. We model this information loss
as the Kullback-Leibler (KL) divergence between distributions S and Lw. In the case of speaker
certainty (S(t) = 1 for the target number t), this reduces to surprisal:2
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
C(t) = DKL(S||Lw) = ∑
je
S(je) log2
S(je)
Lw(je)
= log2
1
Lw(t)
(1)
2 The same loss function is used in rational speech act (RSA; par exemple., Frank & Homme bon, 2012) models in char-
acterizing the utility of a speaker’s word choice.
OPEN MIND: Discoveries in Cognitive Science
62
Numeral Systems and Efficient Communication Xu et al.
We model the communicative cost for a numeral system as a whole as the expected value of
C over all possible target numbers t:
E[C] = ∑
t
N(t)C(t)
(2)
Ici, N(t) is the need probability of target number t—that is, the probability that a speaker
will need to refer to t rather than some other number. We estimated need probabilities by
the normalized frequencies of English numerals in the Google ngram corpus (Michel et al.,
2011) for the year 2000, as described in the Supplemental Materials. Qualitatively, this yields
need that drops off with increasing numerosity. The distribution of need probabilities may
well vary across languages and cultures, and would ideally be estimated on a per-language
basis. Cependant, we do not have data that would support such per-language estimation of need
probabilities, and so we tentatively assume a universal distribution estimated from English
usage (Kemp & Regier, 2012). The qualitative nature of this distribution—a dropoff in need as
numbers increase—may generalize across cultures even if the specific quantitative shape of
that dropoff does not (Dehaene & Mehler, 1992; Piantadosi, 2016). In our analyses below,
we compare this corpus-based distribution with other hypothetical need distributions.
Tradeoff
We take a numeral system to be simple to the extent that it exhibits low complexity, and we
take it to be informative to the extent that it exhibits low communicative cost E[C]. Given
ce, we consider a numeral system to be near-optimally efficient if it is more informative (c'est à dire.,
exhibits lower communicative cost) than most logically possible hypothetical systems of the
same complexity, or if it is simpler (c'est à dire., exhibits lower complexity) than most logically possible
hypothetical systems that have the same communicative cost.
STUDIES
We test our theory against the data in two steps. We first assess the semantic primitives in
Tableau 2. We do so by testing whether the primitives that represent subitizing and the approx-
imate number system can accommodate fine-grained linguistic data from the one relevant
language for which we have such data, Mundurukú. We then use the full set of primitives to
conduct efficiency analyses on all languages in our data set.
Mundurukú and the Approximate Number System
Pica et al.
(2004) showed that their formalization of the approximate number system, gov-
erned by Weber’s law, accounted well for nonlinguistic numerosity judgments by speakers of
Mundurukú. They also collected fine-grained data on the way speakers of Mundurukú name
different numerosities, but they did not directly test whether their formalization of the ap-
proximate number system also accommodates those linguistic data. We test that question
(2004)—
ici. Figure 2A shows empirical Mundurukú number naming data from Pica et al.
specifically, for numerosities 1 à 15, this figure shows the fraction of times each numerosity
i was named with a given Mundurukú word or locution w. Figure 2B shows the fit to these
data of a model based on subitizing and the approximate number system, grounded in the
relevant semantic primitives from Table 2. The model fit was good (MSE = 0.002), et était
superior to that of other models considered. Model details along with variants of the model us-
ing different Weber fraction values are provided in the Supplemental Materials. These findings
suggest that the model of subitizing and the approximate number system given by the relevant
OPEN MIND: Discoveries in Cognitive Science
63
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
/
.
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
.
/
je
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Numeral Systems and Efficient Communication Xu et al.
Chiffre 2. Modeling Mundurukú naming data. (UN) Empirical data collected by Pica et al.
(2004).
(B) Fit to the empirical data of a model based on primitives that capture subitizing and Weber’s law.
semantic primitives in Table 2 provide a reasonable basis for grounding approximate numeral
systèmes.
Efficiency of Numeral Systems
We wished to test (un) whether all numeral systems in our data set are near-optimally efficient,
et (b) whether the notion of efficiency also helps to explain the distinct classes of system that
appear in the data.
To test whether the attested numeral systems in our data set are near-optimally efficient,
we assessed their simplicity and informativeness relative to a large set of logically possible
hypothetical systems. These hypothetical systems fell in the same three major classes as our
attested systems: approximate, exact restricted, and recursive. Details of these hypothetical
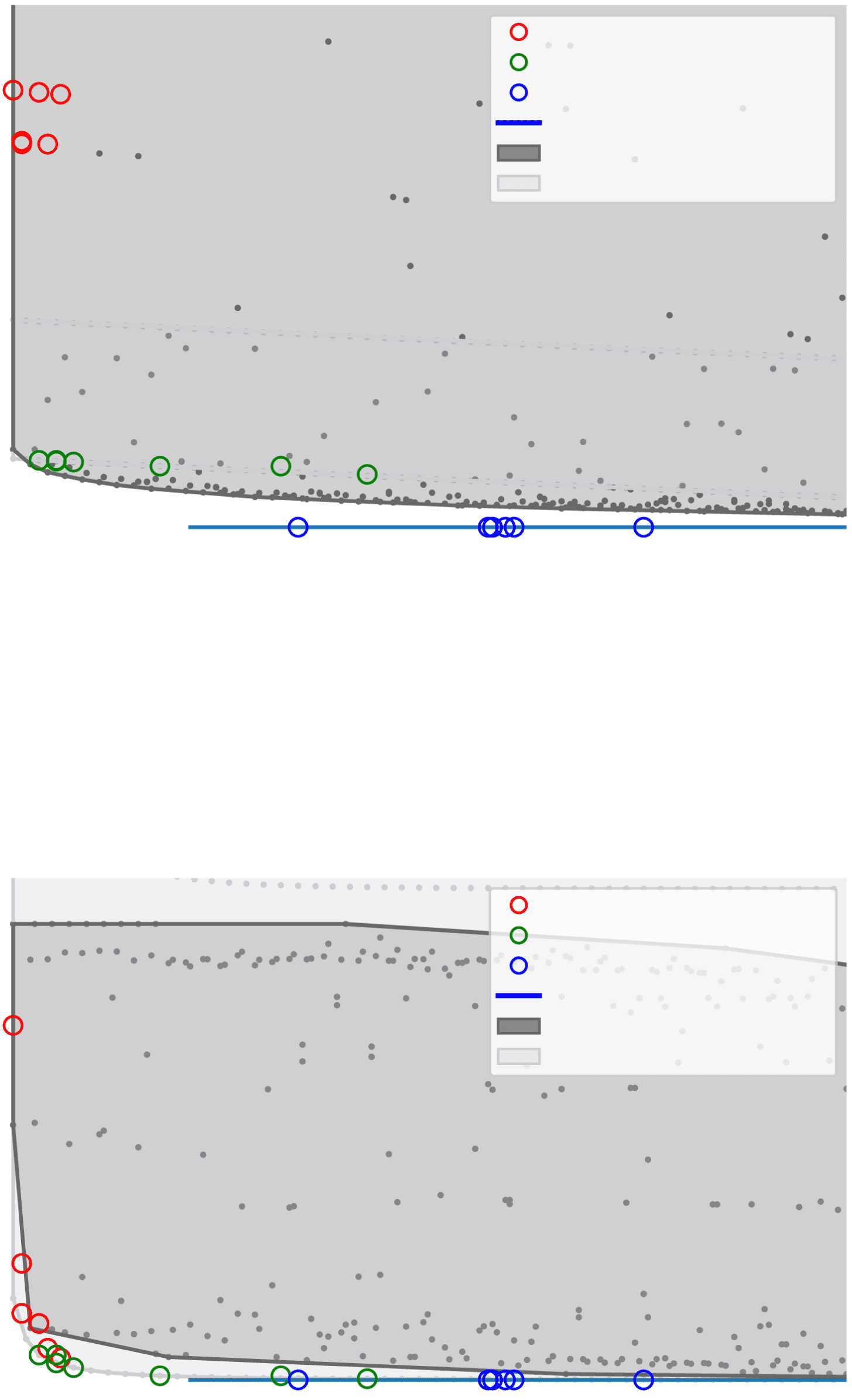
systems are provided in the Supplemental Materials. Figure 3A shows sampled hypothetical
systèmes (in dots), along with the convex hull of those sampled hypothetical systems, for approx-
imate systems and exact restrictive systems, and the full set of hypothetical recursive systems,
plotted according to their complexity and communicative cost, and compared with attested
systèmes (shown as colored circles). The dark gray region denotes the range of costs exhibited
by approximate hypothetical systems of various complexities; the light gray region denotes the
range of costs exhibited by exact restricted hypothetical systems of various complexities; et
the extent of the black horizontal line at communicative cost 0 denotes the range of com-
plexities exhibited by hypothetical recursive systems, all of which have communicative cost
0. It can be seen that, in general, attested numeral systems in our data set tend to be more
informative (show lower communicative cost) than most hypothetical alternatives of the same
complexity. Ainsi, despite their variation, these attested systems all seem to share the capacity
to support near-optimally efficient communication about number, suggesting that they may
reflect adaptation for that function. In the Supplemental Materials, we show that these results
are similar under alternative values of the Weber fraction.
OPEN MIND: Discoveries in Cognitive Science
64
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
/
.
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
/
.
je
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Numeral Systems and Efficient Communication Xu et al.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
.
/
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
.
/
je
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 3. Efficiency analysis of numeral systems. (UN) Near-optimal tradeoff between commu-
nicative cost and complexity across attested numeral systems, compared with corresponding hy-
pothetical approximate, exact restricted, and recursive systems. Several exact restricted systems are
equivalent here, namely, languages with terms for the first three numerals and a higher term (Araona,
Achagua, Baré, Hixkaryana, Martuthunira, Mangarrayi, Pitjantjatjara, !Xóõ), terms for the first four
numerals and a higher term (Awa Pit, Kayardild), and terms for the first six numerals and a higher
term (Rama, Barasano, Imonda, Yidiny). (B) Comparison of sample attested systems to theoretically
optimal systems of the same complexity. (C) Sample of nonoptimal hypothetical approximate (A1–
A4) and exact restricted (E1–E4) systèmes, highlighted in pink in A. In B and C, each hue specifies
the range of a corresponding numeral.
Among the hypothetical recursive systems we considered, canonical base-10 (decimal)
is one of the simpler systems. Par exemple, Mandarin Chinese is a canonical base-10 sys-
tem. The simplicity of base 10 reflects frequency of occurrence among the world’s languages
OPEN MIND: Discoveries in Cognitive Science
65
Numeral Systems and Efficient Communication Xu et al.
(par exemple., Comrie, 2013). In comparison, English as a variant of base-10 system (par exemple., “eleven” and
“twelve” have separate forms and do not derive their meanings from the base “ten”), and re-
cursive systems with base 20 (par exemple., Ainu) or a hybrid of bases 10 et 20 (par exemple., Georgian) tend to
be more complex. These findings are consistent with the suggestion (Ansuini, 2009; Hurford,
1987) that the relative complexity of various types of recursive system may partly explain the
relative frequency of the appearance of such systems. We provide further detail on the relative
complexities of canonical recursive systems in the the Supplemental Materials.
Figure 3B shows sample systems from our data set compared with the theoretically opti-
mally informative (lowest cost) systems of the same complexity—in all cases color-coded such
that a numeral corresponds to a colored region of the number line. It can be seen that the
attested systems resemble these theoretical optima, again suggesting that the attested systems
may have adapted to functional pressure to support efficient communication about number.
In contrast, Figure 3C shows example hypothetical numeral systems (for the range 1–100)
that are further away from the optimal and attested numeral systems, with their exact positions
indicated in Figure 3A. Although these systems are logically possible, they do not appear in
real numeral systems and are generally inefficient because their extensions for the low-order
numerals (par exemple., those below 10) tend to be coarse. En tant que tel, these systems cannot disambiguate
numerals that have the highest communicative need probabilities and therefore are highly
uninformative.
To further examine how need probability influences the efficiency of numeral systems,
we varied the need probability between extremes to assess its impact on the efficiency results.
One extreme was a uniform distribution, as this would remove the advantage of placing exact
terms at the beginning of the number line, increasing the cost for approximate and exact re-
stricted systems. This can be seen in Figure 4A. Another extreme used was a distribution that
was more left-skewed than the one based on corpus counts. This can be seen in Figure 4B.
Using the uniform need probability, all hypothetical systems had higher communicative cost,
and attested systems were further from the frontier as expected. Using the more skewed need
probability, hypothetical systems were lower in communicative cost and attested systems were
near-optimal as in the original case. This indicates that the efficiency of attested systems relies
on the tendency for smaller numeric values to be used more often.
These findings suggest that the pattern of near-optimal efficiency is critically dependent
on communicative need (Gibson et al., 2017; Kemp & Regier, 2012; Zaslavsky, Kemp, Tishby,
& Regier, 2019un, 2019b). We obtain this pattern of near-optimality when assuming a need
distribution that is based on corpus counts, and when assuming a steeper curve as might be
expected for societies with less need to refer often to high numerosities. But we do not obtain
this pattern of near-optimality when instead assuming a uniform need distribution, which is
logically possible but seems intuitively unlikely to characterize the numeral need distribution
for any society.
Our results also support a functional account of why the different classes of numeral
system in the world’s languages appear as they do, namely, as qualitatively different ways of
navigating the tradeoff between simplicity and informativeness. Approximate numeral systems
(shown as red circles in Figure 3A) represent one extreme on a continuum: they are simple (non-
complexe), requiring only a minimal cognitive investment in communicating about number.
These systems support near-optimally informative communication for that level of cognitive
investment—but they do not closely approach perfectly informative (0 coût) communication.
Mundurukú is essentially poised at a tipping point between such approximate systems and ex-
act restricted systems: it is the most complex and most informative of the approximate systems
OPEN MIND: Discoveries in Cognitive Science
66
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
/
.
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
/
.
je
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Numeral Systems and Efficient Communication Xu et al.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
.
/
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
/
.
je
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4. Efficiency of attested numeral systems in comparison to theoretical systems based on a
uniform (UN) and a left-skewed (B) need distribution.
in our data. Exact restricted systems (shown as green circles in the figure) tend to be slightly
more complex and support somewhat more informative communication. Enfin, recursive
systems represent the informative extreme of this continuum: these systems support perfectly
informative communication, because there is a (recursively generated) separate name for each
integer within a large range. Such fine-grained naming would be prohibitively expensive under
a nonrecursive system: there would have to be one rule per integer in the range covered. But a
recursive system supports perfectly informative communication over a large range, at the cost
of only modest complexity.
DISCUSSION AND CONCLUSION
We have seen that the need for efficient communication helps to explain why numeral sys-
tems across languages take the forms they do, by analogy with recent demonstrations in other
OPEN MIND: Discoveries in Cognitive Science
67
Numeral Systems and Efficient Communication Xu et al.
semantic domains—and that the same functional need helps to explain the qualitatively dif-
ferent classes of numeral system found across languages. At the core of this explanation is the
idea that attested numeral systems near-optimally trade off the competing demands of informa-
tiveness and simplicity, given a set of motivated semantic primitives, and a need distribution
grounded in linguistic usage.
The semantic primitives on which we draw support both exact and approximate enumer-
ation. An interesting connection in this regard, for which we thank an anonymous reviewer,
is that the Weber-Fechner law, which characterizes the approximate number system, has itself
been argued to reflect a process of informational optimization (Portugal & Svaiter, 2011; Sun,
Wang, Goyal, & Varshney, 2012). This suggests that there may be related processes operating
at different levels of a single numerical system.
Our results suggest that need probability plays a critical role in explaining why some log-
ically possible partitions of the number line are not attested in the world’s numeral systems. Dans
particular, our results suggest that the dominant need to refer to small rather than high numbers
may explain why some numeral systems make fine distinctions among small numbers while
supporting only imprecise enumeration for higher numbers. This coheres with the centrality of
need probability in accounting for cross-language variation in other semantic domains, tel
as kinship (Kemp & Regier, 2012) and color (Gibson et al., 2017; Zaslavsky, Kemp, et coll.,
2019un, 2019b).
We have made a number of simplifying assumptions in our analyses, and future work
can usefully explore alternatives to some of these assumptions. Par exemple, our efficiency
analyses have focused on one basic function of numeral systems, namely, the communication
of number—but numeral systems also serve other important functions such as arithmetic cal-
culation (Cintreuse & Beller, 2014). De la même manière, we have not explored the influence of physical
tally systems, including those grounded in the human body, such as finger counting (Cintreuse &
Beller, 2012). Enfin, we have assumed that cognitive complexity is well-captured by space
rather than time complexity: we have focused on the representational cost of specifying a nu-
meral grammar, plutôt que, Par exemple, the amount of time it would take to derive numeral
forms using such a grammar. Whether and how our results are critically dependent on these as-
sumptions is an important avenue for future research—as is the question of whether the results
generalize to a broader sample of languages.
Several other questions are left open by these findings. Surtout, given the centrality
of communicative need to our analyses, do different cultures impose different communicative
need distributions on the number line, and if so, do such cultural differences in need explain
more cross-language variation in numeral systems than we have explained here? What sort of
evolutionary process produces the diverse pattern in numeral systems? Future studies address-
ing these questions can help to place our present findings in their proper context. For now,
cependant, our current work suggests that the functional drive for efficient communication may
explain why we see particular numeral systems, and classes of numeral system, in the world’s
languages.
REMERCIEMENTS
We thank Charles Kemp for his role in developing the computational framework we use. Nous
thank Stanislas Dehaene and Charles Kemp for comments on an earlier draft.
INFORMATIONS SUR LE FINANCEMENT
OPEN MIND: Discoveries in Cognitive Science
68
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
.
/
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
/
.
je
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Numeral Systems and Efficient Communication Xu et al.
This work was supported by NSF grant SBE-1041707 and DTRA grant HDTRA11710042 to TR
and NSERC Discovery Grant RGPIN-2018-05872 to YX.
CONTRIBUTIONS DES AUTEURS
YX: Conceptualisation: Equal; Conservation des données: Lead; Analyse formelle: Equal; Méthodologie: Equal;
Writing–Original Draft: Equal; Writing–Review & Editing: Supporting. EL: Conceptualisation:
Supporting; Conservation des données: Supporting; Analyse formelle: Equal; Méthodologie: Supporting;
Writing–Original Draft: Supporting; Writing–Review & Editing: Equal. TR: Conceptualisation:
Equal; Conservation des données: Supporting; Analyse formelle: Supporting; Méthodologie: Equal; Writing–
Original Draft: Equal; Writing–Review & Editing: Equal.
RÉFÉRENCES
Ansuini, UN.
(2009). The complexity of numeral systems (Doctoral
dissertation). Sapienza University of Rome.
Beller, S., & Cintreuse, UN.
(2008). The limits of counting: Numer-
ical cognition between evolution and culture. Science, 319,
213–215.
Cintreuse, UN., & Beller, S. (2012). Nature and culture of finger counting:
Diversity and representational effects of an embodied cognitive
tool. Cognition, 124, 156–182.
Cintreuse, UN., & Beller, S. (2014). Mangarevan invention of binary steps
for easier calculation. Proceedings of the National Academy of
les sciences, 111, 1322–1327.
Berlin, B., & Kay, P.. (1969). Basic color terms: Their universality and
evolution. Berkeley: Presse de l'Université de Californie.
Brooks, N., Audet, J., & Barner, D. (2013). Pragmatic inference, pas
semantic competence, guides 3-year-olds’ interpretation of un-
known number words. Developmental Psychology, 49, 1066–1075.
Comrie, B. (2013). Numeral bases. En M. S. Dryer & M.. Haspelmath
(Éd.), The world atlas of language structures online. Leipzig: Max
Planck Institute for Evolutionary Anthropology. Retrieved from
http://wals.info/chapter/131
Dehaene, S.
(2011). The number sense: How the mind creates
mathematics. New York, New York: Presse universitaire d'Oxford.
Dehaene, S., & Mehler, J.. (1992). Cross-linguistic regularities in the
frequency of number words. Cognition, 43, 1–29.
Fedzechkina, M., Jaeger, T. F., & Newport, E. L. (2012). Language
learners restructure their input to facilitate efficient communi-
cation. Actes de l'Académie nationale des sciences, 109,
17897–17902.
Fodor, J.. UN.
(1975). The language of thought. Cambridge, MA:
Presse universitaire de Harvard.
Frank, M.. C., Everett, D. L., Fedorenko, E., & Gibson, E.
(2008).
Number as a cognitive technology: Evidence from Piraha lan-
guage and cognition. Cognition, 108, 819–824.
Frank, M.. C., & Homme bon, N. D. (2012). Predicting pragmatic rea-
soning in language games. Science, 336, 998.
Gibson, E., Futrell, R., Jara-Ettinger, J., Mahowald, K., Bergen, L.,
(2017). Color naming across languages
Ratnasingam, S., et autres.
reflects color use. Proceedings of the National Academy of Sci-
ences, 114, 10785–10790.
Gibson, E., Futrell, R., Piandadosi, S. T., Dautriche, JE., Mahowald, K.,
Bergen, L., et autres. (2019). How efficiency shapes human language.
Tendances des sciences cognitives, 23, 389–407.
Gordon, P.. (2004). Numerical cognition without words: Evidence
from Amazonia. Science, 306, 496–499.
Hammarström, H.
Greenberg, J.. H. (1978). Generalizations about numeral systems. Dans
J.. H. Greenberg (Ed.), Universals of human language, Vol. 3: Word
structure (pp. 249–295). Stanford, Californie: Stanford University Press.
In J.
Wohlgemuth & M.. Cysouw (Éd.), Rethinking universals: Comment
rarities affect linguistic theory (pp. 11–60). Berlin, Allemagne:
Mouton de Gruyter.
(2010). Rarities in numeral systems.
Haspelmath, M..
(1999). Optimality and diachronic adaptation.
Zeitschrift für Sprachwissenschaft, 18, 180–205.
Hopper, P.. J., & Traugott, E. C. (2003). Grammaticalization (2nd ed.).
Cambridge, ROYAUME-UNI: la presse de l'Universite de Cambridge.
Hurford, J.. (1987). Language and number: The emergence of a cogni-
tive system. Oxford, ROYAUME-UNI: Basil Blackwell.
Kanwal, J., Forgeron, K., Culbertson, J., & Kirby, S. (2017). Zipf’s law of
abbreviation and the principle of least effort: Language users opti-
mise a miniature lexicon for efficient communication. Cognition,
165, 45–52.
Kemp, C., Gaby, UN., & Regier, T. (2019). Season naming and the local
environment. In A. Goel, C. Seifert, & C. Freksa (Éd.), Proceed-
ings of the 41st annual meeting of the Cognitive Science Society
(pp. 539–545). Austin, TX: Cognitive Science Society.
Kemp, C., & Regier, T.
(2012). Kinship categories across lan-
guages reflect general communicative principles. Science, 336,
1049–1054.
Kemp, C., Xu, Y., & Regier, T. (2018). Semantic typology and efficient
communication. Annual Review of Linguistics, 4, 109–128.
Khetarpal, N., Neveu, G., Majid, UN., Michael, L., & Regier, T. (2013).
Spatial terms across languages support near-optimal communi-
cation: Evidence from Peruvian Amazonia, and computational
analyses.
En M. Knauff, M.. Pauen, N. Sebanz, & je. Wachsmuth
(Éd.), Proceedings of the 35th annual meeting of the Cognitive
Science Society (pp. 764–769). Austin, TX: Sciences cognitives
Society.
Kolmogorov, UN. N. (1963). On tables of random numbers. Sankhy ¯a:
The Indian Journal of Statistics, Series A, 25, 369–376.
OPEN MIND: Discoveries in Cognitive Science
69
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
/
/
.
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
/
.
je
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Numeral Systems and Efficient Communication Xu et al.
Levinson, S. C., & Meira, S. (2003). “Natural concepts” in the spa-
tial topologial domain–adpositional meanings in crosslinguistic
perspective: An exercise in semantic typology. Language, 79,
485–516.
Li, M., & Vitányi, P..
(2013). An introduction to Kolmogorov com-
plexity and its applications. New York, New York: Springer.
Michel, J.. B., Shen, Oui. K., Aiden, UN. P., Veres, UN., Gray, M.. K., Le
Google Books Team, et autres. (2011). Quantitative analysis of cul-
ture using millions of digitized books. Science, 331, 176–182.
Piantadosi, S. T.
(2016). A rational analysis of the approximate
number system. Psychonomic Bulletin & Review, 23, 877–886.
Piantadosi, S. T., Tenenbaum, J.. B., & Homme bon, N. D. (2012). Boot-
strapping in a language of thought: A formal model of numerical
concept learning. Cognition, 123, 199–217.
Piantadosi, S. T., Tily, H., & Gibson, E. (2011). Word lengths are op-
timized for efficient communication. Actes de la Nationale
Académie des Sciences, 108, 3526–3529.
Pica, P., Lemer, C., Izard, V., & Dehaene, S. (2004). Exact and ap-
proximate arithmetic in an Amazonian indigene group. Science,
306, 499–503.
Portugal, R., & Svaiter, B. F.
(2011). Weber-Fechner law and the
optimality of the logarithmic scale. Minds and Machines, 21,
73–81.
Regier, T., Kemp, C., & Kay, P.. (2015). Word meanings across lan-
guages support efficient communication.
In B. MacWhinney
& W. O’Grady (Éd.), The handbook of language emergence
(pp. 237–263). Hoboken, New Jersey: Wiley-Blackwell.
Forgeron, K., Tamariz, M., & Kirby, S.
(2013). Linguistic structure is
an evolutionary trade-off between simplicity and expressivity. Dans
M.. Knauff, M.. Pauen, N. Sebanz, & je. Wachsmuth (Éd.), Proceed-
ings of the 35th annual meeting of the Cognitive Science Society
(pp. 1348–1353). Austin, TX: Cognitive Science Society.
Jeux, E. S., & Kinzler, K. D. (2007). Core knowledge. Develop-
mental Science, 10, 89–96.
Sun, J.. Z., Wang, G. JE., Goyal, V. K., & Varshney, L. R..
(2012). UN
framework for Bayesian optimality of psychophysical laws. Jour-
nal of Mathematical Psychology, 56, 495–501.
von der Gabelentz, G. (1901). Sprachwissenschaft, ihre Aufgaben,
Methoden, und bisherige Ergebnisse. Leipzig: Tauchnitz.
Xu, Y., Regier, T., & Malt, B. C. (2016). Historical semantic chain-
ing and efficient communication: The case of container names.
Sciences cognitives, 40, 2081–2094.
Zaslavsky, N., Kemp, C., Regier, T., & Tishby, N.
(2018). Efficient
compression in color naming and its evolution. Proceedings of
the National Academy of Sciences, 115, 7937–7942.
Zaslavsky, N., Kemp, C., Tishby, N., & Regier, T. (2019un). Color nam-
ing reflects both perceptual structure and communicative need.
Topics in Cognitive Science, 11, 207–219.
Zaslavsky, N., Kemp, C., Tishby, N., & Regier, T.
(2019b). Com-
municative need in color naming. Cognitive Neuropsychology.
https://doi.org/10.1080/02643294.2019.1604502
Zaslavsky, N., Regier, T., Tishby, N., & Kemp, C.
(2019). Seman-
tic categories of artifacts and animals reflect efficient coding. Dans
UN. Goel, C. Seifert, & C. Freksa (Éd.), Proceedings of the 41st an-
nual meeting of the Cognitive Science Society (pp. 1254–1260).
Austin, TX: Cognitive Science Society.
Zipf, G. K. (1949). Human behavior and the principle of least effort.
Cambridge, MA: Addison-Wesley.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
o
p
m
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
je
.
/
/
1
0
1
1
6
2
o
p
m
_
un
_
0
0
0
3
4
1
8
6
8
4
2
1
o
p
m
_
un
_
0
0
0
3
4
p
d
.
/
je
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
OPEN MIND: Discoveries in Cognitive Science
70