Predictive Learning, Prediction Errors, and Attention: - Recherche en IA spécialisée au MIT

Predictive Learning, Prediction Errors, and Attention:
Evidence from Event-related Potentials
and Eye Tracking

UN. J.. Wills, UN. Lavric, G. S. Croft, and T. L. Hodgson

Abstrait

& Prediction error (‘‘surprise’’) affects the rate of learning: Nous
learn more rapidly about cues for which we initially make incor-
rect predictions than cues for which our initial predictions are
correct. The current studies employ electrophysiological mea-
sures to reveal early attentional differentiation of events that differ
in their previous involvement in errors of predictive judgment.
Error-related events attract more attention, as evidenced by fea-
tures of event-related scalp potentials previously implicated in se-

lective visual attention (selection negativity, augmented anterior
N1). The earliest differences detected occurred around 120 msec
after stimulus onset, and distributed source localization (LORETA)
indicated that the inferior temporal regions were one source of
the earliest differences. En outre, stimuli associated with the
production of prediction errors show higher dwell times in an eye-
tracking procedure. Our data support the view that early atten-
tional processes play a role in human associative learning. &

INTRODUCTION

Determining the extent to which one event predicts
another is one of the most fundamental
forms of
learning. Classic theorists assumed that predictive learn-
ing occurred whenever two events were contiguous
(Pavlov, 1927). Cependant, more recent analyses indicate
that learning also requires that the second event be
somewhat unexpected (Kamin, 1969). C'est, predictive
learning appears to be driven by prediction errors rather
than simple contiguity, and it occurs at a rate related to
the discrepancy between what is predicted on the basis
of the first event and what actually occurs.

Why does predictive learning appear to be error-
driven? Associative theories assume that prediction
errors affect the rate at which associations between
representations of the two events form (Schultz, Dayan,
& Montague, 1997; Pearce & Hall, 1980; Mackintosh,
1975; Rescorla & Wagner, 1972), whereas reasoning
accounts assume that predictive learning occurs through
a process of high-level reasoning (De Houwer, Beckers,
& Vandorpe, 2005). Proponents of each type of account
have uncovered behavioral phenomena potentially prob-
lematic for the other (Le Pelley, Oakeshott, & McLaren,
2005; De Houwer & Beckers, 2002), and the case for
multiprocess accounts of predictive learning is frequent-
ly made (Ashby, Alfonso-Reese, Turken, & Waldron,
1998; Erickson & Kruschke, 1998). Given this, many neu-
roscientific investigations have understandably sought

University of Exeter, England, ROYAUME-UNI

to examine predictions of particular theories, plutôt
than attempt to distinguish between such broad and
nonexclusive classes of theory. Par exemple, one recent
investigation provided evidence that the blood oxygen
level-dependent (AUDACIEUX) functional magnetic resonance
imaging (IRMf) signal in the prefrontal cortex conforms
to the predictions of the Rescorla–Wagner associative
théorie (Fletcher et al., 2001), and another (O’Doherty,
Dayan, Friston, Critchley, & Dolan, 2003) demonstrated
that activity in the striatum conformed to the predic-
tions of the temporal difference model (Schultz et al.,
1997).

The goal of the studies reported in the current article
was to investigate a prediction made by a number of
associative theories,
including the Pearce–Hall theory
(Pearce & Hall, 1980). The Pearce–Hall theory states that
predictive learning is error-driven because the learner
has limited stimulus processing capacity. In order to
make maximal use of these limited resources, the extent
to which a stimulus is processed is modulated by its
previous involvement in prediction errors. Spécifiquement, un
stimulus whose consequence is well predicted is pro-
cessed to a lesser extent than a stimulus that has
recently been followed by surprising or unexpected
events. This leads to the prediction that stimuli whose
consequences are uncertain receive more attention than
stimuli whose consequences are well predicted.

A different but related proposal (Kruschke, 2001;
Mackintosh, 1975) is that attention is distributed among
the features of a presented stimulus in accordance with
the extent to which those features predict an outcome.

D 2007 Massachusetts Institute of Technology

Journal des neurosciences cognitives 19:5, pp. 843–854

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

D
h
o
t
w
t
p
n
:
o
/
un
/
d
m
e
je
d
t
F
r
p
o
r
m
c
.
h
s
je
p
je
v
d
e
je
r
r
e
c
c
h
t
.
m
un
je
r
e
.
d
c
toi
o
m
o
/
c
j
n
o
un
c
r
t
n
je
c
/
e
un
–
r
p
t
d
je
c
1
je
9
e
5
–
8
p
4
d
3
F
/
1
1
9
9
3
6
/
3
5
0
/
3
8
4
o
3
c
/
n
1
2
7
0
5
0
6
7
6
1
9
9
0
/
5
j
8
o
4
c
3
n
p
.
d
2
0
b
0
oui
7
g
.
toi
1
e
9
s
.
t
5
o
.
n
8
0
4
8
3
S
.
p
e
p
d
F
e
m
b
b
oui
e
r
g
2
toi
0
e
2
s
3
t

/
j

o
n

1
8

M.
un
oui

2
0
2
1

Spécifiquement, features that were previously good predic-
tors of an outcome are assumed to attract more atten-
tion than features that were previously poor predictors
of an outcome. The Mackintosh–Kruschke theory is not
typically framed in terms of limited processing capacity,
although such an interpretation is not unreasonable.
Although the Mackintosh–Kruschke and Pearce–Hall
theories may seem to be contradictory, in that the re-
lationships between prediction error and attention they
postulate are opposite, they can, in fact, be considered
to be complementary. The Mackintosh–Kruschke theory
makes predictions about the relative amounts of atten-
tion different features of the presented stimulus will re-
ceive, whereas the Pearce–Hall theory makes predictions
about changes in the absolute amount of attention di-
rected to the entire stimulus.

Indirect evidence for the presence of Mackintosh–
Kruschke attentional processes in human predictive
learning is provided by the effects of prior predictive-
ness on the rate of subsequent learning. Par exemple,
Lochmann and Wills (2003) trained adults on a task
where some features of the presented stimuli were pre-
dictive of an outcome and other features were non-
predictive. In a subsequent phase, all stimulus features
were fully predictive of a novel outcome; nevertheless,
the previously predictive cues were learned about more
rapidly than the previously nonpredictive cues.

Indirect evidence for the presence of Pearce–Hall
attentional processes in human predictive learning
comes from the BOLD response that is observed in
certain brain regions to the unexpected occurrence
and unexpected omission of outcomes. The Pearce–Hall
theory predicts increased attention as a result of both
the unexpected occurrence and the unexpected omis-
sion of an outcome, Et ainsi, the observation that the
BOLD responses in the hippocampus, the superior
frontal gyrus, and the cerebellum increase to both types
of event (Ploghaus et al., 2000) has been taken by some
as support for this type of associative theory. In other
brain regions, Par exemple, the ventral putamen, unex-
pected occurrence of an outcome leads to an increase in
BOLD signal, whereas the unexpected omission of the
outcome attenuates the BOLD signal (O’Doherty et al.,
2003), which is more in line with the predictions of
nonattentional theories such as temporal difference
théorie (Schultz et al., 1997).

One limitation of Ploghaus et al. (2000), and a number
of other studies (O’Doherty et al., 2003; Fletcher et al.,
2001), is that the unexpected events are more novel
than the expected events. Par exemple, Ploghaus et al.
compare the first trial on which a painful stimulus
follows a colored light with the second trial on which
this occurs. The first trial is assumed to have a higher
prediction error than the second, because the painful
stimulus is less expected on the first trial than on the
second. Cependant, it is also the case that both the light
and the painful stimulus are less novel on the second

trial than on the first. Novel events will tend, on the
whole, to have larger prediction errors than familiar
events, but events of equal frequency can differ in the
hypothesized magnitudes of their prediction errors.
Critique,
it is prediction error rather than frequency
per se that drives learning in most associative theories. UN
number of more complex experimental designs that
employ multiple training phases and multifeature stimuli
allow frequency to be equated while maintaining differ-
ences in prediction error (par exemple., Turner et al., 2004).
Using such a design, Turner et al. (2004) confirmed that
both the unexpected omission and unexpected occur-
rence of an outcome were associated with increased
BOLD activity (in the lateral frontal cortex).

En résumé, behavioral and neuroimaging studies
have thus far provided some indirect evidence of the
involvement of attentional processes in human predic-
tive learning. In Experiment 1, we sought to extend and
strengthen this evidence by exploiting the temporal
resolution of electrophysiological measures to deter-
mine whether stimuli differing in their prediction error
also differ in the amount of early attentional resources
they are allocated. Electrophysiological measures have
previously been used successfully in the study of pre-
dictive learning (par exemple., Holroyd, Nieuwenhuis, Yeung, &
Cohen, 2003).

There is an extensive preexisting literature on the
event-related potential (ERP) correlates of selective atten-
tion. Two sets of ERP components have been implicated
in visual selective attention (Hillyard & Anllo-Vento,
1998). When spatial position determines the amount of
attention allocated to a stimulus, attended and nonat-
tended stimuli differ in the magnitude of the ERP com-
ponents P1, posterior N1, and anterior N1, all three
having a larger amplitude for attended stimuli (Clark &
Hillyard, 1996). The magnitude of components from this
ensemble, often referred to as ‘‘exogenous components,’’ can
also be modulated by increasing the demand on visual
discrimination of the stimulus, even when spatial position
is held constant (Vogel & Luck, 2000). These spatial and
nonspatial modulations of exogenous components are
consistent with their interpretation in terms of a sensory
enhancement mechanism (Hillyard & Anllo-Vento, 1998)
that is relatively nonspecific with regard to individual
features of stimuli, such as color, orientation, and so
en avant. Selective attention to individual features is associ-
ated with another set of ERP components: a selection
negativity (SN), with a posterior scalp distribution, souvent
accompanied by a selection positivity (SP) at anterior
scalp sites (Hillyard & Anllo-Vento, 1998). This set of
components is particularly relevant in the context of the
current studies, in which shape distinguishes the stimuli
to be contrasted. More specifically, support for the
involvement of an early attentional process in human
associative learning would be provided if the magnitude
of the SN and/or SP components to a stimulus previously
involved in many prediction errors was larger than the

844

Journal des neurosciences cognitives

Volume 19, Nombre 5

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

magnitude of the component to a stimulus involved in
relatively few prediction errors (but had occurred with
equal frequency).

It would also seem reasonable to expect prediction
error to modulate the so-called exogenous attentional
components (P1, N1): Early differentiation of the stim-
ulus associated with many prediction errors from the
stimulus associated with few prediction errors may lead
to enhanced subsequent perceptual processing of the
former and/or a suppressed processing of the latter. Comme
discussed, such sensory enhancement/suppression is
reflected in the amplitude of the P1, posterior N1, et
anterior N1 components. Experiment 1 tested these
predictions by using multielectrode electrophysiologi-
cal recordings, and ERP component and distributed
source localization analyses to examine the expected
ERP effects and to establish whether stimuli associated
with many prediction errors result in higher activation
of the cortical circuitry known to be involved in visual
attention than stimuli associated with few prediction
errors.

EXPERIMENT 1

Experiment 1 employed a forward cue competition
conception. Forward cue competition is a design commonly
employed in the study of prediction errors in learning,
and the direction of any reliable effect is well known.
The design employed is summarized in Table 1; le
letters represent the abstract stimuli employed. Ainsi,
in the first part of the experiment, some stimuli predict
an outcome (a fictitious fever), whereas others predict
the absence of that outcome. In the second part of the
experiment, these stimuli are paired with novel stimuli.
On AX trials, participants tend to expect an outcome
from the outset, hence X is involved in few prediction
errors. On BY trials, participants tend not to expect an
outcome initially, hence Y is involved in rather more
prediction errors. As a consequence, participants are
predicted to learn more about Y than X, and this is

Tableau 1. Structure of the Learning Task

Phase 1

Phase 2

Phase 3

UN ! fever (A+)

AX ! fever (AX+)

X ! Data missing (X?)

B ! no fever (B(cid:1))

BY ! fever (BY+)

Oui ! Data missing (Oui?)

je ! no fever (je(cid:1))

IJ ! no fever (IJ(cid:1))

UN ! fever (A+)

B ! no fever (B(cid:1))

AX ! fever (AX+)

BY ! fever (BY+)

Letters represent the abstract forms used as stimuli. Conventional learning theory
notations for each trial type are presented in parentheses.

assessed in the final part of the experiment. Stimuli X
and Y are presented isolation, and participants’ propen-
sity to respond ‘‘fever’’ to X and Y is assessed. Le
prediction of error-driven associative learning (and some
reasoning accounts) is that participants are more likely
to respond ‘‘fever’’ to Y than to X, as a result of Y having
previously been involved in more prediction errors. Dans
this experiment, participants receive ‘‘data missing’’
feedback on the X and Y trial types—in other words,
they are told that it is not known whether the outcome
occurred. The other trial types in Phases 1 et 2 sont
fillers, and the other trial types in Phase 3 maintain the
learning established in Phases 1 et 2.

The forward cue competition design employed has an
advantage over simpler designs in that the target stimuli
which differ in their previous involvement in prediction
errors (X and Y in Phase 3) occur with equal frequency.
Néanmoins, our design is still relatively simple com-
pared to some behavioral-only studies of forward cue
competition and, as such, does not provide as much
information about behavioral performance as these
more complex designs. En particulier, the forward cue
competition design can potentially be broken down into
two subdesigns that are described as forward blocking
(A+ followed by AX+) and reduced overshadowing
(B(cid:1) followed by BY+). The relative contribution of
these two components to forward cue competition can
potentially be assessed by the introduction of further
trial types in Phases 2 et 3. We decided not to include
such trial types in order to keep the difficulty and length
of the task within acceptable limits for our participants.
The constraints of an ERP methodology meant we had
to employ large numbers of small, abstract stimuli in
order to maximize our ability to detect reliable, artifact-
free ERP components, and this limited the complexity of
the behavioral design we could employ.

In a forward cue competition design (Tableau 1), atten-
tional theories of associative learning predict that Y
will attract more attention than X in Phase 3. In the
Mackintosh–Kruschke theory, attention will be directed
away from X in the AX trials of Phase 2 because it is
being presented in the presence of a stimulus that al-
ready predicts the outcome well (UN). This will not hap-
pen to Y in BY trials in Phase 2 because B does not
predict the outcome of BY trials in Phase 2. Ainsi, Y will
attract more attention than X in Phase 2. It is a pre-
diction of the Mackintosh–Kruschke theory that these
attentional differences will persist, at least initially, quand
X and Y are subsequently presented in isolation. Le
behavioral literature suggests that attentional differences
do indeed persist in this way (par exemple., Lochmann & Wills,
2003; Lawrence, 1952).

The Pearce–Hall theory also predicts that Y will attract
more attention than X in Phase 3. In Phase 2, le
outcome of AX trials is well predicted from the outset
so the amount of attention attracted by X will decline
substantially across Phase 2. In contrast, the outcome of

Wills et al.

845

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

BY trials in Phase 2 is not well predicted initially, hence,
the decline in attention to Y will be slower. Although
Pearce–Hall predicts that attention to both X and Y will
eventually decline to zero when learning is complete,
this is a limiting case that arguably may never be reached
in practice. As in the Mackintosh–Kruschke theory,
attentional differences are predicted to persist, at least
initially, when X and Y are presented in isolation.

Although the predictions of attentional theories of
predictive learning concerning X and Y in Phase 3 sont
unambiguous, one might reasonably argue that a more
direct test of these theories would be to measure the
amount of attention X and Y attract during Phase 2,
when learning is occurring, rather than in Phase 3, après
learning has occurred. Such a test is precluded due to
the limitations of ERP methodology. X and Y appear in
compound with other stimuli (A and B) in Phase 2, et
it is extremely difficult to isolate the neurophysiological
response elicited by individual stimuli that are presented
simultaneously. Attentional differences between the AX
and BY stimulus compounds would be relatively unin-
formative because such differences could be due to a
number of different mechanisms. Par exemple, B may
attract more attention than A in Phase 2 because B is
novel in the context of an outcome (having previously
only appeared in the context of no outcome). Atten-
tional differences between X and Y in Phase 2 are as-
sessed in Experiment 2 with eye tracking.

Methods

Participants

Twenty-one students were paid 12 GBP for a 2-hour ses-
sion. All participants were right-handed. One participant’s
data were discarded due to excessive electro-oculogram
(EOG) artifacts. The remaining 20 participants (11 femmes;
âge: mean = 20.85, SD = 3.96, range = 18–36) were the
subject of all subsequent analyses.

Apparatus

Stimulus presentation and response collection was via a
PC-compatible computer and the E-prime package (Ver-
sion 1.1, Psychology Software Tools, Pittsburgh, Etats-Unis).
The electroencephalogram (EEG) was recorded from 64
Ag/AgCl electrodes mounted in an elastic cap (Electro-
Cap International, Eaton, Ohio, Etats-Unis), with a forehead
(AFz) ground and a vertex (Cz) reference. Two of the
disponible 64 channels were used for recording the hor-
izontal EOG (at the outer canthi of both eyes); two for
recording the vertical EOG (supra- and suborbitally at
the right eye) and two were placed on the earlobes for
off-line re-referencing in component amplitude analyses.
Scalp channels (58) were placed in accordance with
the extended 10–20 (10%) convention. The EEG was
sampled at 500 Hz, 0.016 Hz–100 Hz bandpass filtered,

and amplified using BrainAmp amplifiers (BrainProducts,
Munich, Allemagne).

Stimuli

Twenty-four abstract pictures were selected from the 36
used in a previous study (Wills & McLaren, 1997), concernant-
colored red with a yellow outline, and presented against
a black background. The pictures were 0.648 of visual
angle in diameter, presented inside a white outline
square 2.58 in visual angle. On trials where one picture
was presented, it was positioned in the center of the
square. In accordance with attentional theories of pre-
dictive learning, forward cue competition appears to be
facilitated by the spatial separation of the features in
compound stimuli (Glautier, 2002), thus, when two
pictures were presented in this experiment, they were
spatially separated. Spécifiquement, they were vertically
aligned, one appearing 0.368 of visual angle above the
midpoint, and the other an equivalent distance below.

Procedure

Participants were asked to imagine that they worked for
a medical referral service, and that their job was to
predict a fictitious disease (‘‘Jominy fever’’) on the basis
of ‘‘cell bodies’’ in patients’ blood samples (représentée
by abstract pictures). Le 24 pictures of cell bodies were,
separately for each participant, randomly divided into six
cell types (four cell bodies each) corresponding to
stimulus types A, B, je, J., X, and Y in Table 1.

The structure of each trial is illustrated in Figure 1.
Trials began with the presentation of an outline square.
Après 1 sec, one or two ‘‘cell bodies’’ appeared inside the
square. Participants were expected to make either a ‘‘fe-
ver’’ or a ‘‘no fever’’ response by pressing one of two keys
on a standard PC keyboard. Allocation of ‘‘fever’’ and ‘‘no
fever’’ responses to these two keys was counterbalanced
across participants. Once the participant had responded,
the abstract pictures and outline square were replaced
with a feedback message that indicated whether the par-
ticipant’s response was correct or incorrect, and also in-
dicated the correct response. If no response was made
within 2 sec of the onset of the ‘‘cell bodies,’’ the screen

Chiffre 1. Trial structure.

846

Journal des neurosciences cognitives

Volume 19, Nombre 5

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

cleared and the message ‘‘Time out!’’ was presented for
1.5 sec. The next trial followed immediately after this
message. In the final phase of the experiment, X and Y
trials were followed by the uninformative feedback mes-
sage ‘‘????? — DATA MISSING.’’

The experiment had three phases, as shown in Table 1.
Trial order within each phase was randomized within each
of several sequential blocks; starts of blocks were not sig-
naled to participants in any way. Block length was 12 trials
for Phase 1, with each of the three trial types (A+, B(cid:1),
et moi(cid:1)) occurring once for each of the four stimuli that
comprised each stimulus type (c'est à dire., 4 A stimuli, 4 B stimuli,
et 4 I stimuli). Block length in Phase 2 était 24 trials (3 trial
les types (cid:3) 4 pictures (cid:3) 2 screen positions, par exemple., A upper,
X lower and X upper, A lower). For Phase 3, block length
était 48 trials (2 two-picture trial types (cid:3) 4 pictures (cid:3) 2
screen positions + 4 one-picture trial types (cid:3) 4 pictures (cid:3)
2 présentations). Il y avait 16 blocks in Phase 1, 6 blocks
in Phase 2, et 6 blocks in Phase 3.

Electrophysiological Analysis

A 40-Hz low-pass (FIR) filter (12 dB/octave) was applied
to the EEG data off-line. Off-line re-referencing was per-
formed with linked earlobes serving as the new reference
in amplitude analyses, and average reference serving as
the new reference in source localization. ERP segments
(500 msec plus 100 msec prestimulus baseline) were time-
locked to the presentation of X and Y stimuli in Phase 3,
resulting in 48 ERP epochs for each condition. All epochs
were visually inspected and those containing EOG, mus-
clé, amplifier, and other artifacts were removed. Individ-
ual datasets containing less than 30 artifact-free epochs in
either of the conditions were excluded from the analyses
(one participant was excluded in this way). The two con-
ditions did not differ in the number of artifact-free epochs
[X: mean = 43.9, SD = 3.0; Oui: mean = 44.4, SD = 4.1;
t(19) = 0.87, p = .4].

Because the early ERP components under scrutiny
occur in immediate temporal vicinity of each other and
are likely to show substantial overlap, temporal principal
components analysis (APC) was conducted on the ERPs
in order to disentangle temporally overlapping ERP
effects. Le 250 time points were the variables in this
analyse, and there were 2320 cases (20 participants (cid:3) 2
conditions (cid:3) 58 électrodes). Varimax rotation was em-
ployed and an eigenvalue (cid:4)1 was used as the PCA com-
ponent identification criterion. This analysis results in
a number of loading-by-time functions, which are sta-
tistically orthogonal components of the ERP amplitude-
by-time functions from which they are derived. From the
identified PCA components, we selected those whose
loading-by-time function unambiguously corresponded
to the amplitude-by-time function of the ERP compo-
nents under investigation (par exemple., AN1, N1, and SN). Linear
regression was used to obtain factor scores for each
PCA component (Donchin & Heffley, 1978). The scores

of a given PCA component express its magnitude at
each electrode/condition/subject. These PCA compo-
nent scores were then averaged within five scalp re-
gions in each hemisphere: frontal left (Fp1, AF3, F1, F3,
F5, F7), central left (FC1, FC3, FC5, C1, C3, C5), tempo-
ral left (T7, CP5, TP7, P7), parietal left (CP1, CP3, P1,
P3, P5), parieto-occipital left (PO1, PO3, O1, PO7), et
the corresponding symmetric regions/electrodes in the
right hemisphere. Condition (cid:3) Region (cid:3) Hemisphere
analyses of variance (ANOVAs) were run separately on
the scores of PCA components corresponding to the
ERP components of interest. Regionwise t tests were
performed subject to reliable ANOVA effects involving
the condition factor.

Cortical Localization

Low-Resolution Electromagnetic Tomography (LORETA;
Pascual-Marqui, 1999) was used for computing the 3-D
intracerebral distribution of current density underlying
observed scalp ERP effects. LORETA solves the inverse
problem by assuming related strengths and orientations
of sources (no assumption is made about their number).
Mathematically, this is implemented by finding the
smoothest of all possible activity distributions. Le
method has been extensively validated (par exemple., Mulert
et coll., 2004) and is currently one of the most widely
used source localization techniques in EEG. It has been
used previously in cognitive ERP investigations (par exemple.,
Lavric, Pizzagalli, & Forstmeier, 2004).

LORETA computes, at each voxel, current density as
the linear weighted sum of the scalp electric potentials.
The LORETA version used in the present study (Pascual-
Marqui, 1999) was registered to the MNI305 brain atlas.
The computations are restricted to the cortical gray
matter and hippocampi. The spatial resolution of the
method is 7 mm and the solution space consists of 2394
voxels. Brodmann’s area (BA) and region labels are
provided by the LORETA software. For a specific MNI co-
ordinate, LORETA first determines the nearest gray mat-
ter voxel using a lookup table created via the Talairach
Daemon (Lancaster et al., 2000), and then estimates
a conversion from MNI space to Talairach space using
the transform method suggested by Brett, Johnsrude,
and Owen (2002). LORETA solutions were first obtained
for each participant in each condition and for each time
point in the 25-msec time windows defined on the basis
of the observed waveform differences. Subsequently,
time points were averaged to obtain a solution for each
condition and participant. These averaged solutions
were then submitted to voxelwise t tests.

Results

Unless otherwise stated, all tests of statistical significance
are assessed against an a of .05.

Wills et al.

847

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

Behavioral Results

In the final block of Phase 1, mean proportion of ‘‘fever’’
responses was 0.90 to A trials, 0.03 to B trials, et 0.03
to I trials. The difference between A and B trials was
significant, t(19) = 18.92, as was the difference between
A and I trials, t(19) = 18.92. The difference between B
and I did not approach significance, t(19) = 0.

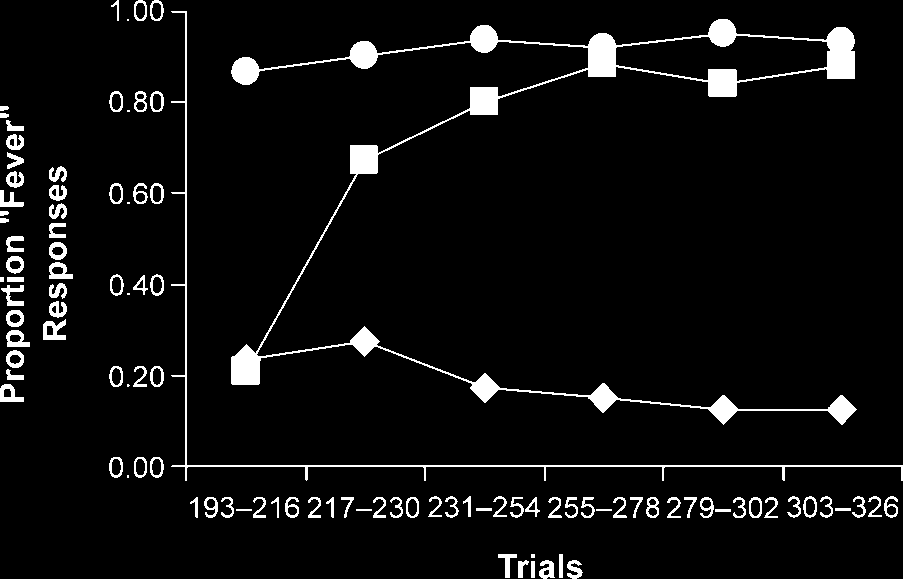
In Phase 2 (voir la figure 2), a two-factor repeated-
measures ANOVA revealed that the proportion of ‘‘fe-
ver’’ responses was significantly affected by trial type,
F(2, 38) = 158.24, and by trial block, F(5, 95) = 25.19.
There was also a significant interaction between these
two factors, F(10, 190) = 40.15. A Greenhouse–Geisser
correction for nonsphericity was applied in this analy-
sis and in all subsequent analyses where it was appro-
priate to do so (uncorrected degrees of freedom are
reported).

In Phase 3, the mean proportion of ‘‘fever’’ responses
était 0.45 to trial type X, et 0.72 to trial type Y. Ce
difference was significant, t(19) = 3.78. Fifteen out of
20 participants made more ‘‘fever’’ responses to trial
type Y than to trial type X. Mean error rates for the other
trial types in this phase were: UN, 4%; AX, 2%; BY, 9%; B,
18%. Mean reaction times were also slightly slower for
trial type X (807 msec) than for trial type Y (767 msec).
This difference was significant, t(19) = 2.34. Mean re-
action times for the other trial types in this phase were:
UN, 705 msec; AX, 835 msec; BY, 889 msec; B, 813 msec.
Across the experiment, 0.3% of trials were lost due to
timeouts.

Event-related Potentials

Attentional associative theories of predictive learning pre-
dict that Y will attract more attention than X in Phase 3.
These theories also make predictions about the amount
of attention attracted by X and Y in Phase 2, but it would

Chiffre 2. Proportion of ‘‘fever’’ responses made across Phase 2
of the experiment, shown for AX+ (.), BY+ (&), and IJ(cid:1) (r) trial
les types.

be extremely difficult to assess these differences through
ERPs, for the reasons outlined earlier. The analyses re-
ported below are therefore based around time-locked
ERPs to the pictures of cell types Y and X presented in
Phase 3. These stimuli were associated with differences
in prediction error in Phase 2 and the ensuing atten-
tional differences were predicted to persist sufficiently
into Phase 3 to be detectable.

Inspection of the middle panel of Figure 3A reveals
that cue type Y was associated with a larger ERP ampli-
tude than cue type X in the temporal range of the N1
component (155–180 msec). Cependant, the difference
between the two cue types persists for about another
100 msec beyond the N1 peak, suggesting the pres-
ence of an SN. SN is most clearly visualized via a dif-
ference waveform, which is also shown in Figure 3A,
middle panel. This difference waveform illustrates the
presence of a SN between about 140 msec and 290 msec
poststimulus onset. The two cue types also diverged
in the anterior N1 component, with larger amplitude
in response to cue type Y than cue type X (see Fig-
ure 3A, top).

The temporal PCA, performed on ERPs to distinguish
between overlapping ERP effects, found three PCA com-
ponents whose time-courses corresponded well to AN1,
N1, and SN, and which accounted for 5.8%, 3.8%, et
9.6% of the variance, respectivement (see Figure 3A, bot-
tom). The scores of these PCA components were ana-
lyzed via three separate ANOVAs, one for each of the
three components (c'est à dire., AN1, N1, and SN), with factors
trial type (X vs. Oui), region, and hemisphere. Given the
preexisting knowledge of the circumscribed scalp distri-
butions of AN1, N1, and SN, each ANOVA involved just
the appropriate subset of scalp regions—anterior re-
gions (frontal and central) for AN1, and posterior re-
gions (parietal and parietal–occipital) for N1 and SN.

For the PCA component corresponding to AN1, un
reliable main effect of trial type was found, F(1, 19) =
5.89; no other main effects or interactions were signifi-
cant. The PCA component corresponding to N1 was
analyzed in a corresponding manner, but no significant
main effects or interactions were found. The PCA com-
ponent corresponding to SN was also analyzed in a
corresponding manner, revealing a significant interac-
tion between trial type and hemisphere, F(1, 19) = 7.03,
and a significant three-way interaction between trial
type, region, and hemisphere, F(1, 19) = 8.66 (no other
main effects or interactions were significant). These
interactions were explored by comparing trial type (X
vs. Oui) in each of the two regions (parietal and parietal–
occipital) over each hemisphere, separately. The X
versus Y differences in the PCA component scores in
the four regions were: 0.21 (parietal left), 0.33 (pariétal
droite), 0.15 (parietal–occipital left), et 0.41 (parietal–
occipital right). The reliability of these four differences
was assessed by t tests; a reliable effect of trial type was
found in the right parietal–occipital region, t(19) = 2.19.

848

Journal des neurosciences cognitives

Volume 19, Nombre 5

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

F
/

t
t

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

Chiffre 3. (UN) The AN1
component at an anterior–
central (FCz) electrode and N1
and SN at a parieto-occipital
électrode (PO4). Below,
the raw loadings from the
temporal PCA are displayed.
The PCA components
corresponding to the ERP
components of interest (AN1,
N1, and SN ) are shown in
bold; PCA components that
differentiated reliably in the
statistical analysis between cue
types Y and X are shown with
solid lines (they correspond to
ERP components AN1 and SN).
(B) Topographic maps of
the difference between
ERPs to cue types Y and X.
(C) Voxel-by-voxel LORETA
t tests comparing X and Y in
the two time windows of
interest; t values thresholded
at p < .01, uncorrected. In (A), there is a difference between conditions Y and X in electrode FCz in a limited substretch of the baseline just preceding the stimulus onset. Every presentation of pictures of fictitious cells X or Y was preceded by a 1000-msec presentation of the empty square, in which cell X or Y was subsequently placed. Thus, the preceding stimulus was constant. To assess whether there were any reliable differences anywhere in the baseline (including the stretch in question), we performed statistical comparisons of the baselines for X and Y (following baseline correction). We used a robust procedure, ideally suited for the identification of global differences across ranges of time points: TANOVA (Pascual-Marqui, Michel, & Lehmann, 1995; see also http://www.unizh.ch/keyinst/ NewLORETA/LORETA01.htm). TANOVA compares the ERPs time point-by-time point and identifies time points showing significant differences, while controlling for alpha inf lation in multiple tests by permutations. No time points in the baseline showed reliable differences across conditions, including the time points in the range under scrutiny (in this range, all p values were >.4). Incidentally, when run on the poststimulus onset
ERPs, TANOVA did find a series of time points showing significantly differences in the N1–SN as well as AN1 ranges.

Cortical Localization (LORETA)

Discussion

Topographic maps of the difference between ERPs to
cue types X and Y across four different time windows
are shown in Figure 3B. As can be seen, ERP differ-
ences appear to be at anterior scalp regions during the
time window of the AN1 component, and at posterior
scalp regions during the N1–SN time window. LORETA
analysis provides a method of estimating the cortical
locations of these differences. For this analysis (see Fig-
ure 3C), two 25-msec time windows were set where
the ERP differences were the largest (AN1 range, 110–
135 msec; N1–SN range, 155–180 msec). In both time
windows of interest, greater current density was found
only for stimulus type Y. Applying a significance level
of p < 0.01 (uncorrected) to voxel-by-voxel t tests re- vealed greater current density to Y than to X in the left inferior temporal region in the earlier time window, and in the left superior parietal region in the later time window. Consistent with our predictions, early ERP components, previously associated with selective attention, distin- guished between cue types X and Y in Phase 3. Because cue types in our experiment can only be differentiated by shape, one would expect the ERP differences ob- served to be those that have previously been associated with selective attention to individual features of stimuli. The SN is one such difference, and we found a signifi- cant SN for cue type Y relative to cue type X in this experiment. The SN we observed extended between 140 and 280 msec poststimulus onset. Given the partial overlap of the observed SN with the posterior N1 peak, we examined and confirmed the reliability of the SN as a statistically independent component using temporal PCA. The presence of an independent posterior N1 difference, in addition to the posterior SN, cannot be ruled out on the basis of these analyses, but no evidence of a reliable difference between the cue types in the Wills et al. 849 D o w n l o a d e d f r o m l l / / / / / j f / t t i t . : / / D h o t w t p n : o / a / d m e i d t f r p o r m c . h s i p l v d e i r r e c c h t . m a i r e . d c u o m o / c j n o a c r t n i c / e a - r p t d i c 1 l 9 e 5 - 8 p 4 d 3 f / 1 1 9 9 3 6 / 3 5 0 / 3 8 4 o 3 c / n 1 2 7 0 5 0 6 7 6 1 9 9 0 / 5 j 8 o 4 c 3 n p . d 2 0 b 0 y 7 g . u 1 e 9 s . t 5 o . n 8 0 4 8 3 S . p e p d f e m b b y e r g 2 u 0 e 2 s 3 t / j . . . . . t f o n 1 8 M a y 2 0 2 1 posterior N1 was obtained when its unique contribution was assessed via PCA. In addition to the SN observed at 140–280 msec after stimulus onset, we observed an even earlier ERP effect— an AN1 (anterior N1) component with a higher ampli- tude for cue type Y than for cue type X. This effect was observed at around 100–150 msec poststimulus onset, and its reliability as an independent effect was confirmed via temporal PCA and ANOVA. It has previously been demonstrated that so-called exogenous components, such as posterior and anterior N1, can be modulated by demand on visual discrimination, even where the stimuli being discriminated appear in the same spatial locations (Vogel & Luck, 2000). The difference observed in our experiment may therefore reflect enhanced visual discrimination of cue type Y, possibly by sensory ampli- fication of all or some of the features of this cue type, as soon as it begins to be differentiated from X by the perceptual system. We believe the difference between the ERPs to images in sets X and Y is a consequence of the participant learning about the images’ differing relationship to the prediction errors made in Phase 2. In Phase 2, partic- ipants predicted the outcome of AX trials throughout, whereas accurate prediction of the outcome of BY trials was acquired more slowly. The greater prediction error in BY trials compared to AX trials is assumed by atten- tional theories of associative learning to result in greater attention to Y images than to X images, which is also what the AN1 and SN differences between these two trial types indicate. The X and Y trials occurred with equal frequency, thus relative novelty is not a confounding factor in this experiment. The specific ‘‘cell bodies’’ used in the X and Y stimulus sets were randomized across participants, so this difference in attention is unlikely to be due to differences in the basic perceptual properties of the X and Y sets. On the basis of current knowledge of functional brain anatomy, it seems reasonable to suggest that the early ERP difference (AN1) reflects early attentional differ- entiation in perceptual identification areas and the as- sociated sensory amplification/suppression, whereas the SN difference reflects the involvement of selective attention circuitry. The LORETA solutions, shown in Figure 3C, are consistent with this view. Although the results from LORETA contrasts only survive the uncor- rected significance threshold and, as such, should be seen as exploratory, the foci they reveal have been pre- viously documented in studies of the functional anat- omy of visual selective attention. In the earlier time window (110–135 msec), we found more activity to Y images than to X images in the inferior temporal region, whereas in the later time window (155–180 msec), we found more activity to Y images than to X images in the posterior parietal cortex. Thus, the functional anatomy reveals the expected shift from differences in early object-identification regions to later differences in regions well known to be implicated in selective visual attention (Nobre, Gitelman, Dias, & Mesulam, 2000; Kim et al., 1999). Our cortical local- izations of attentional differences also have precedents in the study of human predictive learning. Although Turner et al.’s (2004) analysis concentrated on a region of interest in the prefrontal cortex defined by a previous study (Fletcher et al., 2001), they also presented certain differences in other regions, including posterior parietal regions. The current study supports these findings. In addition, it provides a detailed time-course of activity in these regions and links them to scalp waveform compo- nents (SN and AN1) whose functional significance has been extensively investigated. There are also some notable differences between our cortical localizations and those reported in previous studies of predictive learning. For example, previous neuroimaging work on predictive learning emphasizes the role of the striatum (e.g., O’Doherty et al., 2003). However, the absence of localizations in the striatum in our study is unsurprising. The sensitivity of EEG to deep brain regions such as the striatum is very limited (in- deed, the striatum is not even included in the LORETA solution space). Of more interest is the fact that some other human studies (Turner et al., 2004; Fletcher et al., 2001) converge on the observation that the lateral frontal cortex is involved in predictive learning. Al- though EEG and LORETA do detect current density changes originating in the lateral frontal cortex (e.g., Lavric et al., 2004), we did not find differences in this region in the analyzed 500 msec following the presen- tation of the stimulus. It is possible that the activation detected with fMRI reflects a modulation by prefrontal regions of visual attention circuitry. Such modulation is likely to have a more continuous (across trials) and slow character, and thus, is perhaps unlikely to be reflected in rapid event-locked potential changes such as the ones reported here. EXPERIMENT 2 One limitation of Experiment 1 is that its demonstration of attentional differences is confined to Phase 3, by which time learning has been completed. The persist- ence of attentional differences is predicted by certain attentional associative accounts (e.g., Mackintosh, 1975) and there is behavioral evidence that attentional persist- ence can indeed occur in human associative learning tasks (e.g., Lochmann & Wills, 2003). Nevertheless, in order to bridge the gap between prediction error differ- ences and the learning in Phase 2 and the observed attentional ERP effects, it is important to demonstrate the presence of attentional differences in Phase 2. Crucially, in order to provide such evidence, one needs to disentangle the attention to the individual cues X and Y from the cues which appeared on the screen at the 850 Journal of Cognitive Neuroscience Volume 19, Number 5 D o w n l o a d e d f r o m l l / / / / / j t t f / i t . : / / D h o t w t p n : o / a / d m e i d t f r p o r m c . h s i p l v d e i r r e c c h t . m a i r e . d c u o m o / c j n o a c r t n i c / e a - r p t d i c 1 l 9 e 5 - 8 p 4 d 3 f / 1 1 9 9 3 6 / 3 5 0 / 3 8 4 o 3 c / n 1 2 7 0 5 0 6 7 6 1 9 9 0 / 5 j 8 o 4 c 3 n p . d 2 0 b 0 y 7 g . u 1 e 9 s . t 5 o . n 8 0 4 8 3 S . p e p d f e m b b y e r g 2 u 0 e 2 s 3 t / j . . t . f . . o n 1 8 M a y 2 0 2 1 same time (A and B). This is critical because attentional differences between compounds AX and BY in Phase 2 may be due to a simple novelty detection mechanism related to cues A and B: cue B changes its outcome relative to Phase 1 while cue A does not. It would be extremely difficult to use ERPs to measure the correlates of attention to individual cues that appear in com- pounds. Therefore, we turned to a technique that can accomplish this relatively easily: eye tracking. Previous evidence indicates that eye gaze can be used as an overt measure of attention in tasks of this type (e.g., Kruschke, Kappenman, & Hetrick, 2005; Rehder & Hoffman, 2005). Experiment 2 employed very similar behavioral pro- cedures to Experiment 1—the only difference being that the stimuli were enlarged and positioned further apart to facilitate effective eye tracking (in Experiment 1, stimuli were small and tightly positioned to minimize eye-movement artifacts in the EEG). Methods Participants Sixteen students and staff (10 women; age: mean = 25.88 years, SD = 8.82, range = 21–56) took part in Experiment 2. Each participant was paid 4 GBP for a 50-min experimental session. None of the participants had taken part in Experiment 1. Apparatus Stimulus presentation and response collection was via a PC-compatible computer and the E-prime package (Ver- sion 1.1, Psychology Software Tools, Pittsburgh, USA). Eye movements were recorded using an EyeLink II system (SR Research, Osgoode, Canada), a video-based eye-tracker with head movement compensation system. The sampling rate was 500 Hz. Pupil position was monitored (right eye only) via a miniature infrared CCD video camera mounted on an adjustable headband. Participants were instructed to keep head movements to a minimum and no active restraint of head movements was required to obtain sufficiently accurate gaze position recordings. The stimulus presentation PC initiated and terminated eye-tracking recording blocks on each exper- imental trial via a TTL interface box connected to the eye-tracker PC. Stimuli The stimuli were enlarged relative to Experiment 1, but were otherwise identical to those used in that experi- ment. Pictures subtended 6.28 of visual angle and, where two pictures were presented at the same time, one was presented 7.78 of visual angle above the center and the other at an equal distance below the center. There was no white outline square in Experiment 2. Procedure Eye movements were recorded during Phase 1 and Phase 2 of Experiment 2.1 The experimental procedure was identical to that employed in Experiment 1, with the following exceptions. In order to correct for drift in eye- movement position accuracy, experimenter-controlled drift corrections were performed at 24-trial intervals. These drift corrections comprised of a brief 1.5-sec mes- sage telling participants to ‘‘focus on the cross in the center of the screen,’’ followed by a fixation cross. The offset of this cross was controlled by the experimenter, who manually initiated the next trial once the drift cor- rection had been performed by the eye-tracking soft- ware. The time taken to perform this offset correction procedure varied across trials and participants between approximately 3 and 5 sec. Eye-movement Analysis Eye movements were viewed and analyzed off-line using the EyeLink DataViewer software. This software auto- matically detects saccadic eye movements and parses the eye-movement data into individual fixations using a combined position/velocity/acceleration criterion (a sac- cade was defined as a period where eye velocity was greater than 308/sec, eye acceleration was greater than 80008/sec2, and the eye had deviated at least 0.18 from its starting position). Fixations were defined as periods between saccades. Blink artifacts were automatically removed from the data by the DataViewer software. The mean position, duration, and number of fixations in each stimulus ‘‘region of interest’’ on each trial were outputted from the software for further statistical anal- ysis. Regions of interest in this experiment were prede- fined as 210 (cid:3) 210 pixel squares corresponding to the size and positions occupied by the picture stimuli. The total viewing or ‘‘dwell’’ time for each of these regions of interest was calculated for these data for each trial and stimulus of interest (i.e., sum of all individual fixation durations for each stimulus on each trial). D o w n l o a d e d f r o m l l / / / / / j t t f / i t . : / / D h o t w t p n : o / a / d m e i d t f r p o r m c . h s i p l v d e i r r e c c h t . m a i r e . d c u o m o / c j n o a c r t n i c / e a - r p t d i c 1 l 9 e 5 - 8 p 4 d 3 f / 1 1 9 9 3 6 / 3 5 0 / 3 8 4 o 3 c / n 1 2 7 0 5 0 6 7 6 1 9 9 0 / 5 j 8 o 4 c 3 n p . d 2 0 b 0 y 7 g . u 1 e 9 s . t 5 o . n 8 0 4 8 3 S . p e p d f e m b b y e r g 2 u 0 e 2 s 3 t / j . t . f . . . Results All tests of statistical significance were assessed against an a of .05. o n 1 8 M a y 2 0 2 1 Behavioral Results The behavioral results were basically equivalent to those found in Experiment 1. In the final block of Phase 1, the mean proportion of ‘‘fever’’ responses was 0.91 to A trials, 0.05 to B trials, and 0.11 to I trials. The difference between A and B trials was significant, t(15) = 7.582, as was the difference between A and I trials, t(15) = 7.931. The difference between B and I did not approach significance, t(15) = 0.103. In Phase 2, a two-factor Wills et al. 851 repeated-measures ANOVA revealed that the proportion of ‘‘fever’’ responses was significantly affected by trial type, F(2, 30) = 87.087, and by trial block, F(5, 75) = 29.922. There was also a significant interaction between these two factors, F(10, 150) = 14.150. The mean response latencies were also analyzed for each trial type in Phase 2. AX+ trials had a mean la- tency of 1408 and 973 msec, BY+ trials were 1525 and 1019 msec, and IJ(cid:1) trials were 1480 and 1153 msec for the first and last blocks, respectively. A two-factor (trial type, three levels; trial block, six levels) repeated- measures ANOVA was applied to these data and revealed two main effects. There was significant effect of trial type, F(2, 30) = 12.450, and a significant effect of trial block, F(5, 75) = 22.360. The interaction between these two factors was not significant, F(10, 150) = 1.300. In Phase 3, the mean proportion of ‘‘fever’’ responses was 0.50 to trial type X and 0.77 to trial type Y. Thirteen out of 16 participants made more ‘‘fever’’ responses to trial type Y than to trial type X. Mean error rates for the other trial types in Phase 3 were: A, 11%; AX, 5%; BY, 15%; B, 22%. A two-factor (trial type, two levels; trial block, six levels) repeated-measures ANOVA was applied to the proportion of ‘‘fever’’ responses to X and Y stimuli in Phase 3 and yielded a significant difference between these two trial types, F(1, 15) = 11.719. ANOVA found no significant effect of trial block, F(5, 75) = 2.437, and the Trial block (cid:3) Trial type interaction was not significant either, F(5, 75) = 1.576. A further two- factor (trial type, two levels; trial block, six levels) repeated-measures ANOVA applied to the response la- tencies for X and Y in Phase 3 revealed a significant effect of trial block, with response becoming slightly faster for both trial types as Phase 3 progressed, F(5, 75) = 5.570. There was no significant difference between the trial types, F(1, 15) = 0.030; mean response latency was 832 msec to X and 829 msec to Y. The interaction between trial type and trial block was not significant, F(1, 15) = 2.194. Eye-tracking Results Mean total dwell times (see Methods) for the critical stimuli in Phase 2 were calculated. The mean dwell times for X and Y across the phase were 337 and 435 msec per trial, respectively. A two-factor (trial type, two levels; trial block, six levels) repeated-measures ANOVA revealed a significant difference between X and Y, F(1, 15) = 9.346. There was also a significant effect of trial block, F(5, 75) = 13.528, with dwell times decreasing as Phase 2 progressed. The Block (cid:3) Trial type interaction was not significant, F(5, 75) = 1.088. As manual response times were found to vary as a function of block in the experiment (see above), dwell times on regions of interest were also calculated as a percentage of total viewing time for each trial. For each AX trial, percentage dwell time for X was calculated as 100x/(a + x), where x was the dwell time in region of interest for stimulus X, and a was the dwell time in the region of interest for stimulus A. For each BY trial, per- centage dwell time for Y was calculated in the corre- sponding manner: 100y/( y + b). A two-factor (trial type, two levels; trial block, six levels) repeated-measures ANOVA revealed a significant difference between per- centage dwell time on X and Y, F(1, 15) = 9.69. Mean percentage dwell time was 37% for X, and 46% for Y. The effect of block did not approach significance, F(5, 75) = 0.44. The interaction between trial type and block was not significant, F(5, 75) = 1.98, .10 > p > .05, bien que
the trend was toward a divergence of percentage dwell
times as Phase 2 progressed.

A further analysis was carried out to test the hypoth-
esis that what is learned about X and Y (as indexed by
the proportion of ‘‘fever’’ responses to each in Phase 3)
should be linked to the amount of attention directed to
each during learning (as indexed by the mean dwell
times for X and Y in Phase 2). If this hypothesis is cor-
rect, a relationship should be apparent between the
mean differences in dwell times for X and Y in Phase 2
and the mean differences in proportion of ‘‘fever’’
responses in Phase 3 for X and Y. Consistent with the
hypothèse, this analysis revealed significant positive
correlation between these two variables, r(16) = .526.

Discussion

The objective of Experiment 2 was to examine the eye-
movement correlates of attention to cue types X and Y
in Phase 2, separately from cue types with which they
were paired (B and Y). Mean and percentage viewing
(demeurer) times were used as measures of attention to
cues. In accordance with attentional accounts of predic-
tive learning, we expected that early in Phase 2, partic-
ipants would dedicate more time to viewing the cue
associated with larger prediction errors (Oui), compared
to the cue that generated smaller prediction errors (X).
The results unequivocally support this prediction: Both
mean and percentage dwell times were reliably higher
for cue type Y than for cue type X. This difference in
dwell times did not change significantly across Phase 2,
suggesting that the difference arose early on in Phase 2.

GENERAL DISCUSSION

The present studies examined the role of attention in
predictive learning through the measurement of brain
potentials (Experiment 1) and eye movements (Experi-
ment 2). The outcomes from both procedures are
consistent with the idea that the amount of attentional
resources allocated to a cue is positively related to the
size of the prediction error it has previously produced.
D'abord, ERP components that have been implicated in
selective attention were found to have larger amplitudes

852

Journal des neurosciences cognitives

Volume 19, Nombre 5

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

in response to cue types previously associated with
larger prediction errors. The cortical origins of these
differences in scalp-recorded ERPs (as estimated by low-
resolution electromagnetic tomography) were found to
be in areas closely associated with object recognition
and visual attention. Deuxième, participants dedicated
more time to viewing cues that generated larger predic-
tion errors.

The relationship between attention and prediction er-
rors reported in these studies was predicted on the basis
of certain attentional associative theories (Kruschke, 2001;
Pearce & Hall, 1980), and the presence of the effects we
report is consistent with such theories. Inévitablement, other
types of theory can also accommodate our findings if
one allows the introduction of additional assumptions
into those theories. The nature of these assumptions,
and their implications for future research, is discussed
below.

Higher-order reasoning theories of predictive learning
(De Houwer et al., 2005), more or less by definition, faire
not invoke early attentional differences in their explana-
tions of how phenomena such as forward cue compe-
tition occur. Néanmoins, the attentional effects we
have observed could be incorporated within such ac-
counts via the assumption that attentional differences
are the top-down product of high-level reasoning. Dans-
deed, such an argument has recently been forwarded by
De Houwer et al. (2005) and could be seen as deriving
some support from the prefrontal cortex activation
observed in some fMRI studies of predictive learning
(par exemple., Turner et al., 2004). We did not observe prefrontal
involvement in our studies, but this may be due to the
tightly trial-locked and time-specific nature of the ERP
methodology we employed. The question of whether
the attentional differences we observe are the top-down
result of high-level reasoning processes or the result of
the lower-level, automatic processes that are sometimes
assumed to be implied by associative accounts, is an
important topic for future research.

Nonattentional associative learning theories (par exemple.,
Rescorla & Wagner, 1972) could also accommodate our
results by the introduction of certain assumptions. Spe-
cifically, such accounts could postulate that cues with
high associative strength attract more attention than
cues with low associative strength (cue Y is more
likely to produce a ‘‘fever’’ response than cue X in our
experiments, so such associative theories would predict
that cue Y has higher associative strength). Bien que le
introduction of attentional processes into nonattention-
al theories might, at first sight, appear to render the two
types of theory equivalent, the proposal is interesting in
the sense that it appears to make opposite predictions
to the Kruschke–Mackintosh and Pearce–Hall atten-
tional theories in certain situations. Consider, for ex-
ample, a slightly modified design in which AX and BY
predict the absence of fever in Phase 2. In such a design,
nonattentional associative theories would predict that

the associative strength of Y would end up being higher
than the associative strength of X (which would be nega-
tive in order to prevent the prediction of an outcome
on the basis of A). Proponents of nonattentional ac-
counts have previously argued that activation should
be higher for Y than for X in this design, and such an
effect has been observed for dopamine neurons in an
animal model (Tobler, Dickinson, & Schultz, 2003). Dans
contraste, attentional accounts would predict the oppo-
site result—X should attract more attention than Y be-
cause X will have been involved in more prediction
errors in Phase 2 than Y (because participants will ini-
tially and incorrectly predict an outcome on AX trials).
En résumé, the current study provides detailed in-
sights into the electrophysiological correlates (temporal
and anatomical) and the oculomotor correlates of hu-
man associative learning. The more prediction errors an
event has been involved in, the greater the early atten-
tional resources that are directed toward it. The pro-
duction and function of this attentional differentiation is
a matter for further research.

Remerciements

This research was supported by a BBSRC grant 9/S17109, and EC
Framework 6 project grant 516542 (NEST) to the first author.
We thank Jan De Houwer, and two anonymous reviewers, pour
their helpful comments. Related research can be found at www.
willslab.co.uk.

Reprint requests should be sent to A. J.. Wills, School of Psy-
cologie, University of Exeter, Perry Road, Exeter, EX4 4QB,
England, ou par e-mail: a.j.wills@exeter.ac.uk.

Note

1. Eye movements were not recorded during Phase 3. Eye-
tracking data from the target trials in Phase 3 (X and Y) would
have been of limited use, as each stimulus had but a single
component. Measures such as dwell time to that single com-
ponent add relatively little to the information already available
from the participants’ behavioral reaction times. Participant com-
fort was also an issue—our apparatus was too uncomfortable
to be worn for the whole length of this fairly long (45 min)
experiment.

RÉFÉRENCES

Ashby, F. G., Alfonso-Reese, L. UN., Turken, UN. U., & Waldron,
E. M.. (1998). A neuropsychological theory of multiple
systems in category learning. Psychological Review, 105,
442–481.

Brett, M., Johnsrude, je. S., & Owen, UN. M.. (2002). Le

problem of functional localization in the human brain.
Nature Reviews, Neurosciences, 3, 243–249.

Clark, V. P., & Hillyard, S. UN. (1996). Spatial selective
attention affects early extrastriate but not striate
components of the visual evoked potential. Journal
of Cognitive Neuroscience, 8, 387–402.

De Houwer, J., & Beckers, T. (2002). Higher-order

retrospective revaluation in human causal learning.

Wills et al.

853

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

Quarterly Journal of Experimental Psychology, 55B,
137–151.

De Houwer, J., Beckers, T., & Vandorpe, S. N. (2005). Evidence
for the role of higher order reasoning processes in cue
competition and other learning phenomena. Apprentissage &
Behavior, 33, 239–249.

Donchin, E., & Heffley, E. F. (1978). Multivariate analysis of
event-related potential data: A tutorial review. In D. Othon
(Ed.), Multidisciplinary perspectives in event-related
brain potential research (pp. 555–572). Washington, CC:
Government Printing Office.

Erickson, M.. UN., & Kruschke, J.. K. (1998). Rules and exemplars
in category learning. Journal de psychologie expérimentale:
General, 127, 107–140.

Fletcher, P.. C., Anderson, J.. M., Shanks, D. R., Honey, R.,

Carpenter, T. UN., Donovan, T., et autres. (2001). Responses of
human frontal cortex to surprising events are predicted by
formal associative learning theory. Neurosciences naturelles,
4, 1043–1048.

Glautier, S. (2002). Spatial separation of target and competitor
cues enhances blocking of human causality judgements.
Quarterly Journal of Experimental Psychology, 55B,
121–135.

Hillyard, S. UN., & Anllo-Vento, L. (1998). Event-related brain

potentials in the study of visual selective attention.
Actes de l'Académie nationale des sciences, USA.,
95, 781–787.

Holroyd, C. B., Nieuwenhuis, S., Yeung, N., & Cohen, J.. D.
(2003). Errors in reward prediction are reflected in the
event-related brain potential. NeuroReport, 14, 2481–2484.

Kamin, L. J.. (1969). ‘‘Attention-like’’ processes in classical
conditioning. En M. R.. Jones (Ed.), Miami symposium
on the prediction of behavior: Aversive stimulation. Miami,
FL: University of Miami Press.

Kim, Y.-H., Gitelman, D. R., Nobre, UN. C., Parrish, T. B., LaBar,

K. S., & Mesulam, M.. M.. (1999). The large-scale neural
network for spatial attention displays multifunctional
overlap but differential asymmetry. Neuroimage, 9,
269–277.

Kruschke, J.. K. (2001). Toward a unified model of attention in
associative learning. Journal of Mathematical Psychology,
45, 812–863.

Kruschke, J.. K., Kappenman, E. S., & Hetrick, W. P.. (2005).

Eye gaze and individual differences consistent with learned
attention in associative blocking and highlighting. Journal
of Experimental Psychology: Apprentissage, Mémoire, et
Cognition, 31, 830–845.

Lancaster, J.. L., Woldroff, M.. G., Parsons, L. M., Liotti, M.,

Freitas, C. S., Rainey, L., et autres. (2000). Automated Talairach
atlas labels for functional brain mapping. Cerveau humain
Cartographie, 10, 120–131.

Lavric, UN., Pizzagalli, D. UN., & Forstmeier, S. (2004). When ‘‘go’’
and ‘‘nogo’’ are equally frequent: ERP components and
cortical tomography. European Journal of Neuroscience,
20, 2483–2488.

Lawrence, D. H. (1952). The transfer of a discrimination along
a continuum. Journal of Comparative and Physiological
Psychologie, 45, 511–516.

Le Pelley, M.. E., Oakeshott, S. M., & McLaren, je. P.. L. (2005).
Blocking and unblocking in human causal learning. Journal
of Experimental Psychology: Animal Behavior Processes,
31, 56–70.

Lochmann, T., & Wills, UN. J.. (2003). Predictive history in an
allergy prediction task. In F. Schmalhofer, R.. M.. Jeune,
& G. Katz (Éd.), Proceedings of EuroCogSci 03: Le
European Conference of the Cognitive Science Society
(pp. 217–222). Mahwah, New Jersey: Erlbaum.

Mackintosh, N. J.. (1975). A theory of attention: Variations in

the associability of stimuli with reinforcement. Psychological
Review, 82, 276–298.

Mulert, C., Ja¨ger, L., Schmitt, R., Bussfeld, P., Pogarell, O.,

Mo¨ller, H.-J., et autres. (2004). Integration of fMRI and
simultaneous EEG: Towards a comprehensive
understanding of localization and time-course of brain
activity in target detection. Neuroimage, 22, 83–94.

Nobre, UN. C., Gitelman, D. R., Dias, E. C., & Mesulam, M.. M..

(2000). Covert visual spatial orienting and saccades:
Overlapping neural systems. Neuroimage, 11, 210–216.
O’Doherty, J., Dayan, P., Friston, K., Critchley, H., & Dolan, R.. J..
(2003). Temporal difference models and reward-related
learning in the human brain. Neurone, 28, 329–337.

Pascual-Marqui, R.. D. (1999). Review of methods for solving

the EEG inverse problem. Revue internationale de
Bioelectromagnetism, 1, 75–86.

Pascual-Marqui, R.. D., Michel, C. M., & Lehmann, D. (1995).
Segmentation of brain electrical activity into microstates:
Model estimation and validation. IEEE Transactions on
Génie biomédical, 42, 658–665.

Pavlov, je. P.. (1927). Conditioned reflexes. New York: Dover.
Pearce, J.. M., & Hall, G. (1980). A model for Pavlovian learning:
Variations in the effectiveness of conditioned but not of
unconditioned stimuli. Psychological Review, 87, 532–552.
Ploghaus, UN., Tracey, JE., Clare, S., Gati, J.. S., Rawlins, J.. N. P., &
Matthieu, P.. M.. (2000). Learning about pain: The neural
substrate of the prediction error for aversive events.
Actes de l'Académie nationale des sciences, USA.,
97, 9281–9286.

Rehder, B., & Hoffman, UN. B. (2005). Eyetracking and selective
attention in category learning. Psychologie Cognitive, 51,
1–41.

Rescorla, R.. UN., & Wagner, UN. R.. (1972). A theory of Pavlovian

conditioning: Variations in the effectiveness of
reinforcement and nonreinforcement. In A. H. Noir &
W. F. Prokasy (Éd.), Classical conditioning II: Actuel
recherche (pp. 64–99). New York: Appleton-Century-Crofts.

Schultz, W., Dayan, P., & Montague, P.. R.. (1997). A neural

substrate of prediction and reward. Science, 275, 1593–1599.

Tobler, P.. N., Dickinson, UN., & Schultz, W. (2003). Coding

of predicted reward omission by dopamine neurons in a
conditioned inhibition paradigm. Journal des neurosciences,
23, 10402–10410.

Tourneur, D. C., Aitken, M.. R.. F., Shanks, D. R., Sahakian,

B. J., Robbins, T. W., Schwarzbauer, C., et autres. (2004). Le
role of lateral frontal cortex in causal associative learning:
Exploring preventative and super-learning. Cérébral
Cortex, 14, 872–880.

Vogel, E. K., & Luck, S. J.. (2000). The visual N1 component
as an index of a discrimination process. Psychophysiology,
37, 190–203.

Wills, UN. J., & McLaren, je. P.. L. (1997). Generalization in
human category learning: A connectionist explanation
of differences in gradient after discriminative and
non-discriminative training. Quarterly Journal of
Experimental Psychology, 50UN, 607–630.