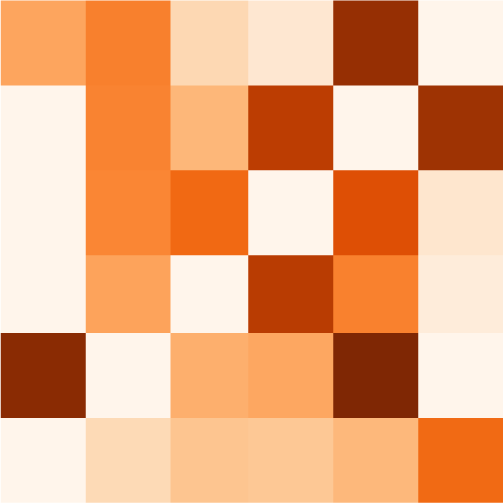PERSPECTIVE
Model-based whole-brain effective connectivity
to study distributed cognition in health
and disease
Matthieu Gilson 1, Gorka Zamora-López1, Vicente Pallarés1, Mohit H. Adhikari1,
Mario Senden2, Adrià Tauste Campo3, Dante Mantini4,5, Maurizio Corbetta6,7,
Gustavo Deco1,8, and Andrea Insabato9
1Center for Brain and Cognition and Department of Information and Communication Technologies, Universitat Pompeu Fabra,
Barcelona, Espagne
2Department of Cognitive Neuroscience, University of Maastricht, Maastricht, The Netherlands
3BarcelonaBeta, Barcelona, Espagne
4Neuroplasticity and Motor Control Research Group, KU Leuven, Leuven, Belgium
5Brain Imaging and Neural Dynamics Research Group, IRCCS San Camillo Hospital, Venice, Italy
6Department of Neuroscience, Venetian Institute of Molecular Medicine (VIMM) and Padova Neuroscience Center (PNC),
University of Padua, Italy
7Department of Neurology, Radiology, and Neuroscience, Washington University School of Medicine, St. Louis, MO, Etats-Unis
8Institució Catalana de la Recerca i Estudis Avançats (ICREA), Barcelona, Espagne
9Institut de Neurosciences de la Timone, CNRS, Marseille, France
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mots clés: IRMf, Cognition, Whole-brain dynamic model, Effective connectivity, Connectivity esti-
mation, Machine learning, Classification, Biomarker, Network theory, Recurrent network, Dynamic
communicability and flow, Community analysis
ABSTRAIT
Neuroimaging techniques are now widely used to study human cognition. The functional
associations between brain areas have become a standard proxy to describe how cognitive
processes are distributed across the brain network. Among the many analysis tools available,
dynamic models of brain activity have been developed to overcome the limitations of
original connectivity measures such as functional connectivity. This goes in line with the
many efforts devoted to the assessment of directional interactions between brain areas from
the observed neuroimaging activity. This opinion article provides an overview of our
model-based whole-brain effective connectivity to analyze fMRI data, while discussing the
pros and cons of our approach with respect to other established approaches. Our framework
relies on the multivariate Ornstein-Uhlenbeck (MOU) process and is thus referred to as
MOU-EC. Once tuned, the model provides a directed connectivity estimate that reflects the
dynamical state of BOLD activity, which can be used to explore cognition. We illustrate this
approach using two applications on task-evoked fMRI data. D'abord, as a connectivity measure,
MOU-EC can be used to extract biomarkers for task-specific brain coordination, understood
as the patterns of areas exchanging information. The multivariate nature of connectivity
measures raises several challenges for whole-brain analysis, for which machine-learning tools
present some advantages over statistical testing. Deuxième, we show how to interpret changes
in MOU-EC connections in a collective and model-based manner, bridging with network
analyse. Our framework provides a comprehensive set of tools that open exciting
perspectives to study distributed cognition, as well as neuropathologies.
RÉSUMÉ DE L'AUTEUR
Brain connectivity measures have been increasingly used to study cognition and
neuropathologies with neuroimaging data. Many methods have been developed with
un accès ouvert
journal
Citation: Gilson, M., Zamora-López, G.,
Pallarés, V., Adhikari, M.. H., Senden, M.,
Campo, UN. T., . . . Insabato, UN. (2020).
Model-based whole-brain effective
connectivity to study distributed
cognition in health and disease.
Neurosciences en réseau, 4(2), 338–373.
https://doi.org/10.1162/netn_a_00117
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00117
Informations complémentaires:
https://doi.org/10.1162/netn_a_00117
https://github.com/mb-BCA/pyMOU
https://github.com/mb-BCA/
NetDynFlow
https://github.com/mb-BCA/
notebooks_review2019
Reçu: 29 Mars 2019
Accepté: 02 Décembre 2019
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Matthieu Gilson
matthieu.gilson@upf.edu
Éditeur de manipulation:
Olaf Sporns
droits d'auteur: © 2019
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
Modeling whole-brain effective connectivity for cognition and disease
particular objectives, in particular predictability to obtain biomarkers (c'est à dire., which brain
regions exhibit changes in their interactions across conditions) and interpretability (relating
the connectivity measures back to the biology). In this article we present our framework for
whole-brain effective connectivity that aims to find the equilibrium between these two
desired properties, relying on a dynamic model that can be fitted to fMRI time series.
Entre-temps, we compare it with previous work. Concretely, we show how machine learning
can be used to extract biomarkers and how network-oriented analysis can be used to
interpret the model estimates in terms of brain dynamics.
INTRODUCTION
The study of cognition has flourished in the recent decades because of the abundance of neu-
roimaging data that give access to brain activity in human subjects. Along the years, tools from
various fields like machine learning and network theory have been brought to neuroimaging
applications in order to analyze data. The corresponding tools have their own strengths, like
predictability for machine learning. This article brings together recent studies based on the
same whole-brain dynamic model in a unified pipeline, which is consistent from the model
estimation to its analysis—in particular, the implications of the model assumptions can be
evaluated at each step. This allows us to naturally combine concepts from several fields, dans
particular for predictability and interpretability of the data. We stress that our framework can
be transposed to other dynamic models, while preserving the concepts underlying its design.
Dans ce qui suit, we first review previous work on connectivity measures to set our formalism
in context. After presenting the dynamic model (the multivariate Ornstein-Uhlenbeck process,
or MOU), we discuss its optimization procedure to reproduce statistics of the fMRI/BOLD
signals (spatiotemporal covariances), yielding a whole-brain effective connectivity estimate
(MOU-EC). Then two MOU-EC-based applications are examined: machine learning to extract
biomarkers and network analysis to interpret the estimated connectivity weights in a collective
manière. Entre-temps, presenting details about our framework, we provide a critical comparison
with previous studies to highlight similarities and differences. We illustrate MOU-EC capabil-
ities in studying cognition in using a dataset where subjects were recorded in two conditions,
watching a movie and a black screen (referred to as rest). We also note that the same tools can
be used to examine cognitive alterations due to neuropathologies.
CONNECTIVITY MEASURES FOR FMRI DATA
Among noninvasive techniques,
imagerie par résonance magnétique fonctionnelle (IRMf) has be-
come a tool of choice to investigate how the brain activity is shaped when performing tasks
(Cohen, 2018; Gonzalez-Castillo & Bandettini, 2017; Li, Wang, Yao, Hu, & Friston, 2012;
Naselaris, Kay, Nishimoto, & Galant, 2011). The blood-oxygen-level-dependent (AUDACIEUX) eux-mêmes-
nals recorded in fMRI measure the energy consumption of brain cells, reflecting modulations in
neural activity (Bartels, Logothetis, & Moutoussis, 2008; Becker, Reinacher, Freyer, Villringer,
& Ritter, 2011; Ekstrom, 2010; Mitra et al., 2018). Since early fMRI analyses, a main focus has
been on identifying with high spatial precision regions of interest (ROI) in the brain that signif-
icantly activate or deactivate for specific tasks (Cordes et al., 2000; Laird et al., 2013; Walther
et coll., 2016). Because the measure of BOLD activity during task requires the quantification
of a baseline, the brain activity for idle subjects became an object of study and developed as
a proper line of research (Biswal, 2012; Snyder & Raichle, 2012). This revealed stereotypical
patterns of correlated activity between brain regions, leading to the definition of the functional
connectivity or FC (Buckner, 2010; Gillebert & Mantini, 2013). Together with studies of the
Neurosciences en réseau
339
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
anatomical connectivity using structural MRI (Hagmann et al., 2008; Sporns, Tononi, & Kötter,
2005), fMRI studies progressively shifted from focusing on specific ROIs to whole-brain anal-
yses (Deco, Jirsa, & McIntosh, 2011). Par exemple, high-order cognition involves changes in
BOLD activity that are distributed across the whole brain (Chang, Gianaros, Manuck, Krishnan,
& Wager, 2015; Rissman & Wagner, 2012), which cannot be restrained to a small set of pre-
selected ROIs. The typical description of the whole-brain activity in these methods is a ROI-
ROI matrix, which we refer to as connectivity measure.
Glossaire
Generative model: Model of (dynamic) equations that generates a signal to be fit to
empirical data. This definition is different from the definition in statistics, où un
generative model describes the joint probability distribution of observed and predicted
variables (here the network activity), as opposed to a discriminative model that de-
scribes the conditional probability of the predicted variables with respect to the ob-
served variables.
Linear Gaussian model (LGM): Generative model of Gaussian variables with linear
relationships. Its output variables have a flat autocovariance (apart from zero time lag)
and is used to model noisy data without temporal structure.
Multivariate autoregressive (MAR) processus: Dynamic generative model in discrete
time with linear relationships. Its output variables have both spatial and temporal
correlations.
Multivariate Ornstein-Uhlenbeck (MOU) processus: Dynamic generative model in con-
tinuous time with linear relationships (referred to as connections). It is the equivalent
of the MAR process in continuous time.
Connections, interactions, and links: In the main text connections refer to a direct and
causal relationship between nodes (ROI) in a dynamic model, whereas interactions
are used to describe network effects that may be mediated by indirect pathways in
the network (for example with FC or dynamic flow). Links are used in the context of
machine learning as a common term for EC connections or FC interactions.
Lyapunov optimization or natural gradient descent: Tuning procedure for the EC weights
in the MOU network that fits the model FC covariance matrices to their empirical
homologues.
Classification pipeline: Succession of machine-learning algorithms that aims to learn
the mapping from input vectors of “features” to output “labels” (or categories). Here we
use neuroimaging connectivity measures to predict cognitive conditions (like the task
performed by a subject).
Multinomial logistic regression (MLR): Linear multicategory classifier that assigns a co-
efficient to each input feature to predict the labels. It reduces to logistic regression for
binary classification.
k-nearest neighbor (kNN): Nonlinear classifier that predicts the category of each new
sample based on the most represented category over the k closest samples from the
train set, given a distance metric or similarity measure.
Biomarker: Subset of observed features (here usually EC/FC links) that enable a robust
classification, often paired with weights as in the case of a linear classifier.
Dynamic communicability: Measure of pairwise interactions between nodes (ROI) dans
a network that takes indirect paths into account. In the present article, it corresponds
to interactions over time for the MOU model.
Dynamic flow: Extension of dynamic communicability that incorporates the effect of
input properties in the MOU model.
Neurosciences en réseau
340
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
Recently, fMRI studies for both rest and tasks have also evolved to incorporate the temporal
structure of BOLD signals in their analysis (Cabral et al., 2017; Ciuciu, Abry, & Il, 2014;
Gilson, Moreno-Bote, Ponce-Alvarez, Ritter, & Deco, 2016; Gonzalez-Castillo & Bandettini,
2017; B. J.. Il, 2011; Hutchison et al., 2013; Mitra, Snyder, Tagliazucchi, Laufs, & Raichle,
2015; Vidaurre et al., 2018), in addition to the spatial structure. Models have also been devel-
oped to formalize the link between the observed BOLD and the neuronal activity (Deco et al.,
2013; Frässle et al., 2018; K. J.. Friston, Harrison, & Penny, 2003; Gilson et al., 2016; Li et al.,
2012; Messé, Rudrauf, Benali, & Marrelec, 2014; Vidaurre et al., 2018). This has led to many
definitions for connectivity measures and variations thereof. In this introductory section we
present fundamental concepts about connectivity measures that set our model-based approach
in context (see also the Glossary for definitions).
Model-Based Versus Model-Free Approaches
A recurrent discussion opposes model-free and model-based approaches in neuroscience,
which also applies for connectivity measures. Par exemple, FC calculated using Pearson corre-
lation between time series (blue matrix in Figure 1A) can be directly calculated from data—see
Equation B.2 in the Supporting Information—and may thus be seen as model-free. Cependant,
the interpretation of the FC values for the pairs of ROIs in the matrix is based on the theory of
linear Gaussian models (LGMs), which assumes multivariate normal distributions for the data.
The Pearson correlation is a connectivity measure that can be directly calculated on the gen-
erated activity. The underlying connectivity in the LGM, called the precision matrix, is closely
related to the partial correlations (PC) represented by the green matrix in Figure 1A. The PC
symmetric matrix describes the undirected linear relationships between Gaussian variables
that result in the observed correlations. Our viewpoint is thus that connectivity measures are
always related to a model, so it is crucial to bear in mind their assumptions when interpret-
ing their values. Note that other classifications of methods have been proposed and discussed
in previous work, like directed functional connectivity measures versus effective connectiv-
ity measures (K. Friston, Moran, & Seth, 2013), state-space models versus structural models
for BOLD dynamics (Valdes-Sosa, Roebroeck, Daunizeau, & Friston, 2011) and network-wise
methods versus pairwise inference methods (Bielczyk et al., 2019).
In the literature of whole-brain modeling, three families of connectivity measures have
emerged:
Structural connectivity (SC): It measures the density or probability of anatomical path-
ways that connect two ROIs, mostly via the white matter (Schmahmann & Pandya, 2007).
This led to the definition of the human connectome at the whole-brain level (Hagmann
et coll., 2008; Sporns et al., 2005).
Functional connectivity (FC): Pairwise statistical dependencies between the observed
activity of ROIs (Buckner, 2010; Gillebert & Mantini, 2013). Apart from the Pearson
correlation of the BOLD signals (Biswal, 2012; Snyder & Raichle, 2012), other common
FC measures include mutual information (Hlinka, Palus, Vejmelka, Mantini, & Corbetta,
2011) and synchrony of instantaneous phases (Cabral, Hugues, Sporns, & Deco, 2011;
Cabral et al., 2017). Conceptually, FC corresponds to a measure that can be applied to
multiple time series, either the data or the model activity.
Effective connectivity (EC): In this article we define EC as a measure of the directional
relationships in a dynamic model. The original concept arises from electrophysiology
(Aertsen, Gerstein, Habib, & Palm, 1989), where EC determines how the stimulation of
a neuron affects a target neuron (par exemple., combining the source-to-target synaptic weight
Neurosciences en réseau
341
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
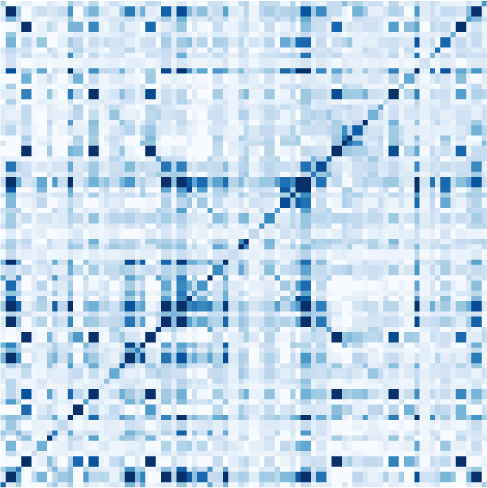
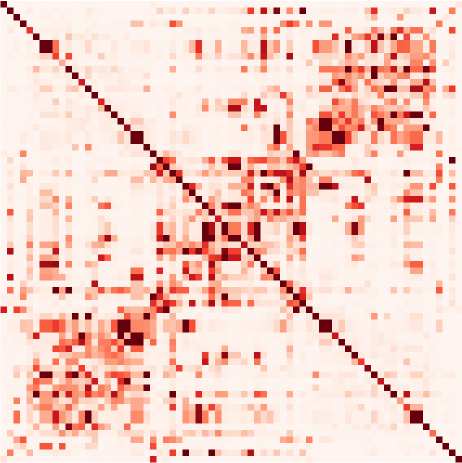
Chiffre 1. Connectivity measures. (UN) Schematic diagram of six brain regions of interest (ROI),
whose fMRI activity is captured by several types of connectivity measures. Here the activity is gen-
erated using a directed matrix. The corresponding structural connectivity (SC, black matrix) indicates
the topology of anatomical connections between the six ROIs, which can be estimated using struc-
tural MRI. Functional connectivity (FC, blue matrix), here calculated using the Pearson correlation
of the BOLD signals. The linear Gaussian model (LGM) assumes activity and corresponds to partial
correlations (PC, green matrix). The multivariate autoregressive (MAR, orange matrix) assumes linear
dynamics while taking the temporal structure of the data into account. Effective connectivity (EC,
red matrix), which is the focus of the present article, depends on the choice for dynamic model, comme
well as input properties. Here the dark brown dashed box groups together the connectivity mea-
sures that involve a model inversion for their estimation, as compared with the light brown box
that can be directly computed from the observed data. (B) Autocorrelograms of the data (in light
brown, left plot) for six ROIs and two network models (middle and right plots). The linear Gaussian
model related to the FC and PC (in green) has a flat autocorrelogram away from the central peak.
In contrast, the profile of the MAR process (in orange) has a decaying exponential profile.
Neurosciences en réseau
342
Modeling whole-brain effective connectivity for cognition and disease
and the excitability of the target). It was then brought to neuroimaging in the 2000s
when building models of the BOLD response and further developed in the context of the
dynamic causal model (DCM), usually interpreted as neuronal coupling (K. Friston, 2011;
K. J.. Friston et al., 2003; Valdes-Sosa et al., 2011). Note that it is also still used close to
its original formulation when measuring stimulation-driven responses in neuroimaging
(Lafleur, Tremblay, Whittingstall, & Lepage, 2016).
To go beyond statistical relationships, the combination of several types of data requires a
model, as with the SC and FC that are combined in the EC model (see Figure 1A). Donc
the choice of the model ingredients, especially their dynamics, has important implications that
we detail in the following.
Choice of Model and Interpretability
In our framework we borrow the EC terminology that can be understood in a broad sense as
the directed connectivity in a generative model, here for BOLD activity. When using the LGM
related to Pearson correlations taken as FC, one can take the partial correlation (PC, vert
matrix in Figure 1A) as “LGM-EC.” As illustrated by the flat green autocorrelogram for nonzero
time lags in Figure 1B, the generated signals by the linear Gaussian model are independently
and identically distributed (i.i.d.) variables and do not have temporal correlations. In contrast,
the multivariate autoregressive process (MAR, in orange in Figure 1A–B) has a directed con-
nectivity (asymmetric matrix) and produces temporally correlated signals. When these models
are fitted to data, they do not capture the same part of the data structure. When the MAR
model is considered, the estimation results in directed connectivity that depends on the spa-
tiotemporal correlation structure of the observed activity (or spatiotemporal FC). Cependant, le
linear Gaussian model does not “naturally” give directed connectivity when fitted to the spatial
FC. Note that techniques based on optimization with regularization have been developed to
enforce directionality in the estimated connectivity (Schiefer et al., 2018), though.
EC usually describes causal and directional relationships that interplay with other dynamic
parameters in the model to determine the global network pattern of activity. When optimizing
a model to reproduce BOLD signals, the parameter can be seen as representations or “projec-
tions” of the BOLD signals, in a top-down or data-driven approach (Valdes-Sosa et al., 2011).
Surtout, the estimated EC depends on the choice for the model dynamics. Par exemple, le
DCM was developed to formalize the link between neural and BOLD activities by explicitly
modeling the hemodynamics (K. Friston, 2011; K. J.. Friston et al., 2003; K. Stephan, Harrison,
Penny, & Friston, 2004). The DCM-EC is thus the directed connectivity between the ROIs and
determines their activities, from which the BOLD signals are generated via a hemodynamic
response function (FRH).
We keep in mind that all interpretations of fMRI signals sit on the hypothesis that correlated
BOLD activity between brain areas reflects the activity of their neuronal populations (David et
al., 2008; Goense & Logothetis, 2008; Oui. He et al., 2018; Matsui, Murakami, & Ohki, 2018),
which in turn mediates the transmission of neuronal information (Fries, 2005). Cependant, many
metabolic mechanisms like breathing (which are usually ignored in whole-brain models) alter
the BOLD signals (Power et al., 2018), and the adequate procedure to minimize the corruption
of data and obtain a satisfactory signal-to-noise ratio is still under debate (Parkes, Fulcher,
Yücel, & Fornito, 2018).
A distinct line of research (Cabral et al., 2011; Deco et al., 2013; Proix et al., 2016; Sanz-
Leon, Knock, Spiegler, & Jirsa, 2015) focuses on the development of whole-brain models in a
Neurosciences en réseau
343
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
more bottom-up fashion (model-driven), combining various datasets and biologically inspired
mechanisms, such as oscillators to produce rhythms observed in the brain. Such approaches
allow for the study of the influence of specific parameters (as ingredients in the model) dans
collectively shaping the global network activity. Compared with connectivity estimation, un
major distinction of many of those models is that SC is taken as the intracortical connectivity
to focus on the influence of the local dynamics in shaping network activity patterns; see Messé
et autres. (2014) for a review.
Consistency of Pipeline From Preprocessed Data to Modeling and Analysis
The incentive for novelty has fostered the development of many methods in computational
neuroscience. This makes results difficult to compare, especially for resting-state fMRI stud-
ies where no ground truth is available. Another caveat concerns network analysis when it is
applied to connectivity estimates from time-varying signals (par exemple., AUDACIEUX) with metrics (par exemple., à
detect communities) that do not genuinely relate to the physical values of the data. Our prac-
tical answer to this point is thus to develop for the same dynamic model a set of analysis tools,
covering parameter inference (Gilson et al., 2016) to machine learning and network analysis.
Although the mathematical tractability of the model limits the richness of its dynamic reper-
toire compared with more elaborate bottom-up models (Deco et al., 2013; Sanz-Leon et al.,
2015), it provides an intuitive understanding of the roles of parameters as well as analytical
derivations for the parameter estimation or model interpretation. We believe that such an effort
for formalization and consistency is beneficial to the field, both for didactic purpose and for
designing tailored methodology for complex models.
The present article follows the pipeline displayed in Figure 2A. The second section presents
the dynamic model and our recent optimization procedure (Gilson, Deco, et coll., 2018; Gilson
et coll., 2016) to estimate MOU-EC for whole-brain fMRI data (Figure 2B). It also discusses tech-
nical aspects in relation with other models used with neuroimaging data. The third section
shows how connectivity measures can be used to predict cognitive states (Figure 2C) and un-
cover their underlying structure. Surtout, the use of datasets with multiple tasks allows for
an in-depth benchmarking of the connectivity measures. It also highlights some advantages
of machine learning over statistical testing in making use of the multivariate nature of con-
nectivity measures, transposing and abstracting concepts presented in a recent study for sub-
ject identification (Pallarés et al., 2018). The fourth section bridges with network analysis
(Gilson et al., 2019; Gilson, Kouvaris, Deco, & Zamora-López, 2018), interpreting changes
in MOU-EC connections in a collective and model-based manner. En particulier, it adapts com-
munity detection to our dynamic model (Figure 2D).
CAPTURING THE WHOLE-BRAIN BOLD DYNAMICS WITH MOU-EC
Using a generative model to reproduce the BOLD statistics, the optimized MOU-EC can be
seen as an estimate that extracts spatiotemporal information about the BOLD dynamics. Dans
fact, the main innovation of the modeling is the optimization procedure in Figure 2B (Gilson
et coll., 2016). This section reviews important points about the underlying multivariate Ornstein-
Uhlenbeck (MOU) dynamic model and its tuning. Further mathematical details can be found in
the Supporting Information (see Figure S1). Our approach aims to combine several key aspects:
Whole-brain connectivity estimates are necessary to properly take into account the ex-
perimentally observed distributed information across distant regions (Chang et al., 2015;
Deco et al., 2011), without a priori selection of ROIs.
Neurosciences en réseau
344
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
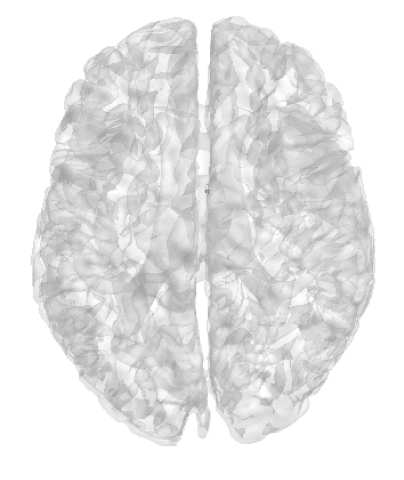
Chiffre 2. EC-based analysis of empirical BOLD signals. (UN) Pipeline for brain coordination analysis
using MOU-EC. For each fMRI session, the model is optimized by tuning its parameters, especially its
connectivité, to reproduce the statistics of the BOLD signals (depicted in the right side of the brain).
A schematic parcellation is represented on the left hemisphere of brain. The estimated MOU-EC can
then be used to predict cognitive states using classification algorithms. On the other hand, MOU-
EC can be analyzed as a graph (or network) to uncover collective properties. A contribution of our
approach is to link the network-oriented analysis with machine-learning techniques. (B) From the
BOLD signals, two FC matrices are calculated, FC0 without time lag in blue and FC1 with a time lag
de 1 TR in green. The model parameters (MOU-EC and Σ) are optimized to reproduce these empirical
FC matrices. Classification focuses on the model connectivity (par exemple., MOU-EC), but the influence of
Σ will be incorporated in the network analysis. See Figure S1 for further details. (C) Schematic
representation of the FC and MOU-EC matrices (one sample per session) in their own spaces for
two cognitive states (R for rest and M for movie). For each connectivity measure, the prediction
of R versus M is robust when the sample distributions represented by the dashed circles do not
overlap. (D) The left diagram represents community detection in a structural undirected network.
The right diagram represents the MOU-EC networks, from which we want to define dynamics-based
communautés.
From the overall spatiotemporal structure of BOLD signals, the dynamic model only
reproduces their covariances (without and with time lag, see Figure 2B). This con-
cerns the same fast timescale as recent studies (Mitra, Snyder, Hacker, & Raichle, 2014;
Mitra et al., 2015), which also demonstrated the influence of behavioral states such as
sleep versus wake. The choice of BOLD covariances to be reproduced by the model
is supported by previous results that showed that most of the information was in the
second-order statistics of BOLD signals (Hlinka et al., 2011).
Neurosciences en réseau
345
Modeling whole-brain effective connectivity for cognition and disease
Causality is inherent to the concept of EC (K. Friston, 2011; K. J.. Friston et al., 2003;
Valdes-Sosa et al., 2011) that is represented by the directed connections in the dynamic
model (red arrows in Figure 2B). From the estimated MOU-EC that best reproduces the
data, we interpret strong MOU-EC weights as causal relationships and can examine their
asymmetry to evaluate for a pair of ROIs which one drives the other. The optimization
can deal with common inputs for ROIs, to explain the observed correlated activity by an
interplay between the directed connectivity and correlated inputs (Gilson, Deco, et coll.,
2018).
The MOU-EC topology is the interregional infrastructure, namely which connections
exist and which do not in the brain network. When SC is available, its binarization (black
matrix in Figure 1A) can be used to constrain the MOU-EC topology in order to reduce
the number of parameters to estimate. This enforces the model to “explain” changes in
the FC by existing connections only, in contrast to PC and MAR (Figure 1A). It is thus
important to remember that MOU-EC estimates are not related to SC values.
The optimization procedure tunes all MOU-EC weights while taking into account net-
work effects. For each fMRI session, we obtain a multivariate estimate of more than 1,000
parameters that represent the dynamical “state” of the brain activity. This contrasts with
previous models that used the symmetric SC as connectivity matrix in dynamic mod-
els and focused on choosing or tuning the nodal dynamics with a few parameters only
(Deco et al., 2013; Messé et al., 2014; Sanz-Leon et al., 2015).
A limitation of the model estimation procedure up to now is the assumption of stationarity
for the BOLD signals over each fMRI session, which limits our approach to ongoing
nonswitching tasks.
Another limitation of MOU-EC for the interpretation in terms of neuronal coupling is the
absence of explicit hemodynamics in the model. This choice comes from the priority
given so far to the estimation robustness (with simpler dynamics) over the biological
interpretability, as will be discussed later.
Multivariate Ornstein-Uhlenbeck Dynamics as Generative Model for BOLD Signals
Officiellement, our model-based analysis is based on the multivariate Ornstein-Uhlenbeck process
that is described by Equation C.1 in the Supporting Information. It corresponds to a network
with linear feedback that is the equivalent in continuous time of the discrete-time multivariate
autoregressive (MAR) processus. These dynamic systems with linear feedback have been widely
used in neuroscience to model the propagation of fluctuating activity, mixing “noise” and struc-
ture, for example in modeling single neuronal dynamics (Burkitt, 2006), relating the connec-
tivity and activity in a network (Galán, 2008) and defining neural complexity (Barnett, Buckley,
& Bullock, 2009; Tononi, Sporns, & Edelman, 1994). It also corresponds to the linearization
of nonlinear population models like Wilson-Cowan neurons (Wilson & Cowan, 1973).
The choice for the MOU dynamics is motivated by the balance between simplicity, lequel
ensures tractable analytical calculation, and richness of the generated activity when modulat-
ing the parameters (especially the MOU-EC weights). Ainsi, it is well adapted to whole-brain
data with parcellation involving many ROIs (≥ 100). En outre, the MOU dynamics implies
exponential decaying autocovariances in the model, which have similar profiles to the empir-
ical data (see the left plot in Figure 1B corresponding to straight lines in log-plot in Figure S1).
Intuitively, it can be understood as a network when fluctuating activity (akin to noise) is gen-
erated at each ROI and propagates via the recurrent EC. Autrement dit, MOU-EC (red matrix in
the bottom box) acts as a “transition matrix” and quantifies the propagation of fluctuating BOLD
Neurosciences en réseau
346
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
activity across ROIs. The MOU-EC matrix is usually sparse when its topology is constrained by
SC (black matrix) to match anatomical white matter connections between ROIs. The fluctuating
activity for all ROIs is described by their (co)variance matrix Σ, which is diagonal in the present
case (see the purple vector of variances). In a previous study, cross-correlations for Σ also
involve common inputs to homotopic sensory ROIs (Gilson, Deco, et coll., 2018).
Parameter Estimation Capturing Network Effects in BOLD Propagation
To capture the BOLD dynamics (c'est à dire., propagation of fluctuating activity), we use the two BOLD
covariance matrices FC0 and FC1 in Figure 2B, without and with time lag, respectivement. Ce
also ensures a one-to-one mapping between an FC configuration (a pair FC0 and FC1) et
a MOU-EC configuration. This choice is in line with previous adjustments of DCM to model
the resting state that relied on the cross-spectrum, namely the Fourier transform of covariances
with all possible time lags (K. Friston, 2011). It is richer than fitting only an FC matrix without
time lag (Deco et al., 2013; Messé et al., 2014) and complies with a recent study of the task-
dependent modification of the BOLD temporal structure at short timescales (Mitra et al., 2015).
The MOU-EC estimate is obtained for the minimum model error in reproducing the em-
pirical FC0 and FC1 for each session (see the fit plot between the boxes in Figure S1). Le
optimization is akin to a “natural” gradient descent (Amari, 1998) in that it takes into account
the nonlinearity of the mapping from MOU-EC to the covariances FC0 and FC1. This arises
because of the network feedback (even though linear) and may result in strong correlations (dans
FC) for disconnected ROIs (EC = 0) provided strong indirect pathways connect them (via other
ROI). Appendix D in the Supporting Information provides the mathematical details of the op-
timization, which applies the gradient descent to both MOU-EC and Σ (Gilson, Deco, et coll.,
2018), extending the initial formulation with a heuristic optimization for Σ (Gilson et al., 2016).
For illustration purpose, this article uses a whole-brain parcellation consisting with 66 ROI.
The SC density is 28%, giving 1,180 MOU-EC weights to estimate (see Appendix A in the
Informations complémentaires). Each fMRI session has 300 time points separated by TR = 2s, so the
number of data points is 66 × 300 ≃ 2.104, à propos 16 times larger than the number of model
parameters. EC should be like a summary of the BOLD signals: informative (not too short),
but extracting and compressing relevant information (not too long). Our method was also suc-
cessfully applied to the AAL (Automated Anatomical Labeling) parcellation with 116 ROIs and
sessions of 5 min (Pallarés et al., 2018). Typiquement, the MOU-EC estimation for a session and
à propos 100 ROIs takes less than a minute of computation time on a desktop computer. Pour
more refined parcellation or shorter sessions, the FC matrices may become quasisingular and
the model estimates are expected to be noisier. The reduction of the number of parameters
to estimate by using SC is crucial to work at the level of individual fMRI session and avoid
overfitting. Ici, overfitting would correspond to the situation where many distinct MOU-EC
configurations in the model give very similar pairs of FC0 and FC1 matrices, giving a larger
overlap for MOU-EC than in Figure 2C and the same small overlap for FC. The comparison be-
tween FC and MOU-EC as multivariate representation of cognitive states will be the focus of the
next section. An important conceptual difference between MOU-EC and SC is that MOU-EC
accounts for the dynamical properties of the brain activity, which are modulated when engag-
ing a task. Autrement dit, MOU-EC is hypothesized to account for the concentration of recep-
tors or neurotransmitters, local excitability, and so on not only the density of the synaptic fibers.
Comparison With Other Approaches to Extract Information From BOLD Signals
Other approaches have been proposed to characterize activity “states” based on the tem-
poral structure of BOLD signals. Par exemple, the “dynamic FC” relies on sliding windows
Neurosciences en réseau
347
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
of several tens of TRs (Gonzalez-Castillo & Bandettini, 2017; Hutchison et al., 2013; Parc &
Friston, 2013; Preti, Bolton, & Van De Ville, 2017), thereby focusing on changes in correlation
patterns over minutes. Shorter timescales have been explored using instantaneous phases ob-
tained using the Hilbert transform on the BOLD signals (Cabral et al., 2017) or hidden Markov
models (HMMs; Bolton, Tarun, Sterpenich, Schwartz, & Van De Ville, 2018; Vidaurre et al.,
2018). In contrast, the MOU-EC describes the BOLD propagation averaged over a session
while assuming stationarity, as calculated in the corresponding statistics (covariances without
lag and with a lag of 1 TR). Note that the “transition matrix” analogy for EC is at the level of the
BOLD activity, not of hidden states as in the case of HMMs. De plus, it does not involve a
dynamic modulation of EC as used in the DCM (K. Friston, 2011; Li et al., 2012; Parc & Friston,
2013).
A key innovation to tackle whole-brain fMRI data is the optimization constrained by SC
that determines the network topology. This means the model has to explain the spatiotemporal
FC structure using the existing connections only. The “prior” information related to SC avoids
the preselection of ROIs and can be seen as an alternative to model comparison in choosing
the best topology using structural equations (James et al., 2009; McIntosh & Gonzalez-Lima,
1994), Granger causality analysis (Goebel, Roebroeck, Kim, & Formisano, 2003), and early
versions of the DCM (K. J.. Friston et al., 2003; Valdes-Sosa et al., 2011)—note that a recent
DCM study incorporates SC for the network topology (Sokolov et al., 2018). De même, le
MOU-EC density usually depends on the threshold applied to SC and the best choice can be
decided using model comparison, although the formulation may not be as natural as in the
Bayesian framework.
Several fundamental properties were discussed a few years ago about the defining concepts
of EC and DCM (Valdes-Sosa et al., 2011). Beyond technical details, three main points are
that DCM-EC corresponds to the connectivity weights in a dynamic model, that the model
incorporates the hemodynamic response function, and that the estimation captures the BOLD
dynamics, including the subsampling related to the low time resolution of BOLD signals. Le
EC terminology was borrowed from the DCM literature (K. Friston, 2011) because of the model-
based aspect. The MOU-EC estimation was developed to solve the trade-off between robust
estimation and application to large brain network (70+ ROI) by using linear dynamics (Gilson
et coll., 2016). Since then, the DCM has been applied to whole-brain fMRI data (Frässle et al.,
2018; Razi et al., 2017).
The FC0 and FC1 matrices in Figure 2B embody the spatiotemporal BOLD structure in
the range of “high” frequencies close to the Nyquist frequency equal to 0.5 Hz. The recent
extension of the DCM to analyze resting-state fMRI data reproduces the BOLD statistics via
the cross-spectrum (Frässle et al., 2018; K. J.. Friston, Kahan, Biswal, & Razi, 2014; Razi et al.,
2017), which is in line with our approach. Recall that this contrasts with earlier versions of the
DCM that reproduced the BOLD time series themselves for stimulation protocols (K. J.. Friston
et coll., 2003; Li et al., 2012). Because it works in continuous time, the MOU model deals with
the BOLD subsampling (Gilson et al., 2016), unlike estimation methods relying on the discrete-
time multivariate autoregressive process that may be sensitive to the subsampling of the BOLD
signals (Seth, Chorley, & Barnett, 2013). De plus, the observed lags between ROIs in FC—
similar to cross-correlograms (Mitra et al., 2014, 2015)—are explained by the combination
between the estimated inputs Σ and MOU-EC (Gilson, 2018).
The time constant τx in the MOU model is identical for all ROIs in Equation C.1 in the
Informations complémentaires, which corresponds to an abstraction of the HRF waveform response
Neurosciences en réseau
348
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
that was reported with a decay of 5 à 10 s (d’Avossa, Shulman, & Corbetta, 2003). An impor-
tant difference of our model compared with the underlying dynamic model behind DCM
(K. J.. Friston et al., 2003; Valdes-Sosa et al., 2011), as well as other bio-inspired network
models (Deco et al., 2013), is the absence of an explicit HRF to link the neural activity to
the measured BOLD signals (Boynton, Ange, Glover, & Heeger, 1996; K. Friston, Mechelli,
Tourneur, & Prix, 2000; K. Stephan et al., 2004). Note that applications of the DCM to resting-
state data involve a linearization of the HRF (Frässle et al., 2018; Razi et al., 2017). Donc,
a foreseen extension of our approach is that of a state-space model with the MOU process
generating the neuronal activity that is convolved with a linear HRF filtering (Sauvage, Hubert,
Touboul, & Ribot, 2017). The challenge is to keep the gradient-descent optimization tractable,
as was previously done with Granger causality analysis (Barnett & Seth, 2015; Faes, Stramaglia,
& Marinazzo, 2017). Incorporating the HRF may improve the reliability of the estimated EC
(Gitelman, Penny, Ashburner, & Friston, 2003; Olszowy, Aston, Rua, & Williams, 2019). Note
that an alternative consists in performing the deconvolution of the BOLD signals with respect
to a HRF before analyzing the obtained neuronal signals, as was done with Granger causal-
ity analysis (David et al., 2008; Goodyear et al., 2016; Sathian, Deshpande, & Stilla, 2013;
Wheelock et al., 2014) or other connectivity analysis (Ryali, Supekar, Chen, & Menon, 2011).
MACHINE LEARNING FOR EXTRACTING MULTIVARIATE BIOMARKER SPECIFIC
TO COGNITIVE STATES
Beyond their goodness of fit and how many “realistic” biological mechanism they might incor-
porate, models can be used to extract information from data in a top-down approach. Once
tuned, the model parameters can indeed be used to discriminate cognitive conditions, as a
representation of the observed data (BOLD signals here). This conceptually differs from find-
ing the generative model of activity with the best fit. Néanmoins, it is expected that a model
with poor fit hardly extracts any relevant information. Many recent studies have used connec-
tivity measures to predict which tasks are performed by the subjects in the scanner (González-
Castillo et al., 2015), the pathological conditions of patients (Kurth, Moyse, Bahri, Salmon,
& Bastin, 2015; Rahim, Thirion, Bzdok, Buvat, & Varoquaux, 2017), and individual iden-
tity (Amico & Goñi, 2018; Calhoun, Lawrie, Mourao-Miranda, & Stephan, 2017; Finn et al.,
2015; Miranda-Dominguez et al., 2014). Machine learning is the standard for identifying bio-
markers of neuropathologies (Varoquaux et al., 2017) and is also widely used in voxel-based
analysis for cognitive tasks (Naselaris et al., 2011; Walther et al., 2016). Cependant, it is less
frequently applied for cognition studies using connectivity measures (Varoquaux & Poldrack,
2019). For a given connectivity measure, a biomarker is a subset of connections (or links) que
enables the robust identification of a category of fMRI sessions, such as a weighted sum of
the matrix elements that exceeds a threshold for the multinational logistic regression (MLR).
In practice, changes in BOLD activity across cognitive conditions are mixed with individual
traits and session-to-session variability. Disentangling these contributions is the key to obtain
efficient biomarkers (Pallarés et al., 2018).
The present section addresses the following questions:
How to cope with the multivariate nature of connectivity measures (par exemple., > 1, 000
MOU-EC links)? We illustrate some advantages of machine learning compared with sta-
tistical testing, about multiple comparisons and beyond.
What does classification tell about the underlying model? Linear and nonlinear classifiers
apply different metrics on the estimated parameters, revealing the distribution of task-
specific changes across brain regions.
Neurosciences en réseau
349
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
In a complex environment (par exemple., many tasks), can we uncover a hierarchy in cognitive
states (subgroups of tasks)?
Adopting the language from machine learning, “samples” refer to fMRI sessions and the
links of the connectivity measures are “features” whose values are used to discriminate “la-
bels”, which are the types of fMRI sessions here. To illustrate our framework, we use data that
were previously analyzed (Demirta¸s et al., 2019; Gilson, Deco, et coll., 2018; Hlinka et al.,
2011; Mantini et al., 2012), whose details are summarized in Appendix A in the Supporting
Information. Subjects in the scanner were recorded fixating on a point in a black screen (deux
rest sessions R1 and R2) or a movie. The entire movie session was divided in three sessions (M1,
M2, and M3), each corresponding to a different part of the movie. The vectorized MOU-EC
estimates are displayed for all subjects and sessions in Figure 3A. The question is then whether
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
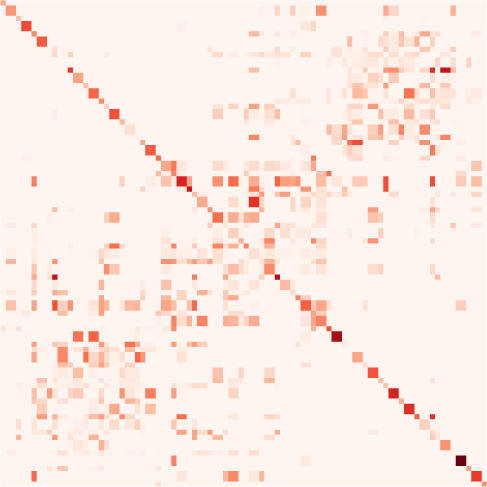
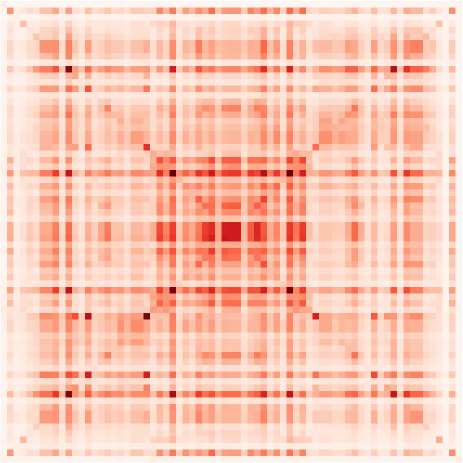
Chiffre 3. Dimensionality reduction of the connectivity measures. (UN) Connectivity estimates (ici
vectorized EC) for five sessions, two for rest and three for movie, for each of the 22 sujets. Each of
the three movie sessions corresponds the three movie sessions each of corresponds to a distinct part
(10 min) of a movie watched and listened to by the subjects. The gray arrow indicates connections
(or links) that strongly differ between rest and movie. (B) Analyse en composantes principales (APC) appliqué
to the vectorized EC, FC, and PC (one for each of the 110 sessions) where the same colors as in panel
A correspond to the 4 tasks. For PCA the task labels are not used in the dimensionality reduction
(unsupervised algorithm). (C) Similar plot to panel B with linear discriminant analysis (LDA) pour
which the labels are used (supervised learning) to separate the four tasks for the 110 sessions. (D)
The silhouette coefficient measures the quality of the clustering for the four dot clouds when varying
the number of LDA components (see x-axis).
Neurosciences en réseau
350
Modeling whole-brain effective connectivity for cognition and disease
connectivity measures can capture information to identify the movie sessions individually. Pour
example, the MOU-EC links indicated by the gray arrow exhibit strong changes between rest
and movie (with small and large values, respectivement).
Variability of Connectivity Measures With Respect to Cognitive Labels
Before classification, the data structure can be explored to evaluate the similarity or distance
across conditions between the connectivity measures, as representations of the BOLD signals.
For this type of (passive) task, BOLD synchronization patterns during movie viewing between
zones du cerveau (par exemple., visual and auditory) as reflected by intersubject correlations (Hasson, Nir,
Levy, Fuhrmann, & Malach, 2004) are expected to be also captured by the connectivity mea-
sures (Gilson, Deco, et coll., 2018). The gray arrow in Figure 3A indicates some MOU-EC links
with strong changes between rest and movie.
A usual technique for multivariate data is dimensionality reduction, for example using prin-
cipal component analysis (APC; Gonzalez-Castillo et al., 2015) and independent component
analyse (ICA; V. D. Calhoun, Liu, & Adali, 2009). Here we compare two linear transformations,
the unsupervised PCA in Figure 3B with the supervised linear discriminant analysis (LDA) dans
Figure 3C. The principal component is the direction in the high-dimension space with largest
variability across the samples, and successive components are ranked in decreasing order for
their corresponding variability. It is called unsupervised because it does not use the task labels
to compute the components, as can be seen for FC where the first component is not related
to the task labels. In comparison, the components for LDA are ranked according to their vari-
ability with respect to task labels. This can be seen for FC where the first component for PCA
does not reflect the separation between movie and rest (the second component does).
The separation of the tasks viewed using the connectivity measures can be evaluated using
silhouette coefficients that measure the clustering quality (Rousseeuw, 1987), ranging from 1
for separated dot clouds to −1 for completely overlapping dot clouds. Applied to the LDA coor-
dinates in Figure 3D, we see a slight increase in silhouette coefficient when incorporating more
components to separate the four clouds. This reflects the difficulty of the four-task discrimina-
tion, as compared with that for the two tasks where a single component is sufficient (Demirta¸s
et coll., 2019). The viewpoint here is that of clustering, assuming that the reduced space allows
for isolating the clouds to characterize the cognitive states (Gonzalez-Castillo et al., 2015). Dans
the following, we rely on various classification techniques for the task discrimination.
Cross-Validation for Assessing the Generalization Capability of Connectivity-Based Classification
Although machine-learning techniques are now increasingly used to analyze neuroimaging
data, the generalization capabilities are not always properly verified (Varoquaux et al., 2017). Pour
example, clustering algorithms applied on reduced-dimension components (see Figure 3B–C)
give a measure for the separation of the tasks viewed using the connectivity measures (Figure 3D).
Notice that all sessions are used for the dimensionality reduction in Figure 3. This is a problem
since the parameters tuning of the model can be influenced by the specific noise of the data
samples and, à son tour, the results will be not generalizable to new samples—a phenomenon
called overfitting. To evaluate the robustness of a classifier, a cross-validation procedure is
the standard for voxel-wise studies for activation maps (Naselaris et al., 2011; Walther et al.,
2016) and for clinical applications (Hohenfeld, Werner, & Reetz, 2018; Rahim et al., 2017).
This procedure consists in splitting the data samples in train and test sets that are respectively
used to fit the classifier and to assess its performance, as described in Figure 4A. Ainsi, un
may have to include preprocessing steps in the cross-validation scheme to properly evaluate
Neurosciences en réseau
351
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
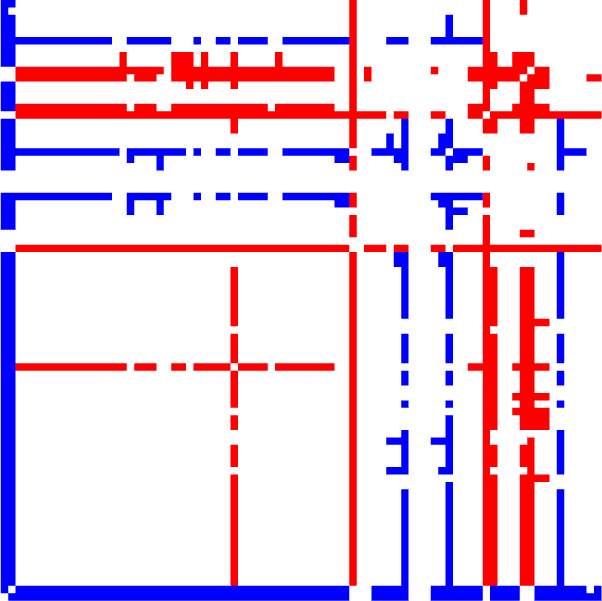
Chiffre 4. Train-test classification for task or subject identification. (UN) The train-test procedure
consists in splitting the sessions in a train set and a test set. The train set is used to optimize the
classifier (here find the best boundaries between labels; see dashed gray lines), whose accuracy
is then measured on the test set. (B) Accuracy for the classification of test sessions to discriminate
movie versus rest (two labels) for the MLR, 1NN, and LDA classifiers, as indicated by the colors.
The connectivity measures are indicated on the x-axis: The masked FC is the subset of FC features
corresponding to the SC mask used for the MOU-EC model; “heur” corresponds to the symmet-
ric connectivity matrix obtained using the heuristic optimization in Appendix D in the Supporting
Information. The classifiers are trained with 80% of the subjects and tested on the remaining sub-
projets, over 40 repetitions. The dashed line indicates the chance level, which corresponds to predict-
ing always movie (three sessions out of five). The MLR gives perfect classification for all connectivity
measures except for MAR. (C) Same as panel B for the classification of session to identify the four
tasks (three movie sessions and rest). The chance level corresponds to predicting always rest (deux
sessions out of five). (D) The left confusion matrix indicates the errors of the MLR classifier trained
with five labels (two labels for rest here), as indicated by the dark green off-diagonal pixels. Comme
expected from panel B, rest and movie are well separated. The movie sessions (M1 to M3) are dis-
tinguishable to some extent, but not the rest sessions (R1 and R2). The right confusion matrix is the
equivalent for the 1NN classifier. (E–F) Same as panels C–D for the identification of the 22 sujets.
Ici 40 splits of the data are considered for two sessions in the train set and three sessions in the test
ensemble, irrespective of rest/movie and individually for each subject. (G) Model error for the MOU-EC
and heuristic optimizations in the two conditions.
Neurosciences en réseau
352
Modeling whole-brain effective connectivity for cognition and disease
the generalization capability of the classification, for example with functional parcellations
derived from the data that should be calculated on the train set only (Brodersen et al., 2011).
For LDA in Figure 3C, this corresponds to setting a linear boundary using the dimensionality
reduction on the train set and evaluating the performance on the test set. The data splitting
can be repeated several times in order to assess the impact of different samples in the training
and test set on the classification performance. Ainsi, the accuracy distribution provides an
estimate of the generalization capability of the classification scheme to new samples. Different
splitting strategies have been proposed, and here we use the recommended one for neuroimag-
ing applications based on a ratio of 80%:20% for train and test sets, respectivement (Varoquaux
et coll., 2017). We repeat the classification for 40 random splitting of the data. This is lower than
the recommended 100 times and is justified by the rather low number of 22 subjects in our
dataset, as explained in the box below together with further technical considerations about
choosing a cross-validation scheme.
Remark on cross-validation schemes
The recommended ratio for neuroimaging applications is 80%:20% for train and test sets, concernant-
spectively, chosen by random draws and repeated about 100 times (Varoquaux et al., 2017).
While we agree on this as a good general practice, we highlight that a slightly different scheme
might be better suited when the number of available samples is rather low, as is often the case
in cognitive studies like here with 22 sujets. Another issue concerns the independence or
absence thereof of the measurements used as inputs for classification. For the example of
Chiffre 3, each subject is scanned in both resting-state and movie conditions, meaning that
fMRI measurements are paired together. Là, random resampling based on fMRI sessions
without separating subjects in train and test sets would lead to more similar samples in the train
and test sets than expected by chance. This would likely inflate the evaluated performance for
generalization. A better solution is to apply the cross-validation to “groups” (subjects in this
case) instead of single samples (fMRI sessions). While it is possible to repeat random resam-
pling of the groups several times, the chance of repeating the cross-validation for the exact
same test set becomes nonnegligible when the number of subjects is not sufficiently large. Pour
our dataset, using four subjects for testing and the remaining 18 for training, there is almost
50% chance of getting the same split twice over 100 repetitions. The consequence would
be an underestimation of performance variability. Dans de tels cas, an alternative valid option
is the leave-one-group-out strategy, using a subject for testing and the remaining subjects for
entraînement, yielding a distribution of 22 accuracies. This procedure also has the advantage of
highlighting individual differences in the dataset, showing for example whether some sub-
jects are easier or more difficult to predict. With our data, we find that repeating 80%:20%
shuffle splits 40 times and performing leave-one-out for each of the 22 subjects leads to very
similar accuracy distributions.
We consider task discrimination in two flavors: movie versus rest (two tasks) in Figure 4B and
the movie sessions individually plus rest (4 tasks) in Figure 4C. For each case, the performance
evaluated using the test set should be considered relative to perfect accuracy and chance level
(dashed line). As expected from Figure 3, the four-task discrimination is more difficult that
the two-task one. The relative performance decreases by about a half of perfect accuracy for
the four tasks compared with the two tasks. There are three interesting points coming from the
comparison of the performances between the connectivity measures.
D'abord, the MLR and LDA perform much better than the 1NN for the four-task discrimination,
with both MOU-EC and FC; this does not change when using kNN instead of 1NN. This agrees
with previous results on subject identification (Pallarés et al., 2018) that are transposed to the
Neurosciences en réseau
353
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
present dataset in Figure 4E. For task identification, the Pearson-correlation similarity for FC
or MOU-EC does not seem the best choice, especially when the environment is complex. UN
technical point here is that LDA takes a long time to be trained for a large number of features or
for many labels (subjects in Figure 4E). Over all these results, the MLR seems the best practical
choice for a classifier, as was found for clinical data (Dadi et al., 2019).
Deuxième, and more importantly, the masked FC performs worse than FC for the four tasks in
Figure 4C, demonstrating that the SC mask (avec 25% density here) cannot be directly used
to preselect the most informative FC links that contribute to the good performance. In con-
trast, MOU-EC has the same number of features as the masked FC and performs as well as FC,
even though the silhouette coefficient in Figure 3D is lower for MOU-EC than FC. De plus,
the MAR connectivity estimate, which extracts temporal information from BOLD signals as
MOU-EC does, gives very poor accuracy, even for the two-task classification. Partial correla-
tions are somewhat in between. For subject identification, MOU-EC performs better than FC
in Figure 4E, in line with previous results (Pallarés et al., 2018). Taken together, these results
show that the dynamic model used for MOU-EC is a representation of the BOLD signals that
extracts relevant information for both cognitive conditions and individual traits. In terms of
dimensionality, MOU-EC can be seen as a more compressed version of the BOLD information
than FC without loss of information.
Last, we consider the symmetric connectivity obtained by the heuristic optimization in
Appendix D (see the Supporting Information) that tunes the MOU model to reproduce the
zero-lag correlation FC. In Figure 4G the goodness of fit is slightly better for the heuristic
method (smaller model error measure by the matrix distance) compared with EC. It is worth
noting that the heuristic estimate leads to perfect accuracy for the “simple” classification rest
versus movie (Figure 4B). Cependant, the accuracy decreases compared with MOU-EC for the
four-task and subject classifications by 5% et 12%, respectivement (Figure 4C, E). This shows
that the choice for the connectivity estimation method (with the corresponding measure on
the BOLD activity) is crucial to efficiently extract information from the BOLD signals.
Capturing the Hierarchy of Cognitive States
The high dimensionality of connectivity measures allows for representing complex environ-
ments, such as the four tasks considered here. Beyond their ability to classify, the important
question is whether MOU-EC or FC can capture the structure of the task categories—rest on
one hand and the group of three movie sessions on the other. A similar goal was sought using
clustering on FC to identify subtypes of depression (Drysdale et al., 2017), although concerns
have been raised about the reproducibility of the results (Dinga et al., 2018). Clustering cor-
responds to unsupervised learning (without cognitive labels) and seeks a structure in the data
for a given metric as with the first two components of PCA in Figure 3B.
Plutôt, we rely on supervised learning and propose labels as an informed guess to a classi-
fier, then assess whether they are meaningful using cross-validation. Beyond the performances
of the two-task and four-task classifications in Figure 4B–C, each classifier thus defines a
similarity metric for the connectivity measures. This is reflected in the confusion matrices in
Figure 4D, where the classification errors (dark off-diagonal green pixels) indicate which cog-
nitive states are difficult to separate. By the naked eye, the structure of the left confusion matrix
for the MLR determines a hierarchy that corresponds to the desired one, similar to the clus-
tering in Figure 3B and C. When asked to discriminate between the two rest sessions, le
classifier gives a negative answer. The three movie sessions are identifiable even though the
Neurosciences en réseau
354
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
MLR classifier makes errors between them. In contrast, the right confusion matrix for the 1NN
does not provide useful information. Similar matrices without a clear hierarchy are obtained
for FC (not shown). This suggests that the Pearson correlation used as a similarity measure in
the 1NN is not well suited to describe the cognitive states with sufficient flexibility. In other
words, it is less the global EC/FC profile than specific links that significantly vary across tasks
and should be the basis for building the task hierarchy. We do not enter into further details
ici, leaving the comparison between unsupervised and supervised learning in estimating la-
bel hierarchies in more depth for future work. As a last comparison, the confusion matrix for
subjects in Figure 4F shows that subjects are well identified and no particular structure in the
errors is observed, indicating an absence of subject groups.
Biomarker Formed of Informative MOU-EC Links: Machine Learning Versus Statistical Testing
The general idea behind a biomarker is the indication of how and where to measure relevant
information in the brain activity for the discrimination of several conditions, here related to
cognition. The biomarkers for the two-task and four-task classifications in Figure 4B–C are
built by identifying the most informative links that contribute to correct classification, aussi
referred to as support network. Practically, we employ recursive feature elimination (RFE) que
efficiently works with the MLR classifier (Guyon, Weston, Barnhill, & Vapnik, 2002). It provides
a ranking of the features in order of importance, and the support network consists of the first
ranked links (with a cutoff when the classification performance based on those selected links
reaches a maximum). A previous study compared these support networks of informative links
for subjects and tasks to see whether the two classifications were biased one by the other
(Pallarés et al., 2018). Here we make another comparison with the two support networks in
Figure 5A, movie versus rest (nine black and two gray links) and for the four tasks (nine black
et 35 red links). The nine common links are also a hallmark of the hierarchy mentioned
in the previous section, in the sense that the more four-task biomarker extends the two-task
biomarker. En outre, the two RFE rankings are robustly aligned (Pearson correlation equal
à 0.46 with p value ≪ 10−10), as illustrated in Figure 5C (left plot). If we compare with the
support network for the FC links in Figure 5B, we observe a similar overlap between the two
support networks. Surtout, five FC links out of the 12 for the two-task classification do not
correspond to anatomical connections in SC, et 20 out of 30 for the four-task classification.
This suggests that FC changes reflect network-wise consequences rather than modulations of
anatomical connections between ROIs (in dashed line). Néanmoins, we find that the RFE
rankings for EC and FC are correlated, with a Pearson coefficient of 0.49 (and p value ≪ 10−10);
see the right plot in Figure 5C.
Now we discuss the pros and cons of machine learning compared with statistical testing
in finding correlates (c'est à dire., link changes) of cognitive tasks. Officiellement, these two methods corre-
spond to distinct questions that relate to opposite mappings from measured variables to con-
ditions: changes in the variables across conditions for statistical testing and the prediction of
conditions based on the variables for machine learning. Cependant, they can be used to address
the same practical question, especially when interpreting data in two conditions (as here with
rest versus movie). In neuroimaging data a crucial point relates to the high dimensionality of
connectivity measures, which leads to repeated hypothesis testing—are MOU-EC values dif-
ferent across two conditions?—over the 1,180 relations. This calls for correction for mul-
tiple comparisons, which is problematic as the number of connections scales with the square
of the number of ROIs in general. We illustrate this point by calculating the p values for the
nonparametric Mann-Whitney test between rest and movie MOU-EC weights for each connec-
tion (left plot in Figure 5D). To identify links that strongly differ across conditions, we use the
Neurosciences en réseau
355
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5. Biomarker for tasks and subjects. (UN) Support network of the 35 most informative
MOU-EC links for the task identification, obtained using recursive feature elimination (RFE). Le
10 black links are common to the easier discrimination between rest and movie, whereas the 29
red links are specific to the four tasks, and the gray link is specific to the two tasks. The ROI colors
indicate anatomical grouping: yellow = occipital, green = parietal, cyan = temporal, gray = central,
orange = frontal, and purple = cingulate. See also Table A.1 for the ROI labels. (B) Same as panel
A for FC links. We obtain eight common black links, three gray links for the two tasks only, et 21
red links for the four tasks only. The links in dashed lines correspond to ROI that are not connected
in SC. (C) Match between EC rankings for the two and four tasks (left plot), as well as between EC
and FC rankings for existing EC links. The Pearson correlation between the matched rankings is
indicated above. (D) Correspondence between p values for Mann-Whitney tests and RFE rankings
for the 1,180 MOU-EC links. For the two tasks, we show two significance thresholds for multiple
comparisons: the Benjamini-Hochberg correction (dashed line) and Bonferroni correction equal to
− log10(0.05/1180) (dashed-dotted line). For the four tasks, the maximum of the p values for the six
pairwise comparisons is plotted, with the same Bonferroni threshold.
significance threshold with Bonferroni correction (dashed-dotted line), here − log10(0.05/1180)
pour 1,180 MOU-EC links, or better with Benjamini-Hochberg correction (Benjamini & Hochberg,
1995; dashed line). The same can be done for the four tasks (right plot), which involves
six pairwise tests between the four cognitive states. For each connection we retain the small-
est p value among the six (as it is informative for at least a pairwise discrimination). For the
Bonferroni correction, this gives 98 connections passing the significance threshold for the four-
task, to be compared with 153 for two tasks. Using Benjamini-Hochberg correction, we find
for the two classifications 554 et 498 links, respectivement. This does not satisfactorily reflect
Neurosciences en réseau
356
Modeling whole-brain effective connectivity for cognition and disease
the increase of complexity of the cognitive labels—more labels require more connections in
the biomarker—while the support network obtained using RFE in Figure 5A provides a satis-
factory description. More importantly, the comparison of the mapping between p values and
the RFE ranking in Figure 5D also illustrates that efficient classification may rely on links with
poor p values, and that this phenomenon may be stronger when the number of categories in-
creases (like labels here). This conclusion also holds when using the parametric Welch t test
instead of the nonparametric Mann-Whitney test. Beyond the details of the present example,
machine learning seems better suited than statistical testing to deal with connectivity measures
in a context of multiple labels.
Another conceptual difference between the two approaches is the Gaussian assumption
for the parameter distribution. Par exemple, DCM relies in many cases on a single generative
model with a distribution for each parameters—typically determined by a mean and a variance
for each connection weight—and selects the model that provides the best evidence for all
observed FC matrices. Plutôt, we estimate a single MOU-EC matrix per session, which builds
a distribution of point samples for each connection. It remains to explore the implications
of the difference in the natures of the estimate distributions and the detection of significant
changes in MOU-EC—using the Bayesian machinery for DCM and standard machine learning
in our case.
NETWORK-ORIENTED ANALYSIS FOR INTERPRETING COLLECTIVE BOLD
DYNAMICS ACROSS CONDITIONS
So far, we have shown how MOU-EC estimates can be used for the classification of cognitive
conditions using machine learning. Now we turn to the collective interpretation of MOU-EC
links as a network. Tools from graph theory have been extensively applied to explore the brain
network and understand how cognitive functions were distributed over subnetworks of ROIs.
The study of both FC and SC has revealed a hierarchical organization of modular networks that
are interconnected by hubs (Hilgetag & Grant, 2010; van den Heuvel & Hulshoff Pol, 2010;
Zamora-López, Zhou, & Kurths, 2011), which can be modulated depending on the subject’s
condition (Bertolero, Yeo, & D'Esposito, 2015; Meunier et al., 2012; Senden, Goebel, & Deco,
2012).
A limitation in many SC and FC studies comes from the direct application of graph measures
defined for binary data. In such cases SC or FC matrices are often binarized using an arbitrary
threshold to obtain a graph, discarding the information conveyed by the graded values. Pour
SC, this gives the skeleton of strong connections. Similar methods have also been used on FC
(de Pasquale et al., 2012; Fair et al., 2007), but the use of a threshold to binarize FC seems
more arbitrary, especially as many pairs of brain regions exhibit strong correlation. Another
important aspect is often overlooked: Brain connectivity measures such as FC are inferred from
signals that have a temporal structure. This means that network analysis should take time into
account. A possibility is to analyze the evolution of snapshot networks over time using dynamic
FC based on sliding windows applied to the observed BOLD signals (Avena-Koenigsberger,
Misic, & Sporns, 2017; Khambhati, Sizemore, Betzel, & Bassett, 2017; Thompson, Brantefors,
& Fransson, 2017).
Going a step further, a particular focus has been on studying the relationship between the SC
and FC (Bettinardi et al., 2017; Sporns, Tononi, & Edelman, 2000), in particular using dynamic
models at the mesoscopic or macroscopic level (Breakspear, 2017; Deco et al., 2011; Frässle
et coll., 2018; Galán, 2008; C. J.. Honey, Kötter, Breakspear, & Sporns, 2007; Messé et al., 2014;
Parc & Friston, 2013; Schmidt, Bakker, Hilgetag, Diesmann, & van Albada, 2018). Following,
Neurosciences en réseau
357
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
graph analysis can be performed on the modeled BOLD activity (Deco & Kringelbach, 2017;
Fransson, Schiffler, & Thompson, 2018). Néanmoins, it can be argued that such “integration”
measures somehow rely on the observed phenomena (in empirical or model activity) rather
than their causes. Plutôt, dynamic models enable the application of graph measures to the
underlying connectivity that generates the dynamics, as was recently proposed (Gilson et al.,
2019; Razi et al., 2017).
Here we follow this novel direction with our adaptation of graph-like measures for the
network dynamics themselves (Gilson et al., 2019; Gilson, Kouvaris, et coll., 2018), whose main
details are presented in the following; see also Appendix E in the Supporting Information for
mathematical details. This section illustrates the following aspects of network-oriented analysis
for MOU-EC:
How can we interpret collective changes in MOU-EC in their contribution to shape the
network dynamics? We introduce dynamic communicability with the notion of “integra-
tion time” that discriminates early and late interactions between ROIs in response to a
(locale) perturbation in the network via MOU-EC.
Are network measures relevant for discriminating cognitive conditions? By doing so we
want to obtain dynamics-specific biomarkers.
Between the level of individual connections and the global network, are intermediate
scales relevant to interpret the MOU-EC estimates? Can we detect functional communi-
ties of ROIs, and are they task-specific?
Dynamic Flow as Graph-Like Measure for Interactions Between ROIs Across Integration Time
Our definition of dynamic flow takes advantage of the information provided by the dynamic
model, here applied to the MOU process (Gilson, Kouvaris, et coll., 2018). As illustrated in
Figure 6A, MOU-EC quantifies the instantaneous causal interactions between pairs of ROIs,
and the Σ matrix measures the spontaneous or input activity level that each ROI receives (ici
represented only for ROI i). Built on those estimates, the dynamic flow measures the influence
of a “perturbation” at a source ROI i onto a target ROI k after a given delay, which we call
integration time. Surtout, it takes into account the network effect (or network response),
meaning the contribution of indirect paths in the network (from ROI i to ROI k via ROI j in the
figure). See Appendix E in the Supporting Information for the mathematical formulation based
on the network impulse response (or Green function), which is analytically tractable for the
MOU process.
The dynamic flow thus aims to capture the dynamic response of the brain to local spon-
taneous activity (or external inputs) as it propagates from region to region in the network. UN
special case of the dynamic flow—termed dynamic communicability—that only depends on
the MOU-EC (and not Σ) can also be defined assuming that all ROIs have independent sponta-
neous activity with the same intensity; it corresponds to a diagonal and homogeneous matrix
Σ. Like the flow, dynamic communicability describes directional interactions, which differs
from the symmetric interactions obtained from the direct application of graph theory to FC or
SC (Gilson et al., 2019). It is worth stressing that the dynamic flow and communicability are
graph-like measures that genuinely capture the properties of weighted networks, similar to the
previously proposed graph communicability (Estrada, 2013; Estrada & Hatano, 2008).
Considering again the fMRI dataset in Appendix A in the Supporting Information, we ex-
amine the dynamic flow at various scales in the brain network for the two conditions, movie
and rest. This complements our previous analysis of the same dataset that showed that the
Neurosciences en réseau
358
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
un
_
0
0
1
1
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 6. Network-oriented analysis of MOU-EC using dynamic flow. (UN) Conceptual illustration
of dynamic communicability and flow. The propagation of extra activity resulting from a perturba-
tion (here applied to ROI i in purple) develops over the integration time and then fades away. Le
dashed purple curve represents the corresponding activity increase for ROI k (for legibility purpose,
the equivalent for ROI j is not displayed). This defines interactions between ROIs that are not directly
connected, like here from ROI i to ROI k. The dynamic communicability corresponds to interactions
determined by the connectivity MOU-EC only, while the dynamic flow incorporates the amplitudes
of ongoing perturbations that is quantified by Σ in the model. (B) Two matrices representing the
pairwise interactions as measured by dynamic communicability for all 66 ROIs at two integration
times, in a single subject. Initially similar to MOU-EC values, the communicability becomes homo-
geneous. (C) Total flow for rest and movie, which is the sum of the interactions between all pairs of
ROI (c'est à dire., sum of all matrix elements in panel B) at each integration time. The error bars indicate the
standard error of the mean over the subjects. The bottom brown horizontal line indicates where the
total flow is larger for movie than for rest with p < 0.01 in a Mann-Whitney test for each integration
time step (without correction). (D) Change in input and output flow as a function of integration time,
which sum all incoming and outgoing flow interactions for each ROI, respectively. The ROIs are or-
dered by anatomical areas and grouped in pairs of left- and right-hemisphere ROIs. The ROIs are
anatomically grouped in the same manner as in Figure 5A–B: yellow = occipital, cyan = temporal,
green = parietal, gray = central, orange = frontal, and purple = cingulate from bottom to top.
modulations of MOU-EC between rest and movie implemented a selection of pathways in the
cortex (Gilson, Deco, et al., 2018). In addition, the stimulus load related to sensory inputs in
the movie condition corresponded to an increase in Σ in the model for occipital and temporal
ROIs. Recall that Σ quantifies the fluctuating BOLD activity intrinsic to each ROI that sub-
sequently propagates via MOU-EC in the model. This motivates the use of the dynamic flow
that incorporates Σ in order to characterize the whole-brain BOLD propagation, as compared
Network Neuroscience
359
Modeling whole-brain effective connectivity for cognition and disease
with dynamic communicability. Note that the “effective drive” defined in our previous study
(Gilson, Deco, et al., 2018) corresponds to the flow at early integration time.
The sum of flow interactions provides insight about how much activity propagates through-
out the whole cortical network, which is higher for movie compared with rest in Figure 6C. An-
alyzing the interactions at the ROI level, the flow changes in Figure 6D indicate differentiated
effects among the ROIs, with increased/decreased listening for input flow and broadcasting
for output flow. Here we observe most of the strongest increases in the output flow for oc-
cipital and temporal ROIs, which makes sense since the subjects both watch and listen to the
movie. A previous analysis based on MOU-EC (Senden et al., 2017) showed task-dependent
changes for the outgoing connections from the rich club of ROIs that have dense anatomical
connectivity, namely the precuneus (PCUN), superior parietal cortex (SP), and superior frontal
cortex (SF), in agreement with previous results about the default mode network also involving
the post-cingulate gyrus (PC Vatansever, Menon, Manktelow, Sahakian, & Stamatakis, 2015;
Vatansever, Menon, & Stamatakis, 2017). Here we only find a slight increase of input flow
for PCUN and SP, which may be explained by the fact that the task is passive viewing and
listening.
Integration in the Brain network
Following experiments on the propagation of stimulus information from sensory areas to
“high-level” brain areas in relation to being conscious of the stimuli (Carhart-Harris et al., 2016;
Dehaene & Naccache, 2001), the concept of integration was defined in models by quantifying
the influence between regions while being in a broader network. Following Figure 6D, we use
the dynamic flow to quantify how the BOLD activity propagates from the occipital and tempo-
ral ROIs, which exhibit an increased visual and auditory stimulus load in movie, to the rest of
the brain. We thus consider the anatomical ROI groups in Figure 7A (same as Figure 5), where
the stimulus load is represented by the purple perturbation applied to OCC and TMP (Gilson,
Deco, et al., 2018). Figure 7B compares the summed flow between the ROI groups for rest
and movie (in black and brown as in Figure 6C). This reveals preferred pathways to the parietal
and frontal ROIs (PAR and FRNT) when sensory information is integrated, as represented by
the thick arrows in Figure 7A.
The machine-learning equivalent of the statistical testing for the summed flow between
subnetworks in Figure 7B gives the green violin plots in Figure 7D. Here a good accuracy
means that the bidirectional flow summed between all considered ROIs is strongly modulated
between rest and movie. The fact that the results are close to chance level indicates strong
variability in the overall flow increase across subjects. A different question, more related to
biomarkers, is to which extent the detailed pattern of flow (multivariate flow, in orange) vary
between movie and rest. This yields robust classification, which strikingly differs from the uni-
variate (summed) flow. This indicates that the modification of interactions between ROIs is
diverse beyond a simple global increase, hinting at the selection of specific pathways. The
flow-based classification even outperforms MOU-EC (in blue) for the same matrix elements
when focusing on particular ROI groups; see Figure 7C for details. The discrepancy between
the flow and MOU-EC shows the importance of network effects, for all three bidirectional path-
ways in Figure 7D. The same classification can be performed with the input and output flows;
see Figure 7E. For interpretation purpose, the better performance for incoming than outgoing
MOU-EC (pink versus cyan) suggests that ROIs change their pattern of listening/broadcasting
communication, especially for PAR and FRNT. However, the overall effect is less pronounced
when considering the dynamic flow that incorporates network effects (red versus purple). These
Network Neuroscience
360
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7.
Integration measured by dynamic flow. (A) Example subset of anatomical ROI groups:
occipital (OCC), temporal (TMP), parietal (PAR), central (CNT), and frontal (FRNT). (B) Comparison
between the flow between the rest (in black) and movie (in brown) conditions. Similar to Figure 6C,
the curves are averages over subjects and corresponding sessions with error bars indicating the stan-
dard error of the mean. Each row corresponds to the flow summed over all ROIs of the indicated
groups (bidirectionally); see also panel A where thick arrows correspond to strong increase in flow
for the movie condition. (C) Example of construction of features for the following classification. At
the top, the EC matrix corresponds to connections for ROIs in groups and gives multivariate features
when vectorized. Below, the flow matrix for the same ROIs equivalently gives multivariate features
or can also be summed to obtain a univariate feature. Moreover, the flow matrix can be summed
over columns or rows to obtain the input and output flows, here taking all 66 ROIs as sources
(y-axis of the matrix) or targets (x-axis). (D) Flow-based classification to discriminate rest versus
movie in multivariate (orange violin plots) and univariate (green), compared with EC-based classi-
fication (blue). The x-axis indicates the ROI subgroups for which the flow interactions are selected.
The dashed black lines indicate chance level, at 60% as in Figure 4B. (E) Same as panel D for the
input flow (in red) and output flow (purple), which are compared with the input and output EC
strengths (pink and cyan, respectively).
Network Neuroscience
361
Modeling whole-brain effective connectivity for cognition and disease
results show that dynamics-based biomarkers that describe the propagation of BOLD activity
can be built in the same way as connectivity-based biomarkers for the discrimination of cog-
nitive tasks. Together with the distributed signature found in Figure 5A, they also highlight
the need for a whole-brain approach to understand the cortical reconfiguration (Betti et al.,
2013), contrasting with previous studies relying on hypothesis testing for a priori selected ROIs
(Ciuciu et al., 2014; Daunizeau, Stephan, & Friston, 2012; Emerson, Short, Lin, Gilmore, &
Gao, 2015; Goebel et al., 2003).
Detection of Functional Communities Determined by Dynamic Flow
In parallel to integration, the concept of complexity has been often used to differentiate brain
states (Barnett et al., 2009; Tononi, Edelman, & Sporns, 1998; Tononi et al., 1994; Zamora-
López, Chen, Deco, Kringelbach, & Zhou, 2016). Intuitively, complexity measures quantify
the diversity of organizational motifs in a network, in the range of interest between the trivial
extremes of full disconnectivity and full connectivity. A proxy for complexity is the detection of
ROI communities because modular networks are a stereotypical model for complex networks,
as was observed with SC (Zamora-López et al., 2011). Here we use the dynamic flow as a
basis for the functional ROI communities in a data-driven manner, which contrasts with the
anatomical grouping in Figure 7A. Such methods developed initially for graphs with a metric
called modularity based on weights (Newman, 2006). Here we consider communities deter-
mined by the flow, namely ROIs with strong exchange of activity in the estimated dynamics
(Gilson, Kouvaris, et al., 2018).
Figure 8A displays the evolution of communities over integration time for rest and movie.
Strong coparticipation values indicate the robustness of the community structure across sub-
jects. It shows a merging of almost all ROIs that eventually exchange flow in an even man-
ner. This agrees with our previous results for resting state only and a different parcellation
(Gilson et al., 2019). This speaks to a transition from segregated processing (within each diag-
onal block of left matrices) to a global integration. The number of communities can be taken as
another proxy for the complexity in the brain network, and our approach provides a dynamical
perspective about it. The community merging goes hand in hand with the homogenization of
the flow matrix in Figure 8B, as quantified by the diversity of the matrix elements in the flow
matrix that decreases and eventually stabilizes (Gilson, Kouvaris, et al., 2018). In our data the
diversity is slightly higher for movie compared with rest.
Going a step further, we can examine the difference between the community structures of
the two conditions; see the bottom row in Figure 8A. This shows that the changes in dynamic
flow for specific pairs of ROIs between rest and movie (Figure 7B, D, and E) have an important
collective impact. The strongest differences appear when the network effects are very strong at
t = 4 TRs. This is confirmed by Figure 8C, where classification shows that the dynamic flow
is most different between rest and movie at integration times corresponding to strong network
effects (the arrow indicates the start of the plateau for maximum performance). These results
speak to an intermediate organization of groups of ROIs between the local and global scales,
which can be captured using our network-oriented analysis of MOU-EC.
CONCLUSIONS
This article illustrates how a model-based approach to whole-brain fMRI analysis combines
the desired properties of predictability and interpretability. This goes beyond the goodness of
fit for fMRI signals that is commonly used to evaluate and compare generative models. To
do so, our framework links tools and concepts from dynamic systems, machine learning, and
Network Neuroscience
362
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. Community detection. (A) Communities correspond to ROIs that bidirectionally ex-
change strong flow. Darker orange pixels indicate stable communities across the subjects for each
condition. The top row corresponds to rest and the middle row to movie for three integration times.
The bottom row displays the significant increases (in red) and decreases (blue) of the community
coparticipation values for movie with respect to rest. Here statistical testing is performed on each
coparticipation value by using the Mann-Whitney test with p < 0.01 (without correction). The ROI
ordering corresponds to the early community structure for rest. (B) Flow diversity for rest (black
curve) and movie (in brown) measuring the heterogeneity within each flow matrix when integra-
tion time increases; see Equation E.4. It is a proxy for the “complexity” of interactions between
ROIs; for details see Gilson et al. (2019) and Gilson, Kouvaris, et al. (2018). (C) Rest-versus-movie
classification based on flow (whole-brain version of multivariate flow in Figure 7C) as a function
of integration time and comparison with EC-based classification. Starting t = 4 TRs indicated by
the arrow, the performance reaches a maximum plateau. Here the train test consists of 20% of the
samples and the test set 80% (the converse compared with before) in order to capture the strongest
changes between rest and movie with classification. This exaggerates the evolution over integration
time of the performance, which is lower compared with the previous plots.
Network Neuroscience
363
Modeling whole-brain effective connectivity for cognition and disease
network theory. This results in a consistent pipeline with controlled hypotheses because we
use the same whole-brain dynamic model from the estimation to the analysis.
General key points for analysis of multivariate neuroimaging data and corresponding results
using MOU-EC
General key points
A dynamic model is a hypothesis on the
structure of the data and is useful to com-
bine several types of data.
Fitting a dynamic network model to time
series captures their dynamics and en-
ables the characterization of network
properties with time involved in the anal-
ysis.
Adequate machine-learning tools (with
cross-validation and feature selection to
build biomarkers) are well adapted to re-
late multivariate neuroimaging data like
fMRI to cognitive states or neuropatholo-
gies.
Graph-like measures can be applied
at multiple scales from the connec-
tion/node level
to communities and
global level in the network.
Presented results using MOU-EC
The MOU process provides a practically use-
ful balance between the richness of the gen-
erated BOLD dynamics, the robustness of the
model optimization, and intuition for inter-
pretability (roles of parameters in the model).
The constraint of MOU-EC topology enforces
the “explanation” of changes in BOLD sig-
nals by modulations of anatomical connec-
tions (Figure 5A compared with Figure 5B).
MOU-EC describes causal relationships in the
network model that collectively explain the
observed BOLD covariance structure, involv-
ing time lags. The MOU-EC estimates can fur-
ther be interpreted in terms of integration in
the network using dynamic communicability
and flow (Figure 6).
Both MOU-EC and dynamic flow can be used
for prediction (Figures 4B–C, 5A, and 7D–E),
as well as exploring the hierarchy of cognitive
states (Figure 4D).
The comparison of classification performance
for tasks using dynamic flow provides in-
sight about the adequate description level of
changes in the network; for example, ROI-
based measures are sufficient to discriminate
the rest and movie conditions (Figure 7D–E).
Spatiotemporal BOLD Structure
By fitting the dynamic model to the spatiotemporal covariance structure of the BOLD signals,
our approach captures the BOLD dynamics averaged over each fMRI session. The estimated
MOU-EC can be seen as a “projection” of the BOLD signals on anatomically constrained con-
nectivity, thereby characterizing the dynamical state of the brain. In contrast, analyses based
on the static FC can be related to a linear Gaussian model, and thus do not take the tem-
poral dimension into account (i.e., BOLD values are considered as i.i.d. variables). Dynamic
FC methods have been developed to incorporate time in the analysis (Cabral et al., 2017;
Gonzalez-Castillo & Bandettini, 2017; Park & Friston, 2013; Preti et al., 2017), but they do not
genuinely capture the propagating nature of BOLD signals. Dynamic causal models have just
been adapted to deal with whole-brain fMRI data (Frässle et al., 2018; Park, Friston, Pae, Park,
& Razi, 2018; Razi et al., 2017), and it will be interesting to compare the estimated connec-
tivities. It is also still unclear how short sessions or observation windows can be to robustly
characterize dynamical states when calculating EC estimates or MAR-like coupling matrices
Network Neuroscience
364
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
in HMMs (Bolton et al., 2018; Vidaurre et al., 2018), in comparison to dynamic FC methods
that are typically used with windows of 30 to 60 TRs.
Biomarkers for Cognition and Neuropathologies
The robust estimation of the (multivariate) parameters allows for a powerful representation of
cognitive states by the MOU-EC estimates (Figure 4), as well as the extraction of task-specific
biomarkers (Figure 5). An important point considering connectivity measures is that machine
learning solves the problem of multiple comparisons: Instead of determining p values and then
a threshold for connections with significant changes, we can characterize which MOU-EC
links—as features—contribute to the correct classification. It has been recently advocated that
machine learning can be used to avoid “excessive reductionism,” namely linking brain ac-
tivity in localized regions to narrow experimental protocols in a way that cannot generalize
to more complex protocols (Varoquaux & Poldrack, 2019). Although the focus has been on
machine-learning techniques, we remind readers that hypothesis testing of significant changes
for preselected ROIs or links can be performed in our framework (see Figure 7B with the dy-
namic flow). In that case, whole-brain changes can also provide a baseline reference for the
considered links or ROIs.
On the technical side, it remains to be explored how the classification performance is
affected by the resolution of various parcellations (Craddock, James, Holtzheimer, Hu, &
Mayberg, 2012; Eickhoff, Thirion, Varoquaux, & Bzdok, 2015; Glasser et al., 2016), as was
recently done with FC-like connectivity measures (Dadi et al., 2019). The trade-off to solve is
between the richness of the connectivity measure (more links can reproduce richer environ-
ments) and their robustness (more parameters may result in noisier estimation). The alignment
of distinct datasets with various MRI protocols also remains a difficult question for practical
application to large datasets (Varoquaux et al., 2018).
In parallel to the study of cognition, the presented framework can be applied to neu-
ropathologies with the aim to inform clinical diagnosis (Matthews & Hampshire, 2016). The
rationale is that BOLD activity specifically reflects neuropathologies, even in the resting state
(Greicius, 2008; Hohenfeld et al., 2018). If SC is increasingly used for strokes or Alzheimer’s
disease that strongly impact the brain anatomy, fMRI may provide additional information
(Habib et al., 2017; Siegel et al., 2016). Other diseases like depression (Drysdale et al., 2017)
or some motor disorders (Rowe & Siebner, 2012) may be better investigated using functional
imaging. Importantly, many neural diseases are likely to affect multiple brain regions and thus
require adequate tools to capture their distributed nature. Another direction where machine
learning is a key tool is the development of personalized medicine, adapting the models to
individual patients beyond group analyses (Yahata, Kasai, & Kawato, 2017).
Network-Oriented Analysis of Dynamics
The network analysis for our dynamic model relies on the dynamic flow, a graph-like con-
nectivity measure that describes the integration of propagating activity at multiple scales in
the network (Figures 7 and 8). In particular, small changes in EC that are not individually
significant can collectively induce large changes in the dynamic flow, especially when feed-
back loops are involved. In this sense, the dynamic flow quantitatively captures the interplay
between parameters, so the resulting communication cannot always be simply understood at
the level of single estimated parameters. As an example, many small changes in EC (below
significance level) may collectively result in a strong dynamical effect, as seen for Task A in
Figure 9. Strong coordinated changes in EC result in large changes in the dynamics (Task B).
Network Neuroscience
365
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
Figure 9.
Schematic representation of the extraction of biomarkers for three tasks compared
with rest. Connection-wise biomarkers correspond to changes in EC, while the bottom row refers
to biomarkers for changes in dynamic flow. Tasks A and B correspond to two modulations of the
connectivity, which lead to similar changes in the dynamic flow (stronger for B). For task C, extra
inputs are received by two nodes, which increase the dynamic flow towards the corresponding two
target nodes.
Moreover, changes in input properties may only be captured by the dynamics, in particular
when the connectivity does not change (Task C). Building biomarkers that capture network
effects is important to make use of the multivariate nature of the fMRI data. This is important
when interpreting data in terms of concepts such as integration, segregation, and complexity
(Deco, Tononi, Boly, & Kringelbach, 2015; Dehaene & Naccache, 2001; Tononi et al., 1998;
Zamora-López et al., 2016). An interesting direction for future work is the study of directional
properties of the flow, especially in the characterization of functional communities.
Limitations and Future Work
As a first warning, we remind readers that any interpretation of BOLD in terms of brain com-
munication relies on the assumption that changes in neuronal activity are reliably reflected in
the BOLD signals, which is still under debate (Goense & Logothetis, 2008; Y. He et al., 2018;
Matsui et al., 2018). In practice, the preprocessing of fMRI signals must strive to increase the
signal-to-noise ratio (Parkes et al., 2018; Power et al., 2018).
Recall also that causal relationships between brain regions come from the directed connec-
tivity in the model, whose “best” parameterization is estimated from the data. The estimation
procedure is crucial, in particular for the dynamic flow here since the asymmetry of MOU-EC
strongly affects the resulting activity propagation in the model. Moreover, without a proper ex-
perimental interaction with the brain activity like using stimulation, the notion of causality is
subject to the initial model assumption (Hughes, 1997; Kaplan, 2011). This remark also applies
to other methods for directed connectivity, such as Granger causality and DCM (Valdes-Sosa
et al., 2011).
A key distinction of our approach compared with DCM is that our MOU-EC (or FC) esti-
mates are calculated for each fMRI session, so we obtain a sample distribution for connection
Network Neuroscience
366
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
weight over all subjects for each condition (e.g., task). In contrast, DCM usually considers a
single model per condition that aims to represent the variability over subjects with a parametric
distribution (mean and variance) for each connection weight. The limitations and advantages
of both approaches in terms of statistical power and generalizability remain to be practically
compared, especially for large datasets.
Regarding the hemodynamics and explicit HRF modeling discussed at the end of the sec-
tion presenting the MOU model, a quantitative comparison between MOU-EC, DCM, and
Granger causality analysis to extract biomarkers or interpret fMRI data in terms of neuronal
coupling is necessary in the future. A particular point concerns the observed heterogeneity
of HRF across different brain regions and how it affects the estimated connectivity and its
directionality (Handwerker, Ollinger, & D’Esposito, 2004). Previous works also suggest that
the HRF is important for the reliability of connectivity analysis (Gitelman et al., 2003; Olszowy
et al., 2019). This may increase the number of parameters in the model, so the robustness of the
estimation should be verified using both forward modeling in synthetic whole-brain networks
(Smith et al., 2011) and with classification from real data with known categories (e.g., subjects
with several sessions each). A first step could be to extend the MOU-EC as a state-space model
with a first-order filter for HRF (Sauvage et al., 2017).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00117.
The analysis tools have been organized in a package written in the open-source language
Python: https://github.com/mb-BCA/pyMOU (Gilson, Zamora-López, & Insabato, 2019) for the
MOU-EC estimation and https://github.com/mb-BCA/NetDynFlow (Zamora-López & Gilson,
2019) for dynamic communicability and flow. The code to reproduce some figures in this paper
using data available on https://github.com/mb-BCA/notebooks_review2019. The classification
uses the library scikit-learn (Abraham et al., 2014).
AUTHOR CONTRIBUTIONS
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
.
t
Matthieu Gilson: Conceptualization; Methodology; Software; Writing - Original Draft. Gorka
Zamora-López: Conceptualization; Methodology; Software; Writing - Original Draft. Vicente
Pallarés: Conceptualization; Methodology; Software; Writing - Original Draft. Mohit H.
Adhikari: Conceptualization; Methodology; Software; Writing - Original Draft. Mario Senden:
Conceptualization; Methodology; Software; Writing - Original Draft. Adrià Tauste Campo:
Conceptualization; Methodology; Software; Writing - Original Draft. Dante Mantini: Resources;
Writing - Review & Editing. Maurizio Corbetta: Resources; Writing - Review & Editing. Gustavo
Deco: Funding acquisition; Writing - Review & Editing. Andrea Insabato: Conceptualization;
Methodology; Software; Writing - Original Draft.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
FUNDING INFORMATION
Mario Senden, Horizon 2020 Framework Programme (http://dx.doi.org/10.13039/100010661),
Award ID: Human Brain Project SGA2 No. 785907. Gorka Zamora-López, Horizon 2020
Framework Programme (http://dx.doi.org/10.13039/100010661), Award ID: Human Brain
Project SGA2 No. 785907. Matthieu Gilson, Horizon 2020 Framework Programme, Award
ID: Human Brain Project SGA2 No. 785907. Gustavo Deco, Horizon 2020 Framework Pro-
gramme (http://dx.doi.org/10.13039/100010661), Award ID: Human Brain Project SGA2 No.
785907. Andrea Insabato, H2020 Marie Skłodowska-Curie Actions (http://dx.doi.org/10.
13039/100010665), Award ID: MSCA grant agreement No. 841684. Gustavo Deco,
Network Neuroscience
367
Modeling whole-brain effective connectivity for cognition and disease
Agencia Estatal de Investigación (http://dx.doi.org/10.13039/501100011033), Award ID:
PSI2016-75688-P. Gustavo Deco, Consell Català de Recercai Innovació (http://dx.doi.org/10.
13039/501100002810), Award ID: AGAUR Programme 2017 899 SGR 1545. Maurizio
Corbetta, Italian Ministry of Research (MIUR), Award ID: Progetto Dipartimenti di Eccellenza
Neuro-DiP. Maurizio Corbetta, Horizon 2020 Framework Programme (http://dx.doi.org/10.
13039/100010661), Award ID: FLAG-ERA JTC.
REFERENCES
Abraham, A., Pedregosa, F., Eickenberg, M., Gervais, P., Mueller,
A., Kossaifi, J., . . . Varoquaux, G. (2014). Machine learning for
neuroimaging with scikit-learn. Frontiers in Neuroinformatics, 8,
14. https://doi.org/10.3389/fninf.2014.00014
Aertsen, A. M., Gerstein, G. L., Habib, M. K., & Palm, G.
(1989).
Dynamics of neuronal firing correlation: Modulation of “effective
connectivity.” Journal of Neurophysiology, 61, 900–917.
Amari, S.-I. (1998). Natural gradient works efficiently in learn-
ing. Neural Computation, 10, 251–276. https://doi.org/10.1162/
089976698300017746
Amico, E., & Goñi, J. (2018). The quest for identifiability in human
functional connectomes. Scientific Reports, 8, 8254. https://doi.
org/10.1038/s41598-018-25089-1
Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2017). Commu-
nication dynamics in complex brain networks. Nature Reviews
Neuroscience, 19, 17–33. https://doi.org/10.1038/nrn.2017.149
Barnett, L., Buckley, C. L., & Bullock, S. (2009). Neural complex-
ity and structural connectivity. Physical Review E, 79, 051914.
https://doi.org/10.1103/PhysRevE.79.051914
Barnett, L., & Seth, A. K. (2015). Granger causality for state-space
models. Physical Review E, 91, 040101. https://doi.org/10.1103/
PhysRevE.91.040101
Bartels, A., Logothetis, N. K., & Moutoussis, K. (2008). fMRI and its
interpretations: An illustration on directional selectivity in area
v5/mt. Trends in Neuroscience,, 31, 444–453. https://doi.org/10.
1016/j.tins.2008.06.004
Becker, R., Reinacher, M., Freyer, F., Villringer, A., & Ritter, P. (2011).
How ongoing neuronal oscillations account for evoked fMRI vari-
ability. Journal of Neuroscience, 31, 11016–11027. https://doi.
org/10.1523/JNEUROSCI.0210-11.2011
Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discov-
ery rate: A practical and powerful approach to multiple testing.
Journal of the Royal Statistical Society, Series B, 57, 289–300.
Benzi, M., & Klymko, C. (2013). Total communicability as a central-
ity measure. Journal of Complex Networks, 1, 124–149. https://
doi.org/10.1093/comnet/cnt007
Bertolero, M. A., Yeo, B. T. T., & D’Esposito, M. (2015). The modular
and integrative functional architecture of the human brain. Pro-
ceedings of the National Academy of Sciences, 112, 6798–6807.
https://doi.org/10.1073/pnas.1510619112
Betti, V., Della Penna, S., de Pasquale, F., Mantini, D., Marzetti, L.,
Romani, G. L., & Corbetta, M. (2013). Natural scenes viewing al-
ters the dynamics of functional connectivity in the human brain.
Neuron, 79, 782–797.
Bettinardi, R. G., Deco, G., Karlaftis, V. M., Van Hartevelt, T. J.,
Fernandes, H. M., Kourtzi, Z., . . . Zamora-López, G. (2017). How
structure sculpts function: Unveiling the contribution of anatom-
ical connectivity to the brain’s spontaneous correlation structure.
Chaos, 27, 047409. https://doi.org/10.1063/1.4980099
Bielczyk, N. Z., Uithol, S., van Mourik, T., Anderson, P., Glennon,
J. C., & Buitelaar, J. K. (2019). Disentangling causal webs in the
brain using functional magnetic resonance imaging: A review of
current approaches. Network Neuroscience, 3, 237–273. https://
doi.org/10.1162/netn_a_00062
Biswal, B. B. (2012). Resting state fMRI: A personal history. Neuro-
Image, 62, 938–944. https://doi.org/10.1016/j.neuroimage.2012.
01.090
Bolton, T. A. W., Tarun, A., Sterpenich, V., Schwartz, S., & Van
De Ville, D. (2018). Interactions between large-scale functional
brain networks are captured by sparse coupled HMMs. IEEE
Transactions on Medical Imaging, 37, 230–240. https://doi.org/
10.1109/TMI.2017.2755369
Boynton, G. M., Engel, S. A., Glover, G. H., & Heeger, D. J. (1996).
Linear systems analysis of functional magnetic resonance imag-
ing in human V1. Journal of Neuroscience, 16, 4207–4221.
Breakspear, M. (2017). Dynamic models of large-scale brain activ-
ity. Nature Neuroscience, 20, 340–352. https://doi.org/10.1038/
nn.4497
Brodersen, K. H., Schofield, T. M., Leff, A. P., Ong, C. S., Lomakina,
E. I., Buhmann, J. M., & Stephan, K. E. (2011). Generative embed-
ding for model-based classification of fMRI data. PLoS Compu-
tational Biology, 7, e1002079. https://doi.org/10.1371/journal.
pcbi.1002079
Buckner, R. L. (2010). Human functional connectivity: New tools,
unresolved questions. Proceedings of the National Academy
of Science, 107, 10769–10770. https://doi.org/10.1073/pnas.
1005987107
Burkitt, A. N. (2006). A review of the integrate-and-fire neuron
model: I. Homogeneous synaptic input. Biological Cybernetics,
95, 1–19. https://doi.org/10.1007/s00422-006-0068-6
Cabral, J., Hugues, E., Sporns, O., & Deco, G. (2011). Role of lo-
cal network oscillations in resting-state functional connectivity.
NeuroImage, 57, 130–139.
Cabral, J., Vidaurre, D., Marques, P., Magalhães, R., Silva Moreira,
P., Miguel Soares, J., . . . Kringelbach, M. L. (2017). Cognitive per-
formance in healthy older adults relates to spontaneous switching
between states of functional connectivity during rest. Scientific
Reports, 7, 5135. https://doi.org/10.1038/s41598-017-05425-7
Calhoun, V. D., Lawrie, S. M., Mourao-Miranda, J., & Stephan,
K. E. (2017). Prediction of individual differences from neuroimag-
ing data. Neuroimage, 145, 135–136. https://doi.org/10.1016/j.
neuroimage.2016.12.012
Calhoun, V. D., Liu, J., & Adali, T. (2009). A review of group ICA
for fMRI data and ICA for joint inference of imaging, genetic, and
Network Neuroscience
368
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
ERP data. Neuroimage, 45, S163–172. https://doi.org/10.1016/
j.neuroimage.2008.10.057
Carhart-Harris, R. L., Muthukumaraswamy, S., Roseman, L.,
Kaelen, M., Droog, W., Murphy, K., . . . Nutt, D. J. (2016). Neural
correlates of the LSD experience revealed by multimodal neu-
roimaging. Proceedings of the National Academy of Sciences,
113, 4853–4858. https://doi.org/10.1073/pnas.1518377113
Chang, L., Gianaros, P., Manuck, S., Krishnan, A., & Wager, T.
(2015). A sensitive and specific neural signature for picture-
induced negative affect. PLoS Biology, 13, e1002180.
Ciuciu, P., Abry, P., & He, B. J. (2014). Interplay between functional
connectivity and scale-free dynamics in intrinsic fMRI networks.
NeuroImage, 95, 248–263.
Cohen, J. R. (2018). The behavioral and cognitive relevance of time-
varying, dynamic changes in functional connectivity. NeuroIm-
age, 180, 515–525. https://doi.org/10.1016/j.neuroimage.2017.
09.036
Cordes, D., Haughton, V. M., Arfanakis, K., Wendt, G. J., Turski,
P. A., Moritz, C. H., . . . Meyerand, M. E. (2000). Mapping func-
tionally related regions of brain with functional connectivity MR
imaging. American Journal of Neuroradiology, 21, 1636–1644.
Craddock, R. C., James, G. A., Holtzheimer, P. E., Hu, X. P., &
Mayberg, H. S. (2012). A whole brain fMRI atlas generated via
spatially constrained spectral clustering. Human Brain Mapping,
33, 1914–1928.
.
Dadi, K., Rahim, M., Abraham, A., Chyzhyk, D., Milham, M.,
Thirion, B.,
. Alzheimer’s Disease Neuroimaging Initia-
tive (2019). Benchmarking functional connectome-based predic-
tive models for resting-state fMRI. NeuroImage, 192, 115–134.
https://doi.org/10.1016/j.neuroimage.2019.02.062
.
Daunizeau, J., Stephan, K., & Friston, K. (2012). Stochastic dynamic
causal modelling of fMRI data: Should we care about neural
noise? NeuroImage, 62, 464–481.
David, O., Guillemain, I., Saillet, S., Reyt, S., Deransart, C., Segebarth,
C., & Depaulis, A. (2008). Identifying neural drivers with func-
tional MRI: An electrophysiological validation. PLoS Biology, 6,
2683–2697. https://doi.org/10.1371/journal.pbio.0060315
d’Avossa, G., Shulman, G. L., & Corbetta, M. (2003). Identification
of cerebral networks by classification of the shape of bold re-
sponses. Journal of Neurophysiology, 90, 360–371. https://doi.
org/10.1152/jn.01040.2002
Deco, G., Jirsa, V., & McIntosh, A. (2011). Emerging concepts for
the dynamical organization of resting-state activity in the brain.
Nature Reviews Neuroscience, 12, 43–56.
Deco, G., & Kringelbach, M. L. (2017). Hierarchy of informa-
tion processing in the brain: A novel “intrinsic ignition” frame-
work. Neuron, 94, 961–968. https://doi.org/10.1016/j.neuron.
2017.03.028
Deco, G., Ponce-Alvarez, A., Mantini, D., Romani, G., Hagmann,
P., & Corbetta, M. (2013). Resting-state functional connectivity
emerges from structurally and dynamically shaped slow linear
fluctuations. Journal of Neuroscience, 33, 11239–11252.
Deco, G., Tononi, G., Boly, M., & Kringelbach, M. L. (2015). Re-
thinking segregation and integration: Contributions of whole-
brain modelling. Nature Reviews Neuroscience, 16, 430–439.
https://doi.org/10.1038/nrn3963
Dehaene, S., & Naccache, L. (2001). Towards a cognitive neu-
roscience of consciousness: Basic evidence and a workspace
framework. Cognition, 79, 1–37.
Demirta¸s, M., Ponce-Alvarez, A., Gilson, M., Hagmann, P., Mantini,
D., Betti, V., . . . Deco, G. (2019). Distinct modes of functional
connectivity induced by movie-watching. NeuroImage, 184,
335–348. https://doi.org/10.1016/j.neuroimage.2018.09.042
de Pasquale, F., Della Penna, S., Snyder, A. Z., Marzetti, L., Pizzella,
V., Romani, G. L., & Corbetta, M. (2012). A cortical core for dy-
namic integration of functional networks in the resting human
brain. Neuron, 74, 753–764.
Dinga, R., Schmaal, L., Penninx, B., van Tol, M. J., Veltman, D., van
Velzen, L., . . . Marquand, A. (2018). Evaluating the evidence for
biotypes of depression: Attempted replication of Drysdale et.al.
2017. bioRxiv. https://doi.org/10.1101/416321
Drysdale, A. T., Grosenick, L., Downar, J., Dunlop, K., Mansouri,
F., Meng, Y., . . . Liston, C. (2017). Resting-state connectivity
biomarkers define neurophysiological subtypes of depression.
Nature Medicine, 23, 28–38. https://doi.org/10.1038/nm.4246
Eickhoff, S. B., Thirion, B., Varoquaux, G., & Bzdok, D. (2015).
Connectivity-based parcellation: Critique and implications. Hu-
man Brain Mapping, 36, 4771–4792.
Ekstrom, A. (2010). How and when the fMRI BOLD signal relates
to underlying neural activity: The danger in dissociation. Brain
Research Reviews, 62, 233–244.
Emerson, R. W., Short, S. J., Lin, W., Gilmore, J. H., & Gao, W.
(2015). Network-level connectivity dynamics of movie watching
in 6-year-old children. Frontiers in Human Neuroscience, 9, 631.
Estrada, E. (2013). Communicability in temporal networks. Physi-
cal Review E, 88, 042811. https://doi.org/10.1103/PhysRevE.88.
042811
Estrada, E., & Hatano, N. (2008). Communicability in complex net-
works. Physical Review E, 77, 036111. https://doi.org/10.1103/
PhysRevE.77.036111
Faes, L., Stramaglia, S., & Marinazzo, D. (2017). On the inter-
pretability and computational reliability of frequency-domain
granger causality. F1000Research, 6, 1710. https://doi.org/10.
12688/f1000research.12694.1
Fair, D. A., Dosenbach, N. U. F., Church, J. A., Cohen, A. L.,
Brahmbhatt, S., Miezin, F. M., . . . Schlaggar, B. L. (2007). De-
velopment of distinct control networks through segregation and
integration. Proceedings of the National Academy of Sciences,
104, 13507–13512. https://doi.org/10.1073/pnas.0705843104
Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M. D., Huang, J.,
Chun, M. M., . . . Constable, R. T. (2015). Functional connectome
fingerprinting: Identifying individuals using patterns of brain con-
nectivity. Nature Neuroscience, 18, 1664–1671. https://doi.org/
10.1038/nn.4135
Fransson, P., Schiffler, B. C., & Thompson, W. H. (2018). Brain
network segregation and integration during an epoch-related
working memory fMRI experiment. NeuroImage, 178, 147–161.
https://doi.org/10.1016/j.neuroimage.2018.05.040
Frässle, S., Lomakina, E. I., Kasper, L., Manjaly, Z. M., Leff, A.,
Pruessmann, K. P., . . . Stephan, K. E. (2018). A generative model
of whole-brain effective connectivity. NeuroImage. https://doi.
org/10.1016/j.neuroimage.2018.05.058
Network Neuroscience
369
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
Fries, P. (2005). A mechanism for cognitive dynamics: Neuronal
communication through neuronal coherence. Trends in Cogni-
tive Sciences, 9, 474–480.
Friston, K. (2011). Functional and effective connectivity: A review.
Brain Connectivity, 1, 8.
Friston, K., Mechelli, A., Turner, R., & Price, C. (2000). Nonlinear re-
sponses in fMRI: The Balloon Model, Volterra kernels, and other
hemodynamics. NeuroImage, 12, 466–477.
Friston, K., Moran, R., & Seth, A. K. (2013). Analysing connectivity
with granger causality and dynamic causal modelling. Current
Opinion in Neurobiology, 23, 172–178. https://doi.org/10.1016/
j.conb.2012.11.010
Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal
modelling. Neuroimage, 19, 1273–1302.
Friston, K. J., Kahan, J., Biswal, B., & Razi, A. (2014). A DCM for
resting state fMRI. NeuroImage, 94, 396–407. https://doi.org/10.
1016/j.neuroimage.2013.12.009
Galán, R. F. (2008). On how network architecture determines the
dominant patterns of spontaneous neural activity. PLoS ONE, 3,
e2148. https://doi.org/10.1371/journal.pone.0002148
Gillebert, C. R., & Mantini, D. (2013). Functional connectivity in the
normal and injured brain. Neuroscientist, 19, 509–522. https://
doi.org/10.1177/1073858412463168
Gilson, M. (2018). Analysis of fMRI data using noise-diffusion net-
work models: A new covariance-coding perspective. Biological
Cybernetics. https://doi.org/10.1007/s00422-017-0741-y
Gilson, M. (2019). PyMOU: Light package for simulation and con-
nectivity estimation using the multivariate Ornstein-Uhlenbeck
process (MOU). GitHub. https://github.com/mb-BCA/pyMOU
Gilson, M., Deco, G., Friston, K., Hagmann, P., Mantini, D., Betti,
V., . . . Corbetta, M. (2018). Effective connectivity inferred from
fMRI transition dynamics during movie viewing points to a bal-
anced reconfiguration of cortical interactions. NeuroImage, 180,
534–546. https://doi.org/10.1016/j.neuroimage.2017.09.061
Gilson, M., Kouvaris, N. E., Deco, G., Mangin, J.-F., Poupon, C.,
Lefranc, S., & Zamora-López, G. (2019). Network analysis of
whole-brain fMRI dynamics: A new framework based on dy-
namic communicability. NeuroImage, 201, e116007. https://doi.
org/10.1016/j.neuroimage.2019.116007
Gilson, M., Kouvaris, N. E., Deco, G., & Zamora-López, G. (2018).
Framework based on communicability and flow to analyze com-
plex network dynamics. Physical Review E, 97, 052301. https://
doi.org/10.1103/PhysRevE.97.052301
Gilson, M., Moreno-Bote, R., Ponce-Alvarez, A., Ritter, P., & Deco,
G. (2016). Estimation of directed effective connectivity from fMRI
functional connectivity hints at asymmetries of cortical connec-
tome. PLoS Computational Biology, 12, e1004762.
Gilson, M., Zamora-López, G., & Insabato, A. (2019). pyMOU:
Light package for simulation and connectivity estimation us-
ing the multivariate Ornstein-Uhlenbeck process (MOU). https://
github.com/mb-BCA/pyMOU
Gitelman, D. R., Penny, W. D., Ashburner, J., & Friston, K. J. (2003).
Modeling regional and psychophysiologic interactions in fMRI:
The importance of hemodynamic deconvolution. NeuroImage,
19, 200–207.
Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D., Harwell,
J., Yacoub, E., . . . Van Essen, D. C. (2016). A multi-modal par-
cellation of human cerebral cortex. Nature, 536, 171–178.
Goebel, R., Roebroeck, A., Kim, D., & Formisano, E. (2003). In-
vestigating directed cortical interactions in time-resolved fMRI
data using vector autoregressive modeling and Granger causality
mapping. Magnetic Resonance Imaging, 21, 1251–1261.
Goense, J. B. M., & Logothetis, N. K. (2008). Neurophysiology of
the bold fMRI signal in awake monkeys. Current Biology, 18(9),
631–640. https://doi.org/10.1016/j.cub.2008.03.054
Gonzalez-Castillo, J., & Bandettini, P. A. (2017). Task-based dy-
namic functional connectivity: Recent findings and open ques-
tions. NeuroImage. https://doi.org/10.1016/j.neuroimage.2017.
08.006
Gonzalez-Castillo, J., Hoy, C. W., Handwerker, D. A., Robinson,
M. E., Buchanan, L. C., Saad, Z. S., & Bandettini, P. A. (2015).
Tracking ongoing cognition in individuals using brief, whole-
brain functional connectivity patterns. Proceedings of the Na-
tional Academy of Sciences, 112, 8762–8767. https://doi.org/10.
1073/pnas.1501242112
Goodyear, K., Parasuraman, R., Chernyak, S., Madhavan, P.,
Deshpande, G., & Krueger, F. (2016). Advice taking from humans
and machines: An fMRI and effective connectivity study. Fron-
tiers in Human Neuroscience, 10, 542. https://doi.org/10.3389/
fnhum.2016.00542
Greicius, M. (2008). Resting-state functional connectivity in neuro-
psychiatric disorders. Current Opinion in Neurology, 21, 424–430.
https://doi.org/10.1097/WCO.0b013e328306f2c5
Guyon, I., Weston, J., Barnhill, S., & Vapnik, V. (2002). Gene se-
lection for cancer classification using support vector machines.
Machine Learning, 46(1), 389–422. https://doi.org/10.1023/A:
1012487302797
Habib, M., Mak, E., Gabel, S., Su, L., Williams, G., Waldman, A.,
. . . O’Brien, J. T. (2017). Functional neuroimaging findings in
healthy middle-aged adults at risk of Alzheimer’s disease. Age-
ing Research Reviews, 36, 88–104. https://doi.org/10.1016/j.arr.
2017.03.004
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6, e159.
Handwerker, D. A., Ollinger, J. M., & D’Esposito, M. (2004). Varia-
tion of BOLD hemodynamic responses across subjects and brain
regions and their effects on statistical analyses. NeuroImage, 21,
1639–1651. https://doi.org/10.1016/j.neuroimage.2003.11.029
Hasson, U., Nir, Y., Levy, I., Fuhrmann, G., & Malach, R. (2004).
Intersubject synchronization of cortical activity during natural vi-
sion. Science, 303, 1634–1640.
He, B. J. (2011). Scale-free properties of the functional magnetic
resonance imaging signal during rest and task. Journal Neuro-
science, 31, 13786–13795.
He, Y., Wang, M., Chen, X., Pohmann, R., Polimeni, J. R., Scheffler,
K., . . . Yu, X. (2018). Ultra-slow single-vessel BOLD and CBV-
based fMRI spatiotemporal dynamics and their correlation with
neuronal intracellular calcium signals. Neuron, 97, 925–939.
https://doi.org/10.1016/j.neuron.2018.01.025
Network Neuroscience
370
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
Hilgetag, C. C., & Grant, S. (2010). Cytoarchitectural differences
are a key determinant of laminar projection origins in the visual
cortex. NeuroImage, 51, 1006–1017. https://doi.org/10.1016/j.
neuroimage.2010.03.006
Hlinka, J., Palus, M., Vejmelka, M., Mantini, D., & Corbetta, M.
(2011). Functional connectivity in resting-state fMRI: Is linear cor-
relation sufficient? NeuroImage, 54, 2218–2225.
Hohenfeld, C., Werner, C. J., & Reetz, K. (2018). Resting-state con-
nectivity in neurodegenerative disorders: Is there potential for an
imaging biomarker? NeuroImage: Clinical, 18, 849–870. https://
doi.org/10.1016/j.nicl.2018.03.013
Honey, C. J., Kötter, R., Breakspear, M., & Sporns, O. (2007). Net-
work structure of cerebral cortex shapes functional connectivity
on multiple time scales. Proceedings of the National Academy
of Sciences, 104, 10240–10245.
Hughes, R. I. G. (1997). Models and representation. Philosophy of
Science, 64, S325–S336. https://doi.org/10.1086/392611
Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A.,
Calhoun, V. D., Corbetta, M.,
(2013). Dy-
namic functional connectivity: Promise, issues, and interpreta-
tions. Neuroimage, 80, 360–378.
. Chang, C.
.
.
Insabato, A., Cunningham, J. P., & Gilson, M. (2018). Bayesian es-
timation for large scale multivariate Ornstein-Uhlenbeck model
of brain connectivity. arXiv: 1805.10050
James, G., Kelley, M., Craddock, R., Holtzheimer, P., Dunlop, B.,
Nemeroff, C., . . . Hu, X. (2009). Exploratory structural equation
modeling of resting-state fMRI: Applicability of group models to
individual subjects. NeuroImage, 45, 778–787.
Kaplan, D. M. (2011). Explanation and description in compu-
tational neuroscience. Synthese, 183, 339. https://doi.org/10.
1007/s11229-011-9970-0
Khambhati, A. N., Sizemore, A. E., Betzel, R. F., & Bassett, D. S.
(2017). Modeling and interpreting mesoscale network dynamics.
NeuroImage. https://doi.org/10.1016/j.neuroimage.2017.06.029
Kurth, S., Moyse, E., Bahri, M. A., Salmon, E., & Bastin, C. (2015).
Recognition of personally familiar faces and functional connec-
tivity in Alzheimer’s disease. Cortex, 67, 59–73. https://doi.org/
10.1016/j.cortex.2015.03.013
Lafleur, L.-P., Tremblay, S., Whittingstall, K., & Lepage, J.-F. (2016).
Assessment of effective connectivity and plasticity with dual-coil
transcranial magnetic stimulation. Brain Stimulation, 9, 347–355.
https://doi.org/10.1016/j.brs.2016.02.010
Laird, A. R., Eickhoff, S. B., Rottschy, C., Bzdok, D., Ray, K. L., &
Fox, P. T. (2013). Networks of task co-activations. NeuroImage,
80, 505–514.
Li, B., Wang, X., Yao, S., Hu, D., & Friston, K.
(2012). Task-
dependent modulation of effective connectivity within the de-
fault mode network. Frontiers in Psychology, 3, 206. https://doi.
org/10.3389/fpsyg.2012.00206
Mantini, D., Hasson, U., Betti, V., Perrucci, M. G., Romani, G. L.,
Corbetta, M., . . . Vanduffel, W. (2012). Interspecies activity cor-
relations reveal functional correspondence between monkey and
human brain areas. Nature Methods, 9, 277–282.
Matsui, T., Murakami, T., & Ohki, K. (2018). Neuronal origin of the
temporal dynamics of spontaneous BOLD activity correlation.
Cerebral Cortex. https://doi.org/10.1093/cercor/bhy045
Matthews, P. M., & Hampshire, A. (2016). Clinical concepts emerg-
ing from fMRI functional connectomics. Neuron, 91, 511–528.
https://doi.org/10.1016/j.neuron.2016.07.031
McIntosh, A., & Gonzalez-Lima, F. (1994). Structural equation mod-
eling and its application to network analysis in functional brain
imaging. Human Brain Mapping, 2, 2–22.
Messé, A., Rudrauf, D., Benali, H., & Marrelec, G. (2014). Relat-
ing structure and function in the human brain: Relative contri-
butions of anatomy, stationary dynamics, and non-stationarities.
PLoS Computational Biology, 10, e1003530.
Meunier, D., Ersche, K. D., Craig, K. J., Fornito, A., Merlo-Pich,
E., Fineberg, N. A., . . . Bullmore, E. T. (2012). Brain func-
tional connectivity in stimulant drug dependence and obsessive-
compulsive disorder. NeuroImage, 59, 1461–1468. https://doi.
org/10.1016/j.neuroimage.2011.08.003
Miranda-Dominguez, O., Mills, B. D., Carpenter, S. D., Grant, K. A.,
Kroenke, C. D., Nigg, J. T., & Fair, D. A. (2014). Connectotyp-
ing: Model based fingerprinting of the functional connectome.
PLoS ONE, 9, e111048. https://doi.org/10.1371/journal.pone.
0111048
Mitra, A., Kraft, A., Wright, P., Acland, B., Snyder, A. Z., Rosenthal,
Z., . . . Raichle, M. E. (2018). Spontaneous infra-slow brain ac-
tivity has unique spatiotemporal dynamics and laminar struc-
ture. Neuron, 98, 297–305. https://doi.org/10.1016/j.neuron.
2018.03.015
Mitra, A., Snyder, A., Hacker, C., & Raichle, M. (2014). Lag structure in
resting-state fMRI. Journal of Neurophysiology, 111, 2374–2391.
Mitra, A., Snyder, A. Z., Tagliazucchi, E., Laufs, H., & Raichle, M.
(2015). Propagated infra-slow intrinsic brain activity reorganizes
across wake and slow wave sleep. eLife, 4.
Naselaris, T., Kay, K. N., Nishimoto, S., & Gallant, J. L. (2011). En-
coding and decoding in fMRI. NeuroImage, 56, 400–410. https://
doi.org/10.1016/j.neuroimage.2010.07.073
Newman, M. E. J. (2006). Modularity and community structure in net-
works. Proceedings of the National Academy of Sciences, 103,
8577–8582.
Olszowy, W., Aston, J., Rua, C., & Williams, G. B. (2019). Accurate
autocorrelation modeling substantially improves fMRI reliabil-
ity. Nature Communications, 10, 1220. https://doi.org/10.1038/
s41467-019-09230-w
Pallarés, V., Insabato, A., Sanjuán, A., Kühn, S., Mantini, D., Deco,
G., & Gilson, M. (2018). Extracting orthogonal subject- and
condition-specific signatures from fMRI data using whole-brain
effective connectivity. NeuroImage, 178, 238–254. https://doi.
org/10.1016/j.neuroimage.2018.04.070
Park, H.-J., & Friston, K. (2013). Structural and functional brain net-
works: From connections to cognition. Science, 342, 1238411.
Park, H.-J., Friston, K. J., Pae, C., Park, B., & Razi, A. (2018).
Dynamic effective connectivity in resting state fMRI. Neuro-
Image, 180, 594–608.https://doi.org/10.1016/j.neuroimage.2017.
11.033
Parkes, L., Fulcher, B., Yücel, M., & Fornito, A. (2018). An evalua-
tion of the efficacy, reliability, and sensitivity of motion correc-
tion strategies for resting-state functional MRI. NeuroImage, 171,
415–436. https://doi.org/10.1016/j.neuroimage.2017.12.073
Network Neuroscience
371
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
Power, J. D., Plitt, M., Gotts, S. J., Kundu, P., Voon, V., Bandettini,
P. A., & Martin, A. (2018). Ridding fMRI data of motion-related
influences: Removal of signals with distinct spatial and physical
bases in multiecho data. Proceedings of the National Academy
of Sciences, 115, E2105–E2114. https://doi.org/10.1073/pnas.
1720985115
Preti, M. G., Bolton, T. A., & Van De Ville, D. (2017). The dy-
namic functional connectome: State-of-the-art and perspectives.
NeuroImage, 160, 41–54. https://doi.org/10.1016/j.neuroimage.
2016.12.061
Proix, T., Spiegler, A., Schirner, M., Rothmeier, S., Ritter, P., &
Jirsa, V. K. (2016). How do parcellation size and short-range
connectivity affect dynamics in large-scale brain network
models? NeuroImage, 142, 135–149. https://doi.org/10.1016/j.
neuroimage.2016.06.016
Rahim, M., Thirion, B., Bzdok, D., Buvat, I., & Varoquaux, G.
(2017). Joint prediction of multiple scores captures better individ-
ual traits from brain images. NeuroImage, 158, 145–154. https://
doi.org/10.1016/j.neuroimage.2017.06.072
Razi, A., Seghier, M. L., Zhou, Y., McColgan, P., Zeidman, P., Park,
H.-J., . . . Friston, K.-J. (2017). Large-scale DCMS for resting-
state fMRI. Network Neuroscience, 1, 222–241. https://doi.org/
10.1162/NETN_a_00015
Rissman, J., & Wagner, A. D. (2012). Distributed representations
in memory: Insights from functional brain imaging. Annual Re-
view Psychology, 63, 101–128. https://doi.org/10.1146/annurev-
psych-120710-100344
Rousseeuw, P. (1987). Silhouettes: A graphical aid to the interpreta-
tion and validation of cluster analysis. Journal of Computational
and Applied Mathematics, 20, 53–65. https://doi.org/10.1016/
0377-0427(87)90125-7
Rowe, J. B., & Siebner, H. R. (2012). The motor system and its dis-
orders. NeuroImage, 61(2), 464–477. https://doi.org/10.1016/j.
neuroimage.2011.12.042
Ryali, S., Supekar, K., Chen, T., & Menon, V. (2011). Multivari-
ate dynamical systems models for estimating causal interactions
in fMRI. NeuroImage, 54, 807–823. https://doi.org/10.1016/j.
neuroimage.2010.09.052
Sanz-Leon, P., Knock, S. A., Spiegler, A., & Jirsa, V. K. (2015). Math-
ematical framework for large-scale brain network modeling in
the virtual brain. NeuroImage, 111, 385–430. https://doi.org/10.
1016/j.neuroimage.2015.01.002
Sathian, K., Deshpande, G., & Stilla, R. (2013). Neural changes with
tactile learning reflect decision-level reweighting of perceptual
readout. Journal of Neuroscience, 33, 5387–5398. https://doi.
org/10.1523/JNEUROSCI.3482-12.2013
Sauvage, A., Hubert, G., Touboul, J., & Ribot, J. (2017). The hemo-
dynamic signal as a first-order low-pass temporal filter: Evidence
and implications for neuroimaging studies. Neuroimage, 155,
394–405. https://doi.org/10.1016/j.neuroimage.2017.03.053
Schiefer, J., Niederbühl, A., Pernice, V., Lennartz, C., Hennig, J.,
LeVan, P., & Rotter, S.
(2018). From correlation to causation:
Estimating effective connectivity from zero-lag covariances of
brain signals. PLoS Compututaional Biology, 14, e1006056.
https://doi.org/10.1371/journal.pcbi.1006056
Schmahmann, J. D., & Pandya, D. N. (2007). Cerebral white matter–
historical evolution of facts and notions concerning the organ-
ization of the fiber pathways of the brain. Journal of the His-
tory of the Neurosciences, 16, 237–267. https://doi.org/10.1080/
09647040500495896
Schmidt, M., Bakker, R., Hilgetag, C. C., Diesmann, M., & van
Albada, S. J.
(2018). Multi-scale account of the network struc-
ture of macaque visual cortex. Brain Structure and Function, 223,
1409–1435. https://doi.org/10.1007/s00429-017-1554-4
Senden, M., Goebel, R., & Deco, G. (2012). Structural connectivity
allows for multi-threading during test: The structure of the cor-
tex leads to efficient alternation between resting state exploratory
behavior and default mode processing. NeuroImage, 60, 2274–
2284. https://doi.org/10.1016/j.neuroimage.2012.02.061
Senden, M., Reuter, N., van den Heuvel, M. P., Goebel, R., Deco,
G., & Gilson, M. (2017). Task-related effective connectivity re-
veals that
the cortical rich club gates cortex-wide commu-
nication. Human Brain Mapping. https://doi.org/10.1002/hbm.
23913
Seth, A. K., Chorley, P., & Barnett, L. C. (2013). Granger causal-
ity analysis of fMRI BOLD signals is invariant to hemodynamic
convolution but not downsampling. NeuroImage, 65, 540–555.
https://doi.org/10.1016/j.neuroimage.2012.09.049
Siegel, J. S., Ramsey, L. E., Snyder, A. Z., Metcalf, N. V., Chacko,
R. V., Weinberger, K., . . . Corbetta, M. (2016). Disruptions
in multiple be-
of network connectivity predict
the National
havioral domains after stroke. Proceedings of
Academy of Sciences, 113, 4367–4376. https://doi.org/10.1073/
pnas.1521083113
impairment
Smith, S., Miller, K., Salimi-Khorshidi, G., Webster, M., Beckmann,
C., Nichols, T., . . . Woolrich, M. (2011). Network modelling
methods for fMRI. NeuroImage, 54, 875–891.
Snyder, A. Z., & Raichle, M. E. (2012). A brief history of the resting
state: The washington university perspective. Neuroimage, 62,
902–910. https://doi.org/10.1016/j.neuroimage.2012.01.044
Sokolov, A. A., Zeidman, P., Erb, M., Ryvlin, P., Pavlova, M. A., &
Friston, K. J. (2018). Linking structural and effective brain connec-
tivity: Structurally Informed Parametric Empirical Bayes (si-PEB).
Brain Structure and Function. https://doi.org/10.1007/s00429-
018-1760-8
Sporns, O., Tononi, G., & Edelman, G. M. (2000). Theoretical neu-
roanatomy: Relating anatomical and functional connectivity in
graphs and cortical connection matrices. Cerebral Cortex, 10,
127–141.
Sporns, O., Tononi, G., & Kötter, R. (2005). The human connec-
tome: A structural description of the human brain. PLOS Com-
putational Biology, 1, 0010042. https://doi.org/10.1371/journal.
pcbi.0010042
Stephan, K., Harrison, L., Penny, W., & Friston, K. (2004). Biophys-
ical models of fMRI responses. Current Opinion in Neurology,
14, 629–635.
Thompson, W. H., Brantefors, P., & Fransson, P. (2017). From static
to temporal network theory: Applications to functional brain con-
nectivity. Network Neuroscience, 1(2), 69–99. https://doi.org/10.
1162/NETN_a_00011
Tononi, G., Edelman, G. M., & Sporns, O. (1998). Complexity and
coherency: Integrating information in the brain. Trends in Cogni-
tive Science, 2, 474–484.
Network Neuroscience
372
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling whole-brain effective connectivity for cognition and disease
Tononi, G., Sporns, O., & Edelman, G. M. (1994). A measure for
brain complexity: Relating functional segregation and integration
in the nervous system. Proceedings of the National Academy of
Sciences, 91, 5033–5037.
Valdes-Sosa, P., Roebroeck, A., Daunizeau, J., & Friston, K. (2011).
Effective connectivity: Influence, causality and biophysical mod-
eling. NeuroImage, 58, 339–361.
van den Heuvel, M. P., & Hulshoff Pol, H. E. (2010). Exploring the
brain network: A review on resting-state fMRI functional con-
nectivity. European Neuropsychopharmacology, 20, 519–534.
https://doi.org/10.1016/j.euroneuro.2010.03.008
Varoquaux, G., & Poldrack, R. A.
(2019). Predictive models
avoid excessive reductionism in cognitive neuroimaging. Cur-
rent Opinion in Neurobiology, 55, 1–6. https://doi.org/10.1016/
j.conb.2018.11.002
Varoquaux, G., Raamana, P. R., Engemann, D. A., Hoyos-Idrobo,
A., Schwartz, Y., & Thirion, B. (2017). Assessing and tuning
brain decoders: Cross-validation, caveats, and guidelines. Neuro-
Image, 145, 166–179.https://doi.org/10.1016/j.neuroimage.2016.
10.038
Varoquaux, G., Schwartz, Y., Poldrack, R. A., Gauthier, B., Bzdok,
D., Poline, J.-B., & Thirion, B. (2018). Atlases of cognition with
large-scale human brain mapping. PLoS Computational Biology,
14, e1006565. https://doi.org/10.1371/journal.pcbi.1006565
Vatansever, D., Menon, D. K., Manktelow, A. E., Sahakian, B. J., &
Stamatakis, E. A. (2015). Default mode dynamics for global func-
tional integration. Journal of Neuroscience, 35, 15254–15262.
https://doi.org/10.1523/JNEUROSCI.2135-15.2015
Vatansever, D., Menon, D. K., & Stamatakis, E. A. (2017). Default
mode contributions to automated information processing. Pro-
ceedings of the National Academy Sciences, 114, 12821–12826.
https://doi.org/10.1073/pnas.1710521114
Vidaurre, D., Abeysuriya, R., Becker, R., Quinn, A. J., Alfaro-
Almagro, F., Smith, S. M., & Woolrich, M. W. (2018). Discovering
dynamic brain networks from big data in rest and task. Neuro-
Image, 180, 646–656.https://doi.org/10.1016/j.neuroimage.2017.
06.077
Walther, A., Nili, H., Ejaz, N., Alink, A., Kriegeskorte, N., &
Diedrichsen, J. (2016). Reliability of dissimilarity measures for
multi-voxel pattern analysis. NeuroImage, 137, 188–200. https://
doi.org/10.1016/j.neuroimage.2015.12.012
Wheelock, M., Sreenivasan, K., Wood, K., Hoef, L. V., Deshpande,
G., & Knight, D. (2014). Threat-related learning relies on distinct
dorsal prefrontal cortex network connectivity. NeuroImage, 102,
904–912. https://doi.org/10.1016/j.neuroimage.2014.08.005
Wilson, H., & Cowan, J. (1973). A mathematical theory of the func-
tional dynamics of nervous tissue. Kybernetik, 13, 55–80.
Yahata, N., Kasai, K., & Kawato, M. (2017). Computational neu-
roscience approach to biomarkers and treatments for mental
disorders. Psychiatry and Clinical Neurosciences, 71, 215–237.
https://doi.org/10.1111/pcn.12502
Zamora-López, G., Chen, Y., Deco, G., Kringelbach, M. L., & Zhou,
C. (2016). Functional complexity emerging from anatomical con-
straints in the brain: The significance of network modularity and
rich-clubs. Science Reports, 6, 38424. https://doi.org/10.1038/
srep38424
Zamora-López, G., & Gilson, M. (2019). NetDynFlow: A package
to study complex networks based on the temporal evolution of
their Dynamic Communicability and Flow. https://github.com/
mb-BCA/NetDynFlow
Zamora-López, G., Zhou, C., & Kurths, J. (2011). Exploring brain
function from anatomical connectivity. Frontiers in Neuro-
science, 5, 83. https://doi.org/10.3389/fnins.2011.00083
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
3
3
8
1
8
6
6
6
3
9
n
e
n
_
a
_
0
0
1
1
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
373