Numbers within Our Hands: Modulation of - Recherche en IA spécialisée au MIT

Numbers within Our Hands: Modulation of
Corticospinal Excitability of Hand Muscles
during Numerical Judgment

Marc Sato, Luigi Cattaneo, Giacomo Rizzolatti, and Vittorio Gallese

Abstrait

& Developmental and cross-cultural studies show that finger
counting represents one of the basic number learning strategies.
Cependant, despite the ubiquity of such an embodied strategy,
the issue of whether there is a neural link between numbers
and fingers in adult, literate individuals remains debated. Ici,
we used transcranial magnetic stimulation to study changes of
excitability of hand muscles of individuals performing a visual

parity judgment task, a task not requiring counting, on Arabic
numerals from 1 à 9. Although no modulation was observed for
the left hand muscles, an increase in amplitude of motor-evoked
potentials was found for the right hand muscles. This increase
was specific for smaller numbers (1 à 4) as compared to larger
numbers (6 à 9). These findings indicate a close relationship
between hand/finger and numerical representations. &

INTRODUCTION

The issue of how numbers are represented (and manip-
ulated) in the human brain has been for a long time
a matter of debate. Recently, thanks to the combined
efforts of developmental psychology, psychophysics,
and neuroscience, our understanding of numerical abil-
ities and their neural basis has significantly improved. Il
has been shown that numerical competence related to
approximate processing of quantity can be considered as
a basic independent faculty, present early in infancy
(Nieder, 2005; Dehaene, 1997). This competence, comment-
jamais, appears to be limited in its representational power,
failing to support certain numerical concepts, tel que
negative numbers or even exact integers (Feigenson,
Dehaene, & Jeux, 2004). The development and mat-
uration of these concepts are thought to depend on
cultural and educational processes. From this perspec-
tive, a fundamental question concerns the role of lan-
guage in developing numerical concepts and arithmetic
abilities. Studies on numerical competence in popula-
tions in which the verbal counting system is limited have
underlined a distinction between a system of number
approximation not linked to language and a language-
based counting system for exact number and arithmetic
(Gordon, 2004; Pica, Lemer, Izard, & Dehaene, 2004).
Individuals of these populations are unable to perform
exact calculation when the answer exceeds their naming
range, but exhibit normal approximate number process-
ing. These results suggest that numerical competence

Universita` degli studi di Parma, Italy

depends on a language-based counting system, et
reinforces the long-standing idea that learning a com-
municable number notation with exact numerical refer-
ences may play a role in the emergence of a fully formed
conception of number (Gelman & Butterworth, 2004;
Gelman & Gallistel, 2004).

Neuropsychological and brain imaging studies fo-
cusing on the localization of numerical processing and
arithmetic in the brain also support the distinction
between a verbal code for exact arithmetic processing
and a language-independent analog magnitude code
for approximate processing. Neuroimaging studies
with healthy individuals show that number processing
rests on a distinct neural circuitry,
involving a set of
pariétal, frontal, and cingulate areas (Pinel, Piazza, Le
Bihan, & Dehaene, 2004; Eger, Sterze, Russ, Giraud, &
Kleinschmidt, 2003; Simon, Mangin, Cohen, Le Bihan, &
Dehaene, 2002; Zago et al., 2001; Stanescu-Cosson et al.,
2000; Chochon, Cohen, van de Moortele, & Dehaene,
1999; Dehaene et al., 1996; Rueckert et al., 1996).
Although the cortex lying in the horizontal segment
of the intraparietal sulcus seems to play a crucial role
in language-independent semantic representation of
numerical quantity, the activation of the left inferior
frontal gyrus, a region commonly associated with lan-
guage functions, has been suggested to reflect exact
mental calculation and to be involved in retrieval of
arithmetic facts (Dehaene, Molko, Cohen, & Wilson,
2004; Dehaene, Piazza, Pinel, & Cohen, 2003). Consist-
ent with these findings is the observation that patients
with lesions in the left frontal cortical areas are unable
to perform exact calculations such as multiplication, mais

D 2007 Massachusetts Institute of Technology

Journal des neurosciences cognitives 19:4, pp. 684–693

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

F
/

t
t

je
t
.

:
/
/

D
h
o
t
w
t
p
n
:
o
/
un
/
d
m
e
je
d
t
F
r
p
o
r
m
c
.
h
s
je
p
je
v
d
e
je
r
r
e
c
c
h
t
.
m
un
je
r
e
.
d
c
toi
o
m
o
/
c
j
n
o
un
c
r
t
n
je
c
/
e
un
–
r
p
t
d
je
c
1
je
9
e
4
–
6
p
8
d
4
F
/
1
1
9
9
3
6
/
3
4
0
/
1
6
8
o
4
c
/
n
1
2
8
0
1
0
6
7
4
1
2
9
6
/
4
j
6
o
8
c
4
n
p
.
d
2
0
b
0
oui
7
g
.
toi
1
e
9
s
.
t
4
o
.
n
6
0
8
7
4
S
.
p
e
p
d
F
e
m
b
b
oui
e
r
g
2
toi
0
e
2
s
3
t

/
j

o
n

1
8

M.
un
oui

2
0
2
1

do not exhibit significant difficulties in quantity com-
parisons (Lemer, Dehaene, Jeux, & Cohen, 2003;
Dehaene & Cohen, 1997). In contrast, patients with
damage to areas within the inferior parietal
lobe are
proficient at performing exact numerical computations
involving rote retrieval but may have striking deficits in
their ability to perform tasks requiring a representation
of numerical quantity (Lemer et al., 2003; Dehaene &
Cohen, 1997; Delazer & Benke, 1997). Altogether, ces
studies provide convincing evidence that number com-
prehension and calculation are mediated by both ana-
logue magnitude and verbal codes.

Another important semiotic means for representing
numbers, also described in populations with extremely
limited or no verbal counting, is the one based on the
use of body parts, such as fingers or hands. Several lines
of evidence argue in favor of a close relationship be-
tween number and hand/finger representations. Devel-
opmental and cross-cultural studies have shown that
finger counting is a basic numerical
learning strategy
that develops spontaneously (Butterworth, 1999). Aussi,
performance on finger discrimination tasks (par exemple., digital
gnosia and digital discrimination) dans 5- to 6-year-old chil-
dren is considered as one of the best predictor of arith-
metic abilities (Fayol, Barouilette, & Marinthe, 1998).
Another connection between hand/finger representa-
tion and numerical knowledge stems from the study of
Gerstmann syndrome (Mayer et al., 1999; Gerstmann,
1924, 1940) and of Developmental Gerstmann Syndrome
(Suresh & Sebastian, 2000; Kinsbourne & Warrington,
1963), where an association of finger agnosia and dys-
calculia can be observed. Accordingly, a recent repetitive
transcranial magnetic stimulation (SMTr) étude (Rusconi,
Walsh, & Butterworth, 2005) on healthy volunteers
showed that stimulation of the left angular gyrus dis-
rupts the capacity to execute tasks requiring access to
finger representations and numerical judgment. Enfin,
several functional imaging studies showed that arithme-
tic tasks activate that part of the left precentral gyrus
where hand movements are represented (Pinel et al.,
2004; Zago et al., 2001; Pesenti, Thioux, Seron, & de
Volder, 2000; Stanescu-Cosson et al., 2000; Dehaene
et coll., 1996; Rueckert et al., 1996).

In the present study, we explored whether numerical
judgment may automatically induce changes in the ex-
citability of corticospinal output to hand muscles of
educated adults despite the absence of any conscious
necessity to use an embodied strategy for solving the
task. In a first experiment, we used single-pulse TMS
applied to the hand region of the motor cortex in
individuals orally performing a visual parity judgment
task on Arabic numerals from 1 à 9 (5 excluded). Le
parity judgment task was chosen because a motor
strategy is irrelevant in order to perform the task. Le
focal TMS was delivered 200 msec after the onset of the
number presentation to either the left or right hemi-
sphère, and motor-evoked potentials (MEPs) were re-

corded from the contralateral abductor pollicis brevis
(APB) and abductor digiti minimi (ADM) hand mus-
clés. These two muscles were chosen within the com-
plex system of intrinsic hand muscles in order to select
a broad spectrum of counting-like hand postures (Blanc
& Flanders, 2004). We hypothesized that changes in
the corticospinal excitability of hand muscles during
the task could be directly related to the way of repre-
senting numbers by means of fingers. Preliminary be-
havioral observations showed a clear tendency for Italian
adults to use their right hand to represent numbers from
1 à 5 et, subsequently, their left hand to represent
numbers from 6 à 10. Accordingly, processing smaller
digits (c'est à dire., depuis 1 à 4) and larger digits (c'est à dire., depuis 6 à
9) should induce an increase in corticospinal excitability
of the right and left hand muscles, respectivement. Enfin,
a behavioral experiment measuring reaction time (RT)
in a parity judgment task was performed in order to as-
sess possible differences in terms of complexity when
processing smaller and larger digits.

EXPERIMENT 1: TMS STUDY

Methods

Participants

Two separate groups of eight subjects (9 les hommes et 7
femmes; mean age ± SD, 24 ± 4 années) participated
in Experiment 1A and Experiment 1B. All were right-
handed according to a standard handedness inventory
(Oldfield, 1971) and had normal or corrected-to-normal
vision. Participants were screened for neurological, psy-
chiatric, and other medical problems, as well as con-
traindications to TMS (Wassermann, 1998). Informed
consent was obtained for all subjects and they were
paid for their participation. The protocol was approved
by the Parma University Ethical Committee and was
carried out in accordance with the ethical standards of
le 1964 Declaration of Helsinki.

Electromyography

Continuous electromyography (EMG) recordings from
the APB and ADM muscles were simultaneously acquired
with a CED Micro 1401 analog-to-digital converting unit
(Cambridge Electronic Design, Cambridge, ROYAUME-UNI). Le
EMG signal was amplified (1000(cid:1)), digitized (sampling
rate: 8 kHz, off-line band-pass filter: 5–4000 Hz), et
stored on a computer for off-line analysis. The APB and
ADM muscles were recorded from either the right or the
left hand, according to the experimental session, en utilisant
Ag/AgCl surface electrodes with a bipolar montage. Le
active electrode was placed on the muscle belly and the
reference electrode on the corresponding tendon. Elec-
trodes were therefore placed laterally to the metacarpal
bone of the thumb for APB and on the medial border
of the palm for ADM.

Sato et al.

685

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

Transcranial Magnetic Stimulation

Either the left or the right hemisphere was magnetically
stimulated by means of monophasic single pulses deliv-
ered through a figure-of-eight coil connected to a trans-
cranial magnetic stimulator (ESAOTE Biomedica, Italy).
The coil was moved over the scalp in order to deter-
mine the optimal site from which maximal amplitude
MEPs were elicited in the APB and ADM muscles. Pour
optimal stimulation of the hand motor cortex, the inter-
section of the coil was placed tangentially to the scalp,
with the handle pointing backward and laterally at a
458 angle away from the midline (Mills, Boniface, &
Schubert, 1992). The coil handle was fixed on a me-
chanical arm to suppress movements of the coil itself
from the original position on the scalp. The resting
motor threshold (rMTh) of the APB and ADM muscles
was determined according to standard methods as the
minimal intensity capable of evoking MEPs (Rossini et al.,
1994) dans 5 out of 10 consecutive trials from the two
relaxed muscles with an amplitude of at least 50 AV. UN
single optimal spot on the scalp was searched for in
order to evoke MEPs from the two muscles with simi-
lar thresholds. In this way, no individual differences in
rMTh between the two muscles on the same side were
found in any subject. The output of the stimulator was
set to 120% of rMTh for the stimulations applied during
the experimental session. The complete muscle relaxa-
tion before TMS was verified by means of on-line visual
monitoring of the EMG signal by the experimenter.

Procedure

The experiments were programmed using Matlab (Math-
travaux, Natick, MA), Cogent (Functional Imaging Labo-
ratory, Queen Square, Londres), and Signal (Cambridge
Electronic Design) software to control the stimulus pre-
sentation and to trigger the TMS and EMG recordings.

Participants were comfortably seated on an armchair
with their elbow flexed at 908 and their hands half-
pronated in a totally relaxed position. The head was
lying on a headrest in order to maintain a comfortable
and stable position. They were required to orally make a
parity judgment on one-digit Arabic numerals. Stimuli
were single Arabic digits ranging from 1 à 9 (5 exclud-
éd), presented one at a time in the center of the screen
and written in black Arial font on a white screen ((cid:2)0.38 (cid:1)
0.38). Stimulus presentation was delivered through a
19-dans. monitor with a viewing distance of approximately
60 cm.

Each trial started with a fixation cue (the ‘‘+’’ symbol,
presentation time 500 msec) followed by the target
number (presentation time 500 msec) and by a blank
screen (presentation time 1000 msec). Then a question
mark (the ‘‘?’’ symbol, presentation time 2500 msec) était
shown, followed by a blank screen (presentation time
1000 msec). The question mark prompted the partic-

ipants to tell whether the observed number was odd
or even.

Both Experiment 1A and Experiment 1B consisted of
two different experimental sessions in which the hand
motor cortex of the left and right hemispheres was
separately stimulated while recording from the contra-
lateral hand muscles. The order of sessions was counter-
balanced across subjects. In Experiment 1A, every digit
was presented five times in a randomized sequence for a
total of 40 trials in both sessions. In each trial, the TMS
pulse was delivered 200 msec after the onset of the
number presentation. The delay of 200 msec was ex-
trapolated on the basis of previous studies, indicating
that lexical and semantic processes during word recog-
nition entail activation in the frontal cortex as early as
150–200 msec after onset of written word stimuli (Hauk
et coll., 2006; Pulvermuller, Shtyrov, & Ilmoniemi, 2005).
This interval also appears to be consistent with ERP
studies focusing on the time course of access to numer-
ical representations (Temple & Posner, 1998; Dehaene,
1996). Experiment 1B was identical to Experiment 1A,
except for an additional control condition where TMS
was applied simultaneously with stimulus presentation.
Each digit was presented nine times in a randomized
sequence for a total of 72 trials. For each digit, the TMS
pulse was delivered 200 msec after the onset of the
number presentation in six trials and at 0 msec from the
onset of the number presentation in the three other
trials. Trials for which the pulse was delivered at the
onset of the stimulus presentation were considered as
control trials.

Data Analysis

Data were processed off-line. The mean percentage of
errors was 1% in both Experiment 1A and Experiment 1B
(SD: 0.58/0.90). Error trials and trials with EMG activity
before TMS were discarded from the analyses (overall
less than 5% in both experiments). The negative to posi-
tive peak amplitude of the MEPs was measured and,
subsequently, z-score normalized to the grand average
of all MEPs from the same muscle and the same hemi-
sphere within the same subject in order to allow a com-
parison between subjects. In Experiment 1A, data were
averaged for each subject within the same muscle and
hemisphere according to both the numerical and parity
catégories (c'est à dire., small/odd,
‘‘2/4’’;
‘‘6/8’’). A four-way anal-
large/odd,
ysis of variance (ANOVA) was performed on these data.
The considered within-factors were related to the stim-
ulated side (left hemisphere and right hemisphere), le
numerical category (smaller digits, c'est à dire., 1 à 4, and larger
digits, c'est à dire., 6 à 9), the parity category (odd and even
digits), and the recorded muscle (APB and ADM). Dans
Experiment 1B, two distinct ANOVAs were performed.
In the first analysis, data were averaged for each sub-
ject within the same muscle and hemisphere according

‘‘1/3’’; small/even,

‘‘7/9’’; large/even,

686

Journal des neurosciences cognitives

Volume 19, Nombre 4

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

to the numerical category (c'est à dire., smaller digits,
larger
digits, and control trials). A three-way ANOVA was per-
formed on these data with the stimulated side, le
numerical category, and the recorded muscles as with-
in-factors. To further investigate a possible parity effect
in Experiment 1B, data related to smaller and larger
numbers were averaged within the same muscle and
hemisphere according to the numerical and parity cat-
egories (c'est à dire., small/odd, ‘‘1/3’’; small/even, ‘‘2/4’’; large/
odd, ‘‘7/9’’; large/even, ‘‘6/8’’), and submitted to a four-
way ANOVA. The considered within-factors were re-
lated to the stimulated side, the numeral category, le
parity category, and the recorded muscle. Whenever
appropriate, post hoc analyses were performed using
Bonferroni correction. The significance level was always
set at p = .05. For each analysis, a Mauchly test showed
that the sphericity assumption was not violated.

Results

Two TMS experiments were carried out. Experiment 1A
consisted of two sessions in which we stimulated the
motor cortex representations of the right and left hands,
respectivement, while recording EMG from the contralateral
APB and ADM muscles. In each trial, the TMS pulse was
delivered 200 msec after the onset of the number
presentation. A four-way ANOVA (with the hemisphere,
the numerical category, the parity category, et le
recorded muscle as within-factors) showed that the
presentation of smaller (1–4) and larger numbers (6–9)
(the digit 5 was not used) differentially affected the MEP
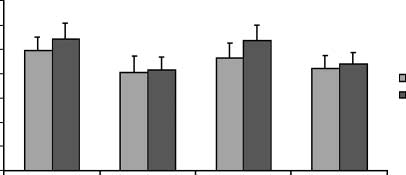
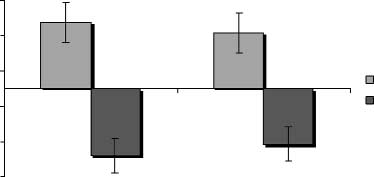
amplitude of hand muscles [F(1,7) = 12.02, p < .01]. A significant interaction was present between the side of stimulation and the numerical category [F(1,7) = 7.78, p < .03]. Post hoc analysis revealed that the interaction was due to the fact that, during stimulation of the left hemisphere, mean MEP amplitudes were larger when processing smaller numbers than larger numbers ( p < .02; see Figure 1A), whereas during stimulation of the right hemisphere, mean MEP amplitudes were not in- fluenced by the two numerical categories ( p > .68; voir
Figure 1B). No interaction was observed between the
recorded muscle and the numerical category [F(1,7) =
0.25], nor between the recorded muscle, the side of
stimulation, and the numerical category [F(1,7) = 0.12].
These later results indicate that the MEP modulation
equally affected both APB and ADM muscles. Enfin,
neither the effect of the parity category [F(1,7) = 0.16]
nor the interaction between the parity and numerical
categories was significant [F(1,7) = 0.43]. All the remain-
ing interactions were not significant.

In Experiment 1B, we further investigated the excit-
ability of the right and left hand muscles during the
parity judgment task by adding a control condition, dans
which the pulse was delivered simultaneously with the
stimulus onset. As in the first experiment, the motor
cortex representations of the right and left hands were

Chiffre 1. Average value of normalized MEP amplitudes of the
contralateral abductor digiti minimi and abductor pollicis brevis
muscles during parity judgment for smaller (1–4) and larger (6–9)
numbers in Experiment A. (UN) Stimulation of the left motor cortex;
(B) Stimulation of the right motor cortex. Les barres d'erreur représentent
standard errors of the mean (n = 8).

respectively stimulated while recording from the contra-
lateral APB and ADM muscles. MEPs induced by focal
TMS, delivered either 0 msec or 200 msec after the onset
of the number presentation, were recorded simulta-
neously from the APB and ADM muscles. ANOVA
showed a significant interaction between the side of
stimulation and the numerical category [F(2,14) = 8.79,
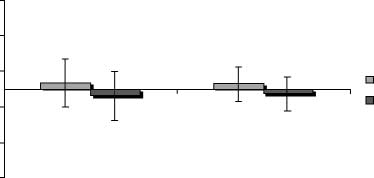
p < .003], but no effect of the numerical category [F(2,14) = 0.93]. Post hoc analysis revealed that the interaction was due to the fact that, during stimulation of the left hemisphere, mean MEP amplitudes were larger when processing smaller numbers than both larger numbers and control trials (small vs. large: p < .05; small vs. control: p < .05; large vs. control: p > .99;
see Figure 2A), whereas during stimulation of the right
hemisphere, mean MEP amplitudes were not influenced
by the three numerical categories (small vs. grand: p >
.99; small vs. control: p > .49; large vs. control: p > .52;
see Figure 2B). Ces résultats, coming from a separate
group of subjects, thus replicate those observed in
Experiment 1A. No interaction was observed between
the recorded muscle and the numerical category
[F(2,14) = 0.04], as well as between the recorded
muscle, the side of stimulation, and the numerical
catégorie [F(2,14) = 0.45]. As in Experiment 1A, ces
latter results indicate that the MEP modulation affected
equally both the APB and ADM muscles.

To further investigate a possible parity effect in Ex-
periment 1B, data related to smaller and larger numbers

Sato et al.

687

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

EXPERIMENT 2: BEHAVIORAL STUDY

Methods

Participants

Twenty-four subjects (15 les hommes et 9 femmes; mean
age ± SD, 27 ± 4 années) participated in Experiment 2.
All were right-handed and had normal or corrected-to-
normal vision. None of them participated in the previous
TMS experiments.

Procedure

The experiment was carried out in a sound-attenuated
room. Participants were seated at a table with the monitor
placed in front of them with a viewing distance of ap-
proximately 60 cm. The experiment, requiring a uniman-
ual go/no-go paradigm, consisted of four experimental
sessions (Hand (cid:1) Parity judgment) in which participants
were asked to make either an odd or an even parity
judgment to one-digit Arabic numerals by pressing a key
aligned with their midline with either their right hand
or left hand. Participants were instructed to give a motor
response, as fast and accurately as possible, when the
stimulus fulfilled the parity criteria response instructions
and refrain from responding when not. The order of ses-
sions was fully counterbalanced across subjects (latin-
square randomization). Stimuli were single Arabic digits
ranging from 1 à 9 (5 excluded), presented one at a time
in the center of the screen and written in black Arial
font on a white screen ((cid:2)0.38 (cid:1) 0.38). Each trial started
with a fixation cue (the ‘‘+’’ symbol) presented during
500 msec, immediately followed by the target number.
The maximum response time was 2 sec. The intertrial
interval, consisting of a blank screen, était 2 sec. For each
session, every digit was presented eight times for a total
de 40 trials organized in a randomized sequence.

Data Analysis

The mean percentage of errors was 1% (SD = 1.21),
no subjects exceeded the limit of 10% of errors. Pour
each participant, median RT values were calculated for
correct trials in relation to each session and numerical
catégorie (c'est à dire., small/odd, ‘‘1/3’’; small/even, ‘‘2/4’’; large/
odd, ‘‘7/9’’; large/even, ‘‘6/8’’). A three-way ANOVA was
conducted on these data with the effector (left or right
main), the parity category (odd/even), and the numer-
ical category (smaller/larger digits) as within-factors.
The significance level was always set at p = .05. UN
Mauchly test showed that the sphericity assumption
was not violated.

Results

Statistical analyses of RTs showed a reliable effect of
the parity category [F(1,21) = 8.17, p < .01], with RTs Figure 2. Average value of normalized MEP amplitudes of the contralateral abductor digiti minimi and abductor pollicis brevis muscles during parity judgment for smaller (1–4) and larger (6–9) numbers and control trials in Experiment B. (A) Stimulation of the left motor cortex; (B) Stimulation of the right motor cortex. Error bars represent standard errors of the mean (n = 8). were entered into a further ANOVA (see Methods). This analysis showed a significant interaction between the side of stimulation and the numerical category [F(1,7) = 6.98, p < .04], but no effect of the numerical category [F(1,7) = 2.06]. Post hoc analysis revealed that the in- teraction was due to the fact that, during stimulation of the left hemisphere, mean MEP amplitudes were larger when processing smaller numbers than when pro- cessing larger numbers ( p < .05), whereas during stimulation of the right hemisphere, mean MEP am- plitudes were not influenced by the two numerical categories ( p > .99). No interaction was observed be-
tween the recorded muscle and the numerical category
[F(1,7) = 0.04], as well as between the recorded mus-
clé, the side of stimulation, and the numerical cate-
gory [F(1,7) = 0.41]. Enfin, neither the effect of the
parity category [F(1,7) = 0.52] nor the interaction be-
tween the parity and numerical categories [F(1,7) =
2.38] was significant. All the remaining interactions were
not significant.

At the end of both TMS experiments, participants
were asked to ‘‘count with their fingers from 1 to 10,’’
without indications on the hand(s) to be used. All sub-
jects but two (14 out of 16) used first their right hand
to count from 1 à 5 and then their left hand to count
depuis 6 à 10. The two other subjects used a counting
strategy involving only the right hand. None of the sub-
jects stated to have used such an embodied strategy to
perform the task during the experimental session.

688

Journal des neurosciences cognitives

Volume 19, Nombre 4

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

F
/

t
t

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

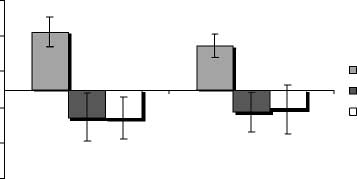
slower when responding for odd than for even num-
bers (average: 456 msec vs. 436 msec), but no reliable
effect of the numerical category [F(1,21) = 3.46] ni
interaction between the two factors [F(1,21) = 1.61].
Enfin, neither significant effect of the hand response
[F(1,21) = 0.01] nor interactions between the indepen-
dent variables were found (voir la figure 3).

As in the TMS experiments, participants were asked
at the end of the behavioral experiment to ‘‘count with
their fingers from 1 to 10,’’ without indications con-
cerning the hand(s) to be used. All subjects but two (22
out of 24) used first their right hand to count from 1 à
5 and then their left hand to count from 6 à 10. The two
other subjects used a counting strategy involving first
the left hand then the right hand. These subjects were
discarded from the analysis.

DISCUSSION

The present results highlight a close relationship be-
tween number and finger cortical representations by
showing a specific increase of the corticospinal excitabil-
ity of the right hand muscles during a visual parity judg-
ment task on Arabic numerals. This excitability increase
was very robust across the two TMS experiments. Three
main results were observed. D'abord, the increase of excit-
ability of right hand muscles was observed only during
the presentation of smaller numbers (1–4), as compared
to larger numbers (6–9) or to a control condition. Sec-
ond, no modulation due to presentation of smaller or
larger numbers was observed when stimulating the right
motor cortex. Troisième, the modulation observed for the
right hand muscles was present 200 msec after the onset
of the number presentation. Because pre-TMS electro-
myography activities showed complete relaxation of
the hand muscles and no participant stated to have used
a strategy based on finger counting to perform the
task, these results clearly demonstrate that number
processing for smaller numbers automatically induces
an increase of the corticospinal excitability of the right
hand muscles.

Chiffre 3. Mean reaction times observed in Experiment 2 according
to the hand response (left/right) and the parity criteria (odd/even).
Error bars represent standard errors of the mean (n = 22).

What is the relation between the numerical judgment
and the enhanced motor output to the right hand mus-
clés, and how can this relationship be explained? In our
voir, the finger/number relation derives from an embod-
ied finger counting strategy developed during numerical
acquisition in childhood to represent, manipulate, et
communicate numbers, and still unconsciously recalled
by adults when dealing with numbers.

Evidence in favor of this interpretation comes from
different sources. Body parts, such as hands, fingers, ou
even toes, appear as a natural means for counting and
representing numbers in many cultures (Butterworth,
1999). At the ontogenetic level, the acquisition of nu-
merical skills and arithmetical knowledge can be seen as
an increasingly sophisticated understanding of numer-
osity that begins well before the development of full
competent language (Butterworth, 2005). From this
voir, developmental research provided converging evi-
dence on the relationship between gesturing and the
acquisition of mathematical knowledge. It is well estab-
léché,
Par exemple, that hand/arm gesturing helps
preschoolers in improving their knowledge of one-to-
one correspondence, and contributes to accurate count-
ing performance (Butterworth, 2005; Alibali & DiRusso,
1999). De la même manière, the study of hand gestures/speech mis-
matches, produced by school children when solving
mathematical problems, showed that they possess math-
ematical knowledge they cannot articulate in speech
(Goldin-Meadow & Wagner, 2005; Goldin-Meadow,
Kim, & Chanteur, 1999; Goldin-Meadow, Alibali, & Church,
1993). Taken together, these findings suggest a tight
connection between the development of symbolic rep-
resentations of numbers and the use of fingers. Plus loin-
plus, in many cultures, manipulating and representing
numbers by means of fingers precedes the use of more
abstract codes, such as the verbal or written codes, et
therefore provides a bridge between the child’s likely
innate capacity for numerosity and more advanced
mathematical achievements (Fuson, 1988; Siegler &
Shrager, 1984). As previously noted, it is also worthwhile
to point out that performance on finger discrimination
tasks (par exemple., digital gnosia and digital discrimination) dans 5-
to 6-year-old children is considered as one of the best
predictor of arithmetic abilities (Fayol et al., 1998).

Another source of evidence for a close relationship
between numbers and hand/finger representations is
given by brain imaging studies. A functional magnetic res-
onance imaging (IRMf) signal increase in the part of the
left precentral gyrus, where hand movements are repre-
sented (Binkofski et al., 1999), was repeatedly reported
during numerical processing. This activation was de-
scribed during additions (Pesenti et al., 2000; Stanescu-
Cosson et al., 2000), multiplications (Zago et al., 2001;
Dehaene et al., 1996), subtractions (Rueckert et al., 1996),
and number comparisons (Pinel et al., 2004; Pesenti et al.,
2000; Dehaene et al., 1996). In agreement with our view,
some authors have suggested that the activations of the

Sato et al.

689

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

F
/

t
t

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

left precentral gyrus, together with those observed in the
parietal cortex, might reflect the involvement of a finger-
movement network, et, par extension, underlie a finger
counting strategy used during the tasks (Zago et al., 2001;
Pesenti et al., 2000). Cependant, because the precentral
gyrus was also found to be activated during a comparative
judgment task on numbers on the basis of their lumi-
nance properties,
it has been argued that this region
might rather reflect response selection and decision
processes (Pinel et al., 2004). In the light of the present
résultats, the fact that the task did not involve any hand
response and, most importantly, that the observed mod-
ulation of the corticospinal excitability of right hand
muscles was strictly related to smaller numbers seems
to rule out the idea that the activation of the precentral
gyrus was exclusively based on response selection and
decision processes. De plus, the fact that the modula-
tion of the corticospinal excitability of the right hand
muscles was observed 200 msec after the onset of the
number presentation suggests that this modulation was
present during early representational processing stages.
The finger embodiment hypothesis has also been di-
rectly investigated in a recent behavioral study where
Italian adults had to identify Arabic digits by pressing 1 de
10 keys with the corresponding finger (Di Luca, Grana,
Semenza, Seron, & Pesenti, 2006). These results showed
que, when any of the 10 fingers can be used, a mapping
congruent with the prototypical finger-counting strategy
reported by the participants (c'est à dire., using first their right
hand to count from 1 à 5 and then their left hand to
count from 6 à 10) leads to better performance than
does a mapping congruent with a left-to-right oriented
mental number line. These results thus provide evidence
that finger-counting strategies may influence the way that
numerical information is mentally represented and pro-
cessed. In our Experiment 2, given that the participants
started to count with their right hand when asked to do
il, one could expect faster responses to smaller numbers
when using the right hand compared to the left one, et
inversement. Cependant, the results did not confirm such
prediction, possibly because number and finger interac-
tions were restricted to unimanual
left or right index
presses. Fait intéressant, both experiments failed to reveal
an interaction between the magnitude of the digit and
the hand used to respond. This finding contradicts the
well-established effect of Spatial–Numerical Association
of Response Code (SNARC) effet, originally described
by Dehaene, Bossini, and Giraux (1993). This effect—
interpreted as evidence that the relative magnitude of
numbers is encoded analogically in terms of left–right
spatial–numerical associations along a mental number
line—refers to the fact that, when participants were
required to make bimanual parity judgments on digits
by pressing a left or a right key, smaller numbers were
responded to faster with the left hand than with the right
main, whereas larger numbers were responded to faster
with the right hand than with the left hand. Although

they do not rule out the existence of numerical repre-
sentation based on a left-to-right oriented mental line,
both our Experiment 2 and the study of Di Luca et al.
(2006) stress the importance of controlling the finger-
counting preference of subjects, together with the ex-
perimental protocol, when studying space and number
interactions.

Although the present TMS findings fit well with these
developmental, behavioral, neuropsychological, et
neuroimaging data, and suggest a close relationship
between number and finger representations, alternative
interpretations of our results have to be discussed.

Firstly, the observed cortical modulation might be due
to possible differences in terms of complexity when
processing smaller and larger numbers. The fact that
RTs were significantly faster when responding to even
numbers than to odd numbers in Experiment 2 may
indeed reflect the higher complexity required for pro-
cessing odd numbers. A similar effect has been previ-
ously reported during a parity judgment task and
attributed to the linguistic complexity of the odd con-
cept (Nuerk, Iversen, & Willmes, 2004; Hines, 1990).
Cependant, the fact that no reliable effect of the parity
category was found in both Experiments 1A and 1B
rules out a possible interpretation of our TMS results
on the basis of a higher complexity for processing odd
numbers.

Deuxièmement, the present modulation was confined to the
left hemisphere and might thus reflect some verbal–
motor components related to covert naming of numbers
or retrieval of numerical knowledge on the basis of ver-
bal routines. Accordingly, an increase in the cortico-
spinal excitability of the right hand muscles has been
previously described during reading aloud (Tokimura,
Tokimura, Oliviero, Asakura, & Rothwell, 1996) and even
during silent reading (Papathanasiou, Filipovic, Whurr,
Rothwell, & Jahanshahi, 2004). The observed increased
motor output might therefore reflect a linguistic contri-
bution of the left hemisphere, with the observed asym-
metry reflecting the lateralized cortical organization
of language. The specificity of the present modulation,
strictly related to smaller numbers, argues against this
hypothèse. Cependant, a more cautious interpretation
of the present results could be based on the lexical
frequency of numbers. En effet, it has been shown that
the lexical frequency of counting words is inversely
correlated with their numerosity: thus, the word one
is more frequent than the word two, two is more fre-
quent than three, and so forth (Dehaene & Mehler,
1992). Donc, one could argue that, because of lower
lexical frequencies, the visual presentation of larger
Arabic digits might activate, to a lesser extent, the sym-
bolic representations involved in covert naming. Comment-
jamais, this prediction does not fit well with our results.
En effet, previous brain imaging studies investigating
the effect of lexical frequency on visual word process-
ing during a lexical decision task have reported an

690

Journal des neurosciences cognitives

Volume 19, Nombre 4

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

increased activation of the left inferior frontal gyrus
for low-frequency words as compared to high-frequency
mots (par exemple., Nakic, Forgeron, Busis, Vythilingam, & Blair,
2006; Prabhakaran, Blumstein, Myers, Hutchison, &
Britton, 2006; Fiebach, Friederici, Muller, & von Cramon,
2002). These results are thought to reflect the role of
the left inferior frontal gyrus in grapheme-to-phoneme
conversion and, more generally, in phonological pro-
cessation, and are consistent with the view that lexical
search for high-frequency words requires less phonolog-
ical mediation because they can be rapidly identified
on the basis of visual word information. En outre, un
recent fMRI study failed to show any significant effects
of low versus high lexical frequency words during read-
ing aloud (Carreiras, Mechelli, & Prix, 2006). Given
these results, it is difficult to interpret the increase in
the corticospinal excitability of the right hand muscles
here reported for smaller numbers as compared to
larger numbers as reflecting greater demand on lexical/
phonological processes involved in covert naming. Fur-
thermore, this interpretation based on lexical frequency
does not appear to be in accordance with the results
of Experiment 1B, in which no significant differences
between larger numbers and control trials were found
when stimulating the left motor cortex.

Another possible interpretation of our results could
come from an elegant neuroimaging study by Long-
camp, Anton, Roth, and Velay (2003), montrant que
the visual presentation of letters automatically activates
writing-related areas in the left premotor cortex. Le
increased corticospinal excitability found in the present
study could then result from the implicit activation of
handwriting movements in response to the visual pre-
sentation of digits. Cependant, the absence of modulation
between larger numbers and control trials observed in
Experiment 1B makes this interpretation unlikely.

Ainsi, although the present study does not allow
to fully reject a linguistic contribution of the left hemi-
sphère, either through covert naming of the presented
number or by implicit activation of handwriting move-
ments, this modulation is much more likely to reflect
the more frequent use of a finger embodiment strategy
for representing smaller numbers. Accordingly, the use
of the embodiment strategy should then primarily in-
volve, at least for right-handed subjects, the right hand
rather than the left one. This is particularly evident
during childhood. At an early stage, it is obvious that
representing numbers by means of finger is firstly re-
stricted to numbers from 1 à 5 (Butterworth, 2005;
Gelman & Gallistel, 2004). This period is considered to
be crucial for the acquisition of meanings of cardinal
numbers and, donc, might represent a fundamental
passage toward the development of a mature language-
based counting system and the mastery of arithmetical
opérations. Also consistent with this view is the fasci-
nating case report of a child who was born without
forearms but experienced phantom hands and actually

used their phantom fingers to count and solve arith-
metic problems (Poek, 1969, cited by Ramachandran &
Hirstein, 1998).

Enfin, an important question raised by the present
study concerns the specificity of the effect. En effet, le
use of only one ordinal sequence, that of numbers, does
not allow us to distinguish between number-related
processes in particular and ordinal sequence processing
in general (par exemple., when processing months, days of the
week, or letters) for which the necessity of a one-to-one
mapping is the common factor. Further experiments are
required to test whether ordinal sequences other than
numbers might also be embodied to some degree in the
sensory–motor system.

In conclusion, we suggest that the present results may
reflect a trace, an echo, of a finger embodiment strategy,
developed in childhood and used to represent and
manipulate numbers. This strategy, constrained by our
bodily experience (Lakoff & Nunez, 2000) and mapped
within the sensory–motor system, might still be auto-
matically evoked during number processing.

Remerciements

This work was supported by MIUR (Ministero Italiano
dell’Istruzione, dell’Universita e della Ricerca) et, as part of
the European Science Foundation EUROCORES Programme
OMLL, was supported by funds to V. G. and G. R.. from the
Italian C.N.R.

Reprint requests should be sent to Marc Sato, School of Com-
munication Sciences and Disorders, Center for Research on
Langue, Esprit, and Brain, 3640 rue de la Montague, Montre´al,
Québec, Canada H3G 2 A8, ou par e-mail: marc.sato@mail.
mcgill.ca.

RÉFÉRENCES

Alibali, M.. W., & DiRusso, UN. UN. (1999). The function of

gesture in learning to count: More than keeping track.
Cognitive Development, 14, 37–56.

Binkofski, F., Buccino, G., Posse, S., Seitz, R.. J., Rizzolatti, G.,
& Freund, H. J.. (1999). A fronto-parietal circuit for object
manipulation in man: Evidence from an fMRI-study.
European Journal of Neuroscience, 11, 3276–3286.
Butterworth, B. (1999). The mathematical brain. Londres:

Macmillan.

Butterworth, B. (2005). The development of arithmetical

abilities. Journal of Child Psychology and Psychiatry, 46,
3–18.

Carreiras, M., Mechelli, UN., & Prix, C. J.. (2006). Effect of word
and syllable frequency on activation during lexical decision
and reading aloud. Human Brain Mapping, 27, 963–972.
Chochon, F., Cohen, L., van de Moortele, P.. F., & Dehaene, S.

(1999). Differential contributions of the left and right
inferior parietal lobules to number processing. Journal
of Cognitive Neuroscience, 11, 617–630.

Dehaene, S. (1996). The organization of brain activations in
number comparison: Event-related potentials and the
additive-factors method. Journal des neurosciences cognitives,
8, 47–68.

Dehaene, S. (1997). The number sense. New York: Oxford

Presse universitaire.

Sato et al.

691

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

Dehaene, S., Bossini, S., & Giraux, P.. (1993). The mental

representation of parity and number magnitude. Journal
of Experimental Psychology: General, 122, 371–396.
Dehaene, S., & Cohen, L. (1997). Cerebral pathways for
calculation: Double dissociation between rote verbal
and quantitative knowledge of arithmetic. Cortex, 33,
219–250.

Dehaene, S., & Mehler, J.. (1992). Cross-linguistic regularities
in the frequency of number words. Cognition, 43, 1–29.
Dehaene, S., Molko, N., Cohen, L., & Wilson, UN. J.. (2004).

Arithmetic and the brain. Current Opinion in
Neurobiology, 214, 218–224.

Dehaene, S., Piazza, M., Pinel, P., & Cohen, L. (2003).

Three parietal circuits for number processing. Cognitive
Neuropsychology, 20, 487–506.

Dehaene, S., Tzourio, N., Frack, F., Raynaud, L., Cohen, L.,

Mehler, J., et autres. (1996). Cerebral activations during
number multiplications and comparisons: A PET study.
Neuropsychologie, 34, 1097–1106.

Delazer, M., & Benke, T. (1997). Arithmetic facts without

meaning. Cortex, 33, 697–710.

Di Luca, S., Grana, UN., Semenza, C., Seron, X., & Pesenti, M..

(2006). Finger-digit compatibility in Arabic numeral
traitement. Quarterly Journal of Experimental Psychology,
59, 1648–1663.

Eger, E., Sterze, P., Russ, M.. O., Giraud, UN. L., & Kleinschmidt,

UN. (2003). A supramodal number representation in
human intraparietal cortex. Neurone, 37, 719–725.

Fayol, M., Barouillet, P., & Marinthe, C. (1998). Predicting

arithmetical achievement from neuropsychological
performance: A longitudinal study. Cognition, 68, 63–70.

Feigenson, L., Dehaene, S., & Jeux, E. (2004). Core

systems of number. Tendances des sciences cognitives, 8,
307–314.

Fiebach, C. J., Friederici, UN. D., Muller, K., & von Cramon,

D. Oui. (2002). fMRI evidence for dual routes to the mental
lexicon in visual word recognition. Journal of Cognitive
Neurosciences, 14, 11–23.

Fuson, K. C. (1988). Children’s counting and concept of

number. New York: Springer.

Gelman, R., & Butterworth, B. (2004). Number and language:
How are they related. Tendances des sciences cognitives, 9,
7-dix.

Gelman, R., & Gallistel, C. R.. (2004). Language and the origin

of numerical concepts. Science, 306, 441–443.

Gerstmann, J.. (1924). Fingeragnosie: Eine umbschriebene
stoerung der orienterung am eigenen koerper. Wiener
Clinische Whochenschrift, 37, 1010–1012.

Gerstmann, J.. (1940). Syndrome of finger agnosia:

Disorientation for right and left, agraphia and acalculia.
Archives of Neurology and Psychiatry, 44, 398–408.
Goldin-Meadow, S., Alibali, M.. W., & Church, B. B. (1993).
Transitions in concept acquisition: Using the hand to
read the mind. Psychological Review, 100, 279–297.
Goldin-Meadow, S., Kim, S., & Chanteur, M.. (1999). What

the teacher’s hands tell the student’s mind about math.
Journal of Educational Psychology, 91, 720–730.

Goldin-Meadow, S., & Wagner, S. M.. (2005). How our hands
help us learn. Tendances des sciences cognitives, 9, 234–241.

Gordon, P.. (2004). Numerical cognition without words:

Evidence from amazonia. Science, 306, 496–499.
Hauk, O., Davis, M.. H., Ford, M., Pulvermuller, F., &

Marslen-Wilson, W. D. (2006). The time course of visual
word recognition as revealed by linear regression analysis
of ERP data. Neuroimage, 30, 1383–1400.

Hines, T. M.. (1990). An odd effect: Lengthened reaction

times for judgments about odd digits. Mémoire & Cognition,
18, 40–46.

Kinsbourne, M., & Warrington, E. K. (1963). The developmental
Gerstmann syndrome. Annales de neurologie, 8, 490–501.

Lakoff, G., & Nunez, R.. E. (2000). Where mathematics

comes from. New York: Livres de base.

Lemer, C., Dehaene, S., Jeux, E., & Cohen, L. (2003).
Approximate quantities and exact number words:
Dissociable systems. Neuropsychologie, 41, 1942–1958.
Longcamp, M., Anton, J.. L., Roth, M., & Velay, J.. L. (2003).
Visual presentation of single letters activates a premotor
area involved in writting. Neuroimage, 19, 1492–1500.

Mayer, E., Martory, M.. D., Pegna, UN. J., Landis, T., Delavelle, J.,
& Annoni, J.. M.. (1999). A pure case of Gerstmann syndrome
with a subangular lesion. Cerveau, 122, 1107–1120.

Mills, K. R., Boniface, S. J., & Schubert, M.. (1992). Magnetic
brain stimulation with a double coil: The importance of
coil orientation. Electroencephalography and Clinical
Neurophysiologie, 85, 17–21.

Nakic, M., Forgeron, B. W., Busis, S., Vythilingam, M., & Blair,
R.. J.. R.. (2006). The impact of affect and frequency on
lexical decisions: The role of the amygdala and inferior
frontal cortex. Neuroimage, 31, 1752–1761.

Nieder, UN. (2005). Counting on neurons: The neurobiology
of numerical competence. Nature Revues Neurosciences,
6, 177–190.

Nuerk, H. C., Iversen, W., & Willmes, K. (2004). Notational

modulation of the SNARC and MARC (linguistic markedness
of response codes) effet. Quarterly Journal of
Experimental Psychology, Series A, 57, 835–863.
Oldfield, R.. C. (1971). The assessment and analysis of

handedness: The Edinburgh inventory. Neuropsychologie,
9, 97–114.

Papathanasiou, JE., Filipovic, S. R., Whurr, R., Rothwell, J.. C.,
& Jahanshahi, M.. (2004). Changes in corticospinal motor
excitability induced by non-motor linguistic tasks.
Experimental Brain Research, 154, 218–225.

Pesenti, M., Thioux, M., Seron, X., & de Volder, UN. (2000).

Neuroanatomical substrates of arabic number processing,
numerical comparison and simple addition: A PET study.
Journal des neurosciences cognitives, 12, 461–479.

Pica, P., Lemer, C., Izard, V., & Dehaene, S. (2004). Exact
and approximate arithmetic in an amazonian indigene
group. Science, 306, 499–503.

Pinel, P., Piazza, M., Le Bihan, D., & Dehaene, S. (2004).

Distributed and overlapping representations of number,
size, and luminance during comparative judgments.
Neurone, 41, 983–993.

Poeck, K. (1969). Phantom limbs after amputation and in

congenital missing limbs. Deutsche Medizinische
Wochenschrift, 94, 2367–2374.

Prabhakaran, R., Blumstein, S. E., Myers, E. B., Hutchison, E.,
& Britton, B. (2006). An event-related fMRI investigation
of phonological–lexical competition. Neuropsychologie,
44, 2209–2221.

Pulvermuller, F., Shtyrov, Y., & Ilmoniemi, R.. (2005). Cerveau
signatures of meaning access in action word recognition.
Journal des neurosciences cognitives, 17, 884–892.

Ramachandran, V. S., & Hirstein, W. (1998). The perception

of phantom limbs. Cerveau, 121, 1603–1630.

Rossini, P.. M., Barker, UN. T., Berardelli, UN., Caramia, M.. D., Caruso,
G., Cracco, R.. Q., et autres. (1994). Non-invasive electrical and
magnetic stimulation of the brain, spinal cord and roots: Basic
principles and procedures for routine clinical application.
Report of an IFCN committee. Electroencephalography
and Clinical Neurophysiology, 91, 79–92.

Rueckert, L., Lange, N., Partiot, UN., Appolonio, JE., Litvan, JE.,
Le Bihan, D., et autres. (1996). Visualizing cortical activation
during mental calculation with functional MRI. Neuroimage,
3, 97–103.

692

Journal des neurosciences cognitives

Volume 19, Nombre 4

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

F
/

t
t

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

Rusconi, E., Walsh, V., & Butterworth, B. (2005). Dexterity
with numbers: rTMS over left angular gyrus disrupts
finger gnosis and number processing. Neuropsychologie,
43, 1609–1624.

Temple, E., & Posner, M.. je. (1998). Brain mechanisms of
quantity are similar in 5-year-old children and adults.
Actes de l'Académie nationale des sciences, USA.,
95, 7836–7841.

Siegler, R.. S., & Shrager, J.. (1984). Strategy choices in addition

Tokimura, H., Tokimura, Y., Oliviero, UN., Asakura, T., & Rothwell,

and subtraction: How do children know what to do?
In C. Sophian (Ed.), Origin of cognitive skills. Hillsdale,
New Jersey: Erlbaum.

Simon, O., Mangin, J.-F., Cohen, L., Le Bihan, D., & Dehaene, S.

(2002). Topographical layout of hand, eye, calculation,
and language-related areas in the human parietal lobe.
Neurone, 33, 475–487.

Stanescu-Cosson, R., Pinel, P., van de Moortele, P.-F., Le Bihan,

D., Cohen, L., & Dehaene, S. (2000). Compréhension
dissociations in dyscalculia: A brain imaging study of the
impact of number size on the cerebral networks for exact
and approximate calculation. Cerveau, 123, 2240–2255.

Suresh, P.. UN., & Sebastian, S. (2000). Developmental
Gerstmann’s Syndrome: A distinct clinical entity of
learning disabilities. Pediatric Neurology, 22, 267–278.

J.. C. (1996). Speech-induced changes in corticospinal
excitability. Annales de neurologie, 40, 628–634.

Wassermann, E. M.. (1998). Risk and safety of repetitive

transcranial magnetic stimulation: Report and suggested
guidelines from the international workshop on the
safety of repetitive transcranial magnetic stimulation,
June 5–7, 1996. Electroencephalography and Clinical
Neurophysiologie, 108, 1–16.

Blanc, E. J., & Flanders, M.. (2004). Muscular and postural

synergies of the human hand. Journal de neurophysiologie,
92, 523–535.

Zago, L., Pesenti, M., Mellet, E., Crivello, F., Mazoyer, B.,
& Tzourio-Mazoyer, N. (2001). Neural correlates of
simple and complex mental calculation. Neuroimage,
13, 314–327.

D
o
w
n
je
o
un
d
e
d

F
r
o
m

/
j

t
t

F
/

je
t
.

:
/
/

/
j

o
n

1
8

M.
un
oui

2
0
2
1

Sato et al.

693 Numbers within Our Hands: Modulation of image

Télécharger le PDF