Near-optimal Integration of Magnitude
in the Human Parietal Cortex
Hannah Tickle1, Maarten Speekenbrink1, Konstantinos Tsetsos2,
Elizabeth Michael2, and Christopher Summerfield2
Abstrait
■ Humans are often observed to make optimal sensorimotor
decisions but to be poor judges of situations involving explicit
estimation of magnitudes or numerical quantities. Par exemple,
when drawing conclusions from data, humans tend to neglect
the size of the sample from which it was collected. Ici, nous
asked whether this sample size neglect is a general property
of human decisions and investigated its neural implementation.
Participants viewed eight discrete visual arrays (samples) de-
picting variable numbers of blue and pink balls. They then
judged whether the samples were being drawn from an urn
in which blue or pink predominated. A participant who neglects
the sample size will integrate the ratio of balls on each array,
giving equal weight to each sample. Cependant, we found that
human behavior resembled that of an optimal observer, giving
more credence to larger sample sizes. Recording scalp EEG sig-
nals while participants performed the task allowed us to assess
the decision information that was computed during integration.
We found that neural signals over the posterior cortex after
each sample correlated first with the sample size and then with
the difference in the number of balls in either category. Plus-
over, lateralized beta-band activity over motor cortex was pre-
dicted by the cumulative difference in number of balls in each
category. Ensemble, these findings suggest that humans achieve
statistically near-optimal decisions by adding up the difference
in evidence on each sample, and imply that sample size neglect
may not be a general feature of human decision-making. ■
INTRODUCTION
Decisions often involve integration of evidence from mul-
tiple sources. Optimal choices are made when information
is weighted by the trustworthiness (or reliability) of each
source. When human sensorimotor behavior is refined
through experience, it often resembles that of an ideal ob-
server (Pouget, Beck, Mame, & Latham, 2013; Kording, 2007).
Par exemple, humans pointing toward a target assign more
weight to prior knowledge about its location when sensory
evidence is indistinct, as an ideal observer should (Kording
& Wolpert, 2004). Humans and monkeys can learn to
weight a train of symbolic cues in direct proportion to
the informativeness with which they predict a rewarded re-
sponse (Gould, Nobre, Wyart, & Rushworth, 2012; Wyart,
de Gardelle, Scholl, & Summerfield, 2012; Lequel & Shadlen,
2007). When visual and haptic cues offer potentially con-
flicting information about the size of an object, visual infor-
mation is less influential when corrupted by noise (Ernst &
Banks, 2002). These findings have prompted the claim that
humans and monkeys have evolved to make optimal deci-
sions, c'est, those that account for the relative uncertainty
associated with each source of choice-relevant information.
Cependant, human choices are not always optimal. Pour
exemple, when asked to evaluate hypothetical scenarios
involving numerical magnitudes, humans often make
1University College London, 2University of Oxford
© 2016 Massachusetts Institute of Technology
biased or inaccurate responses (Griffin & Tversky, 1992).
Consider the problem of estimating whether men out-
number women on a university degree course. The ap-
proximate male–female ratio from a small seminar group
is a less reliable estimator than that from a large lecture
class, because our confidence in an estimate should be
determined by its standard error, which is inversely related
to n, c'est, to the sample size. Given both observations
(small seminar vs. large lecture), an optimal solution to this
problem—which is given by combining the binomial prob-
ability associated with each sample—will afford the larger
sample more weight; simply averaging the two ratios may
lead to a biased decision. Cependant, when confronted with
problems of this nature, humans are excessively reliant on
the relative balance of evidence, overlooking the infor-
mation about sample size and drawing erroneous conclu-
sions from data (Griffin & Tversky, 1992; Kahneman,
Slovic, & Tversky, 1982). Nor is this phenomenon limited
to binomial estimation problems; when asked to judge
whether the average height of a group of humans exceeds
a fixed value, humans disregard whether the group is com-
posed of 10, 100, ou 1000 individuals. Even researchers
who use statistics regularly to evaluate data have been
observed to display this “sample size neglect” (Tversky &
Kahneman, 1971).
Why, alors, do humans account for the reliability of in-
formation in some situations and not in others? One possi-
bility is that simple sensorimotor decisions (par exemple., pointing
Journal des neurosciences cognitives 28:4, pp. 589–603
est ce que je:10.1162/jocn_a_00918
D
o
w
n
je
o
un
d
e
d
F
r
o
m
je
je
/
/
/
/
j
F
/
t
t
je
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
je
n
t
o
p
un
r
d
c
e
.
d
s
F
je
r
o
je
m
v
e
h
r
c
p
h
un
d
je
je
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
un
n
r
un
t
r
je
t
je
c
c
je
e
e
–
p
–
d
p
d
2
F
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
un
/
_
j
0
o
0
c
9
n
1
8
_
un
p
_
d
0
0
b
9
oui
1
g
8
u
.
e
p
s
t
d
o
F
n
b
0
oui
7
S
M.
e
je
p
T
e
m
L
je
b
b
e
r
r
un
2
r
0
je
2
3
e
s
/
j
t
F
.
/
u
s
e
r
o
n
1
7
M.
un
oui
2
0
2
1
toward a target) and higher-level cognitive judgments (par exemple.,
estimating gender ratios) rely on qualitatively distinct com-
putations. Par exemple, optimal performance might be
possible when uncertainty arises early in processing (par exemple.,
from sensory noise), but neglect of sample size might oc-
cur when judgments are limited by more cognitive factors.
Alternativement, sample size neglect might not be a ubiquitous
phenomenon but might depend instead on contextual fac-
tors, such as the format in which the decision information
is provided. Par exemple, sample size neglect might occur
when decision problems are presented as descriptions of
hypothetical scenarios, but not when participants learn to
make decisions in an experience-dependent fashion, que
est, through feedback that reveals whether a classification
judgment was correct or incorrect (Hertwig & Erev, 2009).
Ici, we asked whether humans performing a psycho-
physical task display sample size neglect or whether they
integrate information about numerical magnitudes opti-
mally. Our task was an expanded judgment task, variants
of which have previously been used to interrogate informa-
tion integration during perceptual decision-making (Wyart,
de Gardelle, et coll., 2012; Lequel & Shadlen, 2007). Our ap-
proach thus investigates sample size neglect via an ex-
perimental framework that has been widely used to
understand the neural and computational mechanisms by
which perceptual inputs are integrated and categorized
(Gold & Shadlen, 2007). Observers viewed a succession
of eight discrete visual events (“samples”) in which a vari-
able number of pink and blue balls were displayed and sub-
sequently decided whether they had been drawn from a
larger pool of predominantly pink or predominantly blue
balls. Our initial question was whether humans gave more
credence to samples that contained more balls. For exam-
ple, consider two different samples each offering a 2:1 ratio
of blue–pink balls, one with three balls (two blue, un
pink) and one with 12 balls (eight blue, four pink). If hu-
mans exhibit a sample size bias, their choices would reflect
the integration of these ratios of evidence (c'est à dire., they would
weight samples with 3 et 12 balls equally). Cependant, si
humans are optimal, they will give more weight to samples
with more balls.
We initially predicted that humans would show sample
size neglect during integration of magnitude information.
Cependant, we found strong support for the opposing hy-
pothesis: Human choices were “near optimal,” in that
their choices resembled those that might be made by
an ideal observer (in this case, one who was calculating
the binomial probability of the dots on each sample be-
ing drawn from one urn as opposed to the other). In the
light of this finding, we turned our attention to under-
standing how this behavior might be achieved at the neu-
ral and computational levels. In our task, two simple
strategies would allow participants to arrive at the near-
optimal solution. D'abord, participants could add up the ab-
solute evidence for either response, by integrating the
blue and pink dots independently and comparing the re-
sulting tallies (we call this the tally model; it is related to
the “race” model of perceptual decision-making; Forgeron &
Vickers, 1988; Vickers, 1979). Alternativement, participants
could add up the relative evidence for either choice, par
integrating the difference in the number of blue or pink
dots on each sample (we call this the difference model;
it is related to the drift diffusion model of perceptual
choice; Ratcliff & McKoon, 2008). Because the behavioral
data did not allow us to arbitrate among these possibilities,
we turned to neural recordings and measured the scalp
EEG while participants performed the task. Although we
observed a correlate of the absolute number of pink or
blue dots over posterior electrode sites, this was rapidly
followed by a correlate of their relative difference. Sur
centroparietal sites previously implicated in perceptual cat-
egorization, we observed stronger correlates of both the
momentary and integrated difference signal. Ensemble,
these findings suggest that humans solved the task by ac-
cumulating the relative difference in magnitudes of evi-
dence on each sample, allowing them to perform the
task near-optimally via a computationally tractable
strategy.
MÉTHODES
Participants
Fifty-four participants (31 femmes, 23 men) were recruit-
éd. All reported normal or corrected-to-normal vision and
no history of neurological or psychiatric disorders and
gave written informed consent in accordance with local
ethical guidelines. Participants for the behavioral pilot
(n = 15) and control experiment (n = 19) received
£10 in compensation, and those undergoing EEG (n =
20) received £25. Data from four EEG participants were
excluded (before preprocessing) because of excessive
movement and/or electrical interference, leaving n =
16 for that experiment. For behavioral analyses, we in-
cluded all pilot and valid EEG participants (total n = 31).
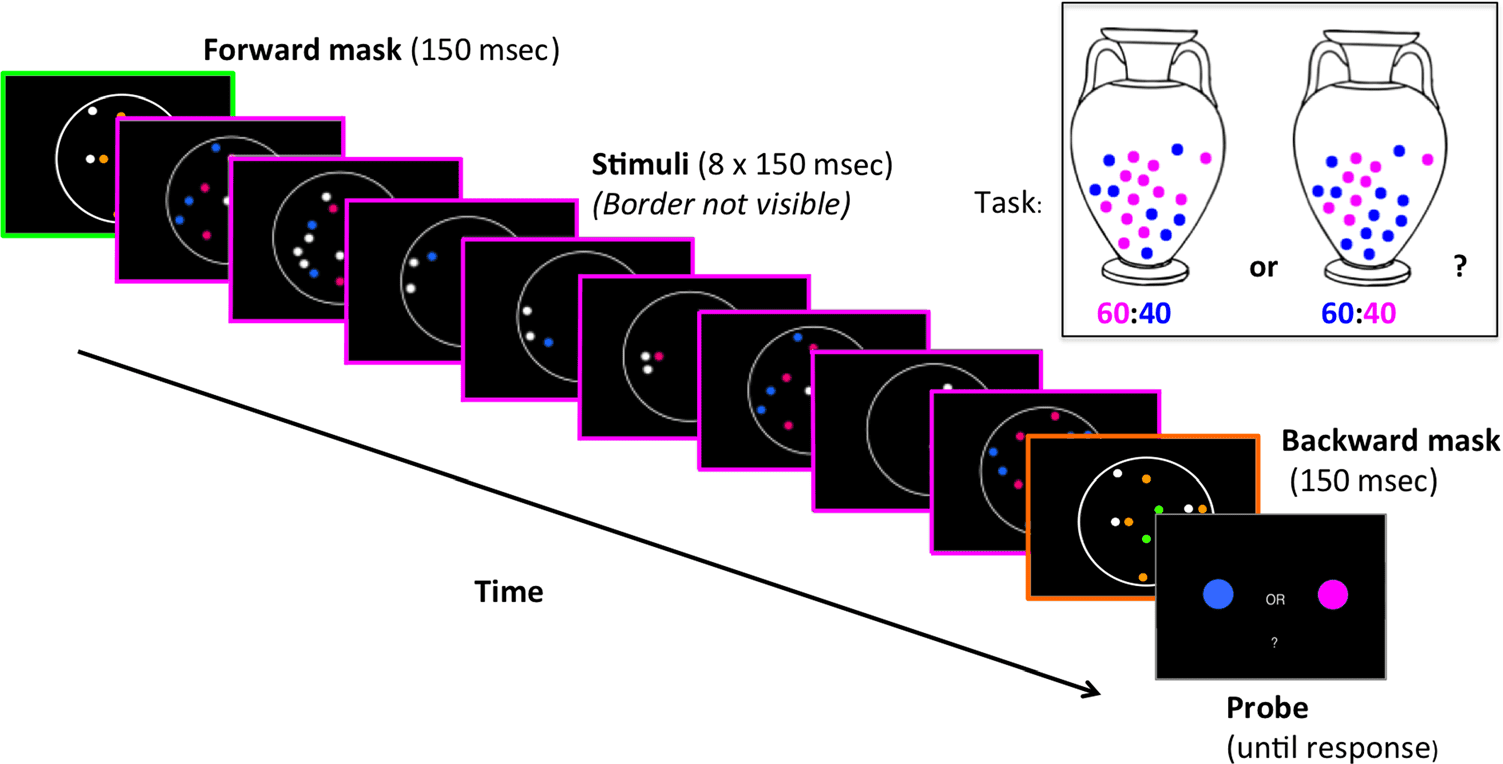
Task Design and Stimuli
In both behavioral and EEG experiments, participants
completed a probabilistic decision-making task (Chiffre 1).
On each trial, one of two virtual “urns” was pseudoran-
domly selected: either one with a 60:40 predominance
of pink balls (50% trials) or one with a 60:40 predomi-
nance of blue balls (50% trials). Eight draws (with re-
placement) de 2, 4, 6, 8, 10, ou 12 balls were made
from the relevant urn. The blue and pink balls drawn
were represented as dots in a circular aperture on each
of the eight sample screens for each trial. After viewing
the eight samples, participants indicated whether the
samples were drawn from the predominantly pink urn
or predominantly blue urn.
The visual stimuli were presented using the Psychophys-
ics 3 Toolbox (Brainard, 1997) running in MATLAB (Le
MathWorks, Natick, MA) on a 17-in. CRT monitor with
590
Journal des neurosciences cognitives
Volume 28, Nombre 4
D
o
w
n
je
o
un
d
e
d
F
r
o
m
je
je
/
/
/
/
j
t
t
F
/
je
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
je
n
t
o
p
un
r
d
c
e
.
d
s
F
je
r
o
je
m
v
e
h
r
c
p
h
un
d
je
je
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
un
n
r
un
t
r
je
t
je
c
c
je
e
e
–
p
–
d
p
d
2
F
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
un
/
_
j
0
o
0
c
9
n
1
8
_
un
p
_
d
0
0
b
9
oui
1
g
8
u
.
e
p
s
t
d
o
F
n
b
0
oui
7
S
M.
e
je
p
T
e
m
L
je
b
b
e
r
r
un
2
r
0
je
2
3
e
s
/
j
/
t
.
F
u
s
e
r
o
n
1
7
M.
un
oui
2
0
2
1
Chiffre 1. Experimental
protocol. Each trial commenced
with a blank black screen for
1 sec, followed by a central
fixation cross for 1 sec. Eight
draws (with replacement) de 2,
4, 6, 8, 10, ou 12 balls were
made from a virtual “urn” either
avec un 60:40 predominance of
pink balls (50% trials) or with a
60:40 predominance of blue
balls (50% trials), and each draw
was represented on screen as
colored dots within a circular
aperture. Each screen also
contained between one and six
white distractor dots and was
displayed for 150 msec with
150-msec ISI. These target
screens were preceded and
followed by a forward and
backward mask created in an identical fashion, except that the colored dots were orange and green, and participants were instructed to ignore them.
At the end of the sample series, participants saw a screen prompting them to respond with a keyboard press. Feedback was given on each trial, avec un
high-pitched (800 Hz) tone for correct response and low-pitched (400 Hz) for incorrect response.
resolution of 1024 × 768 pixels and a refresh rate of 60 Hz.
All stimuli were presented on a black background. Partici-
pants viewed the stimuli in a quiet darkened room approx-
imately 70 cm from the screen. Before the experiment
began, instructions were presented to participants on
screen, including a visual cue indicating the ratio of pink–
blue balls in the two urns. Each trial began with a white
central fixation cross with lines of length 60 pixels (pour
1000 msec), followed by a blank screen (1000 msec). Sub-
sequently, participants viewed a forward mask, eight se-
quentially occurring sample screens, and a backward
mask, each occurring for 150 msec with 150-msec ISI. Chaque
sample screen consisted of an array of blue, pink, and white
dots, chaque 20 pixels in diameter, randomly spatially distrib-
uted (minimum separation of 10 pixels) among 71 possible
locations within a circular aperture of 300-pixel diameter.
The number of blue and pink dots was determined by ran-
domly drawing between 2 et 12 balls from one of two vir-
tual urns as described above. White balls were distracters,
which served to decorrelate decision information from
low-level visual input; one to six white balls were randomly
added to each sample. The mask screens were identical to
sample screens except that the colored balls were green
and orange, and participants were instructed to ignore
eux. These screens helped ensure that participants were
not unduly swayed by the first or last sample (c'est à dire., avoided
perceptual primacy/recency effects).
After the presentation of the samples, participants in-
dicated via a key press whether they thought the balls on
that trial were drawn from the mainly pink urn (“m” key,
with the right hand) or from the mainly blue urn (“z” key,
with the left hand). Auditory feedback was given with a
high tone (800 Hz) for correct answers and a low tone
(400 Hz) for incorrect answers. Before they began the
task, participants were given clear instructions, a visual
representation of the decision problem and urns, et
two practice trials with feedback.
The behavioral pilot differed from the EEG experiment in
three ways: (je) the presentation time and ISI were 250 msec
each rather than 150 msec, (ii) each participant completed
288 plutôt que 570 trials, et (iii) the forward and back-
ward masks were omitted.
Statistically Optimal Solution
Let us denote the number blue and pink balls on sample
k as d1k and d2k, respectivement, with nk = d1k + d2k. Le
probability of drawing a blue ball from Urn 1 (predomi-
nantly blue) was p, and the probability of drawing a blue
ball from Urn 2 (predominantly pink) était 1 − p. Le
converse was true for pink balls. By design, p = .6.
The statistically optimal solution to the task is given by
the integration of binomial probabilities. For any sample
k, the likelihood that the balls are drawn from the blue
urn is given by
p0
k
Þ
¼ B d1k; nk; p
ð
The optimal decision rule is defined by whether the sum
of the log likelihood ratios of each sample coming from
either urn is greater or less than zero. On any sample k,
the evidence or optimal decision update (DU) for or
against each response can be quantified as the log-
likelihood ratio:
(cid:1)
B d1k; nk; p
Þ
ð
ð
B d1k; nk; 1−p
(cid:3)
Þ
enregistrer
Tickle et al.
591
D
o
w
n
je
o
un
d
e
d
F
r
o
m
je
je
/
/
/
/
j
F
/
t
t
je
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
je
n
t
o
p
un
r
d
c
e
.
d
s
F
je
r
o
je
m
v
e
h
r
c
p
h
un
d
je
je
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
un
n
r
un
t
r
je
t
je
c
c
je
e
e
–
p
–
d
p
d
2
F
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
un
/
_
j
0
o
0
c
9
n
1
8
_
un
p
_
d
0
0
b
9
oui
1
g
8
u
.
e
p
s
t
d
o
F
n
b
0
oui
7
S
M.
e
je
p
T
e
m
L
je
b
b
e
r
r
un
2
r
0
je
2
3
e
s
/
j
F
t
.
/
u
s
e
r
o
n
1
7
M.
un
oui
2
0
2
1
Models of Evidence Integration
We considered three models of evidence integration and
choice that human observers could be using to solve the
task: a suboptimal model and two models that arrived at
the statistically optimal solution via two qualitatively dif-
ferent computations. Ainsi, these latter two make identi-
cal behavioral predictions but different predictions about
the neural activity that would accompany each sample.
We first defined the suboptimal model, one in which ev-
idence was not weighted by sample size. In the ratio
model, the momentary DU, DUk,ratio, was based on the
log ratio of blue-to-pink dots:
DUk;ratio ¼ log
(cid:3)
(cid:1)
d1k
d2k
Ainsi, the ratio model ignores the sample size: For exam-
ple, the same value of DU is obtained for d1k = 1 et
d2k = 3 (where the number of balls nk = 4) as for d1k =
3 and d2k = 9 (where nk = 12). Choices were made
according to whether the decision variable (DV), DVratio,
was greater or less than zero:
X
DVratio ¼
8
k¼1
DUk;ratio
This policy accounts for the behavior of participants in
the experiments of Tversky and colleagues described
au-dessus de.
Suivant, we considered two models that are formally
equivalent to the statistically optimal solution but that
solve the task via more biologically plausible mecha-
nisms. We call these the difference and tally models.
The difference model computes the difference between
the number of blue and pink dots on each sample and
adds up these differences to form the DV. Choices are
then made according to whether this DV is greater or less
than zero:
DUdifference ¼ d1k−d2k
DVdifference ¼
X
8
k¼1
DUk;différence
This model predicts that brain signals accompanying
each sample should correlate with the difference
between the number of pink dots and the number of
blue dots, c'est, d1k − d2k.
Par contre, the tally model adds up the number of blue
and pink dots in each stream without computing their dif-
ference. This model thus computes two momentary DVs
for each sample, and the choice is made according to
whether the sum of blue dots (DU1) exceeds the sum of
pink dots (DU2) or vice versa (c'est à dire., according to the sign
of the DV):
DU1tally ¼ d1k
DU2tally ¼ d2k
DVtally ¼
X
8
k¼1
DU1tally−
X
8
k¼1
DU2tally
This model predicts that brain signals accompanying
each sample should correlate with the total number of
blue dots and the total number of pink dots, c'est,
d1k and d2k.
Ainsi, although the quantity DV on which decisions are
based is identical for the difference and tally models, être-
cause they arrive at this DV via different computations
they make different predictions about the neural activity
that will accompany each sample. The difference and tally
models are related (but not identical) to the diffusion
and race models often used to model RTs in psychophys-
ical tasks (Ratcliff & McKoon, 2008; Forgeron & Vickers, 1989;
Vickers, 1979).
For comparison with human data, DVmodel was cor-
rupted with values drawn from a Gaussian distribution,
with mean of zero and a standard deviation of σ, before
being used to generate categorical (model) choices. Le
noise parameter σ was fit to group performance sepa-
rately for the tally and difference models versus the ratio
model but yielded very similar values (in log units: 0.51 pour
the ratio model and 0.59 for the tally and difference
modèles). Note that varying this parameter simply changed
overall model performance without affecting the quali-
tative pattern of results. The distributions of DV associated
with the tally and difference models were very similar;
each was roughly normally distributed and ranged from
−3 to 3 in log units.
Behavioral Analyses
We compared human and model performance in a
number of ways. D'abord, we plotted psychometric func-
tions to envisage how the probability of responding
pink, p(pink), varied as a function of the DVs predicted
by the ratio, différence, and tally models (each binned
into deciles). Deuxième, we used probit regression model
to estimate the influence that each of the sample posi-
tion (from first to last in the sequence) had on choice
and plotted how p(pink) was predicted by the number
of blue and pink balls on each of the eight samples, comme
follows:
je
Þ ¼ ϕ b þ
X
ð
p pink
8
k¼1
where ϕ denotes the standard normal cumulative distri-
bution function.
wk⋅d1k þ wk⋅d2k
Enfin, we tested how the influence of each sample on
choice differed as a function of the total number of dots,
d1k + d2k = nk. The ratio model predicts that all samples
should have the same weight, irrespective of nk. The dif-
ference and tally models predict that the weight carried
by each sample should increase as a function of nk, dans
line with the statistically optimal (binomial) processus. Sur
each trial, we sorted the eight samples according to nk, depuis
lowest to highest, denoting the rank of each sample j, et
m
592
Journal des neurosciences cognitives
Volume 28, Nombre 4
D
o
w
n
je
o
un
d
e
d
F
r
o
m
je
je
/
/
/
/
j
F
/
t
t
je
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
je
n
t
o
p
un
r
d
c
e
.
d
s
F
je
r
o
je
m
v
e
h
r
c
p
h
un
d
je
je
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
un
n
r
un
t
r
je
t
je
c
c
je
e
e
–
p
–
d
p
d
2
F
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
un
/
_
j
0
o
0
c
9
n
1
8
_
un
p
_
d
0
0
b
9
oui
1
g
8
u
.
e
p
s
t
d
o
F
n
b
0
oui
7
S
M.
e
je
p
T
e
m
L
je
b
b
e
r
r
un
2
r
0
je
2
3
e
s
/
j
F
t
/
.
u
s
e
r
o
n
1
7
M.
un
oui
2
0
2
1
used probit regression to calculate the coefficients that
best mapped DUratio onto the choices made by humans
and the various computational models:
h
Þ ¼ ϕ b þ
ð
p pink
X
8
j¼1
je
wj⋅DUratio;j
The logic of this analysis is that if humans are integrating
the ratio of evidence, then the resulting coefficients
should be flat across different values of nk (c'est à dire., over the
ranks j), whereas if they are performing (near-) optimally,
then the coefficients should grow with j.
EEG Acquisition and Preprocessing
A Neuroscan (El Paso, TX) EEG system with NuAmps
digital amplifiers was used to record EEG signals from
32 Ag–AgCl electrodes, located at FP1, FPz, FP2, F7, F3,
Fz, F4, F8, FT7, FC3, FCz, FC4, FT8, T7, C3, Cz, C4, T8,
TP7, CP3, CPz, CP4, TP8, P7, P3, Pz, P4, P8, POz, O1, Oz,
and O2, plus four additional electrodes used in a bipolar
montage as horizontal and vertical EOGs and two elec-
trodes located at the mastoids used as reference. Le
electrode impedances were kept below 10 kΩ. EEG sig-
nals were recorded at a sampling rate of 1 kHz and high-
pass filtered online at 0.1 Hz.
Preprocessing was carried out using the EEGLAB tool-
box for MATLAB (Delorme & Makeig, 2004) and custom
scripts. The data were downsampled to 250 Hz and
epoched from 1 sec before the onset of the first sample
à 6 sec after it, thereby covering the entire trial of eight
samples (including masks). The data were then visually
inspected to remove trials containing nonstereotypical arti-
facts and to identify electrodes showing electrical artifacts
and therefore requiring interpolation. After this, the data
were bandpass filtered between 1 et 30 Hz and rerefer-
enced to the average signal over all electrodes.
An independent component analysis was then conduct-
ed using EEGLAB, and the resulting independent compo-
nent analysis components were visually inspected for
artifacts, particularly stereotypical artifacts such as blinks
and sustained high-frequency noise. Trials with artifacts
were excluded from all further analysis, leaving an aver-
age of 492 (range = 378–544) trials per participant, chaque
consisting of eight overlapping stimulus events (sample
onsets).
Unless otherwise stated, we report statistical tests on EEG
data averaged across occipital (O1, O2, and Oz) and parietal
(P3, Pz, P4, and POz) electrode sites. We chose this
approach because previous studies have identified dissocia-
ble patterns of activity over occipital and parietal electrodes
in discrete-sample integration tasks ( Wyart, Nobre, &
Summerfield, 2012). To correct for multiple comparisons
across time, we used a nonparametric cluster correction
technique, implementing a familywise error (FWE) avec
an alpha of α = .05 (Maris & Oostenveld, 2007).
EEG Analyses: Encoding
We used EEG to investigate how the quantities predicted
by the difference and tally models were encoded in neu-
ral signals, with a view to arbitrating between them, en utilisant
a “model-based” approach to the analysis of brain imag-
ing data. Both of these models made identical predictions
about choice behavior but made different predictions
about the neural activity that would accompany each sam-
ple. Rather than calculating ERPs, we estimated how deci-
sion information was encoded in EEG signals using a
single-trial approach. This “encoding” methodology
involves using parametric predictors (such as DUmodel)
within a general linear regression model to predict the
sample-to-sample variability in the EEG signal, at suc-
cessive time points (−100 to 700 msec) surrounding the
onset of each sample.
D'abord, we took model-predicted quantities |DUdifference|
et |DUratio| and standardized these by z transformation.
Using rectified DUs |DUk| ensures that we identify neural
signals that encode absolute decision information, pas
those that favor one choice over another (c'est à dire., blue vs.
pink), as we were aiming to elucidate the nature of the
mechanism rather than the nature of the choice per se.
(Considérer, as an analogy, random dot kinematogram mo-
tion discrimination tasks: The neural signal of interest
from EEG recordings is one that correlates with the coher-
ence level of the dots, c'est à dire., decision information indepen-
dent of direction of motion, rather than one which
correlates with the extent to which the information favors
leftward vs. rightward motion). We then regressed these
quantities in a point-by-point fashion against the single-
trial EEG activity after each corresponding sample. Le
resulting parameter estimates (slopes of the best-fitting
regression line) provide an estimate of how strongly the
EEG signal (at each time point over the course of the
sample) varies with these model-predicted quantities.
This thus allowed us to assess the difference in neural
processing of reliability-weighted and non-reliability-
weighted information. Although the analysis epochs after
each sample are overlapping, we took careful steps to en-
sure that the correlation between the variables of interest
between adjacent samples was minimized. Ainsi, because
the decision information provided by each sample is suf-
ficiently uncorrelated, responses to adjacent stimulus
events (samples) can be disambiguated, much as they can
in parametric event-related functional neuroimaging de-
signes (Joseph, Tourneur, & Friston, 1997).
Subsequently, we repeated this procedure, y compris
in the same regression the two quantities that are pre-
dicted by the difference and tally models, respectivement:
the total number of blue balls and the total number of
pink balls (tally model) and the absolute difference in
blue/pink balls (difference model). The aim of this analysis
was to determine which of the two models was best able
to account for the neural activity; including these predic-
tors in the same regression ensured that they competed
Tickle et al.
593
D
o
w
n
je
o
un
d
e
d
F
r
o
m
je
je
/
/
/
/
j
F
/
t
t
je
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
je
n
t
o
p
un
r
d
c
e
.
d
s
F
je
r
o
je
m
v
e
h
r
c
p
h
un
d
je
je
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
un
n
r
un
t
r
je
t
je
c
c
je
e
e
–
p
–
d
p
d
2
F
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
un
/
_
j
0
o
0
c
9
n
1
8
_
un
p
_
d
0
0
b
9
oui
1
g
8
u
.
e
p
s
t
d
o
F
n
b
0
oui
7
S
M.
e
je
p
T
e
m
L
je
b
b
e
r
r
un
2
r
0
je
2
3
e
s
/
j
.
t
/
F
u
s
e
r
o
n
1
7
M.
un
oui
2
0
2
1
for unshared variance, allowing us to determine whether
neural signals scaled more faithfully with the tally of evi-
dence or the difference of evidence.
In all of these analyses, decision information from the
preceding and succeeding samples was included as addi-
tional nuisance covariates. This helped ensure that the re-
sulting parameter estimates reflected neural encoding on
the current sample and were not corrupted by decision in-
formation from adjacent samples that overlapped in time
with the epoch. This step, combined with the fact that
the partial correlation between adjacent samples was very
low as described, meant that we could be confident that
the encoding analysis avoided confounding the influence
of future and preceding samples. The resulting parameter
estimates (slopes) for each time point (−100 msec pre-
stimulus to +700 msec post-stimulus) were then averaged
across samples and entered into a second-level statistical
analysis for comparison at the group level. Regions of
temps (and space, c'est à dire., électrodes) where these curves devi-
ate reliably from zero across the cohort indicate where
decision information is reliably encoded in neural signals.
This process is also detailed in our earlier publications
using this method (Wyart, Nobre, et coll., 2012).
EEG Analyses: Decoding
In a subsequent analysis step, we assessed how the
strength of the relationship between decision informa-
tion and neural signals assessed above (EEG encoding)
predicted participants’ choices. This analysis step is close-
ly related to the calculation of “choice probabilities” of
single-cell recording data (Nienborg & Cumming, 2010)
and to an analysis of the psychophysiological interaction
between behavioral and neural variables in fMRI analysis
(Gitelman, Penny, Ashburner, & Friston, 2003). Here and
in previous publications, we have called this analysis
“EEG decoding” ( Wyart, Myers, & Summerfield, 2015;
Wyart, Nobre, et coll., 2012) because it allows us to quantify
how fluctuations in EEG encoding of DU are “decoded”
in downstream brain structures and consequently mani-
fest in choice. Such an analysis involves the use of multi-
variate parametric regression to quantify the extent of the
modulatory influence of the EEG signal on the relation-
ship between DUmodel and choice. A decoding analysis
allows us to see whether samples that are encoded with
higher-than-average strength (autrement dit, with pos-
itive residual variance) are more predictive of choice
than those which are encoded with lower-than-average
strength; if they are, we would see a clear decoding curve
(c'est à dire., a significant effect of the residual EEG signal on
choice). This method of estimating how the single-trial
relationship between input (psychological variable) et
brain activity (physiological variable) predicts choices
allows a more direct measurement of how brain activity
mediates the link between stimulus inputs and the weight
or influence that a sample of information wields over
choices.
To calculate these “decoding” curves, we took the time
course of the unexplained variance (residuals) of the re-
gression of DUtally and DUdifference on the EEG signal. Nous
then entered this quantity, r, into a probit regression,
alongside decision information, as a predictor of partici-
pants’ choices for each sample k and time point t:
Þ ¼ ϕ½ bþ
X
ð
p pink
8
k¼1
wk⋅DUk;model
wk; t⋅DUk;model (cid:2) rk; tÞ(cid:3)
X
8
k¼1
þ
Encore une fois, averaging across samples and participants af-
forded a grand average and the opportunity to conduct
group-level statistics. Positive deviations of r from zero
indicate times at which brain activity not only scaled with
decision information but did so more strongly than on
average (c'est à dire., the gain of encoding of a particular sample
was above average in comparison with the overall encod-
ing curve). If this stronger neural encoding of the DU re-
sults in a stronger effect of the DU on choice, then this
should show as a significant positive interaction between
r and DU, as reflected in the weight wk,t. The methods
used here have been used successfully in previous
articles from our laboratory ( Wyart et al., 2015; Wyart,
de Gardelle, et coll., 2012).
EEG: Lateralized Beta-Band Activity
On the basis of previous studies, which have shown that
oscillatory activity in the beta-band range accompanies
the buildup of information to a decision threshold, nous
investigated the encoding of momentary and cumulative
decision information in time-frequency transformed signals.
We measured how signed DUs (DUtally and DUdifference)
and the corresponding signed DVs were encoded in latera-
lized beta-band activity (∼10–40 Hz), using a comparable
technique to the encoding regressions above, dans lequel
these quantities were regressed together against relative
lateralized single-trial spectral power over the motor cortex
dans 10 logarithmically spaced frequency bands between
9 et 43 Hz. The response made with the left index finger
always corresponded to “blue,” whereas the right index
response always corresponded to “pink.” Thus, l'utilisation
of signed DUs for analyzing lateralized beta-band activity
is crucial in this analysis because, unlike the signals inter-
rogated in previous encoding analyses, ici, the two alter-
natives (pink vs. bleu) map onto putative neural signals that
can be disambiguated at the whole-brain level using scalp
EEG (c'est à dire., hemispherically lateralized patterns of beta-band
desynchronization over the motor and premotor cortices).
For each participant, we computed the interhemispheric
difference in beta activity at lateral central electrodes by
subtracting the spectral log power of (CP + CP3) depuis
(C4 + CP4).
594
Journal des neurosciences cognitives
Volume 28, Nombre 4
D
o
w
n
je
o
un
d
e
d
F
r
o
m
je
je
/
/
/
/
j
t
t
F
/
je
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
je
n
t
o
p
un
r
d
c
e
.
d
s
F
je
r
o
je
m
v
e
h
r
c
p
h
un
d
je
je
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
un
n
r
un
t
r
je
t
je
c
c
je
e
e
–
p
–
d
p
d
2
F
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
un
/
_
j
0
o
0
c
9
n
1
8
_
un
p
_
d
0
0
b
9
oui
1
g
8
u
.
e
p
s
t
d
o
F
n
b
0
oui
7
S
M.
e
je
p
T
e
m
L
je
b
b
e
r
r
un
2
r
0
je
2
3
e
s
/
j
/
F
t
.
u
s
e
r
o
n
1
7
M.
un
oui
2
0
2
1
Control Analyses
In a further effort to determine that our results from the
main experiments were not being driven by low-level vi-
sual properties of the stimuli, we took the number of
pink, bleu, and white balls, respectivement, on each sample
and standardized these by z transformation. We then
asked whether behavioral choice was significantly influ-
enced by the white dots and whether neural signals en-
coded more strongly those quantities that were decision
relevant (pink and blue balls) relative to those that were
irrelevant (white balls).
Previous studies that have focused on the neural repre-
sentation of number have found a parietal ERP that reflects
the difference in magnitude (c'est à dire., the total number of stim-
uli) between one group of dots and the next (Piazza &
Izard, 2009; Piazza, Izard, Pinel, Le Bihan, & Dehaene,
2004). To control for similar effects in our data, we re-
gressed the absolute difference in total number of dots
(bleu + pink + blanc) between one sample and the next
against the EEG signal (using the regression methods
described above, including samples 2–8 in the stream).
En particulier, we were interested in whether any decision-
related signals observed in our experiment could be tri-
vially explained by previously described neural adaptation
to number.
Behavioral Control Experiment
In the experiments described above, all dots were
equally sized, and so the number of dots was correlated
with the pixel area of the colored dots on the display
screen. Ainsi, one question that arises is whether
choices are driven principally by low-level visual proper-
ties of the stimuli, c'est, the area (number of pixels)
that the colored dots take up on screen, or by the num-
ber of dots per se. To arbitrate among these possibili-
liens, we conducted a further behavioral experiment in
which we varied the size of the pink and blue dots from
sample to sample. This ensured that the number of
dots and the number of pixels favoring each choice
were decorrelated.
The design (including timing of stimuli and number of
trials) of this behavioral control task, which was conduct-
ed on a new cohort of 19 participants, was identical to
the first EEG experiment except for the size and position
of the dot array. Dots were randomly spatially distributed
(minimum separation of 10 pixels) among 46 possible lo-
cations within a circular aperture of 500-pixel diameter.
The diameter of the blue dots on each sample was ran-
domly selected from a range of 11–45 pixels (35 possible
sizes), and the same process was applied independently
to both the pink dots and the white dots on each sample,
thus ensuring that the pixel area of each color separately
on each sample, as well as the total filled pixel area, était
decorrelated from the respective number of dots (Pearson’s
correlation ∼.65).
This control allowed us to regress both the number of
dots and the size of the dots on each sample against
choice, thereby allowing us to determine whether sample
size exerted an influence over and above the physical size
of the dots on screen.
RÉSULTATS
Behavior
Participants chose the correct urn on 83 ± 6% of trials,
with RTs averaging 407 msec. After the addition of
performance-limiting noise to the DV, all three models
achieved comparable accuracy to humans (85% for the
tally and difference models and 83% for the ratio model)
and were able to predict psychometric functions well. Nous
calculated how participants’ choices varied as a function
of the z-transformed DVs predicted by the tally and
difference models and the ratio model, DVdifference,
DVtally, and DVratio. The models performed equivalently
(Figure 2A). The tally and difference models behaved in
line with the optimal solution, and both (as described)
made equivalent predictions with the exception of noise.
We next used probit regression on the behavioral data
to estimate the impact that the number of pink and blue
balls in each sample (1–8) had on choice, as a function of
its serial position. As expected, “pink” choices were pre-
dicted positively by the number of pink balls and nega-
tively by the number of blue balls (Figure 2B); ce
analysis suggested that all the samples contributed at
least in part to the decision (all gray bars deviated signif-
icantly from 0).
Enfin, to test our main hypothesis, we determined
whether participants accounted for sample size (number
of dots) when making decisions. To this end, we used
probit regression to estimate the impact that each sam-
ple had on choice, ranked not by its position but by the
total number of colored dots, nk (= d1k + d2k), c'est,
by its overall reliability. We used DUratio, the DU as calcu-
lated by the ratio model, as a predictor. This ensured that
the resulting coefficients for observers who did not weight
information by sample size would be flat over ranks of nk,
whereas an observer who weighted information by reliabil-
ity would show a profile of steadily increasing weights
(note that a mathematically equivalent alternative would
be to use the statistically optimal solution as a predictor,
in which case an ideal observer would show a flat profile
of weights, whereas those for an observer who integrated
the ratio of evidence would decline with n). Par conséquent,
for the ratio model (Figure 2C, orange points), the weights
did not vary with ranks of nk, but the weight given to each
sample ranked by nk grew steadily for both the models that
arrived at the statistically optimal solution (tally model, pur-
ple points; difference model, green points). Encore, le
values predicted by these latter two models are equivalent
to the statistically optimal solution, with any residual vari-
ability because of the noise term σ.
Tickle et al.
595
D
o
w
n
je
o
un
d
e
d
F
r
o
m
je
je
/
/
/
/
j
t
t
F
/
je
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
je
n
t
o
p
un
r
d
c
e
.
d
s
F
je
r
o
je
m
v
e
h
r
c
p
h
un
d
je
je
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
un
n
r
un
t
r
je
t
je
c
c
je
e
e
–
p
–
d
p
d
2
F
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
un
/
_
j
0
o
0
c
9
n
1
8
_
un
p
_
d
0
0
b
9
oui
1
g
8
u
.
e
p
s
t
d
o
F
n
b
0
oui
7
S
M.
e
je
p
T
e
m
L
je
b
b
e
r
r
un
2
r
0
je
2
3
e
s
/
j
F
t
/
.
u
s
e
r
o
n
1
7
M.
un
oui
2
0
2
1
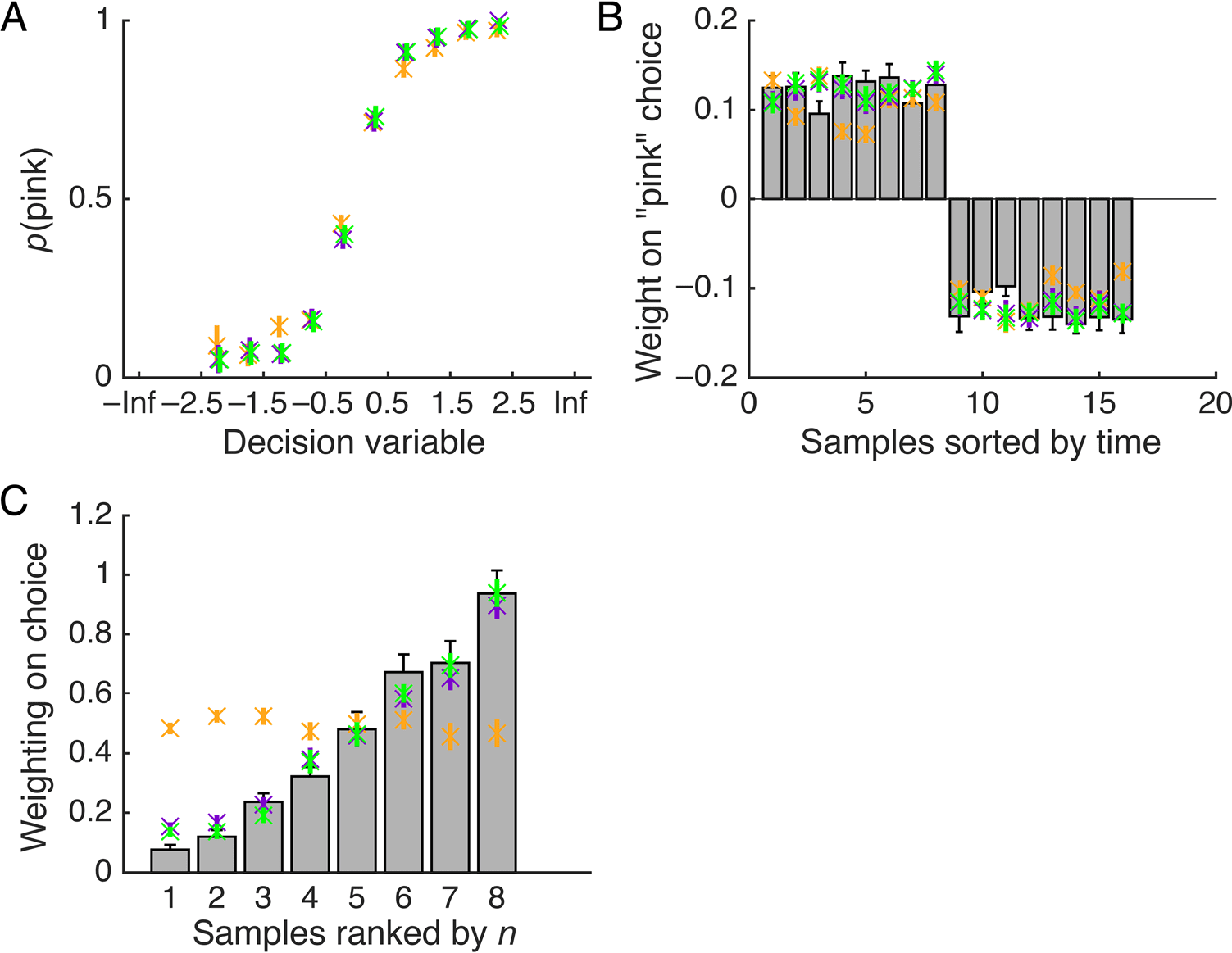
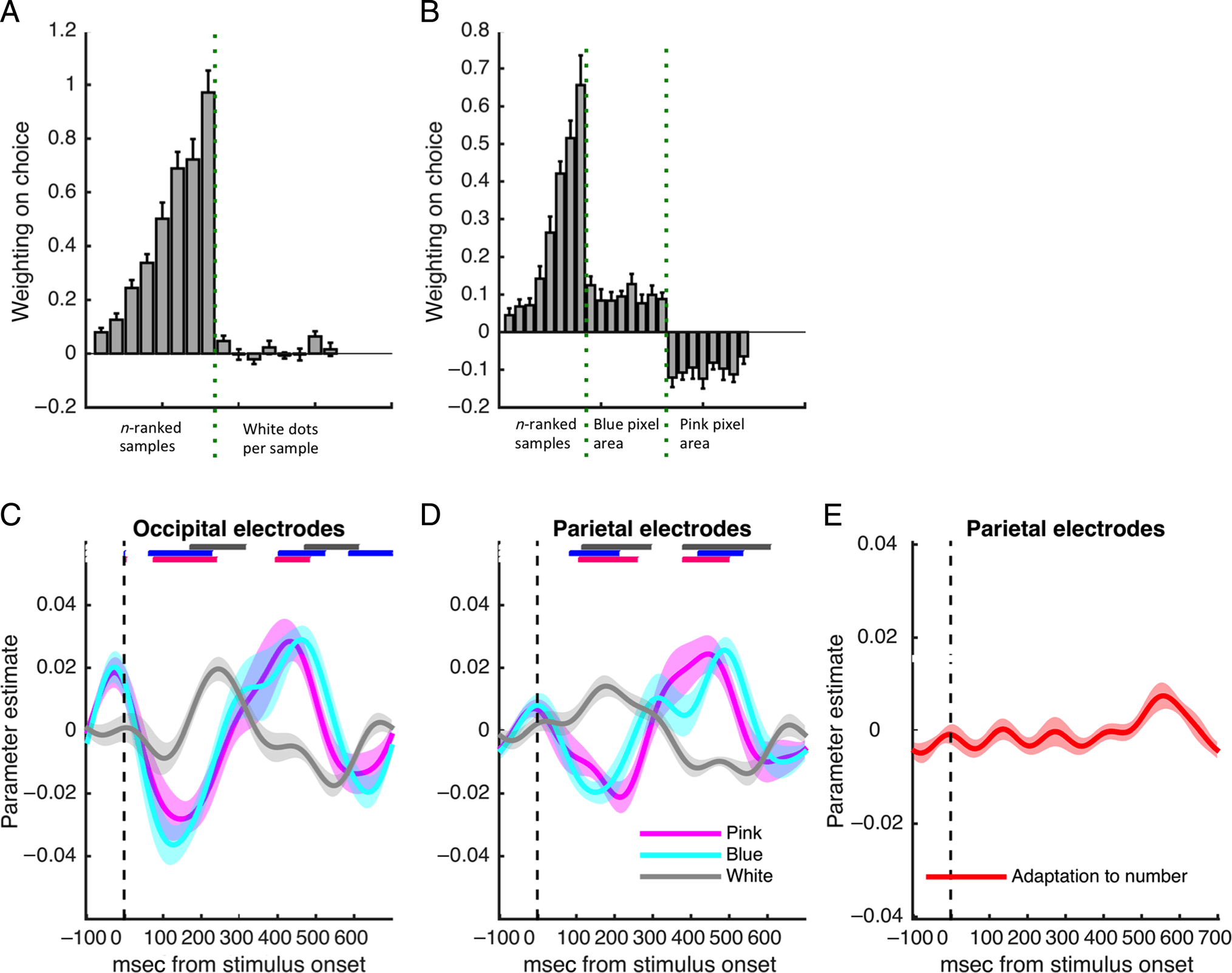
Chiffre 2. Behavioral results
and model predictions. (UN)
Probability of selecting “pink” as
predicted by the DVs for the
ratio model (orange dots) et
the two reliability weighted
modèles (tally model, purple
crosses; difference model,
green crosses); a DV below zero
corresponds to responding
“blue” and above zero
corresponds to a “pink”
response. (B) Impact (beta
coefficient) of each sample on
“pink” choices, ranked by serial
position (1–8), as a function of
the number of pink balls (d'abord
eight bars) and the number of
blue balls (last eight bars) dans le
sample. Estimates were
generated using probit
regression. Gray bars show
human data and orange-/
purple-/green-colored crosses
show predictions of the ratio/
tally/difference models,
respectivement. (C) Weights (beta
coefficients) given to each
sample as ranked by sample size
(smallest to largest) in evidence
l'intégration, calculated using probit regression. Gray bars correspond to human behavior; colored crosses show model estimates for weight given to
the ranked samples. The ratio model, given that it does not reliably weight the samples, is flat across ranks. In all figures, bars show SEM.
Critique, the impact that each sample wielded over
choices for humans depended on the sample size, as it
did for the statistically optimal solution and the two
models that approximated it; this was confirmed by an
ANOVA on the weights over ranks, F(7, 240) = 51.6,
p < .001. The beta weight in the human data for the
largest samples was significantly higher than that of the
smallest samples: t(30) = 13.1, p < .001. In the sub-
sequent neural analyses, we seek to distinguish which
of the two approximations of the optimal (binomial)
solution best describes human brain activity during per-
formance of the task. The reasoning behind this ap-
proach is that it is implausible that neurons explicitly
compute binomial probabilities but rather derive the
solution via a computationally tractable mechanism, such
as those described by both the tally and difference
models. Furthermore, it allows us to tease apart the dif-
ference and tally models that make indistinguishable be-
havioral predictions.
EEG: Encoding of DU in Broadband Occipital and
Parietal Signals
How did humans achieve near-optimal performance on
the task? Although the tally and difference models both
derive the statistically optimal solution with predictions
that match human behavior, they make different predic-
tions about the quantities that are computed en route to
a decision. We thus analyzed the link between decision
information, neural signals, and choices to provide an in-
sight into the mechanisms by which humans were mak-
ing decisions.
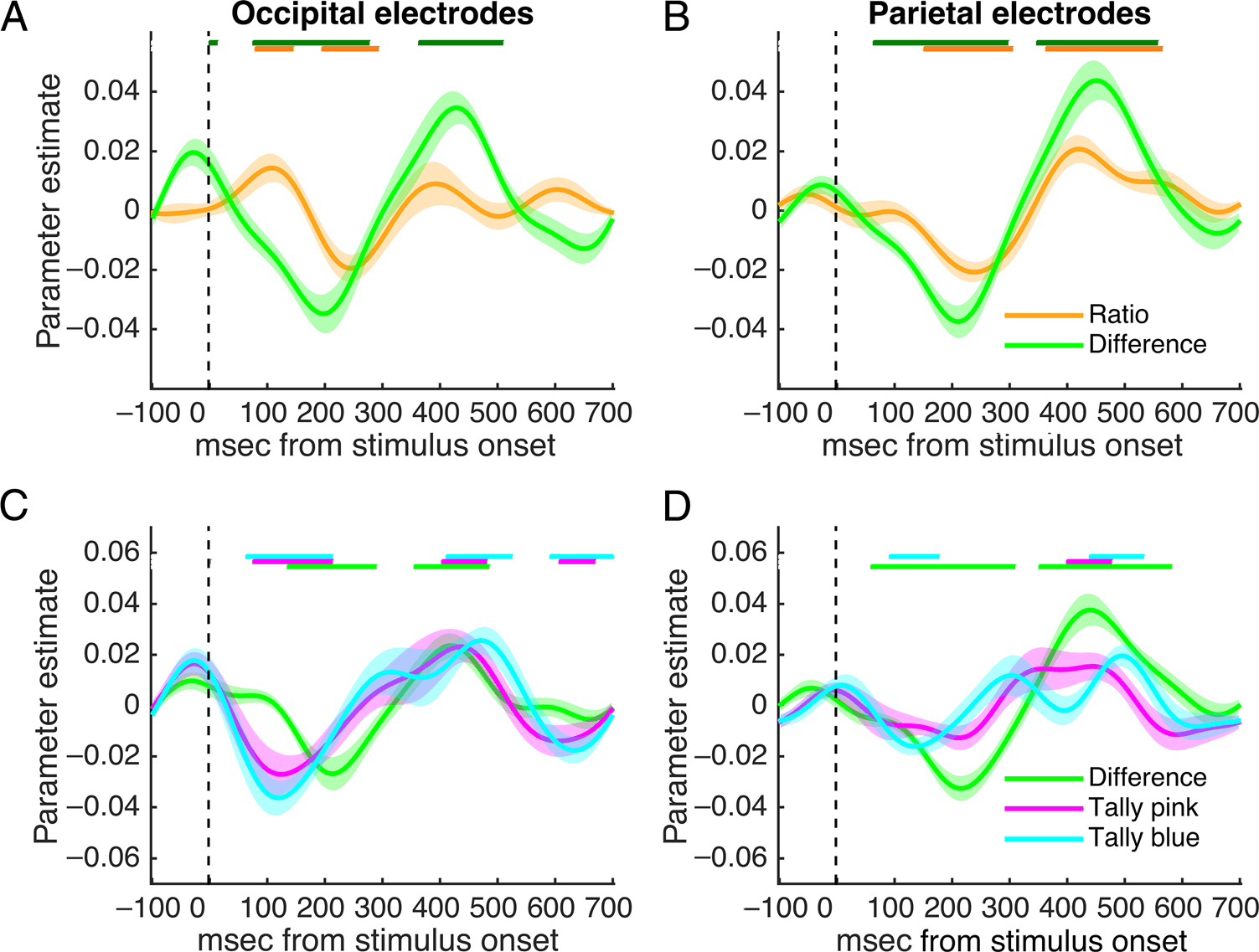
First, we sought to correlate EEG activity with the DU
(i.e., the momentary information conveyed by each
sample) predicted by each of the models. Initially, we
focused on comparing the ratio model with the dif-
ference model, only the latter of which predicts reli-
ability-weighted behavior. To this end, we regressed
|DUdifference| and |DUratio| separately against the single-
trial EEG data for each sample and averaged over the
resulting coefficients at each post-stimulus time point.
The use of rectified predictors allows us to identify neural
signals that correlate with the absolute decision informa-
tion, rather than favoring one choice over another (e.g.,
pink over blue). Standardization ensured that the result-
ing coefficients were directly comparable. Consistent with
participants’ behavioral tendency to act as if they were
weighting the evidence by its reliability (Figure 2A), the
response to |DUdifference| was significantly greater than
that to |DUratio| (Figure 3A and B). In other words, behav-
ioral data indicate that humans pursue a near-optimal
strategy, and neural data suggest that they do so by inte-
grating reliability-weighted evidence rather than only the
ratio of evidence on each sample.
Subsequently, we asked whether humans performed
near-optimally by (i) adding up the differences in num-
bers of balls and deciding whether this quantity was
greater or less than zero (difference model) or (ii) adding
596
Journal of Cognitive Neuroscience
Volume 28, Number 4
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
a
/
_
j
0
o
0
c
9
n
1
8
_
a
p
_
d
0
0
b
9
y
1
g
8
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
i
2
3
e
s
/
j
.
f
t
/
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
up the total information in each stream in parallel and
deciding which was greater (tally model). The former ac-
count predicts that participants compute DUdifference on
each sample; the latter account predicts that only DUtally
is updated on a sample-by-sample basis. We thus entered
|DU1tally|, |DU2tally|, and |DUdifference| as competitive
predictors of the EEG signal at each scalp electrode
and time point from 100 msec preceding sample onset
to 700 msec after its onset (see Methods). We observed
that the neural variance accounted for by |DUdifference|
in parietal electrodes outweighed that accounted for by
|DU1tally| and |DU2tally|, in that the beta weights were
larger for the former and reached significance for longer,
with a first negative deflection peaking at 230 msec and a
second positive deflection at 470 msec after stimulus on-
set (Figure 3D). It is important to note that these curves
are not ERPs but single-trial estimates of the encoding of
decision information by brain activity. Interestingly, the
same regression in occipital electrodes (Figure 3C)
showed an initial negative deflection for |DU1tally| and
|DU2tally| followed 150 msec later by a negative deflec-
tion for |DUdifference| (Figure 3C). One might expect,
even under the difference model, that there would be
an early representation of the total number of pink and
blue dots, as this quantity is required to calculate the dif-
ference. Thus, our interpretation of this finding is that
the initial encoding of the absolute information is fol-
lowed by the emergence of the decision-relevant quantity
DUdifference.
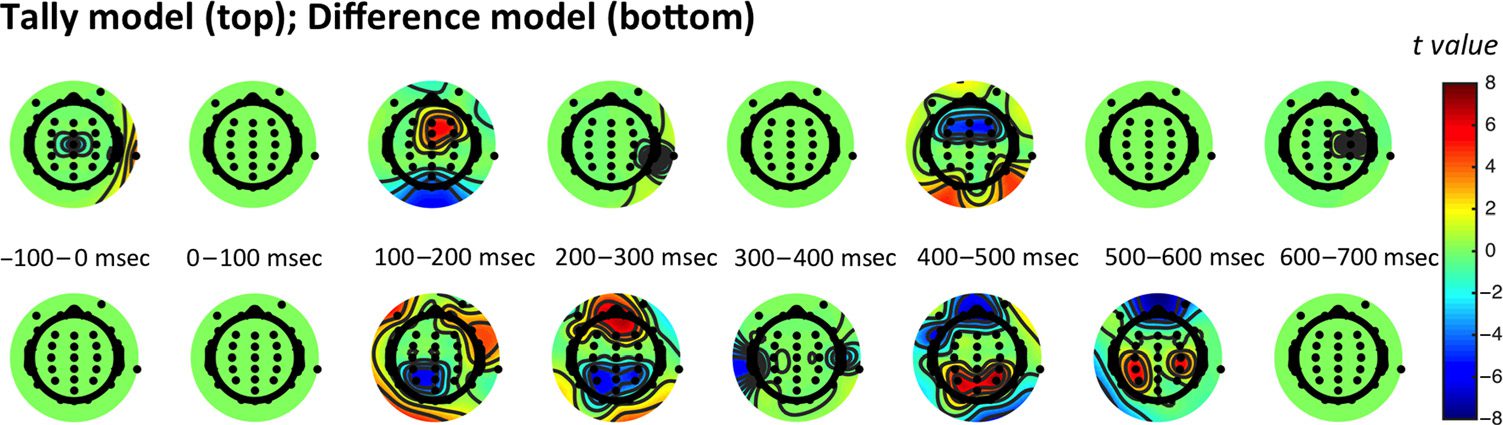
Repeating the above analysis at each electrode provided
a topography of encoding of |DUdifference| and |DUtally|
across the scalp, which we collapsed into bins of 100 msec
(Figure 4; note that the two quantities DU1tally and DU2tally
are combined for ease of presentation given their similar-
ity). The spatial distribution of the resulting weights can be
interpreted as the spatial topography of the underlying
decision-related component in the EEG signal. The result-
ing patterns of significant activation were in accordance
with the results from the regressions above, with the re-
sponse to |DUdifference| (bottom row) outweighing that
to |DUtally| (top row). In other words, these neural obser-
vations suggest that participants use a strategy that involves
encoding the difference in information provided by each
sample. This allows them to derive the near-optimal solu-
tion, weighting information by its reliability.
EEG: Decoding of DU in Broadband Parietal Signals
The encoding regressions suggested that more of the neu-
ral variance was accounted for by the difference model,
which encoded the relative evidence on each sample, than
by the tally model, which encoded the absolute evidence.
Figure 3. Neural encoding
curves. (A and B) Curves
showing correlation between
the predictions of the ratio
model (orange curve) and the
difference model (green curve),
which approximates the
binomial (optimal) solution,
with EEG data after each
sample. Shaded areas in the
curves denote SEM. The bars at
the top show periods from
stimulus onset in which the
curves consistently deviate
significantly from zero across
participants for difference
(green) and ratio (orange)
models. (C and D) Correlation
between EEG signals and the
DUs predicted by the tally
model (blue and pink ball
totals, blue and pink curves)
and the difference model (blue
balls–pink balls, green curve).
Shaded areas in the curves
denote SEM. The bars at the top
show periods from stimulus
onset in which the curves
consistently deviate significantly
from zero across participants for
difference (green bar) and tally (blue and pink bars) models. Note that, for occipital electrodes, there is a period of significant activation
corresponding to the tally model after stimulus onset, followed by significant activation corresponding to the difference model around 200 msec, as
though all evidence is being processed initially followed by the formation of the decision-relevant difference signal. For all panels, statistics were
computed using a nonparametric cluster-correction technique implementing an FWE correction with an alpha of α = .05 (see Methods).
Tickle et al.
597
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
a
/
_
j
0
o
0
c
9
n
1
8
_
a
p
_
d
0
0
b
9
y
1
g
8
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
i
2
3
e
s
/
j
/
f
.
t
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
Figure 4. Scalp topographies.
Scalp-wide significant
correlations between the EEG
signal predicted by the tally
model (top row) and difference
model (bottom row). Note that
the tally model predicts that two
quantities are encoded (number
of pink balls and number of
blue balls); these two quantities
have been combined in this
figure for ease of viewing, but
plotting them separately yields a
qualitatively similar pattern. The plots show the t values corresponding to times and regions at which (on average in that time bin) the correlation for
each model deviated significantly from zero.
D
o
w
n
l
o
a
d
e
d
f
r
o
m
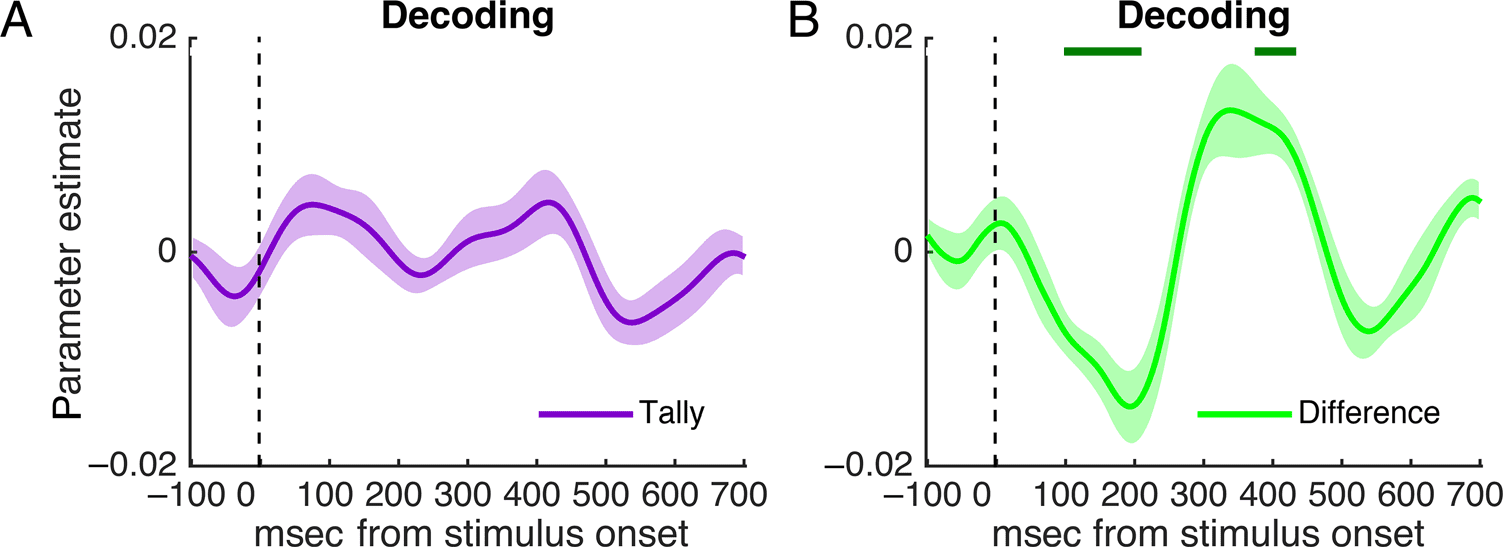
To support this notion further, decoding analyses—which
are able to link the psychological variable (human choice)
with the physiological variable (neural encoding of DU in
the run up to choice)—were used to assess the relation-
ship between the residual variance not accounted for by
the encoding regressions and human choice (see
Methods). This technique allows the link between the neu-
ral transformation of DU and choice behavior (“choice
probabilities”) to be made more explicit. Decoding analysis
asks how residual variance in the encoding (described
above) of model-predicted quantities impacts choices, over
and above the influence of stimulus choices. Although the
decoding analysis for the tally model showed no significant
effect (Figure 5A), the time courses of the decoding regres-
sions for DUdifference were in accordance with those seen in
encoding in parietal electrodes (Figure 5B). This analysis
therefore provides support for the difference model over
the tally model and suggests that variation in encoding of
the difference signals is predictive of participants’ re-
sponses. We note that this finding also rules out spurious
explanations for the observed decision encoding curves,
such as the view that the apparent relationship between
decision information and brain activity is somehow second-
ary to differences in attention or arousal.
EEG: Lateralized Beta-Band Activity
Previous studies have observed that oscillatory activity in
the beta-band range accompanies the buildup of informa-
tion to a decision threshold (O’Connell, Dockree, &
Kelly, 2012). Next, thus, we measured how lateralized
beta-band activity over the motor cortex varied with the
cumulative decision evidence in favor of either choice.
To this end, we wavelet-transformed EEG data into its
spectral components in 10 logarithmically spaced fre-
quency bands between 9 and 43 Hz (i.e., encompassing
the approximate beta-band range extending into lower
gamma). First, we confirmed that lateralized beta-band
activity was present in the preparation of the motor
response (made from 3500 msec after the onset of the
first stimulus in each trial) by computing the interhemi-
spheric difference in EEG activity in the 9- to 43-Hz range
between the lateral central electrodes (see Methods).
The results confirmed that the difference in power in
preparation for responding “pink” (the choice made with
the right index finger) minus responding “blue” (made
with the left index finger) was positive in the contralateral
hemisphere and negative in the ipsilateral hemisphere
(Figure 6A), with a focus between ∼20 and ∼30 Hz.
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
a
/
_
j
0
o
0
c
9
n
1
8
_
a
p
_
d
0
0
b
9
y
1
g
8
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
i
2
3
e
s
/
j
f
/
t
.
Figure 5. Neural decoding
curves. The unexplained
variance (i.e., the residual error)
in the EEG signal from the
encoding regressions in parietal
regions for the tally model
(purple curve) and the
difference model (green) were
used as predictors of choice in
the decoding regressions,
allowing us to link neural
activity (in parietal electrodes)
with behavior choice. See
Methods for more detail on this
procedure. Shaded areas in the
curves denote SEM. The dark
green bar shows periods in which the correlation significantly deviated from zero in the parietal signal; note that, for the tally model, there was
no such period of significance.
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
598
Journal of Cognitive Neuroscience
Volume 28, Number 4
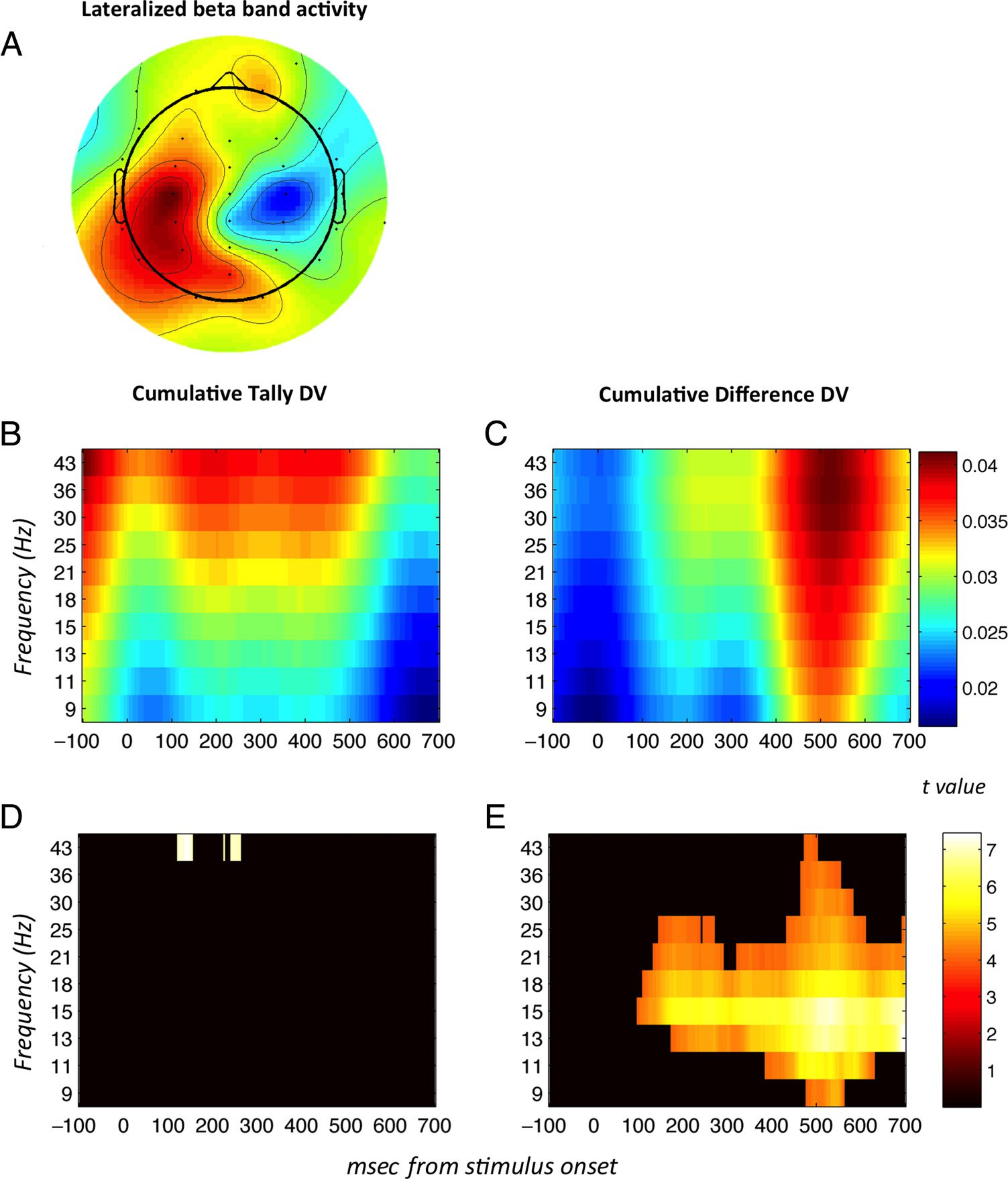
Figure 6. Time–frequency
analyses. Interhemispheric
difference in log spectral power
at 9–43 Hz (i.e., mainly
overlapping the beta band
frequency, approx. 15–30 Hz)
between “blue” choices, which
were always made with the right
index finger, and “pink”
choices, made with the left
index finger. The resulting
quantity was positive in the
contralateral hemisphere to the
hand with which the choice was
made and negative in the
ipsilateral hemisphere. The
period displayed is 2.6–3.2 sec
after first stimulus onset, that is,
close to execution of motor
response. Tally and difference
model DVs were generated by
computing the cumulative sum
of the model-derived sample-
by-sample quantities DUtally and
DUdifference, respectively, across
the trial. Note that the tally
model predicts that two
quantities are encoded (number
of pink balls and number of
blue balls); these two quantities
have been combined in this
figure for ease of viewing. The
resulting predictors were then
regressed against the log
spectral power difference
between centroparietal
electrodes C3 + CP3 and C4 +
CP4, that is, a motor region that
should correspond with motor
preparatory activity. B shows
the correlation between the
predictions of the cumulative
tally DV and the difference in
power between the two
hemispheres, and C depicts the
same but in relation to the difference model DV. D and E show times/frequencies at which the respective quantities plotted in B and C deviate
significantly from zero.
Finally, we tested whether beta-band activity correlated
with the accumulated decision-relevant evidence predicted
by each of the models. To this end, we conducted further
regression analyses in which the momentary (DUdifference)
and cumulative (DVdifference) predictions, as well as the
momentary (DUtally) and cumulative (DVtally) predic-
tions, were both entered as predictors of the inter-
hemispheric difference in lateralized log power in the
10 selected frequency bands (see Methods). Note that,
for these analyses, we used the signed decision quanti-
ties (not rectified) to predict the leftwards versus right-
ward response. Consistent with the view that participants
solve the task by integrating a difference signal, the cumu-
lative difference signal DVdifference, but not the cumulative
tally signal DVtally, was a reliable predictor of beta-band
lateralization over the motor cortex: Figure 6B and C depict
how lateralized beta-band power depends on the cumula-
tive DVtally (Figure 6B) and DVdifference (Figure 6C). The re-
lationship with DVdifference (Figure 6E), unlike that with
DVtally (Figure 6D), showed a period of significance from
100 msec onward.
Control Analyses
Next, to ensure further that the neural responses were
driven by decision-relevant information rather than other
low-level factors, we measured how both behavior and
brain activity correlated with the number of white distrac-
tor dots in comparison with pink and blue dots. These
analyses allowed us to distinguish the behavioral and
neural response to decision information (blue and pink
dots) from that elicited by task-irrelevant sensory input
Tickle et al.
599
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
a
/
_
j
0
o
0
c
9
n
1
8
_
a
p
_
d
0
0
b
9
y
1
g
8
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
i
2
3
e
s
/
j
t
.
f
/
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
(distractor white dots). Entering these quantities (white,
blue, and pink dots) together into the regression ensured
that they competed for unshared variance. In the behav-
ior data, the response to white dots was minimal in com-
parison with that evoked by reliability-weighted colored
dots (Figure 7A). In the neural data, the time course of
the resulting regression coefficients showed that the
number of white (distractor) dots drove a visual response
(Figure 7C and D, gray curve) peaking around 250 msec
post-stimulus. Although the neural encoding of the white
dots was significant, it followed a qualitatively different pat-
tern from the encoding responses to the decision-relevant
quantities (pink and blue dots; indicated in Figure 7C
and D by pink and blue curves, respectively) in both pari-
etal and occipital electrodes. Combined with the behavior
analysis showing limited effect of white dots on choice, the
qualitatively different neural encoding pattern suggests
that the white dots were being processed via a different,
decision-irrelevant mechanism. The responses to the col-
ored dots were characterized by negative and positive de-
flections peaking at ∼100 and ∼400 msec post-stimulus,
respectively.
We also examined the relationship between brain activ-
ity and the difference in magnitude (i.e., the total num-
ber of dots on each sample, both decision relevant [blue
and pink] and decision irrelevant [white]) from one sam-
ple to the next, regressing the absolute difference in
magnitude from sample to sample against the EEG signal
over parietal electrodes (see Methods). Perhaps surpris-
ingly, we found no correlation between the change in
magnitude and parietal EEG signals, with no time window
reaching statistical significance (Figure 7E). This suggests
that our neural data are dominated by decision-related
effects rather than the influence of passive adaptation to
number.
Control Experiment
Finally, to determine whether the observed effects of
sample size were driven by the number of dots, rather
than low-level visual signals such as the total pixel area
taken up by the colored dots, we conducted a further
control experiment. In this experiment, a new cohort of
participants (n = 19) performed the same urn choice
task, with one difference: The pink and blue dots were
different sizes, ensuring that the pixel area taken up by
the dots and the number of dots were dissociable on
each sample, for each color individually (correlation be-
tween number of pink dots and pink pixel area: r = .65,
correlation between number of blue dots and blue pixel
area: r = .66) and overall without white dots (r = .68)
and with white dots (r = .65). This enabled us to inves-
tigate sample size effects using the same regression ap-
proach, in which we predicted choices as a function of
the ratio of dots, sorting samples into predictors by their
sample size (see above) but now partialing out that por-
tion of the variance that could be ascribed to pixel area.
To achieve this, we entered the sample-wise pixel area
for blue and pink categories as additional regressors into
the design matrix. The resulting coefficients could be in-
terpreted in the same fashion as in Figure 2C. The results
show that, although decisions are partly influenced by
number of pixels, the sample size effect on dots remains
robust to the inclusion of these additional regressors
(Figure 7B), following the same pattern of increasing
weight on choice with increasing sample size as seen in
the previous analyses (cf. Figure 2C). This was confirmed
by an ANOVA on the weights over ranks: for the weights
corresponding to sample size, F(7, 144) = 32.6, p < .001.
As before, the beta weight in the human data for the larg-
est samples was significantly higher than that of the smal-
lest samples: t(18) = 7.8, p < .001. However, the same
was not the case for the beta weights corresponding to
pixel area: Although the weights deviated significantly
from zero, the weights did not deviate significantly from
each other, unlike the weights corresponding to sample
size (F = 0.71, p = .66 for blue pixel area; F = 0.67, p = .7
for pink pixel area).
DISCUSSION
Humans making decisions are often faced with informa-
tion that is indistinct, weak, or ambiguous. During senso-
rimotor choices, humans rely more heavily on inputs
coming from sources that are clearly discernable, for ex-
ample, by weighting haptic information over visual infor-
mation when the latter has been corrupted by noise
(Ernst & Banks, 2002). In one sense, it is remarkable that
human behavior has been optimized over evolutionary
history to weight information by its reliability, as a statisti-
cally ideal observer should. On the other hand, it is perhaps
natural that human decisions rely more on information that
can be easily detected than that which cannot. Indeed, un-
certainty can arise at multiple stages during information
processing, and so decision-relevant evidence can be ren-
dered unreliable by other means than corruption from low-
level input noise. Consider, for example, a juror evaluating
evidence in a court of law. On the one hand, a witness
whose testimony is rendered incomprehensible will be un-
likely to hold much sway over the jury, compared with one
that can be clearly understood (uncertainty because of low-
level sensory noise). However, even where testimony is
clearly perceptible, a juror might question whether a lone
witness (rather than, say, 10 consistent testimonies) is suf-
ficient to condemn the accused (uncertainty because of
high-level knowledge of sample size). Here, we tested
whether humans integrate information optimally when un-
certainty arises at a higher, rather than lower, level. Unlike
previous studies using description-based scenarios, we
found that participants automatically weighed the informa-
tion by sample size, behaving in a fashion that resembled
an ideal observer.
Previous research has revealed that humans often
disregard the quantity or quality of information when
600
Journal of Cognitive Neuroscience
Volume 28, Number 4
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
a
/
_
j
0
o
0
c
9
n
1
8
_
a
p
_
d
0
0
b
9
y
1
g
8
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
i
2
3
e
s
/
j
/
f
t
.
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
a
/
_
j
0
o
0
c
9
n
1
8
_
a
p
_
d
0
0
b
9
y
1
g
8
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
i
2
3
e
s
/
j
f
/
t
.
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
Figure 7. Control analyses. The first eight gray bars show weights (beta coefficients) given to the colored (decision-relevant) dots in each sample,
ranked by sample size (smallest to largest). The second set of eight gray bars show the weight given to white (decision-irrelevant) dots in each
sample. The response to the colored dots clearly outweighs the response to the white dots. (B) Gray bars depict the weight (beta coefficients) on
choosing “blue” of various aspects of the decision array. The first set of eight bars show weights given to each sample as ranked by sample size
(smallest to largest), the second set of eight bars show the weight of total pixel area of blue dots per sample, and the final set of eight bars show the
weight of the total pixel area of pink dots per sample, on choosing “blue.” All quantities were entered into the same (probit) regression to ensure
they competed for unshared variance. In all, black bars denote SEM. (C and D) Correlation between decision-relevant (blue and pink dots) and
decision-irrelevant (white dots) information and the EEG signal in occipital electrodes (C) and parietal electrodes (D). Shaded areas in the curves
denote SEM. The bars at the top show periods in which the curves consistently deviate significantly from zero across participants and trials; the colors
of these bars correspond to the colors of the curves they reflect. (E) We regressed a quantity corresponding to the difference in number of dots (blue +
pink + white) between one sample and the next against the EEG signal over parietal electrodes. The curve shows that the correlation between this
quantity and the neural activity was small with no time points reaching significance. Shaded areas in the curve denote SEM. This suggests that the parietal
encoding signal (see Figure 3) is indeed likely to reflect decision-related effects, rather than the influence of passive adaptation to number.
making judgments (Griffin & Tversky, 1992). This “sample
size neglect” can be considered as a special case of a
more general bias by which humans neglect the duration
or extent over which information is available (Kahneman
et al., 1982). However, this classic research presented
decision problems in the form of descriptive scenarios,
making it unclear whether optimality was limited by the
format of decision information (description vs. experience
based) or by the locus of uncertainty (low-level vs. high-lev-
el uncertainty). Here, we assessed human decisions using
an expanded judgment task in which discrete samples of
information arrived in sequence, after which participants
made a categorical judgment about their provenance. We
found that participants paid more heed to samples that
offered better quality information: For example, decisions
were more influenced by samples on which there were
12 balls, rather than three balls, even if the ratio of blue to
pink balls was 2:1 in both cases. In other words, this classic
demonstration of suboptimal behavior from the decision-
making literature may owe more to the format in which
information was presented, rather than the locus of un-
certainty in information processing. This has important
Tickle et al.
601
implications for a range of real-word situations, including
medicine, economics, and public policy, where sample
size neglect might lead to poor or biased decisions.
The optimal solution to the urn-and-balls problem
described here is to estimate the binomial odds ratio that
the balls were drawn from either of the two urns and
decide according to the sign of its logarithm. Note that
samples were presented at 3 Hz, too fast to rely on ex-
plicit mathematical calculation; any integration must be
of approximate number or magnitude (Piazza & Izard,
2009). Thus, although humans behaved near-optimally,
it is implausible that they were explicitly computing bi-
nomial probabilities to solve the task. Rather, there are
two mechanisms that arrive at the binomial solution that
participants could have used. The first is simply to tally
up the approximate number of pink and blue dots inde-
pendently and respond whichever is greater (tally model).
The second is to estimate the approximate difference be-
tween pink and blue dots on each sample and respond
according to whether it is greater or less than zero (differ-
ence model). Where the experimenter, rather than the
observer, determines the viewing time that precedes
choices (as in this experiment), these models make very
similar predictions (identical, except for added stochas-
ticity) regarding behavioral data but differ in their neural
predictions. The computational approaches described by
the tally and difference models are related respectively to
the “race” and “diffusion” accounts of the integration pro-
cess that is a prelude to human categorical choices (Ratcliff
& McKoon, 2008; Vickers, 1979).
The tally model requires that independent totals of blue
and pink dots are registered, but not their relative differ-
ence. Nevertheless, we witnessed neural signals over the
parietal cortex that scaled with the difference in the total
number of blue and pink dots, even when other confound-
ing factors had been taken into account. This supports the
difference model but not the tally model. Indeed, a closer
look at the encoding of information over occipital elec-
trodes suggested that the number of blue and pink dots
was encoded early (100 msec), followed by the difference
signal, exactly as if the brain first estimated independent
totals for each sample and then compared them. This is
reminiscent of the successive encoding of absolute and
relative economic value in magnetoencephalographic
activity observed during a gambling task (Hunt et al.,
2012). In the parietal cortex, the decision information pre-
dicted by the difference model exhibited a temporal profile
characterized by an early dip (at ∼220 msec post-stimulus)
and a later peak (at ∼450 msec). The same pattern of EEG
activity has previously been shown to scale with decision
information in a task involving discrimination of the mean
orientation of a stream of tilted gratings, with a negative
deflection at ∼250 msec and a positive peak at ∼500 msec
after each sample (Wyart, Nobre, et al., 2012).
A wealth of research in humans and nonhuman primates
has implicated the parietal cortex in the representation of
approximate number (Piazza & Izard, 2009). At the single-
cell level, individual neurons show bell-shaped tuning
curves over the number line (Nieder & Miller, 2003). In hu-
man imaging studies, neural signals localized to the parietal
cortex scale with the numerical disparity between two suc-
cessively or simultaneously occurring stimuli (i.e., sets of
dots), even in the absence of an overt estimation task
(Piazza et al., 2004). The focus of our experiment was not
to distinguish accounts based on number from those based
on magnitude per se. Nevertheless, it is unlikely that our
neural findings simply reflect low-level adaptation to num-
ber or magnitude, for four reasons. First, a control experi-
ment in which the pixel area taken up by the colored
dots and the number of colored dots were decorrelated
still showed a strong sample size effect, even when the
lower level factor (pixel area) was included as a nuisance
covariate in the regression. Second, the gain of encoding
of number was qualitatively different for blue and pink
stimuli, which were decision relevant, than for white stim-
uli, which were not. Third, our decoding analysis suggested
that the strength with which neural signals encoded the
difference in number of pink and blue dots was predictive
of later choices, as would be expected of a decision signal.
Fourth, we observed a distinct neural signal over motor
regions that reflected the buildup in magnitude differ-
ences over time. These findings suggest that the parietal
signal observed here instead reflects the relative differ-
ence between decision information in favor of either cat-
egory. One way of linking our findings with this literature
is to assume that, in the absence of an overt task, partic-
ipants implicitly compare information arriving in sequence,
calculating their difference as an implicit decision signal.
Indeed, a similar pattern of adaptation to numerosity is
obtained when participants make same–different judg-
ments on successive stimuli. In other words, the repre-
sentation of numerosity in the parietal cortex might
reflect a more general representation of the magnitude
of the information relevant for a decision (Wyart, Nobre,
et al., 2012).
In summary, we show that humans integrate approxi-
mate number in a near-optimal (reliability-weighted)
fashion. Our study has implications for research in a
number of domains, including economics and medical di-
agnosis, in which it is widely assumed that humans esti-
mate numerical quantities in a biased and suboptimal
fashion. Humans can make near-optimal judgments
about values or other numerical estimates if the informa-
tion is presented in an appropriate format.
Acknowledgments
We thank Nick Yeung for providing access to EEG equipment.
This work was funded by an ERC Starter grant to C. S.
Reprint requests should be sent to Christopher Summerfield,
Department of Experimental Psychology, University of Oxford,
South Parks Road, Oxford, United Kingdom of Great Britain
and Northern Ireland, OX1 3UD, or via e-mail: christopher.
summerfield@psy.ox.ac.uk.
602
Journal of Cognitive Neuroscience
Volume 28, Number 4
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
a
/
_
j
0
o
0
c
9
n
1
8
_
a
p
_
d
0
0
b
9
y
1
g
8
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
i
2
3
e
s
/
j
t
f
.
/
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
REFERENCES
Brainard, D. H. (1997). The psychophysics toolbox. Spatial
Vision, 10, 433–436.
Delorme, A., & Makeig, S. (2004). EEGLAB: An open source
toolbox for analysis of single-trial EEG dynamics including
independent component analysis. Journal of Neuroscience
Methods, 134, 9–21.
Ernst, M. O., & Banks, M. S. (2002). Humans integrate visual
and haptic information in a statistically optimal fashion.
Nature, 415, 429–433.
Gitelman, D. R., Penny, W. D., Ashburner, J., & Friston, K. J.
(2003). Modeling regional and psychophysiologic
interactions in fMRI: The importance of hemodynamic
deconvolution. Neuroimage, 19, 200–207.
Gold, J. I., & Shadlen, M. N. (2007). The neural basis of
decision making. Annual Review of Neuroscience,
30, 535–574.
Gould, I. C., Nobre, A. C., Wyart, V., & Rushworth, M. F. (2012).
Effects of decision variables and intraparietal stimulation on
sensorimotor oscillatory activity in the human brain. Journal
of Neuroscience, 32, 13805–13818.
Griffin, D., & Tversky, A. (1992). The weighting of evidence and
the determinants of confidence. Cognitive Psychology, 24,
411–435.
Hertwig, R., & Erev, I. (2009). The description-experience
gap in risky choice. Trends in Cognitive Sciences,
13, 517–523.
Hunt, L. T., Kolling, N., Soltani, A., Woolrich, M. W., Rushworth,
M. F., & Behrens, T. E. (2012). Mechanisms underlying
cortical activity during value-guided choice. Nature
Neuroscience, 15, 470–476.
Josephs, O., Turner, R., & Friston, K. (1997). Event-related fMRI.
Human Brain Mapping, 5, 243–248.
Kahneman, D., Slovic, P., & Tversky, A. (1982). Judgment under
uncertainty: Heuristics and biases. New York: Cambridge
University Press.
Kording, K. P. (2007). Decision theory: What “should” the
nervous system do? Science, 318, 606–610.
Kording, K. P., & Wolpert, D. M. (2004). Bayesian integration in
sensorimotor learning. Nature, 427, 244–247.
Maris, E., & Oostenveld, R. (2007). Nonparametric statistical
testing of EEG- and MEG-data. Journal of Neuroscience
Methods, 164, 177–190.
Nieder, A., & Miller, E. K. (2003). Coding of cognitive
magnitude: Compressed scaling of numerical information in
the primate prefrontal cortex. Neuron, 37, 149–157.
Nienborg, H., & Cumming, B. (2010). Correlations between the
activity of sensory neurons and behavior: How much do they
tell us about a neuron’s causality? Current Opinion in
Neurobiology, 20, 376–381.
O’Connell, R. G., Dockree, P. M., & Kelly, S. P. (2012). A supramodal
accumulation-to-bound signal that determines perceptual
decisions in humans. Nature Neuroscience, 15, 1729–1735.
Piazza, M., & Izard, V. (2009). How humans count: Numerosity
and the parietal cortex. The Neuroscientist, 15, 261–273.
Piazza, M., Izard, V., Pinel, P., Le Bihan, D., & Dehaene, S.
(2004). Tuning curves for approximate numerosity in the
human intraparietal sulcus. Neuron, 44, 547–555.
Pouget, A., Beck, J. M., Ma, W. J., & Latham, P. E. (2013).
Probabilistic brains: Knowns and unknowns. Nature
Neuroscience, 16, 1170–1178.
Ratcliff, R., & McKoon, G. (2008). The diffusion decision model:
Theory and data for two-choice decision tasks. Neural
Computation, 20, 873–922.
Smith, P. L., & Vickers, D. (1988). The accumulator model of
two-choice discrimination. Journal of Mathematical
Psychology, 32, 135–168.
Smith, P. L., & Vickers, D. (1989). Modeling evidence
accumulation with partial loss in expanded judgment.
Journal of Experimental Psychology: Human Perception
and Performance, 15, 797–815.
Tversky, A., & Kahneman, D. (1971). Belief in the law of small
numbers. Psychological Bulletin, 76, 105–110.
Vickers, D. (1979). Decision processes in visual perception.
London: Academic Press.
Wyart, V., de Gardelle, V., Scholl, J., & Summerfield, C. (2012).
Rhythmic fluctuations in evidence accumulation during
decision making in the human brain. Neuron, 76, 847–858.
Wyart, V., Myers, N. E., & Summerfield, C. (2015). Neural
mechanisms of human perceptual choice under focused and
divided attention. Journal of Neuroscience, 35, 3485–3498.
Wyart, V., Nobre, A. C., & Summerfield, C. (2012). Dissociable
prior influences of signal probability and relevance on visual
contrast sensitivity. Proceedings of the National Academy of
Sciences, U.S.A., 109, 3593–3598.
Yang, T., & Shadlen, M. N. (2007). Probabilistic reasoning by
neurons. Nature, 447, 1075–1080.
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
d
o
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
8
/
4
2
8
5
/
8
4
9
/
1
5
9
8
5
9
0
/
3
1
1
7
6
8
o
4
c
6
n
4
_
7
a
/
_
j
0
o
0
c
9
n
1
8
_
a
p
_
d
0
0
b
9
y
1
g
8
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
i
2
3
e
s
/
j
/
t
.
f
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
Tickle et al.
603