MÉTHODES
Network dynamics in the healthy and
epileptic developing brain
Richard Rosch1,2, Torsten Baldeweg2, Friederike Moeller3, and Gerold Baier4
1Wellcome Trust Centre for Neuroimaging, University College London, United Kingdom
2Developmental Neurosciences Programme, UCL Great Ormond Street Institute of Child Health,
University College London, United Kingdom
3Department of Clinical Neurophysiology, Great Ormond Street Hospital, Londres, United Kingdom
4Cell and Developmental Biology, University College London, United Kingdom
Mots clés: EEG, Dynamic network, Epilepsy, State transitions, Computational analysis
un accès ouvert
journal
ABSTRAIT
Electroencephalography (EEG) allows recording of cortical activity at high temporal
resolution. EEG recordings can be summarized along different dimensions using
network-level quantitative measures, such as channel-to-channel correlation, or band power
distributions across channels. These reveal network patterns that unfold over a range of
different timescales and can be tracked dynamically. Here we describe the dynamics of
network state transitions in EEG recordings of spontaneous brain activity in normally
developing infants and infants with severe early infantile epileptic encephalopathies (n = 8,
âge: 1–8 months). We describe differences in measures of EEG dynamics derived from band
pouvoir, and correlation-based summaries of network-wide brain activity. We further show
that EEGs from different patient groups and controls may be distinguishable on a small set of
the novel quantitative measures introduced here, which describe dynamic network state
switching. Quantitative measures related to the sharpness of switching from one correlation
pattern to another show the largest differences between groups. These findings reveal that the
early epileptic encephalopathies are associated with characteristic dynamic features at the
network level. Quantitative network-based analyses like the one presented here may in the
future inform the clinical use of quantitative EEG for diagnosis.
INTRODUCTION
Epilepsy is the most common primary neurological disorder globally, with a particularly high
incidence in infancy and childhood (Olafsson et al., 2005). In a group of epilepsy syndromes,
the burden of epileptic discharges can cause severe, persistent brain dysfunction, c'est, un
recognizable encephalopathy. When these occur in early infancy, they are known as early
infantile epileptic encephalopathies (EIEE) (Ben-Ari & Holmes, 2006; Jette et al., 2015). Within
the category of severe epilepsies, there are several discrete electroclinical syndromes that
follow specific developmental timelines, occurring mainly in the neonatal period or very
early infancy (par exemple., Ohtahara syndrome), later during infancy (par exemple., infantile spasms / West
syndrome), or in early childhood (par exemple., Lennox-Gastaut syndrome). This developmental pat-
tern can also be observed in individual patients, such that a syndromic pattern may evolve,
such as from Ohtahara to West syndrome during development. This suggests that despite an
individually persistent cause for the epilepsy (such as a genetic mutation or structural lesion),
it is specific stages of brain development that translate the abnormality into age-specific, rec-
ognizable electroclinical phenotypes (Kodera et al., 2016; Ohtahara & Yamatogi, 2006).
Citation: Rosch, R., Baldeweg, T.,
Moeller, F., & Baier, G. (2017). Réseau
dynamics in the healthy and epileptic
developing brain. Réseau
Neurosciences, 2(1), 41–59.
https://doi.org/10.1162/netn_a_00026
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00026
Informations complémentaires:
https://doi.org/10.5281/zenodo.887316
https://www.mathworks.com/products/
new_products/release2016a.html
Reçu: 5 May 2017
Accepté: 9 Septembre 2017
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Richard Rosch
r.rosch@ucl.ac.uk
Éditeur de manipulation:
Olaf Sporns
droits d'auteur: © 2017
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
un
_
0
0
0
2
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network dynamics in the healthy and epileptic developing brain
Early infantile epileptic
encephalopathy (EIEE):
A group of severe epilepsies that
start in early infancy and in which
epileptic activity is so severe that
it disrupts normal brain function
and development.
Electroclinical syndrome:
A set of recognizable clinical and
EEG characteristics that consistently
occur together, that define a
distinctive and recognizable
condition.
Functional network:
A network description of the brain
based on the temporal correlation
between brain regions.
Microstate:
A transient global pattern of activity
measureable with EEG that appears
quasistable at short, subsecond
timescales.
Dynamics matrix:
A correlation matrix of measures
taken at successive time points that
aims to visualize correlation between
network-wide states over time
Feature space:
The number of dimensions required
to capture features of a single
observation. A feature is a
quantifiable property of an observed
phenomenon.
Electroencephalography (EEG) gives a rich picture of dynamic neuronal function and re-
gionally distinct oscillatory brain behavior in frequency ranges that span several orders of mag-
nitude (Lopes da Silva, 1991). In clinical practice, EEG analysis is focused on visual pattern
recognition of specific waveform abnormalities (par exemple., epileptiform discharges) associated with
specific clinical correlates (par exemple., increased risk of epileptic seizures). Visual analysis—while
essential—is biased towards certain observable features: Par exemple, between-channel cor-
relation of low-frequency, high-amplitude discharges is much more readily apparent than that
of high-frequency, low-amplitude discharges. Quantitative, automatic analysis may reveal
some of these EEG features usually overlooked by visual analysis alone (Tong & Thakor, 2009).
Graph theory, or network-based approaches to understanding neuronal function in terms
of functional networks, have recently emerged in imaging neuroscience. Particularly in func-
tional magnetic resonance imaging (IRMf) of the resting state, this has led to the discovery
that neuronal networks show functionally relevant and quantifiable fluctuation between dif-
ferent constellations, or states over time (Allen et al., 2014; Krienen, Yeo, & Buckner, 2014).
Similar methods based on graph theory have now been applied to electrophysiological sig-
nals from EEG and MEG (magnetoencephalography) recordings in humans (Boersma et al.,
2011; Brookes et al., 2011; Maldjian, Davenport, & Whitlow, 2014), and suggest that the
high temporal resolution in these signals can be harnessed to identify recognizable micro-
states at millisecond-to-second timescales and characterize the switching between them
(Baker et al., 2014; Khanna, Pascual-Leone, Michel, & Farzan, 2015; Koenig et al., 2002;
Van De Ville, Britz, & Michel, 2010; Vidaurre et al., 2016).
Dynamic features not directly visible in EEG analysis—such as the microstate dynamics
described above—are not commonly considered in the analysis of clinical EEG record-
ings. There is an emerging literature on the computational analysis of EIEE phenotypes
(Japaridze et al., 2013;
Japaridze et al., 2016) and related abnormal EEG patterns (Ching,
Purdon, Vijayan, Kopell, & Brun, 2012; Liu & Ching, 2017; Zubler et al., 2014). But our
understanding of intrinsic network dynamics in these phenotypes is still limited. Encore, ces
network dynamics are potentially important to understand whole-brain dysfunction as seen in
the EIEEs, where there is often not a sharp distinction between seizure patterns and interictal
abnormalities.
We build on the existing literature by evaluating simple quantitative summary measures of
the network dynamics in spontaneous brain activity in the healthy and epileptic developing
brain. A formally related approach has previously been introduced by Betzel et al. (2012),
where temporal similarity/dynamics matrices were calculated for specific frequency bands for
short EEG segments. We further evaluate the relationship between these correlation-based
network dynamics and power distribution in early infantile EEG.
The work presented in this paper thus has two main goals:
(un) to describe a method to
quantify network dynamics in terms of dynamical switches between EEG states based on cor-
relation patterns and power distributions, thus deriving a multivariate feature space capturing
network-level brain dynamics; et (b) to evaluate whether this approach captures pathological
brain dynamics by mapping two distinct EIEE electroclinical syndromes (Ohtahara syndrome,
West syndrome) onto this brain dynamics feature space. In the future, such an approach may
prove valuable for resolving diagnostic uncertainties (par exemple., in neonatal epilepsy), but it may
also inform computational models of neuronal populations, and thus help identify the neuro-
biological mechanisms underlying the phenotypes seen in this group of severe epilepsies.
Neurosciences en réseau
42
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
un
_
0
0
0
2
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network dynamics in the healthy and epileptic developing brain
MÉTHODES
Sujets
This study is focused on establishing estimates that describe EEG microstate dynamics using
different network measures, and thus illustrates the methodology on a small number of partic-
ipants with profound EEG abnormalities. Both patients and control EEGs were selected from
previously recorded standard pediatric clinical EEGs. The selection was based on classification
by a clinical neurophysiologist with expertise in pediatric EEG (FM).
Subject characteristics are detailed in Table 1. Two control subjects were identified from
routine clinical service in a tertiary pediatric hospital providing specialist regional neurophysi-
ology services, based on their age and an EEG within normal limits without evidence of epi-
leptiform abnormalities. Patients with Ohtahara syndrome were selected based on (un) clinical
history of seizures, (b) neonatal or early infantile onset of the epilepsy, et (c) evidence of
a burst-suppression pattern on standard clinical EEG. Patients with West syndrome were se-
lected based on (un) clinical history of infantile spasms, (b) infantile onset of the epilepsy, et
(c) evidence of hypsarrhythmia on standard clinical EEG. Examples of the EEGs from patients,
compared with the age-matched healthy controls, are shown in Figure 1. Where identified,
underlying causes for the epilepsy ranged from genetic abnormalities to localized brain
lesions and brain malformations.
All EEG recordings were performed with informed consent from the patients’ legal guardians,
and as necessitated by the patients’ clinical course. Use of anonymized EEGs from the clini-
cal database for quantitative analysis was reviewed and approved by the UCL Great Ormond
Street Institute of Child Health Joint Research and Development Office.
EEG Recordings and Preprocessing
Routine clinical EEG recordings were used for the analysis. Each patient had 19–21 scalp
electrodes placed according to the International 10–20 system. Recordings lasted for up to
30 min during task-free resting with the subjects’ parent or guardian. Data were recorded
with a sampling frequency of 256 ou 512 Hz and Butterworth bandpass filtered to a 1–80 Hz
frequency band for visual analysis.
For each individual subject a total of five artefact-free 10-s segments of EEG were selected
for further analysis, excluding periods of visually apparent deep sleep. No distinction was
made for light sleep and awake segments in the EEGs where no obvious electrographic sleep
architecture was appreciated on visual analysis. Because of the severity of the EEG abnormal-
ities, sleep stages were not apparent for some of the patients.
Tableau 1. EEG and clinical features of participants included in the analysis.
ID
1
2
3
4
5
6
7
8
EEG classification
Normal for age
Normal for age
Ohtahara syndrome
Ohtahara syndrome
Ohtahara syndrome
West syndrome
West syndrome
West syndrome
Age (mois)
2
6
1
2
2
5
6
8
EEG abnormality
–
–
Burst suppression
Burst suppression
Burst suppression
Hypsarrhythmia
Hypsarrhythmia
Hypsarrhythmia
43
Neurosciences en réseau
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
un
_
0
0
0
2
6
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network dynamics in the healthy and epileptic developing brain
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
Chiffre 1. EEG recordings of healthy controls (UN,C) and patients with EIEEs (B,D). Compared with
healthy controls at 2 mois (UN), Ohtahara syndrome is associated with abnormal burst-suppression
patterns disrupting the ongoing background, characterized by widespread, intermittent bursts of
high-amplitude activity (B). Compared with healthy controls at 6 mois (C), West syndrome is as-
sociated with chaotic and disorganized high-amplitude activity with mixed-frequency components
(hypsarrhythmia, D). All EEGs are shown in average referential montage.
F
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
un
_
0
0
0
2
6
p
d
t
.
Further analysis was performed on these data segments, each filtered to six different stan-
dard EEG frequency bands: broadband (0.1–60 Hz); delta band (1–4 Hz), theta band (4–8 Hz),
alpha band (8–13 Hz), beta band (13–30 Hz), and gamma band (30–60 Hz). Quantitative anal-
ysis was performed on an average montage with each channel referenced to the overall mean
scalp activity.
Selection of the EEG segments was made pseudorandomly by visually selecting artefact-free
10-s EEG epochs. No specific focus was made to include disease-specific EEG segments; comment-
jamais, the abnormalities for all patients were pervasive throughout the entirety of the recordings.
All data segments included in the analysis can be reviewed in full in the analysis repository at
Rosch (2017).
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Quantitative Network Analysis
Analysis was performed using customized scripts written by the authors running on
Matlab 2016a (MathWorks, 2016), as well as the k-Wave toolbox (Treeby, Varslot, Zhang,
Laufer, & Beard, 2011) for quantification of matrix sharpness and contrast. Existing routines to
generate surrogate time series written by Temu Gautama and based on Schreiber & Schmitz
(1996, 1999) were used to evaluate stationarity in the features described here (https://uk.
mathworks.com/matlabcentral/fileexchange/4612-surrogate-data). Mixed-effects ANOVA to
model repeated measure group differences were performed with routines written by Matthew
44
Stationarity:
A time series is considered stationary
if its statistical properties (par exemple., mean,
variance, autocorrelation) do not
change over time.
Neurosciences en réseau
Network dynamics in the healthy and epileptic developing brain
Johnson,
available online (https://uk.mathworks.com/matlabcentral/fileexchange/27080-
mixed–between-within-subjects–anova). All scripts are available to download and free to use
at doi.org/10.5281/zenodo.887316 (Rosch, 2017). Each feature was calculated separately for
each frequency band.
Spatial inference from EEG is often confounded by issues regarding volume conduction and
the choice of reference (Bastos & Schoffelen, 2015). The analysis presented here is specifically
designed to allow inference on network dynamics rather than topology in order to identify
robust quantitative features shared between patients with very different brain abnormalities
(Bialonski & Lehnertz, 2013). Classical pitfalls, such as volume conduction, are not expected
to introduce an artificial group difference or bias between groups, which is essential for the
future potential use of this approach as a biomarker.
In order to identify changes in network states,
Estimating dynamic correlation pattern changes.
dynamic correlation patterns were estimated (summary of the analysis pipeline shown in
Chiffre 2). For each EEG segment a sliding window approach was used to estimate dynamic
changes in the patterns of correlation between channels. Starting at each sampling point
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
un
_
0
0
0
2
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
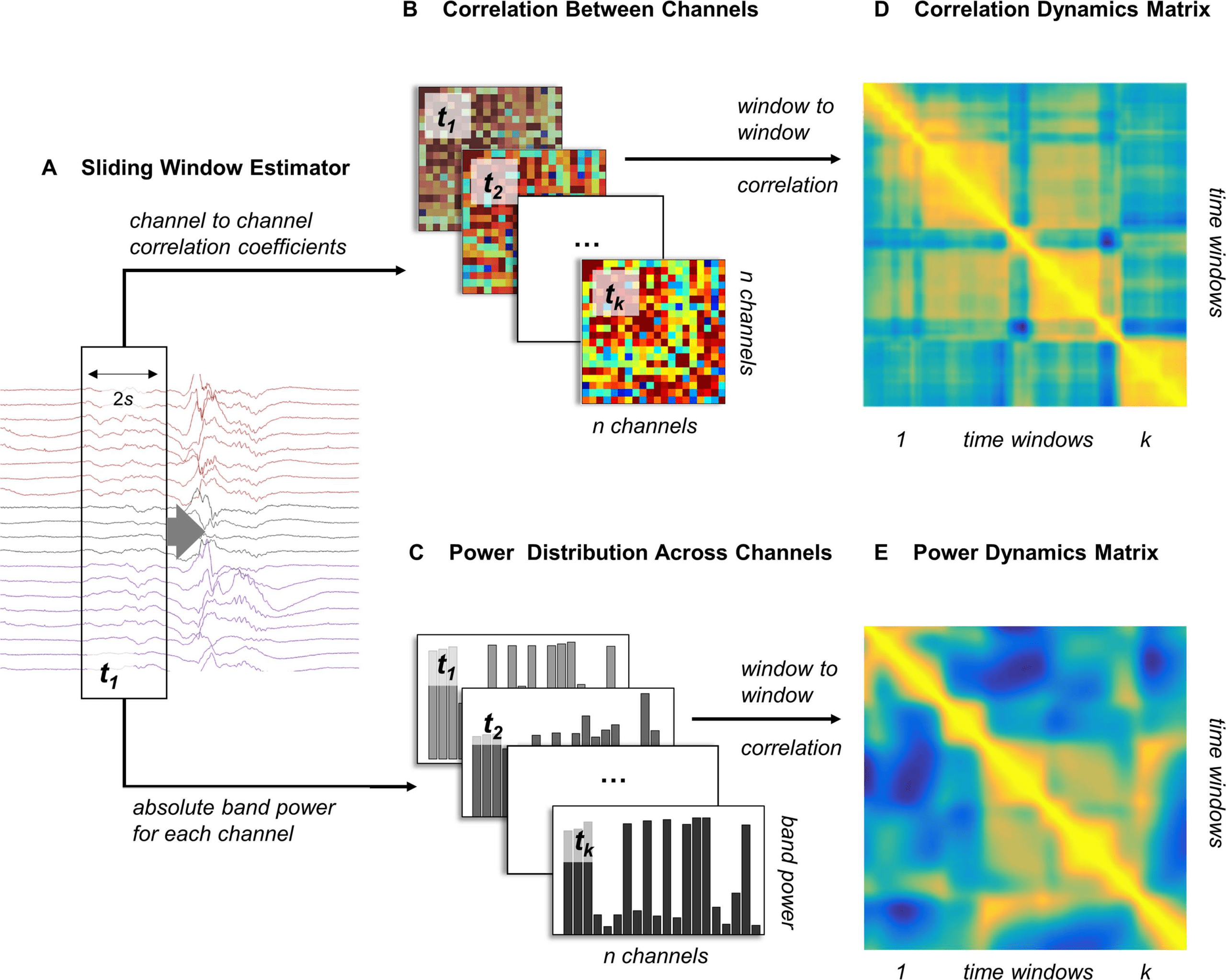
Chiffre 2. Dynamics of band power fluctuations and changing network correlations can be esti-
mated separately. This figure summarizes the estimation of dynamic changes in the power distri-
bution, and correlation patterns over a single 10-s window containing broadband frequencies: (UN)
A sliding window estimator (window length: 2s; step size: 1/512s) is used for feature extraction.
(B) Channel-by-channel correlations are estimated using Pearson’s linear correlation coefficients for
each time window.
(C) The average power within the specified frequency band is estimated for
each channel independently, resulting in a specific band power distribution for each time window.
(D, E) Estimating window-to-window correlation based on these measures yields two n × n dynamics
matrices describing correlation dynamics (D: CDM) and power dynamics (E: PDM), respectivement.
Neurosciences en réseau
45
Network dynamics in the healthy and epileptic developing brain
entre 0 et 8 s of any 10-s EEG segment, a 2-s window was extracted, yielding k short
segments. For each short segment, pairwise Pearson’s correlation indices between individual
channels were calculated, yielding a total of k correlation matrices that were n × n elements
large each (Figure 2B, where k = number of steps for sliding window, n = number of channels).
To identify transitions between network states defined by specific scalp-electrode correla-
tion patterns, a single k × k correlation dynamics matrix (CDM) was calculated: For this, nous
reshaped each of the k separate n × n matrices into k vectors of ∑n−1
i = 1 i unique elements
from the upper triangle of the adjacency matrix (avoiding duplications as the original n × n
adjacency matrix is symmetrical). The pairwise cross-correlation for all k vectors was then
calculated to derive the full k × k CDM. This approach helps to identify temporal changes
in the correlation patterns of the channel-to-channel correlation matrices (Figure 2D). Plus loin
statistical analysis was based on a single such CDM for each 10-s time window.
Similar to the correlation dynamics analysis, nous
Estimating dynamic power distribution changes.
established a related measure describing the power distribution changes over time (also shown
in Figure 2). For each EEG segment, a sliding window approach was used to calculate mean
band power for each channel within the respective frequency band. This yielded k vectors of
length n (Figure 2C, with k = number of steps for sliding window, n = number of channels).
A k × k power dynamics matrix (PDM) was calculated by estimating the pairwise correlation
between each of the k power distribution vectors (Figure 2E). Further statistical analysis was
based on a single PDM for each 10-s time window.
Statistical Analysis
To quantify features in the dynamics matrices, a set of scalar mea-
Quantifying matrix features.
sures was calculated for each dynamics matrix; these are summarized in Table 2. Briefly, ils
include the matrix mean (c'est à dire., dynamic correlation averaged in time); matrix contrast; et
matrix sharpness (defined as the Brenner Operator; Treeby et al., 2011). Contrast and sharp-
ness measures are derived from image analyses, and in this context they represent measures
describing the transition between correlated network states in time. They are differentially
sensitive to regional amplitude differences (where contrast is more robustly sensitive) et
smoothness of transition between states (where sharpness is more robustly sensitive), comme
illustrated in Figure 3.
To evaluate whether the dynamics matrix fea-
Testing for stationarity and statistical differences.
tures reflect nonstationary processes, they were statistically evaluated against a set of sta-
tionary surrogate time series of the same overall frequency and cross-correlation composition
Tableau 2. Measures used for quantification of dynamics matrix features.
Mean values
Contrast*
Sharpness (Brenner operator)**
fx,oui / k2
(cid:0) fx,y − fx+1, y+1(cid:1)
2
( fx+2,y − fx,oui)2 + ( fx,y+2 − fx,oui)2
∑
X,oui
∑
X,oui
∑
X,oui
* Derived indirectly from the gray-level co-occurrence matrix.
** Modified from Treeby et al. (2011).
fx,y = f (X, oui), the scalar value of the matrix at column x, row y. k is the number of rows in
the matrix.
Neurosciences en réseau
46
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
un
_
0
0
0
2
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network dynamics in the healthy and epileptic developing brain
(Schreiber & Schmitz, 1999). For each individual time window included in the analysis, le
following analysis steps were performed in order to derive a stationary normal distribution of
the measures illustrated above (mean values, contraste, and sharpness):
1. A total of 100 sets of amplitude and cross-correlation-adjusted surrogate time series were
generated for each 10-s window (yielding a total of 1,000–1,500 sets of EEG surrogates
per group).
2. Each set of synthetic time series were then analyzed using the same sliding window
analysis applied to the original datasets, thus deriving 100 surrogate sets of the measures
described above for each 10-s time window analyzed.
3. Z-scores were calculated for each measurement derived from the empirical time series,
based on the distribution of synthetically generated surrogate measurement sets.
If a dynamics matrix measure reflects only stationary processes caused by random fluctua-
tions around steady-state frequency distributions, empirical values are expected to fall within
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
un
_
0
0
0
2
6
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
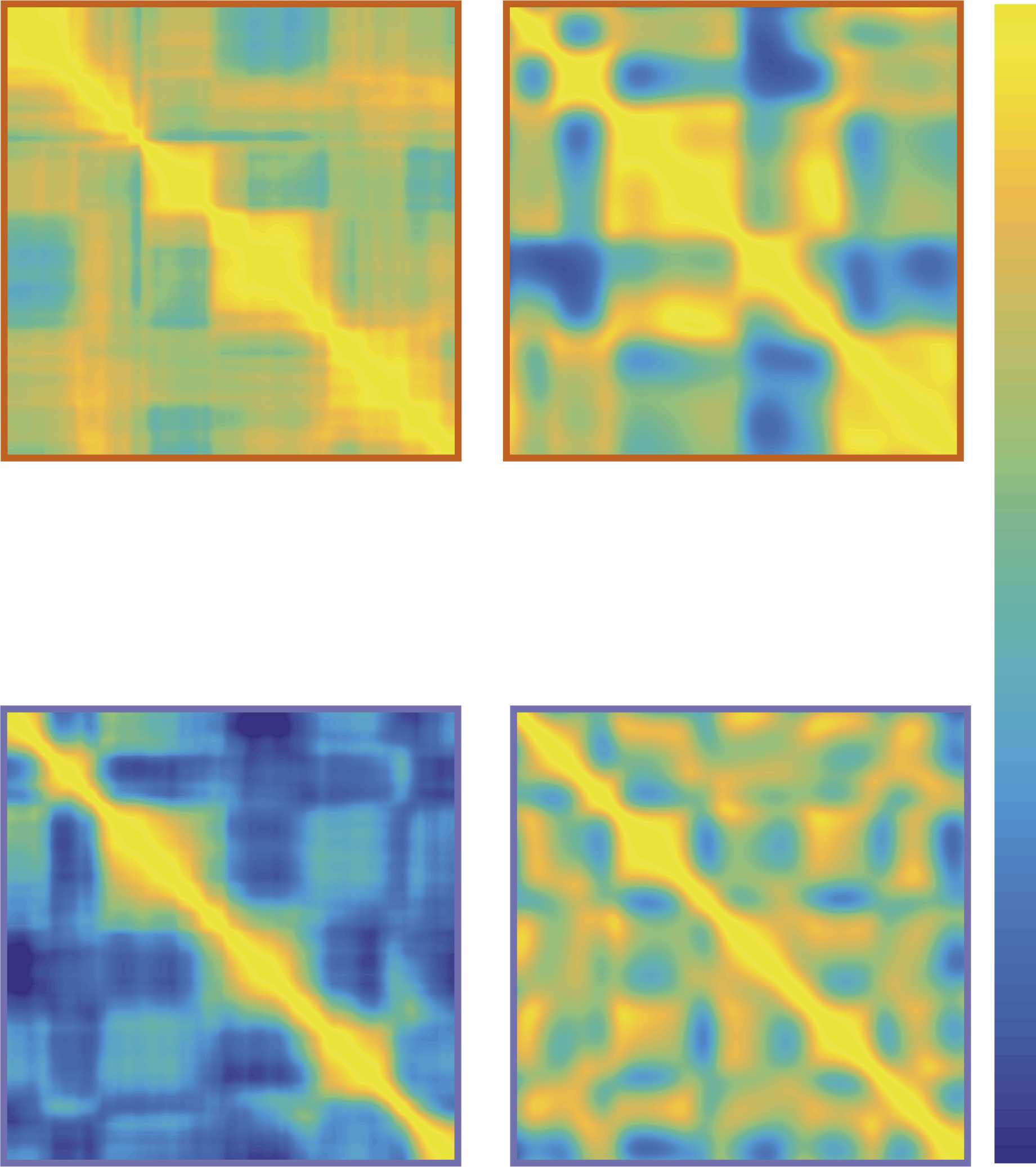
Chiffre 3. Contrast and sharpness measures encode related but different matrix features. Analysis
of example matrices with different levels of Gaussian smoothing (left vs. right panels), and different
signal amplitudes (top vs. bottom panels) shows differential sensitivity of the measures employed
(normalized values shown): Contrast changes mainly with the amplitude of the regional signal dif-
ferences, while sharpness is affected by both amplitude and smoothness modulations.
Neurosciences en réseau
47
Network dynamics in the healthy and epileptic developing brain
Purity:
An external validation for clustering
algorithm that quantifies the
proportion of observations that
are classified correctly.
k-means clustering:
An unsupervised clustering algorithm
that partitions a number of
observations into a predefined
number (k) of clusters.
the normal distribution of the surrogate data, c'est, roughly within the −2 to 2 z-score
interval. We also used the z-score normalized data to test for differences between individ-
ual measures using two-sided t tests.
The approach taken above yields several distinct mea-
Clustering based on network dynamics.
sures for each EEG time window: three dynamics matrix measures (mean, contraste, sharpness)
for two different matrix types (CDM, PDM), for six frequency bands (broadband, delta, theta,
alpha, beta, gamma) resulting in a total of 36 feature measures for each EEG window. À
identify dynamic network measures that capture discriminatory features between the EEG ab-
normalities analyzed here, nous (un) measured how well they can be used to classify individual
EEG segments into distinct groups, et (b) used a subset of the highest ranking measures to
automatically identify clusters within the data using machine-learning approaches.
For each measure we identified thresholds that optimize the classification of EEG windows
into three clusters corresponding to the three participant groups (c'est à dire., Ohtahara syndrome, West
syndrome, and healthy controls). To that effect, the purity of the classification, P., resulting
from a set of two threshold parameters was maximized using a simulated annealing approach.
P ranges from 0 (no element is correctly categorized) à 1 (all elements are correctly categories)
and is calculated as follows:
P. (Ω,C) =
1
N
∑
k
maximum
j
|ω
k ∩ cj| ,
where Ω = {ω1, ω2, . . . , ω
the set of given classes.
k} is the set of estimated clusters, and C = = {c1, c2, . . . , cj} est
The maximally achieved value for P was recorded for each measure and used to rank the
36 individual dynamics measures according to how well they can be used to cluster EEGs into
patient groups. As a second step, we then used subsets of the high-ranking dynamics measures
to automatically cluster the EEGs into different groups using k-means clustering. Cette approche
partitions a dataset into a set of k clusters automatically, given a set of observations. We use
this approach to quantify how well the measures we identified in the first steps can be used to
categorize 10-s segments of EEG into the appropriate participant categories (using the purity
measure P), and how well they distinguish between normal and abnormal (Ohtahara and West
syndromes combined) catégories (using sensitivity and specificity estimates). This does not aim
to assess individual measures in terms of their diagnostic accuracy, but to quantify how much
information about the original classification based on full EEG recordings is retained in this
low-dimensional feature space.
RÉSULTATS
Correlation and Band Power Dynamics
A total of five relatively artefact-free EEG segments were selected randomly and analyzed for
each participant, yielding separate CDM and PDM for each segment and each frequency band.
Across all subjects and segments there are visible differences in the temporal dynamics of cor-
relation patterns and band power distribution patterns (shown in Figure 4A–B), which can be
quantified in the difference between the two matrices: if band power distribution and channel-
to-channel correlation followed the same dynamics, the differences would be expected to cen-
ter around 0. The mean of the CDM – PDM difference is shown for each time window in the
analysis in Figure 4C. This suggests that in healthy controls, PDM values are overall higher than
CDM values, which is also seen in Figure 4B. In both patient groups, there is more temporal
Neurosciences en réseau
48
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
un
_
0
0
0
2
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network dynamics in the healthy and epileptic developing brain
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
un
_
0
0
0
2
6
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4. Network correlation states and band power distribution show different recurrence pat-
terns in time. The dynamics matrices show recurrent correlation or band power distribution patterns
in time. (UN) Shows CDM and PDM for a single 10-s EEG segment of a patient with West syndrome
containing broadband frequencies. Both show high correlation values outside of the leading di-
agonal (c'est à dire., between different time segments). (B) In healthy controls, high between-time-window
correlation is largely restricted to the leading diagonal in the CDM, but not the PDM, suggérant
that network correlation patterns are less recurrent than band power distribution patterns for broad-
band frequencies. (C) Mean CDM – PDM difference values suggest that for healthy controls, but not
the patient groups, recurrent band power patterns recur more across time than network correlation
motifs (c'est à dire., the CDM – PDM difference is negative).
Neurosciences en réseau
49
Network dynamics in the healthy and epileptic developing brain
cross-correlation in network correlation states than in the band power distribution, resulting
in positive mean difference values (which only achieve significance in the West syndrome
patients).
A closer analysis of the temporal patterns underlying these differences is shown for a single
healthy control EEG segment in Figure 5. Transitions between network motifs as measured
through CDM or PDM show a dissociation: Observed band power distribution across the
scalp may change without closely associated corresponding changes in the network correlation
patterns and vice versa.
CDM Nonstationarity and Group Differences
Randomly generated stationary time series of the same spectral composition as the empirical
recordings were used to assess for nonstationarity in different measures applied to the EEG
segments. For each measure, z-scores were calculated from a distribution generated based on
analysis of 100 synthetic datasets for each individual EEG segment, and are shown in Figure 6.
Some of the dynamics measures derived from the PDM can be explained as random fluctu-
ations around a stationary distribution, while all CDM-derived measures differ significantly
from the stationary distributions; c'est, they show nonstationarity.
There are significant group differences in the mean correlation in the CDMs, but not
the PDMs: Mixed-effects ANOVA for repeated measures – PDMs, between subjects factor
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
un
_
0
0
0
2
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5. Dissociation of band power and network correlation dynamics. (UN) Shows the CDM for
a single 10-s EEG broadband segment in healthy control aged 2 mois. (B) Shows the PDM for the
same EEG segment. (C) Channel-to-channel correlation patterns are shown for three separate time
windows, with big differences between time point 1 and the others, and more similarities between
time points 2 et 3. (D) Correlations are shown between a single time window (indicated by the
dashed lines in A, B) and all other time windows based on correlation dynamics (c'est à dire., CDM) et
power dynamics (c'est à dire., PDM). (E) Shows the band power distribution across channels over time.
While there are broad similarities in the temporal trajectories of power and correlation dynamics,
there are discrete instances where similar band power distribution patterns (at t1and t3) are asso-
ciated with very different correlation patterns, and vice versa (at t2 and t3).
Neurosciences en réseau
50
Network dynamics in the healthy and epileptic developing brain
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
un
_
0
0
0
2
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 6. Correlation dynamics are nonstationary. Large proportions of PDM-derived measures
of band power dynamics for windows containing broadband frequencies (UN,C,E) fall within a 95%
confidence interval derived from stationary surrogate synthetic datasets (shown as green shading),
indicating that their variation at least in part may represent random fluctuations around stationary
processes. Groups of measurements that differ significantly from stationary surrogate distribution
are highlighted with asterisks. CDM-derived measures derived from windows containing broad-
band frequencies (B,D,F) are not fully explained by stationary correlation patterns. Red bars indi-
cate the standard deviation around the means of the individual groups; black bars show the group
mean. Asterisks illustrate results of a t test whether distributions differ significantly from mean = 0:
* p < 0.05; ** p < 0.01.
Network Neuroscience
51
Network dynamics in the healthy and epileptic developing brain
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
a
_
0
0
0
2
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
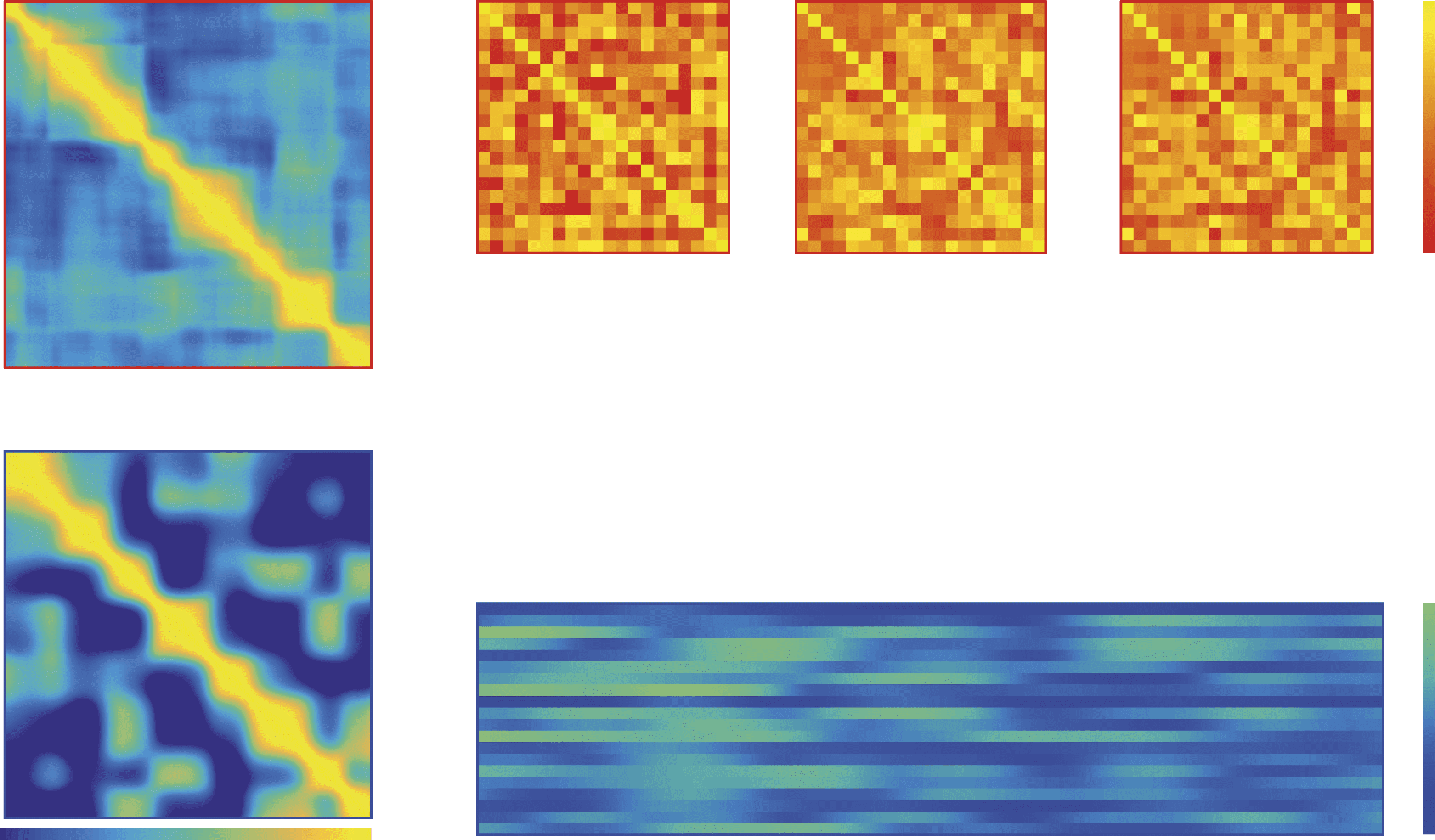
Figure 7. Recurrent and persistent motifs of network correlation states are more apparent in both
patient groups. (A) Broadband Cz-electrode time series and CDMs are shown for single 10-s EEG
segments for representatives of both Ohtahara and West syndrome cohorts and healthy age matched
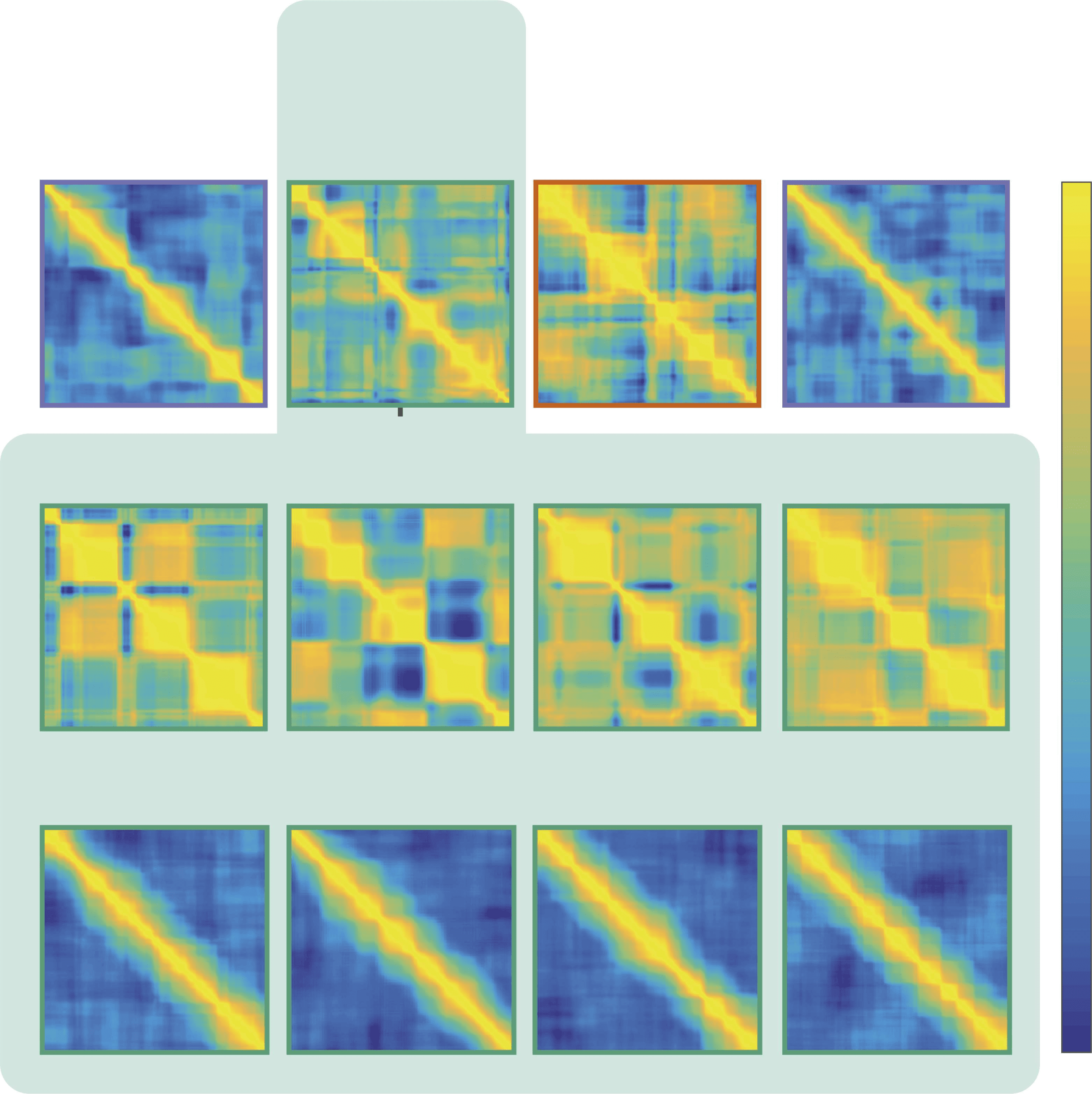
controls. (B) CDMs derived from bandpass filtered data for the EEG segment from the Ohtahara
patient show distinct dynamics patterns for each frequency band. (C) CDMs derived from station-
ary surrogate data are largely restricted to the leading diagonal, thus indicating few persistent or
recurrent network patterns in any of the frequency bands.
F(2) = 0.41, p = 0.68; CDMs, between subjects factor F(2) = 6.74, p = 0.038. Mean correla-
tions (+/− standard error around the mean) in CDMs of both patient groups are higher than in
the healthy controls (Ohtahara syndrome: 0.59 (+/− 0.05), West syndrome: 0.75 (+/− 0.02),
Healthy controls: 0.44 (+/− 0.02). The nonstationarity is expressed across frequency bands
as persistent motifs, as shown for an example segment of the EEG of a patient with Ohtahara
syndrome in Figure 7.
Network Dynamics in EIEE Patients
A complete set of dynamics measures derived from both CDM and PDM were collated for
each EEG segment, resulting in 36 measures (3 measures × 2 matrix types × 6 filter bands)
per EEG segment. For each individual value, thresholds were identified that could be used
to separate the data into three clusters that best reproduced the original participant groups
(Ohtahara syndrome, West syndrome, and healthy controls). Table 3 shows the 10 highest
Network Neuroscience
52
Network dynamics in the healthy and epileptic developing brain
Table 3. Rank of dynamics measures based on clustering ability.
Rank
1
2
3
4
5
6
7
8
9
10
Measure
sharpness
sharpness
sharpness
sharpness
sharpness
mean
mean
mean
contrast
sharpness
Matrix type
PDM
CDM
PDM
CDM
CDM
CDM
CDM
PDM
CDM
CDM
Filter band
alpha
delta
theta
all
theta
all
all
theta
theta
alpha
Purity
0.725
0.700
0.700
0.675
0.625
0.600
0.600
0.600
0.600
0.600
ranking measures based on maximum purity achieved after automatic threshold optimization.
Several of these variables can be used in conjunction to map out distinct groups’ distributions
in a low-dimensional feature space. As an example, Figure 8 shows each individual EEG seg-
ment mapped onto the three highest ranked dynamics measures from Table 3. In order to ver-
ify how well these measures separate distinct subgroups, we evaluated results from a k-means
automatic clustering algorithm based on increasingly large subsets (range: 1 to 20 parameters)
of the dynamics measures. Results of this unsupervised clustering approach were then com-
pared with the known disease category, using overall classification purity, as well as sensitivity
and specificity of separating healthy controls segments from patients (Figure 8B). An exam-
ple of such a clustering is shown for just two parameters in Figure 8C. Using the top-ranking
four parameters, this approach can reach a classification purity of 75.0%, with a disease clas-
sification sensitivity of 96.7% and a specificity of 80.0% (Figure 8B).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
a
_
0
0
0
2
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. Clustering using dynamics measures separates patient groups. (A) Dynamics matrix
measures can be used to visualize clustering of the EEG segments in a three-dimensional feature
space. Here all EEG segments are mapped onto the three most discriminatory dynamics measures,
producing distinct clusters in this three-dimensional feature space. (B) Classification purity, as well
as sensitivity and specificity of classifying patients and healthy controls in separate groups, is shown
for a range of parameters included in the automated clustering. (C) One example clustering solu-
tion is shown using only the two highest ranking parameters with limited separation between West
syndrome and healthy control EEGs.
Network Neuroscience
53
Network dynamics in the healthy and epileptic developing brain
DISCUSSION
This report presents a quantitative analysis approach for identifying temporal patterns in net-
work states in the developing brain. Using electrographically distinct epilepsy syndromes af-
fecting most of the background EEG dynamics as illustrative cases, we show that (a) temporal
correlation analysis can reveal distinct patterns from high-dimensional datasets such as EEG;
(b) band power and channel-to-channel correlation dynamics can be dissociated, even in the
healthy brain; (c) quantitative summary measures derived from this analysis can capture EEG
differences between different electroclinical syndromes.
The novel measures introduced here describe quantitatively the temporal dynamics of whole-
brain network states. Even structurally very different networks may show similarities in dynam-
ics, which makes the measures introduced here particularly useful for identifying similarities in
highly heterogeneous clinical populations. Early infantile EEGs are furthermore characterized
by activity in a variety of spatial distributions (rather than the more typical posterior dominant
rhythms seen in the mature EEG), indicating that analysis of the dynamics of different network
patterns unfolding may be particularly informative in this age group.
Dynamics Matrices Can Reveal Hidden Temporal Structure in High-Dimensional Data
Network-based analyses have been the conceptual basis for the recent success in resting-state
fMRI in humans (Van Dijk et al., 2010). Furthermore, computational modeling approaches
have enabled an understanding of the relationship of observable, macroscopic whole-brain
network dynamics and local, mesoscale neuronal dynamics (Deco, Jirsa, & McIntosh, 2011).
Many of the network features first described based on resting-state fMRI are also present in
the analysis of EEG/MEG recordings, where they can be measured with very high temporal
resolution, revealing fast, subsecond recurrent network switching (Baker et al., 2014). These
fast network dynamics can be task related (O’Neill et al., 2017), and approaches similar to
the one presented here have demonstrated that they are modulated by cognitive tasks, even in
children (Dimitriadis, Laskaris, & Micheloyannis, 2015).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
a
_
0
0
0
2
6
p
d
.
t
The analysis presented here is focused on identifying quantitative EEG features that (a) can
show differences between pathological and healthy brain dynamics even at the level of in-
dividual subjects, and (b) can be applied to task-free resting-state EEG recordings routinely
performed in a clinical setting. Given the heterogeneities in the clinical sample, the aim is not
to identify specific neuroanatomical networks that reproduce between these patients, but to
describe the visually apparent dynamic features using novel quantitative measures and to iden-
tify whether other, less directly visible, features can also be useful discriminators.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The dynamics matrices reveal structured patterns that capture the recurrence of correlated
network states over different timescales. The dynamics of these transitions can be visually rep-
resented and, importantly, quantified using image metrics (such as sharpness and contrast)
that intuitively capture features of the microstate transitions. This approach summarizes spe-
cific aspects of the multichannel, highly time resolved EEG recordings that are less amenable to
standard visual analysis. While these quantitative measures may depend to some extent on the
particular preprocessing steps performed on the EEG data, the identifiable group differences
indicate that they are potentially useful as biomarkers to separate different disease categories.
Band Power and Correlation Patterns Represent Different Aspects of Neuronal Circuitry Function
Correlations between channels and power distribution across channels are likely to repre-
sent physiologically separate processes that can follow distinct dynamic patterns. The spectral
Network Neuroscience
54
Network dynamics in the healthy and epileptic developing brain
composition of the EEG signal (and thus its regionally specific band power distribution) is
believed to result from synchronous firing within local neuronal populations; statistical cor-
relation between distant channels is believed to be caused by direct or indirect, long-range
synaptic connectivity (Buzsáki, Anastassiou, & Koch, 2012; Vanhatalo & Kaila, 2006). A dif-
ference between power- and correlation-derived network dynamics can therefore be under-
stood to represent separately the dynamics of synaptic connectivity at the local and the network
levels. The choice of cross-correlation means that when estimating the functional connectivity,
the data are scaled by the total power of the time series; thus, this measure specifically reveals
temporal structure in the correlations that is independent of the dynamics of power alone.
Across all participant groups, there are visible differences between dynamic patterns as
derived from band power distributions (PDM) and network correlation patterns (CDM). These
differences suggest that a particular band power distribution across the scalp does not cor-
respond to network correlation patterns—that is, functional connectivity motifs—in the devel-
oping brain, both in patients and in normally developing controls. Using the approach shown
here, changes in correlation patterns and band power patterns over time can be tracked sep-
arately and reveal divergent trajectories. Most of the dynamic variance contained within the
PDM can be explained as random fluctuations of an overall stationary process, while correla-
tion patterns over time differ significantly from those observed in a stationary signal, thus the
product of a nonstationary process.
The first year of life is associated with a range of developmental changes affecting both
local microcircuitry (e.g., synaptic pruning, neurotransmitter and receptor changes) as well
as global network integration (e.g., myelinization of large white matter tracts) Chu, Leahy,
Pathmanathan, Kramer, & Cash, 2014; Dehaene-Lambertz & Spelke, 2015). Identifying devel-
opmental changes in the dynamics at different neuronal scales may thus provide insight into
the relationship between neurobiological changes and observed EEG patterns, particularly
where there are visible EEG changes, as is the case in the EIEEs discussed here. Applied to
a larger cohort, the approach illustrated here with just a small sample of pathological EEG
patterns may in the future also reveal more subtle developmental patterns in the healthy devel-
oping brain by allowing quantification of network dynamic behaviors in simple network-based
measures, such as the transition sharpness.
Quantifying Abnormal Brain States in Clinical Populations
Our results suggest that as few as four measures may be sufficient to distinguish EEG segments
from different disease categories with reasonable accuracy. Both Ohtahara and West syndrome
are characterized by pervasive neuronal abnormalities that disrupt normal background EEG
function. Their associated EEG phenotypes (i.e., burst suppression patterns and hypsarrhyth-
mia) are readily apparent throughout most EEG segments. Thus, the analysis approach pre-
sented here is not designed to resolve diagnostic uncertainty; the distinct phenotypes included
in the analysis were utilized to test whether our novel dynamics measures can reveal apparent
differences in the EEG dynamics quantitatively.
As the measures derived from the dynamics matrices are quantifiable, they allow for statisti-
cal testing and the application of simple machine-learning tools. As illustrated in the approach
taken here, individual measures can be ranked according to their discriminative power for
clustering into disease categories, thereby identifying the features that most help differentiate
different pathologies from the dynamics in the normal developing brain.
Network Neuroscience
55
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
a
_
0
0
0
2
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network dynamics in the healthy and epileptic developing brain
Dynamical systems:
A set of variables whose change over
time can be described by differential
equations.
Of the 10 measures that are most distinct between different groups, 8 are measures of
sharpness in either the CDMs or the PDMs—thus different patient groups and healthy controls
show particular differences in their transition between different network states. The majority
of the useful measures are derived from the CDMs (which are also most nonstationary), sug-
gesting that it is specifically the temporal dynamics of the switch between discrete functional
connectivity patterns that separates the groups. Notably, each of the top 10 ranking measures
either were broadband measures or were restricted to the lower frequencies (delta, theta,
alpha), which may be related to the window length of 2 s, as this will average out changes
in high-frequency correlation patterns that are only a few cycles long. However, most of
the physiological and abnormal activity we were aiming to capture is within the lower fre-
quency ranges, which the window length appears to capture well. Both patients with Ohtahara
syndrome and patients with West syndrome show abnormally high persistence of network
states (Figure 4C). These observations suggest that the EIEE brain is susceptible to enter recur-
rent and abnormally stable functional connectivity states.
This approach complements existing computational modeling of epilepsy and seizure ac-
tivity (Kramer & Cash, 2012; Schindler, Bialonski, Horstmann, Elger, & Lehnertz, 2008). The
application of dynamical systems mathematical approaches to neuronal oscillators has led
to the recognition of certain stereotypical seizure patterns as mathematically predictable os-
cillatory patterns (Izkhikevich 2000) that can be reproduced in computational simulations
(Jirsa, Stacey, Quilichini, Ivanov, & Bernard, 2014). Using these in silico simulations means
that we can explain the effects of genetic mutations (Peters, Rosch, Hughes, & Ruben, 2016),
specific seizure responses to stimulation (Taylor et al., 2014), or seizure spread patterns (Baier,
Goodfellow, Taylor, Wang, & Garry, 2012) using full generative models that bridge observ-
able and nonobservable (hidden) spatial and temporal scales. Such approaches focus on repro-
ducing specific features observed in empirical data—typically the particular, directly visible
oscillatory patterns and their relationship to neuronal function (Breakspear, 2005; Jirsa et al.,
2014). Here we offer quantitative descriptions of network-level dynamic features that appear
to be modulated by both the epilepsy (i.e., persistent network states as seen in the examples in
Figure 7A, resulting in the differences in Figure 4C) and the developmental stage (i.e., transition
dynamics differences between the younger Ohtahara syndrome, and the older West syndrome
cohort)—features that can be specifically included in future models of EIEE.
The EEG phenotypes analyzed here are distinctive and easily classified by visual analysis
alone; they appear as generalized EEG features that may arise from focal brain abnormalities.
Thus our analysis aimed to introduce and validate a set of simple measures of whole-brain
dynamics that are not specifically dependent on individual patients’ topology, but capture the
readily apparent EEG abnormalities. In addition to the power components, there are bivariate
features exemplified by the cross-correlation in our analysis that are not readily accessible by
visual analysis alone. While the approach is more complex than a simple stationary power
analysis, it also allows us to extract frequency-band-specific dynamic patterns. Taken together,
these features might allow the identification of disease-specific network states (Betzel et al.,
2012). This work will be the foundation for future computational work aiming to reproduce
some of these intrinsic dynamics to explore the relationship between putative neurobiological
mechanisms of disease and the observed EEG patterns.
Future Applications in the Clinic and in Epilepsy Research
First, the EEG phenomenology-based clustering approach may aid in resolving diagnostic
uncertainties in neonatal EEG analysis, where the difference between abnormal patterns and
Network Neuroscience
56
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
a
_
0
0
0
2
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network dynamics in the healthy and epileptic developing brain
normal developmental variants are more difficult to identify visually (Mathieson et al., 2016;
Stevenson et al., 2015; Torres & Anderson, 1985). Correct diagnosis currently relies on the ex-
pertise of clinicians trained in pediatric (and specifically neonatal) clinical neurophysiology,
who are not available in all clinical settings where accurate diagnosis of neonatal EEG pat-
terns could be valuable. Yet there is a recent focus on improving neurological outcomes of
neonatal care, which is likely to involve a significant increase in EEG recordings and moni-
toring in neonates at risk of seizures, requiring a corresponding scaling up of EEG interpre-
tation capacities (Sands & McDonough, 2016; Vesoulis et al., 2014). Utilizing quantitative,
computational approaches as presented here may be able to support correct diagnosis in
those settings and play a role in improving clinical outcomes (Mathieson et al., 2016; Temko,
Thomas, Marnane, Lightbody, & Boylan, 2011).
Second, the epilepsy syndromes under investigation here have a close relationship to
developmental stages: Ohtahara syndrome typically is restricted to the neonatal or early
infantile period, while West syndrome emerges in later infancy, typically between 3 and
10 months. Both share genetic causes (e.g., GABRA1 mutations; Kodera et al., 2016), and
individual patients can evolve from Ohtahara syndrome to West syndrome during their
development (Ohtahara & Yamatogi, 2006). Thus, understanding the neurobiological pro-
cesses underlying the EEG phenotypes offers a window into the interactions between brain
development and early onset pathological processes. By being able to quantify differences
in network dynamics, we can identify features that are crucial in distinguishing patient
groups. These quantitative features can be used as benchmarks for adapting existing mod-
els of neuronal dynamics (Baier et al., 2012; Papadopoulou et al., 2015; Proix, Bartolomei,
Chauvel, Bernard, & Jirsa, 2014) to reproduce the empirical observations. With those mod-
els we will be able to test mechanistic hypotheses that link recent discoveries on the genetic
basis of many of the EIEEs and our understanding of developmental processes in the infant
brain, to the identifiable EEG syndromes seen in patients.
Limitations
This study is not an attempt at testing the dynamics measures in terms of their clinical validity.
The EIEE syndromes included here were deliberately chosen because of their wide-ranging
impact on the background EEG and the disruption of normal brain dynamics; they are used to
illustrate the validity of the method and the possibility to identify less visible group differences
as a possible basis for a biomarker to separate different EIEE syndromes. Visually observed
EEG differences are large; thus we have included only a small number of subjects, aiming to
identify group differences with large effect sizes that are likely to be useful in future applica-
tions in clinical samples where predictive power at the single individual is required. We have
used several EEG segments from the same patient. These are more likely to cluster than truly
independent samples from a larger population of patients. The clustering approach therefore
is not meant as a comprehensive evaluation of the diagnostic potential of this approach, but il-
lustrates the use of a small set of quantitative measures of network dynamics in segregating EEG
segments. Further evaluation of this approach will require formal analysis on a larger sample
of patients.
FUNDING INFORMATION
RER is funded by a Wellcome Trust Clinical Research Fellowship (106556/Z/14/Z). This study
was supported by the National Institute for Health Research Biomedical Research Centre at
Network Neuroscience
57
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
a
_
0
0
0
2
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network dynamics in the healthy and epileptic developing brain
Great Ormond Street Hospital for Children NHS Foundation Trust and University College
Hospital.
AUTHOR CONTRIBUTIONS
Richard E. Rosch: Conceptualization; Formal analysis; Methodology; Software; Visualization;
Writing – original draft; Writing – review & editing. Torsten Baldeweg: Supervision; Writing –
review & editing. Friederike Moeller: Conceptualization; Formal analysis; Writing – review &
editing. Gerold Baier: Conceptualization; Formal analysis; Supervision; Writing – review &
editing.
REFERENCES
Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele, T., &
(2014). Tracking whole-brain connectivity dy-
Calhoun, V. D.
namics in the resting state. Cerebral Cortex, 24(3), 663–676.
Baier, G., Goodfellow, M., Taylor, P. N., Wang, Y., & Garry, D. J.
(2012). The importance of modeling epileptic seizure dynamics
as spatio-temporal patterns. Frontiers in Physiology, 3(July), 1–7.
Baker, A. P., Brookes, M. A., Rezek, A., Smith, S. M., Behrens, T.,
Probert Smith, P. J., & Woolrich, M. (2014). Fast transient net-
works in spontaneous human brain activity. eLife, 3(3), 1–18.
Bastos, A. M., & Schoffelen, J.-M. (2015). A tutorial review of func-
tional connectivity analysis methods and their interpretational
pitfalls. Frontiers in Systems Neuroscience, 9(January), 175.
Ben-Ari, Y., & Holmes, G. L. (2006). Effects of seizures on develop-
mental processes in the immature brain. The Lancet Neurology,
5(12), 1055–1063.
Betzel, R. F., Erickson, M. A., Abell, M., O’Donnell, B. F., Hetrick,
W. P., & Sporns, O. (2012). Synchronization dynamics and evi-
dence for a repertoire of network states in resting EEG. Frontiers
in Computational Neuroscience, 6(September), 1–13.
Bialonski, S., & Lehnertz, K. (2013). Assortative mixing in functional
brain networks during epileptic seizures. Chaos, 23(3), 033139.
Boersma, M., Smit, D. J., de Bie, H. M., Van Baal, G. C., Boomsma,
D. I., de Geus, E. J., . . . Stam, C. J. (2011). Network analysis of
resting state EEG in the developing young brain: Structure comes
with maturation. Human Brain Mapping, 32(3), 413–425.
Breakspear, M. (2005). A unifying explanation of primary general-
ized seizures through nonlinear brain modeling and bifurcation
analysis. Cerebral Cortex, 16(9), 1296–1313.
Brookes, M. J., Woolrich, M., Luckhoo, H., Price, D., Hale, J. R.,
Investigating the
Stephenson, M. C., . . . Morris, P. G.
electrophysiological basis of resting state networks using mag-
netoencephalography. Proceedings of the National Academy of
Sciences, 108(40), 16783–16788.
(2011).
Buzsáki, G., Anastassiou, C., & Koch, C. (2012). The origin of extra-
cellular fields and currents—EEG, ECog, LFP and spikes. Nature
Reviews Neuroscience, 13(6), 407–420.
Ching, S., Purdon, P. L., Vijayan, S., Kopell, N. J., & Brown, E. N.
(2012). A neurophysiological-metabolic model for burst suppres-
sion. Proceedings of the National Academy of Sciences, 109(8),
3095–3100.
Chu, C. J., Leahy, J., Pathmanathan, J., Kramer, M. A., & Cash,
S. S. (2014). The maturation of cortical sleep rhythms and net-
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
a
_
0
0
0
2
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
works over early development. Clinical Neurophysiology, 125(7),
1360–1370.
Deco, G., Jirsa, V. K., & McIntosh, A. R.
(2011). Emerging con-
cepts for the dynamical organization of resting-state activity in
the brain. Nature Reviews Neuroscience, 12(1), 43–56.
Dehaene-Lambertz, G., & Spelke, E. S. (2015). The infancy of the
human brain. Neuron, 88(1), 93–109.
Dimitriadis, S. I., Laskaris, N. A., & Micheloyannis, S. (2015). Tran-
sition dynamics of EEG-based network microstates during mental
arithmetic and resting wakefulness reflects task-related modu-
lations and developmental changes. Cognitive Neurodynamics,
9(4), 371–387.
Izkhikevich, E.
International
ing.
1171–1266.
(2000). Neural excitability, spiking and burst-
Journal of Bifurcation and Chaos, 10(06),
Japaridze, N., Muthuraman, M., Moeller, F., Boor, R., Anwar,
A. R., Deuschl, G., . . . Siniatchkin, M. (2013). Neuronal net-
works in West syndrome as revealed by source analysis and
renormalized partial directed coherence. Brain Topography,
26(1), 157–170.
Japaridze, N., Muthuraman, M., Dierck, C., von Spiczak, S., Boor,
R., Mideksa, K. G., . . . Siniatchkin, M. (2016). Neuronal net-
works in epileptic encephalopathies with CSWS. Epilepsia, 57(8),
1245–1255.
Jette, N., Beghi, E., Hesdorffer, D., Moshé, S. L., Zuberi, S. M.,
Medina, M. T., & Bergen D. (2015). ICD coding for epilepsy:
Past, present, and future—A report by the International League
Against Epilepsy Task Force on ICD codes in epilepsy. Epilepsia,
56(3), 348–355.
Jirsa, V. K., Stacey, W. C., Quilichini, P. P., Ivanov, A. I., & Bernard,
C. (2014). On the nature of seizure dynamics. Brain, 137(8),
2210–2230.
Khanna, A., Pascual-Leone, A., Michel, C. M., & Farzan, F. (2015).
Microstates in resting-state EEG: Current status and future direc-
tions. Neuroscience & Biobehavioral Reviews, 49, 105–113.
Kodera, H., Ohba, C., Kato, M., Maeda, T., Araki, K., Tajima, D., . . .
Matsumoto, N. (2016). De novo GABRA1 mutations in Ohtahara
and West syndromes. Epilepsia, 57(4), 566–573.
Koenig, T., Prichep, L., Lehmann, D., Sosa, P. V., Braeker, E.,
Kleinlogel, H., . . . John, E. R. (2002). Millisecond by millisec-
ond, year by year: Normative EEG microstates and developmen-
tal stages. NeuroImage, 16(1), 41–48.
Network Neuroscience
58
Network dynamics in the healthy and epileptic developing brain
Kramer, M. A., & Cash, S. S. (2012). Epilepsy as a disorder of cortical
network organization. The Neuroscientist, 18(4), 360–372.
Krienen, F. M., Yeo, B. T., & Buckner, R. L. (2014). Reconfigurable
functional coupling modes cluster around a
task-dependent
core functional architecture. Philosophical Transactions of the
Royal Society of London B: Biological Sciences, 369(1653),
20130526.
Liu, S., & Ching, S. (2017). Homeostatic dynamics, hysteresis and
synchronization in a low-dimensional model of burst suppres-
sion. Journal of Mathematical Biology, 74(4), 1011–1035.
Lopes da Silva, F.
(1991). Neural mechanisms underlying brain
waves: From neural membranes to networks. Electroencephalog-
raphy and Clinical Neurophysiology, 79(2), 81–93.
Maldjian, J. A., Davenport, E. M., & Whitlow, C. T. (2014). Graph
theoretical analysis of resting-state MEG data: Identifying inter-
hemispheric connectivity and the default mode. NeuroImage,
96, 88–94.
Mathieson, S. R., Stevenson, N. J., Low, E., Marnane, W. P., Rennie,
J. M., Temko, A., . . . Boylan, G. B. (2016). Validation of an auto-
mated seizure detection algorithm for term neonates. Clinical
Neurophysiology, 127(1), 156–168.
MathWorks. (2016). Matlab R2016a release updates. https://www.
mathworks.com/products/new_products/release2016a.html
Ohtahara, S., & Yamatogi, Y. (2006). Ohtahara syndrome: With
special reference to its developmental aspects for differentiat-
ing from early myoclonic encephalopathy. Epilepsy Research, 70,
58–67.
Olafsson, E., Ludvigsson, P., Gudmundsson, G., Hesdorffer, D.,
Kjartansson, O., & Hauser, W. A. (2005). Incidence of unpro-
voked seizures and epilepsy in Iceland and assessment of the
epilepsy syndrome classification: A prospective study. The Lancet
Neurology, 4(10), 627–634.
O’Neill, G. C., Tewarie, P. K., Colclough, G. L., Gascoyne, L. E.,
Hunt, B. A. E., Morris, P. G., . . . Brookes, M. J. (2017). Measure-
ment of dynamic task related functional networks using MEG.
NeuroImage, 146, 667–678.
Papadopoulou, M., Leite, M., van Mierlo, P., Vonck, K., Lemieux, L.,
Friston, K., & Marinazzo, D. (2015). Tracking slow modulations
in synaptic gain using dynamic causal modelling: Validation in
epilepsy. NeuroImage, 107, 117–126.
Peters, C., Rosch, R. E., Hughes, E., & Ruben, P. C. (2016).
Temperature-dependent changes in neuronal dynamics in a
patient with an SCN1A mutation and hyperthermia induced
seizures. Scientific Reports, 6(1), 31879.
Proix, T., Bartolomei, F., Chauvel, P., Bernard, C., & Jirsa, V. K.
(2014). Permittivity coupling across brain regions determines
seizure recruitment in partial epilepsy. Journal of Neuroscience,
34(45), 15009–15021.
Rosch, R. E. (2017). Dynamics matrices. Supplemental material
for “Network dynamics in the healthy and epileptic developing
brain.” Network Neuroscience. Advance publication. https://doi.
org/10.5281/zenodo.887316
Sands, T. T., & McDonough, T. L. (2016). Recent advances in neo-
natal seizures. Current Neurology and Neuroscience Reports,
16(10), 92.
Schindler, K. A., Bialonski, S., Horstmann, M. T., Elger, C. E., &
Lehnertz, K. (2008). Evolving functional network properties and
synchronizability during human epileptic seizures. Chaos, 18(3),
033119.
Schreiber, T., & Schmitz, A.
(1996).
Improved surrogate data for
nonlinearity tests. Physical Review Letters, 77(4), 635–638.
Schreiber, T., & Schmitz, A. (1999). Surrogate time series. Physica D,
142, 346–382.
Stevenson, N. J., Clancy, R. R., Vanhatalo, S., Rosén, I., Rennie,
for
J. R., & Boylan, G. B.
(2015).
neonatal seizure detection using multichannel EEG. Annals of
Clinical and Translational Neurology, 2(11), 1002–1011.
Interobserver agreement
Taylor, P. N., Wang, Y., Goodfellow, M., Dauwels, J., Moeller, F.,
(2014). A computational study of
Stephani, U., . . . Baier, G.
stimulus driven epileptic seizure abatement. PLoS ONE, 9(12),
e114316.
Temko, A., Thomas, E., Marnane, W., Lightbody, G., & Boylan,
(2011). EEG-based neonatal seizure detection with support
G.
vector machines. Clinical Neurophysiology, 122(3), 464–473.
Tong, S., & Thakor, N. V. (2009). Quantitative EEG analysis methods
and clinical applications. Norwood, MA: Artech House.
Torres, F., & Anderson, C. (1985). The normal EEG of the human
newborn. Journal of Clinical Neurophysiology, 2(2), 89–103.
Treeby, B. E., Varslot, T. K., Zhang, E. Z., Laufer, J. G., & Beard,
P. C. (2011). Automatic sound speed selection in photoacoustic
Journal of
image reconstruction using an autofocus approach.
Biomedical Optics, 16(9), 090501.
Van De Ville, D., Britz, J., & Michel, C. M. (2010). EEG microstate
sequences in healthy humans at rest reveal scale-free dynam-
ics. Proceedings of the National Academy of Sciences, 107(42),
18179–18184.
Van Dijk, K. R., Hedden, T., Venkataraman, A., Evans, K. C., Lazar,
S. W., & Buckner, R. L. (2010). Intrinsic functional connectivity
as a tool for human connectomics: Theory, properties, and opti-
mization. Journal of Neurophysiology, 103(1), 297–321.
Vanhatalo, S., & Kaila, K.
(2006). Development of neonatal EEG
activity: From phenomenology to physiology. Seminars in Fetal
and Neonatal Medicine, 11(6), 471–478.
Vesoulis, Z. A., Inder, T. E., Woodward, L. J., Buse, B., Vavasseur,
C., & Mathur, A. M. (2014). Early electrographic seizures, brain
injury, and neurodevelopmental risk in the very preterm infant.
Pediatric Research, 75(4), 564–569.
Vidaurre, D., Quinn, A. J., Baker, A. P., Dupret, D., Tejero-Cantero,
A., & Woolrich, M. W. (2016). Spectrally resolved fast tran-
sient brain states in electrophysiological data. NeuroImage, 126,
81–95.
Zubler, F., Gast, H., Abela, E., Rummel, C., Hauf, M., Wiest, R.,
. . . Schindler, K. (2014). Detecting functional hubs of ictogenic
networks. Brain Topography, 28(2), 305–317.
Network Neuroscience
59
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
1
4
1
1
0
9
1
9
8
3
n
e
n
_
a
_
0
0
0
2
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3