MÉTHODES

3M_BANTOR: A regression framework for
multitask and multisession brain
network distance metrics

Chal E. Tomlinson1

, Paul J. Laurienti2,3, Robert G. Lyday2,3, and Sean L. Simpson2,4

1Department of Biostatistics, University of North Carolina at Chapel Hill, Chapel Hill, Caroline du Nord, Etats-Unis
2Laboratory for Complex Brain Networks, Wake Forest University School of Medicine, Winston-Salem, Caroline du Nord, Etats-Unis
3Department of Radiology, Wake Forest University School of Medicine, Winston-Salem, Caroline du Nord, Etats-Unis
4Department of Biostatistics and Data Science, Wake Forest University School of Medicine, Winston-Salem, Caroline du Nord, Etats-Unis

un accès ouvert

journal

Mots clés: Graph theory, Connectivity, IRMf, Neuroimaging, Jaccard, Kolmogorov–Smirnov, Log-
Euclidean Riemannian metric, Riemannian manifold distance, Mixed model, Repeated observations,
Human Connectome Project (HCP), Pearson correlation distance

ABSTRAIT

Brain network analyses have exploded in recent years and hold great potential in helping us
understand normal and abnormal brain function. Network science approaches have facilitated
these analyses and our understanding of how the brain is structurally and functionally
organized. Cependant, the development of statistical methods that allow relating this
organization to phenotypic traits has lagged behind. Our previous work developed a novel
analytic framework to assess the relationship between brain network architecture and
phenotypic differences while controlling for confounding variables. More specifically, ce
innovative regression framework related distances (or similarities) between brain network
features from a single task to functions of absolute differences in continuous covariates and
indicators of difference for categorical variables. Here we extend that work to the multitask
and multisession context to allow for multiple brain networks per individual. We explore
several similarity metrics for comparing distances between connection matrices and adapt
several standard methods for estimation and inference within our framework: standard F test,
F test with scan-level effects (SLE), and our proposed mixed model for multitask (et
multisession) BrAin NeTwOrk Regression (3M_BANTOR). A novel strategy is implemented to
simulate symmetric positive-definite (SPD) connection matrices, allowing for the testing of
metrics on the Riemannian manifold. Via simulation studies, we assess all approaches for
estimation and inference while comparing them with existing multivariate distance matrix
regression (MDMR) méthodes. We then illustrate the utility of our framework by analyzing the
relationship between fluid intelligence and brain network distances in Human Connectome
Project (HCP) data.

INTRODUCTION

As brain network analyses have exploded in recent years, neuroimaging researchers often face
the need to statistically compare brain networks (Simpson et al., 2013un). Many approaches for
relating brain networks to clinical outcomes or demographical variables have been developed.
Such methods include but are not limited to traditional network models (par exemple., exponential

Citation: Tomlinson, C. E., Laurienti,
P.. J., Lyday, R.. G., & Simpson, S. L.
(2023). 3M_BANTOR: A regression
framework for multitask and
multisession brain network distance
metrics. Neurosciences en réseau, 7(1),
1–21. https://doi.org/10.1162/netn_a
_00274

EST CE QUE JE:
https://doi.org/10.1162/netn_a_00274

Informations complémentaires:
https://doi.org/10.1162/netn_a_00274;
https://github.com/applebrownbetty
/ braindist_regression

Reçu: 29 Avril 2022
Accepté: 22 Août 2022

Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.

Auteur correspondant:
Sean L. Simpson
slsimpso@wakehealth.edu

Éditeur de manipulation:
Daniele Marinazzo

droits d'auteur: © 2022
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence

La presse du MIT

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

random graph models; Lehmann et al., 2021; Simpson et al., 2011, 2012), tensor regression
works on brain network (par exemple., Zhang et al., 2018, 2019), Bayesian approaches (par exemple., Dai &
Guo, 2017; Wang et al., 2017), statistical learning techniques (Craddock et al., 2015; Varoquaux
& Craddock, 2013; Xia et al., 2020), and testing based on distance correlation (Székely et al.,
2007; Székely & Rizzo, 2009). Despite the advances made, analysis methods are still needed
that enable relating brain network organization to phenotypic traits. In order to develop such
an analysis, we can exploit the fact that brain networks often exhibit consistent organizations
across subjects. Toward this end, in previous work we developed a permutation testing frame-
work that detects whether the spatial location of network features (such as the location of high
degree nodes) mapped back into brain space differs between two groups of networks, et
whether distributions of topological properties vary by group (Simpson et al., 2013b). We then
proposed an innovative regression framework to relate distances between brain network features
from a single task to functions of absolute differences in continuous covariates and indicators
of difference for categorical variables (Tomlinson et al., 2022). Here we extend that work to the
multitask and multisession context to allow for multiple brain networks per individual.

We considered several different types of metrics for establishing distances (c'est à dire.,
similarity/dissimilarity) between networks. The first type compares degree distributions. Nous
accomplish this by summarizing similarities in connection-based degree distributions across
multiple networks with the Kolmogorov–Smirnov statistic (KS statistic), a measure that quan-
tifies the distance between two cumulative distribution functions (Kolmogorov, 1933; Smirnov,
1948). The second type takes into account consistency of key edge sets. We do so by summa-
rizing similarities in edge sets across multiple networks with the Jaccard distance (or Jaccard
index), a metric that quantifies difference (or similarity) in partitions of a set (Joyce et al., 2010;
Meunier et al., 2009). The third type of metric measures differences in network edges by
employing the Euclidean distance between connectivity matrices (Lance & Williams, 1966).
The fourth type of metric (similar to the third) measures correlations in network edges by
employing the Pearson correlation distance between connectivity matrices (van Dongen &
Enright, 2012). The fourth metric is also edge-based but measures differences between con-
nectivity matrices with the log-Euclidean Riemannian metric (Arsigny et al., 2006). The log-
Euclidean Riemannian metric (LERM) is a metric not considered in our previous work and is
used as a computationally friendly approximation of the affine-invariant Riemannian metric
(AIRM). Riemannian metrics are used to measure representational connectivity (Shahbazi
et coll., 2021) and require the use of symmetric positive-definite (SPD) matrices.

While our previous work summed over the rows of connection matrices to show the utility
of comparing nodal degree vectors, this work focuses solely on distance metrics utility by
using entire connection matrices. This changes the interpretation of what a difference means,
c'est, switching the individual comparisons from nodal degrees to edge weights. Cependant, tous
metrics discussed here, except for LERM, are able to handle nodal degree vectors as well.
There is evidence of edge-centric functional connectivity exhibiting consistent organizations
across subjects over multiple scan sessions (Finn et al., 2015; Shen et al., 2017).

Within our regression framework we adapt several methods for estimation and inference:
standard F test, F test with SLE, and our proposed mixed model for multitask (and multisession)
BrAin NeTwOrk Regression (3M_BANTOR). Each observation in the regression framework
includes a “distance” between two individuals, so observations that share individuals are cor-
related. Ainsi, the standard F test is generally not appropriate but presented for comparison.
Since distances between individuals will be repeated, as individuals have multiple scans each,
we should not expect including fixed SLE within the regression to render the F test valid. C'est
presented here for comparison as well, as this was our chosen method when each individual

Permutation testing framework:
A method to test statistical
significance utilizing permutation
(switching labels).

Degree distribution:
The probability distribution of the
degree of nodes across a network.

Symmetric matrix:
A matrix which entry aij = aji for all
i and j. In the connectivity matrix
espace, this lets us know we are
considering an undirected network.

Mixed model:
Statistical model containing both
fixed (population-level) and random
(individual-level) effects used to
model multivariate data.

Neurosciences en réseau

2

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

Fixed effects:
Variables whose effects are constant
across individuals.

Random effect:
Variable whose effect varies across
individuals.

had only one scan (Tomlinson et al., 2022). 3M_BANTOR includes scan-level fixed effects as
well as random effects to account for repetitions among individuals in an attempt to handle the
correlation induced by including multiple scans per individual.

As mentioned previously, many existing methods exist for relating network metrics and phe-
notypes. We believe our method most closely relates to multivariate distance matrix regression
(MDMR). MDMR tests the significance of associations of response profile (dis)similarities and a
set of predictors. Originally this was done using only permutation tests (Anderson, 2001), mais
later extended to analytic p values and nonindependent observations (McArtor, 2017). These
MDMR methods will be considered for comparison with our proposed methods (F test, F test
with SLE, and 3M_BANTOR).

In this paper, we detail our regression framework and discuss several methods for estima-
tion and inference to be used with a variety of network similarity/dissimilarity metrics within
the framework. A novel strategy is implemented to simulate SPD connection matrices, allow-
ing for the testing of metrics on the Riemannian manifold. We assess all combinations of
methods and metrics within this framework by using simulated fMRI data with known differ-
ences in connectivity matrix distributions. We then apply our framework to multitask and mul-
tisession functional brain networks derived from the HCP dataset to investigate the relationship
between fluid intelligence and network distances after accounting for known confounders.

MÉTHODES

Please note the following notational choices: bold font is used to denote vectors or matrices,
n = number of observations, np = number of participants, nn = number of nodes, nt = number
of tasks, nr = number of repetitions (of a given task), p = number of covariates (y compris
intercept, if included).

Step 1: Network Construction

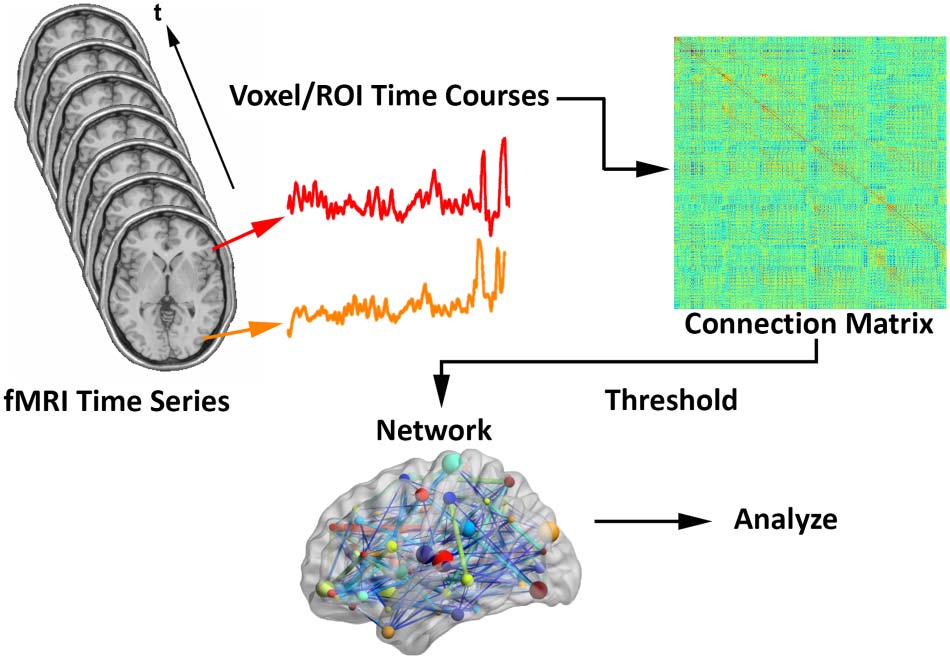
Assuming fMRI connection matrices have already been obtained (voir la figure 1 recreated from
Fornito et al., 2012; Simpson et al., 2013un), let Cijk represent a weighted nn × nn connection

Schematic for generating brain networks from fMRI time series data (recreated from
Chiffre 1.
Fornito et al., 2012; Simpson et al., 2013un). Functional connectivity between brain areas is esti-
mated based on time series pairs to produce a connection matrix. A threshold is commonly applied
to the matrix to remove negative and/or “weak” connections.

Neurosciences en réseau

3

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

matrix for individual i within-task j on repetition k, with matrix entries ranging from −1 (perfect
negative correlation) à 1 (perfect positive correlation). We only considered undirected net-
travaux, so matrices were symmetric, avec le # of row = # of columns = # of nodes (méthodes
are adaptable if directed networks are desired).

Let Bijk represent an nn × nn binary graph for individual i within-task j on repetition k, avec
an entry of 1 representing a key connection and 0 a connection that is not key. Key connec-
tions are most frequently identified with thresholding, where all connections greater than a
certain value get mapped to 1, while the rest get mapped to 0. Since key connections were
compared across subjects, it was important to employ the same criterion in all the networks
(par exemple., top 10% highest connection strengths, correlation > 0.5, etc.).

It should be noted that none of the methods employed here, except for the manifold dis-
tances, are specific to differences between connection matrices. C'est, these methods could
also be implemented on differences between nodal degree vectors or nodal scaled inclusivity,
Par exemple.

Step 2: Establish Similarity/Dissimilarity Between Networks

This section covers some of the metrics we used to gauge distances between individual net-
works given the insight they can provide into brain network organizational differences.

Kolmogorov–Smirnov statistic. Degree distributions, which help quantify the topology of net-
travaux, are likely more similar within distinctive groups than they are between these groups.
We again employed the log of the KS statistic to quantify this potential dissimilarity as we did
for our single-task approach.
(cid:1)

(cid:3)

log KSabc;def

¼ log supx Fabc xð Þ − Fdef xð Þ

ð

j

Þ
j

Empirical distribution function:
Estimate of the cumulative
distribution function using the data.

Logarithmic transformation:
A fancy way of saying we took
the log.

Power:
Probability of correctly rejecting the
null hypothesis.

KSabc,def, a scalar, is the KS statistic between connectivity matrix Cabc (individual a, task b,
repetition c) and connectivity matrix Cdef. Fabc(X) represents the empirical distribution function
for observations from the off-diagonal upper (or lower) triangular portion of Cabc. Donc, supx
|Fabc(X) − Fdef (X)| gives the biggest difference between the empirical edge connectivity distri-
butions between Cabc and Cdef. Bigger values indicate more dissimilarity.

A note on the logarithmic transformation of the KS statistic: when all distances are nonneg-
ative, it is common practice to take a log transformation. Within our simulations, KS was the
only metric that saw improvements in power or type I error when taking such a transformation.
For ease of interpretability, none of the other distances presented here utilized a logarithmic
transformation.

Jaccard distance.

JDabc;def ¼

M01 þ M10
M11 þ M01 þ M10

JDabc,def, a scalar, is the Jaccard distance ( JD) between binary graph Babc (individual a, task b,
repetition c) and binary graph Bdef. M11 is the number of off-diagonal upper (or lower) trian-
gular connections such that Babc and Bdef both have a value of 1, M01 is the number of con-
nections where Babc = 0 and Bdef = 1, and M10 is the number of connections where Babc = 1
and Bdef = 0. JDabc,def gives the proportion of key edges (in either set) that do not share key
status between Babc and Bdef. Values of JDabc,def range from 0 (perfect overlap) à 1 (Non
overlap).

Neurosciences en réseau

4

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

Log-Euclidean Riemannian metric (LERM).

LERMabc;def ¼ log Cabc

ð

(cid:4)
(cid:4)

(cid:1)
Þ − log Cdef

(cid:4)
(cid:3)
(cid:4)

F

LERMabc,def, a scalar, is the log-Euclidean distance between connectivity matrix Cabc and con-
nectivity matrix Cdef, where the exponential of a matrix A is defined by eA ≡
i¼0 An=n!: B is
said to be a matrix logarithm of C if eB ¼ C (Hall, 2015); ‖·‖F, the Frobenius or Euclidean matrix
norm, is defined as the square root of the sum of the absolute squares of its elements (Golub &
Loan, 1996). An in-depth look at Riemannian geometry on SPD matrices and its applications
for the analysis of functional connectivity can be found here (You & Parc, 2021). LERM was
calculated using the pdDist function in the pdSpecEst package in R (Chau, 2020).

P∞

Pearson correlation distance.

PCDabc;def ¼

1 − corr Cabc; Cabc
ð
2

Þ

PCDabc,def, a scalar, is the Pearson correlation distance (PCD) between connectivity matrix
Cabc and connectivity matrix Cdef, where corr (Cabc, Cabc) represents the Pearson correlation
coefficient between the vectorized off-diagonal values of the two matrices. The above equa-
tion is calculated for the off-diagonal upper triangular portion of the matrices (easily adaptable
to upper and lower triangular if nonsymmetric). Values of PCDabc,def range from 0 à 1.

Euclidean distance (EUC).

Eabc;def ¼¼

Xnn

Xnn

i¼1

j¼iþ1

jCabc i; j
½

(cid:2) − Cdef i; j

½

2
(cid:2)j

!1
2

Eabc,def, a scalar, is the Euclidean distance between connectivity matrix Cabc and connectivity
matrix Cdef, where Cabc[je, j] represents the connectivity matrix value (edge weight) entre
node i and node j for individual a, task b, and repetition c. The above equation is
calculated for the off-diagonal upper triangular portion of the matrices (easily adaptable to
upper and lower triangular if nonsymmetric). Bigger values of Euclidean distance indicate
more dissimilarity.

Step 3: Evaluating Differences Between Networks

Standard F test.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Distabc;dbf ¼ X T

abc;dbf ;conβb;con þ X T

abc;dbf ;coiβb;coi þ εabc;dbf

Distabc,dbf represents the distance between connectivity matrix Cabc and connectivity matrix
Cdef (distinct individuals a and d, same-task b, and all combinations of repetitions c and f ).
Distabc,dbf is a generic placeholder for any metric outlined previously in Step 2, c'est, Jaccard
distance ( JDabc,dbf ), KS statistic (KSabc,dbf ), et ainsi de suite.

X T

abc;dbf ;con, un 1 × (p − 1) vector, contains the intercept and differences in confounding
covariables (par exemple., for our data, sex, educational attainment, âge, and body mass index) entre
distinct individuals a and d, same-task b, and all combinations of repetitions c and f (with cor-
responding unknown (p − 1) × 1 task b parameter vector β
b,con) to control for differences that
may confound the relationship between the covariate of interest and the given distance.

Neurosciences en réseau

5

A regression framework for multitask brain network distance metrics

X T
abc;dbf ;coi, a scalar, contains the difference in the covariate of interest (or an indicator of
different group membership for group-based analyses) between distinct individuals a and d,
same-task b, and all combinations of repetitions c and f (with corresponding unknown task
b parameter βb,coi).

Splitting the design matrix Xb, an n × p matrix, into confounding and of interest covariates is
abc;dbf ;coi can be combined into the 1 × p

abc;dbf ;con and X T

purely a notational preference. X T
vector X T

abc;dbf (with corresponding unknown p × 1 parameter vector βb).

εabc,dbf accounts for the random error in the distance ( Jaccard, KS, etc.) valeur. If the random
errors were independent, homoscedastic, and approximately normally distributed, the F test of
a standard linear regression would be an appropriate test. Cependant, here we have correlated
observations, so this standard testing procedure was just included for comparison.

As an example, to test (specifically for task b) whether there is an association between IQ
(continu) and the spatial consistency of network edges (top 20% highest positive correla-
tion) after controlling for age (continu), sex (binary), and treatment (binary) status, notre
model would be

JDabc;dbf ¼ βb;0 þ Ageabc − Agedbf
j
þ IQabc − IQdbf

j

jβb;4 þ εabc;dbf

jβb;1 þ 1 Sexabc ≠ Sexdbf

F

gβb;2 þ 1 Trtabc ≠ Trtdbf

F

gβb;3

with the associated null hypothesis H0 : βb,4 = 0.

Note that there are task-specific design matrices. The aggregated model looks as follows:

Dist ¼ X T β þ (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2) ¼ X T
b1

βb1 þ … þ X T
bnt

βbnt þ (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)

C'est, we will have task-specific inference (parameter estimates, p values, etc.).

Standard F test with scan-level fixed effects (F test with SLE).

Dist ¼ X T β þ SCANID1;1;1α1;1;1 þ … þ SCANIDnp;nt;nrαnp;nt;nr þ (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

Dist is an n × 1 vector of known distance metrics (as outlined in Step 2). XT is the n × ntp design
matrice (intercepts optional) of known covariates with corresponding ntp × 1 unknown param-
eter vector β. SCANIDi,j,k is the n × 1 known indicator variable for the brain scan of individual
je, task j and repetition k, with corresponding unknown parameter αi,j,k. Accounting for SLE
allowed for an F test to appropriately evaluate the covariates of interest in our previous method
(Tomlinson et al., 2022). Given that there are now repeated within-task comparisons between
distinct individuals, we do not expect this approach to still render the F test appropriate. Ce
testing procedure was included here mainly for comparison and to highlight that multiple
brain scans per individual will require additional considerations.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Mixed model for multitask (and multisession) BrAin NeTwOrk regression (3M_BANTOR).

Dist ¼ X T β þ SCANIDT α þ (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2) þ ID1;1 ID2;1b1;1;2;1 þ ID1;1 ID3;1b1;1;3;1 þ …
þ ID1;1 IDnp;1b1;1;np;1 þ ID2;1 ID3;1b2;1;3;1 þ ID2;1 ID4;1b2;1;4;1 þ …
þ ID2;1 IDnp;1b2;1;np;1 þ … þ IDnp−1;nt

IDnp;nt bnp−1;nt ;np;nt

Dist is an n × 1 vector of known distance metrics (as outlined in Step 2). XTβ and SCANIDTα
are combined versions of what was outlined in the previous section. IDa,b_IDd,b is the n × 1
known indicator variable for comparisons between distinct individuals a and d on same-task b,
with ba,b;d,b ∼ N(0, gb) being the corresponding random effect. Linear mixed effects modeling
was done with REML using the lmer function of the R package lme4 (Bates et al., 2015);

Neurosciences en réseau

6

A regression framework for multitask brain network distance metrics

p values were calculated using Satterthwaite’s method (Fai & Cornelius, 2007) using the R pack-
age lmerTest (Kuznetsova et al., 2020).

Please note, if one attempted to use 3M_BANTOR with single-task cross-sectional data (c'est à dire.,
just one task and no repeated scans per subject), there would be one random effect for each
observation (and your statistical software of choice would likely report an error or warning
telling you something along the lines of “the number of levels of a grouping factor for the ran-
dom effects must be less than the number of observations”). Dans ce cas, all random effects
should be dropped, and 3M_BANTOR effectively turns into the model shown in the previous
section, a standard F test with scan-level fixed effects. This is equivalent to the recommended
testing method from our previous method (Tomlinson et al., 2022).

MDMR permutation and mixed-MDMR. Multivariate distance matrix regression (MDMR) is an
existing method that has been included here for comparison. It tests the significance of asso-
ciations of response profile (dis)similarities and a set of predictors. Originally this was done
using only permutation tests (Anderson, 2001), but has been extended to analytic p values
and nonindependent observations (McArtor, 2017). We ran both MDMR permutation and
mixed-MDMR (for nonindependent observations) méthodes.

For our previously mentioned methods, distances were limited to within-task comparisons.
Since MDMR methods require a complete distance matrix, we instead ran MDMR separately
for each task. En plus, in the above methods, observations were limited to distinct indi-
viduals. For similar reasoning (methods require a complete distance matrix), this is not possible
in the MDMR framework and within-individual distances were included. Inputs into each
(individual-task) model were with the npnr × npnr distance matrix D (the distance matrix analog
of Dist) and the npnr × p design matrix Xp (covariates of interest for each participant).

MDMR permutation was run using the mdmr function in the MDMR package in R (McArtor,
2018) using the permutation method with 5,000 permutations. This method does not account
for correlation among individuals and was included mainly for comparison. Mixed-MDMR
accounts for nonindependent observations, and was run with individual-level random inter-
cepts (analogous to section Mixed model for multitask (and multisession) BrAin NeTwOrk
regression (3M_BANTOR)) using the mixed.mdmr function in the MDMR package in R (McArtor,
2018). In its current form, mixed-MDMR does not allow for mixed level models. C'est, random
intercepts can be included at the individual level or at the group level, but not both.

For a summarization of why previous methods are not suitable methods for relating co-

variates to distances in the multitask and multisession context, please see Table 1.

SIMULATION STUDIES

The following simulation study is done using a factorial approach. There are three different
task states (named Tasks 1–3). For each simulation setting, we explore four different metrics

Tableau 1. A summarization of why previous methods are not suitable methods for relating covariates to distances in the multitask and
multisession context

Method
F test

Correlated observations

Limitation in the multitask and multisession context

F test with SLE

Repeated within-task comparisons between distinct individuals

MDMR

Requires complete distance matrix, which means assessing the distance across task/rest connectomes

Neurosciences en réseau

7

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

Fair coin:
A coin which has a 50% chance of
landing on either side.

(KS, JD, EUC, and LERM). For each task and metric combination, five different methods are
considered (F test, F test SLE, 3M_BANTOR, MDMR permutation, and mixed-MDMR). Subse-
quent sections will present details and results for each of these “factors.” (Note: F test, F test
SLE, and 3M_BANTOR are run with all three tasks included in each method. Both MDMR
methods are run separately for each Task. See Methods section for more information.)

Données

We varied simulation settings to assess how well our proposed approaches could detect rela-
tionships between brain network properties and covariates of interest. Each simulation con-
tained 100 sujets, with four covariates of interest. A fair coin was flipped for each subject
to determine their sex (SEX = male or female) and treatment status (TRT = treatment or pla-
cebo). IQ and Age were both simulated from a normal distribution with mean of 100 and a
standard deviation of 15 (rounded to the nearest integer). This resulted in two binary (SEX,
TRT ) and two continuous (AGE, IQ) covariates—variables were given names purely for pur-
poses of explication.

We simulated fMRI connectivity matrices with 268 nodes to mimic the experimental data
detailed in the next section. In each simulation, 12 (4 repetitions for each of the 3 tasks) 268 ×
268 symmetric matrices (with entries ranging from −1 to 1) were generated for each subject.

Time series of 2,500 points (to mimic fMRI BOLD signal) were simulated for each node and

were drawn from three types of distributions:

1) où 0 is the 268 × 1 0-vector, and Σ

1. A low-connectivity noise distribution: low-connectivity noise nodes were drawn from a
1 is the 268 × 268 random correlation

Normal(0, Σ
matrix detailed below.
Defining Σ1: Let Q be the 268 × 268 random orthonormal matrix generated using methods
based on a QR decomposition (Mezzadri, 2007). This was done using the randortho func-
tion in the pracma package in R (Borchers, 2021). Let D be the 268 × 268 diagonal matrix
(cid:3)
(cid:1)
−1/2
with diagonal entries simulated from a Beta 3
4 ; 2
where A = QTDQ and B is the 268 × 268 diagonal matrix with diagonal entries matching
the diagonal of A. Enfin, correlation smoothing (Bock et al., 1988; Wothke, 1993) était
done on Σ
1 using the cor_smooth function in the correlation package in R (Makowski
et coll., 2022) which utilizes the cor.smooth function in the psych package in R (Revelle,
2021). Tolerance for correlation smoothing was chosen to be 10−6.

multiplied times 50. Let Σ

−1/2AB

1 = B

2. A high-connectivity noise distribution: high-connectivity noise nodes were drawn from a
Normal(0, Σ2) où 0 is the 15 × 1 0-vector and Σ2 is the 15 × 15 correlation matrix with
1’s down the diagonal and all off-diagonal entries equal a single draw from a Beta(5, 5)
distribution.

3. A signal distribution dependent on covariates and signal percentage: signal and covariate-
3) où 0 is the 15 × 1 0-vector and Σ
dependent nodes were drawn from a Normal(0, Σ
3
is the 15 × 15 correlation matrix with 1’s down the diagonal. All off diagonals equal a
single draw from a (1 − sp) ∙ Sample(Σ
1) + sp · Beta(ai, 15) distribution where ai = min
(5.95, maximum (−5.95, (IQi − 100) * .15 + (Trti == “Treatment ”) * 2 − (Trti == “Placebo”) * 2))
represented the covariate-dependent parameter, sp represented the signal percentage (depuis
0 à 100%), and Sample(Σ
1. Quand
the signal percent (sp) était 100%, (1 − sp) · Sample(Σ1) + sp · Beta(7 + ai, 7 − ai) = Beta(7 +
ai, 7 − ai). De la même manière, when signal percent was 0%, (1 − sp) · Sample(Σ
1) + sp · Beta(ai, 15) =
Sample(Σ
1), and was therefore identical to the low-connectivity noise distribution and no
longer dependent on covariates.

1) represented a random draw from the off-diagonal of Σ

Neurosciences en réseau

8

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

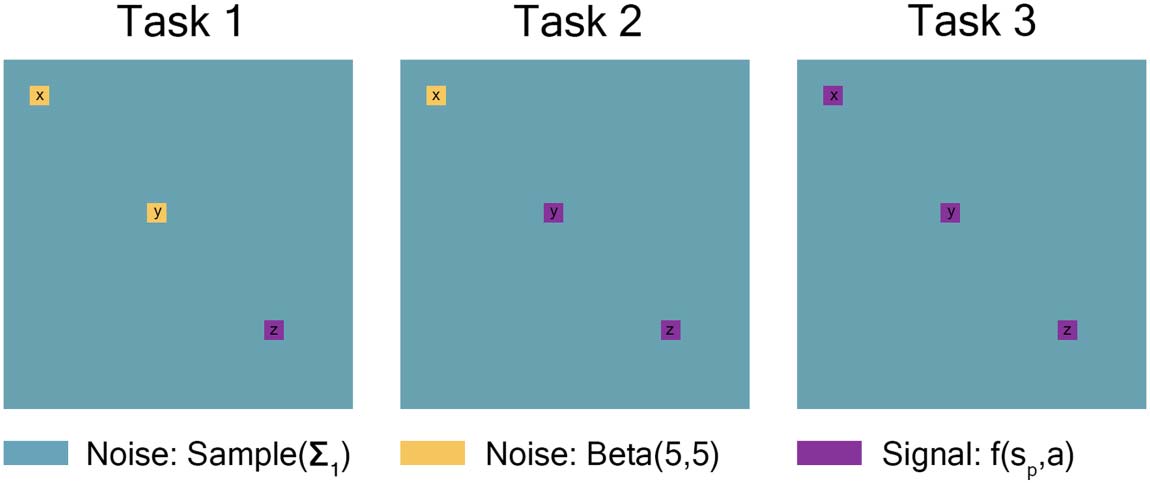
Each Task had three 15-node regions from either the high-connectivity noise distribution or a
covariate-dependent signal distribution. Task 1 had two 15-node regions (node regions x and y)
where all individuals had the same high-connectivity noise distribution, one 15-node region
(node region z) where the signal distribution was dependent on covariates. Task 2 had one
15-node region (X) where all individuals had the same high-connectivity noise distribution
and two 15-node regions (y and z) where the signal distribution was dependent on covariates.
Task 3 had three 15-node regions (X, oui, and z) where the signal distribution was dependent on
covariables. Each node region was correlated in the following way: 12 quantiles (four repetitions
for each of the three tasks) were drawn from a standard multivariate-normal distribution with a
12 × 12 covariance matrix: 1’s down the diagonal, 0.7 for within-task, 0.3 for within-repetition,
et 0 otherwise (see Table 2). These quantiles were then used to draw from either the high-
connectivity noise distribution or the signal distribution dependent on covariates and signal
percentage detailed in the preceding paragraphs.

The remaining time series for nodes from all tasks were directly drawn from the low-
connectivity noise distribution. Pearson correlation matrices were then calculated from the
simulated time series and smoothed using the cor_smooth function in the correlation package
in R (Makowski et al., 2022) which utilizes the cor.smooth function in the psych package in R
(Revelle, 2021). Tolerance for correlation smoothing was chosen to be 10−6.

For a drawn to scale representation of these simulations, voir la figure 2. It should be
noted that connectivity matrices are symmetric, with entries of 1 along the diagonal. Fur-
ther, low-connectivity noise (teal) entries along the rows and columns of high-connectivity

Tableau 2. Within- and between-task correlation table used for simulations

Task 1

Task 2

Task 3

Task 1

Rep. 1

Rep. 1
1

Rep. 2
0.7

Rep. 3
0.7

Rep. 4
0.7

Rep. 1
0.3

Rep. 2
0

Rep. 3
0

Rep. 4
0

Rep. 1
0.3

Rep. 2
0

Rep. 3
0

Rep. 4
0

Rep. 2

Rep. 3

Rep. 4

Task 2

Rep. 1

Rep. 2

Rep. 3

Rep. 4

0.7

0.7

0.7

0.3

0

0

0

Task 3

Rep. 1

0.3

Rep. 2

Rep. 3

Rep. 4

0

0

0

1

0.7

0.7

0

0.3

0

0

0

0.3

0

0

0.7

1

0.7

0

0

0.3

0

0

0

0.3

0

0.7

0.7

1

0

0

0

0.3

0

0

0

0.3

0

0

0

1

0.7

0.7

0.7

0.3

0

0

0

0.3

0

0

0.7

1

0.7

0.7

0

0.3

0

0

0

0.3

0

0.7

0.7

1

0.7

0

0

0.3

0

0

0

0.3

0.7

0.7

0.7

1

0

0

0

0.3

0

0

0

0.3

0

0

0

1

0.7

0.7

0.7

0.3

0

0

0

0.3

0

0

0.7

1

0.7

0.7

0

0.3

0

0

0

0.3

0

0.7

0.7

1

0.7

0

0

0.3

0

0

0

0.3

0.7

0.7

0.7

1

Note. Each node region (X, oui, and z) was correlated in the following way: 12 quantiles (four repetitions for each of the three tasks) were drawn from a standard
multivariate-normal distribution with a 12 × 12 covariance matrix: 1’s down the diagonal, 0.7 for within-task, 0.3 for within-repetition, et 0 otherwise. These
quantiles were then used to draw from either the high-connectivity noise distribution or the signal distribution dependent on covariates and signal percentage
detailed in the proceeding paragraphs.

Neurosciences en réseau

9

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

Chiffre 2. Task 1 had two 15-node regions where all individuals had the same high-connectivity
noise distribution, and one 15-node region where the signal distribution was dependent on covar-
iates. Task 2 had one 15-node region where all individuals had the same high-connectivity noise
distribution and two 15-node regions where the signal distribution was dependent on covariates.
Task 3 had three 15-node regions where the signal distribution was dependent on covariates. Le
remaining nodes from all tasks were drawn from the low-connectivity noise distribution. It should
be noted that connectivity matrices are symmetric, with entries of 1 along the diagonal. Plus loin,
low-connectivity noise (teal) entries along the rows and columns of high-connectivity noise (yellow)
and signal-dependent (purple) regions will be affected by those “yellow” and “purple” entries. Ce
figure is drawn to scale.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Beta distribution:
A family of continuous probability
distributions defined on the closed
interval [0, 1].

bruit (yellow) and signal-dependent (purple) regions will be affected by those “yellow” and
“purple” entries.

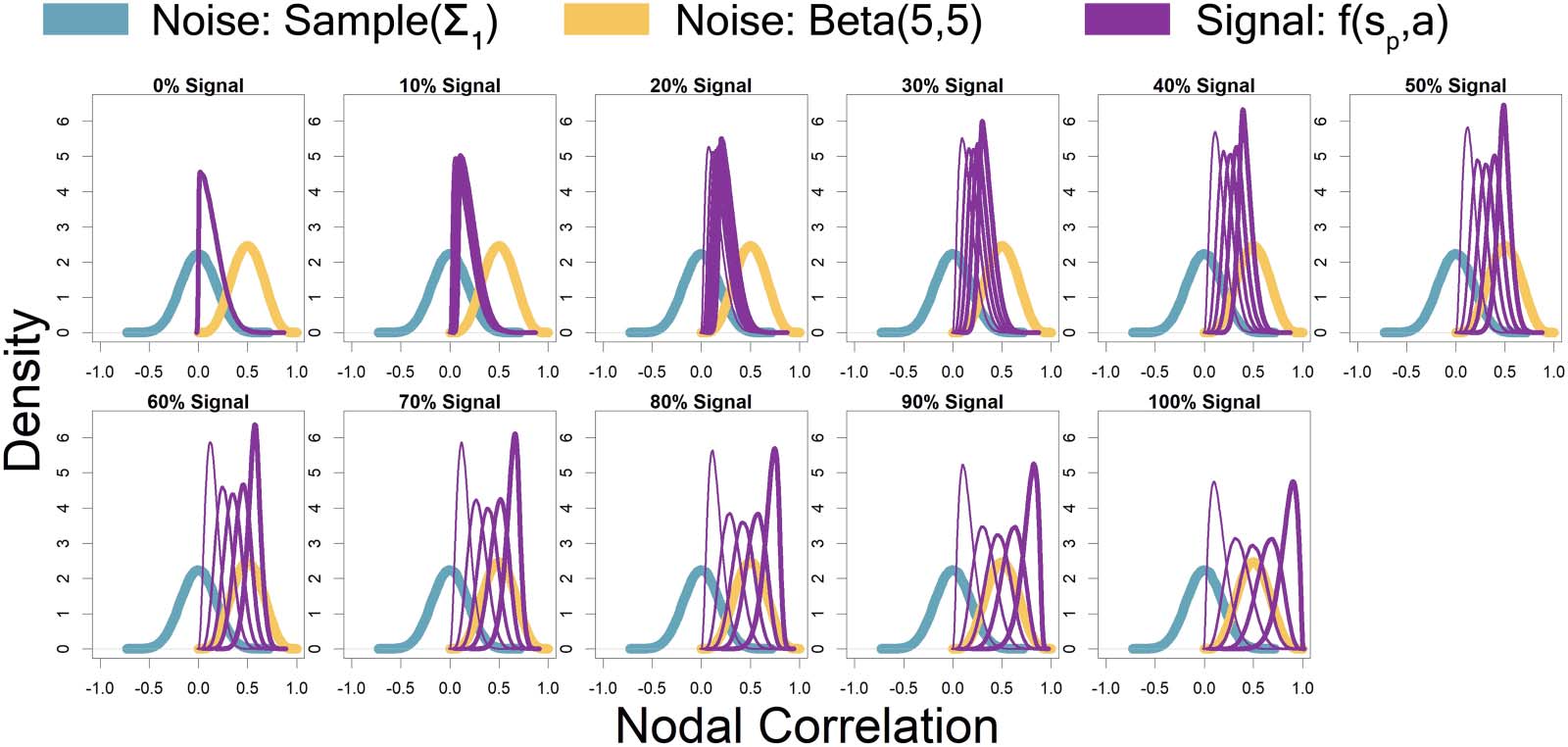
Represented by the same colors from Figure 2 simulated connectivity matrices, Chiffre 3
displays the distributions used for those matrices as signal percentage increased. The low-
connectivity noise distribution was distributed Sample(Σ
1), which represents a random draw
from the off-diagonal of a random correlation matrix Σ
1, and was shown in teal (not affected
by signal percentage). The high-connectivity noise distribution was distributed Beta(5, 5) and is
in yellow (not affected by signal percentage). The “covariate-dependent” signal region can be
seen in purple and was distributed (1 − sp) · Sample(Σ
1) + sp · Beta(7 + un, 7 − a). The a param-
eter had some distribution based on the underlying covariate distribution and signal percent-
âge. There are five purple distributions in each plot representing the 0.05, 0.25, 0.5, 0.75, et
0.95 quantiles (shown in increasing thickness) from the a distribution (Par exemple, le 0.25
quantile distribution is represented by an individual with an IQ of 70 and a “Treatment” status
or an individual with an IQ of 100 and a “Placebo” status; le 0.75 quantile distribution is
represented by an individual with an IQ of 100 and a “Treatment” status or an individual with
an IQ of 130 and a “Placebo” status). Plus loin, the “covariate-dependent” (purple) signal
region’s distribution goes from being the same as the absolute value of the low-connectivity
noise region’s distribution (à 0% signal) to more and more different than the noise region’s
distribution as signal percentage increases.

Results

We assessed methods with 2,500 simulations as detailed in the previous section. Key con-
nections of interest (binary graphs used for the Jaccard distance) based on edge correlation
were identified, selecting the top 20% and top 0.05% highest (positive) correlations and
mapping those to 1 while mapping all remaining edges to 0. The KS statistic, LERM, PCD,
and Euclidean distance were calculated for each pair of same-task connectivity matrices. Le
Jaccard distance was calculated for each pair of same-task binary graphs. MDMR methods
requires inclusion of same-individual comparisons, while all other methods throw these com-
parisons out.

Neurosciences en réseau

10

A regression framework for multitask brain network distance metrics

Chiffre 3. Represented by the same colors from Figure 2 simulated connectivity matrices, Chiffre 3 displays the distributions used for those
matrices as signal percentage increased. The low-connectivity noise distribution was distributed Sample(Σ
1), which represents a random draw
from the off-diagonal of a random correlation matrix Σ
1, and was shown in teal (not affected by signal percentage). The high-connectivity noise
distribution was distributed Beta(5,5) and is in yellow (not affected by signal percentage). The “covariate-dependent” signal region can be seen
in purple and was distributed (1 − sp) · Sample(Σ
1) + sp · Beta(un, 15). The a parameter had some distribution based on the underlying covariate
distribution and signal percentage. There are five purple distributions in each plot representing the 0.05, 0.25, 0.5, 0.75, et 0.95 quantiles
(shown in increasing thickness) from the a distribution (Par exemple, le 0.25 quantile distribution is represented by an individual with an IQ of
70 and a “Treatment” status or an individual with an IQ of 100 and a “Placebo” status; le 0.75 quantile distribution is represented by an
individual with an IQ of 100 and a “Treatment” status or an individual with an IQ of 130 and a “Placebo” status). Plus loin, the “covariate-
dependent” (purple) signal region’s distribution goes from being the same as the absolute value of the low-connectivity noise region’s distri-
bution (à 0% signal) to more and more different than the noise region’s distribution as signal percentage increases.

Type I error rate:
probability of incorrectly rejecting
the null hypothesis.

The percentages of p values less than α = 0.05 for the covariates of interest were recorded
for each combination of signal percent (0%, 10%, …, 100%), distance metric (KS, JD, EUC,
and LERM), and testing framework (F test, F test with SLE, 3M_BANTOR, MDMR Permutation,
and MDMR-mixed). Dans cette section, we discuss whether type I error rate was controlled and at
what signal percent the 80% power threshold was reached. For a visual display of the results,
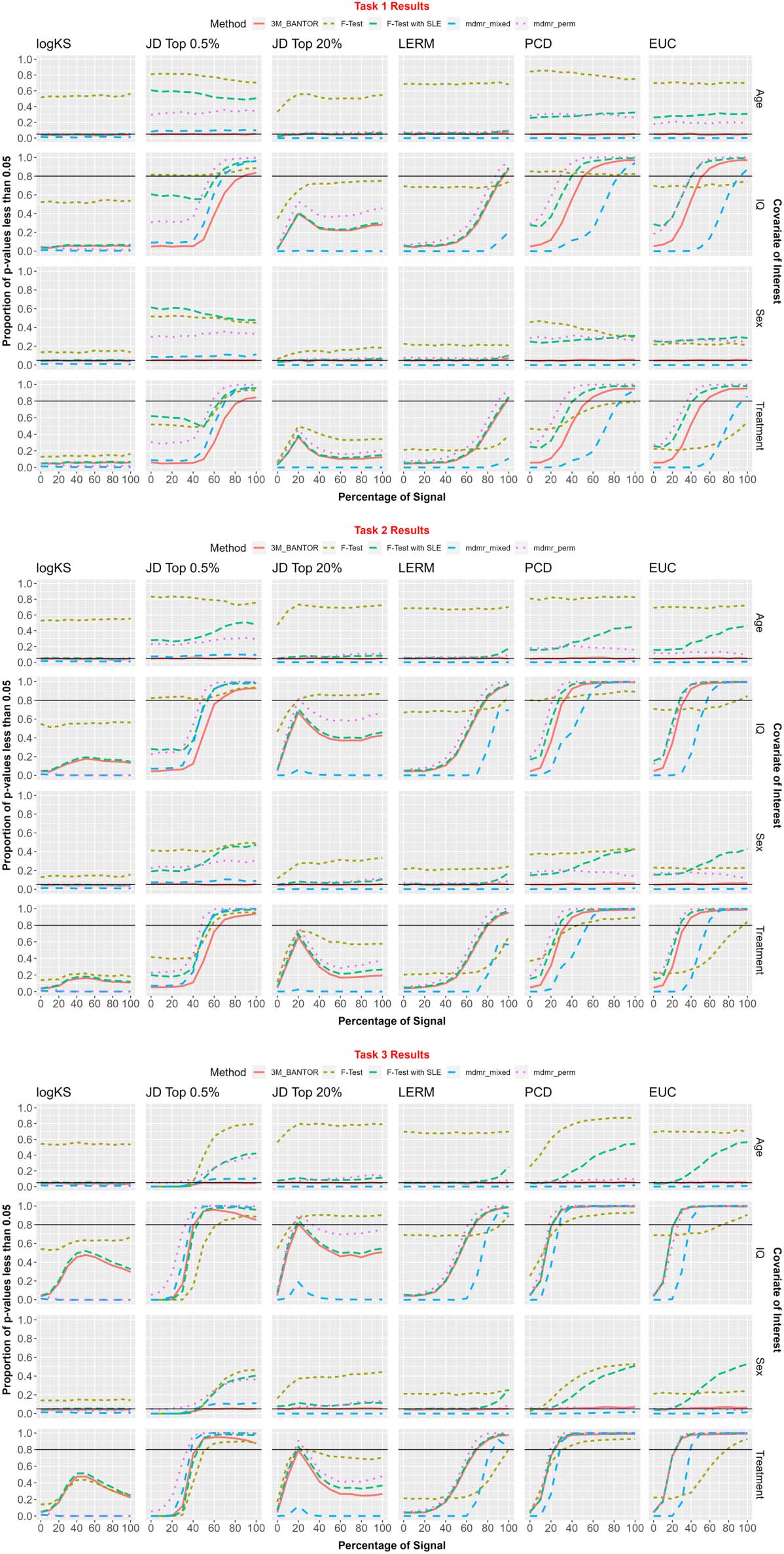
voir la figure 4.

The standard F test, F test with SLE, and MDMR permutation did not control type I error
when testing age and sex. They were included in the figure for reference, but not mentioned any
further in this section. Ainsi, the following is a comparison among the methods 3M_BANTOR
and MDMR-mixed.

Kolmogorov–Smirnov. For the KS metric, 3M_BANTOR adequately controlled type I error
while MDMR-mixed had type I error close to 0. Task 1–3: neither method reached 80% pouvoir
on continuous or binary covariates.

Jaccard top 0.5%. For the Jaccard top 0.5% metric, 3M_BANTOR adequately controlled type I
error while MDMR-mixed did not control type I error for either Age or Sex. Donc, we only
discuss power for 3M_BANTOR here. Task 1: 3M_BANTOR reached the power threshold at
90% of signal for continuous and binary covariates. Task 2: 3M_BANTOR reached the power
threshold at 70% of signal for continuous and binary covariates. Task 3: 3M_BANTOR reached
the power threshold at 50% of signal for continuous and binary covariates.

Neurosciences en réseau

11

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 4. We assessed methods with 2,500 simulations, as detailed in the previous section. The percentages of p values less than α = 0.05 pour
the covariates of interest were recorded for each combination of signal percent (0%, 10%, …, 100%), distance metric (KS, Jaccard distance Top
0.5%, Jaccard distance Top 20%, log-Euclidean Riemannian metric, Pearson correlation distance, Euclidean), and testing framework (F test,
F test with scan-level effects, 3M_BANTOR, MDMR permutation, and MDMR-mixed). It should be noted here that age and sex are “null” covar-
iates (that have no bearing on the data generating process) and are included to assess type I error control of the methods on both continuous and
categorical variables. Black horizontal lines are shown at 5% et 80% for aid in referencing type I error and power, respectivement.

Neurosciences en réseau

12

A regression framework for multitask brain network distance metrics

Jaccard top 20%. For the Jaccard top 20% metric, 3M_BANTOR adequately controlled type I
error while MDMR-mixed had type I error close to 0. Task 1 et 2: neither method reached the
power threshold for continuous nor binary covariates. Task 3: 3M_BANTOR reached the
power threshold at 20% of signal for continuous and binary covariates but fell back below
the threshold as signal increased. MDMR-mixed never reached the power threshold.

LERM. For the LERM metric, 3M_BANTOR adequately controlled type I error while MDMR-
mixed had type I error close to 0. Task 1: 3M_BANTOR reached the power threshold at 100%
of signal for continuous and binary covariates. MDMR-mixed did not reach the power thresh-
vieux. Task 2: 3M_BANTOR reached the power threshold at 80% of signal for continuous and
binary covariates. MDMR-mixed did not reach the power threshold. Task 3: 3M_BANTOR
reached the power threshold at 70% of signal for continuous and binary covariates.
MDMR-mixed reached the power threshold at 90% of signal for continuous and binary
covariables.

Pearson correlation distance. For the PCD, 3M_BANTOR adequately controlled type I error
while MDMR-mixed had type I error close to 0. Task 1: 3M_BANTOR reached the power
threshold at 60% of signal for continuous and binary covariates. MDMR-mixed reached the
power threshold at 100% of signal for continuous and binary covariates. Task 2: 3M_BANTOR
reached the power threshold at 40% of signal for continuous and binary covariates. MDMR-
mixed reached the power threshold at 60% of signal for continuous and binary covariates.
Task 3: 3M_BANTOR and MDMR-mixed reached the power threshold at 30% of signal for
continuous and binary covariates.

Euclidean. For the Euclidean metric, 3M_BANTOR adequately controlled type I error while
MDMR-mixed had type I error close to 0. Task 1: 3M_BANTOR reached the power threshold
à 60% of signal for continuous and binary covariates. MDMR-mixed reached the power
threshold at 90% of signal for continuous and binary covariates. Task 2: 3M_BANTOR reached
the power threshold at 40% of signal for continuous and binary covariates. MDMR-mixed
reached the power threshold at 60% of signal for continuous and binary covariates. Task 3:
3M_BANTOR reached the power threshold at 30% of signal for continuous and binary covar-
iates. MDMR-mixed reached the power threshold at 40% of signal for continuous and binary
covariables.

EXPERIMENTAL STUDIES

Données

The fMRI data used for this project come from the HCP Young Adult 1,200 subjects Minimally
Processed Data Release (Van Essen et al., 2013). Subjects were selected from the Retest subset
to include a second set of fMRI scan data. Each subject completed two scan sessions. A chaque
session, resting-state and working memory fMRI data were collected, in addition to other HCP
tasks that are not used here. Two scans were collected sequentially for each paradigm with
different phase encoding (right to left and left to right). After quality checks of head motion and
the minimal processing, we had 45 subjects with these scans available. The HCP dataset con-
tains subjects belonging to the same family group. To ensure between-subject independence,
we performed a random selection of one subject in each family. This left us with 26 sujets
used for our analyses.

The resting-state paradigm had participants quietly view a fixation cross. The working mem-
ory paradigm had participants complete randomized 0-back and 2-back tasks in a paired

Neurosciences en réseau

13

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

Tableau 3.

Summarization and explanation of HCP covariates treated as continuous (within the regression framework)

Age

BMI

Éducation

Fluid intelligence

Handedness

Income

Mean (SD)
30.2 (3.3)

26.7 (6.1)

15.2 (1.8)

15.1 (5.4)

58.1 (57.2)

4.8 (2.3)

Remarques

In Years

Body Mass Index

Integer Values 11 à 17 (years pf education completed)

Integer valued from 4 à 24

Values range from −100 to 100 par 5 (−100, −95, …, 95, 100)

SSAGA income score – Total household income:

<$10,000 = 1, 10K–19,999 = 2, 20K–29,999 = 3, 30K–39,999 = 4, 40K–49,999 = 5, 50K–74,999 = 6, 75K–99,999 = 7, > = 100,000 = 8

block design interleaved with a rest block. The working memory blocks were also randomized
with photos from one of four types (faces, body parts, houses, and tools). Prior to each block,
participants were alerted to the format of the block. Our analyses only used the 2-back blocks
from this paradigm as described below. During the 2-back, participants were instructed to
respond if the current stimulus matched the stimulus two trials back. Both the fMRI para-
digms were collected as blood oxygenation level–dependent (AUDACIEUX)-weighted images with
TR = 720 ms, LE = 33.1 ms, voxel size 2 mm3, 72 slices. The resting state collected 1,200
volumes and the working memory collected 405 volumes.

The main covariate of interest for this analysis was fluid intelligence. Other covariates
included in the model formulation were age, BMI, éducation, handedness, revenu, course,
sex, and smoking status (alcohol abuse, alcohol dependence, and ethnicity were left out
due to homogeneity). For a summarization and explanation of the variables, see Table 3
and Table 4.

Data Processing and Network Generation

The Minimally Processed Data Release (Van Essen et al., 2013) was used here. Additional pro-
cessing included the removal of the first 14 volumes from each scan, ICA-Aroma (Pruim et al.,
2015) for motion correction, and band-pass filtering (0.009–0.08 Hz). The two scans collected

Tableau 4.

Summarization and explanation of HCP covariates treated as categorical (within the regression framework)

Alcohol abuse

Alcohol dep.

Ethnicity

Race

Sex

Smoking status

1 met the DSM4 criteria for alcohol abuse, 25 did not

0 met the DSM4 criteria for alcohol dependence, 26 did not

26 Not Hispanic/Latino

1 Asian/Nat. Hawaiian/Other Pacific Is., 4 Black or African Am., 21 Blanc

17 Femelle, 9 Male

3 reported as still smoking, 25 did not

Neurosciences en réseau

14

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

at different phase encodings were then concatenated, and a regression was preformed to
account for the effects of the two concatenated scans, whole-brain average signals by tissue
(gray matter, white matter, and cerebral spinal fluid), as well the realignment parameters and
their derivatives. Additional work was needed for the working memory scans. It was necessary
to account for the block design of the task, so we modeled the design in SM12 resulting in
regressors for the 0-back and rest blocks and the cues before every block. These regressors
were added to the regression analysis previously mentioned. After regression, the residual sig-
nal was only kept for volumes that aligned with the 2-back block design. The blocks were then
concatenated, resulting in a time series of 274 volumes. The resulting resting-state time series
contained 2,372 volumes. We averaged the signal from all voxels within each region from the
Shen Atlas (Shen et al., 2013) to create a 268-node time series for each scan. Functional net-
works were constructed for each participant by computing the Pearson (full) correlation
between the resultant time series for each region pair.

Results

Key edges of interest (binary connection matrices used for the Jaccard distance) based on cor-
relation were identified, selecting the top 0.05% highest and mapping those to 1 while map-
ping all remaining edges to 0. The KS statistic, LERM, and Euclidean distance were calculated
for each pair of scans by using their connection matrices. The Jaccard distance was calculated
for each pair of individuals by using their binary graphs.

Distance covariates for each pair of individuals were calculated. A continuous variable’s
distance (âge, par exemple) was calculated as |Agei − Agej| for the pair of individuals i and j.
A binary or categorical variable’s distance (Éducation, par exemple) was calculated as
(cid:5)
1 Edui ≠ Eduj

for the pair of individuals i and j.

(cid:6)

We evaluated differences between networks with our proposed 3M_BANTOR approach.
Resting-state fMRI were compared between all individuals for both sessions (1 et 2) et
phases (LR and RL). Working memory block design was different between the RL and LR
phases, so we did not compare working memory connection matrices between phases. Ainsi,
covariates were estimated for resting state (combining both phases), working memory (phase
LR), and working memory (phase RL). Parameter and standard error estimates can be found in
Supporting Information Tables S1, S2, and S3. Each parameter estimate represented the aver-
age amount the given brain distance metric (KS, Jaccard, etc.) changed based on a one-unit
difference in the respective covariate, after controlling for other covariates. A complete list of
p values for both resting state and working memory can be seen in Table 5. Given the high
degree of dependence between these results, and the illustrative and exploratory nature of
our analysis, there have been no adjustments for multiple comparisons.

After adjusting for the other confounding variables, the covariate of interest, fluid intelli-
gence, had a statistically significant relationship for LERM during working memory (Phase
LR), but did not have a statistically significant relationship with any other distance metric
(KS, JAC, LERM, EUC) for resting-state or working memory fMRI.

In the Supporting Information, we show the 3M_BANTOR approach using nodal degree
vectors rather than connectivity matrices. Fluid intelligence had a statistically significant rela-
tionship for Jaccard distance (top 20%) during working memory (Phase RL), but did not have a
statistically significant relationship with any other distance metric (KS, Jaccard distance (top
5%), Euclidean) for resting-state or working memory fMRI when distances were calculated
using nodal degree vectors (see Supporting Information).

Neurosciences en réseau

15

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

Tableau 5.
using the standard F test with fixed individual-level effects

P values for HCP resting-state and working memory brain scans when modeled with our given regression framework and tested

Resting State

FluidIntl

Age

BMI

Éducation

Gender

Handedness

Income

Race

SmokeStatus

KS
4.87E−01

4.31E−01

9.90E−01

4.80E−01

7.73E−01

2.39E−01

5.06E−01

8.68E−01

9.11E−01

JAC
6.80E−01

6.35E−01

8.43E−01

4.88E−01

1.92E−01

6.93E−02

7.08E−01

7.85E−02

4.25E−01

EUC
4.08E−01

9.35E−01

4.14E−01

4.27E−01

2.53E−01

7.35E−01

7.51E−01

3.10E−03

6.40E−01

LERM
6.98E−01

4.57E−01

4.34E−01

2.51E−01

1.40E−01

2.92E−01

4.71E−01

1.08E−02

2.88E−01

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Working Memory (Phase LR)

Working Memory (Phase RL)

KS

JAC

EUC

LERM

KS

JAC

EUC

LERM

FluidIntl

8.61E−01

3.47E−01

1.93E−01

1.32E−02

7.45E−01

8.44E−01

2.26E−01

3.29E−01

Age

BMI

1.74E−01

1.02E−01

1.19E−01

7.29E−01

7.50E−01

3.41E−01

9.84E−01

1.85E−01

4.82E−01

1.32E−01

1.82E−01

3.27E−01

5.50E−01

2.72E−02

7.23E−02

2.20E−02

Éducation

3.34E−01

8.47E−01

7.72E−01

7.04E−01

6.57E−01

5.08E−01

2.86E−01

8.88E−01

Gender

8.45E−02

4.94E−01

3.50E−01

4.39E−01

8.67E−01

9.38E−01

3.70E−01

4.26E−01

Handedness

6.62E−02

8.14E−01

5.04E−01

9.61E−01

9.84E−01

5.72E−01

4.02E−02

8.26E−01

Income

Race

8.89E−01

7.67E−01

6.05E−01

4.20E−01

4.67E−01

7.19E−01

7.11E−01

8.81E−01

7.93E−01

2.12E−01

3.10E−01

6.36E−01

9.18E−01

9.04E−01

1.10E−02

1.51E−02

SmokeStatus

9.97E−01

7.05E−01

4.77E−01

6.42E−01

5.30E−01

2.60E−01

8.36E−01

7.84E−02

Legend:

0

0.05

1

Note. Parameter estimates and standard errors can be found in the Supporting Information.

DISCUSSION

Our previous work developed a novel analytic framework to assess the relationship between
brain network architecture and phenotypic differences while controlling for confounding var-
iables (Tomlinson et al., 2022). More specifically, this innovative regression framework related
distances (or similarities) between brain network features from a single task to functions of abso-
lute differences in continuous covariates and indicators of difference for categorical variables.

Neurosciences en réseau

16

A regression framework for multitask brain network distance metrics

Here we extended that work to the multitask and multisession context to allow for multiple brain
networks per individual, and explored several similarity metrics for comparing distances
between connection matrices. While our previous work summed over the rows of connection
matrices to create and show the utility of comparing nodal degree vectors, this work focused
solely on the utility of distance metrics using entire connection matrices. This changed the inter-
pretation of what a difference meant, c'est, switching the individual comparisons from nodal
degrees to edge weights. Cependant, all metrics discussed here (except for LERM as it requires SPD
matrices), are able to handle nodal degree vectors as well. En plus, examining the entire
connection matrix allows assessing how more global/systemic properties of networks are related
to covariates, as distinct from node- or edge-based analyses (Simpson & Laurienti, 2016). The KS
statistic measures how different distributions of topological properties vary between two individ-
uals. Key-node metrics (like the Jaccard distance) quantify how much the spatial location of key
brain network edges differ between two networks. The PCD and Euclidean norm measure
whether the spatial location of degree-weighted brain network edges differ. The log-Euclidean
Riemannian metric (LERM) is used as a computationally friendly approximation of the affine-
invariant Riemannian metric (AIRM). Riemannian metrics are used to measure representational
connectivity and “captures representational relationships more accurately when there are rela-
tively small number of response channels (par exemple., voxels)» (Shahbazi et al., 2021). Many other dis-
tances or similarity metrics could be used. Future work might include testing other metrics and
taking a deeper dive into understanding when and how to choose a distance metric.

Several standard methods for estimation and inference were adapted to fit into our regres-
sion framework: standard F test, F test with scan-level effects (ILE), MDMR permutation, mixed-
MDMR, and our proposed 3M_BANTOR approach. All combinations of these approaches and
the distance metrics were assessed via three simulation scenarios. The KS statistic was found to
have low power (relative to the other distance metrics) in all our simulations as we tested
location-specific differences only for connection matrices. Our previous work has shown if
one is interested in comparing nodal degree distributions, the KS statistic is preferred. The Jac-
card top 20% distance did not have consistent or predictable power. This was due to the per-
centage of signal-dependent edges being considerably less than 20% (covariate-dependent
signal was present in approximately 0.3% of edges in Task 1, 0.6% in Task 2, et 0.9% dans
Task 3), et, as signal percentage increased, most signal-dependent edges ended up in the
top 20% (which were mapped to 1). If low signal edges have greater values than the noise,
and the top percentage is high enough to contain all signal-dependent edges, then the Jaccard
distance cannot differentiate between high and low signal connections. To account for the
percentage of signal-dependent edges being considerably less than 20%, the Jaccard top
0.5% distance was explored and had consistent and predictable power as there was a good
spread of signal-dependent edges both in and out of the key-node set (covariate-dependent
signal was present in approximately 0.3% of edges in Task 1, 0.6% in Task 2, et 0.9% dans
Task 3). Two very different choices of thresholding for the Jaccard metric were chosen here
to highlight that the threshold does matter and that thought should be put into what an appro-
priate threshold should be for the given context. Plus loin, we should note that a top percent is
only one type of thresholding; several other approaches have been used in the literature, mais
there is no consensus on the best approach (Simpson et al., 2013un). In our simulations (testing
location-based differences), the Pearson correlation and Euclidean distances had the best com-
bination of type I error control and power (unsurprising considering our previous work and the
nature of our simulation method). Riemannian metrics look to capture several types of differ-
ences within functional connectivity, and the LERM metric showed in our simulations that it
does capture location-specific distances well. As evidenced by the variety of results here,

Neurosciences en réseau

17

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

future work should include a further investigation into how and when to choose specific dis-
tance metrics. The “best” metric to choose in this framework will largely depend on the types
of differences one is looking to detect.

Regarding the comparison of estimation and testing methods (standard F test, F test with
SLE, etc.), our proposed 3M_BANTOR approach was the only method to control type I error
across all metrics. The standard F test, as in our previous work, was not able to control type I
error in a distance regression framework. F test with SLE and MDMR permutation, méthodes
that worked well in our previous work, were not able to control type I error well when multiple
scans were present for each individual. MDMR-mixed did not control type I error when testing
the Jaccard top 20%. MDMR-Mixed with other metrics had the strange property we noticed
with MDMR in our previous work; it had a type I error rate near 0. As for power, our proposed
3M_BANTOR beat MDMR-mixed across all metrics in our simulations.

An analysis of the HCP data was completed using 3M_BANTOR and several distance met-
rics. After adjusting for the other confounding variables, the covariate of interest, fluid intelli-
gence, had a statistically significant relationship for LERM during working memory (Phase LR),
but did not have a statistically significant relationship with any other distance metric (KS, Jaccard
distance, Euclidean, LERM) for resting-state or working memory fMRI when distances were
calculated using connectivity matrices. Fluid intelligence, had a statistically significant rela-
tionship for Jaccard distance (top 20%) during working memory (Phase LR), but did not have
a statistically significant relationship with any other distance metric (KS, Jaccard distance (top
5%), Euclidean) for resting-state or working memory fMRI when distances were calculated
using nodal degree vectors (see Supporting Information). This is somewhat counter to our pre-
vious work, and could be due to power issues from a low sample size or the different (possibly
noisier) set of processed data. Extending our approach to account for familial correlation
would allow increasing our sample size with the HCP data and is planned for future work.
De plus, it is important to note that this modeling approach provides unique and comple-
mentary insight to others, and thus the properties it examines may in fact not be related to
covariates that other network properties may be related to.

Our methodology has applicability to a wide set of clinical populations. Par exemple,
connectome-wide association studies have become very popular, where regions are identified
by the statistical association of their whole-brain patterns with given phenotypic traits (Shehzad
et coll., 2014). This has been implemented mainly using MDMR and successfully applied to
different pathological populations (Alzheimer’s disease, schizophrenia, etc.) and using differ-
ent brain network measures (par exemple., structural connectivity). A few recent examples include
common and dissociable mechanisms of executive system dysfunction across psychiatric dis-
orders in youth (Shanmugan et al., 2016), cerebellar-prefrontal network connectivity and neg-
ative symptoms in schizophrenia (Brady et al., 2019), group-level progressive alterations in
brain connectivity patterns revealed by diffusion-tensor brain networks across severity stages
in Alzheimer’s disease (Rasero et al., 2017un), connectome-wide investigation of altered
resting-state functional connectivity in war veterans with and without posttraumatic stress dis-
order (Misaki et al., 2018), multivariate regression analysis of structural MRI connectivity
matrices in Alzheimer’s disease (Rasero et al., 2017b), and aberrant temporal connectivity
in persons at clinical high risk for psychosis (Colibazzi et al., 2017). Our regression framework
could also be used for connectome-wide association studies in a manner similar to those stud-
ies described above, with the advantage of being in principle more suitable than MDMR, comme
this article shows. It is also important to note that our regression framework can accommodate
any type of connectome data—for example, structural or functional connectomes from other
modalities like EEG and MEG—and data from different atlases, providing additional flexibility.

Neurosciences en réseau

18

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

One could also average the distance for the rest and task conditions to take advantage of
shared features (Elliott et al., 2019; Gao et al., 2019), but it is also possible that network fea-
tures unique to one condition may be specifically associated with the study variables of inter-
est while the other may not. Ainsi, more work needs to be done in this area, and it is certainly
possible that the validity of averaging over conditions is a study-specific issue that depends on
the hypothesis being examined. Future work will examine our framework’s implementation in
different contexts.

Our previous work developed a testing framework that detects whether the spatial location
of key brain network regions and distributions of topological properties differ by phenotype
(continuous and discrete) after controlling for confounding variables in single-task static net-
travaux. This work extends this framework to the multitask and multisession context by allowing
it to handle multiple networks per individual while also displaying the utility of distance met-
rics using entire connection matrices (our previous work showed comparisons of nodal degree
vectors). Plus généralement, this framework allows relating distances between repeated observa-
tions of individual’s networks (par exemple., Jaccard, KS distance) to their covariates of interest. Notre
proposed 3M_BANTOR method is computationally feasible and generally interpretable. Nous
believe this extends an already convenient tool in the neuroscience toolbox to a more general
class of problems.

INFORMATIONS À L'APPUI

Supporting Information for this article is available at https://doi.org/10.1162/netn_a_00274.
Simulation and HCP code is available at https://github.com/applebrownbetty/ braindist
_regression (Tomlinson et al., 2022). HCP data is publicly available for download.

CONTRIBUTIONS DES AUTEURS

Chal E. Tomlinson: Conceptualisation; Conservation des données; Analyse formelle; Enquête; Method-
ology; Gestion de projet; Ressources; Surveillance; Validation; Visualisation; En écrivant -
brouillon original; Rédaction – révision & édition. Paul J. Laurienti: Conservation des données; Ressources; En écrivant -
brouillon original; Rédaction – révision & édition. Robert G. Lyday: Conservation des données; Écriture – originale
brouillon; Rédaction – révision & édition. Sean L. Simpson: Conceptualisation; Conservation des données; Formal
analyse; Acquisition de financement; Enquête; Méthodologie; Gestion de projet; Ressources;
Surveillance; Validation; Visualisation; Rédaction – ébauche originale; Rédaction – révision & édition.

INFORMATIONS SUR LE FINANCEMENT

Sean L. Simpson, National Institute of Biomedical Imaging and Bioengineering (https://dx.doi
.org/10.13039/100000070), Award ID: R01EB024559. Sean L. Simpson, Wake Forest Clinical
and Translational Science Institute, Wake Forest School of Medicine (https://dx.doi.org/10
.13039/100019340), Award ID: UL1TR001420.

RÉFÉRENCES

Anderson, M.. J.. (2001). A new method for non-parametric multivar-
iate analysis of variance. Austral Ecology, 26(1), 32–46. https://
doi.org/10.1111/j.1442-9993.2001.01070.pp.x

Arsigny, V., Fillard, P., Pennec, X., & Ayache, N. (2006). Log-Euclidean
metrics for fast and simple calculus on diffusion tensors. Magnetic

Resonance in Medicine, 56(2), 411–421. https://doi.org/10.1002
/mrm.20965, PubMed: 16788917

Bates, D., Mächler, M., Bolker, B., & Walker, S. (2015). Fitting linear
mixed-effects models using lme4. Journal of Statistical Software,
67(1), 1–48. https://doi.org/10.18637/jss.v067.i01

Neurosciences en réseau

19

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

Bock, R.. D., Gibbons, R., & Muraki, E. (1988). Full-information
item factor analysis. Applied Psychological Measurement, 12(3),
261–280. https://doi.org/10.1177/014662168801200305

Borchers, H. W. (2021). Package “pracma” Title Practical Numeri-

cal Math Functions Depends R (>= 3.1.0) (2.3.6). CRAN.

Brady, R.. O., Gonsalvez, JE., Lee, JE., Öngür, D., Seidman, L. J.,
Schmahmann, J.. D., Eack, S. M., Keshavan, M.. S., Pascual-
Leone, UN., & Halko, M.. UN. (2019). Cerebellar-prefrontal network
connectivity and negative symptoms in schizophrenia. Le
American Journal of Psychiatry, 176(7), 512–520. https://doi.org
/10.1176/appi.ajp.2018.18040429, PubMed: 30696271

Chau, J.. (2020). Package “pdSpecEst” Type Package Title An
Analysis Toolbox for Hermitian Positive Definite Matrices.
https://github.com/JorisChau/pdSpecEst

Colibazzi, T., Lequel, Z., Horga, G., Yan, C. G., Corcoran, C. M.,
Klahr, K., Brucato, G., Girgis, R.. R., Abi-Dargham, UN., Milham,
M.. P., & Peterson, B. S. (2017). Aberrant temporal connectivity
in persons at clinical high risk for psychosis. Biological Psychia-
try. Cognitive Neuroscience and Neuroimaging, 2(8), 696–705.
https://doi.org/10.1016/j.bpsc.2016.12.008, PubMed: 29202110
Craddock, R.. C., Tungaraza, R.. L., & Milham, M.. P.. (2015). Con-
nectomics and new approaches for analyzing human brain func-
tional connectivity. GigaScience, 4(1). https://doi.org/10.1186
/s13742-015-0045-x, PubMed: 25810900

Dai, T., & Guo, Oui. (2017). Predicting individual brain functional
connectivity using a Bayesian hierarchical model. NeuroImage,
147, 772–787. https://doi.org/10.1016/j.neuroimage.2016.11
.048, PubMed: 27915121

Elliott, M.. L., Knodt, UN. R., Cooke, M., Kim, M.. J., Melzer, T. R.,
Keenan, R., Ireland, D., Ramrakha, S., Poulton, R., Caspi, UN.,
Moffitt, T. E., & Hariri, UN. R.. (2019). General functional connec-
tivité: Shared features of resting-state and task fMRI drive reliable
and heritable individual differences in functional brain networks.
NeuroImage, 189, 516–532. https://est ce que je.org/10.1016/j
.neuroimage.2019.01.068, PubMed: 30708106

Fai, UN. H. T., & Cornelius, P.. L. (2007). Approximate F-tests of mul-
tiple degree of freedom hypotheses in generalized least squares
analyses of unbalanced split-plot experiments. Journal of Statisti-
cal Computation and Simulation, 54(4), 363–378. https://doi.org
/10.1080/00949659608811740

Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M.. D., Huang, J., Chun,
M.. M., Papademetris, X., & Constable, R.. T. (2015). Functional
connectome fingerprinting: Identifying individuals using patterns
of brain connectivity. Neurosciences naturelles, 18(11), 1664–1671.
https://doi.org/10.1038/nn.4135, PubMed: 26457551

Fornito, UN., Zalesky, UN., Pantelis, C., & Bullmore, E. T. (2012).
Schizophrenia, neuroimaging and connectomics. NeuroImage,
62(4), 2296–2314. https://doi.org/10.1016/j.neuroimage.2011
.12.090, PubMed: 22387165

Gao, S., Vert, UN. S., Constable, R.. T., & Scheinost, D. (2019).
Combining multiple connectomes improves predictive modeling
of phenotypic measures. NeuroImage, 201, 116038. https://est ce que je
.org/10.1016/j.neuroimage.2019.116038, PubMed: 31336188
Golub, G. H., & Loan, C. F. Van. (1996). Matrix computations (3rd ed.,
pp. 208–209). Baltimore, MARYLAND: The Johns Hopkins University Press.
Hall, B. C. (2015). Lie groups, lie algebras, and representations: Un
elementary introduction (2nd ed.). Cham, Suisse: Springer.
https://doi.org/10.1007/978-3-319-13467-3

Joyce, K. E., Laurienti, P.. J., Burdette, J.. H., & Hayasaka, S. (2010). UN
new measure of centrality for brain networks. PLoS One, 5(8),
e12200. https://doi.org/10.1371/journal.pone.0012200,
PubMed: 20808943

Kolmogorov, UN. (1933). Sulla determinazione empirica di una legge
di distribuzione. Giornale dell’Istituto Italiano degli Attuari, 4,
83–91.

Kuznetsova, UN., Brockhoff, P.. B., Christensen, R.. H. B., & Jensen,
S. P.. (2020). lmerTest Package: Tests in linear mixed effects
models. Journal of Statistical Software, 82(13), 1–26. https://est ce que je
.org/10.18637/jss.v082.i13

Lance, G. N., & Williams, W. T. (1966). Computer programs for
hierarchical polythetic classification (“similarity analyses”). Le
Computer Journal, 9(1), 60–64. https://doi.org/10.1093/comjnl/9
.1.60

Lehmann, B. C. L., Henson, R.. N., Geerligs, L., Cam-CAN, & Blanc,
S. R.. (2021). Characterising group-level brain connectivity: UN
framework using Bayesian exponential random graph models.
NeuroImage, 225, 117480. https://doi.org/10.1016/j.neuroimage
.2020.117480, PubMed: 33099009

Makowski, D., Wiernik, B., & Patil, je. (2022). Package “correlation”

Methods for Correlation Analysis. CRAN.

McArtor, D. B. (2017). Extending a distance-based approach to mul-
tivariate multiple regression. Notre Dame, IN: University of Notre
Dame.

McArtor, D. B. (2018). Package “MDMR” Type Package Title Mul-

tivariate Distance Matrix Regression.

Meunier, D., Lambiotte, R., Fornito, UN., Ersche, K. D., & Bullmore,
E. T. (2009). Hierarchical modularity in human brain functional
réseaux. Frontiers in Neuroinformatics, 3, 37. https://est ce que je.org/10
.3389/neuro.11.037.2009, PubMed: 19949480

Mezzadri, F. (2007). How to generate random matrices from the
classical compact groups. Notices of the AMS, 54(5), 592–604.
https://doi.org/10.48550/arXiv.math-ph/0609050

Misaki, M., Phillips, R., Zotev, V., Wong, C. K., Wurfel, B. E., Krueger,
F., Feldner, M., & Bodurka, J.. (2018). Connectome-wide investiga-
tion of altered resting-state functional connectivity in war veterans
with and without posttraumatic stress disorder. NeuroImage: Clin-
ical, 17, 285–296. https://doi.org/10.1016/j.nicl.2017.10.032,
PubMed: 29527476

Pruim, R.. H. R., Mennes, M., van Rooij, D., Llera, UN., Buitelaar, J.. K.,
& Beckmann, C. F. (2015). ICA-AROMA: A robust ICA-based
strategy for removing motion artifacts from fMRI data. Neuro-
Image, 112, 267–277. https://doi.org/10.1016/j.neuroimage
.2015.02.064, PubMed: 25770991

Rasero, J., Alonso-Montes, C., Diez, JE., Olabarrieta-Landa, L.,
Remaki, L., Escudero, JE., Mateos, B., Bonifazi, P., Fernandez,
M., Arango-Lasprilla, J.. C., Stramaglia, S., & Cortes, J.. M..
(2017un). Group-level progressive alterations in brain connectivity
patterns revealed by diffusion-tensor brain networks across
severity stages in Alzheimer’s disease. Frontiers in Aging Neuro-
science, 9, 215. https://doi.org/10.3389/fnagi.2017.00215,
PubMed: 28736521

Rasero, J., Amoroso, N., La Rocca, M., Tangaro, S., Bellotti, R., &
Stramaglia, S. (2017b). Multivariate regression analysis of struc-
tural MRI connectivity matrices in Alzheimer’s disease. PLoS
Un, 12(11), e0187281. https://doi.org/10.1371/journal.pone
.0187281, PubMed: 29135998

Neurosciences en réseau

20

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A regression framework for multitask brain network distance metrics

Revelle, W. (2021). Package “psych” Procedures for Psychological,
Psychometric, and Personality Research (2.1.9). CRAN. https://
personality-project.org/r/psych/

Shahbazi, M., Shirali, UN., Aghajan, H., & Nili, H. (2021). Using
distance on the Riemannian manifold to compare representations
in brain and in models. NeuroImage, 239, 118271. https://doi.org
/10.1016/j.neuroimage.2021.118271, PubMed: 34157410

Shanmugan, S., Loup, D. H., Calkins, M.. E., Moore, T. M., Ruparel,
K., Hopson, R.. D., Vandekar, S. N., Roalf, D. R., Elliott, M.. UN.,
Jackson, C., Gennatas, E. D., Leibenluft, E., Pine, D. S., Shinohara,
R.. T., Hakonarson, H., Gur, R.. C., Gur, R.. E., & Satterthwaite, T. D.
(2016). Common and dissociable mechanisms of executive sys-
tem dysfunction across psychiatric disorders in youth. Le
American Journal of Psychiatry, 173(5), 517–526. https://est ce que je
.org/10.1176/appi.ajp.2015.15060725, PubMed: 26806874
Shehzad, Z., Kelly, C., Reiss, P.. T., Cameron Craddock, R., Émerson,
J.. W., McMahon, K., Copland, D. UN., Xavier Castellanos, F., &
Milham, M.. P.. (2014). An multivariate distance-based analytic
framework for connectome-wideassociation studies. Neuro-
Image, 93, 74–94. https://doi.org/10.1016/j.neuroimage.2014
.02.024, PubMed: 24583255

Shen, X., Finn, E. S., Scheinost, D., Rosenberg, M.. D., Chun, M.. M.,
Papademetris, X., & Constable, R.. T. (2017). Using connectome-
based predictive modeling to predict individual behavior from
brain connectivity. Nature Protocols, 12(3), 506–518. https://est ce que je
.org/10.1038/nprot.2016.178, PubMed: 28182017

Shen, X., Tokoglu, F., Papademetris, X., & Constable, R.. T. (2013).
Groupwise whole-brain parcellation from resting-state fMRI data
for network node identification. NeuroImage, 82, 403–415.
https://doi.org/10.1016/j.neuroimage.2013.05.081, PubMed:
23747961

Simpson, S. L., Bowman, F. D., & Laurienti, P.. J.. (2013un). Analyzing
complex functional brain networks: Fusing statistics and network
science to understand the brain. Statistics Surveys, 7, 1–36.
https://doi.org/10.1214/13-SS103, PubMed: 25309643

Simpson, S. L., Hayasaka, S., & Laurienti, P.. J.. (2011). Exponential
random graph modeling for complex brain networks. PLoS One,
6(5), e20039. https://doi.org/10.1371/journal.pone.0020039,
PubMed: 21647450

Simpson, S. L., & Laurienti, P.. J.. (2016). Disentangling brain graphs:
A note on the conflation of network and connectivity analyses.
Brain Connectivity, 6(2), 95–98. https://doi.org/10.1089/ brain
.2015.0361, PubMed: 26414952

Simpson, S. L., Lyday, R.. G., Hayasaka, S., Marais, UN. P., & Laurienti,
P.. J.. (2013b). A permutation testing framework to compare groups
of brain networks. Frontiers in Computational Neuroscience, 7,
171. https://doi.org/10.3389/fncom.2013.00171, PubMed:
24324431

Simpson, S. L., Moussa, M.. N., & Laurienti, P.. J.. (2012). An exponen-
tial random graph modeling approach to creating group-based
representative whole-brain connectivity networks. NeuroImage,

60(2), 1117–1126. https://doi.org/10.1016/j.neuroimage.2012
.01.071, PubMed: 22281670

Smirnov, N. (1948). Table for estimating the goodness of fit of
empirical distributions. The Annals of Mathematical Statistics,
19(2), 279–281. https://doi.org/10.1214/aoms/1177730256

Székely, G. J., & Rizzo, M.. L. (2009). Brownian distance covariance.
Annals of Applied Statistics, 3(4), 1236–1265. https://est ce que je.org/10
.1214/09-AOAS312

Székely, G. J., Rizzo, M.. L., & Bakirov, N. K. (2007). Measuring and
testing dependence by correlation of distances. Annales de
Applied Statistics, 35(6), 2769–2794. https://doi.org/10.1214
/009053607000000505

Tomlinson, C. E., Laurienti, P.. J., Lyday, R.. G., & Simpson, S. L.
(2022). A regression framework for brain network distance met-
rics. Neurosciences en réseau, 6(1), 49–68. https://est ce que je.org/10.1162
/netn_a_00214, PubMed: 35350586

van Dongen, S., & Enright, UN. J.. (2012). Metric distances derived
from cosine similarity and Pearson and Spearman correlations.
ArXiv. https://doi.org/10.48550/arXiv.1208.3145

Van Essen, D. C., Forgeron, S. M., Barch, D. M., Behrens, T. E. J.,
Yacoub, E., & Voiture d'Ugur, K. (2013). The WU-Minn Human Connec-
tome Project: An overview. NeuroImage, 80, 62–79. https://est ce que je
.org/10.1016/j.neuroimage.2013.05.041, PubMed: 23684880
Varoquaux, G., & Craddock, R.. C. (2013). Learning and comparing
functional connectomes across subjects. NeuroImage, 80, 405–415.
https://doi.org/10.1016/j.neuroimage.2013.04.007, PubMed:
23583357

Wang, L., Durante, D., Jung, R.. E., & Dunson, D. B. (2017). Bayesian
network–response regression. Bioinformatics, 33(12), 1859–1866.
https://doi.org/10.1093/ bioinformatics/ btx050, PubMed:
28165112

Wothke, W. (1993). Nonpositive definite matrices in structural

modeling. Sage Focus Editions, 154, 256–256.

Xia, C. H., Ma, Z., Cui, Z., Bzdok, D., Thirion, B., Bassett, D. S.,
Satterthwaite, T. D., Shinohara, R.. T., & Witten, D. M.. (2020).
Multi-scale network regression for brain-phenotype associations.
Human Brain Mapping, 41(10), 2553–2566. https://est ce que je.org/10
.1002/hbm.24982, PubMed: 32216125

You, K., & Parc, H. J.. (2021). Re-visiting Riemannian geometry of
symmetric positive definite matrices for the analysis of functional
connectivité. NeuroImage, 225, 117464. https://est ce que je.org/10.1016
/j.neuroimage.2020.117464, PubMed: 33075555

Zhang, J., Sun, W. W., & Li, L. (2018). Network response regression
for modeling population of networks with covariates. ArXiv.
https://www.researchgate.net/publication/328161028_Network
_Response_Regression_for_Modeling_Population_of_Networks
_with_Covariates

Zhang, Z., Allen, G. JE., Zhu, H., & Dunson, D. (2019). Tensor net-
work factorizations: Relationships between brain structural con-
nectomes and traits. NeuroImage, 197, 330–343. https://doi.org
/10.1016/j.neuroimage.2019.04.027, PubMed: 31029870

Neurosciences en réseau

21

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
1
2
0
7
2
0
1
1
n
e
n
_
un
_
0
0
2
7
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Télécharger le PDF