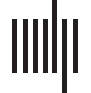MÉTHODES
Path analysis: A method to estimate altered
pathways in time-varying graphs of
neuroimaging data
Haleh Falakshahi1,2
, Hooman Rokham1,2
, Zening Fu1, Armin Iraji1, Daniel H. Mathalon3,4,
Judith M. Ford3,4, Bryon A. Mueller5, Adrian Preda6, Theo G. M.. van Erp6,7,
Jessica A. Turner1,8, Sergey Plis1,9, and Vince D. Calhoun1,2,9
1Tri-Institutional Center for Translational Research in Neuroimaging and Data Science (TReNDS), Georgia State University,
Georgia Institute of Technology, and Emory University, Atlanta, GA, Etats-Unis
2School of Electrical and Computer Engineering, Georgia Institute of Technology, Atlanta, GA, Etats-Unis
3Département de psychiatrie, Université de Californie, San Francisco, Californie, Etats-Unis
4San Francisco VA Medical Center, San Francisco, Californie, Etats-Unis
5Département de psychiatrie, University of Minnesota, Minneapolis, MN, Etats-Unis
6Department of Psychiatry and Human Behavior, University of California Irvine, Irvine, Californie, Etats-Unis
7Center for the Neurobiology of Learning and Memory, University of California Irvine, Irvine, Californie, Etats-Unis
8Département de psychologie, Georgia State University, Atlanta, GA, Etats-Unis
9Department of Computer Science, Georgia State University, Atlanta, GA, Etats-Unis
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
un
_
0
0
2
4
7
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mots clés: Brain graph, Functional connectivity, Gaussian graphical model, Joint estimation,
Resting-state fMRI, Schizophrenia
ABSTRAIT
Graph-theoretical methods have been widely used to study human brain networks in psychiatric
disorders. Cependant, the focus has primarily been on global graphic metrics with little attention
to the information contained in paths connecting brain regions. Details of disruption of these
paths may be highly informative for understanding disease mechanisms. To detect the absence
or addition of multistep paths in the patient group, we provide an algorithm estimating edges that
contribute to these paths with reference to the control group. We next examine where pairs of
nodes were connected through paths in both groups by using a covariance decomposition
method. We apply our method to study resting-state fMRI data in schizophrenia versus controls.
Results show several disconnectors in schizophrenia within and between functional domains,
particularly within the default mode and cognitive control networks. En plus, we identify
new edges generating additional paths. De plus, although paths exist in both groups, ces
paths take unique trajectories and have a significant contribution to the decomposition. Le
proposed path analysis provides a way to characterize individuals by evaluating changes in
paths, rather than just focusing on the pairwise relationships. Our results show promise for
identifying path-based metrics in neuroimaging data.
INTRODUCTION
The human brain is one of the most complex networks, comprising about 86 billion neurons
connected by about 150 trillion synapses allowing neurons to communicate and pass chem-
ical or electrical signals to each other (Azevedo et al., 2009; Farahani, Karwowski, & Lighthall,
2019; Fornito, Zalesky, & Bullmore, 2016). Advances in graph-theoretical analysis provide an
un accès ouvert
journal
Citation: Falakshahi, H., Rokham, H.,
Fu, Z., Iraji, UN., Mathalon, D. H., Ford,
J.. M., Mueller, B. UN., Preda, UN., van Erp,
T. G. M., Tourneur, J.. UN., Plis, S., &
Calhoun, V. D. (2022). Path analysis: UN
method to estimate altered pathways in
time-varying graphs of neuroimaging
data. Neurosciences en réseau, 6(3),
634–664. https://doi.org/10.1162/netn_a
_00247
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00247
Informations complémentaires:
https://doi.org/10.1162/netn_a_00247
Reçu: 3 Juin 2021
Accepté: 23 Mars 2022
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Haleh Falakshahi
hfalakshahi@gatech.edu
Éditeur de manipulation:
Alex Fornito
droits d'auteur: © 2022
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
A method to estimate altered pathways in time-varying brain networks
Brain functional
(réseau) connectivité:
Temporal statistical relationships
between brain regions or networks.
opportunity to examine and understand this complex network in human cognition and behav-
ior as well as neurological and psychiatric disorders (Farahani, Karwowski, & Lighthall, 2019;
Fornito, 2016; Yu et al., 2015, 2018). Graph theory provides a simple and powerful way to
model, estimate and simulate the structure and dynamics of brain networks (Falakshahi,
Rokham, et coll., 2020; Fornito, 2016; Fornito, Zalesky, & Bullmore, 2016; van den Heuvel &
Fornito, 2014; van den Heuvel et al., 2017). A brain network or brain graph is composed of a
set of nodes (vertices) as brain regions connected by a set of edges (links) as some measure of
structural or functional interaction between those brain regions (Farahani, Karwowski, &
Lighthall, 2019; Fornito, 2016).
The combination of graph theory and state-of-the-art noninvasive brain imaging techniques
has shown promise in the detection of potential biomarkers of mental disorders (Farahani,
Karwowski, & Lighthall, 2019; Yu et al. 2018). Brain function can be localized through func-
tional magnetic resonance imaging (IRMf) that assesses the blood oxygenation level–
dependent (AUDACIEUX) signal from the brain (Hillman, 2014). There is a vast literature on using
graph–based methods to analyze brain functional (réseau) connectivity patterns applying
fMRI data (Farahani, Karwowski, & Lighthall, 2019; Fornito, 2016; Karwowski, Vasheghani
Farahani, & Lighthall, 2019; Yu et al., 2018). Different graph metrics were used in these studies
to characterize the brain graphs, such as clustering coefficient, modularity, characteristic path
length, small-world, and assortativity (Farahani, Karwowski, & Lighthall, 2019; Yu et al., 2018).
Par exemple, clustering coefficient, local efficiency, and global efficiency have been shown to
be lower in functional brain graphs in people with schizophrenia (SZ) compared to controls
(Fu, Iraji, et coll., 2021; Fu, Sui, et coll., 2021; Liu et al., 2008). Topological alterations in basal
ganglia and limbic systems in patients with sleep-related hyper-motor epilepsy have been
reported using resting-state fMRI data (Evangelisti et al., 2018). There are numerous reports
on graph-based abnormalities in autism spectrum disorder (ASD) using resting-state fMRI data
that have shown lower modularity and clustering coefficient in ASD compared to controls (Di
Martino et al., 2013; Farahani, Karwowski, & Lighthall, 2019; Keown et al., 2017; Rudie et al.,
2013; van den Heuvel et al., 2017).
Cependant, the focus in neuroimaging data has primarily been on edge and nodal changes or
global graphic metrics, with little focus on the information contained in paths connecting brain
régions. A path from node X to node Y in a graphical model is a sequence of adjacent edges
between nodes X and Y. Paths are of great importance in brain graphs, and details of disruption
of these paths in patient group graph may be highly informative for understanding disease
mechanisms. Surtout, since different edges in the same path may drop out in different indi-
viduals, path-based analysis has the potential to capture information that is typically invisible
to approaches that focus only on pairwise relationships.
Our main contribution in this study is to show that a comprehensive path (as opposed to
individual edge) analysis may help identify putative path-based biomarkers from neuroimag-
ing data. We compare and analyze paths between the brain graphs of control and patient
groupes. Interactions in graphs often happen in groups of three or more nodes that cannot
be explained clearly in terms of pairwise relationships or single links. Paths analyses allow
us to analyze the network beyond pairwise interaction. We provide an algorithm to estimate
edges that trigger absent paths (disconnection) and additional paths (abnormal integration) dans
the patient group with reference to the control group graph. En outre, to examine path
differences that are common across groups, we propose the use of a previously reported
covariance decomposition method (Jones & West, 2005) in which the covariance between
two nodes can be decomposed into a sum of weights associated with each of the paths
connecting those two nodes.
Neurosciences en réseau
635
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
un
_
0
0
2
4
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
Gaussian graphical model (GGM):
An undirected graph of partial
correlation that illustrates the
conditional independences of
multiple random variables. Edges are
regarded as the conditional
dependencies between the nodes.
Static functional (réseau)
connectivité:
A statistical relationship between
brain regions or networks using the
entire length of the data.
We conduct our path analyses under the Gaussian graphical model (GGM) framework to
have an interpretable model of brain graphs from resting-state fMRI data. GGM is frequently
used to explore networks among multiple random variables and, in this study, represents the
interaction between brain components. In a GGM, two variables are conditionally indepen-
dent given all other variables, if and only if their corresponding off-diagonal element in the
precision matrix (inverse of the covariance matrix) is zero, and there is no edge between them.
Donc, the precision matrix in GGM summarizes the conditional dependence of network
structure (He et al., 2019).
Previous studies for network analysis, for the most part, focused on Pearson correlation–
based matrices to measure the strength of association between nodes in a network. GGM is
used to study the partial correlation structure of a set of variables and is a better way to model a
complex network because of its interpretation with conditional dependence between two ran-
dom variables after removing the effect of all other controlling variables. Pearson correlation,
on the contrary, ignores the effect of all other variables (He et al., 2019). There are many
methods for estimating GGM. Dans cette étude, we chose to use the joint graphical lasso, lequel
is a technique for jointly estimating multiple graphical models corresponding to distinct but
related classes (Danaher, Wang, & Witten, 2014; Guo, Levina, Michailidis, & Zhu, 2011; Shan
& Kim, 2018). The joint estimation borrows strength across classes to boost the estimation of
multiple graphical models that share certain characteristics while retaining support for class-
specific structures. En plus, estimating control and patient graph separately using the
group-specific data does not consider similarity between the group models. Jointly estimat-
ing control and patient group graphs improves identifying the differences between groups
by considering the assumption of similarity between the models.
Recent brain imaging studies have demonstrated that brain functional connectivity is
dynamic over time (Allen et al., 2014; Bhinge, Long, Calhoun, & Adali, 2019; Damaraju
et coll., 2014; Iraji et al., 2020). Cependant, prior brain graph–based studies focused predominantly
on static functional (réseau) connectivity with an implicit assumption of stationary brain inter-
actions during the scanning period. Although static functional connectivity has disclosed a
great deal of knowledge, evaluating brain connectivity changes across time can reveal addi-
tional valuable insight into the inherent dynamic connectivity of the human brain. Donc,
in addition to static, we analyze paths on time-varying GGMs for control and patient groups.
To the best of our knowledge, no study has provided a dynamic path–based comparison of
time-varying brain graphs in group studies to identify possible brain abnormalities.
Application of the Proposed Method to Schizophrenia
We illustrate the utility of the proposed method on resting-state fMRI data of SZ patients. SZ is
commonly distinguished as a disorder of brain connectivity (Fornito, Zalesky, Pantelis, &
Bullmore, 2012), although its diagnosis is mostly dependent on qualitative symptom–based
measures (Rokham et al., 2020). It is characterized by functional disconnectivity (Friston,
1998) or abnormal integration between distant brain regions (Damaraju et al., 2014;
Skudlarski et al., 2010). Prior studies have shown functional connectivity abnormalities in
SZ in a broad spectrum of systems that frequently involve prefrontal brain regions (Cole,
Anticevic, Repovs, & Barch, 2011; Fornito et al., 2013; Skaatun et al., 2017; van den Heuvel
& Fornito, 2014). Toujours, little is known about how this disconnection or abnormal integration
manifests. We estimate time-varying and static graphs of the control and SZ group and apply
our proposed method for comprehensive path analysis. A preliminary version of this work has
been reported in Falakshahi, Vergara, et autres. (2020).
Neurosciences en réseau
636
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
un
_
0
0
2
4
7
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
The remainder of the paper is structured as follows: Materials and Methods describes
the details of our method, including estimating static and time-varying graphs of control and
patient groups and our proposed algorithm for path analysis; Results provides details of our
path analysis results on resting-state fMRI data of individuals with SZ and control groups;
Discussion reviews our results and implications. We provide concluding remarks in
Conclusion.
MATERIALS AND METHODS
The methods consist of two parts: identifying static and dynamic graphs from resting-state fMRI
data and “path analysis,” including identifying edges that are associated with disconnection or
abnormal integration in patient group graph and the novel use of a covariance decomposition
method to examine the case where there is at least one path between two specific brain com-
ponents in both control and patient groups. In Figure 1, we illustrate the main steps, and each
section will be explained in detail in the following subsections.
Data Information, Preprocessing, and Intrinsic Connectivity Network Extraction
In this work, we analyzed eyes-closed resting-state fMRI data collected from
Data information.
160 controls and 151 âge, genre, and mean framewise displacement (FD)–matched individ-
uals with schizophrenia (SZ) (âge: p = 0.18; genre: p = 0.39; mean FD: p = 0.97) by the
Function Biomedical Informatics Research Network (fBIRN) (Keator et al., 2016). fBIRN dem-
ographics are available in Supporting Information Table S1. Written informed consent was
obtained from all subjects. Data were collected using 3T scanners with a repetition time
(TR) de 2 s, voxel spacing size of 3.44 × 3.44 × 4 mm, a slice gap of 1 mm, and a total of
162 volumes at seven different sites. Data for six of the seven sites were collected on a 3T
Siemens Tim Trio System, and for one other site, a 3T General Electric DiscoveryMR750
scanner was used. Further details on the dataset can be found in Fu, Iraji, et autres. (2021) et
Fu, Sui et al. (2021).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
un
_
0
0
2
4
7
p
d
.
t
Data preprocessing. Data preprocessing was performed using the SPM 12 (https://www.fil.ion
.ucl.ac.uk/spm/) toolbox. We performed rigid body motion correction to correct subject head
motion, followed by the slice-timing correction to account for timing difference in slice
acquisition. The fMRI data were normalized to the EPI template and resampled to 3-mm3
isotropic voxels. Data were spatially smoothed using a Gaussian kernel with a 6-mm full
width at half maximum. Subjects with head motion < = 3° and < = 3 mm, and with func-
tional data providing near full brain successful normalization (by comparing the individual
mask with the group mask) were selected for further analysis. More details on preprocessing
and subject selection can be found in Damaraju et al. (2014), Fu, Iraji, et al. (2021), and Fu,
Sui, et al., (2021).
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Intrinsic connectivity network extraction. We use independent component analysis (ICA) to
determine the nodes of a graph (Yu et al., 2017), which decomposes the whole-brain fMRI
into independent spatial components known as ICN. Each ICN is composed of a set of voxels
that shows a strong coupling of spontaneous fluctuations in the BOLD signal that can be
considered as one functional unit (Iraji et al., 2019). Using fully blind ICA as a method
for ICN extraction estimation of functional connectivity measures might result in different
components identified across data. This inconsistency of identified components may impede
finding replication or comparison. To address this and obtain the same set of ICNs for both
control and SZ groups, we used the fully automated Neuromark pipeline, which is a spatially
637
Intrinsic connectivity network (ICN):
An estimation of a set of voxels
obtained using ICA with coherent
functional activity over time that can
be considered as one functional unit.
Independent component
analysis (ICA):
A statistical technique that is used for
estimating maximally independent
components.
Network Neuroscience
A method to estimate altered pathways in time-varying brain networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Method outline. (A) data preprocessing and intrinsic connectivity networks (ICNs) extraction using the Neuromark templates, (B)
Static functional network connectivity analysis for each subject. (C) Dynamic functional network connectivity estimation using sliding window
approach and identification of functional brain states (patterns) via k-means clustering algorithm. (D) Evaluating group differences between
patient and control groups in dFNC and sFNC by using two-sample t test in univariate way. (E) Estimation of inverse of the covariance matrices
for control and patient groups by using joint graphical lasso method for static and dynamic states. For the static, the whole time point across all
the subjects of each group was concatenated and then joint estimator was applied on them. In dynamic scene, for each state the joint estimator
was applied on the aggregate corresponding time point of that state across subjects. The parametric test for statistical significance of the partial
correlation was applied for each element of the partial correlation matrix to determine the significant edges. The edge was considered between
two brain components only where the corresponding false discovery rate (FDR) corrected p value was significant ( p < 0.05). (F) Path-based
differential analysis investigated on control and patient groups graphs.
constrained ICA informed by reliable network templates (Du et al., 2020). To generate the
Neuromark templates and to identify robust and reproducible ICNs, spatial ICA was applied
to two large datasets of typical controls (Human Connectome Project [HCP; 823 subjects
after the subject selection] and Genomics Superstruct Project [GSP; 1,005 subjects after
Network Neuroscience
638
A method to estimate altered pathways in time-varying brain networks
the subject selection]). Group ICA with model order 100 was performed on each dataset
separately to obtain group-level components. Then independent components from HCP and
GSP were matched based on the spatial similarity (correlation > = 0.4), and reproducible ICNs
were chosen as the network templates. ICNs identification and functional domain labeling
were performed by five neuroscience experts. More details of the Neuromark templates can
be found in Du et al. (2020). Suivant, spatial maps and time courses (TCs) for the fBIRN dataset
were obtained by the network templates as prior information within a spatially constrained ICA
algorithme. For the spatially constrained ICA algorithm, we used multivariate objective opti-
mization independent component analysis with reference (MOO-ICAR), implemented in the
GIFT toolbox from TReNDS (https://trendscenter.org/software/gift) (Iraji et al., 2020), as it
shows good performance based on our previous studies (Du & Fan, 2013; Du, Allen,
et coll., 2016).
Static Functional Network Connectivity
To create a static functional network connectivity (sFNC) matrix for each subject, pairwise cor-
relations were calculated using the entire length of the ICNs time course. We then calculated
the mean of sFNC matrices across subjects for control and patient groups. Further analysis on
sFNC, including group differences using univariate statistical test, estimating group graphs and
path analysis described in sections D and E.
Dynamic Functional Network Connectivity
Dynamic functional network connectivity (dFNC) investigates the time-varying interactions
between brain networks and has been studied extensively (Bhinge, Long, Calhoun, & Adali,
2019; Sakoğlu et al., 2010). dFNC analysis enables us to evaluate how FNCs between ICNs
evolve over time. A sliding window approach with square window type was applied to the
selected ICNs’ TCs to study the connectivity between selected ICNs in a dynamic manner.
ICNs’ TCs were localized by a sliding window size of 20 TR and a window step size of 5 TR
to reduce computational demands, which led to 28 windows capturing changes in connectivity
au fil du temps.
Suivant, we used the joint graphical lasso (Danaher, Wang, & Witten, 2014) to estimate the
inverse of the covariance matrix (precision matrix) for windowed TCs of each subject. Nous
chose to use a joint graphical lasso, which is a technique for jointly estimating multiple
graphical models corresponding to distinct but related classes (windows of each subject)
(Danaher, Wang, & Witten, 2014; Guo, Levina, Michailidis, & Zhu, 2011; Shan & Kim,
2018). As the simulation study suggested in Danaher, Wang, and Witten (2014), we resample
each window data point by using the fast Fourier transform method to augment the sample
time from 20 à 400 to robustly estimate covariance matrices and improve the accuracy
of estimation. Having the estimated covariance matrix, we then computed the correlation
matrix for each window; the detailed formulation is provided as Supporting Information
Formula 1.
Recent resting-state studies have shown that fluctuations in the brain networks are not ran-
dom and reoccur across and within subjects (Damaraju et al., 2014). These dynamic brain
states or patterns can be identified by grouping windowed FNC using a k-means clustering
algorithmv (Allen et al., 2014; Bhinge, Long, Calhoun, & Adali, 2019; Iraji et al., 2020). Là-
fore, each cluster contains similar functional connectivity patterns. We identified these func-
tional brain states from computed dFNC matrices across all subjects. D'abord, we flatten the upper
diagonal part of each FNC matrix to obtain a feature vector. Alors, pour chaque sujet, the variance
Brain states:
Brain connectivity patterns (states)
that reoccur over time and subjects
and can be identified by applying
k-means clustering algorithm.
Neurosciences en réseau
639
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
un
_
0
0
2
4
7
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
Dynamic functional
(réseau) connectivité:
A statistical relationship between
brain regions or networks using a
portion of the data to study time-
resolved changes in connectivity.
across the feature was computed. Similar to what has been done previously (Allen et al., 2014;
Damaraju et al., 2014), initial clustering was applied on a subset of data exhibiting maximal
deviation from the mean called subject exemplars. The clustering algorithm was applied to
these subject exemplars by using the L1 distance function (Manhattan distance) as the distance
measure with random initialization of centroid positions and replicated 50 times to increase the
chances of escaping local minima. As the k-means algorithm is very sensitive to the starting
indiquer, we applied subject exemplars to select the peaks (strongest contributors) as initialization.
Manhattan distance was chosen as it has been suggested that it might be more effective to
estimate similarity measures for high-dimensional data (Allen et al., 2014). The centroids from
clustering the subject exemplars were used as initial points to cluster all dFNC windows from
all subjects (Allen et al., 2014; Damaraju et al., 2014). The optimal number of clusters was
determined using the elbow criterion.
Evaluating Group Differences in sFNC and dFNC Between Groups
We performed the univariate test in static and dynamic functional (réseau) connectivity to
evaluate differences between the control and patient groups. Regarding sFNC, we applied a
two-sample t test in a univariate manner on estimated sFNC matrices. To obtain group differ-
ences in dFNC, we first computed a subject mean for each state from the subject FNC win-
dows assigned to that state as a representative pattern of connectivity of the subject for that
state. Alors, to identify significant differences between patient and control groups, we per-
formed t tests per ICN pair of the averaged dFNC for each state. We corrected for multiple
comparisons by using the FDR with a threshold of 0.05.
Estimating Static and Time-Varying Graphs for Control and Patient Groups
We used GGM for modeling the brain and identifying the graph structure of control and
patient groups. The brain graphs gained from GGM are used for encoding relationships among
brain components, wherein nodes represent ICNs and edges that demonstrate a partial corre-
lation between nodes. In a GGM, two nodes are conditionally independent, given all other
nodes if and only if their corresponding off-diagonal element in the precision matrix is zero.
To estimate the precision matrix, we used joint graphical lasso (Danaher, Wang, & Witten,
2014) on ICNs’ time courses.
To estimate static group graphs of control and patient, we concatenated ICNs’ time
courses across the subjects of control and patient groups separately and estimated the pre-
cision matrix by performing joint graphical lasso estimation on concatenated ICN time
courses. To estimate time-varying group graphs of control and patient groups, we extracted
a GGM for each state. Clustering the windowed dFNC results in each windowed dFNC being
assigned to a specific cluster. Suivant, the time points of the windows located in one cluster
were concatenated to estimate group graphs for each state. Using the concatenated ICN time
courses of corresponding windows in each state, we jointly estimated precision matrices for
control and patient groups applying the joint estimation presented in Danaher, Wang, et
Witten (2014).
Having the precision matrices for each group in static and dynamic states, we computed the
partial correlation matrices. The detailed formulation is provided as Supporting Information
Formula 2. To obtain the adjacency matrices, the parametric test for statistical significance
of the partial correlation was applied for each element of the partial correlation matrix to deter-
mine the significant edges. The edge was considered between two ICNs only where the
corresponding FDR corrected p value was significant ( p < 0.05).
Network Neuroscience
640
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
Path-Based Differential Analysis
We compared paths between the graphs of control and patient groups for estimated static and
time-varying in four possible cases:
1. Disconnection: In this case, two ICNs are reachable from each other, which means
there is at least one path between them in the control group graph, but there is no
path between them in the patient group graph.
2. Abnormal integration: In contrast to case 1, case 2 occurs when there is no path
between two specific ICNs in the control group graph, but there is at least one path
between those ICNs’ pair in the patient group graph.
3. Connection in both control and SZ patients: In this case there is at least one path
between specific pairs of ICNs in both control and SZ patient group graphs.
4. Disconnection in both control and SZ patients: The last case is when there is no path
between two ICNs in both control and patient group graphs.
We considered case 4 as a trivial case and focused on cases 1–3. For cases 1 and 2, we
proposed an algorithm to estimate edges associated with disconnection and abnormal integra-
tion by mimicking the structure of paths in the control group graph. For case 3, to make the
comparison between control and patient graphs, we applied the covariance decomposition in
GGM (Jones & West, 2005). We first describe our proposed method for cases 1 and 2 in detail,
and then we discuss the proposed method for case 3.
Identifying edges associated with disconnection and abnormal integration. Our proposed method
can be applied to estimated patients and control group graphs obtained through GGM to iden-
tify which links are associated with mental illness across the fMRI dataset. There are some
edges in the control group graph that contribute to creating path(s) between some nodes
(ICNs). However, the absence of those edges in the patient group graph leads to the absence
of some paths between some nodes. We labeled those edges as disconnectors that are asso-
ciated with disconnection in the patient group graph. On the contrary, there are some addi-
tional edges in the patient group graph that contribute to creating some new paths that do not
exist in the healthy group graph. We labeled those edges as connectors that trigger abnormal
integration in the patient group graph.
To compare the paths between nodes of estimated graphs, we utilized the concept of the
connected component in graph theory. A connected component of an undirected graph is a
subgraph in which there is a path between every pair of nodes in that subgraph (Balakrishnan
& Ranganathan, 2012). Hence, when two nodes are in the same connected component, it can
be concluded that there is at least one path between them.
A precise and succinct description of our method is summarized in Algorithm 1, which
receives two graphs as inputs, Graph1 and Graph2 (Line 1 of pseudo-code). The order of
the inputs is important. Disconnectors associated with disconnectivity can be obtained by set-
ting the Graph1 and Graph2 inputs as control and patient group graphs, respectively. On the
contrary, abnormal integration can be obtained by swapping the inputs and setting Graph1
and Graph2 as patient and control group graphs, respectively.
Algorithm 1 first identifies all connected components in Graph1 and Graph2 (lines 3 and 4
of pseudo-code). Then, for each connected component in Graph1, it checks whether the nodes
of that connected component are spread into multiple connected components in Graph2 or
not. One way to check this is to see if the nodes set of that connected component in Graph1
Connected component:
A set of nodes in a graph in which
there is at least one path between
them. That is, it is possible to get from
one node to another within a
connected component.
Network Neuroscience
641
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
intersects with more than one connected component nodes sets in Graph2 (lines 6–12 of
pseudo-code). The “Container” set (line 11 of pseudo-code) keeps those connected compo-
nents in Graph2 that intersects with the current connected component of Graph1 (c1). Then,
if the cardinality of the Container set becomes greater than or equal to two (line 12 of pseudo-
code), it indicates that the nodes of the current connected component of Graph1 (c1) are
observed in at least two connected components in Graph2, and it reveals that the separation
between the nodes of c1 occurred in Graph2. Next, to identify edges associated with discon-
nection, all combinations of two connected components in the Container will be investigated
(lines 13–23 of pseudo-code). Then for each 2-combination of connected components in the
Container set, the union of their nodes is stored in set “N” (line 14 of pseudo-code). Using node-
set N, induced subgraphs of Graph1 and Graph2 will be formed (lines 15–16 of pseudo-code).
Next, differences between the edge sets of these two subgraphs will be obtained (set “E”) (line
17 of pseudo-code). As not all the edges in set E cause separation, from the set E, those
edges will be considered as edges associated with disconnection if their end points belong
to two distinct connected components in Graph2. They also should be part of the current
connected component in Graph1 (c1) that we are currently analyzing (line 18–23 of pseudo-
code). If set E becomes empty, it indicates that the two connected components in Graph2
have become separated indirectly through another connected component.
Network Neuroscience
642
A method to estimate altered pathways in time-varying brain networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
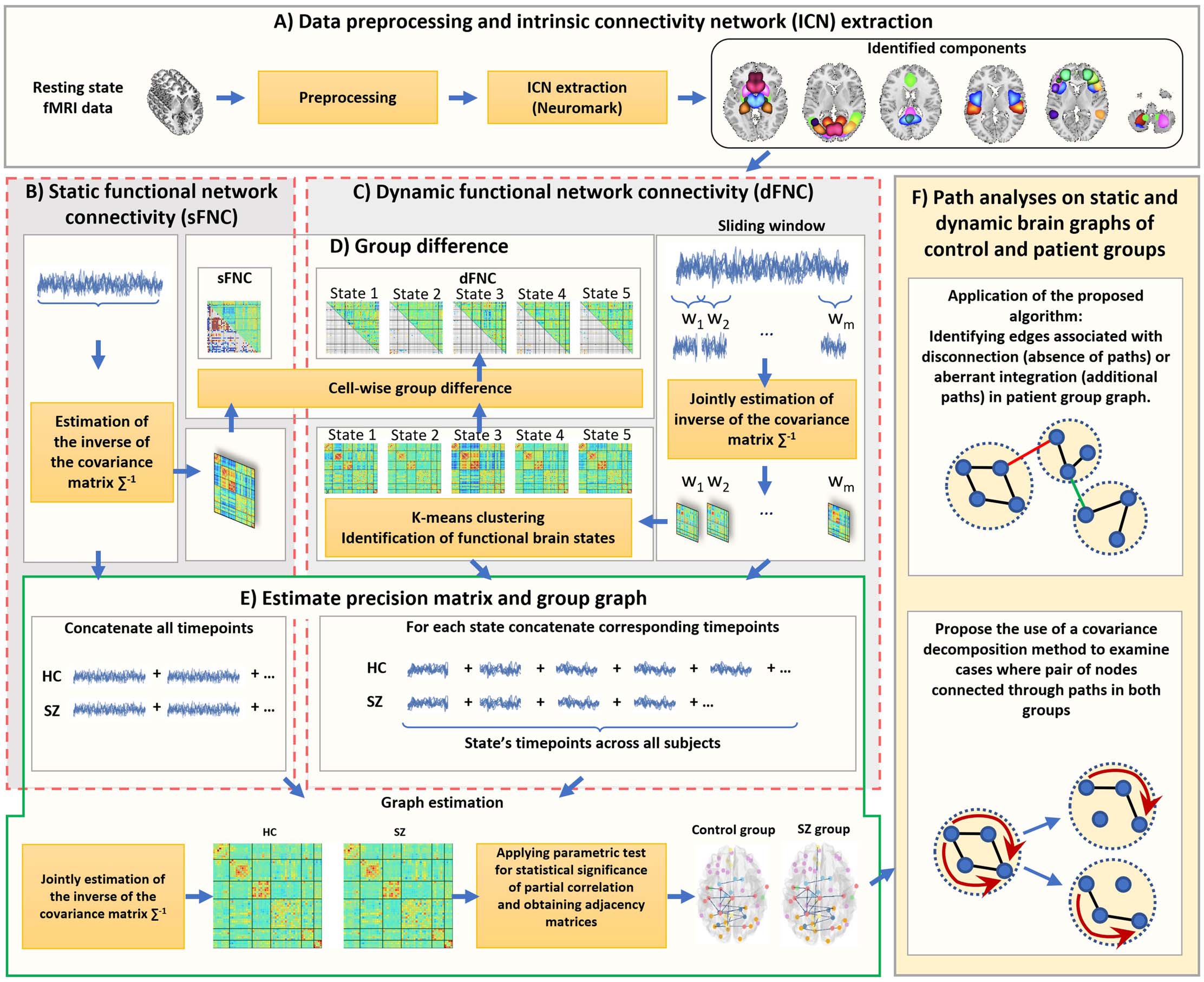
Figure 2. The top-left is an example of the control graph, and the top-right is an example of the patient graph. Bottom row red and green
edges are edges that our algorithm returns as disconnector and connector. Note that the edge (8, 10) depicted in green dashed line is a new
edge in the patient group graph, but it does not contribute to create new path(s) between separated connected components. Similarly, the edge
(1, 4) shown with red dashed line is missing edge in patient group graph, but its absence does not lead to disconnectivity between nodes of its
connected components, and, indeed, the nodes will still be connected through different paths. Therefore, not all missing edges and new edges
in the patient graph are associated with disconnection or abnormal integration.
As an example, to identify disconnectors, consider two fixed graphs of a control group (left)
and a patient group (right) in Figure 2. To identify disconnectors, Graph1 and Graph2 are set as
control and patient group graph as the input, respectively. As illustrated, there are two con-
nected components in the control and patient group graphs. The nodes set of “control con-
nected component 1” intersects with more than one connected component nodes sets in
Graph2:
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nodes of control connected component 1 ∩ Nodes of patient connected component 1
¼ 1; 2; 3; 4
f
g
Nodes of control connected component 1 ∩ Nodes of patient connected component 2
¼ 5; 6; 7
g
f
As the nodes of connected component 1 spread into multiple connected components in the
patient group graph (jContainer j ≥ 2), we can conclude that disconnection happened. Then,
Network Neuroscience
643
A method to estimate altered pathways in time-varying brain networks
using the union of the nodes of patient connected components 1 and 2 (set N), subgraphs of
control and patient groups will be induced, and the differences of their edges will be obtained
with subtraction (set E).
N ¼ 1; 2; 3; 4
f
g ∪ 5; 6; 7; 8; 9; 10
f
g ¼ 1; 2; 3; 4; 5; 6; 7; 8; 9; 10
g
f
E ¼ Edges set of control subGraph − Edges set of patient subGraph ¼ 1; 4ð
f
Þ; 2; 5ð
Þ
g
As not all the edges in set E cause separation, from the set E, those edges will be accepted as
edges associated with disconnection if their end points belong to two distinct connected com-
ponents in Graph2. They also should be the part of the current connected component in
Graph1 (c1) that we are currently analyzing (line 18–23 of pseudo-code). In this example, only
edge (2, 5) belongs to two different connected components in the patient groups graph.
Although the edge (1, 4) is a missing edge, its end points belong to one connected component
in the patient group graph, and its absence did not create any separation between nodes of that
connected component.
The whole procedure needs to be repeated for all the connected components of Graph1.
Therefore, for the second connected component in the control group, the algorithms checks if
spreads occurred for control connected component 2:
Nodes of control connected component 2 ∩ Nodes of patient connected component 1 ¼ fg
Nodes of control connected component 2 ∩ Nodes of patient connected component 2
¼ 8; 9; 10
g
f
Because the nodes of connected component 2 intersect with just one connected component in
the patient group graph, no disconnection happened for control connected component 2.
Edges associated with abnormal integration (connectors) can be identified similarly, by
swapping the order of input variables of the algorithm. In Figure 2, edge (6, 8) shown with
green is associated with abnormal integration.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
Applying covariance decomposition approach. To examine case 3, where two distinct brain com-
ponents are connected and reachable from each other in both control and patient groups, we
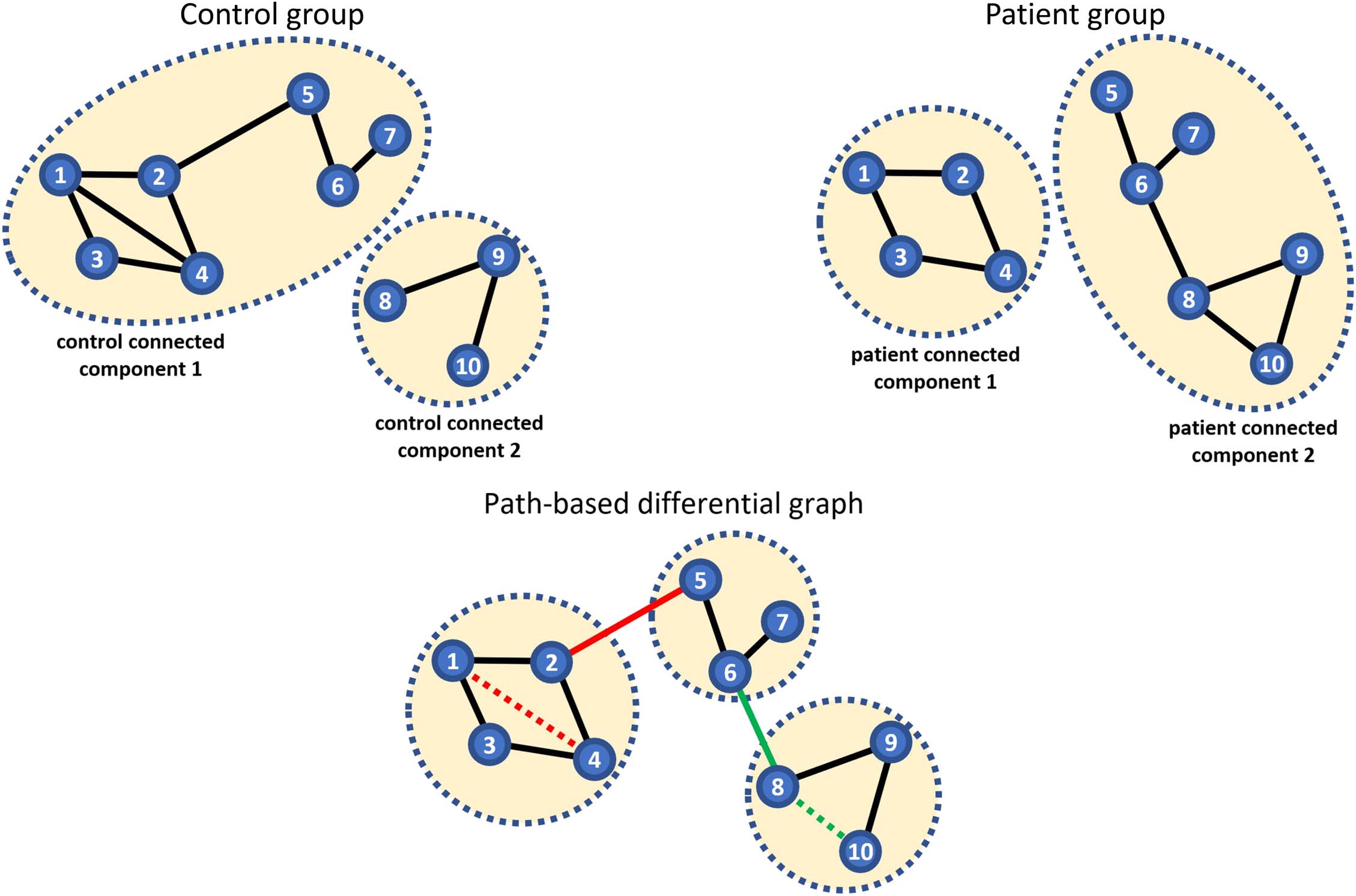
first need to introduce a theorem proposed in Jones and West (2005).
Theorem 1 (Jones & West, 2005): Let (cid:1) denote the covariance matrix corresponding to a
GGM with a set of nodes {1, 2, …, n} with precision matrix Ω, which is the inverse of the
covariance matrix (cid:1)−1. Also, let σxy denote the element of covariance matrix corresponding
to the covariance between variables x and y.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
σxy ¼
X
P(cid:2)Pxy
−1ð
Þtþ1ωp1p2
ωp2p3
…ωpt −1pt
jΩnP j
jΩj
(1)
where Pxy is the set of all paths that exist between variables (nodes) x and y. If we define a path
as a sequence of the nodes, then for all path P in the set Pxy, p1 = x and pt = y where t refers to
the last node in the path. The element of precision matrix between node pi and pj is denoted
by ωpipj and |Ω\P| represents the determinant of the matrix Ω\P that rows and columns
correspond to the nodes of the path P excluded. The proof can be found in Jones and West
(2005). Figure 3 is an example of applying the covariance decomposition approach.
We applied the covariance decomposition approach for case 3 where paths exist between
specific brain components in both control and patient groups to obtain covariance weights for
each path between two nodes in both groups. To be able to compare different paths between
Network Neuroscience
644
A method to estimate altered pathways in time-varying brain networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. There are three paths between node “a” and “b” as illustrated with three different colors. According to the covariance matrix the
covariance between node “a” and “b” is −0.235. Applying the explained formula in Theorem 1 in Jones and West (2005), the covariance
between two nodes (in here as an example “a” and “b”) decomposed into a sum of weights associated with each of the paths connecting those
two nodes. Sum of weights of a-x-b, a-b, and a-y-b paths will be equal to −0.235.
groups, we used alternative correlation weights, which are constant multiples of the
covariance-based weights (Jones & West, 2005). Unlike the covariance-based weights, the
correlation-based weights are comparable between paths with different end points.
To identify the differences between control and patient group in case 3, we computed all the
paths between each pair of ICNs in both groups and calculated their corresponding correlation
weights by using the decomposition method. Lastly, we investigated which paths took unique
trajectories in control or patient graphs and studied how their corresponding correlation weights
contribute over the whole correlation between the two end points. To this end, for each pair of
ICNs that are connected in both control and patient groups, we obtain correlation weights for all
simple paths between them via the decomposition method. Next, we identified those brain com-
ponents that took a distinct path trajectory in comparison with other group and have a significant
contribution (more than 50%) to the correlation between paths end points.
RESULTS
ICN Extraction
We applied the proposed method to resting-state fMRI data collected from control and schizo-
phrenia groups. We selected 53 out of 100 as ICNs for further analysis and categorized them
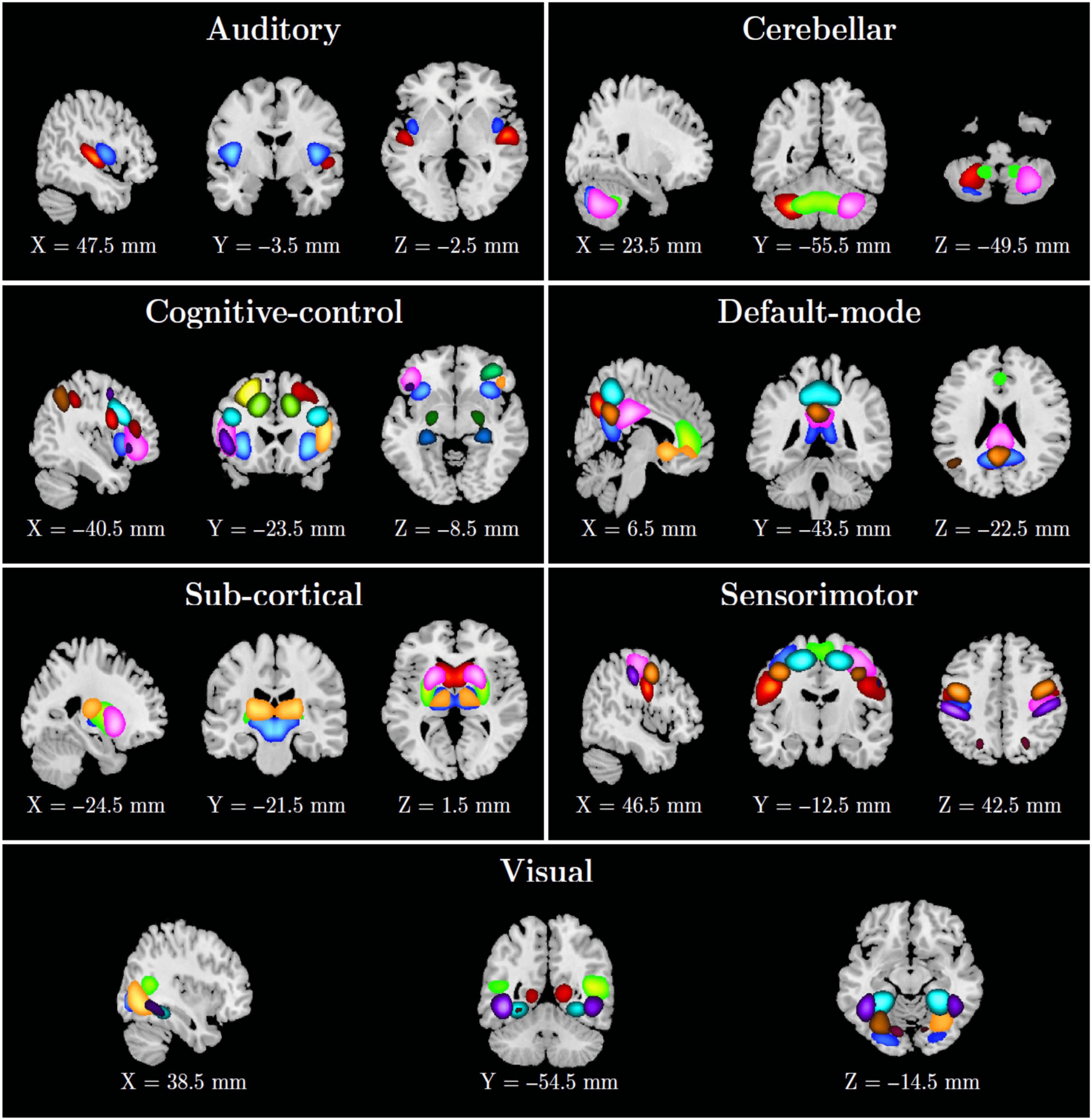
into seven functional domains. The seven labeled functional domains comprise the auditory,
subcortical, sensorimotor, visual, cognitive control, cerebellar, and default mode as depicted
in Figure 4, and ICN numbers, labels, and domains are presented in Table 1.
Network Neuroscience
645
A method to estimate altered pathways in time-varying brain networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Fifty-three ICNs categorized into seven functional domains. ICN numbers, labels, and domains are presented in Table 1.
sFNC Analysis and Group Differences Evaluation Between Control and Patient Groups
To identify significant differences between patient and control groups, we performed two-
sample t tests per ICN pair of sFNC matrices. We corrected for multiple comparisons by using
the FDR with a threshold at 0.05. Figure 5A shows the group-specific mean of sFNC matrices
Network Neuroscience
646
A method to estimate altered pathways in time-varying brain networks
Table 1.
Fifty-three extracted ICNs
ID
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Domain
ICNs
Subcortical
Subcortical
Subcortical
Subcortical
Subcortical
Auditory
Auditory
Sensorimotor
Sensorimotor
Sensorimotor
Sensorimotor
Sensorimotor
Sensorimotor
Sensorimotor
Sensorimotor
Sensorimotor
Visual
Visual
Visual
Visual
Visual
Visual
Visual
Visual
Visual
SC
SC
SC
SC
SC
AU
AU
SM
SM
SM
SM
SM
SM
SM
SM
SM
VI
VI
VI
VI
VI
VI
VI
VI
VI
Caudate
Subthalamus/hypothalamus
Putamen
Caudate
Thalamus
Superior temporal gyrus
Middle temporal gyrus
Postcentral gyrus
Left postcentral gyrus
Paracentral lobule
Right postcentral gyrus
Superior parietal lobule
Paracentral lobule
Precentral gyrus
Superior parietal lobule
Postcentral gyrus
Calcarine gyrus
Middle occipital gyrus
Middle temporal gyrus
Cuneus
Right middle occipital gyrus
Fusiform gyrus
Inferior occipital gyrus
Lingual gyrus
Middle temporal gyrus
ID
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
Domain
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Cognitive control
Default mode
Default mode
Default mode
Default mode
Default mode
Default mode
Default mode
Cerebellar
Cerebellar
Cerebellar
Cerebellar
ICNs
Inferior parietal lobule
Insula
Superior medial frontal gyrus
Inferior frontal gyrus
Right inferior frontal gyrus
Middle frontal gyrus
Inferior parietal lobule
Left inferior parietal lobe
Supplementary motor area
Superior frontal gyrus
Middle frontal gyrus
Hippocampus
Left inferior parietal lobe
Middle cingulate cortex
Inferior frontal gyrus
Middle frontal gyrus
Hippocampus
Precuneus
Precuneus
Anterior cingulate cortex
Posterior cingulate cortex
Anterior cingulate cortex
Precuneus
Posterior cingulate cortex
Cerebellum
Cerebellum
Cerebellum
Cerebellum
CC
CC
CC
CC
CC
CC
CC
CC
CC
CC
CC
CC
CC
CC
CC
CC
CC
DM
DM
DM
DM
DM
DM
DM
CB
CB
CB
CB
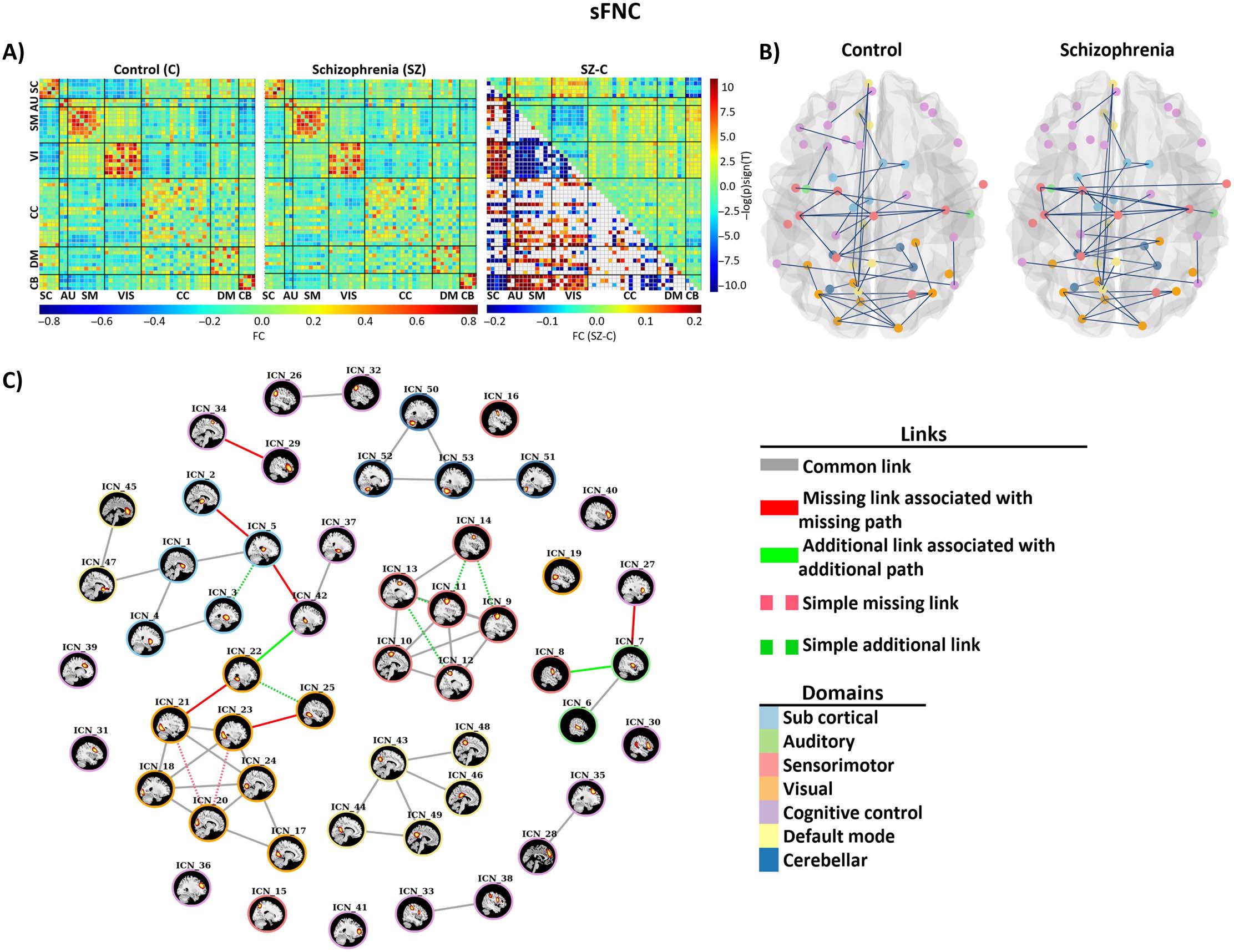
and the group differences results. The sFNC analysis results show that the schizophrenia group
had weaker functional connectivity between sensory domains (AUD, SM, VIS) in comparison
with the control group. Similarly, the connectivity between subcortical and cerebellar domains
was lower in the patient group. However, the schizophrenia group showed stronger
Network Neuroscience
647
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
(A) Mean sFNC maps for control and individuals with SZ groups and the result of group differences. The upper triangle is the group
Figure 5.
difference (SZ-HC) in sFNC, and the lower triangle is the results of multiple comparison test. (B) Estimated static graphs of the control and
SZ groups. (C) Results of applying our proposed algorithm on stating graphs of control and patient groups. Disconnectors associated with
disconnectivity are shown as solid red edges, and additional edges associated with abnormal integration are shown with solid green edges.
The simple missing and simple additional edges are shown with dashed red and green line, respectively.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
connectivity between sensory domains and subcortical domain. In addition, the connectivity
between sensory domains and cerebellar domain was stronger in schizophrenia group.
dFNC Analysis and Group Differences Between Control and Patient Groups
Within subject, windowed FNC matrices were computed as described earlier. We computed
the variance across the windowed FNC matrices for each subject and selected windows
corresponding to local maxima that resulted in 7.2 ± 1.3 (mean ± SD) windows per subject with
a range of 3 to 11; k-means clustering was applied to subjects exemplars, and the centroids from
this clustering were used as initial points to cluster all dFNC windows from all subjects. The
optimal number of clusters was determined as five by the elbow criterion, which is within a
Network Neuroscience
648
A method to estimate altered pathways in time-varying brain networks
reasonable range of previous dFNC studies (Allen et al., 2014; Fiorenzato et al., 2019; Fu et al.,
2018; Tu et al., 2019). The elbow plot can be seen in Supporting Information Figure S1.
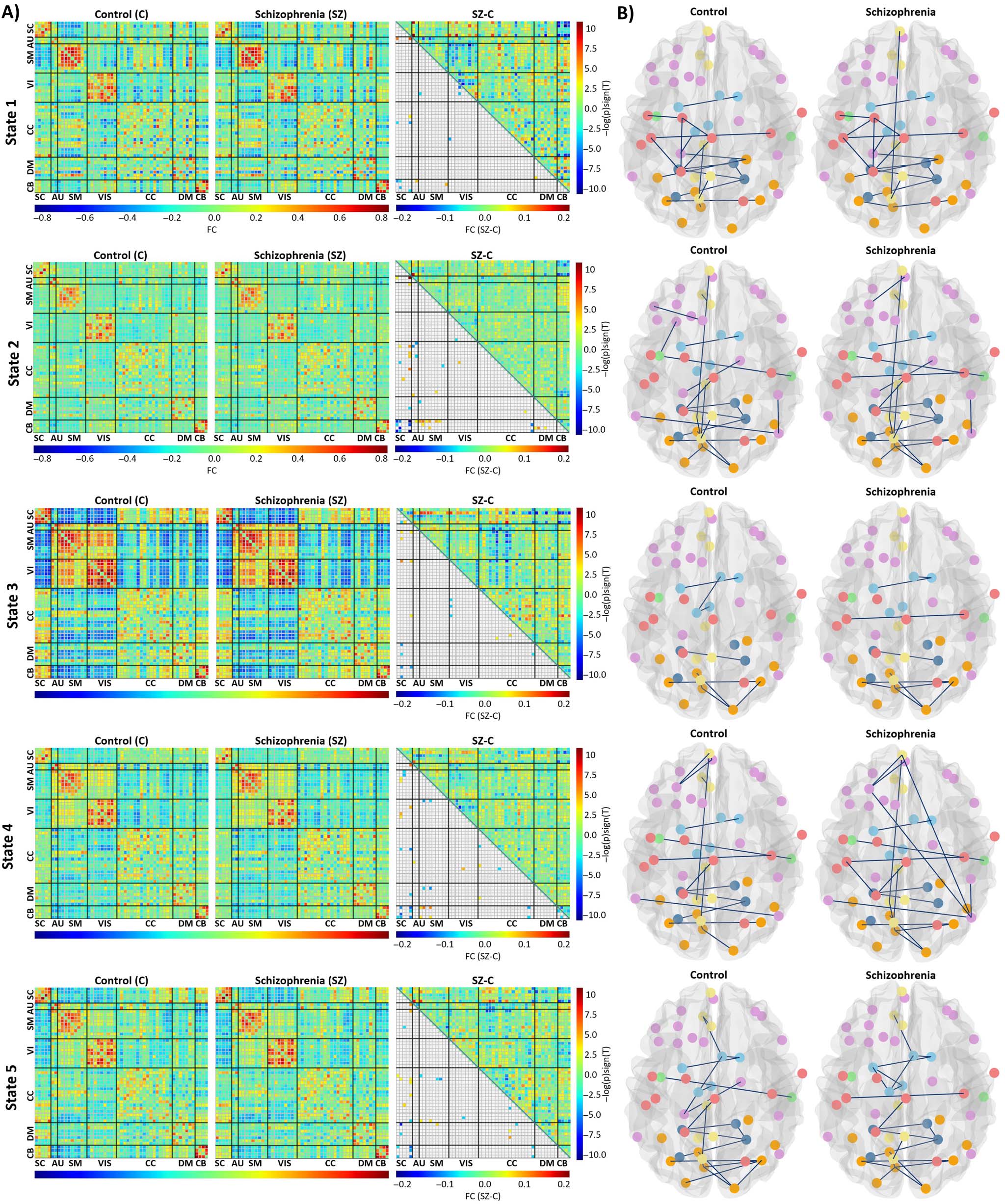
The average of functional connectivity for each state are shown in Figure 6A. In group
difference evaluations, the number of significant FDR corrected p values were 16 for State 1,
44 for State 2, 19 for State 3, 37 for State 4, and 30 for State 5. Figure 6A also illustrates the
results of the multiple comparison test for the control and SZ groups.
State 2 is the weak-connected state among all states as it shows the weak correlation between
all domains. States 1, 4, and 5 have moderate connectivity and State 3 is a strong-connected
state. States 5, 4, and 3 have moderate to high functional connectivity among sensory domains
(AUD, SM, VIS). The antagonism correlation between SC and sensory domains increases from
State 4 to 5 and reaches to its highest value in State 3. Cell-wise differences between each cluster
median (FC state) have been illustrated in Supporting Information Figure S2.
Table 2 shows the occupancy measure of a given state as the percentage of windowed
FNC that had been labeled with the cluster represented by the given state. About 52% of the
windowed dFNCs were clustered as State 2 and State 4, and the occupancy of control group
for State 2 and State 4 were 44% and 51%, respectively. In general, the occupancy of different
states shows the SZ group were mostly located in weakly connected states (State 1, State 2) in
comparison with control, which were observed in strong-connected states (State 3). State 1 was
occupied mostly by SZ patients such that 78% of windowed dFNCs of the State 1 belonged to SZ
patients, and the occupancy of control group in that state was only 22%. However, 74% of win-
dowed dFNCs in State 3 belonged to the control group. Similarly, the occupancy level of SZ for
State 5 was 26% and was lower than the control group. The connectivity between SM and VIS
domain in State 3 was stronger than in State 1. In addition, the connectivity between SC and CC,
DM, and CB in State 3 was higher than State 1. However, the connectivity between sensory
(AUD, SM, VIS) and CB, and between VIS and SB in State 1 was higher than State 3.
Estimating Static and Time-Varying Graphs for Control and Patient Groups
We estimated static brain graphs for control and patient groups by using GGM. Figure 5B illus-
trated the estimated static graphs of control and patient group. The estimated graphs for each
state (time-varying graphs) of control and patient groups are illustrated in Figure 6B.
Identifying Edges Associated with Disconnection and Abnormal Integration in Static and
Time-Varying Graphs
We applied our proposed algorithm to identify missing edges that are associated with discon-
nection and additional edges that are associated with abnormal integration. In static graph
analysis, we identified six missing edges and two additional edges that trigger absent paths
and additional paths in the SZ group, both within and between functional domains. We found
four missing links associated with blocked paths within visual, subcortical, and cognitive control
networks and one missing link between cognitive control and auditory (Insula, Middle temporal
gyrus) and one between subcortical and cognitive control (Thalamus, Hippocampus). Two
additional edges identified between subcortical, auditory, and visual networks. Figure 5C
illustrates differential graphs obtained by our proposed method. Table 3 shows details of
missing and additional links (edges) associated with SZ in our static analysis.
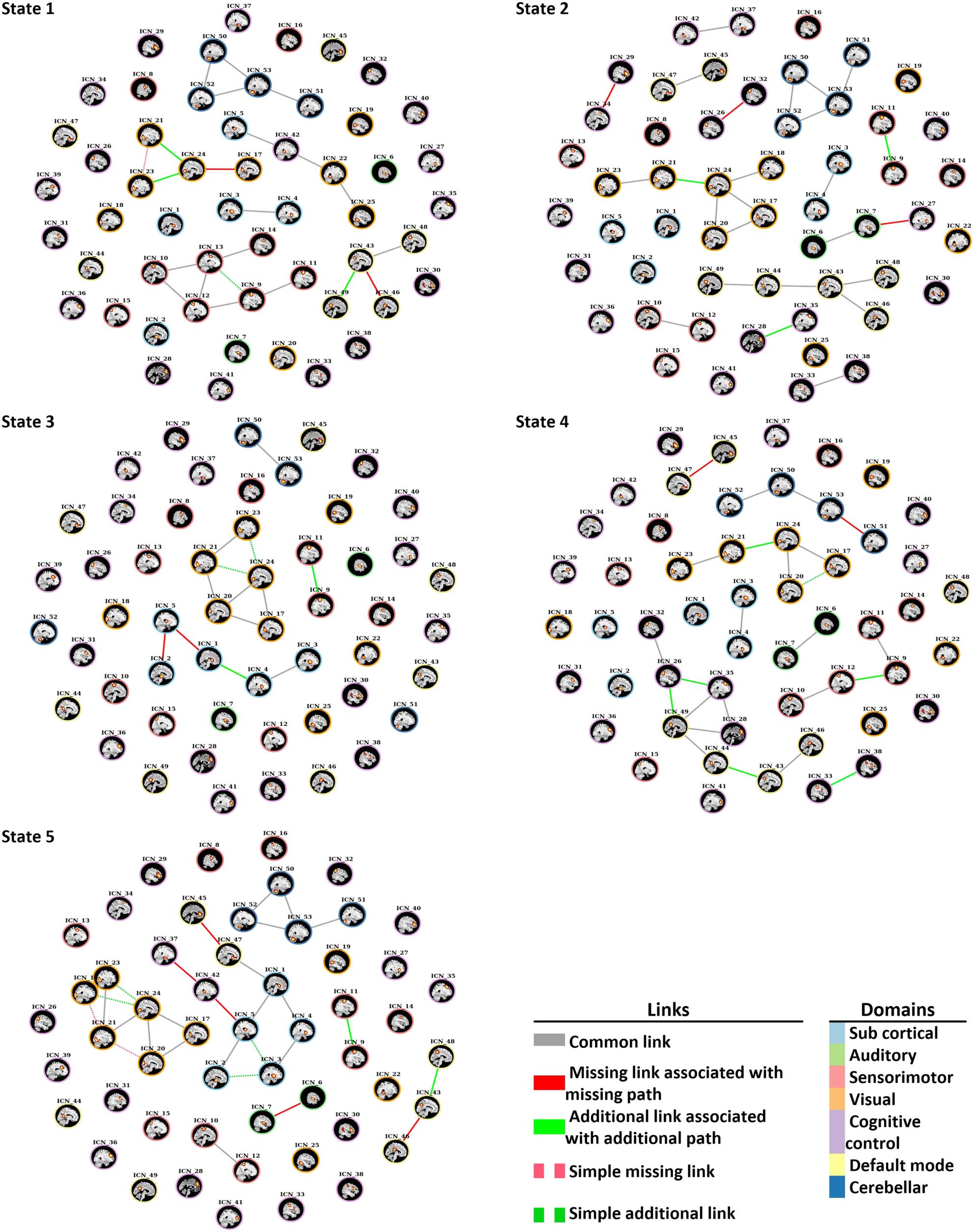
The disconnectors and connectors that were identified through dynamic approach are
shown in Figure 7, and Table 4 shows details of these edges. In State 1, two missing and three
additional edges were identified within the default mode and visual domain. The results show
Network Neuroscience
649
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(A) Each state’s results include parts of averaged correlation matrices for control and SZ and group differences. The upper triangle is
Figure 6.
the differences between averaged correlation matrix of SZ and control (SZ-C), and the lower triangle is the result of multiple comparison test.
(B) Parts of estimated graphs of the control and SZ groups.
Network Neuroscience
650
A method to estimate altered pathways in time-varying brain networks
Table 2.
State occupancy
State 1
(C = 22%,
SZ = 78%)
State 2
(C = 44%,
SZ = 56%)
State 3
(C = 74%,
SZ = 26%)
State 4
(C = 51%,
SZ = 49%)
State 5
(C = 74%,
SZ = 26%)
State-wise percentage
All
Control
Schizophrenia
16%
7%
26%
36%
31%
41%
14%
20%
7%
16%
16%
16%
18%
26%
10%
Table 3.
analysis
The endpoint of links associated with disconnectivity and abnormal integration and their associated functional domain of static
Missing links associated with disconnectivity (v1, v2)
Additional links associated with abnormal integration (v1, v2)
v1
Domain
SC
ICN
Thalamus
v2
ICN
Hippocampus
v1
v2
Domain
CC
Domain
CC
ICN
Hippocampus
ICN
Fusiform gyrus
VIS
VIS
SC
CC
CC
Inferior occipital
Middle temporal
VIS
AU
Middle temporal
gyrus
gyrus
gyrus
Postcentral
gyrus
Right middle
Fusiform gyrus
occipital gyrus
Subthalamus/
hypothalamus
Thalamus
Supplementary
motor area
Inferior frontal
gyrus
VIS
SC
CC
Insula
Middle temporal
AU
gyrus
Note. DM, default mode network; VIS, visual; CC, cognitive control; SM, sensorimotor; AU, auditory; SC, subcortical; CB, cerebellar.
Domain
VIS
VIS
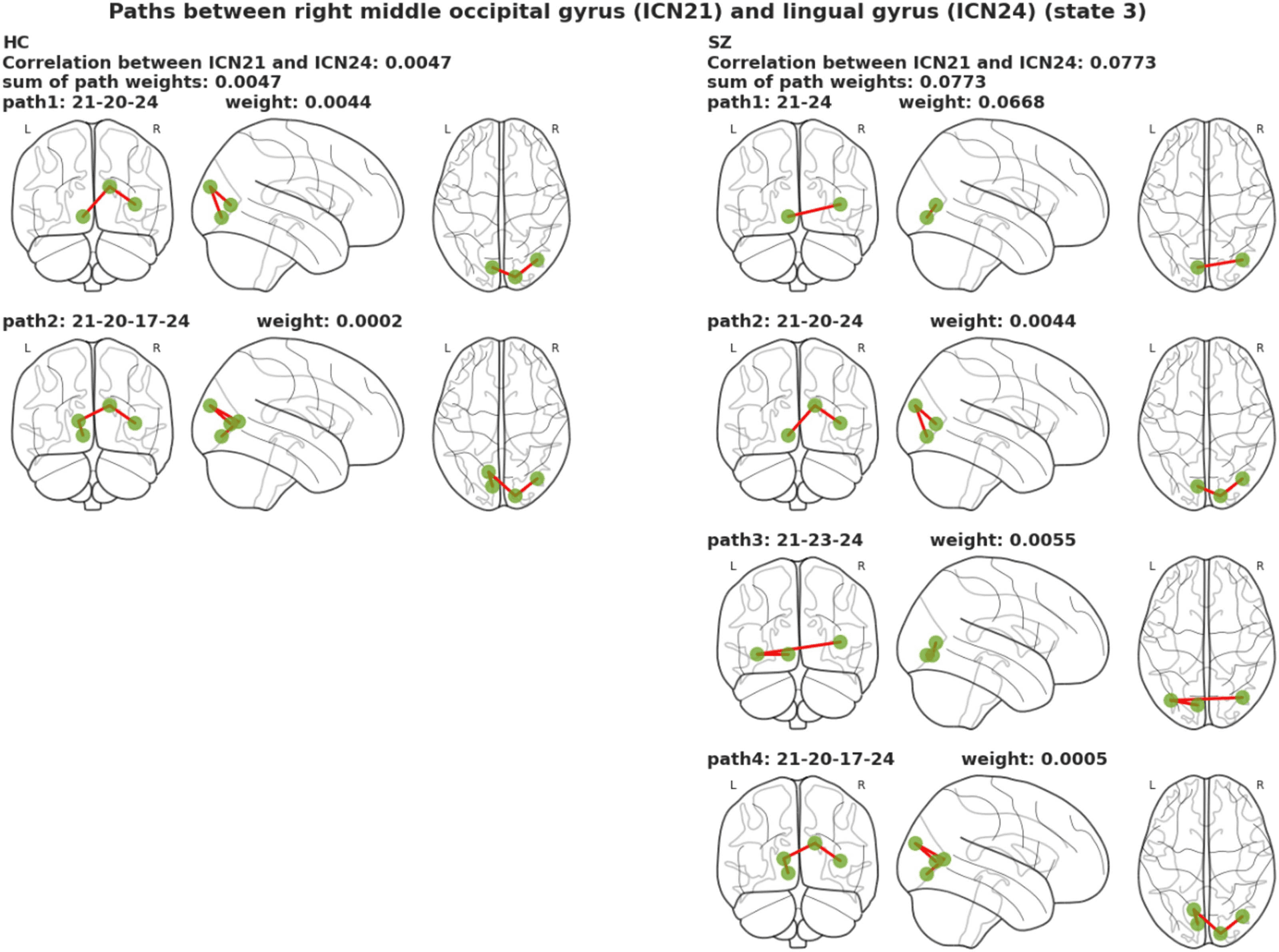
that the connection between the lingual gyrus and the calcarine gyrus in the SZ group was
disrupted, and the lingual gyrus and the right middle occipital gyrus and the inferior occipital
gyrus connected with new additional edges.
In State 2, two missing links were observed within the cognitive control domain. In addi-
tion, one missing link was identified between the insula of the cognitive control domain and
the middle temporal gyrus of the auditory domain. In addition, three new connectors were
observed in the SZ group within ICNs of the cognitive control, the visual, and the sensorimotor
domains.
In State 3, different connections within the subcortical domain were observed in the
SZ group. The connection between the caudate and the thalamus and the subthalamus/
hypothalamus were disrupted in the SZ group, and new connection between the caudate
and the putamen were identified in the SZ group through an additional link. An additional
new connection in the SZ group was observed within the sensorimotor domain between
the left and the right postcentral gyrus.
Network Neuroscience
651
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Disconnectors and connectors that were identified in each state. Solid red links trigger disconnection (absence of paths), and solid
green links trigger abnormal integration (additional paths) in SZ group with reference to the control group graph.
Network Neuroscience
652
A method to estimate altered pathways in time-varying brain networks
Table 4.
analysis
The endpoint of links associated with disconnection and abnormal integration and their associated functional domain of dynamic
Missing links associated with disconnectivity (v1, v2)
Additional links associated with abnormal integration (v1, v2)
v1
v2
State
1
Domain
DM
ICN
Precuneus
VIS
Calcarine gyrus
2
CC
Supplementary
motor area
CC
Insula
ICN
Posterior
cingulate
cortex
Lingual
gyrus
Inferior
frontal
gyrus
Middle
temporal
gyrus
Domain
DM
Domain
DM
v1
ICN
Posterior
cingulate
cortex
v2
ICN
Precuneus
Domain
DM
VIS
VIS
Right middle
Lingual gyrus
occipital gyrus
VIS
Inferior occipital
Lingual gyrus
gyrus
CC
CC
Superior frontal
gyrus
Superior medial
frontal gyrus
VIS
VIS
CC
AU
VIS
Right middle
Lingual gyrus
VIS
occipital gyrus
CC
Inferior parietal
Inferior
CC
SM
Left postcentral
Right postcentral
SM
lobule
parietal
lobule
gyrus
gyrus
3
4
SC
SC
Caudate
Thalamus
Subthalamus/
Thalamus
hypothalamus
SC
SC
SC
SM
Caudate
Caudate
Left postcentral
Right postcentral
gyrus
gyrus
DM
Anterior
cingulate
cortex
Anterior
cingulate
cortex
DM
CC
Left inferior
Left inferior
parietal lobule
parietal lobule
CB
Cerebellum
Cerebellum
CB
VIS
Right middle
Lingual gyrus
occipital gyrus
CC
Superior frontal
Inferior parietal
gyrus
lobule
DM
Posterior
cingulate
cortex
Inferior parietal
lobule
DM
SM
Precuneus
Precuneus
Left postcentral
Superior parietal
gyrus
lobule
SC
SM
CC
VIS
CC
CC
DM
SM
5
DM
Anterior
cingulate
cortex
DM
Precuneus
Anterior
cingulate
cortex
Posterior
cingulate
cortex
DM
SM
Left postcentral
Right postcentral
SM
gyrus
gyrus
DM
DM
Precuneus
Precuneus
DM
Network Neuroscience
653
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
Table 4.
(continued )
Missing links associated with disconnectivity (v1, v2)
Additional links associated with abnormal integration (v1, v2)
v1
v2
v1
v2
State
Domain
CC
ICN
Hippocampus
ICN
Hippocampus
Domain
CC
Domain
ICN
ICN
Domain
SC
AU
Thalamus
Hippocampus
Superior
temporal
gyrus
Middle
temporal
gyrus
CC
AU
Note. DM, default mode network; VIS, visual; CC, cognitive control; SM, sensorimotor; AU, auditory; SC, subcortical; CB, cerebellar.
In State 4, two disconnectors were identified within the cerebellar and the default mode
domains. Five additional links were observed within the cognitive control, the visual, the
default mode, and the sensorimotor domains. Also, one additional link was identified between
the cognitive and the default mode network domains. The missing links triggered separation
within some ICNs of the default mode and the cerebellar domains. However, the additional
edges created more connections within the sensorimotor, the visual, and the cognitive control
ICNs. Three new additional edges of (superior frontal gyrus, inferior parietal lobule; posterior
cingulate cortex, inferior parietal lobule; and precuneus, precuneus) were created for new
additional paths between nodes of the cognitive control and the default mode domains in
the SZ group.
In State 5, four disruptions within the default mode, the cognitive control, and the auditory
domains and one disruption between the cognitive control and the subcortical domains were
observed in the SZ group. Three disconnectors were identified that triggered disconnections
between nodes of a connected component in the control group that belongs to the default
mode, the cognitive control, and the subcortical domains. Two additional integrations also
were observed within the sensorimotor and the default mode domains in the SZ group.
Applying Covariance Decomposition Approach
We also examined the case that paths exist between two specific brain components in both
groups by using the covariance decomposition method. In static analysis of control and SZ
group graphs, 67 pairs of ICNs were identified between which paths exist in both control
and SZ groups. Ten of these pairs took unique path trajectories in at least in one group and
have a contribution of more than 50% of the correlation between path end points obtained via
the decomposition method. Table 5 summarize the results of those ICN pairs in static analysis.
Results of static analysis showed significant differences within the sensory motor, the subcor-
tical, and the visual domains. The SZ groups are connected through higher number of paths
that took unique trajectories, with higher correlation weight in comparison with the control
group in the sensory motor and the subcortical domains. However, within the visual domain
the control group showed a higher number of paths with higher correlation weights.
In time-varying graphs of control and SZ analysis, 127 pairs of ICNs were identified
between which paths exist in both control and SZ groups. States 3 and 5 revealed that pair
4 and 13 took unique path trajectories at least in one group, respectively, which have a con-
tribution of more than 50% of the correlation between path end points obtained via decom-
position. Table 6 summarizes the results of those ICN pairs. Within the visual domain in State
3, the SZ group showed a higher number of paths than the control group in all four cases. Also,
Network Neuroscience
654
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
t
N
e
w
o
r
k
N
e
u
r
o
s
c
e
n
c
e
i
Table 5.
Paths that took unique path trajectory and have a significant contribution to the decomposition in static analysis
No. of
paths
Distinct paths
ICN pair
v1
v2
Domain
SC
ICN
Caudate
ICN
Thalamus
Domain
SC
HC
1
SZ
2
33
48
Left postcentral
Precentral gyrus
gyrus
Paracentral
lobule
Precentral gyrus
SM
SM
6
6
Right postcentral
gyrus
Paracentral
lobule
SM
10
27
Right postcentral
Precentral gyrus
SM
10
33
gyrus
Superior parietal
lobule
Paracentral
lobule
SM
10
32
Superior parietal
Precentral gyrus
SM
10
48
lobule
Cuneus
Right middle
occipital gyrus
VIS
21
15
Cuneus
Inferior occipital
VIS
21
15
gyrus
Fusiform gyrus
Middle temporal
VIS
22
1
gyrus
Number
of common
paths
1
No.
0
HC
Weight
contribution
0.00%
6
6
10
10
10
10
15
15
0
0
0
0
0
0
0
6
6
0.00%
0.00%
0.00%
0.00%
0.00%
0.00%
82.71
81.44
22
1
SZ
Weight
contribution
74.96%
Correlation
difference
HC-SZ
−0.0012
91.16%
−0.0311
56.11%
−0.0045
74.04%
−0.0376
98.09%
−0.0275
66.14%
−0.0385
89.17%
−0.0065
0.00%
0.103
0.00%
0.0852
100%
−0.0313
No.
1
27
42
17
23
22
38
0
0
1
SM
SM
SM
SM
SM
SM
VIS
VIS
VIS
6
5
5
A
m
e
t
h
o
d
t
o
e
s
t
i
m
a
t
e
a
l
t
e
r
e
d
p
a
t
h
w
a
y
s
i
n
t
i
m
e
-
v
a
r
y
i
n
g
b
r
a
i
n
n
e
t
w
o
r
k
s
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
t
N
e
w
o
r
k
N
e
u
r
o
s
c
e
n
c
e
i
Table 6.
Paths between groups that took unique path trajectory and have a significant contribution to the decomposition in dynamic analysis
ICN pair
v1
v2
State
3
Domain
VIS
ICN
Calcarine gyrus
ICN
Right middle
Domain
VIS
C SZ
6
2
occipital gyrus
No. of
paths
Distinct paths
No. of
common
paths
2
Control
Weight
No.
0
contribution No.
0%
4
SZ
Weight
contribution
66.39%
Correlation
difference
(C-SZ)
−0.0106
3
3
3
5
5
5
5
5
5
5
5
5
5
5
5
5
VIS
VIS
Calcarine gyrus
Inferior occipital gyrus
Right middle
Lingual gyrus
occipital gyrus
VIS
Inferior occipital
Lingual gyrus
gyrus
SC
Subthalamus/
Putamen
hypothalamus
SC
Subthalamus/
Caudate
hypothalamus
SC
SC
VIS
VIS
VIS
VIS
Putamen
Caudate
Thalamus
Thalamus
Calcarine gyrus
Inferior occipital gyrus
Inferior occipital
Lingual gyrus
gyrus
Calcarine gyrus
Middle occipital gyrus
Middle occipital
Cuneus
gyrus
VIS
Middle occipital
Right middle
gyrus
occipital gyrus
VIS
VIS
VIS
SC
SC
SC
SC
VIS
VIS
VIS
VIS
VIS
VIS
Middle occipital
Inferior occipital gyrus
VIS
gyrus
VIS
Middle occipital
Lingual gyrus
gyrus
Cuneus
Cuneus
VIS
VIS
Inferior occipital gyrus
Right middle
occipital gyrus
VIS
VIS
VIS
2
2
2
1
1
1
1
4
3
4
3
1
1
3
3
3
7
4
4
3
4
3
3
4
2
2
2
2
2
1
4
4
2
2
2
1
1
1
1
2
1
0
0
0
0
0
2
2
0
0
0
0
0
0
0
2
2
4
3
1
1
3
1
1
0%
0%
0%
0%
0%
0%
0%
31.41%
9.14%
100%
100%
100%
100%
100%
85.12%
85.12%
5
2
2
2
3
2
2
2
1
2
2
2
2
1
2
2
92.14%
93.61%
−0.0071
−0.0726
98.86%
−0.053
99.82%
−0.0376
96.98%
−0.0088
97.64%
70.17%
83.8%
83.8%
100%
100%
−0.0609
−0.0152
−0.0102
−0.0597
−0.0091
−0.0043
100%
0.047
100%
0.0024
100%
−0.0531
83.8%
6.77%
−0.0029
0.0292
6
5
6
A
m
e
t
h
o
d
t
o
e
s
t
i
m
a
t
e
a
l
t
e
r
e
d
p
a
t
h
w
a
y
s
i
n
t
i
m
e
-
v
a
r
y
i
n
g
b
r
a
i
n
n
e
t
w
o
r
k
s
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
distinct paths in terms of the sequence of the nodes in the SZ group account for more than 50%
of the total correlation weight between path end points. For example, the number of paths
between the calcarine gyrus (ICN17) and the right middle occipital gyrus (ICN 21) was six
in the SZ group, while the number of paths between these two ICNs was two in the control
group. Two paths in the SZ group were common to the control group, and the other four took
some unique path trajectories, and decomposition revealed that those distinct paths in the SZ
group have a significant contribution (66.39%). As an example, Figure 8 depicts the result of
covariance decomposition analysis between the right middle occipital gyrus and the lingual
gyrus in State 3. The correlation between these two ICNs in the control and SZ groups is
0.0046 and 0.0772, and the number of paths between them in the control and SZ groups is
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. There are two paths between the right middle occipital gyrus and lingual gyrus in the control group in State 3. The number of paths
identified between these two ICNs in the SZ group is four. The correlation between path endpoints in control is 0.0046, and the decomposition
approach assigned correlation weights of 0.0044 and 0.0002 to each path in control. The correlation between path end points in SZ is 0.0772,
and the decomposition approach assigned correlation weights of 0.0668, 0.0044, 0.0055, and 0.0005 to the four paths in SZ. The decom-
position approach shows that the two new paths in the patient group contribute 86.51% and 7.1% to the correlation between path end points.
A total of 93.61% of correlation weight belongs to these two new paths in the SZ group, and two other paths in SZ that take the same
trajectories as controls have a correlation weight of 6.39% of the path end point correlation.
Network Neuroscience
657
A method to estimate altered pathways in time-varying brain networks
two and four, respectively. The decomposition approach shows that two new paths in the
patient group contribute 93.61% of correlation weight. The other two paths in SZ group that
took the same trajectories as the control group contribute 6.39% of correlation weight.
Similar scenarios were observed within the subcortical and the visual domain in State 5.
Four cases show that the SZ group has more paths between components of putamen, caudate,
and thalamus, which also involve a significant proportion of total correlation between those
end points. In addition, two cases that involve the inferior occipital gyrus as one of the path
end points show that the distinct paths in the SZ group had a significant effect on the total
correlation between the path endpoints.
Five cases in State 5 show the paths from the middle occipital gyrus to other visual domain
components have totally different trajectories in control and SZ groups and do not share any
common paths between control and SZ groups. Moreover, the path analysis between the
cuneus and the right middle occipital gyrus shows that the SZ group has more paths than
the control group; however, the unique path of control significantly contributes to the total
correlation weights between end points. Similar results were observed between the cuneus
and the inferior occipital gyrus, but the distinct paths of both control and SZ groups had a
significant contribution to the decomposition.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
DISCUSSION
In this study, we estimated static and dynamic brain graphs from resting-state fMRI data. We
applied a data-driven approach for determining the nodes and edges of the graphs. Spatial
brain components evaluated by group ICA was used to define data-driven nodes, and for esti-
mating graphs edges, we employed statistical tests and mitigated the bias of relying on ad hoc
thresholds for correlation values. After estimation of a partial correlation matrix, we obtain the
corresponding p values, and we only considered an edge between two nodes if it passes a
significance level (0.05) after multiple comparison correction (FDR). This contribution reduces
the need for subjective choices as in other widely used approaches (Karwowski, Vasheghani
Farahani, & Lighthall, 2019).
Existing methods for identifying differences between control and SZ patient groups in func-
tional brain imaging literature are limited to correlation networks and pairwise functional con-
nectivity comparison. Most studies focus only on pairwise relationships or “single links.” The
path in such networks cannot reveal meaningful interpretation in comparison with the GGM,
in which the conditional dependency plays an important role in determining connection and
paths between nodes.
We analyzed paths on both static and dynamic manner of control and patient group graphs.
We provide an algorithm to estimate edges associated with disconnection (absence of paths) or
aberrant integration (additional paths) in dynamic patient group graphs by mimicking the
structure of control group graphs. We used the concept of the connected component in graph
theory to examine the presence or absence of a path between two nodes of a graph, as there is
at least one path between every pair of nodes in a connected component. This results in time
complexity reduction of path analysis in comparison with checking the absence or presence of
paths for every pair of nodes of a graph. In the first part of the algorithm, we identified con-
nected components in graphs using the NetworkX python package (Hagberg, Swart, & Chult,
2008). Next, through multiple steps in the proposed algorithm, we checked if the nodes of
each connected component separated or joined to a new connected component in the second
graph. Then, if any separation or abnormal integration occurred, the edges associated with
Network Neuroscience
658
A method to estimate altered pathways in time-varying brain networks
those cases would be returned as an output of the algorithm. This algorithm can be applied to
either static or dynamic graphs.
In addition, we studied the cases where two nodes (ICNs) connected in both control and
patient groups. We investigated which paths take unique trajectories and computed their cor-
responding correlation weights by using the covariance decomposition method in a GGM. We
applied our method to both static and dynamic time-varying graphs to analyze changes in
paths over time.
We illustrated the utility of our proposed method on resting-state fMRI data of SZ patients.
Previous studies have been demonstrated that SZ is associated with a disruption of the con-
nections present in the healthy brain (Hunt, Kopell, Traub, & Whittington, 2017; Pearlson,
1997; van den Heuvel & Fornito, 2014; van den Heuvel, Mandl, Stam, Kahn, & Pol, 2010).
Since SZ is a psychiatric disorder that can be distinguished by functional disconnectivity or
abnormal integration between distant brain components (Damaraju et al., 2014; Friston,
1998; Skudlarski et al., 2010), we analyzed additional and blocked paths in estimated SZ
time-varying graphs. However, the proposed method can be applied to any data related to
other conditions that can be distinguished by disconnectivity or abnormal integration. Using
our proposed algorithm, we found several disconnectors and connectors associated with
disconnectivity and abnormal integration (see Table 3 and Table 4).
Our findings show 14 disconnectors and 16 connectors, both within and between functional
domains, across all five states in time-varying brain graphs analysis. Static approach reveals six
disconnectors and two connectors. Table 7 summarizes the number of identified connector and
disconnector across all states in dynamic and static analysis. In static analysis, the disconnec-
tion observed within the nodes of the visual, the subcortical, and the cognitive control domains
and between nodes of the subcortical, the cognitive control, and the auditory domains. In addi-
tion, two abnormal integrations observed between the cognitive control, the visual, and the
auditory domains. In dynamic graph analysis within the default mode network, we found four
missing links associated with blocked paths in States 1, 4, and 5. Several of the observed dis-
connectors showed agreement between static and dynamic approach. Four of six disconnec-
tions in static analysis, which were observed within and between the subcortical, the cognitive
control, and the auditory domain, were also identified in different states of dynamic analysis. In
dynamic approach, the disruption identified between the thalamus (SC) and the hippocampus
(CC) in State 5; between the insula (CC) and the middle temporal gyrus (AU), and between
the supplementary motor area (CC) and the inferior frontal gyrus (CC) in State 2; and between
Table 7. Number of identified links associated with disconnection and abnormal integration in
static and dynamic analysis
Static analysis
State 1
State 2
State 3
State 4
State 5
Number of missing
links associated with
missing paths
6
Number of additional
links associated with
additional paths
2
2
3
2
2
5
3
3
2
6
2
Network Neuroscience
659
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
the subthalamus/hypothalamus (SC) and the thalamus (SC) in State 3 were observed in static
analysis as well. However, results dynamic approach can capture more detailed information
regarding the disconnection and abnormal integration that would be missed in static analysis.
Therefore, path analysis on time-varying graphs extends findings from static analysis and pro-
vides additional results that are complementary to, and extend, a static analysis.
The default mode network describes a distributed large-scale functional brain network that
consists of brain components such as the medial prefrontal cortex, posterior cingulate cortex,
and precuneus (Fox, 2007) that is more active during rest or internal cognitive processing com-
pared to external goal-directed cognitive tasks (Raichle et al., 2001). Previous fMRI studies in
SZ have consistently reported the disruption and aberrant functioning of the default mode net-
work (Du, Pearlson, et al., 2016; Fornito, Zalesky, Pantelis, & Bullmore, 2012; Mars et al.,
2012; Ö ngür et al., 2010; Pankow et al., 2015). Interestingly, our approach identified three
new links associated with additional paths within the default mode network and one new link
between the default mode network and cognitive control in precisely the same states as dis-
connectors were found in dynamic approach, which may be related to a compensatory
response in the SZ group that warrants future study.
In addition, disruption in the subcortical domain is consistent with and significantly extends
recent reports (Damaraju et al., 2014; Woodward, Karbasforoushan, & Heckers, 2012). In
more detail, disconnection between the thalamus and the hippocampus, which were identi-
fied by our method in both dynamic and static analysis, has been reported previously in
Woodward, Karbasforoushan, and Heckers (2012).
Furthermore, the most significant alteration was observed in cognitive control. Cognitive
dysfunction in schizophrenia (McTeague et al., 2017) supports the cognitive control discon-
nections identified by our method, which were observed both in static and dynamic analysis.
In dynamic approach, there were five links associated with blocked paths, of which four were
within cognitive control, and one was between the cognitive control and auditory network.
Also, three new links were observed associated with additional paths within cognitive control,
and one new link was between the default mode network and cognitive control networks.
Cognitive control is a cognitive and neural mechanism that contributes to the ability to adapt
information processing and regulating behavior according to one’s current goals (Miller,
2000), and according to prior studies, cognitive impairments are the main feature of SZ
(Cho, Konecky, & Carter, 2006; Ray, Gold, Silverstein, Barch, & Carter, 2017). Our results thus
are consistent with and extend findings from prior studies.
To examine case 3, where two distinct brain components are connected and reachable
from each other in both control and patient groups, we applied the covariance decomposition
method. The dynamic approach results showed that (only) States 3 and 5 have significant
group differences (Jones & West, 2005). Although the paths existed between pairs of brain
components, particularly within the subcortical and visual domain in both groups, these paths
take unique trajectories, and the decomposition method revealed that those distinct paths have
significant weight. The results of both static and dynamic analysis suggest that despite the con-
nection between the nodes in both groups in subcortical domain, schizophrenia have a dif-
ferent type of connection, in terms of unique paths trajectories, and the decomposition method
showed that those distinct paths have significant weight between the thalamus and the cau-
date. In addition, dynamic analysis provided more additional differences, which were not
revealed in static analysis in the subcortical domain.
Our work shows that differences between control and patient groups are likely the result of
“multilink” disruptions in the paths. The results highlight the importance of studying longer
Network Neuroscience
660
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
path links, especially in the context of complex mental illness such as schizophrenia. Hence,
in comparison with the existing methods, more detailed interpretation regarding the differ-
ences between control and SZ patients can be obtained using our proposed method. Future
work should focus on expanding the approach and replicating our results in additional
datasets.
In this work, we analyzed undirected graphs based on partial correlation. Although the
graph-theoretical approach can be used to either assess functional or effective connectivity
patterns, most human brain graph investigations have applied undirected networks
because of inference constraints of directed graphs (Farahani, Karwowski, & Lighthall, 2019;
Karwowski, Vasheghani Farahani, & Lighthall, 2019; Liao, Vasilakos, & He, 2017). Future work
could utilize directed network analysis that might provide more information on human brain
connectivity.
CONCLUSION
In sum, we provide an approach using GGM to estimate static and time-varying graphs in
control and SZ patient groups on resting-state fMRI data. We comprehensively analyze paths
and propose an algorithm to estimate links associated with disconnectivity and abnormal inte-
gration in the patient group graphs. Also, in cases in which paths exist between two nodes in
two groups, we suggest using a covariance decomposition method. We apply our method to
study resting-state fMRI data in SZ versus controls, as SZ is a disorder characterized by discon-
nectivity. We provided detailed information about how reduced integration or abnormal inte-
gration manifests in the SZ group. Several missing links associated with disconnectivity were
identified in the SZ group, both within and between functional domains, particularly within
the default mode network and cognitive control domains. Also, our proposed algorithm iden-
tified additional new edges within these domains associated with abnormal integration, which
may be related to a compensatory brain response in the schizophrenia group. In analyzing
cases in which paths exist between two specific brain components in both groups, these paths
in some cases took unique trajectories, and the decomposition method showed that those dis-
tinct paths have significant weight. The proposed path analysis provides a way to characterize
individuals by evaluating changes in paths, rather than just focusing on pairwise relationships.
As the edges within a path might be distinct in different individuals, a path-based approach
can capture important information that is ignored by approaches that focus on pairwise rela-
tionships. Our first dynamic path analysis found path-based differences between individuals
with schizophrenia and healthy controls, indicating its promise for identifying path-based
abnormalities in dynamic connectivity in the healthy and disordered brains. Path analysis
on time-varying graphs extends findings from static graphs and provides additional results that
are complementary to, and extend, a static analysis.
ACKNOWLEDGMENTS
Data collection was supported by the National Center for Research Resources at the National
Institutes of Health (grant numbers: NIH 1 U24 RR021992, NIH 1 U24 RR025736-01).
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00247.
Network Neuroscience
661
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
AUTHOR CONTRIBUTIONS
Haleh Falakshahi: Formal analysis; Methodology; Software; Validation; Visualization;
Writing – original draft; Writing – review & editing. Hooman Rokham: Conceptualization;
Writing – review & editing. Zening Fu: Data curation; Writing – review & editing. Armin
Iraji: Writing – review & editing. Daniel H. Mathalon: Resources; Writing – review &
Judith M. Ford: Resources; Writing – review & editing. Bryon A. Mueller:
editing.
Resources; Writing – review & editing. Adrian Preda: Resources; Writing – review & editing.
Theo G. M. van Erp: Resources; Writing – review & editing. Jessica A. Turner: Writing – review
& editing. Sergey Plis: Writing – review & editing. Vince D. Calhoun: Conceptualization;
Funding acquisition; Investigation; Supervision; Validation; Writing – review & editing.
FUNDING INFORMATION
Vince D. Calhoun, National Institutes of Health (https://dx.doi.org/10.13039/100000002),
Award ID: R01MH118695. Vince D. Calhoun, National Science Foundation (https://dx.doi
.org/10.13039/100000001), Award ID: 2112455.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
REFERENCES
Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele, T., &
Calhoun, V. D. (2014). Tracking whole-brain connectivity
dynamics in the resting state. Cerebral Cortex, 24(3), 663–676.
https://doi.org/10.1093/cercor/bhs352, PubMed: 23146964
Azevedo, F. A., Carvalho, L. R., Grinberg, L. T., Farfel, J. M., Ferretti, R. E.,
Leite, R. E., … Herculano-Houzel, S. (2009). Equal numbers of neuro-
nal and nonneuronal cells make the human brain an isometrically
scaled-up primate brain. Journal of Comparative Neurology, 513(5),
532–541. https://doi.org/10.1002/cne.21974, PubMed: 19226510
Balakrishnan, R., & Ranganathan, K. (2012). Paths and connected-
ness. In A textbook of graph theory (p. 13). New York, NY: Springer.
Bhinge, S., Long, Q., Calhoun, V. D., & Adali, T. (2019). Spatial
dynamic functional connectivity analysis identifies distinctive
biomarkers in schizophrenia. Frontiers in Neuroscience. https://
doi.org/10.3389/fnins.2019.01006, PubMed: 31607848
Cho, R., Konecky, R., & Carter, C. S. (2006). Impairments in frontal
cortical gamma synchrony and cognitive control in schizophre-
nia. Proceedings of the National Academy of Sciences, 103(52),
19878–19883. https://doi.org/10.1073/pnas.0609440103,
PubMed: 17170134
Cole, M. W., Anticevic, A., Repovs, G., & Barch, D. (2011). Vari-
able global dysconnectivity and individual differences in schizo-
phrenia. Biological Psychiatry, 70(1), 43–50. https://doi.org/10
.1016/j.biopsych.2011.02.010, PubMed: 21496789
Damaraju, E., Allen, E. A., Belger, A., Ford, J. M., McEwen, S.,
Mathalon, D. H., … Calhoun, V. D. (2014). Dynamic functional
connectivity analysis reveals transient states of dysconnectivity in
schizophrenia. NeuroImage: Clinical, 5, 298–308. https://doi.org
/10.1016/j.nicl.2014.07.003, PubMed: 25161896
Danaher, P., Wang, P., & Witten, D. M. (2014). The joint graphical
lasso for inverse covariance estimation across multiple classes.
Journal of the Royal Statistical Society: Series B (Statistical Meth-
odology), 76(2), 373–397. https://doi.org/10.1111/rssb.12033,
PubMed: 24817823
Di Martino, A., Zuo, X.-N., Kelly, C., Grzadzinski, R., Mennes, M.,
Schvarcz, A., … Milham, M. P. (2013). Shared and distinct intrin-
sic functional network centrality in autism and attention-deficit/
hyperactivity disorder. Biological Psychiatry, 74(8), 623–632.
https://doi.org/10.1016/j.biopsych.2013.02.011, PubMed:
23541632
Du, Y., Allen, E. A., He, H., Sui, J., Wu, L., & Calhoun, V. D. (2016).
Artifact removal in the context of group ICA: A comparison of
single-subject and group approaches. Human Brain Mapping,
37(3), 1005–1025. https://doi.org/10.1002/ hbm.23086,
PubMed: 26859308
Du, Y., & Fan, Y. (2013). Group information guided ICA for fMRI
data analysis. NeuroImage, 69, 157–197. https://doi.org/10
.1016/j.neuroimage.2012.11.008, PubMed: 23194820
Du, Y., Fu, Z., Sui, J., Gao, S., Xing, Y., Lin, D., … Alzheimer’s Dis-
ease Neuroimaging Initiative. (2020). NeuroMark: An automated
and adaptive ICA based pipeline to identify reproducible fMRI
markers of brain disorders. NeuroImage: Clinical, 28, 102375.
https://doi.org/10.1016/j.nicl.2020.102375, PubMed: 32961402
Du, Y., Pearlson, G. D., Yu, Q., He, H., Lin, D., Sui, J. A., &
Calhoun, V. D. (2016). Interaction among subsystems within
default mode network diminished in schizophrenia patients: A
dynamic connectivity approach. Schizophrenia Research, 170(1),
55–65. https://doi.org/10.1016/j.schres.2015.11.021, PubMed:
26654933
Evangelisti, S., Testa, C., Ferri, L., Gramegna, L. L., Manners, D. N.,
Rizzo, G., … Lodi, R. (2018). Brain functional connectivity in
sleep-related hypermotor epilepsy. NeuroImage: Clinical, 17,
873–881. https://doi.org/10.1016/j.nicl.2017.12.002, PubMed:
29527492
Falakshahi, H., Rokham, H., Fu, Z., Mathalon, D. H., Ford, J. M.,
Voyvodic, J., … Calhoun, V. D. (2020). Time-varying graphs: A
method to identify abnormal integration and disconnection in
functional brain connectivity with application to schizophrenia.
Network Neuroscience
662
A method to estimate altered pathways in time-varying brain networks
2020 IEEE 20th International Conference on Bioinformatics and
Bioengineering (BIBE). https://doi.org/10.1109/BIBE50027.2020
.00074
Falakshahi, H., Vergara, V. M., Liu, J., Mathalon, D. H., Ford, J. M.,
Voyvodic, J., … Calhoun, V. D. (2020). Meta-modal information
flow: A method for capturing multimodal modular disconnectivity
in schizophrenia. IEEE Transactions on Biomedical Engineering.
https://doi.org/10.1109/TBME.2020.2964724, PubMed: 31944934
Farahani, F. V., Karwowski, W., & Lighthall, N. R. (2019). Applica-
tion of graph theory for identifying connectivity patterns in
human brain networks: A systematic review. Frontiers in Neuro-
science, 13, 585. https://doi.org/10.3389/fnins.2019.00585,
PubMed: 31249501
Fiorenzato, E., Strafella, A. P., Kim, J., Schifano, R., Weis, L.,
Antonini, A., & Biundo, R. (2019). Dynamic functional connec-
tivity changes associated with dementia in Parkinson’s disease.
Brain, 142(9), 2360–2872. https://doi.org/10.1093/ brain
/awz192, PubMed: 31280293
Fornito, A. (2016). Graph theoretic analysis of human brain networks.
In FMRI techniques and protocols (pp. 283–314). New York, NY:
Springer. https://doi.org/10.1007/978-1-4939-5611-1_10
Fornito, A., Harrison, B. J., Goodby, E., Dean, A., Ooi, C., Nathan,
P. J., … Bullmore, E. T. (2013). Functional dysconnectivity of
corticostriatal circuitry as a risk phenotype for psychosis. JAMA
Psychiatry, 70(11), 1143–1151. https://doi.org/10.1001
/jamapsychiatry.2013.1976, PubMed: 24005188
Fornito, A., Zalesky, A., & Bullmore, E. (2016). Fundamentals of
brain network analysis. Boston, MA: Academic Press.
Fornito, A., Zalesky, A., Pantelis, C., & Bullmore, E. T. (2012).
Schizophrenia, neuroimaging and connectomics. NeuroImage,
62(4), 2296–2314. https://doi.org/10.1016/j.neuroimage.2011
.12.090, PubMed: 22387165
Fox, M. D. (2007). Spontaneous fluctuations in brain activity
observed with functional magnetic resonance imaging. Nature
Reviews Neuroscience, 8(9), 700–711. https://doi.org/10.1038
/nrn2201, PubMed: 17704812
Friston, K. J. (1998). The disconnection hypothesis. Schizophrenia
Research. https://doi.org/10.1016/S0920-9964(97)00140-0,
PubMed: 9549774
Fu, Z., Iraji, A., Turner, J. A., Sui, J., Miller, R., Pearlson, G. D., &
Calhoun, V. D. (2021). Dynamic state with covarying brain
activity-connectivity: On the pathophysiology of schizophrenia.
NeuroImage, 224, 117385. https://doi.org/10.1016/j.neuroimage
.2020.117385, PubMed: 32950691
Fu, Z., Sui, J., Turner, J. A., Du, Y., Assaf, M., Pearlson, G. D., &
Calhoun, V. D. (2021). Dynamic functional network reconfigura-
tion underlying the pathophysiology of schizophrenia and autism
spectrum disorder. Human Brain Mapping, 42(1), 80–94. https://
doi.org/10.1002/hbm.25205, PubMed: 32965740
Fu, Z., Tu, Y., Di, X., Du, Y., Pearlson, G. D., Turner, J. A., …
Calhoun, V. D. (2018). Characterizing dynamic amplitude of
low-frequency fluctuation and its relationship with dynamic
functional connectivity: An application to schizophrenia. Neuro-
Image, 180, 619–631. https://doi.org/10.1016/j.neuroimage
.2017.09.035, PubMed: 28939432
Guo, J., Levina, E., Michailidis, G., & Zhu, J. (2011). Joint estimation
of multiple graphical models. Biometrika, 98(1), 1–15. https://doi
.org/10.1093/biomet/asq060, PubMed: 23049124
Hagberg, A., Swart, P., & Chult, D. S. (2008). Exploring network
structure, dynamics, and function using NetworkX. Proceedings
of the 7th Python in Science Conference (SciPy2008), Pasadena,
CA, USA.
He, H., Cao, S., Zhang, J., Shen, H., Wang, Y.-P., & Deng, H.
(2019). A statistical test for differential network analysis based
on inference of Gaussian graphical model. Scientific Reports,
9(1), 1–8. https://doi.org/10.1038/s41598-019-47362-7,
PubMed: 31350445
Hillman, E. M. (2014). Coupling mechanism and significance of the
BOLD signal: A status report. Annual Review of Neuroscience,
37, 161–181. https://doi.org/10.1146/annurev-neuro-071013
-014111, PubMed: 25032494
Hunt, M. J., Kopell, N. J., Traub, R. D., & Whittington, M. A. (2017).
Aberrant network activity in schizophrenia. Trends in Neurosci-
ences, 40(6), 371–382. https://doi.org/10.1016/j.tins.2017.04
.003, PubMed: 28515010
Iraji, A., Faghiri, A., Lewis, N., Fu, Z., Rachakonda, S., & Calhoun,
V. D. (2020). Tools of the trade: Estimating time-varying connec-
tivity patterns from fMRI data. Social Cognitive and Affective
Neuroscience, 16(8), 849–874. https://doi.org/10.1093/scan
/nsaa114, PubMed: 32785604
Iraji, A., Fu, Z., Damaraju, E., DeRamus, T. P., Lewis, N., Bustillo,
J. R., … Calhoun, V. D. (2019). Spatial dynamics within and
between brain functional domains: A hierarchical approach to
study time-varying brain function. Human Brain Mapping, 40(6),
1969–1986. https://doi.org/10.1002/ hbm.24505, PubMed:
30588687
Jones, B., & West, M. (2005). Covariance decomposition in undi-
rected Gaussian graphical models. Biometrika, 92(4), 779–786.
https://doi.org/10.1093/biomet/92.4.779
Karwowski, W., Vasheghani Farahani, F., & Lighthall, N. (2019).
Application of graph theory for identifying connectivity patterns
in human brain networks: A systematic review. Frontiers in Neu-
roscience, 13, 585. https://doi.org/10.3389/fnins.2019.00585,
PubMed: 31249501
Keator, D. B., van Erp, T. G. M., Turner, J. A., Glover, G. H., Mueller,
B. A., Liu, T. T., … FBIRN. (2016). The function biomedical infor-
matics research network data repository. NeuroImage, 124,
1074–1079. https://doi.org/10.1016/j.neuroimage.2015.09.003,
PubMed: 26364863
Keown, C. L., Datko, M. C., Chen, C. P., Maximo, J. O., Jahedi, A.,
& Muller, R.-A. (2017). Network organization is globally atypical
in autism: A graph theory study of intrinsic functional connec-
tivity. Biological Psychiatry: Cognitive Neuroscience and Neuro-
imaging, 2(1), 66–75. https://doi.org/10.1016/j.bpsc.2016.07
.008, PubMed: 28944305
Liao, X., Vasilakos, A. V., & He, Y. (2017). Small-world human brain
networks: Perspectives and challenges. Neuroscience & Biobe-
havioral Reviews, 77, 286–300. https://doi.org/10.1016/j
.neubiorev.2017.03.018, PubMed: 28389343
Liu, Y., Liang, M., Zhou, Y., He, Y., Hao, Y., Song, M., … Jiang, T.
(2008). Disrupted small-world networks in schizophrenia. Brain,
131(4), 945–961. https://doi.org/10.1093/ brain/awn018,
PubMed: 18299296
Mars, R. B., Neubert, F.-X., Noonan, M. P., Sallet, J., Toni, I., &
Rushworth, M. F. (2012). On the relationship between the
“default mode network” and the “social brain.” Frontiers in
Network Neuroscience
663
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A method to estimate altered pathways in time-varying brain networks
Human Neuroscience, 6, 189. https://doi.org/10.3389/fnhum
.2012.00189, PubMed: 22737119
McTeague, L. M., Huemer, J., Carreon, D. M., Jiang, Y., Eickhoff,
S. B., & Etkin, A. (2017). Identification of common neural cir-
cuit disruptions in cognitive control across psychiatric disor-
ders. American Journal of Psychiatry, 174(7), 676–685.
https://doi.org/10.1176/appi.ajp.2017.16040400, PubMed:
28320224
Miller, E. K. (2000). The prefontral cortex and cognitive control.
Nature Reviews Neuroscience, 1(1), 59–65. https://doi.org/10
.1038/35036228, PubMed: 11252769
Ö ngür, D., Lundy, M., Greenhouse, I., Shinn, A. K., Menon, V.,
Cohen, B. M., & Renshaw, P. F. (2010). Default mode network
abnormalities in bipolar disorder and schizophrenia. Psychiatry
Research: Neuroimaging, 183(1), 59–68. https://doi.org/10.1016
/j.pscychresns.2010.04.008, PubMed: 20553873
Pankow, A., Deserno, L., Walter, M., Fydrich, T., Bermpohl, F.,
Schlagenhauf, F., & Heinz, A. (2015). Reduced default mode net-
work connectivity in schizophrenia patients. Schizophrenia
Research, 165(1), 90–93. https://doi.org/10.1016/j.schres.2015
.03.027, PubMed: 25892719
Pearlson, G. D. (1997). Superior temporal gyrus and planum
temporale in schizophrenia: A selective review. Progress in
Neuro-Psychopharmacology and Biological Psychiatry, 21(8),
1203–1229. https://doi.org/10.1016/S0278-5846(97)00159-0,
PubMed: 9460087
Raichle, M. E., MacLeod, A. M., Snyder, A. Z., Powers, W. J., Gusnard,
D. A., & Shulman, G. L. (2001). A default mode of brain function.
Proceedings of the National Academy of Sciences, 98(2), 676–682.
https://doi.org/10.1073/pnas.98.2.676, PubMed: 11209064
Ray, K. L., Gold, J. M., Silverstein, S. M., Barch, D. M., & Carter,
C. S. (2017). Functional network changes and cognitive control
in schizophrenia. NeuroImage: Clinical, 15, 161–170. https://doi
.org/10.1016/j.nicl.2017.05.001, PubMed: 28529872
Rokham, H., Pearlson, G., Abrol, A., Falakshahi, H., Plis, S., &
Calhoun, V. D. (2020). Addressing inaccurate nosology in mental
health: A multilabel data cleansing approach for detecting label
noise from structural magnetic resonance imaging data in mood
and psychosis disorders. Biological Psychiatry: Cognitive Neuro-
science and Neuroimaging, 5(8), 819–832. https://doi.org/10
.1016/j.bpsc.2020.05.008, PubMed: 32771180
Rudie, J. D., Brown, J., Beck-Pancer, D., Hernandez, L., Dennis, E.,
Thompson, P., … Dapretto, M. (2013). Altered functional and
structural brain network organization in autism. NeuroImage:
Clinical, 2, 79–94. https://doi.org/10.1016/j.nicl.2012.11.006,
PubMed: 24179761
Sakoğlu, Ü., Pearlson, G. D., Kiehl, K. A., Wang, Y. M., Michael,
A. M., & Calhoun, V. D. (2010). A method for evaluating
dynamic functional network connectivity and task-modulation:
Application to schizophrenia. Magnetic Resonance Materials in
Physics, Biology and Medicine, 23, 351–366. https://doi.org/10
.1007/s10334-010-0197-8, PubMed: 20162320
Shan, L., & Kim, I. (2018). Joint estimation of multiple Gaussian
graphical models across unbalanced classes. Computational
Statistics & Data Analysis, 121, 89–103. https://doi.org/10.1016
/j.csda.2017.11.009
Skaatun, K. C., Kaufmann, T., Doan, N. T., Alnaes, D., Cordova-
Palomera, A., Jonsson, E. G., … Westlye, L. T. (2017). Consistent
functional connectivity alterations in schizophrenia spectrum
disorder: A multisite study. Schizophrenia Bulletin, 43(4), 914–924.
https://doi.org/10.1093/schbul/sbw145, PubMed: 27872268
Skudlarski, P., Jagannathan, K., Anderson, K., Stevens, M. C.,
Calhoun, V. D., Skudlarska, B. A., & Pearlson, G. (2010). Brain
connectivity is not only lower but different in schizophrenia: A
combined anatomical and functional approach. Biological Psy-
chiatry, 68(1), 61–69. https://doi.org/10.1016/j.biopsych.2010
.03.035, PubMed: 20497901
Tu, Y., Fu, Z., Zeng, F., Maleki, N., Lan, L., Li, Z., … Kong, J. (2019).
Abnormal thalamocortical network dynamics in migraine. Neu-
rology, 92(23), e2706–e2716. https://doi.org/10.1212/ WNL
.0000000000007607, PubMed: 31076535
van den Heuvel, M. P., & Fornito, A. (2014). Brain networks in
schizophrenia. Neuropsychology Review, 24(1), 32–48. https://
doi.org/10.1007/s11065-014-9248-7, PubMed: 24500505
van den Heuvel, M. P., de Lange, S. C., Zalesky, A., Seguin, C.,
Yeo, B. T., & Schmidt, R. (2017). Proportional thresholding in
resting-state fMRI functional connectivity networks and conse-
quences for patient-control connectome studies: Issues and rec-
ommendations. NeuroImage, 152, 437–449. https://doi.org/10
.1016/j.neuroimage.2017.02.005, PubMed: 28167349
van den Heuvel, M. P., Mandl, R. C., Stam, C. J., Kahn, R. S., & Pol,
H. E. (2010). Aberrant frontal and temporal complex network
structure in schizophrenia: A graph theoretical analysis. Journal
of Neuroscience, 30(47), 15915–15926. https://doi.org/10.1523
/JNEUROSCI.2874-10.2010, PubMed: 21106830
Woodward, N. D., Karbasforoushan, H., & Heckers, S. (2012).
Thalamocortical dysconnectivity in schizophrenia. American
Journal of Psychiatry, 169(10), 1092–1099. https://doi.org/10
.1176/appi.ajp.2012.12010056, PubMed: 23032387
Yu, Q., Du, Y., Chen, J., He, H., Sui, J., Pearlson, G., & Calhoun,
V. D. (2017). Comparing brain graphs in which nodes are regions
of interest or independent components: A simulation study. Jour-
nal of Neuroscience Methods, 291, 61–68. https://doi.org/10
.1016/j.jneumeth.2017.08.007, PubMed: 28807861
Yu, Q., Du, Y., Chen, J., Sui, J., Adale, T., Pearlson, G. D., & Calhoun,
V. D. (2018). Application of graph theory to assess static and
dynamic brain connectivity: Approaches for building brain
graphs. Proceedings of the IEEE, 106(5), 886–906. https://doi.org
/10.1109/JPROC.2018.2825200, PubMed: 30364630
Yu, Q., Erhardt, E. B., Sui, J., Du, Y., He, H., Hjelm, D., … Calhoun,
V. D. (2015). Assessing dynamic brain graphs of time-varying
connectivity in fMRI data: Application to healthy controls and
patients with schizophrenia. NeuroImage, 107, 345–355. https://
doi.org/10.1016/j.neuroimage.2014.12.020, PubMed: 25514514
Network Neuroscience
664
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
6
3
4
2
0
3
6
0
4
6
n
e
n
_
a
_
0
0
2
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3