MÉTHODES - Recherche en IA spécialisée au MIT

MÉTHODES

Neuronal classification from network connectivity
via adjacency spectral embedding

Ketan Mehta1*
Joshua T. Vogelstein4

, Rebecca F. Goldin2*

, David Marchette3,
, Carey E. Priebe4, and Giorgio A. Ascoli1

1Department of Bioengineering and Center for Neural Informatics, Structures, and Plasticity,
George Mason University, Fairfax, VA, Etats-Unis
2Department of Mathematical Sciences and Center for Neural Informatics, Structures, and Plasticity,
George Mason University, Fairfax, VA, Etats-Unis
3Naval Surface Warfare Center, Dahlgren, VA, Etats-Unis
4Department of Applied Mathematics and Statistics, Université Johns Hopkins, Baltimore, MARYLAND, Etats-Unis
*These authors contributed equally to this work.

un accès ouvert

journal

Mots clés: Directed graphs, Expectation maximization, Neural circuits, Stochastic block models,
Cell-type classification, Spectral embedding

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
3
6
8
9
1
9
6
0
5
2
5
n
e
n
_
un
_
0
0
1
9
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

ABSTRAIT

This work presents a novel strategy for classifying neurons, represented by nodes of a directed
graph, based on their circuitry (edge connectivity). We assume a stochastic block model (SBM)
in which neurons belong together if they connect to neurons of other groups according to the
same probability distributions. Following adjacency spectral embedding of the SBM graph,
we derive the number of classes and assign each neuron to a class with a Gaussian mixture
model-based expectation maximization (EM) clustering algorithm. To improve accuracy, nous
introduce a simple variation using random hierarchical agglomerative clustering to initialize
the EM algorithm and picking the best solution over multiple EM restarts. We test this procedure
on a large (≈212–215 neurons), sparse, biologically inspired connectome with eight neuron
classes. The simulation results demonstrate that the proposed approach is broadly stable to the
choice of embedding dimension, and scales extremely well as the number of neurons in the
network increases. Clustering accuracy is robust to variations in model parameters and highly
tolerant to simulated experimental noise, achieving perfect classifications with up to 40% de
swapped edges. Ainsi, this approach may be useful to analyze and interpret large-scale brain
connectomics data in terms of underlying cellular components.

INTRODUCTION

A functionally relevant, quantitative description of cellular diversity in the brain remains a
pressing open problem in neuroscience. Traditionnellement, investigators have classified neurons
by subsets of multifarious properties, including physiology, biochemistry, and morphology
(par exemple., a fast-spiking, parvalbumin-expressing, aspiny interneuron). In spite of the widespread
and foundational use of the notion of cell class, there is no formal definition of this concept,
and how exactly a cell class relates to network connectivity remains a matter of considerable
debate in the community (DeFelipe et al., 2013; Petilla Interneuron Nomenclature Group
et coll., 2008). En particulier, given a “solved” connectome (a complete list of all neurons and

Citation: Mehta, K., Goldin, R.. F.,
Marchette, D., Vogelstein, J.. T., Priebe,
C. E., & Ascoli, G. UN. (2021). Neuronal
classification from network
connectivity via adjacency spectral
embedding. Neurosciences en réseau,
5(3), 689–710. https://est ce que je.org/10.1162
/netn_a_00195

EST CE QUE JE:
https://doi.org/10.1162/netn_a_00195

Informations complémentaires:
https://doi.org/10.1162/netn_a_00195

Reçu: 17 Décembre 2020
Accepté: 2 Avril 2021

Auteur correspondant:
Giorgio A. Ascoli
ascoli@gmu.edu

Éditeur de manipulation:
Olaf Sporns

droits d'auteur: © 2021
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence

La presse du MIT

Neuronal classification from network connectivity

their connections), is it possible to objectively find the number of neuronal connectivity classes,
and to assign each neuron to a class? This would also answer the related open question of how
many cell classes there are from the connectomics perspective (Hamilton, Shepherd, Martone,
& Ascoli, 2012).

In this work we introduce a novel strategy for classifying neurons based on their circuitry. Dans
particular, after formalizing the concept of cell class based on network connectivity, we present
a technique to derive the number of cell classes from a neuronal connectome, and to assign
each neuron to a class. Using neurobiologically realistic surrogate data, we demonstrate that
this technique is robust and efficient.

We begin by asking a mathematical question derived from the neuroscientific one. Recall that
a directed graph (V, E ) consists of vertices V (a finite set), and directed edges E, a subset of ordered
pairs of V × V. We assume the directed graph is simple, c'est, there is at most one edge between
any two distinct vertices, and no edge from a vertex to itself, though we allow the possibility of
edges in either direction. For the purpose of our analysis, each connectome may be represented
by such a directed graph, wherein the vertex represents a neuron and the edge represents a
directed synaptic (usually axon-dendrite) connection. Plus loin, we adopt a generative model
approach by using a stochastic block model (SBM) to add additional structure to the directed
graph. In this model vertices are partitioned into nonoverlapping groups called blocks, tel
that the probability of an edge between two vertices depends only on their respective block
memberships. Vertices in the same block are thus stochastically equivalent. Given a directed
SBM graph, our goal is then to estimate the number of blocks and assign each vertex to its
respective block.

Recently, SBMs have been successfully used to model connectomes (Moyer et al., 2015;
Pavlovic, Vértes, Bullmore, Schafer, & Nichols, 2014), as well as to identify network community
structures within connectomes (Betzel, Medaglia, & Bassett, 2018; Faskowitz, Yan, Zuo, &
Sporns, 2018). Our approach here, cependant, is different from these studies in two important
aspects. D'abord, we use surrogate connectomic data loosely inspired by the entorhinal-CA1 circuit
of the rodent hippocampal formation. The scale and structure of the neuronal network analyzed
in this work is therefore vastly different, with substantially larger graphs (≈212–215 vertices) et
sparse (≈4%) connectivité. Deuxième, and more fundamentally, our focus is on developing a robust
mathematical framework using spectral graph clustering to capture the latent block structure of
the directed graph. We are motivated by recent results (Priebe et al., 2017, 2019; Sussman, Tang,
Fishkind, & Priebe, 2012) that demonstrate the use of adjacency spectral embedding (ASE) dans
conjunction with Gaussian mixture model (GMM)-based clustering to estimate block member-
ship. Here we adopt and modify the GMM(cid:1)ASE framework, and present a strategy to cluster
grand, sparse graphs modeled from surrogate connectomic data.

Given a graph, we begin by embedding it into a much lower dimensional space by computing
the singular value decomposition of a slightly modified version of the adjacency matrix. Since we
consider directed graphs, we embed a concatenation of the left and right singular vectors, lequel
correspond to the outgoing (presynaptic) and incoming (postsynaptic) relations, respectivement.
Following the embedding, the latent vectors are modeled as a GMM and clustered using the ex-
pectation maximization (EM) algorithme. Cependant, the convergence of the EM algorithm is highly
sensitive to the starting values chosen to initialize the algorithm, especially for the multivariate
GMM case (Biernacki, Celeux, & Govaert, 2003; Kwedlo, 2015; Shireman, Steinley, & Brusco,
2017), and often gets trapped in a local optimum. Donc, we propose using a multiple restart
approach wherein we apply hierarchical agglomerative clustering to randomly initialize and start
the EM algorithm multiple times, and subsequently pick the model with the largest value of
Bayesian information criterion (BIC) over multiple restarts.

690

Surrogate data:
Synthetic data generated using a
mathematical model.

Graph:
A formalization of a network in
which the nodes and their
interactions are represented as
vertices and edges, respectivement.

Stochastic:
The property of being described by
a random probability distribution.

Spectral embedding:
Mapping of a high-dimensional
matrix into a relatively low-
dimensional space by making use
of its spectrum (singular values).

Latent vector:
A vector of “hidden” variables (souvent
in a lower dimensional space) que
capture the underlying properties of
the data.

Expectation maximization algorithm:
An iterative probability density
estimation technique to find the
best fit of the assumed statistical
model to the observed data.

Bayesian information criterion:
A criterion for model selection that
measures the trade-off between
model fit and complexity of model.

Neurosciences en réseau

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
3
6
8
9
1
9
6
0
5
2
5
n
e
n
_
un
_
0
0
1
9
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal classification from network connectivity

We perform a series of experimental simulations with surrogate data to validate the effective-
ness of the proposed multiple random restart EM. The simulation results demonstrate the pro-
posed clustering strategy to be extremely effective in successfully recovering the true number of
classes and individual class assignment of the vertices. The random multiple restart approach
also heavily outperforms GMM-based hierarchical partition initialization (Scrucca & Raftery,
2015), while having the advantage of being broadly stable over a wide selection of embedding
dimensions, as choosing an optimal value for dimensional embedding remains an open problem
with spectral graph clustering in general. The proposed approach is also robust to variations in
model parameters and scales extremely well as the number of neurons in the network increases.
De plus, our analysis shows this method to be highly tolerant to noise in the form of edge
swaps akin to experimental errors in pre- or postsynaptic neuron identification.

MODELING THE CONNECTOME

Stochastic Block Models

Consider a directed graph (V, E ) that consists of vertices V (a finite set), and directed edges E, un
subset of ordered pairs of V × V. We write (v, w) 2 E for v, w 2 V if there is a directed edge from
v to w. Plus loin, we assume the graph to be simple, c'est, (v, w) 2 E implies v 6¼ w. As E is a set
of ordered pairs, there is at most one directed edge from any vertex v to a distinct vertex w.
We allow the possibility of edges (v, w) et (w, v). We formally define a partitioned directed
graph as follows:

For a vertex set V, a block assignment τ is an assignment of a group membership, denoted

by an integer 1, 2, …, k, to each vertex in V. Explicitly, for a fixed positive integer k ≤ |V|,
τ : V ! 1; 2; …; k
F

où |V| is the size of the vertex set. A block assignment associates a class to each vertex v,
indicated by the value τ(v). En particulier, two vertices are in the same class if and only if they
have identical values under τ. We formally define a partitioned directed graph as follows:

Definition 1. A partitioned directed graph is a triple (V, E, τ), où (V, E ) is a simple directed
graph and τ : V ! {1, …, k} is a block assignment that partitions the vertices into k ≤ |V| disjoint
(sans chevauchement) subsets

Vj :¼ v 2 V : τ vð Þ ¼ j

for j ¼ 1; …; k:

The set Vj consists of vertices in class j.

Our functional assumption here is that the structural connectome can be represented as a
graph with unweighted (binary) edges, c'est, a synaptic connection is either present or absent.
Plus loin, we assume that the probability of a pre- to postsynaptic connection from neuron v to
neuron w depends solely on the classes τ(v) and τ(w). This is well modeled by a stochastic block
model (Holland, Laskey, & Leinhardt, 1983; Holland & Leinhardt, 1981), in which stochastically
equivalent vertices are partitioned together into classes. En particulier, a SBM assumes that
edges between vertices from the ith class to those in the jth class can be modeled as indepen-
dent Bernoulli trials with parameter pij. Let P = ( pij) be a matrix collecting these parameters.
We then formally define the generative model of the standard directed SBM as follows.

Definition 2. A directed stochastic block model is a generative model for directed graphs. Let
n be the number of nodes (vertices), k the number of groups (classes), P = ( pij) 2 [0, 1]k×k the
block connectivity probability matrix (edge probabilities), and τ : V ! {1, …, k} the assignment

Bernoulli trials:
Independent random experiments,
each with exactly two possible
outcomes occurring with
probabilities p and 1 − p,
respectivement.

Neurosciences en réseau

691

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
3
6
8
9
1
9
6
0
5
2
5
n
e
n
_
un
_
0
0
1
9
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal classification from network connectivity

of each node to a group. A directed SBM graph is a partitioned directed graph G = (V, E, τ)
whose edges are independent Bernoulli draws with probability P{(v, w) 2 E} = pτ(v),τ(w).

Let ρj := |Vj|/n be the proportion of vertices in the jth group. The k-tuple ρ := (r

1, …, ρk)
indicates the proportional sizes of these classes. Note that {V1, …, Vk} and ρ depend only on τ.

In a general SBM (Abbe, 2017) (often referred to simply as a SBM, such as in Sussman et al.,
2012) the vertex assignment, and thus the class size |Vj| of the generated graph, is subject to a
random process. Cependant, in our generative model the assignment is instead specified by the
block assignment function τ. While in theory the number of classes is bounded above by the
size of the vertex set, most practical implementations of SBM inference (Abbe, 2017; Funke &
Becker, 2019; McDaid, Murphy, Friel, & Hurley, 2013) constrain k << |V|. This constraint allows for successful prediction of the block assignments using the limited vertex set size, as well as, in our case, a meaningful resulting neuronal classification. Connectome Generation The experimental design begins with using a directed SBM to generate stochastic realizations (simulations) of the biological connectome. The surrogate model used is loosely inspired by the entorhinal-CA1 circuit of the rodent hippocampal formation based on Hippocampome.org data (Wheeler et al., 2015). Specifically, we consider a directed neuronal network consisting of n cells, where n varies, and k = 8 distinct cell types. Each cell type is briefly described in Table 1. The model is parametrized by the connectivity probability matrix 1 0 B B B B B B B B B B @ P ¼ :02 :02 :02 :02 :02 :00 :04 :00 :02 :006666667 :00 :006666667 :00 :006666667 :00 :006666667 :02 :006666667 :00 :00 :00 :00 :01333333 :00 :00 :02 :04 :04 :02 :02 :00 :00 :00 :00 :00 :00 :00 :00 :00 :02 :00 :00 :00 :00 :00 :02 :00 :00 :00 :00 :00 :04 :04 :02 :04 :00 :02 :02 :01 :00 :00 :02 :02 :01 C C C C C C ; C C C C A (1) and a block membership vector ρ that denotes the proportions of the cells (vertices) assigned each cell type (class), ρ ¼ 0:48120; 0:12207; 0:03052; 0:09155; 0:06104; 0:07629; 0:07629; 0:06104 ð Þ: (2) We chose the specific values of P as rounding approximations of recently published exper- imental data derived from the measured lengths of spatially overlapping presynaptic axons and postsynaptic dendrites from the indicated neuron types in the appropriate anatomical volumes (Tecuatl, Wheeler, Sutton, & Ascoli, 2020). Furthermore, we selected the proportions of neu- rons in each type defined in the individual components of ρ based on estimates obtained by numerical optimization of evidence sourced from Hippocampome.org using a recently intro- duced operations research approach (Attili, Mackesey, & Ascoli, 2020). The assignment τ of cells to cell types simply maps the first nρ 2 cells to the second type, and so on. 1 cells to the first type, then next nρ Partitioned directed graphs are generated using SBM, with the vertices proportioned into blocks according to ρ (2), and edges drawn as per the block probabilities specified in P (1). We label the vertices of V by v1, …, vn. Each directed graph is uniquely associated with an adjacency matrix A, an n × n binary matrix with the ℓmth entry given by 1 if (vℓ, vm) 2 E and 0 otherwise. Network Neuroscience 692 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 8 9 1 9 6 0 5 2 5 n e n _ a _ 0 0 1 9 5 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuronal classification from network connectivity Table 1. The eight cell classes CA1 Pyramidal Principal output neurons of the hippocampus. One of the most studied and best characterized excitory neurons of the mammalian brain. CA1 Oriens/Lacunosum-Moleculare Local inhibitory neurons. Dendrites are in the oriens layer and axons start in the oriens and go up to lacunosum-moleculare. CA1 Basket Local peri-somatic inhibitory interneurons. Axons target pyramidal and basket cells. Dendrites span all layers of CA1. CA1 Perforant Pathway-Associated Local inhibitory interneurons with axons and dendrites confined to the lacunosum-moleculare layer. CA1 Oriens Local inhibitory interneurons with dendrites and axons confined to the oriens layer. Entorhinal Cortex Layer 5 Pyramidal Deep layer excitatory neurons with dendrites and axons extending through the deep and superficial layers of the entorhinal cortex. Entorhinal Cortex Layer 3 Pyramidal Superficial layer excitatory neurons. Dendrites span through the deep and superficial layers of the entorhinal cortex; axons start in layer 3 and project to CA1 lacunosum-moleculare. Entorhinal Cortex GABAergic Cells Inhibitory local interneurons with axons and dendrites through the deep and superficial layers of the entorhinal cortex. ADJACENCY SPECTRAL EMBEDDING Given an n × n adjacency matrix A generated by a directed SBM, the goal is to predict the number of classes and recover the class assignment for each individual vertex of the graph, with no prior knowledge of k, P, or ρ. The first step is to embed the adjacency matrix into a lower dimensional Euclidean space via singular value decomposition. Singular Value Decomposition Any real valued matrix A may be decomposed into a product A = UDV t, where D is a diagonal matrix with nonnegative real entries, and U and V are real valued orthogonal matrices, called a singular value decomposition. We may choose D so that its entries, called the singular values, are nonnegative and weakly decreasing, in which case D is uniquely determined by A. The columns of U and V are called singular vectors. In contrast, U and V are not unique; if the entires of D are distinct and nonzero, then U and V are determined up to a simultaneous factor of ±1 in each column of U and V. If there are repeating nonzero entries of D, the corresponding singular vectors span a subspace of dimen- sion given by the number of copies of the repeated singular value. Any set of orthonormal vectors spanning this subspace can be used as the singular vectors in U, with a resulting choice in V. If any singular values vanish, the corresponding singular vectors in U and V may be chosen independently. For any d ≤ rank(A), one can approximate A by a rank d decomposition A (cid:3) UdDdV t d ; in which Ud and Vd are n × d matrices, and Dd is a d × d diagonal matrix with nonnegative entries. Let X := Ud , so that A (cid:3) XY t. and Y := Vd ﬃﬃﬃﬃﬃﬃﬃ Dd ﬃﬃﬃﬃﬃﬃﬃ Dd p p Network Neuroscience 693 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 8 9 1 9 6 0 5 2 5 n e n _ a _ 0 0 1 9 5 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuronal classification from network connectivity Embedding in a Lower Dimension We use a singular value decomposition of a slight perturbation of the adjacency matrix to capture the most salient data in a low-dimensional space. Since we only consider simple graphs with no self edges, all diagonal entries of the adjacency matrix are zero. It has been shown (Marchette, Priebe, & Coppersmith, 2011; Scheinerman & Tucker, 2010) for undirected graphs that artificially augmenting the diagonal with imputed values may improve the embed- ding in certain cases, in turn leading to fewer misassignments. While similar results have not been proven for the case of directed graphs, we nevertheless modify the adjacency matrix by replacing the diagonal entries via Aii = deg+(vi)/(n − 1), where deg+(vi) is the outgoing degree of the ith vertex, vi 2 V. The outgoing degree of the ith vertex is the number of outgoing edges incident to the vertex, and is calculated by simply summing up all entries of the ith row of A. However, since in general for large, sparse graphs deg+(vi) << n, this change in diagonal value has only a small impact on the matrix decomposition. For each directed graph (V, E ) and choice of embedding dimension d, the vectors forming the columns in the augmented matrix X := [X|Y]t provide a dot product embedding of A in a 2d-dimensional space. The columns of the concatenated matrix X are called latent vectors. The optimal choice of d is a known open problem in literature, with no consensus on a best strategy. The necessity of selecting an optimum d is based on the fact that only a subset of the singular values of the high-dimensional data are informative and relevant to the subsequent statistical inference. Choosing a low d can result in discarding important information, while choosing a higher d than required not only increases computational cost but can adversely effect clustering performance due to the presence of extraneous variables that contribute to- wards noise in the data. For SBM graphs with large n, it has been shown (Fishkind, Sussman, Tang, Vogelstein, & Priebe, 2013) that the optimal choice of d is the rank of the block con- nectivity matrix P, however in our context we assume no prior knowledge of P. A general methodology to choose the optimum value for d is then to examine the scree plot, the plot of the singular values in weakly decreasing order, and look for an “elbow point” that deter- mines the cutoff between relevant and nonrelevant dimensions based on the magnitude of the singular value. The scree plot for a SBM graph generated using the parameters of our surrogate model (1), (2) is shown in Figure 1. Estimating the elbow point using the unit-invariant knee method (Christopoulos, 2016) yields an optimum value of d = 4. This choice of d = 4 is also consistent if we instead use an alternative method (Satopaa, Albrecht, Irwin, & Raghavan, 2011) of estimating the distance from each point in the scree plot to a line joining the first and last points of the plot, and then selecting the elbow point where this distance is the largest. Figure 1. Model selection: d = 4 based on the elbow point of the scree plot of singular values (n = 16,384). The top d singular values and their associated left- and right-singular vectors are concatenated to embed the graph in R2d. Network Neuroscience 694 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 8 9 1 9 6 0 5 2 5 n e n _ a _ 0 0 1 9 5 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuronal classification from network connectivity We apply singular value decomposition directly to A before clustering, rather than to its Laplacian. For the case of a symmetric A (undirected graphs), under certain assumptions (Sussman et al., 2012), clustering of the resulting singular value decomposition converges to a negligible number of misclassified vertices. Such results have also been found in similar work applied to the Laplacian (Rohe, Chatterjee, & Yu, 2011; Vogelstein et al., 2019). However, to the best our knowledge, analogous results for directed graphs have not been explored. GAUSSIAN MIXTURE MODEL-BASED CLUSTERING Let A be an n × n adjacency matrix and A (cid:3) XYt be a singular decomposition with d-singular values. 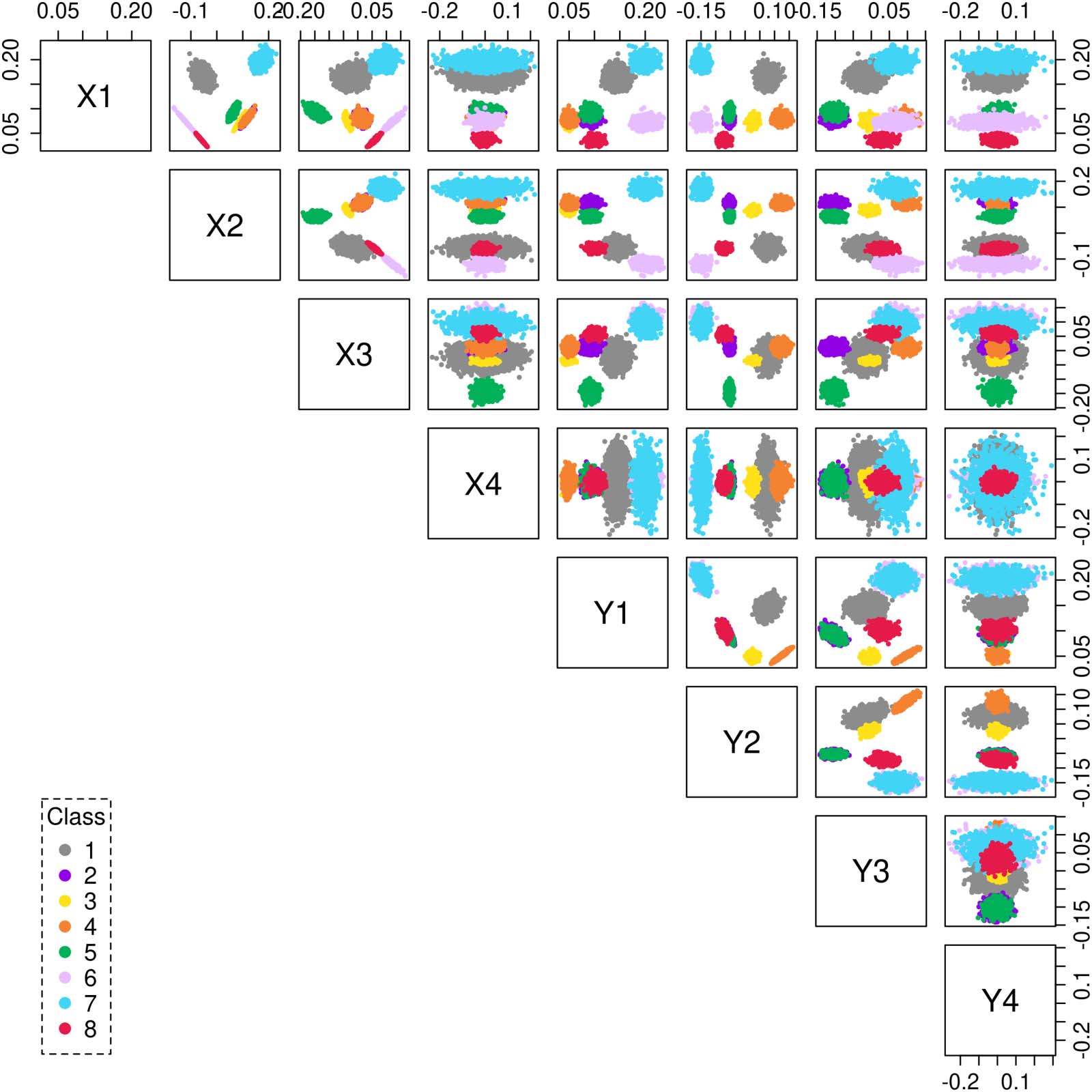We denote by X = ((cid:2)x1, (cid:2)x2, …, (cid:2)xn)t the data (latent vectors) obtained from this decom- position of A, where (cid:2)xi 2 R2d denotes the concatenation of the ith row of X followed by the ith row of Y. Figure 2 shows a scatterplot matrix of the latent vectors distributed in R2d, for the choice of embedding d = 4. The scatterplot depicts the data projected as points onto a two- dimensional subspace, whose coordinates are composed of a pair of the orthogonal singular l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 3 6 8 9 1 9 6 0 5 2 5 n e n _ a _ 0 0 1 9 5 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 2. Scatterplot matrix showing the latent vectors of a SBM graph with k = 8 classes embedded in 2d = 8 dimensions. Each data point (n = 16,384) is color coded as per its original class assignment. Network Neuroscience 695 Neuronal classification from network connectivity vectors. The colors represent the original class assignment associated with each data point. The SBM graph was generated using the surrogate model (1), (2) for k = 8 classes, and n = 16,384. Expectation Maximization (EM) Algorithm We cluster the data by modeling the latent vectors as a multivariate Gaussian mixture model (GMM) in order to predict the number of components, and the SBM block partition function. For sufficiently dense graphs, and large n, the adjacency spectral embedding (ASE) central limit theorem demonstrates that (cid:2)xi behaves approximately as a random sample from a k-component GMM (Athreya et al., 2016). j μ (cid:2)(cid:2) (cid:2)((cid:2)x; Let fj((cid:2)x) = π j), where (cid:2)((cid:2)x; j, Σ j, Σ variate normal distribution with mean vector weight π components is given by j) is the probability density function for the multi- j, and a component j for j = 1, …, κ. The probability density function for the multivariate GMM with κ 2 Z+ j 2 R2d, covariance matrix Σ μ (cid:2)(cid:2) μ (cid:2)(cid:2) Xκ f ð(cid:2)xiÞ ¼ j¼1 fjð(cid:2)xiÞ: The Gaussian mixture model is fitted to the data using the expectation maximization (EM) algo- rithm. We assume the Gaussian distributions may have aspherical covariances to address clus- ters in ellipsoidal shapes. The clusters are centered at the mean vector j, while other geometric features, such as the volume, shape, and orientation, of each cluster are allowed to vary. Assuming the n data points (cid:2)x1, (cid:2)x2, …, (cid:2)xn are independent draws, μ (cid:2)(cid:2) Yn Xk f Xð Þ ¼ i¼1 j¼1 πj(cid:2)ð(cid:2)xi; μj; ΣjÞ: (cid:2) After an initialization of the mixture parameters Θκ = {π 1, μ (cid:2)(cid:2) τij ¼ (cid:3) j ¼ fjðx iÞ f ðx iÞ Xn i¼1 for i ¼ 1; …n; τj ¼ τijx i ; Σj ¼ j, Σ1, …, πκ, (cid:3) μκ, Σκ}, we set (cid:2)(cid:2) (cid:4) fjðx1Þ f ðx1Þ (cid:6) þ (cid:5) fjðx2Þ f ðx2Þ − (cid:3) j − (cid:3) x i j fjðx nÞ f ðx nÞ þ … þ (cid:6) t ; Xn 1 n i¼1 1 n − 1 τij ¼ Xn 1 n (cid:5) τij x i i¼1 where the product ((cid:2)xi − μ j)((cid:2)xi − (cid:2)(cid:2) μ j)t occurring in Σj is the tensor (outer) product. (cid:2)(cid:2) The EM algorithm is used to iteratively improve upon the estimates by maximizing the log- likelihood of the joint probability density function ‘ X; Θκ ð Þ ¼ ln f X; Θκ ð Þ Xn Xk ¼ ln i¼1 j¼1 (cid:5) πj(cid:2) x i (cid:6) : ; (cid:3) ; Σj j (3) (4) We iterate this process until convergence. After the first iteration, (cid:3) ij = 1. This model assumes that (cid:2)xi has an associated probability τij to be in each of the jth group. Indeed from this description we can define the estimated class assignment as follows: Let τ : V ! {1,…,k} be given by τ(vi) = arg maxj τ j = 1, and (cid:3) π ij. τ j j Network Neuroscience 696 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 8 9 1 9 6 0 5 2 5 n e n _ a _ 0 0 1 9 5 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuronal classification from network connectivity Estimating the Number of Clusters The model fitting procedure discussed above relies on a given number of GMM components κ, among which to distribute the n data points. Indeed, assigning each data point to its own clus- ter (κ = n) would uniquely identify connectivity behavior of each vertex, but would not illu- minate common attributes. At the other extreme, κ = 1 provides no distinguishing information among vertices. Let κmin and κmax denote the smallest and largest values of practical interest for κ, respectively. We estimate the number of clusters by selecting the value of κ 2 {κmin, …, κmax} that maximizes the Bayesian information criterion. BIC penalizes the model based on the number of free parameters, (cid:3) (cid:3) (cid:4) (cid:4) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 8 9 1 9 6 0 5 2 5 n e n _ a _ 0 0 1 9 5 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 pκ ¼ κ−1ð Þ þ 2dκ þ 2d 2 þ d κ; (5) which grows linearly with κ and depends quadratically on the number of singular values d. Specifically, let ^Θκ be the maximum likelihood estimate of the parameters given the data (cid:2)x1, (cid:2)x2, …, (cid:2)xn under the assumption that they are modeled by a multivariate Gaussian mixture model with κ components. The estimated number of classes is defined as ^ k ¼ arg max κmin≤κ≤κmax (cid:9) (cid:7) 2‘ X; ^Θκ (cid:8) (cid:10) − pκ ln nð Þ : (6) For each κ, the GMM fit results in a class assignment ^τ of each vector (cid:2)xi to a group labeled {1, …, κ}. EM Initializations Using Multiple Restarts The final parameter estimates of the fitted model are often sensitive to the initial values chosen to start the EM algorithm, especially for the case of finite mixture models (Melnykov & Melnykov, 2012; Shireman et al., 2017). A poor initial choice of the model parameters may cause the EM algorithm to converge to a local but not a global maximum of the likelihood function (Biernacki et al., 2003). A workaround to the problem of EM initialization is the multiple restart approach (Biernacki et al., 2003; Kwedlo, 2015). Specifically, given a set of data points, the EM algorithm is run T times (trials), each trial starting with different initial parameters. Each trial is run across all κ ^ k, ^τ, and a maximum BIC value for the trial. The final values with κmin ≤ κ ≤ κmax, resulting in clustering is selected as the model with the highest BIC across all T trials. Considering the high prevalence of local maxima in the log-likelihood function, optimal solutions resulting from different trials are typically different. The highest BIC observed across a sufficiently large num- ber of trials corresponds to the best estimate of the global maximum among local optima. For each trial, an initial estimate of the model parameters is obtained by applying another preliminary clustering to the data. Towards this extent, we compare two variations of agglom- erative hierarchical clustering. Inherent advantages of agglomerative hierarchical clustering are that it partitions the data simultaneously into any number of desired clusters, and that, for any trial, the initial clusters are similar across values of κ. In the first method, initial param- eters are obtained by partitioning the data using random hierarchical agglomerative clustering (RHAC). In the second approach, initial parameters are obtained by applying model-based hierarchical agglomerative clustering (MBHAC) to a random subset of the data points. Both methods are described in further detail in the following subsections. Restarts using random hierarchical agglomerative clustering (RHAC). At the outset RHAC begins with every data point (cid:2)x1, (cid:2)x2, …, (cid:2)xn in its own cluster. Random pairs of clusters are then Hierarchical agglomerative clustering: A “bottom-up” approach where each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy. Network Neuroscience 697 Neuronal classification from network connectivity † Algorithm 1 mRHEM Input: X = ((cid:2)x1, (cid:2)x2, …, (cid:2)xn)t 1: Begin tth trial, t 2 {1, 2, …, T} 2: 3: 4: 5: 6: Apply RHAC † to initialize model parameters Θκ, {8κ 2 Z+ : κmin ≤ κ ≤ κmax} Loop κ 2 {κmax, κmax − 1, …, κmin + 1, κmin} Run EM: iteratively maximizing ℓ(X; Θκ) until convergence End loop BIC(t) = maxκ {2ℓ(X; ^Θκ) − pκ ln(n)} 7: End trial 8: Select model with highest BIC across all trials, max (BIC(1), BIC(2), …, BIC(T )) Output: number of classes ^ k, and class assignment ^τ † For mMBEM, instead apply MBHAC on a random subset of X to obtain parameters in Step 2. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 8 9 1 9 6 0 5 2 5 n e n _ a _ 0 0 1 9 5 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 successively merged (with a uniform probability of choosing any two clusters for merging) until all n data points have been grouped into a single cluster. Equivalently, we could also start RHAC from a specific number of clusters, and successively proceed to form larger clusters. Since we do not know the true number of clusters we run EM for all values of κ 2 Z+, in the range κmin ≤ κ ≤ κmax. Starting with an initial choice of κmax number of clusters, RHAC assigns each data point randomly to any one of the clusters, with uniform assignment proba- bility 1/κmax. At each subsequent hierarchical agglomerative clustering stage, any two randomly picked clusters are combined, resulting in a total of κ − 1 clusters. This process is successively repeated until all data points have been grouped into κmin clusters. RHAC is computationally very efficient with a fast runtime, and a low memory usage cost of O(2n). During each trial we run the EM algorithm multiple (κmax − κmin + 1) times on the data, successively decreasing the value of κ by one during each run, for the entire range of κ 2 {κmax, …, κmin}. For each κ, the parameters of the randomly created RHAC partitions are used to start the EM. The EM algorithm is then run iteratively, maximizing the log-likelihood esti- mate, until convergence to an optimal solution. The proposed multiple restart RHAC based EM (mRHEM) algorithm is summarized in Algorithm 1. Restarts using MBHAC on a random subset. Model-based hierarchical agglomerative clustering (MBHAC) uses a Gaussian mixture model to obtain a partition of the data (Fraley, 1998; Scrucca & Raftery, 2015), and is the default EM initialization method for the mclust R pack- age (Scrucca, Fop, Murphy, & Raftery, 2016). Starting with each data point of the subset in its own cluster, MBHAC merges a pair of maximum likelihood clusters at each successive stage of the hierarchical clustering, resulting in a partition for each κ 2 {n, …, 1}. The parameters of these clusters obtained using MBHAC can then be used to initialize the EM algorithm across the desired range of κ. Applying MBHAC to the full dataset is deterministic, and computationally expensive with the memory usage cost being proportional to the square of the number of data points, O(n2) (Fraley, 1998). As an alternate for large values of n, the initial model parameters can be ob- tained by applying MBHAC to a smaller subset of the data points chosen at random (with Network Neuroscience 698 Neuronal classification from network connectivity uniform probability) (Fraley, 1998; Scrucca & Raftery 2015). The GMM is then fitted to all n data points by starting the EM algorithm with this choice of initial parameters. We extend this randomized MBHAC approach to implement a multiple random restart ver- sion of the EM algorithm (mMBEM). Specifically, we run many trials on each dataset. For each trial we choose a random subset from among the n data points and apply MBHAC to obtain the initial EM parameters for the desired range of mixture components κ. Finally, we select the model with the highest BIC across all trials. The mMBEM algorithm is therefore identical to mRHEM outlined in the previous section, with the only difference being the use of MBHAC applied to a random subset to initialize the model parameters (in Step 2 of Algorithm 1). The Probability Estimates We obtain an estimate of the block connectivity probability matrix P^ using the proportion of connected vertices given by our graph and using the partition τ^. We define the ijth entry of this matrix by p^ ij :¼ v; wð j f Þ 2 E : ^τ vð Þ ¼ i and ^τ wð in^ n^ j Þ ¼ j; j g ; (7) where n^ i = |{v 2 V : τ^(v) = i}|. The ratio in Equation 7 defines a value from 0 to 1. The probability estimate is compared with the original parameters that generated the graph. Recall that ρi is the proportion of vertices originally in the ith group, and pij is the probability that a specified element of the ith group has a directed edge to a specified element in the jth group. The corresponding relative error rate is defined as 8 >>>< >>>:

ΔP^

ij ¼

2 _

(cid:11)
(cid:11)
(cid:11)
(cid:11)
pij − p^
(cid:11)
(cid:11)
ij
pij þ p^
ij

;

for pij ¼ p^

ij ¼ 0

otherwise:

(8)

The percentage relative error in estimating the block connection probabilities is a weighted

average using the class proportions,

δ^
P ¼

100%
W

je;j¼1

r
je

r
j

ΔP^
ij;

(9)

where W =

je;jð

Þ2I

ρi ρj, with the index set I = {(je, j ) : pij 6¼ 0, and p^
ij

6¼ 0}.

When the clustering is perfect, the expected difference δP^(cid:4) 0.000 because perfect clus-
ij is the proportion of connected vertices in a size ninj random sample

tering implies that p^
from a binomial distribution with parameter pij.

SIMULATION RESULTS

In order to validate the effectiveness of the proposed approach, we performed multiple simula-
tions using our surrogate connectome model. During the course of these simulations we ran-
domly generated SBM graphs by systematically varying each of the parameters (n, P., r) of our
surrogate model (1), (2). For each graph we performed ASE followed by GMM-based EM clus-
tering. We compared the effects of EM initialization on clustering performance by applying the
mRHEM and mMBEM algorithms, to the same graphs, respectivement. En plus, we also tested
the robustness of our model to choices of embedding dimension d, the addition of noise, et le

Neurosciences en réseau

699

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
3
6
8
9
1
9
6
0
5
2
5
n
e
n
_
un
_
0
0
1
9
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal classification from network connectivity

Tableau 2. Clustering accuracy for EM initialization using MBHAC for a single trial, T = 1. The initial parameters were obtained by applying
MBHAC to all n data points. d is the number of singular values chosen for ASE. A total of 50 graphs were used for each n.

n
212 (4,096)

213 (8,192)

214 (16,384)

215 (32,768)

d = 2
2 (7.63)

14 (1.85)

28 (1.94)

34 (1.65)

% Perfect clustering (% vertices misclassified)
d = 4
2 (15.48)

d = 3
0 (14.55)

d = 5
0 (18.18)

24 (7.45)

22 (2.76)

16 (2.76)

12 (8.58)

12 (7.95)

12 (6.37)

4 (10.83)

6 (8.11)

0 (5.26)

d = 6
0 (18.23)

2 (16.87)

2 (7.30)

0 (7.52)

effect of varying the number of trials when applying multiple restart EM. We describe these
results in detail below.

Varying the Embedding Dimension d

We first assess the impact that the choice of embedding dimension has on the clustering per-
formance when using GMM-based hierarchical clustering. We generated 50 random graphs
for each value of n using the surrogate model (1), (2), and then cluster them by embedding
them in R2d using ASE (varying the value of d each time).

For the sake of comparison, clustering was first performed by running the EM algorithm with
initial parameters obtained by applying MBHAC to all n data points, implemented using the
mclust R package (Scrucca et al., 2016). Note that applying MBHAC to all data points cre-
ates deterministic partitions resulting in just a single trial, T = 1. Tableau 2 shows the percentage
de 50 graphs in which the vertices were perfectly clustered (c'est à dire., each vertex vi was correctly
assigned to its true class τ(vi) by the algorithm) and the percentage of vertices that were mis-
classified across these graphs. The results indicate that using this approach to initialize the EM
algorithm performed rather poorly, and was in general unsuccessful in clustering the latent
vectors correctly. Fait intéressant, the method performed better for lower values of d and large
n, with the misclassification rate being very low for these values.

Tables 3 et 4 show the results when using the proposed multiple restart variations
mMBEM, and mRHEM algorithms, respectivement. Both algorithms were implemented with aid
of the mclust package. A total of 100 trials were used to cluster each graph. We observe a
drastic improvement in the clustering performance when using the random multiple restart
approche. Also as expected, and in contrast to MBHAC, the clustering performance improves
as n increases (Athreya et al., 2016).

Tableau 3. Clustering accuracy using mMBEM with T = 100 trials, wherein each trial was initialized using parameters obtained by applying
MBHAC to a random subset of 2,000 points de données. A total of 50 graphs were used for each n.

n
212 (4,096)

213 (8,192)

214 (16,384)

215 (32,768)

d = 2
0 (19.96)

0 (12.48)

14 (5.53)

100 (0.00)

Neurosciences en réseau

% Perfect clustering (% vertices misclassified)
d = 4
14 (14.00)

d = 3
36 (6.10)

d = 5
40 (0.04)

100 (0.00)

58 (17.36)

78 (18.65)

26 (20.36)

98 (0.01)

100 (0.00)

d = 6
44 (0.04)

98 (0.01)

100 (0.00)

700

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
3
6
8
9
1
9
6
0
5
2
5
n
e
n
_
un
_
0
0
1
9
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal classification from network connectivity

Tableau 4. Clustering accuracy using mRHEM with T = 100 trials. d is the number of singular values chosen for ASE. A total of 50 graphs were
used for each n.

n
212 (4,096)

213 (8,192)

214 (16,384)

215 (32,768)

d = 2
50 (0.03)

100 (0.00)

% Perfect clustering (% vertices misclassified)
d = 4
22 (5.05)

d = 3
46 (0.63)

d = 5
10 (10.56)

100 (0.00)

98 (5.08)

100 (0.00)

d = 6
0 (9.72)

92 (7.17)

98 (3.31)

100 (0.00)

For the results in Table 3, the size of the random subset used for mMBEM initialization was
kept constant at 2,000 points de données, irrespective of the value of n. Rather surprisingly though,
mMBEM performed poorly for the choice of embedding dimension d = 4, which from
Chiffre 1 is the target dimension of interest. For the particular case of d = 4, we observed a con-
sistent error pattern for all graphs that were not perfectly clustered. For these graphs the final

clustering always resulted in

^
k = 9, with the largest cluster being split into two.

The clustering results improved when we increased the size of the random subset, but so did
the computation time. In Table 5 we compare the performance of mMBEM as a function of the
random subset size used for initialization, by applying it to the same 50 graphs each with n = 215,
and d = 4. The average CPU elapsed time shown is the time taken to perform agglomerative
hierarchical clustering given data X, and does not include the time taken to perform any other
operation such as ASE, iterating EM, calculating the BICs, et ainsi de suite. Doubling the size of the
random subset to 4,000 data points led to approximately a sixfold increase in CPU computation
time to perform randomized MBHAC, with only a marginal improvement in clustering accuracy.
MBHAC initialization for subsets larger than 2,000 points results in diminishing gain.

In contrast, mRHEM was largely insensitive to the choice of embedding dimensionality. It was
also extremely consistent in its performance with near perfect clustering accuracy for n ≥ 213.
While we list results for 100 trials, a larger number of mRHEM trials resulted in even stronger
résultats. En outre, mMBEM is subject to an additional parameter (viz., size of the random
subset used for initialization), which directly affects its clustering accuracy and computational
complexity, while mRHEM is straightforward to implement and extremely efficient computa-
tionally. We use mRHEM exclusively for the remainder of the analysis.

Varying the Number of Vertices n

To examine the effects of varying n in further detail, we fixed the choice of embedding dimen-
sionality at a constant d = 4, as selected from Figure 1. Tableau 6 shows the clustering perfor-
mance of mRHEM with T = 100 trials for a varying number of vertices. Misclassified vertices

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
3
6
8
9
1
9
6
0
5
2
5
n
e
n
_
un
_
0
0
1
9
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Tableau 5. Average CPU
were used each with n = 215, and d = 4.

†

temps (in seconds) taken to perform different variations of agglomerative hierarchical clustering. A total of 50 graphs

Intialization method
CPU time (secs.)

RHAC
7.36

MBHAC (2,000)
1.87

MBHAC (4,000)
12.19

MBHAC (8,000)
83.22

MBHAC (215)*
4,554.31

% Perfect clustering

100

12*

†

Desktop AMD Ryzen 2700x (3.7 GHz) avec 32 GB RAM (DDR4, 3200 MHz), and mclust version 5.4.2.
* Applying MBHAC to all n points, results in a single trial.

Neurosciences en réseau

701

Neuronal classification from network connectivity

Tableau 6. Varying n: Clustering accuracy using mRHEM with T = 100 trials for d = 4, as the number of vertices n is increased while keeping
other parameters constant. A total of 50 graphs were used for each n.

n
211 (2,048)

212 (4,096)

213 (8,192)

214 (16,384)

215 (32,768)

^
k = 8
14

100

Perfect classification %

100

When imperfect classification

Avg. number (%) misclassfied vertices
315.60 (15.41%)

Avg. δP^
47.385

(%)

Overall Avg. ARI
0.9032

206.95 (5.05%)

1.510

0.000

0.9346

1.0000

were measured from maximal BIC among trials, and averaged over 50 graphs. En plus,
we also include the percentage relative error in estimating the block connection probabilities
(9), and measure the adjusted Rand index (ARI) (Hubert & Arabie, 1985). Here the ARI was
calculated in comparison to the true class memberships, and serves as an estimate for the over-
all accuracy of classification. ARI is a popular similarity score for comparing two partitioning
schemes for the same data points, with a higher value of ARI indicating high similarity; 1 dans-
dicating that they are identical; et 0 for randomly generated partitions.

Varying the Proportions ρ
To test the robustness of the approach, we varied the SBM parameters, such that first ρ = (r
1,
…, ρk) was varied while keeping P constant, and then P was varied while keeping ρ constant.
To vary the class proportions we used a Dirichlet distribution Dir(rρ · ρ + J1,k), where rρ is a
constant, and Ji,j is an i × j matrix of all ones. When rρ = 1 we have the original membership
proportions in (2), and when rρ = 0 the proportions are sampled from a uniform distribution.
Tableau 7 shows the clustering results using mRHEM with 100 trials as ρ was varied. A total of 50
graphs were generated for each ρ, while keeping P, n = 214, and d = 4 constant for each graph.
We include the data for r = 1 for comparison.

Varying the Probability Matrix P

To vary the connectivity probability matrix we used another Dirichlet distribution centered on
P., with parameter rp, such that the probabilities are sampled from a uniform distribution when

Tableau 7. Varying ρ: Clustering accuracy using mRHEM with 50 graphs and T = 100 trials, with varied block membership proportions. Total
number of vertices was kept constant n = 214, and d = 4.

rρ
1

10,000

1,000

100

^
k = 8
100

Perfect classification %
100

100

Neurosciences en réseau

When imperfect classification

Avg. number (%) misclassfied vertices

3,026.455 (18.47%)

^
Avg. δP
0.000

(%)

Overall Avg. ARI
1.0000

0.000

2.743

1.0000

0.9960

702

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
3
6
8
9
1
9
6
0
5
2
5
n
e
n
_
un
_
0
0
1
9
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal classification from network connectivity

rp = 0, and is given by the matrix P when rp = 1. En plus, to ensure that the sampled
graphs remain sparse we put bounds on the Dirichlet sampled ijth entry of the probability ma-
trix, pD

ij , such that

(cid:7)

maximum 0; pij − 0:2

(cid:8)

≤ pD
ij

≤ pij þ 0:2:

(10)

Tableau 8 shows the clustering results for varying P while keeping ρ constant for n = 4,096.
Alternativement, when the number of vertices is increased to n = 8,192, we observed that the
mRHEM performance did not essentially deteriorate as block connection probabilities were
varied relative to the original values; when the number of vertices is set to n = 16,384,
mRHEM achieves perfect classification over the entire range of rp.

Effect of Adding Noise

To test the tolerance of the proposed clustering algorithm under experimentally realistic model
misspecification, we simulate errors in pre- or postsynaptic neuron identification. In order to do this
we add noise to our model by randomly moving edges within the adjacency matrix. Spécifiquement, un
directed edge in the adjacency matrix is moved by flipping the corresponding 1 into a 0, et
simultaneously flipping a randomly chosen 0 somewhere else in the matrix into a 1. Donc,
the total number of edges before and after the addition of noise in a graph remains the same.

The percentage of edge misspecification in a noisy graph indicates the fraction of edges,
relative to the total number of edges in the graph, that are moved. The percentage misspeci-
fication thus determines the size of the subset of edges moved. The subset of edges (and cor-
responding subset of non-edges) to be flipped are chosen using a uniform random distribution
among all possible subsets of the determined size. This ensures that over several instances of
random noisy graphs, the average number of edges removed from each pair of neuronal clas-
ses is proportional to the total number of connections (edges) in between that pair of classes.
Since the graph is sparse, the average number of corresponding edges added has comparatively
small differences across different pairs of neuronal classes. Consequentially, on average, pairs of
neuronal classes with more connections have more noise introduced.

We measured how well mRHEM with T − 100 trials was able to estimate the original class
assignment in the presence of noise. Chiffre 3 shows the average classification accuracy as a
function of the fraction of edges moved, for a total of 10 graphs each with n = 214, and d = 4.
The clustering results demonstrate mRHEM to be extremely tolerant towards added noise, avec
near perfect classification even with 50% edge misspecification.

Tableau 8.
Total number of vertices was kept constant n = 212, and d = 4.

Varying P: Clustering accuracy for using mRHEM with 50 graphs and T = 100 trials, with varied block connection probabilities.

rp
1

10,000

1,000

100

^
k = 8
56

100

Neurosciences en réseau

Perfect classification %
22

Avg. number (%) misclassfied vertices
206.95 (5.05%)

When imperfect classification

Avg. δP^
1.510

(%)

Overall Avg. ARI
0.9346

100

252.35 (6.16%)

162.05 (3.96%)

62.71 (1.53%)

11.184

11.000

6.754

0.000

0.9116

0.9636

0.9954

1.0000

703

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
3
6
8
9
1
9
6
0
5
2
5
n
e
n
_
un
_
0
0
1
9
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal classification from network connectivity

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
3
6
8
9
1
9
6
0
5
2
5
n
e
n
_
un
_
0
0
1
9
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 3. Adding noise: Average percentage of vertices that were misclassified versus the amount
of noise introduced, c'est, fraction of edges moved. Also shown are the percentage of graphs
whose clustering resulted in correctly estimating
, averaged over all
graphs.

^
^
k = 8, and relative error δP

The model’s robustness to noise is partly attributed to the fact that not all neuron types con-
tribute equally to the network connectivity. If ρ is skewed with disproportionately sized groups,
then the process of flipping random edges has a higher probability (than evenly sized classes)
that the removal and addition happens within the same pair of vertex classes. De la même manière, le
greater the differences among entries in P, the more robust the clustering is to the addition of
bruit. Plus généralement, asymmetry in the parameter specifications increases the tolerance of
the model to edge misspecification.

Chiffre 4. Varying number of trials: Percentage of perfectly clustered graphs when running T trials
of mRHEM. A total of 50 graphs were used for different values of rρ (with rp = 1, n = 214, and d = 4
held constant).

Neurosciences en réseau

704

Neuronal classification from network connectivity

Influence of Number of Trials on mRHEM Performance

A fundamental disadvantage of using multiple restart EM is the computational cost associated
with running multiple trials. To the best of our knowledge there is no theoretical solution avail-
able in the literature to determine the number of random initializations that would be sufficient
to ensure a full examination of the likelihood function (Biernacki et al., 2003; Shireman et al.,
2017). In the absence of an analytical solution, we perform an empirical analysis to help de-
termine the number of trials needed for mRHEM to converge to an optimal solution. Chiffre 4

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
3
6
8
9
1
9
6
0
5
2
5
n
e
n
_
un
_
0
0
1
9
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 5. Number of misclassified vertices versus mRHEM trial number for a single graph for (UN) rρ = 1, (B) rρ = 100, et (C) rρ = 0 (avec
rp = 1, n = 214, and d = 4 held constant). The trials are sorted in increasing magnitude of BIC(t). Aussi, shown for comparison is BICM
corresponding to initialization using MBHAC applied to all n data points.

Neurosciences en réseau

705

Neuronal classification from network connectivity

shows the percentage of graphs that are perfectly clustered as a function of the number of trials
used to run mRHEM. Only 37 trials were needed to achieve perfect clustering for over 95% de
the graphs for rρ = 1, and rρ = 100.

We also investigate the empirical relation between BIC and clustering accuracy, as a func-
tion of the number of trials. For a single randomly chosen graph generated with the original
parameters, Figure 5A shows the number of misclassified vertices and the resulting BIC values
pour 100 trials of mRHEM. The trials have been sorted along the horizontal axis in ascending
order of their resulting BIC(t) valeurs, such that the random trial with the lowest BIC corresponds
to t = 1, while the random trial with the highest BIC is t = 100. Aussi, shown on the same plot is
the misclassification error and corresponding BICM value when initializing using MBHAC on
the same graph. A similar comparison is done for a single graph generated with rρ = 100
(Figure 5B) and for a single graph generated with rρ = 0 (Figure 5C).

We observe from Figure 5 that while BICM > BIC(t) pour (cid:4)80% of the trials, its ability to suc-
cessfully predict class assignment is worse than (cid:4)90% of the mRHEM trials, evidenced by the
small number of data points among the mRHEM trials above the horizontal (pink) line indicat-
ing the number of misclassified vertices when initializing using MBHAC. BICM could be used
as a reference when deciding whether additional trials are needed. If the BIC values of all
random trials are less than BICM, more trials may be needed. Enfin, we choose the model
with the highest BIC. Note that the number of misclassifications is not a monotonic function
w.r.t. BIC, c'est, a higher BIC does not necessarily guarantee better clustering.

The time penalty and availability of computational resources are other important factors to
consider when choosing the number of random trials. Despite the added computational cost
associated with running EM several times, 100 mRHEM trials entails only a contained ((cid:4)270%
on average) increase in CPU computation time. En plus, since mRHEM is performing
multiple quick trials, it allows for a relatively easy parallel-processing implementation (as op-
posed to one intensive trial using MBHAC). This could allow future CPU-intensive calculations
to be performed simultaneously, resulting in significant time savings for mRHEM.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
3
6
8
9
1
9
6
0
5
2
5
n
e
n
_
un
_
0
0
1
9
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

DISCUSSION

Understanding the types of neurons that comprise nervous systems is a fundamental step to-
wards a more comprehensive understanding of neural circuits (Armañanzas & Ascoli, 2015).
The need for cell type classification from brain data is demonstrated by it being the first high-
priority research area identified by the Brain Research through Advancing Innovative
Neurotechnologies (BRAIN) Initiative working group interim report (NIH, 2013) and the result-
ing launch of the BRAIN Initiative Cell Census Network (https://biccn.org). Previous approaches
to classifying cell types have largely focused on the analysis of morphological, physiological, ou
genetic properties. Ici, we promote a complementary strategy that directly leverages connec-
tivité. Our methodology effectively recovered the true number of clusters and cluster assign-
ments as the number of vertices increased, even under experimentally realistic model
misspecifications, corroborating its potential utility for analyzing real connectomic data.

Neuronal classification has traditionally relied on axonal and dendritic morphology, molec-
ular expression, and electrophysiology for characterizing cellular properties in the nervous sys-
tem (Petilla Interneuron Nomenclature Group et al., 2008). D'une part, the expedient
abundance of such data has allowed the creation of increasingly unbiased descriptive taxon-
omies (DeFelipe et al., 2013; Yuste et al., 2020). On the other, these experimentally accessible
dimensions are only indirect proxies for the mechanistically more relevant features of network

Neurosciences en réseau

706

Neuronal classification from network connectivity

connectivité, developmental control, and experience-dependent plasticity (Armañanzas &
Ascoli, 2015; Shepherd et al., 2019). En particulier, a community consensus has been coalescing
that the complete synaptic circuitry of a neural system constitutes the fundamental architectural
underpinning of its in vivo dynamics and functions (Abbott et al., 2020). From this perspective, un
quantitative specification of neuron types based on network connectivity such as that proposed
in this work may constitute the most fundamental parts list for deconstructing brain computation.
This raises the important question of mapping the connectomics-based neuron classification to
other well-studied biological dimensions, including transcriptomics and spiking activity pat-
terns. Addressing this problem remains an open challenge in neuroscience.

Our ability as a community to estimate connectomes from real brain data has recently been
transformed by breathtaking advances in techniques such as nanoscale electron microscopy
(Bock et al., 2011; Denk & Horstmann, 2004; Jarrell et al., 2012; Takemura et al., 2013), struc-
tural multicolor microscale light microscopy (Livet et al., 2007) paired with tissue clearing
(Chung & Deisseroth, 2013), functional mesoscale light microscopy (Ahrens, Orger, Robson,
Li, & Keller, 2013; Schrödel, Prevedel, Aumayr, Zimmer, & Ministre, 2013), macroscale functional
and diffusion magnetic resonance imaging (Craddock et al., 2013), computational morphology
and anatomy (Peng et al., 2017; Ropireddy & Ascoli, 2011), and optical coherence tomography
(Magnain et al., 2014). These technological breakthroughs require new approaches to analyze
the resulting data, at scale, using principled statistical tools.

Our work illustrates the value of graph theoretic tools for discovering and assigning cell types
in large scale simulations using connectivity information alone (Ascoli & Atkeson, 2005). Au pair-
particulier, we show that these methods can be used to recover class assignment for neural cells
connected in biologically plausible proportions, at practical graph sizes for which data are
emerging. The analysis and results of these surrogate data suggest that, at least in some circum-
stances, applying singular value decomposition and clustering techniques to the adjacency ma-
trix rather than to its Laplacian results in consistent outcomes. Cependant, there is a clear need for
a theoretical framework that guarantees convergence for data that are asymmetric adjacency
matrices representing directed graphs.

For GMM-based EM clustering of the surrogate data, the proposed mRHEM approach heavily
outperforms the default MBHAC initialization used by mclust (Scrucca et al., 2016; Scrucca &
Raftery, 2015). We show that initializing the EM algorithm with random hierarchical agglomer-
ative clustering multiple times is more effective than standard model-based hierarchical cluster-
ing at identifying the correct classification, as quantified by key measures of accuracy, tel que
clustering into the correct number of groups and misclassifying as few vertices as possible.

While the proposed approach scales extremely well for large networks with 212 ≤ n ≤ 215
vertices, a practical limitation of applying our SBM inference model to real connectomic data
is that it requires the size of the dataset (number of vertices in the network) to be much larger than
the number of model parameters. The number of model parameters grows linearly with the num-
ber of blocks k and depends quadratically on the embedding dimension d (5). While performing
ASE on a sparse graph ensures d << n, there is no guarantee that k << n holds for real data. Our described approach would still attempt to find the most parsimonious model (smallest k) that fits the given data. Recent attempts of applying the SBM framework with small values of k to model connectomic data (Priebe et al., 2017, 2019) and detect community structure (Betzel et al., 2018; Faskowitz et al., 2018; Moyer et al., 2015; Pavlovic et al., 2014) have yielded promising results. It remains necessary, however, to further examine the relationship between the param- eter k and the required n to accurately model networks with even wider range and complexity. Such assessments could drive experimental efforts to reach benchmarked data-collection goals. Network Neuroscience 707 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 8 9 1 9 6 0 5 2 5 n e n _ a _ 0 0 1 9 5 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuronal classification from network connectivity In future work, we will extend these results both theoretically and methodologically. We hope to characterize the circumstances in which one could expect better performance by mRHEM compared with MBHAC, and in particular find a probabilistic characterization of the optimal number of trials needed to obtain perfect clustering. We also intend to extend these results to include not only connectivity information, but also various other vertex and edge attributes of the network, such as spatial, morphological, electrophysiological, and ge- netic properties. While the contribution of this paper was methodological in scope, the lack of experimental validation at this time prevents a definitive assessment of its full scientific impact. Future work will strive to apply the approach introduced here to estimated connectomes from biological data, allowing an empirical test of its ability to foster novel neuroscientific insights. SUPPORTING INFORMATION R code: Self-contained R-script [.r filetype] to generate surrogate data and replicate all simulation results described in the article is available at https://doi.org/10.1162/netn_a_00195. AUTHOR CONTRIBUTIONS Ketan Mehta: Conceptualization; Investigation; Methodology; Software; Validation; Visualization; Writing – original draft; Writing – review & editing. Rebecca F. Goldin: Conceptualization; Funding acquisition; Investigation; Methodology; Software; Supervision; Validation; Visualization; Writing – original draft; Writing – review & editing. David Marchette: Conceptualization; Investigation; Methodology; Software; Validation; Visualization; Writing – original draft; Writing – review & editing. Joshua T. Vogelstein: Conceptualization; Investigation; Methodology; Validation; Visualization; Writing – original draft; Writing – review & editing. Carey E. Priebe: Conceptualization; Investigation; Methodology; Validation; Visualization; Writing – original draft; Writing – review & editing. Giorgio A. Ascoli: Conceptualization; Data curation; Funding acquisition; Investigation; Methodology; Project administration; Resources; Supervision; Validation; Visualization; Writing – original draft; Writing – review & editing. FUNDING INFORMATION Giorgio A. Ascoli, National Institutes of Health (https://dx.doi.org/10.13039/100000002), Award ID: R01NS39600. Giorgio A. Ascoli, National Institutes of Health (https://dx.doi.org /10.13039/100000002), Award ID: U01MH114829. Rebecca F. Goldin, National Science Foundation (https://dx.doi.org/10.13039/100000001), Award ID: 1201458. REFERENCES Abbe, E. (2017). Community detection and stochastic block models: Recent developments. Journal of Machine Learning Research, 18(1), 6446–6531. https://dl.acm.org/doi/10.5555/3122009.3242034 Abbott, L. F., Bock, D. D., Callaway, E. M., Denk, W., Dulac, C., Fairhall, A. L., … Van Essen, D. C. (2020). The mind of a mouse. Cell, 182(6), 1372–1376. https://doi.org/10.1016/j.cell.2020.08 .010, PubMed: 32946777 Ahrens, M. B., Orger, M. B., Robson, D. N., Li, J. M., & Keller, P. J. (2013). Whole-brain functional imaging at cellular resolution using light-sheet microscopy. Nature Methods, 10(5), 413–420. https://doi.org/10.1038/nmeth.2434, PubMed: 23524393 Armañanzas, R., & Ascoli, G. A. (2015). Towards the automatic clas- sification of neurons. Trends in Neurosciences, 38(5), 307–318. https://doi.org/10.1016/j.tins.2015.02.004, PubMed: 25765323 Ascoli, G. A., & Atkeson, J. C. (2005). Incorporating anatomically realistic cellular-level connectivity in neural network models of the rat hippocampus. Biosystems, 79(1), 173–181. https://doi.org /10.1016/j.biosystems.2004.09.024, PubMed: 15649602 Athreya, A., Priebe, C. E., Tang, M., Lyzinski, V., Marchette, D. J., & Sussman, D. L. (2016). A limit theorem for scaled eigenvectors of random dot product graphs. Sankhya A, 78(1), 1–18. https://doi .org/10.1007/s13171-015-0071-x Network Neuroscience 708 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 3 6 8 9 1 9 6 0 5 2 5 n e n _ a _ 0 0 1 9 5 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuronal classification from network connectivity Attili, S. M., Mackesey, S. T., & Ascoli, G. A. (2020). Operations research methods for estimating the population size of neuron types. Annals of Operations Research, 289, 33–50. https://doi .org/10.1007/s10479-020-03542-7, PubMed: 33343053 Betzel, R. F., Medaglia, J. D., & Bassett, D. S. (2018). Diversity of meso-scale architecture in human and non-human connectomes. Nature Communications, 9(346), 1–14. https://doi.org/10.1038 /s41467-017-02681-z, PubMed: 29367627 Biernacki, C., Celeux, G., & Govaert, G. (2003). Choosing starting values for the EM algorithm for getting the highest likelihood in multivariate Gaussian mixture models. Computational Statistics and Data Analysis, 41(3), 561–575. https://doi.org/10.1016 /S0167-9473(02)00163-9 Bock, D. D., Lee, W.-C. A., Kerlin, A. M., Andermann, M. L., Hood, G., Wetzel, A. W., … Reid, R. C. (2011). Network anatomy and in vivo physiology of visual cortical neurons. Nature, 471(7337), 177–182. https://doi.org/10.1038/nature09802, PubMed: 21390124 Christopoulos, D. (2016). Introducing unit invariant knee (UIK) as an objective choice for elbow point in multivariate data analysis techniques. Available at SSRN 3043076. https://doi.org/10.2139 /ssrn.3043076 Chung, K., & Deisseroth, K. (2013). CLARITY for mapping the ner- vous system. Nature Methods, 10(6), 508–513. https://doi.org/10 .1038/nmeth.2481, PubMed: 23722210 Craddock, R. C., Jbabdi, S., Yan, C.-G., Vogelstein, J. T., Castellanos, F. X., Di Martino, A., … Milham, M. P. (2013). Imaging human connectomes at the macroscale. Nature Methods, 10(6), 524–539. https://doi.org/10.1038/nmeth.2482, PubMed: 23722212 DeFelipe, J., López-Cruz, P. L., Benavides-Piccione, R., Bielza, C., Larrañaga, P., Anderson, S., … Ascoli, G. A. (2013). New insights into the classification and nomenclature of cortical GABAergic interneurons. Nature Reviews Neuroscience, 14(3), 202–216. https://doi.org/10.1038/nrn3444, PubMed: 23385869 Denk, W., & Horstmann, H. (2004). Serial block-face scanning electron microscopy to reconstruct three-dimensional tissue nanostructure. PLoS Biology, 2(11), e329. https://doi.org/10 .1371/journal.pbio.0020329, PubMed: 15514700 Faskowitz, J., Yan, X., Zuo, X.-N., & Sporns, O. (2018). Weighted stochastic block models of the human connectome across the life span. Scientific Reports, 8(1), 1–16. https://doi.org/10.1038 /s41598-018-31202-1, PubMed: 30158553 Fishkind, D. E., Sussman, D. L., Tang, M., Vogelstein, J. T., & Priebe, C. E. (2013). Consistent adjacency-spectral partitioning for the stochastic block model when the model parameters are unknown. SIAM Journal on Matrix Analysis and Applications, 34(1), 23–39. https://doi.org/10.1137/120875600 Fraley, C. (1998). Algorithms for model-based Gaussian hierarchical clustering. SIAM Journal on Scientific Computing, 20(1), 270–281. https://doi.org/10.1137/S1064827596311451 Funke, T., & Becker, T. (2019). Stochastic block models: A compar- ison of variants and inference methods. PLoS ONE, 14(4), e0215296. https://doi.org/10.1371/journal.pone.0215296, PubMed: 31013290 Hamilton, D., Shepherd, G., Martone, M., & Ascoli, G. (2012). An on- tological approach to describing neurons and their relationships. Frontiers in Neuroinformatics, 6, 1–15. https://doi.org/10.3389 /fninf.2012.00015, PubMed: 22557965 Holland, P. W., Laskey, K. B., & Leinhardt, S. (1983). Stochastic blockmodels: First steps. Social Networks, 5(2), 109–137. https:// doi.org/10.1016/0378-8733(83)90021-7 Holland, P. W., & Leinhardt, S. (1981). An exponential family of probability distributions for directed graphs. Journal of the American Statistical Association, 76(373), 33–50. https://doi.org /10.1080/01621459.1981.10477598 Hubert, L., & Arabie, P. (1985). Comparing partitions. Journal of Classification, 2(1), 193–218. https://doi.org/10.1007/BF01908075 Jarrell, T. A., Wang, Y., Bloniarz, A. E., Brittin, C. A., Xu, M., Thomson, J. N., … Emmons, S. W. (2012). The connectome of a decision-making neural network. Science, 337(6093), 437–444. https://doi.org/10.1126/science.1221762, PubMed: 22837521 Kwedlo, W. (2015). A new random approach for initialization of the multiple restart EM algorithm for Gaussian model-based clus- tering. Pattern Analysis and Applications, 18(4), 757–770. https:// doi.org/10.1007/s10044-014-0441-3 Livet, J., Weissman, T. A., Kang, H., Draft, R. W., Lu, J., Bennis, R. A., … Lichtman, J. W. (2007). Transgenic strategies for combinatorial expression of fluorescent proteins in the nervous system. Nature, 450(7166), 56–62. https://doi.org/10.1038/nature06293, PubMed: 17972876 Magnain, C., Augustinack, J. C., Reuter, M., Wachinger, C., Frosch, M. P., Ragan, T., … Fischl, B. (2014). Blockface histology with optical coherence tomography: A comparison with Nissl stain- ing. NeuroImage, 84, 524–533. https://doi.org/10.1016/j .neuroimage.2013.08.072, PubMed: 24041872 Marchette, D., Priebe, C., & Coppersmith, G. (2011). Vertex nom- ination via attributed random dot product graphs. Proceedings of the 57th ISI World Statistics Congress, 6, 16. McDaid, A. F., Murphy, T. B., Friel, N., & Hurley, N. J. (2013). Improved Bayesian inference for the stochastic block model with application to large networks. Computational Statistics and Data Analysis, 60, 12–31. https://doi.org/10.1016/j.csda.2012.10.021 Melnykov, V., & Melnykov, I. (2012). Initializing the EM algorithm in Gaussian mixture models with an unknown number of com- ponents. Computational Statistics and Data Analysis, 56(6), 1381–1395. https://doi.org/10.1016/j.csda.2011.11.002 Moyer, D., Gutman, B., Prasad, G., Faskowitz, J., Steeg, G. V., & Thompson, P. (2015). Blockmodels for connectome analysis. In 11th international symposium on medical information processing and analysis ( Vol. 9681, pp. 62–70). Cuenca, Ecuador: SPIE. https://doi.org/10.1117/12.2211519 NIH. (2013). Brain Research through Advancing Innovative Neurotechnologies (BRAIN) Initiative working group interim report. Retrieved from https://braininitiative.nih.gov/sites/default/files/pdfs /11252013_interim_report_exec_sum_508c.pdf Pavlovic, D. M., Vértes, P. E., Bullmore, E. T., Schafer, W. R., & Nichols, T. E. (2014). Stochastic blockmodeling of the modules and core of the Caenorhabditis elegans connectome. PLoS ONE, 9(7), e97584. https://doi.org/10.1371/journal.pone.0097584, PubMed: 24988196 Peng, H., Zhou, Z., Meijering, E., et al. (2017). Automatic tracing of ultra-volumes of neuronal images. Nature Methods, 14, 332– 333. https://doi.org/10.1038/nmeth.4233 Petilla Interneuron Nomenclature Group, Ascoli, G., Alonso- Nanclares, L., Anderson, S. A., Barrionuevo, G., Benavides- Piccione, R., Burkhalter, A., … Yuste, R. (2008). Petilla terminology: Network Neuroscience 709 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 3 6 8 9 1 9 6 0 5 2 5 n e n _ a _ 0 0 1 9 5 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuronal classification from network connectivity Nomenclature of features of GABAergic interneurons of the cere- bral cortex. Nature Reviews Neuroscience, 9(7), 557–568. https:// doi.org/10.1038/nrn2402, PubMed: 18568015 Priebe, C. E., Park, Y., Tang, M., Athreya, A., Lyzinski, V., Vogelstein, J. T., … Cardona, A. (2017). Semiparametric spectral modeling of the Drosophila connectome. arXiv:1705.03297. https://arxiv.org/abs/1705.03297 Priebe, C. E., Park, Y., Vogelstein, J. T., Conroy, J. M., Lyzinski, V., Tang, M., … Bridgeford, E. (2019). On a two-truths phenomenon in spectral graph clustering. Proceedings of the National Academy of Sciences, 116(13), 5995–6000. https://doi.org/10 .1073/pnas.1814462116, PubMed: 30850525 Rohe, K., Chatterjee, S., & Yu, B. (2011). Spectral clustering and the high-dimensional stochastic blockmodel. The Annals of Statistics, 39(4), 1878–1915. https://doi.org/10.1214/11-AOS887 Ropireddy, D., & Ascoli, G. (2011). Potential synaptic connectivity of different neurons onto pyramidal cells in a 3d reconstruction of the rat hippocampus. Frontiers in Neuroinformatics, 5, 1–5. https://doi.org/10.3389/fninf.2011.00005, PubMed: 21779242 Satopaa, V., Albrecht, J., Irwin, D., & Raghavan, B. (2011). Finding a “Kneedle” in a haystack: Detecting knee points in system behavior. In 31st International Conference on Distributed Computing Systems Workshops (pp. 166–171). Minneapolis, MN, USA. https://doi.org /10.1109/ICDCSW.2011.20 Scheinerman, E. R., & Tucker, K. (2010). Modeling graphs using dot product representations. Computational Statistics, 25(1), 1–16. https://doi.org/10.1007/s00180-009-0158-8 Schrödel, T., Prevedel, R., Aumayr, K., Zimmer, M., & Vaziri, A. (2013). Brain-wide 3D imaging of neuronal activity in Caenorhabditis elegans with sculpted light. Nature Methods, 10(10), 1013–1020. https://doi.org/10.1038/nmeth.2637, PubMed: 24013820 Scrucca, L., Fop, M., Murphy, T. B., & Raftery, A. E. (2016). Mclust 5: Clustering, classification and density estimation using Gaussian finite mixture models. The R Journal, 8(1), 289–317. https://doi.org/10.32614/RJ-2016-021, PubMed: 27818791 Scrucca, L., & Raftery, A. E. (2015). Improved initialisation of model-based clustering using Gaussian hierarchical partitions. Advances in Data Analysis and Classification, 9(4), 447–460. https://doi.org/10.1007/s11634-015-0220-z, PubMed: 26949421 Shepherd, G. M., Marenco, L., Hines, M. L., Migliore, M., McDougal, R. A., Carnevale, N. T., … Ascoli, G. A. (2019). Neuron names: A gene- and property-based name format, with special reference to cortical neurons. Frontiers in Neuroanatomy, 13, 1–25. https://doi .org/10.3389/fnana.2019.00025, PubMed: 30949034 Shireman, E., Steinley, D., & Brusco, M. J. (2017). Examining the effect of initialization strategies on the performance of Gaussian mixture modeling. Behavior Research Methods, 49(1), 282–293. https://doi.org/10.3758/s13428-015-0697-6, PubMed: 26721666 Sussman, D. L., Tang, M., Fishkind, D. E., & Priebe, C. E. (2012). A con- sistent adjacency spectral embedding for stochastic blockmodel graphs. Journal of the American Statistical Association, 107(499), 1119–1128. https://doi.org/10.1080/01621459.2012.699795 Takemura, S. Y., Bharioke, A., Lu, Z., Nern, A., Vitaladevuni, S., Rivlin, P. K., … Chklovskii, D. B. (2013). A visual motion de- tection circuit suggested by Drosophila connectomics. Nature, 500(7461), 175–181. https://doi.org/10.1038/nature12450, PubMed: 23925240 Tecuatl, C., Wheeler, D. W., Sutton, N., & Ascoli, G. A. (2020). Comprehensive estimates of potential synaptic connections in local circuits of the rodent hippocampal formation by axonal- dendritic overlap. Journal of Neuroscience, 41(8), 1665–1683. https://doi.org/10.1523/ JNEUROSCI.1193-20.2020, PubMed: 33361464 Vogelstein, J. T., Bridgeford, E. W., Pedigo, B. D., Chung, J., Levin, K., Mensh, B., & Priebe, C. E. (2019). Connectal coding: Discovering the structures linking cognitive phenotypes to indi- vidual histories. Current Opinion in Neurobiology, 55, 199–212. https://doi.org/10.1016/j.conb.2019.04.005, PubMed: 31102987 Wheeler, D. W., White, C. M., Rees, C. L., Komendantov, A. O., Hamilton, D. J., & Ascoli, G. A. (2015). Hippocampome.org: A knowledge base of neuron types in the rodent hippocampus. eLife, 4, e09960. https://doi.org/10.7554/eLife.09960, PubMed: 26402459 Yuste, R., Hawrylycz, M., Aalling, N., Aguilar-Valles, A., Arendt, D., Armañanzas, R., … Lein, E. (2020). A community-based tran- scriptomics classification and nomenclature of neocortical cell types. Nature Neuroscience, 23(12), 1456–1468. https://doi.org /10.1038/s41593-020-0685-8, PubMed: 32839617 Network Neuroscience 710 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 8 9 1 9 6 0 5 2 5 n e n _ a _ 0 0 1 9 5 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 METHODS image

Télécharger le PDF