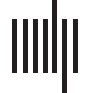MÉTHODES

A morphospace of functional configuration to
assess configural breadth based on brain
functional networks

Duy Duong-Tran1,2, Kausar Abbas1,2, Enrico Amico1,2,3,4, Bernat Corominas-Murtra5,
Mario Dzemidzic6, David Kareken6, Mario Ventresca1,7, and Joaquín Goñi1,2,8

1School of Industrial Engineering, Purdue University, West Lafayette, IN, Etats-Unis
2Purdue Institute for Integrative Neuroscience, Purdue University, West Lafayette, IN, Etats-Unis
3Institute of Bioengineering/Center for Neuroprosthetics, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Suisse
4Department of Radiology and Medical Informatics, University of Geneva, Suisse
5Department of Zoology, Institute of Biology, Karl-Franzens University Graz, Graz, Austria
6Department of Neurology, Indiana University School of Medicine, Indianapolis, IN, Etats-Unis
7Purdue Institute of Inflammation, Immunology, and Infectious Disease, Purdue University, West Lafayette, IN, Etats-Unis
8Weldon School of Biomedical Engineering, Purdue University, West Lafayette, IN, Etats-Unis

Mots clés: Functional reconfiguration, Functional configural breadth, Resting-state networks,
Functional connectomes

ABSTRAIT

The quantification of human brain functional (concernant)configurations across varying cognitive
demands remains an unresolved topic. We propose that such functional configurations may be
categorized into three different types: (un) network configural breadth, (b) task-to task transitional
reconfiguration, et (c) within-task reconfiguration. Such functional reconfigurations are rather
subtle at the whole-brain level. Ainsi, we propose a mesoscopic framework focused on
functional networks (FNs) or communities to quantify functional (concernant)configurations. To do so, nous
introduce a 2D network morphospace that relies on two novel mesoscopic metrics, trapping
efficiency (TE) and exit entropy (EE), which capture topology and integration of information
within and between a reference set of FNs. We use this framework to quantify the network
configural breadth across different tasks. We show that the metrics defining this morphospace
can differentiate FNs, cognitive tasks, and subjects. We also show that network configural
breadth significantly predicts behavioral measures, such as episodic memory, verbal episodic
mémoire, fluid intelligence, and general intelligence. En substance, we put forth a framework to
explore the cognitive space in a comprehensive manner, for each individual separately, and at
different levels of granularity. This tool that can also quantify the FN reconfigurations that result
from the brain switching between mental states.

RÉSUMÉ DE L'AUTEUR

Understanding and measuring the ways in which human brain connectivity changes to
accommodate a broad range of cognitive and behavioral goals is an important undertaking.
We put forth a mesoscopic framework that captures such changes by tracking the topology
and integration of information within and between functional networks (FNs) du cerveau.
Canonically, when FNs are characterized, they are separated from the rest of the brain
réseau. The two metrics proposed in this work, trapping efficiency and exit entropy, quantify
the topological and information integration characteristics of FNs while they are still

un accès ouvert

journal

Citation: Duong-Tran, D., Abbas, K.,
Amico, E., Corominas-Murtra, B.,
Dzemidzic, M., Kareken, D., Ventresca,
M., & Goñi, J.. (2021). A morphospace of
functional configuration to assess
configural breadth based on brain
functional networks. Réseau
Neurosciences, 5(3), 666–688. https://est ce que je
.org/10.1162/netn_a_00193

EST CE QUE JE:
https://doi.org/10.1162/netn_a_00193

Informations complémentaires:
https://doi.org/10.1162/netn_a_00193

Reçu: 2 Janvier 2020
Accepté: 17 Mars 2021

Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.

Auteur correspondant:
Joaquín Goñi
jgonicor@purdue.edu

Éditeur de manipulation:
Claus C. Hilgetag

droits d'auteur: © 2021
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence

La presse du MIT

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A morphospace framework to assess brain functional networks

embedded in the overall brain network. Trapping efficiency measures the module’s ability
to preserve an incoming signal from escaping its local topology, relative to its total exiting
weights. Exit entropy measures the module’s communication preferences with other modules/
networks using information theory. When these two metrics are plotted in a 2D graph as a
function of different brain states (c'est à dire., cognitive/behavioral tasks), the resulting morphospace
characterizes the extent of network reconfiguration between tasks (functional reconfiguration),
and the change when moving from rest to an externally engaged “task-positive” state (functional
preconfiguration), to collectively define network configural breadth. We also show that these
metrics are sensitive to subject, task, and functional network identities. Dans l'ensemble, this method is a
promising approach to quantify how human brains adapt to a range of tasks, and potentially
to help improve precision clinical neuroscience.

INTRODUCTION

Human behavior arises out of a complex interplay of functional dynamics between different
brain networks (Bassett & Gazzaniga, 2011). These interactions are reflected in functional net-
travail (FN) reconfigurations as subjects perform different tasks or are at rest (Amico, Abbas,
et coll., 2019; Amico et al., 2020; Cole, Bassett, Power, Plus courageux, & Petersen, 2014). One of
the network neuroscience challenges is to develop a comprehensive framework to quantify
the brain network (concernant)configurations across different mental states and cognitive tasks. To that
end, configurations across a collection of cognitive tasks can be conceptualized at three dis-
tinct levels of granularity:

▪ Network configural breadth represents, for an FN, a given individual’s repertoire of cog-
nitive and emotional states through functional configurations while performing different
tasks. In practice, how well the entire “cognitive space” (Varona & Rabinovich, 2016;
Varoquaux et al., 2018) is sampled depends on the number and choice of the tasks.
This concept is inspired by Schultz and Cole (2016).

▪ Task-to-task transitional reconfiguration represents the specific shift in network functional
configuration when a subject switches between cognitive/mental tasks (Douw, Wakeman,
Tanaka, Liu, & Stufflebeam, 2016; Gonzalez-Castillo et al., 2015). Par exemple, task tran-
sitions and accompanying reconfigurations will occur when a subject transitions from
quiet reflection to engage in a spatial problem-solving task, or from a lexical retrieval to
a decision-making paradigm.

▪ Within-task reconfiguration represents specific network functional configuration changes
that may occur within a single task. This phenomenon has been assessed at the whole-
brain level, showing the presence of distinct brain states within a task (Bassett et al.,
2011; Betzel, Satterthwaite, Gold, & Bassett, 2017; J.. M.. Shine et al., 2016; J.. M.. Shine
et coll., 2019; J.. M.. Shine & Poldrack, 2018).

While brain network configural properties are task and subject dependent (Schultz & Cole,
2016), task-induced functional (concernant)configurations are rather subtle in whole-brain functional
connectomes, even when comparing task with rest (Cole et al., 2014). En outre, mesoscopic
structures (par exemple., functional networks of the brain) exhibit modular characteristics that adapt to
cognitive demands without significantly affecting the rest of the system where higher levels of
cognition emerge through the changing interactions of subsystems, instead of pairwise edge-

667

Network configural breadth:
Represents, for an FN, a given
individual’s repertoire of cognitive
and emotional states through
functional configurations while
performing different tasks. Dans
pratique, how well the entire
“cognitive space” is sampled
depends on the number and nature
of the tasks. The functional network
configural breadth, for a given
subject and a given FN, est
compartmentalized into two
components: (un) FN (task)
reconfiguration and (b) FN rest-
to-[task-positive] preconfiguration.

Task-to-task transitional
reconfiguration:
Represents the specific shift in the
network functional configuration of
an FN when a subject switches
between distinct cognitive/mental
tasks. Par exemple, task transitions
and accompanying reconfigurations
will occur when a subject transitions
from quiet reflection to engage in a
spatial problem-solving task, or from
a lexical retrieval to a decision-
making paradigm.

Within-task reconfiguration:
Represents specific network
functional configuration changes of
an FN that may occur within a single
task. This phenomenon has been
assessed at the whole-brain level,
showing the presence of distinct
brain states within a task. Pour
instance, within-task reconfiguration
can be tracked by using dynamic
(sliding-window) functional
connectivité.

Neurosciences en réseau

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A morphospace framework to assess brain functional networks

Module trapping efficiency (TE):
Quantifies the capacity of an FN to
act as a segregated module and
hence contain (or trap) a signal
within its local topology.

Module exit entropy (EE):
Quantifies the uncertainty of a signal
in taking a specific exiting node
while escaping the local topology of
an FN.

Functional magnetic resonance
imaging (IRMf):
A noninvasive imaging modality that
estimates brain activity by detecting
changes associated with levels of
blood oxygenation. The rationale of
this technique relies on the fact that
there is an association between
blood oxygenation and neuronal
activation.

Functional reconfiguration:
Quantifies the flexibility of an FN as
a subject adapts to different cognitive
tasks (excluding rest). In this work, it
is represented by a two-dimensional
spatial volume derived from a given
FN’s EE and TE coordinate values
across different cognitive tasks.

Resting-state networks:
Spontaneous brain activity is
organized into a robust and
reproducible (across subjects) set of
localized and distributed networks,
denoted resting-state networks
(RSNs). One of the most common
sets of RSNs divides the cortex
into seven RSNs: visuel ( VIS),
somatomotor (SM), dorsal attention
(DA), ventral attention ( VA), limbic
(LIM), frontoparietal (FP), and default
mode network (DMN). RSNs can be
characterized by their functional
connectivity in terms of within-
network cohesion and between-
network integration. RSNs can also
be referred to as functional networks
(FNs).

Neurosciences en réseau

level interactions (Bassett et al., 2011). Ainsi, a mesoscopic scale (as the one provided by func-
tional networks or communities/modules) may uncover differential patterns of (concernant)configuration
(Mohr et al., 2016), across functional subcircuits, which might otherwise not be detectable at other
scales. Traditionnellement, a mesoscopic assessment of functional brain networks would involve the
detection of functional communities (Sporns & Betzel, 2016) either based on topology (density-
based; Newman, 2006un, 2006b) or based on the information flow (flow-based; Rosvall, Axelsson,
& Bergstrom, 2009; Rosvall & Bergstrom, 2008). These approaches, cependant, are not designed to
track the dynamic behavior of a priori set of communities across time, tasks, and/or subjects. Le
primary aim of this work is to clearly define and quantify different configurations that FNs can
assume, as well as measure their nature of reconfigurations switching between a seemingly infinite
number of cognitive states. From a graph-theoretical perspective, FNs and their corresponding
reconfigurations are described by two attributes: topology and communication. From a system
dynamic perspective, FNs can be characterized by segregation and integration (Sporns, 2013)
properties across which the human brain reconfigures across varied cognitive demands
(J.. Shine et al., 2018; J.. M.. Shine et al., 2016; J.. M.. Shine et al., 2019; J.. M.. Shine & Poldrack,
2018). To formally capture these diverse characteristics of FNs, we constructed a mathematically
well-defined and well-behaved 2D “mesoscopic morphospace” based on two novel measures
defined for nonnegative, undirected, weighted functional connectomes: trapping efficiency (TE)
and exit entropy (EE). Trapping efficiency captures the level of segregation/integration of a func-
tional network embedded in the rest of the functional connectome and quantifies the extent to
which a particular FN “traps” an incoming signal. Exit entropy captures the specificity of integra-
tion of an FN with the rest of the functional connectome, and quantifies the uncertainty as to where
(in terms of exit nodes) that same signal would exit the FN. En résumé, this mesoscopic morpho-
space is a representation of the cognitive space as explored within and between cognitive states, comme
reflected by brain activity in fMRI. Such representation relies on FN reconfigurations that can be
tracked, at an individual level, and at different granularity levels in network (concernant)configurations.

By using this 2D TE, EE-based morphospace, we formally study network configural breadth
(Figure 1A), the most global and coarse grain exploration of the cognitive space, and its sub-
sequent functional configuration components. To that end, we formally define measures of (un)
functional reconfiguration (capacity of an individual to reconfigure across widely differing
cognitive operations) et (b) functional preconfiguration (efficiency of transition from resting
state to task-positive state (Schultz & Cole, 2016)), for potentially any community or FN. These
measures are quantified for resting-state networks (Yeo et al., 2011) on the 100 unrelated sub-
jects from the Human Connectome Project (HCP) dataset. We then study how such quantifi-
cation is related to measures of cognitive abilities, such as fluid intelligence.

A MESOSCOPIC MORPHOSPACE OF FUNCTIONAL CONFIGURATIONS

The mesoscopic morphospace proposed here is a two-dimensional space built upon trapping
efficiency and exit entropy measures for assessing functional networks or communities of func-
tional connectomes. In this framework, functional connectomes must be undirected (symmetrical)
weighted graphs, with nonnegative functional couplings. This framework allows for any a priori
partition into functional communities. In this work, we assess the resting-state functional networks
as proposed by Yeo et al. (2011) as the a priori FNs. Aussi, we use functional connectivity (without
incorporating structural connectivity information), which is a quantification of statistical depen-
dencies between BOLD time series of brain regions, and it can be used as a proxy of communi-
cation dynamics in the brain (Fornito, Zalesky, & Bullmore, 2016). Under this section, further
technical details that are not mentioned in the main text will be directed to different subsections
in the Supporting Information.

668

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A morphospace framework to assess brain functional networks

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 1. The three types of brain (concernant)configurations that can be represented by a mathematical space parameterized by, in this case, deux
generic phenotypic measures of functional communities of the brain: (UN) network configural breadth, which represents changes across a num-
ber of cognitive demands; (B) task-to-task transitional reconfiguration; et (C) within-task reconfiguration.

Functional connectome/connectivity
(FC) matrice:
A network representation of the
functional coupling between brain
régions. Such coupling is usually
measured by quantifying the
statistical dependencies between
time series of brain regions (par exemple.,
pairwise Pearson’s correlation,
mutual information) as obtained by
functional magnetic resonance
imaging (IRMf).

Computing Mechanistic Components for Morphospace Measures

A mesoscopic morphospace is constructed to assess functional network behaviors through two focal
lenses: level of segregation/integration (using graph topology), and specificity of integration (en utilisant
information theory). We first define all necessary components to compute TE and EE as follows:

(un) The whole-brain functional connectome (FC) is graph-theoretically denoted by G(V, E ),
where V is the set of vertices (represented by the regions of interest, ROI) and E is the set
of edges (quantified by functional couplings between pairs of ROIs). The whole-brain FC
is mathematically represented by an adjacency structure denoted as A = [wij], where i, j
are indexed over vertex set V and wij

2 [0, 1] are functional couplings.

(b) Using a predefined set of FNs, a functional community (graph-theoretically denoted as
GC(VC, EC) or for short) is defined to have the corresponding node set VC (cid:2) V and edge set
EC (cid:2) E for which the union over all FNs exhaust the vertex and edge set of G such that
[VC ¼ V and [ EC ¼ E:

(c) For a given functional community C (cid:2) G, define the set of states (or equivalently, ver-
tices) S that contains the set of transient states (denoted as Strans = VC), and absorbing
states (denoted as Sabs = {j | wij > 0; j =2 VC, 8 je 2 VC}) such that

S ¼ Strans [ Sabs:

(d) We mathematically denote a whole-brain FC as A = [wij] (see the Constructing
Functional Connectomes section of the Supporting Information for more details), où

Neurosciences en réseau

669

A morphospace framework to assess brain functional networks

i and j are brain regions (from now on denoted as vertices or states) of the specified
parcellation or atlas. Each matrix A represents a single subject, single session, single task
whole-brain FC. We assess the whole-brain FC with respect to organizations into FNs,
here denoted by C. For a specific A and a specific C, we obtain an induced submatrix AC
by extracting the corresponding rows and columns of matrix A using only the vertices
that belong to S, which results in the following matrix:

AC 2 0; 1ð

Þ Sj j(cid:3) Sj j:

We note that the row and column order of the states (or vertices) of AC respects the order
[ Sabs with transient states followed by absorbing ones, which results in a
of S = Strans
blockage structure:

AC ¼

Transient

Absorbing

ð

Transient
Absorbing
(cid:1)
Þ A Strans; Sabs
ð
A Strans; Strans
Þ
Þ
ð
A Sabs; Sabs
Þ
ð
; Strans
A Sabs

(cid:3)
;

where A(Strans, Strans) means that we extract the submatrix of A that corresponds to states
in Strans for the rows (first argument) and Strans for the columns (second argument).
(e) For any functional network C, using the induced adjacency structure AC in the previous
step, define each vertex in S to be a state in the stochastic process and construct the
corresponding terminating Markov chain by computing the following:

▪ the normalization of AC by the nodal connectivity strength:

Q ¼ D−1

C AC 2 0; 1ð

Þ Sj j(cid:3) Sj j;

where DC is the weighted degree sequence matrix filled with the node strength (defined
by the row [or equivalently, column] sum of AC) in the diagonal entries and zeros for the
off-diagonal elements:

(cid:4)

DC ¼ dij

(cid:5)

¼

(

P.

j

j¼ VCj
j¼1 wij; 8i ¼ j

0; 8i≠j

;

where i, j are indexed over S. Note that the order of rows and columns of Q and DC also
respect the order of S.

▪ the transition probability matrix of the terminating Markov chain:

P ¼

Transient

Absorbing

Transient
Q Strans; Strans

ð

0 Sabs
j

j
j(cid:3) Strans

j

ð

Absorbing
Þ Q Strans; Sabs
I Sabs
j

j

Þ

!

;

où 0|Sabs|×|Strans| is the matrix of all zeros (size |Sabs| rows by |Strans| columns); je|Sabs| est
identity matrix of size |Sabs|; the index C for Q and P is dropped for simplicity.

(F) Using matrix P, we extract the submatrix induced by states in Strans (denoted by P|Strans).
Note that P|Strans = Q (Strans, Strans) because rows and columns of P respect the order of S. Nous
then compute the fundamental matrix (denoted as Z; Kemeny & Snell, 1960), which con-
tains the mean number of steps a specific transient state in Strans is visited, for any pair of
transient states in Strans, before the random walker is absorbed by one of the states in Sabs:

Z ¼ ðIjStrans

− Pj

Strans

Þ−1 2 R Strans

j
þ

j
j(cid:3) Strans

j

:

Neurosciences en réseau

670

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A morphospace framework to assess brain functional networks

(g) Compute the mean time to absorption (denoted as τ), which contains the mean number of
steps that the random particle needs to be absorbed by one of the states in Sabs, given that it
starts in some state in Strans:

τ ¼ Z1 Strans

j

j
j 2 R Strans
þ

j(cid:3)1

;

où 1|Strans| is the all one vector of size |Strans|.

(h) Compute the absorption probability matrix (denoted as Ψ ), which contains the likelihood of
being absorbed by one of the absorbing states, given that the stochastic process starts in
some transient state:

je

h
P.

(cid:6)
(cid:6)

Strans;Sabs

Ψ ¼ Z

j
2 R Strans
þ

j
j(cid:3) Sabs

j

;

where P|Strans,Sabs is the subtransition probability matrix induced from (row) state Strans and
(column) state Sabs. Ainsi, P.|Strans,Sabs = Q(Strans, Sabs).

Module Trapping Efficiency

Module trapping efficiency, denoted as TE (unit: steps
weight), quantifies a module’s capacity to contain
a random particle from leaving its local topology, c'est, C. Spécifiquement, through FN topology,
we want to assess its level of segregation/integration, measured by the L2 norm of τ (unit: steps),
c'est, the mean time to absorption of nodes in C, normalized by its total exiting strength (unit:
weight), measured by

X

LC ¼

ð
Aij ¼ A Strans; Sabs

Þ:

i2Strans;j2Sabs

Mathematically, trapping efficiency is quantified as follows:

TE ¼

τk k
2
LC

:

(1)

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

t

.

We see that the mean time to absorption vector, τ, is dependent on both density-based
(Fortunato, 2010; Newman, 2006b) and flow-based (Malliaros & Vazirgiannis, 2013;
Rosvall et al., 2009; Rosvall & Bergstrom, 2008) modularity. The mean-time-to-absorption vec-
tor τ for which τ
i contains the average number of steps a random walker needs to escape the
FN topology, given that it starts from node i. This means that the numerical values in τ are
always greater than or equal to 1. We chose to use L2 norms because it squares the input
values of the vector and thus enhances our capacity to quantify FN (concernant)configuration. Sur
the other hand, the denominator LC is a simple statistical summary of the module “leakages”
to the rest of the cortex. Since all the values in LC are between (0, 1), L2 norm would have
diminished the differences across FNs. Ainsi, we chose L1 norm for the denominator. The role
of LC is to account for potential differences in trapping efficiency due to community size.
Numerically, higher TE indicates that a module is more segregated (or equivalently, less inte-
grated). This is because the FN topology traps the incoming signal efficiently, relative to its
exiting edges when embedded in the cortex. TE value ranges are given in Figure 2.

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Module Exit Entropy
Module exit entropy (denoted as EE, and in the range EE 2 (0, 1] and unitless) assesses the
normalized level of uncertainty in selecting an exiting node in Sabs of a random particle that
starts in C. The exit entropy, denoted as H
e, measures the level of uncertainty exiting node

Neurosciences en réseau

671

A morphospace framework to assess brain functional networks

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

t

.

Chiffre 2. Morphospace measurements, examples. All three induced subgraphs have the same cardinality (|C| = 8) with a different number of
exits (connections to G \ C). Néanmoins, depending on their topological structures, the corresponding morphospace measurements (TE and
EE) have rather distinct values.

j 2 Sabs (outside of the module) is preferred. Module exit entropy is mathematically formal-
ized as

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

P.

EE ¼

−

¼

Il
N C

j

j
Sabs
ψ
i¼1
ð
j
log Sabs

i log ψ
ð
Þ
j

Þ

je

;

(2)

P.

The numerator of EE(C), c'est, −

where preferential exit probability is the probability vector that contains |Sabs| entries that repre-
sents the likelihood that exit signal selects a specific exiting state j 2 Sabs such that (cid:1)
j = 1.
j

i log(ψ
je), measures the degree to which channels of
communication between nodes in Strans and Sabs are preferred for a fixed task/subject. It is note-
worthy that EE is not influenced by the (cumulative) magnitudes (of functional connectivity
valeurs) that connect nodes from within the FN to outside (exiting) nodes. It is only affected by
the distribution of such values. En particulier, homogeneous distributions display high entropy
levels, and uneven distributions favoring certain exiting node(s) display low entropy. À

j
Sabs
i¼1

j2Sabs

ψ

ψ

Neurosciences en réseau

672

A morphospace framework to assess brain functional networks

demonstrate this point, an example is provided in the Supporting Information under the Module
Exit Entropy section. The normalizer, N C = log(|Sabs|), is the maximum entropy obtained from a
module in which all exit nodes have the same absorption rate. Numerically, a high EE would
denote the homogeneous integration within the rest of the system, whereas a low EE would in-
dicate a preferential communication or integration of the module with the rest of the system. Dans
terms of functional brain networks, module exit entropy facilitates the understanding of collec-
tive behavior from C to other FNs through its outreach channels (edges formed by nodes in C and
exiting nodes in G \ C. This is because entropy measures the level of uncertainty in communi-
cation; hence, lower entropy means higher specificity in communication between the FN with
the rest of the cortex. EE value ranges are given in Figure 2.

The Definition of the Mesoscopic Morphospace Ω
The two distinct features of each FN in brain graphs are addressed by a point u(C ) in Ω (cid:2) (0, M. ) ×
[0, 1] (cid:2) R2 as follows:

u Cð Þ ¼ TE Cð Þ; EE Cð Þ

ð

Þ 2 Ω;

(3)

where M < ∞. For a given subject and task, a functional brain network G is obtained with a pre- defined parcellation that results in l induced subgraph C (cid:2) G. We can then obtain l points u(C) corresponding to l FNs in network G. In general, trapping efficiency TE(C ) is finitely bounded by construction (see more details in the Module Trapping Efficiency section in the Supporting Information). However, a better bound is possible for the HCP dataset used for this study. This is due to two driving factors: connectome sparsity and edge weights (Avena-Koenigsberger, Goñi, Solé, & Sporns, 2015). We address the upper bound for TE as max(TE(C)) = M = 1. In terms of EE(C), its numerical range EE(C) 2 (0, 1]. Hence, Ω (cid:2) (0, 1) × [0, 1] for this dataset. THE NETWORK CONFIGURAL BREADTH FORMALISM Studying the manifold topology defined in this 2D mesoscopic morphospace theoretically re- quires an infinite amount of points. In finite domain with discrete sampling of the morpho- space, polytope theory, a mathematical branch that studies object geometry, allows us to create a reasonable scaffold presentation with well-defined properties to formally define and quantify configural components of the functional networks. Polytope theory is a branch of mathematics that studies the geometry of shapes in a d- dimensional Euclidean space, Rd. Given a set of points in this space, W = {x1, x2, …, x|W|}, a convex hull formed by W is represented by l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 6 6 1 9 6 0 5 1 4 n e n _ a _ 0 0 1 9 3 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 ( Conv Wð Þ ¼ XWj j XWj j αjxjj αj ¼ 1; αj ≥ 0 ) : j¼1 j¼1 One can compute the notion of volume of the convex hull enclosed by Conv(W ), denoted as Vol(Conv(W )). Given that the morphospace is 2D, the manifold dimension can be from 0 up to 2. In the Supporting Information under the Polytope Theory section, further details on volume computation are defined. 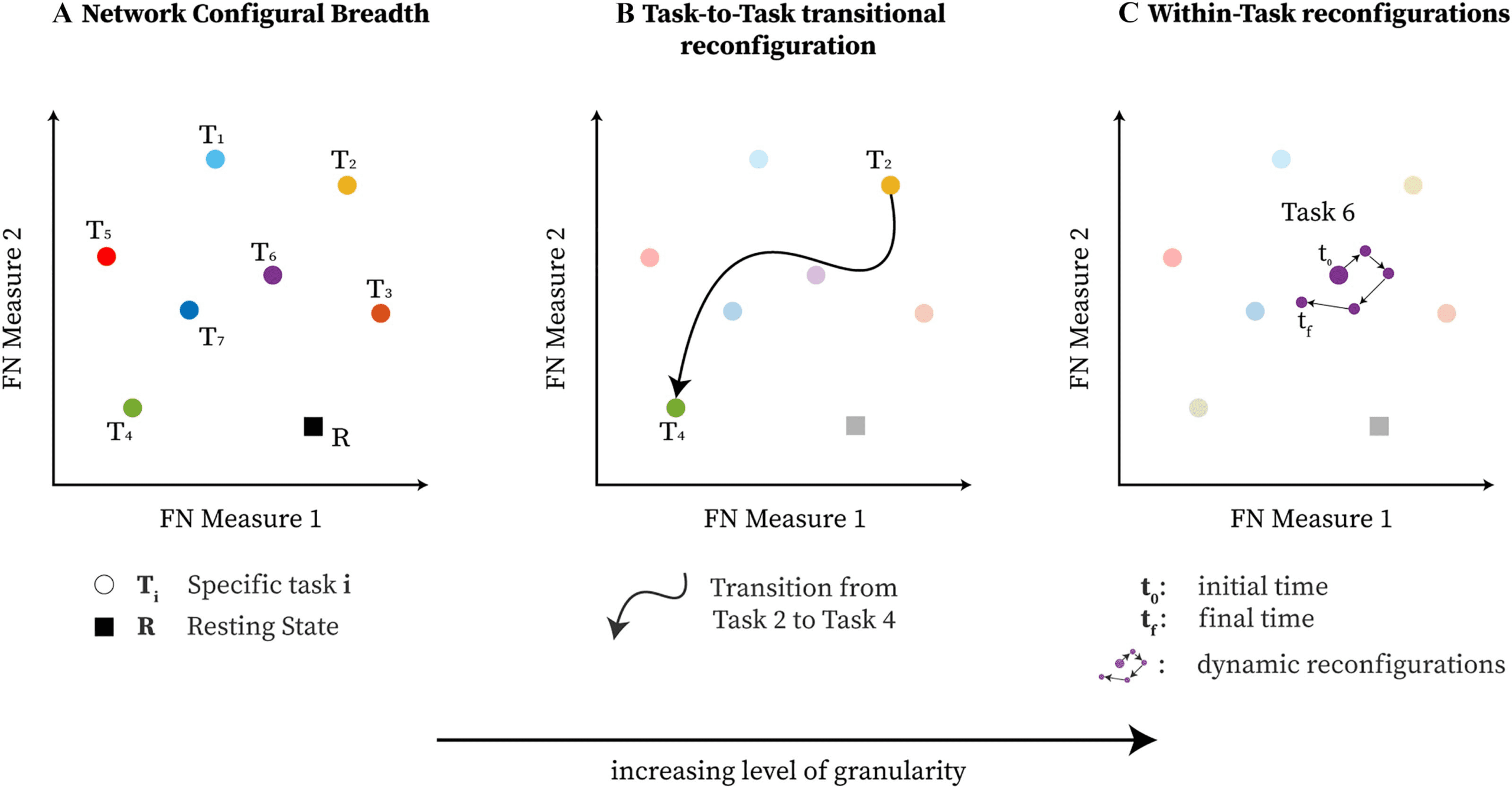The functional network configural breadth, for the ith subject, is compartmentalized into two components: ▪ FN (task) reconfiguration and ▪ FN rest-to-[task-positive] preconfiguration. Network Neuroscience 673 A morphospace framework to assess brain functional networks We then propose a mathematical relation between network configural breadth with FN re- configuration and preconfiguration as follows: (cid:7) F i ¼ f RFN i (cid:8) ; ; PFN i (4) where F i represents configural breadth for subject ith. Here, we provide directly the measures that quantify (functional) reconfiguration and preconfiguration of FNs for ith subject’s config- ural breadth. Tasks are assigned the same level of importance, and hence, no task is weighted more than others. Functional Reconfiguration Definition 1. Functional reconfiguration in this work is represented by a two-dimensional spatial volume derived from given FN’s EE and TE coordinate values across different cognitive tasks. As such, it represents an example of “cognitive space” (Varona & Rabinovich, 2016; Varoquaux et al., 2018) within a functional domain that spans a variety of network states under various task-evoked conditions. We quantify this as (cid:7) (cid:7) (cid:8) (cid:8) RFN i ¼ Vol Conv W FN i ; (5) where W FN Vol(Conv(W FN i i represents the set containing all investigated task coordinates of subject i’s FN; )) is the convex hull volume induced by points in W FN i . For a given subject ith’s FN, note that Conv(W FN i represents the broad span (breadth) of task configurations for a given functional community. Subsequently, RFN represents the amount of breadth as measured by the volume of Conv(W ). Functional reconfiguration for a given sub- ject’s FN, denoted as RFN , is geometrically depicted in Figure 3. i i Functional Preconfiguration Definition 2. Functional preconfiguration reflects the topologically distributed equipotentiality that is theoretically designed to enable an efficient switch from a resting-state configuration to a task-positive state (Schultz & Cole, 2016), and is quantified as follows: PFN i ¼ RestFN i − η W FN i ; (6) (cid:9) (cid:9) (cid:9) (cid:9) (cid:9) (cid:9) 2 is the geometrical centroid of W FN W FN i where η general position (represented by η W FN i it is the 2 norm in Euclidean space. ; PFN i i measures the distance between rest to task ). It is defined with the selected metric space, in this case Functional preconfiguration: Reflects, for an FN, the ease of functional transition from a resting- state configuration to a task-positive state. In this work, it is represented using Euclidean distance between TE and EE coordinates of resting state and geometric centroid of the cognitive tasks. Note that functional preconfiguration can be viewed as Vol(Conv(W )) where the convex hull is defined solely by two points: FN’s rest and FN’s geometrical centroid of task convex hull, that is, W = {RFN }. In such regards, the notion of Vol(Conv(W )) is also suitable to , η i W FN i describe the configural breadth between rest and task-positive location. Functional preconfi- guration is geometrically depicted in Figure 3. RESULTS The mesoscopic morphospace formalized in the Mesoscopic Morphospace of Functional Configurations section is used to assess network configural breadth in terms of functional pre- configuration and reconfiguration for the 100 unrelated subjects of the HCP 900-subject data release (Van Essen et al., 2013; Van Essen et al., 2012). This dataset includes (test and retest) Network Neuroscience 674 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 6 6 1 9 6 0 5 1 4 n e n _ a _ 0 0 1 9 3 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 A morphospace framework to assess brain functional networks Figure 3. Functional network configural breadth is geometrically represented using two predefined morphospace measures. Specifically, for mesoscopic structures such as communities in functional brain networks, the first measure is trapping efficiency (TE) while the second is exit entropy (EE). In this case, tasks T1 to T5 belong to the convex hull (e.g., Pareto front; further details are available in the Supporting Information under the Polytope Theory section), while T6 and T7 are in the interior enclosed by the convex hull. sessions for resting state and seven fMRI tasks: gambling (GAM), relational (REL), social (SOC), working memory ( WM), language processing (LANG), emotion (EMOT), and motor (MOT). Whole-brain functional connectomes estimated from this fMRI dataset include 360 cortical brain regions (Glasser et al., 2016) and 14 subcortical regions. The functional communities evaluated in the morphospace include seven cortical resting-state FNs from Yeo et al. (2011); visual ( VIS), somatomotor (SM), dorsal attention (DA), ventral attention ( VA), fronto- parietal (FP), limbic (LIM), default mode (DMN), and one composed of subcortical regions (SUBC). Additional details about the dataset are available in the Supporting Information, HCP Dataset and HCP Functional Data sections. 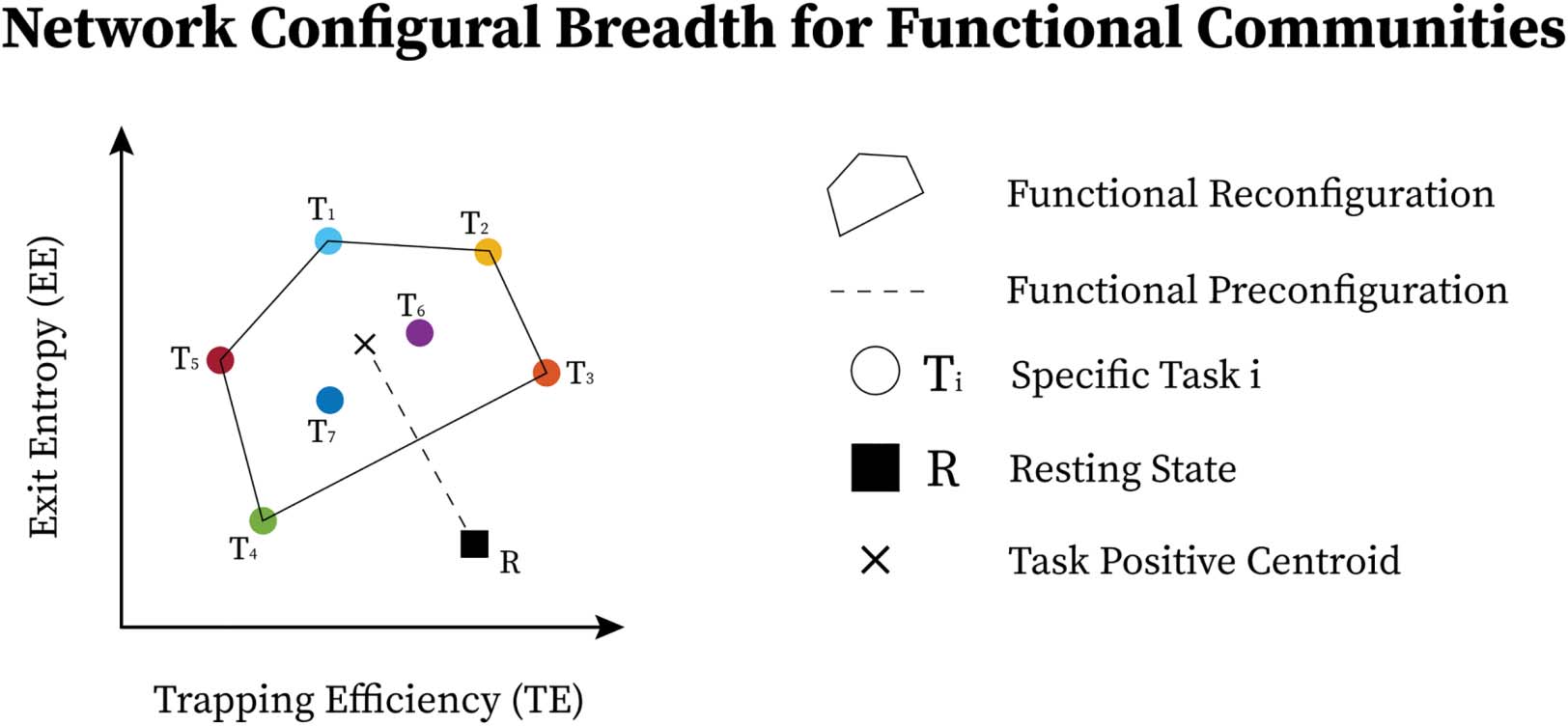Task and Subject Sensitivity Within- and between-subject task sensitivity. We first evaluate the capacity of module trapping efficiency and exit entropy to differentiate between tasks within subject (Figure 4A). For both test and retest sessions of each subject, we compute the TE and EE metrics for each FN. We compute these values for all eight fMRI conditions. We compute the intraclass correlation co- efficient (ICC), with test and retest (per subject) being the repeated measurements and task being the class variable (TE in Figure 4A, top and EE in Figure 4A, bottom, respectively, where each ICC is computed using a 2 [test, retest] by 7 [tasks] design, and the ICC reflects task within-subject sensitivity). For most subjects, ICC values in all FNs are high and positive values. EE displays a higher within-subject task sensitivity than TE. Specifically, TE in VIS, DA, and DMN most distinguished between the cognitive tasks, whereas EE in VA and FP was best at distinguishing the within-subject task-based configural changes. The ICC values for both coordinates were the lowest for LIM. We then evaluate the degree to which morphospace metrics capture cohort-level config- ural changes. To test this, for each morphospace metric (TE or EE), we compute ICC of each FN with subjects as the repeated measures and task as the class variable (Figure 4B). We per- formed the evaluation separately for test and retest sessions as denoted by gray and dark bars, respectively, for TE (Figure 4B, top) and EE (Figure 4B, bottom). EE captures cohort-level task- Network Neuroscience 675 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 6 6 1 9 6 0 5 1 4 n e n _ a _ 0 0 1 9 3 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 A morphospace framework to assess brain functional networks Figure 4. Morphospace measures and their task and subject sensitivity measured by intraclass correlation coefficients for each functional network. (A) Within-subject task sensitivity of module trapping efficiency (TE) and exit entropy (EE) for each FN per subject. (B) Between-subject task sensitivity of TE (top) and EE (bottom). (C) Subject-sensitivity ICC of TE (top) and EE (bottom). based signatures as ICC values are consistently higher than those of TE. Interestingly, LIM has the lowest cohort-level task-based sensitivity for both morphospace metrics. Subject sensitivity across tasks. Here, we compute ICC considering the tasks (fMRI conditions) the repeated measurements and considering subjects the class variable (Figure 4C). It is note- worthy that TE is superior in uncovering subject fingerprints, compared with EE, for the ma- jority of FNs. This is complementary to EE being more task-sensitive. TE and EE are disjoint features. Results in the Task and Subject Sensitivity section suggest that TE and EE have the differentiating capacity to highlight nonoverlapping characteristics of objects under consideration, that is, task- and subject-based FNs. First of all, for within-subject task differentiation (Figure 4A), FNs with high ICC values in one measure do not necessarily show a similar tendency in the other. For instance, VA has the third lowest mean TE value in char- acterizing within-subject task differentiation but it has the highest mean EE score. Similarly, FP has the second lowest average TE score and the third highest EE score, indicating that each of the two measures captures unique aspects of a given FN. Second, evidence of disjoint features is shown through the ICC results in cohort-level task-sensitivity (Figure 4B) and subject- sensitivity (Figure 4C) configural changes. Indeed, TE is superior in detecting subject finger- prints, while EE is better in unraveling task fingerprints. The idea is that, for a given studied object (i.e., task-based FNs), configurations are shown to “stretch” in exclusive/disjoint direc- tions (subject-sensitive trapping efficiency and task-sensitive exit entropy). Quantifying Network Configural Breadth on Functional Networks The mesoscopic morphospace allows the quantification of network configural breadth. For a given functional community, we compute functional reconfiguration (degree of configurations across tasks) and preconfiguration (distance from rest to task-positive state), using Formulas 5 and 6, respectively. Group-average results. The group-average behavior of functional communities is shown in Figure 5. Functional reconfiguration of FNs are shown as filled convex hulls, whereas precon- figuration of FNs are shown as dashed lines from rest to the corresponding task hull geometric centroid. To facilitate comparing network configural breadth across all functional networks, Network Neuroscience 676 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 3 6 6 6 1 9 6 0 5 1 4 n e n _ a _ 0 0 1 9 3 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 A morphospace framework to assess brain functional networks l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 3 6 6 6 1 9 6 0 5 1 4 n e n _ a _ 0 0 1 9 3 p d . t Figure 5. Visualization of network configural breadth. Functional reconfiguration and preconfiguration for all FNs are represented using group average of individual subjects’ coordinates. Task coordinates in this space are represented by either an asterisk (*) or a plus (+) symbol. The asterisk symbol is used for those tasks that are part of the Pareto front of the convex hull; the plus symbol represents either the resting state or task that belongs to the interior of the convex hull. Note that x- and y-axis are purposely not scaled in the same range so that the full range of values for all tasks, task-centroid, and rest can be more easily visualized. 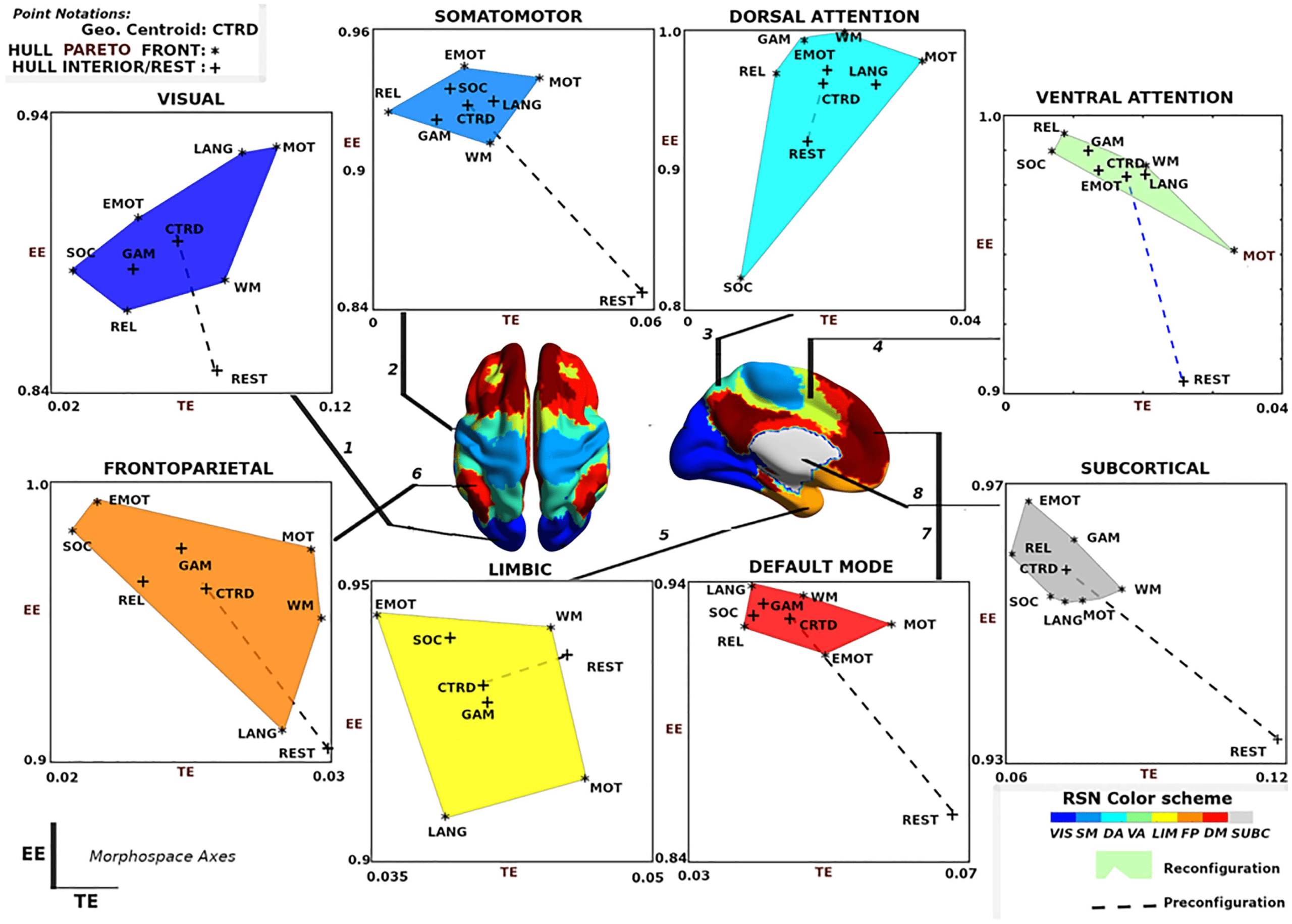f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 these same convex hulls are shown in Figure 6A with the same x- and y-axis values. VIS net- work polytope, representing group-average behavior, is lower in EE relative to other FNs. With the exception of VIS and SUBC, all other FNs cluster in a similar, high EE / low TE area of the morphospace (Figure 6A). It should be noted that different tasks and subject populations (e.g., older or clinical groups) might cluster FNs differently. We also note that the subcortical polytope is relatively high in exit entropy. However, the subcortical parcellation might not optimally reflect the functional and/or structural makeup of various subcortical regions (e.g., role of the basal ganglia in the motor system), so these results should be interpreted cautiously. 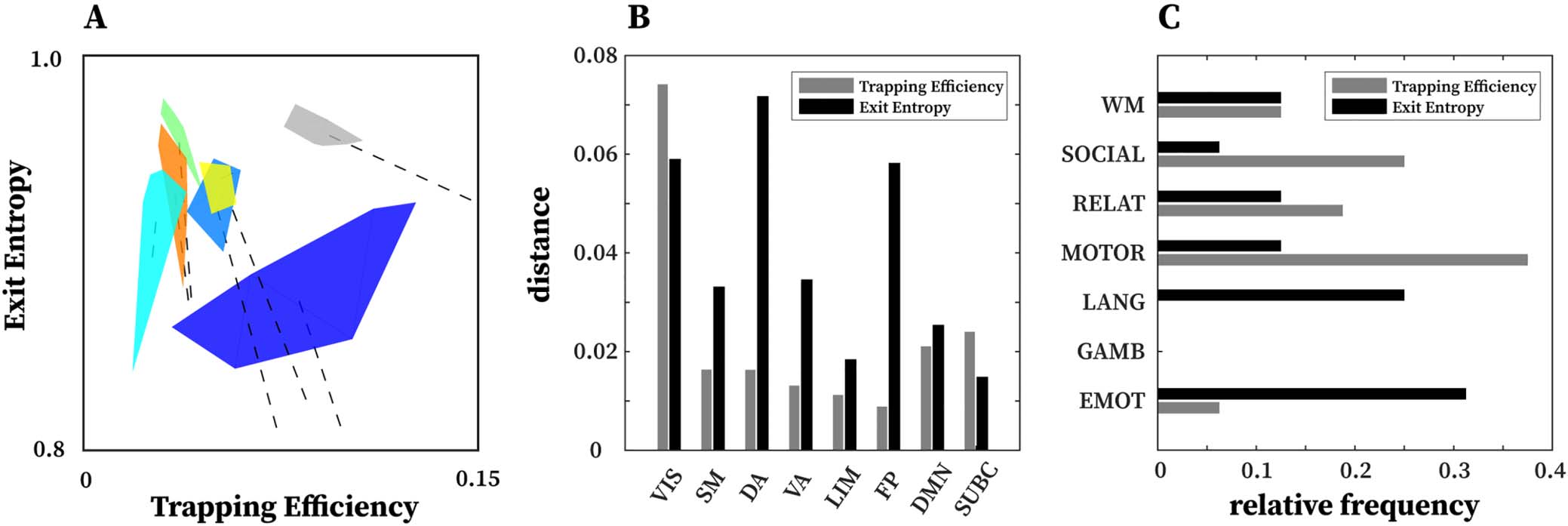One observation drawn from such a presentation is that the morphospace framework re- confirms, quantitatively, that functional dichotomy of the brain between task-positive and rest Network Neuroscience 677 A morphospace framework to assess brain functional networks Figure 6. Network configural breadth insights on functional networks and tasks. (A) An illustration of network configural breadth for all functional communities. Polytope colors are analogous to the scheme shown in Figure 5. For each functional community, the dashed line represents the amount of functional preconfiguration, whereas the polytope volume represents the amount of functional reconfiguration. (B) Maximal distance is computed using the maximum pairwise distance between two tasks for a given functional network. (C) Relative frequency with which a task appears in the maximal distance normalized by 16 (8 FNs and 2 tasks per FN). state (Fox et al., 2005). Specifically, the default mode network acts more as a segregated mod- ule with high level of integration specificity at rest - as seen in the lower right regime with high TE, low EE values - as opposed to under task-evoked conditions - as seen in the top left corner with low TE, high EE values (Figure 5, default mode; Fox et al., 2005; Greicius, Krasnow, Reiss, & Menon, 2003). Another observation is that in terms of segregation level measured by TE, the lower bound of subcortical convex hull is, approximately, the upper bound of other FNs, with the exception of the visual network. Figures 7.1A and 7.2A also summarize functional reconfiguration and pre- configuration, respectively, for test and retest fMRI sessions in all subjects and FNs. Here, the VIS system displays the largest functional reconfiguration (see Figure 7.1A). From Figure 7.2A, func- tional preconfigurations display a more comparable magnitude among all FNs. Further evidence of disjoint feature is also displayed in Figure 6B and 6C. In Figure 6B, maximal distance is computed using pairwise distances for two given tasks for a specific FN. The result shows that for a given FN, the two measures complement each other and in many cases, stretch the cognitive space in one direction or the other. For instance, in the case of DA and FP, the maximal distance in EE is very high but low for TE, whereas in VIS and SUBC, TE maximal distance is higher than that of EE. Furthermore, in Figure 6C, only specific tasks (e.g., motor and emotion) push the cognitive space in a particular direction (which is captured by maximal distance computation). Evidence of disjoint features is also illustrated by the relative frequency of motor and emotion tasks for which TE and EE are complementary. Subject specificity of pre- and reconfiguration of functional networks. The formulation of network configural breadth (in terms of preconfiguration and reconfiguration) enables us to assess these properties at the subject level. In Figure 7.1B and 7.2B, we use ICC to analyze the ability of morphospace measures (in the form of reconfiguration, panels Figure 7.1, and preconfiguration, panels Figure 7.2) to reflect subject identity within each FN. For all FNs from Yeo et al. (2011), the ICCs suggest that Network Neuroscience 678 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 6 6 1 9 6 0 5 1 4 n e n _ a _ 0 0 1 9 3 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 A morphospace framework to assess brain functional networks l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 3 6 6 6 1 9 6 0 5 1 4 n e n _ a _ 0 0 1 9 3 p d t . 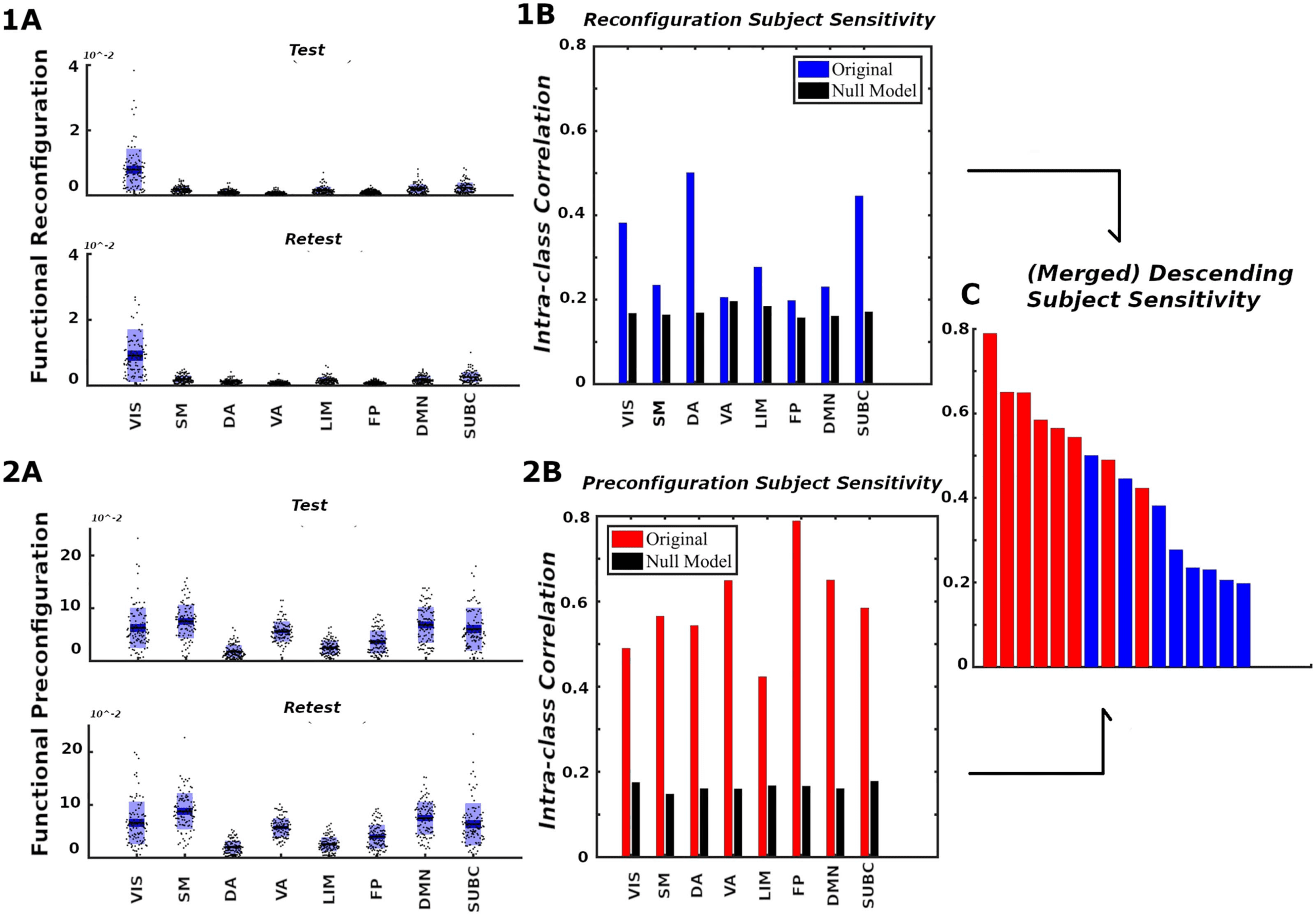Figure 7. Network configural breadth, subject specificity analysis. Panels 1 and 2 show functional reconfiguration and preconfiguration, respectively, from both magnitude and subject-sensitivity viewpoints. For each functional network, the (A) panels report subject’s preconfi- guration and reconfiguration values whereas the (B) panels quantify subject sensitivity. Reconfiguration and preconfiguration measures are displayed in blue and red, respectively. Panel (C) merges all 16 configural breadth terms in descending order of subject sensitivity. f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 subjects can be differentiated from each other when contrasted against a corresponding null model (for details, see the Supporting Information, Subject Sensitivity section). We see that subject-sensitivity scores of all eight FNs for both pre- and reconfigurations are higher than their corresponding null models. Finally, for a fixed FN, functional preconfigurations dominated the subject sensitivity ranking, as illustrated by Figure 7C. Furthermore, FP, DMN, and VA pre- configurations are among the FNs with the highest subject fingerprints in overall subject- sensitivity ranking. Network Configural Breadth and Behavior Network configural breadth, compartmentalized into FN reconfiguration RFN and preconfi- guration P FN, shows a high level of subject sensitivity. This allows us to assume that F i is associated with an individual’s behavioral measures (denoted as :>
i for subject ith). Several

Neurosciences en réseau

679

A morphospace framework to assess brain functional networks

studies reported that FP and DMN networks are associated with memory and intelligence
(Gray, Chabris, & Plus courageux, 2003; Schultz & Cole, 2016; Tschentscher, Mitchell, & Duncan,
2017). Donc, we evaluated whether the outlined framework reflects four widely studied
cognitive/behavioral measures, related to memory and intelligence: episodic memory, verbal
episodic memory (verb. epi. mem.), fluid intelligence gF, and general intelligence g. While
fluid intelligence reflects subject capacity to solve novel problems, general intelligence, g, concernant-
flects not only fluid intelligence, gF, traits but also crystallized (c'est à dire., acquired) connaissance
(Cattell, 1963, and typically denoted as gC ). The early notion of general intelligence is con-
ceptualized by Spearman’s positive manifold (Spearman, 1904) that cannot be fully described
using a single task. Quantification of g can be accomplished using subspace extraction tech-
niques such as explanatory factor analysis (Dubois, Galdi, Paul, & Adolphs, 2018) or principal
component analysis (APC; Schultz & Cole, 2016). In this work, we quantified g using the PCA
approach described in Schultz and Cole (2016). Mathematically, we propose the following
composite relationship:

(cid:7)
:>i ¼ ϒ RFN

je

; PFN
je

(cid:8)

:

(7)

Having established a plausible connection between behavioral measures and P FN, RFN,
Équation 7 can be viewed as a multilinear model (MLM) using FN preconfiguration and recon-
figuration as independent variables (or predictors). The MLM is constructed iteratively, starting

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

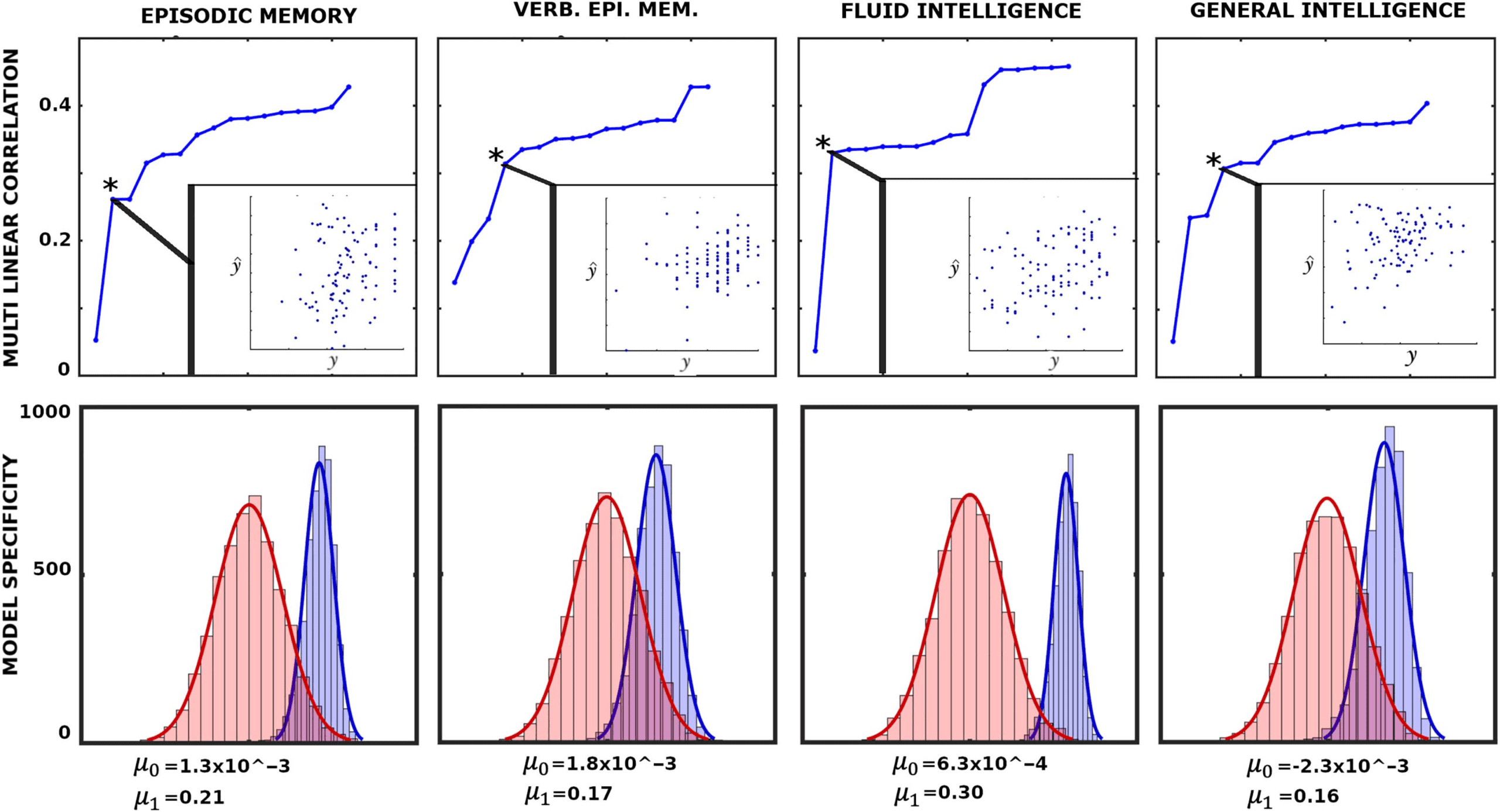
Chiffre 8. Associations between network configural breadth and behavior. The x-axis represents functional network preconfiguration and
reconfiguration terms, c'est, PFN
, ordered in decreasing subject fingerprints (as shown in Figure 7C). The top panels illustrate iterative
multilinear regression model (MLM), while the bottom panels show model specificity (MS) for corresponding behavioral measures. Asterisk
represents the optimal MLM with lowest p value. Further details are available in the Supporting Information, Behavioral Measure Analysis
section.

i and RFN

je

Neurosciences en réseau

680

A morphospace framework to assess brain functional networks

with the descriptor with the highest individual fingerprints in Figure 7C. In each iteration, le
subsequently ranked descriptor (according to Figure 7C) is appended to the existing ones. Le
best MLM (denoted with an asterisk in Figure 8), which determines the number of linear de-
scriptors included the model, is selected based on the model p value.

To test the level of specificity in the model, we performed 2,000 simulations of k-fold cross
validation where k = 5 between the selected MLM and the corresponding behavioral measure.
Spécifiquement, for each cross validation (per simulation), we obtain a correlation between the 20
left-out values (oui) with the predicted values (y^). Ainsi, in each simulation we obtained five
correlations and their mean value. It can be shown that those means follow a normal distri-
bution (details shown in the Supporting Information). Dernièrement, to provide the level of specificity
of linear descriptors, we present a corresponding null model where the same descriptors are
evaluated to predict random vectors of appropriate size. To test our model and its ability to
predict the behavioral measures, we rely completely on network configural breadth predictors
ranked in descending order of subject specificity.

The top panels in Figure 8 show that as more linear descriptors (FN’s functional pre- et
reconfigurations) are added to iterative MLMs, variance associating with behavioral/cognitive
performance measures decreases with linear descriptors that bear less subject sensitivity. Ce
result highlights the importance of appending linear predictors in descending order with re-
spect to the subject sensitivity. Spécifiquement, as individual specificity reduces from left to right
(Figure 7C), the differential correlations, c'est, the difference between two consecutive cor-
relation values, decreases.

DISCUSSION

In this work, we fill an existing gap in the field of network neuroscience by proposing a math-
ematical framework that captures the extent to which subject-level functional networks, comme
estimated by fMRI, reconfigure across diverse mental/emotional states. We first propose that
brain networks can undergo three different types of (concernant)configurations: (un) network configural
breadth, (b) task-to-task transitional reconfiguration, et (c) within-task reconfiguration.
Unlike other existing frameworks (Schultz & Cole, 2016; J.. M.. Shine et al., 2019; J.. M..
Shine & Poldrack, 2018), the framework presented here can be applied to all three reconfig-
uration types. As a first step, we focus on assessing the broadest aspect of reconfiguration, que
est, network configural breadth. We postulate, based on previous literature (Cole et al., 2014),
that macroscale (whole-brain) and microscale (edge-level) reconfigurations of brain networks
are subtle, and hence difficult to disentangle. En même temps, mesoscopic structures in the
brain (par exemple., functional networks, FNs) reconfigure substantially across different
mental/emotional states as elicited by different tasks (Mohr et al., 2016). The framework pre-
sented here constitutes the first attempt to formalize such (concernant)configurations of mesoscopic
structures of the brain, and quantify the behavior of a reference set of FNs with changing men-
états tal. We set forth a mathematically well-defined and well-behaved 2D network morpho-
space using novel mesoscopic metrics of trapping efficiency (TE) and exit entropy (EE). Ce
morphospace characterizes not only the topology of FNs but also the flow of information with-
in and between FNs. We show that this morphospace is sensitive to FNs, tasks, sujets, et
the levels of cognitive performance. We show that both of these measures are highly subject-
sensitive for some FNs, while preconfiguration is highly subject-sensitive for all of them. Dernièrement,
we also formalize and quantify the concepts of functional reconfiguration (the extent to which
an FN has the capacity to reconfigure across different tasks) and functional preconfiguration
(amount of transition from resting-state to a task-positive centroid). We thus construct a

Neurosciences en réseau

681

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A morphospace framework to assess brain functional networks

formalism that can explore FN changes across different cognitive states in a comprehensive
manner and at different levels of granularity.

Ideally, a morphospace framework (Avena-Koenigsberger et al., 2015; Avena-Koenigsberger,
Misic, & Sporns, 2018; Corominas-Murtra, Goñi, Solé, & Rodríguez-Caso, 2013; Goñi et al., 2013;
McGhee, 1999; Morgan, Achard, Termenon, Bullmore, & Vértes, 2018; Schuetz, Zamboni,
Zampieri, Heinemann, & Sauer, 2012; Shoval et al., 2012; Thomas, Shearman, & Stewart,
2000) would have a minimal complexity and, in this particular case, capture distinct features of
functional network changes. As discussed in Avena-Koenigsberger et al. (2015), metrics parame-
trizing a given morphospace should be disjoint. We see that, for any specific FN, high within-
subject task sensitivity of TE does not necessarily imply a high value in EE and vice versa (par exemple.,
VA and FP in Figure 4A). En outre, we see that both TE and EE offer their unique insights in
capturing nonoverlapping features, with TE being more subject-sensitive and EE more task-
sensitive at the cohort level (Figure 4B, 4C). Figure 6B highlights the disjoint nature of the two
metrics as well, where we compute maximal distance per FN polytope in the TE and the EE axes
separately. Results show that corresponding TE and EE maximal distances are disjoint and FN de-
pendent. Autrement dit, for a specific FN, the polytope is “stretched” in a particular task direction,
where each morphospace measurement (TE or EE) unravels distinct properties. In Figure 6C, nous
further see that a subset of tasks dominantly contribute to the maximal distance computation, tel
as motion, langue, and social tasks. Fait intéressant, we see that motion and language tasks can be
considered “orthogonal” tasks with respect to TE and EE.

Fait intéressant, the limbic network possesses the lowest ability to distinguish between tasks
(Chiffre 4). Similar behavior has been observed in Amico, Arenas, and Goñi (2019) when using
Jensen-Shannon divergence as a distance metric of functional connectivity. En outre, le
limbic network seems to work as a “relay” in brain communication (Amico, Abbas, et coll.,
2019). One potential explanation for this unique behavior is that the limbic network maintains
a minimal cognitive load across various tasks, most of which comprises relaying information
from one part of the brain to the others; it thus does not reconfigure as much across different
mental states.

Brain network configuration is typically studied considering a specific task at multiple spa-
tial and temporal scales (see Bassett et al., 2011; Betzel et al., 2017; Mohr et al., 2016; J.. Shine
et coll., 2018; J.. M.. Shine et al., 2016; J.. M.. Shine et al., 2019; J.. M.. Shine & Poldrack, 2018).
Previous investigations have mainly focused on the mechanism of how the brain traverses be-
tween high/low cognitive demands (Amico, Arenas, & Goñi, 2019; Avena-Koenigsberger
et coll., 2018; Bertolero, Yeo, & D'Esposito, 2015; J.. M.. Shine et al., 2019; Sporns, 2013), ou
on periods of integration and segregation at rest (J.. Shine et al., 2018; J.. M.. Shine et al.,
2019; J.. M.. Shine & Poldrack, 2018), defined in this paper as within-task reconfigurations.
On the other hand, whole-brain configurations have also been investigated across different
tasks (one configuration per task) with respect to rest, which led to the concept of general ef-
ficiency (Schultz & Cole, 2016). This approach would belong to a wider category that we for-
mally generalize as the network configural breadth. The idea of general efficiency in Schultz
and Cole (2016) relied on whole-brain FC correlations between task(s) and rest. While intuitive
in quantifying similarity/distance between a single task and rest, quantification across multiple
tasks becomes a challenge. Spécifiquement, note that in Schultz and Cole (2016), general efficiency
is quantified using the first eigenmode, which explains most of the variance, after measuring
the correlation between resting FC and three distinct task FCs. As more and more tasks are
included, using the first eigenmode would become less and less representative of the task-
related variations present in the data (in this paper summarized as the network configural

Neurosciences en réseau

682

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A morphospace framework to assess brain functional networks

breadth). The proposed network morphospace overcomes these limitations and can be used to
study brain network (concernant)configurations across any number of tasks. It allows us to study differ-
ent types of brain network (concernant)configurations, as mentioned above, using one comprehensive
mathematical framework, which also facilitates a meaningful comparison between these
seemingly disparate kinds of (concernant)configurations. Schultz and Cole (2016) proposed that config-
urations can be compartmentalized into two differentiated concepts: functional reconfigura-
tion and preconfiguration. Note that although the term reconfiguration is also used in Schultz
and Cole (2016), it is not referring to the action of switching among multiple mental/emotional
states, c'est, as represented by task-to-task transitional reconfiguration or within-task recon-
figuration (as shown in Figure 1B and 1C). Plutôt, it refers to the overall competence in ex-
ploring the total repertoire of task space of each subject given its resting configuration. C'est
why when we translate the corresponding idea into the mesoscopic morphospace, we call it
the network configural breadth. We have also incorporated the two concepts of functional pre-
and reconfigurations into a well-defined mathematical space, which solves some of the tech-
nical difficulties (as discussed in the Mesoscopic Morphospace of Functional Configurations
section) and generalizes these concepts to mesoscopic structures.

Brain network within-task reconfigurations have been almost exclusively qualitatively as-
sessed. Par exemple, J.. M.. Shine et al. (2016) show that the whole-brain functional connec-
tome traverses segregated and integrated states as it reconfigures while performing a task. Ils
also found that integrated states are associated with faster, more effective performance. Notre
formalism of within-task reconfigurations permits assessing such reconfigurations in a quanti-
tative manner. Potentially, such within-task reconfigurations could also be used to assess cog-
nitive fatigue, effort, or learning across time.

Cole et al. (2014) have shown that the resting architecture network modifies itself to fit task
requirements through subtle changes in functional edges. Numerically, small changes consti-
tuted by functional edges between rest and task-based connectivity might not be statistically
significant when looking at edge level. De plus, we also observe that while such changes
might be negligible on a whole-brain global scale, they are more evident when looking at
subsystems or functional brain networks, as clearly observed in the VIS network, relative to
others. For functional preconfiguration (Chiffre 5, Chiffre 6, Figure 7.2A), this effect is observ-
able in all the FNs. En substance, we are postulating that a mesoscopic exploration of changes in
brain network configurations with changing mental states is more informative than a macro-
scopic or microscopic exploration.

A key feature of this morphospace is that, in order to study brain network (concernant)configuration,
an FN is not removed from the overall network for exploration. On the contrary, both metrics
that define the morphospace, namely TE and EE, account for a particular FN’s place embedded
within the overall functional brain network, in terms of both topological structure and flow of
information. That is why it is important to begin with a reference set of FNs (par exemple., RSNs), so as
to study how these FNs adapt to changing mental states within the context of the overall
réseau.

Another benefit of a mesoscopic framework is that we can compare individual cognitive traits
in each FN, instead of the whole brain (Figure 7.1B, 7.2B). Spécifiquement, after quantifying recon-
figuration and preconfiguration for all FNs, we determine whether these quantities incorporate
information about individual traits (Figure 7C). We observe different levels of subject fingerprint
in different FNs for both re- and preconfiguration measures. This subject fingerprint heterogene-
ity across different FNs is consistent with previous literature on functional connectome finger-
impression (Amico & Goñi, 2018; Finn et al., 2015). Fait intéressant, functional preconfiguration

Neurosciences en réseau

683

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A morphospace framework to assess brain functional networks

Tableau 1. Multilinear regression models with corresponding standardized β coefficients.

Dependent variables for each model are episodic memory, verbal episodic memory, fluid
intelligence ( gF ), and general intelligence ( g).

MLM terms/coefficients
Episodic memory

Verbal episodic memory

gF

g

Constant
β
0
0.6

0.5

0.7

0.8

PFP
β

1
2.9

11.8

5.1

3.9

PDMN
β
2
−9.3

−1.1

−12

−5.5

PVA
β

3

PSUBC
β
4

−8.8

−6.1

−3.6

−5.7

(amount of transition from a resting state to a task-positive state) displayed greater subject finger-
print than functional reconfiguration for all FNs. Based on this observation, we argue that to have
better subject differentiability, we need to design tasks where the subject transitions from a stable
resting state to a task-positive state and/or vice versa (Amico et al., 2020). This could be a sig-
nificant step forward in precision psychiatry (Fraguas, Díaz-Caneja, Pina-Camacho, Janssen, &
Arango, 2016), where we can identify regional brain dysfunction more precisely as a function of
the type and degree of cognitive or emotional load.

Subject sensitivity of the proposed network morphospace framework is also supported by
significant associations of the frontoparietal and default mode networks with fluid intelligence;
see Tables 1 et 2. Spécifiquement, as pointed out by Tschentscher et al. (2017), high fluid intel-
ligence is associated with a greater frontoparietal network activation, which is also consistent
with findings from a three-back working memory task (Gray et al., 2003). In the domain of
network configural breadth, we observe a higher reconfiguration as represented by a positive
frontoparietal functional preconfiguration coefficient (Tableau 1).

This study has several limitations. The framework was tested specifically on the Human
Connectome Project dataset and using a single whole-brain parcellation. Alternative parcella-
tion (Schaefer et al., 2018; Tian, Margulies, Breakspear, & Zalesky, 2020), additional fMRI
tasks to better sample the cognitive space, and other datasets might offer further insights about
the mesoscopic network morphospace (see Avena-Koenigsberger et al., 2015; Corominas-
Murtra et al., 2013). En outre, we did not perform a sensitivity analysis on how small fluc-
tuations in functional connectomes affect mapping into the network morphospace. À cause de
the nature of module trapping efficiency and exit entropy metrics, negative functional cou-
plings were not considered, and hence were set to zero. In future work, other combinations
of L1 and L2 norms, or even other norm choices, should be evaluated when defining trapping

Tableau 2. Multilinear models with corresponding p values. Note that we do not use stepwise linear model which discards descriptors that are
not statistically significant. Column entire model shows the significance of the entire model.

MLM terms/p values
Episodic memory

Verbal episodic memory

gF

g

Neurosciences en réseau

Constant
p0
0

0

0

0.03

PFP

p1
0.57

0.02

0.30

0.44

PDMN

p2
0.01

0.77

9 × 10

−4

PVA

p3

PSUBC

p4

0.17

0.03

0.16

0.57

0.05

Entire model
0.03

0.04

0.004

0.05

684

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A morphospace framework to assess brain functional networks

efficiency. This would impact not only the magnitude of the morphospace measure but also
the differentiating capacity of configuration across different functional networks.

Future studies should incorporate a sensitivity study of the behavior of this network mor-
phospace with respect to small fluctuations in the input functional connectomes. Further stud-
ies could also incorporate structural connectivity information to inform both TE and EE
measures when assessing the morphospace coordinates of functional reconfiguration.
Additional exploration of different aspects of this morphospace could provide further insights.
Par exemple, location of the polytopes in the morphospace might improve individual finger-
print. An important aspect of the proposed mesoscopic network morphospace is that it allows
for an exhaustive and continuous exploration of network reconfigurations, including those that
are continuous in time (Douw et al., 2016; J.. M.. Shine et al., 2019), Par exemple, if the subject
performs several tasks within the same scanning session, including extended resting-state pe-
riods (such as the fMRI experiment done at Barnes, Bullmore, & Suckling, 2009). This would
allow us to fully explore the cognitive space and gain a valuable insight into how different
subjects adapt to different levels of cognitive demands. One can also study the trajectory of
changing mental states using dynamic functional connectivity (Gonzalez-Castillo et al., 2015),
which can easily be mapped to this morphospace for additional insights. Another potential
avenue could be the application of this framework to characterize and understand different
brain disorders.

En résumé, this mesoscopic network morphospace is our first attempt to create a mathe-
matically well-defined framework to explore an individual’s cognitive space at different levels
of granularity. It allows us to characterize the structure and dynamics of specific subsystems in
the brain. This type of framework can be extremely helpful in characterizing brain dynamics at
the individual level, in healthy and pathological populations, which in turn would pave the
way for the development of personalized medicine for brain disorders.

METHODOLOGY

We provide detailed information on materials and methods in the Supporting Information. Dans
short, all necessary mechanics collected from multiple disciplines and general setup for matrix
computations are described in main text under the Mesoscopic Morphospace of Functional
Configurations section and Supporting Information Preliminaries and Data sections. The data-
set consists of high-resolution functional connectivity matrices describing human cerebral cor-
tex and subcortex (see Supporting Information, Données). The construction of morphospace and
the formalized notion of configural breadth are described in the Supporting Information,
Morphospace Analysis section. Multilinear model and model specificity are described in
Informations complémentaires, Behavioral Measure analysis section.

REMERCIEMENTS

Data were provided (in part) by the Human Connectome Project, WU-Minn Consortium (prin-
cipal investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16
NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by
the McDonnell Center for Systems Neuroscience at Washington University. JG acknowledges
financial support from NIH R01EB022574 and NIH R01MH108467 and the Indiana Clinical
and Translational Sciences Institute (Grant Number UL1TR001108) from the National
Institutes of Health, National Center for Advancing Translational Sciences, Clinical and
Translational Sciences Award. MV and JG acknowledge financial support from Purdue
Industrial Engineering Frontier Teams Network Morphospace Award and from Purdue

Neurosciences en réseau

685

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A morphospace framework to assess brain functional networks

Discovery Park Data Science Award “Fingerprints of the Human Brain: A Data Science
Perspective.” We thank Dr. Olaf Sporns and Meenusree Rajapandian for valuable comments.

INFORMATIONS À L'APPUI

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00193.

CONTRIBUTIONS DES AUTEURS

Duy Anh Duong-Tran: Conceptualisation; Analyse formelle; Enquête; Méthodologie;
Rédaction – ébauche originale. Kausar Abbas: Enquête; Rédaction – ébauche originale. Enrico Amico:
Conceptualisation; Analyse formelle; Méthodologie; Visualisation. Bernat Corominas-Murtra:
Conceptualisation; Analyse formelle; Enquête; Méthodologie. Mario Dzemidzic: Données
curation; Méthodologie; Rédaction – ébauche originale. David Kareken: Conceptualisation;
Surveillance; Rédaction – ébauche originale. Mario Ventresca: Conceptualisation; Surveillance.
Joaquin Goñi: Conceptualisation; Conservation des données; Analyse formelle; Acquisition de financement;
Enquête; Méthodologie; Gestion de projet; Surveillance; Rédaction – ébauche originale.

INFORMATIONS SUR LE FINANCEMENT

Joaquin Goñi, National Institutes of Health (https://dx.doi.org/10.13039/100000002), Award
ID: NIH R01EB022574. Joaquin Goñi, National Institutes of Health (https://dx.doi.org/10
.13039/100000002), Award ID: R01MH108467.

RÉFÉRENCES

Amico, E., Abbas, K., Duong-Tran, D. UN., Tipnis, U., Rajapandian,
M., Chumin, E., … Goñi, J.. (2019). Towards a mathematical theory
of communication for the human connectome. arXiv:1911.02601
Amico, E., Arenas, UN., & Goñi, J.. (2019). Centralized and distributed
cognitive task processing in the human connectome. Réseau
Neurosciences, 3(2), 455–474. https://doi.org/10.1162/netn_a
_00072, PubMed: 30793091

Amico, E., Dzemidzic, M., Oberlin, B. G., Carron, C. R., Harezlak,
J., Goñi, J., & Kareken, D. UN. (2020). The disengaging brain:
Dynamic transitions from cognitive engagement and alcoholism
risk. NeuroImage, 209, 116515. https://est ce que je.org/10.1016/j
.neuroimage.2020.116515, PubMed: 31904492

Amico, E., & Goñi, J.. (2018). The quest for identifiability in human
functional connectomes. Rapports scientifiques, 8(1), 8254. https://
doi.org/10.1038/s41598-018-25089-1, PubMed: 29844466

Avena-Koenigsberger, UN., Goñi, J., Solé, R., & Sporns, Ô. (2015).
Network morphospace. Journal of the Royal Society Interface,
12(103), 20140881. https://doi.org/10.1098/rsif.2014.0881,
PubMed: 25540237

Avena-Koenigsberger, UN., Misic, B., & Sporns, Ô. (2018).
Communication dynamics in complex brain networks. Nature
Reviews Neuroscience, 19(1), 17. https://doi.org/10.1038/nrn
.2017.149, PubMed: 29238085

Barnes, UN., Bullmore, E. T., & Suckling, J.. (2009). Endogenous hu-
man brain dynamics recover slowly following cognitive effort.
PLoS ONE, 4(8), e6626. https://doi.org/10.1371/journal.pone
.0006626, PubMed: 19680553

Bassett, D. S., & Gazzaniga, M.. S. (2011). Understanding complexity
in the human brain. Tendances des sciences cognitives, 15(5), 200–209.
https://doi.org/10.1016/j.tics.2011.03.006, PubMed: 21497128
Bassett, D. S., Wymbs, N. F., Porter, M.. UN., Mucha, P.. J., Carlson,
J.. M., & Grafton, S. T. (2011). Dynamic reconfiguration of human
brain networks during learning. Actes de la Nationale
Académie des Sciences, 108(18), 7641–7646. https://est ce que je.org/10
.1073/pnas.1018985108, PubMed: 21502525

Bertolero, M.. UN., Yeo, B. T., & D'Esposito, M.. (2015). The modular
and integrative functional architecture of the human brain.
Actes de l'Académie nationale des sciences, 112(49),
E6798–E6807. https://doi.org/10.1073/pnas.1510619112,
PubMed: 26598686

Betzel, R.. F., Satterthwaite, T. D., Gold, J.. JE., & Bassett, D. S. (2017).
Positive affect, surprise, and fatigue are correlates of network
flexibility. Rapports scientifiques, 7(1), 520. https://est ce que je.org/10.1038
/s41598-017-00425-z, PubMed: 28364117

Cattell, R.. B. (1963). Theory of fluid and crystallized intelligence: UN
critical experiment. Journal of Educational Psychology, 54(1), 1.
https://doi.org/10.1037/h0046743

Cole, M.. W., Bassett, D. S., Power, J.. D., Plus courageux, T. S., & Petersen,
S. E. (2014). Intrinsic and task-evoked network architectures of
the human brain. Neurone, 83(1), 238–251. https://est ce que je.org/10
.1016/j.neuron.2014.05.014, PubMed: 24991964

Corominas-Murtra, B., Goñi, J., Solé, R.. V., & Rodríguez-Caso, C.
(2013). On the origins of hierarchy in complex networks.
Actes de l'Académie nationale des sciences, 110(33),

Neurosciences en réseau

686

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A morphospace framework to assess brain functional networks

13316–13321. https://doi.org/10.1073/pnas.1300832110,
PubMed: 23898177

Douw, L., Wakeman, D. G., Tanaka, N., Liu, H., & Stufflebeam,
S. M.. (2016). State-dependent variability of dynamic functional
connectivity between frontoparietal and default networks relates
to cognitive flexibility. Neurosciences, 339, 12–21. https://doi.org
/10.1016/j.neuroscience.2016.09.034, PubMed: 27687802

Dubois, J., Galdi, P., Paul, L. K., & Adolphs, R.. (2018). A distributed
brain network predicts general intelligence from resting-state hu-
man neuroimaging data. Philosophical Transactions of the Royal
Society of London, Série B: Sciences biologiques, 373(1756),
20170284. https://doi.org/10.1098/rstb.2017.0284, PubMed:
30104429

Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M.. D., Huang, J.,
Chun, M.. M., … Constable, R.. T. (2015). Functional connectome
fingerprinting: Identifying individuals using patterns of brain con-
nectivity. Neurosciences naturelles, 18(11), 1664. https://est ce que je.org/10
.1038/nn.4135, PubMed: 26457551

Fornito, UN., Zalesky, UN., & Bullmore, E. (2016). Fundamentals of

brain network analysis. Academic Press.

Fortunato, S. (2010). Community detection in graphs. Physics
Reports, 486(3), 75–174. https://doi.org/10.1016/j.physrep.2009
.11.002

Fox, M.. D., Snyder, UN. Z., Vincent, J.. L., Corbetta, M., Van Essen, D. C.,
& Raichle, M.. E. (2005). The human brain is intrinsically organized
into dynamic, anticorrelated functional networks. Proceedings of
the National Academy of Sciences, 102(27), 9673–9678. https://
doi.org/10.1073/pnas.0504136102, PubMed: 15976020

Fraguas, D., Díaz-Caneja, C. M., Pina-Camacho, L., Janssen, J., &
Arango, C. (2016). Progressive brain changes in children and ad-
olescents with early-onset psychosis: A meta-analysis of longitu-
dinal MRI studies. Schizophrenia Research, 173(3), 132–139.
https://doi.org/10.1016/j.schres.2014.12.022, PubMed:
25556081

Glasser, M.. F., Coalson, T. S., Robinson, E. C., Hacker, C. D.,
Harwell, J., Yacoub, E., … Van Essen, D. C. (2016). A multi-modal
parcellation of human cerebral cortex. Nature, 536(7615), 171–178.
https://doi.org/10.1038/nature18933, PubMed: 27437579

Goñi, J., Avena-Koenigsberger, UN., de Mendizabal, N. V., van den
Heuvel, M.. P., Betzel, R.. F., & Sporns, Ô. (2013). Exploring the
morphospace of communication efficiency in complex networks.
PLoS ONE, 8(3), e58070. https://doi.org/10.1371/journal.pone
.0058070, PubMed: 23505455

Gonzalez-Castillo, J., Hoy, C. W., Handwerker, D. UN., Robinson,
M.. E., Buchanan, L. C., Saad, Z. S., & Bandettini, P.. UN. (2015).
Tracking ongoing cognition in individuals using brief, whole-
brain functional connectivity patterns. Actes du
Académie nationale des sciences, 112(28), 8762–8767. https://est ce que je
.org/10.1073/pnas.1501242112, PubMed: 26124112

Gray, J.. R., Chabris, C. F., & Plus courageux, T. S. (2003). Neural mecha-
nisms of general fluid intelligence. Neurosciences naturelles, 6(3),
316. https://doi.org/10.1038/nn1014, PubMed: 12592404

Greicius, M.. D., Krasnow, B., Reiss, UN. L., & Menon, V. (2003).
Functional connectivity in the resting brain: A network analysis
of the default mode hypothesis. Actes de la Nationale
Académie des Sciences, 100(1), 253–258. https://doi.org/10.1073
/pnas.0135058100, PubMed: 12506194

Kemeny, J.. G., & Snell, J.. L. (1960). Finite Markov chains (Vol. 356).

Princeton, New Jersey: van Nostrand.

Malliaros, F. D., & Vazirgiannis, M.. (2013). Clustering and commu-
nity detection in directed networks: A survey. Physics Reports,
533(4), 95–142. https://doi.org/10.1016/j.physrep.2013.08.002
McGhee, G. R.. (1999). Theoretical morphology: The concept and

its applications. Columbia University Press.

Mohr, H., Wolfensteller, U., Betzel, R.. F., Mišic(cid:3), B., Sporns, O.,
Richiardi, J., & Ruge, H. (2016). Integration and segregation of
large-scale brain networks during short-term task automatization.
Communications naturelles, 7(1), 1–12. https://est ce que je.org/10.1038
/ncomms13217, PubMed: 27808095

Morgan, S. E., Achard, S., Termenon, M., Bullmore, E. T., & Vértes,
P.. E. (2018). Low-dimensional morphospace of topological motifs in
human fMRI brain networks. Neurosciences en réseau, 2(2), 285–302.
https://doi.org/10.1162/netn_a_00038, PubMed: 30215036

Newman, M.. E. (2006un). Finding community structure in networks
using the eigenvectors of matrices. Physical Review E, 74(3), 036104.
https://doi.org/10.1103/PhysRevE.74.036104, PubMed: 17025705
Newman, M.. E. (2006b). Modularity and community structure in
réseaux. Actes de l'Académie nationale des sciences,
103(23), 8577–8582. https://doi.org/10.1073/pnas.0601602103,
PubMed: 16723398

Rosvall, M., Axelsson, D., & Bergstrom, C. T. (2009). The map
equation. The European Physical Journal: Special Topics, 178(1),
13–23. https://doi.org/10.1140/epjst/e2010-01179-1

Rosvall, M., & Bergstrom, C. T. (2008). Maps of random walks on
complex networks reveal community structure. Proceedings of
the National Academy of Sciences, 105(4), 1118–1123. https://
doi.org/10.1073/pnas.0706851105, PubMed: 18216267

Schaefer, UN., Kong, R., Gordon, E. M., Laumann, T. O., Zuo, X.-N.,
Holmes, UN. J., … Yeo, B. T. (2018). Local-global parcellation of
the human cerebral cortex from intrinsic functional connectivity
IRM. Cortex cérébral, 28(9), 3095–3114. https://est ce que je.org/10.1093
/cercor/bhx179, PubMed: 28981612

Schuetz, R., Zamboni, N., Zampieri, M., Heinemann, M., & Sauer,
U. (2012). Multidimensional optimality of microbial metabolism.
Science, 336(6081), 601–604. https://doi.org/10.1126/science
.1216882, PubMed: 22556256

Schultz, D. H., & Cole, M.. W. (2016). Higher intelligence is asso-
ciated with less task-related brain network reconfiguration.
Journal des neurosciences, 36(33), 8551–8561. https://est ce que je.org/10
.1523/JNEUROSCI.0358-16.2016, PubMed: 27535904

Shine, J., Breakspear, M., Cloche, P., Ehgoetz, K. M., Shine, R., Koyejo,
O., … Poldrack, R.. (2018). The dynamic basis of cognition: Un
integrative core under the control of the ascending neuromodu-
latory system. https://doi.org/10.1101/266635

Shine, J.. M., Bissett, P.. G., Cloche, P.. T., Koyejo, O., Balsters, J.. H.,
Gorgolewski, K. J., … Poldrack, R.. UN. (2016). The dynamics of
functional brain networks: Integrated network states during cog-
nitive task performance. Neurone, 92(2), 544–554. https://doi.org
/10.1016/j.neuron.2016.09.018, PubMed: 27693256

Shine, J.. M., Breakspear, M., Cloche, P.. T., Martens, K. UN. E., Shine, R.,
Koyejo, O., … Poldrack, R.. UN. (2019). Human cognition involves
the dynamic integration of neural activity and neuromodulatory
systèmes. Neurosciences naturelles, 22(2), 289. https://est ce que je.org/10
.1038/s41593-018-0312-0, PubMed: 30664771

Neurosciences en réseau

687

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A morphospace framework to assess brain functional networks

Shine, J.. M., & Poldrack, R.. UN. (2018). Principles of dynamic net-
work reconfiguration across diverse brain states. NeuroImage,
180, 396–405. https://doi.org/10.1016/j.neuroimage.2017.08
.010, PubMed: 28782684

Shoval, O., Sheftel, H., Shinar, G., Hart, Y., Ramote, O., Mayo, UN.,
… Alon, U. (2012). Evolutionary trade-offs, pareto optimality,
and the geometry of phenotype space. Science, 1217405.
https://doi.org/10.1126/science.1217405, PubMed: 22539553
Spearman, C. (1904). “General intelligence,” objectively deter-
mined and measured. American Journal of Psychology, 15(2),
201–292. https://doi.org/10.2307/1412107

Sporns, Ô. (2013). Network attributes for segregation and integration in
the human brain. Opinion actuelle en neurobiologie, 23(2), 162–171.
https://doi.org/10.1016/j.conb.2012.11.015, PubMed: 23294553
Sporns, O., & Betzel, R.. F. (2016). Modular brain networks. Annual
Review of Psychology, 67, 613–640. https://doi.org/10.1146
/annurev-psych-122414-033634, PubMed: 26393868

Thomas, R., Shearman, R.. M., & Stewart, G. W. (2000).
Evolutionary exploitation of design options by the first animals
with hard skeletons. Science, 288(5469), 1239–1242. https://
doi.org/10.1126/science.288.5469.1239, PubMed: 10817998
Tian, Y., Margulies, D. S., Breakspear, M., & Zalesky, UN. (2020).
Hierarchical organization of the human subcortex unveiled with
functional connectivity gradients. bioRxiv. https://est ce que je.org/10
.1101/2020.01.13.903542

Tschentscher, N., Mitchell, D., & Duncan, J.. (2017). Fluid intelligence
predicts novel rule implementation in a distributed frontoparietal

control network. Journal des neurosciences, 37(18), 4841–4847.
https://doi.org/10.1523/ JNEUROSCI.2478-16.2017, PubMed:
28408412

Van Essen, D. C., Forgeron, S. M., Barch, D. M., Behrens, T. E.,
Yacoub, E., & Voiture d'Ugur, K. (2013). The WU-Minn Human
Connectome Project: An overview. NeuroImage, 80, 62–79.
https://doi.org/10.1016/j.neuroimage.2013.05.041, PubMed:
23684880

Van Essen, D. C., Voiture d'Ugur, K., Auerbach, E., Barch, D., Behrens, T.,
Bucholz, R., … WU-Minn HCP Consortium. (2012). The Human
Connectome Project: A data acquisition perspective.
NeuroImage, 62(4), 2222–2231. https://est ce que je.org/10.1016/j
.neuroimage.2012.02.018, PubMed: 22366334

Varona, P., & Rabinovich, M.. je. (2016). Hierarchical dynamics of
informational patterns and decision-making. Actes du
Royal Society B: Sciences biologiques, 283(1832), 20160475.
https://doi.org/10.1098/rspb.2016.0475, PubMed: 27252020
Varoquaux, G., Schwartz, Y., Poldrack, R.. UN., Gauthier, B., Bzdok,
D., Poline, J.-B., & Thirion, B. (2018). Atlases of cognition with
large-scale human brain mapping. Biologie computationnelle PLoS,
14(11), e1006565. https://doi.org/10.1371/journal.pcbi
.1006565, PubMed: 30496171

Yeo, B. T., Krienen, F. M., Sepulcre, J., Sabuncu, M.. R., Lashkari, D.,
Hollinshead, M., … Buckner, R.. L. (2011). The organization of the
human cerebral cortex estimated by intrinsic functional connectiv-
ville. Journal de neurophysiologie, 106(3), 1125–1165. https://doi.org
/10.1152/jn.00338.2011, PubMed: 21653723

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
3
6
6
6
1
9
6
0
5
1
4
n
e
n
_
un
_
0
0
1
9
3
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neurosciences en réseau

688

Télécharger le PDF