Membership Inference Attacks on Sequence-to-Sequence Models:

Membership Inference Attacks on Sequence-to-Sequence Models:
Is My Data In Your Machine Translation System?

Sorami Hisamoto∗
Works Applications
s@89.io

Kevin Duh
Matt Post
Université Johns Hopkins
{post,kevinduh}@cs.jhu.edu

Abstrait

Data privacy is an important issue for
‘‘machine learning as a service’’ provid-
ers. We focus on the problem of mem-
bership inference attacks: Given a data
sample and black-box access to a model’s
API, determine whether the sample ex-
isted in the model’s training data. Notre
contribution is an investigation of this
problem in the context of sequence-to-
sequence models, which are important in
applications such as machine translation
and video captioning. We define the mem-
bership inference problem for sequence
generation, provide an open dataset based
on state-of-the-art machine translation mod-
le, and report initial results on whether
these models leak private information against
several kinds of membership inference
attacks.

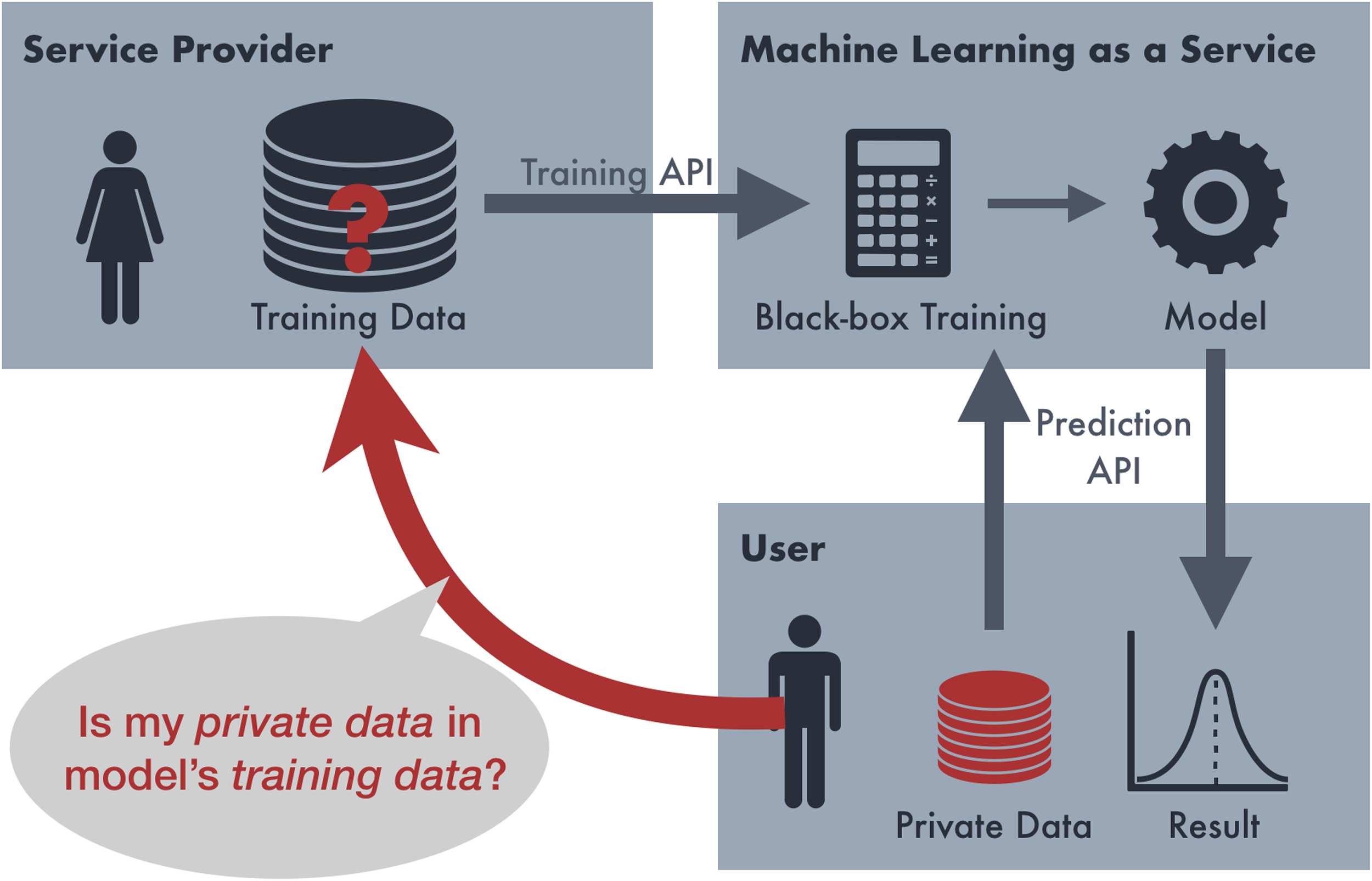
1 Motivation

There are many situations in which private entities
are worried about the privacy of their data. Pour
example, many companies provide black-box
training services where users are able to upload
their data and have customized models built
for them, without requiring machine learning
expertise. A common concern in these ‘‘machine
learning as a service’’ offerings is that the up-
loaded data be visible only to the client that
owns it.

Actuellement, these entities are in the position of
having to trust that service providers abide by the
terms of their agreements. Although trust is an
important component in relationships of all kinds,
it has its limitations. En particulier, it falls short
of a well-known security maxim, originating in
a Russian proverb that translates as, Trust, mais

verify.1 Ideally, customers would be able to verify
that their private data was not being slurped up
by the serving company, whether by design or
accident.

This problem has been formalized as the mem-
bership inference problem, first introduced by
Shokri et al. (2017) and defined as: ‘‘Given a
machine learning model and a record, determine
whether this record was used as part of the model’s
training dataset or not.’’ The problem can be
tackled in an adversarial framework: The attacker
is interested in answering this question with high
accuracy, whereas the defender would like this
question to be unanswerable (voir la figure 1). Since
alors, researchers have proposed many ways to
attack and defend the privacy of various types of
models. Cependant, the work so far has only focused
on standard classification problems, where the
output space of the model is a fixed set of labels.
In this paper, we propose to investigate member-
ship inference for sequence generation problems,
where the output space can be viewed as a chained
sequence of classifications. Prime examples of
sequence generation includes machine translation
and text summarization: In these problems, le
output is a sequence of words whose length is un-
determined a priori. Other examples include speech
synthesis and video caption generation. Sequence
generation problems are more complex than clas-
sification problems, and it is unclear whether the
methods and results developed for membership
inference in classification problems will transfer.
Par exemple, one might imagine that whereas a
flat classification model might leak private in-
formation when the output is a single label, un
recurrent sequence generation model might ob-
fuscate this leakage when labels are generated
successively with complex dependencies.

We focus on machine translation (MT) as the
example sequence generation problem. Recent

1Popularized by Ronald Reagan in the context of nuclear

∗Work done while visiting Johns Hopkins University.

disarmament.

Transactions of the Association for Computational Linguistics, vol. 8, pp. 49–63, 2020. https://doi.org/10.1162/tacl a 00299
Action Editor: Colin Cherry. Submission batch: 5/2019; Revision batch: 10/2019; Published 3/2020.
c(cid:13) 2020 Association for Computational Linguistics. Distributed under a CC-BY 4.0 Licence.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Alice (the service provider) builds a sequence-
to-sequence model based on an undisclosed
dataset Atrain and provides a public API. Pour
MT, this API takes a foreign sentence f as input
and returns an English translation ˆe.

Bob (the attacker)
is interested in discerning
whether a data sample was included in Alice’s
training data Atrain by exploiting Alice’s API.
This sample is called a ‘‘probe’’ and consists of
a foreign sentence f and its reference English
translation, e. Together with the API’s output
ˆe, Bob has to make a binary decision using a
membership inference classifier g(·), whose goal
is to predict:3

g(F, e, ˆe) =

if probe ∈ Atrain

dans
out otherwise

(

(1)

We term in-probes to be those probes where
the true class is in, and out-probes to be those
whose true class is out. Surtout, note that
Bob has access not only to f but also to e in
the probe. Intuitively, if ˆe is equivalent to e, alors
Bob may believe that the probe was contained
in Atrain; cependant, it may also be possible that
Alice’s model generalizes well to new samples
and translates this probe correctly. The challenge
for Bob is to make this distinction; the challenge
for Alice is to prevent Bob from doing so.

Carol (the neutral third-party)
is in charge of
setting up the experiment between Alice and Bob.
She decides which data samples should be used
as in-probes and out-probes and evaluates Bob’s
classification accuracy. Carol is introduced only
to clarify the exposition and to set up a fair
experiment for research purposes. In practical
scenarios, Carol does not exist: Bob decides his
own probes, and Alice decides her own Atrain.

2.1 Detailed Specification

In order to be precise about how Carol sets
up the experiment, we will explain in terms of
machine translation, but note that the problem
definition applies to any sequence-to-sequence
problem. A training set for MT consists of a
set of sentence pairs {(F (d)
je )}. We use a
label d ∈ {ℓ1, ℓ2, . . .} to indicate the domain

, e(d)

3In the experiments, we will also consider extending
the information available to Bob. Par exemple, if Alice
additionally provides the translation probabilities ρ in the
API, then Bob can exploit that in the classifier as g(F, e, ˆe, r).

Chiffre 1: Membership inference attack.

advances in neural sequence-to-sequence models
have improved the quality of MT systems sig-
nificantly, and many commercial service pro-
viders are deploying these models via public
API’s. We pose the main question in the following
formulaire:

Given black-box access to an MT model,
is it possible to determine whether a
particular sentence pair was in the
training set for that model?

Dans ce qui suit, we define membership infer-
ence for sequence generation problems (§2) et
contrast with prior work on classification (§3).
Next we present a novel dataset (§4) based on
state-of-the-art MT models.2 Finally, we propose
several attack methods (§5) and present a series
of experiments evaluating their ability to answer
the membership inference question (§6). Notre
conclusion is that simple one-off attacks based
on shadow models, which proved successful in
classification problems, are not successful on
sequence generation problems; this is a result that
favors the defender. Nevertheless, we describe the
specific conditions where sequence-to-sequence
models still leak private information, and discuss
the possibility of more powerful attacks (§7).

2 Problem Definition

We now define the membership inference attack
problem for sequence-to-sequence models in de-
tail. Following tradition in the security research
literature, we introduce three characters:

2We release the data to encourage further research in
this new problem: https://github.com/sorami/
tacl-membership

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(the subcorpus or the data source), and an index
i ∈ {1, 2, . . . , je(d)} to indicate the sample id in
the domain (subcorpus). Par exemple, e(d)
i with
d = ℓ1 and i = 1 might refer to the first sentence in
the Europarl subcorpus, while e(d)
i with d = ℓ2
and i = 1 might refer to the first sentence in the
CommonCrawl subcorpus. je(d) is the maximum
number of sentences in the subcorpus with label d.
The distinction among subcorpora is not necessary
in the abstract problem definition, but is important
in practice when differences in data distribution
may reveal signals in membership.

Without

loss of generality,

in this section
assume that Carol has a finite number of samples
from two subcorpora d ∈ {ℓ1, ℓ2}. D'abord, elle
creates an out-probe of k samples from subcorpus
ℓ1:

Aout probe =

(F (d)
je

, e(d)

je ) :

(

d = ℓ1, ℓ2
i = 1, . . . , k)

(2)

Then Carol creates the data for Alice to train

Alice’s MT model, using subcorpora ℓ1 and ℓ2:

(

je ) :

, e(d)

(F (d)
je

Atrain =

d = ℓ1, ℓ2
i = k + 1, . . . , je(d))
(3)
Surtout, the two sets are totally disjoint:
c'est à dire., Aout probe ∩ Atrain = ∅. By definition,
out-probes are sentence pairs that are not
dans
Alice’s training data. Enfin, Carol creates the
in-probe of k samples by drawing from Atrain,
c'est à dire. Ain probe ⊂ Atrain, which is defined to be
samples that are included in training:

(

je ) :

, e(d)

(F (d)
je

Ain probe =

d = ℓ1, ℓ2
i = k + 1, . . . , 2k)
(4)
Note that both Ain probe and Aout probe are
sentence pairs that come from the same subcorpus;
the only difference is that the former is included
in Atrain whereas the latter is not.

There are several ways in which Bob’s data
can be created. For this work, we will assume
that Bob also has some data to train MT models,
in order to mimic Alice and design his attacks.
This data could either be disjoint from Atrain,
or contain parts of Atrain. We choose the latter,
which assumes that there might be some public
data that is accessible to both Alice and Bob. Ce
scenario slightly favors Bob. In the case of MT,
parallel data can be hard to come by, and datasets

like Europarl are widely accessible to anyone,
so presumably both Alice and Bob would use it.
Cependant, we expect that Alice has an in-house
dataset (par exemple., crawled data) that Bob does not have
access to. Ainsi, Carol creates data for Bob:

Ball =

(F (d)
je

, e(d)

je ) :

(

d = ℓ1
i = 2k + 1, . . . , je(d))

(5)
Note that this dataset is like Atrain but with
two exceptions: All samples from subcorpora ℓ2
and all samples from Ain probe are discarded. Un
can view ℓ2 as Alice’s own in-house corpus which
Bob has no knowledge of or access to, and ℓ1
as the shared corpus where membership inference
attacks are performed.

To summarize, Carol gives Atrain to Alice,
who uses it in whatever way she chooses to build
a sequence-to-sequence model M [Atrain, Ème]. Le
model is trained on Atrain with hyperparameters
Ème (par exemple., neural network architecture) known only
to Alice. In parallel, Carol gives Ball to Bob, OMS
uses it to design various attack strategies, resulting
in a classifier g(·) (see Section 5). When it is
time for evaluation, Carol provides both probes
Ain probe and Aout probe to Bob in randomized
order and asks Bob to classify each sample as in
or out. For each probe (F (d)
), Bob is allowed
to make one call to Alice’s API to obtain ˆe(d)

, e(d)
je

As an additional evaluation, Carol creates a
third probe based on a new subcorpus ℓ3. We call
this the ‘‘out-of-domain (OOD) probe’’:

Aood =

(

(F (d)
je

, e(d)

je ) :

d = ℓ3
i = 1, . . . , k)

(6)

Both Aout probe and Aood should be classified
as out by Bob’s classifier. Cependant, it has been
known that sequence-to-sequence models behave
very differently on data from domains/genre that
is significantly different from the training data
(Koehn and Knowles, 2017). The goal of having
two out probes is to quantify the difficulty or ease
of membership inference in different situations.

2.2 Summary and Alternative Definitions

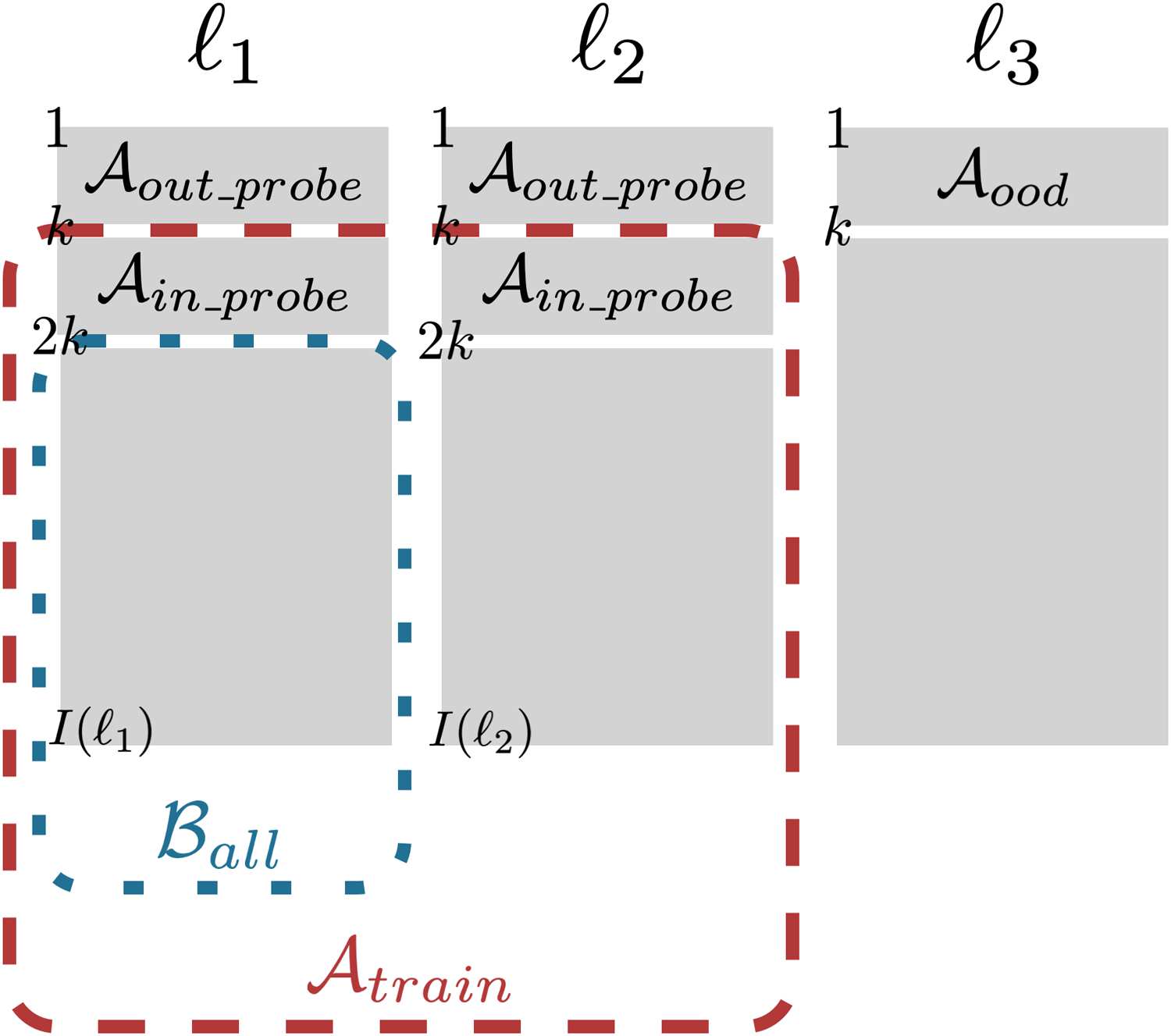
Chiffre 2 summarizes the problem definition. Le
probes Aout probe and Aood are by construction
outside of Alice’s training data Atrain, alors que
the probe Ain probe is included. Bob’s goal is to
produce a classifier that can make this distinction.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

providers may support customized engines if users
upload their own bitext training data. The provider
promises that the user-supplied data will not be
used in the customized engines of other users,
and can play both Alice and Bob, attacking its
own model to provide guarantees to the user. If it
is possible to construct a successful membership
inference mechanism, then many ‘‘good guys’’
would be able to provide the aforementioned
fairness (1, 2) and privacy guarantees (3).

3 Related Work

Shokri et al. (2017) introduced the problem of
membership inference attacks on machine learn-
ing models. They showed that with shadow models
trained on either realistic or synthetic datasets, Bob
can build classifiers that can discriminate Ain probe
and Aout probe with high accuracy. They focus
on classification problems such as CIFAR image
recognition and demonstrate successful attacks on
both convolutional neural net models as well as
the models provided by Amazon ML.

Why do these attacks work? The main infor-
mation exploited by Bob’s classifier is the out-
put distribution of class labels returned by Alice’s
API. The prediction uncertainty differs for data
samples inside and outside the model training
data, and this can be exploited. Shokri et al.
(2017) propose defense strategies for Alice, tel
as restricting the prediction vector to top-k classes,
coarsening the values of the output probabilities,
and increasing the entropy of the prediction vec-
tor. The crucial difference between their work and
ours, besides our focus on sequence generation
problems, is the availability of this kind of output
distribution provided by Alice. Although it is com-
mon to provide the whole distribution of out-
put probabilities in classification problems, ce
is not possible in sequence generation problems
because the output space of sequences is expo-
nential in the output length. At most, séquence
models can provide a score for the output pre-
diction ˆe(d)
, for example with a beam search
procedure, but this is only one number and not
normalized. We do experiment with having Bob
exploit this score (Tableau 3), but it appears far infe-
rior to the use of the whole distribution available
in classification problems.

Subsequent work on membership inference has
focused on different angles of the problem. Salem
et autres. (2018) investigated the effect of training the

Chiffre 2: Illustration of data splits for Alice and Bob.
There are k samples each for Ain probe, Aout probe, et
Aood. Alice’s training data Atrain excludes Aout probe
and ℓ3, while including Ain probe. Bob’s data Ball is a
subset of Alice’s data, excluding Ain probe and ℓ2.

He has at his disposal a smaller dataset Ball, lequel
he can use in whatever way he desires.

There are alternative definitions of this mem-
bership inference problem. Par exemple, one can
allow Bob to make multiple API calls to Alice’s
model for each probe. This enlarges the repository
of potential attack strategies for Bob. Or, one could
evaluate Bob’s accuracy not on a per-sample basis,
but allow for a coarser granularity where Bob
can aggregate inferences over multiple samples.
There is also a distinction between white-box
and black-box attacks: We focus on the black-
box case where Bob has no internal access to
the internal parameters of Alice’s model, but can
only guess at likely model architectures. In the
white-box case, Bob would have access to Alice’s
model internals, so different attacks would be
possible (par exemple., backpropagation of gradients). Dans
these respects, our problem definition makes the
problem more challenging for Bob the attacker.

Enfin, note that Bob is not necessarily always
the ‘‘bad guy’’. Some examples of who Alice and
Bob might be in MT are: (1) Organizations (Bob)
that provide bitext data under license restrictions
might be interested to determine whether their
licenses are being complied with in published
models (Alice). (2) The organizers (Bob) of an
annual bakeoff (par exemple., WMT) might wish to confirm
that the participants (Alice) are following the rules
of not training on test data. (3) ‘‘MT as a service’’

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

les types,

shadow model and datasets that match or do not
match the distribution of Atrain, and compared
training a single shadow model as opposed to
many. Truex et al. (2018) present a comprehensive
evaluation of different model
entraînement
data, and attack strategies. Borrowing ideas from
adversarial learning and minimax games, Hayes
et autres. (2017) propose attack methods based on gen-
erative adversarial networks, while Nasr et al. (2018)
provide adversarial regularization techniques for
the defender. Nasr et al. (2019) extend the anal-
ysis to white-box attacks and a federated learning
setting. Pyrgelis et al. (2018) provide an empirical
study on location data. Veale et al. (2018) dis-
cuss membership inference and the related
model inversion problem, in the context of data
protection laws like GDPR.

Shokri et al. (2017) note a synergistic connec-
tion between the goals of learning and the goals of
privacy in the case of membership inference: Le
goal of learning is to generalize to data outside
the training set (par exemple., so that Aout probe and Aood
are translated well), while the goal of privacy is
to prevent leaking information about data in the
training set. The common enemy of both goals
is overfitting. Yeom et al. (2017) analyze how
overfitting by Alice’s increases the risk privacy
leakage; Long et al. (2018) showed that even
a well-generalized model holds such risks in
classification problems, implying that overfitting
by Alice is a sufficient but not necessary condition
for privacy leakage.

A large body of work exists in differential
privacy (Dwork, 2008; Machanavajjhala et al.,
2017). Differential privacy provides guarantees
that a model trained on some dataset Atrain will
produce statistically similar predictions as a model
trained on another dataset which differs in exactly
one sample. This is one way in which Alice can
defend her model (Rahman et al., 2018), but note
that differential privacy is a stronger notion and
often involves a cost in Alice’s model accuracy.
Membership inference assumes that content of
the data is known to Bob and only is concerned
whether it was used. Differential privacy also
protects the content of the data (c'est à dire., the actual
words in (F (d)

) should not be inferred).

, e(d)
je

Song and Shmatikov (2019) explored the mem-
bership inference problem of natural language
text, including word prediction and dialog gen-
eration. They assume that the attacker has access
to a probability distribution or a sequence of dis-

tributions over the vocabulary for the generated
word or sequence. This is different from our work
where the attacker gets only the output sequence,
which we believe is a more realistic setting.

4 Data and Evaluation Protocol

4.1 Données: Subcorpora and Splits

Based on the problem definition in Section 2, nous
construct a dataset to investigate the possibility of
the membership inference attack on MT models.
We make this dataset available to the public to
encourage further research.4

There are various considerations to ensure the
benchmark is fair for both Alice and Bob: We need
a dataset that is large and diverse to ensure Alice
can train state-of-the-art MT models and Bob
can test on probes from different domains. Nous
used corpora from the Conference on Machine
Translation (WMT18) (Bojar et al., 2018). Nous
chose the German–English language pair because
it has a reasonably large amount of training
data, and previous work demonstrate high BLEU
scores.

We now describe how Carol prepares the data
for Alice and Bob. D'abord, Carol selects four sub-
corpora for the training data of Alice, namely,
CommonCrawl, Europarl v7, News Com-
mentary v13, and Rapid 2016. A subset of
these four subcorpora are also available to Bob (ℓ1
in § 2.1). En outre, Carol gives ParaCrawl to
Alice but not Bob (ℓ2 in §2.1). We can think of it
as in-house data that the service provider holds.
For all these subcorpora, Carol first performs
basic preprocessing: (un) tokenization of both the
German and English sides using the Moses tok-
enizer, (b) de-duplication of sentence pairs so that
only unique pairs are present, et (c) randomly
shuffling all sentences prior to splitting into probes
and MT training data.5

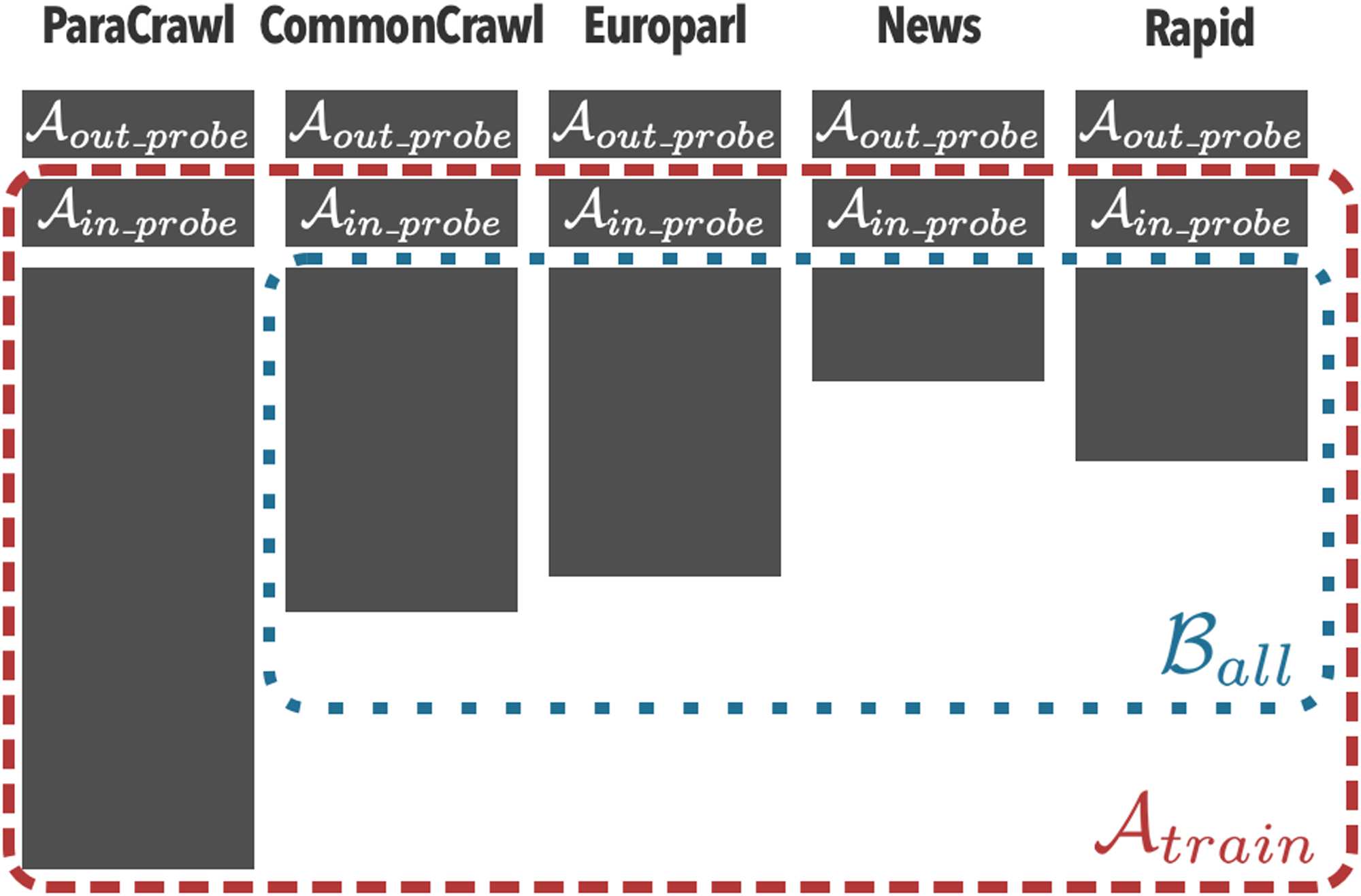
Chiffre 3 illustrates how Carol splits subcorpora
for Alice and Bob. For each subcorpus, Carol splits

4https://github.com/sorami/tacl-

membership

5These are design decisions that balance between simple
experimentation vs.
realistic condition. Carol doing a
common tokenization removes some of the MT-specific
complexity for researchers who want to focus on the Alice
or Bob models. Cependant, in a real-world public API, Alice’s
tokenization is likely to be unknown to Bob. We decided on a
middle ground to have Carol perform a common tokenization,
but Alice and Bob do their own subword segmentation.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

trained until perplexity on newstest2017
(Bojar et al., 2017) had not improved for five
consecutive checkpoints, computed every 5,000
batches.

The BLEU score (Papineni et al., 2002) sur
newstest2018 was 42.6, computed using
sacreBLEU (Post, 2018) with the default settings.8

4.3 Evaluation Protocol

To evaluate membership inference attacks on
Alice’s MT models, we use the following
procedure: D'abord, Bob asks Alice to translate f .
Alice returns her result ˆe to Bob. Bob also has
access to the reference e and use his classifier
g(F, e, ˆe) to infer whether (e, F ) was in Alice’s
training data. The classification is reported to
Carol, who computes ‘‘attack accuracy’’. Given a
probe set P containing a list of (F, e, ˆe, je), where l
is the label (in or out), this accuracy is defined as:

accuracy(g, P. ) =

1
|P. |

[g(F, e, ˆe) = l]

(7)

X
the accuracy is 50%,

then the binary
classification is same as random, and Alice is
safe. An accuracy slightly above 50% can be
considered a potential breach of privacy.

5 Membership Inference Attacks

5.1 Shadow Model Framework

Bob’s initial approach for attack is to use ‘‘shadow
models’’, similar to Shokri et al. (2017). Le
idea is that Bob creates MT models with his
data to mimic (shadow) the behavior of Alice’s
MT model, then train a membership inference
classifier on these shadow models. To do so,
Bob splits his data Ball into his own version of
in-probe, out-probe, and training set in multiple
ways to train MT models. Then he translates these
probe sentences with his own shadow MT models,
and use the resulting (F, e, ˆe) with its in or out
label to train a binary classifier g(F, e, ˆe). If Bob’s
shadow models are sufficiently similar to Alice’s
in behavior, this attack can work.

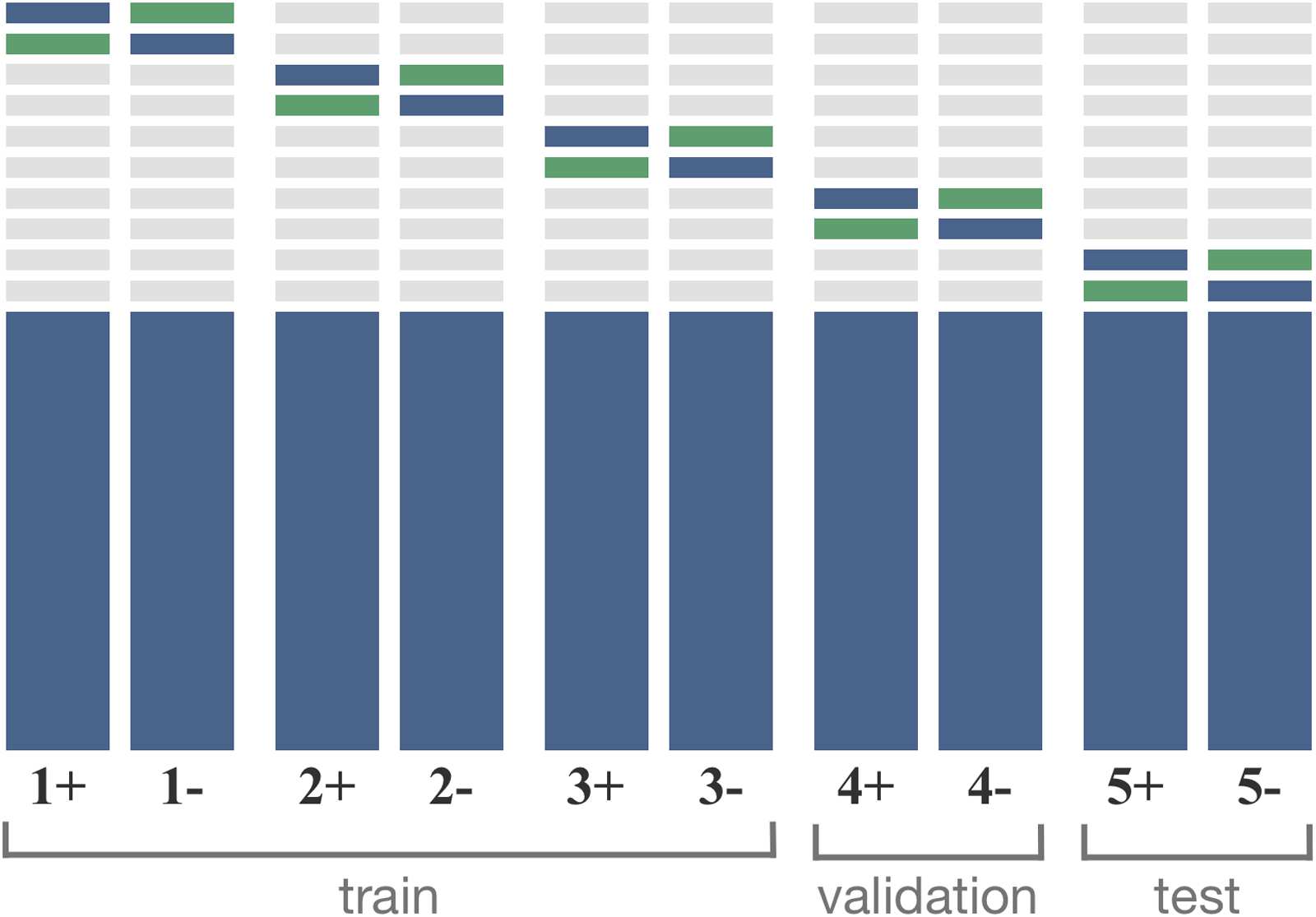
Bob first selects 10 sets of 5,000 phrases
per subcorpus in Ball. He then chooses two sets
and uses one as in-probe and the other as out-
sonde, and combines in-probe and the rest (Balle
minus 10 sets) as a training sets. We use notations

8Version 1.2.12, case-sensitive, ‘‘13a’’ tokenization for

comparability with WMT.

Chiffre 3: Illustration of actual MT data splits. Atrain
does not contain Aout probe, and Ball is a subset of
Atrain with Ain probe and ParaCrawl excluded.

them to create probes Ain probe and Aout probe, et
Atrain and Ball. Carol sets k = 5, 000, meaning
each probe set per subcorpus has 5,000 samples.
For each subcorpus, Carol selects 5,000 samples to
create Aout probe. She then uses the rest as Atrain
and select 5,000 from it as Ain probe. She excludes
Ain probe and ParaCrawl from Atrain to create
a dataset for Bob, Ball.6 In addition, Carol has
four other domains to create out-of-domain probe
set Aood, namely, EMEA and Subtitles 18
(Tiedemann, 2012), Koran (Tanzil), and TED
(Duh, 2018). These subcorpora are equivalent to
ℓ3 in § 2.1. The size of Aood is 5,000 per subcorpus,
same as Ain probe and Aout probe. The number of
samples for each set is summarized in Table 1.

4.2 Alice MT Architecture

Alice uses her dataset Atrain (consisting of
four subcorpora and ParaCrawl) to train her
own MT model. Because Paracrawl is noisy,
Alice first applies dual conditional cross-entropy
filtering (Junczys-Dowmunt, 2018), retaining the
top 4.5 million lines. Alice then trains a joint
BPE subword model (Sennrich et al., 2016) en utilisant
32,000 merge operations. No recasing is applied.
is a six-layer Transformer
(Vaswani et al., 2017) using default parameters in
Sockeye (Hieber et al., 2017).7 The model was

Alice’s model

6We prepared two different pairs of Ain probe and
Aout probe. Thus Ball has 10k fewer samples than Atrain,
and not 5k fewer. For the experiment we used only one pair,
and kept the other for future use.

7Three-way tied embeddings, model and embedding size
512, eight attention heads, 2,048 hidden states in the feed
forward layers, layer normalization applied before each self-
attention layer, and dropout and residual connections applied
afterward, word-based batch size of 4,096.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Aout probe Ain probe

Atrain

Balle

ParaCrawl
CommonCrawl
Europarl
News
Rapide
EMEA
Koran
Subtitles
TED

5,000
5,000
5,000
5,000
5,000
N/A
N/A
N/A
N/A

4,518,029
2,389,123
1,865,271
273,702
1,062,214
N/A
N/A
N/A
N/A

0
2,379,123
1,855,271
263,702
1,052,214
N/A
N/A
N/A
N/A

Aood

N/A
N/A
N/A
N/A
N/A
5,000
5,000
5,000
5,000

TOTAL

25,000

10,108,339

5,550,310

20,000

Tableau 1: Number of sentences per set and subcorpus. For each subcorpus, Atrain
includes Ain probe and does not include Aout probe. Ball is a subset of Atrain,
excluding Ain probe and ParaCrawl. Aood is for evaluation only, and only
Carol has access to it.

sample if it was in or out of the training data for
the MT model used to translate that sentence.

5.2 Bob MT Architecture

Bob’s model is a 4-layer Transformer, with no
tied embedding, model/embedding size 512, 8
attention heads, 1,024 hidden states in the feed
forward layers, word-based batch size of 4,096.
The model is optimized with Adam (Kingma and
Ba, 2015), regularized with label smoothing (0.1),
and trained until perplexity on newstest2016
(Bojar et al., 2016) had not improved for 16
consecutive checkpoints, computed every 4,000
batches. Bob has BPE subword models with
vocab size 30k for each language. The mean
BLEU scores of the ten shadow models on news-
test2018 is 38.6±0.2 (compared with 42.6 pour
Alice).

5.3 Membership Inference Classifier

Bob extracts features from (F, e, ˆe) for a binary
classifier. He uses modified 1- to 4-gram preci-
sions and smoothed sentence-level BLEU score
(Lin and Och, 2004) as features. Bob’s intuition
is that if an unusually large number of n-grams
in ˆe matches e, then it could be a sign that this
was in the training data and Alice memorized it.
Bob calculates n-gram precision by counting the
number of n-grams in translation that appear in the
reference sentence. In the later investigation Bob
also considers the MT model score as an extra
feature.

Chiffre 4: Illustration of how Bob splits Ball for each
shadow model. Blue boxes are the in-probe Bin probe
and training data Btrain, where small box is the in-probe
and small and large boxes combined is the training data.
Green box indicates the out-probe Bout probe. Bob uses
models from splits 1 à 3 as a train, 4 as a validation,
et 5 as a test sets for his attack.

out probe, and B1+

in probe B1+
B1+
train for the first group
of in-probe, out-probe, and training sets. Bob then
swaps the in-probe and out-probe to create another
group. We notate this as B1−
out probe, et
B1−
train. With 10 sets of 5,000 phrases, Bob can
create 10 different groups of in-probe, out-probe,
and training sets. Chiffre 4 illustrates the data
splits.

in probe, B1−

For each group of data, Bob first trains a shadow
MT model using the training set. He then uses this
model to translate sentences in the in-probe and
out-probe sets. Bob has now a list of (F, e, ˆe) depuis
different shadow models, and he knows for each

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Algorithm 1: Construction of A Membership
Inference Classifier
Données: Balle
Result: g(·)
Split Ball into multiples groups of (Bi
out probe, Bi
Bi
foreach i in 1+, 1−, 2+, 2−, 3+, 3− do
Train a shadow model Mi using Bi
in probe, Bi
Translate Bi

train ;
out probe with Mi ;

in probe,

train) ;

end
Use Bi
translations to train g(·) ;

in probe, Bi

out probe, and their

Bob tries different types of classifiers, namely,
Perceptron (P.), Decision Tree (DT), Na¨ıve Bayes
(NB), Nearest Neighbors (NN), and Multi-layer
Perceptron (MLP). DT uses GINI impurity for
the splitting metrics, and the max depth to be 5.
Our NB uses Gaussian distribution. For NN we
set the number of neighbors to be 5 and use
Minkowski distance. For MLP, we set the size of
the hidden layer to be 100, the activation function
to be ReLU, and the L2 regularization term α to
être 0.0001.

Algorithm 1 summarizes the procedure to
construct a membership inference classifier g(·)
using Bob’s dataset Ball. For training the binary
classifiers, Bob uses models from data splits 1
à 3 for training, 4 for validation, et 5 for his
own internal testing. Note that the final evaluation
of the attack is done using the translations of
Ain probe and Aout probe with Alice’s MT model,
by Carol.

6 Attack Results

We now present a series of results based on
the shadow model attack method described in
Section 5. In Section 6.1 we will observe that Bob
has difficulty attacking Alice under our definition
of membership inference. In Sections 6.2 et
6.3 we will see that Alice nevertheless does leak
some private information under more nuanced
conditions. Section 6.4 describes the possibility
of attacks beyond sentence-level membership.
Section 6.5 explores the attacks using external
ressources.

6.1 Main Result

Tableau 2 shows the accuracy of the membership
inference classifiers. Il y a 5 different types

Alice Bob:train Bob:valid Bob:test

P.
DT
NB
NN
MLP

50.0
50.4
50.4
49.9
50.2

50.0
51.4
51.2
61.6
50.8

50.0
51.2
51.1
50.5
50.8

50.0
51.1
51.0
50.0
50.8

Tableau 2: Accuracy of membership inference per
classifier type, Perceptron (P.), Decision Tree (DT),
Na¨ıve Bayes (NB), Nearest Neighbors (NN), et
Multi-layer Perceptron (MLP). Alice column shows
the accuracy of attack on Alice probes Ain probe
and Aout probe. Bob columns show the accuracy on
the classifiers’ train, validation, and test set. Note
que, following the evaluation protocol explained in
Section 4.3, only Carol the evaluator can observe
the accuracy of the attacks on Alice model.

of classifiers, as described in Section 5.3. Le
numbers in the Alice column shows the attack
accuracy on Alice probes Ain probe and Aout probe;
these are the main results. The numbers in Bob
columns show the results on the Bob classifiers’
train, validation, and test sets, as described in
Section 5.3.

The results of the attacks on the Alice model
show that it is around 50%, meaning that the attack
is not successful and the binary classification is
almost the same as a random choice.9 The ac-
curacy is around 50% for Bob:valid, meaning that
Bob also has difficulty attacking his own sim-
ulated probes, therefore the poor performance on
Ain probe and Aout probe is not due to mismatches
between Alice’s model and Bob’s model.

The accuracy is around 50% for Bob:train as
well, revealing that the classifier g(·) is under-
fitting.10 This suggests that the current features
do not provide enough information to distinguish
in-probe and out-probe sentences. Chiffre 5 shows

9Some numbers are slightly over 50%, which may be
interpreted as small leak of privacy. Although the desired
accuracy levels depend on the application, for the MT
scenarios described in Section 2.2 Bob would need much
higher accuracies. Par exemple, if Bob is a bakeoff organizer,
he might want accuracy above 60% in order to determine
si
whether to manually check the submission. Cependant,
Bob is providing ‘‘MT as a service’’ with strong privacy
guarantees, he may need to provide the client with accuracy
higher than 90%.

10The higher accuracy for k-NN is an exception, but is due
to having the exact same datapoint in the model as the input,
which always becomes the nearest neighbor. When the k
value is increased, the accuracy on in-sample data decreased.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 5: Confusion matrices of the attacks on Alice model per classifier type.

Alice Bob:train Bob:valid Bob:test

P.
DT
NB
NN
MLP

49.7
50.4
50.1
50.2
50.4

49.2
51.5
50.2
67.1
51.2

49.3
51.1
50.1
50.2
51.2

49.4
51.2
50.2
50.0
51.1

Tableau 3: Membership inference accuracy when MT
model score is added as an extra classifier feature.

the confusion matrices of the classifier output
on Alice probes. We see that for all classifiers,
whatever prediction they make is incorrect half of
le temps.

Tableau 3 shows the result when MT model score
is added as an extra feature for classification. Le
result indicates that this extra information does
not improve the attack accuracy. En résumé,
these results suggest that Bob is not able to reveal
membership information at the sentence/sample
level. This result is in contrast to previous work on
membership inference in ‘‘classification’’ prob-
lems, which demonstrated high accuracy with
Bob’s shadow model attack.

En plus, note that although accuracies are
close to 50%, the number of Bob:test tend to be
slightly higher than Alice’s for some classifiers.
This may reflect the fact that Bob:test is a matched
condition using the same shadow MT architecture,
while Alice probes are from a mismatched con-
dition using an unknown MT architecture. C'est
important to compare both numbers in the exper-
iments: accuracy on Alice probes is the real eval-
uation and accuracy on Bob:test is a diagnostic.

6.2 Out-of-Domain Subcorpora

Carol prepared OOD subcorpora, Aood, that are
separate from Atrain and Ball. The membership
inference accuracy of each subcorpus is shown
in Table 4. The accuracy for OOD subcor-
pora are much higher than that of original in-
domain subcorpora. Par exemple, the accuracy

with Decision Tree was 50.3% et 51.1% pour
ParaCrawl and CommonCrawl (in-domain),
whereas accuracy was 67.2% et 94.1% for EMEA
and Koran (out-of-domain). This suggests that
for OOD data Bob has a better chance to infer the
membership.

In Table 4 we can see that Perceptron has
accuracy 50% for all in-domain subcorpora and
100% for all OOD subcorpora. Note that the OOD
subcorpora only have out-probes. By definition
none of the samples from OOD subcorpora are in
the training data. We get such accuracy because
our Perceptron is always predicting out, as we can
see in Figure 5. We believe this behavior is caused
by applying Perceptron to inseparable data, et
this particular model happened to be trained to
act this way. To confirm this we have trained
variations of Perceptrons by shuffling the training
data, and observed that the resulting models had
different output ratios of in and out, and in some
cases always predicting in for both in and OOD
subcorpora.

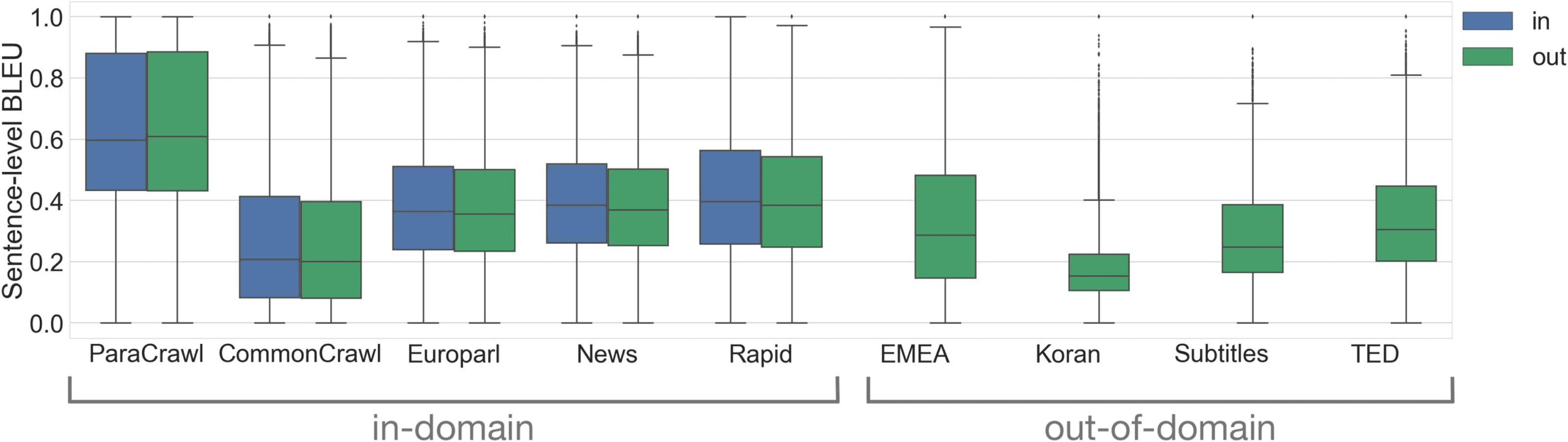
Chiffre 6 shows the distribution of sentence-
level BLEU scores per subcorpus. The BLEU
scores tend to be lower for OOD subcorpora,
and the classifier may exploit this information to
distinguish the membership better. But note that
EMEA (out-of-domain) and CommonCrawl (dans-
domain) have similar BLEU scores, but vastly
different membership accuracies, so the classifier
may also be exploiting n-gram match distributions.

Dans l'ensemble, these results suggest that Bob’s accu-
racy depends on the specific type of probe being
tested. If there is a wide distribution of domains,
there is a higher chance that Bob may be able to
reveal membership information. Note that in the
actual scenario Bob will have no way of knowing
what is OOD for Alice, so there is no signal that
is exploitable for Bob. This section is meant as
an error analysis that describes how membership
inference classifiers behave differently in case the
probe is OOD.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

ParaCrawl CommonCrawl Europarl News Rapid EMEA Koran Subtitles TED

P.
DT
NB
NN
MLP

50.0
50.3
50.1
49.4
49.6

50.0
51.1
51.2
50.7
50.8

50.0
49.7
49.9
50.3
49.9

50.0
50.7
50.6
49.7
50.3

50.0
50.0
50.2
49.2
50.7

100.0 100.0
94.1
96.1
52.6
97.9

67.2
69.5
43.3
73.6

100.0
80.2
81.7
48.7
84.8

100.0
67.1
70.5
49.9
85.0

Tableau 4: Membership inference accuracy per subcorpus. The right-most 4 columns are results for
out-of-domain subcorpora. Note that ParaCrawl is out-of-domain for Bob and his classifier,
although it is in-domain for Alice and her MT model.

Chiffre 6: Distribution of sentence-level BLEU per subcorpora for Ain probe (blue boxes), Aout probe (vert, gauche
five boxes), and Aood (vert, right four boxes).

6.3 Out-of-Vocabulary Words

We also focused on the samples that contain the
words that never appear in the training data of
the MT model used for translation, c'est, out-of-
vocabulary (OOV) words. For this analysis, nous
focus only on vocabulary that does not exist in the
training data of Bob’s shadow MT models, rather
than Alice’s, since Bob does not have access
to her vocabulary. By definition there are only
out-probes in OOV subsets.

For Bob’s shadow models, 7.4%, 3.2%, et
1.9% of samples in the probe sets had one or
more OOV words in source, reference, or both
phrases, respectivement. Tableau 5 shows the mem-
bership inference accuracy of the OOV subsets
from the Bob test set, which is generally very high
(>70%). This implies that sentences with OOV
words are translated idiosyncratically compared
with the ones without OOV words, and the classi-
fier can exploit this.

6.4 Alternative Evaluation: Grouping Probes

Section 6.1 showed that it is generally difficult
for Bob to determine membership for the strict
definition of one sentence per probe. What if we

OOV in src OOV in ref OOV in both

P.
DT
NB
NN
MLP

100.0
73.9
77.4
49.9
89.0

100.0
74.1
77.0
49.2
85.8

100.0
68.0
70.3
49.3
80.4

Tableau 5: Membership inference accuracy on the
sentences in Bob:test containing out-of-vocabulary
(OOV) words for the MT model used for translation.

loosen the problem, letting the probe be a group
of sentences?

We create probes of 500 sentences each to
investigate this hypothesis. Bob randomly samples
500 sentences with the same label from Bob’s
training set to form a probe group. To create suf-
ficient training data for his classifier, Bob repeats
sampling and creates 6,000 groupes. Bob uses
sentence BLEU bin percentage and corpus BLEU
as features for classification. For each group, Bob
counts the sentence BLEU for each bin. The bin
size is set to 0.01. Bob also uses all 500 translations
together to calculate the group’s corpus BLEU
score. Bob trains the classifiers using these fea-
photos, and applies it to Bob’s validation and test

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bob
train valid

Alice

test

original

adjusted

71.6
P.
70.4
DT
72.9
NB
NN
77.4
MLP 73.0

69.4
65.6
67.5
66.9
68.8

68.1
64.4
70.0
62.5
70.0

50.0
52.0
50.0
51.0
50.0

59.0
61.0
50.0
50.0
52.0

Tableau 6: Attack accuracy on probe groups. Dans
addition to the original Alice set, we have the
adjusted set where the feature values are adjusted
by subtracting the mean BLEU difference be-
tween Alice and Bob models.

sets, and Alice sets. These sets are evenly split into
groups of 500, not sampled as done in training.

Tableau 6 shows the accuracy on probe groups.
We can see that the accuracy is much higher
que 50%, not only for Bob’s training set but
also for his validation and test sets. Cependant,
for Alice, we found that classifiers were almost
always predicting in, resulting the accuracy to be
autour 50%. This is due to the fact that classifiers
were trained on shadow models that have lower
BLEU scores than Alice. This suggests that we
need to incorporate the information about the
Alice / Bob MT performance difference.

One way to adjust

the difference is to di-
rectly manipulate the input feature values. Nous
adjusted the feature values, compensating by the
difference in mean BLEU scores, and accuracy
on Alice probes increased to 60% for P and DT
as shown in the ‘‘adjusted’’ column of Table 6.
If the classifier took advantage of the absolute
values in its decision, the adjustment may provide
improvements. If that is not the case, then im-
provements are less likely. Before the adjustment,
all classifiers were predicting everything to be in
for Alice probes. Classifiers like NB and MLP
apparently did not change how often they predict
in even after the normalization, whereas classifiers
like P and DT did. In a real scenario this BLEU
difference can be reasonably estimated by Bob,
since he can use Alice’s translation API to calcu-
late the BLEU score on a held-out set, and com-
pare it with his shadow models.

Another possible approach to handle the prob-
lem of classifiers always predicting in is to con-
sider the relative size of classifier output score.
We can rank the samples by the classifier output
scores, and decide top N% to be in and rest to

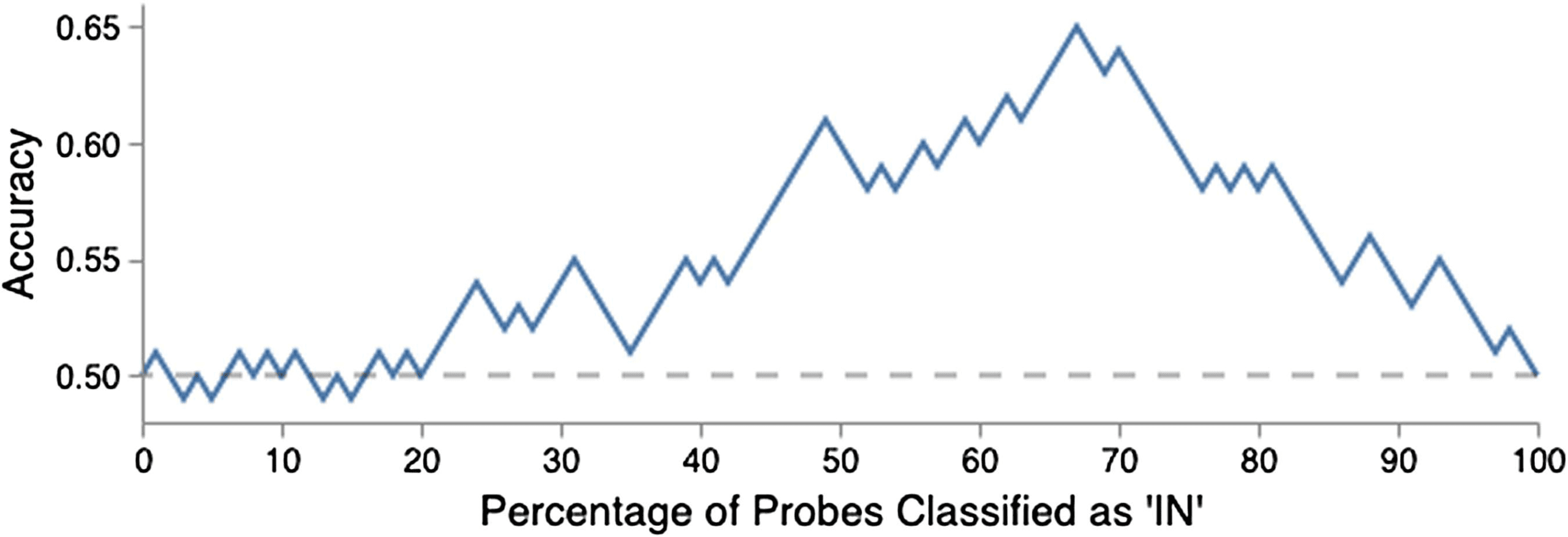
Chiffre 7: How the attack accuracy on Alice set changes
when probe groups are sorted by Perceptron output
score and the threshold to classify them as in is varied.

be out. Chiffre 7 shows how the accuracy changes
when varying the in percentage. We can see that
the accuracy can be much higher than the original
result, especially if Bob can adjust the threshold
based on his knowledge of in percentage in the
sonde.

This is the first strong general result for Bob,
suggesting the membership inference attacks are
possible if probes are defined as groups of sen-
tences.11 Importantly, note that
the classifier
threshold adjustment is performed only for the
classifiers in this section, and is not relevant for
the classifiers in Section 6.1 à 6.3.

6.5 Attacks Using External Resources

Our results in Section 6.1 demonstrate the dif-
ficulty of general membership inference attacks.
One natural question is whether attacks can be im-
proved with even stronger features or classifiers, dans
particular by exploiting external resources beyond
the dataset Carol provided to Bob. We tried two
different approaches: one using a Quality Esti-
mation model
trained on additional data, et
another using a neural sequence model with a
pre-trained language model.

Quality Estimation (QE) is a task of predicting
the quality of a translation at the sentence or
word level. One may imagine that a QE model
might produce useful feature to tease apart in and
out because in translations may have detectable
improvements in quality. To train this model, nous
used the external dataset from the WMT shared
task on QE (Specia et al., 2018). Note that for
our language pair, German to English, the shared
task only had a labeled dataset for the SMT

11We can imagine an alternative definition of this group-
level membership inference where Bob’s goal is to predict
the percentage of overlap with respect to Alice’s training
data. This assumes that model trainers make corpus-level
decisions about what data to train on. Reformulation of a
binary problem to a regression problem may be useful for
some purposes.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Alice Bob:train Bob:valid Bob:test

50.0
P.
50.3
DT
50.4
NB
49.8
NN
MLP
50.4
BERT 50.0

49.9
51.4
51.2
66.1
51.0
50.0

50.0
51.1
51.1
50.0
51.0
50.0

50.0
51.1
51.0
50.1
50.8
50.0

Tableau 7: Membership inference accuracies for clas-
sifiers with Quality Estimation sentence score as
an extra feature, and a BERT classifier.

système. Our models are NMT, so the estimation
quality may not be optimally matched, but we
ce
believe this is the best data available at
temps. We applied the Predictor-Estimator (Kim
et coll., 2017) implemented in an open source QE
framework OpenKiwi (Kepler et al., 2019). Il
consists of a predictor that predicts each token
of the target sentence given the target context
and the source, and estimator that takes features
produced by the predictor to estimate the labels;
both are made of LSTMs. We used this model
as this is one of the best models seen in the
shared tasks, and it does not require alignment
information. The model metrics on the WMT18
dev set, namely, Pearson’s correlation, Mean
Average Error, and Root Mean Squared Error
for sentence-level scores, sont 0.6238, 0.1276, et
0.1745, respectivement.

We used the sentence score estimated by the QE
model as an extra feature for classifiers described
in Section 6.1. The results are shown in Table 7.
We can see that this extra feature did not provide
any significant influence to the accuracy. In a
more detailed analysis, we find that the reason is
that our in and out probes both contain a range of
translations from low to high quality translations,
and our QE model may not be sufficiently fine-
grained to tease apart any potential differences.
En fait, this may be difficult even for a human
estimator.

Another approach to exploit external resources
is to use a language model pre-trained on a large
amount of text. En particulier, we used BERT
(Devlin et al., 2019), which has shown competitive
results in many NLP tasks. We used BERT directly
as a classifier, and followed a fine-tuning setup
similar to paraphrase detection: For our case the
inputs are the English translation and reference

phrases, and the output is the binary membership
label. This setup is similar to the classifiers we
described in Section 5.3, where rather than train-
ing Perceptron or Decision Tree on manually
defined features, we directly applied BERT-based
sequence encoders on the raw sentences.

to previous results,

We fine-tuned the BERT Base,Cased English
model with Bob:train. The results are shown
le
in Table 7. Similar
accuracy is 50% so the attack using BERT as
classifier was not successful. Detailed exam-
ination of the BERT classifier probabilities show
that they are scattered around 0.5 for all cases,
but in general are quite random for both Bob and
Alice probes. This result is similar to the other
simpler classifiers in Section 6.1.

En résumé, from these results we can see that
even with external resources and more complex
classifiers, sentence-level attack is still very diffi-
cult for Bob. We believe this attests to the inherent
difficulty of the sentence-level membership infer-
ence problem.

7 Discussions and Conclusions

We formalized the problem of membership infer-
ence attacks on sequence generation tasks, et
used machine translation as an example to investi-
gate the feasibility of a privacy attack.

Our results in Section 6.1 and Section 6.5 show
that Alice is generally safe and it is difficult for
Bob to infer the sentence-level membership. Dans
contrast to attacks on standard classification prob-
lems (Shokri et al., 2017), sequence generation
problems maybe be harder to attack because the
input and output spaces are far larger and complex,
making it difficult to determine the quality of
the model output or how confident the model is.
Aussi, the output distribution of class labels is an ef-
fective feature for the attacker for standard clas-
sification problems, but is difficult to exploit in
the sequence case.

Cependant, this does not mean that Alice has no
risk of leaking private information. Our analyses
in Sections 6.2 et 6.3 show that Bob’s accuracy
on out-of-domain and out-of-vocabulary data is
above chance, suggesting that attacks may be
feasible in conditions where unseen words and
domains cause the model to behave differently.
Plus loin, Section 6.4 shows that for a looser defini-
tion of membership attack on groups of sentences,
the attacker can win at a level above chance.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Our attack approach was a simple one, en utilisant
shadow models to mimic the target model. Bob
can attempt more complex strategies, Par exemple,
by using the translation API multiple times per
sentence. Bob can manipulate a sentence, pour
example, by dropping or adding words, and ob-
serve how the translation changes. We may also
use the metrics proposed by Carlini et al. (2018) comme
features for Bob; they show how recurrent models
might unintentionally memorize rare sequences
in the training data, and propose a method to
detect it. Bob can also add ‘‘watermark sentences’’
that have some distinguishable characteristics to
influence the Alice model, making attack easier.
To guard against these attacks, Alice’s protection
strategy may include random subsampling of
training data or additional regularization terms.

Enfin, we note some important caveats when
interpreting our conclusions. The translation qual-
ity of the Alice and Bob MT models turned out to
be similar in terms of BLEU. This situation favors
Bob, but in practice Bob is not guaranteed to be
able to create shadow models of the same standard,
nor verify how well it performs compared with
the Alice model. We stress that when one is to
interpret the results, one must evaluate both on
Bob’s test set and Alice probes side-by-side, like
those shown in Tables 2, 3, et 7, to account for
the fact that Bob’s attack on his own shadow model
translations is likely an optimistic upper-bound on
the real attack accuracy on Alice’s model.

We believe our dataset and analysis is a good
starting point for research in these privacy ques-
tion. Although we focused on MT, the formula-
tion is applicable to other kinds of sequence
generation models such as text summarization
and video captioning; these will be interesting as
future work.

Remerciements

The authors thank the anonymous reviewers and
the action editor, Colin Cherry, for their comments.

Les références

Ondˇrej Bojar, Rajen Chatterjee, Christian
Federmann, Yvette Graham, Barry Haddow,
Shujian Huang, Matthias Huck, Philipp Koehn,
Qun Liu, Varvara Logacheva, Christof Monz,
Matteo Negri, Matt Post, Raphael Rubino,
Lucia Specia, and Marco Turchi. 2017. Find-

ings of
le 2017 conference on machine
translation (WMT17). In Proceedings of the
Second Conference on Machine Translation,
pages 169–214, Copenhagen, Denmark. Asso-
ciation for Computational Linguistics.

Ondˇrej Bojar, Rajen Chatterjee, Christian
Federmann, Yvette Graham, Barry Haddow,
Matthias Huck, Antonio Jimeno Yepes, Philipp
Koehn, Varvara Logacheva, Christof Monz,
Matteo Negri, Aurelie Neveol, Mariana Neves,
Martin Popel, Matt Post, Raphael Rubino,
Carolina Scarton, Lucia Specia, Marco Turchi,
Karin Verspoor, and Marcos Zampieri. 2016.
Findings of the 2016 conference on machine
translation. In Proceedings of the First Confer-
ence on Machine Translation, pages 131–198,
Berlin, Allemagne. Association for Computa-
tional Linguistics.

Ondˇrej Bojar, Christian Federmann, Mark Fishel,
Yvette Graham, Barry Haddow, Philipp Koehn,
and Christof Monz. 2018. Findings of the 2018
conference on machine translation (WMT18).
In Proceedings of the Third Conference on
Machine Translation: Shared Task Papers,
pages 272–303, Belgium, Brussels. Association
for Computational Linguistics.

Nicholas Carlini, Chang Liu, Jernej Kos, ´Ulfar
Erlingsson, and Dawn Xiaodong Song. 2018.
The secret sharer: Measuring unintended neural
network memorization & extracting secrets.
CoRR, abs/1802.08232.

Jacob Devlin, Ming-Wei Chang, Kenton Lee, et
Kristina Toutanova. 2019. BERT: Pre-training
of deep bidirectional transformers for language
understanding. In Proceedings of the 2019 Con-
ference of the North American Chapter of the
Association for Computational Linguistics:
Human Language Technologies, Volume 1
(Long and Short Papers), pages 4171–4186,
Minneapolis, Minnesota. Association for Com-
putational Linguistics.

Kevin Duh. 2018. The multitarget TED talks task.
http://www.cs.jhu.edu/∼kevinduh/
a/multitarget-tedtalks/.

Cynthia Dwork. 2008. Differential privacy: UN
survey of results. Manindra Agrawal, Dingzhu
Du, Zhenhua Duan, and Angsheng Li, editors,
In Theory and Applications of Models of

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computation, pages 1–19. Springer Berlin
Heidelberg.

Jamie Hayes, Luca Melis, George Danezis, et
Emiliano De Cristofaro. 2017. LOGAN: Eval-
uating privacy leakage of generative models
using generative adversarial networks. CoRR,
abs/1705.07663.

Felix Hieber,

Tobias Domhan, Michael
Denkowski, David Vilar, Artem Sokolov, Ann
Clifton, and Matt Post. 2017. Sockeye: UN
toolkit for neural machine translation. CoRR,
abs/1712.05690.

Marcin Junczys-Dowmunt. 2018. Dual condi-
tional cross-entropy filtering of noisy parallel
the Third Con-
corpora. In Proceedings of
ference on Machine Translation: Shared Task
Papers, pages 888–895, Belgium, Brussels.
Association for Computational Linguistics.

Fabio Kepler, Jonay Tr´enous, Marcos Treviso,
Miguel Vera, and Andr´e F. T. Martins. 2019.
OpenKiwi: An open source framework for qual-
the 57th
ity estimation. In Proceedings of
Annual Meeting of the Association for Com-
putational Linguistics: System Demonstrations,
pages 117–122, Florence, Italy. Association for
Computational Linguistics.

Hyun Kim, Jong-Hyeok Lee, and Seung-Hoon
Na. 2017. Predictor-estimator using multilevel
task learning with stack propagation for neural
le
quality estimation.
Second Conference on Machine Translation,
pages 562–568, Copenhagen, Denmark. Asso-
ciation for Computational Linguistics.

In Proceedings of

Diederik P. Kingma and Jimmy Ba. 2015. Adam:
A method for stochastic optimization. CoRR,
abs/1412.6980.

Philipp Koehn and Rebecca Knowles. 2017. Six
challenges for neural machine translation. Dans
Proceedings of the First Workshop on Neural
Machine Translation.

Chin-Yew Lin and Franz Josef Och. 2004.
Automatic evaluation of machine translation
quality using longest common subsequence and
skip-bigram statistics. In Proceedings of the
the Association for Com-
42nd Meeting of
putational Linguistics (ACL’04), Main Volume,
pages 605–612, Barcelona, Espagne.

Yunhui Long, Vincent Bindschaedler, Lei Wang,
Diyue Bu, Xiaofeng Wang, Haixu Tang, Carl A.
Gunter, and Kai Chen. 2018. Understand-
ing membership inferences on well-generalized
learning models. CoRR, abs/1802.04889.

Ashwin Machanavajjhala, Xi He, and Michael
Hay. 2017. Differential privacy in the wild: UN
tutorial on current practices & open challenges.
In Proceedings of the 2017 ACM International
Conference on Management of Data, SIGMOD
’17, pages 1727–1730, New York, New York. ACM.

Milad Nasr, Reza Shokri, and Amir Houmansadr.
2018. Machine learning with membership
privacy using adversarial regularization. En Pro-
ceedings of the 2018 ACM SIGSAC Conference
on Computer and Communications Security,
CCS ’18, pages 634–646, New York, New York. ACM.

Milad Nasr, Reza Shokri, and Amir Houmansadr.
2019. Comprehensive privacy analysis of deep
learning: Passive and active white-box infer-
ence attacks against centralized and federated
learning. Dans 2019 IEEE Symposium on Security
and Privacy (SP).

Kishore Papineni, Salim Roukos, Todd Ward, et
Wei-Jing Zhu. 2002, Jul. BLEU: a method for
automatic evaluation of machine translation. Dans
Proceedings of 40th Annual Meeting of the
Association for Computational Linguistics,
pages 311–318, Philadelphia, Pennsylvanie. Association
for Computational Linguistics.

Matt Post. 2018, Oct. A call for clarity in reporting
the Third
BLEU scores. In Proceedings of
Conference on Machine Translation: Research
Papers, pages 186–191, Belgium, Brussels.
Association for Computational Linguistics.

Apostolos Pyrgelis, Carmela Troncoso, et
Emiliano De Cristofaro. 2018. Knock knock,
who’s there? Membership inference on aggre-
gate location data. CoRR, abs/1708.06145.

Md Atiqur Rahman, Tanzila Rahman, Robert
Laganiere, Noman Mohammed, and Yang Wang.
2018. Membership inference attack against dif-
ferentially private deep learning model. Trans-
actions on Data Privacy, 11:61–79.

Ahmed Salem, Yonghui Zhang, Mathias Humbert,
Mario Fritz, and Michael Backes. 2018. Ml-
leaks: Model and data independent membership

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
2
9
9
1
9
2
3
5
4
7

/
t

un
c
_
un
_
0
0
2
9
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

inference attacks and defenses on machine
learning models. CoRR, abs/1806.01246.

Rico Sennrich, Barry Haddow, and Alexandra
Birch. 2016. Neural machine translation of rare
words with subword units. In Proceedings of
the 54th Annual Meeting of the Association
for Computational Linguistics (Volume 1: Long
Papers), pages 1715–1725, Berlin, Allemagne.
Association for Computational Linguistics.

R.. Shokri, M.. Stronati, C. Song, and V. Shmatikov.
2017. Membership inference attacks against
machine learning models. Dans 2017 IEEE Sym-
posium on Security and Privacy (SP), pages 3–18.

Congzheng Song and Vitaly Shmatikov. 2019.
Auditing data provenance in text-generation
the 25th ACM
models.
SIGKDD International Conference on Knowl-
edge Discovery & Data Mining, KDD ’19,
pages 196–206. New York, New York, ACM.

In Proceedings of

Lucia Specia, Varvara Logacheva, Frederic Blain,
Ramon Fernandez, and Andr´e Martins. 2018.
WMT18 quality estimation shared task training
and development data. LINDAT/CLARIN digi-
tal library at the Institute of Formal and Applied
Linguistics ( ´UFAL), Faculty of Mathematics
and Physics, Charles University.

J¨org Tiedemann. 2012. Parallel data, tools and
interfaces in opus. In Proceedings of the Eight
International Conference on Language Re-
sources and Evaluation (LREC’12), Istanbul,
Turkey. European Language Resources Asso-
ciation (ELRA).

Stacey Truex, Ling Liu, Mehmet Emre Gursoy,
Lei Yu, and Wenqi Wei. 2018. Towards
demystifying membership inference attacks.
CoRR, abs/1807.09173.

Ashish Vaswani, Noam Shazeer, Niki Parmar,
Jakob Uszkoreit, Llion Jones, Aidan N. Gomez,
Łukasz Kaiser, and Illia Polosukhin. 2017.
Attention is all you need. In I. Guyon, U. V.
Luxburg, S. Bengio, H. Wallach, R.. Fergus,
S. Vishwanathan, et R. Garnett, editors,
Advances in Neural Information Processing
Systems 30, pages 5998–6008. Curran Asso-
ciates, Inc.

Michael Veale, Reuben Binns, and Lilian Edwards.
2018. Algorithms that remember: Model inver-
sion attacks and data protection law. Philo-
sophical Transactions. Series A, Mathématique,
Physical, and Engineering Sciences, 376.

Samuel Yeom, Matt Fredrikson, and Somesh
Jha. 2017. The unintended consequences of
overfitting: Training data inference attacks.
CoRR, abs/1709.01604.