Maxence Larrieu
Litt ´eratures, savoirs et arts (LISAA)
Universit ´e Gustave Eiffel
5 Boulevard Descartes, 77420
Champs-sur-Marne, France
maxence@larri.eu
An Analysis of “nyx”
(2017), a Computer Music
Work by Kerry Hagan
Abstrait: Kerry Hagan composed “nyx,” a real-time computer music work, dans 2017. The key inspiration of “nyx” is
bruit, which Hagan achieves through chaos theory. In Greek mythology, Nyx was born from Chaos, and she is the
deity of the night. In the same way, two key materials of the work are chaotic synthesis and, at a higher level, the use
of several random algorithms. To analyze “nyx,” I apply a specific methodology that considers both the sound and the
computer code. En fait, I consider code as a medium through which Hagan has realized her musical ideas, that is to say,
seeing code as a support for musical ideas, and not only as a computing object.
This article has two main sections: The first describes Hagan’s techniques through Pure Data code, and in the second
the music is analyzed in its canonical form, describing the structure of the work. Enfin, I argue that “nyx” involves
many levels of noise, from the sound design, to the use of random algorithms, and lastly to the inspiration from Greek
mythology to structure the work.
Kerry Hagan’s computer music work “nyx” (2017)
has been publicly presented in well-known music
venues including BEAST FEaST (at the University
of Birmingham in the UK), the Cube (at the School
of Performing Arts, Virginia Tech), and in other
facilities with advanced spatialization systems.
The work is shared by Hagan on her website,
kerrylhagan.net, where one can find a stereophonic
audio file as well as the Pure Data patch that permits
us to see the computations and hear the work.
The work “nyx” is part of a series of computer
works by Hagan that were inspired by noise:
“Morphons and Bions” (2011), “. . .of pulses and
times. . .» (2012), “s/d” (2015), and finally “nyx.”
The pieces in this “noise series” strictly use digital
synthesis, without any recorded samples, and are
“real-time compositions” in the sense that they
contain random algorithms so that each realization
of a particular composition is different, at least in
part. Hagan has explained her aesthetic inspiration
from noise (Hagan 2012) et, for the first work of
the series, “Morphons and Bions,” she has explained
how noise has been used for the material of the work
(Hagan 2013). In both papers, Hagan also explains
the reason behind this series.
At first, there is a wish to extend musical material
with synthesis:
All artwork in this article is covered by Creative Commons
license CC BY 4.0, https://creativecommons.org/licenses/by/4.0.
Computer Music Journal, 44:2/3, pp. 118–132, Summer/Fall 2020
est ce que je:10.1162/COMJ a 00569
c(cid:2) 2021 Massachusetts Institute of Technology.
I always worked with recorded sound for my
electroacoustic compositions. The richness and
variety of acoustic sounds provided enough
sonic data for processing and manipulation.
Synthesis sound seemed flat, mundane, et
plain by comparison. I decided that working
with synthesis would be my next challenge
(Hagan 2013).
And then, with a goal to make rich noise synthe-
sis, comes the deep inspiration from noise:
I decided that it was the noise of acoustic
sounds that made them richer. . . I approached
synthesis from the basis of noise, using noise
as the foundation of every synthesis method
(Hagan 2013).
Donc, the use of noise with synthesis tech-
niques is crucial in the works of the series. With
“nyx,” Hagan used new material that is coherent
with noise, namely, chaotic mathematical functions.
Two standard chaotic functions, Gingerbreadman
and Ikeda, are used. De plus, all the sound sources
of the work come from those chaotic functions. Même
if the sound design level is essential for “nyx,” this is
not the only level influenced by the notion of noise.
I can see two others: one concerning the mesoform
(c'est à dire., a middle layer of musical form) and another for
the aesthetic. For the mesoform, in each work there
is the use of random algorithms to determine, within
a section, the behavior of the synthesis techniques.
In this way, each realization of the same work will
be different, within constraints. As we will see, ce
noise at the mesoform level poses problems for the
118
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
analyse, as it becomes inappropriate to consider
only one realization of the work—this is one good
reason for considering the patch in analysis: “nyx”
exists not only as an audio signal but also as a
patch.
The highest level of noise concerns aesthetics. Dans
relation to the preceding chaotic functions, Hagan
finds inspiration in Greek mythology, from which
the name of the work comes: Nyx is the name of
the Goddess of night and—together with her brother
Erebus, the god of darkness—was born from Chaos.
They were the first two divinities who gave birth
to the Greek gods. I suggest that the structure of
the work can be seen in this “creation process,»
starting from chaos, with the raw noise of the
chaotic functions at the beginning, and proceeding
to creation, with one last pitch gesture from low to
haut.
Before discussing the work, I will introduce two
points that explain the method used to analyze
computer music work.
My first point can be explained if one considers
the material objects of computer music. The first
obvious material object one can think of is the audio
signal of the work. In our digital era, the audio signal
is stored in computer files, permitting anyone to
hear the music, if the files are publicly accessible.
This object is perhaps obvious, because it is a more
convenient way to permit people to appreciate the
work—as Pierre Schaeffer said, “music is made
to be heard” (cf. Chion 2009, p. 35). The second
material object of computer music is the code
(c'est à dire., the instructions written by the composer in a
programming language), which computes the audio
signal of the work. My first point is related to the
existence of this code in computer music. Following
the argument made in Otto Laske’s article, “The
Computer as the Artist’s Alter Ego” (Laske 1990),
I see the code as an object with which composers
create and think of their music. Donc, to analyze
computer music, the code has to be studied, because
it sheds light on the work in a different way than
the listening does (cf. Di Scipio 1995; Risset 2001;
Battier 2003; Zattra 2015). Nevertheless, there could
be a danger in following this route, in which one can
be dazzled by the code and can forget to listen to the
travail. To avoid this, my first point is that to analyze
computer music, both code and audio signal have to
be considered. They enrich each other (for a deeper
viewpoint, cf. Larrieu 2019).
My second point is related to the analysis of
computer music works that contain indeterminate
elements. In “nyx” we find random processes, donc
that each computation, each calculation of the audio
signal, is different. Another way to explain this is to
focus on the relationship between the code and the
audio signals: One program can produce many audio
signals, and all of them belong to “nyx,” between
code and audio signals there is a one-to-many
relationship. To reveal this relationship, I call the
result of one computation an actualization, so that
the actualizations of one work are the many audio
files that the code can produce. This one-to-many
relationship impacts the way of analyzing a work. Dans
fact, an analysis focusing only on one actualization,
dealing with time and sound morphology, will
not be suitable, because it does not account for
the production of actual sounds or the level of
randomness in their production. One sound present
at a specific time in one actualization will not
necessarily be present in another actualization. My
second point is that the analysis of works containing
indeterminate processes has to consider many
actualizations, so that the analyst can evaluate the
level of randomness in the production. Nick Collins
(2008) addresses the same questions in the context
of generative computer music.
The analysis presented in this article contains two
main sections. The first, Music Modules, concerns
those of Hagan’s techniques captured inside the
Pure Data (Pd) patch, for which I use the concept
of music modules. Music modules are understood
here as the grouping of many elements inside the
patch, which a composer uses to realize musical
matériel. In this definition, music modules are not
merely technological, they belong to a musical
level and result from the subjective understanding
of the analyst or composer. I differentiate music
modules, which are higher-level constructs by a
composer, from lower-level technological modules,
like reverberation, which are common to the field
of sound engineering (for further discussion, voir
Larrieu 2018, p. 99). The second main section,
Music Analysis, concerns the actualization of the
Larrieu
119
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
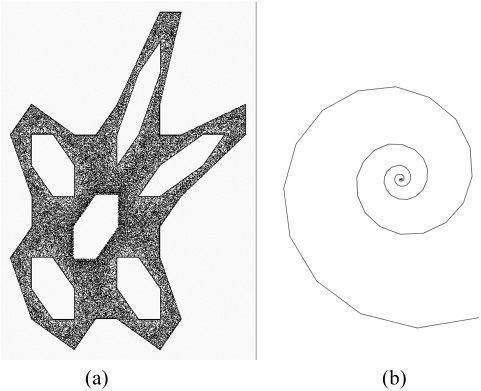
Chiffre 1. Sample
representations of two
chaotic functions:
Gingerbreadman function
with x0 = −0.1 and
y0 = 0.2 (un); Ikeda function
with x0 = 1, y0 = 0.3, et
u = 0.94 (b).
travail; there I will analyze the temporal structure
and the sounding elements of the work.
Enfin, because “nyx” has been played on im-
portant multichannel systems with highly specific
configurations—for example, at the Cube in the
School of Performing Arts at Virginia Tech, le
spatialization was on 124 chaînes (cf. Lyon 2016)—
there are several versions of the work. En fait, quand
Hagan is invited to play the work on such a system,
she rewrites the spatialization, thus composing a
new, ad hoc version. In this analysis, plutôt que
considering multichannel spatialization, I will focus
on the stereophonic version of “nyx.”
The Pd patch has been made publicly
available by Hagan on a scientific repository
(https://doi.org/10.5281/zenodo.3971610) using a
Creative Commons license, so that now anyone can
download, share, and cite the patch; thanks to the
persistent identifier, people can be sure of referring
to the same version. The patch runs on Vanilla
Pd, the version distributed by Miller Puckette, comme
opposed to versions from other developers, OMS
build on and extend Puckette’s version.
Music Modules
One can differentiate three music modules in “nyx.”
The first is a chaotic synthesis module, generating
noise with chaotic functions; the second is a phase
vocoder module, which applies time-scaling and
pitch-shifting to the previous signals; and the last is
a spatialization module.
Chaotic Synthesis
Using chaotic functions as synthesis techniques is
not new in computer music. Par exemple, dans le
1990s one can find an article (Slater 1998) where the
author combines a chaotic function (named “Ueda
attractor”) with frequency modulation techniques.
With “nyx,” the use of chaotic functions is different:
The idea is not to combine chaotic functions with
synthesis techniques but to directly use these
functions to produce sound signals—and moreover
to use them as musical material. Hagan used two
standard functions, named Gingerbreadman and
Ikéda, both discrete and in two dimensions.
Gingerbreadman and Ikeda Functions
To use these chaotic functions, the two cor-
responding equations must be implemented.
Gingerbreadman:
xn+1 = 1 − yn + |xn|,
yn+1 = xn.
and Ikeda:
xn+1 = 1 + toi(xn cos(tn) − yn sin(tn)),
yn+1 = u(xn sin(tn) + yn cos(tn)),
where u is a parameter and tn is defined as
tn = 0.4 −
6
1 + x2
n
.
+ y2
n
As one can easily see, the Gingerbreadman func-
tion is computationally quite simple, with only
an absolute value function and simple arithmetic.
The Ikeda function is more complex, with lay-
ered trigonometric functions, as well as a specific
parameter called u.
Because these functions are discrete with two
dimensions (x and y), it is appropriate to represent
them in a two-dimensional space. In Figure 1a,
120
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
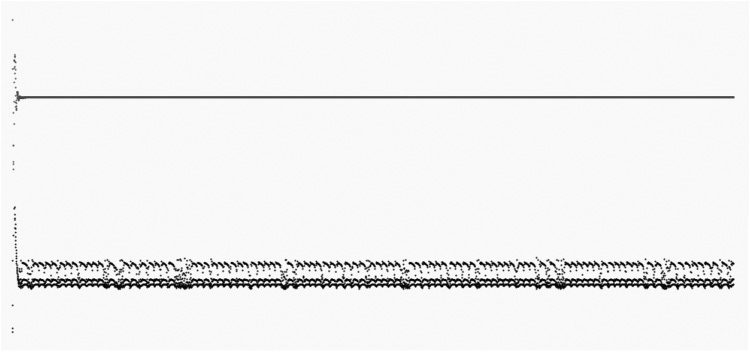
Chiffre 2. Waveform of
Ikeda × signal: avec le
original function (un) et
the modified function (b).
The time span is nearly
135 msec.
the Gingerbreadman function is represented with
100,000 iterations, with each of the outcomes (xn,
yn) as coordinates of one point.
The shape of a gingerbread man can be better
recognized if one rotates the figure 135 degrees
clockwise.
Figure 1b represents the Ikeda function. It was
obtained with 10,000 iterations and by connecting
each successive point, (xn, yn) à (xn+1, yn+1).
The Ikeda function looks like a spiral, and as
the value of u increases, the tighter the resulting
spiral—a value of 0.2 will give something like a line,
and a value of 0.99 will give many spiral loops.
Sound Synthesis with Chaotic Functions
Hagan’s idea is not to combine the chaotic functions
with oscillators, but to listen directly to the chaotic
functions–as it were, “to plunge into the chaos.” To
réaliser cela, the outputs of the functions are directly
used as sample values. The functions are, donc,
computed near the sample rate (44.1 kHz in “nyx”).
This is done with one peculiarity of Pd, where one
can set a metronome measured by samples. Enfin,
to avoid artifacts such as clicks, an audio ramp is
used when the function runs slower than the sample
rate.
As we have seen, the functions have two dimen-
sions, x and y, which is suitable for image rendering.
To adapt these functions to the audio domain, chaque
dimension is used as a separate audio signal: Le
output values from the x dimension produce one
audio signal and those for the y dimension another.
Ainsi, each chaos function implemented produces
two independent audio signals, referred to as x and y.
Before going further, I must note a mathematical
error in the patch that occurs in the implementation
of the Ikeda function. One principle of the Ikeda
function is that, as the iteration progresses, le
difference between results diminishes (c'est à dire., plus
they tend towards an attractor). Donc, because
we are concerned with audio samples, it is apparent
that after 1 second of sound (iteration 44,101)
the sample values would be almost static, thus
producing no sounds. Cependant, the implementation
made by Hagan does produce sounds. This comes
from a small error inside the calculation of tn, où
one can read tn = 0.4 − 6/(1 + 2 × y2
tn = 0.4 − 6/(1 + x2
n). Chiffre 2 compares results
n
de 6,000 iterations for the original function and the
function as actually implemented. As is apparent,
the waveform of Ikeda’s original function is quickly
null, whereas the one with the error in the tn
calculation produces sound.
n) instead of
+ y2
Describing the resulting sound is not an easy task
because it is unrelated to perceptible components,
such as sine waves, formants, or spectral distri-
bution. Indeed those “perceptible components”
cannot shed light on signals produced by chaotic
les fonctions. Unlike the visualization in Figure 1, le
Larrieu
121
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
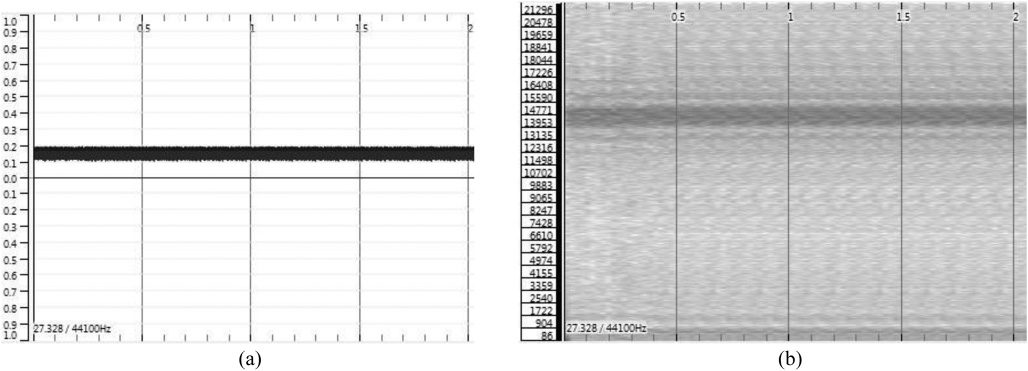
Chiffre 4. Waveform (un) et
spectrogram (b) of Ikeda x
signal for 2 seconds.
Chiffre 3. Waveform (un) et
spectrogram (b) de
Gingerbreadman × signal
pour 2 seconds. (All spectral
analyses are made with a
Hann window: size 1,024
samples, threshold
−43 dB.)
Chiffre 3
Chiffre 4
sound produced does not have a familiar pattern.
Ici, what is produced is fundamentally noise: Nous
cannot immediately hear any spectral or temporal
organization.
As can be seen, the Gingerbreadman signal (voir
Chiffre 3) is complex, with a pattern that repeats
itself vertically in the spectrogram. It is impossible,
cependant, to hear any patterns. The sound we hear
is high (cf. the black line near 9.5 kHz) and made
of infinitesimal movements dispersed across the
spectrum scale. The Ikeda function is also high and
clearly evinces a fast cyclic pattern (voir la figure 4).
I describe these signals here only for an analytical
but, cependant; one cannot hear them indepen-
dently in “nyx.” In fact, to add complexity, Hagan
implemented three distinct Gingerbreadman and
122
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
two distinct Ikeda functions, which can be run at
different rates. Ainsi, the chaotic synthesis module
produces no fewer than ten signals: Five chaotic
functions are implemented (three Gingerbreadman
and two Ikeda) with each producing two signals
(x and y).
Contrôle
At this point in the analysis, it would be fruitful
to focus on the controls present in the chaotic
synthesis. D'abord, because Hagan deals with math-
ematical functions, there is a series of low-level
parameters that must be noted. Each x0 and y0 of the
Gingerbreadman functions and each x0, y0, and u of
the Ikeda functions must be defined at the start of
the computation. This is done during initialization,
when the patch is open or reset. Even if these values
are at a low level, it is important to note them,
because it is through these values that the module
produces different signals. The last low-level pa-
rameters are the ones that modify the amplitude of
the signals. There is one on each signal, with vari-
ables 1gingXfl and 1ikedXfl. The variable naming
convention is: instance number, function name, X
or y signal, “f” for a fader, and “l” for line object
generating a ramp. They are worth noting because,
as we will see, random processes are applied to them.
The next control is at a higher level of abstraction
and is more closely linked to the perception of the
sound: the computational rate of the functions.
There are five variables for controlling the rates
of the five instances, named 1gingratel, 2gingratel,
3gingratel, 1ikedratel and 2ikedratel. Again the
ending “l” stands for line, meaning a ramp function
is used. Functions with changing rates are signifi-
cantly more perceptible to the listener than are the
low-level parameters noted above. The standard rate
is the sampling rate, 44.1 kHz, and one key action
Hagan executes is to slow down these particular
rates, which will decrease the perceived pitch of
both the x and the y signals.
Algorithms
Two simple algorithms with the same behaviors
are present in the module. The first affects signal
Tableau 1. Scales of Random Amplitude Algorithm
Variables
Minimum Value Maximum Value
1gingxfl, 1gingyfl
2gingxfl, 2gingyfl
3gingxfl, 3gingyfl
1ikedaxfl, 1ikedayfl
2ikedaxfl, 2ikedayfl
50
70
46
80
70
74
94
70
104
94
Values are in decibels, avec 100 corresponding to unity gain,
following Pure Data conventions.
Tableau 2. Scales of Random Rate Algorithms
Variables Minimum Value Maximum Value
1gingrate
2gingrate
3gingrate
1ikedarate
2ikedarate
5
45
1
60
1
9
55
5
100
10
amplitude, the second affects the computational
rates of the chaotic functions. Both algorithms
simply generate a pairs of points (X, oui) where x
is a destination value and y a time in seconds to
achieve that destination. Aussi, once the point x
has been achieved in the desired time y, a new pair
of values is generated. Ainsi, once activated—with
Boolean variables randlevelsorig and randrate for
amplitudes and rates, respectively—the algorithm
will continuously generate new values. Each chaos
function changes independently in amplitude and
rate with these variables.
For amplitude, time y is selected randomly in
each implementation in the interval [1, 5] seconds
with a step of one, and amplitude values are selected
randomly in an interval that changes according
to instances. Tableau 1 describes the amplitude
calculation.
For the rate algorithm, the time is selected
randomly in interval [10, 29] seconds and the
destination point x is selected randomly with the
distribution shown in Table 2.
Tableau 3 describes the meaning of chaotic module
controls.
Larrieu
123
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Tableau 3. Meanings of Chaotic Synthesis Controls
Variable
1gingratel
2gingratel
3gingratel
1ikedratel
2ikedratel
1gingXfll
2gingXfll
3gingXfll
1gingYfl
2gingYfl
3gingYfl
1ikedXfl
2ikedXfl
1ikedYfl
2ikedYfl
Type
Meaning
float or list
Change the rate of one Gingerbreadman instance
float or list
Change the rate of one Ikeda instance
float or list
Change the amplitude of the x signal from one Gingerbreadman instance
float or list
Change the amplitude of the y signal from one Gingerbreadman instance
float or list
Change the amplitude of the x signal from one Ikeda instance
float or list
Change the amplitude of the y signal from one Ikeda instance
randlevelsorig
Boolean
Activate random amplitude algorithm
randrate
Boolean
Activate random rate algorithm
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
Phase Vocoder
Usage
The second module is a phase vocoder, which is
applied to the chaotic synthesis signals. It permits
one to change, independently and in real time,
the duration and tuning of an incoming signal via
time stretching and pitch shifting, respectivement.
The implementation is taken from the description
given by Miller Puckette (2006, p. 292) in his
seminal publication The Theory and Technique
of Electronic Music, and is also present as an
example in the Pd library (see the patch named
I07.phase.vocoder.pd). In this analysis I will not
describe Miller Puckette’s implementation. UN
higher level of mathematics would be needed
(complex numbers, fast Fourier transform) et,
more importantly, it is not something developed by
Hagan for “nyx.” I will therefore focus on how she
has used this technology in her work.
The phase vocoder is applied independently to each
of the ten signals produced by chaotic synthesis. Il
is used to change both speed and tuning (see Table 4
to view all phase vocoder controls). Speed, once set,
remains static throughout, whereas tuning changes
all through the work. Concerning the speed, chaque
signal of the chaotic module is slowed down to one
fifth of its original speed. Slowing down all noise
signals is valuable, because the raw signals are made
up of infinitesimal movements. The goal, cependant,
is not to produce something identifiable. En effet,
these new slowed-down signals do not replace the
“raw” signal but are distributed simultaneously
instead.
Concurrently, the tuning parameter is used
to add short gestures in pitch. It will basically
change the perceived pitch of noise signals. All
the transformations lower the pitch, transposing the
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
124
Computer Music Journal
Tableau 4. Phase Vocoder Controls
Variable
1speedl
2speedl
. . .
10speedl
1gpvXfl
2gpvXfl
3gpvXfl
1gpvYfl
2gpvYfl
3gpvYfl
1ikedXfl
2ikedXfl
1ikedYfl
2ikedYfl
Type
Meaning
float or list
Changes the speed of incoming signal (stretching)
float or list
Changes the amplitude of the x signal from one Gingerbreadman instance
float or list
Changes the amplitude of the y signal from one Gingerbreadman instance
float or list
Changes the amplitude of the x signal from one Ikeda instance
float or list
Changes the amplitude of the y signal from one Ikeda instance
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
randlevelspvoc
Boolean
Activates random detuning algorithm
decreasedetune
Boolean
Activates a sequence to continuously reduce detunes range
signals downward between 0 et 8,000 cents (presque
seven octaves). Donc, the phase vocoder, avec
its speed reduction and lowering of pitch, est utilisé pour
add another layer of noise, intensely enriching the
noise of the chaotic synthesis.
Algorithms
There are also two random algorithms inside
the phase vocoder. The first is the same as that
used in the chaotic synthesis, which changes the
amplitude of the x and y signal pairs. The second
permits modification of the tuning signals. Ce
modification also uses randomness, but in a new
chemin.
The random detuning algorithm generates a pair
of values (X, oui), with x being the transposition value
and y the time. The transposition value is reached
directly, without a duration value. The second value,
oui, is a time lapse before a new transposition value
x is calculated. Donc, this random detuning
algorithm does not generate a ramp of values, mais un
instantaneous change.
The time lapse is selected randomly in the
interval [10, 19] seconds, and the transposition
is also selected randomly in the interval [−8000,
−1] cents. The values are generated once the
algorithm is activated, with a variable named
detune.
Enfin, there is a second input inside this
algorithm that, once activated, progressively reduces
the range of detuning values. At first, the range will
ramp continuously from [−8000, −1] à [−7000, −1]
dans 60 seconds, then to [−6000, −1] dans 36 seconds,
and so forth, creating a sequence of 3:30 minutes
with this key correlation. The more time progresses,
the smaller the range of random detuning. En effet, à
the end of the main section (duration of 3:30 min),
detuning values are zero, and there is no more
transposition.
Spatialization
The last module of “nyx” to discuss is that of
spatialization. It allows the placement of a signal in
Larrieu
125
Chiffre 5. Pseudocode
illustrating the
spatialization algorithm.
Chiffre 6. Pd patches for the
spatialization model (un)
and the expon abstraction
(b).
Run randomDur() and spat() les fonctions, wait for duration and start them again, etc..
randomDur() function is
d = random(0.001, 1) with a step of 0.001
duration = -log(d) / 0.0009
spat() function is
x = random(0.001, 0.999) with step of 0.001
smoothx = line(X, duration)
// line() outputs a floating point value that ramps
// continuously to x within the specified time duration.
// Once x is reached, the output stops ramping.
leftChannel = cos(smoothx * PI/2)
rightChannel = sin(smoothx * PI/2)
Chiffre 5
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
stereophonic space. It is applied each time a signal
is diffused, so on the ten signals coming from the
chaotic synthesis module and the ten signals coming
from the phase vocoder module. Par conséquent, un
can see that spatialization is not made “by hand”
but with the use of small random algorithms.
These algorithms have the same behavior as those
previously discussed. They generate a pair of values
(X, oui) where x is a position in the stereophonic space
and y a duration. What is new here, cependant, is that
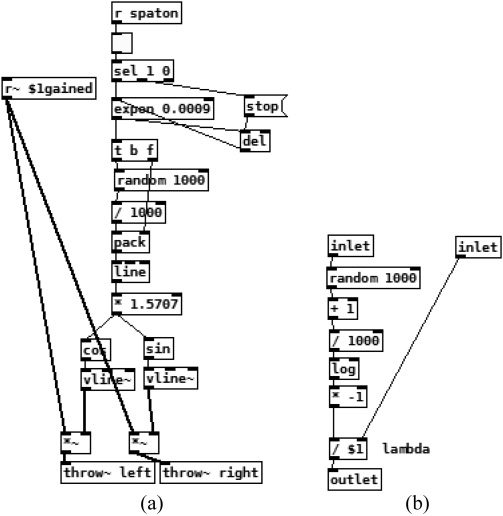
duration is calculated with an exponential function.
Figures 5, 6, et 7 describe calculations made by the
algorithme.
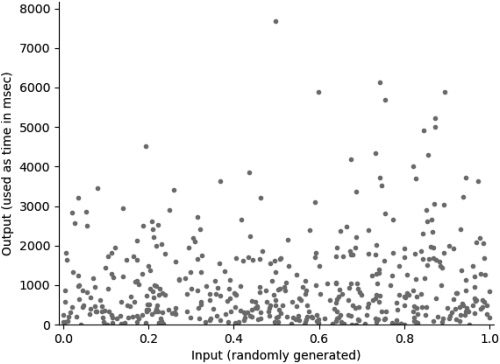
As shown in Figure 7, the use of the exponential
function allows Hagan to incorporate noncyclic
behavior (Hagan 2018, p. 119). The mean of outcomes
is nearly 770 millisecondes (mean = 0.69315 / 0.0009)
but because of the exponential function it will vary
widely. Donc, the spatial movement occurs at
the scale of a “note”: near to one second. Because
movements are not going from full left to full right,
cependant, and because the listener will hear at least
ten spatial movements at the same time, it should be
hard to hear precisely one “spatial movement.” We
should, cependant, hear a whole series of movements.
En fait, the spatialization module is a way for Hagan
to add, one more time, additional noise within the
stereophonic space.
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 6
Routing
Routing—that is to say, connections between
modules—is fixed throughout the work. I suggest
126
Computer Music Journal
Chiffre 7. Outputs of the
randomDur() fonction
during one actualization
for one instance of spat
(471 outputs).
Chiffre 8. Audio flow chart
for one of the ten voices
from the Pd Patch. Chaque
voice produces two audio
signals, one coming
directly from chaotic
synthesis and the other
after the output from the
chaotic synthesis has been
processed by a phase
vocoder module.
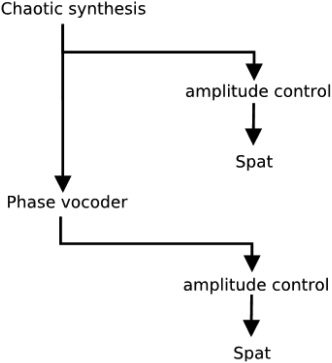
therefore describing the patch as a set of voices.
Each voice is basically made of one signal from one
chaos function, one phase vocoder instance, et
two spatializer instances. The first spatialization
is applied to the chaotic synthesis output and
the second to the phase vocoder output. Chiffre 8
represents one voice.
The patch contains ten voices; donc, le
composition is made with 20 different signals.
Musical Analysis
Even if “nyx” is largely based on noise, this does not
imply that there is a lack of organization. One can
easily perceive structure when listening to this work
lasting 8:15 min. This structure is largely gestural,
with a prominent gesture going from low to high
pitch, or from high to low, at significant points in
the work. This gesture is implemented via one of
the most important controls yet to be addressed:
the rate of chaotic synthesis. Hagan decreases or
increases the five chaotic rates that produce an
important sliding in pitch. The first gesture appears
near the beginning at 1:00 and the last one at 7:30.
These two gestures encapsulate the main section
of the work. The two resulting short fragments at
the opening and closing are essentially introductory
and closing materials. Par conséquent, the structure
of “nyx” approximates an ABA’ structure, avec le
central section constituting the largest and most
developmental.
Before explaining these three sections it is
important to note precisely how the composition
is realized in time. There is a sequencer, made
of messages boxes and connected through delay
objets, that contains all the changes over time of
all variables described. Ainsi, there is one way to
compose with time that is determinate: Each time
“nyx” is computed, the same sounding elements
appear at the same times (par exemple., the two prominent
gestures in pitch noted above). Cependant, as we
have seen with the many random algorithms,
there is another way to compose with time that is
indeterminate, in which we cannot know exactly
what will happen each time the work is computed
(for interesting questions related to indeterminacy
and real time in computer music, see Hagan 2016).
The structure of “nyx” reflects this fundamental
opposition: The opening and closing are determinate
and do not contain random algorithms, whereas the
main section is partially indeterminate and contains
all the random algorithms. Analyzing determinate
computer music does not present new problems,
because the audio signal is fixed. Problems arise
with the analysis of indeterminate computer music,
cependant, when the audible elements can be different
in another actualization. To accommodate this
challenge, I have chosen a methodology outlined
immediately following the discussion of the opening
section.
Larrieu
127
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 9. Spectrogram of
the first prominent gesture.
À 1:00 min Hagan
decreases the rates of the
chaotic functions, lequel
produce an important
glissando from high to low
pitch. This gesture marks
the end of the opening of
the piece.
of indeterminate elements produced by algorithms.
Concretely, it means that the sounds I am listening
to as “the work” can be different (or completely
missing) in another actualization. Par exemple, si
I hear a harmonic interval at a precise moment,
nothing permits me to say that it will present in
another actualization. Because “nyx” is real-time
computer music, audio files must be understood as
one of many possible actualizations: One trap for
the analyst would be to over-consider any audio file
in particular, and to analyze “nyx” as an acousmatic
travail. Another danger would be to only consider the
algorithms, the computer writings made by Hagan,
without considering sound at all in the six minutes
of the main section.
Ainsi, for this section I will consider both what
is written and what is heard. D'abord, I will describe
what is written, when and how long the algorithms
are launched, and then I will, à son tour, describe
the sound manifestation in the section. To avoid
focusing on one actualization, I have realized
six actualizations and I will take them all into
account.
Analysis of Written Materials
Chiffre 10 represents all the writing of the algorithms.
As one can see, the main section is constructed with
an accumulation of algorithms. D'abord, just after the
prominent gesture, the random rates algorithm is
triggered at 1:45, generating long lines of pitched
bruit. En même temps, the phase vocoder fades in,
doubling the chaotic signals with a deceleration by
a factor of five. Then the two random amplitudes
algorithms are added at 2:15 et 3:15, respectivement.
The last algorithm is started at 3:30; it is the
random detuning algorithm from the phase vocoder.
Until this moment, the phase vocoder was only
slowing down the original noise signals. With this
last algorithm, the phase vocoder’s signals become
independent in pitch, randomly detuning each
chaotic signal. Near the middle of the section, à
3:45, the sequence to reduce random detuning is
launched. The range will decrease progressively
from a maximum of −8,000 cents to zero at 6:45.
The last part of the section consists of progressively
switching off all the algorithms.
Opening
The opening section of “nyx” spans one minute and
immediately immerses the listeners in the work’s
bruit, confronted as they are by ten signals from
the chaotic synthesis module. Signals are diffused
raw, with no phase vocoding, only spatialization.
Ainsi, during the first minute, the listener is totally
thrown into a noise environment. Noise is the
only element present, without alteration or effect,
for one minute. This opening is like an invitation
“to go inside the noise” and stop considering it as
something undesirable.
The opening finishes with the first prominent
gesture from high to low pitch, at one minute. Hagan
smoothly decreases rates of chaotic synthesis. Elle
generates a ramp from a frequency of calculation
of once per sample to one calculation for every 50
samples. The effect is an important decrease in the
perceived pitch, as Figure 9 shows.
After the raw noise, we now have an important fa-
miliar gesture in the pitch dimension, the glissando,
which encourages anticipation in the listener.
Main Section
As stated earlier, this main section contains diffi-
culties for musical analysis because there are a host
128
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 10. Algorithm states
(above timeline) et
sounding elements (below
timeline).
Analysis of Generated Sound
Even if the development is made with random
algorithms, one can hear some persistent sonic
elements when one listens to a few different
actualizations. After the prominent pitch gesture
that opens the section, à 1:45 there is a new set
of pitch lines. These come from the random rate
algorithme, which produces new rate values with
longer durations (entre 10 et 30 seconds).
This element is reminiscent of the prominent
structural gesture, but it is considerably more
subtle. Rates here are not synchronized: Their
instructions (up or down) are set randomly. The listener
discovers herein yet another compositional idea in
the work, whose character is situated between the
raw noise of the opening and the prominent pitch
gesture.
À 2:00 more new material is introduced, dans-
riching the experience thus far. The material comes
from the phase vocoder, which is softly faded in. Le
deceleration effect adds a deep lower layer of noise.
For one minute all the materials of the work find
exposition: the raw noise with random rates lines
plus random fades, and the last deep noise coming
from the phase vocoder.
À 3:35 there appears a new movement. The deep
noise of the phase vocoder suddenly fades out to give
way to a quiet region. The spectrogram of this area
contains less energy; low noises are less present and
there are untidy short sound events, with different
pitches, which appear and disappear after a few
seconds. This is visible in Figure 11, which shows
the spectrogram of six actualizations.
At this point in the work, all materials and
algorithms have been exposed; one might say in
this movement “the composer lets the algorithms
speak.” Because of the two random-amplitude
algorithms (which generate ramps between 1 et
5 seconds in length), many short sounds appear
and disappear, and occasionally moments with
less energy, of relative calm, appear. En outre,
the random detuning algorithms transpose these
short sounds. Ainsi, sometimes the succession of
two sounds forms a clear pitch interval. Là
est, moreover, a tension building as a result of the
detuning algorithms: The more time passes, le
smaller the transposition. En effet, à 6:32 detunings
fall within the interval [−1000, 0] and finally at 6:45
there is no more transposition.
With these calm areas, clear pitch intervals, et
the aforementioned tension that builds from full to
null transposition, this main section is the richest
part of the composition. It is the opposite of the
raw noise sounds from the opening. There are now
sounds of a few seconds, with different pitches, que
attract the listener’s attention.
The main section finishes with a small gesture at
à propos 6:50, in which pitch goes from high to low.
This is produced with the phase vocoder module and
in an original manner. Because the detuning is null
Larrieu
129
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 11. Spectrograms of
the main section for six
actualizations of “nyx.”
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
at that time, the pitch should go from low to high;
cependant, the gestures one can hear are going to be
low because of aliasing. Signals are indeed going up
but the frequencies are over the Nyquist frequency,
22.05 kHz, and because of aliasing they are reflected
and essentially mirrored into the audible spectrum.
Closing
The end of the main section is marked by the
second prominent gesture at 7:35, from low to
high pitch this time (voir la figure 12). Encore, ce
is made by increasing the rate of the instances of
130
Computer Music Journal
Chiffre 12. Spectrogram of
the last gesture.
chaotic synthesis module. Bien sûr, the beginning
of this gesture recalls the first gesture and places the
listener in a situation of considerable anticipation.
The gesture finishes beautifully: Just after its end,
in a very high pitch, the raw noise signals return,
much like the opening. Hearing chaotic noise here
does not create an impression of chaos, cependant:
The noise signals only last a few seconds and then
slowly fade out. Ici, noise is used constructively,
to finish the last important gesture.
Conclusion
Analyzing a real-time computer music work
presents unique challenges, because one must
fundamentally question what constitutes the ap-
propriate object for analysis. Do we engage with
the sound manifestation or computer music code?
Considering Risset (2001), Battier (2003), and Zattra
(2015), I have developed an analysis that answers
that question: Both the sound manifestation and the
computer music code must be taken into account.
Donc, the purpose of the research was explain-
ing both what is contained with the patch and how
it is used, as well as providing a sonic analysis of the
music via listening.
In the Music Modules section, I described the
patch and its contents: three music modules in-
cluding chaotic synthesis that produces raw noise,
a phase vocoder that is used for time-stretching and
transposition, and finally a spatialization module
that spatializes these signals within a stereophonic
espace. The key controls of these modules are the
rate of chaotic synthesis, the detune of the phase
vocoder, et, to a lesser extent, amplitude for both
chaotic synthesis and phase vocoder. Dernièrement, tous
these modules include random algorithms that are
applied to the aforementioned key controls for the
chaotic and phase vocoder modules, as well as to the
spatialization, resulting in random rates, random
detuning, random amplitudes, and random spatial
positions. Another way to shed light on the “nyx”
artifact (the patch) is to see four successive levels
of noise: (1) the use of chaotic functions to produce
sound, (2) the use of phase vocoder for noise signals,
(3) the realization of a map of 20 noise signals, et
(4) the use of random algorithms to produce music.
In the Musical Analysis section I engaged with the
work in terms of duration. Even if “nyx” is realized
with chaos, the work nonetheless contains an ABA’
structure. De plus, during the work there is a clear
direction: It begins with raw noises for one minute
and finishes with an important expressive gesture.
This direction is clearly one of organization and
corresponds nicely with a narration of mythology:
“Verily at the first Chaos came to be, but next
wide-bosomed Earth, the ever-sure foundations
of all” (from Hesiod’s Theogony). The important
gesture at the very end of the work, from low pitch
to high, easily corresponds with something like this
creation.
Larrieu
131
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Enfin, three main areas of note in “nyx,” the
most obvious being the use of chaotic functions to
produce noise and to use that noise as music mate-
rial. The second point to note is the implementation
of random algorithms, so that the work contains
significant indeterminate elements that vary across
realizations. Troisième, there is the use of the meaning of
chaos in Greek mythology to structure the musical
travail. These three areas can be understood as three
facets of the totality of noise, which make “nyx” a
captivating computer music work.
Remerciements
I would like to thank Kerry Hagan for the discussions
we had and the embassy of France in Ireland, lequel
contributed to the funding of this work.
Les références
Proceedings of the Music, Esprit, and Invention Work-
shop, Paper 20. Available online at owd.tcnj.edu/∼mmi/
papers/Paper20.pdf. Accessed March 2021.
Hagan, K. 2013. “The Noise of ‘Morphons and Bions’.”
Proceedings of the International Computer Music
Conference, pp. 376–379.
Hagan, K. 2016. “The Intersection of ‘Live’ and ‘Real
Time’.” Organised Sound 21(2):138–146.
Hagan, K. 2018. Computer Music for Absolute Begin-
ners: Real-Time Sound Synthesis, Manipulation and
Composition. Teaching materials. Department of Com-
puter Science and Information Systems, Université de
Limerick, Ireland.
Larrieu, M.. 2018. “Analyse des musiques d’informatique,
vers une int ´egration de l’artefact: Propositions
th ´eoriques et application sur Jupiter (1987) de Philippe
Manoury. PhD dissertation, Universit ´e Paris-Est,
Musique, musicologie et arts de la sc `ene. Available on-
line at hal.archives-ouvertes.fr/tel-01757277. Accessed
May 2021.
Larrieu, M.. 2019. “A Consideration of the Code of
Computer Music as Writing and Some Thinking on
Analytical Theories.” Organised Sound 24(3):319–328.
Laske, Ô. 1990. “The Computer as the Artist’s Alter Ego.”
Battier, M.. 2003 “A Constructivist Approach to the
Leonardo 23(1):53–66.
Analysis of Electronic Music and Audio Art: Entre
Instruments and Faktura.” Organised Sound 8(3):249–
255.
Chion, M.. 2009. Guide to Sound Objects: Pierre Schaeffer
and Musical Research, trans. J.. Dack and C. North.
Leicester, ROYAUME-UNI: EARS/De Montfort University. Available
online at www.ears.dmu.ac.uk. Accessed March 2001.
(Orig. Chion, M.. 1983. Guide des objets sonores:
Pierre Schaeffer et la recherche musicale. Paris:
Buchet/Chastel.)
Collins, N. 2008. “The Analysis of Generative Music
Programs.” Organised Sound 13(3):23–248.
Di Scipio, UN. 1995. “Inseparable Models of Materials and
of Musical Design in Electroacoustic and Computer
Music.” Journal of New Music Research 24(1):34–50.
Hagan, K. 2012. “Aesthetic and Philosophical Implica-
tions of Noise in ‘Morphons and Bions’ (2011).” In
Lyon, E. 2016. “Genesis of the Cube: The Design and
Deployment of an HDLA-Based Performance and
Research Facility.” Computer Music Journal 40(4):62–
78.
Puckette, M.. 2006. The Theory and Technique of Elec-
tronic Music. Singapore: World Scientific.
Risset, J.-C. 2001. “Probl `emes pos ´es par l’analyse
d’œuvres musicales dont la r ´ealisation fait appel `a
l’informatique.” In Analyse et cr ´eation musicales:
Actes du Troisi `eme congr `es europ ´een d’Analyse Musi-
cale, pp. 131–160.
Slater, D. 1998. “Chaotic Sound Synthesis.” Computer
Music Journal 22(2):12–19.
Zattra, L. 2015. “G ´en ´etiques de la computer music.” In
N. Donin, UN. Gr ´esillon, J.-L. Lebrave, éd.. Gen `eses mu-
sicale. Paris: Presses Universitaires de Paris-Sorbonne,
pp. 213–238.
132
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
2
–
3
1
1
8
2
0
0
5
4
2
0
/
c
o
m
_
un
_
0
0
5
6
9
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3