Locally Typical Sampling

Clara Meister1 Tiago Pimentel2 Gian Wiher1 Ryan Cotterell1,2

1ETH Z¨urich, Suisse

2University of Cambridge, ROYAUME-UNI

clara.meister@inf.ethz.ch tp472@cam.ac.uk

gian.wiher@inf.ethz.ch ryan.cotterell@inf.ethz.ch

Abstrait

Today’s probabilistic language generators fall
short when it comes to producing coherent and
fluent text despite the fact that the underlying
models perform well under standard metrics
(par exemple., perplexity). This discrepancy has puzzled
the language generation community for the last
few years. In this work, we posit that the ab-
straction of natural language generation as a
discrete stochastic process—which allows for
an information-theoretic analysis—can pro-
vide new insights into the behavior of probabi-
listic language generators, Par exemple, why
high-probability texts can be dull or repetitive.
Humans use language as a means of com-
municating information, aiming to do so in a
simultaneously efficient and error-minimizing
manière;
in fact, psycholinguistics research
suggests humans choose each word in a string
with this subconscious goal in mind. We for-
mally define the set of strings that meet this
criterion: Those for which each word has an
information content close to the expected in-
the conditional
formation content, namely,
entropy of our model. We then propose a sim-
ple and efficient procedure for enforcing this
criterion when generating from probabilistic
models, which we call locally typical sam-
pling. Automatic and human evaluations show
que, in comparison to nucleus and top-k sam-
pling, locally typical sampling offers com-
petitive performance (in both abstractive
summarization and story generation) in terms
of quality while consistently reducing degen-
erate repetitions.

1

Introduction

ity is the choice of decoding strategy—that is,
the decision rule used to extract strings from a
model. Perhaps surprisingly, for many language
generation tasks, decoding strategies that aim to
find the highest-probability strings produce text
that is undesirable (Holtzman et al., 2020; Voir
et coll., 2019; Eikema and Aziz, 2020; Zhang
et coll., 2021; DeLucia et al., 2021). Par exemple,
Stahlberg and Byrne (2019) report that in their neu-
ral machine translation experiments, the highest-
probability string is usually the empty string. Sur
the other hand, stochastic strategies, which take
random samples from the model, often lead to text
with better qualitative properties (Fan et al., 2018;
Holtzman et al., 2020; Basu et al., 2021). Comment-
jamais, stochastic strategies still have a host of other
problems, while not entirely dispensing with those
seen in maximization-based approaches.1
it

is unintuitive that high-
probability strings are often neither desirable nor
human-like. Due to this pathology, a number of
studies have concluded that there must be faults
in the training objective or architecture of the
probabilistic models behind language generators
(Welleck et al., 2020; Guan et al., 2020; Li et al.,
2020, inter alia). Encore, this conclusion is at odds
with these models’ performance in terms of other
metrics. The fact that modern models can place
high probability on held-out text suggests that
they provide good estimates (in at least some as-
pects) of the probability distribution underlying
human language. We posit that looking at lan-
guage generation through an information-theoretic
lens may shed light on this paradox.

At first glance,

Modern probabilistic models have repeatedly
demonstrated their prowess at modeling natural
langue, placing high probability on held-out
corpora from many different domains (Brun
et coll., 2020; Hoffmann et al., 2022; Chowdhery
et coll., 2022). Yet when used as text generators,
their performance is far from perfect. One of the
largest determinants of the generated text’s qual-

Communication via natural language can in-
tuitively be cast in information-theoretic terms.
En effet, there is a long history of studying language
through the lens of information theory (Shannon,

1While maximization-based strategies can produce text
that is generic or degenerate, stochastic strategies occasion-
ally produce nonsensical text. Both types of strategies tend
to eventually fall into repetitive loops.

102

Transactions of the Association for Computational Linguistics, vol. 11, pp. 102–121, 2023. https://doi.org/10.1162/tacl a 00536
Action Editor: Ehud Reiter. Submission batch: 3/2022; Revision batch: 6/2022; Published 1/2023.
c(cid:2) 2023 Association for Computational Linguistics. Distributed under a CC-BY 4.0 Licence.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
5
3
6
2
0
6
7
8
6
5

/

/
t

je

un
c
_
un
_
0
0
5
3
6
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

1948, 1951; Hale, 2001; Piantadosi et al., 2011;
Pimentel et al., 2020, inter alia). In this para-
digm, linguistic strings are messages used to con-
vey information, and their information content
can be quantified as a function of their proba-
bility of being uttered—often driven by context.
Assuming that humans use language in order to
transmit information in an efficient yet robust
manière (Zaslavsky et al., 2018; Gibson et al.,
2019), the subset of strings typically used by hu-
mans should encode information at some (peut-être
near-optimal) rate.2 In fact, prior works studying
the uniform information density hypothesis (Levy
and Jaeger, 2007; Mahowald et al., 2013) empir-
ically observed this property in humans’ use of
natural language.

These insights lead us to re-think what it means
to be a probabilistic language generator. D'abord, nous
contend that language generators, in some cases,
can be thought of as discrete stochastic processes.
Ce, à son tour, allows us to cleanly define typicality
(and the typical set) for these processes. We ar-
gue, cependant, that due to discrepancies between
the model behind these generators and the true
distribution over natural language strings, directly
sampling from the typical set is not a good idea.
En effet, for language generators that do not use
an end-of-string (EOS) state, this is exactly what is
done by ancestral sampling—a decoding strategy
not known for providing high-quality text. Dans-
spired by research on human sentence processing,
we then define the more restrictive notion of local
typicality, and argue that if we want text generated
from a model to be ‘‘human-like,’’ we should per-
haps enforce this information-theoretic criterion
in generations ourselves. To this end, we develop
a new algorithm, which we call locally typi-
cal sampling. Concretely, we hypothesize that
for text to be perceived as natural, each word
should have an information content close to its
expected information content given prior context.
When sampling from probabilistic language gen-
erators, we should limit our options to strings
that adhere to this property. In experiments on
abstractive summarization and story generation,
we observe that, compared to nucleus and top-k
sampling: (je) locally typical sampling reduces the
number of degenerate repetitions, giving a REP

2Information rate may be defined with respect to time
(as is the case with spoken language) or with respect to
a specific linguistic unit, such as a word (as is the case
with text).

valeur (Welleck et al., 2020) on par with human
text, et (ii) text generated using typical sam-
pling is generally closer in quality to that of hu-
man text.3

2 Two Views of Language Modeling

In this work, we discuss language models4 in an
information-theoretic light. Our first step towards
this goal is to re-frame their presentation. Con-
cretely, we put forth that there are actually two
lenses through which we can view language mod-
eling productively. Under the traditional lens, nous
can think of a language model as a distribution
over full strings: A language model constitutes
the distribution of a single string-valued random
variable. Under an alternative lens, we can think
of a language model as a discrete stochastic pro-
cess: a collection of indexed random variables.
We compare and contrast these views formally,
and then show how to use the language process
view to derive a new sampling algorithm in §5.

2.1 A Single String-Valued
Random Variable

We codify the traditional view of language mod-
eling in the following definition. Let V be an
alphabet—a non-empty, finite set.

Definition 2.1 (Language Model). A language
model p is a probability distribution over all
strings y ∈ V ∗.5 Under this view, we can think
of a language model as describing a single V ∗-
valued random variable.

Under Definition 2.1, it is common to express a
language model in the following factorized form

p(y = y1 · · · yT ) =

T(cid:2)

t=1

p(yt | oui 0. In slight abuse of notation
but out of convention, we take Yt for t ≤ 0 to be
BOS, c'est à dire., conditioning p on just BOS signifies the
initial distribution of the process.

Definition 2.2 is very generic. In words, it
just says that a language process is any discrete
process where we sample a new word9 given the
previously sampled words. The first question that
naturally comes to mind is when the definitions of
a language model and a language process coincide.
As it turns out, there is a simple answer.

Definition 2.3 (Tightness). Let Y = {Yt}∞
t=1
be a language process over alphabet V with dis-

6The ubiquity of Eq. (1) has led some authors to defining
language models in the locally normalized form, even though
globally normalized language models are also perfectly fine
to consider (Goyal et al., 2019).

7Some authors erroneously omit EOS from their definition.
Cependant, we require a distinguished symbol EOS to be able
to locally normalize the language model and make it a valid
probability distribution.

8This process is discrete both in time and in value.
9One could just as easily define a language process over

subwords, morphemes, or characters.

tribution p. A language process is tight (Booth
and Thompson, 1973) if and only if

(cid:3)

|oui|(cid:2)

y∈(V ∗⊗{EOS})

t=1

p(Yt = yt | Oui 0. In plain terms,
this just says that we can always reach every word
in our alphabet via some path no matter where
we currently are. In our context, ergodicity also
relates to the problem with EOS. If we convert a lan-
guage model into a language process (as discussed

11Note that, in principle, human language is not Markov,
in so far as many linguists believe human language is capa-
ble of arbitrarily deep center-embeddings (Chomsky, 1957,
1995). Yet research suggests that humans do not make use
of this property in practice (Reich, 1969; Karlsson, 2010),
and so we do not consider the Markovian property of most
models as a limitation to their ability to model natural lan-
guage in practice.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
5
3
6
2
0
6
7
8
6
5

/

/
t

je

un
c
_
un
_
0
0
5
3
6
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

in §2.1) and make the EOS state absorbing,12 ce
language process must be non-ergodic, as once it
encounters EOS, no other state is reachable.

2.4 Estimating a Language Model from Data

Language models are typically estimated from
language data. The standard method for estimating
the parameters of p is via maximization of the
log-likelihood of a training corpus S

L(je; S) = −

(cid:3)

|oui|(cid:3)

y∈S

t=1

log p(yt | oui 0, pour
sufficiently large T , the following conditions hold:

(cid:4)

je)

y∈T (T )
ε

p(oui) > 1 − ε

ii) (1 − ε)2T (H(Oui )−ε) ≤ |T (T )

ε

| ≤ 2T (H(Oui )+ε)

12This would be done by setting the transition probability

p(Yt = EOS | Oui 0. In words,
this means that we should expect every word
in natural-sounding sentences to be close to the
expected information content under ˜p, c'est à dire., le
conditional entropy given prior context.

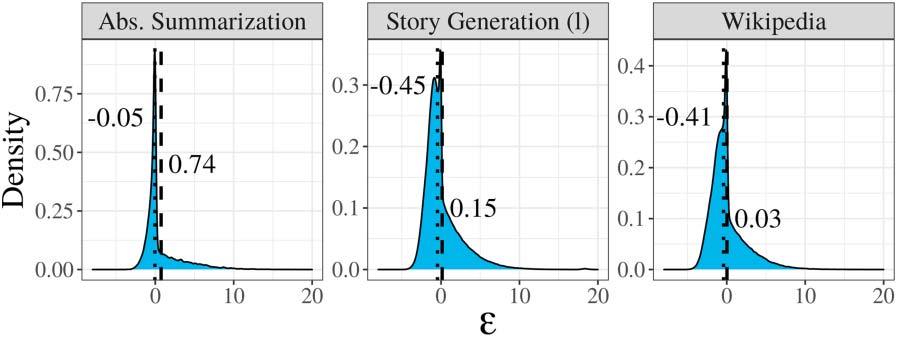
ε

We verify this relationship empirically using
data from human language processes. In Figure 1,
we show the distribution of the difference between
the information content of yt and the expected
information content of Yt, namely, − log ˆp(yt |
oui$15/hour. 6.2 Results Quantitative Performance. Tables 1 et 2 show the results of our different evaluation met- rics. Human scores are averaged across the qual- itative metrics to give an aggregate score; the value in parentheses is the standard error of the estimate. We show full breakdowns of score dis- tributions in Table 5. We see that in general, lo- cally typical sampling performs on par with or better than other sampling techniques, producing text with human quality ratings closest to that of the reference among the stochastic decoding strategies. Fait intéressant, beam search still outper- forms locally typical sampling in abstractive sum- marization, albeit by a small margin. This could perhaps be attributed to the deterministic nature of beam search, which suggests that an interesting di- rection for future research may be a deterministic version of locally typical sampling, Par exemple, where the highest-probability word within the truncated set is always chosen. Surtout, all the strategies we explore are quite close to human- level performance—in some cases even surpass- ing human references in terms of ratings. At this level, it is perhaps only reasonable to expect that the differentiation between the top strategies is small. Accordingly, we also consider how robust locally typical sampling is to hyperparameter 112 l Téléchargé à partir du site Web : / / direct . m je t . e d u / t a c l / l a r t i c e – pdf / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 5 3 6 2 0 6 7 8 6 5 / / t l a c _ a _ 0 0 5 3 6 pd . f par invité 0 7 Septembre 2 0 2 3 PPL (g) Abstractive Summarization PPL (je) MAUVE (↑) REP (↓) Reference 10.29 34.21 Beam (k=5) Temperature (τ =0.5) Temperature (τ =1) Nucleus (η=0.9) Nucleus (η=0.95) Top-k (k=30) Top-k (k=40) Typical (τ =0.2) Typical (τ =0.95) 1.39 (−8.90) 7.10 (−3.19) 6.46 (−3.83) 2.97 (−7.32) 3.96 (−6.33) 3.13 (−7.16) 3.26 (−7.03) 3.80 (−6.49) 3.86 (−6.43) 34.21 (−0.00) 55.31 (+21.1) 35.96 (+1.75) 33.63 (−0.58) 56.43 (+22.22) 34.79 (+0.58) 28.38 (−5.83) 62.33 (+28.12) 56.67 (+22.46) – 0.90 0.97 0.95 0.90 0.99 0.98 0.96 0.72 0.96 0.13 0.14 0.15 0.14 0.17 0.15 0.16 0.16 0.14 0.15 Zipf D (↑) Human (↑) 0.76 0.77 (+0.01) 0.75 (−0.01) 0.75 (−0.01) 0.93 (+0.17) 0.91 (+0.15) 0.93 (+0.17) 0.93 (+0.17) 0.91 (+0.15) 0.92 (+0.16) 0.97 0.97 0.97 0.97 0.96 0.97 0.97 0.97 0.97 0.97 4.31 (±0.03) 4.35 (±0.03) 4.25 (±0.03) 4.29 (±0.03) 4.26 (±0.03) 4.26 (±0.03) 4.31 (±0.03) 4.29 (±0.03) 4.27 (±0.03) 4.32 (±0.03) Tableau 2: Automatic quality and diversity metrics, as described in §6.1, along with human ratings on the CNN/DAILYMAIL dataset. Human ratings are averaged across criteria to form a single metric. Bolded values are the best results among decoding strategies, where for perplexity (PPL) and Zipf’s coefficient, we take this to be the delta from measurements on human text (numbers in purple). Numbers in blue are standard error estimates. l Téléchargé à partir du site Web : / / direct . m je t . e d u / t a c l / l a r t i c e – pdf / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 5 3 6 2 0 6 7 8 6 5 / / t l a c _ a _ 0 0 5 3 6 pd . f par invité 0 7 Septembre 2 0 2 3 Chiffre 2: REP (Welleck et al., 2020) values for different k and τ /η (lower is better). Lines indicate REP measurement for reference text and Mirostat (gauche)/beam search (droite). choice. Chiffre 2 shows REP measurements for different values of the hyperparameters k, η, and τ for top-k, nucleus, and locally typical sampling, respectivement. Fait intéressant, REP appears to be far less sensitive to τ than to k and η. While many values of k and η appear to lead to degenerate repetitions in story generation, most values of τ lead to text with a REP value on par with human text, demonstrating that an advantage of our tech- nique is its robustness to hyperparameter choice. Voir la figure 3 in the Appendix for a larger explo- ration of how other quality metrics vary as a func- tion of τ . Qualitative Performance. We present some examples of text generated according to each of the decoding strategies in Tables 3 et 4. For both of the tasks, we choose the example with ID 1 in the respective test set and provide examples from each of the decoding strategies, employing the hyperparameter values that lead to the best human scores in Tables 2 et 1. For the summa- rization task, we see that locally typical sampling provides a comprehensive and coherent summary of the article, quite similar to that of beam search. In comparison, the text produced by temperature sampling is not necessarily coherent; text from nu- cleus sampling and top-k sampling misses some of the important information in the article, Par exemple, the charges of burglary and arson. While the qualitative performance in story generation is much more subjective, locally typical sampling arguably provides the most fluent story among all the decoding strategies. Other stories lack coher- ence and, even within the first few sentences, we see repeated phrases and words. Ensemble, these results suggest that locally typical sampling may indeed produce more desirable text. 113 Prompt Abstractive Summarization (CNN/DailyMail) (CNN) The attorney for a suburban New York cardiologist charged in what authorities say was a failed scheme to have another physician hurt or killed is calling the allegations against his client ‘‘completely unsubstantiated.’’ Appearing Saturday morning on CNN’s ‘‘New Day,’’ Randy Zelin defended his client, Docteur. Anthony Moschetto, who faces criminal solicitation, conspiracy, burglary, arson, criminal prescription sale and weapons charges in connection to what prosecutors called a plot to take out a rival doctor on Long Island. ‘‘None of anything in this case has any evidentiary value,’’ Zelin told CNN’s Christi Paul… Beam k = 5 Nucleus η = 0.95 Top-k k = 30 Reference A lawyer for Dr. Anthony Moschetto says the charges against him are baseless. Moschetto, 54, was arrested for selling drugs and weapons, prosecutors say. Authorities allege Moschetto hired accomplices to burn down the practice of former associate. Docteur. Anthony Moschetto faces criminal solicitation, conspiracy, burglary, arson and weapons charges. ‘‘None of anything in this case has any evidentiary value,’’ his attorney says. Docteur. Anthony Moschetto, 54, pleaded not guilty to charges Wednesday. Two men – identified as James Chmela and James Kalamaras – were named as accomplices. Docteur. Anthony Moschetto is accused of providing police with weapons and prescription drugs. Authorities say he was part of a conspiracy to harm or kill a rival doctor. His attorney calls the allegations against his client ‘‘completely unsubstantiated’’ Dr. Anthony Moschetto is charged with crimes including arson, conspiracy, burglary, prescription sale, weapons charges. His attorney says ‘‘none of anything in this case has any evidentiary value’’ Typical τ = 0.95 Tableau 3: Sample generations for abstractive summarization; examples correspond to ID 1 in the test set. Decoding strategy hyperparameters are chosen based off of performance in human evaluations shown in Table 2. 7 Conclusion In this work, we analyze decoding from prob- abilistic language generators in the information- theoretic framework. We equate a language model to a discrete stochastic process, and use the known properties of such processes to quantitatively de- scribe the samples we should expect. Motivated by results in psycholinguistics, we hypothesize that—with the goal of communicating efficiently and robustly—humans produce text whose per- word information content is within a close range of the expected information content of a word given prior context. Current language models may fall short in capturing this property, which is a possible explanation for why the corresponding language processes often do not lead to human- like text. Encore, this observation provides a simple new criterion for decoding more human-like text from probabilistic language generators: Constrain- ing the sampling space to words that meet this criterion. In experiments on two language genera- tion tasks, we find that our strategy—called locally typical sampling—leads to text of comparable or better quality than other stochastic decoding strategies according to human ratings. Plus loin, when compared to these other decoding strate- gies, several quantitative properties of typically- sampled text more closely align with those of human text. Acknowledgments We would like to thank Jason Eisner, Tim Vieira, Jennifer White, and Ari Holtzmann for early conversations about the relationship between in- formation theory and sampling. We would also like to thank Ehud Reiter, who served as our TACL action editor, and the the anonymous re- viewers for their insightful feedback during the review process. Plus loin, we are grateful to Eleanor Chodroff, Cl´ement Guerner, and Lucas Torroba Hennigen for their feedback on the manuscript of this work. Ethical Concerns In order to complete our human evaluation, we used a crowdsourcing platform. For each task, we made sure that the crowdworkers would be paid (at minimum) a wage of $15 per hour.

114

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
5
3
6
2
0
6
7
8
6
5

/

/
t

je

un
c
_
un
_
0
0
5
3
6
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Prompt

Reference

Nucleus
η = 0.95

Top-k
k = 30

Temp
τ = 1.0

Mirostat
τ = 3

Typical
τ = 0.2

Story Generation (WritingPrompts)

A kid doodling in a math class accidentally creates the world’s first functional magic circle
in centuries.
It was dark and Levi was pretty sure he was lying on his back. There was firelight flickering
off of what was left of a ceiling. He could hear something but it was muffled. He was almost
positive it was screaming. When he tried to move he felt an excruciating pain in his left side
that caused him to cry out…
‘‘Why do you draw a circle?’’ He asked as he handed the piece of paper over to her. Elle
rolled her eyes and looked down at the picture, ‘‘Because I like math!’’ ‘‘Then what?’’ ‘‘I like
to draw the circles.’’ She ran a hand through her curls and looked away. ‘‘See, I have three
circles.’’ ‘‘Hmph, I didn’t think I saw that in your class.’’ A younger student brought up the
ceiling and murmured…
‘‘Aha. Aah! That makes three.’’ Professor Gosh sighed. ‘‘Oh my God, you had to have been
there.’’ ‘‘Well, I’m not sure if that’s the right term, but this circle is going to work.’’ ‘‘But I
just told you that it wasn’t working, didn’t you, you little sh**? I’m not kidding! That circle
is gon na work!’’ ‘‘So what now?’’…
It was teachers duty to ensure that our kingdom is pure and pure and successful, however it
does not mean we do not try to be as rebellious as any other kingdom. Most of our teachers
are suitable for rulership, being knowledgeable in sadistic rec thunking of time stopping
magic circle created by several apprentices…
ready to go home, when a little kid starts to sketch a circle. ‘‘No. Just stop. It’s not working.’’
‘‘But the circle turns to smoke and then to a flame. It’s not working, I know it is!’’ Another
kid, who was also drawing a circle with his phone, starts to scream. The teacher, looking at
the circle, lost his patience and started to yell…
As soon as he got the clock on his desk he jumped up. The noise it was making had changed
his day forever. His hair, normally unkempt, now glistened and he had to have more hair
because of it. ‘‘Yes!’’ He had declared triumphantly as he watched his father fumble around
in the backpack in search of a little compass he always kept with him. He took it from the
desk and quickly walked out the door to see what had happened. He wasn’t the first child in
the world to draw something…

Tableau 4: Sample generations for story generation from GPT-2 large finetuned on the WRITINGPROMPTS
dataset; examples correspond to ID 1 in the test set. Decoding strategy hyperparameters are chosen
based off of best performance in human evaluations shown in Table 1.

Another ethical consideration worth discussing
concerns the use of language models for text gen-
eration. Text generated by these models may con-
tain malicious content, either by design of the user
or as a byproduct of the training data/algorithm.

While we hope the results of our work will not be
misused, they may nonetheless provide insights
for those employing these models with ill-intent
as to how machine-generated text can be made
more ‘‘human-like,’’ and thus more convincing.

115

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
5
3
6
2
0
6
7
8
6
5

/

/
t

je

un
c
_
un
_
0
0
5
3
6
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A Additional Results

Decoder

Reference
Beam (k=5)

Story Generation (je)

Story Generation (m)

Coherence
4.36 (±0.31)
−

Fluency
4.25 (±0.23)
−

Interestingness Coherence
4.02 (±0.27)
−

4.56 (±0.25)
−

Fluency
4.2 (±0.27)
−

Interestingness
4.15 (±0.2)
−

Summarization

Fluency
4.43 (±0.25)
4.47 (±0.24)

Relevance
4.18 (±0.27)
4.23 (±0.28)

Temperature (τ =0.9)

4.32 (±0.25)

4.16 (±0.19)

4.47 (±0.27)

4.02 (±0.22)

4.26 (±0.29)

4.19 (±0.24)

4.36 (±0.25)

4.13 (±0.26)

Temperature (τ =1)

4.36 (±0.28)

4.25 (±0.22)

4.47 (±0.30)

4.02 (±0.32)

4.2 (±0.29)

4.18 (±0.22)

4.42 (±0.26)

4.15 (±0.28)

Nucleus (η=0.9)

4.32 (±0.25)

4.28 (±0.24)

4.48 (±0.31)

3.99 (±0.27)

4.16 (±0.32)

4.13 (±0.21)

4.39 (±0.27)

4.13 (±0.3)

Nucleus (η=0.95)

4.3 (±0.28)

4.28 (±0.29)

4.49 (±0.26)

4.00 (±0.19)

4.24 (±0.35)

4.14 (±0.17)

4.44 (±0.26)

4.08 (±0.29)

Top-k (k=30)

Top-k (k=40)

Mirostat (τ =3)

Typical (τ =0.2)

4.35 (±0.25)

4.21 (±0.24)

4.53 (±0.27)

4.03 (±0.24)

4.2 (±0.3)

4.16 (±0.22)

4.44 (±0.24)

4.18 (±0.26)

4.34 (±0.27)

4.24 (±0.23)

4.53 (±0.25)

4.00 (±0.27)

4.17 (±0.31)

4.11 (±0.18)

4.39 (±0.27)

4.26 (±0.23)

4.55 (±0.27)

4.02 (±0.22)

4.16 (±0.32)

4.17 (±0.22)

4.41 (±0.25)
−

4.17 (±0.33)
−

4.36 (±0.29)

4.24 (±0.24)

4.55 (±0.25)

4.07 (±0.26)

4.23 (±0.32)

4.14 (±0.26)

4.37 (±0.28)

4.16 (±0.29)

Typical (τ =0.95)

4.35 (±0.28)

4.24 (±0.23)

4.53 (±0.26)

4.04 (±0.21)

4.18 (±0.31)

4.18 (±0.22)

4.42 (±0.28)

4.22 (±0.27)

Tableau 5: Breakdown of human ratings on quality metrics per task; results for story generation are from
finetuned versions of GPT-2 medium (m) and large (je). Values in blue are variances.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
5
3
6
2
0
6
7
8
6
5

/

/
t

je

un
c
_
un
_
0
0
5
3
6
p
d

.

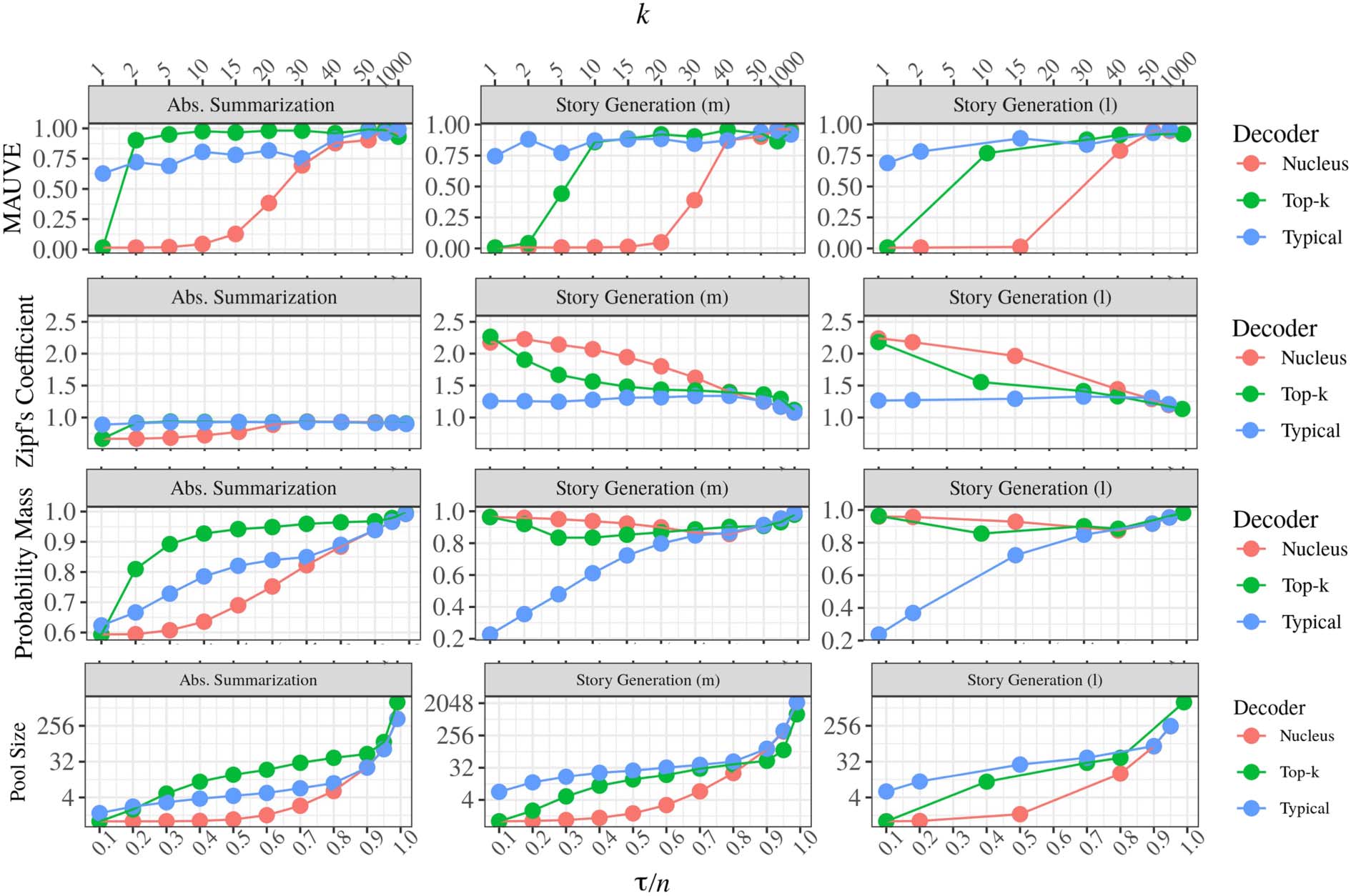
Chiffre 3: MAUVE, Zipf’s coefficient, (average) probability mass of candidate token pool, et (average)
candidate token pool size as a function of decoder hyperparameters for nucleus, top-k, and locally
typical sampling.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

116

Les références

Matthew Aylett and Alice Turk. 2004. Le
smooth signal redundancy hypothesis: A func-
tional explanation for relationships between re-
dundancy, prosodic prominence, and duration
in spontaneous speech. Language and Speech,
47(1):31–56. https://est ce que je.org/10.1177
/00238309040470010201, PubMed: 15298329

Sourya

Basu, Govardana

Sachitanandam
Ramachandran, Nitish Shirish Keskar, et
Lav R. Varshney. 2021. Mirostat: A perplexity-
controlled neural text decoding algorithm. Dans
Proceedings of the 9th International Confer-
ence on Learning Representations.

Taylor L. Booth and Richard A. Thompson.
1973. Applying probability measures to abstract
languages. IEEE Transactions on Computers,
C-22(5):442–450. https://est ce que je.org/10
.1109/T-C.1973.223746

Mark Braverman, Xinyi Chen, Sham Kakade,
Karthik Narasimhan, Cyril Zhang, and Yi
Zhang. 2020. Calibration, entropy rates, et
memory in language models. In Proceedings
of the 37th International Conference on Ma-
chine Learning, volume 119, pages 1089–1099.
PMLR.

Leo Breiman. 1957. The individual ergodic theo-
rem of information theory. The Annals of Math-
ematical Statistics, 28(3):809–811. https://
doi.org/10.1214/aoms/1177706899

Tom Brown, Benjamin Mann, Nick Ryder,
Melanie Subbiah, Jared D. Kaplan, Prafulla
Dhariwal, Arvind Neelakantan, Pranav Shyam,
Girish Sastry, Amanda Askell, Sandhini
Agarwal, Ariel Herbert-Voss, Gretchen Krueger,
Tom Henighan, Rewon Child, Aditya Ramesh,
Daniel Ziegler, Jeffrey Wu, Clemens Winter,
Chris Hesse, Mark Chen, Eric Sigler, Mateusz
Litwin, Scott Gray, Benjamin Chess, Jack
Clark, Christopher Berner, Sam McCandlish,
Alec Radford,
Ilya Sutskever, and Dario
Amodei. 2020. Language models are few-
Dans-
shot
formation Processing Systems, volume 33,
pages 1877–1901. Curran Associates, Inc.

In Advances in Neural

learners.

Noam Chomsky. 1957. Syntactic Structures.
Mouton and Co., The Hague. https://est ce que je
.org/10.1515/9783112316009

117

Noam Chomsky. 1995. The Minimalist Program.

AVEC Presse, Cambridge, MA.

Aakanksha Chowdhery, Sharan Narang, Jacob
Devlin, Maarten Bosma, Gaurav Mishra, Adam
Roberts, Paul Barham, Hyung Won Chung,
Charles Sutton, Sebastian Gehrmann, Parker
Schuh, Kensen Shi, Sasha Tsvyashchenko,
Joshua Maynez, Abhishek Rao, Parker
Barnes, Yi Tay, Noam Shazeer, Vinodkumar
Prabhakaran, Emily Reif, Nan Du, Ben
Hutchinson, Reiner Pope, James Bradbury,
Jacob Austin, Michael Isard, Guy Gur-Ari,
Pengcheng Yin, Toju Duke, Anselm Levskaya,
Sanjay Ghemawat, Sunipa Dev, Henryk
Michalewski, Xavier Garcia, Vedant Misra,
Kevin Robinson, Liam Fedus, Denny Zhou,
Daphne Ippolito, David Luan, Hyeontaek Lim,
Barret Zoph, Alexander Spiridonov, Ryan
Sepassi, David Dohan, Shivani Agrawal, Mark
Omernick, Andrew M. Dai, Thanumalayan
Sankaranarayana Pillai, Marie Pellat, Aitor
Lewkowycz, Erica Moreira, Rewon Child,
Oleksandr Polozov, Katherine Lee, Zongwei
Zhou, Xuezhi Wang, Brennan Saeta, Mark
Diaz, Orhan Firat, Michele Catasta, Jason
Wei, Kathy Meier-Hellstern, Douglas Eck, Jeff
Dean, Slav Petrov, and Noah Fiedel. 2022.
PaLM: Scaling language modeling with path-
ways. CoRR, abs/2204.02311.

Christophe Coup´e, Yoon Mi Oh, Dan Dediu,
and Franc¸ois Pellegrino. 2019. Different lan-
guages, similar encoding efficiency: Com-
parable information rates across the human
communicative niche. Science Advances, 5(9).
https://doi.org/10.1126/sciadv.aaw2594,
PubMed: 32047854

Thomas M. Cover and Joy A. Thomas. 2012.
Elements of Information Theory. John Wiley
& Fils.

Alexandra DeLucia, Aaron Mueller, Xiang Lisa
Li, and Jo˜ao Sedoc. 2021. Decoding methods
for neural narrative generation. In Proceedings
of the 1st Workshop on Natural Language Gen-
eration, Evaluation, and Metrics (GEM 2021),
pages 166–185, En ligne. Association for Com-
putational Linguistics. https://doi.org
/10.18653/v1/2021.gem-1.16

Sander Dieleman. 2020. Musings on typicality.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
5
3
6
2
0
6
7
8
6
5

/

/
t

je

un
c
_
un
_
0
0
5
3
6
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sergey Edunov, Myle Ott, Michael Auli, et
David Grangier. 2018. Understanding back-
translation at scale. In Proceedings of
le
2018 Conference on Empirical Methods in
Natural Language Processing, pages 489–500,
Brussels, Belgium. Association for Computa-
tional Linguistics. https://est ce que je.org/10
.18653/v1/D18-1045

Bryan Eikema and Wilker Aziz. 2020. Is MAP
decoding all you need? The inadequacy of
the mode in neural machine translation. Dans
Proceedings of the 28th International Confer-
ence on Computational Linguistics, COLING,
pages 4506–4520, Barcelona, Espagne (En ligne).
International Committee on Computational Lin-
guistics. https://doi.org/10.18653/v1
/2020.coling-main.398

Angela Fan, Mike Lewis, and Yann Dauphin.
2018. Hierarchical neural story generation. Dans
Proceedings of the 56th Annual Meeting of
the Association for Computational Linguis-
tics (Volume 1: Long Papers), pages 889–898,
Melbourne, Australia. Association for Compu-
tational Linguistics.

August Fenk and Gertraud Fenk. 1980. Konstanz
im Kurzzeitged¨achtnis-Konstanz im sprach-
f¨ur ex-
lichen Informationsfluß. Zeitschrift
perimentelle und angewandte Psychologie,
27(3):400–414.

Edward Gibson, Richard Futrell, Steven T.
Piantadosi, Isabelle Dautriche, Kyle Mahowald,
Leon Bergen, and Roger Levy. 2019. Comment
efficiency shapes human language. Trends in
Cognitive Sciences, 23(5):389–407. https://
doi.org/10.1016/j.tics.2019.02.003,
PubMed: 31006626

Kartik Goyal, Chris Dyer, and Taylor Berg-
Kirkpatrick. 2019. An empirical investigation
of global and local normalization for recur-
rent neural sequence models using a continu-
ous relaxation to beam search. In Proceedings
of the 2019 Conference of the North American
Chapter of
the Association for Computa-
tional Linguistics: Human Language Tech-
nologies, Volume 1 (Long and Short Papers),
pages 1724–1733, Minneapolis, Minnesota.
Association for Computational Linguistics.

Jian Guan, Fei Huang, Zhihao Zhao, Xiaoyan
Zhu, and Minlie Huang. 2020. A knowledge-
enhanced pretraining model for commonsense

story generation. Transactions of the Associa-
tion for Computational Linguistics, 8:93–108.

John Hale. 2001. A probabilistic Earley parser
as a psycholinguistic model. In Second Meet-
le
ing of
Association for Computational Linguistics.
https://doi.org/10.3115/1073336
.1073357

the North American Chapter of

Jordan Hoffmann, Sebastian Borgeaud, Arthur
Mensch, Elena Buchatskaya, Trevor Cai, Eliza
Rutherford, Diego de Las Casas, Lisa Anne
Hendricks, Johannes Welbl, Aidan Clark, Tom
Hennigan, Eric Noland, Katie Millican, George
van den Driessche, Bogdan Damoc, Aurelia
Guy, Simon Osindero, Karen Simonyan, Erich
Elsen, Jack W. Rae, Oriol Vinyals, and Laurent
Sifre. 2022. Training compute-optimal large
language models. CoRR, abs/2203.15556.

Ari Holtzman, Jan Buys, Li Du, Maxwell Forbes,
and Yejin Choi. 2020. The curious case of
text degeneration. In Proceedings of
neural
the 8th International Conference on Learning
Representations.

Fred Karlsson.

2010.

3. Syntactic

recur-
In Recursion and Hu-
sion and iteration.
man Language. De Gruyter Mouton, Berlin,
New York. https://doi.org/10.1515
/9783110219258.43

Urvashi Khandelwal, He He, Peng Qi, and Dan
Jurafsky. 2018. Sharp nearby, fuzzy far away:
How neural language models use context. Dans
Proceedings of the 56th Annual Meeting of
the Association for Computational Linguis-
tics (Volume 1: Long Papers), pages 284–294,
Melbourne, Australia. Association for Compu-
tational Linguistics. https://est ce que je.org/10
.18653/v1/P18-1027

Konrad Knopp. 1954. Theory and Application of
Infinite Series. Londres, Blackie & Son Ltd.

Jey Han Lau, Alexander Clark, and Shalom
Lappin. 2017. Grammaticality, acceptabil-
ville, and probability: A probabilistic view
of linguistic knowledge. Sciences cognitives,
41(5):1202–1241. https://est ce que je.org/10
.1111/cogs.12414, PubMed: 27732744

Roger Levy and T. Florian Jaeger. 2007. Speakers
optimize information density through syntactic

118

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
5
3
6
2
0
6
7
8
6
5

/

/
t

je

un
c
_
un
_
0
0
5
3
6
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

reduction. In Advances in Neural Information
Processing Systems, volume 19. AVEC Presse.

https://doi.org/10.18653/v1/2020
.acl-main.615

Mike Lewis, Yinhan Liu, Naman Goyal, Marjan
Ghazvininejad, Abdelrahman Mohamed, Omer
Levy, Veselin Stoyanov, and Luke Zettlemoyer.
2020. BART: Denoising sequence-to-sequence
pre-training for natural language generation,
translation, and comprehension. In Proceed-
le
ings of
Association for Computational Linguistics,
pages 7871–7880, En ligne. Association for
Computational Linguistics. https://doi.org
/10.18653/v1/2020.acl-main.703

the 58th Annual Meeting of

Jiwei Li, Michel Galley, Chris Brockett,
Jianfeng Gao, and Bill Dolan. 2016. UN
diversity-promoting objective function for neu-
ral conversation models. In Proceedings of
le 2016 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
pages 110–119, San Diego, California. Associ-
ation for Computational Linguistics.

Margaret Li, Stephen Roller, Ilia Kulikov, Sean
Welleck, Y-Lan Boureau, Kyunghyun Cho, et
Jason Weston. 2020. Don’t say that! Making
inconsistent dialogue unlikely with unlikeli-
hood training. In Proceedings of
the 58th
Annual Meeting of the Association for Compu-
tational Linguistics, pages 4715–4728, En ligne.
Association for Computational Linguistics.

Kyle Mahowald, Evelina Fedorenko, Steven
T. Piantadosi, and Edward Gibson. 2013.
choose
Info/information theory: Speakers
shorter words in predictive contexts. Cogni-
tion, 126(2):313–318. https://est ce que je.org/10
.1016/j.cognition.2012.09.010, PubMed:
23116925

Brockway McMillan. 1953. The basic theorems
of information theory. The Annals of Mathe-
matical Statistics, 24(2):196–219. https://
doi.org/10.1214/aoms/1177729028

Clara Meister, Elizabeth Salesky, and Ryan
Cotterell. 2020un. Generalized entropy regular-
ization or: There’s nothing special about label
smoothing. In Proceedings of the 58th An-
nual Meeting of the Association for Computa-
tional Linguistics, pages 6870–6886, En ligne.
Association for Computational Linguistics.

Clara Meister, Tim Vieira, and Ryan Cotterell.
2020b. If beam search is the answer, what
was the question? In Proceedings of the 2020
Conference on Empirical Methods in Natural
Language Processing, En ligne. Association for
Computational Linguistics. https://doi.org
/10.18653/v1/2020.emnlp-main.170

Clara Meister, Gian Wiher, Tiago Pimentel,
and Ryan Cotterell. 2022. On the probability–
quality paradox in language generation. En Pro-
ceedings of the 60th Annual Meeting of the
Association for Computational Linguistics (Vol-
ume 2: Short Papers), pages 36–45, Dublin,
Ireland. Association for Computational Lin-
guistics. https://doi.org/10.18653/v1
/2022.acl-short.5

Stephen Merity, Caiming Xiong,

James
Bradbury, and Richard Socher. 2017. Pointer
sentinel mixture models. In Proceedings of
the 5th International Conference on Learning
Representations.

the 1st Conference of

Moin Nadeem, Tianxing He, Kyunghyun Cho,
and James Glass. 2020. A systematic char-
acterization of sampling algorithms for open-
ended language generation. In Proceedings
de
the Asia-Pacific
Chapter of the Association for Computational
Linguistics and the 10th International Joint
Conference on Natural Language Processing,
pages 334–346, Suzhou, Chine. Association
for Computational Linguistics.

Ramesh Nallapati, Bowen Zhou, Cicero dos
Santos, Caglar Gulc¸ehre, and Bing Xiang.
2016. Abstractive text summarization using
sequence-to-sequence RNNs and beyond. Dans
Proceedings of The 20th SIGNLL Conference
on Computational Natural Language Learning,
pages 280–290, Berlin, Allemagne. Association
for Computational Linguistics. https://est ce que je
.org/10.18653/v1/K16-1028

Nathan Ng, Kyra Yee, Alexei Baevski, Myle Ott,
Michael Auli, and Sergey Edunov. 2019. Face-
book FAIR’s WMT19 news translation task
submission. In Proceedings of the Fourth Con-
ference on Machine Translation (Volume 2:
Shared Task Papers, Day 1), pages 314–319,

119

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
5
3
6
2
0
6
7
8
6
5

/

/
t

je

un
c
_
un
_
0
0
5
3
6
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Florence, Italy. Association for Computational
Linguistics.

Gabriel Pereyra, George Tucker, Jan Chorowski,
Łukasz Kaiser, and Geoffrey E. Hinton. 2017.
Regularizing neural networks by penalizing
confident output distributions. In Proceedings
of the 5th International Conference on Learn-
ing Representations.

Steven T. Piantadosi, Harry Tily, and Edward
Gibson. 2011. Word lengths are optimized for
efficient communication. Proceedings of the Na-
tional Academy of Sciences, 108(9):3526–3529.
https://doi.org/10.1073/pnas.1012551108,
PubMed: 21278332

Krishna Pillutla, Swabha Swayamdipta, Rowan
Zellers, John Thickstun, Sean Welleck, Yejin
Choi, and Zaid Harchaoui. 2021. MAUVE:
Measuring the gap between neural text and
Dans
human text using divergence frontiers.
Advances in Neural Information Processing
Systems, volume 34, pages 4816–4828. Curran
Associates, Inc.

Tiago Pimentel, Clara Meister,

and Ryan
Cotterell. 2022. Cluster-based evaluation of
automatically generated text. arXiv preprint
arXiv:2205.16001.

Tiago Pimentel, Clara Meister, Elizabeth Salesky,
Simone Teufel, Dami´an Blasi, and Ryan
Cotterell. 2021. A surprisal–duration trade-off
across and within the world’s languages. Dans
Actes du 2021 Conference on Em-
pirical Methods in Natural Language Process-
ing, pages 949–962, Online and Punta Cana,
Dominican Republic. Association for Compu-
tational Linguistics. https://est ce que je.org/10
.18653/v1/2021.emnlp-main.73

Tiago Pimentel, Brian Roark,

and Ryan
Cotterell. 2020. Phonotactic complexity and its
trade-offs. Transactions of the Association for
Computational Linguistics, 8:1–18. https://
doi.org/10.1162/tacl a 00296

Alec Radford, Jeffrey Wu, Rewon Child, David
Luan, Dario Amodei, and Ilya Sutskever.
2019. Language models are unsupervised mul-
titask learners.

Peter A. Reich. 1969. Le

finiteness of
langue. Language, 45(4):831–843.

naturel
https://doi.org/10.2307/412337

Carson T. Sch¨utze. 2016. The empirical base of
linguistics: Grammaticality judgments and lin-
guistic methodology. Classics in Linguistics 2.
Language Science Press, Berlin. https://
doi.org/10.26530/OAPEN 603356

Abigail See, Aneesh Pappu, Rohun Saxena,
Akhila Yerukola, and Christopher D. Manning.
2019. Do massively pretrained language mod-
els make better storytellers? In Proceedings of
the 23rd Conference on Computational Natural
Language Learning (CoNLL), pages 843–861,
Hong Kong, Chine. Association for Computa-
tional Linguistics.

Claude E. Shannon. 1948. A mathematical the-
ory of communication. Bell System Technical
Journal, 27:623–656.

Claude E. Shannon. 1951. Prediction and en-
tropy of printed English. Bell System Technical
Journal, 30(1):50–64. https://est ce que je.org/10
.1002/j.1538-7305.1951.tb01366.x

Felix Stahlberg and Bill Byrne. 2019. On NMT
search errors and model errors: Cat got your
tongue? In Proceedings of
le 2019 Con-
ference on Empirical Methods in Natural
Language Processing and the 9th International
Joint Conference on Natural Language Pro-
cessation (EMNLP-IJCNLP), pages 3356–3362,
Hong Kong, Chine. Association for Computa-
tional Linguistics. https://est ce que je.org/10
.18653/v1/D19-1331

Chris van der Lee, Albert Gatt, Emiel van
Miltenburg, Sander Wubben,
and Emiel
Krahmer. 2019. Best practices for the hu-
man evaluation of automatically generated
text. In Proceedings of the 12th International
Conference on Natural Language Generation,
pages 355–368, Tokyo, Japan. Association for
Computational Linguistics. https://est ce que je
.org/10.18653/v1/W19-8643

Sean Welleck, Ilia Kulikov, Stephen Roller, Emilie
Dinan, Kyunghyun Cho, and Jason Weston.
2020. Neural text generation with unlikelihood
entraînement. In Proceedings of the 8th International
Conference on Learning Representations.

Thomas Wolf, Lysandre Debut, Victor Sanh,
Julien Chaumond, Clement Delangue, Antoine
Moi, Pierric Cistac, Tim Rault, R´emi Louf,
Morgan Funtowicz, Joe Davison, Sam Shleifer,

120

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
5
3
6
2
0
6
7
8
6
5

/

/
t

je

un
c
_
un
_
0
0
5
3
6
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Patrick von Platen, Clara Ma, Yacine Jernite,
Julien Plu, Canwen Xu, Teven Le Scao,
Sylvain Gugger, Mariama Drame, Quentin
Lhoest,
and Alexander M. Rush. 2020.
Transformers: State-of-the-art natural language
traitement. In Proceedings of the 2020 Con-
ference on Empirical Methods in Natural
Language Processing: System Demonstrations,
pages 38–45, En ligne. Association for Compu-
tational Linguistics. https://est ce que je.org/10
.18653/v1/2020.emnlp-demos.6

Yonghui Wu, Mike Schuster, Zhifeng Chen,
Quoc V. Le, Mohammad Norouzi, Wolfgang
Macherey, Maxim Krikun, Yuan Cao, Qin Gao,
Klaus Macherey, Jeff Klingner, Apurva Shah,
Melvin Johnson, Xiaobing Liu, Lukasz Kaiser,
Stephan Gouws, Yoshikiyo Kato, Taku Kudo,
Hideto Kazawa, Keith Stevens, George Kurian,
Nishant Patil, Wei Wang, Cliff Young, Jason
Forgeron, Jason Riesa, Alex Rudnick, Oriol
Vinyals, Gregory S. Corrado, Macduff Hughes,

and Jeffrey Dean. 2016. Google’s neural ma-
chine translation system: Bridging the gap
between human and machine translation.
CoRR, abs/1609.08144.

Noga Zaslavsky, Charles Kemp, Terry Regier, et
Naftali Tishby. 2018. Efficient compression
in color naming and its evolution. Proceed-
ings of
the National Academy of Sciences,
115(31):7937–7942. https://est ce que je.org/10
.1073/pnas.1800521115, PubMed: 30021851

Hugh Zhang, Daniel Duckworth, Daphne
Ippolito, and Arvind Neelakantan. 2021. Trad-
ing off diversity and quality in natural language
generation. In Proceedings of the Workshop
on Human Evaluation of NLP Systems (Hum-
Eval), pages 25–33, En ligne. Association for
Computational Linguistics.

George Kingsley Zipf. 1949. Human Behavior
and the Principle of Least Effort. Addison-
Wesley Press, Oxford, ROYAUME-UNI.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
5
3
6
2
0
6
7
8
6
5

/

/
t

je

un
c
_
un
_
0
0
5
3
6
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

121

Télécharger le PDF