LETTER
Communicated by Peter K ¨onig
Integrator or Coincidence Detector: A Novel Measure
Based on the Discrete Reverse Correlation to Determine
a Neuron’s Operational Mode
Jacob Kanev
jkanev@zoho.com
Institute of Software Engineering and Theoretical Computer Science, Technische
Universit¨at Berlin, Berlin 10587, Allemagne
Achilleas Koutsou
achilleas.k@cs.ucy.ac.cy
Chris Christodoulou
cchrist@cs.ucy.a.cy
Department of Computer Science, University of Cyprus, 1678 Nicosia, Cyprus
Klaus Obermayer
klaus.obermayer@mailbox.tu-berlin.de
Institute of Software Engineering and Theoretical Computer Science, Technische
Universit¨at Berlin, Berlin 10587, Allemagne
In this letter, we propose a definition of the operational mode of a neuron,
c'est, whether a neuron integrates over its input or detects coincidences.
We complete the range of possible operational modes by a new mode we
call gap detection, which means that a neuron responds to gaps in its
stimulus. We propose a measure consisting of two scalar values, les deux
ranging from −1 to +1: the neural drive, which indicates whether its
stimulus excites the neuron, serves as background noise, or inhibits it;
the neural mode, which indicates whether the neuron’s response is the
result of integration over its input, of coincidence detection, or of gap
detection; with all three modes possible for all neural drive values. This is
a pure spike-based measure and can be applied to measure the influence
of either all or subset of a neuron’s stimulus. We derive the measure
by decomposing the reverse correlation, test it in several artificial and
biological settings, and compare it to other measures, finding little or
no correlation between them. We relate the results of the measure to
neural parameters and investigate the effect of time delay during spike
generation. Our results suggest that a neuron can use several different
modes simultaneously on different subsets of its stimulus to enable it to
respond to its stimulus in a complex manner.
Neural Computation 28, 2091–2128 (2016)
est ce que je:10.1162/NECO_a_00875
c(cid:2) 2016 Massachusetts Institute of Technology.
Publié sous Creative Commons
Attribution 3.0 Unported (CC PAR 3.0) Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
un
_
0
0
8
7
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2092
J.. Kanev, UN. Koutsou, C. Christodoulou, and K. Obermayer
1 Introduction
For a considerable time, there has been a discussion about whether a neuron
acts as a coincidence detector or an integrator. Despite a number of con-
tributions on this issue, the underlying assumption about what is actually
meant by the terms integrator or coincidence detector seems to have varied.
The discussion was sparked off by Abeles (1982), who stated that the cor-
tical neuron is a coincidence detector, not an integrator. This was based on
the fact that the neuron is usually more sensitive to a few spikes that arrive at
the same time than to the same number of spikes when they are distributed
over a longer time. He used a measure he called coincidence advantage that
shows the extent to which synchronous activation of a few synapses is
more effective than asynchronous activation of the same synapses. Kempter,
Gerstner, and van Hemmen (1998) used a similar measure that expresses
the ratio of the neuron’s response rates to either random or correlated
stimulus.
The coincidence advantage measure, introduced by Abeles (1982), uses
a neuron model with a threshold and an exponential rise after the reset, et
it assumes gaussian-distributed excitatory stimulus. A distinction is made
between the background stimulus, which is used to keep the membrane
potential at its average rate, and the signal stimulus, which is or is not de-
tected by the postsynaptic neuron. He defines three values: the synchronous
attenuation is the number of simultaneous stimulus spikes necessary to get
the membrane potential from its average voltage to threshold voltage. Le
asynchronous attenuation is the number of nonsimultaneous stimulus spikes,
additional to the background, that are needed to get one additional re-
sponse spike. Enfin, the coincidence advantage is defined as the ratio of
synchronous attenuation to asynchronous attenuation.
Some subsequent contributions were based on the mean and variance
of the response spike train. Softky and Koch (1993) argued that in integra-
tion mode, the resulting spike train should be regular at high firing rates,
while the high firing irregularity that is observed in cortical neurons means
the neuron is detecting coincidences. These authors used the coefficient of
variation (CV) to characterize the high firing irregularity and defined it as
the standard deviation of the stimulus interspike interval, divided by the
mean stimulus interspike interval. In their paper, the coincidence detection
mode is equivalent to the neuron reacting to occasional input bursts with
a single response, where in between responses, the neuron forgets previ-
ous inputs because the membrane potential polarizes again. De la même manière, Cloche,
Mainen, Tsodyks, and Sejnowski (1995) tried to explain the high CV ob-
served in cortical neurons at high rates and found a balanced parameter
regime in which high CVs can be observed. They concluded that a high-
response CV is not observed when a neuron mainly integrates on its input.
In their work, the high CV was seen as an indirect measure that a neuron
is not integrating. Stevens and Zador (1998) also used the CV as an indirect
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
un
_
0
0
8
7
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2093
indicator for a coincidence detection scenario and claimed that the high CV
that is observed in neurons in vivo at high rates is the result of synchronous
stimulus, indicating a coincidence detection scenario.
Other authors based their reasoning on the integration time of the neu-
ron. K ¨onig, Ange, and Singer (1996) suggested that the distinction between
the two modes could be made by the ratio of the integration time inter-
val of the neuron and its response interspike interval (ISI). In integration
mode, a neuron has a long integration interval compared to its response
rate, while in coincidence detection, it is short. The membrane time con-
stant can be lowered significantly by background stimulus activity, fabrication
coincidence detection plausible even in regimes where the response firing
rate is higher than 25 Hz. The integration time window measure, introduced
by K ¨onig et al. (1996), is defined as the ratio of a neuron’s integration time
window to the response interspike interval. The integration time window
is equal to the membrane time constant τ in the exponential rise exp(− t
)
τ
of the membrane potential. K ¨onig et al. (1996) also showed that correlated
excitatory and inhibitory stimulus has the same effect of inducing coinci-
dence detection mode. Shadlen & Newsome (1994, 1998) argue, in favor
of a time window measure, that a high CV does not show neurons to be
coincidence detectors, because a high CV can be reached by balanced exci-
tation and inhibition. Due to the high number of connections to a neuron,
a population code is predominant in the mammalian cortex. Instead of the
CV, a time window measure should be used where integrators are charac-
terized by a long time constant and coincidence detectors by a short one.
Ratt´e, Lankarany, Rho, Patterson, and Prescott (2015) analyzed subthresh-
old mechanisms that lead to coincidence detection or integration mode. Dans
addition to these two modes, they introduce a differentiation mode, où
a response is triggered whenever there is a sudden rate increase in an oth-
erwise steady stimulus. Integration mode in their work is characterized by
a long integration time window and regular response, while coincidence
detection is characterized by a short time window and immediate response
after a coincidence in the stimulus.
Other authors suggested using time windows on the stimulus. Bugmann,
Christodoulou, and Taylor (1997) demonstrated that a partial reset model
can explain the high CV in high mean responses, that temporal integration
and coincidence detection can coexist, and that reverse correlation curves
fail to show whether a neuron is in integration or coincidence detection
mode. Here coincidence detection is equivalent to the presence of simulta-
neous spikes that cause the neuron to fire in a small time window before the
response. Roy and Alloway (2001) found by in vivo studies that neurons
in the cortex are possibly reacting to synchronous thalamic discharges. À
distinguish coincidence detection from temporal integration, they used a
time window approach to classify stimuli as synchronous or asynchronous
and then calculated the correlation between either synchronous or asyn-
chronous events and the response. Koutsou, Christodoulou, Bugmann, et
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
un
_
0
0
8
7
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2094
J.. Kanev, UN. Koutsou, C. Christodoulou, and K. Obermayer
Kanev (2012) found that neurons can act as integrators even in a high-rate
and high-response variance setting. They proposed a new measure, the nor-
malized prespike slope (NPSS), based on the mean of a normalized membrane
slope during a small time window before the response. More specifically,
the NPSS is based on the mean slope of the membrane potential in the last n
milliseconds before the response, n being a parameter of the method. That
slope is normalized for each response spike, using a theoretical slope for
perfect integration as a lower bound and a theoretical slope for perfect co-
incidence detection as an upper bound. The lower bound is defined as the
slope that results if the response spike were the result of integration over
constant input during the interresponse spike interval. The upper bound is
defined as the slope that results if the neuron had received all its stimulus
in the time window before the response. The linearly normalized slope is
averaged over many responses, yielding the NPSS. A neuron is a perfect
integrator if its membrane potential is driven to the threshold by a constant
stimulus and a perfect coincidence detector if the membrane rises from the
static mean to the threshold within the preresponse time window of n ms. Dans
addition, Koutsou, Kanev, and Christodoulou (2013) investigated whether
correlations in the input can be estimated by looking at the membrane po-
tential and the neural response. They found that large parts of stimulus
synchrony are reflected by a neuron’s response. In that work, a neuron was
considered to be a coincidence detector if the synchrony of the stimulus
could be recreated from the neuron’s response.
Investigations were also done using actual spike-wise input-output re-
lations. Rudolph and Destexhe (2003) concluded that a neuron operates in
continuum between both modes, and the main influence on the mode is
synchrony in the stimulus. Using a compartmental model and stimulating
with gaussian spike volleys of a certain standard deviation, they proposed
a reliability measure R as the ratio of number of responses over number of
spike volleys. In integration mode, a neuron responds with R = 1 to a stimu-
lus with large standard deviation. In coincidence detection mode, a neuron
responds with R = 1 to a stimulus with a small standard deviation. Kreuz,
Haas, Morelli, Abarbanel, and Politi (2007), Kreuz, Chicharro, Andrzejak,
Haas, and Abarbanel (2009), Kreuz, Chicharro, Greschner, and Andrzejak
(2011), and Kreuz, Chicharro, Houghton, Andrzejak, and Mormann (2013)
have suggested several stimulus correlation measures. While they make
no claim about the predominant mode of cortical neurons, they underline
the idea that synchrony plays an important role in neural coding. Kreuz,
Mulansky, and Bozanic (2015) have suggested a new coincidence measure,
the SPIKE-synchronization distance, and Mulansky, Bozanic, Sburlea, et
Kreuz (2015) have investigated its mathematical properties. This measure
is a pure similarity measure between neural spike trains and is not related
to neural response modes. Ici, a coincidence is a close pair of spikes from
different neurons, distanced fewer than half of the previous or following
interspike intervals in each of both neurons, respectivement.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
un
_
0
0
8
7
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2095
Considerably fewer studies looked at Fourier transformations of spike
trains into frequency space. Hsu, Borst, and Theunissen (2004) argued that a
rate-based code is at work in the cortex but with constantly changing rates.
As a measure for the integration mode, they proposed a special form of co-
herence between stimulus and response. Ostojic, Brunel, and Hakim (2009)
investigated the influence of various parameters on spike train correlations
using a Fourier transform approach.
We believe that if a measure for the neural operational mode is to serve
as a basis of a broad discussion and aid investigation and understanding
of neural behavior, it should have certain properties: (1) it should be as
general as possible—in particular, it should be independent of a specific
neuron model, its parameters, or details of a real biological neuron to be
measured; (2) it should be as simple as possible; et (3) the concept of a
coincidence should be well defined and in a general and intuitive way.
In this letter, we try to clarify the concept of a neural operational mode.
We propose a definition of the neural mode that is as simple and direct as
possible, leading to a mathematical way to distinguish coincidence detec-
tion from temporal integration and to quantify what kind of influence a
presynaptic spike train has had on a neuron’s response.
In section 2, we derive a new definition from the standard reverse cor-
relation and formulate the measure. In section 3, we present and discuss
the measure’s behavior under different conditions, in relation to existing
measures and its performance on biological data. The letter finishes with a
discussion of the measure, our results, and further implications in section 4.
An appendix gives technical details of the numerical experiments.
2 Materials and Methods
2.1 Decomposing the Response-Stimulus Correlation. We base our
measure of the neural operational mode on a decomposed form of the
response-stimulus (or reverse) correlation (RSC). The RSC is estimated by
averaging time windows of the stimulus that have the same length and
are centered at observed response spikes. Continuous RSC shows the con-
ditional mean stimulus just before a neuron’s response. Unfortunately the
RSC cannot show whether the neuron operates as a temporal integrator or a
coincidence detector (Mainen & Sejnowski, 1995; Bugmann et al., 1997). À
overcome this, we decompose the RSC into the contributions of the single
spikes before a response.
Consider an ordered set of stimulus spike times
S = {s0
< s1
< s2
< . . .}
and an ordered set of response spike times
T = {t0
< t1
< t2
< . . .}
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2096
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
generated by a neuron. Let si be the time of the last stimulus spike before a
response spike at tj,
si
= max
k
{sk
|sk
< t j
}.
Consider distances from the nth stimulus spike before tj to tj itself:
t j
− si−n
.
These distances have a distribution (see Figure 1, middle). We calculate
the temporal mean for each distribution separately,
Rn
= 1
J
(cid:2)
j
(t j
− si−n
),
where J is the number of response spikes used in the average; tj are their
times; and si−n are the times of the preceding nth stimulus spike before the
(T, S), a series of time
response. The result is a decomposed discrete RSC, Rn
distances to an observed response spike, where R0 is the distance between
the response and the last stimulus before the response, R−1 is the distance
between the response and the penultimate stimulus before the response,
and so on (see Figure 1, bottom).
Note, however, that if, instead of building temporal means per distribu-
− si−n (see Figure 1, middle)
tion, the distributions of the spike distances t j
are added up for each point in time separately and divided by the mean
stimulus rate λ, they yield the normalized expected number of spikes at that
certain time before the observed response spike. The result is the standard
nondecomposed reverse correlation (see Figure 1, top).
As a last step we use the decomposed correlation Rn to define the time
series rn of stimulus intervals, where each rn is the (positive-valued) time
interval of the nth stimulus spike pair preceding a response,
r0
r1
r2
,
= −R0
= R0
= R−1
. . .
,
− R−1
− R−2
,
rn
= R−(n−1) − R−n
.
The first two elements of this series, r0 and r1, will form our proposed
measure of the neuron’s operational mode.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2097
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
Figure 1: Decomposed response-stimulus correlation. (Top) Reverse correla-
tion, built from single per-spike distributions of a simulated conductance-based
neuron, as shown in the middle part. (Middle) Distributions of arrival times of
the nth spike of the same neuron before the response. Adding all curves will
result in the reverse correlation shown in the top part of the figure. (Bottom)
Temporal mean of each of the single distributions from the middle panel. This
is a decomposed discrete form of the RSC, showing the mean arrival time of
each nth preresponse stimulus, as is used in our later analysis. The data was
produced by a numerical simulation of a conductance-based integrate-and-fire
neuron according to equation 3.1 with a reset of −50 mV (partial reset according
to Bugmann et al., 1997), resting potential of −60 mV, membrane time constant
of 20.0 ms, threshold of −42.0 mV, an excitatory conductance at 0 mV with
synaptic weight of 0.3 driven by a Poisson process of rate 100 Hz, and an in-
hibitory conductance at −75 mV with synaptic weight of 0.6 driven by a Poisson
process of rate 200 Hz.
2.2 Neural Mode and Drive. What is a neuron doing when it is consid-
ered to be integrating or detecting coincidences? We think the most natural
answer would be to say that a neuron detects coincidences when it responds
whenever spikes in its stimulus appear at the same time or are very close
to each other. It integrates when it fires with a steady rate in response to
fairly steady regular stimulus and its response rate somehow reflects the
rate of its stimulus. The context of the whole spike train decides whether a
succession of stimulus spikes is an episode of rapidity within an otherwise
calm input or whether it is part of a totally homogeneous but high-rate
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2098
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
stimulus. Because of this, a neuron’s operational mode measure must be
independent of temporal scaling of both stimulus and response.
We define a neuron’s neural drive as follows: (1) a neuron is positively
driven by a stimulus when a response spike is fired almost immediately
after the last preceding stimulus spike, (2) a neuron is negatively driven by
a stimulus when the response delay after the last preceding stimulus spike
is a lot longer than what is to be expected if the stimulus and response were
independent processes, and (3) a neuron is not driven by a stimulus when
the response delay after the last stimulus spike is what would be expected
if both processes were independent. These correspond loosely to excitation
(for positive drive), hyperpolarizing inhibition (for negative drive), and
either independence or shunting inhibition (for no drive); differences will
be made clear in section 3.
Looking at the last two stimulus spikes before a response, we define a
neuron’s operational mode as follows:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
• Coincidence detection is the operational mode where the neural drive
is positive and the neuron responds to pairs of stimulus spikes that
are significantly closer than expected
• Integration is the operational mode where the neural drive is posi-
tive and the neuron responds to pairs of stimulus spikes that are an
average time apart
• Gap detection is the operational mode where the neural drive is
positive and the neuron responds to a pair of stimulus spikes that are
significantly farther apart than expected.
The width of this last interval is relative to the rate of the stimulus in
question.
Our proposed measure RM,D for the operational stimulus-response mode
consists of these two values: the neural mode RM, denoting gap detec-
tion/integration/coincidence detection, and the neural drive RD denoting
negative/positive drive. Both values should range from −1 to 1.
To achieve a range from −1 to 1 for the neural drive, the distance r0 of
the last stimulus spike to the response is normalized by dividing it by the
expected distance if stimulus and response were independent and scaled
= 0, the mode is 1 (the neuron is driven
exponentially so that when r0
= ∞, the mode is −1 (the neuron responds only
directly), and when r0
when stimulus is missing). This yields the neural drive RD,
= 21−r0
/r∗
0 − 1,
RD
(2.1)
where r∗
0 is the mean distance between the response and the last preceding
stimulus spike if both stimulus and response were independent. If the
stimulus spike train were periodic (with the standard deviation of the ISI
distribution σ = 0), this distance would be 1
2λ , while if the stimulus spike
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2099
train were Poisson distributed (σ λ = 1), it would be 1
between these two extremes, we get an expected distance of
λ . Using σ λ to scale
∗
r
0
= 1 + σ λ
2λ
.
(2.2)
This theoretical value for r∗
0 is accurate under the assumption that the stim-
ulus is a mixture of regular and Poisson processes. If the stimulus has more
complex time dependencies (e.g., is a sparse succession of fixed-length high-
frequency bursts as in section 3.4), r∗
0 should be computed numerically.
To achieve a range from −1 to 1 for the neural mode, the relative mean
−
= 0, the mode is 1 (coincidence
= ∞, the
time interval of the last pair of stimulus spikes before the response, r1
R−1, is scaled exponentially so that when r1
detection), when r1
mode is −1 (gap detection). This yields the neural mode RM:
= 1 the mode is 0 (integration), and when r1
= R0
= 21−r1
/r∗
1 − 1.
RM
(2.3)
2.3 Modes of Operation. To discern different modes of operation, we
propose some boundaries in the RM,D plane (see Figure 2).
= −0.1. Values below RD
The neural drive RD, based on the normalized distance r0 of the last
preresponse spike to the response, provides information on the timing of
the response with respect to the stimulus trigger. Large values mean a re-
sponse is fired relatively late, inside an unusually big gap in the stimulus
spike train; small values mean a response is fired relatively quickly after
the triggering stimulus. We suggest two boundaries to discern inhibition:
independence and excitation. One border divides inhibition from inde-
< −0.1 indicate that the mean
pendence, at RD
response is triggered when there has been no stimulus for 115% longer than
expected. The reference for this expectation is the mean interval that would
be measured if stimulus and response were independent. If the presence
of a response indicates the absence of stimulus, the stimulus in question
< −0.1 indicate inhibition (see
has an inhibitory effect; hence, values of RD
Figure 2, left column). Another border divides independence from excita-
< +0.1 indicate that
tion, at RD
the mean response is triggered at between 115% and 86% of its expected
distance to the preceding stimulus. This area suggests independence (see
> 0.1 indicate that the mean re-
Chiffre 2, middle column). Values of RD
sponse is fired faster after the trigger than expected, at less than 86% de
the independence reference value, suggesting excitation (voir la figure 2, droite
column).
= 0.1. Values between RD
> −0.1 and RD
The neural mode RM, based on the normalized distance r1 of the two
last preresponse spikes, provides information on the rate of the stimulus
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
un
_
0
0
8
7
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2100
J.. Kanev, UN. Koutsou, C. Christodoulou, and K. Obermayer
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
un
_
0
0
8
7
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2: Overview of neural modes. The plane defined by the neural mode
and the neural drive (see section 2.2 and equations 2.1 et 2.3). Areas are
labeled according to the behavior of the responding neuron. For discussion, voir
section 2.3.
immediately before the response. Large values mean a response is a re-
action to a drop in the stimulus rate (a gap in the stimulus), and small
values mean a response is a reaction to a sudden increase in the rate (un
coincidence). We suggest two boundaries to discern coincidence detection:
temporal integration and gap detection. One border divides coincidence de-
> 0.5 indicate that
tection from integration, at RM
the mean response is triggered by a stimulus spike pair that is less than 42%
wide, compared to its expected width. This corresponds to an increase in
the local rate by a factor of 2.4. If a response indicates the presence of an
unusually close spike pair, the response is marking a coincidence; hence,
> 0.5 indicate coincidence detection (voir la figure 2, top row).
values of RM
= 0.5. Values above RM
Integrator or Coincidence Detector
2101
< 0.5 and RM
= −0.5.
The other border divides integration from gap detection, at RM
> −0.5 indicate that the mean response
Values between RM
reacts to stimulus spike pairs that are between 115% et 86% of their ex-
pected width apart. The response does not indicate any sudden changes of
the local stimulus rate; this area suggests temporal integration (voir la figure 2,
< −0.5 indicate that the mean response is fired
middle row). Values of RM
after a stimulus gap (in contrast to inhibition, where the response is fired
inside a stimulus gap), with the preceding spike pair being more than 200%
of its expected value apart, corresponding to a drop in the stimulus rate
< −0.5 indicate gap detection (see Figure 2,
by a factor of 0.5. Values of RM
bottom row).
Altogether, there are nine areas in the RM,D plane. On the inhibitory side,
there is an area where a coincidence precedes a quiescence in stimulus (see
Figure 2, top left). We have termed this fast inhibition. There is an area where
the response is triggered by one quiescence in an otherwise normally paced
stimulus (see Figure 2, middle left), and there is an area where the mean
response is an answer to a general slowdown of the stimulus—at least one
longer gap before the quiescence (see Figure 2, bottom left)—termed slow
inhibition.
In the central column, there is an area where a response marks a coinci-
dence, but the stimulus does not trigger the response directly (see Figure 2,
middle top), an area where the response does not mark any change in stim-
ulus at all (see Figure 2, middle), and an area where the response marks
a gap in the stimulus but is not triggered directly (see Figure 2, middle
bottom). These areas suggest independence, possibly in the coincidence,
and in the gap detection case, there are indirect influences (populations, or
connections via more than one neuron).
Within the area of excitation is an area of coincidence detection (see
Figure 2, top right), defined by excitation and the detection of coincidences;
an area of integration (see Figure 2, middle right), defined by excitation
and the absence of coincidences; and an area of gap detection (see Figure 2,
bottom right), defined by the detection of gaps in the stimulus.
3 Results
To explore the behavior of our new measure, several numerical simulations
were carried out, as well as one experiment using publicly available record-
ings from a cat’s cortex. All numerical simulations were run in C++ and
NeuroLab.1 The results are presented in this section; technical settings and
parameters are described in the appendix.
1NeuroLab is an open source C++ class library for numerical simulation and analysis of
stochastic processes in neuroscience, available online since 2005 and continually evolving.
Source code and documentation can be downloaded from GitHub at https://github.com
/jkanev/neurolab; precompiled packages are available on the first author’s home page.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2102
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
3.1 Corner Cases of the Measure. To demonstrate the measure on some
corner cases, we used artificial spike trains and measured their RM,D. No
neuron was simulated; rather, stimulus and response time series were com-
pared directly.
When a neuron responds to relatively closely arriving spikes within
a slower spike train, and only then, we would say it is in a coincidence
detection mode. The results of Figure 3, trace A, show the value for the
neural mode RM to be near 1; the value for the neural drive RD is near 1 as
well. In this case, the neuron separates coincidences from a noncoincident
background.
In contrast, when a neuron receives only coincidences and responds to
each one of them, it no longer separates coincidences from the background.
The mean width of the spike pair preceding the response is close to the
width that can be expected if the response were independent of the stimu-
lus. This is because random independent events would most likely fall in
between two coincidence pairs. Only in the unlikely case of a random event
falling inside a coincidence pair does the preceding spike pair span the gap
between two coincidences. The value for RM is much nearer to zero (see
Figure 3, trace B), so the neuron integrates over coincidences.
When a neuron responds regularly to regularly timed stimulus spikes,
with a response directly after a stimulus, it is integrating. In agreement with
this, the example in Figure 3, trace C, shows a value near zero for the neural
mode RM and a high neural drive RD.
If a neuron is reacting only to stimulus pairs that are relatively wide
apart compared to the mean time interval (e.g., because synaptic sensitivity
is increased while the synapse is quiescent), we would say it is detecting
gaps. Figure 3, trace D shows a sample train, and the resulting RM,D values
show a negative value for the neural mode and a positive value for the
neural drive (note that the response spike is emitted after the gap).
When a neuron’s firing is independent of the timing of its stimulus, it
shows a neural drive of zero, indicating independence. Our examples show
two Poisson-distributed independent spike trains (see Figure 3, trace E) and
two regular independent spike trains (see Figure 3, trace F). RD is zero for
both the regular and the irregular cases.
In the case of inhibition, the neuron does not respond directly after a
stimulus spike, but a long time later, due to the suppressive effect of the
stimulus (see Figure 3, traces H and I). In gap detection mode, the neuron
responds directly after a stimulus spike, but only when there was a large
gap before that last spike (see Figure 3, trace D). Inhibition occurs when the
stimulating synapse has a very low reversal potential, while gap detection
occurs when the synapse’s sensitivity is increased by a quiescent stimulus.
3.2 Inhibition, Subthreshold, and Superthreshold Excitation. The bi-
ological mechanism for the excitation or inhibition of a neuron’s response is
the reversal potential of the stimulating synapse: stimulus at high reversal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2103
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3: Corner cases of integration, gap detection and coincidence detec-
tion. (a) Artificial example spike trains. (b) Details of trains from panel a—one
preresponse interval r0 marked orange and the preceding interval r1 marked
green. (c) Measure in the RM,D plane. Spike trains: A, stimulus of coincidences
within random stimulus; response at the coincidences: coincidence detection.
B, stimulus of coincidences only; responses at the coincidence: integration over
coincidences. C, regular stimulus, regular response: integration. D, stimulus
with gaps, responses after gaps: gap detection. E, irregular stimulus, indepen-
dent irregular response: independence. F, regular stimulus, independent regu-
lar response: independence. G, stimulus with coincidences followed by gaps,
response during gap: fast inhibition. H, stimulus with gaps, response during
gaps: inhibition. I, stimulus with successive gaps, response during gap: slow
inhibition.
potential excites, and stimulus at low reversal potentials inhibits the re-
sponse. The value of RD reflects this behavior. To demonstrate this, we ran
a numerical simulation using a leaky integrate-and-fire neuron model with
conductances,
=
dVt
(cid:2)
i
(cid:3)
w
i
v
i
− Vt
(cid:4)
,
dGi
t
(3.1)
2104
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
Figure 4: Mode and drive in relation to excitation versus inhibition. (a) Behavior
of neural mode and drive (RM,D) during the change of the signal synapse’s
reversal potential from −75 mV to 0 mV. (b) Behavior of neural mode (RM) and
drive (RD) separately, in relation to the reversal potential.
where Vt is the membrane voltage, wi are weights, vi are reversal potentials,
and dGi
t are derivatives of stochastic processes (for parameter details, see
section A.1). The results are shown in Figure 4. The neuron was driven
by excitatory and inhibitory background noise and a signal, the reversal
potential of which we changed in several runs. While changing the signal’s
influence on the neuron’s response from excitatory to inhibitory, the neural
drive reacts accordingly: an excitatory reversal potential corresponds to a
> 0.0, while an inhibitory reversal potential corresponds
neural drive RD
< 0.0. While the reversal potential is changed and
to a neural drive RD
the neural drive value changes accordingly, the neural mode stays mostly
unaffected.
A neuron can operate in two distinctly different regimes. In the sub-
threshold regime, the membrane potential mean is lower than the thresh-
old, the neuron is driven by fluctuations in the membrane potential, and the
neuron spikes with a lower rate and higher variance. In the superthreshold
regime, the membrane potential mean is above the threshold, the neuron
is driven by the membrane potential mean, and the neuron spikes with
a higher rate and lower variance. The subthreshold regime is commonly
associated with coincidence detection and the superthreshold regime with
temporal integration (Kempter, Gerstner, & van Hemmen, 1998; Kempter,
Gerstner, van Hemmen et al., 1998; Tchumatchenko, Malyshev, Geisel, Vol-
gushev, & Wolf, 2010). The value of RM reflects this. To demonstrate this,
we ran a numerical simulation exploring different values of the membrane
spiking threshold (see section A.2 for detailed parameter settings). The re-
sults (see Figure 5) clearly show that according to the value of RM, the
neuron used in the example integrates when in superthreshold regime and
detects coincidences when in subthreshold regime. For any neuron, RM will
be higher when the neuron is in a subthreshold regime and lower when
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2105
Figure 5: Mode and drive in relation to sub- versus superthreshold regime.
(a) Behavior of neural mode and Drive (RM,D) during the change of the regime
from subthreshold to superthreshold. (b) Behavior of neural mode (RM) and
drive (RD) separately, in relation to the response rate.
the neuron is in a superthreshold regime, although exact values of RM may
vary depending on other neural parameters. The kink in the RM curve near
= 0.5 appears when the threshold is well above the mean membrane
RM
potential.
3.3 Comparison with Other Measures: Random Test. To compare our
new measure with other measures that are used in the literature, we ran a
numerical simulation using the same neuron model as before (conductance-
based leaky integrate-and-fire; see equation 3.1). Between 100 and 150 trials
were run and parameter values were chosen randomly (see section A.3 for
technical details). We investigated the following measures:
1. The normalised prespike slope (NPSS, according to Koutsou et al., 2012).
The original measure is based on a current-based neuron, in contrast to the
conductance-based neuron model used in this study. Our calculation devi-
ates from the original form as follows. For each response spike, a test neuron
was created, and two membrane trajectories were calculated numerically—
for ideal integration (the membrane potential reaches the threshold using
a constant scalar stimulus) and for ideal coincidence detection (the neuron
reaches the threshold because all stimuli are received within a 2 ms time
window before the response). The actual voltage difference m in a 2 ms
time window before the response was scaled by the respective values for
the ideal integrator (mlower) and the ideal coincidence detector (mupper):
NPSS = m − mlower
mupper
− mlower
.
(3.2)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2106
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
2. The coefficient of variation (CV, used by Bell et al., 1995, and others)
which in the current study we did not scale or normalise.
3. The normalized coincidence advantage (according to Abeles, 1982) shows
the extent to which synchronous activation of a few synapses is more ef-
fective than asynchronous activation of the same synapses. A synchronous
advantage aC was obtained by calculating how many stimulus spikes would
bring the membrane potential from its mean to the threshold vθ ,
= 1
λ
aC
vθ − (cid:5)Vt
− (cid:5)Vt
v
S
(cid:6)
(cid:6)
,
(3.3)
where vS is the synaptic reversal potential of the synapses carrying the
signal. Then the neuron was simulated without signal stimulus, only with
background noise. Using r for the normal response rate measured previ-
ously and rs for the response rate without stimulus, the integration advan-
tage aI is the gain of the response rate created by a single nonsynchronous
stimulus spike,
= r − rs
λ
.
aI
(3.4)
The normalized coincidence advantage is the relation between the syn-
chronous advantage aC and the asynchronous advantage aI:
a = 1
2
.
aC
aI
(3.5)
4. For the integration time window measure (ITWM, according to K ¨onig,
Engel, & Singer, 1996) the membrane time constant was calculated, with the
notable difference that the effective membrane time constant was used—
that is, the effect of background noise on the time constant was taken into
account. The result was exponentially scaled to achieve a value of 0 for pure
integration and a value of 1 for pure coincidence detection:
(cid:5)
ITWM = exp
−
(cid:6)
.
r
+ w
1
τ
μ
B
B
(3.6)
Here r is the mean response rate, τ is the membrane time constant, wB is the
weight of the background synapses, and μ
B is the mean of the background
(cid:3)
(cid:4)
stimulus rate. The expression 1/
μ
is the adjusted time constant,
B
taking the change by the background noise into account.
+ w
1
τ
B
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
These coincidence detection measures
into two categories:
like NPSS and integration time window
fall
membrane-based measures,
Integrator or Coincidence Detector
2107
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
Figure 6: Comparison of neural drive and mode to different measures. (a) Com-
= 0.035. The Pearson correlation coeffi-
parison of NPSS and neural mode. ρ
= 0.030. (b) Comparison of coefficient of variation and neural mode,
cient ρ
= 0.083. (c) Comparison of the coincidence advantage according to Abeles
ρ
x,y
(1982) and the neural mode. (d) Comparison of integration time window and
neural mode, ρ
= 0.245.
x,y
x,y
x,y
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
(ITWM), and pure spike-based measures like coincidence advantage, CV,
and neural mode. Using a model neuron with random but biologically plau-
sible parameter settings, we generated stimulus and response spike trains
and assessed neural mode and drive. Figure 6 shows the value of each in-
vestigated measure plotted against the neural mode, where each point is
the result of one simulation. No strong correlation can be seen between the
2108
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
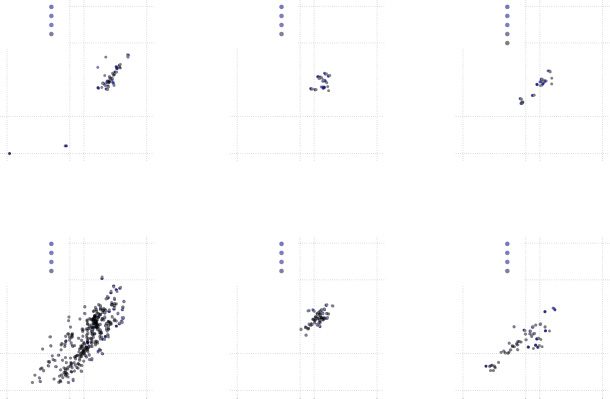
Figure 7: Pairwise comparison of different measures. (a) Comparison of coef-
= 0.581. Pearson correla-
ficient of variation and integration time window; ρ
= 0.313. (b) Comparison of NPSS and integration time win-
tion coefficient ρ
dow. (c) Comparison of integration time window and coincidence advantage,
= 0.265.
ρ
x,y
x,y
= 0.017. (f) Compari-
(e) Comparison of NPSS and coincidence advantage, ρ
= −0.202.
son of coefficient of variation and coincidence advantage, ρ
= 0.020. (d) Comparison of NPSS and coefficient of variation, ρ
x,y
x,y
x,y
x,y
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
neural mode and any of the other measures. Figure 7 shows the correlation
of each measure with every other measure.
The plots suggest a correlation between the CV and the ITWM (ρ
=
0.581; see Figure 7a), a weaker correlation between NPSS and ITWM (ρ
=
0.313; see Figure 7b), and a weak nonlinear correlation of the ITWM and
the coincidence advantage (ρ
= 0.020; see Figure 7c). None of the tests
show a really strong correlation between any of the tested measures. This
suggests that each measure measures something different, as we explain
below.
x,y
x,y
x,y
The NPSS measure is a measure based on the membrane potential. In
contrast to all other measures, its calculation is response-interval based.
It classifies the behavior of the membrane potential, placing it in a con-
tinuum between the two extremes of an integrator (a neuron spiking in
response to totally scalar stimulus) and a coincidence detector (a neuron
responding only when all input has arrived just before the response). It
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2109
operates on the complete system stimulus-neuron-response. A neuron re-
ceiving a regular stimulus and responding to each stimulus spike would
be classified as a coincidence detector. The random test shows no rela-
tion to the neural mode but a relation to the neural drive (see Figure 6a).
When a neuron is not directly driven by its input, it is classified as an
integrator. The NPSS measures how the behavior of the membrane poten-
tial reflects synchrony in the stimulus. While a high NPSS measure is an
indicator that a neuron might be detecting coincidences, a neuron might
still react solely to coincidences and have a low NPSS, for example, when
a stream of coincidences is responded to with a low response frequency
(integrating over coincidences; see also Koutsou, Kanev, Economidou, &
Christodoulou, 2016). Therefore we feel that the NPSS does not measure
the neural mode directly, but is one of the means to achieve it. We found a
weak correlation with the ITWM (ρ
= 0.313; see Figure 7b), which is not
x,y
surprising as both measures operate on preresponse time windows. The
NPSS operates on a timescale defined by the length of the 2 ms preresponse
window and the length of the response interval. The relationship between
these lengths determines the neural mode, independent of the stimulus
rate. This is in contrast to the other measures, and, in particular, the neural
mode, which operates on a relative timescale defined by the stimulus. This
explains the fact that there is no correlation of the NPSS with the neural
mode.
Although it was never used as a direct measure of the neuron’s opera-
tional mode, it was argued that a high CV (close to 1) in the case of high
firing rates means that a neuron is not integrating (Softky & Koch, 1993).
The CV is the only measure investigated that looks only at the response
spike train. A neuron producing a regular response spike train (low CV)
would be classified as an integrator, independent of whether it responds to
regular close spike pairs or bursts, or not. Using the CV to classify a neuron
makes sense only when the stimulus statistics are in a certain very narrow
range, that is, when they show a Poisson-like distribution. The random test
shows no relation to the neural mode but a relation to the neural drive
(see Figure 6b). We also found a connection to the ITWM (ρ
= 0.581; see
Figure 7a). When a neuron is not directly driven by its input, the CV classi-
fies it as integrator, although not as extremely as done by the NPSS measure.
While a high CV can possibly be the result of coincidence detection, it is also
conceivable that a high CV is the result of integration over short episodes
of different stimulus rates or of bursting activity in the responding neuron.
Therefore we think that the CV is a possible consequence of a certain mode
of operation, with a weak connection to coincidence detection, even though
other studies also show that integration is possible with a high response
CV (Koutsou et al., 2012). The CV operates on a timescale defined by the
neural response. Like the neural mode proposed in this letter, it is a relative
measure, but the neural mode’s timescale is determined by the stimulus.
This is why there is no correlation between the two.
x,y
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2110
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
The ITWM states whether the neuron acts as a strong or a weak high-
pass filter. Like the CV, it works independent of the stimulus and takes only
the neuron’s response into account. The results of the random test show a
weak correlation to the CV, which suggests that time-based filtering and
response CV are connected, but there is no correlation with neural mode
or drive (see Figure 6b). The ITWM is a measure purely about the neural
mechanism and independent of the characteristics of the stimulus. While
a long integration time constant may hint at integration mode, it is still
possible that due to balanced input, a neuron’s membrane potential hovers
near the threshold, making the neuron sensitive to coincidences. In that
case, a neuron would be detecting coincidences, while the ITWM would
classify it as an integrator. We feel that the ITWM, similar to the NPSS,
does not measure the neural computation mode, but is a means to achieve
it. The timescale the ITWM operates on is determined by the membrane
time constant. In the way we conducted the simulation, this was influenced
by the stimulus rate. Nevertheless, the timescale is absolute, while the
timescale of the neural mode measure is relative. This explains the missing
correlation between the two.
The coincidence advantage is the only measure that discerns signal and
background within the stimulus. It operates on a neuron with random
background input and measures how the neuron would react to an input
signal on top of that background noise. It does not classify the complete
system stimulus-neuron-response. An integrator is a neuron that treats a
signal similar to background noise, while a coincidence detector is a neuron
that uses its background to detect coincidences in its stimulus signal. The
results of the random test show a weak correlation to the ITWM, which
suggests a link between the idea of utilization of background noise for
signal detection and the idea of filtering. There seems to be no relation to
the neural mode, but a relation to the neural drive (see Figure 6c). It is biased
toward coincidence detection and is the only measure that classifies neurons
that operate independent of their stimulus as coincidence detectors. The
coincidence advantage is a relative measure weighing how much a neuron
amplifies a signal spike against a background stimulus. While related, this is
a different concept of coincidence detection than any of the later proposed
measures we found in the literature. The coincidence advantage uses an
absolute timescale; in particular, it regards only those spikes as coincident
that happen at exactly the same time. This is in contrast to the proposed
neural mode and explains the missing correlation between neural mode
and coincidence advantage.
3.4 Naturalistic Setting. A single incoming stimulus spike raises the
neural membrane potential of a typical cortical neuron in vivo only by
fractions of a millivolt. The density of stimulus is usually very high, and
many stimulus spikes take part in raising the voltage to the threshold in the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2111
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
Figure 8: Neural mode in a realistic setting: Sample of stimulus and response.
(Top to bottom) Exc: scatter plot of excitatory background stimulus spikes; each
spike is one dot. Inh: scatter plot of inhibitory background stimulus spikes. Sgn:
scatter plot of signal stimulus spikes, 10 Hz, 16 Hz, . . . , 153 Hz—responses of
the five different neurons from the simulation. At 10 Hz, each response spike
marks a signal spike packet. At higher response rates, spikes are increasingly
caused by background fluctuations.
last milliseconds before the response. Our measure takes only the two very
last stimulus spikes into account.
To test whether this approach is feasible in a realistic setting, we ran a
numerical simulation of five leaky integrate-and-fire neurons with conduc-
tances linked to 5000 excitatory and 5000 inhibitory presynaptic background
spike trains at 5 Hz each (see section A.4 for further details). In addition to
that background, a signal consisting of 124 signal neurons where either 4,
20, or 100 neurons fired nearly simultaneously, with spikes 1
100 ms apart,
was added to the excitatory conductance. Each of the packets of 4, 20, or 100
spikes occurred with a rate of 3 Hz, adding up to a total of 9 Hz for the in-
coming spike packets. The five simulated neurons had different thresholds,
making them respond at different rates. The first neuron fired at 10 Hz,
picking up only the coincident spike packets in the signal and ignoring
everything else. The second neuron fired at 16 Hz, in addition slightly re-
sponding to the background. The other three neurons fired at 32 Hz, 73 Hz,
and 153 Hz, where the last neuron responded largely on the excitatory
background (see Figure 8 for a sample of the spike trains). We analyzed
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2112
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
the result using the neural mode and drive. To get a complete picture, we
measured how different parts of the input contribute in different ways to
generate the observed response.
Looking at all the stimuli combined—excitatory, inhibitory, and signal—
and measuring against the response, we find that the neuron that responds
with 10 Hz performs coincidence detection, while the others are mainly
integrating (see Figure 9g). This is in agreement with the fact that this
neuron responds solely to the signal, while the other neurons also respond
to the background, and it clearly shows how coincidence detection is used
as a means to separate a weak signal from a strong background.
Looking at only the background, we find that the high-rate neurons op-
erate as integrators on the background stimulus, while the low-rate neurons
seem independent of the background. This is because they are driven by the
signal and not by the background noise, and because inhibitory and excita-
tory effects of the background cancel out (see Figure 9d). Looking at only the
excitatory stimulus and ignoring inhibition, the neural drive is much higher
and coincidence detection is much more pronounced (see Figure 9f). Ignor-
ing the excitatory background and analyzing only inhibitory background
and signal, versus the response, leads to a result where the low-frequency
neurons are coincidence detectors (responding to the signal), while the in-
put to the high-rate neurons seems characterized by inhibition, meaning
their response times are largely independent of the spike timing of the
stimulus (see Figure 9e).
As expected, analyzing the effect of the excitatory background only re-
sults in integration for all neurons. This shows how neurons use integra-
tion on one part of their stimulus to become sensitive to another part (see
Figure 9b). Also as expected, looking at the inhibitory background produces
a similar result in the inhibitory range of the neural drive (see Figure 9c).
We measured how the signal itself influenced the neuron’s response, ne-
glecting the background. Because of the far-reaching temporal correlations
(regular-spaced spike packets of up to 100 spikes, arriving in a random
manner), the signal process is clearly not Poisson nor regular and cannot
be estimated using equation 2.2. For this reason, we used a numerical esti-
mation (see Figure 9a). As a comparison, we also show the regular/Poisson
approximation of equation 2.2 (see Figure 9h). Interestingly, measuring how
the neuron operates purely on the signal itself results in independence for
the high-rate neurons (as expected) but in gap detection or integration for
the low-rate neurons (see Figure 9a). The gap detection is a result of the
structure of the stimulus. The neuron is so sensitive that it responds to
the first spike of the stimulus spike volleys, thus detecting when the gap
between the two volleys has finished. All this shows how coincidence de-
tection can be used by a neuron to first separate signal from background
and then process that separated signal using a different mode of operation
(gap detection or temporal integration in our example). Here the neuron
operates in a stochastic resonance scenario where background noise is used
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2113
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9: Neural mode in a realistic setting: Plane defined by RM,D. (a) RM,D
of signal versus response, using a numerical estimation for r∗
0 in equation 2.1.
(b) RM,D of excitatory background versus response. (c) RM,D of inhibitory back-
ground versus response. (d) RM,D of excitatory and inhibitory background com-
bined versus response. (e) RM,D of signal and inhibitory background combined
versus response. (f) RM,D of excitatory stimulus only (background and signal)
versus response. (g) RM,D of all stimulus (excitatory, inhibitory, and signal) com-
bined versus response. (h) RM,D of signal versus response, using a regular/
Poisson calculation according to equation 2.2.
to achieve sufficient sensitivity to respond to small fluctuations in the signal
(Plesser & Tanaka, 1997; Rudolph & Destexhe, 2001; Wenning & Obermayer,
2003).
2114
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
3.5 Time Delay. An intrinsic problem of the way the new measure op-
erates is that it relies on the immediate response after the last stimulus spike
before that response: one single response spike is triggered by one single
last stimulus spike occurring immediately before the response. This could
pose a problem in the case of biological neurons where spike generation
may take some time after being initiated. Stimulus occurring during this
time would not contribute to the spike generation, but would be falsely
identified by the new measure as stimulus that has triggered a response.
To overcome this problem we suggest calculating the neural drive and
mode after adding a time delay d to each stimulus spike time. This time
delay should match the time needed by the spike generation mechanism of
the neuron. Unfortunately in most cases, d will not be known and can only
be estimated. Here several measurements should be made using different
values for d, and the value for d with the highest absolute drive should
be used. This is the value that will most accurately fit the time distance
between the last significant spike and the response.
Previous research has found that in the dendritic tree, active and pas-
sive properties counterbalance the different delay times caused by spatial
distribution of the synapses. Depending on the location of the synapses,
excitatory postsynaptic potentials (EPSPs) reach the soma with different
amplitudes, but with no difference in time delay (Williams & Stuart, 2000;
Magee, 2000). While it would be possible to find optimal time delay com-
pensation values for spike trains on the basis of the spatial location of the
respective synapses on the dendrite, we believe, on the grounds of men-
tioned research results, integration differences in the dendritic tree can be
neglected.
To test the effect of less optimal values for d, we ran a numerical sim-
ulation with a conductance-based LIF neuron model as above, but with a
delay after the threshold crossing to mimic the spike generation time. When
the membrane potential Vt exceeds the threshold, the neuron is frozen for
a small time period d and input stimuli during that time are ignored. After
that time has passed, a spike is emitted and the neuron proceeds normally.
In the simulation, we used the same background activity and neural pa-
rameters as in the naturalistic experiment (see section 3.4), except that there
was no extra signal stimulus. Various studies have found a wide range of
the first spike latency—values for pyramidal cells in the neocortex range
from 0.32 ms (Waterhouse, Mouradian, Sessler, & Lin, 2000) to 137 ms
(Kumar & Ohana, 2008). In our experiment, we used an arbitrary value
for the spike generation delay of d = 5 ms. (see section A.5 for detailed
parameter settings).
Figure 10a shows a sample of the neural membrane voltage. The voltage
stays at the threshold for 5 ms before the spike is emitted. Figures 10b and 10c
show the result with various values of d used in the analysis, while the delay
of the tested neuron was always fixed. A delay in the analysis that matched
the delay of the neural membrane turned out to be optimal and yielded
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2115
Figure 10: Time delay. (a) Membrane voltage sample, showing a threshold hit
at 67 ms and subsequent freeze for 5 ms. (b) Calculated RM,D for the excitatory
stimulus. Labels show different time delays of 5 ms to 4.92 ms. (c) Calculated
RM,D for the inhibitory stimulus. Labels show different time delays of 5 ms to
4.92 ms.
the highest absolute drive in both the excitatory and the inhibitory cases.
Delays that were slightly smaller reduced the neural drive, but increased
the absolute neural mode. If the delay is too large, the causality is lost and
the neural drive will equal zero (not shown).
The sensitivity of the neural drive and neural mode to time delay is
proportional to the stimulus rate. As soon as several stimulus spikes get
in between the last stimulus spike that has triggered the response, and
the delayed response itself, the intervals r0 and r1 are calculated using the
wrong stimulus spikes. An extreme case is a neuron responding to sparse
single spike pairs in an otherwise evenly spaced stimulus spike flow. The
causality is totally lost as soon as the neuron introduces a time delay that
is larger than the stimulus rate. A more common case would be a neuron
responding to spike volleys from a presynaptic neural population. Here the
causality is lost only if the time delay is larger than the length of a spike
volley.
Reducing the delay in the analysis shows a deterioration of both neural
mode and neural drive to zero. The nonlinearity, that is, the rising of the
neural mode in the excitatory and the falling in the inhibitory case, is a
result of additional stimulus spikes being accounted for between the actual
triggering spike and the response. In the case of excitation, if the delay time d
is less than the mean distance of the last spike pair that triggered a response,
additional spikes will produce a (wrongly accounted for) spike pair that is
smaller than the actual one. Hence the neural mode will be slightly lifted
toward coincidence detection. In the case of inhibition, the reverse of this
effect takes place.
3.6 In Vivo Recordings. In this section, we demonstrate how the mea-
sure could be used to analyze data from in vivo measurements. Extracellular
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2116
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
recordings use multitrodes with several recording sites to record spikes that
are produced in different local areas and are created by many different neu-
rons. It is not clear whether recorded spikes are being used as inhibitory or
excitatory stimulus by any postsynaptic neuron. It is also not clear whether
a recording site has picked up the activity of a whole neural population,
or just part of it, or activity from several populations. The approach we
propose deals with this situation by combining one or several recording
sites to sets and regarding each as a black box. The neural mode and neural
drive are measured between pairs of black boxes. The combined spike train
of one set’s recording sites acts as a stimulus and the spike train of the
other (usually single recording site) as response. The measure will indicate
whether one group excites the other or inhibits it, whether coincidences
trigger responses, or whether both groups are independent. That way, the
ideas of temporal integration, coincidence detection, excitation, inhibition,
and independence are applied to larger neural groups.
Different populations may be interconnected with a time lag due to
their spatial separation. Our analysis is able only to apply fixed time lags
per group. To find the optimal time lag compensation per neuron set, we
explored five values between zero and 2 ms delay. An ideal analysis would
measure each possible pair of subsets of recording sites against each other
and explore many different time lags. Such an analysis was beyond the
scope of this letter.
We used publicly available recordings from the NSF-funded CRCNS
Data Sharing website (https://crcns.org/data-sets/vc/pvc-3). Neural data
were recorded by Tim Blanche in the laboratory of Nicholas Swindale,
University of British Columbia. We used the CRNS-PVC3 data set, which
consists of several recordings from a cat’s cortex done with a multitrode and
one spike train for each of the multitrode’s recording sites (more details are
in section A.6). We do not make any statements about actual neural behavior
in the mammalian cortex. We had no knowledge of the underlying neural
connectivity or about how many neurons had contributed to the spike train
from each recording site of the multitrode.
The data set contains several in vivo recordings in different situations.
We measured each recording twice. In a first run, we measured all possible
pairs of one response group consisting of a single recording site, and a
stimulus consisting of all remaining recording sites (see Figures 11a to
11c). In a second run, we analyzed all possible triplets and measured the
stimulus of two recording sites combined against the response of a third
site (see Figures 11d to 11f). The analysis was done at different time lags,
d = 0, 0.5, . . . , 2 ms.
Figures 11a to 11c show mainly integration with a little bit of inhibition.
Looking at all-to-one connections gives a very broad picture of what is
going on inside a cortical column in total. If the dominant neural mode is
integration, as it seems in our example, smaller subgroups showing other
modes, like inhibition, would get lost.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2117
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
Figure 11: In vivo recordings of cat cortex. (Top row) All (N-1)-to-one elec-
trode pairs. (a) Spontaneous activity in area 18. (b) Watching a natural movie.
(c) Watching a drifting bar. (Bottom row) All two-to-one electrode pairs. (d)
Spontaneous activity in area 18. (e) Watching a natural movie. (f) Watching a
drifting bar.
Figures 11d to 11f show integration and slow inhibition but little coin-
cidence detection. Looking at two-to-one connections gives a very detailed
view of where each recording site will be measured against many possible
stimulus pairs. Larger groups of signaling neural populations could get
broken up, and, for example, a strong coincidence detection effect could be
reduced in the analysis. Missing coincidence detection could be due to this
fact or could simply not be present. Analysis also shows a high amount of
slow inhibition: the response group responds only after the stimulus has
slowed down for more than two spikes.
We explored various time delay values below 2 ms (the width of a spike
of a typical CA2 pyramidal neuron; Scorza et al., 2011). Time delays below
2 ms had almost no effect on the neural mode and drive. The low sensitivity
can be explained by two observations, the first being that the stimulus
rate was below 500 Hz in all the measured groups, in both the two-to-
one connections and all-to-one connections. Moving the response within a
range of 2 ms would not change the intervals r0 and r1 a lot. The second
observation justifying the low sensitivity was that none of the neurons was
≈ 1. The interval r0 was much larger
driven directly, with a neural drive RD
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2118
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
than 2 ms, and a time shift below 2 ms would have had little effect on its
relative value R0.
4 Summary and Discussion
4.1 Neural Mode and Drive. We believe the operational mode of a
neuron should be the description of the mathematical operation of turning
stimulus spikes into response spikes, independent of the physical nature
of the computing neuron. An assessment of whether a response spike train
is the result of coincidence detection or temporal integration should be
possible to be made without knowledge of the producing neuron’s inner
working or the parameter settings of a certain model.
In this letter, we suggested a clear concept of coincidence detection, based
entirely on spike trains. Coincidence detection is the mathematical opera-
tion of creating a response event time series where each response event
marks a relative coincidence in the stimulus. We defined coincidence as two
relatively close spikes compared to the rate of the spike train they occur in,
and we defined detection as eliciting a response spike. This led to a spike-
based definition of excitation, which we defined as responding to a stimulus
faster than expected if stimulus and response were independent. To com-
plete this, we also included independence as responding as fast as expected,
inhibition as responding more slowly than expected, and gap detection as
responding to two spikes that are relatively far apart.
These definitions lead to a two-dimensional measure RM,D, where the
neural mode RM quantifies whether the eliciting events are coincidences,
normally distanced spikes, or gaps, and where the neural drive RD quan-
tifies whether the response timing is excitatory, independent, or inhibitory
(see equations 2.1 to 2.3).
4.2 Modes of Operation. Dividing the RM,D plane into several areas,
we suggested different modes of neural operation. For a low value of the
neural drive, near −1, when the neuron responds long after the last response
spike was received, we have suggested slow inhibition (responding after
the stimulus has died down for a bit), normal inhibition (responding as
soon as the stimulus leaves a large gap), and fast inhibition (responding to
an increase and subsequent silence of the stimulus). For a drive of zero, we
have suggested independence, although the cases of a very high or a very low
mode RM are still interesting. In the case of high RM, the neuron is reacting
to coincidences among neurons to which it may be connected indirectly,
while in the case of a low RM, it may be sensitive to a signal with a special
temporal structure (compare the simulation result in section 3.4, Figure
9a, for independent gap detection as a result of temporal correlations in
the stimulus). For a high value of RD, near 1, we have suggested coincidence
detection (responding to coincidences in the stimulus, when RM is also high),
integration (responding, but not detecting particular patterns, when RM is
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2119
near zero), or gap detection (responding to the first stimulus spike after a gap
in the stimulus, when RM is low).
4.3 Corner Cases of the Measure. We tested the behavior of the mea-
sure by applying it to extreme cases. Situations of perfect integration, perfect
coincidence detection, gap detection, slow and fast inhibition, and two
forms of independence were tested, and the resulting measure was in ac-
cordance with our theory.
4.4 Inhibition and Subthreshold and Superthreshold Excitation. Run-
ning numerical simulations, we also found that whether a neuron is in a sub-
threshold or a superthreshold regime is reflected by the neural mode. While
all other parameters were fixed, applying the measure in a superthreshold
regime resulted in integration; in a subthreshold regime, the result was coin-
cidence detection. Looking at excitation or inhibition, the measure behaved
as expected: subthreshold reversal potentials were classified as inhibitory,
while superthreshold reversal potentials were classified as excitatory. A
change of the reversal potential of a stimulating synapse results in a change
of the neural drive, and changing the spiking threshold results in a change
of neural mode.
4.5 Comparison with Other Measures. We compared the suggested
measure with four selected measures from the literature and also com-
pared these measures among themselves. We found some correlation, but
no convincing agreement between any two measures. We have come to the
conclusion that existing measures do not measure the operational mode of
a neuron directly. As explained in section 3, they either quantify parameter
settings or other mechanisms a neuron may use to execute a certain opera-
tional mode, or they quantify possible consequences of certain operational
modes.
The CV measures the irregularity of a neuron’s response. Under certain
conditions, this can be an indicator of the neuron’s operational mode. These
conditions are quite restrictive: the stimulus must be a Poisson distributed
flow of spikes with a static mean and variance and without any temporal
correlations. The neuron’s firing irregularity may be a possible consequence
of the neural mode but not the neural mode itself. The coincidence advan-
tage (CA) is a relative measure weighing how much a neuron amplifies a
signal spike against a background stimulus and, in particular, at what dis-
tance to the threshold its mean membrane voltage lies. We believe the CA
measures whether a neuron operates in a stochastic resonance scenario—or
whether it does not. While these concepts are related, stochastic resonance
is a result of coincidence detection, but both concepts are not identical.
The integration time window measure (ITWM) measures whether a neu-
ron works in a superthreshold or a subthreshold regime. The ITWM is a
measure purely about the neural mechanism and independent of statistical
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2120
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
characteristics of the stimulus. The idea of the regime is related to the neural
mode, but the ITWM does not measure the neural mode. The normalized
prespike slope (NPSS) measures how the behavior of the membrane poten-
tial reflects synchrony in the stimulus. The idea to average the membrane
potential slope before a response and the idea to average the last two stim-
ulus spikes before the response are related. We believe the NPSS measures
a biological mechanism—the use of the neural membrane as a high-pass
filter—that is used to achieve coincidence detection or integration but not
the neural mode itself.
Because of these slight differences of concept, none of the definitions
from the literature we looked at are highly correlated between themselves.
Moreover, apart from the CV, none of them is extendable to measure the
spiking behavior of more abstract spike generators, like neural populations,
artificial spike trains, or spike models that do not incorporate a neural
membrane.
4.6 Naturalistic Setting and In Vivo Recordings. In the historic discus-
sion of whether neurons act as integrators or coincidence detectors, there
seems to be a consensus that a neuron operates somewhere in a contin-
uum between these extremes (Koutsou et al., 2012, 2013; Ratt´e et al., 2015;
Rudolph & Destexhe, 2003). There does not seem to be a consensus, though,
on what the term coincidence detection actually refers to: a mode of a neuron
only or a mode of a system consisting of stimulus, neuron, and response.
We would argue that a neuron can use different neural modes at the same
time, just as excitation and inhibition are used at the same time, depending
on which subset of its stimuli is being investigated. An example would be
a neuron operating in a stochastic resonance scenario and using integration
on some of its input to enable it to execute either coincidence detection
or gap detection on another part of its input. We propose the terms neural
drive and neural mode to refer to a system consisting of a deliberately chosen
subset of a neuron’s stimulus and the neuron’s response.
This modular approach enables an investigation of how stimulus groups
that differ by a property like the reversal potential of their synapses are
used differently by a responding neuron. By regarding the sources of a
set of stimulus spike trains as a black box, analysis of relations between
larger population becomes possible. It is conceivable to measure the com-
bined stimulus spike train from one neural population against the com-
bined response spike train from another population. A whole population
may act as an integrator over the stimulus of another whole population
or as a coincidence detector; populations may be excited or inhibited by
the stimulus of other populations. A neuron inside a population may use
coincidence detection to stay in sync with the firing of other population
members, while at the same time, the whole population may be integrating
over population-external background noise to get near a reaction threshold
to start synchronous spiking.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2121
The proposed measure takes only the two very last stimulus spikes
before a response into account. In a typical high-density stimulus, many
stimulus spikes may take part in raising the voltage to the threshold in the
last milliseconds before the response. We still believe that looking at the
last two spikes is sufficient. Averaging a small random sample over many
trials to get information about the whole population is a common idea in
statistical analysis. By constructing a measure from an average over just the
two last spikes before a response, we apply that idea to the investigation
into preresponse stimulus dynamics. Even if the elicitation of a response is
done by a spike burst of several hundred spikes, the last two spikes will
carry general information about spike timing and dispersion within the
whole burst. By building an average of an interstimulus relation (the neural
mode) and a stimulus-response relation (the neural drive) from these two
spikes, we extract information about time dispersal within the burst, as well
as information about the burst’s relation to the response. Still, the approach
is general enough to work in scenarios where a response is triggered by just
one spike.
The experiment in section 3.4 was run to demonstrate both the concept
of modularity and the idea that the last spike pair can serve as an estimator
for the preresponse stimulus dynamics. We have measured the stimulus
in seven groupings against the response of a single neuron. We believe
the results clearly demonstrate the feasibility of the idea of grouping the
stimulus into different larger sets and the idea of sampling by using just
two spikes. The composition of the respective groups, and the way spikes
were triggered, were well reflected in the final measure (see Figure 9 and
text in section 3.4). The same idea was applied to an in vivo recording
(see section 3.6), although a complete and extensive investigation into dif-
ferent groups and populations would have been outside the scope of this
work.
A problem we have not addressed yet is the fact that in a high-density
stimulus scenario, the last two spikes are very close together. The numerical
simulation in section 3.4 was run with a time resolution of 2 nanoseconds.
Measuring in in vivo or in vitro setups at such a resolution could be very
demanding, if not unfeasible. There may be several ways to overcome this
obstacle.
One way is to use prior knowledge about neural populations. If it can be
assumed that a neuron receives a stimulus from a whole presynaptic neural
population, the spike train of a small subgroup of that population may be
used as an estimator for the whole group’s stimulus-response relation with
the neuron in question. The neural mode and drive from that small group’s
spike train would be measured against the response of the postsynaptic
neuron. The small subgroup fires in the same way as the whole population,
but with a much lower frequency. As the measure is independent of the
actual stimulus rate, the value of neural mode and drive would be the same
as for the entire population. To refine this approach, several such samples
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2122
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
could be taken and a total neural mode and drive built by averaging over
those samples.
In a similar way, it is conceivable to use smaller, arbitrary subgroups
of presynaptic neurons. However, in that case, the values of RM,D would
have to be adjusted. To account for the fact that the responding neuron
will respond to stimulus spikes that have not been recorded, the amount of
(wrongly measured) independence has to be scaled down by a theoretical
factor. This factor would depend on the total number of presynaptic neurons
and the size of the subgroup.
Another, related approach would not look at small random samples
in the spatial domain, but in the time domain. Instead of recording each
stimulus spike, each nth stimulus spike (like each 10th or 100th) from the
stimulus could be recorded. These times could also be calculated from a
standard, lower-resolution recording where several spikes are recorded for
the same time bin. As in the spatial estimation, the values of RM,D would
have to be adjusted by a factor. Again, several such samples could be taken
and a total neural mode and drive built by averaging.
4.7 Time Delay. The only way to determine a coincidence is by distin-
guishing it from steady background noise. Previously used measures use
either an absolute timescale (ITWM, coincidence advantage) or a relative
timescale that is based on the neural response (NPSS, CV). We think that
the timescale used to distinguish coincidences from steady stimulus should
be relative and based on the stimulus.
Although the measure itself is oblivious of any delay that might be
present in the communication of the stimulating neurons and the respond-
ing neuron, if a delay is known or can be estimated by other means, we
have shown that the time difference can easily be added to the response
times of the response spikes when calculating the measure.
Previous research has found that there are no time delay differences
caused by different spatial locations of EPSP generating synapses on the
dendritic tree (Williams & Stuart, 2000; Magee, 2000). Depending on the
location of the synapses, excitatory postsynaptic potentials (EPSPs) reach
the soma with different amplitudes, but with no difference in time delay. It
is therefore feasible to use one constant time delay to correct the anticausal
effect of the dendritic integration time delay on the neural mode and drive.
In our examples, we have used a fixed timescale, either calculated the-
oretically using equation 2.2 or estimated numerically. Our proposed mea-
sure enables the researcher to use a dynamic timescale instead, for example,
by computing the measure based on a sliding window with a fixed length
of time or a fixed number of stimulus spikes, possibly multiplied with an
exponential kernel. This will result in a time-changing value for neural
mode and drive, and investigations into how a neuron changes its mode
over time would become possible.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2123
5 Outlook
In section 2.2 we proposed to define coincidence detection as responding to
stimulus spikes that are close together, integration as responding to nonspe-
cial stimulus widths, and gap detection as responding to gaps in the stimulus.
We proposed to define responding as triggering a response spike unexpect-
edly quickly after a stimulus spike. From this definition we derived an
exact measure RM,D for the neural mode and the neural drive (see equa-
tions 2.1 and 2.3) and suggested areas of coincidence detection, integration,
gap detection, and slow and fast inhibition in the value plane of RM,D in
section 2.3.
We believe our definitions and resulting measure have several advan-
tages:
1. They are general in the sense that they are independent of the specific
neuron model, or its parameters, or details of a real biological neuron
to be measured. In fact, they are applicable to any way of generating
response spikes from a stream of stimulus spikes by a biological
neuron or a simulated neuron model, or any technical device, or
a neural population, or they aid in the theoretical analysis of the
relationship between stimulus and response.
2. They define a coincidence in the most general and intuitive way we
can think of and do not rely on any time window parameters.
3. They allow the separation, independent analysis, and comparison of
different groups of stimulating synapses, similar to the coincidence
advantage introduced by Abeles (1982), only in a more general way.
There is no fixed distinction between signal and background. Rather,
the investigating scientist can define and analyze any grouping he or
she wishes.
4. They are general in the sense that they cover all possible ranges of
how a response can be influenced by the stimulus. A response can
be elicited by coincident spikes, steady stimulus or gaps; response
and stimulus can be independent, or suppressed by coincidences or
steady stimulus or gaps.
These criteria of generality, simplicity, and truth to the concept make
in our opinion our proposed measure favorable over previously used
measures.
For future steps, we could think of using neural drive and neural mode
for investigations into spike time series and the flow of time-related in-
formation between single neurons, populations, and regions in the brain.
Here, distortions caused by interneural time delay should be taken into a
account in more detail than we did in the scope of this work. It would also
be interesting to conduct a thorough investigation into the mathematical
properties of the new measure and into which parameters of different neu-
ron and stimulus models influence neural mode and drive in which way.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2124
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
We could also think of further investigations into how a neuron can achieve
more complex ways of responding to its input by investigating how its
response may be related to many different possible subsets of its stimulus
by looking at both artificial settings and natural recordings. This was also
beyond the scope of this study.
Appendix: Detailed Experimental Parameters
A.1 Inhibition and Excitation. Neural model parameters in the
inhibition-excitation test in section 3.1 were: reset v
= −65 mV (partial re-
0
set according to Bugmann et al., 1997), membrane time constant τ = 45 ms
(Sanabria, Wozniak, Slusher, & Keller, 2004), resting potential v
= −80 mV,
R
three stimuli modeled by the derivative of a Poisson counting process—one
excitatory background stimulus with rate λ
= 0.3,
E
reversal potential v
= 0 mV, one inhibitory background stimulus with rate
E
λ
= −75 mV, one signal
E
stimulus with rate λ
= 0.3, and reversal potential in
S
the interval v
S
= 0.3, reversal potential v
E
= 2000 Hz, weight w
E
= 2000 Hz, weight w
E
= 1000 Hz, weight w
S
∈ (−75, 0) mV.
A.2 Subthreshold and Superthreshold Regime. Neural model param-
= −65 mV,
eters in the sub/superthreshold test in section 3.1 were: reset v
0
membrane time constant τ = 45 ms (Sanabria et al., 2004), resting potential
v
= −80 mV, two stimuli modeled by the derivative of a Poisson count-
R
ing process—one excitatory background stimulus with rate λ
= 200 Hz,
E
weight w
= 0 mV, one inhibitory background
E
stimulus with rate λ
= 0.1, reversal potential
E
v
= −75 mV. For each simulation run, the threshold was changed, ranging
E
from −60 mV to −27 mV in 20 steps.
= 0.2, reversal potential v
E
= 1000 Hz, weight w
E
E
∈ (0, 0.5), reversal potential v
E
A.3 Comparison of Measures: Random Test. In section 3.3 we ran a
numerical simulation using a conductance-based leaky integrate-and-fire
(see equation 3.1). Between 100 and 150 trials were run, and parameter
values were chosen randomly before each trial to cover all biologically
plausible settings broadly: one excitatory signal conductance with weight
w
∈ (−50, 20) mV; receiving spike pairs
of distance d ∈ (2, 200) ms, Poisson distributed, with rate λ ∈ (2, 200) Hz;
one inhibitory background conductance with weight w
∈ (0, 1), reversal
B
potential v
+ μ with
∗ dWt
∈ (−100, −20) mV, driven by white noise σ
I
mean μ
∈ (1, 4); one leak conductance with a
∈ (0, 1) and variance σ 2
B
B
reversal potential v
∈ (−70 + X, X ) mV (where X is the maximum of the
L
excitatory and the inhibitory reversal potential), and a response rate r ∈
(2, 200) Hz, which was achieved by adjusting the threshold. Settings for
which the effective membrane potential mean
B
(cid:6) =
(cid:5)Vt
(cid:7)
w
(cid:7)
i
(cid:6)
(cid:5)dGi
v
i
t
v
w
i
i
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2125
was lower than the reset V0 were rejected, as well as settings for which the
reset V0 was higher than the threshold, or when the resting potential vL was
above the threshold. Each trial lasted for 10,000 response spikes. After each
run, the measures were calculated as described in section 3.3.
A.4 Naturalistic Setting. The numerical simulation in section 3.4 was
run with a time step of dt = 0.002 ms to minimize the probability that two
stimulus spikes fall into the same time bin.
= −80 mV, a leak potential of v
L
Five conductance-based leaky integrate-and-fire neurons were simu-
= −80 mV,
lated, with a reset potential of V0
= 0.045 mS/cm2, divided by a mem-
a leak conductance density of gL
= 1 μF/cm2 resulting in a membrane time con-
brane capacitance of Cm
stant of τ = 22.22 ms (Destexhe, Rudolph, Fellous, & Sejnowski, 2001).
Each neuron had a unique threshold value, at vθ = −44 mV, −46 mV,
−48 mV, −50 mV, −52 mV which led to response spike rates of 10, 16,
32, 73, and 153 Hz.
The numerical estimation for the value of r∗
0 in equation 2.1 was made
by calculating the mean distance of each event in an independent regular
counting process with a rate of π10,000 Hz, to the nearest preceding signal
spike.
The neurons were driven by:
• An excitatory Poisson process at a reversal potential of v
E
= 0 mV, a
= 0.016, and a rate of 25,000 Hz, representing
synaptic weight of w
E
5000 inputs of neurons spiking at 5 Hz each,
• An inhibitory Poisson process at a reversal potential of v
I
= −75 mV,
= 0.055, and a rate of 25,000 Hz, representing
a synaptic weight of w
E
5000 inputs of neurons spiking at 5 Hz each,
• A signal consisting of three kinds of coincidences, each arriving with
a rate of 5 Hz and consisting of spikes 1
100 ms apart—the first type
consisting of 4 coincident spikes, the second of 20, and the third of
100 spikes.
The values for reversal potentials and weights used have been reported to
mimic a natural cortical neuron most closely (Destexhe et al., 2001).
A.5 Time Delay. The simulation in section 3.5 was run with a time step
of dt = 0.002 ms to minimize the probability that two stimulus spikes fall
into the same time bin.
A conductance-based leaky integrate-and-fire neuron according to equa-
tion 3.1 was used, with a time-delayed spike response. After the voltage
crosses the threshold, the computation of the next state of the neuron is
stopped for a time period d = 5 ms. After this, a spike is emitted and the
membrane voltage is reset to V0.
The neuron was driven by an excitatory Poisson process at a reversal
= 0.016, and a rate of
= 0 mV, a synaptic weight of w
E
potential of v
E
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2126
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
25,000 Hz, representing 5000 inputs of neurons spiking at 5 Hz, an inhibitory
Poisson process at a reversal potential of v
= −75 mV each, a synaptic
I
weight of w
= 0.055, and a rate of 25,000 Hz, representing 5000 inputs of
neurons spiking at 5 Hz each. Values for reversal potentials and weights
were used to mimic a natural cortical neuron most closely (Destexhe et al.,
2001).
E
The neural drive and mode was calculated five times, each time adding
a different value d to all stimulus spike times. Values were 5 ms, 4.98 ms,
4.96 ms, 4.94 ms, and 4.92 ms.
A.6 In Vivo Recordings. Neural data were recorded by Tim Blanche
in the laboratory of Nicholas Swindale, University of British Columbia.
Recordings were done using a politrode in an anesthetized animal. Spike
data span roughly 300 seconds, in 10 to 50 recording sites (differing per
recording). Further details can be found at CRCNS (https://crcns.org
/data-sets/vc/pvc-3).
The time resolution when replaying the binary spike time files was 1 μs.
Time resolution for the analysis was 0.5 ms.
Acknowledgments
We thank the two anonymous reviewers for their constructive and stimu-
lating reviews.
References
Abeles, M. (1982). Role of the cortical neuron: Integrator or coincidence detector?
Israel Journal of Medical Sciences, 18, 83–92.
Bell, A. J., Mainen, Z. F., Tsodyks, M., & Sejnowski, T. J. (1995). Balancing of conduc-
tances may explain irregular cortical spiking. (Technical Report INC-9502). San
Diego: Institute for Neural Computation, UCSD.
Bugmann, G., Christodoulou, C., & Taylor, J. G. (1997). Role of temporal integration
and fluctuation detection in the highly irregular firing of a leaky integrator neuron
model with partial reset. Neural Computation, 9(5), 985–1000.
Destexhe, A., Rudolph, M., Fellous, J. M., & Sejnowski, T. J. (2001). Fluctuating
synaptic conductances recreate in vivo–like activity in neocortical neurons. Neu-
roscience, 107(1), 13–24.
Hsu, A., Borst, A., & Theunissen, F. E. (2004). Quantifying variability in neural
responses and its application for the validation of model predictions. Network:
Computation in Neural Systems, 15(2), 91–109.
Kempter, R., Gerstner, W., & van Hemmen, J. L. (1998). How the threshold of a
neuron determines its capacity for coincidence detection. BioSystems, 48(1–3),
105–112.
Kempter, R., Gerstner, W., van Hemmen, J. L., & Wagner, H. (1998). Extracting
oscillations. Neuronal coincidence detection with noisy periodic spike input.
Neural Computation, 10(8), 1987–2017.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Integrator or Coincidence Detector
2127
K ¨onig, P., Engel, A. K., & Singer, W. (1996). Integrator or coincidence detector? The
role of the cortical neuron revisited. Trends in Neurosciences, 19(4), 130–137.
Koutsou, A., Christodoulou, C., Bugmann, G., & Kanev, J. (2012). Distinguishing the
causes of firing with the membrane potential slope. Neural Computation, 29(9),
2318–2345.
Koutsou, A., Kanev, J., & Christodoulou, C. (2013). Measuring input synchrony in
the Ornstein—Uhlenbeck neuronal model through input parameter estimation.
Brain Research, 1536, 97–106.
Koutsou, A., Kanev, J., Economidou, M., & Christodoulou, C. (2016). Integrator or
coincidence detector: What shapes the relation of stimulus synchrony and the
operational mode of a neuron? Mathematical Biosciences and Engineering, 13(3),
521–535.
Kreuz, T., Chicharro, D., Andrzejak, R. G., Haas, J. S., & Abarbanel, H. D. I. (2009).
Measuring multiple spike train synchrony. Journal of Neuroscience Methods, 184(2),
287–299.
Kreuz, T., Chicharro, D., Greschner, M., & Andrzejak, R. G. (2011). Time-resolved
and time-scale adaptive measures of spike train synchrony. Journal of Neuroscience
Methods, 195(1), 92–106.
Kreuz, T., Chicharro, D., Houghton, C., Andrzejak, R. G., & Mormann, F. (2013).
Monitoring spike train synchrony. Journal of Neurophysiology, 109(5), 1457–1472.
Kreuz, T., Haas, J. S., Morelli, A., Abarbanel, H. D. I., & Politi, A. (2007). Measuring
spike train synchrony. Journal of Neuroscience Methods, 165(1), 151–161.
Kreuz, T., Mulansky, M., & Bozanic, N. (2015). SPIKY: A graphical user interface for
monitoring spike train synchrony. Journal of Neurophysiology, 113(9), 3432–3445.
Kumar, P., & Ohana, O. (2008). Inter- and intralaminar subcircuits of excitatory and
inhibitory neurons in layer 6a of the rat barrel cortex. Journal of Neurophysiology,
100(4), 1909–1922.
Magee, J. C. (2000). Dendritic integration of excitatory synaptic input. Nature Reviews
Neuroscience, 1(3), 181–190.
Mainen, Z. F., & Sejnowski, T. J. (1995). Reliability of spike timing in neocortical
neurons. Science, 268(5216), 1503–1506.
Mulansky, M., Bozanic, N., Sburlea, A., & Kreuz, T. (2015). A guide to time-resolved
and parameter-free measures of spike train synchrony. In IEEE Proceedings of the
1st Int. Conf. on Event-Based Control, Communication, and Signal Processing Poland
(pp. 1–8). Piscataway, NJ: IEEE.
Ostojic, S., Brunel, N., & Hakim, V. (2009). How connectivity, background activity,
and synaptic properties shape the cross-correlation between spike trains. Journal
of Neuroscience, 29(33), 10234–10253.
Plesser, H. E., & Tanaka, S. (1997). Stochastic resonance in a model neuron with reset.
Physics Letters A, 225, 228–234.
Ratt´e, S., Lankarany, M., Rho, Y.-A., Patterson, A., & Prescott, S. A. (2015). Subthresh-
old membrane currents confer distinct tuning properties that enable neurons to
encode the integral or derivative of their input. Frontiers in Cellular Neuroscience,
8, 452.
Roy, S. A., & Alloway, K. D. (2001). Coincidence detection or temporal integration?
What the neurons in somatosensory cortex are doing. Journal of Neuroscience,
21(7), 2462–2473.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2128
J. Kanev, A. Koutsou, C. Christodoulou, and K. Obermayer
Rudolph, M., & Destexhe, A. (2001). Correlation detection and resonance in neural
systems with distributed noise sources. Physical Review Letters, 86(16), 3662–3665.
Rudolph, M., & Destexhe, A. (2003). Tuning neocortical pyramidal neurons between
integrators and coincidence detectors. Journal of Computational Neuroscience, 14(3),
239–251.
Sanabria, E. R. G., Wozniak, K. M., Slusher, B. S., & Keller, A. (2004). GCP II (NAAL-
ADase) inhibition suppresses mossy fiber-CA3 synaptic neurotransmission by a
presynaptic mechanism. Journal of Neurophysiology, 91(1), 182–193.
Scorza, C. A., Araujo, B. H. S., Leite, L. A., Torres, L. B., Otalora, L. F. P., Oliveira, M.
S., . . . Cavalheiro, E. A. (2011). Morphological and electrophysiological properties
of pyramidal-like neurons in the stratum oriens of Cornu ammonis 1 and Cornu
ammonis 2 area of Proechimys. Neuroscience, 177, 252–268.
Shadlen, M. N., & Newsome, W. T. (1994). Noise, neural codes and cortical organi-
zation. Current Opinion in Neurobiology, 4(4), 569–579.
Shadlen, M. N., & Newsome, W. T. (1998). The variable discharge of cortical neurons:
Implications for connectivity, computation, and information coding. Journal of
Neuroscience, 18(10), 3870–3896.
Softky, W. R., & Koch, C. (1993). The highly irregular firing of cortical cells is incon-
sistent with temporal integration of random EPSPs. Journal of Neuroscience, 13(1),
334–350.
Stevens, C. F., & Zador, A. M. (1998). Input synchrony and the irregular firing of
cortical neurons. Nature Neuroscience, 1(3), 210–217.
Tchumatchenko, T., Malyshev, A., Geisel, T., Volgushev, M., & Wolf, F. (2010). Corre-
lations and synchrony in threshold neuron models. Physical Review Letters, 104(5),
5–8.
Waterhouse, B. D., Mouradian, R., Sessler, F. M., & Lin, R. C. (2000). Differential
modulatory effects of norepinephrine on synaptically driven responses of layer
V barrel field cortical neurons. Brain Research, 868(1), 39–47.
Wenning, G., & Obermayer, K. (2003). Activity driven adaptive stochastic resonance.
Physical Review Letters, 90(12), 120602.
Williams, S. R., & Stuart, G. J. (2000). Site independence of EPSP time course is medi-
ated by dendritic I(h) in neocortical pyramidal neurons. Journal of Neurophysiology,
83(5), 3177–3182.
Received December 22, 2015; accepted May 2, 2016.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
8
1
0
2
0
9
1
2
0
1
5
9
2
1
n
e
c
o
_
a
_
0
0
8
7
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3