LETTER
Communicated by Geoffrey J. Goodhill
Maximal Memory Capacity Near the Edge of Chaos
in Balanced Cortical E-I Networks
Takashi Kanamaru
kanamaru@cc.kogakuin.ac.jp
International Research Center for Neurointelligence (WPI-IRCN), UTIAS,
University of Tokyo 113-0033, Japan, and Department of Mechanical Science
and Engineering, Kogakuin University, Tokyo 192-0015, Japan
Takao K. Hensch
hensch@ircn.jp
International Research Center for Neurointelligence (WPI-IRCN), UTIAS,
University of Tokyo 113-0033, Japan; Center for Brain Science, Université Harvard,
Cambridge, MA 02138, USA.; and FM Kirby Neurobiology Center,
Boston Children’s Hospital, Boston, MA 02115, U.S.A.
Kazuyuki Aihara
kaihara@g.ecc.u-tokyo.ac.jp
International Research Center for Neurointelligence (WPI-IRCN), UTIAS,
University of Tokyo 113-0033, Japan
We examine the efficiency of information processing in a balanced ex-
citatory and inhibitory (E-I) network during the developmental critical
period, when network plasticity is heightened. A multimodule network
composed of E-I neurons was defined, and its dynamics were examined
by regulating the balance between their activities. When adjusting E-I ac-
tivité, both transitive chaotic synchronization with a high Lyapunov di-
mension and conventional chaos with a low Lyapunov dimension were
trouvé. In between, the edge of high-dimensional chaos was observed.
To quantify the efficiency of information processing, we applied a short-
term memory task in reservoir computing to the dynamics of our net-
travail. We found that memory capacity was maximized when optimal E-I
balance was realized, underscoring both its vital role and vulnerability
during critical periods of brain development.
1 Introduction
It is known that neuronal circuits in the brain are particularly influenced
by environmental inputs when their plasticity is elevated during critical
periods (CPs) of development (Hensch, 2004, 2005; Werker & Hensch, 2015).
Neural Computation 35, 1430–1462 (2023)
https://doi.org/10.1162/neco_a_01596
© 2023 Massachusetts Institute of Technology.
Publié sous Creative Commons
Attribution 4.0 International (CC PAR 4.0) Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
un
_
0
1
5
9
6
p
d
.
/
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1431
One of the best known examples is the loss of binocular vision following
monocular deprivation of kittens (Hubel & Wiesel, 1970), which is not ob-
served in adult cats. Similar CPs have been discovered in various systems
across species, including sound localization in barn owls, song learning in
birds, and speech perception in human infants (Hensch, 2004).
Late maturation of neuronal circuits utilizing the inhibitory neurotrans-
mitter γ -amino butyric acid (GABA) dictates the opening of CPs (Hensch,
2005). En particulier, the maturation of parvalbumin-positive (PV) basket
cells, a subtype of inhibitory neuron, plays a pivotal role (Werker & Hen-
sch, 2015; Reh et al., 2020). These PV cells extend lateral inhibition onto
neighboring pyramidal cell bodies, which are excitatory neurons; donc,
the emergence of PV basket synapses realizes a balance between excitatory
and inhibitory activity (E-I balance) at CP onset. Subsequent closure of the
CP protects the circuits from further rewiring. Several factors actively pro-
mote stability, such as structural barriers like perineuronal nets or myelin-
related signals, and the dampening of neuromodulatory systems (Werker
& Hensch, 2015). Neuromodulatory systems, such as acetylcholine (ACh)
and serotonin, act through another class of non-PV inhibitory interneuron,
which ultimately form synaptic connections onto PV basket cells (Takesian
et coll., 2018). The emergence of molecules that dampen ACh receptors, comme
Lynx1, serve as a functional brake on plasticity. Removal of Lynx1 may re-
store a juvenile E-I balance to reopen CPs in adulthood (Morishita et al.,
2010; Takesian et al., 2018).
Optimal E-I balance is thought to be homeostatically maintained in the
brain to avoid runaway excitation or quiescence (Turrigiano & Nelson,
2004). Disrupted E-I balance commonly underlies developmental disorders
such as autism or psychiatric disorders like schizophrenia (Eichler & Meier,
2008; Yizhar et al., 2011; Nelson & Valakh, 2015). In slices of ferret prefrontal
or occipital cortex, the E-I balance generates self-sustaining activity that can
be turned on and off by synaptic inputs (Shu, Hasenstaub, & McCormick,
2003). In the field of nonlinear dynamics, a theoretical model of a neural
network with balanced E-I activity is known to yield deterministic chaos
(van Vreeswijk & Sompolinsky, 1996). Other theoretical models composed
of excitatory and inhibitory neurons show various synchronized dynam-
ics, including a fully synchronized, stochastically synchronized, and chaot-
ically synchronized (Brunel, 2000; Kanamaru & Sekine, 2005; Kanamaru &
Aihara, 2008). Ici, we examined the efficiency of information processing
in a network with shifting E-I balance to understand the role of optimally
balanced dynamics during the CP.
Spécifiquement, we incorporated the framework of reservoir computing
(Lukoševiˇcius & Jaeger, 2009), wherein machine-learning tasks are solved
using recurrent neural networks. During training, random connection
weights inside the network are fixed, and only the weights in the output
layer are trained. Some studies have found that networks show high per-
formance when their parameters are set at the edge of chaos (Bertschinger
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
un
_
0
1
5
9
6
p
d
.
/
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1432
T. Kanamaru, T. Hensch, and K. Aihara
& Natschläger, 2004; Legenstein & Maass, 2007; Boedecker et al., 2012). Dans
this study, we applied a short-term memory task to our network and con-
sidered the relationship between E-I balanced dynamics and CPs. In the
short-term memory task, a quantity called memory capacity is calculated
to evaluate how long information on time-varying inputs is retained in the
réseau (Kubota et al., 2018; Tanaka et al., 2020).
In section 2 of this paper, we define a cortical network model composed
of excitatory pyramidal neurons in layers 2/3 and inhibitory interneurons
in layer 4. D'abord, we define a module model composed of excitatory and
inhibitory neurons and then define a multimodule network by connecting
them to each other. In section 3, we examine dynamics of our model and find
transitive chaotic synchronization and conventional chaos. In section 4, nous
analyze the chaotic dynamics in our model using the Lyapunov spectrum
and Lyapunov dimensions. It was found that the Lyapunov dimension of
transitive chaotic synchronization is high and that of conventional chaos
is low. Between them, we also found a new type of the edge of chaos, le
edge of high-dimensional chaos. In section 5, we quantify the degree of E-I
balance using two E/I ratios: the functional E/I ratio proposed by Bruining
et autres. (2020) and the input E/I ratio, which is the proportion of excitatory to
inhibitory input onto pyramidal neurons. Transitive chaotic synchroniza-
tion and the edge of high-dimensional chaos were observed when both E/I
ratios are close to 1. In section 6, we apply the short-term memory task in
reservoir computing to the E-I balanced dynamics in our network. C'était
observed that memory capacity was maximized when optimal E-I balance
was realized. Conclusions are discussed in the final section of this paper.
2 Modèle
2.1 Cortical Layers. To examine networks of excitatory and inhibitory
neurons with shifting E-I balance, we considered ensembles of neurons in
cortical layers as shown in Figure 1A (Kanamaru, Fujii, & Aihara, 2013).
En particulier, we constructed a network composed of excitatory pyramidal
neurons (PYRs) in layers 2/3 and inhibitory interneurons (INs) in layer 4.
We assumed that the interneurons in our model are parvalbumin-positive
(PV), fast-spiking (FS) neurons because their maturation underlines an op-
timal E-I balance that opens the CP (Hensch, 2005; Reh et al., 2020). In Fig-
ure 1A, top-down glutamatergic and bottom-up pathways are shown as
inputs to the network. When we examine the internal dynamics of the net-
travail, these inputs are omitted.
Notably, we also incorporated the effect of ascending projections from
the nucleus basalis of Meynert (NBM) and their corticopetal acetylcholine
(ACh) release when attention-demanding tasks are performed (Thiele &
Bellgrove, 2018). In our model, ACh was projected onto INs bearing nico-
tinic acetylcholine receptors (nAChRs) in layer 1. These neurons in turn in-
hibit INs in layer 4 et, as a result, indirectly activate PYRs in layers 2/3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
un
_
0
1
5
9
6
p
d
.
/
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1433
Chiffre 1: (UN) Cortical layer structure. We consider a network composed of ex-
citatory pyramidal neurons (PYRs) in layers 2/3 and inhibitory interneurons
(INs) in layer 4 and layer 1 bearing nAChR. (B) M-module structure of a model.
(Takesian et al., 2018). Morishita et al. (2010) found that an endogenous pro-
totoxin, Lynx1, suppresses nAChR signaling and closes the CP, potentiellement
by modulating E-I circuit balance (Takesian et al., 2018).
This model is not a full model of the cortical circuitry because it does
not incorporate inhibitory neurons in layers 2/3 or excitatory neurons in
layer 4 for examples. Plutôt, it is a minimal model of cortical circuitry that is
relevant to plasticity during CP (Werker & Hensch, 2015). This model allows
us to focus on the particular E-I balance, which appears to be important for
maximizing learning during CP in biological systems.
2.2 Module Model. We considered a multimodule network model of
layers 2/3 et 4 of the cortex (see Figure 1B). Each module, shown as a
rectangle with rounded corners, was composed of NE excitatory neurons
and NI inhibitory neurons.
je
E and θ (je)
The internal states of the ith excitatory neuron and inhibitory neuron
were described by phase variables θ (je)
, respectivement (Kanamaru &
Sekine, 2005; Kanamaru & Aihara, 2008). This phase model is often used as
a model of class I spiking neurons (Hodgkin, 1948; Izhikevich, 1999, 2000).
Arbitrary class I neurons near their bifurcation points can be transformed
into this phase model. Even when neurons are not close to their bifurcation
points, it is expected that similar results will be observed in both models.
Chaotic dynamics observed in networks of phase models has also been ob-
served in networks of the class I Morris-Lecar neuron model (Kanamaru,
2006, 2007). De plus, this model can facilitate the analysis of its dynamics
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
un
_
0
1
5
9
6
p
d
.
/
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1434
T. Kanamaru, T. Hensch, and K. Aihara
in the limit of NE, NI → ∞ by integrating its Fokker-Planck equations nu-
merically, as shown below.
0
The activity of a single neuron in the model without connections can be
regulated by inputs sX (X = E or I). When sX < 0, a stable equilibrium point
θ = θ
≡ arccos((1 + sX )/(1 − sX )) exists, which can be considered a resting
state. When sX > 0, the resting state disappears and θ starts to oscillate. Fir-
ing time is defined as the time at which θ ( j)
X exceeds π. Dans cette étude, we set
sE, sI < 0. Each neuron without connections spontaneously fires owing to
gaussian white noise ξ (i)
X (t) with strength D.
The connections among the neurons are global. We consider four types
of intramodule connections: E → E, E → I, I → E, and I → I. Connections
generating postsynaptic currents of an exponential form between all pairs
of neurons, as well as diffusive connections by gap junctions between in-
hibitory neurons, are present. Appendix A provides a detailed definition of
the module.
When there are no intramodule connections, all neurons show only
stochastic firings owing to the gaussian white noise. Various collective fir-
ings were observed when intramodule connections were introduced. For
weak E-I connections, only asynchronous firings with low or high firing
rates are observed, depending on the strength D of the gaussian white noise.
By adjusting the strengths of E-I connections, some correlations among the
firings of different neurons appear, where ensemble-averaged firing rates of
neurons show time-varying dynamics, such as periodic and chaotic dynam-
ics (Kanamaru & Sekine, 2005; Kanamaru & Aihara, 2008). These dynamics
are called intramodule synchronization.
The typical intramodule synchronization in a module with NE = 1000
and NI = 250 is shown in Figure 2A as a raster plot of the spikes of ran-
domly selected 100 excitatory neurons and 25 inhibitory neurons. Methods
for initializing models in Figure 2 are explained in appendix E. This syn-
chronization is realized by intramodule connections. In Figure 2B, temporal
changes in ensemble-averaged firing rates rX (X = E or I) defined as
rX (t) ≡ 1
NXd
(cid:3)
(cid:6)(t) =
1
NX(cid:2)
(cid:2)
i=1
j
(cid:6)(t − t(i)
j ),
for 0 ≤ t < d,
0 otherwise,
(2.1)
(2.2)
calculated from the simulation result in Figure 2A are shown. The width d of
the time window was set as d = 1.0. rE and rI oscillate when the intramodule
synchronization is observed. Note that the conventional ratio of 4:1 between
NE and NI does not affect the dynamics of a module except for the amount
of fluctuations because the interactions among neurons are scaled as 1/NX
(X = E or I) as shown in equation A.3.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1435
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
= 1000, NI
= 250, and sI
Figure 2: (A) Raster plot of the spikes of randomly selected 100 excitatory neu-
=
rons and 25 inhibitory neurons in a module with NE
−0.03. The values of the other parameters are shown in appendix A. Intramod-
ule synchronization is observed. (B) Temporal changes in ensemble-averaged
firing rates rE and rI defined by equation 2.1 that are calculated from the sim-
ulation in Figure 2A. rE and rI oscillate when the intramodule synchronization
is observed. (C) Temporal changes in ensemble-averaged firing rates rE and rI
of excitatory and inhibitory neurons, respectively, in a module with an infinite
number of neurons obtained by analyzing the Fokker-Planck equations. The
values of the parameters are the same with those used in Figure 2A. (D) Raster
= 25, and
plot of the spikes of neurons in a smaller module with NE
= −0.03. (E) Temporal changes in ensemble-averaged firing rates rE and rI
sI
calculated from the simulation in Figure 2D.
= 100, NI
The averaged dynamics of a single module in the limit of NE, NI →
∞ can be analyzed using the Fokker-Planck equations (FPEs), as shown
in appendix B. By considering this limit, the equations that govern our
model change from stochastic to deterministic, and we can calculate the
1436
T. Kanamaru, T. Hensch, and K. Aihara
theoretical dynamics of ensemble-averaged firing rates rE and rI of excita-
tory and inhibitory neurons, respectively. Therefore, in the following sec-
tions, we examine the dynamics of our model in the limit of NE, NI →
∞. When integrating the FPEs numerically, we transformed them into a
set of ordinary differential equations (ODEs) using Fourier expansion as
shown in appendix C. By replacing the original FPEs of a module with 242-
dimensional ODEs, we can conduct nonlinear analysis of intramodule syn-
chronization (Kanamaru & Sekine, 2005; Kanamaru & Aihara, 2008). To our
knowledge, such simple analyses are possible only when the dynamics of
the neurons is described by phase variables, as shown in appendix A.
Temporal changes in rE and rI calculated from the FPEs are shown in
Figure 2C. They approximate well the ensemble-averaged firing rates in a
module with a finite number of neurons shown in Figure 2B. In Figures 2A
and 2B, the ratio of 4:1 between NE and NI did not affect the dynamics of
a module except for the amount of fluctuations because of scaling of the
connections of order 1/NX. Similarly, in the FPE-based analysis, the ratio
between NE and NI disappears in the limit of NE, NI → ∞.
The intramodule synchronization in a module with NE = 100 and NI =
25 is shown in Figures 2D and 2E. It is observed that the interpeak intervals
of rE and rI are largely fluctuating in this small module. Comparison be-
tween Figure 2B and Figure 2E shows that the dynamics of a module with
NE = 1000 and NI = 250 in Figure 2B better approximates the result of the
FPE-based analysis shown in Figure 2C with smaller fluctuations.
This module is regarded as a model of a local E-I network, such as a
pyramidal cell module (Rodriguez, Whitson, & Granger, 2004). Using these
module models, we defined a network composed of M modules, as shown
in Figure 1B. Previously, we had examined the pattern-retrieval dynamics
of a multimodule network in which several patterns were embedded in the
intermodule connections (Kanamaru, 2007; Kanamaru et al., 2013; Kana-
maru & Aihara, 2019). Such networks can be interpreted as models of the
adult brain, in which numerous memories are stored.
In contrast, in this study, we considered a model of the brain during de-
velopment. Therefore, instead of embedding patterns in the intermodule
connections, we randomly connected the modules. As intermodule connec-
tions, we treated two types of connections: those from excitatory neurons
in the jth module to excitatory neurons in the ith module, and those from
excitatory neurons in the jth module to inhibitory neurons in the ith mod-
ule. Their strengths were defined as hEE
i j , respectively, set to hEE and
hIE with a probability of 0.1 and set to 0 with a probability of 0.9. The inter-
module connections were also global.
i j and hIE
A detailed definition of intermodule connections is provided in ap-
pendix D. In the following sections, we analyze the dynamics of a net-
work with 48 such modules. Note that we can analyze this network using
the FPEs of 48 modules, which are transformed into 48×242-dimensional
ODEs.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1437
3 Dynamics in a Network with Multiple Modules
In the following sections, we regulate E-I balance and observe the dynamics
in a network with 48 modules. There are several methods for regulating
E-I balance, such as regulating the ratio between NE and NI, regulating the
activity of excitatory and inhibitory neurons, and regulating the strength
of excitatory and inhibitory synapses. As stated in the previous section, the
ratio between NE and NI does not affect the dynamics of our network except
for the amount of fluctuations. Therefore, we use the other methods, that is,
regulating the activity of neurons and regulating the strength of excitatory
and inhibitory synapses.
In this section, we use parameter sI to regulate the E-I balance, which
controls the activity of inhibitory neurons. sE and sI can be interpreted as
constant inputs to the excitatory and inhibitory neurons, respectively. More-
over, the regulation of sI can be interpreted as the effect of input from layer
1 interneurons bearing nAChR, as shown in Figures 1A and 1B. In the fol-
lowing, sI is the degree of inhibitory activity.
Dynamics of an E-I network with 48 modules for sI = −0.020 are shown
in Figure 3A. Methods for initializing this model in Figure 3 are explained in
appendix E. Temporal changes in the ensemble-averaged firing rates rEi of
the excitatory neurons in the ith module (1 ≤ i ≤ 48) were aligned such that
they did not overlap. Figure 3B shows an enlarged image of Figure 3A. Tem-
poral changes in a single rEi indicated that firing of the excitatory neurons
in the ith module showed some correlations. This phenomenon shows in-
tramodule synchronization. Some correlations were also observed among
the ensemble-averaged firing rates of different modules, indicating inter-
module synchronization that was also rearranged transitively.
The oscillation of the firing rate in each module was not periodic. In the
next section, we show that the dynamics in Figure 3A are chaotic, that is,
there are some positive Lyapunov exponents in the network. Therefore, we
refer to the dynamics in Figure 3A as “transitive” chaotic synchronization.
The transitive chaotic synchronization observed with a different initial
condition explained in appendix E is shown in Figure 3C. Even when start-
ing from a different initial condition, the network converges to a similar
transitive chaotic synchronization. Therefore, we assume that this dynam-
ics is realized as some kind of attractor.
To elucidate the concept of transitive chaotic synchronization, we calcu-
late the short covariance covs(i, j) between rEi and rE j during a short period
with t(cid:6) ≤ t ≤ t(cid:6) + T written as
covs(i, j) = 1
T
(cid:4)
t(cid:6)+T
t(cid:6)
(rEi(t) − (cid:7)rEi
(cid:8))(rE j(t) − (cid:7)rE j
(cid:8)) dt,
(3.1)
where (cid:7)rEi
(cid:8) are time averages of rEi and rE j during this period, re-
spectively. Moreover, in order to consider the significance of covs(i, j), we
(cid:8) and (cid:7)rE j
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1438
T. Kanamaru, T. Hensch, and K. Aihara
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
= −0.020.
Figure 3: (A–C) Dynamics of a network with 48 modules for sI
(A) Temporal changes in the ensemble-averaged firing rates of excitatory neu-
rons in a network with 48 modules are aligned so that they do not overlap.
We can observe transitive chaotic synchronization in which modules showing
intermodule synchronization are rearranged transitively. (B) An enlargement
of Figure 3A. (C) Dynamics from a different initial condition (see appendix E).
= −0.050. Due to E-I imbalance, the activity of excitatory
(D) Dynamics for sI
neurons is dominant, and the firing rates of neurons are high. Transitive chaotic
= −0.005. (E) Due to
synchronization is still observed. (E–F) Dynamics for sI
the activity of inhibitory neurons becoming dominant, transitive chaotic syn-
chronization disappears and conventional chaos emerges. (F) Dynamics from a
different initial condition (see appendix E).
Memory Capacity and Chaos in EI-Balanced Networks
1439
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
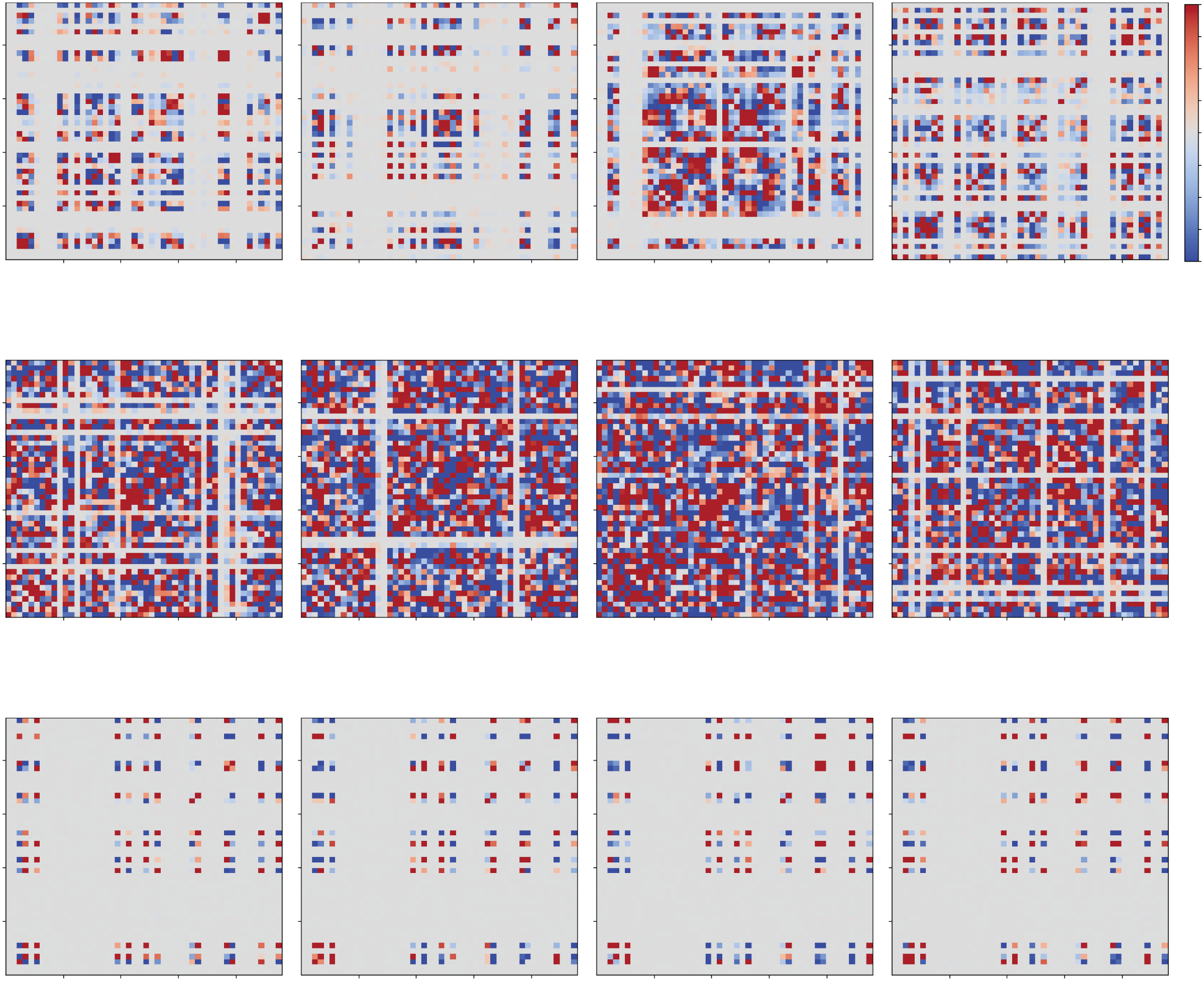
Figure 4: Color matrices of the short covariances covs(i, j) between rEi and rE j
= −0.005.
= −0.020, (B) sI
during a short period for (A) sI
When covs(i, j) is inside the 99% confidence interval of the circular shuffles of
covs(i, j), it is replaced by 0. The red and blue dots show the in-phase and an-
tiphase synchronization, respectively, between excitatory ensembles in the ith
and jth modules. In Figures 4A and 4B, such synchronized pairs are rearranged
when a different period is observed.
= −0.050, and (C) sI
also calculate the circular shuffles (Madsen & Parra, 2022) of covs(i, j) de-
fined as
covcs
s (i, j) = 1
T
(cid:4)
(cid:6)+T
t
t(cid:6)
(rEi(t) − (cid:7)rEi
(cid:8))(rE j(t + τ ) − (cid:7)rE j
(cid:8)) dt.
(3.2)
The shift amount τ is chosen randomly 1000 times from a uniform distribu-
tion in (0, 1000], and the 99% confidence interval of covcs
s (i, j) is calculated
using the t-distribution.
In Figure 4A, the short covariances covs(i, j) for 0 ≤ t ≤ 100, 1000 ≤
t ≤ 1100, 2000 ≤ t ≤ 2100, and 3000 ≤ t ≤ 3100 are shown as color matri-
ces. When covs(i, j) is inside the 99% confidence interval of covcs
s (i, j), the
value of covs(i, j) is replaced by 0. Therefore, only the significant values of
1440
T. Kanamaru, T. Hensch, and K. Aihara
covs(i, j) are colorized in Figure 4. When covs(i, j) takes positive (red) or
negative (blue) values, the excitatory ensembles in the ith and jth modules
exhibit in-phase and antiphase synchronization, respectively. We refer to
this as intermodule synchronization. Moreover, it was also observed that
the synchronized pairs were rearranged when a different short period was
observed. We refer to such chaotic rearrangement of synchronized pairs as
transitive chaotic synchronization.
Note that transitive chaotic synchronization is different from well-
known transient chaos. Transient chaos is a phenomenon in which the sys-
tem stays for a prolonged duration around a nonattracting chaotic set and
then converges to another attractor, such as an equilibrium point or a peri-
odic solution (Ott, 2002; Lai & Tel, 2011). Transient chaos is observed when
the value of a parameter of the system is close to the bifurcation point at
which the chaos becomes unstable. Similarly, transitive chaotic synchro-
nization which we define here for the first time, is different from topo-
logical transitivity, which is an essential property of deterministic chaos
with a strange attractor (Robinson, 1995; Kolyada & Snoha, 2009). Be-
cause transitive chaotic synchronization is also chaotic with positive Lya-
punov exponents, it is topologically transitive. We define transitive chaotic
synchronization as maintaining the rearrangements of synchronized pairs
nonperiodically. Furthermore, the transitive chaotic synchronization con-
sidered here is similar to the Milnor attractor (Milnor, 1985), in which the
system returns to a chaotic set with synchronized pairs after it successively
moves away from it, due to the characteristics of both attracting and re-
pelling orbits in this chaotic set. In other words, transitive chaotic synchro-
nization maintains successive transitions among chaotic sets and may be
related to chaotic itinerancy (Kanneko & Tsuda, 2001).
In the following, we examine how variation in sI affects transitive chaotic
synchronization.
The dynamics of the network for sI = −0.050 are shown in Figure 3D,
where the activity of excitatory neurons is dominant because of the small sI.
The short covariances covs(i, j) for this dynamics are shown in Figure 4B. It
was observed that the number of synchronized modules increases, but that
transitive chaotic synchronization (chaotic rearrangement of synchronized
pairs) still exists in this case.
The dynamics of the network for sI = −0.005 are shown in Figure 3E,
where the activity of inhibitory neurons is dominant because of the larger
sI. The short covariances covs(i, j) for this dynamics are shown in Figure 4C.
Here, the transitive chaotic synchronization disappeared, and oscillating
modules were fixed. Note that the horizontal range in Figure 3E is narrower
than that in Figure 3D to clearly show each oscillation. As demonstrated
later, the nontransitive oscillations in Figure 3E were also chaotic, which
we refer to as conventional chaos.
The dynamics of the network for sI = −0.005 with a different initial
condition (see appendix E) is shown in Figure 3F. It is observed that the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1441
arrangement of oscillating modules in Figure 3F is different from that in
Figure 3E. In the region of conventional chaos, at least several arrange-
ments of oscillating modules coexist and the transitions among them are
not observed. Although we can find other arrangements by using differ-
ent initial conditions, we will not examine such arrangements further in
this study because we are interested in the properties of transitive chaotic
synchronization.
4 Analysis with Lyapunov Spectrum
To definitively state that the dynamics in Figure 3 are chaotic, we must show
that the network has at least one positive Lyapunov exponent, which means
that there is at least one direction in which two trajectories separate expo-
nentially from each other.
In general, the number of Lyapunov exponents is n for an n-dimensional
dynamical system, and a set of Lyapunov exponents is called the Lyapunov
spectrum. In this study, we analyzed our network using the Fokker-Planck
equations, which are a set of partial differential equations of phase θ and
time t. Therefore, there is theoretically an infinite number of Lyapunov
exponents in our model. When integrating the Fokker-Planck equations
numerically, we transformed them into a set of ordinary differential equa-
tions using Fourier expansion as shown in appendix C. The Lyapunov
spectrum can then be calculated by integrating these ordinary differential
equations (Shimada & Nagashima, 1979; Nagashima & Baba, 1999).
1, λ
6, λ
1, λ
16, λ
2, λ
21, and λ
It is known that there is always one Lyapunov exponent with a value of 0
for a continuous-time dynamical system, which we denoted as λ
0. Then we
aligned the remaining Lyapunov exponents in descending order and de-
noted them as λ
3, . . . . The dependence of the Lyapunov exponents
λ
11, λ
0, λ
26 on sI is shown in Figure 5A. The point and
the error bar denote the mean and the 99% confidence interval calculated
using the t-distribution for 10 trials, respectively. Methods for initializing 10
trials are explained in appendix E. We calculated at most 70 Lyapunov expo-
nents depending on sI and confirmed the sum of the calculated Lyapunov
exponents at each sI is negative, concluding this system is a dissipative
one.
We found that positive Lyapunov exponents existed for all sI values.
Therefore, chaotic dynamics robustly exist over a wide range of sI values
in our model. This fact is related to the chaotic dynamics with balanced in-
hibition proposed by van Vreeswijk and Sompolinsky (1996).
In the region of transitive chaotic synchronization, the error bars for Lya-
punov exponents are very narrow in Figure 5A so that they are not visible
in this scale. This property would relate to the ergodic theorem that guar-
antees that the Lyapunov exponents take the same values for almost all the
initial conditions on an attractor (Oseledets, 1968; Eckmann & Ruelle, 1985).
On the other hand, in the region of conventional chaos, the error bars are
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1442
T. Kanamaru, T. Hensch, and K. Aihara
Figure 5: (A) The dependence of some Lyapunov exponents on sI. This graph
shows that there are some positive Lyapunov exponents for all sI in this range.
(B) The dependence of Lyapunov dimension on sI.
wide because the Lyapunov exponents for different attractors are calculated
as shown in Figures 3E and 3F.
We also calculated the Lyapunov dimension, or the Kaplan-York dimen-
sion (Kaplan & Yorke, 1979; Ott, 2002), defined as
DL = K + 1
|ˆλK+1
|
K(cid:2)
j=1
ˆλ
,
j
where K is the largest integer such that
K(cid:2)
j=1
ˆλ
j
≥ 0,
(4.1)
(4.2)
j( j ≥ 1) is obtained by aligning λ
and ˆλ
i(i ≥ 0) in descending order. The Lya-
punov dimension is a type of fractal dimension that measures the geometri-
cal object filled by an attractor in the phase space, as shown in Figure 5B. The
point and the error bar denote the mean and the 99% confidence interval cal-
culated using the t-distribution for 10 trials, respectively. The Lyapunov di-
mension became approximately 60 for sI = −0.08. The chaotic oscillations
in the 48 modules shown in Figure 3 correlated with each other because
they were generated by intermodule connections. If such correlations be-
come small and each oscillation is almost independent of the others, the
Lyapunov dimension becomes large. Therefore, the modules for sI (cid:10) −0.08
would show relatively independent chaotic oscillations compared to those
for other values of sI.
When sI was increased toward −0.017, it was observed that DL monoton-
ically decreased, and when sI > −0.017, the dependence of DL on sI became
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
un
_
0
1
5
9
6
p
d
.
/
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1443
Chiffre 6: Intermittent switching between transitive chaotic synchronization
= −0.017, which would be related to the edge
and conventional chaos for sI
of chaos.
complicated. These results imply that transitive chaotic synchronization for
sI < −0.017 and conventional chaos for sI > −0.017 were qualitatively dif-
ferent phenomena. As stated above, for sI > −0.017, several arrangements
of the oscillating modules can coexist. In this region, the Lyapunov dimen-
sion depends on the number of largely oscillating modules (par exemple., 13 mod-
ules in Figure 3E and 12 modules in Figure 3F). Donc, in the region
of conventional chaos, the Lyapunov dimensions take different values for
10 trials.
De plus, a transition from high ((cid:10)22) dimensional chaos to low ((cid:10)8) di-
mensional chaos took place at sI (cid:10) −0.017. Around this transition point, nous
observed intermittent switching between transitive chaotic synchronization
and conventional chaos, as shown in Figure 6.
Such intermittent switching is often observed at the edge of chaos. Le
“edge of chaos” refers to the area between order and disorder in the field
of cellular automata and is also used in the field of dynamical systems
(Pierre & Hübler, 1994; Melby et al., 2000). The edge of chaos in dynami-
cal systems is typically observed when the largest positive Lyapunov ex-
ponent of the system approaches zero. Dans ce cas, intermittent switching
between chaotic and nonchaotic dynamics was observed. Cependant, in our
model, intermittent switching between high-dimensional chaotic dynamics
and low-dimensional chaotic dynamics was observed, as shown in Figure 6.
Donc, it is more appropriate to use the term “edge of high-dimensional
chaos” in our system rather than “edge of chaos,” but we will use the latter
simpler term below to indicate this meaning.
To confirm the robustness of the observed phenomena, we regulated the
strength of the connections instead of sI. D'abord, the strengths of the connec-
tions from the inhibitory neurons gEI and gII are replaced by γ
fromIgEI and
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
un
_
0
1
5
9
6
p
d
.
/
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1444
T. Kanamaru, T. Hensch, and K. Aihara
fromI and γ
= γ
c
fromIgII, respectivement, and γ
fromI is regulated. De la même manière, the connections from
excitatory neurons to inhibitory neurons, gIE and hIE, are replaced by γ
toIgIE
and γ
toIhIE, respectivement. gEI, gII, and gIE are the strengths of intramodule
relations, and hIE is the strength of intermodule connections, as shown
in appendixes A and D. c
fromI is related to the maturation of inhibitory neu-
rons, and γ
toI is related to the regulation of inhibitory neurons by excitatory
neurons. The dependence of some Lyapunov exponents and Lyapunov di-
mensions on γ
toI is shown in Figure 7. The values of the param-
eters for γ
toI = 1 were the same as those used in Figure 3A. Le
fromI
point and the error bar denote the mean and the 99% Intervalle de confiance
calculated using the t-distribution for 10 trials, respectivement. Methods for
initializing 10 trials are explained in appendix E. Similar to Figure 5, le
largest positive Lyapunov exponents and Lyapunov dimensions become
small when regulating γ
toI, c'est, a transition between transitive
chaotic synchronization and conventional chaos occurs. Donc, we re-
garded this transition as a robust phenomenon. Note that the Lyapunov
dimension of the conventional chaos for γ
= 0.8 is larger than 10 être-
cause the number of largely oscillating modules tend to become large in
this setting, as shown in Figure 7E, où 19 modules are oscillating.
fromI or γ
Transitive chaotic synchronization is stable for large γ
toI.
It is somewhat difficult to understand the opposite dependence of dynam-
ics on the parameters, because the dynamics in our network is generated
by reciprocal excitatory and inhibitory connections. Cependant, the regula-
tion of sI yields clear results because it directly modulates the firing rates
of inhibitory neurons. Donc, as described in the following sections, nous
subsequently used sI to regulate the E-I balance.
fromI and small γ
fromI
5 Measuring E-I Balance
In the previous sections, we identified several dynamics in our model by
regulating the degree of inhibitory activity, sI. With particular values of sI,
an optimal E-I balance in the network can be realized.
To measure the degree of E-I balance, we use two E/I ratios: the func-
tional E/I ratio ( f E/I) proposed by Bruining et al. (2020) and the input E/I
ratio (iE/I), which is the proportion of excitatory to inhibitory input onto
pyramidal neurons.
f E/I relates to detrended fluctuation analysis (DFA) (Peng et al., 1995;
Linkenkaer-Hansen et al., 2001; Hardstone et al., 2012) to analyze the long-
term correlations and scale-free properties of time series obtained from neu-
ral systems. In DFA, a time series is divided into bins with width w, et le
trend in each bin is removed. Then the average (cid:7)F(w)(cid:8) over bins of standard
deviation F(w) of the detrended data in each window is calculated. Quand
scaling (cid:7)F(w)(cid:8) ∼ wα
is observed, α is called the DFA exponent. Typical val-
ues of the DFA exponent are 0.5 for white noise, 1 pour 1/ f fluctuations, et
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
un
_
0
1
5
9
6
p
d
.
/
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1445
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
un
_
0
1
5
9
6
p
d
.
/
Chiffre 7: The dependence of (UN, C) some Lyapunov exponents and (B, D) Lya-
punov dimensions on the strengths of connections. The strengths of connections
fromIgEI and γ
(UN, B) from inhibitory neurons (c
fromIgII) ou (C, D) from excitatory
toIgIE and γ
to inhibitory neurons (c
toIhIE) are regulated. The values of the param-
= 1 are the same as those used in Figure 3A. (E) Temporal
eters for γ
fromI
changes in the ensemble-averaged firing rates of excitatory neurons in a net-
work with 48 modules for γ
= 0.8.
= γ
toI
fromI
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1446
T. Kanamaru, T. Hensch, and K. Aihara
1.5 for Brownian motion. When the DFA exponent takes large values in the
range (0.5, 1], the original time series has long-term correlations.
The DFA exponent carries some disadvantages when measuring the de-
gree of E-I balance. D'abord, a long time series is required to calculate the DFA
exponent. Deuxième, even when the DFA exponent can be obtained, the ratio
of excitatory and inhibitory activity cannot be uniquely determined. Le
f E/I was then proposed to overcome these disadvantages (Bruining et al.,
2020).
It takes a value of 1 when the DFA exponent reaches a maximum value by
regulating the ratio of E-I activity. It is assumed that long-term correlation is
maximal when optimal E-I balance is realized and that the maximal value of
the DFA exponent is in the range (0.5, 1]. When the DFA exponent increases
with an increase in excitatory activity, f E/I is defined as f E/I < 1. When
the DFA exponent decreases with an increase in excitatory activity, f E/I is
defined as f E/I > 1. The detailed method for calculating f E/I is presented
in appendix F. When calculating it, the ensemble-averaged firing rate rEi for
the ith module was used, and the average and standard deviation over the
48 modules were calculated.
For further comparison, we also calculated the simple input E/I ratio
iE/I of the excitatory to inhibitory input onto pyramidal neurons, defined
comme
iE/I =
InputE→Ei
InputI→Ei
(cid:6)
,
je
(cid:5)
(cid:7)
InputE→Ei
=
(gEE − hEE )IEi
+
InputI→Ei
(cid:9)
=
gEIIIi
(cid:10)
t
,
M.(cid:2)
j=1
hEE
i j IE j
(cid:8)
,
t
(5.1)
(5.2)
(5.3)
where InputE→Ei and InputI→Ei are sums of excitatory and inhibitory synap-
tic inputs to the ith excitatory module and (cid:7)·(cid:8)t and (cid:7)·(cid:8)
i denote an average
over time t and an average over 48 modules, respectivement. Note that they
include both intra- and intermodule synaptic inputs. The meanings of the
other parameters are explained in appendixes A, B, and D.
Although the definition of iE/I can be easily interpreted, it cannot be
applied to experimental data in many cases. Inversement, f E/I can be cal-
culated only from time series data obtained from neural systems because
it quantifies long-term correlations and scale-free properties of data. Pour
exemple, Bruining et al. (2020) applied f E/I to EEGs of healthy adults. Nous
calculated both E/I ratios in our network for comparison. f E/I becomes im-
portant when we compare our theoretical results with experimental ones.
The dependence of f E/I and iE/I on sI in our model is shown in Figure 8.
The excitatory activity is dominant for small sI because both f E/I and iE/I
are larger than 1. The typical dynamics are shown in Figure 3D.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
un
_
0
1
5
9
6
p
d
.
/
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1447
Chiffre 8: The dependence of f E/I and iE/I on sI. Error bars denote the standard
deviations over 48 modules.
It is observed that both f E/I and iE/I approach 1 when sI is increased.
iE/I (cid:10) 1 means that the network shows neither runaway excitation nor a
quiescent state (Turrigiano & Nelson, 2004). Cependant, the property of the
dynamics with iE/I (cid:10) 1 is not clear when only iE/I is observed. En revanche,
f E/I is calculated based on the analysis of the long-term correlations and
scale-free properties of the data. Donc, f E/I (cid:10) 1 means that the transi-
tive chaotic synchronization shown in Figures 3A, 3B, and 3C has a long-
term correlation.
For sI > −0.017, both f E/I and iE/I become smaller than 1 (c'est à dire., the in-
hibitory activity is dominant), and the conventional chaos in Figures 3E and
3F is observed.
Dans la rubrique suivante, we show that transitive chaotic synchronization
with f E/I, iE/I (cid:10) 1 is suitable for information processing.
6 Storing Randomly Varying Inputs via Reservoir Computing
Ici, we demonstrate that transitive chaotic synchronization and the dy-
namics at the edge of chaos are suitable for information processing. Specifi-
cally, we consider the response of the network to time-varying inputs using
the framework of reservoir computing (Lukoševiˇcius & Jaeger, 2009) avec
respect to a short-term memory task. We demonstrate that a network show-
ing transitive chaotic synchronization or dynamics at the edge of chaos dis-
plays a large memory capacity.
We define a time-varying input u(t) as a binary signal whose value
changes randomly every ws,
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
un
_
0
1
5
9
6
p
d
.
/
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1448
T. Kanamaru, T. Hensch, and K. Aihara
(cid:3)
u(t) =
+1 with probability 0.5
−1 otherwise
,
(6.1)
for mws ≤ t < (m + 1)ws (m = 0, 1, 2, . . .). We set ws = 10 so that the dynam- ics of the network can follow changes in u(t). i We define the weights g(in) i u(t). Weights g(in) for the ith module as following a uniform distribution [−Is, Is], where Is = 0.03. u(t) is assigned to the excitatory neu- rons in all modules by replacing the degree of excitatory activity sEi with sEi + g(in) In the following, we denote u(t) for mws ≤ t < (m + 1)ws as um for dis- crete time steps m = 0, 1, 2, . . .. Similarly, we obtain the output of the net- work for a discrete time step m as follows. First, the ensemble-averaged firing rate rEi(t) of the excitatory ensemble in the ith module is binarized as follows: i were fixed during the simulations. (cid:3) θ Ei(t) = if rEi(t) > 0.01,
1
0 otherwise.
(6.2)
Ei(t) is averaged in the range mws ≤ t < (m + 1)ws, and we denote it
Then θ
as ˆrEim as follows:
ˆrEim
= 1
ws
(cid:4)
(m+1)ws
mws
θ
Ei(t) dt.
(6.3)
Finally, the output om of the network for time step m is defined as a linear
combination of 48 modules with a bias of
om = g0
+
48(cid:2)
i=1
gi ˆrEim
.
(6.4)
Then the data for 0 ≤ m < 1000 were discarded, the data for 1000 ≤ m <
2000 were used to train gi (0 ≤ i ≤ 48), and the data for 2000 ≤ m < 3000
were used as test data. We used the previous values of input um−k (k =
1, 2, 3, . . .) for the target of om.
The weights gi were trained to maximize the coefficient of determination
between om and um−k for 1000 ≤ m < 2000. The maximum of the coefficient
of determination is denoted as MFk as follows:
MFk
= max
gi
cov2(om, um−k)
σ 2(om)σ 2(um−k)
,
(6.5)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1449
Figure 9: The dependence of MFk on the time delay k for sI
transitive chaotic synchronization is observed.
= −0.020, where
where σ 2(om) and σ 2(um−k) are the variances of om and um−k, respectively,
and cov(om, um−k) is the covariance between om and um−k.
The dependence of MFk on the time delay k for sI = −0.020 where tran-
sitive chaotic synchronization is observed is shown in Figure 9. MFk for the
test data is also shown, which was obtained by calculating the coefficient of
determination with the test data using gi obtained from the training data.
Whereas MFk for the training data always takes positive values, MFk for the
test data takes positive values only when k ≤ 10.
Using MFk, the memory capacity MC is defined as the sum of MFk over
k as
MC =
kmax(cid:2)
k=1
,
MFk
(6.6)
where kmax
= 50 in this study.
The dependence of MC on sI for the training data (1000 ≤ m < 2000) and
the test data (2000 ≤ m < 3000) is shown in Figure 10. We have shown MC
before training for comparison, where the values of weights gi are set fol-
lowing a uniform distribution [−1, 1]. All results were obtained by averag-
ing 10 experiments for different u(t).
Figure 10 shows that MC increases when sI is close to −0.017 where
transitive chaotic synchronization or dynamics at the edge of chaos are ob-
served. For such values of sI, both f E/I and iE/I are close to 1; therefore,
it can be concluded that MC increases when an optimal E-I balance is re-
alized. Although MC for test data was relatively small, it was larger than
that before training. To obtain larger MC, all connections inside the net-
work should be trained. Such training of the entire network is important
for future comparison to the actual brain.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1450
T. Kanamaru, T. Hensch, and K. Aihara
Figure 10: The dependence of MC on sI. MCs for the training data (1000 ≤ m <
2000) and the test data (2000 ≤ m < 3000) are shown. MC before training is also
shown for comparison. MC increases when sI is close to −0.017, where transitive
chaotic synchronization or dynamics at the edge of high-dimensional chaos is
observed.
7 Conclusions and Discussion
In the field of nonlinear dynamics, it is well known that network mod-
els with balanced excitation and inhibition yield deterministic chaos (van
Vreeswijk & Sompolinsky, 1996). The novelty of our study lies in the anal-
ysis of the Lyapunov spectrum and Lyapunov dimension, and the find-
ing of more detailed properties of the chaotic dynamics with E-I balance
(van Vreeswijk & Sompolinsky, 1996), namely, transitive chaotic synchro-
nization, conventional chaos, and their intermittent switching at the edge
of high-dimensional chaos with respect to the CP.
To understand the role of optimal E-I balance during the CP, we exam-
ined the dynamics of a network composed of excitatory pyramidal neu-
rons (PYRs) in layers 2/3 and inhibitory interneurons (INs) in layer 4. INs
with nicotinic acetylcholine receptors (nAChRs) in layer 1 were further con-
nected to INs in layer 4. The effect of ACh was incorporated into the regu-
lation of a parameter sI of INs in layer 4.
In a randomly connected network of 48 such modules, transitive chaotic
synchronization was observed in which modules that showed intermod-
ule synchronization were rearranged transitively. When the activity of in-
hibitory neurons was dominant for a large sI, conventional chaos was
observed, in which modules that showed intramodule synchronization
were fixed.
The parameter sI can be interpreted as a constant input to inhibitory neu-
rons, and we used it to regulate the E-I balance. Other methods for reg-
ulating E-I balance are available, such as regulating the ratio between the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1451
numbers of excitatory and inhibitory neurons and regulating the strength of
excitatory and inhibitory synapses. The former method cannot be applied
to our model because the interactions among neurons are scaled as 1/NX
(X = E or I), as shown in equation A.3. The latter method can be realized
by regulating the strengths of the connections gEE, gIE, gEI, gII, hEE, and hIE.
In Figure 7, the transition between transitive chaotic synchronization and
conventional chaos was also observed when the strengths of connections
from inhibitory neurons (gEI and gII) or from excitatory to inhibitory neu-
rons (gIE and hIE) were regulated. Therefore, we regarded this transition as
a robust phenomenon.
The Lyapunov dimension of transitive chaotic synchronization was high
and that of conventional chaos was low. Around the boundary between
these two regions, intermittent switching between transitive chaotic syn-
chronization and conventional chaos was observed. Typical dynamics at
the edge of chaos are intermittent switching between chaotic and non-
chaotic dynamics (Pierre & Hübler, 1994; Melby et al., 2000). However,
in our model, intermittent switching between high- and low-dimensional
chaotic dynamics was observed. Therefore, a more suitable term than “edge
of chaos” would be “edge of high-dimensional chaos.”
To further investigate the relationship between E-I balance and chaotic
dynamics in our network, we calculated two E/I ratios: the functional E/I
ratio f E/I proposed by Bruining et al. (2020) and the input E/I ratio (iE/I)
onto pyramidal neurons. Transitive chaotic synchronization and dynamics
at the edge of high-dimensional chaos were observed when f E/I, iE/I (cid:10) 1.
While iE/I (cid:10) 1 indicates neither runaway excitation nor a quiescent net-
work state (Turrigiano & Nelson, 2004), the dynamics is not clear when
only this ratio is taken. In contrast, f E/I is calculated based on the anal-
ysis of long-term correlations and scale-free properties of the data. Thus, it
can be concluded that transitive chaotic synchronization and the dynam-
ics at the edge of high-dimensional chaos with f E/I (cid:10) 1 show long-term
correlations.
Finally, to examine the efficiency of information processing, a framework
of reservoir computing (Lukoševiˇcius & Jaeger, 2009) was introduced. A
short-term memory task was performed by the network in which a time-
varying random input was given, and the previous values of the input were
obtained as the output of the network. It was found that memory capac-
ity takes large values when transitive chaotic synchronization or dynam-
ics at the edge of high-dimensional chaos were observed, where both f E/I
and iE/I are close to 1. Therefore, it can be concluded that a network with
optimal E-I balance offers large memory capacity. This result is similar to
those of previous studies in which dynamics at the edge of chaos showed
high performance in some tasks of the reservoir computing (Bertschinger
& Natschläger, 2004; Legenstein & Maass, 2007; Boedecker et al., 2012).
While previous studies have analyzed the dynamics at the edge of low-
dimensional chaos, our network shows high-dimensional chaos with large
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1452
T. Kanamaru, T. Hensch, and K. Aihara
Lyapunov dimensions, realized by the network’s multiple-module struc-
ture. The edge of high-dimensional chaos is a novel phenomenon that ex-
ists between transitive and conventional chaos. The dimension of chaos is
expected to increase when the number of modules increases. Such high-
dimensional chaos may be effective for certain tasks in reservoir computing.
Uncovering such tasks will be investigated in future studies.
In the brain, the maturation of perisomatic GABA circuits achieves the
optimal E-I balance that opens the CP (Hensch, 2005; Reh et al., 2020). Our
finding that a network with E-I balance holds a large memory capacity in-
directly supports the heightened learning capacity during these windows
of brain development. When training a network under the reservoir com-
puting framework, all connections in the network were fixed except those
to the output neuron. To more accurately model learning during the CP,
all connections inside the network should be trained. A procedure called
force learning has been proposed to train recurrent neural networks, which
successfully generates complex time-varying output patterns (Sussillo &
Abbott, 2009). Such training of the entire network is important for future
comparison to the actual brain.
Notably, CP timing is staggered across brain regions as each modality se-
quentially attains E-I balance (Reh et al., 2020). Mistimed or misaligned CP
milestones may then amplify the progression toward cognitive disorders.
In the literature on reservoir computing, various tasks, such as classifica-
tion, parity check, and systems modeling, have been used as benchmarks
(Bertschinger & Natschläger, 2004; Legenstein & Maass, 2007; Lukoševiˇcius
& Jaeger, 2009; Boedecker et al., 2012). As shown by Cramer et al. (2020)
and Shi et al. (2022), the importance of “criticality” might depend on the
complexity of the tasks. Similarly, the importance of the dynamics of the E-I
balance might also depend on the properties of the tasks involving multiple
brain areas. Analyses of such task dependence are planned for our future
work.
Appendix A: Definition of a Single Module
In this appendix, we provide a detailed definition of the module model. A
module of a network composed of NE pyramidal neurons and NI interneu-
rons is defined using the following equations:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
τE
˙θ (i)
E
τI
˙θ (i)
I
= (1 − cos θ (i)
× (sE + ξ (i)
E ) + (1 + cos θ (i)
E )
E (t) + gEEIE (t) − gEIII(t)),
= (1 − cos θ (i)
I
× (sI + ξ (i)
I
) + (1 + cos θ (i)
I
(t) + gIEIE (t) − gIIII(t) + ggapI(i)
)
gap(t)),
(A.1)
(A.2)
Memory Capacity and Chaos in EI-Balanced Networks
(cid:11)
− t − t( j)
κX
k
(cid:12)
,
1
κX
exp
IX (t) = 1
2NX
NX(cid:2)
(cid:2)
j=1
k
(cid:13)
gap(t) = 1
I(i)
NI
NI(cid:2)
j=1
sin
θ ( j)
I
(t) − θ (i)
(cid:14)
I (t)
,
(cid:7)ξ (i)
X (t)ξ ( j)
Y (t
(cid:6)
)(cid:8) = Dδ
XY
δ
i j
δ(t − t
(cid:6)
).
1453
(A.3)
(A.4)
(A.5)
I
E and θ (i)
The internal states of the ith pyramidal neurons and ith interneurons are
described by the phase variables θ (i)
, respectively (Kanamaru &
Sekine, 2005). The activity of a single neuron in the model can be regu-
lated by sX (X = E or I) when all connections are omitted, that is, gEE =
≡
gEI = gIE = gII = ggap = 0. When sX < 0, a stable equilibrium point θ = θ
0
arccos((1 + sX )/(1 − sX )) exists and can be considered a resting state. When
sX > 0, the resting state disappears and θ starts to oscillate. Firing time is
defined as the time at which θ ( j)
X exceeds π. Dans cette étude, we set sE, sI < 0.
Each neuron without connections spontaneously fires owing to gaussian
white noise ξ (i)
X (t) with strength D.
The connections among the neurons are global. We consider four types
of intramodule connections: E → E, E → I, I → E, and I → I. Connections
generating postsynaptic currents of an exponential form between all pairs
of neurons, as well as diffusive connections between inhibitory neurons,
are present. These two types of connections model chemical and electrical
synapses with gap junctions, respectively. The form of the connections of
the gap junctions is sinusoidal, following the Kuramoto model (Kuramoto,
1984) because our network is described by phase variables. t( j)
is the kth
k
firing time of the jth neuron. gEE, gIE, −gEI, and −gII are connection weights
within the excitatory and inhibitory ensembles, respectively, and ggap is the
strength of the gap junctions. τE and τI are the membrane time constants,
and κE and κI are the time constants of the synaptic currents.
We set the values of the parameters as sE = −0.019, D = 0.0025, gEE = 6,
gIE = gEI = 2.8, gII = 1, ggap = 0.1, τE = 1, τI = 0.5, κE = 1, and κI = 1.
Appendix B: The Fokker-Planck Equations
The averaged dynamics of a single module in the limit of NE, NI → ∞ can
be analyzed using the Fokker-Planck equations (FPEs) (Kuramoto, 1984;
Kanamaru & Sekine, 2005), defined as follows:
∂nE
∂t
∂nI
∂t
= −
= −
∂
∂θE
∂
∂θI
(AEnE ) + D
2
(AInI ) + D
2
∂
∂θE
(cid:15)
∂
∂θI
(cid:15)
BE
∂
∂θE
(cid:16)
,
(BEnE )
(cid:16)
BI
∂
∂θI
(BInI )
,
(B.1)
(B.2)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1454
T. Kanamaru, T. Hensch, and K. Aihara
AE (θE, t) = 1
τE
× (sE + gEEIE (t) − gEIII(t)),
(1 − cos θE ) + 1
τE
(1 + cos θE )
AI(θI, t) = 1
τI
× (sI + gIEIE (t) − gIIII(t) + ggapIgap(θI, t)),
(1 − cos θI ) + 1
τI
(1 + cos θI )
BE (θE, t) = 1
τE
BI(θI, t) = 1
τI
(1 + cos θE ),
(1 + cos θI ),
Igap(θI, t) = (cid:7)sin θI(cid:8) cos θI − (cid:7)cos θI(cid:8) sin θI,
(cid:7) f (θI )(cid:8) =
(cid:4)
2π
0
f (θI ) nI(θI, t) dθI,
(B.3)
(B.4)
(B.5)
(B.6)
(B.7)
(B.8)
for the normalized number densities nE (θE, t) and nI(θI, t) of the excitatory
and inhibitory neurons, respectively. In the limit of NE, NI → ∞, nE (θE, t)
and nI(θI, t) are defined as follows:
nE (θE, t) ≡ 1
NE
nI(θI, t) ≡ 1
NI
(cid:2)
δ(θ (i)
E
− θE ),
(cid:2)
δ(θ (i)
I
− θI ).
(B.9)
(B.10)
The probability fluxes for excitatory neurons and inhibitory neurons are
defined as
rE (θE, t) = AEnE − D
2
rI(θI, t) = AInI − D
2
BI
BE
∂
∂θE
∂
∂θI
(BInI ).
(BEnE ),
(B.11)
(B.12)
rE ≡ rE (π, t) and rI ≡ rI(π, t) can be interpreted as ensemble-averaged fir-
ing rates for excitatory and inhibitory neurons.
Using rE and rI, the excitatory current IE (t) and the inhibitory current II(t)
in the intramodule connections are governed by the following equations:
˙IX (t) = − 1
κX
(cid:17)
(cid:18)
.
IX (t) − 1
2
rX
(B.13)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1455
Using FPEs, we can obtain the theoretical dynamics of ensemble-
averaged firing rates rE and rI, and various methods for nonlinear analysis
can be used.
In this study, we examined the network in the limit of NE, NI → ∞ by
analyzing FPEs B.1 and B.2, which describe the dynamics of globally con-
nected E-I neurons governed by equations A.1 and A.2. The dynamics of
randomly connected E-I neurons with probability p is also described by
FPEs B.1 and B.2. In such a network, NX in the denominator and the sum-
mation over j in equation A.3 are replaced by pNX and summation over
a set of pNX neurons, respectively. This equivalence between a global net-
work and a random network is caused by the scaling factor 1/NX in equa-
tion A.3 and the large NX limit. The infinitesimally small connections of
order 1/NX differ from the strong connections of order 1/
NX in previ-
ous studies (Renart et al., 2010; van Vreeswijk & Sompolinsky, 1996). De-
spite the different orders of connections, the E-I balance is important in all
networks.
√
Appendix C: Numerical Integration of the Fokker-Planck Equations
In this appendix, we describe a method for the numerical integration of
FPEs B.1 and B.2 (Kanamaru & Sekine, 2005; Kanamaru & Aihara, 2008).
Because the two densities nE and nI are 2π-periodic functions of θE and θI,
respectively, they can be expanded as
nE (θE, t) = 1
2π
nI(θI, t) = 1
2π
+
+
∞(cid:2)
k=1
∞(cid:2)
k=1
(aE
k (t) cos(kθE ) + bE
k (t) sin(kθE )),
(aI
k(t) cos(kθI ) + bI
k(t) sin(kθI )),
(C.1)
(C.2)
and by substituting them, equations B.1 and B.2 are transformed into a set
of ordinary differential equations of aX
k and bX
k as follows:
da(X )
k
dt
= −(sX + ˜IX + 1)
− (sX + ˜IX − 1)
k
2τX
(b(X )
k−1
+ b(X )
k+1)
b(X )
k
k
τX
πggapk
4τX
− Dk
8τ 2
X
f (a(X )
k
) +
(−b1g1(b(X )
k
) + a1g2(a(X )
k
))δXI,
(C.3)
db(X )
k
dt
= (sX + ˜IX + 1)
k
τX
a(X )
k
+ (sX + ˜IX − 1)
k
2τX
(a(X )
k−1
+ a(X )
k+1)
− Dk
8τ 2
X
f (b(X )
k
) +
πggapk
4τX
(b1g1(a(X )
k
) + a1g2(b(X )
k
))δXI,
(C.4)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1456
T. Kanamaru, T. Hensch, and K. Aihara
f (xk) = (k − 1)xk−2
+ 2(2k − 1)xk−1
+ 2(2k + 1)xk+1
+ 2xk−1
+ 2xk−1
+ (k + 1)xk+2
+ 2xk+1
− xk+2
+ 2xk
− 2xk+1
,
+ xk+2
,
g1(xk) = xk−2
g2(xk) = xk−2
+ 6kxk
,
˜IX ≡ gXEIE − gXIII,
a(X )
0
b(X )
0
a(X )
−n
b(X )
−n
≡ 1
π
,
≡ 0,
,
≡ a(X )
n
≡ −b(X )
n
,
(C.5)
(C.6)
(C.7)
(C.8)
(C.9)
(C.10)
(C.11)
(C.12)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
where X = E or I. Using a vector x = (IE, II, aE
, . . .)t,
1
the ordinary differential equations ˙x = f (x) are defined by equations B.13,
C.3, and C.4. By numerically integrating these ordinary differential equa-
tions, the time series of the ensemble-averaged firing rates rE and rI are ob-
tained. For the numerical calculations, each Fourier series is truncated at
the first 60 terms; therefore, x is approximated by a 242-dimensional vector.
, aE
2
, bE
2
, bE
1
, bI
1
, bI
2
, aI
1
, aI
2
Appendix D: Connections among Modules
To obtain a network of M modules, we defined the connection strengths
TEi and TIi of the input to the excitatory and inhibitory neurons in the ith
module as follows:
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
TEi
= (gEE − hEE )IEi
− gEIIIi
+
M(cid:2)
j=1
hEE
i j IE j
,
TIi
= (gIE − hIE )IEi
− gIIIIi
+
M(cid:2)
j=1
hIE
i j IE j
,
(D.1)
(D.2)
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
where IEi and IIi are the sums of the postsynaptic currents of the ith mod-
ule defined by equation A.3. We replaced the inputs to the excitatory and
inhibitory neurons used in equations A.1 and A.2 with TEi and TIi.
In the definitions above, the intramodule connection weights gEE and
gIE are decreased by subtracting hEE and hIE, respectively, to maintain the
chaotic dynamics observed in a module.
The intermodule connection weights hEE
i j and hIE
i j are defined randomly
as follows:
Memory Capacity and Chaos in EI-Balanced Networks
1457
⎧
⎪⎨
⎪⎩
⎧
⎪⎨
⎪⎩
1
Mp
0,
1
Mp
0,
hEE
i j
=
=
hIE
i j
hEE, with probability p,
otherwise.
hIE, with probability p,
otherwise.
(D.3)
(D.4)
We set the values of the parameters as M = 48, p = 0.1, hIE = 1.2, and hEI =
1.9.
Appendix E: Initialization of Models
In this appendix, we explain methods for initializing our models.
In Figures 2A, 2B, 2D, and 2E, the dynamics of a module model com-
posed of NE excitatory neurons and NI inhibitory neurons defined by equa-
tions A.1 and A.2 is shown. In this model, θ (i)
I were initialized to
random values obtained from a uniform distribution in [0, 2π]. Discarding
the transient data until t = 1000, the results in Figures 2A, 2B, 2D, and 2E
were obtained.
E and θ (i)
In Figure 2C, a module model was analyzed by FPEs. As shown in ap-
pendix C, FPEs can be analyzed by ordinary differential equations B.13,
C.3, and C.4 for a vector x = (IE, II, aE
, . . .)t, which in-
, bE
1
1
cludes Fourier series of probability densities nE and nI. This vector x cannot
be initialized randomly because it should satisfy the following conditions
for probability density nX (X = E of I):
, aE
2
, bE
2
, bI
2
, bI
1
, aI
2
, aI
1
nX (θX, 0) ≥ 0,
nX (θX, 0) = 1.
(cid:4)
2π
0
Instead, we initialized x to 0, which corresponds to a uniform distribution
nX (θX, 0) = 1
2π
,
as shown in equations C.1 and C.2. When the transient data until t = 1000
are discarded, the result in Figure 2C was obtained.
In Figure 3, the dynamics of a network with 48 modules is analyzed by
FPEs. When all the vectors x of 48 modules are initialized to 0, the simulation
starts from a fully synchronized state of 48 modules. To avoid such a fully
synchronized initial condition, we prepared 48 different vectors x using the
following method. First, we simulated a single module for sI with an initial
condition x = 0 until t = t1, and we denote the obtained vector as x1(t1
; sI ).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1458
T. Kanamaru, T. Hensch, and K. Aihara
; sI )
Then we initialized the ith module of 48 modules to x1(t1
(i = 1, 2, . . . , 48), and we simulated the network with 48 modules until
t = t2. The obtained vector is denoted as x48(t1
; sI ), and it can be used
as an initial vector for the network with 48 modules. In Figures 3A, 3B, 3D,
and 3E, x48(10,000, 0.01, 10,000; −0.013) was used for initialization. In Fig-
ures 3C and 3F, x48(10,000, 0.01, 10,000; −0.020) was used for initialization.
When the transient data until t = 4000 were discarded, the results in Fig-
ure 3 were obtained.
+ (i − 1)dt1
, dt1
, t2
In Figures 4 and 6, x48(10,000, 0.01, 10,000; −0.013) was used for initial-
ization, and the transient data until t = 4000 were discarded.
When calculating NL Lyapunov exponents as shown in Figures 5, 7A,
7B, 7C, and 7D, we have to compute NL + 1 trajectories. We calculate
them for 10 trials. We initialized the network to x48(10,000, 0.01, 10,000 +
0.1(i − 1); −0.013)
trial, and we ini-
tialized them to x48(10,000, 0.01, 10,000 + 0.1(i − 1); −0.020 − 0.001( j − 2))
(i = 1, 2, . . . NL + 1) for the jth ( j = 2, 3, . . . , 10) trial. Discarding transient
data until t = 4000, Lyapunov exponents were calculated by using the dy-
namics until t = 50,000.
(i = 1, 2, . . . NL + 1)
for the first
In Figure 7E, x48(10,000, 0.01, 10,000; −0.021) was used for initialization,
and the transient data until t = 4000 were discarded.
In Figures 8, 9, and 10, x48(10,000, 0.01, 10,000; −0.013) was used for ini-
tialization, and the transient data until t = 4000 were discarded.
Appendix F: Calculation of f E/I
Here, we introduce a method for calculating f E/I (Bruining et al., 2020).
1. Typically, a bandpass filter is applied to the data. Bruining et al. (2020)
applied a bandpass filter with a frequency range of 8 to 13 Hz to
electroencephalogram data. However, in this study, a bandpass fil-
ter was not applied because our data were obtained from numerical
simulations.
2. The envelope of the data is obtained by applying the Hilbert trans-
form. We denote the obtained envelope as A(t) (t = 1, 2, 3, . . .) and
denote its average over time as (cid:7)A(cid:8).
3. The cumulative sum S(t) of A(t) is calculated as follows:
S(t) =
t(cid:2)
k=1
(A(k) − (cid:7)A(cid:8)).
(F.1)
4. The time axis is divided into bins of width w, and S1(t) = S(t)/(cid:7)A(cid:8)w
is calculated, where (cid:7)A(cid:8)w is the average of A(t) in each bin.
5. A linear fit lw(t) of S1(t) in each bin was calculated, and S2(t) =
S1(t) − lw(t) was calculated.
6. The standard deviation nF of S2(t) in each bin is calculated.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1459
7. The correlation coefficient C of (cid:7)A(cid:8)w and nF is calculated. Subse-
quently, f E/I is defined as f E/I = 1 − C.
Acknowledgments
We thank the anonymous reviewers for their valuable comments, which
have greatly improved the quality of this paper. This work was supported
by the International Research Center for Neurointelligence (WPI-IRCN) at
the University of Tokyo Institutes for Advanced Study (UTIAS), JST Moon-
shot R&D grant JPMJMS2021, AMED under grant JP22dm0307009, Institute
of AI and Beyond of UTokyo, and JSPS KAKENHI grants JP20H05920 and
JP20H05921.
References
Bertschinger, N., & Natschläger, T. (2004). Real-time computation at the edge of
chaos in recurrent neural networks. Neural Computation, 16, 1413–1436. 10.1162/
089976604323057443
Boedecker, J., Obst, O., Lizier, J. T., Mayer, N. M., & Asada, M. (2012). Information
processing in echo state networks at the edge of chaos. Theory in Biosciences, 131,
205–213. 10.1007/s12064-011-0146-8
Bruining, H., Hardstone, R., Juarez-Martinez, E. L., Sprengers, J., Avramiea, A.-
E., Simpraga, S., . . . Linkenkaer-Hansen, K. (2020). Measurement of excitation-
inhibition ratio in autism spectrum disorder using critical brain dynamics. Scien-
tific Reports, 10, 9195. 10.1038/s41598-020-65500-4
Brunel, N. (2000). Dynamics of sparsely connected networks of excitatory and
inhibitory spiking neurons. Journal of Computational Neuroscience, 8, 183–208.
10.1023/A:1008925309027
Cramer, B., Stöckel, D., Kreft, M., Wibral, M., Schemmel, J., Meiner, K., & Priese-
mann, V. (2020). Control of criticality and computation in spiking neuromorphic
networks with plasticity. Nature Communications, 11, 2853.
Eckmann, J. P., & Ruelle, D. (1985). Ergodic theory of chaos and strange attractors.
Reviews of Modern Physics, 57, 617–656. 10.1103/RevModPhys.57.617
Eichler, S. A., & Meier, J. C. (2008). E-I balance and human diseases—from
molecules to networking. Frontiers in Molecular Neuroscience, 1, 1–5. 10.3389/
neuro.02.002.2008
Hardstone, R., Poil, S.-S., Schiavone, G., Jansen, R., Nikulin, V. V., Mansvelder, H.
D., & Linkenkaer-Hansen, K. (2012). Detrended fluctuation analysis: A scale-free
view on neuronal oscillations. Frontiers in Physiology, 3, 450. 10.3389/fphys.2012
.00450
Hensch, T. K. (2004). Critical period regulation. Annual Review of Neuroscience, 27,
549–579. 10.1146/annurev.neuro.27.070203.144327
Hensch, T. K. (2005). Critical period plasticity in local cortical circuits. Nature Reviews
Neuroscience, 6, 877–888. 10.1038/nrn1787
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1460
T. Kanamaru, T. Hensch, and K. Aihara
Hodgkin, A. L. (1948). The local electric changes associated with repetitive ac-
tion in a non-medullated axon. Journal of Physiology, 107, 165–181. 10.1113/
jphysiol.1948.sp004260
Hubel, D. H., & Wiesel, T. N. (1970). The period of susceptibility to the physiologi-
cal effects of unilateral eye closure in kittens. Journal of Physiology, 206, 419–436.
10.1113/jphysiol.1970.sp009022
Izhikevich, E. M. (1999). Class 1 neural excitability, conventional synapses, weakly
connected networks, and mathematical foundations of pulse-coupled models.
IEEE Transactions on Neural Networks and Learning Systems, 10, 499–507. 10.1109/
72.761707
Izhikevich, E. M. (2000). Neural excitability, spiking and bursting. International Jour-
nal of Bifurcation and Chaos, 10, 1171–1266.
Kanamaru, T. (2006). Blowout bifurcation and on-off intermittency in pulse neural
networks with multiple modules. International Journal of Bifurcation and Chaos, 16,
3309–3321. 10.1142/S021812740601680X
Kanamaru, T. (2007). Chaotic pattern transitions in pulse neural networks. Neural
Networks, 20, 781–790. 10.1016/j.neunet.2007.06.002
Kanamaru, T., & Aihara, K. (2008). Stochastic synchrony of chaos in a pulse coupled
neural network with both chemical and electrical synapses among inhibitory neu-
rons. Neural Computation, 20, 1951–1972. 10.1162/neco.2008.05-07-516
Kanamaru, T., & Aihara, K. (2019). Acetylcholine-mediated top-down attention im-
proves the response to bottom-up inputs by deformation of the attractor land-
scape. PLOS ONE, 14, e0223592. 10.1371/journal.pone.0223592
Kanamaru, T., Fujii, H., & Aihara, K. (2013). Deformation of attractor landscape via
cholinergic presynaptic modulations: A computational study using a phase neu-
ron model. PLOS ONE, 8, e53854. 10.1371/journal.pone.0053854
Kanamaru, T., & Sekine, M. (2005). Synchronized firings in the networks of class 1
excitable neurons with excitatory and inhibitory connections and their depen-
dences on the forms of interactions. Neural Computation, 17, 1315–1338. 10.1162/
0899766053630387
Kaneko, K., & Tsuda, I. (2001). Complex systems: Chaos and beyond. Springer.
Kaplan, J. L., & Yorke, J. A. (1979). Chaotic behavior of multidimensional difference
equations. In H. O. Peitgen & H. O. Walther (Eds.), Functional differential equations
and approximations of fixed points. Lecture Notes in Mathematics, vol. 730. Springer.
Kolyada, S., & Snoha, L. (2009). Topological transitivity. Scholarpedia, 4, 5802.
Kubota, T., Nakajima, K., & Takahashi, H. (2018). Information processing using a
single Izhikevich neuron. In Proceedings of ALIFE 2018: The 2018 Conference on Ar-
tificial Life (pp. 550–557).
Kuramoto, Y. (1984). Chemical oscillations, waves, and turbulence. Springer.
Lai, Y.-C., & Tel, T. (2011). Transient chaos, complex dynamics on finite time scales.
Springer.
Legenstein, R., & Maass, W. (2007). Edge of chaos and prediction of computational
performance for neural circuit models. Neural Networks, 20, 323–334. 10.1016/
j.neunet.2007.04.017
Linkenkaer-Hansen, K., Nikouline, V. V., Palva, J. M., & Ilmoniemi, R. J. (2001). Long-
range temporal correlations and scaling behavior in human brain oscillations.
Journal of Neuroscience, 15, 1370–1377. 10.1523/JNEUROSCI.21-04-01370.2001
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory Capacity and Chaos in EI-Balanced Networks
1461
Lukoševiˇcius, M., & Jaeger, H. (2009). Reservoir computing approaches to recurrent
neural network training. Computer Science Review, 3, 127–149.
Madsen, J., & Parra, L. C. (2022). Cognitive processing of a common stimulus syn-
chronizes brains, hearts, and eyes. PNAS Nexus, 1, pgac020. 10.1093/pnasnexus/
pgac020
Melby, P., Kaidel, J., Weber, N., & Hübler, A. (2000). Adaptation to the edge of chaos
in the self-adjusting logistic map. Physical Review Letters, 84, 5991–5993. 10.1103/
PhysRevLett.84.5991
Milnor, J. (1985). On the concept of attractor. Communications in Mathematical Physics,
99, 177–195. 10.1007/BF01212280
Morishita, H., Miwa, J. M., Heintz, N., & Hensch, T. K. (2010). Lynx1, a cholinergic
brake, limits plasticity in adult visual cortex. Science, 330, 1238–1240. 10.1126/
science.1195320
Nagashima, H., & Baba, Y. (1999). Introduction to chaos. Institute of Physics
Publishing.
Nelson, S. B., & Valakh, V. (2015). Excitatory/inhibitory balance and circuit home-
ostasis in autism spectrum disorders. Neuron, 87, 684–698. 10.1016/j.neuron.2015
.07.033
Oseledets, V. I. (1968). A multiplicative ergodic theorem. Characteristic Ljapunov,
exponents of dynamical systems. Transactions of the Moscow Mathematical Society,
19, 197–231.
Ott, E. (2002). Chaos in dynamical systems (2nd ed.). Cambridge University Press.
Peng, C.-K., Havlin, S., Stanley, H. E., & Goldberger, A. L. (1995). Quantification
of scaling exponents and crossover phenomena in nonstationary heartbeat time
series. Chaos, 5, 82–87. 10.1063/1.166141
Pierre, D., & Hübler, A. (1994). A theory for adaptation and competition applied to
logistic map dynamics. Physica D, 7, 343–360. 10.1016/0167-2789(94)90292-5
Reh, R. K., Dias, B. G., Nelson, C. A. III, Kaufer, D., Werker, J. F., Kolb, B., . . . Hensch,
T. K. (2020). Critical period regulation across multiple timescales. In Proceedings of
the National Academy of Sciences USA, 117, 23242–23251. 10.1073/pnas.1820836117
Renart, A., Rocha, J., Bartho, P., Hollender, L., Parga, N., Reyes, A., & Harris, K. D.
(2010). The asynchronous state in cortical circuits. Science, 327, 587–590. 10.1126/
science.1179850
Robinson, C. (1995). Dynamical systems: Stability, symbolic dynamics, and chaos. CRC
Press.
Rodriguez, A., Whitson, J., & Granger, R. (2004). Derivation and analysis of basic
computational operations of thalamocortical circuits. Journal of Cognitive Neuro-
science, 16, 856–877. 10.1162/089892904970690
Shi, J., Kirihara, K., Tada, M., Fujioka, M., Usui, K., Koshiyama, D., . . . Aihara, K.
(2022). Criticality in the healthy brain. Frontier in Network Physiology, 1, 755685.
Shimada, I., & Nagashima, H. (1979). A numerical approach to ergodic problem
of dissipative dynamical systems. Progress of Theoretical Physics, 61, 1605–1616.
10.1143/PTP.61.1605
Shu, Y., Hasenstaub, A., & McCormick, D. A. (2003). Turning on and off recurrent
balance cortical activity. Nature, 423, 288–293. 10.1038/nature01616
Sussillo, D., & Abbott, L. F. (2009). Generating coherent patterns of activity from
chaotic neural networks. Neuron, 63, 544–557. 10.1016/j.neuron.2009.07.018
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1462
T. Kanamaru, T. Hensch, and K. Aihara
Takesian, A. E., Bogart, L. J., Lichtman, J. W., & Hensch, T. K. (2018). Inhibitory cir-
cuit gating of auditory critical period plasticity. Nature Neuroscience, 21, 218–227.
10.1038/s41593-017-0064-2
Tanaka, T., Nakajima, K., & Aoyagi, T. (2020). Effect of recurrent infomax on the in-
formation processing capability of input-driven recurrent neural networks. Neu-
roscience Research, 156, 225–233. 10.1016/j.neures.2020.02.001
Thiele, A., & Bellgrove, M. A. (2018). Neuromodulation of attention. Neuron, 97, 769–
785. 10.1016/j.neuron.2018.01.008
Turrigiano, G. G., & Nelson, S. B. (2004). Homeostatic plasticity in the developing
nervous system. Nature Reviews Neuroscience, 5, 97–107. 10.1038/nrn1327
van Vreeswijk, C., & Sompolinsky, H. (1996). Chaos in neuronal networks with bal-
anced excitatory and inhibitory activity. Science, 274, 1724–1726. 10.1126/science
.274.5293.1724
Werker, J. F., & Hensch, T. K. (2015). Critical periods in speech perception: new
directions. Annual Review of Psychology, 66, 173–196. 10.1146/annurev-psych
-010814-015104
Yizhar, O., Fenno, L. E., Prigge, M., Schneider, F., Davidson, T. J., O’Shea, D. J.,
. . . Deisseroth, K. (2011). Neocortical excitation/inhibition balance in information
processing and social dysfunction. Nature, 477, 171–178. 10.1038/nature10360
Received July 27, 2022; accepted March 23, 2023.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
4
3
0
2
1
4
3
2
4
9
n
e
c
o
_
a
_
0
1
5
9
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3