LETTER
Communicated by Litian Liu
Understanding Dynamics of Nonlinear Representation
Learning and Its Application
Kenji Kawaguchi
kkawaguchi@fas.harvard.edu
Université Harvard, Cambridge, MA 02138, U.S.A.
Linjun Zhang
linjun.zhang@rutgers.edu
Rutgers University, New Brunswick, New Jersey 08901
Zhun Deng
zhundeng@g.harvard.edu
Harvard University Cambridge, MA 02138, U.S.A.
Representations of the world environment play a crucial role in artifi-
cial intelligence. It is often inefficient to conduct reasoning and infer-
ence directly in the space of raw sensory representations, such as pixel
values of images. Representation learning allows us to automatically dis-
cover suitable representations from raw sensory data. Par exemple, given
raw sensory data, a deep neural network learns nonlinear representations
at its hidden layers, which are subsequently used for classification (ou
regression) at its output layer. This happens implicitly during training
through minimizing a supervised or unsupervised loss. In this letter, nous
study the dynamics of such implicit nonlinear representation learning.
We identify a pair of a new assumption and a novel condition, appelé
the on-model structure assumption and the data architecture alignment
condition. Under the on-model structure assumption, the data architec-
ture alignment condition is shown to be sufficient for the global conver-
gence and necessary for global optimality. De plus, our theory explains
how and when increasing network size does and does not improve the
training behaviors in the practical regime. Our results provide practi-
cal guidance for designing a model structure; Par exemple, the on-model
structure assumption can be used as a justification for using a particu-
lar model structure instead of others. As an application, we then derive a
new training framework, which satisfies the data architecture alignment
condition without assuming it by automatically modifying any given
training algorithm dependent on data and architecture. Given a stan-
dard training algorithm, the framework running its modified version is
empirically shown to maintain competitive (practical) test performances
while providing global convergence guarantees for deep residual neural
Neural Computation 34, 991–1018 (2022)
https://doi.org/10.1162/neco_a_01483
© 2022 Massachusetts Institute of Technology.
Publié sous Creative Commons
Attribution 4.0 International (CC PAR 4.0) Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
992
K. Kawaguchi, L. Zhang, and Z. Deng
networks with convolutions, skip connections, and batch normalization
with standard benchmark data sets, including MNIST, CIFAR-10, CIFAR-
100, Semeion, KMNIST, and SVHN.
1 Introduction
LeCun, Bengio, and Hinton (2015) described deep learning as one of hier-
archical nonlinear representation learning approaches:
Deep-learning methods are representation-learning methods with multi-
ple levels of representation, obtained by composing simple but non-linear
modules that each transform the representation at one level (starting with
the raw input) into a representation at a higher, slightly more abstract
level (p. 436).
In applications such as computer vision and natural language process-
ing, the success of deep learning can be attributed to its ability to learn hi-
erarchical nonlinear representations by automatically changing nonlinear
features and kernels during training based on the given data. This is in con-
trast to classical machine-learning methods where representations or equiv-
alently nonlinear features and kernels are fixed during training.
Deep learning in practical regimes, which has the ability to learn nonlin-
ear representation (Bengio, Courville, & Vincent, 2013), has had a profound
impact in many areas, including object recognition in computer vision (Ri-
fai et al., 2011; Hinton, Osindero, & Teh, 2006; Bengio, Lamblin, Popovici,
& Larochelle, 2007; Ciregan, Meier, & Schmidhuber, 2012; Krizhevsky,
Sutskever, & Hinton, 2012), style transfer (Gatys, Ecker, & Bethge, 2016;
Luan, Paris, Shechtman, & Bala, 2017), image super-resolution (Dong, Loy,
Il, & Tang, 2014), speech recognition (Dahl, Ranzato, Mohamed, & Hinton,
2010; Deng et al., 2010; Seide, Li, & Yu, 2011; Mohamed, Dahl, & Hinton,
2011; Dahl, Yu, Deng, & Acero, 2011; Hinton et al., 2012), machine transla-
tion (Schwenk, Rousseau, & Attik, 2012; Le, Oparin, Allauzen, Gauvain, &
Yvon, 2012), paraphrase detection (Socher, Huang, Pennington, Ng, & Homme-
ning, 2011), word sense disambiguation (Bordes, Glorot, Weston, & Bengio,
2012), and sentiment analysis (Glorot, Bordes, & Bengio, 2011; Socher, Stylo-
nington, Huang, Ng, & Manning, 2011). Cependant, we do not yet know the
precise condition that makes deep learning tractable in the practical regime
of representation learning.
To initiate a study toward such a condition, we consider the following
problem setup that covers deep learning in the practical regime and other
nonlinear representation learning methods in general. We are given a train-
∈ Y ⊆ Rmy
ing data set ((xi
are the ith input and the ith target, respectivement. We would like to learn a pre-
dictor (or hypothesis) from a parametric family H = { F (·, je ) : Rmx → Rmy |
θ ∈ Rd} by minimizing the objective L,
i=1 of n samples where xi
∈ X ⊆ Rmx and yi
, yi))n
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
L(je ) = 1
n
n(cid:2)
je = 1
(cid:3)( F (xi
, je ), yi),
993
(1.1)
où (cid:3) : Rmy × Y → R≥0 is the loss function that measures the discrepancy
, je ) and the target yi for each sample. Dans ce
between the prediction f (xi
= xi (for i = 1, . . . , n) to include the setting of
letter, it is allowed to let yi
unsupervised learning. The function f is also allowed to represent a wide
, je )
range of machine learning models. For a (deep) neural network,
represents the preactivation output of the last layer of the network, et
the parameter vector θ ∈ Rd contains all the trainable parameters, y compris
weights and bias terms of all layers.
F (xi
Par exemple, one of the simplest models is the linear model in the form
(cid:6)je , where φ : X → Rd is a fixed function and φ(X) is a non-
of f (X, je ) = φ(X)
linear representation of input data x. This is a classical machine learning
model where much of the effort goes into the design of the handcrafted
feature map φ via feature engineering (Tourneur, Fuggetta, Lavazza, & Loup,
1999; Zheng & Casari, 2018). In this linear model, we do not learn the rep-
resentation φ(X) because the feature map φ is fixed without dependence on
the model parameter θ that is optimized with the data set ((xi
, yi))n
je = 1.
Similar to many definitions in mathematics, where an intuitive notion in
a special case is formalized to a definition for a more general case, we now
abstract and generalize this intuitive notion of the representation φ(X) of the
linear model to that of all differentiable models as follows:
Definition 1. Given any x ∈ X and differentiable function f , we define
be the gradient representation of the data x under the model f at θ .
∂ f (X,je )
∂θ
à
(cid:6)je
∂ f (X,je )
∂θ
= ∂φ(X)
∂θ
This definition recovers the standard representation φ(X) in the linear
= φ(X) and is applicable to all differentiable non-
model as
linear models in representation learning. De plus, this definition captures
the key challenge of understanding the dynamics of nonlinear representa-
tion learning well, as illustrated below. Using the notation of dθ t
= (cid:6)t, le
dt
dynamics of the model f (X, θ t ) over the time t can be written by
d
dt
F (X, θ t ) =
∂ f (X, θ t )
∂θ t
dθ t
dt
=
∂ f (X, θ t )
∂θ t
(cid:6)t.
(1.2)
Ici, we can see that the dynamics are linear in (cid:6)t if there is no gradient
≈ ∂ f (X,je 0 )
. Cependant, with representation
representation learning as
∂θ 0
∂ f (X,θ t )
∂θ t
changes depending on t (et
learning, the gradient representation
(cid:6)t), resulting in the dynamics that are nonlinear in (cid:6)t. Donc, the defini-
tion of the gradient representation can distinguish fundamentally different
dynamics in machine learning.
∂ f (X,θ t )
∂θ t
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
994
K. Kawaguchi, L. Zhang, and Z. Deng
In this letter, we initiate the study of the dynamics of learning gradi-
ent representation that are nonlinear in (cid:6)t. C'est, we focus on the regime
∂ f (X,θ t )
at the end of training time t dif-
where the gradient representation
∂θ t
∂ f (X,je 0 )
∂θ 0
fers greatly from the initial representation
. This regime was stud-
ied in the past for the case where the function φ(X) (cid:8)→ f (X, je ) is affine for
some fixed feature map φ (Saxe, McClelland, & Ganguli, 2014; Kawaguchi,
2016, 2021; Laurent & Brecht, 2018; Bartlett, Helmbold, & Long, 2019; Zou,
Long, & Gu, 2020; Xu et al., 2021). Unlike any previous studies, we focus
on the problem setting where the function φ(X) (cid:8)→ f (X, je ) is nonlinear and
nonaffine, with the effect of nonlinear (gradient) representation learning.
The results of this letter avoid the curse of dimensionality by studying the
global convergence of the gradient-based dynamics instead of the dynamics
of global optimization (Kawaguchi et al., 2016) and Bayesian optimization
(Kawaguchi, Kaelbling, & Lozano-Pérez, 2015). Surtout, we do not re-
quire any wide layer or large input dimension throughout this letter. Notre
main contributions are summarized as follows:
1. In section 2, we identify a pair of a novel assumption and a new
condition, called the common model structure assumption and the data-
architecture alignment condition. Under the common model structure
assumption, the data-architecture alignment condition is shown to
be a necessary condition for the globally optimal model and a suffi-
cient condition for the global convergence. The condition is depen-
dent on both data and architecture. De plus, we empirically verify
and deepen this new understanding. When we apply representation
learning in practice, we often have overwhelming options regarding
which model structure to be used. Our results provide a practical
guidance for choosing or designing model structure via the common
model structure assumption, which is indeed satisfied by many rep-
resentation learning models used in practice.
2. In section 3, we discard the assumption of the data-architecture
alignment condition. Plutôt, we derive a novel training framework,
called the exploration-exploitation wrapper (EE wrapper), which sat-
isfies the data-architecture alignment condition time-independently
a priori. The EE wrapper is then proved to have global convergence
guarantees under the safe-exploration condition. The safe-exploration
condition is what allows us to explore various gradient represen-
tations safely without getting stuck in the states where we cannot
provably satisfy the data-architecture alignment condition. The safe-
exploration condition is shown to hold true for ResNet-18 with stan-
dard benchmark data sets, including MNIST, CIFAR-10, CIFAR-100,
Semeion, KMNIST, and SVHN time-independently.
3. In section 3.4, the EE wrapper is shown to not degrade practical per-
formances of ResNet-18 for the standard data sets, MNIST, CIFAR-10,
CIFAR-100, Semeion, KMNIST, and SVHN. To our knowledge, ce
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
995
letter provides the first practical algorithm with global convergence
guarantees without degrading practical performances of ResNet-18
on these standard data sets, using convolutions, skip connections,
and batch normalization without any extremely wide layer of the
width larger than the number of data points. To the best of our knowl-
bord, we are not aware of any similar algorithms with global conver-
gence guarantees in the regime of learning nonlinear representations
without degrading practical performances.
It is empirically known that increasing network size tends to improve
training behaviors. En effet, the size of networks correlates well with the
training error in many cases in our experiments (par exemple., see Figure 1b). Comment-
jamais, the size and the training error do not correlate well in some ex-
periments (par exemple., see Figure 1c). Our new theoretical results explain that
the training behaviors correlate more directly with the data-architecture
alignment condition instead. The seeming correlation with the network
size is caused by another correlation between the network size and the
data-architecture alignment condition. This is explained in more detail in
section 2.3.
2 Understanding Dynamics via Common Model Structure
and Data-Architecture Alignment
Dans cette section, we identify the common model structure assumption and
study the data-architecture alignment condition for the global convergence
in nonlinear representation learning. We begin by presenting an overview
of our results in section 2.1, deepen our understandings with experiments
in section 2.2, discuss implications of our results in section 2.3, and establish
mathematical theories in section 2.4.
2.1 Overview. We introduce the common model structure assumption
in section 2.1.1 and define the data-architecture alignment condition in sec-
tion 2.1.2. Using the assumption and the condition, we present the global
convergence result in section 2.1.3.
2.1.1 Common Model Structure Assumption. Through examinations of
representation learning models used in applications, we identified and for-
malized one of their common properties as follows:
Assumption 1 (Common Model Structure Assumption). There exists a sub-
set S ⊆ {1, 2, . . . , d} such that f (xi
for any i ∈
, je ) =
{1, . . . , n} and θ ∈ Rd.
k=1 1{k ∈ S}je
(cid:4) ∂ f (xi
,je )
k
(cid:3)
∂θ
(cid:5)
d
k
Assumption 1 is satisfied by common machine learning models, tel
as kernel models and multilayer neural networks, with or without convo-
lutions, batch normalization, pooling, and skip connections. Par exemple,
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
996
K. Kawaguchi, L. Zhang, and Z. Deng
d
k(
k=1 1{k ∈ S}je
consider a multilayer neural network of the form f (X, je ) = Wh(X, toi) + b,
where h(X, toi) is an output of its last hidden layer and the parameter
vector θ consists of the parameters (W, b) at the last layer and the pa-
rameters u in all other layers as θ = vec([W, b, toi]). Ici, for any matrix
M ∈ Rm× ¯m, we let vec(M.) ∈ Rm ¯m be the standard vectorization of the ma-
trix M by stacking columns. Alors, assumption 1 holds because f (X, je ) =
(cid:3)
∂ f (xi
,je )
k : k ∈ S} = {vec([W, b])k :
), where S is defined by {je
∂θ
k
k = 1, 2, . . . , ξ } with vec([W, b]) ∈ Rξ
. Since h is arbitrary in this example,
the common model structure assumption holds, Par exemple, for any mul-
tilayer neural networks with a fully connected last layer. En général, être-
cause the nonlinearity at the output layer can be treated as a part of the
loss function (cid:3) while preserving convexity of q (cid:8)→ (cid:3)(q, oui) (par exemple., cross-entropy
loss with softmax), this assumption is satisfied by many machine learning
models, including ResNet-18 and all models used in the experiments in this
letter (as well as all linear models). De plus, assumption 1 is automatically
satisfied in the next section by using the EE wrapper.
, . . . , oui(cid:3)
n)
2.1.2 Data-Architecture Alignment Condition. Given a target matrix Y =
(cid:6) ∈ Rn×my and a loss function (cid:3), we define the modified tar-
, y2
, . . . , yn)
(y1
, oui(cid:3)
(cid:6) ∈ Rn×my by Y(cid:3) = Y for the squared loss (cid:3),
get matrix Y(cid:3) = (oui(cid:3)
2
1
− 1 for the (binary and multiclass) cross-entropy losses
= 2Yi j
and by (Oui(cid:3))i j
(cid:6) ∈ Rn×mx , le
(cid:3) with Yi j
∈ {0, 1}. Given input matrix X = (x1
output matrix fX (je ) ∈ Rn×my is defined by fX (je )i j
∈ R. For any
matrix M ∈ Rm× ¯m, we let Col(M.) ⊆ Rm be its column space. With these
notations, we are now ready to introduce the data-architecture alignment
condition:
, . . . , xn)
, je ) j
= f (xi
, x2
Definition 2 (Data-Architecture Alignment Condition). Given any data set
(X, Oui), differentiable function f , and loss function (cid:3), the data-architecture align-
ment condition is said to be satisfied at θ if vec(Oui(cid:3)) ∈ Col(
∂vec( fX (je ))
∂θ
).
The data-architecture alignment condition depends on both data
(through the target Y and the input X) and architecture (through the model
F ). It is satisfied only when the data and architecture align well to each
(cid:6)θ ∈ R, le
other. Par exemple, in the case of linear model f (X, je ) = φ(X)
condition can be written as vec(Oui(cid:3)) ∈ Col((cid:8)(X )) où (cid:8)(X ) ∈ Rn×d and
(cid:8)(X )i j
= φ(xi) j. In definition 2, fX (je ) is a matrix of the preactivation out-
puts of the last layer. Ainsi, in the case of classification tasks with a nonlinear
activation at the output layer, fX (je ) and Y are not in the same space, lequel
is the reason we use Y(cid:3) here instead of Y.
Surtout, the data-architecture alignment condition does not make
∈ Rnmy×d:
any requirements on the the rank of the Jacobian matrix
is allowed to be smaller than nmy and d. Ainsi, for ex-
the rank of
ample, the data-architecture alignment condition can be satisfied depend-
ing on the given data and architecture even if the minimum eigenvalue of
∂vec( fX (je ))
∂θ
∂vec( fX (je ))
∂θ
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
997
(
∂vec( fX (je ))
∂θ
∂vec( fX (je ))
∂θ
)(cid:6) is zero, in both cases of overparameteriza-
the matrix
tion (par exemple., d (cid:9) n) and underparameterization (par exemple., d (cid:10) n). This is further
illustrated in section 2.2 and discussed in section 2.3. We note that we fur-
ther discard the assumption of the data-architecture alignment condition in
section 3 as it is automatically satisfied by using the EE wrapper.
2.1.3 Global Convergence. Under the common model structure assump-
tion, the data-architecture alignment condition is shown to be what lets us
avoid the failure of the global convergence and suboptimal local minima.
More concretely, we prove a global convergence guarantee under the data-
architecture alignment condition as well as the necessity of the condition
for the global optimality:
Theorem 1 (Informal Version). Let assumption 1 hold. Then the following two
statements hold for gradient-based dynamics:
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
(je) The global optimality gap bound decreases per iteration toward zero at the
|T |) for any T such that the data-architecture alignment con-
√
rate of O(1/
dition is satisfied at θ t for t ∈ T .
(ii) For any θ ∈ Rd, the data-architecture alignment condition at θ is necessary
to have the globally optimal model fX (je ) = ηY(cid:3) at θ for any η ∈ R.
Theorem 1i guarantees the global convergence without the need to sat-
isfy the data-architecture alignment condition at every iteration or at the
limit point. Plutôt, it shows that the bound on the global optimality gap
decreases toward zero per iteration whenever the data-architecture align-
ment condition holds. Theorem 1ii shows that the data-architecture align-
ment condition is necessary for the global optimality. Intuitively, this is
because the expressivity of a model class satisfying the common model
structure assumption is restricted such that it is required to align the archi-
tecture to the data in order to contain the globally optimal model fX (je ) =
ηY(cid:3) (for any η ∈ R).
To better understand the statement of theorem 1i, consider a counterex-
ample with a data set consisting of the single point (X, oui) = (1, 0), the model
F (X, je ) = θ 4 − 10θ 2 + 6je + 100, and the squared loss (cid:3)(q, oui) = (q − y)2. Dans
this example, we have L(je ) = f (X, je )2, which has multiple suboptimal
local minima of different values. Alors, via gradient descent, the model
converges to the closest local minimum and, in particular, does not neces-
sarily converge to a global minimum. En effet, this example violates the com-
mon model structure assumption (assumption 1) (although it satisfies the
data-architecture alignment condition), showing the importance of the
common model structure assumption along with the data-architecture
alignment. This also illustrates the nontriviality of theorem 1i in that the
data-architecture alignment is not sufficient, and we needed to understand
what types of model structures are commonly used in practice and formal-
ize the understanding as the common model structure assumption.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
998
K. Kawaguchi, L. Zhang, and Z. Deng
To further understand the importance of the common model structure
assumption in theorem 1, we now consider the case where we do not re-
quire the assumption. En effet, we can guarantee the global convergence
without the common model structure assumption if we ensure that the min-
imum eigenvalue of the matrix
is nonzero. This can be
proved by the following derivation. Let θ be an arbitrary stationary point
of L. Then we have 0 = ∂L(je )
n
, which implies
je = 1(
que
∂vec( fX (je ))
∂θ
∂vec( fX (je ))
∂θ
∂(cid:3)(q,yi )
∂q
= 1
n
∂ f (xi
∂θ
q= f (xi
,je ))
(cid:6)
)
(cid:3)
,je )
∂θ
(
|
∂vec( fX (je ))
∂θ
v = 0,
(2.1)
|
,je ))
q= f (x1
∂(cid:3)(q,u1 )
∂q
(cid:6), . . . , (
where v = vec((
∂(cid:3)(q,uN )
∂q
is nonzero,
if the minimum eigenvalue of the matrix
= 0 for all i ∈ {1, 2, . . . , n}. Using the con-
then we have v = 0:
vexity of the map q (cid:8)→ (cid:3)(q, oui) (which is satisfied by the squared loss and
cross-entropy loss), this implies that for any q1
) ∈ Rnmy . Donc,
, . . . , qn ∈ Rmy ,
(cid:6)
q= f (xn,je ))
∂vec( fX (je ))
∂θ
∂vec( fX (je ))
∂θ
∂(cid:3)(q,ui )
∂q
q= f (xi
, q2
(cid:6)
)
,je )
(
|
|
n(cid:2)
(cid:3)( F (xi
, je ), yi)
(cid:3)(qi
, yi) −
(cid:6)
∂(cid:3)(q, ui)
∂q
(cid:8)
(cid:7)
(cid:7)
(cid:7)
(cid:7)
q= f (xi
,je )
(2.2)
(cid:8)
(qi
− f (xi
, je ))
(2.3)
(cid:3)(qi
, yi).
(2.4)
L(je ) = 1
n
≤ 1
n
≤ 1
n
je = 1
n(cid:2)
(cid:6)
je = 1
n(cid:2)
je = 1
(
(cid:6)
)
the minimum eigenvalue of
Since f (x1), F (x2), . . . , F (xn) ∈ Rmy , this implies that any stationary point
θ is a global minimum if
the matrix
∂vec( fX (je ))
∂vec( fX (je ))
is nonzero, without the common model structure as-
∂θ
∂θ
sumption (see assumption 1). En effet, in the above example with the model
F (X, je ) = θ 4 − 10θ 2 + 6je + 100, the common model structure assumption is
violated, but we still have the global convergence if the minimum eigen-
F (X, je ) = y = 0 at any stationary point θ
value is nonzero—for example,
such that the minimum eigenvalue of the matrix
est
nonzero. In contrast, theorem 1 allows the global convergence even when
the minimum eigenvalue of the matrix
is zero by uti-
lizing the common model structure assumption.
∂vec( fX (je ))
∂θ
∂vec( fX (je ))
∂θ
∂vec( fX (je ))
∂θ
∂vec( fX (je ))
∂θ
(cid:6)
)
(cid:6)
)
(
(
The formal version of theorem 1 is presented in section 2.4 and is proved
in appendix A in the supplementary information that relies on the addi-
tional previous works of Clanuwat et al. (2019), Krizhevsky and Hinton
(2009), Mityagin (2015), Netzer et al. (2011), Paszke et al. (2019un, 2019b),
and Poggio et al. (2017). Before proving the statement, we first examine the
meaning and implications of our results through illustrative examples in
sections 2.2 et 2.3.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
999
2.2 Illustrative Examples in Experiments. Theorem 1 suggests that
data-architecture alignment condition vec(Oui(cid:3)) ∈ Col(
) has the abil-
ity to distinguish the success and failure cases, even when the minimum
is zero for all t ≥ 0. Dans ce
eigenvalue of the matrix
section, we conduct experiments to further verify and deepen this theoret-
ical understanding.
∂vec( fX (θ t ))
∂θ t
∂vec( fX (θ t ))
∂θ t
∂vec( fX (θ t ))
∂θ t
(cid:6)
)
(
We employ a fully connected network having four layers with 300 nouveau-
rons per hidden layer, and a convolutional network, LeNet (LeCun et al.,
1998), with five layers. For the fully connected network, we use the two-
moons data set (Pedregosa et al., 2011) and a sine wave data set. To create
the sine wave data set, we randomly generated the input xi from the uni-
form distribution on the interval [−1, 1] and set yi
= 1{sin(20xi) < 0} ∈ R
for all i ∈ [n] with n = 100. For the convolutional network, we use the Se-
meion data set (Srl & Brescia, 1994) and a random data set. The random
data set was created by randomly generating each pixel of the input im-
∈ R16×16×1 from the standard normal distribution and by sampling
age xi
yi uniformly from {0, 1} for all i ∈ [n] with n = 1000. We set the activation
functions of all layers to be softplus ¯σ (z) = ln(1 + exp(ςz))/ς with ς = 100,
which approximately behaves as the ReLU activation as shown in appendix
C in the supplementary information. See appendix B in the supplementary
information for more details of the experimental settings.
The results of the experiments are presented in Figure 1. In each panel
of the figure, the training errors and the values of QT are plotted over time
T. Here, QT counts the number of Y(cid:3) not satisfying the condition vec(Y(cid:3)) ∈
Col(
) during t ∈ {0, 1, . . . , T} and is defined by
∂vec( fX (θ t ))
∂θ t
QT =
T(cid:2)
t=0
(cid:9)
1
vec(Y(cid:3)) /∈ Col
(cid:10)
∂vec( fX (θ t ))
∂θ t
(cid:11)(cid:12)
.
(2.5)
Figure 1a shows the results for the fully connected network. For the two-
moons data set, the network achieved the zero training error with QT = 0
for all T (i.e., vec(Y(cid:3)) ∈ Col(
) for all T). For the sine wave data
set, it obtained high training errors with QT = T for all T (i.e., vec(Y(cid:3)) /∈
) for all T). This is consistent with our theory. Our theory ex-
Col(
plains that what makes a data set easy to be fitted or not is whether the
condition vec(Y(cid:3)) ∈ Col(
) is satisfied or not.
∂vec( fX (θ T ))
∂θ T
∂vec( fX (θ T ))
∂θ T
∂vec( fX (θ t ))
∂θ t
Figures 1b and 1c show the results for the convolutional networks with
two random initial points using two different random seeds. In the fig-
ure panels, we report the training behaviors with different network sizes
mc = 1, 2, and 4; the number of convolutional filters per convolutional layer
is 8 × mc and the number of neurons per fully connected hidden layer is
128 × mc. As can be seen, with the Semeion data set, the networks of all
sizes achieved zero error with QT = 0 for all T. With the random data set,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
a
_
0
1
4
8
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1000
K. Kawaguchi, L. Zhang, and Z. Deng
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
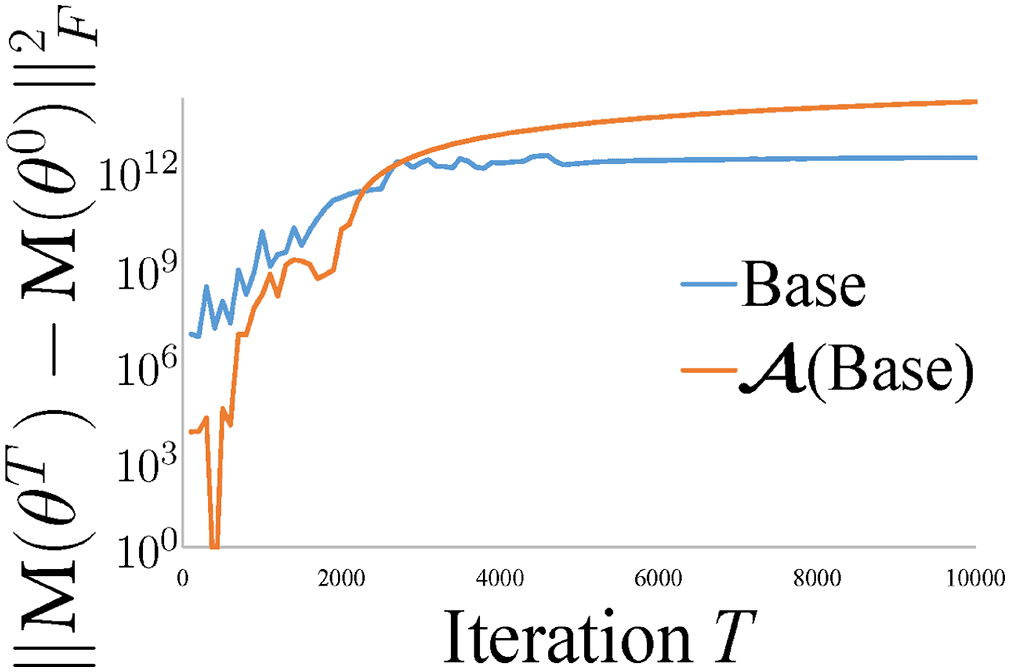
Figure 1: Training error and the value of QT over time steps T. The legend
of panel b is shown in panel c. The value of QT measures the number of Y(cid:3)
not satisfying the condition of vec(Y(cid:3)) ∈ Col(
). This figure validates
our theoretical understanding that the bound on the global optimality gap de-
creases at any iteration when QT does not increase at the iteration—that is,
when the QT value is flat. The minimum eigenvalue of the matrix M(θ t ) =
∂vec( fX (θ ))
)(cid:6) is zero at all iterations in Figures 1b and 1c for all cases
∂θ
with mc
∂vec( fX (θ ))
(
∂θ
= 1.
∂vec( fX (θt ))
∂θt
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
a
_
0
1
4
8
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
the deep networks yielded the zero training error whenever QT is not lin-
early increasing over the time or, equivalently, whenever the condition of
vec(Y(cid:3)) ∈ Col(
) holds sufficiently many steps T. This is consistent
with our theory.
∂vec( fX (θ T ))
∂θ T
Finally, we also confirmed that gradient representation
significantly from the initial one
∂ f (x,θ 0 )
∂θ 0
in our experiments. That is, the
∂ f (x,θ t )
∂θ t
changed
Understanding Nonlinear Representation Learning
1001
Table 1: The Change of the Gradient Representation during Training, (cid:13)M(θ ˆT ) −
∂vec( fX (θ ))
M(θ 0)(cid:13)2
∂θ
)(cid:6) and ˆT Is the Last Time Step.
F, Where M(θ ) := ∂vec( fX (θ ))
∂θ
(
a. Fully-Connected Network
Data Set
Two moons
Sine wave
2.09 × 1011
3.95 × 109
b. Convolutional Network
mc = 4
mc = 2
mc = 1
seed#1
Data Set
Semeion 8.09 × 1012
Random 3.73 × 1012
seed#2
5.19 × 1012
1.64 × 1012
seed#1
9.82 × 1012
3.43 × 107
seed#2
3.97 × 1012
4.86 × 1012
seed#1
2.97 × 1012
1.40 × 107
seed#2
5.41 × 1012
8.57 × 1011
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
values of (cid:13)M(θ T ) − M(θ 0)(cid:13)2
F were significantly large and tended to increase
as T increases, where the matrix M(θ ) ∈ Rnmy×nmy is defined by M(θ ) =
∂vec( fX (θ ))
)(cid:6). Table 1 summarizes the values of (cid:13)M(θ T ) − M(θ 0)(cid:13)2
∂θ
F
∂vec( fX (θ ))
∂θ
(
at the end of the training.
2.3 Implications. In section 2.1.3, we showed that an uncommon model
structure f (x, θ ) = θ 4 − 10θ 2 + 6θ + 100 does not satisfy assumption 1, and
assumption 1 is not required for global convergence if the minimum eigen-
value is nonzero. However, in practice, we typically use machine learning
models that satisfy assumption 1 instead of the model f (x, θ ) = θ 4 − 10θ 2 +
6θ + 100, and the minimum eigenvalue is zero in many cases. In this con-
text, theorem 1 provides the justification for common practice in nonlinear
representation learning. Furthermore, theorem 1i contributes to the litera-
ture by identifying the common model structure assumption (assumption
1) and the data-architecture alignment condition (definition 1) as the novel
and practical conditions to ensure the global convergence even when the
minimum eigenvalue becomes zero. Moreover, theorem 1ii shows that this
condition is not arbitrary in the sense that it is also necessary to obtain the
globally optimal models. Furthermore, the data-architecture alignment con-
dition is strictly more general than the condition of the minimum eigen-
value being nonzero, in the sense that the latter implies the former but not
vice versa.
Our new theoretical understanding based on the data-architecture align-
ment condition can explain and deepen the previously known empirical
observation that increasing network size tends to improve training be-
haviors. Indeed, the size of networks seems to correlate well with the
training error to a certain degree in Figure 1b. However, the size and the
training error do not correlate well in Figure 1c. Our new theoretical under-
standing explains that the training behaviors correlate more directly with
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
a
_
0
1
4
8
3
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1002
K. Kawaguchi, L. Zhang, and Z. Deng
∂vec( fX (θ t ))
∂θ t
the data-architecture alignment condition of vec(Y(cid:3)) ∈ Col(
) in-
stead. The seeming correlation with the network size is indirect and caused
by another correlation between the network size and the condition of
vec(Y(cid:3)) ∈ Col(
)
more likely tends to hold when the network size is larger because the matrix
∂vec( fX (θ t ))
is of size nmy × d where d is the number of parameters: that is, by
∂θ t
) to increase
). That is, the condition of vec(Y(cid:3)) ∈ Col(
increasing d, we can increase the column space Col(
the chance of satisfying the condition of vec(Y(cid:3)) ∈ Col(
∂vec( fX (θ t ))
∂θ t
∂vec( fX (θ t ))
∂θ t
∂vec( fX (θ t ))
∂θ t
∂vec( fX (θ t ))
∂θ t
that
∂vec( fX (θ ))
∂θ
the minimum eigenvalue of
the matrix M(θ t ) =
Note
∂vec( fX (θ ))
)(cid:6) is zero at all iterations in Figures 1b and 1c for
∂θ
all cases of mc = 1. Thus, Figures 1b and 1c also illustrate the fact that while
having the zero minimum eigenvalue of the matrix M(θ t ), the dynamics
can achieve the global convergence under the data-architecture alignment
condition. Moreover, because the multilayer neural network in the lazy
training regime (Kawaguchi & Sun, 2021) achieves zero training errors
for all data sets, Figure 1 additionally illustrates that our theoretical and
empirical results apply to the models outside of the lazy training regime
and can distinguish “good” data sets from “bad” data sets given a learning
algorithm.
).
(
In sum, our new theoretical understanding has the ability to explain
and distinguish the successful case and failure case based on the data-
architecture alignment condition for the common machine learning mod-
els. Because the data-architecture alignment condition is dependent on data
and architecture, theorem 1, along with our experimental results, shows
why and when the global convergence in nonlinear representation learning
is achieved based on the relationship between the data (X, Y) and architec-
ture f . This new understanding is used in section 3 to derive a practical
algorithm and is expected to be a basis for many future algorithms.
2.4 Details and Formalization of Theorem 1. This section presents the
precise mathematical statements that formalize the informal description of
theorem 1. In the following sections, we devide the formal version of theo-
rem 1 into theorem 2, theorem 3, and proposition 1.
2.4.1 Preliminaries. Let (θ t )∞
t=0 be the sequence defined by θ t+1 = θ t −
αt ¯gt with an initial parameter vector θ 0, a learning rate αt, and an update
vector ¯gt. The analysis in this section relies on the following assumption on
the update vector ¯gt:
Assumption 2. There exist ¯c, c > 0 such that c(cid:13)∇L(θ t )(cid:13)2 ≤ ∇L(θ t )
(cid:13) ¯gt(cid:13)2 ≤ ¯c(cid:13)∇L(θ t )(cid:13)2 for any t ≥ 0.
(cid:6) ¯gt and
Assumption 2 is satisfied by using ¯gt = Dt∇L(θ t ), where Dt
positive-definite symmetric matrix with eigenvalues in the interval [c,
is any
√
¯c].
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
1003
If we set Dt = I, we have gradient descent, and assumption 2 is satisfied
with c = ¯c = 1. This section also uses the standard assumption of differen-
tiability and Lipschitz continuity:
Assumption 3. For every i ∈ [n], the function (cid:3)
tiable and convex, the map fi : je (cid:8)→ f (xi
)(cid:13) ≤ L(cid:13)θ − θ (cid:16)(cid:13) for all θ , je (cid:16)
∇L(je (cid:16)
je : q (cid:8)→ (cid:3)(q, yi) is differen-
, je ) is differentiable, et (cid:13)∇L(je ) −
in the domain of L for some L ≥ 0.
The assumptions on the loss function in assumption 3 are satisfied by
using standard loss functions, including the squared loss, logistic loss, et
cross-entropy loss. Although the objective function L is nonconvex and
non-invex, the function q (cid:8)→ (cid:3)(q, yi) is typically convex.
, y∗
For any matrix Y∗ = (y∗
2
1
(cid:6) ∈ Rn×my , we define
, . . . , y∗
n)
L∗
∗
(Oui
) = 1
n
n(cid:2)
je = 1
(cid:3) (oui
∗
je
, yi) .
(2.6)
Par exemple, for the squared loss (cid:3), the value of L∗
minimum value of L as
(Oui(cid:3)) is at most the global
(2.7)
L∗
(Oui(cid:3)) ≤ L(je ), ∀θ ∈ Rd,
(cid:3)
(cid:13)2
2
n
je = 1
− yi
(Oui(cid:3)) = 1
n
∂vec( fX (je ))
∂θ
since L∗
(cid:13)yi
= 0 ≤ L(je ) ∀θ ∈ Rd. This letter also uses
the notation of [k] = {1, 2, . . . , k} for any k ∈ N+
et (cid:13) · (cid:13) = (cid:13) · (cid:13)
2 (Euclidean
norm). Enfin, we note that for any η ∈ R, the condition of vec(Oui(cid:3)) ∈
) is necessary to learn a near-global optimal model fX (je ) =
Col(
ηY(cid:3):
Proposition 1. Suppose assumption 1 holds. If vec(Oui(cid:3)) /∈ Col(
fX (je ) (cid:19)= ηY(cid:3) for any η ∈ R.
Proof. All proofs of this letter are presented in appendix A in the supple-
(cid:2)
mentary information.
∂vec( fX (je ))
∂θ
), alors
(ηY∗
) for any Y∗
such that vec(Y∗
2.4.2 Global Optimality at the Limit Point. The following theorem shows
that every limit point ˆθ of the sequence (θ t )t achieves a loss value L( ˆθ ) Non
worse than infη∈R L∗
) pour
all t ∈ [τ, ∞) with some τ ≥ 0:
Theorem 2. Suppose assumptions 1 à 3 hold. Assume that the learning rate se-
quence (αt )t satisfies either (je) (cid:14) ≤ αt ≤ c(2−(cid:14))
for some (cid:14) > 0 ou (ii) limt→∞ αt =
αt = ∞. Then for any Y∗ ∈ Rn×my , if there exists τ ≥ 0 such that
0 et
vec(Y∗
) for all t ∈ [τ, ∞), every limit point ˆθ of the sequence
(θ t )t satisfies
(cid:3)∞
t=0
) ∈ Col(
∂vec( fX (θ t ))
∂θ t
∂vec( fX (θ t ))
∂θ t
) ∈ Col(
L ¯c
L( ˆθ ) ≤ L∗
(ηY
∗
), ∀η ∈ R.
(2.8)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1004
K. Kawaguchi, L. Zhang, and Z. Deng
Par exemple, for the squared loss (cid:3)(q, oui) = (cid:13)q − y(cid:13)2, theorem 2 implique
that every limit point ˆθ of the sequence (θ t )t is a global minimum as
L( ˆθ ) ≤ L(je ), ∀θ ∈ Rd,
(2.9)
if vec(Oui(cid:3)) ∈ Col(
L( ˆθ ) ≤ L∗
∂vec( fX (θ t ))
∂θ t
) for t ∈ [τ, ∞) with some τ ≥ 0. This is because
(Oui(cid:3)) ≤ L(je ) ∀θ ∈ Rd from theorem 2 and equation 2.7.
In practice, one can easily satisfy all the assumptions in theorem 2 ex-
cept for the condition that vec(Y∗
) for all t ∈ [τ, ∞). Ac-
) ∈ Col(
cordingly, we now weaken this condition by analyzing optimality at each
iteration so that the condition is verifiable in experiments.
∂vec( fX (θ t ))
∂θ t
2.4.3 Global Optimality Gap at Each Iteration. The following theorem states
that under standard settings, the sequence (θ t )t∈T converges to a loss value
no worse than infη∈R L∗
) at the rate of O(1/
tel
that vec(Y∗) ∈ Col(
) for t ∈ T :
Theorem 3. Suppose assumptions 1 et 3 hold. Let (αt, ¯gt ) = ( 2un
L
an arbitrary α ∈ (0, 1). Then for any T ⊆ N
) for all t ∈ T , it holds that
Col(
, ∇L(θ t )) avec
0 and Y∗ ∈ Rn×my such that vec(Y∗) ∈
|T |) for any T and Y∗
(ηY∗
∂vec( fX (θ t ))
∂θ t
∂vec( fX (θ t ))
∂θ t
√
L(θ t ) ≤ L∗
(ηY
∗
min
t∈T
) + 1√
|T |
(cid:13)
LζηL(θ t0 )
2un(1 − un)
,
(2.10)
for any η ∈ R, where t0
η)(cid:13)2),
ˆβ(je , η) := η((
je
k for all k ∈ S and ν(je )k
tion 1.
= min{t : t ∈ T }, ζη := 4 maxt∈T max((cid:13)ν(θ t )(cid:13)2, (cid:13) ˆβ(θ t,
∂vec( fX (je ))
=
∂θ
= 0 for all k /∈ S with the set S being defined in assump-
(cid:6) ∂vec( fX (je ))
)
∂θ
), and ν(je )k
∂vec( fX (je ))
∂θ
vec(Y∗
)†(
(cid:6)
)
For the squared loss (cid:3), theorem 3 implies the following for any T ≥ 1: pour
any T ⊆ [T] such that vec(Oui(cid:3)) ∈ Col(
∂vec( fX (θ t ))
∂θ t
) for all t ∈ T , we have
min
t∈[T]
L(θ t ) ≤ inf
θ ∈Rd
(cid:14)
L(je ) + Ô(1/
|T |).
This is because L∗
≤ mint∈T L(θ t ) from T ⊆ [T].
(Oui(cid:3)) ≤ infθ ∈Rd L(je ) from equations 2.7 and mint∈[T]
(2.11)
L(θ t )
De la même manière, for the binary and multiclass cross-entropy losses, theorem 3
implies the following for any T ≥ 1: for any T ⊆ [T] such that vec(Oui(cid:3)) ∈
Col(
) for all t ∈ T , we have that for any η ∈ R,
∂vec( fX (θ t ))
∂θ t
L(θ t ) ≤ L∗
min
t∈[T]
(cid:14)
(ηY(cid:3)) + Ô(η2/
|T |).
(2.12)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
1005
Given any desired (cid:14) > 0, since L∗
(ηY(cid:3)) → 0 as η → ∞, setting η to be suf-
ficiently large obtains the desired (cid:14) value as mint∈T L(θ t ) ≤ (cid:14) in equation
2.12 comme
|T | → ∞.
√
3 Application to the Design of Training Framework
The results in the previous section show that the bound on the global
optimality gap decreases per iteration whenever the data-architecture
alignment condition holds. Using this theoretical understanding, in this
section, we propose a new training framework with prior guarantees while
learning hierarchical nonlinear representations without assuming the data-
architecture alignment condition. Par conséquent, we made significant improve-
ments over the most closely related study on global convergence guarantees
(Kawaguchi & Sun, 2021). En particulier, whereas the related study requires a
wide layer with a width larger than n, our results reduce the requirement to
n. Par exemple, the MNIST data set has
a layer with a width larger than
n = 60,000 and hence previous studies require 60,000 neurons at a layer,
60,000 ≈ 245 neurons at a layer. Our require-
whereas we only require
ment is consistent and satisfied by the models used in practice that typically
have from 256 à 1024 neurons for some layers.
√
√
We begin in section 3.1 with additional notations and then present the
training framework in section 3.2 and convergence analysis in section 3.3.
We conclude in section 3.4 by providing empirical evidence to support our
théorie.
(je)
3.1 Additional Notations. We denote by θ
∈ Rdl the vector of all the
trainable parameters at the lth layer for l = 1, . . . , H where H is the depth or
the number of trainable layers (c'est à dire., one plus the number of hidden layers).
C'est, the Hth layer is the last layer containing the trainable parameter
(H) at the last layer. For any pair (je, je(cid:16)) such that 1 ≤ l ≤ l(cid:16) ≤ H, nous
vector θ
define θ
(je:je(cid:16) )
(je)
if l = l(cid:16)
. We consider a family of training algorithms that update the param-
eter vector θ as follows: for each l = 1, . . . , H,
(cid:16) —for example, je
(je(cid:16) )](cid:6) ∈ Rdl:je
= θ and θ
= [je (cid:6)
(je)
, . . . , je (cid:6)
= θ
(je:je(cid:16) )
(1:H)
θ t+1
(je)
= θ t
(je)
− gt
(je)
,
gt
(je)
∼ G
(je)(θ t, t),
(3.1)
(je) outputs a distribution over the vector gt
where the function G
(je) and dif-
fers for different training algorithms. Par exemple, pour (minibatch) stochas-
tic gradient descent (SGD), gt
(je) represents a product of a learning rate
(je) at the time t. We define G =
and a stochastic gradient with respect to θ
(G
(H)) to represent a training algorithm.
, . . . , G
For an arbitrary matrix M ∈ Rm×m(cid:16)
tor in Rm, Mi∗ be its ith row vector in Rm(cid:16)
We define M ◦ M(cid:16)
, we let M∗ j be its jth column vec-
, and rank(M.) be its matrix rank.
to be the Hadamard product of any matrices M and M(cid:16)
.
(1)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1006
K. Kawaguchi, L. Zhang, and Z. Deng
For any vector v ∈ Rm, we let diag(v ) ∈ Rm×m be the diagonal matrix with
diag(v )ii
i for i ∈ [m]. We denote by Im the m × m identity matrix.
= v
3.2 Exploration-Exploitation Wrapper. Dans cette section, we introduce the
exploration-exploitation (EE) wrapper A. The EE wrapper A is not a stand-
alone training algorithm. Plutôt, it takes any training algorithm G as its
input and runs the algorithm G in a particular way to guarantee global con-
vergence. We note that the exploitation phase in the EE wrapper does not
optimize the last layer; instead, it optimizes hidden layers, whereas the ex-
ploration phase optimizes all layers. The EE wrapper allows us to learn the
representation
that differs significantly from the initial representa-
∂ f (X,je 0 )
∂θ 0 without making assumptions on the minimum eigenvalue of
the matrix
by leveraging the data-architecture align-
ment condition. The data-architecture alignment condition is ensured by
the safe-exploration condition (defined in section 3.3.1), which is time inde-
pendent and holds in practical common architectures (as demonstrated in
section 3.4).
∂vec( fX (je ))
∂θ
∂vec( fX (je ))
∂θ
∂ f (X,θ t )
∂θ t
tion
(cid:6)
)
(
3.2.1 Main Mechanisms. Algorithm 1 outlines the EE wrapper A. During
the exploration phase in lines 3 à 7 of algorithm 1, the EE wrapper A freely
explores hierarchical nonlinear representations to be learned without any
restrictions. Alors, during the exploitation phase in lines 8 à 12, it starts
exploiting the current knowledge to ensure vec(Oui(cid:3)) ∈ Col(
) for all
t to guarantee global convergence. The value of τ is the hyperparameter
that controls the time when it transitions from the exploration phase to the
exploitation phase.
∂vec( fX (θ t ))
∂θ t
In the exploitation phase, the wrapper A only optimizes the parame-
ter vector θ t
(H−1) à la (H − 1)th hidden layer, instead of the parameter
vector θ t
(H) at the last layer or the Hth layer. Malgré cela, the EE wrap-
per A is proved to converge to global minima of all layers in Rd. The ex-
ploitation phase still allows us to significantly change the representations
as M(θ t ) (cid:19)≈ M(θ τ
) for t > τ . This is because we optimize the hidden layers
instead of the last layer without any significant overparameterizations.
The exploitation phase uses an arbitrary optimizer ˜G with the update
(H−1)(θ t, t) with ˜gt = αt ˆgt ∈ RdH−1 . During the two phases, nous
vector ˜gt ∼ ˜G
can use the same optimizers (par exemple., SGD for both G and ˜G) or different opti-
mizers (par exemple., SGD for G and L-BFGS for ˜G).
3.2.2 Model Modification. This section defines the details of the model
modification at line 2 of algorithm 1. Given any base network ¯f , le
wrapper A first checks whether the last two layers of the given network
¯f are fully connected. If not, one or two fully connected last layers are
added such that the output of the network ¯f can be written by ¯f (X, ¯θ ) =
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
1007
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
(1:H−2))). Ici, z(X, je
¯W (H) ¯σ ( ¯W (H−1)z(X, je
(1:H−2)) is the output of the (H − 2)ème
layer, and the function z is arbitrary and can represent various deep net-
travaux. De plus, ¯σ is a nonlinear activation function, and ¯W (H−1) and ¯W (H)
are the weight matrices of the last two layers. The wrapper A then modi-
fies these last two layers as follows. In the case of my = 1, the model ¯f is
modified to
F (X, je ) = W (H)p (W (H−1), z(X, je
(1:H−2))),
(3.2)
where W (H−1) ∈ RmH ×mH−1 and W (H) ∈ Rmy×mH are the weight matrices of the
last two layers. The nonlinear activation σ is defined by σ (q, q(cid:16)
) ◦
(qq(cid:16)
), where ˜σ is some nonlinear function. Par exemple, we can set ˜σ (q) =
q (sigmoid) with any hyperparameter ς (cid:16) > 0, for which it holds that as
1
1+e−ς (cid:16)
ς (cid:16) → ∞,
) = ˜σ (qq(cid:16)
F (X, je ) → W (H)relu(W (H−1)z(X, je
(1:H−2))).
(3.3)
1008
K. Kawaguchi, L. Zhang, and Z. Deng
We generalize equation 3.2 to the case of my ≥ 2 comme
F (X, je ) j
= W (H)
j∗ σ
j(W (H−1, j), z(X, je
(1:H−2))),
(3.4)
j
= σ until line 10. At line 10, the wrapper A replaces σ
R.( j) (q, q(cid:16)
for j ∈ [mon] where W (H−1, j) ∈ RmH ×mH−1 is the weight matrix at the (H − 1)ème
layer and σ
j by
p
=
R.( j) where σ
(W (H−1, j))(cid:6). To consider the bias term, we include the constant neuron to the
(1:H−2))(cid:6), 1](cid:6) ∈ RmH−1 ,
output of the (H − 1)th layer as z(X, je
where ¯z(X, je
(1:H−2)) is the output without the constant neuron.
) with R( j) = θ τ
(1:H−2)) = [ ¯z(X, je
(H−1, j) and θ
) = ˜σ (R.( j)q(cid:16)
) ◦ (qq(cid:16)
(H−1, j)
3.3 Convergence Analysis. Dans cette section, we establish global conver-
gence of the EE wrapper A without using assumptions from the previous
section. Let τ be an arbitrary positive integer and ε be an arbitrary posi-
tive real number. Let (θ t )
t=0 be a sequence generated by the EE wrapper A.
(H)) and B ¯(cid:14) = minθ
−
We define ˆL(je
(1:H−2)
θ τ
(H−1)), ¯(cid:14)) for any ¯(cid:14) ≥ 0.
(H−1)
(H−1)) = L(θ τ
¯(cid:14) = argminθ
, θ τ
, je
(H−1)
maximum( ˆL(je
(cid:13) où (cid:19)
(H−1)
∈(cid:19) ¯(cid:14)
(cid:13)je
(H−1)
∞
(H−1)
3.3.1 Safe-Exploration Condition. The mathematical analysis in this sec-
tion relies on the safe-exploration condition, which allows us to safely
explore deep nonlinear representations in the exploration phase with-
out getting stuck in the states of vec(Oui(cid:3)) /∈ Col(
). The safe-
exploration condition is verifiable, time-independent, data-dependent, et
architecture-dependent. The verifiability and time independence make the
assumption strong enough to provide prior guarantees before training. Le
data dependence and architecture dependence make the assumption weak
enough to be applicable for a wide range of practical settings.
∂vec( fX (θ t ))
∂θ t
For any q ∈ RmH−1
×mH , we define the matrix-valued function φ(q, je
(1:H−2))
∈ Rn×mH mH−1 by
⎡
⎢
⎢
⎣
φ(q, je
(1:H−2)) =
˜σ (z(cid:6)
˜σ (z(cid:6)
1
1 q∗1)z(cid:6)
…
n q∗1)z(cid:6)
n
· · ·
. . .
· · ·
⎤
⎥
⎥
⎦ ,
˜σ (z(cid:6)
˜σ (z(cid:6)
1
1 q∗mH )z(cid:6)
…
n q∗mH )z(cid:6)
n
, je
= z(xi
(1:H−2)) ∈ RmH−1 and ˜σ (z(cid:6)
∈ R1×mH−1 for all i ∈ [n] et
where zi
k ∈ [mH]. Using this function, the safe exploration condition is formally
stated as:
Assumption 4 (Safe-Exploration Condition). There exist a q ∈ RmH−1
and a θ
∈ Rd1:H−2 such that rank(φ(q, je
i q∗k)z(cid:6)
(1:H−2))) = n.
(1:H−2)
×mH
je
The safe-exploration condition asks for only the existence of one param-
(1:H−2))) = n. Il
eter vector in the network architecture such that rank(φ(q, je
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
1009
is not about the training trajectory (θ t )t. Since the matrix φ(q, je
(1:H−2)) est
of size n × mHmH−1, the safe-exploration condition does not require any
wide layer of size mH ≥ n or mH−1
≥ n. Plutôt, it requires a layer of size
≥ n. This is a significant improvement over the most closely re-
mHmH−1
lated study (Kawaguchi & Sun, 2021) where the wide layer of size mH ≥
≥ n does not imply the safe-
n was required. Note that having mHmH−1
≥ n is a necessary condition to sat-
exploration condition. Plutôt, mHmH−1
isfy the safe-exploration condition, whereas mH ≥ n or mH−1
≥ n was a nec-
essary condition to satisfy assumptions in previous papers, including the
most closely related study (Kawaguchi & Sun, 2021). The safe-exploration
condition is verified in experiments in section 3.4.
3.3.2 Additional Assumptions. We also use the following assumptions:
je(q) − ∇(cid:3)
Assumption 5. For any i ∈ [n], the function (cid:3)
et (cid:13)∇(cid:3)
Assumption 6. For each i ∈ [n], the functions θ
q (cid:8)→ ˜σ (q) are real analytic.
)(cid:13) ≤ L(cid:3)(cid:13)q − q(cid:16)(cid:13) for all q, q(cid:16) ∈ R.
je(q(cid:16)
je : q (cid:8)→ (cid:3)(q, yi) is differentiable,
(1:H−2)
(cid:8)→ z(xi
, je
(1:H−2)) et
dy
(cid:3)
(cid:3)
k=1 yk log exp(qk )
(cid:16) exp(qk
Assumption 5 is satisfied by using standard loss functions such
as the squared loss (cid:3)(q, oui) = (cid:13)q − y(cid:13)2 and cross-entropy loss (cid:3)(q, oui) =
−
(cid:16) ) . The assumptions of the invexity and convex-
ity of the function q (cid:8)→ (cid:3)(q, yi) in sections 3.3.3 et 3.3.4 also hold
for these standard loss functions. Using L(cid:3) in assumption 5, we de-
fine ˆL = L(cid:3)
(H, j)) ⊗
n
ImH−1 ](φ(θ τ
(cid:13)Z(cid:13)2, where Z ∈ Rn is defined by Zi
(cid:6)
= (W (H)
j∗ )
= max j∈[mon]
(cid:6)(cid:13) avec θ
(cid:13)[diag(θ τ
(1:H−2))i∗)
(H−1, j)
(H, j)
, θ τ
.
k
Assumption 6 is satisfied by using any analytic activation function
such as sigmoid, hyperbolic tangents, and softplus activations q (cid:8)→ ln(1 +
exp(ςq))/ς with any hyperparameter ς > 0. This is because a composition
of real analytic functions is real analytic, and the following are all real ana-
lytic functions in θ
(1:H−2): the convolution, affine map, average pooling, skip
connection, and batch normalization. Donc, the assumptions can be sat-
isfied by using a wide range of machine learning models, including deep
neural networks with convolution, skip connection, and batch normaliza-
tion. De plus, the softplus activation can approximate the ReLU activation
for any desired accuracy, c'est, ln(1 + exp(ςq))/ς → relu(q) as ς → ∞,
where ReLU represents the ReLU activation.
3.3.3 Global Optimality at the Limit Point. The following theorem proves
the global optimality at limit points of the EE wrapper with a wide range
of optimizers, including gradient descent and modified Newton methods:
Theorem 4. Suppose assumptions 4 à 6 hold and that the function (cid:3)
je : q (cid:8)→
(cid:3)(q, yi) is invex for any i ∈ [n]. Assume that there exist ¯c, c > 0 such that
(H−1))(cid:13)2 for any t ≥ τ .
c(cid:13)∇ ˆL(θ t
(cid:6) ˆgt and (cid:13) ˆgt(cid:13)2 ≤ ¯c(cid:13)∇ ˆL(θ t
(H−1))(cid:13)2 ≤ ∇ ˆL(θ t
(H−1))
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1010
K. Kawaguchi, L. Zhang, and Z. Deng
Assume that the learning rate sequence (αt )t≥τ satisfies either (je) (cid:14) ≤ αt ≤ c(2−(cid:14))
ˆL ¯c
for some (cid:14) > 0 ou (ii) limt→∞ αt = 0 et
t=τ αt = ∞. Then with probabil-
ity one, every limit point ˆθ of the sequence (θ t )t is a global minimum of L as
L( ˆθ ) ≤ L(je ) for all θ ∈ Rd.
(cid:3)∞
3.3.4 Global Optimality Gap at Each Iteration. We now present global con-
vergence guarantees of the EE wrapper A with gradient decent and SGD:
Theorem 5. Suppose assumptions 4 à 6 hold and that the function (cid:3)
je : q (cid:8)→
(cid:3)(q, yi) is convex for any i ∈ [n]. Alors, with probability one, the following two
statements hold:
(je) (Gradient descent) if ˆgt = ∇ ˆL(θ t
(H−1)) and αt = 1
ˆL
for t ≥ τ , then for any
¯(cid:14) ≥ 0 and t > τ ,
L(θ t ) ≤ inf
θ ∈Rd
¯(cid:14) ˆL
maximum(L(je ), ¯(cid:14)) + B2
2(t − τ )
.
(ii) (SGD) if E[ ˆgt|θ t] = ∇ ˆL(θ t
(cid:3)∞
t=τ (αt )2 < ∞ and (H−1)) (almost surely) with E[(cid:13) ˆgt(cid:13)2] ≤ G2, and t=τ αt = ∞ for t ≥ τ , then for any ¯(cid:14) ≥ 0 (cid:3)∞ if αt ≥ 0, and t > τ ,
E[L(θ t∗
)] ≤ inf
θ ∈Rd
maximum(L(je ), ¯(cid:14)) + B2
¯(cid:14) + G2
(cid:3)
t
2
(cid:3)
t
k=τ α2
k
k=τ α
k
(3.5)
where t∗ ∈ argmink∈{τ,τ +1,…,t}L(θ k).
√
In theorem 5ii, with αt ∼ O(1/
t), the optimality gap becomes
∗
E[L(θ t
)] − inf
θ ∈Rd
maximum(L(je ), ¯(cid:14)) = ˜O(1/
t).
√
3.4 Experiments. This section presents empirical evidence to support
our theory and what is predicted by a well-known hypothesis. We note
that there is no related work or algorithm that can guarantee global con-
vergence in the setting of our experiments where the model has convolu-
tion, skip connections, and batch normalizations without any wide layer
(of the width larger than n). De plus, unlike any previous studies that pro-
pose new methods, our training framework works by modifying any given
method.
3.4.1 Sine Wave Data Set. We have seen in section 2.2 that gradient de-
scent gets stuck at suboptimal points for the sine wave data set. Using the
same setting as that in section 2.2 with ε = 0.01, τ = 2000, and ˜G = G, nous
confirm in Figure 2 that the EE wrapper A can modify gradient descent to
avoid suboptimal points and converge to global minima as predicted by our
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
1011
Chiffre 2: Training errors for three random trials.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
Chiffre 3: Changes of the representations where M(je ) := ∂vec( fX (je ))
∂θ
∂vec( fX (je ))
∂θ
(
)(cid:6).
théorie. Chiffre 3 shows the value of the change of the gradient representa-
tion, (cid:13)M.(θ T ) − M(je 0)(cid:13)2
F, for each time step T. As can be seen, the values of
(cid:13)M.(θ T ) − M(je 0)(cid:13)2
F are large for both methods. Notably, the EE wrapper A
of the base case significantly increases the value of (cid:13)M.(θ T ) − M(je 0)(cid:13)2
F even
in the exploitation phase after τ = 2000 as we are optimizing the hidden
layer. See appendix B in the supplementary information for more details of
the experiments for the sine wave data set.
3.4.2 Image Data Sets. The standard convolutional ResNet with 18 layers
(Il, Zhang, Ren, & Sun, 2016) is used as the base model ¯f . We use ResNet-
18 for the illustration of our theory because it is used in practice and it has
convolution, skip connections, and batch normalization without any width
larger than the number of data points. This setting is not covered by any of
the previous theories for global convergence. We set the activation to be the
softplus function q (cid:8)→ ln(1 + exp(ςq))/ς with ς = 100 for all layers of the
base ResNet. This approximates the ReLU activation well, as shown in ap-
pendix C in the supplementary information. We employ the cross-entropy
loss and ˜σ (q) = 1
1+e−q . We use a standard algorithm, SGD, with its standard
hyperparameter setting for the training algorithm G with ˜G = G—that is,
−5, the mo-
we let the minibatch size be 64, the weight decay rate be 10
mentum coefficient be 0.9, the learning rate be αt = 0.1, and the last epoch
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1012
K. Kawaguchi, L. Zhang, and Z. Deng
Tableau 2: Verification of the Safe-Exploration Condition (Assumption 4).
Data Set
n
mH−1
MNIST
CIFAR-10
CIFAR-100
Semeion
KMNIST
SVHN
60,000
50,000
50,000
1,000
60,000
73,257
513
513
513
513
513
513
mH
234
195
195
4
234
286
Assumption 4
Verified
Verified
Verified
Verified
Verified
Verified
= (cid:23)2(n/mH−1 )(cid:24) where n is the number of
Note: mH
training data, mH is the width of the last hidden layer,
and mH−1 is the width of the penultimate hidden layer.
0 ˆT were selected from ε ∈ {10
ˆT be 200 (with data augmentation) et 100 (without data augmentation).
−5} et
The hyperparameters ε and τ = τ
τ
∈ {0.4, 0.6, 0.8} by only using training data. C'est, we randomly divided
0
each training data set (100%) into a smaller training data set (80%), and a
validation data set (20%) for a grid search over the hyperparameters. Voir
appendix B in the supplementary information for the results of the grid
search and details of the experimental setting. This standard setting satis-
fies assumptions 5 et 6, leaving assumption 4 to be verified.
−3, 10
Verification of Assumption 4. Tableau 2 summarizes the verification results
of the safe-exploration condition. Because the condition only requires an
existence of a pair (je , q) satisfying the condition, we verified it by using
a randomly sampled q from the standard normal distribution and a θ re-
= 513
turned by a common initialization scheme (He et al., 2015). As mH−1
(512 + the constant neuron for the bias term) for the standard ResNet, nous
set mH = (cid:23)2(n/mH−1)(cid:24) throughout all the experiments with the ResNet. Pour
each data set, the rank condition was verified twice by the two standard
méthodes: one from Press, Teukolsky, Vetterling, and Flannery (2007) et
another from Golub and Van Loan (1996).
Test Performance. One well-known hypothesis is that the success of deep-
learning methods partially comes from its ability to automatically learn
deep nonlinear representations suitable for making accurate predictions
from data (LeCun et al., 2015). As the EE wrapper A keeps this ability of
representation learning, the hypothesis suggests that the test performance
of the EE wrapper A of a standard method is approximately comparable to
that of the standard method. Unlike typical experimental studies, our ob-
jective here is to confirm this prediction instead of showing improvements
over a previous method. We empirically confirmed the prediction in Tables
3 et 4 where the numbers indicate the mean test errors (and standard de-
viations are in parentheses) over five random trials. As expected, the values
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
1013
Tableau 3: Test Error (%): Data Augmentation.
Data Set
Standard
UN(Standard)
MNIST
CIFAR-10
CIFAR-100
Semeion
KMNIST
SVHN
0.40 (0.05)
7.80 (0.50)
32.26 (0.15)
2.59 (0.57)
1.48 (0.07)
4.67 (0.05)
0.30 (0.05)
7.14 (0.12)
28.38 (0.42)
2.56 (0.55)
1.36 (0.11)
4.43 (0.11)
Tableau 4: Test Error (%): No Data Augmentation.
Data Set
Standard
UN(Standard)
MNIST
CIFAR-10
CIFAR-100
0.52 (0.16)
15.15 (0.87)
54.99 (2.29)
0.49 (0.02)
14.56 (0.38)
46.13 (1.80)
Chiffre 4: Training Loss with Data Augmentation.
de (cid:13)M.(θ ˆT ) − M(je 0)(cid:13)2
2 were also large—for example, 4.64 × 1012 for the stan-
dard method and 3.43 × 1012 for wrapper A of the method with the Semeion
data set.
Training Behavior. Chiffre 4 shows that the EE wrapper A can improve
training loss values of the standard SGD algorithm in the exploitation phase
without changing its hyperparameters because ˜G = G in these experiments.
In the figure, the plotted lines indicate the mean values over five random
trials, and the shaded regions show error bars with 1 standard deviation.
Computational Time. The EE wrapper A runs the standard SGD G in the
exploration phase and the SGD ˜G = G only on the subset of the weights
je
(H−1) in the exploitation phase. Ainsi, the computational time of the EE
wrapper A is similar to that of the SGD in the exploration phase, and it
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1014
K. Kawaguchi, L. Zhang, and Z. Deng
Tableau 5: Total Wall-Clock Time in a Local GPU Workstation.
Data Set
Standard
UN(Standard)
Semeion
CIFAR-10
364.60 (0.94)
3616.92 (10.57)
356.82 (0.67)
3604.5 (6.80)
Tableau 6: Test Errors (%) of A(Standard) with ˜G = L-BFGS.
(un) with data augmentation
(b) without data augmentation
τ
0
ε
−3
−5
10
10
0.4
0.6
0.8
0.26
0.37
0.38
0.32
0.37
0.37
τ
0
ε
−3
−5
10
10
0.4
0.6
0.36
0.42
0.43
0.35
0.8
0.42
0.35
tends to be faster than the SGD in the exploitation phase. To confirm this,
we measure computational time with the Semeion and CIFAR-10 data sets
under the same computational resources (par exemple., without running other jobs
in parallel) in a local workstation for each method. The mean wall-clock
temps (in seconds) over five random trials is summarized in Table 5, où
the numbers in parentheses are standard deviations. It shows that the EE
wrapper A is slightly faster than the standard method, as expected.
Effect of Learning Rate and Optimizer. We also conducted experiments on
the effects of learning rates and optimizers using the MNIST data set with
data augmentation. Using the best learning rate from {0.2, 0.1, 0.01, 0.001}
for each method (with ˜G = G = SGD), the mean test errors (%) over five ran-
dom trials were 0.33 (0.03) for the standard base method and 0.27 (0.03) pour
the A wrapper of the standard base method (the numbers in parentheses
are standard deviations). De plus, Tableau 6 reports the preliminary results
on the effect of optimizers with ˜G being set to the limited-memory Broyden–
Fletcher–Goldfarb–Shanno algorithm (L-BFGS) (with G = the standard
SGD). By comparing Tables 3 et 6, we can see that using a different op-
timizer in the exploitation phase can potentially lead to performance im-
provements. A comprehensive study of this phenomenon is left to future
travail.
4 Conclusion
Despite the nonlinearity of the dynamics and the noninvexity of the objec-
tive, we have rigorously proved convergence of training dynamics to global
minima for nonlinear representation learning. Our results apply to a wide
range of machine learning models, allowing both underparameterization
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
1015
and overparameterization. Par exemple, our results are applicable to the
)(cid:6) est
case where the minimum eigenvalue of the matrix
zero for all t ≥ 0. Under the common model structure assumption, models
that cannot achieve zero error for all data sets (except some “good” data
sets) are shown to achieve global optimality with zero error exactly when
the dynamics satisfy the data-architecture alignment condition. Our results
provide guidance for choosing and designing model structure and algo-
rithms via the common model structure assumption and data-architecture
alignment condition.
∂vec( fX (θ t ))
∂θ t
∂vec( fX (θ t ))
∂θ t
(
The key limitation in our analysis is the differentiability of the func-
tion f . For multilayer neural networks, this is satisfied by using stan-
dard activation functions, such as softplus, sigmoid, and hyperbolic tan-
gents. Whereas softplus can approximate ReLU arbitrarily well, the direct
treatment of ReLU in nonlinear representation learning is left to future
travail.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
Our theoretical results and numerical observations uncover novel math-
ematical properties and provide a basis for future work. Par exemple,
we have shown global convergence under the data-architecture alignment
. The EE wrapper A is only one way
condition vec(Oui(cid:3)) ∈ Col
to ensure this condition. There are many other ways to ensure the data-
architecture alignment condition, and each way can result in a new algo-
rithm with guarantees.
(cid:4) ∂vec( fX (θ t ))
∂θ t
(cid:5)
Les références
Bartlett, P.. L., Helmbold, D. P., & Long, P.. M.. (2019). Gradient descent with identity
initialization efficiently learns positive-definite linear transformations by deep
residual networks. Neural Computation, 31(3), 477–502. 10.1162/neco_a_01164,
PubMed: 30645179
Bengio, Y., Courville, UN., & Vincent, P.. (2013). Representation learning: A review and
new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence,
35(8), 1798–1828. 10.1109/TPAMI.2013.50, PubMed: 23787338
Bengio, Y., Lamblin, P., Popovici, D., & Larochelle, H. (2007). Greedy layerwise train-
ing of deep networks. In B. Schölkopf, J.. Platt, & T. Hoffman (Éd.), Advances in
neural information processing systems, 19 (p. 153). Red Hook. New York: Curran.
Bordes, UN., Glorot, X., Weston, J., & Bengio, Oui. (2012). Joint learning of words and
meaning representations for open-text semantic parsing. In Proceedings of the
15th International Conference on Artificial Intelligence and Statistics, 22 (pp. 127–
135).
Ciregan, D., Meier, U., & Schmidhuber, J.. (2012). Multi-column deep neural networks
for image classification. In Proceedings of the 2012 IEEE Conference on Computer Vi-
sion and Pattern Recognition (pp. 3642–3649). Piscataway, New Jersey: IEEE.
Clanuwat, T., Bober-Irizar, M., Kitamoto, UN., Lamb, UN., Yamamoto, K., & Ha, D.
(2019). Deep learning for classical Japanese literature. In NeurIPS Creativity Work-
shop 2019.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1016
K. Kawaguchi, L. Zhang, and Z. Deng
Dahl, G., Ranzato, M., Mohamed, A.-r., & Hinton, G. E. (2010). Phone recogni-
tion with the mean-covariance restricted Boltzmann machine. In J. Lafferty, C.
Williams, J.. Shawe-Taylor, R.. Zemel, & UN. Culotta (Éd.), Advances in neural infor-
mation processing systems, 23 (pp. 469–477). Red Hook, New York: Curran.
Dahl, G. E., Yu, D., Deng, L., & Acero, UN. (2011). Context-dependent pre-trained deep
neural networks for large-vocabulary speech recognition. IEEE Transactions on
Audio, Speech, and Language Processing, 20(1), 30–42. 10.1109/TASL.2011.2134090
Deng, L., Seltzer, M.. L., Yu, D., Acero, UN., Mohamed, A.-r., & Hinton, G. (2010). Binary
coding of speech spectrograms using a deep auto-encoder. In Proceedings of the
Eleventh Annual Conference of the International Speech Communication Association.
Red Hook, New York: Curran.
Dong, C., Loy, C. C., Il, K., & Tang, X. (2014). Learning a deep convolutional net-
work for image super-resolution. In Proceedings of the European Conference on Com-
puter Vision (pp. 184–199). Berlin: Springer.
Gatys, L. UN., Ecker, UN. S., & Bethge, M.. (2016). Image style transfer using convolu-
tional neural networks. In Proceedings of the IEEE Conference on Computer Vision
and Pattern Recognition (pp. 2414–2423). Piscataway, New Jersey: IEEE.
Glorot, X., Bordes, UN., & Bengio, Oui. (2011). Domain adaptation for large-scale senti-
ment classification: A deep learning approach. In Proceedings of the International
Conference on Machine Learning. New York: ACM.
Golub, G. H., & Van Loan, C. F. (1996). Matrix computations. Baltimore, MARYLAND: Johns
Hopkins University Press.
Il, K., Zhang, X., Ren, S., & Sun, J.. (2015). Delving deep into rectifiers: Surpassing
human-level performance on ImageNet classification. In Proceedings of the IEEE
International Conference on Computer Vision (pp. 1026–1034). Piscataway, New Jersey: IEEE.
Il, K., Zhang, X., Ren, S., & Sun, J.. (2016). Identity mappings in deep residual net-
travaux. In Proceedings of the European Conference on Computer Vision (pp. 630–645).
Berlin: Springer.
Hinton, G., Deng, L., Yu, D., Dahl, G. E., Mohamed, A.-r., Jaitly, N., . . . Kingsbury,
B. (2012). Deep neural networks for acoustic modeling in speech recognition: Le
shared views of four research groups. IEEE Signal Processing Magazine, 29(6), 82–
97. 10.1109/MSP.2012.2205597
Hinton, G. E., Osindero, S., & Teh, Y.-W. (2006). A fast learning algorithm for deep
belief nets. Neural Computation, 18(7), 1527–1554. 10.1162/neco.2006.18.7.1527,
PubMed: 16764513
Kawaguchi, K. (2016). Deep learning without poor local minima. In D. Lee, M..
Sugiyama, U. Luxburg, je. Guyon, & R.. Garnett (Éd.), Advances in neural infor-
mation processing systems, 29 (pp. 586–594). Red Hook, New York: Curran.
Kawaguchi, K. (2021). On the theory of implicit deep learning: Global conver-
gence with implicit layers. In Proceedings of the International Conference on Learning
Representations.
Kawaguchi, K., Kaelbling, L. P., & Lozano-Pérez, T. (2015). Bayesian optimization
with exponential convergence. In C. Cortes, N. Lawrence, D. Lee, M.. Sugiyama,
& R.. Garnett (Éd.), Advances in neural information processing systems, 28 (pp. 2809–
2817). Red Hook. New York: Curran.
Kawaguchi, K., Maruyama, Y., & Zheng, X. (2016). Global continuous optimization
with error bound and fast convergence. Journal of Artificial Intelligence Research,
56, 153–195. 10.1613/jair.4742
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Understanding Nonlinear Representation Learning
1017
Kawaguchi, K., & Sun, Q. (2021). A recipe for global convergence guarantee in deep
neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, 35
(pp. 8074–8082). Palo Alto, Californie: AAAI.
Krizhevsky, UN., & Hinton, G. (2009). Learning multiple layers of features from tiny images
(Technical report). Citeseer.
Krizhevsky, UN., Sutskever, JE., & Hinton, G. E. (2012). ImageNet classification with
deep convolutional neural networks. In F. Pereira, C. J.. C. Burges, L. Bottou, &
K. Q. Weinberger (Éd.), Advances in neural information processing systems, 25 (pp.
1097–1105). Red Hook. New York: Curran.
Laurent, T., & Brecht, J.. (2018). Deep linear networks with arbitrary loss: All local
minima are global. In Proceedings of the International Conference on Machine Learning
(pp. 2902–2907).
Le, H.-S., Oparin, JE., Allauzen, UN., Gauvain, J.-L., & Yvon, F. (2012). Structured output
layer neural network language models for speech recognition. IEEE Transactions
on Audio, Speech, and Language Processing, 21(1), 197–206.
LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–444.
10.1038/nature14539, PubMed: 26017442
LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P.. (1998). Gradient-based learning
applied to document recognition. In Proceedings of the IEEE, 86(11), 2278–2324.
10.1109/5.726791
Luan, F., Paris, S., Shechtman, E., & Bala, K. (2017). Deep photo style transfer. Dans
Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp.
4990–4998). Piscataway, New Jersey: IEEE.
Mityagin, B. (2015). The zero set of a real analytic function. arXiv:1512.07276.
Mohamed, A.-r., Dahl, G. E., & Hinton, G. (2011). Acoustic modeling using deep
belief networks. IEEE Transactions on Audio, Speech, and Language Processing, 20(1),
14–22. 10.1109/TASL.2011.2109382
Netzer, Y., Wang, T., Coates, UN., Bissacco, UN., Wu, B., & Ng, UN. Oui. (2011). Reading
digits in natural images with unsupervised feature learning. In NIPS Workshop
on Deep Learning and Unsupervised Feature Learning.
Paszke, UN., Gross, S., Massa, F., Lerer, UN., Bradbury, J., Chanan, G., . . . Chintala, S.
(2019un). Pytorch: An imperative style, high-performance deep learning library. Dans
H. Wallach, H. Larochelle, UN. Beygelzimer, F. d’Alché-Buc, E. Fox, & R.. Garnett
(Éd.), Advances in neural information processing systems, 32 (pp. 8026–8037). Red
Hook. New York: Curran.
Paszke, UN., Gross, S., Massa, F., Lerer, UN., Bradbury, J., Chanan, G., . . . Chintala, S.
(2019b). Pytorch: An imperative style, high-performance deep learning library. Dans
H. Wallach, H. Larochelle, UN. Beygelzimer, F. d’Alché-Buc, E. Fox, & R.. Garnett
(Éd.), Advances in neural information processing systems, 32 (pp. 8024–8035). Red
Hook. New York: Curran.
Pedregosa, F., Varoquaux, G., Gramfort, UN., Michel, V., Thirion, B., Grisel, . . . Duches-
nay, E., (2011). Scikit-learn: Machine learning in Python. Journal of Machine Learn-
ing Research, 12, 2825–2830.
Poggio, T., Kawaguchi, K., Liao, Q., Miranda, B., Rosasco, L., Boix, X., Hidary, J., &
Mhaskar, H. (2017). Theory of deep learning III: Explaining the non-overfitting puzzle.
arXiv:1801.00173.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1018
K. Kawaguchi, L. Zhang, and Z. Deng
Presse, W. H., Teukolsky, S. UN., Vetterling, W. T., & Flannery, B. P.. (2007). Numerical
recipes: The art of scientific computing. (3rd ed.). Cambridge: L'université de Cambridge
Presse.
Rifai, S., Dauphin, Oui. N., Vincent, P., Bengio, Y., & Muller, X. (2011). The manifold tan-
gent classifier. In J. Shawe-Taylor, R.. Zemel, P.. Bartlett, F. Pereira, & K. Q. Wein-
berger (Éd.), Advances in neural information processing systems, 24 (pp. 2294–2302).
Red Hook. New York: Curran.
Saxe, UN. M., McClelland, J.. L., & Ganguli, S. (2014). Exact solutions to the nonlinear
dynamics of learning in deep linear neural networks. In Proceedings of the Inter-
national Conference on Learning Representations.
Schwenk, H., Rousseau, UN., & Attik, M.. (2012). Large, pruned or continuous space
language models on a GPU for statistical machine translation. In Proceedings of
the NAACL-HLT 2012 Workshop: Will We Ever Really Replace the N-gram Model? Sur
the Future of Language Modeling for HLT (pp. 11–19). Stroudsburg, Pennsylvanie: Association
for Computational Linguistics.
Seide, F., Li, G., & Yu, D. (2011). Conversational speech transcription using context-
dependent deep neural networks. In Proceedings of the Twelfth Annual Conference
of the International Speech Communication Association. New York: ACM.
Socher, R., Huang, E. H., Pennington, J., Ng, UN. Y., & Manning, C. D. (2011). Dy-
namic pooling and unfolding recursive autoencoders for paraphrase detection.
In J. Shawe-Taylor, R.. Zemel, P.. Bartlett, F. Pereira, & K. Q. Weinberger (Éd.),
Advances in neural information processing systems, 24 (pp. 801–809). Red Hook, New York:
Curran.
Socher, R., Pennington, J., Huang, E. H., Ng, UN. Y., & Manning, C. D. (2011). Semi-
supervised recursive autoencoders for predicting sentiment distributions. En Pro-
ceedings of the 2011 Conference on Empirical Methods in Natural Language Processing
(pp. 151–161). Stroudsburg, Pennsylvanie: Association for Computational Linguistics.
Srl, B. T., & Brescia, je. (1994). Semeion handwritten digit data set. Rome, Italy: Semeion
Research Center of Sciences of Communication.
Tourneur, C. R., Fuggetta, UN., Lavazza, L., & Loup, UN. L. (1999). A conceptual ba-
sis for feature engineering. Journal of Systems and Software, 49(1), 3–15. 10.1016/
S0164-1212(99)00062-X
Xu, K., Zhang, M., Jegelka, S., & Kawaguchi, K. (2021). Optimization of graph neural
réseaux: Implicit acceleration by skip connections and more depth. In Proceed-
ings of the International Conference on Machine Learning.
Zheng, UN., & Casari, UN. (2018). Feature engineering for machine learning: Principles and
techniques for data scientists. Sebastopol, Californie: O’Reilly Media.
Zou, D., Long, P.. M., & Gu, Q. (2020). On the global convergence of training
deep linear ResNets. In Proceedings of the International Conference on Learning
Representations.
Received July 16, 2021; accepted November 24, 2021.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
4
4
9
9
1
2
0
0
3
0
8
5
n
e
c
o
_
un
_
0
1
4
8
3
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3