LETTER
Communicated by Hiroki Mori
Completion of the Infeasible Actions of Others:
Goal Inference by Dynamical Invariant
Takuma Torii
tak.torii@jaist.ac.jp
Shohei Hidaka
shhidaka@jaist.ac.jp
Japan Advanced Institute of Science and Technology,
Nomi, Ishikawa 923-1211, Japan
To help another person, we need to infer his or her goal and intention and
then perform the action that he or she was unable to perform to meet the
intended goal. Dans cette étude, we investigate a computational mechanism
for inferring someone’s intention and goal from that person’s incomplete
action to enable the action to be completed on his or her behalf. As a mini-
mal and idealized motor control task of this type, we analyzed single-link
pendulum control tasks by manipulating the underlying goals. By ana-
lyzing behaviors generated by multiple types of these tasks, we found
that a type of fractal dimension of movements is characteristic of the dif-
ference in the underlying motor controllers, which reflect the difference
in the underlying goals. To test whether an incomplete action can be com-
pleted using this property of the action trajectory, we demonstrated that
the simulated pendulum controller can perform an action in the direc-
tion of the underlying goal by using the fractal dimension as a criterion
for similarity in movements.
1 Introduction: Imitation of Action
As a method of social learning from others, children imitate their parents’
movements in early development (Meltzoff, 1995). Imitation, as a behav-
ioral basis for understanding other’s goals and intentions, is considered a
mechanism for preserving social and cultural knowledge. From the per-
spective of cultural evolution, it plays a key role as a “latchet,” which
preserves the skills and knowledge obtained by our ancestors, prevent-
ing human cultural knowledge from moving backward (Tomasello, 2001).
Teaching techniques that show and mimic a demonstration are commonly
adopted in not only education but also robot learning (Schaal, 1999).
In a typical imitation (Breazeal & Scassellati, 2002), a demonstrator (par exemple.,
parent) shows the imitator (par exemple., enfant) an action with an intention. Dans ce
letter, we employ the definition of intention and action described by Bern-
stein (1996): intention means either motor planning or motor control to
Neural Computation 33, 2996–3026 (2021) © 2021 Massachusetts Institute of Technology.
https://doi.org/10.1162/neco_a_01437
Publié sous Creative Commons
Attribution 4.0 International (CC PAR 4.0) Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Completion of the Infeasible Actions of Others
2997
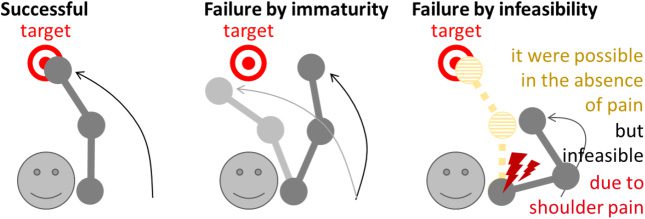
Chiffre 1: Two types of failure illustrated using the reaching task. Successful:
The actor accurately reaches the target. Failure by immaturity: The actor is un-
able to accurately reach the target due to poor control. Failure by infeasibility:
The actor is unable to reach the target due to the presence of pain. The actor
would be able to reach the target if he or she had no pain.
achieve a certain goal, leading to a series of choices or a movement toward
a certain goal, and action means a movement with an intention to achieve
a certain goal. Using these terms, we operationally define the “success” or
optimality of an action as consistency between the generated movement
and the goal of the motor control system, and define the “failure” of an ac-
tion as inconsistency between them. In this definition, we differentiate the
decision to use motor control from actual task performance and define the
success or failure of an action in terms of the former. We further refine our
definition of the failure of actions for two distinct causes below (illustrated
in Figure 1).
Consider two scenarios in which a human demonstration can end in fail-
ure without completing a given task. The actor intended to reach a target
but could not do so because of inaccurate motor control or could not move
her arm freely due to an injury.
Although the action ends in failure in both scenarios, the reasons under-
lying why the actor failed to complete the given task are totally different.
In scenario 1 (voir la figure 1, failure by immaturity), the reason for the failure
is an insufficiency in the accuracy of the actor’s motor control for the given
task, which can likely be overcome with additional motor learning. Comment-
jamais, in scenario 2 (voir la figure 1, failure by infeasibility), the reason for the
failure is temporary or permanent inability to perform an appropriate ac-
tion. By our definition, the action in scenario 2 is considered a hypothetical
success because the actor’s motor control is optimal for the task in question
and her action would be successful if she were not injured. Dans cette étude, nous
refer to the former type of failure as “failure by immaturity” and the latter
as “failure by infeasibility.”
While problems closely related to imitation have been studied in
robotics, the majority of these have been classified as failure by immaturity.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2998
T. Torii and S. Hidaka
Par exemple, Schaal proposed a scheme called learning from demonstra-
tion (LFD; Schaal, 1997, 1999), which aimed to utilize human demon-
stration to initialize and improve a robot controller. Typiquement, combined
with reinforcement learning (Sutton & Barto, 1998; Doya, 1999), a set of
human-demonstrated trajectories is used to provide an initial guess of con-
troller parameters such as the Q function to leverage learning (Schaal, 1997)
and/or update trained controllers based on human performance evaluation
(Argall, Browning, & Veloso, 2007). The idea of LFD has been extended to in-
verse reinforcement learning (IRL; Ng & Russell, 2000; Abbeel & Ng, 2004),
whose aim is to infer the unknown reward function given a task struc-
ture (states, actions, and environment) and a set of trajectories produced
by experts of the given task. The recent development of IRL algorithms
(Ziebart, Maas, Bagnell, & Dey, 2008; Babes-Vroman, Marivate, Subrama-
nian, & Littman, 2011; Ho, Littman, MacGlashan, Cushman, & Austerweil,
2016) has led to great success in such applications.
LFD and IRL studies have typically examined certain tasks under
the failure-by-immaturity class. Both LFD and IRL typically assume that
all given action trajectories are successful or fall under the failure-by-
immaturity class with respect to an unknown but fixed task. Recent studies
(Grollman & Billard, 2011; Shiarlis, Messias, & Whiteson, 2016) on learn-
ing from “failed” demonstrations (reviewed in Zhifei & Joo, 2012) have at-
tempted to utilize nonexpert trajectories in failure-by-immaturity.
In detail, Grollman and Billard (2011) studied how a robot can learn only
from nonexpert demonstrations of failure by immaturity. Namely, they as-
sumed that the provided “failed” demonstrations are distributed around
the “successful” trajectory in space. In this sense, they assumed that the
failed trajectories were similar to the successful ones and on average con-
tained information about the successful ones. A subsequent study found
that a handcrafted reward function for the target task or human perfor-
mance evaluation is required to train an acceptable robot controller (Groll-
man & Billard, 2012). Recently, Shiarlis et al. (2016) studied how nonexpert
demonstrations can be used to improve the performance of existing IRL al-
gorithms. Shiarlis et al. (2016) utilized nonexpert demonstrations of failure
by immaturity as auxiliary information and successful demonstrations to
train IRL systems as a set of positive and negative samples, respectivement,
to behave more like successful ones and less like failed ones. Shiarlis et al.
(2016) showed that successful demonstrations must be provided to facilitate
learning of a controller from demonstrations.
Most previous studies on learning from (failed) demonstrations assumed
that the demonstration was either successful or a case of failure by imma-
turity rather than failure by infeasiblity. Ainsi, the learner or imitator in this
scheme can access an optimal or near-optimal (with noise) demonstration.
Cependant, enfants, even in early development, can go further: they can
learn and complete a failed demonstration by infeasibility, which has no
action at its goal state. Dans ce cas, what the imitator has to infer is the goal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Completion of the Infeasible Actions of Others
2999
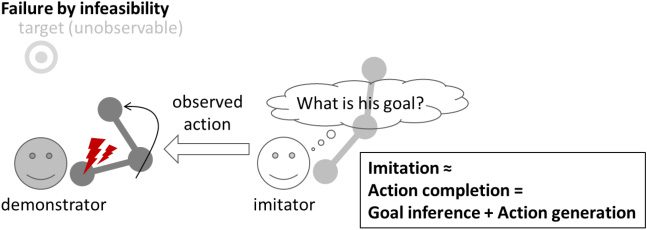
Chiffre 2: Problem setting for this study: goal inference and action generation
from an action that failed by infeasibility. This is a model of a typical situation
in which the demonstrator needs the help of the imitator. To help the demon-
strator, the imitator has to infer the goal of the demonstrator and complete the
demonstrator’s action that failed by infeasibility.
underlying the demonstrator’s nonoptimal movement, in which the goal
state is absent. We think that failure by infeasibility (scénario 2) is needed
to help others—that is, it is necessary to complete an action in the course
of meeting its goal without knowing the goal state. Relevant developmen-
tal studies have shown that two-year-olds can “help” others by completing
their action (Meltzoff, 1995; Warneken & Tomasello, 2006).
Dans cette étude, we examine a computational mechanism for imitation
learning from an action that failed by infeasibility, where the imitator does
not know the demonstrator’s goal or the intention behind his action (comme
illustrated in Figure 2). Given our proposed setting, imitation learning re-
quires solving the following two major classes of problems: (1) identifica-
tion of action features, in which two actions with different intentions can be
discriminated, et (2) completion of observed action, in which an incomplete
part of someone’s action to meet a goal is extrapolated and an appropri-
ate action to meet that goal is performed. The first problem, identification
of features, requires identifying features correlated with the intentional dif-
ference (functional difference in motor control) behind the observed action
rather than features that just describe apparent movements. Inferring an in-
tention or goal behind an action is, cependant, generally an ill-posed problem:
a pair of similar movements can be produced by two very different inten-
tions and/or with two different goals. The second problem, action comple-
tion, requires not only the identification of features but also ensuring that
the imitator’s own action meets an inferred goal for some observed portion
of the demonstrator’s incomplete action that the demonstrator intended but
failed to complete.
In this letter, we aim to address the two problems we posed above in
imitation learning: (1) action recognition and (2) action completion by per-
forming a numerical study on a task that involves controlling a physical
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3000
T. Torii and S. Hidaka
object—a single-stick pendulum. We suppose that this simple control task
is minimally sufficient to capture the essential aspects of goal imitation: comment
one recognizes the intention (motor control) behind a given action and how
one performs the action. The primary objective of this letter is to provide
computational proofs-of-concept for our hypothesis that some degrees-of-
freedom (DoF) is critical for characterizing the underlying goal and inten-
tion of an observed action (described in the next section). Donc, dans le
computer simulation studies in this letter, we suppose that the imitator can
obtain sufficient trajectory data from the demonstrator to learn action fea-
photos. This allows us to explore the primary problem, the principle of the
computational possibility of goal inference, separately from other technical
problems, such as learning from a small training data set. This assumption
may be a limitation of our study and is discussed in section 5.
Although the control task involving a pendulum may be considered
overly simple in its structural complexity compared to the human body,
we think this task has very similar characteristics to the experimental task
reported by Warneken and Tomasello (2006). In their experiment, Warneken
and Tomasello exposed 18-month-old children to an adult (experimenter)’s
goal-failed action and investigated whether these children could infer the
adult’s latent goal, which was not demonstrated, and could help the adult
complete the goal-failed action. The research suggested that children of this
age can infer others’ goals and complete others’ actions.
En principe, children in such an experiment are required to (1) recognize
the adult’s failed goal and/or intention and (2) perform their own action
by controlling their own body to meet the adult’s goal. In this letter, tasks
1 et 2 sont, respectivement, called recognition and completion tasks for goal im-
itation. We illustrate how our simulation framework captures the goal im-
itation behavior and report two simulation studies for our recognition and
completion task.
2 Simulation Design
2.1 A Situation That Requires Recognition and Completion of Other’s
Action. D'abord, we briefly introduce the psychological experiment per-
formed by Warneken and Tomasello (2006) (abbreviated as WT hereafter) comme
a representative situation against which we modeled our theoretical frame-
travail. WT investigated whether children can infer a demonstrator’s goal
and the intention behind their behavior. In the experimental (goal-failed)
condition, called out-of-reach, the demonstrator accidentally dropped a
marker on the floor and was unable to reach for it. In the control (goal-
achieved) condition, the demonstrator intentionally dropped a marker on
the floor. The former condition implicitly calls for the child to help the
demonstrator achieve her unsuccessful intention/goal, namely, to pick
up the marker, while the latter does not. The experimental and control
conditions were designed such that the demonstrator’s apparent bodily
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Completion of the Infeasible Actions of Others
3001
movements were similar (par exemple., both dropped a marker), whereas the un-
derlying intention/goal behind the action was different. WT showed that
the children more frequently showed helping behaviors in the experimental
condition than the control condition.
2.2 A Model of Recognition and Completion of Other’s Action. Dans
this study, we designed a simulation framework to capture the essence of
WT’s experimental design in minimal form. Spécifiquement, we employed a
single-link pendulum as a simplified human body. The imitator (c'est à dire., le
hypothetical child) and the demonstrator must both control a pendulum to
perform an action (c'est à dire., a goal-directed movement). The demonstrator’s goal
is to keep the body of the pendulum at the top-most position of its trajectory
(opposite to gravity) as much as possible subject to given bodily constraints,
a set of physical parameters for the pendulum (par exemple., mass and length). Le
demonstrator’s intention is motor control (or policy in terms of reinforce-
ment learning) of the pendulum, which gives angular acceleration (force)
as a function of the angle and angular velocity of the pendulum. An action
of the demonstrator is to manipulate the movement (trajectory) of the pen-
dulum, as represented by either an orbit of the (X, oui) coordinates or a vector
of the angle and angular velocity, which are generated using a given pair of
initial conditions and the demonstrator’s controller.
We hypothesize that the essential difference between the experimental
(goal-failed) and control (goal-achieved) conditions in the study conducted
by WT is captured by the degree of optimality of the intention and action
with respect to the given goal. Suppose there are controllers A and B, lequel
are optimal for the distinct goals GA and GB, respectivement. If the demon-
strator uses controller A for goal GA, the generated movement would be
optimal and considered a successful action. In contrast, if the demonstrator
uses controller B for goal GA, the generated movement would in general
be suboptimal and would be considered a failed action. We consider the
former case to be analogous to the control (goal-achieved) condition in the
experiment conducted by WT in which a successful action was performed
and did not lead the child to help the demonstrator and the latter to be anal-
ogous to the experimental (goal-failed) condition that led the child to help
the demonstrator.
Accordingly, we designed two tasks for demonstrators with different
combinations of task goals and constraints. We called the first task (UN) le
swing-up task, in which the goal is to keep the mass of the pendulum as
close as possible to the top of the angle space without any obstruction (voir
Figure 3A). The goal is implicitly defined by the maximum of the reward
function r(je ) = cos θ of the angle θ ∈ R, which takes the maximum at the
top-most position θ = 2 nπ for any n ∈ Z in this angle coordination. Nous
called the second task (B) the swing-up-no-hit task, in which the movement
of the pendulum is constrained within a given angle range, called the fea-
sible angle space. The remaining angle space, in which the pendulum is not
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3002
T. Torii and S. Hidaka
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
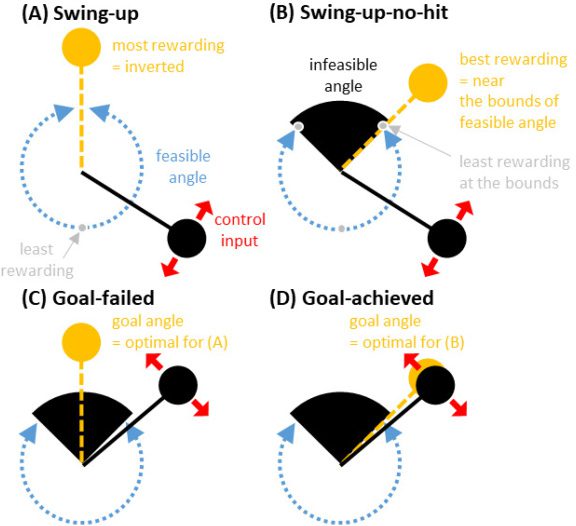
Chiffre 3: Simulation design analogous to experimental tasks in Warneken and
Tomasello (2006). (UN) The swing-up task. The most rewarding angle is when
the mass of the pendulum is at the top-most position of the angle space (θ = 0),
and the least rewarding angle is at the bottom of the angle space (θ = π ). (B) Le
swing-up-no-hit task. The least rewarding angles are when the mass of the pen-
dulum is at the bottom of the angle space (θ = π ) and at the bounds of the infea-
sible region (black: θ = ±π /8). The most rewarding angle is somewhere close to
the top of the angle space within the feasible region. It is optimal to keep the pen-
dulum swinging without touching the bounds. (C) Goal-failed demonstration:
performing task B with the control that is optimal for task A. (D) Goal-achieved
demonstration: performing task B with the control that is optimal for task B.
allowed to enter in the swing-up-no-hit task, is called the infeasible angle
espace. The black region in Figure 3B shows the infeasible angle space. Le
goal of the swing-up-no-hit task is to keep the mass of the pendulum as
close as possible to the top of the angle space while remaining within the
feasible angle space. In the swing-up-no-hit task (B), the demonstrator will
be given the least reward r(je ) = −1 = r(π ) for any θ in the infeasible angle
space including its boundary; otherwise, the demonstrator is given at each
time step the reward r(je ) = cos θ as a function of angle with the least value
r(π ) = −1. The degree of optimality (c'est à dire., numerical indicator of match or
Completion of the Infeasible Actions of Others
3003
mismatch between the goal of the task and the action) is defined as the cu-
mulative sum of rewards for a given action trajectory over time relative to
the largest cumulative sum of the theoretically best action trajectory for the
given task.
Given these two types of tasks, we defined the goal-failed condition as
a mismatch between the task and action in which the demonstrator is per-
forming the swing-up-no-hit task (with the infeasible region) by controlling
the pendulum using a controller that is optimal for the swing-up task (voir
Figure 3C). We consider this goal-failed condition to be analogous to the
experimental condition in the study conducted by WT in which a failed ac-
tion was demonstrated. We also defined the goal-achieved condition, lequel
we consider to be analogous to WT’s control condition, as a match between
the task and action in which the demonstrator is performing the swing-up-
no-hit task by controlling the pendulum using a controller that is optimal
for the swing-up-no-hit task (see Figure 3D). We expect that the demonstra-
tor in our goal-failed condition (see Figure 3C), but not the goal-achieved
condition (see Figure 3D), will perform an action that is suboptimal for the
swing-up-no-hit task, which may appear similar on the surface but is es-
sentially different from the action intended to be optimal for the swing-up
task.
The imitator, à son tour, observes two types of goal-failed and goal-achieved
actions, which are potentially different, and analyzes their potential differ-
ence based only on the observed action trajectories. This situation corre-
sponds to simulation I (see section 3), in which we investigated recognition
of the potential difference between goal-failed and goal-achieved actions.
After some visual inspection of actions, the imitator is expected to per-
form his or her own actions to complete the demonstrator’s action (c'est à dire.,
“help” the demonstrator) if the action is incomplete or goal-failed. This sit-
uation corresponds to simulation II (see section 4) in which we investigated
action generation based on observation of the demonstrator’s incomplete
or goal-failed actions.
2.3 Pendulum Control. A mathematical model of a simple pendulum
is composed of a link of length l = 1 with one end fixed at the origin and a
point mass m = 1 at the other end. The state of this pendulum is identified
by the angle θ ∈ R of the link, relative to angle zero, which corresponds to
the top-most position of the angle space, and the angular velocity ˙θ ∈ R, le
first-order time derivative of the angle. The equation of motion is given by
ml2 ¨θ − mgl sin θ = f (je , ˙θ ) + ε,
(2.1)
where g = 9.8 is the gravity constant, F (je , ˙θ ) is the state-dependent control
input (torque) from a controller f , and ε ∼ N(0, p ) is the intrinsic noise of
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3004
T. Torii and S. Hidaka
the system, time independently sampled from a normal distribution with
variance σ 2.
The pendulum swing-up task is classically used in feedback control the-
ory (Doya, 1999), originally used to design a controller f that can swing
the pendulum and maintain it at about the top-most position where θ = 0.
The controller for this task is defined by the function f , which outputs
torque f (je , ˙θ ) ∈ R for any given state (je , ˙θ ) ∈ (−π, π] × (−2π, 2π]. The goal
of the task is implicitly and quantitatively represented by the reward func-
tion r (see equation 2.4 ou 2.5). With this reward function, we can define the
goal-meeting action as an action with the maximal reward value (or large
t r(θt ) as a
enough to be considered an approximation of the maximum)
function of the controller (see the next section for details). In each run of the
simulation, the initial position of the pendulum was set such that ˙θ = 0 et
angle θ drawn from the uniform distribution ranged by θ ∈ ±[π/8, π ).
(cid:2)
2.4 Energy-Based Swing-Up Controller. The simple pendulum de-
fined in the previous section is well characterized by the mechanical energy
of the system—that is, the sum of the kinetic and potential energy:
E(je , ˙θ ) = 1
2
ml2 ˙θ 2 + mgl (cos θ − 1).
(2.2)
In the pendulum swing-up task, its goal state or the most rewarding state
(c'est à dire., the pendulum is inverted with the mass at the top-most position θ = 0
with zero velocity ˙θ = 0) corresponds to the state with energy E(0, 0) = 0.
The simple pendulum preserves the mechanical energy over time in this
state if the control input is set to u = 0 without any noise (σ = 0). Ainsi, un
way to meet the goal of the swing-up task is to keep the mechanical energy
at zero (E(je , ˙θ ) = 0). Based on this observation, Astrom and Furuta (2000)
defined the energy-based controller of the simple pendulum as
fG(je , ˙θ ) = −(E(je , ˙θ ) − E(G, 0)) ˙θ ,
(2.3)
with which one can reduce the difference between the energy E(je , ˙θ ) of the
current state and the target energy E(G, 0) with the goal angle G ∈ R. In our
simulation, we employed this energy-based controller to generate an action
toward the goal angle G.
In our previous work (Torii & Hidaka, 2017), we adopted a controller
(or policy) based on reinforcement learning to study the action recognition
task described in section 3. We obtained the same qualitative results to those
in this letter. To study the action completion task described in section 4,
we adopted the energy-based controller throughout the study, whose scalar
parametric form is very convenient compared to reinforcement learning,
which requires computationally expensive training of the policy function.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Completion of the Infeasible Actions of Others
3005
2.5 Goal-Achieved and Goal-Failed Action. For each of the demon-
strators in the swing-up and swing-up-no-hit tasks, two different reward
functions r(je ) are assumed as described in section 2.2. In the swing-up task,
the reward function is
r(je ) = cos θ ,
(2.4)
which indicates that the top-most position θ = 0 is the most rewarding posi-
tion for the pendulum. In the swing-up-no-hit task with an infeasible angle
space of [−θ
min], the reward function is
, +je
min
(cid:3)
rθ
min (je ) =
cos(π ) = −1
cos θ
if θ ∈ [−θ
otherwise
min
, +je
min]
.
(2.5)
min
= π/8 in the swing-up-no-hit task. The optimal con-
Spécifiquement, we set θ
trollers are different for the two tasks with the different reward functions r
and rθ
min . The optimal energy-based controller for the swing-up task and the
swing-up-no-hit task is the controller (see equation 2.3) with the goal angle
G = 0 and G = θ
min, respectivement.
For both the swing-up and swing-up-no-hit tasks, we applied the
energy-based controller (Astrom & Furuta, 2000) with some goal angle G
introduced in the previous section. Since the energy-based controller with
the goal angle G = 0 was originally designed for the pendulum swing-up
task with no angle constraint, this energy-based controller is not optimal for
the swing-up-no-hit task with the constrained pendulum: it does not sup-
ply sufficient torque to hold the pendulum against gravity. Par conséquent, it
produces a repeated swinging movement, unlike the behavior without the
infeasible boundary, in which it holds the pendulum still at the goal angle.
For visual inspection of the movements generated by these two dis-
tinct controllers with G = 0 or G = θ
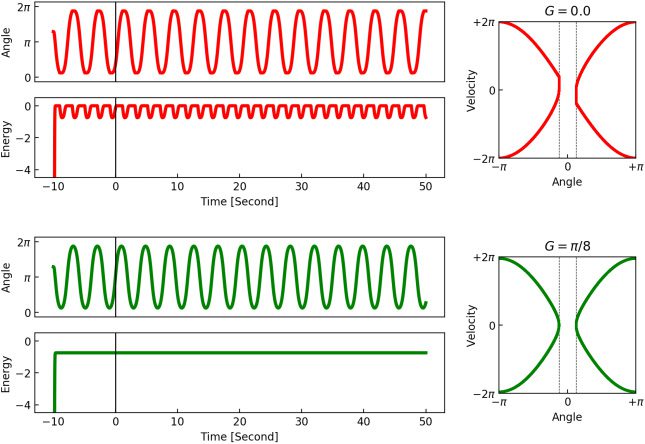
min, Chiffre 4 shows the two typical
angular time series generated by these controllers. Chiffre 4 (top) shows
the typical actions (time series of angles) performed by the goal-failed
demonstrator with the goal angle G = 0 in the swing-up task (see Fig-
ure 3C). Chiffre 4 (bottom) shows the typical actions performed by the goal-
achieved demonstrator with the goal angle G = θ
min in the swing-up-no-hit
task (see Figure 3D). Both movements result in swinging within the range
θ ∈ ±[maximum{G, je
}, π], despite having different goal angles and feasible an-
gle spaces. These movements look similar in their angle dynamics, lequel
simulate the movement similarity in the experiment by WT (par exemple., dropping
a marker accidentally and intentionally). Cependant, as shown in Figure 4,
their mechanical energy, a direct indicator of their controller, can reveal dif-
ferences between the two actions.
min
When the pendulum collides with the bounds, some loss of mechan-
ical energy occurs because the height of the pendulum forcibly remains
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3006
T. Torii and S. Hidaka
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
Chiffre 4: A typical time series of angle and mechanical energy generated by the
goal-failed demonstrator (top panels) with G = 0 and the goal-achieved demon-
strator (bottom panels) with G = θ
min. The dashed lines in the right panels indi-
cate the bound θ
min
= π /8.
unchanged and the body decelerates to an angular velocity of zero, lequel
can be visually observed in both the energy-time series and the trajectory
in the angle-velocity plane in the top panel of Figure 4. In contrast, no such
loss of energy is observed in the bottom panel because the pendulum rarely
collides with the bounds.
2.6 Features for Detecting Intentional Differences. According to our
definition of the goal-failed and goal-achieved conditions, the intention be-
hind a movement that is optimal for the swing-up task does not match
that for the swing-up-no-hit task (see Figure 3C). Other than in this par-
ticular case, many other actions that fail by infeasibility, including those in
the study by WT, essentially display this type of mismatch between some
originally intended task and the actual performed task. One of the critical
features common to these types of tasks is that the task to work has an addi-
tional unexpected obstacle that is absent in the original task, for which the
controller is optimal.
Beyond specific differences across different tasks, we hypothesize that
these types of failures may be characterized by the existence of some
additional factor complicating the originally intended task. In WT’s
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Completion of the Infeasible Actions of Others
3007
condition in which a marker was accidentally dropped, the demonstrator
was not ready for the situation in which he or she was required to pick up
the dropped marker; the accidental dropping of the marker introduces an
additional complexity to the originally intended task: to carry the marker
to some location (without dropping it). This is analogous to the goal-failed
condition in our pendulum simulation: the additional obstacle, the limita-
tion in the feasible angle, causes suboptimality of the original motor control
in this unexpected new task.
What characteristics can be used to detect such suboptimality in an ac-
tion? Dans cette étude, we hypothesize that this additional factor of complexity
can be detected in the degrees-of-freedom (DoF) of the given system.
Let us consider a successful action, Par exemple, the goal-achieved con-
dition of the pendulum control task. Such an action is expected to flow
smoothly, without any sudden change in its motion trajectory. Ainsi, le
movement can be closely approximated using a set of differential equations
with a relatively small number of variables. In contrast, an action that fails
by infeasibility, Par exemple, the goal-failed condition of the pendulum con-
trol task, is expected to have some discontinuous or nonsmooth change in
its motion trajectory, such as at the time point before or after an unexpected
accident for the given system. Ainsi, before and after this change, such a sys-
tem would be better described using two or more distinct sets of differential
equations.
Although it is technically difficult to identify such differences in the un-
derlying systems (or sets of differential equations) in full detail here, it
should be clear that the underlying controller in these two cases would dif-
fer in their DoF. This consideration leads us to the hypothesis that some
difference in the DoF of movement is diagnostic of successful and failed
actions.
In this letter, we specifically employ a type of fractal dimension, appelé
pointwise dimension (see section 3.1), of the actions as an indicator of the
DoF of the underlying controller and test whether it is characteristic of the
difference in intention underlying the actions. In the following two sections,
we examine our hypothesis by analyzing the movement data generated by
the simulated pendulum control task. We divided our analyses into action
recognition and action completion.
D'abord, we analyzed the recognition task from the imitator’s perspective
by examining which features of the movements the imitator (observer of
the actions) was able to discriminate between the goal-achieved and goal-
failed actions. Success recognition, the ability to tell the difference between
two qualitatively different actions, is considered necessary to complete an-
other’s failed action.
Deuxième, we analyzed the completion task by asking whether the char-
acteristic features of the intention underlying actions, as identified in the
first analysis, are sufficient to generate an action to complete a goal-failed
action. Ici, completion of the action means that the imitator performs an
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3008
T. Torii and S. Hidaka
action that meets the goal that an observed demonstrator’s action failed
rencontrer. En tant que tel, a goal-failed action is incomplete by definition and not
fully observed by the imitator; thus, the imitator is required to extrapolate
the observed action to generate the originally intended action. This action
completion task needs not just recognition of the qualitative difference in
actions but also some identification of the demonstrator’s failed action and
the imitator’s action.
3 Simulation I: Action Recognition Task
In simulation I, we investigate whether the imitator can tell the difference
between the two different intentions underlying the actions performed by
the demonstrators in the goal-failed and goal-achieved conditions. The goal
of this simulation is to analyze and identify the feature that is most charac-
teristic of the latent intention of actions.
Spécifiquement, we listed several features typically used in time series anal-
ysis, such as angle (or angular position), angular velocity, angular accel-
eration, angular jerk, power spectrum, mechanical energy, and pointwise
dimension. We hypothesized that pointwise dimension would be most
characteristic of the latent intention of actions for this analysis. Angle, un-
gular velocity, and power spectrum are commonly employed features of
movements in the literature. They are also fitting for our simulation, as mo-
tor control is a function of angle and angular velocity, and the generated
movement is periodic. Mechanical energy is the very concept defining the
motor control task (see equation 2.3), and we thus expect mechanical en-
ergy to be the best possible feature in theory to characterize the intention
(motor control). Cependant, a naive imitator, such as a child, who is ignorant
of the demonstrator’s physical properties may not have direct access to the
mechanical energy because of the need for knowledge of the physical pa-
rameters of the pendulum (c'est à dire., mass m and length l in equation 2.1, lequel
are necessary to compute the mechanical energy of the pendulum system).
Ainsi, we treated mechanical energy as an indicator of the best possible (mais
unlikely to be directly accessible) reference feature for the recognition task
in our analysis.
Enfin, given that the pointwise dimension indicates the latent DoF of
an underlying dynamical system, we hypothesize that it is an indicator of
task-system complexity and is characteristic of the intentional difference
between movements performed in the goal-failed and goal-achieved con-
ditions. We tested this hypothesis by evaluating recognition performance
using the pointwise dimension compared to that using the reference fea-
ture: mechanical energy in the classification of movements with different
intentions.
3.1 Pointwise Dimensions. To characterize complexity in each demon-
le
strator’s movements, we analyzed the attractor dimension of
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Completion of the Infeasible Actions of Others
3009
movements by treating it as a dynamical system. Spécifiquement, we exploited a
type of fractal dimension called pointwise dimension for classification anal-
ysis. The pointwise dimension is a type of dimension defined for a small,
open set or measure in the set, including a point in a given set (see Cutler,
1993; Jeune, 1982, for details). Officiellement, for a set of points X in a topolog-
ical space Rn, the pointwise dimension d(X) at point x ∈ X is defined (if it
exists) by the local scaling exponent of the associated probability measure
μ on X such that μ(B(X, (cid:6))) ∼ (cid:6)d(X) comme (cid:6) → 0, commonly expressed as
d(X) = lim
(cid:6)→0
log μ(B(X, (cid:6)))
log (cid:6)
,
(3.1)
where B(X, (cid:6)) ⊆ X gives a subset of points around x within distance (cid:6). Point-
wise dimension is invariant under arbitrary smooth transformation. As it is
associated with each point, we can analyze the distribution of the pointwise
dimension across points. Informally speaking, the pointwise dimension of
a point characterizes the measurable space of a certain dimension that sur-
rounds the point. We have developed a statistical technique to estimate the
pointwise dimension for a set of data points (Hidaka & Kashyap, 2013). Us-
ing this technique, each point in the data set is assigned a positive value of
pointwise dimension.
3.2 Two-Class Classification. We performed classification analyses of
demonstrator types based on each of the features described. Performance
of the classification is used as a measure of how well each feature discrim-
inates among demonstrator types. Spécifiquement, for this two-class classifica-
tion task, the imitator is exposed to a time series of a pair of angles that
reflect each movement demonstrated in the goal-achieved and goal-failed
conditions. Part of each time series corresponding to the first 10 seconds of
the task was excluded from the training data because these were transient
periods that were heavily dependent on the initial state. The rest of the time
series, corresponding to the last 50 seconds of the movement (de 5000 sam-
ple points), was used as the training data for classification. We used a single,
long time series because the system is expected to be ergodic, defined as a
time series with any initial starting state that eventually converges to the
same stationary near-periodic dynamical system (with some intrinsic noise
in motor control).
For classification, we considered the following features: angle (or angu-
lar position), angular velocity, angular acceleration, angular jerk (the third
derivative of angle), power spectrum, mechanical energy, and pointwise
dimension. Given a time series of angle (or angular position), le temps
series of angular velocity, acceleration, and jerk was calculated by taking
the first-, second-, and third-order difference of the angle time series. Le
third derivative of the position, called “jerk,” is a notable feature that is
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3010
T. Torii and S. Hidaka
hypothesized to be critical in the minimum jerk and/or minimum torque-
change trajectory for human motor control of reaching (Hogan, 1984; Uno,
Kawato, & Suzuki, 1989). The data points for the power spectrum feature
were constructed as a collection of frequencies with the largest powers in
the power spectrum of angles computed within a moving time window size
de 5 seconds. Details of the construction of the pointwise dimension feature
are described later. In contrast to the features described, which can only be
computed using the observable time series, computation of mechanical en-
ergy requires knowledge of the physical properties, such as the body mass
and length, of the pendulum system, as evident from equation 2.2.
To analyze the degree of contribution of pointwise dimension to recog-
nizing the underlying controller of the system, the pointwise dimension
associated with each data point was estimated from a time series of coordi-
nate values (xt, yt ) = (sin θt, cos θt ) of the pendulum. As pointwise dimen-
sion is an invariant under arbitrary smooth transformation, we obtained
essentially the same estimate as that from the time series of angle. In dy-
namical systems theory, Takens’s embedding theorem states that a diffeo-
morphism of a smooth attractor in a latent high-dimensional space can be
reconstructed from a univariate or low-dimensional time series, which is a
projection on a subset of the original high-dimensional state space, en utilisant
time-delay coordinates with a sufficiently high dimension for embedding
the attractor. Donc, the positional time series {(xt, yt )}t was first em-
bedded into the time-delay coordinates of the embedding dimension 2k,
{(xt, yt, xt+1
, yt+k−1)}t. Then the embedded 2k-dimensional
time series (de 5000 − k + 1 sample points) was used to estimate the point-
wise dimension, equation 3.1, for the time series. We mostly adopted k = 20
for the pendulum system with a controller.
, . . . , xt+k−1
, yt+1
For the recognition (two-class classification) task, the feature points in a
feature time series are treated as independent samples. The classification
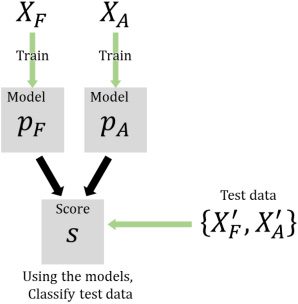
procedure is illustrated in Figure 5. XF and X(cid:6)
F denote two distinct sets
of feature points in the training and test data set, respectivement, which are
constructed from distinct actions generated by the goal-failed demonstra-
tor. De la même manière, XA and X(cid:6)
A denote those of the goal-achieved demonstrator.
For features other than those for pointwise dimension, given a set of fea-
ture points as training data, either XF or XA, we used the gaussian mixture
model, in which each class of data is distributed as one or more multivari-
ate normal distribution(s) over a given feature space. We chose the gaussian
mixture model because of its computational simplicity for constructing two
sample probability functions of a variable (c'est à dire., a feature). We denoted the
probability density function of a certain feature x estimated with the goal-
failed action(s) XF as pF (X) and that estimated with goal-achieved action(s)
XA as pA(X). Using these sample probability density functions, the imita-
tor asserts that a given test feature x ∈ X(cid:6)
A belongs to the goal-failed
F
demonstrator if pF (X) > pA(X); otherwise, it belongs to the goal-achieved
demonstrator. The classification accuracy is defined as the proportion of
∪ X(cid:6)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Completion of the Infeasible Actions of Others
3011
Chiffre 5: Procedure for the recognition task.
correct responses, which is defined by the equality between the underlying
class and the asserted class for each unit of a given time series. Precisely, le
correct response was defined by pF (X) > pA(X) if a test feature x was indeed
sampled from x ∈ X(cid:6)
UN, the correct response was
pF (X) < pA(x). For each feature, we reported the classification accuracy of
the gaussian mixture model, with the number of multivariate normal dis-
tributions in the gaussian mixture model selected based on the minimum
Akaike information criterion (Akaike, 1974).
F; otherwise, namely, x ∈ X(cid:6)
To perform the recognition task using pointwise dimension as a fea-
ture, we used the statistical model underlying the dimension estimation
method proposed by Hidaka and Kashyap (2013). The method or dimen-
sion estimator constructs a model for given data as a mixture of multiple
Weibull-gamma distributions, each of which has an associated parameter
representing the fractal dimension. This method can also be used to calcu-
late the probability that a sample data point x with time-delay embedding
belongs to the mixture model. Therefore, for the probability density func-
tions of the pointwise dimension feature, we adopted the Weibull-gamma
mixture model rather than the gaussian mixture model used for the other
features. The training and test data for, say, XF and X(cid:6)
F, were both obtained
by time-delay embedding the positional time series. For this recognition
task, the spatial neighborhood of a sample point x ∈ X(cid:6)
A was calcu-
F
lated within the feature space spanned by training data XF (or XA) as-
sociated with the probability density function pF (or pA). The number of
mixture components of the Weibull-gamma mixture model was selected
based on the minimum Akaike information criterion (Akaike, 1974).
∪ X(cid:6)
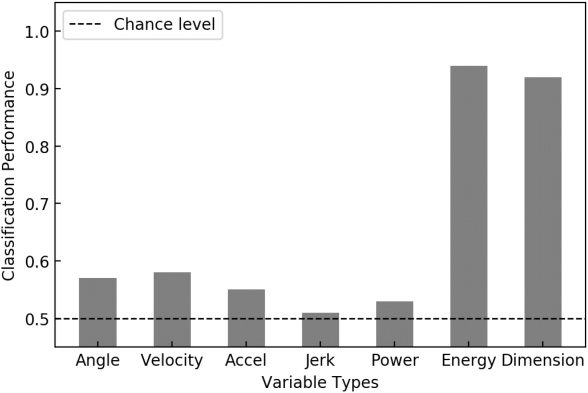
3.3 Classification Results. Figure 6 shows the classification accuracy
for each feature of the test data set. As both the training and test data contain
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3012
T. Torii and S. Hidaka
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6: Results of classification tasks with several features.
an equally balanced number of samples from the two classes (5000 − k + 1
sample points for each class), the chance level for classification was 50%.
The classification accuracy with angle (angular position), angular veloc-
ity, angular acceleration, angular jerk, and power spectrum was near or
slightly above chance level. The accuracy with mechanical energy was ap-
proximately 95%, significantly higher than the chance level. This result is
as expected: two classes of data generated using two distinct controllers
that represent two distinct goals (i.e., goal angle G in equation 2.3) defined
by mechanical energy. We treated this accuracy with mechanical energy as
the best-possible reference accuracy in this classification task. Compared
with this best-possible accuracy, the classification accuracy with pointwise
dimension was approximately 92%, which was comparable. Note that un-
like mechanical energy, which requires prior knowledge of the demonstra-
tor’s physical properties, pointwise dimension was computable using only
a time series of angles formed by the pendulum that were observable to a
naive imitator. This result suggests that pointwise dimension is a potentially
useful feature for recognizing the intentions (controllers) behind observed
movements that can be ascertained using only observable data.
To determine why both mechanical energy and pointwise dimension
were effective for discriminating the latent underlying controllers, we fur-
ther visualized how those features characterize the observable trajectories
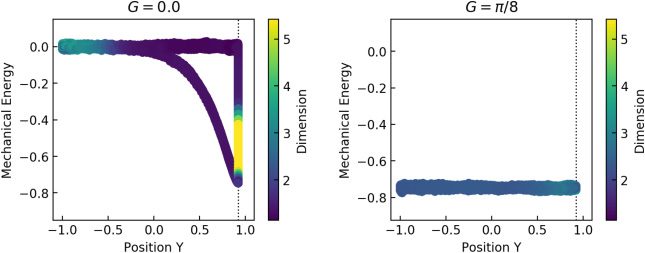
of the pendulums. Figure 7 shows how the position yt = cos θt of the ma-
nipulated pendulum, its mechanical energy, and pointwise dimension are
correlated within the training data XF for pF (or XA for pA). For visibility, the
Completion of the Infeasible Actions of Others
3013
Figure 7: Dynamics of the pendulums in the plane of the y position and me-
chanical energy. The color of the data points indicates the pointwise dimension.
The dashed lines indicate the bound cos θ
min.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
value of the pointwise dimension d(x) for each data point x ∈ XF (or XA) in
the figure was spatially averaged over the 100 nearest neighbors of x on the
plane of the y position and mechanical energy. For the goal-achieved con-
troller, in Figure 7 (right), the mechanical energy was mostly maintained at
E(G, 0) with G = θ
min, based on the design of the energy-based controller.
The estimated pointwise dimension was also mostly constant over time.
In contrast, for the goal-failed controller, in Figure 7 (left), the mechanical
energy and pointwise dimension both dramatically changed over time. Ac-
cording to the design of the controller, the mechanical energy was main-
tained at about E(G, 0) with G = 0 for the feasible angle space θt > je
min,
≈ 0.923, but decreased when the pendulum touched
c'est, yt < cos θ
the bounds, remaining so until it started to leave the bounds with E(θ
, 0).
We think this difference in mechanical energy could contribute to high clas-
sification accuracy based on the mechanical energy.
min
min
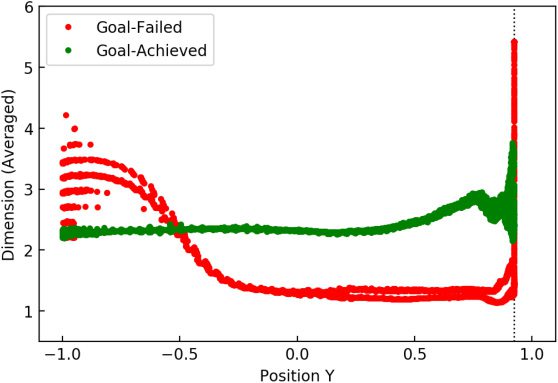
Additionally, Figure 8 shows the direct relationship between the y posi-
tion and the pointwise dimension when spatially averaged in the manner
above. As shown in Figures 7 (left) and 8, the pointwise dimension first
decreased around the time the pendulum touched the bounds and later
increased when the pendulum started to leave the bounds, that is, the
energy-based controller regained control of the pendulum. This tendency
for a dramatic change in the pointwise dimension near the bounds can be
observed in almost all other simulation runs. Thus, we hypothesized that
the pointwise dimension characterizes such participation of the additional
number of control variables, at least near the bounds of the infeasible an-
gle space. Again, the great difference in pointwise dimension illustrated in
these figures is expected to contribute to the high classification accuracy
based on the pointwise dimension.
3014
T. Torii and S. Hidaka
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8: Dynamics of the pointwise dimension (averaged) of the pendulums
as a function of their y position.
4 Simulation II: Action Completion Task
One of the key observations in the experiment conducted by WT is that the
children could perform an action to achieve the demonstrator’s “goal” by
simply observing their incomplete action. Because the children did not ob-
serve the complete action in the experiment, they needed to identify the pu-
tative complete action by extrapolating the observed incomplete action. To
explore the mechanism of the action completion task, we asked, how does
the imitator observing the goal-failed demonstration produce an action that
achieves the unobserved goal? As pointwise dimension was found to be
reasonably characteristic of the intentions behind observed movements in
simulation I, we examined an extended use of the pointwise dimension for
the action completion task in this simulation.
In the action completion task, exact identification of the intention is not
necessarily required or beneficial because the imitator (e.g., child) does not
necessarily have the same body as the demonstrator (e.g., adult), and the
motor controllers of different bodies required to meet the same goal may
generally differ. Thus, in the action completion task, the imitator needs to
identify two actions that have similar goals but may have different physical
properties and latent motor control.
4.1 Action Completion Model. Based on the requirement described
above, here we propose using the similarity in the dynamic transition pat-
terns in the DoF of the two action-generating systems. Specifically, we
Completion of the Infeasible Actions of Others
3015
hypothesize that the imitator observes an action and extracts the dynam-
ics of the DoFs, defined by pointwise dimension, from the action as esti-
mated for the recognition task in simulation I. Next, the imitator (mentally)
simulates a movement by a given pendulum for each set of candidate con-
trollers. Then the imitator performs an action by choosing the controller
that can generate the action that is most similar to the demonstrated action.
In this way, this action completion model uses a similarity in DoF dynam-
ics rather than a similarity in apparent features such as angle and angular
velocity patterns, which were found to be less characteristic of intentional
differences in actions.
Specifically, we suppose that the imitator is exposed to one time series of
angles generated in the goal-failed condition (see Figure 3C), which is sub-
optimal for the swing-up-no-hit task. We assume that the imitator performs
an action by choosing a controller (see equation 2.3) with goal angle G as
the parameter. In one condition, the other physical parameters, mass m and
length l, of the pendulum are fixed at (m, l) = (1, 1), the same values used by
the demonstrator. In the two other pendulum conditions, the imitator uses
either (m, l) = (4, 1) or (m, l) = (1, 2), which differ in mass or length to that
used by the demonstrator. These three conditions are designed to investi-
gate the robustness of the action completion model compared to differences
in the physical features of the imitator’s and demonstrator’s pendulums.
Given the goal-failed action, the action completion task of the imitator is
to choose the controller fG with the goal angle G that will most likely gen-
erate a movement similar to the demonstrated movement in terms of DoF
dynamics. We let a set of controllers with the goal angles 0, 0.05, 0.1, . . . , 0.9
represent the imitator’s options. The similarity in DoF dynamics of actions
is described in the next section.
4.2 Similarity in DoF Dynamics. In this study, the DoF dynamics of a
system are defined by the temporal change in the pointwise dimension es-
timated in the time series generated by the system. Specifically, a pointwise
dimension estimator was constructed for a given demonstrated movement
using the method proposed by Hidaka and Kashyap (2013), and used to es-
timate a series of pointwise dimensions for each of the demonstrated and
candidate movements. The constructed pointwise dimension estimator is a
mixture of multiple Weibull-gamma distributions, where each probability
distribution Pi corresponds to a particular pointwise dimension and assigns
for each point xt in a trajectory the probability Pi(xt ) that the point belongs
to the ith distribution.
In our action completion model, the imitator is expected to perform an
action controlled by the goal angle G that maximizes the log-likelihood
function (defined by equation 4.4), which indicates some similarity in DoF
dynamics between the demonstrated and simulated trajectory. Specifically,
the log-likelihood is defined and maximized using the following steps
(illustrated in Figure 9):
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3016
T. Torii and S. Hidaka
Figure 9: Our computational framework used for maximum likelihood infer-
ence for unknown parameters of the demonstrator behind the observed demon-
strated trajectory. See text for details.
1. Given the demonstrated trajectory {xt}t∈T as primary data, construct
the pointwise dimension estimator/classifier {Pi
}
i∈{1,...,k} for a recon-
structed attractor by the method of time-delay coordinates with suffi-
ciently high embedding dimension. The number of Weibull-gamma
distributions k is chosen based on the Akaike information criterion
(Akaike, 1974).
2. The demonstrated trajectory {xt}t is transformed into a state sequence
{st}t, where each symbol st ∈ {1, . . . , k} is the index of the most likely
distribution:
st = arg max
i
Pi(xt ).
(4.1)
3. Denote ns
i, j as the number of transitions from state st = i to state st+1
=
j in {st}t. Then the state transition joint probability matrix Q ∈ Rk×k
for all pairs of states is defined by
Qi j
=
(cid:2)
ns
i, j
(cid:2)
k
j(cid:6)=1 ns
i(cid:6), j(cid:6)
.
k
i(cid:6)=1
(4.2)
4. Given a candidate controller including its parameters (e.g., goal an-
gle G), a simulated trajectory {yt}t∈T is generated and transformed
into another state sequence {ut}t = {arg maxi Pi(yt )}t. To calculate the
probability Pi(yt ), the simulated trajectory was first transformed by
the method of time-delay coordinates with the same embedding
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
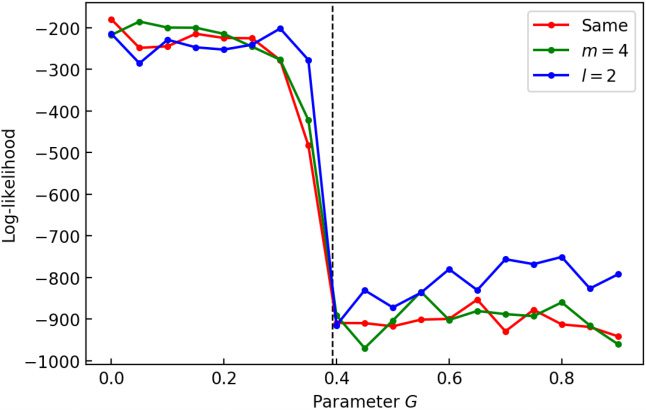
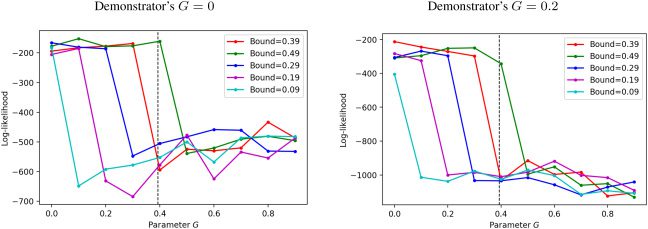
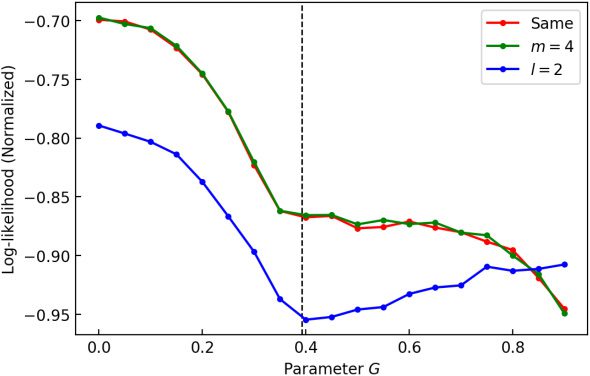
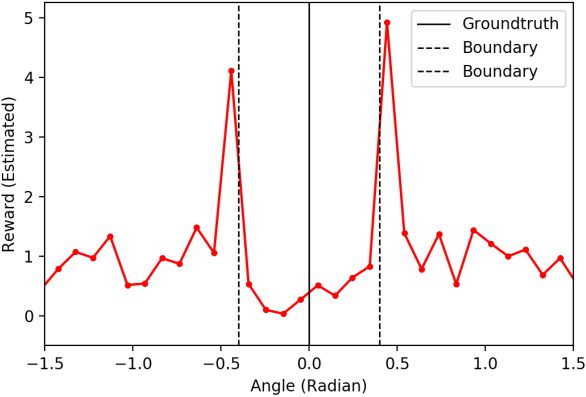
Completion of the Infeasible Actions of Others
3017
dimension, and the spatial neighborhood of sample point yt was cal-
culated within the feature space spanned by {yt}t∈T itself. Then the
state transition frequency matrix H ∈ Nk×k
is defined by
0
Hi j
= nu
i, j
,
(4.3)
where nu
i, j is the number of transitions from state i to state j in {ut}t.
5. The likelihood of the candidate controller is defined by the multi-
nomial distribution of a transition frequency H generated by the
unknown controller showing the transition probability Q of the
pointwise dimension estimator. Specifically, the log-likelihood func-
tion of the candidate controller with the goal angle parameter G is
given by
log L(G) = CH +
k(cid:4)
k(cid:4)
i=1
j=1
Hi j log Qi j
,
(4.4)
where CH is the multinomial coefficient for the multinomial distribu-
tion. To obtain comparable log-likelihoods for trajectories of unequal
length, the log-likelihoods should be normalized by the numbers of
state transitions, that is,
(cid:2)
i, j Hi, j.
6. Repeat steps 4 and 5 for other candidate controllers with different
parameters.
This method is designed to abstract away differences in the absolute
value of the pointwise dimension at each step between the two systems and
compute similarities in the temporal change in the relative degrees of free-
dom. In our simulations below, the imitator is expected to generate an action
trajectory controlled by the goal angle G that maximizes the log-likelihood
function, equation 4.4.
We have two remarks on the procedure described above. First, in step
4, the spatial neighborhood of the sample point was calculated so as to ab-
stract away differences in the physical properties of the pendulum, such as
the absolute value of the positional data, such as differences in the pendu-
lum length between the imitator and demonstrator. In the previous section,
the neighborhood was calculated within the space spanned by the train-
ing data for the dimension estimator. However, this is valid only for the
recognition task, in which we assumed the same physical properties for
the two demonstrators. Second, in this method, we constructed Q from a
demonstrated and H from a simulated trajectory. In terms of imitation or
mimicry in biology, the demonstrator is actually the “model” or “exem-
plar” to be imitated by the imitator or “mimic”; hence, the mimic H can
be seen as a realization of the model Q. However, the opposite view is also
acceptable: the imitator forms a hypothesis Q(cid:6)
and tests it using a realiza-
tion H(cid:6)
by the demonstrator. The same result will be obtained using either
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3018
T. Torii and S. Hidaka
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 10: Results of the action completion task. The log-likelihood was com-
puted using the action completion model. For the same-pendulum condition,
the ground truth is G = 0. The vertical dashed line is the boundary of the feasi-
= π /8. For the different-pendulum conditions, candidate move-
ble angle θ
ments were generated using an imitator’s pendulum of either (m, l) = (4, 1) or
(1, 2).
min
view because similarity is a symmetric measure between the demonstrator
and imitator, or the model and mimic. In the proposed method, we take the
former view for the practical reason that the dimension estimation is com-
putationally expensive and the estimation is required only once. This is in
contrast to the latter view, which requires as many estimations as there are
hypotheses.
4.3 Results of Action Completion. In this simulation, we assumed that
the demonstrator had a controller with goal angle G = 0 but failed to meet
the goal due to the infeasible region with its boundary at θ
≈ 0.39. Thus,
we set the ground truth at an estimated G = 0, as the latent goal angle of
the controller used by the goal-failed demonstrator was G = 0. In the action
completion task, the imitator is expected to generate an action that matches
the latent intention of the demonstrator. The imitator employs the action
completion model described above to produce the action most likely to dis-
play DoF dynamics similar to that of the demonstrator’s.
For each goal angle G in the candidate set {0, 0.05, . . . , 0.9}, we computed
the log-likelihood function, equation 4.4, based on the similarity in DoF dy-
namics between demonstrated and simulated movements (see Figure 10).
min
Completion of the Infeasible Actions of Others
3019
min than others G ≥ θ
For each G, the figure shows the average of 20 log-likelihood values over
sampled simulated actions with different initial values. In the action com-
pletion model, a controller with some G with higher log-likelihood is more
likely to be chosen as the action produced by the imitator. Figure 10 (red
points) shows the log-likelihood of goal angle G in the same-pendulum
condition, that is, when the demonstrator and imitator control the same
pendulum with the same physical parameters (m = 1, l = 1). Although the
log-likelihood was not the highest at G = 0, it was generally higher for
one range of angles 0 ≤ G < θ
min. When we separated
these angles into two groups at the boundary angle θ
min, we found the log-
likelihood values on average were significantly different (t(376) = 39.76,
p < 0.01). Thus, based on the similarity in DoF dynamics, these results sug-
gest that the imitator can generally differentiate between two latent types of
candidate action, which correspond to the difference between the swing-up
and swing-up-no-hit task. In other words, the imitator can estimate that the
demonstrator’s latent intention is to move up beyond the infeasible bound-
ary rather than to stop at the boundary as suggested in direct observation.
To what extent does this action completion model depend on the same-
ness of physical parameters of the demonstrator’s and imitator’s pendu-
lums? To examine the robustness of this action completion model against
deviations from the identical physical setting (m = 1, l = 1) between the
demonstrator and imitator, we analyzed the same action completion task
when the imitator controls pendulums with different physical parameters
(m = 4 and l = 1, and, m = 1 and l = 2). In both cases, we obtained es-
sentially the same results (green and blue points in Figure 10) as those in
the same-pendulum condition (red points in Figure 10). The two groups of
log-likelihood values were on average both significantly different (t(375) =
40.93, p < 0.01 for the condition with m = 4; t(374) = 34.88, p < 0.01 for
the condition with l = 2). That is, even with physically different pen-
dulums, the imitator can differentiate between the two general types of
intentions (i.e., swing-up versus swing-up-no-hit). Thus, by using DoF
dynamics as an indicator of similarity in movements, the imitator can suc-
cessfully abstract away differences in physical features of the two pendu-
lums. Note that when using two physically different pendulums, the motor
controller has no “ground truth” of goal inference or no actual way of pro-
ducing a movement that is exactly the same as the demonstrator’s. Thus,
in these different-pendulum conditions, it would be difficult for a simple
movement-matching strategy to reproduce some unseen action performed
by the demonstrator.
The previous experiment in which G = 0 and bounds of the infeasible
region θ
= ±π/8 ≈ 0.39 was conducted to test the robustness of the ac-
tion completion model against nonidentical latent body parameters, l and
m. Because the bounds of the infeasible region can also be latent bodily pa-
rameters, we conducted a similar line of experiments with G = 0 and var-
ious hypothetical bounds θ
min for the imitator’s pendulum, or the “mental
min
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3020
T. Torii and S. Hidaka
Figure 11: Results of the action completion task. The log-likelihood was com-
puted using the action completion model. The ground truth is G = 0 for the
chart on the left and G = 0.2 for the chart on the right. The vertical dashed
= π /8. Candidate movements
line is the boundary of feasible angle range θ
were generated by the imitator’s pendulum with various hypothetical bounds
θ
min
= 0.09, 0.19, 0.29, π /8 ≈ 0.39, 0.49.
min
min
simulator.” In these experiments, the imitator can also manipulate the infea-
sible bounds parameter θ
min, called the hypothetical bounds. Figure 11 (left)
shows the goal inference results using pendulums with different bounds for
the infeasible region θ
= 0.09, 0.19, 0.29, π/8 ≈ 0.39, 0.49. The ground
truth parameter (of the demonstrator’s pendulum) is θ
= π/8 ≈ 0.39.
This experiment showed that the imitator inferred that some goal angle
greater than her pendulum’s hypothetical bounds is more likely, regard-
less of the pendulum’s actual hypothetical bounds. Figure 11 (right) shows
the results for the same line of experiments with G = 0.2. The results are
similar to those in Figure 11 (left) despite the difference in goal G. Thus, our
proposed method for goal inference can be performed without knowledge
of the physical parameters l, m or the bounds of the infeasible region θ
min.
However, our method cannot currently be used to identify the exact goal G,
but simply to infer a range within which the goal G falls.
min
An additional point that should be examined is whether goal inference
is possible from the observation of nonrepeated actions. The new goal in-
ference task will be referred to as single-shot goal inference, in which the
demonstrator does not repeat a similar (goal-failed/achieved) movement
but provides only one swing of the pendulum such that it moves from
the bottom to the top-most position and then to the bottom again. In this
task, the imitator observed a batch of one-swing movements performed by
the demonstrator aiming to obtain the same goal angle; the imitator sub-
sequently inferred the latent goal angle. For training, 30 one-swing move-
ments by the demonstrator were provided, and an embedding dimension
of 20 was used. For inference, we restricted our imitator such that it like-
wise could produce only one-swing movements in his mental simulation.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Completion of the Infeasible Actions of Others
3021
Figure 12: Results of the single-shot action completion task. The normalized
log-likelihood was computed. See the Figure 10 caption for details.
A batch of one-swing movements, except for the final one, for training can
be interpreted as a collection of the imitator’s past experiences in the same
or a similar situation as that of the demonstrator. Similar to Figure 10, Fig-
ure 12 shows the average of 20 normalized values of the log-likelihood of
goal angle G in the same and different pendulum conditions. The results
for nonrepeated actions in general show a similar tendency to our previ-
ous results for repeated actions. This result suggests the robustness of the
proposed goal inference scheme against this type of data shortage.
4.4 Goal Inference via Inverse Reinforcement Learning. One of the
standard techniques used to infer a goal from observed data on an action
is inverse reinforcement learning (IRL) (Ng & Russell, 2000). In IRL, the re-
ward function is inferred from a large number of state-transition sequences
based on the assumption that those sequences were sampled from an un-
known Markov decision process. We adopted one IRL algorithm (Ziebart
et al., 2008) that has been frequently reported to be robust and efficient in the
IRL literature. The basic idea of IRL is often represented as frequency match-
ing: in general, IRL algorithms estimate a higher reward for a more fre-
quently visited state. Because the pendulum swing-up task is quite common
in reinforcement learning (Sutton & Barto, 1998; Doya, 1999), we adopted
the simplest state-space discretization method, called tile coding. The state
space (θ , ˙θ ) ∈ (−π, π] × (−2π, 2π] is divided equally into 64 × 64 equally
spaced tiles. Time series are sampled every three time steps.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3022
T. Torii and S. Hidaka
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
a
_
0
1
4
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 13: Reward function predicted by an IRL algorithm. The ground truth is
=
G = 0. The vertical dashed lines are the boundaries of the feasible angle θ
π /8.
min
Figure 13 shows the reward function estimated by the IRL algorithm
for observed state sequences generated from a movement performed by
the goal-failed demonstrator with goal angle G = 0. Since her pendulum
is constrained by the infeasible region, the controller constantly hits the
bounds of the infeasible region, and thus the most frequently visited states
are those in which the pendulum stops at the bounds of the feasible re-
gion (θ , ˙θ ) ≈ (±π/8, 0). As shown in Figure 13, the IRL algorithm estimated
that the highest reward states were at the bounds of the feasible region
θ = ±π/8, and the actual G = 0 was estimated as a low-reward state, which
is unlikely to be the demonstrator’s goal angle. This result is expected, as
IRL generally works as a “frequency-matching” algorithm. Therefore, our
findings suggest that a frequency-matching algorithm such as IRL works
poorly when it is used to complete an unobserved action (with zero fre-
quency) in the goal-failed situation.
5 Discussion
Inspired by the psychological experiment conducted by Warneken and
Tomasello (2006), we designed a minimal simulation framework to account
for the mechanism of action recognition and action completion. We showed
that the simulated imitator can discriminate between goal-failed and goal-
achieved actions, which have apparently similar movements but different
Completion of the Infeasible Actions of Others
3023
intentions and goals (simulation I). Then we proposed an action comple-
tion model that can perform an action comparable to the optimal action
for the swing-up task simply by observing the goal-failed action, which is
suboptimal with the pendulum in the infeasible region (simulation II). Both
recognition and completion can be the basis of goal inference from an un-
successful demonstration.
In these two simulations, we used DoF dynamics in actions, or a type
of abstraction of bodily movements using a dynamical invariant, as a fea-
ture of the underlying motor controllers. For this abstraction, the obtained
DoF dynamics can effectively ignore apparent positional variation among
observed movements while extracting the dynamical/mechanical charac-
teristics behind the movements. Our simulations comparing action com-
pletion based on DoF dynamics versus the frequency of spatial/positional
states (see Figure 10 versus Figure 13) suggested that our abstraction to DoF
dynamics allowed the imitator to identify a range of controllers (with the
parameter G > je
min) including the optimal controller for the demonstrator’s
latent goal. Our additional simulations (voir la figure 11) suggested that this
abstraction may not allow the imitator to exactly identify the demonstra-
tor’s goal. We consider that this limitation of our proposed method is ac-
ceptable, as even we humans cannot infer another’s hidden goal exactly
but can rather identify the general direction of the demonstrator’s intended
goal. Par exemple, consider the case in which you seeing a man kicking a
closed door many times while both of his hands are full. You may think
that he wants to open the door. But how can you infer exactly where he is
heading after he goes through the door? It is difficult for you to determine
this without any prior knowledge of his goal. In our simple pendulum sim-
ulations, the imitator successfully inferred that the demonstrator wanted to
go beyond the infeasible bounds (the door) but could not exactly identify
the demonstrator’s goal angle (where he is heading). Given the theoretical
results of this letter—that DoF dynamics are effective in both action recog-
nition and action completion—we predict that this feature will also play a
crucial role in understanding human action and imitation. This hypothesis
will be tested in future work.
Enfin, we add two remarks on why a dynamical invariant is effective for
completing a goal-failed action compared with existing approaches. D'abord,
our approach using a dynamical invariant does not presume any kind of op-
timality of observed actions, whereas existing approaches, such as inverse
optimal control (Wolpert, Doya, & Kawato, 2003) and IRL (Ng & Russell,
2000), faire. This difference between the approaches is crucial, because the
observed action, to be completed, failed in its original goal in our task.
Deuxième, our approach using a dynamical invariant is likely to be use-
ful for estimating the point-to-control underlying the goal-failed or goal-
achieved actions. En général, bodily movements need to be more carefully
controlled when the movement is at a state closer to the final goal. Consider
reaching, Par exemple. Finer control is needed near the point to be reached,
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3024
T. Torii and S. Hidaka
more so than at the beginning of the action. This necessary control gain may
be reflected by the observable granularity in the fluctuation of an action and
can be quantified using a type of fractal dimension of trajectories.
As Bernstein (1996) pointed out, while the DoF of our bodies can be a
source of flexibility in our movements, generally a system with a very large
number of DoF is likely to be intractable. Donc, organisms must reduce
their body’s DoF to be tractable (Bernstein, 1996). We predict that a reduc-
tion in DoF is crucial especially when accuracy of movement is required or
when one is close to the task goal state. Ainsi, we speculate that a dynamic
decrease or increase in DoF might inform the imitator about whether the
current state of the observed system is near or far from the unknown task
goal state. Spécifiquement, the goal-failed actions we adopted in this letter can
have their own characteristic dynamic pattern of DoF—for example, le
different ways by which the pendulum touches the boundaries of the in-
feasible space. Donc, our approach can successfully infer the hidden
goal of an observed action, even if the observed action is suboptimal and
goal-failed.
A review of IRL (Zhifei & Joo, 2012) proposed that learning from goal-
failed or imperfect or incomplete demonstrations is a challenging new prob-
lem in related research fields. Our approach based on a dynamical system
is expected to bring new insights to this class of problems.
The proposed model, at least in a minimal physical model such as a pen-
dulum control task, is reasonably effective for an action completion task.
Although we hypothesized that DoF can be a commonly effective feature
for goal inference, the evidence for this claim (c'est à dire., the results from our sim-
ulation models) is limited as we supposed that the simple pendulum was a
physical body and that we had a sufficient amount of training data, among
other assumptions. Given that the simple pendulum is a mechanical sys-
tem with only one DoF, this assumption greatly simplifies the problem of
imitation, which may require a large number of DoFs to control the body. Dans
imitating systems with high DoF, an ill-posed problem, in which there are
multiple different ways to achieve the same goal, is another fundamental
problem that we have not addressed in this letter. En outre, we only
quantitatively studied simple stage goal-directed actions with no need for
explicit subgoals, as opposed to complex actions composed of multiple
stages with the need for explicit subgoals. Whether DoF can be generally
effective or how it can be effectively exploited for goal inference from com-
plex actions of high DoF systems should be explored in the future. We ex-
pect to extend the current work to more complex action-generating systems
in the future.
Remerciements
We thank the anonymous reviewer. This work was supported by JSPS KAK-
ENHI grants JP 20H04994 and JP 16H05860.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Completion of the Infeasible Actions of Others
3025
Les références
Abbeel, P., & Ng, UN. (2004). Apprenticeship learning via inverse reinforcement learn-
ing. In Proceedings of the 21th International Conference on Machine Learning (pp. 1–8).
PMLR. https://doi.org/10.1145/1015330.1015430
Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions
on Automatic Control, 19(6), 716–723. https://doi.org/10.1109/TAC.1974.1100705
Argall, B., Browning, B., & Veloso, M.. (2007). Learning by demonstration with cri-
tique from a human teacher. In Proceedings of the ACM/IEEE International Confer-
ence on Human-Robot Interaction (pp. 57–64). New York ACM. https://est ce que je.org/10.
1145/1228716.1228725
Astrom, K. J., & Furuta, K. (2000). Swinging up a pendulum by energy control. Au-
tomatica, 36(2), 287–295. https://doi.org/10.1016/S1474-6670(17)57951-3
Babes-Vroman, M., Marivate, V., Subramanien, K., & Littman, M.. (2011). Appren-
ticeship learning about multiple intentions. In Proceedings of the 28th International
Conference on Machine Learning (pp. 897–904).
Bernstein, N. UN. (1996). Dexterity and its development. Londres: Psychology Press.
Breazeal, C., & Scassellati, B. (2002). Robots that imitate humans. Tendances cognitives
les sciences, 6(11), 481–487. https://est ce que je.org/10.1016/S1364-6613(02)02016-8
Cutler, C. D. (1993). A review of the theory and estimation of fractal dimension.
In H. Tong (Ed.), Dimension estimation and models (pp. 1–107). Singapore: Monde
Scientific.
Doya, K. (1999). Reinforcement learning in continuous time and space. Neural Com-
putation, 12, 243–269. https://doi.org/10.1162/089976600300015961
Grollman, D. H., & Billard, UN. (2011). Donut as I do: Learning from failed demon-
strations. In Proceedings of the IEEE International Conference on Robotics and Au-
tomation (pp. 3804–3809). Piscataway, New Jersey: IEEE. https://doi.org/10.1109/ICRA.
2011.5979757
Grollman, D. H., & Billard, UN. (2012). Robot learning from failed demonstra-
tion. International Journal of Social Robotics, 4, 331–342. https://doi.org/10.1007/
s12369-012-0161-z
Hidaka, S., & Kashyap, N.
(2013). On the estimation of pointwise dimension.
arXiv:1312.2298.
Ho, M.. K., Littman, M., MacGlashan, J., Cushman, F., & Austerweil, J.. L. (2016).
Showing versus doing: Teaching by demonstration. In D. Lee, M.. Sugiyama, U.
Luxburg, je. Guyon, & R.. Garnett (Éd.), Advances in neural information processing
systèmes, 29 (pp. 3027–3035). Red Hook, New York: Curran.
Hogan, N. (1984). An organizing principle for a class of voluntary movements.
Journal des neurosciences, 4(11), 2745–2754. https://doi.org/10.1523/JNEUROSCI.
04-11-02745.1984, PubMed: 6502203
Meltzoff, UN. N. (1995). Understanding the intentions of others: Re-enactment of in-
tended acts by 18-month-old children. Developmental Psychology, 31(5), 838–850.
https://doi.org/10.1023/A:1013251112392
Ng, UN., & Russell, S. J.. (2000). Algorithms for inverse reinforcement learning. En Pro-
ceedings of the 17th International Conference on Machine Learning (pp. 663–670).
Schaal, S. (1997). Learning from demonstration. En M. Mozer, M.. Jordan, & T. Petsche
(Éd.), Advances in neural information processing systems, 9 (pp. 1040–1046). Came-
pont: AVEC Presse.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3026
T. Torii and S. Hidaka
Schaal, S. (1999). Is imitation learning the route to humanoid robots? Trends in Cogni-
tive Sciences, 3(6), pp. 233–242. https://doi.org/10.1016/s1364-6613(99)01327-3,
PubMed: 10354577
Shiarlis, K., Messias, J., & Whiteson, S. (2016). Inverse reinforcement learning from
failure. In Proceedings of the 15th International Conference on Autonomous Agents and
Multiagent Systems (pp. 1060–1068). New York: ACM.
Sutton, R.. S., & Barto, UN. G. (1998). Reinforcement learning: An introduction. Came-
pont, MA: AVEC Presse.
Tomasello, M.. (2001). The cultural origins of human cognition. Cambridge, MA: Cheveux-
vard University Press. https://doi.org/10.2307/j.ctvjsf4jc
Torii, T., & Hidaka, S. (2017). Toward a mechanistic account for imitation learning:
An analysis of pendulum swing-up. New Frontiers in Artificial Intelligence, 10247,
327–343. https://doi.org/10.1007/978-3-319-61572-1_22
Uno, Y., Kawato, M., & Suzuki, R..
(1989). Formation and control of op-
trajectory in human multijoint arm movement: minimum torque-
timal
change model. Biological Cybernetics, 61(2), 89–101. https://doi.org/10.1007/
BF00204593, PubMed: 2742921
Warneken, F., & Tomasello, M.. (2006). Altruistic helping in human infants and young
chimpanzees. Science, 311, 1301–1303. https://doi.org/10.1126/science.1121448,
PubMed: 16513986
Wolpert, D. M., Doya, K., & Kawato, M.. (2003). A unifying computational framework
for motor control and social interaction. Philosophical Transactions of the Royal So-
ciety B: Sciences biologiques, 358(1431), 593-602.
Jeune, L.-S.
(1982). Dimension, entropy, and Lyapunov exponents. Ergodic
Theory and Dynamical Systems, 2(1), 109–124. https://doi.org/10.1017/
S0143385700009615
Zhifei, S., & Joo, E. M.. (2012). A review of inverse reinforcement learning: théorie
and recent advances. In Proceedings of the IEEE World Congress on Computational
Intelligence (pp. 1–8). Piscataway, New Jersey: IEEE. https://doi.org/10.1109/CEC.2012.
6256507
Ziebart, B. D., Maas, UN., Bagnell, J.. UN., & Dey, UN. K. (2008). Maximum entropy inverse
reinforcement learning. In Proceedings of the 23rd National Conference on Artificial
Intelligence (vol. 3, pp. 1433–1438). Palo Alto, Californie: AAAI Press.
Received October 23, 2020; accepted June 4, 2021.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
9
9
6
1
9
6
6
6
4
1
n
e
c
o
_
un
_
0
1
4
3
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3