LETTER
Communicated by Peer Neubert
Simulating and Predicting Dynamical Systems
With Spatial Semantic Pointers
Aaron R. Voelker
arvoelke@uwaterloo.ca
Peter Blouw
peter.blouw@appliedbrainresearch.com
Xuan Choo
xuan.choo@appliedbrainresearch.com
Applied Brain Research, Waterloo, ON N2L 3G1, Canada
Nicole Sandra-Yaffa Dumont
ns2dumont@uwaterloo.ca
École d'informatique de Cheriton, Université de Waterloo,
Waterloo, Ontario, N2L 3G1, Canada
Terrence C. Stewart
terrence.stewart@nrc-cnrc.gc.ca
National Research Council of Canada, Université de Waterloo
Collaboration Centre, Waterloo, ON N2L 3G1 Canada
Chris Eliasmith
celiasmith@uwaterloo.ca
Centre for Theoretical Neuroscience, Université de Waterloo,
Waterloo, Ontario, N2L 3G1, Canada
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
While neural networks are highly effective at learning task-relevant rep-
resentations from data, they typically do not learn representations with
the kind of symbolic structure that is hypothesized to support high-level
cognitive processes, nor do they naturally model such structures within
problem domains that are continuous in space and time. To fill these gaps,
this work exploits a method for defining vector representations that bind
discrete (symbol-like) entities to points in continuous topological spaces
in order to simulate and predict the behavior of a range of dynamical sys-
thèmes. These vector representations are spatial semantic pointers (SSPs),
and we demonstrate that they can (1) be used to model dynamical sys-
tems involving multiple objects represented in a symbol-like manner
et (2) be integrated with deep neural networks to predict the future of
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A.V. and P.B. contributed equally.
Neural Computation 33, 2033–2067 (2021) © 2021 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01410
2034
UN. Voelker et al.
physical trajectories. These results help unify what have traditionally ap-
peared to be disparate approaches in machine learning.
1 Introduction
A considerable amount of recent progress in AI research has been driven
by the fact that artificial neural networks are highly effective function ap-
proximators when trained with sufficient amounts of data. Cependant, it is
generally acknowledged that there remain important aspects of intelligent
behavior that are not naturally described by static functions applied to dis-
crete sets of inputs. Par exemple, LeCun, Bengio, and Hinton (2015) have
decried the lack of methods for combining representation learning with
complex reasoning (see also Bottou, 2014), an avenue of research that has
traditionally motivated researchers to posit the need for structured sym-
bolic representations (Marcus, 1998; Smolensky & Legendre, 2006; Hadley,
2009). Others have noted such methods do not effectively capture the dy-
namics of cognitive information processing in continuous space and time
(Eliasmith, 2013; Schöner, 2014). Par conséquent, extending neural networks
to manipulate structured symbolic representations in task contexts that in-
volve dynamics over continuous space and time is an important unifying
goal for the field.
In this work, we take a step toward this goal by exploiting a method for
defining vector representations that encode blends of continuous and dis-
crete structures in order to simulate and predict the behavior of a range of
dynamical systems in which multiple objects move continuously through
space and time. These vector representations are spatial semantic pointers
(SSPs), and we provide analyses of both their capacity to represent com-
plicated spatial topographies and their ability to learn and model arbitrary
dynamics defined with respect to these topographies. More specifically, nous
show how SSPs can be used to (1) simulate continuous trajectories involving
multiple objects, (2) simulate interactions between these objects and walls,
et (3) learn the dynamics governing these interactions in order to predict
future object positions.
Mathematically, SSPs are built on the concept of a vector symbolic ar-
chitecture (VSA; Gayler, 2004), in which a set of algebraic operations is
used to bind vector representations into role-filler pairs and to group such
pairs into sets (Smolensky, 1990; Plate, 2003; Kanerva, 2009; Frady, Kleyko,
& Sommer, 2020; Schlegel, Neubert, & Protzel, 2020). Traditionnellement, VSAs
have been characterized as a means of capturing symbol-like discrete repre-
sentational structures using vector spaces. Recent extensions to VSAs have
introduced fractional binding operations that define SSPs as distributed
representations in which both roles and fillers can encode continuous quan-
tities (Komer, Stewart, Voelker, & Eliasmith, 2019; Frady, Kanerva, & Som-
mer, 2018). SSPs have previously been used to model spatial reasoning
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2035
tasks (Lu, Voelker, Komer, & Eliasmith, 2019; Blanc, Cheung, & Olshausen,
2016), model path planning and navigation (Komer & Eliasmith, 2020),
and model grid cell and place cell firing patterns in the context of spik-
ing neural networks (Dumont & Eliasmith, 2020). Storage capacity analy-
ses with SSPs have also been performed (Mirus, Stewart, & Conradt, 2020).
Ici, we extend this prior work to model continuous dynamical systems
with SSPs and thereby integrate perspectives on AI that alternatively focus
on deep learning (LeCun, Bengio, and Hinton, 2015; Goodfellow, Bengio,
& Courville, 2016; Schmidhuber, 2015), symbolic structure (Marcus, 1998,
2019; Hadley, 2009), and temporal dynamics (Eliasmith, 2013; Voelker, 2019;
McClelland et al., 2010).
We begin by introducing VSAs and fractional binding. We then use these
concepts to define SSPs and discuss methods for visualizing them. We dis-
cuss their relevance for neurobiological representations (c'est à dire., grid cells) et
feature representation in deep learning. After this introductory material,
we turn to our contributions, which expose new methods for representing
and learning arbitrary trajectories in neural networks. We then demonstrate
how arbitrary trajectories can be simulated dynamically for both single and
multiple objects. Suivant, we derive partial differential equations (PDEs) que
can simulate continuous-time trajectories by way of linear transformations
embedded in recurrent spiking neural networks. We also introduce two
methods for simulating multiple objects, and compare and contrast them.
Enfin, we show how SSPs can be combined with Legendre memory units
(LMUs; Voelker, Kaji´c, & Eliasmith, 2019) to predict the future trajectory of
objects moving along paths with discontinuous changes in motion.
2 Structured Vector Representations
2.1 Vector Symbolic Architectures. Vector symbolic architectures
(VSAs) were developed in the context of long-standing debates surround-
ing the question of how symbolic structures might be encoded with dis-
tributed representations of the sort manipulated by neural networks (Fodor
& Pylyshyn, 1988; Marcus, 1998; Smolensky & Legendre, 2006). To provide
an answer to this question, a VSA first defines a mapping from a set of
primitive symbols to a set of vectors in a d-dimensional space, V ⊆ Rd. Ce
mapping is often referred to as the VSA’s “vocabulary.” Typically the vec-
tors in the vocabulary are chosen such that by the similarity measure used
in the VSA, each vector is dissimilar and thus distinguishable from every
other vector in the vocabulary. A common method for generating random
d-dimensional vectors involves sampling each element from a normal dis-
tribution with a mean of 0 and a variance of 1/d (Muller, 1959). Choosing
vector elements in this way ensures both that the expected L2-norm of the
vector is 1 and that performing the discrete Fourier transform (DFT) on the
vector results in Fourier coefficients uniformly distributed around 0 avec
identical variance across all frequency components.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2036
UN. Voelker et al.
En plus, VSAs define algebraic operations that can be performed on
vocabulary items to enable symbol manipulation. These operations can be
grouped into five types: (1) a similarity operation that computes a scalar
measure of how alike two vectors are; (2) a collection operation that com-
bines two vectors into a new vector that is similar to both inputs; (3) un
binding operation that compresses two vectors into a new vector that is
dissimilar to both inputs; (4) an inverse operation that decompresses a vec-
tor to undo one or more binding operations; et (5) a cleanup operation
that maps a noisy or decompressed vector to the most similar “clean” vec-
tor in the VSA vocabulary. We discuss each of these operations in turn and
focus on a specific VSA that uses vector addition for collection and circular
convolution for binding, and whose vectors are commonly referred to as
holographic reduced representations (HRRs; Plate, 2003):
Similarity. To measure the similarity (s) between two vectors, VSAs typ-
ically use the inner product operation in Euclidean space (a.k.a., le
dot product):
s = A · B = ATB.
(2.1)
When the two vectors are unit length, this becomes identical to the
“cosine similarity” measure. When this measure is used, two identi-
cal vectors have a similarity of 1, while two orthogonal vectors will
have a similarity of 0. We note that when the dimensionality, d, est
grand, then two randomly generated unit vectors are expected to be
approximately orthogonal, or dissimilar, to one another (Gosmann,
2018).
Collection. A collection operation is defined to map any pair of input
vectors to an output vector that is similar to both inputs. This is
useful for representing unordered sets of symbols. Vector superposi-
tion (c'est à dire., element-wise addition) is commonly used to implement this
operation.
Binding. A binding operation is defined to map any pair of input vec-
tors to an output vector that is dissimilar to both input vectors.
This is useful for representing the conjunction of multiple symbols.
Common choices for a binding operation include circular convolu-
tion (Plate, 2003), element-wise multiplication (Gayler, 2004), vector-
derived transformation binding (Gosmann & Eliasmith, 2019), et
exclusive-or (Kanerva, 2009), though some of these choices impose
requirements on the vocabularly vectors they apply to. With circular
convolution ((cid:2)), the binding of A and B can be efficiently computed
comme
UN (cid:2) B = F −1{F{UN} (cid:3) F{B}},
(2.2)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2037
where F{·} is the DFT operator and (cid:3) denotes the element-wise mul-
tiplication of two complex vectors. Ensemble, collection via addition
and binding via circular convolution obey the algebraic laws of com-
mutativity, associativity, and distributivity (Gosmann, 2018).
En plus, because circular convolution produces an output vec-
tor for which each element is a dot product between one input vec-
tor and a permutation of the elements in the other input vector, it
possible to permute the elements of A to construct a fixed “binding
matrice,” T(UN) ∈ Rd×d that can be used to implement this binding op-
eration (Plate, 2003):
UN (cid:2) B = T(UN)B.
(2.3)
More specifically, T(UN) is a special kind of matrix called a “circulant
matrix” that is fully specified by the vector A. Its first column is A, et
remaining columns are cyclic permutations of A with offset equal to
the column index.
Inverse. The inverse, or “unbinding,” operation can be thought of as
creating a vector that undoes the effect of a binding operation, tel
that if ∼A is the inverse of A, then binding ∼A to a vector that binds
together A and B will return B. For a VSA that uses circular convo-
lution, the inverse of a vector is calculated by computing the com-
plex conjugate of its Fourier coefficients. Fait intéressant, performing the
complex conjugate in the Fourier domain is equivalent to perform-
ing an involution operation1 on the individual elements of the vector.
Since the exact inverse of a vector must take into account the mag-
nitude of its Fourier coefficients, while the complex conjugate does
pas, the inverse operation in general only computes an approximate
inverse of the vector, c'est, ∼A ≈ A−1, where A−1 is the exact inverse
of A.2
Cleanup. When the inverse operation is approximate, binding a vec-
tor with its inverse introduces noise into the result. Performing the
binding operation on a vector that has collected together multiple
other vectors also introduces potentially unwanted output terms3
1
2
The involution operation preserves the order of the first element in a vector and re-
verses the order of the remaining elements. As an example, the involution of the vector
[0, 1, 2, 3] est [0, 3, 2, 1].
Computing the exact inverse of a vector can occasionally result in large Fourier
coefficient magnitudes, since the Fourier coefficients of the input vector are uniformly dis-
tributed around 0. The large Fourier coefficient magnitudes consequently generate vectors
with “misbehaved” vector magnitudes (c'est à dire., they do not conform to the assumption that
the vector magnitudes should be approximately 1).
An algebraic analogy to these extraneous symbolic terms is to consider using (un + b)2
to compute a2 + b2. In this analogy, the expanded form of (un + b)2 contains the “desired”
a2 and b2 terms and an “extraneous” 2ab term.
3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2038
UN. Voelker et al.
into the symbolic computation. Par conséquent, VSAs define a cleanup
operation that can be used to reduce the noise accumulated through
the application of binding and unbinding operations and to remove
unwanted vector terms from the results of these operations. To per-
form a cleanup operation, an input vector is compared to all the
vectors within a desired vocabulary, with the output of the cleanup
operation being the vector within the vocabulary that has the high-
est similarity to the input vector. This operation can be learned from
data using a deep neural network (Komer & Eliasmith, 2020) or im-
plemented directly by combining a matrix multiplication (to compute
the dot product) with a thresholding function (Stewart, Tang, & Elia-
smith, 2011) or a winner-take-all mechanism (Gosmann, Voelker, &
Eliasmith, 2017).
Until recently, VSAs have been largely used to map discrete structures
into high-dimensional vector spaces using slot-filler representations created
through the application of binding and collection operations. Such repre-
sentations are quite general and capture a variety of data types familiar
to neural and cognitive modelers, including lists, trees, graphs, grammars,
and rules. Cependant, there are many natural tasks for which discrete rep-
resentational structures are not appropriate. Consider the example of an
agent moving through an unstructured spatial environment (par exemple., a forest).
Ideally, the agent’s internal representations of the environment would be
able to incorporate arbitrary objects (par exemple., notable trees or rocks) while bind-
ing these objects to arbitrary spatial locations or areas. To implement such
representations with a VSA, the slots should ideally be continuous (c'est à dire.,
mapping to continuous spatial locations) even if the fillers are not. Con-
tinuous slots of this sort would allow for representations that bind specific
objets (par exemple., a symbol-like representation of a large oak tree) to particular
spatial locations. To develop this kind of continuous spatial representation,
it is useful to exploit certain additional properties of VSAs that use circular
convolution as binding operator.
2.1.1 Unitary Vectors. Within the set of vectors operated on by circular
convolution, there exists a subset of “unitary” vectors (Plate, 2003) that ex-
hibit the following two properties: their L2-norms are exactly 1, et le
magnitudes of their Fourier coefficients are also exactly 1. Surtout, ces
properties ensure that (1) the approximate inverse of a unitary vector is
equal to its exact inverse, hence we can use A−1 = ∼A interchangeably,
(2) the dot product between two unitary vectors becomes identical to their
cosine similarity, et (3) binding one unitary vector with another uni-
tary vector results in yet another unitary vector; hence, unitary vectors are
“closed” under binding with circular convolution.
Since the approximate inverse is exact for these vectors, binding a uni-
tary vector with its inverse does not introduce noise in the result. Ainsi,
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2039
unitary vectors support lossless binding and unbinding operations. Arbi-
trary sequences of these operations are perfectly reversible without the use
of a cleanup operation as long as the operands that need to be inverted are
known in advance.
2.1.2 Iterative Binding. One particularly useful application of unitary
vectors involves iterating a specific binding operation to generate a set of
points that are closed under a linear transformation (Komer, 2020). Typi-
cally, this involves binding a given vector to itself some number of times
such that if k is a natural number and A is a vector, alors
Ak = A (cid:2) UN (cid:2) UN . . . (cid:2) UN
(cid:5)
(cid:2)
(cid:3)(cid:4)
A appears k times
.
(2.4)
This process is sometimes referred to as a repeated “autoconvolution”
(Plate, 2003).
The significance of this definition lies in the fact that when A is unitary, it-
erative binding creates a closed sequence of approximately orthogonal vec-
tors that can be easily traversed. Par exemple, moving from the vector Ak
in the sequence to the vector Ak+1 is as simple as performing the binding
Ak (cid:2) UN; moving back to Ak from Ak+1 is as simple as performing the bind-
ing Ak+1 (cid:2) A−1 due to the fact that the inverse is exact for unitary vectors.
+k2 = Ak1 (cid:2) Ak2 for all integers k1 and k2, a single
Plus généralement, because Ak1
binding operation suffices to move between any two vectors in the closed
sequence corresponding to self-binding under A.
Because further binding operations can be used to associate the points in
this sequence with other representations, it becomes very natural to encode
a list of elements in a single vector using these techniques. Par exemple, à
encode the list X, Oui, Z . . ., one could bind each vector in this list to neighbor-
ing points as follows: A1 (cid:2) X + A2 (cid:2) Oui + A3 (cid:2) Z . . . The retrieval of specific
elements from this list can then be performed by moving to the desired cue
in the set of vectors defined by A closed under self-binding (par exemple., A2), et
then unbinding this cue to extract the corresponding element from the en-
coded list (par exemple., Oui). This method has been used in several neural models of
working memory (Choo, 2010; Eliasmith et al., 2012; Gosmann & Eliasmith,
2020).
2.1.3 Fractional Binding. It is possible to further generalize iterative bind-
ing by allowing k to be a real-valued number rather than an integer. Mathe-
matically, a fractional number of binding iterations can be expressed in the
Fourier domain as
Ak DEF= F −1
(cid:6)
(cid:7)
,
F{UN}k
(2.5)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2040
UN. Voelker et al.
where F{UN}k is the element-wise exponentiation of a set of complex Fourier
coefficients. This definition is equivalent to equation 2.4 when k is a positive
integer but generalizes it to allow k to be real.
Assuming A is unitary, we often find it convenient to restate this defini-
tion by using Euler’s formula and the fact that exponentiating a unit-length
complex number is equivalent to scaling its polar angle,
Ak = F −1
(cid:7)
(cid:6)
eikφ
,
(2.6)
where φ are the polar angles of F {UN}. De même, binding two unitary vec-
tors is equivalent to adding their polar angles, as is made implicit in equa-
tion 2.2.
One consequence of this definition is that for any k1
algebraic property holds:
, k2
∈ R, the following
Ak1 (cid:2) Ak2 = Ak1
+k2 .
(2.7)
Ainsi, fractional binding can be used to generate a closed sequence of vec-
tors that can easily be traversed or continuously shifted by any (cid:3)k. Comment-
jamais, the vectors are not all approximately orthogonal to one another. Plutôt,
for nearby values of k, the pointers Ak will be highly similar to one an-
other (Komer, 2020). En particulier, as the dimensionality becomes suffi-
ciently high, the expected similiarity approaches:
Ak1 · Ak2 = sinc(k2
− k1)
(2.8)
for unitary A with independent φ ∼ U (−π, π ) (Voelker, 2020). We address
these latter points in section A.1.
The most significant consequence of being able to perform fractional
binding using real values for k is that vectors of the form Ak can encode con-
tinuous quantities. Such continuous quantities can then be bound into other
representations, thereby allowing for vectors that encode arbitrary blends
of continuous and discrete elements. Par exemple, a discrete pair of contin-
(cid:2) Ak2 . De la même manière, a contin-
uous values could be represented as P1
uous three-dimensional value could be represented as Ak1 (cid:2) Bk2 (cid:2) Ck3 . Le
point to draw from such examples is that the use of fractional binding sig-
nificantly expands the class of data structures that can be encoded and ma-
nipulated using a vector symbolic architecture, namely, to those definable
over continuous spaces (c'est à dire., with continuous slots).
(cid:2) Ak1 + P2
2.2 Spatial Semantic Pointers. To best make use of the above features
of VSAs in the context of spatial reasoning tasks, we incorporate fractional
binding operations into a cognitive modeling framework called the se-
mantic pointer architecture (SPA; Eliasmith, 2013). The SPA provides an
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2041
architecture and methodology for integrating cognitive, perceptual, et
motor systems in spiking neural networks. The SPA defines vector repre-
sentations, named semantic pointers (SPs), que (1) are produced via com-
pression and collection operations involving representations from arbitrary
modalities, (2) express semantic features, (3) “point to” additional repre-
sentations that are accessed via decompression operations, et (4) can be
neurally implemented (Eliasmith, 2013). By integrating symbolic structures
of the sort defined by conventional VSAs with richer forms of sensorimo-
tor data, the SPA has enabled the creation of what still remains the world’s
largest functioning model of the human brain (Eliasmith et al., 2012; Choo,
2018), along with a variety of other models focused on more specific cogni-
tive functions (Rasmussen & Eliasmith, 2011; Stewart, Choo, & Eliasmith,
2014; Crawford, Gingerich, & Eliasmith, 2015; Blouw, Solodkin, Thagard, &
Eliasmith, 2016; Gosmann & Eliasmith, 2020).
SSPs extend the class of representational structures defined within the
SPA by binding arbitrarily complex representations of discrete objects to
points in continuous topological spaces (Komer et al., 2019; Lu, Voelker,
Komer, & Eliasmith, 2019; Komer & Eliasmith, 2020). The SPA provides
methods for realizing and manipulating these representations in spiking
(and nonspiking) neural networks.
For convenience, we introduce the shorthand notation for encoding a
position (X, oui) in a continuous space,
P.(X, oui)
DEF= Xx (cid:2) Yy,
(2.9)
where X, Y ∈ V are randomly generated, but fixed, unitary vectors repre-
senting two axes in Euclidean space. Our definitions naturally generalize
to multidimensional topological spaces, but we restrict our focus here to
two-dimensional Euclidean space for purposes of practical illustration.
Mathematically, an SSP that encodes a set of m objects on a plane can be
defined as
M =
m(cid:8)
je = 1
OBJi
(cid:2) Si
.
(2.10)
In equation 2.10, OBJi
∈ V is an arbitrary SP representing the ith object, et
Si
= P(xi
, yi),
où (xi, yi) is its position in space, ou
(cid:9)
=
Si
P.(X, oui) dx dy,
(X,oui)∈Ri
where Ri
⊆ R2 is its region in two-dimensional space.
(2.11)
(2.12)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2042
UN. Voelker et al.
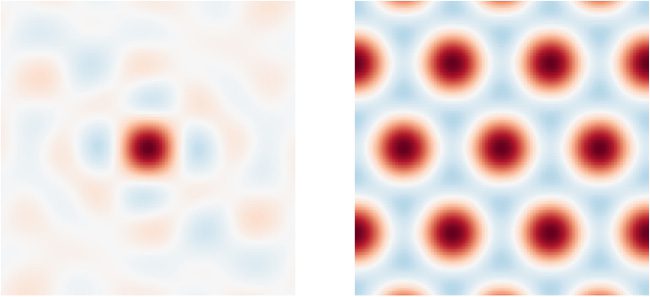
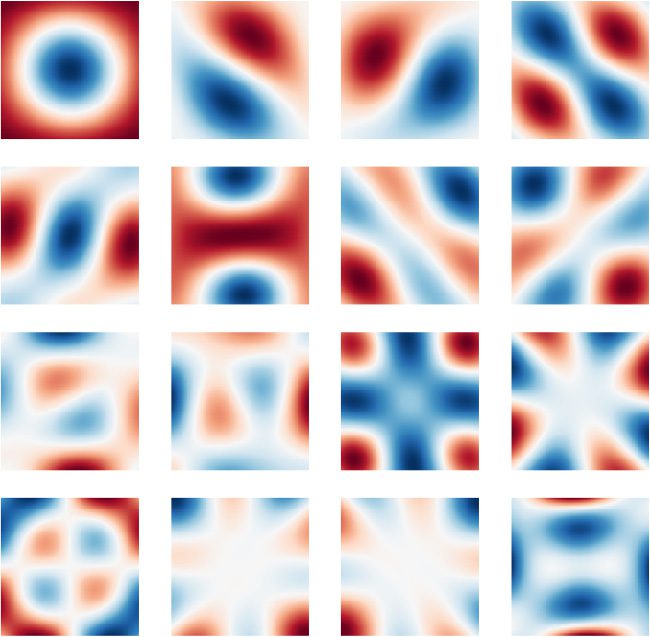
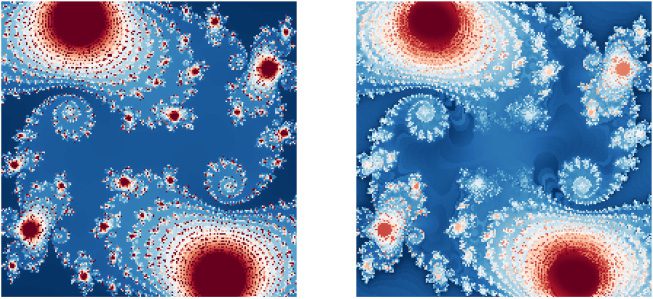
Chiffre 1: Example similarity maps for two different SSPs, each encoding a sin-
gle object at position (0, 0) on a square map of size 6
2. Gauche: A 512-dimensional
SSP is constructed using randomly generated unitary axis vectors. Droite: UN
7-dimensional SSP is constructed using axis vectors that produce a hexagonal
lattice (see section 2.2.2).
√
The integral defining Si can range over a set of points, in which case arbi-
trary regions can be encoded into the SSP (also see section 2.2.1); otherwise,
Si encodes a single point in the plane. The sum ranging from 1 to m can fur-
ther include null entity and spatial representations (c'est à dire., the identity seman-
tic pointer) such that the SSP is able to include entity representations not
associated with particular locations in space, along with spatial representa-
tions not associated with particular entities. These features of the definition
allow SSPs to flexibly encode information about a wide range of spatial (et
other continuous) environnements.
SSPs can be manipulated to, Par exemple, shift or locate multiple objects
in space (Komer et al., 2019) and to query the spatial relationships between
objets (Lu, Voelker, Komer, & Eliasmith, 2019). To provide a simple exam-
ple, an object located at (X, oui) can be retrieved from an SSP by computing
M. (cid:2) P.(X, oui)−1 and then cleaning up the result to the most similar SP in the
vocabulary {OBJi
}m
je = 1. De même, the ith point or region in space, Si, can be
−1
retrieved by computing M (cid:2) OBJ
, with an optional cleanup on the result.
je
As a final example, equation 2.7 can be exploited to shift all coordinates in
M by the same amount, ((cid:3)X, (cid:3)oui), with the binding M (cid:2) P.((cid:3)X, (cid:3)oui).
2.2.1 Visualizing SSPs with Similarity Maps. To visualize some object’s
point or region in space (Si, from equations 2.11 ou 2.12), we often plot what
we refer to as the “similarity map” (voir la figure 1). This is computed by se-
lecting some set of two-dimensional coordinates that one wishes to evalu-
ate and then for each (X, oui) coloring the corresponding pixel by the value
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2043
of P(X, oui)T Si, c'est, the similarity between the pointer and the correspond-
ingly encoded point in space. Typically the colors are chosen from a diverg-
ing color palette, normalized to [−1, 1], the limits for the similarity between
two unitary vectors.
More formally, the similarity map is a linear operator that consumes an
SSP, S, and produces a function of (X, oui) for that particular SSP, which we
can denote mathematically as
M.(S) = P(X, oui)T S.
(2.13)
Chiffre 1 illustrates example similarity maps for two different choices of
axis vectors (X, Oui), giving different P(X, oui). In each case, we are plotting
M. (P.(0, 0)), où (X, oui) are evenly tiled across a square grid of size 6
2,
centered at (0, 0).
√
These illustrations are useful for understanding and visualizing what a
particular SSP is representing. It is important to note that SSPs themselves
are not discretized sets of pixels; they are essentially compressed represen-
tations thereof using Fourier basis functions. The similarity map is primar-
ily a tool for visualization.
That said, the similarity map does provide an important insight: equa-
tion 2.11 ou 2.12 are sufficient but not necessary ways of constructing SSPs
that encode points or regions of space. C'est, S can be any vector such that
M.(S) approximates some desired function of (X, oui), so that the similarity
between S and P(X, oui) represents that spatial map. We provide an example
of an interesting application of this insight in section A.1.
The similarity map also has a number of important properties. D'abord,
shifting the similarity map of A is equivalent to shifting A by the same
amount, depuis
P.(X + X
(cid:8), oui + oui
(cid:8)
)T S =
(cid:10)
P.(X, oui) (cid:2) P.(X
(cid:10)
= P(X, oui)T
(cid:10)
= M
S (cid:2) P.(X
T
(cid:8)
(cid:8)
(cid:8), oui
(cid:11)
)
(cid:8), oui
S (cid:2) P.(X
(cid:11)
(cid:8), oui
.
)
(cid:8)
S
(cid:11)
)
(2.14)
Deuxième, since the dot product is a linear operator, the function that produces
a similarity map, M.(·), is in fact a linear function; taking a linear combi-
nation of similarity maps is equivalent to taking the similarity map of that
same linear combination of vectors. Troisième, the peak(s) in the plot, over some
spatial domain, correspond to the ideal target(s) for a cleanup that is to out-
put the most similar P(X, oui) given that domain as its vocabulary.
2.2.2 Relevance of SSPs to Neurobiological Representations. SSPs can also be
used to reproduce the same grid cell firing patterns (Dumont & Eliasmith,
2020) that have been famously identified as a basis for the brain’s spatial
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2044
UN. Voelker et al.
representation system (Moser, Kropff, & Moser, 2008). This is accomplished
by generating the axis vectors, (X, Oui), in the following manner.
Consider the similarity map of a d-dimensional SSP representing a single
indiquer, noting that the dot product between two vectors is equal (up to a
constant) to the dot product of their Fourier transforms,
M.(P.(x0
, y0)) = P(X, oui)T P(x0
, y0) ∝
d(cid:8)
j=1
ei(K j,1(x+x0 )+K j,2(y+y0 )),
(2.15)
where K j,1 is the polar angle of the jth component of the Fourier transform
of the axis vector X, and K j,2 is the polar angle for the axis vector Y.
Sorscher, Mel, Ganguli, and Ocko (2019, see equation 2.10) and Dumont
and Eliasmith (2020, see equations 2.11–2.13) provide the conditions on
these phases such that the similarity map is a regular hexagonal lattice pat-
tern across the (X, oui) plane. The core building block is a matrix K ∈ R3×2
that holds the three two-dimensional coordinates of an equilateral triangle
inscribed in a unit circle:
⎛
⎞
⎟
⎠ .
(2.16)
⎜
⎝
K =
√
1
0
3/2 −1/2
√
3/2 −1/2
−
Using these values for the polar angles in equation 2.15 produces hexag-
onally tiled similarity maps. Cependant, to ensure the resulting axis vectors
are real and unitary, additional polar angles are needed. En particulier, le
Fourier transform of the axis vectors must have Hermitian symmetry (c'est à dire.,
contain the complex conjugates of the coefficients given by K) and a zero-
frequency term of one. This results in seven-dimensional axis vectors.
Scaled and/or rotated versions of the K matrix can be used to set the
resolution and orientation, respectivement, of the resulting hexagonal pattern.
Ici, scaling means multiplying K by a fixed scalar, and rotating means
applying a 2D rotation matrix to the columns of K. Par exemple, to produce
place or grid cell bumps with a diameter of
2 (voir la figure 1, droite), le
scaling factors should have a mean of 2π/
6.4
√
√
While these 7-dimensional SSPs can be used to create spiking neural net-
works with grid cell–like firing patterns, this patterned similarity means
that such SSPs can only uniquely represent a small area of (X, oui) valeurs.
To increase the representational power of the SSPs and produce place cell–
like similarity maps, the dimensionality must be increased by combining
4
Using the fact that the distance between peaks in the hexagonal lattice is 4π /
où |k| is the scaling factor on K (Dumont & Eliasmith, 2020).
(cid:18)√
(cid:19)
3|k|
,
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2045
a variety of grids with different resolutions and orientations. Scaled and
rotated versions of K can be stacked in the Fourier domain n times to gen-
erate the x- and y-axis vectors. The final dimensionality of the axis vectors
is d = 6n + 1 (6 from each 3-dimensional K block of different scale/rotation
and their complex conjugates, et 1 from the zero frequency term). SSPs
that use such axis vectors will be referred to as hexagonal SSPs. Neurons
in networks representing hexagonal SSP can pick out the different grids it
contains. This reproduces grid cell–like tuning distributions and provides
more accurate place cell representations using SSPs in spiking neural net-
travaux (Dumont & Eliasmith, 2020).
2.2.3 SSPs as Features for Deep Learning. SSPs, used within the greater SPA
framework, provide a general method for encoding continuous variables
in high-dimensional vector spaces in which algebraic operations have se-
mantic interpretations. Ainsi, these vectors and operations can be used to
craft complex cognitive models. Beyond this, SSPs are a useful tool in deep
learning as a method for embedding data in a feature space with desirable
propriétés.
The data used to create features and the way in which features are rep-
resented can potentially have a large impact on performance of a neural
réseau (Komer, 2020). Ici, “features” refers to the initial vector input
provided to a network. Each layer of a network receives information rep-
resented as a vector and projects it into another vector space. The neurons
in a layer can be thought of as the basis of its space. If half (ou plus) de
the neurons are active, that means most of the dimensions of the vector
space are needed to represent the information. Such a layer would contain
a dense coding of the incoming information. If only one neuron was acti-
vated in a layer, it would represent a local coding. One-hot encoding and
feature hashing are examples of heuristics for encoding discrete data that
correspond to a local and dense coding, respectivement. Anything in between
a dense and local code is called a sparse code. Sparse codes are an advan-
tageous balance between the two extremes; they have a higher representa-
tional capacity and better generalizability than local codes and are gener-
ally easier to learn functions from compared to dense codes (Foldiak, 2003).
Autrement dit, such feature vectors have a reasonable dimensionality and
result in better performance when used in downstream tasks.
Feature learning (par exemple., with an autoencoder) can be used to learn useful
representations, mais, as is often the case in deep learning, the result is usu-
ally uninterpretable. A well-known model for word embedding is word2vec,
which takes a one-hot encoding of a word and outputs a lower-dimensional
vector. An important property of the resultant vectors is that their cosine
similarity corresponds to the encoded words’ semantic similarity. Distinct
inputs have a similarity close to zero. When word embeddings with this
property are used, it is easy to learn a sparse coding with a single layer of
neurons.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2046
UN. Voelker et al.
How can features with such properties be constructed from continuous
variables, in particular, low-dimensional variables? Continuous numeric
values can be fed directly into a neural network, but this raw input is in
the form of a dense coding, and so generally larger/deeper networks are
needed for accurate function approximation. To obtain a sparse encoding
from continuous data, it must be mapped onto a higher-dimensional vec-
tor space. This is exactly what is done when encoding variables as SSPs. UN
simple autoencoder cannot solve this problem; autoencoders work by using
an informational bottleneck, and if their embedding had a higher dimen-
sion than the input, it would just learn to pass the input through. Meth-
ods such as tile coding and radial basis function representation can be used
to encode continuous variables in higher-dimensional spaces, but SSPs has
been found to have better performance over such coding on an array of
deep learning tasks (Komer, 2020). Much like word2vec embeddings, SSPs
of variables with a high distance in Euclidean space will have a low cosine
similarité, and so a sparse code can be obtained from them. En outre,
SSPs can be bound with representations of discrete data without increasing
their dimensionality to create structured symbolic representations that are
easy to interpret and manipulate. These properties of SSPs motivate extend-
ing the theory of SSPs to represent trajectories and dynamic variables. Ce
will fill the gap in methods for structured, dynamic feature representation.
3 Methods for Simulating Dynamics with SSPs
Prior work on SSPs has focused on representing two-dimensional spatial
maps (Komer et al., 2019; Lu et al., 2019; Komer & Eliasmith, 2020; Dumont
& Eliasmith, 2020; Komer, 2020). Some of that work has also shown that
on machine learning problems requiring continuous representations, SSPs
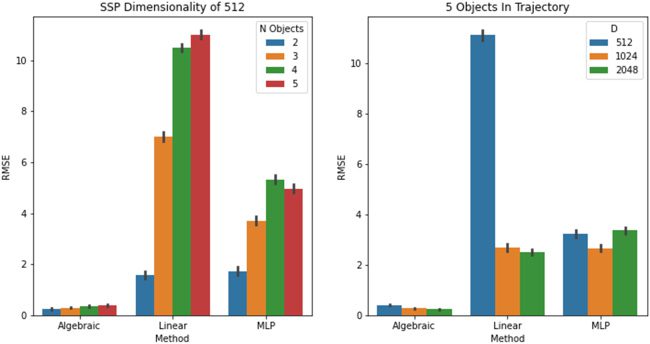
most often should be the preferred choice. Spécifiquement, Komer (2020) com-
pared SSPs to four other standard encoding methods across 122 different
tasks and demonstrated that SSPs outperformed all other methods on 65.7%
of regression and 57.2% of classification tasks. Ici, we extend past work
by introducing methods for representing arbitrary single-object trajectories
and methods for simulating the dynamics of one or more objects following
independent trajectories.
3.1 Representing Arbitrary Trajectories. For many problems, un
needs to encode data that are dynamic, not static. Time is a continuous vari-
capable, much like space, and so it too can be included in an SSP as an addi-
tional axis,
P.(X, oui, t) = Ct (cid:2) Xx (cid:2) Yy,
(3.1)
where C is a randomly chosen unitary SP. This time pointer can be manip-
ulated and decoded the same way as any other SSP.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2047
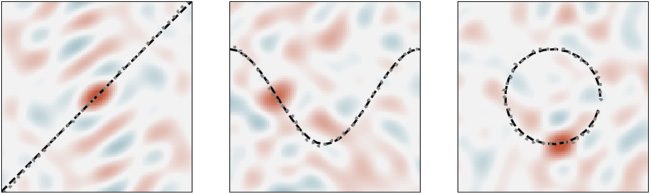
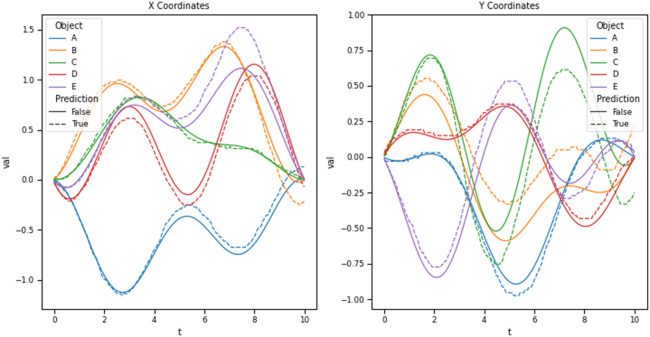
Chiffre 2: Decoding trajectories represented by SSPs (gauche: linear; middle: cosine;
droite: circle). Twenty-five sample points from a continuous trajectory (shown as
a black dotted line) are bound with a “cue” trajectory (par exemple., temps) and summed
together as an SSP. To decode the interpolated position from the SSP, 144 cue
points are used. These decoded positions (after the cleanup procedure) are plot-
ted with a dotted gray line. Snapshots of the similarity plots computed using
decoded positions are plotted underneath.
A sequence of such time-dependent SSPs is an encoding of an entire ar-
bitrary trajectory. The equation to encode such trajectories is
m(cid:8)
je = 1
Cti (cid:2) Si
.
(3.2)
It is a sum over a discrete collection of m points, where Si is the encoding
of each point spatially and ti is the relative time of that point within the
trajectory. If we wanted to encode an ordered sequence of SSPs, order could
be used as “time,” and ti would be the position of the spatial SSPs within
the list.
Continuous trajectories may also be encoded with a natural generaliza-
tion of equation 3.2:
(cid:9)
t
0
τ (cid:2) S(τ ) dτ,
C
(3.3)
where S(τ ) produces the encoding for each point within some trajectory of
points defined over a continuous interval of time, τ ∈ [0, t].
An SSP that implements a transformation that moves smoothly along
this trajectory can then be used to decode information that interpolates be-
tween the points in the original nonlinear trajectory. When few and distant
sample points are used, this interpolation resembles a linear interpolation,
although the result of decoding outside the time range of the samples points
(c'est à dire., extrapolating) decays to zero. Chiffre 2 shows three continuous trajec-
tories being decoded from SSPs. The first traces out a linear y = x function,
the second traces out a cosine function, and third traces out a circle.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2048
UN. Voelker et al.
The smoothness of the replay depends on the number of sample points
used to learn the trajectory, the distances between sample points, the di-
mensionality of the SSP, and the scaling of the time and space variables. Le
amount of noise in the visualization also depends on these factors since, pour
exemple, a lower-dimensional SSP will not be able to encode a large num-
ber of trajectory sample points without incurring a significant amount of
compression loss.
The method presented here for encoding an entire sequence of dynamic
variables as a fixed-length vector could be used in many domains. Co-Reyes
et autres. (2018) provide an example of where performance in continuous state
and action reinforcement learning problems can be improved using tra-
jectory encodings. They use trained autoencoders to encode sequences of
state-space observations and generate action trajectories. Encoding a trajec-
tory with an SSP does not require any learning. Despite not being learned,
SSPs have been found to perform better on navigation tasks compared to
learned encodings (Komer & Eliasmith, 2020).
3.2 Simulating Arbitrary Trajectories. Dans cette section, we move from
encoding specific trajectories to simulating these trajectories online using
some specification of the dynamics governing each object represented by
an SSP.
3.2.1 Simulating Single Objects with Continuous PDEs. D'abord, we illustrate
how to simulate partial differential equations in the SSP space by applying
transformations to an initial SSP that encodes a single object at a particular
point in space. In the discrete-time case, a transformation will be applied to
the SSP at every timestep to account for the movement of the object it rep-
resents. Mathematically, these updates to the initial SSP take the following
form over time.
Mt+(cid:3)t =
(cid:10)
(cid:3)xt (cid:2) Oui
X
(cid:3)yt
(cid:11)
(cid:2) Mt = P((cid:3)xt, (cid:3)yt ) (cid:2) Mt,
(3.4)
où (cid:3)xt and (cid:3)yt are derived from differential equations that relate x and
y to t in some way. Par exemple, if the underlying dynamics are linear, nous
have (cid:3)x = dx
(cid:3)t. Assuming Mt = Xxt (cid:2) Yyt , then the algebraic properties
dt
of SSPs ensure that Xxt (cid:2) Yyt (cid:2) X(cid:3)xt (cid:2) Oui(cid:3)yt = Xxt +(cid:3)xt (cid:2) Yyt +(cid:3)yt = Mt+(cid:3)t, comme
required.
An important observation is that binding with P((cid:3)xt, (cid:3)yt ) is equiv-
alent to applying a matrix transformation to the SSP (see equation 2.3).
Spécifiquement,
Mt+(cid:3)t = T (P.((cid:3)xt, (cid:3)yt )) Mt,
(3.5)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2049
where T(·) is the linear operator that produces the binding matrix for a
given SP (c'est à dire., T(UN)B = A (cid:2) B). Although we have assumed above that the
differential equations are expressed over discrete time, we can also do the
same over continuous time. We omit the proof and simply state the result,
using ln to denote the principal branch of the matrix logarithm:
dM
dt
(cid:20)
(cid:20)
=
=
(cid:20)
(cid:20)
P.
dx
, dy
dt
dt
ln T(X ) + dy
dt
ln T
dx
dt
(cid:21)(cid:21)(cid:21)
M.
(cid:21)
ln T(Oui)
M..
(3.6)
Donc, the continuous-time partial differential equation that evolves an
SSP over time with respect to dx/dt and dy/dt is the addition of two fixed
matrix transformations of the SSP that are each scaled by their respective
derivatives. Équation 3.6 is thus equivalent to a linear dynamical system,
with two time-varying integration time constants controlling the velocity
of x and y—a system that can be implemented accurately and efficiently by
recurrent spiking neural networks (Eliasmith & Anderson, 2003; Voelker,
2019).
We can alternatively express the above continuous-time linear system as
a binding, by first introducing the following definition, which is analogous
to equation 2.5:
ln A
dM
dt
(cid:20)
DEF= F −1{ln F{UN}}.
ln X + dy
dt
dx
dt
=
(cid:21)
ln Y
(cid:2) M..
(3.7)
(3.8)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
The system of equation 3.6 maps directly onto a recurrent neural network
with two recurrent weight matrices, ln T(X ) and ln T(Oui), with gain factors
dx/dt and dy/dt that independently scale the respective matrix-vector mul-
tiplications. In our examples, we simulate the dynamics of equation 3.8 us-
ing a spiking neural network. When simulating with spiking neurons, le
presynaptic activity must be filtered to produce the postsynaptic current.
This filtering must be accounted for in recurrent networks.
The neural engineering framework (NEF; Eliasmith & Anderson, 2003)
provides a methodology for representing vectors via the collective activity
of a population of spiking neurons and for implementing dynamics via re-
current connections. Assuming a first-order low-pass filter is used, a neural
population representing a vector M can evolve according to some dynam-
ics dM
dt via a recurrent connection with weights set to perform the trans-
+ M., where τ is the filter time constant. Optimal weights
formation τ dM
dt
to perform a transformation with one layer can be found via least-squares
optimization.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2050
UN. Voelker et al.
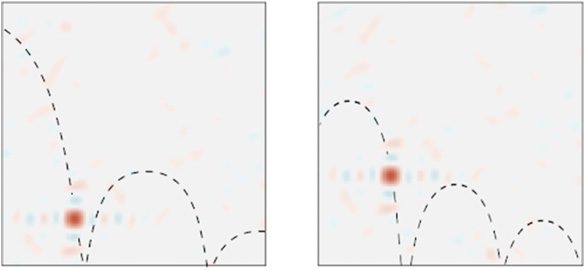
Chiffre 3: A neural network that implements the dynamical system of equa-
tion 3.8 using the binding network described in Stewart, Bekolay, and Eliasmith
(cid:11) + 1) neural populations (where d
(2011). The binding network consists of 4((cid:10) d
2
is the size of the SSP). The weights connecting the inputs to these populations
are set to compute the Fourier transform. Each population performs one of the
element-wise multiplications of the two inputs in the Fourier domain. Weights
outgoing from these populations to the output of the network perform the in-
verse Fourier transform.
Chiffre 4: Using a spiking neural network to simulate a continuous-time partial
differential equation that maps onto the oscillation of a single object. The neu-
ral network consists of a single recurrently connected layer of 30,400 spiking
neurons.
dt ln X + dy
Prior work has used the NEF to construct a neural network that pre-
forms circular convolution (Stewart, Bekolay et al., 2011). The system of
equation 3.8 maps onto such a network, as shown in Figure 3. The network
binds an input vector dx
dt ln Y (passed in through connection 1 dans
the diagram) with an internal state vector that represents the SSP M. Using
two recurrent connections, one that feeds the result of the binding scaled
by τ back into the network as input (connection 2) and another that feeds
the internally represented M (prebinding) to the input as well (connection
3), the dynamics of equation 3.8 are realized. Ainsi, the methods presented
here can be used to build neural networks that move any SSP around space
by integrating dx/dt and dy/dt over time, akin to neural models of path in-
tegration (Conklin & Eliasmith, 2005).
To provide an example, we use these methods to simulate an SSP oscil-
lating in two-dimensional space (voir la figure 4), similar to a controlled cyclic
attractor (Eliasmith, 2005). Hexagonal SSPs (described in section 2.2.2) sont
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2051
Chiffre 5: Simulating trajectories governed by differential equations and elastic
collisions. Each trajectory is generated by binding an SSP encoding the object’s
state to a “transformation” SSP at every time step that encodes its instantaneous
velocity in accordance with the effects of initial velocity, gravity, and collisions
with the bottom of the plane.
used with n = 25 (from having five scalings of K uniformly ranging from 0.9
à 1.5, and five rotations; this results in d = 151) et 100 spiking integrate-
and-fire neurons per element-wise product in the Fourier domain (30,400
neurons total). In this example, the partial derivatives dx/dt and dy/dt are
determined by a 0.2 Hz oscillation with a radius of five spatial units.
It is also possible to impose collision dynamics whenever the simulated
trajectory of a represented object encounters a solid surface (par exemple., a floor or
a wall). Spécifiquement, the instantaneous velocity imposed by a given trans-
formation is inverted and scaled on impact with a surface in accordance
with a simple model of the physics of elastic collisions. Autrement dit, le
((cid:3)xt, (cid:3)yt) ou (dx/dt, dy/dt) corresponding to times at which collisions occur
can be determined in a context-dependent manner. In Figure 5, snapshots
from simulations of balls being dropped (gauche) and tossed (droite) with dif-
ferent initial conditions before bouncing on a hard surface are shown. Ici,
sequences of transformation SSPs are derived assuming (1) an initial object
position and velocity, (2) a differential equation for the effect of gravity, et
(3) a simple model of elastic collisions that reverses and scales the object’s
movement along the y-axis when it reaches of the bottom of the represented
plane.
To summarize, we can model both discrete time and continuous time
differential equations over space by using linear transformations (see equa-
tion 3.5 et 3.6) or bindings (equations 3.4 et 3.8) that are applied to
the SSP over time. Note that the dynamics themselves are driven by the
velocity inputs. The purpose of the methods presented here is to simulate
such dynamics in the space of SSPs and demonstrate that this is possible us-
ing spiking neural networks. These methods can be used in various ways.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2052
UN. Voelker et al.
In the case where the dynamics are self-motion of an animal, this simula-
tion is a biologically plausible path integration model, the result of which
could be used in downstream cognitive tasks. When hexagonal SSPs are
used, the model will have grid cell–like firing patterns, consistent with neu-
robiological findings. En outre, simulating dynamics in the SSP space
circumvents the issue of limits on the representational radius of neural
populations, which prevents dynamics in Euclidean space from being sim-
ulated directly with such networks. En outre, encodings of dynamically
evolving quantities can be used as features in a deep learning network. UN
dynamic encoding could be quite useful for certain problems, such as an on-
line reinforcement learning task, where keeping track of moving obstacles
may be important, or problems that involve predicting future trajectories.
3.2.2 Predicting Future Object Positions. While simulating a dynamical
system can be used to perform prediction, we can also directly tackle the
problem without using knowledge of underlying dynamics by training a
network to output a prediction of the future state of a moving object. Ici,
we briefly describe a technique that exploits SSP representations to enable
prediction of a bouncing ball in a square environment. Spécifiquement, for this
réseau, we provided the SSP representation of a ball bouncing around a
square environment as an online input time series to a recently developed
type of recurrent neural network called a Legendre memory unit (LMU;
Voelker, Kaji´c, & Eliasmith, 2019).
The LMU has been shown to outperform other kinds of recurrent net-
works in a variety of benchmark tasks for time series processing. Il a
also been shown to be optimal at compressing continuous signals over ar-
bitrary time windows, which lends itself well to dynamic prediction. Le
LMU works by using a linear time-invariant system (defined by matrices
A ∈ Rn×n and B ∈ Rn×1) to orthogonalize input signals across a sliding time
window of some fixed length θ . The windowed signal is projected to a basis
that resembles the first n Legendre polynomials (that are shifted, normal-
dimensionné, and discretized).
Assume we have an SSP varying over time, Mt ∈ Rd, and let [Mt] j be its
jth component. At each time step, the LMU will update its internal memory,
m( j)
t
, for each component of the SSP as follows:
m( j)
t
= Am( j)
t−1
+ B [Mt] j
.
The matrices that defined the LTI system are given by
(cid:22)
[UN]i j
= (2je + 1)
je
−1
(−1)i− j+1
if i ≤ j
else
= (2je + 1)(−1)je
je
.
[B]je
(3.9)
(3.10)
(3.11)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2053
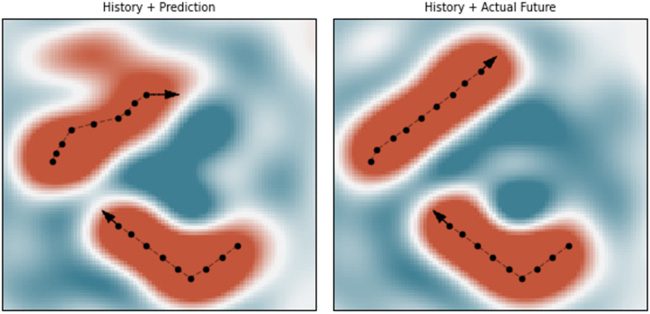
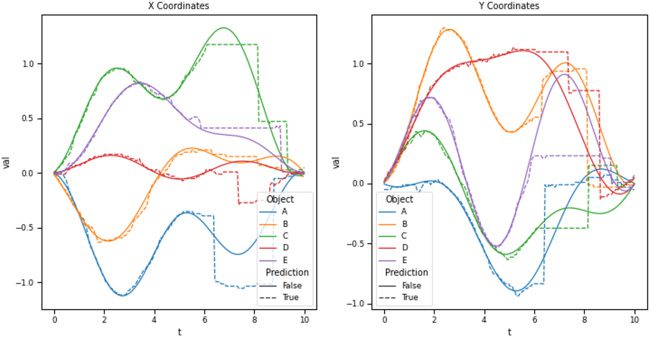
Chiffre 6: Similarity maps of the sum of the history of a bouncing ball (a time
window of SSPs) et (droite) its future or (gauche) a prediction of this future com-
puted using the Legendre memory unit (LMU) and the history. Plotted are
dashed lines indicating the positions represented by these time windows of
SSPs, which are computed using a cleanup procedure.
The LMU that we employ here has a history window θ of 4 s and uses
12 Legendre bases (par exemple., n = 12). A hexagonal 541-dimensional SSP is used
avec 10 scalings of K uniformly ranging from 0.9 à 3.5, et 9 rotations.
The model predicts the same window of time but 6 s into the future
(hence, there is a 2 s gap between the current time and the start of the pre-
dicted future states). The output of the LMU is fed into a neural network
with three dense layers. Input to the network are the d memory vectors
∈ Rn×1, one for each dimension of the SSP, comme
computed via the LMU, m( j)
t
a single flattened vector with size 6492. The first two layers have a hidden
size of 1024 and are followed by an ReLU activation function. The last layer
has a hidden size of 6492. The output of this network is projected onto n Leg-
endre polynomials to obtain a prediction of the SSP at 10 time points equally
spaced over the future window. The network has a total of 14,352,732 train-
able parameters.
The network is trained on 4000 s of bouncing dynamics within a 1 par
1 box. The training data are a time series of SSPs encoding the ball’s po-
sition at 0.4 s intervals. The ball’s trajectory is generated by a simulation
with random initial conditions (position within the box and velocity) et
the dynamics of boundary collisions.
An example simulation is shown in Figure 6, in which the LMU pre-
diction and the actual future SSP representations are compared. We found
that it was able to accurately represent sliding windows of the ball’s history
while simultaneously predicting the sliding window of its future. We con-
sider this a proof-of-principle demonstrating the potential to successfully
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2054
UN. Voelker et al.
marry SSPs with deep learning methods for dynamic simulation and pre-
diction. As a demonstration, we leave quantitative analysis and comparison
to integration with other deep networks for future work (see Komer, 2020,
for evidence of the general utility of SSPs for regression and classification
problems).
3.3 Simulating Multiple Objects. While equation 2.10 establishes that
a single SSP can be used to encode and decode the positions of multiple ob-
projets, further steps are required to simulate continuous dynamics defined
with respect to these objects. Ici, we illustrate that it is possible to de-
fine unique operators or functions that concurrently simulate the dynamics
of multiple objects, such that each object follows its own independent tra-
jectory. Spécifiquement, we describe a method for simulating the dynamics of
multiple objects algebraically, along with a method for simulating such dy-
namics using a trained function approximator.
In the context of SSPs that encode multiple objects, it is essential to
use cleanup operations given that whenever a specific object’s position
is extracted from an SSP, the extracted position will be a lossy approx-
−1
imation of the true position, since M (cid:2) OBJ
≈ Xxi (cid:2) Yyi . De plus, le
je
amount of compression loss observed in such cases will be proportional
to the number of encoded objects, making the application of transforma-
tions to SSPs encoding multiple objects difficult. Cependant, by leverag-
ing knowledge about the specific methods used to generate these SSPs, it
is possible to define cleanup methods that significantly ameliorate these
challenges.
−1 to return the point (xi
3.3.1 Cleanup Methods. In this section we introduce two cleanup meth-
ods for SSPs. The first method involves precomputing Xxi (cid:2) Yyi at a discrete
number of points along a fixed grid, and then taking the dot product of each
vector with M (cid:2) OBJ
, yi) with maximal cosine simi-
larity to the given SSP. This can be implemented by a single layer in a neural
réseau, whose weights are Xxi (cid:2) Yyi , followed by an argmax, threshold, ou
some other winner-take-all mechanism. The main disadvantage of this ap-
proach is that it does not naturally handle continuous outputs, bien que
one can weigh together neighboring dot product similarities to interpolate
between the grid points.
The second cleanup method takes advantage of the fact that it is usually
only important to retrieve Xxi (cid:2) Yyi and not necessarily (xi
, yi). Spécifiquement,
we need to learn a function f that takes the noisy result of unbinding an
object from an SSP as input and outputs a “clean” SSP:
−1
F (M. (cid:2) OBJ
) = Xxi (cid:2) Yyi ,
je
−1
where M (cid:2) OBJ
je
−1
= Xxi (cid:2) Yyi + η (cid:2) OBJ
je
,
(3.12)
(3.13)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2055
and η is some “noisy” vector standing for the superposition of all other ob-
jects in the SSP to which the unbinding operation applies. This function f
can be trained in the same manner as an autoencoding denoiser, with mean
squared error (MSE) loss and gaussian noise (σ = 0.1/d) included on the
training inputs (Komer & Eliasmith, 2020). We find that a network com-
prising one layer of ReLUs, with as many neurons as there are dimensions
in the SSP, is sufficient. We also normalize the output of the cleanup to force
it to remain unitary. The benefit of this approach is that it has a continuous
output (as opposed to a discrete set of possible outputs). The cleanup can
also be trained to return a continuous (xi
, yi) as opposed to Xxi (cid:2) Yyi .
3.3.2 Simulating Multiple Objects Algebraically. The algebraic properties
of SSPs introduce a number of possibilities for applying transformations
to the spatial positions of multiple objects. Recall from section 2.2 that for
an SSP encoding a set of object positions, it is possible to shift all of these
positions by (cid:3)x and (cid:3)y as follows:
M = M (cid:2) X
(cid:3)X (cid:2) Oui
(cid:3)oui.
(3.14)
The drawback of this method is that it makes it impossible to apply dif-
ferent updates to each object position, since there is no way to distinguish
which update should be applied to which position (due to the fact that ad-
dition is commutative).
An alternative method involves tagging each pair of coordinates with a
representation of the corresponding object and then applying transforma-
tions to update the position of each object independently. The use of tagging
allows each object position to be extracted and updated separately, after
which these updated positions can rebound to their corresponding objects
and summed together to produce a new SSP. Mathematically, this process
is described as follows,
M ←
m(cid:8)
je = 1
OBJi
−1
(cid:2) F (M. (cid:2) OBJ
je
) (cid:2) X
(cid:3)xi (cid:2) Oui
(cid:3)yi ,
(3.15)
where f is the cleanup from equation 3.12. We find that this approach works
well as long as the cleanup function is sufficiently accurate. The main draw-
back is that m applications of the cleanup are required at every time step,
although these can be applied in parallel and added together.
An even more effective method involves tagging each set of coordinates
with a representation of the corresponding object and then applying addi-
tive shifts to update the position of each object independently as follows:
M ← M (cid:2) OBJi
(cid:2) (cid:3)Pi
,
(3.16)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2056
UN. Voelker et al.
Chiffre 7: Using separate algebraic updates (see equation 3.16) with the first
cleanup method to simulate the trajectories of five different objects within a
single SSP. One starts with an SSP representation of all five object initial po-
sitions. A chaque 0.05 s time step, the SSP is algebraically updated to simulate
the objects’ motion. The dashed lines represent the object trajectories decoded
from this simulation, while the solid lines represent the ground-truth object
trajectories.
où
(cid:3)Pi
= Xxi
+(cid:3)xi (cid:2) Yyi
+(cid:3)yi − f (M. (cid:2) OBJ
−1
je
).
This works because
OBJi
= OBJi
(cid:2) Xxi (cid:2) Yyi + OBJi
+(cid:3)xi (cid:2) Yyi
(cid:2) Xxi
+(cid:3)yi .
(cid:2) (Xxi
+(cid:3)xi (cid:2) Yyi
−1
+(cid:3)yi − f (M. (cid:2) OBJ
je
))
(3.17)
(3.18)
The drawback of this approach is that multiple operations are needed
to update the SSP (one for each encoded object). Otherwise the approach is
similar to the previous method, although the update defined here is itera-
tive (subtracting out each past position one at a time), in contrast to hav-
ing all past position information replaced at once with a new sum. Both
algebraic methods can be naturally implemented as a neural network. figue-
ure 7 demonstrates the use of additive shifts to move five objects along dis-
tinct trajectories within an SSP. The decoded trajectories are accurate over
short time spans but eventually drift due to accumulation of errors. Given
its good performance characteristics, we use this method of additive shifts
as our favored algebraic approach for simulating the motion of multiple
objets (see the benchmarking results described below).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2057
3.3.3 Simulating Multiple Objects with a Learned Model. An alternative to
relying on the algebraic properties of SSPs involves approximating a func-
tion that repeatedly transforms an SSP by mapping it to a new SSP corre-
sponding to the next point along some trajectory:
M ← g(M., (cid:3)M.),
(3.19)
where g is a neural network trained to minimize the MSE loss in equa-
tion 3.19 from separate training data, et (cid:3)M encodes all of the object ve-
locities as follows:
(cid:3)M =
m(cid:8)
je = 1
OBJi
(cid:2) X
(cid:3)xi (cid:2) Oui
(cid:3)yi .
(3.20)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
(cid:24)
(cid:23)
M.
(cid:3)M.
En substance, this method is equivalent to learning the algebraic shifts de-
scribed above such that the updates are performed in a single “step.” We
simulate trajectories using a linear model for g (par exemple., g(M., (cid:3)M.) = A
+
b with matrix A ∈ Rd×2d and bias vector b ∈ Rd×1), and with g being a mul-
tilayer perceptron (MLP). The MLP’s first layer has a number of neurons
equal to four times the SSP dimension and is followed by a ReLU nonlinear-
ville, and its second layer’s number of neurons is equal to the SSP dimension.
An example trajectory containing five objects and simulated with the MLP
trained on five trajectories is shown in Figure 8. The first cleanup procedure
is used on the output of the MLP at every time step. If the cleanup fails (c'est à dire.,
a decoded object’s position is dissimilar to all SSPs in the area checked),
then the position estimate at the previous time step is carried over. Ce
method performs quite well on training data. Cependant, even here, the de-
coded positions flat-line at times. For some input, unbinding the objects’ SPs
from the model’s output results in a vector that does not lie in the space of
SSPs.
3.3.4 Results of Simulating Multiple Objects. To perform an analysis of SSP
capacity and accuracy trade-offs when simulating multiobject dynamics,
we focus on a comparison between the algebraic approach of performing
additive shifts and learned approaches involving a function approximator,
g(M., (cid:3)M.).
The models are trained on 100 random trajectories, each with 200 temps
steps and represented by a sequence of SSPs and velocity SSPs (Mt and
(cid:3)Mt). To be precise, these random trajectories are two-dimensional band-
limited white noise signals that lie in a two-by-two box. Test performance
is reported as the RMSE between the true time series of SSPs representing
the trajectory and the trajectories simulated using the algebraic method or
g, averaged over 50 random test trajectories.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2058
UN. Voelker et al.
Chiffre 8: Using a multilayer perciptron (MLP) in combination with the first
cleanup method to simulate the trajectories of five different objects within a
single SSP. The MLP takes in the last estimate of SSP and the object’s velocities
represented as a single SSP as input and estimates the SSP at the next time step.
Starting with the initial SSP, at each 0.05 s time step, the SSP is updated using the
MLP and then “cleaned up” to simulate the objects’ motion. The dashed lines
represent the object trajectories decoded from this simulation, while the solid
lines represent the ground-truth object trajectories.
Chiffre 9 shows the results of the comparison between the algebraic and
learned function approximator approaches while both varying the number
of encoded objects while holding the dimensionality of the SSPs fixed, et
varying the dimensionality of the SSPs while holding the number of en-
coded objects fixed. Both the linear model and MLP perform adequately on
small training sets but do not generalize to the test data. Fait intéressant, le
linear model performs better than the MLP when the dimensionality of the
SSP is high enough.
Dans l'ensemble, this suggests that the algebraic method performs better than the
learned models from an MSE perspective. Another advantage of the alge-
braic approach is that it is compositional, which can be critical for flexibly
scaling to larger problems. Spécifiquement, once any one trajectory has been
learned, it can be combined with other trajectories in parallel, while adding
together the SSP representations. The only limits on the compositionality
are determined by the dimensionality of the SSP. As shown in Figure 9, 512
dimensions can effectively handle at least five objects.
In conclusion, by using SSPs, a structured, symbol-like representation,
neural networks can be constructed to perform algebraic operations that use
this structure to accurately perform computations. The resultant network
is completely explainable; it is no black box. Structured representations in
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2059
Chiffre 9: Benchmarking the simulation of separate dynamical trajectories ap-
plied to a number of objects encoded in a single SSP. The algebraic approach
(c'est à dire., additive shifting) is compared against several methods of learning a model
of the trajectory. Gauche: Model error as a function of the number of objects in the
SSP. Droite: Model error as a function of SSP dimensionality.
vector form, like SSPs, allow for this marriage of symbol-like reasoning and
deep networks.
4 Conclusion
Spatial semantic pointers (SSPs) are an effective means of constructing con-
tinuous spatial representations that can be naturally extended to represen-
tations of dynamical systems. We have extended recent SSP methods to
capture greater spatial detail and encode dynamical systems defined by dif-
ferential equations or arbitrary trajectories. We have applied these methods
to simulate systems with multiple objects and predict the future of trajecto-
ries with discontinuous changes in motion.
More specifically, we show that it is possible to represent and continu-
ously update the trajectories of multiple objects with minimal error using
a single SSP when that SSP is updated using an appropriate algebraic con-
struction and cleanup. En plus, we showed that coupling SSPs with
the LMU allowed the prediction of the future trajectory of a moving object
as it was being observed.
There are several ways in which these results could be extended. Pour dans-
position, it would be interesting to experiment with dynamics defined over
higher-dimensional spaces and with more complex representations of the
objects located in these spaces. Par exemple, it might be possible to define at-
tributes that determine the dynamics of specific object types, such that novel
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2060
UN. Voelker et al.
object dynamics could be predicted solely on the basis of these attributes.
It would be useful to extend our work on predicting object interactions to
improve both the range of different interaction types that can be predicted
and the accuracy with which they can be predicted.
On a more theoretical level, SSPs help to unify currently disparate ap-
proaches to modeling intelligent behavior within a common mathematical
framework. En particulier, the combination of binding operations that sup-
port continuous role-filler structure with neural networks provides a point
of common ground between approaches to AI that focus on machine learn-
ing, dynamical systems, and symbol processing. Exploiting this common
ground is likely to be necessary for continued progress in the field over the
long terme.
Software Packages
Utilities for generating and manipulating spatial semantic pointers (SSPs)
are built into the software package NengoSPA (Applied Brain Research,
2020), which supports neural implementations for a number of VSAs and
is part of the Nengo ecosystem (Bekolay et al., 2014), a general-purpose
Python software package for building and simulating both spiking and
nonspiking neural networks.
To integrate Nengo models with deep learning, NengoDL (Rasmussen,
2019) provides a TensorFlow (Abadi et al., 2016) back end that enables
Nengo models to be trained using backpropagation, run on GPUs, et
interfaced with other networks such as Legendre memory units (LMUs;
Voelker et al., 2019). We make use of Nengo, NengoSPA, TensorFlow, et
LMUs throughout.
Software and data for reproducing reported results are available at
https://github.com/abr/neco-dynamics.
Appendix: Additional Simulation Experiments
A.1 Recursive Spatial Semantic Pointers (rSSPs). An important limi-
−
tation of SSPs is that P(x1
y1)2 ≤ 2, c'est, the dot product of nearby points is close to one (Komer,
2020). This occurs regardless of the dimensionality (d) of the SP.
, y1) is similar to P(x2
, y2) quand (x2
− x1)2 + (y2
Plus généralement, there is a fundamental limitation regarding the kinds
of similarity maps that can be represented via the function produced
by equation 2.13, as determined by linear combinations of vectors in
(cid:7)
(cid:6)
, R ⊆ R2; this set of vectors does not necessarily span
P.(X, oui) : (X, oui) ∈ R
all of Rd. Autrement dit, since vectors that are encoding different parts of
the space are often linearly dependent, there are fewer than d degrees of
freedom that determine the kinds of spatial maps that can be represented
given fixed axis vectors within finite regions of space.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2061
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 10: D'abord 16 principal components of Xx (cid:2) Yy for x2 + y2 ≤ 2. These ba-
sis vectors are independent of dimensionality and independent of the absolute
position in space. Only the first 21 vectors have singular values greater than
un.
2,
√
est,
√
que
(cid:7)
. A circle of radius
Chiffre 10 makes this precise by plotting the principal components
within a circle of radius
the left singular vectors of
(cid:6)
P.(X, oui) : x2 + y2 ≤ 2
2 approximates the invertible do-
main of sinc(X) sinc(oui) (Voelker, 2020; also see Komer, 2020, Chiffre 3.21).
Intuitively, any P(X, oui) within this circle can be accurately represented by
a linear combination of this spatial basis. We find that—assuming d is suf-
ficiently large—only ≈21 principal components are needed to accurately
represent this subspace (singular values greater than 1); there are far fewer
degrees of freedom than there are dimensions in the SSP (par exemple., d = 1024 dans
Chiffre 10), et, most important, increasing d does not create any new de-
grees of freedom.
2062
UN. Voelker et al.
√
One solution is to simply rescale all (X, oui) coordinates such that points
that must be nearly orthogonal to one another are separated by a Euclidean
distance of at least
2. Cependant, this is not practical if the SSP has already
been encoded (there is no known way of rescaling the coordinates without
first cleaning the SSP up to some particular vocabulary) and leads to unfa-
vorable scaling in d for certain kinds of spatial maps through inefficient use
of the continuous surface.
An alternative solution is to vary the axis vectors, (X, Oui), as a function of
(X, oui). A convenient way to do this is to use SSPs in place of each axis vector.
We refer to this as a recursive spatial semantic pointer (rSSP). En général, un
rSSP uses the following formula to encode positions:
P.(X, oui) = (cid:9)(X, oui; X )X (cid:2) (cid:9)(X, oui; Oui)oui,
(A.1)
où (cid:9)(X, oui ; UN) is some function that produces an SSP. (cid:9)(·) may be pre-
determined or computed by a neural network—feedforward or recurrent—
that is optionally trained via backpropagation. Par exemple,
(cid:9)(X, oui ; UN) = A
|h(X,oui)|/3+2
(A.2)
generates axes that oscillate between A2 and A3 using the hexagonal lattice
from equations 2.15 et 2.16, which are then used to encode (X, oui) as usual
via equation A.1. We find that this increases the degrees of freedom from
≈21 to ≈36 within a radius of
2, given the same dimensionality, map scale,
and singular value cutoff.
√
En substance, this formulation enables the encoding to use different axis
vectors in different parts of the space. Since (Aa)b (cid:14)= Aab in general for a, b ∈
R., this is not the same as rescaling (X, oui). Plutôt, depuis (cid:9)(·) is a nonlinear
operation with potentially infinite complex branching, this increases the
representational flexibility of the surface by decreasing the linear depen-
dence in P(X, oui) and thus allows rSSPs to capture fine-scaled spatial struc-
tures through additional degrees of freedom.
We illustrate by encoding a fractal from the Julia (1918) set—a com-
plex dynamical system—using a single rSSP (d = 1,024). Specifically we
define (cid:9)(X, oui ; UN) = AJ(x+iy) where J(z) is an affine transformation of the
number of iterations required for z ← z2 + c to escape the set |z| ≤ R (c =
−0.1 + 0.65je, R ≈ 1.4527, 1000 iterations). We then solve for the vector that
best reconstructs J(X + iy) in its similarity map by optimizing a regularized
least-squares problem, which is possible because equation 2.13 is a linear
operator. The solution produces a map that is perceptually quite similar
to the ideal fractal (voir la figure 11), thus demonstrating the effectiveness
of rSSPs in representing intricate spatial structures using relatively few
dimensions.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2063
(un) Ideal Julia Set Fractal
(b) Recursive Spatial Semantic
Pointer (rSSP)
Chiffre 11: Representing a fractal from the Julia set within the similarity map
of a recursively-generated SSP (d = 1,024). Rendered images are 501 × 501 (c'est à dire.,
251,001 pixels). See text for details.
A.2 Axis-Specific Algebraic SSP Updates. One option for applying dif-
ferent updates to different objects encoded in an SSP involves representing
the axes of the plane for each object separately as follows:
SSP = Xx1
1
(cid:2) Yy1
1
+ Xx2
2
(cid:2) Yy2
2
. . .
(A.3)
With this representation, it is possible to define a transformation SSP that
acts on each object separately:
(cid:3)x1
SSP = SSP (cid:2) (X
1
(cid:3)y1
(cid:2) Oui
1
(cid:3)x2
+ X
2
(cid:3)y2
(cid:2) Oui
2
. . .).
(A.4)
The effect of applying this transformation is to produce an updated SSP
with m2 − m noise terms if m is the number of encoded objects, since each
term in the bracketed sum would apply to a corresponding term in SSP and
combine with the other m − 1 terms in the SSP to yield noise. There are m
terms in the bracketed sum, so the creation of m − 1 noise terms occurs m
times, leading to a total of O(m2) noise terms overall. Such scaling is unlikely
to permit the successful manipulation of SSPs encoding large numbers of
objets, even if the noise is zero-mean.
Officiellement, we can describe the growth of noise terms over time as follows:
as just mentioned, each term in the bracketed sum described above applies
to one corresponding term in SSP and combines with the other m − 1 termes
in SSP to yield noise. There are m terms in the bracketed sum, so the creation
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2064
UN. Voelker et al.
of m − 1 noise terms occurs m times, leading to a total of m2 − m noise terms
after a single time step. On the next time step, each term in the bracketed
sum applies to one corresponding term in the SSP, and then combines with
the m − 1 other encoding terms and the m2 − m noise terms created by the
previous time step; again, these combinations occur m times. This yields
a total of m(m − 1 + m2 − m = O(m3) noise terms on the second time step.
After t time steps, the number of noise terms is O(mt+1).
Dans l'ensemble, axis-specific shifts are unsatisfactory in the absence of cleanup
méthodes, since the noise terms compound at each time step, quickly push-
ing the signal-to-noise ratio towards zero.
Les références
Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, UN., Dean, J., . . . Zheng, X. (2016).
TensorFlow: A system for large-scale machine learning. In Proceedings of the 12th
USENIX Symposium on Operating Systems Design and Implementation (pp. 265–283),
PeerJ.
Applied Brain Research. (2020). Nengo spa. https://www.nengo.ai/nengo-spa/.
Bekolay, T., Bergstra, J., Hunsberger, E., DeWolf, T., Stewart, T. C., Rasmussen, D.,
& Eliasmith, C. (2014). Nengo: A Python tool for building large-scale functional
brain models. Frontiers in Neuroinformatics, 7, 48.
Blouw, P., Solodkin, E., Thagard, P., & Eliasmith, C. (2016). Concepts as semantic
pointers: A framework and computational model. Sciences cognitives, 40(5), 1128–
1162.
Bottou, L. (2014). From machine learning to machine reasoning: An essay. Machine
Apprentissage, 94(2), 133–149.
Choo, X. (2010). The ordinal serial encoding model: Serial memory in spiking neurons. Mas-
ter’s thesis, Université de Waterloo.
Choo, X. (2018). Spaun 2.0: Extending the World’s Largest Functional Brain Model. PhD
diss., Université de Waterloo.
Co-Reyes, J.. D., Liu, Y., Gupta, UN., Eysenbach, B., Abbeel, P., & Levine, S. (2018). Self-
consistent trajectory autoencoder: Hierarchical reinforcement learning with trajectory
embeddings. arXiv:1806.02813.
Conklin, J., & Eliasmith, C. (2005). A controlled attractor network model of path in-
tegration in the rat. Journal of Computational Neuroscience, 18(2), 183–203.
Crawford, E., Gingerich, M., & Eliasmith, C. (2015). Biologically plausible, human-
scale knowledge representation. Sciences cognitives, 40, 782–821.
Dumont, N. S.-Y., & Eliasmith, C. (2020). Accurate representation for spatial cog-
nition using grid cells. In Proceedings of the 42nd Annual Meeting of the Cognitive
Science Society. Red Hook, New York: Curran.
Eliasmith, C. (2005). A unified approach to building and controlling spiking attractor
réseaux. Neural Computation, 17(6), 1276–1314.
Eliasmith, C. (2013). How to build a brain: A neural architecture for biological cognition.
New York: Presse universitaire d'Oxford.
Eliasmith, C., & Anderson, C. H. (2003). Neural engineering: Computation, representa-
tion, and dynamics in neurobiological systems. Cambridge, MA: AVEC Presse.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2065
Eliasmith, C., Stewart, T. C., Choo, X., Bekolay, T., DeWolf, T., Tang, Y., & Ras-
mussen, D. (2012). A large-scale model of the functioning brain. Science, 338, 1202–
1205.
Fodor, J., & Pylyshyn, Z. (1988). Connectionism and cognitive architecture: A critical
analyse. Cognition, 28(1–2), 3–71.
Foldiak, P.. (2003). Sparse coding in the primate cortex. En M. UN. Arbib (Ed.), Le
handbook of brain theory and neural networks. Cambridge, MA: AVEC Presse.
Frady, E. P., Kleyko, D., & Sommer, F. (2020). Variable binding for sparse distributed
representations: Theory and applications. arXiv:abs/2009.06734.
Frady, P., Kanerva, P., & Sommer, F. (2018). A framework for linking computations
and rhythm-based timing patterns in neural firing, such as phase precession in
hippocampal place cells. In Proceedings of the Conference on Cognitive Computational
Neurosciences.
Gayler, R.. (2004). Vector symbolic architectures answer Jackendoff’s challenges for cognitive
neuroscience. arXiv preprint cs/0412059.
Goodfellow, JE., Bengio, Y., & Courville, UN. (2016). Deep learning, vol. 1. Cambridge,
MA: AVEC Presse.
Gosmann, J.. (2018). An integrated model of context, short-term, and long-term memory.
PhD diss., Université de Waterloo.
Gosmann, J., & Eliasmith, C. (2019). Vector-derived transformation binding: An im-
proved binding operation for deep symbol-like processing in neural networks.
Neural Computation, 31(5), 849–869.
Gosmann, J., & Eliasmith, C. (2020). CUE: A unified spiking neuron model of short-
term and long-term memory. Psych. Review, 128, 104–124.
Gosmann, J., Voelker, UN. R., & Eliasmith, C. (2017). A spiking independent accu-
mulator model for winner-take-all computation. In Proceedings of the 39th Annual
Conference of the Cognitive Science Society. Londres, ROYAUME-UNI: Cognitive Science Society.
Hadley, R.. (2009). The problems of rapid variable creation. Neural Computation, 21,
510–532.
Julia, G. (1918). Memoire sur l’itération des fonctions rationnelles. J.. Math. Pures
Appl., 8, 47–245.
Kanerva, P.. (2009). Hyperdimensional computing: An introduction to computing
in distributed representation with high-dimensional random vectors. Cognitive
Computation, 1(2), 139–159.
Komer, B. (2020). Biologically inspired spatial representation. PhD diss., Université de
Waterloo.
Komer, B., & Eliasmith, C. (2020). Efficient navigation using a scalable, biologically
inspired spatial representation. In Proceedings of the 42nd Annual Meeting of the
Cognitive Science Society. Londres, ROYAUME-UNI: Cognitive Science Society.
Komer, B., Stewart, T., Voelker, UN. R., & Eliasmith, C. (2019). A neural representation
of continuous space using fractional binding. In Proceedings of the 41st Annual
Meeting of the Cognitive Science Society. Londres, ROYAUME-UNI: Cognitive Science Society.
LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–
444.
Lu, T., Voelker, UN. R., Komer, B., & Eliasmith, C. (2019). Representing spatial relations
with fractional binding. In Proceedings of the 41st Annual Meeting of the Cognitive
Science Society. Londres, ROYAUME-UNI: Cognitive Science Society.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2066
UN. Voelker et al.
Marcus, G. (1998). Rethinking eliminative connectionism. Psychologie Cognitive, 37,
243–282.
Marcus, G. F. (2019). The algebraic mind: Integrating connectionism and cognitive science.
Cambridge, MA: AVEC Presse.
McClelland, J., Botvinick, M., Noelle, D., Plaut, D., Rogers, T., Seidenberg, M., &
Forgeron, L. (2010). Letting structure emerge: Connectionist and dynamical sys-
tems approaches to cognitive modelling. Tendances des sciences cognitives, 14(8), 348–
356.
Mirus, F., Stewart, T., & Conradt, J.. (2020). Analyzing the capacity of distributed
vector representations to encode spatial information. In Proceedings of the 2020
International Joint Conference on Neural Networks (pp. 1–7). Piscataway, New Jersey: IEEE.
Moser, E. JE., Kropff, E., & Moser, M.-B. (2008). Place cells, grid cells, and the brain’s
spatial representation system. Annu. Rev. Neurosci., 31, 69–89.
Muller, M.. E. (1959). A note on a method for generating points uniformly on n-
dimensional spheres. Comm. Assoc. Comput. Mach., 2(1–2), 19–20.
Plate, T. (2003). Holographic Reduced Representation: Distributed Representation for Cog-
nitive Structures. Stanford, Californie: CSLI Publications.
Rasmussen, D. (2019). NengoDL: Combining deep learning and neuromorphic mod-
elling methods. Neuroinformatics, 17(4), 611–628.
Rasmussen, D., & Eliasmith, C. (2011). A neural model of rule generation in inductive
raisonnement. Topics in Cognitive Science, 3(1), 140–153.
Schlegel, K., Neubert, P., & Protzel, P.. (2020). A comparison of vector symbolic architec-
photos. arXiv:2001.11797.
Schmidhuber, J.. (2015). Deep learning in neural networks: An overview. Neural Net-
travaux, 61, 85–117.
Schöner, G. (2014). Embodied cognition, neural field models of. In Encyclopedia of
computational neuroscience (pp. 1084–1092). Berlin: Springer.
Smolensky, P.. (1990). Tensor product variable binding and the representation of
symbolic structures in connectionist systems. Artificial Intelligence, 46(1–2), 159–
216.
Smolensky, P., & Legendre, G. (2006). The harmonic mind: From neural computation to
optimality-theoretic grammar. Cambridge, MA: AVEC Presse.
Sorscher, B., Mel, G., Ganguli, S., & Ocko, S. (2019). A unified theory for the origin
of grid cells through the lens of pattern formation. In H. Wallach, H. Larochelle,
UN. Beygelzimer, F. d’Alché-Buc, E. Fox, & R.. Garnett (Éd.), Advances in neural
information processing systems, 32 (pp. 10003–10013). Red Hook, New York: Curran.
Stewart, T., Bekolay, T., & Eliasmith, C. (2011). Neural representations of composi-
tional structures: Representing and manipulating vector spaces with spiking neu-
rons. Connection Science, 23, 145–153.
Stewart, T. C., Choo, X., & Eliasmith, C. (2014). Sentence processing in spiking neu-
rons: A biologically plausible left-corner parser. In Proceedings of the 36th Annual
Conference of the Cognitive Science Society (pp. 1533–1538). Londres, U.K.: Cognitive
Science Society.
Stewart, T. C., Tang, Y., & Eliasmith, C. (2011). A biologically realistic cleanup mem-
ory: Autoassociation in spiking neurons. Cognitive Systems Research, 12(2), 84–92.
Voelker, UN. R.. (2019). Dynamical systems in spiking neuromorphic hardware. PhD diss.,
Université de Waterloo.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical Systems With Spatial Semantic Pointers
2067
Voelker, UN. R.. (2020). A short letter on the dot product between rotated Fourier transforms.
arXiv:2007.13462.
Voelker, UN. R., Kaji´c, JE., & Eliasmith, C. (2019). Legendre memory units: Continuous-
time representation in recurrent neural networks. In H. Wallach, H. Larochelle,
UN. Beygelzimer, F. d’Alché-Buc, E. Fox, & R.. Garnett (Éd.), Advances in neural
information processing systems, 32 (pp. 15544–15553). Red Hook, New York: Curran.
Blanc, E., Cheung, B., & Olshausen, B. (2016). A neural architecture for represent-
ing and reasoning about spatial relationships. In Proceedings of the International
Conference on Learning Representations—Workshop Track. La Jolla, Californie: ICLR.
Received November 4, 2020; accepted March 15, 2021.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
c
o
_
un
_
0
1
4
1
0
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3