LETTER - Recherche en IA spécialisée au MIT

LETTER

Communicated by Raoul-Martin Memmesheimer

The Remarkable Robustness of Surrogate Gradient
Learning for Instilling Complex Function in Spiking
Neural Networks

Friedemann Zenke
friedemann.zenke@fmi.ch
Centre for Neural Circuits and Behaviour, University of Oxford,
Oxford OX1 3SR, U.K., and Friedrich Miescher Institute for
Biomedical Research, 4058 Bâle, Suisse

Tim P. Vogels
tim.vogels@ist.ac.at
Centre for Neural Circuits and Behaviour, University of Oxford,
Oxford OX1 3SR, U.K., and Institute for Science and Technology,
3400 Klosterneuburg, Autriche

Brains process information in spiking neural networks. Their intricate
connections shape the diverse functions these networks perform. Yet how
network connectivity relates to function is poorly understood, et le
functional capabilities of models of spiking networks are still rudimen-
tary. The lack of both theoretical insight and practical algorithms to find
the necessary connectivity poses a major impediment to both studying
information processing in the brain and building efficient neuromorphic
hardware systems. The training algorithms that solve this problem for
artificial neural networks typically rely on gradient descent. But doing so
in spiking networks has remained challenging due to the nondifferen-
tiable nonlinearity of spikes. To avoid this issue, one can employ surro-
gate gradients to discover the required connectivity. Cependant, the choice
of a surrogate is not unique, raising the question of how its implementa-
tion influences the effectiveness of the method. Ici, we use numerical
simulations to systematically study how essential design parameters of
surrogate gradients affect learning performance on a range of classifica-
tion problems. We show that surrogate gradient learning is robust to dif-
ferent shapes of underlying surrogate derivatives, but the choice of the
derivative’s scale can substantially affect learning performance. When we
combine surrogate gradients with suitable activity regularization tech-
niques, spiking networks perform robust information processing at the
sparse activity limit. Our study provides a systematic account of the re-
markable robustness of surrogate gradient learning and serves as a prac-
tical guide to model functional spiking neural networks.

Neural Computation 33, 899–925 (2021)
https://doi.org/10.1162/neco_a_01367

© 2021 Massachusetts Institute of Technology.
Publié sous Creative Commons
Attribution 4.0 International (CC PAR 4.0) Licence.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

900

1 Introduction

F. Zenke and T. Vogels

The computational power of deep neural networks (LeCun, Bengio, & Hin-
ton, 2015; Schmidhuber, 2015) has reinvigorated interest in using in-silico
systems to study information processing in the brain (Barrett, Morcos, &
Macke, 2019; Richards et al., 2019). Par exemple, performance-optimized
artificial neural networks bear striking representational similarity with
the visual system (Maheswaranathan et al., 2018; McClure & Kriegesko-
rte, 2016; McIntosh, Maheswaranathan, Nayebi, Ganguli, & Baccus, 2016;
Pospisil, Pasupathy, & Bair, 2018; Tanaka et al., 2019; Yamins & DiCarlo,
2016; Yamins et al., 2014) and serve to formulate hypotheses about their
mechanistic underpinnings. De la même manière, the activity of artificial recurrent neu-
ral networks optimized to solve cognitive tasks resembles cortical activ-
ity in prefrontal (Cueva et al., 2019; Mante, Sussillo, Shenoy, & Newsome,
2013), medial frontal (Wang, Narain, Hosseini, & Jazayeri, 2018), and motor
domaines (Michaels, Schaffelhofer, Agudelo-Toro, & Scherberger, 2019; Stroud,
Porter, Hennequin, & Vogels, 2018), thus providing us with new vistas for
understanding the dynamic properties of computation in recurrent neural
réseaux (Barrett et al., 2019; Sussillo & Barak, 2012; Williamson, Doiron,
Forgeron, & Yu, 2019).

All of these studies rely on conventional artificial neural networks with
graded activation functions as commonly used in machine learning. Le
recipe for building a deep neural network is straightforward. The value
of a scalar loss function defined at the output of the network is decreased
through gradient descent. Deep neural networks differ from biological neu-
ral networks in important respects. Par exemple, they lack cell type diver-
sity and do not obey Dale’s law while ignoring the fact that the brain uses
spiking neurons. We generally accept these flaws because we do not know
how to construct more complicated networks. Par exemple, gradient de-
scent works only when the involved system is differentiable. This is not the
case for spiking neural networks (SNNs).

Surrogate gradients have emerged as a solution to build functional SNNs
capable of solving complex information processing problems (Bellec, Salaj,
Subramoney, Legenstein, & Maass, 2018; Cramer, Stradmann, et coll., 2020;
Esser et al., 2016; Hunsberger & Eliasmith, 2015; Lee, Delbruck, & Pfeiffer,
2016; Neftci, Mostafa, & Zenke, 2019; Pfeiffer & Pfeil, 2018; Shrestha & Or-
chard, 2018). To that end, the actual derivative of a spike, which appears in
the analytic expressions of the gradients, is replaced by any well-behaved
fonction. There are many possible choices of such surrogate derivatives,
et par conséquent, the resulting surrogate gradient is, unlike the true gradi-
ent of a system, not unique. A number of studies have successfully applied
different instances of surrogate derivatives to various problem sets (Bellec
et coll., 2018; Esser et al., 2016; Huh & Sejnowski, 2018; Shrestha & Orchard,
2018; Wo´zniak, Pantazi, Bohnstingl, & Eleftheriou, 2020; Zenke & Ganguli,
2018). While this suggests that the method does not crucially depend on

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Robustness of Surrogate Gradients

901

the specific choice of surrogate derivative, we know relatively little about
how the choice of surrogate gradient affects the effectiveness and whether
some choices are better than others. Previous studies did not address this
question because they solved different computational problems, thus pre-
cluding a direct comparison. In this letter, we address this issue by pro-
viding benchmarks for comparing the trainability of SNNs on a range of
supervised learning tasks and systematically vary the shape and scale of
the surrogate derivative used for training networks on the same task.

2 Results

To systematically evaluate the performance of surrogate gradients, nous
sought to repeatedly train the same network on the same problem while
changing the surrogate gradient. Toward this end, we required a demand-
ing spike-based classification problem with a small computational foot-
print to serve as benchmark. There are only few established benchmarks for
SNNs. One approach is to use analog-valued machine learning data sets as
input currents directly (Hunsberger & Eliasmith, 2015) or to first convert
them to Poisson input spike trains (Lee et al., 2016; Pfeiffer & Pfeil, 2018).
These input paradigms, cependant, do not fully capitalize on the ability to
encode information in spike timing, an important aspect of spiking pro-
cessation. Gütig (2016) addressed this point with the Tempotron by classify-
ing randomly generated spike timing patterns in which each input neuron
fires a single spike. Yet completely random timing precludes the possibility
of assessing generalization performance, c'est, the ability to generalize to
previously unseen inputs.

2.1 Random Manifolds as Basis for Flexible Benchmarks. To assess if
SNNs could learn to categorize spike patterns and generalize to unseed pat-
terns, we created a number of synthetic classification data sets with added
temporal structure. Spécifiquement, we created spike rasters for a given set of
input afferents. Each afferent only fired one spike, and the spike times of
all afferents were constrained to lie on a low-dimensional smooth, random
manifold in the space of all possible spike timings. All data points from the
same manifold were defined as part of the same input class, whereas differ-
ent manifolds correspond to different classes.

The spike-timing manifold approach has several advantages: D'abord, le
temporal structure in the data permits studying generalization, a deci-
sive advantage over using purely random spike patterns. Deuxième, the task
complexity is seamlessly adjustable by tuning the number of afferents,
manifold’s smoothness parameter α (see Figure 1a), the intrinsic manifold
dimension D, and the number of classes n (see Figure 1b). Troisième, we en-
sure that each input neuron spikes exactly once (see Figure 1c), guaran-
teeing that the resulting data sets are purely spike-timing-dependent and
thus cannot be classified from firing rate information. Enfin, sampling an

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

902

F. Zenke and T. Vogels

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

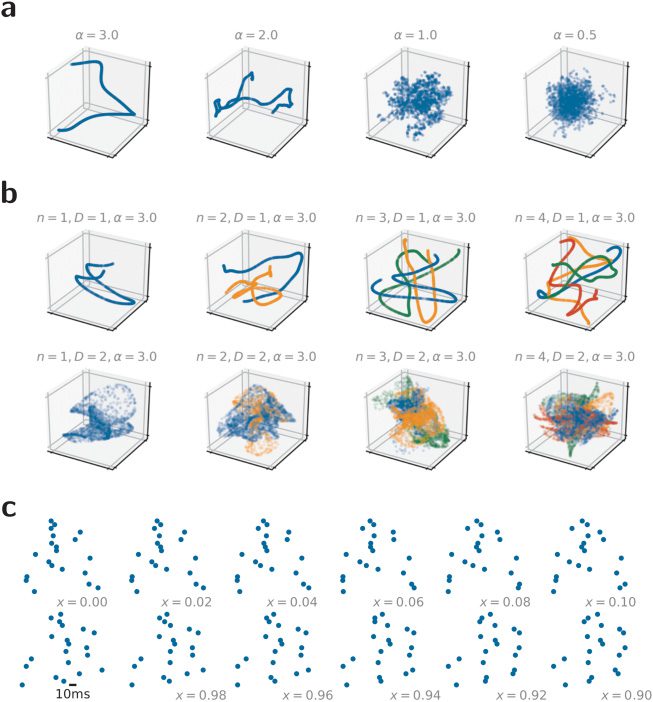
Chiffre 1: Smooth random manifolds provide a flexible way of generating syn-
thetic spike-timing data sets. (un) Four one-dimensional example manifolds for
different smoothness parameters α in a three-dimensional embedding space.
From each manifold, we plotted 1000 random data points. (b) Same as in panel
un, but keeping α = 3 fixed while changing the manifold-dimension D and the
number of random manifolds (different colors). By sampling different random
manifolds, it is straight-forward to build synthetic multiway classification tasks.
(c) Spike raster plots corresponding to 12 samples along the intrinsic manifold
coordinate x of a one-dimensional smooth random manifold (α = 3) par lequel
we interpreted the embedding space coordinates as firing times of the individ-
ual neurons.

arbitrary number of data points from each class is computationally cheap,
and it is equally easy to generate an arbitrary number of different data sets
with comparable properties.

Robustness of Surrogate Gradients

903

To demonstrate the validity of our approach, we tested it on an SNN with
a single hidden layer on a simple two-way classification problem (see Fig-
ure 2a and section 4). We modeled the units of the hidden layer as current-
based leaky integrate-and-fire neurons. Between layers, the connectivity
was strictly feedforward and all-to-all. The output layer consisted of two
leaky integrators that did not spike, allowing us to compute the maximum
of the membrane potential (Gütig & Sompolinsky, 2006) and interpret these
values as the inputs for a standard classification loss function for supervised
learning (see section 4). In this setup, the readout unit with the highest ac-
tivity level signals the putative class-membership of each input (Cramer,
Stradmann, Schemmel, & Zenke, 2020).

We first confirmed that learning is poor when we used the actual gra-
dient. To that end, we computed it using the derivative of the hard thresh-
old nonlinearity of the spikes. As expected, the hard threshold nonlinear-
ity prevented gradient flow into the hidden layer (Neftci et al., 2019) et
consequently led to poor performance (see Figures 2b and 2c). In contrast,
when we used surrogate gradients to train the same network, le problème
disappeared. Learning took place in both the hidden and output layers and
resulted in a substantial reduction of the loss function (see Figures 2b to 2e).

2.2 Surrogate Gradient Learning Is Robust to the Shape of the Surro-
gate Derivative. A necessary ingredient of surrogate gradient learning is a
suitable surrogate derivative. To study the effect of the surrogate derivative
comparably, we generated a random manifold data set with 10 classes. Nous
chose the remaining parameters, c'est, the number of input units, the man-
ifold dimension, and the smoothness α to make the problem impossible to
solve for a network without a hidden layer while at the same time keeping
the computational burden minimal. We trained multiple instances of the
= 1) using the derivative of a
same network with a single hidden layer (nh
fast sigmoid as a surrogate derivative (see Figure 3a “SuperSpike”; Zenke
& Ganguli, 2018) on this data set. In each run, we kept both the data set and
the initial parameters of the model fixed but varied the slope parameter β,
of the surrogate. For each value of β, we performed a parameter sweep over
the learning rate η. Following training, we measured the classification accu-
racy on held-out data. This search revealed an extensive parameter regime
of β and η in which the system was able to solve the problem with high accu-
racy (see Figure 3b). The addition of a second hidden layer only marginally
improved on this result, et, as expected, a network without a hidden layer
performed poorly (see Figure 3c). The extent of the parameter regime yield-
ing high performance suggests remarkable robustness of surrogate gradi-
ent learning to changes in the steepness of the surrogate derivative. While
a steep approach to the threshold could be seen as a closer, hence better,
approximation of the actual derivative of the spike, the surrogate gradient
remains largely unaffected by how closely the function resembles the exact
derivative as long as it is not a constant.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

904

F. Zenke and T. Vogels

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 2: Surrogate gradient descent allows building functional SNNs.
(un) Sketch of the network model with two readout units at the top. The su-
pervised loss function L
sup is defined by first taking the maximum activation
over time of the readout units U out
(orange and blue) and then applying a Soft-
max and cross-entropy loss L
CE (see section 4 for details). (b) Learning curves of
the network when using the actual gradient (“true,” gray) or a surrogate gradi-
ent (red) to train an SNN on a binary random manifold classification problem.
(c) Snapshot of network activity before training. Bottom: Spike raster of the in-
put layer activity. Four different inputs corresponding to two different classes
are plotted in time (orange/blue). Middle: Spike raster of the hidden-layer activ-
ville. Top: Readout unit membrane potential. The network erroneously classifies
the two “orange” inputs as belonging to the “blue” class, as can be read off from
the maximum activity of its readout units. (d) Same as in panel c, but following
training of the network with surrogate gradient descent. (e) Example membrane
potential traces from seven randomly selected hidden-layer neurons during a
single trial.

Robustness of Surrogate Gradients

905

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

Chiffre 3: Surrogate gradient learning is robust to the shape of the surrogate
derivative. (un) Three different surrogate derivative shapes that have been used
for training on the synthetic smooth random manifold spiking data set. Depuis
left to right: SuperSpike (Zenke & Ganguli, 2018), the derivative of a fast sig-
moid function, Sigma(cid:2), the derivative of a standard sigmoid function, and “Esser
et al.,” a piece-wise linear function (Bellec et al., 2018; Esser et al., 2016). Col-
ors correspond to different values of the slope parameter β. (b) Accuracy on
held-out data as a function of the learning rate η and the slope β for the corre-
= 1).
sponding surrogates in panel a for a network with one hidden layer (nh
(c) Test accuracy for the five best parameter combinations obtained from a grid
recherche, as shown in panel b for different surrogates and numbers of hidden
layers nh. While a network without a hidden layer is unable to solve the classi-
fication problem (black), networks trained with a wide range of different surro-
gates and slope parameters (β > 0) have no problem solving the task with high
accuracy (shades of blue). Cependant, the problem is not solved with high accu-
racy by a network with a hidden layer in which the surrogate derivative was
a constant during training (β = 0; gray). Error bars correspond to the standard
deviation (n = 5). (d) Whisker plot of classification accuracy for a network with
one hidden layer over five different realizations of the random manifold data
sets (“Datasets”) and for the same data set, but using different weight initial-
= 2) hidden
izations (“Inits.”) in networks with either one (nh
layers.

= 1) or two (nh

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

906

F. Zenke and T. Vogels

(cid:2)

Next we tested different surrogate derivative shapes, namely a standard
sigmoid (Sigmoid
) and piece-wise linear function (Esser et al., 2016; voir
Figure 3a; Bellec et al., 2018). This manipulation led to a reduction of the
size of the parameter regime in β in which the network was able to perform
the task, which is presumably due to vanishing gradients (Hochreiter, 1998).
Cependant, there was no substantial reduction in maximum performance (voir
Figures 3b and 3c). Using a piece-wise linear surrogate derivative (Esser
et coll.) led to a further reduction of viable parameters β (see Figure 3b), mais
did not affect maximum performance, regardless of whether we used one or
two hidden layers (see Figure 3c). To check whether a surrogate derivative
was required at all for solving the random manifold problem, we assayed
the learning performance for β = 0, which corresponds to setting the func-
tion to 1. This change resulted in a significant drop in performance compa-
rable to a network without hidden units (see Figure 3c) suggesting that a
nonlinear voltage dependence is crucial to learn useful hidden-layer repre-
sentations. Enfin, we confirmed that these findings were robust to differ-
ent initial network parameters and data sets (see Figure 3d) apart from only
= 2).
a few outliers with low performance in the two-hidden-layer case (nh
These outliers point at the vital role of proper initialization (Il, Zhang, Ren,
& Sun, 2015; Mishkin & Matas, 2016).

2.3 Surrogate Gradient Learning Is Sensitive to the Scale of the Surro-
gate Derivative. In most studies that rely on surrogate gradients, the surro-
gate derivative is normalized to 1 (Bellec et al., 2018; Esser et al., 2016; Neftci
et coll., 2019; Shrestha & Orchard, 2018; Zenke & Ganguli, 2018) (see Fig-
ure 3a), markedly different from the actual derivative of a spiking threshold
which is infinite (see Figure 5a). The scale of the substituted derivative has
a strong effect on the surrogate gradient due to both explicit and implicit
forms of recurrence in SNNs (voir la figure 4; Neftci et al., 2019). Most notably,
the scale may determine whether gradients vanish or explode (Hochreiter,
1998). Cependant, it is unclear to what extent such differences translate into
performance changes of the trained networks.

To gain a better understanding of how derivative scales larger than one
affect surrogate gradient learning, we trained networks on a fixed random
manifold task (see Figures 3a to 3c), using an asymptotic version of the Su-
perSpike surrogate (aCtl; voir la figure 3) and our well-tested standard Super-
Spike function (sCtl; voir la figure 3) as a control (sCtl). As we expected, le
difference in scale to manifest itself primarily in the presence of recurrence,
we compared networks in which we treated the spike reset as differentiable
(DR) with networks in which its contribution was ignored by detaching
it from the computational graph. Technically speaking, we prevented Py-
Torch’s auto-differentiation routines (Paszke et al., 2019) from considering
connections in the computational graph that correspond to the spike reset
when computing the gradient with backpropagation through time (BPTT)
(see equation 4.1). While both the normalized (sCtl) and the asymptotic

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Robustness of Surrogate Gradients

907

Chiffre 4: SNNs can have both implicit and explicit recurrence. Schematic of the
computational graph of a single SNN layer composed of leaky integrate-and-
fire (LIF) neurons (see section 4). Input spike trains S(0) enter at the bottom and
affect the synaptic current variable I(1) through the feedforward weights W (1).
Time flows from left to right. Any link that connects temporally adjacent nodes
in the graph constitutes a form of recurrence in the computation whereby the
synaptic connections V (1) contribute explicit recurrence to the graph. Implicit re-
currence is contributed, par exemple, by the decay of synaptic current variables
and the membrane potentials U (1). En plus, the spike reset contributes an-
other form of implicit recurrence by coupling the future states to the output
spike train S(1). Recurrences involving the surrogate derivative (e.g. the reset)
depend on both the shape and the scale of the surrogate chosen and can sub-
stantially alter the surrogate gradient.

surrogate (aCtl) performed equally well when the reset was detached, com-
bining a differentiable reset with an asymptotic surrogate derivative (aDR)
led to impaired performance (see Figures 5b and 5c). This adverse effect on
learning was amplified in deeper networks (see Figure 5d). Ainsi, the scale
of the surrogate derivative plays an important role in learning success if im-
plicit recurrence, as contributed by the spike reset, is present in the network.
Since the spike reset constitutes a specific form of implicit recurrence (cf.
voir la figure 4), we were wondering whether we would observe a similar phe-
nomenon for explicit recurrence through recurrent synaptic connections. À
that end, we repeated the performance measurements in networks with re-
current connections but kept the spike reset term detached to prevent gra-
dient flow. We observed a small but measurable reduction in accuracy for
the best-performing networks (see Figures 5c and 5e). Surtout, comment-
jamais, there was a substantial decrease in classification performance when
gradients were allowed to flow through recurrent connections and the

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

908

F. Zenke and T. Vogels

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

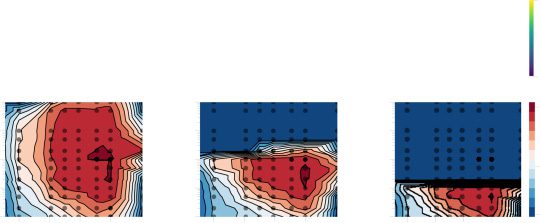
Chiffre 5: Surrogate gradient learning is sensitive to the scale of the surrogate
derivative. (un) Illustration of pseudo-derivatives σ (cid:2) that converge toward the
actual derivative of a hard spike threshold β → ∞. Note that in contrast to
Figure 3a, their maximum value grows as β increases. (b) Training accuracy
= 1) during training on a synthetic classifica-
of several spiking networks (nh
tion task. The gray curves comprise control networks in which the surrogate
derivative was either normalized to one or in which we used an asymptotic sur-
rogate derivative but prevented surrogate gradients from flowing through the
spike reset. Orange curves correspond to networks with asymptotic pseudo-
derivatives with differentiable spike reset (aDR). In all cases, we plot the five
best-performing learning curves obtained from an extensive grid search over
β and the learning rate η (cf. Chiffre 3). (c) Quantification of the test accuracy of
the different learning curves shown in panel b. We trained all networks using
a SuperSpike nonlinearity. The reset term was either ignored (sCtl) or a differ-
entiable reset was used (aDR). De la même manière, we considered an asymptotic variant
of SuperSpike that does converge toward the exact derivative of a step func-
tion for β → ∞, without (aCtl) or with a differentiable reset term (aDR). Le
results shown correspond to the 10 best results from a grid search. The error
bars denote the standard deviation. (d) A similar comparison of control cases
in which reset terms were ignored (gray) or could contribute to the surrogate
gradient (orange) for different numbers of hidden layers. (e) Test accuracy as in
panel c, but comparing SuperSpike s and the asymptotic a case in which gra-
dients can flow through recurrent connections (Soutenir) versus the detached case
(Ctl). (F) Test accuracy for asymptotic SuperSpike as a function of the number of
hidden layers for networks in which gradients were flowing through recurrent
relations (orange) versus the detached case (gray).

Robustness of Surrogate Gradients

909

Chiffre 6: Surrogate gradient learning is effective on different loss functions, dans-
put paradigms, et ensembles de données. Bar plots showing the test classification accuracy
for different data sets (a–e). The plots further distinguish models by their read-
out configuration (Sum versus Max) and whether they use purely feedforward
(FF) or explicitly recurrent (RC) synaptic connectivity. Each bar corresponds to
the mean over the 10 best-performing models on held-out validation data, et
error bars signify the standard deviation.

asymptotic SuperSpike variant was used (see Figure 5e). Unlike in the dif-
ferentiable reset (DR) case, the effect was severe enough to drop network
performance to chance level even for a network with a single hidden layer
(see Figure 5f). En résumé, surrogate gradients are sensitive to the scale of
the surrogate derivative. More specifically, when the scale of the surrogate
derivative is too large, and either implicit or explicit recurrence is present
in the network, the effect on learning can be detrimental.

2.4 Surrogate Gradient Learning Is Robust to Changes in the Loss
Functions, Input Paradigms, and Data Sets. So far we have investigated
synthetic random manifold data sets in strictly feedforward networks
trained with loss functions that were defined on the maximum over time
(Max) of the readout units. Suivant, we performed additional simulations in
which the loss was computed by summation over time (“Sum”; see section
4). Based on our findings above, we limited our analysis to the SuperSpike
surrogate with β = 10 and detached reset terms. As before, we performed
a grid search over the learning rate η and selected the 10 best-performing
models using held-out validation data. We then computed their classifica-
tion performance on a separate test set. We repeated our simulation exper-
iments on the above random manifold task and did not observe any sub-
stantial difference in the accuracy for the Max and Sum type readout heads
(see Figure 6a).

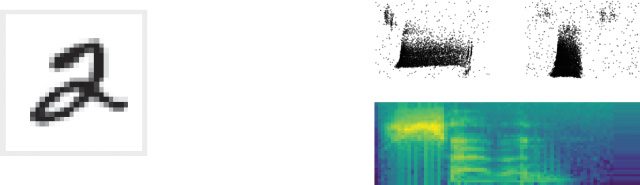
To check the validity of these findings on a different data set, we trained
networks on MNIST by converting pixel values into spike latencies (see Fig-
ures 7a and 7b and section 4). In this paradigm, each input neuron fires
either a single or no spike for each input. The networks reached a test ac-
curacy of (98.3 ± 0.9) %, which is comparable to a conventional artificial
neural network with the same number of neurons and hidden layers and to

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

910

F. Zenke and T. Vogels

Chiffre 7: Examples of different input paradigms. (un) One example image from
MNIST handwritten digit data set. (b) Spike raster plot of the corresponding
spike latency encoding for the 28 × 28 = 784 input neurons. (c) Spike raster of
two example inputs for the spoken digits “three” and “seven” taken from the
SHD data set (Cramer, Stradmann et al., 2020). (d) Mel-scaled spectrogram of an
utterance of the number “seven” as used for simulations using raw audio input.

previous SNN studies using temporal coding (Mostafa, 2018). We did not
observe any discernible performance differences between the two readout
types we tested (see Figure 6b).

Plus loin, to study the effect of explicit recurrence, we ran separate exper-
iments for recurrently connected networks (RC). Surtout, we did not
observe any substantial performance differences between strictly feedfor-
ward and recurrently connected networks either (see Figures 6a and 6b).

We speculated that the absence of an effect may be due to the short dura-
tion of the input spike trains considered so far (environ 50 ms). Re-
current connections are typically thought to provide neural networks with
longer timescale dynamics, effectively giving the network a working mem-
ory. Ainsi, the beneficial effects of recurrent connections may only emerge
when using stimuli of longer duration, with potentially multiple spikes
from any given input neuron.

To test this hypothesis, we trained networks on the Spiking Hei-
delberg Digits (SHD) data set (Cramer, Stradmann et al., 2020), lequel
consists of simulated input spikes from the auditory pathway of varied
duration between 0.6 et 1.4 s (see Figure 7c). En effet, we found that the
best-performing models in this case were recurrent and achieving state-of-
the-art classification accuracy of (0.82 ± 0.02) % (see Figure 6c). These data
are consistent with the notion that working memory plays a vital role in
classifying longer input patterns.

2.5 Surrogate Gradient Learning in Networks with Current-Based
Input. Until now, we have considered spike-based data sets. While spik-
ing inputs are arguably the most natural input to SNNs, they come with an
important caveat. All spiking data sets assume a specific encoding model,
which is used to convert analog input data into a spiking representation.
The chosen model, cependant, may not be optimal and thus adversely affect

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Robustness of Surrogate Gradients

911

classification performance. To avoid this issue, we sought to learn the spike
encoding by directly feeding current-based input to a set of spiking units
(Zimmer, Pellegrini, Singh, & Masquelier, 2019). To test this idea, we con-
verted the raw audio data of the Heidelberg Digits (Cramer, Stradmann
et coll., 2020) to Mel-spaced spectrograms (see Figure 7d and section 4). À
reduce overfitting, we decreased the number of channels and time steps to
values commonly used in artificial speech recognition systems. Spécifiquement,
we used 40 channels and 80 time frames, corresponding to compression in
time by a factor of about five (see section 4). The networks trained on this
RawHD data set showed reduced overfitting yet still benefited from recur-
rent connections compared to strictly feedforward networks (see Figure 6d).
Concretely, recurrent networks reached (94 ± 2) % test accuracy, alors que
the feedforward networks reached only (85 ± 3) %. In agreement with the
results on Randman and MNIST, there were no significant differences be-
tween the Sum and Max readout configurations (voir la figure 6).

We wanted to know whether the discrepancy between feedforward and
recurrent networks would increase for more challenging data sets. This was
made possible by the performance gain from reducing the input dimen-
sion to 40 chaînes, which allowed us to train SNNs on the larger Speech
Command data set (Warden, 2018; see section 4). This data set contains over
100,000 utterances from 35 classes, including “yes,” “no,” and “left.” In con-
trast to the original intended use for keyword spotting, here we assayed its
top-1 classification accuracy over all classes, a more challenging problem
than accurate detection of only a subset of words. The best SNNs achieved
(85.3 ± 0.3) % on this challenging benchmark (see Figure 6e). On the same
task, the spiking feedforward network performed at (70 ± 2) %. There was
a clear benefit from adding recurrent connections to the network, avec le
performance of the Max ((85.3 ± 0.3) %) being slightly better than the Sum
((80.7 ± 0.4) %) readout configuration.

These findings illustrate that surrogate gradient learning is robust to
changes in the input paradigm, including spiking and nonspiking data sets.
For more complex data sets, recurrently connected networks performed bet-
ter than strictly feedforward networks. Enfin, in the majority of cases, sur-
rogate gradient learning was robust to the details of how the output loss
was defined.

2.6 Optimal Sparse Spiking Activity Levels in SNNs. Up to now,
we have focused on maximizing classification accuracy while ignoring the
emerging activity levels in the resulting SNNs. Cependant, we found that for
some solutions, the neurons in these networks displayed implausibly high
firing rates (see Figure 8a). Experimental results suggest that most biolog-
ical networks exhibit sparse spiking activity, a feature that is presumed to
underlie their superior energy efficiency (Boahen, 2017; Cramer, Billaudelle
et coll., 2020; Neftci, 2018; Roy, Jaiswal, & Panda, 2019; Schemmel et al., 2010;
Sterling & Laughlin, 2017).

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

912

F. Zenke and T. Vogels

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

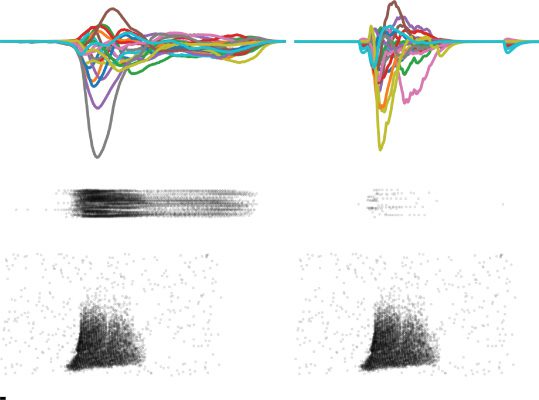
Chiffre 8: Activity regularization renders hidden-layer activity sparse while
maintaining functionality. (un) Activity snapshot of one example input from SHD
in a trained network. Spike raster plots of the input and hidden-layer units are
shown at the bottom and in the middle. The activity of the 20 readout units is
plotted at the top, with the brown line corresponding to the correct output for
this example. Without any specific regularization, spiking activity in the hid-
den layer is pathologically high. (b) As in panel (un), but for a network trained
with a penalty term for high spiking activity. This form of activity regulariza-
tion drastically alters the hidden-layer activity for the same input, while leaving
the winning output of the network unchanged (brown line). (c) Distribution of
the number of spikes emitted by individual hidden neurons in the unregular-
ized network over all trials of the test data set. The maximum firing rate in this
simulation was 500 Hz. (d) Same as in panel c, but for the regularized network.

We investigated whether surrogate gradients could instantiate SNNs in
this biologically plausible, sparse activity regime. To that end, we trained
SNNs with added activity regularization that penalized high spiking ac-
tivité (see Figure 8b and section 4) and recorded their hidden-layer activ-
ville. While neurons in the unregularized network frequently emityed the

Robustness of Surrogate Gradients

913

Chiffre 9: Classification accuracy degrades below a critical number of hidden-
layer spikes. Plots showing classification accuracy as a function of the average
number of hidden-layer spikes per input. The different columns correspond to
the different data sets (see Figures 6 et 7). Top row: Networks with feedfor-
ward connectivity. Bottom row: Networks with recurrent synapses. Blue data
points correspond to networks with one hidden layer, whereas orange data
points come from networks with two hidden layers. The solid lines correspond
to fitted sigmoid functions.

maximally possible number of 500 spikes per trial (see Figure 8c), regular-
ization drastically reduced both the maximal spike count per event and the
overall probability of high spike count events (see Figure 8d).

Despite a sizable reduction in spike count, many networks retained high
classification accuracy. In most cases, the number of spikes could be reduced
by approximately two orders of magnitude before there was a notable de-
cline in performance, and we found a critical transition in the average num-
ber of hidden-layer spikes below which networks performed poorly (voir
Chiffre 9). Par exemple, in the random manifold task, the transition occurred
at approximately 36 hidden-layer spikes per input in a single hidden layer
and approximately 76 spikes in a two-hidden-layer feed-forward network.
In the recurrent network, this number was reduced to 26 (nh

= 1).

In the case of MNIST, fewer than 10 spikes were sufficient on average to
achieve the point of diminishing returns beyond which additional spiking
activity did not improve classification performance.

This trend could be replicated for all other data sets, with varying de-
grees of spike reduction. Adding a hidden layer generally required more
spikes for the same performance. Recurrency generally did not have a great
effect on the minimum number of spikes and did not improve performance
except on RawSC. On RawSC, 80% classification accuracy was achieved
only by a few feedforward networks with more than 2000 spikes on av-
erage. In the recurrent network, this level was already attained with about
150 spikes (voir la figure 9).

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

914

F. Zenke and T. Vogels

In all cases, the transition from chance level to maximum accuracy oc-
curred in less than one order of magnitude change in the mean number of
spikes. On all data sets we tested, the addition of a second hidden layer led
to an overall increase in mean spiking activity, which did not yield a no-
table performance change on Randman and MNIST but resulted in small
improvements on RawHD and RawSC.

These results illustrate that activity-regularized SNNs can perform with
high accuracy down to some critical activity threshold at which their per-
formance degrades rapidly. Surtout, we found several network config-
urations that showed competitive performance with an average number of
spikes substantially lower than the number of hidden units. Par exemple, à
classify MNIST with high accuracy, an average of 10 à 20 action potentials
was sufficient. Such low activity levels are more consistent with the sparse
neuronal activity observed in biological neural circuits and illustrate that
surrogate gradients are well suited to building SNNs that use such plausi-
ble sparse activity levels for information processing.

3 Discussion

Surrogate gradients offer a promising way to instill complex functions in ar-
tificial models of spiking networks. This step is imperative for developing
brain-inspired neuromorphic hardware and using SNNs as in silico models
to study information processing in the brain. In this letter, we have focused
on two aspects of surrogate gradient learning in SNNs. We showed, us-
ing a range of supervised classification problems, that surrogate gradient
learning in SNNs is robust to different shapes of surrogate derivatives. Dans
contraste, inappropriate choice of scale adversely affected learning perfor-
mance. Our results imply that for practical applications, surrogate deriva-
tives should be appropriately normalized. Deuxième, by constraining their
activity through regularization, we showed that surrogate gradients could
produce SNNs capable of efficient information processing with sparse spik-
ing activity.

Surrogate gradients have been used by a number of studies to train SNNs
(Neftci et al., 2019), solve small-scale toy problems with fractionally predic-
tive neurons (Bohte, 2011), train convolutional SNNs on challenging neu-
romorphic (Amir et al., 2017; Orchard, Jayawant, Cohen, & Thakor, 2015)
and vision benchmarks (Esser et al., 2016), or train recurrent SNNs on tem-
poral problems requiring working memory (Bellec et al., 2018; Shrestha &
Orchard, 2018). These studies used different surrogate derivatives ranging
from exponential (Shrestha & Orchard, 2018), piece-wise linear (Bellec et al.,
2018), or tanh (Wo´zniak et al., 2020), sometimes with a nonstandard neuron
model with a constant leak term (Esser et al., 2016), but due to the differ-
ent function choices and data sets, they are not easily comparable. Here we
provide such a comprehensive comparison.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Robustness of Surrogate Gradients

915

Towards this end, we had to make some compromises. Our study, like
previous ones, is limited to supervised classification problems, because su-
pervised learning offers a well-defined and intuitive quantification of com-
putational performance. To keep the number of model parameters tractable,
we focused on current-based LIF neurons. De plus, we entirely dispensed
with Dale’s law and relied solely on all-to-all connectivity. Cependant, nous
believe that most of our findings will carry over to more realistic neu-
ronal, synaptic, and connectivity models. Our study thus provides a set of
blueprints and benchmarks to accelerate the design of future studies.

An alternative way of training SNNs, which does not rely on surrogate
gradients, was introduced by Huh and Sejnowski (2018), who put forward a
differentiable formulation of the neuronal spiking dynamics, thus allowing
gradient descent with exact gradients. Cependant, thus far, the approach has
only been demonstrated for theta neurons, and nonleaky integrate-and-fire
neurons and an extension to neuron models with nondifferentiable reset
dynamics, like the LIF neurons we used here, is still pending.

Although considered biologically implausible (Crick, 1989), we have
limited our study to training SNNs with backpropagation, the de facto
standard for computing gradients in systems involving recurrence and hid-
den neurons. Although there exist more plausible forward-in-time algo-
rithms like real-time recurrent learning (RTRL) (Williams & Zipser, 1989)
they are prohibitively expensive or require additional approximations that
affect learning performance (Bellec et al., 2019; Murray, 2019; Neftci et al.,
2019; Zenke & Ganguli, 2018). Plutôt, using BPTT enabled the targeted
manipulation of gradient flow through different elements of the network,
which allowed us to dis-entwine some of the complexity of surrogate
gradient learning. Enfin, our study was purely numerical, and several
important questions remain open. Par exemple, how does one optimally
initialize hidden-layer weights? How well do these findings translate to
convolutional neural networks? And why do the surrogate gradients work
so well, despite ignoring the spike reset in their evaluation? Answering
these questions requires additional numerical experiments and a rigorous
theoretical understanding of surrogate gradient learning in SNNs, both of
which remain for future work.

En résumé, surrogate gradients allow translating the success of deep
learning to biologically inspired SNNs by optimizing their connectivity to-
ward functional complexity through end-to-end optimization. The in-depth
study of both surrogate gradients and the resulting functional SNNs will
occupy scientists for years to come and will likely prove transformative for
neural circuit modeling.

4 Methods

4.1 Supervised Learning Tasks. Dans cette étude, we used a number of syn-
thetic and real-world learning tasks with the overarching aim of balancing

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

916

F. Zenke and T. Vogels

computational feasibility and practical relevance. To that end, we focused
on synthetic data sets generated from random manifolds and real-world
auditory datasets.

4.1.1 Smooth Random Manifold Data Sets. We generated a range of syn-
thetic classification data sets based on smooth random manifolds. Suppose
we want to generate a smooth random manifold of dimension D in an
embedding space of dimension M. We are looking for a smooth random
function f : RD → RM defined over the finite interval 0 ≤ x < 1 in each in- trinsic manifold coordinate axis. Moreover, we would like to keep its val- ues bounded in a similar (0 ≤ x < τ randman)M box in the embedding space. To achieve this, we first generate M smooth random functions fi : RD → R and then combine them to f : RD → RM. Specifically, we generate the fi from the Fourier basis as follows: (cid:3) (cid:7) fi((cid:2)x) = (cid:2) ncutoff(cid:4) j∈D k=1 1 kα (cid:5) (cid:5) (cid:6)(cid:6) θ A i jk sin 2π kx j θ B i jk + θ C i jk , i jk for L ∈ {A, B, C} were drawn independent and where the parameters θ L identically distributed from a uniform distribution U (0, 1). We set ncutoff = 1000, which leaves α as a parameter that controls the smoothness of the manifold. Larger values of α lead to more slowly varying manifolds, whereas smaller values increase the high-frequency content (see Figure 1a). In addition to α, the complexity of the learning problem can be seamlessly adjusted by either increasing the intrinsic dimension D of the manifold or the number of random manifolds whereby each random manifold corre- sponds to a separate class of the classification problem (see Figure 1b). Concretely, we generated spike trains by randomly and uniformly sam- pling points from a D-dimensional hypercube with a side length of one. We then interpreted these points as intrinsic manifold coordinates and con- verted them to the corresponding embedding space coordinates. We next standardized these values along all embedding dimensions to lie between 0 and τ randman and interpreted these M-dimensional coordinates as the fir- ing times of M distinct input neurons belonging to the same class of the classification problem (see Figure 1c). Example code to generate smooth random manifolds following this procedure is available at https://github. com/fzenke/randman. We chose a default parameter set for most of our experiments that struck a good balance between minimizing both the embedding dimension and the number of samples needed to solve the problem while simultaneously not being solvable by a two-layer network without hidden units. Specifi- cally, we chose a 10-way problem with D = α = 1, M = 20, and τ = 50 ms and fixed the random seed in situations in which we reused the same data set. In practice, the spike time tc i of input neuron i in a given trial of randman l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 3 4 8 9 9 1 9 0 2 2 9 4 n e c o _ a _ 0 1 3 6 7 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Robustness of Surrogate Gradients 917 = f c i (X ), where the f c class c is tc i are fixed random functions and X is a i uniformly distributed random number between zero and one. For all sim- ulation experiments, we generated 1000 data points for each class, out of which we used 800 for training and two sets of 100 each for validation and testing purposes. 4.1.2 Spike Latency MNIST Data Set. To convert the analog valued MNIST data set (LeCun, Cortes, & Burges, 1998) to firing times, we proceeded as μ follows. We first standardized all pixel values x i to lie within the interval 0 ≤ x < τ eff. We then computed the time to first spike latency T as the time to reach firing threshold of a leaky integrator, T(x) = (cid:8) τ eff log (cid:10) (cid:9) x x−ϑ x > ϑ

∞

otherwise

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

and in our simulations, we used ϑ = 0.2 and τ
and 7b).

eff

= 50 ms (see Figures 7a

4.1.3 Auditory Data Sets. We used both spiking and nonspiking auditory
data sets of digit and word utterances. Spécifiquement, we used the SHDs with-
out any further preprocessing (Cramer, Stradmann et al., 2020). For per-
formance reasons and to dispense with the spike conversion process, nous
ran additional simulations with nonspiking auditory inputs. Spécifiquement,
we worked with the raw Heidelberg Digits (RawHD) and Pete Warden’s
Speech Commands data set (RawSC) (Warden, 2018) which were prepro-
cessed as follows. We first applied a preemphasis filter to the raw audio sig-
nal x(t) by computing y(t) = x(t) − 0.95x(t − 1). We then computed 25 ms
frames with a 10 ms stride from the resulting signal and applied a Ham-
ming window to each frame. For each frame, we computed the 512-point
fast Fourier transform to obtain its power spectrum. From the power spec-
trum, we further computed the filter banks by applying 40 triangular fil-
ters on a Mel-scale (Huang, Acero, Hon, & Reddy, 2001). After cropping or
padding to 80 (RawHD) ou 100 (RawSC) steps by repeating the last frame,
the analog-valued filter banks were fed directly to the SNNs.

4.2 Network Models. To train SNN models with surrogate gradients,
we implemented them in PyTorch (Paszke et al., 2019). To that end, all mod-
els were explicitly formulated in discrete time with time step (cid:10)t.

4.2.1 Neuron Model. We used leaky integrate-and-fire neurons with
current-based exponential synapses (Gerstner, Kistler, Naud, & Paninski,
2014; Vogels & Abbott, 2005). The membrane dynamics of neuron i in layer
l were characterized by the following update equations,

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

918

F. Zenke and T. Vogels

(cid:5)

U (je)
je

[n + 1] =

memU (je)
β
je

[n] + (1 − β

mem) je(je)

je [n]

(cid:6) (cid:5)

(cid:6)
je [n]

1 − S(je)

(4.1)

(cid:6)

[n] − 1

je [n] ≡ (cid:11)

where U (je)
[n] corresponds to the membrane potential of neuron i in layer
l at time step n and is its S(je)
je [n], the associated output spike train defined
(cid:5)
U (je)
via the Heaviside step function (cid:11) as S(je)
. Note that in
je
this formulation, the membrane dynamics are effectively rescaled such that
the resting potential corresponds to zero and the firing threshold of one.
This choice simplifies the implementation of the neuronal reset dynamics
through the factor on the right-hand side. During the backward pass of
gradient computation with BPTT, the derivative of the step function is ap-
proximated using a surrogate, as explained later. In situations in which we
ignored the reset term, this was done differently for the output spike train
and the spike train underlying the reset term by detaching it from the com-
putational graph. The membrane decay variable β
mem is associated with
(cid:6)
the membrane time constant τ
. Enfin, le
variable I(je)
je

mem
[n] is the synaptic current defined as

mem through β

(cid:5)
− (cid:10)t
τmem

≡ exp

je(je)
je [n + 1] = β

synI(je)

je [n] +

(cid:4)

W (je)

i j S(l−1)

[n] +

(cid:4)

i j S(je)
V (je)

j [n],

(cid:6)

(cid:5)
− (cid:10)t
τsyn

with feedforward afferent weights Wi j and the optional recurrent weights
≡
Vi j. In analogy to the membrane decay constant, β
= 5 ms. Together the computa-
exp
tions involved in each time step can be summarized in the computational
graph of the model (voir la figure 4).

syn is defined as β

= 10 ms and τ

. We set τ

mem

syn

4.2.2 Readout Layer. The readout units in our models are identical to the
above neuron model, but without the spike and associated reset. Addition-
ally, we allow for a separate membrane time constant τ
= 20 ms with
β

. Dans l'ensemble, their dynamics are described by

(cid:5)
− (cid:10)t
τ

≡ exp

readout

dehors

(cid:6)

readout

U (dehors)
je

[n + 1] = β

outU (dehors)
je

[n] + (1 − β

dehors) je(dehors)
je

[n].

4.2.3 Connectivity and Initialization. We used all-to-all connectivity in all
simulations without bias terms unless mentioned explicitly. The weights
were initialized from a uniform distribution U (−
where ninputs is the number of afferent connections.

k) with k = 1

ninputs

√

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

4.2.4 Readout Heads and Supervised Loss Function. We trained all our net-

works by minimizing a standard cross-entropy loss L

sup defined as

Robustness of Surrogate Gradients

919

sup

= − 1
N

N(cid:4)

C(cid:4)

μ=1

je = 1

m
i log

oui

(cid:9)

(cid:10)

m
p
je

i is the one-hot encoded target for input μ, N is the number of input
where y
m
samples, and C is the number of classes. The output probabilities p
i were
given by the Softmax function

m
p
je

m
je

ea
(cid:11)
C
k=1 ea

m
k

m
in which the logits a
m
figuration either given by the sum over all time steps a
je

i for each input μ were depending on the readout con-
(cid:6)
[n]

(cid:5)
U (dehors)
je

(cid:11)

= maxn

m
or defined as the maximum a
, a notion inspired by the
je
Tempotron (Gütig & Sompolinsky, 2006). It is worth noting that in the case
of the Tempotron, the maximum over time is combined with a hinge loss
fonction, which allows for binary classification only. In contrast, the Soft-
max formulation that we used throughout this letter enables our framework
to perform multiway classification.

[n]

(cid:5)
U (dehors)
je

(cid:6)

4.2.5 Activity Regularization. To control spiking activity levels in the hid-
den layers, we employed two forms of activity regularization. D'abord, to pre-
vent quiescent units in the hidden layers, we introduced a lower-activity
threshold ν

lower at the neuronal level defined as

m
g
lower

lower
M.

M.(cid:4)

(cid:5)(cid:12)
ν
lower

− ζ (je),m
je

(cid:13)

(cid:6)
2

with the neuronal spike count ζ (je)
and the number of neu-
rons M in hidden-layer l. De la même manière, we defined an upper threshold at the
population level as

n S(je)

≡

(cid:5)(cid:11)

(cid:6)
je [n]

m
g
upper

= −λ

upper

⎛

(cid:3)

⎝

1
M.

M.(cid:4)

ζ (je),m
je

− ν

upper

(cid:7)

⎞
L
⎠

(cid:11)

for which we explored both values of L ∈ {1, 2}. The overall reg-
ularization loss was computed by summing and averaging L
=
m
+ g
1
upper
N
by dint of surrogate gradient descent.

(cid:10)
. Finally we optimized the total loss L

m
g
lower

reg
+ L

= L

sup

reg

tot

(cid:9)

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

920

F. Zenke and T. Vogels

1
0
.
0

,
3
−

0
1
×
5

,
3
−

3
−

0
1
×
1

3
−

0
1
/
0
.
0
0
1

0
1
×
1

1
−

2
≤

3
−

0
1
×
1

3
−

0
1
/
0
.
0
0
1

)
3
−

0
0
0
1
–
0

1
,
0

0
0
1
,
0
1

0
1
,
1

,
6
0
.
0

0
1
,
1
0
.
0
(
/
0
.
0
0
1

0
0
1
,
0
2
,
0
1

,
0

0
0
1
,
1

,
5
.
0

,
2
.
0

,
1
.
0
,
0

—

6
0
.
0

0
0
0
1
–
0

—

C
S
w
un
R.

D
H
w
un
R.

0
4

6
5
2

5
3

0
4

6
5
2

0
2

D
H
S

0
0
7

6
5
2

0
2

5
0
0
1
1
/
1
8
9
9
/
9
4
8
4
8

8
8
0
2
/
3
3
8
/
8
9
4
7

k
0
1
/
k
5
/
k
5
4

0
0
1
/
s

m
2

0
8
/
s

m
2

0
0
5
/
s

m
2

0
0
1
/
s

m
1

2
1
5

0
5

8
2
1

0
5

6
5
2

0
0
2

6
5
2

0
0
1

T
S
je
N
M.

n
un
m
d
n
un
R.

r
e
t
e
m
un
r
un
P.

.
s
n
o
je
t
un
je
toi
m
je
S
k
r
o
w
t
e
N

F
o
s
e
toi
je
un
V
r
e
t
e
m
un
r
un
P.

:
1
e
je
b
un
T

4
8
7

0
0
1

0
1

3
≤

0
2

0
0
1

0
1

0
0
1
/
s

m
1

0
5
2
,
8
2
1

0
0
1
–
0
5

k
2
/
k
2
/
k
8

2
≤

s
t
je
n
toi
n
e
d
d
h
F
o
r
e
b
m
toi
N

s
t
je
n
toi
t
toi
p
n

F
o
r
e
b
m
toi
N

s
t
je
n
toi
t
toi
o
d
un
e
r

F
o
r
e
b
m
toi
N

s
p
e
t
s

F
o
r
e
b
m
toi
N
/
t

(cid:10)

h
n
s
r
e
oui
un
je

n
e
d
d
h
F
o
r
e
b
m
toi
N

)
t
s
e
t
/
d

je
je
un
v
/
n

je
un
r
t
(

t
e
s
un
t
un
D

s
h
c
o
p
e

F
o
r
e
b
m
toi
N

e
z
je
s
h
c
t
un
b
je

n
M.

p
e
e
w
s

e
t
un
r
g
n

n
r
un
e
L

1
0
.
0

—

0
0
1
–
0

0
0
0
1
–
0

1
,
1
.
0

,
1
0
0
.
0
,
0

0
0
1

,
1
.
0

3
−

5
0
.
0

0
1
/
0
.
0
0
1

0
0
1
,
1

0
0
0
1
–
0

0
0
1
,
1
,
0

0
0
1
–
0

r
e
p
p
toi

ν
d
je
o
h
s
e
r
h
t
1
L
r
e
p
p
U

ν
d
je
o
h
s
e
r
h
t
2
L
r
e
p
p
U

λ
h
t
g
n
e
r
t
s
2
L
r
e
p
p
U

λ
h
t
g
n
e
r
t
s
1
L
r
e
p
p
U

ν
/

r
e
w
o
je

:
2
L
r
e
w
o
L

t
s
e
B

1
≤
η
≤

4
−

0
1
×
2

1
−

1
≤
η
≤

4
−

0
1
×
2

0
≤
η
≤

3
−

0
1

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Robustness of Surrogate Gradients

921

4.2.6 Surrogate Gradient Descent. We minimized the loss L

tot by ad-
justing the parameters W and V in the direction of the negative surro-
gate gradients using Adam with default parameters (Kingma & Ba, 2014).
Surrogate gradients were computed with backpropagation through time
using PyTorch’s automatic differentiation capabilities. To deal with the
nondifferential spiking nonlinearity of the hidden-layer neurons, we ap-
(cid:10)
(cid:9)
m
proximated their derivatives S(cid:2)
je [n]
U
with suitable sur-
(cid:10)
(cid:10)
(cid:9)
(cid:9)
m
rogates σ (cid:2)
je [n] − 1
je [n]
U
U
. Throughout, we used the following
functions h(X):

(cid:9)
je [n] − 1
U

= (cid:11)(cid:2)

= h

(cid:10)

SuperSpike: h(X) =
Sigmoid(cid:2): h(X) = s(X) (1 − s(X)) with the sigmoid function s(X) =

1
(β|X|+1)2

1
1+exp(−βx)

Esser et al.: h(X) = max(0, 1.0 − β |X|)

where β is a parameter that controls the slope of the surrogate deriva-
tive. In Figure 5, we additionally considered an asymptotic variant of Su-
perSpike defined as h(X) =
(β|X|+1)2 . Unless mentioned otherwise, we set
β = 10. Tableau 1 specifies the relevant hyperparameters used in the differ-
ent simulations. An example of how these manipulations can be achieved
easily with PyTorch can be found at https://github.com/fzenke/spytorch
(Zenke, 2019). All simulations and parameter sweeps were performed on
compute nodes equipped with Nvidia Quadro RTX 5000 and V100 GPUs.

Remerciements

F.Z. was supported by the Wellcome Trust (110124/Z/15/Z) and the No-
vartis Research Foundation. T.P.V. was supported by a Wellcome Trust
Sir Henry Dale Research fellowship (WT100000), a Wellcome Trust Senior
Research Fellowship (214316/Z/18/Z), and an ERC Consolidator Grant
SYNAPSEEK.

Les références

Amir, UN., Taba, B., Berger, D., Melano, T., McKinstry, J., Di Nolfo, C., . . . Kusnitz, J..
(2017). A low power, fully event-based gesture recognition system. In Proceedings
of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 7243–7252).
Piscataway, New Jersey: IEEE.

Barrett, D. G., Morcos, UN. S., & Macke, J.. H. (2019). Analyzing biological and artificial
neural networks: Challenges with opportunities for synergy? Current Opinion in
Neurobiology, 55, 55–64, 2019. est ce que je:10.1016/j.conb.2019.01.007.

Bellec, G., Salaj, D., Subramoney, UN., Legenstein, R., & Maass, W. (2018). Long short-
term memory and learning-to-learn in networks of spiking neurons. In S. Bengio,
H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, & R.. Garnett (Éd.),

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

922

F. Zenke and T. Vogels

Advances in neural information processing systems, 31 (pp. 795–805). Red Hook, New York:
Curran.

Bellec, G., Scherr, F., Hajek, E., Salaj, D., Legenstein, R., & Maass, W. (2019). Biolog-
ically inspired alternatives to backpropagation through time for learning in recurrent
neural nets. arXiv: 1901.09049.

Boahen, K. (2017). A neuromorph’s prospectus. Comput. Sci. Eng., 19(2), 14–28. est ce que je:10.

1109/MCSE.2017.33.

Bohte, S. M.. (2011). Error-backpropagation in networks of fractionally predictive
spiking neurons. In Artificial Neural Networks and Machine Learning—ICANN 2011,
Lecture Notes in Computer Science, pages 60–68. Berlin: Springer. est ce que je:10.1007/
978-3-642-21735-78.

Cramer, B., Billaudelle, S., Kanya, S., Leibfried, UN., Grübl, UN., Karasenko, V., . . .
Zenke, F. (2020). Training spiking multi-layer networks with surrogate gradients on
an analog neuromorphic substrate. arXiv:2006.07239.

Cramer, B., Stradmann, Y., Schemmel, J., & Zenke, F. (2020). The Heidelberg spiking
data sets for the systematic evaluation of spiking neural networks. IEEE Trans-
actions on Neural Networks and Learning Systems, 1–14. est ce que je:10.1109/TNNLS.2020.
3044364.

Crick, F. (1989). The recent excitement about neural networks. Nature, 337(6203), 129–

132. est ce que je:10.1038/337129a0.

Cueva, C. J., Marcos, E., Saez, UN., Genovesio, UN., Jazayeri, M., Romo, R., . . .
Fusi, S. (2019). Low dimensional dynamics for working memory and time encoding.
bioRxiv:504936. est ce que je:10.1101/504936.

Esser, S. K., Merolla, P.. UN., Arthur, J.. V., Cassidy, UN. S., Appuswamy, R., Andreopou-
los, UN., . . . Modha, D. S. (2016). Convolutional networks for fast, energy-efficient
neuromorphic computing. In Proc. Natl. Acad. Sci. USA., 113(41), 11441–11446.
est ce que je:10.1073/pnas.1604850113.

Gerstner, W., Kistler, W. M., Naud, R., & Paninski, L. (2014). Neuronal dynamics: Depuis
single neurons to networks and models of cognition. Cambridge: Cambridge Univer-
sity Press.

Gütig, R.. (2016). Spiking neurons can discover predictive features by aggregate-label

learning. Science, 351(6277), aab4113. est ce que je:10.1126/science.aab4113.

Gütig, R., & Sompolinsky, H. (2006). The tempotron: A neuron that learns spike

timing-based decisions. Nat. Neurosci., 9(3), 420–428. est ce que je:10.1038/nn1643.

Il, K., Zhang, X., Ren, S., & Sun, J.. (2015). Delving deep into rectifiers: Surpassing
human-level performance on imagenet classification. In Proceedings of the IEEE
International Conference on Computer Vision (pp. 1026–1034). Piscataway, New Jersey: IEEE.
Hochreiter, S. (1998). The vanishing gradient problem during learning recurrent neu-
ral nets and problem solutions. Int. J.. Unc. Fuzz. Knowl. Based Syst., 6(2), 107–116.
est ce que je:10.1142/S0218488598000094.

Huang, X., Acero, UN., Hon, H.-W., & Reddy, R.. (2001). Spoken language processing: UN
guide to theory, algorithm and system development. Upper Saddle River, New Jersey: Prentice
Hall.

Huh, D., & Sejnowski, T. J.. (2018). Gradient descent for spiking neural networks. Dans
S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, & R.. Garnett
(Éd.), Advances in neural information processing systems, 31 (pp. 1440–1450). Red
Hook, New York: Curran.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Robustness of Surrogate Gradients

923

Hunsberger, E., & Eliasmith, C. (2015). Spiking deep networks with LIF neurons.

arXiv:1510.08829.

Kingma, D., & Ba, J.. (2014). Adam: A method for stochastic optimization. arXiv:1412.6980.
LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–444.

est ce que je:10.1038/nature14539.

LeCun, Y., Cortes, C., & Burges, C. J.. (1998). The MNIST database of handwritten digits.

1998.

Lee, J.. H., Delbruck, T., & Pfeiffer, M.. (2016). Training deep spiking neural networks

using backpropagation. Front. Neurosci., 10. est ce que je:10.3389/fnins.2016.00508.

Maheswaranathan, N., McIntosh, L. T., Kastner, D. B., Melander, J., Brezovec, L.,
Nayebi, UN., . . . Baccus, S. UN. (2018). Deep learning models reveal internal struc-
ture and diverse computations in the retina under natural scenes. bioRxiv. est ce que je:10.1101/
340943.

Mante, V., Sussillo, D., Shenoy, K. V., & Newsome, W. T. (2013). Context-dependent
computation by recurrent dynamics in prefrontal cortex. Nature, 503(7474), 78–84.
est ce que je:10.1038/nature12742.

McClure, P., & Corps de guerre, N. (2016). Representational distance learning for deep
neural networks. Front. Comput. Neurosci., 10. est ce que je:0.3389/fncom.2016.00131.
McIntosh, L., Maheswaranathan, N., Nayebi, UN., Ganguli, S., & Baccus, S. (2016).
Deep learning models of the retinal response to natural scenes. In D. Lee, M..
Sugiyama, U. Luxburg, je. Guyon, & R.. Garnett (Éd.), Advances in neural infor-
mation processing systems, 29 (pp. 1369–1377). Red Hook, New York: Curran.

Michaels, J.. UN., Schaffelhofer, S., Agudelo-Toro, UN., & Scherberger, H. (2019). A neural
network model of flexible grasp movement generation. bioRxiv. est ce que je:10.1101/742189.

Mishkin, D., & Matas, J.. (2016). All you need is a good init. arXiv:151106422.
Mostafa, H. (2018). Supervised learning based on temporal coding in spiking neural
réseaux. Trans. Neural Netw. Learn. Syst., 29(7), 3227–3235. est ce que je:10.1109/TNNLS.
2017.2726060.

Murray, J.. M.. (2019). Local online learning in recurrent networks with random feed-

back. eLife, 8, e43299. est ce que je:10.7554/eLife.43299.

Neftci, E. Ô. (2018). Data and power efficient intelligence with neuromorphic learn-

ing machines. iScience, 5, 52–68. est ce que je:10.1016/j.isci.2018.06.010.

Neftci, E. O., Mostafa, H., & Zenke, F. (2019). Surrogate gradient learning in spiking
neural networks: Bringing the power of gradient-based optimization to spiking
neural networks. IEEE Signal Process. Mag., 36(6), 51–63. est ce que je:10.1109/MSP.2019.
2931595.

Orchard, G., Jayawant, UN., Cohen, G. K., & Thakor, N. (2015). Converting static im-
age datasets to spiking neuromorphic datasets using saccades. FrontNeurosci., 9.
est ce que je:10.3389/fnins.2015.00437.

Paszke, UN., Gross, S., Massa, F., Lerer, UN., Bradbury, J., Chanan, . . . Chintala, S. (2019).
PyTorch: An imperative style, high-performance deep learning library. In H. Wal-
lach, H. Larochelle, UN. Beygelzimer, F. d’Alché-Buc, E. Fox, & R.. Garnett (Éd.),
Advances in neural information processing systems, 32 (pp. 8026–8037). Red Hook,
New York: Curran.

Pfeiffer, M., & Pfeil, T. (2018). Deep learning with spiking neurons: Opportunities

and challenges. Front. Neurosci., 12. est ce que je:10.3389/fnins.2018.00774.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

924

F. Zenke and T. Vogels

Pospisil, D. UN., Pasupathy, UN., & Bair, W. (2018). “Artiphysiology” reveals V4-like
shape tuning in a deep network trained for image classification. eLife, 7:e38242.
est ce que je:10.7554/eLife.38242.

Richards, B. UN., Lillicrap, T. P., Beaudoin, P., Bengio, Y., Bogacz, R., Christensen, UN., . . .
Kording, K. P.. (2019). A deep learning framework for neuroscience. Nat. Neurosci.,
22(11), 1761–1770. est ce que je:10.1038/s41593-019-0520-2.

Roy, K., Jaiswal, UN., & Panda, P.. (2019). Towards spike-based machine intelli-
gence with neuromorphic computing. Nature, 575(7784), 607–617. est ce que je:10.1038/
s41586-019-1677-2.

Schemmel, J., Briiderle, D., Griibl, UN., Hock, M., Meier, K., & Millner, S. (2010). UN
wafer-scale neuromorphic hardware system for large-scale neural modeling. Dans
Proceedings of 2010 IEEE International Symposium on Circuits and Systems (pp. 1947–
1950). Piscataway, New Jersey: IEEE.

Schmidhuber, J.. (2015). Deep learning in neural networks: An overview. Neural

Netw., 61, 85–117. est ce que je:10.1016/j.neunet.2014.09.003.

Shrestha, S. B., & Orchard, G. (2018). SLAYER: Spike layer error reassignment in
temps. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, &
R.. Garnett (Éd.), Advances in neural information processing systems, 31 (pp. 1419–
1428). Red Hook, New York: Curran.

Sterling, P., & Laughlin, S. (2017). Principles of neural design. Cambridge, MA: AVEC

Presse.

Stroud, J.. P., Porter, M.. UN., Hennequin, G., & Vogels, T. P.. (2018). Motor primitives in
space and time via targeted gain modulation in cortical networks. Nature Neuro-
science, 21(12), 1774. est ce que je:10.1038/s41593-018-0276-0.

Sussillo, D., & Barak, Ô. (2012). Opening the black box: Low-dimensional dynamics
in high-dimensional recurrent neural networks. Neural Comput., 25(3), 626–649.
est ce que je:10.1162/NECO_a_00409.

Tanaka, H., Nayebi, UN., Maheswaranathan, N., McIntosh, L., Baccus, S., & Ganguli,
S. (2019). From deep learning to mechanistic understanding in neuroscience: Le
structure of retinal prediction. In H. Wallach, H. Larochelle, UN. Beygelzimer, F.
d’Alché-Buc, E. Fox, & R.. Garnett (Éd.), Advances in neural information processing
systèmes, 32 (pp. 8535–8545). Red Hook, New York: Curran.

Vogels, T. P., & Abbott, L. F. (2005). Signal propagation and logic gating in net-
works of integrate-and-fire neurons. J.. Neurosci., 25(46), 10786. est ce que je:10.1523/
JNEUROSCI.3508-05.2005.

Wang, J., Narain, D., Hosseini, E. UN., & Jazayeri, M.. (2018). Flexible timing by tem-
poral scaling of cortical responses. Nat. Neurosci., 21(1), 102–110. est ce que je:10.1038/
s41593-017-0028-6.

Warden, P.. (2018). Speech commands: A dataset for limited-vocabulary speech recognition.

arXiv:1804.03209.

Williams, R.. J., & Zipser, D. (1989). A learning algorithm for continually running

fully recurrent neural networks. Neural Computation, 1(2), 270–280.

Williamson, R.. C., Doiron, B., Forgeron, M.. UN., & Yu, B. M.. (2019). Bridging large-
scale neuronal recordings and large-scale network models using dimensional-
ity reduction. Opinion actuelle en neurobiologie, 55, 40–47. est ce que je:10.1016/j.conb.2018.
12.009.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
3
4
8
9
9
1
9
0
2
2
9
4
n
e
c
o
_
un
_
0
1
3
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Robustness of Surrogate Gradients

925

Wo´zniak, S., Pantazi, UN., Bohnstingl, T., & Eleftheriou, E. (2020). Deep learning in-
corporating biologically inspired neural dynamics and in-memory computing.
Nature Machine Intelligence, 2(6), 325–336. est ce que je:10.1038/s42256-020-0187-0.

Yamins, D. L. K., & DiCarlo, J.. J.. (2016). Using goal-driven deep learning models to
understand sensory cortex. Nat. Neurosci., 19(3), 356–365. est ce que je:10.1038/nn.4244.
Yamins, D. L. K., Hong, H., Cadieu, C. F., Solomon, E. UN., Seibert, D., & DiCarlo,
J.. J.. (2014). Performance-optimized hierarchical models predict neural responses
in higher visual cortex. In Proc. Natl. Acad. Sci. USA., 111(23), 8619–8624. est ce que je:10.
1073/pnas.1403112111.
Zenke, F. (2019). SpyTorch.
Zenke, F., & Ganguli, S. (2018), SuperSpike: Supervised learning in multilayer spik-

ing neural networks. Neural Comput., 30(6), 1514–1541.

Zimmer, R., Pellegrini, T., Singh, S. F., & Masquelier, T. (2019). Technical re-
port: Supervised training of convolutional spiking neural networks with PyTorch.
arXiv:1911.10124.

Received July 24, 2020; accepted November 6, 2020.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d