LETTER - Recherche en IA spécialisée au MIT

LETTER

Communicated by Hugo G. Schnack

Brain Morphometry Methods for Feature Extraction
in Random Subspace Ensemble Neural Network
Classification of First-Episode Schizophrenia

Roman Vyškovský
vyskovsky@iba.muni.cz
Daniel Schwarz
schwarz@iba.muni.cz
Masaryk University, Faculty of Medicine, Institute of Biostatistics and Analyses,
625 00, Brno, Czech Republic

Tomáš Kašpárek
tkasparek@fnbrno.cz
Masaryk University and University Hospital Brno, Département de psychiatrie,
625 00, Brno, Czech Republic

Machine learning (ML) is a growing field that provides tools for auto-
matic pattern recognition. The neuroimaging community currently tries
to take advantage of ML in order to develop an auxiliary diagnostic tool
for schizophrenia diagnostics. In this letter, we present a classification
framework based on features extracted from magnetic resonance imag-
ing (IRM) data using two automatic whole-brain morphometry methods:
voxel-based (VBM) and deformation-based morphometry (DBM). Le
framework employs a random subspace ensemble-based artificial neu-
ral network classifier—in particular, a multilayer perceptron (MLP). Le
framework was tested on data from first-episode schizophrenia patients
and healthy controls. The experiments differed in terms of feature extrac-
tion methods, using VBM, DBM, and a combination of both morphom-
etry methods. Ainsi, features of different types were available for model
adaptation. As we expected, the combination of features increased the
MLP classification accuracy up to 73.12%—an improvement of 5% versus
MLP-based only on VBM or DBM features. To further verify the findings,
other comparisons using support vector machines in place of MLPs were
made within the framework. Cependant, it cannot be concluded that any
classifier was better than another.

1 Introduction

Schizophrenia (SZ) is a severe mental disorder that affects people most of-
ten in early adulthood (Andreasen, 1995). It is characterized by hallucina-
tions and delusions, which impose a profound psychological burden on the

Neural Computation 31, 897–918 (2019)
est ce que je:10.1162/neco_a_01180

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

898

R.. Vyškovský, D. Schwarz, and T. Kašpárek

patients, their surroundings, and caregivers. If the patient is left untreated
for a longer period of time, psychosis is associated with lower levels of
symptomatic and functional recovery from the first psychotic episode and
also corresponds to the severity of negative symptoms (Perkins, Gu, Boteva,
& Lieberman, 2005). Ainsi, early detection of schizophrenia and administra-
tion of antipsychotics is critical.

Computer science is a progressive discipline enabling auxiliary diag-
nostics through a wide range of tools, such as high-resolution neuroimag-
ing devices and high-speed computers, that are able to run computation-
ally demanding algorithms for image processing, analyse, and pattern
reconnaissance. Many papers have revealed the morphological changes in the
brain affected by schizophrenia versus the healthy brain, as in Gaser, Volz,
Kiebel, Riehemann, and Sauer (1999) and Wright et al. (1995). These differ-
ences may enable development of a model applicable in computer-aided
diagnostics.

Analysis of brain morphology is an important step on the way to creating
a classification framework. The underlying computational neuroanatomy
méthodes, such as voxel- and deformation-based morphometry (Ashburner
& Friston, 2000; Ashburner et al., 1998) are widely used for spatial normal-
ization of brain images and detection of morphological abnormalities based
on comparisons made between patients and healthy controls.

Voxel-based morphometry (VBM) involves several image processing
steps. The first step is spatial normalization of images, c'est, registration
to a standard template followed by resampling to isotropic voxels and res-
olution typically set to 1.5 mm or 1.0 mm. This step ensures that global
differences in position, orientation, size, and shape are removed while
maintaining local differences. The registered images are segmented into tis-
sue types—white matter, gray matter, and cerebrospinal fluid—that are sub-
sequently smoothed by the gaussian filter, and the resulting tissue densities
are analyzed statistically. The significant differences identified between tis-
sue densities in healthy and diseased subjects are interpreted as the impact
of the disease (Schwarz & Kašpárek, 2011). Following the spatial normaliza-
tion and segmentation, a step called “modulation” may be incorporated in
order to scale the normalized tissue maps by the macroscopic deformations,
and thus preserve local volume.

The VBM approach has been validated several times, showing consis-
tent findings obtained from VBM and by means of volumetric calculations
over regions of interest (Giuliani, Calhoun, Pearlson, Francis, & Buchanan,
2005; Gong et al., 2005; Keller et al., 2002). Cependant, the underlying method-
ology of VBM was criticized for being susceptible to errors and false-
positive results due to imprecise and possibly erroneous image registrations
(Bookstein, 2001) et, subsequently, argued and advocated for (Ashburner
& Friston, 2001; Davatzikos, 2004). Criticism against VBM is also allevi-
ated if the SPM package (Statistical Parametric Mapping toolbox for Mat-
laboratoire: http://www.fil.ion.ucl.ac.uk/spm/) is used. The package offers the

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Morphometry Methods for Ensemble-Based Schizophrenia Classification 899

standard VBM implementation, which includes a precise intersubject regis-
tration algorithm DARTEL (diffeomorphic anatomical registration through
exponentiated lie algebra) (Ashburner, 2007). Nevertheless, the heterogene-
ity of the results obtained from VBM analyses is still very high, and the neu-
roimaging community lacks a gold-standard configuration applicable to all
image processing steps within the VBM pipeline, including the choice of a
registration algorithm, inclusion of the modulation step, and setting of the
gaussian filter smoothing.

The other method for detection of morphological abnormalities pre-
sented in this letter is deformation-based morphometry (DBM). The method
is based on the analysis of deformation fields obtained from the registration
step (Schwarz & Kašpárek, 2011). Unlike VBM, DBM can detect differences
in shape and volume within the whole brain. It must be noted that the DBM
was originally used (Ashburner et al., 1998) as a method for detecting global
brain shape differences in different populations. Several DBM methods dif-
fer in the registration algorithm and spatial deformation model. In the early
études (Ashburner & Friston, 2000; Ashburner et al., 1998), smooth para-
metric transformations with low-frequency sine basis functions were used.
Cette approche (low-resolution DBM) did not take account of all anatomical
variability, and therefore it was unable to encode all subtle differences into
spatial transformations. Introduction of high-resolution deformable regis-
tration has made it possible to describe the complex brain morphology. Ce
high-resolution DBM includes spatial deformation models based on high-
dimension parametric transformations or models inspired by similarity to
continuum mechanics. There are several ways to analyze the resulting de-
formation fields. One of the frequently used approaches to the analysis is
based on independent univariate tests applied voxel-wise to Jacobian deter-
minants, which quantify changes in voxel volume and can be calculated di-
rectly from the deformation fields. In this manner, significant local volume
changes between diseased and healthy brains can be detected (Schwarz &
Kašpárek, 2011).

Recognizing a mental disease from imaging data, particularly first-
episode schiozophrenia, is a complex task employing multivariate algo-
rithms that unveil patterns of subtle differences in the images and use them
to assign a class label. Machine learning (ML), which represents the state-
of-the-art methodology in the field, encompasses self-adaptive classifica-
tion algorithms, y compris, Par exemple, support vector machines (SVM),
artificial neural networks (ANN), decision trees, and clustering meth-
ods. Promising results from several studies have already been published,
showing that ML classifier accuracy can exceed 70%, c'est, it is higher
than a random guess (accuracy rates are in the brackets): ANNs based
on diffusion imaging data (100%; Charpentier, & Savio, 2010), functional
magnetic resonance imaging (IRMf) data and features from independent
component analysis (75.6%; Jafri & Calhoun, 2006); SVM with wavelet fea-
tures extracted from MRI (73.20%; Dluhoš, Schwarz, & Kašpárek, 2014); et

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

900

R.. Vyškovský, D. Schwarz, and T. Kašpárek

search-light-based feature extraction from fMRI (91%; Bleich-Cohen et al.,
2014). Nieuwenhuis et al. (2012) used SVM and features selected from a
gray matter (GM) densities and removed those with low weights in the
SVM model (less than 70%). Neural networks also reveal good accuracy for
other brain diseases, including Alzheimer’s disease (AD): backpropagation
network based on MRI and principal component analysis (100%; Huang,
Yan, Jiang, & Wang, 2008), radial basis function network, probabilistic neu-
ral networks, and learning vector quantization network based on MRI
(66–83%; Savio, García-Sebastián, Hernández, Graña, & Villanúa, 2009).
Recognition tools for Parkinson’s disease include SVM in combination with
principal component analysis and MRI (plus que 90%, depending on the
number of components used; Salvatore et al., 2014).

Ensemble learning represents a methodology that generally employs
multiple classifiers, which either differ in principle or share the same prin-
ciple but differ in some parameter values or are identical but trained on
different subsets of data. The underlying algorithms combine individual
classifiers’ outputs to reach a final decision and thus mimic the thought
process of an ensemble. The ensemble learning methods have already been
applied in the detection of schizophrenia based on brain imaging data.
Lequel, Liu, Sui, Pearlson, and Calhoun (2010) achieved classification accu-
racy of 87% with SVMs governed by the AdaBoost algorithm. Janousova,
Schwarz, and Kasparek (2015) employed three different classifiers with a
maximum uncertainty linear discriminant analysis, centroid, and average
linkage methods. The experiments combined three different imaging fea-
photos (image intensities, GM densities, and local volume changes), et le
best accuracy achieved was 81.6%, showing an insignificant improvement
compared to a single classifier accuracy of 80.6%.

Ensemble learning has also been used for the detection of other neuro-
logical diseases. Liu, Zhang, and Shen (2012) proposed a local patch-based
subspace ensemble method to diagnose Alzheimer’s disease and improved
the accuracy by 3% versus a single classifier. Lebedev et al. (2014) reached
91% with random forests for the same disease, and Liu, Shang, Zheng, et
Wen (2016) combined linear regression, linear SVM, naive Bayes, positron
emission tomography (ANIMAL DE COMPAGNIE), and MRI for dementia diagnosis. They found
96.7% specificity for AD versus HC and more than 60% specificity for mild
cognitive impairment versus HC. Gould et al. (2014) used resampling and
created an ensemble of SVMs to ensure result stability while classifying the
cognitive subtypes of schizophrenia.

Ici, we use an ensemble learning method to improve the classification
accuracy of an ANN, particularly a multilayer perceptron (MLP). Although
there are many types of ensemble learning techniques in use, we adapt the
random subspace ensemble (RSE) method (Ho, 1998) due to its expected
applicability to the problem known as the curse of dimensionality in brain
image classification (Lemm, Blankertz, Dickhaus, & Müller, 2011). Plus loin-
plus, we compare random subspace ensemble neural networks with SVM,

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Morphometry Methods for Ensemble-Based Schizophrenia Classification 901

one of the most common approaches used in pattern recognition. We re-
fer to the combination of these methods as RSE-MLP and RSE-SVM in the
following text.

The letter is organized into five sections. Section 2 describes the math-
ematical background—brain image preprocessing and the design of the
ensemble learning classification framework including feature selection,
classification and validation. Section 3 shows the results, section 4 discusses
the outcomes, and section 5 concludes.

2 Methods

This section presents the data used for the experiment and summarizes the
mathematical issues, which are important for the classification pipeline pre-
sented here.

2.1 Image Acquisition. The MR images were collected in the Univer-
sity Hospital Brno. Patients were interviewed in compliance with the Inter-
national Statistical Classification of Disease and Related Health Problems
(ICD-10), and subsequently their blood and urine samples were collected
for toxicological, hematological, and biochemical testing. Subjects with ab-
normal findings were excluded from the data set. None of the subjects had
a family or personal history of axis I psychiatric conditions. All subjects
signed the informed consent, and the study was approved by the ethics
committee (Janousova et al., 2016).

The data set contained 104 (52 SZ + 52 healthy controls (HC)) T1-
weighted images of the entire head obtained with a 1.5 T MR device and the
following parameters: sagittal tomographic plane thickness of 1.17 mm, le
in-plane resolution was 0.48 mm × 0.48 mm, a 3D field of view contained
160 × 512 × 512 voxels, inversion recovery/gradient recalled (IR/GR) avec-
quence, repetition time (TR) était 1700 ms, echo time (TE) était 3.93 ms, inver-
sion time was 1100 ms, flip angle was 15◦
, and the field of view (FOV) était
246 × 246 mm. The data were matched for age median (min-max): SZ 22.9
(17–40), HC 23.0 (18.2–37.8), and sex because all subjects were men. Plus
details about the data set and image acquisition can be found in Janousova
et autres. (2016).

2.2 Feature Extraction Based on Brain Morphometry Methods. Le
GM tissue segments were obtained from all images following bias field
inhomogeneity correction, spatial normalization, and segmentation (Ash-
burner & Friston, 2005) with the use of the VBM8 toolbox (http://dbm
.neuro.uni-jena.de/vbm/) implemented in the SPM8 software package.
Spatial normalization steps involved affine registration to standard sta-
tistical parametric mapping (SPM) T1 template followed by the fast dif-
feomorphic registration algorithm DARTEL. The gray matter (GM) tissue
segments were modulated with Jacobian determinants calculated from the

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

902

R.. Vyškovský, D. Schwarz, and T. Kašpárek

obtained spatial transformations to account for registration-related changes
in local volumes. The modulated GM segment images were subsequently
smoothed with an 8 mm full width at half maximum (FWHM) gaussian
kernel to enable intersubject comparisons and to make the data distribu-
tion more normal.

Spatial normalization steps in DBM included the same affine registration
algorithm as in VBM. After transforming all bias-corrected images into the
stereotaxic space, our original high-dimensional deformable registration
technique (Schwarz, Kasparek, Provaznik, & Jarkovsky, 2007) avait l'habitude de
compute the vector displacement fields that maximized the normalized mu-
tual information between the images and the high-resolution single-subject
template retrieved from the database of International Consortium for Brain
Cartographie (ICBM). The registration algorithm calculated local forces in each
voxel and their regularization via a modified Rogelj’s elastic-incremental
spatial deformation model (for more details, see Schwarz et al., 2007). Le
resulting 3D displacement vector fields were converted to scalar fields by
computing Jacobian determinants in each voxel of the stereotaxic space. Af-
ter logarithmic transformation, the resulting positive and negative values
refer to local volume changes caused by the deformation (c'est à dire., expansions
and contractions, respectivement), whereas no deformation effect is observed
where the values are close to zero.

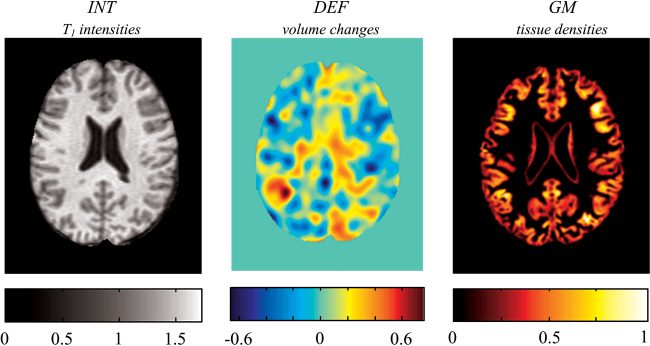
Examples of the gray matter tissue densities (GM) and the local volume
changes (DEF) in a 2D slice are shown with MR intensities of a normalized
image (INT) in Figure 1.

2.3 Mathematical Formalization of Artificial Neural Networks. Neu-
ral networks offer many algorithms inspired by neurophysiological neu-
rons. Ici, we focused on the traditional neural network type consisting of
neurons that can be described by the equation corresponding to the model

(cid:2)

y = ϕ

(cid:4)

ixi

n(cid:3)

je = 1

(2.1)

where y is an output, ϕ is a hyperbolic tangent activation function, w
i is the
ith weight, xi is the ith component of the input vector, and w
0 is a bias. Le
neurons are organized in a network and form layers. The applied archi-
tecture consists of input units that equal the number of features—10 hid-
den neurons and 2 output neurons. This architecture resulted from our
preliminary experiments (Vyškovský, Schwarz, Janoušová, & Kašpárek,
2016), which involved a wide range of ANN configurations parameterized
with learning algorithms, number of layers, hidden neurons, and training
epochs. The input neurons in the first layer receive the image data and pass
the information farther inside the network. Ici, each neuron transforms
the data via equation 2.1. Only two neurons are in the output layer, depuis

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Morphometry Methods for Ensemble-Based Schizophrenia Classification 903

Chiffre 1: A representative 2D slice of stereotaxic space showing three types of
features used in the classification experiments. The MR intensities are features
extracted by spatial normalization of T1-weighted images. The DEF are features
representing local volume changes extracted by deformation-based morphom-
etry. The GM are features representing gray matter tissue densities extracted by
voxel-based morphometry.

the first one represents SZ and the second represents HC. The class is de-
termined by the output neuron that is excited by the input image. In other
mots, the neuron with a higher value defines the class. The values can
be interpreted as posterior probabilities because the output of these two
neurons is rescaled by the softmax function to always return nonnegative
numbers that total one (Duda, 2001).

The weights are adapted during the learning process using a scaled con-
jugate gradient backpropagation algorithm that is much faster than the tra-
ditional backpropagation algorithm, as shown in Møller (1993) and verified
experimentally in our previous study (Vyškovský et al., 2016). The learning
rate is set to 0.01, and two stopping conditions are given: d'abord, when the
minimum gradient drops below 10−6, et deuxieme, when the total number
of training epochs exceeds 1000. The cost function minimized during the
learning is the cross-entropy (CE) function defined as

CE = −t log (oui) − (1 − t ) log (1 − y),

(2.2)

where y is the output vector and t is the target vector. Équation 2.2 exces-
sively penalizes outputs that deviate extremely from the target. Outputs
that deviate slightly are also penalized, but less so. Recently, cross-entropy
has replaced the more traditional squared error, as it has better convergence

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

904

R.. Vyškovský, D. Schwarz, and T. Kašpárek

propriétés (Golik, Doetsch, & Ney, 2013). Other parameters (par exemple., regular-
ization or dropout techniques) are not optimized due to the high computa-
tional complexity.

Support vector machines serve here as a reference classifier. The config-
uration includes the maximum number of iterations, which was increased
from the default 15,000 à 100,000 to ensure convergence of each SVM in-
position; linear kernel; constraint C = 1; and the sequential minimal opti-
mization algorithm for training. The optimization of the C parameter could
potentially affect the results, but this was not considered for the same rea-
son given in the previous paragraph.

2.4 Classification Framework of Random Subspace Ensemble Neural
Networks. The goals of this study include understanding (1) how the num-
ber of classifiers in an ensemble, size of a feature pool (FP), and length of
feature input vector improve classification performance measures—overall
accuracy (OA), sensitivity (SEN), and specificity (SPE); (2) which morphom-
etry method, VBM or DBM, better suits the proposed classification scheme;
et (3) if the combination of both morphometry methods (VBM and DBM)
improves the classification success rate. Despite the differing nature of these
morphometry methods, they seem to be complementary, and the combi-
nation of them could yield more variable information, making better con-
ditions for finding complex discriminative information for adaptation of
ensemble-based classifiers.

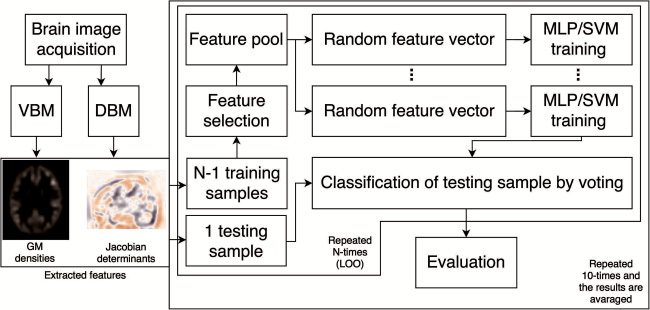
The experimental design is shown in Figure 2. The first part of the ex-
periment involved random subspace ensembles combined with ANNs and
SVM trained with the GM features extracted using the VBM pipeline. De-
tails and results of this task were reported in Vyškovský et al. (2016). Ici,
we employed the DBM pipeline to extract the DEF features and obtain infor-
mation different from the GM features. The next logical step was to employ
both morphometry methods concurrently. This combination allowed us to
extract information from both morphometry methods and thus to feed the
classifiers with more variable features to create a decision boundary.

Feature selection and model adaptation followed brain image prepro-
cessing using morphometry methods. These two steps were included in a
validation loop of leave-one-out cross-validation (LOO-CV). Ici, one sub-
ject serves as a testing sample, and the others are used for training. Ce
process is repeated N times. The performance of the classifiers is then mea-
sured on the test set. This validation method is widely used in neuroimag-
ing; cependant, it is recommended that a more robust validation approach
should be used, involving images acquired from different medical centers
and devices with the same parameter settings (Nieuwenhuis et al., 2012).

The feature selection step chooses only the features with high discrimina-
tion power and is determined by a selected discrimination criterion—here,
a simple two-sample t-test is used. This univariate method basically reveals
the voxels in which the two groups significantly differ. We do not draw a

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Morphometry Methods for Ensemble-Based Schizophrenia Classification 905

Chiffre 2: Classification scheme showing the experimental design implemented
in this study. After the acquisition, the images are preprocessed using both VBM
and DBM to extract GM densities and Jacobian determinants. Features are fur-
ther selected from the training sample using a two-sample t-test, and a feature
pool is created. Several feature vectors are chosen to train the classifiers. Le
testing subject is then classified by voting and the results evaluated. The in-
ner frame comprises the process validated using leave-one-out cross-validation,
and the outer frame indicates a process that is repeated 10 times. The results
gained are averaged.

line between significant and insignificant features, but we sort the features
in ascending order based on the p-value and use the most significant ones.
This application justifies the use of a parametric test, which is computation-
ally faster than the Mann-Whitney U test. Since the images are smoothed
during the VBM and DBM morphometry pipelines, autocorrelation among
neighboring voxels may appear. Cependant, the ability of single voxels to
discriminate the patients from healthy controls is neither searched for nor
interpreted (unlike, Par exemple, logistic regression model coefficients in
many applications). En outre, simplicity of the classification algorithm is
preferred. The voxels are therefore not checked for autocorrelation.

After feature extraction and selection, a feature pool is prepared and clas-
sifiers are adapted. This is also where the ensemble learning is held. Le
algorithm of these processes has several steps:

1. The feature pool is created from the specified number of the most sig-
nificant features. Dans cette étude, the influence of the size of FP on the
performance measures was explored. The defined sizes were 10,000
et 100,000 voxels. Another way to define a feature pool size could
be to subject all the significant voxels selected to the two-sample
t-test applying FDR correction. This approach is not feasible here as
it yields different numbers of voxels in each fold of cross-validation.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

906

R.. Vyškovský, D. Schwarz, and T. Kašpárek

The numbers of significant voxels (level of significance = 0.05) in our
data set are min = 194, max = 10,320, median = 1537.5 for VBM and
min = 0, max = 86, median = 0 for DBM. Donc, a sufficient num-
ber of input features for classifiers cannot be guaranteed.

2. This FP played the role of a bag from which a feature vector (FV) était
randomly chosen. Since the length of an FV directly affects the re-
sults, the three options of this parameter were defined and explored:
100, 1000, et 10,000.

3. The feature vector of each training subject and the corresponding la-
bel of the group were applied in the adaptation of the classification al-
gorithms. This particular vector was designed to train both MLP and
SVM to ensure the comparativeness of the results. After the adap-
tation phase, the testing subject was classified, and its predicted la-
bel was stored. Due to the random initialization of weights in MLP,
this adaptation was performed 11 times, and the predicted class was
based on voting. Ainsi, this step also included ensemble learning in
which the variability was gained by random weight initialization.
4. Mesures 2 et 3 were repeated 31 times, and thus many predictions
based on randomly chosen feature vectors from FP were gained and
could be used to vote on the final class for the testing subject. Le
number of voting classifiers (31) proved sufficient to demonstrate the
overall trend toward greater accuracy when ensembles of classifiers
were used to vote for the final class.

During these four steps, the results of single classifiers trained on dif-
ferent features were gained. In the next step, these results were used for
voting. Since 31 single classifications were computed, any odd number of
these results between 1 et 31 could be used for voting. Aussi, any combi-
nation could vote. Donc, in order to generate smooth trend curves, tous
the trained classifiers were used for evaluation. Par exemple, there is only
one ensemble of size 31, but there are 4495 ensembles containing three clas-
sifiers. All possible combinations, but not more than 10,000 (this limitation
was added to save computational time), were used to compute the perfor-
mance measures, and the outcomes were averaged. En outre, the ex-
periment was performed 10 times because the feature vectors were chosen
randomly from the FP and the results were averaged.

3 Results

In this letter, we experimented with VBM and DBM morphometry methods,
individually and in combination, adding other parameters, such as the size
of the feature pool, the length of the feature vector, and the type of classifier.
We studied the influence of these parameters on performance measures.
The results are presented here.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Morphometry Methods for Ensemble-Based Schizophrenia Classification 907

The experiment was performed in Matlab R2015b on a computer with 2×
Intel Xeon CPU E5-2640 2.5 GHz and RAM 64 GB. To train one iteration of a
framework, both MLP and SVM included, took around 20 hours (evaluation
not included).

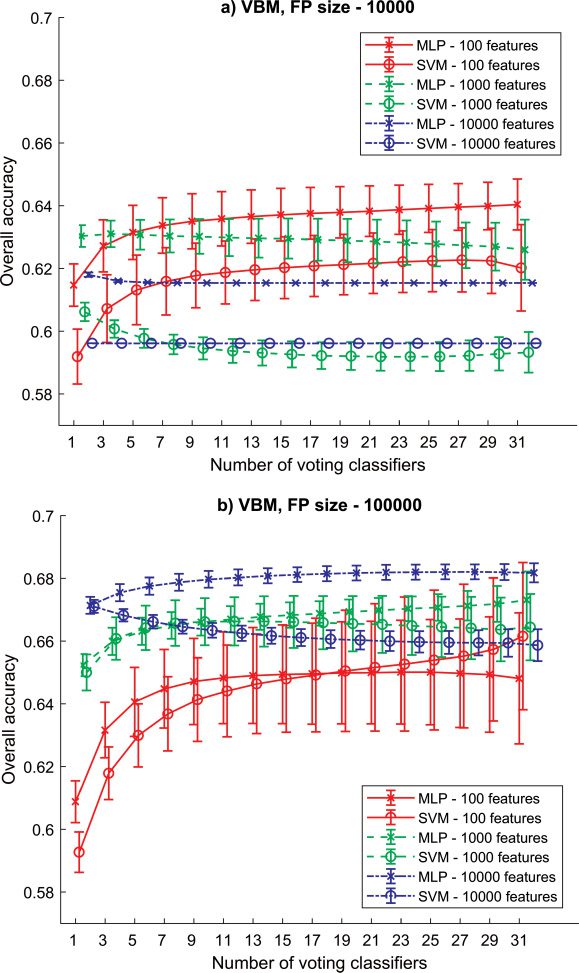
3.1 RSE-MLP/SVM Based on VBM. The first experiment was carried
out on the features extracted from MRI images using VBM. A feature pool
of size 10,000 (see Figure 3a) reached a maximal overall accuracy around
64.04 ± 0.81% (MLP, SEN = 60.00%, SPE = 68.08%). The use of shorter fea-
ture vectors revealed better outcomes compared to the use of the longest
one for training the same classifier except for the SVM with 1000 inputs;
the accuracy fell below SVM with 10,000 inputs. The ANN performed bet-
ter than SVM when compared to models with the same number of input
features. When the FP size was increased to 100,000 (see Figure 3b), the ac-
curacy was increased in all models and reached 68.20 ± 0.24% (MLP, SEN
= 67.09%, SPE = 69.32%). This time, models adapted on longer FV were
better than those adapted on the shortest one. The neural network was a
better model than SVM; cependant, SVM with 100 inputs improved the ac-
curacy when more single models voted in the ensemble. With 19 voters, it
outperformed the MLP. In both FP sizes, the RSE significantly helped with
the classification accuracy only when short vectors were used.

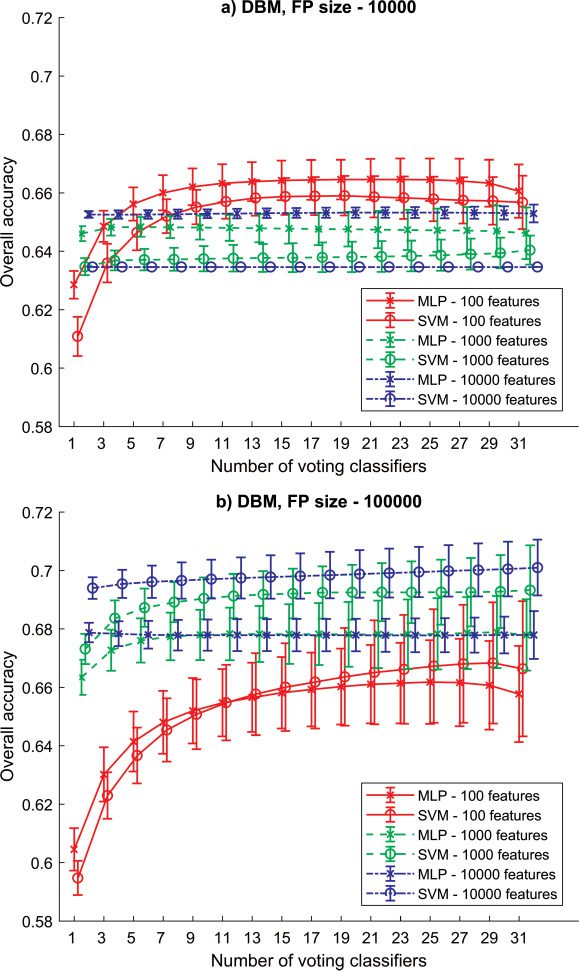
3.2 RSE-MLP/SVM Based on DBM. In the second part of the experi-
ment, we focused on the images preprocessed by DBM (voir la figure 4). Ici,
the parameter settings are comparable to those in Figure 3. Regarding the
FP of size 10,000 (see Figure 4a), the MLP in all cases was the better classi-
fier when the same features were used (maximum. OA = 66.46 ± 0.70%, SEN =
64.88%, SPE = 68.04%). The shorter the feature vector used to train the mod-
le, the higher the accuracy achieved except for the SVM trained on FV of
the middle size. This was better than the SVM trained on the longest FV.
The bigger feature pool (see Figure 4b) helped to increase the OA to 70.10 ±
0.96% (SEN =70.58%, SPE = 69.62%). Cependant, this time, the SVM yielded
better results than MLP. The longer FV helped to gain better results than
the shortest FV. A random subspace ensemble method helped only in the
case of the shorter FV in both Figures 4a and 4b. Nevertheless, this improve-
ment did not outperform models adapted on the longest FV in Figure 4b.
The features extracted using DBM provided better information for the clas-
sification task than VBM because the accuracy increased to 70%.

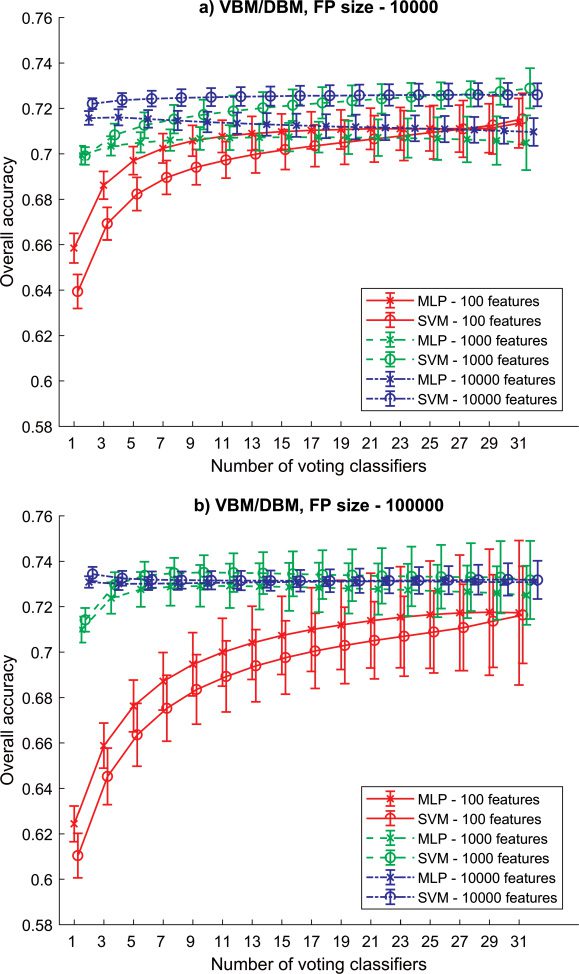
3.3 RSE-MLP/ SVM Based on the Combination of VBM and DBM.
The last experiment took advantage of both morphometry methods. Feature
pools created from VBM and DBM were combined with 50% of the feature
vector selected from FP based on VBM; the other 50% were selected from FP
based on DBM. Ainsi, the sizes of FV were equal to previous experiments,
which makes the models comparable (voir la figure 5). In Figure 5a, the better

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

908

R.. Vyškovský, D. Schwarz, and T. Kašpárek

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 3: Results (mean and standard deviation) for RSE-MLP and RSE-SVM
based on GM extracted using the VBM pipeline. (un) Results obtained based on
small FP with 10,000 features. (b) Results obtained based on big FP with 100,000
features.

Morphometry Methods for Ensemble-Based Schizophrenia Classification 909

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 4: Results (mean and standard deviation) for RSE-MLP and RSE-SVM
based on Jacobian determinants extracted using the DBM pipeline. (un) Results
obtained based on small FP with 10,000 features. (b) Results obtained based on
big FP with 100,000 features.

910

R.. Vyškovský, D. Schwarz, and T. Kašpárek

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 5: Results (mean and standard deviation) for RSE-MLP and RSE-SVM
based on both GM extracted using VBM and Jacobian determinants extracted
using DBM. (un) Results obtained based on small FP with 10,000 features. (b) Re-
sults obtained based on big FP with 100,000 features.

Morphometry Methods for Ensemble-Based Schizophrenia Classification 911

Tableau 1: Statistical Comparison of the Two Morphometry Methods (N1
N2

= 10, FP = 100 000 in All Cases).

= 10,

Number of Classifiers Number

Morphometry
Method

in Ensemble/Type
of Classifier

VBM
DBM
VBM
VBM/DBM
DBM
VBM/DBM

27 MLP
31 SVM
27 MLP
9 SVM
31 SVM
9 SVM

de
Inputs

10,000
10,000
10,000
1000
10,000
1000

Mean (SD)

p-value

68.20 (0.24)
70.10 (0.96)
68.20 (0.24)
73.51 (0.76)
70.10 (0.96)
73.51 (0.76)

9.688e-06

∼0

5.64e-08

classifier is SVM, especially for longer FV. The shortest FV in the MLP is bet-
ter, but the gap between ANN and SVM decreases with the increasing num-
ber of voting models. This time, the classifiers based on longer FV reached
OA of 72.88 ± 0.88% (SVM, SEN = 67.69%, SPE = 78.08%). In Figure 5b, les deux
classifiers revealed similar results. Increasing the number of voters seemed
to help only when the short FV were used, but this did not help to outper-
form classifiers based on longer FV. The combination of VBM and DBM im-
proved the accuracy to 73.12 ± 0.16% (MLP, SEN = 71.14%, SPE = 75.10%)
et 73.51 ± 0.76% (SVM, SEN = 72.97%, SPE = 74.05%).

3.4 Statistical Comparison of the Two Morphometry Methods. Le
impact of the morphometry methods on classification accuracy was sta-
tistically assessed as follows. A number of classifiers were trained on the
features using VBM, DBM, and the combination of both morphometry
méthodes. The classifier that outperformed the other classifiers was chosen.
Following that, a two-sample t-test was run to determine whether the differ-
ence in accuracy is statistically significant at the 0.05 alpha level. The results
presented in Table 1 demonstrate that the DBM feature extraction method is
better than VBM in terms of classification accuracy. What is more, the com-
bination of both morphometry methods showed even better results, dehors-
performing either method alone.

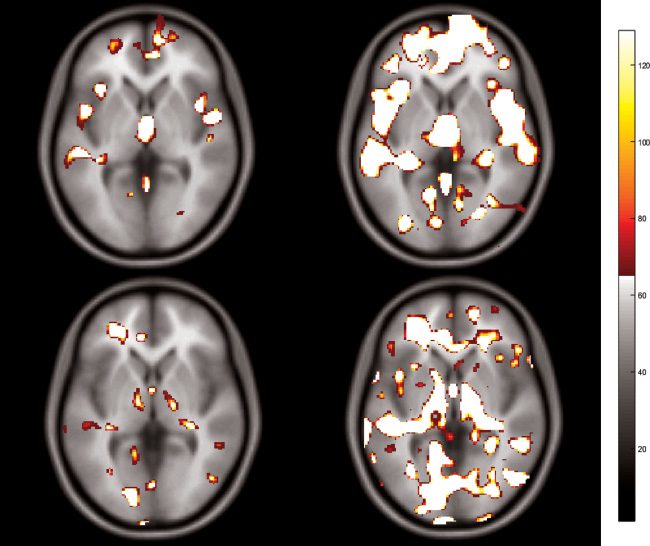
3.5 Brain Structures in the Feature Pool. Dans cette section, the feature
pools were analyzed and visualized in this way. The FPs were computed
for each fold of leave-one-out cross-validation separately, because even one
subject separated during LOO-CV changes the shape of the feature pool.
The frequency of voxel occurrence in a feature pool is visualized in 2D axial
slices in Figure 6, demonstrating which parts of the brain were involved in
training the classifiers.

Regarding VBM, the FPs overlapped mainly with these structures:
frontal lobe (inferior frontal gyrus, medial frontal gyrus, superior frontal

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

912

R.. Vyškovský, D. Schwarz, and T. Kašpárek

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 6: The first row represents the feature pool selected with VBM: feature
pool size 10,000 voxels (gauche) et 100,000 voxels (droite). The second row repre-
sents the feature pool selected with DBM: feature pool size 10,000 voxels (gauche)
et 100,000 voxels (droite).

gyrus, middle frontal gyrus, and precentral gyrus), temporal lobe (supe-
rior temporal gyrus, and middle temporal gyrus), limbic lobe (cingulate
gyrus), occipital lobe, and parietal lobe (mainly in 100,000 FP). In the case
of DBM, the FPs overlapped with the following structures: frontal lobe, oc-
cipital lobe (cuneus, lingual gyrus, and middle Occipital Gyrus), temporal
lobe (mainly in 100,000 FP), parietal lobe (mainly in 100,000 FP), cerebellum
anterior lobe, culmen, limbic lobe (anterior cingulate), pons, temporal lobe
(mainly in 100,000 FP), and parietal lobe (mainly in 100,000 FP).

As shown in Figure 6, the voxels were selected from multiple structures
using both morphometry methods, even when the 10,000 most significant
voxels were selected. VBM selected voxels from outer parts of the brain,
while DBM did not. The differences identified between the feature extrac-
tion processes of the studied morphometry methods may be attributed to
the fact that, DBM, unlike VBM, takes the whole brain approach and is thus
able to detect abnormalities not only in gray matter but also in all brain

Morphometry Methods for Ensemble-Based Schizophrenia Classification 913

compartments at once. This fact may also contribute to better accuracy
achieved when a combination of both morphometry methods is used to
extract the imaging features.

4 Discussion

This letter extends our previous study (Vyškovský et al., 2016), where RSE-
MLPs were applied in first-episode schizophrenia recognition in brain im-
ages preprocessed by VBM. Ici, two novel contributions are presented:
(1) RSE-MLP and RSE-SVM methods are employed to detect schizophrenia
in MRI data preprocessed using DBM and (2) both VBM and DBM prepro-
cessing methods are combined to provide features for subsequent classifi-
cation. As expected, the resulting classification accuracy was influenced by
all parameters: type of morphometry, size of feature pool, length of feature
vector, and type of classifier.

Classifiers adapted on short feature vectors were similarly successful for
both FP sizes. En outre, they were improved along with increasing en-
semble size, especially when a few voters were added. The bigger size of the
ensembles did not help that much. This was not the case of the classifiers
using longer FV (1000, 10,000) for their adaptation. Their performance was
improved negligibly using RSE-MLP and RSE-SVM. Cependant, they per-
formed much better when they had bigger FP available. These trends may
be explained by the fact that a bigger feature pool provides uncorrelated
features from many different parts of the brain, which may offer variable
discriminative information. The classifiers needed to use more of these vec-
tors to converge because the shorter FV were constituted of fewer voxels,
and they are less likely to hold sufficient information from different parts of
le cerveau. This is consistent with the literature (Liu et al., 2012) classifying
Alzheimer’s disease with faster convergence with longer FV. The multilayer
perceptron seems to be better than SVM when short FV and VBM are used
for adaptation.

Besides the dimension of the feature vector, feature pool, and type of
classifier, the classification accuracy was influenced by methods for feature
extraction. While models created on the basis of VBM reached an overall ac-
curacy of 68.20%, models that took information from DBM reached 70.10%.
Although the difference in accuracy was only around 2%, this suggested
that there was variability in the information provided by these two meth-
ods. When both methods were combined, the accuracy improved to 73.12%
(MLP) et 73.51% (SVM). As expected, the combination of morphometry
methods added features with positive influence on the discrimination of
patients in the first episode of schizophrenia (FES) and HC.

The best results were achieved by MLP (FP = 100,000; length of FV,
10,000; number of MLPs in ensemble, 21); OA = 73.12%; SEN = 71.14%,
SPE = 75.10%, and SVM (FP = 100,000; length of FV, 1000; number of SVMs
in ensemble, 9); OA = 73.51%, SEN = 72.97%, and SPE = 74.05%. Cependant,

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

914

R.. Vyškovský, D. Schwarz, and T. Kašpárek

similar accuracies were achieved using single MLP (OA = 73.09%, SEN =
71.10%, SPE = 75.07%) and single SVM (OA = 73.43%, SEN = 73.86%, SPE
= 73.00%), both with 10,000 input features. Ainsi, the RSE did not help in an
important way. The performance measures reached in this study are consis-
tent with the results reported in (Ashburner et al. (1998), Bleich-Cohen et al.
(2014), and Dluhoš et al. (2014).

A statistical comparison test done on the best-performing ensemble clas-
sifiers trained on the features extracted using two different morphom-
etry methods and their combination revealed that the set of imaging
features obtained using the combination of VBM and DBM yielded a sta-
tistically significant better overall accuracy than the features obtained by
either morphometry method alone. This suggests that either morphome-
try method provides different information that can be used to distinguish
between the schizophrenic patients and healthy controls.

En outre, DBM provides features with higher discrimination capa-
bilities than VBM. The distinction in feature quality stems from the differing
nature of these data extraction techniques. While DBM takes all brain tis-
sue types into account, VBM can extract features only from separated gray
matter, white matter, or cerebrospinal fluid. The findings might have impor-
tant implications for further research employing morphometry methods in
schizophrenia diagnostics.

Compared to other studies mentioned in section 1, our method achieved
similar accuracy to Dluhoš et al. (2014), and Jafri and Calhoun (2006). Quelques
other papers (Bleich-Cohen et al., 2014; Nieuwenhuis et al., 2012; Charp-
entier & Savio, 2010; Yang et al., 2010) achieved better results but suffered
from small sample sizes (20–53 subjects), which can lead to high accuracy
in some parameter settings (Nieuwenhuis et al., 2012; Schnack & Kahn,
2016). Studies based on the same data set as ours reported similar outcomes.
Dluhoš et al. (2017) achieved accuracy between 65% (gray matter densities
as features) et 70% (Jacobian determinants as features), though they im-
proved the accuracy to 76% when weights of SVM models were averaged
from multiple models adapted on data sets obtained from three different
clinical sites. Malheureusement, we did not have a multisite data set available.
Janousova et al. (2016) selected features using penalized linear discriminant
analysis with resampling and obtained classification accuracy around 66%
when adhering to the correct procedure of cross-validation. In a different
étude, Janousova et al. (2015), the achieved accuracy exceeded 80%. Besides
gray matter densities and local deformations, they used MR intensities, et
the features were extracted using intersubject principal component analy-
sis. The results of this study suggest that adding further feature extraction
methods to our framework may improve the outcomes.

Although good classification accuracy was reached, confounding factors
and limitations must be taken into consideration. The possible confounders
include age, sex, long-term antipsychotic treatment, and disease progres-
sion. These were excluded because the patients were age matched, all male,

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Morphometry Methods for Ensemble-Based Schizophrenia Classification 915

and in FES. The first limitation is related to the sample size. Nieuwen-
huis et al. (2012) experimented with bootstrapping of samples and rec-
ommended at least 130 samples to gain robust and stable outcomes. Le
second limitation regarding the sample is that the validation was not done
on the images acquired from different medical centers and devices with the
same parameter settings, which would be considered a more appropriate
validation method (Nieuwenhuis et al., 2012). Troisième, the classifiers used in
the proposed framework depend on several parameters. The performance
of SVM is influenced by C-parameter (Franke, Ziegler, Klöppel, & Gaser,
2010), and MLP’s success depends on the number of neurons, layers, les types
of activation functions, and other training parameters. All of these param-
eters were fixed here because the computational cost to investigate them
would have risen markedly otherwise.

The success of RSE-based classification of FES is dependent on several
crucial steps, including brain preprocessing and feature extraction, size of
the feature pool, length of the feature vector, and type of classifier. Dans ce
étude, VBM and DBM feature extraction methods and their combination
were employed to provide data for learning. As expected, their combination
enabled the classifiers to capture more complex discriminative information
compared to separate variants. Other information, Par exemple, from psy-
chological tests, could further improve the outcomes. In all the presented
experiments, random subspace ensemble-based approaches helped only
when the feature vectors were short. More suitable classifiers among MLP
and SVM were not found, their success depended on other parameters in
the proposed design.

Remerciements

This work was supported by research grant 17-33136A from the Ministry of
Health, Czech Republic.

Les références

Andreasen, N. C. (1995). Symptoms, signes, and diagnosis of schizophrenia. Lancet,

346(8973), 477–481.

Ashburner, J.. (2007). A fast diffeomorphic image registration algorithm. NeuroImage,

38(1), 95–113. https://doi.org/10.1016/j.neuroimage.2007.07.007

Ashburner, J., & Friston, K. J.. (2000). Voxel-based morphometry—the methods. Neu-

roImage, 11(6), 805–821. https://doi.org/10.1006/nimg.2000.0582

Ashburner, J., & Friston, K. J.. (2001). Why voxel-based morphometry should be used.

NeuroImage, 14(6), 1238–1243. https://doi.org/10.1006/nimg.2001.0961

Ashburner, J., & Friston, K. J.. (2005). Unified segmentation. NeuroImage, 26(3), 839–

851. https://doi.org/10.1016/j.neuroimage.2005.02.018

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

916

R.. Vyškovský, D. Schwarz, and T. Kašpárek

Ashburner, J., Hutton, C., Frackowiak, R., Johnsrude, JE., Prix, C., & Friston, K. (1998).
Identifying global anatomical differences: Deformation-based morphometry. Hu-
man Brain Mapping, 6(5–6), 348–357.

Bleich-Cohen, M., Jamshy, S., Sharon, H., Weizman, R., Intrator, N., Poyurovsky,
M., & Hendler, T. (2014). Machine learning fMRI classifier delineates subgroups
of schizophrenia patients. Schizophrenia Research, 160(1–3), 196–200. https://est ce que je
.org/10.1016/j.schres.2014.10.033

Bookstein, F. L. (2001). “Voxel-based morphometry” should not be used with imper-
fectly registered images. NeuroImage, 14(6), 1454–1462. https://doi.org/10.1006
/nimg.2001.0770

Charpentier, J., & Savio A. (2010). Neural classifiers for schizophrenia diagnostic

support on diffusion imaging data. Neural Network World, 20, 935–949.

Davatzikos, C. (2004). Why voxel-based morphometric analysis should be used with
great caution when characterizing group differences. NeuroImage, 23(1), 17–20.
https://doi.org/10.1016/j.neuroimage.2004.05.010

Dluhoš, P., Schwarz, D., Cahn, W., van Haren, N., Kahn, R., Španiel, F., . . . Schnack, H.
(2017). Multi-center machine learning in imaging psychiatry: A meta-model ap-
proach. NeuroImage, 155, 10–24. https://doi.org/10.1016/j.neuroimage.2017.03
.027

Dluhoš, P., Schwarz, D., & Kašpárek, T. (2014). Wavelet features for recognition of
first episode of schizophrenia from MRI brain images. Radioengineering, 23(1),
274–281.

Duda, R.. Ô. (2001). Pattern classification (2nd ed). New York: Wiley.
Franke, K., Ziegler, G., Klöppel, S., & Gaser, C. (2010). Estimating the age of healthy
subjects from T1-weighted MRI scans using kernel methods: Exploring the in-
fluence of various parameters. NeuroImage, 50(3), 883–892. https://est ce que je.org/10
.1016/j.neuroimage.2010.01.005

Gaser, C., Volz, H.-P., Kiebel, S., Riehemann, S., & Sauer, H. (1999). Detecting struc-
tural changes in whole brain based on nonlinear deformations: Application
to schizophrenia research. NeuroImage, 10(2), 107–113. https://doi.org/10.1006
/nimg.1999.0458

Giuliani, N. R., Calhoun, V. D., Pearlson, G. D., Francis, UN., & Buchanan, R.. W. (2005).
Voxel-based morphometry versus region of interest: A comparison of two meth-
ods for analyzing gray matter differences in schizophrenia. Schizophrenia Research,
74(2–3), 135–147. https://doi.org/10.1016/j.schres.2004.08.019

Golik, P., Doetsch, P., & Ney, H. (2013). Cross-entropy vs. squared error training: UN
theoretical and experimental comparison. In Proceedings of the 14th Annual Confer-
ence of the International Speech Communication Association (pp. 1756–1760). Baixas,
France: International Speech Communication Association.

Gong, Q.-Y., Sluming, V., Mayes, UN., Keller, S., Barrick, T., Cezayirli, E., & Roberts, N.
(2005). Voxel-based morphometry and stereology provide convergent evidence of
the importance of medial prefrontal cortex for fluid intelligence in healthy adults.
NeuroImage, 25(4), 1175–1186. https://doi.org/10.1016/j.neuroimage.2004.12.044
Gould, je. C., Shepherd, UN. M., Laurens, K. R., Cairns, M.. J., Carr, V. J., & Vert,
M.. J.. (2014). Multivariate neuroanatomical classification of cognitive subtypes in
schizophrenia: A support vector machine learning approach. NeuroImage. Clini-
cal, 6, 229–236. https://doi.org/10.1016/j.nicl.2014.09.009

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Morphometry Methods for Ensemble-Based Schizophrenia Classification 917

Ho, T. K. (1998). The random subspace method for constructing decision forests.
IEEE Transactions on Pattern Analysis and Machine Intelligence, 20(8), 832–844.
https://doi.org/10.1109/34.709601

Huang, C., Yan, B., Jiang, H., & Wang, D. (2008). Combining voxel-based mor-
phometry with artificial neural network theory in the application research of
diagnosing Alzheimer’s disease. In Proceedings of the International Conference on
BioMedical Engineering and Informatics (vol. 1, pp. 250–254). Piscataway, New Jersey: IEEE.
https://doi.org/10.1109/BMEI.2008.245

Jafri, M.. J., & Calhoun, V. D. (2006). Functional classification of schizophrenia using
feed forward neural networks. In Proceedings of the Annual International Confer-
ence de la IEEE Engineering in Medicine and Biology Society (Supplément, pp. 6631–6634).
Piscataway, New Jersey: IEEE. https://doi.org/10.1109/IEMBS.2006.260906

Janousova, E., Montana, G., Kasparek, T., & Schwarz, D. (2016). Supervised, mul-
tivariate, whole-brain reduction did not help to achieve high classification per-
formance in schizophrenia research. Frontiers in Neuroscience, 10, 392. https://est ce que je
.org/10.3389/fnins.2016.00392

Janousova, E., Schwarz, D., & Kasparek, T. (2015). Combining various types of classi-
fiers and features extracted from magnetic resonance imaging data in schizophre-
nia recognition. Psychiatry Research: Neuroimaging, 232(3), 237–249. https://est ce que je
.org/10.1016/j.pscychresns.2015.03.004

Keller, S. S., Mackay, C. E., Barrick, T. R., Wieshmann, U. C., Howard, M.. UN., &
Roberts, N. (2002). Voxel-based morphometric comparison of hippocampal and
extrahippocampal abnormalities in patients with left and right hippocampal at-
rophy. NeuroImage, 16(1), 23–31. https://doi.org/10.1006/nimg.2001.1072

Lébédev, UN. V., Westman, E., Van Westen, G. J.. P., Kramberger, M.. G., Lundervold,
UN., Aarsland, D., . . . Simmons, UN. (2014). Random Forest ensembles for detection
and prediction of Alzheimer’s disease with a good between-cohort robustness.
NeuroImage: Clinique, 6, 115–125. https://doi.org/10.1016/j.nicl.2014.08.023

Lemm, S., Blankertz, B., Dickhaus, T., & Müller, K.-R. (2011). Introduction to machine
learning for brain imaging. NeuroImage, 56(2), 387–399. https://est ce que je.org/10.1016
/j.neuroimage.2010.11.004

Liu, J., Shang, S., Zheng, K., & Wen, J.-R. (2016). Multi-view ensemble learning for
dementia diagnosis from neuroimaging. Neurocomput., 195, 112–116. https://est ce que je
.org/10.1016/j.neucom.2015.09.119

Liu, M., Zhang, D., & Shen, D. (2012). Ensemble sparse classification of Alzheimer’s
maladie. NeuroImage, 60(2), 1106–1116. https://doi.org/10.1016/j.neuroimage
.2012.01.055

Møller, M.. F. (1993). A scaled conjugate gradient algorithm for fast supervised learn-
ing. Neural Networks, 6(4), 525–533. https://doi.org/10.1016/S0893-6080(05)
80056-5

Nieuwenhuis, M., van Haren, N. E. M., Hulshoff Pol, H. E., Cahn, W., Kahn, R.. S., &
Schnack, H. G. (2012). Classification of schizophrenia patients and healthy con-
trols from structural MRI scans in two large independent samples. NeuroImage,
61(3), 606–612. https://doi.org/10.1016/j.neuroimage.2012.03.079

Perkins, D. O., Gu, H., Boteva, K., & Lieberman, J.. UN. (2005). Relationship between
duration of untreated psychosis and outcome in first-episode schizophrenia: UN
critical review and meta-analysis. American Journal of Psychiatry, 162(10), 1785–
1804. https://doi.org/10.1176/appi.ajp.162.10.1785

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
1
5
8
9
7
2
0
1
5
0
5
1
n
e
c
o
_
un
_
0
1
1
8
0
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

918

R.. Vyškovský, D. Schwarz, and T. Kašpárek

Salvatore, C., Cerasa, UN., Castiglioni, JE., Gallivanone, F., Augimeri, UN., Lopez, M.,
. . . Quattrone, UN. (2014). Machine learning on brain MRI data for differential
diagnosis of Parkinson’s disease and progressive supranuclear palsy. Journal de
Neuroscience Methods, 222, 230–237. https://doi.org/10.1016/j.jneumeth.2013.11.
016

Savio, UN., García-Sebastián, M., Hernández, C., Graña, M., & Villanúa, J.. (2009). Clas-
sification results of artificial neural networks for Alzheimer’s disease detection.
In E. Corchado & H. Yin (Éd.), Intelligent data engineering and automated learning—
IDEAL 2009 (pp. 641–648). Berlin: Springer. http://link.springer.com/chapter
/10.1007/978-3-642-04394-9_78

Schnack, H. G., & Kahn, R.. S. (2016). Detecting neuroimaging biomarkers for
psychiatric disorders: Sample size matters. Neuroimaging and Stimulation, 7.
https://doi.org/10.3389/fpsyt.2016.00050

Schwarz, D., & Kašpárek, T. (2011). Comparison of two methods for automatic brain

morphometry analysis. Radioengineering, 20(4), 996–1001.

Schwarz, D., Kasparek, T., Provaznik, JE., & Jarkovsky, J.. (2007). A deformable reg-
istration method for automated morphometry of MRI brain images in neu-
ropsychiatric research. IEEE Transactions on Medical Imaging, 26(4), 452–461.
https://doi.org/10.1109/TMI.2007.892512

Vyškovský, R., Schwarz, D., Janoušová, E., & Kašpárek, T. (2016). Random subspace
ensemble artificial neural networks for first-episode schizophrenia classification.
In Proceedings of the 2016 Federated Conference on Computer Science and Information
Systems (pp. 317–321). Piscataway, New Jersey: IEEE.

Wright, je. C., McGuire, P.. K., Poline, J.. B., Travere, J.. M., Murray, R.. M., Frith, C. D., . . .
Friston, K. J.. (1995). A voxel-based method for the statistical analysis of gray and
white matter density applied to schizophrenia. NeuroImage, 2(4), 244–252. https:
//doi.org/10.1006/nimg.1995.1032

Lequel, H., Liu, J., Sui, J., Pearlson, G., & Calhoun, V. D. (2010). A hybrid ma-
chine learning method for fusing fMRI and genetic data: Combining both im-
proves classification of schizophrenia. Frontiers in Human Neuroscience, 4, 1–9.
https://doi.org/10.3389/fnhum.2010.00192

Received August 3, 2018; accepted January 4, 2019.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d