Learning Lexical Subspaces in a Distributional Vector Space
Kushal Arora∗
Aishik Chakraborty∗
Jackie C. K. Cheung
School of Computer Science, Université McGill
Qu´ebec AI Instuite (Mila)
{kushal.arora,aishik.chakraborty}@mail.mcgill.ca,
jcheung@cs.mcgill.ca
Abstrait
In this paper, we propose LEXSUB, a novel
approach towards unifying lexical and dis-
tributional semantics. We inject knowledge
about lexical-semantic relations into distribu-
tional word embeddings by defining subspaces
of the distributional vector space in which
a lexical relation should hold. Our frame-
work can handle symmetric attract and repel
relations (par exemple., synonymy and antonymy,
respectivement), as well as asymmetric relations
(par exemple., hypernymy and meronomy). In a suite of
intrinsic benchmarks, we show that our model
outperforms previous approaches on related-
ness tasks and on hypernymy classification and
detection, while being competitive on word
similarity tasks. It also outperforms previous
systems on extrinsic classification tasks that
benefit from exploiting lexical relational cues.
We perform a series of analyses to understand
the behaviors of our model.1
1 Introduction
Pre-trained word embeddings are the bedrock of
modern natural language processing architectures.
This success of pre-trained word embeddings
is attributed to their ability to embody the
distributional hypothesis (Harris, 1954; Firth,
1957), which states that ‘‘the words that are used
in the same contexts tend to purport similar
meanings’’ (Harris, 1954).
The biggest strength of the embedding methods—
their ability to cluster distributionally related
words—is also their biggest weakness. Ce
contextual clustering of words brings together
words that might be used in a similar context in the
∗Equal contribution.
1C ode
a va i l a bl e
aishikchakraborty/LexSub.
a t https://github.com/
311
text, but that might not necessarily be semantically
similar, ou pire, might even be antonyms (Lin
et coll., 2003).
Several techniques have been proposed in the
literature to modify word vectors to incorporate
lexical-semantic relations into the embedding
espace (Yu and Dredze, 2014; Xu et al., 2014; Frit
and Duh, 2014; Faruqui et al., 2015; Mrkˇsi´c et al.,
2016; Mrkˇsi´c et al., 2017; Glavaˇs and Vuli´c,
2018). The common theme of these approaches is
that they modify the original distributional vector
space using auxiliary lexical constraints to endow
the vector space with a sense of lexical relations.
Cependant, a potential limitation of this approach is
that the alteration of the original distributional
space may cause a loss of the distributional
information that made these vectors so useful
in the first place, leading to degraded performance
when used in the downstream tasks.
This problem could be further exacerbated when
multiple relations are incorporated, especially as
different lexical-semantic relations have different
mathematical properties. Par exemple, synonymy
is a symmetric relation, whereas hypernymy and
meronymy are asymmetric relations. It would be
difficult to control the interacting effects that
constraints induced by multiple relations could
have on the distributional space.
The solution that we propose is to enforce a
separation of concerns, in which distributional
information is addressed by a central main vector
espace, whereas each lexical relation is handled by a
separate subspace of the main distributional space.
The interface between these components is then a
projection operation from the main distributional
space into a lexical subspace. Our framework,
LEXSUB, thus formulates the problem of enforcing
lexical constraints as a problem of learning a
Transactions of the Association for Computational Linguistics, vol. 8, pp. 311–329, 2020. https://doi.org/10.1162/tacl a 00316
Action Editor: Katrin Erk. Submission batch: 10/2019; Revision batch: 1/2020; Published 6/2020.
c(cid:13) 2020 Association for Computational Linguistics. Distributed under a CC-BY 4.0 Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
je
un
c
_
un
_
0
0
3
1
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
metric, repel-symmetric, and attract-asymmetric.
We demonstrate that our approach outperforms
or is competitive with previous approaches on
intrinsic evaluations, and outperforms them on a
suite of downstream extrinsic tasks that might
benefit from exploiting lexical relational infor-
mation. Enfin, we design a series of experiments
to better understand the behaviors of our model
and provide evidence that the separation of con-
cerns achieved by LEXSUB is responsible for its
improved performance.
2 Related Work
Several approaches have been proposed towards
unifying the lexical and distributional semantics.
These approaches can broadly be classified into
two categories: 1) post-hoc, et 2) ad-hoc ap-
proaches. Post-hoc approaches finetune pre-trained
embeddings by fitting them with lexical relations.
On the other hand, ad-hoc models add auxiliary
lexical constraints to the distributional similarity
perte. Both post-hoc and ad-hoc approaches rely on
lexical databases such as WordNet (Miller, 1995),
FrameNet (Baker et al., 1998), BabelNet (Navigli
and Ponzetto, 2012), and PPDB (Ganitkevitch
et coll., 2013; Pavlick et al., 2015) for symbolically
encoded lexical relations that are translated into
lexical constraints. These lexical constraints en-
dow the embeddings with lexical-semantic rela-
tional information.
Post-hoc Approaches.
In the post-hoc ap-
proach, pre-trained word vectors such as GloVe
(Pennington et al., 2014), Word2Vec (Mikolov
et coll., 2013), FastText (Bojanowski et al., 2017),
or Paragram (Wieting et al., 2015) are fine-tuned
to endow them with lexical relational information
(Faruqui et al., 2015; Jauhar et al., 2015; Rothe and
Sch¨utze, 2015; Wieting et al., 2015; Mrkˇsi´c et al.,
2016, 2017; Jo, 2018; Jo and Choi, 2018; Vuli´c
and Mrkˇsi´c, 2017; Glavaˇs and Vuli´c, 2018). Dans ce
papier, we primarily discuss LEXSUB as a post-hoc
model. This formulation of LEXSUB is similar to the
other post-hoc approaches mentioned above with
the significant difference that the lexical relations
are enforced in a lexical subspace instead of the
original distributional vector space. Rothe et al.
(2016) explores the idea of learning specialized
subspaces with to reduce the dimensionality
of distributional space such that it maximally
task-specific information at
preserves relevant
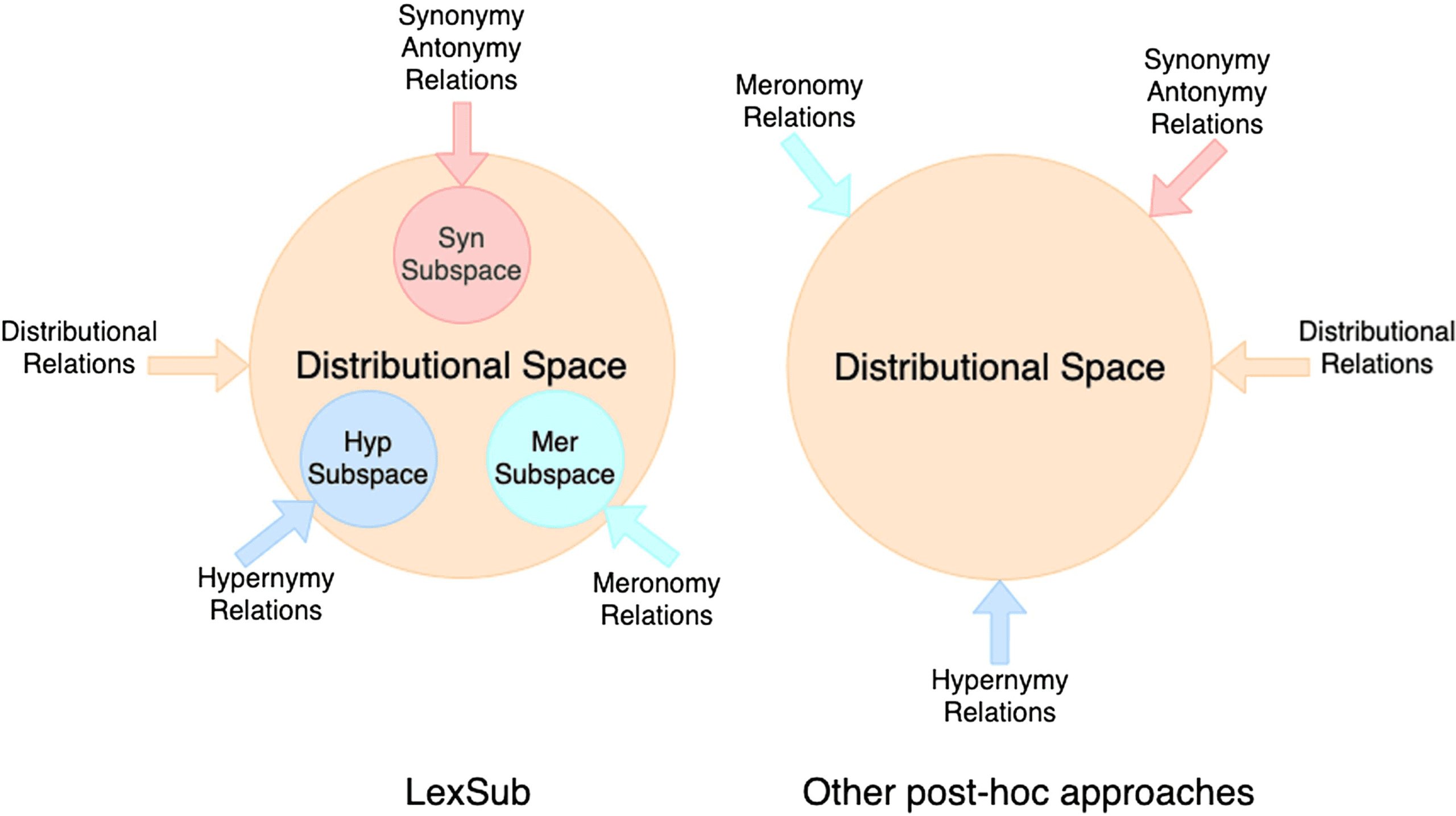
Chiffre 1: A concept diagram contrasting other
post-hoc approaches with our LEXSUB framework.
Our LEXSUB framework enforces the lexical
constraints in lexical relation-specific subspaces,
whereas the other approaches try to learn lexical
relations in the original distributional vector space.
linear subspace for each of the lexical relations
within the distributional vector space. Chiffre 1
shows a conceptual diagram of the relationship
between the distributional space and the lexical
subspaces in LEXSUB.
We show that LEXSUB outperforms previous
methods in a variety of evaluations, particularly
on intrinsic relatedness correlation tasks, et en
extrinsic evaluations in downstream settings. Nous
also show that LEXSUB is competitive with existing
models on intrinsic similarity evaluation tasks.
We run a series of analyses to understand why our
method improves performance in these settings.
Our experimental results suggest that explicitly
separating lexical
into their own
relations
subspaces allows the model to better capture the
structure of each lexical relation without being
polluted by information from the distributional
espace. Inversement, the main distributional vector
space is not polluted by the need to model
lexical relations in the same space, as is the case
for previous models. En outre, the explicit
linear projection that is learned ensures that a
relation-specific subspace exists in the original
distributional vector space, and can thus be
discovered by a downstream model if the extrinsic
task requires knowledge about lexical-semantic
relations.
Cotisations.
En résumé, we propose LEXSUB,
a framework for learning lexical linear subspaces
within the distributional vector space. The pro-
posed framework can model all major kinds of
lexical-semantic relations, namely, attract-sym-
312
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
je
un
c
_
un
_
0
0
3
1
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
the expense of distributional information. Unlike
Rothe et al. (2016), our proposed method tries
to retain the distributional
information in the
embeddings so that
they can be used as a
general-purpose initialization in any NLP pipeline.
Embeddings from Rothe et al. (2016)’s method
can only be used for the task on which they were
trained.
Ad-hoc Approaches. The ad-hoc class of
approaches add auxiliary lexical constraints to
the distributional similarity loss function, usually,
a language modeling objective like CBOW
(Mikolov et al., 2013) ou
recurrent neural
network language model (Mikolov et al., 2010;
Sundermeyer et al., 2012). These constraints can
either be viewed as a prior or as a regularizer to
the distributional objective (Yu and Dredze, 2014;
Xu et al., 2014; Bian et al., 2014; Kiela et al.,
2015un; Fried and Duh, 2014). In other work, le
original language modeling objective is modified
to incorporate lexical constraints (Liu et al., 2015;
Osborne et al., 2016; Bollegala et al., 2016;
Ono et al., 2015; Nguyen et al., 2016, 2017; Tifrea
et coll., 2018). We discuss the ad-hoc formulation
of LEXSUB in Appendix A.
lexical
types of
An alternate axis along which to classify
these approaches is by their ability to model
different types of lexical relations. These types can
be enumerated as symmetric-attract (synonymy),
symmetric-repel (antonymy), and asymmetric-
attract (hypernymy, meronymy). Most approaches
mentioned above can handle symmetric-attract
type relations, but only a few of them can
model other
relations. Pour
(2015) can exclusively
example, Ono et al.
(2018) et
model antonymy, Tifrea et al.
Nguyen et al. (2017) can only model hypernymy
whereas Mrkˇsi´c et al. (2016); Mrkˇsi´c et al.
(2017) can model synonymy and antonymy,
and Vuli´c and Mrkˇsi´c (2017) can handle
synonymy, antonymy, and hypernymy relations.
Our proposed framework can model all types
of lexical relations, namely, symmetric-attract,
symmetric-repel, and asymmetric-attract, and uses
of all four major lexical relations found in lexical
resources like WordNet, namely, synonymy,
antonymy, hypernymy, and meronymy, and could
flexibly include more relations. To our knowledge,
we are the first to use meronymy lexical relations.
Other Approaches. Several approaches do not
fall into either of the categories mentioned above.
A subset of these approaches attempts to learn
lexical relations, especially hypernymy, directly
by embedding a lexical database, Par exemple,
Poincar´e Embeddings (Nickel and Kiela, 2017)
or Order-Embeddings (Vendrov et al., 2015).
Another set of approaches, like DIH (Chang et al.,
2018) or Word2Gauss (Vilnis and McCallum,
2014; Athiwaratkun and Wilson, 2017) attempt
to learn the hypernymy relation directly from the
corpus without relying on any lexical database.
The third set of approaches attempt to learn a scor-
ing function over a sparse bag of words (SBOW)
features. These approaches are summarized by
Shwartz et al. (2017).
3 Model
3.1 Task Definition
que
similarity as well as
Given a vocabulary set V {x1, x2, x3, . . . .xn},
our objective is to create a set of vectors
{x1, x2, x3, . . . , xn} ∈ Rd
respect both
lexical-
distributional
semantic relations. We refer to these vectors as
the main vector space embeddings. Let R be the
relation set corresponding to a lexical-semantic
relation r. The elements of this relation set are
ordered pairs of words (xi, xj) ∈ V × V ; que
est, si (xi, xj) ∈ R, then xi and xj are related by
the lexical relation r. For symmetric relations
like synonymy and antonymy, (xi, xj) ∈ R
implique (xj, xi) ∈ R. De la même manière, for asymmetric
relations like hypernymy and meronymy, xj is
related to xi by relation r if (xi, xj) ∈ R and
(xj, xi) /∈ R.
Our model has two components. The first
component helps the model
learn the lexical
subspaces within the distributional vector space.
These subspaces are learned using a loss function
Llex defined in Section 3.2.4. The second com-
ponent helps the model learn the distributional
vector space. The training of this vector space
is aided by a loss function Ldist defined in
Section 3.3. The total loss that we optimize is
therefore defined as: Ltotal = Ldist +Llex.
Distance Function.
In the subsequent subsec-
tion, we will build lexical subspace distance
functions using the cosine distance function,
d(X, oui) = 1 − x · y/(kxkkyk) where x and y are
embeddings for the word x and y, respectivement.
313
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
je
un
c
_
un
_
0
0
3
1
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3.2 Learning Lexical Subspaces in the
Distributional Space
Dans cette section, we discuss three types of abstract
lexical losses—attract symmetric, attract asym-
metric, and repel symmetric—that are commonly
found in lexical databases like WordNet. We then
discuss a negative sampling loss that prevents the
model from finding trivial solutions to the lexical
objective.
3.2.1 Abstract Lexical Relation Loss
Let xi and xj be a pair of words related by a lexical
relation r. We project their embeddings xi, xj ∈
Rd to an h-dimensional lexical subspace (h < d)
using a learned relation-specific projection matrix
W proj
with dimensions h × d. The distance
r
between any two words xi and xj in the lexical
subspace is defined as a distance between their
projected embeddings. We define this lexico-
relational subspace specific distance function
dproj
r
as
dproj
r
(xi, xj) = d(W proj
r
xi, W proj
r
xj)
(1)
The lexical subspaces can be categorized into
three types: attract symmetric, attract asymmetric,
and repel symmetric. In an attract symmetric
subspace, the objective is to minimize the distance
between the lexically related word pair xi and xj.
The corresponding loss function is:
Latt-sym
r
=
1
|R| X
xi,xj ∈R
dproj
r
(xi, xj)
(2)
Similarly, for repel symmetric lexical relations
such as antonymy, the goal is to maximize the
distance (up to a margin γ) between the two
projected embeddings. We define a repel loss for
r, Lrep
r
, as:
Lrep
r =
1
|R| X
xi,xj ∈R
max
(cid:0)
0, γ − dproj
r
(xi, xj)
(cid:1)
(3)
In the case of attract asymmetric relations,
we encode the asymmetry of the relationship
between xi and xj by defining an asymmetric
distance function dasym
in terms of this affine
transformation of embeddings of xi and xj as:
r
dasym
r
(xi, xj) = dproj
r
(W asym
r
xi + basym
r
, xj)
(4)
314
r
(an h × d matrix) and basym
where W asym
(an
h-dimensional vector) are the parameters of the
affine function.
r
The attract asymmetric loss function is then
defined in terms of dasym
r
as:
Latt-asym
r
=
1
|R| X
xi,xj ∈R
dasym
r
(xi, xj) +
max (cid:16)0, γ − dasym
r
(xj, xi)(cid:17)
(5)
r
The first term of the Latt-asym
brings xi’s
projected embedding closer to the embedding of
xj. The second term avoids the trivial solution
of parameterized affine function collapsing to a
identity function. This is achieved by maximizing
the distance between xi and the affine projection
of xj.
3.2.2 Negative Sampling
We supplement our lexical loss functions with a
negative sampling loss. This helps avoid the trivial
solutions such as all words embeddings collapsing
to a single point for attract relations and words
being maximally distant in the repel subspace.
We generate negative samples by uniformly
sampling n words from the vocabulary V . For
attract subspaces (both attract symmetric and
attract asymmetric), we ensure that negatively
sampled words in the subspace are at a minimum
distance δmin
for repel
subspaces, we ensure that negative samples are
at a distance of at-most δmax
from xi. The attract
and repel negative sampling losses are:
from xi. Similarly,
r
r
Lattr-neg
r
Lrep-neg
r
n
X
l=1
n
X
l=1
=
X
xi,xj
=
X
xi,xj
max(cid:16)0, δmin
r − dproj
r
(xi, xl)(cid:17)
max(cid:16)0, dproj
r
(xi, xl) − δmax
r
(cid:17)
where xl indicates the negative sample drawn
from a uniform distribution over vocabulary.
3.2.3 Relation-Specific Losses
Synonymy Relations. As
synonymy is an
attract symmetric relation, we use Lattr-sym
as our
syn
lexical loss and Lattr-neg
as our negative sampling
loss, with the negative sampling loss weighted by
a negative sampling ratio hyperparameter µ.
syn
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Lsyn = Lattr-sym
syn
+ µLattr-neg
syn
(6)
Antonymy Relations. Antonymy relation is the
mirror image of the synonymy relation; hence,
we use the same subspace for both the relations;
ant = W proj
(i.e., W proj
syn ). As antonymy is a repel
lexical relation, we use Lrep
syn as our lexical loss
and Lrep-neg
syn
as our negative loss.
Lexical Relation
Synonyms
Antonyms
Hypernyms/Hyponyms
Meronyms/Holonyms
Num Pairs
239,100
12,236
20,887
31,181
Table 1: Statistics for lexical relation pairs ex-
tracted from WordNet.
Lant = Lrep
syn + µLrep-neg
syn
(7)
4 Training Setup
Hypernymy Relations. Hypernymy
an
attract asymmetric relation, hence, we use
Lattr-asym
as
negative sampling loss.
as the lexical loss and Lattr-neg
hyp
hyp
is
Lhyp = Lattr-asym
hyp
+ µLattr-neg
hyp
(8)
Meronymy Relations. Meronymy is also an
attract-asymmetric relation. Therefore, in a similar
manner, the lexical loss will be Lattr-asym
and
mer
negative sampling loss will be Lattr-neg
:
mer
Lmer = Lattr-asym
mer
+ µLattr-neg
mer
(9)
3.2.4 Total Lexical Subspace Loss
Based on the individual lexical losses defined
above, the total lexical subspace loss defined as
follows:
Llex = νsynLsyn+νantLant+νhypLhyp+νmerLmer
(10)
where νsyn, νant, νhyp, νmer ∈ [0, 1] are lexical
relation ratio hyperparameters weighing the im-
portance of each of the lexical relation.
3.3 Preserving the Distributional Space
1, x′
2, . . . , x′
from pre-
In the post-hoc setting, we start
trained embeddings X = [x1, x2, . . . , xn]T ∈
Rn×d to learn retrofitted embeddings X′ =
n]T ∈ Rn×d. The Ldist component
[x′
aims to minimize the change in L2 distance
between the word embeddings in order to preserve
the distributional information in the pre-trained
embeddings:
Ldist =
1
n
kX − X ′k2
2
(11)
3.4 Overall Loss Function
The overall loss of LEXSUB is Ltotal = Ldist+Llex.
315
In this section, we describe the datasets and models
that we use in our experiments. The output of our
model is the main vector space embedding that is
endowed with the specialized lexical subspaces.
All our evaluations are done on the main vector
space embeddings unless stated otherwise.
4.1 Training Dataset
Our experiments were conducted using GloVe
embeddings (Pennington et al., 2014) of 300-
dimension trained on 6 billion tokens from the
Wikipedia 2014 and Gigaword 5 corpus. The vo-
cabulary size for GloVe embeddings is 400,000.
4.2 Lexical Resource
We use WordNet (Miller, 1995) as the lexical
database for all experiments. We consider all four
types of lexical relations: synonymy, antonymy,
hypernymy, and meronymy. Only those relation
triples where both words occur in the vocabulary
are considered. We consider both instance and
concept hypernyms for hypernymy relations, and
for meronomy relations, part, substance, as well as
member meronyms were included as constraints.
Table 1 shows the relation-wise split used in the
experiments.
4.3 Models and Hyperparameters
We learn 300-dimensional embeddings during
training. We use Adagrad (Duchi et al., 2011)
as our optimizer with learning rate 0.5. We train
the models for 100 epochs. For the lexical losses,
we take n = 10, µ = 10, γ = 2, δsyn
max = 1.5,
δsyn
min = 1, δhyp
min = 0.5, δmer
min = 1.0, and νsyn = 0.01,
νhyp = 0.01, νmer = 0.001.
We rely on the validation sets corresponding
to our extrinsic tasks (Section 6.2) for choosing
these hyperparameter values. We ran a grid search
on the hyperparameter space and selected the final
set of hyperparameters by first ranking validation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
results for each task in descending order, then
calculating the mean rank across the tasks. We
selected the hyperparameters that achieved the
best (i.e., lowest) mean rank.
5 Baselines
Vanilla. The Vanilla baselines refer
to the
original GloVe word embeddings without any
lexical constraints.
Retrofitting. Retrofitting (Faruqui et al., 2015)
uses similarity constraints from lexical resources
to pull similar words together. The objective
function that retrofitting optimizes consists of a
reconstruction loss Ldist and a symmetric-attract
loss Lsyn
syn = Ih, and
d = k · k2.
att-sym with d = h, W proj
Counterfitting. Counterfitting (Mrkˇsi´c et al.,
2016) builds up on retrofitting but also support
repel symmetric relations. Their objective func-
tion consists of three parts: Synonym Attract,
Antonym Repel, and a Vector Space Preservation
att-sym, Lsyn
loss, similar to Lsyn
rep-sym, and Ldist,
respectively.
LEAR. LEAR (Vuli´c
and Mrkˇsi´c, 2017)
expands the counterfitting framework by adding
a Lexical Entailment (LE) loss. This LE loss
encodes a hierarchical ordering between con-
cepts (hyponym-hypernym relationships) and can
handle attract asymmetric relations.
We train each of the baseline models using the
lexical resources described in Section 4.2. LEAR,
LEXSUB, and Counterfitting were trained on all
four lexical relations whereas the Retrofitting
was trained only on attract relations, namely,
synonymy, hypernymy, and meronymy. This is
due to Retofitting’s inability to handle repel
type relations. We also report
the results of
our experiments with LEXSUB and the baselines
trained on the lexical resource from LEAR in
Appendix B.
6 Evaluations
6.1 Intrinsic Tasks
WordSim353 dataset (Agirre et al., 2009) to
measure the ability of the embedding’s to retain the
distributional information. We use the SimLex-
999 dataset (Hill et al., 2015) and SimVerb 3500
(Gerz et al., 2016) to evaluate the embedding’s
ability to detect graded synonymy and antonymy
relations. Both the relatedness and similarity tasks
were evaluated in the main vector space for
LEXSUB.
Hypernymy Tasks. Following Roller et al.
(2018), we consider three tasks involving hyper-
nymy: graded hypernymy evaluation, hypernymy
classification, and directionality detection. We use
the hypernymy subspace embeddings for LEXSUB
for these experiments.
For graded hypernymy evaluation, we use
the Hyperlex dataset (Vuli´c et al., 2017) and
report the results on the complete hyperlex dataset.
We measure Spearman’s ρ between the cosine
similarity of embeddings of the word pairs and the
human evaluations.
The hypernymy classification task is an
unsupervised task to classify whether a pair of
words are hypernym/hyponym of each other. We
consider four of the five benchmark datasets
considered in Roller et al. (2018); namely, BLESS
(Baroni and Lenci, 2011), LEDS (Baroni et al.,
2012), EVAL (Santus et al., 2014), and WBLESS
(Weeds et al., 2014). We do not consider the
SHWARTZ dataset (Shwartz et al., 2016), as the
number of OOV was high (38% for LEXSUB,
Retrofitting, and LEAR and 60% for Counter-
fitting for GloVe). The evaluation is done by
ranking the word pairs by cosine similarity and
computing the mean average precision over the
ranked list.
The hypernymy directionality detection task
is designed to detect which of the two terms is the
hypernym of the other; that is, given two words w1
and w2, is w1 the hypernym of w2 or vice versa.
We consider two of the three datasets from Roller
et al., (2018); namely, WBLESS and BIBLESS
(Kiela et al., 2015b). The classification setup is
similar to Roller et al. (2018) and is done using
the open source package provided by the authors.2
6.2 Extrinsic Tasks
Word Similarity Task. We use four popular
to evaluate word
word similarity test
similarity. We use the men3k dataset by (Bruni
et al., 2014) and the relatedness section of the
sets
We evaluate our embeddings on five extrinsic
tasks that could benefit from the lexical relational
2https://github.com/facebookresearch/
hypernymysuite.
316
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
cues. We do so by injecting our embeddings into
recent high-performing models for those tasks.
The tasks and models are:
NER Classification. We use the CoNLL 2003
NER task (Tjong Kim Sang and De Meulder,
2003) for the Named Entity Recognition (NER)
Task. The dataset consists of news stories from
Reuters where the entities have been labeled into
four classes (PER, LOC, ORG, MISC). We use
the model proposed by Peters et al. (2018) for the
NER task.
Sentiment Classification. We use the Bi-
Attentive Classification Network (BTN) by
McCann et al. (2017) to train a sentiment classifier.
We train all models for sentiment classification on
the Stanford Sentiment Treebank (SST) (Socher
et al., 2013). We use a two-class granularity
where we remove the ‘‘neutral’’ class following
McCann et al. (2017) and just use the ‘‘positive’’
and ‘‘negative’’ classes for classification.
Textual Entailment. For
textual entailment
experiments, we use the Decomposable Attention
model by Parikh et al. (2016) for our experiments.
We train and evaluate the models on the
Stanford Natural Language Inference (SNLI)
dataset (Bowman et al., 2015) using the standard
train, test and validation split.
Question Answering. We use the SQUAD1.1
question answering dataset (Rajpurkar et al.,
2016). The dataset contains 100k+ crowd-sourced
question answer pairs. We use the BiDAF model
(Seo et al., 2016) for the question answering task.
We report the accuracy on the development set for
SQuAD.
Paraphrase Detection. For
the paraphrase
detection task, we use the BIMPM model by
Wang et al. (2017) for our experiments. We train
and evaluate the models on the Quora Question
Pairs (QQP) dataset3 using the standard splits.
Method For the above models, we use the
reference implementations of the models provided
by the AllenNLP toolkit (Gardner et al., 2018).
We replace the input layer of these models with
the embeddings we want to evaluate. We use two
different setups for our extrinsic experiments and
report results for both.
3https://www.kaggle.com/c/quora-question-
pairs.
Setup 1:
In our first setup, we standardize
several representational and training decisions
to remove potential confounding effects. This
ensures that performance differences in the
extrinsic tasks are reflective of the quality of
the embeddings under evaluation. We achieve this
by making the following changes to all extrinsic
task models. First, for the Vanilla models, we use
pretrained GloVe embeddings of 300 dimensions,
trained on 6 billion tokens. Similarly, we train
all post-hoc embeddings using the 6 billion token
300-dimensional pretrained GloVe embeddings
and plug these post-hoc embeddings into the
extrinsic task model. Second, we remove character
embeddings from the input layer. Finally, we do
not fine-tune the pretrained embeddings.
Setup 2:
In order to demonstrate that we are
not unfairly penalizing the base models, we
also conduct a second set of experiments where
models for all the extrinsic tasks are trained in
the original settings (i.e., without the changes
mentioned above). In these experiments, we do
not remove character embeddings from any model,
nor do we put any restrictions on fine-tuning of
the pretrained word embeddings. These results for
both the experiments are reported in Table 4.
7 Results
We now report on the results of our comparisons
of LEXSUB to Vanilla embeddings and baselines
trained on the same lexical resource as LEXSUB.
We use the main vector space embeddings
in all our experiments except for hypernymy
experiments, for which we use the hypernymy
space embeddings.
Intrinsic Evaluations. Table 2 shows that our
model outperforms the Vanilla baseline on both
relatedness and similarity tasks, outperforms
all
the other baselines on relatedness, and is
competitive with the other baselines on all the
word similarity tasks. Table 3 demonstrates that
we considerably outperform Vanilla as well as
other baseline post-hoc methods on hypernymy
tasks. Thus, our subspace-based approach can
learn lexical-semantic relations and can perform
as well or better than the approaches that enforce
lexical constraints directly on the distributional
space.
Another important result from Table 2 is the
poor performance of LEAR and Counterfitting
317
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Models
Vanilla
Retrofitting
Counterfitting
LEAR
LEXSUB
Relatedness Tasks
Similarity Tasks
men3k(ρ)
0.7375
0.7437
0.6487
0.6850
0.7493
WS-353R(ρ)
0.4770
0.4701
0.2497
0.3385
0.4956
Simlex(ρ)
0.3705
0.4435
0.4870
0.5998
0.5044
Simverb(ρ)
0.2275
0.2976
0.4119
0.5637
0.3983
Table 2: Similarity and relatedness results for baselines and LEXSUB. The results indicate that LEXSUB
outperforms all the baselines on relatedness tasks and is competitive on the similarity tasks. This
indicates that our model retains the distributional information better than the other models while also
learning synonymy and antonymy relations.
Models
Similarity (ρ) Directionality (Acc)
Classification (Acc)
Vanilla
Retrofitting
Counterfitting
LEAR
LEXSUB
Hyperlex
0.1352
0.1055
0.1128
0.1384
0.2615
wbless
0.5101
0.5145
0.5279
0.5362
0.6040
bibless
0.4894
0.4909
0.4934
0.5024
0.4952
bless
0.1115
0.1232
0.1372
0.1453
0.2072
leds
0.7164
0.7279
0.7246
0.7399
0.8525
eval
0.2404
0.2639
0.2900
0.2852
0.3946
weeds
0.5335
0.5547
0.5734
0.5872
0.7012
Table 3: Hypernymy evaluation results for baselines and LEXSUB. LEXSUB considerably outperforms all
the other methods and the Vanilla on nearly all hypernymy tasks. We attribute this performance to our
novel loss function formulation for asymmetric relations and the separation of concerns imposed by the
LEXSUB.
tasks
on relatedness
like men3k and WS-
353R. We hypothesize that enforcing symmetric-
(Counterfitting) and asymmetric-attract
repel
(Counterfitting and LEAR) constraints directly
on the distributional space leads to distortion
of the distributional vector space, resulting in
poor performance on relatedness tasks. LEXSUB
performs competitively on similarity tasks without
sacrificing its performance in relatedness tasks,
sacrifice
that
unlike contemporary methods
relatedness by optimizing for similarity.
first
setup—that
the results
Extrinsic Evaluations. Table 4 presents the
results of the extrinsic evaluations. Rows 3–7
present
is,
for
experiments without confounds (Setup 1) such as
character embeddings and further fine-tuning of
the input embeddings. The results for the models
trained with the original setting (Setup 2) are
presented in rows 9–14. In the original setting,
the model for QQP, SQuAD, and NER contains
additional trainable character embeddings in the
layer. The original NER model further
input
fine-tunes the input embeddings.
In our first set of experiments, we find that the
LEXSUB model outperforms the baseline methods
on every extrinsic task and Vanilla on every
extrinsic task except SNLI. In the case of our
second experiment, LEXSUB outperforms previous
post-hoc methods in all extrinsic tasks but does
worse than GloVe in NER. We hypothesize
the relatively poor performance of LEXSUB with
respect to GloVe on NER might be due to the
task-specific fine-tuning of the embeddings.
In fact, we find that the baseline approaches,
with a few exceptions, do worse than Vanilla
across the whole suite of extrinsic tasks in both
the settings. Taken together, this indicates that
our subspace-based approach is superior if the
objective is to use these modified embeddings in
downstream tasks.
We hypothesize that these results are indicative
of the fact that the preservation of distributional
information is crucial to the downstream perfor-
mance of the embeddings. The baseline approaches,
318
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Models
NER(F1) SST-2(Acc) SNLI(Acc) SQuAD(EM) QQP(Acc)
Vanilla
Retrofitting
Counterfitting
LEAR
LEXSUB
Vanilla
Retrofitting
Counterfitting
LEAR
LEXSUB
State of the Art
87.88
86.16
80.09
83.20
88.06
89.83
85.56
84.44
85.47
89.76
93.50
Experiments with Setup 1
87.31
88.58
86.77
88.08
88.91
85.00
84.68
84.99
83.74
85.00
Experiments with Setup 2
87.31
88.58
86.77
88.08
88.91
95.60
85.00
84.68
84.99
83.74
85.00
91.60
64.23
64.01
62.86
63.10
64.65
66.62
66.21
66.51
65.71
66.94
88.95
87.08
87.01
87.10
86.06
87.31
88.45
88.54
88.44
87.67
88.69
90.10
Table 4: Extrinsic evaluation results for baselines and LEXSUB. Setup 1 refers to the experiments
without extrinsic model confounds such as character embeddings and further fine-tuning of the input
embeddings. Setup 2 refers to the experiments in the original AllenNLP setting where the model for
QQP, SQuAD, and, NER contains additional trainable character embeddings in the input layer, and the
original NER model further fine-tunes the input embeddings. In both the setups, we see that LEXSUB
outperforms the baselines on most of the extrinsic tasks. We hypothesize the relatively poor performance
of LEXSUB compared to Vanilla on NER might be due to the task-specific fine-tuning of the embeddings.
which learn the lexical-semantic relations in
the
the original distributional space, disrupt
poor
information,
distributional
extrinsic task performance. We expand on this
point in Section 8.3.
leading to
State-of-the-Art Results in Extrinsic Tasks.
We have also added the current state-of-the-
art results for the respective extrinsic tasks in
Table 4 (last row). The current state of the art
for NER is Baevski et al. (2019). The authors
also use the model proposed by Peters et al.
(2018) but initialize the model with contextualized
transformer.
embeddings from a bi-directional
Similarly, the current state of the art for SST-2 and
QQP (ERNIE 2.0; Sun et al., 2019), SNLI (MT-
DNN; Liu et al., 2019), and SQuAD (XLNet; Yang
et al., 2019) are all initialized with contextualized
embeddings from a bidirectional
transformer-
based model trained on a data that is orders of
magnitude larger than the GloVe variant used in
our experiments. The contextualized embeddings,
because of their ability to represent the word in
the context of its usage, are considerably more
powerful than GloVe, hence the models relying
on them are not directly comparable to our model
or the other baselines.
319
8 Analysis
In this section, we perform several analyses
to understand the behaviors of our model and
the baselines better, focusing on the following
questions:
Q1: How well do LEXSUB’s lexical subspaces
capture the specific lexical relations for which
they were optimized, as opposed to the other
relations?
Q2: Can the lexical subspaces and the manifolds
in the main distributional space be exploited by a
downstream neural network model?
Q3: How well do the models preserve relatedness
in the main distributional space?
8.1 LEXSUB Subspace Neighborhoods (Q1)
Table 5 lists the top five neighbors for selected
query words for each of the lexical subspaces of
the LEXSUB, as well as the main vector space. The
distance metric used for computing the neighbors
for main vector space, synonymy, hypernymy,
and meronymy subspaces are d, dproj
, and
dasym
, respectively. We see that most of the closest
r
neighbors in the learned subspace are words that
are in the specified lexical relation with the query
words.
, dasym
r
r
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Neighbors
Syn Sub.
Hyp Sub.
Mer Sub.
Main V.S.
poem
poems, frameworks, artist,
poetry, letters
elegy, sonnet, aria, epic,
ditty
canto, verses, cantos,
rime, prosody
poems, verse, poetry,
verses, prose
automobile
motorcar, auto, car,
automobiles, cars
minivan, suv, coupe,
two-seater, phaeton
gas, highs, throttles,
pod, accelerator
auto, automobiles, car,
cars, automotives
church
churches, churchs, infirmary,
microstates, prelims
duomo, cathedral, abbey,
kirk, jamestown
apsis, chancel, christian,
bema, transept
churches, episcopal, cathedral,
catholic, chapel
Table 5: Neighborhoods for the query words for the main vector space, as well as each of the lexical
subspaces. Words in bold letters indicate that the given word is related to the query word by the
said lexical relation. The distance metric used for computing the neighbors for main vector space,
synonymy, hypernymy, and meronymy subspaces are d, dproj
, respectively.
, and dasym
r
, dasym
r
r
Models
Vanilla
Retrofitting
Counterfitting
LEAR
LEXSUB
Syn Subspace.
Hyp Subspace.
Mer Subspace.
syn
0.1512
0.2639
0.3099
0.4338
0.2108
0.4574
0.0162
0.0125
hyp .
0.0842
0.1999
0.3194
0.3443
0.0794
0.0392
0.4180
0.0102
mer
0.1191
0.1896
0.2641
0.2713
0.1307
0.0977
0.0048
0.4908
Table 6: MAP@100 scores for query words taken
from Hyperlex and Simlex999.
To systematically quantify these results, we
compute the mean average precision (MAP) over
the top 100 neighbors for a list of query words.
We use the words from the Hyperlex (Vuli´c et al.,
2017) and Simlex (Hill et al., 2015) datasets as the
query words for this experiment. For each query
word and for each lexical relation, we obtain a list
of words from WordNet which are related to the
query word through that particular lexical relation.
These words form the gold-standard labels for
computing the average precision for the query
word. Table 6 shows the MAP scores for the top
100 neighborhood words for the baselines, for
LEXSUB, and for its lexical subspaces. The main
vector space subspace does worse than all the
baselines, which is expected because the baselines
learn to fit their lexical relations in the original
distributional space. However, if we look at the
individual lexical subspaces, we can see that the
synonymy, hypernymy, and meronymy subspaces
have the best MAP score for their respective
relation, demonstrating the separation of concerns
property that motivated our approach.
8.2 Lexical Relation Prediction Task (Q2)
One of the motivations behind enforcing explicit
lexical constraints on the distributional space is
to learn lexico-relational manifolds within the
distributional vector space. On any such lexico-
relational manifold, the respective lexical relation
will hold. For example, on a synonymy manifold,
all the synonyms of a word would be clustered
together and the antonyms would be maximally
distant. The deep learning based models then will
be able to exploit these lexico-relational manifolds
to improve generalization on the downstream
tasks. To evaluate this hypothesis, we propose
a simplified classification setup of predicting
the lexical relation between a given word pair.
If a downstream model is able to detect these
manifolds, it should be able to generalize beyond
the word pairs seen in the training set.
Lexical Relation Prediction Dataset. The
lexical relation prediction dataset is composed
of word pairs as input and their lexical relation
as the target. The problem is posed as a
four-way classification problem between the
relations synonymy, antonymy, hypernymy, and
meronomy. The dataset is collected from WordNet
and has a total of 606,160 word pairs and labels
split in 80/20 ratio into training and validation.
The training set contains 192,045 synonyms,
9,733 antonyms, 257,844 hypernyms, and 25,308
meronyms. Similarly, the validation set by relation
split
is 96,022 synonyms, 4,866 antonyms,
128,920 hypernyms, and 12,652 meronyms.
We use the word pairs with lexical relation
labels from the Hyperlex (Vuli´c et al., 2017)
as our test set. We only consider synonymy,
320
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Models
Vanilla
Retrofitting
Counterfitting
LEAR
LEXSUB
Val(F1)
0.5905
0.6546
0.6366
0.6578
0.7962
Test(F1)
0.2936
0.2899
0.3275
0.3211
0.4050
Table 7: Macro-averaged F1 across four lexical
relation classes, namely, synonymy, antonymy,
hypernymy, and meronymy, for lexical relation
prediction task.
antonymy, meronomy, and degree-1 hypernymy
relations from the Hyperlex as these directly map
to our training labels. We remove all the word
pairs that occur in the training set. This leads to
917 examples with 194 synonym, 98 antonym,
384 hypernym, and 241 meronym pairs.4
Lexical Relation Prediction Model. We use a
Siamese Network for the relation classification
task. The input to the model is a one-hot encoded
word pair, which is fed into the embedding
layer. This embedding layer is initialized with
the embedding that is to be evaluated and is not
fine-tuned during training. This is followed by
a 1,500-dimensional affine hidden layer with
a ReLU activation function that
is shared by
both word embeddings. This shared non-linear
layer is expected to learn a mapping from the
distributional vector space to lexico-relational
manifolds within the distributional vector space.
The shared layer is followed by two different
sets of two-dimensional 125 × 4 affine layers,
one for each word. These linear layers are put
in place to capture the various idiosyncrasies of
lexical relations such as asymmetry and attract
and repel nature. Finally, the cosine similarity of
the hidden representation corresponding to two
words is fed into the softmax layer to map the
output to probabilities. The models are trained for
30 epochs using the Adagrad (Duchi et al., 2011)
optimizer with an initial learning rate of 0.01 and
a gradient clipping ratio of 5.0.
Table 7 shows the results of our
lexical
relation prediction experiments. All the post-hoc
the
models except for retrofitting can exploit
Models
Retrofitting
Counterfitting
LEAR
LEXSUB
mean shift
32.12
32.97
32.09
1.13
Table 8: Mean shift comparison between baselines
and LEXSUB models.
lexical relation manifold to classify word pairs
by their lexical relation. The LEXSUB model again
outperforms all the baseline models in the task.
We hypothesize that this is because LEXSUB learns
the lexical relations in a linear subspace which
happens to be the simplest possible manifold.
Hence, it might be easier for downstream models
to exploit it for better generalization.
8.3 Preserving the Distributional Space (Q3)
As previously discussed, one of
the main
motivations of LEXSUB is to separate the learning
of lexical relations into subspaces, so that the
main distributional vector space is not deformed
to as great a degree. We directly measure this
deformation by computing the mean shift in the
learned embedding space. We define the mean
shift as the average L2-distance between the
learned and the Vanilla embeddings. We find
that the mean shift for LEXSUB is about 30 times
lower than the baselines (Table 8). This shows that
LEXSUB better preserves the original distributional
space, which may explain its better performance
in intrinsic relatedness evaluations and extrinsic
evaluations.
9 Conclusion
various
We presented LEXSUB, a novel framework for
learning lexical subspaces in a distributional
vector space. The proposed approach properly
separates
from
the main distributional
space, which leads
to improved downstream task performance,
interpretable learned subspaces, and preservation
of distributional information in the distributional
space.
relations
lexical
4The Lexical Relation Prediction Dataset can be downloaded
from https://github.com/aishikchakraborty/
LexSub.
In future work, we plan to extend our framework
to contextualized embeddings and expand the
framework to support hyperbolic distances, which
321
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Models
Vanilla
ad-hoc LEXSUB
Relatedness Tasks
Similarity Tasks
men3k(ρ) WS-353R(ρ) Simlex(ρ) Simverb(ρ)
0.5488
0.5497
0.3917
0.3943
0.3252
0.3489
0.2870
0.3215
(a) Intrinsic evaluation results for ad-hoc models in word similarity and relatedness tasks.
Models
Similarity (ρ) Directionality (Acc)
Classification (Acc)
Vanilla
adhoc LEXSUB
Hyperlex
0.1354
0.1639
wbless
0.5309
0.5362
bibless
0.5129
0.5220
bless
0.1202
0.1237
leds
0.6987
0.7029
eval
0.2402
0.2456
weeds
0.5473
0.5476
(b) Intrinsic evaluation results for ad-hoc models in hypernymy classification tasks.
Models
Vanilla
ad-hoc LEXSUB
NER(F1) SST(Acc) SNLI(Acc)
85.78
86.00
86.67
86.73
83.99
84.00
SQuAD(EM) QQP(Acc)
68.22
68.50
87.83
88.33
(c) Extrinsic Evaluation results (Setup 1) for ad-hoc models.
Table 9: Intrinsic and extrinsic experiment results for the ad-hoc LEXSUB. The Vanilla model here refers
to language model embeddings trained on Wikitext-103 without the lexical constraints. Ad-hoc LEXSUB
outperforms the Vanilla embeddings on both intrinsic and extrinsic tasks indicating the gains from
post-hoc LEXSUB can be extended to the ad-hoc formulation.
can better model hierarchical
hypernymy.
relations
like
Acknowledgments
We would like to thank the reviewers for their
valuable comments. This work is supported by
funding from Samsung Electronics. The last
author is supported by the Canada CIFAR AI
Chair program. This research was enabled in
part by support provided by Calcul Qu´ebec,5 and
Compute Canada.6 We would also like to thank
Prof. Timothy O’Donnell, Ali Emami, and Jad
Kabbara for their valuable input.
Appendix A: Ad-hoc LEXSUB
In this section, we show how LEXSUB can be
extended to the ad-hoc setting. We achieve this by
substituting the GloVe reconstruction loss from
Section 3.3 with a language modeling objective
that enables us to learn the embedding matrix X′
from scratch.
5https://www.calculquebec.ca.
6https://www.computecanada.ca.
The Ad-hoc Distributional Space. Given a set
of tokens in a corpus C = (w1, w2, . . . , wt), we
minimize the negative log likelihood function:
Ladhoc
dist = −
k
X
i=1
log P (wi|wi−k, · · · , wi−1; θ)
where k is the size of the sequence under con-
sideration, and the conditional probability P is
modeled using a neural language model with θ
parameters which includes the embedding matrix
X′ = [x′
1, · · · , x′
n]T .
Ad-hoc LEXSUB Loss. The total loss in case of
ad-hoc LEXSUB is thus: Ltotal = Ladhoc
dist + Llex,
where Llex is defined by equation 10.
Training Dataset. The ad-hoc model is trained
on the Wikitext-103 dataset (Merity et al., 2016).
We preprocess the data by lowercasing all the
tokens in the dataset across the splits, and limiting
the vocabulary to top 100k words.
Ad-Hoc LEXSUB Model. The distributional
component of our ad-hoc model is a two-layer
QRNN-based language model (Bradbury et al.,
2016) with a 300-dimensional embedding layer
and a 1,200-dimensional hidden layer. The batch-
size, BPTT length, and dropout ratio values for
322
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Models
Vanilla
Retrofitting
Counterfitting
LEAR
LEXSUB
Relatedness Tasks
Similarity Tasks
men3k(ρ) WS-353R(ρ) Simlex(ρ) Simverb(ρ)
0.7375
0.7451
0.6034
0.5024
0.7562
0.4770
0.4662
0.2820
0.2300
0.4787
0.3705
0.4561
0.5605
0.7273
0.4838
0.2275
0.2884
0.4260
0.7050
0.3371
(a) Intrinsic evaluation results for for baselines and LEXSUB trained with lexical resource from LEAR.
Models
Similarity (ρ) Directionality (Acc)
Classification (Acc)
Vanilla
Retrofitting
Counterfitting
LEAR
LEXSUB
Hyperlex
0.1352
0.1718
0.3440
0.4346
0.5327
wbless
0.5101
0.5603
0.6196
0.6779
0.8228
bibless
0.4894
0.5469
0.6071
0.6683
0.7252
bless
0.1115
0.1440
0.1851
0.2815
0.5884
leds
0.7164
0.7337
0.7344
0.7413
0.9290
eval
0.2404
0.2648
0.3296
0.3623
0.4359
weeds
0.5335
0.5846
0.6342
0.6926
0.9101
(b) Hypernymy evaluation results for baselines and LEXSUB trained with lexical resource from LEAR.
Models
Vanilla
retrofitting
Counterfitting
LEAR
LEXSUB
NER(F1) SST-2(Acc) SNLI(Acc)
87.31
87.26
87.53
88.08
88.69
87.88
85.88
80.00
80.23
88.02
85.00
84.61
84.93
83.70
85.03
SQuAD(EM) QQP(Acc)
64.23
64.91
63.70
62.96
64.95
87.08
86.98
86.82
86.01
87.65
(c) Extrinsic evaluation results (Setup 1) for baselines and LEXSUB trained with lexical resource from LEAR.
Table 10: Intrinsic and extrinsic experiment results for baselines and LEXSUB trained with lexical
resource from LEAR. We observe a similar trend in the intrinsic and the extrinsic evaluation as to when
the models were trained on lexical resources from Section 4.2. This indicates that the LEXSUB stronger
performance is due to our novel subspace-based formulation rather than its ability to better exploit a
specific lexical resource.
our model are 30, 140, and 0.1 respectively. We
train our model for 10 epochs using the Adam
(Kingma and Ba, 2014) optimizer with an initial
learning rate of 0.001, which is reduced during
training by a factor of 10 in epochs 3, 6, and 7.
We use the same set of hyperparameters that were
used for the post-hoc experiments.
9c
the
presents
Results Table
extrinsic
evaluations of the ad-hoc LEXSUB model. Vanilla,
in this case, refers to embeddings from the
language model trained on Wikitext-103 without
any lexical constraints. We observe that ad-hoc
LEXSUB outperforms Vanilla on all extrinsic tasks,
demonstrating that learning lexical relations in
subspaces is also helpful in the ad-hoc setting.
We observe similar gains for ad-hoc LEXSUB on
intrinsic evaluation in Table 9a and 9b.
Appendix B: Experiments with Lexical
Resource from Vuli´c and Mrkˇsi´c (2017)
In Section 7, we discussed the performance
of LEXSUB and the baselines trained on the
lexical resource presented in Section 4.2. In this
section, we repeat the same set of experiments
but with the LEXSUB and the baselines trained
on lexical resource from LEAR, our strongest
competitor. The objective of these experiments
is to ascertain that
the LEXSUB’s competitive
advantage is due to our novel subspace-based
323
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
formulation rather than its ability to better exploit
the lexical resource discussed in Section 4.2.
The hyperparameters used to train the models is
the same as Section 4.3. For baselines, we use the
hyperparameters reported in the respective papers.
We observe a similar trend in intrinsic and
extrinsic evaluation. LEXSUB outperforms all the
baselines on relatedness (Table 10a), hypernymy
intrinsic tasks (Table 10b), and all the extrinsic
tasks
(Table 10c). We again observe that
LEAR and Counterfitting perform poorly in the
relatedness tasks. We suspect the poor relatedness
score of LEAR and Counterfitting is because these
models distort the original distributional space.
References
Eneko Agirre, Enrique Alfonseca, Keith Hall, Jana
Kravalova, Marius Pas¸ca, and Aitor Soroa.
2009. A study on similarity and relatedness
using distributional and WordNet-based ap-
proaches. In Proceedings of Human Language
Technologies: The 2009 Annual Conference of
the North American Chapter of the Association
for Computational Linguistics on - NAACL ’09,
page 19, Boulder, Colorado. Association for
Computational Linguistics.
Ben Athiwaratkun and Andrew Wilson. 2017.
Multimodal Word Distributions. In Proceed-
ings of the 55th Annual Meeting of the Associa-
tion for Computational Linguistics (Volume 1:
Long Papers), pages 1645–1656.
Alexei Baevski, Sergey Edunov, Yinhan Liu,
Luke Zettlemoyer, and Michael Auli. 2019.
Cloze-driven Pretraining of Self-attention Net-
works. In Proceedings of the 2019 Conference
on Empirical Methods in Natural Language
Processing and the 9th International Joint
Conference on Natural Language Process-
ing (EMNLP-IJCNLP), pages 5360–5369,
Hong Kong, China. Association for Compu-
tational Linguistics.
Collin F. Baker, Charles J. Fillmore, and John B.
Lowe. 1998. The Berkeley FrameNet Project.
In Proceedings of the 17th International Con-
ference on Computational Linguistics - Vol-
ume 1, COLING ’98, pages 86–90, Montreal,
Quebec, Canada. Association for Computa-
tional Linguistics.
Marco Baroni, Raffaella Bernardi, Ngoc-Quynh
Do, and Chung-chieh Shan. 2012. Entailment
above the word level in distributional semantics.
In Proceedings of the 13th Conference of the
European Chapter of
the Association for
Computational Linguistics, pages 23–32.
Marco Baroni and Alessandro Lenci. 2011. How
We BLESSed Distributional Semantic Eval-
the GEMS 2011
uation. In Proceedings of
Workshop on GEometrical Models of Natural
Language Semantics, GEMS ’11, pages 1–10,
Edinburgh, Scotland. Association for Compu-
tational Linguistics.
Jiang Bian, Bin Gao, and Tie-Yan Liu. 2014.
Knowledge-powered Deep Learning for Word
the 2014th
In Proceedings of
Embedding.
European Conference on Machine Learning
and Knowledge Discovery in Databases - Vol-
ume Part I, ECMLPKDD’14, pages 132–148,
Nancy, France. Springer-Verlag.
Piotr Bojanowski, Edouard Grave, Armand Joulin,
and Tomas Mikolov. 2017. Enriching Word
Vectors with Subword Information. Transac-
tions of
the Association for Computational
Linguistics, 5:135–146.
Danushka Bollegala, Alsuhaibani Mohammed,
Takanori Maehara, and Ken-ichi Kawarabayashi.
2016. Joint Word Representation Learning
Using a Corpus and a Semantic Lexicon. In
the Thirtieth AAAI Confer-
Proceedings of
ence on Artificial
Intelligence, AAAI’16,
pages 2690–2696, Phoenix, Arizona. AAAI
Press.
Samuel Bowman, Gabor Angeli, Christopher
Potts, and Christopher D. Manning. 2015. A
large annotated corpus for learning natural lan-
guage inference. In Conference Proceedings -
EMNLP 2015: Conference on Empirical
Methods in Natural Language Processing,
pages 632–642. Association for Computational
Linguistics (ACL).
James Bradbury, Stephen Merity, Caiming Xiong,
and Richard Socher. 2016. Quasi-Recurrent
Neural Networks. arXiv:1611.01576 [cs].
Elia Bruni, Nam Khanh Tran, and Marco Baroni.
2014. Multimodal Distributional Semantics.
Journal of Artificial
Intelligence Research,
49(1):1–47.
324
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Haw-Shiuan Chang, Ziyun Wang, Luke Vilnis,
and Andrew McCallum. 2018. Distributional
Inclusion Vector Embedding for Unsupervised
Hypernymy Detection. In Proceedings of the
2018 Conference of the North American Chap-
the Association for Computational
ter of
Linguistics: Human Language Technologies,
Volume 1 (Long Papers), pages 485–495,
New Orleans, Louisiana. Association for Com-
putational Linguistics.
John Duchi, Elad Hazan, and Yoram Singer. 2011.
Adaptive Subgradient Methods for Online
Learning and Stochastic Optimization. Jour-
nal of Machine Learning Research, 12(Jul):
2121–2159.
Manaal Faruqui, Jesse Dodge, Sujay Kumar
Jauhar, Chris Dyer, Eduard Hovy, and Noah A.
Smith. 2015. Retrofitting Word Vectors to
Semantic Lexicons. In Proceedings of the 2015
Conference of the North American Chapter
of
the Association for Computational Lin-
guistics: Human Language Technologies,
pages 1606–1615.
J. R. Firth. 1957. A synopsis of linguistic theory,
1930–1955. Studies in Linguistic Analysis.
Daniel Fried and Kevin Duh. 2014. Incorporating
Both Distributional and Relational Semantics in
Word Representations. arXiv:1412.4369 [cs].
In Proceedings of
Juri Ganitkevitch, Benjamin Van Durme, and
Chris Callison-Burch. 2013. PPDB: The Para-
the
phrase Database.
the North American
2013 Conference of
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
pages 758–764. Atlanta, Georgia. Association
for Computational Linguistics.
Matt Gardner, Joel Grus, Mark Neumann, Oyvind
Tafjord, Pradeep Dasigi, Nelson Liu, Matthew
Peters, Michael Schmitz, and Luke Zettlemoyer.
2018. AllenNLP: A Deep Semantic Natural
Language Processing Platform. arXiv:1803.
07640 [cs].
Daniela Gerz, Ivan Vuli´c, Felix Hill, Roi Reichart,
and Anna Korhonen. 2016. SimVerb-3500: A
Large-Scale Evaluation Set of Verb Similarity.
In Proceedings of the 2016 Conference on Em-
pirical Methods in Natural Language Processing,
pages 2173–2182, Austin, Texas. Association
for Computational Linguistics.
Goran Glavaˇs and Ivan Vuli´c. 2018. Explicit
Retrofitting of Distributional Word Vectors.
In Proceedings of the 56th Annual Meeting of
the Association for Computational Linguistics
(Volume 1: Long Papers), pages 34–45.
Zellig S. Harris. 1954. Distributional Structure.
WORD, 10(2-3):146–162.
Felix Hill, Roi Reichart, and Anna Korhonen.
2015. SimLex-999: Evaluating Semantic Models
With (Genuine) Similarity Estimation. Compu-
tational Linguistics, 41(4):665–695.
Sujay Kumar Jauhar, Chris Dyer, and Eduard
Hovy. 2015. Ontologically Grounded Multi-
sense Representation Learning for Semantic
Vector Space Models. In Proceedings of the
2015 Conference of the North American Chap-
ter of
the Association for Computational
Linguistics: Human Language Technologies,
pages 683–693, Denver, Colorado. Association
for Computational Linguistics.
Hwiyeol
Jo. 2018. Expansional Retrofitting
for Word Vector Enrichment. arXiv:1808.
07337 [cs].
Hwiyeol Jo and Stanley Jungkyu Choi. 2018.
Extrofitting: Enriching Word Representation
and its Vector Space with Semantic Lexicons.
In Proceedings of The Third Workshop on Rep-
resentation Learning for NLP, pages 24–29,
Melbourne, Australia. Association for Compu-
tational Linguistics.
Douwe Kiela, Felix Hill, and Stephen Clark.
2015a. Specializing Word Embeddings for Sim-
ilarity or Relatedness. In Proceedings of the
2015 Conference on Empirical Methods in Nat-
ural Language Processing, pages 2044–2048,
Lisbon, Portugal. Association for Computa-
tional Linguistics.
Douwe Kiela, Laura Rimell, Ivan Vuli´c, and
Stephen Clark. 2015b. Exploiting Image Gen-
erality for Lexical Entailment Detection. In
Proceedings of the 53rd Annual Meeting of the
Association for Computational Linguistics and
the 7th International Joint Conference on Nat-
ural Language Processing (Volume 2: Short
325
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Papers), pages 119–124, Beijing, China, Asso-
ciation for Computational Linguistics,
Diederik P. Kingma and Jimmy Ba. 2014.
Adam: A Method for Stochastic Optimization.
arXiv:1412.6980 [cs].
Dekang Lin, Shaojun Zhao, Lijuan Qin, and Ming
Zhou. 2003. Identifying Synonyms Among
Distributionally Similar Words. In Proceed-
ings of
the 18th International Joint Con-
ference on Artificial Intelligence, IJCAI’03,
pages 1492–1493. Acapulco, Mexico. Morgan
Kaufmann Publishers Inc..
Quan Liu, Hui Jiang, Si Wei, Zhen-Hua Ling,
and Yu Hu. 2015. Learning Semantic Word
Embeddings based on Ordinal Knowledge
Constraints. In Proceedings of the 53rd Annual
Meeting of the Association for Computational
Linguistics and the 7th International Joint
Conference on Natural Language Processing
(Volume 1: Long Papers), pages 1501–1511.
Beijing, China. Association for Computational
Linguistics.
Xiaodong Liu, Pengcheng He, Weizhu Chen, and
Jianfeng Gao. 2019. Multi-Task Deep Neural
Networks for Natural Language Understanding.
In Proceedings of the 57th Annual Meeting of
the Association for Computational Linguistics,
pages 4487–4496, Florence, Italy. Association
for Computational Linguistics.
Bryan McCann, James Bradbury, Caiming Xiong,
and Richard Socher. 2017. Learned in Trans-
lation: Contextualized Word Vectors. In I. Guyon,
U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus,
S. Vishwanathan, and R. Garnett, editors,
Advances in Neural Information Processing
Systems 30, pages 6294–6305. Curran Asso-
ciates, Inc.
Stephen Merity, Caiming Xiong, James Bradbury,
and Richard Socher. 2016. Pointer Sentinel
Mixture Models. arXiv:1609.07843 [cs].
Tomas Mikolov, Kai Chen, Greg Corrado,
and Jeffrey Dean. 2013. Efficient Estimation
of Word Representations in Vector Space.
arXiv:1301.3781 [cs].
Tomas Mikolov, Martin Karafi´at, Luk´as Burget,
and Sanjeev Khudanpur.
Jan Cernock´y,
2010. Recurrent neural network based lan-
guage model. In Eleventh Annual Conference
of
the International Speech Communication
Association.
George A. Miller. 1995. WordNet: A Lexical
Database for English. Communications of ACM,
38(11):39–41.
Nikola Mrkˇsi´c, Diarmuid ´O S´eaghdha, Blaise
Thomson, Milica Gaˇsi´c, Lina M. Rojas-Barahona,
Pei-Hao Su, David Vandyke, Tsung-Hsien Wen,
and Steve Young. 2016. Counter-fitting Word
In Pro-
Vectors to Linguistic Constraints.
ceedings of the 2016 Conference of the North
American Chapter of
the Association for
Computational Linguistics: Human Language
Technologies, pages 142–148.
Nikola Mrkˇsi´c, Ivan Vuli´c, Diarmuid ´O S´eaghdha,
Ira Leviant, Roi Reichart, Milica Gaˇsi´c, Anna
Korhonen, and Steve Young. 2017. Semantic
Specialization of Distributional Word Vector
Spaces using Monolingual and Cross-Lingual
Constraints. Transactions of the Association for
Computational Linguistics, 5(0):309–324.
Roberto Navigli and Simone Paolo Ponzetto.
2012. BabelNet: The automatic construction,
evaluation and application of a wide-coverage
multilingual semantic network. Artificial Intel-
ligence, 193:217–250.
Kim Anh Nguyen, Maximilian K¨oper, Sabine
Schulte im Walde, and Ngoc Thang Vu.
2017. Hierarchical Embeddings for Hypernymy
Detection and Directionality. In Proceedings of
the 2017 Conference on Empirical Methods in
Natural Language Processing, pages 233–243.
Kim Anh Nguyen, Sabine Schulte im Walde,
and Ngoc Thang Vu. 2016. Integrating Distribu-
tional Lexical Contrast into Word Embeddings
for Antonym-Synonym Distinction. In Pro-
ceedings of the 54th Annual Meeting of the
Association for Computational Linguistics
(Volume 2: Short Papers), pages 454–459,
Berlin, Germany. Association for Computa-
tional Linguistics.
Maximillian Nickel and Douwe Kiela. 2017.
Poincar´e Embeddings for Learning Hierar-
chical Representations. In I. Guyon, U. V.
Luxburg, S. Bengio, H. Wallach, R. Fergus,
326
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Vishwanathan, and R. Garnett, editors,
Advances in Neural Information Processing
Systems 30, pages 6338–6347. Curran Asso-
ciates, Inc.
Masataka Ono, Makoto Miwa, and Yutaka Sasaki.
2015. Word Embedding-based Antonym
Detection using Thesauri and Distributional
Information. In Proceedings of the 2015 Con-
ference of the North American Chapter of the
Association for Computational Linguistics:
Human Language Technologies, pages 984–989,
Denver, Colorado. Association for Computa-
tional Linguistics.
Dominique Osborne, Shashi Narayan, and Shay B.
Cohen. 2016. Encoding Prior Knowledge with
Eigenword Embeddings. Transactions of the
Association for Computational Linguistics,
4:417–430.
Ankur Parikh, Oscar T¨ackstr¨om, Dipanjan Das,
and Jakob Uszkoreit. 2016. A Decomposable
Attention Model for Natural Language Infer-
ence. In Proceedings of the 2016 Conference
on Empirical Methods in Natural Language
Processing, pages 2249–2255, Austin, Texas.
Association for Computational Linguistics.
Ellie Pavlick, Pushpendre Rastogi, Juri Ganitkevitch,
Benjamin Van Durme, and Chris Callison-Burch.
2015. PPDB 2.0: Better paraphrase ranking,
fine-grained entailment relations, word embed-
dings, and style classification. In Proceedings
of the 53rd Annual Meeting of the Association
for Computational Linguistics and the 7th In-
ternational Joint Conference on Natural Lan-
guage Processing (Volume 2: Short Papers),
pages 425–430, Beijing, China. Association for
Computational Linguistics.
Jeffrey Pennington, Richard Socher, and Christopher
Manning. 2014. Glove: Global Vectors for
Word Representation. In Proceedings of the
2014 Conference on Empirical Methods
in Natural Language Processing (EMNLP),
pages 1532–1543, Doha, Qatar. Association for
Computational Linguistics.
Matthew Peters, Mark Neumann, Mohit Iyyer,
Matt Gardner, Christopher Clark, Kenton Lee,
and Luke Zettlemoyer. 2018. Deep Contex-
tualized Word Representations. In Proceedings
of the 2018 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
Volume 1 (Long Papers), pages 2227–2237.
New Orleans, Louisiana. Association for Com-
putational Linguistics.
Pranav Rajpurkar,
Jian Zhang, Konstantin
Lopyrev, and Percy Liang. 2016. SQuAD:
100,000+ Questions for Machine Comprehen-
the 2016
sion of Text. In Proceedings of
Conference on Empirical Methods in Natural
Language Processing, pages 2383–2392.
Stephen Roller, Douwe Kiela, and Maximilian
Nickel. 2018. Hearst Patterns Revisited: Auto-
matic Hypernym Detection from Large Text
Corpora. In Proceedings of the 56th Annual
Meeting of
the Association for Computa-
tional Linguistics (Volume 2: Short Papers),
pages 358–363. Melbourne, Australia. Associ-
ation for Computational Linguistics.
Sascha Rothe, Sebastian Ebert, and Hinrich
Sch¨utze. 2016. Ultradense Word Embeddings
by Orthogonal Transformation. arXiv:1602.
07572 [cs].
Sascha Rothe
and Hinrich Sch¨utze. 2015.
AutoExtend: Extending Word Embeddings to
Embeddings for Synsets and Lexemes.
In
Proceedings of the 53rd Annual Meeting of
the Association for Computational Linguistics
and the 7th International Joint Conference on
Natural Language Processing (Volume 1: Long
Papers), pages
1793–1803, Beijing, China.
Association for Computational Linguistics.
Enrico Santus, Alessandro Lenci, Qin Lu, and
Sabine Schulte im Walde. 2014. Chasing
Hypernyms in Vector Spaces with Entropy.
In Proceedings of
the 14th Conference of
the European Chapter of the Association for
Computational Linguistics, Volume 2: Short
Papers, pages 38–42, Gothenburg, Sweden.
Association for Computational Linguistics.
Minjoon Seo, Aniruddha Kembhavi, Ali Farhadi,
and Hannaneh Hajishirzi. 2016. Bidirectional
Attention Flow for Machine Comprehension.
arXiv:1611.01603 [cs].
Vered Shwartz, Yoav Goldberg, and Ido Dagan.
2016. Improving Hypernymy Detection with
327
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
an Integrated Path-based and Distributional
Method. In Proceedings of the 54th Annual
Meeting of the Association for Computational
Linguistics
Long Papers),
pages 2389–2398.
(Volume
1:
Vered Shwartz, Enrico Santus, and Dominik
Schlechtweg. 2017. Hypernyms under Siege:
Linguistically-motivated Artillery for Hyper-
nymy Detection. In Proceedings of the 15th
Conference of
the European Chapter of
the Association for Computational Linguis-
tics: Volume 1, Long Papers, pages 65–75.
Valencia, Spain. Association for Computational
Linguistics.
Richard Socher, Alex Perelygin, Jean Wu, Jason
Chuang, Christopher D. Manning, Andrew Ng,
and Christopher Potts. 2013. Recursive Deep
Models for Semantic Compositionality Over a
Sentiment Treebank. In Proceedings of the 2013
Conference on Empirical Methods in Natural
Language Processing, pages 1631–1642.
Yu Sun, Shuohuan Wang, Yukun Li, Shikun Feng,
Hao Tian, Hua Wu, and Haifeng Wang. 2019.
ERNIE 2.0: A Continual Pre-training Frame-
work for Language Understanding. arXiv:1907.
12412 [cs].
Martin Sundermeyer, Ralf Schl¨uter, and Hermann
Ney. 2012. LSTM neural networks for language
modeling. In Thirteenth Annual Conference
of
the International Speech Communication
Association.
Alexandru Tifrea, Gary B´ecigneul, and Octavian-
Eugen Ganea. 2018. Poincar´e GloVe: Hyper-
bolic Word Embeddings. arXiv:1810.06546 [cs].
Erik F. Tjong Kim Sang and Fien De Meulder.
2003. Introduction to the CoNLL-2003 Shared
Task: Language-independent Named Entity Rec-
ognition. In Proceedings of the Seventh Con-
ference on Natural Language Learning at
HLT-NAACL 2003 - Volume 4, CONLL ’03,
pages 142–147, Edmonton, Canada. Associa-
tion for Computational Linguistics.
Ivan Vendrov, Ryan Kiros, Sanja Fidler, and
Raquel Urtasun. 2015. Order-Embeddings of
Images and Language. arXiv:1511.06361 [cs].
328
Luke Vilnis and Andrew McCallum. 2014. Word
Representations via Gaussian Embedding.
arXiv:1412.6623 [cs].
Ivan Vuli´c, Daniela Gerz, Douwe Kiela, Felix Hill,
and Anna Korhonen. 2017. HyperLex: A Large-
Scale Evaluation of Graded Lexical Entailment.
Computational Linguistics, 43(4):781–835.
Ivan Vuli´c and Nikola Mrkˇsi´c. 2017. Specialising
Word Vectors for Lexical Entailment. arXiv:
1710.06371 [cs].
Zhiguo Wang, Wael Hamza, and Radu Florian.
2017. Bilateral Multi-perspective Matching for
Natural Language Sentences. In Proceedings of
the 26th International Joint Conference on Arti-
ficial Intelligence, IJCAI’17, pages 4144–4150,
Melbourne, Australia. AAAI Press.
Julie Weeds, Daoud Clarke, Jeremy Reffin,
David Weir, and Bill Keller. 2014. Learn-
ing to Distinguish Hypernyms and Co-Hyponyms.
In Proceedings of COLING 2014, the 25th
International Conference on Computational
Linguistics: Technical Papers, pages 2249–2259.
John Wieting, Mohit Bansal, Kevin Gimpel,
and Karen Livescu. 2015. From Paraphrase
Database to Compositional Paraphrase Model
and Back. Transactions of the Association for
Computational Linguistics, 3:345–358.
Incorporating Knowledge
Chang Xu, Yalong Bai, Jiang Bian, Bin Gao,
Gang Wang, Xiaoguang Liu, and Tie-Yan
Liu. 2014. RC-NET: A General Framework
into Word
for
Representations. In Proceedings of the 23rd
ACM International Conference on Conference
on Information and Knowledge Management -
CIKM ’14, pages 1219–1228, Shanghai, China.
ACM Press.
Zhilin Yang, Zihang Dai, Yiming Yang, Jaime
Carbonell, Russ R Salakhutdinov, and Quoc V.
Le. 2019. XLNet: Generalized Autoregressive
Pretraining for Language Understanding. In
H. Wallach, H. Larochelle, A. Beygelzimer,
F. d’ Alch´e-Buc, E. Fox, and R. Garnett, editors,
Advances in Neural Information Processing
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Systems 32, pages 5753–5763. Curran Asso-
ciates, Inc.
Mo Yu and Mark Dredze. 2014. Improving Lex-
ical Embeddings with Semantic Knowledge.
In Proceedings of the 52nd Annual Meeting
of the Association for Computational Linguis-
tics (Volume 2: Short Papers), pages 545–550,
Baltimore, Maryland. Association for Compu-
tational Linguistics.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
1
6
1
9
2
3
0
8
9
/
/
t
l
a
c
_
a
_
0
0
3
1
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
329