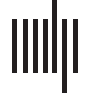FONCTION DE MISE AU POINT:
Linking Experimental and Computational Connectomics
An architectonic type principle integrates
macroscopic cortico-cortical connections
with intrinsic cortical circuits
of the primate brain
Claus C. Hilgetag
1,2, Sarah F. Beul1, Sacha J. van Albada3, and Alexandros Goulas1
1Institute of Computational Neuroscience, University Medical Center Eppendorf, Hamburg University, Allemagne
2Department of Health Sciences, Université de Boston, Boston, MA, Etats-Unis
3Institute of Neuroscience and Medicine (INM-6), Institute for Advanced Simulation (IAS-6), and JARA-Institute of Brain
Structure-Function Relationships (INM-10), Jülich Research Centre, Allemagne
Mots clés: Cortical connectome, Wiring principles, Cortical structural gradients, Cytoarchitecture
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
ABSTRAIT
The connections linking neurons within and between cerebral cortical areas form a
multiscale network for communication. We review recent work relating essential features
of cortico-cortical connections, such as their existence and laminar origins and terminations,
to fundamental structural parameters of cortical areas, such as their distance, similarity in
cytoarchitecture, defined by lamination or neuronal density, and other macroscopic and
microscopic structural features. These analyses demonstrate the presence of an architectonic
type principle. Across species and cortices, the essential features of cortico-cortical
connections vary consistently and strongly with the cytoarchitectonic similarity of cortical
domaines. Par contre, in multivariate analyses such relations were not found consistently for
distance, similarity of cortical thickness, or cellular morphology. Gradients of laminar
cortical differentiation, as reflected in overall neuronal density, also correspond to regional
variations of cellular features, forming a spatially ordered natural axis of concerted
architectonic and connectional changes across the cortical sheet. The robustness of findings
across mammalian brains allows cross-species predictions of the existence and laminar
patterns of projections, including estimates for the human brain that are not yet available
experimentally. The architectonic type principle integrates cortical connectivity and
architecture across scales, with implications for computational explorations of cortical
physiology and developmental mechanisms.
RÉSUMÉ DE L'AUTEUR
The mammalian cortex possesses multiple dimensions of organization, par exemple, le
connectional and the cytoarchitectonic dimension. Are there principles that link the
different dimensions? Here we review an architectonic type principle that links
cytoarchitectonic aspects of the cerebral cortex, such as neuron density or morphology
across the cortical layers, to large-scale interregional cortical connection patterns. Le
reviewed findings highlight the existence of a natural axis of spatially ordered, concerted
changes of multiple architectonic, connectional, and functional features stretching from less
to more differentiated cortical areas. This framework comprises species-general, mais aussi
un accès ouvert
journal
Citation: Hilgetag, C. C., Beul, S. F.,
van Albada, S. J., & Goulas, UN. (2019).
An architectonic type principle
integrates macroscopic cortico-cortical
connections with intrinsic cortical
circuits of the primate brain. Réseau
Neurosciences, 3(4), 905–923.
https://doi.org/10.1162/netn_a_00100
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00100
Reçu: 13 Décembre 2018
Accepté: 7 Juin 2019
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Claus C. Hilgetag
c.hilgetag@uke.de
Éditeur de manipulation:
Jochen Triesch
droits d'auteur: © 2019
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
An Architectonic Type Principle of the Primate Brain
species-specific, principles of the organization of the mammalian, and particularly the
primate, cerebral cortex and highlights potential developmental underpinnings as well as
functional ramifications of such principles.
SEARCHING FOR PRINCIPLES OF CORTICAL CONNECTIVITY
Why Search for Principles of Brain Organization
The wiring of the cerebral cortex appears highly structured, but its precise organization is over-
whelmingly difficult to discern. En particulier, the large number of neural elements and the vast
number of intricate interactions among them obscure potential regularities. A similar level of
complexity exists in other aspects of brain organization, such as the diversity and distribution of
different cell types (Cembrowski & Menon, 2018; Molyneaux, Arlotta, Menezes, & Macklis,
2007), the arrangement of neurotransmitters and receptors (Palomero-Gallagher & Zilles, 2017;
Zilles & Palomero-Gallagher, 2017), and diverse morphological features at the micro- (cellular)
(Elston, 2002, 2003) and macro- (régional) scale. Ainsi, at first sight, it appears almost impos-
sible to integrate the many different dimensions of brain organization. Heureusement, cependant,
some of these aspects are intrinsically related through fundamental organizational principles,
substantially reducing the dimensionality of the problem. Ainsi, underlying principles of cor-
tical wiring and architecture curb the complexity of cortical organization. De plus, the dis-
covery of such integrative principles, linking the different dimensions of cortical organization,
may hint at central mechanisms of brain evolution and development and may facilitate the
understanding of brain function.
Motivated by the wish to integrate different dimensions of brain organization and the hope
to understand mechanisms of development and evolution that produce the complex neural
substrate, several groups including ours have been striving to identify regularities and prin-
ciples in the organization of brain connectivity, particularly the macroscopic interareal con-
nections of the mammalian cerebral cortex, frequently guided by a cross-species mammalian
perspective (Goulas, Majka, Rose, & Hilgetag, 2019; Goulas, Zilles, & Hilgetag, 2018; van den
Heuvel, Bullmore, & Sporns, 2016). In this context they have also investigated the relation of
connection features to other structural aspects of the brain. Note that here we reserve the term
“principle” for regularities that can be supported by mechanistic explanations of their occur-
rence. En particulier, principles of cortical wiring may be explained by mechanisms of brain
development and plasticity, and may allow the integration of cortical structure, connectivité,
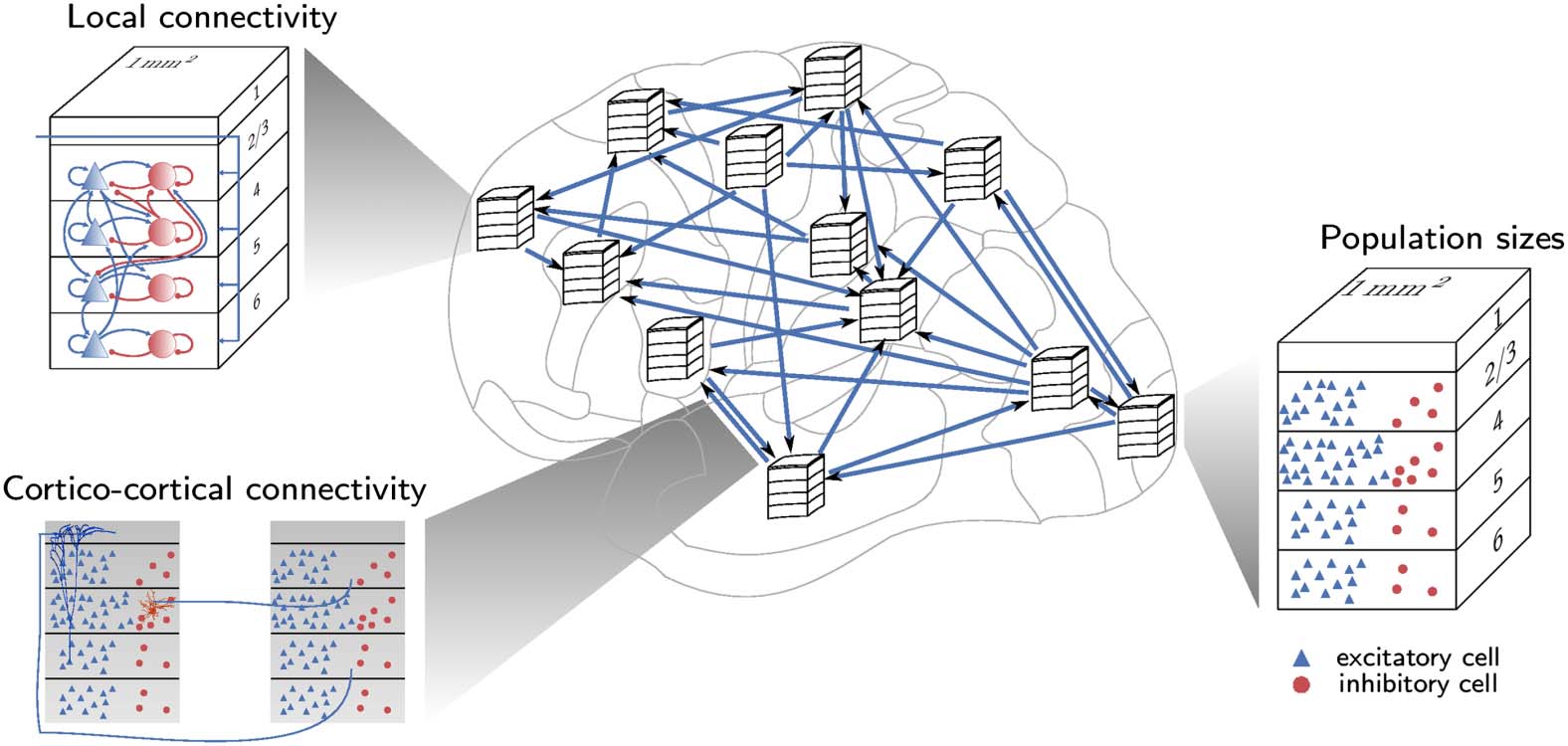
and function (Chiffre 1).
While there are many possible aspects of wiring that could be addressed, a helpful initial
goal is to explain basic features of cortical connections, such as the existence and density of
connections as well as the patterns of laminar origins and terminations of projections. Another
such feature would be the direction of projections (Kale, Zalesky, & Gollo, 2018). Ainsi, dans
the present review, we do not primarily focus on high-order organizational features of cortical
brain networks, tel que, Par exemple, their rich-club topology, which are worthwhile features
to explain in their own right, but may in fact arise from the more basic aspects of brain network
organization (Rubinov, 2016).
Physical Embedding of Connectivity and Minimal Wiring
One well-established and intuitive idea is that brain connectivity is shaped by the physical
embedding of the brain in space (Henderson & Robinson, 2011; Roberts et al., 2016), lequel
Neurosciences en réseau
906
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
Chiffre 1. Principles of cortical wiring integrate regularities of cortical architecture, connectivité,
and function through mechanistic explanations. Connections create functions of brain areas, et
functional interactions among areas, from the structural substrate of the brain, and specifically the
cortical sheet. En particulier, areas are linked through connections which have a laminar composition
that is appropriate for the laminar microenvironment within the respective areas as well as the type of
information exchange between these areas. Ainsi, local cortical architecture, the connection features
of a cortical area, and an area’s functional role within the cortical network are tightly intertwined.
Adapted from Beul and Hilgetag (2019).
constrains the development of neural connections (kaiser & Hilgetag, 2004; kaiser, Hilgetag,
& van Ooyen, 2009). The idea of a strong influence of the spatial layout on the organization
of connections is also related to the engineering-inspired concept of minimal wiring (Ramón y
Cajal, 1899), which suggests that the length and volume of wiring reflects a substantial cost in
brain development and function and should thus be as small as possible (reviewed in Sterling
& Laughlin, 2015). While numerous studies have demonstrated that wiring economy indeed
appears to affect the organization of brain connectivity, as reviewed in Bullmore and Sporns
(2012), it is also clear that minimal wiring is not the only structural or functional constraint on
brain organization (kaiser & Hilgetag, 2006; Roberts et al., 2016; Rubinov, 2016). Plutôt, le
brain is subject to multiple structural and functional evolutionary constraints that may be partly
antagonistic (Chen, Wang, Hilgetag, & Zhou, 2013, 2017), as well as constraints imposed by
the evolutionary history and dynamic stability of the nervous system (Gollo et al., 2018).
Embedding of Cortical Connectivity in Brain Architecture
One alternative perspective on brain organization also has a long tradition in brain research,
particularly in the investigation of the cerebral cortex. Classical neuroanatomists, such as Brod-
mann, the Vogts, or von Economo and Koskinas, used regional variations in architectonic fea-
tures of the brain, such as neuronal density or thickness of cortical layers, in order to parcellate
and characterize brain regions. This work was founded on the central tenet of biology, déjà
recognized by Aristotle1 (350 AD), that differences in biological function should vary with
1 “The thinkers however to whom we are referring attempt to state the nature of the soul only: with regard
to the nature of the body which is to receive the soul they determine nothing in particular. And thus, bien que
every body seems to possess a distinctive form and character, they act as if it were possible for any soul to cloth
itself in any body…” (Peri psych ¯es I, 3).
Neurosciences en réseau
907
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
differences of structure. Ainsi, the architectonic differences of cortical areas were used to de-
lineate structural parcels that may also operate as specialized functional units.
Such anatomical approaches observed that there may be systematic variations, in terms of
spatially defined gradients of brain architecture, as expressed by the differential density of neu-
ral populations across the cortical layers. En particulier, von Economo and Koskinas categorized
areas into so-called cortical types (von Economo, 1927; von Economo & Koskinas, 1925), et
Sanides (1962) linked gradients of cortical types to their evolutionary origins. It was also sug-
gested that such architectonic gradients shape basic features of connectivity (Pandya & Sanides,
1973). En particulier, in her “structural model of connections” (García-Cabezas, Zikopoulos, &
Barbas, 2019), H. Barbas proposed that laminar terminations and origin patterns of prefrontal
cortical areas in the primate brain are directly linked to the relative differences in the lami-
nar differentiation and organization of cortical areas (Barbas, 1986; Barbas & Rempel-Clower,
1997).
Relations of Connectivity to Other Aspects of Brain Structure
Several further factors that may be related to connectivity have been tested. These factors in-
clude covariation of the overall cortical thickness of different regions as a proxy for connectiv-
ville (Il, Chen, & Evans, 2007; Lerch et al., 2006) or MR-based measurements (Seidlitz et al.,
2018) indicating structural similarity. Cependant, the actual relation of these “morphological
networks” to structural or functional connectivity warrants further investigation, as these mea-
sures do not map directly onto each other (Reid et al., 2016), et, donc, “connectivity”
in the different contexts is used with different meanings and potentially reflects different
neurobiological aspects.
Patterns of gene expression may also be directly linked to connectivity (Fulcher & Fornito,
2016) or structural covariation (Romero-Garcia et al., 2018). De plus, several studies have
explored which cellular properties are related to connectivity (Scholtens, Schmidt, de Reus,
& van den Heuvel, 2014; van den Heuvel, Scholtens, Barrett, Hilgetag , & de Reus, 2015). Dans
particular, these studies found a relation of the cell size of layer III pyramidal cells in different
cortical areas with features of connectivity, such as the number of connections that these areas
formulaire. Generally, while there are findings that several architectonic features at the macroscale
(such as cortical thickness) or microscale (cell size, density) may be related to cortico-cortical
connectivité, the systematic relations among these features and connectivity are still unclear.
In any case, the potential linkages among these measures necessitate the joint multivariate
analysis of as many available features as possible.
Based on these potential correlates of connectivity, our goal has been to systematically test
different concepts of cortical connectivity organization. Ainsi, we performed a series of stud-
ies in various cortical regions and across mammalian species, which are summarized in the
following sections. We used a wide range of variables to investigate the embedding of fun-
damental features of connectivity in brain space or brain architecture. En particulier, we used
Euclidean and geodesic distance as well as border distance as measures of spatial separation
and characterized essential features of cortical architecture categorically as well as quantita-
tivement. In this context, we focused on a fundamental characterization of cortical architecture
as reflected in cortical type. Cortical type is a classical, comprehensive characterization of
cortical parcels and comprises the apparent density of cellular populations across the cortical
layers (Hilgetag, Medalla, Beul, & Barbas, 2016). A simple quantitative proxy of cortical type
is neuronal density, measured across all cortical layers (Medalla & Barbas, 2006). It is already
known that the classical measure of neuronal density is the most characteristic measure for
Laminar differentiation:
The extent to which the cellular
density and morphology of cortical
layers differ and allow the layers to
be discriminated.
Cortical type:
An ordinal description and
classification of cortical areas by the
density and appearance of their
cortical layers, ranging from less
clearly differentiated agranular
and dysgranular areas to more
differentiated “eulaminate” areas
(García-Cabezas et al., 2019;
Hilgetag et al., 2016). Dans l'ensemble
neuron density may be employed as
a metric indicator of cortical type
(Hilgetag, Medalla, Beul, & Barbas,
2016; Medalla & Barbas, 2006).
Neurosciences en réseau
908
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
Architectonic type principle:
The systematic relationships of
essential cortical connection features
to the cytoarchitecture of the
mammalian cerebral cortex. These
relationships manifest as variations of
connectional features, tel que
existence or laminar origin and
termination of projections, avec
spatially ordered, concerted
variations of structural features, tel
as neuron density and cellular
morphology, across the cortical
feuille.
identifying cortical areas (Dombrowski, Hilgetag, & Barbas, 2001). En outre, we considered
further morphological and cellular markers of the structural organization of cortical areas, tel
as cortical thickness, and cellular features, such as layer III pyramidal cell soma cross section,
dendritic synapse count, dendritic synapse density, and dendritic tree size.
THE ARCHITECTONIC TYPE PRINCIPLE UNDERLIES THE CONNECTIVITY OF
THE PRIMATE CONNECTOME
In order to assess the relations between essential features of cortical connections and cortical
architecture, we investigated a comprehensive, quantitative compilation of connectivity data (un
connectome) for cortico-cortical connections of the macaque monkey brain (Markov, Ercsey-
Ravasz, et coll., 2014; Markov, Vezoli, et coll., 2014) together with quantitative measures of various
aspects of cortical structure. Present and absent pathways differ in terms of the features of the
potentially connected cortical areas. Areas linked by a connection are more similar in terms
of neuronal density and cortical thickness, and in terms of cellular morphological features
such as spine density and dendritic arborization. De plus, connected areas are also spatially
closer to each other than unconnected areas (Beul & Hilgetag, 2019). Cependant, all of these
structural features are related to each other (cf. Chiffre 4). Donc, multivariate analyses are
required to disentangle the essential structural contributions to connectivity features. Using
such an analysis (multivariate regression), we found that the most fundamental contributions
came from just two factors, neuronal density and distance, where in fact neuronal density was
the cortical dimension that was more consistently related to the existence and laminar origin
of connections (Beul & Hilgetag, 2019).
These insights can be used to predict connections by regression based on the proximity and
architectonic similarity of cortical areas. This approach allows one to assess the individual and
combined contributions of the different structural factors to explaining the existence of corti-
cal connections. The measures showed that architectonic similarity as well as distance were
individually strongly predictive of connections, while similarity of cortical thickness was not.
Cependant, the best prediction performance was achieved by combining architectonic similarity
with distance, leading to high classification accuracy (Beul, Barbas, & Hilgetag, 2017).
Notably, the number of connections of an area (the area’s degree, in graph-theoretical terms)
was found to be inversely correlated to the area’s type or neuronal density, with less dense
(low-type) areas having more connections than dense (high-type) domaines (Beul et al., 2017).
En outre, core or rich-club areas (Ercsey-Ravasz et al., 2013; Harriger, van den Heuvel, &
Sporns, 2012) are of low type; c'est, they possess low neuronal density.
Another essential feature of cortico-cortical projections is the pattern of their origins and
terminations in the cortical layers, which shapes spectral channels of interareal communication
(Bastos et al., 2015) and is a central feature in theories of brain function such as predictive
coding (Bastos et al., 2012). The only factor that was significantly correlated with the patterns
of laminar origins of primate cortico-cortical projections (Markov, Vezoli, et coll., 2014) was the
relative neuronal density of the source versus the target area of the projection (Beul & Hilgetag,
2019). Larger positive differences in neuron density from connection source to connection
target were associated with projections mainly originating from upper cortical layers, alors que
negative neuron density differences were associated with projection origins in deep cortical
layers. None of the other tested parameters showed a systematic correlation with the laminar
projection patterns. Ainsi, the cytoarchitectonic gradients of the cerebral cortex, reflected in
graded neuronal density differences, are the fundamental dimensions across which systematic
Neurosciences en réseau
909
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
shifts in the laminar origin of connections occur (Barbas, 1986; Barbas & Rempel-Clower,
1997; Beul & Hilgetag, 2019; Goulas et al., 2018).
EVIDENCE FOR THE ARCHITECTONIC TYPE PRINCIPLE ACROSS CORTICES
AND SPECIES
Cat Cortical Connectome
Analyses of further datasets widely confirm the findings from the primate connectome. Au pair-
particulier, an analysis of the cat cortico-cortical connectome (Scannell, Blakemore, & Jeune,
1995) yielded very similar results (Beul, Grant, & Hilgetag, 2015). In a multivariate linear dis-
criminant analysis (LDA), border distance as well as architectonic type difference were found
to be associated with the presence or absence of connections, type difference more so than
distance, but the best classification accuracy was achieved by combining the two factors.
As in the primate, the type of an area was inversely associated with the number of connec-
tions formed by the area, with low-type areas, including the core of the cat cortex (Zamora-
López, Zhou, & Kurths, 2010), forming more connections.
Type differences were also significantly associated with the laminar projection patterns of
the cortico-cortical connections, such that projections from a higher type to a lower type area
formed forward pathways, while projections from the lower type to a higher type area formed
feedback projections (Beul et al., 2015; Hilgetag & Grant, 2010), once again highlighting the
cytoarchitectonic gradients of the cortex as a fundamental dimension across which systematic
changes of the laminar origin of connections manifest.
Mouse Cortical Macroconnectome
As in the primate and the cat, the existence of cortico-cortical connections in the mouse was as-
sociated with spatial proximity as well as similarity of cortical type of the potentially connected
domaines (Goulas, Uylings, & Hilgetag, 2017). Fait intéressant, distance appeared to contribute more
strongly to the prediction of ipsilateral projections, while architectonic similarity contributed
more strongly for contralateral projections. Tests of the relationship between cortical types and
the laminar projection patterns in the mouse await the full release of such projection informa-
tion. Néanmoins, the architectonic type principle and its accentuation across the spectrum of
mammalian cortical architecture (Goulas et al., 2018) allow predictions of laminar projection
patterns in presently untested connectomes. Specifically, for rodents, who have architecton-
ically less well-differentiated upper cortical layers than species such as the cat or macaque
monkey, we predict that the laminar origin of connections will be less varied across the corti-
cal sheet, with most projections having a bilaminar origin or originating from the deep cortical
layers (cf. Hilgetag & Grant, 2010).
Findings for Further Connectivity Data
In addition to the studies already described above, there is a wealth of evidence supporting
the architectonic type principle across different cortical regions and across different species.
Originally, Barbas (1986) demonstrated the correlation between the laminar origin patterns
of projections and the cortical type of the projection origin for projections to the prefrontal
cortex in the primate brain. These findings were later extended to terminations of prefrontal
relations (Barbas & Rempel-Clower, 1997) and connections of the prefrontal cortex with
other lobes. De plus, the architectonic type principle also applies to the laminar origins
of projections to the amygdala (Ghashghaei, Hilgetag, & Barbas, 2007), and to the laminar
Neurosciences en réseau
910
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
patterns and existence of cortico-cortical connections with the contralateral hemisphere in the
primate (Barbas, Hilgetag, Saha, Dermon, & Suski, 2005). In a study of the laminar patterns of
parietal-prefrontal projections, Medalla and Barbas (2006) demonstrated that overall neuronal
density can be used as a metric proxy of cortical type, and that this variable also explained
small variations of the laminar patterns. Using this proxy, Schmidt, Bakker, Hilgetag, Diesmann,
and van Albada (2018) predicted laminar origin patterns in macaque vision-related cortex. Le
analysis further showed laminar termination patterns from the CoCoMac database (Bakker,
Wachtler, & Diesmann, 2012) to relate to the laminar origin patterns, consistent with the clas-
sic work of Felleman and Van Essen (1991). Ainsi, differences in neuronal density or architec-
tonic type are also predictive of laminar termination patterns among the vision-related areas
of macaque cortex (Hilgetag et al., 2016).
En outre, the architectonic type principle was observed for laminar origin patterns of
extrastriate projections in the cat visual cortex (Hilgetag & Grant, 2010), as well as for the
existence and absence of connections and laminar origin patterns of the entire cat cortical
connectome (see above). Ainsi, there is widespread evidence across mammalian species and
different types of cortex of the relation of architectonic differentiation with essential features of
macroscopic cortical connectivity, giving rise to the hypothesis that this association may also
be present in the human brain (Goulas et al., 2016; Solari & Stoner, 2011).
These findings may be summarized in cortical wiring diagrams (Chiffre 2) that show the
arrangement of cortical areas and their connections according to cortical types, with the most
highly differentiated areas on the outside and more poorly differentiated areas on the inside of
the diagram.
Surtout, if differences in cortical architecture are to be predictive for connectivity fea-
photos, such as the existence and laminar profiles of projections, there need to exist architectonic
differences between the cortical territories in the first place. Par conséquent, in species such as
rodents that show less pronounced differences between different cortical regions, a less pro-
nounced alignment between cortical architecture and connectivity is expected. Indeed Goulas
et autres. (2019) showed that the cytoarchitectonic similarity of cortical areas relates to the exis-
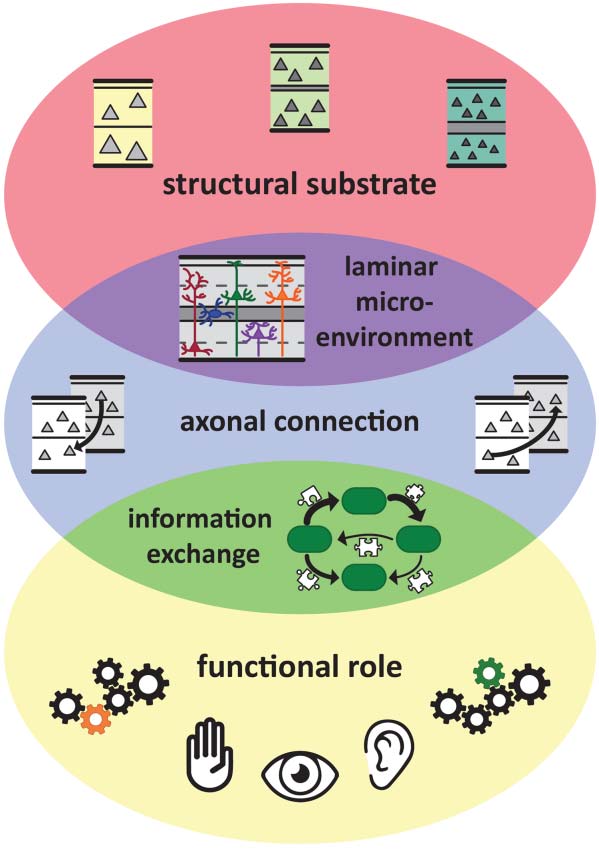
tence of cortical connections in a species-specific manner (Chiffre 3). A species-specific relation
between cytoarchitecture and connectivity is also apparent at the level of the global network
topology of mammalian connectomes. Core areas, c'est, areas tightly interconnected among
themselves as well as with the rest of the brain, differ in terms of cytoarchitecture in relation to
peripheral areas (less interconnected areas) in the cat and macaque monkey, with core areas
also constituting the less differentiated and less neuronally dense areas (Chiffre 2, lower panels).
Cependant, this cytoarchitectonic segregation of core and periphery areas is statistically absent
in the marmoset monkey and completely absent in the mouse. Cytoarchitecture varies system-
atically with other cytological features, such as spine density, and overall myelination. Ainsi,
the synergy between topological segregation (core vs. periphery) and cytological properties
or its absence across species might have species-specific functional implications and denote
differences in the degree of vulnerability to pathology of these cortical areas across species
(see Goulas et al., 2019 for details).
INTEGRATION OF INTRINSIC CORTICAL ARCHITECTURE AND CIRCUITS WITH
MACROSCOPIC CONNECTIONS
Cortical
type indicates the intrinsic cytoarchitectonic organization of cortical areas as
well as patterns of extrinsic, cortico-cortical connections of the areas. De plus, the organi-
zation of area-intrinsic cortical circuits varies with type. En particulier, eulaminate areas, with a
Neurosciences en réseau
911
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2. Architectonic type principle across species. Upper panels: Maps of the cat and macaque cortex, indicating the variation of architec-
tonic differentiation across the cortex of these two species. Differentiation is represented as architectonic type in the cat cortex and as neuron
density in the macaque cortex. Lower panels: Visualization of cortico-cortical connections in the cat and macaque cortex. Cat connections
are shown as collated in Scannell et al. (1995); macaque connections are shown as published by Markov, Ercsey-Ravasz, et autres. (2014). Gray
rings correspond to degree of architectonic differentiation (determined as cortical type for the cat and by neuron density for the macaque) et
cortical areas are placed accordingly, with differentiation increasing from center to periphery. Projections are color coded according to the
difference in architectonic differentiation between connected areas. Node sizes indicate the areas’ degree (c'est, the number of connections
associated with them). For the cat cortex, ordinal projection strength (sparse, intermédiaire, or dense) is coded by increasing projection width
and nodes are grouped and color coded according to anatomical modules as indicated. Hub-module areas, as classified by Zamora-López
et autres. (2010) in the cat and Ercsey-Ravasz et al. (2013) in the macaque, are marked by a white outline or red fill, respectivement. Panels adapted
from Beul et al. (2017, 2015).
Neurosciences en réseau
912
An Architectonic Type Principle of the Primate Brain
well-defined laminar structure and high neuronal density, feature an intricate intrinsic circuitry
that has been described as a canonical microcircuit (Binzegger, Douglas, & Martine, 2009;
Douglas, Martine, & Whitteridge, 1989; Douglas & Martine, 2004; Potjans & Diesmann, 2012),
in which intra- as well as interlaminar excitation are well balanced by populations of excitatory
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 3. Cytoarchitectonic similarity relates to the existence of connections in a species-specific
manière. (UN) Increasing cytoarchitectonic dissimilarity of cortical areas results in a decrease of the
probability of the existence of a connection. This decrease is more pronounced for the cat when
compared with the mouse, as indicated by the larger probability decrease (shaded areas) for the
same increase of cytoarchitectonic dissimilarity. (B) Same relation as in (UN), but for the comparison
of mouse versus macaque monkey. The shaded areas highlight the differences of probability of ex-
istence of a connection with an increase of cytoarchitectonic dissimilarity in the different species.
Note that the illustrated differences of probability of existence can be visually demonstrated in other
intervals, such as 0.4–0.5 or 0.7–0.8. The decrease of the probability of the existence of a connection
is more pronounced for the macaque monkey when compared with the mouse. (C) Same relation
as in (UN), but for the comparison of cat versus macaque monkey. In this comparison, no species-
specific differences of the effect of cytoarchitectonic similarity on the probability of connections
were observed. (D) Brain size and phylogenetic distance of the mouse, macaque monkey, and cat.
Adapted from Goulas et al. (2019).
Neurosciences en réseau
913
An Architectonic Type Principle of the Primate Brain
Externopyramidization:
The rate of change of the ratio of
soma size of supragranular versus
infragranular pyramidal neurons. Ce
rate can be calculated from the
amount of change in soma size ratio
across the cortical sheet.
and inhibitory neurons. Despite the idea that this circuit may form a constant template across
the cortical sheet, there exist variations of this template. Particularly, limbic (agranular and
dysgranular) domaines, which are characterized by the absence or a less marked appearance of a
granular layer and generally show fewer apparent layers and a lower overall neuronal density,
comprise a reduced microcircuit, which particularly appears to possess reduced interlaminar
inhibition (Beul & Hilgetag, 2015).
De plus, the findings described above demonstrate that several of the macroscopic and
intrinsic structural features of cortical areas are linked. Par exemple, higher neuronal density
goes along with smaller cell cross sections and less elaborate morphological dendritic features,
while lower density coincides with larger cell cross sections and more elaborate dendritic mor-
phology (Beul & Hilgetag, 2019). The relations of connection features with the intrinsic con-
nectional and structural organization of areas offer an opportunity for integrating microscopic
and macroscopic architecture and connection features of cortical areas. These features are
summarized in Figure 4. In terms of interareal connectivity, more frequent and denser connec-
tions exist between areas that are similar in cortical type, with similar overall neuron density.
The projections originate in a bilaminar fashion from the upper and deep cortical layers of the
source area, but predominantly in the upper cortical layers of the higher type areas, et ils
terminate across all layers of the target area, but predominantly in the middle layers (granu-
lar layer IV, where it exists) of the lower type areas. Par contre, areas of markedly different
type are either not connected or only sparsely connected. Ici, the projections arise mostly
in a unilaminar fashion from the upper cortical layers of the source area and terminate on the
middle to deep layers of the lower type target area. Such projections are complemented by
projections from the deep layers of the lower type area that terminate in the upper layers of
the higher type area.
Along with the regularities between cortical type or neuronal density and local morpho-
logical features, such as arborization of dendritic trees, these organizational principles of mi-
croscopic connectivity integrate microscopic cortico-cortical connections with the intrinsic
circuits of each cortical area. Such generic rules can be used to inform particularly the de-
velopment of large-scale cortical models. A first example of such a model has already been
constructed (see “Implications of the Architectonic Type Principle for Large-Scale Simulations
of Cortical Dynamics” herein; Schmidt, Bakker, Hilgetag, et coll., 2018; Schmidt, Bakker, Shen,
et coll., 2018).
DEVELOPMENTAL UNDERPINNINGS
Both within and across mammalian species, systematic covariation of multiple features of
cellular morphology has been observed. This includes a higher number and higher density
of spines and more complex dendritic arbors in prefrontal cortices of nonhuman primates
(Bianchi et al., 2013; Elston, 2003, 2007, 2011) and higher total dendritic length, dendritic
spine density, and dendritic spine numbers in the prefrontal cortex of the human brain (Jacobs,
2001). De plus, it has been observed that with increasing soma size, the amount of hete-
rochromatin in the nucleus decreases, while axon length and size of nucleus and nucleolus
increase (García-Cabezas, Barbas, & Zikopoulos, 2018). Such gradual changes in cell morphol-
ogy are aligned with the overall degree of architectonic differentiation across cortical areas. Dans
the human brain, this systematic architectonic variation observed across the cortex has been
directly linked to the timing of development (Barbas & García-Cabezas, 2016). Across species,
differences in spine head size, spine neck length, and spine density have been reported be-
tween mouse and human cortex (Benavides-Piccione, Ballesteros-Yáñez, DeFelipe, & Yuste,
Neurosciences en réseau
914
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Integration of cortical macro- and microarchitecture with cortical connections. Less architectonically differentiated, agranular,
Chiffre 4.
cortical areas (yellow) are characterized by lower neuron density and different morphology of layer III pyramidal cells than more strongly
differentiated, eulaminate, domaines (dark green), with gradual changes across the spectrum. (UN) Macroscopic and microscopic architectonic
features show concerted changes along spatial cortical gradients, indicating a natural axis of cortical organization. En particulier, higher neuron
density tends to correlate with smaller cross sections of the soma and the dendritic tree as well as with lower total spine count and lower peak
spine density. (B) Relations of architectonic types with connection features. Within cortical areas, the ratio of supra- versus infragranular soma
size of projection neurons tends to increase as one transitions from less to more differentiated areas (externopyramidization; Goulas et al.,
2018). Also note that projection neurons are displayed with relatively larger soma cross section than nonprojection neurons in the same cortical
area and layer. Surtout, connections exist predominantly between areas of similar cortical type, and agranular and dysgranular regions
(yellow) tend to form more connections than eulaminate regions (dark green). Hence agranular and dysgranular regions tend to be part of the
network core, while eulaminate regions tend to be part of the network periphery (cf. Chiffre 2). De plus, laminar patterns of projection origins
are related to differences in architectonic differentiation. Connections between areas of distinct differentiation show a skewed unilaminar
projection pattern, with projections originating predominantly in the infragranular or supragranular layers depending on the direction of the
projection (agranular to eulaminate projections and eulaminate to agranular projections, respectivement), while connections between areas of
similar architectonic differentiation show a bilaminar projection origin pattern (connections between middle panels), where the dominating
laminar compartment again depends on the connected areas’ relative differentiation. In sum, there are concurrent changes of macro- et
microstructural cellular and connectional features across the cortical sheet, forming spatially ordered gradients, confirming and expanding
observations from classic neuroanatomy studies (gradation principle of Sanides, 1962). Panels adapted from Beul and Hilgetag (2019).
Neurosciences en réseau
915
An Architectonic Type Principle of the Primate Brain
2002). Plus généralement, a successive increase in dendritic complexity has been reported from
New World monkeys to Old World monkeys to hominids (Bianchi et al., 2013; Elston, 2003,
2007; reviewed in Charvet & Finlay, 2014). These observations are consistent with an overall
increase in neuron density as the length of developmental time schedules and brain size in-
crease (reviewed in Caviness, Bhide, & Nowakowski, 2008, and Charvet & Finlay, 2014). À
summarize, many features of cellular morphology seem to be tightly interlinked, correspond-
ing to the overall degree of architectonic differentiation as well as differences in developmental
timing. Together with this precise orchestration of cell specification during ontogenesis, lequel
results in morphological features of neurons being attuned to the architectonic differentiation
of an area as a whole, also the development of cortical connections appears to be closely cou-
pled to architectonic differentiation. In data from two tract-tracing studies probing the develop-
mental time course of projections within the visual cortex of the macaque monkey (Batardiere
et coll., 2002; Kennedy, Bullier, & Dehay, 1989), it can be observed that, even in the immature
(prenatal or neonate) cortex, the fraction of projection neurons originating in supragranular
layers is correlated with the difference in architectonic differentiation (as indicated by cortical
type or neuronal density) between connected areas, and that immature laminar patterns of
projection origins strongly correlate with eventual adult levels of supragranular contribution
(Beul et al., observation inédite). These observations indicate that the architectonic type
principle successfully predicts the laminar origins of projections even at early stages of brain
development. Donc, basic ontogenetic mechanisms likely underlie its emergence.
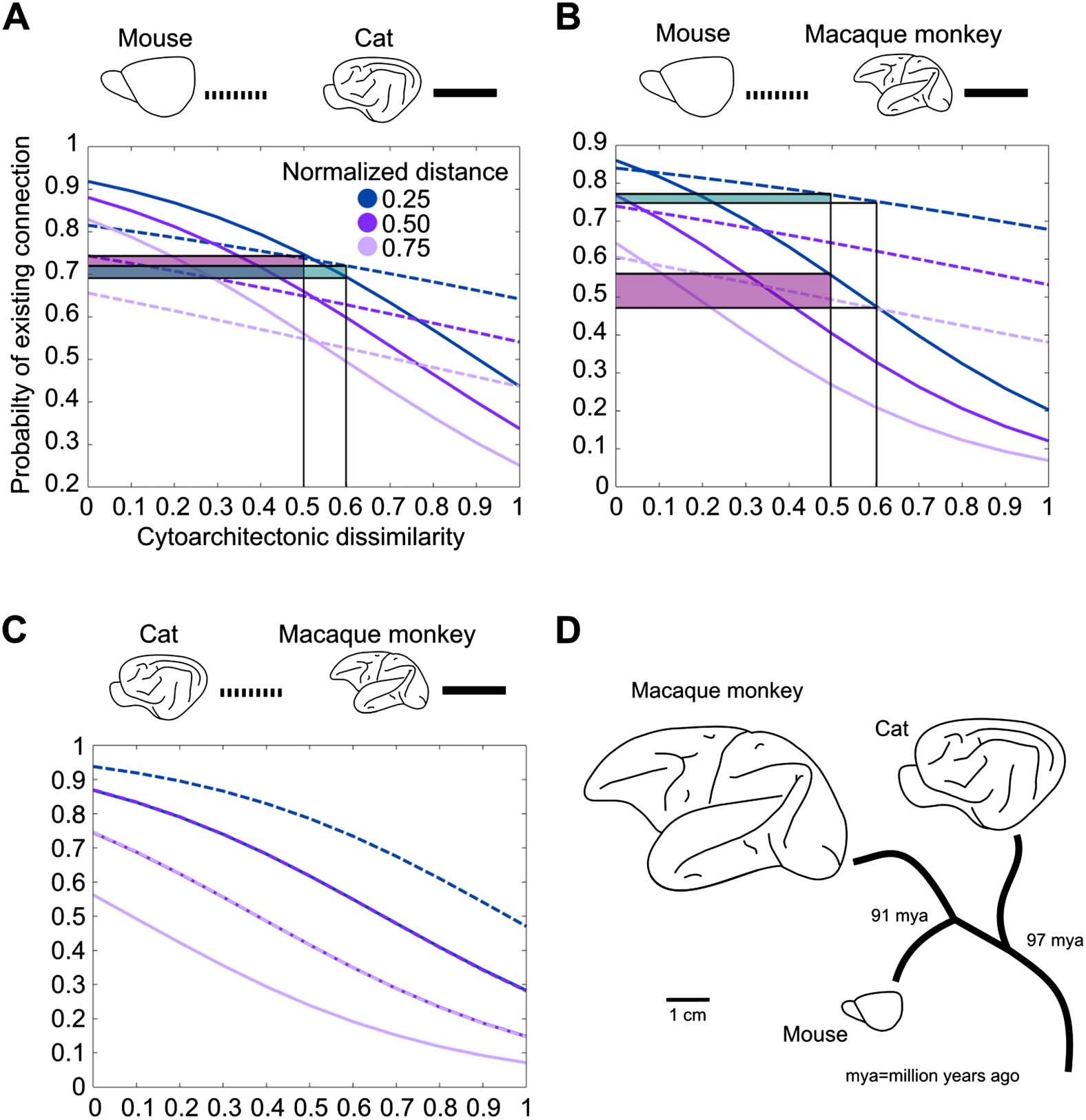
In recent simulation experiments (Beul, Goulas, & Hilgetag, 2018), we explored whether
spatiotemporal interactions in the forming cortical sheet could lead to the empirically observed
connectivity consistent with the architectonic type principle. In an in silico model of cortical
sheet growth and the concurrent formation of cortico-cortical connections, we systematically
varied the spatiotemporal trajectory of neurogenesis and the relation between architectonic dif-
ferentiation and time of origin of neural populations. We showed that, for realistic assumptions
about neurogenesis, successive tissue growth and stochastic connection formation interacted
to produce realistic cortico-cortical connectivity (Chiffre 5). The implication is that precise
targeting of interareal connection terminations is not necessary to produce connectivity that
resembles real brain networks within a cortical hemisphere. Using classifiers trained on such
simulated cortico-cortical connection networks consistent with the architectonic type princi-
ple, we could successfully predict empirically observed connectivity in two species, cat and
macaque. In similar simulations (Goulas, Betzel, & Hilgetag, 2019), we also demonstrated that
interactions of structured spatial gradients and developmental time windows during ontogeny
can explain the widely known features of homophily (Betzel et al., 2016) and distance depen-
dence of connection strength, as well as a host of empirically observed patterns of network
topology of vertebrate and invertebrate nervous systems. In sum, we demonstrated a possible
mechanism of how relative architectonic differentiation and central features of connectivity
become linked during development through spatiotemporal interactions (Beul et al., 2018),
which supports previously stated hypotheses about the mechanistic underpinnings of the ar-
chitectonic type principle (Barbas, 1986; Barbas, 2015; Hilgetag et al., 2016).
IMPLICATIONS OF THE ARCHITECTONIC TYPE PRINCIPLE FOR LARGE-SCALE
SIMULATIONS OF CORTICAL DYNAMICS
In addition to revealing wiring principles of the primate cerebral cortex, the exposed regu-
larities of cortical structure can be employed to construct large-scale computational models
of the cerebral cortex that are a unique tool for gaining novel insights into cortical dynamics
and function (Chiffre 6). En particulier, these regularities, including the systematic association of
Neurosciences en réseau
916
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
Chiffre 5. Developmental origins of the architectonic type principle. Summary of computational
modeling of the ontogenetic development of cortical architecture and connections (Beul et al.,
2018). The simulations indicate that the presence of two spatial origins of neurogenesis, resulting in
two neurogenetic (temporal) and architectonic gradients, is necessary for the close correspondence
of the in silico model to the empirical relations between connectivity and architectonic differentia-
tion. Surtout, the empirically observed relations are replicated in silico only if the less-to-more
differentiated architectonic gradients align with early-to-late ontogenetic gradients. Ainsi, the sug-
gested mechanism is consistent with correspondence of time of neurogenesis to architectonic dif-
ferentiation (par exemple., Dombrowski, Hilgetag, & Barbas, 2001) and a dual origin of the cerebral cortex
(Pandya, Seltzer, Pétrides, & Cipolloni, 2014; Sanides, 1962).
connectivity with cortical type or neuron density differences, enable connectomes underlying
dynamical network simulations to be derived from incomplete experimental connectivity data.
Schmidt, Bakker, Hilgetag, et autres. (2018) used this approach, predicting laminar origin patterns
of cortico-cortical connections from relative neuron densities of connected areas, to derive a
layer-resolved connectivity matrix for all vision-related areas in one hemisphere of macaque
cortex. En outre, the work exposed a close correlation between neuron density and corti-
cal thickness, which was used to estimate missing thickness data and to help determine neural
population sizes. As mentioned in the preceding, neurons in prefrontal cortices have a compar-
atively high number of dendritic spines in both humans and nonhuman primates (Bianchi et al.,
2013; Elston, 2003, 2007, 2011; Jacobs, 2001). This feature is part of a more general upward
gradient in the number of spines per neuron from high to low architectural types (Elston, 2002,
2003). The comparative constancy of the volume density of synapses across cortical areas
(Harrison, Hof, & Wang, 2002) logically links the decrease in neuron density with the increase
in the number of spines per neuron across areas of different architectonic type (Schmidt, Bakker,
Hilgetag, et coll., 2018). Ainsi, the gradient of architectonic types and associated morphological
trends allow educated guesses for the full specification of cortical network models.
Such specification of complete connectivity graphs at the level of cortical areas and layers
enables network simulations taking into account the corresponding detailed connectivity, comme
done by Schmidt, Bakker, Shen, et autres. (2018) for all vision-related areas in one hemisphere
of macaque cortex. This work studies resting-state activity in a network of interconnected mi-
crocircuits each with the full density of neurons and synapses, so that both the microscopic
spiking activity and the macroscopic activity at the level of areas can be directly compared with
experimental data. Good agreement with experimental observations was achieved simultane-
ously for microscopic and macroscopic activity at a metastable state of the network. The close
Neurosciences en réseau
917
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
Chiffre 6. The architectonic type principle enables the generation of large-scale cortical models
that integrate microscopic and macroscopic cortical architecture and connections. Schematic rep-
resentation of a multiarea spiking model of macaque vision-related cortex, with laminar patterns of
cortico-cortical connectivity determined in part from relative neuron densities of connected areas.
Interarea and local connectivity together form polysynaptic pathways through the network. Chiffre
reproduced from Schmidt, Bakker, Hilgetag, et autres. (2018).
correspondence with experimental activity data provides additional support for the underlying
assumptions on the network structure. Such results, in conjunction with recent similar studies
(par exemple., Joglekar, Mejias, Lequel, & Wang, 2018), showcase the need for computational models
embodying the graded changes of micro- and macrostructure of cortex for more thoroughly
explaining experimental observations at the functional level.
The fact that the architectonic type principle enables connectivity to be predicted not only
at the level of cortical areas, but also at the laminar level, helps to identify polysynaptic path-
ways through the multiarea cortical network. A necessary step for this identification is to link
cortico-cortical to intrinsic connectivity, by mapping cortico-cortical synapses to their target
neurons and tracking the strongest pathways between areas that may pass through several inter-
mediate populations within the same area. Following this approach, Schmidt, Bakker, Hilgetag,
et autres. (2018) found that the strongest paths between areas of similar type are like feedforward
pathways in their start-to-end patterns, but like feedback pathways in terms of laminar patterns
in intermediate areas.
The association of denser connectivity with lower architectonic types carries with it dif-
ferences in spiking patterns of low- and high-type areas. En particulier, Schmidt, Bakker, Shen,
et autres. (2018) found low-type areas to be more prone to bursting, which implies generally longer
intrinsic time constants in line with a hierarchical organization of the width of single-neuron
autocorrelation functions (Murray et al., 2014). This contribution of differential connection
density to the hierarchy of intrinsic timescales may complement effects of area-specific recep-
tor densities (Duarte, Seeholzer, Zilles, & Morrison, 2017).
Various studies have shown that a hierarchical separation of timescales at the level of neu-
ral populations or cortical areas matches nested frequencies present in the sensory environ-
ment and in motor behavior (Gordon, Koenig-Robert, Tsuchiya, van Boxtel, & Hohwy, 2017;
Hasson, Lequel, Vallines, Heeger, & Rubin, 2008; Kiebel, Daunizeau, & Friston, 2008; Victor &
Neurosciences en réseau
918
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
Purpura, 1996). These population- or area-level timescales mainly reflect correlations between
neurons, rather than single-neuron autocorrelations, as the number of correlations grows with
the square of the number of neurons (Hagen et al., 2016). Computational studies have linked
the hierarchical trend in connection density (Chaudhuri, Knoblauch, Gariel, Kennedy, & Wang,
2015) or the topology of a rich-club core and less densely connected periphery (Gollo, Zalesky,
Hutchison, van den Heuvel, & Breakspear, 2015) to hierarchically organized timescales, lequel
in turn likely relate to layer-specific high-frequency feedforward and low-frequency feedback
communication (Bastos et al., 2015; Mejias, Murray, Kennedy, & Wang, 2016; Michalareas
et coll., 2016; van Kerkoerle et al., 2014). Cependant, these studies represent each area using
coarse-grained equations, and thus do not distinguish between single-neuron and population-
level dynamics, which can be markedly different. Direct comparison with the experimentally
observed hierarchy of timescales in the sense of single-neuron autocorrelations (Murray et al.,
2014) requires model predictions at the level of individual neurons. En outre, proper si-
multaneous predictions of single-neuron dynamics and pairwise cross-correlations in neural
network models require using the full density of neurons and synapses (van Albada, Helias, &
Diesmann, 2015). As shown by Schmidt, Bakker, Hilgetag, et autres. (2018) and Schmidt, Bakker,
Shen, et autres. (2018), connectivity matrices informed by the architectonic type principle can help
make such neuron-level predictions along with accurate predictions of large-scale dynamics.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dans l'ensemble, relationships between cortical types and their connectivity inform various aspects
of dynamic network simulations of the mammalian brain. For simulating the human brain,
where invasive connectivity data are not available, predictive connectomics is inevitable in
order to fully specify the network connectivity, implying even greater relevance of the archi-
tectonic type principle.
CONCLUSIONS
Various aspects of macroscopic and microscopic cortical organization, such as architectonic
type, cellular density, and size as well as dendritic size and spine density, are closely interre-
lated and present in spatially ordered gradients of cortical structure, defining a natural axis of
cortical organization along which many macroscopic and microscopic cortical architectonic
features covary. De plus, these architectonic features are also related to the intrinsic cortical
circuitry, as well as to features of the extrinsic, cortico-cortical connections. Ainsi, the archi-
tectonic type principle, which may derive from basic properties of spatially and temporally
ordered cortical development, allows the integration of cortical architecture and connectiv-
ity across scales of organization, and provides specifications of multiscale models of cortical
dynamics. Despite these intriguing findings; cependant, we are still at the beginning of under-
standing all the developmental, structural, and functional implications of this fundamental
principle of cortical organization.
REMERCIEMENTS
We thank Helen Barbas and Miguel A. García-Cabezas for helpful comments on the manuscript.
CONTRIBUTIONS DES AUTEURS
Enquête; Surveillance;
Claus C. Hilgetag: Conceptualisation; Acquisition de financement;
Writing – Original Draft; Writing – Review & Editing. Sarah F. Beul: Analyse formelle; Investiga-
tion; Méthodologie; Logiciel; Visualisation; Writing – Review & Editing. Sacha J. van Albada:
Conceptualisation; Analyse formelle; Acquisition de financement; Enquête; Méthodologie; Soft-
Neurosciences en réseau
919
An Architectonic Type Principle of the Primate Brain
ware; Visualisation; Writing – Review & Editing. Alexandros Goulas: Analyse formelle; Funding
acquisition; Enquête; Méthodologie; Writing – Review & Editing.
INFORMATIONS SUR LE FINANCEMENT
Alexandros Goulas, Alexander von Humboldt Foundation, Humboldt Research Fellowship.
Claus C. Hilgetag, Human Brain Project, Award ID: HBP/SGA2. Claus C. Hilgetag, German
Research Council DFG, Award ID: SFB 936/A1. Claus C. Hilgetag, German Research Council
DFG, Award ID: TRR 169/A2. Sacha J. van Albada, German Research Council DFG, Award
ID: SPP 2041. Claus C. Hilgetag, German Research Council DFG, Award ID: SPP 2041, HI
1286/7-1.
RÉFÉRENCES
Aristotle. (350 AD). Peri psych ¯es.
Bakker, R., Wachtler, T., & Diesmann, M.. (2012). CoCoMac 2.0 et
the future of tract-tracing databases. Frontiers in Neuroinformatics,
6. https://doi.org/10.3389/fninf.2012.00030
Barbas, H. (1986). Pattern in the laminar origin of corticocortical con-
nections. Journal of Comparative Neurology, 252(3), 415–422.
https://doi.org/10.1002/cne.902520310
Barbas, H. (2015). General cortical and special prefrontal connec-
tion: Principles from structure to function. Annual Review of
Neurosciences, 38, 269–289. https://doi.org/10.1146/annurev-neuro-
071714-033936
Barbas, H., & García-Cabezas, M.. À.
(2016). How the prefrontal
executive got its stripes. Opinion actuelle en neurobiologie, 40,
125–134. https://doi.org/10.1016/j.conb.2016.07.003
Barbas, H., Hilgetag, C. C., Saha, S., Dermon, C. R., & Suski,
J.. L. (2005). Parallel organization of contralateral and ipsilateral
prefrontal cortical projections in the rhesus monkey. BMC Neuro-
science, 6, 32. https://doi.org/10.1186/1471-2202-6-32
Barbas, H., & Rempel-Clower, N. (1997). Cortical structure predicts
the pattern of corticocortical connections. Cortex cérébral, 7(7),
635–646.
Bastos, UN. M., Usrey, W. M., Adams, R.. UN., Mangun, G. R., Fries,
P., & Friston, K. J.. (2012). Canonical microcircuits for predictive
coding. Neurone, 76(4), 695–711. https://est ce que je.org/10.1016/j.neuron.
2012.10.038
Bastos, UN. M., Vezoli,
J., Bosman, C. UN., Schoffelen,
J.-M.,
Oostenveld, R., Dowdall, J.. R., . . . Fries, P.. (2015). Visual areas
feedforward and feedback influences through distinct
exert
frequency channels. Neurone, 85(2), 390–401. https://est ce que je.org/10.
1016/j.neuron.2014.12.018
Batardiere, UN., Barone, P., Knoblauch, K., Giroud, P., Berland, M.,
Dumas, UN. M., & Kennedy, H. (2002). Early specification of the
hierarchical organization of visual cortical areas in the macaque
monkey. Cortex cérébral, 12(5), 453– 465.
Benavides-Piccione, R., Ballesteros-Yáñez, JE., DeFelipe, J., & Yuste,
R.. (2002). Cortical area and species differences in dendritic spine
morphology. Journal of Neurocytology, 31(3–5), 337–346.
Betzel, R.. F., Avena-Koenigsberger, UN., Goñi, J., Il, Y., de Reus,
M.. UN., Griffa, UN., . . . Sporns, Ô. (2016). Generative models of
the human connectome. NeuroImage, 124, 1054–1064. https://
doi.org/10.1016/j.neuroimage.2015.09.041
Beul, S. F., Barbas, H., & Hilgetag, C. C. (2017). A predictive struc-
tural model of the primate connectome. Scientific Reports, 7,
43176. https://doi.org/10.1038/srep43176
Beul, S. F., Goulas, UN., & Hilgetag, C. C.
(2018). Comprehensive
computational modelling of the development of mammalian cor-
tical connectivity underlying an architectonic type principle.
Biologie computationnelle PLoS, 14(11), e1006550. https://est ce que je.org/
10.1371/journal.pcbi.1006550
Beul, S. F., Grant, S., & Hilgetag, C. C. (2015). A predictive model of
the cat cortical connectome based on cytoarchitecture and dis-
tance. Structure et fonction du cerveau, 220(6), 3167–3184. https://
doi.org/10.1007/s00429-014-0849-y
Beul, S. F., & Hilgetag, C. C. (2015). Towards a “canonical” agran-
ular cortical microcircuit. Frontiers in Neuroanatomy, 8. https://
doi.org/10.3389/fnana.2014.00165
Beul, S. F., & Hilgetag, C. C. (2019). Neuron density fundamentally
relates to architecture and connectivity of the primate cerebral
cortex. https://doi.org/10.1101/117051
Bianchi, S., Stimpson, C. D., Bauernfeind, UN. L., Schapiro, S. J.,
(2013).
Baze, W. B., McArthur, M.. J., . . . Sherwood, C. C.
Dendritic morphology of pyramidal neurons in the chimpanzee
neocortex: Regional specializations and comparison to humans.
Cortex cérébral, 23(10), 2429–2436. https://est ce que je.org/10.1093/
cercor/bhs239
Binzegger, T., Douglas, R.. J., & Martine, K. UN. C.
(2009). Topol-
ogy and dynamics of the canonical circuit of cat v1. Neural
Networks, 22(8), 1071–1078. https://doi.org/10.1016/j.neunet.
2009.07.011
Bullmore, E., & Sporns, Ô. (2012). The economy of brain network
organization. Nature Revues Neurosciences, 13(5), 336–349.
https://doi.org/10.1038/nrn3214
Caviness, V. S., Bhide, P.. G., & Nowakowski, R.. S. (2008). Histoge-
netic processes leading to the laminated neocortex: Migration is
only a part of the story. Developmental Neuroscience, 30(1–3),
82–95. https://doi.org/10.1159/000109854
Cembrowski, M.. S., & Menon, V.
(2018). Continuous variation
within cell types of the nervous system. Trends in Neurosciences,
41(6), 337–348. https://doi.org/10.1016/j.tins.2018.02.010
Charvet, C. J., & Finlay, B. L. (2014). Evo-devo and the primate iso-
cortex: The central organizing role of intrinsic gradients of neu-
rogenesis. Cerveau, Behavior and Evolution, 84(2), 81–92. https://
doi.org/10.1159/000365181
Neurosciences en réseau
920
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
Chaudhuri, R., Knoblauch, K., Gariel, M.-A., Kennedy, H., & Wang,
X.-J.
(2015). A large-scale circuit mechanism for hierarchical
dynamical processing in the primate cortex. Neurone, 88(2),
419–431. https://doi.org/10.1016/j.neuron.2015.09.008
Chen, Y., Wang, S., Hilgetag, C. C., & Zhou, C. (2013). Trade-
off between multiple constraints enables simultaneous forma-
tion of modules and hubs in neural systems. PLoS Computa-
tional Biology, 9(3), e1002937. https://doi.org/10.1371/journal.
pcbi.1002937
Chen, Y., Wang, S., Hilgetag, C. C., & Zhou, C.
(2017). Features
of spatial and functional segregation and integration of the pri-
mate connectome revealed by trade-off between wiring cost and
efficiency. Biologie computationnelle PLoS, 13(9), e1005776. https://
doi.org/10.1371/journal.pcbi.1005776
Dombrowski, S. M., Hilgetag, C. C., & Barbas, H. (2001). Quanti-
tative architecture distinguishes prefrontal cortical systems in the
rhesus monkey. Cortex cérébral, 11(10), 975–988.
Douglas, R.. J., Martine, K. UN. C., & Whitteridge, D. (1989). A canonical
microcircuit for neocortex. Neural Computation, 1(4), 480–488.
https://doi.org/10.1162/neco.1989.1.4.480
Douglas, R., & Martine, K. (2004). Neuronal circuits of the neocor-
tex. Revue annuelle des neurosciences, 27, 419–451.
Duarte, R., Seeholzer, UN., Zilles, K., & Morrison, UN. (2017). Synap-
tic patterning and the timescales of cortical dynamics. Actuel
Opinion in Neurobiology, 43, 156–165. https://est ce que je.org/10.1016/
j.conb.2017.02.007
Elston, G. N. (2002). Cortical heterogeneity: Implications for visual
processing and polysensory integration. Journal of Neurocytology,
31, 317–335.
Elston, G. N. (2003). Cortex, cognition and the cell: New insights into
the pyramidal neuron and prefrontal function. Cortex cérébral,
(13), 111124–1138. https://doi.org/10.1093/cercor/bhg093
Elston, G. N. (2007). Specialization of the neocortical pyramidal
cell during primate evolution. In Evolution of nervous systems
(pp. 191–242). https://doi.org/10.1016/B0-12-370878-8/00164-6
(2011). Pyramidal cells in prefrontal cortex of pri-
mates: Marked differences in neuronal structure among species.
Frontiers in Neuroanatomy. https://doi.org/10.3389/fnana.2011.
00002
Elston, G. N.
Ercsey-Ravasz, M., Markov, N. T., Lamie, C., Van Essen, D. C.,
Knoblauch, K., Toroczkai, Z., & Kennedy, H. (2013). A predic-
tive network model of cerebral cortical connectivity based on a
distance rule. Neurone, 80(1), 184–197. https://est ce que je.org/10.1016/
j.neuron.2013.07.036
Felleman, D. J., & Van Essen, D. C. (1991). Distributed hierarchical
processing in the primate cerebral cortex. Cortex cérébral, 1(1),
1–47. https://doi.org/10.1093/cercor/1.1.1
Fulcher, B. D., & Fornito, UN. (2016). A transcriptional signature of
hub connectivity in the mouse connectome. Actes du
Académie nationale des sciences, 113(5), 1435–1440. https://est ce que je.
org/10.1073/pnas.1513302113
García-Cabezas, M.. UN., Barbas, H., & Zikopoulos, B. (2018). Paral-
lel development of chromatin patterns, neuron morphology, et
relations: Potential for disruption in autism. Frontiers in Neu-
roanatomy, 12. https://doi.org/10.3389/fnana.2018.00070
García-Cabezas, M.. UN., Zikopoulos, B., & Barbas, H. (2019). Le
Structural Model: A theory linking connections, plasticity, pathol-
ogy, development and evolution of the cerebral cortex. Cerveau
Structure and Function, 224(3), 985–1008. https://est ce que je.org/10.
1007/s00429-019-01841-9
Ghashghaei, H., Hilgetag, C. C., & Barbas, H.
(2007). Sequence
of information processing for emotions based on the anatomic
dialogue between prefrontal cortex and amygdala. NeuroImage,
34(3), 905–923. https://doi.org/10.1016/j.neuroimage.2006.09.046
Gollo, L. L., Roberts, J.. UN., Cropley, V. L., Di Biase, M.. UN., Pantelis,
C., Zalesky, UN., & Breakspear, M.. (2018). Fragility and volatility of
structural hubs in the human connectome. Neurosciences naturelles,
21(8), 1107–1116. https://doi.org/10.1038/s41593-018-0188-z
Gollo, L. L., Zalesky, UN., Hutchison, R.. M., van den Heuvel, M., &
Breakspear, M.. (2015). Dwelling quietly in the rich club: Cerveau
network determinants of slow cortical fluctuations. Philosoph-
ical Transactions of the Royal Society B: Sciences biologiques,
370(1668), 20140165. https://doi.org/10.1098/rstb.2014.0165
Gordon, N., Koenig-Robert, R., Tsuchiya, N., van Boxtel, J.. J., &
Hohwy, J..
(2017). Neural markers of predictive coding under
perceptual uncertainty revealed with Hierarchical Frequency
Tagging. eLife, 6, e22749. https://doi.org/10.7554/eLife.22749
Goulas, UN., Betzel, R.. F., & Hilgetag, C. C.
(2019). Spatiotempo-
ral ontogeny of brain wiring. Science Advances, 5(6), eaav9694.
https://doi.org/10.1126/sciadv.aav9694
Goulas, UN., Majka, P., Rose, M.. G., & Hilgetag, C. C. (2019). UN
blueprint of mammalian cortical connectomes. PLoS Biology,
17(3), e2005346. https://doi.org/10.1371/journal.pbio.2005346
(2017). Princi-
ples of ipsilateral and contralateral cortico-cortical connectivity
in the mouse. Structure et fonction du cerveau. https://est ce que je.org/10.
1007/s00429-016-1277-y
Goulas, UN., Uylings, H. B. M., & Hilgetag, C. C.
Goulas, UN., Werner, R., Beul, S. F., Saering, D., van den Heuvel, M.,
Triarhou, L. C., & Hilgetag, C. C. (2016). Cytoarchitectonic simi-
larity is a wiring principle of the human connectome. https://est ce que je.
org/10.1101/068254
Goulas, UN., Zilles, K., & Hilgetag, C. C. (2018). Cortical gradients
and laminar projections in mammals. Trends in Neurosciences,
41(11), 775–788. https://doi.org/10.1016/j.tins.2018.06.003
Hagen, E., Dahmen, D., Stavrinou, M.. L., Lindén, H., Tetzlaff, T.,
van Albada, S. J., . . . Einevoll, G. T.
(2016). Hybrid scheme
for modeling local field potentials from point-neuron networks.
Cortex cérébral, 26(12), 4461– 4496. https://est ce que je.org/10.1093/
cercor/bhw237
Harriger, L., van den Heuvel, M.. P., & Sporns, Ô. (2012). Rich club
organization of macaque cerebral cortex and its role in network
communication. PLoS ONE, 7(9), e46497. Retrieved from https://
doi.org/10.1371/journal.pone.0046497
Harrison, K. H., Hof, P.. R., & Wang, S. S.-H. (2002). Scaling laws in
the mammalian neocortex: Does form provide clues to function?
Journal of Neurocytology, 31(3–5), 289–298.
Hasson, U., Lequel, E., Vallines, JE., Heeger, D. J., & Rubin, N. (2008).
A hierarchy of temporal receptive windows in human cortex.
Journal des neurosciences, 28(10), 2539–2550. https://est ce que je.org/10.
1523/JNEUROSCI.5487-07.2008
Il, Y., Chen, Z. J., & Evans, UN. C.
(2007). Small-world anatomi-
cal networks in the human brain revealed by cortical thickness
from MRI. Cortex cérébral, 17(10), 2407–2419. https://est ce que je.org/
10.1093/cercor/bhl149
Neurosciences en réseau
921
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
Henderson, J.. UN., & Robinson, P.. UN. (2011). Geometric effects on
complex network structure in the cortex. Physical Review Letters,
107(1), 018102.
Hilgetag, C. C., & Grant, S.
(2010). Cytoarchitectural differences
are a key determinant of laminar projection origins in the visual
cortex. NeuroImage, 51(3), 1006–1017. https://est ce que je.org/10.1016/
j.neuroimage.2010.03.006
Hilgetag, C. C., Medalla, M., Beul, S. F., & Barbas, H. (2016). Le
primate connectome in context: Principles of connections of the
cortical visual system. NeuroImage, 134, 685–702. Retrieved
from https://doi.org/10.1016/j.neuroimage.2016.04.017
Jacobs, B. (2001). Regional dendritic and spine variation in human
cerebral cortex: A quantitative Golgi study. Cortex cérébral,
11(6), 558–571. https://doi.org/10.1093/cercor/11.6.558
Joglekar, M.. R., Mejias, J.. F., Lequel, G. R., & Wang, X.-J. (2018). Inter-
areal balanced amplification enhances signal propagation in a
large-scale circuit model of the primate cortex. Neurone, 98(1),
222–234.e8. https://doi.org/10.1016/j.neuron.2018.02.031
kaiser, M., & Hilgetag, C. C. (2004). Spatial growth of real-world
réseaux. Physical Review E, Statistical, Nonlinear, and Soft
Matter Physics, 69(3 Pt. 2), 036103.
kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component place-
ment, but short processing paths, due to long-distance projec-
tions in neural systems. Biologie computationnelle PLoS, 2(7), e95.
https://doi.org/10.1371/journal.pcbi.0020095
kaiser, M., Hilgetag, C. C., & van Ooyen, UN. (2009). A simple rule
for axon outgrowth and synaptic competition generates realistic
connection lengths and filling fractions. Cortex cérébral, 19(12),
3001–3010. https://doi.org/10.1093/cercor/bhp071
Kale, P., Zalesky, UN., & Gollo, L. L. (2018). Estimating the impact
of structural directionality: How reliable are undirected connec-
tomes? Neurosciences en réseau, 02(02), 259–284. https://est ce que je.org/
10.1162/netn_a_00040
Kennedy, H., Bullier, J., & Dehay, C. (1989). Transient projec-
tion from the superior temporal sulcus to area 17 in the new-
born macaque monkey. Proceedings of the National Academy of
les sciences, 86(20), 8093–8097.
Kiebel, S. J., Daunizeau, J., & Friston, K. J.. (2008). A hierarchy of time-
scales and the brain. Biologie computationnelle PLoS, 4(11), e1000209.
Lerch, J.. P., Worsley, K., Shaw, W. P., Greenstein, D. K., Lenroot,
R.. K., Giedd, J., & Evans, UN. C. (2006). Mapping anatomical cor-
relations across cerebral cortex (MACACC) using cortical thick-
ness from MRI. NeuroImage, 31(3), 993–1003. https://est ce que je.org/
10.1016/j.neuroimage.2006.01.042
Markov, N. T., Ercsey-Ravasz, M.. M., Ribeiro Gomes, UN. R., Lamie,
C., Magrou, L., Vezoli, J., . . . Kennedy, H. (2014). A weighted
and directed interareal connectivity matrix for macaque cerebral
cortex. Cortex cérébral, 24(1), 17–36. https://est ce que je.org/10.1093/
cercor/bhs270
Markov, N. T., Vezoli, J., Chameau, P., Falchier, UN., Quilodran, R.,
Huissoud, C., . . . Kennedy, H.
(2014). Anatomy of hierarchy:
Feedforward and feedback pathways in macaque visual cortex.
Journal of Comparative Neurology, 522(1), 225–259. https://est ce que je.
org/10.1002/cne.23458
Medalla, M., & Barbas, H.
(2006). Diversity of laminar connec-
tions linking periarcuate and lateral intraparietal areas depends
on cortical structure. European Journal of Neuroscience, 23(1),
161–179. https://doi.org/10.1111/j.1460-9568.2005.04522.x
Mejias, J.. F., Murray, J.. D., Kennedy, H., & Wang, X.-J.
(2016).
Feedforward and feedback frequency-dependent interactions in
a large-scale laminar network of the primate cortex. Science
Advances, 14.
Michalareas, G., Vezoli, J., van Pelt, S., Schoffelen, J.-M., Kennedy,
H., & Fries, P.. (2016). Alpha-beta and gamma rhythms subserve
feedback and feedforward influences among human visual cortical
domaines. Neurone. https://doi.org/10.1016/j.neuron.2015.12.018
Molyneaux, B. J., Arlotta, P., Menezes, J.. R.. L., & Macklis, J.. D.
(2007). Neuronal subtype specification in the cerebral cortex.
Nature Revues Neurosciences, 8(6), 427–437. https://est ce que je.org/10.
1038/nrn2151
Murray, J.. D., Bernacchia, UN., Freedman, D. J., Romo, R., Wallis,
J.. D., Cai, X., . . . Wang, X.-J.
(2014). A hierarchy of intrinsic
timescales across primate cortex. Neurosciences naturelles, 17(12),
1661–1663. https://doi.org/10.1038/nn.3862
Palomero-Gallagher, N., & Zilles, K. (2017). Cyto-, myelo-, receptor-
and synaptic architecture in human cortical areas. NeuroImage.
https://doi.org/10.1016/j.neuroimage.2017.08.035
Pandya, D. N., & Sanides, F.
(1973). Architectonic parcellation
of the temporal operculum in rhesus monkey and its projection
pattern. Zeitschrift Für Anatomie Und Entwicklungsgeschichte,
139(2), 127–161. https://doi.org/10.1007/BF00523634
Pandya, D. N., Seltzer, B., Pétrides, M., & Cipolloni, P.. B. (2014).
Cerebral cortex: Architecture, relations, and the dual origin
concept Oxford. Oxford United Kingdom: Oxford University
Presse.
Potjans, T. C., & Diesmann, M.. (2012). The cell-type specific cor-
tical microcircuit: Relating structure and activity in a full-scale
spiking network model. Cortex cérébral. https://est ce que je.org/10.1093/
cercor/bhs358
Ramón y Cajal, S. (1899). Textura del sistema nervioso del hombre
y de los vertebrados. (Madrid:Nicolas Moya.[Texture of the ner-
vous system of man and the vertebrates](P.. Pasik & T. Pasik, Trans.,
1999, New York: Springer)
Reid, UN. T., Lewis,
J., Bezgin, G., Khundrakpam, B., Eickhoff,
S. B., McIntosh, UN. R., . . . Evans, UN. C. (2016). A cross-modal,
cross-species comparison of connectivity measures in the pri-
mate brain. NeuroImage, 125, 311–331. https://est ce que je.org/10.1016/
j.neuroimage.2015.10.057
Roberts, J.. UN., Perry, UN., Lord, UN. R., Roberts, G., Mitchell, P.. B.,
Forgeron, R.. E., . . . Breakspear, M..
(2016). The contribution of
geometry to the human connectome. NeuroImage, 124(Pt. UN),
379–393. https://doi.org/10.1016/j.neuroimage.2015.09.009
Romero-Garcia, R., Whitaker, K. J., Váša, F., Seidlitz, J., Shinn, M.,
Fonagy, P., . . . Vértes, P.. E. (2018). Structural covariance networks
are coupled to expression of genes enriched in supragranular lay-
ers of the human cortex. NeuroImage, 171, 256–267. https://est ce que je.
org/10.1016/j.neuroimage.2017.12.060
Rubinov, M.. (2016). Constraints and spandrels of interareal connec-
tomes. Communications naturelles, 7(1). https://doi.org/10.1038/
ncomms13812
Sanides, F. (1962). Die Architektonik des menschlichen Stirnhirns.
Berlin, Allemagne: Springer.
Scannell, J.. W., Blakemore, C., & Jeune, M.. P.. (1995). Analysis of
connectivity in the cat cerebral cortex. Journal des neurosciences,
15(2), 1463–1483.
Neurosciences en réseau
922
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
An Architectonic Type Principle of the Primate Brain
Schmidt, M., Bakker, R., Hilgetag, C. C., Diesmann, M., & van Albada,
S. J.. (2018). Multi-scale account of the network structure of
macaque visual cortex. Structure et fonction du cerveau, 223(3),
1409–1435. https://doi.org/10.1007/s00429-017-1554-4
Schmidt, M., Bakker, R., Shen, K., Bezgin, G., Diesmann, M., & van
Albada, S. J.. (2018). A multi-scale layer-resolved spiking network
model of resting-state dynamics in macaque visual cortical areas.
Biologie computationnelle PLoS, 14(10), e1006359. https://est ce que je.org/
10.1371/journal.pcbi.1006359
Scholtens, L. H., Schmidt, R., de Reus, M.. UN., & van den Heuvel,
M.. P.. (2014). Linking macroscale graph analytical organization
to microscale neuroarchitectonics in the macaque connectome.
Journal des neurosciences, 34(36), 12192–12205. https://est ce que je.org/
10.1523/JNEUROSCI.0752-14.2014
Seidlitz, J., Váša, F., Shinn, M., Romero-Garcia, R., Whitaker, K. J.,
Vértes, P.. E., . . . Bullmore, E. T. (2018). Morphometric similar-
ity networks detect microscale cortical organization and predict
inter-individual cognitive variation. Neurone, 97(1), 231–247.e7.
https://doi.org/10.1016/j.neuron.2017.11.039
Solari, S. V. H., & Stoner, R..
(2011). Cognitive consilience: Pri-
mate non-primary neuroanatomical circuits underlying cogni-
tion. Frontiers in Neuroanatomy, 5, 65. https://doi.org/10.3389/
fnana.2011.00065
Sterling, P., & Laughlin, S. (2015). Principles of neural design.
Cambridge, MA: AVEC Presse.
van Albada, S. J., Helias, M., & Diesmann, M..
(2015). Scalabil-
ity of asynchronous networks is limited by one-to-one mapping
between effective connectivity and correlations. PLoS Computa-
tional Biology, 11(9), e1004490. https://doi.org/10.1371/journal.
pcbi.1004490
van den Heuvel, M.. P., Bullmore, E. T., & Sporns, Ô. (2016). Compara-
tive connectomics. Tendances des sciences cognitives, 20(5), 345–361.
https://doi.org/10.1016/j.tics.2016.03.001
van den Heuvel, M.. P., Scholtens, L. H., Barrett, L. F., Hilgetag, C. C.,
& de Reus, M.. UN. (2015). Bridging cytoarchitectonics and con-
Journal des neurosciences,
nectomics in human cerebral cortex.
35(41), 13943–13948. Extrait de http://www.jneurosci.org/
content/35/41/13943.long
van Kerkoerle, T., Self, M.. W., Dagnino, B., Gariel-Mathis, M.-A.,
Poort, J., van der Togt, C., & Roelfsema, P.. R..
(2014). Alpha
and gamma oscillations characterize feedback and feedforward
processing in monkey visual cortex. Actes de la Nationale
Académie des Sciences, 111(40), 14332–14341. https://est ce que je.org/
10.1073/pnas.1402773111
Victor, J.. D., & Purpura, K. P.. (1996). Nature and precision of tem-
poral coding in visual cortex: A metric-space analysis. Journal de
Neurophysiologie, 76(2), 1310–1326. https://est ce que je.org/10.1152/jn.
1996.76.2.1310
von Economo, C. (1927). Zellaufbau der Grosshirnrinde des Men-
schen. Zehn Vorlesungen. Berlin, Allemagne: Springer.
von Economo, C., & Koskinas, G. N. (1925). Die Cytoarchitektonik der
Hirnrinde des Erwachsenen Menschen. Berlin, Allemagne: Springer.
Zamora-López, G., Zhou, C., & Kurths, J.. (2010). Cortical hubs form
a module for multisensory integration on top of the hierarchy of
cortical networks. Frontiers in Neuroinformatics, 4, 1. https://
doi.org/10.3389/neuro.11.001.2010
Zilles, K., & Palomero-Gallagher, N.
(2017). Multiple transmitter
receptors in regions and layers of the human cerebral cortex.
Frontiers in Neuroanatomy, 11. https://doi.org/10.3389/fnana.
2017.00078
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
4
9
0
5
1
8
6
6
7
7
7
n
e
n
_
un
_
0
0
1
0
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Neurosciences en réseau
923