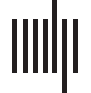FONCTION DE MISE AU POINT: - Recherche en IA spécialisée au MIT

FONCTION DE MISE AU POINT:
Topological Neuroscience

Generating dynamical neuroimaging spatiotemporal
representations (DyNeuSR) en utilisant
topological data analysis

Caleb Geniesse1,2, Olaf Sporns3, Giovanni Petri4,5, and Manish Saggar1,2

1Biophysics Program, Université de Stanford, Stanford, Californie, Etats-Unis
2Department of Psychiatry and Behavioral Sciences, Université de Stanford, Stanford, Californie, Etats-Unis
3Department of Psychological and Brain Sciences, Indiana University, Bloomington, IN, Etats-Unis
4ISI Foundation, Turin, Italy
5ISI Global Science Foundation, New York, New York, Etats-Unis

un accès ouvert

journal

Mots clés: Brain dynamics, TDA, IRMf, Brain networks, Mapper

ABSTRAIT

In this article, we present an open source neuroinformatics platform for exploring, analyzing,
and validating distilled graphical representations of high-dimensional neuroimaging data
extracted using topological data analysis (TDA). TDA techniques like Mapper have been
recently applied to examine the brain’s dynamical organization during ongoing cognition
without averaging data in space, in time, or across participants at the outset. Such TDA-based
approaches mark an important deviation from standard neuroimaging analyses by distilling
complex high-dimensional neuroimaging data into simple—yet neurophysiologically valid
and behaviorally relevant—representations that can be interactively explored at the
single-participant level. To facilitate wider use of such techniques within neuroimaging and
general neuroscience communities, our work provides several tools for visualizing,
interacting with, and grounding TDA-generated graphical representations in neurophysiology.
Through Python-based Jupyter notebooks and open datasets, we provide a platform to assess
and visualize different intermittent stages of Mapper and examine the inﬂuence of Mapper
parameters on the generated representations. We hope this platform could enable researchers
and clinicians alike to explore topological representations of neuroimaging data and
generate biological insights underlying complex mental disorders.

RÉSUMÉ DE L'AUTEUR

To develop biologically grounded psychiatric diagnosis, researchers and clinicians need tools
for distilling complex high-dimensional neuroimaging data into simple yet interactive and
clinically relevant representations. Plus loin, for translational outcomes, these representations
should be conceivable at the single-participant level. Topological data analysis techniques
such as Mapper allow generation of these representations. Ici, we introduce a set of tools
that can facilitate wider acceptance of Mapper within the neuroscience community and
provide a series of easy-to-follow steps for visualizing Mapper-generated graphical
representations. We provide detailed examples to reveal the “under-the-hood” workings of
Mapper.

INTRODUCTION

Capturing and quantifying dynamic ﬂuctuations in neuronal activity is critical for under-
standing how the brain dynamically reorganizes during ongoing cognition. Although current

Citation: Geniesse, C., Sporns, O.,
Petri, G., & Saggar, M.. (2019).
Generating dynamical neuroimaging
spatiotemporal representations
(DyNeuSR) using topological data
analyse. Neurosciences en réseau, 3(3),
763–778. https://est ce que je.org/10.1162/
netn_a_00093

EST CE QUE JE:
https://doi.org/10.1162/netn_a_00093

Informations complémentaires:
https://doi.org/10.1162/netn_a_00093
http://bdl.stanford.edu/projects/
dyneusr

Reçu: 1 Novembre 2018
Accepté: 25 Avril 2019

Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.

Auteur correspondant:
Manish Saggar
saggar@stanford.edu

Éditeur de manipulation:
Morten Kringelbach

droits d'auteur: © 2019
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence

La presse du MIT

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamical neuroimaging spatiotemporal representations using TDA

neuroimaging technologies enable us to measure brain function at very high spatiotempo-
ral resolutions, most traditional approaches to neuroimaging data analysis invariably collapse
high-resolution neuroimaging data across spatiotemporal scales at the outset (Preti, Bolton,
& Van De Ville, 2016). The resulting loss of spatiotemporal precision impedes the interpreta-
tion of such high-dimensional neuroimaging data and may obscure important detail related
to temporal dynamics and individual differences. For better translational outcomes, there is a
need for interactive data-driven methods for analyzing and visualizing neuroimaging data that
are capable of delivering behaviorally relevant insights at the single-participant level without
collapsing spatiotemporal data at the outset.

Several innovative methods have been proposed to examine and quantify ﬂuctuations in
both functional activity (Karahano˘glu & Van De Ville, 2015; Liu & Duyn, 2013; Liu, Zhang,
Chang, & Duyn, 2018) and connectivity (Preti et al., 2016; Shine et al., 2015; Xu & Lindquist,
2015). These approaches provide valuable insights; cependant, they cannot uncover the threshold-
free optimal spatiotemporal scale that best captures behaviorally relevant dynamics (Preti
et coll., 2016). Plus récemment, an approach based on topological data analysis (TDA) called
Mapper (Carlsson, 2009; Lum et al., 2013; Singh, Mémoli & Carlsson, 2007) has been used to
graphically represent the brain’s overall dynamical organization (c'est à dire., the shape graph) without
arbitrarily collapsing data in space or time (Saggar et al., 2018). Intuitively, Mapper helps con-
struct a skeletonized graph of a high-dimensional dataset to encapsulate the original shape of
the data by representing similar points as more closely linked than dissimilar points in the gen-
erated shape graph. Par exemple, in case of studying anatomical heterogeneity across partici-
pants, the data points could be individual participants themselves and the Mapper-generated
graph would link participants with similar anatomical features closer as compared with par-
ticipants with dissimilar anatomy. Mapper-generated representation is analogous to generating
a subway map that can capture the essential features of a system while potentially reduc-
ing the effect of noisy data. Plus loin, the generated representations can be interactively visual-
ized, quantiﬁed in a variety of ways using graph theory, validated by anchoring them to brain
anatomy, and constructed at the level of individual participants or populations, making them
suitable for exploratory and translational research purposes.

Although several different Mapper software allow construction of such shape graphs for any
kind of data that can be represented as a matrix (including neuroimaging data), to our knowl-
bord, none of these tools were designed with explicit built-in support for visualization and
analysis of those graphs in the context of neuroscience (see Table 1). De plus, while software
packages have been developed speciﬁcally for neuroimaging data analysis and visualization,
none of these tools were designed speciﬁcally to work with shape graphs produced by Mapper.
En tant que tel, integrating Mapper with existing neuroimaging tools into a full data analysis pipeline
poses a steep learning curve and a signiﬁcant challenge for many neuroscience researchers. À
overcome these hurdles, we believe researchers need tools that connect Mapper with existing
neuroimaging software.

In light of this need, we developed DyNeuSR, an open source platform for exploring, un-
alyzing, and validating topological properties and neurophysiological correlates of Mapper-
generated graphs (voir la figure 1). The DyNeuSR toolkit and source code are available at our
website (Geniesse, Sporns, Petri, & Saggar, 2018).

In this paper, we provide some examples to illustrate the key features of DyNeuSR. D'abord,
we introduce Mapper and its workings using a synthetic 3-D trefoil knot dataset. Using the
trefoil dataset, we also compare Mapper with other traditional dimensionality reduction

764

Topological data analysis (TDA):
Applied mathematical approach to
analyzing datasets using techniques
from algebraic topology and
providing information about the
shape of complex data.

Mapper:
TDA-based technique for extracting
graphical descriptions of point cloud
data based on the idea of
ﬁlter-guided partial clustering.

Shape graph:
Compressed network representation
generated by Mapper; nodes
correspond to local clusters and
edges connect nodes that share data
points.

Dimensionality reduction:
Process of selecting and extracting
features from data to reduce the
number of random variables under
consideration.

Neurosciences en réseau

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamical neuroimaging spatiotemporal representations using TDA

Logiciel

Ayasdi

KeplerMapper

Python Mapper

TDAmapper

MapperTools

Tableau 1. A survey of available Mapper software.

Programming language

License

Built-in support for neuroscience

Link

Python

Proprietary

AVEC

GPL

Non

ayasdi.com

github.com/MLWave/kepler-mapper

danifold.net/mapper

github.com/paultpearson/TDAmapper

github.com/alpatania/MapperTools

The table provides a quick overview of existing Mapper software, including whether the respective software has built-in support for
neuroscience applications (par exemple., relating shape graphs of neuroimaging data to neurophysiology correlates).

techniques. Deuxième, we introduce the features of DyNeuSR using a real neuroimaging dataset
(Haxby et al., 2001). Speciﬁcally, we show how to (un) visualize and annotate shape graphs
with meta-information; (b) anchor shape graphs into brain anatomy and physiology; et (c)
quantify shape graphs to capture transitions in brain activity. Ensemble, these demonstrations
highlight how DyNeuSR provides a simple interface between Mapper and neuroimaging data
analysis and visualization.

RÉSULTATS

The results are presented in two parts. D'abord, we use DyNeuSR to introduce, visualize, et
motivate Mapper on a synthetic 3-D trefoil knot. Deuxième, we use DyNeuSR to analyze and
interpret shape graphs generated from a real neuroimaging dataset. To view the respective
code and results, please refer to the Jupyter notebook provided in Supplemental Data 1 et 2
(Informations complémentaires).

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 1. Overview of DyNeuSR. Once the Mapper graph is generated using any of the existing
tools listed in Table 1, DyNeuSR allows for annotating using meta information, anchoring graph
nodes in to neurophysiology, and capturing temporal (or over samples) variations.

Neurosciences en réseau

765

Dynamical neuroimaging spatiotemporal representations using TDA

Cover:
Set of overlapping bins of data points
produced by the partitioning of the
data along one or more ﬁlters
deﬁned on that data.

Filtering:
First stage of Mapper where
low-dimensional views (embeddings)
of data are constructed in order to
guide partial clustering in later
étapes.

Introducing and Visualizing Mapper

Officiellement, Mapper produces the topological skeleton of a dataset by combining together the
dataset and a map deﬁned on it (Carlsson, 2009; Lum et al., 2013; Singh et al., 2007). With
these two elements, it computes a cover of the codomain of the map, which is the actual
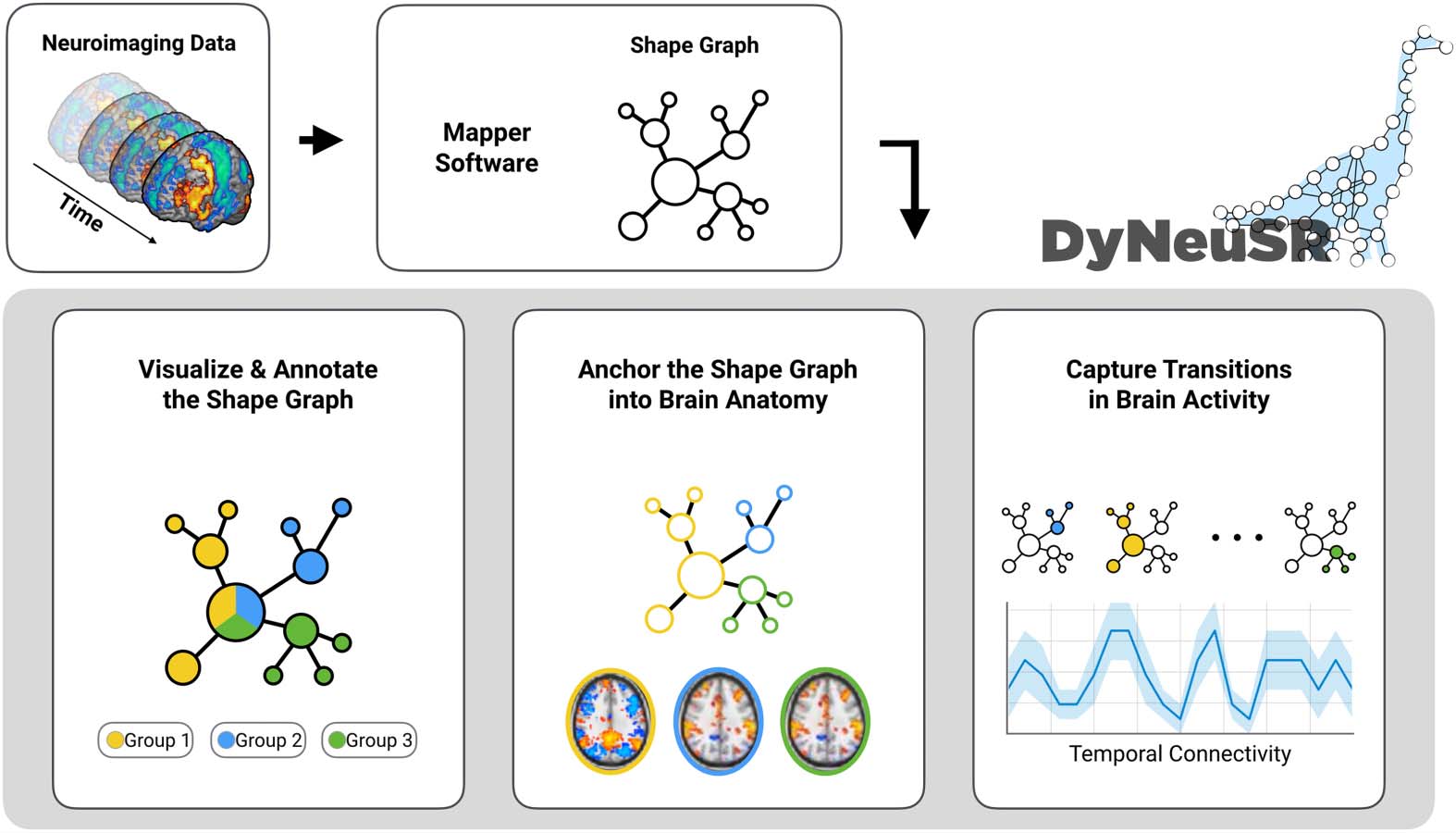
skeleton. In practice, this process can be summarized in four stages: (un) slicing the data;
(b) binning data points according to slices from the ﬁrst stage; (c) clustering data points within
each bin; et (d) linking the clusters that share points across bins.

To better understand these stages, DyNeuSR provides tools for visualizing how data are
transformed at each stage. Voir la figure 2 for a visual representation of each stage. In the fol-
lowing section, we discuss how the trefoil knot data are transformed during each of the four
stages of Mapper. We then highlight the advantages of Mapper as compared with standard
dimensionality reduction methods.

Stages of Mapper. High-dimensional data are transformed into a lower dimensional graphical
representation as it passes through the four stages of the Mapper algorithm. The ﬁrst stage of
Mapper involves ﬁltering high-dimensional data into a lower dimension. Note that this ﬁltering
step is not equivalent to standard dimensionality reduction; instead, the ﬁlters in Mapper are
used as lenses to slice the data. The shape of the data captured in the later stages and ﬁnal
output of Mapper often depend on how the data were sliced, Et ainsi, the choice of ﬁlter
function and Mapper parameters is critical (see the Discussion section). The ability to slice
data in several ways, cependant, makes this tool extremely versatile for data exploration and
feature extraction (Phinyomark, Ibanez-Marcelo, & Petri, 2017). For the 3-D trefoil knot data,
ﬁltering along any subset of the three dimensions will produce a simple lens that is easy to
visualize (voir la figure 2). The shape graph shown in Figure 2 was generated using the ﬁrst and
second dimensions of the 3-D trefoil knot data as a lens; cependant, other pairs of dimensions
produce similar results (see Supplemental Figure 1A; Informations complémentaires).

After ﬁltering the data using a lens, the data are sliced or binned along each ﬁlter dimension
in the lens into overlapping bins, c'est, a cover parameterized by resolution (R.) and gain (G).
Ici, the resolution corresponds to the number of bins and the gain to the relative overlap
between them. The shape graph of the trefoil data shown in Figures 2 et 3 was generated
using a low resolution (R = 6) and a high gain equivalent to an 80% overlap between bins

Chiffre 2. Visualizing the Stages of Mapper. This ﬁgure shows the results from a visual inspection
of Mapper intermediates for synthetic data sampled from a 3-D trefoil knot.

Neurosciences en réseau

766

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamical neuroimaging spatiotemporal representations using TDA

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

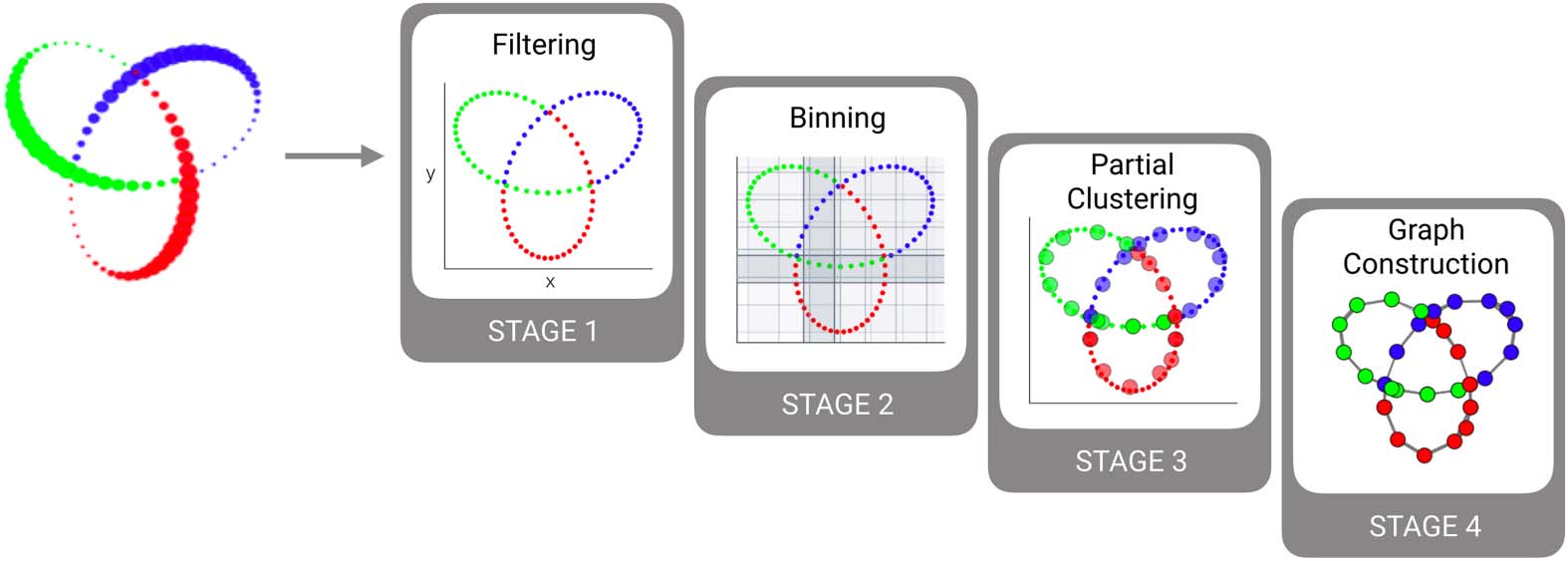
Chiffre 3. Visualizing the advantages of Mapper. This ﬁgure compares representations of the syn-
thetical 3-D trefoil knot generated using traditional dimensionality reduction techniques, y compris
linear (par exemple., APC) and nonlinear (par exemple., t-SNE) approaches with one generated using Mapper. A sub-
set of the data points can be mapped from the high-dimensional space (top) to each of the low-
dimensional representations (bottom). Note, blue and green points within the subset of data are
separated by the third dimension in the high-dimensional space. APC (UN) and t-SNE (B) both fail to
resolve this separation—the blue and green points are positioned similarly in the reduced-dimension
espace. In contrast, Mapper (C) represents these points as two different unconnected nodes in the
shape graphs. Since Mapper performs clustering on the original three-dimensional data, the blue
and green points are assigned to different clusters because of the separation in the third dimen-
sion. Plus loin, the same shape graph is shown in two different layouts, revealing that the result is in
fact a circle. For additional results showing how Mapper recovers an actual topological circle, voir
Supplemental Figure 1 (Informations complémentaires).

(G = 5). Supplemental Figure 1B (Informations complémentaires) provides similar results using differ-
ent resolution and gain parameters.

importantly,

The third stage pertains to partial clustering of data points within each bin. Any cluster-
ing method can be used, et,
the clustering is performed in the original
high-dimensional space. This clustering step compresses the original data by grouping similar
data. Because of the overlap between bins, any two adjacent bins along each ﬁlter dimension
can share data points. In the last step, adjacent bins with non-empty intersection (c'est à dire., avec
common data points) are joined together into a simpliﬁed skeleton representation of the
original data.

Advantages of Mapper. With respect
to standard dimensionality reduction techniques,
Mapper is advantageous because it combines dimensionality reduction with clustering in
the original high-dimensional space. Standard dimensionality reduction techniques can only
project data points to a lower dimensional space, where the analysis is then performed. Ainsi,
regardless how accurate the projection, these methods are bound to lose some of the in-
formation contained in the dataset for the sake of interpretability. Inversement, Mapper uses

Neurosciences en réseau

767

Dynamical neuroimaging spatiotemporal representations using TDA

Stochastic Neighborhood
Embedding:
Nonlinear method for projecting
high-dimensional data into a
low-dimensional space in a way
that preserves local structure in
the original space.

information from the lower dimensional lens to augment the information present in the origi-
nal high-dimensional space.

The trefoil knot example is particularly illustrative. Standard dimensionality reduction tech-
niques yield complicated overlapping patterns in two dimensions (Figure 3A and 3B), alors que
Mapper utilizes two-dimensional projection information jointly with clustering in three dimen-
sions to return nonoverlapping clusters at the intersection points of the knot (emphasized in
Figure 3C). This allows Mapper to tease apart the real structure of the trefoil knot: a topological
circle. For additional results, see Supplemental Figure 1 (Informations complémentaires).

Analyzing and Interpreting Shape Graphs

Dans cette section, we demonstrate three different ways to extract insights from shape graph rep-
resentations of real brain activity data with DyNeuSR. Speciﬁcally, we explore the functional
magnetic resonance imaging (IRMf) dataset from a study on face and object recognition in the
human ventral temporal cortex (Haxby et al., 2001). Data were collected while visual stim-
uli from eight different categories (par exemple., faces, cats, ﬁve categories of man-made objects, et
scrambled control) were presented to six different subjects across 12 sessions (per subject).
Ici, we applied Mapper to the fMRI brain activity patterns of response measured in the ven-
tral stream, which is a major pathway involved with object identiﬁcation and recognition. Pour
each of the six subjects, the input to Mapper was a matrix with time frames as rows and voxels
as columns. Speciﬁcally, we used 242 time frames from Sessions 4 et 5, and voxels from each
subjects’ ventral temporal cortex (par exemple., 577 voxels for the ﬁrst subject). KeplerMapper (Saul &
van Veen, 2017) was used to generate the shape graphs. We used Stochastic Neighborhood
Embedding (t-SNE; Maaten & Hinton, 2008) as a nonlinear lens for ﬁltering, and a resolution
de 17 and gain of 3 (c'est à dire., 66.7% overlap) as cover parameters for binning. We also explored a
linear lens (APC) to examine the Haxby dataset; please see Supplemental Figure 2 (Supporting
Information) for more information.

In the following subsections, we will describe three different ways that the shape graph
can be related to neurophysiology using DyNeuSR. Supplemental Data 2 (Supporting Infor-
mation) includes a Jupyter notebook containing the code used to download and prepare the
data, generate the shape graphs using Mapper, and perform the analyses of the shape graphs
using DyNeuSR.

The shape graphs generated by Mapper provide a
Visualizing and Annotating Shape Graphs.
mapping between data points in the original dataset and nodes in the shape graph. This map-
ping can also be used to annotate the shape graph using additional meta-information not used
in the analysis (par exemple., target variables or outcomes). DyNeuSR makes it easy to annotate and
color nodes in the shape graph based on the meta-information.

To demonstrate this, we annotated nodes in each of the six subjects’ shape graphs based
on the categories of stimuli presented at each time frame. For each time frame, we know the
category of visual stimulus presented. Ainsi, every node can be assigned a set of stimulus labels
corresponding to the set of time frames contained in that node. These assignments can be used
for annotating (or coloring) the shape graph. To represent the relative proportion of the different
stimulus labels assigned, DyNeuSR represents each node as a pie chart.

DyNeuSR provides a user interface for visualizing and interacting with the shape graph (voir
Supplemental Figure 4 for an example; Informations complémentaires). Using this interface, we were
able to quickly visualize the different proportions of visual stimuli associated with the nodes

Neurosciences en réseau

768

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamical neuroimaging spatiotemporal representations using TDA

in the shape graph, as well as different regions of the shape graph corresponding to differ-
ently colored nodes. With this visualization alone, researchers can glean insights into how sep-
arable (ou non) different kinds of visual stimuli are based on their respectively evoked brain
activation patterns.

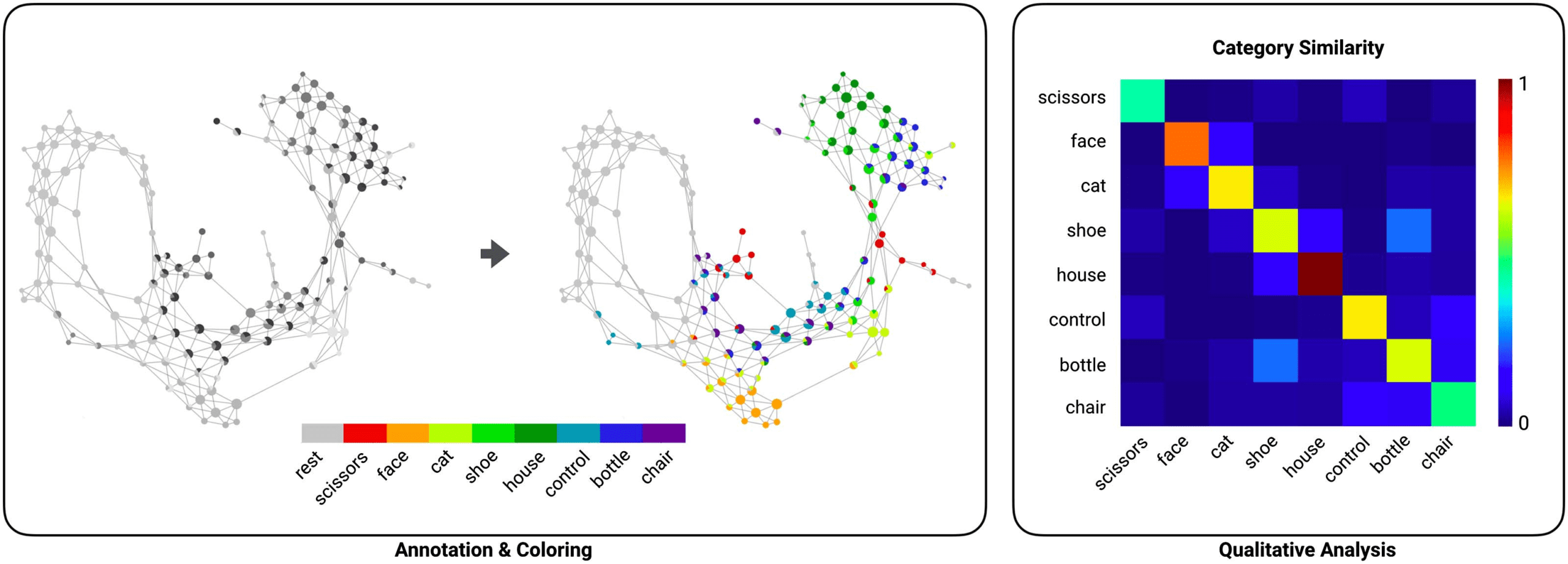
Par exemple, Chiffre 4 shows the shape graph generated and annotated for the ﬁrst Haxby
participant. The nodes corresponding to time frames during which the brain was processing
images of faces (annotated using orange color) appear to be highly interconnected and local-
ized in the shape graph. In comparison, the nodes corresponding to houses (annotated using
green color) are localized in a different part of the graph and entirely disconnected from the
orange-colored nodes for face stimuli. From this comparison, we might hypothesize that the
brain processes these two categories quite differently. Supplemental Figure 3 (Supporting In-
formation) provides shape graphs for all participants in the Haxby dataset.

The annotated shape graph can be further analyzed to study similarities within and between
partitions of the data based on the connectivity of nodes in the shape graph. Par exemple,
Chiffre 4 (right panel) shows the similarity of data associated with visual stimuli within the same
category and between different categories. This similarity matrix can be estimated for a single
subject by examining connectivity of nodes within and between each stimulus category. Pour
example, the heatmap shown in Figure 4 (right panel) implies slightly higher similarity of nodes
associated with faces and cats stimuli, suggesting some overlap in how the brain processes and
represents these stimuli categories in the ventral temporal cortex—reminiscent of the represen-
tational overlap proposed in the original study (Haxby et al., 2001). This example illustrates a
potential use of the annotation property of DyNeuSR to both qualitatively and quantitatively
examine hidden relationships between different event types in neuroimaging data.

Though annotation and visualization alone can provide some initial insight, it is important
to interpret the shape graph in context of the data that were used to generate it. Dans ce cas,

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 4. Annotating the shape graph with meta-information. The left panel shows how the shape graph can be annotated and colored with
DyNeuSR. Nodes in the shape graph are represented as pie charts to help visualize the different categories of visual stimuli associated with
each node (par exemple., faces, houses). The annotated shape graph can be analyzed, Par exemple, to examine category speciﬁcity. In the right panel,
the similarity of categories is shown for the ﬁrst subject from the Haxby dataset. This similarity can be estimated by comparing the connectivity
of nodes corresponding to the different stimulus categories in the Mapper-generated shape graph.

Neurosciences en réseau

769

Dynamical neuroimaging spatiotemporal representations using TDA

images of the brain can be mapped to the nodes for a more neuroscientiﬁc interpretation of
brain processing across these categories, as discussed next.

To anchor the shape graph properties into anatomy
Anchoring Shape Graphs into Brain Anatomy.
and neurophysiology, spatial maps of brain activity from samples (or time frames) within each
shape graph node and the corresponding neighboring nodes can be averaged and overlaid onto
an anatomical image of the brain. In addition to mere averaging, more advanced techniques
like Spatial Mixture Modeling can also be used (Saggar et al., 2018).

Chiffre 5 shows several spatial brain activation patterns in the ventral stream estimated from
nodes corresponding to resting state, three different categories of visual stimuli, and control
stimuli (c'est à dire., scrambled images). These anatomical overlays were estimated by averaging over
spatial maps of brain activity associated with time frames sharing (or linking to) one or more
similar nodes in the shape graph. It is important to note that because nodes in the shape graph
contain samples (or time frames) that are very similar, and not necessarily sequential, averaging
over these samples has been previously shown to be effective in capturing task-related brain
activation patterns at the highest temporal resolution (Saggar et al., 2018).

Using the Haxby dataset as an example, one could explore how spatial maps of brain activ-
ity evolve over time as the participant transitions from one kind of stimuli to another. Plus loin,
the individual variations in such evolution could be used a potential biomarker for var-
ious mental disorders. In Supplemental Movie 1 (Informations complémentaires), we provide such
an exploration of brain activation patterns over time extracted from the Mapper-generated
shape graph.

Capturing Temporal Transitions in Brain Activity. DyNeuSR can also be used to capture tempo-
ral dynamics and transitions in data based on the shape graph. To estimate temporal transitions
in brain activity, the compressed shape graph can be transformed back to the original space

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 5. Anchoring the shape graph into brain anatomy. Ici, average spatial maps of brain activity in the ventral temporal cortex esti-
mated for individual time frames associated with different categories of visual stimuli are shown for the ﬁrst subject from the Haxby study.
Supplemental Figure 5 (Informations complémentaires) depicts this feature with the user interface.

Neurosciences en réseau

770

Dynamical neuroimaging spatiotemporal representations using TDA

of samples (or time frames). Such transformation then allows for examining relationships in
the data at the highest level of temporal resolution (Saggar et al., 2018). This transformation is
done by converting a Mapper-generated shape graph into an adjacency matrix in the tempo-
ral domain (c'est à dire., a temporal connectivity matrix, TCM). Ici, the time frames are considered
connected (or similar) if they share a node in the shape graph or if the nodes containing these
time frames are connected by an edge in the shape graph. Remarquablement, the degree of TCM
corresponds to the similarity of brain activation patterns captured at individual time frames
and can be used to identify temporal transitions between different states of brain activity
(at the level of individual time frames).

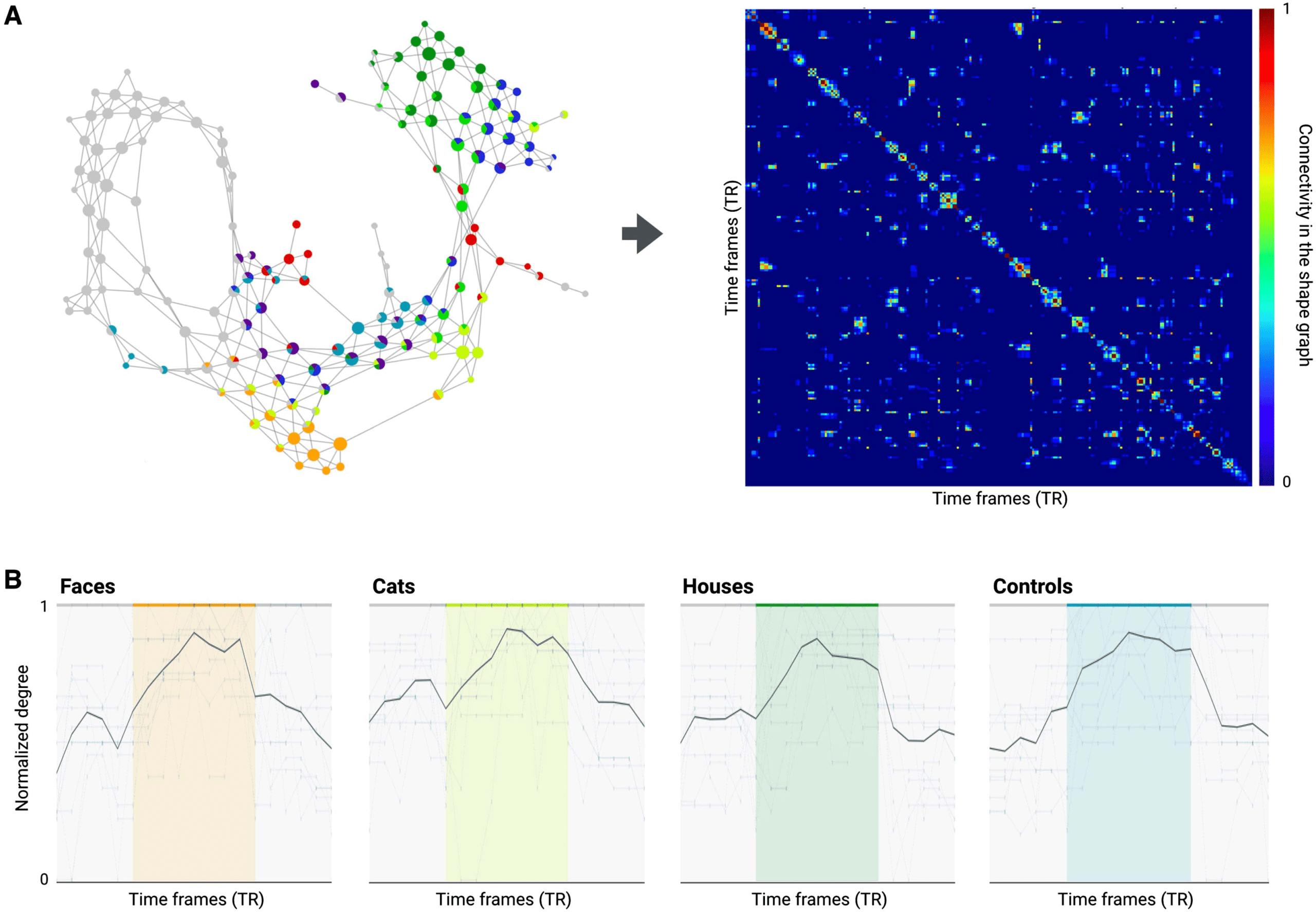
Chiffre 6 shows the temporal connectivity matrix from the ﬁrst Haxby participant. The onset,
duration, and offset of stimulus blocks and the associated temporal connectivity and degree of
TCM are shown for four different categories of visual stimuli. Qualitative analysis conﬁrms that
the temporal connectivity can reveal these temporal transitions at the level of individual time

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 6. Capturing temporal transitions with shape graphs. (UN) The shape graph and the temporal connectivity matrix (TCM) are shown for
the ﬁrst subject to illustrate how the shape graph can be projected back into the time domain. (B) The average temporal connectivity across
subjects is shown for time frames associated with each of the different stimulus categories, illustrating how the degree of TCM can capture the
onset and offset of stimulus blocks. The colored bars represent different categories of visual stimuli, and white space between colored bars
represents rest.

Neurosciences en réseau

771

Dynamical neuroimaging spatiotemporal representations using TDA

frames, and a time frame by time frame analysis suggests that the degree of TCM can capture
both onset and offset of stimulus blocks for different categories of visual stimuli (colored bars
in Figure 6). These results are similar to those reported by Saggar et al. (2018), where transitions
between different types of cognitive tasks were captured from whole-brain activity. Our results
help to validate this approach to characterizing dynamic aspects of brain activity. More work
will be required, cependant, to extend the approach to capture transitions in brain activity when
no stimulus information is provided, Par exemple, during rest.

DISCUSSION

In this paper, we introduce DyNeuSR, an open source Python platform for exploring, ana-
lyzing, and anchoring Mapper-generated topological graphs into known neurophysiological
correlates. Speciﬁcally, DyNeuSR was designed to help users (un) annotate Mapper-generated
shape graphs with meta-information; (b) anchor shape graphs to known neuroanatomical cor-
relates; et (c) study topological properties of shape graphs to capture temporal transitions
between coactivated brain patterns. We hope DyNeuSR will enable and encourage the larger
neuroscience community to harness Mapper-based methods more effectively.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Prior Work

Although TDA-based Mapper technique was recently developed (Singh et al., 2007), it has
already been successfully applied to a variety of datasets. Outside of the neuroscience ﬁeld,
Mapper has been productively applied to reveal the shape of genetic data in breast cancer
patients, where the shape graph was used to identify a unique subgroup of patients that ex-
hibit 100% survival and no metastasis (Nicolau, Levine, & Carlsson, 2011). Mapper has also
been used to characterize transient intermediate or transition states of biomolecular folding
pathways (Yao et al., 2009), and to reveal implicit subgroups within the U.S. House of Repre-
sentatives based on voting behavior (Lum et al., 2013).

Within neuroscience and neuroimaging ﬁelds, Mapper has been mostly employed at the
population or group level to parse heterogeneity in data and identify subgroups that portray
unique characteristics. Par exemple, Mapper has been recently used to parse heterogeneity in
patient populations and to identify clinically distinct neurophenotypes in children with fragile
X syndrome (Bruno et al., 2017; Romano et al., 2014); patients with osteoarthritis (Pedoia et al.,
2018; Rossi-deVries et al., 2018); patients with myalgic encephalomyelitis/chronic fatigue syn-
drome (Nagy-Szakal et al., 2017); inpatients with serious mental illness (Madan et al., 2017);
patients with mild traumatic brain injury (Nielson et al., 2015); and individuals diagnosed with
attention-deﬁcit/hyperactivity disorder (Kyeong et al., 2015).

Unlike group-based studies, one unique feature of Mapper is that it allows users to extract
insights at the level of individual participants, thereby helping users better understand individ-
ual differences in the brain’s dynamical organization (Saggar et al., 2018). Whereas standard
neuroimaging analyses typically average or collapse the data into lower dimensional repre-
sentations early on during the analysis, Mapper retains information about the original high-
dimensional space throughout the analysis. Ainsi, the representations produced by Mapper
could thereby provide novel measures of the neurophysiology underlying observed behavior.
In the future, research should be done to assess whether Mapper-generated representations are
robust and sensitive for predicting translational outcomes as well as for grounding psychiatric
illnesses in biological mechanisms. DyNeuSR is designed to support both group-based and
individual-based applications of Mapper.

Neurosciences en réseau

772

Dynamical neuroimaging spatiotemporal representations using TDA

Mapper has also been hypothesized to help visualize neural state-space traversal using dy-
namical networks (Khambhati, Sizemore, Betzel, & Bassett, 2018). As shown here, when ap-
plied to the Haxby visual decoding dataset, the DyNeuSR platform allows exploration of the
continuous unfolding of brain dynamics across each time frame. Plus loin, by allowing annota-
tion of shape graphs based on meta-information (par exemple., category of visual stimuli presented),
DyNeuSR also enables multimodal data exploration. Dernièrement, individual nodes in the shape
graph can be anchored into neurophysiological correlates and examined across the period
of one or more scans using interactive tools provided in the DyNeuSR platform.

Future Applications

Over the last 10 années, there has been a huge surge in collecting and aggregating spatio-
temporally rich neuroimaging data. Plus loin, advances in technology have enabled more shar-
ing of data across the world. Dans 2014, plus que 8,000 MRI datasets alone were shared
online (Poldrack & Gorgolewski, 2014). To take advantage of this widespread access to spatio-
temporally rich high-dimensional datasets, novel methods are needed to extract computational
insights that are robust against noise, reproducible, and biologically valid. The ultimate aim is
to produce methods that can translate neuroscientiﬁc knowledge into clinical applications.

We argue that methods like TDA-based Mapper are well-suited for this challenge. Comme indiqué
previously, Mapper can be employed at the population level to parse out heterogeneity and
reveal the underlying structure of the data when applied at the individual level. Plus loin, unlike
traditional machine learning algorithms, Mapper makes fewer assumptions about the under-
lying data; represents the underlying structure as a combinatorial object (c'est à dire., graph), dont
topological properties can be easily quantiﬁed; and provides coordinate and deformation in-
variance properties, making it suitable for examining within and between participants’ data
(Carlsson, 2009). Dernièrement, because of the partial clustering step, Mapper-based analysis is com-
putationally robust to handle very large datasets.

Cognitive and clinical neuroscientists have started incorporating macroscopic imaging
methods into assessments of brain dynamics to develop more personalized diagnostic and ther-
apeutic strategies (Williams, 2017). DyNeuSR anchors topological data analysis into anatom-
ical structure, enabling potentially quick data analysis for practical clinical use. Par exemple,
there are many cases of brain dysfunction or disease that manifest as changes in the dynamical
landscape of brain activity (Du et al., 2018, 2017). Ainsi, it should be possible to discriminate
between these dysfunctional brain dynamics and disordered cognitive states, and DyNeuSR
has the potential to enable such discrimination in a research or clinical setting.

Topological data analysis offers compact and insightful visualization of high-dimensional
neuroimaging data, and as a result, facilitates the characterization of large-scale structural
and functional brain networks. Although the examples presented here focus on fMRI data,
the core components of DyNeuSR can be easily extended to a diversity of other applications
and data types. Par exemple, future research plans include extending DyNeuSR to structural
connectivity estimated from diffusion tensor imaging (DTI). It should also be noted that TDA
approaches are amenable to other sources of neuroscience data as well, including invasive
neurophysiological, optical imaging, and spike recordings obtained from model organisms.

Limitations

One of the major limitations of Mapper is that the topology of shape graph highly depends
on the chosen ﬁlter function (par exemple., linear vs. nonlinear) and resolution/gain parameters. While
the topological observables are typically robust by construction to parameter perturbations, comme

Neurosciences en réseau

773

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamical neuroimaging spatiotemporal representations using TDA

shown in Saggar et al. (2018), it would be still very useful to quantify the effect of perturbations
in parameter or ﬁlter space. Carrière, Michel, & Oudot (2018) attempted to automate parameter
selection; cependant, it remains unclear how to compare Mapper graphs obtained from different
ﬁlter functions. Such comparisons would likely require information-theoretic methods based
on clustering comparison (par exemple., Gates, Wood, Hetrick, & Ahn, 2017), or graph-size agnostic
topological methods, such as distances in persistent homology (Bergomi, Ferri, & Zufﬁ, 2017;
Reininghaus, Huber, Bauer, & Kwitt, 2015). Plus loin, random null models that constrain speciﬁc
properties of the Mapper graph can be used to establish the signiﬁcance of the observed
features, analogous to how random network models are used in network science. While
random topological models have been proposed (Costa & Farber, 2016; Kahle, 2009; Zuev,
Eisenberg, & Krioukov, 2015), few can be directly compared with the (typically irregular)
structures obtained from data (par exemple., Jeune, Petri, Vaccarino, & Patania, 2017). Par conséquent,
the inability to make these direct comparisons could potentially impede statistical validation
of Mapper results.

Néanmoins, like any other machine learning technique, interpretation of Mapper results
should always be taken in the context of model parameters. Plus loin, choice of ﬁlter functions
and other Mapper parameters also make this tool extremely versatile for both data exploration
and feature extraction in large, complex datasets (Phinyomark et al., 2017), for example by
providing topological maps of feature spaces that can guide the choice of relevant features.
Finalement, the choice of ﬁlter function depends on both the data itself and the research ques-
tions at hand. Par exemple, Supplemental Figure 2 (Informations complémentaires) shows how using
PCA as a linear ﬁlter function, Mapper is able to capture global differences in the data, tel que
rest versus stimuli presentation. In addition to this global structure in the data, cependant, en utilisant
t-SNE as a nonlinear ﬁlter function, Mapper is able to capture additional local structure in the
data, as indicated by more ﬁne-scale differentiation of different stimulus categories.

Conclusions

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

DyNeuSR is still in the early stages of development, and it has the potential to grow in exciting
and novel ways. Some future research directions include (un) developing a new ﬁlter function
for neuroimaging data that utilizes structural connectome; (b) linking the neurophysiological
correlates obtained from the Mapper shape graph to standard dynamic functional connectivity;
et (c) applying persistent homology to analyze DyNeuSR results.

As we continue to develop and reﬁne DyNeuSR, we invite others to contribute. By making
DyNeuSR an open source tool, we hope that future work on DyNeuSR will be a collaborative
and productive effort. Ainsi, to accelerate such efforts and encourage distributed open source
development, our priorities include refactoring, testing, and documenting the codebase. Future
code development will also include integrating other tools from topological data analysis.

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

To help share this software with the neuroimaging community, we plan on developing
additional tutorials and examples demonstrating the use of Mapper in other neuroimaging
datasets. Par exemple, in other disciplines, researchers often leverage Mapper to visualize
high-dimensional datasets and detect outliers in the data. We plan on exploring how re-
searchers can leverage DyNeuSR’s visualization tools to detect outliers in raw fMRI data
during preprocessing. We hope researchers can use DyNeuSR in combination with other
software packages for fMRI data preprocessing, such as fMRIPrep (Esteban et al., 2018) et
C-PAC (Sikka et al., 2014).

Neurosciences en réseau

774

Dynamical neuroimaging spatiotemporal representations using TDA

We think DyNeuSR can offer unique insight into neuroimaging data analysis and visual-
ization. To this end, we also hope to integrate DyNeuSR with widely used Python software,
such as Nilearn (nilearn.github.io) and nipy (github.com/nipy/nipy). Enfin, to improve the de-
scriptive power of DyNeuSR, we welcome the addition of network and simplicial packages
within DyNeuSR’s analytical framework, such as graph-tool (graph-tool.skewed.de), GUDHI
(gudhi.gforge.inria.fr), and SNAP (snap.stanford.edu).

MATERIALS AND METHODS

Datasets

We used the following two datasets: (un) synthetic 3-D trefoil knot data; et (b) real neuro-
imaging data from the Haxby visual decoding experiment. Below, we will brieﬂy describe
each of these datasets.

The ﬁrst dataset consists of a synthetic set of data points sampled from a three-
Trefoil Knot.
dimensional trefoil knot. The space is parameterized by a set of sin and cos functions over
the domain (0, 2π) deﬁning the position of n sampled points in x−, y−, and z−dimensions.
Speciﬁcally, the following equations describe the parameters:

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

φ ∈ [0, 2π]
x = sin (φ) + 2 cos (2φ)
y = sin (φ) − 2 cos (2φ)
z = − sin (3φ)

The code to sample data from these equations was implemented using the Numerical Python
(NumPy) software package. To see the Python code used to load and prepare the data, please
refer to the Jupyter notebook provided in Supplemental Data 1 (Informations complémentaires).

Haxby fMRI Dataset. We also explored a fMRI dataset from a study on face and object recog-
nition in the human ventral temporal cortex (Haxby et al., 2001). Dans cette étude, visual stimuli
from eight different categories were shown to six different subjects over 12 sessions per subject.
In each session, fMRI data were collected while subjects passively viewed grayscale images
from the eight different categories grouped into stimulus blocks and separated by periods of
repos. Speciﬁcally, during each 24-s block of images, each image was presented for 500 ms and
followed by an interstimulus interval (ISI) de 1,500 ms. The data were collected with a volume
repetition time (TR) de 2,500 ms, which means around nine volumes were collected for each
stimulus category per session. The fMRI data were stored as a 4-D NIfTI time series image,
consisting of 1,452 volumes with 40 × 64 × 64 voxels (c'est à dire., corresponding to a voxel size =
3.5 × 3.75 × 3.75 mm). A NIfTI image mask of the ventral temporal cortex was used to extract
a subset of voxels relevant to visual decoding.

To download the Haxby dataset, we used Nilearn’s API. We also used Nilearn to load and
preprocess the NIfTI time series images and extract NumPy matrix representations for input
to Mapper. For each of the six subjects, we used as the input to Mapper a matrix with time
frames as rows and voxels as columns. Speciﬁcally, we used 242 time frames from Sessions 4
et 5, and we used voxels from each subjects’ ventral temporal cortex (par exemple., 577 voxels for the
ﬁrst subject, 348 voxels for the sixth subject). We used subject-speciﬁc NIfTI anatomical masks
provided with the dataset to identify the speciﬁc voxels corresponding to each subjects’ ventral
cortex temporal. We used Stochastic Neighborhood Embedding (t-SNE; Maaten & Hinton,

Neurosciences en réseau

775

Dynamical neuroimaging spatiotemporal representations using TDA

2008) as a lens for ﬁltering, and a resolution of 17 and gain of 3 (c'est à dire., 66.7% overlap) as cover
parameters for binning. To see the Python code used to load and prepare the data, please refer
to the Jupyter notebook provided in Supplemental Data 2 (Informations complémentaires).

Mapper Implementation

In this work, we generated all shape graphs with the open source KeplerMapper Python
package (Saul & van Veen, 2017).

Overview of DyNeuSR

DyNeuSR is a Python package for interactive graph visualization and neuroscientiﬁc analysis
of Mapper-generated shape graphs.

Installation. DyNeuSR can be installed as a Python module and imported into any Python
environment. The current implementation requires Python 3.

The primary way to visualize and interact with
Visualizing and Interacting with Shape Graphs.
the shape graph is through DyNeuSR’s web-based interface. This interface is automatically gen-
erated using a combination of HTML, JavaScript, and D3. As shown in Supplemental Figure 4
(Informations complémentaires), the interface is composed of three main parts: (un) an annotated shape
graph with a force-directed layout; (b) a panel with information about the shape graph (par exemple.,
source ﬁle name, color legend); et (c) a hover box that displays information about individual
nodes (par exemple., labels). De plus, every node assigned more than a single color (or annotation) est
represented as a pie chart with slices proportional to the number of samples in each group.

To anchor the Mapper-generated graphical repre-
Anchoring Shape Graphs into Brain Anatomy.
sentation in neurophysiology, DyNeuSR provides different ways to estimate and visualize rep-
resentative brain activation (and deactivation) maps for each node in the shape graph. Users
can generate plots of the estimated brain activation patterns using Nilearn, and the resulting
images can be included in the hover box assigned to each node in the shape graph.

Capturing Temporal Transitions in Brain Activity. DyNeuSR provides methods for capturing tem-
poral dynamics and transitions in data based on the shape graph. By default, after constructing
a NetworkX graphical object representation of the shape graph, DyNeuSR creates a temporal
connectivity matrix (TCM) based on the node membership and connectivity of time frames (ou
samples). Speciﬁcally, the TCM encodes the similarity between all the time frames (or across
samples). The degree of nodes in the TCM can then be used to identify temporal transitions
associated with task-related brain activity (Saggar et al., 2018). For each node in the TCM,
the degree is estimated as the number of connecting nonzero edges. This approach can also
be used to describe the temporal (or sample) evolution of other graph metrics. At this time,
DyNeuSR only offers tools for estimating temporal connectivity using the normalized degree
of nodes in the shape graph. Cependant, the code could easily be extended to leverage other
graph measures.

INFORMATIONS À L'APPUI

DyNeuSR is an open source project. The code, documentation, and example tutorials are
publicly available at http://bdl.stanford.edu/projects/dyneusr.

Supplementary ﬁgures, data, and movies are available at https://doi.org/10.1162/netn_a_
00093.

Neurosciences en réseau

776

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamical neuroimaging spatiotemporal representations using TDA

CONTRIBUTIONS DES AUTEURS

Caleb Geniesse:
Enquête; Méthodologie; Logiciel; Visualisation; En écrivant – Review &
Editing. Olaf Sporns: Méthodologie; Validation; En écrivant – Review & Editing. Giovanni Petri:
Méthodologie; Validation; En écrivant – Review & Editing. Manish Saggar: Conceptualisation; Données
curation; Acquisition de financement; Enquête; Méthodologie; Gestion de projet; Logiciel;
Surveillance; Validation; Visualisation; En écrivant – Original Draft; En écrivant – Review & Editing.

INFORMATIONS SUR LE FINANCEMENT

Manish Saggar, National Institute of Mental Health (http://dx.doi.org/10.13039/100000025),
Award ID: R00 MH104605. Caleb Geniesse, National Institute of General Medical Sciences
(http://dx.doi.org/10.13039/100000057), Award ID: T32 GM008294. Manish Saggar, National
Institutes of Health (http://dx.doi.org/10.13039/100000002), Award ID: DP2 MH119735.

RÉFÉRENCES

Bergomi, M.. G., Ferri, M., & Zufﬁ, L. (2017). Topological graph per-

sistence. arXiv:1707.09670.

Bruno, J.. L., Romano, D., Mazaika, P., Lightbody, UN. UN., Hazlett,
H. C., Piven, J., & Reiss, UN. L. (2017). Longitudinal identiﬁca-
tion of clinically distinct neurophenotypes in young children
with fragile X syndrome. Proceedings of the National Academy of
les sciences, 114(40), 10767–10772. https://doi.org/10.1073/pnas.
1620994114

Carlsson, G. (2009). Topology and data. Bulletin of the American
Mathematical Society, 46(2), 255–308. https://doi.org/10.1090/
S0273-0979-09-01249-X

Carrière, M., Mitchel, B., & Oudot, S. (2018). Statistical analysis
and parameter selection for mapper. Journal of Machine Learning
Research, 19, 1–39.

Costa, UN., & Farber, M.. (2016). Random simplicial complexes. Dans
F. Callegaro, F. Cohen, C. De Concini, E. Feichtner, G. Gaifﬁ, &
M.. Salvetti (Éd.), Conﬁguration spaces (Springer INdAM series,
Vol. 14, pp. 129–153). Cham, Suisse: Springer International
Édition. https://doi.org/10.1007/978-3-319-31580-5_6
J.,

.
Calhoun, V. D. (2018). Dynamic functional connectivity impair-
ments in early schizophrenia and clinical high-risk for psychosis.
NeuroImage, 180, 632–645. https://doi.org/10.1016/j.neuroimage.
2017.10.022

Du, Y., Fryer, S. L., Fu, Z., Lin, D., Sui,

J., Chen,

Du, Y., Pearlson, G. D., Lin, D., Sui, J., Chen, J., Salman, M., . . .
Calhoun, V. D. (2017). Identifying dynamic functional connec-
tivity biomarkers using GIG-ICA: Application to schizophrenia,
schizoaffective disorder, and psychotic bipolar disorder. Human
Brain Mapping, 38(5), 2683–2708. https://doi.org/10.1002/hbm.
23553

Esteban, O., Markiewicz, C., Blair, R.. W., Moodie, C., Isik, UN. JE.,
Aliaga, UN. E., . . . Gorgolewski, K. J.. (2018). FMRIPrep: A ro-
bust preprocessing pipeline for functional MRI. bioRxiv:306951.
https://doi.org/10.1101/306951

Gates, UN. J., Wood, je. B., Hetrick, W. P., & Ahn, Y.-Y. (2017).
On comparing clusterings: An element-centric framework uni-
ﬁes overlaps and hierarchy. arXiv:1706.06136.

Geniesse, C., Sporns, O., Petri, G., & Saggar, M.. (2018). Gen-
erating dynamical neuroimaging spatiotemporal representations
(DyNeuSR) using topological data analysis. http://bdl.stanford.
edu/projects/dyneusr

Haxby, J.. V., Gobbini, M.. JE., Furey, M.. L., Ishai, UN., Schouten, J.. L., &
Pietrini, P.. (2001). Distributed and overlapping representations of
faces and objects in ventral temporal cortex. Science, 293(5539),
2425–2430. https://doi.org/10.1126/science.1063736

Kahle, M.. (2009). Topology of random clique complexes. Discrete
Mathematics, 309(6), 1658–1671. https://doi.org/10.1016/j.disc.
2008.02.037

Karahano˘glu, F. JE., & Van De Ville, D. (2015). Transient brain activ-
ity disentangles fMRI resting-state dynamics in terms of spatially
and temporally overlapping networks. Communications naturelles,
6(1), 7751. https://doi.org/10.1038/ncomms8751

Khambhati, UN. N., Sizemore, UN. E., Betzel, R.. F., & Bassett, D. S.
(2018). Modeling and interpreting mesoscale network dynam-
ics. NeuroImage, 180(Pt. B), 337–349. https://est ce que je.org/10.1016/
j.neuroimage.2017.06.029

Kyeong, S., Parc, S., Cheon, K.-A., Kim, J.-J., Song, D.-H., & Kim,
E. (2015). A new approach to investigate the association be-
tween brain functional connectivity and disease characteristics of
attention-deﬁcit/hyperactivity disorder: Topological neuroimag-
ing data analysis. PloS ONE, 10(9), e0137296. https://est ce que je.org/
10.1371/journal.pone.0137296

Liu, X., & Duyn, J.. H. (2013). Time-varying functional network
instances of spontaneous
information extracted from brief
brain activity. Proceedings of
the National Academy of
les sciences, 110(11), 4392–4397. https://doi.org/10.1073/pnas.
1216856110

Liu, X., Zhang, N., Chang, C., & Duyn, J.. H. (2018). Co-activation
patterns in resting-state fMRI signals. NeuroImage, 180(Pt. B),
485–494. https://doi.org/10.1016/j.neuroimage.2018.01.041
Lum, P.. Y., Singh, G., Lehman, UN., Ishkanov, T., Vejdemo-Johansson,
M., Alagappan, M., . . . Carlsson, G. (2013). Extracting insights
from the shape of complex data using topology. Scientiﬁc Re-
ports, 3, 1236. https://doi.org/10.1038/srep01236

Neurosciences en réseau

777

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamical neuroimaging spatiotemporal representations using TDA

Maaten, L., & Hinton, G. (2008). Visualizing data using t-SNE. Jour-

nal of Machine Learning Research, 9, 2579–2605.

Madan, UN., Fowler, J.. C., Patriquin, M.. UN., Salas, R., Baldwin, P.. R.,
Velasquez, K. M., . . . Frueh, C. (2017). A novel approach
to identifying a neuroimaging biomarker
for patients with
serious mental illness. Journal of Neuropsychiatry and Clinical
Neurosciences, 29(3), 275–283. https://doi.org/10.1176/appi.
neuropsych.16090174

Nagy-Szakal, D., Williams, B. L., Mishra, N., Che, X., Lee, B.,
Bateman, L., . . . Lipkin, W. je. (2017). Fecal metagenomic proﬁles
in subgroups of patients with myalgic encephalomyelitis/chronic
fatigue syndrome. Microbiome, 5(1), 44. https://doi.org/10.1186/
s40168-017-0261-y

Nicolau, M., Levine, UN. J., & Carlsson, G. (2011). Topology based
data analysis identiﬁes a subgroup of breast cancers with a
unique mutational proﬁle and excellent survival. Proceedings of
the National Academy of Sciences, 108(17), 7265–7270.

Nielson, J.. L., Paquette, J., Liu, UN. W., Guandique, C. F., Tovar, C. UN.,
Inoué, T., . . . Ferguson, UN. R.. (2015). Topological data analysis for
discovery in preclinical spinal cord injury and traumatic brain in-
jury. Communications naturelles, 6, 8581. https://doi.org/10.1038/
ncomms9581

Pedoia, V., Haefeli, J., Morioka, K., Teng, H.-L., Nardo, L., Souza,
R.. B., . . . Majumdar, S. (2018). MRI and biomechanics multi-
dimensional data analysis reveals R2-R1ρ as an early predictor
of cartilage lesion progression in knee osteoarthritis. Journal de
Magnetic Resonance Imaging, 47(1), 78–90. https://est ce que je.org/10.
1002/jmri.25750

Phinyomark, UN., Ibanez-Marcelo, E., & Petri, G. (2017). Resting-
state fMRI functional connectivity: Big data preprocessing pipe-
lines and topological data analysis. IEEE Transactions on Big Data,
3(4), 415–428. https://doi.org/10.1109/tbdata.2017.2734883
Poldrack, R.. UN., & Gorgolewski, K. J.. (2014). Making big data open:
Data sharing in neuroimaging. Neurosciences naturelles, 17(11),
1510–1517. https://doi.org/10.1038/nn.3818

Preti, M.. G., Bolton, T. UN., & Van De Ville, D. (2016). The dy-
namic functional connectome: State-of-the-art and perspectives.
NeuroImage. https://doi.org/10.1016/j.neuroimage.2016.12.061
Reininghaus, J., Huber, S., Bauer, U., & Kwitt, R.. (2015). A sta-
ble multi-scale kernel for topological machine learning (Vol. 7,
pp. 4741–4748). Presented at the Proceedings of the IEEE Com-
puter Society Conference on Computer Vision and Pattern Recog-
nition, IEEE. https://doi.org/10.1109/CVPR.2015.7299106

Romano, D., Nicolau, M., Quintin, E.-M., Mazaika, P.. K.,
Lightbody, UN. UN., Cody Hazlett, H., . . . Reiss, UN. L. (2014).
Topological methods reveal high and low functioning neuro-

phenotypes within fragile X syndrome. Human Brain Mapping.
https://doi.org/10.1002/hbm.22521

Rossi-deVries, J., Pedoia, V., Samaan, M.. UN., Ferguson, UN. R., Souza,
R.. B., & Majumdar, S. (2018). Using multidimensional topologi-
cal data analysis to identify traits of hip osteoarthritis. Journal de
Magnetic Resonance Imaging, 48(4), 1046–1058. https://est ce que je.org/
10.1002/jmri.26029

Saggar, M., Sporns, O., Gonzalez-Castillo, J., Bandettini, P.. UN.,
Carlsson, G., Glover, G., & Reiss, UN. L. (2018). Towards a new
approach to reveal dynamical organization of the brain using
topological data analysis. Communications naturelles, 9(1), 1399.
Saul, N., & van Veen, H. J.. (2017). MLWave/kepler-mapper: 186F.

Zenodo. https://doi.org/10.5281/zenodo.1054444

Shine, J.. M., Koyejo, O., Cloche, P.. T., Gorgolewski, K. J., Gilat,
M., & Poldrack, R.. UN.
(2015). Estimation of dynamic func-
tional connectivity using Multiplication of Temporal Derivatives.
NeuroImage, 122, 399–407. https://doi.org/10.1016/j.neuroimage.
2015.07.064

Sikka, S., Cheung, B., Khanuja, R., Ghosh, S., Yan, C., Li, Q.,
. . . Milham, M.. (2014). Towards automated analysis of con-
nectomes: The conﬁgurable pipeline for the analysis of con-
nectomes (C-PAC). Frontiers in Neuroinformatics. Conference
abstract: 5th INCF Congress of Neuroinformatics. https://est ce que je.org/
10.3389/conf.fninf.2014.08.00117

Singh, G., Mémoli, F., & Carlsson, G. E. (2007). Topological meth-
ods for the analysis of high dimensional data sets and 3d object
reconnaissance. Symposium on Point Based Graphics.

Williams, L. M.. (2017). Getting personalized: Brain scan biomark-
ers for guiding depression interventions. American Journal of
Psychiatry, 174(6), 503–505. https://doi.org/10.1176/appi.ajp.
2017.17030314

Xu, Y., & Lindquist, M.. UN. (2015). Dynamic connectivity detection:
An algorithm for determining functional connectivity change
points in fMRI data. Frontiers in Neuroscience, 9(143), 285.
https://doi.org/10.3389/fnins.2015.00285

Yao, Y., Sun, J., Huang, X., Bowman, G. R., Singh, G., Lesnick,
M., . . . Carlsson, G. (2009). Topological methods for explor-
ing low-density states in biomolecular folding pathways. Journal
of Chemical Physics, 130(14), 144115. https://doi.org/10.1063/
1.3103496

Jeune, J.. G., Petri, G., Vaccarino, F., & Patania, UN. (2017). Construc-
tion of and efﬁcient sampling from the simplicial conﬁguration
model. Physical Review E, 96(3), 477. https://doi.org/10.1103/
PhysRevE.96.032312

Zuev, K., Eisenberg, O., & Krioukov, D. (2015). Exponential ran-
dom simplicial complexes. Journal of Physics A: Mathématique
and Theoretical, 48(46), 465002. https://doi.org/10.1088/1751-
8113/48/46/465002

Neurosciences en réseau

778

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

3
3
7
6
3
1
0
9
2
4
9
3
n
e
n
_
un
_
0
0
0
9
3
p
d