Feature-Frequency–Adaptive On-line
Training for Fast and Accurate Natural
Language Processing
Xu Sun∗
Peking University
Wenjie Li∗∗
Hong Kong Polytechnic University
Houfeng Wang†
Peking University
Qin Lu‡
Hong Kong Polytechnic University
Training speed and accuracy are two major concerns of large-scale natural language processing
systèmes. Typiquement, we need to make a tradeoff between speed and accuracy. It is trivial to improve
the training speed via sacrificing accuracy or to improve the accuracy via sacrificing speed.
Nevertheless, it is nontrivial to improve the training speed and the accuracy at the same time,
which is the target of this work. To reach this target, we present a new training method, feature-
frequency–adaptive on-line training, for fast and accurate training of natural language process-
ing systems. It is based on the core idea that higher frequency features should have a learning rate
that decays faster. Theoretical analysis shows that the proposed method is convergent with a fast
convergence rate. Experiments are conducted based on well-known benchmark tasks, y compris
named entity recognition, word segmentation, phrase chunking, and sentiment analysis. These
tasks consist of three structured classification tasks and one non-structured classification task,
with binary features and real-valued features, respectivement. Experimental results demonstrate
that the proposed method is faster and at the same time more accurate than existing methods,
achieving state-of-the-art scores on the tasks with different characteristics.
∗ Key Laboratory of Computational Linguistics (Peking University), Ministry of Education, Beijing, Chine,
and School of EECS, Peking University, Beijing, Chine. E-mail: xusun@pku.edu.cn.
∗∗ Department of Computing, Hong Kong Polytechnic University, Hung Hom, Kowloon 999077, Hong
Kong. E-mail: cswjli@comp.polyu.edu.hk.
† Key Laboratory of Computational Linguistics (Peking University), Ministry of Education, Beijing, Chine,
and School of EECS, Peking University, Beijing, Chine. E-mail: wanghf@pku.edu.cn.
‡ Department of Computing, Hong Kong Polytechnic University, Hung Hom, Kowloon 999077, Hong
Kong. E-mail: csluqin@comp.polyu.edu.hk.
Submission received: 27 Décembre 2012; revised version received: 30 May 2013; accepted for publication:
16 Septembre 2013.
est ce que je:10.1162/COLI a 00193
© 2014 Association for Computational Linguistics
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
je
je
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
je
je
_
un
_
0
0
1
9
3
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 40, Nombre 3
1. Introduction
Training speed is an important concern of natural language processing (NLP) systèmes.
Large-scale NLP systems are computationally expensive. In many real-world applica-
tion, we further need to optimize high-dimensional model parameters. Par exemple,
the state-of-the-art word segmentation system uses more than 40 million features (Sun,
Wang, and Li 2012). The heavy NLP models together with high-dimensional parameters
lead to a challenging problem on model training, which may require week-level training
time even with fast computing machines.
Accuracy is another very important concern of NLP systems. Nevertheless, usually
it is quite difficult to build a system that has fast training speed and at the same time
has high accuracy. Typically we need to make a tradeoff between speed and accuracy,
to trade training speed for higher accuracy or vice versa. In this work, we have tried
to overcome this problem: to improve the training speed and the model accuracy at the
same time.
There are two major approaches for parameter training: batch and on-line. Standard
gradient descent methods are normally batch training methods, in which the gradient
computed by using all training instances is used to update the parameters of the model.
The batch training methods include, Par exemple, steepest gradient descent, conjugate
gradient descent (CG), and quasi-Newton methods like limited-memory BFGS (Nocedal
and Wright 1999). The true gradient is usually the sum of the gradients from each
individual training instance. Donc, batch gradient descent requires the training
method to go through the entire training set before updating parameters. This is why
batch training methods are typically slow.
On-line learning methods can significantly accelerate the training speed compared
with batch training methods. A representative on-line training method is the stochastic
gradient descent method (SGD) and its extensions (par exemple., stochastic meta descent) (Bottou
1998; Vishwanathan et al. 2006). The model parameters are updated more frequently
compared with batch training, and fewer passes are needed before convergence. Pour
large-scale data sets, on-line training methods can be much faster than batch training
méthodes.
Cependant, we find that the existing on-line training methods are still not good
enough for training large-scale NLP systems—probably because those methods are
not well-tailored for NLP systems that have massive features. D'abord, the convergence
speed of the existing on-line training methods is not fast enough. Our studies show that
the existing on-line training methods typically require more than 50 training passes
before empirical convergence, which is still slow. For large-scale NLP systems, le
training time per pass is typically long and fast convergence speed is crucial. Deuxième,
the accuracy of the existing on-line training methods is not good enough. We want to
further improve the training accuracy. We try to deal with the two challenges at the
same time. Our goal is to develop a new training method for faster and at the same time
more accurate natural language processing.
In this article, we present a new on-line training method, adaptive on-line gradient
descent based on feature frequency information (ADF),1 for very accurate and fast
on-line training of NLP systems. Other than the high training accuracy and fast train-
ing speed, we further expect that the proposed training method has good theoretical
1 ADF source code and tools can be obtained from http://klcl.pku.edu.cn/member/sunxu/index.htm.
564
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
je
je
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
je
je
_
un
_
0
0
1
9
3
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sun et al.
Feature-Frequency–Adaptive On-line Training for Natural Language Processing
properties. We want to prove that the proposed method is convergent and has a fast
convergence rate.
In the proposed ADF training method, we use a learning rate vector in the on-line
updating. This learning rate vector is automatically adapted based on feature frequency
information in the training data set. Each model parameter has its own learning rate
adapted on feature frequency information. This proposal is based on the simple intu-
ition that a feature with higher frequency in the training process should have a learning
rate that decays faster. This is because a higher frequency feature is expected to be
well optimized with higher confidence. Ainsi, a higher frequency feature is expected to
have a lower learning rate. We systematically formalize this intuition into a theoretically
sound training algorithm, ADF.
The main contributions of this work are as follows:
r
r
On the methodology side, we propose a general purpose on-line training
method, ADF. The ADF method is significantly more accurate than
existing on-line and batch training methods, and has faster training speed.
De plus, theoretical analysis demonstrates that the ADF method is
convergent with a fast convergence rate.
On the application side, for the three well-known tasks, including named
entity recognition, word segmentation, and phrase chunking, the proposed
simple method achieves equal or even better accuracy than the existing
gold-standard systems, which are complicated and use extra resources.
2. Related Work
Our main focus is on structured classification models with high dimensional features.
For structured classification, the conditional random fields model is widely used. À
illustrate that the proposed method is a general-purpose training method not limited to
a specific classification task or model, we also evaluate the proposal for non-structured
classification tasks like binary classification. For non-structured classification, the max-
imum entropy model (Berger, Della Pietra, and Della Pietra 1996; Ratnaparkhi 1996)
is widely used. Ici, we review the conditional random fields model and the related
work of on-line training methods.
2.1 Conditional Random Fields
The conditional random field (CRF) model is a representative structured classification
model and it is well known for its high accuracy in real-world applications. The CRF
model is proposed for structured classification by solving “the label bias problem”
(Lafferty, McCallum, and Pereira 2001). Assuming a feature function that maps a pair of
observation sequence xxx and label sequence yyy to a global feature vector fff, the probability
of a label sequence yyy conditioned on the observation sequence xxx is modeled as follows
(Lafferty, McCallum, and Pereira 2001):
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
je
je
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
je
je
_
un
_
0
0
1
9
3
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
P.(yyy|xxx, www) =
where www is a parameter vector.
∑
⊤
exp {www
fff (yyy, xxx)}
′
′
′y
′ exp {www⊤fff (oui
oui
′
′y
∀y
oui
, xxx)}
(1)
565
Computational Linguistics
Volume 40, Nombre 3
Given a training set consisting of n labeled sequences, zzzi = (xxxi, yyyi), for i = 1 . . . n,
parameter estimation is performed by maximizing the objective function,
L(www) =
n∑
je = 1
log P(yyyi
|xxxi, www) − R(www)
(2)
The first term of this equation represents a conditional log-likelihood of training
data. The second term is a regularizer for reducing overfitting. We use an L2 prior,
||www||2
R.(www) =
2(cid:27)2 . In what follows, we denote the conditional log-likelihood of each sample
|xxxi, www) as ℓ(zzzi, www). The final objective function is as follows:
as log P(yyyi
L(www) =
n∑
je = 1
ℓ(zzzi, www) −
||www||2
2σ2
(3)
2.2 On-line Training
The most representative on-line training method is the SGD method (Bottou 1998;
Tsuruoka, Tsujii, and Ananiadou 2009; Sun et al. 2013). The SGD method uses a
randomly selected small subset of the training sample to approximate the gradient of
an objective function. The number of training samples used for this approximation is
called the batch size. By using a smaller batch size, one can update the parameters
more frequently and speed up the convergence. The extreme case is a batch size of 1,
and it gives the maximum frequency of updates, which we adopt in this work. Dans ce
case, the model parameters are updated as follows:
wwwt+1 = wwwt + γt
∇
wwwt
L
stoch(zzzi, wwwt)
(4)
where t is the update counter, γt is the learning rate or so-called decaying rate, et
L
stoch(zzzi, wwwt) is the stochastic loss function based on a training sample zzzi. (More details
of SGD are described in Bottou [1998], Tsuruoka, Tsujii, and Ananiadou [2009], et
Sun et al. [2013].) Following the most recent work of SGD, the exponential decaying
rate works the best for natural language processing tasks, and it is adopted in our
implementation of the SGD (Tsuruoka, Tsujii, and Ananiadou 2009; Sun et al. 2013).
Other well-known on-line training methods include perceptron training (Freund
and Schapire 1999), averaged perceptron training (Collins 2002), more recent devel-
opment/extensions of stochastic gradient descent (par exemple., the second-order stochastic
gradient descent training methods like stochastic meta descent) (Vishwanathan et al.
2006; Hsu et al. 2009), et ainsi de suite. Cependant, the second-order stochastic gradient descent
method requires the computation or approximation of the inverse of the Hessian matrix
of the objective function, which is typically slow, especially for heavily structured classi-
fication models. Usually the convergence speed based on number of training iterations
is moderately faster, but the time cost per iteration is slower. Thus the overall time cost
is still large.
Compared with the related work on batch and on-line training (Jacobs 1988;
Sperduti and Starita 1993; Dredze, Crammer, and Pereira 2008; Duchi, Hazan, et
Chanteur 2010; McMahan and Streeter 2010), our work is fundamentally different. Le
proposed ADF training method is based on feature frequency adaptation, and to the best
of our knowledge there is no prior work on direct feature-frequency–adaptive on-line
566
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
je
je
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
je
je
_
un
_
0
0
1
9
3
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sun et al.
Feature-Frequency–Adaptive On-line Training for Natural Language Processing
entraînement. Compared with the confidence-weighted (CW) classification method and its
variation AROW (Dredze, Crammer, and Pereira 2008; Crammer, Kulesza, and Dredze
2009), the proposed method is substantially different. While the feature frequency
information is implicitly modeled via a complicated Gaussian distribution framework
in Dredze, Crammer, and Pereira (2008) and Crammer, Kulesza, and Dredze (2009),
the frequency information is explicitly modeled in our proposal via simple learning
rate adaptation. Our proposal is more straightforward in capturing feature frequency
information, and it has no need to use Gaussian distributions and KL divergence,
which are important in the CW and AROW methods. En outre, our proposal is a
probabilistic learning method for training probabilistic models such as CRFs, alors que
the CW and AROW methods (Dredze, Crammer, and Pereira 2008; Crammer, Kulesza,
and Dredze 2009) are non-probabilistic learning methods extended from perceptron-
style approaches. Ainsi, the framework is different. This work is a substantial extension
of the conference version (Sun, Wang, and Li 2012). Sun, Wang, and Li (2012) focus on
the specific task of word segmentation, whereas this article focuses on the proposed
training algorithm.
3. Feature-Frequency–Adaptive On-line Learning
In traditional on-line optimization methods such as SGD, no distinction is made for
different parameters in terms of the learning rate, and this may result in slow conver-
gence of the model training. Par exemple, in the on-line training process, suppose the
high frequency feature f1 and the low frequency feature f2 are observed in a training
sample and their corresponding parameters w1 and w2 are to be updated via the same
learning rate γt. Suppose the high frequency feature f1 has been updated 100 times
and the low frequency feature f2 has only been updated once. Alors, it is possible that
the weight w1 is already well optimized and the learning rate γt is too aggressive for
updating w1. Updating the weight w1 with the learning rate γt may make w1 be far
from the well-optimized value, and it will require corrections in the future updates. Ce
causes fluctuations in the on-line training and results in slow convergence speed. Sur
the other hand, it is possible that the weight w2 is poorly optimized and the same learn-
ing rate γt is too conservative for updating w2. This also results in slow convergence
speed.
To solve this problem, we propose ADF. In spite of the high accuracy and fast
convergence speed, the proposed method is easy to implement. The proposed method
with feature-frequency–adaptive learning rates can be seen as a learning method with
specific diagonal approximation of the Hessian information based on assumptions of
feature frequency information. In this approximation, the diagonal elements of the
diagonal matrix correspond to the feature-frequency–adaptive learning rates. Accord-
ing to the aforementioned example and analysis, it assumes that a feature with higher
frequency in the training process should have a learning rate that decays faster.
3.1 Algorithm
In the proposed ADF method, we try to use more refined learning rates than traditional
SGD training. Instead of using a single learning rate (a scalar) for all weights, we extend
the learning rate scalar to a learning rate vector, which has the same dimension as the
weight vector www. The learning rate vector is automatically adapted based on feature
567
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
je
je
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
je
je
_
un
_
0
0
1
9
3
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 40, Nombre 3
frequency information. By doing so, each weight has its own learning rate, and we will
show that this can significantly improve the convergence speed of on-line learning.
In the ADF learning method, the update formula is:
wwwt+1 = wwwt + γγγt
··· gggt
(5)
The update term gggt is the gradient term of a randomly sampled instance:
gggt = ∇
wwwt
stoch(zzzi, wwwt) = ∇
L
wwwt
ℓ(zzzi, wwwt) −
{
}
||wwwt
||2
2nσ2
En outre, γγγt
component-wise (Hadamard) product of two vectors.
+ is a positive vector-valued learning rate and ··· denotes the
∈ R f
The learning rate vector γγγt is automatically adapted based on feature frequency
information in the updating process. Intuitively, a feature with higher frequency in the
training process has a learning rate that decays faster. This is because a weight with
higher frequency is expected to be more adequately trained, hence a lower learning
rate is preferable for fast convergence. We assume that a high frequency feature should
have a lower learning rate, and a low frequency feature should have a relatively higher
learning rate in the training process. We systematically formalize this idea into a theoret-
ically sound training algorithm. The proposed method with feature-frequency–adaptive
learning rates can be seen as a learning method with specific diagonal approximation
of the inverse of the Hessian matrix based on feature frequency information.
Given a window size q (number of samples in a window), we use a vector vvv to record
the feature frequency. The kth entry vvvk corresponds to the frequency of the feature k in
this window. Given a feature k, we use u to record the normalized frequency:
u = vvvk/q
For each feature, an adaptation factor η is calculated based on the normalized frequency
information, as follows:
η = α − u(α − β)
where α and β are the upper and lower bounds of a scalar, avec 0 < β < α < 1. Intu-
itively, the upper bound α corresponds to the adaptation factor of the lowest frequency
features, and the lower bound β corresponds to the adaptation factor of the highest
frequency features. The optimal values of α and β can be tuned based on specific real-
world tasks, for example, via cross-validation on the training data or using held-out
data. In practice, via cross-validation on the training data of different tasks, we found
that the following setting is sufficient to produce adequate performance for most of the
real-world natural language processing tasks: α around 0.995, and β around 0.6. This
indicates that the feature frequency information has similar characteristics across many
different natural language processing tasks.
As we can see, a feature with higher frequency corresponds to a smaller scalar via
linear approximation. Finally, the learning rate is updated as follows:
γγγk
← ηγγγk
568
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sun et al.
Feature-Frequency–Adaptive On-line Training for Natural Language Processing
ADF learning algorithm
stoch(zzzi, www)
www ← 0, t ← 0, vvv ← 0, γγγ ← c
repeat until convergence
. Draw a sample zzzi at random from the data set ZZZ
. vvv ← UPDATEFEATUREFREQ(vvv, zzzi)
if t > 0 and t mod q = 0
.
. γγγ ← UPDATELEARNRATE(γγγ, vvv)
.
. vvv ← 0
.
. ggg ← ∇
L
www
. www ← www + γγγ ··· ggg
t ← t + 1
.
return www
1: procedure ADF(ZZZ, www, q, c, un, β)
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:
12:
13:
14: procedure UPDATEFEATUREFREQ(vvv, zzzi)
for k ∈ features used in sample zzzi
15:
. vvvk
16:
return vvv
17:
18:
19: procedure UPDATELEARNRATE(γγγ, vvv)
20:
21:
22:
23:
24:
for k ∈ all features
. u ← vvvk/q
. η ← α − u(α − β)
← ηγγγk
. γγγk
return γγγ
← vvvk + 1
Chiffre 1
The proposed ADF on-line learning algorithm. In the algorithm, ZZZ is the training data set; q, c, un,
and β are hyper-parameters; q is an integer representing window size; c is for initializing the
learning rates; and α and β are the upper and lower bounds of a scalar, avec 0 < β < α < 1.
With this setting, different features correspond to different adaptation factors based
on feature frequency information. Our ADF algorithm is summarized in Figure 1.
The ADF training method is efficient because the only additional computation
(compared with traditional SGD) is the derivation of the learning rates, which is simple
and efficient. As we know, the regularization of SGD can perform efficiently via the opti-
mization based on sparse features (Shalev-Shwartz, Singer, and Srebro 2007). Similarly,
the derivation of γγγt can also perform efficiently via the optimization based on sparse
features. Note that although binary features are common in natural language processing
tasks, the ADF algorithm is not limited to binary features and it can be applied to real-
valued features.
3.2 Convergence Analysis
We want to show that the proposed ADF learning algorithm has good convergence
properties. There are two steps in the convergence analysis. First, we show that the
ADF update rule is a contraction mapping. Then, we show that the ADF training is
asymptotically convergent, and with a fast convergence rate.
To simplify the discussion, our convergence analysis is based on the convex loss
function of traditional classification or regression problems:
L(www) =
n∑
i=1
ℓ(xxxi, yi, www · fff i) −
||www||2
2σ2
569
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 40, Number 3
where fff i is the feature vector generated from the training sample (xxxi, yi). L(www) is a func-
tion in www · fff i, such as 1
− www · fff i)2 for regression or log[1 + exp(−yiwww · fff i)] for binary
classification.
2 (yi
To make convergence analysis of the proposed ADF training algorithm, we need to
introduce several mathematical definitions. First, we introduce Lipschitz continuity:
Definition 1 (Lipschitz continuity)
A function F : X → R is Lipschitz continuous with the degree of D if |F(x) − F(y)| ≤
D|x − y| for ∀x, y ∈ X . X can be multi-dimensional space, and |x − y| is the distance
between the points x and y.
Based on the definition of Lipschitz continuity, we give the definition of the
Lipschitz constant ||F||
Lip as follows:
Definition 2 (Lipschitz constant)
||F||
Lip := inf{D where |F(x) − F(y)| ≤ D|x − y| for ∀x, y}
In other words, the Lipschitz constant ||F||
that makes the function F Lipschitz continuous.
Lip is the lower bound of the continuity degree
Further, based on the definition of Lipschitz constant, we give the definition of
contraction mapping as follows:
Definition 3 (Contraction mapping)
A function F : X → X is a contraction mapping if its Lipschitz constant is smaller than
1: ||F||
Lip < 1.
Then, we can show that the traditional SGD update is a contraction mapping.
Lemma 1 (SGD update rule is contraction mapping)
−1,
Let γ be a fixed low learning rate in SGD updating. If γ ≤ (||x2
i
the SGD update rule is a contraction mapping in Euclidean space with Lipschitz con-
tinuity degree 1 − γ/σ2.
|| · ||∇
′ℓ(xxxi, yi, y
′
′y
y
y
Lip)
)||
′
The proof can be extended from the related work on convergence analysis of parallel
SGD training (Zinkevich et al. 2010). The stochastic training process is a one-following-
one dynamic update process. In this dynamic process, if we use the same update rule F,
we have wwwt+1 = F(wwwt) and wwwt+2 = F(wwwt+1). It is only necessary to prove that the dynamic
update is a contraction mapping restricted by this one-following-one dynamic process.
That is, for the proposed ADF update rule, it is only necessary to prove it is a dynamic
contraction mapping. We formally define dynamic contraction mapping as follows.
Definition 4 (Dynamic contraction mapping)
Given a function F : X → X , suppose the function is used in a dynamic one-following-
∈ X . Then, the function F is a
one process: xt+1 = F(xt) and xt+2 = F(xt+1) for ∀xt
| for ∀xt
− xt+1
dynamic contraction mapping if ∃D < 1, |xt+2
| ≤ D|xt+1
∈ X .
− xt
We can see that a contraction mapping is also a dynamic contraction mapping, but
a dynamic contraction mapping is not necessarily a contraction mapping. We first show
570
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sun et al.
Feature-Frequency–Adaptive On-line Training for Natural Language Processing
that the ADF update rule with a fixed learning rate vector of different learning rates is
a dynamic contraction mapping.
Theorem 1 (ADF update rule with fixed learning rates)
Let γγγ be a fixed learning rate vector with different learning rates. Let γmax be the max-
imum learning rate in the learning rate vector γγγ: γmax := sup{γi where γi
∈ γγγ}. Then
−1, the ADF update rule is a dynamic contraction
if γmax
mapping in Euclidean space with Lipschitz continuity degree 1 − γmax/σ2.
The proof is sketched in Section 5.
′
|| · ||∇
′ℓ(xxxi, yi, y
′
′y
y
y
≤ (||x2
i
Lip)
)||
)||
Lip)
Further, we need to prove that the ADF update rule with a decaying learning
rate vector is a dynamic contraction mapping, because the real ADF algorithm has a
|| ·
decaying learning rate vector. In the decaying case, the condition that γmax
−1 can be easily achieved, because γγγ continues to decay with an
′
||∇
′ℓ(xxxi, yi, y
′
′y
y
y
exponential decaying rate. Even if the γγγ is initialized with high values of learning rates,
after a number of training passes (denoted as T) γγγT is guaranteed to be small enough so
−1. Without
that γmax := sup{γi where γi
losing generality, our convergence analysis starts from the pass T and we take γγγT as γγγ0
in the following analysis. Thus, we can show that the ADF update rule with a decaying
learning rate vector is a dynamic contraction mapping:
′
|| · ||∇
′ℓ(xxxi, yi, y
′
′y
y
y
} and γmax
≤ (||x2
i
≤ (||x2
i
∈ γγγT
Lip)
)||
Theorem 2 (ADF update rule with decaying learning rates)
Let γγγt be a learning rate vector in the ADF learning algorithm, which is decaying
over the time t and with different decaying rates based on feature frequency infor-
≤
mation. Let γγγt start from a low enough learning rate vector γγγ0 such that γmax
−1, where γmax is the maximum element in γγγ0. Then, the ADF
(||x2
i
update rule with decaying learning rate vector is a dynamic contraction mapping in
Euclidean space with Lipschitz continuity degree 1 − γmax/σ2.
The proof is sketched in Section 5.
′
|| · ||∇
′ℓ(xxxi, yi, y
′
′y
y
y
Lip)
)||
Based on the connections between ADF training and contraction mapping, we
demonstrate the convergence properties of the ADF training method. First, we prove
the convergence of the ADF training.
Theorem 3 (ADF convergence)
ADF training is asymptotically convergent.
The proof is sketched in Section 5.
Further, we analyze the convergence rate of the ADF training. When we have the
lowest learning rate γγγt+1 = βγγγt, the expectation of the obtained wwwt is as follows (Murata
1998; Hsu et al. 2009):
E(wwwt) = www
∗ +
t∏
m=1
∗
(III − γγγ0βmHHH(www
))(www0
∗
− www
)
∗
where www
is the optimal weight vector, and HHH is the Hessian matrix of the objective
function. The rate of convergence is governed by the largest eigenvalue of the function
CCCt =
)). Following Murata (1998) and Hsu et al. (2009), we can
derive a bound of rate of convergence, as follows.
m=1(III − γγγ0βmHHH(www
∏
t
∗
571
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 40, Number 3
Theorem 4 (ADF convergence rate)
m=1(III − γγγ0βmHHH(www
Assume ϕ is the largest eigenvalue of the function CCCt =
proposed ADF training, its convergence rate is bounded by ϕ, and we have
∏
t
∗
)). For the
ϕ ≤ exp { γγγ0λβ
β − 1
}
∗
where λ is the minimum eigenvalue of HHH(www
The proof is sketched in Section 5.
).
The convergence analysis demonstrates that the proposed method with feature-
frequency-adaptive learning rates is convergent and the bound of convergence rate
is analyzed. It demonstrates that increasing the values of γγγ0 and β leads to a lower
bound of the convergence rate. Because the bound of the convergence rate is just an
up-bound rather than the actual convergence rate, we still need to conduct automatic
tuning of the hyper-parameters, including γγγ0 and β, for optimal convergence rate in
practice. The ADF training method has a fast convergence rate because the feature-
frequency-adaptive schema can avoid the fluctuations on updating the weights of high
frequency features, and it can avoid the insufficient training on updating the weights of
low frequency features. In the following sections, we perform experiments to confirm
the fast convergence rate of the proposed method.
4. Evaluation
Our main focus is on training heavily structured classification models. We evaluate the
proposal on three NLP structured classification tasks: biomedical named entity recogni-
tion (Bio-NER), Chinese word segmentation, and noun phrase (NP) chunking. For the
structured classification tasks, the ADF training is based on the CRF model (Lafferty,
McCallum, and Pereira 2001). Further, to demonstrate that the proposed method is
not limited to structured classification tasks, we also perform experiments on a non-
structured binary classification task: sentiment-based text classification. For the non-
structured classification task, the ADF training is based on the maximum entropy model
(Berger, Della Pietra, and Della Pietra 1996; Ratnaparkhi 1996).
4.1 Biomedical Named Entity Recognition (Structured Classification)
The biomedical named entity recognition (Bio-NER) task is from the BIONLP-2004
shared task. The task is to recognize five kinds of biomedical named entities, including
DNA, RNA, protein, cell line, and cell type, on the MEDLINE biomedical text mining
corpus (Kim et al. 2004). A typical approach to this problem is to cast it as a sequential
labeling task with the BIO encoding.
This data set consists of 20,546 training samples (from 2,000 MEDLINE article
abstracts, with 472,006 word tokens) and 4,260 test samples. The properties of the data
are summarized in Table 1. State-of-the-art systems for this task include Settles (2004),
Finkel et al. (2004), Okanohara et al. (2006), Hsu et al. (2009), Sun, Matsuzaki, et al.
(2009), and Tsuruoka, Tsujii, and Ananiadou (2009).
Following previous studies for this task (Okanohara et al. 2006; Sun, Matsuzaki,
et al. 2009), we use word token–based features, part-of-speech (POS) based features,
and orthography pattern–based features (prefix, uppercase/lowercase, etc.), as listed in
Table 2. With the traditional implementation of CRF systems (e.g., the HCRF package),
the edges features usually contain only the information of yi−1 and yi, and ignore the
572
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sun et al.
Feature-Frequency–Adaptive On-line Training for Natural Language Processing
Table 1
Summary of the Bio-NER data set.
#Abstracts
#Sentences
#Words
Train
Test
2,000
404
20,546 (10/abs)
4,260 (11/abs)
472,006 (23/sen)
96,780 (23/sen)
Table 2
Feature templates used for the Bio-NER task. wi is the current word token on position i. ti is the
POS tag on position i. oi is the orthography mode on position i. yi is the classification label on
position i. yi−1yi represents label transition. A × B represents a Cartesian product between
two sets.
}
}
Word Token–based Features:
{wi−2, wi−1, wi, wi+1, wi+2, wi−1wi, wiwi+1
×{yi, yi−1yi
Part-of-Speech (POS)–based Features:
{ti−2, ti−1, ti, ti+1, ti+2, ti−2ti−1, ti−1ti, titi+1, ti+1ti+2, ti−2ti−1ti, ti−1titi+1, titi+1ti+2
×{yi, yi−1yi
Orthography Pattern–based Features:
{oi−2, oi−1, oi, oi+1, oi+2, oi−2oi−1, oi−1oi, oioi+1, oi+1oi+2
×{yi, yi−1yi
}
}
}
}
information of the observation sequence (i.e., xxx). The major reason for this simple real-
ization of edge features in traditional CRF implementation is to reduce the dimension
of features. To improve the model accuracy, we utilize rich edge features following Sun,
Wang, and Li (2012), in which local observation information of xxx is combined in edge
features just like the implementation of node features. A detailed introduction to rich
edge features can be found in Sun, Wang, and Li (2012). Using the feature templates,
we extract a high dimensional feature set, which contains 5.3 × 107 features in total.
Following prior studies, the evaluation metric for this task is the balanced F-score
defined as 2PR/(P + R), where P is precision and R is recall.
4.2 Chinese Word Segmentation (Structured Classification)
Chinese word segmentation aims to automatically segment character sequences into
word sequences. Chinese word segmentation is important because it is the first step
for most Chinese language information processing systems. Our experiments are based
on the Microsoft Research data provided by The Second International Chinese Word
Segmentation Bakeoff. In this data set, there are 8.8 × 104 word-types, 2.4 × 106 word-
tokens, 5 × 103 character-types, and 4.1 × 106 character-tokens. State-of-the-art systems
for this task include Tseng et al. (2005), Zhang, Kikui, and Sumita (2006), Zhang and
Clark (2007), Gao et al. (2007), Sun, Zhang, et al. (2009), Sun (2010), Zhao et al. (2010),
and Zhao and Kit (2011).
The feature engineering follows previous work on word segmentation (Sun, Wang,
and Li 2012). Rich edge features are used. For the classification label yi and the label
transition yi−1yi on position i, we use the feature templates as follows (Sun, Wang, and
Li 2012):
r
Character unigrams located at positions i − 2, i − 1, i, i + 1, and i + 2.
573
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 40, Number 3
r
r
r
r
r
r
r
Character bigrams located at positions i − 2, i − 1, i and i + 1.
Whether xj and xj+1 are identical, for j = i − 2, . . . , i + 1.
Whether xj and xj+2 are identical, for j = i − 3, . . . , i + 1.
The character sequence xj,i if it matches a word w ∈ U, with the constraint
i − 6 < j < i. The item xj,i represents the character sequence xj . . . xi.
U represents the unigram-dictionary collected from the training data.
The character sequence xi,k if it matches a word w ∈ U, with the constraint
i < k < i + 6.
The word bigram candidate [xj,i−1, xi,k] if it hits a word bigram
[wi, wj] ∈ B, and satisfies the aforementioned constraints on j and k.
B represents the word bigram dictionary collected from the training data.
The word bigram candidate [xj,i, xi+1,k] if it hits a word bigram
[wi, wj] ∈ B, and satisfies the aforementioned constraints on j and k.
All feature templates are instantiated with values that occurred in training samples.
The extracted feature set is large, and there are 2.4 × 107 features in total. Our evaluation
is based on a closed test, and we do not use extra resources. Following prior studies, the
evaluation metric for this task is the balanced F-score.
4.3 Phrase Chunking (Structured Classification)
In the phrase chunking task, the non-recursive cores of noun phrases, called base NPs,
are identified. The phrase chunking data is extracted from the data of the CoNLL-2000
shallow-parsing shared task (Sang and Buchholz 2000). The training set consists of 8,936
sentences, and the test set consists of 2,012 sentences. We use the feature templates
based on word n-grams and part-of-speech n-grams, and feature templates are shown
in Table 3. Rich edge features are used. Using the feature templates, we extract 4.8 × 105
features in total. State-of-the-art systems for this task include Kudo and Matsumoto
(2001), Collins (2002), McDonald, Crammer, and Pereira (2005), Vishwanathan et al.
(2006), Sun et al. (2008), and Tsuruoka, Tsujii, and Ananiadou (2009). Following prior
studies, the evaluation metric for this task is the balanced F-score.
4.4 Sentiment Classification (Non-Structured Classification)
To demonstrate that the proposed method is not limited to structured classification, we
select a well-known sentiment classification task for evaluating the proposed method
on non-structured classification.
Table 3
Feature templates used for the phrase chunking task. wi, ti, and yi are defined as before.
}
Word-Token–based Features:
{wi−2, wi−1, wi, wi+1, wi+2, wi−1wi, wiwi+1
×{yi, yi−1yi
Part-of-Speech (POS)–based Features:
{ti−1, ti, ti+1, ti−2ti−1, ti−1ti, titi+1, ti+1ti+2, ti−2ti−1ti, ti−1titi+1, titi+1ti+2
×{yi, yi−1yi
}
}
}
574
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sun et al.
Feature-Frequency–Adaptive On-line Training for Natural Language Processing
Generally, sentiment classification classifies user review text as a positive or neg-
ative opinion. This task (Blitzer, Dredze, and Pereira 2007) consists of four subtasks
based on user reviews from Amazon.com. Each subtask is a binary sentiment clas-
sification task based on a specific topic. We use the maximum entropy model for
classification. We use the same lexical features as those used in Blitzer, Dredze, and
Pereira (2007), and the total number of features is 9.4 × 105. Following prior work, the
evaluation metric is binary classification accuracy.
4.5 Experimental Setting
As for training, we perform gradient descent with the proposed ADF training method.
To compare with existing literature, we choose four popular training methods, a rep-
resentative batch training method, and three representative on-line training methods.
The batch training method is the limited-memory BFGS (LBFGS) method (Nocedal and
Wright 1999), which is considered to be one of the best optimizers for log-linear models
like CRFs. The on-line training methods include the SGD training method, which we
introduced in Section 2.2, the structured perceptron (Perc) training method (Freund
and Schapire 1999; Collins 2002), and the averaged perceptron (Avg-Perc) training
method (Collins 2002). The structured perceptron method and averaged perceptron
method are non-probabilistic training methods that have very fast training speed due
to the avoidance of the computation on gradients (Sun, Matsuzaki, and Li 2013). All
training methods, including ADF, SGD, Perc, Avg-Perc, and LBFGS, use the same set
of features.
We also compared the ADF method with the CW method (Dredze, Crammer, and
Pereira 2008) and the AROW method (Crammer, Kulesza, and Dredze 2009). The CW
and AROW methods are implemented based on the Confidence Weighted Learning
Library.2 Because the current implementation of the CW and AROW methods do not
utilize rich edge features, we removed the rich edge features in our systems to make
more fair comparisons. That is, we removed rich edge features in the CRF-ADF setting,
and this simplified method is denoted as ADF-noRich. The second-order stochastic
gradient descent training methods, including the SMD method (Vishwanathan et al.
2006) and the PSA method (Hsu et al. 2009), are not considered in our experiments
because we find those methods are quite slow when running on our data sets with high
dimensional features.
We find that the settings of q, α, and β in the ADF training method are not sensitive
among specific tasks and can be generally set. We simply set q = n/10 (n is the number
of training samples). It means that feature frequency information is updated 10 times
per iteration. Via cross-validation only on the training data of different tasks, we find
that the following setting is sufficient to produce adequate performance for most of
the real-world natural language processing tasks: α around 0.995 and β around 0.6.
This indicates that the feature frequency information has similar characteristics across
many different natural language processing tasks.
Thus, we simply use the following setting for all tasks: q = n/10, α = 0.995, and
β = 0.6. This leaves c (the initial value of the learning rates) as the only hyper-parameter
that requires careful tuning. We perform automatic tuning for c based on the training
data via 4-fold cross-validation, testing with c = 0.005, 0.01, 0.05, 0.1, respectively, and
the optimal c is chosen based on the best accuracy of cross-validation. Via this automatic
2 http://webee.technion.ac.il/people/koby/code-index.html.
575
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 40, Number 3
tuning, we find it is proper to set c = 0.005, 0.1, 0.05, 0.005, for the Bio-NER, word
segmentation, phrase chunking, and sentiment classification tasks, respectively.
To reduce overfitting, we use an L2 Gaussian weight prior (Chen and Rosenfeld
1999) for the ADF, LBFGS, and SGD training methods. We vary the σ with different
values (e.g., 1.0, 2.0, and 5.0) for 4-fold cross validation on the training data of different
tasks, and finally set σ = 5.0 for all training methods in the Bio-NER task; σ = 5.0 for
all training methods in the word segmentation task; σ = 5.0, 1.0, 1.0 for ADF, SGD,
and LBFGS in the phrase chunking task; and σ = 1.0 for all training methods in the
sentiment classification task. Experiments are performed on a computer with an Intel(R)
Xeon(R) 2.0-GHz CPU.
4.6 Structured Classification Results
4.6.1 Comparisons Based on Empirical Convergence. First, we check the experimental re-
sults of different methods on their empirical convergence state. Because the perceptron
training method (Perc) does not achieve empirical convergence even with a very large
number of training passes, we simply report its results based on a large enough number
of training passes (e.g., 200 passes). Experimental results are shown in Table 4.
As we can see, the proposed ADF method is more accurate than other training
methods, either the on-line ones or the batch one. It is a bit surprising that the ADF
method performs even more accurately than the batch training method (LBFGS). We
notice that some previous work also found that on-line training methods could have
Table 4
Results for the Bio-NER, word segmentation, and phrase chunking tasks. The results and the
number of passes are decided based on empirical convergence (with score deviation of adjacent
five passes less than 0.01). For the non-convergent case, we simply report the results based on a
large enough number of training passes. As we can see, the ADF method achieves the best
accuracy with the fastest convergence speed.
Bio-NER
Prec
Rec
F-score
Passes
Train-Time (sec)
LBFGS (batch)
SGD (on-line)
Perc (on-line)
Avg-Perc (on-line)
ADF (proposal)
67.69
70.91
65.37
68.76
71.71
70.20
72.69
66.95
72.56
72.80
68.92
71.79
66.15
70.61
72.25
400
91
200
37
35
152,811.34
76,549.21
20,436.69
3,928.01
27,490.24
Segmentation
Prec
Rec
F-score
Passes
Train-Time (sec)
LBFGS (batch)
SGD (on-line)
Perc (on-line)
Avg-Perc (on-line)
ADF (proposal)
97.46
97.58
96.99
97.56
97.67
96.86
97.11
96.03
97.05
97.31
97.16
97.34
96.50
97.30
97.49
102
27
200
16
15
13,550.68
6,811.15
8,382.606
716.87
4,260.08
Chunking
Prec
Rec
F-score
Passes
Train-Time (sec)
LBFGS (batch)
SGD (on-line)
Perc (on-line)
Avg-Perc (on-line)
ADF (proposal)
94.57
94.48
93.66
94.34
94.66
94.09
94.04
93.31
94.04
94.38
94.33
94.26
93.48
94.19
94.52
105
56
200
12
17
797.04
903.88
543.51
33.45
282.17
576
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sun et al.
Feature-Frequency–Adaptive On-line Training for Natural Language Processing
better performance than batch training methods such as LBFGS (Tsuruoka, Tsujii, and
Ananiadou 2009; Schaul, Zhang, and LeCun 2012). The ADF training method can
achieve better results probably because the feature-frequency–adaptive training schema
can produce more balanced training of features with diversified frequencies. Traditional
SGD training may over-train high frequency features and at the same time may have
insufficient training of low frequency features. The ADF training method can avoid
such problems. It will be interesting to perform further analysis in future work.
We also performed significance tests based on t-tests with a significance level of
0.05. Significance tests demonstrate that the ADF method is significantly more accurate
than the existing training methods in most of the comparisons, whether on-line or
batch. For the Bio-NER task, the differences between ADF and LBFGS, SGD, Perc,
and Avg-Perc are significant. For the word segmentation task, the differences between
ADF and LBFGS, SGD, Perc, and Avg-Perc are significant. For the phrase chunking
task, the differences between ADF and Perc and Avg-Perc are significant; the differences
between ADF and LBFGS and SGD are non-significant.
Moreover, as we can see, the proposed method achieves a convergence state with
the least number of training passes, and with the least wall-clock time. In general, the
ADF method is about one order of magnitude faster than the LBFGS batch training
method and several times faster than the existing on-line training methods.
4.6.2 Comparisons with State-of-the-Art Systems. The three tasks are well-known bench-
mark tasks with standard data sets. There is a large amount of published research on
those three tasks. We compare the proposed method with the state-of-the-art systems.
The comparisons are shown in Table 5.
As we can see, our system is competitive with the best systems for the Bio-NER,
word segmentation, and NP-chunking tasks. Many of the state-of-the-art systems use
extra resources (e.g., linguistic knowledge) or complicated systems (e.g., voting over
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
Table 5
Comparing our results with some representative state-of-the-art systems.
Bio-NER
Method
F-score
Semi-Markov CRF + global features
(Okanohara et al. 2006)
(Hsu et al. 2009)
CRF + PSA(1) training
(Tsuruoka, Tsujii, and Ananiadou 2009) CRF + SGD-L1 training
Our Method
CRF + ADF training
71.5
69.4
71.6
72.3
Segmentation
(Gao et al. 2007)
(Sun, Zhang, et al. 2009)
(Sun 2010)
Our Method
Method
F-score
Semi-Markov CRF
Latent-variable CRF
Multiple segmenters + voting
CRF + ADF training
97.2
97.3
96.9
97.5
Chunking
(Kudo and Matsumoto 2001)
(Vishwanathan et al. 2006)
(Sun et al. 2008)
Our Method
Method
F-score
Combination of multiple SVM
CRF + SMD training
Latent-variable CRF
CRF + ADF training
94.2
93.6
94.3
94.5
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
577
Computational Linguistics
Volume 40, Number 3
multiple models). Thus, it is impressive that our single model–based system without
extra resources achieves good performance. This indicates that the proposed ADF
training method can train model parameters with good generality on the test data.
4.6.3 Training Curves. To study the detailed training process and convergence speed, we
show the training curves in Figures 2–4. Figure 2 focuses on the comparisons between
the ADF method and the existing on-line training methods. As we can see, the ADF
method converges faster than other on-line training methods in terms of both training
passes and wall-clock time. The ADF method has roughly the same training speed per
pass compared with traditional SGD training.
Figure 3 (Top Row) focuses on comparing the ADF method with the CW method
(Dredze, Crammer, and Pereira 2008) and the AROW method (Crammer, Kulesza, and
Dredze 2009). Comparisons are based on similar features. As discussed before, the ADF-
noRich method is a simplified system, with rich edge features removed from the CRF-
ADF system. As we can see, the proposed ADF method, whether with or without rich
edge features, outperforms the CW and AROW methods. Figure 3 (Bottom Row) focuses
on the comparisons with different mini-batch (the training samples in each stochastic
update) sizes. Representative results with a mini-batch size of 10 are shown. In general,
we find larger mini-batch sizes will slow down the convergence speed. Results demon-
strate that, compared with the SGD training method, the ADF training method is less
sensitive to mini-batch sizes.
Figure 4 focuses on the comparisons between the ADF method and the batch
training method LBFGS. As we can see, the ADF method converges at least one order
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2
Comparisons among the ADF method and other on-line training methods. (Top Row)
Comparisons based on training passes. As we can see, the ADF method has the best accuracy
and with the fastest convergence speed based on training passes. (Bottom Row) Comparisons
based on wall-clock time.
578
0204060801006667686970717273Number of Passes) ADFSGDPerc0204060801009696.296.496.696.89797.297.497.6Segmentation (ADF vs. on-line)Number of Passes) ADFSGDPerc02040608010092.59393.59494.5Chunking (ADF vs. on-line)Number of Passes) ADFSGDPerc0123456x1046667686970717273Training Time (sec)) ADFSGDPerc02,0004,0006,0008,00010,0009696.296.496.696.89797.297.497.6Segmentation (ADF vs. on-line)Training Time (sec)) ADFSGDPerc020040060080092.59393.59494.5Chunking (ADF vs. on-line)Training Time (sec)) ADFSGDPerc
Sun et al.
Feature-Frequency–Adaptive On-line Training for Natural Language Processing
Figure 3
(Top Row) Comparing ADF and ADF-noRich with CW and AROW methods. As we can see,
both the ADF and ADF-noRich methods work better than the CW and AROW methods.
(Bottom Row) Comparing different methods with mini-batch = 10 in the stochastic learning
setting.
magnitude faster than the LBFGS training in terms of both training passes and wall-
clock time. For the LBFGS training, we need to determine the LBFGS memory parameter
m, which controls the number of prior gradients used to approximate the Hessian
information. A larger value of m will potentially lead to more accurate estimation
of the Hessian information, but at the same time will consume significantly more
memory. Roughly, the LBFGS training consumes m times more memory than the ADF
on-line training method. For most tasks, the default setting of m = 10 is reasonable. We
set m = 10 for the word segmentation and phrase chunking tasks, and m = 6 for the
Bio-NER task due to the shortage of memory for m > 6 cases in this task.
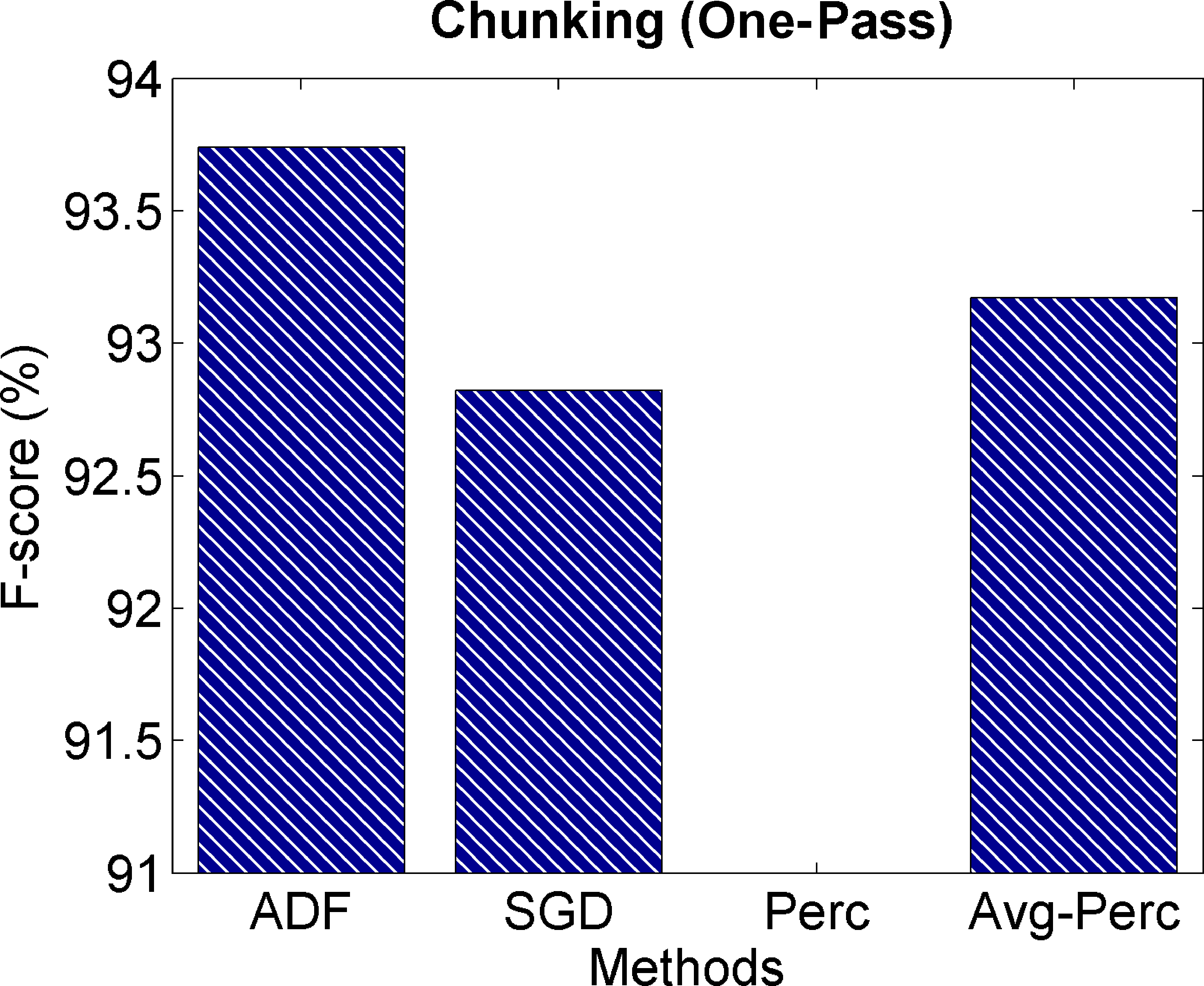
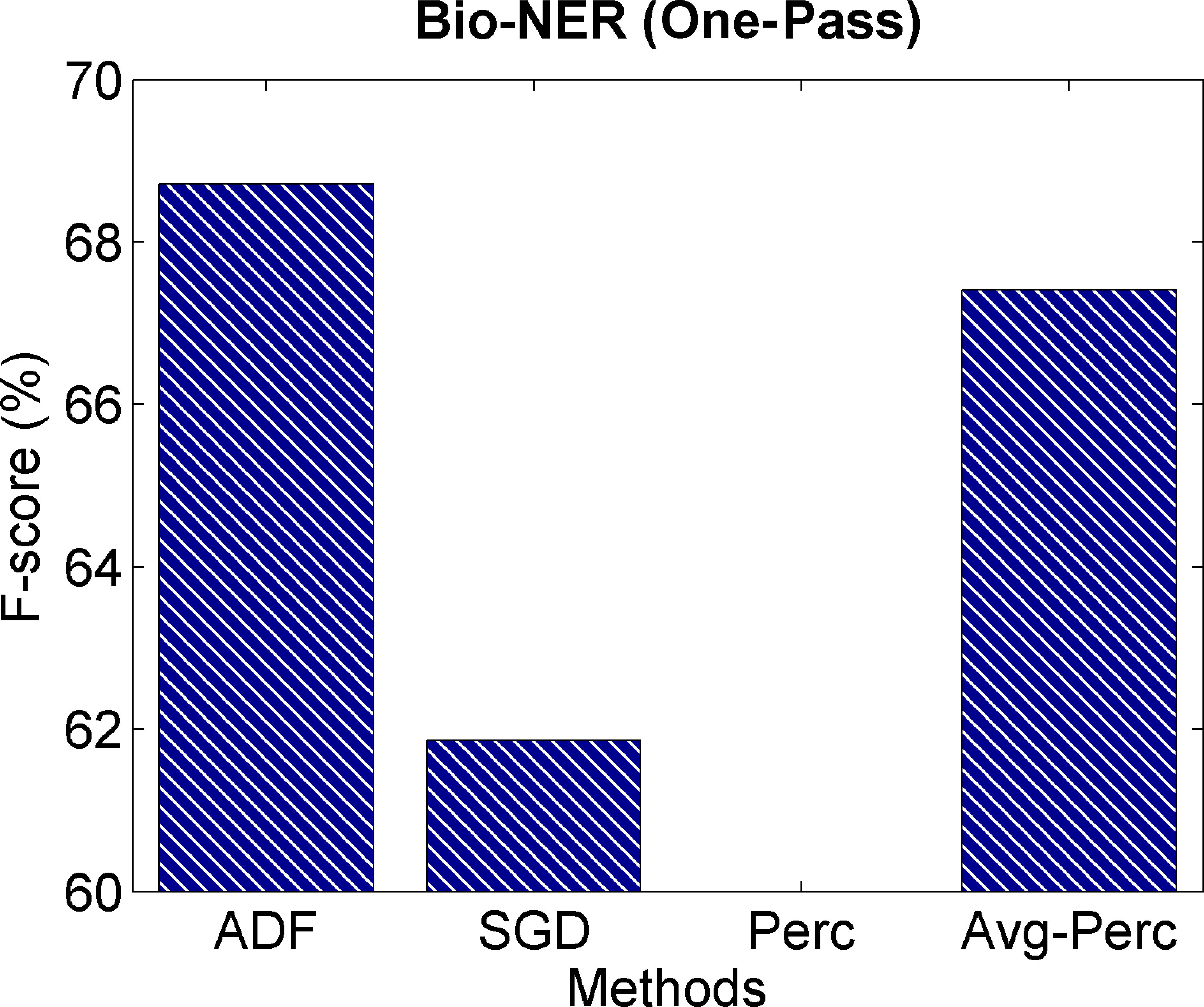
4.6.4 One-Pass Learning Results. Many real-world data sets can only observe the training
data in one pass. Par exemple, some Web-based on-line data streams can only appear
once so that the model parameter learning should be finished in one-pass learning (voir
Zinkevich et al. 2010). Ainsi, it is important to test the performance in the one-pass
learning scenario.
In the one-pass learning scenario, the feature frequency information is computed
“on the fly” during on-line training. As shown in Section 3.1, we only need to have
a real-valued vector vvv to record the cumulative feature frequency information, lequel
is updated when observing training instances one by one. Alors, the learning rate
vector γγγ is updated based on the vvv only and there is no need to observe the training
instances again. This is the same algorithm introduced in Section 3.1 and no change is
required for the one-pass learning scenario. Chiffre 5 shows the comparisons between
the ADF method and baselines on one-pass learning. As we can see, the ADF method
579
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
je
je
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
je
je
_
un
_
0
0
1
9
3
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
02040608010060626466687072Bio−NER (ADF vs. CW/AROW)Number of PassesF−score (%) ADFADF−noRichCWAROW02040608010092939495969798Segmentation (ADF vs. CW/AROW)Number of PassesF−score (%) ADFADF−noRichCWAROW02040608010092.59393.59494.595Chunking (ADF vs. CW/AROW)Number of PassesF−score (%) ADFADF−noRichCWAROW020406080100686970717273Bio−NER (MiniBatch=10)Number of PassesF−score (%) ADFSGD02040608010096.496.696.89797.297.497.6Segmentation (MiniBatch=10)Number of PassesF−score (%) ADFSGD02040608010093.293.493.693.89494.294.494.6Chunking (MiniBatch=10)Number of PassesF−score (%) ADFSGD
Computational Linguistics
Volume 40, Nombre 3
Chiffre 4
Comparisons between the ADF method and the batch training method LBFGS. (Top Row)
Comparisons based on training passes. As we can see, the ADF method converges much faster
than the LBFGS method, and with better accuracy on the convergence state. (Bottom Row)
Comparisons based on wall-clock time.
consistently outperforms the baselines. This also reflects the fast convergence speed of
the ADF training method.
4.7 Non-Structured Classification Results
In previous experiments, we showed that the proposed method outperforms existing
baselines on structured classification. Nevertheless, we want to show that the ADF
method also has good performance on non-structured classification. En outre, ce
task is based on real-valued features instead of binary features.
Chiffre 5
Comparisons among different methods based on one-pass learning. As we can see, the ADF
method has the best accuracy on one-pass learning.
580
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
je
je
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
je
je
_
un
_
0
0
1
9
3
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
01002003004006667686970717273Bio−NER (ADF vs. batch)Number of PassesF−score (%) ADFLBFGS01002003004009696.296.496.696.89797.297.497.6Segmentation (ADF vs. batch)Number of PassesF−score (%) ADFLBFGS010020030040093.693.89494.294.4Chunking (ADF vs. batch)Number of PassesF−score (%) ADFLBFGS051015x 1046667686970717273Bio−NER (ADF vs. batch)Training Time (sec)F−score (%) ADFLBFGS012345x 1049696.296.496.696.89797.297.497.6Segmentation (ADF vs. batch)Training Time (sec)F−score (%) ADFLBFGS01,0002,0003,00092.59393.59494.5Chunking (ADF vs. batch)Training Time (sec)) ADFLBFGS
Sun et al.
Feature-Frequency–Adaptive On-line Training for Natural Language Processing
Tableau 6
Results on sentiment classification (non-structured binary classification).
Accuracy
Passes
Train-Time (sec)
LBFGS (batch)
SGD (on-line)
Perc (on-line)
Avg-Perc (on-line)
ADF (proposal)
87.00
87.13
84.55
85.04
87.89
86
44
25
46
30
72.20
55.88
5.82
12.22
57.12
Experimental results of different training methods on the convergence state are
shown in Table 6. As we can see, the proposed method outperforms all of the on-line
and batch baselines in terms of binary classification accuracy. Here again we observe
that the ADF and SGD methods outperform the LBFGS baseline.
The training curves are shown in Figure 6. As we can see, the ADF method con-
verges quickly. Because this data set is relatively small and the feature dimension is
much smaller than previous tasks, we find the baseline training methods also have
fast convergence speed. The comparisons on one-pass learning are shown in Fig-
ure 7. Just as for the experiments for structured classification tasks, the ADF method
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
je
je
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
je
je
_
un
_
0
0
1
9
3
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 6
F-score curves on sentiment classification. (Top Row) Comparisons among the ADF method and
on-line training baselines, based on training passes and wall-clock time, respectivement. (Bottom
Row) Comparisons between the ADF method and the batch training method LBFGS, based on
training passes and wall-clock time, respectivement. As we can see, the ADF method outperforms
both the on-line training baselines and the batch training baseline, with better accuracy and
faster convergence speed.
581
0204060801008283848586878889Sentiment (ADF vs. on-line)Number of PassesAccuracy (%) ADFSGDPerc0204060808283848586878889Sentiment (ADF vs. on-line)Training Time (sec)Accuracy (%) ADFSGDPerc0501001508283848586878889Sentiment (ADF vs. batch)Number of PassesAccuracy (%) ADFLBFGS0501001508283848586878889Sentiment (ADF vs. batch)Training Time (sec)Accuracy (%) ADFLBFGS
Computational Linguistics
Volume 40, Nombre 3
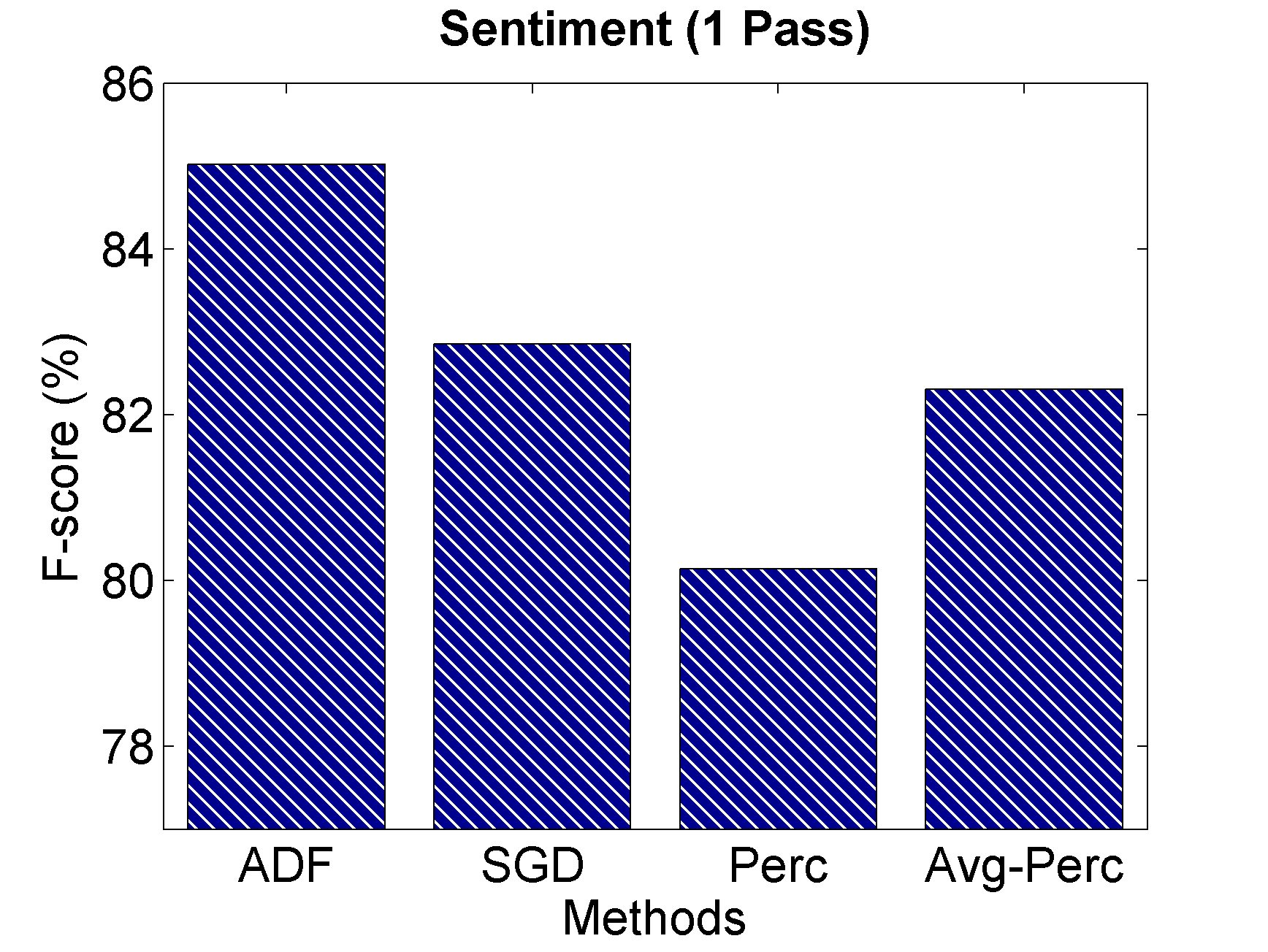
Chiffre 7
One-pass learning results on sentiment classification.
outperforms the baseline methods on one-pass learning, with more than 12.7% error
rate reduction.
5. Proofs
This section gives proofs of Theorems 1–4.
Proof of Theorem 1 Following Equation (5), the ADF update rule is F(wwwt) := wwwt+1 =
wwwt + γγγ ··· gggt. For ∀wwwt
∈ X ,
|
|
|
− wwwt+1
|F(wwwt+1) − F(wwwt)|
= |F(wwwt+1) − wwwt+1
= |wwwt+1 + γγγ ··· gggt+1
= |γγγ ··· gggt+1
= [(a1b1)2 + (a2b2)2 + · · · + (af bf )2]1=2
≤ [(γmaxb1)2 + (γmaxb2)2 + · · · + (γmaxbf )2]1=2
= |γmaxgggt+1
= |FSGD(wwwt+1) − FSGD(wwwt)|
|
(6)
where ai and bi are the ith elements of the vector γγγ and gggt+1, respectivement. FSGD is the
SGD update rule with the fixed learning rate γmax such that γmax := sup{γi where γi
∈
γγγ}. Autrement dit, for the SGD update rule FSGD, the fixed learning rate γmax is derived
from the ADF update rule. According to Lemma 1, the SGD update rule FSGD is a
contraction mapping in Euclidean space with Lipschitz continuity degree 1 − γmax/σ2,
′
|| · ||∇
′ℓ(xxxi, yi, oui
given the condition that γmax
′
′y
oui
oui
−1. Ainsi, it goes to
≤ (||x2
je
Lip)
)||
|FSGD(wwwt+1) − FSGD(wwwt)| ≤ (1 − γmax/σ2)|wwwt+1
− wwwt
|
(7)
Combining Equations (6) et (7), it goes to
|F(wwwt+1) − F(wwwt)| ≤ (1 − γmax/σ2)|wwwt+1
− wwwt
|
Ainsi, according to the definition of dynamic contraction mapping, the ADF update rule
is a dynamic contraction mapping in Euclidean space with Lipschitz continuity degree
⊓⊔
1 − γmax/σ2.
582
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
je
je
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
je
je
_
un
_
0
0
1
9
3
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sun et al.
Feature-Frequency–Adaptive On-line Training for Natural Language Processing
Proof of Theorem 2 As presented in Equation (5), the ADF update rule is F(wwwt) :=
wwwt+1 = wwwt + γγγt
··· gggt. For ∀wwwt
∈ X ,
|
··· gggt+1
|F(wwwt+1) − F(wwwt)|
= |γγγt+1
= [(a1b1)2 + (a2b2)2 + · · · + (af bf )2]1=2
≤ [(γmaxb1)2 + (γmaxb2)2 + · · · + (γmaxbf )2]1=2
= |FSGD(wwwt+1) − FSGD(wwwt)|
(8)
where ai is the ith element of the vector γγγt+1. bi and FSGD are the same as before.
Similar to the analysis of Theorem 1, the third step of Equation (8) is valid because γmax
is the maximum learning rate at the beginning and all learning rates are decreasing
when t is increasing. The proof can be easily derived following the same steps in the
⊓⊔
proof of Theorem 1. To avoid redundancy, we do not repeat the derivation.
Proof of Theorem 3 Let M be the accumulative change of the ADF weight vector wwwt:
Mt :=
∑
t′=1,2,:::,t
|wwwt′+1
− wwwt′|
To prove the convergence of the ADF, we need to prove the sequence Mt converges as
t → ∞. Following Theorem 2, we have the following formula for the ADF training:
|F(wwwt+1) − F(wwwt)| ≤ (1 − γmax/σ2)|wwwt+1
− wwwt
|
where γmax is the maximum learning rate at the beginning. Let d0 := |www2
q := 1 − γmax/σ2, then we have:
− www1
| et
Mt =
∑
t′=1,2,:::,t
|wwwt′+1
− wwwt′|
≤ d0 + d0q + d0q2 + · · · + d0qt−1
= d0(1 − qt)/(1 − q)
(9)
When t → ∞, d0(1 − qt)/(1 − q) goes to d0/(1 − q) because q < 1. Hence, we have:
Mt
≤ d0/(1 − q)
Thus, Mt is upper-bounded. Because we know that Mt is a monotonically increasing
function when t → ∞, it follows that Mt converges when t → ∞. This completes the
⊓⊔
proof.
583
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 40, Number 3
Proof of Theorem 4 First, we have
eigen(CCCt) =
t∏
(1 − γγγ0βmλ)
m=1
{
≤ exp
− γγγ0λ
}
βm
t∑
m=1
0 ≤
n∏
j=1
(1 − aj) ≤
n∏
j=1
−
−aj = e
e
∑
n
j=1 aj
Then, we have
This is because 1 − aj
t → ∞, we have
≤ e
−aj given 0 ≤ aj < 1. Finally, because
{
eigen(CCCt) ≤ exp
− γγγ0λ
t∑
}
βm
{
→ exp
m=1
}
−γγγ0λβ
1 − β
∑
t
m=1 βm → (cid:12)
1−(cid:12) when
This completes the proof.
6. Conclusions
⊓⊔
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
In this work we tried to simultaneously improve the training speed and model accuracy
of natural language processing systems. We proposed the ADF on-line training method,
based on the core idea that high frequency features should result in a learning rate that
decays faster. We demonstrated that the ADF on-line training method is convergent
and has good theoretical properties. Based on empirical experiments, we can state the
following conclusions. First, the ADF method achieved the major target of this work:
faster training speed and higher accuracy at the same time. Second, the ADF method
was robust: It had good performance on several structured and non-structured classifi-
cation tasks with very different characteristics. Third, the ADF method worked well on
both binary features and real-valued features. Fourth, the ADF method outperformed
existing methods in a one-pass learning setting. Finally, our method achieved state-
of-the-art performance on several well-known benchmark tasks. To the best of our
knowledge, our simple method achieved a much better F-score than the existing best
reports on the biomedical named entity recognition task.
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Acknowledgments
This work was supported by the National
Natural Science Foundation of China
(no. 61300063, no. 61370117), the Doctoral
Fund of Ministry of Education of China
(no. 20130001120004), a Hong Kong
Polytechnic University internal grant
(4-ZZD5), a Hong Kong RGC Project
(no. PolyU 5230/08E), the National High
Technology Research and Development
Program of China (863 Program,
no. 2012AA011101), and the Major National
Social Science Fund of China (no. 12&ZD227).
This work is a substantial extension of the
conference version presented at ACL 2012
(Sun, Wang, and Li 2012).
584
Sun et al.
Feature-Frequency–Adaptive On-line Training for Natural Language Processing
References
Berger, Adam L., Vincent J. Della Pietra, and
Stephen A. Della Pietra. 1996. A maximum
entropy approach to natural language
processing. Computational Linguistics,
22(1):39–71.
Blitzer, John, Mark Dredze, and Fernando
Pereira. 2007. Biographies, Bollywood,
boom-boxes and blenders: Domain
adaptation for sentiment classification.
In Proceedings of the 45th Annual Meeting of
the Association of Computational Linguistics,
pages 440–447, Prague.
Bottou, L´eon. 1998. Online algorithms
and stochastic approximations. In
D. Saad, editor. Online Learning and Neural
Networks. Cambridge University Press,
pages 9–42.
Chen, Stanley F. and Ronald Rosenfeld.
1999. A Gaussian prior for smoothing
maximum entropy models. Technical
Report CMU-CS-99-108, Carnegie
Mellon University.
Collins, Michael. 2002. Discriminative
training methods for hidden Markov
models: Theory and experiments with
perceptron algorithms. In Proceedings of
EMNLP’02, pages 1–8, Philadelphia, PA.
Crammer, Koby, Alex Kulesza, and Mark
Dredze. 2009. Adaptive regularization of
weight vectors. In NIPS’09, pages 414–422,
Vancouver.
Dredze, Mark, Koby Crammer, and
Fernando Pereira. 2008. Confidence-
weighted linear classification. In
Proceedings of ICML’08, pages 264–271,
Helsinki.
Duchi, John, Elad Hazan, and Yoram Singer.
2010. Adaptive subgradient methods
for online learning and stochastic
optimization. Journal of Machine
Learning Research, 12:2,121–2,159.
Finkel, Jenny, Shipra Dingare, Huy Nguyen,
Malvina Nissim, Christopher Manning,
and Gail Sinclair. 2004. Exploiting context
for biomedical entity recognition: From
syntax to the Web. In Proceedings of
BioNLP’04, pages 91–94, Geneva.
Freund, Yoav and Robert Schapire. 1999.
Large margin classification using the
perceptron algorithm. Machine Learning,
37(3):277–296.
Gao, Jianfeng, Galen Andrew, Mark Johnson,
and Kristina Toutanova. 2007. A comparative
study of parameter estimation methods for
statistical natural language processing. In
Proceedings of the 45th Annual Meeting of the
Association of Computational Linguistics
(ACL’07), pages 824–831, Prague.
Hsu, Chun-Nan, Han-Shen Huang, Yu-Ming
Chang, and Yuh-Jye Lee. 2009. Periodic
step-size adaptation in second-order
gradient descent for single-pass on-line
structured learning. Machine Learning,
77(2-3):195–224.
Jacobs, Robert A. 1988. Increased rates of
convergence through learning rate
adaptation. Neural Networks, 1(4):295–307.
Kim, Jin-Dong, Tomoko Ohta, Yoshimasa
Tsuruoka, and Yuka Tateisi. 2004.
Introduction to the bio-entity recognition
task at JNLPBA. In Proceedings of
BioNLP’04, pages 70–75, Geneva.
Kudo, Taku and Yuji Matsumoto. 2001.
Chunking with support vector machines.
In Proceedings of NAACL’01, pages 1–8,
Pittsburgh, PA.
Lafferty, John, Andrew McCallum, and
Fernando Pereira. 2001. Conditional
random fields: Probabilistic models for
segmenting and labeling sequence
data. In ICML’01, pages 282–289,
Williamstown, MA.
McDonald, Ryan, Koby Crammer, and
Fernando Pereira. 2005. Flexible text
segmentation with structured multilabel
classification. In Proceedings of HLT/
EMNLP’05, pages 987–994, Vancouver.
McMahan, H. Brendan and Matthew J.
Streeter. 2010. Adaptive bound
optimization for online convex
optimization. In Proceedings of COLT’10,
pages 244–256, Haifa.
Murata, Noboru. 1998. A statistical study
of on-line learning. In D. Saad, editor.
Online Learning in Neural Networks.
Cambridge University Press, pages 63–92.
Nocedal, Jorge and Stephen J. Wright.
1999. Numerical optimization. Springer.
Okanohara, Daisuke, Yusuke Miyao,
Yoshimasa Tsuruoka, and Jun’ichi Tsujii.
2006. Improving the scalability of
semi-Markov conditional random
fields for named entity recognition.
In Proceedings of COLING-ACL’06,
pages 465–472, Sydney.
Ratnaparkhi, Adwait. 1996. A maximum
entropy model for part-of-speech tagging.
In Proceedings of the Conference on Empirical
Methods in Natural Language Processing
1996, pages 133–142, Pennsylvania.
Sang, Erik Tjong Kim and Sabine Buchholz.
2000. Introduction to the CoNLL-2000
shared task: Chunking. In Proceedings
of CoNLL’00, pages 127–132, Lisbon.
Schaul, Tom, Sixin Zhang, and Yann LeCun.
2012. No more pesky learning rates. CoRR,
abs/1206.1106.
585
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 40, Number 3
Settles, Burr. 2004. Biomedical named entity
recognition using conditional random
fields and rich feature sets. In Proceedings
of BioNLP’04, pages 104–107, Geneva.
Shalev-Shwartz, Shai, Yoram Singer, and
Nathan Srebro. 2007. Pegasos: Primal
estimated sub-gradient solver for SVM.
In Proceedings of ICML’07, pages 807–814,
Corvallis, OR.
Sperduti, Alessandro and Antonina Starita.
1993. Speed up learning and network
optimization with extended back
propagation. Neural Networks, 6(3):365–383.
Sun, Weiwei. 2010. Word-based and
character-based word segmentation
models: Comparison and combination.
In COLING’10 (Posters), pages 1,211–1,219,
Beijing.
Sun, Xu, Takuya Matsuzaki, and Wenjie Li.
2013. Latent structured perceptrons
for large-scale learning with hidden
information. IEEE Transactions on
Knowledge and Data Engineering,
25(9):2,063–2,075.
Sun, Xu, Takuya Matsuzaki, Daisuke
Okanohara, and Jun’ichi Tsujii. 2009.
Latent variable perceptron algorithm for
structured classification. In Proceedings
of the 21st International Joint Conference
on Artificial Intelligence (IJCAI 2009),
pages 1,236–1,242, Pasadena, CA.
Sun, Xu, Louis-Philippe Morency, Daisuke
Okanohara, and Jun’ichi Tsujii. 2008.
Modeling latent-dynamic in shallow
parsing: A latent conditional model with
improved inference. In Proceedings of
COLING’08, pages 841–848, Manchester.
Sun, Xu, Houfeng Wang, and Wenjie Li. 2012.
Fast online training with frequency-
adaptive learning rates for Chinese word
segmentation and new word detection.
In Proceedings of ACL’12, pages 253–262,
Jeju Island.
Sun, Xu, Yaozhong Zhang, Takuya
Matsuzaki, Yoshimasa Tsuruoka, and
Jun’ichi Tsujii. 2009. A discriminative
latent variable Chinese segmenter with
hybrid word/character information.
In Proceedings of NAACL-HLT’09,
pages 56–64, Boulder, CO.
Sun, Xu, Yao Zhong Zhang, Takuya
Matsuzaki, Yoshimasa Tsuruoka, and
Jun’ichi Tsujii. 2013. Probabilistic Chinese
word segmentation with non-local
information and stochastic training.
Information Processing & Management,
49(3):626–636.
Tseng, Huihsin, Pichuan Chang, Galen
Andrew, Daniel Jurafsky, and Christopher
Manning. 2005. A conditional random
field word segmenter for SIGHAN bakeoff
2005. In Proceedings of the Fourth SIGHAN
Workshop, pages 168–171, Jeju Island.
Tsuruoka, Yoshimasa, Jun’ichi Tsujii, and
Sophia Ananiadou. 2009. Stochastic
gradient descent training for
l1-regularized log-linear models with
cumulative penalty. In Proceedings of
ACL’09, pages 477–485, Suntec.
Vishwanathan, S. V. N., Nicol N.
Schraudolph, Mark W. Schmidt, and
Kevin P. Murphy. 2006. Accelerated
training of conditional random
fields with stochastic meta-descent.
In Proceedings of ICML’06, pages 969–976,
Pittsburgh, PA.
Zhang, Ruiqiang, Genichiro Kikui, and
Eiichiro Sumita. 2006. Subword-based
tagging by conditional random fields for
Chinese word segmentation. In Proceedings
of the Human Language Technology
Conference of the NAACL, Companion
Volume: Short Papers, pages 193–196,
New York City.
Zhang, Yue and Stephen Clark. 2007.
Chinese segmentation with a word-based
perceptron algorithm. In Proceedings of the
45th Annual Meeting of the Association of
Computational Linguistics, pages 840–847,
Prague.
Zhao, Hai, Changning Huang, Mu Li,
and Bao-Liang Lu. 2010. A unified
character-based tagging framework for
Chinese word segmentation. ACM
Transactions on Asian Language Information
Processing, 9(2): Article 5.
Zhao, Hai and Chunyu Kit. 2011. Integrating
unsupervised and supervised word
segmentation: The role of goodness
measures. Information Sciences,
181(1):163–183.
Zinkevich, Martin, Markus Weimer,
Alexander J. Smola, and Lihong Li.
2010. Parallelized stochastic gradient
descent. In Proceedings of NIPS’10,
pages 2,595–2,603, Vancouver.
586
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
0
3
5
6
3
1
8
0
3
7
9
7
/
c
o
l
i
_
a
_
0
0
1
9
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3