Evolving Virtual Creatures
and Catapults
Abstract We present a system that can evolve the morphology
and the controller of virtual walking and block-throwing creatures
(catapults) using a genetic algorithm. The system is based on Sims’
travail, implemented as a flexible platform with an off-the-shelf
dynamics engine. Experiments aimed at evolving Sims-type walkers
resulted in the emergence of various realistic gaits while using fairly
simple objective functions. Due to the flexibility of the system,
drastically different morphologies and functions evolved with only
minor modifications to the system and objective function. Pour
example, various throwing techniques evolved when selecting for
catapults that propel a block as far as possible. Among the strategies
and morphologies evolved, we find the drop-kick strategy, aussi
as the systematic invention of the principle behind the wheel, quand
allowing mutations to the projectile.
Nicolas Chaumont
De´partement d’informatique
Universite´ de Sherbrooke
Sherbrooke, Que´bec, Canada J1K 2R1
et
Keck Graduate Institute of Applied
Life Sciences
Claremont, Californie, 91711
nicolas_chaumont@kgi.edu
Richard Egli
De´partement d’informatique
Universite´ de Sherbrooke
Sherbrooke, Que´bec, Canada J1K 2R1
Richard.Egli@USherbrooke.CA
Christoph Adami
Keck Graduate Institute of Applied
Life Sciences
Claremont, Californie 91711
christoph_adami@kgi.edu
Mots clés
Artificial life, genetic algorithm, catapults,
walkers, dynamics simulator, coevolution
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1 Introduction
Use of the power of evolutionary techniques such as genetic algorithms is critical for solving
particularly complex problems in which the search for a solution has to be performed in a high-
dimensional space of almost unknown structure. This is especially true when an artificial creature’s
morphology has to be evolved along with its controller. The research presented in this article
addresses this problem using a system able to evolve complex behaviors in a three-dimensional
environment that simulates rigid body dynamics and body-brain coevolution.
The hope is ultimately to create a mature, highly flexible open-source framework specifically
designed for conducting experiments of arbitrary complexity where body-brain coevolution plays a
central role. To fulfill this goal, the system has to be composed of an initial set of components that
capture the complexity necessary to evolve elaborated behaviors. These components have to be
combined in a modular way to provide the flexibility and extensibility that allow users to perform
more complex experiments with a minimum of programming overhead. The initial (prototype)
version of the code is available at: http://sourceforge.net/projects/evol.
Dans la section suivante, we begin by relating this work to previous efforts in the field. Section 3
demonstrates the system’s initial ability to evolve complex behaviors by evolving walking blocky
n 2007 Massachusetts Institute of Technology
Artificial Life 13: 139 – 157 (2007)
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
creatures very similar to those of Sims [30, 31]. Taking advantage of the system’s modularity, only a
few modifications to the first experiment were necessary to set up a second where the initial
creature’s structure was slightly modified to allow it to detach a block from the main body. As the
new creatures are put in an environment that rewards individuals in proportion to the distance they
can impart to the detached block, various block-throwing strategies emerged. These modifications as
well as the results are discussed in Section 4. Important details about setting up similar experiments
with the dynamics engine ODE [24] are explained in Section 5.
Enfin, the general performance of the system is discussed in Section 6 along with future
extensions that allow more complex and real-life-like experiments.
2 Previous Work
The use of physics in three-dimensional environments for simulating realistic virtual agents is not a new
approche [21] and has been applied to the animation of various kinds of agents [33, 9, 26]. Much at-
tention has been focused on the evolution of autonomous agents in two-dimensional worlds [43, 36–38],
but surprisingly little progress has been made in the automatic evolution of three-dimensional virtual
creatures—morphology and behavior—simulated in a dynamics simulator where their bodies simul-
taneously coevolve with their controller. Two reasons can explain this shortcoming. D'abord, programming
a realistic dynamics simulator and the data structure for the creatures and the genetic algorithm is a te-
dious and complex endeavor, et deuxieme, the optimization process requires considerable computational
pouvoir. Cependant, both the tools and sufficient computer power are now at hand. Par exemple, several
off-the-shelf dynamics simulators are now available [24, 11, 7, 41], as well as software that embeds a set
of tools to model a creature, the simulation environment, and the optimization algorithm [14, 5].
Taylor and Massey [32] give a good overview of the work in the field that is still up to date at the time
of writing of this article. Cependant, we would like to mention the work by Kim and Shim [28, 29], OMS
successfully evolved creatures that are able to fly. Instead of using blocks, these authors used the plane
and the cylinder as primitives to evolve wing structures. The genetic encoding itself is restricted in order
to favor the development of pairs of wings by enforcing symmetry. Kim and Shim used the Open
Dynamics Engine (ODE) [24] as the dynamics engine. This simulator puts a particular emphasis on
numerical stability; cependant, according to the authors, avoiding ‘‘numerical explosions’’ (see below) était
particularly difficult, because simulating wing-flapping flight involves strong torques and low masses.
Miconi and Channon [23] recently presented a nearly exact reimplementation of Sims’ system and
expanded his results by evolving creatures for tasks based on ‘‘box-grabbing.’’
Additionally to these peer-reviewed improvements on Sims’ initial work, there are many suc-
cessful efforts to perform very similar experiments using various dynamics libraries such as
BreveCreatures [15], ODE [8, 2, 39], or Newton Dynamics [42], par exemple.
3 Evolution of Virtual Walkers
3.1 The Original Implementation by Sims
Sims [30, 31] proposed to use a genetic algorithm to coevolve the morphology as well as the
behavior of virtual creatures. The morphology consists of bricklike primitives —more technically,
rectangular parallelepipeds, or cuboids— connected together by motor joints actuated by a neural-
network-based controller (Chiffre 1). Each creature carries a set of genes (genotype), connected
together in a graph, that completely describes its morphology and its controller (phenotype).
The genetic algorithm tries to improve an initial population through successive generations by
altering the genotype of each creature by means of three genetic operators: mutation, grafting, et
crossover. To proceed to the next generation, the genetic algorithm simulates the behavior of each
individual, using a dynamics simulator. The individual’s performances are recorded and evaluated
according to criteria specified through an objective function that returns a single value: the fitness.
The top 20% of the population (elite) with the highest fitness are retained for the next generation,
140
Artificial Life Volume 13, Nombre 2
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
Chiffre 1. Example of a simple blocky creature evolved by Karl Sims.
whereas the remaining 80% are replaced by new individuals from the new generation, generated
from the 20% elite using genetic operators. When the population is regenerated, the new generation
undergoes in turn the same process of evaluation and selection for a fixed maximum of time. In a
typical optimization process, a population of 300 individuals is optimized over 100 generations.
Since the settings used to perform our experiments are close to the description provided in Sims’
original articles [30, 31], only the features that are different are explained in this section and in Section 5.
3.2 Simple Experimental Settings Favor Simple Behaviors
As observed by Taylor and Massey [32], defining an objective function to evolve suitable creatures is
not a trivial task, even for very simple behaviors such as forward progress. For every simulation
performed up to date, the evolution process has been able to find some individuals that perform
correctly with respect to the objective function, but that exhibit unexpected and undesirable
behaviors. During trial runs, almost every time such creatures were able to obtain an instant reward
for distance traveled, without moving any body part. Par exemple, at the beginning of a simulation,
the creatures (suspended over the ground) are falling and acquire momentum.1 At the time they hit
the ground, part of their vertical kinetic energy is converted into horizontal speed depending on the
creatures’ shape and position, causing some of them to roll farther than others. At early generations,
this distance is often longer than any distance travelled by moving individuals that possess a primitive
controller that may develop a gait. Systematically, the evolutionary algorithm favors the rolling
strategy over developing a gait, optimizing the individual’s position and/or shape to roll even longer;
never does the individual develop a controller that actuates the limbs. Behaviors based on this
principle are much easier to evolve and preclude potentially more promising creatures —that need
time to develop a controller complex enough to become efficient— from evolving.
The standard objective function Fw for forward motion can be defined as
Fw ¼ Dw;
where Dw is the distance traveled by a creature, c'est, the distance between the initial position of the
center of mass of its root block (first block created by its first gene) and its position at the time when
the simulation ends. In order to obtain more elaborate behaviors, we used methods and protocols
that consist in modifying the objective function and activating/deactivating the creature’s controller
in a sequence synchronized with its state.
3.3 Controller’s Activation Sequence
As discussed above, in order to evolve efficient locomotion strategies, we must prevent undesir-
capable (or cheater) behavior. These unwanted behaviors suggested an efficient penalizing sequence of
timings in which an individual’s controller is sequentially activated and deactivated. Dans cette section, nous
1 It is not possible in ODE to place an individual directly on the surface and avoid interpenetration between the creature’s body parts
and the ground, which will cause the creature to fly off due to the repulsion generated by the interpenetration. Plutôt, we drop
individuals from a safe position above the ground.
Artificial Life Volume 13, Nombre 2
141
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
describe the experience acquired designing the activation sequence and provide insights to the
practitioner who may face similar problems.
When an individual is instantiated in the simulator, its neural network is immediately activated (chaque
sensor, neuron, and actuator processes its inputs and output) and then dropped to the surface. Souvent,
the genetic algorithm takes advantage of a creature’s shape and momentum acquired during the fall
(after being dropped) in such a way that it rolls without actively moving a block. Some creatures were
able to roll as long as the simulation time itself (10 seconds). For this reason, we decided that the
evaluation of a creature should begin after its motion has stabilized. Because of inaccuracies in the
simulation of the cancellation of forces after the drop, every block continuously vibrates, even at rest.
Ainsi, we cannot use movement alone as a criterion for rest. While the controller is still deactivated
after releasing a creature, we record the displacement of the center of gravity of every block. The largest
of these displacements is compared with a threshold value, given by the inaccuracy of the dynamics
simulator. We thus deem that motion has stopped if the only detectable motion is due to simulator
artifacts. Typiquement, this accuracy is Dx ¼ 1/300 for a time Dt ¼ 1/60.
The following problem also emerged: Some creatures fall almost standing still. They appear stable
for some time after they hit the ground, but they progressively lose balance and fall over at last. Because
the algorithm described above would have deemed the creature to be stable, the subsequent falling
motion is interpreted as genuine motion even though no blocks are actively moved. The solution we
adopted to discard such unstable creatures was to tighten the definition of stability, by requiring
subthreshold motion for at least 0.5 seconds of simulation time (30 consecutive steps for Dt ¼ 1/60).
Toujours, some new individuals that land on the ground after being dropped may have freely oscillating body
parties. As the simulation environment does not take into account joint friction, these oscillating body
parts will move indefinitely. Such individuals will never be considered stable, and no distance will ever be
recorded for them, so their fitness will be zero, which will automatically disqualify the individual from
the evolution. While such elimination may reduce diversity, it does not appear to constrain evolution.
Once this algorithm is implemented, a new type of undesirable creatures can arise that perform a
single jump and remain stationary for the rest of the simulation. It appears to be easier for the
genetic algorithm to evolve single-impulse controllers — giving rise to jerks — than controllers
producing periodic repetitive motions. Such creatures are also easy to eliminate. Individuals are
given the opportunity to jump by activating the neural network for a short period of time — less than
10 time steps — after equilibration, but without recording the distance traveled. After an additional
equilibration period, the true distance measurement begins.
After implementing this start-up sequence, the genetic algorithm still manages to find some unexpected
creatures that arose in many simulations. These are individuals that land on the ground and are stable
enough to keep their balance even after the first (short) activation of the neural controller that test for
jumpers. During the subsequent activation of the controller, block motion can destabilize a balanced crea-
ture so that it topples after all, reaching a decent distance. Evolution can quickly optimize such cheaters by
elongating the main body, thus preventing the evolution of more sophisticated locomotion strategies. À
eliminate such cheaters, we simply increase the interval for the initial controller activation to 1 second.
Ainsi, our preparation sequence can be summarized as follows:
(cid:2) First stabilization period of 0.5 second.
(cid:2) Activation of the creature’s controller for 1 second.
(cid:2) Second stabilization period of 0.5 second.
(cid:2) Permanent activation of the creature’s controller throughout the simulation.
This sequence manages to eliminate a significant fraction of uninteresting strategies, reducing their
proportion to a small minority. Some unwanted behaviors still appear in a very few tests like those
mentioned by Taylor and Massey [32] (snakelike individuals that unfold and thus shift their center of
gravity without moving on the ground at all), but such cases are so isolated that we can ignore them.
142
Artificial Life Volume 13, Nombre 2
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
3.4 Modification of the Objective Function
Many creatures that emerge from the initial population are very simple, typically composed of only
two or three large blocks. The fact that larger creatures tend to be more successful can be explained
by the larger amplitude of their movements, which allows them to travel farther within a single move.
A solution would be to scale each creature’s Dw by a coefficient Cl related to its size: If two
individuals have exactly the same morphology and move in exactly the same way, but one is twice as
large as the other (in the length of its blocks), the bigger one will travel twice as far. It would be fair
to normalize their distances Dw by a coefficient Cl in order to obtain two normalized distances that
are equal. The heuristic chosen to compute Cl is to take the average of each creature’s block lengths:
Ct ¼
1
N
XN
(cid:2)
i¼1
x þ Bi
Bi
y þ Bi
z
(cid:3)
;
where N is the total number of a creature’s blocks, and Bi
the block i.
X; Bi
oui; and Bi
z are the three dimensions of
The fitness value normalized by Cl is given by
Fw ¼
Dw
Cl
:
The simple sum of the block sizes appears to narrow the diversity of individuals, favoring those with
fewer blocks. Donc,
it is also important to take into account that each joint strength is
proportional to the cross section of the bigger block (which is an area) and that a creature’s weight
scales with its volume [30, 31]. Ainsi, when an individual is stretched to twice its original size, le
strength of its joints is multiplied by four while its weight is multiplied by eight, and the bigger
individual will move with more difficulty, since the ratio strength/weight has decreased. À
counterbalance this disadvantageous ratio, two other coefficients Cs and Cv are used: the average
of the sum of each creature’s block areas,
Cs ¼
1
N
XN
i¼1
(cid:2)
2 Bi
xBi
y þ Bi
xBi
z þ Bi
yBi
z
(cid:3)
;
and the average of the sum of each creature’s block volumes,
Cv ¼
1
N
XN
i¼1
xBi
Bi
yBi
z :
The fitness value normalized by the three coefficients Cl, Cs, and Cv is
Fw ¼ Dw
(cid:4)
(cid:5)
:
Cv
Cl Cs
As the numbers of neurons, sensors, and actuators tend to increase with the number of blocks,
simpler creatures are likely to evolve faster and gain speed earlier than more complex ones. The last
Artificial Life Volume 13, Nombre 2
143
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
coefficient Cc allows creatures that would not otherwise survive the first generations to develop their
potential and eventually outperform the simpler ones that quickly reached a lower fitness peak. Comme
each new block brings additional complexity to the creature, it seems reasonable that Cc should
depend on the number of blocks, N, comme
Cc ¼ kN ;
where k is a user-specified constant. Note that if k is close to 1, the N-scaling is mostly linear as long
as N is not too large. En effet, we obtain the best results for k ¼ 1.02. If k is too high, the genetic
algorithm puts too much emphasis on creatures with many blocks, even if they are poorly
performing, while a value too close to 1 is ineffective. The final expression of the objective function
Fw that we used is given by
Fw ¼ Dw
(cid:4)
Cv
CsCl
(cid:5)
Cc :
ð1Þ
3.5 Simulation Time and Periodic Motion
The simulation time during which an individual’s performance is evaluated is critical for finding candi-
dates with periodic motion. It turns out that for a simulation time of 10 seconds, the genetic algorithm
finds creatures that perform correctly inside this period but stop moving in most of the cases when
evaluated for a longer period. Taylor and Massey [32] suggest increasing the simulation time, and indeed,
when it was raised to 20 seconds, almost every resultant creature exhibited periodic motion and was able
to perform for a much longer period than the simulation time itself (from the order of minutes to what
appears to be infinite). Typiquement, 40% à 50% of the creatures stop moving not because the actuators do
not receive any signal from the controller, but instead because they become unstable after several cycles.
3.6 Results for Walkers
Several replicate simulations were started with exactly the same simulation parameters, except for the
random seed. We defined the solution as the fittest individual in the last generation. Not only are the
initial populations different, but the actual solutions and their fitnesses differ systematically across
runs. De plus, even though in some cases solutions are similar to Sims’, none of them are identical
either in their morphology or in their behavior. This clearly indicates that the fitness landscape has
many local optima disseminated in different regions. Cependant, these solutions display similarities
that naturally suggest grouping them in categories or families.
The most common family consists of two blocks (Figure 2a), where the smallest block is used as
an appendage to push the larger one. This appendage sometimes develops into several blocks and is
used to push the organism, in a manner reminiscent of caterpillars (Figure 2b). Another common
family consists of creatures that use the corners of two or more blocks in an antiphase scheme to
either crawl on the ground (Figure 2c) or roll over (Figure 2d). Some more complex creatures use an
additional appendage to counterbalance the opposite part of their body and amplify their crawling or
oscillating motion to move faster (Figure 2e). Others are initially standing upright and are able to
shuffle forward while keeping their balance, or use the two opposite sides of two blocks and rotate
each of them in almost perfect synchrony to walk in a quadruped-like manner (Figure 2f ). Because
the friction parameter was set high, almost no sliding organisms emerged from the optimization
runs. The few that did progress painfully and perform very poorly in general. Evolution found a way
around this difficulty by developing controllers that minimize ground contacts.
In the scope of 100 generations, each run produced individuals that are significantly different from
each other and that correspond to trajectories in the search space with distinctive end points. It is also
obvious that the population never exhausted all the possible innovations in any optimization run.
144
Artificial Life Volume 13, Nombre 2
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
Chiffre 2. Samples of various evolved locomotion strategies.
A natural question arises from these results: Would the evolution process perform much better
sampling of a region of a particular subspace (local optimum) if it kept going for hundreds of
thousands of generations? In that case, would the evolution trajectories of different runs tend to
meet in a few basins of attraction (convergence to a few families of similar species), or would each
run follow its own path and the trajectories converge to as many local optima (specialization of
species)? This is a fundamental question about the structure and topology of genetic space that has
occupied the experimental evolution community for many years [19, 34, 41].
The answer is certainly not straightforward and may depend on several parameters, such as the
similarity between initial populations (influence of proximity between starting points of different tra-
jectories) or whether interaction between species occurs during a simulation run (influence of proximity
between trajectories). An experiment spanning over 100,000 generations would be impractical, as it
would take (on our current platform, a Pentium 4, 3.0 GHz) entre 1 et 3 months to complete.
4 Evolution of Catapults
In order to study the emergence of behaviors significantly different from the walking and swimming
behaviors studied by Sims, we introduced small modifications to the way blocks are connected to
allow for the evolution of throwing strategies. The modifications to the system as well as the results are
discussed in the next subsections.
4.1 Differences from Walkers
A catapult is composed of three parts: a main body that is structurally identical to a walker’s body, un
arm in which a mechanism controls the release of the block that has to be thrown, and the projectile
lui-même (Chiffre 3). The mechanism consists of four neurons that can be activated after a predefined
delay (30 time steps, ou 0.5 seconds) or else earlier if there is an incoming signal from the body’s
neural network (Chiffre 4). Once the mechanism is fired, a special kind of effector breaks the link
between the projectile and the arm. This mechanism ensures that the projectile will always be
released before a maximum amount of time and lets the creature modify this time for potential
synchronization to another event. The projectile is a standard block without neurons.
In order to keep the catapult’s structure consistent, genetic operators have to be slightly modified
as well so that mutations do not affect the arm’s inner mechanism, except its connection to the
neural network. In some experiments, mutations are allowed on the size and shape of the projectile.
Artificial Life Volume 13, Nombre 2
145
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
Chiffre 3. Schematic representation of catapult’s genotype, where each circle is a gene. The arm (dotted circle) is the root
of the graph to which the projectile (black circle) and the remainder of the body (white circles) are connected.
Grafting (Chiffre 5) and crossover (Chiffre 6) operators are applied in order to keep one arm and one
projectile only for each creature.
4.2 Description of Tasks
For the evolution of the catapults, two kinds of tasks are tested, and for each of them, mutations on
the projectile are allowed in some simulations and prohibited in others. The first task simply consists
in optimizing the distance covered by the projectile, while the second is to aim at a specific direction
as vigorously as possible.
The distance Dp traveled by the projectile is measured by recording the position of the projectile’s
center of mass when the block is released and when it comes to rest, discarding the vertical
component z. (If elevation is taken into account, the projectile will traverse a distance simply by being
released, and evolution just tends to maximize this elevation by selecting motionless catapults that
simply release their projectile from an elevated point.) The fitness given by the objective function is
FD ¼ Dp:
ð2Þ
In that way, it is possible to immediately stop the simulation when the last position is recorded, lequel
significantly reduces the real time spent for each simulation run to 1(cid:6)3 hours. The creatures are
usually tested very quickly in the early generations. The simulation times increase later to about
5 seconds, but on average they are still much below the 20 seconds spent for each walker. Sur-
prisingly, this simple measure (Équation 2) is enough to obtain interesting results. There is no need
to eliminate any individuals with undesirable behavior either.
Cependant, a recurrent problem in dynamics simulations is the risk of numerical explosion, which is a
numerical instability leading to forces so large that they overwhelm the joints that keep the blocks
ensemble. Such creatures literally explode, with body parts flying off in all directions (voir la figure 7). Un-
fortunately, evolution of throwers is likely to generate individuals with strategies involving fast motions
that raise the risk of numerical explosion. (Numerical explosions are discussed in detail in Section 5.4.)
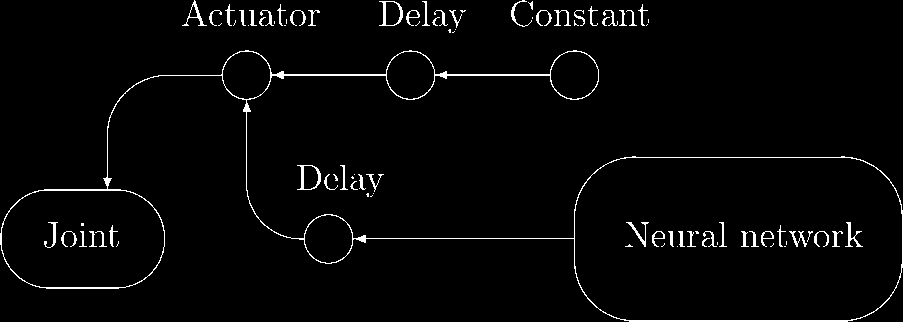
Chiffre 4. Schematic representation of the catapult’s ignition mechanism that releases the projectile. A constant coupled
with a delay neuron ensures that a signal will reach the actuator. A signal could also come from the creature’s neural
network and reach the actuator before the delay to allow eventual synchronization.
146
Artificial Life Volume 13, Nombre 2
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
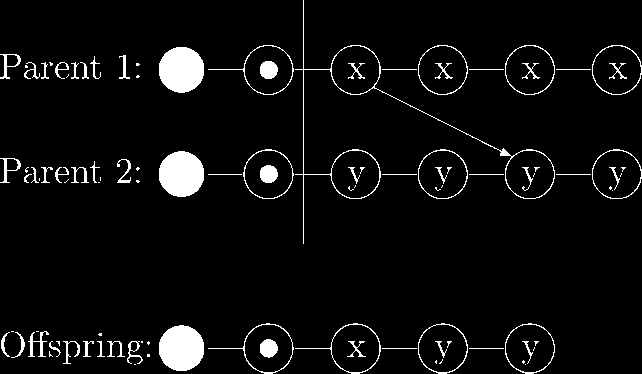
Chiffre 5. The grafting operator chooses the arm (white circle) and the projectile (dotted circle) from parent 1, alors que
treating the other genes (right side of the vertical line) in the standard manner.
A test for eliminating such creatures is absolutely necessary because the optimization process tends
to select for individuals with increasingly higher throwing impulses, ultimately reaching a level leading
to numerical explosions. To prevent this from happening, we test the speed of every moving body part,
and eliminate those creatures that have body parts moving faster than a particular threshold. Note that
this puts an upper limit on the speed of the throwing arm, because the test does not distinguish between
fast throwers and creatures that blow apart due to numerical instabilities. Souvent, the optimization pro-
cess selects individuals that have high impulses in the early generations until it finds one that exhibits a
motion fast enough to trigger a numerical explosion that eliminates the individual. Once this upper
limit on the speed is reached, the optimization process chooses descendants that exhibit almost the
same arm speed, but with a better throwing technique or a projectile with a more advantageous combi-
nation of weight (lighter) and shape (still rolls easily), as these are the only ways to increase the distance.
At the time the optimization process reaches this point, a significant portion of the catapult arms move
at a speed close to the threshold (see Section 5.4), leading to a significant increase in the proportion of
discarded individuals in the population compared to the beginning of the optimization process.
For the tests where creatures have to aim at a specific direction, their performance is evaluated on
how close the projectile’s trajectory is to the target, without necessarily stopping at that particular
indiquer; it is actually more suitable if the block continues: the idea is to hit the target. For that reason,
the fitness of a catapult, Fa, takes into account the distance the projectile traveled, Dp, et le
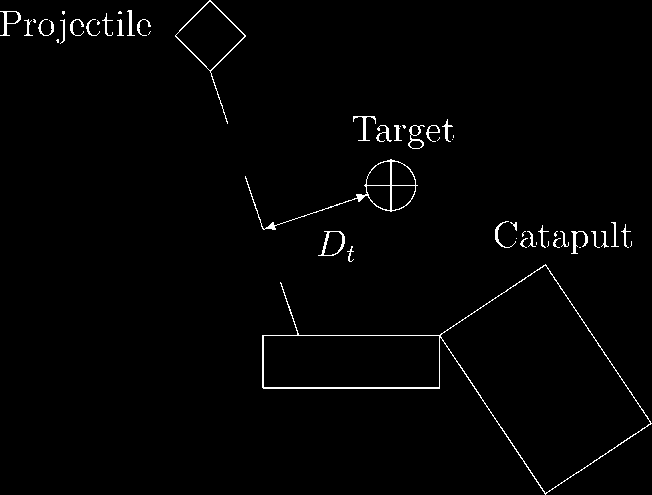
minimum distance Dt between the target and the trajectory (voir la figure 8):
Fa ¼ apDp (cid:6) at Dt :
ð3Þ
We set ap ¼ at ¼ 1 throughout. No further simulations were performed to refine the values of these
constants.
4.3 Results for the Catapults
In the simulation presented here, for every new seed a different individual emerges, and no throwing strat-
egies are alike. While some of the strategies can be guessed from the catapult’s shape (Figures 9 et 10),
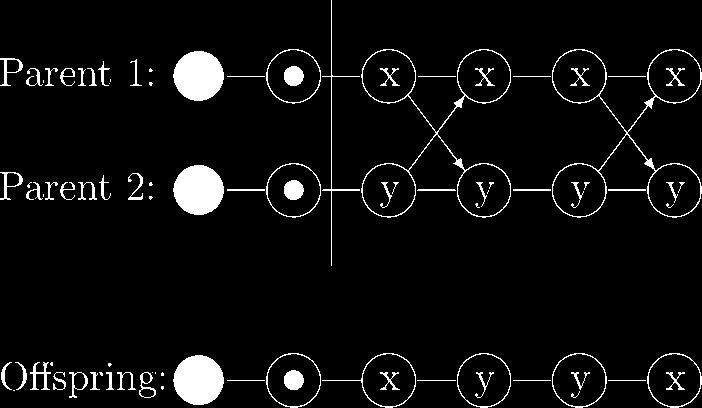
Chiffre 6. The crossover operator for the catapults.
Artificial Life Volume 13, Nombre 2
147
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
Chiffre 7. When a numerical explosion happens, the creature’s spatial configuration and motion are inconsistent. Le
simulator cannot keep the blocks close to their joints.
evolution exploited some morphologies in a surprising manner. We describe here a few examples, but every
strategy is interesting to observe. A video of several of these strategies can be seen at http://public.kgi.edu/
~nchaumon. Among the most spectacular throwing strategies, the following caught our attention:
(cid:2) The drop-kicker releases its projectile, letting it fall on the ground, without moving
(Chiffre 11). At the moment the projectile touches the ground, the catapult actuates a
block to kick the projectile, in the manner of a drop kick. This is an obvious example of
synchronization between an event that happens in the external environment (the projectile
touches the ground) and the ignition mechanism (Chiffre 4) triggered by the controller.
(cid:2) The spinner, before throwing its block, spins it first with two of its appendages to make
it roll much farther on the ground, as one would roll a die before throwing it.
(cid:2) The acrobat curiously begins by standing on its projectile (Chiffre 12), then suddenly imparts
a violent impulse to its whole body so as to spin into a somersault, thereby achieving
a large amplitude and finally releasing the projectile just at the right time. This is also a
demonstration of synchronization between the controller and an event in the environment.
(cid:2) The double-contact hitter uses its big flat arm to hit the projectile with one corner and, on reaching
some initial speed, hits it again with another corner of the arm to increase the speed further.
When mutations are allowed on the projectile, evolution systematically flattens it while keeping its
almost perfect square shape. When thrown, such a block rolls on the edge, like a plate. In this way,
creatures are able to increase the moment of inertia of the projectile while taking advantage of its
diminished weight, as if it were a wheel.
Chiffre 8. Minimum distance Dt between a projectile’s trajectory and the target.
148
Artificial Life Volume 13, Nombre 2
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
Chiffre 9 . Block thrower using lateral momentum.
Among the different morphologies, the most efficient catapults are the ones that use a technique
that consists in propelling the block very close to the ground to maximize the horizontal component
of the velocity. Some of them are able to make their block roll for almost 20 seconds, which is a
particularly long period for this simulation. When the projectile finally stabilizes, it rests in perfect
balance on its edge, without falling.
Only two deceiving strategies with a high fitness score emerged from the experiments performed on
the first task (maximization of Dw). (Perhaps ‘‘deceiving’’ is not the right word, because the only one being
deceived is the one designing the fitness landscape.) In the first one a creature released its block, lequel
subsequently rolled on one of its inclined parts, and in the other a creature fell along with its block and
released it at the very last moment, when its speed reached its maximum. These two strategies involve no
limb actuation at all; evolution was instead very keen at optimizing initial positions of inert bodies.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 10. Example of a creature that uses a throwing strategy similar to that of real-world catapults.
Artificial Life Volume 13, Nombre 2
149
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
Chiffre 11. The drop-kicker.
The second task involves throwing, but with the added complexity of aim. A point in the
simulation environment is defined as the target. Even though the individuals do not have sensors to
retrieve information about the target, aiming is indirectly evolved through selection using the
parameter Dt (see Equation 3). The creatures are evolved over 100 generations. Most of the
solutions aim almost perfectly towards the target, but the distances traveled by the blocks are on
average half those obtained on the previous task. As in the earlier experiments with the catapults, le
strategies that emerge from the simulations are all different from each other. The genetic algorithm
found only one suboptimal strategy that does not involve actual throwing. This strategy consists in
pushing a projectile rather than throwing it.
No individual detached its projectile without any synchronization with an external event. In the
majority of the cases, the projectile was released before the maximum time. This clearly indicates that
the controllers successfully coevolved with respect to three key components: the catapult’s morphol-
Chiffre 12. The acrobat.
150
Artificial Life Volume 13, Nombre 2
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
un
r
t
je
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R.. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
ogy, its motion, and finally the delay after which the ignition mechanism disconnects the projectile
from the body.
5 Methods
5.1 Choice of the Hardware and the Software
The software was coded in C++ without parallelization, and the experiments were carried out on a dual
Pentium-4 Xeon 2.6-GHz workstation with 2 GB of RAM. The creature’s 3D environment and physics
are simulated by Russel Smith’s Open Dynamics Engine [24], version 0.25 (ODE). Since ODE does not
simulate fluid dynamics, the experiments concentrate on the evolution of ground-dwelling creatures only.
To ensure a maximum of stability, chaque (ball and socket) joint has only one degree of freedom.
5.2 Population Size and Generations
Several trials were performed for the walkers and the catapults, varying the population size and the
number of generations in such a way that the product of population size and number of generations was
held constant, ensuring almost constant simulation time. While the simulation time scales roughly lin-
early with each of these parameters, it turns out that fastest improvements were obtained with a popu-
lation of 300 individuals evolved over 100 generations. Cependant, we noticed that the final efficiency of
an individual is much more sensitive to the population size than it is to the number of generations.
5.3 Modified Motor Response in ODE
As we evolve individuals with organic motions, the creature’s effectors should behave as if controlled
by muscle forces. Cependant, ODE is intended to simulate ideal mechanical devices, and the signal
that reaches the effector (from the neural controller) is interpreted as a desired velocity (Vdes):
Vdes ¼ V0 þ
Fdes
m
Dt:
Ici, Fdes is the required force, m the mass of the effector, V0 its initial velocity, and Dt the time
interval during which the force is applied. This velocity is reached instantly by the effector by applying
the required force F within a single time step Dt. In order to avoid singularities, the force cannot
exceed a maximum value Fmax, which is specified for each joint at each time step.
If the desired velocity cannot be achieved because it would require a force F > Fmax, then the
motor saturates, c'est,
Vmax ¼ V0 þ
Fmax
m
Dt < Vdes:
Naturally, if the desired velocity oscillates rapidly, this mechanism leads to violently shaking or-
ganisms. Interestingly, this feature is exploited very rapidly by the selection process, because such
vibrations can lead to forward motion very easily because ideal effectors vibrate without damping.
Such a setup precludes the evolution of more interesting modes of locomotion.
Instead of varying the velocity Vdes by applying a force F, we can operate the motor at saturation
by varying Fmax instead, keeping Vdes fixed and high. Because the effective friction introduced by
running the motor at saturation dampens the input signal, violent vibrations can be avoided.
It is possible that the neural signal itself evolves to be smooth rather than oscillating in the long
run. However, we did not check whether this is the case, or whether oscillations are always
suppressed by the motors.
Artificial Life Volume 13, Number 2
151
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
a
r
t
l
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
5.4 Avoiding Catastrophic Numerical Instabilities in the Simulation
Throughout a simulation, ODE uses a numerical integrator to predict the objects’ positions and
velocities interacting in the dynamical simulation. The integrator computes the amount of force and
torque that accumulates on contact points, using a constant time step size that is often a tradeoff:
small time steps allow more accurate and more stable simulations, whereas large ones accelerate the
simulation while deteriorating the computation accuracy. In the worst case, the intensity of forces or
torques that accumulate on a point can diverge over time, leading to astronomically high values that
break the simulation consistency (see Figure 7). We call this phenomenon numerical explosion.
Even though the time step chosen for the experiments presented here is rather small (0.016 second,
compared to 0.05 second for Taylor and Massey [32]), there are still some creatures that could find weak-
nesses in the simulator and take advantage of the numerical explosions to propel themselves significantly
farther than any other could in a realistic situation. Since in most of the cases the displacement resulting from
a numerical explosion is easy to detect, each part of a creature’s body is monitored, and its displacement is
compared with a maximum threshold. Each displacement larger than this threshold is considered a numer-
ical explosion; the creature is discarded from the population by setting its fitness to an arbitrary low value.
5.5 Genotypic and Phenotypic Constraints
Besides the test for valid motion, a test is also carried out to avoid impossible phenotypes. Each time a
new individual is created, its morphology is tested in ODE for self-collisions. If such collisions occur,
the creature is eliminated and the system generates a new one until it finds a valid candidate. Contrary
to Sims’ implementation, there is no attempt to repel the creatures’ body parts from each other.
Although systematically discarding individuals with self-penetrating parts is computationally faster than
Sims’ test for valid new creatures, it fails to retain potentially interesting creatures that are close to being
valid. Still, there is no evidence at this time that such a test narrows the population diversity.
In Sims’ work, a creature is eliminated if the number of blocks that compose its body exceeds a
predefined maximum number. In our simulation (unlike in previous works [30 – 32]), we specify a
maximum number of genes instead: nmax ¼ 20. While genomes with 20 genes can give rise to
creatures with any number of blocks, those with a disproportionately large number of blocks are
normally eliminated due to poor performance.
5.6 The Controller
The set of neurons used in this work is simpler than those used in [28, 30 –32]. A description is
provided in the Appendix.
When a new creature is generated, no garbage collection is performed to eliminate the unconnected
parts of the controller. In this way, a new connection can take advantage of previously disconnected
parts that are ready to be used without re-creating a whole new part of the network from scratch.
5.7 The Genetic Operators
The same genetic operators as Sims’ are used in the simulations that evolve walking creatures, but a
slightly modified version, explained in Section 4.1, has to be used to allow the evolution of catapults. The
same probabilities of choosing a particular operator are used in each experiment: every new creature has
a 40% chance of being generated from mutations only (asexually), 30% from crossovers, and 30% from
grafting. The asexual operator chooses a parent among the survivor population, copies it, and considers
each of its parameters for mutation with a 10% probability. After a crossover or grafting, the new
individual has a 10% chance of undergoing mutations, with a per-site mutation probability of 5%.
6 Discussion and Future Work
The diversity of evolved organisms, whether they are walkers or catapults, proves that our system can
automatically generate diversified and complex individuals with complex behaviors. When evolving
catapults—in contrast with walkers—no refinements such as a controller’s activation/deactivation
152
Artificial Life Volume 13, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
a
r
t
l
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
sequence or a nontrivial fitness measure is necessary to obtain interesting throwing strategies. This fact is
unexpected if the complexity of the experiment setup grows with the individual’s structure. Catapults
and walkers share the same body structure that has to be evolved to perform a specific motion.
Catapults have in addition a throwing arm with a projectile. This structural addition might have made
catapults more difficult to evolve, and we might have expected the experimental setup to have to be
even more sophisticated than the setup required for evolving walkers. This intuition turns out to be
erroneous: there is no evidence in our experiments of a direct correlation between the individual’s
structural complexity and the amount of computation needed to evolve it towards satisfactory behavior.
We suppose instead that the individual’s structural suitability for the task constitutes a better pre-
dictor of how hard it is to obtain suitable behavior. Indeed, the constraints imposed on a catapult’s
structure provide a shortcut from which evolution can elaborate subsequent innovations directly
relevant to throwing strategies; every catapult evolved strategies around the throwing arm and the
detachable projectile. This advantage provides a head start for every catapult, avoiding the struggle
for newly generated individuals to evolve this mechanism de novo. The walkers do not benefit from
such structural guidance — primitive limbs, for example — that could support locomotion strategies.
In order to have more evidence regarding this conjecture, one could design an experiment to
evolve catapults (requiring them) to evolve a throwing arm and a detachable projectile (from scratch).
Some individuals might never evolve such components, just as some walkers do not evolve useful
limbs. Additionally, if such constraints on the catapult’s structure effectively facilitated their evolu-
tion, it would be interesting to assess how tightly these constraints determine evolution’s course by
removing a variable number of a catapult’s structural constraints (some formerly fixed parameters
describing a catapult’s constraints could be subjected to genetic alterations) and measuring the fre-
quency of successful convergences to throwing strategies.
In previous work [30 –32], few or no individuals could evolve actuating controllers. To overcome
this shortcoming, actuators generated at the initial generation were built up with a particularly large
number of oscillators. This bias in oscillator proportion increases the chance an oscillator is connected
to an actuator. In our work, no particular bias of any sort was required to evolve suitable behaviors.
This observation may be explained by the absence of garbage collection in the creature’s controller:
No part of the neural network is eliminated by garbage collection if a disconnection occurs. Recon-
nections are easier, which makes the overall network configuration more stable against genetic
alteration. The drawback of this choice is that creatures carry useless components. Typically, only a
quarter of the genotype is used to express the phenotype. However, this significant overhead in gene
manipulations remains unnoticed, as most of the CPU time is consumed by the dynamics simulation.
The basic structure of the system is very modular to allow maximum versatility in the design of body-
brain coevolution experiments. For that reason, future scientific endeavors with this system will often
require the implementation of system extensions. The following discussion suggests possible experi-
ments that will require new features to be implemented. Implementation will build upon the three main
components that already exist: the virtual creatures, the environment, and the optimization algorithm.
In the short term, it would be easy to add new kinds of neurons, as in [17, 18, 25, 30], to see how
new neural functions impact the evolution process. New sensors can also be added that reveal the
direction of a particular point—for example, to let catapults exploit information directly originating
from the target. More extensive tests can be carried out to evolve catapults to aim at moving targets,
rather than at a fixed location. On that basis, it should also be possible to optimize catapults to obey
rules of a game such as curling, for example. Moreover, no comparative analysis has been performed
of the efficiency of individuals that are built from primitives of different shapes (spheres, cubes, sticks,
tetrahedra, etc.). This extension is quite straightforward, since all the necessary functions already exist in
ODE to build individuals with heterogeneous primitives, manage collision detection, and so on.
In the longer term, the system can easily take advantage of more profound modifications to
investigate questions that have not yet been addressed. These modifications can affect each of the
three major components of the system (virtual creatures, optimization algorithm, and environment).
Modification of the virtual creatures: The creatures may take advantage of new kinds of evolvable
sensors, sensitive to different kinds of stimuli (contact, light, smell, etc.), and let them evolve with the
Artificial Life Volume 13, Number 2
153
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
a
r
t
l
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
creature. To our knowledge, no work has been reported about optimizing sensor efficiency for a
given task by varying its position and characteristics.
The existing neural network can be replaced by other types of controllers, such as gene regulation
networks. The gene regulation network can not only define the actual individual’s configuration, but
also control its development, as in the work of Bongard and Pfeifer [3, 4]. Such an approach has the
advantage of systematically generating consistent individuals, making the tests for validating the
viability of each new individual obsolete.
The optimization process can also be given a more restricted set of primitives, as in the work by
Lipson and Pollack [20]. These primitives are the virtual counterpart of real mechanical parts that
can be assembled to build actual robots. These robots and their controllers are the mechanical
equivalent of virtual robots evolved in silico to accomplish predefined tasks. This represents a
promising avenue that has yet to be explored.
The optimization algorithm: In the field of body-brain coevolution, the genetic space has been searched
almost exclusively with genetic algorithms using traditional genetic operators. In some cases in biology,
recombination turns out to slow down the evolution process [10]; even if this operator has the potential
to relocate two beneficial innovations on a single individual, it may also disrupt the efficiency of two
parents that are structurally very different. Moreover, no investigation has been conducted to assess the
superiority of this technique over others such as evolution strategy [16], simulated annealing [13], genetic
algorithms [22] combined with gradient descent [1], cultural algorithms [27], evolutionary diffusion
algorithms [35], particle swarm optimization [12], and ant colony optimization [6]. The current version
can easily be extended to allow the user to perform experiments with various search methods.
The environment: As is typical of evolution experiments in simulated environments, a large fraction of
the population obtains its initial fitness by exploiting the numerical instabilities of the simulator for
forward movement. We measured the potential efficiency of such creatures: A run was started in which
each individual’s controller was disabled, while keeping the same step size (1/60 second). The evolved
creature was simple (composed of two blocks) and used amplified vibrations caused by a bigger block
pushing a smaller one into the ground. Only one edge of the smaller block penetrated the ground, and it
did not point precisely downwards, so the repulsion and gravitational forces that caused the vibration
were applied to the block almost but not quite vertically. This imperfect alignment caused the block’s
position to be offset by a small distance each time a gravitational or a repulsion force was applied. Friction
forces due to the ground reduced the offset when a penetration happened, leaving the repulsion offset
often larger. The repetitive application of gravitational and repulsion forces to the smaller block caused the
individual to move in a preferred direction quite fast. Fortunately, that kind of individual is eliminated in
ODE at the early stages of the evolution process, provided the simulator’s inaccuracies are small enough.
Depending on the computational model (integration strategy, collision response, etc.), each
simulator has its own strengths and weaknesses, which make it suitable for a specific kind of physics
interaction. In ODE, for example, it is obvious that evolving catapults is feasible and involves less
computation than evolving walkers. This may not be true for another simulator that cannot deal with
contacts with projectiles that hit the ground abruptly at high velocities. Conversely, a simulator may
generate large inaccuracies when simulating walkers that would take advantage of this weakness by
evolving violent vibrations. As evolving simple controllers that exploit quakes is easier than evolving
more complex controllers that generate smooth periodic motions, the former may outperform the
latter in the early generations, resulting in a population composed of vibrating individuals in the
subsequent generations. Depending on the task, a particular simulator may fail systematically while
another may be much more successful; having the choice of several simulators is critical.
Finally, simulations can be carried out in more realistic environments that combine air and water,
complex terrain, and so on, and that allow energy exchange between creatures and their environment
as well as between creatures (creatures feeding on energy resources present in the environment, on
other creatures’ waste products, or even the creatures themselves). These features could allow
experiments where the effects of habitat diversity together with different kinds of resources cause
a homogeneous ancestral population to split up to occupy several niches. Allopatric speciation,
adaptive radiation, and predator-prey interactions may also be observed.
154
Artificial Life Volume 13, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
a
r
t
l
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
Ultimately, we believe that systems capable of displaying nearly open-ended evolution of complex
morphologies and behaviors should be used to study basic questions in evolutionary biology that
cannot be addressed by any other means, such as the mode and manner of speciation via niche
speciation, its relation to mate selection, and the emergence of ecologies. We hope to use this system
in that manner in the future.
7 Conclusion
We have described a system to perform experiments exploring the coevolution of morphology and
behavior of artificial agents. As examples, we successfully evolved walking and block-throwing
creatures that exploit a rich diversity of efficient locomotion and block-throwing strategies. These
goals are achieved thanks to the modularity of our system, which allows us to implement a simple
controller activation/deactivation sequence for evolving walkers, and to modify a walker’s structure
for evolving block-throwing individuals. The wealth of evolved throwing strategies is further
evidence of the complexity of simulated 3D physical environments and hints at a promising path
towards quasi-open-ended evolution. The juxtaposition of the locomotion and throwing experiments
also revealed fundamental differences in the evolvability of prototypes that can be traced back to the
suitability of the structure for these tasks rather than the complexity of the tasks themselves.
Evolvability is only one of the many basic concepts in evolutionary biology that can be addressed
in a quantitative manner using our system. It is particularly well suited to designing experiments that
would be impossible, impractical, or unethical to perform on biological organisms and communities.
We hope that our framework will ultimately alleviate the traditional programming burden that turns
experimentation with simulated 3D physical environments into real challenges.
Acknowledgments
Thanks to Russel Smith for making the ODE engine available for an open-source project. The
research of the second author was supported by a grant from the Natural Sciences and Engineering
Research Council of Canada.
References
1. Arfken, G. (1985). Mathematical methods for physicists (3rd ed.), (pp. 428 – 436). Orlando, FL:
Academic Press.
2. Autonomous Virtual Humans. http://www.vrac.iastate.edu/~streeter/avh/avh.html.
3. Bongard, J. C., & Pfeifer, R. (2001). Repeated structure and dissociation of genotypic and
phenotypic complexity in artificial ontogeny. In L. Spector, et al. (Eds.), Proceedings of the Genetic
and Evolutionary Computation Conference (pp. 829 – 836). San Francisco: Morgan Kaufmann.
4. Bongard, J. C., & Pfeifer, R. (2003). Evolving complete agents using artificial ontogeny. In F. Hara &
R. Pfeifer (Eds.), Morpho-functional machines: The new species (designing embodied intelligence) (pp. 237 – 258).
Berlin: Springer-Verlag.
5. Darwin2k. http://darwin2k.sourceforge.net (accessed January 2007).
6. Dorigo, M., & Gianni, D. C. (1999). The ant colony optimization meta-heuristic. In I. D. Corne,
M. Dorigo, & F. Glover (Eds.), New ideas in optimization (pp. 11 – 32). London: McGraw-Hill.
7. DynaMechs. http://dynamechs.sourceforge.net (accessed January 2007).
8. Evolving Robots. http://www.erachampion.com/ai/ (accessed January 2007).
9. Faloutsos, P., van de Panne, M., & Terzopolous, D. (2003). Autonomous reactive control for
simulated humanoids. In IEEE International Conference on Robotics and Automation (pp. 917 – 924).
Piscataway, NJ: IEEE.
10. Froissart, P., Wilke, C. O., Montville, R., Remold, S. K., Chao, L., & Turner, P. E. (2004). Co-infection
weakens selection against epistatic mutations in RNA viruses. Genetics, 168, 9 – 19.
11. Havok. http://www.havok.com/products/physics.php (accessed January 2007).
Artificial Life Volume 13, Number 2
155
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
a
r
t
l
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
12. Kennedy, J. (1997). The particle swarm: Social adaptation of knowledge. In R. Eberhart & P. Angeline
(Eds.), Proceedings of the 1997 International Conference on Evolutionary Computation (pp. 303 – 308). Piscataway,
NJ: IEEE.
13. Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220,
671 – 680.
14. Klein, J. (2003). BREVE: A 3D environment for the simulation of decentralized systems and artificial
life. In K. Standish, M. A. Bedau, & A. Abbass (Eds.), Proceedings of the Eighth International Conference on
Artificial Life (pp. 329 – 334). Cambridge, MA: MIT Press.
15. Klein, J. (2006). BreveCreatures. http://www.spiderland.org/breve/breveCreatures.html (accessed
January 2007).
16. Knowles, J., & Corne, D. (1999). The Pareto archived evolution strategy: A new baseline algorithm for
Pareto multiobjective optimization. Evolutionary Computation, 1, 98 – 105.
17. Komosin´ski, M. (2003). The Framsticks system: Versatile simulator of 3D agents and their evolution.
Kybernetes: The International Journal of Systems & Cybernetics, 32, 156 – 173.
18. Komosin´ski, M., & Ulatowski, S. (1999). Framsticks: Towards a simulation of a nature-like world,
creatures and evolution. Lecture Notes in Artificial Intelligence, 1674, 261 – 265.
19. Lenski, R. E., & Tavisano, M. (1994). Dynamics of adaptation and diversification: A 10,000-generation
experiment with bacterial populations. Proceedings of the National Academy of Sciences of the U.S.A., 91,
6808 – 6814.
20. Lipson, H., & Pollack, J. B. (2000). Automatic design and manufacture of artificial lifeforms. Nature,
406, 974 – 978.
21. McKenna, M., & Zeltzer, D. (1990). Dynamic simulation of autonomous legged locomotion.
In F. Baskett (Ed.), Proceedings of the 17th Annual Conference on Computer Graphics and Interactive Techniques,
SIGGRAPH 1990 (pp. 29 – 38). New York: ACM Press.
22. Michalewicz, Z. (1996). Genetic algorithms + data structures ¼ evolution programs (3rd ed.),
New York: Springer-Verlag.
23. Miconi, T., & Channon, A. (2006). An improved system for artificial creatures evolution. In L. Rocha,
L. Yaeger, M. Bedau, D. Floreano, R. Goldstone, & A. Vespignani (Eds.), Proceedings of the 10th Conference on
the Simulation and Synthesis of Living Systems, ALIFE X (pp. 255 – 261). Cambridge, MA:
MIT Press.
24. Open Dynamics Engine. http://ode.org (accessed January 2007).
25. Ray, T. S. (2000). Aesthetically evolved virtual pets. In C. C. Maley & E. Boudreau (Eds.), Artificial Life
VII Workshop (pp. 158 – 161). Cambridge, MA: MIT Press.
26. Reynolds, C. (1987). Flocks, herds, and schools: A distributed behavioral model. In M. C. Stone
(Ed.), Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 1987
(pp. 25 – 34). New York: ACM Press.
27. Reynolds, R. G. (1994). An introduction to cultural algorithms. In A. V. Sebald & L. J. Fogel (Eds.),
Proceedings of the 3rd Annual Conference on Evolutionary Programming (pp. 131 – 139). River Edge, NJ:
World Scientific Publishing.
28. Shim, Y.-S., & Kim, C.-H. (2003). Generating flying creatures using body-brain coevolution.
In A. P. Rockwood (Ed.), Proceedings of ACM SIGGRAPH/Eurographics Symposium on Computer
Animation (pp. 267 – 285). San Diego, CA: Eurographics Association.
29. Shim, Y.-S., Kim, S.-J., & Kim, C.-H. (2004). Evolving flying creatures with path following behavior.
In J. Pollack, et al. (Eds.), Proceedings of Artificial Life IX (pp. 125 – 132). Cambridge, MA: MIT Press.
30. Sims, K. (1994). Evolving virtual creatures. In A. Glassner (Ed.), Proceedings of the 21st Annual Conference
on Computer Graphics and Interactive Techniques, SIGGRAPH 1994 (pp. 15 – 22). New York: ACM Press.
31. Sims, K. (1994). Evolving 3D morphology and behavior by competition. Artificial Life, 1(4), 353 – 372.
32. Taylor, T., & Massey, C. (2001). Recent developments in the evolution of morphologies and controllers
for physically simulated creatures. Artificial Life, 7(1), 77 – 87.
33. Terzopoulos, D., Tu, X., & Grzeszczuk, R. (1994). Artificial fishes: Autonomous locomotion,
perception, behavior, and learning in a simulated physical world. Artificial Life, 1(4), 327 – 351.
156
Artificial Life Volume 13, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
a
r
t
l
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N. Chaumont, R. Egli, and C. Adami
Evolving Virtual Creatures and Catapults
34. Travisano, M., Mongold, J. A., Benett, A. F., & Lenski, R. E. (1995). Experimental tests of the role
of adaptation, chance and history in evolution. Science, 267, 87 – 90.
35. Tsui, K. C., & Liu, J. (2002). Evolutionary diffusion optimization, part I: Introduction to the algorithm.
In D. Fogel, et al. (Eds.), Proceedings of the IEEE Congress on Evolutionary Computation (pp. 169 – 174).
Piscataway, NJ: IEEE.
36. Ventrella, J. (1994). Disney meets Darwin: An evolution-based interface for exploration and design of expressive animated
behavior. Master’s thesis, MIT Media Lab, Massachusetts Institute of Technology, Cambridge, MA.
37. Ventrella, J. (1994). Explorations in the emergence of morphology and locomotion behavior in
animated figures. In M. A. Brooks & P. Maes (Eds.), Proceedings of Artificial Life IV (pp. 436 – 441).
Cambridge, MA: MIT Press.
38. Ventrella, J. (1996). Sexual swimmers (emergent morphology and locomotion without a fitness function).
In P. Maes, et al. (Eds.), From Animals to Animats: Proceedings of the Fourth International Conference on Simulation
of Adaptive Behavior (pp. 484 – 493). Cambridge, MA: MIT Press.
39. Virtual Biped. http://fy.chalmers.se/~wolff/simulatedhumanoid.html.
40. Vortex. http://www.cm-labs.com (accessed January 2007).
41. Wagenaar, A., & Adami, C. (2004). Influence of chance, history, and adaptation on digital evolution.
Artificial Life, 10, 181 – 190.
42. Walker Demo (Newton Dynamics). http://www.newtondynamics.com/downloads.html (accessed
January 2007).
43. Yaeger, L. (1994). Computational genetics, physiology, metabolism, neural systems, learning, vision,
and behavior or PolyWorld: Life in a new context. In C. Langton (Ed.), Proceedings of Artificial Life III
(pp. 263 – 298). Reading, MA: Addison-Wesley.
Appendix
Table 1 . Neuron description. Every input value lies in the interval [(cid:6)1, 1], every output value is also restricted to the same
interval. Bold letters are user-defined internal values specified at the neuron instantiation. t is the internal simulator time.
Neuron type
Input
Output O
sen
None O =
8
<
1 if a contact is detected on the block’s
face the sensor is attached to,
:
(cid:6)1 otherwise.
sumT
a, b
O =
(cid:9)a + b
0
if (a + b) z T,
otherwise.
div
eff
mem
wav
mul
sum
cst
a, b
O =
(cid:9)1
if b V q,
a/b otherwise.
a
a
An impulse of intensity a is sent to
the actuator assigned to the motor.
O = a after n time steps.
a, b, c O = b sin(at + c).
a, b
O = ab.
a, b
O = a + b.
None O = V.
Artificial Life Volume 13, Number 2
157
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
a
r
t
l
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
2
1
3
9
1
6
6
2
3
8
8
a
r
t
l
.
/
.
.
2
0
0
7
1
3
2
1
3
9
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3