Eduardo R. Miranda, Alexis Kirke, et
Qijun Zhang
Interdisciplinary Centre for Computer
Music Research (ICCMR)
University of Plymouth
Plymouth, PL4 8AA United Kingdom
{eduardo.miranda, alexis.kirke,
qijun.zhang}@plymouth.ac.uk
Artificial Evolution
of Expressive Performance
of Music: An Imitative
Multi-Agent Systems
Approach
As early as the 1950s and early 1960s, pioneers such
as Lejaren Hiller, Gottfried Michael Koenig, Iannis
Xenakis, and Pietro Grossi, among a few others,
started to gain access to computers to make music.
It soon became clear that to render music with a so-
called “human feel,” computers needed to process
information about performance (par exemple., deviations in
tempo and loudness), in addition to the symbols
that are normally found in a traditional musical
score (par exemple., pitch and rhythm). This was especially
relevant for those interested in using the computer
to play back scores.
En effet, the first ever attempt at creating a
computer-music programming language, by Max
Mathews at Bell Telephone Laboratories in 1957,
was motivated by his wish to “write a program
to perform music on the computer” (Parc 2009
p. 10). It appears that this development began after
Mathews and John Pierce went to a piano concert
ensemble. During the intermission, Pierce suggested
that perhaps a computer could perform as well
as the pianist. Mathews took up the challenge,
which resulted in Music I, the ancestor of music
programming languages such as Csound (Boulanger
2000).
Research into computational models of expres-
sive performance of music (Widmer and Goebl 2004)
is still an active area of study—particularly, recherche
into devising increasingly more sophisticated auto-
mated and semi-automated computer systems for
expressive music performance, hereinafter referred
to as CSEMP.
A CSEMP is able to generate expressive perfor-
mances of music. Par exemple, software for music
typesetting is often used to write a piece of mu-
sic, but most packages play back the music in a
Computer Music Journal, 34:1, pp. 80–96, Spring 2010
c(cid:2) 2010 Massachusetts Institute of Technology.
“robotic” way, without expressive performance.
The provision of a CSEMP engine would enable
such systems to produce more realistic playback.
A variety of techniques have been used to
implement CSEMPs (Widmer and Goebl 2004;
Kirke and Miranda 2009; in press). These include
(1) rule and grammar-based approaches (Sundberg,
Askenfelt, and Fryd ´en 1983; Clynes 1986; Bresin
and Friberg 2000; Livingstone et al. 2007), y compris
expert systems (Johnson 1991); (2) linear and non-
linear regression systems (Canazza et al. 2000;
Ishikawa et al. 2000), including artificial neural
réseaux (Bresin and Vecchio 1995; Camurri,
Dillon, and Saron 2000), Hidden Markov Models
(Grindlay 2005), Bayesian Belief Networks (Raphael
2001), Sequential Covering methods (Widmer and
Tobudic 2003), and Regression Trees (Ramirez
and Hazan 2005); et (3) evolutionary computing
méthodes (Zhang and Miranda 2006; Ramirez et al.
2008). In this article, we introduce a new approach
using the imitative multi-agents paradigm.
Expressive Music Performance
How do humans make their performances sound so
different from the so-called “robotic” performance
a machine would normally give? In this article, le
strategies and changes that are not marked in a score
but which performers apply to the music are referred
to as expressive performance actions. Two of the
most common expressive performance actions in
Western classical music are changing the tempo
and the loudness of the piece as it is played. These
are tempo and loudness changes not marked on the
score; they are additional to notated tempo or loud-
ness changes, such as accelerando or mezzo-forte.
Par exemple, a common expressive performance
strategy is for the performer to slow down as they
approach the end of the piece (Friberg and Sundberg
80
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1999). Another expressive performance action is
the use of expressive articulation—for instance,
when a performer chooses to play notes in a more
staccato (short and pronounced) or legato (lisse)
chemin. Those who play instruments with continu-
ous tuning, for example string players, can also
use expressive intonation, making notes slightly
sharper or flatter, and such instruments also allow
for expressive vibrato. Many instruments provide
the ability to expressively change timbre as well.
There have been a number of studies into Western
pre-20th-century classical music performance, Non-
tably involving the music of the Baroque, Classical,
and Romantic periods. On of the earliest systematic
studies was developed in the late 1930s (Seashore
1938), and more recently good reviews have been
published (par exemple., Palmer 1997; Gabrielsson 2003).
One element of these studies has been to discover
what aspects of a piece of music are related to a per-
former’s use of expressive performance actions. Un
important factor of expressive music performance
is the performer’s structural interpretation of the
piece. Performers have a tendency to express this
structure in their performances (Palmer 1997). Ils
often slow down at boundaries in the hierarchy,
with the amount of slowing being correlated to the
importance of the boundary (Clarke 1988). Ainsi, un
performer would tend to slow more at a boundary be-
tween sections than between phrases. There are also
regularities relating to other musical features in per-
formers’ expressive strategies. Par exemple, in some
cases, higher-pitched notes tend to be played more
loudly. Aussi, notes that introduce tension relative
to the key may be played more loudly. Cependant, pour
every rule, there are always exceptions. For a discus-
sion of other factors involved in human expressive
performance, we refer the reader to Juslin (2003).
Evolutionary Computation
Evolutionary Computation (EC) methods have been
successfully applied to algorithmic composition
(please refer to Miranda and Biles 2007 for an
introduction to a number of such systems). The great
majority of these systems use genetic algorithms
(Goldberg 1989), or GA, to produce melodies and
rhythms. In these systems, music parameters are
represented as “genes” of software agents, and GA
operators are applied to “evolve” music according to
given fitness criteria.
Plus récemment, progress in applying EC to CSEMP
has been reported (Ramirez and Hazan 2005; Zhang
and Miranda 2006; Ramirez et al. 2008). EC-based
CSEMPs have all applied the neo-Darwinian ap-
proach of selecting the musically fittest genes to be
carried into the next generation. We are interested,
cependant, in investigating the application of an alter-
native EC approach to expressive performance—one
that is based on cultural transmission rather than
genetic transmission.
Musical behavior in human beings is based both
in our genetic heritage and also our cultural heritage
(Dissanayake 2001). One way of achieving a cultural,
as opposed to genetic, transmission is through
imitation of behavior (Zentall and Galef 1988; Boyd
and Richerson 2005). Work on the application of
this imitative cultural approach to algorithmic
composition was initiated by Miranda (2002). Dans
this article, we follow up the cultural transmission
methodology with an application of an imitative
multi-agent systems approach to expressive music
performance. We have developed a system referred
to as Imitative Multi-Agent Performer, or IMAP,
which is introduced subsequently.
In the GA model of behavior transmission, un
population of agents is generated having its own
behavior defined by their “genetic” code. Le
desirability of the behavior is evaluated by a global
fitness function, and agents with low fitness are
often discarded, depending on which version of the
algorithm is adopted (Goldberg 1989). Alors, a new
population of agents is generated by combination and
deterministic or non-deterministic transformation
of the genes of the highest-scoring agents.
Inversement, in the imitation model of behavior
transmission, an agent interacts with one or more
other agents using a protocol that communicates
the first agent’s behavior to the other agents. Le
other agents evaluate the first agent’s behavior based
on some evaluation function, and if the evaluation
scores highly enough, one or more of the other
agents will change their own behaviors based on the
first agent’s behavior. The evaluation function in the
Miranda et al.
81
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
imitation model plays a similar role to the fitness
function in the GA model. Cependant, in imitative
multi-agent systems, the evaluation function is
particularly suited for the design of EC systems
using a non-global fitness function, Par exemple, par
giving each agent their own evaluation function.
The potential for diversity is a desirable trait
in a system for generating novel expressive music
performances—as opposed to replicating existing
ones—because there is no objectively defined op-
timal performance for a musical score (Bresin and
Friberg 2000; Ramirez et al. 2008). Performance is
a subjective, creative act. Previous work on genetic
transmission in generating expressive music per-
formance has been significantly motivated by the
desire to generate a variety of performances. As will
be demonstrated herein, there is even more scope for
such variety in IMAP because a multiplicity of eval-
uation functions is used. En outre, there is scope
for easily controlling the level of diversity in IMAP.
It is not our intention to compare the imitative
approach with the GA approach, because both
approaches have their own merits and should be
considered as complementary approaches. Ramirez
et autres. (2008) demonstrated the validity of a GA
model, and the experiments later in this article
demonstrate the validity of our imitative approach.
One obvious measure of validity is whether the
system generates performances that are expres-
sive. The other two measures of validity relate to
those elements of the imitative approach, lequel
differentiate it from the standard GA approach—in
particular, the ability to easily provide the system
with a number of parallel interacting fitness func-
tion. Ainsi, IMAP will be evaluated in terms of
(1) the expressiveness of IMAP-generated perfor-
mances (note, cependant, that this is not assessed
by means of experiments with human subjects; nous
assess how well the agents can generate perfor-
mances that embody their preference weights); (2)
performance-diversity generation and control of the
level of diversity; et (3) the ability to control diver-
sity when it is being affected by multiple musical
elements simultaneously.
Imitative learning has been frequently used in
other multi-agent systems research (De Boer 2000;
Noble and Franks 2004). Cependant, to the best of our
connaissance, IMAP is the first application of such
methods to the generation of expressive musical
les performances.
Imitative Multi-Agent Performer: IMAP
Each agent has two communication functions: Il
can listen to the performance of another agent,
and it can perform to another agent. All agents
are provided with the same monophonic melody—
the melody from which expressive performances
will be generated. In all interactions, all agents
perform the same melody, usually with different
expressive actions. Agents in IMAP have two types
of expressive actions: changes in tempo and changes
in note loudness. Each agent also has a musical
evaluation function based on a collection of rules,
where different agents give different weightings
to the rules and use the combination to evaluate
the performances they hear. Initially, agents will
perform with random expressive actions. If they
evaluate another agent’s expressive performance
highly enough through their evaluation function,
then they will adjust their own future performances
toward the other agent’s expressive actions. As this
process continues, a repertoire of different expressive
performances evolves across the population.
Agent Evaluation Functions
The agents’ evaluation functions could be generated
in a number of ways. One of the most common
methods used in CSEMPs is learning from human
examples using machine-learning techniques (Bresin
and Vecchio 1995; Widmer and Tobudic 2003;
Grindlay 2005). A second common method is
providing agents with rules describing what features
an expressive performance should have (Sundberg,
Askenfelt, and Fryd ´en 1983; Todd 1985; Hashida,
Nagata, and Katayose 2006; Livingstone et al. 2007).
The second approach was chosen for IMAP because
we wanted to provide the means to explicitly change
the influence of various musical factors on the
final expressive performance. Machine-learning
approaches, such as those based on artificial neural
82
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
réseaux, tend to develop a more implicit reasoning
système (Ben-David and Mandel 1995). An explicitly
described rule set allows for simpler controllability
of a multi-agent system. Cependant, unlike many
rule-based CSEMPs, the agents in IMAP do not
use their rules to generate their performances.
Plutôt, they use them to evaluate performances
(their own and those of other agents) and therefore
choose which other agents to imitate. This will
become clearer as we introduce the system. In short,
the more highly another agent’s performance is
scored by the parameterized evaluation function of a
listening agent, the more highly the listening agent
will regard the performing agent.
An agent’s evaluation function is defined at
two stages: the Rule Level and the Analytics
Level. The first stage—the Rule Level—involves
a series of five rules derived from previous work
on generative performance. The second stage—
the Analytics Level—involves a group of musical
analysis functions that the agent uses to represent
the structure of the musical score. The Rule Level
and the Analytics Level are both parameterized to
allow the user to control which elements have most
influence on the resulting performances.
For the Rule Level, we could have selected
a large number of rules available from previous
research into CSEMP. To keep the rule list of IMAP
manageable, only five rules were selected, bearing
in mind the application and controllability of the
imitative approach. One should note, cependant, que
these rules are not absolute; as will be demonstrated
plus tard, the agents often create performances that do
not fully conform to all rules. For this reason we
refer to these rules as preference rules.
The five preferences rules of the Rule Level
relate to Performance Curves, Note Punctuation,
Loudness Emphasis, Accentuation, and Boundary
Remarques. Each preference rule is based on previous
research into music performance, as follows.
Rule 1: Performance Curves
Performance deviations for tempo between note
group boundaries (par exemple., motif and phrase boundaries)
should increase for the beginning part of the group
and decrease for the second part of the group; comment
these “parts” are defined is explained later. This is
consistent with the expressive shapes, which are
well established in the field of CSEMP (Todd 1985;
Friberg, Bresin, and Sundberg 2006; Hashida, Nagata,
and Katayose 2006; Livingstone et al. 2007). Ce
shape should also occur for the loudness deviations
(Todd 1992).
Rule 2: Note Punctuation
According to this rule, the ending note of a group
of notes should be lengthened (Friberg, Bresin, et
Sundberg 2006).
Rule 3: Loudness Emphasis
Performance deviations for loudness should empha-
sise the metrical, melodic, and harmonic structure
(Clarke 1988; Sundberg et al. 1983).
Rule 4: Accentuation
Any note at a significantly accentuated position
(as defined later) must either have a lengthened
duration value or a local loudness maximum (Clarke
1988; Cambouropoulos 2001).
Rule 5: Boundary Notes
The last note in a note grouping should have an
expressive tempo, which is either a local minimum
or local maximum (Clarke 1988).
Evaluation Equations
These five preference rules of the Rule Level were
implemented as a set of evaluation equations, lequel
are detailed in the following sections. The user can
change the influence of a preference rule in the
final evaluation through the setting of weights. Le
rules take as input the result of a musical score
analysis done by four analysis functions in the
Analytics Level, namely Local Boundary Detection
Model (LBDM), Metric Hierarchy, Melodic Accent,
and Key Change. A detailed explanation of these
analysis functions is beyond the scope of this article;
the reader is invited to consult the given references.
Miranda et al.
83
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Local Boundary Detection Model (LBDM)
The first of these, LBDM, takes a monophonic
melody as input and returns a curve that estimates
the grouping structure of the music; c'est à dire., where the
note–group boundaries are and how important each
boundary is (Cambouropoulos 2001). Each adjacent
note pair is given an LBDM value. The higher the
valeur, the more likely that the interval is at a
grouping boundary; and the higher the value at a
boundary, the more important the boundary is. Ce
function allows an agent to express aspects of the
grouping structure of the music.
Metric Hierarchy
The second function is the Metric Hierarchy func-
tion, which uses the Lerdahl and Jackendoff (1983)
method of assigning notes a position in a metric
hierarchy. In most Western European classical mu-
sic, each note has a position in a metric hierarchy.
Par exemple, a piece in 4/4 time might have a note
with a strong beat at the start of every bar and a
weaker beat half way through each bar. The Metric
Hierarchy function is implemented in IMAP as a
function that takes as input a melody and returns
the strength of each beat. (A detailed explanation
of the implementation is beyond the scope of this
article; it suffices to say that the representation
does not explicitly include information about bar
lines and time signatures.) Ainsi, it allows an agent
to express aspects of the metric structure in its
performance.
Melodic Accent
Another form of accent analysis used in the Analysis
Level is the Melodic Accent. Thomassen (1982) pro-
poses a methodology for analyzing the importance
of each note in a melody; each note is assigned an
importance value. This allows an agent to express
aspects of the melodic structure in its performance.
Key Change
The fourth function in the Analysis Level is the
Key Change analysis. Krumhansl (1991) introduces
an algorithm, based on perceptual experiments,
for analyzing changes of key in a melody. Ce
algorithm allows an agent to express aspects of the
harmonic structure in its performance.
Donc, an agent will represent the score by its
note groupings, metric hierarchy, melodic accents,
and key changes, although different agents may
see the music score differently depending on how
they parameterize the functions in the Analytics
Level. Alors, based on the five preference rules,
the agents will prefer certain expression deviations
for different parts of the musical score, where the
types of expressive deviations preferred depend on
an agent’s parameterization of the preference rules
in the Rules Level.
Agent Function Definitions
The evaluation function E(P.) of an agent evaluating
a performance P is defined as
E(P.) = wTem ∗ ETem(P.) + wLou ∗ E Lou(P.)
(1)
Ici, ETem and ELou are the agent’s evaluation
of how well a performance fits with its preference
for expressive deviations in tempo and loudness,
respectivement. (Although the weights in this two
parameter equation are designed to add to unity
and could therefore be rewritten in a single weight
form with multipliers of w and 1–w, both weights
are explicitly written for reasons of clarity and for
conformity with the format of the other equations
below.) The preference weights wTem and wLou define
how much an agent focuses on timing elements
of expression in relation to loudness elements of
expression. The evaluation functions for tempo and
loudness are defined using evaluation sub-functions
EiTem and EiLou, which evaluate all five preference
rules discussed earlier. Subscripts 1–5 relate to
preference rules 1–5, respectivement:
ETem = w1Tem ∗ E1Tem + w2Tem ∗ E2 + w4Tem
∗E4Tem + w5Tem ∗ E5
E Lou = w1Lou ∗ E1Lou + w3Lou ∗ E3
+ w4Lou ∗ E4Lou
(2)
(3)
84
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The E1Tem and E1Lou functions refer to preference
rule 1 and affect both tempo and loudness, respecter-
tivement. Function E2 refers to preference rule 2 et
affects only tempo. De la même manière, function E3 refers to
preference rule 3 and affects only loudness. Func-
tions E4Tem and E4Lou refer to preference rule 4 et
affects both loudness and tempo, and function E5
refers to rule 5 and affects only tempo.
The weights wiTem, and wiLou allow the setting of
agent preferences for each of the five rules, though
not all rules need to be part of both functions,
because some apply only to tempo or only to
loudness. The sub-functions are defined in terms
of the deviations of tempo and loudness from the
nominal score values found in a performance. Le
sub-functions are given in Equations 4–10. Equations
4 et 5 implement preference rule 1:
⎛
n(cid:2)
⎝
(cid:5)
stur n−1(cid:2)
E1Tem =
1 (devTem(je + 1) > devTem(je))
0 (devTem(je + 1) ≤ devTem(je))
(cid:6)
1 (devTem(je + 1) < devTem(i))
0 (devTem(i + 1) ≥ devTem(i))
i=sstar t
(cid:5)
send−1(cid:2)
1
+
i=stur n
⎛
(cid:5)
n(cid:2)
⎝
stur n−1(cid:2)
E1Lou =
1 (devLou(i + 1) > devLou(je))
0 (devLou(je + 1) ≤ devLou(je))
(cid:6)
1 (devLou(je + 1) < devLou(i))
0 (devLou(i + 1) ≥ devLou(i))
i=sstar t
(cid:5)
send−1(cid:2)
1
+
i=stur n
(4)
(5)
The ith note’s tempo and loudness expressive
deviations are written as devTem(i) and devLou(i)
in the sub-functions. By virtue of the first (outer)
summation in each equation, the calculations are
applied to each note grouping separately, and the
scores are added across the whole performance. The
index values sstar t and send are the note indices at
which a note grouping starts and ends, and stur n is
its turning point.
There is no fixed threshold for defining boundaries
using the LBDM method. We opted for one that was
found sufficient for the purposes of IMAP: for a
note to be a boundary note, its LBDM value must
be greater than the average LBDM value of the
whole melody. The turning point of a grouping is
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
the point at which the expressive tempo defined by
preference rule 1 peaks before dropping; it is not
defined explicitly by LBDM either. In IMAP, the
“third most important note” in the group is selected
as representing a boundary between the first part of
the group and the last part. So the turning point is
defined as the note having the third highest LBDM
in the group; the start and end notes will be the two
highest LBDM values. This definition of turning
point was found to be more musically meaningful
than simply taking the mid-point between the start
and end notes. To ensure that every note grouping
has at least one potential turning point, another
constraint is placed on note groupings: they must
contain at least four notes; i.e., three intervals.
Equation 6 is added over all note groups in the
melody. This sub-function implements preference
rule 2. A tempo deviation value of unity means the
performance is the same as the nominal value in
the score; a value greater than unity means louder
or faster than the score. This is applied to each note
group in the melody.
(cid:5)
E2 =
n(cid:2)
1
1 (devTem(send) < 1)
0 (devTem(send) ≥ 1)
(6)
Equation 7 implements preference rule 3. The
curve sA(i) used in this equation is the accentuation
curve, which is generated by a weighted sum of three
other curves: melodic accent, metrical hierarchy,
and the key change, thus representing multiple
musical elements. (Note: the notion of “curve” here
is broadly metaphorical; it is not a mathematical
curve in the strict sense of the term.)
E3 =
(cid:5)
q−1(cid:2)
i=1
1 ((cid:2)d ∗ (cid:2)devLou > 0)
0 ((cid:2)d ∗ (cid:2)devLou ≤ 0)
où
(cid:2)d = sA(i+1) − sA(je)
(cid:2)devLou = devLou(je + 1) − devLou(je)
(7)
The melodic-accent curve moves higher for more
important melodic notes (Thomassen 1982), alors que
the metrical hierarchy curves move higher for notes
that are more important in the metrical hierarchy
(Lerdahl and Jackendoff 1983). The key-change
curve moves higher the further away the melody
Miranda et al.
85
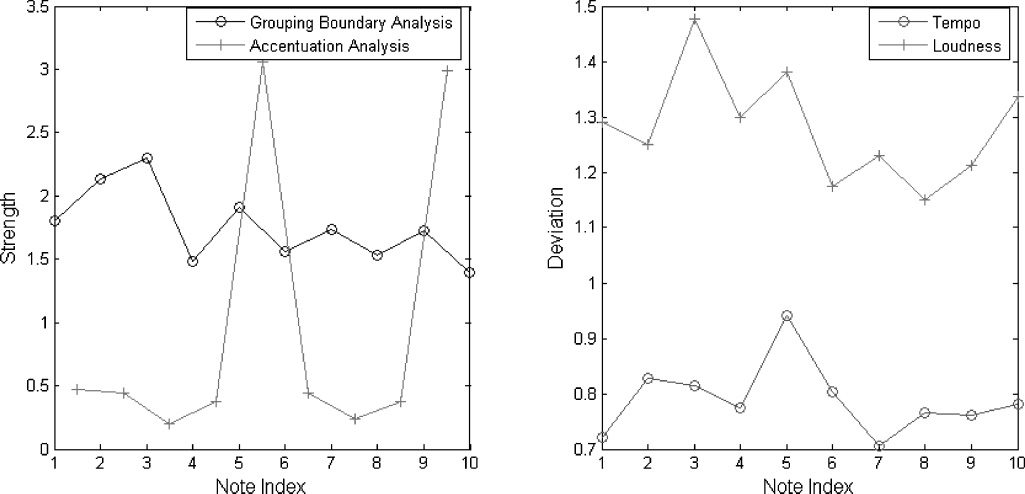
Chiffre 1. Exemple
characteristics of a single
agent with respect to a
given sequence of ten
notes.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
moves from the estimated key (Krumhansl 1990)
of the previous N bars, the default being two bars.
These three curves are normalized, then weighted
based on an agent’s preferences, and finally added
to generate the accentuation curve sA(je). Équation 7
will evaluate to a larger number if the loudness-
deviation curve of a performance follows the same
direction as this accentuation curve, encouraging
the emphasis of the parts of the performance based
on elements of their melodic, metric, and harmonic
properties.
Chiffre 1 shows examples of accentuation and
loudness curves (as well as the LBDM and tempo-
deviation curves) for a single agent, given a sequence
of ten notes. This sort of analysis is done once per
agent.
In Figure 1, both x-axes refer to note index, où
1 is the first note in the score, 2 is the second
note, etc.. The left side of Figure 1 shows part of an
example LBDM curve (circled points) used to define
grouping boundaries, and an accentuation curve
(crossed points) used for expressive loudness. Le
y-axis is the normalized strengths of the curves. Le
absolute strength is not important, but rather the
relative values. The right side of Figure 1 shows the
resulting deviation curves for tempo (circles) et
loudness (crosses) after a number of iterations. UN
deviation greater than unity implies an increase in
tempo, or an increase in loudness; a deviation less
than unity implies a decrease in tempo or loudness.
Equations 8 et 9 implement preference rule 4.
The rule is only applied to accentuated notes {a1,. . .,
am}, which are defined as those notes i whose value
on the accentuation curve sA(je) is a local maximum
on the sA curve. This definition chooses notes whose
metric, melodic, or harmonic properties make them
more significant than the notes surrounding them.
The values of Equations 8 et 9 are higher if an
accentuated note is reduced in tempo more than its
neighbor notes (Équation 8), or played with a higher
loudness (Équation 9).
E4Tem =
E4Lou =
⎧
⎪⎨
⎪⎩
⎧
⎪⎨
⎪⎩
am(cid:2)
j=a1
am(cid:2)
j=a1
1 (devTem( j) < devTem( j − 1) and devTem( j) < devTem( j + 1)) (8) 0 (otherwise) 1 (devLou( j) ≥ devLou( j − 1) and devLou( j) ≥ devLou( j + 1)) (9) 0 (otherwise) 86 Computer Music Journal Figure 2. The core algorithm of the agents’ interaction cycle. Begin of Cycle 1 An agent is selected to perform, say agent A1 Agent A1 performs All agents Aj apart from A1 evaluate A1’s performance, to get Ej1 If an agent Aj’s evaluation Ej1 is greater than its evaluation of its own performance, then Aj moves its own expressive performance deviations closer to A1’s performance by an amount defined by the learning rate. An agent is selected to perform, say agent A2 Agent A2 performs All agents Aj apart from A2 evaluate A2’s performance, to get Ej2 If an agent Aj’s evaluation Ej2 is greater than its evaluation of its own performance, then Aj moves its own expressive performance deviations closer to A2’s performance by an amount defined by the learning rate. (cid:129) (cid:129) (cid:129) Continue this process until all agents have performed, then Cycle 1 is complete End of Cycle 1 Repeat cycles until some user-defined stopping condition is met. Equation 10 implements preference rule 5, checking that notes at the end of a group have a higher or lower tempo deviation, compared to the notes on either side. ⎧ ⎪⎨ 1 (devTem(send) − devTem(send − 1)) n(cid:2) E5 = ⎪⎩ 1 ∗ (devTem(send) − devTem(send + 1)) > 0.
0 (otherwise)
(10)
With Equations 1–10, a user can set weights
to control how an agent represents or, speaking
metaphorically, “sees” the score. A user can also
control how the agent prefers such a “seen” score to
be performed.
Agent Cycle
Agents are initialized with evaluation weights for
their evaluation functions and with a common
monophonic score in MIDI form that they will
perform. Agents are also initialized with an initial
performance. This will be a set of expressive
deviations from the score in loudness and tempo,
which are implemented when the agent plays to
another agent. These initial deviations are usually
set randomly, but they can be set by the user
should one wish. Default values used for tempo are
55–130% of nominal and 75–125% for loudness.
These values were established intuitively after
experimenting with different ranges. Agents have
a learning rate between 0% et 100%. If an agent
with a learning rate L% hears a performance P that
it prefers to its own, then it will move its own
performance deviations linearly toward P by L%.
An agent with a learning rate of 100% will allow
another agent’s performance to influence 100% de
its own performance. C'est, the agent will replace
its performance entirely with any it hears, lequel
it prefers to its own. An agent with a learning
taux de 0% will ignore all other performances it
hears.
The core algorithm of the agents’ interaction
cycle is given in Figure 2. Note that the algorithm
shown here is sequential, but in reality the agents
are asynchronous, in the sense that all agents are
operating simultaneously in separate threads.
User-Generated Performances with IMAP
Before describing how to generate expressive perfor-
mances with IMAP, we would like to discuss some
Miranda et al.
87
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
of the issues with practical performance genera-
tion. Kirke and Miranda (2009) introduced the term
“performance creativity” to refer to the ability of a
CSEMP to generate novel and original performances,
as opposed to simulating previous human strategies.
Such creative and novel performance is often ap-
plauded in human performers. Par exemple, Glenn
Gould created highly novel expressive performances
of pieces of music and has been described as having
a vivid musical imagination. Expressive computer
performance provides possibilities for even more
imaginative experimentation with performance
strategies. Many CSEMPs, for example the Artificial
Neural Network Piano System (Bresin and Vecchio
1995; Bresin 1998), are designed to simulate human
performances—an important research goal—but
not to create novel performances. IMAP is less
constrained in the generation of performances than
a number of systems that learn from human exam-
ples. It also has a parameterization ability, lequel
can be manipulated creatively to generate entirely
novel performances.
There are two important provisos here. D'abord,
“novel” does not necessarily mean “pleasant.”
Deuxième, flexibility does not necessarily lead to
creativity. A system that is totally manual would
seem at first glance to have a high creativity
potential, because the user could entirely shape
every element of the performance. Cependant, ce
potential may never be realized owing to the
excessively time-consuming manual effort required
to implement a performance. Not all CSEMPs
are able to act in a novel way that is practically
controllable. A number of them generate a model of
performance, which is basically a vector or matrix
of coefficients. Changing this matrix by hand (c'est à dire.,
“hacking” it) would allow the technically savvy
to generate novel performances. Toujours, the changes
would entail an excessive amount of manual effort—
or the results of such changes could be excessively
unpredictable—thus requiring too many iterations
or “try-outs.” For performance creativity, a balance
needs to exist between automation and creative
flexibility.
As described earlier, in IMAP there are a number
of weights that need to be defined for an agent’s
evaluation function. Tableau 1 lists all the weights
Tableau 1. IMAP Weights That Can Be Set in
Equations 1, 2, et 3 by the User to Influence the
Final Expressive Performance
Preference Rule
Weight Equation
wTem
All tempo-based effects
All loudness-based effects wLou
w1Tem
Rule 1 tempo effects
w2Tem
Rule 2 tempo effects
w4Tem
Rule 4 tempo effects
w5Tem
Rule 5 tempo effects
w1Lou
Rule 1 loudness effects
w3Lou
Rule 3 loudness effects
w4Lou
Rule 4 loudness effects
Équation 1
Équation 1
Équation 2, Tempo
Équation 2, Tempo
Équation 2, Tempo
Équation 2, Tempo
Équation 3, Loudness
Équation 3, Loudness
Équation 3, Loudness
These nine weights define the effects of the five preference rules
in the Rules Level.
that must be set in IMAP. Although a set of
nine weights may seem too large for practical
performance creativity, in reality, many of these
weights can be fitted to default values, et le
remaining weights would still provide a wide scope
for creativity. Par exemple, users could simply adjust
the top two weights of the equation hierarchy (wTem
and wLou) in Equation 1, fixing all other weights to
their default values. This two-weight set could be
simply extended by also allowing the user to adjust
the weights w4Tem and w4Lou in Equations 2 et 3 à
change the amount of tempo and loudness emphasis,
respectivement, of accentuated notes. It is worth noting
that the parameters in the Analytics Level can also
be made available to users. Par exemple, the user
could set weights that would indirectly change the
shape of the accentuation curve shown in Figure 1.
Another key element of IMAP is how agents
can have different “views” of what makes a good
expressive performance. This provides an ability,
which will be demonstrated later in this article, pour
generating and controlling diversity in the results of
the population learning. Par exemple, a population
with similar initial preference weights will tend to
learn a group of far more similar performances than a
population whose initial weight values differ widely.
We now describe how to generate expressive
performances with IMAP. Before the first cycle of
IMAP, a population size is defined—for example
3, 10, ou 50 agents. (Larger populations may have
88
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
the advantage of greater statistical stability and a
larger choice of performances.) Alors, a learning rate
must be set. In this article, a global learning rate
is used: All agents have the same learning rate, un
default of 10%. A low learning rate was desired
to allow agents to build up a good combination of
performances through imitation. A learning rate
closer to 100% would turn the system into more of
a performance-swapping population rather than one
for performance combining. Cependant, too low a rate
would result in slow convergence.
Concerning the question of how many cycles
to run the system, one approach would be to
define a fixed number of cycles. Another approach
would be to define a more sophisticated stopping
condition. A common form of stopping condition is a
convergence criterion—for example, stopping when
agents are no longer updating their performance
deviations during the interactions. This normally
occurs when no agent is hearing a performance
better than its own performance. Yet another
option is to base convergence on the average
performance, c'est à dire., the average deviations across the
entire population. Once this ceases to change by a
significant amount per cycle (that amount defined
by the user), convergence can be considered to have
been achieved.
Three experiments with IMAP are detailed in this
article that test the system in terms of capability of
expression generation, generation of diversity, et
controlling the direction of the diversity.
Experiments and Evaluation
The melody of ´Etude No. 3, Op. 10 by Fr ´ed ´eric
Chopin was used in the experiments that follow.
Although IMAP is able to process whole pieces of
(monophonic) musique, for the sake of clarity, only
the first five bars of Chopin’s piece were considered
herein.
Experiment 1: Can Agents Generate Performances
Expressing Their “Preference” Weights?
The purpose of this experiment is to demonstrate
that the agents generate performances that express
their “preference” weights. To show this clearly,
two weight sets were used: set A, in which wTem = 1,
w1Tem = 1, and all other weights are 0; and set B, dans
which wLou = 1, w3Lou = 1, and all other weights are 0.
The first of set of weights will only lead to preference
rule 1 being applied (and only to tempo). The second
set of weights will lead to preference rule 3 être
appliqué (and only to loudness). If agents express
the music structure through their weights, then a
multi-agent system where agents have only weight
set A should generate performances whose tempo
deviations clearly express the grouping structure
(LBDM) of the music as defined by preference rule 1.
De la même manière, if the agents are given weight set B, alors
the generated loudness deviations should express the
accentuation curve as implemented by preference
rule 3.
Two groups of experiments were run: five with
weight set A and five with weight set B. A system
de 15 agents was used, et 20 iterations were used
for each run. For each run in the experiment with
weight set A, the initial agent performances were
randomized. For comparison purposes, exactly the
same set of initial performances was used for the
parallel run with weight set B; hence, the ten runs
only use five sets of 15 random initial performances.
To enable meaningful results for the scenario with
weight set A, a new curve is defined: the transferred
LBDM curve. The transferred LBDM curve is our
own adaptation of the LBDM curve into a form more
easily comparable with the grouping expression.
The transferred curve will have maxima at the
boundary points on the LBDM curve and minima
at the turning points within each note group. Le
transferred LBDM is concave between boundary
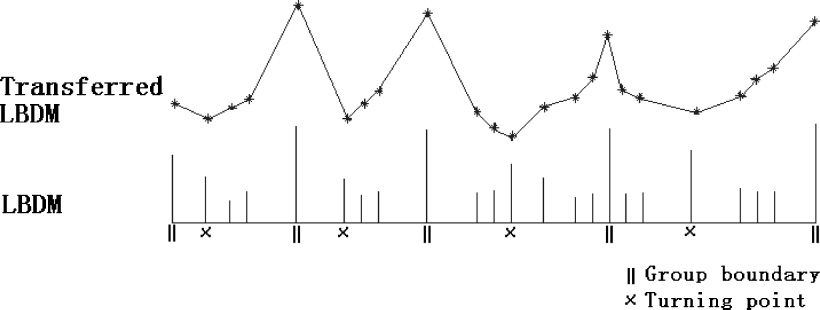
points. An example is shown in Figure 3. Preference
rule 1 can then be interpreted as saying that tempo
curves should move in the opposite direction to the
transferred LBDM curve—or equivalently, that the
reciprocal of the tempo curve should move in the
same direction as the transferred LBDM curve.
In Figure 3, the horizontal axis represents time.
On the vertical axis, LBDM values do not have units
as such. They indicate relative “boundary strength”
rather than absolute values. The fitness function
only needs to know the direction of the transferred
LBDM curve rather than its absolute value. In the
Miranda et al.
89
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 3. Example of a
transferred LBDM curve
for a melody from Chopin’s
´Etude No. 3, Op. 10.
lower graph, the LBDM values are plotted for each
note pair/interval. The group boundaries and turning
points are shown on the horizontal axis. Note that
the transferred LBDM curve in the upper graph
is concave between boundaries; it has maxima at
boundaries and minima at the turning points.
In this experiment, the average performance
across all agents was used to represent the perfor-
mances evolved by the system. Ainsi, the deviations
of the tempo and loudness generated by the system
are represented by the deviations of the tempo and
loudness in the average performance. The results
of scenarios with weight sets A and B can be seen
in Table 2, which shows the average correlations
Corr(X, oui) across the five runs for x set to the trans-
ferred LBDM curve tLBDM; x set to the accentuation
curve Acc; y set to the reciprocal of performance
tempo rTem; and y set to the performance loudness
Lou.
It can be seen that for weight set A (a weight set
that should cause grouping structure to be expressed
using tempo deviations to express it), there is an
increase in correlation between the transferred
LBDM and the reciprocal performance tempo:
Corr(tLBDM, rTem) = 0.11. For weight set B (un
weight set that should cause the accentuation curve
to be expressed by loudness deviations), the only
increase in correlation is between the accentuation
curve and the loudness: Corr(Acc, Lou) = 0.2. These
results show that the average agent performances
are expressing the preference weights in the system.
Chiffre 4 shows expressive deviations evolved by two
agents for the Chopin melody.
Tableau 2. Results from Experiment 1 Showing
Correlations for Average Performance Across a
Population of Agents
Before
Iterations
After
Iterations
Increase
Weight Set A (Tem)
Corr(tLBDM, rTem)
Corr(tLBDM, Lou)
Corr(Acc, Lou)
0.49
0.52
0.5
0.61
0.52
0.52
Weight Set B (Lou)
Corr(tLBDM, rTem)
Corr(tLBDM, Lou)
Corr(Acc, Lou)
0.49
0.52
0.5
0.49
0.48
0.7
0.11
0
0.02
0
–0.04
0.2
An increase in correlation between the transferred LDBM and
reciprocal performance tempo shows that the tempo deviations
are expressing the grouping structure of the music. An increase
in correlation between the accentuation curve and loudness
shows that the loudness is expressing elements of the metric,
melodic structure, and harmonic structure of the music, comme
defined in the accentuation curve.
Experiment 2: Can One Control the Extent
of the Performances’ Diversity?
The purpose of this experiment was to demonstrate
that IMAP can generate a diversity of performances
and that the user can control that diversity. In the
experiment, a group of 15 agents was used, chaque
with randomly initialized performance deviations.
A set of default weights W for Table 1 was defined.
The experiment was set with two conditions. Dans
Condition 1, agents were assigned weights that could
vary by no more than 10% from the corresponding
90
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
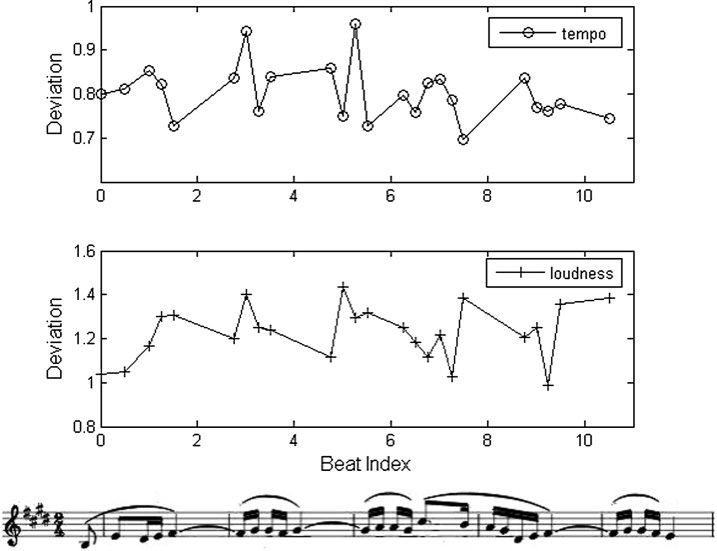
Chiffre 4. Expressive
deviations of two agents
from Experiment 1 after 20
iterations for the first 5
bars of the melody of
Chopin’s ´Etude No. 3, Op.
10. (Each point in the plots
corresponds to a note in
the score, excepting the
last point in each plot.)
The top graph (circles)
shows the weight set A of
an agent (tempo
expression only), hence
only tempo expression is
plotted. The bottom graph
(crosses) shows the weight
set B of another agent
(loudness evaluation only),
hence only loudness
expression is plotted.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
default weight in set W. In Condition 2, ce
variation was raised to 60%. Ainsi, in Condition 2,
the preference weights varied much more widely
across agents than in Condition 1. In each condition,
30 iterations were performed, and the coefficient
of variation (c'est à dire., the ratio of standard deviation to
mean for both tempo and loudness deviations) était
calculated for deviations across the population. Ce
experiment was repeated 10 times, each time with
different initial random performance deviations.
After 30 iterations of Condition 1, the resulting
average coefficient of variation for tempo and for
loudness deviations was 0.2%. In Condition 2, avec
more diverse preference weights, the value was
1.9%. This supports the ability of IMAP to generate
a diversity of performances and to control that
diversity using the spread of preference weights.
Experiment 3: Controlling the Direction
of the Performances’ Diversity
a subset of the population, then the resulting per-
formances will become affected by that preference.
This demonstrated that, although a diversity of per-
formances can be produced as shown by Experiment
2, changing the distribution of weights enables one
to change the distribution of outcomes in a coherent
chemin. To show this, we used the same two weight
sets as in Experiment 1: set A, in which wTem = 1,
w1Tem = 1, and all other weights are 0; and set B,
in which wLou = 1, w3Lou = 1, and all other weights
sont 0. Ainsi, weight set A only affects timing, et
weight set B only affects loudness. The two weight
sets do not overlap in their effect. In this experi-
ment, the population of 15 agents from Experiment
1 had another 5 agents added to it. Le 15 agents
(labeled group G2) are assigned weight set B, et le
5 additional agents (labeled group G1) are assigned
weight set A. The objective is to demonstrate that
the addition of G1 to G2 leads to G1 influencing the
performances of G2, despite the fact that G1 and G2
have mutually exclusive weight sets.
The purpose of this experiment was to demonstrate
that if agent preferences are biased a certain way in
Before running the experiment, il faut
to benchmark the level of random relative increase
Miranda et al.
91
Tableau 3. The Results of Benchmarking the Level of Random Fluctuations
Run1
Run2
Run3
Run4
Run5
Set B
Lou
Tem
Lou
Tem
Lou
Tem
Lou
Tem
Lou
Tem
Before
After
Changement
TempoRatio
0.19
0.315
0.125
0.19
0.19
0
0
0.213
0.325
0.112
0.213
0.19
–0.02
–0.205
0.223
0.306
0.083
0.223
0.248
0.025
0.301
0.21
0.35
0.137
0.213
0.208
–0.005
–0.037
0.301
0.374
0.073
0.301
0.292
–0.009
–0.123
After 25 iterations, the increase in loudness evaluation and tempo evaluation were measured with Equations 3 et 2, respectivement.
The ratio of tempo evaluation increase to loudness evaluation increase was calculated.
in evaluation that can be generated in the system.
Spécifiquement, given an agent system of 15 agents
with preference weights that only affect loudness,
how much would we expect their expressive tempo
evaluation to increase relative to the increase in their
expressive loudness evaluation, solely due to random
fluctuations in tempo during iterations? These
random fluctuations come from the randomized
initial performances influencing each other. Ce
was measured by taking a system of 15 agents with
loudness-only weights (c'est à dire., weight set B) and doing
five runs of 25 cycles. (The authors ran a number of
versions of this experiments, and it was clear that
as few as five runs of 25 cycles were sufficient to
generate meaningful random fluctuations in this
context.)
The results are shown in Table 3. The column
and row headings in this table are defined as follows:
“Lou” refers to the expressive loudness evaluation
by Equation 3, “Tem” refers to the expressive
tempo evaluation by Equation 2, “Before” is the
average evaluation before iterations, “After” is the
average evaluation after 25 iterations, “Change”
is the change in evaluation before and after 20
iterations, and “TempoRatio” is the change in
tempo evaluation divided by the change in loudness
evaluation. Essentially, this ratio is a measure of
the increase of tempo expressiveness relative to the
increase of loudness expressiveness:
TempoRatio(P.) = Increase in ETem(P.)
Increase in E Lou(P.)
(11)
The average value of TempoRatio across the
five runs is equal to –0.013. This will be used as a
measure of relative tempo evaluation increase owing
to random fluctuations in performance, because
during these five runs there was no evaluation
function pressure to increase tempo expressiveness.
This particular TempoRatio = −0.013 is referred to
as the baseline value of TempoRatio.
Suivant, another set of runs were performed with 5
agents added to the system of 15 agents described
previously. As mentioned, le 5 agents (group G1)
were assigned tempo-only weight set A, as opposed
to the 15 agents (group G2), which had loudness-
only weight set B. The results after 25 iterations
are shown in Table 4. The column heading “AP2”
is the average performance deviation of agents in
G2. Par exemple, G1(AP2) = 0.255 is G1’s average
evaluation of G2’s performances in Run 2 after 25
iterations.
The key measurements in Table 4 are G1’s
evaluations of G2’s performances AP2; this is
written as G1(AP2). Note that all values in “Increase
G1(AP2)” row are smaller than all the values in the
“Increase G2(AP2)” row. These values are shown
before and after iterations in rows 1 et 2 of Table 4,
respectivement. G1(AP2) is calculated using Equation
12, but this equation can be simplified into Equation
13, because wLouG1 is equal to 0 and wTemG1 is equal
à 1 (weight set A):
G1(AP2) = EG1(AP2) = wTemG1 ∗ ETemG1(AP2)
+ wLouG1 ∗ E LouG1(AP2)
(12)
G1(AP2) = ETemG1(AP2)
(13)
Ainsi, because G1’s evaluation functions mea-
sure only tempo expressivity, G1(AP2) provides
a measure of the expressive tempo evaluation of
G2’s performance. The difference between G1(AP2)
92
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Tableau 4. Results of Experiment 3
Run1 Run2 Run3 Run4 Run5
AP2 AP2 AP2 AP2 AP2
Before 0.245 0.273 0.239 0.269 0.255
0.252 0.255 0.274 0.276 0.291
After
0.236 0.284 0.24
Before 0.21
0.234
0.335 0.307 0.349 0.322 0.305
After
0.007 –0.018 0.035 0.007 0.036
0.125 0.071 0.065 0.082 0.071
0.056 –0.253 0.538 0.085 0.507
G1(AP2)
G2(AP2)
Increase G1(AP2)
Increase G2(AP2)
Cross-Group
TempoRatio
Results for a 20-agent system made up of 15 agents with weight
set B (labeled G2), et 5 agents with weight set A (labeled G1).
After 25 iterations, the increase in loudness evaluation and
tempo evaluation for the average performance of G2 was
measured for both groups. The ratio of tempo evaluation
increase to loudness evaluation increase (Cross-Group
TempoRatio) was then calculated.
before and after the iterations is a measure of
how much G2’s expressive tempo evaluation has
increased, as evaluated by G1. De la même manière, the mea-
sure of G2’s expressive loudness evaluation is found
by calculating G2’s evaluation of its own perfor-
mance, G2(AP2), comme le montre l'équation 14, lequel
can be simplified into Equation 15, because wTemG2
is equal to 0 and wLouG1 is equal to 1 (weight set B):
G2(AP2) = E2G2(AP2) = wTemG2 ∗ ETemG2(AP2)
+ wLouG2 ∗ E LouG2(AP2)
(14)
G2(AP2) = E LouG2(AP2)
(15)
The increase in G2(AP2) before and after itera-
tions gives the increase in G2’s loudness expressivity
as a result of iterations. The ratio of these two values
is shown in Equation 16 and is the increase of expres-
siveness of G2’s tempo deviations relative to the in-
crease in expressiveness of G2’s loudness deviations:
Increase in G1(AP2)
Increase in G2(AP2)
TempoRatio as defined in Equation 11; otherwise,
the numerator in Equation 16 would have to be
increase in ETemG2(AP2). A TempoRatio based on
this numerator would always be equal to 0, because
G2’s evaluation function ETemG2 is defined by weight
set B, in which all weights in ETemG2 are set to 0.
Donc, the only meaningful tempo ratio has G1’s
ETemG1 in the numerator. This is not just meaningful,
but also relevant: the purpose of this experiment
was to investigate how G1’s view of expressive
performance has influenced G2. Ainsi, when looking
at the influence of G1’s evaluation function on G2,
we use G1’s evaluation function—hence the use
of the cross-group TempoRatio, or CGTR. This is
calculated in the last row of the Table 4. La moyenne
value of CGTR for G2’s performance is 0.219.
It would be tempting to say that the average
CGTR = 0.219 supports the hypothesis that G1’s
tempo weights have influenced G2’s tempo expres-
sion, just because it is a positive value. Cependant,
on its own, this positive average CGTR might just
represent the result of random fluctuations in G2’s
tempo deviations caused during the iterations. Mais
recall that we have shown in a previous set of five
runs that the baseline value TempoRatio owing
to random fluctuations in a dynamics-only agent
set was on the order of –0.013. By comparing G2’s
CGTR of 0.219 to the baseline value TempoRatio
of –0.013, and considering that G1 and G2 have
mutually exclusive weight sets, one can see that
the expressiveness of G2’s tempo deviations relative
to the expressiveness of G2’s loudness deviations is
significantly larger than could likely be explained by
random fluctuations. This supports the hypothesis
that G1 has significantly influenced the increase in
G2’s tempo expressivity relative to its loudness ex-
pressivity. This in turn supports the idea that if agent
preferences are biased a certain way in a subset of the
population, then the whole system’s performances
will become affected by that preference.
= Increase in ETemG1(AP2)
Increase in E LouG2(AP2)
= CGT R(AP2)
(16)
Conclusions and Recommendations
for Further Work
This could be interpreted as a form of “cross-
group” TempoRatio (CGTR) of G2’s performance
AP2. Cependant, Équation 16 is not G1’s actual
This article introduced an imitative multi-agent sys-
tem approach to generate expressive performances
Miranda et al.
93
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
of music, based on agents’ individual parameterized
musical rules. We have developed a system called
IMAP to demonstrate the approach. Aside from
investigating the usefulness of such an application
of the imitative multi-agent paradigm, there was
also a desire to investigate the inherent feature of
diversity and control of diversity in this methodol-
ogy: a desirable feature for a creative application,
such as synthesized musical performance. To aid
this control of diversity, parameterized rules based
on previous expressive-performance research were
used. These were implemented in the agents using
previously developed musical-analysis algorithms.
When experiments were run, we found that agents
were expressing their preferences through their
music performances and that diversity could be
generated and controlled.
In addition to the possibility of using IMAP
in practical applications, there are also potential
applications of IMAP in an area in which multi-
agent systems are frequently used: modeling for
sociological study, specifically in the sociological
study of music performance (Clarke and Davidson
1998). Cependant, the focus of this article was on
the practical application of imitative multi-agent
systems to generate expressive performance, rather
than to investigate social modeling.
A priority piece of future work for IMAP would be
to conduct formal listening tests to measure human
judgments of automatically generated performances.
Only then we would be in a better position to eval-
uate whether IMAP would indeed be more practical
and more beneficial for music-making than simply
allowing the user to control parameters directly. Un-
other area of work would be listening experiments
on how adjusting parameters such as the pitch and
inter-onset intervals weights in the LBDM would
affect performances, and how other variables such as
the number-of-bars horizon in the key-change part
of the accentuation curve impacts performances.
The effectiveness of IMAP is to a significant
degree decided by the effectiveness of the Analysis
Level. We acknowledge that the algorithms we
have used are not absolutely perfect; Par exemple,
LBDM is known to only be a partial solution to
the detection of local boundaries. Different analysis
algorithms should be tested. The same could be said
of the Rule Level: other sets of rules could be used
in experiments. In both the case of the Rule Level
and the Analysis Level, such work could include
the investigation of explicitly polyphonic analysis
functions and rules. En outre, despite the initial
experience and thoughts regarding convergence
criteria for the system, such criteria are by no means
obvious in a creative application; thus, further work
should be done at this front.
We believe that advanced learning rate functional-
ity would be a fruitful area for further investigation.
Par exemple, agents with learning rates of 0% have
the power to influence but not be influenced by
the system. Another area of investigation is inter-
action control. The system currently assumes that
all agents can always interact with all agents. Dans
multi-agent systems, there are often “popularity”
or “connection” measures (Kirke 1997; Wooldridge
2002) that define which agents interact with which.
The addition of a social network, which could
change conditionally over time, would be worth
investigating.
IMAP has the potential to be influenced by human
les performances, and this is certainly an area worth
investigating further. Suppose the system is set
up with 50% of agents supplied with performance
deviations from a single performance M by a human
performer A. The other 50% would have random
les performances. Depending on preference weightings,
the resulting performances would be influenced to
a degree by Performer A’s performance. Another
approach would be to reverse engineer evaluation
function weights from Performer A’s performance,
using a parameter search optimization technique
(Winston and Venkataramanan 2002). Performer A’s
preference weights would affect the performances
more strongly than just using Performer A’s initial
les performances. The preference function would not
necessarily contain Performer A’s real preference,
and there would not be a one-to-one relationship
between function weights and a single performance.
Nevertheless, such an approach would be worth
investigating as a tool for generating new expressive
les performances. En fait, one could envision a “recipe
book” of different agent preferences generated by
deviations from different professional performers.
These agents could then be added to IMAP in the
94
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
proportions desired by the user. Par exemple, a user
might specify “I would like a performance repertoire
of Bach’s Piano Partita No. 2 based 30% on Daniel
Barenboim’s performance, 50% on Glenn Gould’s
performance, et 20% based on the preference
weights I explicitly specify.”
Another suggested future work for IMAP would
be to study the effect of agent communication noise
on the convergence of the system. Par exemple,
Kirke and Miranda (in press) have introduced a
multi-agent system in which agents communicate
musical ideas and generate new ideas partially
through errors in the communication. De la même manière,
allowing agents in IMAP to make small errors in
their performances could be viewed as an imitative
equivalent of a GA mutation operator. This would
potentially lead to agents generating performances
that more closely match their preferences.
Aussi, one should consider extending IMAP to
expressive performance indicators other than tempo
and loudness. Cependant, the limitations of MIDI
make this difficult with our current framework.
Ideally, we should address this extension once we
are in a position to deal directly with audio rather
than MIDI.
Remerciements
This work was financially supported by the EPSRC-
funded project “Learning the Structure of Music,»
grant EPD063612-1. Qijun Zhang was partially
supported by the Faculty of Technology, University
of Plymouth.
Les références
Ben-David, UN., and J. Mandel. 1995. “Classification
Accuracy: Machine Learning vs. Explicit Knowledge
Acquisition.” Machine Learning 18(1):109–114.
Boulanger, R., éd. 2000. The Csound Book: Perspectives in
Software Synthesis, Sound Design, Signal Processing,
and Programming. Cambridge, Massachusetts: AVEC
Presse.
Boyd, R., and P. J.. Richerson. 2005. “Solving the Puzzle
of Human Cooperation.” In S. Levinson, éd. Evolution
and Culture. Cambridge, Massachusetts: AVEC Presse,
pp. 105–132.
Bresin, R.. 1998. “Artificial Neural Network Based Models
for Automatic Performance of Musical Scores.” Journal
of New Music Research 27(3):239–270.
Bresin, R., et un. Friberg. 2000. “Emotional Coloring of
Computer-Controlled Music Performances.” Computer
Music Journal 24(4):44–63.
Bresin, R., and C. Vecchio. 1995. “Neural Networks
play Schumann.” Proceedings of the KTH Symposium
on Grammars for Music Performance. Stockholm:
Department of Speech Communication and Music
Acoustics, KTH, pp. 5–14.
Cambouropoulos, E. 2001. “The Local Boundary Detection
Model (LBDM) and Its Application in the Study of Ex-
pressive Timing.” Proceedings of the 2001 International
Computer Music Conference. San Francisco, California:
International Computer Music Association. Available
online at hdl.handle.net/2027/spo.bbp2372.2001.021.
Camurri, UN., R.. Dillon, et un. Saron. 2000. “An Exper-
iment on Analysis and Synthesis of Musical Expres-
sivity.” Proceedings of 13th Colloquium on Musical
Informatics. L’Aquila, Italy: Istituto Gramma. Available
online at ftp://infomus.dist.unige.it/Pub/Publications/
CIM2000CDS.PDF.
Canazza, S., et autres. 2000. “Audio Morphing Different
Expressive Intentions for Multimedia Systems.” IEEE
Multimedia 7(3):79–83.
Clarke, E. F. 1988. “Generative Principles in Music
Performance.” In J. Sloboda, éd. Generative Processes in
Music: The Psychology of Performance, Improvisation,
and Composition. Oxford: Clarendon Press, pp. 1–
26.
Clarke, E. F., and J. W. Davidson. 1998. “The Body in
Music as Mediator Between Knowledge and Action.” In
W. Thomas, éd. Composition, Performance, Reception:
Studies in the Creative Process in Music. Oxford:
Presse universitaire d'Oxford, pp. 74–92.
Clynes, M.. 1986. “Generative Principles of Musical
Thought: Integration of Microstructure with Structure.”
Communication and Cognition 3:185–223.
De Boer, B. 2000. “Emergence of Vowel Systems through
Self-Organisation.” AI Communications 13:27–29.
Dissanayake, E. 2001. “Birth of the Arts.” Natural History
109(10):84–92.
Friberg, UN., R.. Bresin, and J. Sundberg. 2006. “Overview
of the KTH Rule System for Musical Performance.”
Advances in Cognitive Psychology 2(2):145–161.
Friberg, UN., and J. Sundberg. 1999. “Does Music Per-
formance Allude to Locomotion? A Model of Final
Ritardandi Derived from Measurements of Stopping
Runners.” Journal of the Acoustical Society of America
105(3):1469–1484.
Miranda et al.
95
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Gabrielsson, UN. 2003. “Music Performance Research at
the Millennium.” Psychology of Music 31:221–272.
Goldberg, D. E. 1989. Genetic Algorithms in Search,
Optimization, and Machine Learning. Cholchester:
Addison-Wesley.
Grindlay, G. C. 2005. “Modeling Expressive Musical
Performance with Hidden Markov Models.” Master’s
Thesis, University of California Santa Cruz.
Hashida, M., N. Nagata, and H. Katayose. 2006. “Pop-E:
A Performance Rendering System for the Ensemble
Music that Considered Group Expression.” Proceedings
of 9th International Conference on Music Perception
et cognitif. Bologna: ESCOM, pp. 526–534.
Ishikawa, O., et autres. 2000. “Extraction of Musical Perfor-
mance Rule Using a Modified Algorithm of Multiple
Regression Analysis.” Proceedings of the 2000 Inter-
national Computer Music Conference. San Francisco,
California: International Computer Music Association,
pp. 348–351.
Johnson, M.. L. 1991. “Toward an Expert System for Ex-
pressive Musical Performance.” Computer 24(7):30–34.
Juslin, P.. 2003. “Five Facets of Musical Expression: UN
Psychologist’s Perspective on Music Performance.”
Psychology of Music 31(3):273–302.
Kirke, UN. 1997. “Learning and Co-operation in Mobile
Multi-Robot Systems.” PhD Thesis, Université de
Plymouth.
Kirke, UN., and E. R.. Miranda. 2009. “A Survey of
Computer Systems for Expressive Music Performance.”
ACM Surveys 42(1): Article 3.
Kirke, UN., and Miranda, E. R.. In press. “Using a
Biophysically Constrained Multi-Agent System to
Combine Expressive Performance with Algorithmic
Composition.” In E. R.. Miranda, éd. A-Life for Music:
Music and Computer Models of Living Systems.
Middleton, Wisconsin: A-R Editions.
Krumhansl, C. 1991. Cognitive Foundations of Musical
Pitch. Oxford: Presse universitaire d'Oxford.
Lerdahl, F., and Jackendoff, R.. 1983. A Generative Theory
of Tonal Music. Cambridge, Massachusetts: AVEC Presse.
Livingstone, S. R., et autres. 2007. “Controlling Musical Emo-
tionality: An Affective Computational Architecture
for Influencing Musical Emotions.” Digital Creativity
18(1):43–53.
Miranda, E. R.. 2002. “Emergent Sound Repertoires in
Virtual Societies.” Computer Music Journal 26(2):77–90.
Miranda, E. R., and J. UN. Biles, éd.. 2007. Evolutionary
Computer Music. Londres: Springer.
Noble, J., and D. W. Franks. 2004. “Social Learning in
a Multi-Agent System.” Computing and Informatics
22(6):561–574.
Palmer, C. 1997. “Music Performance.” Annual Review
of Psychology 48:115–138.
Parc, T. H. 2009. “An Interview with Max Mathews.”
Computer Music Journal 33(3):9–22.
Ramirez, R., et un. Hazan. 2005. “Modeling Expressive
Performance in Jazz.” Proceedings of 18th Interna-
tional Florida Artificial Intelligence Research Society
Conference. Menlo Park, California: Association for the
Advancement of Artificial Intelligence Press, pp. 86–
91.
Ramirez, R., et autres. 2008. “A Genetic Rule-Based Model of
Expressive Performance for Jazz Saxophone.” Computer
Music Journal 32(1):38–50.
Raphael, C. 2001. “Synthesizing Musical Accompani-
ments with Bayesian Belief Networks.” Journal of New
Music Research 30(1):59–67.
Seashore, C. E. 1938. Psychology of Music. New York:
McGraw-Hill.
Sundberg, J., UN. Askenfelt, and L. Fryd ´en. 1983. “Musical
Performance: A Synthesis-by-Rule Approach.”
Computer Music Journal 7:37–43.
Thomassen, J.. M.. 1982. “Melodic Accent: Experiments
and a Tentative Model.” Journal of the Acoustical
Society of America 71(6):1596–1605.
Todd, N. P.. 1985. “A Model of Expressive Timing in Tonal
Music.” Music Perception 3:33–58.
Todd, N. P.. 1992. “The Dynamics of Dynamics: A Model
of Musical Expression.” Journal of the Acoustical
Society of America 91(6):3540–3550.
Widmer, G., et W. Goebl. 2004. “Computational Models
of Expressive Music Performance: The State of the
Art.” Journal of New Music Research 33(3):203–
216.
Widmer, G., et un. Tobudic. 2003. “Playing Mozart
by Analogy: Learning Multi-Level Timing and
Dynamics Strategies.” Journal of New Music Research
32(3):259–268.
Winston, W. L., and M. Venkataramanan. 2002. Introduc-
tion to Mathematical Programming: Applications and
Algorithms. Pacific Grove, California: Duxbury Press.
Wooldridge, M.. 2002. An Introduction to Multi-Agent
Systems. Hoboken, New Jersey: Wiley.
Zentall, T., et B. G. Galef. 1988. Social Learning:
Psychological and Biological Perspectives. Hillsdale,
New Jersey: Lawrence Erlbaum.
Zhang, Q., and E. R.. Miranda. 2006. “Evolving Musical
Performance Profiles Using Genetic Algorithms
with Structural Fitness.” Proceedings of the 8th
Annual Conference on Genetic and Evolutionary
Computation. New York: Association for Computing
Machinery, pp. 1833–1840.
96
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
3
4
1
8
0
1
8
5
5
4
8
2
/
c
o
m
j
.
.
2
0
1
0
3
4
1
8
0
p
d
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3