Does Computer-Aided Instruction Improve
Children’s Cognitive and Noncognitive Skills?
Hirotake Ito, Keiko Kasai, Hiromu Nishiuchi, et
Makiko Nakamuro∗
This paper examines the causal effects of computer-aided instruction (CAI) sur
children’s cognitive and noncognitive skills. We ran a clustered randomized
controlled trial at five elementary schools with more than 1,600 students
near Phnom Penh, Cambodia. After 3 months of intervention, we find that
the average treatment effects on cognitive skills are positive and statistically
significant, while hours of study were unchanged both at home and in the
classroom. This indicates that CAI is successful in improving students’ learning
productivity per hour. En outre, we find that CAI raises students’ subjective
expectation to attend college in the future.
Mots clés: clustered randomized controlled trial, computer-assisted instruction,
noncognitive skills
Codes JEL: I21, I25, I30
je. Introduction
The World Bank recently made reference to a “learning crisis” (World Bank
2017), arguing that a large proportion of students in developing countries are
failing to acquire even foundational skills at school, Par exemple, basic math that
is required when buying and selling in markets, handling household budgets, ou
transacting with banks or other financial institutions (Hanushek and Woessmann
2016).
∗Hirotake Ito (corresponding author): Graduate School of Media and Governance, Keio University. E-mail:
itouhrtk@keio.jp; Keiko Kasai: School of International Development, University of East Anglia. E-mail:
keikokasai131@gmail.com; Hiromu Nishiuchi: Graduate School of International Management, Yokohama City
University. E-mail: hiromunishiuchi@gmail.com; Makiko Nakamuro: Faculty of Policy Management, Keio
University. E-mail: makikon@sfc.keio.ac.jp. This study was conducted as part of the project “Research on the
Improvement in Resource Allocation and Productivity among the Healthcare and Education Service Industries”
undertaken at the Research Institute of Economy, Trade and Industry (RIETI). We thank Hanamaru Lab, especially
Kei Kawashima, Kodai Tokumaru, and Daiki Watanabe for their support of the experiment in Cambodia. Nous
also thank the managing editor, the anonymous referee, and participants in the Asian Development Bank (ADB)-
International Energy Agency (IEA) roundtable, Makoto Yano, Masayuki Morikawa, Kyoji Fukao, and Tomohiko
Inui for helpful comments and suggestions. We also gratefully acknowledge the financial support received from the
MEXT/JSPS KAKENHI Grant Number: 18H05314. The usual ADB disclaimer applies.
Revue du développement en Asie, vol. 38, Non. 1, pp. 98–118
https://doi.org/10.1162/adev_a_00159
© 2021 Asian Development Bank and
Asian Development Bank Institute.
Publié sous Creative Commons
Attribution 3.0 International (CC PAR 3.0) Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Does Computer-Aided Instruction Improve Children’s Skills? 99
While many low-income countries have rapidly increased primary school
enrollments in recent decades, they often face substantial obstacles in avoiding a
learning crisis. D'abord, increases in primary school enrollments have occurred along
with increases in education inputs, such as teachers and other school resources.
Cependant, any decline in per capita inputs will likely reduce the quality of primary
éducation. Deuxième, hiring high-quality teachers is difficult in many developing
countries because they are paid less than other comparably qualified professionals,
particularly in urban areas. Troisième, any substantial gap between the abilities of
faible- and high-achieving students makes it difficult for teachers to set their level of
instruction appropriately. Such situations produce a mismatch between a teacher’s
level of instruction and students’ level of proficiency (Glewwe and Muralidharan
2016).
New technologies offer promising ways to mitigate such problems
in developing countries. Although computer access in classrooms does not
improve students’ learning, as shown in Barrera-Osorio and Linden (2009),
well-designed computer-assisted learning (CAL) allows students to access high-
quality instructional materials even in the presence of severe teacher shortages and
learn at their own pace and proficiency. Cependant, the empirical evidence on the
effect of computer-aided instruction (CAI) is mixed. In India, CAI was found to
improve student performance substantially, especially for low-achieving students
(Linden 2008), while the One Laptop per Child programs in Peru and Uruguay
had no impact on student reading or math abilities (Cristia et al. 2017; De Melo,
Machado, and Miranda 2014).
This study was designed to rigorously estimate the causal impact of CAI on
students’ cognitive and noncognitive skills, in collaboration with the Government
of Cambodia, the Japan International Cooperation Agency, and Hanamaru Lab,
a Japanese private company that developed a personalized computer-assisted
software called Think!Think! The primary objective of Think!Think! is to develop
foundational math skills for elementary school students.
To examine the effect of Think!Think!, we ran a clustered randomized
controlled trial (RCT) involving 1,656 students from grade 1 (G1) to G4 at five
public elementary schools near Phnom Penh from May to August 2018. Because
each school has two classes in each grade, students were randomly assigned
during the 3-month intervention to either one of the 20 treatment classes that used
Think!Think! or one of the 20 control classes.
Our results show that the average treatment effects on cognitive skills
measured by several types of math achievement tests and intelligence quotient
(IQ) tests are positive and statistically significant. The size of the effect is large,
especially compared with previous studies conducted in developing countries:
our study’s preferred point estimates are 0.68–0.77 standard deviation for student
achievements and 0.66 standard deviation for IQ scores, even after controlling for
prior scores in the baseline survey, genre, grade, birth month, parental education,
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
100 Revue du développement en Asie
and schools’ time-invariant characteristics. En outre, the CAI-based software
raises students’ subjective expectations of attending college in the future. Cependant,
there is no significant effect on noncognitive skills, namely motivation and self-
esteem.
Our contribution to the literature can be mainly summarized as follows:
(je) While prior literature has focused more on test score gains, our paper examines
the effect of CAI on a wide variety of outcome variables, including cognitive skills
measured by test scores and IQ scores, noncognitive skills measured by motivation
and self-esteem, and other habits such as hours spent studying at home. (ii) While
the demand for new technologies is growing in education, especially in developing
des pays, more rigorous research is required to establish their external validity.
To our knowledge, ours is the first study that has been rigorously designed and
implemented in Cambodia. (iii) Unlike prior literature which provided after-school
CAI as part of remedial education, students in our study were allowed to access CAI
only during class. We are thus able to identify whether CAI caused an improvement
in students’ cognitive abilities because of increased learning productivity per hour,
not because of increased hours available for instruction.
The remainder of this paper will proceed as follows. Section II provides
a literature review. Section III explains the research design and data. Section IV
presents empirical specifications and the main results on cognitive and noncognitive
skills. Section V concludes and provides policy implications.
II. Literature Review
Previous studies have defined investment in computers by schools as either
information communication technology or CAI. Au cours des dernières années, CAI programs,
which do not necessarily require an internet connection, have become more
widely used in public schools. Cependant, while several studies have shown that
well-designed CAI programs appear to have strong and positive effects on math
or science abilities of weaker students, especially in developing countries, other
studies have found insignificant effects on reading and language test scores. Pour
example, Rouse and Krueger (2004) ran a large-scale RCT using the computer
software program Fast For Word for G3 to G6 students in an urban district in
northwestern United States. Their results showed that the effect of this program
on language and reading skills is small and statistically significant. Banerjee et al.
(2007) examined the effect of a CAI program for G4 students in urban India. Le
students who were randomly assigned to treatment schools increased their math
achievements by 0.47 standard deviation, mainly because of improvement among
poorer performing children. Surprisingly, this positive effect remained even after
the programs were terminated, although the size of the effect decreased to about
0.10 standard deviation.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Does Computer-Aided Instruction Improve Children’s Skills? 101
In economics, investments in computers, the internet, software, et autre
technologies have been analyzed typically in the context of an education production
fonction. Bulman and Fairlie (2016) pointed out that the binding constraint in the
model is often the amount of time available for instruction, which is regarded
as one of the educational inputs. Autrement dit, this trade-off between time
spent using a computer in class and time spent on traditional instruction makes
it more difficult to determine whether schools should use CAI programs or more
traditional instruction. Cependant, many studies, including Rouse and Krueger (2004)
and Banerjee et al. (2007), have estimated the effect of supplemental education or
remedial education with CAI programs outside of class.
To deal with these issues, Barrow, Markman, and Rouse (2009) developed a
trial in which middle school students in randomly assigned treatment classes were
taught using CAI, while students in the control classes were taught traditionally in
class. This enabled a comparison of the effects of the newly developed CAI program
and more traditional instruction under limited school resources and time constraints.
The 2-year experiment found that the treatment students improved their math ability
by at least 0.17 standard deviation more than their counterparts. Carrillo, Onofa,
and Ponce (2011) conducted a similar experiment in Ecuador for elementary school
students. Using CAI in class, instead of traditional instruction, helped to improve
math performance, but not language acquisition. Cependant, a recent study on middle
schools in urban India showed that using CAI in class has a greater impact on
both math and language abilities (Muralidharan, Singh, and Ganimian 2019). Le
authors’ instrumental variable estimates find that treatment students performed 0.37
standard deviation higher in math and 0.23 standard deviation higher in Hindi
during the 5-month intervention. They also found that the achievement gains were
greater for academically weaker students. Our empirical analysis follows that of
Muralidharan, Singh, and Ganimian (2019) and tests whether CAI programs are
effective for younger children in relatively disadvantaged areas of a developing
country.
III. Methodology and Data
UN.
Background
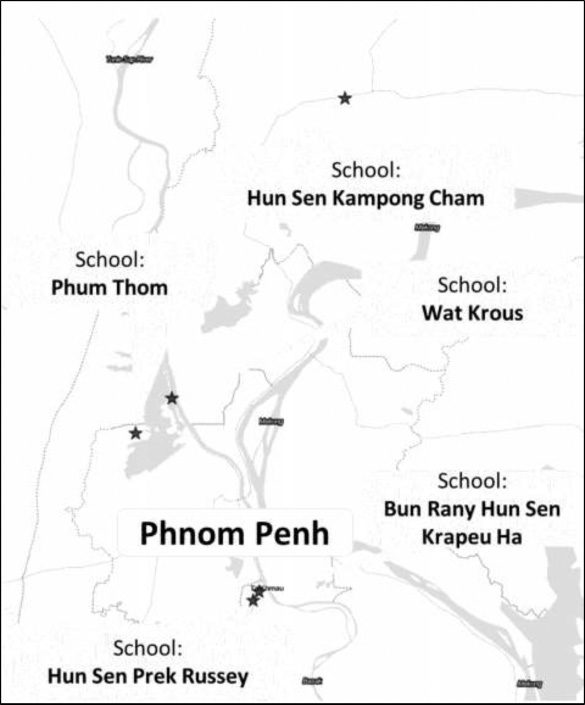
Our study targets five public elementary schools located within a radius of
environ 10 kilometers around Phnom Penh. Because these schools did not
receive any aid or assistance from other development agencies during the period
of our intervention, we can rule out any confounding factors from other external
interventions. The majority of households around the schools engage in farming
and fishing to generate income. Only a small proportion of parents have tertiary
éducation. The locations of these five schools are illustrated in Figure 1.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
102 Revue du développement en Asie
Chiffre 1. Locations of Target Schools
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Note: This map was not produced by the cartography unit of the Asian Development Bank. The boundaries, colors,
denominations, and any other information shown on this map do not imply, on the part of the Asian Development
Bank, any judgment on the legal status of any territory, or any endorsement or acceptance of such boundaries, colors,
denominations, or information.
Source: Stamen Maps. http://maps.stamen.com/.
B.
Baseline and Follow-Up Surveys
Prior to the intervention, we conducted baseline surveys in class from
21–25 May 2018 with the full cooperation of teachers and staff. The baseline survey
included two sets of 40-minute achievement tests for G3 and G4 students, 40-minute
IQ tests for all students, and 20-minute surveys for all students and parents.
To measure students’ cognitive skills, two sets of achievement tests were
used: the National Assessment Test (NAT) administered by Cambodia’s Ministry
of Education, Youth and Sports for G3 students; and Trends in International
Does Computer-Aided Instruction Improve Children’s Skills? 103
Mathematics and Science Study (TIMSS) administered by the International
Association for the Evaluation of Educational Achievement (IEA) for G4 students.
We selected exams that the students in our intervention had not previously taken.
As there are no standardized tests to measure the cognitive abilities of younger
students, we did not administer achievement tests for G1 and G2 students. Plutôt,
we administered two sets of age-appropriate IQ tests in the baseline survey. One of
the IQ tests—the “new Tanaka B-type intelligence test” (Tanaka, Okamoto, et
Tanaka 2003)—has long been used in Japan and other countries in Asia as an
age-appropriate measure of children’s cognitive skills. The Tanaka B-type
intelligence test was translated into the local
language and also modified
appropriately for the local environment (par exemple., illustrations of local banknotes, food,
people, etc.). The other intelligence test conducted during the baseline survey
was the Goodenough Draw-a-Man (DAM) test (Goodenough 1926). In this test,
students are asked to complete drawings of a whole person(s) on a piece of paper
for 10–15 minutes. Several examples of children’s drawings collected during our
baseline survey appear in Figure 2. Although the validity of this test as a measure of
intelligence has been criticized, the literature suggests that the DAM test is effective
in screening for lower levels of intelligence in 5- to 12-year-old children (Scott
1981).
The survey of all G1 to G4 students asked them to provide demographic
information, including gender, grade, birth month, hours of study at home, et
subjective likelihood of attending college in the future. The survey also included
a set of questionnaires to measure noncognitive skills, in particular the Rosenberg
self-esteem scale (Rosenberg 1965) and an internal and external motivation scale
(Sakurai and Takano 1985). The survey of parents asked about socioeconomic
status, such as their educational backgrounds.
Following the 3-month intervention, a follow-up survey was conducted from
Août 16 à 25. We again administered the same sets of achievement tests, IQ tests,
and questionnaires for students, focusing only on time-varying variables, tel que
willingness to attend college and time spent studying at home.
Out of 1,656 students who officially registered in our target schools, 77.2%
of them participated both in the baseline and follow-up surveys, bien que 6.3%
did the baseline survey only. The sample attrition may be a great threat to reduce
the comparability of treatment and control. If our intervention is successful, le
low-achieving students assigned to the treatment group may not drop out during the
intervention, while their counterpart low-achieving students assigned to the control
group may drop out of school altogether. Dans ce cas, the estimated impact of this
intervention may be downward biased. We calculated the attrition rate for both
treatment and control groups and checked whether the students who dropped out
of the two groups had different characteristics. Heureusement, there is no evidence
of differential attrition rates and different types of attrition in the treatment and
control groups. Cependant, we still do not know much about the 9.2% of students who
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
104 Revue du développement en Asie
Chiffre 2. Samples of Draw-a-Man Test
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Source: Figures by four anonymous students selected from the Draw-a-Man tests conducted during the baseline
survey.
completed neither baseline nor follow-up surveys. According to the latest World
Bank Indicators, the school dropout rate in Cambodia nationwide was 9.4% dans 2017.
Because our intervention was implemented in the last 3 months of the semester,
some may have dropped out of school before or during the intervention. To deal
with this problem, we created a dummy variable which we set to 0 if the baseline
data is missing and then controlled for it in our analysis of covariance (ANCOVA)
estimate as a robustness check (models 2 et 3 in Tables 2 et 3, and model 2 dans
Tables 4 et 5).
Does Computer-Aided Instruction Improve Children’s Skills? 105
Chiffre 3. Sample Problem
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Source: Wonder Lab (formerly Hanamaru Lab). https://wonderlabedu.com/.
C.
Education Software: Think!Think!
The software called Think!Think! used in our intervention was originally
developed by Hanamaru Lab, taking full advantage of its substantial experience in
operating a large number of cramming schools for school-aged children in Japan.
This software is especially designed to develop the foundational math skills of
elementary school students (Chiffre 3). Why math? As a number of studies have
suggested, math and science skills are highly related to economic growth across
des pays (par exemple., Jamison, Jamison, and Hanushek 2007; Hanushek and Woessmann
2016). The benefits of mathematical proficiency not only drive economic growth
but also raise individual earnings. Par exemple, Joensen and Nielsen (2009)
exploited an institutional reduction in the costs of acquiring advanced high school
math in Denmark and provide evidence that the choice of a more math-intensive
high school specialization has a causal effect on future labor market earnings.
More specifically, Think!Think! incorporates adaptive learning using an original
algorithm and provides math problems, materials, and instructions to reflect the
proficiency level of each individual student.
Think!Think! was modified for elementary school students in Cambodia to
meet local curriculum standards and was translated into the local language, Khmer.
Students who were assigned to treatment classes were provided with free access to a
tablet or laptop to use Think!Think! in class. CAI often requires additional teaching
staff in class. In our intervention, we provided three additional staff with no teaching
experience to advise students on technical matters and time management.
106 Revue du développement en Asie
We carefully compared Think!Think! with a CAL program called Mindspark
used in a study by Muralidharan, Singh, and Ganimian (2019) and found
that it had many features that were very similar to Think!Think! According
to the authors,
the advantages of using Mindspark are (je) its high-quality
instructional materials; (ii) its adaptive contents which allow them to implement
“Teaching at a Right Level” for each individual student; (iii) that it alleviates a
student-specific conceptual bottleneck; et (iv) its interactive user interface, tous
of which also characterize the attractive features of Think!Think! (Muralidharan,
Singh, and Ganimian 2019, 1431–32). One slight difference is that Mindspark
provides Hindi (langue) programs as well as math for middle school students
(G6 to G9), while Think!Think! specializes in math for younger primary school
students (G1 to G4).
Because of these similarities, our results are, in fact, very consistent with
Muralidharan, Singh, and Ganimian (2019). Cependant, one of the most significant
differences between our study and Muralidharan, Singh, and Ganimian (2019)
is in the implementation. The authors’ intervention was a “blended learning”
program, meaning “a combination of the Mindspark CAL program, group-based
instruction and extra instructional time” (Muralidharan, Singh, and Ganimian 2019,
1429). Their results, donc, could not disentangle the pure effect of CAL from
additional inputs and investigate whether the technology could have a positive effect
on test scores in the absence of a constraint. Assuming that the amount of time
available for instruction is fixed at a school, whether schools choose the optimal
level of technology relative to traditional instruction in class may be a more relevant
policy question for governments in developing countries.
D.
Clustered Randomized Controlled Trial
If we were to allow students to access the CAI based on their own
preferences, the software would most likely be used by higher-achieving students.
Students who have sought to access a higher quality of education, including the
exposure to new technology, are much more enthusiastic to study, on average, que
those who never did. Random assignment of access to the CAI-based software
avoids this selection bias.
Students in the treatment classes used Think!Think! for approximately 30
minutes each day. Peer effects are a potential threat to the internal validity of this
experiment, and interactions between students may violate the stable unit treatment
value assumption. To avoid this situation, besides the fact that clustered RCT is
more common in education as noted in the literature, we randomized classrooms
rather than individual students within them.1
1Cependant, as pointed out by Imbens and Wooldridge (2009), it is technically difficult to separate the direct
effect of the intervention on an individual from the indirect effect of peers on that individual.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Does Computer-Aided Instruction Improve Children’s Skills? 107
Because each school has two classes in each grade, we used a stratified
randomization: we picked one treatment in each grade at each school. This created
20 treatment classes (avec 840 students) et 20 control classes (avec 816 students)
across the five schools.2 However, there is still the concern that students in the
treatment classes would talk to their friends in the control classes at the same
school about what they had learned. To reduce the risk of such spillovers, nous
did not allow the treatment students to access Think!Think! outside of class.
En outre, they were not allowed to take their tablet or laptop home. Cependant, notre
class-level clustered randomization may not be enough to contain the spillovers
between treatment and control groups. The unbiased estimate may be larger
if there exists a positive spillover within treated peers and a secondary effect
on those who are not treated in the same schools. Despite the relatively short
period of intervention of 3 mois, the students were enthusiastic about using
Think!Think! The drawbacks of our study may be the presence of evaluation-driven
behavioral changes in the treatment group called the Hawthorn effect and/or in the
control group called the John-Henry effect. Because the Hawthorn effect artificially
improves student’s outcomes in the treatment group, the impact of CAI compared to
its true impact may be overestimated, although we do not find any significant change
in motivation within the treatment group. On the other hand, the John-Henry effect
boosts outcomes among students in the control group, which may underestimate the
impact of CAI.
IV. Econometric Specification and Results
UN.
Econometric Specification
To identify the causal effect of using Think!Think!, we conduct ANCOVA
using the following model and identify the effect of using CAI. Our equation of
interest is
Faire, j,t = α + βTi, j,t + γ Yi, j,t−1 + δMissingBaselinei, j,t
+ Xi, j,tσ + ∈i, j,t
(1)
where Yi, j,t is the outcome variable of student i in school j at time t. Ti, j,t is access to
CAI and the key independent variable of interest. MissingBaselinei, j,t is a dummy
variable to indicate whether student i participated in the baseline survey or not.
Xi, j,t is a vector of control variables, while ∈i, j,t is the idiosyncratic error term.
Xi, j,t includes the basic demographic controls, such as gender, grade, birth month,
parental education, and school-grade time-invariant fixed effects. According to
2While there can be unobserved correlations between the outcomes of students in the same classroom,
clustered standard errors can be used to correct for such correlations. Cependant, we cannot calculate clustered standard
errors because there are only 40 classrooms in our experiments and the calculation of this type of standard errors
requires at least 42 clusters, as suggested by Angrist and Pischke (2008).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
108 Revue du développement en Asie
McKenzie (2012), ANCOVA is preferred for experimental designs, rather than the
difference-in-difference approach, when the autocorrelation in outcome variables
between the baseline and the follow-up survey is low. Because our data are only
weakly autocorrelated, we apply ANCOVA for our estimation.
The crucial identifying assumption in this empirical model is that the
relationship between exposure to the CAI-based software and students’ unobserved
ability is orthogonal to the error term, conditional on the controls. Under this
assumption, the estimate of β in equation (1) can be interpreted as the causal impact
of the CAI-based software on student outcomes.
B.
Variable Definitions
Tableau 1 presents a balance check for the baseline survey. There is no
statistically significant difference in the results of the NAT between the G3 students
assigned to treatment classes and those assigned to control classes, although the G4
students in the control classes performed slightly better on the TIMSS than those
in the treatment classes, even after controlling for school-by-grade fixed effects,
following Bruhn and McKenzie (2009).
Another outcome variable is IQ test scores: the results of the Tanaka
B-type IQ test and the DAM test are converted to a mental age, and the IQ scores
are then calculated as mental age divided by chronological age multiplied by 100.
According to the descriptive statistics, the mean of the Tanaka B-type IQ test score
est 78.612 with a standard deviation of 13.451, and the mean of the DAM type IQ
score is 0.692 with a standard deviation of 0.207. There is no statistically significant
difference between the Tanaka B-type IQ test score and the DAM score.
The next set of outcome variables, measures of noncognitive skills, are coded
as the mean of a set of questionnaires specific to self-esteem and motivation.
The self-esteem measure is slightly higher for the treatment students, tandis que le
motivation measure is similar across the two groups of students. All cognitive and
noncognitive outcome measures are normalized to a mean of 0 and a standard
deviation of 1 when we run the regression analysis.
Willingness to attend college is measured on a 3-point scale (depuis 1 = not
likely to 3 = very likely) based on students’ subjective expectations. Hours spent
studying at home is measured on a 6-point scale (depuis 1 = not at all to 6 = more
que 4 hours). We set the minimum of this variable to 0 and the maximum to 4
hours, and then we took the median value for categories between 2 (less than 30
minutes) et 5 (2–3 hours) on the 6-point scale. The key independent variable of
interest denoted by Ti, j,t is a dummy variable coded as 1 if students are assigned to
a treatment class and 0 otherwise.
The demographic variables denoted by Xi, j,t, such as gender, âge, et
parental educational backgrounds, are very similar between the treatment and
control students. The variable on parental education represents the highest level of
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Does Computer-Aided Instruction Improve Children’s Skills? 109
Tableau 1. Descriptive Statistics and Balance Test
Achievement test (NAT, G3)
Achievement test (TIMSS, G4)
IQ test (Tanaka-B)
IQ test (Draw-a-Man)
Self-esteem
Motivation
Willingness to go to college
Minutes of studying at home
per week
Gender (male = 1, female = 0)
Age
Highest parental education
College or graduate school
High school
Junior high school
Elementary school
No education (ref)
Birth month
Jan–Mar
Apr–Jun
Jul–Sep
Oct–Dec
All
0.538
(0.207, 356)
0.292
(0.203, 347)
78.612
(13.451, 1,385)
0.692
(0.207, 1,217)
2.762
(0.549, 1,150)
0.656
(0.142, 996)
2.410
(0.771, 1,051)
168.667
(117.005, 949)
0.525
(0.500, 1,643)
8.485
(1.553, 1,620)
0.023
(0.149, 1,236)
0.457
(0.498, 1,236)
0.299
(0.458, 1,236)
0.220
(0.414, 1,236)
0.002
(0.040, 1,236)
0.234
(0.423, 1,620)
0.246
(0.431, 1,620)
0.249
(0.433, 1,620)
0.270
(0.444, 1,620)
Contrôle
(UN)
Treatment
(B)
Différence
(B)-(UN)
0.522
(0.198, 177)
0.330
(0.187, 174)
78.432
(13.131, 700)
0.678
(0.206, 594)
2.726
(0.596, 535)
0.652
(0.150, 471)
2.342
(0.809, 482)
170.142
(108.975, 423)
0.530
(0.499, 813)
8.501
(1.573, 803)
0.016
(0.127, 610)
0.474
(0.500, 610)
0.292
(0.455, 610)
0.215
(0.411, 610)
0.003
(0.057, 610)
0.223
(0.416, 803)
0.263
(0.440, 803)
0.255
(0.436, 803)
0.259
(0.438, 803)
0.554
(0.214, 179)
0.252
(0.211, 173)
78.795
(13.777, 685)
0.705
(0.207, 623)
2.794
(0.502, 615)
0.660
(0.133, 525)
2.467
(0.734, 569)
167.481
(123.173, 526)
0.519
(0.500, 830)
8.470
(1.535, 817)
0.029
(0.167, 626)
0.441
(0.497, 626)
0.305
(0.461, 626)
0.225
(0.418, 626)
0.000
(0.000, 626)
0.245
(0.430, 817)
0.230
(0.421, 817)
0.244
(0.430, 817)
0.282
(0.450, 817)
0.031
(0.039)
−0.067*
(0.035)
0.401
(1.647)
0.026
(0.033)
0.039
(0.043)
0.01
(0.013)
0.108
(0.109)
−3.111
(13.628)
−0.01
(0.016)
−0.034
(0.048)
0.009*
(0.004)
−0.028
(0.031)
0.011
(0.019)
0.009
(0.022)
−0.004
(0.003)
0.018
(0.021)
−0.034
(0.022)
−0.016
(0.019)
0.021
(0.021)
CAI = computer-aided instruction, G3 = grade 3, G4 = grade 4, IQ = intelligence quotient, NAT = National
Assessment Test, TIMSS = Trends in International Mathematics and Science Study.
Remarques: Treatment and control refer to whether students are randomly assigned into classes with CAI. Variables
used in this table are from the baseline survey in May 2018. The data are combined from three pieces of survey
conducted: (je) student survey, (ii) parent survey, et (iii) skill assessment. The numbers reported in each cell represent
means along with the standard deviation and the number of observations in parentheses (in this order). The column
“Difference” shows the estimates drawn from regressing outcomes on a treatment dummy coded 1 if students are
randomly assigned into classes with CAI and school-by-grade fixed effects. ***, **, et * represent 0.1%, 1%, et
5% significance levels, respectivement.
Source: Authors’ estimates.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
110 Revue du développement en Asie
education of either one of the parents. Note that this information is retrieved from
the parental survey conducted at the same time as the student survey. Cependant,
unlike the 100% response rate of the student survey administered during class, le
response rate of the parental survey was approximately 85%.
Although the observable characteristics are similar between the two groups,
several outcome variables, namely the achievement score for G4 students, DAM
type IQ scores, and self-esteem scale, are not comparable in the baseline
survey.
Because heterogeneity across groups can occur by chance even when
randomization is implemented correctly and the chance of achieving homogeneity
when we randomize at the group level increases with sample size, we are not
concerned by heterogeneity in four of the 15 variables. Cependant, although schools
randomize the change in class composition annually, heterogeneity between the
treatment and control groups may still exist because of dropouts or absences on the
day of the baseline survey. We thus control for this using the demographic variables
we use for the heterogeneity check to enable a “pure” comparison.
students. Pour
The average treatment effect may depend on the interests of particular
subgroups of
familiar with
computer-related equipment, the effect may be stronger for boys than girls. Ce
kind of heterogeneous effect is important for policy makers in designing policy
to reflect the needs of particular subgroups. We will discuss this point in the next
section.
are more
example,
if boys
C.
Results
1.
Effect on Cognitive Skills
We start by estimating the effect of CAI on student achievement.
The ordinary least squares estimates are reported in Table 2 along with
heteroskedasticity-robust standard errors. Our primary focus is the estimated effect
of access to Think!Think! on the NAT for G3 students and on the TIMSS for G4
students in the first row of the table.
Model 1 provides unconditional ANCOVA estimates. Model 2 controls for
prior achievement scores in the baseline survey and the missing baseline dummy.
Model 3 controls for basic demographic controls, such as gender, grade, birth
month, parental education, and school-grade time-invariant fixed effects, in addition
to prior test scores and the missing baseline dummy.
The results clearly show that the estimated coefficients on the standardized
test scores are positive and statistically significant at the 0.1% level (Tableau 2, NAT).
The estimated coefficients for the sample of G3 students indicate that exogenous
exposure to the CAI raises average test scores by about 0.77 standard deviation in
model 3.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Does Computer-Aided Instruction Improve Children’s Skills? 111
Tableau 2. Effect of Treatment: Cognitive Skills
NAT
TIMSS
Dependent Variable Model 1 Model 2 Model 3 Model 1 Model 2 Model 3
Treatment
Baseline score
Contrôle
Observations
Adjusted R2
0.814***
(0.291)
0.723***
(0.204)
√
0.767***
(0.223)
√
√
0.522***
(0.135)
0.630***
(0.091)
√
0.681***
(0.104)
√
√
369
0.131
369
0.619
298
0.695
350
0.051
350
0.096
303
0.213
NAT = National Assessment Test, TIMSS = Trends in International Mathematics and Science Study.
Remarques: The coefficients for the treatment group are reported above. The unit of observation is student. Columns
labeled models 1–3 show ordinary least squares estimates. Model 2 controls for prior score and missing baseline
dummy. Model 3 controls for prior score, genre, grade, birth months, parental education, missing baseline
dummy, and school-grade fixed effects. Standard errors are in parentheses and clustered by school. ***, **, et
* represent 0.1%, 1%, et 5% significance levels, respectivement.
Source: Authors’ estimates.
Adding demographic controls and school-by-grade fixed effects to model 3
neither changes the magnitude of the coefficients across specifications nor improves
the precision of our estimates in explaining the variation in test scores. Once
we include the interaction term and test for heterogeneous effects for gender,
grade, and parental education, we obtain small point estimates on nearly all the
interaction terms, and the differences between these coefficients do not support
the hypothesis of significant heterogeneous effects on test scores. En outre,
the achievement gains are homogeneous for academically weaker students. These
results are available upon request.
The results are consistent with our expectations for the G4 sample (Tableau
2, TIMSS). Access to the CAI improves standardized test scores by 0.68 standard
deviation per 3-month exposure in model 3. Adding controls increases the point
estimates and decreases the standard errors of these estimates. En même temps,
we do not find any significant heterogeneous effects of gender, grade, parental
éducation, or initial achievement on test scores.
In Table 3, the estimated coefficient on the Tanaka B-type IQ score is positive
and statistically significant at the 0.1% level. Tableau 3 shows that the effect on the
IQ score from model 3 est 0.66 standard deviation. The estimated coefficient is
unchanged after controlling for demographic characteristics in model 3. Cependant,
the coefficients of the DAM score are not statistically significant, regardless of the
model specification. Dans l'ensemble, our results indicate that the magnitude in cognitive
skills appears to be very large, compared with evidence from previous literature
where the intervention lasted for at least a year.
Because Muralidharan, Singh, and Ganimian (2019) applied very similar
CAL software to relatively poor students in Delhi, India, it is worth comparing their
results with ours. The comparable intent-to-treat estimates in Muralidharan, Singh,
and Ganimian (2019) indicate that lottery-winner-treated students scored 0.23
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Baseline score
Contrôle
Observations
Adjusted R2
112 Revue du développement en Asie
Tableau 3. Effect of Treatment: Intelligence Quotient (IQ)
IQ
Draw-a-Man
Treatment
Dependent Variable Model 1 Model 2 Model 3 Model 1 Model 2 Model 3
−0.003
(0.105)
√
√
0.664***
(0.111)
√
√
0.692***
(0.111)
√
0.705***
(0.117)
0.022
(0.097)
√
0.071
(0.080)
1,404
0.076
1,404
0.4
1,146
0.51
1,390
0.001
1,390
0.182
1,133
0.287
Remarques: The coefficients for the treatment group are reported above. The unit of observation is student. Columns
labeled models 1–3 show ordinary least squares estimates. Model 2 controls for prior score and missing
baseline dummy. Model 3 controls for prior score, genre, grade, birth months, parental education, missing
baseline dummy, and school-grade fixed effects. Standard errors are in parentheses and clustered by school.
***, **, et * represent 0.1%, 1%, et 5% significance levels, respectivement.
Source: Authors’ estimates.
standard deviation higher than control students after 4.5 mois, while our results
in model 3 show an improvement of 0.77, 0.68, et 0.66 standard deviation for G3
students who took the NAT, G4 students who took the TIMSS, and G1–G4 students
who took the Tanaka-B IQ test, respectivement. Muralidharan, Singh, and Ganimian
(2019) recruited the sample students from a cramming school called Mindspark
center in Delhi, and parents were told that their children would be chosen by lottery
to receive a tuition waiver (₹200 per month, equivalent to $3). Their participants
were self-selected (and perhaps highly motivated) and the administrative data
suggested they performed better than nonparticipants. Muralidharan, Singh, et
Ganimian (2019) found considerable heterogeneity in student progress by initial
learning level and that test score gains were much larger for initially low-achieving
students. The true estimates drawn from the representative sample containing more
low-performing students in our study may be much larger than the estimates
reported in their paper. On the other hand, because we covered all students in public
schools, the participants were not self-selected into the intervention.
Using kernel density estimation, we obtain the probability density function
for both achievement test scores and IQ scores to compare the score distributions
after the 3-month intervention (Figures A1–A3). Although the difference in the
DAM scores for the entire sample and even the interaction term with grades are not
statistically significant, the skills of younger students seem to improve.
2.
Effect on Noncognitive Skills and Inputs for Study
We then repeated the above approach using a set of noncognitive skills as
résultats. Unlike the results for cognitive skills, we do not find any significant
effect for noncognitive skills, measured by motivation and self-esteem (Tableau 4).
Cependant, it is clear that the estimated coefficient on willingness to attend college
is positive and statistically significant at the 5% level (Tableau 5), indicating that
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Does Computer-Aided Instruction Improve Children’s Skills? 113
Tableau 4. Effect of Treatment: Noncognitive Skills
Motivation
Self-Esteem
Dependent Variable Model 1 Model 2 Model 1 Model 2
Treatment
Baseline score
Contrôle
Observations
Adjusted R2
−0.023
(0.070)
√
−0.031
(0.069)
√
√
0.023
(0.052)
√
1402
0.274
1125
0.377
1396
0.025
0.014
(0.059)
√
√
1121
0.138
Remarques: The coefficients for the treatment group are reported above. The unit
of observation is student. Columns labeled models 1 et 2 show ordinary
least squares estimates. Model 1 controls for prior score and missing baseline
dummy. Model 2 controls for prior score, genre, grade, birth months, parental
éducation, missing baseline dummy, and school-grade fixed effects. Standard
errors are in parentheses and clustered by school. ***, **, et * represent 0.1%,
1%, et 5% significance levels, respectivement.
Source: Authors’ estimates.
Tableau 5. Effect of Treatment: Study Input
Study Time (minutes) Willingness to Go to College
Dependent Variable Model 1 Model 2 Model 1
−0.032
(0.097)
√
0.136*
(0.073)
√
Treatment
−0.099
(0.101)
√
√
1,299
0.05
1,057
0.09
1,367
0.033
Baseline score
Contrôle
Observations
Adjusted R2
Model 2
0.139*
(0.083)
√
√
1,094
0.048
Remarques: The coefficients for the treatment group are reported above. The unit of observation
is student. Columns labeled models 1 et 2 show ordinary least squares estimates. Model
1 controls for prior score and missing baseline dummy. Model 2 controls for prior score,
genre, grade, birth months, parental education, missing baseline dummy, and school-grade
fixed effects. Standard errors are in parentheses and clustered by school. ***, **, et *
represent 0.1%, 1%, et 5% significance levels, respectivement.
Source: Authors’ estimates.
students who used the CAI during class are more likely to believe they would
undertake more advanced education in the future. The coefficient remains constant
after controlling for demographic characteristics in model 2, which suggests that
heterogeneous effects in terms of gender, grade, and parental education do not exist.
Although the results do not indicate a positive effect of the CAI on noncognitive
skills, the estimated probability density functions (Figures A4–A5) suggest a slight
improvement in younger grades.
We also estimated the effect on time spent studying at home (Tableau 5), lequel
is considered an important input of an education production function. As already
mentioned above, students were not allowed to bring the tablet or personal computer
to their own homes. It is thus convincing that we do not find any significant effect
on studying longer at home. Cependant, students in treatment classes sharply raised
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
114 Revue du développement en Asie
their achievements, even though their hours of study did not change both at home
and in the classroom. This indicates that CAI is successful in improving students’
learning efficiency and productivity.
V. Conclusion
We examined the causal effect of CAI on children’s cognitive and
noncognitive skills. In collaboration with the Government of Cambodia, we ran
a clustered RCT at five elementary schools around Phnom Penh over a period of 3
mois. Students were randomly assigned to either one of 20 treatment classes that
were allowed to use the CAI instead of regular math classes during the intervention
or one of 20 control classes. Our empirical results show that the average treatment
effect on cognitive skills measured by several types of math achievement tests and
IQ tests is positive and statistically significant. The effect size is large, especially
compared with those in previous studies for developing countries: the estimated
coefficients are 0.68–0.77 standard deviation for student achievement and 0.66
standard deviation for IQ scores even after controlling for demographic factors.
En outre, we found that the CAI can raise students’ subjective expectation
of attending college in the future. Cependant, there is no significant effect on
noncognitive skills, namely motivation and self-esteem.
Because we ran this clustered RCT for only 3 mois, whether these effects
remain in the longer term requires further investigation. Nevertheless, our results
suggest that CAI has tremendous potential to improve students’ math scores in both
the short term and possibly the longer term.
Les références
Angrist, Joshua D., and Jörn-Steffen Pischke. 2008. Mostly Harmless Econometrics: Un
Empiricist’s Companion. Princeton: Princeton University Press.
Banerjee, Abhijit V., Shawn Cole, Esther Duflo, and Leigh Linden. 2007. “Remedying Education:
Evidence from Two Randomized Experiments in India.” The Quarterly Journal of
Economics 122 (3): 1235–64.
Barrera-Osorio, Felipe, and Leigh L. Linden. 2009. “The Use and Misuse of Computers
in Education: Evidence from a Randomized Controlled Trial of a Language Arts
Program.” Abdul Latif Jameel Poverty Action Lab (JPAL). https://www.povertyactionlab.
org/evaluation/use-and-misuse-computers-education-evidence-randomized-controlled-
trial-language-arts.
Barrow, Lisa, Lisa Markman, and Cecilia Elena Rouse. 2009. “Technology’s Edge: Le
Educational Benefits of Computer-Aided Instruction.” American Economic Journal:
Economic Policy 1 (1): 52–74.
Bruhn, Miriam, and David McKenzie. 2009. “In Pursuit of Balance: Randomization in Practice in
Development Field Experiments.” American Economic Journal: Applied Economics 1 (4):
200–32.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Does Computer-Aided Instruction Improve Children’s Skills? 115
Bulman, George, and Robert W. Fairlie. 2016. “Technology and Education: Computers, Logiciel,
and the Internet.” In Handbook of the Economics of Education, edited by Eric A. Hanushek,
Stephen Machin, and Ludger Woessmann, 5: 239–80. Amsterdam: Elsevier.
Carrillo, Paul E., Mercedes Onofa, and Juan Ponce. 2011. “Information Technology and Student
Achievement: Evidence from a Randomized Experiment in Ecuador.” IDB Working Paper
Non. 78.
Cristia, Julian, Pablo Ibarrarán, Santiago Cueto, Ana Santiago, and Eugenio Sever’in. 2017.
“Technology and Child Development: Evidence from the One Laptop per Child Program.”
American Economic Journal: Applied Economics 9 (3): 295–320.
De Melo, Gioia, Alina Machado, and Alfonso Miranda. 2014. “The Impact of a One Laptop per
Child Program on Learning: Evidence from Uruguay.” IZA Discussion Paper No. 8489.
Glewwe, Paul, and Karthik Muralidharan. 2016. “Improving Education Outcomes in Developing
Countries: Evidence, Knowledge Gaps, and Policy Implications.” In Handbook of the
Economics of Education, edited by Eric A. Hanushek, Stephen Machin, and Ludger
Woessmann, 5: 653–743. Amsterdam: Elsevier.
Goodenough, Florence Laura. 1926. Measurement of Intelligence by Drawings. Yonkers-on-
Hudson, New York: World Book Company.
Hanushek, Eric A., and Ludger Woessmann. 2016. “Knowledge Capital, Growth, and the East
Asian Miracle.” Science 351 (6271): 344–45.
Imbens, Guido W., and Jeffrey M. Wooldridge. 2009. “Recent Developments in the Econometrics
of Program Evaluation.” Journal of Economic Literature 47 (1): 5–86.
Jamison, Eliot A., Dean T. Jamison, and Eric A. Hanushek. 2007. “The Effects of Education
Quality on Income Growth and Mortality Decline.” Economics of Education Review 26 (6):
771–88.
Joensen, Juanna Schrøter, and Helena Skyt Nielsen. 2009. “Is There a Causal Effect of High
School Math on Labor Market Outcomes?” Journal of Human Resources 44 (1): 171–98.
Linden, Leigh L. 2008. “Complement or Substitute? The Effect of Technology on Student
Achievement in India.” InfoDev Working Paper No. 17. World Bank Group.
McKenzie, David. 2012. “Beyond Baseline and Follow-Up: The Case for More T in Experiments.”
Journal of Development Economics 99 (2): 210–21.
Muralidharan, Karthik, Abhijeet Singh, and Alejandro J. Ganimian. 2019. “Disrupting Education?
Experimental Evidence on Technology-Aided Instruction in India.” American Economic
Review 109 (4): 1426–60.
Rosenberg, Morris. 1965. Society and the Adolescent Self-Image. New Jersey: Princeton
Presse universitaire.
Rouse, Cecilia Elena, and Alan B. Krueger. 2004. “Putting Computerized Instruction to the Test:
A Randomized Evaluation of a ‘Scientifically Based’ Reading Program.” Economics of
Education Review 23 (4): 323–38.
Sakurai, Shigeo, and Seijun Takano. 1985. “A New Self-Report Scale of Intrinsic versus Extrinsic
Motivation toward Learning in Children.” Tsukuba Psychological Research 7: 43–54.
Scott, Linda H. 1981. “Measuring Intelligence with the Goodenough-Harris Drawing Test.”
Psychological Bulletin 89 (3): 483–505.
Tanaka, Kanichi, Kenroku Okamoto, and Hidehiko Tanaka. 2003. The New Tanaka B Intelligence
Scale. Tokyo: Kaneko shobo.
World Bank. 2017. World Development Report 2018: Learning to Realize Education’s Promise.
Washington, CC.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
116 Revue du développement en Asie
Appendix. Effect of Treatment: Estimated Probability Density Functions
Figure A1. NAT and TIMSS Scores
G3 = grade 3, G4 = grade 4, NAT = National Assessment Test, TIMSS = Trends in International Mathematics and
Science Study.
Remarques: This graph shows the estimated probability density functions for the National Assessment Test (NAT) et
Trends in International Mathematics and Science Study (TIMSS) test given at the follow-up surveys. The light gray
function represents treatment groups and the dark gray function represents control groups.
Source: Authors’ calculation.
Figure A2.
Intelligence Quotient (IQ) Scores (End-line)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
G1 = grade 1, G2 = grade 2, G3 = grade 3, G4 = grade 4.
Remarques: This graph shows the estimated probability density functions for the IQ tests given at the follow-up surveys.
The light gray function represents treatment groups and the dark gray function represents control groups.
Source: Authors’ calculation.
Does Computer-Aided Instruction Improve Children’s Skills? 117
Figure A3. Draw-a-Man Test Scores (End-line)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
G1 = grade 1, G2 = grade 2, G3 = grade 3, G4 = grade 4.
Remarques: This graph shows the estimated probability density functions for the Draw-a-Man test given at the follow-up
surveys. The light gray function represents treatment groups and the dark gray function represents control groups.
Source: Authors’ calculation.
Figure A4. Motivation (End-line)
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
G1 = grade 1, G2 = grade 2, G3 = grade 3, G4 = grade 4.
Remarques: This graph shows the estimated probability density functions for motivation measured at the follow-up
surveys. The light gray function represents treatment groups, and the dark gray function represents control groups.
Source: Authors’ calculation.
118 Revue du développement en Asie
Figure A5. Self-Esteem (End-line)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
G1 = grade 1, G2 = grade 2, G3 = grade 3, G4 = grade 4.
Remarques: This graph shows the estimated probability density functions for self-esteem measured at the follow-up
surveys. The light gray function represents treatment groups and the dark gray function represents control groups.
Source: Authors’ calculation.
/
e
d
toi
un
d
e
v
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
8
1
9
8
1
8
9
7
7
2
7
un
d
e
v
_
un
_
0
0
1
5
9
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3