Discontinuous Combinatory Constituency Parsing
Zhousi Chen and Mamoru Komachi
Faculty of Systems Design
Tokyo Metropolitan University
6-6 Asahigaoka, Hino, Tokyo 191-0065, Japan
{chen-zhousi@ed., komachi@}tmu.ac.jp
Abstrait
We extend a pair of continuous combinator-
based constituency parsers (one binary and
one multi-branching) into a discontinuous
pair. Our parsers iteratively compose con-
stituent vectors from word embeddings with-
out any grammar constraints. Their empirical
complexities are subquadratic. Our extension
includes 1) a swap action for the orientation-
based binary model and 2) biaffine attention
for the chunker-based multi-branching model.
In tests conducted with the Discontinuous
Penn Treebank and TIGER Treebank, nous
achieved state-of-the-art discontinuous accu-
racy with a significant speed advantage.
1
Introduction
Discontinuity is common in natural languages,
as illustrated in Figure 1. Children from a discon-
tinuous constituent are not necessarily consecu-
tive because each can group with its syntactic
cousins in the sentence rather than its two adja-
cent neighbors. Although this relaxation makes
discontinuous parsing more challenging than con-
tinuous parsing, it becomes more valuable for
studies and applications in non-configurational
languages (Johnson, 1985), where word order does
not determine grammatical function. With gradu-
ally saturated continuous parsing accuracy (Zhou
and Zhao, 2019; Kitaev and Klein, 2018, 2020;
Xin et al., 2021), discontinuous parsing has started
gaining more attention (Fern´andez-Gonz´alez and
G´omez-Rodr´ıguez, 2020un, 2021; Corro, 2020).
Typiquement, constituency parsers are divided into
two genres (not including methods employing de-
pendency parsing, par exemple., Fern´andez-Gonz´alez and
G´omez-Rodr´ıguez [2020b]): 1) Global parsers use
a fixed chart to search through all parsing possi-
bilities for a global optimum. 2) Local parsers
rely on fewer local decisions, which leads to
lower complexities. The global parser complexi-
ties start at least from binary O(n3) (Kitaev and
Klein, 2018) or m-ary O(n4) (Xin et al., 2021),
resulting in low speeds for long parses. Global
parsers introduce numerous hypotheses, whereas a
local shift-reduce process or incremental parse ex-
hibits more linguistic interests with fewer outputs
(Yoshida et al., 2021; Kitaev et al., 2022). Neu-
ral global parsers dominate both continuous and
discontinuous parsing (Corro, 2020; Ruprecht and
M¨orbitz, 2021) in terms of F1 score, but they do
not exhibit a strong accuracy advantage over other
parsers. Although local parsers may in some cases
produce ill-formed trees, global parsers do not
guarantee the selection of gold-standard answers
from their charts.
We propose extending a pair of local parsers
to achieve high speed, accuracy, and convenient
investigation for both binary and multi-branching
parses. Chen et al. (2021) proposed a pair of
continuous parsers employing bottom-up vector
compositionality. We dub these as neural combi-
natory constituency parsers (NCCP) with binary
CB and multi-branching CM. To the best of our
connaissance, they possess the top parsing speeds
for continuous constituency. CB reflects a linguis-
tic branching tendency, whereas CM represents
unsupervised grammatical headedness through
composition weight. CM is among the few parsers
that do not require preprocessing binarization
(Xin et al., 2021) but possess a high parsing speed.
We dub our extension as DCCP with binary DB
and multi-branching DM. The mechanisms with
neural discontinuous combinators are shown in
Chiffre 2.
Spécifiquement, our combinators take a sentence-
representing vector sequence as input and pre-
dict layers of concurrent tree-constructing actions.
Two mechanisms are employed. DB triggers an
action if the orientations of two neighboring vec-
tors agree. A swap action exchanges the vectors;
267
Transactions of the Association for Computational Linguistics, vol. 11, pp. 267–283, 2023. https://doi.org/10.1162/tacl a 00546
Action Editor: Carlos G´omez-Rodr´ıguez. Submission batch: 8/2022; Revision batch: 12/8/2022; Published 3/2023.
c(cid:2) 2023 Association for Computational Linguistics. Distributed under a CC-BY 4.0 Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
complexity h. Par conséquent, a binary continuous
h=0(n − h) · h ∼ O(n3)
chart parser has a fixed Σn
complexity for the CKY decoding algorithm.
In m-ary and/or discontinuous cases (c'est à dire., pour
multi-branching arity m and/or fan-out k of each
constituent), the chart is superior to that of bi-
nary continuous parsing in terms of complexity.
Both horizontal and vertical axes expand to di-
versify the combination of discrete bits of each
lexical node. Because of the expansion, m-ary
continuous global parsing (Xin et al., 2021) a
Ô(n4) complexity, whereas binary discontinuous
parsing has exponential complexity at O(n3k)
(Corro, 2020; Stanojevic and Steedman, 2020),
where k ∈ {1, 2} are special cases for binary CFG
(likely in Chomsky Normal Form [CNF]) and bi-
nary Linear Context-Free Rewriting Systems with
maximum fan-out 2 (Stanojevic and Steedman,
2020, LCFRS-2). M -ary discontinuous parsing,
which certainly has a higher complexity, is not yet
available for global parsing.
For efficiency, expensive rules are commonly
restricted by LCFRS-2 parsers (Corro, 2020;
Stanojevic and Steedman, 2020; Ruprecht and
M¨orbitz, 2021). A tricky O(n3) variant of Corro
(2020) covering major rules has produced the best
résultats. Cependant, the variant excludes 2% sophis-
ticated discontinuous rules on TIGER Treebank.
Limited by the simplified grammar, their discon-
tinuous scores are low, especially for recalls. UN
global optimum does not guarantee a gold parse,
leaving room for local parsing.
Local Parsing. Local parsers do not observe the
chart framework and only consider one greedy
or a few hypotheses. Transition-based parsers
with a swap or gap action have sequential actions
and low complexities (Maier, 2015; Coavoux and
Crabb´e, 2017). Multiple swaps or gaps combine
to construct a large discontinuous constituent. Dans
contraste, stack-free parsing can directly pick up
a distant component with one attachment search
(Coavoux and Cohen, 2019). Easy-first (Nivre
et coll., 2009; Versley, 2014) and chunker-based
(Ratnaparkhi, 1997; Collobert, 2011) run rapidly.
Fern´andez-Gonz´alez and G´omez-Rodr´ıguez
(2020un) redirected discontinuity to dependency
parsing via pointer networks and obtained signifi-
cant accuracy improvement among greedy parsers.
Cependant, it is difficult to determine whether such
improvement originates from the model or the
extra head information. In contrast, Fern´andez-
Chiffre 1: Evang and Kallmeyer (2011, DPTB) concernant-
cover discontinuity from continuous Penn Treebank
(Marcus et al., 1993, PTB) with trace nodes (blue).
a joint action composes a new vector with them.
CB only possesses a joint action. Entre-temps, DM
takes discontinuous vectors to form biaffine at-
tention matrices and decides their groups collec-
tivement; the remaining continuous vectors resort
to chunking decisions, as with CM. NCCP and
DCCP are unlexicalized supervised greedy parsers.
The contributions of our study are as follows:
• We propose a pair of discontinuous parsers1
(c'est à dire., binary and multi-branching) by ex-
tending continuous parsers of Chen et al.
(2021).
• We demonstrate the effectiveness of our work
on the Discontinuous Penn Treebank (Evang
and Kallmeyer, 2011, DPTB) and the TIGER
Treebank (Brants et al., 2004). Our parsers
achieve new state-of-the-art discontinuous
F1 scores and parsing speeds with a small
set of training and inferring tricks, y compris
discontinuity as data augmentation, unsuper-
vised headedness, automatic hyperparameter
tuning, and pre-trained language models.
2 Related Work
Global Parsing. The chart for binary continuous
parsing (Kitaev and Klein, 2018) is triangular,
as shown in black in Figure 3. The horizontal
dimension enumerates the position of each node
(c'est à dire., each bit as a word). The vertical C indicates
the number of continuous cases included in each
node. Nodes at height h share combinatorics of
1 Our code with all model configuration files is available
at https://github.com/tmu-nlp/UniTP.
268
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2: Mechanism examples. Gauche: DB produces swap to facilitate traveling of discontinuous nodes and joint
to combine adjacent nodes. Droite: DM leverages biaffine attention to identify and combine discontinuous groups.
Chiffre 3: Fan-out and input sizes increase Continuous
and Discontinuous combinatory global parser cases.
Gonz´alez and G´omez-Rodr´ıguez (2020b) reor-
dered input words in at most O(n2) complexity
and redirected to various continuous parsers.
3 Discontinuous Combinatory Parsing
We call a level of partial derivations or subtrees
a ply (Jurafsky and Martin, 2009), as depicted in
Chiffre 4. Similar to the state of a transition-based
parser, each of which leads to an action, ply is the
state for DCCP, each of which leads to a sequence
of concurrent actions for itself.
Starting with a sequence of words (x1, · · · , xn)
as an initial ply, we assemble an unlabeled dis-
continuous parse tree in a bottom–up manner by
applying concurrent actions to the roots of sub-
trees in the ply and iterating until sequence length
n = 1.
3.1 Binary Ply: Joint and Swap
For a binary tree, two actions are sufficient:
action(xi ⊕ xi+1) ∈ {joint, swap}
joint : compose(xi, xi+1) → xi
swap : (xi, xi+1) → (xi+1, xi) .
(1)
Chiffre 4: DCCP plies with concurrent actions.
One joint reduces the sequence length by one;
the swap does not affect the sequence length but
affects its order. The binary function compose is
a binary neural combinator. The concatenation
‘‘⊕’’ only works for adjacent nodes.
Cependant, concurrent adjacent actions would
conflict in a ply (par exemple., two swaps for (x1, x2, x3)
leaves an undecidable x2). Autrement dit, ils
need a resolution. We adopt a solution of
orientation(xi) ∈ {0, 1}
orientation(xi) − orientation(xi+1) = 1 ,
(2)
where each orientation indicates either left (0) ou
droite (1) and the adjacent node pair of (xi, xi+1)
contains the agreeing orientations. Ainsi, only un-
der this circumstance, DB activates joint or swap
by action(xi ⊕ xi+1) without conflict.
Résumé. All nodes in a DB ply are derived
by Formula 1 under the condition of Formula 2
to form a new ply. As exemplified in Figure 4
for DB, (x1, x2) et (x4, x5) meet the condition
of Formula 2 and have respective joint and swap
actes. Entre-temps, x3 takes neither action and
remains in the ply, because the orientations of x2
269
and x4 do not agree with x3, regardless of x3’s
orientation.
3.2 Multi-branching Ply: Affinity and Chunk
We characterize whether xi and xj from a ply are
two siblings of the same parent constituent as
affinity(xi, xj) ∈ {0, 1} ,
(3)
où 0 denotes false and 1 denotes true. Ainsi,
DM decides a discontinuity action of xi and
then forwards it
to a group action for either
a discontinuous or continuous constituent as in
Formula 4:
action(xi) ∈ {discontinuous, continu}
discontinuous :
G = {xj | affinity(xi, xj) = 1}
medoid ∈ {j | xj ∈ G}
compose(G) → xmedoid
(4)
continu :
G = {xj | lb < i ≤ rb, lb < j ≤ rb, and
affinity(xj, xj+1) = 1(j /∈ {lb, rb})}
compose(G) → xlb+1 ,
whereas ‘‘1(·)’’ is the indicator function. We
select one medoid for each discontinuous con-
stituent to determine its position in the modified
ply, whereas the choice of medoid for continu-
ous constituents makes no difference. Continuous
· · ·, xrb)
nodes split into segments of (xlb+1,
lb + 1) and (rb, rb + 1) as bound-
with (lb,
aries. Function compose is a flexible m-ary neural
combinator with m ∈ N.
Dozat and Manning (2017) characterized each
dependency tree as a sparse asymmetric matrix via
biaffine attention, with each sole positive signal
in a row (or column) indicating a lexical depen-
dency (from a word to its head or vice versa).
Nevertheless, lexical dependency is not available
for constituency parsing, and biaffine attention
becomes expensive at O(n2) complexity.
In contrast, we designate discontinuous affinity
as a small dense symmetric biaffine attention
matrix and control its computational size of O(n2).
Otherwise, continuous affinity for adjacent nodes
takes a special form of
chunk(xi ⊕ xi+1) = affinity(xi, xi+1)
with a simpler O(n) complexity.
Summary. Via fast chunking or a small bi-
affine attention matrix, DM balances to increase
its efficiency. As exemplified in Figure 4 for
DM, discontinuous (x1, x2, x5) are grouped as
one because of their mutual affinity, which is
equivalent to a 3 × 3 biaffine attention matrix
of ones. Node x2 is selected as the medoid for
the constituent’s location in the new ply. Mean-
while, continuous (x3, x4) forms a constituent for
chunk(xi ⊕ xi+1) = affinity(xi, xi+1) = 1(i /∈
{2, 4}) and i ∈ [2, 4].
3.3 Oracle
We state the conversion from tree into layers
of action signals for fully supervised training.
For convenience, we merge DM’s chunk seman-
tics into joint to unify DB’s and DM’s interstice
signals. The common signals are
(cid:2)
x1:n, t1:n, l1:H
1:nh
, j1:H−1
1:nh−1
(cid:3)
,
where x represents a sentence with n words, n
POS tags, H layers of labels, and H − 1 layers of
joints, respectively. ‘‘:’’ indicates sequence range
(e.g., ply height h ∈ [1, H]). DB features in
(cid:2)
(cid:3)
o1:H−1
1:nh
,
containing H − 1 layers of orientations. For DM,
our extension includes discontinuity and affinity
biaffine attention matrices with medoids,
(cid:4)
d1:H−1
1:nh
, a1:H−1
[1:dh, 1:dh]
(cid:5)
,
(cid:6)
nh
i=1 dh
i
≤ nh indicates a number
where dh =
of discontinuous nodes that is no larger than the
number of total nodes in layer h.
Empty Node and Unary Branch. Similar to a
range of previous works (Chen et al., 2021; Shen
et al., 2018; Kitaev and Klein, 2020; Corro, 2020),
we adopt an empty label ‘‘∅’’ for our substructure
(e.g., binarization). Additionally, we collapse each
unary branch into a single node and join their
constituent labels according to their hierarchical
order (e.g., S+VP as derivation S→VP) with easy
restoration during inference. Unary collapse is
productive for label type, as shown in Table 1.
Binarization ρDB. C children of a constituent
join one by one via their orientation and joint
signals. For c ∈ [1, C), [1, c]-th children are set
to orientation right (1) and (c, C]-th are set to
270
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
l
a
c
_
a
_
0
0
5
4
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
l
a
c
_
a
_
0
0
5
4
6
p
d
.
Figure 5: Examples illustrating the principle of stratification. The original m-ary tree (c) is binarized and stratified
into (a) and (b) with numeric factors ρDB, whereas (c) is stratified into (d) with a categorical medoid factor random.
In (d), w2 and w5 are randomly selected as medoids for discontinuous parents l2
2 with more or less twisted
descendant lines. We color constituent components and show disabled joints with light blue ‘‘ ’’ and ‘‘(cid:8).’’
1 and l2
Corpus
DPTB
TIGER
Label Type
Total Collapsed
Label Token
Frequency%
126
80
99
55
3.82%
0.72%
Table 1: Label type and token in our oracle format.
orientation left (0). Neighboring children have
positive joint signals if they are siblings. Oth-
erwise, negative joints swap them toward their
siblings. We normalize a factor ρDB = c−1
∈
C−2
[0, 1] for treebank binarization. In continuous
parsing, ρDB ∈ {0, 1} implies CNF.
As illustrated in Figure 5 (a) & (b), we obtain
layers of action signals from the binarization of
(c). As an extension to CNF, we use the beta distri-
bution ρDB ∼ Beta(αleft, αright) ∈ (0, 1) to create
augmented samples with αleft, αright ∈ (0, +∞).
Medoid ρDM. We use a set of categorical medoid
factors ρDM ∈ {random, leftmost, rightmost} to
stratify a multi-branching tree: 1) random picks a
random child with uniform probability, whereas
2) leftmost and 3) rightmost take the two ends of
a discontinuous group.
2 and l2
In Figure 5 (d), w1 and w4 are randomly selected
as medoids. Meanwhile, l1
2 would exchange
their places if w3 and w4 were selected. Medoid
is different from headedness (Zwicky, 1985). It
is an intermediate variable for locating a discon-
tinuous constituent.
3.4 Model Implementation
NCCP and DCCP have the same bottom–up
iteration on a ply and share two types of neu-
Algorithm 1: Combinatory Parsing
1 Function PARSE(x1:n):
2
ply ← [] and nh ← n with height h ← 1;
xh
1:nh
for i ← 1 to n do
← BiLSTMcxt(embeddings of x1:n);
i );
← FFNNlabel(xh
ˆti ← FFNNtag(xh
ˆlh
i
append a tree with (xi, ˆti, ˆlh
i );
i ) to ply;
while nh > 1 faire
);
← BiLSTMply(xh
1:nh
← FOLD(ply, xh
zh
1:nh
xh+1
1:nh+1
h ← h + 1;
for i ← 1 to nh do
, zh
1:nh
);
1:nh
← FFNNlabel(xh
ˆlh
je
label i-th tree of ply with ˆlh
je ;
je );
return the sole tree in ply;
3
4
5
6
7
8
9
10
11
12
13
14
15
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
ral components: bidirectional Long Short-Term
Mémoire (BiLSTM) and feedforward neural net-
travail (FFNN).
In Algorithm 1, BiLSTMcxt contextualizes the
sequence of words x1:n as embeddings x1
1:n1 and
BiLSTMply contextualizes the ply sequence xh
1:nh
for either DB FOLD in Algorithm 2 or DM FOLD
in Algorithm 3, either of which modifies ply and
constructs new layers of embeddings xh+1
. Le
necessity of BiLSTMcxt and BiLSTMply contex-
tualization was empirically examined with NCCP.
Entre-temps, FFNNtag and FFNNlabel predict the
lexical tags and constituent labels based on contex-
tualized individual embeddings without grammar
constraint.
1:nh+1
When actions do not modify ply at inference
phase, PARSE terminates with a VROOT label
for the current ply. We define CONDENSE as a
271
Algorithm 2: Binary Ply
1 Function FOLD(ply, x1:n, z1:n):
2
for i ← 1 to n do
3
4
5
6
← FFNNori(zi);
← FFNNjoint(zi ⊕ zi+1);
ˆoh
je
ˆjh
je
w.r.t. Subsection 3.1, apply actions to ply
and xi ← COMPOSE(xi, xi+1);
return CONDENSE(x1:n);
7 Function COMPOSE(xL, xR):
8
λ ← σ FFNNbinary(xL ⊕ xR);
return λ (cid:11) xL + (1 − λ) (cid:11) xR;
9
process reenumerating ply nodes regardless their
inconsecutive and unordered indices following
the actions (par exemple., CONDENSE(x1, x3, x5, x4) →
(x1, x2, x3, x4))
CONDENSE : (n ply nodes) → (x1, . . . , xn)
Binary Combinator. The FOLD of DB is shown
in Algorithm 2. The COMPOSE function uses
sigmoid activation ‘‘σ’’ to create a pair of com-
plementary gates λ and (1 − λ) for xL and xR. λ
is a vector of the same size as the embeddings.
Multi-branching Combinator. The DM FOLD
has vectors z1:n and Δ1:n in exchangeable shapes
in Algorithm 3. We choose Δ1:n because it per-
forms empirically optimal. Otherwise, Algorithms
2 et 3 should look more identical. Entre-temps,
(cid:6)G
λi in COMPOSE with
i λi= 1 from Softmax
is the adaptive gating vector for xi. We consider
the average of λi (c'est à dire., ¯λi) as the unsupervised
headedness for inference and visualization. Ainsi,
DM is able to infer with a special factor:
ρDM = uhead ,
which takes medoid ← arg maxi∈G ¯λi as the
group medoid.
[1:D,1:D] for value range (0, 1) (D =
To identify discontinuous groups in the affin-
ity biaffine attention matrix, DM takes M =
ˆdh
σˆah
je )
and booleanizes it into B ← M > θ. Il 1) tries
default threshold θ = 0.5 as the natural selection
for sigmoid activation and checks whether all the
following statements are true:
(cid:6)
je
• B is symmetric (c'est à dire., B = B(cid:2)),
• any rows v, w ∈ B are v (cid:12)= 0,
• either v = w or v(cid:2) · w = 0.
Algorithm 3: Multi-branching Ply
1 Function FOLD(ply, x1:n, z1:n):
2
((cid:7)z1:n ⊕ (cid:7)z1:n) ← z1:n (avant & backward);
for i ← 1 to n do
← FFNNdisc(zi);
ˆdh
je
Δi ← ((cid:7)zi − (cid:7)zi−1) ⊕ ((cid:7)zi − (cid:7)zi+1);
ˆjh
← FFNNjoint(Δi ⊕ Δi+1);
je
v,w do
· W aff · Δw + baff ;
foreach i, j-th discontinuous ˆdh
← x(cid:2)
v
ˆah
[je,j]
find discontinuous groups by checking ˆah;
foreach group indices G and its medoid do
w.r.t Subsection 3.2, apply actions to ply
and xmedoid ← COMPOSE(ΔG, xG);
return CONDENSE(x1:n);
3
4
5
6
7
8
9
10
11
12
13 Function COMPOSE(ΔG, xG):
14
λG ← Softmax (FFNNmulti(ΔG));
return
(cid:6)G
i λi (cid:11) xi;
15
It succeeds in most cases. Otherwise, il 2) tries
a value from M as θ, checks and loops again.
We order the thresholds by their distances to the
default 0.5. If all 2) échouer, il 3) simply falls back into
grouping all nodes as one and counts one FAIL.
Basic Losses. We choose HINGE-LOSS for
binary prediction and CROSS-ENTROPY for
multi-class prediction, following NCCP. Respect-
ing the context in Algorithms 1–3, our basic loss
items are
Ltag, Llabel, Lori, Ljnt, Ldisc, LD
aff
(cid:6)
by accumulating their items across all layers.
Par exemple, LD
[je,j],
aff
ˆah
[je,j]) with D for discontinuous affinity. Nous avons
additional loss items in the next subsection.
je,j,h HINGE-LOSS(ah
←
Complexity. Extreme cases provide the upper
bounds for our theoretical complexity. DB takes
2 fully swapping plies and n
n
2 fully joining plies.
Each ply costs O(n) recurrency; the bound is
Ô(n2). Every DM ply involves a matrix for all
nodes and decreases n only by one. Assume that
we limit check 2) to some fixed sizes. Each ply
costs O(n2); the bound is O(n3).
Cependant, DCCP has an empirical O(n2) com-
plexity with strong linearity, as shown in Figure 6.
DB has higher linear coefficients because of its
slow binary combination. Entre-temps, DM shows
stronger quadratic tendency because of biaffine
272
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 6: Quadratic linear regression (LR) on sentence
length vs. parsing node count on stratified DCCP tree-
banks. DM counts in biaffine attention matrix nodes.
Colors show binarization and medoid strategies. Cubic
LR gives all negative cubic terms highly close to zero.
attention. Encore, their coefficient magnitudes are on
par with one another.
3.5 Training Tricks
Data Augmentation. Chiffre 7 first summarizes
(e) basic data augmentation with binarization for
DB and medoid for DM (y compris (un), (b), et (d)
in Figure 5). The beta distribution can resemble a
uniform random distribution or other biased dis-
tributions to detect linguistic branching tendency
with specific (αleft, αright).
Alors, we further leverage the intermediate non-
terminal node ‘‘∅’’ to create more ∅-subtrees.
The augmentation is an inspiration of CM’s de-
terministic SUB node, which balances subtree
heights and boosts both accuracy and efficiency.
(Non- SUB trees remain at their original heights.)
Cependant, (g) ∅-subtree is random and creates
imbalance. It creates only one stretching branch
by iteratively grouping nodes with possibility ρ∅,
which has three significant impacts:
• Random stretching branches add mild vari-
ations to the context as states for robust ply
actions in FOLD.
• Random discontinuity creates DB orienta-
tion layers that cannot be created by ρDB
binarization.
• They reduce large (possibly continuous)
constituents into smaller (possibly discon-
tinuous) pieces without adding a large pay-
load to the biaffine attention, which narrows
the gap between DB and DM (DM is
more vulnerable to dramatic many-to-one
COMPOSE).
Taking NP ‘‘a good day’’ for instance, any of
‘‘a day,’’ ‘‘a good,’’ and ‘‘good day’’ can be an
intermediate option for creating the NP. On the
one hand, these options create varied contexts for
the remaining parts of a ply. D'autre part,
assume that ‘‘a day’’ (which is not a ρDB product)
is selected. DM learns to discern it with the other
possible ‘‘a day’’ in biaffine attention based on
their context.
ori and Lshfl
jnt. It shuffles xh
Model Robustness. To further randomize DB
entraînement, we introduce (F) ply shuffle and its resul-
tant losses Lshfl
avec
respect to each constituent, takes the new sequence
to BiLSTMply and FOLD, and reuses the ply of
orientation and joint for those additional losses.
Par exemple, a VP to the left of an NP gets shuf-
fled to the right with the same ply ‘‘right (cid:3) left’’
producing the additional loss items.
1:nh
Continuous affinity and discontinuous affinity
in DM undergo different identification processes.
To minimize the difference, we introduce (h) LC
aff
and LX
aff for continuous and interply affinity, dans
addition to cardinal LD
aff. These reduce the risk
of biaffine attention forwarding incorrect nodes,
which would evoke exposure bias. We use posi-
je ) and βx · σ(xh(cid:2)
tive rates βc and βx for βc · σ( ˆdh
·
W aff · Δ¯h
w + baff) to limit the sample size, où
layers ¯h (cid:12)= h contain discontinuous nodes. Fal-
lible signals are more likely to form losses via
HINGE-LOSS.
w
En résumé, the additional loss items are
ori, Lshfl
Lshfl
jnt, LC
aff, LX
aff .
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
4 Experiment
DCCP takes frozen pre-trained FastText as static
word embedding (PWE) or fine-tuned 12-layer
pre-trained XLNet and BERT as contextualized
embedding of pre-trained language models (PLM)
as lexical input 2 and parses on English DPTB and
German TIGER treebanks. See Table 2.
Two-stage Training for a PWE Model. Le
first stage (S1) requires approximately 300 epochs
2To compare to other parsers with a lexical component,
NCCP used pre-trained FastText or FastText trained on PTB.
The former slightly increased F1 score by 0.2. We choose
BERT (https://www.deepset.ai/german-bert)
for German and adopt FFNNcxt instead of BiLSTMcxt for
model connection following NCCP.
273
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(e) Beta distribution is equivalent to uniform random when αleft = αright = 1. Otherwise, it is
Chiffre 7:
for detecting branching tendency with DB. (F) Constituent children get shuffled and create additional losses.
(A1, A2, A3), B1, et (C1, C2) belong to three different constituents. (g) ∅-subtree creates discontinuity from
continuity with a random stretching branch. (h) In-ply continuous nodes and interply nodes are chosen for DM
biaffine attention.
DCCP model dimension
BiLSTMctx / BiLSTMply layers
FFNN{tag, label, ori, jnt, disc} layers
300
6 / 2
2
Optimizer
Adam
(1-epoch γ warm-up, linear decay, and early stop.)
The second stage (S2) involves 100 short trials
with a Bayesian optimization (BO) tool (Akiba
et coll., 2019, optuna); each trial requires less than
30 epochs and brings hyperparameter adjustment:
Drop out rate (recurrent)
Batch size (non-training)
Parameter sizes (w/o PLM)
BiLSTMcxt
+CB
+CM +DB
0.4 (0.2)
80 (160)
+DM
3.25M.
0.36M 0.55M 1.32M 1.45M
Tableau 2: Fixed model hyperparameters and model
parameter sizes of NCCP and DCCP. CB & CM
have a single-layer BiLSTMply of fewer model
parameters.
with general hyperparameters. Loss functions are
sum of all loss items:
DB = Ltag + Llabel + Ljnt + Lori + Lshfl
LS1
DM = Ltag + Llabel + Ljnt + Ldisc +
ori + Lshfl
jnt
(cid:7)
Li
aff
LS1
i∈D,X,C
Adam optimizer’s learning rate is γ = 10−3.
DB uses uniform binarization αleft = αright = 1.
DM uses ∅-subtree ratio ρ∅ = 0.25, robustness
βc = 0.1, and βx = 1 for both efficiency and
accuracy.
274
DB = αtag · Ltag + · · · + αshfl
LS2
jnt
(cid:7)
DM = βtag · Ltag + · · · +
LS2
· Lshfl
jnt
(βi · Li
aff).
i∈D,X,C
Trials follow practical constraints: learning rate
γ ∈ (10−6, 10−3), beta’s αleft, αright ∈ (10−3, 103)
instead of (0, +∞), et [0, 1] for the others.
PLM models also use general hyperparameters
with learning rate 10−6 at S1. PLMs are frozen
during the first 50 epochs to avoid noise pollution
and then are fine-tuned with learning rate 3×10−6.
They inherit explored hyperparameters from PWE
models at S2, except for learning rate 3 × 10−6.
4.1 Overall Results
Tableau 3 shows F1 scores of recent neural dis-
continuous parsers under comparable conditions
on test sets. We follow their reported number of
significant digits and reduce the effects of random
initialization with an average of five runs. Le
details are shown in Table 4.
DCCP models achieved state-of-the-art per-
formance in terms of discontinuous F1 scores
and parsing speeds. Although speed tests are
Type
Trans-Gap
Stack-Free
Seq-Labeling
Model
without pre-trained language model
Coavoux et al. (2019)
Coavoux and Cohen (2019)
Pointer-based VG20 w/ Ling et al. (2015)
Pointer-based FG22 w/ Ling et al. (2015) Multitask†
Stanojevic and Steedman (2020)
Corro (2020)
Ruprecht and M¨orbitz (2021) w/ flair
DB w/ FastText (dans & de)
DM w/ FastText (dans & de)
with pre-trained language model
Pointer-based VG20 w/ BERTBASE
Pointer-based FG22 w/ BERTBASE
Corro (2020) w/ BERT
Ruprecht and M¨orbitz (2021) w/ BERT
FG21 w/ XLNet (dans) or BERTBASE (de)
FG21 w/ XLNet (dans) or BERTBASE (de)
DB w/ XLNet (dans) or BERTBASE (de)
DM w/ XLNet (dans) or BERTBASE (de)
Seq-Labeling
Multitask†
Chart
Chart
Reorder-Chart
Reorder-Trans
Combinator
Combinator
Chart
Chart
Chart
Combinator
Combinator
Complexity
Ô(n)
Ô(n2)
Ô(n2)
Ô(n2)
Ô(n6)
Ô(n3)
–
Ô(n2)
Ô(n3)
DPTB test set
D.F1
71.3
67.3
45.8
–
67.1
64.9
76.1
75.6
78.1
Speed
80
38
611
–
–
355
86
940
970
F1
91.0
90.9
88.8
–
90.5
92.9
91.8
92.0
92.1
TIGER test set
D.F1
55.9
55.9
39.5
62.6
53.5
51.2
61.0
60.1
62.0
Speed
126
64
568
–
–
474
80
1160
1300
F1
82.7
82.5
77.5
86.6
83.4
85.2
85.1
84.9
85.1
Ô(n2)
Ô(n2)
Ô(n3)
–
Ô(n3)
Ô(n2)
Ô(n2)
Ô(n3)
91.9
–
94.8
93.3
95.1
95.5
94.8
95.0
50.8
–
68.9
80.5
74.1
73.4
76.6
83.0
80
–
–
57
179
133
275
375
84.6
89.8
90.0
88.3
88.5
88.5
89.5
89.6
51.1
71.0
62.1
69.0
63.0
62.7
69.7
70.9
80
–
–
60
238
157
424
535
Tableau 3: Overall performance of recent discontinuous parsers. Speeds in sentences per second
were obtained in tests conducted on incomparable hardware and software platforms. Ours and
Vilares and G´omez-Rodr´ıguez (2020, VG20) were conducted on a GeForce GTX 1080 Ti with a
PyTorch implementation, and that of Fern´andez-Gonz´alez and G´omez-Rodr´ıguez (2021, FG21) était
conducted on a GeForce RTX 3090. Fern´andez-Gonz´alez and G´omez-Rodr´ıguez (2022, FG22) involved
lexical dependency information†.
PWE
F1
DPTB (test)
91.97±0.05
DB
DM 92.06±0.10
94.84±0.24
DB
DM 95.04±0.06
PLM
PWE
F1
TIGER (test)
84.88±0.08
DB
DM 85.11±0.13
89.48±0.16
DB
DM 89.61±0.09
PLM
D.F1
75.62±0.82
78.14±0.69
76.62±2.07
83.04±0.79
D.F1
60.08±0.37
62.02±0.71
69.68±0.55
70.93±0.63
Tableau 4: Means and standard deviations of five
runs on test sets with four significant digits. DM
outperforms DB. Development sets reflect similar
variability.
conducted on different platforms, our parsers lead
by a significant margin. In terms of overall F1
score, our parsers outperform some chart parsers
(Stanojevic and Steedman, 2020; Ruprecht and
M¨orbitz, 2021) and slightly underperform the
overall best outline, as characterized in boldface.
4.2 Ablation Study
We ablate the PWE models in two-stage training,
as shown in Table 5. We only show one repre-
275
Model
(Stage)
DPTB (dev)
D.F1
F1
TIGER (dev)
D.F1
F1
DB
(S1)
(S2)
DM
(S1)
(S2)
(0, 0, 0)
(0, 1, 1)
(1, 0, 1)
(1, 1, 0)
‡ (1, 1, 1)
(cid:10)→ optuna
(0, 0, 0)
(0, 1, 1)
(1, 0, 1)
(1, 1, 0)
‡ (1,1,1)
(cid:10)→ optuna
90.93
91.61
91.62
91.48
91.72
92.25
91.62
91.44
91.74
91.84
92.16
92.37
63.28
69.84
74.25
70.97
66.82
76.60
79.37
78.70
79.02
77.37
80.29
82.76
87.73
88.70
87.93
89.05
89.28
89.59
88.30
88.61
89.64
89.78
89.77
89.84
56.49
61.15
59.85
63.32
63.49
66.03
62.41
65.10
67.40
67.78
68.20
68.45
Tableau 5: Ablation in two-stage training on de-
velopment F1 scores. Triplets in {0, 1} indicate
turning on and off (ρ∅, ρDB ∼ Beta(1, 1), shuffle)
for DB and (ρ∅, βc, βx) for DM. Variants of
‘‘‡’’ are S1—the start of S2.
sentative run with ablation because of the similar
low variability on development sets. DB has two
data augmentation items ρ∅ and ρDB as well as one
model item ply shuffle. On ρ∅ refers to ρ∅ = 0.25
and off ρ∅ = 0. Off Beta(1, 1) refers to a static
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Model
Dev set
ρ∅ = 0
0.1
DB
DM
DPTB
TIGER
DPTB
TIGER
91.61
88.70
91.44
88.61
91.79
89.04
91.80
89.45
‡0.25
91.72
89.28
92.16
89.77
0.5
91.95
89.25
89.86
88.61
Tableau 6: DM is sensitive to ρ∅ with dev F1 scores.
All variants are based on (ρ∅, 1, 1) in Table 5
with specific ρ∅ as the variable for DB and DM.
Test set DM Medoid ρDM
F1
DPTB
TIGER
uhead
leftmost
rightmost
random (min)
random (maximum)
uhead
leftmost
rightmost
random (min)
random (maximum)
95.05
95.00
95.03
95.01
95.04
89.62
89.56
89.56
89.55
89.61
D.F1
83.58
81.64
82.47
82.18
83.17
71.61
71.43
70.92
71.26
71.52
Tableau 7: DM medoid factor ρDM = uhead offers
stable gains even without head information during
entraînement. We tested ρDM = random five times.
ρDB = 0.5 et (0, 0, 0) shows the performance of
bare DB models.
On the flip side, DM’s (0, 0, 0) contains ran-
domness because of ρDM = random. We do not
intend to examine a static ρDM as DB yields nega-
tive results. Based on effective training tricks, le
variants enter the BO process at S2. DCCP shows
its sensitivity to ρ∅ in Table 6.
4.3 Inference with Unsupervised Headedness
Both CM and DM provide unsupervised head-
edness ¯λ. Chen et al. (2021) were unable to test
the benefits of CM’s unsupervised headedness
because it is a final product that cannot affect
parsing. Cependant, DM’s medoid affects parsing
performance. On PLM DM, we select different
ρDM categories, which affect the location of all
discontinuous constituent, and examine their gen-
eralization on test sets, as shown in Table 7. All
models are trained with ρDM = random but infer-
ence with ρDM = uhead exerts positive gains on
accuracy.
Chiffre 8: DB and DM’s discontinuity and multi-
branching performance. Because the TIGER Treebank
is richer in discontinuity, DM exhibits higher F1 scores.
5 Discussion
Properties of DCCP Models. Tableau 3 exhibits
high speeds and near state-of-the-art accuracies of
DCCP compared to recent works. DCCP inher-
its many properties from NCCP. CB and CM are
special cases of DB and DM without swap and dis-
continuous actions. All models contain compact
components without grammar restriction. Chaque
model has no more than 4.7M parameters apart
from PWE or PLM, as listed in Table 2.
The variability of all models is low, except for
the discontinuous F1 score of PLM DB on DPTB,
as shown in Table 4. The main cause may not be
the random initialization but the different train-
ing processes of PWE and PLM models—PLM
models use the configuration of PWE models at
S2. Those degraded PLM models adopted low ρ∅
configurations (par exemple., ρ∅ = 0.078). Because DPTB
has less discontinuity and overall F1 scores are
used for model evaluation, high variability in
discontinuous F1 scores becomes more common
without several BO trials; this phenomenon is also
reflected in Table 5. DB lacks explicit disconti-
nuity, and the selection of hyperparameters seems
to be necessary on DPTB.
Chiffre 8 presents the F1 scores for discontinu-
ity and multi-branching. We select PLM models
276
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parent (#)
Head child by maximum weight
NP (14.4K)
from CM
NP(14.3K)
from DM
DT (4.5K); NP (4.3K); NNP (1.6K);
JJ (922); NN (751); NNS (616);
etc.. (1.6K; 12 de 50 types with ‘‘*’’)
NP (4.7K); DT (4.5K); NNP (1.6K);
JJ (786); NN (715); NNS (565);
etc.. (1.4K; 15 de 49 types with ‘‘*’’)
Tableau 8: CM & DM unsupervised NP headedness
depuis (D)PTB test sets. ‘‘*’’ denotes minority NPs
having DTs as non-head children (c'est à dire., DTs are
strong NP heads).
seems to cascade to multi-branching prediction,
resulting in degradation of both properties. Mean-
alors que, DPTB is largely transformed from PTB
by typed traces and automatic rules, where the
multi-branching accuracy stays more stable.
As seen in Table 7, ρDM = rightmost, leftmost
yielded the second best F1 and D.F1 scores on
DPTB and TIGER, respectivement. The reversed
setting yielded poor results, even if not the worst.
The observation implies that many English heads
locate rightward (right-branching) and that Ger-
man heads tend to locate leftward (verb-second
word order, V2). German has abundant separable
verbs with their prefixes at the right-hand side of
the clauses.
Error Rates of DCCP. Greedy parsers allow
ill-formed outputs without a single root, especially
in case of single-model inference. Our models
yielded a few invalid parses, as demonstrated
in Table 11. DM models produce more errors.
Cependant, unsuccessful decomposition of biaffine
attention matrices might not be the direct cause,
as also shown in Figure 11. ρ∅ > 0 variants
cleared the matrices that could not be decomposed
with any θ (FAIL). Similar to CM, this genre
suffers from more failures. Spécifiquement, the ply
size cannot be reduced to one during the iteration.
Greedy parsers must suffer the defect because
of their simplicity. Cependant, invalid parses can
contribute positive F1 scores and global parsers
can yield inaccurate parses.
We applied methods such as Boolean matrix
factorization and singular value decomposition.
Cependant, they did not provide any improvement
and significantly slowed down the speed. This is
Chiffre 9: Beta distribution visualization for TIGER DB
at S2. See their hyperparameters in Figure 10.
whose overall F1 scores are close (c'est à dire., most F1
differences are less than 0.1 and DB’s performance
is high). DM exhibits persistent advantages over
DB when these properties are frequent. We fur-
ther determined that CM has the same gains over
CB starting identically from 4-ary nodes with mi-
nor score differences on (D)PTB under the same
ρ∅ = 0 condition, as shown in Table 9. The result
supports the argument of Xin et al. (2021), lequel
asserts that m-ary constituency parsing without
binarization preserves some natural advantages,
par exemple., predicate-argument structure. Spécifiquement,
ρ∅ > 0 shifts DM’s multi-branching advantage
to frequent low-arity trees, favoring the overall
scores on DPTB, while it enhances both disconti-
nuity and multi-branching advantages on TIGER,
as shown in Table 10, in agreement with Table 6.
The training process of CB with CNF bina-
rization has a slight impact on parsing accuracy.
Chen et al. (2021) obtained the best CB with
Bernoulli distribution P (ρDB = 0) = 0.85 (c'est à dire.,
P. (ρDB = 1) = 0.15 or L85R15 in their for-
mat ‘‘L%R%’’) on PTB. They argued that such
binarization brings orientation balance.
De la même manière, DB’s S2 exhibits a slightly leftward
exploration with the beta distribution, as shown
in Figure 9. DPTB has a similar situation. Encore,
the optimized distributions are relatively uniform
and symmetric, which qualifies our uniform ran-
domness with ρDB at S1 and indicates a desired
property for future language-agnostic practice.
For unsupervised headedness, Chen et al.
(2021) reported that CM absolutely picks deter-
miners (DT) as heads for major NP. DM contin-
ues and further grammatically picks more noun
phrases (NP) as NP heads, as shown in Table 8.
Linguistic Properties by DCCP. From Fig-
ure 8, we learned that TIGER is more challenging
in discontinuity. Incorrect discontinuity prediction
277
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 10: The BO process starts with S1 dev F1 scores (c'est à dire., a small dot at each legend bottom) and ends with a
range of scores in S2. While the models are not sensitive to hyperparameters (par exemple., all gains are less than 0.54),
their preferences are different on respective corpora. On TIGER, αori < αshfl
ori and high (βC, βX ) are preferable.
Prop.
M -ary
1
2
3
4
5
6
7
8
9
k > 1
All
Gold
Tree
9,073
26,338
7,009
1,490
344
96
32
12
3
731
44,397
PWE
ρ∅ = 0
ρ∅ > 0
PLM
ρ∅ = 0
ρ∅ > 0
CB
92.25
90.41
84.17
77.87
74.19
70.05
64.71
64.00
100.00
–
92.54
CM
92.02
89.94
83.56
78.95
77.29
78.35
86.15
72.73
75.00
–
92.08
DB
91.43
89.87
83.50
78.19
76.14
72.90
73.53
81.82
100.00
73.95
91.99
DM
91.35
89.68
83.34
79.82
78.46
80.63
87.10
85.71
75.00
77.60
92.02
DB
91.68
89.95
83.60
78.50
74.97
77.39
76.47
75.00
100.00
75.68
92.00
DM
91.53
90.02
83.79
78.86
78.87
76.29
71.43
80.00
50.00
78.94
92.00
CB
93.80
94.41
90.27
87.42
81.42
78.64
76.47
78.26
100.00
–
95.71
CM
94.33
94.33
89.81
86.51
84.06
80.00
70.18
86.96
75.00
–
95.44
DB
93.36
93.47
88.31
83.98
78.61
79.23
75.76
78.57
100.00
78.62
94.70
DM
93.41
93.65
88.60
86.50
85.15
83.50
77.42
83.33
85.71
83.04
94.79
DB
93.91
93.77
88.57
83.88
81.38
79.02
80.60
91.67
85.71
78.65
95.08
DM
93.82
93.92
88.87
85.90
83.17
76.44
54.90
63.16
100.00
82.71
95.09
Tableau 9: Multi-branching and discontinuous F1 scores of NCCP and DCCP on (D)PTB test sets. Nous
grouped k > 1 because only one tree has fan-out k = 2 in the test set. The scores of CB and CM are
from Chen et al. (2021).
Soutenir.
M -ary
1
2
3
4
5
6
7
8
9
k = 1
k = 2
k = 3
All
Gold
Tree
470
15,379
13,497
6,166
2,202
602
130
20
6
36,317
1,963
194
38,474
PWE ρ∅ = 0
DM
DB
49.14
45.37
82.57
81.83
80.58
80.41
73.43
73.34
64.14
63.66
52.85
50.72
43.38
36.25
24.39
11.24
66.60
12.90
85.95
85.92
59.88
59.64
59.83
57.46
84.56
84.50
ρ∅ > 0
DB
51.64
82.25
80.95
74.04
64.27
51.62
40.53
16.44
21.43
86.41
59.95
58.89
84.99
DM
55.32
83.36
81.05
74.36
65.15
55.13
44.91
19.51
28.57
86.39
62.05
60.61
85.08
PLM ρ∅ = 0
DM
DB
56.84
55.16
86.34
85.91
85.96
85.35
80.71
79.93
72.40
71.09
63.61
59.30
55.02
45.51
24.32
24.24
33.33
16.67
89.85
89.75
71.15
67.53
68.23
63.91
88.82
88.57
ρ∅ > 0
DB
54.45
86.50
86.93
81.76
73.37
61.32
43.59
16.67
12.90
90.69
69.78
69.21
89.55
DM
57.48
87.31
86.89
81.92
73.88
64.79
50.37
20.00
54.55
90.66
70.85
68.95
89.58
Tableau 10: Multi-branching and discontinuous test F1 scores of DCCP on TIGER. Fan-out is de-
tailed in k.
278
Test set
Total trees
DB’s ill-formed parses
DM’s ill-formed parses
Biaffine attention matrices
θ = 0.5 solutions
Average of tries if θ (cid:12)= 0.5
FAIL + identity matrices
DPTB TIGER
2,416
1
15
594
587
12.4
0+4
4,998
2
47
7,278
7,114
42.9
0+81
Tableau 11: Errors in DCCP PLM models with
ρ∅ > 0. A FAIL causes a matrix of ones, alors que
a θ close to one yields an identity matrix—an
expensive null action.
Chiffre 11: The numbers of tries to decompose biaffine
attention matrices on test sets. ‘‘(cid:4)’’ marks FAILs.
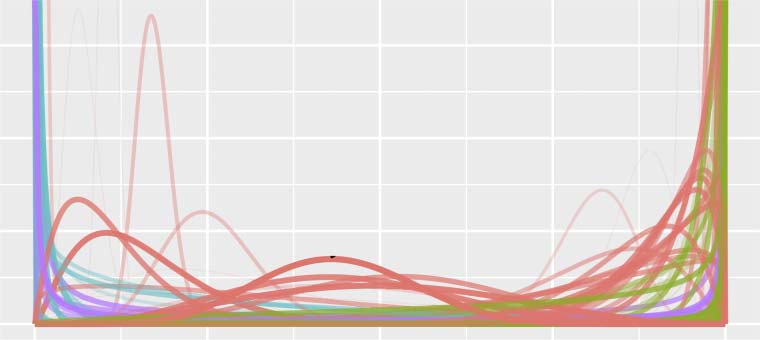
Chiffre 12: Signal polarity in corpora DPTB (sections
2–24) and TIGER. Top: DB signal polarity to ρDB
with orientation right ‘‘•’’ and joint ‘‘(cid:4)’’ Bottom:
DM signal polarity to stratifying medoid factor ρDM
with affinity ‘‘•,’’ joint ‘‘(cid:4)’’ and discontinuity ‘‘ .’’
Continuous and head are referential only, looking for
the least discontinuity and leveraging head information.
(All ρ∅ = 0.)
279
Chiffre 13: An exact matched DPTB sample from PLM
DB and DM models versus CM on PTB. The parse
contains complex nested clauses that CM must fail
to capture, and it becomes ungrammatical in the con-
tinuous scenario. DB’s outputs include orientations
depicted as arrows and their traveling traces colored
for groups. Entre-temps, DM produces two biaffine
attention matrices, one of which has a highly biased
but correct threshold θ = 0.99. Bar heights indicate
values in matrices and their colors indicate the
relationship to θ.
because θ (cid:12)= 0.5 cases are few. Notre
avec-
quential tries to decompose might be na¨ıve, mais
they are effective. In Figure 11, the number of
tries does not significantly increase under θ < 0.9
within 50 tries. For θ ≥ 0.9, although some tries
are expensive, we will see that they are worthy
in the next section. The imbalanced signals from
both datasets account for the bias of θ—more than
92% of the biaffine attention signals are ones,
as shown in Figure 12. All affinity biases (i.e.,
baff ∈ [−1.60, −0.84]) are significant negative
numbers for counteraction.
Weakness. The design of affinity as biaffine
attention is an initial but coarse attempt, which
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
l
a
c
_
a
_
0
0
5
4
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
l
a
c
_
a
_
0
0
5
4
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 14: A TIGER parse. DB natively with ∅-subtrees achieved the exact match but DM erred with ρ∅ = 0.
brings imbalance. If one encoded dependency
within constituent to biaffine attention instead,
both signal balance and multi-grammar parsing
might be better addressed. However, based on
the context of constituency parsing, we leave this
topic for future study.
6 Sample Analysis
Continuous vs. Discontinuous Parsing. Fig-
ure 13 highlights the value of discontinuous pars-
ing by demonstrating the respective CM parse.
Conspicuously, the branching tendency of the
continuous parse is to the right, while it is not obvi-
ous for the discontinuous parsing. Meanwhile, we
observed instances of similar unsupervised head-
edness weights. This sample is not trivial, which
challenges our PLM DCCP models.
In Figure 13, DB
Parsing Process of DCCP.
shows sinuous travel traces of ‘‘I,’’ ‘‘was,’’ and
larger ∅-subtree nodes that involve the turning
of orientations. The varying context leads them
to achieve complex movement. DB also cre-
ated some grammatical substructures for ‘‘How,’’
‘‘referred,’’ ‘‘to,’’ ‘‘was,’’ ‘‘in,’’ and ‘‘school.’’
Meanwhile, the DM parse is more dramatic. The
formation of the lower discontinuous VP involves
five nodes, two of which are irrelevant words
‘‘How’’ and ‘‘referred’’ triggered by incorrect
discontinuity signals. They are discontinuous but
for the higher VP. The two nodes create a noisy bi-
affine attention matrix because their grammatical
roles are compatible with the lower VP. Trained for
extra robustness, the matrix decomposition with
five tries found the right θ to identify the correct
VP members excluding ‘‘How’’ and ‘‘referred.’’
The interply loss and the decoding process gave
this parse a chance for perfection.
In Figure 14 for German, DB achieved a
long distant constituent in a more subtle way.
The word ‘‘zwar’’
joins ‘‘registriert’’ as an
∅-subtree when the formation of intermediate
NP shortens their distance and prevents a travel
through. ‘‘Gegenw¨artig’’ follows and forms a VP.
However, DM failed.
The ρ∅ > 0 matters. The above failure ex-
plains why DM is inferior to DB with ρ∅ = 0.
DB’s orientation system allows some free travel
before joining with correct mates. The constituent
formation through steps of accumulation creates
280
timization framework. In Proceedings of the
25th ACM SIGKDD International Conference
on Knowledge Discovery & Data Mining,
pages 2623–2631. https://est ce que je.org/10
.1145/3292500.3330701
Sabine Brants, Stefanie Dipper, Peter Eisenberg,
Silvia Hansen-Schirra, Esther K¨onig, Wolfgang
Lezius, Christian Rohrer, George Smith, et
Hans Uszkoreit. 2004. TIGER: Linguistic in-
terpretation of a German corpus. Research on
Language and Computation, 2(4):597–620.
https://doi.org/10.1007/s11168-004
-7431-3
Zhousi Chen, Longtu Zhang, Aizhan Imankulova,
and Mamoru Komachi. 2021. Neural combina-
tory constituency parsing. In Findings of the
Association for Computational Linguistics: ACL/
IJCNLP, pages 2199–2213. https://doi.org
/10.18653/v1/2021.findings-acl.194
Maximin Coavoux and Shay B. Cohen. 2019.
Discontinuous constituency parsing with a
stack-free transition system and a dynamic ora-
clé. In Proceedings of the 2019 Conference of
the North American Chapter of the Association
for Computational Linguistics: Human Lan-
guage Technologies, pages 204–217. https://
doi.org/10.18653/v1/n19-1018
Maximin Coavoux and Benoˆıt Crabb´e. 2017.
Incremental discontinuous phrase structure
parsing with the GAP transition. In Proceed-
ings of the 15th Conference of the European
Chapter of the Association for Computational
Linguistics, pages 1259–1270. https://est ce que je
.org/10.18653/v1/e17-1118
Maximin Coavoux, Benoˆıt Crabb´e, and Shay B.
Cohen. 2019. Unlexicalized transition-based
discontinuous constituency parsing. Transac-
tions of
the Association for Computational
Linguistics, 7:73–89. https://est ce que je.org/10
.1162/tacl a 00255
Ronan Collobert. 2011. Deep learning for effi-
cient discriminative parsing. In Proceedings
of the Fourteenth International Conference on
Artificial Intelligence and Statistics, volume
15 of JMLR Proceedings, pages 224–232.
http://proceedings.mlr.press/v15
/collobert11a/collobert11a.pdf
Chiffre 15: A semantic ∅-subtree by DM with ρ∅ > 0.
Copula ‘‘were’’ has less affinity than ‘‘when’’ and
‘‘due.’’
a more stable context. Cependant, DM’s group ac-
tion happens all at once. An incorrect composition
might create a quite different context, which leads
to unseen reaction chains. The strange unsuper-
vised headedness weights reflect the issue. On the
other side, with ρ∅ > 0, DM can also gradually
build and discover some semantic substructures,
as shown in Figure 15. In contrast, DB is not
sensitive to ρ∅ because of its nature, in agreement
with Table 6.
7 Conclusion
We proposed a pair of efficient and effective
discontinuous combinatory constituency parsers
and extended the neural combinator family of
NCCP. A binary combinator DB is based on
orientation extended into a joint-swap system.
A multi-branching combinator DM leverages bi-
affine attention adapted for constituency. Notre
models (as in Table 2) achieved state-of-the-
art discontinuous F1 scores with a significant
advantage in speed.
In the future, we will aim to extend DCCP
into a multilingual tool for directed acyclic graph
(DAG) parsing with function tag prediction for
predicate-argument structure.
Remerciements
We extend special thanks to our action editor,
anonymous reviewers, and Prof. Yusuke Miyao
for their invaluable comments and suggestions.
This work was partly supported by TMU research
fund for young scientists.
Les références
Takuya Akiba, Shotaro Sano, Toshihiko Yanase,
Takeru Ohta, and Masanori Koyama. 2019.
Optuna: A next-generation hyperparameter op-
281
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Caio Corro. 2020. Span-based discontinuous
constituency parsing: A family of exact
chart-based algorithms with time complexities
from O(n∧6) down to O(n∧3). In Proceed-
ings of
le 2020 Conference on Empirical
Methods in Natural Language Processing,
pages 2753–2764. https://est ce que je.org/10
.18653/v1/2020.emnlp-main.219
Timothy Dozat and Christopher D. Manning.
2017. Deep biaffine attention for neural depen-
dency parsing. In 5th International Confer-
ence on Learning Representations.
Kilian Evang and Laura Kallmeyer. 2011.
PLCFRS parsing of english discontinuous
constituents. In Proceedings of the 12th Inter-
national Conference on Parsing Technologies,
pages 104–116.
Daniel
et
Fern´andez-Gonz´alez
Carlos
G´omez-Rodr´ıguez. 2020un. Discontinuous con-
stituent parsing with pointer networks. In The
Thirty-Fourth AAAI Conference on Artificial
Intelligence, The Thirty-Second Innovative
Applications of Artificial Intelligence Confer-
ence, The Tenth AAAI Symposium on Edu-
cational Advances in Artificial Intelligence,
pages 7724–7731. https://est ce que je.org/10
.1609/aaai.v34i05.6275
Daniel
Fern´andez-Gonz´alez
Carlos
G´omez-Rodr´ıguez. 2020b. Multitask pointer
network for multi-representational parsing.
CoRR, abs/2009.09730.
et
Daniel
et
2021. Reducing
Fern´andez-Gonz´alez
Carlos
G´omez-Rodr´ıguez.
dis-
continuous to continuous parsing with pointer
network reordering. In Proceedings of the 2021
Conference on Empirical Methods in Natural
Language Processing, pages 10570–10578.
https://doi.org/10.18653/v1/2021
.emnlp-main.825
Daniel Fern´andez-Gonz´alez and Carlos G´omez-
Rodr´ıguez. 2022. Multitask pointer network
for multi-representational parsing. Knowledge-
Based Systems, 236:107760. https://est ce que je
.org/10.1016/j.knosys.2021.107760
Marc Johnson. 1985. Parsing with discontinuous
constituents. In Proceedings of the 23rd An-
nual Meeting of the Association for Computa-
tional Linguistics, pages 127–132. https://
doi.org/10.3115/981210.981225
282
Dan Jurafsky and James H. Martine. 2009. Speech
and Language Processing: An Introduction
to Natural Language Processing, Computa-
tional Linguistics, and Speech Recognition,
2nd Edition. Prentice Hall series in artificial
intelligence, Prentice Hall, Pearson Education
International.
Nikita Kitaev and Dan Klein. 2018. Constituency
parsing with a self-attentive encoder. En Pro-
ceedings of
the 56th Annual Meeting of
the Association for Computational Linguistics,
pages 2676–2686. https://est ce que je.org/10
.18653/v1/P18-1249
Nikita Kitaev and Dan Klein. 2020. Tetra-tagging:
Word-synchronous parsing with linear-time
inference. In Proceedings of the 58th Annual
Meeting of the Association for Computational
Linguistics, pages 6255–6261. https://est ce que je
.org/10.18653/v1/2020.acl-main.557
Nikita Kitaev, Thomas Lu, and Dan Klein. 2022.
Learned incremental representations for pars-
ing. In Proceedings of the 60th Annual Meeting
of the Association for Computational Linguis-
tics, pages 3086–3095. https://doi.org
/10.18653/v1/2022.acl-long.220
Wang Ling, Chris Dyer, Alan W. Noir, et
Isabel Trancoso. 2015. Two/too simple adap-
tations of word2vec for syntax problems. Dans
Le 2015 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
pages 1299–1304. https://est ce que je.org/10
.3115/v1/n15-1142
Wolfgang Maier. 2015. Discontinuous incremen-
tal shift-reduce parsing. In Proceedings of the
53rd Annual Meeting of the Association for
Computational Linguistics and the 7th Interna-
tional Joint Conference on Natural Language
Processing of the Asian Federation of Natu-
ral Language Processing, pages 1202–1212.
https://doi.org/10.3115/v1/p15-1116
Mitchell P. Marcus, Beatrice Santorini, and Mary
Ann Marcinkiewicz. 1993. Building a large
annotated corpus of English: The Penn Tree
bank. Computational Linguistics, 19(2):313–330.
https://doi.org/10.21236/ADA273556
Joakim Nivre, Marco Kuhlmann, and Johan Hall.
2009. An improved oracle for dependency
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
parsing with online reordering. In Proceedings
of the 11th International Workshop on Parsing
Technologies, pages 73–76. https://est ce que je
.org/10.3115/1697236.1697250
Adwait Ratnaparkhi. 1997. A linear observed
time statistical parser based on maximum
entropy models. In Second Conference on Em-
pirical Methods in Natural Language Process-
ing. https://aclanthology.org/W97
-0301/
Thomas Ruprecht
and Richard M¨orbitz.
2021. Supertagging-based parsing with linear
context-free rewriting systems. In Proceedings
of the 2021 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
pages 2923–2935. https://est ce que je.org/10
.18653/v1/2021.naacl-main.232
Yikang Shen, Zhouhan Lin, Athul Paul Jacob,
Alessandro Sordoni, Aaron C. Courville, et
Yoshua Bengio. 2018. Straight
to the tree:
Constituency parsing with neural syntactic dis-
tance. In Proceedings of
the 56th Annual
Meeting of the Association for Computational
Linguistics, pages 1171–1180. https://est ce que je
.org/10.18653/v1/P18-1108
Milos Stanojevic and Mark Steedman. 2020.
Span-based LCFRS-2 parsing. In Proceedings
of the 16th International Conference on Pars-
ing Technologies and the IWPT 2020 Shared
Task on Parsing into Enhanced Universal De-
pendencies, pages 111–121. https://est ce que je
.org/10.18653/v1/2020.iwpt-1.12
Yannick Versley. 2014.
Incorporating semi-
supervised features into discontinuous easy-
first constituent parsing. CoRR, abs/1409.3813.
David Vilares and Carlos G´omez-Rodr´ıguez.
2020. Discontinuous constituent parsing as
sequence labeling. In Proceedings of the 2020
Conference on Empirical Methods in Natu-
ral Language Processing, pages 2771–2785.
https://doi.org/10.18653/v1/2020
.emnlp-main.221
Xin Xin, Jinlong Li, and Zeqi Tan. 2021. N-ary
constituent tree parsing with recursive semi-
Markov model. In Proceedings of the 59th
Annual Meeting of the Association for Com-
putational Linguistics and the 11th Interna-
tional Joint Conference on Natural Language
Processing, pages 2631–2642. https://est ce que je
.org/10.18653/v1/2021.acl-long.205
Ryo Yoshida, Hiroshi Noji, and Yohei Oseki.
2021. Modeling human sentence processing
with left-corner recurrent neural network gram-
mars. In Proceedings of the 2021 Conference
on Empirical Methods in Natural Language
Processing, pages 2964–2973. https://est ce que je
.org/10.18653/v1/2021.emnlp-main.235
Junru Zhou and Hai Zhao. 2019. Head-driven
phrase structure grammar parsing on Penn
Treebank. In Proceedings of the 57th Confer-
ence of the Association for Computational Lin-
guistics, pages 2396–2408. https://est ce que je
.org/10.18653/v1/P19-1230
Arnold M. Zwicky. 1985. Heads. Journal de
Linguistics, 21(1):1–29. https://doi.org
/10.1017/S0022226700010008
283
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
4
6
2
0
7
5
7
3
9
/
/
t
je
un
c
_
un
_
0
0
5
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3