Designing an Automatic Agent for Repeated Language–based
Persuasion Games
Maya Raifer, Guy Rotman, Reut Apel, Moshe Tennenholtz, Roi Reichart
Technion—Israel Institute of Technology, Israel
{mayatarno, grotman, reutapel}@campus.technion.ac.il
{roiri, moshet}@technion.ac.il
Abstrait
Persuasion games are fundamental in eco-
nomics and AI research and serve as the basis
for important applications. Cependant, work on
this setup assumes communication with styl-
ized messages that do not consist of rich human
langue. In this paper we consider a repeated
sender (expert) – receiver (decision maker)
game, where the sender is fully informed about
the state of the world and aims to persuade the
receiver to accept a deal by sending one of
several possible natural language reviews. Nous
design an automatic expert that plays this re-
peated game, aiming to achieve the maximal
payoff. Our expert is implemented within the
Monte Carlo Tree Search (MCTS) algorithme,
with deep learning models that exploit behav-
ioral and linguistic signals in order to predict
the next action of the decision maker, et le
future payoff of the expert given the state of the
game and a candidate review. We demonstrate
the superiority of our expert over strong base-
lines and its adaptability to different decision
makers and potential proposed deals.1
1 Introduction
Natural Language Processing (NLP) has made
substantial progress in recent years, excelling on text
understanding applications such as machine trans-
lation (Bahdanau et al., 2015; Johnson et al., 2017),
information extraction (Stanovsky et al., 2018),
and question answering (Andreas et al., 2016;
Kwiatkowski et al., 2019). Cependant, these appli-
cations do not assume that language is used for
interaction between strategic participants whose
objectives overlap only partially.
In contrast, in the fields of economics and artificial
intelligence (AI), such setups have been widely
explored. Par exemple, the settings of person-
alized advertising and targeted recommendation
systèmes (Shapiro and Varian, 1998; Emek et al.,
1Our code and data are available at: https://github
.com/mayaraifer/automatic agent.
307
2014; Bahar et al., 2016) suggest personalized
services for their customers, and solutions are
formed as strategic sender–receiver interactions
(Arieli and Babichenko, 2019). Cependant, ce
work assumes stylized messaging that does not
involve real-world natural language.
In this paper we address the setting of sender–
receiver interaction, mais, in contrast to previous
recherche, we assume natural language interaction
between the players in an iterative non zero-sum
persuasion game. In our setting the two partici-
pants are strategic players with their own private
utilities. Surtout, the sender has more informa-
tion about the world than the receiver does. Taking
the NLP perspective, we are particularly interested
in the persuasion game setting, where the sender’s
objective is to persuade the receiver, using natural
language messages, to select an action from a set
of alternatives. The receiver, à son tour, has different
payoffs for the different actions. The receiver’s
payoff depends on properties of the setup that are
unavailable to her, and she has a higher level of
uncertainty about the setup than the sender has.
Our focus is on repeated non-cooperative se-
tups, where the utilities of the players do not fully
overlap. Consider a repeated persuasion game
where the interests of the players are aligned. Dans
such a case, the sender should reveal the complete
information she possesses, letting the receiver take
an action that maximizes both their payoffs. In a
repeated non-cooperative setup, in contrast, le
sender opts to reveal a piece of information that
should yield her a high payoff but also maintain a
trustful relationship with the receiver, pour
avoid damaging her reputation and hence possibly
also her future payoff.
Designing agents to play games is a long stand-
ing goal of deep reinforcement learning (RL)
these games are typically
recherche. Cependant,
zero-sum games, modeled as a utility maximiza-
tion problem (voir, par exemple., Silver et al. [2018] et
Transactions of the Association for Computational Linguistics, vol. 10, pp. 307–324, 2022. https://doi.org/10.1162/tacl a 00462
Action Editor: Liang Huang. Submission batch: 10/2021; Revision batch: 12/2021; Published 3/2022.
c(cid:2) 2022 Association for Computational Linguistics. Distributed under a CC-BY 4.0 Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
the references within). In contrast, in economic
contexts like ours, games are rarely zero-sum. UN
commerce Web site that aims to recommend a
hotel cares about the customer choosing the ho-
tel, while the customer cares about the hotel quality;
their incentives are non-identical, but are also
non-opposite. These games cannot be solved as
a maximization problem, and there is in fact no
optimal player in such problems (Fudenberg and
Tirole, 1991). Incontrast to economic games where
the communication among agents is typically
through formal signals or bids (Mansour et al.,
2015; Bahar et al., 2020), we focus on natural
language communication, which is very natural to
persuasion games.
Recently, Apel et al. (2020) were the first to
adapt the aforementioned setup to natural language
messaging. Spécifiquement, they designed a repeated
persuasion game in which an expert (travel agent)
repeatedly interacts with a decision-maker (DM,
customer). At each trial of the interaction the ex-
pert observes a hotel alongside its scored textual
reviews, and should choose a single review to
reveal to the DM, in a hope to convince her
to choose the hotel. The DM, à son tour, can choose
to either accept or reject the hotel, and her payoff
stochastically depends on the review score distri-
bution available to the expert only. Enfin, les deux
players observe their payoffs and proceed to the
next, similar, step of the game.
While Apel et al. (2020) focus on predicting the
DM’s actions, we adapt their setting and aim to
design an artificial expert (AE) that should take
the expert role in a way that maximizes its payoff.
Our AE is implemented within the Monte Carlo
Tree Search (MCTS) algorithme, which has been
extensively used in AI-based game playing (§4.1).
We present language- and behavior-based deep
learning models for two crucial components of the
MCTS: (un) A Decision Making Model (DMM),
which predicts the actions taken by the DM given
the current state of the game; et (b) A Value
Model (VM), which predicts the future payoff of
the AE given the current state of the game and
a potential review that can be presented at the
current step.
We focus on three questions: (1) Can our AE
achieve a high payoff? (2) Does our AE adapt its
strategy to different decision maker types? et (3)
Do our automated AE’s strategies resemble those
of human AEs?
We test our AE against various types of artifi-
cial DMs, compare it to strong alternative experts,
and demonstrate its superiority. We further show
that our AE is able to adapt its strategy to the DM it
faces. We evaluate the impact of proper modeling
of the linguistic signal (revealed reviews), com-
paring a BERT-based approach to hand-crafted
features, and show that the later are generally bet-
ter. Plus loin, we analyze the reviews chosen by our
AE, shedding light on its strategy.
Dernièrement, we also test our AE against human
DMs, comparing its performance to a strong base-
line. We provide a detailed analysis of the pros
and cons of our AE, and discuss the differences
between evaluation with human and simulation-
based DMs.
2 Related Work
Some previous work addressed language-based
communication in games where the participants
have matched or mismatched objectives (Golland
et coll., 2010; Frank and Goodman, 2012; Lewis
et coll., 2017), while other work addressed commu-
nication in iterated games (Hawkins et al., 2017).
The main novelty of our setup is the intersec-
tion between mismatched objectives and iterative
games. We survey relevant works along three
lines: Human decision predictions, NLP-based
persuasion, and artificial agents in textual games.
Human Decision-Making Predictions Previ-
ous work used machine learning to predict
human decisions based on non-textual information
(Altman et al., 2006; Hartford et al., 2016; Plonsky
et coll., 2017), as well as textual signals—for ex-
ample, for judicial decisions (Aletras et al., 2016;
Zhong et al., 2018; Medvedeva et al., 2020; Lequel
et coll., 2019b) and decisions of leading figures
(Bak and Oh, 2018). These studies formulate the
problem as a classification task where the clas-
sifier is based on textual (and potentially also
other) signals. Unlike in our work, these predic-
tions are not made in a strategic environment,
where participants have objectives that affect
their decisions.
Several studies aim to draw predictions of hu-
man decisions in competitive games given textual
signals (Ben-Porat et al., 2020; Oved et al., 2020).
Par exemple, Niculae et al. (2015) proposed an
algorithm for predicting actions in an online strat-
egy game based on the language produced by the
players as part of the inter-player communication
308
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
required in the game. The setups of these studies
differ from ours, et, particularly, they do not
address persuasion and repeated games.
The most relevant work to ours is that of
Apel et al. (2020): We use their setup and data
(§3). Cependant, Apel et al. (2020) only focused
on predicting the decisions of the decision-maker.
En outre, while they based their predictions on
past and future game information, we perform
more realistic predictions based on past informa-
tion only.
Persuasion in NLP Hidey et al. (2017) pro-
posed an annotation scheme to differentiate claims
and premises using different persuasion strate-
gies in an online persuasive forum (Tan et al.,
2016). Hidey and McKeown (2018) tried to pre-
dict persuasiveness in social media posts contain-
ing sequential arguments. Yang et al. (2019un),
Wang et al. (2019), and Chen and Yang (2021)
aimed to quantify persuasiveness and to identify
persuasive strategies. This line of study, lequel
aims to analyze and predict persuasive aspects
is a step towards developing
langue,
de
persuasive agents.
Several studies examined persuasion dialogue
tasks. While models for task-oriented dialogue
have achieved promising performance on tasks
where the users and the system are coordi-
nated in their goals, persuasion dialogue tasks
are less common. Hiraoka et al. (2014) focused
on learning a policy which satisfies both user and
system goals in a cooperative persuasive dialogue.
Li et al. (2020) proposed an end-to-end neural
network to generate diverse coherent responses
for non-collaborative dialogue tasks, where users
and systems do not share a common goal.
Efstathiou and Lemon (2014) developed a dia-
logue agent that learns to perform non-cooperative
dialogue turns for utility maximization in a
stochastic trading game with very simple linguistic
messages. Lewis et al. (2017) trained end-to-end
models for negotiation in a semi-cooperative
setup. These studies differ from ours because we
focus on designing an artificial agent in a repeated
persuasion game setting, where the expert should
construct a long-term strategy as its choice in a
specific trial affects both the outcome of that trial
and its future reputation.
(Lazaridou et al., 2017; Havrylov and Titov,
2017), where agents should interactively develop
a shared language in order to communicate with
each other and solve a joint task. Another line
of work designs agents for games inspired by
Wittgenstein’s (1953) language games (Wang
et coll., 2016), where a human aims to accomplish
a task (par exemple., achieving a certain configuration of
blocks), but is only able to communicate with an
artificial agent which performs the actual actions.
Such games are cooperative in nature as the play-
ers share their goals. Enfin, Narasimhan et al.
(2015) address text-based games, where natural
language is used both to describe the state of the
world and the actions of the participating play-
ers. They design a deep RL agent that jointly
learns state representations and action policies us-
ing game rewards as feedback. This game is also
very different from ours.
3 Task Definition
We consider a two-player, travel agent (expert)
and customer (decision-maker, DM), repeated
persuasion game. The game, first introduced by
Apel et al. (2020), consists of a sequence of ten
trials. In each trial, the expert observes seven re-
views of a given hotel, alongside their scores, et
she then sends the DM one of the reviews, without
its score. Based on this review, the DM decides
between two options: Accepting or rejecting the
hotel. If the hotel is not accepted by the DM, le
payoff of both players is 0. Otherwise, the expert’s
payoff is 1, and the DM’s payoff is a score ran-
domly sampled from the seven scores presented
to the expert at the beginning of this trial, referred
to as the lottery result, minus the constant 8. Ce
constant imposes a zero expected payoff for a
DM who chooses to accept the hotel in all the
ten trials.2
A more abstract description of each trial in this
multi-stage game would be as follows. Every hotel
is associated with an unknown distribution over
payoffs, corresponding to the distribution over
experiences that guests will have at this hotel. Le
scored reviews are sampled from this distribution,
and the DM’s reward is another sample from the
distribution. Because in our setting we do not have
access to the real payoff distribution of each hotel,
Artificial Agents in Textual Games Several
studies designed agents for referential games
2For full information of the train and test hotels, y compris
their review scores, see Table 1 of Apel et al. (2020).
309
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
we approximate it using the empirical distribution
from the payoffs observed by the expert.
Officiellement, denote the suggested hotel at trial t
by ht, the DM’s decision at this trial by at, où
at = 1 if the DM accepts the hotel, and the seven
2, ..st
scores attached to the reviews of ht by st
7,
where st
1, st
i ∈ [0, 10]. The players’ payoffs are:
expert-payoff =
(cid:0){at=1},
dm-payoff =
(cid:0){at=1} · (st
i − 8),
i ∼ unif orm[1, 7].
While the two players would ideally like to gain
the highest possible payoff (c'est à dire., this is not a
zero-sum game), their strategies are not necessar-
ily coordinated. Particularly, while the expert aims
to sell as many hotels as possible, the DM aims to
accept only hotels that are likely to yield a posi-
tive payoff. Note that the DM is not fully informed
of the hotel state, and should make her decision
based on the partial information provided by the
expert. The repeated nature of the game adds com-
plexity to the decisions, as the expert’s choice in
a specific trial affects not only the DM’s decision
in this trial but also the expert’s reputation in the
next trials.
Let us consider the game from the expert’s point
de vue. Consider an expert who cares solely about
the present and reveals a high-score review in
order to tempt the DM to choose the hotel, even if
the acceptance decision is likely to yield a negative
payoff. This expert is likely to gain a high payoff
at the first few rounds. Cependant, as the game
proceeds the DM would probably understand that
the expert is unreliable. On the other hand, if the
expert reveals only reviews that reliably describe
the hotel (par exemple., the median scoring reviews), le
DM is likely not to choose the hotel when she is
presented with mediocre reviews.
Apel et al. (2020) provide an equilibrium anal-
ysis of our game. This is a theoretical analysis,
under some constraining assumptions and, as the
authors demonstrate, the players do not follow it in
pratique. This further motivates our work, lequel
aims to design an NLP-based agent of the expert
in this game. Note, that our approach is different
from that of Apel et al. (2020), who aimed to pre-
dict individual decisions of the DM, plutôt que
constructing an artificial DM or expert.
310
Chiffre 1: An example review from the Apel et al.
(2020) dataset. Each review consists of a continuous
score ranging from 0 à 10, alongside positive and
negative textual descriptions.
le
utiliser
dataset
collected
Data We
par
Apel et al. (2020) using Amazon Mechanical
Turk.3 The dataset is composed of 509 ten-trial
games. The participants were randomly and
anonymously paired, and each of
them was
randomly selected to be in one of the two roles:
DM or expert.
The training set consists of 408 games. Dans ces
games the same hotels and reviews were used,
but the hotels were randomly permuted between
le 10 trials. The test set consists of 101 games,
played with a different set of hotels and reviews,
such that the hotels are again randomly permuted.
Each participant was allowed to participate in the
experiment only once, such that the training and
test sets consist of different players.
Each hotel is accompanied by seven reviews
collected from the Booking.com Web site along
with their scores, continuously ranging between
0 et 10 (see an example review in Figure 1).
All the reviews contain at least 100 characters
and are separated into positive and negative parts.
Chiffre 1 demonstrates a sampled review from the
dataset. The order in which each of these parts
were presented to the experts was also assigned at
random. For more details, see Apel et al. (2020).
4 Method
We design an AE that aims to maximize its payoff
in the persuasion game.
The High-level Structure of our Algorithm
Our algorithm is composed of three components:
(un) MCTS – an online search algorithm that looks
for the best action out of a predefined set (dans
terms of maximum expected payoff) at each game
trial. In our setting, actions correspond to review
selection, so the MCTS determines which review
should be revealed to the DM in each trial.
3https://github.com/reutapel/Predicting
-Decisions-in-Language-Based-Persuasion-Games.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
(b) The DM Model (DMM) – a model that pre-
dicts the decision made by the DM in each trial
of the game. This model allows the MCTS algo-
rithm to simulate the DM’s response to revealed
reviews.
(c) The Value Model (VM) – a model that pre-
dicts the expert’s future payoff in each trial of
the game. It is used by the MCTS to initialize
the expected return values of new explored deci-
sion paths.
Note that MCTS is the core component of
our AE and the two other models are integrated
into it after they have been trained offline. Nous
next describe these three components in detail,
concluding the section with a description of the
two feature sets used by the DMM and the VM.
4.1 The MCTS Algorithm
MCTS (Coulom, 2006) is a heuristic search tech-
nique, presented in the field of RL. It has received
considerable attention due to its success in the
difficult problem of computer Go (Gelly et al.,
2006) and has been used widely in challenging
domains such as general game playing (Finnsson
and Bj¨ornsson, 2008; Kim and Kim, 2017; Baier
and Cowling, 2018; Sironi et al., 2018) et
real-time strategy games (Balla and Fern, 2009;
Ontan´on, 2016). We briefly describe MCTS in
the context of our game settings. A detailed sur-
vey can be found in Coulom (2006) and Browne
et autres. (2012).
The MCTS determines the best action out
of a set of available actions by balancing the
exploration-exploitation trade-off. It constructs a
search tree, node-by-node, starting from a root
node defined by the current state of the game.
In our setting, s(v), the state of the node v, est
uniquely defined by the complete history of the
game and the current suggested hotel h. Là-
fore, the action space A(s(v)) of s(v) consists of
the corresponding reviews of its current suggested
hotel h, UN(s(v)) = {rhi|i ∈ {1, ..7}}, where rhi
denotes the i(cid:5)th review of hotel h.
We initialize the values of each state node
variable s(v) according to our VM function, à
predict its expected future payoff. For each trial t
of the game the MCTS is provided with the new
candidate hotel, and the next steps of the game are
simulated with the VM and DMM. Basé sur ceci
simulation the algorithm selects the optimal expert
action, c'est, the optimal review that should be
revealed to the DM.
4.2 The DMM and VM Models
The DMM and the VM are applied in each trial
of the game, for predicting the DM’s decision
(DMM) and the expert’s future payoff (VM). Le
predictions at trial t are based on information
about the previous trials and the current trial. Both
models have identical architectures, and they are
trained off-policy on the training set of Apel et al.
(2020). Due to the different nature of prediction,
cependant, they are trained to optimize different
loss functions: Binary cross entropy (DMM) et
mean squared error (VM). In both cases train-
ing is done with the Adagrad algorithm (Duchi
et coll., 2011).
We consider two architectures (Chiffre 2). Due
to the sequential nature of the decision mak-
ing process, we based the two models on the
Long Short-Term Memory (LSTM) architecture
(Hochreiter and Schmidhuber, 1997). We feed the
first LSTM variant, denoted by HC-LSTM, avec
two types of features: (un) statistical game features,
representing the information about the previous
and the current trials; et (b) hand-crafted tex-
tual features (Apel et al., 2020), automatically
extracted from the review. A detailed description
of both types of features is provided in §4.3. Le
binary hand-crafted features are passed through
the Sigmoid activation function and are concate-
nated to the continuous statistical game features
before being passed to the LSTM encoder.
The second architecture, denoted by BERT-
is an LSTM fed by the statistical
LSTM,
game features and the pooler output of BERT
(Devlin et al., 2019). Because the encoded out-
put of BERT is processed by the Tanh activation
fonction, we pass the statistical game features
through it before performing the concatenation and
passing the resulted vectors to the LSTM encoder.
4.3 Features
We explore two types of hand-crafted features:
Hand-crafted textual features (HC), capturing tex-
tual knowledge from the reviews, and statistical
game features (SG), capturing properties of the
human interactions during the game.
The HC set, consisting of 42 binary features
that can be split into three feature types, was cre-
ated by Apel et al. (2020). Features of the first
type indicate whether some predefined topics are
311
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2: Illustration of our two model architectures. HCt, SGt, and Rt denote the hand-crafted features, le
statistical game features and the presented review in trial t, respectivement. For DMM, yt is the DM’s decision in
trial t, and for VM, yt is the expert’s future payoff in trial t.
mentioned in the positive and negative parts of
the review (facilities, price, location, staff, trans-
portation, food, etc.). Features of the second type
correspond to predefined textual properties of the
positive and negative parts of the review, for exam-
ple, the length of each part (short/medium/long),
existence of words with high, medium or low in-
tensity, and so forth. Enfin, features of the third
type capture the structural properties of the overall
revoir, Par exemple, the ratio between the lengths
of the positive and negative parts. While these
features are hand-crafted, they are automatically
extracted from the text. We refer the reader to
Apel et al. (2020) for further details.
Tableau 1 provides a detailed description of the
SG features, some of which are a contribution of
this paper. The SG set includes two main types
of features: (un) Features that represent information
about the DM’s behavior up to trial t. Par exemple,
HotelAcceptance measures the proportion of trials
where the DM accepted a hotel; et (b) Features
that represent general information about the game
up to trial t. Par exemple, the proportion of trials
where the lottery result was low, high or medium
and whether the proposed hotel has a low, high or
medium average score.
5 Experiments
Experimental Setting Evaluating our AE against
humans is highly expensive and time-consuming,
and hence infeasible at large scales. We hence
start with another, widely used solution: Human
simulations (Jung et al., 2008; Ai and Weng, 2008;
Gonz´alez et al., 2010; Shi et al., 2019; Zhang and
Balog, 2020). In this approach we evaluate the
AE against an automatic algorithm that simulates
human DMs. Although this evaluation is not per-
formed against actual humans, it allows us to
evaluate the AE against various types of players,
by changing the data-driven DM in a controlled
manière. We perform 1000 simulated games over
the test set per DM simulator, where the order
in which the hotels are presented to the AE is
randomly permuted at each simulation.
We employ two DMMs (HC-LSTM and
BERT-LSTM) as our basic DM simulators, comme
they are trained to imitate the human DM’s behav-
ior in the game. We further modify the behavior
of these ‘‘human like’’ DMMs, by changing their
hotel acceptance probability in a controlled man-
ner. We consider: (un) α-compromised DMMs,
where the acceptance probability is increased by
α = 0.1 or α = 0.2 over the prediction of the
basic DMM; et (b) α-inflexible DMMs, où
the acceptance probability is similarly decreased.
Baselines We next describe the baselines for
the AE and for its components, the DMM variants
(HC-LSTM and BERT-LSTM), and the VM
variants (HC-LSTM and BERT-LSTM).
DMM. The DMM decides in each trial whether
to accept a suggested hotel or not. We propose
four different DMM variants, differing in their
decision strategy, architecture and features: (un)
HC-SVM – a Support Vector Machine (SVM;
Cortes and Vapnik, 1995) based on the HC and
SG features. It allows us to evaluate the power
312
Feature Name
Behavioral Features
Feature Description
Feature Formulation
HotelAcceptance
Avg #trials where the hotel was accepted
HotelAcceptance
Earn
Avg #trials where the hotel was accepted and the DM
achieved a negative payoff.*
HotelAcceptance
Lose
¬HotelAcceptance
Earn
¬HotelAcceptance
Lose
BadHotel
Acceptance
¬ExcellentHotel
Acceptance
DMPayoff
General Features
LotteryLow
LotteryMed
LotteryHigh
CompletedTrials
GoodHotel
MedHotel
BadHotel
HighScore
MedScore
LowScore
TopReview
BottomReview
Avg #trials where the hotel was accepted and the DM
achieved a positive payoff.*
Avg #trials where the hotel was not accepted but
the payoff would have been positive if the DM had
accepted it.*
Avg #trials where the hotel was not accepted but
the payoff would have been negative if the DM had
accepted it.*
Avg #trials where a hotel with average score lower
que 7.5 was accepted.
Avg #trials where a hotel with average score higher
que 9.5 was accepted.
Avg DM’s payoff pet trial
Avg #trials where the lottery result was lower than
3.*
Avg #trials where the lottery result was between 3 à
5.*
Avg #trials where the lottery result was higher than 8.*
The proportion of trials that have already been played.
Avg score of the current hotel is higher than 8.5.
Avg score of the current hotel is between 7.8 à 8.5.
Avg score of the hotel is lower than 7.5.
The attached score of the presented review is higher
que 8.5.
The attached score of the presented review is between
7.5 à 8.5.
The attached score of the presented review is lower
que 7.5.
The attached score of the presented review is in the
top 3 scoring reviews.
The attached score of the presented review is not in
the top 3 scoring reviews.
(cid:2)t−1
je = 1 (cid:0){ai=1}
t−1
(cid:2)t−1
je = 1 (cid:0){ai=1∩dmpi>0}
(cid:2)t−1
(cid:2)t−1
t−1
t−1
t−1
je = 1 (cid:0){ai=1∩dmpi<0} i=1 (cid:0){ai=0∩dmpi>0}
(cid:2)t−1
je = 1 (cid:0){ai=0∩dmpi<0} t−1 i=1 (cid:0){ai=1∩s(hi)<7.5} (cid:2)t−1 (cid:2)t−1 t−1 t−1 i=1 (cid:0){ai=0∩s(hi)>9.5}
(cid:2)t−1
i=1 dmpi
t−1
(cid:2)t−1
je = 1 (cid:0){li<3}
t−1
(cid:2)t−1
i=1 (cid:0){li≥3∩li<5}
t−1
(cid:2)t−1
i=1 (cid:0){li≥8}
t−1
t−1
10
(cid:0){s(ht)≥8.5}
(cid:0){s(ht)<8.5∩s(ht)≥7.5}
(cid:0){s(ht)≤7.5}
(cid:0){s(rt)≥8.5}
(cid:0){s(rt)<8.5∩s(rt)≥7.5}
(cid:0){s(rt)<7.5}
(cid:0){s(rt)∈ top 3 scores}
(cid:0){s(rt)/∈ top 3 scores}
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
l
a
c
_
a
_
0
0
4
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Table 1: SG features of trial t. ai, li, and dmpi denote the DM’s action, lottery result, and DM’s payoff
in trial t, respectively. s(ht) is the average score of the suggested hotel in trial t, rt is its revealed review,
and s(rt) is the revealed review score. * indicates that the feature is taken from Apel et al. (2020).
of a non-DNN and non-sequential modeling ap-
proach; (b) BERT-SVM – This model is similar to
HC-SVM, except that the text is represented with
BERT; (c) Expected Weighted Guess (EWG) – a
random baseline that applies the hotel acceptance
probability of the training set (p = 0.72); and (d)
Previous Decisions (PD) – a deterministic base-
line which predicts that the DM accepts the hotel
313
only if it accepted at least half of the previous
hotels.
VM. The VM predicts the expert’s future payoff
in each trial. We propose five different variants
of it: (a) HC-SVR – a Support Vector Regres-
sion (SVR) (Drucker et al., 1997) model based on
the HC and SG features. This is a non-DNN and
non-sequential approach; (b) BERT-SVR – an
SVR model based on the SG and the encoded
BERT features; (c) Maximal Future Payoff
(MFO) – a deterministic baseline that assumes
that all future hotels will be accepted and hence
the future payoff at each trial is maximal; (d)
Average Value (AV) – a deterministic baseline
that assigns the value in trial t to the average
expert’s future payoff as observed in the training
set; and (e) History Proportion (HP) – a deter-
ministic baseline which predicts that the future
hotel choice rate is identical to the choice rate in
previous steps.4
AE. We compare our AE to ten alternatives,
divided to four groups: (a-d) static rules; (e-g)
dynamic rules, which adjust their predictions ac-
cording to the behavior of the DM; (h) a greedy
baseline that tests the VM classifier without the
MCTS; and (i-j) variants of our original AE.
(a) RAND – an expert that randomly chooses a
review from the available set; (b) MEDIAN – an
expert that chooses the median scoring review at
each trial. This baseline honestly communicates
the value of the hotel; (c) HIGHEST – an expert
that chooses the highest scoring review at each
trial. This expert always overestimates the value
of the hotel; (d) EXTREMIST – an expert that
chooses the highest scoring review if the average
review score is at least 8, and otherwise chooses
the lowest scoring review. This expert makes the
strongest positive recommendation when the ho-
tel crosses the ‘‘likely gain’’ threshold, and the
strongest negative recommendation otherwise. (e)
ADAPTIVE LIAR (A-LIAR) – An expert that
reveals the highest scoring review as long as the
DM keeps accepting the hotels. After the first re-
jection by the DM, the expert chooses randomly
between the second and third highest scoring re-
views. After the second rejection it reveals the
median review for the remaining hotels; (f+g)
PERSONAL TASTE DETECTION (PTD) –
this expert selects the review that is most similar
to the average review representation, among the
hotels accepted in previous trials. We consider
either the HC features (PTD-HC) or the BERT
features (PTD-BERT) of the reviews, and com-
pute similarity with the cosine operator;5 (h) VM
SOFTMAX (VM-SM) – a greedy expert that at
each trial selects a review with a probability pro-
portional to the expected expert payoff associated
with it according to the VM. This expert helps us
quantify the added value of MCTS over a greedy
strategy; (i+j) our AE when using the second
best DMM (AE-DM2) and the second best VM
(AE-VM2).
Numerical Communication The success of our
AE depends both on our modeling approach and
on the use of text-based communication between
the expert and the DM. In order to separate the im-
pact of these two characteristics, we replicate our
experiments where the communication between
the expert and the DM is purely numerical. To
achieve this goal we utilize another dataset col-
lected by Apel et al. (2020). The authors collected
data from 493 games (392 train and 101 test) with
the same hotels and reviews discussed in § 3 (in-
cluding the split to training and test hotels), but
with a different set of participants. In these numer-
ical communication experiments the experts are
presented with all seven reviews but are told that
they can only reveal to the DM the score of one of
them, rather than its text. The DM, in turn, decides
whether or not to accept the hotel based solely on
the revealed numerical score. Other than that the
experimental setup in this condition is identical to
that of the textual communication experiments.
This data allows us to test a numerical commu-
nication version of our AE. To this end we trained
the following models: (a) DMM: SG-LSTM: Our
original LSTM-based DMM trained on the nu-
merical communication training set, employing
only the SG features; and (b) VM: SG-LSTM:
Our original LSTM-based VM trained on the nu-
merical communication training set, employing
only the SG features. Finally, we test the AE-SG
model, an MCTS-based expert identical to our
AE, except that it uses the SG-LSTM variants of
the DMM and VM. The test setup is identical to
the above, except that the simulations are based
on the numerical communication DMM and VM.
4In this baseline, as well as in the PD decision maker
baseline, the past experiences are based on the gold standard.
5In the first round the review is randomly selected.
314
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
l
a
c
_
a
_
0
0
4
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Training Procedure and Hyperparameters
We apply a 5-fold cross validation protocol on
the training set, and determine the optimal config-
uration of hyperparameters according to the best
average F1 score of the minority class—hotel re-
jection. Next, we train the DMM and VM with
their optimal configurations on the entire training
set, and report results on the test set.
For the HC-LSTM models we optimize the
hidden layer size (64, 128, 256), the batch size
(5, 10, 15, 20, 25), and the dropout value
(0.3, 0.4, 0.5, 0.6). Training is carried out for
100 epochs with an early stopping criterion.
For the BERT-LSTM models we use Hugging-
Face’s implementation of the pre-trained uncased
BERT-Base model.6 We tune the hidden layer size
(64, 128, 256) and the dropout value (0.3, 0.4, 0.5,
0.6) of the LSTM component, and set the batch
size to 5. During the training of BERT-LSTM
we keep BERT’s parameters fixed for the first 8
epochs, and fine-tune them for additional 4 to 12
epochs with early stopping.
For MCTS we set the exploration constant c
to 0.5, after normalizing the rewards to be in the
[0,1] range, and the time limit constant to 1.5 min-
utes. Our AE uses the MCTS with the HC-LSTM
variant for DMM and VM, which were selected in
cross-validation experiments on the training data.
Likewise, VM-SM uses the HC-LSTM model.
6 Results
This section presents our results. We would first
like (§6.1) to evaluate the performance of our
DMM and VM models, since they are key ele-
ments of our AE. After verifying their quality, we
turn to present our main results (§6.2), comparing
our AE to the various baselines. This will allow
us to answer our three research questions (§1),
related to the AE performance (Q1), its adaptation
to different decision maker types (Q2), and its
strategy compared to humans (Q3).
6.1 The DMM and VM Models
DMM Results Table 2 (top) presents the accu-
racy and macro average F1-score results of the
DMM variants on the binary task of predicting
whether or not a human DM will choose to ac-
cept a suggested hotel. The results show that the
best performing model is the HC-LSTM, which
yields an accuracy of 82.40% and a macro average
6https://github.com/huggingface/transformers.
DMM
HC-LSTM
BERT-LSTM
SG-LSTM
HC-SVM
BERT-SVM
PD
EWG
VM
HC-LSTM
BERT-LSTM
SG-LSTM
HC-SVR
BERT-SVR
AVG
DO
HP
Accuracy ↑ F1-score ↑
82.40%
80.80%
77.00%
79.50%
75.80%
69.90%
60.00%
Accuracy ↑
38.90%
16.70%
33.95%
35.40%
25.54%
33.70%
26.20%
29.10%
73.20
68.30
65.70
68.50
52.00
45.21
50.00
RMSE ↓
1.11
2.14
1.40
1.13
1.41
1.08
1.94
1.90
Table 2: Evaluation of DMM and VM variants.
F1-score of 73.20. This result reflects the value of
the hand-crafted textual features, a pattern that was
also reported by Apel et al. (2020). BERT-LSTM
lags a bit behind (accuracy of 80.80%, macro F1
score of 68.30), demonstrating that clever feature
design can outperform this strong language en-
coder. In general, the SVM baselines fall short
of the neural networks, whereas the deterministic
baselines PD and EWG are not very successful.
the second-best model
VM Results Table 2 (bottom) presents the exact
accuracy and Root Mean Square Error (RMSE)
of the VM variants on the task of predicting
the experts’ future payoff. The strongest model
is HC-LSTM (best exact accuracy, second-best
RMSE). Moreover,
is
HC-SVR, which also exploits the hand-crafted
textual features. In contrast, the BERT-based mod-
els perform quite poorly. This illustrates once
again the strong positive impact of the HC fea-
tures, which are very effective even when the task
classifier does not model the structure of the data.
Interestingly, the same features and architecture
perform best both for the DMM and for the VM.
The AVG baseline, which always predicts the
average score, obtains the lowest RMSE score,
but it is not as accurate as our HC-based models.
DO and HP, which are based on simple statistical
rules, also perform quite poorly.
315
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
l
a
c
_
a
_
0
0
4
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Expert/DM
AE
HC-LSTM
7.12 [7.02, 7.22]
BERT-LSTM HC-LSTM+0.1
8.10 [8.02, 8.19]
7.04 [7.03, 7.29]
HC-LSTM+0.2
8.77 [8.70, 8.84]
HC-LSTM-0.1
6.04 [5.93, 6.20]
HC-LSTM-0.2 AVG
7.02
5.02 [4.90, 5.13]
6.54 [6.49, 6.70]
RAND
6.46 [6.37, 6.54]
MEDIAN
HIGHEST
6.77 [6.65, 6.89]
EXTREMIST 6.21 [6.11, 6.32]
A-LIAR
PTD-HC
PTD-BERT
VM-SM
AE-DM2
AE-VM2
AE-SG
6.54 [6.42, 6.65]
6.88 [6.78, 6.99]
6.79 [6.67, 6.88]
6.58 [6.50, 6.71]
7.05 [6.93, 7.14]
7.03 [6.93, 7.13]
7.53 [7.39, 7.64]
6.67 [6.56, 6.77]
6.85 [6.76, 6.96]
7.82 [7.73, 7.92]
6.86 [6.76, 6.96]
7.14 [7.06, 7.28]
7.03 [6.86, 7.06]
6.59 [6.51, 6.73]
7.00 [6.91, 7.12]
7.23 [7.13, 7.33]
7.05 [6.96, 7.17]
7.56 [7.47, 7.65]
7.24 [7.16, 7.33]
7.94 [7.84, 8.04]
7.24 [7.14,7.34]
7.15 [7.06, 7.28]
7.68 [7.63, 7.80]
7.72 [7.63, 7.82]
7.70 [7.60, 7.77]
7.94 [7.86, 8.02]
8.00 [7.93, 8.09]
8.31 [8.24, 8.38]
8.02 [7.96, 8.11]
8.82 [8.74, 8.89]
7.99 [7.92, 8.09]
8.69 [8.61, 8.77]
8.49 [8.43, 8.57]
8.46 [8.38, 8.54]
8.34 [8.26, 8.41]
8.66 [8.58, 8.73]
8.76 [8.72, 8.85]
5.58 [5.47, 5.68]
5.45 [5.37, 5.54]
5.55 [5.42, 5.68]
5.14 [5.04, 5.26]
5.40 [5.28, 5.51]
5.83 [5.72, 5.95]
5.77 [5.64, 5.88]
5.65 [5.58, 5.79]
5.92 [5.84, 6.07]
5.98 [5.88, 6.09]
4.49 [4.38, 4.60]
4.66 [4.56, 4.76]
4.46 [4.33, 4.58]
4.08 [3.97, 4.19]
4.35 [4.24, 4.47]
4.92 [4.79, 5.02]
4.82 [4.71, 4.93]
4.67 [4.57, 4.80]
4.97 [4.89, 5.10]
4.98 [4.90, 5.12]
–
8.63 [8.48, 8.65]
9.10 [9.09, 9.22]
6.02 [5.93, 6.23]
4.85 [4.61, 4.93]
6.53
6.45
6.89
6.25
6.55
6.83
6.69
6.66
6.96
6.97
7.23
Table 3: Average expert’s payoff over 1000 simulations against different DMs. The table is split
into five sections, from top to bottom: Our model (AE), static rules, dynamic rules, algorithms, and
the results in the numerical communication setup, which are not directly comparable to the above,
text-based communication results. For each condition, we report the average expert payoff over our
1000 simulations, as well as 95% CI (in brackets, using bootstrap re-sampling with 1000 re-samples
of our original 1000 simulations; see Dror et al., 2018). The human experts in the experiments of
Apel et al. (2020) achieve an average payoff of 7.36.
6.2 Main Results: Automated Expert
Performance against Different DMs
Table 3 presents AE results (averaged over 1000
simulated games) when playing with 6 different
DMs. Notice that our AE employs the HC-LSTM
based DMM and VM variants at all times—the
columns of the table correspond to the different
DMs it plays with. Recall that the AE can adapt
itself to its rival through the statistical game fea-
tures, which reflect the behavior of the rival DM
at previous trials. This allows us to test how well
our AE generalizes to new players with different
strategies than those it assumes.
The results suggest that our AE is the best
expert, reaching the best average payoff overall,
the best average payoff when playing against 4 of
the 6 DMs, and the second- and fifth-best payoffs
when playing against the remaining 2 DMs. These
encouraging results indicate the capability of our
AE to adapt itself to various DM types, providing
a positive answer for Q1 and Q2.
The human experts in the experiments of
Apel et al. (2020) achieved an average payoff
of 7.36, somewhat higher than the 7.02 average of
our AE. Note, however, that the human experts of
Apel et al. (2020) played against human DMs and
hence the results are not directly comparable. Yet,
hoping that the various automated DMs provide
a representation of the prominent types of hu-
man DMs, we consider the small gap between the
two numbers to provide an optimistic indication
that the answer to Q3 may be positive and our
AE performs similarly to human experts, at least
with respect to its payoff. Below (§7) we further
analyze the choices made by our AE, demonstrat-
ing interesting properties of its revealed texts and
comparing its decisions to those of the human
experts of Apel et al. (2020).
Interestingly,
the HIGHEST baseline per-
forms best and third-best, respectively, against
HC-LSTM+0.2 and HC-LSTM+0.1. This is be-
cause these compromised DMs tend to accept
the hotel for almost every review that
they
are presented with. However, for HC-LSTM,
and for the inflexible DMs, HC-LSTM-0.1 and
HC-LSTM-0.2, HIGHEST is far from being the
best model.
Additionally, the EXTREMIST and MEDIAN
baselines, which aim to select the review that best
reflects the different hotel scores, are inferior to
our AE in all setups. Two possible explanations
can be considered. First, unlike the AE that is
trained to maximize its payoff, EXTREMIST and
MEDIAN favor the DM by being transparent in
their choices at the expense of their own benefits.
Second, unlike the AE, these baselines do not
exploit the textual features of the reviews. The
strong performance of the AE is an indication
of the importance of textual features for strategy
design.
Finally, the dynamic rules (A-LIAR, PTD-HC,
and PTD-BERT), the greedy VM-SM, and the
AE-DM2 and AE-VM2 versions of our AE, which
use the second best DMM (BERT-LSTM) or VM
316
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
l
a
c
_
a
_
0
0
4
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
(HC-SVR), respectively, are inferior to our AE.
We consider this an indication of the importance
of a wise search procedure, that carefully balances
the long (explore) and the short (exploit) terms,
and of careful selection of suitable DMM and VM.
7 Ablation Analysis
In this section we analyze several aspects of the
main results presented above. We start by ana-
lyzing the impact of text-based communication
on our results, evaluating the performance of our
AE when performing numerical communication.
Then, we analyze different aspects of the observed
behavior of our AE in our main text-based com-
munication experiments: The average payoff of
the DMs (indicating whether our AE facilitates
fairness), the decision patterns of our AE when
playing against the various DMs (shedding more
light on Q2—does the AE adapt to the DM it
plays with), comparing the reviews revealed by
our AE to those revealed by the human experts in
Apel et al. (2020) (thus shedding more light on
Q3), and, finally, analyzing the textual properties
of the reviews revealed by our AE.
Numerical Communication Results To put our
textual communication results in context, we also
report results for the numerical communication
setup (Table 3, bottom line). As above, we report
results for the DMM and VM models, based on
the SG-LSTM architecture, and for the eventual
AE-SG expert. We cannot compare these results
directly to the textual communication numbers, as
they are based on another set of games and a differ-
ent type of communication, but we do hope to learn
about the difference between the communication
types based on the observed patterns.
The numerical communication DMM:SG-
LSTM and VM:SG-LSTM models achieve accu-
racy scores of 77.00% and 33.95%, respectively.
The F1-score of the DMM is 65.70 and the RMSE
score of the VM is 1.4. Interestingly, these num-
bers are substantially lower than the comparable
numbers of the leading textual communication
models (see Table 2). This is an indication that it
is harder to predict the DM behavior as well as
the future AE payoff when the communication is
numerical and hence only behavioral features can
be used for prediction.
Interestingly, the AE-SG model achieved payoffs
of 7.53, 8.63, 9.1, 6.02, and 4.85 against the numer-
ical HC-LSTM, HC-LSTM+0.1, HC-LSTM+0.2,
317
Figure 3: Average expert payoff as a function of the
average payoff of the DMs it played with.
HC-LSTM-0.1, and HC-LSTM-0.2, respectively
(there is no BERT-LSTM simulation when com-
munication is numerical). These payoffs are higher
than the best AE payoff in the textual communi-
cation setups in the first 3 cases, but are lower in
the last 2 setups where the acceptance probability
of the simulated DM is decreased.
Although this comparison between numerical
and textual communication is interesting, we
notice that in many real-life scenarios the com-
munication is either numerical or verbal. Hence,
it is important to design effective models for
both cases.
Average DM Payoff Figure 3 presents the av-
erage payoff of each expert as a function of the
average payoff of the DMs it played with. The
figure suggests that DMs who played with the two
experts with the lowest average payoff (MEDIAN
and EXTREMIST) achieve the highest payoff on
average. Our AE, in contrast, the highest-paid ex-
pert on average, leads to one of the lowest average
DM payoffs. Generally, we observe a strong neg-
ative correlation of −0.76 between the average
payoffs of the expert and the DM. As discussed in
§1, our game is not a zero-sum game. Yet, the neg-
ative correlation between the payoffs of the expert
and the DM, even for experts that were not trained
to maximize their own payoffs (like our AE and
the numerical communication AE-SG), demon-
strates the competitive nature of our task. A major
goal of future research is to design an expert that
can balance the payoffs of the two players, ideally
maximizing them at the same time.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
l
a
c
_
a
_
0
0
4
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Low Scoring Hotels Medium Scoring
Location-Positive
(92.5%)
Metro-Positive
(52.5%)
Staff-Positive
(46.8%)
Staff-Negative
(45.0%)
Facilities-Negative
(44.6%)
Hotels
Room-Positive
(67.6%)
Staff-Positive
(64.2%)
Location-Positive
(48.9%)
Metro-Positive
(38.2%)
Facilities-Negative
(31.2%)
High Scoring
Hotels
Staff-Positive
(81.3%)
Location-Positive
(74.9%)
Room-Positive
(47.3%)
Facilities-Positive
(29.4%)
Metro-Positive
(23.9%)
Table 4: The top 5 topics (ordered by frequency)
discussed in the reviews revealed by the AE for
low, medium, or high scoring hotels.
bin. The figure indicates that both experts con-
sistently prefer to present highly ranked reviews
and tend to reveal reviews that overestimate the
hotels’ average scores. Nonetheless, in all cases,
the HEs output higher estimations, whereas the
AE’s scores are more diverse and closer to the
average review score. This analysis sheds light
on our AE’s behavior, providing an initial answer
to Q3.
Textual Analysis of the AE-revealed Reviews
We also analyze the textual features of the re-
views that our AE chose when played against the
LSTM-HC DM. Table 4 presents the top 5 topics
discussed in the revealed reviews for low (average
score (as) < 7.5), medium (7.5 ≤ as ≤ 8.5),
or high (as > 8.5) scoring hotels. The topics are
based on the HC features, that encode topics such
as facilities, staff, location, food, conception, and price,
which are reviewed positively or negatively.
Fait intéressant, location, staff, and metro are all
discussed positively in the revealed reviews of
the three hotel groups. Cependant, the lower the
hotel score is, the lower the rank of its staff
and the higher the rank of the metro, among the
top 5 topics. It hence seems that for low-scoring
hotels the AE communicates positive aspects
of their outer surroundings. Negative topics are
more discussed in low and medium scoring ho-
tels, with facilities being negatively discussed
in many revealed reviews of low-scoring and
medium-scoring hotels.
8 Human Experiments
Enfin, we evaluate our AE when playing with
human DMs. We do believe that simulation-based
evaluation is crucial for our setting as it allows
us to test our AE against DMs with a variety of
Chiffre 4: Revealed review score distributions for the
AE and the human experts (HEs), for four represen-
tative hotels. The reviews are grouped into three bins
according to their attached score: Low (L), moyen
(M.), ou élevé (H), and the average score of the reviews
in each bin is in parentheses.
Analysis of AE Personalization A desirable
characteristic of an AE is the ability to personalize
its decisions to the DM it faces. We analyze
this behavior by measuring the average review
score that our AE chooses to reveal to the five
HC-LSTM variants of Table 3.
Our analysis reveals that the higher the ten-
dency of the DM to accept hotels, the higher are
the scores of the reviews sent by the AE. Nous
normalize the scores of each hotel to the [0, 1]
range and compute the average review score se-
lected across all hotels, for each of the DMs.
The average scores are 0.483 (HC-LSTM-0.2),
0.485 (HC-LSTM-0.1), 0.487 (HC-LSTM), 0.488
(HC-LSTM+0.1), et 0.491 (HC-LSTM+0.2).
This favorable behavior of our AE serves as an
evidence to its generalizability (Q2).
AE vs. Human Experts One of the most inter-
esting aspects of designing an AE is its similarity
to human experts (HEs). To address this aspect
(Q3), we compare between the AE and the HEs
that participated in the experiments of Apel et al.
(2020). Notice that the HEs play against human
DMs, while our AE plays against artificial DMs,
which makes them not directly comparable.
Chiffre 4 depicts the score distributions of the
reviews as revealed by the AE and the HEs
pour 4 representative test set hotels. We cluster
the scores per hotel into 3 bins—Low, moyen,
and high—and present the average score of each
318
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5: Average AE payoff for average hotel scores (Gauche) and for revealed review scores (Middle) that are
up to a certain threshold (x-axis). (Droite) Average DM payoff for revealed review scores that are at least of a
certain threshold (x-axis).
controlled characteristics at a relatively low-cost
(see §5). Encore, human-based evaluation, even if it is
small-scale due to its high cost, provides important
complementary information.
Following Apel et al. (2020), our AE plays
avec 100 different human DMs on the Amazon
Mechanical Turk (AMT) platform,7 such that no
DM competes against more than one expert.8 We
follow the same experimental setting as in our
simulations, and particularly use the same test-set
hotels. We compare the performance of our AE to
those of the strongest alternative: HIGHEST, le
second best baseline in our simulations (in terms
of average performance; the various AE agents
are not considered as baselines in this definition).
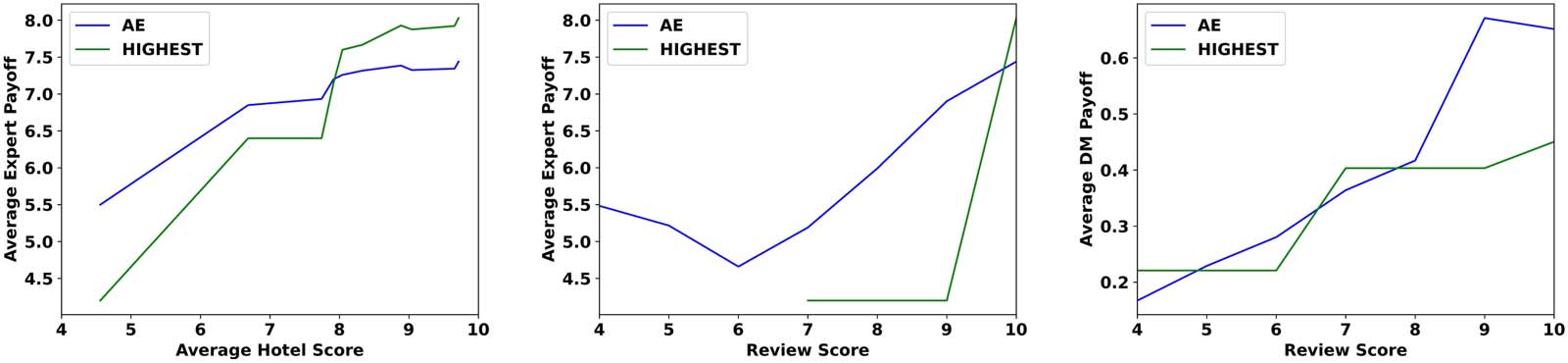
Chiffre 5 (Gauche) illustrates the average expert
payoff for hotels with an average review score
of at most s ∈ {4, . . . , 10}. The results suggest
that our AE achieves the highest average payoffs
for the 4 hotels with the lowest average review
score (average score of up to 8), c'est, the hotels
for which the expected DM payoff is negative.
This observation implies that our AE is able to
maximize its payoff on the most challenging ho-
tels. The HIGHEST agent excels on the other 6
hotels, those with an average review score higher
que 8 and hence a positive expected DM payoff.
Fait intéressant, 5 of these 6 hotels have a review
with the maximal score of 10, which is chosen by
HIGHEST.
est,
We next analyze the scores of the revealed
reviews—that
the reviews that were cho-
sen by the experts and presented to the DMs.
Chiffre 5 (Middle) presents the average expert
payoff when its revealed review score is at most
7https://www.mturk.com.
8We followed the exact same AMT experimental setup
as in Apel et al. (2020). Particularly, we filtered the AMT
workers according to the two attention checks described in
Section 4.1 of their paper.
319
7.44
8.03
All Games
Expert Payoff DM Payoff Num. Players
1.03
2.21
Acceptance Rate ≤ 80%
Expert Payoff DM Payoff Num. Players
0.70
0.72
6.51
6.60
100
100
70
50
AE
HIGHEST
AE
HIGHEST
Tableau 5: Average payoffs for all games (top) et
when the acceptance rate ≤ 80% (bottom).
s ∈ {4, . . . , 10}. While the HIGHEST agent
achieves the best payoff when it reveals a re-
view with the maximal score of 10, when moving
to lower scores we see that our agent maintains a
higher average payoff. For such cases where the
hotel does not have any review with the score of
10, the HIGHEST agent achieves a low average
payoff of 4.2.
The final analysis (Chiffre 5 (Droite)) is similar
to first two, except that now we are focusing
on the average DM payoff, when the revealed
review score is at least s ∈ {4, . . . , 10}. Le
leftmost point, corresponding to all experiments,
suggests that in total the human DMs who played
with our AE achieve the lowest average payoff.
Cependant, we notice that as the AE chooses to
reveal reviews with higher scores the average DM
payoff increases and surpasses the average payoff
of the DMs who played with the HIGHEST agent.
This is an interesting pattern, given that the AE
is trained to maximize its own payoff, and its
objective does not take the DM’s payoff into
account.
Enfin, Tableau 5 presents the average DM and
expert payoffs, considering all the experiments
(top) and those experiments where the DMs ac-
cepted at most 8 hotels. The table demonstrates
that the HIGHEST agent yielded the highest av-
erage payoffs for both player types, but this is
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
mostly due to a large number of DMs who ac-
cepted 9 ou 10 hotels. En effet, when focusing only
on DMs who considered the hotels more care-
fully (bottom table), the average of both the DM
and the expert payoffs are quite similar for both
agents. The results reflect an interesting property
of the HIGHEST agent: It makes many more hu-
man DMs accept all (or almost all) of the hotels.
This may reflect an interesting difference between
human and simulation DMs, to be explored in
l'avenir.
9 Conclusions
We consider the problem of automatic expert de-
sign for a repeated non-cooperative persuasion
game. Our AE is based on the MCTS search
algorithm with deep learning models for DM
decision and expert’s future payoff predictions.
Our experiments quantitatively and qualitatively
analyze the performance of our AE in compar-
ison to a large variety of alternatives. While
our main evaluation is with simulated (auto-
matic) DMs, we also examine the generalizability
of our results to experiments with human DMs.
Our work relies on the dataset of Apel et al.
(2020) for training and testing the various ex-
pert models. One limitation of
this dataset
is its size: It is based on only 10 training and 10 test
hotels, each with 7 scored reviews. De plus, le
training set, which is used for training our DMM
and VM models, consists of only 408 ten-trial
games. We aimed to compensate for this by per-
forming a large number of simulations (1000)
for each expert/DM pair, and by reporting 95%
intervalles de confiance (CIs), demonstrating limited
overlap between the 95% CI of our AE and the
baselines. Encore, richer datasets in terms of the
size and diversity of the hotel sets, ainsi que
the richness of interaction between the human
players, are required in order to further validate
our results.
In future we would like to extend our AE in
three main directions: (un) Designing end-to-end
architectures, where the DMM and VM are jointly
trained in order to maximize the AE’s payoff;
(b) Letting the AE generate persuasive language
rather than choosing from pre-written reviews;
et (c) Considering other AE strategies such as
fair payoff division between the expert and the
DM, instead of maximizing the AE’s payoff.
Remerciements
We would like to thank the action editor and
the reviewers, as well as the members of the
IE@Technion NLP group for their valuable feed-
back and advice. We are also extremely thank-
ful for the valuable guidance and assistance of
Christian K¨onig-Kersting in conducting the hu-
man experiments. This research is partially funded
by an ISF personal grant no. 1625/18. The work of
R.. Apel and M. Tennenholtz is funded by the Euro-
pean Research Council (ERC) under the European
Union’s Horizon 2020 research and innovation
programme (grant agreement no. 740435).
Les références
Hua Ai and Fuliang Weng. 2008. User simula-
tion as testing for spoken dialog systems. Dans
Proceedings of the 9th SIGdial Workshop on
Discourse and Dialogue, pages 164–171.
Nikolaos Aletras, Dimitrios Tsarapatsanis, Daniel
Preot¸iuc-Pietro, and Vasileios Lampos. 2016.
Predicting judicial decisions of the European
Court of Human Rights: A natural language pro-
cessing perspective. PeerJ Computer Science,
2:e93.
Alon Altman, Avivit Bercovici-Boden, and Moshe
Tennenholtz. 2006. Learning in one-shot strate-
gic form games. In European Conference on
Machine Learning, pages 6–17. Springer.
Jacob Andreas, Marcus Rohrbach, Trevor Darrell,
and Dan Klein. 2016. Learning to compose
neural networks for question answering. Dans
Actes du 2016 Conference of the
North American Chapter of the Association for
Computational Linguistics: Human Language
Technologies, pages 1545–1554.
Reut Apel, Ido Erev, Roi Reichart, and Moshe
Tennenholtz. 2020. Predicting decisions in lan-
guage based persuasion games. arXiv preprint
arXiv:2012.09966.
Itai Arieli and Yakov Babichenko. 2019. Pri-
vate Bayesian persuasion. Journal of Economic
Theory, 182:185–217.
Gal Bahar, Itai Arieli, Rann Smorodinsky, et
Moshe Tennenholtz. 2020. Multi-issue so-
cial learning. Mathematical Social Sciences,
104:29–39.
320
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Gal Bahar, Rann Smorodinsky, and Moshe
Tennenholtz. 2016. Economic recommendation
systèmes: One page abstract. In Proceedings of
le 2016 ACM Conference on Economics and
Computation, pages 757–757.
Dzmitry Bahdanau, Kyung Hyun Cho, et
Yoshua Bengio. 2015. Neural machine trans-
lation by jointly learning to align and translate.
In International Conference on Learning
Representations.
Hendrik Baier and Peter
je. Cowling. 2018.
Evolutionary MCTS for multi-action adver-
sarial games. Dans 2018 IEEE Conference on
Computational Intelligence and Games (CIG),
pages 1–8. IEEE.
JinYeong Bak and Alice Oh. 2018. Conversa-
tional decision-making model for predicting
the king’s decision in the Annals of
le
Joseon Dynasty. In Proceedings of the 2018
Conference on Empirical Methods in Nat-
ural Language Processing, pages 956–961.
https://www.aclweb.org/anthology
/D18-1115.pdf.
Radha-Krishna Balla and Alan Fern. 2009. UCT
for tactical assault planning in real-time strategy
games. In Proceedings of the 21st Interna-
tional Jont Conference on Artifical Intelligence,
pages 40–45.
Omer Ben-Porat, Sharon Hirsch, Lital Kuchi, Guy
Elad, Roi Reichart, and Moshe Tennenholtz.
2020. Predicting strategic behavior from free
text. Journal of Artificial Intelligence Research,
68:413–445.
Cameron B. Browne, Edward Powley, Daniel
Whitehouse, Simon M. Lucas, Peter I. Cowling,
Philipp Rohlfshagen, Stephen Tavener, Diego
Perez, Spyridon Samothrakis, and Simon
Colton. 2012. A survey of Monte Carlo tree
search methods. IEEE Transactions on Com-
in Games,
Intelligence and AI
putational
4(1):1–43.
Jiaao Chen and Diyi Yang. 2021. Weakly-
supervised hierarchical models for predict-
ing persuasive strategies in good-faith textual
requests. arXiv preprint arXiv:2101.06351.
Corinna Cortes and Vladimir Vapnik. 1995.
Support vector machine. Machine Learning,
20(3):273–297.
R´emi Coulom. 2006. Efficient selectivity and
backup operators in Monte-Carlo tree search.
In International Conference on Computers and
Games, pages 72–83. Springer.
Jacob Devlin, Ming-Wei Chang, Kenton Lee, et
Kristina Toutanova. 2019. Bert: Pre-training of
deep bidirectional transformers for language
understanding. In Proceedings of
le 2019
Conference of the North American Chapter of
the Association for Computational Linguistics:
Human Language Technologies, Volume 1
(Long and Short Papers), pages 4171–4186.
Rotem Dror, Gili Baumer, Segev Shlomov, et
Roi Reichart. 2018. The hitchhiker’s guide to
testing statistical significance in natural lan-
guage processing. In Proceedings of the 56th
Annual Meeting of the Association for Compu-
tational Linguistics (Volume 1: Long Papers),
pages 1383–1392.
Harris Drucker, Chris
J.. C. Burges, Linda
Kaufman, Alex Smola, and Vladimir Vapnik.
1997. Support vector
regression machines.
Advances in Neural Information Processing
Systems, 9:155–161.
John Duchi, Elad Hazan, and Yoram Singer.
2011. Adaptive subgradient methods for online
learning and stochastic optimization. Journal de
Machine Learning Research, 12(7).
Ioannis Efstathiou and Oliver Lemon. 2014.
Learning non-cooperative dialogue behaviours.
In Proceedings of the 15th Annual Meeting of
the Special Interest Group on Discourse and
Dialogue (SIGDIAL), pages 60–68.
Yuval Emek, Michal Feldman, Iftah Gamzu,
Renato PaesLeme, and Moshe Tennenholtz.
2014. Signaling schemes for revenue maxi-
mization. ACM Transactions on Economics and
Computation (TEAC), 2(2):1–19.
Hilmar Finnsson and Yngvi Bj¨ornsson. 2008.
Simulation-based approach to general game
playing. In Proceedings of
the AAAI Con-
ference on Artificial Intelligence, volume 8,
pages 259–264.
Michael C. Frank and Noah D. Homme bon. 2012.
Predicting pragmatic reasoning in language
games. Science, 336(6084):998–998.
Drew Fudenberg and Jean Tirole. 1991. Game
théorie. Cambridge, MA: AVEC Presse.
321
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Sylvain Gelly, Yizao Wang, R´emi Munos, et
Olivier Teytaud. 2006. Mogo: Improvements
in Monte-Carlo computer-go using UCT and
sequence-like simulations. Presentation given
at the University of Alberta.
Dave Golland, Percy Liang, and Dan Klein. 2010.
A game-theoretic approach to generating spa-
tial descriptions. In Proceedings of the 2010
Conference on Empirical Methods in Natural
Language Processing, pages 410–419.
Meritxell Gonz´alez, Silvia Quarteroni, Giuseppe
Riccardi, and Sebastian Varges. 2010. Co-
operative user models in statistical dialog
simulators. In Proceedings of
the SIGDIAL
2010 Conference, pages 217–220.
Jason S. Hartford, James R. Wright, and Kevin
Leyton-Brown. 2016. Deep learning for predict-
ing human strategic behavior. In Proceedings
of the 30th International Conference on Neural
Information Processing Systems.
Serhii Havrylov and Ivan Titov. 2017. Émer-
gence of language with multi-agent games:
Learning to communicate with sequences of
symbols. In Proceedings of
the 31st Inter-
national Conference on Neural Information
Processing Systems, pages 2146–2156.
Robert X. D. Hawkins, Mike Frank, and Noah
D. Homme bon. 2017. Convention-formation in
iterated reference games. In CogSci.
Christopher Hidey and Kathleen McKeown. 2018.
Persuasive influence detection: The role of
argument sequencing. In Proceedings of the
AAAI Conference on Artificial Intelligence,
volume 32.
Christopher Hidey, Elena Musi, Alyssa Hwang,
Smaranda Muresan, and Kathleen McKeown.
2017. Analyzing the semantic types of claims
and premises in an online persuasive forum. Dans
Proceedings of the 4th Workshop on Argument
Mining, pages 11–21.
Takuya Hiraoka, Graham Neubig, Sakriani Sakti,
Tomoki Toda, and Satoshi Nakamura. 2014.
Reinforcement
learning of cooperative per-
suasive dialogue policies using framing. Dans
Proceedings of COLING 2014, the 25th In-
ternational Conference on Computational Lin-
guistics: Technical Papers, pages 1706–1717.
Sepp Hochreiter and J¨urgen Schmidhuber. 1997.
Long short-term memory. Neural Computation,
9(8):1735–1780.
Melvin Johnson, Mike Schuster, Quoc V.
Le, Maxim Krikun, Yonghui Wu, Zhifeng
Chen, Nikhil Thorat, Fernanda Vi´egas, Martine
Wattenberg, Greg Corrado, Macduff Hughes,
and Jeffrey Dean. 2017. Google’s multi-
lingual neural machine translation system:
Enabling zero-shot translation. Transactions of
the Association for Computational Linguistics,
5:339–351.
Sangkeun Jung, Cheongjae Lee, Kyungduk Kim,
and Gary Geunbae Lee. 2008. An integrated dia-
log simulation technique for evaluating spoken
dialog systems. In COLING 2008: Proceed-
ings of the Workshop on Speech Processing
for Safety Critical Translation and Pervasive
Applications, pages 9–16.
Man-Je Kim and Kyung-Joong Kim. 2017. Op-
ponent modeling based on action table for
MCTS-based fighting Game AI. Dans 2017 IEEE
Conference on Computational Intelligence and
Games (CIG), pages 178–180. IEEE.
Tom Kwiatkowski, Jennimaria Palomaki, Olivia
Redfield, Michael Collins, Ankur Parikh, Chris
Illia Polosukhin,
Alberti, Danielle Epstein,
Jacob Devlin, Kenton Lee, Kristina Toutanova,
Llion Jones, Matthew Kelcey, Ming-Wei
Chang, Andrew M. Dai, Jakob Uszkoreit, Quoc
Le, and Slav Petrov. 2019. Natural ques-
tion: A benchmark for question answering
recherche. Transactions of the Association for
Computational Linguistics, 7:453–466.
Angeliki Lazaridou, Alexander Peysakhovich,
and Marco Baroni. 2017. Multi-agent coopera-
tion and the emergence of (naturel) langue.
In International Conference on Learning
Representations.
Mike Lewis, Denis Yarats, Yann Dauphin, Devi
Parikh, and Dhruv Batra. 2017. Deal or no deal?
End-to-end learning of negotiation dialogues. Dans
Actes du 2017 Conference on Empir-
ical Methods in Natural Language Processing,
pages 2443–2453.
Yu Li, Kun Qian, Weiyan Shi, and Zhou Yu.
2020. End-to-end trainable non-collaborative
dialog system. In Proceedings of the AAAI Con-
ference on Artificial Intelligence, volume 34,
pages 8293–8302.
322
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Yishay Mansour, Aleksandrs Slivkins,
et
Vasilis Syrgkanis. 2015. Bayesian incentive-
compatible bandit exploration. In Proceedings
of the Sixteenth ACM Conference on Economics
and Computation, pages 565–582.
Masha Medvedeva, Michel Vols, and Martijn
Wieling. 2020. Using machine learning to
predict decisions of the European court of
droits de l'homme. Artificial Intelligence and Law,
28(2):237–266.
Karthik Narasimhan, Tejas Kulkarni, and Regina
Barzilay. 2015. Language understanding for
text-based games using deep reinforcement
learning. In Proceedings of
le 2015 Con-
ference on Empirical Methods in Natural
Language Processing, pages 1–11.
Vlad Niculae, Srijan Kumar, Jordan Boyd-Graber,
and Cristian Danescu-Niculescu-Mizil. 2015.
Linguistic harbingers of betrayal: A case study
on an online strategy game. In Proceedings
of the 53rd Annual Meeting of the Associa-
tion for Computational Linguistics and the 7th
International Joint Conference on Natural Lan-
guage Processing (Volume 1: Long Papers),
pages 1650–1659, Beijing, Chine. Association
for Computational Linguistics.
Santiago Ontan´on. 2016. Informed Monte Carlo
tree search for real-time strategy games. Dans
2016 IEEE Conference on Computational In-
telligence and Games (CIG), pages 1–8. IEEE.
Nadav Oved, Amir Feder, and Roi Reichart. 2020.
Predicting in-game actions from interviews
of NBA players. Computational Linguistics,
46(3):667–712.
Ori Plonsky, Ido Erev, Tamir Hazan, and Moshe
Tennenholtz. 2017. Psychological forest: Pre-
dicting human behavior. In Proceedings of
the AAAI Conference on Artificial Intelligence,
volume 31.
Carl Shapiro, and Hal R. Varian. 1998. Infor-
mation rules: A strategic guide to the network
economy, Harvard Business Press.
Weiyan Shi, Kun Qian, Xuewei Wang, and Zhou
Yu. 2019. How to build user simulators to
train RL-based dialog systems. In Proceed-
le 2019 Conference on Empirical
ings of
Methods in Natural Language Processing and
the 9th International Joint Conference on
Natural Language Processing (EMNLP-IJCNLP),
pages 1990–2000.
David Silver, Thomas Hubert, Julian Schrittwieser,
Ioannis Antonoglou, Matthew Lai, Arthur
Guez, Marc Lanctot, Laurent Sifre, Dharshan
Kumaran, Thore Graepel, Timothy Lillicrap,
Karen Simonyan, and Demis Hassabis. 2018. UN
general reinforcement learning algorithm that
masters chess, shogi, and go through self-play.
Science, 362(6419):1140–1144.
Chiara F. Sironi, Jialin Liu, Diego Perez-Liebana,
Raluca D. Gaina, Ivan Bravi, Simon M. Lucas,
and Mark H. M.. Winands. 2018. Self-adaptive
mcts for general video game playing. In In-
ternational Conference on the Applications of
Evolutionary Computation, pages 358–375.
Gabriel Stanovsky,
Julian Michael, Luke
Zettlemoyer, and Ido Dagan. 2018. Supervised
open information extraction. In Proceedings of
le 2018 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
Volume 1 (Long Papers), pages 885–895.
Chenhao Tan, Vlad Niculae, Cristian Danescu-
Niculescu-Mizil, and Lillian Lee. 2016. Win-
Interaction dynamics and
ning arguments:
persuasion strategies
in good-faith online
discussions. In Proceedings of the 25th In-
ternational Conference on World Wide Web,
pages 613–624.
Sida I. Wang, Percy Liang, and Christopher
D. Manning. 2016. Learning language games
through interaction. In Proceedings of the 54th
Annual Meeting of the Association for Compu-
tational Linguistics (Volume 1: Long Papers),
pages 2368–2378.
Xuewei Wang, Weiyan Shi, Richard Kim,
Yoojung Oh, Sijia Yang, Jingwen Zhang, et
Zhou Yu. 2019. Persuasion for good: Towards
a personalized persuasive dialogue system for
social good. In Proceedings of the 57th Annual
Meeting of the Association for Computational
Linguistics, pages 5635–5649.
Ludwig Wittgenstein. 1953. Philosophical
dans-
vestigations. philosophische untersuchungen.
Macmillan.
Diyi Yang, Jiaao Chen, Zichao Yang, Dan
Jurafsky, and Eduard Hovy. 2019un. Let’s
make your request more persuasive: Modeling
323
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
le 2019 Conference of
persuasive strategies via semi-supervised neural
nets on crowdfunding platforms. In Proceed-
ings of
the North
American Chapter of
the Association for
Computational Linguistics: Human Language
Technologies, Volume 1 (Long and Short
Papers), pages 3620–3630.
Ze Yang, Pengfei Wang, Lei Zhang, Linjun
Shou, and Wenwen Xu. 2019b. A recurrent
attention network for judgment prediction. Dans
International Conference on Artificial Neural
Networks, pages 253–266. Springer.
Shuo Zhang and Krisztian Balog. 2020. Eval-
uating conversational recommender systems
via user simulation. In Proceedings of
le
26th ACM SIGKDD International Conference
on Knowledge Discovery & Data Mining,
pages 1512–1520.
Haoxi Zhong, Zhipeng Guo, Cunchao Tu,
Chaojun Xiao, Zhiyuan Liu, and Maosong
Sun. 2018. Legal judgment prediction via topo-
logical learning. In Proceedings of the 2018
Conference on Empirical Methods in Natural
Language Processing, pages 3540–3549.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
4
6
2
2
0
0
4
0
6
3
/
/
t
je
un
c
_
un
_
0
0
4
6
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
324