Data-driven Model Generalizability in Crosslinguistic Low-resource

Data-driven Model Generalizability in Crosslinguistic Low-resource
Morphological Segmentation

Zoey Liu
Department of Computer Science
Boston College, Etats-Unis
zoey.liu@bc.edu

Emily Prud’hommeaux
Department of Computer Science
Boston College, Etats-Unis
prudhome@bc.edu

Abstrait

Common designs of model evaluation typi-
cally focus on monolingual settings, où
different models are compared according to
their performance on a single data set that is
assumed to be representative of all possible
data for the task at hand. While this may be
reasonable for a large data set, this assump-
tion is difficult to maintain in low-resource
scenarios, where artifacts of the data col-
lection can yield data sets that are outliers,
potentially making conclusions about model
performance coincidental. To address these
concerns, we investigate model generalizabil-
ity in crosslinguistic low-resource scenarios.
Using morphological segmentation as the test
case, we compare three broad classes of models
with different parameterizations, taking data
depuis 11 languages across 6 language fami-
lies. In each experimental setting, we evaluate
all models on a first data set, then examine
their performance consistency when introduc-
ing new randomly sampled data sets with the
same size and when applying the trained mod-
els to unseen test sets of varying sizes. Le
results demonstrate that the extent of model
generalization depends on the characteristics
of the data set, and does not necessarily rely
heavily on the data set size. Among the charac-
teristics that we studied, the ratio of morpheme
overlap and that of the average number of
morphemes per word between the training and
test sets are the two most prominent factors.
Our findings suggest that future work should
adopt random sampling to construct data sets
with different sizes in order to make more
responsible claims about model evaluation.

Introduction

In various natural
language processing (NLP)
études, when evaluating or comparing the per-
formance of several models for a specific task,
the current common practice tends to examine
these models with one particular data set that is

393

deemed representative. The models are usually
trained and evaluated using a predefined split
of training/test tests (with or without a develop-
ment set), or using cross-validation. Given the
results from the test set, authors typically con-
clude that certain models are better than others
(Devlin et al., 2019), report that one model is gen-
erally suitable for particular tasks (Rajpurkar et al.,
2016; Wang et al., 2018; Kondratyuk and Straka,
2019), or state that large pretrained models have
‘‘mastered’’ linguistic knowledge at human levels
(Hu et al., 2020).

Par conséquent, the ‘‘best’’ models, while not
always surpassing other models by a large mar-
gin, are subsequently cited as the new baseline
or adopted for state-of-the-art comparisons in
follow-up experiments. These new experiments
might not repeat the comparisons that were carried
out in the work that identified the best model(s).
This model might be extended to similar tasks
in different domains or languages, regardless
of whether these new tasks have characteris-
tics comparable to those where the model was
demonstrated to be effective.

That being said, just because a self-proclaimed
authentic Chinese restaurant is very good at cook-
ing orange chicken, does not mean that its orange
chicken will be delicious on every visit to the
restaurant. De la même manière, common implementations
of model comparisons have been called into
question. Recent work by Gorman and Bedrick
(2019) (see also Szyma´nski and Gorman [2020]
and Søgaard et al. [2021]) analyzed a set of the
best part-of-speech (POS) taggers using the the
Wall Street Journal (WSJ) from the Penn Tree-
bank (Marcus et al., 1993). They demonstrated
inconsistent model performance with randomly
generated splits of the WSJ data in contrast to the
predefined splits as used in previous experiments
(Collins, 2002).

Transactions of the Association for Computational Linguistics, vol. 10, pp. 393–413, 2022. https://doi.org/10.1162/tacl a 00467
Action Editor: Luke Zellemoyer. Submission batch: 9/21; Revision batch: 12/2021; Published 4/2022.
c(cid:2) 2022 Association for Computational Linguistics. Distributed under a CC-BY 4.0 Licence.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
4
6
7
2
0
0
6
9
7
9

/
t

un
c
_
un
_
0
0
4
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Others (see Linzen [2020] for a review) have
argued that the majority of model evaluations are
conducted with data drawn from the same distri-
bution—that is, the training and the test sets bear
considerable resemblance in terms of their statis-
tical characteristics—and therefore these models
will not generalize well to new data sets from dif-
ferent domains or languages (McCoy et al., 2019,
2020; Jia and Liang, 2017). Autrement dit, à
evaluate the authenticity of a Chinese restaurant,
one would need to not only try the orange chicken,
but also order other traditional dishes.

Previous work on model evaluation, cependant,
has focused on high-resource scenarios, dans lequel
there is abundant training data. Very little ef-
fort has been devoted to exploring whether the
performance of the same model will generalize
in low-resource scenarios (Hedderich et al., 2021;
Ramponi and Plank, 2020). Concerns about model
evaluation and generalizability are likely to be
even more fraught when there is a limited amount
of data available for training and testing.

Imagine a task in a specific domain or language
that typically utilizes just one specific data set,
which is common in low-resource cases. We will
refer to the data set as the first data set. Quand
this first data set is of a reasonable size, it may
well be the case (though it might not be true)
that the data is representative of the population
for the domain or language, and that the training
and the test sets are drawn more or less from the
same distribution. The performance of individual
models and the rankings of different models can
be expected to hold, at the very least, for new data
from the same domain.

Now unfold that supposition to a task in a spe-
cific domain or language situated in a low-resource
scénario. Say this task also resorts to just one par-
ticular data set, which we again call the first data
ensemble. Considering the limitation that the data set
size is relatively small, one might be skeptical of
the claim that this first data set could represent the
population distribution of the domain or language.
Accordingly, within the low-resource scenario,
model evaluations obtained from just the first data
set or any one data set could well be coincidental
or random. These results could be specific to the
characteristics of the data set, which might not
necessarily reflect the characteristics of the do-
main or language more broadly given the small
size of the data. This means that even within the
same domain or language, the same model might

not perform well when applied to additional data
sets of the same sizes beyond the first data set, et
the best models based on the first data set might
not outperform other candidates when facing new
data. Continuing the Chinese restaurant analogy,
the same orange chicken recipe might not turn out
well with a new shipment of oranges.

As an empirical illustration of our concerns
raised above, this paper studies model generaliz-
ability in crosslinguistic low-resource scenarios.
For our test case, we use morphological segmen-
tation, the task of decomposing a given word into
individual morphemes (par exemple., modeling → model +
ing). En particulier, we focus on surface segmen-
tation, where the concatenation of the segmented
sub-strings stays true to the orthography of the
word (Cotterell et al., 2016b).1 This also involves
words that stand alone as free morphemes (par exemple.,
free → free).

Leveraging data from 11 languages across six
language families, we compare the performance
consistency of three broad classes of models
(with varying parameterizations) that have gained
in popularity in the literature of morphologi-
cal segmentation. In each of the low-resource
experimental settings (Section 6.1), we ask:

(1) To what extent do individual models gener-
alize to new randomly sampled data sets of
the same size as the first data set?

(2) For the model that achieves the best results
overall across data sets, how does its perfor-
mance vary when applied to new test sets of
different sizes?

2 Prior Work: Model Generalizability

A number of studies have noted inconsistent per-
formance of the same models across a range of
generalization and evaluation tasks. Par exemple,
McCoy et al. (2020) demonstrated that the same
pretrained language models, when paired with
classifiers that have different initial weights or are
fine-tuned with different random seeds, can lead to

1This includes segmentation for both inflectional and
derivational morphology; we used the term ‘‘sub-strings’’,
since not all elements in the segmented forms will be a
linguistically defined morpheme due to the word formation
processes. Therefore surface segmentation is in opposition
to canonical segmentation; see Cotterell et al. (2016b) pour
detailed descriptions of the differences between the two
tasks.

394

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
4
6
7
2
0
0
6
9
7
9

/
t

un
c
_
un
_
0
0
4
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

drastically unstable results (McCoy et al., 2019).
This pattern seems to hold for both synthetic
(Weber et al., 2018; McCoy et al., 2018) and natu-
ralistic language data (Zhou et al., 2020; Reimers
and Gurevych, 2017). Using approximately 15,000
training examples, Lake and Baroni
artificial
(2018) showed that sequence-to-sequence mod-
els do not generalize well with small data sets
(see also Akyurek and Andreas, 2021). Through a
series of case studies, Dodge et al. (2019) demon-
strated that model performance showed a different
picture depending on the amount of computation
associated with each model (par exemple., number of it-
erations, computing power). They suggested that
providing detailed documentation of results on
held-out data is necessary every time changes in
the hyperparameters are applied.

Another line of research has focused on test-
ing the generalizability of large language models
with controlled psycholinguistic stimuli such as
subject-verb agreement (Linzen et al., 2016),
filler-gap dependencies (Wilcox et al., 2019), et
garden-path sentences (Futrell et al., 2019), où
the stimuli data share statistical similarities with
the training data of the language models to dif-
ferent degrees (Wilcox et al., 2020; Hu et al.,
2020; Thrush et al., 2020). This targeted evalua-
tion paradigm (Marvin and Linzen, 2018; Linzen
and Baroni, 2021) tends to compare model perfor-
mance to behaviors of language users. It has been
claimed that this approach is able to probe the
linguistic capabilities of neural models, ainsi que
shed light on humans’ ability to perform gram-
matical generalizations. Thus far, related studies
have mainly investigated English, with notable
exceptions of crosslinguistic extensions to other
typologically diverse languages, such as Hebrew
(Mueller et al., 2020), Finnish (Dhar and Bisazza,
2021), and Mandarin Chinese (Wang et al., 2021;
Xiang et al., 2021).

As fruitful as the prior studies are, ils sont
mostly targeted towards evaluating models that
have access to a large or at least reasonable amount
of training data. In contrast, there is, as yet, Non
concrete evidence regarding whether and to what
extent models generalize when facing limited data.
En plus, although recent work has pro-
posed different significance testing methods in
order to add statistical rigor to model evalua-
tion (Gorman and Bedrick, 2019; Szyma´nski and
Gorman, 2020; Dror et al., 2018), most tests make
assumptions on the distributional properties or the

sampling process of the data (par exemple., data points are
sampled independently [Søgaard, 2013]), and a
number of these tests such as bootstrapping are
not suitable when data set size is extremely small
due to lack of power (see also Card et al., 2020).

3 Morphological Surface Segmentation

Why morphological surface segmentation? D'abord,
previous work has demonstrated that morpho-
logical supervision is useful for a variety of
NLP tasks, including but not limited to machine
translation (Clifton and Sarkar, 2011), depen-
dency parsing (Seeker and C¸ etino˘glu, 2015),
bilingual word alignment (Eyig¨oz et al., 2013),
and language modeling (Blevins and Zettlemoyer,
2019). For languages with minimal training re-
sources, surface or subword-based segmentation
is able to effectively mitigate data sparsity issues
(Tachbelie et al., 2014; Ablimit et al., 2010).
For truly low-resource cases, such as endan-
gered and indigenous languages, morpheme-level
knowledge has the potential
to advance de-
language technologies such as
velopment of
automatic speech recognition (Afify et al.,
2006) in order to facilitate community language
documentation.

Deuxième, information about morphological struc-
tures is promising for language learning. Espe-
cially for indigenous groups, prior studies have
proposed incorporating morphological annotation
into the creation of online dictionaries as well
as preparing teaching materials, with the goal
of helping the community’s language immersion
programs (Garrett, 2011; Spence, 2013).

Troisième, despite its utility in different

tasks,
semi-linguistically informed subword units are
not as widely used as they might be, depuis
acquiring labeled data for morphological seg-
including the case of
mentation in general,
surface segmentation,
requires extensive lin-
guistic knowledge from native or advanced
speakers of the language. Linguistic expertise
can be much more difficult
to find for criti-
cally endangered languages, lequel, by definition
(Meek, 2012), are spoken by very few peo-
ple, many of whom are not native speakers of
the language. These aforementioned limitations
necessitate better understanding of the perfor-
mance for different segmentation models and
how to reliably estimate their effectiveness.

395

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
4
6
7
2
0
0
6
9
7
9

/
t

un
c
_
un
_
0
0
4
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Language

Language family Morphological feature(s) N of types

Data set sizes

New test set sizes

Yorem Nokki Yuto-Aztecan

Polysynthetic

Nahuatl

Wixarika

Polysynthetic

English

Indo-European

Fusional

German

Persian

Russian

Fusional

95,922

in initial data

1,050

1,096

1,350

1,686

1,751

32,292

{500, 1,000}

–

{500, 1,000}

{50, 100}

{500, 1,000, 1,500}

{50, 100}

{500, 1,000, 1,500}

{50, 100}

{500, 1,000, 1,500
{2,000, 3,000, 4,000}

{500, 1,000, 1,500}
2,000, 3,000, 4,000}

{50, 100, 500, 1,000}

Turkish

Turkic

Agglutinative

Finnish

Uralic

Agglutinative

1,760

1,835

{500, 1,000, 1,500}

{50, 100}

{500, 1,000, 1,500}

{50, 100}

Zulu

Niger-Congo

Agglutinative

10,040

Indonesian

Austronesian

Agglutinative

3,500

{500, 1,000, 1,500}
{2,000, 3,000, 4,000}

{50, 100, 500, 1,000}

{500, 1,000, 1,500}
{2,000, 3,000}

{50, 100, 500}

Tableau 1: Descriptive statistics for the languages in our experiments. Data set sizes apply to both sampling
strategies (with and without replacement). New test set sizes (sampled without replacement) refer to the
different sizes of constructed test sets described in Section 6.2.

4 Meet the Languages

A total of eleven languages from six language
families were invited to participate in our
experiments. Following recently proposed scien-
tific practices for computational linguistics and
NLP (Bender and Friedman, 2018; Gebru et al.,
2018), we would like to introduce these languages
and their data sets explored in our study (Tableau 1).
First we have three indigenous languages
from the Yuto-Aztecan language family (Boulanger,
1997),
including Yorem Nokki (Southern di-
alect) (Freeze, 1989) spoken in the Mexican
states of Sinaloa and Sonora, Nahuatl (Oriental
branch) (de Su´arez, 1980) spoken in Northern
Puebla, and Wixarika (G´omez and L´opez, 1999)
spoken in Central West Mexico. These three
Mexican languages are highly polysynthetic with
agglutinative morphology. The data for these
languages was originally digitized from the book
collections of Archive of Indigenous Language.
Data collections were carried out and made

publicly available by the authors of Kann et al.
(2018) given the narratives in their work.

Next are four members from the Indo-European
language family: English, German, Persian, et
Russian, all with fusional morphological char-
acteristics. The data for English was provided
by the 2010 Morpho Challenge (Kurimo et al.,
2010), a shared task targeted towards unsupervised
learning of morphological segmentation. Le
German data came from the CELEX lexical data-
base (Baayen et al., 1996) and was made available
by Cotterell et al. (2015). The Persian data from
Ansari et al. (2019un) (see also Ansari et al., 2019b)
contains crowd-sourced annotations, tandis que le
data for Russian was extracted from an online
dictionary (Sorokin and Kravtsova, 2018).

The remaining languages each serve as a repre-
sentative of a different language family. The data
sets for Turkish from the Turkic language fam-
ily and Finnish from the Uralic language family
were again provided by the 2010 Morpho Chal-
lenge (Kurimo et al., 2010). The data collection

396

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
4
6
7
2
0
0
6
9
7
9

/
t

un
c
_
un
_
0
0
4
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

for both Zulu and Indonesian was carried out by
Cotterell et al. (2015). The Zulu words were taken
from the Ukwabelana Corpus (Spiegler et al.,
2010), and the segmented Indonesian words were
derived via application of a rule-based mor-
to an Indonesian-English
phological analyzer
bilingual corpus.2 All four of these languages
have agglutinative morphology.

5 Meet the Models

compared three

Nous
categories of models:
sequence-to-sequence (Seq2seq) (Bahdanau et al.,
2015), conditional random field (CRF) (Lafferty
et coll., 2001), and Morfessor (Creutz and Lagus,
2002).

Seq2seq The first guest in our model suite is a
character-based Seq2seq recurrent neural network
(RNN) (Elman, 1990). Previous work (Kann et al.,
2018; Liu et al., 2021) has demonstrated that this
model is able to do well for polysynthetic indige-
nous languages even with very limited amount
of data. Consider the English word papers as an
illustration. With this word as input, the task of
the Seq2seq model is to perform:

papers → paper + s.

As we are interested in individual models,
the training setups are constant for the data of
tous
languages. We adopted an attention-based
encoder-decoder (Bahdanau et al., 2015) où
the encoder consists of a bidirectional gated
recurrent unit (GRU) (Cho et al., 2014), et le
decoder is composed of a unidirectional GRU.
The encoder and the decoder both have two hid-
den layers with 100 hidden states in each layer. All
embeddings have 300 dimensions. Model training
was carried out with OpenNMT (Klein et al.,
2017), using ADADELTA (Zeiler, 2012) and a
batch size of 16.

Order-k CRF The second guest is the order-k
CRF (hereafter k-CRF) (Lafferty et al., 2001;
Ruokolainen et al., 2013), a type of log-linear
discriminative model that treats morphological
segmentation as an explicit sequence tagging task.
Given a character wt within a word w, where t is
the index of the character, CRF gradually predicts
the label yt of the character from a designed feature
set xt that is composed of local (sub-)strings.

2https://github.com/desmond86/Indonesian

-English-Bilingual-Corpus

397

In detail, k-CRF takes into consideration the
label(s) of k previous characters in a word
(Cuong et al., 2014; Cotterell et al., 2015). Ce
means that when k = 0 (c'est à dire., 0-CRF), the label yt
is dependent on just the feature set xt of the current
character wt. On the other hand, when k ≥ 1, dans
our settings, the prediction of yt is context-driven
and additionally considers a number of previous
labels {yt−k, . . . , yt−1}.

Prior work (Vieira et al., 2016) (see also Mueller
et coll., 2013) has claimed that, with regard to
choosing a value of k, 2-CRF usually yields good
résultats; increasing k from 0 à 1 leads to large
improvements, while increasing from 1 à 2 concernant-
sults in a significant yet weaker boost in model
performance. With that in mind, we investigated
five different values of k (k = {0, 1, 2, 3, 4}).

In training the CRFs, the feature set for every
character in a word is constructed as follows. Chaque
word is first appended with a start ((cid:5)w(cid:6)) and an end
((cid:5)/w(cid:6)) symbol. Then every position t of the word
is assigned a label and a feature set. The feature
set consists of the substring(s) occurring both on
the left and on the right side of the current position
up to a maximum length, d. As a demonstration,
take the same English word above (papers) as an
example. For the third character p in the word,
with δ having a value of 3, the set of substrings on
the left and right side would be, respectivement, {un,
Pennsylvanie, (cid:5)w(cid:6)Pennsylvanie} et {p, pe, par}. The concatenation of
these two sets would be the full feature set of the
character p. In our experiments, we set δ to have
a constant value of 4 across all languages.

Depending on the position index t and the mor-
pheme that this index occurs in, each character can
have one of six labels: {START (start of a word),
B (beginning of a multi-character morpheme), M.
(middle of a multi-character morpheme), E (end of
a multi-character morpheme), S (single-character
morpheme), END (end of a word)}. Donc,
papers has the following segmentation label
representation, and the training objective of the
CRF model is to learn to correctly label each
character given its corresponding feature set.

(cid:5)/w(cid:6)
(cid:5)w(cid:6)
p
START B M M M E S END

Dans notre étude, all linear-chain CRFs were im-
plemented with CRFsuite (Okazaki, 2007) avec
modifications. Model parameters were estimated

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
4
6
7
2
0
0
6
9
7
9

/
t

un
c
_
un
_
0
0
4
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

with L-BFGS (Liu and Nocedal, 1989) and L2 reg-
ularization. Encore, the training setups were kept
the same for all languages.

Supervised Morfessor The last participating
model
is the supervised variant of Morfes-
sor (Creutz and Lagus, 2002; Rissanen, 1998)
which uses algorithms similar to those of the
semi-supervised variant (Kohonen et al., 2010),
except that, given our crosslinguistic low-resource
scenarios, we did not resort to any additional un-
labeled data. For the data of every language, tous
Morfessor models were trained with the default
parameters.

In the remainder of this paper, to present clear
narratives, in cases where necessary, we use the
term model alternative(s) to refer to any of the
seven alternatives: Morfessor, Seq2seq, 0-CRF,
1-CRF, 2-CRF, 3-CRF, and 4-CRF.

6 Experiments

6.1 Generalizability Across Data Sets

Our first question concerns the generalizability of
results from the first data set across other data sets
of the same size. For data set construction, nous
took an approach similar to the synthetic method
from Berg-Kirkpatrick et al. (2012). Given the
initial data for each language, we first calculated
the number of unique word types; after comparing
this number across languages, we decided on a
range of data set sizes that are small in general
(Tableau 1), then performed random sampling to
construct data sets accordingly.

The sampling process is as follows, using Rus-
sian as an example. For each data set size (par exemple.,
500), we randomly sampled words with replace-
ment to build one data set of this size; this data
set was designated the first data set; and then an-
other 49 data sets were sampled in the same way.
We repeated a similar procedure using sampling
without replacement. Each sampled data set was
randomly assigned to training/test sets at a 3:2
ratio, five times. In what follows, we use the term
experimental setting to refer to each unique com-
bination of a specific data set size and a sampling
strategy.

Compared with Berg-Kirkpatrick et al. (2012),
our data set constructions differ in three aspects.
D'abord, our sampling strategies include both with
in order to simulate
and without replacement
realistic settings (par exemple., real-world endangered lan-
guage documentation activities) where the training

and the test sets may or may not have overlapping
items. Deuxième, in each augmented setting with a
specific sampling strategy and a data set size, un
total of 250 models were trained given each model
alternative (5 random splits ∗ 50 data sets); ce
contrasts with the number of models for different
tasks in Berg-Kirkpatrick et al. (2012), ranging
depuis 20 for word alignment to 150 for machine
translation. Troisième, we aim to build data sets of very
small sizes to suit our low-resource scenarios.

For every model trained on each random split,
five metrics were computed to evaluate its perfor-
mance on the test set: full form accuracy, mor-
pheme precision, recall, and F1 (Cotterell et al.,
2016un; van den Bosch and Daelemans, 1999),
and average Levenshtein distance (Levenshtein,
1966). The average of every metric across the
five random splits of each data set was then com-
puted. For each experimental setting, given each
metric, we measured the consistency of model
performance from the first data set as follows:

(1) the proportion of times the best model alter-
native based on the first data set is the best
across the 50 data sets;

(2) the proportion of times the model ranking of
the first data set holds across the 50 data sets.

If a particular model A is indeed better than
alternative B based on results from the first data
ensemble, we would expect to see that hold across the
50 data sets. En outre, the model ranking drawn
from the first data set would be the same for the
other data sets as well.

While we examined the results of all metrics,
for the sake of brevity, we focus on F1 scores
when presenting results (Section 7).3

6.2 Generalizability Across New Test Sets

In addition to evaluating model performance
across the originally sampled data sets of the
same sizes, we also investigated the generalizabil-
ity of the best model alternatives from Section 6.1
when facing new unseen test sets. Taking into
consideration the type counts of the initial data for
every language and the sizes of their sampled data
sets in our experiments, a range of test set sizes
that would be applicable to all data set sizes was
decided, shown in Table 1. (Note that no new test
sets were created for Yorem Nokki and Nahuatl,

3Code and full results are in quarantine at https://

github.com/zoeyliu18/orange chicken.

398

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
4
6
7
2
0
0
6
9
7
9

/
t

un
c
_
un
_
0
0
4
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
4
6
7
2
0
0
6
9
7
9

/
t

un
c
_
un
_
0
0
4
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 1: Generalizability results for the Russian example in Section 7.1.

since it would be feasible for these two languages
only when the data set size is 500.) Alors, for every
data set, we selected all unique words from the
initial data that did not overlap with those in the
data set. From these words, given a test set size,
we performed random sampling without replace-
ment 100 times. Autrement dit, each data set had
correspondingly 100 new test sets of a particu-
lar size.

After constructing new test sets, for each ex-
perimental setting, we picked the overall best
performing model alternative based on average
observations across the 50 data sets from Sec-
tion 6.1. For each data set, this model alternative
was trained five times (via 5 random splits). Le
trained models were then evaluated with each of
le 100 new test sets for the data set and the same
five metrics of segmentation performance were
computed. Encore, due to space constraints, nous
focus on F1 in presentations of the results.

7 Results

7.1 A Walk-through

To demonstrate the two ways of evaluating
model generalizability outlined above, take Rus-
sian again as an example, when the data set size is
2,000 and the evaluation metric is F1 score. For the
first data set, when sampled with replacement, le
best model is Seq2seq, achieving an average F1
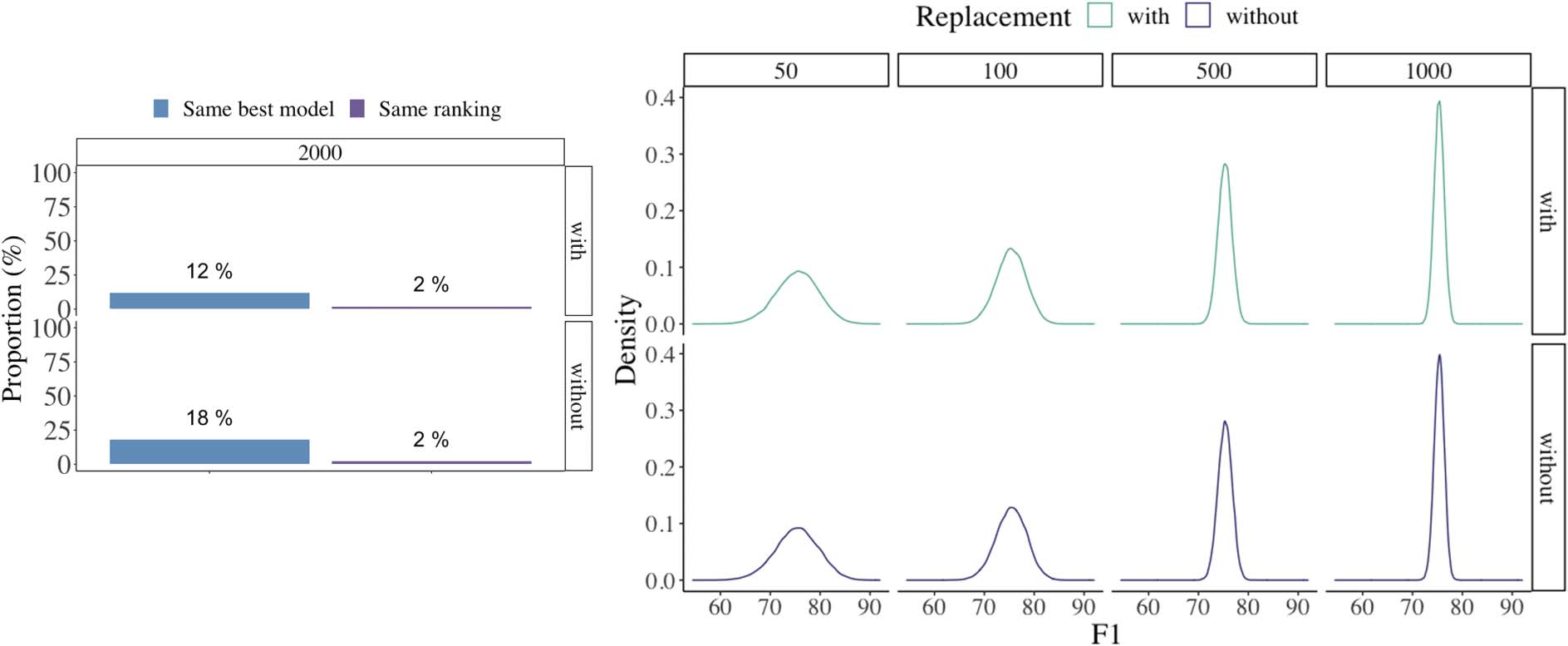
score of 74.26. As shown in Figure 1a, the propor-
tion of times Seq2seq is the best model across the

50 data sets is 12%. The model performance rank-
ing for the first data set is Seq2seq > 1-CRF >
4-CRF > 2-CRF > 3-CRF > 0-CRF > Mor-
fessor, a ranking that holds for 2% of all 50
data sets.

By comparison, when the first data set was
sampled without replacement, the best model is
1-CRF with an average F1 score of 74.62; le
proportion of times this model has the best results
across the 50 data sets is 18%. The best model
ranking is 1-CRF > 3-CRF > 2-CRF > 4-CRF >
Seq2seq > 0-CRF > Morfessor, and this pattern
accounts for 2% of all model rankings considering
le 50 data sets together.

Taking a closer look at the performance of each
model for the first data set given each sampling
strategy (Tableau 2), while the average F1 scores of
Morfessor and 0-CRF are consistently the lowest,
the performance of the other models is quite simi-
lar; the difference of F1 scores between each pair
of models is less than one.

Now turn to patterns across the 50 data sets as
a whole. It seems that for the Russian example,
whether sampling with or without replacement,
the best model is instead 4-CRF (Tableau 2), lequel
is different from the observations derived from the
respective first data set of each sampling method.
The differences in the proportion of times 4-CRF
ranks as the best model and that of other model al-
ternatives are quite distinguishable, although their
mean F1 scores are comparable except for Mor-
fessor and 0-CRF. With CRF models, it does not

399

Sampling

Model

Avg. F1 for
the first data set

Avg. F1 across
le 50 data sets

F1 range across
le 50 data sets

F1 std. across
le 50 data sets

% of times
as the best model

avec
replacement

Morfessor

0-CRF

1-CRF

2-CRF

3-CRF

4-CRF

Seq2seq

without
replacement

Morfessor

0-CRF

1-CRF

2-CRF

3-CRF

4-CRF

Seq2seq

34.61

58.75

74.20

74.02

73.71

74.06

74.26

34.16

59.10

74.62

74.53

74.60

74.48

74.00

36.52

59.59

75.38

75.46

75.48

75.54

74.86

36.04

59.41

75.08

75.15

75.18

75.21

74.39

(34.61, 38.36)

(57.83, 62.65)

(73.93, 76.66)

(74.02, 76.68)

(73.71, 76.52)

(74.06, 76.73)

(73.48, 76.45)

(34.16, 38.17)

(57.15, 60.95)

(73.72, 76.72)

(73.75, 76.89)

(73.77, 76.76)

(73.79, 77.14)

(72.54, 76.99)

0.76

0.87

0.65

0.67

0.68

0.85

0.88

0.96

0.72

0.81

0.79

0.83

0.89

Tableau 2: Summarization statistics of model performance for the Russian example in Section 7.1.

appear to be the case that a higher-order model
leads to significant improvement in performance.
Comparing more broadly, CRF models are better
overall than the Seq2seq models.

In spite of the small differences on average
between the better-performing model alternatives,
every model alternative presents variability in
its performance: The score range (c'est à dire., the dif-
ference of the highest and the lowest metric
score across the 50 data sets of each experi-
mental setting) spans from 2.66 for 2-CRF to 2.97
for Seq2seq. The difference between the average
F1 for the first data set and the highest average
F1 score of the other 49 data sets is also no-
ticeable. When sampling with replacement, le
value spans from 2.19 for Seq2seq to 3.90 pour
0-CRF; and when sampling without replacement,
the value ranges from 1.85 for 0-CRF to 2.99
for Seq2seq.

In contrast, in this Russian example, we see
a different picture for each model alternative if
comparing their results for the first data set to
the averages across all the data sets instead; le
largest mean F1 difference computed this way
est 1.91 when sampling with replacement, et
1.89 for sampling without replacement, both from

scores of Morfessor; and these difference val-
ues are smaller than the score range from all
data sets.

While we focused on F1 scores, we analyzed
the other four metrics in the same way. Given
each metric, the generalizability of the observa-
tions from the first data set, regardless of the
specific score of each model alternative and their
differences, is still highly variable; the most gen-
eralizable case, where the best model from the first
data set holds across the 50 data sets, is relying on
full form accuracy when sampling with replace-
ment (36%). When contrasting results from the
first data set to the other 49 data sets, there are
again noticeable differences between the average
score of the former and the highest average score
of the latter. Par exemple, when using morpheme
precision and sampling with replacement, the dif-
ference ranges from 1.98 for Seq2seq to 4.00 pour
Morfessor; with full form accuracy and sampling
without replacement, the difference spans from
2.12 for 0-CRF to 4.78 for Morfessor.

Given each sampling method, we applied the
250 trained models of the best performing model
alternative across the 50 data sets (Tableau 2) to new
test sets of four different sizes. As presented in

400

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
4
6
7
2
0
0
6
9
7
9

/
t

un
c
_
un
_
0
0
4
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 1b, for this Russian example, the distribu-
tions of the F1 scores demonstrate variability to
different extents for different test set sizes. Quand
the data was sampled with replacement, the results
are the most variable with a test set size of 50,
where the F1 scores span from 57.44 à 90.46;
and the least variable F1 scores are derived when
the test set size is 1,000, ranging from 70.62 à
79.36. On the other hand, the average F1 across
the different test sizes is comparable, spanning
depuis 75.30 when the test size is 50 à 75.41 quand
the test size is 500. Encore, we observed similar
results when the data sets were sampled without
replacement.

7.2 An Overall Look

The results for the data sets of all languages were
analyzed in exactly the same way as described
for the Russian example given in Section 7.1.
When not considering how different the average
F1 score of each model alternative is compared to
every other alternative within each experimental
setting (82 settings in total; 41 for each sampling
method), in most of the settings the performance
of the model alternatives for the first data set is
not consistent across the other data sets; the pro-
portions of cases where the best model alternative
of the first data set holds for the other 49 data
sets are mostly below 50%, except for most of the
cases for Zulu (data set size (cid:2) 1,000) where the
proportion values approximate 100%. The obser-
vations for model rankings are also quite variable;
the proportion of times the model ranking of the
first data set stays true across the 50 data sets
va de 2% for those in Russian containing
2,000 words sampled with replacement, à 56%
for data sets in Zulu including 4,000 words sam-
pled without replacement. (The high variability
derived this way persists despite of the particular
metrics applied.)

Considering all the experimental settings, quand
sampling with replacement, the two best per-
forming models for the first data sets are 4-CRF
(13 / 41 = 31.71%) and Seq2seq (36.59%); 2-CRF
(26.83%) and 4-CRF (36.59%) are more favorable
if sampling without replacement. The differences
between the best model alternatives are in general
petit; the largest difference score between the
top and second best models is 1.89 for data sets
in Zulu with 1,500 words sampled with replace-
ment. Across the 50 data sets within each setting,

overall, higher-order CRFs are the best per-
forming models.

Similar findings of performance by different
model alternatives were observed for other metrics
aussi, except for average Levenshtein distance
where CRF models are consistently better than
Seq2seq, even though the score differences are
mostly small. This is within expectation given
that our task is surface segmentation, and Seq2seq
models are not necessarily always able to ‘‘copy’’
every character from the input sequence to the
output. Previous work has tried to alleviate this
problem via multi-task learning (Kann et al., 2018;
Liu et al., 2021), où, in addition to the task
of morphological segmentation, the model is also
asked to learn to output sequences that are exactly
the same as the input. We opted not to explore
multi-task learning here in order to have more
experimental control for data across languages.

When analyzing the performance range of the
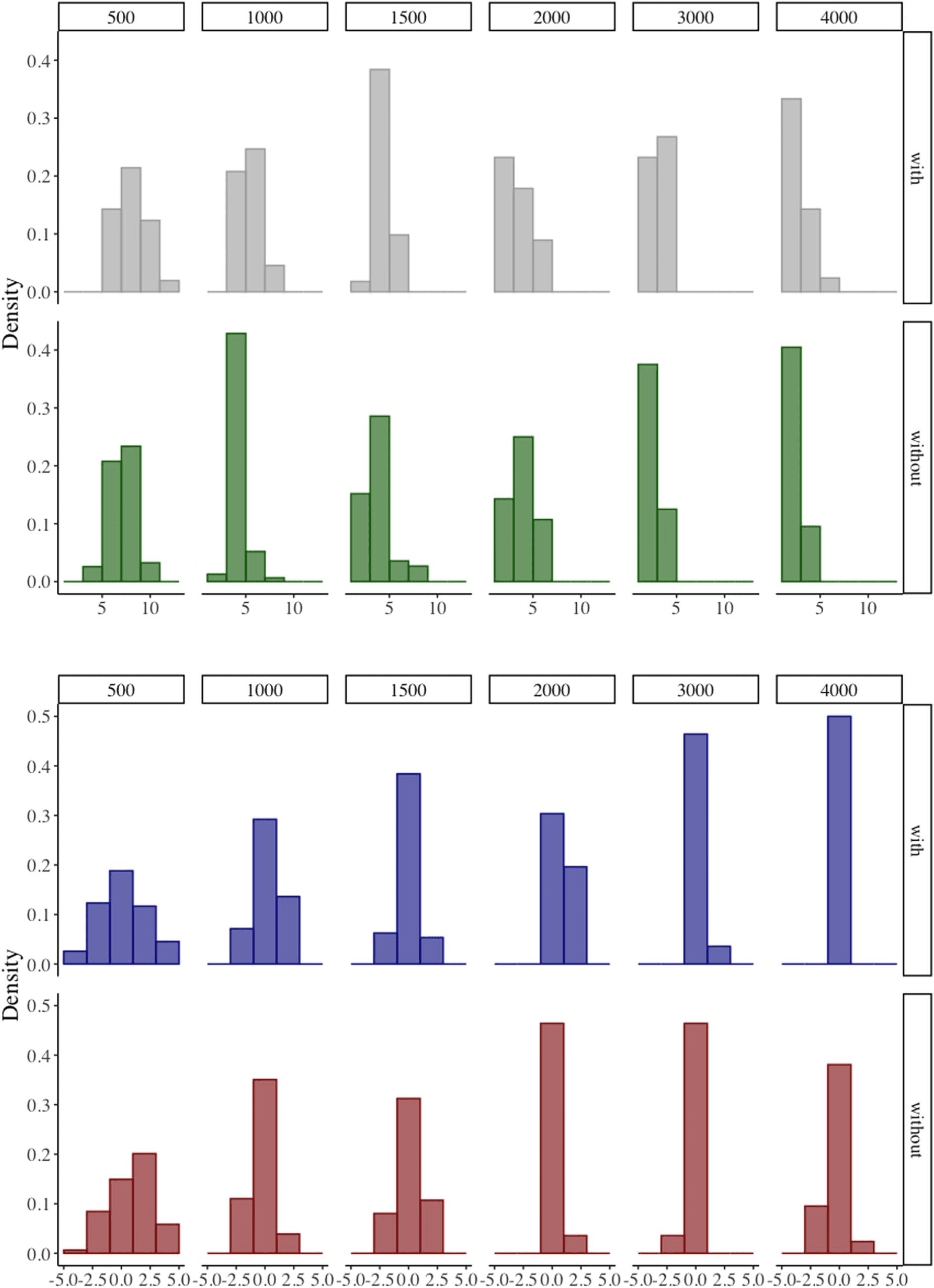
models, we see variability as well. Figure 2a
presents the distribution of F1 score ranges ag-
gregating the results for all the models across
the score ranges of
all experimental settings;
individual model alternatives are additionally
demonstrated in Figure 3. Larger score ranges
exist especially when data sets have a size of 500,
irrespective of the specific model (whether it is
non-neural or neural). Par exemple, 3-CRF has a
score range of 11.50 for data in Persian sampled
with replacement and the range of Seq2seq in this
setting is 11.24. As the data set sizes increase, le
score ranges become smaller.

Across all experimental settings, we also an-
alyzed the difference between the average F1
score of the first data set and that across all 50
data sets (Figure 2b). While in most of the cases
the differences for the same model alternative
are very small, the values of the differences ap-
pear to be more distinguishable when the data
set size is small. On the other hand, as shown
in Figure 3, these differences are by comparison
(much) smaller than the average F1 score range
(the triangles are consistently below the circles),
an observation that also aligns with what we have
seen from the Russian example.

Encore, similar results hold for the other four
evaluation metrics as well; different model alter-
natives demonstrate large score range across all
experimental settings regardless of the particular
metric. As an illustration, we performed linear

401

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
4
6
7
2
0
0
6
9
7
9

/
t

un
c
_
un
_
0
0
4
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
4
6
7
2
0
0
6
9
7
9

/
t

un
c
_
un
_
0
0
4
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 2: Some distribution statistics of the average F1 score of all models across all experimental settings.

402

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi

/
t

un
c
je
/

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

1
0
1
1
6
2

/
t

un
c
_
un
_
0
0
4
6
7
2
0
0
6
9
7
9

/
t

un
c
_
un
_
0
0
4
6
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 3: Some summary statistics for the performance of all models across all experimental settings. Within each
setting, circle represents the average F1 score range; variability exists in the score range regardless of the model
alternative applied or the data set size, though the range appears to be larger when data set sizes are small. Par
comparison, triangle represents the difference between the average F1 score of the first data set and that across
tous 50 data sets; the values of the differences seem to be more noticeable when data set sizes are small, yet these
differences are in general smaller than the score range.

403

regression modeling analyzing the relationships
between other evaluation metrics and the average
F1 score. Take morpheme recall as an example.
Given all the data of a language, the regression
model predicts the score range of average mor-
pheme recall across data sets in an experimental
setting as a function of the score range of av-
erage F1 in the same experimental setting. Le
same procedure was carried out for each of the
other metrics as well. Significant effects were
trouvé (p < 0.01 or p < 0.001) for the score range of average F1, indicating strong compara- bility of model performance in terms of different evaluation metrics. In addition, besides average F1, there are also noticeable differences between a given metric score for the first data set and that across all 50 data sets within each experimental setting, yet these differences are also smaller than the score range. Our regression models predicting these differences as a function of the differences of average F1 score also show significant effects for the latter, again lending support to the comparability between these metrics when characterizing model evaluation in our study here. When we applied the trained models of the overall best model alternative to new test sets, all settings demonstrate a great amount of variability that seems to be dependent on both the size of the data set used to train the models and that of the new test sets. The extent of variation does not ap- pear to be constrained by the sampling strategy. The difference in the resulting F1 scores ranges from around 6.87, such as the case with Indonesian when the data set size is 3,000 sampled without replacement and the test set size is 500, to approx- imately 48.59, as is the case for Persian when the data set size is 500 sampled with replacement and the test set size is 50. That being said, as in the Russian example, the average results among the different test sizes for each setting of every lan- guage are also comparable to each other.4 4In addition to testing the best model alternatives, for every experimental setting of Persian, Russian, and Zulu, the three languages that have the largest range of data set sizes and new test set sizes in our study, we also experimented with the second or third best model alternatives based on their average performance and computing power. The observations of these alternatives are comparable to those of the best models. 404 7.3 Regression Analysis One question arises from the aforementioned find- ings: Why is there variable performance for each model alternative across all the experimental set- tings of each language? With the observations in our study thus far, it seems that the results are dependent on the data set size or test set size. But is that really the case, or is sample size simply a confounding factor? To address the questions above, we studied several data characteristics and how they affect model performance. It is important to note that, as discussed in Section 1, we do not wish to claim these features are representative of the full language profile (e.g., how morphologically com- plex the language is as a whole). For instance, one might expect that on average, languages that are agglutinative or polysynthetic have larger num- bers of morphemes per word when compared to fusional languages. While that might be true for cases with ample amounts of data, the same as- sumption does not always seem to be supported by the data sets in our experiments. For each experi- mental setting, the average number of morphemes per word across the 50 data sets of Indonesian (classified as agglutinative) is mostly comparable to that of Persian (fusional); on the other hand, in all experimental settings that are applicable, the average number of morphemes per word for data sets of Russian (fusional) is always higher than that for data of the Mexican indigenous lan- guages (polysynthetic). These patterns resonate again with the our main point, that when data set size is small, the first data set or just one data set might not suffice to reflect the language features overall. Thus here we consider the characteristics to be specific to the small data sets in our experiments. For each random split (including a training and a test set) of every data set, we investigated: (1) word overlap, the proportion of words in the test set that also occur in the training set (only applicable to sam- pling with replacement); (2) morpheme overlap, the proportion of morphemes in the test set that also appear in the training set; (3) the ratio of the average number of morphemes per word between the training and test sets; (4) the distance between the distribution of the average number of mor- phemes per word in the training set and that in the test set; for this feature we used the Wasserstein distance for its ease of computation (Arjovsky l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 6 7 2 0 0 6 9 7 9 / / t l a c _ a _ 0 0 4 6 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Language Word overlap Morpheme overlap Ratio of avg. N Distance between distributions of morphemes of N of morphemes Ratio of avg. morpheme length Yorem Nokki 11.68** 17.10 13.64** Nahuatl 13.15** 49.56*** 14.22*** Wixarika 21.57*** 63.69*** −2.58 English 9.97** 50.35*** 26.01*** German 10.03** 61.09*** 21.44*** Persian 26.90*** 21.56*** 26.15*** Russian 3.38 69.49*** 11.96*** Turkish 15.88*** 44.31*** 1.37 Finnish 9.47** 60.58*** 10.49** Zulu 15.48*** 79.07*** 11.34*** Indonesian 8.12* 25.53*** 19.55*** −7.19 −3.16 −0.70 −6.78* 2.29 −3.82* −2.88** −0.73 −1.95 −4.14*** −6.46** 4.81 −1.15 −11.06** 8.44* 3.25 −3.09 3.19 0.30 −3.90 4.11 7.64* Table 3: Regression coefficients for random splits of data sets in all languages; a positive coefficient value corresponds to higher metric scores; the numbers in bold indicate significant effects; the number of * suggests significance level: * p < 0.05, ** p < 0.01, *** p < 0.001. et al., 2017; Søgaard et al., 2021); and (5) the ratio of the average morpheme length per word between the training and the test sets. To measure the individual effect of each fea- ture, we used linear regression. Because of the relatively large number of data sets that we have and our areas of interest, we fit the same regression model to the data of each lan- guage rather than combining the data from all languages. The regression predicts the metric scores of all models for each random split as a function of the five characteristics, described above, of the random split. Meanwhile we con- trolled for the roles of four other factors: the model alternatives, the metrics used, sampling methods, and data set size—the latter two of which also had interaction terms with the five characteristics. Given the components of our regression model, a smaller/larger value of the coefficient for the same factor here does not necessarily mean that this factor has a weaker/stronger role. In other words, the coefficients of the same feature are not comparable across the data for each language. Rather, our goal is simply to see whether a fea- ture potentially influences metric scores when other factors are controlled for (e.g., data set size) within the context of the data for every language. The regression results are presented in Table 3. It appears that the features with the most promi- nent roles are the proportion of morpheme overlap as well as the ratio of the average number of morphemes per word. Word overlap also has sig- nificant effects, though this is applicable only to data sets sampled with replacement. In com- parison, data set size does not appear to have significant positive effects in all cases; the excep- tions include the data for Yorem Nokki, Nahuatl, Wixarika, and Turkish. In scenarios where data set size does have an effect, its magnitude is much smaller compared to the characteristics in Table 3 that we studied. Thus, while data set size potentially plays a role in the results, it does not appear to be the sole or even the most important factor. The range of model performance is more dependent on the specific features of, or what is available in, the data sets. For example, larger training and test sets do not necessarily lead to higher morpheme overlap ratio. We adopted similar approaches to investigate the variability in the results when trained segmen- tation models were applied to new test sets of different sizes (Section 6.2). In these cases, the 405 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 6 7 2 0 0 6 9 7 9 / / t l a c _ a _ 0 0 4 6 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 five characteristics described before were mea- sured taking into account the training set of the segmentation model and each of the new test sets (100 in total for each training set). In contrast to the previous regression model, since the new test sets were sampled without replacement and since we are focusing on predictions derived from the best model alternative (but see Section 7.2), word overlap ratios and the model alternatives were not included in the regression. We additionally con- trolled for the effect of the new test set size. Again the same regression model was fit to the data of each language. Comparing the different features, morpheme overlap ratio and the average number of morphemes per word are again the two most pronounced factors in model performance, while the role of test set size is much less pronounced or even negligible. 7.4 Alternative Data Splits Our experiments so far involved random splits. While the heuristic or adversarial splits proposed in Søgaard et al. (2021) are also valuable, the success of these methods requires that the same data could be split based on heuristics, or be separated into training/test sets such that their distributions are as divergent as possible. To illustrate this point for morphological seg- mentation, we examined the possibility of the data sets being split heuristically and adversarially. For the former, we relied on the metric of the average number of morphemes per word, based on regres- sion results from Section 7.3. Given each data set within every experimental setting, we tried to automatically find a metric threshold so that the words in the data set are able to be separated by this threshold into training/test sets at the same 3:2 ratio, or a similar ratio; words in which the number of morphemes goes beyond this thresh- old were placed in the test set. We note that it is important (same as for adversarial splits) that the number of words in the resulting training and test sets follows a similar ratio to that for random splits. This is in order to ensure that the size of the training (or the test) set would not be a fac- tor for potential differences in model performance derived from different data split methods. In most of the data sets across settings, however, such a threshold for the average number of morphemes per word does not seem to exist. The exceptions are Wixarika, where the maximum number of data sets that are splittable this way is 35, for data sets containing 1,000 words sampled without replacement; and certain cases in Finnish, where the maximum number of data sets suitable for heuristic splitting is 11, when the data sets have 500 words sampled with replacement. For adversarial splitting, we split each data set (for five times, as well) via maximization of the Wasserstein distance between the training and the test sets (Søgaard et al., 2021). We then calculated the word overlap ratio between the test sets of the adversarial splits and those from the random splits. Across most of the experimental settings, the average word overlap ratios center around or are lower than 50%. This suggests that the training and test sets of adversarial splits are reasonably different from those derived after random splits; in other words, these data sets could be split adversarially. Although it is not the focus in this study to com- pare different ways of splitting data, we carried out adversarial splits for the data of Persian and Rus- sian, two of the languages with the largest range of data set sizes and new test set sizes. The models applied were second-order and fourth-order CRFs because of their overall good performance (Sec- tion 7). For each experimental setting, the results are still highly variable. Compared to splitting data randomly, the average metric scores of adversar- ial splits are lower (e.g., the mean difference of the average F1 scores between the two data split methods is 17.85 across settings for the data of Zulu, and 6.75 for the data of Russian), and the score ranges as well as standard deviations are higher. That being said, the results from these two data split methods are, arguably, not directly comparable, since with adversarial splits the test sets are constructed to be as different or distant as possible from the training sets. When applying the trained models to the same new test sets sampled from Section 6.2, the ob- servations are similar to the descriptions above, except the differences between the two data split methods regarding the mean metric scores, score ranges, and variances are much smaller. The most pronounced average difference in F1 is approxi- mately 7.0 when the experimental settings yield small data set sizes. On the other hand, within each setting, despite the model performance variability, the average results of the different test sizes are again comparable. 406 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 6 7 2 0 0 6 9 7 9 / / t l a c _ a _ 0 0 4 6 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 8 Discussion and Conclusion Using morphological segmentation as the test case, we compared three broad classes of models with different parameterizations in crosslinguistic low-resource scenarios. Leveraging data from 11 languages across six language families, our re- sults demonstrate that the best models and model rankings for the first data sets do not generalize well to other data sets of the same size, though the numerical differences in the results of the better-performing model alternatives are small. In particular, within the same experimental setting, there are noticeable discrepancies in model predic- tions for the first data set compared to the averages across all data sets; and the performance of each model alternative presents different yet signifi- cant score ranges and variances. When examining trained models on new test sets, considerable vari- ability exists in the results. The patterns described above speak to our concerns raised at the begin- ning, namely, that when facing a limited amount of data, model evaluation gathered from the first data set—or essentially any one data set—could fail to hold in light of new or unseen data. To remedy the observed inconsistencies in model performance, we propose that future work should consider utilizing random sampling from initial data for more realistic estimates. We draw support for this proposal from two patterns in our study. First, in each experimental setting, the difference between the average F1 score of the first data set and that across all 50 data sets is in general smaller than the range of the scores. Second, the average metric scores across unseen test sets of varying sizes in every setting are com- parable to each other; this holds for models trained from random splits and those trained using adver- sarial splits. Therefore, depending on the initial amount of data, it is important to construct data sets and new test sets of different sizes, then evaluate mod- els accordingly. Even if the size of the initial data set is small, as is the case with most en- dangered languages, it is worthwhile to sample with replacement in order to better understand model performance. Based on these observations, it would be interesting to analyze the potential factors that lead to the different degrees of gen- eralization, which could in turn provide guidance on what should be included or sampled in the training sets in the first place. Thorough compar- isons of different models should be encouraged even as the amount of data grows, particularly if the experimental settings are still situated within low-resources scenarios for the task at hand (Hedderich et al., 2021). Lastly, while we did not perform adversarial splits for all experimental settings here, for the cases that we have investigated, model perfor- mance from adversarial splits also yields high variability both across data sets of the same size and in new test sets. Though our criteria for heuristic splits were not applicable with the data explored, we would like to point out that for future endeavors, it would be necessary to at least check the applicability of different data splits, as we did in Section 7.4. As long as the data set possesses the properties that allow it to be divided by different split methods, it is worthwhile to further explore the influence of these splits, coupled with ran- dom sampling. Acknowledgments We are grateful to the reviewers and the action editor for their insightful feedback. This material is based upon work supported by the National Science Foundation under Grant # 2127309 to the Computing Research Association for the CIFel- lows Project, and Grant # 1761562. Any opinions, findings, and conclusions or recommendations ex- pressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation nor the Computing Research Association. References M. Ablimit, G. Neubig, M. Mimura, S. Mori, T. Kawahara, and A. Hamdulla. 2010. Uyghur morpheme-based language models and ASR. In ICASSP, pages 581–584. https://doi .org/10.1109/ICOSP.2010.5656065 Mohamed Afify, Ruhi Sarikaya, Hong-Kwang Jeff Kuo, Laurent Besacier, and Yuqing Gao. 2006. On the use of morphological analy- sis for dialectal Arabic speech recognition. In Ninth International Conference on Spoken Lan- guage Processing. https://doi.org/10 .21437/Interspeech.2006-87 407 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 6 7 2 0 0 6 9 7 9 / / t l a c _ a _ 0 0 4 6 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Ekin Akyurek and Jacob Andreas. 2021. Lexicon Learning for Few Shot Sequence Modeling. In Proceedings of the 59th Annual Meet- ing of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), pages 4934–4946, Online. Association for Computational Linguis- tics. https://doi.org/10.18653/v1 /2021.acl-long.382 Ebrahim Ansari, Zdenˇek ˇZabokrtsk´y, Hamid Haghdoost, and Mahshid Nikravesh. 2019a. Persian Morphologically Segmented Lexicon 0.5. LINDAT/CLARIAH-CZ digital library at the Institute of Formal and Applied Linguistics ( ´UFAL), Faculty of Mathematics and Physics, Charles University. using rich In Proceedings of Ebrahim Ansari, Zdenˇek ˇZabokrtsk´y, Mohammad Mahmoudi, Hamid Haghdoost, and Jon´aˇs 2019b. Supervised morphological Vidra. segmentation lexi- the International con. Conference on Recent Advances in Natu- ral Language Processing (RANLP 2019), pages 52–61, Varna, Bulgaria. INCOMA Ltd. https://doi.org/10.26615/978-954 -452-056-4 007 annotated Martin Arjovsky, Soumith Chintala, and L´eon Bottou. 2017. Wasserstein generative adver- sarial networks. In International Conference on Machine Learning, pages 214–223. PMLR. R. Harald Baayen, Richard Piepenbrock, and Leon Gulikers. 1996. The CELEX lexical database (cd-rom). Dzmitry Bahdanau, Kyung Hyun Cho, and Yoshua Bengio. 2015. Neural machine translation by In jointly learning to align and translate. 3rd International Conference on Learning Representations, ICLR 2015. Mark C. Baker. 1997. Complex predicates and agreement in polysynthetic languages. Complex predicates, pages 247–288. Emily M. Bender and Batya Friedman. 2018. Data statements for natural language pro- cessing: Toward mitigating system bias and enabling better science. Transactions of the Association for Computational Linguistics, 6:587–604. https://doi.org/10.1162 /tacl_a_00041 408 Taylor Berg-Kirkpatrick, David Burkett, and Dan Klein. 2012. An empirical investigation of statistical significance in NLP. In Pro- ceedings of the 2012 Joint Conference on Empirical Methods in Natural Language Pro- cessing and Computational Natural Language Learning, pages 995–1005, Jeju Island, Korea. Association for Computational Linguistics. Terra Blevins and Luke Zettlemoyer. 2019. Better character language modeling through morphology. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 1606–1613, Florence, Italy. Association for Computational Linguistics. https://doi.org/10.18653/v1/P19 -1156 Dallas Card, Peter Henderson, Urvashi Khandelwal, Robin Jia, Kyle Mahowald, and Dan Jurafsky. 2020. With little power comes great responsibility. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 9263–9274, Online. Association for Computational Linguistics. https://doi . o r g / 1 0 . 1 8 6 5 3 / v 1 / 2 0 2 0 . e m n l p - m a i n . 7 4 5 Kyunghyun Cho, Bart van Merri¨enboer, Caglar Gulcehre, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, and Yoshua Bengio. 2014. Learning phrase representations using RNN encoder–decoder for statistical machine trans- lation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Lan- guage Processing (EMNLP), pages 1724–1734, Doha, Qatar. Association for Computational Linguistics. Ann Clifton and Anoop Sarkar. 2011. Com- bining morpheme-based machine translation with post-processing morpheme prediction. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, pages 32–42, Portland, Oregon, USA. Association for Com- putational Linguistics. Michael Collins. 2002. Discriminative training methods for Hidden Markov Models: Theory and experiments with perceptron algorithms. In Proceedings of the 2002 Conference on Empir- ical Methods in Natural Language Processing (EMNLP 2002), pages 1–8. Association for l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 6 7 2 0 0 6 9 7 9 / / t l a c _ a _ 0 0 4 6 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Computational Linguistics. https://doi .org/10.3115/1118693.1118694 Ryan Cotterell, Arun Kumar, and Hinrich Sch¨utze. 2016a. Morphological segmentation inside-out. In Proceedings of the 2016 Conference on in Natural Language Empirical Methods Processing, pages 2325–2330, Austin, Texas. Association for Computational Linguistics. h t t p s : / / d o i . o r g / 1 0 . 1 8 6 5 3 / v 1 / D 1 6 - 1 2 5 6 In Proceedings of Ryan Cotterell, Thomas M¨uller, Alexander Fraser, and Hinrich Sch¨utze. 2015. Labeled mor- phological segmentation with semi-Markov the Nineteenth models. Conference on Computational Natural Lan- guage Learning, pages 164–174, Beijing, China. Association for Computational Linguis- tics. https://doi.org/10.18653/v1 /K15-1017 Ryan Cotterell, Tim Vieira, and Hinrich Sch¨utze. 2016b. A joint model of orthography and morphological segmentation. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pages 664–669, San Diego, California. Association for Computational Linguistics. h t t p s : / / d o i . o r g / 1 0 . 1 8 6 5 3 / v 1 / N 1 6 - 1 0 8 0 discovery of morphemes. Mathias Creutz and Krista Lagus. 2002. Un- In supervised Proceedings of the ACL-02 Workshop on Morphological and Phonological Learning, pages 21–30. Association for Computational Linguistics. https://doi.org/10.3115 /1118647.1118650 Nguyen Viet Cuong, Nan Ye, Wee Sun Lee, and Hai Leong Chieu. 2014. Conditional random field with high-order dependencies for sequence labeling and segmentation. Journal of Machine Learning Research, 15(1):981–1009. Yolanda Lastra de Su´arez. 1980. N´ahuatl de Acaxochitl´an (Hidalgo), El Colegio de M´exico. Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguis- tics: Human Language Technologies, Volume 409 1 (Long and Short Papers), pages 4171–4186, Minneapolis, Minnesota. Association for Com- putational Linguistics. recurrent neural networks. Prajit Dhar and Arianna Bisazza. 2021. Un- derstanding cross-lingual syntactic transfer in multilingual In Proceedings of the 23rd Nordic Conference on Computational Linguistics (NoDaLiDa), Iceland (Online). pages 74–85, Reykjavik, Link¨oping University Electronic Press, Sweden. Jesse Dodge, Suchin Gururangan, Dallas Card, Roy Schwartz, and Noah A. Smith. 2019. Show your work: Improved reporting of ex- perimental results. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Pro- cessing (EMNLP-IJCNLP), pages 2185–2194, Hong Kong, China. Association for Computa- tional Linguistics. https://doi.org/10 .18653/v1/D19-1224 Rotem Dror, Gili Baumer, Segev Shlomov, and Roi Reichart. 2018. The hitchhiker’s guide to testing statistical significance in natural language processing. In Proceedings of the 56th Annual Meeting of the Association for Compu- tational Linguistics (Volume 1: Long Papers), pages 1383–1392, Melbourne, Australia. Association for Computational Linguistics. h t t p s : / / d o i . o r g / 1 0 . 1 8 6 5 3 / v 1 / P 1 8 - 1 1 2 8 Jeffrey L. Elman. 1990. Finding structure in time. Cognitive Science, 14(2):179–211. https:// doi.org/10.1207/s15516709cog1402 1 Elif Eyig¨oz, Daniel Gildea, and Kemal Oflazer. 2013. Simultaneous word-morpheme align- ment for statistical machine translation. In Proceedings of the 2013 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pages 32–40, Atlanta, Georgia. Association for Computational Linguistics. Ray A. Freeze. 1989. Mayo de Los Capomos, Sinaloa. El Colegio de M´exico. Richard Futrell, Ethan Wilcox, Takashi Morita, Peng Qian, Miguel Ballesteros, and Roger language models as Levy. 2019. Neural psycholinguistic subjects: Representations of the 2019 syntactic state. In Proceedings of l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 6 7 2 0 0 6 9 7 9 / / t l a c _ a _ 0 0 4 6 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Conference of the North American Chapter of the Association for Computational Linguis- tics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 32–42, Minneapolis, Minnesota. Association for Com- putational Linguistics. https://doi.org /10.18653/v1/N19-1004 Andrew Garrett. 2011. An online dictionary with texts and pedagogical tools: The Yurok language project at Berkeley. International Journal 24(4):405–419. https://doi.org/10.1093/ijl/ecr018 of Lexicography, Timnit Gebru, Jamie Morgenstern, Briana Vecchione, Jennifer Wortman Vaughan, Hanna Wallach, Hal Daum´e III, and Kate Crawford. 2018. Datasheets for datasets. In Proceedings of the 5th Workshop on Fairness, Accountability, and Transparency in Machine Learning. Paula G´omez and Paula G´omez L´opez. 1999. Huichol de San Andr´es Cohamiata, Jalisco. El Colegio de M´exico. Kyle Gorman and Steven Bedrick. 2019. We need to talk about standard splits. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 2786–2791, Florence, Italy. Association for Computa- tional Linguistics. https://doi.org/10 .18653/v1/P19-1267 Michael A. Hedderich, Lukas Lange, Heike Adel, Jannik Str¨otgen, and Dietrich Klakow. 2021. A survey on recent approaches for natural language processing in low-resource scenar- ios. In Proceedings of the 2021 Conference of the North American Chapter of the Associ- ation for Computational Linguistics: Human Language Technologies, pages 2545–2568, Online. Association for Computational Linguis- tics. https://doi.org/10.18653/v1 /2021.naacl-main.201 Jennifer Hu, Jon Gauthier, Peng Qian, Ethan Wilcox, and Roger Levy. 2020. A systematic assessment of syntactic generalization in neural language models. In Proceedings of the 58th Annual Meeting of the Association for Compu- tational Linguistics, pages 1725–1744, Online. Association for Computational Linguistics. Robin Jia and Percy Liang. 2017. Adversarial ex- amples for evaluating reading comprehension systems. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, pages 2021–2031, Copenhagen, Denmark. Association for Computational Lin- guistics. https://doi.org/10.18653 /v1/D17-1215 Katharina Kann, Jesus Manuel Mager Hois, Ivan Vladimir Meza-Ruiz, and Hinrich Sch¨utze. 2018. Fortification of neural morphologi- cal segmentation models for polysynthetic minimal-resource languages. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers), pages 47–57, New Orleans, Louisiana. Association for Computa- tional Linguistics. Guillaume Klein, Yoon Kim, Yuntian Deng, Jean Senellart, and Alexander Rush. 2017. OpenNMT: Open-source toolkit for neural machine translation. In Proceedings of ACL 2017, System Demonstrations, pages 67–72, Vancouver, Canada. Association for Computa- tional Linguistics. https://doi.org/10 .18653/v1/P17-4012 Oskar Kohonen, Sami Virpioja, and Krista Lagus. 2010. Semi-supervised learning of concatena- tive morphology. In Proceedings of the 11th Meeting of the ACL Special Interest Group on Computational Morphology and Phonol- ogy, pages 78–86. https://doi.org/10 .18653/v1/P17-4012 Dan Kondratyuk and Milan Straka. 2019. 75 languages, 1 model: Parsing universal depen- dencies universally. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Pro- cessing (EMNLP-IJCNLP), pages 2779–2795, Hong Kong, China. Association for Computa- tional Linguistics. https://doi.org/10 .18653/v1/D19-1279 Mikko Kurimo, Sami Virpioja, Ville Turunen, and Krista Lagus. 2010. Morpho Challenge 2005-2010: Evaluations and results. In Pro- ceedings of the 11th Meeting of the ACL Special Interest Group on Computational Morphology and Phonology, pages 87–95, Uppsala, Sweden. Association for Computational Linguistics. John D. Lafferty, Andrew McCallum, and Fernando C. N. Pereira. 2001. Conditional ran- dom fields: Probabilistic models for segmenting 410 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 6 7 2 0 0 6 9 7 9 / / t l a c _ a _ 0 0 4 6 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 and labeling sequence data. In Proceedings of the Eighteenth International Conference on Machine Learning, pages 282–289. Brenden M. Lake and Marco Baroni. 2018. Generalization without systematicity: On the compositional skills of sequence-to-sequence the recurrent networks. 35th International Conference on Machine ICML 2018, Stockholmsm¨assan, Learning, Stockholm, Sweden, July 10-15, 2018, vol- ume 80 of Proceedings of Machine Learning Research, pages 2879–2888. PMLR. In Proceedings of Vladimir I. Levenshtein. 1966. Binary codes capa- ble of correcting deletions, insertions, and rever- sals. Soviet Physics Doklady, 10(8):707–710. Tal Linzen. 2020. How can we accelerate progress towards human-like linguistic gener- alization? In Proceedings of the 58th Annual Meeting of the Association for Computa- tional Linguistics, pages 5210–5217, Online. Association for Computational Linguistics. https://doi.org/10.18653/v1/2020 .acl-main.465 Tal Linzen and Marco Baroni. 2021. Syntactic structure from deep learning. Annual Review of Linguistics, 7(1):195–212. https://doi .org/10.1146/annurev-linguistics -032020-051035 Tal Linzen, Emmanuel Dupoux, and Yoav Goldberg. 2016. Assessing the ability of LSTMs to learn syntax-sensitive dependencies. Trans- actions of the Association for Computational Linguistics, 4:521–535. https://doi.org /10.1162/tacl_a_00115 Dong C. Liu and Jorge Nocedal. 1989. On the limited memory BFGS method for large scale optimization. Mathematical Program- ming, 45(1):503–528. https://doi.org /10.1007/BF01589116 Zoey Liu, Robert Jimerson, and Emily Prud’hommeaux. 2021. Morphological seg- mentation for Seneca. In Proceedings of the First Workshop on Natural Language Process- ing for Indigenous Languages of the Americas, pages 90–101, Online. Association for Compu- tational Linguistics. https://doi.org/10 .18653/v1/2021.americasnlp-1.10 Mitchell Marcus, Beatrice Santorini, and Mary Ann Marcinkiewicz. 1993. Building a large an- notated corpus of English: The Penn Treebank. 411 Computational Linguistics, 19(2):313–330. https://doi.org/10.21236/ADA273556 Rebecca Marvin and Tal Linzen. 2018. Targeted language models. syntactic evaluation of the 2018 Conference on In Proceedings of Empirical Methods in Natural Language Pro- cessing, pages 1192–1202, Brussels, Belgium. Association for Computational Linguistics. https://doi.org/10.18653/v1/D18-1151 R. Thomas McCoy, Robert Frank, and Linzen Tal. 2018. Revisiting the poverty of the stimulus: Hi- erarchical generalization without a hierarchical bias in recurrent neural networks. In Proceed- ings of the Cognitive Science Society, pages 2093–2098. Madison, WI. the 40th Annual Conference of R. Thomas McCoy, Junghyun Min, and Tal Linzen. 2020. BERTs of a feather do not generalize together: Large variability in gen- eralization across models with similar test the set performance. Third BlackboxNLP Workshop on Analyzing and Interpreting Neural Networks for NLP, pages 217–227, Online. Association for Com- putational Linguistics. https://doi.org /10.18653/v1/2020.blackboxnlp-1.21 In Proceedings of Tom McCoy, Ellie Pavlick, and Tal Linzen. 2019. Right for the wrong reasons: Diagnos- ing syntactic heuristics in natural language inference. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 3428–3448, Florence, Italy. Association for Computational Linguistics. https://doi.org/10.18653/v1/P19-1334 Barbra A. Meek. 2012. We Are Our Language: An Ethnography of Language Revitalization in a Northern Athabaskan Community. University of Arizona Press. Aaron Mueller, Garrett Nicolai, Panayiota and Tal Petrou-Zeniou, Natalia Talmina, Linzen. 2020. Cross-linguistic syntactic eval- uation of word prediction models. In Proceed- ings of the Association for Computational Linguistics, pages 5523–5539, Online. Association for Computational Linguistics. https://doi .org/10.18653/v1/2020.acl-main.490 the 58th Annual Meeting of Thomas Mueller, Helmut Schmid, and Hinrich Sch¨utze. 2013. Efficient higher-order CRFs for l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 6 7 2 0 0 6 9 7 9 / / t l a c _ a _ 0 0 4 6 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 morphological tagging. In Proceedings of the 2013 Conference on Empirical Methods in Nat- ural Language Processing, pages 322–332, Seattle, Washington, USA. Association for Computational Linguistics. Naoaki Okazaki. 2007. CRFsuite: A fast im- random Fields plementation of conditional (CRFs). Pranav Rajpurkar, Jian Zhang, Konstantin Lopyrev, and Percy Liang. 2016. SQuAD: 100,000+ questions for machine comprehen- the 2016 sion of Conference on Empirical Methods in Natu- ral Language Processing, pages 2383–2392, Austin, Texas. Association for Computational Linguistics. In Proceedings of text. In Proceedings of Alan Ramponi and Barbara Plank. 2020. Neural unsupervised domain adaptation in NLP—A the 28th Inter- survey. national Conference on Computational Lin- guistics, pages 6838–6855, Barcelona, Spain (Online). International Committee on Compu- tational Linguistics. https://doi.org/10 .18653/v1/2020.coling-main.603 Nils Reimers and Iryna Gurevych. 2017. Re- porting score distributions makes a difference: performance study of LSTM-networks for Se- quence Tagging. In Proceedings of the 2017 Conference on Empirical Methods in Nat- ural Language Processing, pages 338–348, Copenhagen, Denmark. Association for Com- putational Linguistics. https://doi.org /10.18653/v1/D17-1035 Jorma Rissanen. 1998. Stochastic Complexity in Statistical Inquiry, volume 15. World scientific. Teemu Ruokolainen, Oskar Kohonen, Sami Virpioja, and Mikko Kurimo. 2013. Supervised morphological segmentation in a low-resource learning setting using conditional random the Seventeenth In Proceedings of fields. Conference on Computational Natural Lan- guage Learning, pages 29–37, Sofia, Bulgaria. Association for Computational Linguistics. Wolfgang Seeker and ¨Ozlem C¸ etino˘glu. 2015. A graph-based lattice dependency parser for joint morphological segmentation and syntac- tic analysis. Transactions of the Association for Computational Linguistics, 3:359–373. https://doi.org/10.1162/tacl a 00144 412 Anders Søgaard. 2013. Estimating effect size across datasets. In Proceedings of the 2013 Con- ference of the North American Chapter of the Association for Computational Linguistics: Hu- man Language Technologies, pages 607–611. Association for Computational Linguistics, Atlanta, Georgia. Anders Søgaard, Sebastian Ebert, Jasmijn Bastings, and Katja Filippova. 2021. We need In Proceed- to talk about random splits. ings of the 16th Conference of the European Chapter of the Association for Computational Linguistics: Main Volume, pages 1823–1832, Online. Association for Computational Linguis- tics. https://doi.org/10.18653/v1 /2021.eacl-main.156 Alexey Sorokin and Anastasia Kravtsova. 2018. Deep convolutional networks super- vised morpheme segmentation of Russian language. In Conference on Artificial Intel- ligence and Natural Language, pages 3–10. https://doi.org/10.1007 Springer. /978-3-030-01204-5_1 for Justin Spence. 2013. Language Change, Contact, and Koineization in Pacific Coast Athabaskan. Ph.D. thesis, University of California, Berkeley. Sebastian Spiegler, Andrew van der Spuy, and Peter A. Flach. 2010. Ukwabelana - An open-source morphological Zulu corpus. In Proceedings of the 23rd International Con- ference on Computational Linguistics (Coling 2010), pages 1020–1028, Beijing, China. Coling 2010 Organizing Committee. Piotr Szyma´nski and Kyle Gorman. 2020. Is the best better? Bayesian statistical model comparison for natural language process- ing. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 2203–2212, On- line. Association for Computational Linguis- tics. https://doi.org/10.18653/v1 /2020.emnlp-main.172 Martha Tachbelie, Solomon Teferra Abate, and Laurent Besacier. 2014. Using differ- ent acoustic, lexical and language model- ing units for ASR of an under-resourced language - Amharic. Speech Communica- tion, 56. https://doi.org/10.1016/j .specom.2013.01.008 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 6 7 2 0 0 6 9 7 9 / / t l a c _ a _ 0 0 4 6 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Tristan Thrush, Ethan Wilcox, and Roger Levy. 2020. Investigating novel verb Learn- ing in BERT: Selectional preference classes and alternation-based syntactic generalization. In Proceedings of the Third BlackboxNLP Workshop on Analyzing and Interpreting Neural Networks for NLP, pages 265–275, Online. Association for Computational Linguis- tics. https://doi.org/10.18653/v1 /2020.blackboxnlp-1.25 Antal van den Bosch and Walter Daelemans. 1999. Memory-based morphological analysis. the 37th Annual Meet- In Proceedings of ing of the Association for Computational Linguistics, pages 285–292, College Park, Maryland, USA. Association for Computational Linguistics. https://doi.org/10.3115 /1034678.1034726 Tim Vieira, Ryan Cotterell, and Jason Eisner. 2016. Speed-accuracy tradeoffs in tagging with variable-order CRFs and structured sparsity. the 2016 Conference on In Proceedings of Empirical Methods in Natural Language Processing, pages 1973–1978, Austin, Texas. Association for Computational Linguistics. https://doi.org/10.18653/v1/D16-1206 Alex Wang, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel Bowman. 2018. GLUE: A multi-task benchmark and language un- analysis platform for natural the 2018 In Proceedings of derstanding. EMNLP Workshop BlackboxNLP: Analyz- ing and Interpreting Neural Networks for NLP, pages 353–355, Brussels, Belgium. Association for Computational Linguistics. https://doi.org/10.18653/v1/W18-5446 Yiwen Wang, Jennifer Hu, Roger Levy, and Peng Qian. 2021. Controlled evaluation of grammatical knowledge in Mandarin Chinese language models. In Proceedings of the 2021 Conference on Empirical Methods in Natu- ral Language Processing, pages 5604–5620, Online and Punta Cana, Dominican Repub- lic. Association for Computational Linguis- tics. https://doi.org/10.18653/v1 /2021.emnlp-main.454 Noah Weber, Leena Shekhar, and Niranjan Balasubramanian. 2018. The fine line be- tween linguistic generalization and failure in seq2seq-attention models. In Proceedings of the Workshop on Generalization in the Age of Deep Learning, pages 24–27, New Orleans, Louisiana. Association for Computa- tional Linguistics. https://doi.org/10 .18653/v1/W18-1004 the 2019 Conference of Ethan Wilcox, Peng Qian, Richard Futrell, Miguel Ballesteros, and Roger Levy. 2019. Structural supervision improves learning of non-local grammatical dependencies. In Pro- ceedings of the North American Chapter of the Association for Computational Linguistics: Human Lan- guage Technologies, Volume 1 (Long and Short Papers), pages 3302–3312, Minneapo- lis, Minnesota. Association for Computa- tional Linguistics. https://doi.org/10 .18653/v1/N19-1334 Ethan Wilcox, Peng Qian, Richard Futrell, Ryosuke Kohita, Roger Levy, and Miguel Ballesteros. 2020. Structural supervision im- proves few-shot learning and syntactic gen- language models. eralization in neural In Proceedings of the 2020 Conference on in Natural Language Empirical Methods Processing (EMNLP), pages 4640–4652, On- line. Association for Computational Linguis- tics. https://doi.org/10.18653/v1 /2020.emnlp-main.375 Beilei Xiang, Changbing Yang, Yu Li, Alex Warstadt, and Katharina Kann. 2021. CLiMP: A benchmark for Chinese language model evaluation. In Proceedings of the 16th Confer- ence of the As- the European Chapter of sociation for Computational Linguistics: Main Volume, pages 2784–2790, Online. Association for Computational Linguistics. https://doi.org/10.18653/v1/2021.eacl -main.242 Matthew D. Zeiler. 2012. Adadelta: An adap- tive learning rate method. arXiv preprint arXiv:1212.5701v1. Xiang Zhou, Yixin Nie, Hao Tan, and Mohit Bansal. 2020. The curse of performance instability in analysis datasets: Consequences, In Proceedings and suggestions. source, on Empirical 2020 Conference the of Methods in Natural Language Process- ing (EMNLP), pages 8215–8228, Online. for Computational Linguis- Association tics. https://doi.org/10.18653/v1 /2020.emnlp-main.659 413 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 6 7 2 0 0 6 9 7 9 / / t l a c _ a _ 0 0 4 6 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Data-driven Model Generalizability in Crosslinguistic Low-resource image

Télécharger le PDF