Communicated by David A. Robinson
A Control Systems Model of Smooth Pursuit Eye
Movements with Realistic Emergent Properties
R.. J.. Krauzlis
S. G. Lisberger
Department of Physiology and Neuroscience Graduate Program,
University of California, San Fkancisco, C A 94143, Etats-Unis
Visual tracking of objects in a noisy environment is a difficult problem
that has been solved by the primate oculomotor system, but remains
unsolved in robotics. In primates, smooth pursuit eye movements
match eye motion to target motion to keep the eye pointed at smoothly
moving targets. We have used computer models as a tool to investigate
possible computational strategies underlying this behavior. Ici, nous
present a model based upon behavioral data from monkeys. The model
emphasizes the variety of visual signals available for pursuit and, dans
particular, includes a sensitivity to the acceleration of retinal images.
The model was designed to replicate the initial eye velocity response
observed during pursuit of different target motions. The strength of
the model is that it also exhibits a number of emergent properties that
are seen in the behavior of both humans and monkeys. This suggests
that the elements in the model capture important aspects of the mech-
anism of visual tracking by the primate smooth pursuit system.
1 Introduction
Computer models have advanced our understanding of eye movements
by providing a framework in which to test ideas suggested by behavioral
and physiological studies. Our knowledge of the smooth pursuit system
is at a stage where such models are especially useful. We know that
pursuit eye movements are a response to visual motion and that they are
used by primates to stabilize the retinal image of small moving targets.
Lesion and electrophysiological studies have identified several cortical
and subcortical sites that are involved in pursuit (see Lisberger et al.
1987 for review), but the precise relationship between the visual motion
signals recorded at these sites and those used by pursuit remain unclear.
We present a model that was designed to replicate the monkey’s initial
eye velocity response as a function of time for different pursuit target
motions. The model emphasizes the variety of visual signals available
for pursuit and minimizes the computations done by motor pathways.
The structure of the model is based upon behavioral experiments which
Neural Computation 1,116122 (1989) @ 1989 Massachusetts Institute of Technology
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
1
6
8
1
1
8
0
5
n
e
c
o
1
9
8
9
1
1
1
1
6
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Control Systems Model of Smooth Pursuit Eye Movements
117
have characterized how different aspects of visual motion act to initiate
pursuit. In monkeys, the pursuit system responds not only to the velocity
of retinal images, but also to smooth accelerations and to the abrupt
accelerations that accompany the onset of target motion (Krauzlis and
Lisberger 1987; Lisberger and Westbrook 1985). Donc, the model
includes three parallel pathways that are sensitive to these three aspects
of visual motion.
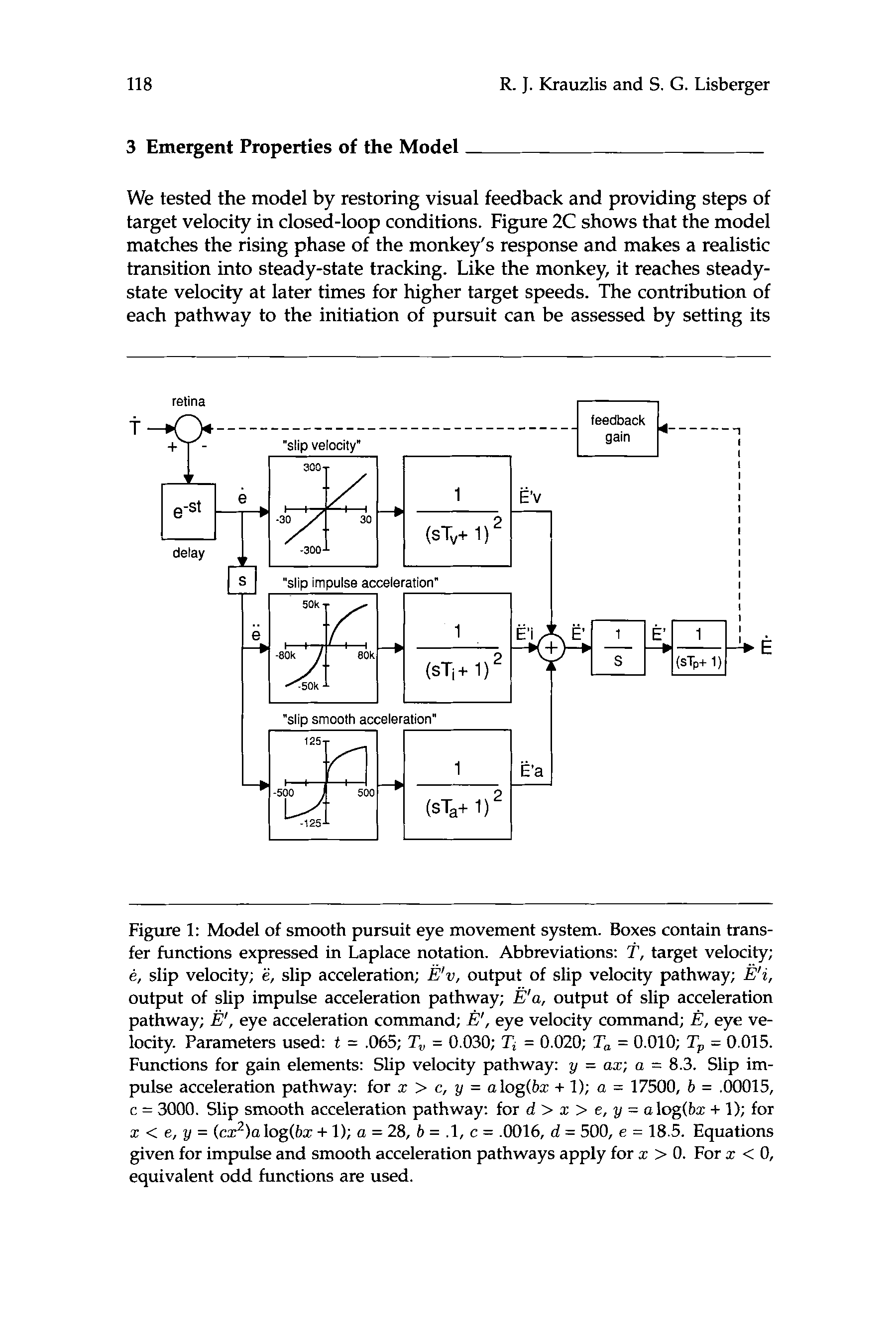
2 Structure of the Model
Our model is drawn in figure 1. Within each pathway, a time-delayed
signal related to the motion of retinal images (?’ – E , called retinal “slip”)
is processed by a nonlinear gain element derived from our behavioral ex-
periments and a filter. The first pathway is sensitive to slip velocity (C)
and its gain is linear. The second and third pathways are both sensitive to
slip acceleration (il, but in different ways. The impulse acceleration path-
way is sensitive to the large accelerations that accompany step changes
in target velocity, but has a dead zone in the gain element that renders it
insensitive to smaller accelerations. The smooth acceleration pathway is
sensitive to gradual changes in image velocity. The outputs of the gain
elements in each pathway are low pass filtered to produce three signals
with different dynamics (&w, Pi, p a ) that are then summed and inte-
grated to give a command for eye velocity (je?). The integrator makes
our model reproduce the fact that the pursuit system interprets visual
inputs as commands for eye accelerations (Lisberger et al. 1981). Eye
velocity ( E ) is obtained by passing the eye velocity command through a
low pass filter that represents the eye muscles and orbital tissues.
The behavior of the model was refined by matching its performance
under open-loop conditions to that of the monkey. We removed visual
feedback by setting the value of feedback gain to zero, and compared
the model’s output to averages of the monkey’s eye velocity in behav-
ioral trials where visual feedback was electronically eliminated for 200 ms
(methods in Morris and Lisberger 1987). D'abord, we stimulated the model
with steps in target velocity, which activate the slip velocity and impulse
acceleration pathways. We adjusted the filters in these pathways to ob-
tain the fit in figure 2A, where the rising phase of the model’s output
(dotted lines) matches the rising phase of the monkey’s eye velocity (solid
lines) during the open-loop portion of the monkey’s response. Alors, nous
stimulated the model with steps in target acceleration, which activates
the slip velocity and smooth acceleration pathways, and adjusted the
filter in the smooth acceleration pathway (figue. 2B).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
1
6
8
1
1
8
0
5
n
e
c
o
1
9
8
9
1
1
1
1
6
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
118
R.. J.. Krauzlis and S. G. Lisberger
3 Emergent Properties of the Model
We tested the model by restoring visual feedback and providing steps of
target velocity in closed-loop conditions. Figure 2C shows that the model
matches the rising phase of the monkey’s response and makes a realistic
transition into steady-state tracking. Like the monkey, it reaches steady-
state velocity at later times for higher target speeds. The contribution of
each pathway to the initiation of pursuit can be assessed by setting its
retina
m
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
1
“sib smooth acceleration”
je
F
/
/
/
/
/
1
1
1
1
6
8
1
1
8
0
5
n
e
c
o
1
9
8
9
1
1
1
1
6
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 1: Model of smooth pursuit eye movement system. Boxes contain trans-
fer functions expressed in Laplace notation. Abbreviations: T , target velocity;
e, slip velocity; e, slip acceleration; E’v, output of slip velocity pathway; B’i,
output of slip impulse acceleration pathway; p a , output of slip acceleration
pathway; e’, eye acceleration command; je?', eye velocity command; E , eye ve-
locity. Parameters used: t = .065; T, = 0.030; Ti = 0.020; T, = 0.010; Tp = 0.015.
Functions for gain elements: Slip velocity pathway: y = az; a = 8.3. Slip im-
pulse acceleration pathway: for z > c, y = alog(bz + 1); a = 17500, b = .00015,
c = 3000. Slip smooth acceleration pathway: for d > z > e, y = alog(bz + 1); pour
z < e, y = (cz2)alog(bz + 1); a = 28, b = .l, c = .0016, d = 500, e = 18.5. Equations
given for impulse and smooth acceleration pathways apply for z > 0. For z < 0,
equivalent odd functions are used.
A Control Systems Model of Smooth Pursuit Eye Movements
119
gain to zero, effectively “lesioning” that limb of the model. When the slip
impulse acceleration pathway is lesioned, the rising phase is delayed and
more sluggish, but the transition to steady-state tracking is unchanged
(Fig. 2D, open arrow). This pathway contributes exclusively to the initial
25-50 ms of the response to steps in target velocity and allows the model
to reproduce the observation that the earliest component of the pursuit
response is sensitive to target direction, but relatively insensitive to target
speed (Lisberger and Westbrook 1985). When the smooth acceleration
pathway is eliminated, the rising phase is unchanged, but there is a large
overshoot in the transition to steady-state tracking (Fig. 2D, filled arrow).
Thus, the smooth acceleration pathway normally decelerates the eye as
eye velocity approaches target velocity. This is an emergent property of
the model, since this pathway was tuned by adjusting its contribution to
the acceleration of the eye as shown in figure 2B.
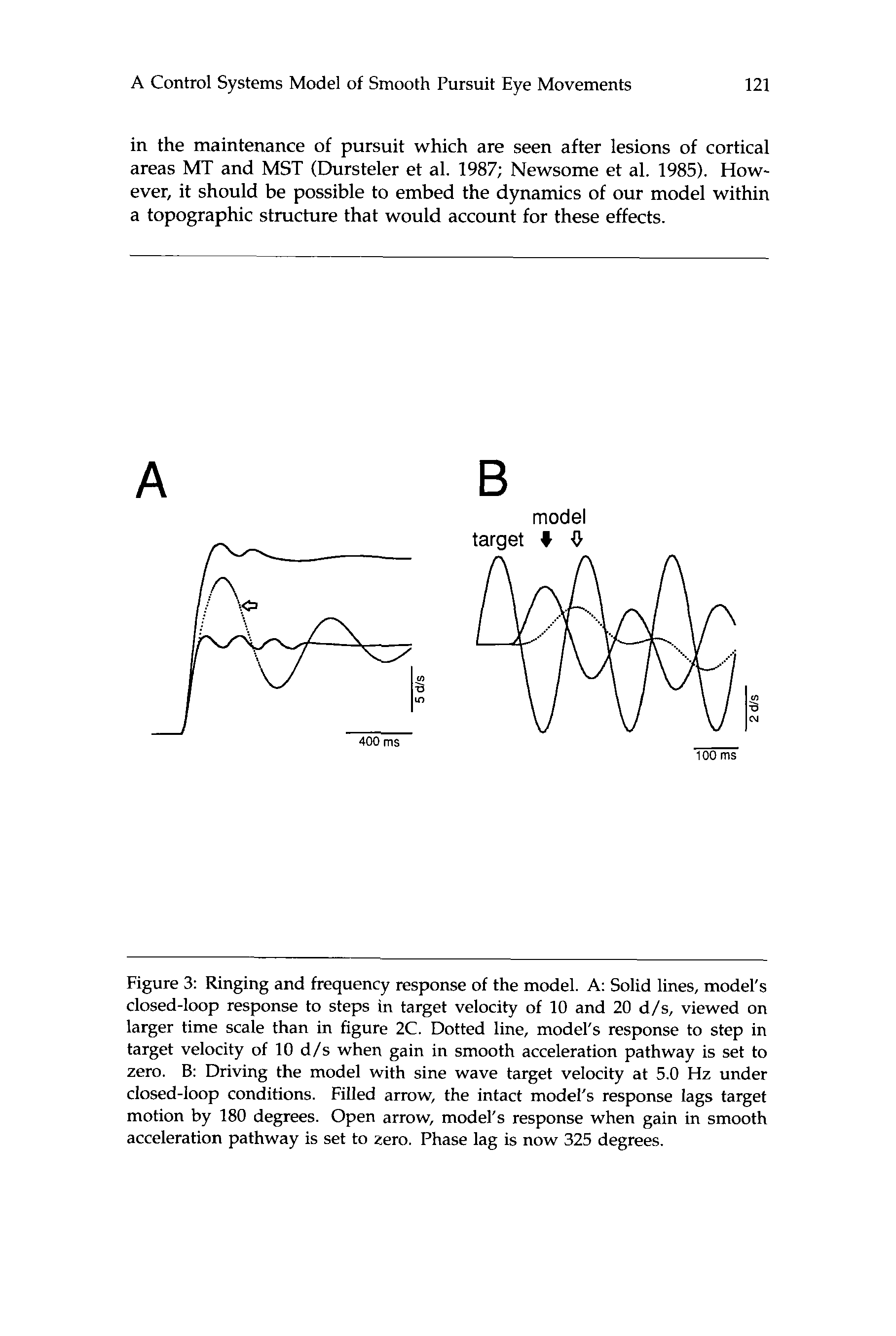
The model rings at a relatively high frequency, 5 Hz, in response to
steps in target velocity (solid lines in figure 3A). Similar oscillations are
seen in the behavior of both humans and monkeys (Goldreich and Lis-
berger 1987; Robinson et al. 1986). If the model is driven at this resonant
frequency, the output lags target velocity by 180 degrees (Fig. 3B, filled
arrow), an effect that is also seen in the monkey’s behavior (Goldreich
and Lisberger 1987). The high frequency properties of the model depend
upon the presence of the smooth acceleration pathway. If this pathway
is eliminated, the spontaneous oscillations still occur, but now at only 1.6
Hz (Fig. 3A, open arrow), and the phase lag in the response to sinusoidal
inputs increases (Fig. 3B, open arrow).
4 Discussion
An important property of our model is that it allows independent control
over the initiation and maintenance phases of pursuit. The rising phase
is determined mainly by the slip velocity and impulse acceleration path-
ways. The steady-state behavior is determined primarily by the smooth
acceleration pathway. Since the differentiator in the smooth accelera-
tion pathway introduces a phase lead, the steady-state behavior of the
model has a higher frequency response than the rising phase. The exact
frequency of ringing depends upon the total delay around the smooth
acceleration pathway. For example, if the delay in the visual input is
increased by 30 ms, the model will ring at 3.8 Hz, similar to what is nor-
mally observed in humans (Robinson et al. 1986) or in monkeys when the
delay in visual feedback is increased (Goldreich and Lisberger 1987). The
amount of ringing depends upon the gain element in the smooth accel-
eration pathway. Lowering the gain dampens or eliminates the ringing,
increasing the gain produces persistent ringing. Such variations are also
seen on individual trials in the monkey’s behavior.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
1
1
6
8
1
1
8
0
5
n
e
c
o
1
9
8
9
1
1
1
1
6
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
120
R. J. Krauzlis and S. G. Lisberger
25 B
15
5
120
64
45
...--.. ..
'..
;.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
Figure 2: Comparison of the eye velocity output from the model and the mon-
key. In all panels, dotted lines show the model's output and solid lines show
the monkey's eye velocity. A: Steps in target velocity of 5, 15, and 25 d/s under
open-loop conditions. The monkey's open-loop response lasts for the first 200
ms of his response. B: Steps in target acceleration of 45, 64, and 120 d/s2 un-
der open-loop conditions. C: Steps in target velocity of 5, 15, and 25 d/s under
closed-loop conditions. D Effect of lesioning either acceleration pathway on the
model's response to a step in target velocity of 20 d/s. Open arrow, model's
response when gain in slip impulse acceleration pathway is set to zero. Closed
arrow, model's response when gain in slip smooth acceleration pathway is set
to zero.
The strength of our model is that it uses open-loop behavioral data
to embody the pursuit system's sensitivity to different aspects of visual
motion. Although it was designed to replicate the dynamics of the initi-
ation of pursuit, the model also serendipitously solves a problem noted
by Robinson (Robinson et al. 1986), namely, that the rising phase of pur-
suit is sluggish compared to the frequency of its ringing. The emergence
of realistic steady-state properties in the model indicates that the visual
elements in its pathways capture important aspects of signal processing
within the smooth pursuit system. Our model does not include a sensitiv-
ity to position errors, which can affect steady-state tracking in monkeys
(Morris and Lisberger 1987). It also does not include the topographic
organization of the visual system and therefore cannot reproduce the
retinotopic deficits in the initiation of pursuit or the directional deficits
/
/
/
/
1
1
1
1
6
8
1
1
8
0
5
n
e
c
o
1
9
8
9
1
1
1
1
6
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Control Systems Model of Smooth Pursuit Eye Movements
121
in the maintenance of pursuit which are seen after lesions of cortical
areas MT and MST (Dursteler et al. 1987; Newsome et al. 1985). How-
ever, it should be possible to embed the dynamics of our model within
a topographic structure that would account for these effects.
A
B
model
target 4 U
400 ms
-
100 ms
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
1
1
6
8
1
1
8
0
5
n
e
c
o
1
9
8
9
1
1
1
1
6
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3: Ringing and frequency response of the model. A: Solid lines, model's
closed-loop response to steps in target velocity of 10 and 20 d/s, viewed on
larger time scale than in figure 2C. Dotted line, model's response to step in
target velocity of 10 d / s when gain in smooth acceleration pathway is set to
zero. 8: Driving the model with sine wave target velocity at 5.0 Hz under
closed-loop conditions. Filled arrow, the intact model's response lags target
motion by 180 degrees. Open arrow, model's response when gain in smooth
acceleration pathway is set to zero. Phase lag is now 325 degrees.
122
R. J. Krauzlis and S. G. Lisberger
Acknowledgments
This research was supported by NIH Grants EY03878 a n d EY07058.
References
Dursteler, M.R., R.H. Wurtz, and W.T. Newsome. 1987. Directional Pursuit
Deficits Following Lesions of the Foveal Representation within the Superior
Temporal Sulcus of the Macaque Monkey. J. Neurophysiol 57, 1262-1287.
Goldreich, D. and S.G. Lisberger. 1987. Evidence that Visual Inputs Drive
Oscillations in Eye Velocity during Smooth Pursuit Eye Movements in the
Monkey. SOC. Neurosci. Abstr. 13, 170.
Krauzlis, R.J. and S.G. Lisberger. 1987. Smooth Pursuit Eye Movements are Not
Driven Simply by Target Velocity. SOC. Neurosci. Abstr. 13, 170.
Lisberger, S.G., C. Evinger, G.W. Johanson, and A.F. Fuchs. 1981. Relationship
between Eye Acceleration and Retinal Image Velocity during Foveal Smooth
Pursuit Eye Movements in Man and Monkey. J. Neurophysiol. 46,229-249.
Lisberger, S.G., E.J. Morris, and L. Tychsen. 1987. Visual Motion Processing and
Sensory-motor Integration for Smooth Pursuit Eye Movements. Ann. Rev.
Neurosci. 10, 97-129.
Lisberger, S.G. and L.E. Westbrook.
1985. Properties of Visual Inputs that
Initiate Horizontal Smooth Pursuit Eye Movements in Monkeys. J. Neurosci.
5, 1662-1673.
Morris, E.J. and S.G. Lisberger. 1987. Different Responses to Small Visual Errors
during Initiation and Maintenance of Smooth-pursuit Eye Movements in
Monkeys. J. Neurophysiol. 58, 1351-1369.
Newsome, W.T., R.H. Wurtz, M.R. Dursteler, and A. Mikami. 1985. Deficits
in Visual Motion Processing Following Ibotenic Acid Lesions of the Middle
Temporal Area of the Macaque Monkey. J. Neurosci. 5, 825-840.
Robinson, D.A., J.L. Gordon, and S.E. Gordon. 1986. A Model of the Smooth
Pursuit Eye Movement System. Biol. Cybern. 55, 43-57.
Received 15 August; accepted 1 October 1988.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
1
1
6
8
1
1
8
0
5
n
e
c
o
1
9
8
9
1
1
1
1
6
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3