Beyond Hemispheric Dominance: Brain Regions
Underlying the Joint Lateralization of Language
and Arithmetic to the Left Hemisphere

Philippe Pinel1,2,3 and Stanislas Dehaene1,2,3,4

Abstrait

& Language and arithmetic are both lateralized to the left
hemisphere in the majority of right-handed adults. Encore, does
this similar lateralization reflect a single overall constraint of
brain organization, such an overall ‘‘dominance’’ of the left
linguistic and symbolic operations? Est-ce
hemisphere for all
related to the lateralization of specific cerebral subregions? Or
is it merely coincidental? To shed light on this issue, nous
performed a ‘‘colateralization analysis’’ over 209 healthy sub-
projets: We investigated whether normal variations in the degree
of left hemispheric asymmetry in areas involved in sentence
listening and reading are mirrored in the asymmetry of areas
involved in mental arithmetic. Within the language network,
a region-of-interest analysis disclosed partially dissociated
patterns of lateralization, inconsistent with an overall ‘‘domi-

nance’’ model. Only two of these areas presented a lateraliza-
tion during sentence listening and reading which correlated
strongly with the lateralization of two regions active during
calculation. Spécifiquement, the profile of asymmetry in the pos-
terior superior temporal sulcus during sentence processing
covaried with the asymmetry of calculation-induced activation
in the intraparietal sulcus, and a similar colateralization linked
the middle frontal gyrus with the superior posterior parietal
lobule. Given recent neuroimaging results suggesting a late
emergence of hemispheric asymmetries for symbolic arithmetic
during childhood, we speculate that these colateralizations
might constitute developmental traces of how the acquisition
of linguistic symbols affects the cerebral organization of the
arithmetic network. &

INTRODUCTION

Strong left hemispheric asymmetry is a striking character-
istic of the cerebral regions involved in language process-
ing, both at the functional and at the anatomical level,
noticeably around the peri-sylvian and temporal struc-
photos (Toga & Thompson, 2003; Geschwind & Levitsky,
1968). The left hemisphere also plays a key role in mental
arithmetic, as revealed by both lesion patterns (acalculia
being strongly linked to left parietal lesions, as shown by
Jackson & Warrington, 1986) and by more recent fMRI
(Chochon, Cohen, van de Moortele, & Dehaene, 1999).
Based on the observation of joint deficits in language and
calculation following unilateral brain lesions, the classical
neurological wisdom stipulates that the left hemisphere is
‘‘dominant’’ for both language and calculation. Dans ce
vein, Semenza et al. (2006) reported, in the special case of
right hemisphere aphasia, a co-occurrence of language
and arithmetic impairments.

The neuropsychological concept of ‘‘dominance,’’
cependant, seems very coarse in the face of our recent
ability to finely dissect, with neuroimaging methods, le
specific areas involved in language and arithmetic tasks.

1INSERM, Gif-sur-Yvette, France, 2CEA, Gif-sur-Yvette, France,
3Universite´ Paris-Sud, Gif-sur-Yvette, France, 4Colle`ge de France,
Paris, France

Are all of these areas equally lateralized to the left hemi-
sphère, as would be predicted by a single overarching
‘‘dominance’’ factor? Or are there much more specific
patterns of colateralization between language and arith-
metic, restricted to a small subset of brain areas linking
the two domains? Enfin, a third possibility is that al-
though both language and arithmetic relate to the left
hemisphere, these are two independent patterns that
just happen to coincide. Par exemple, the left hemi-
spheric lateralization for language could result from an
early asymmetry in structure and functions of the tem-
poral lobe (Tervaniemi & Hugdahl, 2003; Chi, Dooling,
& Gilles, 1977), whereas the parietal hemispheric spe-
cialization for quantities processing (the left parietal lobe
being more involved in exact calculation and the right
one more involved in judgment on analogical quantities;
Piazza, Mechelli, Prix, & Butterworth, 2006; Stanescu-
Cosson et al., 2000) may mirror an initial left hemispheric
advantage for processing stimuli as categories, alors que
the right hemisphere shows a preference for process-
ing analogical dimensions (Kosslyn et al., 1989; see also
Vauclair, Yamazaki, & Gu¨ntu¨rku¨n, 2006 for an extension
to animals studies).

In the present work, we aimed to further specify the
anatomical bases of the joint lateralization of language
and arithmetic to the left hemisphere, using as a source

D 2009 Massachusetts Institute of Technology

Journal des neurosciences cognitives 22:1, pp. 48–66

D
o
w
n
je
o
un
d
e
d

je

je

/

/

/

/
j

F
/

t
t

je
t
.

:
/
/

F
r
o
m
D
h
o
t
w
t
n
p
o
:
un
/
d
/
e
m
d
je
F
t
r
o
p
m
r
c
h
.
s
p
je
je
d
v
je
e
r
e
r
c
c
t
.
h
m
un
je
r
e
d
.
toi
c
o
o
m
c
/
n
j
un
o
r
c
t
je
n
c
/
e
un
–
p
r
d
t
je
2
c
2
je
1
e
–
4
p
8
d
1
F
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
oui
0
g
0
toi
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
F
e
m
b
oui
b
e
g
r
toi
2
e
0
2
s
3
t

/
j

t

.

F

/

.

.

o
n

1
8

M.
un
oui

2
0
2
1

of data the normal interindividual variability in functional
lateralization. Using a very large database of fMRI activa-
tion from 209 healthy subjects, we could study the inter-
correlations between the lateralization indices of many
brain regions active during either sentence listening, sen-
tence reading, or mental arithmetic tasks. As we shall see,
this ‘‘colateralization analysis’’ suggests that functional
lateralization is not a simple issue of one hemisphere
‘‘dominating’’ over the other, but a more subtle phe-
nomenon linking specific cortical areas.

Our interest in the lateralization of arithmetic stemmed
from a much broader debate, which concerns whether
mental arithmetic is shaped by the organization of the
language system (Gordon, 2004; Pica, Lemer, Izard, &
Dehaene, 2004). Although arithmetical procedures are
mainly based on a language-like system with a dedicated
set of symbols and syntax, several published results un-
derline the relative independence of linguistic and ar-
ithmetical abilities. Mastery of arithmetical procedures,
par exemple, has been reported to be dissociable from lan-
guage impairment in many different neurological cases,
including aphasic patients (Cohen, Dehaene, Chochon,
Lehe´ricy, & Naccache, 2000), patients affected by semantic
dementia (Cappelletti, Butterworth, & Kopelman, 2001),
or agrammatic patients (Varley, Klessinger, Romanowski,
& Siegal, 2005). This suggests that, at least for adult
sujets, the core system for number manipulation is largely
independent from the language network (Butterworth,
2005).

According to some theories, the extent to which cal-
culation relies on a linguistic coding of numbers may
depend on the arithmetic task. It is assumed in the
triple-code model (Dehaene & Cohen, 1995), based on
neurological dissociation reports, that quantity manipu-
lations rely on a nonverbal analogical representation of
numbers, used for instance to compare numbers or to
approximate simple operations, whereas the memoriza-
tion of exact arithmetical facts relies on a verbal memory
store (Lefevre, 1996). To support this model, Dehaene,
Piazza, Pinel, and Cohen (2003) published a meta-analysis
of numerical paradigms and reported two distinct sites
located in the fundus of the horizontal part of the in-
traparietal sulcus (hIPS) and in the angular gyrus (AG),
which may be the correlates of quantity manipulation
and of arithmetical fact storage, respectivement. In agree-
ment with the model, activation during a mental calcu-
lation task shifts from the hIPS to the AG after arithmetic
entraînement, as subjects rely less on active number manipu-
lation and more on fact retrieval ( Venkatraman, Siong,
Chee, & Ansari, 2006; Delazer et al., 2003). The core
system of ‘‘number sense,’’ located in the hIPS, would
thus be anatomically and functionally distinct from the
language areas, usually described as belonging to the
inferior frontal, peri-sylvian, and superior temporal re-
gions (Binder et al., 2000; Hickok & Poeppel, 2000).

Recently, cependant, it has become apparent that even
within the domain of simple nonsymbolic calculations

accessible to preverbal infants (Barth, La Mont, Lipton, &
Jeux, 2005; McCrink & Wynn, 2004), the acquisition of
number symbols and of a verbal counting routine ex-
tends arithmetic performance and leads to a radical
development of human arithmetical abilities. Compared
to uneducated adults who live in remote areas of the
Amazon and whose language has few number words,
Western children and adults represent numerical quan-
tities in a more precise manner (Gordon, 2004; Pica et al.,
2004) and understand that numbers map onto space
in a linear rather than in logarithmic manner (Dehaene,
Izard, Jeux, & Pica, 2008; Siegler & Booth, 2004). Dur-
ing development, the integration of different codes for
number (verbal and Arabic symbols, preverbal quanti-
liens, and ordinal concepts) leads to massive changes in
children’s performance of simple numerical tasks such
as the ‘‘give a number’’ task, where one simply asks a
child ‘‘give me five objects’’ ( Wynn, 1992). En résumé,
current theories of numerical cognition propose that the
preverbal coding of numbers is profoundly changed and
refined by education with numerical symbols (Dehaene,
2007; Pica et al., 2004; Carey, 1998). Although the ma-
ture systems for language and numbers appear largely
dissociated in the adult brain, these views predict that
they should be interdependent in the course of devel-
opération. Ici, we investigated whether consistent func-
intercorrelations of these two systems across
tional
intersubject variability, in adulthood, may shed light on
that issue as traces of a linked development.

As a first and simple marker of cerebral organization,
we used an asymmetry index which evaluates, dans un
given cortical area, the extent to which functional acti-
vation is stronger in one hemisphere relative to the
other. Reasoning that developmental constraints would
be reflected in long-lasting correlations at the brain level
(Andresen & Marsolek, 2005), we examined, across very
different language comprehension and calculation tasks,
whether language-related areas colateralize with the
main areas related to mental arithmetic. Bien sûr, le
activation levels of the left and right hemispheres may
also be affected by a variety of other factors such as
subjects’ performance, strategies, or attention that may
partially mask the predicted correlation. To mitigate this
problem, we used an unusually large-scale database of
209 subjects which contains individual functional mag-
netic resonance images and behavioral scores (Pinel
et coll., 2007). Reliable networks for sentence compre-
hension and for simple calculation, both across the
visual and auditory modalities, were available for each
sujet. Considering the large number of fMRI data, nous
hoped that our analysis would be sensitive to subtle
anatomo-functional links between the two sets of lan-
guage and calculation circuits.

We computed profiles of asymmetry (c'est à dire., variations in
the degree of hemispheric lateralization over the group
of subjects) for each of the main areas activated during
the language comprehension and calculation tasks. Ce

Pinel and Dehaene

49

D
o
w
n
je
o
un
d
e
d

je

je

/

/

/

/
j

F
/

t
t

je
t
.

:
/
/

F
r
o
m
D
h
o
t
w
t
n
p
o
:
un
/
d
/
e
m
d
je
F
t
r
o
p
m
r
c
h
.
s
p
je
je
d
v
je
e
r
e
r
c
c
t
.
h
m
un
je
r
e
d
.
toi
c
o
o
m
c
/
n
j
un
o
r
c
t
je
n
c
/
e
un
–
p
r
d
t
je
2
c
2
je
1
e
–
4
p
8
d
1
F
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
oui
0
g
0
toi
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
F
e
m
b
oui
b
e
g
r
toi
2
e
0
2
s
3
t

/
j

.

.

.

/

t

F

o
n

1
8

M.
un
oui

2
0
2
1

region-of-interest (ROI) approach allowed us to establish
a detailed region-based description of the lateralization
of the two networks. Using an intratask correlation anal-
ysis, we first examined whether a single ‘‘dominance’’
factor accounted for the data, or whether regional pat-
terns of asymmetry could be isolated within the activa-
tions evoked by our paradigms. In a second step, nous
analyzed the correlations of the lateralization profiles
across the language and arithmetic tasks, pour
isolate the areas that presented a significant joint colat-
eralization. These pairs of areas were then specifically
explored in a voxel-based whole-brain analysis to deter-
mine more precisely which voxels exhibited, in one task,
an asymmetry that was well predicted by the asymmetry
profile of another region in the other task. Enfin, to test
whether these joint colateralization patterns could be
related to a structural basis, we extracted, on an inde-
pendent sample of diffusion tensor images (DTI), le
white matter fiber tracks linking these areas.

MÉTHODES

Subjects and Protocol

We used fMRI data collected from 209 French healthy
adult volunteers (all were right-handed, 60% women/
40% men, âge moyen = 23.8 ± 4.4 années). The databasing
procedure and the experimental protocol are detailed
in Pinel et al., 2007; basically, we used a 5-minute-long
functional localizer to isolate in a reliable way individual
correlates of sentence reading, speech listening, et
mental calculation. Twenty short sentences and 20 sub-
traction problems were presented via visual or auditory
stimulation (half of the trials each) in a random-like
order (a symbolic subtraction task was selected to en-
sure a strong activation of the various components of
the number processing system; see Chochon et al., 1999).
Twenty flashing checkerboards were also displayed and
served as control for the reading task.

Imaging Data Processing

Anatomical and fMRI data were acquired on a 3-Tesla
scanner (Brucker; TR = 2400 msec, 34 slices of 4-mm
thickness covering the whole brain). Images were pre-
processed (realignment, normalization to the Montreal
Neurological Institute [MNI] template, resampled voxel
size to 3 mm, 5 mm smoothing) with SPM2 (www.fil.ucl.
ac.uk) and analyzed according to the SPM general linear
model (hemodynamic response function plus its deriva-
tive), resulting in five functional contrasts: visual sentence–
checkerboard for the reading task, sentence listening–rest
for speech listening task, visual calculation–visual sen-
tence for visual mental calculation, auditory calculation–
auditory sentence for auditory mental calculation, et
overall calculation–sentence for calculation task. Individ-
ual conjunction image were computed to isolate amodal

components of language comprehension (Boolean in-
tersection of the visual and the auditory language con-
trasts) and mental calculation (Boolean intersection of
the visual and the auditory calculation contrasts).

We also computed individual whole-brain images of
the degree of left/right asymmetry of activation for each
of these contrasts. To this aim, the standard SPM nor-
malization procedure was used to align each individual
flipped normalized anatomy (along the y axis) onto the
corresponding normalized anatomy image. This should
maximize alignment of homolog anatomical structures
in the two hemispheres despite macroscopic anatomical
asymmetry (petalia and torque effects). Alors, the func-
tional contrast activation images were also realigned
using the same matrix, and activation from the right
hemisphere was subtracted voxel by voxel from the
corresponding left hemisphere activation.

Group Analysis

Random effect analyses (RFX) were performed with
SPM2 on the whole brain for group-level analyses ( p < .05 after family-wise error correction for multiple com- parisons, 20 voxels cluster extent). An RFX was per- formed onto the 209 individual contrasts images to show task-related activation, and a left hemisphere RFX was performed onto the 209 left–right asymmetry images to test for any significant group-level asymmetry of the func- tional circuits. In order to report asymmetry of activation only, displays of asymmetry RFX maps were masked by the corresponding RFX activation map. A two-sample t-test analysis was performed on asymmetry images to test for different pattern of lateralization between men and women. SPM-based regression analyses were also performed on the individual asymmetry images to assess at the whole-brain hemisphere level which voxels presented an asymmetry of activation during the calculation task that correlated with the laterality index (LI) of a given ROI in reading task. To ensure that these regression analyses were unaffected by subjects’ performance, which may affect level of activation especially in left parietal cortex (Menon et al., 2000), individual calculation score (avail- able on a subset of 174 subjects) was added as a covari- ate (defined as the number of correct two-digit additions and subtractions solved in a limited time outside of the scanner). To benefit from the entire set of fMRI data and to maintain comparability with the ROI’s LI analysis (described in the next paragraph), simple regressions with LI are also reported. Finally, to ensure that the re- ported colateralization were not due to a main effect of sex, we performed a third regression analysis on asym- metry images using both reading ROI’s LI and subjects’ sex as regressor. Similar analyses were performed on the reading task asymmetry images, using a predictor the LI from the cal- culation task. We limited this SPM exploration to areas 50 Journal of Cognitive Neuroscience Volume 22, Number 1 D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j t . . . f / o n 1 8 M a y 2 0 2 1 that presented a significant correlation across tasks in the LI correlation analysis (see below). Calculation of Laterality Index The choice of an LI was constrained by the following aims. First, the index must be robust in the face of inter- individual variability in activation topography. In partic- ular, it must take into account the fact that homologous areas of the left and right hemispheres do not necessar- ily occupy perfect mirror-image locations. Second, the LI should be a normalized index, not influenced by overall changes in amount of activation. Third, it must be un- affected by the presence of deactivation in some subjects and/or hemispheres which can create misinterpretation in term of activation asymmetry (Seghier, 2008). These issues were addressed as follows. For each func- tional peak of interest, we selected two symmetrical spheres (radius = 4 voxels, i.e., 12 mm, based on the anatomical variability of individual peak reported for this paradigm in Pinel et al., 2007) respectively in the left and right hemispheres, centered on the peak coordinates of the group-level analysis. For a given subject, within each of these spheres, we then eliminated inactive or deacti- vated voxels with a loose criterion that their t value should be superior to 1. This procedure ensured that the activation values entered in the LI formula were al- ways positive, thus alleviating potential problems arising from the presence of deactivation in some subjects and/ or areas. Within those active voxels, we then selected the most activated voxels by keeping only up to 5% of the original sphere volume. Finally, the LI was computed by the classical formula LI = (R (cid:1) L)/(L + R) where L and R are, respectively, the left and right average activations of the selected voxels. The index ranged from (cid:1)1 (total left lateralization) to +1 (total right lateralization), with 0 re- flecting perfect symmetry of activation. In this formula, activation for one hemisphere was set to zero if no voxels passed the criterion of having a t value > 1. Dans ce cas, the LI always reached its max-
imum (plus or minus 1), regardless of the amount of
activation in the other hemisphere. This can add noise
to the analysis because even very small activations, quand
passing threshold in one hemisphere and not the other,
are considered maximally asymmetrical. To mitigate this
problem, an LI defined from a total of less than 15 ac-
tivated voxels was excluded from analysis. Note that this
procedure rejected about 5% of subjects for most ROI,
and up to 15–30% for areas found active in only a sub-
group of subjects, such as the putamen, inferior parietal,
or cingulate. Critique, the main reading–calculation cor-
relations reported here were calculated from 98% of the
subjects for pSTS–hIPS and 85% for mFG–precuneus
pair.

To characterize the leftward lateralization of the lan-
guage comprehension cerebral network, we computed
the LI from seven local peaks of the RFX analysis for

reading lateralization, which were also part of the most
activated sites (6 maxima were present in both language
modalities). To explore the lateralization of the calcula-
tion network, we computed the LI from all nine local
peaks of the RFX analysis for areas active during cal-
culation. For each of these peaks, we performed a
two-sample t test on LI values with sex as independent
variable to test for a putative difference of lateralization
between male and female subjects.

We first investigated the colateralization patterns with-
in the seven language-related ROIs, both within and
across modalities of sentence presentation (visual and
auditory stimulation). We then calculated the matrix of
correlation corresponding to the 7 (cid:2) 9 combinations of
LI from reading and calculation tasks respectively. Nous
report matrices of p values testing the null hypothesis
of no correlation.

Fiber Tracking

To explore whether colateralization of brain areas may
be sustained by direct connections via anatomical fiber
bundles, we performed fiber tracking with the Brainvisa
software (Cointepas et al., 2003; http://brainvisa.info/) sur
six subjects’ DTIs acquired in another protocol (Siemens
Trio 3-T whole-body scanner): TE/TR = 81 msec/14 sec,
0/700 s mm(cid:1)2 b1/b2 factor, 41 instructions, FOV = 240,
1.9 (cid:2) 1.9 (cid:2) 2 mm voxel size, 60 slices.

Tracking was performed starting from five functionally
defined seed regions: middle frontal and posterior su-
perior temporal spheres (4 mm), centered on the peak
defined by the previously described reading task RFX,
and intraparietal, superior parietal and precuneus spheres
defined by the calculation task. Spheres were defined
in MNI space and then unnormalized to match the
individual diffusion-weighted images. To estimate how
these areas were linked, fiber trees were labeled accord-
ing to the pair of seed regions they crossed. Resulting
tracks were then converted into 3-D images, normalized
to MNI coordinates and added up for a group-level
description.

RÉSULTATS

Language Lateralization

The overall networks activated during reading, speech
listening, and calculation reported in Figure 1 resembled
those classically reported in the literature (see Pinel
et coll., 2007, for a detailed description of these networks).
Nearly all activated areas were strongly leftward lateral-
ized in these three cognitive tasks (Chiffre 1, bottom
row). Two interesting and heretofore unreported ex-
ceptions were right postcentral cortex for reading and a
right middle temporal area for speech listening.

Based on those asymmetry images, the seven bilateral
ROIs which reflected both strong lateralization and

Pinel and Dehaene

51

D
o
w
n
je
o
un
d
e
d

je

je

/

/

/

/
j

F
/

t
t

je
t
.

:
/
/

F
r
o
m
D
h
o
t
w
t
n
p
o
:
un
/
d
/
e
m
d
je
F
t
r
o
p
m
r
c
h
.
s
p
je
je
d
v
je
e
r
e
r
c
c
t
.
h
m
un
je
r
e
d
.
toi
c
o
o
m
c
/
n
j
un
o
r
c
t
je
n
c
/
e
un
–
p
r
d
t
je
2
c
2
je
1
e
–
4
p
8
d
1
F
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
oui
0
g
0
toi
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
F
e
m
b
oui
b
e
g
r
toi
2
e
0
2
s
3
t

/
j

F

.

t

.

/

.

o
n

1
8

M.
un
oui

2
0
2
1

D
o
w
n
je
o
un
d
e
d

je

je

/

/

/

/
j

t
t

F
/

je
t
.

:
/
/

F
r
o
m
D
h
o
t
w
t
n
p
o
:
un
/
d
/
e
m
d
je
F
t
r
o
p
m
r
c
h
.
s
p
je
je
d
v
je
e
r
e
r
c
c
t
.
h
m
un
je
r
e
d
.
toi
c
o
o
m
c
/
n
j
un
o
r
c
t
je
n
c
/
e
un
–
p
r
d
t
je
2
c
2
je
1
e
–
4
p
8
d
1
F
9
/
3
2
8
2
4
/
1
1
1
/
o
4
c
8
n
/
1
2
7
0
0
6
9
9
1
2
1
1
5
1
/
8
4
j
o
p
c
d
n
.
b
2
oui
0
g
0
toi
9
e
.
s
t
2
o
1
n
1
8
0
4
8
.
S
p
e
d
p
F
e
m
b
oui
b
e
g
r
toi
2
e
0
2
s
3
t

/
j

.

.

F

/

.

t

o
n

1
8

M.
un
oui

2
0
2
1

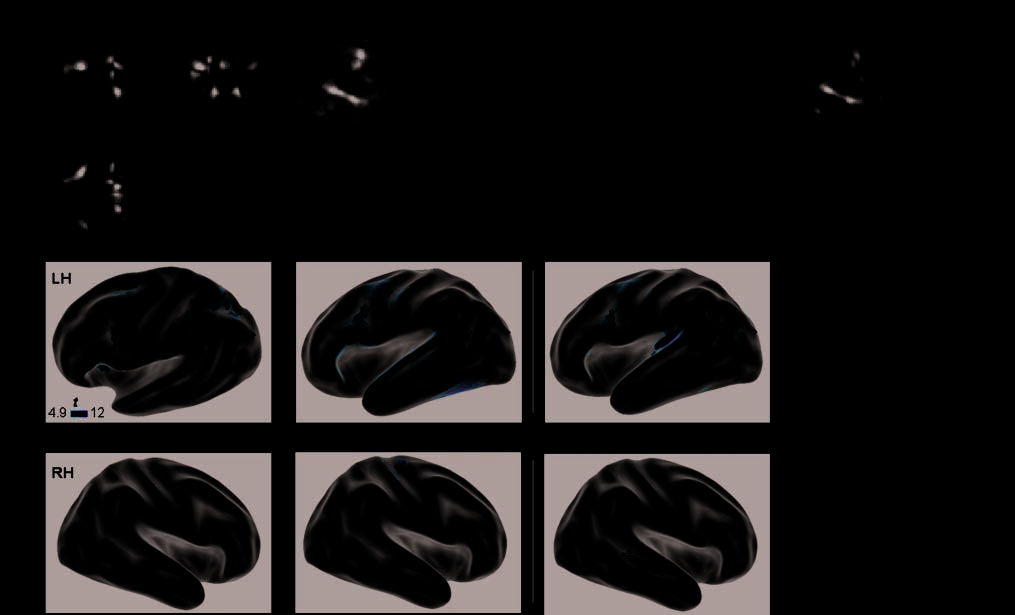
Chiffre 1. Hemispheric asymmetries during language and calculation. The first row (glass brains) shows sagittal, axial, and coronal views of the
brain networks active during calculation, reading, speech listening, and core language comprehension, respectivement ( pcorr. < .05). Red numbers indicate regions of interest of the calculation circuit for which a laterality index was computed: putamen (1), insula (2), middle frontal (3), precentral (4), superior frontal (5), cingulate (6), hIPS (7), superior parietal lobule (8), and precuneus (9). Blue numbers indicate ROI of the reading circuit: inferior frontal area (1), precentral area (2), middle frontal area (3), fusiform gyrus (4), pSTS (5), aSTS (6), and cingulate (7). Note that all but one of these regions was also present in the core system of language comprehension. On the next two rows are displayed series of left (LH) and right (RH) inflated hemisphere with projections of cortical sites of significant asymmetry, respectively, in favor of the left or of the right hemisphere ( pcorr. < .05). activation of the language cerebral organization were centered on the following peaks: inferior frontal area (close to Broca’s area; see Lindenberg, Fangerau, & Seitz, 2007, for a recent meta-analysis; MNI: x = (cid:1)43, y = 22, z = (cid:1)2), precentral area (x = (cid:1)47, y = 6, z = 25), mid- dle frontal gyrus (mFG, x = (cid:1)48, y = (cid:1)3, z = 53), fusi- form gyrus (about 3 mm from the visual word form area; Cohen & Dehaene, 2004; x = (cid:1)45, y = (cid:1)56, z = (cid:1)10), posterior STS (pSTS; x = (cid:1)58, y = (cid:1)44, z = 8), anterior STS (aSTS; x = (cid:1)57, y = (cid:1)3, z = (cid:1)9), and cingulate (x = (cid:1)6, y = 3, z = 63). Only the fusiform gyrus activation was specific to the visual modality. No significant difference was observed between male and female subjects in the voxel-based analysis (voxel puncorr. < .001, pcorr. < .05 for cluster extent). The only area associated with a sex effect with a p value < .1 in the ROI analysis was the inferior frontal area ( p = .09 in reading and p = .01 in speech listening condition, 206 degrees of freedom) with a trend toward a larger left lateralization for men (median LI = (cid:1)0.24 and (cid:1)0.11 for reading and speech listening, respectively) than for women (median LI = (cid:1)0.16 and (cid:1)0.06). Table 1 gives the correlation of the LIs across areas, both within and across the language tasks. Looking first at the diagonal values (bottom of Table 1), we see that for all areas, the LIs were highly correlated across the two modalities of linguistic input (visual or auditory), suggesting that left lateralization in most areas arises from amodal levels of language processing. Even the fusiform peak, which did not survive corrected thresh- old for activation during the auditory trials, presented a trend toward leftward asymmetry during speech listen- ing that correlated with reading activation asymmetry in this region (perhaps corresponding to a top–down acti- vation of orthographic processing in the visual word form area during speech listening; Cohen, Jobert, Le Bihan, & Dehaene, 2004). This analysis also demonstrated that, for each subject, the LI of each selected ROI was reli- ably measured by our paradigm over two independent language-related conditions. In view of this high reproducibility of the LI within each area, it is surprising that the LI across areas are sometimes weakly correlated, suggesting that many re- gions present relative independent pattern of hemispheric 52 Journal of Cognitive Neuroscience Volume 22, Number 1 Table 1. Reproducibility and Colateralization of Asymmetries during Language Processing LI Correlation within Each Language Task Reading Inferior Frontal Precentral Mid-frontal Fusiform Posterior STS Anterior STS Cingulate Inferior Frontal Precentral Mid-frontal Fusiform Posterior STS Anterior STS Cingulate g n i d a e R g n i n e t s i l h c e e p S Inferior Frontal Precentral Mid-frontal Fusiform Posterior STS Anterior STS Cingulate – – – – – – – .008 – – – – – – .077 .001 – – – – – .185 .061 <10(cid:1)3 – – – – <10(cid:1)3 .005 <10(cid:1)3 <10(cid:1)3 – – – Speech Listening .001 .167 .033 .013 .002 – – <10(cid:1)3 <10(cid:1)3 .007 .783 <10(cid:1)3 .213 – Inferior Frontal Precentral Mid-frontal Fusiform Posterior STS Anterior STS Cingulate – – – – – – – <10(cid:1)3 – – – – – – .004 <10(cid:1)3 – – – – – .012 <10(cid:1)3 .006 .001 – – – .002 .140 .021 .506 .628 – – .047 .003 <10(cid:1)3 .579 .046 .352 – .393 .429 .951 – – – – Reading LI Correlation across the Two Language Tasks Inferior Frontal Precentral Mid-frontal Fusiform Posterior STS Anterior STS Cingulate Inferior Frontal <10(cid:1)3 g n i n e t s i l h c e e p S Precentral Mid-frontal Fusiform Posterior STS Anterior STS Cingulate .027 .082 .381 .005 .016 .120 .019 <10(cid:1)3 .429 .585 .246 .103 .637 .472 .132 <10(cid:1)3 .178 .289 .503 .031 .041 .622 .352 .023 .031 .710 .796 .092 .307 .563 .050 <10(cid:1)3 .410 .476 .372 .101 .177 .695 .025 <10(cid:1)3 .664 .380 .012 .903 .666 .080 .737 <10(cid:1)3 The table shows the p values of the correlation between the lateralization indices (LI) of the seven main language-related ROIs during language comprehension tasks. The upper part of the table reports the correlations within the same modality of language input (visual sentence reading and auditory speech listening). Bold values indicate correlation values that are similarly significant ( p < .05) for the same pairs across modalities. The bottom part reports the correlations across two independent trial types with visual and auditory language inputs. Bold values on the diagonal highlight the level of LI reliability across modalities. asymmetries, perhaps reflecting multiple determinants of left hemispheric bias for language in the course of development. For instance, although all of these regions are highly asymmetrically activated, always in favor of the left hemisphere, correlations between the LI of the fusiform gyrus and of frontal areas are weak, as well as those between aSTS and precentral gyrus, cingulate and fusiform gyrus, cingulate and aSTS. It is remarkable that this pattern of weak correlation was largely similar across the two modalities of sentence presentation. Similarly, Pinel and Dehaene 53 D o w n l o a d e d l l / / / / j t t f / i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j . / . t f . o n 1 8 M a y 2 0 2 1 there were notable patterns of extremely high correla- tion across areas, both for the reading and the speech listening tasks. Such consistently high correlations were found between the pSTS and both fusiform and frontal areas; within the frontal lobe, between precentral and both the mFG and the inferior frontal area; and finally, between the aSTS and both the mFG and the inferior frontal area. Only a few pairs of areas presented incon- sistent level of LI correlation across modalities, notice- ably the fusiform and mFG as well as the aSTS and pSTS, probably due to the partially modality-specific involve- ment of these areas, respectively, in orthographic and phonological processing. Arithmetic Lateralization The nine ROIs from activation for the calculation task were centered on the following maxima (Figure 1): puta- men (x = (cid:1)18, y = 11, z = 4), insula (x = (cid:1)32, y = 20, z = 6), mFG (x = (cid:1)44, y = 39, z = 15), precentral (x = (cid:1)48, y = 8, z = 33), superior frontal gyrus (sFG close to frontal eye fields; Simon et al., 2004; x = (cid:1)25, y = 2, z = 59), cingulate (x = 0, y = 14, z = 47; left and right parts of the sphere were here considered), hIPS (virtually iden- tical to the location reported from in the meta-analysis of Dehaene et al., 2003; x = (cid:1)40, y = (cid:1)47, z = 47), superior parietal lobule (sPL, close to the posterior sPL from Dehaene et al., 2003; x = (cid:1)27, y = (cid:1)69, z = 44), and precuneus (x = (cid:1)14, y = (cid:1)72, z = 54). Because lateralization of calculation is less well char- acterized than language lateralization, Figure 2 details the RFX lateralization map of the calculation task with a series of axial slices. All activated areas showed at least a trend toward left lateralization, often reaching very high degrees of significance: t(208) = 17.23 in cingular cortex slightly posterior to the activation peak, t = 16.00 in pre- central, t = 12.98 in the posterior parietal lobule close to the sPL, t = 12.34 posterior to putamen peak, t = 11.90 about 3 voxels under the insula peak, t = 10.40 in the sFG, t = 8.75 in the hIPS, and t = 8.19 in the middle frontal area. Examination of the distributions of the LI across subjects allowed for a more detailed and anatomy- free analysis of the lateralization of these sites. A gradi- ent emerged in the extent of lateralization for arithmetic, with the highest value for the precentral area (median LI = (cid:1)0.218); medium lateralization for sPL ((cid:1)0.148), hIPS ((cid:1)0.125), cingulate ((cid:1)0.125), sFG ((cid:1)0.119), and middle frontal ((cid:1)0.110); and low LI for the subcortical system: putamen ((cid:1)0.028) and insula ((cid:1)0.012). The par- tial discrepancy of the latter finding with the RFX asymmetry map may be due to the fact that subcortical peaks had approximately equal levels of BOLD activa- tions in both hemispheres, but with a more extended activation in the left hemisphere. No significant differences were observed between male and female subjects in the voxel-based analysis (voxel puncorr. < .001, pcorr. < .05 for cluster extent). The only areas associated to a sex effect with a p value < .1 in the ROI analysis was the putamen area ( p = .04, 206 de- grees of freedom), with a trend toward a larger, al- though weak, left lateralization for men (median LI = (cid:1)0.04) than for women (median LI = 0.01). Colateralization of Language and Arithmetic: ROI Analysis To examine how arithmetic and language colateralized, we first examined the full correlation matrix between the asymmetry of activation in the above-selected ROI, known to be asymmetrically activated during one or both of these activities. As a proxy for language asymmetry, we used the LI obtained during reading because (1) the diagonal of Table 2 indicates a very highly correlation with the LI obtained during language listening in all regions; (2) in one region (left fusiform), reading yielded stronger and more asymmetrical activation than lan- guage listening (corresponding to the putative ortho- graphic role of this region as the visual word form area). Surprisingly, the correlation matrix between reading and calculation LIs indicated that most of the language- and calculation-related areas varied independently in their degree of lateralization (Table 2). However, a few pairs of areas presented a significant positive correlation across tasks: The mFG LI during reading correlated with the precuneus LI during calculation (r = .25); the pSTS LI during reading correlated with the precentral area (r = .28), sFG (r = .23), hIPS (r = .21), and precuneus (r = .23) LI during calculation; and finally, the cingulate LI during reading correlated with the sFG LI during calculation (r = .22). When considering separately the auditory and visual modalities for calculation trials, only a subset of correlations survived across these two inde- pendent sets of data. On the one hand, lateralization in the pSTS during reading was reliably correlated with lat- eralization in the hIPS during calculation. On the other hand, mFG lateralization during reading correlated with precuneus lateralization during calculation. D o w n l o a d e d l l / / / / j t t f / i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j t / . . . f Colateralization of Language and Arithmetic: Voxel-based Analyses We first confirmed our results by a voxel-based regres- sion approach, which consisted in examining how the LI of a selected region predicted, at the whole-brain level, the asymmetry in activation in another task. o n 1 8 M a y 2 0 2 1 Link 1: sFG and hIPS Even when exploring the entire left hemisphere, only the sFG and the hIPS exhibited profiles of asymmetry during the calculation task that were significantly pre- dicted by the lateralization index of the pSTS during 54 Journal of Cognitive Neuroscience Volume 22, Number 1 D o w n l o a d e d l l / / / / j t t f / i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j t . . / . 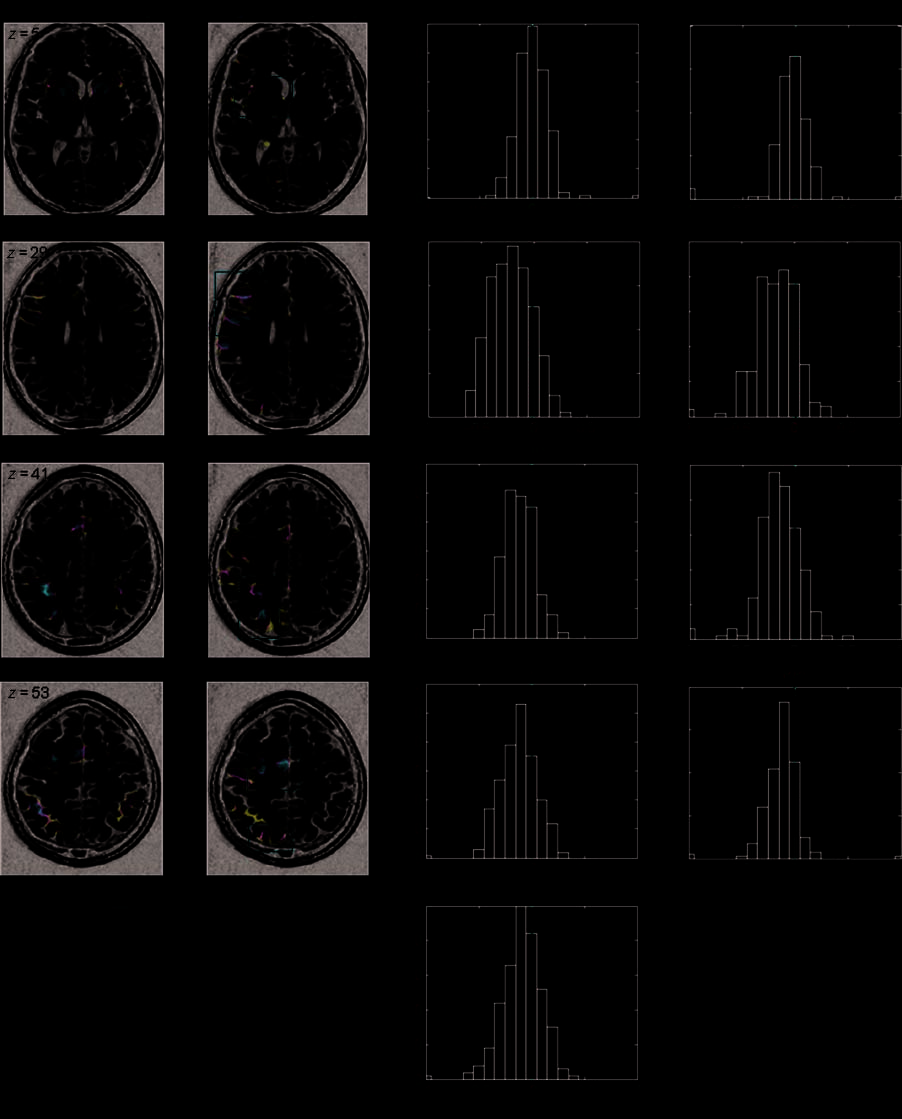f o n 1 8 M a y 2 0 2 1 Figure 2. Quantifying functional asymmetries in the calculation network. Axial slices describe the entire pattern of activation and asymmetry for the calculation task (neurological convention) from bottom to the top of the brain (RFX group analysis, pcorr. < .05). The histograms at right show the distribution of LI across subjects for each of the nine selected ROIs. Red rectangles help locate these ROIs on the corresponding slices. ppl = posterior parietal lobule; superior frontal = superior frontal cortex. reading ( p < .05, corrected for multiple comparisons; see Figure 3A, Table 3). Note that, in this analysis, the subjects’ arithmetical performance was regressed out as a covariate of noninterest, and thus, performance variabil- ity did not contribute to this significant colateralization. At a lower voxelwise threshold ( p < .01, uncorrected), additional voxels were found in the precentral gyrus and in the caudate nucleus (Table 3). A number of control analyses were run to assess the significance of these findings. First, a simple regression Pinel and Dehaene 55 Table 2. Colateralization of Asymmetries during Calculation and Reading Reading Inferior Frontal Precentral Mid-frontal Fusiform Posterior STS Anterior STS Cingulate l n o i t a u c l a C l n o i t a u c l a c o e d i V l n o i t a u c l a c o i d u A Putamen Insula Mid-frontal Precentral Superior Frontal Cingulate hIPS Superior Parietal Precuneus Putamen Insula Mid-frontal Precentral Superior Frontal Cingulate hIPS Superior Parietal Precuneus Putamen Insula Mid-frontal Precentral Superior Frontal Cingulate hIPS Superior parietal Precuneus .010* .307 .077 .077 .101 .235 .288 .465 .146 .685 .226 .143 .566 .540 .860 .319 .953 .053 .551 .449 .349 .086 .100 .077 .184 .186 .265 .384 .203 .137 .464 .138 .830 .602 .222 .703 .391 .578 .170 .175 .943 .616 .644 .013 .433 .160 .443 .523 .942 .028 .167 .303 .899 .433 .653 .137 .838 .155 .080 .030 .026 .510 <10(cid:1)3** .117 .445 .778 .064 .671 .025 .040 .756 .001** .763 .332 .250 .198 .009* .304 .107 .251 <10(cid:1)3** .083 .456 .698 .736 .390 .069 .174 .784 .710 .151 .713 .763 .746 .913 .388 .510 .981 .930 .721 .407 .846 .466 .150 .053 .073 .971 .283 .394 .633 .050 .010* .001** .060 .002* .035 .002* .278 .725 .013 .133 .284 .007* <10(cid:1)3** .564 <10(cid:1)3** .073 .896 .094 .020 .002* .364 .005* .067 .018 .678 .012 .993 .506 .166 .191 .248 .373 .100 .920 .002* .480 .892 .766 .407 .783 .988 .038 .756 .297 .189 .283 .113 .040 .106 .433 .285 .015 .184 .922 .053 .004* .018 .226 .486 .293 .016 .311 .311 .034 .231 .013 .146 .982 .069 .106 .463 .786 .158 .009* .308 .284 .340 .815 The table shows the p values of the correlation between the lateralization indices (LI) of the reading and calculation ROIs. In each case, we report the correlation of activation asymmetry on two independent sets of trials, the reading trials (horizontally) versus the calculation trial (vertically). Significance is reported both for overall calculation trials (first part of the table), visually presented calculations only (second part) and auditory presented calculations only (third part). Bold values highlight the two correlation patterns that were deemed reliable enough. *p value < .01. **p value < .001. with the LI of the pSTS during reading, computed with- out any behavioral regressor but applied to the whole population images, gave comparable results. Three peaks survived a corrected p value of .05 for cluster extent: hIPS [(cid:1)36, (cid:1)48, 42; t(207) = 4.70, voxel pcorr. < .05], sFG [(cid:1)18, 3, 66; t(207) = 5.10, voxel puncorr. < .001], and precentral peak [(cid:1)51, 3, 27; t(207) = 4.30, voxel puncorr. < .001]. Second, we checked whether the pos- itive correlation found for calculation minus sentence processing was, in fact, due to a negative correlation with lateralization in the control task of visual sentence pro- cessing. When analyzing the contrast of sentence reading minus rest, no voxel of the superior frontal or parietal sites presented any significant asymmetry predicted by 56 Journal of Cognitive Neuroscience Volume 22, Number 1 D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j f . . . 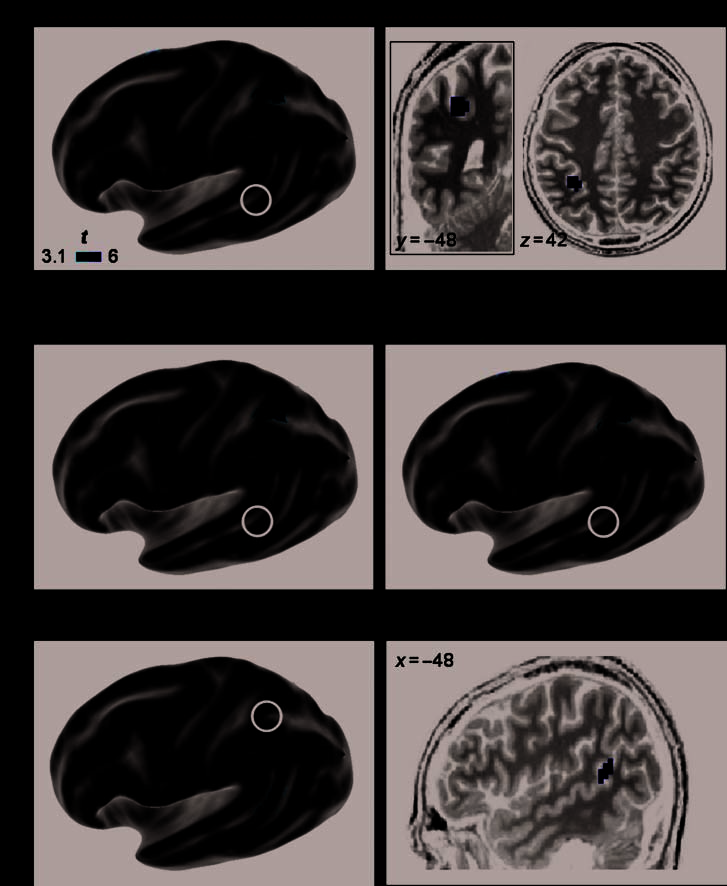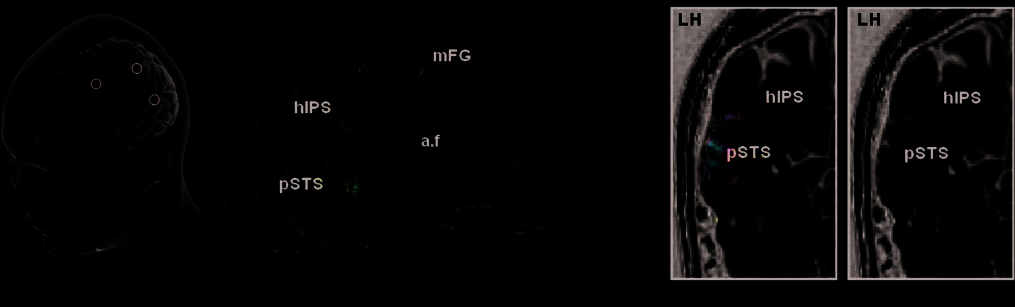t / o n 1 8 M a y 2 0 2 1 Figure 3. Colateralized regions for reading and calculation: pSTS and hIPS. Whole-brain regression analysis of the colateralization between the reading temporal area (pSTS) and the calculation intraparietal area (hIPS; p < .001, uncorrected at the voxel level, p < .05, corrected for the cluster extent). (A) The first row shows a 3-D rendering of which voxels from the global calculation–sentence contrast showed an asymmetry that was significantly predicted by the LI of the pSTS region during reading (this ‘‘source’’ region is enclosed with a black circle). The SPM statistical map was projected onto an inflated left hemisphere of the template brain of the Caret software. The observed intraparietal cluster is detailed on coronal and axial slices. On the second row, similar analyses are shown separately for the auditory and visual calculation, respectively. (B) 3-D rendering of the converse analysis: reading–checkerboard contrast asymmetry predicted by the LI of the hIPS during calculation (black circle). The observed temporal cluster is detailed on the sagittal view of one subject’s anatomy. the pSTS LI, even at a low threshold at the voxel level ( p > .01, uncorrected). En outre, when we directly
regressed the asymmetry of calculation versus rest to the
LI of the pSTS during reading, with calculation score as a
covariate (voxel puncorr. < .001, pcorr. < .05 for cluster ex- tent), we still isolated the hIPS [(cid:1)36, (cid:1)48, 42; t(173) = 4.63], in addition to a broad sentence comprehension cir- cuit that encompassed the pSTS [(cid:1)54, (cid:1)48, 15; t(173) = 5.63], the fusiform gyrus [(cid:1)42, (cid:1)63, (cid:1)12; t(173) = 5.16], and an occipito-parietal area [(cid:1)36, (cid:1)48, 42; t(173) = 4.63]. Third, and most crucially, the hIPS was the only area whose asymmetry during calculation was significantly predicted by the LI of the pSTS during reading when we did separate analyses on auditory and on visual calcula- tion trials (Figure 3A, Table 3). Finally, the multiregres- sion analysis with sex as a second regressor gave strictly similar results with no sex effect at the selected threshold. The converse regression analysis, starting with the LI of the hIPS region during calculation and using it as a regressor of the images of asymmetry during reading, revealed a small set of voxels in the pSTS, close to the maxima of asymmetry during the reading task (Figure 3B, Table 3). Another significant cluster was found in the anterior cingulum, but in a region not reported here as a part of the reading network. Link 2: mFG and Superior Parietal/Precuneus Similar multiple regression analyses used the LI of the mFG during reading as a predictor of calculation asym- metry images, with behavioral calculation performance as a covariate of noninterest. This SPM analysis isolated two superior parietal/precuneus clusters (Figure 4A). The regression was weaker and did not survive a corrected p value at the voxel level, but approached significance at the cluster level (Table 4). Here again, a simple regression to the reading mFG LI, computed without any behavioral regressor but applied to the whole population images, Pinel and Dehaene 57 D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j . / f t . . o n 1 8 M a y 2 0 2 1 Table 3. Whole-brain Analysis of Colateralization with pSTS Coordinates Voxel Brain Area x y z puncorr. pFWE-corr. t(173) Calculation Asymmetry Regressed by the Reading pSTS LI puncorr. < .001 Intraparietal sulcus Superior frontal gyrus puncorr. < .01 Precentral gyrus Caudate nucleus (cid:1)36 (cid:1)18 (cid:1)48 (cid:1)18 (cid:1)48 3 0 (cid:1)9 42 66 30 24 Video Calculation Asymmetry Regressed by the Reading pSTS LI puncorr. < .001 Superior frontal gyrus Intraparietal sulcus puncorr. < .01 Precentral gyrus (cid:1)15 (cid:1)36 (cid:1)48 3 (cid:1)48 0 66 42 30 Audio Calculation Asymmetry Regressed by the Reading pSTS LI puncorr. < .001 Intraparietal sulcus (cid:1)33 (cid:1)48 puncorr. < .01 Precentral gyrus (cid:1)36 x (cid:1)6 y Reading Asymmetry Regressed by the Calculation hIPS LI puncorr. < .001 Anterior cingulum (cid:1)15 33 puncorr. < .01 Mid-temporal gyrus (cid:1)48 (cid:1)54 42 63 z 6 15 Cluster pcorr. .001 .011 .019 .030 .020 .040 .049 .007 .002 <.001 <.001 <.001 <.001 <.001 <.001 .004* .010* .117 .974 .012* .054* <.001 .638 <.001 <.001 .070 .093 5.26 4.73 4.61 3.70 5.11 4.48 4.12 4.98 4.66 puncorr. pFWE-corr. t(208) pcorr. <.001 <.001 .075 .666 4.68 4.05 .006 .017 Brain areas where the leftward asymmetry during calculation was significantly predicted by the lateralization index of the pSTS during reading (whole left hemisphere analysis). Regression was performed separately for the overall images of asymmetry during calculation (pooling over visual and auditory trials), for visual calculation trials only, and for auditory calculation trials only. For an exhaustive description of the regression, we reported for each case statistical mapping results with a voxel threshold of .001 and with a more liberal threshold of .01, keeping .05 as a corrected threshold for cluster extent. The bottom part of the table reports the converse analysis, that is, areas with a leftward asymmetry during reading that was significantly predicted by the lateralization index of the hIPS during calculation. gave comparable results: sPL [(cid:1)24, (cid:1)66, 54; t(207) = 3.44, voxel puncorr. < .001], precuneus [(cid:1)9, (cid:1)69, 54; t(207) = 3.42, voxel puncorr. < .001], and postcentral gyrus [(cid:1)27, (cid:1)45, 51; t(207) = 3.67, voxel puncorr. < .001]. Finally, the multiregression analysis with sex as a second regressor gave strictly similar results with no sex effect at the se- lected threshold in active areas. The converse regression analysis, considering the LI from the sPL during calculation as the regressor of the reading asymmetry images, showed that only a cluster of voxels in the mFG exhibited an asymmetry during the reading task that was significantly predicted by this LI. The region clearly encompassed the ROI selected for its asymmetry during the reading task (Figure 3B, Table 3). Relation between Colateralization and Anatomical Connectivity In this final analysis, we wondered whether the observed patterns of colateralization between two areas related to 58 Journal of Cognitive Neuroscience Volume 22, Number 1 D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j f t . / . . 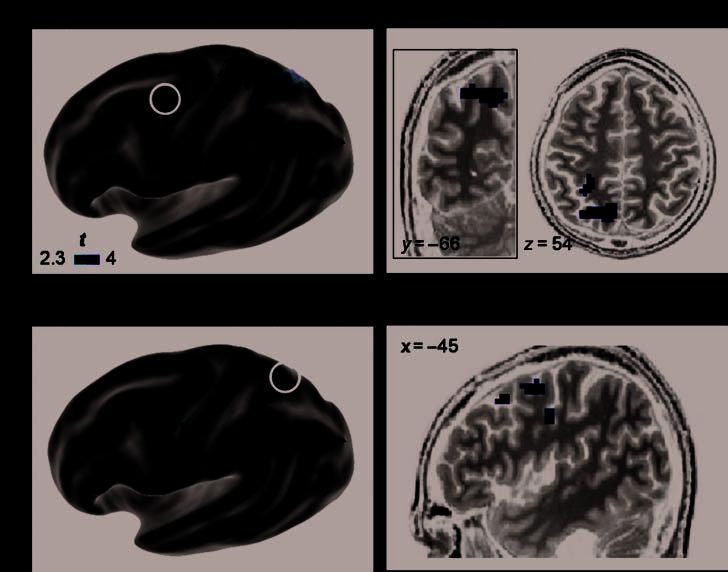o n 1 8 M a y 2 0 2 1 Figure 4. Colateralized regions for reading and calculation: mFG and posterior parietal/precuneus. Whole-brain regression analysis of the colateralization between the reading middle frontal area (mFG) and the calculation posterior parietal lobe/precuneus ( p < .01, uncorrected at the voxel level; p < .05 correct for the cluster extent). (A) 3-D rendering of which voxels from the calculation–sentence contrast showed an asymmetry that was significantly predicted by the LI of the mFG during reading (black circle). The most posterior cluster is detailed on coronal and axial slices. (B) 3-D rendering of the converse analysis: reading–checkerboard contrast asymmetry predicted by the LI of the precuneus during calculation (black circle). The observed frontal clusters are detailed on the sagittal view of one subject’s anatomy. the existence of actual anatomical connections between them, such that if one area grew more asymmetrical in the course of development, the other would also tend to develop a growing asymmetry. Fiber tracking from DTIs provided clear structural support for our first finding of a strong pSTS–hIPS co- lateralization: In all of the six subjects, projections were found from the pSTS to inferior parietal cortex. As for Cluster pcorr. .050 .080 Table 4. Whole-brain Analysis of Colateralization with the mFG Coordinates Voxel Brain Area x y z puncorr. pFWE-corr. t(173) Calculation Asymmetry Regressed by the Reading mFG LI puncorr. < .01 Postcentral gyrus Superior parietal gyrus Precuneus (cid:1)21 (cid:1)24 (cid:1)9 x (cid:1)39 (cid:1)66 (cid:1)63 y 66 54 54 z Reading Asymmetry Regressed by the Calculation Precuneus LI <.001 <.001 <.001 .864 .999 1.0 3.90 3.46 3.46 puncorr. pFWE-corr. t(208) pcorr. puncorr. < .01 Mid-frontal gyrus Mid-frontal gyrus (cid:1)45 (cid:1)48 15 (cid:1)3 51 57 <.001 <.001 .275 .596 4.38 4.11 .030 Brain areas where the leftward asymmetry during calculation was significantly predicted by the lateralization index of the mFG during reading (whole left hemisphere analysis). Regression was performed on the images of asymmetry during calculation, pooled over visual and auditory trials. For an exhaustive description of the regression, we reported for each case statistical mapping results with a voxel threshold of .01 and .05 as a corrected threshold for cluster extent (except for the superior parietal gyrus reported in ROI analysis). The bottom part of the table reports the converse analysis, that is, areas with a reading leftward asymmetry during reading that was significantly predicted by the lateralization index of the precuneus during calculation. Secondary peaks are reported in italic. Pinel and Dehaene 59 D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j / f . . t . o n 1 8 M a y 2 0 2 1 D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j f . . / . t o n 1 8 M a y 2 0 2 1 Figure 5. Anatomical connections putatively supporting the observed colateralization patterns. (A) Location on a 3-D left hemisphere of the three frontal, parietal, and temporal seed regions used for tracking. (B) Left hemisphere fibers of interest (from an internal view): long segment of the arcuate fasciculus (a.f., in blue), posterior segment linking the pSTS and hIPS (red), superior segment linking the hIPS and mFG (green), and projections connecting the mFG and pSTS (purple). (C) Coronal view of the projections to the left parietal region, respectively, from seed regions in the pSTS (left) and the mFG (right). Color scale corresponds to the amount of overlap from five different individuals. The pSTS clearly connects to the banks of the intraparietal sulcus, whereas the mFG projects more dorsally toward superior parietal cortex. hIPS = horizontal segment of the intraparietal sulcus; mFG = middle frontal gyrus; pSTS = posterior superior temporal sulcus. the second finding, as detailed in Figure 5A, white mat- ter tracks also connected the mFG to the dorsal parietal region (as well as, in some subjects, the mFG to the pSTS). Although no direct connections were found from the mFG to the sPL and the precuneus, dense local U-shaped fibers were found linking the three parietal seed regions (intra- parietal, superior parietal, and precuneus). Furthermore, crucially, a close look at the organization of projections to parietal cortex showed an anatomical segregation of fibers originating from the pSTS and from the mFG, mir- roring the parietal parcellation found by correlation with the LI (Figure 5B). Projections from the pSTS were lo- cated laterally in the inferior parietal lobule, often ex- tending to the banks of the intraparietal sulcus, whereas those from the mFG region projected more dorsally into the sPL. DISCUSSION We studied the profile of functional brain asymmetries for language and calculation over a large population of 200 subjects. Our goal was to study the colateralization of these two functions across subjects, possibly reflect- ing an influence of language organization onto the cerebral architecture for calculation. Purposely, our starting point was the definition of two distinct and distributed networks; a vast language net- work, defined by its activation to simple spoken or writ- ten sentences and supported by frontal and peri-sylvian areas, and a calculation network, defined by areas showing more activity to verbally presented subtraction problems (e.g., ‘‘compute 11 minus 3’’) than to other nonnumerical sentences and supported by frontal, parietal, and subcor- tical regions. Although both circuits showed significant left hemispheric asymmetry, our results indicate that the concept of a single hemispheric ‘‘dominance,’’ determin- ing the lateralization of all regions of the language and cal- culation networks, does not suffice to explain the patterns of hemispheric asymmetries across individuals. In our data, lateralization appears as a local regional phenomenon, even within a given task. LIs are often uncorrelated across distant areas, and therefore, probably have multiple de- terminants. Indeed, interestingly, only two anatomically restricted sets of areas showed a correlated asymmetry across the language comprehension and the arithmetic tasks: The lateralization profile of the pSTS during read- ing correlated with the lateralization of the fundus of the hIPS during calculation, and the lateralization of the mFG during reading correlated with that of the sPL and the precuneus during calculation. Although the asymmetry of language areas only explained a relatively small propor- tion of the variance in left/right parietal organization for arithmetic, this amount was comparable to the correla- tion observed within some areas of the language net- work. Importantly, both findings were reproducible over two separate sets of data (spoken and written arith- metic problems), and both ROI-based and voxel-based analysis. These patterns of colateralization were further sup- ported by the presence of anatomical connections, re- spectively linking the pSTS with the hIPS, and the mFG with the sPL, Notably, the pattern of white matter pro- jections from the pSTS and mFG areas toward the parie- tal lobe matched the pattern of colateralization between parietal voxels and those two temporal and frontal sites. Overall, these results underline an interesting subdivi- sion of superior parietal cortex into two distinct regions that could be subject to different influences in their de- velopment and maturation. 60 Journal of Cognitive Neuroscience Volume 22, Number 1 Colateralization of the Language-related pSTS and the Core Numerical System The global tasks used in the present study did not allow us to precisely delineate the processing stages subtended by the various brain areas reported here. However, a striking aspect of our results is that language lateraliza- tion in the pSTS is significantly related to those of the frontal and parietal regions known to be crucial for the representation and processing of numerical quantities. The intraparietal site of colateralization reported here, especially the fundus of the intraparietal sulcus, has been systematically reported in various numerical tasks (Venkatraman, Ansari, & Chee, 2005; Dehaene et al., 2003; Delazer et al., 2003) and its neuronal coding properties have been recently investigated in humans and non- humans primates (Nieder, Diester, & Tudusciuc, 2006; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004). Contrary to posterior parietal areas, which are shared with visuo- spatial tasks, and to the AG, which is thought to relate to the verbal coding of arithmetical facts, the intraparietal location reported here is thought to house an amodal rep- resentation of quantities (Piazza et al., 2006; Venkatraman et al., 2005; Eger, Sterzer, Russ, Giraud, & Kleinschmidt, 2003; Pinel, Dehaene, Riviere, & Le Bihan, 2001). We found the hIPS to be linked to the pSTS by a white matter track that could correspond to the posterior segment of the arcuate fasciculus, first described by Catani, Jones, and Ffytche (2005) in their dissection of the human peri- sylvian language network. The second site of colateralization with the pSTS, lo- cated in the precentral gyrus, although found at a lower level of significance, has been repeatedly reported as being coactivated with the hIPS in nearly all arithmetic tasks requiring an active manipulation of numbers, by opposition to mere priming or adaptation paradigms (Pinel, Piazza, Le Bihan, & Dehaene, 2004; Delazer et al., 2003; Stanescu et al., 2000). It is noteworthy that the pSTS is quite remote from the precentral site (although probably connected to it via the arcuate fasciculus; see Schmahmann et al., 2007). Conversely, the precentral site shows an asymmetry entirely independent of the nearby sFG. Thus, covariations of asymmetry profiles, as identified by the present ‘‘colateralization analysis,’’ may reflect functionally significant connectivity rather than spatial proximity. It is interesting that the superior temporal language area that colateralizes with the hIPS has been identified as important for mapping linguistic inputs onto the amodal representation of their meaning in adults. The pSTS can be activated by either written and spoken words or sentences (Beauchamp, Argall, Bodurka, Duy, & Martin, 2004), it appears essential for semantic-level processing of words and pictures (Vandenbulcke, Peeters, Dupont, Van Hecke, & Vandenberghe, 2007; Vandenberghe, Price, Wise, Josephs, & Frackowiak, 1996), and it may form a linking symbolic and high-level ‘‘convergence zone’’ nonsymbolic information (Damasio & Damasio, 1994). If so, the correlation between pSTS and hIPS asymmetry may reflect the mapping of abstract representations of number symbols (perhaps shared by Arabic numerals and by spoken and written number words), putatively coded in the left pSTS, to the corresponding numerical quantities, putatively coded in the hIPS. According to this scenario, although both left and right parietal lobes appear to encode numerosity, the left parietal region may be more susceptible to changes induced by the acquisition of number symbols because of more direct links with left hemispheric parietal and temporal areas involved in word processing. Piazza, Pinel, Le Bihan, and Dehaene (2007) first probed the convergence of sym- bolic and nonsymbolic representations of numbers us- ing a cross-notation paradigm of fMRI adaptation (Arabic digits and sets of dots). They observed that the numeri- cal information was transferred across those two nota- tions in both the left and right hIPS, at a site only 6 mm from the present parietal area whose asymmetry corre- lates with the pSTS lateralization. Critically, Piazza et al. (2007) found a hemispheric asymmetry, suggesting that the coding of Arabic numerals was more precise in the left hIPS than in the right hIPS. They suggested that although both the left and right hIPS are involved in the coding of numerical quantities, the quantity code in the left hIPS is progressively refined through a direct inter- action with number symbols coded in the left hemi- sphere, such as words or Arabic numerals. Verguts and Fias (2004) indeed showed in a neural network simula- tion how the interaction of symbolic and nonsymbolic codes for number could yield to such a refinement of the precision of number coding. A developmental study by Ansari and Dhital (2006) also observed that the left, but not the right, IPS exhibited an increase in the size of the numerical distance effect during a number com- parison task—again compatible with the hypothesis that the left IPS is the target of a particular development, possibly including an increase in the precision of nu- merical coding induced by the concomitant acquisition of number symbols. Our study is compatible with this assumption and tentatively suggests that the primary source of this developmental change in the hIPS may be its direct connection with a high-level representation of numerical symbols in the pSTS. Colateralization of the Language-related mFG and the sPL We now turn to our second finding, the colateralization of the mFG during reading with a large extent of ac- tivation in the sPL and the precuneus during calculation. Although the sPL had been tentatively associated to visuospatial mechanisms in the context of fronto-parietal circuits (Astafiev et al., 2003; Simon et al., 2002), the mFG implicated here is much more inferiorly positioned, making this correlation of asymmetry more difficult to Pinel and Dehaene 61 D o w n l o a d e d l l / / / / j t t f / i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j . f . / . t o n 1 8 M a y 2 0 2 1 interpret. The mFG site that we observed, located dor- sally to Broca’s region, has repeatedly been reported for both speech listening and word reading tasks (Mechelli et al., 2005; Binder et al., 2000), yet those studies did not isolate which specific linguistic process is involved. This site is also frequently activated during calculation tasks (see details in Pinel et al., 2007). It may tentatively reflect general working memory processes for storage and in- tegration of information contained in a complex and extended verbal stimulus. Interestingly, it is known that although the frontal lobe supports working memory pro- cesses independently of the nature of inputs (Owen et al., 1998), additional posterior areas may be involved according to the nature of the content. For instance, Klingberg (2006) reported a developmental increase of the white matter connections linking frontal and supe- rior parietal areas involved in a visuospatial memory task. Considering current theories that postulate shared mechanisms for numerical and visuospatial processing (Hubbard, Piazza, Pinel, & Dehaene, 2005), it may be pro- posed that, in the case of our arithmetical operations (dis- played in a sentence-like presentation), which consisted of a simple canonical structure (first operand one, sign, second operand), the relation between these quantities would be jointly encoded syntactically in the mFG and spatially in the sPL. This recruitment of spatial networks would explain why numerical operations often elicit spa- tial attentional and motor biases (for a review, see Hubbard et al., 2005). Although speculative, this account fits with reports of impaired arithmetic procedural skills with pre- servation of number knowledge in the case of a frontal lesion (Lucchelli & De Renzi, 1993), and may also par- tially explain the spatial deficits reported in children with mathematical disabilities (Geary, Hoard, Byrd-Craven, & DeSoto, 2004; Noe¨l, Seron, & Trovarelli, 2004). DTI analysis showed that the colateralized mFG and sPL areas are connected by the anterior segment of the arcuate fasciculus (Catani et al., 2005). Note that al- though they showed similar profile of lateralization, no fibers were found to link the mFG and the precuneus. Because long-distance association fibers such as the superior longitudinal fasciculus are known to connect the frontal and posterior parietal lobes (Jellison et al., 2004), it is likely that dense local parietal connections may have artifactually limited the tracking algorithm to the anterior hIPS portion. It is also plausible that a cascade of local connections inside the parietal lobe propagates from the superior parietal lobe toward the precuneus via U-shaped association fibers. Implications for the Development of Symbolic Arithmetic It is tempting, although obviously speculative, to inter- pret the present across tasks colateralizations within a causal developmental framework. Although a detailed lateralization analysis similar to the present one remains to be done with fMRI data from children, studies of early brain lesions and time windows for recovering linguistic abilities suggest that the hemispheric organization for language is already established within the first 5 years of life (Bates & Roe, 2001). Indeed, recent neuroimaging data indicate that a leftward lateralization of the tempo- ral lobe can be observed during speech listening in infancy as early as 2 to 3 months after birth (Dehaene- Lambertz, Dehaene, & Hertz-Pannier, 2004; Pen˜a et al., 2003). A shift toward left hemispheric processing has been reported during a lexical task around 14 to 20 months old (Mills, Coffey-Corina, & Neville, 1997), and a strictly left- lateralized set of fronto-inferotemporal activations has been seen during an auditory semantic task in 5-year-olds (Balsamo, Xu, & Gaillard, 2006). Contrariwise, in 5-year-old children, the number pro- cessing networks of the parietal lobe are equally activated in both hemispheres, for both digits and dots manipu- lation (Temple & Posner, 1998). With nonsymbolic pre- sentations of numbers as sets of objects, activation during number processing may even show a rightward laterali- zation in 4-year-olds and even in infants (Izard, Dehaene- Lambertz, & Dehaene, 2008; Cantlon et al., 2007). One possible interpretation of these lateralization patterns is that the pSTS lateralization for language precedes and progressively biases the lateralization of the hIPS for number. This implies that, although the pSTS is not part of the mature arithmetic circuit in the adult brain, proper functioning of the temporo-parietal language system may be crucial for the normal develop- ment and acquisition of mathematics. Such a develop- mental model would seem to fit well with the scarce developmental data available, to date, on how the num- ber system evolves with age. Rivera, Reiss, Eckert, and Menon (2005) observed that the fMRI correlates of performance in a simple arithmetical task shifted from the frontal lobe toward a more focused temporo-parietal network as the age of the subjects varied from 8 to 19 years of age. The only two areas that increased in activity with age were a left inferior/middle temporal region and a left supramarginal/IPS region that both fall close to those observed in the present study. This fMRI result concurs with behavioral studies that indicate a progressive automatization and strengthening of the link between digit shapes and the corresponding quantities from first- to fifth-grade children (Rubinsten, Henik, Berger, & Shahar-Shalev, 2002). Indeed, in adults, this interference effect of an irrelevant Arabic digit onto a physical size comparison task has been related to intra- parietal cortex (Pinel et al., 2004). Based on this developmental scenario, it is then pos- sible that the pivotal role of the left STS for symbol processing decreases later in life in the special case of number symbols, as number processing becomes highly automatized. Such a decrease would fit with the clinical dissociation between numerical and nonnumerical mean- ing reported at the adult age: Zamarian, Karner, Benke, 62 Journal of Cognitive Neuroscience Volume 22, Number 1 D o w n l o a d e d l l / / / / j t t f / i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j . . t f . / o n 1 8 M a y 2 0 2 1 Donnemiller, and Delazer (2006) described a single-case study of a patient with of severe atrophy of the tempo- ral lobe, who presented great difficulties in understand- ing or finding some words but performed at ceiling in number tasks, notably with all numerical formats in transcoding tasks. Under the speculative hypothesis presented here, lateralization of the left STS would serve as a seed that constrains a subsequent cascade of secondary lateraliza- tion in the associative parietal cortices to which it is tightly interconnected (Andresen & Marsolek, 2005). It should be remembered, however, that the present correlational method is unable to assess the causality of these events. Genuinely testing this developmental model will therefore require an adaptation of the pres- ent methods to future longitudinal developmental fMRI data. A Mosaic of Lateralizations in all, our study questions the very concept of All hemispheric ‘‘dominance.’’ This concept, indeed, has been already challenged by occasional case studies that reported interhemispheric dissociations between lan- guage production and comprehension tasks (Dongwook et al., 2008; Jansen et al., 2006). Here we showed that, even within a given experimental situation such as sentence comprehension, the strongly left-lateralized speech processing network may be dissected into a com- plex combination of distinct patterns of asymmetry. Sur- prisingly, these patterns allow dissociating even closely located areas. For instance, the profile of asymmetry of the mFG is similar, during the reading task, to that of the fusiform area, but is uncorrelated with that of inferior frontal cortex. On the contrary, the latter region colater- alizes strongly with remote sites in superior temporal and cingulate cortex. Thus, our results suggest that func- tional lateralization relates to a mosaic of partially inde- pendent left/right shifts, and results from a complex sum of regional events rather than a single overall ‘‘domi- nance’’ factor. The observed networks of long-range colateralizations may also reflect structural connections. For instance, the independent patterns of colateraliza- tion respectively associated with the pSTS and the aSTS appear to reflect fiber pathways that link the middle and posterior part of the superior temporal region to dif- ferent areas of the frontal lobe in the monkey brain (Petrides & Pandya, 1988). Our results refine the recent claim of Cai, Lavidor, Brysbaert, Paulignan, and Nazir (2008) and Hunter, Brysbaert, and Knecht (2007), who suggested that hemi- spheric dominance for spoken language production in the frontal lobe plays a causal role in the lateralization of the posterior reading system. Cai et al. (2008) based their claim on the observation of a colateralization of event-related potentials associated with orthographic processing (occipito-temporal N170) with those associ- ated with verb generation (late frontal negativity), in a population of right-handed or left-handed subjects se- lected for their strong lateralization either to the left or to the right hemisphere in the latter task. Likewise, in a similar population, Hunter et al. (2007) found a shift in the optimal viewing position for reading to the hemifield contralateral the hemisphere that was found dominant (in frontal areas) for a verbal fluency task. In our pop- ulation of normal right-handers, during reading we also found a strong colateralization of the fusiform activation with the mFG. However, there was no such collaterali- zation with nearby inferior frontal or precentral sites, therefore indicating that lateralization must be consid- ered at a finer scale than at the lobe level. Furthermore, the fronto-fusiform correlation vanished during the au- ditory speech listening task, whereas the pSTS–fusiform correlation remained very high (indeed it was the only one shared by the reading and speech listening tasks; see Table 1). These data suggest that the lateralization of orthographic processes in the fusiform may be driven much more strongly by the temporal lobe than by the frontal lobe. The tight degree of colateralization of the pSTS with essentially all other language-related areas, especially during reading (Table 1), suggests that it represents a central node in the asymmetry of these subnetworks. This central role could be a direct consequence of the structural asymmetry which is already detectable prena- tally in the planum temporale (Chi et al., 1977) and superior temporal sulcus (Dubois et al., 2008). An early asymmetry in the processing of speech sounds may create a subtle initial bias that contributes, during the development, to the establishment of a leftward asym- metry at other levels of the language system (Tervaniemi & Hugdahl, 2003; Bates & Roe, 2001). Among the other possible determinants of the mosaic of asymmetry, our data suggest that sex is not a crucial one. We only observed a weak trend to a greater leftward asymmetry in the inferior frontal area for men (especially during speech listening) in an ROI approach, yet this was not replicated in the voxel-based analysis. This result is in accordance with a series of large-scale and meta-analysis studies (Sommer, Aleman, Bouma, & Kahn, 2004; Pujol, Deus, Losilla, & Capdevila, 1999), that found no significant sex differences for language laterali- zation at the population level across tasks, challenging widespread beliefs on men/women functional brain dif- ferences (Kimura, 1999; Shaywitz et al., 1995). This ab- sence of sex effect was extended here to the left/right cortical organization of mental arithmetic. However, the lateralization of other numerical skills, such as arith- metical fact retrieval or approximate nonsymbolic cal- culation, should be explored further before concluding that men and women use strictly similar networks during arithmetic. Recent results showed that many genes are expressed asymmetrically early on in fetal development (Sun, Pinel and Dehaene 63 D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j f / . . t . o n 1 8 M a y 2 0 2 1 Collura, Ruvolo, & Walsh, 2006), and that different cor- tical areas, noticeably peri-sylvian regions, may be char- acterized by different patterns of genetic expression (Abrahams et al., 2007) which, for some genes, seem specific to humans. These data indicate that the later- alization of the widespread human language networks is probably under various local genetic influences, per- haps through a cascade of successive influences on sulcal shape and connectivity patterns (Leonard, Eckert, & Kuldau, 2006). Indeed, the present fMRI analysis is part of a larger databasing effort for which fMRI, but also behavioral, connectivity and genetic data are also col- lected from hundreds of subjects (see Pinel et al., 2007). A next step will therefore be to clarify to what extent the patterns of collateralization reported here result from structural constraints, and at which level (fiber tracks, sulci, neural microstructures, or functional biases) do genetic factors induce local hemispheric preferences in regional brain organization. Acknowledgments We thank all the investigators at Service Hospitalier Fre´de´ric Joliot and the NeuroSpin center for sharing fMRI scanning time and subjects with us, and particularly A. D. Devauchelle, J. B. Poline, and B. Thirion for supporting this database project. We also thank the NUMBRA Network student Alex Lopez Rolon for his assistance in this project. Reprint requests should be sent to Philippe Pinel, INSERM, U562, Cognitive Neuroimaging Unit, CEA/Saclay/Neurospin, Bat. 145, 91191 Gif-sur-Yvette, France, or via e-mail: philippe.pinel@cea.fr. REFERENCES Abrahams, B. S., Tentler, D., Perederiy, J. V., Oldham, M. C., Coppola, G., & Geschwind, D. H. (2007). Genome-wide analyses of human perisylvian cerebral cortical patterning. Proceedings of the National Academy of Sciences, U.S.A., 104, 17849–17854. Andresen, D. R., & Marsolek, C. J. (2005). Does a causal relation exist between the functional hemispheric asymmetries of visual processing subsystems? Brain and Cognition, 59, 135–144. Ansari, D., & Dhital, B. (2006). Age-related changes in the activation of the intraparietal sulcus during nonsymbolic magnitude processing: An event-related functional magnetic resonance imaging study. Journal of Cognitive Neuroscience, 18, 1820–1828. Astafiev, S. V., Shulman, G. L., Stanley, C. M., Snyder, A. Z., Van Essen, D. C., & Corbetta, M. (2003). Functional organization of human intraparietal and frontal cortex for attending, looking, and pointing. Journal of Neuroscience, 23, 4689–4699. Balsamo, L. M., Xu, B., & Gaillard, W. D. (2006). Language lateralization and the role of the fusiform gyrus in semantic processing in young children. Neuroimage, 31, 1306–1314. Barth, H., La Mont, K., Lipton, J., & Spelke, E. (2005). Abstract number and arithmetic in preschool children. Proceedings of the National Academy of Sciences, U.S.A., 102, 14116–14121. Bates, E., & Roe, K. (2001). Language development in children with unilateral brain injury. In C. Nelson & M. Luciana (Eds.), Handbook of developmental cognitive neuroscience (pp. 281–307). Cambridge, MA: MIT Press. Beauchamp, M. S., Argall, B. D., Bodurka, J., Duy, J. H., & Martin, A. (2004). Unraveling multisensory integration: Patchy organization within human STS multisensory cortex. Nature Neuroscience, 7, 1190–1192. Binder, J. R., Frost, J. A., Hammeke, T. A., Bellgowan, P. S. F., Springer, J. A., Kaufman, J. N., et al. (2000). Human temporal lobe activation by speech and nonspeech sounds. Cerebral Cortex, 10, 512–528. Butterworth, B. (2005). The development of arithmetical abilities. Journal of Child Psychology and Psychiatry, 46, 3–18. Cai, Q., Lavidor, M., Brysbaert, M., Paulignan, Y., & Nazir, T. A. (2008). Cerebral lateralization of frontal lobe language processes and lateralization of the posterior visual word processing system. Journal of Cognitive Neuroscience, 20, 672–681. Cantlon, J. F., Libertus, M. E., Pinel, P., Dehaene, S., Brannon, E. M., & Pelphrey, K. A. (2007). Symbolic & non-symbolic number in the developing brain. Poster presented at the Cognitive Neuroscience Society, New York. Cappelletti, M., Butterworth, B., & Kopelman, M. (2001). Spared numerical abilities in a case of semantic dementia. Neuropsychologia, 39, 1224–1239. Carey, S. (1998). Knowledge of number: Its evolution and ontogeny. Science, 282, 641–642. Catani, M., Jones, D. K., & Ffytche, D. H. (2005). Perisylvian language networks of the human brain. Annals of Neurology, 57, 8–16. Chi, J., Dooling, E., & Gilles, F. (1977). Left–right asymmetries of the temporal speech areas of the human fetus. Archives of Neurology, 34, 346–348. Chochon, F., Cohen, L., van de Moortele, P. F., & Dehaene, S. (1999). Differential contributions of the left and right inferior parietal lobules to number processing. Journal of Cognitive Neuroscience, 11, 617–630. Cohen, L., & Dehaene, S. (2004). Specialization within the ventral stream: The case for the visual word form area. Neuroimage, 22, 466–476. Cohen, L., Dehaene, S., Chochon, F., Lehe´ricy, S., & Naccache, L. (2000). Language and calculation within the parietal lobe: A combined cognitive, anatomical and fMRI study. Neuropsychologia, 38, 1426–1440. Cohen, L., Jobert, A., Le Bihan, D., & Dehaene, S. (2004). Distinct unimodal and multimodal regions for word processing in the left temporal cortex. Neuroimage, 23, 1256–1270. Cointepas, Y., Poupon, C., Maroy, R., Riviere, D., Le Bihan, D., & Mangin, J. F. (2003). A freely available Anatomist/ BrainVISA package for analysis of diffusion MR data [Proceedings of the 9th HBM Scientific Meeting, New York, USA]. Neuroimage, 19, S810. Damasio, A. R., & Damasio, H. (1994). Cortical systems for retrieval of concrete knowledge: The convergence zone framework. In C. Koch & J. L. Davis (Eds.), Large-scale neuronal theories of the brain (pp. 61–74). Cambridge, MA: MIT Press. Dehaene, S. (2007). Symbols and quantities in parietal cortex: Elements of a mathematical theory of number representation and manipulation. In P. Haggard & Y. Rossetti (Eds.), Attention & performance: XXII. Sensori-motor foundations of higher cognition (pp. 527–574). Cambridge, MA: Harvard University Press. Dehaene, S., & Cohen, L. (1995). Towards an anatomical and functional model of number processing. Mathematical Cognition, 1, 83–120. 64 Journal of Cognitive Neuroscience Volume 22, Number 1 D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j f . / . t . o n 1 8 M a y 2 0 2 1 Dehaene, S., Izard, V., Spelke, E., & Pica, P. (2008). Log or linear? Distinct intuitions of the number scale in Western and Amazonian indigene cultures. Science, 320, 1217–1220. Dehaene, S., Piazza, M., Pinel, P., & Cohen, L. (2003). Three parietal circuits for number processing. Cognitive Neuropsychology, 20, 487–506. Dehaene-Lambertz, G., Dehaene, D., & Hertz-Pannier, L. (2004). Functional neuroimaging of speech perception in infants. Science, 298, 2013–2015. Delazer, M., Domahs, F., Bartha, L., Brenneis, C., Lochy, A., Trieb, T., et al. (2003). Learning complex arithmetic—An fMRI study. Cognitive Brain Research, 18, 76–88. Dongwook, L., Swanson, S. J., Sabsevitz, D. S., Hammeke, A., Winstanley, F. S., Possing, E. T., et al. (2008). Functional MRI and Wada studies in patients with interhemispheric dissociation of language functions. Epilepsy & Behavior, 13, 350–356. Dubois, J., Benders, M., Cachia, A., Lazeyras, F., Ha-Vinh Leuchter, R., Sizonenko, S. V., et al. (2008). Mapping the early cortical folding process in the preterm newborn brain. Cerebral Cortex, 18, 1444–1454. Eger, E., Sterzer, P., Russ, M. O., Giraud, A. L., & Kleinschmidt, A. (2003). A supramodal number representation in human intraparietal cortex. Neuron, 37, 719–725. Geary, D. C., Hoard, M. K., Byrd-Craven, J., & DeSoto, C. M. (2004). Strategy choices in simple and complex addition: Contributions of working memory and counting knowledge for children with mathematical disability. Journal of Experimental Child Psychology, 88, 121–151. Geschwind, N., & Levitsky, W. (1968). Left–right asymmetry in temporal speech region. Science, 161, 186–187. Gordon, P. (2004). Numerical cognition without words: Evidence from Amazonia. Science, 306, 496–499. Hickok, G., & Poeppel, D. (2000). Towards a functional neuroanatomy of speech perception. Trends in Cognitive Sciences, 4, 131–138. Hubbard, E. M., Piazza, M., Pinel, P., & Dehaene, S. (2005). Interactions between number and space in parietal cortex. Nature Reviews Neuroscience, 6, 435–448. Hunter, Z. R., Brysbaert, M., & Knecht, S. (2007). Foveal word reading requires interhemispheric communication. Journal of Cognitive Neuroscience, 19, 1373–1387. Izard, V., Dehaene-Lambertz, G., & Dehaene, S. (2008). Distinct cerebral pathways for object identity and number in human infants. PLoS Biology, 6, e11. doi:10.1371/journal. pbio.0060011. Lefevre, J. A. (1996). Selection of procedures in mental addition: Reassessing the problem size effect in adults. Journal of Experimental Psychology: Learning, Memory, and Cognition, 22, 216–230. Leonard, C. M., Eckert, M. A., & Kuldau, J. M. (2006). Exploiting human anatomical variability as a link between genome and cognome. Genes, Brain, and Behavior, 5, 64–77. Lindenberg, R., Fangerau, H., & Seitz, R. J. (2007). ‘‘Broca’s area’’ as a collective term? Brain and Language, 102, 22–29. Lucchelli, F., & De Renzi, E. (1993). Primary dyscalculia after a medial frontal lesion of the left hemisphere. Journal of Neurology and Psychiatry, 56, 304–307. McCrink, K., & Wynn, K. (2004). Large-number addition and subtraction by 9-month-old infants. Psychological Science, 15, 776–781. Mechelli, A., Crinion, J. T., Long, S., Friston, K. J., Lambon Ralph, M. A., Patterson, K., et al. (2005). Dissociating reading processes on the basis of neuronal interactions. Journal of Cognitive Neuroscience, 17, 1–13. Menon, V., Rivera, S. M., White, C. D., Eliez, G. H., Glover, G. H., & Reiss, A. L. (2000). Functional optimization of arithmetic processing in perfect performers. Cognitive Brain Research, 9, 343–345. Mills, D. L., Coffey-Corina, S., & Neville, H. J. (1997). Language comprehension and cerebral specialization from 13 to 30 months. Developmental Neuropsychology, 13, 397–445. Nieder, A., Diester, L., & Tudusciuc, O. (2006). Temporal and spatial enumeration processes in the primate parietal cortex. Science, 313, 1431–1435. Noe¨l, M. P., Seron, X., & Trovarelli, F. (2004). Working memory as a predictor of addition skills and addition strategies in children. Current Psychology of Cognition, 22, 3–25. Owen, O. M., Stern, C. E., Look, R. B., Tracey, I., Rosen, B. R., & Petrides, M. (1998). Functional organization of spatial and nonspatial working memory processing within the human lateral frontal cortex. Proceedings of the National Academy of Sciences, U.S.A., 95, 7721–7726. Pen˜a, M., Maki, A., Kovacic´, D., Dehaene-Lambertz, G., Koizumi, H., Bouquet, F., et al. (2003). Sounds and silence: An optical topography study of language recognition at birth. Proceedings of the National Academy of Sciences, U.S.A., 100, 11702–11705. Petrides, M., & Pandya, D. N. (1988). Association fiber pathways to the frontal cortex from the superior temporal region in the rhesus monkey. Journal of Comparative Neurology, 273, 52–66. Jackson, M., & Warrington, E. K. (1986). Arithmetic skills in Piazza, M., Izard, V., Pinel, P., Le Bihan, D., & Dehaene, S. patients with unilateral cerebral lesions. Cortex, 22, 611–620. Jansen, A., Deppe, M., Schwindt, W., Mohammadi, S., Sehlmeyer, C., & Knecht, S. (2006). Interhemispheric dissociation of language regions in a healthy subject. Archive of Neurology, 63, 1344–1346. Jellison, B. J., Field, A. S., Medow, J., Lazar, M., Salamat, M. S., & Alexander, A. L. (2004). Diffusion tensor imaging of cerebral white matter: A pictorial review of physics, fiber tract anatomy, and tumor imaging patterns. American Journal of Neuroradiology, 25, 356–369. Kimura, D. (1999). Sex and cognition. Cambridge, MA: MIT Press. Klingberg, T. (2006). Development of a superior frontal–intraparietal network for visuo-spatial working memory. Neuropsychologia, 44, 2171–2177. Kosslyn, S. M., Koenig, O., Barrett, A., Cave, C. B., Tang, J., & Gabrieli, J. D. E. (1989). Evidence for two types of spatial representations: Hemispheric specialization for categorical and coordinate relations. Journal of Experimental Psychology: Human Perception and Performance, 15, 723–735. (2004). Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron, 44, 547–555. Piazza, M., Mechelli, A., Price, C. J., & Butterworth, B. (2006). Exact and approximate judgements of visual and auditory numerosity: An fMRI study. Brain Research, 1106, 177–188. Piazza, M., Pinel, P., Le Bihan, D., & Dehaene, S. (2007). A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron, 2, 293–305. Pica, P., Lemer, C., Izard, V., & Dehaene, S. (2004). Exact and approximate arithmetic in an Amazonian indigene group. Science, 306, 499–503. Pinel, P., Dehaene, S., Riviere, D., & Le Bihan, D. (2001). Modulation of parietal activation by semantic distance in a number comparison task. Neuroimage, 14, 1013–1026. Pinel, P., Piazza, M., Le Bihan, D., & Dehaene, S. (2004). Distributed and overlapping cerebral representations of number, size, and luminance during comparative judgments. Neuron, 41, 983–993. Pinel, P., Thirion, B., Meriaux, S., Jobert, A., Serres, J., Le Bihan, D., et al. (2007). Fast reproducible identification and Pinel and Dehaene 65 D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j / f . . . t o n 1 8 M a y 2 0 2 1 large-scale databasing of individual functional cognitive networks. BMC Neuroscience, 8, 91. Pujol, J., Deus, J., Losilla, J. M., & Capdevila, A. (1999). Cerebral lateralization of language in normal left-handed people studied by functional MRI. Neurology, 52, 1038–1043. Rivera, S. M., Reiss, A. L., Eckert, M. A., & Menon, V. (2005). Developmental changes in mental arithmetic: Evidence for increased functional specialization in the left inferior parietal cortex. Cerebral Cortex, 15, 1779–1790. Rubinsten, O., Henik, A., Berger, A., & Shahar-Shalev, S. (2002). The development of internal representations of magnitude and their association with Arabic numerals. Journal of Experimental Child Psychology, 81, 74–92. Schmahmann, D. D., Pandya, D. N., Wang, R., Dai, G., D’Arceuil, H. E., de Crespigny, A. J., et al. (2007). Association fibre pathways of the brain: Parallel observations from diffusion spectrum imaging and autoradiography. Brain, 130, 630–653. Seghier, M. (2008). Laterality index in functional MRI: Methodological issues. Magnetic Resonance Imaging, 26, 594–601. Semenza, C., Delazer, M., Bertella, L., Grana`, A., Mori, I., Conti, F. M., et al. (2006). Is math lateralised on the same side as language? Right hemisphere aphasia and mathematical abilities. Neuroscience Letters, 406, 285–288. Shaywitz, B. A., Shaywitz, S. E., Pugh, K. R., Constable, R. T., Skudlarski, P., Fulbright, R. K., et al. (1995). Sex differences in the functional organisation of the brain for language. Nature, 373, 607–609. Siegler, R. S., & Booth, J. L. (2004). Development of numerical estimation in young children. Child Development, 75, 428–444. Simon, O., Kherif, F., Flandin, G., Poline, J. B., Riviere, D., Mangin, J. F., et al. (2004). Automatized clustering and functional geometry of human parietofrontal networks for language, space, and number. Neuroimage, 23, 1192–1202. Simon, O., Mangin, J. F., Cohen, L., Le Bihan, D., & Dehaene, S. (2002). Topographical layout of hand, eye, calculation, and language-related areas in the human parietal lobe. Neuron, 33, 475–487. calculation processes: Impact of number size on the cerebral circuits for exact and approximate calculation. Brain, 123, 2240–2255. Sun, T., Collura, R. V., Ruvolo, M., & Walsh, C. A. (2006). Genomic and evolutionary analyses of asymmetrically expressed genes in human fetal left and right cerebral cortex. Cerebral Cortex, 16(Suppl. 1), i18–i25. Temple, A., & Posner, E. (1998). Brain mechanisms of quantity are similar in 5-year-old children and adults. Proceedings of the National Academy of Sciences, U.S.A., 95, 7836–7841. Tervaniemi, M., & Hugdahl, K. (2003). Lateralization of auditory-cortex function. Brain Research Review, 43, 231–246. Toga, A. W., & Thompson, P. M. (2003). Mapping brain asymmetry. Nature Reviews Neuroscience, 4, 37–48. Vandenberghe, R., Price, C., Wise, R., Josephs, O., & Frackowiak, R. (1996). Functional anatomy of a common semantic system for words and pictures. Nature, 383, 254–256. Vandenbulcke, M., Peeters, R., Dupont, P., Van Hecke, P., & Vandenberghe, R. (2007). Word reading and posterior temporal dysfunction in amnesic mild cognitive impairment. Cerebral Cortex, 17, 542–551. Varley, R. A., Klessinger, N. J., Romanowski, C. A., & Siegal, M. (2005). Agrammatic but numerate. Proceedings of the National Academy of Sciences, U.S.A., 102, 3519–3524. Vauclair, J., Yamazaki, Y., & Gu¨ntu¨rku¨n, O. (2006). The study of hemispheric specialization for categorical and coordinate spatial relations in animals. Neuropsychologia, 44, 1524–1534. Venkatraman, V., Ansari, D., & Chee, M. W. (2005). Neural correlates of symbolic and nonsymbolic arithmetic. Neuropsychologia, 43, 744–753. Venkatraman, V., Siong, S. C., Chee, M. W., & Ansari, D. (2006). Effect of language switching on arithmetic: A bilingual fMRI study. Journal of Cognitive Neuroscience, 18, 64–74. Verguts, T., & Fias, W. (2004). Representation of number in animals and humans: A neural model. Journal of Cognitive Neuroscience, 16, 1493–1504. Wynn, K. (1992). Addition and subtraction by human infants. Sommer, I. E. C., Aleman, A., Bouma, A., & Kahn, R. S. (2004). Nature, 358, 749–750. Do women really have more bilateral language representation than men? A meta-analysis of functional imaging studies. Brain, 127, 1845–1852. Stanescu-Cosson, R., Pinel, P., van de Moortele, P. F., Le Bihan, D., Cohen, L., & Dehaene, S. (2000). Cerebral bases of Zamarian, L., Karner, E., Benke, T., Donnemiller, E., & Delazer, M. (2006). Knowing 7 (cid:2) 8, but not the meaning of ‘‘elephant’’: Evidence for the dissociation between numerical and non-numerical semantic knowledge. Neuropsychologia, 44, 1708–1723. D o w n l o a d e d l l / / / / j t t f / i t . : / / f r o m D h o t w t n p o : a / d / e m d i f t r o p m r c h . s p i l d v i e r e r c c t . h m a i r e d . u c o o m c / n j a o r c t i n c / e a - p r d t i 2 c 2 l 1 e - 4 p 8 d 1 f 9 / 3 2 8 2 4 / 1 1 1 / o 4 c 8 n / 1 2 7 0 0 6 9 9 1 2 1 1 5 1 / 8 4 j o p c d n . b 2 y 0 g 0 u 9 e . s t 2 o 1 n 1 8 0 4 8 . S p e d p f e m b y b e g r u 2 e 0 2 s 3 t / j . f t . . / o n 1 8 M a y 2 0 2 1 66 Journal of Cognitive Neuroscience Volume 22, Number 1

Télécharger le PDF