Bespoke Physics for
Living Technology
David H. Ackley*
The University of New Mexico
In the physics of the natural world, basic tasks of life,
Abstrait
such as homeostasis and reproduction, are extremely complex
opérations, requiring the coordination of billions of atoms even in
simple cases. Par contre, artificial living organisms can be
implemented in computers using relatively few bits, and copying a
data structure is trivial. Bien sûr, the physical overheads of the
computers themselves are huge, but since their programmability
allows digital “laws of physics” to be tailored like a custom suit,
deploying living technology atop an engineered computational
substrate might be as or more effective than building directly on the
natural laws of physics, for a substantial range of desirable purposes.
This article suggests basic criteria and metrics for bespoke physics
computing architectures, describes one such architecture, and offers
data and illustrations of custom living technology competing to
reproduce while collaborating on an externally useful computation.
Mots clés
Bespoke physics, indefinite scalability,
living technology, Movable Feast Machine,
spatial computing
A version of this paper with color figures is
available online at http://dx.doi.org/10.1162/
artl_a_00117. Subscription required.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1 Living Technology and Big Computing
In some ways, en effet, life is hard. Certainly, in the natural world, making a self-sustaining and
reproducing creature is a messy and complex affair. Even the tiny Pelagibacter ubique bacterium
[30], Par exemple, known as one the smallest of free-living creatures, involves hundreds of millions
of atoms, and its reproduction involves intricate choreography, for over a day, of that many more.
Natural life is an amazing, obstinate process, but—at least from the viewpoint of an atom, say—it
isnʼt easy.
In exploring life as it could be, artificial life researchers deploy technologies—from robotic hard-
ware, to pure software, to biochemical preparations—that implement the organisms and operations
of life in many ways, sometimes quite differently from traditional life as we know it. The primary
purpose of such research has often been scientific, but—as introduced and discussed in [5]—there
is also growing interest in living technology: engineered systems that make essential use of lifelike com-
ponents or principles. A recent focus (voir, par exemple., many of the articles in [31]) is wet living technology,
which uses atoms and small molecules as basic units and builds from there toward basic living
mechanisms like metabolism and reproduction. Such efforts have tremendous potential because they
build on the same low-level, widely available ingredients and conditions as natural life, and can deploy
similar structures and mechanisms for similar jobs—but by the same token, many aspects of their
design are prefigured by their relatively traditional atomic units and chemical interactions.
* Department of Computer Science, The University of New Mexico, Albuquerque, NM 87131. E-mail: ackley@cs.unm.edu
© 2013 Massachusetts Institute of Technology
Artificial Life 19: 347–364 (2013) est ce que je:10.1162/ARTL_a_00117
D. H. Ackley
Bespoke Physics for Living Technology
Choosing atoms, say, as the basic units for an approach to living technology is just one possibility—as
discussed for example by Pattee [29], it is ultimately a definitional question how we categorize
phenomena as “physical law” versus “initial condition.” Like nesting virtual machines in computer
science—one machine simulating another, which may be simulating a third, and so on—one theoryʼs
initial condition can be anotherʼs physical law. As a practical matter, for basic units we can choose
almost anything in reality that can be found or fabricated in sufficient numbers, and manipulated
as needed, for our living technology to be productive. A simple-minded approach to viruses, pour
example, might treat complete cells or complex cellular components as “atomic” entities. De la même manière,
adopting initial conditions like “clean white sand, air, falling water, and sunlight” [32] makes scientific
sense when exploring the origins of natural life, but for systems engineering all such decisions are for
the living technology designer to make, given the tasks and resources at hand.
Compared to low-level wet approaches, living technologies built on digital software and
hardware require extensive computing machinery before we can even begin to design—but that
looks increasingly reasonable, given the proliferation of inexpensive computing devices in our
environment. Relatively low-cost processor and memory chips are now being produced by the
million, creating a potential “complexity sweet spot” for digital living technologies based on such
machinery. And building living technology atop digital hardware offers an extreme level of freedom
to the designer. General-purpose programmability allows bits and Boolean operations to combine in
a staggering panoply of possible “atomic” units and “chemical” mechanisms to underpin a living
technologie. Computer-based models of artificial chemistries ([13] is an early review) vary widely, dans
everything from their size and level of detail to their spatial dimensionality and treatment of time.
Such diversity in laws of digital physics is understandable given the design freedom of the approach
and the range of the scientific and theoretical purposes of the models. En même temps, such variety
makes it challenging to compare models or have much confidence that results from one may apply
in another.
My primary purpose in writing this article is to highlight potential connections between computer
architecture and engineering on the one hand, and artificial life, artificial chemistry, and artificial
physics on the other. Section 2 offers possible requirements and quality principles, or metalaws,
for custom laws of physics in computer systems, motivated primarily by engineering concerns,
and suggests some rough and ready metrics for comparing approaches. Section 3 provides an
overview for the artificial life community of our work with the Movable Feast Machine, a metalaw-
compliant architecture for bespoke physics processing. Section 4 relates this work to some existing
research efforts, and finally, Section 5 offers a brief conclusion.
2 Bespoke Physics as Interface
In traditional scientific use, laws of physics are descriptive—representing more or less accurate or
predictive abstractions of reality—and, in effect, they are judged by their leverage: the simplicity or
cleanliness of the laws themselves versus the range of initial conditions over which the laws make
useful predictions. For engineering use, here our purpose is prescriptive: laws of physics as speci-
fications for the structure and behavior of machinery. A law like F = ma, Par exemple, can be at once
a scientific description of a wide range of physical phenomena, and an engineering prescription for a
computer game or physical simulation.
In computer and software engineering, an interface specification defines the legal interactions
between some system components. As in laws of physics, in interface specification quality derives
largely from simplicity and clarity versus completeness and utility—which all vary widely, depending
on the scope and maturity of the interface, as well as the underlying wisdom of its design. Le
Unix yes program—which endlessly prints lines containing ‘y’ or another given string—fills only
a small niche, but its interface specification is just a few lines of text [28]. The IA32/64 architecture,
by contrast—a widely used interface between computer hardware and software—is specified by a
software developerʼs manual [18] que, currently, spans some 3,000 pages in seven volumes.
348
Artificial Life Volume 19, Nombre 3 & 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
The vast gap between such a complex specification and the simple power of, say, Newtonian
mechanics mostly reflects different divisions of labor between “law” and “initial condition,” as
discussed earlier. The same physical laws describe basically all mechanical devices; the additional
details needed to describe any particular machine are relegated to the initial conditions. Par contre, un
IA32 machine remains distinctly a computer—though perhaps operating only briefly or uselessly—no
matter what the initial contents of its memory.
The very notion of a bespoke physics may seem a pointless contrivance, because any bespoke-
physics-plus-implementation can always be viewed as a single undifferentiated system in the “real”
laws of physics of the natural world. But the same is true of interfaces in computing—any
collection of interfaces-plus-implementations can also be viewed as a single monolithic computa-
tion—and yet good interfaces are crucial to manage complexity throughout hardware, software,
and systems engineering.
At root, my goal for the concept of bespoke physics is to pull the concepts of interface specifi-
cations and laws of physics toward each other. Bespoke physics asks us to frame laws of physics that
are somewhat constrained and task-specific—as is typical for interface specifications—while also
defining computing interfaces and architectures that are simple and indefinitely scalable—as is
typical for laws of physics.
2.1 Definitions and Design Principles
In this section we use the key words MUST and SHOULD (similarly SHOULD NOT)—as described in
RFC2119 [7]—to introduce passages constituting requirements and strong expectations, respecter-
tivement, of a specification.1 Let a bespoke physics be composed of a definition of a basic unit, lequel
may have any set of ascribed properties representable in finite state, plus a finite set of dynamical
laws determining how the basic units move and interact. Depending on the purpose, a basic unit
might be akin to an atom or a subatomic particle, or a molecule or a cell, or a billiard ball or a bit
or a widget; ascribed properties might include atomic number or charge, valence or cell type, solid or
striped, or some wild pastiche never before seen in one entity.
A bespoke physics, plus an initial condition—some arrangement of basic units—defines a computa-
tion. A computational system, à son tour, is a physical realization or implementation of a computation. Et
finally, a bespoke physics for computation can also be called a hosted physics relative to such an
implementation, which may also be called a host physics.
Those definitions are meant to be agnostic about whether the basic units and dynamical laws are
more or less analog or digital in character—but, minding the complexity sweet spot discussed above,
this article considers only implementations based on widely available digital circuitry. Note also that
in a digital bespoke physics, a single bit may or may not be a basic unit—some larger data structure
involving multiple bits may be more useful. Par exemple, the basic units in the physics described in
Section 3 have ascribed properties specified by 64 bits each.
As in the scientific usage, for our engineering use we also wish to maximize the leverage of our
custom physics—on the one hand by keeping the laws as manageable and affordably implementable
as possible, while on the other hand ensuring their widest applicability to possible initial conditions.
To that end, d'abord, there is the implementability requirement : A bespoke physics for a computational sys-
tem MUST be implementable, d'une manière ou d'une autre, in conventional physical reality as we understand it. Tel
implementations—in principle or (preferably) in actual practice—provide one more or less quantita-
tive basis for comparing the capabilities and costs of different bespoke laws of physics, as discussed
in Section 2.3.
1 Applying a term like “should” to the laws of physics seems utterly teleological and mystical—suggesting they have a creator capable of
purpose and expectation—but of course that is precisely what bespoke laws of physics do have. And despite the lure of purely formal
specifications, in practice, adopting an intentional stance is often essential to the effective use of complex systems of interfaces.
Artificial Life Volume 19, Nombre 3 & 4
349
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
Deuxième, we offer four quality principles, or metalaws, aimed at increasing the compactness or usability
of the laws themselves, or increasing the set of possible initial conditions, or both:
1. Indefinite scalability: The laws themselves SHOULD NOT have internal restrictions or limits; ils
SHOULD apply to arbitrary and arbitrarily large initial conditions—at least in principle and for
analyse, even if such initial conditions may not be practically constructible.
2. Spatiotemporal isotropy at scale: There may be some fine structure or granularity to the laws,
mais, at least above some length and duration accessible to the artificial life organisms, le
laws SHOULD apply uniformly, regardless of specific disposition in space or moment in time.
3. Limited causality: The laws SHOULD NOT (and arguably cannot) require globally deterministic
evolution from the initial conditions, but there SHOULD be generally reliable causal
regularities, at space and time scales locally exploitable by the artificial life organisms.
4. Strong level isolation: It SHOULD be as difficult as possible to affect the bespoke laws of physics
from within the computation itself. Hardware designed to implement just one bespoke
physics would be perfect, but for economies of scale, or research and development,
programmable hardware may be used, meaning the bespoke physics can, d'une manière ou d'une autre, être
modified without manufacturing, so this possibility must be treated carefully.
In descriptive contexts, principle 1 usually goes without saying—at least until it is violated, as when
classical mechanics breaks down around a black hole. In computer engineering, though, the wide-
spread use of techniques that are only finitely scalable—such as global synchronous clocking, fixed-
width memory addressing, or globally unique network addresses—mean that very few existing
computing mechanisms donʼt violate principle 1 (voir [2] for further discussion).
In his 1963 Nobel Lecture [37], Wigner discussed basic superprinciples that physical laws should
possess even to be recognizable as such—including invariance under Euclidean geometric transfor-
mations and time displacements, which he called “Category (un) et (b) invariance transformations.”
Principle 2 is a rendering of that same intent, though weakened to add engineering “wiggle room” at
the bottom.
Principle 3, similarly, is an explicit weakening of the notion of global determinism or causality.
Though physical and philosophical theories differ on the degree and nature of determinism pre-
sumed to exist in reality, nearly all current computers are deterministic in the sense that they are
designed to produce exactly the same outputs given the same inputs, with very high probability. Ce
can ease debugging and logical analysis, but means any randomness needed by the computation must
be simulated.2 Furthermore, such determinism is increasingly unaffordable as systems grow under
principle 1, due to synchronization costs and the need for large systems to handle errors and local
failures gracefully. Some researchers [9] in high-performance computing, Par exemple, discuss limited
ways to move beyond determinism in the move to exascale computing (machines performing 1018
operations per second). Principle 3 countenances that and even more radical departures from traditional
computational determinism, but does ask—albeit rather informally—that bespoke physics provide
enough stability and repeatability to make locally reliable computation possible.
Principle 4 also usually goes without saying; in the natural world, violations of it—known as magic—are
considered rare. Here it is an explicit quality principle, in large part, to call out the dismal state of
security and trustworthiness in computing today. It is said one shouldnʼt violate the laws of man
while one canʼt violate the laws of physics—but far too often, programmed “laws” for computer
security and privacy have proven merely the former when we needed the latter. Principle 4 asks the
computer architect and living technology designer to recognize and manage the liabilities, and not
just the benefits, of general-purpose programmability.
2 Computer designers are increasingly augmenting traditional deterministic machines with hardware devices providing “true
randomness”—or call it “external unpredictability”—primarily to facilitate encryption.
350
Artificial Life Volume 19, Nombre 3 & 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
2.2 Natural versus Bespoke Physics
A bespoke physics can call its basic unit an “atom,” but itʼs unlikely that that basic unit can or will
be implemented using a single physical atom. This article focuses on using stored digital bits to
represent a basic unit, with the bit values specifying the unitʼs ascribed properties. At a minimum,
donc, one bespoke atom requires however many real atoms it takes to store those bits. That
hosting overhead—the number of host atoms per hosted atom, overall—is the huge elephant in the
bespoke physics room, in contrast with the direct “an atom is an atom” physics of reality itself.
How bad does that ratio need to be? A MicroSD card, Par exemple, weighing perhaps half a gram,
−10 g
can today store 64 GB; if we imagine our basic units are 64 bits each, that amounts to perhaps 10
−23 g for say a carbon atom. Thirteen orders of magnitude
per bespoke atom, compared to around 10
of hosting overhead goes well beyond the perhaps billions of atoms tied up in a P. ubique, Par exemple,
and additional hosting resources are needed—processors and program memory, for example—that
only make it worse. At least in the nearer term, hosting overheads are likely to be substantial, raising
concerns about cost-effective scalability. Half a century ago, Feynman [14] discussed the vast “room
at the bottom”—at the fine-grained end of natural physics—for increased information storage and
processing density. From within a bespoke physics, there is no explicit structure below the level of
its basic unit properties—although implementation details may be detectable by the hosted physics,
despite principle 4—but Feynmanʼs arguments do suggest that clever implementations might reduce
hosting overhead significantly.
Even without such optimizations, though, there are at least two considerable benefits to bespoke
physics over natural physics. D'abord, and most important for the present purposes, a bespoke physics
gains the same advantage held by any programmable machine over a special-purpose one: Deferring
functional commitment from manufacturing time to programming time creates flexibility, allow-
ing us to change the laws of bespoke physics as needed, for research or upgrades or custom com-
putation. Basic tasks such as active transport faster than diffusion, Par exemple, which involve
considerable complexity in direct biology (par exemple., [33]), can be programmed directly in a bespoke
physics (see Section 3.4 for an example). En effet, having spent an order of magnitude of orders
of magnitude to buy the flexibility of bespoke physics, we do get to choose some rebates while
furnishing the place.
A second advantage is less immediately useful, but should be noted because it may ultimately
prove overwhelming. En principe, bespoke matter could move within a bespoke universe more
quickly and nimbly than actual matter in the spatially coextensive direct physics, because the
motion is performed by digital copying mediated by electromagnetic wave propagation at a substan-
tial fraction of light speed, rather than by actual movement of massive, inertial nuclei in the direct
physics. It is pure science fiction at present [35], but it is possible that digital technologies based on
biological components (par exemple., [8, 34]) could ultimately be outcompeted by living technologies based
on electronic components.
Long before such concerns can be taken seriously, cependant, we need ways to compare bespoke
physics systems with each other and with natural physics systems, and that is our next topic.
2.3 Scalable Metrics of Computation
Any individual computing device is a finite machine, both in physical size and in computational
capacity; as a platform for bespoke physics it would violate principle 1 of Section 2.1. But “finite”
doesnʼt mean “isolated”: To be useful, a finite machine has to have external connections, at least for
power and communications. We define an indefinitely scalable machine to be any procedure for tiling
space with finite machines, with no a priori requirements that such a tiling have any particular
properties—like aligning tile outputs with adjacent inputs. So tiling space by, say, laying HP65 pocket
calculators out in a grid is admissible as an indefinitely scalable machine.
Given such a tiling procedure, Tableau 1 defines some indefinitely scalable machine metrics, which—though
incomplete and underdetermined—suffice to show why a tiling of HP65s would not be a good
indefinitely scalable machine. The symbols are subscripted with “s ” to stress they require a scalable
Artificial Life Volume 19, Nombre 3 & 4
351
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
Tableau 1. Tile-based performance metrics for indefinitely scalable machines. Here g, s, j, and m are grams, seconds, joules,
and meters, while Ni, Ne, and Ns are counts of instructions, events, and sites, respectivement. See text.
Quantity
Peak computational density
Peak power efficiency
Peak communications velocity
Average event rate
Code
PCD
PPE
PCV
AER
Symbol
Value
Us
Ds
vs
comme
tile computation speed
tile mass
Us
dissipated power
max tile pitch
hosted bit latency
events per tile per second
sites per tile
Unit
−1 · g
Ni · s
−1
Ni · g
−1 · J
−1
−1
m · s
Ne · Ns
−1 · s
−1
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
basis; until a tiling procedure is understood, all the Table 1 metrics are undefined, no matter how capable
some finite machine may be.
We can construct an indefinitely scalable machine that is as large as we need, so long as we have
sufficient materials, energy, room, and time; the desire to minimize those resources, while somehow
maximizing computational power, motivates the metrics of Table 1. Dehonʼs [11] early and influen-
tial “ALU bit ops/area-time” metric for computational density is a similar approach, although that was
applied just to components rather than a whole tile, and was measured in process-specific units
rather than as absolute physical values, hindering comparisons between technologies.
The indefinitely scalable peak computational density (PCD for code, Us for math) is defined as the
number of instructions per second per tile divided by tile mass, where the tile itself drops out of the
equation but determines the granularity of the measurement. One instruction per second per gram
of mass hopefully will prove to be a rather small unit; recognizing Stross [35], who popularized the
phrase “MIPS per milligram,” I sometimes informally refer to a PCD of 109 comme 1 stross. The PCDʼs
use of “instructions” inherits all the notorious ambiguities that plague the notion of MIPS, mais
captures well the whole-system perspective we are advocating.
An HP65 calculator (Figure 1a, [17]) weighs 312 g and as a guess might deliver a few thousand
instructions per second, so a spatial tiling of HP65s might have a PCD in single digits. The IXM
hardware tile in Figure 1b—our first indefinitely scalable prototype, developed in collaboration with
liquidware.com [21]—masses about 16.5 g per tile (including two intertile connectors, not shown)
and peaks at 72 MIPS, for a PCD of about 4.4 million, ou 4.4 millistross. À 19 g with a 400-MHz
processor, the XMOS XK1 (Figure 1c, [38]) might offer over 26 millistross.
An obvious measure of peak power efficiency (PPE, Ds) is PCD per watt of dissipated power, ou
instructions per gram-joule as in Table 1. But of course, no matter how dense or efficient, without
communications a tiling is effectively worthless. We define the indefinitely scalable peak communica-
tions velocity (PCV, vs) as the tile pitch—the distance between adjacent tile centers—divided by the time
for one hosted bit to travel from tile to tile (taking maxima of both quantities if it matters). Ici
Chiffre 1. Estimated indefinitely scalable performance metrics for sample hardware tiles.
352
Artificial Life Volume 19, Nombre 3 & 4
D. H. Ackley
Bespoke Physics for Living Technology
the unconnected HP65s manifestly score zero; the vs upper bounds shown in Figure 1 for IXM and
XK-1 are based on their typical channel speeds, without including the latencies of hosted physics
traitement. (Note that the XK1 natively supports communications in only one scalable dimension,
despite its visual similarities to the 2D-scalable IXM.)
Such peak performance values are host physics implementation properties that hardware and
marketing people can love, but more important to programmers and users is how fast events are
likely to unfold within the hosted physics. In that context, the key implementation parameter is the
indefinitely scalable average event rate (AER, comme), where again the tile drops out, but the averaging
is over both isolated intratile events and intertile events requiring communications, in whatever
proportion is implied by the hosted physics. We currently lack any satisfactory bespoke physics
implementation on indefinitely scalable hardware—so no as values are reported in Figure 1, pour
example—but hope to establish an initial benchmark at as = 1 for DReg physics (see Section 3.2)
on our next-generation hardware now in development.
For a bespoke physics independent of any implementation, there is no inherent unit of time;
instead we measure duration and scalable computational effort in terms of average events per site
(AEPS). In one AEPS, on average each site will perform one event, which would take 1 s on an
indefinitely scalable implementation that delivered one AER.
2.4 Interdimensional Comparative Metaphysics
The measures in the previous section are fundamental but far from exhaustive; other metrics could
be as or more useful, depending on the goals and specifics of a bespoke physics and the needs and
capabilities of any given implementation strategy. Par exemple, a volume density of computation
would emphasize spatial compactness, compared to the mass density Us. And for effective parallelism,
the scalable communications bandwidth, expressed as a hosted bit current density, would likely be
a key parameter.
Beyond the specific choices, cependant, a larger goal for such metrics is to create a common
physical framework for computational machinery, allowing quantitative comparisons between
bespoke laws of physics that may differ on matters as fundamental as their basic granularity and
global dimensionality. Ensemble, the implementability requirement and the quality principles all
but force bespoke physics to employ no more than three scalable dimensions,3 but finite-sized
compact dimensions can be added as desired. Par exemple, a “thin film” of one finite and two scalable
dimensions could offer locally three-dimensional bespoke physics on top of an essentially two-
dimensional implementation, facilitating construction and maintenance and the routing of energy
and heat. As another perspective, the bespoke physics presented in the next section is purely
two-dimensional and differs from traditional 3D physics in many ways—but those differences
may be problematic, irrelevant, or advantageous, depending on the computational purposes and
techniques involved.
3 Living Technology in the Movable Feast Machine
Traditional deterministic and synchronous computer architectures, viewed as bespoke physics, sont
blatantly incompatible with the principles of the previous section—so much so it may be unclear
what a conforming architecture might look like. This section highlights one concrete approach,
illustrating how robust and indefinitely scalable computation—perhaps inevitably—will look far
more lifelike than most computation has to date. We expect that mature computer architectures will
necessarily manifest ongoing concerns with distributed agents building, preserving, and growing
3 At least, simple-minded approaches to encoding multiple scalable dimensions into fewer ultimately run afoul of principle 2. Time,
arguably, could provide a fourth scalable dimension, if it is acceptable to impose some fixed time limit on individual computations
occurring within the physics.
Artificial Life Volume 19, Nombre 3 & 4
353
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
their own mechanisms and relationships, rather than presuming a computation can be set up once
and for all in the finite style.
We have previously reported [2, 3] on the Movable Feast Machine (MFM), a computer architec-
ture for an indefinitely scalable machine. Here we give a high-level introduction and then briefly step
through three connected examples of building a living technology “ecosystem” using custom laws of
physics, with simulation-based data and observations illustrating both more obvious and more sur-
prising aspects of MFM-style living technology.
Figure 2a is an overview of the MFM. The hardware structure is a spatially distributed, deux-
dimensional parallel processing array, designed with the Section 2 principles first and foremost:
1. Indefinite scalability: Each tile is internally clocked; direct communications are asynchronous
and to adjacent tiles only; there is no global clocking or long-range routing fabric.
2. Isotropy: Uniform scalability in two symmetric spatial dimensions (see Figure 2a) avec
relative coordinates only; there is no global coordinate origin. Tiles are completely fungible,
with no hardware-defined unique identifiers. Time is structured as an open-ended sequence
of brief atomic events (see Figure 2b).
3. Limited causality: Hosted physics processing has no inherent global sequential structure.
A single atomic event runs sequentially to completion, providing a bounded event window
of causality to ease local programming and analysis, but interevent scheduling is
randomized and subject to acquiring any necessary intertile locks. Tiles are hot-pluggable
without requiring a global restart.
4. Level isolation: Strict Harvard architecture separating code and data; the code implementing
the laws of hosted physics is treated as firmware and is stored, accessed, and updated
separately from all bespoke physics processing.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2. Architectural overview and event details.
354
Artificial Life Volume 19, Nombre 3 & 4
D. H. Ackley
Bespoke Physics for Living Technology
3.1 Model Details
In the current version of the MFM (using the P1 parameter set [3]), data is stored in structured
form within atoms each containing 64 bits. Sixteen of those bits specify the atomic format, lequel
in turn specifies the interpretation of the remaining 48 bits and determines the dynamics of events
centered on an atom of this type. Each tile contains an array of sites, each of which may hold one
atom. Figure 2b illustrates the event window processing cycle as seen from the MFM programmerʼs
point of view. Mesures 1 through 7 are a critical section—so although the sequencing between events is
unpredictable, the bespoke element programmer does not have to worry about race conditions within
a single space-time event window.
An atomic bond denotes a linkage between two atoms, and is offered in two types: Long bonds can
connect atoms up to a Manhattan distance of four, while short bonds reach distance two. When an
atom diffuses (step 4 in Figure 2b), bond length limits are respected and all involved bond coordi-
nates are updated automatically.
Behavior in the MFM is determined by the set of custom elements defined by the programmer,
plus initial conditions4 including the size and shape of the available computational space and the
distribution of elements within that space. Unlike much work in artificial life, in the MFM there
are no a priori mechanisms forcing computations to display adaptive or evolutionary or indeed
any particular behaviors, though, as we will see, lifelike behaviors such as homeostasis and reproduc-
tion can readily be programmed as bespoke physics.
The MFM exposes a flexible and reasonably familiar sequential programming model at the level
of elements, providing significant power and expressiveness for creating sets of hosted physical laws.
Here we present three sample case studies, illustrating simple living technologies and how such low-
level mechanisms can interact and coexist with each other and with larger computational goals, en utilisant
space sharing within a grid.
For reference throughout the following subsections, Chiffre 3 presents a partial “table of elements”
for the examples we consider; Figure 3a in particular illustrates the basic structural properties shared
by MFM atoms. Le 48 user-programmable bits of an atom are divided on a per-element basis among
four uses: type bits to represent the unique type number of this element, long bonds connecting
atoms up to four sites apart, short bonds stretching up to two sites, and state bits to record miscella-
neous information as needed.
3.2 Regulating Occupied Site Density
The ability of atoms to move within the grid is critical for reactions, and thus computations,
to occur, and atomic mobility is strongly affected by how crowded the grid is, as measured, pour
example, by the occupied-site density (OSD) expressed as a percentage of occupied sites over some
region of interest.
We have explored managing the OSD using a simple dynamic regulator element we call DReg,
whose dynamical law is depicted5 in Figure 4: A random nearby location is selected (at Manhattan
distance 1, c'est à dire., the Moore neighborhood) and examined. If it is empty, there is a low probability of
creating another DReg; otherwise there is a somewhat higher probability of creating a Res, a basic
resource element designed to be transmuted into more useful forms by other elements in a more
complex system. On the other hand, if the chosen location is occupied by a DReg, there is a
significant chance of destroying it, while anything else has a lower probability of being destroyed.
Recasting that dynamical law in the style of an artificial chemistry, Chiffre 5 summarizes the pos-
sible DReg reactions. Unlike traditional chemical notation, here there is explicit accounting of empty
space in the reaction diagrams, because the MFM physics allows creation of an atom on the fly—but
only if there is a place to put it. The reaction rates shown in Figure 5—which restate the odds
4 Since indefinitely scalability offers no guarantee of a single global starting time, these are probably better described as “boundary conditions.”
5 In pseudocode for now; an actual Movable Feast Assembler is currently under development.
Artificial Life Volume 19, Nombre 3 & 4
355
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
Chiffre 3. Sample bespoke elements: (un ) illustrates the notational structure; (b) et (c) are discussed in Section 3.2;
(d), (e), et (F ) are discussed in Section 3.3; (g) et (h) are discussed in Section 3.4.
parameters in Figure 4—are inexact, because the sequential checking in the DReg dynamical
law causes some reactions to interact. Par exemple, the create/other reaction that produces Res
will actually occur in less than 0.5% of its opportunities, because sometimes a DReg will be
created instead.
A grid initialized with such a DReg gradually fills with Res and DReg atoms, until their
concentrations—and the overall OSD—equilibrate at a level determined by the reaction rates. With
the create/other reaction running about half the rate of destroy/other, as shown, the OSD settles
somewhat above 33%, including about a percent of DReg. The OSD is higher than might be
expected, despite the reduced create/other reaction rate, because absent stirring, a DReg has
a higher than average chance of reencountering the results of its own actions, producing a bias
toward 50% OSD.
Chiffre 6 illustrates dynamic regulation at work, showing approaches to equilibrium from various
initial concentrations of DReg and Res. The data shows that, as intended, the high destroy/self
reaction rate causes excess DReg to be eliminated quickly (Figure 6b and 6c); a surprise was the
significant DReg undershoot and slow recovery visible in Figure 6d, leading to its incomplete con-
vergence even after 25K AEPS. The reason, again, is local deviations induced by the computation
lui-même: With initial OSD so very high, the few existing DReg end up migrating to or being created in
small pockets within dense fields of Res, causing much higher rates of destroy/self than the global
concentrations would predict. Toujours, the Figure 6d initial OSD is so far above typical system opera-
tions that this pathology seems mostly a minor concern.
Chiffre 4. Movable Feast Assembler pseudocode of a dynamic regulator element. See text.
356
Artificial Life Volume 19, Nombre 3 & 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
Chiffre 5. Dreg reactions.
DReg and Res are a simple autocatalytic set [20] driving a basic metabolic cycle, creating new
bottom-of-the-food-chain Res, and randomly destroying arbitrary atoms to maintain the OSD—while
controlling DReg levels to preserve the reaction system itself. Such autocatalytic regulation—involving
“birth” and “death” at the lowest level—is a durable and basic living technology mechanism for
robust, indefinitely scalable computing. In addition to managing grid liquidity, DReg creates an envi-
ronment of continuous training, forcing the other elements to handle a basic class of attacks on an
ongoing basis, long before any power failure, cosmic ray, or malicious intruder must be confronted.
3.3 Base Chains, Polymerization, and Interpretation
DReg specifically creates Res and DReg and nothing else—it is robust, but not flexible. Shifting to
the other direction, we have drawn inspiration from natural information carriers such as RNA and
DNA, and developed a simple molecular carrier of arbitrary digital information that we call a base
chain (BC, Figure 3d). It possesses left and right long bonds to chain BCs together, a dock short bond
allowing other elements to grab hold, and a data field that carries 16 bits of arbitrary data.
Chiffre 6. Typical approaches to equilibrium to DReg and Res systems. Four separate runs shown in (un)–(d); in each run
all grid sites are initialized at random with given odds.
Artificial Life Volume 19, Nombre 3 & 4
357
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
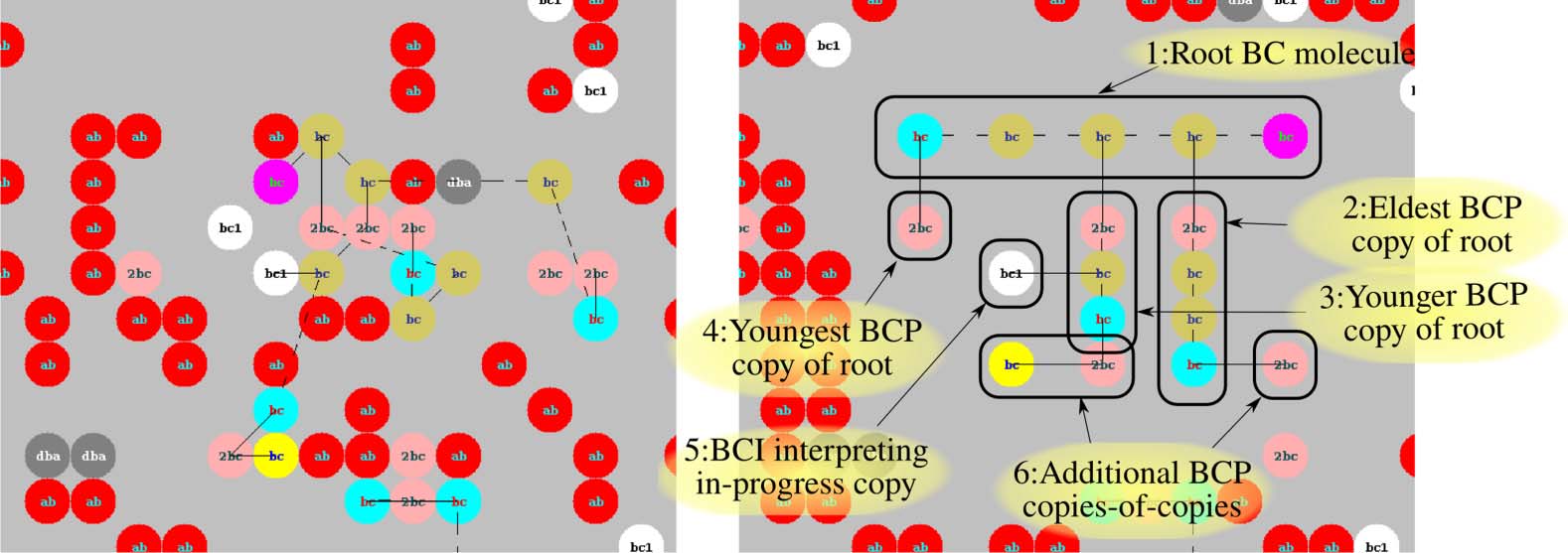
Chiffre 7. A base chain molecule complex as found in the wild (gauche), and the same manually “denatured” and annotated
(droite). See text.
We made a base chain polymerase (BCP, Figure 3e) atom that—over the course of many events, si
not disrupted—is capable of copying any preexisting, well-formed BC chain, by capturing Res
atoms from the environment and transmuting them into copied BCs as it works from left to right.
And finally, to put it all together, we made a simple base chain interpreter (BCI, Figure 3e) element that
incrementally executes the data contained in a chain of BC molecules, treating each four bits as an
opcode for one of various operations: Shift a value into a register (field r0 of BCI), wait for a Res
and capture it, transmute a captured atom into an atom whose type is specified by r0, and so forth.
Given an initial configuration containing a DReg, some BCI, and a BC-encoded program that
specifies making a BCI and a BCP (and perhaps other things), an entire autocatalytically sustained
population of reproducing and executing programs usually develops, except for rare “infant mortal-
ities” in which DReg erases all the BCIs or breaks the primordial BC chain before copies proliferate.
Chiffre 7, drawn from a program discussed in the next section, illustrates some of the surprising
complexity that is generated.
These first two examples suggest some of the low-level mechanisms and techniques we are ex-
ploring: DReg provides resilient grid density management, while BC, BCP, and BCIs provide a mea-
sure of robust programmability within the grid. But those tasks are only living technology support
mechanisms—they establish, preserve, and regulate themselves, which is indeed crucial, mais ils
accomplish nothing else.
3.4 Demon Horde Sort
Our final example shows how these living technology pieces can be put together to perform an
externally facing computation—a simple stream-sorting task, in which an endless stream of numbers
are injected near the right edge of a 128 × 64 rectangular grid, with each 32-bit number encoded in a
Datum atom (Figure 3g). The stream of Datums are to be sorted on the fly so that by the time they
are absorbed at the left edge of the grid, the smaller numbers have risen to the top, and the larger
are farther down.
Our sorting strategy, inspired by Maxwellʼs demon, is based on the Sorter element depicted in
Figure 8—a whole horde of such Sorters, generated by a BC program designed to produce two
Sorters as a payload before producing the BCP and BCI that keep the population robust.6 Each
Sorterʼs threshold is just the value of the last Datum that it moved.
Chiffre 9 is a typical illustration of how the demon horde performs in simulation, both when the
system is peaceful, and when it is subjected to a series of shocks to test robustness. The y axis is
the sorting performance on the left and the data throughout on the right, while the x axis is
6 In the online version, all of the red atoms marked with type ab in Figure 7 are Sorters. Note also that the demon horde sort
discussed and demonstrated in [3, 1] is simplified compared to this approach.
358
Artificial Life Volume 19, Nombre 3 & 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
Chiffre 8. A right-to-left sorting demon (center) discovers that datum 79 in its upper right region is larger than its current
threshold (43), and it moves to an empty location in the left lower. The demon would be willing to move 24 to the upper
gauche, but no empty locations are currently available.
abstract time in units of 1,000 AEPS (see the end of Section 2.3). The grid has 32 Datum sources
near the right edge, each of which probabilistically emits uniform random numbers from 0 à
999,999, et 32 Datum sinks at the left edge, each of which absorbs (and scores for statistical
purposes) any Datums that appear within its short bond range. We measure performance by
computing an average bucket error (dashed, green curve in the online version) based on how far
each absorbed Datum is from its “perfect” bucket (derived using our experimenterʼs knowledge of
the input data distribution). We also compute the categorization error rate (dotted, blue curve in the
online version), which is the percentage of Datums that are absorbed by a sink more than a third
of the total number of sinks away from the correct bucket, approximating just a high-medium-low
categorization. Enfin, we also compute the data throughput (solid, red curve in the online version) comme
the ratio of data absorbed to data emitted per unit time (which can be greater than 100%, due to
variable buffering in the grid).
The program initial configuration contains simply data sources and sinks and small blocks of DRegs,
Res, BCIs, and preprogrammed BCs. At first we see the system warming up as the elements gradually
approach equilibrium concentrations; it will “boot” much more rapidly if initialized to a near-equilibrium
state by about 15K AEPS, the average error is a little over two buckets out of 32, the categorization
error is perhaps a percent or two, and the data throughout hovers right around 100%.
At equilibrium we observe about 40–50 complete BC chains in the grid at any given time,
typically in large complexes as exemplified by Figure 7. That count is an important measure of
system resilience, as became evident when we began to stress the system. First we hit it with five
“cosmic ray blasts” from 20K to 22K AEPS, each blast flipping about 0.1% of the grid bits—hundreds
of bits per blast—and then a flash “power outrage” at 30K AEPS that reset two-thirds of the grid
sites.7 The system recovers from both of those events, more or less quickly, but then at 50K AEPS,
25 more closely spaced “cosmis ray blasts” occur, ultimately disrupting the last of the BC chains
containing the master program, after which the system degrades and fails.
Though we managed to kill the demon horde in that demonstration, it is indeed strikingly robust—
sometimes in ways we had not anticipated. We initially picked a data input probability that seemed high
enough that the system had to actively transport the Datums from right to left, faster than diffusion, ou
7 Though the data sources and sinks do not diffuse, they are also vulnerable to these events; they employ custom autocatalysis to
repopulate themselves at their designed spacing.
Artificial Life Volume 19, Nombre 3 & 4
359
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
Chiffre 9. The demon horde continues to sort in the face of transient hardware failures—until it doesnʼt. See text
for details.
else the array of data sources would get clogged and data injections would begin failing, punishing the
throughput.
Later on, seeking an additional system stressor, we thought of increasing the data input rate, but were
surprised to find (voir la figure 10) that this MFM programʼs performance improved with increasing data
rate over a fairly wide range, before it was ultimately unable to avoid input grid clogging. In retrospect,
at least this behavior is understandable. Higher data rates both help the in-grid data better match the
distribution used for scoring, and also cause the sorters to move data more frequently compared to
their diffusion rate, tending to keep their thresholds more appropriate to their grid positions.
This is adaptation of a rather fundamental and inherent and, we think, satisfying variety: un
programmed computation that naturally improves when worked harder, while deteriorating with
idleness—a sorting muscle.
4 Related Work
The present work is perhaps unusual in its use of living technology for robustness and scalability in
computer architecture and computer engineering, but its approach and mechanisms are related to
existing work in several areas; here we briefly touch on three.
Chiffre 10. The demon hordeʼs sorting performance improves with increased workload, until capacity is reached, causing
throughput to decline. See text for discussion.
360
Artificial Life Volume 19, Nombre 3 & 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
4.1 Cellular Automata
Cellular automata (CAs) are a typically fine-grained and spatiotemporally isotropic model of compu-
tation. They have been extensively studied in many variations [16], some of which can satisfy all the
quality principles of Section 2. The MFM can be viewed as an asynchronous, stochastic CA [24],
using the random independent updates [10] strategy.8 But while CA models often focus on theore-
tical parsimony and existence proofs, the MFM focuses instead on resilient programming expres-
siveness for scalable hardware. Par conséquent, instead of minimizing the automata alphabet or
neighborhood size on a problem-specific basis, we establish those parameters once, based on hard-
ware and software engineering concerns.
Par conséquent, the MFM atom size and event window size—though minuscule in comparison with
the addressable random access memory of a von Neumann machine—is also gargantuan in CA
termes. The “P1 parameters” mentioned in Section 3.1 specify 64 bits in a site, et 41 sites in a
(Manhattan distance 4) neighborhood. That would imply a hopelessly infeasible CA state table with
à propos 10800 rows, so the formal equivalence between the MFM and a CA, in practical terms, may
rarely be of great use. But computer science and software engineering have learned much about how
to express contingent behavior in compact and expressive programming language forms; the MFM
applies that knowledge to CA-style state transition programming, while shedding the global deter-
minism that traditionally accompanied it.
4.2 Artificial Chemistry
Artificial chemistries (ACs) are models inspired in some way by chemical systems (voir [13] for a
revoir), et, like CAs, vary widely in the intent and in the broad mechanisms and fine details of
their presumed physics. Early influential AC work such as E-chemistry [15] used explicit molecules
in a “flow reactor” physics that was finite, non-spatialized, and globally randomized—which was
wise for its scientific purposes, but is not indefinitely scalable; many other ACs are similar.
Graph-based models such as random reaction networks (par exemple., [19]) are even more abstract and
inherently descriptive, explicitly representing not individual molecules but potential chemical reactions.
Among ACs, lattice molecular systems [13] are sometimes designed with explicit sensitivity to
computer engineering concerns (par exemple., [25]), and often postulate physics that comes close to satisfying
the Section 2.1 metalaws—although presumptions of global clocking and deterministic operation
remain common. The MFM is a lattice molecular system, and its physics is clearly related to influ-
ential early lattice models such as the autopoiesis model [36] (with its important later corrections
[26]). To date we have explored a few bespoke physics programs that support membranes to create
spatial boundaries (voir [3])—rather than for variable-length information-carrying as in Section 3.3—and
it would be interesting to develop a more fully autopoietic cell template in the MFM.
4.3 Spatial Computing
Though aspects of space—geometry and location, distance, and direction—are central to particular
tasks like mapping, the inherently spatial properties of a physical computing system are abstracted
from and ignored by most of computer science. Cependant, as clock speed growth stalls, and distrib-
uted computer networks proliferate at multiple spatial scales, continuing to marginalize space be-
comes increasingly myopic. Primarily in the last decade, an increasing number of researchers have
begun to focus on spatial computing models that retain space as a first-class concern ([12] is an
introduction). Diverse avenues have been explored, from continuous spatial models (par exemple., [4, 22]),
to models aimed at wireless and mobile computing (par exemple., [6, 23]), to fine-grained spatially organized
machines such as FPGAs (par exemple., [11]).
Compared to many spatial computing approaches, a primary distinguishing feature of the MFM is
its focus on inherent resilience, employing stochastic execution and emphasizing autocatalytic and
8 At least in the current simulator; our hardware implementations may vary.
Artificial Life Volume 19, Nombre 3 & 4
361
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
concentration-based reliability—much in the spirit of [27], except with reified agents in extended
espace, rather than a well-stirred reactor.
5 Call to Action
Living technologies based on robotic hardware or biochemical wetware have the potential for huge
applications across society, but are mostly in the early stages of research and development. Computer-
based soft ALife research has explored many models, but its influence on computer science and
engineering has been limited. It is distressing that the highest-impact lifelike computational objects
today—though not springing from overtly ALife research—are the computer viruses and other
digital vermin of the Internet.
Life is the most practically scalable semiprogrammable behavior generation system we have
encountered—and that is why artificial life can and should play a central role in the design of
post-von Neumann architectures and computations capable of open-ended growth. À ce jour, though,
typically each ALife model specifies its own co-designed custom physics as an integral component,
creating a “universe of Babel” problem among models that hampers scientific generalization and
engineering interoperability.
A common physics could offer tremendous leverage for building and combining ALife models
and mechanisms, but what type of physics should that be? Design decisions like global synchronous
clocking and deterministic error-free operation can be tempting, to simplify logical and combinatoric
reasoning, and they may seem like harmless conveniences—especially for computations offered only
as existence proofs anyway, as many artificial life models have been, explicitly or implicitly. But to the
contrary, although ALife models built on unscalable physics have inspired and informed us, ils
have also importantly deluded and misled us—both generally about how much of the problem
we have solved, and specifically about what architectural directions to pursue for enduring progress.
For artificial life to advance future computing and contribute powerfully to the emergence of
living technologies, we must ground our physics in something other than the needs of any particular
ALife model. As an affirmative effort to help stiffen our spines to do better, the Section 2 principles
of bespoke physics offer one such grounding. Moving beyond synchronous and error-free deter-
minism is not a small matter; the imperatives of robustness and indefinite scalability influence com-
putational design from top to bottom and back again. Compare Figure 7 with Figure 11. Both depict
implementations of programmed reproduction in a discrete two-dimensional environment—and yet
Chiffre 11. The Langton loop: Programmed reproduction in a synchronous deterministic physics (cf. Chiffre 7).
362
Artificial Life Volume 19, Nombre 3 & 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
they are utterly different in character. Et, I suggest, the former is far more suggestive of life in
the wild.
Architecture is destiny.
Les références
1. Ackley, D. H. (2013). Robust-first computing: Demon horde sort (full version). Online video, available at
http://www.youtube.com/watch?v=helScS3coAE (accessed May 2013).
2. Ackley, D. H., & Cannon, D. C. (2011). Pursue robust indefinite scalability. In Proceedings of the
Thirteenth Workshop on Hot Topics in Operating Systems (HotOS XIII).
3. Ackley, D. H., Cannon, D. C., & Williams, L. R.. (2013). A movable architecture for robust spatial
computing. The Computer Journal, Advance Access, EST CE QUE JE: 10.1093/comjnl/bxs129.
4. Beal, J., & Bachrach, J.. (2007). Programming manifolds. In A. DeHon, J.-L. Giavitto, & F. Gruau (Éd.),
Computing media and languages for space-oriented computation. Schloss Dagstuhl, Allemagne: Internationales
Begegnungs- und Forschungszentrum für Informatik (IBFI).
5. Bedau, M.. UN., McCaskill, J.. S., Packard, N. H., & Rasmussen, S. (2010). Living technology: Exploiting lifeʼs
principles in technology. Artificial Life, 16(1), 89–97.
6. Borcea, C., Intanagonwiwat, C., Kang, P., Kremer, U., & Iftode, L. (2004). Spatial programming using smart
messages: Design and implementation. In International Conference on Distributed Computing Systems (ICDCS04)
(pp. 690–699). IEEE.
7. Bradner, S. (1997). Key words for use in RFCs to indicate requirement levels. RFC 2119 (best current practice).
Available at http://www.ietf.org/rfc/rfc2119.txt (accessed May 2013).
8. Canton, B., Labno, UN., & Endy, D. (2008). Refinement and standardization of synthetic biological parts and
devices. Nature Biotechnology, 26(7), 787–793.
9. Cappello, F., Geist, UN., Gropp, B., Kal, L. V., Kramer, B., & Snir, M.. (2009). Toward exascale resilience.
International Journal of High Performance Computing Applications, 23(4), 374–388.
10. Cornforth, D., Vert, D. G., & Newth, D. (2005). Ordered asynchronous processes in multi-agent
systèmes. Physica D: Nonlinear Phenomena, 204(1–2), 70–82.
11. DeHon, UN. (1996). Reconfigurable architectures and general-purpose computing in the MOS VLSI era (Transit
note 131). Cambridge, MA: MIT Artificial Intelligence Laboratory.
12. DeHon, UN., Giavitto, J.-L., & Gruau, F. (2007). Executive report: Computing media languages for
space-oriented computation. In A. DeHon, J.-L. Giavitto, & F. Gruau (Éd.), Computing media and
languages for space-oriented computation. Schloss Dagstuhl, Allemagne: Internationales Begegnungs- und
Forschungszentrum für Informatik (IBFI).
13. Dittrich, P., Ziegler, J., & Banzhaf, W. (2001). Artificial chemistries: A review. Artificial Life, 7(3),
225–275.
14. Feynman, R.. P.. (1992). Thereʼs plenty of room at the bottom. Journal of Microelectromechanical Systems, 1(1),
60–66.
15. Fontana, W., & Buss, L. W. (1994). “The arrival of the fittest”: Toward a theory of biological organization.
Bulletin of Mathematical Biology, 56(1), 1–64.
16. Ganguly, N., Sikdar, B. K., Deutsch, UN., Canright, G., & Chaudhuri, P.. P.. (2003). A survey on cellular automata
(Technical report). Centre for High Performance Computing, Dresden University of Technology.
17. Hicks, D. G. (curator ). (1995). The museum of HP calculators: HP-65 features. Available at
http://www.hpmuseum.org/features/65f.htm (accessed May 2013).
18. Intel Corporation. (2012). Intel 64 and IA-32 architectures software developers manual combined volumes: 1, 2UN, 2B,
2C, 3UN, 3B and 3C. Order number: 325462-044NOUS. Santa Clara, Californie: Intel. Available at http://www.intel.com/
content/www/us/en/processors/architectures-software-developer-manuals.html (accessed December 2012).
19. Kauffman, S. UN. (1969). Metabolic stability and epigenesis in randomly constructed genetic nets. Journal de
Theoretical Biology, 22(3), 437–467.
20. Kauffman, S. UN. (1986). Autocatalytic sets of proteins. Journal of Theoretical Biology, 119(1), 1–24.
21. Liquidware.com. (2011). Illuminato X machina. Available at http://illuminatolabs.com (accessed May 2013).
Artificial Life Volume 19, Nombre 3 & 4
363
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley
Bespoke Physics for Living Technology
22. MacLennan, B. (1990). Field computation: A theoretical framework for massively parallel analog computation, Parts I–IV
(Technical report CS-90-100). Knoxville: University of Tennessee, Department of Computer Science.
23. Mamei, M., & Zambonelli, F. (2009). Programming pervasive and mobile computing applications: Le
TOTA approach. ACM Transactions on Software Engineering and Methodology, 18(4), 1–56.
24. Marroquin, J.. L., & Ramirez, UN. (1991). Stochastic cellular automata with Gibbsian invariant measures.
IEEE Transactions on Information Theory, 37(3), 541–551.
25. Mayer, B., & Rasmussen, S. (1996). Lattice molecular automaton (LMA): A physico-chemical simulation system for
constructive molecular dynamics (Working paper ). Santa Fe, NM: Santa Fe Institute.
26. McMullin, B., & Varela, F. J.. (1997). Rediscovering computational autopoiesis. In P. Husbands & je. Harvey
(Éd.), 4th European Conference on Artificial Life (ECALʼ97) (pp. 38–47). Cambridge, MA: AVEC Presse.
27. Meyer, T., Yamamoto, L., & Tschudin, C. (2008). An artificial chemistry for networking. In Bio-Inspired
Computing and Communication: First Workshop on Bio-Inspired Design of Networks, BIOWIRE 2007, Cambridge, ROYAUME-UNI,
April 2–5, 2007, Revised Selected Papers (pp. 45–57). Berlin: Springer-Verlag.
28. OpenBSD Foundation. (2012). OpenBSD Reference Manual: yes(1). Edmonton, Canada: The OpenBSD
Fondation. Available at http://www.openbsd.org/cgi-bin/man.cgi?query=yes (accessed May 2013).
29. Pattee, H. H. (1995). Artificial life needs a real epistemology. In Proceedings of the Third European Conference on
Advances in Artificial Life (pp. 23–38). Berlin: Springer-Verlag.
30. Rappé, M.. S., Connon, S. UN., Vergin, K. L., & Giovannoni, S. J.. (2002). Cultivation of the ubiquitous SAR11
marine bacterioplankton clade. Nature, 418(6898), 630–633.
31. Rasmussen, S., Bedau, M.. UN., Chen, L., Deamer, D., Krakauer, D. C., Packard, N. H., & Stadler, P.. F. (Éd.).
(2009). Protocells: Bridging nonliving and living matter. Cambridge, MA: AVEC Presse.
32. Ray, T. S. (1994). An evolutionary approach to synthetic biology: Zen and the art of creating life.
Artificial Life, 1(1–2), 179–209.
33. Sellers, J.. R., & Veigel, C. (2006). Walking with myosin V. Current Opinion in Cell Biology, 18(1), 68–73.
34. Stojanovic, M.. N., & Stefanovic, D. (2003). A deoxyribozyme-based molecular automaton. Nature
Biotechnology, 21(9), 1069–1074.
35. Stross, C. (2005). Accelerando. New York: Ace Books. Available at http://www.antipope.org/charlie/
blog-static/fiction/accelerando/accelerando-intro.html (accessed May 2013).
36. Varela, F. J., Maturana, H. R., & Uribe, R.. (1974). Autopoiesis: The organization of living systems, its
characterization and a model. Biosystems, 5(4), 187–196.
37. Wigner, E. P.. (1964). Events, laws of nature, and invariance principles. Science, 145(3636), 995–999.
38. XMOS Corporation. (2010). XK-1 development kit. Available at https://www.xmos.com/products/
development-kits/xk-1-development-kit (accessed May 2013).
364
Artificial Life Volume 19, Nombre 3 & 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
9
3
_
4
3
4
7
1
6
6
3
9
7
3
un
r
t
je
/
_
un
_
0
0
1
1
7
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3