ARTICLE
Communicated by Christopher Buckley
A Novel Predictive-Coding-Inspired Variational RNN Model
for Online Prediction and Recognition
Ahmadreza Ahmadi
ar.ahmadi62@gmail.com
Okinawa Institute of Science and Technology, Okinawa, Japan 904-0495, and School
of Electrical Engineering, Korea Advanced Institute of Science and Technology,
Daejeon, 305-701, Republic of Korea
Jun Tani*
tani1216jp@gmail.com
Okinawa Institute of Science and Technology, Okinawa, Japan 904-0495
This study introduces PV-RNN, a novel variational RNN inspired by
predictive-coding ideas. The model learns to extract the probabilistic
structures hidden in fluctuating temporal patterns by dynamically chang-
ing the stochasticity of its latent states. Its architecture attempts to address
two major concerns of variational Bayes RNNs: how latent variables can
learn meaningful representations and how the inference model can trans-
fer future observations to the latent variables. PV-RNN does both by
introducing adaptive vectors mirroring the training data, whose values
can then be adapted differently during evaluation. De plus, prediction
errors during backpropagation—rather than external inputs during the
forward computation—are used to convey information to the network
about the external data. For testing, we introduce error regression for
predicting unseen sequences as inspired by predictive coding that lever-
ages those mechanisms. As in other variational Bayes RNNs, our model
learns by maximizing a lower bound on the marginal likelihood of the
sequential data, which is composed of two terms: the negative of the ex-
pectation of prediction errors and the negative of the Kullback-Leibler
divergence between the prior and the approximate posterior distribu-
tion. The model introduces a weighting parameter, the meta-prior, à
balance the optimization pressure placed on those two terms. We test the
model on two data sets with probabilistic structures and show that with
high values of the meta-prior, the network develops deterministic chaos
through which the randomness of the data is imitated. For low values,
the model behaves as a random process. The network performs best on
intermediate values and is able to capture the latent probabilistic struc-
ture with good generalization. Analyzing the meta-prior’s impact on the
*auteur correspondant.
Neural Computation 31, 2025–2074 (2019) © 2019 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01228
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2026
UN. Ahmadi and J. Tani
network allows us to precisely study the theoretical value and practical
benefits of incorporating stochastic dynamics in our model. We demon-
strate better prediction performance on a robot imitation task with our
model using error regression compared to a standard variational Bayes
model lacking such a procedure.
1 Introduction
Predictive coding has attracted considerable attention in cognitive neu-
roscience as a neuroscientific model unifying possible neuronal mecha-
nisms of prediction, reconnaissance, and learning (Rao & Ballard, 1999; Lee &
Mumford, 2003; Clark, 2015; Friston, 2018). Predictive coding suggests that,
first agents predict future perception through a top-down internal process.
Alors, prediction errors are generated by comparing the actual perception
and the predicted ones. These errors are propagated through a bottom-up
process to update agents’ internal states such that the error is minimized
and the actual perceptual inputs are recognized. Learning may then be
achieved by optimizing the internal model.
Tani and colleagues (Tani & Nolfi, 1999; Tani & Ito, 2003; Tani, Ito, &
Sugita, 2004) have investigated neural networks, which may be considered
analogous to the predictive-coding framework, especially for learning tem-
poral patterns in robotic experiments. They used recurrent neural networks
(RNNs) (Elman, 1990; Jordan, 1997; Hochreiter & Schmidhuber, 1997) depuis
RNNs are capable of learning long-term dependencies in temporal patterns.
Cependant, their predictive ability is limited in real-world applications where
high uncertainty is involved. This limitation is mainly because conventional
RNNs are able to predict only perceptual inputs deterministically.
To help solve this, Murata and colleagues (Murata, Namikawa, Arie,
Sugano, & Tani, 2013; Murata et al., 2017) proposed a stochastic RNN. Dans
this RNN, the uncertainty in data is estimated by the mean and variance
of a gaussian distribution in the output layer via learning. The hidden lay-
ers remained deterministic, cependant, because there was no known way to
do backpropagation through random variables. This therefore limited the
network from fully extracting the probabilistic structures of the target data
during learning.
To work around this limitation, Kingma and Welling (2013), in their work
on variational Bayes autoencoders (VAEs), developed a technique called the
reparameterization trick, which allows backpropagating errors through hid-
den layers with random variables, thus allowing for internal stochasticity
in neural networks.
Kingma and Welling (2013) used this method in an autoencoder in order
to approximate a posterior distribution of latent variables. The variational
Bayes (VB) approach optimizes the network by maximizing a variational
lower bound on the marginal likelihood of the data, and the prior distri-
bution is sampled from a standard normal gaussian. This lower bound is
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2027
composed of two terms: the negative of the prediction error and the nega-
tive of the Kullback-Leibler (KL) divergence between the approximate pos-
terior and prior distributions.
Various RNNs have been proposed based on the VAE. The first varia-
tional Bayes RNNs proposed sampling the prior distribution from a stan-
dard normal gaussian at each time step (Fabius & van Amersfoort, 2014;
Bayer & Osendorfer, 2014). Plus tard, Chung et al. (2015) proposed a VAE RNN,
the variational RNN (VRNN), which used a conditional prior distribution
derived from the state variables of an RNN to account for temporal depen-
dencies within the data. Since then, various attempts have been made to the
approximate posterior of the VRNN. Some recent studies proposed approx-
imate posteriors that had more similar structures to the true posterior by
considering future dependencies on sequential data by using two RNNs—
one forward and one backward (Fraccaro, Sønderby, Paquet, & Winther,
2016; Goyal, Sordoni, Côté, Ke, & Bengio, 2017; Shabanian, Arpit, Trischler,
& Bengio, 2017). Another issue targets VRNN-based models: they have a
tendency to ignore the stochasticity introduced by their random variables
and to rely only on deterministic states. To remedy this, there have been
several attempts to force the latent variables to learn meaningful informa-
tion in the approximate posteriors (Bowman et al., 2015; Karl, Soelch, Bayer,
& van der Smagt, 2016; Goyal et al., 2017).
This article proposes a novel network model, referred to as the
predictive-coding-inspired variational RNN (PV-RNN), that integrates
ideas from recent variational RNNs and predictive coding. In this model,
the prior distribution is computed using conditional parameterization sim-
ilar to Chung et al. (2015), whereas the posterior is approximated using a
new adaptive vector A, which forces the latent variables to represent mean-
ingful information. This new vector also provides the approximate poste-
rior with the future dependency information via backpropagation through
temps (BPTT; Werbos, 1974; Rumelhart, Hinton, & Williams, 1985) without a
backward RNN. All model variables and A are optimized by maximizing a
variational lower bound on the marginal likelihood of the data.
Our model also incorporates a process inspired by the predictive cod-
ing framework, error regression, which is used online during testing in our
experiments after learning is finished. During error regression, the model
constantly makes predictions, and the resulting prediction errors are back-
propagated up the network hierarchy to update the internal states A of the
model in order to maximize both negative terms of the lower bound.
Many studies have assumed that the brain may use predictive coding
to minimize a free energy or maximize a lower bound on surprise (Friston,
2005, 2010; Hohwy, 2013; Clark, 2015). By incorporating features inspired
by predictive coding principles, our model may be considered to be more
consistent with the ideas of computational neuroscience than other VAE-
based models. While most models propagate inputs through the network
during the forward computation, our model only propagates prediction er-
rors through backpropagation through time (BPTT).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2028
UN. Ahmadi and J. Tani
One important motivation in this study is to clarify how uncertainty
or probabilistic structure hidden in fluctuating temporal patterns can be
learned and then internally represented in the latent variables of an RNN.
Surtout, randomness hidden in sequences can be accounted for by ei-
ther deterministic chaos or a stochastic process. Donc, if we consider
that we may observe sensory data with only finite resolution (Crutchfield,
1992), then if the original dynamics are chaotic, the symbolic dynamics ob-
served through Markov partitioning involved with the coarse-graining may
be ergodic, generating stochasticity (Sinai, 1972). Inversely, if a determinis-
tic RNN acts as a generative model to reconstruct such stochastic sequences
through learning, the RNN may do so by embedding the sequences into in-
ternal, deterministic chaos by leveraging initial sensitivity (Tani & Fuku-
mura, 1995). An interesting question, cependant, est, If a generative model
contains an adaptive mechanism to estimate first-order statistics—as in our
proposed model and other variational Bayes RNNs—how may the com-
ponents of deterministic and stochastic dynamics be used to account for
observed stochasticity in the model’s output?
To examine this question, we introduce a variable, the meta-prior, que
weights the minimization of the divergence between the posterior and the
prior against that of the prediction error in the computation of the varia-
tional lower bound. We investigate how the meta-prior influences devel-
opment of different types of information processing in the model. D'abord, nous
conduct a simulation experiment using a simple probabilistic finite state
machine (PFSM) and observe how different settings of the meta-prior af-
fect representation of uncertainty in the latent state of the model. Suivant, nous
examine how different representations of latent states in the model can lead
to the development of purely deterministic dynamics, random processes, ou
something in between these two extremes. En particulier, we examine how
generalization capabilities correlate with such differences.
Suivant, we consider a more complex setup, where the data embed multi-
timescale information and the network features multiple layers, each with
its own time constant. This allows the model to deal with fluctuating tempo-
ral patterns that consist of sequences of hand-drawn primitives with prob-
abilistic transitions among them. We conduct simulation experiments to
examine if the multiple-layer model exhibits qualitatively the same abil-
ity as the one of the previous experiment to extract the latent probabilistic
structures of such compositionally organized sequence data.
Enfin, we evaluate the performance of the proposed model in a real-
world setting by conducting a robotic experiment. On a task where a
robot learns to imitate another, imitation performance is compared between
PV-RNN with error regression for posterior inference, and VRNN, lequel
uses a variational autoencoder. This experiment aims to evaluate our hy-
pothesis that the posterior inference calculated through error regression
provides better estimates than an autoencoder-based model.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2029
2 Model
We now describe in detail the generative and inference models, ainsi que
the learning procedure. The generative model produces predictions based
on the latent state of the network. Inversement, the inference model, given
an observation, estimates what should be the latent state in order to pro-
duce the observation. The learning process concerns itself with discovering
good values for the learnable variables of both the generative and inference
models.
2.1 Generative Model. As with many published variational Bayes
models, the generative model Pθ of PV-RNN is an RNN with stochas-
tic latent variables. Ici, θ denotes the learnable variables of the gen-
erative model, which is illustrated in Figure 1A by black lines. Le
variables θ are distributed among the components X , Z, d of the genera-
tive model, as θX, θZ, je
d. Z and d are the stochastic and deterministic la-
tent states, respectivement, and X is the generated prediction. For a prediction
, . . . , X T ), the generative model factorizes as
X 1:T = (X 1
, X 2
Pθ (X 1:T , Z1:T , d1:T | Z0
, d0)
= PθX (X 1:T | d1:T , Z1:T )PθZ (Z1:T | d1:T , Z0)Pθ
d (d1:T | Z1:T , d0)
=
T(cid:2)
t=1
PθX (X t | dt, Zt )PθZ (Zt | dt−1)Pθ
d (dt | dt−1
, Zt )
(2.1)
The initial values of Z and d at time step zero, Z0 and d0, are set to zero in
our experiments. The latent state dt is recursively computed using an RNN
model:
dt = fθ
d (dt−1
, Zt ).
(2.2)
In this article, we use a multiple timescale recurrent neural network
(MTRNN) (Yamashita & Tani, 2008) as fθ
d , but any type of RNN, tel que
long short term memory (LSTM) or gated recurrent units (GRUs) could be
used instead. MTRNNs are a type of RNNs composed of several hierar-
chical layers, with each layer using a different time constant. The internal
dynamic of an MTRNN model is computed as
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
)hk
t−1
= (1 − 1
τ
k
= tanh(hk
t ),
hk
t
dk
t
+ 1
τ
k
(W kk
dddk
t−1
+ W kk
dzZk
t
+ W kk+1
dd dk+1
t−1
+ W kk−1
dd dk−1
t−1 )
(2.3)
where hk
at time t, W kk
t is the vector of the internal state values of the kth context layer
dd is the matrix of the connectivity weights from the d units in
2030
UN. Ahmadi and J. Tani
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
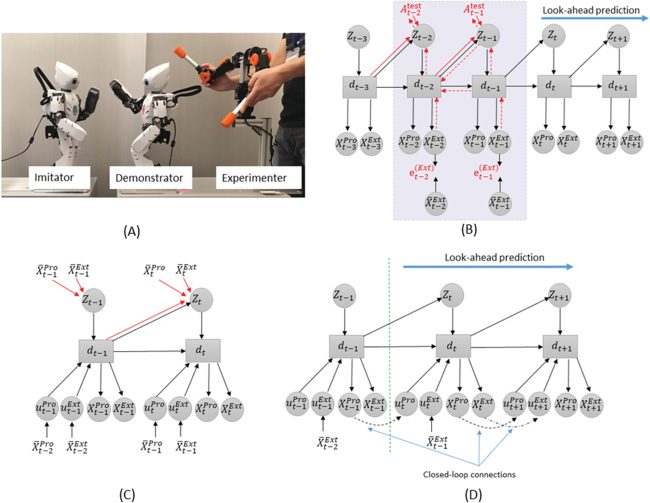
Chiffre 1: (UN) The generative and inference models of PV-RNN in an MTRNN
setting, (B) the error regression graph during tests, et (C) the error regres-
sion process. In panels A and B, black lines represent the generative model and
red lines show the inference model, with solid red lines showing the feedfor-
ward computations of the inference model and dashed red lines showing the
BPTT that is used to update AX in panel A and Atest in panel B. The gray area in
panel B represents a two-step temporal window of the immediate past in which
Atest
t−2:t−1 is modified to maximize the lower bound. Panel C illustrates the er-
ror regression process. At t = 6, predictions are generated (gauche) after observing
1:6 . The three-time step time window is slid by one time step to [4, 7] (middle;
X
now, t = 7), and an error is observed between the prediction X pred
4:7 and the target
test
value X
4:7 . The lower bound is computed, and backpropagation is performed;
4:7 is then optimized, and the prediction X pred
Atest
is updated (droite). This back-
propagation/optimization/prediction cycle can be repeated multiple times be-
fore moving on to the [5, 8] time window.
test
4:7
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2031
dd
dd
the kth context layer to itself, W kk
dz the connectivity weights from Z to d in
layer k, W kk+1
is the matrix of the connectivity weights from the d units of
the k + 1th context layer to the ones in the kth layer, et, similarly, W kk−1
is the matrix for the one coming from layer k − 1, and τ is the time con-
stant. Bias terms are not shown in equation 2.3 for clarity. In this article,
we consider networks with no more than three layers. Aussi, as is common
with MTRNNs, the lower layer will have a faster time constant than the
higher layer. In that context, we refer to the lowest layer, with the fastest
time constant, as the fast layer, and symmetrically, to the highest layer, avec
the slowest time constant, as the slow layer. The slow (highest) layer does
not have any layer above it, and so, obviously, in equation 2.3, the term
W kk+1
dd dk+1
t−1 is removed. The same thing applies for the fast (lowest) layer and
the term W kk−1
t−1 . Figure 1A shows the PV-RNN model implemented with
a two-layer MTRNN. We extended the original MTRNN model (Yamashita
& Tani, 2008) by adding stochastic units Z to each layer. Each layer commu-
nicates only with the layer above and the one below to create a hierarchical
structure.
dd dk−1
Enfin, the prior distribution PθZ (Zt | dt−1) is a gaussian with a diagonal
covariance matrix, which depends on dt−1. Priors depending on the pre-
vious state were used in Chung et al. (2015), and it outperformed the in-
dependent standard gaussian prior used in STORN (Bayer & Osendorfer,
2014),
PθZ (Zt | dt−1) = N (Zt; m(p)
t
, p (p)
t
) où [m(p)
t
, log σ (p)
t
] = f (p)
θZ
(dt−1),
(2.4)
t
denotes a one-layer feedforward neural network and μ(p)
where f (p)
et
θZ
p (p)
are the mean and standard deviation of Zt. We use the reparameteri-
t
zation trick (Kingma & Welling, 2013) such that the latent value Z in both
posterior and prior are reparameterized as Z = μ + σ ∗ ε, where ε is sam-
pled from N (0, je). Dans cette étude, PθX (X t | d1
t ) is obtained by a one-layer
t
feedforward model f (X)
θX
, Z1
One peculiar detail about the generative model is that it does not accept
any external inputs. En effet, the generative model, unlike many other vari-
ational Bayes RNN models, generates sequences based on the latent state
exclusively. Rather than using external inputs, the PV-RNN model prop-
agates the errors between the predictions and the observations via back-
propagation through time. To understand this clearly, we need to explain
the inference model first.
.
2.2 Inference Model. Based on the generative model, the true posterior
distribution of Zt depends on X t:T , which can be verified using d-separation
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2032
UN. Ahmadi and J. Tani
(Geiger, Verma, & Pearl, 1990). Computing the true posterior is intractable,
so an inference model is designed to compute an approximate posterior.
To compute Zt, the network considers the deterministic state of the net-
work during the previous time step, dt−1. In all other variational Bayes
RNNs, d units are fed training patterns directly, but in our case, we removed
those inputs to force d not to ignore Z. We need another method to feed the
network with information specific to the current pattern. To that end, pour
a training sequence of T time steps X 1:T , we introduce the adaptive vec-
tors AX
1:T . For each time step X t of X , we have a corresponding vector AX
t .
This vector is specific to the sequence X. Autrement dit, the model is going
to have T × NX adaptive vectors like this, with NX the number of training
sequences.
Each AX
t
is going to be adapted through BPTT, and the changes made
through BPTT will depend on the prediction errors between X and X from
T to t, et:T . Naturellement, the other learning variables of the network θX, θZ, je
d,
and φ (see equation 2.5 for φ) will also be affected during BPTT by the in-
formation contained in e1:T . But those variables are trained on all training
motifs. Only AX will be specifically trained on the prediction errors rela-
tive to X. En tant que tel, AX
is able to specifically capture information about the
t
future time steps X t:T of the training sample and their existing dependen-
cies with the current time step t. Alors, during inference, AX
t and dt−1 are
and σ (q)
combined to compute the mean and standard deviation μ(q)
que
t
t
define the distribution from which Zt will be drawn. It is to this mechanism
that we will be referring in the rest of the article when we claim that we
do not directly feed the external inputs to the network during the forward
computation; instead, the prediction errors, and thus information about fu-
ture observations, are propagated through the network via BPTT. The idea
to convey information about future observations is also present in varia-
tional Bi-LSTMs (Fraccaro et al., 2016; Goyal et al., 2017; Shabanian et al.,
2017), although they use a backward RNN for this purpose, and therefore
a feedforward mechanism, rather than backpropagation, as we do here.
The approximate posterior is obtained as
qφ (Zt | dt−1
, et:T ) = N (Zt; m(q)
t
] = f (q)
, AX
φ (dt−1
, p (q)
t
t ),
[m(q)
t
, log σ (q)
t
) où
(2.5)
is a one-layer feedforward network, and φ denotes the posterior
are given in
and log σ (q)
t
where f (q)
φ
parameters. Detailed computations of AX
t
appendix A.
Using AX
t vectors in our model presents another advantage. In all other
variational Bayes RNNs, d units are fed the training patterns directly, et
in μ(q)
t
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2033
the network can solely rely on d to regenerate the training pattern, ignor-
ing Z during learning and making it largely irrelevant in the computation
(Bowman et al., 2015; Karl et al., 2016; Kingma et al., 2016; Chen et al., 2016;
Zhao, Zhao, & Eskenazi, 2017; Goyal et al., 2017). In our proposed model,
if d ignores Z, then it has no access to pattern-specific information. Ce
is one reason why AX
t vectors target Zt and not dt: to avoid ignoring Zt
during training. On top of that, in our implementation, Zt has a 10 times
smaller dimension than dt, making it more efficient for AX
t to target Zt than
dt. One might wonder if rather than introducing new latent vectors AX
t , nous
might have directly replaced Zt by AX
t during the posterior computation.
We did not do this for two reasons. D'abord, we wanted to keep the structure
of the prior and posterior as close as possible. Deuxième, we assumed that
providing the information about the past dt−1 to the posterior computa-
tion of Zt would be beneficial in some context. This assumption is tested in
appendix G.
2.3 Learning Process. To learn the variables θ and φ of the generative
and inference models, we need to define a loss function. For variational
Bayes neural networks, it has been shown that models’ variables can be
jointly learned by maximizing a lower bound on the marginal likelihood of
training data (Kingma & Welling, 2013; Bayer & Osendorfer, 2014; Chung
et coll., 2015; Fraccaro et al., 2016; Goyal et al., 2017). We maximize a lower
bound because maximizing the marginal likelihood directly is intractable.
We now derive the lower bound.
Based on equation 2.1, the marginal likelihood or evidence can be ex-
pressed as
Pθ (X 1:T |Z0
(cid:3) (cid:3) T(cid:2)
, d0)
[PθX (X t | dt, Zt )PθZ (Zt | dt−1)Pθ
d (dt | dt−1
, Zt )]dZ1:T dd1:T .
(2.6)
=
t=1
Given dt−1 and Zt, the value of dt is deterministic. Donc, if we de-
, Zt ), as per equa-
, Zt ) is a Dirac distribution centered on ˜dt. By replacing
d (dt | dt−1
, Zt ) by the Dirac delta function δ(dt − ˜dt ) in equation 2.6, we can
note the value of the variable dt as ˜dt (equal to fθ
tion 2.2), Pθ
d (dt | dt−1
Pθ
remove the integral over d:
d (dt−1
Pθ (X 1:T |Z0
, d0) =
(cid:3) T(cid:2)
t=1
(cid:4)
(cid:5)
PθX (X t | ˜dt, Zt )PθZ (Zt | ˜dt−1)
dZ1:T .
(2.7)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2034
UN. Ahmadi and J. Tani
If we factorize the integral over time and take the logarithm of the marginal
likelihood, we will have
log Pθ (X 1:T |Z0
, d0) = log
=
T(cid:8)
t=1
(cid:6)(cid:3)
T(cid:2)
(cid:6)(cid:3)
t=1
log
(cid:7)
PθX (X t | ˜dt, Zt )PθZ (Zt | ˜dt−1)dZt
(cid:7)
PθX (X t | ˜dt, Zt )PθZ (Zt | ˜dt−1)dZt
. (2.8)
We now multiply the inside of the integral by 1 = qφ (Zt | ˜dt−1
qφ (Zt | ˜dt−1
,et:T )
,et:T )
pour
obtain an expectation form. Aussi, this introduces the inference model into
equations that were generative-model-only so far, allowing for the joint op-
timization of both models:
log Pθ (X 1:T |Z0
T(cid:8)
(cid:9)(cid:3)
, d0)
=
log
t=1
(cid:11)
qφ (Zt| ˜dt−1
, et:T )
(cid:10)
PθX (X t | ˜dt, Zt )dZt
.
PθZ (Zt | ˜dt−1)
qφ (Zt| ˜dt−1
, et:T )
(cid:12)(cid:13)
(cid:6)
Eqφ (Zt
| ˜dt−1
,et:T )
Pθ
Z
qφ (Zt
(Zt
| ˜dt−1
| ˜dt−1 )
,et:T )
(cid:7)
X (X t | ˜dt ,Zt )
Pθ
(cid:14)
(2.9)
Since a logarithm is a concave function, we can apply Jensen’s inequality:
log(E[X]) ≥ E[log(X )]:
log Pθ (X 1:T |Z0
T(cid:8)
(cid:9)(cid:3)
, d0)
log
qφ (Zt| ˜dt−1
, et:T )
PθZ (Zt | ˜dt−1)
qφ (Zt| ˜dt−1
, et:T )
(cid:9)
(cid:10)
PθX (X t | ˜dt, Zt )dZt
(cid:10)
PθX (X t | ˜dt, Zt )
qφ (Zt| ˜dt−1
, et:T ) log
PθZ (Zt | ˜dt−1)
qφ (Zt| ˜dt−1
, et:T )
(cid:12)(cid:13)
L(je ,φ): Variational Evidence Lower Bound
=
≥
t=1
T(cid:8)
(cid:3)
t=1
(cid:11)
.
dZt
(cid:14)
(2.10)
Now the variational evidence lower bound (ELBO) L(je , φ) can be maxi-
mized instead of the logarithm of the marginal likelihood Pθ (X 1:T |Z0
, d0)
in order to optimize the learning variables of the generative model and
the approximate posterior. This formula for maximizing the lower bound is
equivalent to the principle of free energy minimization provided by Friston
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2035
(2005). L(je , φ) can be rewritten as
(cid:15) (cid:3)
T(cid:8)
L(je , φ) =
qφ (Zt | ˜dt−1
, et:T ) log PθX (X t | ˜dt, Zt )dZt
t=1
(cid:3)
−
(cid:15)
T(cid:8)
=
t=1
qφ (Zt | ˜dt−1
, et:T ) log
(cid:16)
qφ (Zt | ˜dt−1
, et:T )
PθZ (Zt | ˜dt−1)
dZt
Eqφ (Zt | ˜dt−1
,et:T )[log PθX (X t | ˜dt, Zt )]
− KL[qφ (Zt | ˜dt−1
(cid:16)
, et:T ) (cid:4) PθZ (Zt | ˜dt−1)]
,
(2.11)
where the first term on the right-hand side is the expected log likelihood
under qφ (Zt | ˜dt−1
, et:T ) or the negative of the expected prediction error
(Kingma & Welling, 2013), and the second term is the negative Kullback-
Leibler (KL) divergence between the posterior and prior distributions of the
latent variables. Only the summation over time is shown in this equation,
but the lower bound is also summed over the number of training samples.
We divided the first term by the dimension of X and the second term by
the dimension of Z during experiments. The KL divergence is computed
analytically as
KL[qφ (Zt | ˜dt−1
+ (m(p)
t
, et:T ) (cid:4) PθZ (Zt | ˜dt−1)]
− μ(q)
)2 + (p (q)
t
)2
= log
t
2(p (p)
t
)2
p (p)
t
p (q)
t
− 1
2
,
(2.12)
which is simply the KL divergence between two gaussian distributions. Le
detailed derivation of the KL divergence is in appendix B.
The variables of the prior θZ are optimized through the KL divergence
term, whereas variables of the posterior φ are optimized through both
termes. We can exploit this asymmetry. By weighting the two terms differ-
ently, we can increase or decrease the explicit optimization pressure on the
learning variables corresponding to the prior or the posterior. To that end,
we introduce a weighting parameter, the meta-prior w, in the lower bound
(see equation 2.11) to regulate the strength of the KL divergence, producing:
T(cid:8)
Lw(je , φ) =
(Eqφ (Zt | ˜dt−1
,et:T )[log PθX (X t | ˜dt, Zt )]
t=1
− w · KL[qφ (Zt | ˜dt−1
, et:T ) (cid:4) PθZ (Zt | ˜dt−1)]).
(2.13)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2036
UN. Ahmadi and J. Tani
In the experiments, all model variables and A are optimized in order
to maximize the lower bound using ADAM (Kingma & Ba, 2014). We use
the same parameter setting for the ADAM optimizer as the original pa-
par: α = 0.001, β
= 0.999 in training. In both experiments,
1
the latent units Z were 10 times smaller than the number of deterministic
units d.
= 0.9, and β
2
2.4 Error Regression. Testing the network on unseen training se-
quences is not straightforward:
it does not accept any input during
the forward computation. It does, cependant, propagate errors during
backpropagation, so we leverage this mechanism during testing.
While training the inference model, we created sequences of adaptive
vectors AX
1:T —one for each training observation. The purpose was to capture
the relevant information about the training observation into AX
1:T and train
the other weights of the network, θ and φ, to use this information to make
useful predictions. Another way to understand this is that AX
1:T are building
good representations that the rest of the network, shared among all training
sequences, learns to use. In that sense, the adaptive vectors AX
1:T on one side,
and the weights θ and φ on the other side, are fulfilling vastly different roles.
And as we will see, once the training is done, the values of AX
1:T are no longer
needed to process unseen testing sequences.
When processing an unseen testing sequence, the weights θ and φ are
fixed, and the adaptive vectors AX
1:T are unavailable. We initialize the adap-
tive vector Atest
1:T (cid:5) to zero values; we are going to optimize Atest
1:T (cid:5) online, pendant
the processing of X test, to maximize our ability to predict it. This online opti-
mization is done incrementally, inside a time window of size m. Le processus
is illustrated in Figure 1C.
1:m is then compared to X
Using the m (et, for now, zero-valued) Atest
1:m values, we can generate
1:m using the inference model qφ (see equation 2.5) and compute dpred
Zpred
1:m us-
1:m can also be computed using Zpred
ing equation 2.3. The prediction X pred
1:m and
test
1:m . X pred
dpred
1:m, and the resulting prediction errors e1:m
are backpropagated through the network to update the values of Atest
1:m. Le
update is done the same way the network is trained—by computing the
lower bound and using BPTT—except that the variables θ and φ are fixed
and are not modified. The new values of Atest
1:m are used to generate a new
prediction X pred
1:m , and a new optimization cycle can occur. The number of
optimization cycles of Atest
1:m for a given time window can depend on reach-
ing a given error threshold, be fixed beforehand, ou, in a real-time context,
depend on the available computational time. Suivant, the time window is slid
à [2, m + 1], and Atest
2:m+1 and are optimized. Im-
portantly, only the part of Atest
2:m+1—is
optimized. En particulier, Atest
2:m+1,
the time window moves to [3, m + 2] et ainsi de suite.
1:T (cid:5) inside the time window—here Atest
is now fixed. After the optimization of Atest
2:m+1 are used to generate X pred
1
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2037
At any point in this process, for a time window [t − m, t − 1], the pre-
, . . . can be generated
, X t+2
diction steps outside the time window X t, X t+1
, . . . using the generative model (see equation
by computing Zt, Zt+1
, Zt+2
, Atest
, . . . lequel
, Atest
2.4), which does not depend on the values of Atest
t+1
t+2
t
sont, at this point, zero. The predictions X t, X t+1
, . . . correspond to un-
, X t+2
observed parts of the testing sequence at this point and therefore are the
model’s prediction of the future. These additional predictions have no im-
pact on the BPTT process of error regression.
Enfin, we note that the optimization can begin before the time window
is at full size and start with time windows [1, 1], [1, 2], . . . , [1, m], [2, m + 1]
et ainsi de suite. En plus, the optimization does not need to happen at every
time step and can, par exemple, be triggered every 10 time steps, with time
windows [1, 10], [1, 20], . . . , [1, m], [11, m + 10], [21, m + 20], . . . (assuming
here that m is a multiple of 10).
The error regression process was implemented in deterministic RNNs,
and it was shown how it could help the generalization capability of those
models (Tani & Ito, 2003; Murata et al., 2017; Ahmadi & Tani, 2017b). Ce
testing process through error regression bears similarities to, and is inspired
par, predictive coding. Predictive coding proposes that the brain is continu-
ally making predictions about incoming sensory stimuli and that error be-
tween the prediction and the real stimuli is propagated back up through
the layers of the processing hierarchy. Those error signals are then used
to update the internal state of the brain, with impacts on future predic-
tion. Our network goes through similar stages during error regression:
predictions are made (X pred), compared to actual observations (X test), et
the errors (e1:m) are backpropagated to update the internal state of the net-
travail (Atest
1:m). To be very clear, our network is not a model of the brain; it
does not claim to explain any existing neurological data or make any useful
predictions about animal brains. We are merely drawing inspiration from
the predictive coding ideas to design new machine learning networks. Dans
particular, in neurological models of predictive coding (Rao & Sejnowski,
2000), each layer makes an independent prediction and propagates the er-
ror signal to the upper processing layer only. In our network, the predic-
tion error from the raw sensory data is backpropagated through the entire
network hierarchy. This is deliberate, because we use BPTT: we adapted
the ideas of predictive coding to the classical tools of recurrent neural
réseaux.
2.5 Related Work. RNNs are widely used to model temporal sequences
due to their ability to capture long dependencies in data. Cependant, un
, X t−1) can have problems when modeling
deterministic RNN dt = f (dt−1
stochastic sequences with a high signal-to-noise ratio (Chung et al., 2015).
In an attempt to solve this problem, Bayer and Osendorfer (2014) intro-
duced a model called STORN by inserting a set of independent latent
variables (sampled from a fixed distribution) into the RNN model. Plus tard,
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2038
UN. Ahmadi and J. Tani
t
t
, log(p (p)
the VRNN model was proposed using conditional prior parameterization
(Chung et al., 2015). In their model, the prior distribution is obtained using
a nonlinear transformation of the previous hidden state of the forward net-
work as [m(p)
)] = f (p)(dt−1). VRNN outperformed STORN by using
this type of conditional prior. Cependant, in VRNN, the posterior is inferred
at each time step without using information from future observations. UN
posterior inferred in such a way would be different from the true posterior.
Plus tard, this issue was considered by using two RNNs: a forward RNN and
a backward one. The backward RNN was used in the posterior to transfer
future observations for the current prediction (Fraccaro et al., 2016; Goyal
et coll., 2017; Shabanian et al., 2017). As explained, our model manages this
by updating AX through backpropagation of the error signal.
Recent studies of generative models show that extracting a meaningful
latent representation can be difficult when using a powerful decoder. Le
d units ignore the latent variables Z and capture most of the entropy in the
data distribution (Goyal et al., 2017). Many researchers have addressed this
issue by either weakening the decoder or annealing the KL divergence term
during training (Bowman et al., 2015; Karl et al., 2016; Kingma et al., 2016;
Chen et al., 2016; Zhao et al., 2017). In a recent attempt, the authors of Z-
forcing also proposed an auxiliary training signal for latent variables alone,
which forces the latent variables to reconstruct the state of the backward
RNN (Goyal et al., 2017). This method introduces an additional generative
model and, as a result, an additional cost on the lower bound. Compara-
tivement, our model captures information about external inputs in AX and the
information flows to d through Z, rendering the model unable to ignore its
latent variables.
Donc, in our model, those two issues, capturing future dependencies
and avoiding having the network ignore its latent states, are addressed with
the same mechanism: the adaptive vectors AX .
Introducing adjustable parameters in the lower bound has been studied
for variational Bayes neural networks previously. KL annealing does this
(Bowman et al., 2015), linearly increasing the weight of the KL-divergence
term from 0 à 1 during the training process to avoid ignoring the latent
variables and to improve convergence. Higgins et al. (2017) showed that the
degree of the disentanglement in latent representations of VAE models can
be improved by strengthening the importance of the KL divergence term in
the lower bound. The generative factors in an image of a dog, Par exemple,
can be its color, size, and breed. Disentangling the generative factors in the
model can be beneficial, as it creates latent units sensitive to the changes in a
single generative factor while being relatively invariant to changes in other
factors (Bengio, Courville, & Vincent, 2013). Our model considers weight-
ing the KL divergence term for a purpose different from KL annealing or
disentanglement: to influence the balance between a deterministic and a
stochastic representation of the data in the model.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2039
The current study is a continuation of our previous work (Ahmadi &
Tani, 2017un) that proposed a predictive-coding variational Bayes RNN and
studied the effect of weighting the KL divergence term. This model, comment-
jamais, was composed of only the latent variables Z and did not use the de-
terministic units d; it also used a prior distribution with a fixed mean and
standard deviation that has been shown not to be plausible for models that
deal with time-series data (Chung et al., 2015). This led us to consider sepa-
rating stochastic and deterministic states in the current model. It allows us
to have a conditional prior.
Separating deterministic and stochastic states provides an additional ad-
vantage: it allows having a number of Z units significantly smaller than d
units. In our test, having 10 times more d units than Z units was the best bal-
ance between performance and computational time; the number of A units
was always the same as the number of Z units. We use this ratio in all our
experiments.
3 Simulation Experiments
We conducted simulation experiments to examine how learning in the
proposed model depends on the meta-prior w. The first experiment
investigates how the proposed model could learn to extract the latent prob-
abilistic structure from discrete (0 ou 1) data sequences generated from a
simple probabilistic finite state machine (PFSM) under different settings of
the meta-prior w. The purpose of this relatively simple experiment is to
conduct a detailed analysis of the underlying mechanism of the PV-RNN
when embedding the latent probabilistic structure of the data into mixtures
of deterministic and stochastic dynamics. In the second experiment, a more
complex situation is considered where the model is required to extract la-
tent probabilistic structures from continuous sequence patterns (mouvement
trajectories). For this purpose, trajectory data were generated by consider-
ing probabilistic switching of primitive movement patterns based on an-
other predefined PFSM in which each primitive was generated with fluc-
tuations in amplitude, velocity, and shape. Encore, we examined how the
performance depends on the meta-prior w.
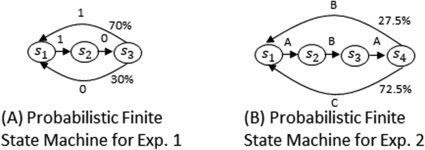
3.1 Experiment 1. The PFSM shown in Figure 2A was used as the target
generator. Transitions from s1 to s2 and s2 to s3 were deterministically deter-
mined with 1 et 0 as output, respectivement. Cependant, the transitions from
s3 to s1 were randomly sampled with 30% et 70% probabilities for output
0 et 1, respectivement. Ten target sequence patterns, de 24 time steps each,
were generated and provided to the PV-RNN as training data. Each model
had only one context layer consisting of 10 d units and a single Z unit. Le
time constant τ for all d units was set to 2.0. The output of the network,
X 1:T , was discretized during testing, with outputs less than 0.5 assigned to
zero and the ones equal to or larger than 0.5 assigned to one. Finding an
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2040
UN. Ahmadi and J. Tani
Chiffre 2: The probabilistic finite state machines used to generate training pat-
terns for PV-RNNs in the (UN) first and (B) second experiments.
adequate range of w at the beginning of an experiment depends on the net-
work parameter settings, the data set, and the task. For this experiment, le
most interesting behavior was observed in the range [0.0001, 0.1]. For w set
to larger values such as 0.5 et 1.0, the networks showed the same qualita-
tive behavior to the network with w set to 0.1. Training was conducted on
seven models with the different meta-prior w set to 0.1, 0.05, 0.025, 0.015,
0.01, 0.001, et 0.0001, respectivement. In this experiment, we used an MTRNN
to be consistent with our other experiments. Cependant, it is possible to do
this experiment with a simple RNN as well. Similar results were obtained
by using a simple RNN and are shown in appendix D.
After training for 500,000 epochs, given a training sequence X , le
learned value of AX
1 is fed to the network, generating Z1 via equation 2.5.
Then the remaining latent states Z2:T and the output X 1:T are generated from
the generative model (see equation 2.4). The purpose is to study if provid-
ing AX
1 is enough for the trained network to regenerate X accurately. Nous
refer to this procedure as target regeneration.
Chiffre 3 compares one target sequence pattern and its corresponding re-
generation by the PV-RNN model trained with different values of the meta-
prior. For large values of w, the network reproduced the training pattern
accurately. As the value of w decreases, divergences appear earlier and ear-
lier, and for low values even the deterministic steps show errors.
For a given reconstruction, one can compute the diverging step as the
time t of the first difference between the target and the reconstruction. If
both target and reconstruction are identical, the diverging step is equal to
the length of the reconstruction. For each training pattern, we compute the
diverging step 10 times and compute the mean of all results to obtain the
average diverging step (ADS) over the training data set.
To characterize the deterministic nature of the network behavior, nous
compute the variance of the divergence (VD), which shows diversity among
sequence patterns regenerated from the same value of AX
1 . For a given
value of AX
1 , we ran the regeneration 50 times and computed the mean
variance (across all 50 runs and all time steps) of the generated X before
discretization.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2041
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
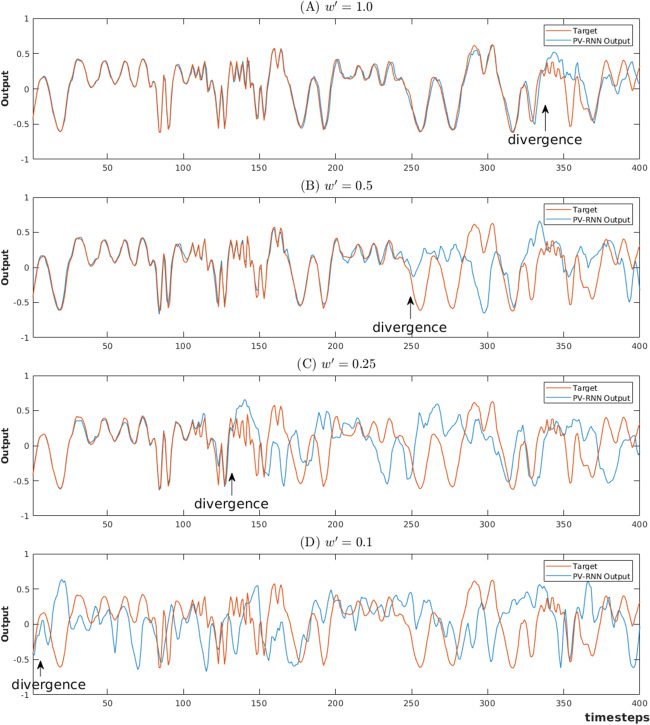
Chiffre 3: Larger values of the meta-prior translate into better reconstruction of
the training patterns. The four graphs show a training pattern (in orange) et
its reconstruction by PV-RNN (in blue) for different values of w. Overlapping
sections are in dark gray. For w = 0.1, the target sequence is completely regen-
erated. When w is equal to 0.025 et 0.01, all deterministic steps are correctly
reproduced, but regenerated patterns begin to diverge at the 11th and 8th step,
respectivement. When w is set to 0.0001, even the deterministic transition rules fail
to be reproduced, and the signals diverge at the 6th time step.
ADS and VD for different values of w are shown in Table 1. ADS de-
creases while VD increases as w decreases. For w = 0.1, VD is near zero; le
network reproduces the same pattern with little variation, and the behav-
ior developed can be regarded as deterministic. The relatively high value
of VD for w = 0.0001, cependant, points to highly stochastic dynamics.
In Table 1, we examine the ability of the network to extract the latent
probabilistic structure from the data by computing the KL divergence be-
tween the probability distributions of sequences of length 12 généré par
the PFSM, P.(X t:t+11) and the one generated by the PV-RNN, P.(X t:t+11) (thus
characterizing how similar they are). To compute the probability distribu-
tion P(X t:t+11), we set A1 randomly and generate a sequence of 50,000 steps
using the generative model. We refer to this as free generation. We consider
the distribution of the 49,989 sequences of length 12 X t:t+11 present in the
sequence and compute their distribution. For the probability distribution
2042
UN. Ahmadi and J. Tani
Tableau 1: Evaluation of the Regeneration and Generalization Capabilities of the
PV-RNN Model Trained with Different Values for w.
Meta-Prior w
0.05
0.025
0.015
0.01
0.001
0.0001
0.1
22
Average diverging step (ADS)
Variance of divergence (VD)
KL divergence of test phase
19
14
12
11
0.00003 0.00155 0.0480 0.0499 0.0618 0.134
0.0684 0.120
5.040
0.148
2.276
9
8
0.172
1.0679 5.607
Remarques: The average diverging step (ADS) and variance of divergence (VD) measures point
to better reconstruction performance when w is high. Cependant, taking into account the KL
divergence between the probabilistic distribution of the generated pattern P(X t:t+11 ) et
the one of the training data, P.(X t:t+11 ) paints another picture: the network best captures
the probabilistic structure of the data for an average value of w. The bold numbers in rows
1 et 2 show the model with the best regeneration capability. The bold numbers in row 3
shows the model with best generalization capability.
P.(X t:t+11), we concatenate the 10 training sequences in one sequence of 240
time steps (which is a valid output sequence of the PFSM) and compute
the distribution of the 229 sequences of the length 12 we could extract from
it. The resulting KL divergence measures from those two distributions for
all PV-RNN models show that average values of the meta-prior capture
the underlying transition probability of the PFSM from the training data
best.
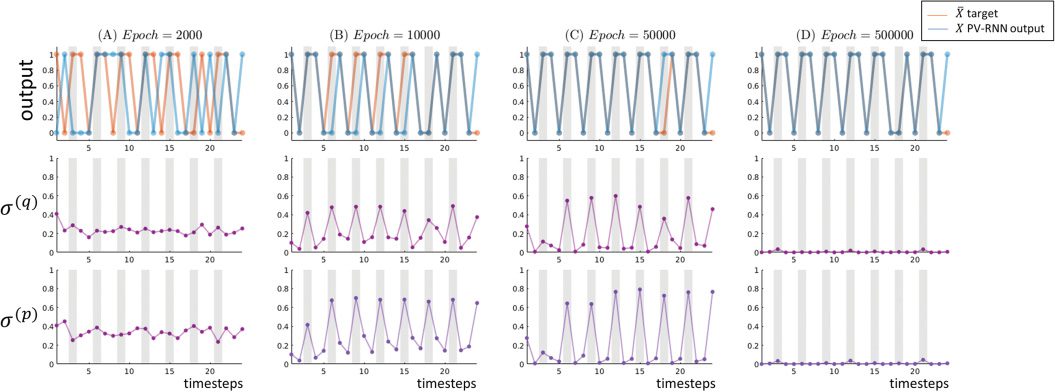
Chiffre 4 displays the mean and variance of the latent state during re-
generation of a target sequence for w equal to 0.1 et 0.025 and confirms
this analysis. With w = 0.1, the network possesses deterministic dynamics
that amount to rote learning. With w = 0.025, the network distinguishes be-
tween deterministic and probabilistic states, and captures the probabilis-
tic structure in its internal dynamics. Plots showing the cases of w set to
0.001 et 0.0001 are provided in Figure 11 in appendix H. With w = 0.0001,
the value of sigma becomes high even for the deterministic case; the net-
work does not distinguish anymore between deterministic and probabilis-
tic states, and behaves as a random process.
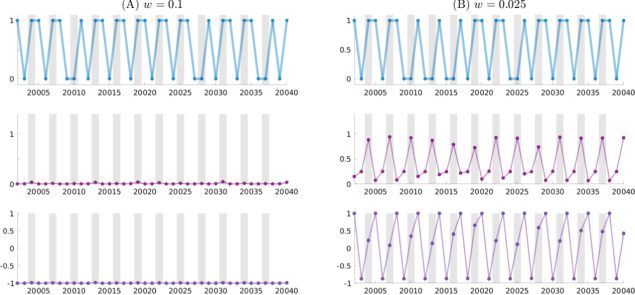
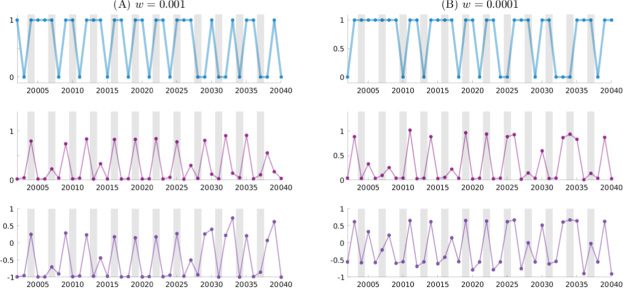
Chiffre 5 illustrates the generated output, the mean μ(p), and the standard
deviation σ (p) of the Z unit for PV-RNNs trained with w equal to 0.1 et
0.025 from time steps 20,002 à 20,040. The behaviors of μ(p) and σ (p) in both
cases are similar to those shown in Figure 4. In the case of w set to 0.025, le
network was most successful at extracting the latent probabilistic structure
from the data by detecting both the uncertain and deterministic states in the
séquence. The same figure for w equal to 0.001 et 0.0001 is shown in Fig-
ure 12 in appendix H. The transition rules defined in the PFSM were mostly
broken for the case with the minimum w value (0.0001) and frequently for
the case of w equal to 0.001 as the model wrongly estimated the uncertainty
as high even for the deterministic states.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2043
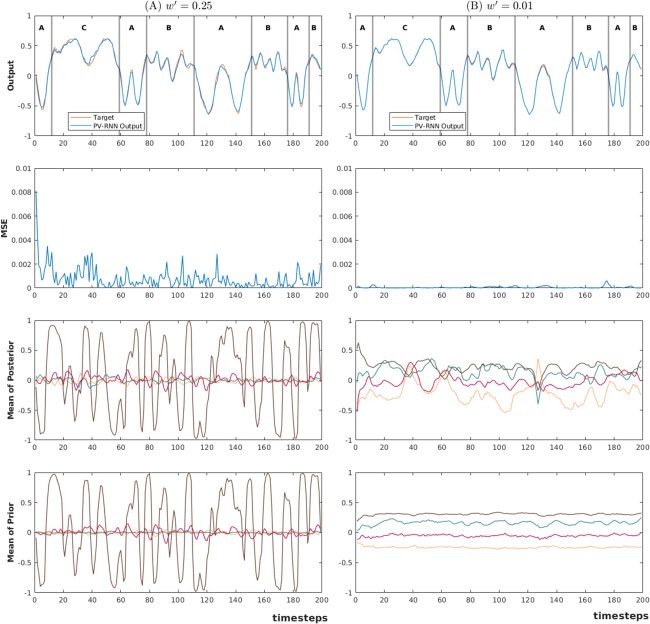
Chiffre 4: A high meta-prior forces the network into deterministic dynamics.
With an average value of w, the probabilistic structure of the data is captured.
The mean μ(p) (middle row) and variance σ (p) (bottom row) of the latent state
during regeneration of a given X (top row) for w equal to 0.1 et 0.025 sont
shown. With w = 0.1, the σ (p) is near zero. It amounts to rote learning by the
network of the training pattern. m(p), on the other hand, varies only during the
first few time steps, suggesting that the information identifying which training
pattern to regenerate is transferred to the network early on, and thereafter, le
value of Z is disregarded. With w = 0.025, the variance σ (p) is much larger over-
all and significantly higher for the probabilistic states (gray bars). This suggests
that PV-RNN with w set to 0.025 is capable of discriminating between deter-
ministic and probabilistic steps in the sequence. This effect is reflected in μ(p)
aussi, with most deterministic states having a μ(p) close to either 1 or −1 and
probabilistic states mostly confined to the range [0, 0.75], the asymmetry over
the range possible range ([−1, 1]) possibly even reflecting the 70%/30% differ-
ence in transition probability.
We observed that the deterministic network developed with w set to 0.1
generated nonperiodic output patterns. This can be roughly seen in Fig-
ure 5A. We assumed that deterministic chaos or transient chaos developed
in this learning condition. To confirm this, the Lyapunov exponents were
computed using the method in Alligood, Sauer, and Yorke (1996). Inter-
estingly, the largest Lyapunov exponent was positive. We evaluated this
by generating patterns (using free generation) pour 50,000 steps twice: once
as usual and once with the random variable generating the value of the
Z unit, ε
1:50000, set to zero (so that the value of σ (p) is irrelevant). This was
done to verify that the noise generation was not affecting the value of the
Lyapunov exponent. In both cases, the largest Lyapunov exponents were
positive (autour 0.1). The method for computing Lyapunov exponents is
described in appendix C.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2044
UN. Ahmadi and J. Tani
Chiffre 5: The generated output, the mean μ(p), and the standard deviation σ (p)
from time steps 20,002 à 20,040 of two PV-RNNs trained with the meta-prior
w set to 0.1 (UN) et 0.025 (B). Gray bars show the time steps corresponding to
uncertain states.
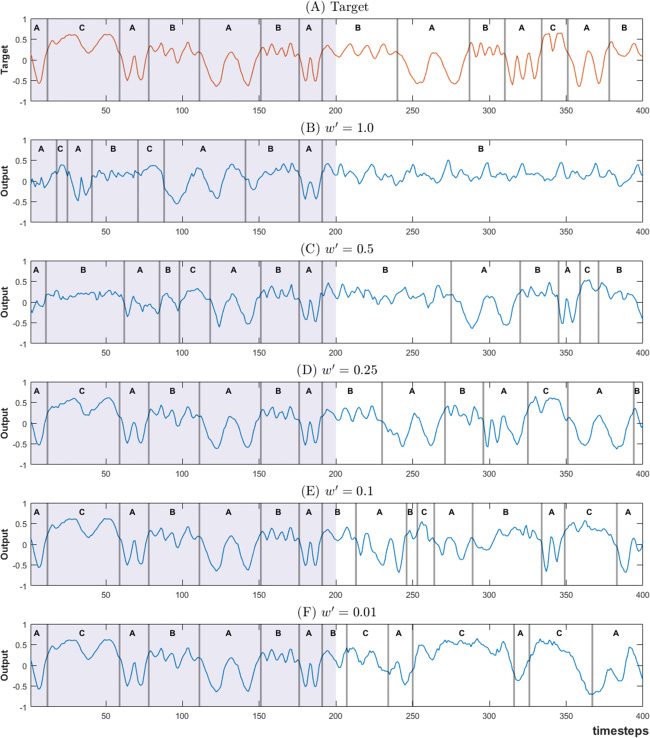
The results of this experiment can be summarized as follows. It was
shown that different types of internal dynamics can be developed in the
current model depending on the value of the meta-prior w used during
training on stochastic sequences. When w is set to a large value (0.1), deter-
ministic dynamics were generated by minimizing σ (p) in the prior to nearly
0 for all time steps. The deterministic aspect of the developed dynamics
was further confirmed by observing that they generated the least diver-
sity when generation was run multiple times starting from the same initial
A1. The finding of the maximum Lyapunov exponent of the dynamics as
a positive value confirmed that those dynamics developed into determin-
istic chaos. It was also found that the average diverging steps (ADS) être-
came larger when w was set to a larger value: each training target sequence
was captured exactly for relatively long time steps, in a fashion akin to rote
learning.
On the other hand, decreasing w generated stochastic dynamics, même
approaching the random process for low values of the meta-prior, as evi-
denced by the increase of diversity in sequences generated from the same
latent initial state. It was found, cependant, that the best generalization in
learning took place with w set to an intermediate value. The analysis of the
latent variable in this condition revealed that low values of w translated
into high values of σ (p) for probabilistic and deterministic state transitions.
For intermediate values of the meta-prior, cependant, high values of σ (p) étaient
mostly observed for probabilistic state transition, indicating that the model
did discriminate between the two in that case. To understand why this is the
case, one must observe that the KL divergence term of equation 2.13 acts as
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2045
a pressure for σ (p) to be close to σ (q) and μ(p) to be close to μ(q) and for the
posterior and prior distributions to be similar to one another.
When w is small, the pressure that the KL divergence term has on the
backpropagation process is small to almost nonexistent. Donc, the pairs
p (p), p (q) and μ(p), m(q) are free to be uncorrelated. The other term of equation
2.13, the reconstruction error, puts learning pressure on σ (q) and μ(q). Là-
fore, there is little learning pressure on the prior distribution, and it mostly
stays close to its initialization values. In our implementation, those values
are random, and therefore the network acts as a random process when the
Z states are generated by the generative model.
When w is high, the pressure is high for the posterior and prior distribu-
tions to be similar. Deterministic states are easier for the network to learn,
and therefore both the σ (q) and σ (p) can converge to small values so as to
reduce both the KL divergence term and the reconstruction error term of
equation 2.13. Probabilistic states take longer to learn. Looking at the close-
form solution of the KL divergence term, equation 2.12, one way to reduce
the KL divergence between the posterior and prior distributions is to in-
crease σ (p) when μ(q) and μ(p) are different. And this is the temporary solu-
tion that the network seems to be using, when looking at the evolution of
p (p) in Figure 14 in appendix H. Eventually the network makes σ (q) and σ (p)
converge to zero in order to minimize the KL divergence further.
For the network with w set to an intermediate value, the pressure is
less for the posterior and prior distributions to be similar. p (q) and σ (p) faire
not converge to zero, and the network seems to stay in the intermediate
solution.
3.2 Experiment 2. In this experiment, the PV-RNN was required to ex-
tract latent probabilistic structures from observed continuous sequence data
(movement trajectories). We generated 48,400-time-step data sequences and
one of length 6400 time steps were generated using the PFSM depicted in
Figure 2B, where the primitive pattern A, B, and C corresponded to a circle,
a Figure 8, and a triangle, respectivement. The sequences were based on hu-
man hand-drawn patterns with naturally varying amplitude, velocity, et
shape. One such sequence can be seen in Figure 13 in appendix H. Sixteen
of the 48,400-step sequences were used to train the model, tandis que le 32 concernant-
maining ones were reserved for testing. The details of the generation are in
appendix E.
For this experiment, the most interesting behavior was observed with
w in the range [1.0 × 10−3, 0.01 × 10
−3]. To avoid excessive notation in the
following text, we introduce w(cid:5) = w × 103, so that when w evolves in the
range [1.0 × 10
evolves in [1.0, 0.01].
−3, 0.01 × 10
Six PV-RNN models were trained with w(cid:5)
set to 1.0, 0.5, 0.25, 0.15, 0.1,
et 0.01. Each model had three context layers consisting of 80 d units and
8 Z units for the fast context (FC) layer, 40 d units and 4 Z units for the
−3], w(cid:5)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2046
UN. Ahmadi and J. Tani
middle context (MC) layer, et 20 d units and 2 Z units for the slow context
(SC) layer. The time constants of FC, MC, and SC units were set to 2, 4,
et 8, respectivement. Training ran for 250,000 epochs in each case. We also
conducted experiments using two context layers for two PV-RNN models
with w(cid:5)
set to 0.25. The results are in appendix F.
During testing, the capability of the generative model to reproduce the
training patterns was evaluated through target regeneration. For this pur-
pose, target patterns were regenerated by providing the initial latent state
A1 with the value obtained during training, as we did in experiment 1. Le
latent states Z2:T and X 1:T were computed by the generative model. Chiffre 6
illustrates how the regeneration is affected by different values of the meta-
prior, and Table 2 shows the ADS for those values, c'est, in the continu-
ous case, the time step at which the mean square error between the target
and the generated pattern exceeded a threshold (0.01) over 10 repetitions
of each training sequence, as well as the mean activity of the variance σ (p)
for the whole training set. We obtain results in accordance with the ones of
experiment 1: the PV-RNN model trained with the largest meta-prior value
(w(cid:5) = 1.0) exhibits deterministic dynamics, while the one trained with low
values w(cid:5)
approaches random process behavior.
To test the generalization capabilities of the models, the prediction per-
formance using error regression was evaluated. The test pattern of length
6400 steps was given to each PV-RNN model to make predictions from 1
à 5 steps ahead. The size of the time window was set to 50, and Atest
t−50:t−1
was optimized 30 times at every time step. The time window was contin-
uously sliding one step forward at a time to generate the whole sequence
X 1:6400. The MSE between the test pattern and the generated output for all
prediction steps is given in Table 3. The PV-RNN trained with w(cid:5)
set to 0.25
outperforms other models in all cases except for the one-step-ahead predic-
tion where w(cid:5) = 0.1 has a small lead. Two-dimensional visualizations of the
test for one-step- and five-step-ahead predictions with w(cid:5)
set to 1.0, 0.25,
et 0.1 are shown in Figure 7. As expected, predicting five steps ahead is
challenging for all models. Cependant, in this case, the network with w(cid:5)
set to
0.25 performs best at preserving the structure of the target. When w(cid:5)
is set
à 0.1, the network predicting five steps ahead generates a quite noisy pat-
tern. The structure looks qualitatively wrong in some areas for both cases
of prediction when w(cid:5)
is set to 1.0.
Previous performance measures focus on the model’s ability to quanti-
tatively reproduce or predict each time step. To characterize the ability of
the model to qualitatively reproduce and predict the correct patterns, nous
designed an experiment using error regression with a longer but fixed time
window. Contrary to previous experiments with error regression when the
time window would gradually grow to full size m and then slide over the
whole test sequence, here we consider one time window starting at time
step 1 and ending at time step 200 (included). En particulier, we do not con-
sider time windows [1, 1], [1, 2], . . . , [1, 199]. One thousand optimization
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2047
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 6: PV-RNN regenerates training patterns better when the meta-prior has
a high value. The four graphs show one dimension (oui, ici) of a training pattern
(in orange) and the output regenerated by PV-RNN (in blue), obtained by boot-
strapping the value of A1 with the one obtained during training, and computing
predictions X 1:T using the generative model exclusively for the remaining time
steps. Black arrows point to the diverging steps in which the regenerated output
diverges from the target pattern.
steps of Atest
1:200 are performed in this error regression time window. Alors
the generative model is used to generate 200 additional steps, producing
X 201:400. This predicted 2D output is then analyzed and labeled by a hu-
man with the three primitive pattern types A, B, or C, and compared to
the ground truth of the corresponding testing pattern. Chiffre 8 shows one
2048
UN. Ahmadi and J. Tani
Tableau 2: Evaluation of the Regeneration Capability of the PV-RNN Model
Trained with Different Values for w.
w(cid:5)
1.0
0.5
0.25
0.15
0.1
0.01
ADS
Mean of Variance
343
0.0007
229
0.0015
103
0.0039
17
0.005
4
0.021
1
0.1126
Remarques: High meta-prior translates into deterministic dynamics, while low
values produce random-process-like behavior. When w(cid:5) = 1.0, the diver-
gence starts from the 343th step driven by low stochasticity, and as w(cid:5)
becomes smaller, the divergence starts earlier. When w(cid:5) = 0.01, the diver-
gence starts immediately after the onset and the variance is high. The bold
numbers show the model with the best regeneration capacity.
Tableau 3: MSE between the Target and Look Ahead Prediction.
w(cid:5)
1.0
0.5
0.25
0.15
0.1
0.01
1-step prediction
2-steps prediction
3-steps prediction
4-steps prediction
5-steps prediction
0.0101
0.0171
0.0222
0.0279
0.0325
0.00726
0.0127
0.0183
0.0233
0.0274
0.00418
0.00907
0.0140
0.0189
0.0234
0.00376
0.00918
0.0152
0.0212
0.0270
0.00341
0.0116
0.0205
0.0301
0.0375
0.00834
0.0229
0.0378
0.0497
0.0578
Remarques: The best predictions are produced by the model trained with an interme-
diate value of the meta-prior (w(cid:5) = 0.25). The table shows the MSE between the
unseen test targets and the one-step- to five-steps-ahead generated predictions.
The networks with minimum MSE are shown in bold numbers.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
instance of the labeling of a test pattern, and illustrates the effects of differ-
ent values of the meta-prior.
If a model produces the right primitive after the error regression win-
dow, it has 1-primitive prediction capability. If it produces the correct two
primitive in the right order, it has 2-primitive prediction capability, and so
sur. Primitive reproduction is not rated on how long it lasts or if it would
coincide temporally with the test pattern. Tableau 4 shows the aggregated pre-
diction performance of each PV-RNN model over the 32 patterns of the test-
ing data set. The prediction capability is best when w(cid:5)
is set to 0.25. Ce
indicates that generalization in predicting at the primitive sequence level
can be achieved to the highest degree by extracting the latent probabilis-
tic structure in primitive sequences adequately when w(cid:5)
balances well the
two optimization terms of the lower bound. Previous work with MTRNN
models has shown that higher layers (middle and slow) can learn the
transitions between primitive patterns, while the lowest (fast) layer learns
detailed information about primitive patterns (Yamashita & Tani, 2008;
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2049
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 7: Only the w(cid:5) = 0.25 case retains good qualitative behavior for both
one-step- and five-step-ahead predictions. Target and prediction outputs of
PV-RNNs with w(cid:5) set to 1.0, 0.25, et 0.1 during error regression when pre-
dictions are made (UN) one step ahead and (B) five steps ahead. Only the first
200 steps are shown to retain clarity.
Ahmadi & Tani, 2017b). Ici, it is probable that PV-RNN was able to
predict long-term primitive sequences by using the slow timescale dynam-
ics developed in the higher layers of the network hierarchy.
2050
UN. Ahmadi and J. Tani
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
Chiffre 8: w(cid:5) = 0.25 produces the most faithful qualitative reproduction of se-
quence of primitives in terms of both order and timing. It is the only one that re-
produces the correct deterministic part of the target sequence ∗, UN, B, UN, ∗, UN, B
(as well as producing possible stochastic steps, c'est, not producing B on a
stochastic step). In all these graphs, error regression is done once over the [1200]
time window, pour 1000 optimization steps (shaded area). Then the generative
model produces the remaining 200 time steps, which are labeled to one of the
three A, B, or C primitives, based on their similarity to them. While here, only
the y dimension is displayed, the labeling was done on the 2D signal. Gray bars
display perceived transition primitive patterns (and actual ones for the target
pattern).
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2051
Tableau 4: Percent Accuracy for Primitive Prediction for Models Trained with Dif-
ferent Values for w.
w(cid:5)
1.0
0.5
0.25
0.15
0.1
0.01
1-primitive prediction (%)
2-primitive prediction (%)
3-primitive prediction (%)
81.25
62.50
40.63
90.63
78.13
53.13
100
84.38
59.38
93.75
68.75
37.50
90.63
59.38
21.88
81.25
37.50
9.38
Remarques: Intermediate values of the meta-prior reproduce best the sequence of
primitives. The table shows the percent accuracy for one, deux, and three prim-
itive prediction for models trained with different values for w(cid:5)
. The network
with the best accuracy is shown in bold numbers.
t
, and the mean of prior μ(p)
One issue remains unclear in Figure 8: Why did the predictability worsen
even though the reconstruction becomes better when w(cid:5)
goes from 0.25 à
0.01? To answer this, we compare the divergence between the posterior and
the prior in the regression window of the w(cid:5) = 0.25 and w(cid:5) = 0.01 models.
Chiffre 9 shows the target patterns, the reconstructed outputs, the MSE be-
tween the target patterns and reconstructed outputs, the mean of posterior
m(q)
for the middle layer on the same test se-
t
quence. The reconstruction is more effective with w(cid:5)
set to 0.01, but the ac-
tivities of the prior and posterior differ much more, as the activity of the
mean of the middle layer indicates. Low values of the meta-prior lead to
a low optimization pressure on the KL divergence term between the prior
and posterior of the lower bound, and thus less pressure for the prior and
posterior to coincide, and thus poor learning for the prior (the activity of
the mean of the prior for w(cid:5) = 0.01 is poor), leading to poor prediction ca-
pabilities. Instead the optimization pressure concentrates on the reconstruc-
tion error term, leading to a lower MSE for the reconstruction. This analysis
strongly suggests that a good balance between minimizing the reconstruc-
tion error and minimizing the KL divergence between the posterior and the
prior by setting the meta-prior in an intermediate range is the best way to
ensure the best performance of the network across a range of tasks.
One question that may arise is how to find the optimal meta-prior at the
beginning of the training. We do not have a good answer for that, as the
optimal value depends on the task and the network topology. In the exper-
iments of this article, we conducted a simple grid search; this method does
not guarantee finding the optimal value and is time-consuming. We may
employ optimization techniques such as evolutionary algorithms, ou con-
sider the meta-prior as one of the training parameters of the network, et
optimize it through backpropagation. Our preliminary experiments with
learning the meta-prior did not show any satisfactory results, and the net-
work did not converge. We have left this issue as future work.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2052
UN. Ahmadi and J. Tani
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 9: While the reconstruction is better for w(cid:5) = 0.01 (lower MSE), the prior
and posterior activity of the middle layer are significantly more different than
for w(cid:5) = 0.25, and the prior activity in particular seems to be constant. Ici,
we take a closer look at the activity of the w(cid:5) = 0.25 and w(cid:5) = 0.01 models pre-
sented in Figure 8. Ici, we consider only the part happening during the time
window [1200]. Only the y dimension of the 2D patterns is illustrated in the first
row of the graphs; cependant, the MSE (second row) is computed for both dimen-
sions. The two bottom rows show the mean μ(q)
(prior) de
t
the middle layer.
(posterior) and μ(p)
t
4 Robot Experiment
As explained in the previous section, PV-RNN was able to deal with
probabilistic patterns during simulation experiments. We also conducted a
robotics experiment involving synchronous imitation between two robots.
This experiment allows us to do several things at once. One is to pro-
vide a more realistic test case, in higher dimensions (12), with complex
A Novel Predictive-Coding-Inspired Variational RNN Model
2053
perceptual noise source (par exemple., hardware variations, motor noise, tempera-
ture, small synchronization discrepancies, and variations introduced when
capturing training sequences from human movement). Another is to con-
sider a context where actions need to be performed. The action space and
sensory space are different in this experiment, leading us to adapt and ap-
ply the model in new ways. A final one is to compare PV-RNN with VRNN
(Chung et al., 2015) and thus to contrast the effectiveness of error regression
versus an autoencoder-based approach. For this, synchronous imitation is
considered to be an ideal task because it involves predicting both future
perceptual sequences to compensate possible perceptual delay and recog-
nizing others intention via posterior inference.
4.1 Experimental Settings. We used two identical OP2 humanoid
robots placed face-to-face. One robot was the demonstrator and the other
the imitator. To generate the training data, 15 movement primitives of 200
time steps, different from one another, were designed. A human then exe-
cuted each primitive on both robots at the same time, in mirror fashion, tel
that the movement of the left arm of one robot was executed on the right
arm of the other (see Figure 10A). The imitator was then given training se-
quences composed of proprioception data—the joint angles of its own arms
during movement, X Pro
t —and exteroception data—the XYZ coordinate of
the hand tip of the demonstrator robot, from the perspective of the imitator
robot, X Ext
.
t
The testing data were generated by a human, creating a movement se-
quence by repeating a movement primitive a few times (seven cycles on
average) and then switching at random to another primitive, so that all 15
primitives were used. The human strived to produce qualitatively the same
mouvement, but not quantitatively: speed, amplitude and shape could differ.
The resulting testing sequence is 4641 time steps long.
t
, but not, crucially, the X Pro
During testing, the demonstrator would play the prerecorded testing se-
quence, and the imitator robot would receive, at each time step t, the corre-
sponding exteroception data X Ext
t proprioception
data. The imitator would use the PV-RNN model to make predictions about
both the exteroception and the proprioception data. The proprioception
predictions would be sent to the PID controller to be executed on the im-
itator robot, while the exteroception predictions would be compared with
the actual observed one, X Ext
, and the resulting error would be propagated
through the network to perform error regression. We insist that the errors
propagated through the network are only relative to X Ext
, as the target pro-
prioception sequence is unavailable during testing. An important challenge
in this setup is the switching, in the sequence, between different primitive
motifs; the imitator must be able to recognize when they happen and up-
date the internal state of the network, Atest, appropriately (see Figure 10B).
The same training and testing data were used on the same setup to train
t
t
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2054
UN. Ahmadi and J. Tani
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 10: Robotic experiment of synchronous imitation. One OP2 robot imi-
tates the other OP2 teleoperated by the experimenter (UN), graph of computation
and information flow using PV-RNN during testing (B), VRNN during train-
ing (C), and VRNN during testing (D). The red lines in panels B and C show
the inference models of PV-RNN and VRNN, and the dashed lines in panel D
show how the closed-loop generation is computed. The models in panels B–D
are depicted with only one context layer for clarity. uPro
represent the
proprioception and exteroception input units at time step t that are fed by X Pro
t−1
and X Ext
and uExt
t−1, respectivement.
t
t
a VRNN model; Figures 10C and 10D show how VRNN was used in the
training and testing, respectivement.
To fairly compare the PV-RNN and VRNN, the same MTRNN-type net-
work layer structure was used for both networks. The internal dynamic of
the MTRNN used in VRNN was computed as in equation 2.3, but for the
lowest layer, there is an added term W duut to feed the input ut to the net-
travail. ut is composed of uPro
. In that case, equation 2.3 becomes
and uExt
t
t
(cid:15)
(cid:16)
=
1 − 1
τ
1
t ).
= tanh(h1
h1
t
d1
t
h1
t−1
+ 1
τ
1
(W 1,1
dd d1
t−1
+ W 1,1
dz Z1
t
+ W 1,2
dd d2
t−1
+ W duut )
(4.1)
A Novel Predictive-Coding-Inspired Variational RNN Model
2055
t
= X Pro
t−1 and uExt
In variational Bayes autoencoder RNNs (Chung et al., 2015; Fraccaro
et coll., 2016; Goyal et al., 2017; Shabanian et al., 2017), the previous time
step target X t−1 is provided as the current input to predict X t in the output.
= X Ext
As can be seen in Figure 10C, during training, uPro
t−1.
The look-ahead predictions for multiple steps were conducted by closed-
loop generation (Tani, 1996) wherein both prediction of the proprioception
and exteroception at a particular future time step are obtained by feeding
the prediction outputs of them at the previous time step into the inputs at
this step. Officiellement, during testing, for one-step-ahead prediction, we retain
uExt
t−1, but the proprioception data come from the prediction of the
t
network itself, such that uPro
t−1. For two-steps-or-more-ahead predic-
tion, we do not have access to exteroception targets. Donc, both the
proprioception and exteroception data come from the prediction of the net-
t:T−1 and uExt
work itself, such that uPro
The approximate posterior of the VRNN is obtained as (Chung et al.,
= X Ext
= X Ext
= X Pro
= X Pro
t:T−1.
t+1:T
t+1:T
t
t
2015)
qφ (Zt | dt−1
, X t ) = N (Zt; m(q)
, p (q)
t
t
, X t ),
] = f (q)
φ (dt−1
) où
(4.2)
[m(q)
t
, log σ (q)
t
where f (q), X, and φ denote a one layer feedforward neural network, the tar-
get, and the posterior variables, respectivement. This means that in the VRNN
(during training), the current time step target (observation) is directly pro-
vided to the approximate posterior, whereas in the PV-RNN, not only the
current time step target but also future ones are indirectly provided to the
approximate posterior through BPTT. The prior computation of VRNN is
the same as equation 2.4.
We used the same number of d and Z units for the VRNN and PV-RNN
models. Each model had three context layers consisting of 120 d units and
12 Z units for the fast context (FC) layer, 60 d units and 6 Z units for the
middle context (MC) layer, et 30 d units and 3 Z units for the slow context
(SC) layer. Time constants of FC, MC, and SC units were set to 2, 10, et 50,
respectivement. In each model case, the training ran for 50,000 epochs.
t
For testing, we performed prediction from one to five steps ahead. Le
motor controllers of the robot receive the last proprioception predictions as
control targets: if we do one-step-ahead predictions, the motor controllers
will receive X Pro
at time t. If we do five-step-ahead predictions, they will
receive X Pro
t+4 at time t. This would allow correction for perceptual and pro-
cessing delay. For error regression in PV-RNN, the size of the time window
m was set to 10, et 100 regression steps were performed at each time step.
Not providing VRNN with any proprioception information led to poor per-
formance. To remedy this, we provided VRNN with 20 steps of propriocep-
tion information at the beginning of the test sequence. PV-RNN does not
have access to any proprioception information.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2056
UN. Ahmadi and J. Tani
Tableau 5: MSE between the Target and Look-Ahead Prediction.
Number of Prediction Steps
1 Step
2 Mesures
3 Mesures
4 Mesures
5 Mesures
PV-RNN 0.00254
0.00641
VRNN
0.00259
0.00702
0.00339
0.00779
0.00395
0.00852
0.00473
0.00943
Remarques: PV-RNN outperforms VRNN regardless of the number
of prediction steps. The table shows the MSE between the tar-
get and look-ahead prediction with different time steps ahead
for PV-RNN and VRNN. The network with minimum MSE is
shown in bold numbers.
Synchronized imitation with PV-RNN could not be done online because
the error regression with 100 optimization steps costs about twice the com-
putational time (205 ms) than real time would allow. Donc, in the case
of using PV-RNN, the test was conducted on prerecorded data sequence
of exteroception. Although the VRNN case could be performed in real
temps, we also used the prerecorded target sequences to ensure the fairest
comparison.
4.2 Experimental Results. For PV-RNN and VRNN, we compared the
performance for different values of the meta-prior w: 1.0, 0.5, 0.25, 0.2, et
0.1. We present here the results for the best value of w for each model, 0.5
for PV-RNN and 0.25 for VRNN.
The mean square error (MSE) between the target (exteroception and pro-
prioception targets) and the predicted outputs (exteroception and proprio-
ception outputs) with different look-ahead step length is shown for both
cases of using PV-RNN and VRNN in Table 5.
In both PV-RNN and VRNN, the error increases as the model predicts
more steps ahead, as is expected. PV-RNN consistently outperforms VRNN,
showing the effectiveness of error regression for prediction performance.
We recorded two videos—one-step-(Video 1) and five-steps-ahead
(Video 2) predictions—of the movement patterns of three robots. One robot
(middle) was the demonstrator robot, and the others were the imitator
robots: one controlled by the PV-RNN (gauche) and one by the VRNN (droite).
PV-RNN convincingly outperforms VRNN in the video of the one-step-
ahead prediction. The PV-RNN robot synchronously imitates the target
robot, whereas the VRNN does not always perform a smooth, or correct, im-
itation. One-step-ahead prediction (50 ms) seems to be enough to overcome
the perceptual delay in this setting, as delay is difficult to observe between
demonstrator and imitator. In the five-step-ahead prediction, PV-RNN
still shows better prediction performance than VRNN. Cependant, it also
fails to imitate the target robot for several movements and exhibits brusk
changes of speed, accelerating and slowing down around the target pattern.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2057
Looking at the video of a successful imitation frame by frame, one can see
that the imitator robot movements seem to be ahead of the target one.
5 Discussion
This article examines how uncertainty or probabilistic structure hidden in
observed temporal patterns can be captured in an RNN through learn-
ing. To that end, it proposes a novel, predictive-coding-inspired variational
Bayes RNN. Our model possesses three main features that distinguish it
from the existing variational Bayes RNN. The first is the use of a weight-
ing parameter, the meta-prior, between the two terms of the lower bound to
control the optimization pressure. The second is propagating errors through
backpropagation instead of propagating inputs during the forward com-
putation. And the third is the error regression procedure during testing,
performing online optimization of the internal state of the network during
prediction.
The idea of weighting the KL divergence term of the lower bound has
been employed before, most notably in KL annealing (Bowman et al., 2015).
However in this article, it is used for a different purpose. Through two
experiments, the first one involving a finite state machine and the second
one continuous temporal patterns composed of probabilistic transitions be-
tween a set of hand-generated movement, we showed that by changing the
value of the meta-prior, we could achieve either a deterministic or a ran-
dom process behavior. The deterministic behavior reconstructed training
sequences well and imitated the stochasticity of the data through deter-
ministic chaos but could not generalize to unseen testing sequences. Le
random process behavior could neither reconstruct training sequences nor
generalize to unseen ones; its behavior was dominated by noise. The best
value of the meta-prior could be found between those two extremes, où
we showed that the network displayed both good reconstruction and gener-
alization capability. It can be summarized that although probabilistic tem-
poral patterns can be imitated by either deterministic chaos or stochastic
processus, as suggested by the ergodic theory of chaos (Crutchfield, 1992),
the best representation can be developed by mixing the deterministic and
stochastic dynamics via iterative learning of the proposed RNN model.
We employed the idea of propagating errors instead of propagating in-
puts to address two important issues in variational Bayes RNNs: how to
provide the future dependency information to the latent states and how to
avoid ignoring the latent states during learning. We addressed both issues
by introducing an adaptive vector AX in the inference model. AX is opti-
mized through BPTT and captures the future dependencies of the external
observation. This was verified in both simulated experiments, as providing
the first time step AX
1 was sufficient to reconstruct the training sequences.
En outre, because information from AX flows to Z and the information
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2058
UN. Ahmadi and J. Tani
from Z flows through the deterministic states d, which are ultimately re-
sponsible for the output sequences, the network is forced to construct good
representations in the latent state Z. This phenomenon was shown in the
first experiment when looking at the activity of mean μ(p) and variance σ (p)
of Z.
Enfin, we used an error regression procedure during testing for mak-
ing predictions about unseen sequences. In the second experiment, le
PV-RNN, based on a network architecture with multiple layers, was eval-
uated for look-ahead prediction in primitive sequences. We found that rel-
atively long sequences of primitive transitions were successfully predicted
despite some discrepancies when w was set to an adequate intermediate
valeur. Ce, cependant, required a window of a sufficient length (200 steps)
and a high number of iterations for error regression (1000 iterations). Ce
suggests that a good balance between minimizing reconstruction error and
divergence between the prior and posterior distributions can result in ac-
curate prediction of future primitive sequences.
En outre, the error regression procedure we employed bears a lot
of similarities to the predictive coding principle. En particulier, it shares the
same processing cycle: making predictions, propagating prediction errors
through the network hierarchy, and updating its internal state online to im-
prove future predictions. Some important differences exist with predictive-
coding implementations closer to the neurobiology of the brain (Rao &
Sejnowski, 2000); in our model, errors are propagated globally rather than
locally. This is deliberate, to take advantage of the canonical tools of varia-
tional Bayes RNNs.
Other autoencoder-based variational Bayes RNNs infer the latent vari-
able at each time step through a recurrent mapping of the hidden state of
the previous step, fed with inputs with the current time step (Fabius &
van Amersfoort, 2014; Bayer & Osendorfer, 2014; Chung et al., 2015). Dans
the robotic experiment for an imitation learning task, we showed that our
model outperforms VRNN (Chung et al., 2015). This demonstrated the ef-
fectiveness of the error regression.
The learning vector AX addressed two issues but introduces another. Dans-
deed, as described in section 2.2, the dimension of AX increases linearly
with the length and the number of training samples. It seems to preclude
working with large data sets as a naive implementation might exceed any
reasonable available memory. Cependant, with each vector AX correspond-
ing to a specific training pattern, it can be dynamically loaded and unloaded
into memory whenever needed during training, resulting in a memory re-
quirement equal to the one of the largest training batch. En outre, le
trained values of the AX vectors are not needed for predicting unseen test-
ing sequences and can be discarded entirely. If one wishes to perform re-
construction of the training patterns, only the first time step AX
1 is needed.
Enfin, although we did not do it in this article, AX vectors may not be
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2059
needed for every time step and we could consider having AX vectors every
10 steps, par exemple. The implications are not necessarily trivial, and this
is a subject of ongoing study.
While the memory requirement of the model may not be a fundamental
problem, perhaps a more serious issue lies in the computational require-
ment of the error regression process. En effet, compared to most models that
only need forward computations for evaluation, our model still needs to
backpropagate and perform optimization. This can severely hamper its abil-
ity to be deployed on a variety of platforms. It can also be an issue for real-
time robotics, as was the case in our robotic experiment. We are currently
investigating ways to reduce the computational burden of error regression.
An intriguing consideration is that the current results showing that the
generalization capability of PV-RNN depend on the setting of the meta-
prior w bears parallels to observational data about autism spectrum dis-
ordres (ASD) and may suggest possible accounts of its underlying mech-
anisms. ASD is a wide-ranging pathology including deficits in communi-
cation, abnormal social interactions, and restrictive or repetitive interests
and behaviors (DiCicco-Bloom & Crabtree, 2006). Recently, there has been
an emerging view suggesting that deficits in low-level sensory processing
may cascade into higher-order cognitive competency, such as in language
and communication (Stevenson et al., 2014; Lawson, Rees, & Friston, 2014;
Robertson & Baron-Cohen, 2017. Van de Cruys et al. (2014) have suggested
that ASD might be caused by overly strong top-down prior potentiation to
minimize prediction errors (thus increasing precision) in perception, lequel
can enhance capacities for rote learning while resulting in the loss of the
capacity to generalize what is learned, a common ASD symptom.
This account by Van de Cruys et al. (2014) corresponds to some extent
to the situation of PV-RNN when learning with w set to a larger value.
PV-RNN is able to exactly reconstruct complex training sequences by em-
bedding them in deterministic dynamics, while being unable to generalize
to unseen sequences. With a larger value of w, the optimization pressure
on the KL divergence term, and therefore on the prior to be similar to the
posterior, is stronger. This pushes the network to reduce uncertainty in the
réseau (low σ), increasing the precision of the predictions, resulting in a
stronger top-down prior. Such a phenomenon could explain how ASD pa-
tients in social contexts might frequently suffer from overamplified error
in predicting behaviors of others; this results from overestimated precision
in prediction due to overfitting in learning. For this reason, such patients
may tend to indulge in their own repetitive behaviors that generate a tol-
erable amount of error. Alors, mechanisms akin to the inability of adapt-
ing w adequately may result in the pathology. Lawson et al. (2014) propose
that maladaptation of precision itself in hierarchical message passing in the
brains may contribute to many features of autistic perception in a study
using a hierarchical Bayesian model built on the predictive coding frame-
travail. If a neural mechanism indeed exists that corresponds to adapting w,
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2060
UN. Ahmadi and J. Tani
study about the precise feedback mechanisms to regulate w within an op-
timal range could be an important research question for ASD. It could also
shed light on how the brain handles various cognitive tasks using statistical
inference.
Various robotics applications would be interesting for future study. Un
of the main features of the proposed model is that it can learn the latent
probabilistic structure of data; this should translate into high performance
at learning skilled behaviors through supervised teaching, such as manual
manipulation d'objets. En effet, a crucial component in generating skilled
behavior is that precision in movement control must change depending on
the situation during task execution. Par exemple, when an individual is
grasping an object, the precision during reaching can be low, but it must
become much higher at the moment of contact with the object to establish a
good grasp. It is highly likely that PV-RNN can learn to extract such statis-
tical structure by inferring the necessary precision in generating movement
trajectories from the set of training trajectories.
Another interesting direction for future study would be the introduction
of goal-directed planning mechanisms into the current model. Arie, Endo,
Arakaki, Sugano, and Tani (2009) showed that the deterministic MTRNN
model can generate goal-directed plans. It does that by starting from a de-
sired goal state for a future time step and backpropagating the error to in-
fer the necessary context state of the current time step to achieve this goal.
From this inferred initial context state, a proprioception sequence (joint an-
gles of the robot) can be predicted and used to directly specify what ac-
tions the robot should undertake. En outre, Butz, Bilkey, Humaidan,
Knott, and Otte (2019) recently proposed, a retrospective and prospective
inference schEme (REPRISE), which can infer both retrospectively for past
contextual event states and prospectively for future optimal motor com-
mand sequences satisfying some given goal states. REPRISE is built on
their previous work, which included the prospective phase using an RNN
(Otte, Zwiener, & Butz, 2017). In the new proposed model, an RNN is aug-
mented with contextual neurons in order to encode continuous sensori-
motor dynamics into sequences of discrete events. The contextual neurons
are adapted during the retrospective phase in order to minimize the loss
between predicted and actual sensory information. Then the motor com-
mands in the future time steps are adapted via BPTT during the prospec-
tive phase in order to minimize the discrepancies between predicted future
states and desired goal states. Such a mechanism could also be realized in
PV-RNN by inferring the optimal adaptive vector A sequence accounting
for both past sensory experience and the specified future goal states. Fu-
ture study should examine how the extended PV-RNN can perform goal-
directed planning tasks, including online replanning ones, compared to
existing models such as REPRISE Butz et al. (2019).
The robotic experiment presented in this article was limited in many
ways. We are now working on a two-robot setup where, rather than one
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2061
demonstrator and one imitator, there are two imitators imitating each other.
In the context of active inference (Friston, Daunizeau, & Kiebel, 2009; Fris-
ton, Daunizeau, Kilner, & Kiebel, 2010; Pezzulo, Rigoli, & Friston, 2015;
Baltieri & Buckley, 2017), an agent interacting with an environment has
two choices when its predictions do not agree with its observations: either
modify its internal state to produce predictions that better align with obser-
vations, or perform an adequate intervention in the environment to make
observations better correspond to the predictions. Autrement dit, quand
the world does not fit our expectations, we can change our expectations or
change the world by acting adequately on it. In a context where a demon-
strator performs for an imitator, the imitator has no choice but to change
its internal state when prediction errors occur. But in a situation with two
imitators, robot A may learn how robot B responds to its own actions, es-
pecially when robot A’s actions generate prediction errors for robot B. If
robot B is only updating its internal state, robot A might end up continu-
ously performing interventions on robot B’s behavior rather than changing
its own internal state. The most interesting case should happen when both
robots are able to learn to predict the consequences of their own actions on
the other robots and perform interventions to influence one another’s ac-
tion. The circular causality developed between those two may lead to am-
biguity in determining which one drives the other, which one demonstrates,
and which one imitates, with possibly continuous switching between those
roles. The early results we obtained on such a setup are encouraging. Stud-
ies examining such aspects could greatly contribute to understanding the
underlying mechanisms of social cognition and how to engineer the au-
tonomous development of collaborative actions among multiple agents.
6 Conclusion
We proposed a predictive-coding-inspired variational Bayes RNN to cap-
ture the stochasticity of time-series data. To that end, the cost function of
the network is composed of two terms: the expected prediction error and
the KL divergence (measuring how similar two distributions are) entre
the posterior and prior distributions. The relative importance of those two
terms is weighted by a parameter w, the meta-prior.
D'abord, in a simple task, we demonstrated that increasing the value of the
meta-prior w, and therefore the optimization pressure on the KL diver-
gence term in the cost function, led to the model’s behaving increasingly
deterministically, leading to development of deterministic chaos, with low
generalization capabilities. Inversement, lowering the value of w led to a net-
work’s behaving increasingly stochastically. Stochastic models are better at
generalization, but at the extreme, they turn into random generators that
disregard the structure of the input data.
The best behavior is found when the value of w is between those two ex-
tremes: the network was able to achieve the best generalization capability
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2062
UN. Ahmadi and J. Tani
with an intermediate value of the meta-prior. We confirmed this observa-
tion on more complex tasks using both hand-drawn patterns and robotic
motions and on a more complex model using a higher number of context
layers.
Our approach provides interesting solutions to two issues that vari-
ational Bayes RNNs typically have: latent variables are ignored during
entraînement, and they do not have access to information about the future de-
pendencies of the data. Our network solves those two issues by avoiding
feeding inputs to the network during the forward computation, preferring
to propagate prediction errors during BPTT to dedicated latent variables.
These variables are leveraged when predicting unseen testing sequences:
we use an error regression procedure during evaluation, which performs
online optimization of the internal state of the network based on observed
prediction errors. Donc, the predictions are constantly reevaluated as
new external data become observable. We have shown that our model out-
performs the VRNN model (Chung et al., 2015) on a robotic imitation task.
Appendix A: Posterior Computation
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
qφ (Zt | dt−1
, et:T ) = N (Zt; m(q)
t
, AX
] = f (q)(dt−1
t )
, p (q)
t
)
où
[m(q)
t
, log σ (q)
t
The equation for μ and log σ of posterior can be written as
(cid:17)
μk
t
log σk
t
= tanh (W kk
μd
˜dk
= W kk
t−1
σ d
˜dk
t−1
+ AX,k
p,t
+ AX,k
m,t )
,
(A.1)
(A.2)
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
where μk
t is the vector of the mean values of the kth context layer at time
t, W kk
μd is the matrix of the connectivity weights from the d units in the kth
context layer to μ units in the same context layer, and W kk
σ d is the matrix
of the connectivity weights from the d units in the kth context layer to the
σ units in the same context layer. The notation (q) was omitted from the
equation for simplicity. AX,k
p,t are obtained as follows,
m,t and AX,k
⎧
⎪⎨
⎪⎩
AX,k
m,t
AX,k
p,t
= AX,k
m,t
= AX,k
p,t
+ α ∂L
∂AX,k
m,t
+ α ∂L
∂AX,k
p,t
,
(A.3)
where α is the learning rate. Based on equation A.2, we can rewrite equation
A.3 to have the derivatives with respect to mean and standard deviation
values as
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2063
⎧
⎪⎪⎪⎨
⎪⎪⎪⎩
AX,k
m,t
= AX,k
m,t
+ un
(cid:22)
1 − tanh2
(cid:22)
W kk
μd
˜dk
t−1
+ AX,k
m,t
AX,k
p,t
= AX,k
p,t
+ un
∂L
∂ log σk
t
(cid:23)(cid:23) (cid:15)
(cid:16)
∂L
∂μk
t
.
(A.4)
Appendix B: KL Divergence
We let each posterior and prior distribution be a gaussian with a diagonal
covariance matrix, donc:
KL[qφ (Zt ) (cid:4) PθZ (Zt )] = Eqφ [log qφ (Zt )] − Eqφ [log PθZ (Zt )],
qφ (Zt ) =
PθZ (Zt ) =
1(cid:24)
2π (σq
t )2
1(cid:24)
2π (σ p
t )2
e
e
−(Zt
t )2
−μq
t )2
2(σq
−(Zt
t )2
−μp
t )2
2(σ p
,
.
(B.1)
(B.2)
(B.3)
For simplicity, we removed parentheses from p and q. Based on equations
B.1 to B.3,
Eqφ [log qφ (Zt )] = Eqφ
Eqφ [log PθZ (Zt )] = − 1
2
log 2π − 1
2
(cid:6)
− 1
2
(cid:6)
log 2π + log (σ p
Eqφ
log (σq
(cid:6)
log 2π + log (σ p
= − 1
2
Eqφ
t )2
t )2 +
−(Zt − μq
2(σq
t )2
(cid:7)
t )2 + (Zt − μp
t )2
(σ p
t )2
t )2 + (Zt )2 + 2Ztμp
t
(σ p
t )2
,
Variance and E[Z2
t ] can be written as
σ2
t
= E[(Zt − μt )2], E[Z2
t ] = μ2
t
+ σ2
t
,
so equations B.4 and B.5 can be rewritten as
(cid:15)
Eqφ [log qφ (Zt )] = − 1
2
log 2π + log (σq
(cid:16)
t )2 + (σq
t )2
(σq
t )2
(cid:26)
(cid:25)
= − 1
2
log 2π + log (σq
t )2 + 1
,
(cid:7)
,
(B.4)
− (μp
t )2
(cid:7)
.
(B.5)
(B.6)
(B.7)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2064
UN. Ahmadi and J. Tani
(cid:15)
Eqφ [log PθZ (Zt )] = − 1
2
log 2π + log (σ p
t )2
+ (μq
t )2 + (σq
t )2 − 2μq
(σ p
t )2
t
μp
t
+ (μp
t )2
(cid:16)
.
(B.8)
Now, equation B.1 can be rewritten as
KL[qφ (Zt ) (cid:4) PθZ (Zt )] = − 1
2
(cid:15)
log (σq
t )2 + 1 − log (σ p
t )2
− (μq
t )2 + (σq
(cid:16)
+ (μp
t )2
t
μp
t
t )2 − 2μq
(σ p
t )2
)2 + (p (q)
t
− μ(q)
t
2(p (p)
t
)2
= log
p (p)
t
p (q)
t
+ (m(p)
t
)2
− 1
2
.
(B.9)
Appendix C: Lyapunov Exponent Computation
For simplicity, let us consider a PV-RNN consisting of 2 d units and 1 Z unit.
We need to first compute Jacobian matrices at each time step as
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
∂Zt+1,1
∂Zt,1
∂dt+1,1
∂Zt,1
∂dt+1,2
∂Zt,1
∂Zt+1,1
∂dt,1
∂dt+1,1
∂dt,1
∂dt+1,2
∂dt,1
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
.
∂Zt+1,1
∂dt,2
∂dt+1,1
∂dt,2
∂dt+1,2
∂dt,2
Jt =
It can be noted that X does not exist in the Jacobian matrices because in
the generative model, X 1:T are not given to the context layers. We can now
. . . J1U of the unit
resort to the approximation of the image ellipsoid JT JT−1
sphere by a computational algorithm. (More details can be seen in Alligood
et coll., 1996.) Ici, the computation of the first-largest Lyapunov exponent
is given. Let us start with an orthonormal basis r = [1.0 0.0 0.0]T , and use
the Gram-Schmidt orthogonalization procedure, so we have algorithm 1,
où (cid:4).(cid:4) and LE denote Euclidean length and the first largest Lyapunov
exponent, respectivement. T was 50,000 in our experiments.
Appendix D: Experiment 1 with a Simple RNN
We conducted experiment 1 again using the same data sets and network
parameter settings with the exception of the time constant. We set the time
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2065
Tableau 6: Evaluation of the Regeneration and Generalization Capabilities of the
PV-RNN Model Trained with Different Values for w.
Meta-Prior w
0.1
0.05
0.025
0.015
0.01
0.001
0.0001
Average diverging step (ADS)
KL divergence of test phase
23
12
6.8589 1.6515 0.1106 0.1306 0.359 0.8758 2.8845
15
19
11
8
7
Remarques: The average diverging step (ADS) points to better reconstruction performance
when w is high. Cependant, taking into account the KL divergence between the probabilistic
distribution of the generated pattern P(X t:t+11 ) and the one of the training data P(X t:t+11 )
paints another picture: the network best captures the probabilistic structure of the data
for an average value of w. The bold number in the first row shows the model with the
best regeneration capability. The bold numbers in the second row shows the model with
best generalization capability.
constant in equation 2.3 à 1.0, which removes the leaky integrator and the
d unit becomes a simple RNN. ADS and KL divergence of the test phase for
different values of w are shown in Table 6. The results are in line with the
ones shown in section 3.1 where the MTRNN with time constant 2.0 était
used.
Appendix E: Experiment 2 Data Set
The data set for experiment 2 data sequences was generated in three stages
as follows.
D'abord, three different 2D movement primitive patterns and a PFSM of
defining the transition probability among those patterns were prepared.
Then a human subject was asked to draw patterns in 2D using a tablet
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2066
UN. Ahmadi and J. Tani
device by sequentially concatenating the primitive patterns by following
the transition probability defined in the PFSM of Figure 2B. Each drawing
of hand-drawing primitive patterns necessarily contains fluctuations in am-
plitude, velocity, and shape. Primitive patterns A, B, C were circles, a rotated
figure eight, and triangles similar to those depicted in the first row of Fig-
ure 7. Each of them is a cyclic pattern with periodicity 2. The PFSM adopted
in this experiment is shown in Figure 2B. The total number of A, B, C primi-
tive patterns generated was 160 (4458 time steps). The branching after s4 by
generating either a primitive B or C was randomly chosen by the human.
We measured the conditional probabilities in the data after the generation,
and they were P(B|ABA) = 0.275% and P(C|ABA) = 0.725%.
Suivant, a target generator was built using the human-generated data for
the purpose of producing training and testing patterns used for evaluating
the PV-RNN. An MTRNN was used as the target generator by training it
with using the human-generated data as the teaching target sequences. Af-
ter the training, the closed-loop operation of the MTRNN (feeding next step
inputs with current step prediction outputs) generated sample sequence
patterns while adding gaussian noise with zero mean and constant σ of
0.05 to the internal state of each context unit at each time step. This makes
the outputs of the network stochastic while preserving the probabilistic
structure, not necessarily exactly the same as the one in the training pat-
terns prepared. More details and implementations of this target generator
MTRNN can be seen in Ahmadi and Tani (2017un). Due to the noise inserted
into the internal dynamics of the MTRNN, the output patterns were nois-
ier and fluctuated more than the human-generated patterns, and those pat-
terns could have different numbers of cycles than two. Enfin, three groups
of patterns were sampled from the MTRNN-generated output patterns,
one consisting of 16 sequence patterns, each with a 400 step-length for the
training of the PV-RNN, another comprising 1 sequence patterns with a
6400-step length for the first test phase of the PV-RNN, and the last one
consisting of 32 sequence patterns, each with a 400-step length for the sec-
ond test phase of the PV-RNN. The main reason that the target generator
was used instead of using human-generated trajectory data was that signif-
icantly more target data were used (up to 128 sequences) while designing
the model, more than could be reasonably created using human generation.
The target generator, MTRNN, can effortlessly generate as many instances
of patterns as one needs.
Appendix F: Experiment 2 with Two Context Layers
Two PV-RNN models were trained with w(cid:5)
set to 0.25. The first model had
two context layers consisting of 80 d units and 8 Z units for the fast context
(FC) layer and 40 d units and 4 Z units for the slow context (SC) layer. Le
time constants of FC and SC units were set to 2 et 4, respectivement. Le
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2067
Tableau 7: MSE between the Unseen Test Targets and the One-Step- to Five-Steps-
Ahead Generated Predictions for Models with Two Context Layers.
Number of Prediction Steps
1-Step
Prediction
2-Mesures
Prediction
3-Mesures
Prediction
4-Mesures
Prediction
5-Mesures
Prediction
First model
Second model
0.00439
0.0041
0.00912
0.00865
0.014
0.013
0.0183
0.0178
0.02236
0.0223
Tableau 8: Accuracy for One, Deux, and Three Primitive Prediction for Models with
Two Context Layers.
Number of Prediction Primitives
Un
90.62%
100
Deux
75%
81.25
Three
46.87%
50
First model
Second model
second model had two context layers consisting of 90 d units and 9 Z units
for the fast context (FC) layer and 50 d units and 5 Z units for the slow
contexte (SC) layer. The time constants of FC and SC units were set as in the
first model. Training ran for 300,000 epochs in each case. The first model
is equivalent to removing the slow context layer from the PV-RNN model
of section 3.2 with w(cid:5)
set to 0.25. De plus, the summations of d units and
Z units in the second model and the PV-RNN model of section 3.2 with w(cid:5)
set to 0.25 are equal, although the second model has 3640 more learnable
weights.
The prediction performance using error regression was evaluated for
both models as in section 3.2. Tables 7 et 8 show the error regression re-
sults of the one-step- to five-steps-ahead predictions and the one-primitive
to three-primitives predictions, respectivement. Both networks show similar
results to the network with three context layers (see Table 3) for predicting
each time step. Cependant, it can be seen by comparing Table 4 with Table 8
that the network with three context layers outperforms the networks with
two context layers for predicting correct patterns.
Appendix G: Experiment 2 with an Alternate Inference Model
We examined how providing the past dt−1 to the inference model could be
beneficial by deleting dt−1 information. The new approximate posterior is
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2068
UN. Ahmadi and J. Tani
Tableau 9: MSE between the Unseen Test Targets and the One-Step- to Five-Steps-
Ahead Generated Predictions for an Inference Model without dt−1 Information.
Number of Prediction Steps
1-Step
3-Mesures
Prediction Prediction Prediction Prediction Prediction
2-Mesures
5-Mesures
4-Mesures
Alternate inference model
0.0105
0.02116
0.02977
0.03414
0.03911
obtained as
qφ (Zt | et:T ) = N (Zt; m(q)
t
, p (q)
t
) où
[m(q)
t
, log σ (q)
t
] = f (q)
φ (AX
t )
(G.1)
A PV-RNN model was trained with w(cid:5)
set to 0.25. Other network param-
eters were exactly the same as the PV-RNN models in section 3.2. Tableau 9
shows the error regression results of the one-step- to five-steps-ahead pre-
dictions. By comparing these results with the error regression results of the
PV-RNN with w(cid:5)
set to 0.25 shown in Table 3, it can be seen that the model
presented here significantly underperforms (it is almost twice as bad) le
model with dt−1 information.
Appendix H: Additional Figures
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 11: The target and the regenerated outputs, the mean μ(p), and the stan-
dard deviation σ (p) of two PV-RNNs trained with meta-prior w set to 0.01 × 10−1
(UN) et 0.001 × 10−1 (B). The gray bars show the time steps corresponding to
uncertain states.
A Novel Predictive-Coding-Inspired Variational RNN Model
2069
Chiffre 12: The generated output, the mean μ(p), and the standard deviation σ (p)
from time steps 20,002 à 20,040 of two PV-RNNs trained with the meta-prior
w set to 0.01 × 10−1 (UN) et 0.001 × 10−1 (B). The gray bars show the time steps
corresponding to uncertain states.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 13: The A, B, and C patterns generated based on PFSM shown in Figure
2B. The whole pattern is 1000 time steps, y compris 20 of pattern A, 13 of pattern
B, et 7 of pattern C: Each pattern has two cycles. The patterns are not identical
and contain fluctuations in amplitude, velocity, and shape.
2070
UN. Ahmadi and J. Tani
c
je
t
s
je
n
je
m
r
e
t
e
d
e
h
t
d
n
un
)
s
r
un
b
oui
un
r
g
(
e
h
t
r
o
F
r
e
h
g
je
h
oui
je
t
n
un
c
fi
je
n
g
je
s
e
r
un
)
p
(
s
e
t
un
t
s
p
d
n
un
)
q
(
p
c
je
t
s
je
je
je
b
un
b
o
r
p
e
h
t
h
t
o
b
r
o
F
e
g
r
un
je
e
r
un
)
p
(
p
d
n
un
)
q
(
p
,
g
n
je
n
je
un
r
t
e
h
t
F
o
e
g
un
t
s
oui
je
r
un
e
e
h
t
t
UN
:
4
1
e
r
toi
g
je
F
,
s
h
c
o
p
e
0
0
0
,
0
1
r
e
t
F
UN
.
n
e
k
o
r
b
oui
je
t
s
o
m
e
r
un
M.
S
F
P.
e
h
t
n
je
d
e
n
fi
e
d
s
e
je
toi
r
n
o
je
t
je
s
n
un
r
t
e
h
t
;
s
e
t
un
t
s
e
h
t
n
o
e
n
o
d
oui
je
je
toi
F
s
s
e
c
c
toi
s
s
je
s
n
r
e
t
t
un
p
g
n
je
n
je
un
r
t
e
h
t
F
o
n
o
je
t
c
toi
r
t
s
n
o
c
e
r
.
d
e
t
un
r
e
n
e
g
e
r
oui
je
e
t
e
je
p
m
o
c
s
je
e
c
n
e
toi
q
e
s
t
e
g
r
un
t
e
h
t
d
n
un
o
r
e
z
r
un
e
n
e
r
un
)
p
(
p
d
n
un
)
q
(
p
e
h
t
,
e
r
o
F
e
r
e
h
T
.
s
e
n
o
c
je
t
s
je
n
je
m
r
e
t
e
d
e
h
t
n
un
h
t
s
e
t
un
t
s
c
je
t
s
je
je
je
b
un
b
o
r
p
,
g
n
je
n
je
un
r
t
e
h
t
F
o
e
g
un
t
s
je
un
n
fi
e
h
t
t
UN
.
s
e
t
un
t
s
c
je
t
s
je
je
n
m
r
e
t
e
d
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
.
t
s
r
fi
s
n
r
e
t
t
un
p
g
n
je
n
je
un
r
t
e
h
t
F
o
s
e
t
un
t
s
c
je
t
s
je
n
je
m
r
e
t
e
d
e
h
t
s
t
c
toi
r
t
s
n
o
c
e
r
k
r
o
w
t
e
n
e
h
t
t
un
h
t
w
o
h
s
s
t
je
toi
s
e
r
e
s
e
h
T
A Novel Predictive-Coding-Inspired Variational RNN Model
2071
Remerciements
We give special thanks to people who helped us with this study. First and
foremost, we are particularly grateful for great assistance and insightful
advice given by Fabien Benureau for improving the content and language
of the article. We sincerely express our appreciation to Tom Burns, Nadine
Wirkuttis, Wataru Ohata, Takazumi Matsumoto, and Siqing Hou for their
great help in improving this work as well.
Les références
Ahmadi, UN., & Tani, J.. (2017un). Bridging the gap between probabilistic and determin-
istic models: A simulation study on a variational Bayes predictive coding recur-
rent neural network model. In Proceedings of the International Conference on Neural
Information Processing (pp. 760–769). Berlin: Springer.
Ahmadi, UN., & Tani, J.. (2017b). How can a recurrent neurodynamic predictive cod-
ing model cope with fluctuation in temporal patterns? Robotic experiments on
imitative interaction. Neural Networks, 92, 3–16.
Alligood, K. T., Sauer, T. D., & Yorke, J.. UN. (1996). Chaos. Berlin: Springer.
Arie, H., Endo, T., Arakaki, T., Sugano, S., & Tani, J.. (2009). Creating novel goal-
directed actions at criticality: A neuro-robotic experiment. New Mathematics and
Natural Computation, 5(1), 307–334.
Baltieri, M., & Buckley, C. L. (2017). An active inference implementation of photo-
taxis. In Proceedings of the European Conference on Artificial Life (vol. 14, pp. 36–43).
Cambridge, MA: AVEC Presse.
Bayer, J., & Osendorfer, C. (2014). Learning stochastic recurrent networks. arXiv:1411.
7610.
Bengio, Y., Courville, UN., & Vincent, P.. (2013). Representation learning: A review and
new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence,
35(8), 1798–1828.
Bowman, S. R., Vilnis, L., Vinyals, O., Dai, UN. M., Jozefowicz, R., & Bengio, S. (2015).
Generating sentences from a continuous space. arXiv:1511.06349.
Butz, M.. V., Bilkey, D., Humaidan, D., Knott, UN., & Otte, S. (2019). Apprentissage, planning,
and control in a monolithic neural event inference architecture. Neural Networks,
117, 135–144.
Chen, X., Kingma, D. P., Salimans, T., Duan, Y., Dhariwal, P., Schulman, J., . . . Abbeel,
P.. (2016). Variational lossy autoencoder. arXiv:1611.02731.
Chung, J., Kastner, K., Dinh, L., Goel, K., Courville, UN. C., & Bengio, Oui. (2015). A recur-
rent latent variable model for sequential data. In C. Cortes, N. D. Lawrence, D. D.
Lee, M.. Sugiyama, & R.. Garnett (Éd.), Advances in neural information processing
systèmes, 28 (pp. 2980–2988). Red Hook, New York: Curran.
Clark, UN. (2015). Surfing uncertainty: Prediction, action, and the embodied mind. Nouveau
York: Presse universitaire d'Oxford.
Crutchfield, J.. P.. (1992). Semantics and thermodynamics. En M. Casdagli & S. Eubank
(Éd.), Nonlinear modeling and forecasting (p. 317). Reading, MA: Addison-Wesley.
DiCicco-Bloom, B., & Crabtree, B. F. (2006). The qualitative research interview. Med-
ical Education, 40(4), 314–321.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2072
UN. Ahmadi and J. Tani
Elman, J.. L. (1990). Finding structure in time. Sciences cognitives, 14(2), 179–211.
Fabius, O., & van Amersfoort, J.. R.. (2014). Variational recurrent auto-encoders.
arXiv:1412.6581.
Fraccaro, M., Sønderby, S. K., Paquet, U., & Winther, Ô. (2016). Sequential neural
models with stochastic layers. In D. D. Lee, M.. Sugiyama, U. V. Luxburg, je. Guyon,
& R.. Garnett (Éd.), Advances in neural information processing systems, 29 (pp. 2199–
2207). Red Hook, New York: Curran.
Friston, K. (2005). A theory of cortical responses. Philosophical Transactions of the Royal
Society of London B: Sciences biologiques, 360(1456), 815–836.
Friston, K. (2010). The free-energy principle: A unified brain theory? Nature Reviews
Neurosciences, 11(2), 127.
Friston, K. (2018). Does predictive coding have a future? Neurosciences naturelles, 21(8),
1019.
Friston, K. J., Daunizeau, J., & Kiebel, S. J.. (2009). Reinforcement learning or active
inference? PloS One, 4(7), e6421.
Friston, K. J., Daunizeau, J., Kilner, J., & Kiebel, S. J.. (2010). Action and behavior: UN
free-energy formulation. Biological Cybernetics, 102(3), 227–260.
Geiger, D., Verma, T., & Pearl, J.. (1990). Identifying independence in Bayesian net-
travaux. Networks, 20(5), 507–534.
Goyal, UN., Sordoni, UN., Côté, M.-A., Ke, N., & Bengio, Oui. (2017). Z-forcing: Training
stochastic recurrent networks. In I. Guyon, U. Von Luxburg, S. Bengio, H. Wal-
lach, R.. Fergus, S. V. N. Vishwanathan, & R.. Garnett (Éd.), Advances in neural
information processing systems, 30 (pp. 6713–6723). Red Hook, New York: Curran.
Higgins, JE., Matthey, L., Pal, UN., Bourgeois, C., Glorot, X., Botvinick, M., . . . Lerchner,
UN. (2017). Beta-vae: Learning basic visual concepts with a constrained variational
framework. In Proceedings of the International Conference on Learning Representa-
tion.
Hochreiter, S., & Schmidhuber, J.. (1997). Long short-term memory. Neural Computa-
tion, 9(8), 1735–1780.
Hohwy, J.. (2013). The predictive mind. New York: Presse universitaire d'Oxford.
Jordan, M.. je. (1997). Serial order: A parallel distributed processing approach. In J. W.
Donahoe & V. P.. Dorsel (Éd.), Advances in psychology (vol. 121, pp. 471–495). Am-
sterdam: Elsevier.
Karl, M., Soelch, M., Bayer, J., & van der Smagt, P.. (2016). Deep variational Bayes filters:
Unsupervised learning of state space models from raw data. arXiv:1605.06432.
Kingma, D. P., & Ba,
arXiv:1412.6980.
J..
(2014). Adam: A method for stochastic optimization.
Kingma, D. P., Salimans, T., Jozefowicz, R., Chen, X., Sutskever, JE., & Welling,
M.. (2016). Improved variational inference with inverse autoregressive flow. Dans
D. D. Lee, M.. Sugiyama, U. V. Luxburg, je. Guyon, & R.. Garnett (Éd.), Ad-
vances in neural information processing systems, 29 (pp. 4743–4751). Red Hook, New York:
Curran.
Kingma, D. P., & Welling, M.. (2013). Auto-encoding variational Bayes. arXiv:1312.6114.
Lawson, R.. P., Rees, G., & Friston, K. J.. (2014). An aberrant precision account of
autism. Frontiers in Human Neuroscience, 8, 302.
Lee, T. S., & Mumford, D. (2003). Hierarchical Bayesian inference in the visual cortex.
Journal of the Optical Society of America, 20(7), 1434–1448.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
A Novel Predictive-Coding-Inspired Variational RNN Model
2073
Murata, S., Yamashita, Y., Arie, H., Ogata, T., Sugano, S., & Tani, J.. (2017). Apprentissage
to perceive the world as probabilistic or deterministic via interaction with others:
A neuro-robotics experiment. IEEE Trans. Neural Netw. Learning Syst., 28(4), 830–
848.
Murata, S., Namikawa, J., Arie, H., Sugano, S., & Tani, J.. (2013). Learning to repro-
duce fluctuating time series by inferring their time-dependent stochastic proper-
liens: Application in robot learning via tutoring. IEEE Transactions on Autonomous
Mental Development, 5(4), 298–310.
Otte, S., Zwiener, UN., & Butz, M.. V. (2017). Inherently constraint-aware con-
trol of many-joint robot arms with inverse recurrent models. In Proceedings of
the International Conference on Artificial Neural Networks (pp. 262–270). Berlin:
Springer.
Pezzulo, G., Rigoli, F., & Friston, K. (2015). Active inference, homeostatic regulation
and adaptive behavioural control. Progrès en neurobiologie, 134, 17–35.
Rao, R.. P., & Ballard, D. H. (1999). Predictive coding in the visual cortex: A functional
interpretation of some extra-classical receptive-field effects. Neurosciences naturelles,
2(1), 79.
Rao, R.. P., & Sejnowski, T. J.. (2000). Predictive sequence learning in recurrent neo-
cortical circuits. In S. UN. Solla, T. K. Leen, & K.-R. Müller (Éd.), Advances in neural
information processing systems, 12 (pp. 164–170). Cambridge, MA: AVEC Presse.
Robertson, C. E., & Baron-Cohen, S. (2017). Sensory perception in autism. Nature
Reviews Neuroscience, 18(11), 671.
Rumelhart, D. E., Hinton, G. E., & Williams, R.. J.. (1985). Learning internal represen-
tations by error propagation. La Jolla: Université de Californie, San Diego, Institut
for Cognitive Science.
Shabanian, S., Arpit, D., Trischler, UN., & Bengio, Oui. (2017). Variational Bi-LSTMs.
arXiv:1711.05717.
Sinai, Oui. G. (1972). Gibbs measures in ergodic theory. Russian Mathematical Surveys,
27(4), 21.
Stevenson, R.. UN., Siemann, J.. K., Schneider, B. C., Eberly, H. E., Woynaroski, T. G.,
Camarata, S. M., & Wallace, M.. T. (2014). Multisensory temporal integration in
autism spectrum disorders. Journal des neurosciences, 34(3), 691–697.
Tani, J.. (1996). Model-based learning for mobile robot navigation from the dynamical
systems perspective. IEEE Transactions on Systems, Homme, and Cybernetics, Part B
(Cybernetics), 26(3), 421–436.
Tani, J., & Fukumura, N. (1995). Embedding a grammatical description in deter-
ministic chaos: An experiment in recurrent neural learning. Biological Cybernetics,
72(4), 365–370.
Tani, J., & Ito, M.. (2003). Self-organization of behavioral primitives as multiple at-
tractor dynamics: A robot experiment. IEEE Transactions on Systems, Homme, et
Cybernetics—Part A: Systems and Humans, 33(4), 481–488.
Tani, J., Ito, M., & Sugita, Oui. (2004). Self-organization of distributedly represented
multiple behavior schemata in a mirror system: Reviews of robot experiments
using RNNPB. Neural Networks, 17(8–9), 1273–1289.
Tani, J., & Nolfi, S. (1999). Learning to perceive the world as articulated: An ap-
proach for hierarchical learning in sensory-motor systems. Neural Networks, 12(7-
8), 1131–1141.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2074
UN. Ahmadi and J. Tani
Van de Cruys, S., Evers, K., Van der Hallen, R., Van Eylen, L., Boets, B., de Wit, L.,
& Salariés, J.. (2014). Precise minds in uncertain worlds: Predictive coding in
autism. Psychological Review, 121(4), 649.
Werbos, P.. (1974). Beyond regression: New tools for prediction and analysis in the
behavioral sciences. PhD diss., Université Harvard.
Yamashita, Y., & Tani, J.. (2008). Emergence of functional hierarchy in a multiple
timescale neural network model: A humanoid robot experiment. PLoS Compu-
tational Biology, 4(11), e1000220.
Zhao, T., Zhao, R., & Eskenazi, M.. (2017). Learning discourse-level diversity for neural
dialog models using conditional variational autoencoders. arXiv:1703.10960.
Received November 4, 2018; accepted June 24, 2019.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
1
1
1
2
0
2
5
1
8
6
4
8
0
0
n
e
c
o
_
un
_
0
1
2
2
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3