ARTICLE - Recherche en IA spécialisée au MIT

ARTICLE

Communicated by Manuel Beiran

Heterogeneity in Neuronal Dynamics Is Learned by Gradient
Descent for Temporal Processing Tasks

Chloe N. Winston
wincnw@gmail.com
Departments of Neuroscience and Computer Science, University of Washington,
Seattle, WA 98195, USA., and University of Washington Computational
Neuroscience Center, Seattle, WA 98195, U.S.A.

Dana Mastrovito
dana.mastrovito@alleninstitute.org
Allen Institute for Brain Science, Seattle, WA 98109, U.S.A.

Eric Shea-Brown
etsb@uw.edu
Stefan Mihalas
stefanm@alleninstitute.org
University of Washington Computational Neuroscience Center, Seattle, WA 98195,
USA.; Allen Institute for Brain Science, Seattle, WA 98109, USA.; and Department
of Applied Mathematics, University of Washington, Seattle, WA 98195, U.S.A.

Individual neurons in the brain have complex intrinsic dynamics that
are highly diverse. We hypothesize that the complex dynamics produced
by networks of complex and heterogeneous neurons may contribute to
the brain’s ability to process and respond to temporally complex data.
To study the role of complex and heterogeneous neuronal dynamics
in network computation, we develop a rate-based neuronal model, le
generalized-leaky-integrate-and-fire-rate (GLIFR) model, which is a rate
equivalent of the generalized-leaky-integrate-and-fire model. The GLIFR
model has multiple dynamical mechanisms, which add to the complex-
ity of its activity while maintaining differentiability. We focus on the
role of after-spike currents, currents induced or modulated by neuronal
spikes, in producing rich temporal dynamics. We use machine learning
techniques to learn both synaptic weights and parameters underlying in-
trinsic dynamics to solve temporal tasks. The GLIFR model allows the
use of standard gradient descent techniques rather than surrogate gradi-
ent descent, which has been used in spiking neural networks. After es-
tablishing the ability to optimize parameters using gradient descent in
single neurons, we ask how networks of GLIFR neurons learn and per-
form on temporally challenging tasks, such as sequential MNIST. Nous
find that these networks learn diverse parameters, which gives rise to

Neural Computation 35, 555–592 (2023)
https://doi.org/10.1162/neco_a_01571

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

556

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

diversity in neuronal dynamics, as demonstrated by clustering of neu-
ronal parameters. GLIFR networks have mixed performance when com-
pared to vanilla recurrent neural networks, with higher performance in
pixel-by-pixel MNIST but lower in line-by-line MNIST. Cependant, ils
appear to be more robust to random silencing. We find that the ability to
learn heterogeneity and the presence of after-spike currents contribute
to these gains in performance. Our work demonstrates both the compu-
tational robustness of neuronal complexity and diversity in networks and
a feasible method of training such models using exact gradients.

1 Introduction

1.1 Background. Artificial neural networks (ANNs) have been used to
emulate the function of biological networks at a system level (Yamins et al.,
2014; Rajan et al., 2016). Such models rely on the fantastic capacity of ANNs
to be trained to solve a task via backpropagation, using tools developed
by the machine learning community (Goodfellow et al., 2016). Cependant,
the way in which the neurons in recurrent ANNs integrate their inputs
over time differs from neuronal computation in the brain (see Figures 1A
and 1B).

Primarily, biological neurons are dynamic, constantly modulating inter-
nal states in a nonlinear way while responding to inputs. A biological neu-
ron maintains a membrane potential that varies not only with input currents
but also through history-dependent transformations. When its voltage ex-
ceeds some threshold, a neuron produces a spike, a rapid fluctuation in volt-
age that is considered the basis of neuronal communication. While these are
the defining features of a neuron, neurons exhibit additional, more complex
types of dynamics, including threshold variability and bursting. Threshold
adaptation gives rise to threshold variability and thus modulates the sen-
sitivity of a neuron to inputs. A proposed mechanism is that the thresh-
old fluctuates in a voltage-dependent manner, possibly due to the gating
mechanisms of various ion channels (Fontaine et al., 2014). Another type of
dynamic is responsible for bursting and related spiking behaviors. Bursting
results from depolarizing currents, which can be induced by prior spikes. UN
broader array of spiking patterns can be explained by considering both hy-
perpolarizing and depolarizing after-spike currents, currents that are mod-
ulated by a neuron’s spiking activity (Mihala¸s & Niebur, 2009).

In sum, biological neuronal dynamics can be thought of as continuous,
nonlinear transformations of internal neural states, such as ionic currents
and voltage. This is in contrast to a typical artificial neuron that maintains a
single state resulting from a static, linear transformation of an input vector.
De plus, diversity in intrinsic neuronal mechanisms gives rise to hetero-
geneity in the dynamics that biological neurons express. Par exemple, pas
all neurons in the brain display bursting behavior or threshold adaptation.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal Heterogeneity Learned by Gradient Descent

557

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 1: (UN) Schematic of a “vanilla” RNN cell or neuron. An RNN neuron
maintains a hidden state r(t) that is computed at each timestep by linearly
weighting the input signal and the previous output of itself and neighbor-
ing neurons through a recurrent connection. The output S(t) is computed by
applying a nonlinear transformation (par exemple., ReLU, tanh, or sigmoid) to r(t).
(B, C) Schematics of a GLIFR neuron. Each neuron maintains a synaptic current
Isyn that is computed at each timestep by linearly weighting the input signal by
Win, as well as the previous output of its neuron layer through a lateral or recur-
rent connection by Wlat. The neuron’s voltage V decays over time according to
membrane decay factor km and integrates synaptic currents and after-spike cur-
rents I j over time based on membrane resistance Rm and the membrane decay
factor. En plus, the voltage tends toward Vreset through a continuous reset
mechanism based on the firing rate at a given time. An exponential transfor-
mation of the difference between the voltage and the threshold voltage yields
a continuous-valued normalized firing rate, which varies between 0 et 1. Le
normalized firing rate, along with terms a j and r j, is used to modulate the after-
spike currents that decay according to decay factor k j. The dynamics present in
a GLIFR neuron give rise to its key differences from RNN neurons; GLIFR neu-
rons can express heterogeneous dynamics, in contrast to the fixed static trans-
formations utilized in RNN neurons.

558

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

The brain also exhibits diversity in neuronal properties, such as ionic con-
ductances, threshold, and membrane properties. This diversity is evident
from experiments fitting neuronal models to spiking behavior observed in
the mouse cortex (Teeter et al., 2018). Heterogeneity of such neural charac-
teristics further amplifies the diversity in neuronal dynamics. In contrast,
the only diversity in typical recurrent neural networks (RNNs), ANNs that
incorporate information over time, lies in synaptic weights. Typical RNN
neurons do not exhibit intrinsic dynamics, and each neuron responds iden-
tically to input with a common, fixed activation function.

Vanilla RNNs, which employ linear weighting of inputs and nonlinear
transformation of hidden states over time (see Figure 1A), have managed
to perform quite well on complex tasks without incorporating the complex-
ity and heterogeneity prominent in biological networks. RNNs have been
successful at classifying text (Liu et al., 2016) and images from a pixel-by-
pixel presentation (Goodfellow et al., 2016; Li et al., 2018; LeCun et al., 2015).
This raises the question of what, if any, the advantage of neuronal dynamics
and the diversity thereof is. Do neuronal dynamics enable the modeling of
more temporally complex patterns? Does neuronal heterogeneity improve
the learning capacity of neural networks?

We propose that neuronal dynamics, such as after-spike currents, aussi
as heterogeneity in the properties of these dynamics across a network, dans-
hance a network’s capacity to model temporally complex patterns. More-
over, we hypothesize that heterogeneity in dynamics, resulting from the
diversity of single-neuron parameters, will be optimal when parameters are
optimized in conjunction with synaptic weights during training. In order
to evaluate these hypotheses, we develop and test a neuronal model whose
parameters can be optimized through gradient descent.

A set of approaches has been previously used to develop neuronal mod-
els that encapsulate the above-mentioned biological complexities. These
range from models that include a dynamical description of at the level of
membrane channels (Hodgkin & Huxley, 1952; Morris & Lecar, 1981) à
more compact models that synthesize the complexities into more abstract
dynamical systems (Izhikevich, 2003) or hybrid systems (Mihala¸s & Niebur,
2009). While networks of such neurons have been constructed (Markram
et coll., 2015; Billeh et al., 2020), they are often difficult to optimize, either to
solve a task or to fit biological data.

Small increases in dynamical complexity can have significant benefits.
Adaptation dynamics can help neural networks perform better on predic-
tive learning tasks (Burnham et al., 2021) and achieve better fits of neuronal
and behavioral data in mice (Hu et al., 2021). Inroads have been made to
allow the optimization of spiking models using backpropagation via sur-
rogate gradients (Huh & Sejnowski, 2018; Neftci et al., 2019). Such meth-
ods have revealed the importance of neuronal integration and synaptic
timescales (Perez-Nieves et al., 2021) and adaptation (Salaj et al., 2021; Bellec
et coll., 2020) in network computation. Previous models (Perez-Nieves et al.,

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal Heterogeneity Learned by Gradient Descent

559

2021; Burnham et al., 2021) have also shown the importance of timescale
diversity in temporal tasks. Cependant, these models are still significantly
simpler than those found to fit single-neuron data well (Teeter et al., 2018).
To allow larger-scale dynamics to fit well, we want to be able to optimize
neural networks with the type of dynamics proven to fit such complexi-
liens. Here we focus on the addition of after-spike currents, which are cur-
rents modulated by a neuron’s spiking behavior leading to a wide variety
of observed dynamics, including bursting (Gerstner et al., 2014; Mihala¸s &
Niebur, 2009).

While spiking neurons are more biologically realistic, they are gener-
ally more difficult to optimize. Ainsi, we develop a model that is typi-
cally differentiable but becomes a spiking model in the limit of taking a
parameter to 0. We refer to this novel neuronal model as the generalized
leaky-integrate-and-fire-rate (GLIFR) model. The GLIFR model is built on
the spike-based generalized-leaky-integrate-and-fire (GLIF) models. GLIF
models introduce several levels of complexity to leaky-integrate-and-fire
models, which only model a neuron’s leaky integration of input currents.
We focus on the GLIF3 model (Teeter et al., 2018), which accounts for
after-spike currents through additive and multiplicative effects of spiking.
Our proposed GLIFR model translates the GLIF3 model into a rate-based
scheme. Unlike the GLIF model, the differentiability of the GLIFR model
enables the application of standard deep learning techniques to optimize
parameters underlying intrinsic neuronal dynamics. Ainsi, we explore two
aspects of the GLIFR model. D'abord, we explore the addition of complex neu-
ral dynamics. After-spike currents act like a feedback mechanism in a neu-
ron, being directly affected by a neuron’s firing pattern and simultaneously
being integrated into the voltage along with synaptic currents. Deuxième, nous
study the effects of heterogeneity in dynamics resulting from heterogeneity
in underlying neuronal parameters learned by gradient descent. For exam-
ple, different after-spike currents may lead to different neuronal timescales.
Beyond after-spike currents, differences in the membrane time constant and
firing thresholds across neurons may add to the rich repertoire of firing pat-
terns produced by a network.

To explore these two aspects introduced by the GLIFR neurons, we use
gradient descent to optimize networks of GLIFR neurons on several tem-
poral tasks and assess the performance and robustness of these networks
in comparison to that of vanilla RNNs as well as long short-term-memory
(LSTM) réseaux, which use a gating mechanism to promote memory over
timescales (Hochreiter & Schmidhuber, 1997). While the GLIFR networks
are outperformed by LSTM networks, our networks have mixed perfor-
mance when compared to vanilla RNNs on a pattern generation task and
a temporally complex sequential MNIST task. We find that it is possible
to optimize both intrinsic neuronal parameters and synaptic weights us-
ing gradient descent. Optimization of neuronal parameters generally leads
to diversity in parameters and dynamics across networks. De plus, quand

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

560

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

we compare among several variations of the GLIFR model, we find that
both the presence of after-spike currents and the heterogeneity in neuronal
properties improve performance, suggesting an important computational
role for neuronal complexity and heterogeneity in the brain. We provide
code for creating and optimizing GLIFR models in Python.

1.2 Related Work. In our work, we assess how, if at all, the presence
of neuronal dynamics, as well as the heterogeneity thereof, confers per-
formance improvements in RNNs. Prior work has developed RNNs that
express biologically realistic dynamics, giving rise to a class of networks
known as spiking neural networks (SNNs). One example of an SNN (Zenke
& Vogels, 2021) uses a leaky-integrate-and-fire dynamic across its neurons.
In these neurons, the membrane potential was modulated according to
equation 1.1 where S represents whether the neuron is spiking and V rep-
resents the neuron’s membrane potential:

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

V (t + dt) = (e

−dt/τmV (t) + (1 − e

−dt/τ

)je(t))(1 − S(t)),

S(t) = H(V (t) − Vth),

je(t + dt) = e

−dt/τsyn I(t) + WSpresynaptic(t) + WrecS(t).

(1.1)

At each timestep, the voltage exponentially decays toward zero while
being increased by the neurons’ synaptic currents that also decay exponen-
tially. Spiking drives the voltage to zero. In this work, only synaptic weights
were trained, and a surrogate gradient was employed to address the dif-
ficulty presented by the undifferentiable Heaviside function. Spécifiquement,
when computing gradients of the loss with respect to parameters, the gra-
dient of the Heaviside function was approximated by a smoother function
(see equation 1.2). Using these approximated surrogate gradients, this SNN
(Zenke & Vogels, 2021) achieved high performance on auditory tasks (SHD,
RawHD, and RawSC) and an MNIST task where inputs are converted to
spiking times:

F (X) =

1
(β|X| + 1)2

(1.2)

As an alternative to spiking models, a number of rate-based models have
also been developed, including those that incorporate forms of after-spike
currents. Muscinelli et al. (2019) and Beiran and Ostojic (2019) model after-
spike currents in a form similar to equation 1.3 where I j represents the after-
spike current and s represents the firing rate. This form enables a neuron’s
firing behavior to have an additive effect on the after-spike current but not
a multiplicative effect. In contrast, our model includes both an additive and
multiplicative term as in Table 1:

dI j(t)
dt

= −k jI j(t) + a js(t).

(1.3)

Neuronal Heterogeneity Learned by Gradient Descent

561

Tableau 1: Equations Describing the GLIFR Model.

S(t) =

1
−(V (t)−Vth )/p
V

1+e

= −kmV (t) + RmkmItot (t) − (V (t) − Vreset )Sr(t)
(cid:3)

(cid:2)

dV (t)
dt
dI j
+ r jI j (t)
dt
Isyn(t) = WinSpre(t) + Wlat S(t)

= −k jI j (t) +

a j

Sr(t)

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

En outre, in these works, parameter optimization by gradient descent
was not explored. Other work has explored the effect of spike frequency
adaptation on network performance using a different mode of spike fre-
quency adaptation, mediated by threshold adaptation rather than after-
spike currents (Salaj et al., 2021). Spike-frequency adaptation improved the
performance of LIF SNNs on temporally challenging tasks, such as a se-
quential MNIST task, where the network must classify images of handwrit-
ten digits based on a pixel-by-pixel scan, an audio classification task where
the network must identify silence or spoken words from the Google Speech
Commands data set, and an XOR task where the network must provide the
answer after a delay following the inputs. These networks were found to
approach RNN performance on the second audio classification task.

While the work described thus far used spiking models of biological dy-
namics, it did not explore the advantage that heterogeneity could confer.
Several approaches have been taken to this end. One approach is to ini-
tialize an SNN with heterogeneous dynamics but optimize only synaptic
weights. This method achieved comparable or higher performance than
ANNs that employed convolutional or recurrent transformations on an
object detection task (She et al., 2021). A second approach is to optimize
intrinsic neuronal parameters in addition to synaptic weights. Under the
hypothesis that neuronal heterogeneity is computationally advantageous,
the learned parameters will be diverse across the trained network. To this
end, one study extended the surrogate gradient technique for LIF SNNs
to also optimize membrane and synaptic time constants across networks
(Perez-Nieves et al., 2021). It was found that these networks learned hetero-
geneous parameters across the network when trained on temporal MNIST
tasks, a gesture classification task, and two auditory classification tasks. Sur
some tasks, particularly the temporally complex tasks that relied on precise
timing of spikes, learning parameters improved performance over learning
synaptic weights alone. Cependant, in this work, learning parameters relied
on surrogate gradients, and a simpler neuron model (LIF) was used.

Recent work has proposed a novel approach, event-based backpropaga-
tion, to compute exact gradients despite the discrete spiking (Wunderlich
& Pehle, 2021). While promising, this approach requires complex compu-
tational techniques. In contrast, our work establishes a method of training

562

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

neuronal parameters with standard gradient descent by using a rate-based
neuronal model; moreover, this model additionally expresses after-spike
currents as schematized in Figures 1A and 1B.

To summarize, previous work has suggested that heterogeneity in in-
tegration and synaptic timescales improves network performance. Ce
opens the door to the questions we address here: whether after-spike cur-
rents that produce complex dynamics within individual neurons can be
trained, whether these after-spike currents improve network performance,
and whether training naturally leads to their heterogeneity. It also invites
the question of whether neuronal models with these complex dynamics can
be designed that learn using standard gradient descent. In what follows, nous
show that this is possible, and illustrate how this results in heterogeneous
neuronal dynamics as well as mixed performance relative to vanilla RNNs.

2 Generalized Leaky-Integrate-and-Fire-Rate (GLIFR) Model

2.1 Model Definition. We develop a neuronal model that exhibits after-
spike currents and is conducive to training with gradient descent (see Fig-
ures 1B and 1C). Pour faire ça, we build on a previously described spike-based
GLIF model that incorporates after-spike currents (Teeter et al., 2018). Nous
transform this GLIF model into what we term a GLIFR model, which is rate-
based to facilitate optimizing neuronal parameters with traditional gradient
descent mechanisms. Spécifiquement, we modify the GLIF3 model from Teeter
et autres. (2018) to produce firing rates rather than discrete spikes. In order to do
ce, we define the normalized firing rate of a GLIFR neuron as a sigmoidal
transformation of the voltage (S(t) =
V ). This may be interpreted
as an instantaneous normalized firing rate (varying between 0 et 1), as a
spiking probability, or as a smoothed spike (voir la figure 2). A raw firing rate
can be derived from S(t) as follows: Sr(t) = S(t)
τ where τ (ms) represents
how often we check if the neuron has crossed the threshold. The parame-
ter σV (mV) controls the smoothness of the voltage-spike relationship, avec
low values (σV (cid:2) 1 mV) enabling production of nearly discrete spikes and
higher values enabling more continuous output. This rate-based approach
enables the use of exact gradients rather than surrogate gradients across
the spiking function. En plus, it is more akin to vanilla RNNs that use
smooth activation functions, thereby motivating the application of standard
deep learning techniques.

1
−(V (t)−Vth )/p

1+e

We model voltage similar to its definition in the spiking GLIF model, mais
instead of the discrete reset rule in the GLIF model, we let voltage continu-
ously tend toward the reset voltage Vreset (mV) at a rate proportional to the
= −kmV (t) + RmkmItot (t) −
firing rate Sr. Ainsi, voltage is modeled as dV (t)
dt
(V (t) − Vreset )Sr(t), where Itot (t) is the total current produced by the sum
of a constant baseline current I0, the after-spike currents, and the synaptic
current.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal Heterogeneity Learned by Gradient Descent

563

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

, a2

= 5000 pA, a2

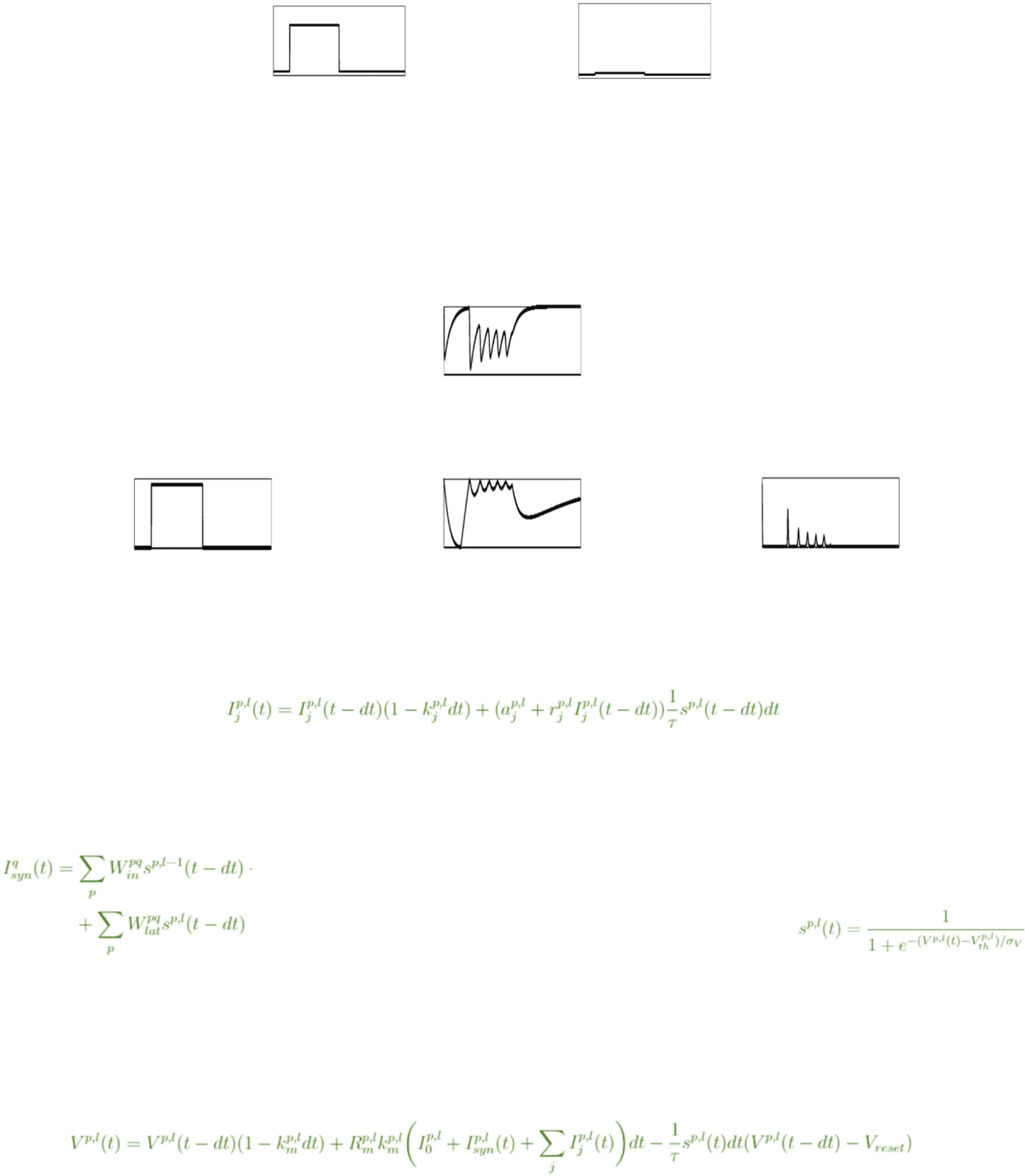
Chiffre 2: (UN) Sample responses to constant input. These plots show exam-
ple outputs of two neurons when provided with a constant input over a
40 ms time period. The two neurons share identical membrane-related pa-
rameters and decay factors for after-spike currents. The two neurons differ
only in the multiplicative and additive terms for after-spike currents (r j, a j).
The neuron whose output is traced in purple has the following after-spike
= −5000 pA. The neuron whose
= −1; a1
, r2
current related parameters: r1
= 1,
output is represented in green has the following parameters: r1
= −5000 pA. The difference in after-spike current parameters
a1
gives rise to different types of dynamics. The lefthand column contains outputs
= 1, whereas the righthand column contains out-
produced by neurons with σ
V
= 0.001 mV, demonstrating the ability of
puts produced by neurons with σ
V
the GLIFR neuron to produce spike-like behavior while maintaining its general
differentiability. Both I1(t) and I2(t) are plotted for each parameter combination.
Ainsi, we plot two purple traces corresponding to j = 1, 2 and two green traces
corresponding to j = 1, 2. (B) Sample responses to different amplitude inputs.
These plots show example outputs of a neuron when provided with different
magnitudes of constant input over a 40 ms time period. Larger inputs appear to
yield higher-frequency oscillations in the neuron’s output. The lefthand column
= 1 mV, whereas the righthand
contains outputs produced by neurons with σ
V
= 0.001 mV.
column contains outputs produced by neurons with σ
V

= −1, r2

564

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

After-spike currents are modeled as a set of separate ionic cur-
+ r jI j(t))Sr(t). The de-
rents indexed by j as follows:
cay factor k j (ms−1) captures the continuous decay of the current. Le
“spike-dependent” component of the current is determined by the com-
bination of the multiplicative parameter r j and the additive parameter a j
(pA), scaled by the raw firing rate 1

= −k jI j(t) + (a j

dI j
dt

τ s.

Synaptic currents, those resulting from input from the previous layer as
well as lateral connections, are modeled according to Isyn(t) = WinSpre(t) +
WlatS(t), where Spre represents either the normalized firing rate of the presy-
naptic neuron layer or the input to the network. The weights Win describe
how the input to the neuron layer should be weighted, and the lateral
weights Win describe the connections between neurons in the same layer.
We do not include a temporal dependence for simplicity as we focus on
cellular properties. These equations are summarized in Table 1.

Applying gradient descent, we simultaneously optimize both synaptic
weights and parameters underlying the GLIFR model. The parameters we
train are listed in Table 5. The GLIFR model is also publicly released as a
PyTorch model (further details on its implementation are in section 6).

2.2 Effect of Parameters on Model Behavior. The effects of the param-
eters on model behavior have been previously described in the discrete
spiking scheme (Mihala¸s & Niebur, 2009). In this work, we translate to a
continuous spiking scheme. Ainsi, we visualize the effect of σV on model
behavior (see Figures 2A and 2B). Comme indiqué, lower values of σV approxi-
mate discrete spikes, while higher values of σV result in smoother changes
in the firing rate.

Varying the values of a j and r j can give rise to a variety of com-
plex patterns including bursting. As shown in Figure 2A, hyperpolarizing
(negative) values enable the neuronal firing rate to oscillate slightly, et
a combination of hyperpolarizing and depolarizing (positive) after-spike
currents enables regular oscillations in firing rate. Because we model firing
rates rather than individual spikes, we take this as a form of bursting. Nous
furthermore find that for a given set of neuronal parameters, larger inputs
yield higher-frequency oscillations in firing rate (see Figure 2B). We note
that in these simulations and later in trained networks, the GLIFR model is
theoretically capable of producing both biologically plausible patterns and
less biologically realistic activity.

2.3 Optimization of Neuronal Parameters for Learning Realizable Sig-
nals. We first confirm the ability of neuronal parameters to be optimized
through gradient descent in a theoretically simple task: learning a target
that is known to be realizable by a GLIFR.

As shown in Figure 3A, we initialize a single GLIFR neuron and record
its response to a constant input stimulus over a fixed period of time (10 ms

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal Heterogeneity Learned by Gradient Descent

565

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

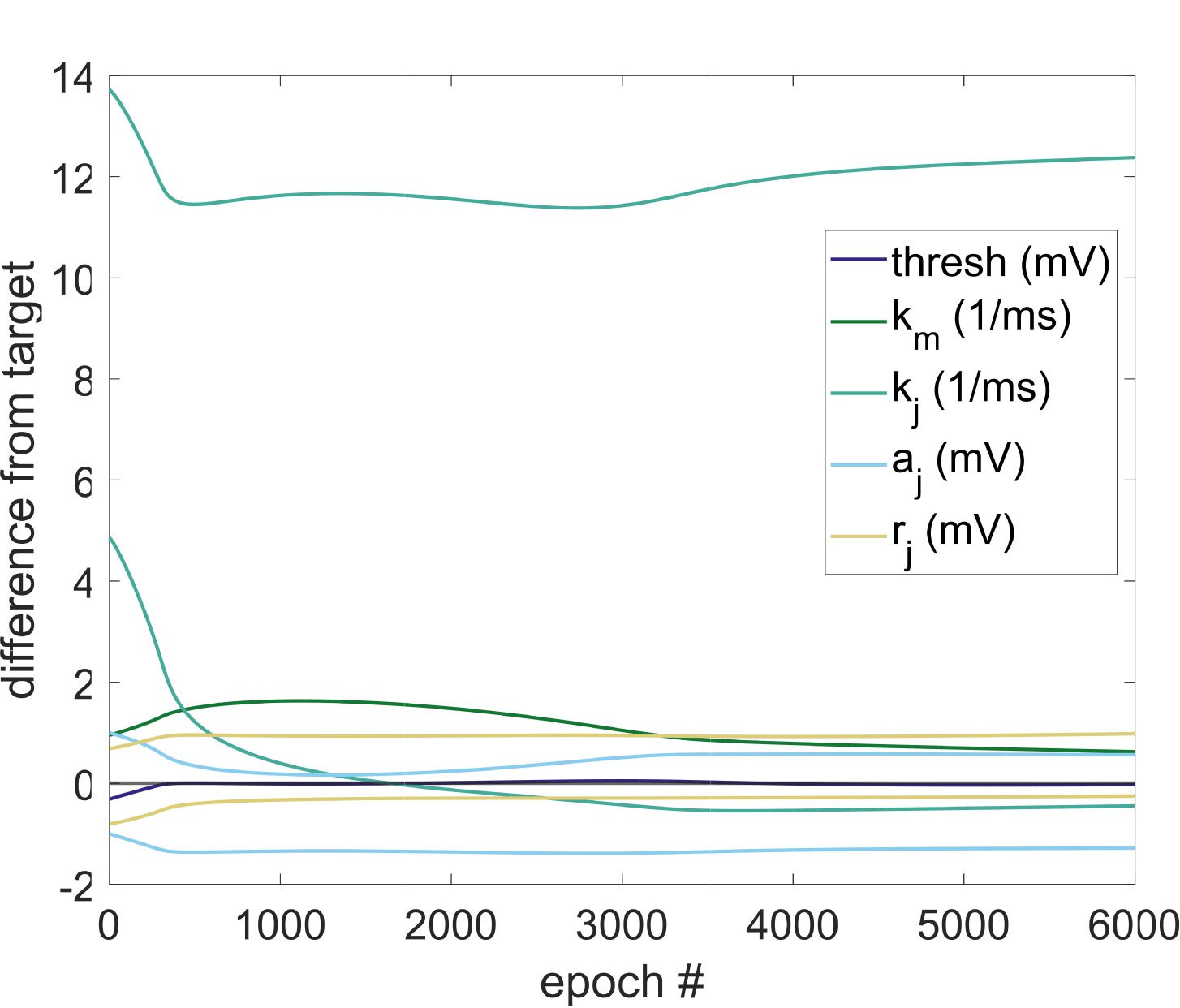
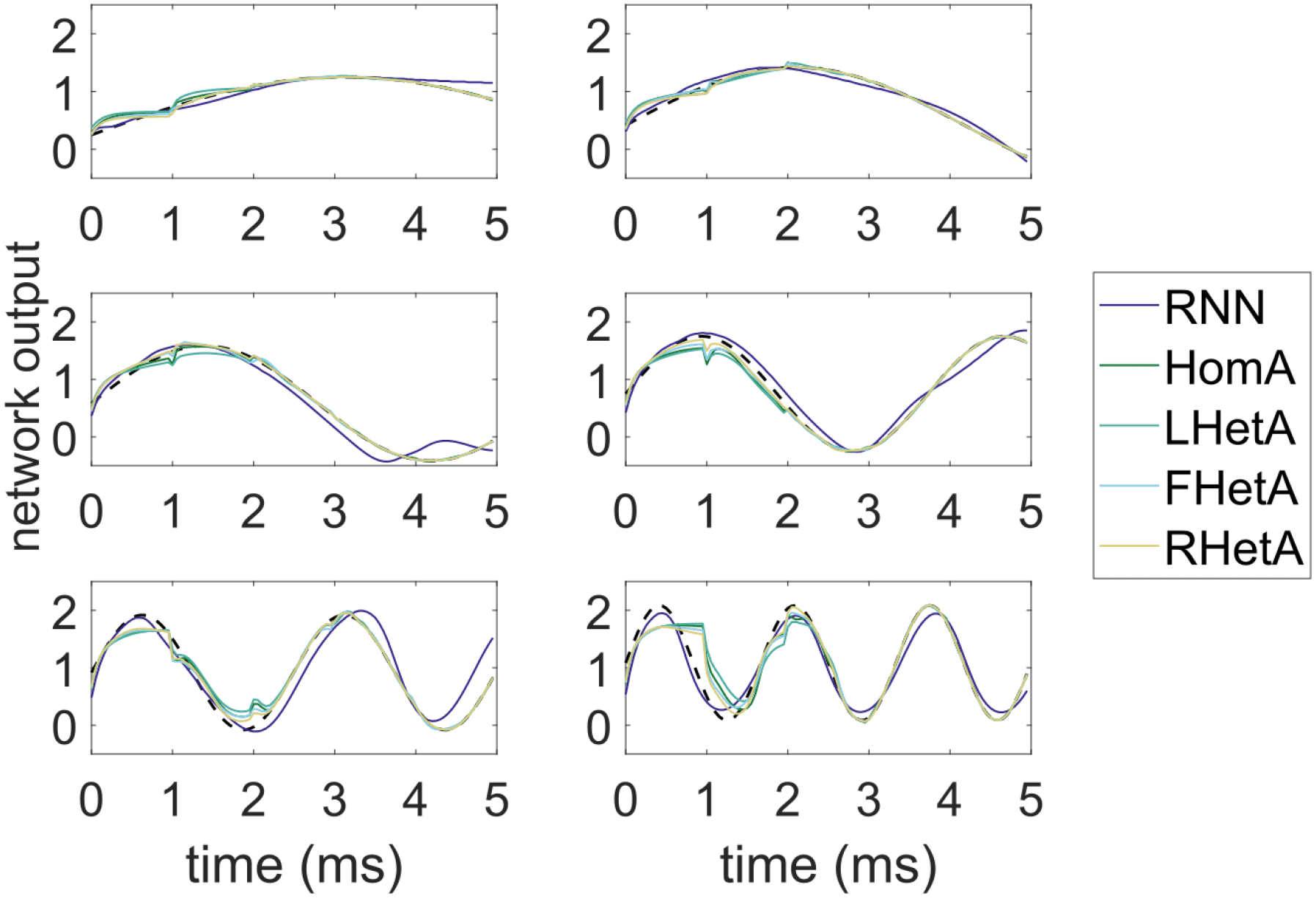
Chiffre 3: (UN) Testing optimization in single neurons for realizable signals. Dans
the realizable pattern generation task depicted here, a neuron (the target neu-
ron) is used to create the target firing pattern. A second neuron (the learn-
ing neuron) is initialized with different parameters and learns parameters to
produce the target. (B) Training loss. This plot shows an example trace of mean-
squared error over training of a single neuron. (C) Output of the learning neu-
ron. This plot shows the output of the learning neuron prior to training and
after training, along with the target, demonstrating the ability of a single GLIFR
neuron to learn simple patterns. (D) Learned parameters. This plot depicts the
difference between the values of the trainable parameters in the learning neuron
and the corresponding values in the target neuron over training epochs. Note
that a value of zero represents equivalence to the target network in a particular
parameter.

566

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

with timestep duration of 0.05 ms.) This is our target neuron. We then create
a second neuron (learning neuron) that is equivalent to the target neuron
only in the incoming weights used. We train the learning neuron to produce
the target neuron’s output, using Adam optimization and a learning rate of
0.001, allowing it to learn the neural parameters (Kingma & Ba, 2014).

We tested the ability of the learning neuron to reproduce the pattern of
the target neuron. Figures 3B and 3C show that the learning neuron suc-
cessfully learned to approximate the dynamics of the target neuron. Comment-
jamais, the final parameters learned by the learning neuron differed from the
parameters of the target neuron (see Figure 3D), illustrating that different
internal mechanisms can lead to similar dynamics (Prinz et al., 2004). Ce
supports the idea that for the proposed model, when optimizing indepen-
dently the time constants and the additive and multiplicative parameters
for after-spike currents, varying distributions of trained parameters across
a network may nevertheless lead to similar network function.

3 Results

3.1 Strategy for Analyzing Task Learning and Performance. After ver-
ifying the theoretical ability to optimize neuronal parameters in single
GLIFR systems, we turn to more complex tasks. As in previous work (Perez-
Nieves et al., 2021), we aimed to assess the role of several factors in network
computation while evaluating our networks: (1) the presence of biologically
realistic dynamics (c'est à dire., membrane dynamics, voltage reset), (2) the presence
of after-spike currents, (3) random heterogeneity of neuronal parameters
across the network, et (4) optimized heterogeneity of neuronal parame-
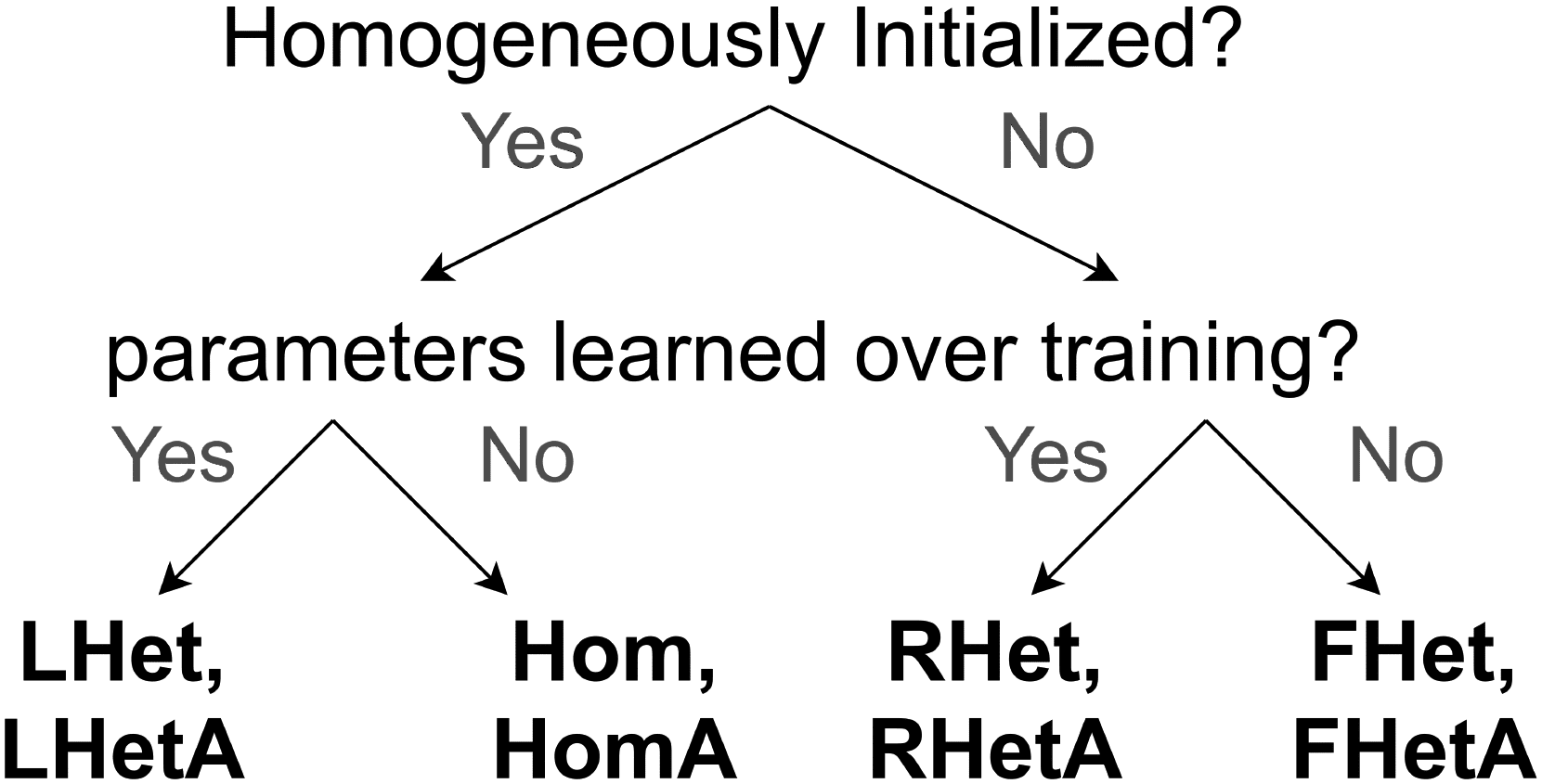
ters across the network. Ainsi, we use multiple network types. As a baseline,
we use a vanilla recurrent neural network (RNN). We also use the following
variations of the GLIFR network: a GLIFR network with fixed heterogeneity
with after-spike currents (FHetA) or without (FHet), a GLIFR network with
refined heterogeneity with after-spike currents (RHetA) or without (RHet),
and a GLIFR network with learned heterogeneity with after-spike currents
(LHetA) or without (LHet). We define fixed heterogeneity as heterogene-
ity that a network is initialized with and does not alter over training, concernant-
fined heterogeneity as heterogeneity that a network is initialized with but
is altered (“fine-tuned”) over training, and learned heterogeneity as hetero-
geneity that a network is not initialized with but is learned over training. À
achieve heterogeneous initialization, we permute the parameters learned in
a corresponding LHet/LHetA network and initialize a new network with
the resulting parameters. These distinctions are illustrated in Figure 4. Fi-
enfin, we use an LSTM network as another baseline whose mechanisms im-
prove the ability to model complex temporal dynamics without emulating
biology. For each experiment, we set the number of neurons for each net-
work type to yield comparable numbers of learnable parameters.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal Heterogeneity Learned by Gradient Descent

567

Chiffre 4: GLIFR schemes. A flowchart describes the variations of the GLIFR
networks we explored. These are based on whether the network neuronal pa-
rameters were homogeneously initialized or heterogeneously initialized as well
as whether these intrinsic neuronal parameters were learned over training. Ce
classification enables us to isolate effects of the expression of after-spike currents
(models with names ending in A), a complex type of dynamic, and the learning
of heterogeneous parameters.

Each network, including RNNs, GLIFR networks, and LSTM networks,
consists of a single recurrent hidden layer of the appropriate neuron type,
whose outputs at each time point are passed through a fully connected lin-
ear transformation to yield the final output. The recurrence is incorporated
into the GLIFR networks through the term WlatS(t) in the synaptic currents,
equation 1.1, and the W pq

lat sp,je (t − (cid:5)t) term in equation 6.5.
Code for the GLIFR model is publicly available at https://github.com/
AllenInstitute/GLIFS_ASC. The model is implemented in PyTorch, and we
rely on the underlying autodifferentiation engine to backpropagate through
the model.

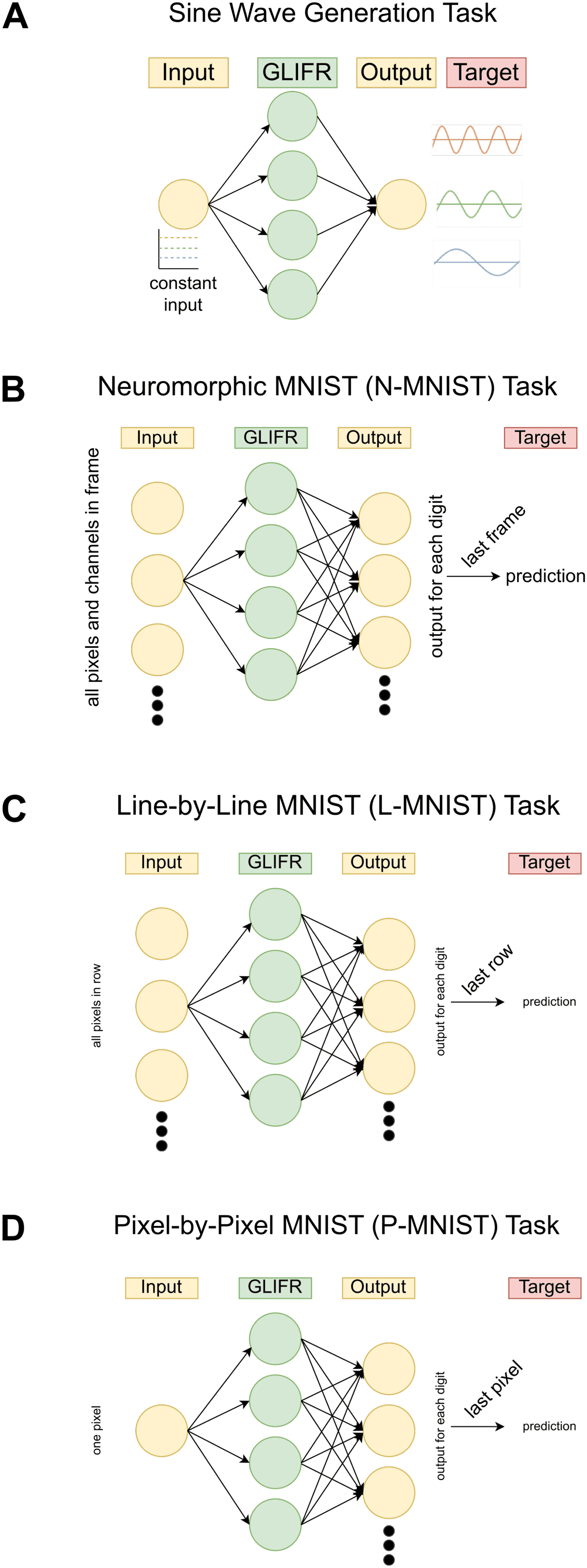
3.2 Performance on Tasks. In this work, we study five tasks: a sine gen-
eration task, a neuromorphic MNIST (N-MNIST) task, a line-by-line MNIST
(L-MNIST) task, and a pixel-by-pixel MNIST (P-MNIST) task. We choose
these tasks due to their varying complexity and timescales. The sine gen-
eration task tests the ability of a network to learn sine waves whose fre-
quencies are determined by the amplitude of the input signal. This requires
memory over a relatively small time period. The N-MNIST task is based
on the scanning of an MNIST image using a digital vision sensor, lequel
senses changes in pixel intensity along two dimensions. The resulting input
to the model is along 15 timesteps, where for each timestep, the network
is input a 34 × 34 × 2 binary vector representing two channels capturing
the change in pixel intensity over the 34 × 34 image. In the L-MNIST and
P-MNIST tasks, networks are expected to classify the digit represented by
an MNIST digit after receiving the input image either line-by-line or pixel-
by-pixel. Ainsi, the L-MNIST task engages memory over 28 timesteps (un
timestep is used to process each line of the image), whereas the P-MNIST
task engages memory over 576 timesteps. The setup of each of these tasks
is depicted in Figure 5, and details of each of these tasks, along with the

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

568

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 5: Setup of tasks explored. These schematics illustrate the setup of the
sine wave generation task (UN), the neuromorphic MNIST task (B), the line-by-
line MNIST task (C), and the pixel-by-pixel task (D). In each schematic, the input
to the network as well as the readout (produced by a linear transformation of
the output of the neuron layer) are denoted in yellow, and the hidden layer
of neurons (GLIFR, RNN, or LSTM neurons) is denoted in green. The lateral
connections are not visualized for clarity, but in each task, lateral connections
between neurons exist. Enfin, the target signal is shown, along with how the
readout is transformed.

Neuronal Heterogeneity Learned by Gradient Descent

569

hyperparameters used, are in section 6. Due to the computation time re-
quired to train networks on the P-MNIST task, we limit our training to
50 epochs and analyze the performance of only RNNs and the LHetA and
RHetA GLIFR networks.

We run 10 training simulations for each task and network type, and we
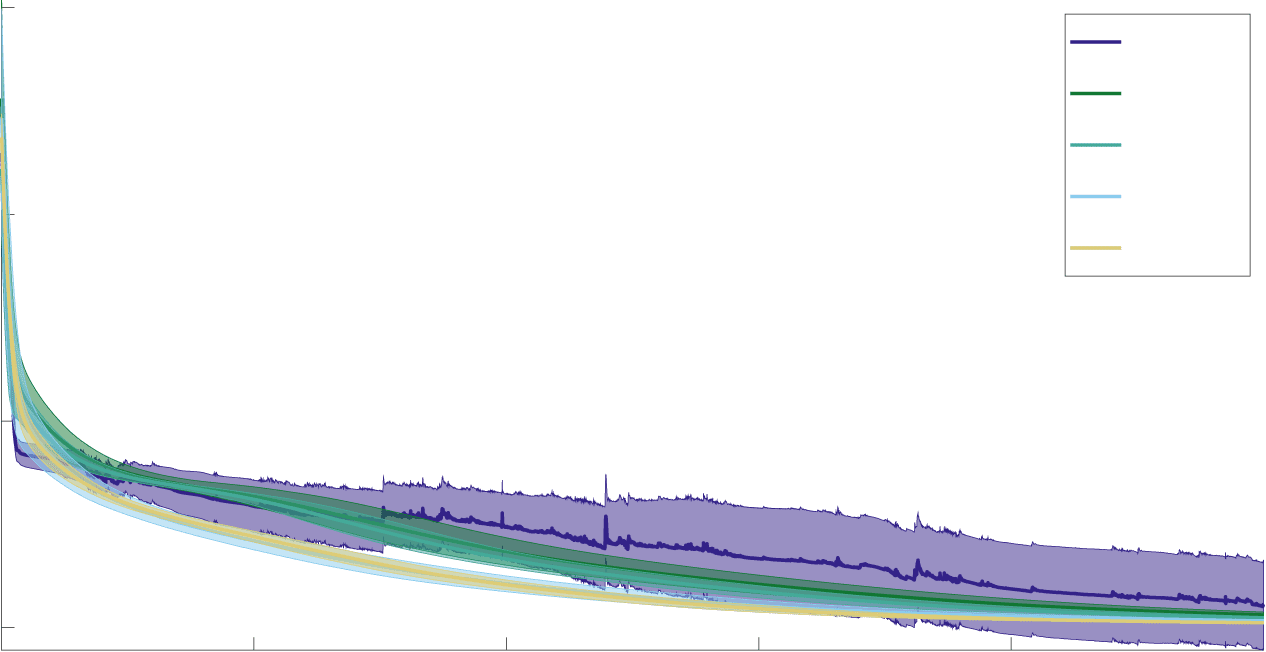
use two-sample t-tests to analyze the results (α = 0.05). As shown in Fig-
ure 6 and Table 2 (see also Figures 10 et 11), all networks train to close to
convergence within the given training epochs except on the P-MNIST task
due to the limited training time. The GLIFR networks, regardless of their
initialization and whether they learn parameters over training, outperform
RNNs on the N-MNIST and P-MNIST tasks. Within the variations of the
GLIFR networks, we find that after-spike currents appear to improve per-
formance only in the L-MNIST task, particularly in the LHet, RHet, et
FHet schemes. On the other hand, learned heterogeneity appears to have
a much more consistent benefit to performance. On all tasks except for the
N-MNIST task, RHetA networks outperform LHetA networks, indicating
a benefit of heterogeneous initialization, and LHetA and RHetA networks
outperform HomA networks, indicating a benefit of learned heterogene-
ville. Oddly, we find the reverse pattern in the N-MNIST task, where among
the eight variations of the GLIFR networks studied, Hom networks per-
form best. We hypothesize that heterogeneous and complex dynamics are
advantageous. Cependant, due to the complicated error landscape, gradient
descent is capable of optimizing the heterogeneity of neuronal parameters
only in some settings. Exploring in detail the optimization setting that ben-
efits such complex neuron models is beyond the scope of this study.

3.3 Robustness to Silencing. GLIFR dynamics enable more complex
temporal interactions within and among neurons. What is the resulting im-
pact on the robustness of GLIFR networks’ random “deletions” (or silenc-
ing) of individual neurons? We test this by evaluating the robustness of
networks to random silencing of neurons. Spécifiquement, for various propor-
tions p, we randomly select a subset of the neurons in the network with
proportion p to silence in a trained network throughout testing. For each
subset, we clamp the neurons’ firing rates to zero, preventing their contribu-
tion in both forward and lateral connections, and compute the performance
of the network on the task. We run this experiment on the sine wave genera-
tion, N-MNIST, and L-MNIST tasks (voir la figure 7). In all tasks, silencing im-
paired performance, but we analyze the extent to which each network was
impaired. Lower impairment implies greater robustness to silencing. In the
sine wave generation task, several variations of the GLIFR network appear
more robust than the RNN when small percentages of neurons are silenced.
The GLIFR networks do not appear to maintain this advantage for the
N-MNIST task. We see the greatest differences in the L-MNIST task, où
we find that when silencing proportions of neurons with p ≥ 0.2, all forms
of GLIFR networks show an advantage over the RNN. En général, RHetA

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

570

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 6: Training loss curves. The training mean-squared error (sine wave gen-
eration) or cross-entropy loss (MNIST tasks) of the network averaged over 10
random initializations is plotted over training epochs. The shading indicates a
moving average of the standard deviation. En moyenne, all network types con-
verge on a solution within the training time except for the P-MNIST task.

Neuronal Heterogeneity Learned by Gradient Descent

571

Tableau 2: Performance on Tasks.

Sine Generation Task N-MNIST

L-MNIST

P-MNIST

RNN
LSTM
Hom
HomA
LHet
LHetA
FHet
FHetA
RHet
RHetA

0.0561
0.0094
0.0348
0.0309
0.0233
0.0227
0.0164
0.0166
0.0115
0.0121

84.1740%
85.9230%
88.0000%
87.9560%
87.7470%
87.8330%
87.2160%
87.2240%
87.4020%
87.3070%

N/A
N/A
N/A
N/A

97.7920% 25.6400%
98.6620%
93.6540%
93.6420%
93.7750%
94.1700% 61.6780%
93.7220%
94.1160%
93.7520%
94.8140% 67.2090%

N/A
N/A
N/A

Note: This table lists the testing performance (mean-squared error for
the sine wave generation task and accuracy for the remaining tasks) de
each task explored.

networks perform the best. This observation suggests that neuronal com-
plexity and heterogeneity improve network robustness despite the reduced
baseline performance induced by silencing when compared with vanilla
RNNs.

Arguably, the poorer robustness of the RNNs may be anticipated due
to the lack of dropout during training (Hinton et al., 2012). Ainsi, nous
performed additional experiments on the L-MNIST task. For each prob-
ability p, we trained each network with dropout with probability p and
tested its performance when random sets of neurons (proportion p) étaient
silenced through the entirety of each testing simulation. En effet, we see
that the performance of these networks trained with dropout is better than
that observed without dropout, but the trends discussed above hold (voir
Chiffre 12).

3.4 Optimization in Discrete Spiking Regime. In all the experiments
so far, we have kept σV a constant during training. As previously noted, le
parameter σV can be modified such that as σV (cid:2) 1, the model approaches
discrete spiking dynamics.

We take a simulated annealing approach to assess whether this setup can
be utilized to learn a nearly discrete model that would more closely repro-
duce biologically realistic, rapid spiking. Spécifiquement, we train an LHetA
GLIFR network on the L-MNIST task while gradually decreasing the σV
−3). We find that the LHetA networks
parameter over training (depuis 1 à 10
still learn the task well, achieving an average accuracy of 74.49% (n = 10;
standard deviation of 1.90%). This is lower than the previously achieved
accuracy of 94.17% using relatively high values of σV but better than when
using a constant but low value of σV throughout training. We also note that
this approach does not converge once σV is reduced past a certain amount

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

572

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 7: Model performance when neurons were silenced through testing. UN
single random network initialization was trained on the L-MNIST task. During
testing, a random subset of neurons in the network was silenced, and the net-
work was tested. This was repeated 10 times with different random subsets of
the same percentage. The average accuracy of each network with varying per-
centages of their neurons silenced is shown for each task. Bars represent stan-
dard deviation across trials.

Neuronal Heterogeneity Learned by Gradient Descent

573

Chiffre 8: Training loss curves with lower σ
V . The training cross-entropy loss of
the LHetA and RHetA networks on the L-MNIST task averaged over 10 random
initializations is plotted over training epochs where either σ
V is maintained at
a constant value of 10−3 (UN) or the simulated annealing approach is taken for
learning with small values of σ
V (B). The shading indicates a moving average
of the standard deviation.

(voir la figure 8). Ainsi, further work is needed to identify the optimal anneal-
ing procedure for learning tasks with low σV , but this annealing experiment
demonstrates the ability of GLIFR networks to produce spiking behavior
and still perform well despite being a fundamentally rate-based model.

3.5 Heterogeneity Learned over Training. Based on the performance
values above, neuronal heterogeneity seemed to contribute to the GLIFR
networks’ performance. To further elucidate whether and how the learned
heterogeneity in parameters may have reshaped neuronal dynamics, nous
determined the extent to which the GLIFR networks had learned truly di-
verse parameters in each task context. For the homogeneously initialized
réseaux, both a js and r js had been initialized with limited diversity to pro-
mote neuronal stability, and the remaining neuronal parameters had been
set homogeneously. We hypothesized that the diversity in all parameters
would have developed over training. The heterogeneously initialized net-
works were set with distributions of parameters learned by the LHet and
LHetA networks, but we expected the distribution to shift over the course
of training as the model fine-tuned its shuffled parameters and weights to
the particular task.

We found that training did result in heterogeneous parameter values for
all tasks (data shown for L-MNIST; see Figures 13A and 13B) such that the
variance of the trained a j and r j parameters is much larger than at initial-
ization (standard deviation of initial distribution was 0.01). De la même manière, nous
observe shifts in the distribution of some parameters when heterogeneity
is “refined.” We wanted to determine how well this diversity in neuronal
parameters mapped to diversity in neuronal dynamics. Pour faire ça, we con-
structed f-I curves representing the average firing rate of each neuron over

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

574

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

a time period (5 ms) when the neuron was injected with varying levels of
current (see Figure 13B). We found a diversity in shapes of these curves, il-
lustrating the diversity in the neuronal dynamics produced by neurons in
the trained networks.

Enfin, we used Ward’s hierarchical clustering to capture in other ways
the variation in neuronal dynamics. Spécifiquement, we performed hierarchi-
cal clustering on the neuronal parameters of networks trained on the each
task. We used the Calinski-Harabasz (CH) index as a measure of clustering.
For the pattern generation task, we were unable to find a number of clus-
ters that produced the optimal CH score. Cependant, we found that the CH
score was maximized using five clusters in the LHetA network trained on
the N-MNIST task and using four clusters in the LHetA network trained
on the L-MNIST task (see Figure 14A). After clustering these neurons, nous
examined their parameters. Arguably, the classes of neurons for both tasks
appear to lie on a continuum rather than discretely clustering, but they ap-
peared to be separated primarily based on after-spike current parameters
a j and k j (see Figure 9B). In the networks trained on the L-MNIST task, un
class (UN) expresses slow depolarizing after-spike currents, a second class
(B) expresses fast after-spike currents with hyperpolarizing values of a j and
depolarizing values of r j, a third class (C) expresses smaller and faster after-
spike currents, and a final class (D) expresses after-spike currents with small
hyperpolarizing values of a j and depolarizing values of r j. As shown in Fig-
ure 15D, this results in saturating behavior for class A, oscillating or burst-
ing behavior for class B, and relatively stable behavior for the other two
classes. We noted that each pair of parameters corresponding to after-spike
≈ a2). We suggest
currents tended to be similar (c'est à dire., for a given neuron, a1
that this is a result of the gradient descent technique. Potentially, the gra-
dients over both after-spike currents were similar, resulting in both sets of
parameters progressing in the same direction. We found similar clustering
for the N-MNIST task but not the sine wave generation task, for which we
were unable to find an optimal number of clusters.

We also found that the classes based on parameters separated the
f-I curves (see Figure 9B). Par exemple, the neurons with hyperpolariz-
ing after-spike currents tended to exhibit low maximal firing rates. Et
the neurons with depolarizing after-spike currents tended to exhibit firing
rates that rapidly saturated to relatively high values. While we cannot ex-
tend these results to identify each category as discrete cell types, this further
suggests that the learned diversity in parameters enabled a diversity in dy-
namics as well.

4 Discussion

This work explored the role of neuronal complexity and heterogeneity in
network learning and computation using a novel paradigm. Spécifiquement,
we developed the GLIFR model, a differentiable rate-based neuronal model

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal Heterogeneity Learned by Gradient Descent

575

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 9: Heterogeneity in learned networks for the sine wave generation task
(UN), the N-MNIST task (B), and the L-MNIST task (C). For each task, various
pairs of parameters in a representative trained LHetA network are plotted. Le
points are colored according to clusters produced by Ward’s hierarchical clus-
tering on learned parameters using optimal cluster number (based on the CH
index). These plots are displayed in the left column of the figure. The black point
in each scatterplot represents the parameter distribution the network was ini-
tialized to. On the right column of the figure, f-I curves are plotted for each
neuron in a representative trained LHetA network. The black traces represent
those produced by the initial network. Ensemble, these data demonstrate the het-
erogeneity in parameters and dynamics that result from the training.

that expresses after-spike currents in addition to the simple types of dynam-
ics. While past work (Perez-Nieves et al., 2021; Salaj et al., 2021) has studied
neuronal complexity and heterogeneity, here we demonstrated the ability

576

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

to learn both synaptic weights and individual neuronal parameters under-
lying intrinsic dynamics with traditional gradient descent for models with
more complex internal neuron dynamics generated by after-spike currents.
While it is generally rate-based, the GLIFR model retains the ability to pro-
duce spiking outputs and thus is a powerful model for studying neuronal
dynamics.

We demonstrated the ability for networks of GLIFR neurons to learn
tasks ranging in complexity from a sine wave generation task to the pixel-
by-pixel MNIST task. In each task, heterogeneous parameters and dynam-
ics were learned. We tested the effects of the ability to learn parameter
heterogeneity and the ability to express after-spike currents on model
performance. Learning heterogeneous parameter distributions generally
improved performance, and modeling after-spike currents improved per-
formance on the L-MNIST task. Regardless of whether heterogeneous
parameters or after-spike currents were learned, the GLIFR models outper-
formed vanilla RNNs in the N-MNIST and P-MNIST tasks. We hypothesize
that the differences in results among tasks reflect differences in complexity
and engagement of memory between tasks. Par exemple, we only observe
improvements in GLIFR networks over RNN networks in N-MNIST and
P-MNIST tasks, but not in the sine wave generation task and the L-MNIST
task. Since the N-MNIST and P-MNIST tasks theoretically engage more
memory than the other two tasks, we suggest that the RNN may simply
do well enough for the other two tasks that improvement over it would be
inattendu. It is difficult to explain why neuronal heterogeneity appeared
to be disadvantageous in the N-MNIST task, but perhaps neuronal hetero-
geneity complicated the error landscape and hindered the network’s learn-
ing ability in this setting. We also found that GLIFR networks trained on the
L-MNIST task were more robust to neuronal loss. Spécifiquement, when we si-
lenced fixed fractions of neurons, the GLIFR networks generally performed
better than vanilla recurrent neural networks. Enfin, we found that learn-
ing parameters across a network in response to a temporally challenging
task enabled the network to develop neurons with differing intrinsic pa-
rameters and dynamics.

These findings support the hypothesis that neuronal heterogeneity and
complexity have a computational role in learning complex tasks. The im-
plications of this are two-fold. On one hand, neuronal heterogeneity may
allow more powerful computing in artificial neural networks. Vanilla recur-
rent networks, Par exemple, rely on a single type of dynamic—typically the
ReLU, sigmoid, or tanh activation function. Cependant, the use of activation
functions that can be “learned” over time, such that the trained network
exhibits diverse dynamics across its neurons, may confer a computational
advantage (Geadah et al., 2020). Here we demonstrated several computa-
tional advantages of more biologically realistic neurons for some specific
temporally challenging tasks while using traditional gradient descent train-
ing techniques. Other learning techniques may be required for other tasks,

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal Heterogeneity Learned by Gradient Descent

577

where the complex error landscape hinders the ability of gradient descent
to optimize both the neuronal parameters and the synaptic weights.

On the other hand, our results provide further insight into the purpose
of complexity and diversity of neural dynamics seen in the brain. Notre
brains are responsible for integrating various sensory stimuli, each vary-
ing in their temporal structures. Intuitively, heterogeneity in the types of
dynamics used by neurons across the brain may enable robust encoding of
a broad range of stimuli. The ability of diverse networks to encode infor-
mation more efficiently is supported by several studies (Hunsberger et al.,
2014; Shamir & Sompolinsky, 2006; Tripathy et al., 2013). Certain types of
complex dynamics may also affect synaptic strengths and improve the net-
work’s robustness to damage.

We believe that with the GLIFR model in the research domain, we have
opened the door to more intriguing studies that will identify further roles
for complex neural dynamics in learning tasks. In future work, testing the
GLIFR models on additional tasks may provide additional insight into the
computational advantages of neuronal heterogeneity and complexity. Ad-
ditionally, it would be interesting to pursue a theoretical explanation of
the computational role of heterogeneity and complexity. Past experimen-
tal work (Tripathy et al., 2013) found that neuronal heterogeneity increased
the amount of information carried by each neuron and reduced redundancy
in the network. Exploring this in computational models would be valuable,
as it may suggest additional ways in which the computational advantages
of biological dynamics can be harnessed to improve artificial neural net-
works and yield insights into the mechanisms of computation in biological
réseaux.

5 Code Availability

Modeling, entraînement, and analysis code is available at https://github.com/
AllenInstitute/GLIFS_ASC.

6 Methods

6.1 GLIFR Model.

6.1.1 Development of the Single-Neuron Model. As previously described,
the GLIFR model encapsulates the concepts behind the GLIF3 model (Teeter
et coll., 2018), while producing continuous outputs. We describe how state
variables are computed at each timestep in the GLIFR model, comparing
the computation to that in the GLIF model. We use a subscript s for the
GLIF state variables and no subscript for the equivalent GLIFR variables.
We use superscript p to represent the index of the neuron in consideration
and l for the associated layer, where postsynaptic layers are indexed with

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

578

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

larger numbers than are presynaptic layers. Par exemple, Sp,je (t) defines the
normalized firing rate of the pth neuron in the lth layer.

The discrete spiking equation can be expressed as in equation 6.1. H
refers to the Heaviside function where H(X) = 1 when x > 0 and H(X) = 0
when x ≤ 0. Ainsi, spiking is a binary event, and neurons produce a spike
when the voltage exceeds a certain threshold. In the GLIFR model, we de-
fine Sp,je (t), the normalized firing rate that is unitless and varies continu-
ously between 0 et 1 (see equation 6.2). A raw firing rate Sp,je
τ Sp,je (t)
may be derived where τ (ms) represents how often we check if the neurons
has crossed the threshold, and we set τ to dt throughout the study. While S
represents a normalized firing rate, for simplicity of terminology, we refer
to it as the firing rate. The parameter σV (mV) controls the smoothness of
the voltage-spiking relationship, and we used σV = 1 mV for all simulations
unless otherwise noted. Ainsi, for the GLIF and GLIFR models, respectivement,
spiking is defined as

r (t) = 1

s (t) = H(V p,je (t) − V p,je
Sp,je
ème ),

Sp,je (t) =

1 + e−(V p,je (t)−V p,je

ème )/σV

(6.1)

(6.2)

After-spike currents are modeled as a set of separate ionic currents
(corresponding to j = 1, 2, . . .) as in equation 6.4. We use two after-spike
currents with arbitrary ionic current equivalents, but this model can theoret-
ically be extended to more currents. As in the GLIF model (see equation 6.3),
decay factor kp,je
−1) is used to capture the continuous decay of the cur-
rent, and the “spike-dependent current” is determined by multiplicative pa-
rameter rp,je
(pA). In the GLIFR model, though,
this “spike-dependent current” is scaled by the raw firing rate 1

j and additive parameter ap,je

(ms

τ sp,je:

dI p,je
s, j (t)
dt
dI p,je
j
dt

(t)

= −kp,je

j I p,je

= −kp,je

j I p,je

(t) + (ap,je

+ rp,je

j I p

j (t))Sp,je

s (t),

+ rp,je

j I p,je

(t))Sp

r (t).

(6.3)

(6.4)

Synaptic currents, currents resulting from input from the previous layer
as well as lateral connections, are modeled according to equation 6.6. Le
first term in this equation represents the integration of firing inputs from the
presynaptic layer, and the second term describes the integration of firing in-
puts from the same layer through lateral connections. Wpq (pA) defines how
much the presynaptic spiking outputs (of neuron p) affect the postsynap-
tic current (of neuron q). While we model this synaptic transmission as be-
ing nearly instantaneous (the delay being just one timestep), we model the

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal Heterogeneity Learned by Gradient Descent

579

Tableau 3: States in GLIFR Neurons and Their Units.

s(t)
V (t)
I j (t)
Isyn(t)

normalized firing rate
voltage
after-spike current
synaptic current

1
mV
pA
pA

lateral transmission as having a synaptic delay denoted (cid:5)t. Autrement dit,
syn(t) depends on Sp,l−1(t) and Sp,je (t − (cid:5)t):
Iq
(cid:4)

(cid:4)

Iq
s,syn(t) =

W pq

in Sp,l−1

(t − dt) +

W pq

lat Sp,je

s (t − (cid:5)t),

Iq
syn(t) =

p
(cid:4)

W pq

in Sp,l−1(t − dt) +

p
(cid:4)

W pq

lat Sp,je (t − (cid:5)t).

(6.5)

(6.6)

Enfin, voltage is modeled in much the same way as in a traditional GLIF
model (see equation 6.7), but in order to facilitate gradient descent, we ig-
nore the more complex reset rule that is used in the GLIF model (Teeter
et coll., 2018). Plutôt, we set fr = 1 in equation 6.8:

(t)

dV p,je
s
dt

dV p,je (t)
dt

= −kp,je

m V p,je (t − dt) + Rmkp,je

(cid:5)

+ I p,je

syn(t) +

− fr(V p,je (t − dt) − Vreset )Sp,je
s (t),
(cid:5)

= −kp,je

m V p,je (t − dt) + Rmkp,je

+ I p,je

syn(t) +

− (V p,je (t − dt) − Vreset )Sp,je

r (t − dt).

(cid:6)

I p,je

(t)

(cid:6)

I p,je

(t)

(cid:4)

(6.7)

(6.8)

Ici, V p,je (t) decays according to km (ms

−1) and integrates current based
on resistance Rm (G(cid:7)). Voltage also tends toward the reset voltage Vreset (mV)
at a rate proportional to the firing rate sp,je. This is a continuous equivalent
of the discrete voltage reset.

A summary of these equations and the states and parameters describing

the GLIFR equations is in Tables 1, 3, et 4.

6.1.2 Effect of σV on Model Behavior. As described earlier, the parameter σV
controls the smoothness of the relationship between voltage and firing rate.
As σV approaches 0, the GLIFR equations in the continuous space approach
the equivalent GLIF equations in the discrete space. This is established in
equations 6.9 à 6.11:

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
5
4
5
5
5
2
0
7
5
3
3
3
n
e
c
o
_
un
_
0
1
5
7
1
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

580

C. Winston, D. Mastrovito, E. Shea-Brown, et S. Mihalas

Tableau 4: List of Parameters Describing GLIFR Networks, along with Their Units.

Spiking related

V p,je
ème
p
V

Voltage related

kp,je
m
Rm
Vreset
I0

threshold
smoothness

voltage decay factor
membrane resistance
reset voltage
baseline current

After-spike current related

ap,je
rp,je
kp,je

additive constant in after-spike current

multiplicative constant in after-spike current

unitless

decay factor for after-spike current

mV
mV

−1
ms
G(cid:7)
mV
pA

−1

pA
pA

Synaptic current related

W pq
dans
W pq
lat

input weight
lateral weight

Note: Ici, indices p, l refer to neuron p in layer l.

lim
σV →0

sp,je (t) = lim
σV →0
⎧
⎨

ème )/σV

1 + e−(V p,je (t)−V p,je
1 V p,je (t) > V p,je
0 V p,je (t) < V p,l th th = ⎩ lim σV →0 V p,l (t) = lim σV →0 (cid:5) V p,l (t − dt)(1 − kp,l m dt) = H(V p,l (t) − V p,l th ) (6.9) + Rp,l m kp,l m (cid:5) I p,l 0 + I p,l syn(t) + (cid:4) (cid:6) I p,l j (t) dt − dt (cid:6) τ sp,l (V p,l (t − dt) − Vreset ) j = V p,l (t − dt)(1 − kp,l m dt) + Rp,l m kp,l m (cid:5) I p,l 0 + I p,l syn(t) + (cid:6) I p,l j (t) dt (cid:4) j − dt τ lim σV →0 (sp,l )(V p,l (t − dt) − Vreset ) = V p,l (t − dt)(1 − kp,l m dt) + Rp,l m kp,l m (cid:5) I p,l 0 + I p,l syn(t) + (cid:6) I p,l j (t) dt (cid:4) j − dt τ H(V p,l (t) − V p,l th )(V p,l (t − dt) − Vreset ) (6.10) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuronal Heterogeneity Learned by Gradient Descent 581 (cid:5) lim σV →0 I p,l j (t) = lim σV →0 + (ap,l j (cid:5) I p,l j (t − dt)(1 − kp,l j dt) + rp,l j I p,l j (t − dt)) (cid:6) dt τ sp,l (t − dt) = lim σV →0 I p,l j (t − dt)(1 − kp,l j dt) + rp,l j I p,l j (t − dt)) dt τ lim σV →0 + (ap,l j (cid:5) = lim σV →0 I p,l j (t − dt)(1 − kp,l j dt) (cid:6) (sp,l (t − dt)) (cid:6) + (ap,l j + rp,l j I p,l j (t − dt)) dt τ H(V p,l (t) − V p,l th ) (6.11) 6.1.3 Discretization of GLIFR Equations. In order to compute efficiently across large networks of GLIFR neurons, we discretize the equations de- fined previously for the GLIFR model so that the required computations are approximated using forward Euler. The resulting equations are defined in equations 6.12 to 6.15: Sp,l[t] = 1 1 + e−(V p,l [t]−V p,l th )/σV , V p,l[t] = V p,l[t − dt](1 − kp,l m dt) + Rp,l m kp,l m (cid:10) I p,l 0 + I p,l syn[t] + (cid:11) I p,l j [t] dt (cid:4) j r [t]dt(V p,l[t − dt] − Vreset ), − Sp,l j [t − dt](1 − kp,l j [t] = I p,l I p,l (cid:4) Iq syn[t] = W pq in Sp,l−1[t − dt] + j dt) + (ap,l j (cid:4) j [t − dt])Sp,l + rp,l j I p,l lat Sp,l[t − (cid:5)t]. W pq r [t − dt]dt (6.12) (6.13) (6.14) (6.15) p p 6.2 GLIFR Optimization. We use standard gradient descent to opti- mize networks of GLIFR neurons, training both synaptic weights and pa- rameters in each neuron separately, similar to Perez-Nieves et al. (2021). In this way, the network can learn heterogeneous parameters across neurons. We introduce several changes in variables to enable training multiplica- tive terms and promote stability. Because multiplicative terms can pose challenges for optimization by gradient descent, we keep resistance fixed and do not optimize it. Instead, while we do optimize km, we optimize the product WpqRmkqdt rather than Wpq (for either incoming weight or lateral weights) or Rm individually, and we refer to this product as ωpq. Thus, the l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 582 C. Winston, D. Mastrovito, E. Shea-Brown, and S. Mihalas Table 5: Trained Parameters. j lat V p,l th ω pq in , ω pq ap,l rp,l,∗ kp,l,∗ kp,l,∗ j j m threshold combined synaptic weights additive constant in after-spike current mV mV pA transformed multiplicative constant in after-spike current unitless transformed decay factor for after-spike current transformed voltage decay factor −1 ms −1 ms Notes: List of trainable parameters in GLIFR networks, along with their units. Here, indices p, l refer to neuron p in layer l, so that individual neuron parameters are trained separately. voltage and synaptic current equations can be combined as in the following equation: V p,l[t] = V p,l[t − dt](1 − kp,l m dt) + Rp,l m kp,l m (cid:10) I p,l 0 (cid:4) + j (cid:11) I p,l j [t] dt (cid:4) + p in Sp,l−1[t − dt] + ω pq (cid:4) p latSp,l[t − (cid:5)t] ω pq − Sp,l r [t]dt(V p,l[t − dt] − Vreset ). (6.16) We also add biological constraints to several parameters to maintain sta- bility through training. In biological systems, km and k j are restricted to be positive since they represent rates of decay. Moreover, to maintain stabil- ity, decay factors should be kept between 0 and 1 dt throughout training. To achieve this constraint without introducing discontinuities in the loss func- 1−kdt ) for each decay factor k. Thus, t∗ can be any tion, we optimize t∗ = ln( kdt real number, whereas k = sigmoid(t∗ dt is the decay factor we use when simulating neural activity. In this way, the value of k that is used is always between 0 and 1 dt . ) · 1 The term r j can also introduce instability, so we use a similar method to 1−r j constrain r j to [−1, 1]. We optimize t∗ = ln( = 1+r j 1 − 2 · sigmoid(t∗ ), which is bounded between −1 and 1. Other instabilities may be encountered, for example, by large synaptic weights, but we find these approaches sufficient for training networks of GLIFR neurons. ) and retrieve r j using r j The parameters we optimize-after making the above changes are listed in Table 5. When training on complex tasks, we create networks of neurons, each consisting of a single hidden layer of GLIFR neurons whose outputs at each time point are passed through a fully connected linear transforma- tion to yield the final output. The weights and biases used for this linear transformation are additionally optimized. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuronal Heterogeneity Learned by Gradient Descent 583 Table 6: Parameter Initialization. Parameter Homogeneous Initialization Vth ω pq ap j rp j kp j kp m N ) mV U(− 1 N 1 mV , 1 U(−0.01, 0.01) pA U(−0.01, 0.01) 0.1 dt dt Notes: This table describes how each trainable parameter was initialized in GLIFR neurons either homogeneously or heterogeneously across neurons. Note that in both schemes, ω, r j, and k j were initialized with at least some amount of heterogeneity. 6.3 Evaluation Setup. When optimizing our model on tasks, we use multiple network types. First, as a baseline, we use a vanilla recurrent neu- ral network (RNN). The neurons used by RNNs are modeled as in equa- tion 6.17. Here, Wih represents the weights applied to the input signal, Whh refers to the recurrent weights, and b refers to the bias term. In contrast to GLIFR neurons, we set the synaptic delay (cid:5)t to dt in RNNs for some tasks in order to enable the modeling of nonlinear transformations at the begin- ning of a simulation. In other words, instead of incorporating dynamics from several timesteps prior, the synaptic delay is a single timestep in du- ration. This enables the RNN to perform better than it would if we used (cid:5)t = 1 ms: h(t) = tanh(Wihx(t) + Whhh(t − (cid:5)t) + b). (6.17) We additionally study multiple variations of the GLIFR networks, vary- ing in whether parameters are homogeneously initialized and whether pa- rameters are learned over training. When initializing homogeneously, we employ a deterministic initialization scheme to decrease the likelihood that the network will learn parameters underlying exploding or saturating fir- ing rates; specifically, we initialize the network with small decay constants and thresholds close to the reset voltage of 0 mV. The homogeneous initial- ization scheme is described in Table 6. Note that the neuron described is in a layer with N neurons. When initializing heterogeneously, we initialize both parameters and input and lateral weights by randomly sampling from the distribution of parameters and weights in a trained LHet or LHetA model. This also decreases the likelihood of learning parameters that lead to ex- ploding or saturating firing rates while erasing any learned patterns in the parameters or connectivity patterns in the network. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 584 C. Winston, D. Mastrovito, E. Shea-Brown, and S. Mihalas Table 7: Size of Networks. Sine Generation L-MNIST P-MNIST N-MNIST RNN LSTM Hom HomA LHet LHetA FHet FHetA RHet RHetA 128(16,769) 63(16,696) 128(16,641) 128(16,641) 127(16,638) 124(16,617) 128(16,641) 128(16,641) 127(16,638) 124(16,617) 256(75,530) 122(75,406) 256(75,274) 256(75,274) 255(75,235) 252(75,106) 256(75,274) 256(75,274) 255(75,235) 252(75,106) 256(75,530) 122(75,406) 256(75,274) 256(75,274) 255(75,235) 252(75,106) 256(75,274) 256(75,274) 255(75,235) 252(75,106) 256(75,530) 122(75,406) 256(75,274) 256(75,274) 255(75,235) 252(75,106) 256(75,274) 256(75,274) 255(75,235) 252(75,106) Notes: This table lists the size of networks trained on each task. These are listed as number of neurons (number of parameters). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . Table 8: Hyperparameters. Model hyperparameters (cid:5)t (GLIFR/RNN) dt Optimization technique Sine Generation L-MNIST P-MNIST N-MNIST 1 ms/0 ms 0.05 ms 1 ms/0 ms 0.05 ms 15 ms/15 ms 0.05 ms 0 ms/0 ms 1 ms Loss function Technique Mean-squared error Cross-entropy loss Adam optimization (Kingma & Ba, 2014) Optimization hyperparameters Learning rate Betas Batch size Number of epochs 0.0001 6 5000 0.001 (0.9, 0.999) 256 30 0.0001 0.001 512 50 512 30 Notes: This table lists the hyperparameters used for each task. The only hyperparameter that varies between networks is the synaptic delay ((cid:5)t), and this is denoted as ((cid:5)t for GLIFR and LSTM/(cid:5)t for RNN). 6.4 Tasks. In this work, we explore multiple tasks, analyzing and com- paring the performance of RNNs, LSTMs, and variations of GLIFR net- works. The chosen tasks range in complexity. When training networks on these tasks, we parameter-match them, thus using the hidden sizes listed in Table 7. The hyperparameters used for each task are listed in Table 8. Below, we discuss each task in detail. 6.4.1 Sine Generation Task. In the sine generation task, each network was trained to generate 5 ms sinusoidal patterns whose frequencies are deter- mined by the amplitudes of the corresponding constant inputs. We trained / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuronal Heterogeneity Learned by Gradient Descent 585 each network to produce six sinusoids with frequencies ranging from 80 Hz to 600 Hz. The ith sinusoid was associated with a constant input of am- plitude (i/6) + 0.25. Previous work (Sussillo & Barak, 2013) tackles a more complex version of this task using RNNs but uses Hessian-free optimiza- tion, while we limit our training technique on both the RNN and the GLIFR networks to simple gradient descent. 6.4.2 Line-by-Line MNIST (L-MNIST) Task. In the L-MNIST task, a net- work takes in a 28-dimensional input at each timestep corresponding to a row of a MNIST image, which is sized 28 × 28. At each of the 28 timesteps, the network produces a 10-dimensional output (1 dimension for each digit 0–9), whose softmax would represent a one-hot encoding of the digit. The network is trained so that the 10-dimensional output at the last time point correctly indicates the input digit. 6.4.3 Pixel-by-Pixel MNIST (P-MNIST) Task. We analyze a variation of the L-MNIST task in which at each timestep, a network takes in a 1-dimensional input corresponding to a single pixel of an MNIST image. Thus, the number of timesteps processed for a single sample is 28 × 28 = 784. Similar to the L-MNIST setup, the network produces a 10-dimensional output for each timestep, and the network is trained so that the output at the last time point correctly indicates the input digit. 6.4.4 Neuromorphic MNIST (N-MNIST) Task. In the N-MNIST task, a net- work is trained to identify the digit represented by an MNIST image cap- tured by a dynamic vision sensor (DVS) (Orchard et al., 2015). The image is smoothly moved in front of a DVS camera, while for each frame, the DVS camera senses changes in pixel intensity in two directions and translates these into spiking events. As a result, a single image is represented by a 34 × 34 × 2 × T matrix, where T is the number of frames and each image is 34 × 34. Due to the large T accompanying samples from this data set, we employ the strategy taken in He et al. (2020). Specifically, for a timestep duration dt, we summarize each consecutive nonoverlapping window of t Xi jk(t)) for each pixel coordinates i, j and length dt by computing sign( channel k. We define sign(x) to be 0 for x = 0, positive for x > 0, and neg-
ative for x < 0. After summarizing each consecutive window, we use the first 15 timesteps for training. (cid:12) 6.5 Hardware. To accelerate training networks on the L-MNIST and P- MNIST tasks, we use the NVIDIA RTX 2080Ti GPU (two GPUs and eight CPUs). With GPU acceleration, one epoch on the L-MNIST task takes un- der 1 minute, and one epoch on the P-MNIST task takes approximately 2 minutes. We trained the sine wave generation task, which was and the N-MNIST task, which took around 20 minutes per epoch, on CPU only. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 586 C. Winston, D. Mastrovito, E. Shea-Brown, and S. Mihalas 7 Supplementary Data l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 10: Distribution of final loss. For each result listed in Table 2, the distri- bution of MSEs/accuracies across the 10 trials conducted is displayed. Neuronal Heterogeneity Learned by Gradient Descent 587 Figure 11: Predictions on sine wave generation task. A representative trace is shown for the predictions made by five networks trained on the sine wave gen- eration task. The black dashed line denotes the target pattern. All network types perform reasonably on this task. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 12: Effect of dropout on ablation results. Testing accuracy under ran- dom neuron silencing is recorded when dropout is used during training (B) and when it is not applied (A). 588 C. Winston, D. Mastrovito, E. Shea-Brown, and S. Mihalas l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 13: A–D. Learned parameter distributions. The initial (yellow) and learned (green) distributions of parameters across neurons in single example networks are shown for the L-MNIST task. Results are shown for both homo- geneous initialization (A) and heterogeneous initialization (B). Under both ini- tialization schemes, heterogeneity in neuronal parameters is learned. Neuronal Heterogeneity Learned by Gradient Descent 589 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 14: The CH scores for different cluster numbers are plotted for the pa- rameters learned on the sine wave generation task (A), the N-MNIST task (B), and the L-MNIST task (C), demonstrating optimal cluster counts of one, five, and four, respectively. 590 C. Winston, D. Mastrovito, E. Shea-Brown, and S. Mihalas Figure 15: Sample responses. Two neurons from each cluster in the LHetA net- work trained on the L-MNIST task were chosen and exposed to a constant stimulus of magnitude 0.001 pA. The resulting S(t) is plotted here. The colors represent the different clusters of neurons as identified in Figure 9. Acknowledgments We acknowledge the following sources of funding and support: the Uni- versity of Washington Mary Gates Research Endowment, NIH training grant T90 DA 32436-10, and NIH BRAIN initiative grant 1RF1DA055669. We thank the Allen Institute founder, Paul G. Allen, for his vision, encour- agement, and support. References Beiran, M., & Ostojic, S. (2019). Contrasting the effects of adaptation and synaptic fil- tering on the timescales of dynamics in recurrent networks. PLOS Computational Biology, 15(3), e1006893. 10.1371/journal.pcbi.1006893 Bellec, G., Scherr, F., Subramoney, A., Hajek, E., Salaj, D., Legenstein, R., & Maass, W. (2020). A solution to the learning dilemma for recurrent networks of spiking neurons. Nature Communications, 11(1). 10.1038/s41467-020-17236-y Billeh, Y. N., Cai, B., Gratiy, S. L., Dai, K., Iyer, R., Gouwens, N. W., . . . Arkhipov, A. (2020). Systematic integration of structural and functional data into multi- scale models of mouse primary visual cortex. Neuron, 106(3), 388–403. 10.1016/ j.neuron.2020.01.040, PubMed: 32142648 Burnham, D., Shea-Brown, E., & Mihalas, S. (2021). Learning to predict in networks with heterogeneous and dynamic synapses. bioRxiv. Fontaine, B., Peña, J. L., & Brette, R. (2014). Spike-threshold adaptation predicted by membrane potential dynamics in vivo. PLOS Computational Biology, 10(4), e1003560. 10.1371/journal.pcbi.1003560 Geadah, V., Kerg, G., Horoi, S., Wolf, G., & Lajoie, G. (2020). Advantages of biologically- inspired adaptive neural activation in RNNs during learning. arXiv:2006.12253. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuronal Heterogeneity Learned by Gradient Descent 591 Gerstner, W., Kistler, W. M., Naud, R., & Paninski, L. (2014). Neuronal dynamics: From single neurons to networks and models of cognition. Cambridge University Press. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. MIT Press. He, W., Wu, Y., Deng, L., Li, G., Wang, H., Tian, Y., . . . Xie, Y. (2020). Comparing SNNs and RNNs on neuromorphic vision datasets: Similarities and differences. Neural Networks, 132, 108–120. 10.1016/j.neunet.2020.08.001, PubMed: 32866745 Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R. R. (2012). Improving neural networks by preventing co-adaptation of feature detectors. arXiv:1207.0580. Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural Computa- tion, 9(8), 1735–1780. 10.1162/neco.1997.9.8.1735, PubMed: 9377276 Hodgkin, A. L., & Huxley, A. F. (1952). A quantitative description of membrane cur- rent and its application to conduction and excitation in nerve. Journal of Physiol- ogy, 117(4). 10.1113/jphysiol.1952.sp004764 Hu, B., Garrett, M. E., Groblewski, P. A., Ollerenshaw, D. R., Shang, J., Roll, K., . . . Mihalas, S. (2021). Adaptation supports short-term memory in a visual change detection task. PLOS Computational Biology, 17(9). 10.1371/journal.pcbi.1009246 Huh, D., & Sejnowski, T. J. (2018). Gradient descent for spiking neural networks. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, & R. Garnett (Eds.), Advances in neural information processing systems, 31. Curran. Hunsberger, E., Scott, M., & Eliasmith, C. (2014). The competing benefits of noise and heterogeneity in neural coding. Neural Computation, 26(8), 1600–1623. 10.1162/ NECO_a_00621, PubMed: 24877735 Izhikevich, E. (2003). Simple model of spiking neurons. IEEE Transactions on Neural Networks, 14(6), 1569–1572. 10.1109/TNN.2003.820440, PubMed: 18244602 Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv:1412. 6980. LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–444. 10.1038/nature14539, PubMed: 26017442 Li, S., Li, W., Cook, C., Zhu, C., & Gao, Y. (2018). Independently recurrent neural network (INDRNN): Building a longer and deeper RNN. arXiv:1803.04831. Liu, P., Qiu, X., & Huang, X. (2016). Recurrent neural network for text classification with multi-task learning. arXiv:1605.05101. Markram, H., Muller, E., Ramaswamy, S., Reimann, M. W., Abdellah, M., Sanchez, C. A., . . . Schürmann, F. (2015). Reconstruction and simulation of neocortical mi- crocircuitry. Cell, 163(2), 456–492. 10.1016/j.cell.2015.09.029 Mihala¸s, ¸S., & Niebur, E. (2009). A generalized linear integrate-and-fire neural model produces diverse spiking behaviors. Neural Computation, 21(3), 704–718. 10.1162/ neco.2008.12-07-680 Morris, C., & Lecar, H. (1981). Voltage oscillations in the barnacle giant muscle fiber. Biophysical Journal, 35(1). 10.1016/S0006-3495(81)84782-0 Muscinelli, S. P., Gerstner, W., & Schwalger, T. (2019). How single neuron proper- ties shape chaotic dynamics and signal transmission in random neural networks. PLOS Computational Biology, 15(6), e1007122. 10.1371/journal.pcbi.1007122 Neftci, E. O., Mostafa, H., & Zenke, F. (2019). Surrogate gradient learning in spiking neural networks: Bringing the power of gradient-based optimization to spiking neural networks. IEEE Signal Processing Magazine, 36(6). 10.1109/ MSP.2019.2931595 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 592 C. Winston, D. Mastrovito, E. Shea-Brown, and S. Mihalas Orchard, G., Jayawant, A., Cohen, G. K., & Thakor, N. (2015). Converting static im- age datasets to spiking neuromorphic datasets using saccades. Frontiers in Neu- roscience, 9, 437. 10.3389/fnins.2015.00437 Perez-Nieves, N., Leung, V. C., Dragotti, P. L., & Goodman, D. F. (2021). Neural heterogeneity promotes robust learning. Nature Communications, 12(1). 10.1038/ s41467-021-26022-3 Prinz, A. A., Bucher, D., & Marder, E. (2004). Similar network activity from dis- parate circuit parameters. Nature Neuroscience, 7(12), 1345–1352. 10.1038/nn1352, PubMed: 15558066 Rajan, K., Harvey, C. D., & Tank, D. W. (2016). Recurrent network models of sequence generation and memory. Neuron, 90(1). 10.1016/j.neuron.2016.02.009 Salaj, D., Subramoney, A., Kraisnikovic, C., Bellec, G., Legenstein, R., & Maass, W. (2021). Spike frequency adaptation supports network computations on tempo- rally dispersed information. eLife, 10. 10.7554/eLife.65459 Shamir, M., & Sompolinsky, H. (2006). Implications of neuronal diversity on popu- lation coding. Neural Computation, 18(8), 1951–1986. 10.1162/neco.2006.18.8.1951, PubMed: 16771659 She, X., Dash, S., Kim, D., & Mukhopadhyay, S. (2021). A heterogeneous spiking neural network for unsupervised learning of spatiotemporal patterns. Frontiers in Neuroscience, 14, 1406. 10.3389/fnins.2020.615756 Sussillo, D., & Barak, O. (2013). Opening the black box: Low-dimensional dynamics in high-dimensional recurrent neural networks. Neural Computation, 25(3), 626– 649. 10.1162/NECO_a_00409, PubMed: 23272922 Teeter, C., Iyer, R., Menon, V., Gouwens, N., Feng, D., Berg, J., . . . Mihalas, S. (2018). Generalized leaky integrate-and-fire models classify multiple neuron types. Na- ture Communications, 9(1). 10.1038/s41467-017-02717-4 Tripathy, S. J., Padmanabhan, K., Gerkin, R. C., & Urban, N. N. (2013). Intermediate intrinsic diversity enhances neural population coding. In Proceedings of the Na- tional Academy of Sciences, 110(20), 8248–8253. 10.1073/pnas.1221214110 Wunderlich, T. C., & Pehle, C. (2021). Event-based backpropagation can compute ex- act gradients for spiking neural networks. Scientific Reports, 11(1), 1–17. 10.1038/ s41598-021-91786-z, PubMed: 34145314 Yamins, D. L. K., Hong, H., Cadieu, C. F., Solomon, E. A., Seibert, D., & DiCarlo, J. J. (2014). Performance-optimized hierarchical models predict neural responses in higher visual cortex. In Proceedings of the National Academy of Sciences, 111(23), 8619–8624. 10.1073/pnas.1403112111 Zenke, F., & Vogels, T. P. (2021). The remarkable robustness of surrogate gradient learning for instilling complex function in spiking neural networks. Neural Com- putation, 33(4), 899–925. 10.1162/neco_a_01367, PubMed: 33513328 Received January 19, 2022; accepted November 2, 2022. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 4 5 5 5 2 0 7 5 3 3 3 n e c o _ a _ 0 1 5 7 1 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Image de l'ARTICLE

Télécharger le PDF