ARTICLE - Recherche en IA spécialisée au MIT

ARTICLE

Communicated by Terrence Sejnowski

Disentangled Representation Learning and Generation
With Manifold Optimization

Arun Pandey
arun.pandey@esat.kuleuven.be
KU Leuven, Department of Electrical Engineering, STADIUS Center for Dynamical
Systems, Signal Processing and Data Analytics, B-3001 Leuven, Belgium

Michaël Fanuel
michael.fanuel@univ-lille.fr
Université de Lille, CNRS, Centrale Lille, F-59000 Lille, France

Joachim Schreurs
joachim.schreurs@esat.kuleuven.be
Johan A. K. Suykens
johan.suykens@esat.kuleuven.be
KU Leuven, Department of Electrical Engineering, STADIUS Center for Dynamical
Systems, Signal Processing and Data Analytics, Kasteelpark Arenberg 10,
B-3001 Leuven, Belgium

Disentanglement is a useful property in representation learning, lequel
increases the interpretability of generative models such as variational
autoencoders (VAE), generative adversarial models, and their many vari-
ants. Typically in such models, an increase in disentanglement perfor-
mance is traded off with generation quality. In the context of latent
space models, this work presents a representation learning framework
that explicitly promotes disentanglement by encouraging orthogonal
directions of variations. The proposed objective is the sum of an autoen-
coder error term along with a principal component analysis reconstruc-
tion error in the feature space. This has an interpretation of a restricted
kernel machine with the eigenvector matrix valued on the Stiefel man-
ifold. Our analysis shows that such a construction promotes disentan-
glement by matching the principal directions in the latent space with
the directions of orthogonal variation in data space. In an alternating
minimization scheme, we use the Cayley ADAM algorithm, a stochastic
optimization method on the Stiefel manifold along with the Adam opti-
mizer. Our theoretical discussion and various experiments show that the
proposed model is an improvement over many VAE variants in terms of
both generation quality and disentangled representation learning.

Neural Computation 34, 2009–2036 (2022) © 2021 Massachusetts Institute of Technology.
https://doi.org/10.1162/neco_a_01528
Publié sous Creative Commons
Attribution 4.0 International (CC PAR 4.0) Licence.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2010

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

1 Introduction

Latent space models are popular tools for sampling from high-dimensional
distributions. Souvent, only a small number of latent factors are sufficient
to describe data variations. These models exploit the underlying struc-
ture of the data and learn explicit representations that are faithful to the
data-generating factors. Popular latent space models are variational autoen-
coders (VAEs; Kingma & Welling, 2014), restricted Boltzmann machines
(RBMs; Salakhutdinov & Hinton, 2009), normalizing flows (Rezende &
Mohamed, 2015), and their many variants.

In latent variable models, one is often interested in modeling the data in
terms of uncorrelated or independent components, yielding a so-called dis-
entangled representation (Bengio, Courville, & Vincent, 2013), which is of-
ten studied in the context of VAEs. Generative adversarial networks (GAN)
have also been extended to perform disentangled representation learning,
par exemple, with Info-GANs. It is a GAN that also maximizes the mutual
information between a small subset of the discrete latent codes and the
true images. En principe, disentanglement corresponds to identifying the
underlying factors that generate the data. Components corresponding to
the orthogonal directions in latent space may be interpreted as generating
distinct factors in the input space (e.g. lighting conditions, style, colors).
An illustration of a latent traversal is shown in Figure 1, where one ob-
serves that only one specific feature of the image is changing as one moves
along a component in the latent space. Par exemple, in Figure 1, we ob-
serve that moving along the first component (vector u1) generates images
where only floor color is varying, alors que, all other features, such as shape,
scale, wall color, and object color, are constant, whereas traversing along
the sixth component (vector u6), par exemple, generates images where only
the object scale changes as shown in the second row. As we explain later,
the components here refer to the principal components given by the princi-
pal component analysis (APC). Donc, these principal directions encode
the directions of maximum variance. Since the floor color is encoded by the
largest number of pixels, it gets represented by the first principal compo-
nent u1. De la même manière, the other components correspond to the directions with
smaller variance. An advantage of such a representation is that the different
latent units impart more interpretability to the model. Disentangled models
are useful for the generation of plausible pseudo-data with certain desir-
able properties (par exemple., generating new car designs with a predefined color or
height).

Now we introduce the mathematical setting to formalize our discussion
throughout the paper. We start by introducing a VAE (Kingma & Welling,
2014). Let p(X) be the distribution of the data x ∈ Rd and consider latent
vectors z ∈ R(cid:2)
with the prior distribution p(z), typically a standard nor-
mal distribution. Alors, one defines an encoder q(z|X) that can be deter-
ministic or probabilistic, Par exemple, given by N (z|φθ (X), γ 2I), where the

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stiefel-Restricted Kernel Machine

2011

Chiffre 1: Images by the decoder of the latent space traversal: ψξ (tui) for t ∈
[un, b] with a < b and for some i ∈ {1, . . . , m}. Green and black dashed lines repre- sent the walk along u1 and u6, respectively. At every step of the walk, the output of the decoder generates the data in the input space. The images were generated by St-RKM with σ = 10−3 on 3Dshapes dataset. See Figure 5 for traversal along other components. mean1 is given by the neural network φθ parametrized by θ. A random de- coder p(x|z) = N (x|ψξ (z), σ 2 I) is associated with the decoder neural net- 0 work ψξ, parameterized by ξ, which maps latent codes to the data points. A VAE is trained by maximizing the lower bound to the idealized log- likelihood as: E z∼q(z|x)[log(p(x|z))] − βKL(q(z|x), p(z)) ≤ log p(x). (1.1) This lower bound is often called as the evidence lower bound (ELBO) when β = 1. Higgins et al. (2017) show that the larger values of β > 1 promote
more disentanglement but at the expense of generation quality. In this arti-
clé, we attempt to reconcile the generation quality with disentanglement. À
introduce the model, we first make explicit the connection between β-VAEs
and standard autoencoders (AEs). Let the data set be {xi
∈ Rd.
Let q(z|X) = N (z|φθ (X), γ 2I) be an encoder, where z ∈ R(cid:2)
. For a fixed γ > 0,
the maximization problem 1.1 is then equivalent to the minimization of the
regularized AE,

}n
i=1 with xi

min
je,ξ

(cid:3)
E(cid:6)(cid:5)xi

1
n

n(cid:2)

je = 1

− ψξ (φθ (xi) + (cid:6))(cid:5)2
2

+ un(cid:5)φθ (xi)(cid:5)2
2

(cid:4)
,

(1.2)

where α = βσ 2
0 , (cid:6) ∼ N (0, γ 2I) and additive constants depending on γ have
been omitted. The first term in equation 1.2 can be interpreted as an AE loss,
whereas the second term can be viewed as a regularization. This regularized
AE interpretation motivates our method as introduced in section 3.

A typical implementation of VAE includes another neural network (after the primary
réseau) for parametrizing the covariance matrix. To simplify this introductory discus-
sion, this matrix is here chosen as a constant diagonal γ 2I.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2012

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

The rest of the article is organized as follows. In section 2 we discuss the
closely related work on disentangled representation learning and genera-
tion in the context of autoencoders. Further in section 3, we describe the
proposed model along with the connection between PCA and disentangle-
ment. In section 3.2, we discuss our contributions. In section 4, we derive
the evidence lower bound of the proposed model and show connections
with the probabilistic models. In section 5, we describe our experiments
and discuss the results.

2 Related Work

Related works can be broadly classified into two categories: Variational au-
toencoders (VAE) in the context of disentanglement and Restricted Kernel
Machines (RKM), a recently proposed modeling framework that integrates
kernel methods with deep learning.

2.1 VAE. As discussed in the section 1 (Higgins et al., 2017) suggested
that a stronger emphasis on the posterior to match the factorized unit gaus-
sian prior puts further constraints on the implicit capacity of the latent bot-
tleneck. Burgess et al. (2017) further analyzed the effect of the β term in
depth. Plus tard, Chen, Li, Grosse, and Duvenaud (2018) showed that the KL
term includes the mutual information gap, which encourages disentangle-
ment. Recently, several variants of VAEs promoting disentanglement have
been proposed by adding extra terms to the ELBO. Par exemple, FactorVAE
(Kim & Mnih, 2018) augments the ELBO by a new term enforcing factoriza-
tion of the marginal posterior (or aggregate posterior). Rolínek et al. (2019)
analyzed the reason for the alignment of the latent space with the coor-
dinate axes, as the design of VAE itself does not suggest any such mech-
anism. The authors argue that due to the diagonal approximation in the
encoder, together with the inherent stochasticity, forces the local orthogo-
nality of the decoder. Locatello et al. (2020) considered adding an extra term
that accounts for the knowledge of some partial label information to im-
prove disentanglement. Plus tard, Ghosh, Sajjadi, Vergari, Noir, and Schölkopf
(2020) studied the deterministic AEs, where another quadratic regulariza-
tion on the latent vectors was proposed. In contrast to Rolínek et al. (2019),
where the implicit orthogonality of VAE was studied, our proposed model
has orthogonality by design due to the introduction of the Stiefel manifold.

2.2 RKM. Restricted kernel machines (RKM; Suykens, 2017) provides a
representation of kernel methods with visible and hidden variables sim-
ilar to the energy function of restricted Boltzmann machines (RBM; Le-
Cun, Huang, & Bottou, 2004; Hinton, 2005), thus linking kernel methods
with RBMs. Training and prediction schemes are characterized by the sta-
tionary points for the unknowns in the objective. The equations in these
stationary points lead to solving a linear-system or matrix decomposition

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stiefel-Restricted Kernel Machine

2013

Chiffre 2: Schematic illustration of St-RKM training problem. The length of the
dashed line represents the reconstruction error (see the autoencoder term in
equation 3.3) and the length of the vector projecting on hyperplane represents
the PCA reconstruction error. After training, the projected points tend to be dis-
tributed normally on the hyperplane.

for the training. Suykens (2017) shows various RKM formulations for
doing classification, regression, kernel PCA, and singular value decompo-
sition. Later the kernel PCA formulation of RKM was extended to a mul-
tiview generative model called generative-RKM (Gen-RKM) which uses
convolutional neural networks as explicit feature maps (Pandey, Schreurs,
& Suykens, 2020, 2021). For the joint feature selection and subspace learn-
ing, the proposed training procedure performs eigendecomposition of the
kernel/covariance matrix in every minibatch of the optimization scheme.
Intuitively, the model could be seen as learning an autoencoder with ker-
nel PCA in the bottleneck part. Par conséquent, the computational complexity
scales cubically with the minibatch size and is proportional to the number of
minibatches. De plus, backpropagation through the eigendecomposition
could be numerically unstable due to the possibility of small eigenvalues.
All such limitations are addressed by our proposed model.

3 Proposed Mechanism

The main idea of this article consists of learning an autoencoder, along with
finding an optimal linear subspace of the latent space such that the vari-
ance of the training set in latent space is maximized within this space. (Voir
Chiffre 2 to follow the discussion below.) Note the distinction with linear au-
toencoders, which also project the data into the low-dimensional subspace
although via nonorthogonal transformations. As a consequence, the latent
variables are not guaranteed to be uncorrelated. The encoder φθ : Rd → R(cid:2)
typically sends input data to a latent space, while the decoder ψξ : R.(cid:2) → Rd
goes in the reverse direction and constitutes an approximate inverse. Both
the encoder and decoder are neural networks parameterized by vectors θ

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2014

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

and ξ. Cependant, it is unclear how to define a parameterization or an archi-
tecture of these neural networks so that the learned representation is disen-
tangled. Donc, in addition to these trained parameters, we also jointly
find an m-dimensional linear subspace range(U ) of the latent space R(cid:2)
, tel
that the encoded training points mostly lie within this subspace. This linear
subspace is given by the span of the orthonormal columns of the (cid:2) × m ma-
trix U = [u1
, . . . , um]. The set of such matrices with m orthonormal columns
in R(cid:2)
avec (cid:2) ≥ m defines the Stiefel manifold St((cid:2), m). For a reference about
optimization on Stiefel manifold, we refer to Absil, Mahony, and Sepulchre
(2008). Input data are then encoded into a subspace of the latent space by

(cid:9)
X (cid:8)→ PU φθ (X) = u
1

φθ (X) ×

⎤

⎦ + . . . + toi

(cid:9)
m

φθ (X) ×

⎡

⎣

|
u1
|

⎤

⎦ ,

⎡

⎣

|
um
|

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

where the orthogonal projector onto range(U ) is simply PU = UU (cid:9)

Orthogonal latent directions. Naturellement, given an m × m orthogonal matrix

O and a matrix U ∈ St((cid:2), m), we have

range(U ) = range(UO).

n
je = 1

φθ (xi)φ(cid:9)

, . . . , toi(cid:7),m to be the eigenvectors of the matrix Cθ = 1
n

, . . . , toi(cid:7),m] ∈ St((cid:2), m), we choose
To select a specific matrix U(cid:7) = [toi(cid:7),1
(cid:9)
je (xi),
toi(cid:7),1
associated with the m largest eigenvalues sorted in descending order. Pour
simplicity, we assume that the m largest eigenvalues of Cθ are distinct,
whereas the general case involves minor technicalities. Here the feature
map is assumed to be centered, E
x∼p(X)[φθ (X)] = 0, so that Cθ is interpreted
as a covariance matrix. Suivant, we state a result that we will use extensively
plus tard.
Proposition 1. Let M be an (cid:2) × (cid:2) symmetric matrix. Let ν
, . . . , νm be its m
1
smallest eigenvalues, possibly including multiplicities, with associated orthonor-
mal eigenvectors v
, . . . , vm. Let V be a matrix whose columns are these eigenvec-
tors. Then the optimization problem minU∈St((cid:2),m) Tr(U (cid:9)MU ) has a minimizer at
MU(cid:7) = diag(ν), with ν = (ν
U(cid:7) = V and we have U(cid:7)
1

, . . . , νm)

(cid:9).

(cid:9)

(cid:7) MU (cid:10)

A few remarks follow. D'abord, if U(cid:7) is a minimizer of the optimization prob-
lem in proposition 1 then U (cid:10)
(cid:7) = U(cid:7)O with O orthogonal is also a minimizer,
but U (cid:10)(cid:9)
(cid:7) is not necessarily diagonal. Deuxième, notice that if the eigen-
values of M in proposition 1 have a multiplicity larger than 1, there can
exist several sets of eigenvectors v
, . . . , vm, associated with the m smallest
eigenvalues, spanning distinct linear subspaces. Nevertheless, in practice,
the eigenvalues of the matrices considered in this article are numerically
distinct.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stiefel-Restricted Kernel Machine

2015

We now use proposition 1. For a given positive integer m ≤ (cid:2), the sub-
space spanned by the eigenvectors of Cθ with the m largest eigenvalues is
obtained by solving

min
U∈St((cid:2),m)

Tr (Cθ − PUCθPU ) = 1
n

n(cid:2)

je = 1

(cid:5)P.

U⊥ φθ (xi)(cid:5)2
2

where P
U⊥ = I − PU , as it is explained, par exemple, in section 4.1 of Avron,
Nguyen, and Woodruff (2014). The above objective corresponds to the re-
construction error of kernel PCA, for the kernel kθ (X, oui) = φ(cid:9)
je (X)φθ (oui). Comme
described earlier, we choose a specific U(cid:7) ∈ St((cid:2), m) by requiring that the
following matrix is diagonal,

(cid:9)
(cid:7) CθU(cid:7) = diag(λ),

(3.1)

where λ is a vector containing the m largest eigenvalues sorted in de-
creasing order. If these eigenvalues are distinct, then the U(cid:7) is essentially
unique, up to sign flip of each of its columns. Notice that Tr(U(cid:9)
(cid:7) CθU(cid:7)) =
Tr(U(cid:7)U (cid:9)

(cid:7) CθU(cid:7)U (cid:9)

(cid:7) ).

Orthogonal directions of variation in input space. We want the lines defined
by the orthonormal vectors {toi(cid:7),1
, . . . , toi(cid:7),m} to provide directions associated
with different generative factors of our model. Autrement dit, we conjec-
ture that a possible formalization of disentanglement is that the principal
directions in latent space match orthogonal directions of variation in the
data space (voir la figure 2). C'est, we would like that

(cid:9)
U
(cid:7)

d(cid:2)

(cid:10)

a=1

(cid:9)
∇ψa(yi)∇ψa(yi)

(cid:11)

U(cid:7) is diagonal,

(3.2)

= PU φθ (xi) for i = 1, . . . , n. In equation
for all the points in latent space yi
3.2, ψa(oui) refers to the ath component of the image ψ(oui) ∈ Rd. To sketch this
idea, we study the local motions in the latent space.

= ∇ψ(oui)(cid:9)toi(cid:7),k

∈ Rd be the directional derivative of ψ at point y
in the direction u(cid:7),k with 1 ≤ k ≤ m. Alors, as one moves in the latent space
from a point y in the direction of u(cid:7),k, the generated data change by

Let (cid:9)
k

ψ(oui + tu(cid:7),k) − ψ(oui) = t(cid:9)
k

+ Ô(t2),

∈ Rd and t ∈ R. Consider now a different direction, k(cid:10) (cid:13)= k. As the
avec (cid:9)
k
latent point moves along u(cid:7),k or along u(cid:7),k(cid:10) , we expect the decoder output to
vary in a significantly different manner, (cid:9)(cid:9)
k(cid:10) = 0. We presume this inter-
k
pretation to model the change in floor color and object scale in Figure 1 pour
instance. More explicitly, we can expect uk and uk(cid:10) to model, respectivement,
the change of colors of the floor and of the main object while leaving the
color of the other objects unchanged. Since the floor and the main object

(cid:9)

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2016

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

(cid:9)

do not overlap, c'est, they are different regions in pixel space, nous serions
have (cid:9)(cid:9)
k(cid:10) = 0. Admittedly, the change in object shape in Figure 1 is less
k
obviously interpreted. Now, denote by (cid:9) the matrix obtained by stacking
(cid:9)U(cid:7).
the vector (cid:9)
Ainsi, for all y in the latent space, we expect the Gram matrix (cid:9)(cid:9)(cid:9) to be
diagonal (see equation 3.2). We now discuss how this idea might be realized
by minimizing specific objective functions.

k as columns for 1 ≤ k ≤ m. Explicitly, we have (cid:9) = ∇ψa(oui)

3.1 Objective Function. In this article, we propose to train an objective
function which is composed of an AE loss and a PCA loss. Ainsi, the pro-
posed model is given by

min
U∈St((cid:2),m)
je,ξ

n(cid:2)

je = 1

λ 1
n
(cid:12)

Lξ,PU (xi
(cid:13)(cid:14)

, φθ (xi))
(cid:15)

,
+ Tr (Cθ − PUCθPU )
(cid:15)
(cid:13)(cid:14)

(cid:12)

PCA objective

Autoencoder objective

(3.3)

(cid:9)

n
je = 1

φθ (xi)φ(cid:9)

where λ > 0 is a trade-off parameter and Cθ = 1
je (xi). Natu-
n
rally, the above objective is invariant if U is replaced by UO with O an or-
thogonal matrix. Given a local minimizer, we select U(cid:7) ∈ St((cid:2), m) such that
U (cid:9)
(cid:7) CθU(cid:7) is diagonal as in equation 3.1, to identify the principal directions in
the latent space. This last step is conveniently done with a singular value
decomposition (see step 10 of algorithm 1). In the proposed model, recon-
struction of an out-of-sample point x is given by ψξ
. We call the
procedure to

(cid:11)
PU φθ (X)

(cid:10)

find a triplet (U(cid:7), je, ξ) solving (5) s.t. U

(cid:9)
(cid:7) CθU(cid:7) is diagonal,

St-RKM

the training of a Stiefel-restricted kernel machines, equation 3.3, in view of
our discussion in section 2. The basic idea is to design different AE losses
with a regularization term that penalizes the feature map in the orthogonal
subspace U ⊥
. The choice of the AE losses is motivated by the expression
of the regularized AE in equation 1.2 and by the following lemma, lequel
extends the result of Rolínek et al. (2019). Here we adapt it in the context of
optimization on the Stiefel manifold (see appendix for the proof).
Lemma 1. Let (cid:6) ∼ N (0, Im) a random vector and U ∈ St((cid:2), m). Let ψa(·) ∈
C2(R.(cid:2)
a has La-Lipschitz continuous Hes-
sian for all a ∈ [d], we have

) with a ∈ [d]. If the function [ψ(·) − x]2

E(cid:6)(cid:5)x − ψ(oui + σU(cid:6))(cid:5)2
2

= (cid:5)x − ψ(oui)(cid:5)2
2

(cid:10)
+ σ 2Tr
U

(cid:9)
(cid:9)∇ψ(oui)∇ψ(oui)

(cid:11)

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

−p 2

d(cid:2)

(cid:10)
[x − ψ(oui)]aTr
U

(cid:9)

Hessy[ψa]U

d(cid:2)

(cid:11)

a=1

Ra(p ),

(3.4)

2(m+1)(cid:11)((m+1)/2)
(cid:11)(m/2)

où (cid:11) is Euler’s gamma function.

a=1

√

avec |Ra(p )| ≤ 1
6

σ 3La

Stiefel-Restricted Kernel Machine

2017

In lemma 1, the first term on the right-hand side in equation 3.4 plays
the role of the classical AE loss. The second term is proportional to the trace
of equation 3.2. This is related to our discussion above where we argue that
jointly diagonalizing both U(cid:9)∇ψ(oui)∇ψ(oui)
(cid:9)U and U (cid:9)CθU helps to enforce
disentanglement. Cependant, determining the behavior of the third term in
equation 3.4 is difficult. This is because, for a typical neural network archi-
tecture, it is unclear in practice if the function [x − ψ(·)]2
a has La-Lipschitz
continuous Hessian for all a ∈ [d]. Hence we propose another AE loss (split-
ted loss) in order to cancel the third term in equation 3.4. Nevertheless,
the assumption in lemma 1 is used to provide a meaningful bound on the
remainder in equation 3.4. In the light of these remarks, we propose two
stochastic AE losses.

3.1.1 AE Losses. In analogy with the VAE objective equation 1.2, the first

AE encoder loss function can be chosen as

L(p )
ξ,PU

(X, z) = E(cid:6)∼N (0,Im )

(cid:16)
(cid:16)
x − ψξ

(cid:10)

PU z + σU(cid:6)

(cid:11)(cid:16)
(cid:16)2
2

, with σ > 0.

As motivated by lemma 1, the noise term σU(cid:6) above promotes a smoother
decoder network. To further promote disentanglement, we propose a split
AE loss

L(p ),sl
ξ,PU

(X, z) =

(cid:16)
(cid:16)

x − ψξ

(cid:10)

PU z

(cid:11)(cid:16)
(cid:16)2
2

+ E(cid:6)

(cid:16)
(cid:16)ψξ

(cid:11)

(cid:10)
PU z

(cid:10)

− ψξ

PU z + σU(cid:6)

(cid:11)(cid:16)
(cid:16)2
2

(3.5)

avec (cid:6) ∼ N (0, Im). The first term in equation 3.5 is the classical AE loss while
the second term promotes orthogonal directions of variations. Ainsi, by re-
lating lemma 1 to equation 3.5 we see that

L(p ),sl
ξ,PU

(X, z) =

(cid:16)
(cid:16)

x − ψξ

(cid:10)

PU z

(cid:11)(cid:16)
(cid:16)2
2

(cid:10)
+ σ 2Tr
U

(cid:9)
(cid:9)∇ψ(oui)∇ψ(oui)

d(cid:2)

(cid:11)

a=1

Ra(p ).

In short, the optimization over U in equation 3.3 with the splitted loss aims
to promote a U(cid:7) such that

(cid:9)
(cid:9)
(cid:7) CθU(cid:7) and U
(cid:7)

(cid:17)

n(cid:2)

je = 1

(cid:18)

(cid:9)
∇ψ(yi)∇ψ(yi)

U(cid:7) are jointly diagonal.

Chiffre 3 gives a visualization of the diagonal form of

1
|C|

(cid:2)

i∈C

(cid:9)
(cid:9)
(cid:7) ∇ψ(yi)∇ψ(yi)

U(cid:7), with yi

= PU φθ (xi)

(3.6)

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2018

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 3: Visualizing the matrix, equation 3.6 for St-RKM models after train-
ing on three data sets. The first two rows show, equation 3.6, where U =
U(cid:7) ∈ St((cid:2), m) is the output of algorithm 1. These matrices are effectively close
to being diagonal and especially for St-RKM-sl, as expected. In contrast, le
third row shows the same matrix, equation 3.6, with U ∈ St((cid:2), m) sampled uni-
formly at random (see Table 6 for the corresponding normalized diagonalization
errors).

obtained after training; where C contains the indices of a subset of 50 im-
ages sampled uniformly at random. (For numerical values, Tableau 6 dans le
appendix shows the normalized diagonalization errors.)

Note that we do not simply propose another encoder-decoder architec-
ture, given by U (cid:9)φθ (·) and ψξ (U·). Plutôt, our objective assumes that the
neural network defining the encoder provides a better embedding if we im-
pose that it maps training points on a linear subspace of dimension m < (cid:2) in the (cid:2)-dimensional latent space. In other words, the optimization of the parameters in the last layer of the encoder does not play a redundant role, since the second term in equation 3.3 clearly also depends on P U⊥ φθ (·). The full training involves an alternating minimization procedure, which is de- scribed in algorithm 1. Stiefel-Restricted Kernel Machine 2019 3.2 Contributions. Here is a summary of our contributions. We propose three main changes with respect to the related works. First, to promote dis- entangled representation learning, we propose orthogonal projection in the latent space via a rectangular matrix that is valued on the Stiefel manifold. Then for the training, we use the Cayley ADAM algorithm of Li, Li, and Todorovic (2020) for stochastic optimization on the Stiefel manifold and call our proposed model St-RKM. Second, we propose several objective func- tions to learn the feature map and the pre-image map networks in the form of an encoder and a decoder, respectively. The best configuration for pro- moting a disentangled representation is λ n n(cid:2) i=1 min U∈St((cid:2),m) θ,ξ (splitted) AE loss(xi , PU , θ, ξ) + PCA objective(Cθ, PU ), (cid:9) n i=1 φθ (xi)φ(cid:9) θ (xi) and PU = UU (cid:9) where the covariance matrix reads Cθ = 1 n with U an (cid:2) × m matrix with orthonormal columns. Here λ > 0 is a trade-
off parameter. The final parameters (U(cid:7), je, ξ) give a local minimizer of this
objective with U(cid:7) chosen such that U (cid:9)
(cid:7) CθU(cid:7) is diagonal. Troisième, we validate
through experiments the following statement: The combination of a split
AE loss with a PCA objective by using an explicit optimization on the Stiefel
manifold promotes disentanglement. In this article, disentanglement is in-
terpreted as jointly diagonalizing the matrix representing variations in the
(cid:9)U(cid:7) où
input space with respect to latent motions
φθ (xi) and the covariance matrix of the data set in the latent space
yi
U (cid:9)

(cid:7) ∇ψξ (yi)∇ψξ (yi)

= PU(cid:7)
(cid:7) CθU(cid:7).

i U (cid:9)

(cid:9)

4 Connections with the Evidence Lower Bound

We now discuss the interpretation of the proposed model in the probabilis-
tic setting and the independence of latent factors. In order to formulate an
ELBO, consider the following random encoders,

q(z|X) = N (z|φθ (X), γ 2I(cid:2)) and qU (z|X) = N (z|PU φθ (X), σ 2PU + δ2P

U⊥ ),

where φθ has zero mean on the data distribution. Ici, p 2 plays the role
of a trade-off parameter, while the regularization parameter δ is introduced
for technical reasons and is put to a numerically small absolute value (voir
the appendix for details). Let the decoder be p(X|z) = N (X|ψξ (z), p 2
je) et
0
the latent space distribution is parameterized by p(z) = N (0, (cid:13)) où
(cid:13) ∈ R(cid:2)×(cid:2)
is a covariance matrix. We treat (cid:13) as a parameter of the opti-
mization problem that is determined at the last stage of the training. Alors
the minimization problem 3.3 with stochastic AE loss is equivalent to the

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2020

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

maximization of
(cid:3)

n(cid:2)

1
n

je = 1

E
(cid:12)

qU (z|xi )[log(p(xi

(cid:13)(cid:14)

|z))]
(cid:15)

− KL(qU (z|xi), q(z|xi))
(cid:15)
(cid:13)(cid:14)

(cid:12)

− KL(qU (z|xi), p(z))
(cid:15)
(cid:13)(cid:14)

(cid:12)

(je)

(II)

(III)

(cid:4)
,

(4.1)

which is a lower bound to the ELBO, since the KL divergence in term II
in equation 4.1 is positive. For details of the derivation, see the appendix.
The hyperparameters γ , p, p
0 take a fixed value. Up to additive constants,
the terms I and II of equation 4.1 match the objective, equation 3.3. The third
term (III) in equation 4.1 is optimized after the training of the first two terms.
It can be written as

1
n

n(cid:2)

je = 1

KL(qU (z|xi), p(z)) = 1
2

Tr[(cid:13)
0

(cid:13)−1] + 1
2

log(det (cid:13)) + constants,

= PUCθPU + σ 2PU + δ2P

avec (cid:13)
0
matrix is diagonalized (cid:13) = U(diag(λ) + σ 2Im)U (cid:9) + δ2PU⊥
the principal values of the PCA.

U⊥ . In that case, the optimal covariance
, with λ denoting

Now we briefly discuss the factorization of the encoder. Let h(X) =
U (cid:9)φθ (X) and let the effective latent variable be z(U ) = U (cid:9)z ∈ Rm. Then the
probability density function of qU (z|X) est

fqU (z|X)(z) = e
√

−

(cid:5)U

(cid:9)
⊥ z(cid:5)2
2
2δ2
2πδ2)(cid:2)−m

−
e
√

(U )
j

−h j (X))2
2p 2
2πσ 2

m(cid:19)

j=1

(

where the first factor is approximated by a Dirac delta if δ → 0. Ainsi, le
factorized form of qU shows the independence of the latent variables z(U ).
This factorization is used as a regularization term in the objective by Kim
and Mnih (2018) to promote disentanglement. En particulier, term II in equa-
tion 4.1 is analogous to a “total correlation” loss (Chen et al., 2018).

5 Experiments

Dans cette section, we investigate if St-RKM2 can simultaneously achieve ac-
curate reconstructions on training data, good random generations, et
good disentanglement performance. We use the standard data sets: MNIST
(LeCun & Cortes, 2010), Fashion-MNIST (fMNIST; Xiao, Rasul, & Vollgraf,
2017), and SVHN (Netzer et al., 2011). To evaluate disentanglement, nous
use data sets with known ground-truth generating factors such as dSprites

The source code is available at http://bit.ly/StRKM_code.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stiefel-Restricted Kernel Machine

2021

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(Matthey, Higgins, Hassabis, & Lerchner, 2017), 3DShapes (Bourgeois & Kim,
2018), and 3D cars (Reed, Zhang, Zhang, & Lee, 2015). Plus loin, all fig-
ures and tables report average errors with 1 standard deviation over 10
experiments.

5.1 Algorithm. We use an alternating-minimization scheme as shown
in algorithm 1. D'abord, the Adam optimizer with a learning rate 2 × 10−4 is
used to update the encoder-decoder parameters; alors, the Cayley Adam
optimizer (Li et al., 2020) with a learning rate 10−4 is used to update U. Fi-
enfin, at the end of the training, we recompute U from the singular value
decomposition (SVD) of the covariance matrix as a final correction-step of
the kernel PCA term in our objective (step 10 of algorithm 1). Since the (cid:2) × (cid:2)
covariance matrix is typically small, this decomposition is fast (see Table 3).
In practice, our training procedure only marginally increases the computa-
tion cost, which can be seen from training times in Table 1.

5.2 Experimental Setup. We consider four baselines for comparison:
VAE, β-VAE, FactorVAE, and Info-GAN. An ablation study with the

2022

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

Tableau 1: Training Time in Minutes (pour 1000 Epochs, Mean with 1 Standard De-
viation over 10 Runs) and the Number of Parameters (Nb) of the Generative
Models on the MNIST Data Set.

Model

St-RKM

(β)-VAE

FactorVAE

Info-GAN

Nb parameters
Training time

4164519
21.93 (1.3)

4165589
19.83 (0.8)

8182591
33.31 (2.7)

4713478
45.96 (1.6)

Gen-RKM is shown in section A.4 in the appendix. Extensive experimen-
tation was not computationally feasible since the evaluation and decompo-
sition of kernel matrices scales O(n2) and O(n3) with the data set size (voir
the discussion in section 2).

5.3 Inductive Biases. To be consistent in evaluation, we keep the same
encoder (discriminator) and decoder (generator) architecture and the same
latent dimension across the models. We use convolutional neural networks
due to the choice of image data sets for evaluating generation and disentan-
glement. In the case of Info-GAN, batch normalization is added for training
stability (see section A.3 in the appendix for details). For the determination
of the hyperparameters of other models, we start from values in the range of
the parameters suggested in the authors’ reference implementation. After
trying various values, we noticed that β = 3 and γ = 12 seem to work well
across the data sets that we considered for β-VAE and FactorVAE, respecter-
tivement. En outre, in all the experiments on St-RKM, we keep the recon-
struction weight λ = 1. All models are trained on the entire data set. Note
that for the same encoder-decoder network, the St-RKM model has the least
number of parameters compared to any VAE variants and Info-GAN (voir
Tableau 1).

To evaluate the quality of generated samples, we report the Fréchet in-
ception distance (FID; Heusel et al., 2017) and the sliced Wasserstein dis-
tance (SWD; Karras, Aila, Laine, & Lehtinen, 2017) scores with mean and
standard deviation in Figure 4. Note that FID scores are not necessarily
appropriate for dSprites since this data set is significantly different from Im-
ageNet on which the Inception network was originally trained. (Randomly
generated samples are shown in Figure 8 in the appendix). To generate sam-
ples from the deterministic St-RKM (σ = 0), we sample from a fitted normal
distribution on the latent embedding of the data set; for a similar procedure,
see Ghosh et al., 2020). Chiffre 4 shows that the St-RKM variants perform
better (lower mean scores) on most data sets, and within them, the stochas-
tic variants with σ = 10−3 perform best. This can be attributed to a better
generalization of the decoder network due to the addition of noise term on
latent variables (see lemma 1). The training times for St-RKM variants are
shorter compared to FactorVAE and Info-GAN due to a significantly small
number of parameters.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stiefel-Restricted Kernel Machine

2023

Chiffre 4: Fréchet inception distance (FID; Heusel, Ramsauer, Unterthiner,
Nessler, & Hochreiter, 2017) and sliced Wasserstein distance (SWD) scores
(méchant et 1 standard deviation) pour 8000 randomly generated samples (smaller
is better).

To evaluate the disentanglement performance, various metrics have
been proposed. A comprehensive review by Locatello et al. (2019) shows
that the various disentanglement metrics are correlated, albeit with a dif-
ferent degree of correlation across data sets. In this article, we use three
metrics to evaluate disentanglement: Eastwood’s framework (Eastwood &
Williams, 2018), mutual information gap (MIG; Chen et al., 2018), and sep-
arated attribute predictability (SAP; Kumar et al., 2018) scores. Eastwood’s
framework (Eastwood & Williams, 2018) further proposes three metrics: dis-
entanglement: the degree to which a representation factorizes the underlying
factors of variation, with each variable capturing at most one generative fac-
tor; completeness: the degree to which each underlying factor is captured by
a single code variable; and informativeness: the amount of information that
a representation captures about the underlying factors of variation. Fur-
thermore, we use a slightly modified version of MIG score as proposed by
Locatello et al. (2019). Chiffre 6 shows that St-RKM variants have better dis-
entanglement and completeness scores (higher mean scores). Cependant, le
informativeness scores are higher for St-RKM when using a lasso-regressor
in contrast to mixed scores with a random forest regressor. Chiffre 7 further
complements these observations by showing MIG and SAP scores. Ici,
the St-RKM-sl model has the highest mean scores for every data set. Qual-
itative assessment can be done from Figure 5, which shows the generated
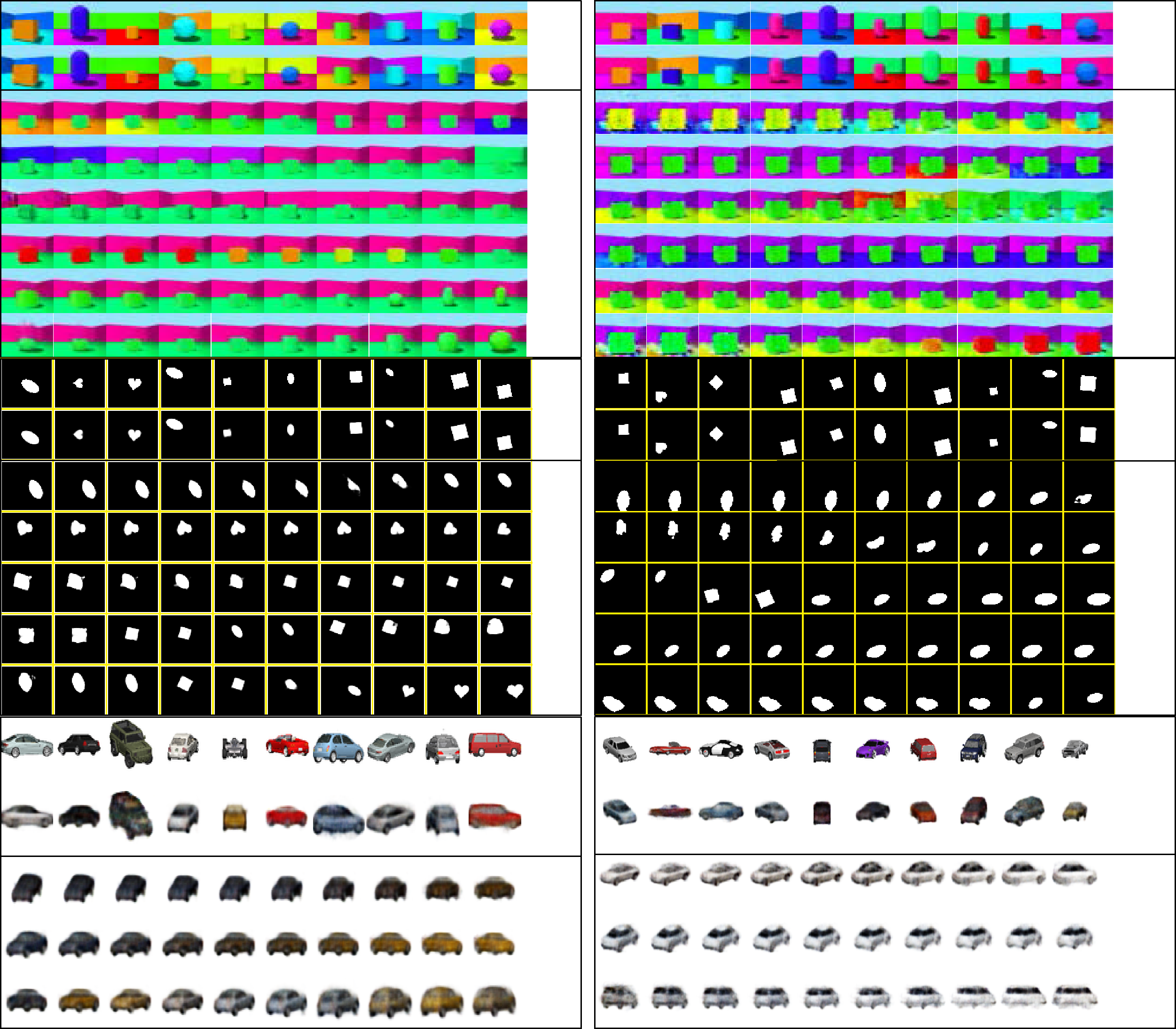
images by traversing along the principal components in the latent space.
In the 3DShapes data set, the St-RKM model captures floor hue, wall hue,
and orientation perfectly but has a slight entanglement in capturing other
factors. This is worse in β-VAE, which has entanglement in all dimensions
except the floor hue, along with noise in some generated images. Similar
trends can be observed in the dSprites and 3D cars data sets.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2024

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 5: Traversals along the principal components. The first two rows show
the ground-truth and reconstructed images. Each subsequent row shows the
generated images by traversing along a principal component in the latent space.
The last column in each subimage indicates the dominant factor of variation.

6 Conclusion

This article proposes he St-RKM model for disentangled representation
learning and generation based on manifold optimization. For the train-
ing, we use the Cayley Adam algorithm of Li et al. (2020) for stochastic
optimization on the Stiefel manifold. Computationally, St-RKM increases
the training time by only a reasonably small amount compared to β-VAE,
par exemple. En outre, we propose several autoencoder objectives and
discuss that the combination of a stochastic AE loss with an explicit opti-
mization on the Stiefel manifold promotes disentanglement. En outre, nous
establish connections with probabilistic models, formulate an evidence
lower bound, and discuss the independence of latent factors. Where the
considered baselines have a trade-off between generation quality and dis-
entanglement, we improve on both of these aspects as illustrated through

Stiefel-Restricted Kernel Machine

2025

Chiffre 6: Eastwood framework’s (Eastwood & Williams, 2018) disentangle-
ment metric with Lasso and random forest (RF) regressor. The plot shows
méchant et 1 standard deviation of scores over 10 iterations. For disentangle-
ment and completeness, a higher score is better; for informativeness, lower is
better. “Info.” indicates (average) root-mean-square error in predicting z.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 7: MIG (Chen et al., 2018; Locatello et al., 2019) and SAP (Kumar, Sat-
tigeri, & Balakrishnan, 2018) scores to evaluate disentanglement performance
showing the mean (standard deviation) over 10 random seeds.

various experiments. The proposed model has some limitations. A first limi-
tation is hyperparameter selection: the number of components in the KPCA,
neural network architecture, and the final size of the feature map. When ad-
ditional knowledge on the data is available, we suggest that the user selects
the number of components close to the number of underlying generating

2026

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

factors. The final size of the feature map should be large enough so that
KPCA extracts meaningful components. Deuxième, we interpret the disentan-
glement as the two orthogonal changes in the latent space corresponding to
two orthogonal changes in input space. Although not perfect, we believe it
is a reasonable mathematical approximation of the loosely defined notion
of disentanglement. De plus, experimental results confirm this assump-
tion. Among the possible regularizers on the hidden features, the model
associated with the squared Euclidean norm was analyzed in detail, alors que
a deeper study of other regularizers is a prospect for further research, dans
particular for the case of spherical units.

Appendix

A.1 Proof of Lemma 1. We first quote a result that is used in the context
of optimization (Nesterov, 2014, lemma 1.2.4). Let f be a function with La-
Lipschitz continuous Hessian. Alors,

(cid:20)
(cid:20)
(cid:9)
(cid:20) F (y1) − f (oui) − ∇ f (oui)
(cid:12)

(y1

(cid:9)
− y)

Hessy[ F ](y1

(cid:20)
(cid:20)
(cid:20)

− y)
(cid:15)

− y) − 1
2
(cid:13)(cid:14)
−y)

r(y1

≤ La
6

(cid:5)y1

− y(cid:5)3
2

(A.1)

Then we calculate the power series expansion of f (oui) = [x − ψ(oui)]2
a and
take the expectation with respect to (cid:6) ∼ N (0, je). D'abord, we have ∇ f (oui) =
−2[x − ψ(oui)]a∇ψa(oui) et

Hessy[ F ] = 2∇ψa(oui)∇ψa(oui)

(cid:9) − 2[x − ψ(oui)]aHessy[ψa].

Then we use equation A.1 with y1
over (cid:6), notice that the order 1 term in σ vanishes since E(cid:6)[(cid:6)] = 0. We find

− y = σU(cid:6). By taking the expectation

E(cid:6)[x − ψ(oui + σU(cid:6))]2
un

= [x − ψ(oui)]2
un

(cid:10)
+ σ 2Tr
U
(cid:10)
−p 2[x − ψ(oui)]aTr
U

(cid:9)∇ψa(oui)∇ψa(oui)
Hessy[ψa]U

(cid:11)

(cid:9)

(cid:11)

+ E(cid:6)r(σU(cid:6)),

where we used that E(cid:6)[(cid:6)(cid:9)M.(cid:6)] = Tr[M.] for any symmetric matrix M since
E(cid:6)[(cid:6)
i j. Suivant, denote Ra(p ) = E(cid:6)r(σU(cid:6)); we can use the Jensen in-
je
equality and subsequently equation A.1:

j] = δ

(cid:6)

|Ra(p )| = |E(cid:6)r(σU(cid:6))| ≤ E(cid:6)|r(σU(cid:6))| ≤ La
6

E(cid:6)(cid:5)σU(cid:6)(cid:5)3
2

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stiefel-Restricted Kernel Machine

2027

= σ ((cid:6)(cid:9)U (cid:9)U(cid:6))1/2 = σ (cid:5)(cid:6)(cid:5)
2. It is useful to notice
2 is distributed according to a chi distribution. By using this remark,

Suivant, we notice that (cid:5)σU(cid:6)(cid:5)
que (cid:5)(cid:6)(cid:5)
we find

|Ra(p )| ≤ σ 3 La
6

E(cid:6)(cid:5)(cid:6)(cid:5)3
2

= σ 3 La
6

√

2(m + 1)(cid:11)((m + 1)/2)
(cid:11)(m/2)

where the last equality uses the expression for the third moment of the chi
distribution and where the gamma function (cid:11) is the extension of the facto-
rial to the complex numbers.

A.2 Details on Evidence Lower Bound for St-RKM model. Now we
discuss the details of ELBO given in section 4. The first term in equation 4.1
est

qU (z|xi )[log(p(xi

|z))] = − 1
2p 2
0

E(cid:6)∼N (0,je)

(cid:5)xi

− ψξ (PU φθ (xi) + σ PU (cid:6) + δP

U⊥ (cid:6))(cid:5)2
2

− d
2

log(2πσ 2

0 ),

where we used the following reparameterization following Kingma and
(cid:22)
Welling (2014): E
U⊥ )(cid:15))
,
with p(X|z) = N (X|ψξ (z), p 2
U⊥ ).
0
Clairement, the above expectation can be written as

je), and qU (z|X) = N (z|PU φθ (X), σ 2PU + δ2P

F (PU φθ (X) + (σ PU + δP

qU (z|xi )[ F (z)] = E(cid:6)∼N (0,je)

(cid:21)

E(cid:6)E(cid:6)⊥

(cid:5)xi

− ψξ (PU φθ (xi) + σU(cid:6) + δU⊥(cid:6)⊥)(cid:5)2
2

avec (cid:6) ∼ N (0, Im) et (cid:6)⊥ ∼ N (0, je(cid:2)−m). Ainsi, we fix σ 2
= 1/2 and take δ >
0
0 to a numerically small value. For the other terms of equation 4.1, we use
the formula giving the KL divergence between multivariate normals. Let N
0
and N
1 and covariance
(cid:13)
, (cid:13)
0

1 être (cid:2)-variate normal distributions with mean μ
0
1, respectivement. Alors,

, m

(cid:23)

KL(N

, N

1) = 1
2

Tr((cid:13)−1
1

(cid:13)

0) + (m
1

− μ

(cid:9)(cid:13)−1

1 (m

− μ

0) − (cid:2) + log

(cid:24)

det (cid:13)
1
det (cid:13)
0

(cid:25)(cid:26)

By using this identity, we find the second term of equation 4.1,

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

KL[qU (z|xi), q(z|xi)] = 1
2

(cid:23)

mσ 2 + ((cid:2) − m)δ2
c 2
(cid:24)

+ 1
c 2
(cid:25)(cid:26)

c 2(cid:2)
σ 2mδ2((cid:2)−m)

− (cid:2) + log

(cid:5)φθ (xi) − PU φθ (xi)(cid:5)2
2

2028

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

Tableau 2: Data Sets and Hyperparameters Used for the Experiments.

Data Set

MNIST
fMNIST
SVHN
dSprites
3DShapes
3D cars

60,000
60,000
73,257
737,280
480,000
17,664

28 × 28
28 × 28
32 × 32 × 3
64 × 64
64 × 64 × 3
64 × 64 × 3

10
10
10
5
6
3

256
256
256
256
256
256

Note: N is the number of training samples, d
the input dimension (resized images), m the sub-
space dimension, and M the minibatch size.

where q(z|X) = N (z|φθ (X), γ 2I(cid:2)). For the third term in equation 4.1, we find

(cid:3)
Tr((σ 2PU + δ2P

KL[qU (z|xi), p(z)] = 1
2
(cid:4)
+ log det((cid:13)) − (cid:2) − log(σ 2mδ2((cid:2)−m))
,

U⊥ )(cid:13)−1) + (PU φθ (xi))

(cid:9)(cid:13)−1(PU φθ (xi))

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

with p(z) = N (0, (cid:13)). By averaging over i = 1, . . . , n, we obtain

1
n

n(cid:2)

je = 1

KL[qU (z|xi), p(z)] = 1
2

(cid:3)
Tr((σ 2PU + δ2P

U⊥ )(cid:13)−1) + Tr(PUCθPU (cid:13)−1)

(cid:4)
+ log det((cid:13)) − (cid:2) − log(σ 2mδ2((cid:2)−m))

where we used the cyclic property of the trace and Cθ = 1
φθ (xi)
n
φθ (xi)(cid:9). This proves the analogous expression in section 4. Enfin, the esti-
mation of the optimal (cid:13) can be done in parallel to the maximum likelihood
estimation of the covariance matrix of a multivariate normal.

n
je = 1

(cid:9)

A.3 Data Sets and Hyperparameters. We refer to Tables 2 et 3 pour
specific details on the model architectures, data sets, and hyperparameters
used in this article. All models were trained on full data sets and for a maxi-
mum of 1000 epochs. En outre, all data sets are scaled between [0-1] et
are resized to 28 × 28 dimensions except dSprites and 3D cars. The PyTorch
library (single precision) in Python was used as the programming language
sur 8 GB NVIDIA QUADRO P4000 GPU. See algorithm 1 for training the
St-RKM model. In the case of FactorVAE, the discriminator architecture is
same as proposed in the original paper (Kim & Mnih, 2018).

A.3.1 Disentanglement Metrics. MIG was originally proposed by Chen
et autres. (2018); cependant, we use the modified metric as proposed in Locatello

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stiefel-Restricted Kernel Machine

2029

Tableau 3: Model Architectures.

Data Set

Architecture

MNIST/fMNIST/

φθ (·) =

/SVHN/3DShapes/
sDprites/3Dcars

⎧

⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎩

Conv [c] × 4 × 4;
Conv [c × 2] × 4 × 4;
Conv [c × 4] × ˆk × ˆk;
FC 256;

FC 50 (Linear)

ψζ (·) =

⎧

⎪⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎪⎩

FC 256;
FC [c × 4] × ˆk × ˆk;
Conv [c × 2] × 4 × 4;
Conv [c] × 4 × 4;
Conv [c] (Sigmoid)

Remarques: All convolutions and transposed convolutions are with stride 2 and padding 1. Un-
less stated otherwise, layers have parametric-RELU (α = 0.2) activation functions, except
output layers of the preimage maps, which have sigmoid activation functions (since in-
put data are normalized [0, 1]). Adam and Cayley ADAM optimizers have learning rates
−4, respectivement. The preimage map/decoder network is always taken as
2 × 10
transposed of the feature map/encoder network. c = 48 for 3D cars; and c = 64 for all oth-
ers. Plus loin, ˆk = 3 and stride 1 for MNIST, fMNIST, SVHN and 3DShapes; and ˆk = 4 pour
others. SVHN and 3DShapes are resized to 28 × 28 input dimensions.

−4 and 10

et autres. (2019). We evaluate this score on 5000 test points across all the con-
sidered data sets. SAP and Eastwood’s metrics use different classifiers to
compute the importance of each dimension of the learned representation
for predicting a ground-truth factor. For these metrics, we randomly sam-
ple 5000 et 3000 training and testing points, respectivement. To compute
these metrics, we use the open source library available at github.com/
google-research/disentanglement_lib.

A.4 Ablation Studies.

A.4.1 Significance of the KPCA Loss. Dans cette section, we show an ablation
study on the KPCA loss and evaluate its effect on disentanglement. We re-
peat the experiments of section 5 on the mini-3DShapes data set (floor hue,
wall hue, object hue, and scale: 8000 samples), where we consider three dif-
ferent variants of the proposed model:

1. St-RKM (σ = 0): The KPCA loss is optimized in a stochastic manner
using the Cayley ADAM optimizer, as proposed in this article.

2. Gen-RKM: The KPCA loss is optimized exactly at each step by per-
forming an eigendecomposition in each minibatch (this corresponds
to the algorithm in Pandey et al., 2021).

3. AE-PCA: A standard AE is used, and a reconstruction loss is mini-
mized for the training. As a postprocessing step, a PCA is performed
on the latent embedding of the training data.

The encoder/decoder maps are the same across all the models, and for the
AE-PCA model, additional linear layers are used to map the latent space to

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2030

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

Tableau 4: Training Timings per Epoch (in minutes) and Disentanglement Scores
(Heusel et al., 2017) for Different Variants of RKM When Trained on the mini-
3Dshapes Data Set.

St-RKM (σ = 0) Gen-RKM AE-PCA

Training time
Disentanglement score

Compliance score

Information score

Lasso
RF
Lasso
RF
Lasso
RF

3.01 (0.71)
0.40 (0.02)
0.27 (0.01)
0.64 (0.01)
0.67 (0.02)
1.01 (0.02)
0.98 (0.01)

9.21 (0.54)
0.44 (0.01)
0.31 (0.02)
0.51 (0.01)
0.58 (0.01)
1.11 (0.02)
1.09 (0.01)

2.87 (0.33)
0.35 (0.01)
0.22 (0.02)
0.42 (0.01)
0.45 (0.02)
1.20 (0.01)
1.17 (0.02)

Remarques: Gen-RKM has the worst training time but gets the highest disentangle-
ment scores. This is due to the exact eigendecomposition of the kernel matrix at
every iteration. This computationally expensive step is approximated by the St-
RKM model, which achieves significant speed-up and scalability to large data
sets. Enfin, the AE-PCA model has the fastest training time due to the absence
of eigendecompositions in the training loop. Cependant, using PCA in the post-
processing step alters the basis of the latent space. This basis is unknown to the
decoder network, resulting in degraded disentanglement performance.

Tableau 5: FID Scores Computed on Randomly Generated 8000 Images When
Trained with Architecture and Hyperparameters.

St-RKM

VAE

β-VAE

FactorVAE

InfoGAN

MNIST
fMNIST

24.63 (0.22)
61.44 (1.02)

36.11 (1.01)
73.47 (0.73)

42.81 (2.01)
75.21 (1.11)

35.48 (0.07)
69.73 (1.54)

45.74 (2.93)
84.11 (2.58)

Remarques: Lower is better with standard deviations. Adapted from Dupont (2018).

the subspace. From Table 4, we conclude that optimizing the KPCA loss
during training improves disentanglement. De plus, using a stochastic
algorithm improves computation time and scalability with only a slight
decrease in disentanglement score. Note that calculating the exact eigen-
decomposition at each step (Gen-RKM) comes with numerical difficul-
liens. En particulier, double floating-point precision has to be used together
with a careful selection of the number of principal components to avoid
ill-conditioned kernel matrices. This problem is not encountered when us-
ing the St-RKM training algorithm.

A.4.2 Smaller Encoder/Decoder Architecture. Dans cette section, we analyze the
impact of the encoder/decoder architecture on the generation quality of
considered models. The generation quality experiment of section 5 is re-
peated on the fMNIST and MNIST data set, where the architecture and hy-
perparameters are adapted from Dupont (2018). From Table 5 and Figure 9,

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stiefel-Restricted Kernel Machine

2031

Tableau 6: Computing the Diagonalization Scores (voir la figure 3).

Models

dSprites

3DShapes

3D cars

St-RKM-sl (σ = 10
St-RKM (σ = 10
St-RKM (σ = 10

−3, U(cid:7))
−3, random U)

−3, U(cid:7))

0.17 (0.05)
0.26 (0.05)
0.61 (0.02)

0.23 (0.03)
0.30 (0.10)
0.72 (0.01)

0.21 (0.04)
0.31 (0.09)
0.69 (0.03)

(cid:9)

i∈C U

φθ (xi ) (cf.
Remarques: Denote M = 1
|C|
F , où
equation 3.6). Then we compute the score as
diag : Rm×m (cid:8)→ Rm×m sets the off-diagonal elements of matrix to zero. Le
scores are computed for each model over 10 random seeds and show the mean
(standard deviation). Lower scores indicate better diagonalization.

(cid:9)
U(cid:7), with yi
(cid:7) ∇ψ(yi )∇ψ(yi )
(cid:16)
(cid:16)
(cid:16)
(cid:16)
M − diag(M.)

= P
U
/ (cid:5)M.(cid:5)

(cid:9)

we see that the overall FID scores and generation quality have improved;
cependant, the relative scores among the models did not change significantly.

A.4.3 Analysis of St-RKM with a Fixed U. We discuss here the role of the
optimization of St((cid:2), m) on disentanglement in the case of a classical AE
perte (σ = 0). To do so, a matrix ˜U ∈ St((cid:2), m) is generated randomly3 and
kept fixed during the training of the following optimization problem,

min
je,ξ

λ 1
n

n(cid:2)

je = 1

L(0)
ξ, ˜U (xi

, φθ (xi)) + 1
n
(cid:12)

n(cid:2)

je = 1

(cid:5)P.(ε)

˜U⊥ φθ (xi)(cid:5)2
2
(cid:15)
(cid:13)(cid:14)

(A.2)

regularized PCA objective

˜U⊥ = ε( ˜U ˜U (cid:9) + εI(cid:2))

with λ = 1 and where ε ≥ 0 is a regularization constant and where the reg-
ularized (or mollified) projector P(ε)
−1 is used in order to
prevent numerical instabilities. En effet, if ε = 0, the second term in equation
A.2 (PCA term) is not strictly convex as a function of φθ, since this quadratic
form has flat directions along the column subspace of ˜U. Our numerical
simulations in single-precision PyTorch with ε = 0 exhibit instabilities, que
est, the PCA term in equation A.2 takes negative values during the training.
Ainsi, the regularized projector is introduced so that the PCA quadratic
is strongly convex for ε > 0. This instability is not observed in the training
of equation 3.3 where U is not fixed. This is one asset of our training pro-
cedure using optimization over Stiefel manifold. Explicitly, the regularized
projector satisfies the following properties:
˜U⊥ u⊥ = u⊥ for all u⊥ ∈ (range(U ))
˜U⊥ u = εu for all u ∈ range(U ).

• P(ε)
• P(ε)

⊥

Using a random ˜U ∈ St((cid:2), m) can be interpreted as sketching the encoder map in the
spirit of randomized orthogonal systems (ROS) sketches (see Yang, Pilanci, & Wainwright,
2017).

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2032

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

Chiffre 8: Samples of randomly generated batch of images used to compute FID
scores and SWD scores (voir la figure 4).

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Thanks to the push-through identity, we have the alternative expression
P.(ε)
P.(ε)
˜U⊥ = I − U(U (cid:9)U + εIm)
˜U⊥ = P ˜U⊥ , as it
−6, the regularized
should. In our experiments, we set ε = 10
PCA objective in equation A.2 takes negative values after a few epochs due
to the numerical instability as mentioned above.

−1U (cid:9). Donc, it holds limε→0

−5. If ε ≤ 10

Stiefel-Restricted Kernel Machine

2033

Chiffre 9: Samples of randomly generated images used to compute the FID
scores. See Table 5.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

Chiffre 10: (un) Loss evolution (log plot) during the training of equation A.2 over
1000 epochs with ε = 10−5 once with Cayley ADAM optimizer (green curve)
and then without (blue curve). (b) Traversals along the principal components
when the model was trained with a fixed U, c'est, with the objective given by
equation A.2 and ε = 10−5. There is no clear isolation of a feature along any of
the principal components, indicating further that optimizing over U is key to
better disentanglement.

In Figure 10a, the evolution of the training objective A.2 is displayed.
It can be seen that the final objective has a lower value [exp(6.78) ≈ 881]
when U is optimized compared to its fixed counterpart [exp(6.81) ≈ 905],
showing the merit of optimizing over Stiefel manifold for the same parame-
ter ε. Ainsi, the subspace determined by range(U ) has to be adapted to the
encoder and decoder networks. Autrement dit, the training over θ, ξ is not

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2034

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

sufficient to minimize the St((cid:2), m) objective with Adam. Figure 10b further
explores the latent traversals in the context of this ablation study. In the top
row of Figure 10b (latent traversal in the direction of u1), both the shape of
the object and the wall hue are changing. A coupling between wall hue and
shape is also visible in the bottom row of this figure.

Remerciements

Most of this work was done when M.F. was at KU Leuven.

EU: The research leading to these results received funding from the Euro-
pean Research Council under the European Union’s Horizon 2020 recherche
and innovation program/ERC Advanced Grant E-DUALITY (787960). Ce
article reflects only the authors’ views, and the EU is not liable for any use
that may be made of the contained information.

Research Council KUL: Optimization frameworks for deep kernel ma-

chines C14/18/068.

Flemish government: (un) FWO: projects: GOA4917N (Deep Restricted
Kernel Machines: Methods and Foundations), PhD/postdoc grant. (b) Ce
research received funding from the Flemish government (AI Research Pro-
gram). We are affiliated with Leuven.AI-KU Leuven institute for AI, B-3000,
Leuven, Belgium.

Ford KU Leuven Research Alliance Project: KUL0076 (stability analysis
and performance improvement of deep reinforcement learning algorithms).
Vlaams Supercomputer Centrum: The computational resources and ser-
vices used in this work were provided by the VSC (Flemish Supercomputer
Centre), funded by the Research Foundation–Flanders (FWO) and the Flem-
ish government department EWI.

Les références

Absil, P.-A., Mahony, R., & Sepulchre, R.. (2008). Optimization algorithms on matrix

manifolds. Princeton, New Jersey: Princeton University Press.

Avron, H., Nguyen, H., & Woodruff, D. (2014). Subspace embeddings for the poly-
nomial kernel. In Z. Ghahramani, M.. Welling, C. Cortes, N. Lawrence, & K. Q.
Weinberger (Éd.), Advances in neural information processing systems, 27 (pp. 2258–
2266). Red Hook, New York: Curran.

Bengio, Y., Courville, UN., & Vincent, P.. (2013). Representation learning: A review and
new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence,
35(8), 1798–1828. 10.1109/TPAMI.2013.50, PubMed: 23787338

Bourgeois, C., & Kim, H. (2018). 3Dshapes dataset. https://github.com/deepmind/

3dshapes-dataset/

Bourgeois, C. P., Higgins, JE., Pal, UN., Matthey, L., Watters, N., Desjardins, G., & Ler-
chner, UN. (2017). Understanding disentangling in β-VAE. In NIPS 2017 Travail-
shop on Learning Disentangled Representations: From Perception to Control. https:
//sites.google.com/view/disentanglenips2017

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stiefel-Restricted Kernel Machine

2035

Chen, R.. T. Q., Li, X., Grosse, R.. B., & Duvenaud, D. K. (2018). Isolating sources
of disentanglement in variational autoencoders. In S. Bengio, H. Wallach, H.
Larochelle, K. Grauman, N. Cesa-Bianchi, & R.. Garnett (Éd.), Advances in neu-
ral information processing systems, 31 (pp. 2610–2620). Red Hook, New York: Curran.
Dupont, E. (2018). Learning disentangled joint continuous and discrete representa-
tion. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, & R..
Garnett (Éd.), Advances in neural information processing systems, 31 (pp. 708–718).
Red Hook, New York: Curran.

Eastwood, C., & Williams, C. K. je. (2018). A framework for the quantitative evalua-
tion of disentangled representations. In Proceedings of the International Conference
on Learning Representations.

Ghosh, P., Sajjadi, M.. S., Vergari, UN., Noir, M., & Schölkopf, B. (2020). From varia-
tional to deterministic autoencoders. In Proceedings of the International Conference
on Learning Representations.

Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B., & Hochreiter, S. (2017). GANs
trained by a two time-scale update rule converge to a local Nash equilibrium. Dans
je. Guyon, Oui. V. Luxburg, S. Bengio, H. Wallach, R.. Fergus, S. Vishwanathan, &
R.. Garnett (Éd.), Advances in neural information processing systems, 30 (pp. 6629–
6640). Red Hook, New York: Curran.

Higgins, JE., Matthey, L., Pal, UN., Bourgeois, C., Glorot, X., Botvinick, M., . . . Lerchner, UN.
(2017). Beta-VAE: Learning basic visual concepts with a constrained variational
framework. In Proceedings of the International Conference on Learning Representations
(vol. 2, p. 6).

Hinton, G. E. (2005). What kind of a graphical model is the brain? In Proceed-
ings of the 19th International Joint Conference on Artificial Intelligence (pp. 1765–
1775).

Karras, T., Aila, T., Laine, S., & Lehtinen, J.. (2017). Progressive growing of GANs
for improved quality, stability, and variation. In Proceedings of the International
Conference on Learning Representations.

Kim, H., & Mnih, UN. (2018). Disentangling by factorising. In Proceedings of the Thirty-

Fifth International Conference on Machine Learning (vol. 80, pp. 2649–2658).

Kingma, D. P., & Welling, M.. (2014). Auto-encoding variational Bayes. In Proceedings

of the International Conference on Learning Representations.

Kumar, UN., Sattigeri, P., & Balakrishnan, UN. (2018). Variational inference of disen-
tangled latent concepts from unlabeled observations. In Proceedings of the Interna-
tional Conference on Learning Representations. https://openreview.net/forum?id=
H1kG7GZAW

LeCun, Y., & Cortes, C. (2010). MNIST handwritten digit database. http://yann.lecun

.com/exdb/mnist/

LeCun, Y., Huang, F. J., & Bottou, L. (2004). Learning methods for generic object
recognition with invariance to pose and lighting. In Proceedings of the Conference
on Computer Vision and Pattern Recognition.

Li, J., Li, F., & Todorovic, S. (2020). Efficient Riemannian optimization on the Stiefel
manifold via the Cayley transform. In Proceedings of the International Conference on
Learning Representations.

Locatello, F., Bauer, S., Luˇci´c, M., Rätsch, G., Gelly, S., Schölkopf, B., & Bachem,
Ô. F. (2019). Challenging common assumptions in the unsupervised learning of

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
c
o
_
un
_
0
1
5
2
8
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2036

UN. Pandey, M.. Fanuel, J.. Schreurs, and J. Suykens

disentangled representations. In Proceedings of the International Conference on Ma-
chine Learning.

Locatello, F., Tschannen, M., Bauer, S., Rätsch, G., Schölkopf, B., & Bachem, Ô. (2020).
Disentangling factors of variations using few labels. In International Conference on
Learning Representations.

Matthey, L., Higgins, JE., Hassabis, D., & Lerchner, UN. (2017). dSprites: Disentanglement

testing Sprites dataset. https://github.com/deepmind/dsprites-dataset/

Nesterov, Oui. (2014). Introductory lectures on convex optimization: A basic course. Berlin:

Springer.

Netzer, Y., Wang, T., Coates, UN., Bissacco, UN., Wu, B., & Ng, UN. Oui. (2011). Reading
digits in natural images with unsupervised feature learning. In NIPS Workshop
on Deep Learning and Unsupervised Feature Learning. http://ufldl.stanford.edu/
housenumbers/nips2011_housenumbers.pdf

Pandey, UN., Schreurs, J., & Suykens, J.. UN. K. (2020). Robust generative restricted
kernel machines using weighted conjugate feature duality. In Proceedings of
the Sixth International Conference on Machine Learning, Optimization, and Data
Science.

Pandey, UN., Schreurs, J., & Suykens, J.. UN. (2021). Generative restricted kernel
machines: A framework for multi-view generation and disentangled feature
learning. Neural Networks, 135, 177–191. 10.1016/j.neunet.2020.12.010, PubMed:
33395588

Reed, S., Zhang, Y., Zhang, Y., & Lee, H. (2015). Deep visual analogy-making. In C.
Cortes, N. Lawrence, D. Lee, M.. Sugiyama, & R.. Garnett (Éd.), Advances in neural
information processing systems, 28. Red Hook, New York: Curran.

Rezende, D. J., & Mohamed, S. (2015). Variational inference with normalizing flows.

In Proceedings of the International Conference on Machine Learning.

Rolínek, M., Zietlow, D., & Martius, G. (2019). Variational autoencoders pursue PCA
instructions (by accident). In Proceedings of the 2019 IEEE/CVF conference on Computer
Vision and Pattern Recognition (pp. 12398–12407).

Salakhutdinov, R., & Hinton, G. (2009). Deep Boltzmann machines. In Proceedings of

the Twelfth International Conference on Artificial Intelligence and Statistics.

Suykens,

J.. UN. K.

(2017). Deep restricted kernel machines using conjugate
feature duality. Neural Computation, 29(8), 2123–2163. 10.1162/neco_a_00984,
PubMed: 28562217

Xiao, H., Rasul, K., & Vollgraf, R.. (2017). Fashion-MNIST: A novel image dataset for

benchmarking machine learning algorithms. arXiv:1708.07747.

Lequel, Y., Pilanci, M., & Wainwright, M.. J.. (2017). Randomized sketches for kernels:
Fast and optimal nonparameteric regression. Annals of Statistics, 45(3), 991–1023.
10.1214/16-AOS1472

Received October 4, 2021; accepted May 24, 2022.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d