ARTICLE - Recherche en IA spécialisée au MIT

ARTICLE

Communicated by Eric T. Shea-Brown

Reduced-Dimension, Biophysical Neuron Models
Constructed From Observed Data

Randall Clark
r2clark@ucsd.edu
Lawson Fuller
llfuller@ucsd.edu
Jason A. Platt
jplatt@ucsd.edu
Department of Physics, University of California San Diego, La Jolla,
Californie 92093-0374, U.S.A.

Henry D. je. Abarbanel
habarbanel@ucsd.edu
Marine Physical Laboratory, Scripps Institution of Oceanography, and Department
of Physics, University of California San Diego, La Jolla, Californie 92093-0374, U.S.A.

Using methods from nonlinear dynamics and interpolation techniques
from applied mathematics, we show how to use data alone to construct
discrete time dynamical rules that forecast observed neuron properties.
These data may come from simulations of a Hodgkin-Huxley (HH) nouveau-
ron model or from laboratory current clamp experiments. In each case, le
reduced-dimension, data-driven forecasting (DDF) models are shown to
predict accurately for times after the training period.

When the available observations for neuron preparations are, for ex-
ample, membrane voltage V(t) only, we use the technique of time delay
embedding from nonlinear dynamics to generate an appropriate space in
which the full dynamics can be realized.

The DDF constructions are reduced-dimension models relative to HH
models as they are built on and forecast only observables such as V(t).
They do not require detailed specification of ion channels, their gating
variables, and the many parameters that accompany an HH model for lab-
oratory measurements, yet all of this important information is encoded in
the DDF model. As the DDF models use and forecast only voltage data,
they can be used in building networks with biophysical connections.
Both gap junction connections and ligand gated synaptic connections
among neurons involve presynaptic voltages and induce postsynaptic
voltage response. Biophysically based DDF neuron models can replace
other reduced-dimension neuron models, say, of the integrate-and-fire
type, in developing and analyzing large networks of neurons.

Neural Computation 34, 1545–1587 (2022) © 2022 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01515

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1546

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

When one does have detailed HH model neurons for network compo-
nents, a reduced-dimension DDF realization of the HH voltage dynamics
may be used in network computations to achieve computational effi-
ciency and the exploration of larger biological networks.

1 Introduction

1.1 General Setting. When we have observed data generated by a com-
plex, nonlinear system, neurons and their networks are a prime example of
ce, but we do not have a model for the detailed neurodynamics of the sys-
thème, it is possible to use those measured data alone to create a dynamical
rule that forecasts the future of the observed quantities beyond the window
in time where the data were measured. We call this data-driven forecasting
(DDF).

Our goal in this article is to demonstrate how to achieve and then use

DDF in the context of neuroscience.

DDF is to be viewed as a way to capture observed aspects of neurobio-
logical data in contrast to the usual method of creating a detailed biophys-
ical model, often of the Hodgkin-Huxley (HH) type, which may or may
not be correct, specifying all of the relevant ion currents, the required gat-
ing variables, and the concentrations of relevant quantities such as [Ca2+
](t)
(Johnston & Wu, 1995; Sterratt, Graham, Gillies, & Willshaw, 2011).

Unknown quantities in such an HH model may be estimated using data
assimilation (DA) (Toth et al., 2011; Kostuk et al., 2012; Meliza et al., 2014;
Nogaret et al., 2016; Abarbanel, 2022). DA requires a model of the observed
complex system and, bien sûr, data from observing that system. The data
are used to train items in the model such as fixed parameters and unob-
served state variables.

DDF does not require a model of all these often unobservable details.
Néanmoins, as it is built on observed data, it encodes those details while
forecasting only the observable properties of the neuron activity. Both
DA and DDF may be seen as a form of supervised learning (Abarbanel,
Rozdeba, & Shirman, 2018). À cet égard, they may also be regarded as
methods of machine learning.

If the construction and analysis of a biophysically detailed HH model
have been achieved, perhaps employing DA, using HH models in large
networks of biological interest may prove computationally quite challeng-
ing. DDF may be utilized to accurately forecast the voltage time course of
this HH model, thus replacing it in the network of interest. Only the volt-
ages across neuron cell membranes are used in the communication among
neurons in a network; thus, DDF neurons are nicely suited for use as the
dynamical elements of functional biological networks. Using a reduced-
dimensional model in network studies can result in significantly decreased
computational tasks.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1547

1.2 Data of Interest. We start with the formulation of DDF models for

individual neurons.

We have in mind data where a neuron is stimulated by a known forc-
ing via an injected current Istim(t), and its membrane voltage response V(t)
is measured, namely, current clamp experiments. One observes V(t) at dis-
+ nh; n = 0, 1, . . . , N. We use these data to build a bio-
crete times tn = t0
physically based, nonlinear discrete time map that takes V (tn) → V (tn+1)
for any selected stimulating current. Surtout, the map must predict well
for n ≥ N + 1.

We demonstrate that this is accomplished in the analysis of numerically
generated data from a standard neuron model and in the analysis of current
clamp data collected in a laboratory environment.

When this is successful, we will have created a DDF dynamical rule mov-
ing V(t) forward in time without regard for gating variable time courses—
parameters such as maximal conductances or reversal potentials, chemical
reaction rates, or any of the other detailed biophysical characteristics of the
HH neuron dynamics. Yet built from observed data, the biophysical infor-
mation is embedded in the DDF model.

As we shall demonstrate here, one is able to accomplish this but, pas
surprisingly, must give up some things that are found in the use of a detailed
model. The method is restricted to forecasting only what is observed.

1.3 Useful Attributes of DDF Neurons. This forecasting construction
V (tn) → V (tn+1), which we call a DDF neuron, may be used in network
models of interest. DDF neurons would be located at the nodes of the net-
travail, leaving only the network connectivity to be determined, possibly by
DA from observed network activity data (Abarbanel, 2022).

In biological networks, the individual neurons are driven by external
currents, if present, and by the currents received from other neurons presy-
naptic to it. The gap junction and synaptic current connections are described
by the presynaptic voltage and the postsynaptic voltages, allowing DDF
neurons to be valuable, efficient network nodes in computational models
of functional neural networks.

If one has the goal of controlling aspects of functional neural networks to
achieve desired goals, DDF neurons provide a computationally inexpensive
way of incorporating the observable properties of such a network. This is
significant as observables are the attributes that control forces may affect.

2 Plan for This Article

1. To begin, we describe the DDF method as applied to individual neu-
ron data and give an example using numerical data from solving a basic
Hodgkin-Huxley (HH) neuron model (Hodgkin & Huxley, 1952; Johnston
& Wu, 1995; Sterratt et al., 2011) with Na, K, and Leak channels. For brevity,
we designate this HH model as an NaKL neuron.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1548

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

2. The time courses for the voltage and the Na and K channel gating vari-
ables {V (t), m(t), h(t), n(t)} from the model are used as “data” and analyzed
in two settings:

• The first setting is a confidence-building exercise, not biologically real-
istic, that assumes we have observed data on the membrane voltage
V(t), as well as on all three of the HH gating variables {m(t), h(t), n(t)}
in the model.

• The second setting conforms to what one can actually do in a cur-
rent clamp experiment, namely, observe only the membrane voltage
V(t) given the stimulating current Istim(t). This requires us to add to
the basic DDF formulation the idea of constructing enlarged state
spaces from the observed variables and their time delays (Takens,
1981; Aeyels, 1981un, 1981b; Abarbanel, 1996; Kantz & Schreiber, 2004).
This method is familiar and essential in the study of nonlinear dy-
namics and will be explained in the present context.

3. We next turn to the DDF analysis of laboratory current clamp data

acquired in the Margoliash laboratory at the University of Chicago.

4. An analysis is then made of how DDF neurons can be used in the
construction and study of networks of neurons. In this article, we first di-
rect our attention to a quite simple two-neuron example with gap junction
relations.

5. Then we present a study of a network segment where a presynaptic
neuron, driven by a stimulating current Istim(t), drives a postsynaptic neu-
ron via a ligand gated synapse.

6. A summary and discussion complete the article.
7. We include three appendixes:

• Appendix A is a brief manual discussing how one builds DDF models

in practice.

• Appendix B has the formulation for incorporating ligand gated

synaptic connections into a DDF-based network model.

• Appendix C contains a short biophysical discussion on the choice of
stimulating currents Istim(t) selected to permit the DDF model to gen-
eralize its response to a wide class of stimulating currents. This ap-
pendix was developed following questions from two reviewers of an
earlier draft of this article.

3 Discussion of the Methods of DDF

Our discussion begins with a broader formulation of DDF than will be re-
quired in neurobiology, where only V(t) is observed in laboratory current
clamp experiments. We return to the realistic scenario of observing only
V(t) after providing the broad perspective. An example of data, au-delà
membrane voltage, where DDF will permit accurate forecasting, includes

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1549

fluorescence associated with Ca concentration variation (Ca2+
)(t) dans le
presence of a Ca indicator (Smetters, Majewska, & Yuste, 1999; Vogelstein
et coll., 2009; MacLean & Yuste, 2009), (Ca2+
)(t). The DDF formulation for
[Ca2+

](t) is described in section 7.

The idea of DDF is to start with the collection of D-dimensional observed
data u(tn) = u(n) = {ua(n)}; a = 1, 2, . . . , D, sampled at discrete times tn
+ nh; n = 0, 1, 2, . . . , N
over an observation window [t0
in time steps of size h.

≤ tn ≤ tN]; tn = t0

Suivant, using only these data, we discuss how to construct a discrete time
map u(n + 1) = u(n) + F(toi(n), χ) for forecasting the future of those data.
The χ are parameters in f(toi(n), χ) that we will estimate (train) on the ob-
served data. The nonlinear function f(toi, χ) is called the vector field (Strogatz,
2015) of the discrete time map.

When we do not have a model of the biophysical processes generating
toi(t), we ask: Can we build a representation of f(toi, χ) and use observed
data to determine the unknown, time-independent quantities χ in that
representation?

We will answer this in the affirmative using applicable developments
in applied mathematics (Hardy, 1971; Broomhead & Lowe, 1988; Casdagli,
1989; Judd & Mees, 1995; Schaback, 1995; Powell, 2002) explored in depth
over many years.

The general idea was well investigated in the context of autonomous
systems where there is no external forcing. This is not the situation that
one addresses in neurobiology, where neurons are stimulated by external
sources and, in functional networks, by the activity of other neurons in the
réseau.

The first step is to select a parameterized representation for f(toi, χ) en utilisant
toi(n + 1) = u(n) + F(toi(n), χ) pour 0 ≤ n ≤ N, to estimate (train) the parame-
ters χ. Once the χ are known, we are able to use this trained discrete time
dynamical rule u(n + 1) = u(n) + F(toi(n), χ) to forecast the behavior of the
observed quantities u(n) for n ≥ N + 1 in time steps of size h.

We use the results of Schaback (1995) and Powell (2002) montrant que

one can accurately represent a multivariate function of u, F(toi, χ), comme

fa(toi, χ) =

J.(cid:2)

j=1

ca j p j(toi) +

Nc(cid:2)

q=1

waqψ((u − uc(q))2, p ); a = 1, 2, . . . , D.

(3.1)

, waq, p } are among the parameters to be estimated or trained using

Le {ca j
the observed data {toi(n)}.

In equation 3.1, the p j(toi) are multivariate polynomials of order j, Le
functions ψ((u − uc(q))2, p ) are called radial basis functions (RBFs). The Nc
{uc(q)} are denoted as centers, and they are selected from the observed data:
Nc ≤ N.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1550

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

In developing this representation of the vector field as a function on u
espace, we may think of the {toi(n); n = 0, . . . , N} as samples of a distribution
in u. The f(toi, χ) are designed to interpolate among these samples.

The training of the {ca j

, waq} is a linear algebra problem (Presse, Teukol-
sky, Vetterling, & Flannery, 2007). The linear algebra problem for Nc (cid:5)= N
requires regularization, and that means we must specify a Tikhonov regu-
larization parameter, which we call β. This is also called ridge regression.
We must also specify any parameters appearing in the functions ψ((u −
uc(q))2, p ). A guide to how we select all parameters of the DDF formulation,
in practice, y compris {ca j
, waq, p, β}, is given in appendix A. When we use
time delay coordinates, as we do in section 6, two more parameters enter:
the time delay τ and the dimension of the time delay vector DE. So χ =
{ca j
, waq, p, β, τ, DE} is the full set of parameters that we must estimate from
the given data.

The representation of the vector field fa(toi, χ) in equation 3.1 has both
what one often finds described as RBFs by themselves (the second term on
the right) and polynomials in u. We first tried to work with the polynomials
alone, but found that when J was only 3 ou 4, they were not able to represent
the kind of nonlinearities found in biophysical models of neurons. As J in-
creases the number of coefficients ca j grows more or less as J!, and even the
linear algebra problem becomes difficult. The more general case in equation
3.1 is discussed in Schaback (1995) and Powell (2002). In practice we only
used the monomial u.

The possibility of including polynomial terms beyond u(n) was not re-
quired to achieve the results we present, so the training (estimation) of χ is
done using

ua(n + 1) = ua(n) +

Nc(cid:2)

q=1

waqψ((toi(n) − uc(q))2, p ), n = 0.1, . . . , N,

(3.2)

and we realize it by minimizing

N−1(cid:2)

D(cid:2)

[ua(n + 1) − ua(n) −

n=0

a=1

Nc(cid:2)

q=1

waqψ((toi(n) − uc(q))]2, p )]2,

(3.3)

which we regularize in a well-established way (Press et al., 2007). The de-
tails of this are presented in appendix A.

Once the linear algebra problem of determining the {waq} is completed,
equation 3.2 becomes our discrete time (in steps of size h) dynamical, non-
linear forecasting rule for times tn ≥ tN.

There are many choices for these RBFs (Hardy, 1971; Powell, 2002;
Schaback, 1995; Buhmann, 2009). Our RBF choice has been the gaussian:
ψ
G((u − uc(q))2) = exp[−R(u − uc(q))2)], R = 1/σ 2. Other choices, et

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1551

there are many (see Table I in Schaback, 1995), have given equivalent re-
sults in practice.

4 Using DDF in Neurobiology

4.1 Data Assimilation. In the study of the ingredients of functional neu-
ronal networks, one is able to measure the time series of voltage V(t) across
the cell membrane of individual neurons in a routine manner. Using ob-
served values of V(t) along with knowledge of the forcing by a stimulating
current Istim(t) presented to the neurons, it is often possible to estimate the
detailed electrophysiological properties of a Hodgkin-Huxley model of an
individual neuron (Hodgkin & Huxley, 1952; Sterratt et al., 2011; Johnston
& Wu, 1995) using data assimilation (Abarbanel, 2022).

The data assimilation estimation involves inferring the unmeasured state
variables, including ionic gating variables, and unknown parameters such
as maximal conductances of ion channels. A model developed and com-
pleted in this manner is validated by comparing its voltage time course
when driven by stimulating currents after the observation window. Only
in the observation window is information passed to the model from mea-
surements of V(t).

4.2 DDF. The DDF perspective selects a related, but also biophysically
grounded, path that emphasizes what can actually be measured and fore-
casts only those aspects of complex neuronal activity.

Approaching the question of biophysical models for the dynamics of
neurons from a DDF perspective provides a way to make predictions or
forecasts of V(t) without the details of the biophysical model. Ce, as noted,
sets aside the knowledge of the details of the model, but for purposes of
building up the dynamics of voltage activity in a network, it may be of great
utility.

One attractive feature of DDF is that it results in significant model reduc-
tion from the many state variables and proliferation of parameters present
in the neuron dynamics (Nogaret, Meliza, Margoiliash, & Abarbanel, 2016)
by focusing on those state variables that can be measured.

4.3 Hodgkin-Huxley Structure for Driven Neurobiological Dynamics.
We continue our discussion of DDF in neurodynamics by attending to how
one can work with numerical and simulated data from a basic, well-studied,
Hodgkin-Huxley (HH) model neuron. Our analysis of experimental current
clamp data will follow this set of numerical examples.

The biophysical HH equations for the dynamics of a single neuron

driven by a simulating current Istim(t) have the structure

dV (t)
dt

= Fintrinsic(V (t), UN(t)) + Istim(t); dA(t)
dt

= FA(V (t), UN(t)).

(4.1)

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1552

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

Fintrinsic(UN(t), V (t)) contains the ion currents and their gating variables,
which satisfy A(t), 0 ≤ A(t) ≤ 1. These quantities, descriptive of the intrin-
sic electrophysiology of a biophysical neuron, are independent of the stim-
ulating current Istim(t). In addition to the HH dynamics, there may be other
state variables in addition to {V (t), UN(t)}, such as concentrations of vari-
ous biochemicals. To proceed, we concentrate on the HH voltage equation
structure in equation 4.1.

In the HH formalism, the equation for the voltage is driven by Istim(t) dans
an additive manner. We use this in formulating our DDF protocol for bio-
physical neuron models. What we do not know from the data alone are the
vector fields {Fintrinsic(V (t), UN(t)), FA(V (t), UN(t))}, whose specification yields
the detailed HH biophysical model.

The solution or flow (Strogatz, 2015) of the HH model, equation 4.1, est
achieved by integrating that equation from tn to tn + h = tn+1 leading us to
the discrete time map {V (tn), UN(tn)} → {V (tn+1), UN(tn+1)} ou {V (n), UN(n)} →
{V (n + 1), UN(n + 1)}:

V (n + 1) = V (n) +

UN(n + 1) = A(n) +

(cid:3)

tn+1

tn
(cid:3)

tn+1

(cid:6) Fintrinsic(UN(t(cid:6)
C

), V (t(cid:6)

))

(cid:3)

tn+1

(cid:6) Istim(t(cid:6)
C

)

(cid:6)

FA(V (t

(cid:6)

), UN(t

(cid:6)

)).

(4.2)

4.4 The Basic NaKL HH Neuron as an Example. We now analyze the
DDF representation of the flow, 4.2 in the NaKL HH model neuron, in two
cases: (1) when we observe all state variables {V (t), UN(t)} et (2) when we
observe only V(t). Case 1 is not a realistic scenario in current clamp ex-
periments, but we include it as a confidence-building exercise in the con-
struction of DDF neurons. Case 2 is the realistic scenario in a current clamp
experiment where a simulating current Istim(t) drives a neuron and only the
membrane voltage V(t) is observed.

Our first step is to work with numerically generated data from the HH

NaKL model neuron (Johnston & Wu, 1995; Sterratt et al., 2011).

This basic, well-studied, detailed biophysical HH neuron model has 4
state variables and the order of 20 parameters (Johnston & Wu, 1995; Toth
et coll., 2011; Kostuk et al., 2012). DDF will replace this with a forecasting
equation for V(t), the experimentally observable quantity, alone. As we have
argued, much is gained by this model reduction.

The equations for this neuron model are

dV (t)
dt

= gNam3(t)h(t)(ENa − V (t)) + gKn4(t)(EK − V (t))

+ gL(EL − V (t)) + IDC

+ Istim(t),

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1553

dm(t)
dt

dn(t)
dt

= m0(V (t)) − m(t)
τm(V (t))
= n0(V (t)) − n(t)
τm(V (t))

; dh(t)
dt

= h0(V (t)) − h(t)
τ
h(V (t))

;

(4.3)

The gating variable functions g0(V ), τg(V ); g = {m, h, n} have the form

g0(V ) = 1
2

(cid:5)

(cid:4)
1 + tanh

(cid:6)(cid:7)

(V − vg)
dvg

τg(V ) = tg0

+ tg1

(cid:5)

(cid:4)
1 − tanh2

(cid:6)(cid:7)

(V − vgt)
dvgt

In these equations, we use the parameters given in Toth et al. (2011) et
Kostuk et al. (2012). Data are generated by solving equation 4.3 using a
fourth-order Runge-Kutta method (Press et al., 2007).

The DDF formulation when we observe w(t) = {V (t), m(t), h(t), n(t)} =
{V (t), UN(t)}, again not the realistic biological feature of a current clamp ex-
periment, is the following (w(tn) = w(n)):

V (n + 1) = V (n) + fV (w(n)) + h
2C
UN(n + 1) = A(n) + fA(w(n)),

[Istim(n + 1) + Istim(n)])

as suggested by equation 4.2. The functions { fV (w), fA(w)} are sums over
the RBFs as in equation 3.1.

We use the trapezoidal rule (Press et al., 2007) for the integration over
Istim(t). We are taking steps of size h in time. There are many improvements
over the trapezoidal rule for the integration from tn to tn+h over Istim(t).
Those improvements require sampling or estimating values at points be-
tween tn and tn + h. We do not have these quantities in our data set.

The task for DDF is to select representations for the vector fields fV (w)
and fA(w), which we do below. Fait intéressant, the constant C, the mem-
brane capacitance, can be estimated in the DDF training protocol as the time
course of the driving force, Istim(tn), must be specified by the user.

Using a gaussian RBF for each of the four vector fields { fv (w), fA(w)},
DDF training provides an estimate of the parameters in each vector field.
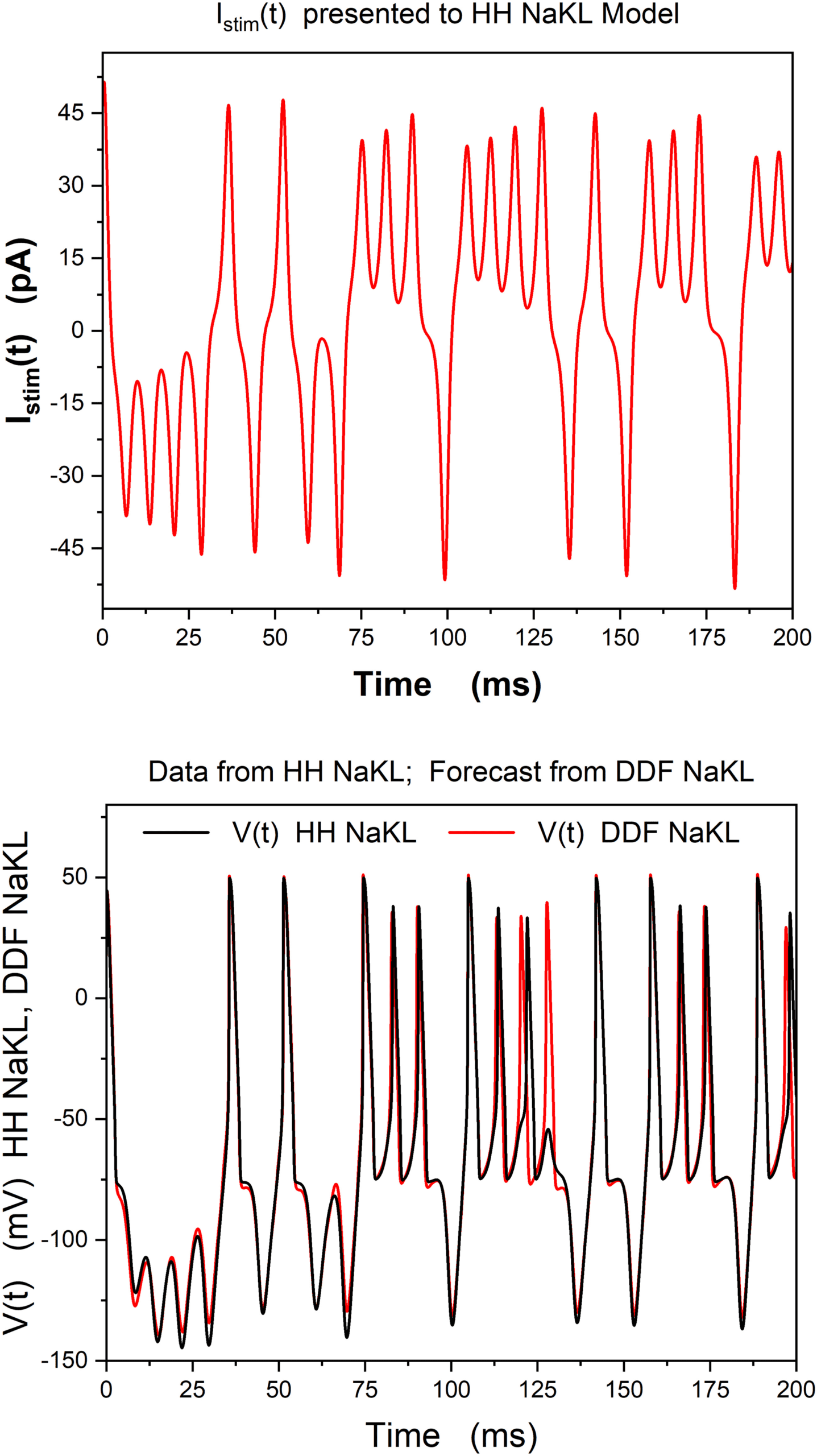
The result from forecasting with the trained DDF model is shown in Fig-
ure 1. It is clear from this result that the DDF when all {V (t), UN(t)} are “ob-
served” does a strikingly good job at forecasting the actual observable V(t).

5 Observing Only V(t): Time-Delay Methods

What is actually measured in current clamp laboratory experiments is V(t)
alone. The neuron dynamics resides in a higher-dimensional space than the
one-dimensional V(t) that is measured. What we observe is the operation of
the full dynamics projected down to the single dimension V(t). To proceed,

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1554

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 1: (Top) Our selection of a stimulating current to an NaKL HH neuron
model (Toth et al., 2011; Kostuk et al., 2012). Data are generated using this Istim(t)
in solving equation 4.3. (Bottom) Forecast using a gaussian RBF model trained
by both the voltage and the gating variables: {V (t), m(t), h(t), n(t)}. (This not a
realistic protocol for a current clamp experiment where Istim(t) is given, but V(t)
alone is observed. This calculation is only a demonstration of the efficacy of
DDF method in neurodynamics.)

Neuron Models Constructed From Observed Data

1555

we must effectively “unproject” the dynamics back to a “proxy space,” com-
prising the voltage and its time delays (Takens, 1981; Aeyels, 1981un, 1981b;
Abarbanel, 1996; Kantz & Schreiber, 2004), which is equivalent to the origi-
nal state space of V(t) and the gating variables for the ion channels.

This is accomplished as follows. If we have observed V(t), we can define
DE-dimensional (“unprojected”) proxy space vectors S(tn) via time de-
lays τ
k of V (tn) (Takens, 1981; Abarbanel, 1996; Kantz & Schreiber, 2004)
(τn+1
> τn):

S(n) = [S1(n), S2(n), . . . , SDE (n)]

= [V (tn − τ

1), V (tn − τ

2), V (n − τ

3), . . . , V (tn − τDE )].

(5.1)

The use of Takens’s theorem in nonlinear dynamics (Takens, 1981) is widely
practiced in the analysis of time series from nonlinear systems (Abarbanel,
1996; Kantz & Schreiber, 2004).

The physics behind the time-delay construction is that as the observed
system moves from time tn − τn+1
→ tn − τn, the dynamics of the system in-
corporates information about the activity of all other variables beyond the
voltage alone. When the quantity V (tn − τn) is approximately statistically
independent of the quantity V (tn − τn+1), each can be used as the compo-
nents in a “proxy vector” S(n) representing the system dynamics as it de-
velops in dimensions higher than V(t) alone.

Using the average mutual information (Fraser & Swinney, 1986; Abar-
banel, 1996; Kantz & Schreiber, 2004) between S j and Sk(cid:5)= j, and choosing
time lags {τ
} giving a minimum of this average mutual information, nous
achieve an approximate information-theoretic, nonlinear independence of
the DE components of S(n) with respect to each other.

, τ
k

In principle in the discussion of Takens’s work, if one has an infinite
amount of noise-free data, any time delay or set of time delays (Hirata,
Suzuki, & Aihara, 2006) would give a proxy state vector S(n) that is equiva-
lent to the original dynamical space of the data source. Bien sûr, we never
have that, so a guide was devised by Fraser and Swinney (1986) suggérer-
ing that choosing the components of S(n) to be nonlinearly independent of
l'un l'autre, using average mutual information as a “nonlinear correlation”
among the components, would provide a good measure of the ability of the
components of S(n) not to be parallel to each other. If that is achieved, alors
they would span the DE-dimensional space of S(n) in a numerically useful
manière. If there are multiple time scales in the data, the method of Hirata
et autres. (2006) could be a useful method to implement.

To estimate DE, one may use the method of false nearest neighbors (Abar-

banel, 1996; Kantz & Schreiber, 2004).

It is typical, but not required, to select τa = (a − 1)τ ; a = 1, 2, . . . , DE. Dans
this standard choice of delay coordinates, there are two parameters that de-
termine the vectors S(t) : {τ, DE}. τ is conveniently taken to be an integer

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1556

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

multiple of h; DE is an integer about twice the dimension of the system gen-
erating V(t). More precise results for these criteria are given in Sauer, Yorke,
and Casdagli (1991); Abarbanel (1996); and Kantz & Schreiber (2004).
+ h:

In S space, we develop a map from time tk

k to time tk

+ τ
k

− τ

Sa(tk

+ h) = Sa(tk) + fa(S(tk), χ) + [Forcinga(tk

, tk

+ h)];

(5.2)

a = 0, 1, . . . , DE. We are interested in making steps of size h to arrive at the
dynamical discrete time map (a = 1, 2, . . . , DE):

Sa(t + h) = Sa(t) + fa(S(t), χ) + h
2C

[Istim(t − τa) + Istim(t − τa + h)],

(5.3)

− τa, tk

as each component of S is a voltage. The last term in equation 5.3 est
the trapezoidal approximation to the integral of Istim(t) over the interval
− τa + h]. Each fa(S, χ) is a function of the DE-dimensional vari-
[tk
ables S and constants χ to be trained as before. The parameters are now
χ = {waq, p, β, τ, DE}. We represent fa(S, χ) using a linear combination of
gaussian RBFs.

In equation 5.3 we have introduced DE vector fields fa(S, χ) whose pa-
rameters χ must be estimated by requiring equation 5.3 to be true over
a training set with {tn}; n = 1, 2, . . . , N − 1. The trained dynamical map
S(n) → S(n + 1) is used to forecast all components of S(k) for k ≥ N.

Since we are representing the development of voltage in each component
of fa(S, χ), these vector fields should be independent of a, et, in practice,
we take that as given and move forward only the component S1(n), namely,
the observed voltage, donc

V (t + h) = V (t) + fV (S(t), χ) + h
2C

[Istim(t) + Istim(t + h)].

(5.4)

We then use that result to evaluate the remaining components of S(n) concernant-
quired in equation 5.3.

6 Results When Only V(t) Is Observed

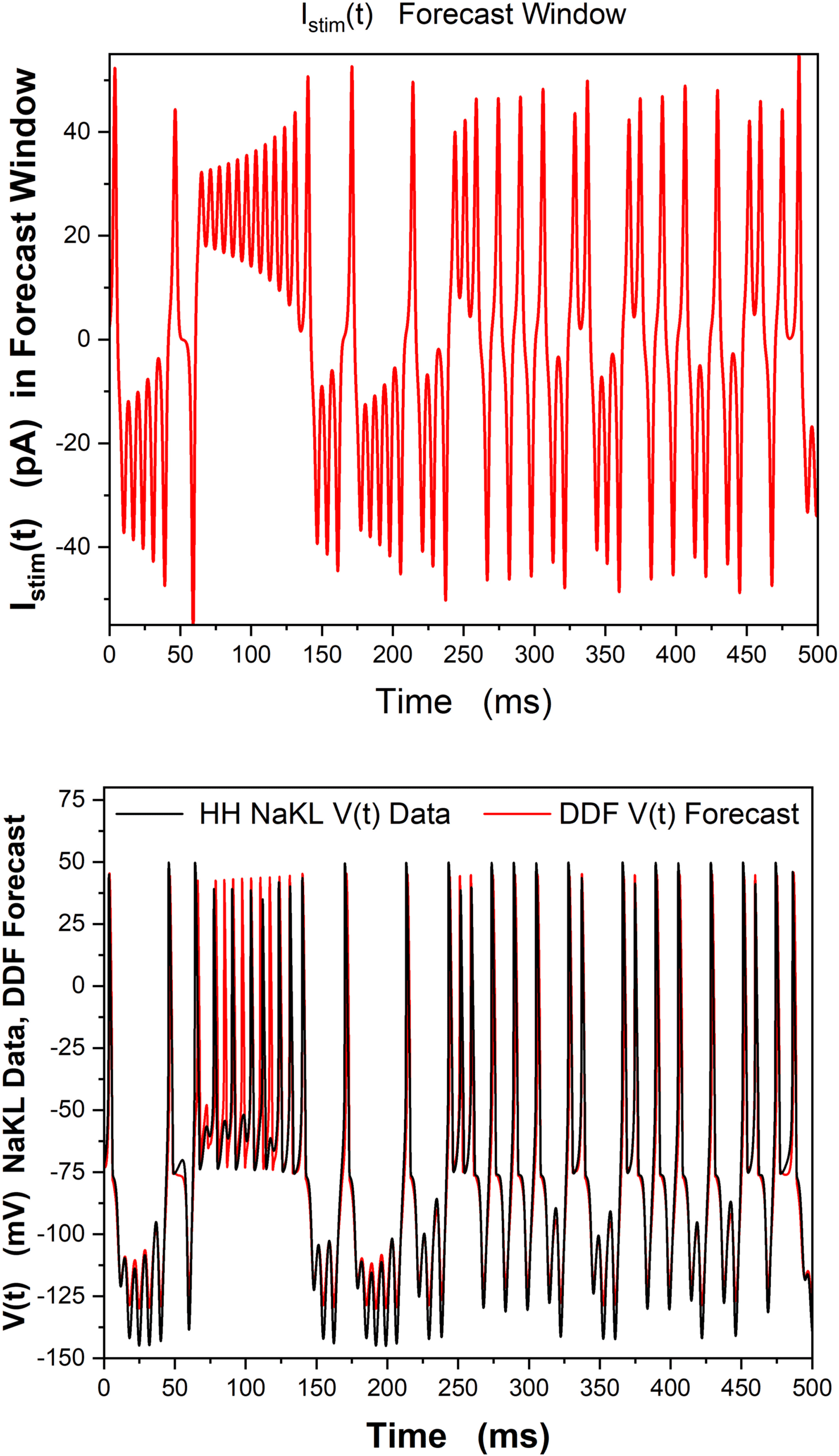
6.1 DDF Analysis of Numerical V(t) Data from an NaKL Neuron. Toujours
using data from the numerical solution of the basic HH equation, equation
4.3, we now train a gaussian RBF via equation 5.3, avec 125 ms of data for
V(t) alone employed in the estimation of the parameters χ of the RBF.

The trained DDF is used to predict the subsequent 500 ms of the V(t) temps

cours.

As in the earlier (unrealistic) example when all state variables from the
NaKL neuron model were available, when V(t) alone is presented, the DDF

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1557

neuron is able to predict the time course of the observable membrane volt-
age with significant accuracy. This result is shown in Figure 2.

Note that one cannot forecast the gating variables {UN(t)} of the HH NaKL
model as we have no observed information about them. Through the time-
delay vector S(tn), the biophysical information in the {UN(t)} is encoded in
the trained parameters χ.

6.1.1 Comparing DDF Forecasting and NaKL Forecasting Times. To assess
the effectiveness of using a trained DDF to forecast V(t) data, Par exemple,
for the efficiency of computational demands on a DDF neuron in a circuit
where it replaces a HH model, we compared the computation time for solv-
ing our HH NaKL model to the forecasting time of a DDF trained on the V(t)
from that HH NaKL model.

We generated HH NaKL data by solving equation 4.3 using a standard
fourth-order Runge-Kutta method (Press et al., 2007; Olver, 2017) with a
time step of h = 0.02 ms. The times taken by the generation of the NaKL
data in a forecast window of 2000 ms (105 time steps) étaient 8.9 s for either
CPU time or wall clock time.

We then forecast in the same window using the same Istim(t) as for the
HH NaKL model but using a trained DDF, trained on V(t) from the HH
NaKL model and forecasting only V(t).

The choice of the number of centers Nc in the training and forecasting
for the DDF is important to the forecasting time of the DDF. If we choose
Nc = 500, then the CPU time for forecasting the 2000 ms with h = 0.02 est 3 s,
while the wall clock time is 2.4 s. If we decrease the number of centers to
Nc = 100, then the CPU time during forecasting is reduced to 2 s, tandis que le
wall clock time drops to 1.5 s.

The training time for the DDF with Nc = 500, on V(t) from the HH NaKL
models is 1.1 s for CPU time and 0.63 s for wall clock time. This decreases
à 135 ms CPU time and 142 ms wall clock time for Nc = 100.

These times will vary as the complexity of the HH model neuron in-
creases from the minimalist NaKL model to a model for observed laboratory
observations. One expects the V(t) trained and forecasting DDF to become
relatively more efficient than our results on the simple NaKL model. Le
training times for a DDF on V(t) data alone are quite fast. In the scenar-
ios where we substitute DDF V(t) neurons for HH neurons in a circuit, le
computational efficiency is what will be of central importance.

6.2 DDF Analysis of Laboratory Data from an HVC Neuron in the
Avian Song System. With these DDF results on numerical data generated
by the solution of the NaKL HH equation in hand, we turn to the use of
DDF when presented with experimental current clamp data.

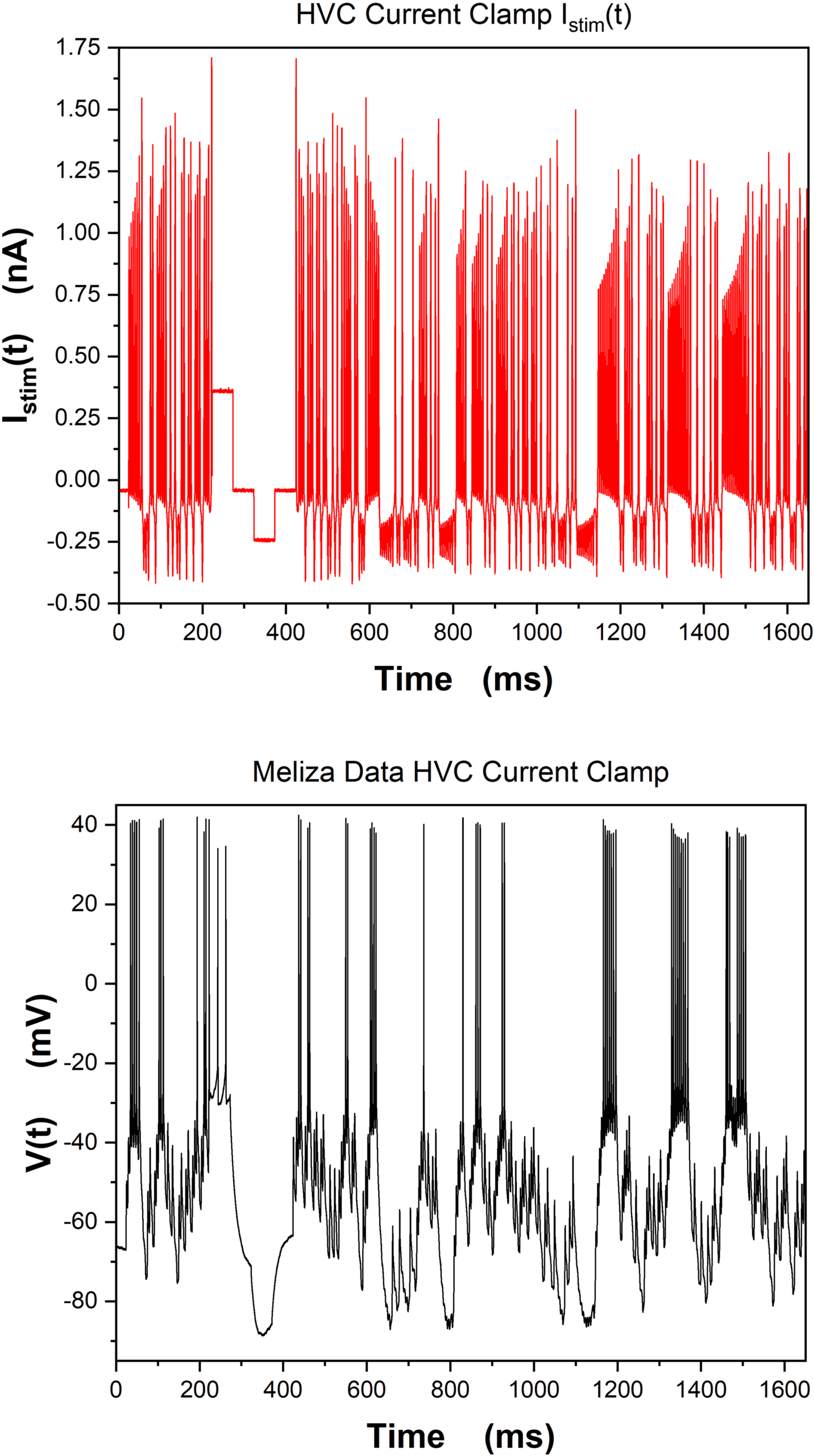
In Figure 3, we show the stimulating current Istim(t) (gauche) and the result-
ing membrane voltage time course (droite) from an in vitro current clamp
experiment on an isolated neuron in the HVC nucleus of the zebra finch
song system (Nogaret et al., 2016).

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1558

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

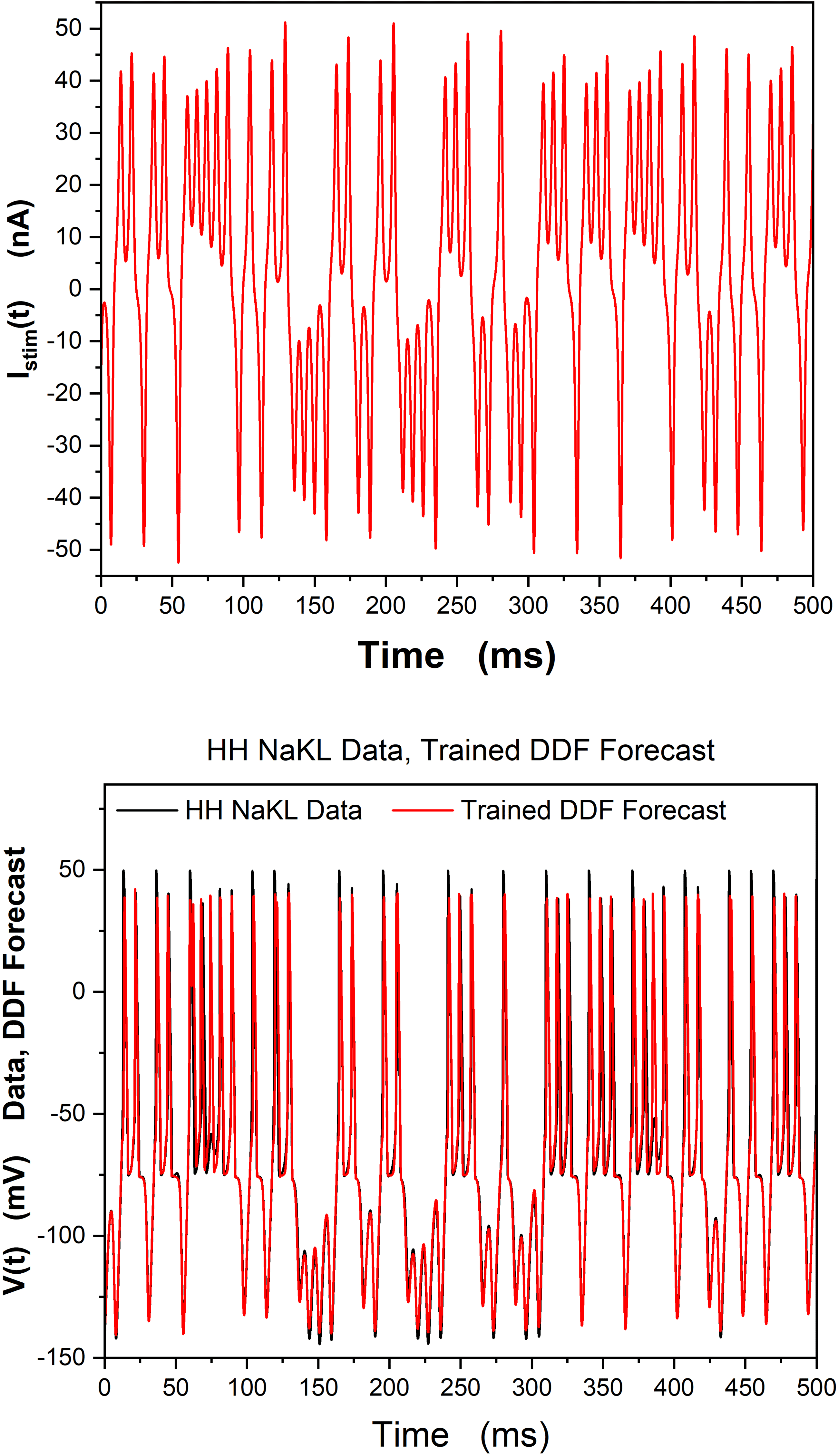
Chiffre 2: Data are generated by solving the HH-NaKL model, equation 4.3. Nous
observe only the membrane voltage, V(t), and use 125 ms of these data for train-
ing the gaussian RBF. (Top) Istim(t) dans le 500 ms forecasting window. (Bottom)
We display the V(t) forecast of the trained DDF-NaKL construct for 500 ms af-
ter the training window and compare it to the HH NaKL model-generated V(t)
data. This is a numerical calculation, but it corresponds to a realistic current
clamp experiment where, given a driving current Istim(t), only V(t) is observed.
h = 5 × 10−3 ms, β = 100, R = 10−3, τ = 8h, Nc

= 5000.

Neuron Models Constructed From Observed Data

1559

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 3: (Top) The stimulating current Istim(t) presented to an isolated neuron
in the HVC nucleus of the zebra finch song system in an in vitro current clamp
experiment at the University of Chicago laboratory of Dan Margoliash. (Bottom)
The recorded membrane voltage response to Istim(t). These data were collected
by C. D. Meliza (now at the University of Virginia) who designed Istim(t) in col-
laboration with M. Kostuk, then a UCSD physics PhD student.

1560

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

6.3 Only V(t) Is Observed in Laboratory Current Clamp Data. Actuel
clamp data were collected by C. D. Meliza at the University of Chicago lab-
oratory of Daniel Margoliash from presenting various stimulating currents
Istim(t) to isolated HVC neurons in a zebra finch in vitro preparation. Le
data were organized into epochs of length about 2 à 6 seconds observed
over several hours.

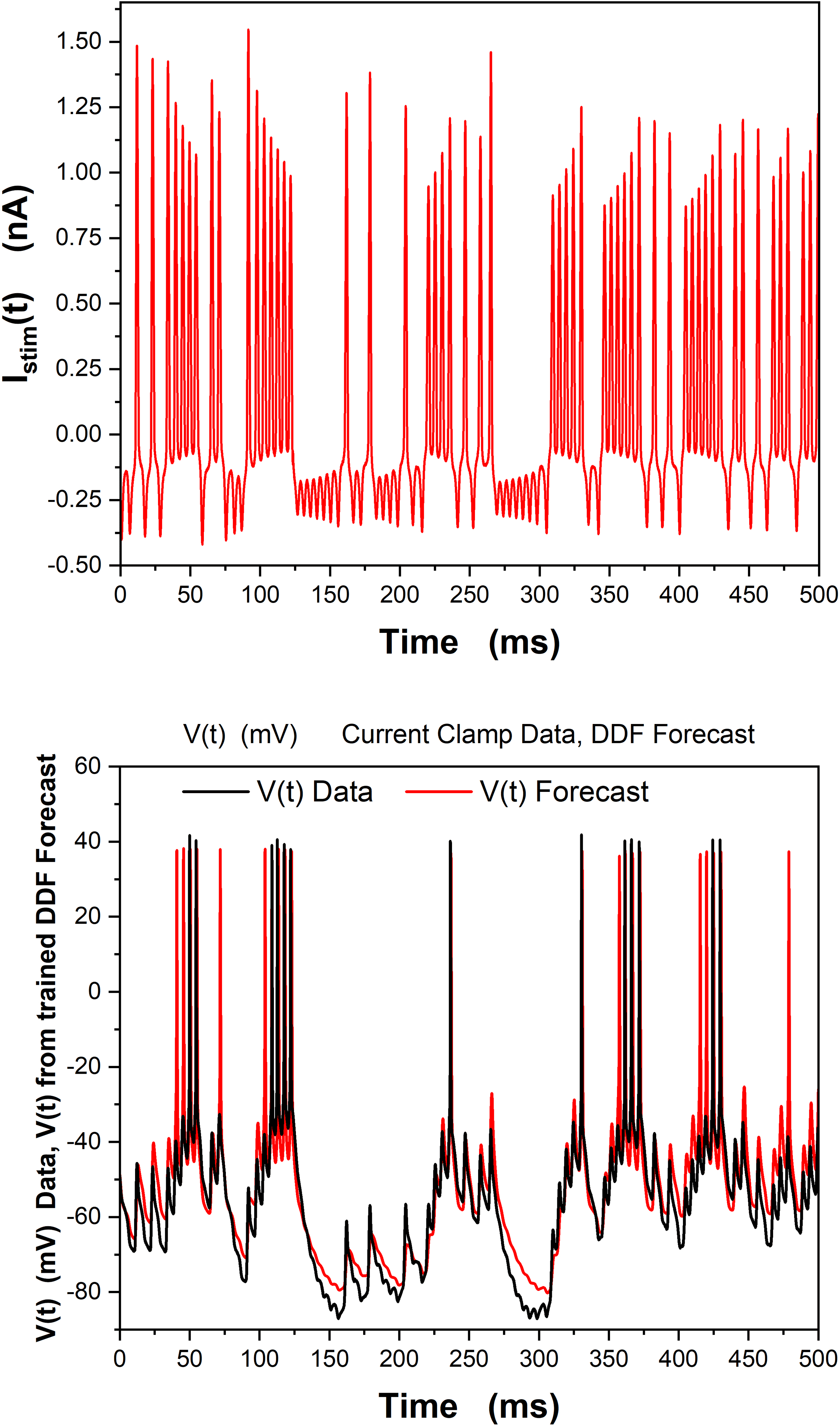
In Figure 4, we show the results of constructing a DDF neuron forecasting
model on these data. The first 500 ms of the stimulating current data and
the V(t) response data (these are not shown) were used to train a DDF RBF
model. In the left panel, we show the stimulating current used in 500 ms
of a prediction window for the same experimental preparation. In the right
panel we show the voltage forecast of V(t) using the trained DDF model
(blue) along with the observed voltage response (black).

Suivant, we provide the same analysis as in Figure 4 using two different
epochs, epoch 25 and epoch 26, of data collected by C. D. Meliza in the
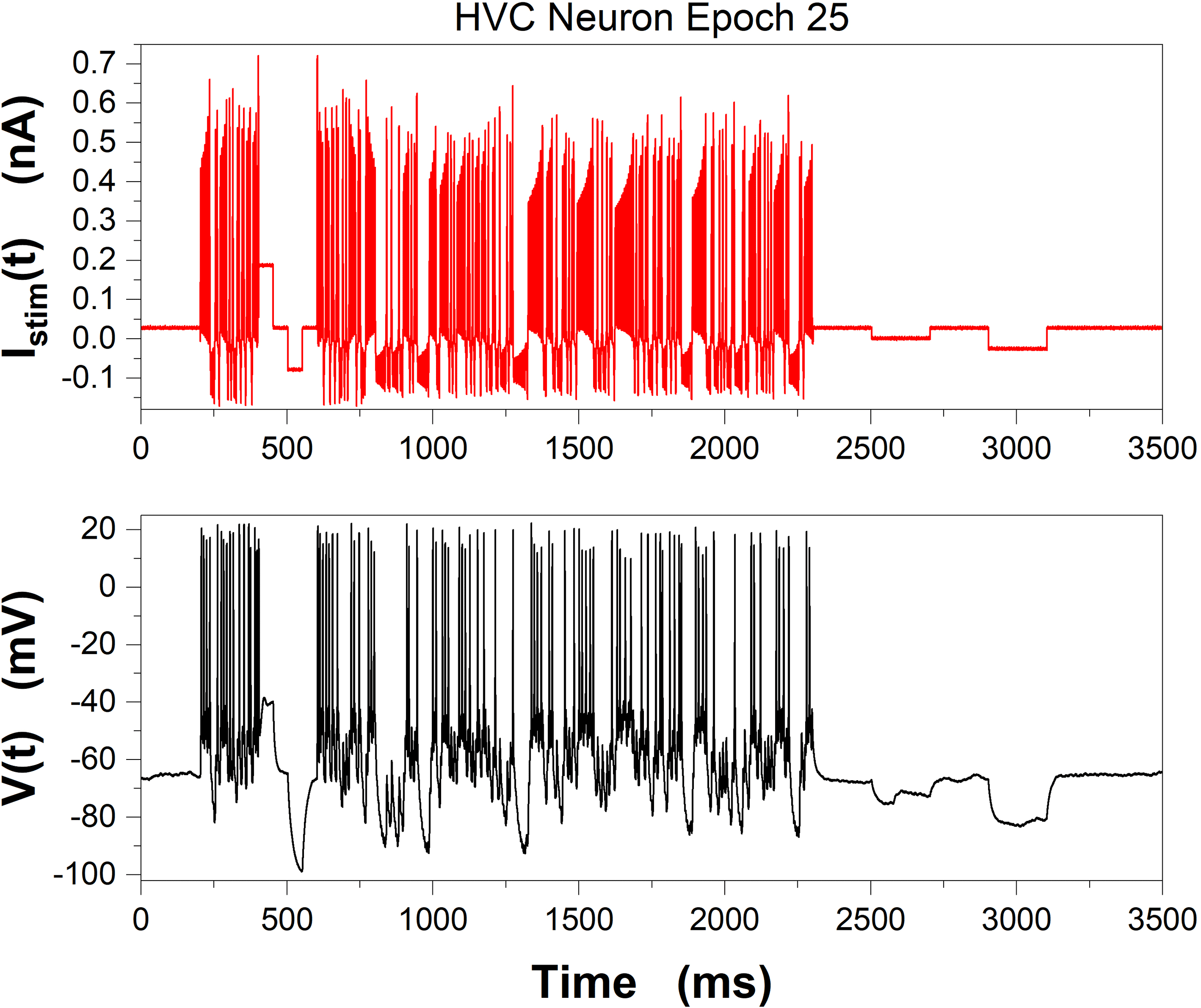
Margoliash laboratory. In Figure 5 we display the stimulating current Istim(t)
used in epoch 25 (top), and the V(t) response of the neuron (bottom). Dans
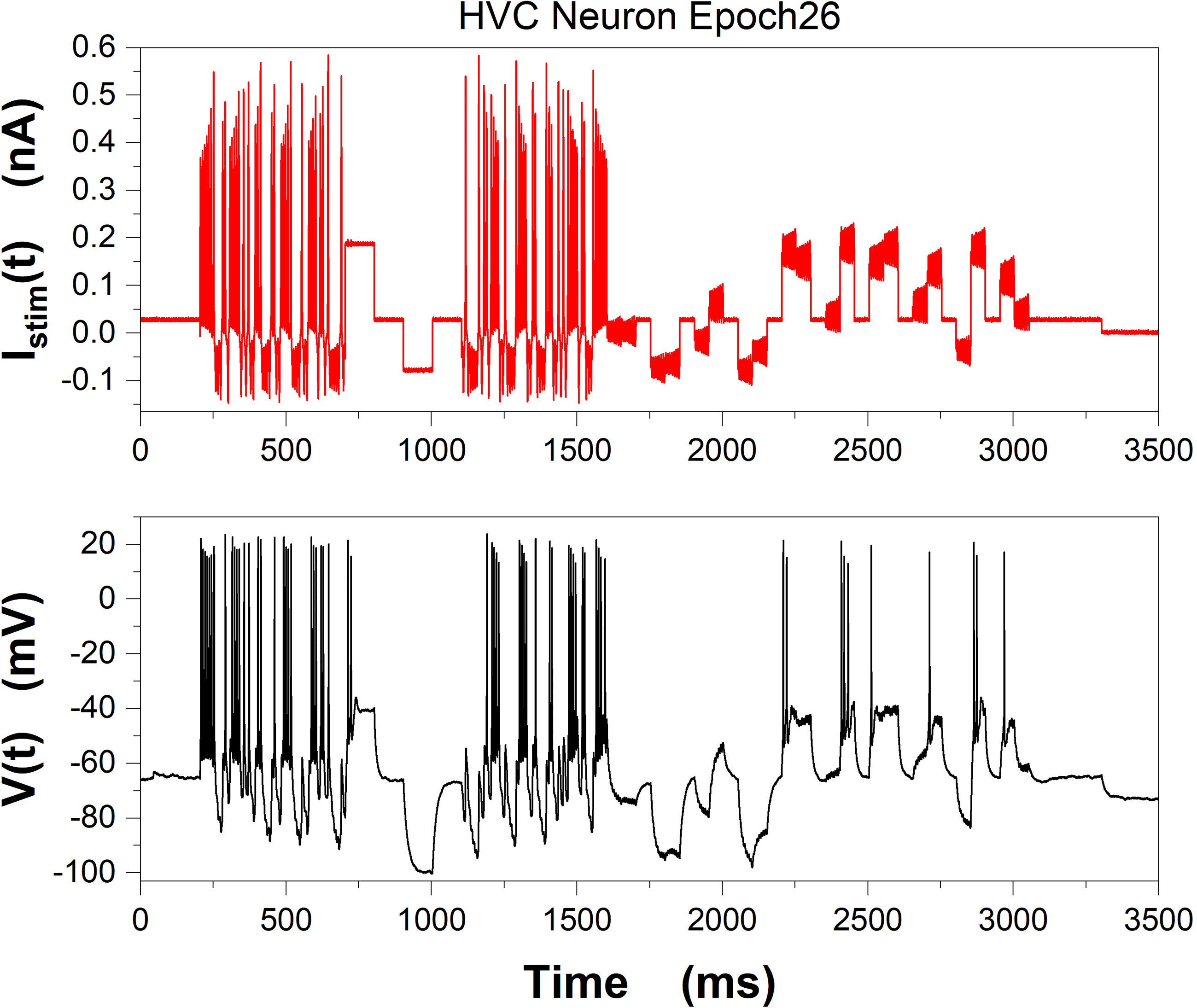
Chiffre 6, we display the stimulating current Istim(t) used in epoch 26 (top),
and the V(t) response of the neuron (bottom). This demonstrates that the
DDF model neuron, just like the HH model neuron, responds appropriately
to changes in the stimulating current. It is the unknown intrinsic properties
of the neuron for which we have introduced a RBF representation.

6.4 Training a DDF Neuron in One Epoch and Using It to Forecast
in Another Epoch on Experimental Current Clamp Data. Another infor-
mative test of the DDF approach is to train a DDF neuron on neuron data
from one time epoch with a selected Istim(t), then using the same parame-
ters χ from the first epoch to forecast the V(t) response to different Istim(t)
presented in a second time epoch. This is a test of the DDF neuron ability
to correctly respond to different stimulating currents.

In Figure 5 (top), we show Istim(t) in epoch 25 and the resulting, VData(t)
(bottom). In Figure 6 (top), we show Istim(t) in epoch 26 and the resulting,
VData(t) (bottom). These data are from two epochs of a current clamp experi-
ment from the Margoliash laboratory (University of Chicago) on an isolated
neuron from the zebra finch HVC nucleus.

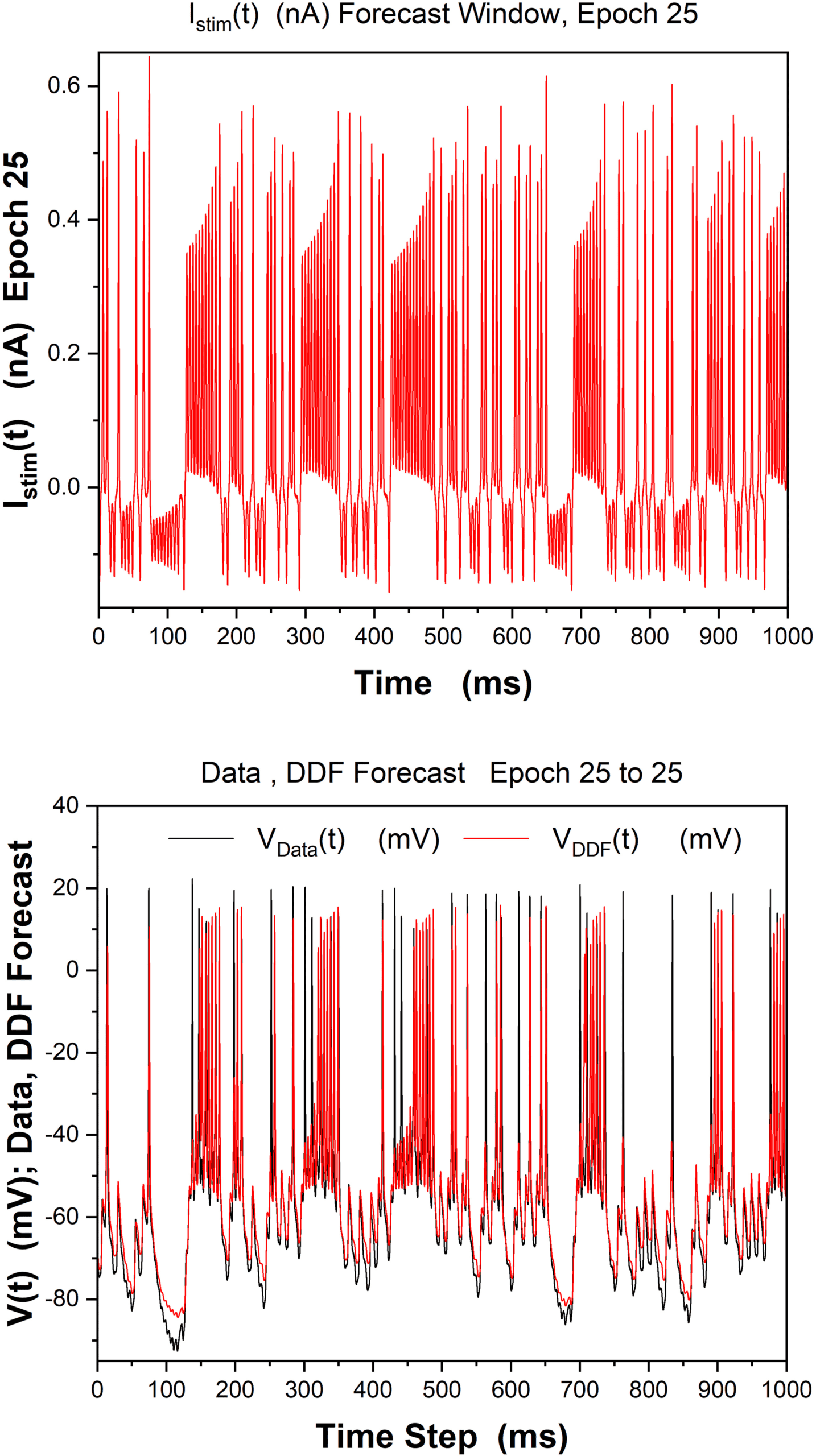
Suivant, in Figure 7, we display the observed data; then we analyze the abil-
ity of DDF trained on data from epoch 25 to forecast within that epoch. Alors
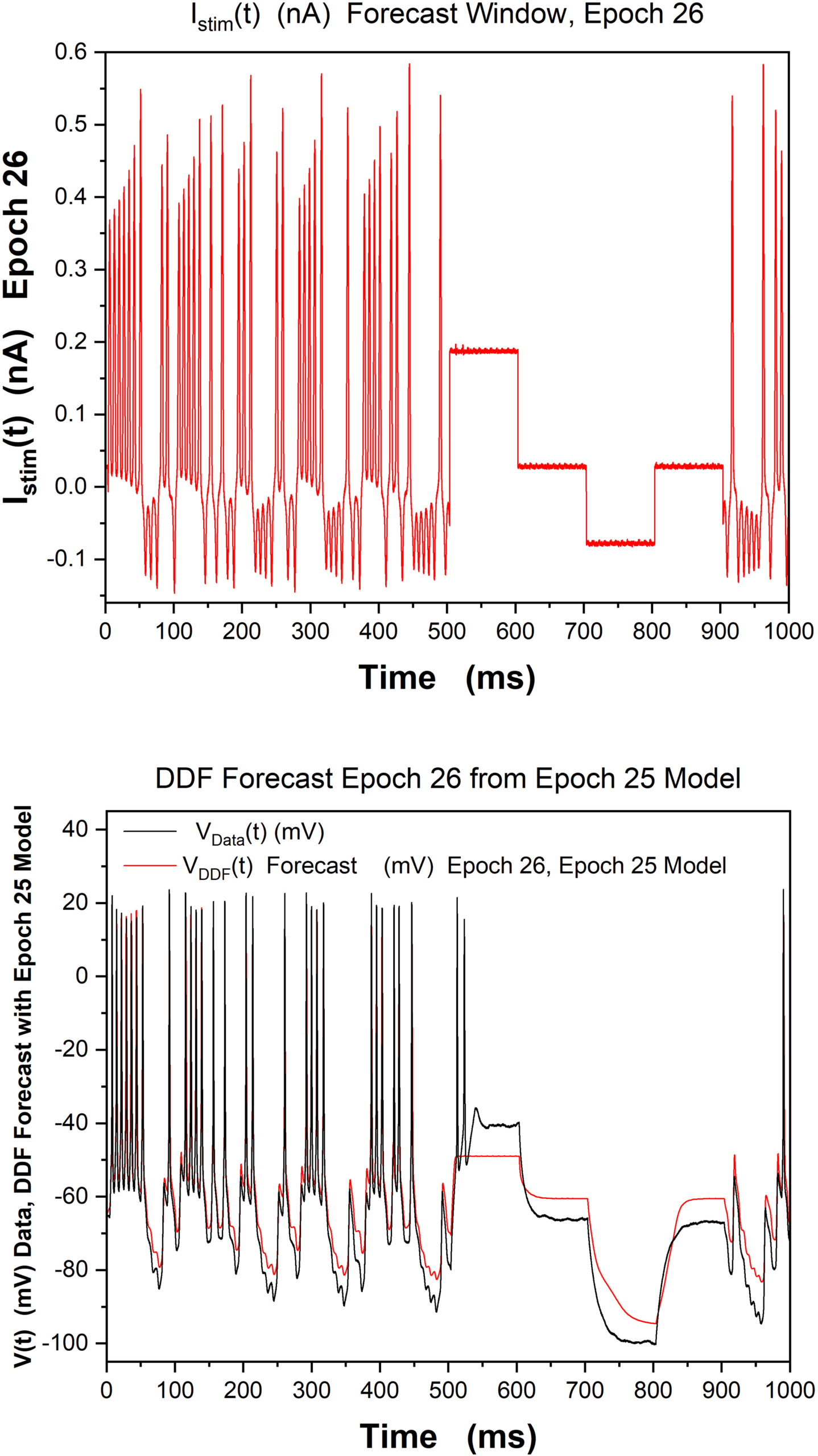
in Figure 8, we show how the DDF model trained on data from epoch 25 est
able to forecast the V(t) for data in epoch 26, where the Istim(t) is different,
though the neuron is the same.

6.5 Comments on the HVC Current Clamp Experiments. There is a
large library of current clamp data from this preparation. The observation
window for the data used here was about 1650 à 3500 ms. Many entries in
the library have a longer window of time over which data were collected,

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1561

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 4: A gaussian RBF representation for the vector field of the membrane
potential dynamics was used to train a DDF. The training used 500 ms of ob-
served V(t) data. (Top) In the 500 ms forecast window Istim(t), data from Figure 3
were used. (Bottom) The V(t) forecast for 500 ms by the trained DDF neuron (dans
red) along with 500 ms of the observed V(t) current clamp data (in black). h =
0.02 ms, τ = 2h, Nc

= 5000, DE

= 3.

1562

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 5: (Top) Stimulating current Istim(t) for a current clamp experiment at
the Margoliash laboratory of the University of Chicago. (Bottom) Membrane
voltage response, V(t), to Istim(t). Data were collected by C. D. Meliza (now at
the University of Virginia) in sequential time epochs from the same HVC neuron
in zebra finch. Between epochs, Istim(t) = 0. Many epochs of varying length in
time and with different stimulating currents Istim(t) were recorded. These data
sont 3500 ms from epoch 25 of the observations.

and this would allow longer training windows to be used. In previous work
with these kinds of data (Kostuk et al., 2012; Nogaret et al., 2016) longer
estimation windows typically result in better forecasting.

The stimulating currents in these data were designed with three biophys-
ical principles in mind. D'abord, the amplitude variations of Istim(t) must be
large enough to generate many action potentials as well as substantial peri-
ods of subthreshold behavior. This guarantees that the full dynamic range
of neuron response is well represented. Deuxième, the observation window
must be long enough in time to ensure the same goals as in the third princi-
ple. Troisième, the frequencies in Istim(t) should be low enough so that properties
of the stimulating signal are not filtered out by the RC low-pass character-
istic of the cell membrane. If these criteria are not met, aspects of Istim(t)
are filtered out by the cell membrane, and the training is likely to be insuf-
ficiently well informed. V(t) data collected with Istim(t) chosen employing
these guidlines were regularly successful in using DA to estimate the prop-
erties of rich HH models (Toth et al., 2011; Kostuk et al., 2012; Nogaret et al.,
2016) from laboratory data.

The context of this discussion is expanded in appendix C.

Neuron Models Constructed From Observed Data

1563

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 6: (Top) Stimulating current Istim(t) for a current clamp experiment at
the Margoliash laboratory of the University of Chicago. (Bottom) Membrane
voltage response, V(t), to Istim(t). Data were collected by C. D. Meliza (now at the
University of Virginia) in sequential time epochs from the same HVC neuron in
zebra finch. These data are 3500 ms from epoch 26 of the observations.

7 Adding Other Observables

In many neurobiological investigations, more observables than just V(t)
may be available. We examine how these may be combined with observa-
tions of V(t) in a DDF framework or used on their own.

As an example, we consider the important quantity of the time course
](t) = Ca(t). This is gov-

of the intracellular concentration of calcium [Ca2+
erned by a conservation equation of the form

dCa(t)
dt

= [Sources of Ca](t) + C0

− Ca(t)
τc

where C0 is an equilibrium or rest state concentration of Ca, and τc is a re-
laxation time for the Ca(t) dynamics.

The equation for the difference (cid:5)(t) = Ca(t) − C0, est

d(cid:5)(t)
dt

= [Sources of Ca](t) −

(cid:5)(t)
τc

The sources of Ca ions are attributed to voltage gated Ca channels with
various properties and release of and uptake of Ca from intracellular stores

1564

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 7: DDF forecasting and observed data, epoch 25. Training window was
1000 ms. Only V(t) was observed and used to train the DDF neuron. (Top) Ob-
served Istim(t) in forecast window. (Bottom) Forecast for 1000 ms by DDF voltage
= 4, R = 10−3, β = 10−3.
on epoch 25 data. h = 0.02 ms, τ = 2h, Nc

= 5000, DE

Neuron Models Constructed From Observed Data

1565

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 8: Analysis of epoch 26 data using a DDF neuron trained on 1000 ms
epoch 25 V(t) data. (Top) Istim(t) for epoch 26 in the forecast window. This is
different from the Istim(t) used in the epoch 25 training window. (Bottom) Ob-
served current clamp data and DDF forecast in the epoch 26 time window using
the epoch 25 trained DDF. The performance is worst for regions of Istim(t) com-
prising square pulses; this is consistent with the observations in Mainen and
Sejnowski (1995). h = 0.02 ms, τ = 2h, Nc

= 4, R = 10−3, β = 10−3.

= 5000, DE

1566

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

such as the endoplasmic reticulum (Houart, Dupont, & Goldbeter, 1999,
2003; Dupont & Goldbeter, 1993; Ye et al., 2014).

Integrate equation 7.1 from time t to time t + h to make a discrete time

map:

(cid:5)(t + h)y+ = (cid:5)(t)y− +

(cid:3)

t+h

(cid:6)

[Sources of Ca](t’),

(cid:5)(t + h)y+ = (cid:5)(t)y− + fCa(D(t), χ).

(7.1)

y± = 1 ± h
2τc

appears here as we identify the appearance of (cid:5)(n) et
(cid:5)(n + 1) on both sides of the equation for the flow of Ca(t). The integral
over (cid:5)(t) uses the trapezoidal approximation, and the unknown dynamics
for the sources and sinks of Ca(t) are represented within the RBF vector field
fCa(D(t), χ).

The Ca(t) time variation is a projection from higher-dimensional dynam-
ics of a neuron, and a time-delay “unprojection” is required here as well.
The time-delay state vector for this situation is

D(t) = [(cid:5)(t − θ
D(t) = [D1(t), D2(t), . . . , CC(t)],

1), (cid:5)(t − θ

2), . . . , (cid:5)(t − θ

C)],

(7.2)

in which the time delays {je
k
“unprojects” the projected observation of Ca(t).

}; k = 1, 2, . . . , DC appear. This construct

If V(t) and Ca(t) were both to be observed, then the unprojection occurs in
the joint time delay space of voltage, S(t), equation 5.1, and D(t), equation
7.2. Further observations, when available, may be added to this framework.

8 Using DDF Neurons in a Network

One important goal of using neuron models trained by data alone (par exemple., DDF
neurons) is to provide a reduced model based on biophysical observations
to employ in building network models.

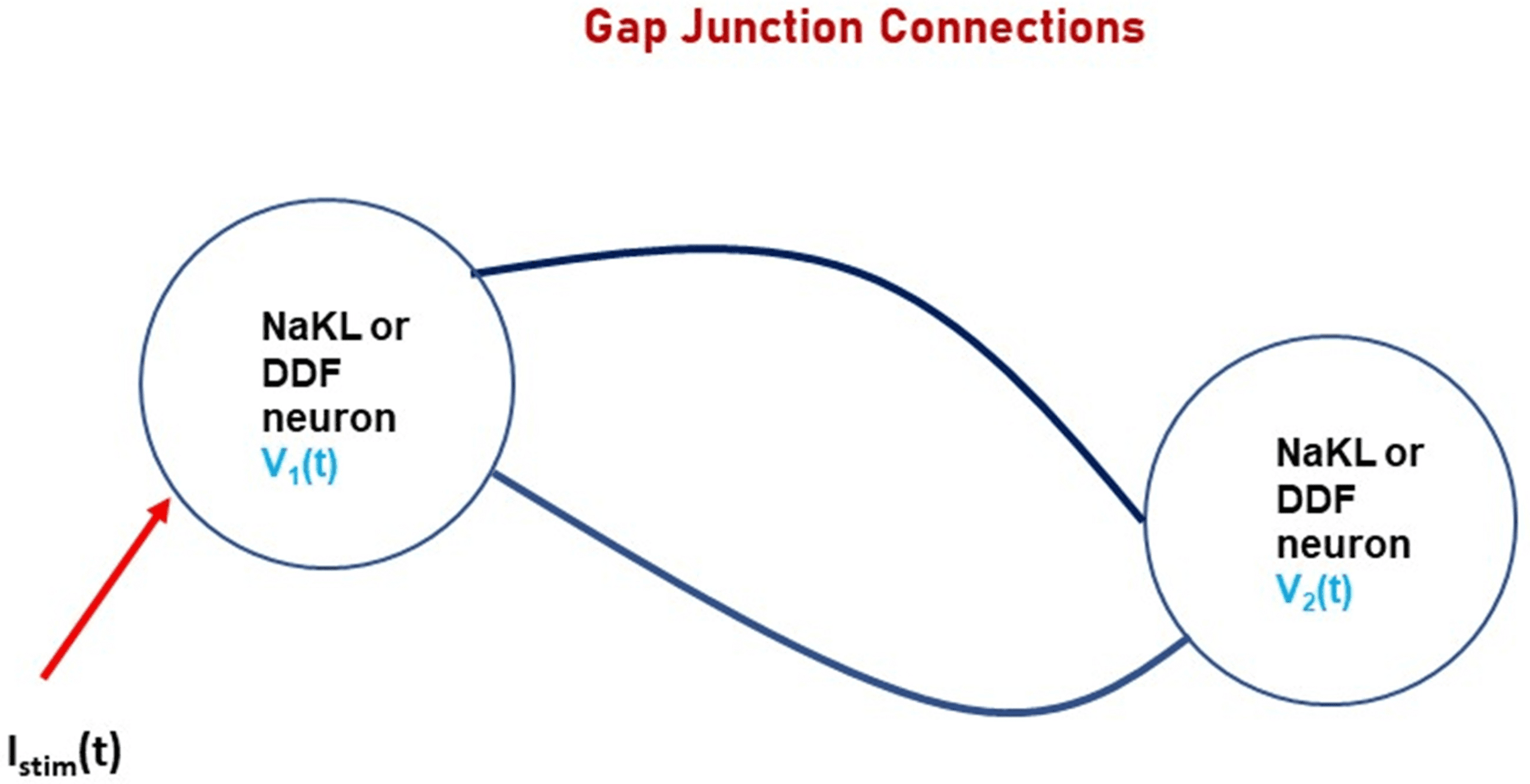
We demonstrate this in the most basic network comprising just two neu-

rons, connected by gap junctions, as shown in Figure 9.

Note that it is only the presynaptic and postsynaptic voltages that convey
information from any neuron in this circuit to others in the circuit. Either the
HH model NaKL neuron or the NaKL-trained DDF neuron may be used in
this small network. Each produces voltage signals that couple the neurons.

8.1 Discrete Time Gap Junction Dynamics. The differential equations

for the two-neuron circuit with gap junction connections are these:

dV1(t)
dt

= FV (V1(t), A1(t)) + IDC1
C

+ g12
C

(V2(t) − V1(t)) + Istim(t)

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1567

Chiffre 9: A two-neuron circuit comprising two NaKL HH neurons or two DDF
neurons trained on NaKL voltage data. There are gap junction connections be-
tween the two neurons in the circuit. The circuit is driven by the stimulating
current Istim(t) presented to neuron 1. An NaKL neuron is a Hodgkin-Huxley
model neuron with Na, K, and leak channels (Johnston & Wu, 1995; Sterratt
et coll., 2011). The DDF neuron is built with RBFs trained with V(t) data from the
HH NaKL model. The computational task using the DDF neurons is substan-
tially simplified as only membrane voltage plays a role and no integration of
HH differential equations is required in establishing the behavior of the neural
circuit. The equations of the map are given in equations 8.2 à 8.4.

dV2(t)
dt

= FV (V2(t), A2(t)) + IDC2
C

+ g21
C

(V1(t) − V2(t)).

(8.1)

Integrating these over the interval [t, t + h], we arrive at

V1(t + h) = V1(t) + fV1(S1(t)) + hIDC1
C

+ h
2C

[Istim(t + h) + Istim(t)]

+ g12h
C

(V2(t + h) + V2(t) − V1(t + h) − V1(t))

V2(t + h) = V2(t) + fV2(S2(t)) + hIDC2
C

+ g21h
C

(V1(t + h) + V1(t) − V2(t + h) − V2(t)),

(8.2)

and then

g12+V1(t + h) = fV1(S1(t)) + g12−V1(t) + hIDC1
C

+ h
2C

[Istim(t) + Istim(t + h)] + g12h
2C

[V2(t) + V2(t + h)],

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1568

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

g21+V2(t + h) = fV2(S2(t)) + g21−
C

V2(t) + hIDC2
C

+ g21h
2C

[V1(t) + V1(t + h)]

g12± = 1 ± g12h
2C

; g21± = 1 ± g21h
2C

(8.3)

Defining the two-dimensional vector v(t) = [V1(t), V2(t)] equation 8.3 may
be put into matrix form,

MLv(t + h) = MRv(t) + J.(t),

dans lequel

(cid:8)

ML =

g12+ − g12h
2
− g21h
g21+
2

(cid:9)

(cid:8)

, MR =

(cid:9)

g12h
2
g21−

g12−
g21h
2

(8.4)

(8.5)

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

and J(t) = [ hIDC1
C

+ fV1(S1(t)) + h

2C [Istim(t) + Istim(t + h)], hIDC2

+ fV2(S(t))].

The desired discrete time map for gap junction coupling in a two-neuron

map is then

v(t + h) = M

(cid:11)
(cid:10)
MRv(t) + J.(t)

−1
L

9 Dynamics of a Simple Two-Neuron Network

(8.6)

We are now prepared to use the dynamical discrete time maps for circuits
such as the one in Figure 9.
This proceeds as follows:

1. Determine the neuron RBFs for the two neurons fV1(S1) and fV2(S2).
In the simplest case, which we adopt here, the neurons are the same,
and the RBFs, fV (S), are the same function as their respective multi-
variate arguments S1(t) and S2(t).
2. Select a stimulating current Istim(t).
3. Select excitatory or inhibitory synaptic connections or gap junction

relations.

4. Using the DDF neurons in place of the HH neurons appearing in the

circuit, use the trained DDF neurons.

5. Evaluate the network behavior using the discrete time map for the
coupled V1(tn) and V2(tn), equations 8.2 et 8.3, when DDF neurons
are at the nodes of the network.

9.1 A Two-Neuron Circuit: HH NaKL Neurons or DDF, NaKL Trained,
Neurons; Gap Junction Connections. We begin by using a selected Istim(t)
to an HH-NaKL neuron and use the resulting V(t) data to train a DDF
discrete time map for V(t) generated from an HH NaKL neuron. Le

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1569

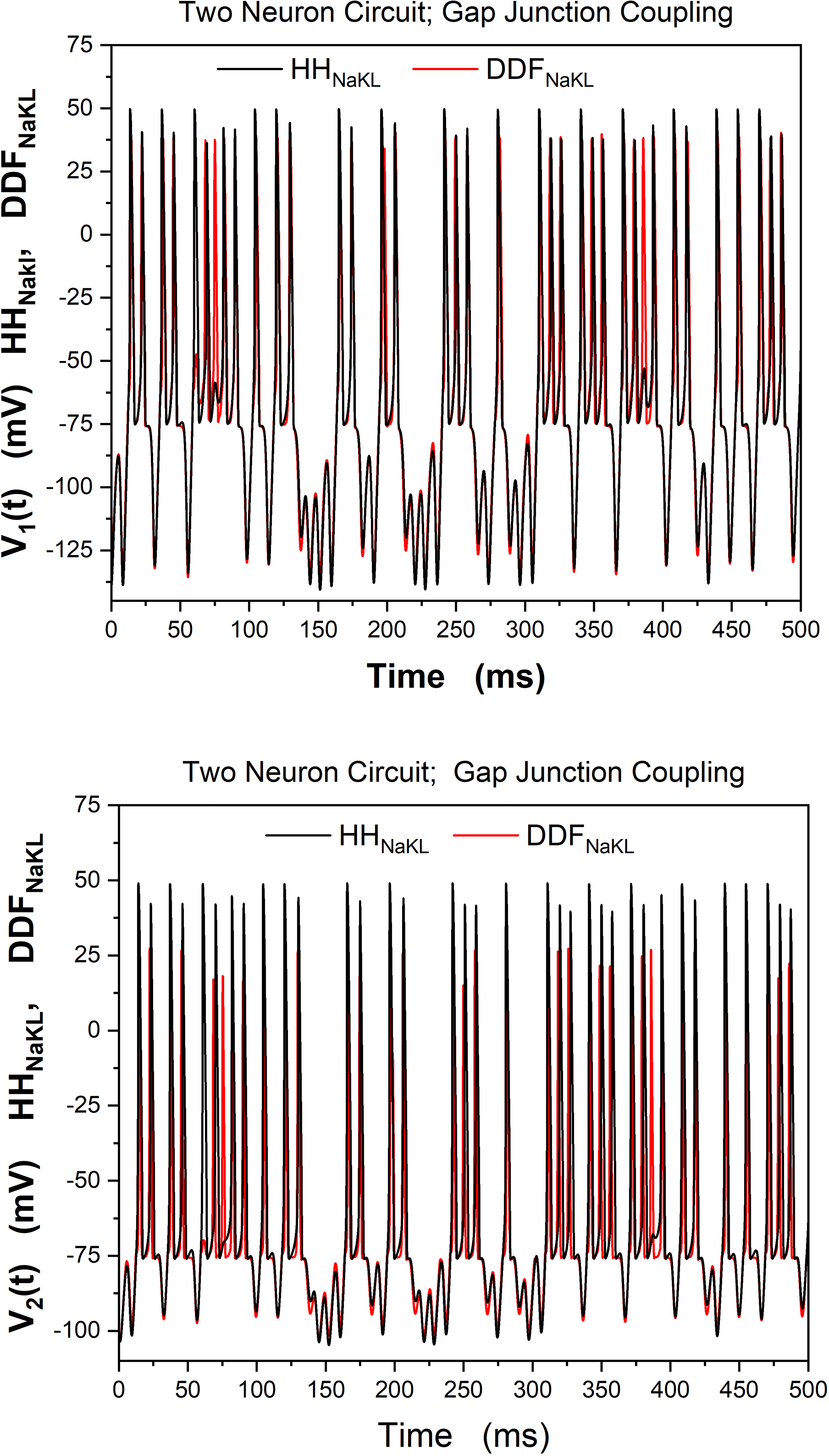
forecasting ability of the DDF is shown in Figure 10. We now have the HH
model NaKL and the DDF model NaKL neuron we require for a comparison
of the circuit using one and then the other at the nodes of the two-neuron
réseau.

Using the HH-NaKL neuron at both nodes of the network (voir la figure 9),
we generated the time course of V1(t) and V2(t). Then replacing the HH-
NaKL neurons with the trained DDF-NaKL neuron, we generated another
set of V1(t) and V2(t) time courses.

A comparison of the results of using these two-neuron models at the
nodes of our simple network is shown in Figure 11. While the “network”
we selected is simple, the idea that we are able to replace an HH neuron
with a trained DDF neuron in a network is now supported by these results.
This result is, as noted, for gap junction couplings between the two neu-
rons. The way one introduces ligand gated synaptic connections into a net-
work is discussed in appendix B.

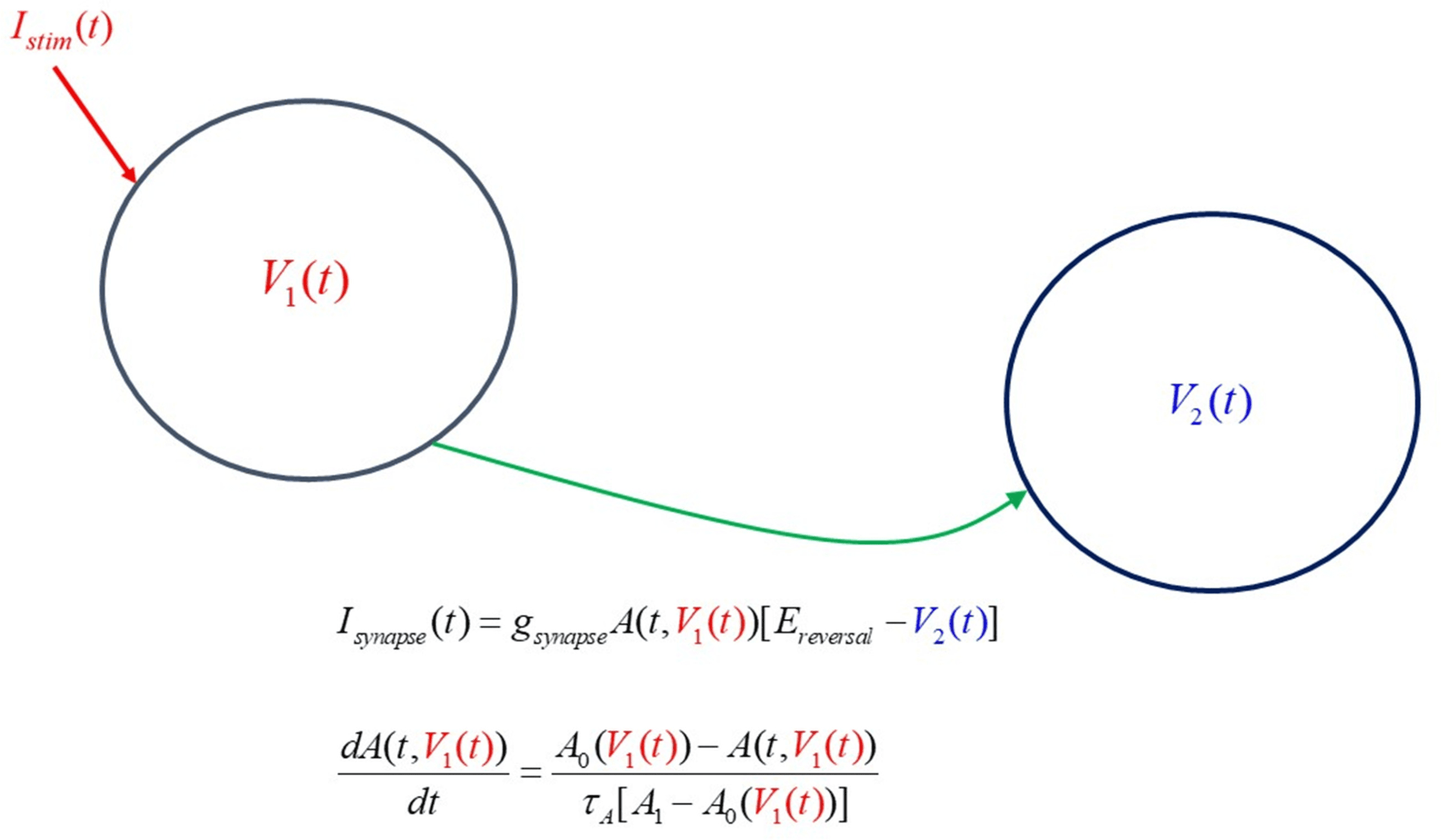
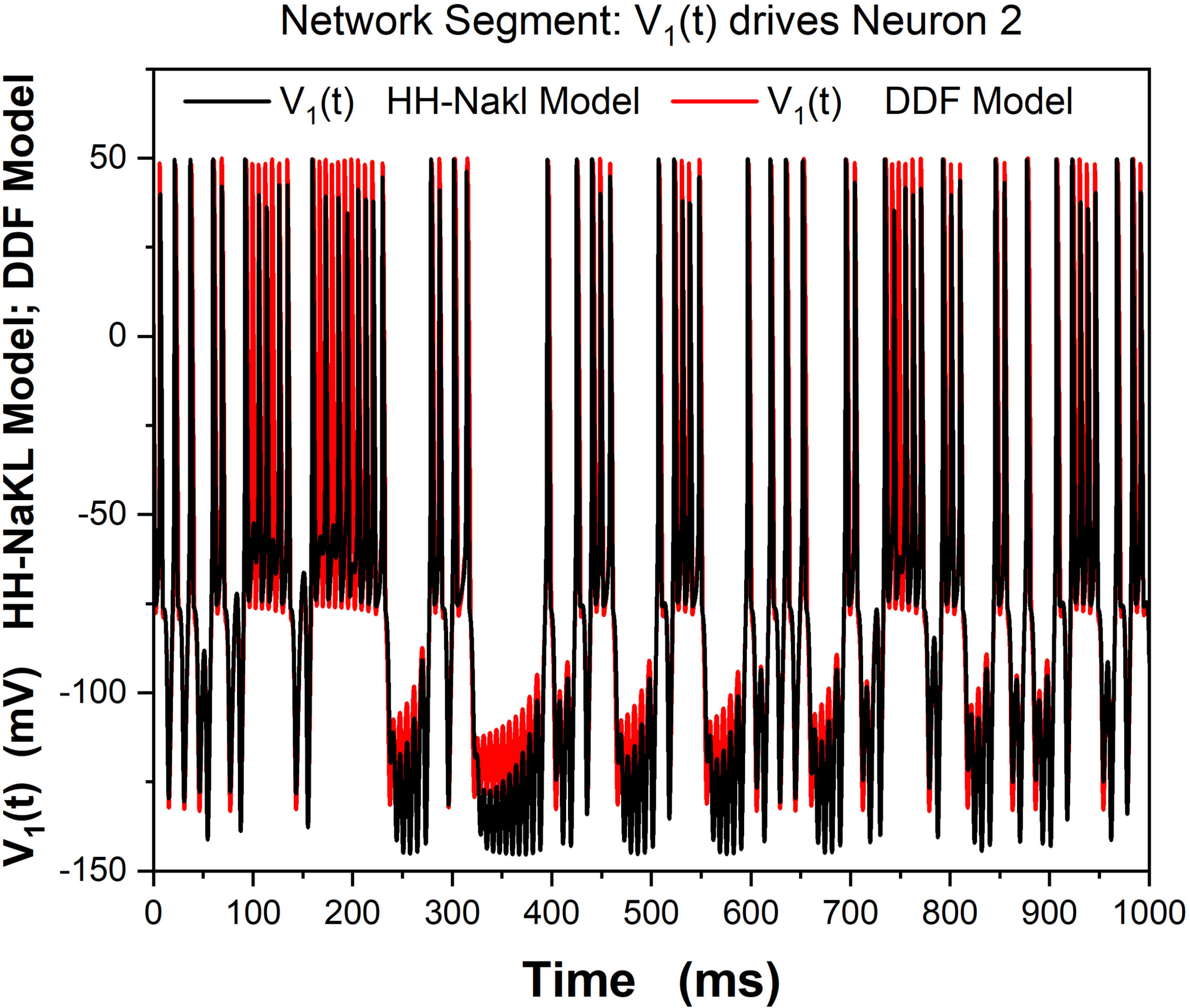
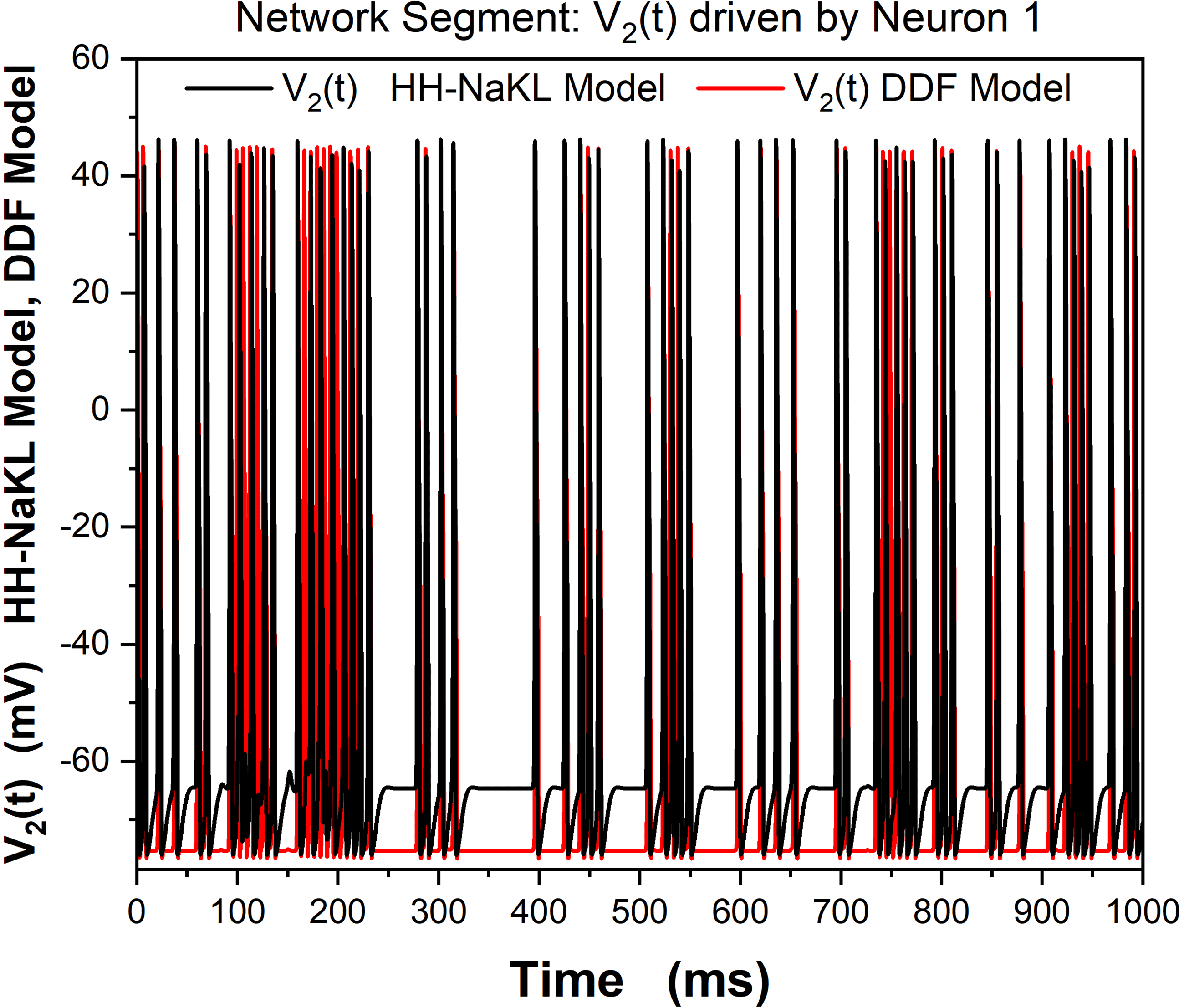
9.2 One DDF Neuron Driving a Second DDF Neuron through a
Synaptic Connection. To explore the ability of DDF neurons to work in a
biological network with ligand gated synaptic connections, we constructed
a network segment in which neuron 1, with membrane voltage V1(t), est
driven by a stimulating current Istim(t), and this neuron drives a second neu-
ron, with membrane voltage V2(t), via an excitatory ligand gated synapse.
This network segment is shown in Figure 12.

The synaptic current from the presynaptic neuron with voltage V1(t) et

driving the postsynaptic neuron with voltage V2(t) is described by

Isynaptic(t) = gsynA(t, V1(t))[Erev − V2(t)],

dA(t, V1(t))
dt

= A0(V1(t)) − A(t, V1(t))

τ
UN(A1

− A0(V1(t))

(9.1)

where A(t, V1(t)) is a synaptic gating variable. It is opened, UN(t, V1(t)) ≈ 1,
when the neurotransmitter binds onto receptors on the postsynaptic cell. Il
is closed, UN(t, V1(t)) ≈ 0, when that neurotransmitter is released from the
postsynaptic receptor.

We represent the driver of this transition in the neighborhood of a tran-

sition at a voltage V0 from closed to open by writing

A0(V ) = 1
2

(cid:4)

(cid:5)
1 + tanh

(cid:7)(cid:6)

V − V0
dV0

(9.2)

This function moves from very near 0 when V (cid:8) V0 to very near 1 quand
V (cid:9) V0, as desired, and it does so over an interval in voltage dV0.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1570

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

= 3, β = 10, τ = 3h, Nc

Chiffre 10: An HH-NaKL model neuron and a DDF-NaKL were driven by the
same Istim(t) in a training window of 500 ms. Only the V(t) data from the HH-
NaKL model neuron were used to train the DDF-NaKL neuron. (h = 0.02 ms,
= 5000.) (Top) We show the Istim(t) in a subsequent
DE
500 ms window used for prediction by the trained DDF-NaKL model. (Bottom)
Comparison of the voltage time courses V(t) from the numerical solution of the
HH-NaKL and the forecast of the trained DDF-NaKL models over a 500 ms
forecasting window. This V(t)-trained DDF-NaKL neuron was used in the two-
neuron gap junction network, Chiffre 9, to replace the HH NaKL neuron.

Neuron Models Constructed From Observed Data

1571

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 11: In the two-neuron circuit with gap junction connections shown in
Chiffre 9, HH-NaKL model neurons were used in the circuit and V1(t) and V2(t)
were recorded. Then we used the trained DDF-NaKL neurons (voir la figure 10) dans
the same circuit with the same Istim(t). V1(t) and V2(t) were recorded with HH-
NaKL neurons and with DDF neurons. (Top) Comparison of the time courses of
V1(t) in the two circuits. (Bottom) Comparison of the voltage time courses V2(t)
in the two circuits.

1572

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

Chiffre 12: A network segment with a presynaptic neuron with membrane volt-
age V1(t) driven by a stimulating current Istim(t) connected to a postsynaptic
neuron with membrane voltage V2(t) by a ligand gated synaptic connection.
The current flowing into neuron 2 is given in equation 9.1.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

For the excitatory synaptic connection, we selected gsyn = 0.5, Erev =

50 mV, τ
UN

= 0.1 ms, A1

= 9/8, V0

= −50 mV and dV0

= 10 mV.

The performance of this network segment was evaluated using the sim-
ple NaKL HH neuron as both the presynaptic neuron and the postsynaptic
neuron. Along with the dynamics of the synaptic gating variable A(t, V (t)),
this is a nine-dimensional dynamical system. Selecting Istim(t) as we have
earlier, we solved for V1(t) and V2(t) and stored these data for later use.

Suivant, using just the V(t) from an isolated NaKL neuron driven by the
selected Istim(t), we built a DDF neuron using the time-delay method de-
scribed earlier. In the construction of the DDF neuron model, we used
Nc = 500, DE = 4, τ = 2, and h = 0.02 ms in the data.

Two of these DDF neurons were then used in the network segment in
place of the simple NaKL HH neurons, and the same network segment was
driven by the same Istim(t) presented to neuron 1 connected by the same
synaptic dynamics to DDF neuron 2. The DDF neurons were trained with
500 ms of HH model V(t) data.

In Figure 13, we display the behavior of V1(t) from the presynaptic HH
neuron and the presynaptic DDF neuron when operating in the network
segment.

In Figure 14, we display the behavior of V2(t) from the postsynaptic HH
neuron and the postsynaptic DDF neuron when operating in the network
segment.

This network segment result indicates that, en effet, we may replace the
more complex HH neuron voltage activity with the reduced dimension,

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1573

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 13: In the network segment shown in Figure 12, neuron 1 with mem-
brane voltage V1(t) is driven by our selected Istim(t). The voltage activity V1(t)
drives neuron 2 through a ligand gated synapse, equation 9.1. In this figure we
show V1(t) comparing V1(t) when HH NaKL neurons are in the network seg-
ment (black) and when DDF neurons, trained on the HH V1(t), are in the neuron
segment (red). Nc

= 500 for the DDF neurons.

biophysically trained, V(t) DDF neuron in synaptic connections occurring
in a network of neurons.

10 Summary and Discussion

This article is a melding of many ideas from nonlinear dynamics and ap-
plied mathematics to the goal of constructing biophysically based models
of observables in neurobiology. These data-driven models encode the full
information in experimental observations on the complex system, the neu-
ron, which is observed in a current clamp experiment, c'est, one with a
given Istim(t) with membrane voltage V(t) observed, and permit forecasting
and predicting the voltage response of the observed neuron to other stimuli.
The method is called data-driven forecasting (DDF), and the model
construction produces a discrete time, nonlinear map V (t) → V (t + (cid:5)t) =
V (t + h) that may be used in a network with synaptic or gap junction con-
nections, as the dynamical function of each is determined by the volt-
ages of the presynaptic and the postsynaptic cells. We have shown this
in a simple network for gap junction neuronal connections and for a net-
work segment where a presynaptic neuron, stimulated by Istim(t), drives a

1574

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 14: In the network segment shown in Figure 12, neuron 1 with mem-
brane voltage V1(t) is driven by our selected Istim(t). The voltage activity V1(t)
drives neuron 2 through a ligand gated synapse, equation 9.1. In this figure we
show V2(t) comparing V2(t) when HH NaKL neurons are in the network seg-
ment (black) and when DDF neurons, trained on the HH V1(t), are in the neuron
segment (red). Nc

= 500 for the DDF neurons.

postynaptic neuron via an excitatory synapse. The formulation of the re-
quired dynamical map for the gating variables of synaptic connections is
given in appendix B.

The DDF-based network permits a computationally efficient network
model where the trained DDF discrete time map, trained on biophysical
data, replaces complex Hodgkin-Huxley models typically used in contem-
porary research. The computational advantage is achieved in two ways:
(1) no differential equations at the network nodes must be solved, et
(2) the nodal models are substantially reduced in complexity as it is only
the observable, V(t) that is forecast.

In the timing comparisons we performed on the use of an HH NaKL
model neuron solved by a standard fourth-order Runge-Kutta ordinary dif-
ferential equation solver compared to the forecasting efficiency of the V(t)
alone DDF for the same time period with the same Istim(t), we found a com-
putational improvement by a factor of 3.7. As the HH NaKL model eval-
uates four state variables {V (t), m(t), h(t), n(t)} while the V(t)-trained DDF
neuron gives only the time course of V(t), V (t) → V (t + h), a factor of about
four in execution of the DDF is sensible.

Neuron Models Constructed From Observed Data

1575

For the data in Figure 3, a detailed Hodgkin-Huxley model with 14 state
variables, V(t), et 13 gating variables was constructed using methods of
data assimilation (Nogaret et al., 2016). The improvement in computational
efficiency in forecasting V(t) using the DDF neuron trained on these data
over the HH model was approximately 10. This suggests the idea that for
an HH neuron with Ngating variables, the computational efficiency of a DDF
neuron accurately forecasting the membrane voltage will be about Ngating
faster than solving the HH model at each node of a functional network.

One must recognize that while much is gained by the DDF neuron con-
struction, something is set aside, and that is the knowledge of the biophysics
in detailed HH models of individual neurons, including the operation of
gating variables for the ion channels selected for the model, parameters de-
termining the dynamics and strength of those ion channels, and other un-
observed yet relevant biophysical properties of the neurons.

In this article, we have presented the formulation of the DDF method.
Many familiar with its ingredients will recognize the provenance of such
a strategy. We have also shown how this approach can be applied to ex-
perimental data from current clamp experiments from an avian songbird
preparation.

The challenges ahead in building large, realistic functional network
models in neurobiology are significant. Encore, as the DDF models are based
on observations of V(t) from experimental data, the biophysical content of
each representation of neuron dynamics is equivalent.

While we certainly have not shown this in this article, it is not inappro-
priate to state that the connectivity of a realistic functional network with
DDF neuron models at the nodes can be established using methods of data
assimilation (Toth et al., 2011; Kostuk et al., 2012; Nogaret et al., 2016; Abar-
banel, 2022).

Data assimilation for such a network requires a model of the connec-
tivity among the component neurons, along with data on the operation of
many neurons in the intact network. The ability to use Ca fluorescence ex-
perimental results (Smetters et al., 1999; MacLean & Yuste, 2009; Vogelstein
et coll., 2009), where a large number of neurons are observed in a data as-
similation environment suggests a path forward for this kind of network
connectivity construction.

Another potential use of DDF arises when one does have detailed HH
model neurons for network components. This may be of value in answer-
ing questions more intricate than computationally efficient neurons at the
nodes of large networks (Daou & Margoliash, 2020; Abarbanel, 2022, chap.
9). It is likely that data assimilation will have been used to create such de-
tailed biophysical models. Using V(t) from such models, one can construct
a reduced dimension DDF V (t) → V (t + h) realization of the biophysics
in the HH model, and then, as we showed, one may replace the com-
plex HH model with the reduced-dimension DDF construct. One can ex-
pect to achieve computational efficiency and allow the exploration of larger

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1576

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

biological networks when using the DDF construction to capture the neu-
ron biophysics.

Appendix A: A Guide for the Implementation of DDF

A.1 Guide to the Use of Radial Basis Functions in Data-Driven Fore-
casting. To provide readers an overview of how we construct and use the
representations of the vector field for the DDF discrete time maps con-
structed from observed data, we present in this appendix a “manual.” Our
manual is more general than the applications in the main body of the arti-
clé, which has as its focus the use of the methods in neuroscience. Ici, nous
identify what is special for neuroscience and what is useful in general:

1. Collect D-dimensional data for the observations on your system
+ (n − 1)h, n =
of interest. We call these data u(tn) = u(n)∈ RD; tn = t0
1, 2, . . . N. We wish to use these data to construct a discrete time map
toi(n) → u(n + 1), which we then use for n > N: to forecast in the dynamical
development of the observations beyond the data that have been collected.
2. Select a training subset of the data {toi(n)}; n = 1, 2, . . . , NT ; NT < N. 3. Select a subset of the observed data to use as “centers” uc(q) q = 1, 2, . . . , Nc; Nc ≤ NT . The RBF was designed to be an accurate interpolat- ing function in u space, and the centers tell us which samples of the distri- bution in u space we utilize. 4. Select a radial basis function (RBF) ψ([u − uc(q)]2, σ ). All of the RBFs have a shape factor σ that is associated with the distance in D-dimensional u space over which the influence of the observed data is important (Wu, Wang, Zhang, & Du, 2012). 5. Represent the vector field f(u(n), χ) for the discrete time dynamics u(n + 1) = u(n) + f(u(n), χ). The χ are a set of parameters that we will learn while training the RBF. 6. The representation of f(u, χ) is fa(u, χ) = Nc(cid:2) q=1 waqψ([u − uc(q)]2, σ ); a = 1, 2, . . . , D, (A.1) and among the parameters in χ are {waq, σ Nc} and others we identify in a moment. A more general RBF formulation (Powell, 2002; Schaback, 1995) allows for a polynomial in u, but we have not used this freedom in this article. 7. Train the elements of χ via ua(n + 1) = ua(n) + Nc(cid:2) q=1 waqψ([u(n) − uc(q)]2, σ); n = 1, 2, . . . , NT − 1. (A.2) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 7 1 5 4 5 2 0 3 0 4 5 1 n e c o _ a _ 0 1 5 1 5 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Neuron Models Constructed From Observed Data 1577 8. This training involves the inversion of a rectangular Nc × NT matrix ψ([u(n) − uc(q)]2, σ ), which is an ill-posed problem and requires regular- ization (Press et al., 2007) to make its inverse well defined. This procedure is also called ridge regression in the literature. The regularization consists of realizing the determination of the {waq} as the minimization of (cid:4) NT(cid:2) n=1 ua(n + 1) − ua(n) − Nc(cid:2) q=1 waqψ([u(n) − uc(q)]2, σ ) , (A.3) (cid:7)2 to which we add a regularization term β (cid:12) (cid:12) NT n=1 Nc q=1 wT aq waq. When Znq = ψ([u(n) − uc(q)]2, σ ) and ya(n) = ua(n + 1) − ua(n), the so- lution to the minimization of equation A.3 is written as waq = (cid:4) Nc(cid:2) q(cid:6)=1 1 ZT Z + β (cid:7) NT −1(cid:2) qq(cid:6) n=1 Zq(cid:6)nya(n); a = 1, 2, . . . , D. (A.4) This enlarges the list of quantities in are required to estimate to {waq, σ Nc, β}. 9. If one is using the time-delay embedding space to “unproject” the D-dimensional measurements into a larger space where the dynamics oper- ates, then we need to estimate two more parameters: the time delay τ and the dimension DE of vectors S(n) in the larger space. For D = 1, the case we encountered in application of DDF to neuroscience problems, where u(n) = V (n), the time delay vectors are S(n) = [u(n), u(n − τ ), u(n − 2τ ), . . . , u(n − (DE − 1)τ )]. (A.5) If D > 1, the time-delay vectors will have components built with time de-
lays of the observed u(n). The full set of parameters we need to estimate in
this practical setting is now {waq, p, Nc, β, τ, DE}.

To implement this protocol, we have proceeded in the following way:
There are many RBFs to choose from. (See Table 1 in Schaback, 1995, pour

a list.) We have not tried them all. We have primarily used the gaussian

G([toi(n) − uc(q)]2, p ) = exp[−R(toi(n) − uc(q))2]

(A.6)

in our calculations. R is the precision of the gaussian.

We also used the multiquadric of Hardy (1971; Micchelli, 1986; Powell,

2002; Schaback, 1995)

(cid:13)

MQ([toi(n) − uc(q)]2, p ) =

([toi(n) − uc(q)]2 + p 2),

(A.7)

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1578

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

and found on some problems essentially equivalent results. In what follows,
and in the work in this article, we remain with ψ

G([toi(n) − uc(q)]2, p ).

A.2 Including Polynomial Terms in the Representation of f(toi). It can
be helpful to include polynomial terms as well as RBFs in the representation
of the discrete vector field (Schaback, 1995; Powell, 2002). The vector field
representation becomes

fa(toi, χ) =

J.(cid:2)

j=1

ca j p j(toi) +

Nc(cid:2)

q=1

waqψ([u − uc(q)]2, p ); a = 1, 2, . . . , D,

(A.8)

which is what we see in equation 3.1.

The addition of polynomials is indicated if we know on other grounds
something about the underlying dynamic of the source of the data that sug-
gests polynomial terms in the vector fields are present. That is not the case
in applying these methods to neuroscience, so except for the term u(n) dans
equation A.2, we do not use the freedom of further polynomials in u.

A.3 How to Choose Centers. The choice of centers, the uc vectors in the
RBF, is constrained by the data points in the training window 1 ≤ n ≤ NT .
We used K-means clustering (Du & Swamy, 2006) to select the uc, and this is
a way of selecting centers where they are needed to sample the distribution
in u space. While there may be more advanced methods, we have found
K-means to work well enough and have used the method in finding all of
the results in this article.

Another aspect to consider is the number of centers Nc. A general rule of
thumb is that the more centers, the better, as the distribution in u space is
better sampled. Cependant, this comes at the cost of both memory and com-
putational time. In this article, we typically chose about 5000 centers for
training lengths NT ≈ 25 − 50 × 104.

There is a possible strategy with regard the selecting Nc that balances a
finely grained sampling of the distribution in u space against the increased
computing cost in evaluating the dynamical map u(n) → u(n + 1) quand
Nc. When a data set that is noisy is presented, the resolution in u space
is coarsely grained when the data arrive. The idea is to recognize that lim-
itation on how well any DDF can perform by evaluating a metric on the
match between the predictions of the trained DDF {uDDF (n) compared to
the known, noisy knowledge we have of the data udata(n) for n ≥ NT . Ce
n>NT [uDDF (n) − udata(n)]2. Noise will limit the im-
could be something like
provements in forecasting quality as Nc increases, and the performance of
the metric should lead to a modest Nc larger than which no increase in fore-
casting skill is seen.

(cid:12)

A.3.1 Centers and RBFs. We found that the obvious choices for DDF
worked out well, namely, choosing gaussian RBFs and K-means clustering.
These strategies are commonly used in the RBF literature.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1579

Cependant, these are far from the only good working ideas there that could
possibly work better. The centers could also be chosen by emphasizing
places where the first or second derivatives in the data u(n) are greatest.
This could work well because it could select more centers where data might
be sparse—for example, when the neuron data are spiking and regions are
traversed at higher speed than in subthreshold regions with smaller deriva-
tives in u(n) (Sánchez, 1995).

A.4 Working with Imposed Driving Forces Acting on the Source of
the Data {toi(n)}: Stimulating Currents Istim(t). We have not found a gen-
eral formulation for DDF in the case of a driven dynamical system. Un
natural idea is to include those forces—call them Kext (t)—on the list of ob-
served quantities in the data: {toi(n)} → {toi(n), Kext (n)} and enter this into the
arguments of the relevant RBFs.

In many interesting situations in physics and neurobiology, cependant, le
forces are additive, so the formulation presented in this article may be ap-
plicable to many interesting problems.

If we were analyzing the underlying detailed dynamical equations of
the processes producing the data, the Kext (t) would have to be provided as
they are not given a differential equation of their own but specified by the
user. This is true when we solve the differential equations for a model of the
driven systems and remains true for DDF.

In the case of the dynamics of neurons, we are in a fortunate situation. Dans
this instance, the forcing is from currents external to the intrinsic currents
associated with the ion channel dynamics. The voltage HH equation is a
statement of current conservation, and currents are additive.

This permitted us to write equation 4.1,

dV (t)
dt

= Fintrinsic(V (t), UN(t)) + Istim(t); dA(t)
dt

= FA(V (t), UN(t)),

(A.9)

and is an example where some knowledge of the biophysics or other physics
of the data source is of value.

A.5 Evaluating the χ. We have two classes of parameters in our repre-
sentation of the vector field f(toi, χ): those coefficients {ca j
} that weight
the polynomial and RBF contributions in equation 3.1. These are deter-
mined by linear algebra from

, w

a j

ua(n + 1) = ua(n) + fa(toi(n), χ) =

J.(cid:2)

j=1

ca j p j(toi(n))

Nc(cid:2)

q=1

waqψ([toi(n) − uc(q)], p ); a = 1, 2, . . . , D,

(A.10)

when the parameters (cid:4) = {R., β, τ, DE} are fixed.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1580

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

We proceeded by selecting a set of (cid:4), making a coarse grid search over
le (cid:4), performing the regularized linear algebra to train the coefficients
ϕ = {ca j
} for each choice of the (cid:4), and using this trained representation
to perform a validation test for each choice. χ = {ϕ, ξ}.

, w

a j

To accomplish this validation step we selected the unused part of the
known data with NV = N − NT elements and calculated a validation set of
forecast values uV (n):

uV (n + 1) = uV (n) + F(uV (n), ϕ, (cid:4)); n ≥ N − NT .

(A.11)

Then we compared the values uV (n), which are dependent on the choice of
(cid:4), with the known data. Effectively we evaluated the cost function,

C((cid:4)) =

1
NV − 1

N(cid:2)

j=N−NT +1

(uV ( j) − u( j))2,

(A.12)

and sought a minimum over the (cid:4).

Our practice has been to examine the quality of uV (n) ≈ u(n), locate re-
gions of the (cid:4) where they match well, and refine the grid search in the (cid:4)
as required.

A.5.1 Differential Evolution to Search for the minimum of C((cid:4)). Differen-
tial evolution is a genetic algorithm that could be implemented in our DDF
construction to improve our ability to create DDF models by more precisely
choosing sets of parameters (cid:4) = {R., β, τ, DE}. The method is described in
Storn and Price (1997).

It works by initiating a parent set of parameters from a user-defined uni-
form distribution. From that start, new “children” sets of (cid:4) are made from
combining the parents in an algorithmic way and comparing the new vali-
dation forecast {uV ( j)} to the old one. A user-defined cost function, tel que
equation A.12, is used to compare the children to their parents.

As generations go by, parents will gradually be replaced by children until
all of the parents converge on a minimum in the cost function. A user who
is able to define a clever cost function could get a result that surpasses those
from the simple grid searching employed so far.

A.6 Code for Our Implementation of DDF. We did all of our testing
and programming in Python. We give links to the code we used published
in GitHub. In the links is a DDF program that was written purely for radial
basis functions; in this repository, we include code for both gaussian and
multiquadric forms of the RBF. There is a link to a DDF neuron repository
that includes code that was built specifically for the study of an NaKL neu-
ron, where only the voltage and the stimulus are known; this means that
the code is built to perform time-delay embedding on a single dimension

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1581

of voltage. The treatment of the stimulus current in this code p. 66: a list of
4 URLs is as we described earlier. The third and final attached link is to a
method of using DDF with polynomial terms in the representation of f(toi, χ)
as an additional resource:

• https://github.com/RandarserousRex/Data-Driven-Forecasting

-Radial-Basis-Function-Method

• https://github.com/RandarserousRex/DDF-Applications-to

-Neurons

• https://github.com/RandarserousRex/Data-Driven-Forecasting

-Taylor-Method

A.7 Memory Management. An important note to consider is the size
of the matrices involved in training, for they can grow to the size of gi-
gabytes. Par exemple, the largest matrix involved in training is that of all
values of the RBFs at all times; NT by Nc can have a standard length of
25,000 data points with 5000 centres. Typically we use float64 for all our
valeurs, resulting in this matrix having a size 25,000(NT ) × 5000(Nc) × 8 = 1
gigabyte. We need another gigabyte for its transpose used in the regular-
ized matrix inversion calculation. This could be a limiting factor if one is
running multiple tests in parallel on a CPU or on a cluster with limited
storage.

A.8 Parallelizing DDF Calculations. This section serves as a sugges-
tion to take advantage of the ability to run DDF code in parallel. The grid
searching method discussed above lends itself readily to parallel program-
ming. Even the differential evolution method can be run in parallel. A sin-
gle trial of DDF does not have much potential for parallel operations as the
training is just matrix multiplication, and the forecasting is a step-by-step
process that relies on the result of the previous step.

Appendix B: Synaptic Dynamics

In the main text, we implemented a simple two-neuron circuit with gap
junction connections between the neurons. A richer network consists of
more neurons and allows for synaptic connections as well. Starting with
an equation for synaptic currents Isynaptic(t), we provide a discrete time map
to update the time dependence in a map for V(t).

B.1 Discrete Time Synaptic Dynamics. In the discrete time dynamical
rules for the membrane voltages of the neurons in a network, we require
the gating variable at discrete time tn and tn + h = tn+1.

The synaptic current between a presynaptic neuron with voltage Vpre(t)

and a postsynaptic neuron with voltage Vpost(t) is described by

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1582

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

Isynaptic(t) = gsynA(t, Vpre(t)[Erev − Vpost (t)],

dA(t, Vpre(t))
dt

= A0(Vpre(t)) − A(t)
− A0(Vpre(t))

τ
UN(A1

(B.1)

where A(t, Vpre(t)) is a synaptic gating variable. The synaptic gating is
opened, meaning is opened A(t, Vpre(t)) ≈ 1 when eneurotransmitter binds
onto receptors on the postsynaptic cell. It is closed, meaning A(t, Vpre(t)) ≈
0, when that neurotransmitter is released from the postsynaptic receptor.
Henceforth we denote the gating variable A(t, Vpre(t)) as A(t) for brevity.

In equation B.1, we have time constants τ (A1

− A0(Vpre(t)) and a function
A0(Vpre(t)) to specify. The function A0(V ) describes the transition of the gat-
ing variable from A(t) ≈ 0, namely a closed synaptic channel, to A(t) ≈ 1,
an open synaptic channel.

We represent this transition in the neighborhood of a transition at a volt-

age V0 from closed to open by writing

A0(Vpre(t)) = 1
2

(cid:4)

(cid:5)
1 + tanh

(cid:7)(cid:6)

Vpre(t) − V0
dV0

(B.2)

This function moves from very near 0 when V (cid:8) V0 to very near 1 quand
Vpre(t) (cid:9) V0, as desired, and it does so over an interval in voltage dV0.

When the width of this transition dV0 is small, A0(V ) is essentially a step

function in voltage.

When Vpre(t) < V0, equation B.1 is approximately dA(t) dt = − A(t) τ AA1 , and when Vpre(t) > V0, it is approximately

dA(t)
dt

= 1 − A(t)
− 1)
τ
UN(A1

(B.3)

(B.4)

By integrating each of these equations from time t to time t + h, we find for
V (cid:8) V0,

UN(t + h) = u−
u+

UN(t); u±1

= 1 ± h
2τ

AA1

(B.5)

For Vpre(t) (cid:9) V0, we find

UN(t + h)w+ = A(t)w− +

h
τ
UN(A1

− 1)

; w±1

= 1 ±

h
UN(A1

2τ

− 1)

(B.6)

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1583

To avoid the discontinuous change in voltage associated with a step func-
tion in Vpre, we write a smoother transition over an interval dV for the synap-
tic gating variable A(t):

UN(t + h) = u−
u+
(cid:4)

UN(t)

(cid:5)

(cid:4)

1
2

1 − tanh

(cid:7) (cid:6)

(Vpre(t) − V0)
dV

(cid:7)(cid:5)

(cid:4)

UN(t)

w−
w+

h
UN(A1

w+τ

− 1)

1
2

1 + tanh

(cid:10)
Vpre(t) − V0
dV

(cid:11)

(cid:7)(cid:6)
,

u±1

= 1 ± h
2τ

AA1

; w±1

= 1 ±

h
UN(A1

2τ

− 1)

(B.7)

B.2 Excitatory and Inhibitory Synaptic Formulation. In equation B.1,
we have two time constants {τ
− 1)} corresponding to the time
UN(A1
it takes for a neurotransmitter to undock from a postsynaptic receptor and
dock at the receptor, respectivement.

AA1

, τ

For an excitatory AMPA receptor, mediated by the neurotransmitter glu-
− 1) ≈ 1 ms.
= 1.5. For an
≈ 8 ms, and of

tamate, the approximate value of τ
So for this excitatory synaptic connection τ
UN
inhibitory synaptic connection, mediated by GABA, τ
τ
= 4/3.
UN(A1

UN(A1
= 2 ms and A1

− 1) ≈ 2 ms, leading to τ
UN

≈ 3 ms, and of τ

= 6 ms and A1

AA1

Appendix C: A Comment on Injected Currents

C.1 What Waveforms Should Be Chosen for Istim(t)? This question
arose in the valuable comments of the reviewers and is certainly an impor-
tant issue in training a DDF model neuron so that it will respond accurately
to any stimulating current it may encounter in a network or from environ-
mental stimulation.

The fact that the stimulating current enters the biophysical (HH) equa-
tions in an additive manner, reflecting the way current conservation works
in all electric circuits, suggests that a judicious choice of Istim(t) is possible.
We do not have a mathematical statement about what stimulating cur-
rents should be used to train a DDF or, d'ailleurs, an HH neuron model
via data assimilation. Cependant, we do have a biophysical argument.

1. If one wanted to learn how a DDF would respond when parameter
value is changed, then presenting data to the DDF training protocol
from a range of parameter values would permit the DDF to inter-
polate through that range. DDFs and radial basis functions (RBFs)
are interpolating mathematical devices by construction. With enough
data sampling enough of the dynamical system attractor, the RBF can
accurately interpolate among the given data points.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1584

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

= t0

2. As we have no differential equation for the stimulating current
+ hk, k = 0, 1, 2, . . . , N are just like parameters in the
Istim(tk)), tk
voltage or any other DDF. If we choose a training I(t), which evokes a
V(t) over the dynamical range expected of a neuron, say, −100 mV to
100 mV, then we will be able to interpolate to new V(t) values within
the training range. That is likely not to be quite enough as Istim(t) est
also a time series, albeit prescribed by the user, so we have found
that the strength of Istim(t) in its Fourier power spectrum must lie in a
range that can be determined by the data presented. Biophysically, si
the Istim(t) frequencies are too high, they would be filtered out by the
cell membranes RC time constant, as that acts as a low-pass filter.

Just this line of thinking led to the stimulating currents one sees in each
of the experimental time courses presented in this article. Before we used
this biophysical heuristic, data assimilation—training an HH model with
data—was unsuccessful. With this heuristic guiding the choices of Istim(t),
successful DA is now routine.

Remerciements

We acknowledge support from the Neurological Disorders and Stroke In-
stitute, National Institutes of Health, “From Ion Channels to Graph The-
ory in Sensorimotor Learning,” grant U01 NS115821-01, and the Office of
Naval Research, grants N00014-20-1-2580 and N00014-19-1-2522. Discus-
sions with Erik Bollt and Daniel Gauthier were instrumental in initiating
this work. C. Dan Meliza (University of Virginia) and Daniel Margoliash
(University of Chicago) kindly provided us with the current clamp data
from experiments on neurons within the nucleus HVC of zebra finch song-
birds. Discussions with Stefan Luther and Ulrich Parlitz gave us insights
into how DDF may have broad applications in biophysics. Two anonymous
referees assisted in improving earlier drafts of this article.

Les références

Abarbanel, H. D. je. (1996). The analysis of observed chaotic data. New York: Springer-

Verlag.

Abarbanel, H. D. je. (2022). The statistical physics of data assimilation and machine learn-

ing. Cambridge: la presse de l'Universite de Cambridge.

Abarbanel, H. D. JE., Rozdeba, P.. J., & Shirman, S. (2018). Machine learning: Deepest
learning as statistical data assimilation problems. Neural Computation, 30, 2025–
2055. 10.1162/neco_a_01094, PubMed: 29894650

Aeyels, D. (1981un). Generic observability of differentiable systems. SIAM J. Contrôle

Optim., 19, 595–603. 10.1137/0319037

Aeyels, D. (1981b). On the number of samples necessary to achieve observability.

Systems Control Lett., 1, 92–94. 10.1016/S0167-6911(81)80042-4

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1585

Broomhead, D. S., & Lowe, D. (1988). Multi-variable functional interpolation and

adaptive networks. Complex Systems, 2, 321–355.

Buhmann, M.. D. (2009). Radial basis functions: Theory and implementations. Cambridge:

la presse de l'Universite de Cambridge.

Casdagli, M.. (1989). Nonlinear prediction of chaotic time series. Physica D, 35, 335–

356. 10.1016/0167-2789(89)90074-2

Daou, UN., & Margoliash, D. (2020). Intrinsic neuronal properties represent song
and error in zebra finch vocal learning. Communications naturelles, 11. 10.1038/
s41467-020-14738-7

Du, K.-L., & Swamy, M.. N. (2006). Neural networks in a softcomputing framework. Nouveau

York: Springer Science & Business Media.

Dupont, G., & Goldbeter, UN. (1993). One-pool model for CA2+

oscillations involving
CA2+ and inositol 1,4,5-trisphosphate as co-agonists for CA2+ release. Cell Cal-
cium, 14, 311–322. 10.1016/0143-4160(93)90052-8, PubMed: 8370067

Fraser, UN. M., & Swinney, H. L. (1986). Independent coordinates for strange at-
tractors from mutual information. Physical Review A, 33, 1134–1140. 10.1103/
PhysRevA.33.1134

Hardy, R.. L. (1971). Multiquadric equations of topography and other irregular sur-
faces. Journal of Geophysical Research, 76, 1905–1915. 10.1029/JB076i008p01905
Hirata, Y., Suzuki, H., & Aihara, K. (2006). Reconstructing state spaces from mul-
tivariate data using variable delays. Physical Review E, 74, 026202. 10.1103/
PhysRevE.74.026202

Hodgkin, UN. L., & Huxley, UN. F. (1952). A quantitative description of membrane cur-
rent and its application to conduction and excitation in nerve. Journal of Physiol-
ogie, 172, 500–544. 10.1113/jphysiol.1952.sp004764

Houart, G., Dupont, G., & Goldbeter, UN. (1999). Bursting, chaos and birhythmicity
originating from self-modulation of the inositol 1,4,5-trisphosphate signal in a
model for intracellular CA2+ oscillations. Bull. Math. Biol., 61, 507–530. 10.1006/
bulm.1999.0095, PubMed: 17883229

Houart, G., Dupont, G., & Goldbeter, UN. (2003). From simple to complex CA2+

oscil-
lations: Regulatory mechanisms and theoretical models. En M. Falcke & D. Mal-
chow (Éd.), Understanding calcium dynamics: Experiments and theory (pp. 31–152).
Berlin: Springer.

Johnston, D., & Wu, S. M.-S. (1995). Foundations of cellular neurophysiology. Came-

pont, MA: Bradford Books, AVEC Presse.

Judd, K., & Mees, UN. (1995). On selecting models for nonlinear time series. Physica

D, 82, 426–444. 10.1016/0167-2789(95)00050-E

Kantz, H., & Schreiber, T. (2004). Nonlinear time series analysis (2nd ed.). Cambridge:

la presse de l'Universite de Cambridge.

Kostuk, M., Toth, B. UN., Meliza, C. D., Margoliash, D., & Abarbanel, H. D.
(2012). Dynamical estimation of neuron and network properties II: Path integral
Monte Carlo methods. Biological Cybernetics, 106(3), 155–167. 10.1007/s00422-012
-0487-5, PubMed: 22526358

MacLean, J.. N., & Yuste, R.. (2009). Imaging action potentials with calcium indica-
tors. Cold Spring Harbor Protocols, 2009(11), pdb.prot5316. 10.1101/pdb.prot5316,
PubMed: 20150055

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1586

R.. Clark, L. Fuller, J.. Platt, and H. Abarbanel

Mainen, Z. F., & Sejnowski, T. J.. (1995). Reliability of spike timing in neocortical neu-

rons. Science, 268, 1503–1506. 10.1126/science.7770778, PubMed: 7770778

Meliza, C. D., Kostuk, M., Huang, H., Nogaret, UN., Margoliash, D., & Abar-
banel, H. D. je. (2014). Estimating parameters and predicting membrane voltages
with conductance-based neuron models. Biological Cybernetics, 108(4), 495–516.
10.1007/s00422-014-0615-5, PubMed: 24962080

Micchelli, C. UN. (1986). Interpolation of scattered data: Distance matrices and condi-
tionally positive definite functions. Constructive Approximation, 2, 11–22. 10.1007/
BF01893414

Nogaret, UN., Meliza, C. D., Margoiliash, D., & Abarbanel, H. D. je. (2016). Automatic
construction of predictive neuron models through large scale assimilation of elec-
trophysiological data. Rapports scientifiques, 6. 10.1038/srep32749, PubMed: 27605157
Olver, P.. J.. (2017). Nonlinear ordinary differential equations (University of Minnesota

technical report). http://www-users.math.umn.edu/∼olver/.

Powell, M.. D. J.. (2002). Radial basis function methods for interpolation to functions
of many variables. In Fifth Hellenic-European Conference on Computer Mathematics
and Its Applications (DAMTP report 11).

Presse, W. H., Teukolsky, S. UN., Vetterling, W. T., & Flannery, B. P.. (2007). Numerical
recipes: The art of scientific computing (3rd ed.) Cambridge: L'université de Cambridge
Presse.

Sánchez, V. D. (1995). Second derivative dependent placement of RBF centers. Neu-

rocomputing, 7(3), 311–317.

Sauer, T. J., Yorke, J.. UN., & Casdagli, M.. (1991). Embedology. Journal of Statistical

Physics, 65, 579–616. 10.1007/BF01053745

Schaback, R.. (1995). Error estimates and condition numbers for radial basis func-
tion interpolation. Advances in Computational Mathematics, 3, 251–264. 10.1007/
BF02432002

Smetters, D., Majewska, UN., & Yuste, R.. (1999). Detecting action potentials in neu-
ronal populations with calcium imaging. Methods: A Companion to Methods in En-
zymology, 18, 215–221. 10.1006/meth.1999.0774

Sterratt, D., Graham, B., Gillies, UN., & Willshaw, D. (2011). Principles of computational

modelling in neuroscience. Cambridge: la presse de l'Universite de Cambridge.

Storn, R., & Prix, K. (1997). Differential evolution—A simple and efficient heuris-
tic for global optimization over continuous spaces. Journal of Global Optimization,
11(4), 341–359. 10.1023/UN:1008202821328

Strogatz, S. H. (2015). Nonlinear dynamics and chaos: With applications to physics, biology,

chemistry, and engineering (2nd ed.). Boca Raton, FL: CRC Press.

Takens, F. (1981). Detecting strange attractors in turbulence. Lecture Notes in Math.,

898, 366–381. 10.1007/BFb0091924

Toth, B. UN., Kostuk, M., Meliza, C. D., Margoliash, D., & Abarbanel, H. D. je.
(2011). Dynamical estimation of neuron and network properties I: Variational
méthodes. Biological Cybernetics, 105(3–4), 217–237. 10.1007/s00422-011-0459-1,
PubMed: 21986979

Vogelstein, J.. T., Watson, B. O., Packer, UN. M., Yuste, R., Bruno Jedynak, B., & Panin-
ski, L. (2009). Spike inference from calcium imaging using sequential Monte Carlo
méthodes. Biophysical Journal, 97, 636–655. 10.1016/j.bpj.2008.08.005

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

F
/

3
4
7
1
5
4
5
2
0
3
0
4
5
1
n
e
c
o
_
un
_
0
1
5
1
5
p
d

b
oui
g
toi
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuron Models Constructed From Observed Data

1587

Wu, Y., Wang, H., Zhang, B., & Du, K.-L. (2012). Using radial basis function networks
for function approximation and classification. ISRN Applied Mathematics, 2012,
324194. 10.5402/2012/324194

Ye, J., Rozdeba, P.. J., Morone, U. JE., Daou, UN., & Abarbanel, H. D. je. (2014). Estimat-
ing the biophysical properties of neurons with intracellular calcium dynamics.
Physical Review E, 89, 062714.

Received December 4, 2021; accepted March 23, 2022.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d