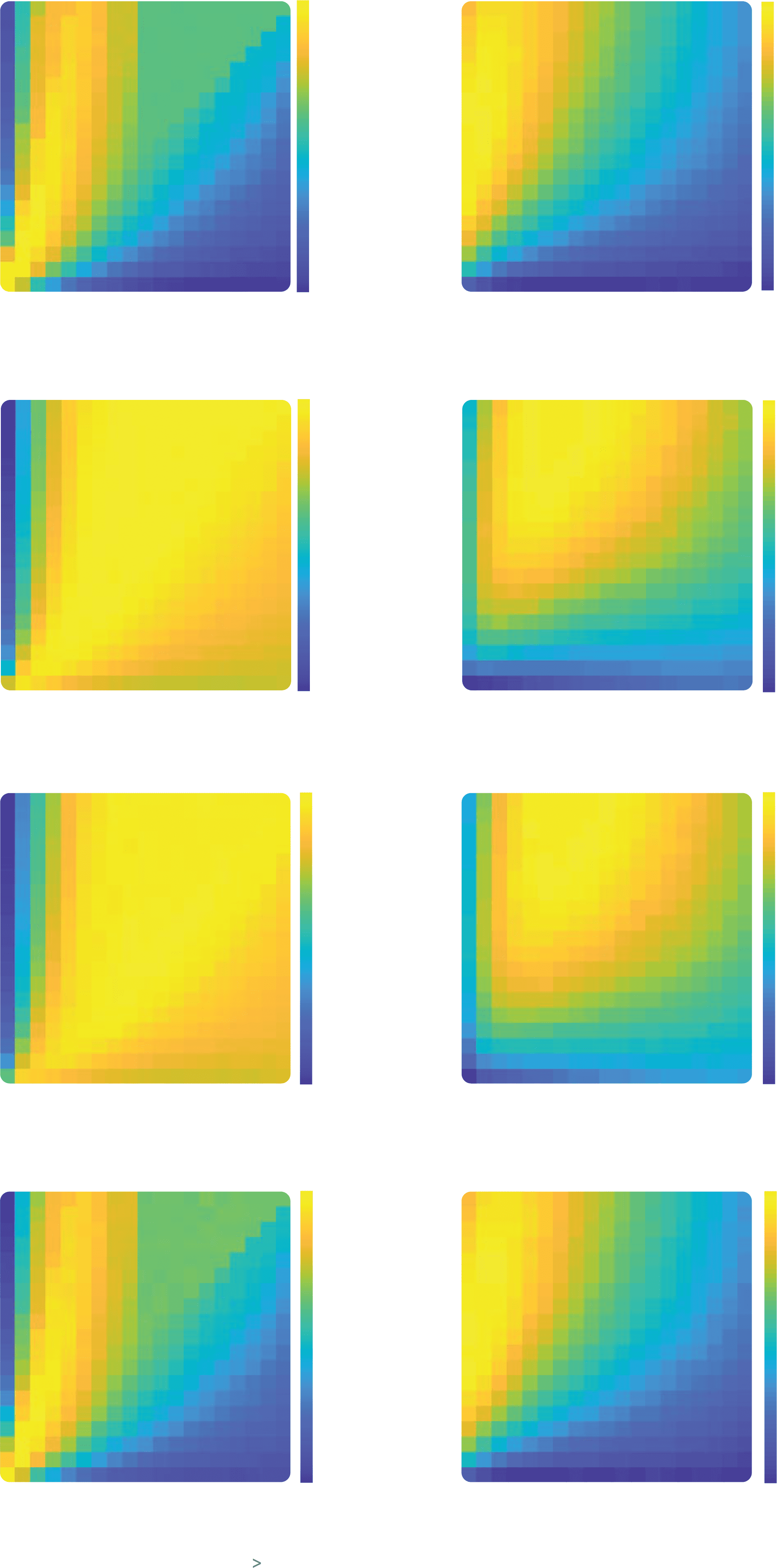ARTICLE

Communicated by Jianqiao Zhu

A Normative Account of Confirmation Bias During
Reinforcement Learning

Germain Lefebvre
germain.lefebvre@outlook.com
MRC Brain Network Dynamics Unit, Nuffield Department of Clinical
Neurosciences, University of Oxford, Oxford OX3 9DU, ROYAUME-UNI.

Christopher Summerfield
christopher.summerfield@psy.ox.ac.uk
Department of Experimental Psychology, University of Oxford,
Oxford OX3 9DU, ROYAUME-UNI.

Rafal Bogacz
rafal.bogacz@ndcn.ox.ac.uk
MRC Brain Network Dynamics Unit, Nuffield Department of Clinical
Neurosciences, University of Oxford, Oxford OX3 9DU, ROYAUME-UNI.

Reinforcement learning involves updating estimates of the value of states
and actions on the basis of experience. Previous work has shown that in
humans, reinforcement learning exhibits a confirmatory bias: when the
value of a chosen option is being updated, estimates are revised more
radically following positive than negative reward prediction errors, mais
the converse is observed when updating the unchosen option value es-
timate. Ici, we simulate performance on a multi-arm bandit task to ex-
amine the consequences of a confirmatory bias for reward harvesting. Nous
report a paradoxical finding: that confirmatory biases allow the agent to
maximize reward relative to an unbiased updating rule. This principle
holds over a wide range of experimental settings and is most influential
when decisions are corrupted by noise. We show that this occurs because
on average, confirmatory biases lead to overestimating the value of more
valuable bandits and underestimating the value of less valuable bandits,
rendering decisions overall more robust in the face of noise. Our results
show how apparently suboptimal learning rules can in fact be reward
maximizing if decisions are made with finite computational precision.

C.S. and R.B. contributed equally.

Neural Computation 34, 307–337 (2022)
https://doi.org/10.1162/neco_a_01455

© 2021 Massachusetts Institute of Technology.
Publié sous Creative Commons
Attribution 4.0 International (CC PAR 4.0) Licence.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

308

G. Lefebvre, C. Summerfield, et R. Bogacz

1 Introduction

Confirmation bias refers to seeking or interpreting evidence in ways that are
influenced by existing beliefs, and it is a ubiquitous feature of human per-
ceptual, cognitive, and social processes and a longstanding topic of study
in psychology (Nickerson, 1998). Confirmatory biases can be pernicious
in applied settings, Par exemple, when clinicians overlook the correct di-
agnosis after forming a strong initial impression of a patient (Groopman,
2007). In laboratory, confirmation bias has been studied with a variety of
paradigms (Nickerson, 1998; Talluri, Urai, Tsetsos, Usher, & Donner, 2018).
One paradigm in which the confirmation bias can be observed and mea-
sured involves reinforcement learning tasks, where participants have to
learn from positive or negative feedback which options are worth taking
(Chambon et al., 2020; Palminteri, Lefebvre, Kilford, & Blakemore, 2017).
This article focuses on confirmation bias during reinforcement learning.

In the laboratory, reinforcement learning is often studied via a “multi-
armed bandit” task in which participants choose between two or more
states that pay out a reward with unknown probability (Daw, O’Doherty,
Dayan, Seymour, & Dolan, 2006). Reinforcement learning on this task can
be modeled with a simple principle known as a delta rule (Rescorla & Wag-
ner, 1972), in which the estimated value V i
t of the chosen bandit i on trial t
is updated according to

V i

t+1

= V i
t

+ α · δi
t

.

(1.1)

In this equation, α is a learning rate in unity range, and δi
prediction error defined as

t is the reward

δi
t

= Ri
t

− V i
t

.

(1.2)

In the above equation, Ri
ciently small, V i
of bandit i (in stationary environments).

t is the payout for option i on trial t. If α is suffi-
t tend to converge over time to the vicinity of expected value

This task and modeling framework have also been used to study the
biases that humans exhibit during learning. One line of research has sug-
gested that humans may learn differently from positive and negative out-
comes. Par exemple, variants of the model above, which include distinct
learning rates for positive and negative updates to V i
t , have been observed
to fit human data from a two-armed bandit task better, even after penal-
izing for additional complexity (Gershman, 2015; Niv, Edlund, Dayan, &
O’Doherty, 2012). Similar differences in learning rates after positive and
negative feedback have also been observed in monkeys (Farashahi, Don-
ahue, Hayden, Lee, & Soltani, 2019) and rodents (Cie´slak, Ahn, Bogacz, &
Parkitna, 2018), suggesting that they reflect an important optimization of a
learning process that occurred earlier in evolution and has been preserved

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Confirmation Bias in Reinforcement Learning

309

across species. When payout is observed only for the option that was cho-
sen, updates seem to be larger when the participant is positively rather than
negatively surprised, which might be interpreted as a form of optimistic
learning (Lefebvre, Lebreton, Meyniel, Bourgeois-Gironde, & Palminteri,
2017). Cependant, a different pattern of data was observed in follow-up stud-
ies in which counterfactual feedback was also offered: the participants were
able to view the payout associated with both chosen and unchosen op-
tion. Following a feedback on the unchosen option, larger updates were
observed for negative prediction errors (Chambon et al., 2020; Palminteri
et coll., 2017; Schuller et al., 2020). This is consistent with a confirmatory
bias rather than a strictly optimistic bias, whereby belief revision helps to
strengthen rather than weaken existing preconceptions about which option
may be better.

One obvious question is why confirmatory biases persist as a feature
of our cognitive landscape. If they promote suboptimal choices, why have
they not been selected away by evolution? One variant of the confirmation
bias, a tendency to overtly sample information from the environment that
is consistent with existing beliefs, has been argued to promote optimal data
selection: where the agent chooses its own information acquisition policy,
exhaustively ruling out explanations (however obscure) for an observation
would be highly inefficient (Oaksford & Chater, 2003). Cependant, this ac-
count is unsuited to explaining the differential updates to chosen and un-
chosen options in a bandit task with counterfactual feedback, because in
this case, feedback for both options is freely displayed to the participant,
and there is no overt data selection problem.

− V 2

It has been demonstrated that biased estimates of value can paradox-
ically be beneficial in two-armed tasks in the sense that under standard
assumptions, they maximize the average total reward for the agent (Caze
& van der Meer, 2013). This happens because with such biased value es-
timates, the difference V 1
t may be magnified, so with a noisy choice
t
rule (typically used in reinforcement learning models), the option with the
higher reward probability is more likely to be selected. Caze and van der
Meer (2013) considered a standard reinforcement learning task in which
feedback is provided only for the chosen option. In that task, the reward
probabilities of the two options in the task determine whether, it is benefi-
cial to have a higher learning rate after positive or negative prediction error
(Caze & van der Meer, 2013). Autrement dit, when only the outcome of
a chosen option is observed, optimistic bias is beneficial for some reward
probabilities and pessimistic bias for other.

In this article, we show that if the participants are able to view the pay-
outs associated with both chosen and unchosen options, reward is typically
maximized if the learning rates follow the pattern of the confirmation bias,
c'est, they are higher when the chosen option is rewarded and the un-
chosen option is unrewarded. We find that this benefit holds over a wide
range of settings, including both stationary and nonstationary bandits, avec

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

310

G. Lefebvre, C. Summerfield, et R. Bogacz

different reward probabilities, across different epoch lengths, et sous
different levels of choice variability. We also demonstrate that such confir-
mation bias tends to magnify the difference V 1
t and hence makes the
t
choice more robust to the decision noise. These findings may explain why
humans tend to revise beliefs to a smaller extent when outcomes do not
match with their expectations.

− V 2

We formalize the confirmation bias in a reinforcement learning model,
compare its performance in simulations with models without confirmation
bias, and formally characterize the biases introduced in value estimates. Nous
also point out that the confirmation bias not only typically increases the
average reward, but may shorten reaction times and thus increase the rate of
obtaining rewards to even higher extent.

2 Reinforcement Learning Models

2.1 Confirmation Model. We analyze properties of a confirmation
model (Palminteri et al., 2017) that describes learning in a two-armed bandit
task where feedback is provided for both options on each trial. The model
updates the corresponding value estimates V i
t according to a delta rule with
two learning rates: αC for confirmatory updates (c'est à dire., following positive pre-
diction errors for the chosen option and negative for the unchosen option)
and αD for disconfirmatory updates (c'est à dire. following negative prediction er-
rors for the chosen option and positive for the unchosen option; Palminteri
et coll., 2017). Ainsi, on each trial t, if the agent chooses option 1, the model
updates the values V 1
t of the chosen and unchosen options, respecter-
tivement, such that

t and V 2

(cid:2)

(cid:2)

V 1

t+1

= V 1
t

+

et

V 2

t+1

= V 2
t

+

,

αC · δ1
t
αD · δ1
t

αD · δ2
t
αC · δ2
t

,

,

,

if δ1
t
if δ1
t

> 0
< 0 if δ2 t if δ2 t > 0
< 0 , (2.1) (2.2) with δi t being the prediction error for bandit i on trial t defined in equation 1.2. We define an agent with a confirmatory bias as one for whom αC > αD,
whereas an agent with a disconfirmatory bias has αC < αD and an agent with no bias (or a neutral setting) has αC = αD. Note that for αC = αD = α, the model amounts to a standard delta-rule model with a unique learning rate α defined in equation 1.1, and we refer to it as unbiased. 2.2 Decaying Learning Rate Model. We compared the performance of the confirmation model in a stable environment to an optimal value l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Confirmation Bias in Reinforcement Learning 311 estimator, which for each option computes the average of rewards seen so far. Such values can be learned by a model using the update given in equa- tion 1.1 with the learning rate α decreasing over trials according to α = 1 t , where t is the trial number (note that with the counterfactual feedback, t is also equal to the number of times the reward for this option has been observed). 2.3 Decision Policies. In this article, we consider three policies for mak- ing a choice on the basis of learned values: hardmax, softmax, and ε-greedy policies. The hardmax is a noiseless policy selecting deterministically the arm associating with the highest value. The softmax is a probabilistic ac- tion selection process associated with each arm a the probability Pa t of being selected based on their respective values such that = Pa t /β ) exp(V a t /β ) + exp(V 2 t exp(V 1 t . /β ) (2.3) In this equation, β is the temperature of the softmax function, and the higher the temperature, the more random the decision is. To mathematically an- alyze properties of the confirmation model, we also consider a simpler stochastic choice rule, ε-greedy, which on the majority of trials selects op- tion with the highest estimated value while with certain fixed probability selects an action randomly. 3 Effects of Confirmation Bias on Average Reward 3.1 Methods of Simulation. Our goal was to test how outcomes vary with a confirmatory, disconfirmatory, or neutral bias across a wide range of settings that have been the subject of previous empirical investigation in humans and other animals. We considered tasks involving choice between two options. Each bandit i may yield reward R = 1 with probability pi and no reward (R = 0) with probability 1 − pi. Importantly, we assumed that the agent observes on each trial the payouts for both options: the chosen one and the not chosen one (see Figure 1a). We consider an agent who chooses among bandits for 2n trials, where n varied from 2 to 10 in simulations (see Figure 1b), and the presented rewards were averaged over these values of n (unless otherwise stated). We considered four ways in which the reward probabilities pi are set, illustrated schematically in Figure 1c. First, we considered stable environ- ments in which reward probabilities were constant. We also considered con- ditions of 1 reversal and 3 reversals where the payout probabilities were reversed to 1 − pi once in the middle of the task (second display in Figure 1c) or three times at equal intervals (third display in Figure 1c). In stable, 1 reversal and 3 reversals conditions, the initial probabilities pi at the start l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 312 G. Lefebvre, C. Summerfield, and R. Bogacz Figure 1: Simulation setup. (a) Reward contingencies. The illustration repre- sents the chosen (orange) and unchosen (blue) bandits, each with a feedback signal (central number). Below, we state the range of possible outcomes and probabilities. (b) Learning periods. The illustration represents the different lengths of the learning periods and the different outcome combinations poten- tially received by the agents. (c) Volatility types. The line plots represent the evolution of the two arms’ probability across trials in the different volatility conditions. of the task were sampled at intervals of 0.1 in the range [0.05, 0.95] such that p1 (cid:2)= p2, and we tested all possible combinations of these probabilities (45 probability pairs). Unless otherwise noted, results are averaged across these initial probabilities. Additionally, we considered the random walk condition where the prob- abilities were initialized to a random number from uniform distribution on an interval from 0 to 1 and then drifted over trials as follows, pi t+1 = pi t + κ · (0.5 − pi t ) + N (0, σ 2), (3.1) with κ being a parameter decaying the reward probability toward 0.5 (here set to κ = 0.001) and σ being the standard deviation of the normal distri- bution from which the fluctuations in probabilities were sampled (here, set to σ = 0.02). Sample probabilities generated from this process are shown in the fourth display in Figure 1c. We conduct all simulations numerically, sampling the initial payout probabilities and experiment length(s) exhaustively, varying αC and αD ex- haustively and noting the average reward obtained by the agent in each set- ting. The model is simulated with all possible combinations of learning rates αC and αD defined in the range [0.05, 0.95] with increments of 0.05, that is 192 learning rate combinations. For each combination of parameters, the sim- ulations were performed 1000 times for all but the random walk condition l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . 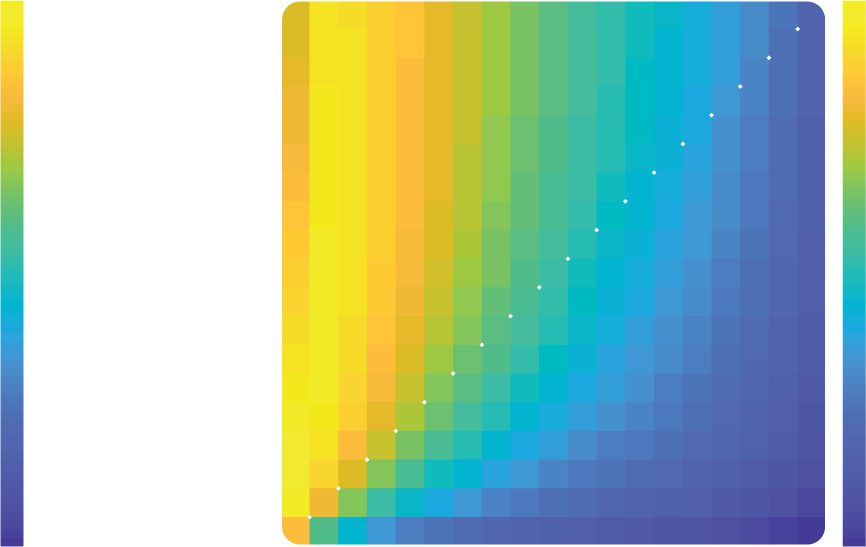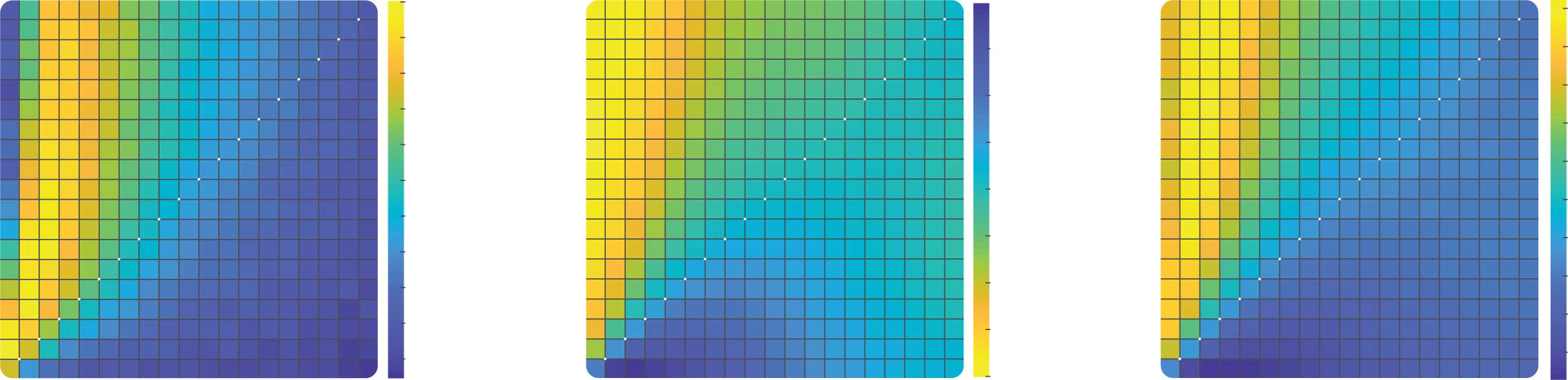/ f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Confirmation Bias in Reinforcement Learning 313 Figure 2: Dependence of reward on learning rate and decision noise in a sta- ble environment. (a, b) Average reward for all learning rate combinations. The heat maps represent the per trial average reward for combinations of αC (y-axis) and αD (x-axis), averaged across all reward contingencies and agents in the sta- ble condition with 1024 trials. Areas enclosed by black lines represent learning rate combinations for which the reward is significantly higher than the perfor- mance of the best equal learning rates combination represented by a black circle, one-tailed independent samples rank-sum tests, p < 0.001 corrected for multiple comparison. (a) Deterministic decisions. Simulated reward is obtained using a noiseless hardmax policy. (b) Noisy decisions. Simulated reward is obtained us- ing a noisy softmax policy with β = 0.1. (c) Comparison with optimal models. The bar plot represents the per trial average reward of the confirmation model, the small learning rate model and the decaying learning rate model for four dif- ferent levels of noise in the decision process. In simulations of the confirmation model, the best learning rates combination was used for each noise level (αC = [0.1, 0.15, 0.3, 0.35] and αD = 0.05). Bars represent the means and error bars the standard deviations across agents; all reward levels are significantly different from each other; two-tailed independent samples rank-sum tests, p < 0.001. where simulations are performed 100,000 times to account for the increased variability. Results are averaged for plotting and analysis. In all cases, infer- ential statistics were conducted using nonparametric tests with an alpha of p < 0.001 and Bonferroni correction for multiple comparisons. At the start of each simulation, the value estimates were initialized to V i 0 = 0.5. 3.2 Results of Simulations. Figure 2 plots total reward obtained in the stationary bandit problem as a function of αC (y-axis) and αD (x-axis), for the sequence length of 1024 and averaged across payout probabilities, for both the hardmax (left) and softmax (right) rules. The key result is that rewards are on average greater when αC > αD (warmer colors above the diagonal)
relative to when they are equal or when αC < αD. We tested this finding sta- tistically by repeating our simulations multiple times with resampled stim- ulus sequences (and choices in the softmax condition) and comparing the accrued reward to a baseline in which αC = αD = 0.05, the most promis- ing unbiased setting for α. The area enclosed by black line in Figures 2a and 2b indicate combinations of learning rates that yield rewards higher l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 314 G. Lefebvre, C. Summerfield, and R. Bogacz than the unbiased setting. Figure 2b confirms that in particular for the more plausible case where decisions are noisy (i.e., softmax temperature β > 0),
there is a reliable advantage for a confirmatory update policy in the bandit
task.

We compared the performance of the confirmation model to the decay-
ing learning rate model described above, which maximizes reward under
the assumption that payout probabilities are stationary and decisions are
noiseless (c'est à dire., under a hardmax choice rule). We confirmed this by plot-
ting the average reward under various temperature values for three mod-
le: one in which a single learning rate was set to a fixed low value α = 0.05
(small learning rate model), one in which it was optimally annealed (decay-
ing learning rate model), and one in which there was a confirmatory bias
(confirmation model; see Figure 2c). As can be seen, only under β = 0 does
the confirmation bias not increase rewards; as soon as decision noise in-
creases, the relative merit of the confirmation model grows sharply. Impor-
tantly, whereas the performance advantage for the decaying learning rate
model in the absence of noise (under β = 0) was very small (on the order of
0.2%), the converse advantage for the confirmatory bias given noisy deci-
sions was numerically larger (1.6%, 4.6%, et 5.5% under β = 0.1, 0.2, 0.3,
respectivement).

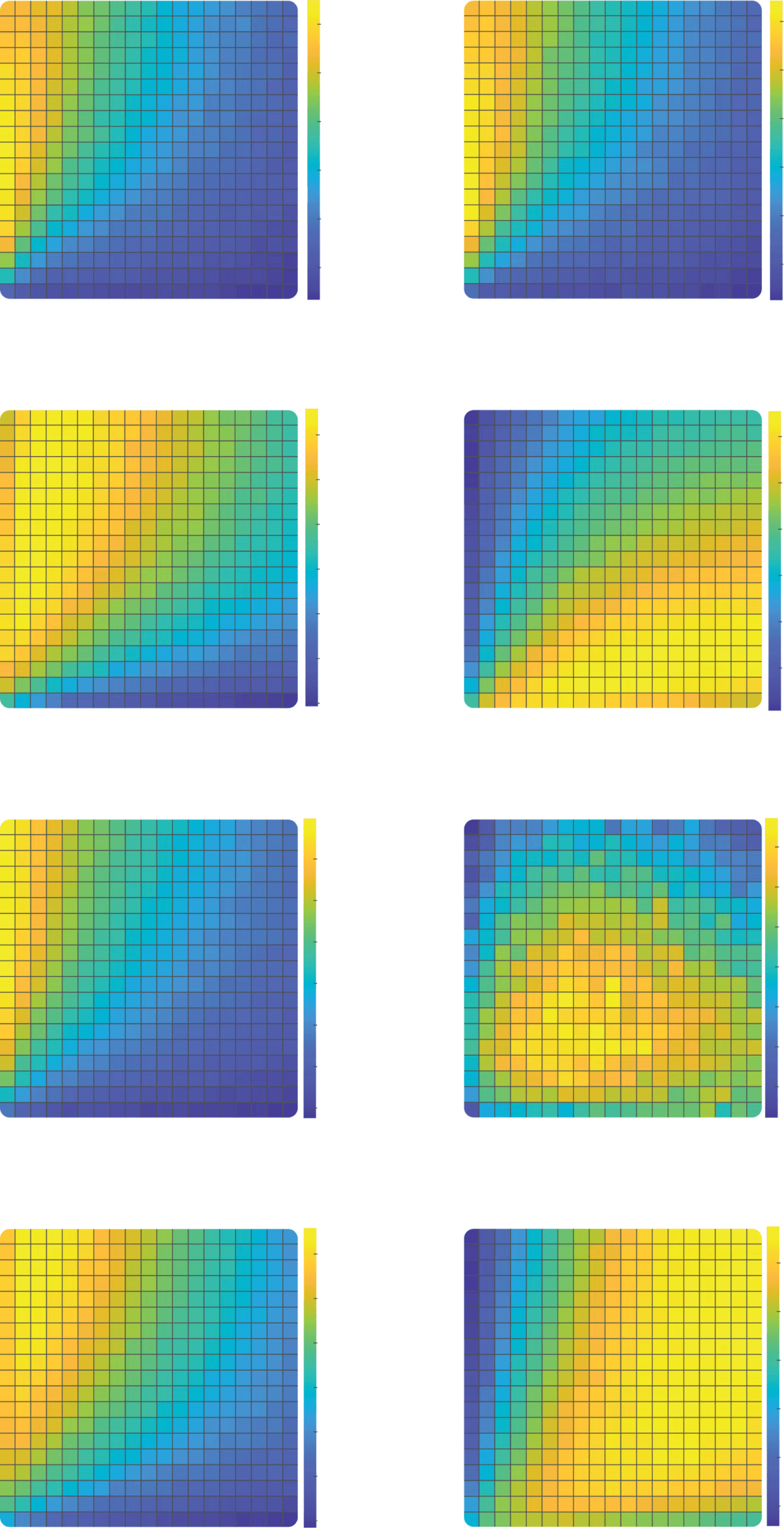
Suivant, we verified that these results held over different trial lengths and
for differing volatility conditions. The results (averaged over different num-
bers of trials) are shown in Figure 3. One can see equivalent results pre-
sented for a paradigm involving stable contingencies (see Figures 3a and
3e), a reversal of probability between the two bandits midway through the
séquence (see Figures 3b and 3f), for three such reversals (see Figures 3c and
3g), and for a random walk in which probabilities drift upward or down-
ward on each trial (see Figures 3d and 3h). When decisions are noisy, dans
all four cases, confirmatory agents reap more rewards than disconfirma-
tory agents do and also than agents for whom there is a single α selected
to maximize reward (see Figures 3e to 3h). When the decisions are based
on the hardmax choice rule, there was no biased combination of learning
rates giving significantly higher rewards than unbiased model (see Figures
3a to 3d). Nevertheless, there were still combinations of parameters with
αC > αD yielding reward similar to that from the unbiased model.

Subsequently, we tested how the sequence length affected the relative
advantage conferred by a confirmatory bias. In Figure 4a, we show that the
advantage for the confirmatory over the unbiased model holds true for all
but the very shortest sequences and continues to grow up to sequences of
1024 trials. Enfin, the confirmatory model is most advantageous at inter-
mediate levels of decision noise (as quantified here by the softmax temper-
ature). As we have seen, the relative numerical and statistical advantage is
lower if we assume no decision noise, but as decision noise grows to the
extent that performance tends toward random, all differences between dif-
ferent update policies disappear (Figure 4b).

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Confirmation Bias in Reinforcement Learning

315

Many decisions that humans and animals face in natural environments
involve choices among multiple options; hence, we investigated if the
confirmation bias also brings an advantage in such situations. The confir-
mation model can be naturally extended to multiple options by applying
the update of equation 2.2 to all unchosen options. Figure S1 in the online
supplementary information shows that confirmation bias also increases
the average outcome for extended learning environments with more than
two options.

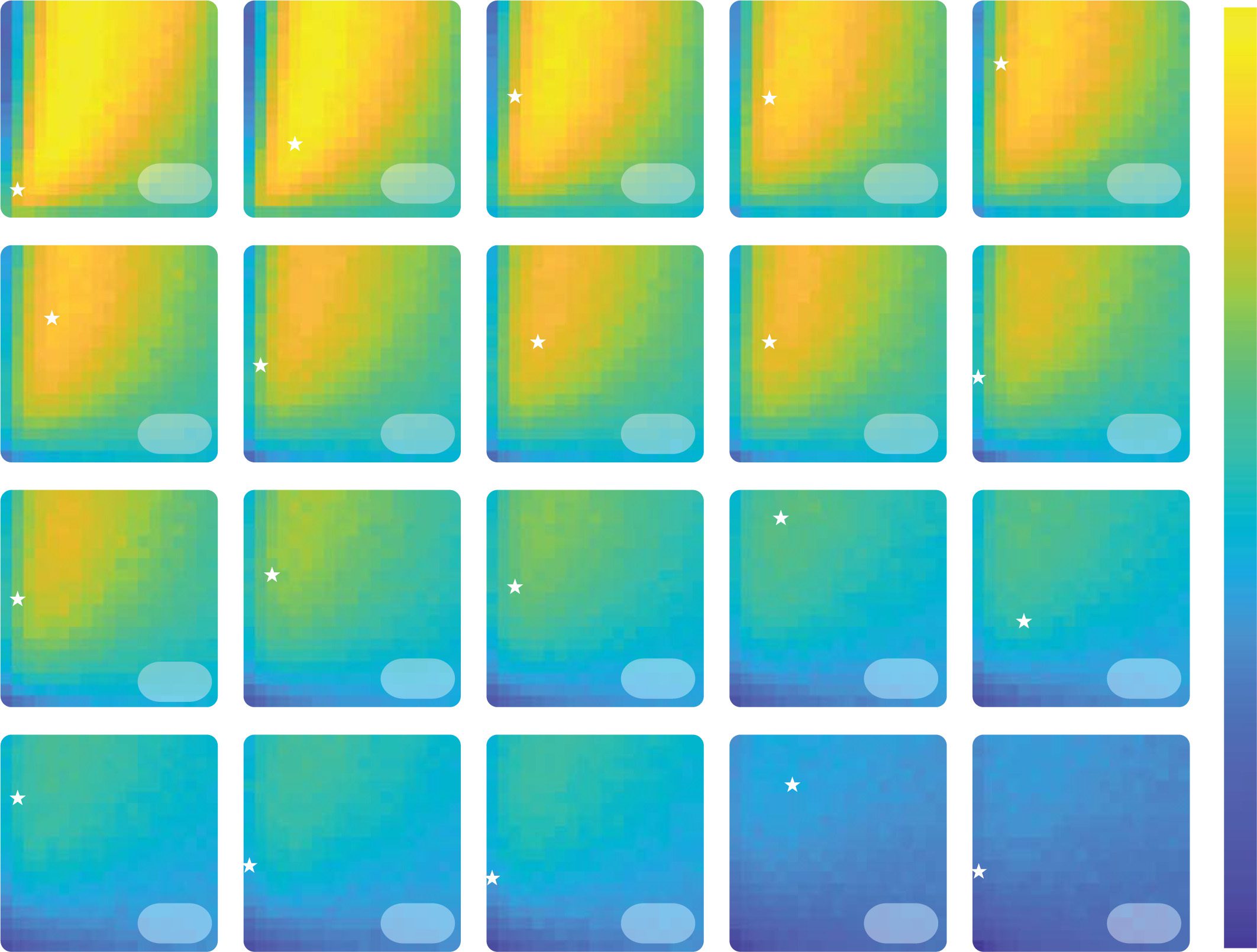
Enfin, we performed simulations of the experiment by Palminteri et al.
(2017) in order to see where human participants’ learning rates combi-
nations stand in terms of performance. Dans cette étude, participants made
choices between two options and received feedback on the outcomes of
both options. The task involved choices in multiple conditions in which
the participants could receive outcomes −1 or 1. In some conditions, le
reward probabilities were constant, while in others, 1 reversal occurred.
We simulated the confirmation model in the same sets of conditions that
participants experienced, with the same number of trials. We used the
values of softmax temperature estimated from individual participants by
fitting the confirmation model to their behavior (data are available at https:
//doi.org/10.6084/m9.figshare.4265408.v1). These estimated parameter
values of the confirmation model were reported by Palminteri et al. (2017).
Chiffre 5 shows for each participant, the simulated performance of all
combinations of learning rates considering their level of decision noise as
observed during the experiment, as well as their fitted learning rates. Comme
expected, most participants’ learning rates combinations fall in the vicinity
of the best-performing learning rates combinations, above the diagonal.

4 Confirmation Bias Magnifies Difference between Estimated Values

The simulations show that a confirmatory update strategy—one that priv-
ileges the chosen over the unchosen option—is reward maximizing across
a wide range of experimental conditions, in particular when decisions are
noisy. Why would this be the case? It is well known, Par exemple, that adopt-
ing a single small value for α will allow value estimates to converge to their
ground-truth counterparts. Why would an agent want to learn biased value
estimates? To answer this question, we demonstrate that the confirmation
bias often magnifies the differences between estimated values and hence
makes choices more robust to decision noise. We first show it on an intu-
itive example and then more formally.

4.1 Example of the Effects of Confirmation Bias. We selected three pa-
rameterizations of the update rules and examined their consequences in
plus de détails. The selected pairs of values for αC and αD are illustrated in
Figure 6a (symbols (cid:8), ×, and ◦). The first corresponded to an unbiased up-
date rule, αC = αD = 0.25; the second to a moderately biased rule, αC = 0.35,

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

316

G. Lefebvre, C. Summerfield, et R. Bogacz

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Confirmation Bias in Reinforcement Learning

317

αD = 0.15; and the third to a severely biased rule, αC = 0.45, αD = 0.05. Nous
refer to the bandit with a higher reward probability as richer and to the
other bandit as poorer. We chose a setting in which the reward probability
for the richer bandit is p+ = 0.65, while for the poorer bandit it is p− = 0.35.
For each update rule, we plotted the evolution of the value estimate for
the richer bandit V +
over trials (see Figure 6b) as well as aggregate choice ac-
curacy (see Figure 6c). Beginning with the choice accuracy data, one can see
that intermediate levels of bias are reward maximizing in the sense that they
increase the probability that the agent chooses the bandit with the higher
payout probability, relative to an unbiased or a severely biased update rule
(see Figure 6c). This is of course simply a restatement of the finding that
biased policies maximize reward (see the shading in Figure 6a). Cependant,
perhaps more informative are the value estimates for V +
under each up-
date rule (see Figure 6b). As expected, the unbiased learning rule allows
the agent to accurately learn the appropriate value estimate, such that after
a few tens of trials, V + ≈ p+ = 0.65 (gray line). Par contre, the confirma-
tory model overestimates the value of the richer option (converging close to
V + ∼ 0.8 despite p+ = 0.65, et (not shown) the model underestimates the
value of the poorer option p− = 0.35). Ainsi, the confirmation model out-
performs the unbiased model despite misestimating the value of both the
better and the worse option. How is this possible?

To understand this phenomenon, it is useful to consider the policy by
which simulated choices are made. In the two-armed bandit case, the soft-
max choice rule of equation 2.3 can be rearranged to the following logistic
fonction:

=

P1
t

1
1 + exp((V 2
t

.

− V 1

t )/β )

(4.1)

Ici, the choice probability depends on both the inverse slope of the choice
function β and the difference in value estimates for bandits 1 et 2. Le
effect of the confirmation bias is to inflate the quantity V 1
t away from
t

− V 2

Chiffre 3: Dependence of reward on learning rate and decision noise in different
environnements. The heat maps represent the per trial average reward for combi-
nations of αC (y-axis) and αD (x-axis) given a hardmax policy (a–d) or a softmax
politique (β = 0.3) (panels e–h). The performance is averaged across all reward
contingencies, period lengths, et 1000 agents in the stable condition (un, e), 1
reversal condition (b, F), 3 reversals condition (c, g), ou 100,000 agents in the
random walk condition (d, h). Areas enclosed by black lines represent learning
rate combinations for which the reward is significantly higher than the reward
of the best equal learning rates combination represented by a black circle, un-
tailed independent samples rank-sum tests, p < 0.001 corrected for multiple comparisons. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 318 G. Lefebvre, C. Summerfield, and R. Bogacz l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Figure 4: Effects of period length and decision noise on the relative perfor- mance of the confirmation model. (a) Effect of period length on reward. The line plot represents the difference in average reward between the confirmation model (with the best confirmatory learning rate combination per period) and the unbiased model (with the best per period single learning rate) in function of the log of the period length and for the four different volatility conditions. The logarithmic transformation of the trial number is for illustrative purpose only. ∗ p < 0.001, two-tailed independent rank-sum tests. (b) Effect of decision noise on performance. The line plot represents the difference in per trial average performances of the confirmation model (with the best confirmatory learning rates combination) and the unbiased model (with the single best learning rate) as function of the log of softmax temperature, and for the four different volatil- ity conditions. The logarithmic transformation of the softmax temperature is for illustrative purposes only. ∗ p < 0.001, two-tailed independent rank-sum tests. zero in either the positive or the negative direction, thereby ensuring choice probabilities that are closer to 0 or 1 even in the presence of decision noise (i.e. larger β). This comes at a potential cost of overestimating the value of Confirmation Bias in Reinforcement Learning 319 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Figure 5: Relation between human and synthetic data. The heat maps represent the per trial average reward for combinations of αC (y-axis) and αD (x-axis) in the experimental environment studied by Palminteri et al. (2017). Simulations have been performed with different softmax temperatures corresponding to the fitted temperature of the participants from that study and are averaged across 1000 agents. The stars represent the combination of fitted learning rates for each participant. the poorer option rather than the richer, which would obviously hurt per- formance. The relative merits of an unbiased versus biased update rule are thus shaped by the relative influence of these factors. When the rule is unbi- ased, the model does not benefit from the robustness conferred by inflated value estimates. When the model is severely biased, the probability of con- firming the incorrect belief is excessive leading to a high probability that the poorer option will be overvalued rather than the richer (see the bimodal dis- tribution of value estimates in Figure 6b, inset). Our simulations show that when this happens, the average reward is low, resulting in bimodal distri- bution of rewards across simulations (see the inset in Figure 6a). However, there exists a “goldilocks zone” for confirmatory bias in which the benefit of the former factor outweighs the cost of the latter. This is why a confirmation bias can help maximize reward. 320 G. Lefebvre, C. Summerfield, and R. Bogacz Figure 6: Mechanism by which confirmation bias tends to increase reward. (a) Average reward and reward distributions for different levels of confirma- tion bias. The heat map represents the per trial average reward of the confir- mation model for all learning rate combinations (confirmatory learning rates are represented on the y-axis whereas disconfirmatory learning rates are rep- resented on the x-axis) associated with a softmax policy with β = 0.1. The rewards concern the stable condition with 128 trials and asymmetric contin- gencies (p− = 0.35 and p+ = 0.65) and are averaged across agents. The three signs inside the heat map ((cid:8), ×, and +) represent the three learning rate com- binations used in the simulations illustrated in panels b and c. The histograms show the distribution across agents of the average per trial reward for the three different combinations. (b) Estimated values. The line plots represent the evo- lution of the best option value V + across trials. The large plot represents the agents-averaged value of the best option across trials for three different learning rate combinations: “unbiased” (αC = αD = 0.25), “biased (low)” (αC = 0.35 and αD = 0.15), and “biased (high)” (αC = 0.45 and αD = 0.05). The lines represent the mean and the shaded areas, the SEM. The small plots represent the value of the best option across trials plotted separately for the three combinations. The thick lines represent the average across agents and the lighter lines the individ- ual values of 5% of the agents. (c) Choice accuracy. The line plots represent the evolution of the probability to select the best option across trials. The large plot represents the agents-averaged probability to select the best option across tri- als for three different learning rates combinations: “unbiased” (αC = αD = 0.25), “biased (low)” (αC = 0.35 and αD = 0.15), and “biased (high)” (αC = 0.45 and αD = 0.05). The lines represent the mean and the shaded areas, the SEM. The small plots represent the probability of selecting the best option across trials plotted separately for the three combinations. The thick lines represent the av- erage across agents and the lighter lines the individual probability for 5% of the agents. 4.2 Analysis of Biases in Estimated Values. This section shows for- mally that the confirmation bias tends to increase the distance between the estimated values, but beyond a certain critical level of confirmation bias, the model may get stuck in a false belief that the poorer option is superior. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Confirmation Bias in Reinforcement Learning 321 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . 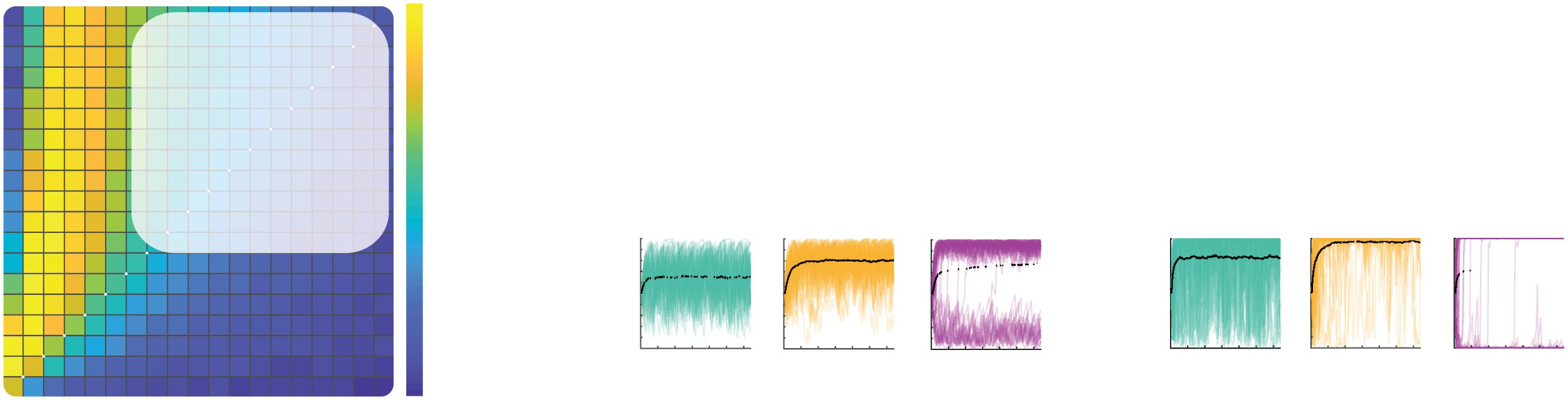/ f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Figure 7: Stochastic fixed points of value estimates. Behavior of the confirma- tion model with ε-greedy choice policy (ε = 0.1) has been analyzed for a stable environment with reward probabilities of the two options equal to p+ = 0.6 and p− = 0.4. (a) Blue and purple lines show the evolution of value estimates over simulated trials. Different displays correspond to different levels of confirma- tion bias b, indicated above the displays. The learning rates were set to αD = 0.01 and αC = bαD. (b) Asymptotic behavior of the confirmation model for different levels of the confirmation bias. The blue and magenta curves show the aver- age estimated values at the end of simulation with 10,000 trials. This average is taken over 100 simulations, and the error bars indicate the standard deviation. The model was simulated with αD = 0.01 and αC = bαD, where the confirmation bias b is shown on x-axes. Red and green curves denote the values of stochastic fixed points. The two displays correspond to different initial estimated values, listed above the displays. We followed the approach from a previous study analyzing biases in values due to unequal learning rates (Caze & van der Meer, 2013) and analyzed the values learned in a stable environment. Due to the stochastic nature of re- wards in the task, V i t constantly fluctuate, but with time, they approach a vicinity of values known as stochastic fixed points, in which they will not change on average, E((cid:8)V i t ) = 0 (E denotes expected value). The fluctuation of estimated values around stochastic fixed points is illustrated in Figure 7a. Different displays correspond to different levels of confirmation bias quan- tified by b = αC αD . For relatively low levels of bias, there exists only a single fixed point V i true for each estimated value corresponding to a true belief that the richer option is superior. Comparing the displays in Figure 7a illustrates 322 G. Lefebvre, C. Summerfield, and R. Bogacz that the distance between these fixed points for the two options increases with the confirmation bias, and this will be shown formally below. For a high level of confirmation bias illustrated in the right display of Figure 7a, there exists another fixed point V i f alse for each value, corresponding to a false belief that the poorer option is superior. In the simulation illustrated in Fig- ure 7a, right, the estimated values initially fluctuate around V i f alse and in − this period V . Due to the stochastic nature of rewards, the values t may switch between fluctuations around V i true, and such a shift happened around trial 500 (see Figure 7a, right). Importantly, we demon- strate formally below that these additional fixed points V i f alse appear for the confirmation bias only above a certain critical value; thus, the confirmation model tends to get stuck in false belief only when the bias is higher than a specific value (dependent on task parameters). f alse and V i + > V
t

We were not able to obtain tractable analytic expressions for stochastic
fixed points of values when the softmax choice rule was assumed; hence,
we considered a simpler ε-greedy choice rule. We denote the probability of
selecting an option with a lower estimated value by ε. To find the stochastic
fixed points, we will assume that it rarely changes which of V
est
higher. En effet, in simulation of Figure 7a, droite, such change occurred only
once in 1000 trials. Donc, we will analyze the behavior within the inter-
−
+
> V
vals on which V
, when the agent’s beliefs on superiority of options
t
t
−
+
< V are true, and within intervals on which V , when the agent’s beliefs t t are false. − + t and V t We first consider a case of true beliefs, where a learned value for the + richer option V . In this t case, the richer option is selected with probability 1 − ε and the poorer op- tion with probability ε. − is higher than the value for the poorer option V t The average change in the value of the richer option is then given by E((cid:8)V + t ) = (1 − ε)[p + ε[p +αC(1 − V + +αD(1 − V t ) + (1 − p + + t ) + (1 − p + t )] + )αD(−V + t )]. )αC(−V (4.2) In this equation, the first line corresponds to changes occurring when the richer option is chosen and the second line when the poorer option is cho- sen. Within each line, the first term in a square bracket corresponds to a change when the richer option yields rewards and the second term when the richer option is not rewarded. To find the value in a stochastic fixed point, we set the left-hand side of the above equation to 0 (because the stochastic fixed point is defined as the value in which the average value change is 0), and so the values in the fixed point V + true need to satisfy l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 0 = (1 − ε)[p + ε[p +αC(1 − V + +αD(1 − V true) + (1 − p + + true) + (1 − p + true)] + )αD(−V + true)]. )αC(−V (4.3) Confirmation Bias in Reinforcement Learning Solving for V + true we obtain, V + true = bp+(1 − ε) + p+ε b(p+(1 − ε) + (1 − p+)ε) + (1 − p+)(1 − ε) + p+ε . 323 (4.4) + The equation shows that the value V true in a stochastic fixed point does not depend on the individual learning rates, but only on their ratio b, as in a previous study (Caze & van der Meer, 2013). Analogous analysis shows that the stochastic fixed point for the poorer option is equal to V − true = bp−ε + p− (1 − ε) b(p−ε + (1 − p−)(1 − ε)) + (1 − p−)ε + p−(1 − ε) . (4.5) We now demonstrate that the confirmation bias increases V creases V we compute true. To evaluate the effect of increasing αC relatively to αD on V − + true and de- + true, dV + true db = p+ (1 − p+ )(1 − 2ε) [b(p+(1 − ε) + (1 − p+)ε) + (1 − p+)(1 − ε) + p+ε]2 . (4.6) This expression is nonnegative because the denominator is nonnegative (as it is a square) and the numerator is a product of nonnegative terms. This derivative will be positive if 0 < p+ < 1, and ε < 1 2 , when the rewards are nondeterministic and the choice policy is not completely random. The − derivative for V true is equal to an analogous expression but with a negative sign: dV − true db = − p− (1 − p− )(1 − 2ε) [b(p−ε + (1 − p−)(1 − ε)) + (1 − p−)ε + p−(1 − ε)]2 . (4.7) + In summary, for stochastic rewards, the confirmation bias increases V true and − decreases V true, and hence it magnifies the difference between these stochas- tic fixed points. This magnification of distance is visible in Figure 7a where the gap between dark green and red lines increases across the displays. − < V t Let us now consider the behavior of the model under false beliefs, during + the intervals when V . In this case, the poorer option is chosen on the t majority of trials because the agent falsely believes it has higher value. Fur- − + thermore, V is updated in the same way V t was updated under the correct t − beliefs. Hence the fixed point under the false beliefs, V f alse, is given by an expression analogous to that for V replaced by p− (see equation 4.5) but with p− − + f alse is given by an expression analogous to that for V true + − f alse and V f alse true (see equation 4.4) but with p+ replaced by p+ . Consequently, V . Similarly, V + l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 324 G. Lefebvre, C. Summerfield, and R. Bogacz + true and V − true their dependence on confirmation bias: V − inherit from V f alse in- + creases with the confirmation bias, while V f alse decreases with the bias. The green and red curves in Figure 7b plot the expressions for the stochastic fixed points for sample parameters. Without the confirmation bias (b = 1), the expressions for true and false fixed points coincide and then diverge with confirmation bias. = V < V + f alse + f alse − f alse and V − f alse. The fixed points V Importantly, the fixed points based on false beliefs exist only when the agent has false beliefs. Thus the agent will tend to stay in these fixed points − only if the false belief is satisfied in these fixed points: V f alse. In Fig- ure 7b, this false belief is only satisfied to the right from the intersection of the bright curves, so the intersection occurs at a critical value of the con- + firmation bias in which V f alse only emerge for the confirmation bias above this critical value, and to highlight + this, the curves plotting expressions for V f alse are shown in solid in Figure 7b when they become fixed points. + − f alse and V f alse only above critical confirma- tion bias is confirmed in simulations shown in Figure 7b. Blue and magenta curves show the mean estimated values at the end of simulations. The left display corresponds to simulations in which the values are initialized to + − a false belief. In this case, the values stay in V f alse and V f alse for sufficiently − + true and V high confirmation bias but move to V true for lower biases. The right display corresponds to a simulation in which the values are initialized to − 0.5. In this case, the values always move toward V true for low bias, + while for large bias, on some simulations they go to V f alse, as in- dicated by larger error bars. + true and V − f alse and V The existence of fixed points V − f alse and V The critical value of bias in which the bifurcation occurs can be found by − + finding the value of bcrit for which V f alse. In general, an analytic ex- f alse pression for bcrit is excessively long and thus uninformative, but an insight- ful expression can be found for the special case of deterministic choices, ε = 0. In this case the stochastic fixed points become = V V − f alse = V + f alse = bp− bp− + (1 − p+) p+ b(1 − p+) + p+ , . (4.8) (4.9) Equating equations 4.8 and 4.9 and solving for bias we find the critical value of the confirmation bias: (cid:3) (cid:4) (cid:4) (cid:5) = bcrit 1 p− − 1 p+ − 1 1 . (4.10) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Confirmation Bias in Reinforcement Learning 325 In this equation, we observe that bcrit increases with p+ and decreases with p− . Therefore, the larger the difference in reward probabilities of the two options, the higher the confirmation bias needs to be for the agent to get stuck in the false belief. 5 Effects of Confirmation Bias on Reward Rate The analysis shown in Figure 6 illustrates why the benefit of confirmation drops off as the bias tends to the extreme: under extreme bias, the agent falls into a feedback loop whereby it confirms its false belief that the lower- valued bandit is in fact the best. Over multiple simulations, this radically increases the variance in performance and thus dampens overall average reward (see Figure 6c). However, it is noteworthy that this calculation is made under the assumption that all trials are made with equivalent re- sponse times. In the wild, incorrect choices may be less pernicious if they are made rapidly, if biological agents ultimately seek to optimize their reward per unit time (or reward rate). Here, we relaxed this assumption and asked how the confirmatory bias affected overall reward rates, under the assumption that decisions are drawn to a close after a bounded accumulation process that is described by the drift-diffusion model This allows us to model not only the choice probabilities but also reaction times. 5.1 Methods of Simulations. We simulated a reinforcement learning drift diffusion model (RLDDM) in which the drift rate was proportional to the difference in value estimates between the two bandits (Pedersen, Frank, & Biele, 2017), which in turn depends on the update policy (confirmatory, disconfirmatory, or neutral). At each trial, the relative evidence x in favor of one of the two options is integrated over time, discretized in finite time step i, until it reaches one of two thresholds at 0 and a, implying the selection of the favored option such that xi+1 = xi + vt ∗ dt + c ∗ √ dt ∗ N (0, 1) (5.1) with x0, the initial evidence defined as x0 2 , dt set to 0.001 and c to 0.1. The drift rate vt is linearly defined from the difference in values such that = a vt = v mod + ∗ (V t − V − t ), (5.2) + t and V − t being the values at trial t, of the correct and incorrect options, V respectively. We used in our simulation a drift rate scaling parameter and a threshold values that make the drift-diffusion model to produce the same choice probabilities as the softmax policy with a temperature β = 0.1. In l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 326 G. Lefebvre, C. Summerfield, and R. Bogacz Figure 8: Effect of confirmation bias on reward rate. (a) The heat map repre- sents the per trial average reward simulated with the confirmation RLDDM for all learning rates combinations (confirmatory learning rates are represented on the y-axis, whereas disconfirmation learning rates are represented on the x-axis). The rewards concern the stable condition with 128 trials and asymmetric contin- gencies (p− = 0.35 and p+ = 0.65) and are averaged across agents. (b) The heat map represents the per trial average reaction time estimated with the confirma- tion RLDDM for all learning rates combinations. (c) The heat map represents the per trial average reward rate simulated with the confirmation RLDDM for all learning rates combinations. particular, the probability of making a correct choice by a diffusion model (Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006) is given by + P t = 1 1 + exp(−avt/c2) . (5.3) mod √ = a = /c2 = 1/β. Thus, The above probability is equal to that in equation 4.1 if av we set v 0.1. The values are updated exactly the same way as in the confirmation model (see equations 2.1 and 2.2). We employed the setting with 128 trials, using stable contingencies with reward probabilities equal to p− = 0.35 and p+ = 0.65. mod 5.2 Results of Simulations. When we plotted the overall accuracy of the model, the results closely resemble those from previous analyses, as is to be expected (see Figure 8a). When we examined simulated reaction times, we observed that confirmatory learning leads to faster decisions (see Figure 8b). This follows naturally from the heightened difference in values esti- mated for each bandit, as shown in Figure 6. Critically, however, responses were faster for both correct and incorrect trials. This meant that confirma- tory biases have the potential to draw decisions to a more rapid close, so that unrewarded errors give way rapidly to new trials which have a chance of yielding reward. This was indeed the case: when we plotted reward rate as a function of confirmatory bias, there was a relative advantage over a neutral bias even for those more extreme confirmatory strategies that were detrimental in terms of accuracy alone (see Figure 8c). Thus, even a severe l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Confirmation Bias in Reinforcement Learning 327 Table 1: Learning Rates in the Confirmation and Alternative Models. Model Confirmation model Valence model Hybrid model Partial feedback Chosen Option i Unchosen Option j (cid:2)= i δi t > 0

δi
t

< 0 δ j t > 0

δ j
t

< 0 αC α+ α+ α+ αD α− α− α− αD α+ α= — αC α− α= — Note: To make the table easier to read, αC and α+ are highlighted in bold. confirmatory bias can be beneficial to reward rates in the setting explored here. However, we note that this may be limited to the case explored here, where the ratio of reward to penalty is greater than one. 6 Comparison with Alternative Models In order to clarify the role of the constraint imposed on the learning rates and of the counterfactual feedback, we performed simulations with three additional models, which differ from the confirmation model in the update of the values of the unchosen option. Table 1 compares how the learning rates depend on the choice and the sign of prediction error in the confirma- tion model and the alternative models. for positive updates and α− All of the alternative models update the value estimate V i t of the cho- sen option similar to the confirmation model—that is, according to a delta rule with two learning rates: α+ for negative updates. The three additional models differ in their updates of the value estimate of the unchosen option. The first model, referred to as the valence model, updates the value estimate of the unchosen option with learning rates depending on the sign of prediction error analogous to that of the chosen option. Thus, in this model, the learning rate depends only on the sign of prediction error, not on whether the option was chosen. The second model, referred to as the hybrid model, updates the value of unchosen option us- ing an unbiased learning rate defined as α= = (α+ + α− )/2. We refer to this model as hybrid because the learning rate for the unchosen option in this model is the average of those in the valence model and the confirmation model (with αC = α+ ). The third model, referred to as partial feedback, does not update the value of the unchosen option; hence, it can de- scribe learning in tasks in which feedback is provided only for the chosen option. We define an agent with a positivity bias as one for whom α+ > a−
,
whereas an agent with a negativity bias has α+ < α− , and an agent with no bias (or a neutral setting) has α+ = α− . Figure 9 shows the performance of all four models separately for re- ward probabilities for both options pi < 0.5 (left panels) and for reward and αD = α− l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 328 G. Lefebvre, C. Summerfield, and R. Bogacz l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Confirmation Bias in Reinforcement Learning 329 probabilities for both options pi > 0.5 (right panels). For low reward proba-
bilities, the simulations gave very similar results in terms of favorable learn-
ing rates combinations (see Figures 9a, 9c, 9e, and 9g), whereas it is not the
case for high probabilities (see Figures 9b, 9d, 9F, and 9h). Two analyses can
be made based on this figure. D'abord, Figures 9a to 9f compare different mod-
els in the case of full feedback (for both the chosen and unchosen options),
et, second, Figures 9g to 9h illustrate the case of partial feedback. We an-
alyze these two cases next.

In the case of full feedback, Figures 9a and 9b show that confirmation
bias in the confirmation model increases average reward regardless of the
range of reward probabilities for the two options. The consistent effect of
confirmation bias contrasts with the opposite effects of biases in learning
rates in the valence model (see Figures 9c and 9d), where positivity bias is
beneficial for low reward probabilities, while negativity bias is beneficial
for high reward probabilities. These effects can be understood on the basis
of a previous study (Caze & van der Meer, 2013). That study analyzed the
reinforcement learning model in which the learning rate depended on the
sign of prediction error as in the valence model. The study showed that if
reward probabilities for both options pi < 0.5, then it is beneficial to have a positivity bias. With such bias, both V 1 and V 2 will be overestimated and, critically, the difference V 1 − V 2 will be magnified, so with a noisy choice rule, the option with the higher reward probability will be more likely to be selected. By contrast, if both pi > 0.5, then overestimating V 1 and V 2 would
actually reduce the difference V 1 − V 2 due to a ceiling effect, because ac-
cording to equation 1.1, reward estimates cannot exceed the maximum re-
ward available, V i ≤ 1. Dans ce cas, it is beneficial to have a negativity bias.
Donc, if one assumes that learning rates can differ between rewarded
and unrewarded trials, the type of reward-increasing bias depends on the
magnitude of reward probabilities in a task (Caze & van der Meer, 2013), un
dependence clearly seen in Figures 9c and 9d.

Chiffre 9: Dependence of reward on contingencies in alternative models. Le
heat maps represent the per trial average reward for combinations of αC (y-axis)
and αD (x-axis) (un, b) or α+ (y-axis) and α− (x-axis) (c–h) with a softmax pol-
icy (β = 0.3) in a stable environment. The performance is averaged across 1000
agents, all period lengths, and low reward contingencies: p1 < 0.5 and p2 < 0.5 (a, c, e, g) or high reward contingencies (p1 > 0.5 and p2 > 0.5 (b, d, F, h). Le
four models are the confirmation model (un, b), the valence model (c, d) the hy-
brid model (e, F), and a model with partial feedback (g, h). Areas enclosed by
black lines represent learning rate combinations for which the reward is sig-
nificantly higher than the reward of the best equal learning rates combination
represented by a black circle, one-tailed independent samples rank-sum tests,
p < 0.001, corrected for multiple comparisons. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 2 3 0 7 2 0 0 6 8 3 3 n e c o _ a _ 0 1 4 5 5 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 330 G. Lefebvre, C. Summerfield, and R. Bogacz Since the learning rates in the hybrid model lie in between those in the valence and the confirmation models, the optimal bias in the hybrid model is in between that in these two models. The positivity or confirmation bias is optimal for low reward probabilities (see Figure 9e), while for high re- ward probabilities the optimal bias is close to b ≈ 1 (see Figure 9f), so it is between the optimal biases for the confirmation (see Figure 9b) and valence (see Figure 9d) models. It is also worth comparing the performance of the models for their opti- mal learning rates. Different panels in Figures 9a to 9f have different color scales that span the range of obtained rewards. Comparing color scales re- veals that the confirmation model can produce the overall highest reward: for low reward probabilities, it achieved higher reward (for its best parame- ters) than the valence model and similar performance to the hybrid model, while for high reward probabilities, it obtained higher reward than both alternative models. In summary, in the case of full feedback, the confirmation model is the only one among models compared in Figures 9a to 9f for which the optimal learning rates lie in the same regions of parameter space for both low and high probabilities. A learner often does not know the task parameters, and the confirmation model is most robust to this uncertainty because it is the only model for which it is possible to choose a combination of learning rates that work relatively well for different tasks. In the case of partial feedback, where only the value of the chosen op- tion is modified, the positivity bias is beneficial for low reward probabili- ties, while the negativity bias is beneficial for high reward probabilities (see Figures 9g and 9h), as expected from a previous theoretic analysis (Caze & van der Meer, 2013). The optimal learning rates with partial feedback are similar to those in the valence model with full feedback (compare Figures 9c and 9d with Figures 9g and 9h) as in both models the learning rate only depends on the sign of prediction error (see Table 1). The optimal learning rates slightly differ between the valence model with full feedback and partial feedback: less negativity bias is required to maximize reward with partial feedback for high probabilities (see Figures 9d and 9h). This difference arises because with full feedback both values are updated equally often, while with partial feedback, the poorer option is chosen less frequently. Hence, with partial feedback, the value of the poorer option moves slowly from its initial value of 0.5, so even if α+ > a−
, le
value of the poorer option may not be overestimated. The difference be-
tween the models disappears if both values are updated with more similar
frequencies (we observed it in simulations, not shown, in which tempera-
ture of the softmax function was increased).

En résumé, in the case of partial feedback, updating values of the
chosen option with the larger learning rate after positive prediction er-
ror is detrimental for higher reward probabilities (see Figure 9h). Ainsi,
the bias that optimizes the confirmation model (see Figure 9b) may be

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Confirmation Bias in Reinforcement Learning

331

detrimental with partial feedback in the model analyzed in this section (voir
Figure 9h). Nevertheless, in the next section, we come back to this issue, et
point out that the optimal bias may differ in other reinforcement learning
models with partial feedback.

7 Discussion

Humans have been observed to exhibit confirmatory biases when choosing
between stimuli or actions that pay out with uncertain probability (Cham-
bon et al., 2020; Palminteri et al., 2017; Schuller et al., 2020). These biases
drive participants to update positive outcomes (or those that are better than
expected) for chosen options more sharply than negative outcomes, but to
reverse this update pattern for the unchosen option. Ici, we show through
simulations that in an extended range of settings traditionally used in hu-
man experiments, this asymmetric update is advantageous in the presence
of noise in the decision process. En effet, agents who exhibited a confirma-
tory bias, rather than a neutral or disconfirmatory bias, were in most cir-
cumstances tested the agents that reaped the largest quantities of reward.
This counterintuitive result directly stems from the update process itself
that biases the value of the chosen and unchosen options (corresponding
overall to the best and worst options respectively), increasing mechanisti-
cally their relative distance from each other and ultimately the probability
of selecting the best option in the upcoming trials.

Exploring the evolution of action values under confirmatory updates of-
fers insight into why this occurs. Confirmatory updating has the effect of
rendering subjective action values more extreme than their objective coun-
terparts; in other words, options that are estimated to be good are over-
valued, and options estimated to be bad are undervalued (voir la figure 6).
This can have both positive and negative effects. The negative effect is that
a sufficiently strong confirmatory bias can drive a feedback loop whereby
poor or mediocre items that are chosen by chance can be falsely updated in
a positive direction, leading them to being chosen more often. The positive
effet, cependant, is that where decisions are themselves intrinsically variable
(par exemple., because they are corrupted by gaussian noise arising during decision
making or motor planning, modeled here with the softmax temperature pa-
rameter), overestimation of value makes decisions more robust to decision
noise because random fluctuations in the value estimated at the time of the
decision are less likely to reverse a decision away from the better of the two
options. The relative strength of these two effects depends on the level of
decision noise: within reasonable noise ranges, the latter effect outweighs
the former and performance benefits overall.

7.1 Relationship to Other Studies. The results described here thus
join a family of recently reported phenomena whereby decisions that dis-
tort or discard information lead to reward-maximizing choices under the

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

332

G. Lefebvre, C. Summerfield, et R. Bogacz

assumption that decisions are made with finite computational precision—
in other words, that decisions are intrinsically noisy (Summerfield & Tset-
sos, 2015). Par exemple, when averaging features from a multi-element
array to make a category judgment, under the assumption that features are
equally diagnostic (and that the decision policy is not itself noisy), then nor-
matively, they should be weighted equally in the choice. Cependant, dans le
presence of “late” noise, encoding models that overestimate the decision
value of elements near the category boundary are reward maximizing, pour
the same reason as the confirmatory bias here: they inflate the value of am-
biguous items away from indifference and render them robust to noise (Li,
Herce Castanon, Solomon, Vandormael, & Summerfield, 2017). A similar
phenomenon occurs when comparing gambles defined by different mon-
etary values: utility functions that inflate small values away from indiffer-
ence (rendering the subjective difference between $2 et $4 greater than
the subjective difference between $102 et $104) have a protective effect
against decision noise, providing a normative justification for convex util-
ity functions (Juechems, Spitzer, Balaguer, & Summerfield, 2020). Related
results have been described in problems that involve sequential sampling
in time, where they may account for violations of axiomatic rationality, tel
as systematically intransitive choices (Tsetsos et al., 2016). De plus, a bias
in how evidence is accumulated within a trial has been shown to increase
the accuracy of individual decisions, making the decision variable more ex-
treme and thus less likely to be corrupted by noise (Zhang & Bogacz, 2010).
Recent studies also report simulations of the confirmation bias model
(Chambon et al., 2020; Tarantola, Folke, Boldt, Perez, & De Martino, 2021).
These simulations paralleled experimental paradigms reported in these pa-
pers and a confirmation model was simulated for parameters (y compris
softmax temperature) corresponding to those estimated for participants of
the studies. The simulated agents employing confirmation bias obtained
higher average reward than unbiased learners, as well as learners described
by other models. Our article suggests the same conclusion using a comple-
mentary approach in which the models have been simulated in a variety of
conditions and analyzed mathematically.

Modeling studies have investigated how learning with rates depending
on the sign of prediction error could be implemented in the basal ganglia
circuits known to underlie reinforcement learning (Collins & Frank, 2014;
Dabney et al., 2020). Models have been developed to describe how positive
and negative prediction errors preferentially engage learning in different
populations of striatal neurons (Mikhael & Bogacz, 2016; Möller & Bogacz,
2019). It would be interesting to investigate the neural mechanisms that lead
to learning rates depending not only on the sign of prediction error but also
on whether options have been chosen.

7.2 Validity of Model’s Assumptions. Reinforcement learning mod-
els fit to human data often assume that choices are stochastic—that

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Confirmation Bias in Reinforcement Learning

333

participants fail to choose the most valuable bandit. In standard tasks
involving only feedback about the value of the chosen option (factual
feedback), some randomness in choices promotes exploration, which in
turns allows information to be acquired that may be relevant for future
decisions. Cependant, our task involves both factual and counterfactual
feedback, and so exploration is not required to learn the value of the two
bandits. Nevertheless, in some simulations, we modeled choices with a
softmax rule, which assumes that decisions are corrupted by gaussian
bruit, or an ε-greedy policy, which introduces lapses to the choice process
with a fixed probability. Implicitly, thus, we are committing to the idea that
value-guided decisions may be irreducibly noisy even where exploration
is not required (Renart & Machens, 2014). En effet, others have shown that
participants continue to make noisy decisions even where counterfactual
feedback is available, even if they have attributed that noise to variability in
learning rather than choice (Findling, Skvortsova, Dromnelle, Palminteri,
& Wyart, 2019).

Due to our assumptions, this study has a number of limitations. D'abord, nous
explored the properties of a confirmatory model that has been previously
shown to provide a good fit to human data performing a bandit task with
factual and counterfactual feedback. Cependant, we acknowledge that this is
not the only possible model that could increase reward by enhancing the
difference between represented values of options. En principe, any other
models producing choice hysteresis might be able to explain these results
(Katahira, 2018; Miller, Shenhav, & Ludvig, 2019; Worthy, Pang, & Byrne,
2013). An analysis of these different models and their respective resilience
to decision noise in different settings is beyond the scope of our study here
but would be an interesting target for future research. Deuxième, the results
described here hold assuming a fixed and equal level of stochasticity (par exemple.,
softmax temperature) in agents’ behaviors, regardless of their bias (c'est à dire., le
specific combination of learning rates). Relaxing this assumption, an unbi-
ased agent could perform equally well as a biased agent subject to more de-
cision noise. Ainsi, the benefit of confirmatory learning is relentlessly linked
to the level of noise, and one level of confirmation bias cannot be thought as
being beneficial overall. Troisième, our study does not investigate the impact on
the performance of other kinds of internal noise such like an update noise
(Findling et al., 2019). The latter, instead of perturbing the policy itself, par-
turbs at each trial the update process of the option’s value (c'est à dire., prediction
errors are blurred with a gaussian noise) and cannot presumably produce
a similar increase in performance, having overall no effect on the average
difference between these option values.

7.3 Confirmation Bias with Partial Feedback. In this article, we have
focused on studying confirmation bias in tasks where the feedback is pro-
vided for both chosen and unchosen options, but in most reinforcement
learning tasks studied in the laboratory and possibly in the real world,

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

334

G. Lefebvre, C. Summerfield, et R. Bogacz

feedback is provided only for the chosen option. With such partial feed-
back, it seems not possible to distinguish between the confirmation and va-
lence models because they make the same update of the value of the chosen
option. Cependant, a recent ingenious experiment suggested that the confir-
mation bias was also present with partial feedback, because the learning
rate was higher after positive prediction errors only if the choice was made
by the participant but not when the choice was made by a computer (Cham-
bon et al., 2020). Analogous effect was also observed outside the laboratory
in a study of heart surgeons who learned more from their own successes
than their failures but not from observed successes of their colleagues (Kc,
Staats, & Gino, 2013). Ainsi, it is important to understand how results from
this article could be generalized to partial feedback.

For partial feedback, previous theoretic work suggests that optimal lean-
ing rates depend on whether the reward probability is high or low (Caze &
van der Meer, 2013), and we confirmed it in simulations in Figures 9g and
9h. Surprisingly, it has been shown that human participants did not follow
this pattern and had similar learning rates regardless if reward probabili-
ties were low or high (Chambon et al., 2020; Gershman, 2015). This poses
a question whether humans do not behave in a way maximizing rewards
(which seems unlikely given the evolutionary pressure for reward maxi-
mization) or the normative theory of learning with partial feedback needs
to be revised. One way to include confirmation bias in models of learning
with partial feedback would be to note that humans and animals are aware
of confidence of their choices (Kiani & Shadlen, 2009)—that is, whether they
are certain the chosen option yields the highest reward or if the choice was
a guess. Ainsi, one could consider models in which learning rate depends
not only on the sign of prediction error but also on the confidence such that
the negative feedback is taken into consideration less when a participant is
confident of his or her choice. Formulating such models would require care-
ful comparison of the models with specially designed experiments; hence,
it is beyond the scope of this article but would be an interesting direction
for future work.

7.4 Limits to the Benefits of Biased Beliefs. It is important to point out
that confirmation bias is beneficial in many, but not all, circonstances. Al-
though in almost all presented simulations, there exists a combination of
biased learning rates giving performance that is higher than or as good as
the best unbiased learner, the optimal learning rates and hence the amount
of bias differ depending on task parameters. At the start of the task, a learner
usually is unable to know the details of the task, so needs to adopt a certain
default combination of learning rates. One could expect that such default
learning rates would be determined by experience or even be to a certain
extent influenced by evolution. Cependant, such a default set of biased learn-
ing rates will lead to detrimental effects on performance in certain tasks.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Confirmation Bias in Reinforcement Learning

335

Par exemple, a recent study estimated average learning rates of human
participants to be αC ≈ 0.15 and αD ≈ 0.05 (Tarantola et al., 2021) giving a
confirmation bias of b ≈ 3. Although such strong confirmation bias in-
creases reward in many simulated scenarios when decisions are noisy (par exemple.,
Figures 3e to 3h), it would have a negative effect on performance when de-
cisions are accurately made on the basis of values and in changing environ-
ments (par exemple., Figures 3a to 3d). If the default confirmation bias is influenced
by evolution, its value is likely to be relatively high because many of the
key decisions of our ancestors had to be quick and thus were noisy due to
the speed–accuracy trade-off. Par contre, in the modern world, we often
can take time to consider important choices, hence the biases that brought
evolutionary advantage to our ancestor may not always be beneficial to us.

Remerciements

This work has been supported by MRC grants MC_UU_12024/5, MC_
UU_00003/1, BBSRC grant BB/S006338/1, and ERC Consolidator grant
725937.

Les références

Bogacz, R., Brun, E., Moehlis, J., Holmes, P., & Cohen, J.. D. (2006). The physics
of optimal decision making: A formal analysis of models of performance
in two-alternative forced-choice tasks. Psychol. Rev., 113(4), 700–765. 10.1037/
0033-295X.113.4.700, PubMed: 17014301

Caze, R.. D., & van der Meer, M.. UN. (2013). Adaptive properties of differential learning
rates for positive and negative outcomes. Biol. Cybern., 107(6), 711–719. 10.1007/
s00422-013-0571-5, PubMed: 24085507

Chambon, V., Théro, H., Vidal, M., Vandendriessche, H., Haggard, P., & Palminteri,
S. (2020). Information about action outcomes differentially affects learning from
self-determined versus imposed choices. Nature Human Behaviour, 4(10), 1067–
1079. 10.1038/s41562-020-0919-5, PubMed: 32747804

Cie´slak, P.. E., Ahn, WYOMING., Bogacz, R., & Parkitna, J.. R.. (2018). Selective effects of the
loss of NMDA or mGluR5 receptors in the reward system on adaptive decision-
fabrication. Eneuro, 5(4).

Collins, UN. G., & Frank, M.. J.. (2014). Opponent actor learning (OpAL): Modeling
interactive effects of striatal dopamine on reinforcement learning and choice in-
centive. Psychological Review, 121(3), 337.

Dabney, W., Kurth-Nelson, Z., Uchida, N., Starkweather, C. K., Hassabis, D., Munos,
R., & Botvinick, M.. (2020). A distributional code for value in dopamine-based
reinforcement learning. Nature, 577(7792), 671–675. 10.1038/s41586-019-1924-6,
PubMed: 31942076

Daw, N. D., O’Doherty, J.. P., Dayan, P., Seymour, B., & Dolan, R.. J.. (2006). Corti-
cal substrates for exploratory decisions in humans. Nature, 441(7095), 876–879.
10.1038/nature04766, PubMed: 16778890

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

336

G. Lefebvre, C. Summerfield, et R. Bogacz

Farashahi, S., Donahue, C. H., Hayden, B. Y., Lee, D., & Soltani, UN. (2019). Flexi-
ble combination of reward information across primates. Nature Human Behaviour,
3(11), 1215–1224. 10.1038/s41562-019-0714-3, PubMed: 31501543

Findling, C., Skvortsova, V., Dromnelle, R., Palminteri, S., & Wyart, V. (2019).
Computational noise in reward-guided learning drives behavioral variability
in volatile environments. Nat. Neurosci., 22(12), 2066–2077. 10.1038/s41593-019-
0518-9, PubMed: 31659343

Gershman, S. J.. (2015). Do learning rates adapt to the distribution of rewards? Psy-
chon. Bull. Rev., 22(5), 1320–1327. 10.3758/s13423-014-0790-3, PubMed: 25582684

Groopman, J.. (2007). How doctors think. Boston: Mariner Books.
Juechems, K., Spitzer, B., Balaguer, J., & Summerfield, C. (2020). Optimal utility and
probability functions for agents with finite computational precision. PsyArXiv. https:
//psyarxiv.com/6yhwg/

Katahira, K. (2018). The statistical structures of reinforcement learning with
asymmetric value updates. J.. Math. Psychol., 87, 31–45. 10.1016/j.jmp.2018.09
.002

Kc, D., Staats, B. R., & Gino, F. (2013). Learning from my success and from others’
failure: Evidence from minimally invasive cardiac surgery. Management Science,
59(11), 2435–2449. 10.1287/mnsc.2013.1720

Kiani, R., & Shadlen, M.. N. (2009). Representation of confidence associated with a
decision by neurons in the parietal cortex. Science, 324(5928), 759–764. 10.1126/
science.1169405, PubMed: 19423820

Lefebvre, G., Lebreton, M., Meyniel, F., Bourgeois-Gironde, S., & Palminteri, S.
(2017). Behavioural and neural characterization of optimistic reinforcement
learning. Nat. Hum. Behav., 1. 10.1038/s41562-017-0067

Li, V., Herce Castanon, S., Solomon, J.. UN., Vandormael, H., & Summerfield, C. (2017).
Robust averaging protects decisions from noise in neural computations. PLOS
Comput. Biol., 13(8), e1005723. 10.1371/journal.pcbi.1005723

Mikhael, J.. G., & Bogacz, R.. (2016). Learning reward uncertainty in the basal gan-
glia. PLOS Computational Biology, 12(9), e1005062. 10.1371/journal.pcbi.1005062,
PubMed: 27589489

Miller, K. J., Shenhav, UN., & Ludvig, E. UN. (2019). Habits without values. Psychol. Rev.,

126(2), 292–311. 10.1037/rev0000120, PubMed: 30676040

Möller, M., & Bogacz, R.. (2019). Learning the payoffs and costs of actions. PLOS

Computational Biology, 15(2), e1006285.

Nickerson, R.. S. (1998). Confirmation bias: A ubiquitous phenomenon in many

guises. Review of General Psychology, 2, 175–220. 10.1037/1089-2680.2.2.175

Niv, Y., Edlund, J.. UN., Dayan, P., & O’Doherty, J.. P.. (2012). Neural prediction errors
reveal a risk-sensitive reinforcement-learning process in the human brain. J.. Neu-
rosci., 32(2), 551–562. 10.1523/JNEUROSCI.5498-10.2012, PubMed: 22238090
Oaksford, M., & Chater, N. (2003). Optimal data selection: revision, revoir,
and reevaluation. Psychon. Bull. Rev., 10(2), 289–318. 10.3758/BF03196492,
PubMed: 12921410

Palminteri, S., Lefebvre, G., Kilford, E. J., & Blakemore, S. J.. (2017). Confirmation
bias in human reinforcement learning: Evidence from counterfactual feedback
traitement. PLOS Comput. Biol., 13(8), e1005684. 10.1371/journal.pcbi.1005684,
PubMed: 28800597

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Confirmation Bias in Reinforcement Learning

337

Pedersen, M.. L., Frank, M.. J., & Biele, G. (2017). The drift diffusion model as
the choice rule in reinforcement learning. Psychon. Bull. Rev., 24(4), 1234–1251.
10.3758/s13423-016-1199-y, PubMed: 27966103

Renart, UN., & Machens, C. K. (2014). Variability in neural activity and behavior. Curr.
Opin. Neurobiol., 25, 211–220. 10.1016/j.conb.2014.02.013, PubMed: 24632334
Rescorla, R.. UN., & Wagner, UN. R.. (1972). A theory of Pavlovian conditioning: Varia-
tions in the effectiveness of reinforcement and nonreinforcement. In B. UN. H. &
W. F. Prokasy (Éd.), Classical conditioning II: Current research and theory (pp. 64–
99). New York: Appleton Century Crofts.

Schuller, T., Fischer, UN. G., Gruendler, T. Ô. J., Baldermann, J.. C., Huys, D., Ullsperger,
M., & Kuhn, J.. (2020). Decreased transfer of value to action in Tourette syndrome.
Cortex, 126, 39–48. 10.1016/j.cortex.2019.12.027

Summerfield, C., & Tsetsos, K. (2015). Do humans make good decisions? Trends Cogn.

Sci., 19(1), 27–34. 10.1016/j.tics.2014.11.005, PubMed: 25488076

Talluri, B. C., Urai, UN. E., Tsetsos, K., Usher, M., & Donner, T. H. (2018). Confirma-
tion bias through selective overweighting of choice-consistent evidence. Actuel
Biology, 28(19), 3128–3135. 10.1016/j.cub.2018.07.052, PubMed: 30220502

Tarantola, T. O., Folke, T., Boldt, UN., Perez, Ô. D., & De Martino, B. (2021). Confirmation

bias optimizes reward learning. bioRxiv.

Tsetsos, K., Moran, R., Moreland, J., Chater, N., Usher, M., & Summerfield, C. (2016).
Economic irrationality is optimal during noisy decision making. In Proc. Natl.
Acad. Sci. Etats-Unis, 113(11), 3102–3107. 10.1073/pnas.1519157113

Worthy, D. UN., Pang, B., & Byrne, K. UN. (2013). Decomposing the roles of persever-
ation and expected value representation in models of the Iowa gambling task.
Front Psychol., 4, 640. 10.3389/fpsyg.2013.00640, PubMed: 24137137

Zhang, J., & Bogacz, R.. (2010). Bounded Ornstein–Uhlenbeck models for two-choice
time controlled tasks. Journal of Mathematical Psychology, 54(3), 322–333. 10.1016/
j.jmp.2010.03.001

Received March 16, 2021; accepted July 26, 2021.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
2
3
0
7
2
0
0
6
8
3
3
n
e
c
o
_
un
_
0
1
4
5
5
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Télécharger le PDF