ARTICLE
Communicated by Terrence Sejnowski
Parametric UMAP Embeddings for Representation
and Semisupervised Learning
Tim Sainburg
timsainb@gmail.com
University of California San Diego, La Jolla, Californie 92093, U.S.A.
Leland McInnes
leland.mcinnes@gmail.com
Tutte Institute for Mathematics and Computing, Ottawa, Ontario Canada
Timothy Q. Gentner
tgentner@ucsd.edu
University of California San Diego, La Jolla, Californie 92093, U.S.A.
UMAP is a nonparametric graph-based dimensionality reduction algo-
rithm using applied Riemannian geometry and algebraic topology to find
low-dimensional embeddings of structured data. The UMAP algorithm
consists of two steps: (1) computing a graphical representation of a data
ensemble (fuzzy simplicial complex) et (2) through stochastic gradient de-
scent, optimizing a low-dimensional embedding of the graph. Ici, nous
extend the second step of UMAP to a parametric optimization over neu-
ral network weights, learning a parametric relationship between data and
embedding. We first demonstrate that parametric UMAP performs com-
parably to its nonparametric counterpart while conferring the benefit of a
learned parametric mapping (par exemple., fast online embeddings for new data).
We then explore UMAP as a regularization, constraining the latent distri-
bution of autoencoders, parametrically varying global structure preser-
vation, and improving classifier accuracy for semisupervised learning by
capturing structure in unlabeled data.1
1 Introduction
Current nonlinear dimensionality reduction algorithms can be divided
broadly into nonparametric algorithms, which rely on the efficient com-
putation of probabilistic relationships from neighborhood graphs to ex-
tract structure in large data sets (UMAP (McInnes, Healy, & Melville, 2018),
t-SNE (van der Maaten & Hinton, 2008), LargeVis (Tang, Liu, Zhang, &
1
Google Colab walkthrough.
Neural Computation 33, 2881–2907 (2021) © 2021 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01434
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2882
T. Sainburg, L. McInnes, and T. Gentner
Mei, 2016)), and parametric algorithms, lequel, driven by advances in deep
learning, optimize an objective function related to capturing structure in a
data set over neural network weights (Ding, Condon, & Shah, 2018; Ding &
Regev, 2019; Hinton & Salakhutdinov, 2006; Kingma & Welling, 2013; Szu-
bert, Cole, Monaco, & Drozdov, 2019).
Au cours des dernières années, a number of parametric dimensionality reduction algo-
rithms have been developed to wed these two classes of methods, learning
a structured graphical representation of the data and using a deep neu-
ral network to capture that structure (discussed in section 3). In partic-
ular, over the past decade, several variants of the t-SNE algorithm have
proposed parameterized forms of t-SNE (Bunte, Biehl, & Hammer, 2012;
Gisbrecht, Lueks, Mokbel, & Hammer, 2012; Gisbrecht, Schulz, & Ham-
mer, 2015; van der Maaten, 2009). Parametric t-SNE (van der Maaten, 2009)
Par exemple, trains a deep neural network to minimize loss over a t-SNE
graph. Cependant, the t-SNE loss function itself is not well suited to neural
network training paradigms. En particulier, t-SNE’s optimization requires
normalization over the entire data set at each step of optimization, fabrication
batch-based optimization and online learning of large data sets difficult. Dans
contraste, UMAP is optimized using negative sampling (Mikolov, Sutskever,
Chen, Corrado, & Dean, 2013; Tang et al., 2016) to sparsely sample edges
during optimization, making it, in principle, better suited to batch-wise
training as is common in deep learning applications. Our proposed method,
Parametric UMAP, brings the nonparametric graph-based dimensionality
reduction algorithm UMAP into an emerging class of parametric topologi-
cally inspired embedding algorithms.
Dans la rubrique suivante, we broadly outline the algorithm underlying
UMAP to explain why our proposed algorithm, Parametric UMAP, is par-
ticularly well suited to deep learning applications. We contextualize our
discussion of UMAP in t-SNE to outline the advantages that UMAP confers
over t-SNE in the domain of parametric neural-network-based embedding.
We then perform experiments comparing our algorithm, Parametric UMAP,
to parametric and nonparametric algorithms. Enfin, we show a novel ex-
tension of Parametric UMAP to semisupervised learning.
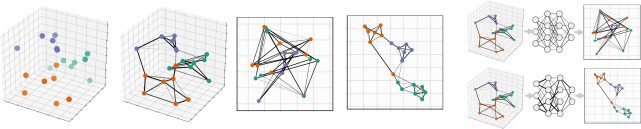
2 Parametric and Nonparametric UMAP
UMAP and t-SNE have the same goal: Given a D-dimensional data set X ∈
RD, produce a d-dimensional embedding Z ∈ Rd such that points that are
close together in X (par exemple., xi and x j) are also close together in Z (zi and z j).
Both algorithms have the same two broad steps: first construct a graph of
local relationships between data sets (see Figure 1A); then optimize an em-
bedding in low-dimensional space that preserves the structure of the graph
(see Figure 1B). The parametric approach replaces the second step of this
process with an optimization of the parameters of a deep neural network
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parametric UMAP
2883
Chiffre 1: Overview of UMAP (A → B) and Parametric UMAP (A → C).
over batches (see Figure 1C). To understand how Parametric UMAP is op-
timized, it is necessary to understand these steps.
2.1 Graph Construction.
2.1.1 Computing Probabilities in X. The first step in both UMAP and t-SNE
is to compute a distribution of probabilities P between pairs of points in X
based on the distances between points in data space. Probabilities are ini-
tially computed as local, one-directional probabilities between a point and
its neighbors in data space, then symmetrized to yield a final probability
representing the relationship between pairs of points.
In t-SNE, these probabilities are treated as conditional probabilities of
) computed using a gaussian distribution centered at
neighborhood (pt-SNE
xi,
je| j
pt-SNE
j|je
=
(cid:4)
(cid:2)
(cid:3)
exp
k(cid:4)=i exp
−d(xi
(cid:2)
, x j )/2p 2
je
, xk)/2p 2
je
−d(xi
(cid:3) ,
(2.1)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
, x j ) represents the distance between xi and x j (par exemple., Euclidean
where d(xi
distance) and σ
i is the standard deviation for the gaussian distribution,
based on the perplexity parameter such that one standard deviation of the
gaussian kernel fits a a set number of nearest neighbors in X.
In UMAP, locale, one-directional probabilities (PUMAP
) are computed be-
tween a point and its neighbors to determine the probability with which an
bord (or simplex) exists, based on an assumption that data are uniformly
distributed across a manifold in a warped data space. Under this assump-
tion, a local notion of distance is set by the distance to the kth nearest neigh-
bor, and the local probability is scaled by that local notion of distance,
je| j
pUMAP
j|je
= exp(−(d(xi
, x j ) −p
je)/p
je),
(2.2)
where ρ
its nearest neighbor, and σ
i is a local connectivity parameter set to the distance from xi to
i is a local connectivity parameter set to match
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2884
T. Sainburg, L. McInnes, and T. Gentner
the local distance around xi upon its k nearest neighbors (where k is a
hyperparameter).
After computing the one-directional edge probabilities for each data
indiquer, UMAP computes a global probability as the probability of either of
the two local, one-directional, probabilities occurring:
pUMAP
i j
=
(cid:2)
(cid:3)
p j|je
+ pi| j
− p j|i pi| j
.
In contrast, t-SNE symmetrizes the conditional probabilities as
= p j|je
pt-SNE
i j
+ pi| j
2N
.
(2.3)
(2.4)
2.2 Graph Embedding. After constructing a distribution of probabilis-
tically weighted edges between points in X, UMAP and t-SNE initialize an
embedding in Z corresponding to each data point, where a probability dis-
tribution (Q) is computed between points as was done with the distribution
(P.) in the input space. The objective of UMAP and t-SNE is then to optimize
that embedding to minimize the difference between P and Q.
2.2.1 Computing Probabilities in Z. In embedding space, the pairwise
probabilities are computed directly without first computing local, un-
directional probabilities.
je| j
is computed in a similar manner to pt-SNE
In the t-SNE embedding space, the pairwise probability between two
points qt-SNE
, but where the gaus-
sian distribution is replaced with the fatter-tailed Student’s t-distribution
(with one degree of freedom), which is used to overcome the crowding
problem (van der Maaten & Hinton, 2008) in translating volume differences
in high-dimensional spaces to low-dimensional spaces:
je| j
qt-SNE
i j
=
(cid:4)
.
(cid:3)−1
(2.5)
(cid:5)
1 +
(cid:2)
k(cid:4)=l
(cid:6)
(cid:6)
zi
− z j
(cid:7)−1
(cid:6)
(cid:6)2
1 + (cid:5)zk
− zl
(cid:5)2
UMAP’s computation of the pairwise probability qUMAP
in the embedding space Z uses a different family of functions:
i j
between points
(cid:2)
qUMAP
i j
=
1 + un (cid:5)zi
− z j
||2b
(cid:3)−1 ,
(2.6)
where a and b are hyperparameters set based on a desired minimum dis-
tance between points in embedding space. Notably, the UMAP probabil-
ity distribution in embedding space is not normalized, while the t-SNE
distribution is normalized across the entire distribution of probabilities,
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parametric UMAP
2885
meaning that the entire distribution of probabilities needs to be calculated
before each optimization step of t-SNE.
2.2.2 Cost Function. Enfin, the distribution of embeddings in Z is opti-
mized to minimize the difference between Q and P.
In t-SNE, a Kullback-Leibler divergence between the two probability
distributions is used, and gradient descent in t-SNE is computed over the
embeddings:
Ct-SNE
=
(cid:8)
je(cid:4)= j
pi j log
.
pi j
qi j
(2.7)
In UMAP, the cost function is cross-entropy, also optimized using gradi-
ent descent:
CUMAP
=
(cid:8)
je(cid:4)= j
pi j log
(cid:10)
(cid:2)
+
(cid:9)
pi j
qi j
1 − pi j
(cid:3)
log
(cid:9)
(cid:10)
.
1 − pi j
1 − qi j
(2.8)
2.3 Attraction and Repulsion. Minimizing the cost function over ev-
ery possible pair of points in the data set would be computationally expen-
sive. UMAP and more recent variants of t-SNE both use shortcuts to bypass
much of that computation. In UMAP, those shortcuts are directly advanta-
geous to batch-wise training in a neural network.
The primary intuition behind these shortcuts is that the cost function
of both t-SNE and UMAP can be broken out into a mixture of attractive
forces between locally connected embeddings and repulsive forces between
nonlocally connected embeddings.
2.3.1 Attractive Forces. Both UMAP and t-SNE utilize a similar strategy
in minimizing the computational cost over attractive forces: they rely on
an approximate nearest neighbors graph.2 The intuition for this approach
is that elements that are farther apart in data space have very small edge
probabilities, which can be treated effectively as zero. Ainsi, edge probabil-
ities and attractive forces only need to be computed over the nearest neigh-
bors; non-nearest neighbors can be treated as having an edge probability of
zero. Because nearest-neighbor graphs are themselves computationally ex-
pensive, approximate nearest neighbors (Dong, Moses, & Li, 2011) produce
effectively similar results.
2
UMAP requires substantially fewer nearest neighbors than t-SNE, which generally
requires three times the perplexity hyperparameter (defaulted at 30 ici), whereas UMAP
computes only 15 neighbors by default, which is computationally less costly.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2886
T. Sainburg, L. McInnes, and T. Gentner
2.3.2 Repulsive Forces. Because most data points are not locally con-
nected, we do not need to waste computation on most pairs of embeddings.
UMAP takes a shortcut motivated by the language model word2vec
(Mikolov et al., 2013) and performs negative sampling over embeddings.
Each training step iterates over positive, locally connected edges and ran-
domly samples edges from the remainder of the data set, treating their edge
probabilities as zero to compute cross-entropy. Because most data points are
not locally connected and have a very low edge probability, these negative
samples are, on average, correct, allowing UMAP to sample only sparsely
over edges in the data set.
In t-SNE, repulsion is derived from the normalization of Q. A few meth-
ods for minimizing the amount of computation needed for repulsion have
been developed. The first is the Barnes-Hut tree algorithm (van der Maaten,
2014), which bins the embedding space into cells and where repulsive forces
can be computed over cells rather than individual data points within those
cells. De la même manière, the more recent interpolation-based t-SNE (FIt-SNE; Lin-
derman, Rachh, Hoskins, Steinerberger, & Kluger, 2017, 2019) divides the
embedding space into a grid and computes repulsive forces over the grid
rather than the full set of embeddings.
2.4 Parametric UMAP. To summarize, both t-SNE and UMAP rely on
the construction of a graph and a subsequent embedding that preserves the
structure of that graph (voir la figure 1). UMAP learns an embedding by min-
imizing cross-entropy sampled over positively weighted edges (attraction)
and using negative sampling randomly over the data set (repulsion), al-
lowing minimization to occur over sampled batches of the data set. t-SNE,
meanwhile, minimizes a KL divergence loss function normalized over the
entire set of embeddings in the data set using different approximation tech-
niques to compute attractive and repulsive forces.
Because t-SNE optimization requires normalization over the distribution
of embedding in projection space, gradient descent can only be performed
after computing edge probabilities over the entire data set. Projecting an
entire data set into a neural network between each gradient descent step
would be too computationally expensive to optimize, cependant. The trick
that Parametric t-SNE proposes for this problem is to split the data set up
into large batches (e.g. 5000 data points in the original paper) that are used
to compute separate graphs that are independently normalized over and
used constantly throughout training, meaning that relationships between
elements in different batches are not explicitly preserved. Inversement, un
parametric form of UMAP, using negative sampling, can in principle be
trained on batch sizes as small as a single edge, making it suitable for mini-
batch training needed for memory-expensive neural networks trained on
the full graph over large data sets as well as online learning.
Given these design features, UMAP loss can be applied as a regulariza-
tion in typical stochastic gradient descent deep learning paradigms without
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parametric UMAP
2887
requiring the batching trick that Parametric T-SNE relies on. Malgré cela,
a parametric extension to the UMAP learning algorithm has not yet been
explored. Ici, we explore the performance of a parametric extension to
UMAP relative to current embedding algorithms and perform several ex-
periments further extending Parametric UMAP to novel applications.3
3 Related Work
Beyond Parametric t-SNE and Parametric UMAP, a number of recent para-
metric dimensionality reduction algorithms utilizing structure-preserving
constraints exist that were not compared here. This work is relevant to ours
and is mentioned here to provide clarity on the current state of parametric
topologically motivated and structure-preserving dimensionality reduction
algorithms.
Moor et al. (2020; topological autoencoders) and Hofer, Kwitt, Nietham-
mer, and Dixit (2019; connectivity-optimized representation learning)
apply an additional topological structure-preserving loss using persistent
homology over minibatches to the latent space of an autoencoder. Jia, Sun,
Gao, Song, and Shi (2015; Laplacian autoencoders) similarly define an au-
toencoder with a local structure-preserving regularization. Mishne, Sha-
ham, Cloninger, and Cohen (2019; Diffusion Nets) define an autoencoder
extension based on diffusion maps that constrains the latent space of the
autoencoder. Ding et al. (2018; scvis) and Graving and Couzin (2020; VAE-
SNE) describe VAE-derived dimensionality reduction algorithms based
on the ELBO objective. Duque, Morin, Loup, and Moon (2020; geometry-
regularized autoencoders) regularize an autoencoder with the PHATE
(potential of heat-diffusion for affinity-based trajectory embedding) embed-
ding algorithm (Moon et al., 2019). Szubert et al. (2019; ivis) and Robinson
(2020; differential embedding networks) make use of Siamese neural net-
work architectures with structure-preserving loss functions to learn embed-
dings. Pai, Talmon, Bronstein, and Kimmel (2019; DIMAL) similarly uses
Siamese networks constrained to preserve geodesic distances for dimen-
sionality reduction. Several of these parametric approaches indirectly con-
dition neural networks (par exemple., autoencoders) on nonparametric embeddings
rather than directly on the loss of the algorithm, which can be applied to ar-
bitrary embedding algorithms. We contrast indirect and direct parametric
embeddings in section 5.6.
4 UMAP as a Regularization
In machine learning, regularization refers to the modification of a learning
algorithm to improve generalization to new data. Ici, we consider both
3
See code implementations: Experiments: https://github.com/timsainb/Parametric
UMAP_paper. Python package: https://github.com/lmcinnes/umap.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2888
T. Sainburg, L. McInnes, and T. Gentner
Chiffre 2: Variants of UMAP used in this letter. Solid lines represent neural net-
travaux. Dashed lines represent error gradients.
regularizing neural networks with UMAP loss, as well as using additional
loss functions to regularize the embedding that UMAP learns. While non-
parametric UMAP optimizes UMAP loss directly over embeddings (see Fig-
ure 2A), our proposed algorithm, Parametric UMAP, applies the same cost
function over an encoder network (see Figure 2B). By applying additional
pertes, we can use regularize UMAP and UMAP to regularize additional
training objectives, which we outline below.
4.1 Autoencoding with UMAP. AEs are by themselves a powerful di-
mensionality reduction algorithm (Hinton & Salakhutdinov, 2006). Ainsi,
combining them with UMAP may yield additional benefits in capturing la-
tent structure. We used an autoencoder as an additional regularization to
Parametric UMAP (see Figure 2C). A UMAP/AE hybrid is simply the com-
bination of the UMAP loss and a reconstruction loss, both applied over the
réseau. VAEs have similarly been used in conjunction with Parametric t-
SNE for capturing structure in animal behavioral data (Graving & Couzin,
2020) and combining t-SNE, which similarly emphasizes local structure,
with AEs aiding in capturing more global structure over the data set
(Graving & Couzin, 2020; van der Maaten & Hinton, 2008).
4.2 Semisupervised Learning. Parametric UMAP can be used to regu-
larize supervised classifier networks, training the network on a combina-
tion of labeled data with the classifier loss and unlabeled data with UMAP
perte (see Figure 2D). Semisupervised learning refers to the use of unlabeled
data to jointly learn the structure of a data set while labeled data are used
to optimize the supervised objective function, such as classifying images.
Ici, we explore how UMAP can be jointly trained as an objective function
in a deep neural network alongside a classifier.
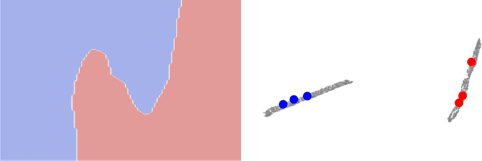
In the example in Figure 3, we show an intuitive example of semisuper-
vised learning using UMAP over the Moons data set (Pedregosa et al., 2011).
By training a Y-shaped network (see Figure 2D) on both the classifier loss
over labeled data points (see Figure 3A, red and blue) and the UMAP loss
over unlabeled data points (see Figure 3A, gray) jointly, the shared latent
space between the UMAP and classifier network pulls apart the two moons
(see Figure 3B), resulting in a decision boundary that divides cleanly be-
tween the two distributions in data space.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parametric UMAP
2889
Chiffre 3: An example of semisupervised learning with UMAP on the moons
data set.
4.3 Preserving Global Structure. An open issue in dimensionality re-
duction is how to balance local and global structure preservation (Becht
et coll., 2019; De Silva & Tenenbaum, 2003; Kobak & Linderman, 2021). Al-
gorithms that rely on sparse nearest neighbor graphs like UMAP focus
on capturing the local structure present between points and their nearest
neighbors, while global algorithms, like multidimensional scaling (MDS),
attempt to preserve all relationships during embedding. Local algorithms
are both computationally more efficient and capture structure that is lost
in global algorithms (par exemple., the clusters corresponding to numbers found
when projecting MNIST into UMAP). While local structure preservation
captures more application-relevant structure in many data sets, the ability
to additionally capture global structure is still often desirable. The approach
used by nonparametric t-SNE and UMAP is to initialize embeddings with
global structure-preserving embeddings such as PCA or Laplacian eigen-
maps embeddings. In Parametric UMAP, we explore a different tactic, im-
posing global structure by jointly training on a global structure preservation
loss directly.
5 Experiments
Experiments were performed comparing parametric UMAP and a
UMAP/AE hybrid, to several baselines: nonparametric UMAP, nonpara-
metric t-SNE (FIt-SNE) (Linderman et al., 2019; Poliˇcar, Stražar, & Zupan,
2019), Parametric t-SNE, an AE, a VAE, and PCA projections. As additional
baselines, we compared PHATE (nonparametric), SCVIS (parametric), et
IVIS (parametric), which we described in section 3. We also compare a sec-
ond nonparametric UMAP implementation that has the same underlying
code as Parametric UMAP, but where optimization is performed over em-
beddings directly rather than neural network weights. This comparison is
made to provide a bridge between the UMAP-learn implementation and
Parametric UMAP, to control for any potential implementation differences.
Parametric t-SNE, Parametric UMAP, the AE, VAE, and the UMAP/AE
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2890
T. Sainburg, L. McInnes, and T. Gentner
hybrid use the same neural network architectures and optimizers within
each data set (described in supplemental materials).
We used the common machine learning benchmark data sets MNIST,
FMNIST, and CIFAR-10 alongside two real-world data sets in areas where
UMAP has proven a useful tool for dimensionality reduction: a single-
cell retinal transcriptome data set (Macosko et al., 2015) and a bioacoustic
data set of Cassin’s vireo song, recorded in the Sierra Nevada mountains
(Hedley, 2016un, 2016b).
5.1 Embeddings. We first confirm that Parametric UMAP produces
embeddings that are of a similar quality to nonparametric UMAP. À
quantitatively measure the quality of embeddings, we compared embed-
ding algorithms on several metrics across data sets. We compared each
method/data set on 2D and 64D projections.4 Each metric is explained
in detail in the supplemental materials. The 2D projection of each data
set/method is shown in Figure 4. The results are given in Supplementary
Figures 1–6 and Supplementary Tables 2–7 and summarized below.
5.1.1 Trustworthiness. Trustworthiness (see supplementary equation 1
and Venna & Kaski, 2006) is a measure of how much of the local structure
of a data set is preserved in a set of embeddings. In 2D, we observe that
each of the UMAP algorithms performs similarly in trustworthiness, avec
t-SNE being slightly more trustworthy in each data set (voir la figure 5, Sup-
plementary Figure 1, and Supplementary Table 2. At 64D, APC, AE, VAE,
and Parametric t-SNE are most trustworthy in comparison to each UMAP
implementation, possibly reflecting the more approximate repulsion (neg-
ative sampling) used by UMAP.
5.1.2 Area under the Curve (AUC) of RNX. To compare embeddings across
scales (both local and global neighborhoods), we computed the AUC of
RNX for each embedding (Lee, Peluffo-Ordóñez, & Verleysen, 2015), lequel
captures the agreement across K-ary neighborhoods, weighting nearest
neighbors as more important than farther neighbors. In 2D we find that
Parametric and nonparametric UMAP perform similarly, while t-SNE has
the highest AUC. At 64D, Parametric and nonparametric UMAP again per-
form similarly, with PCA having the higher AUC.
5.1.3 KNN-Classifier. A KNN-classifier is used as a baseline to mea-
sure supervised classification accuracy based on local relationships in
4
Where possible. In contrast with UMAP, Parametric UMAP, and Parametric t-SNE,
Barnes Huts t-SNE can only embed in two or three dimensions (van der Maaten, 2014),
and while FIt-SNE can in principle scale to higher dimensions (Linderman et al., 2019),
embedding in more than two dimensions is unsupported in both the official implemen-
tation (KlugerLab, 2020) and openTSNE (Poliˇcar et al., 2019)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parametric UMAP
2891
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4: Comparison of projections from multiple data sets using UMAP,
UMAP in tensorflow, parametric UMAP, parametric UMAP with an autoen-
coder loss, parametric t-SNE, t-SNE, SCVIS, IVIS, PHATE, a VAE, an AE, et
APC. (un) Moons. (B) 3D buffalo. (c) MNIST, (d) Cassin’s vireo song segments,
(e) Mouse retina single-cell transcriptomes. (F) Fashion MNIST, (g) CIFAR10.
The Cassin’s vireo data set uses a dynamic time warping loss and an LSTM net-
work for the encoder and decoder for the neural networks. The image data sets
use a convnet for the encoder and decoder for the neural networks. The bison
examples use a t-SNE perplexity of 500 et 150 nearest neighbors in UMAP to
capture more global structure.
embeddings. We find KNN-classifier performance largely reflects trustwor-
thiness (voir la figure 5, Supplementary Figures 3 et 4, and Supplementary
Tables 4 et 5). In 2D, we observe a broadly similar performance between
UMAP and t-SNE variants, each of which is substantially better than the
APC, AE, or VAE projections. À 64 dimensions UMAP projections are sim-
ilar but in some data sets (FMNIST, CIFAR-10) slightly under-perform PCA,
AE, VAE, and Parametric t-SNE.
5.1.4 Silhouette Score. Silhouette score measures how clustered a set of
embeddings is given ground truth labels. In 2D, across data sets, we tend to
see a better silhouette score for UMAP and Parametric UMAP projections
than t-SNE and Parametric t-SNE, which are more clustered than PCA in
all cases but CIFAR-10, which shows little difference from PCA (see Fig-
ure 5, Supplementary Figure 5 and Supplementary Table 5). The cluster-
ing of each data set can also be observed in Figure 4, where t-SNE and
2892
T. Sainburg, L. McInnes, and T. Gentner
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5: Embedding metrics for 2D projections. Full results are given in the
appendix. Accuracy is shown for KNN (k = 1).
Parametric t-SNE are more spread out within the cluster than UMAP. Dans
64D projections, we find the silhouette score of Parametric t-SNE is near
or below that of PCA, which is lower than UMAP-based methods. We note,
cependant, that the poor performance of Parametric t-SNE may reflect setting
the degrees-of-freedom (un) at d − 1, which is only one of three parameter-
ization schemes that van der Maaten (2009) suggests. A learned degrees-
of-freedom parameter might improve performance for parametric t-SNE at
higher dimensions.
5.1.5 Clustering. To compare clustering directly across embeddings, nous
performed k-means clustering over each latent projection and compared
each embedding’s clustering on the basis of the normalized mutual infor-
mation (NMI) between clustering schemes (voir la figure 5, Supplemental Fig-
ure 6, and Supplementary Table 6). In both the 2D and 64D projections, nous
find that NMI corresponds closely to the silhouette score. UMAP and t-SNE
show comparable clustering in 2D, both well above PCA in most data sets.
At 64D, each UMAP approach shows superior performance over t-SNE.
5.2 Training and Embedding Speed.
5.2.1 Training Speed. Optimization in nonparametric UMAP is not in-
fluenced by the dimensionality of the original data set; the dimensionality
Parametric UMAP
2893
Chiffre 6: Training times comparison between UMAP and Parametric UMAP.
All results were obtained with up to 32 threads on a machine with 2 AMD EPYC
Rome 7252 8-core CPU running at 3.1 GHz and a Quadro RTX 6000.
comes into play only in computing the nearest-neighbors graph. In contrast,
training speeds for Parametric UMAP are variable based on the dimen-
sionality of data and the architecture of the neural network used. The di-
mensionality of the embedding does not have a substantial effect on speed.
In Figure 6, we show the cross-entropy loss over time for Parametric and
nonparametric UMAP, for the MNIST, Fashion MNIST, and Retina data
sets. Across each data set, we find that nonparametric UMAP reaches a
lower loss more quickly than Parametric UMAP but that Parametric UMAP
reaches a similar cross-entropy within an order of magnitude of time. Ainsi,
Parametric UMAP can train more slowly than nonparametric UMAP, mais
training times remain within a similar range, making Parametric UMAP a
reasonable alternative to nonparametric UMAP in terms of training time.
5.2.2 Embedding and Reconstruction Speed. A parametric mapping allows
embeddings to be inferred directly from data, resulting in a quicker embed-
ding than nonparametric methods. The speed of embedding is especially
important in signal processing paradigms where near-real-time embedding
speeds are necessary. For example in brain-machine interfacing, bioacous-
tics, and computational ethology, fast embedding methods like PCA or deep
neural networks are necessary for real-time analyses and manipulations;
thus, deep neural networks are increasingly being used (Brun & De Bivort,
2018; Pandarinath et al., 2018; Sainburg, Thielk, & Gentner, 2019). Ici, nous
compare the embedding speed of a held-out test sample for each data set,
as well as the speed of reconstruction of the same held-out test samples.
Broadly, we observe similar embedding times for the nonparametric
t-SNE and UMAP methods, which are several orders of magnitude slower
than the parametric methods, where embeddings are direct projections into
the learned networks (voir la figure 7). Because the same neural networks
are used across the different parametric UMAP and t-SNE methods, nous
show only Parametric UMAP in Figure 7, which is only slightly slower than
APC, making it a viable candidate for fast embedding where PCA is cur-
rently used. De la même manière, we compared parametric and nonparametric UMAP
reconstruction speeds (see Supplemental Figure 7). With the network
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2894
T. Sainburg, L. McInnes, and T. Gentner
Chiffre 7: Comparison of embedding speeds using Parametric UMAP and other
embedding algorithms on a held-out testing data set. Embeddings were per-
formed on the same machine as Figure 6. Values shown are the median times
over 10 runs.
architectures we used, reconstructions of Parametric UMAP are orders
of magnitude faster than nonparametric UMAP, and slightly slower, mais
within the same order of magnitude as PCA.
5.3 Capturing Additional Global Structure in Data. To capture addi-
tional global structure we added a naive global structure preservation loss
to Parametric UMAP, maximizing the Pearson correlation within batches
between pairwise distances in embedding and data spaces,
CPearson
= − cov(dX, dZ)
p
p
dX
dZ
,
(5.1)
where cov(X, Oui) is the covariance of data and embeddings and σX and σZ
are the standard deviations of the data and embeddings. The same notion of
pairwise distance correlation has previously been used directly as a metric
for global structure preservation (Becht et al., 2019; Kobak & Linderman,
2021).
The weight of this additional loss can be used to dictate the balance be-
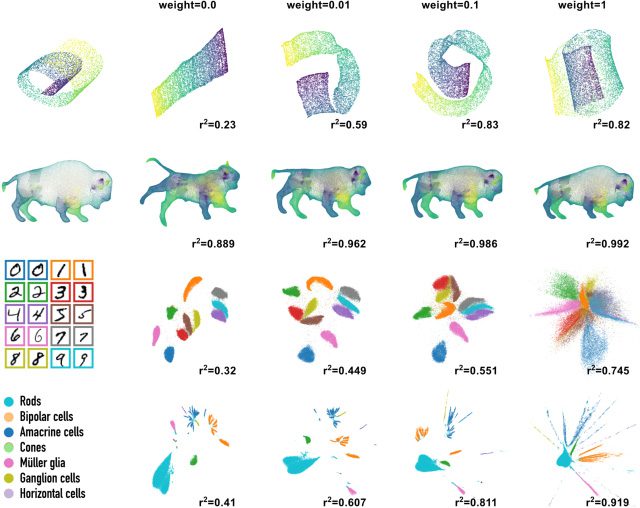
tween capturing global and local structure in the data set. In Figure 8, nous
apply this loss at four different weights, ranging from only UMAP (gauche)
to primarily global correlation (droite). As expected, we observe that as we
weight CPearson more heavily, the global correlation (measured as the correla-
tion of the distance between pairs of points in embedding and data space)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parametric UMAP
2895
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 8: Global loss applied to Parametric UMAP embeddings with different
weights. r2 is the correlation between pairwise distances in data space and em-
bedding space.
increases (indicated in each panel). Notably, when a small weight is used
with each data set, local structure is largely preserved while substantially
improving global correlation.
In Figure 9, we show the global distance correlation plotted against two
local structure metrics (silhouette score and trustworthiness) for the MNIST
and Macosko et al. (2015) data sets corresponding to the projections shown
in Figure 8 in relation to each embedding from Figure 4. En outre, nous
compared TriMap (Amid & Warmuth, 2019), a triplet-loss-based embed-
ding algorithm designed to capture additional global structure, by preserv-
ing the relative distances of triplets of data samples. We also compared
minimum distortion embedding (MDE), which comprises two separate
embedding functions: a local embedding algorithm that preserves relation-
ships between neighbors similar to UMAP and t-SNE and a global embed-
ding algorithm that preserves pairwise distances similar to MDS.
Broadly, with Parametric UMAP, we can observe the trade-off between
captured global and local structure with the weight of CPearson (light blue
line in each panel of Figure 9). We observe that adding this loss can increase
the amount of global structure captured while preserving much of the local
2896
T. Sainburg, L. McInnes, and T. Gentner
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 9: Comparison of pairwise global and local relationship preservation
across embeddings for MNIST and Macosko et al. (2015). Local structure metrics
are silhouette score and trustworthiness. Global structure metric is Spearman
correlation of distances in X and Z. Connected lines are for the different weights
of the correlation loss from Figure 8 in Parametric UMAP and the λ parameter
in TriMap (50, 500, et 5000). MDE (distances) is not given for MNIST because
of memory issues (sur 512 GB RAM).
structure, as indicated by the distance to the top right corner of each panel
in Figure 9, which reflects the simultaneous capture of global and local re-
lationships, relative to each other embedding algorithm.
5.4 Autoencoding with UMAP. The ability to reconstruct data from em-
beddings can aid in understanding the structure of nonlinear embeddings
and allow for manipulation and synthesis of data based on the learned fea-
tures of the data set. We compared the reconstruction accuracy across each
method, which had inverse-transform capabilities (Z → X), as well as the
reconstruction speed across the neural network–based implementations to
nonparametric implementations and PCA. En outre, we performed la-
tent algebra on Parametric UMAP embeddings both with and without an
Parametric UMAP
2897
Chiffre 10: Reconstruction accuracy measured as mean squared error (MSE).
MSE is shown relative to each data set (setting mean at 1).
autoencoder regularization and found that reconstructed data can be lin-
early manipulated in complex feature space.
5.4.1 Reconstruction Accuracy. We measured reconstruction accuracy as
mean squared error (MSE) across each data set (voir la figure 10 and Supple-
mentary Table 7). In two dimensions, we find that Parametric UMAP typi-
cally reconstructs better than nonparametric UMAP, which in turn performs
better than PCA. En outre, the autoencoder regularization slightly im-
proves reconstruction performance. À 64 dimensions, the AE regularized
Parametric UMAP is generally comparable to the AE and VAE and per-
forms better than Parametric UMAP without autoencoder regularization.
The nonparametric UMAP reconstruction algorithm is not compared at 64
dimensions because it relies on an estimation of Delaunay triangulation,
which does not scale well with higher dimensions.
5.4.2 Latent Features. Previous work shows that parametric embedding
algorithms such as AEs (par exemple., variational autoencoders) linearize complex
data features in latent space—for example, the presence of a pair of sun-
glasses in pictures of faces (Radford, Metz, & Chintala, 2015; Sainburg
et coll., 2018; Blanc, 2016). Ici, we performed latent-space algebra and re-
constructed manipulations on Parametric UMAP latent space to explore
whether UMAP does the same.
To do so, we use the CelebAMask-HQ data set which contains anno-
tations for 40 different facial features over a highly structured data set of
human faces. We projected the data set of faces into a CNN autoencoder
architecture based on the architecture defined in Huang, Liu, Belongie, et
Kautz (2018). We trained the network first using UMAP loss alone (Para-
metric UMAP) and then using the joint UMAP and AE loss (voir la figure 11).
We then fit an OLS regression to predict the latent projections of the entire
data set using the 40 annotated features (par exemple., hair color, presence of beard,
smiling). The vectors corresponding to each feature learned by the linear
model were then treated as feature vectors in latent space and added and
subtracted from projected images, then passed through the decoder to ob-
serve the resulting image (as in Sainburg et al., 2018).
We find that complex latent features are linearized in latent space when
the network is trained with UMAP loss alone as well as when the network
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2898
T. Sainburg, L. McInnes, and T. Gentner
Chiffre 11: Reconstruction and interpolation. (UN) Parametric UMAP reconstruc-
tions of faces from a holdout testing data set. (B) The same networks, adding
latent vectors corresponding to image features.
is trained with AE loss. Par exemple, in the third set of images in Figure
10, a pair of glasses can be added or removed from the projected image by
adding or subtracting its corresponding latent vector.
5.5 Semisupervised Learning. Real-word data sets often comprise a
small number of labeled data and a large number of unlabeled data.
Semisupervised learning (SSL) aims to use the unlabeled data to learn the
structure of the data set, aiding a supervised learning algorithm in making
decisions about the data. Current SOTA approaches in many areas of super-
vised learning such as computer vision rely on deep neural networks. Like-
wise, semisupervised learning approaches modify supervised networks
with structure-learning loss using unlabeled data. Parametric UMAP, être
a neural network that learns structure from unlabeled data, is well suited to
semisupervised applications. Ici, we determine the efficacy of UMAP for
semisupervised learning by comparing a neural network jointly trained on
classification and UMAP (see Figure 2D) with a network trained on classi-
fication alone using data sets with varying numbers of labeled data.
We compared data sets ranging from highly structured (MNIST) to un-
structuré (CIFAR-10) in UMAP using a naive distance metric in data space
(par exemple., Euclidean distance over images). For image data sets, we used a deep
convolutional neural network (CNN), which performs with relatively high
accuracy for CNN classification on the fully supervised networks (see Sup-
plementary Table 8 based on the CNN13 architecture commonly used in
SSL (Oliver, Odena, Raffel, Cubuk, & Goodfellow, 2018). For the birdsong
data set, we used a BLSTM network, and for the retina data set, we used a
densely connected network.
5.5.1 Naive UMAP Embedding. For data sets where structure is learned
in UMAP (par exemple., MNIST, FMNIST), we expect that regularizing a classifier
network with UMAP loss will aid the network in labeling data by learning
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parametric UMAP
2899
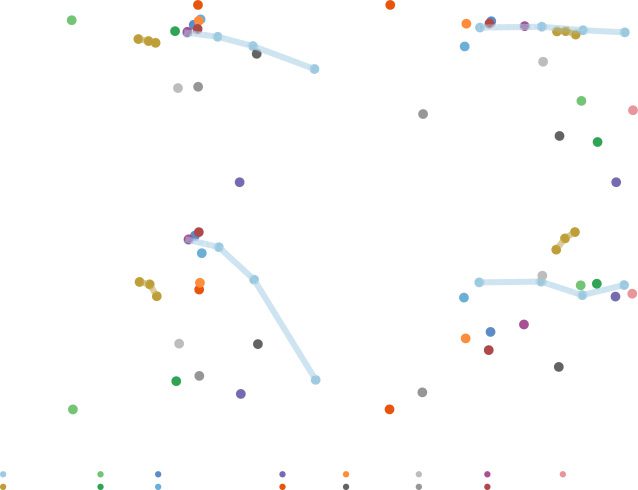
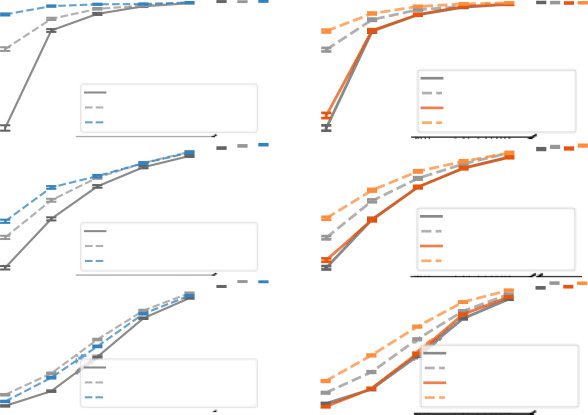
Chiffre 12: Baseline classifier with an additional UMAP loss with different num-
bers of labeled training examples. Nonparametric UMAP projections of the
UMAP graph being jointly trained are shown at the bottom right of each panel.
Error bars show SEM.
the structure of the data set from unlabeled data. To test this, we compared a
baseline classifier to a network jointly trained on classifier loss and UMAP
perte. We first trained the baseline classifier to asymptotic performance on
the validation data set, alors, using the pretrained weights from the base-
line classifier, trained a Y-shaped network (see Figure 2D) jointly on UMAP
over Euclidean distances and a classifier loss over the data set. We find
that for each data set where categorically relevant structure is found in la-
tent projections of the data sets (MNIST, FMNIST, birdsong, retina), classi-
fications are improved in the semisupervised network over the supervised
network alone, especially with smaller numbers of training examples (voir
Chiffre 12 and Supplementary Table 8). In contrast, for CIFAR-10, the addi-
tional UMAP loss impairs performance in the classifier.
5.5.2 Consistency Regularization and Learned Invariance Using Data Aug-
mentation. Several current SOTA SSL approaches employ a technique called
consistency regularization (Sajjadi, Javanmardi, & Tasdizen, 2016) c'est,
training a classifier to produce the same predictions with unlabeled data
that have been augmented and data that have not been augmented (Berth-
elot et al., 2020; Sohn et al., 2020). In a similar vein, for each image data set,
we train the network to preserve the structure of the UMAP graph when
data have been augmented. We computed a UMAP graph over unaug-
mented data and, using augmented data, trained the network jointly us-
ing classifier and UMAP loss, teaching the network to learn to optimize the
same UMAP graph, invariant to augmentations in the data. We observe a
further improvement in network accuracy for MNIST and FMNIST over the
baseline and the augmented baseline (voir la figure 13, left and Supplementary
Tableau 8). For the CIFAR-10 data set, the addition of the UMAP loss, même
over augmented data, reduces classification accuracy.
5.5.3 Learning a Categorically Relevant UMAP Metric Using a Supervised
Réseau. It is unsurprising that UMAP confers no improvement for the
CIFAR-10 data set, as UMAP computed over the pixel-wise Euclidean dis-
tance between images in the CIFAR-10 data set does not capture very much
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2900
T. Sainburg, L. McInnes, and T. Gentner
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
Chiffre 13: Comparison of baseline classifier, augmentation, and augmentation
with an additional UMAP loss (gauche). SSL using UMAP over the learned latent
graph, computed over latent activations in the classifier (droite).
categorically relevant structure in the data set. Because no common distance
metric over CIFAR-10 images is likely to capture such structure, we con-
sider using supervision to learn a categorically relevant distance metric for
UMAP. We do so by training on a UMAP graph computed using distance
over latent activations in the classifier network (as in Carter, Armstrong,
Schubert, Johnson, & Olah, 2019), where categorical structure can be seen in
UMAP projection (voir la figure 14). The intuition is that training the network
with unlabeled data to capture distributional structure within the network’s
learned categorically relevant space will aid in labeling new data.
We find that in all three data sets, without augmentation, the addition
of the learned UMAP loss confers little to no improvement in classification
accuracy over the data (voir la figure 13, droite, and Supplementary Table 8).
When we look at nonparametric projections of the graph over latent activa-
tion, we see that the learned graph largely conforms to the network’s cat-
egorical decision making (par exemple., Chiffre 14 predictions versus ground truth).
In contrast, with augmentation, the addition of the UMAP loss improves
performance in each data set, including CIFAR-10. This contrast in im-
provement demonstrates that training the network to learn a distribution
in a categorically relevant space that is already intrinsic to the network
does not confer any additional information that the network can use in
classification. Training the network to be invariant toward augmentations
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parametric UMAP
2901
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 14: Nonparametric UMAP projections of activations in the last layer of
a trained classifier for MNIST, FMNIST, and CIFAR-10. For each data set, le
top row shows the ground truth labels and the model’s predictions in a light
color map. On top of each projection, the labeled data points used for training
are shown in a darker color map.
in the data, cependant, does aid in regularizing the classifier, more in line with
directly training the network on consistency in classifications (Sajjadi et al.,
2016).
5.6 Comparisons with Indirect Parametric Embeddings. En principe,
any embedding technique can be implemented parametrically by training a
parametric model (par exemple., a neural network) to predict embeddings from the
original high-dimensional data (as in Duque et al., 2020). Cependant, tel
a parametric embedding is limited in comparison to directly optimizing
the algorithm’s loss function. Parametric UMAP optimizes directly over
the structure of the graph with respect to the architecture of the network as
well as additional constraints (par exemple., additional losses). In contrast, training a
2902
T. Sainburg, L. McInnes, and T. Gentner
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 15: Top: Cross-entropy loss for one-hidden-layer instance of Paramet-
ric UMAP versus a neural network trained to predict nonparametric embed-
dings using MSE on MNIST. The same network architectures are used in each
case. The x-axis varies the number of neurons in the network’s single hidden
layer layer. The dashed gray line is the loss for the nonparametric embedding.
Bottom: Projections corresponding to the losses shown in the panel above.
neural network to predict nonparametric embeddings does not take addi-
tional constraints into account.
To exemplify this, in Figure 15 we compare Parametric UMAP to a neu-
ral network trained to predict nonparametric embeddings by minimizing
MSE when the number of neurons in the network is limited. In the case
of parametric UMAP, the objective of the network is to come up with the
best embedding of the UMAP graph that it can, given the constraints of the
architecture of the network. In the indirect/MSE case, information about
the structure of the graph is available only through an intermediary, le
nonparametric embedding; thus, this method cannot be optimized to learn
an embedding of the data that best preserve the structure of the graph. Dans
autres mots, the indirect method is not optimizing the embedding of the
graph with respect to additional constraints. Plutôt, it is minimizing the
distance between two sets of embeddings. The weighted graph is an inter-
mediate topological representation (notably of no specific dimensionality)
and is the best representation of the data under UMAP’s assumptions. Le
process of embedding the data in a fixed dimensional space is necessarily
a lossy one. Optimizing over the graph directly avoids this loss. This issue
also applies when incorporating additional losses (par exemple., a classifier loss or
autoencoder loss) to indirect embeddings.
Parametric UMAP
6 Discussion
2903
In this letter, we propose a novel parametric extension to UMAP. This para-
metric form of UMAP produces embeddings similar to those of nonpara-
metric UMAP, with the added benefit of a learned mapping between data
space and embedding space. We demonstrated the utility of this learned
mapping on several downstream tasks. We showed that parametric re-
lationships can be used to improve inference times for embeddings and
reconstructions by orders of magnitude while maintaining similar embed-
ding quality to nonparametric UMAP. Combined with a global structure
preservation loss, Parametric UMAP captures additional global relation-
ships in data, outperforming methods where global structure is only
imposed upon initialization (par exemple., initializing with PCA embeddings). Com-
bined with an autoencoder, UMAP improves reconstruction quality and
allows for the reconstruction of high-dimensional UMAP projections. Nous
also show that Parametric UMAP projections linearize complex features
in latent space. Parametric UMAP can be used for semisupervised learn-
ing, improving training accuracy on data sets where small numbers of
training exemplars are available. We showed that UMAP loss applied to
a classifier improves semisupervised learning in real-world cases where
UMAP projections carry categorically relevant information (such as stereo-
typed birdsongs or single-cell transcriptomes), but not in cases where
categorically relevant structure is not present (such as CIFAR-10). Nous
devised two downstream approaches based around learned categorically
relevant distances and consistency regularization that show improvements
on these more complex data sets. Parametric embedding also makes UMAP
feasible in fields where dimensionality reduction of continuously gener-
ated signals plays an important role in real-time analysis and experimental
control.
A number of future directions and extensions to our approach have
the potential to further improve upon our results in dimensionality re-
duction and its various applications. Par exemple, to improve global
structure preservation, we jointly optimized over the Pearson correlation
between data and embeddings. Using notions of global structure beyond
pairwise distances in data space (such as global UMAP relationships or
higher-dimensional simplices) may capture additional structure in data.
De la même manière, one approach we used to improve classifier accuracy relied on
obtaining a categorically relevant metric, defined as the Euclidean dis-
tance between activation states of the final layer of a classifier. Recent work
(par exemple., as discussed and proposed in Schulz, Hinder, & Hammer, 2019) have
explored methods for more directly capturing class information in the com-
putation of distance, such as using the Fisher metric to capture category-
and decision-relevant structure in classifier networks. Similar metrics may
prove to further improve semisupervised classifications with Parametric
UMAP.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2904
T. Sainburg, L. McInnes, and T. Gentner
Remerciements
This work was supported by NIH 5T32MH020002-20 to T.S. et
5R01DC018055-02 to T.G. We also thank Kyle McDonald for making avail-
able his translation of Parametric t-SNE to Tensorflow/Keras, which we
used as a basis for our own implementation.
Les références
Amid, E., & Warmuth, M.. K. (2019). Trimap: Large-scale dimensionality reduction using
triplets. arXiv:1910.00204.
Becht, E., McInnes, L., Healy, J., Dutertre, C.-A., Kwok, je. W., Ng, L. G., . . . Newell,
E. W. (2019). Dimensionality reduction for visualizing single-cell data using
UMAP. Nature Biotechnology, 37(1), 38–44. https://doi.org/10.1038/nbt.4314
Berthelot, D., Carlini, N., Cubuk, E. D., Kurakin, UN., Sohn, K., Zhang, H., & Raffel, C.
(2020). Remixmatch: Semi-supervised learning with distribution matching and
augmentation anchoring. In Proceedings of the International Conference on Learning
Representations. https://openreview.net/forum?id=HklkeR4KPB
Brun, UN. E., & De Bivort, B. (2018). Ethology as a physical science. Nature Physics,
14(7), 653–657. https://doi.org/10.1038/s41567-018-0093-0
Bunte, K., Biehl, M., & Hammer, B. (2012). A general framework for dimensionality-
reducing data visualization mapping. Neural Computation, 24(3), 771–804.
https://doi.org/10.1162/NECO_a_00250
Carter, S., Armstrong, Z., Schubert, L., Johnson, JE., & Olah, C. (2019). Activation atlas.
Distill, 4(3), e15.
De Silva, V., & Tenenbaum, J.. B. (2003). Global versus local methods in nonlinear
dimensionality reduction. In S. Becker, S. Thrun, & K. Overmayer (Éd.), Ad-
vances in neural information processing systems, 15 (pp. 721–728). Red Hook, New York:
Curran.
Ding, J., Condon, UN., & Shah, S. P.. (2018). Interpretable dimensionality re-
duction of single cell transcriptome data with deep generative models. Na-
ture Communications, 9(1), 1–13. https://doi.org/10.1038/s41467-018-04368-5,
PubMed: 29784946
Ding, J., & Regev, UN. (2019). Deep generative model embedding of single-cell RNA-Seq
profiles on hyperspheres and hyperbolic spaces. bioRxiv:853457.
Dong, W., Moses, C., & Li, K. (2011). Efficient k-nearest neighbor graph construc-
tion for generic similarity measures. In Proceedings of the 20th International Con-
ference on World Wide Web (pp. 577–586). New York: ACM. https://est ce que je.org/10.
1145/1963405.1963487
Duque, UN. F., Morin, S., Loup, G., & Moon, K. R.. (2020). Extendable and invertible man-
ifold learning with geometry regularized autoencoders. arXiv:2007.07142.
Gisbrecht, UN., Lueks, W., Mokbel, B., & Hammer, B. (2012). Out-of-sample kernel
extensions for nonparametric dimensionality reduction. In Proceedings of the Eu-
ropean Symposium on Artificial Neural Networks, Computational Intelligence, and Ma-
chine Learning. https://doi.org/10.1109/TNNLS.2015.2512277
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parametric UMAP
2905
Gisbrecht, UN., Schulz, UN., & Hammer, B. (2015). Parametric nonlinear dimensionality
reduction using kernel t-SNE. Neurocomputing, 147, 71–82. https://est ce que je.org/10.
1016/j.neucom.2013.11.045
Graving, J.. M., & Couzin, je. D. (2020). Vae-SNE: A deep generative model for simultaneous
dimensionality reduction and clustering. bioRxiv. https://doi.org/10.1101/2020.07.
17.207993
Hedley, R.. W. (2016un). Complexity, predictability and time homogeneity of syntax
in the songs of Cassin’s Vireo (Vireo cassinii). PLOS One, 11(4), e0150822. https:
//doi.org/10.1371/journal.pone.0150822, PubMed: 27050537
Hedley, R.. W. (2016b). Composition and sequential organization of song repertoires
in Cassin’s Vireo (Vireo cassinii). Journal of Ornithology, 157(1), 13–22. https://est ce que je.
org/10.1007/s10336-015-1238-x
Hinton, G. E., & Salakhutdinov, R.. R.. (2006). Reducing the dimensionality of
data with neural networks. Science, 313(5786), 504–507. https://doi.org/10.1126/
science.1127647, PubMed: 16873662
Hofer, C., Kwitt, R., Niethammer, M., & Dixit, M.. (2019). Connectivity-optimized
representation learning via persistent homology. In Proceedings of the International
Conference on Machine Learning (pp. 2751–2760). Berlin: Springer.
Huang, X., Liu, M.-Y., Belongie, S., & Kautz, J.. (2018). Multimodal unsuper-
vised image-to-image translation. In Proceedings of the European Conference
on Computer Vision (pp. 172–189). Berlin: Springer. https://doi.org/10.1007/
978-3-030-01219-9_11
Jia, K., Sun, L., Gao, S., Song, Z., & Shi, B. E. (2015). Laplacian auto-encoders:
An explicit learning of nonlinear data manifold. Neurocomputing, 160, 250–260.
https://doi.org/10.1016/j.neucom.2015.02.023
Kingma, D. P., & Welling, M.. (2013). Auto-encoding variational Bayes. arXiv:1312.6114.
KlugerLab. (2020). Open source survey. https://github.com/KlugerLab/FIt-SNE,
commit=4f57d6a0e4c030202a07a60bc1bb1ed1544bf679.
Kobak, D., & Linderman, G. C. (2021). Initialization is critical for preserving global
data structure in both t-SNE and UMAP. Nature Biotechnology, 1–2. https://est ce que je.
org/10.1038/s41587-020-00809-z
Lee, J.. UN., Peluffo-Ordóñez, D. H., & Verleysen, M.. (2015). Multi-scale similarities
in stochastic neighbour embedding: Reducing dimensionality while preserving
both local and global structure. Neurocomputing, 169, 246–261. https://est ce que je.org/
10.1016/j.neucom.2014.12.095
Linderman, G. C., Rachh, M., Hoskins, J.. G., Steinerberger, S., & Kluger, Oui. (2017). Effi-
cient algorithms for t-distributed stochastic neighborhood embedding. arXiv:1712.09005.
https://doi.org/10.1038/s41592-018-0308-4
Linderman, G. C., Rachh, M., Hoskins, J.. G., Steinerberger, S., & Kluger, Oui. (2019).
Fast interpolation-based t-SNE for improved visualization of single-cell RNA-Seq
data. Nature Methods, 16(3), 243–245. https://doi.org/10.1038/s41592-018-0308-4
Macosko, E. Z., Basu, UN., Satija, R., Nemesh, J., Shekhar, K., Homme d'or, M., . . . McCar-
roll, S. UN. (2015). Highly parallel genome-wide expression profiling of individual
cells using nanoliter droplets. Cell, 161(5), 1202–1214. https://est ce que je.org/10.1016/j.
cell.2015.05.002, PubMed: 26000488
McInnes, L., Healy, J., & Melville, J.. (2018). Umap: Uniform manifold approximation and
projection for dimension reduction. arXiv:1802.03426.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2906
T. Sainburg, L. McInnes, and T. Gentner
Mikolov, T., Sutskever, JE., Chen, K., Corrado, G. S., & Dean, J.. (2013). Distributed rep-
resentations of words and phrases and their compositionality. In C. J.. C. Burges,
L. Bottou, M.. Welling, Z. Ghahramani, & K. Q. Weinberger (Éd.), Advances in
neural information processing systems, 26 (pp. 3111–3119). Red Hook, New York: Curran.
Mishne, G., Shaham, U., Cloninger, UN., & Cohen, je. (2019). Diffusion nets. Applied and
Computational Harmonic Analysis, 47(2), 259–285.
Moon, K. R., van Dijk, D., Wang, Z., Gigante, S., Burkhardt, D. B., Chen, W. S., . . .
Krishnaswamy (2019). Visualizing structure and transitions in high-dimensional
biological data. Nature Biotechnology, 37(12), 1482–1492. https://est ce que je.org/10.
1038/s41587-019-0336-3
Moor, M., Corne, M., Rieck, B., & Borgwardt, K. (2020). Topological autoencoders. Dans
Proceedings of the International Conference on Machine Learning.
Oliver, UN., Odena, UN., Raffel, C. UN., Cubuk, E. D., & Goodfellow, je. (2018). Realistic
evaluation of deep semi-supervised learning algorithms. In S. Bengio, H. Wal-
lach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, & R.. Garnett (Éd.), Advances
in neural information processing systems, 31 (pp. 3235–3246). Red Hook, New York: Curran.
Pai, G., Talmon, R., Bronstein, UN., & Kimmel, R.. (2019). DIMAL: Deep isometric man-
ifold learning using sparse geodesic sampling. In Proceedings of the 2019 IEEE
Winter Conference on Applications of Computer Vision (pp. 819–828). Piscataway, New Jersey:
IEEE.
Pandarinath, C., O’Shea, D. J., Collins, J., Jozefowicz, R., Stavisky, S. D., Kao, J.. C.,
. . . Sussilo, D. (2018). Inferring single-trial neural population dynamics using
sequential auto-encoders. Nature Methods, 15(10), 805–815. https://est ce que je.org/10.
1038/s41592-018-0109-9
Pedregosa, F., Varoquaux, G., Gramfort, UN., Michel, V., Thirion, B., Grisel, O., . . .
Cournapeau, D. (2011). Scikit-learn: Machine learning in Python. Journal of Ma-
chine Learning Research, 12, 2825–2830.
Poliˇcar, P.. G., Stražar, M., & Zupan, B. (2019). openTSNE: A modular Python library for
t-SNE dimensionality reduction and embedding. bioRxiv. https://www.biorxiv.org/
content/early/2019/08/13/731877
Radford, UN., Metz, L., & Chintala, S. (2015). Unsupervised representation learning with
deep convolutional generative adversarial networks. arXiv:1511.06434.
Robinson, je. (2020). Interpretable visualizations with differentiating embedding networks.
arXiv:2006.06640.
Sainburg, T., Thielk, M., & Gentner, T. Q. (2019). Latent space visualization, character-
ization, and generation of diverse vocal communication signals. est ce que je:https://est ce que je.org/
10.1101/870311
Sainburg, T., Thielk, M., Theilman, B., Migliori, B., & Gentner, T. (2018). Generative ad-
versarial interpolative autoencoding: Adversarial training on latent space interpolations
encourage convex latent distributions. arXiv:1807.06650.
Sajjadi, M., Javanmardi, M., & Tasdizen, T. (2016). Regularization with stochastic
transformations and perturbations for deep semi-supervised learning. In D. Lee,
M.. Sugiyama, U. Luxburg, je. Guyon, & R.. Garnett (Éd.), Advances in neural infor-
mation processing systems, 29 (pp. 1163–1171). Red Hook, New York: Curran.
Schulz, UN., Hinder, F., & Hammer, B. (2019). Deepview: Visualizing classification bound-
aries of deep neural networks as scatter plots using discriminative dimensionality reduc-
tion. arXiv:1909.09154.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parametric UMAP
2907
Sohn, K., Berthelot, D., Li, C.-L., Zhang, Z., Carlini, N., Cubuk, E. D., . . . Raffel,
C. (2020). Fixmatch: Simplifying semi-supervised learning with consistency and confi-
dence. arXiv:2001.07685.
Szubert, B., Cole, J.. E., Monaco, C., & Drozdov, je. (2019). Structure-preserving vi-
sualisation of high dimensional single-cell datasets. Rapports scientifiques, 9(1), 1-dix.
https://doi.org/10.1038/s41598-019-45301-0
Tang, J., Liu, J., Zhang, M., & Mei, Q. (2016). Visualizing large-scale and high-
dimensional data. In Proceedings of the 25th International Conference on World Wide
Web (pp. 287–297). New York: ACM. https://doi.org/10.1145/2872427.2883041
van der Maaten, L. (2009). Learning a parametric embedding by preserving local
structure. In Proceedings on the 12th International Conference on Artificial Intelligence
and Statistics (pp. 384–391).
van der Maaten, L. (2014). Accelerating t-SNE using tree-based algorithms. Journal
of Machine Learning Research, 15(1), 3221–3245.
van der Maaten, L., & Hinton, G. (2008). Visualizing data using t-SNE. Journal de
Machine Learning Research, 9, 2579–2605.
Venna, J., & Kaski, S. (2006). Local multidimensional scaling. Neural Networks, 19(6–
7), 889–899.
Blanc, T. (2016). Sampling generative networks. arXiv:1609.04468.
Received April 1, 2021; accepted June 1, 2021.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
1
2
8
8
1
1
9
6
6
6
5
6
n
e
c
o
_
un
_
0
1
4
3
4
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3