ARTICLE
Communicated by Shun-ichi Amari
On the Achievability of Blind Source Separation
for High-Dimensional Nonlinear Source Mixtures
Takuya Isomura
takuya.isomura@riken.jp
Laboratory for Neural Computation and Adaptation and Brain Intelligence Theory
Unit, RIKEN Center for Brain Science, Wako, Saitama 351-0198, Japan
Taro Toyoizumi
taro.toyoizumi@riken.jp
Laboratory for Neural Computation and Adaptation, RIKEN Center for Brain
Science, Wako, Saitama 351-0198, Japan, and Department of Mathematical
Informatics, Graduate School of Information Science and Technology,
University of Tokyo, Bunkyo-ku, Tokyo 113-8656, Japan
For many years, a combination of principal component analysis (APC)
and independent component analysis (ICA) has been used for blind
source separation (BSS). Cependant, it remains unclear why these lin-
ear methods work well with real-world data that involve nonlinear
source mixtures. This work theoretically validates that a cascade of lin-
ear PCA and ICA can solve a nonlinear BSS problem accurately—when
the sensory inputs are generated from hidden sources via nonlinear map-
pings with sufficient dimensionality. Our proposed theorem, termed the
asymptotic linearization theorem, theoretically guarantees that applying
linear PCA to the inputs can reliably extract a subspace spanned by the
linear projections from every hidden source as the major components—
and thus projecting the inputs onto their major eigenspace can effectively
recover a linear transformation of the hidden sources. Then subsequent
application of linear ICA can separate all the true independent hidden
sources accurately. Zero-element-wise-error nonlinear BSS is asymptoti-
cally attained when the source dimensionality is large and the input di-
mensionality is sufficiently larger than the source dimensionality. Notre
proposed theorem is validated analytically and numerically. De plus,
the same computation can be performed by using Hebbian-like plastic-
ity rules, implying the biological plausibility of this nonlinear BSS strat-
egy. Our results highlight the utility of linear PCA and ICA for accurately
and reliably recovering nonlinearly mixed sources and suggest the im-
portance of employing sensors with sufficient dimensionality to identify
true hidden sources of real-world data.
Neural Computation 33, 1433–1468 (2021) © 2021 Massachusetts Institute of Technology.
https://doi.org/10.1162/neco_a_01378
Publié sous Creative Commons
Attribution 4.0 International (CC PAR 4.0) Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1434
1 Introduction
T. Isomura and T. Toyoizumi
Blind source separation (BSS) involves the separation of mixed sensory in-
puts into their hidden sources without knowledge of the manner in which
they were mixed (Cichocki, Zdunek, Phan, & Amari, 2009; Comon & Jut-
ten, 2010). Among the numerous BSS methods, a combination of principal
component analysis (APC) (Pearson, 1901; Oja, 1982, 1989; Sanger, 1989; Xu,
1993; Jolliffe, 2002) and independent component analysis (ICA) (Comon,
1994; Cloche & Sejnowski, 1995, 1997; Amari, Cichocki, & Lequel, 1996; Hy-
varinen & Oja, 1997) is one of the most widely used approaches. Dans ce
combined PCA–ICA approach, PCA yields a low-dimensional concise rep-
resentation (c'est à dire., the major principal components) of sensory inputs that
most suitably describes the original high-dimensional redundant inputs.
Whereas, ICA provides a representation (c'est à dire., encoders) that separates the
compressed sensory inputs into independent hidden sources. A classical
setup for BSS assumes a linear generative process (Cloche & Sejnowski, 1995),
in which sensory inputs are generated as a linear superposition of indepen-
dent hidden sources. The linear BSS problem has been extensively studied
both analytically and numerically (Amari, Chen, & Cichocki, 1997; Oja &
Yuan, 2006; Erdogan, 2009), where the cascade of PCA and ICA is guaran-
teed to provide the optimal linear encoder that can separate sensory inputs
into their true hidden sources, up to permutations and sign-flips (Baldi &
Hornik, 1989; Chen, Hua, & Yan, 1998; Papadias, 2000; Erdogan, 2007).
Another crucial perspective is the applicability of BSS methods to real-
world data generated from a nonlinear generative process. En particulier,
the aim of nonlinear BSS is to identify the inverse of a nonlinear generative
process that generates sensory inputs and thereby infer their true indepen-
dent hidden sources based exclusively on the sensory inputs. Bien que le
cascade of linear PCA and ICA has been applied empirically to real-world
BSS problems (Calhoun, Liu, & Adali, 2009), no one has yet theoretically
proven that this linear BSS approach can solve a nonlinear BSS problem. À
address this gap, this work demonstrates mathematically that the cascade
of PCA and ICA can solve a nonlinear BSS problem accurately when the
source dimensionality is large and the input dimensionality is sufficiently
larger than the source dimensionality so that various nonlinear mappings
from sources to inputs can be determined from the inputs themselves.
En général, there are five requirements for solving the nonlinear BSS
problem. The first two requirements are related to the representation capac-
ity of the encoder: (1) the encoder’s parameter space must be sufficiently
large to accommodate the actual solution that can express the inverse of
the true generative process. (2) Cependant, this parameter space should not
be too large; otherwise, a nonlinear BSS problem can have infinitely many
spurious solutions wherein all encoders are independent but dissimilar to
the true hidden sources (Hyvarinen & Pajunen, 1999; Jutten & Karhunen,
2004). Ainsi, it is important to constrain the representation capacity of the
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1435
encoder in order to satisfy these opposing requirements. A typical approach
for solving the nonlinear BSS problem involves using a multilayer neu-
ral network—with nonlinear activation functions—that learns the inverse
of the generative process (Lappalainen & Honkela, 2000; Karhunen, 2001;
Hinton & Salakhutdinov, 2006; Kingma & Welling, 2013; Dinh, Krueger, &
Bengio, 2014). The remaining three requirements are related to the unsu-
pervised learning algorithms used to identify the optimal parameters for
the encoder: (3) the learning algorithm must have a fixed point at which
the network expresses the inverse of the generative process; (4) the fixed
point must be linearly stable so that the learning process converges to the
solution; et (5) the probability of not converging to this solution should
be small, c'est, most realistic initial conditions must be within the basin of
attraction of the true solution.
Approaches using a nonlinear multilayer neural network satisfy require-
ment 1 when the number of neurons in each layer is sufficient (univer-
sality: Cybenko, 1989; Hornik, Stinchcombe, & Blanc, 1989; Barron, 1993);
moreover, learning algorithms that satisfy requirements 3 et 4 are also
known (Dayan, Hinton, Neal, & Zemel, 1995; Friston, 2008; Friston, Trujillo-
Barreto, & Daunizeau, 2008). Cependant, reliable identification of the true
hidden sources is still necessary because the encoder can have infinitely
many spurious solutions if its representation capacity is too large (c'est à dire., if re-
quirement 2 is violated). As previously indicated, to the best of our knowl-
bord, there is no theoretical proof that confirms a solution for a nonlinear
BSS problem (Hyvarinen & Pajunen, 1999; Jutten & Karhunen, 2004), ex-
cept for some cases wherein temporal information—such that each inde-
pendent source has its own dynamics—is available (Hyvarinen & Morioka,
2016, 2017; Khemakhem, Kingma, Monti, & Hyvarinen, 2020). De plus,
even when requirement 2 is satisfied, there is no guarantee that a learning
algorithm will converge to the true hidden source representation because
it might be trapped in a local minimum wherein outputs are still not inde-
pendent of each other. Ainsi, for a nonlinear BSS problem, it is of paramount
importance to simplify the parameter space of the inverse model in order
to remove spurious solutions and prevent the learning algorithm from at-
taining a local minimum (to satisfy requirements 2 et 5) while retaining
its capacity to represent the actual solution (requirement 1). Ainsi, in this
travail, we apply a linear approach to solving a nonlinear BSS problem in
order to ensure requirements 2 et 5 are satisfied. We demonstrate that the
cascade of PCA and ICA can reliably identify a good approximation of the
inverse of nonlinear generative processes asymptotically under the condi-
tion where the source dimensionality is large and the input dimensionality
is sufficiently larger than the source dimensionality (thus satisfying require-
ments 1–5). Although such a condition is different from the case typically
considered by earlier work—where the sources and inputs have the same
dimensionality—the condition we consider turns out to be apt for the math-
ematical justification of the achievability of the nonlinear BSS.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1436
T. Isomura and T. Toyoizumi
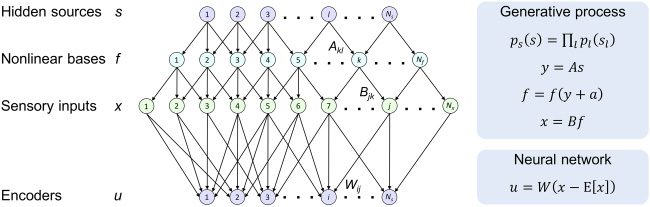
, . . . , fN f )T , where A = {Akl
Chiffre 1: Structures of nonlinear generative process (top) and linear neural
, . . . , sNs )T generate sensory inputs
réseau (bottom). Hidden sources s = (s1
, . . . , xNx )T via nonlinear mappings characterized by nonlinear bases f =
x = (x1
, . . . , aN f )T are gaussian-distributed
( f1
} is a lower-
higher-layer mixing weights and offsets, respectivement, and B = {B jk
layer mixing weight matrix. Encoders comprise a single-layer linear neural net-
} is a synaptic
travail, where u = (u1
weight matrix. Equations on the right-hand-side panels summarize the genera-
tion of sensory inputs from hidden sources through nonlinear mixtures and the
inversion of this process using a linear neural network.
, . . . , uNs )T are neural outputs and W = {Wi j
} and a = (a1
2 Results
2.1 Overview. Our proposed theorem, referred to as asymptotic lin-
earization theorem, is based on an intuition that when the dimensionality
of sensory inputs is significantly larger than that of hidden sources, ces
inputs must involve various linear and nonlinear mappings of all hidden
sources—thus providing sufficient information to identify the true hidden
sources without ambiguity using an unsupervised learning approach. Nous
consider that Ns-dimensional hidden sources s ≡ (s1
, . . . , sNs )T generate Nx-
dimensional sensory inputs x ≡ (x1
, . . . , xNx )T through a generative process
characterized by an arbitrary nonlinear mapping x ≡ F(s) (voir la figure 1).
Ici, the hidden sources are supposed to follow independently an identical
probability distribution with zero mean and unit variance ps(s) ≡
i pi(si).
A class of nonlinear mappings F(s) can be universally approximated by a
×Ns and
specific but generic form of two-layer network. Suppose A ∈ RN f
B ∈ RNx×N f as higher- and lower-layer mixing matrices, respectivement; a ∈
RN f as a constant vector of offsets; y ≡ As as a linear mixture of sources,
F (•) : R. (cid:4)→ R as a nonlinear function; and f ≡ ( f1
, . . . , fN f )T ≡ f (Comme +
un) ≡ f (oui + un) as N f -dimensional nonlinear bases. The sensory inputs are
given as
(cid:2)
x = B f (Comme + un),
(2.1)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1437
ou, equivalently, x = B f (oui + un) = B f . This expression using the two-layer
network is universal in the component-wise sense1 (Cybenko, 1989; Hornik
et coll., 1989; Barron, 1993) and each element of x can represent an arbitrary
mapping x = F(s) as N f increases by adjusting parameters a, UN, et B.
We further suppose that each element of A and a is independently gener-
ated from a gaussian distribution N [0, 1/Ns], which retains its universal-
ville (Rahimi & Recht, 2008un, 2008b) as long as B is tuned to minimize the
mean squared error E[|B f − F(s)|2]. Ici, E[•] describes the average over
ps(s). The scaling of A is to ensure that the argument of f is of order 1.
−1/2
The N
order offset a is introduced to this model to express any genera-
s
tive process F(s); cependant, it is negligibly small relative to As for large Ns.
The whole system, including the generative process and neural network, est
depicted in Figure 1 (gauche). The corresponding equations are summarized in
Chiffre 1 (droite).
For analytical tractability, we decompose nonlinear bases f
into the
sum of linear and nonlinear parts of hidden sources as follows: linear
components of the hidden sources in the bases are defined as Hs using a
coefficient matrix H that minimizes the mean squared error, H ≡
arg minH E[| f − E[ F ] − Hs|2]. Such a coefficient matrix is computed as H =
E[ f sT ]. The remaining part φ ≡ f − E[ F ] − Hs is referred to as nonlinear
components of the hidden sources, which are orthogonal (uncorrelated) à
s (c'est à dire., E[φsT ] = O). This definition of linear and nonlinear components is
unique. Ainsi, the sensory inputs (see equation 2.1) are decomposed into
linear and nonlinear transforms of the hidden sources:
x − E[X] = BHs
(cid:3)(cid:4)(cid:5)(cid:6)
+ Bφ
(cid:3)(cid:4)(cid:5)(cid:6)
.
signal
residual
(2.2)
The first term on the right-hand side represents the signal comprising the
linear components of the hidden sources, whereas the second term repre-
sents the residual introduced by the nonlinearity in the generative process.
Plus loin, because φ is uncorrelated with s, the covariance of the bases is
decomposed into their linear and nonlinear counterparts Cov[ F ] ≡ E[( f −
E[ F ])( f − E[ F ])T ] = Cov[Hs] + Cov[φ] = HHT + (cid:3), où (cid:3) ≡ Cov[φ] dans-
dicates the covariance of φ. Ainsi, the covariance of the sensory inputs
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1
In this work, based on the literature (Cybenko, 1989), we define the universality in the
component-wise sense as the condition wherein each element of x = F(s) is approximated
using the two-layer network with an approximation error smaller than an arbitrary δ > 0,
c'est, sups[|Fj (s) − B j f (Comme + un)|] < δ for j = 1, . . . , Nx when N f is sufficiently large. Note
that Fj (s) is the jth element of F(s) and B j is the jth row vector of B. It is known that when
f is a sigmoidal function and parameters are selected appropriately, the approximation
−1
(Barron, 1993); hence, E[|Fj (s) − B j f (As +
error can be upper-bounded by the order N
f
a)|2] ≤ O(N
(cid:7) Ns (cid:7) 1, irrespective of Nx.
). This relationship holds true when N f
−1
f
1438
T. Isomura and T. Toyoizumi
Cov[x] ≡ BCov[ f ]BT can be decomposed into the signal and residual
covariances:
Cov[x] = BHHT BT
(cid:6)
(cid:4)(cid:5)
(cid:3)
+
B(cid:3)BT
(cid:3) (cid:4)(cid:5) (cid:6)
.
(2.3)
signal covariance
residual covariance
Crucially, the signal covariance has only Ns nonzero eigenvalues when
> Ns owing to low-column-rank matrix H, whereas the eigenvalues of
N f
the residual covariance are distributed in the N f -dimensional eigenspace.
This implies that if the norms of the linear and nonlinear components in the
inputs are in a similar order and Ns is sufficiently large, the eigenvalues of
/Ns order times larger
the signal covariance (c'est à dire., linear components) are N f
than those of the residual covariance (c'est à dire., nonlinear components). We will
prove in the following sections that when Ns (cid:7) 1, this property is derived
from the fact that elements of A are gaussian distributed and singular values
of B are of order 1.
In what follows, we demonstrate that owing to the aforementioned prop-
erty, the first Ns major principal components of the input covariance pre-
cisely match the signal covariance when the source dimensionality is large
and the input dimensionality is sufficiently larger than the source dimen-
sionality. Par conséquent, projecting the inputs onto the subspace spanned
by major eigenvectors can effectively extract the linear components in the
inputs. De plus, the same projection can effectively filter out the nonlin-
ear components in the inputs because the majority of the nonlinear com-
ponents are perpendicular to the major eigenspace. Ainsi, applying PCA to
the inputs enables the recovery of a linear transformation of all the true hid-
den sources of the mixed sensory inputs with a small estimation error. Ce
property, termed asymptotic linearization, enables the reduction of the orig-
inal nonlinear BSS problem to a simple linear BSS problem, par conséquent
satisfying requirements 1 à 5. In the remainder of this article, we mathemat-
ically validate this theorem for a wide range of nonlinear setups and thereby
demonstrate that linear encoder neural networks can perform the nonlin-
ear BSS in a self-organizing manner.2 We assume that Nx = N f
(cid:7) Ns (cid:7) 1
throughout the article.3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2
In this article, we refer to the neural network as the encoder because networks that
convert the input data into a different (lower-dimensional) code or representation are
widely recognized as encoders in the literature on machine learning (Hinton & Salakhut-
dinov, 2006; Goodfellow, Bengio & Courville, 2016). Cependant, one may think that the
generative process encodes the hidden sources into the sensory inputs through nonlin-
ear mixtures. From this viewpoint, one may term the neural network as the decoder that
decodes the inputs to recover the original sources.
Our numerical simulations suggest that the system behaves similarly for Nx ≥ N f
Ns > 1 in some cases, although our theorem holds mathematically only when Nx = N f
Ns (cid:7) 1.
≥
(cid:7)
3
Achievability of Nonlinear Blind Source Separation
1439
2.2 PCA Can Extract Linear Projections of All True Hidden Sources.
Dans cette section, we first demonstrate that the major principal components
(cid:7)
of the input covariance precisely match the signal covariance when N f
Ns (cid:7) 1 by analytically calculating eigenvalues of HHT and (cid:3) for the afore-
mentioned system. For analytical tractability, we assume that f (•) is an odd
nonlinear function. This assumption does not weaken our proposed theo-
rem because the presumed generative process in equation 2.1 remains uni-
versal. We further assume that ps(s) is a symmetric distribution.
Each element of—and any pair of two elements in—a vector y ≡ As is
approximately gaussian distributed for large Ns due to the central limit
, y j ) from the
theorem. The deviation of their marginal distribution p(yi
, y j ) ≡ N [0, ˜A ˜AT ] est
corresponding zero-mean gaussian distribution pN (yi
order N−1
s because the source distribution is symmetric, where ˜A ∈ R2×Ns
indicates a submatrix of A comprising its ith and jth rows (see lemma
1 and its proof in section 4.1). This asymptotic property allows us to
compute H and (cid:3) based on the expectation over a tractable gaussian
, y j )—as
distribution pN (yi
the leading order for large Ns, despite the fact that s actually follows a
, y j )
nongaussian distribution (ensure that p(yi
, y j ) comme
in the large Ns
(cid:7)
to distinguish it from E[•]. The latter can
EN [•] ≡
•pN (yi
be rewritten as E[•] = EN [•(1 + G(yi
, y j )/Ns)] using an order-one function
, y j ); thus,
, y j ) from pN (yi
G(yi
the deviation caused by this approximation is negligibly smaller than the
leading order in the following analyses.
limit). We denote the expectation over pN (yi
, y j )dyidy j
, y j )—as a proxy for the expectation over p(yi
, y j ) that characterizes the deviation of p(yi
, y j ) converges to pN (yi
(cid:7)
(cid:7)
f p(cid:9)
N (oui)T dy AAT =
Owing to this asymptotic property, the coefficient matrix H is com-
puted as follows: the pseudo-inverse of A, A+ ≡ (AT A)−1AT , satisfies
A+A = I and A+T = AT+. Ainsi, we have H = HAT A+T = E[ f yT ]A+T .
It can be approximated by EN [ f yT ]A+T as the leading order from
lemma 1. From the integration by parts, we obtain EN [ f yT ] =
diag[ F (cid:9)]pN (oui)dy AAT = diag[EN [ F (cid:9)]]AAT . Ce
−
relationship is also known as the Bussgang theorem (Bussgang, 1952).
−1/2
Ainsi, EN [ f yT ]A+T = diag[EN [ F (cid:9)]]A is order N
for a generic odd func-
s
tion f (•) (as it is the product of order 1 diagonal matrix diag[EN [ F (cid:9)]] et
−1/2
order N
matrix A). According to lemma 1, the difference between H
s
−3/2
and diag[EN [ F (cid:9)]]A is order N
s order times smaller than the
s
leading order (see remark 1 in section 4.1 for details). Ainsi, we obtain
as it is N−1
H = diag[EN [ F
(cid:9)
]]UN + Ô
(cid:9)
(cid:8)
−3/2
N
s
= f (cid:9)UN + Ô
(cid:8)
(cid:9)
.
−1
N
s
(2.4)
F (cid:9)
In the last equality,
√
(cid:7)
(ξ ) exp(−ξ 2/2)dξ /
able ξ . The order N−1
s
F (cid:9) ≡
the scalar coefficient
2π using the expectation over a unit gaussian vari-
error term includes the nongaussian contributions
is expressed as
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1440
T. Isomura and T. Toyoizumi
s
diagonal matrix (diag[EN [ F (cid:9)]] − f (cid:9)je) and order N
−1/2
deviation of diag[EN [ F (cid:9)]] from f (cid:9),
of y and the effect of the order N
s
where the latter yields the order N−1
error owing to the product of order
−1/2
−1/2
N
s matrix A. Due
s
to the low column rank of matrix A, AAT has Ns nonzero eigenvalues,
/Ns as the leading order, because elements of A are
all of which are N f
independent and identically distributed variables sampled from a gaus-
sian distribution N [0, 1/Ns] (Marchenko & Pastur, 1967). The same scaling
of eigenvalues also holds for HHT because the difference between the
−1/2
nonzero singular values of H and those of f (cid:9)A—caused by the order N
s
deviation of diag[EN [ F (cid:9)
]] from f (cid:9)I—is smaller than order (N f
Suivant, we characterize the covariance matrix (cid:3) = Cov[φ] using the
asymptotic property. The nonlinear components can be cast as a function of
oui, φ(oui) = f (oui + un) − E[ F ] − E[ f yT ]A+T A+y. For large Ns, the covariance of y,
Cov[oui] = AAT , is close to the identity matrix—and the deviation (AAT − I)
−1/2
is order N
for each element—because elements of A are gaussian dis-
s
tributed. This weak correlation between yi and y j (je (cid:11)= j) leads to a weak cor-
relation of their functions φ
j. Ainsi, by computing the Taylor expan-
j] ≡ EN [φ
, φ
sion of CovN [φ
j] with respect to the small
, y j] ≡ EN [yiy j], we obtain (Toyoizumi & Abbott, 2011)
covariance CovN [yi
(see lemma 2 in section 4.2):
i and φ
φ
je
j] − EN [φ
/Ns)1/2.
je]EN [φ
je
CovN [φ
je
, φ
j] =
∞(cid:10)
EN
(cid:12)
(cid:11)
φ(n)
je
EN
(cid:12)
(cid:11)
φ(n)
j
n=1
n!
CovN [yi
, y j]n
(2.5)
je
je
je
je
, φ
, φ
] = O(N−1
s
−n/2
, y j]n is order N
s
) et |EN [φ(n)
. In contrast, the ith diagonal element CovN [φ
. Because EN [φ(1)
for i (cid:11)= j. Ici, CovN [yi
),
−1/2
]| ≤ O(1) for n ≥ 3 hold with a generic
] = O(N
EN [φ(2)
s
odd function f (•) (see remark 2 in section 4.2 for details), CovN [φ
j] est
je
−3/2
order N
je] is order 1.
s
These observations conclude that eigenvalues of CovN [φ]—and therefore
those of (cid:3) according to lemma 1 (see remark 1 in section 4.1 for details)—
−3/2
are not larger than order max[1, N f N
]; thus, all nonzero eigenvalues
s
/Ns—are sufficiently greater than those of (cid:3)
of HHT —which are order N f
(cid:7) Ns (cid:7) 1.
when N f
, y j]n = ((AAT )
One can further proceed to the calculation of (cid:3) by explicitly comput-
ing the coefficients EN [φ(n)
] up to the fourth order. Because f (•) is an
(cid:13)n)i j, equation 2.5 becomes
odd function, using CovN [yi
j] = EN [ F (3)(yi)]EN [ F (3)(y j )]{aia j((AAT )
/6}
/2 + ((AAT )
, φ
CovN [φ
je
−5/2
+ Ô(N
) (see remark 2 in section 4.2 for details). This analytical ex-
s
pression involves the Hadamard (element-wise) power of matrix AAT
(cid:13)3 ≡ (AAT ) (cid:13) (AAT ) (cid:13) (AAT ). Quand
(denoted by (cid:13)), Par exemple, (AAT )
/N2
N f
s
(as the leading order) with the corresponding eigenvectors that match the
(cid:13)3 has Ns major eigenvalues—all of which are 3N f
(cid:7) 1, (AAT )
> N2
s
(cid:13)2)i j
(cid:13)3)i j
je
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1441
(cid:13)3 − diag[(AAT )
− Ns) minor eigenvalues that are negligibly
directions of AAT —and (N f
/N2
smaller than order N f
s (see lemma 3 in section 4.3). This property yields
(cid:13)3] = (3/Ns)(AAT − diag[AAT ])
an approximation (AAT )
(cid:7) 1,
up to the negligible minor eigenmodes. Note that when N2
s
(cid:13)3 are negligible compared to diagonal
off-diagonal elements of (AAT )
(cid:13)2 has one major eigenvalue,
elements of (cid:3) (see below). De la même manière, (AAT )
/Ns, in the direction of (1, …, 1)T , while other minor eigenmodes of it
N f
are negligible. These approximations are used to compute off-diagonal
elements of (cid:3).
> N f
Ainsi, (cid:3) is analytically expressed as
(cid:13)
(cid:3) =
F 2 − f (cid:9)2
(cid:14)
2
je + F (3)
2Ns
(AAT + aaT ) + (cid:7).
(2.6)
(cid:7)
√
) using f 2 ≡
= f 2 − f (cid:9)2 + Ô(N
F (3)(ξ ) exp(−ξ 2/2)dξ /
−1/2
2π up to order N
s
Ici, depuis (cid:3) = Cov[ F ] − HHT and equation 2.4, each diagonal element is
−1/2
expressed as (cid:3)
F 2(ξ ) exp(−ξ 2/2)dξ /
√
ii
s
2π, which yields the first term of equation 2.6 (where the error term is
involved in the third term). The second term is generated from equation
2.5 followed by lemma 3, where EN [ F (3)(yi)] is approximated by f (3) ≡
(cid:7)
. The third term is the er-
ror matrix (cid:7) that summarizes the deviations caused by the nongaussian-
, y j ) (see lemma 1; see also remark 1 in section 4.1), higher-order
ity of p(yi
(cid:13)2 et
terms of the Taylor series in equation 2.5, minor eigenmodes of (AAT )
−1/2
(cid:13)3, and the effect of the order N
(AAT )
deviations of coefficients (par exemple.,
s
E[ F 2
je ]) from their approximations (par exemple., F 2). Due to its construction, eigen-
values of (cid:7) are smaller than those of the first or second term of equation
2.6. This indicates that for large Ns, either the first or second term of equa-
tion 2.6 provides the largest eigenvalue of (cid:3), which is order max[1, N f
/N2
s ].
Ainsi, (cid:7) is negligible for the following analyses.
Accordingly, all nonzero eigenvalues of HHT —that are order N f
/Ns—
are much greater than the maximum eigenvalue of (cid:3)—that is, order
maximum[1, N f
(cid:7) Ns (cid:7) 1. Ainsi, unless B specifically attenuates
one of Ns major eigenmodes of HHT or significantly amplifies a particular
eigenmode of (cid:3), we have
s ]—when N f
/N2
min eig[HT BT BH] (cid:7) max eig[B(cid:3)BT ]
(2.7)
(cid:7) Ns (cid:7) 1. Ici, eig[•] indicates a set of eigenvalues of •.
for Nx = N f
/Ns min eig[BT B],
Because min eig[HT BT BH] is not smaller than order N f
while max eig[B(cid:3)BT ] is not larger than order max[1, N f
/N2
s ] max eig[BT B],
/Ns and Ns are much greater than
inequality 2.7 holds at least when N f
max eig[BT B]/ min eig[BT B]. This is the case, Par exemple, if all the sin-
gular values of B are order 1. We call B sufficiently isotropic when
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1442
T. Isomura and T. Toyoizumi
max eig[BT B]/ min eig[BT B] can be upper-bounded by a (possibly large)
finite constant and focus on such B, because the effective input dimension-
ality is otherwise much smaller than Nx. Autrement dit, one can redefine
Nx of any system by replacing the original sensory inputs with their com-
pressed representation to render B isotropic.
When inequality 2.7 holds, the first Ns major eigenmodes of Cov[X] pre-
cisely match the signal covariance, while minor eigenmodes are negligibly
petit. Ainsi, there is a clear spectrum gap between the largest Ns eigen-
values and the rest. This indicates that one can reliably identify the signal
covariance and source dimensionality based exclusively on PCA of Cov[X]
in an unsupervised manner. Ainsi, quand (cid:8)M ∈ RNs×Ns is a diagonal matrix
that arranges the first Ns major eigenvalues of Cov[X] in descending order,
with the corresponding eigenvector matrix PM ∈ RNx×Ns , we obtain
MP(cid:8)MPT
M.
(cid:14) BHHT BT .
(2.8)
The corrections of (cid:8)M and PM due to the presence of the residual covariance
are estimated as follows: by the first-order perturbation theorem (Griffiths,
2005), the correction of the ith major eigenvalue of Cov[X] is upper-bounded
by max eig[B(cid:3)BT ], while the norm of the correction of the ith eigenvector
is upper-bounded by max eig[B(cid:3)BT ]/ min eig[HT BT BH]. These corrections
are negligibly smaller than the leading-order terms, when inequality 2.7
holds. Further details are provided in section 4.4.
Donc, applying PCA to Cov[X] can extract the signal covariance
as the major principal components with high accuracy when Nx = N f
(cid:7)
Ns (cid:7) 1 and B is sufficiently isotropic. This property is numerically val-
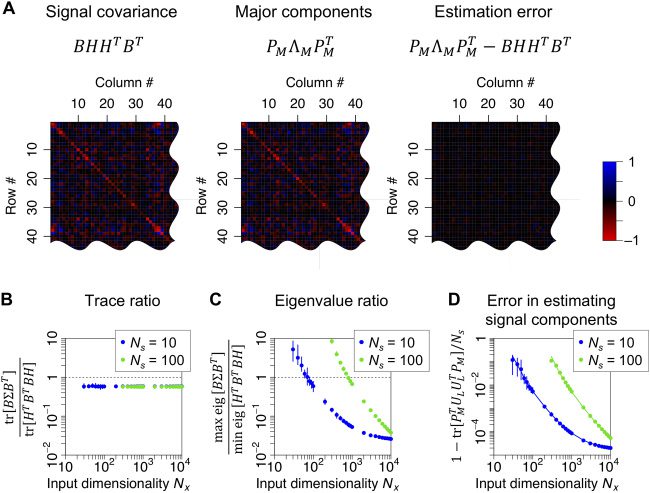
idated. The major principal components of Cov[X] suitably approximate
the signal covariance (see Figure 2A). In the simulations, elements of B
are sampled from a gaussian distribution with zero mean. The trace ra-
tio tr[B(cid:3)BT ]/tr[HT BT BH] (c'est à dire., the ratio of the eigenvalue sum of residual
covariance tr[B(cid:3)BT ] to that of signal covariance tr[HT BT BH]) retains the
value of about 0.6 irrespective of Ns and Nx, indicating that the large-
scale systems we consider are fairly nonlinear (see Figure 2B). In contrast,
the eigenvalue ratio max eig[B(cid:3)BT ]/ min eig[HT BT BH] monotonically con-
verges to zero when Nx increases; thus, inequality 2.7 holds for large Nx (voir
Figure 2C). Par conséquent, PM approximates nonzero eigenmodes of the sig-
nal covariance accurately (see Figure 2D). These results indicate that PCA is
a promising method for reliably identifying the linear components in sen-
sory inputs. In what follows, we explicitly demonstrate that projecting the
inputs onto the major eigenspace can recover true hidden sources of sen-
sory inputs accurately.
2.3 Asymptotic Linearization Theorem. We now consider a linear en-
coder comprising a single-layer linear neural network,
u ≡ W (x − E[X]) ,
(2.9)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1443
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
= 10 and Nx
Chiffre 2: PCA can identify linear components comprising linear projections
from every true hidden source. Ici, hidden sources s are independently gen-
erated from an identical uniform distribution with zero mean and unit vari-
= Nx and f (•) = sign(•) are fixed; elements of A, a are independently
ance; N f
sampled from N [0, 1/Ns]; and elements of B are independently sampled from
N [0, 1/N f ]. PCA is achieved via eigenvalue decomposition. (UN) Comparison be-
tween the signal covariance and major principal components of sensory inputs,
= 103. (B) Trace ratio tr[B(cid:3)BT ]/tr[HT BT BH]. (C) Eigen-
when Ns
value ratio max eig[B(cid:3)BT ]/ min eig[HT BT BH]. (D) Error in extracting nonzero
eigenmodes of signal covariance as major components, which is scored by
∈ RNx×Ns indicates the left-singular vectors of
1 − tr[PT
BH. As Nx increases, PMPT
L reliably and accurately. Solid
lines indicate theoretical values of estimation errors: see equation 4.24 for de-
tails. Circles and error bars indicate the means and areas between maximum
and minimum values obtained with 20 different realizations of s, UN, B, un, où
some error bars are hidden by the circles.
M converges to ULU T
L PM]/Ns, where UL
MULU T
, . . . , uNs )T are Ns-dimensional neural outputs and W ∈
where u ≡ (u1
RNs×Nx is a synaptic weight matrix. Suppose that by applying PCA to the
inputs, one obtains W, which represents a subspace spanned by the ma-
jor eigenvectors, W = (cid:9)M.(cid:8)−1/2
M., où (cid:9)M is an arbitrary Ns × Ns or-
thogonal matrix expressing an ambiguity. A normalization factor (cid:8)−1/2
M PT
M.
1444
T. Isomura and T. Toyoizumi
is multiplied so as to ensure Cov[toi] = I. Neural outputs with this W in-
deed express the optimal linear encoder of the inputs because it is the
solution of the maximum likelihood estimation that minimizes the loss
to reconstruct the inputs from lower-dimensional encoder u using a lin-
ear network under gaussian assumption (see Xu, 1993, and Wentzell, Un-
drews, Hamilton, Faber, & Kowalski, 1997, for related studies). In other
mots, when we assume that the loss follows a unit gaussian distribution,
arg minW E[|x − E[X] − W +u|2] = (cid:9)M.(cid:8)−1/2
M PT
M holds under the constraint
of dim[toi] = Ns and Cov[toi] = I, where W +
indicates the pseudo inverse
of W.
Surtout, equation 2.8 directly provides the key analytical expression to
represent a subspace spanned by the linear components:
W (cid:14) (cid:9)(BH)
+.
(2.10)
+ ≡ (HT BT BH)
−1HT BT is the pseudo inverse of BH, et (cid:9) is an-
Ici, (BH)
+
other arbitrary Ns × Ns orthogonal matrix. Error in approximating (BH)
is negligible for the following calculations as long as inequality 2.7 holds
(see section 4.4 for more details). Équation 2.10 indicates that the directions
of the linear components can be computed under the BSS setup—up to an
arbitrary orthogonal ambiguity factor (cid:9). Ainsi, we obtain the following
theorem:
Theorem 1 (Asymptotic Linearization). When inequality 2.7 holds, from equa-
tion 2.2, 2.9, et 2.10, the linear encoder with optimal matrix W = (cid:9)M.(cid:8)−1/2
M PT
M.
can be analytically expressed as
u = (cid:9)(s + ε)
using a linearization error ε ≡ (BH)
+Bφ with the covariance matrix of
+
Cov[ε] = (BH)
B(cid:3)BT (BH)
+T .
(2.11)
(2.12)
The maximum eigenvalue of Cov[ε] is upper-bounded by max eig[B(cid:3)BT ]/
min eig[HT BT BH], which is sufficiently smaller than one from inequality 2.7. Dans
particular, when ps(s) is a symmetric distribution, F (•) is an odd function, et B
is sufficiently isotropic, using equation 2.6, Cov[ε] can be explicitly computed as
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cov[ε] = Ns
N f
(cid:15)
(cid:16)
− 1
F 2
F (cid:9)2
(je + (cid:11)) + F (3)
2
2Ns f (cid:9)2 je
(2.13)
as the leading order. Symmetric matrix (cid:11) ≡ UT
anisotropy of BT B in the directions of the left-singular vectors of A, UA
UN (BT B − I)2UA characterizes the
×Ns ,
∈ RN f
Achievability of Nonlinear Blind Source Separation
1445
wherein max eig[(cid:11)] is upper-bounded by max eig[(BT B − I)2] = O(1). Ensemble,
we conclude that
u = (cid:9)s + Ô
(cid:15)(cid:17)
(cid:16)
Ns
N f
+ Ô
(cid:18)
(cid:19)
.
1√
Ns
(2.14)
The derivation detail of equation 2.13 is provided in section 4.5. Équation
/Ns
2.13 indicates that the linearization error monotonically decreases as N f
and Ns increase; thus, u converges to a linear mixture of all the true hidden
sources (u → (cid:9)s) in the limit of large N f
/Ns and Ns. Only the anisotropy
of BT B in the directions of UA increases the linearization error. En substance,
applying PCA to the inputs effectively filters out nonlinear components in
the inputs because the majority of nonlinear components are perpendicular
to the directions of the signal covariance.
Although the obtained encoder is not independent of each other because
of the multiplication with (cid:9), it is remarkable that the proposed approach
enables the conversion of the original nonlinear BSS problem to a simple
linear BSS problem. This indicates that u can be separated into each inde-
pendent encoder by further applying a linear ICA method (Comon, 1994;
Cloche & Sejnowski, 1995, 1997; Amari et al., 1996; Hyvarinen & Oja, 1997)
to it, and these independent encoders match the true hidden sources up to
permutations and sign-flips. Zero-element-wise-error nonlinear BSS is at-
/Ns and Ns. As a side note, PCA can indeed
tained in the limit of large N f
recover a linear transformation of true hidden sources in the inputs even
when these sources have higher-order correlations if the average of these
correlations converges to zero with high source dimensionality. This prop-
erty is potentially useful, Par exemple, for identifying true hidden states of
time series data generated from nonlinear systems (Isomura & Toyoizumi,
2021).
En résumé, we analytically quantified the accuracy of the optimal linear
encoder—obtained through the cascade of PCA and ICA—in inverting the
nonlinear generative process to identify all hidden sources. The encoder
/Ns and Ns increase and asymptotically attains
increases its accuracy as N f
the true hidden sources.
The proposed theorem is empirically validated by numerical simula-
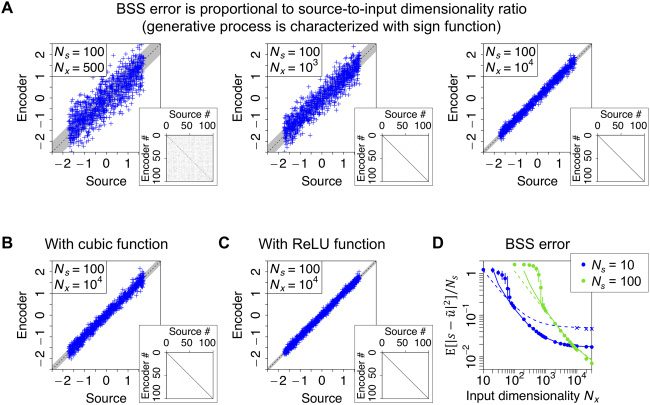
tion. Each element of the optimal linear encoder obtained by the PCA–ICA
cascade represents a hidden source, wherein BSS errors (the difference be-
tween the true and estimated sources) decrease as Nx increases (voir la figure
3UN). The PCA–ICA cascade performs the nonlinear BSS with various types
of nonlinear basis functions (see Figures 3B and 3C). This is a remarkable
property of the PCA–ICA cascade because these results indicate that it can
perform the nonlinear BSS without knowing the true nonlinearity that char-
acterizes the generative process. Although equation 2.13 is not applicable
to non-odd nonlinear basis function f (•), empirical observations indicate
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1446
T. Isomura and T. Toyoizumi
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
Chiffre 3: BSS error can be characterized by the source and input dimensional-
= Nx
ities. In all panels, s is generated by an identical uniform distribution; N f
is fixed; et un, B, a are sampled from gaussian distributions as in Figure 2. En-
, . . . , ˜uNs )T are obtained by applying the PCA–ICA cascade to sen-
coders ˜u = ( ˜u1
sory inputs. For visualization purpose, elements of ˜u are permuted and sign-
flipped to ensure that ˜ui encodes si. (UN) Each element of ˜u encodes a hidden
source, wherein an error in representing a source monotonically decreases when
= 100 and f (•) =
Nx increases. The generative process is characterized with Ns
sign(•). Shaded areas represent theoretical values of the standard deviation
computed using equation 2.13. As elements of B are gaussian distributed, (cid:11) = I
holds. Inset panels depict the absolute value of covariance matrix |Cov[ ˜u, s]|
with gray-scale values ranging from 0 (blanc) à 1 (black). A diagonal covari-
ance matrix indicates the successful identification of all the true hidden sources.
(B, C) Nonlinear BSS when the generative process is characterized by f (•) = (•)3
or f (•) = ReLU(•). ReLU(•) outputs • for • > 0 ou 0 otherwise. In panel C, le
shaded area is computed using equation 2.12. (D) The quantitative relationship
between the source and input dimensionalities and element-wise BSS error is
scored by the mean squared error E[|s − ˜u|2]/Ns. Ici,
F (•) = sign(•) is sup-
posed. Circles and error bars indicate the means and areas between maximum
and minimum values obtained with 20 different realizations of s, UN, B, un, où
some error bars are hidden by the circles. Solid and dashed lines represent
theoretical values computed using equations 2.12 et 2.13, respectivement. These
(cid:7) 1, although some deviations
lines fit the actual BSS errors when Nx
occur when Ns or Nx is small. Blue cross marks indicate actual BSS errors for
= 10 when hidden sources are sampled from a symmetric truncated normal
Ns
distribution.
(cid:7) Ns
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1447
that the PCA–ICA cascade can identify the true hidden sources even with
non-odd function f (•) (see Figure 3C), as long as H = E[ f sT ] is nonzero.
The log-log plot illustrates that the magnitude of element-wise BSS
errors—scored by the mean squared error—decreases inversely propor-
tional to Nx/Ns; cependant, it saturates around Nx = N2
s (see Figure 3D). These
observations validate equation 2.13 which asserts that the linearization er-
ror is determined by the sum of Ns/N f and 1/Ns order terms. Although
equation 2.13 overestimates the BSS error when Ns = 10, this is because
each dimension of As significantly deviates from a gaussian variable due
to small Ns—as s is sampled from a uniform distribution in these simula-
tion. We confirm that when hidden sources are generated from a distribu-
tion close to gaussian, actual BSS errors shift toward the theoretical value
of equation 2.13 even when Ns = 10 (see the cross marks in Figure 3D). Dans-
deed, this deviation disappears for large Ns according to the central limit
theorem. Donc, equation 2.13 is a good approximation of actual BSS
errors for Nx = N f
(cid:7) Ns (cid:7) 1, and the proposed theorem suitably predicts
the performance of the PCA–ICA cascade for a wide range of nonlinear BSS
setups.
2.4 Hebbian-Like Learning Rules Can Reliably Solve Nonlinear BSS
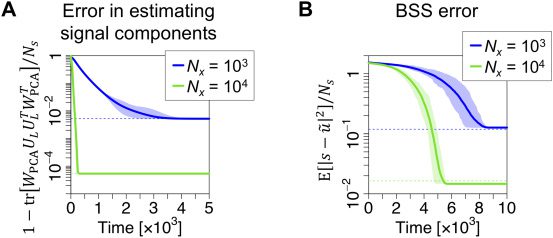
Problem. As a corollary of the proposed theorem, a linear neural network
can identify true hidden sources through Hebbian-like plasticity rules in the
nonlinear BSS setup under consideration. Oja’s subspace rule (Oja, 1989)—
which is a modified version of the Hebbian plasticity rule (see section 4.6)—
is a well-known PCA approach that extracts the major eigenspace without
yielding a spurious solution or attaining a local minimum (Baldi & Hornik,
1989; Chen et al., 1998). Ainsi, with generic random initial synaptic weights,
this Hebbian-like learning rule can quickly and reliably identify an optimal
linear encoder that can recover true hidden sources from their nonlinear
mixtures in a self-organizing or unsupervised manner.
Numerical experiments demonstrate that regardless of the random ini-
∈ RNs×Nx , Oja’s subspace rule up-
tialization of synaptic weight matrix WPCA
dates WPCA to converge to the major eigenvectors, c'est, the directions
of the linear components. The accuracy of extracting the linear compo-
nents increases as the number of training samples increases, and reaches
the same accuracy as an extraction via eigenvalue decomposition (see Fig-
ure 4A). Because the original nonlinear BSS problem has now been trans-
formed to a simple linear BSS problem, the following linear ICA approach
(Comon, 1994; Cloche & Sejnowski, 1995, 1997; Amari et al., 1996; Hyvarinen
& Oja, 1997) can reliably separate all the hidden sources from the features
extracted using Oja’s subspace rule. Amari’s ICA algorithm (Amari et al.,
1996), which is another Hebbian-like rule (see section 4.6), updates synaptic
∈ RNs×Ns to render neural outputs independent of each
weight matrix WICA
other. The obtained independent components accurately match the true
hidden sources of the nonlinear generative process up to their permutations
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1448
T. Isomura and T. Toyoizumi
Chiffre 4: Hebbian-like learning rules can identify the optimal linear encoder.
=
As in Figures 2 et 3, s is generated by an identical uniform distribution; Ns
= Nx, and f (•) = sign(•) are fixed; et un, B, a are sampled from gaus-
100, N f
sian distributions. (UN) Learning process of Oja’s subspace rule for PCA. Synap-
∈ RNs×Nx —initialized as a random matrix—converges
tic weight matrix WPCA
to PT
M up to multiplication of an orthogonal matrix from the left-hand side.
This indicates that Oja’s rule extracts the linear components according to the
proposed theorem. Dashed lines indicate the estimation errors when eigen-
value decomposition is applied (see Figure 2C). (B) Learning process of Amari’s
∈ RNs×Ns —initialized as a random
ICA algorithm. Synaptic weight matrix WICA
matrix—learns to separate the compressed inputs WPCA(x − E[X]) into indepen-
dent signals. Because PCA yields a linear transformation of hidden sources,
the ensuing independent encoder ˜u ≡ WICAWPCA(x − E[X]) identifies all the true
hidden sources with a small BSS error. Elements of ˜u are permuted and sign-
flipped to ensure that ˜ui encodes si. Dashed lines are computed using equation
= 0.02, respecter-
2.13. In panels A and B, learning rates are η
tivement. Solid lines represent the mean estimation errors, while shaded areas rep-
resent areas between maximum and minimum values obtained with 20 different
realizations of s, UN, B, un.
= 10−3 and η
APC
ICA
and sign-flips (see Figure 4B). These results highlight that the cascade of
PCA and ICA—implemented via Hebbian-like learning rules—can self-
organize the optimal linear encoder and therefore identify all the true hid-
den sources in this nonlinear BSS setup, with high accuracy and reliability
when Nx = N f
(cid:7) Ns (cid:7) 1.
3 Discussion
In this work, we theoretically quantified the accuracy of nonlinear BSS
performed using the cascade of linear PCA and ICA when sensory in-
puts are generated from a two-layer nonlinear generative process. D'abord, nous
demonstrated that as the dimensionality of hidden sources increases and
the dimensionalities of sensory inputs and nonlinear bases increase rela-
tive to the source dimensionality, the first Ns major principal components
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1449
approximately express a subspace spanned by the linear projections from
all hidden sources of the sensory inputs. Under the same condition, nous
then demonstrated that the optimal linear encoder obtained by projecting
the inputs onto the major eigenspace can accurately recover all the true
hidden sources from their nonlinear mixtures. This property is termed the
asymptotic linearization theorem. The accuracy of the subspace extraction
/Ns and Ns increase, because the gap between the minimum
increases as N f
eigenvalue of the linear (c'est à dire., signal) components and maximum eigenvalue
of the nonlinear (c'est à dire., residual) components becomes significantly large.
Hebbian-like plasticity rules can also identify the optimal linear encoder
by extracting major principal components in a manner equal to PCA. Sub-
sequent application of linear ICA on the extracted principal components
can reliably identify all the true hidden sources up to permutations and
sign-flips. Unlike conventional nonlinear BSS methods that can yield spu-
rious solutions (Hyvarinen & Pajunen, 1999; Jutten & Karhunen, 2004), le
PCA–ICA cascade is guaranteed to identify the true hidden sources in the
asymptotic condition because it successfully satisfies requirements 1 à 5
specified earlier.
The unique identification of true hidden sources s (up to permutations
and sign-flips) is widely recognized only under the linear BSS setup. Dans
contraste, it is well known that conventional nonlinear BSS approaches us-
ing nonlinear neural networks do not guarantee the identification of true
hidden sources under the general nonlinear BSS setup (Hyvarinen & Pa-
junen, 1999; Jutten & Karhunen, 2004). One may ask if nonlinear BSS meth-
ods may find a component-wise nonlinear transformation of the original
sources s(cid:9) = g(s) instead of s because s(cid:9)
is still an independent source rep-
resentation. This is observed when conventional nonlinear BSS approaches
based on the nonlinear ICA are employed because the nonlinear ICA finds
one of many representations that minimize the dependency among outputs.
Cependant, such nonlinear BSS approaches do not guarantee the identifica-
tion of true sources. This is because when g(cid:9)
(s) is a component-wise nonlin-
ear transformation that renders a nongaussian source gaussian distributed,
a transformation s(cid:9)(cid:9) = g(Rg(cid:9)
(s))—characterized by some orthogonal matrix
R and component-wise nonlinear transformation g—can yield an arbitrary
independent representation s(cid:9)(cid:9)
that differs from the original sources. Le
former (s(cid:9)
). Even in the former case, finding
s(cid:9)
transformed by a highly nonlinear, nonmonotonic function g(s) is prob-
lematic. Ainsi, the general nonlinear BSS is essentially an ill-posed problem.
Having said this, earlier works typically investigated the case in which the
sources and inputs have the same dimensionality, while the other condi-
tions have not been extensively analyzed. Ainsi, in the current work, we fo-
(cid:7) Ns (cid:7) 1.
cused on the nonlinear BSS under the condition where Nx = N f
A remarkable aspect of the proposed nonlinear BSS approach is that
it utilizes the linear PCA to extract the linear components of the orig-
inal sources from the mixed sensory inputs. This is the process that
) is a special case of the latter (s(cid:9)(cid:9)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1450
T. Isomura and T. Toyoizumi
enables the reduction of the original nonlinear BSS to a simple linear BSS
and consequently ensures the reliable identification of the true sources. Dans
autres mots, the proposed approach does not rely on the nonlinear ICA;
thus, no concerns exist regarding the creation of the already noted spurious
solutions. We mathematically demonstrated the absence of such spuri-
(cid:7) Ns (cid:7) 1. Spécifiquement, we adopted a minimal
ous solutions when Nx = N f
assumption about the relationship between B and the system dimen-
/Ns and Ns are much greater than max eig[BT B]/
sionalities such that N f
min eig[BT B]. Our mathematical analyses demonstrate that this condition is
sufficient to asymptotically determine the possible form of hidden sources,
which can generate the observed sensory inputs x, in a unique manner. Dans
/Ns and Ns, no nonlinear transformation of
contraste, in the limit of large N f
s (c'est à dire., s(cid:9)
) can generate the observed sensory inputs while satisfying the
aforementioned condition.4 Thus, when inequality 2.7 holds, the true hid-
den sources s are uniquely determined up to permutations and sign-flips
ambiguities without component-wise nonlinear ambiguity. (Inversement, si
inequality 2.7 does not hold, it might not be possible to distinguish true hid-
den sources and their nonlinear transformations in an unsupervised man-
ner.) Ainsi, under the condition we consider, the nonlinear BSS is formally
reduced to a simple linear BSS, wherein only permutations and sign-flips
ambiguities exist while no nonlinear ambiguity remains. This property is
crucial for identifying the true sources under the nonlinear BSS setup, avec-
out being attracted by spurious solutions such as s(cid:9)
and s(cid:9)(cid:9)
or s(cid:9)(cid:9)
.
The nonlinear generative processes that we considered in this work are
sufficiently generic. Owing to the universality of two-layer networks, chaque
element of an arbitrary generative process x = F(s) can be approximated
using equation 2.1 with a high degree of accuracy in the component-wise
(cid:7) Ns (cid:7) 1.5 This allows one to analyze the achievabil-
sense when Nx = N f
ity of the nonlinear BSS using a class of generative processes comprising
4
(cid:9)
(cid:9)
M PT
/Ns and Ns. En outre, we define s
This property can be understood as follows. Because x is generated through x =
B f (Comme + un) with a sufficiently isotropic B that satisfies inequality 2.7, from the proposed
theorem, the encoder u = (cid:8)−1/2
M.(x − E[X]) = (cid:9)(s + ε) asymptotically becomes u → (cid:9)s
(cid:9) = g(s) ∈ RNs as a nonlinear
in the limit of large N f
(cid:9)
(cid:9) + un
(cid:9)
(cid:9)
transformation of s. If there is another generative process x = B
F
s
(UN
) that can gen-
(cid:9)
(cid:9)
erate the observed x while satisfying inequality 2.7—where A
and a
are gaussian dis-
tributed matrix and vector, F
is a nonlinear function (not the derivative of f , unlike in
(cid:9)
the main text), et B
is a sufficiently isotropic matrix—the encoder can also be expressed
(cid:9) = (cid:8)−1/2
M PT
as u
), which asymptotically becomes u
dans le
limit of large N f
M and PM are the same as above because x does
(cid:9)
not change. Cependant, while u ≡ u
for any orthogonal
matrices (cid:9) et (cid:9)(cid:9)
(cid:9)
because s
is a nonlinear transformation of s. Ainsi, such a generative
(cid:9)
(cid:9) + un
(cid:9)
(cid:9)
process x = B
s
(UN
/Ns and Ns.
It should be noted that unlike the condition we considered (c'est à dire., Nx = N f
(cid:7) Ns (cid:7) 1),
(cid:7) Nx, one may observe a counterexample of the proposed theorem such that
when N f
the major principal components are dissimilar to a linear transformation of the true hid-
den sources, as is well-known in the literature on nonlinear ICA (Hyvarinen & Pajunen,
M.(x − E[X]) = (cid:9)(cid:9)
/Ns and Ns. Note that (cid:8)
holds by construction, (cid:9)s (cid:11)≡ (cid:9)(cid:9)
) does not exist in the limit of large N f
(cid:9) → (cid:9)(cid:9)
(cid:9) + ε(cid:9)
(cid:9)
s
(cid:9)
s
(s
F
5
(cid:9)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1451
random basis functions, as a proxy for investigating x = F(s). As a gen-
eral property of such generative processes, the eigenvalues of the signal
covariance (c'est à dire., linear components) become significantly larger than those
of the residual covariance (c'est à dire., nonlinear components) when Nx = N f
(cid:7)
Ns (cid:7) 1. Sufficient system dimensionalities to exhibit this property are de-
termined depending on matrix B that characterizes the generative pro-
/Ns and Ns
cess. Namely, this observation holds true at least when both N f
are much greater than max eig[BT B]/ min eig[BT B]. The existence of such
Ns and N f is guaranteed if we consider sufficiently isotropic B wherein
max eig[BT B]/ min eig[BT B] is upper-bounded by a large, finite constant.
Entre-temps, with such a large constant, the two-layer networks can approx-
imate each element of x = F(s) accurately. This in turn means that as N f
/Ns
and Ns increase, the proposed theorem becomes applicable to a sufficiently
broad class of nonlinear generative processes.
= Hks + φ
This asymptotic property can be understood as follows. When adding
a new random basis ( fk
k) to the existing large-scale system,
the linear component of fk (Hks) must be placed within the existing low-
dimensional subspace spanned only by Ns ((cid:15) N f ) linear projections of
sources. In contrast, its nonlinear component (φ
k) is almost uncorrelated
with other nonlinear components (φ), as shown in equation 2.6, because
these components are characterized by gaussian distributed A. Ainsi, le
former increases the eigenvalues of the signal covariance in proportion to
/Ns, while the latter adds a new dimension in the subspace of nonlin-
N f
ear components without significantly increasing the maximum eigenvalue
of the residual covariance. Owing to this mechanism, the eigenvalues of
/Ns times larger than those of the residual
the signal covariance become N f
covariance when Ns (cid:7) 1. Ainsi, the linear PCA is sufficient to reduce the
nonlinear BSS to a linear BSS.
Nonlinear variants of PCA such as autoencoders (Hinton & Salakhut-
dinov, 2006; Kingma & Welling, 2013) have been widely used for rep-
resentation learning. Because natural sensory data are highly redundant
and do not uniformly cover the entire input space (Chandler & Field,
2007), finding a concise representation of the sensory data is essential to
characterize its properties (Arora & Risteski 2017). En général, if a large,
nonlinear neural network is used, many equally good solutions will be pro-
duced (Kawaguchi, 2016; Lu & Kawaguchi, 2017; Nguyen & Hein, 2017).
Dans ce cas, there is no objective reason to select one solution over an-
other if they have similar reconstruction accuracy. Cependant, this prop-
erty also leads to infinitely many spurious solutions if the aim is the
(cid:7) Nx, a general B may not be
1999; Jutten & Karhunen, 2004). This is because when N f
(cid:7) Nx corresponds to the case wherein Nx is in-
sufficiently isotropic. Autrement dit, N f
sufficient to ensure inequality, equation 2.7; thus, Nx needs to be greater. Ainsi, it is re-
markable that the proposed theorem specifies the condition under which the achievability
of the nonlinear BSS is mathematically guaranteed.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1452
T. Isomura and T. Toyoizumi
identification of the true hidden sources (Hyvarinen & Pajunen, 1999; Jut-
ten & Karhunen, 2004). Par conséquent, the outcomes of these approaches
using nonlinear neural networks are intrinsically ambiguous, and obtained
solutions highly depend on the heuristic design of the regularization pa-
rameters used in the networks and learning algorithms (Dahl, Yu, Deng,
& Acero, 2012; Hinton, Srivastava, Krizhevsky, Sutskever, & Salakhutdi-
nov, 2012; Wan, Zeiler, Zhang, LeCun, & Fergus, 2013). Cependant, unlike
those nonlinear approaches, we proved that the cascade of linear PCA and
ICA ensures that the true hidden sources of sensory inputs are obtained if
there are sufficient dimensionalities in mappings from hidden sources to
sensory inputs. Ainsi, this linear approach is suitable to solve the nonlin-
ear BSS problem while retaining the guarantee to identify the true solution.
Its BSS error converges in proportion with the source-to-input dimensional-
ity ratio for a large-scale system comprising high-dimensional sources. Fur-
thermore, if needed, its outcomes can be used as a plausible initial condition
for nonlinear methods to further learn the forward model of the generative
processus.
Because most natural data (including biological, chemical, and social
data) are generated from nonlinear generative processes, the scope of ap-
plication of nonlinear BSS is quite broad. The proposed theorem provides a
theoretical justification for the application of standard linear PCA and ICA
to nonlinearly generated natural data to infer their true hidden sources.
An essential lesson from the proposed theorem is that an artificial intelli-
gence should employ a sufficient number of sensors to identify true hidden
sources of sensory inputs accurately, because the BSS error is proportional
to the source-to-input dimensionality ratio in a large-scale system.
In the case of computer vision, low-dimensional representations (typi-
cally 10–104 components) are extracted from up to millions of pixels of the
high-dimensional raw images. Our theory implies that the linear PCA–ICA
cascade can be utilized to identify the true hidden sources of natural im-
age data. This has been demonstrated using video images (Isomura & Toy-
oizumi, 2021). En particulier, a combination of the proposed theorem with
another scheme that effectively removes unpredictable noise from sequen-
tial data (c'est à dire., video sequence) is a powerful tool to identify the true hidden
sources of real-world data. By this combination, one can obtain data with
minimal irrelevant or noise components—an ideal condition for the asymp-
totic linearization theorem—from the original noisy observations. Un tel
combination enables the reliable and accurate estimations of hidden sources
that generate the input sequences, even in the presence of considerable ob-
servation noise. The source estimation performance was demonstrated by
using sequential visual inputs comprising hand-digits, rotating 3D objects,
and natural scenes. These results support the applicability of the proposed
theorem to the natural data and further highlight that the PCA–ICA cas-
cade can extract true or relevant hidden sources when the natural data are
sufficiently high-dimensional. (See Isomura & Toyoizumi, 2021, for details.)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1453
En outre, a few works have cited a preprint version of this article to
justify the application of their linear methods to real-world nonlinear BSS
tasks, in the contexts of wireless sensor networks (van der Lee, Exarchakos,
& de Groot, 2019) and single-channel source separation (Mika, Budzik, &
Józwik, 2020). These works demonstrated that linear methods work well
with nonlinear BSS tasks, as our theorem predicts. The asymptotic lineariza-
tion theorem is of great importance in justifying the application of these
linear methods to real-world nonlinear BSS tasks.
In terms of the interpretability of the outcomes of the PCA–ICA cas-
cade, one may ask if applying the cascade to natural image patches sim-
ply yields less interpretable Gabor-filter-like outputs, which are usually not
considered to be certain nonlinear, higher-order features underlying natural
images. Cependant, when we applied the PCA–ICA cascade—featuring a
separate noise-reduction technique that we developed—to natural image
data with a high-dimensionality reduction rate, we obtained outputs or im-
ages that represent features relevant to hidden sources, such as the cate-
gories of objects (Isomura & Toyoizumi, 2021). Based on our observations,
three requirements to render the PCA–ICA cascade extract features rele-
vant to hidden sources are considered. D'abord, the dimensionality reduction
rate should be high relative to that of the conventional PCA application. Dans-
deed, when the dimensionality reduction rate was low, we observed that the
obtained encoders exhibit Gabor-filter-like patterns. Deuxième, the PCA–ICA
cascade should be applied not to image patches but to entire images. Image
patches contain only a fraction of information about the original hidden
sources; thus, it is likely that the original hidden sources cannot be recov-
ered from image patches. Troisième, PCA should be applied to denoised data
wherein observation noise is removed in advance using a separate scheme,
as in our case. When PCA is applied to noisy data, sufficient information for
recovering hidden sources cannot be extracted as the major principal com-
ponents because PCA preferentially extracts large noise owing to its extra
variance. Ainsi, when the requirements are satisfied, the outcome of the
PCA–ICA cascade can exhibit a high interpretability, wherein the extracted
features are relevant to hidden sources.
As a side note, to utilize the asymptotic linearization theorem to estimate
the accuracy of source separation, one cannot use up-sampling techniques
to increase the input dimensionality beyond the resolution of the origi-
nal data or images. This is because these techniques simply yield linear or
nonlinear transformations of the original data, which typically do not in-
crease information about true hidden sources. Autrement dit, the resolu-
tions of the original data determine the effective input dimensionality, donc
that these up-samplings merely render matrix B singular (thereby violating
the condition of isotropic B).
En outre, an interesting possibility is that living organisms might
have developed high-dimensional biological sensors to perform nonlin-
ear BSS using a linear biological encoder because this strategy guarantees
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1454
T. Isomura and T. Toyoizumi
robust nonlinear BSS. En particulier, this might be the approach taken by the
human nervous system using large numbers of sensory cells, such as ap-
proximately 100 million rod cells and 6 million cone cells in the retina, et
environ 16,000 hair cells in the cochlea, to process sensory signals
(Kandel, Schwartz, Jessell, Siegelbaum, & Hudspeth, 2013).
Neuronal networks in the brain are known to update their synapses by
following Hebbian plasticity rules (Hebb, 1949; Malenka & Bear, 2004), et
researchers believe that the Hebbian plasticity plays a key role in represen-
tation learning (Dayan & Abbott, 2001; Gerstner & Kistler, 2002) and BSS
(Brun, Yamada, & Sejnowski, 2001) in the brain—in particular, the dy-
namics of neural activity and plasticity in a class of canonical neural net-
works can be universally characterized in terms of representation learning
or BSS from a Bayesian perspective (Isomura & Friston, 2020). Ainsi, it fol-
lows that major linear BSS algorithms for PCA (Oja, 1982, 1989) and ICA
(Cloche & Sejnowski, 1995, 1997; Amari et al., 1996; Hyvarinen & Oja, 1997) sont
formulated as a variant of Hebbian plasticity rules. De plus, in vitro neu-
ronal networks learn to separately represent independent hidden sources in
(and only in) the presence of Hebbian plasticity (Isomura, Kotani, & Jimbo,
2015; Isomura & Friston, 2018). Néanmoins, the manner in which the brain
can possibly solve a nonlinear BSS problem remains unclear, even though
it might be a prerequisite for many of its cognitive processes such as vi-
sual recognition (DiCarlo et al., 2012). While Oja’s subspace rule for PCA
(Oja, 1989) and Amari’s ICA algorithm (Amari et al., 1996) were used in this
article, these rules can be replaced with more biologically plausible local
Hebbian learning rules (Foldiak, 1990; Linsker, 1997; Pehlevan, Mohan, &
Chklovskii, 2017; Isomura & Toyoizumi, 2016, 2018, 2019; Leugering & Pipa,
2018) that require only directly accessible signals to update synapses. A re-
cent work indicated that even a single-layer neural network can perform
both PCA and ICA through a local learning rule (Isomura & Toyoizumi,
2018), implying that even a single-layer network can perform a nonlinear
BSS.
En résumé, we demonstrated that when the source dimensionality is
large and the input dimensionality is sufficiently larger than the source di-
mensionality, a cascaded setup of linear PCA and ICA can reliably identify
the optimal linear encoder to decompose nonlinearly generated sensory in-
puts into their true hidden sources with increasing accuracy. This is because
the higher-dimensional inputs can provide greater evidence about the hid-
den sources, which removes the possibility of finding spurious solutions
and reduces the BSS error. As a corollary of the proposed theorem, Hebbian-
like plasticity rules that perform PCA and ICA can reliably update synap-
tic weights to express the optimal encoding matrix and can consequently
identify the true hidden sources in a self-organizing or unsupervised man-
ner. This theoretical justification is potentially useful for designing reliable
and explainable artificial intelligence, and for understanding the neuronal
mechanisms underlying perceptual inference.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1455
4 Methods
4.1 Lemma 1.
Definition 1. Suppose ps(s) is a symmetric distribution, ˜y ≡ (yi
, y j )T ≡ ˜As is a
, . . . , A jNs ) est
two-dimensional subvector of y = As, and ˜A ≡ (Ai1
un 2 × Ns submatrix of A. The expectation of an arbitrary function F( ˜y) over ps(s)
is denoted as E[F( ˜y)], whereas when ˜y is sampled from a gaussian distribution
pN ( ˜y) ≡ N [0, ˜A ˜AT ], the expectation of F( ˜y) over pN ( ˜y) is denoted as EN [F( ˜y)] ≡
(cid:7)
, . . . , AiNs
; A j1
F( ˜y)pN ( ˜y)d ˜y.
Lemma 1. When F( ˜y) is order 1, the difference between E[F( ˜y)] and EN [F( ˜y)] est
upper-bounded by order N−1
as a corollary of the central limit theorem. In partic-
ular, E[F( ˜y)] can be expressed as EN [F( ˜y)(1 + G( ˜y)/Ns)], where G( ˜y) = O(1) est
a function that characterizes the deviation of p( ˜y) from pN ( ˜y).
s
Proof. The characteristic function of p( ˜y) is given as ψ (τ ) ≡ E[eiτ T ˜y] as a
function of τ ∈ R2, and its logarithm is denoted as (cid:15)(τ ) ≡ log ψ (τ ). Le
d'abord- to fourth-order derivatives of (cid:15)(τ ) with respect to τ are provided
comme
(cid:15) (1) = E[i ˜yeiτ T ˜y]/ψ,
(cid:15) (2) = E[(i ˜y)
(cid:15) (3) = E[(i ˜y)
⊗2eiτ T ˜y]/ψ − ((cid:15) (1))
⊗3eiτ T ˜y]/ψ − E[(i ˜y)
⊗2,
⊗2eiτ T ˜y]/ψ ⊗ (cid:15) (1) − (cid:15) (2) ⊗ (cid:15) (1)
− (cid:15) (1) ⊗ (cid:15) (2)
= E[(i ˜y)
(cid:15) (4) = E[(i ˜y)
⊗3eiτ T ˜y]/ψ − 2(cid:15) (2) ⊗ (cid:15) (1) − ((cid:15) (1))
⊗4eiτ T ˜y]/ψ − E[(i ˜y)
⊗3eiτ T ˜y]/ψ ⊗ (cid:15) (1) − 2(cid:15) (3) ⊗ (cid:15) (1)
⊗3 − (cid:15) (1) ⊗ (cid:15) (2),
− 3((cid:15) (2))
− ((cid:15) (1))
⊗2 − (cid:15) (2) ⊗ ((cid:15) (1))
⊗2 ⊗ (cid:15) (2) − (cid:15) (1) ⊗ (cid:15) (3).
⊗2 − (cid:15) (1) ⊗ (cid:15) (2) ⊗ (cid:15) (1)
(4.1)
When τ = 0,
(cid:15) (3)(0) = 0, et (cid:15) (4)(0) = E[ ˜y⊗4] − 3E[ ˜y⊗2]
source distribution ps(s).
they become (cid:15)(0) = 0, (cid:15) (1)(0) = 0, (cid:15) (2)(0) = −E[ ˜y⊗2],
⊗2 owing to the symmetric
They are further computed as E[ ˜y⊗2]=Vec[ ˜A ˜AT ] and E[ ˜y⊗4]=Vec[E[( ˜y ˜yT )
⊗ ( ˜y ˜yT )]] = 3Vec[ ˜A ˜AT ]
k] − 3 dans-
Ns
k=1( ˜A•k ˜AT
•k)
dicates the kurtosis of the source distribution and ˜A•k denotes the kth
˜A. De plus, (cid:15) (2)(0) · τ ⊗2 = −τ T ˜A ˜AT τ and (cid:15) (4)(0) · τ ⊗4 =
column of
(cid:20)
−3/2
κVec[
Ns
)
s
hold. Ici, a quartic function of τ ,
because
k=1(τ T ˜A•k)4 = 3κ (τ T τ )2/Ns + Ô(N
k=1(τ T ˜A•k)4, is order N−1
⊗2], where κ ≡ E[s4
•k)⊗2] · τ ⊗4 = κ
Ns
k=1( ˜A•k ˜AT
⊗2 + κVec[
(cid:20)
(cid:20)
(cid:20)
Ns
s
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1456
T. Isomura and T. Toyoizumi
˜A•k is sampled from N [0, 1/Ns]. Ainsi, the Taylor expansion of (cid:15)(τ ) est
expressed as
(cid:15)(τ ) =
∞(cid:10)
n=0
(cid:15) (n)(0)
n!
· τ ⊗n = − 1
2
τ T ˜A ˜AT τ +
(τ T τ )2 + Ô
(cid:8)
(cid:9)
.
−3/2
N
s
κ
8Ns
(4.2)
−3/2
from ψ (τ ) = exp[−τ T ˜A ˜AT τ /2 + κ (τ T τ )2/8Ns + Ô(N
s
)] =
)), p( ˜y) is computed as follows (le
−3/2
s
Ainsi,
e−τ T ˜A ˜AT τ /2(1 + κ (τ T τ )2/8Ns + Ô(N
inversion theorem):
(cid:21)
p( ˜y) = 1
(2π )2
−iτ T ˜yψ (τ )λ(dτ )
e
(cid:18)
R2
(cid:21)
−iτ T ˜y− 1
e
2
τ T ˜A ˜AT τ
1 +
= 1
(2π )2
= pN ( ˜y)
R2
(cid:18)
(cid:19)
,
1 + G( ˜y)
Ns
κ
8Ns
(τ T τ )2 + Ô
(cid:19)
(cid:9)
(cid:8)
−3/2
N
s
λ(dτ )
(4.3)
where λ denotes the Lebesgue measure. Ici, G( ˜y) = O(1) indicates a func-
tion of ˜y that characterizes the difference between p( ˜y) and pN ( ˜y). Ainsi,
the expectation over p( ˜y) can be rewritten using that over pN ( ˜y):
(cid:21)
(cid:21)
E[F( ˜y)] =
(cid:21)
=
F( ˜y)ps(s)ds =
(cid:18)
F( ˜y)p( ˜y)d ˜y
(cid:19)
F( ˜y)pN ( ˜y)
(cid:22)
(cid:18)
1 + G( ˜y)
Ns
(cid:19)(cid:23)
d ˜y
= EN
F( ˜y)
1 + G( ˜y)
Ns
.
(4.4)
(cid:2)
Remark 1. For equation 2.4, from the Bussgang theorem (Bussgang, 1952),
we obtain
E[ F ( ˜y) ˜yT ] = EN
F ( ˜y) ˜yT
(cid:22)
(cid:18)
(cid:19)(cid:23)
1 + G( ˜y)
Ns
(cid:18)
1 + G( ˜y)
Ns
(cid:8)
( ˜y)]
(cid:9)
(cid:9)
(cid:22)
diag[ F
= EN
(cid:8)
=
diag[EN [ F
( ˜y)]] ˜A + Ô
−3/2
N
s
(cid:19)
(cid:23)
G(cid:9)
( ˜y)T
Ns
˜A ˜AT
(4.5)
+ F ( ˜y)
(cid:9)(cid:9)
˜AT
−1/2
as ˜A is order N
s
−3/2
Ô(N
).
s
. Ainsi, we obtain H = E[ f yT ]A+T = diag[EN [ F (cid:9)
]]UN +
For equation 2.5, because yi and y j are only weakly correlated with
l'un l'autre, (1 + G( ˜y)/Ns) can be approximated as (1 + G( ˜y)/Ns) (cid:14) (1 +
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1457
G(yi)/Ns)(1 + G(y j )/Ns) as the leading order using newly defined functions
G(yi) and G(y j ). Ainsi, we obtain
Cov[φ
je
, φ
j] = E[(φ
je
(cid:22)(cid:24)
− E[φ
je])(φ
j
(cid:14) EN
(φ
je
− E[φ
je])
− E[φ
j])]
(cid:18)
1 + G(yi)
Ns
(cid:19)(cid:25)(cid:24)
(φ
j
− E[φ
j])
(cid:19)(cid:25)(cid:23)
(cid:18)
1 + G(y j )
Ns
= CovN [φ∗
je
(cid:11)
φ∗(n)
je
, φ∗
j ]
(cid:12)
∞(cid:10)
EN
=
n=1
EN
n!
(cid:12)
(cid:11)
φ∗(n)
j
CovN [yi
, y j]n
(4.6)
je
j
je
≡ (φ
− E[φ
− E[φ
] from EN [φ(n)
for i (cid:11)= j as the leading order, where φ∗
je])(1 + G(yi)/Ns) et
≡ (φ
je
φ∗
j])(1 + G(y j )/Ns) are modified nonlinear components. Le
j
last equality holds according to lemma 2 (see below), wherein EN [φ∗(n)
] ap-
]. As a corollary of lemma 1, the deviation of EN [φ∗(n)
proximates E[φ(n)
] (cid:14)
] due to the nongaussianity of yi is order N−1
E[φ(n)
. Be-
s
je
−1/2
] = O(N−1
] = O(N
cause CovN [yi
),
s
et |EN [φ(n)
]| ≤ O(1) for n ≥ 3 hold with a generic odd function f (•) (voir
remark 2 for details), the difference between CovN [φ∗
j]
je
−5/2
is order N
j] can be characterized by computing
s
, φ
CovN [φ
j] as a proxy up to the negligible deviation; par conséquent, equa-
tion 2.6 is obtained.
−n/2
, y j]n = O(N
s
j ] and CovN [φ
. Ainsi, Cov[φ
), EN [φ(2)
), EN [φ(1)
, φ∗
, φ
, φ
s
je
je
je
je
je
je
je
je
je
4.2 Lemma 2.
Lemma 2. Suppose v and w are gaussian variables with zero mean, σv and σw
are their standard deviations, and their correlation c ≡ Cov[v, w]/σv σw is smaller
que 1. For an arbitrary function g(•),
Cov[g(v ), g(w)] =
∞(cid:10)
n=1
v σ n
σ n
wE[g(n)(v )]E[g(n)(w)]
.
cn
n!
(4.7)
√
Proof. Because the correlation between v and w is c, w can be cast as w =
σwcv/σv + σw
1 − c2ξ using a new a zero-mean and unit-variance gaussian
variable ξ that is independent of v. When we define the covariance between
g(v ) and g(w) comme (cid:19)(c) ≡ Cov[g(v ), g(w)], its derivative with respect to c is
given as
(cid:22)
(cid:18)
(cid:19)(cid:9)
(c) = Cov
(cid:22)
(cid:9)
g(v ), g
(cid:26)
+ σw
1 − c2ξ
σwcv
σv
(cid:19) (cid:18)
(cid:19)(cid:23)
σwv
σv
σwcξ
1 − c2
−
√
(cid:19) (cid:18)
= E
(cid:9)
(g(v ) − E[g(v )])g
(cid:18)
σwcv
σv
(cid:26)
+ σw
1 − c2ξ
σwv
σv
−
√
σwcξ
1 − c2
(cid:19)(cid:23)
.
(4.8)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1458
T. Isomura and T. Toyoizumi
By applying the Bussgang theorem (Bussgang, 1952) with respect to v, nous
obtain
(cid:22)
E
(cid:22)
(cid:9)
(g(v ) − E[g(v )])g
(cid:18)
(cid:18)
σwcv
σv
(cid:26)
(cid:26)
(cid:19)
(cid:23)
+ σw
1 − c2ξ
v
(cid:19)
= E
(cid:9)
g
(cid:9)
(v )g
+ σw
1 − c2ξ
σwcv
σv
(cid:9)(cid:9)
+ (g(v ) − E[g(v )])g
(cid:18)
σwcv
σv
(cid:26)
+ σw
1 − c2ξ
(cid:19)
(cid:23)
v .
p 2
σwc
σv
(4.9)
De la même manière, applying the same theorem with respect to ξ yields
(cid:18)
(cid:19)
(cid:23)
(cid:22)
(cid:26)
E
(cid:9)
(g(v ) − E[g(v )])g
(cid:22)
= E
(cid:9)(cid:9)
(g(v ) − E[g(v )])g
(cid:18)
σwcv
σv
σwcv
σv
+ σw
1 − c2ξ
ξ
(cid:26)
(cid:19)
(cid:26)
(cid:23)
+ σw
1 − c2ξ
σw
1 − c2
.
(4.10)
As equation 4.8 comprises equations 4.9 et 4.10, (cid:19)(cid:9)
(c) becomes
(cid:22)
(cid:18)
(cid:19)(cid:9)
(c) = σv σwE
(cid:9)
g
(cid:9)
(v )g
(cid:26)
(cid:19)(cid:23)
+ σw
1 − c2ξ
.
σwcv
σv
Ainsi, for an arbitrary natural number n, we obtain
(cid:19)(n)(c) = σ n
v σ n
wE
(cid:18)
(cid:22)
g(n)(v )g(n)
σwcv
σv
(cid:26)
(cid:19)(cid:23)
+ σw
1 − c2ξ
.
(4.11)
(4.12)
wE[g(n)(v )]E[g(n)(w)]
When c = 0, (cid:19)(n)(c) = σ n
holds, where we again regard σwξ = w. Ainsi, from the Taylor expansion
with respect to c, we obtain
wE[g(n)(v )]E[g(n)(σwξ )] = σ n
v σ n
v σ n
(cid:19)(c) =
∞(cid:10)
n=1
(cid:19)(n)(0)
=
cn
n!
∞(cid:10)
n=1
v σ n
σ n
wE[g(n)(v )]E[g(n)(w)]
.
cn
n!
(4.13)
(cid:2)
Remark 2. For φ(oui) = f (oui + un) − E[ F ] − E[ f yT ]A+T A+y,
coeffi-
cients EN [φ(n)
] can be computed as follows (up to the fourth or-
der): because applying the Bussgang theorem (Bussgang, 1952)
yields EN [ f yT ]A+T A+ = diag[EN [ F (cid:9)
the difference between
E[ f yT ]A+T A+
(due to the nongaussian
]] = O(1),
]] is order N−1
s
and diag[EN [ F (cid:9)
le
je
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1459
contributions of y;
E[ f yT ]A+T A+
, we have
voir
lemma 1). Ainsi,
from φ(1) = diag[ F (cid:9)
] −
EN [φ(1)] = EN
(cid:11)
diag[ F
(cid:9)
] − diag[EN [ F
(cid:9)
−1
]] + Ô(N
s
(cid:12)
)
−1
= O(N
s
).
(4.14)
De plus, for the second- to fourth-order derivatives, we obtain
EN [φ(2)
je
] = EN [ F (2)(yi
+ ai)] = EN [ F (3)(yi)]ai
−3/2
+ Ô(N
s
−1/2
) = O(N
s
),
EN [φ(3)
je
] = EN [ F (3)(yi
EN [φ(4)
je
] = EN [ F (4)(yi
−1
+ ai)] = EN [ F (3)(yi)] + Ô(N
s
−1/2
+ ai)] = O(N
s
).
) = O(1),
(4.15)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
the Taylor expansion with respect
is applied, où
Ici,
EN [ F (2)(yi)] = EN [ F (4)(yi)] = 0 owing to odd function f (•). For n ≥ 5,
(cid:13)n)i j is order
|EN [φ(n)
−n/2
N
s
]| ≤ O(1) holds. Ainsi, because CovN [yi
je
, equation 2.5 becomes
, y j]n = ((AAT )
to ai
CovN [φ
je
, φ
j] = EN [φ(1)
(cid:3)
je
](AAT )i j
(cid:6)
+ 1
2
]EN [φ(1)
j
(cid:4)(cid:5)
−5/2
Ô(N
s
)
EN [φ(2)
je
]EN [φ(2)
j
]((AAT )
(cid:13)2)i j
+ 1
6
+ 1
24
(cid:3)
EN [φ(3)
je
]EN [φ(3)
j
]((AAT )
(cid:13)3)i j
EN [φ(4)
je
]EN [φ(4)
j
(cid:4)(cid:5)
−3
Ô(N
s
)
]((AAT )
(cid:13)4)i j
(cid:6)
−5/2
+ Ô(N
s
)
= EN [ F (3)(yi)]EN [ F (3)(y j )]
(cid:24)
aia j((AAT )
(cid:13)2)i j
1
2
+ 1
6
×
4.3 Lemma 3.
(cid:25)
((AAT )
(cid:13)3)i j
−5/2
+ Ô(N
s
).
(4.16)
×Ns are independently sampled from a gaus-
Lemma 3. When elements of A ∈ RN f
(cid:13)3 ≡ (AAT ) (cid:13) (AAT ) (cid:13)
sian distribution N [0, 1/Ns] and N f
> N2
s
(AAT ) has Ns major eigenmodes—all of which have the eigenvalue of 3N f
s (comme
the leading order) with the corresponding eigenvectors that match the directions
− Ns) randomly distributed nonzero minor eigenmodes
of AAT —and up to (N f
whose eigenvalues are order max[1, N f
s ] on average. Ainsi, the latter are neg-
ligibly smaller than the former when N f
(cid:7) 1, (AAT )
/N3
> N2
s
(cid:7) 1.
/N2
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1460
T. Isomura and T. Toyoizumi
Proof. Suppose N f
≡ (A1k
as A•k
, . . . , AN f k)T ∈ RN f , (AAT )
(cid:13)3 becomes
> N2
s
(cid:7) 1. When the kth column vector of A is denoted
(AAT )
(cid:13)3 =
Ns(cid:10)
Ns(cid:10)
Ns(cid:10)
k=1
l=1
m=1
(A•k
(cid:13) A•l
(cid:13) A•m)(A•k
(cid:13) A•l
(cid:13) A•m)T
Ns(cid:10)
=
(UN
(cid:13)3
•k )(UN
(cid:13)3
•k )T + 3
(cid:10)
k(cid:11)=l
(UN
(cid:13)2
•k
(cid:13)2
(cid:13) A•l )(UN
•k
(cid:13) A•l )T
(A•k
(cid:13) A•l
(cid:13) A•m)(A•k
(cid:13) A•l
(cid:13) A•m)T .
(4.17)
k=1
+ 6
(cid:10)
k
over, we define an orthogonal matrix UN ∈ RNx×(Nx−Ns ) such that it is per-
pendicular to UL and that multiplying it by the residual covariance B(cid:3)BT
from both sides diagonalizes B(cid:3)BT . Ainsi, (UL, UN )(UL, UN )T = I holds, et
NB(cid:3)BTUN ∈ R(Nx−Ns )×(Nx−Ns ) is a diagonal matrix that arranges its
XNN ≡ U T
diagonal elements in descending order. Without loss of generality, B(cid:3)BT is
decomposed into three matrix factors:
B(cid:3)BT = (UL, UN )
(cid:15)
(cid:16) (cid:15)
(cid:16)
XLL XT
NL
XNL XNN
U T
L
U T
N
.
(4.19)
L B(cid:3)BTUL ∈ RNs×Ns
Ici, XLL ≡ U T
is a symmetric matrix and XNL ≡
NB(cid:3)BTUL ∈ R(Nx−Ns )×Ns is a vertically long rectangular matrix. This de-
U T
composition separates B(cid:3)BT into components in the directions of UL and
the rest. From equations 2.3 et 4.19, we obtain the key equality that
links the eigenvalue decomposition with the decomposition into signal and
residual covariances:
(cid:15)
(cid:16) (cid:15)
(cid:16)(cid:15)
(cid:15)
(cid:16)
(cid:16)
(MP, Pm)
(cid:8)M O
Ô (cid:8)m
= (UL, UN )
S2
L
PT
M.
PT
m
+ XLL XT
NL
XNN
XNL
U T
L
U T
N
.
(4.20)
The left-hand side is the eigenvalue decomposition of Cov[X], où (cid:8)M ∈
RNs×Ns and (cid:8)m ∈ R(Nx−Ns )×(Nx−Ns ) are diagonal matrices of major and minor
eigenvalues, respectivement, and PM ∈ RNx×Ns and Pm ∈ RNx×(Nx−Ns ) are their
+ XLL is suf-
corresponding eigenvectors. When inequality 2.7 holds, S2
L
ficiently close to a diagonal matrix and XNL is negligibly small relative
+ XLL; thus, the right-hand side can be viewed as the zeroth-order
to S2
L
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1462
T. Isomura and T. Toyoizumi
approximation of the eigenvalue decomposition of Cov[X]. Owing to the
uniqueness of eigenvalue decomposition, we obtain (MP, Pm) = (UL, UN ),
(cid:8)M = S2
L
+ diag[XLL], et (cid:8)m = XNN as the leading order.
Suivant, we compute an error in the first order by considering a small per-
turbation that diagonalizes the right-hand side of equation 4.20 more accu-
rately. Suppose (je, ET ; −E, je) ∈ RNx×Nx as a block matrix that comprises Ns ×
Ns and (Nx − Ns) × (Nx − Ns) identity matrices and a rectangular matrix
E ∈ R(Nx−Ns )×Ns with small value elements. Comme (je, ET ; −E, je)(je, ET ; −E, je)T =
je + Ô(|E|2), it is an orthogonal matrix as the first-order approximation. Be-
cause the middle matrix on the right-hand side of equation 4.20 has been
almost diagonalized, a small perturbation by (je, ET ; −E, je) can diagonalize
it with higher accuracy. By multiplying (je, ET ; −E, je) and its transpose by
the near-diagonal matrix from both sides, we obtain
(cid:16)
(cid:16) (cid:15)
(cid:16) (cid:15)
(cid:15)
je
−E
ET
je
S2
L
+ XLL XT
NL
XNN
XNL
I −ET
E
je
(cid:15)
=
S2
L
−E(S2
L
+ XLL + ET XNL + XT
NLE
+ XLL) + XNL + XNNE
+ XLL)ET + XT
−(S2
NL
L
−XNLET − EXT
NL
+ ET XNN
+ XNN
(cid:16)
+ Ô(|E|2)
(4.21)
up to the first order of E. Équation 4.21 is diagonalized only when −E(S2
L
XLL) + XNL + XNNE = O. Ainsi, we obtain
+
Vec[E] =
(cid:27)
I ⊗ (S2
L
⇐⇒ E ≈ XNLS
+ XLL) − XNN ⊗ I
−2
L
(cid:28)−1
Vec[XNL] ≈
(cid:9)
(cid:8)
I ⊗ S
−2
L
Vec[XNL]
(4.22)
as the first-order approximation. Substituting E = XNLS
into equation
4.21 yields the first-order approximation of major and minor eigenvalues:
−2
L
(cid:8)
(cid:8)M = S2
L
(cid:8)m = XNN − 2diag[XNLS
(cid:9)
−2
L diag[XLL] + Ô(|E|2)
−2
L XT
je + S
NL] + Ô(|E|2).
,
(4.23)
De plus, the first-order approximation of their corresponding eigenvec-
tors is provided as
(cid:15)
(MP, Pm) = (UL, UN )
(cid:16)
I −ET
E
je
=
=
(cid:8)
UL + UNE, UN − ULET
(cid:8)
UL + UNXNLS
−2
L
(cid:9)
, UN − ULS
(cid:9)
−2
L XT
NL
+ Ô(|E|2).
(4.24)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1463
The accuracy of these approximations is empirically validated using nu-
merical simulations (see Figure 2D), wherein an error in approximating
UL using PM is analytically computed as tr[ET E]/Ns = tr[S
L B(cid:3)BT (I −
−2
L ]/Ns as the leading order. This error is negligibly small
ULU T
relative to the linearization error in equation 2.12 when inequality 2.7
holds.
L )B(cid:3)BTULS
−2
L U T
4.5 Derivation of Linearization Error Covariance. Équation 2.13 is de-
rived as follows: from equation 2.4, (BH)
) holds
when B is sufficiently isotropic. Ainsi, from equations 2.6 et 2.12, nous
obtain
+ + Ô(N−1
s
+ = f (cid:9)
(BA)
−1
Cov[ε] =
(cid:15)
(cid:16)
− 1
+
(BA)
F 2
F (cid:9)2
BBT (BA)
2
+T + F (3)
2Ns f (cid:9)2 je
(4.25)
as the leading order. Ici, aaT and (cid:7) in equation 2.6 are negligibly smaller
than the leading-order eigenmodes when inequality 2.7 holds and B is suf-
×Ns ,
ficiently isotropic. If we define the left-singular vectors of A as UA
/Ns)1/2
because A has Ns singular values with the leading-order term of (N f
/Ns)1/2UA holds approximately. Ainsi,
(Marchenko & Pastur, 1967), A = (N f
−1U T
(BA)
+ = (Ns/N f )1/2(U T
∈ RN f
A BT BUA)
Plus loin, as B is isotropic, UT
A BT BUA)
trix; thus, (U T
proximation. De la même manière, U T
is sufficiently close to the identity matrix. Ainsi,
A BT BBT BUA
= I + U T
UN
−1 ≈ I − U T
A BT holds as the leading order.
A BT BUA is sufficiently close to the identity ma-
UN (BT B − I)UA provides the first-order ap-
{2(BT B − I) + (BT B − I)2}UA
+
(BA)
BBT (BA)
+T ≈ Ns
N f
(cid:27)
je + U T
UN (BT B − I)2UA
(cid:28)
(4.26)
holds as the leading order. Ainsi, en utilisant (cid:11) ≡ UT
equation 2.13.
UN (BT B − I)2UA, we obtain
4.6 Hebbian-Like Learning Rules. Oja’s subspace rule for PCA (Oja,
1989) is defined as
(cid:29)
˙WPCA
∝ E
uPCA(x − E[X] − W T
PCAuPCA)T
(cid:30)
,
(4.27)
∈ RNs×Nx is a synaptic weight matrix, uPCA
≡ WPCA(x − E[X]) ∈
where WPCA
RNs is a vector of encoders, and the dot over WPCA denotes a temporal
derivative. This rule can extract a subspace spanned by the first Ns princi-
pal components (c'est à dire., WPCA
M.) in a manner equal to PCA via eigen-
value decomposition. Although Oja’s subspace rule does not have a cost
fonction, a gradient descent rule for PCA, based on the least mean squared
→ (cid:9)MPT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1464
T. Isomura and T. Toyoizumi
PCAuPCA
error, is known (Xu, 1993), whose cost function is given as E[|x − E[X] −
|2]. En effet, this equals the maximum likelihood estimation of
W T
x − E[X] using a lower-dimensional linear encoder uPCA under the assump-
tion that the loss follows a unit gaussian distribution. The gradient descent
on this cost function is equal to Oja’s subspace rule up to an additional term
that does not essentially change the behavior of the algorithm.
For BSS of uPCA, Amari’s ICA algorithm is considered (Amari et al.,
1996). Using encoders ˜u ≡ WICAuPCA
∈ RNs with synaptic weight ma-
∈ RNs×Ns , the ICA cost function is defined as the Kullback–
trix WICA
Leibler divergence between the actual distribution of ˜u, p( ˜u), and its prior
belief p0( ˜u) ≡
KL[p( ˜u)||p0( ˜u)] ≡ E[log p( ˜u) − log p0( ˜u)].
The natural gradient of D
KL yields Amari’s ICA algorithm,
i p0( ˜ui), D
≡ D
(cid:2)
KL
˙WICA
∝ −
∂D
KL
∂WICA
W T
ICAWICA
= (I − E
(cid:30)
(cid:29)
g( ˜u) ˜uT
)WICA
,
(4.28)
where g( ˜u) ≡ −d log p0( ˜u)/d ˜u is a nonlinear activation function.
Remerciements
This work was supported by RIKEN Center for Brain Science (T.I. and T.T.),
Brain/MINDS from AMED under grant JP21dm020700 (T.T.), and JSPS
KAKENHI grant JP18H05432 (T.T.). The funders had no role in the study
conception, data collection and analysis, decision to publish, or preparation of
the manuscript.
Data Availability
All relevant data are within the article. The Matlab scripts are available at
https://github.com/takuyaisomura/asymptotic_linearization.
Les références
Amari, S. JE., Chen, T. P., & Cichocki, UN. (1997). Stability analysis of learning algo-
rithms for blind source separation. Neural Networks, 10(8), 1345–1351.
Amari, S. JE., Cichocki, UN., & Lequel, H. H. (1996). A new learning algorithm for blind
signal separation. In D. S. Touretzky, M.. C. Mozer, & M.. E. Hasselmo (Éd.), Ad-
vances in neural information processing systems, 8 (pp. 757–763). Cambridge, MA:
AVEC Presse.
Arora, S., & Risteski, UN. (2017). Provable benefits of representation learning. arXiv:1706.
04601.
Baldi, P., & Hornik, K. (1989). Neural networks and principal component analysis:
Learning from examples without local minima. Neural Networks, 2(1), 53–58.
Barron, UN. R.. (1993). Universal approximation bounds for superpositions of a sig-
moidal function. IEEE Trans. Info. Theory, 39(3), 930–945.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1465
Cloche, UN. J., & Sejnowski, T. J.. (1995). An information-maximization approach to blind
separation and blind deconvolution. Neural Comput., 7(6), 1129–1159.
Cloche, UN. J., & Sejnowski, T. J.. (1997). The “independent components” of natural scenes
are edge filters. Vision Res., 37(23), 3327–3338.
Brun, G. D., Yamada, S., & Sejnowski, T. J.. (2001). Independent component analysis
at the neural cocktail party. Trends Neurosci., 24(1), 54–63.
Bussgang, J.. J.. (1952). Cross-correlation functions of amplitude-distorted gaussian signals
(Technical Report 216). Cambridge, MA: MIT Research Laboratory of Electronics.
Calhoun, V. D., Liu, J., & Adali, T. (2009). A review of group ICA for fMRI data and
ICA for joint inference of imaging, genetic, and ERP data. NeuroImage, 45(1), S163–
S172.
Chandler, D. M., & Field, D. J.. (2007). Estimates of the information content and di-
mensionality of natural scenes from proximity distributions. J.. Opt. Soc. Am. UN,
24(4), 922–941.
Chen, T., Hua, Y., & Yan, W. Oui. (1998). Global convergence of Oja’s subspace al-
gorithm for principal component extraction. IEEE Trans. Neural Netw., 9(1), 58–
67.
Cichocki, UN., Zdunek, R., Phan, UN. H., & Amari, S. je. (2009). Nonnegative matrix and
tensor factorizations: Applications to exploratory multi-way data analysis and blind
source separation. Hoboken, New Jersey: Wiley.
Comon, P.. (1994). Independent component analysis, a new concept? Sig. Process,
36(3), 287–314.
Comon, P., & Jutten, C. (2010). Handbook of blind source separation: Independent compo-
nent analysis and applications. Orlando, FL: Academic Press.
Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Math
Control Signals Syst., 2(4), 303–314.
Dahl, G. E., Yu, D., Deng, L., & Acero, UN. (2012). Context-dependent pretrained
deep neural networks for large-vocabulary speech recognition. IEEE Trans. Audio
Speech Lang. Proc., 20(1), 30–42.
Dayan, P., & Abbott, L. F. (2001). Theoretical neuroscience: Computational and mathemat-
ical modeling of neural systems. Cambridge, MA: AVEC Presse.
Dayan, P., Hinton, G. E., Neal, R.. M., & Zemel, R.. S. (1995). The Helmholtz machine.
Neural Comput., 7(5), 889–904.
DiCarlo, J.. J., Zoccolan, D., & Rust, N.C. (2012). How does the brain solve visual
object recognition? Neurone, 73(3), 415–434.
Dinh, L., Krueger, D., & Bengio, Oui. (2014). NICE: Non-linear independent components
estimation. arXiv:1410.8516.
Erdogan, UN. T. (2007). Globally convergent deflationary instantaneous blind source
separation algorithm for digital communication signals. IEEE Trans. Signal Pro-
cess., 55(5), 2182–2192.
Erdogan, UN. T. (2009). On the convergence of ICA algorithms with symmetric orthog-
onalization. IEEE Trans. Signal Process., 57(6), 2209–2221.
Földiák, P.. (1990). Forming sparse representations by local anti-Hebbian learning.
Biol. Cybern., 64(2), 165–170.
Friston, K. (2008). Hierarchical models in the brain. PLOS Comput. Biol., 4, e1000211.
Friston, K., Trujillo-Barreto, N., & Daunizeau, J.. (2008). DEM: A variational treatment
of dynamic systems. NeuroImage, 41(3), 849–885.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1466
T. Isomura and T. Toyoizumi
Gerstner, W., & Kistler, W. M.. (2002). Spiking neuron models: Single neurons, popula-
tion, plasticity. Cambridge: la presse de l'Universite de Cambridge.
Goodfellow, JE., Bengio, Y., & Courville, UN. (2016). Deep learning. (Cambridge, MA:
AVEC Presse).
Griffiths, D. J.. (2005). Introduction to quantum mechanics (2nd ed.). Upper Saddle River,
New Jersey: Pearson Prentice Hall.
Hebb, D. Ô. (1949). The organization of behavior: A neuropsychological theory. New York:
Wiley.
Hinton, G. E., & Salakhutdinov, R.. R.. (2006). Reducing the dimensionality of data
with neural networks. Science, 313(5786), 504–507.
Hinton, G. E., Srivastava, N., Krizhevsky, UN., Sutskever, JE., & Salakhutdinov, R.. R..
(2012). Improving neural networks by preventing co-adaptation of feature detectors.
arXiv:1207.0580.
Hornik, K., Stinchcombe, M., & Blanc, H. (1989). Multilayer feedforward networks
are universal approximators. Neural Netw., 2(5), 359–366.
Hyvärinen, UN., & Morioka, H. (2016). Unsupervised feature extraction by time-
contrastive learning and nonlinear ICA. In D. Lee, M.. Sugiyama, U. Luxburg,
je. Guyon, & R.. Garnett (Éd.), Advances in neural information processing systems, 29
(pp. 3765–3773). Red Hook, New York: Curran.
Hyvärinen, UN. J., & Morioka, H. (2017). Nonlinear ICA of temporally depen-
dent stationary sources. In Proceedings of the Conference on Machine Learn
Research.
Hyvärinen, UN., & Oja, E. (1997). A fast fixed-point algorithm for independent com-
ponent analysis. Neural Comput., 9(7), 1483–1492.
Hyvärinen, UN., & Pajunen, P.. (1999). Nonlinear independent component analysis:
Existence and uniqueness results. Neural Netw., 12(3), 429–439.
Isomura, T., & Friston, K. (2018). In vitro neural networks minimise variational free
energy. Sci. représentant, 8, 16926.
Isomura, T., & Friston, K. (2020). Reverse engineering neural networks to character-
ize their cost functions. Neural Comput., 32(11), 2085–2121.
Isomura, T., Kotani, K., & Jimbo, Oui. (2015). Cultured cortical neurons can perform
blind source separation according to the free-energy principle. PLOS Comput.
Biol., 11(12), e1004643.
Isomura, T., & Toyoizumi, T. (2016). A local learning rule for independent component
analyse. Sci. représentant, 6, 28073.
Isomura, T., & Toyoizumi, T. (2018). Error-gated Hebbian rule: A local learning rule
for principal and independent component analysis. Sci. représentant, 8, 1835.
Isomura, T., & Toyoizumi, T. (2019). Multi-context blind source separation by error-
gated Hebbian rule. Sci. représentant, 9, 7127.
Isomura, T., & Toyoizumi, T. (2021). Dimensionality reduction to maximize predic-
tion generalization capability. Nat. Mach. Intell., in press.
Jolliffe, je. T. (2002). Analyse en composantes principales (2nd ed.). Berlin: Springer.
Jutten, C., & Karhunen, J.. (2004). Advances in blind source separation (BSS) et en-
dependent component analysis (ICA) for nonlinear mixtures. Int. J.. Neural. Syst.,
14(5), 267–292.
Kandel, E. R., Schwartz, J.. H., Jessell, T., M., Siegelbaum, S. UN., & Hudspeth, UN. J..
(2013). Principles of neural science (5th ed.). New York: McGraw-Hill.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Achievability of Nonlinear Blind Source Separation
1467
Karhunen, J.. (2001). Nonlinear independent component analysis. In S. Roberts &
R.. Everson (Éd.), Independent component analysis: Principles and practice (pp. 113–
134). Cambridge: la presse de l'Universite de Cambridge.
Kawaguchi, K. (2016). Deep learning without poor local minima. In D. Lee, M..
Sugiyama, U. Luxburg, je. Guyon, & R.. Garnett (Éd.), Advances in neural infor-
mation processing systems, 29. Red Hook, New York: Curran.
Khemakhem, JE., Kingma, D., Monti, R., & Hyvarinen, UN. (2020). Variational autoen-
coders and nonlinear ICA: A unifying framework. In Proceedings of the Interna-
tional Conference on Artificial Intelligence and Statistics 2207–2217. ML Research
Presse.
Kingma, D. P., & Welling, M.. (2013). Auto-encoding variational Bayes. arXiv:1312.6114.
Lappalainen, H., & Honkela, UN. (2000). Bayesian non-linear independent component
analysis by multi-layer perceptrons. En M. Girolami, (Ed.), Advances in independent
component analysis (pp. 93–121). Londres: Springer.
Leugering, J., & Pipa, G. (2018). A unifying framework of synaptic and intrinsic plas-
ticity in neural populations. Neural Comput., 30(4), 945–986.
Linsker, R.. (1997). A local learning rule that enables information maximization for
arbitrary input distributions. Neural Comput., 9(8), 1661–1665.
Lu, H., & Kawaguchi, K. (2017). Depth creates no bad local minima. arXiv:1702.08580.
Malenka, R.. C., & Bear, M.. F. (2004). LTP and LTD: An embarrassment of riches.
Neurone, 44(1), 5–21.
Marchenko, V. UN., & Pastur, L. UN. (1967). Distribution of eigenvalues for some sets
of random matrices. Mat. Sbornik, 114, 507–536.
Mika, D., Budzik, G., & Józwik, J.. (2020). Single channel source separation with ICA-
based time-frequency decomposition. Sensors, 20(7), 2019.
Nguyen, Q., & Hein, M.. (2017). The loss surface of deep and wide neural networks.
arXiv:1704.08045.
Oja, E. (1982). Simplified neuron model as a principal component analyzer. J.. Math.
Biol., 15(3), 267–273.
Oja, E. (1989). Neural networks, principal components, and subspaces. Int. J.. Neural.
Syst., 1(10), 61–68.
Oja, E., & Yuan, Z. (2006). The FastICA algorithm revisited: Convergence analysis.
IEEE Trans. Neural Netw., 17(6), 1370–1381.
Papadias, C. B. (2000). Globally convergent blind source separation based on a mul-
tiuser kurtosis maximization criterion. IEEE Trans. Signal Process., 48(12), 3508–
3519.
Pearson, K. (1901). On lines and planes of closest fit to systems of points in space.
Philos. Mag., 2(11), 559–572.
Pehlevan, C., Mohan, S., & Chklovskii, D. B. (2017). Blind nonnegative source sepa-
ration using biological neural networks. Neural Comput., 29(11), 2925–2954.
Rahimi, UN., & Recht, B. (2008un). Uniform approximation of functions with random
bases. In Proceedings of the 46th Annual Allerton Conference on Communication, Con-
trol, and Computing (pp. 555–561). Red Hook, New York: Curran.
Rahimi, UN., & Recht, B. (2008b). Weighted sums of random kitchen sinks: Replacing
minimization with randomization in learning. In D. Koller, D. Schuurmans, Oui.
Bengio, & L. Bottou (Éd.), Advances in neural information processing systems, 21
(pp. 1313–1320). Cambridge, MA: AVEC Presse.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1468
T. Isomura and T. Toyoizumi
Sanger, T. D. (1989). Optimal unsupervised learning in a single-layer linear feedfor-
ward neural network. Neural Netw., 2(6), 459–473.
Toyoizumi, T., & Abbott, L. F. (2011). Beyond the edge of chaos: Amplification and
temporal integration by recurrent networks in the chaotic regime. Phys. Rev. E.,
84(5), 051908.
van der Lee, T., Exarchakos, G., & de Groot, S. H. (2019). In-network Hebbian plas-
ticity for wireless sensor networks. In Proceedings of the International Conference on
Internet and Distributed Computing Systems (pp. 79–88). Cham: Springer.
Wan, L., Zeiler, M., Zhang, S., LeCun, Y., & Fergus, R.. (2013). Regularization of neural
networks using DropConnect. In Proceedings of Machine Learning Research (28)3,
1058–1066.
Wentzell, P.. D., Andrés, D. T., Hamilton, D. C., Faber, K., & Kowalski, B. R.. (1997).
Maximum likelihood principal component analysis. J.. Chemom., 11(4), 339–366.
Xu, L. (1993). Least mean square error reconstruction principle for self-organizing
neural–nets. Neural Netw., 6(5), 627–648.
Received July 26, 2020; accepted December 23, 2020.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
6
1
4
3
3
1
9
1
6
3
6
4
n
e
c
o
_
un
_
0
1
3
7
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3