ARTICLE
Communicated by Stefano Panzeri
The Refractory Period Matters: Unifying Mechanisms
of Macroscopic Brain Waves
Corey Weistuch
corey.weistuch@stonybrook.edu
Laufer Center for Physical and Quantitative Biology and Department of Applied
Mathematics and Statistics, Stony Brook University, Stony Brook, New York 11794, U.S.A.
Lilianne R. Mujica-Parodi
lilianne.strey@stonybrook.edu
Laufer Center for Physical and Quantitative Biology, Departments of Biomedical
Engineering and of Physics and Astronomy, Program in Neuroscience, et
Department of Chemistry, Stony Brook University, Stony Brook, New York 11794, USA.,
and Athinoula A. Martinos Center for Biomedical Imaging, Général du Massachusetts
Hospital and Harvard Medical School, Boston, MA 02129, U.S.A.
Ken Dill
dill@laufercenter.org
Laufer Center for Physical and Quantitative Biology, Department of Physics
and Astronomy, and Department of Chemistry, Stony Brook University,
Stony Brook, New York 11794, U.S.A.
The relationship between complex brain oscillations and the dynamics
of individual neurons is poorly understood. Here we utilize maximum
caliber, a dynamical inference principle, to build a minimal yet general
model of the collective (mean field) dynamics of large populations of neu-
rons. In agreement with previous experimental observations, we describe
a simple, testable mechanism, involving only a single type of neuron,
by which many of these complex oscillatory patterns may emerge. Notre
model predicts that the refractory period of neurons, which has often
been neglected, is essential for these behaviors.
1 Introduction
A major interest in neuroscience is understanding how macroscopic brain
les fonctions, such as cognition and memory, are encoded at the microscale of
neurons and their topological connectivities. One of the significant develop-
ments in this direction was the Wilson-Cowan (WC) model, describing the
averaged behavior of large populations of simple excitatory and inhibitory
neurons in terms of a set of coupled, mesoscale differential equations (Des-
texhe & Sejnowski, 2009; Wilson & Cowan, 1972, 1973). With only a few
Neural Computation 33, 1145–1163 (2021) © 2021 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01371
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
un
_
0
1
3
7
1
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1146
C. Weistuch, L. Mujica-Parodi, and K. Dill
physical parameters, WC provided one of the first mechanisms for simple
(single-frequency) oscillations across the brain, such as the hypersynchro-
nized dynamics observed during epileptic seizures (Destexhe & Sejnowski,
2009; Shusterman & Troy, 2008). Plus récemment, generalized WC-like models
have been used to describe heterogeneous populations of neurons ranging
in scale from single regions to networks of activities across the whole brain
(Breskin, Soriano, Moses, & Tlusty, 2006; Deco, Jirsa, Robinson, Breakspear,
& Friston, 2008; Destexhe & Sejnowski, 2009; Hopfield, 1982; Schneidman,
Berry, Segev, & Bialek, 2006; Tkacik, Schneidman, Berry, Michael, & Bialek,
2006; Weistuch, Mujica-Parodi, Amgalan, & Dill, 2020).
But there remain important macroscopic brain behaviors that WC-like
models fail to adequately explain (Chow & Karimipanah, 2019; Muir, 1979).
One example is theta oscillations in the hippocampus, which have multiple
superimposed frequencies and are thought to be critical for memory forma-
tion and storage (Buzsáki, 2002; Buzsáki & Draguhn, 2004; Colgin, 2013).
They are believed to be generated through recurrent feedback involving
excitatory neurons only (Buzsáki, 2002). Another example is gamma oscil-
lations, which are high-frequency chaotic firing patterns associated with a
wide-range of complex brain activities (Buzsáki & Wang, 2012). They are
believed to arise in networks of inhibitory neurons. While WC-like mod-
els can exhibit these complex patterns of brain activity, they require many
different subtypes of neurons to do so (Goles-Chacc, Fogelman-Soulié, &
Pellegrin, 1985; Keeley, Fenton, & Rinzel, 2017; Neves & Monteiro, 2016;
Rajan & Abbott, 2006).
Brain oscillations can be facilitated by the refractory period of a popula-
tion of neurons (Greenberg & Hastings, 1978; Sanchez-Vives & McCormick,
2000). Encore, while the WC model considers both an absolute and a relative
refractory period of neurons, it can only be applied under quasi-steady-
state conditions (Feldman & Cowan, 1975; Muir, 1979). Par conséquent, the WC
model only exhibits simplified, lower-dimensional behaviors. Ici, we de-
scribe a model of similar simplicity to the WC model but that also accounts
for the non-steady-state behaviors induced by the refractory periods of neu-
rons (see Figure 1A compared to the effective WC model in Figure 1B for a
single population of neurons). Related generalizations indeed exhibit com-
plex dynamical features missing from Benayoun, Cowan, van Drongelen,
and Wallace (2010), Pinto and Copelli (2019), and Goychuk and Goychuk
(2015). Cependant, current models make broad assumptions about neural dy-
namics, and their behaviors have yet to be fully determined. The novelty of
this article is two-fold. D'abord, we treat the stochastic dynamics of the model
using maximum caliber (Max Cal), a principle of statistical inference that
applies to systems of pathways or systems of dynamical processes, lequel
draws more directly on data and is freer of unwarranted model assump-
tion (Dixit et al., 2018; Ghosh, Dixit, Agozzino, & Dill, 2020; Pressé, Ghosh,
Lee, & Dill, 2013; Weistuch, Agozzino, Mujica-Parodi, & Dill, 2020). Deuxième,
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
un
_
0
1
3
7
1
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The Refractory Period Matters
1147
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
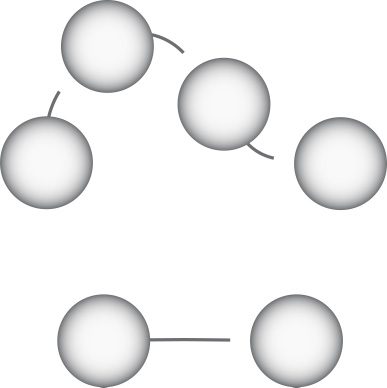
Chiffre 1: Neural oscillations depend on the refractory period. (UN). A network
representation of the model. Gauche: Neural activity represented as a Markov
chain. Here the rates (pQA, pAR, and pRQ) determine the occupation probabili-
ties of the three states: Q, UN, et R. Droite: The fraction of neurons in each state
evolves over time. Active neurons (yellow) can either excite (as shown) ou dans-
hibit neighboring quiescent neurons (blue) by modulating the average firing
probability pQA. Complex oscillations emerge when these neurons must wait to
fire again (red). (B). Without the refractory state (gauche), the fraction of neurons in
each state does not evolve over time (droite).
the model is well characterized and provides a simple, testable mechanism
for both multifrequency and chaotic oscillations.
2 The Physics of the Model
We represent a generic network of N neurons (labeled i = 1, 2, . . . , N) comme
a graph; nodes represent each neuron, and edges are synaptic connections
(voir la figure 1). Each node (je) also has a time-dependent state Si(t), represent-
ing the activity of a neuron. En particulier, the nodes of our network can be
in any one of three states: quiescent (Q), or silent but able to fire; active (UN),
or firing; or refractory (R.), or unable to fire. En plus, the states of each
node evolve stochastically over time: Q → A → R → Q. The rate of each of
these transitions is then chosen to reflect the biophysical dynamics of real
neurons.
F
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
un
_
0
1
3
7
1
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1148
C. Weistuch, L. Mujica-Parodi, and K. Dill
We use the principle of maximum caliber (Max Cal) to infer these tran-
sitions directly from the data (Dixit et al., 2018; Ghosh et al., 2020; Pressé
et coll., 2013). Here Max Cal, the dynamical extension of maximum entropy,
provides the simplest and least-biased model consistent with a few known
transition rates, such as average neuronal firing rates and correlations (Dixit
et coll., 2018; Ghosh et al., 2020; Pressé et al., 2013; Tkacik et al., 2006). Ce
model takes the form of a probability distribution P over different dynam-
ical trajectories (cid:2) of populations of neurons.
Using Max Cal, we model how the fraction of neurons in each state (π
Q,
π
UN, and πR) evolves over time. While our approach is applicable to any num-
ber of neurons, we focus on the case when this number is large. We maintain
our focus here for two reasons. D'abord, it presents an enormous simplification,
as we can study the long-time behavior of our model using mean-field the-
ory (Deco et al., 2008; Gerstner, 2000; Jirsa & Haken, 1997; Omurtag, Knight,
& Sirovich, 2000). Deuxième, it is often a reasonable approximation, as system
behaviors converge to their means when their number of components N is
grand.
2.1 Obtaining the Stochastic Dynamics of the Model Using Maximum
Caliber. Here we ask how simple neuronal interactions might give rise to
complex patterns of brain dynamics. To answer this, we use Max Cal to
build a minimal model of neural dynamics. Ici, the Caliber C is defined as
the path entropy over the probability distribution of trajectories P(cid:2) sujet
to a prespecified set of constraints:
(cid:2)
(cid:2)
C[P.(cid:2)] = −
P.(cid:2) log P(cid:2) +
iAi,(cid:2)P.(cid:2),
λ
(2.1)
(cid:2)
je,(cid:2)
where λ
i are the Lagrange multipliers constraining generic average quan-
tities (cid:3)Ai
(cid:4). Here the quantities that we measure are the transitions of nodes
between different states: lQA
(t), and lRQ
(t) is one
if the ith node transitions from Q to A during the time interval [t, t + 1] et
is otherwise zero; the other transition indicators are defined similarly. Nous
thus want to constrain our model in such a way as to preserve the average
transition rate between each pair of states:
(t). En particulier, lQA
(t), lAR
je
je
je
je
rQA
= 1
N
rAR
= 1
N
rRQ
= 1
N
(cid:4)
lQA
je
(t)
=
(cid:4)
lAR
je
(t)
=
(cid:4)
lRQ
je
(t)
=
(cid:3)
N(cid:2)
(cid:3)
je = 1
N(cid:2)
(cid:3)
je = 1
N(cid:2)
je = 1
(cid:5)
(cid:6)
π
Q(t)pQA(t)
,
(cid:5)
(cid:6)
,
π
UN(t)pAR(t)
(cid:5)
(cid:6)
.
πR(t)pRQ(t)
(2.2)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
un
_
0
1
3
7
1
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The Refractory Period Matters
1149
Ici (cid:3)◦(cid:4) denotes an average over time, and the second set of equalities holds
when the number of neurons N is large. The average rates rQA, rAR, et
rRQ are computed from experimental data as the time-averaged fraction of
nodes transitioning from Q → A, A → R, and R → Q, respectivement. In con-
trast, the right-hand sides of the above equations are computed over the
different trajectories that our inferred model will produce. Ici, these av-
erages are constrained using the Lagrange multipliers hQA, hAR, and hRQ,
respectivement (see appendix A and B).
These Lagrange multipliers can then be incorporated into the transition
probabilities pQA, pAR, and pRQ as discussed in appendix B. Ici, pAR and
pRQ are constants and are functions of their respective Lagrange multipliers.
More directly, pAR (resp. pRQ) can be computed as the average fraction of
refracting A (resp. quiescing R) per unit time. In contrast, a key property
of neurons is their ability to communicate by altering the firing activity of
their neighbors. Spécifiquement, firing neurons can either increase (excite) ou
decrease (inhibit) the probability that other quiescent neurons fire. Here we
include this with the additional constraint
C = 1
N
(cid:3)
N(cid:2)
je = 1
(cid:4)
lQA
je
(t)NA(t)
= N
(cid:5)
Q(t)π
π
(cid:6)
,
UN(t)pQA(t)
(2.3)
where NA(t) is the number of active neurons at time t. A large value of C
thus represents a population of excitatory neurons, as the firing probability
of additional nodes increases with the number of currently active nodes.
Inversement, a small (close-to-zero) value of C represents an inhibitory pop-
ulation, whereby the activation of a few nodes suppresses subsequent firing
of additional nodes. This constraint is enforced by the Lagrange multiplier
J., the coupling constant. Ainsi, the transition probability pQA is a function
of both the raw firing probability of a neuron (controlled by h = hQA) et
the feedback strength, J.. This relationship is given by (see appendix B)
pQA(π
UN) = eh+Jπ
1 + eh+Jπ
UN
UN
.
(2.4)
Ainsi, h and J can be alternatively computed by fitting the shape of pQA
for different values of π
UN. Taken together, our model is a function of four
parameters (pAR, pRQ, h, and J), each uniquely chosen to reproduce our four
experimental constraints.
2.2 The Mean-Field Equations. Here we compute the time evolution
of the average fraction of neurons in each state (π
UN, and πR). Before
proceeding, we make a few notational simplifications to enhance read-
ability. D'abord, we use (cid:5) to refer to the change in a variable over time. Pour
exemple, (cid:5)π
UN(t). And second, aside from their initial
UN(t + 1) − π
UN(t) = π
Q, π
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
un
_
0
1
3
7
1
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1150
C. Weistuch, L. Mujica-Parodi, and K. Dill
UN, et (cid:5)π
definitions, we implicitly assume the time dependence of our variables and
drop (t) when writing our equations. Par exemple, π
UN(t) will just be writ-
ten as π
UN(t) will just be (cid:5)π
UN. Ainsi, after maximizing the caliber
subject to our four constraints and computing the average (mean-field) dy-
namics (see appendixes A and B), we find that our system can be described
by two coupled equations:
(cid:5)π
Q
(cid:5)π
UN
= (1 − π
− π
UN
Q pQA − π
= π
Q)pRQ − π
A pAR.
Q pQA,
(2.5)
Here we have eliminated the corresponding third equation for (cid:5)πR using
the constraint that the fractions of nodes of each type sum to unity (c'est à dire., le
number of neurons is fixed).
In contrast to typical modeling approaches, we have made no assump-
tions in deriving these equations other than the fact that our experimentally
observed constraints are reasonably descriptive of neural dynamics. Ainsi,
we expect our model to be widely applicable, even when other previous
models fail.
Aussi, each of our parameters has a clear biological interpretation. D'abord,
pAR and pRQ control the average amount of time neurons spend (respecter-
tivement) active and refractory. Ainsi, when pAR is large (as might be expected
of real neurons), nodes are only briefly active. On the other hand, pRQ might
be expected to be small, as biological neural oscillation occurs at a relatively
low frequency (an action potential lasts 1 ms, but the fastest oscillations
have a period of about 10 ms). Reflecting these requirements, we fix pAR and
pRQ at 0.8 et 0.01, respectivement. En plus, h, the unit-less average firing
threshold, controls the fraction of neurons that fire spontaneously. Ainsi,
we should have h < 0, reflecting a low-level of baseline activity. Finally, J
reflects feedback, or synaptic coupling, between neighboring neurons and
can be either positive (excitatory) or negative (inhibitory).
We study two general classes of brain oscillations, corresponding to the
network activities of excitatory (J > 0) and inhibitory (J. < 0) neurons. Here,
excitatory oscillations are characterized by high-amplitude waves of activ-
ity followed by long periods of silence during which most neurons are re-
fractory (Buzsáki, 2002; Buzsáki & Draguhn, 2004). In contrast, networks
of inhibitory neurons fire asynchronously, producing low-amplitude, high-
frequency oscillations (Brunel & Hakim, 2008; Buzsáki & Wang, 2012; Korn
& Faure, 2003). And unlike WC, both of these behaviors can be exhibited by
our model using only a single population of neurons (Feldman & Cowan,
1975; Muir, 1979).
3 Model Properties
The formulation of WC-like models is based on quasi-steady-state dy-
namics and requires multiple populations of neurons to exhibit even
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The Refractory Period Matters
1151
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
Q vs π
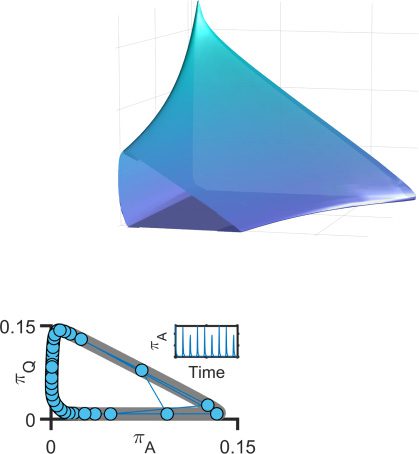
Figure 2: Excitatory couplings produce complex oscillations. (A). The phase
A) for different values of J (at h = −5), illustrating the emer-
plane (π
gence of oscillations (rings). (B). A typical trajectory (blue) in phase space (gray)
and over time (inset). Because π
A vary slightly with each cycle, the os-
cillatory amplitude changes over time. These changes are very sensitive to J.
(C). Examples of different oscillatory patterns for different values of J.
Q and π
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
single-frequency oscillations (see appendix C and Feldman & Cowan, 1975,
and Muir, 1979). In contrast, the behaviors of real neurons are more com-
plex, often involve few neural subtypes, and have been difficult to describe
mechanistically (Buzsáki & Draguhn, 2004; Chow & Karimipanah, 2019).
We next demonstrate the significant improvements of our model over these
previous approaches.
Unlike WC, our model explains how a single population of excitatory
neurons can generate multifrequency oscillation patterns (see Figure 2).
In particular, Figure 2A, depicting the phase plane of our model, shows
the emergence of oscillatory activity (rings) when the coupling J > 0 est
nestled within a critical region. Here the amplitude of each oscillation
can vary with every cycle (see Figure 2B), producing the multifrequency
bands expected of real neurons (Bacak, Kim, Forgeron, Rubin, & Rybak, 2016;
Buzsáki, 2002; Vladimirski, Tabak, O’Donovan, & Rinzel, 2008). Unlike WC,
by only slightly tuning J, our model predicts the emergence of highly dis-
tinct patterns of activity (see Figure 2C). And indeed, a similar mechanism
1152
C. Weistuch, L. Mujica-Parodi, and K. Dill
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
un
_
0
1
3
7
1
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Q vs π
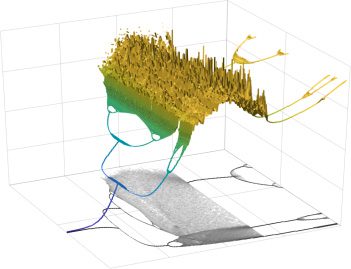
Chiffre 3: Inhibitory couplings produce chaotic oscillations. (UN). The phase
UN) and its projection (black) for different values of J (at h = −1).
plane (π
The number of points (for each J) corresponds to the period of the associated
oscillation. As J is decreased, the oscillations become chaotic and aperiodic (ou-
ange). (B). Comparison of inhibitory (blue) to excitatory (orange) oscillations
produced by our model. (C). Examples of different chaotic oscillatory patterns
along with a histogram of π
A over time (inset). Here information is stored, pas
in the timing but in the probabilities of different amplitudes.
is thought to underlie tremendous information capacity of real networks
of neurons (Averbeck, Latham, & Pouget, 2006; Panzeri, Macke, Gross, &
Kayser, 2015; Vladimirski et al., 2008).
At the other extreme, recurrent inhibitory networks of neurons have
been shown to produce high-frequency and sometimes chaotic firing pat-
terns (Buzsáki & Wang, 2012; Korn & Faure, 2003). In contrast to excita-
tory networks, inhibitory neurons fire in small bands of only a few neurons
at a time. As the strength of this inhibition is increased, these neurons fire
asynchronously and chaotically (Buzsáki & Wang, 2012). And while WC-
like models can produce some inhibitory oscillations, they require multi-
ple subtypes of neurons to do so (Goles-Chacc et al., 1985; Keeley et al.,
2017). Chiffre 3 describes how these features emerge from our model using
only a single subtype of neuron. Ici, Figure 3A. depicts the phase plane of
The Refractory Period Matters
1153
Chiffre 4: The phase diagram of our model, depicting the emergence of excita-
tory (vert) and inhibitory (orange) oscillations. In the blue region, brain activ-
ity is constant over time. In contrast to WC-like models, cependant, oscillations
can be produced by tuning h and J.
our model for different values of J (J. < 0). The number of points for each J
corresponds to the period of the inhibitory oscillations. As J is decreased,
this period continually doubles until it diverges to infinity and chaos
emerges. Because inhibitory neurons fire as far apart as possible, they os-
cillate with a much higher frequency (as well as a lower amplitude) as
compared to excitatory neurons (see Figure 3B; Buzsáki & Draguhn, 2004;
Buzsáki & Wang, 2012).
And despite appearing to have almost noise-like dynamics, these chaotic
firing patterns robustly store information in their probability distributions
of amplitudes (see Figure 3C and inset). And thus, the asynchronous os-
cillations in real networks of inhibitory neurons can be seen as information
transmission that is fast and robust to noise (Brunel & Hakim, 2008; Buzsáki
& Wang, 2012). Also, hidden within the chaotic region are occasional win-
dows of stable oscillations that are seen when J is very negative (see Fig-
ure 3A). Whether pathological or strategic, this suggests that real networks
of neurons may be able to flexibly switch between qualitatively different
patterns of firing activity by only slightly changing their synaptic coupling
(Korn & Faure, 2003).
Taken together, the general behavior of our model changes dramatically,
in biologically expected ways, as its parameters are varied. These findings
are summarized in Figure 4, illustrating how these behaviors change with
h and J (with pRQ and pAR fixed at their previous, biologically plausible
values). In particular, as long as pRQ and pAR are biologically appropri-
ate, our model exhibits roughly three different behaviors (corresponding
to the three colors in Figure 4): constant (equilibrium) activity and both ex-
citatory and inhibitory oscillations (including chaos). In contrast, a single
population of WC neurons exhibits only the former behavior (see appendix
C). And analysis of the locations and properties of each of these regimes
can be easily performed using only standard techniques (see appendix D).
Thus, our model explains a huge variety of complex, natural phenomena
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1154
C. Weistuch, L. Mujica-Parodi, and K. Dill
in a simple and practical way. In particular, h (i.e., the mean firing prob-
ability) can be manipulated experimentally by applying an external volt-
age to a group of neurons (Breskin et al., 2006; Eckmann et al., 2007). Also,
synaptic activity (J) can be manipulated (Breskin et al., 2006). The predic-
tions of our model (and even the phase diagram itself) can be easily tested
experimentally.
4 Discussion
Here we have presented a new treatment of collective neural dynamics
that starts from only the most elementary biophysical of neurons, and basic
stochastic dynamics. We find a broad range of behaviors, even in the sim-
plest case of only a single type of neuron (either excitatory or inhibitory).
Of course, many situations involve both types of neurons. Nevertheless,
some situations involve only a single type. For example, theta-wave neu-
ronal oscillations in the hippocampus are thought to play a considerable
role in memory formation and spatial navigation (Buzsáki, 2002; Colgin,
2013). The currents driving these oscillations are believed to be primarily
generated by recurrent excitatory-excitatory connections within the CA3
region of the hippocampus, whereby these neurons robustly synchronize
using a “relaxation” mechanism akin to our model’s predictions (Buzsáki,
2002; Buzsáki & Draguhn, 2004). Our model suggests how these neurons
can easily toggle between and store the large number of complex oscilla-
tory patterns required for their proper function (Buzsáki & Draguhn, 2004;
Hutcheon & Yarom, 2000; Llinás, 1988).
Similarly, the emergence of chaotic neural dynamics has been seen exper-
imentally and is believed to underlie high-frequency, gamma-band oscilla-
tions across the brain (Aihara, Takabe, & Toyoda, 1990; Brunel & Hakim,
2008; Korn & Faure, 2003). Our model generates these patterns with just
inhibitory neurons (Buzsáki & Wang, 2012). And while chaotic dynamics
might seem counterproductive for the brain, it has been theorized that these
patterns are critical for information storage (Aihara et al., 1990; Brunel &
Hakim, 2008; Jia et al., 2012; Korn & Faure, 2003). And perhaps fluctua-
tions into the occasional window of stability within this chaos play a role in
pathologies such as epilepsy (Sato et al., 2017).
It is also worth noting that our mean-field Max Cal, equation 2.5, resem-
bles the model proposed in Goychuk and Goychuk (2015), but with two key
differences: first, it makes far fewer assumptions and can be rigorously ex-
tended to small, noisy populations of neurons (see appendix B); and second,
it defines time discretely and exhibits richer dynamics (e.g., chaos). At the
same time, this link may provide a new avenue to examine the behaviors of
more general neural networks (Pinto & Copelli, 2019; Goychuk & Goychuk,
2015).
Our model is also readily extended beyond a single type of neuron.
In particular, WC provided the starting point for the Hopfield model of
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The Refractory Period Matters
1155
associative learning, which has itself been an essential starting point for
much of the recent development in artificial neural networks (Destexhe &
Sejnowski, 2009; Hopfield, 1982; Hopfield & Tank, 1986). In that case, each
population of neurons is assigned its own learned coupling Ji j, representing
the storage of unique patterns of activity. In a similar vein, the present may
allow generalization beyond the Hopfield model to include more complex,
dynamical features (Destexhe & Sejnowski, 2009).
Appendix A: Maximizing Caliber for Markovian Processes
Here we summarize how to apply Max Cal to Markovian systems. The tra-
jectories (cid:2) of some variable S are defined as (cid:2) = {S0
, . . . , ST }. Our goal
is to infer P(cid:2) using some given information, or constraints. First, since the
process is Markovian,
, S1
P(cid:2) = π (S0)
T(cid:7)
t=1
P(St|St−1),
(A.1)
where the vertical bar is used to denote the conditional probability. P de-
notes the transition probabilities, and π denotes a distribution over states.
In particular, if the Markov chain is allowed to reach a steady-state distri-
bution π,
(cid:2)
(cid:2)
π (St ) =
P(St|St−1)π (St−1),
π (St ) = 1.
(A.2)
St−1
St
The path entropy E can then be written as
E{P} = −
(cid:2)
(cid:2)
P(cid:2) log P(cid:2) = −
(cid:2)
S0
π (S0) log π (S0)
T(cid:2)
(cid:2)
(cid:2)
−
t=1
St
St−1
π (St−1)P(St|St−1) log P(St|St−1),
(A.3)
which for T large reduces to
E{P} = −
1
T
(cid:2)
(cid:2)
Sa
Sb
π (Sa)P(Sb
|Sa) log P(Sb
|Sa)
(A.4)
for generic subsequent times a and b. We now write our caliber C as
C{P} =
1
T
(cid:2)
(cid:2)
π (Sa)
Sa
Sb
(cid:8)
P(Sb
|Sa)
−log P(Sb
|Sa) + μ(Sa) +
(cid:9)
iAi(Sa, Sb)
λ
.
(cid:2)
i
(A.5)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1156
C. Weistuch, L. Mujica-Parodi, and K. Dill
Here μ(Sa) ensures that the transition probabilities P(Sb
|Sa) are properly
normalized (sum to 1). Additionally the Lagrange multipliers λ
i enforce the
constraints of (cid:3)Ai(Sa, Sb)(cid:4), such as the mean transition rates discussed in the
main text. We find the trajectory distribution that maximizes the caliber C:
∂C
∂P(Sb
|Sa)
= 0 (cid:6)⇒ − log P(Sb
|Sa) + μ(Sa) +
(cid:2)
i
iAi(Sa, Sb) − 1 = 0.
λ
Therefore:
P(Sb
|Sa) = e
μ(Sa )−1+
λ
iAi (Sa,Sb).
i
(cid:10)
Since the distributions need to be normalized, we have that
|Sa) = e
(cid:10)
P(Sb
Sb
(cid:10)
i
λ
iAi (Sa,Sb)
(cid:10)
e
λ
iAi (Sa,Sb)
i
.
(A.6)
(A.7)
(A.8)
Finally, using our original constraints, equation A.5, we can uniquely de-
termine the Lagrange multipliers λ
i.
Appendix B: Deriving the Mean-Field Model from Max Cal
Here our goal is to understand how the constraints, equations 2.2 and
2.3, give rise to our mean-field model, equation 2.5. First, we use S(t) =
{S1(t), S2(t), . . . , SN(t)} to denote the states of all nodes at time t. Second, the
number of nodes in each state are then given (respectively) by NQ(t), NA(t),
and NR(t). And finally, transitions are indicated by the functions lQA
(t),
lAR
(t) as indicated in the main text. We next follow the general
i
procedure laid out in appendix A (see equation A.8) to infer the transition
(cid:12)
(cid:11)
lQA
i
. In particular, each quiescent
|S
, and P
probabilities P
(Q) node fires (Q → A) with probability
(t), and lRQ
(cid:11)
lRQ
i
(cid:11)
lAR
i
|S
|S
, P
(cid:12)
(cid:12)
i
i
(cid:12)
(cid:11)
lQA
i
P
|S
= ehQA+J∗NA
1 + ehQA+J∗NA
= pQA.
(B.1)
Similarly, each active (A) node becomes refractory (A → R) with proba-
bility
(cid:12)
(cid:11)
lAR
i
P
|S
= ehAR
1 + ehAR
= pAR,
(B.2)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The Refractory Period Matters
and each refractory (R) node quiesces (R → Q) with probability
(cid:12)
(cid:11)
lRQ
i
P
|S
= ehRQ
1 + ehRQ
= pRQ.
1157
(B.3)
Equations B.1 to B.3 provide the rules by which our simple network of
neurons evolves over time. However, here we are primarily interested in
how the population dynamics of a group of neurons changes over time—in
particular, NQ, NA, and NR. For example, changes in NQ can occur in two
ways. First, nodes in R can quiesce (R → Q), adding to the total number of
Q nodes. Second, nodes in Q can fire (Q → A), subtracting from the total
number of Q nodes. Here we denote the number of each kind of transition
as NRQ, NQA, and NAR. The number of nodes of each type at time t + 1 is
then given by
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
(cid:5)NQ
= NRQ
(cid:5)NA
= NQA
(cid:5)NR = NAR
− NQA
− NAR
− NRQ
,
,
.
In reality, though, we only have two dynamical equations since
NQ
+ NA
+ NR = N
(B.4)
(B.5)
for all t. Additionally, since each transition is independent, the number of
transitions of each type is binomially distributed:
NRQ
NQA
NAR
∼ B(NR, pRQ),
, pQA),
∼ B(NQ
∼ B(NA
, pAR).
(B.6)
Here we use B(N, p) as shorthand for the two-parameter binomial distri-
bution; N is the number of trials, and p is the probability of each success
(here, a transition of a particular node). We next ask how simple neuronal
interactions might give rise to complex patterns of brain dynamics. In par-
ticular, we use mean-field theory to explore how our previous equations
behave when the number of neurons is large (Deco et al., 2008). To sim-
plify our analysis, we divide equation B.4 by the number of nodes N and
instead follow how the average fraction of nodes in each state (π
A, and
πR) changes over time. Since the mean of a binomially distributed random
variable B(N, p) is N p, the average dynamics of our model are given by
Q, π
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1158
C. Weistuch, L. Mujica-Parodi, and K. Dill
(cid:5)π
Q
Q pQA,
= πR pRQ − π
Q pQA − π
A pAR,
= π
A pAR − πR pRQ.
(cid:5)π
A
(cid:5)πR = π
(B.7)
But we can eliminate contributions from πR using equation B.5. In addi-
tion, to keep all variables in terms of the fractions π, we define J = J∗N and
thus arrive at our final relationships, equations 2.5 and 2.4.
Appendix C: Deriving the Wilson-Cowan Model from Max Cal
Here we show how the widely used Wilson-Cowan (WC) model emerges
as a special case of our more general Max Cal model. For simplicity, we
focus on only a single type of neuron, but the derivation (as well as our
model) can almost trivially be extended to any number of neural types
by adding couplings. Here we start from our mean-field model, equa-
tion 2.5. Suppose that the number of refractory neurons (πR = 1 − π
Q)
is in a quasi-steady state (cid:5)πR ≈ 0. Thus, adding together both parts of
equation 2.5,
− π
A
(1 − π
A
− π
Q)pRQ − π
A pAR = 0 (cid:6)⇒ π
Q
= 1 − π
A
(cid:13)
(cid:14)
.
1 + pAR
pRQ
(C.1)
Next, we define the constant r = 1 + pAR
pRQ . Substituting this back into our
equation for (cid:5)π
A,
(cid:5)π
= pQA(1 − rπ
A) − π
A pAR.
A
(C.2)
Now, defining pAR = 1/τ and rearranging, our equation turns into the ex-
act same form as that from the WC equation (Chow & Karimipanah, 2019;
Wilson & Cowan, 1972). While the original derivation of WC assumes that
all of the variables are in a quasi-steady state (Chow & Karimipanah, 2019),
our re-derivation suggests that it can be applied more generally. Neverthe-
less, WC still breaks down when the rate of change of recovering neurons
is large. In other words, a single population of WC neurons cannot describe
strongly coupled behaviors such as avalanches and intrinsic oscillations.
In contrast, our Max Cal model provides a much more complete picture of
neural dynamics while retaining the simplicity of the original WC model.
Appendix D: Bifurcation Analysis
Here we use local stability analysis to explore how our model transitions be-
tween simple equilibrium behavior and complex oscillatory dynamics as its
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The Refractory Period Matters
1159
parameters are varied. To achieve this, we compute the equilibrium state of
our model and ask how typical trajectories behave in its vicinity. In general,
a system is in equilibrium if it does not change over time. Thus, the equi-
librium states of our model are the coordinates where the left-hand side of
equation 2.5 is 0. After standard algebraic manipulation, we find that the
equilibrium point satisfies
π ∗
A
=
pRQ pQA
pRQ pQA + pQA pAR + pAR pRQ
= pRQ pQA
pD
, π ∗
Q
= π ∗
A
pAR
pQA
.
(D.1)
The behavior of trajectories near this point is then determined by the
∂ (π (cid:11)
A )
A ) . Here we use (cid:11) to denote a sub-
Jacobian matrix of derivatives, J =
Q
∂ (π
sequent time step (t + 1) and bold to denote matrices. For equation 2.5, the
Jacobian is given by
,π (cid:11)
,π
Q
(cid:13)
J (π
, π
A) =
Q
1 − pRQ − pQA
pQA
−pRQ − M
1 − pAR + M)
(cid:14)
.
(D.2)
, π ∗
, π ∗
QJ pQA(1 − pQA). To describe the stability, we must compute the
Here, M = π
eigenvalues of this matrix evaluated at the equilibrium (π ∗
A). In particu-
Q
lar, when the magnitudes of these eigenvalues (whether real or complex) are
both less than one, all trajectories rapidly approach the equilibrium point
(π ∗
A), that is, the dynamics are stable. But when one (or both) of these
Q
eigenvalues has magnitude greater than one, trajectories never reach equi-
librium (the dynamics are unstable). Additionally, this transition can occur
in several different ways, giving rise to the different types of oscillations
we observe. In particular, excitatory oscillations occur when the real part
of this eigenvalue is positive (leading to large oscillations between high π
A
and high π
Q). In contrast, when the real part of this eigenvalue is nega-
tive, high-frequency, inhibitory oscillations occur. To determine when os-
cillatory behaviors occur, we thus need to determine when the eigenvalues
of J change their stability. To simplify the expression of these eigenvalues,
we define
F = pRQ + pQA + pAR − M
2
.
The eigenvalues, λ, are then given by
(cid:15)
λ = 1 − F ±
F2 − pD + pRQM.
(D.3)
(D.4)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1160
C. Weistuch, L. Mujica-Parodi, and K. Dill
We now have three cases to consider: when the unstable eigenvalue is
one (excitatory), when it is −1 (inhibitory), and when it is complex with
|λ| = 1 (either excitatory or inhibitory).
For the first case, we set λ = 1 and solve equation D.4 to find the critical
point Jc,
(cid:13)
Jc = − 1
π ∗
A
W
−eh
pARπ ∗
A
(cid:14)
,
(D.5)
where W (x) is the multivalued Lambert W function. For the λ = −1 (in-
hibitory case), pQA and pRQ are both expected to be small. Solving equation
D.4 after this approximation produces Jc:
Jc = pRQ + pAR − 2
π ∗
A pAR
− 1
π ∗
A
W
− pRQ + pAR − 1
pAR
h+ pRQ +pAR −2
pAR
e
(cid:13)
(cid:14)
.
(D.6)
And finally, solving the complex case exactly produces Jc:
pRQ + pAR
(1 − pRQ)π ∗
A pAR
− 1
π ∗
A
(cid:13)
W
−
pRQ + pAR + 1 − pRQ
π ∗
A
(1 − pRQ)pAR
h+ pRQ +pAR
(1−pRQ )pAR
e
(cid:14)
.
(D.7)
Additionally, if pRQ (cid:12) pQA (which is almost always the case for biologi-
cally plausible sets of parameters),
π ∗
A
≈
pRQ
pRQ + pAR
.
(D.8)
Thus, the three scenarios describe three sets of critical transitions be-
tween different types of oscillations. The first (λ = 1) and last (λ complex)
exclusively correspond to the emergence of excitatory oscillations. In con-
trast, the second case (λ = −1) corresponds to the emergence of inhibitory
oscillations. Most important, the Lambert function W (x) is only defined
when x ≥ e−1. And when −e−1 < x < 0, the Lambert function has two so-
lutions (corresponding to the beginning and end of oscillatory behavior).
Thus, we have found an analytical relationship between our model param-
eters and the emergence of qualitatively distinct biological patterns.
Acknowledgments
The research was funded by the WM Keck Foundation (L.M.P., K.D.), the
NSF BRAIN Initiative (L.M.P., K.D.: ECCS1533257, NCS-FR 1926781), and
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The Refractory Period Matters
1161
the Stony Brook University Laufer Center for Physical and Quantitative
Biology (K.D.).
Competing Interests
We declare no competing financial interests.
References
Aihara, K., Takabe, T., & Toyoda, M. (1990). Chaotic neural networks. Physics Letters
A, 144(6–7), 333–340.
Averbeck, B. B., Latham, P. E., & Pouget, A. (2006). Neural correlations, population
coding and computation. Nature Reviews Neuroscience, 7(5), 358–366.
Bacak, B. J., Kim, T., Smith, J. C., Rubin, J. E., & Rybak, I. A. (2016). Mixed-mode os-
cillations and population bursting in the pre-Bötzinger complex. eLife, 5, e13403.
Benayoun, M., Cowan, J. D., van Drongelen, W., & Wallace, E. (2010). Avalanches in a
stochastic model of spiking neurons. PLOS Computational Biology, 6(7), e1000846.
Breskin, I., Soriano, J., Moses, E., & Tlusty, T. (2006). Percolation in living neural
networks. Physical Review Letters, 97(18), 188102.
Brunel, N., & Hakim, V. (2008). Sparsely synchronized neuronal oscillations. Chaos,
18(1), 015113.
Buzsáki, G. (2002). Theta oscillations in the hippocampus. Neuron, 33(3), 325–340.
Buzsáki, G., & Draguhn, A. (2004). Neuronal oscillations in cortical networks. Science,
304(5679), 1926–1929.
Buzsáki, G., & Wang, X.-J. (2012). Mechanisms of gamma oscillations. Annual Review
of Neuroscience, 35, 203–225.
Chow, C. C., & Karimipanah, Y. (2019). Before and beyond the WilsonCowan equations.
arXiv:1907.07821.
Colgin, L. L. (2013). Mechanisms and functions of theta rhythms. Annual Review of
Neuroscience, 36, 295–312.
Deco, G., Jirsa, V. K., Robinson, P. A., Breakspear, M., & Friston, K. (2008). The dy-
namic brain: From spiking neurons to neural masses and cortical fields. PLOS
Computational Biology, 4(8).
Destexhe, A., & Sejnowski, T. J. (2009). The Wilson–Cowan model, 36 years later.
Biological Cybernetics, 101(1), 1–2.
Dixit, P. D., Wagoner, J., Weistuch, C., Pressé, S., Ghosh, K., & Dill, K. A. (2018). Per-
spective: Maximum caliber is a general variational principle for dynamical sys-
tems. Journal of Chemical Physics, 148(1), 010901.
Eckmann, J.-P., Feinerman, O., Gruendlinger, L., Moses, E., Soriano, J., & Tlusty,
T. (2007). The physics of living neural networks. Physics Reports, 449(1–3), 54–
76.
Feldman, J., & Cowan, J. (1975). Large-scale activity in neural nets I: Theory
with application to motoneuron pool responses. Biological Cybernetics, 17(1), 29–
38.
Gerstner, W. (2000). Population dynamics of spiking neurons: Fast transients, asyn-
chronous states, and locking. Neural Computation, 12(1), 43–89.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1162
C. Weistuch, L. Mujica-Parodi, and K. Dill
Ghosh, K., Dixit, P. D., Agozzino, L., & Dill, K. A. (2020). The maximum caliber vari-
ational principle for nonequilibria. Annual Review of Physical Chemistry, 71, 213–
238.
Goles-Chacc, E., Fogelman-Soulié, F., & Pellegrin, D. (1985). Decreasing energy func-
tions as a tool for studying threshold networks. Discrete Applied Mathematics,
12(3), 261–277.
Goychuk, I., & Goychuk, A. (2015). Stochastic Wilson–Cowan models of neuronal
network dynamics with memory and delay. New Journal of Physics, 17(4), 045029.
Greenberg, J. M., & Hastings, S. (1978). Spatial patterns for discrete models of diffu-
sion in excitable media. SIAM Journal on Applied Mathematics, 34(3), 515–523.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective
computational abilities. In Proceedings of the National Academy of Sciences, 79(8),
2554–2558.
Hopfield, J. J., & Tank, D. W. (1986). Computing with neural circuits: A model. Science,
233(4764), 625–633.
Hutcheon, B., & Yarom, Y. (2000). Resonance, oscillation and the intrinsic frequency
preferences of neurons. Trends in Neurosciences, 23(5), 216–222.
Jia, B., Gu, H., Li, L., & Zhao, X. (2012). Dynamics of period-doubling bifurcation
to chaos in the spontaneous neural firing patterns. Cognitive Neurodynamics, 6(1),
89–106.
Jirsa, V. K., & Haken, H. (1997). A derivation of a macroscopic field theory of the
brain from the quasi-microscopic neural dynamics. Physica D: Nonlinear Phenom-
ena, 99(4), 503–526.
Keeley, S., Fenton, A. A., & Rinzel, J. (2017). Modeling fast and slow gamma oscil-
lations with interneurons of different subtype. Journal of Neurophysiology, 117(3),
950–965.
Korn, H., & Faure, P. (2003). Is there chaos in the brain? II. Experimental evidence
and related models. Comptes Rendus Biologies, 326(9), 787–840.
Llinás, R. R. (1988). The intrinsic electrophysiological properties of mammalian neu-
rons: Insights into central nervous system function. Science, 242(4886), 1654–1664.
Muir, A. (1979). A simple case of the Wilson-Cowan equations. Biophysical Journal,
27(2), 267.
Neves, L. L., & Monteiro, L. H. A. (2016). A linear analysis of coupled Wilson-
Cowan neuronal populations. Computational Intelligence and Neuroscience 2016,
art. 8939218.
Omurtag, A., Knight, B. W., & Sirovich, L. (2000). On the simulation of large popu-
lations of neurons. Journal of Computational Neuroscience, 8(1), 51–63.
Panzeri, S., Macke, J. H., Gross, J., & Kayser, C. (2015). Neural population coding:
Combining insights from microscopic and mass signals. Trends in Cognitive Sci-
ences, 19(3), 162–172.
Pinto, I. L. D., & Copelli, M. (2019). Oscillations and collective excitability in a model
of stochastic neurons under excitatory and inhibitory coupling. Physical Review
E, 100(6), 062416.
Pressé, S., Ghosh, K., Lee, J., & Dill, K. A. (2013). Principles of maximum entropy and
maximum caliber in statistical physics. Review of Modern Physics, 85(3), 1115.
Rajan, K., & Abbott, L. F. (2006). Eigenvalue spectra of random matrices for neural
networks. Physical Review Letters, 97(18), 188104.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The Refractory Period Matters
1163
Sanchez-Vives, M. V., & McCormick, D. A. (2000). Cellular and network mechanisms
of rhythmic recurrent activity in neocortex. Nature Neuroscience, 3(10), 1027–1034.
Sato, Y., Wong, S. M., Iimura, Y., Ochi, A., Doesburg, S. M., & Otsubo, H. (2017).
Spatiotemporal changes in regularity of gamma oscillations contribute to focal
ictogenesis. Scientific Reports, 7(1), 1–9.
Schneidman, E., Berry, M. J., Segev, R., & Bialek, W. (2006). Weak pairwise corre-
lations imply strongly correlated network states in a neural population. Nature,
440(7087), 1007–1012.
Shusterman, V., & Troy, W. C. (2008). From baseline to epileptiform activity: A path
to synchronized rhythmicity in large-scale neural networks. Physical Review E,
77(6), 061911.
Tkacik, G., Schneidman, E., Berry, I., Michael, J., & Bialek, W. (2006). Ising models for
networks of real neurons. arXiv:0611072.
Vladimirski, B. B., Tabak, J., O’Donovan, M. J., & Rinzel, J. (2008). Episodic activity in
a heterogeneous excitatory network, from spiking neurons to mean field. Journal
of Computational Neuroscience, 25(1), 39–63.
Weistuch, C., Agozzino, L., Mujica-Parodi, L. R., & Dill, K. A. (2020). Inferring a net-
work from dynamical signals at its nodes. arXiv:2004.02318.
Weistuch, C., Mujica-Parodi, L. R., Amgalan, A., & Dill, K. A. (2020). Younger, but not
older, brains are poised at a critical point of functional activity. bioRxiv.
Wilson, H. R., & Cowan, J. D. (1972). Excitatory and inhibitory interactions in local-
ized populations of model neurons. Biophysical Journal, 12(1), 1–24.
Wilson, H. R., & Cowan, J. D. (1973). A mathematical theory of the functional dy-
namics of cortical and thalamic nervous tissue. Kybernetik, 13(2), 55–80.
Received August 14, 2020; accepted November 16, 2020.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
5
1
1
4
5
1
9
0
8
9
9
9
n
e
c
o
_
a
_
0
1
3
7
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3