ARTICLE
Communicated by Terrence Sejnowski
A Cerebellar Computational Mechanism for Delay
Conditioning at Precise Time Intervals
Terence D. Sanger
terry@sangerlab.net
Departments of Biomedical Engineering, Neurologie, and Biokinesiology,
University of Southern California, Les anges, Californie 90089, U.S.A.
Mitsuo Kawato
kawato@atr.jp
Brain Information Communication Research Laboratory Group, Advanced
Telecommunications Research Institutes International, Kyoto 619-0288, Japan, et
Center for Advanced Intelligence Project, RIKEN, Chuo-ku, Tokyo, 103-0027, Japan
The cerebellum is known to have an important role in sensing and exe-
cution of precise time intervals, but the mechanism by which arbitrary
time intervals can be recognized and replicated with high precision is
unknown. We propose a computational model in which precise time in-
tervals can be identified from the pattern of individual spike activity in a
population of parallel fibers in the cerebellar cortex. The model depends
on the presence of repeatable sequences of spikes in response to con-
ditioned stimulus input. We emulate granule cells using a population
of Izhikevich neuron approximations driven by random but repeatable
mossy fiber input. We emulate long-term depression (LTD) and long-term
potentiation (LTP) synaptic plasticity at the parallel fiber to Purkinje cell
synapse. We simulate a delay conditioning paradigm with a conditioned
stimulus (CS) presented to the mossy fibers and an unconditioned stimu-
lus (NOUS) some time later issued to the Purkinje cells as a teaching signal.
We show that Purkinje cells rapidly adapt to decrease firing probability
following onset of the CS only at the interval for which the US had oc-
curred. We suggest that detection of replicable spike patterns provides
an accurate and easily learned timing structure that could be an impor-
tant mechanism for behaviors that require identification and production
of precise time intervals.
1 Introduction
With the evolution of vertebrates came the problem of combination of sen-
sory signals and coordination of motor commands that arrive from and are
destined for distant parts of the body. Different body regions are connected
to the central nervous system by neurons whose axons are responsible for
Neural Computation 32, 2069–2084 (2020) © 2020 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01318
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2070
T. Sanger and M. Kawato
differing delays in transmission. This creates the need for recognition and
generation of signals with precise time delays. While some delays are de-
termined by neuroanatomy and therefore unchanging, the need to interact
with a dynamic environment requires the ability to learn and replicate arbi-
trary time intervals (Molinari, Leggio, & Thaut, 2007). This function is often
attributed to the cerebellum (Bareš et al., 2019), and cerebellar injury impairs
the estimation and production of millisecond-precision time intervals up to
à propos 1 à 2 seconds in duration (Buhusi & Meck, 2005; Ivry & Spencer, 2004;
Schwartze, Keller, & Kotz, 2016). A common experimental paradigm is eye-
blink conditioning, in which a behaviorally irrelevant conditioned stimulus
(CS) is repeatedly followed at a predictable interval by a puff of air on the
cornea (unconditioned stimulus, NOUS). After training, presentation of the CS
without the US leads to an eyeblink at the precise interval at which the US
would normally have occurred (Attwell, Ivarsson, Millar, & Yeo, 2002; Ger-
wig, Kolb, & Timmann, 2007; Kim & Thompson, 1997; Kotani, Kawahara,
& Kirino, 2002; Raymond & Medina, 2018).
The mechanism by which time intervals can be learned and replicated is
the subject of multiple models (Yamazaki & Tanaka, 2009). Proposed mecha-
nisms include delays implemented by the time required for axonal conduc-
tion or conduction through neural circuits (Buonomano, 2003; Braitenberg,
1967), rhythmic pattern generators with a known period (Miall, 1989; Panz-
eri, Ince, Diamond, & Kayser, 2014), beat frequency between oscillators at
differing frequencies (Buhusi & Meck, 2005), synchronized firing of groups
of neurons (Hopfield & Brody, 2001), or superimposed time-varying wave-
forms that can be combined to produce temporal sequences (Medina, Gar-
cia, Nores, Taylor, & Mauk, 2000; Narain, Remington, De Zeeuw, & Jazayeri,
2018). A particularly interesting group of models suggests that random but
repeatable dynamics can be generated by feedback loops between granule
cells and Golgi cells, and the resulting time-varying patterns triggered by
the conditioned stimulus allow determination of time intervals (Roössert,
Dean, & Porrill, 2015; Yamazaki & Tanaka, 2007un, 2007b). While most of
these mechanisms are able to approximate smooth temporal sequences,
they do not have the ability to learn a rapid eyeblink at an arbitrary time in-
terval with millisecond precision because they are based on average firing
rates rather than instantaneous spikes (Karmarkar & Buonomano, 2007).
The precision, repeatability, and stability of rate-based models may not
reflect the true challenges of achieving millisecond precision timing with
interconnected populations of spiking neurons Even in a model based on
simulation of populations of spiking neurons, time-varying patterns in
granule cells are expressed as relatively slow variations in firing rates that
cannot be identified at millisecond precision (Yamazaki & Tanaka, 2007b).
We propose a new mechanism for learning time intervals with millisec-
ond precision. This mechanism is based on patterns of activity within pop-
ulations of granule cells, but the patterns are determined by predictable and
repeatable (although random-appearing) sequences of individual spikes
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Timing in Cerebellum
2071
rather than by slower temporal patterns of spike rates, oscillations, or syn-
chrony. The mechanism requires that cerebellar granule cells are able to
produce nearly identical spike trains for similar inputs and that the Purk-
inje cells can recognize specific patterns in the population of granule cells.
If these two conditions are met, then the pattern of spikes in the popula-
tion provides a unique and precise time stamp at any desired time interval,
and the association of a training signal in the climbing fibers at a partic-
ular time interval after the stimulus allows plasticity at the parallel fiber
to Purkinje cell synapses to respond to the pattern of activity at that spe-
cific time. There is accumulating evidence that even though cell spike se-
quences appear to have Poisson statistics, they may not be random and
often have the repeated sequences required for this mechanism (Alstrøm,
Beierholm, Nielsen, Ryge, & Kiehn, 2002; Hires, Gutnisky, Yu, O’Connor, &
Svoboda, 2015; Kayser, Logothetis, & Panzeri, 2010; Mainen & Sejnowski,
1995; Masquelier, 2013; Nolte, Reimann, King, Markram, & Muller, 2019;
Petersen, Panzeri, & Diamond, 2001, 2002; Shmiel et al., 2005). This is con-
sistent with theoretical results showing that for certain classes of nonlinear
systèmes, apparently chaotic but nevertheless repeatable sequences can be
achieved (Rössert et al., 2015; Uchida, McAllister, & Roy, 2004). Although
this phenomenon has not yet been tested in granule cells, we suggest that
the identification of time-stamped patterns of neural activity may provide a
widespread mechanism for the representation of time intervals and the syn-
chronization of events with repeatable time delays within the cerebellum,
as well as elsewhere in the brain.
The model and simulations we propose we have here are intended to
demonstrate the potential for this computational mechanism to generate
and recognize precise time intervals in response to pairings of CS and US.
Although this can be perhaps interpreted as a model for certain behavioral
phenomena including eyeblink conditioning, we emphasize that we do not
attempt to emulate many of the more complex and interesting behavioral
phenomena associated with eyeblink or other conditioned reflexes, we do
not attempt to match the empirically observed firing patterns of granule
or Purkinje cells, and the time intervals we have chosen are intended for
illustration rather than as a specific instance of conditioning. Our intent is
to show in a very simplified model that there is a previously undescribed
computational mechanism based on spike timing that has the potential to
be used to generate time intervals and response patterns with millisecond
precision after relatively short periods of training.
2 Methods
Cerebellar learning is simulated in Matlab, based on common connectivity
and plasticity models (for review, see D’Angelo, 2014; Raymond & Medina,
2018). The network (voir la figure 1) is constructed of 100 mossy fibers, 2000
granule cells, and a single output Purkinje cell. Each granule cell contacts
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2072
T. Sanger and M. Kawato
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 1: Structure of the simplified cerebellar model. The conditioned stimulus
(CS) sur 100 mossy fibers is expansion recoded onto 2000 granule cells, each of
which takes input from four mossy fibers. The granule cell axons are the parallel
fibers that contact the synapses of a Purkinje cell. The climbing fiber from a cell
in the inferior olive contacts the Purkinje cell and supplies the unconditioned
stimulus (NOUS). The output of the Purkinje cell makes an inhibitory synapse with
deep cerebellar nuclei.
four randomly selected mossy fibers via excitatory synapses, and the Purk-
inje cell contacts all granule cells via excitatory synapses. Granule cells do
not synapse on other granule cells. Granule cell membrane potential and
spike generation obey the Izhikevich approximation (Izhikevich, 2003) à
the Hodgkin-Huxley equations integrated at 1 msec timescale, with param-
eters tuned as fast-spiking neurons (a = 0.16, b = 0.225, c = −65, d = 8) avec
5% jitter of each parameter to simulate differences between cells.
We emulate a delay conditioning paradigm in which the conditioned
stimulus (CS) and unconditioned stimulus (NOUS) overlap in time. This is be-
cause in the absence of overlap (trace conditioning), the response may de-
pend on other brain regions, including the hippocampus (Beylin et al., 2001;
Kim, Clark, & Thompson, 1995; Blanc, Bouwmeester, Power, & Disterhoft,
1999), although more recent results suggest that trace and delay condition-
ing may share mechanisms at the Purkinje cell (Halverson, Khilkevich, &
Timing in Cerebellum
2073
Chiffre 2: Pattern of granule cell firing during a single trial. Each row is the
spikes for one of the 2000 granule cells. Cells only fire when driven by the mossy
fiber inputs during the conditioned stimulus (CS), entre 200 et 300 msec.
The pattern repeats, and the intertrial interval is therefore 400 msec between the
end of one CS and the start of the next.
Mauk, 2018). In our model as well as most other models that depend on
temporal patterns of granule cell activity, in the absence of overlap between
CS and US, the CS input drive from the mossy fibers to the granule cells is
absent at the time of the US, so the parallel fibers to Purkinje cell synapses
are not activated and learning cannot be performed.
The conditioned stimulus is presented for 100 msec, and the US is pre-
sented for 10 msec, starting 70 msec after the start of the CS. The US is indi-
cated by climbing fiber input, and we represent this as a 10 msec constant
signal. The CS is a set of 100 independent Poisson spike trains with aver-
age rate of 200 Hz, one for each of the 100 mossy fiber inputs. The same
spike train pattern is given for each presentation of the CS. When the CS
is not present, the mossy fibers are silent. Fifty trials are performed in se-
quence, each with the same pattern of spikes on the set of 100 incoming
mossy fibers. Mossy fiber to granule cell synapses create a depolarizing ex-
citatory postsynaptic current (EPSC) avec 40 msec time constant and av-
erage amplitude of 10 microAmps with 10% random variation in the EPSC
size between different synapses. The intertrial interval is 400 msec, which is
sufficient for the Izhikevich granule cells to return to their fully resting state.
Chiffre 2 shows an example of the pattern of granule cell firing for a single
trial.
The granule cell to Purkinje cell synapses have a variable synaptic
i indicated by a value between 0 et 1. The Purkinje cell exci-
strength w
tatory postsynaptic potential is calculated at each 1 msec time step as
EPSP =
1(cid:2)(cid:3)
(cid:4)
i g2
je
je
w
,
igi
(2.1)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2074
T. Sanger and M. Kawato
(cid:5)(cid:3)
where gi is 1 if the ith granule cell fired and zero otherwise. Granule cell in-
i gi) because the
put is normalized by RMS input power (equivalently,
relatively small number of granule cells in our simulation leads to much
larger variance in the mean input than would be present in the biological
système. The Purkinje cells fire with Poisson statistics such that firing rate
is proportional to the EPSP, adjusted to have a maximum rate of 50 Hz.
Golgi cells, stellate cells, basket cells, plasticity at the mossy fiber to gran-
ule cell synapse, and the effect of nitric oxide and catecholamines are not
modeled.
Plasticity is simulated only at the granule cell to Purkinje cell synapses.
Long-term potentiation (LTP) occurs by adding a value to the synaptic
weight of 0.0001 per spike, whenever there is an incoming spike on a gran-
ule cell, independent of whether the Purkinje cell fires. This simulates the
absence of backpropagating action potentials in the Purkinje cells, so that
synapses are not aware of output firing and thus do not implement a true
Hebbian-type learning rule. Long-term depression (LTD) occurs by sub-
tracting a value of 0.03 per spike for each granule cell spike that occurs dur-
ing the US. Since the US is assumed to trigger activity on climbing fibers,
this simulates the LTD associated with coincident Purkinje cell complex
spikes and incident granule cell firing. All weights w
i are maintained be-
tween 0 et 1. This algorithm can be written as
(cid:2)w(t) = g ∗ ((1 − US(t)) ∗ LTPrate − US(t) ∗ LTDrate) ,
(2.2)
0
2000
. . . w
> is the synaptic vector of weights w
where w =< w
i, (cid:2)w(t) is
the vector change in the weight at time step t, g =< g0
> is a binary
= 1 for every granule cell that fired, NOUS(t) is the scalar value
vector with gi
of the unconditioned stimulus at time t, and LTPrate and LTDrate are scalars
indicating the amounts of LTP or LTD that occur in response to a single spike
event. Équation 2.2 operates continually from the start of the experiment to
la fin, reflecting changes in weights for every US event as these occur.
. . . g2000
Équation 2.2 will drive the Purkinje cell output to zero during times that
correspond to positive values of the unconditioned stimulus US. Cependant,
this same circuitry can be used to approximate desired smooth functions
if instead we use the Widrow-Hoff LMS rule (Widrow & Hoff, 1960) pour
entraînement:
(cid:2)w(t) = LTDrate ∗ g ∗ (1 − US(t) − PCoutput),
(2.3)
where PCoutput is the scalar probability of the Purkinje cell firing, approxi-
mated as proportional to the instantaneous magnitude of its membrane po-
tential. Dans ce cas, the Purkinje cell output will converge through learning
to approximate the time-varying signal US(t).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Timing in Cerebellum
2075
Chiffre 3: Demonstration of time interval recognition from the population pat-
tern. Spike rasters from only 200 granule cells are shown during the first 50 msec
of the conditioned stimulus (CS). The red box illustrates how a particular pat-
tern of spikes can uniquely identify a particular time interval following the start
of the CS.
Following training, the Purkinje cell EPSP is calculated using equation
2.1 while the CS is on but the US is inactive. Successful recognition of the
pattern of granule inputs that had been present during the US will result
in the Purkinje cell firing rate dropping to zero in the absence of the US
whenever the selected pattern occurs (voir la figure 3).
To estimate the probability that an untrained pattern could be mistaken
for a pattern present during the US, we calculate the cross-correlation ma-
trix between each different pattern. We compare the magnitude of the di-
agonal elements of the cross-correlation matrix (responding to the correct
pattern) with the magnitude of the off-diagonal elements (responding to an
incorrect pattern).
Because neither the granule cell to Purkinje cell synaptic weights nor the
granule cell inputs can represent negative numbers, orthogonality of dif-
ferent granule cell patterns occurs only when there is no overlap between
motifs. This substantially reduces the number of possible orthogonal pat-
terns representable in any population. At least 2000 granule cells appear to
be needed for reliable results in our simulation. Since those cells are driven
by only 100 mossy fiber inputs, there needs to be a method to distribute the
inputs randomly across the granule cells. Expansion coding is necessary in
our simulation in order to allow a rich enough representation to achieve a
unique pattern on the parallel fibers for each stimulus at each time.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2076
T. Sanger and M. Kawato
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4: Histogram of magnitudes of elements in the cross-correlation matrix.
Off-diagonal elements (entre 0 et 0.4) have significantly lower magnitudes
than the diagonal elements (peak at 1).
3 Results
Chiffre 4 shows the cross-correlation between different granule cell patterns
at each point in time. The diagonal elements of the cross-correlation matrix
Timing in Cerebellum
2077
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
Chiffre 5: Because of LTD, during training, the Purkinje cell output at the time
of the unconditioned stimulus (NOUS) drops to zero.
are much higher than the off-diagonal elements, with no overlap in the dis-
tributions. Donc, there will not be confusion between different patterns,
and every time interval has a unique pattern signature. In order to obtain
a unique pattern for each time, the granule cells need to be sufficiently dif-
ferent from each other, with sufficiently high firing rates. The mossy fiber
inputs are insufficient for this purpose, since patterns are often replicated
at different time points. Expansion coding to the granule cells generates a
larger variety of independent Poisson-like sequences with a much lower
probability (in this case, zero) of confusion of the patterns for two different
time intervals. This occurs in part because the time constant of the granule
cell EPSC (40 msec in our simulation) allows response to mossy fiber inputs
that occur over a finite time interval, therefore expanding potential granule
cell patterns beyond the instantaneous mossy fiber pattern set.
Chiffre 5 shows the rapid convergence of the Purkinje cell output to
the desired value during eyeblink conditioning. Fewer than 30 trials are
typically required to achieve full suppression of the Purkinje cell outputs.
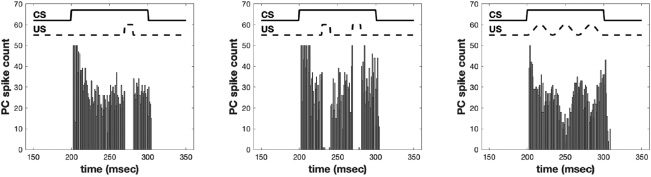
Chiffre 6 shows the resulting Purkinje cell outputs when presented with
the conditioned stimulus (CS) in the absence of the unconditioned stim-
ulus (NOUS) for three different US patterns: single eyeblink, double eyeblink,
and a smooth sinusoidal function. The sinusoidal function is trained using
LMS as in equation 2.3. It is instructive to compare the eyeblink response
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2078
T. Sanger and M. Kawato
Chiffre 6: Purkinje cell outputs after training with different US patterns. Gauche:
Single eyeblink conditioning with US present from 270 à 280 msec. Middle:
Double eyeblink response with US present from 240 à 250 msec and 270 à
280 msec. Droite: Smoothly varying US trained using the LMS algorithm.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 7: Combined output of 20 Purkinje cells trained by LMS to respond to
a smoothly varying US. The combined output population response provides a
much better representation of the desired output than any single Purkinje cell.
to in vivo recordings, such as Figure 3 in Kotani, Kawahara, and Kirino
(2003), Chiffre 3 in Jirenhed, Rasmussen, Johansson, and Hesslow (2017),
and Figure 5 in Kotani, Kawahara, and Kirino (2006). (Matlab code
for this simulation can be downloaded from http://www.sangerlab.net
/TimingModelSangerKawato2019.m.)
Because of the inherent variability in Purkinje cell outputs, the represen-
tation of the desired sinusoidal function in Figure 6 is not very accurate.
Cependant, in the full cerebellum, there would be a population of Purkinje
cells to represent these values. Chiffre 7 shows the summed activity of a
population of 20 Purkinje cells, each of which learned to approximate the
same sinusoidal function. The population statistics are much smoother than
the individual statistics. For the population average to have higher accuracy
than its individual elements, the different Purkinje cells must have slightly
different responses. This is achieved by adding 1% noise to the synaptic
weight change in equation 2.3.
Timing in Cerebellum
2079
4 Discussion
The very simple LTD/LTP learning algorithm emulated here effectively
“deletes” the response to granule cells that tend to be on during the US.
Cependant, once deleted, any subset of the deleted set will also lead to a fall
in Purkinje cell firing. Thus normalization is necessary for the small num-
bers of granule cells in our simulation to ensure that random coincidences of
pauses in granule cell firing do not automatically lead to low Purkinje cell
firing that would be misinterpreted as a conditioned response (CR). Ce
mechanism predicts dense granule cell firing (Badura & De Zeeuw, 2017),
since a sparse code will frequently have very few or absent input firing,
which would lead to lack of Purkinje cell input that would be mistaken for
the decreased firing associated with the CR. Similar to other algorithms,
this mechanism is not a model for trace conditioning, since if the CR occurs
following the end of the CS, then the granule cells would not be driven by
the CS and both granule cells and Purkinje cells would cease firing.
A reasonable analogy is a lock-and-key mechanism. The Purkinje cell
synapses are a lock that causes the Purkinje cell to fire for almost all in-
coming patterns of granule cells. Only when the particular incoming pat-
tern is the key that exactly matches the synapses that have been silenced by
LTD does the Purkinje cell stop firing. Normalization (perhaps performed
by Golgi cells or other cerebellar interneurons) is essential to ensure that a
blank “skeleton” key with little or no granule cell activity would not be able
to emulate a truly matching key.
Successful function of the mechanism we propose depends on several
details of the network, without which the conditioned response can be in-
correct or absent:
1. The pattern of granule cell spike timing during the CS is similar on
each repetition of the CS.
2. There is high variation between the spike time patterns of different
granule cells.
3. Purkinje cell inputs are normalized.
In order to achieve the first detail, the mossy fiber input needs to have a
reliably repeatable pattern for each repetition, there must be no other noise
input to the granule cells, and there must be a sufficient intertrial interval
that the granule cell membrane potentials can return to their original resting
state. In order to achieve the second one, expansion recoding of the mossy
fiber input is needed to create a sufficient number of differing spike trains
from the mossy fiber input, and the US must occur at a sufficient time in-
terval following onset of the CS that initial transient-correlated responses
in the granule cell population have abated. In order to achieve the final de-
tail, there must be either a very large number of granule cells so that in the
absence of the US, the mean Purkinje cell EPSP has low variance, or there
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2080
T. Sanger and M. Kawato
must be feedback onto the granule cells that maintains the total granule cell
activity approximately constant.
The algorithm proposed here shares important features with prior tim-
ing algorithms based on extraction of information from time-varying pop-
ulation responses to the CS input. Tripp and Eliasmith (2006) show that
arbitrary output patterns can be computed based on apparently random
input patterns similar to those used in our simulations, but they did not im-
plement a cerebellar-like learning rule, and although their results depend
on reliable spike timing within the patterns, they do not discuss or simulate
mechanisms that permit such timing. Medina et al. (2000) provide a detailed
simulation of cerebellar circuitry that estimates temporal patterns as linear
combinations of the granule cell patterns. Repeatable patterns of granule
cell average firing rates (but not precise spike timing) are induced by vari-
ations in network properties within the cerebellar granule and molecular
layers. Yamazaki and Tanaka (2007b) demonstrate a spiking neural model
with random interconnectivity between granule and Golgi cells that leads to
a repeatable but random pattern of firing rates, and they show that a spike-
timing-dependent plasticity rule at the parallel fiber to Purkinje cell synapse
leads to the ability to learn time intervals in a delay conditioning task. Le
major difference from the work presented here is that these prior models
depend on Purkinje cells detecting (random or known) temporal patterns
of spike rates but not the spikes themselves (Rössert et al., 2015). Donc,
the temporal precision of such models is limited because determination of
a spike rate requires the generation of multiple spikes over time and cannot
respond at the millisecond level of precision. Par exemple, rate-dependent
models cannot generally model the ability of Purkinje cells to respond to
two different US timings (Jirenhed et al., 2017), whereas we have shown
that our model can yield both multiple responses as well as patterned re-
sponses at precise intervals (voir la figure 6).
Although the granule cell spike trains are repeatable, they appear to have
Poisson statistics. A simple rate code that looks at average firing but ignores
the temporal pattern would identify the average spatial pattern of activity
on the mossy fibers, and this could potentially confuse different conditioned
stimulus inputs. By responding to the precise pattern of spikes, the Purkinje
cell has the ability to recognize not only the pattern of the CS but the timing
aussi. Ainsi, the temporal pattern of spikes on the granule cells identifies
both the what and the when of the incoming input data stream.
The model presented here is not intended to be a complete model of
cerebellar function or the behavior of eyeblink delayed conditioning tasks.
Par exemple, known phenomena, including the effect of interstimulus inter-
val on learning, extinction of learned eyeblink responses, eligibility traces,
and changes in amplitude and reliability, are not modeled (Bareš et al.,
2019). The possibility that Purkinje cells have intrinsic time discrimina-
tion properties is not modeled (Johansson, Jirenhed, Rasmussen, Zucca, &
Hesslow, 2014). The time intervals chosen (100 msec CS with ISIs of 40 ou
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Timing in Cerebellum
2081
70 msec) are not intended to be representative of the values seen in eyeblink
conditioning; plutôt, they are intended as examples of high-precision tim-
ing responses that can be achieved by this mechanism. Our purpose is to
demonstrate the feasibility, precision, and capability of this previously un-
described mechanism without proposing that it is the sole explanation for
the complexity of observed learning behaviors.
This model depends critically on the presence of repeatable spike pat-
terns in response to repeatable inputs. Although we believe that individ-
ual cells do not have true random effects, there are sufficient numbers of
inputs to many cells in the central nervous system that truly repeatable
spike patterns may not occur. Despite this concern, there is emerging ev-
idence of specific instances in which repeatable patterns have been found.
Our results suggest that whenever this occurs, whether within or outside
the cerebellum, there is the potential ability to identify and respond to pre-
cise time intervals identified by the specific patterns of spikes that occur
over the population at each time. Donc, this mechanism has the poten-
tial to form a more widespread interval timer that could be used for syn-
chronization, sequence generation, recognition and matching of intervals in
sensory data, and production of rhythmic sequences. It is tempting to spec-
ulate that such a mechanism could be used to fill in the gaps between suc-
cessive peaks in the theta rhythms generated by thalamus that are thought
to provide a global synchronization signal. This would allow the relatively
low-frequency theta rhythm to provide a global clock that could be subdi-
vided locally to provide a high-resolution synchronization signal suitable
for sensory-motor responses of animals with large bodies and variable pe-
ripheral transmission delays.
Remerciements
Support for this project was provided by Riken AIP, ATR, and the USC De-
partment of Biomedical Engineering.
Les références
Alstrøm, P., Beierholm, U., Nielsen, C. D., Ryge, J., & Kiehn, Ô. (2002). Reliability
of neural encoding. Physica A: Statistical Mechanics and Its Applications, 314(1–4),
61–68.
Attwell, P.. J., Ivarsson, M., Millar, L., & Yeo, C. H. (2002). Cerebellar mechanisms
in eyeblink conditioning. Annals of the New York Academy of Sciences, 978(1), 79–
92.
Badura, UN., & De Zeeuw, C. je. (2017). Cerebellar granule cells: Dense, rich and evolv-
ing representations. Biologie actuelle, 27(11), R415–R418.
Bareš, M., Apps, R., Avanzino, L., Breska, UN., D’Angelo, E., Filip, P., . . . Lusk, N. UN.
(2019). Consensus paper: Decoding the contributions of the cerebellum as a time
machine. From neurons to clinical applications. Cerebellum, 18(2), 266–286.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2082
T. Sanger and M. Kawato
Beylin, UN. V., Gandhi, C. C., Wood, G. E., Talk, UN. C., Matzel, L. D., & Shors, T. J.. (2001).
The role of the hippocampus in trace conditioning: Temporal discontinuity or task
difficulty? Neurobiology of Learning and Memory, 76(3), 447–461.
Braitenberg, V. (1967). Is the cerebellar cortex a biological clock in the millisecond
range? In C. UN. Fox & R.. S. Snider (Éd.), Progress in brain research (Vol. 25, pp.
334–346). Amsterdam: Elsevier.
Buhusi, C. V., & Meck, W. H. (2005). What makes us tick? Functional and neural
mechanisms of interval timing. Nature Revues Neurosciences, 6(10), 755.
Buonomano, D. V. (2003). Timing of neural responses in cortical organotypic slices.
In Proceedings of the National Academy of Sciences, 100(8), 4897–4902.
D’Angelo, E. (2014). The organization of plasticity in the cerebellar cortex: Depuis
synapses to control. In N. Ramnani (Ed.), Progress in brain research (Vol. 210, pp.
31–58). Amsterdam: Elsevier.
Gerwig, M., Kolb, F., & Timmann, D. (2007). The involvement of the human cerebel-
lum in eyeblink conditioning. Cerebellum, 6(1), 38.
Halverson, H. E., Khilkevich, UN., & Mauk, M.. D. (2018). Cerebellar processing com-
mon to delay and trace eyelid conditioning. Journal des neurosciences, 38(33), 7221–
7236.
Hires, S. UN., Gutnisky, D. UN., Yu, J., O’Connor, D. H., & Svoboda, K. (2015). Low-
noise encoding of active touch by layer 4 in the somatosensory cortex. Elife, 4,
e06619.
Hopfield, J.. J., & Brody, C. D. (2001). What is a moment? Transient synchrony as a
collective mechanism for spatiotemporal integration. In Proceedings of the National
Académie des Sciences, 98(3), 1282–1287.
Ivry, R.. B., & Spencer, R.. M.. (2004). The neural representation of time. Current Opinion
in Neurobiology, 14(2), 225–232.
Izhikevich, E. M.. (2003). Simple model of spiking neurons. IEEE Transactions on Neu-
ral Networks, 14(6), 1569–1572.
Jirenhed, D.-A., Rasmussen, UN., Johansson, F., & Hesslow, G. (2017). Learned re-
sponse sequences in cerebellar Purkinje cells. In Proceedings of the National
Académie des Sciences, 114(23), 6127–6132.
Johansson, F., Jirenhed, D.-A., Rasmussen, UN., Zucca, R., & Hesslow, G. (2014). Mem-
ory trace and timing mechanism localized to cerebellar Purkinje cells. In Proceed-
ings of the National Academy of Sciences, 111(41), 14930–14934.
Karmarkar, U. R., & Buonomano, D. V. (2007). Timing in the absence of clocks: En-
coding time in neural network states. Neurone, 53(3), 427–438.
Kayser, C., Logothetis, N. K., & Panzeri, S. (2010). Millisecond encoding precision of
auditory cortex neurons. In Proceedings of the National Academy of Sciences, 107(39),
16976–16981.
Kim, J.. J., Clark, R.. E., & Thompson, R.. F. (1995). Hippocampectomy impairs the
memory of recently, but not remotely, acquired trace eyeblink conditioned re-
sponsors. Behavioral Neuroscience, 109(2), 195.
Kim, J.. J., & Thompson, R.. E. (1997). Cerebellar circuits and synaptic mechanisms
involved in classical eyeblink conditioning. Trends in Neurosciences, 20(4), 177–
181.
Kotani, S., Kawahara, S., & Kirino, Oui. (2002). Classical eyeblink conditioning in de-
cerebrate guinea pigs. European Journal of Neuroscience, 15(7), 1267–1270.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Timing in Cerebellum
2083
Kotani, S., Kawahara, S., & Kirino, Oui. (2003). Purkinje cell activity during learn-
ing a new timing in classical eyeblink conditioning. Brain Research, 994(2), 193–
202.
Kotani, S., Kawahara, S., & Kirino, Oui. (2006). Purkinje cell activity during classi-
cal eyeblink conditioning in decerebrate guinea pigs. Brain Research, 1068(1), 70–
81.
Mainen, Z. F., & Sejnowski, T. J.. (1995). Reliability of spike timing in neocortical neu-
rons. Science, 268(5216), 1503–1506.
Masquelier, T. (2013). Neural variability, or lack thereof. Frontiers in Computational
Neurosciences, 7, 7.
Medina, J.. F., Garcia, K. S., Nores, W. L., Taylor, N. M., & Mauk, M.. D. (2000). Tim-
ing mechanisms in the cerebellum: Testing predictions of a large-scale computer
simulation. Journal des neurosciences, 20(14), 5516–5525.
Miall, C. (1989). The storage of time intervals using oscillating neurons. Neural Com-
putation, 1(3), 359–371.
Molinari, M., Leggio, M.. G., & Thaut, M.. H. (2007). The cerebellum and neural net-
works for rhythmic sensorimotor synchronization in the human brain. Cerebel-
lum, 6(1), 18–23.
Narain, D., Remington, E. D., De Zeeuw, C. JE., & Jazayeri, M.. (2018). A cerebellar
mechanism for learning prior distributions of time intervals. Nature Communica-
tion, 9(1), 1–12.
Nolte, M., Reimann, M.. W., King, J.. G., Markram, H., & Muller, E. B. (2019). Cortical
reliability amid noise and chaos. Communications naturelles, 10(1), 1–15.
Panzeri, S., Ince, R.. UN., Diamond, M.. E., & Kayser, C. (2014). Reading spike timing
without a clock: Intrinsic decoding of spike trains. Philosophical Transactions of the
Royal Society B: Sciences biologiques, 369(1637), 20120467.
Petersen, R.. S., Panzeri, S., & Diamond, M.. E. (2001). Population coding of stimulus
location in rat somatosensory cortex. Neurone, 32(3), 503–514.
Petersen, R.. S., Panzeri, S., & Diamond, M.. E. (2002). Population coding in so-
matosensory cortex. Opinion actuelle en neurobiologie, 12(4), 441–447.
Raymond, J.. L., & Medina, J.. F. (2018). Computational principles of supervised learn-
ing in the cerebellum. Revue annuelle des neurosciences, 41, 233–253.
Roössert, C., Dean, P., & Porrill, J.. (2015). At the edge of chaos: How cerebellar granu-
lar layer network dynamics can provide the basis for temporal filters. PLOS Com-
putational Biology, 11(10).
Schwartze, M., Keller, P.. E., & Kotz, S. UN. (2016). Spontaneous, synchronized, et
corrective timing behavior in cerebellar lesion patients. Behavioural Brain Research,
312, 285–293.
Shmiel, T., Drori, R., Shmiel, O., Ben-Shaul, Y., Nadasdy, Z., Shemesh, M., . . . Abeles,
M.. (2005). Neurons of the cerebral cortex exhibit precise interspike timing in cor-
respondence to behavior. In Proceedings of the National Academy of Sciences, 102(51),
18655–18657.
Tripp, B., & Eliasmith, C. (2006). Neural populations can induce reliable postsynaptic
currents without observable spike rate changes or precise spike timing. Cérébral
Cortex, 17(8), 1830–1840.
Uchida, UN., McAllister, R., & Roy, R.. (2004). Consistency of nonlinear system re-
sponse to complex drive signals. Physical Review Letters, 93(24), 244102.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2084
T. Sanger and M. Kawato
Blanc, C., Bouwmeester, H., Power, J.. M., & Disterhoft, J.. F. (1999). Hippocampal
lesions prevent trace eyeblink conditioning in the freely moving rat. Behavioural
Brain Research, 99(2), 123–132.
Widrow, B., & Hoff, M.. E. (1960). Adaptive switching circuits (Technical Report). Stan-
ford University, Stanford Electronics Labs.
Yamazaki, T., & Tanaka, S. (2007un). The cerebellum as a liquid state machine. Neural
Networks, 20(3), 290–297.
Yamazaki, T., & Tanaka, S. (2007b). A spiking network model for passage-of-time rep-
resentation in the cerebellum. European Journal of Neuroscience, 26(8), 2279–2292.
Yamazaki, T., & Tanaka, S. (2009). Computational models of timing mechanisms in
the cerebellar granular layer. Cerebellum, 8(4), 423–432.
Received December 2, 2019; accepted June 23, 2020.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
2
1
1
2
0
6
9
1
8
6
5
3
9
2
n
e
c
o
_
un
_
0
1
3
1
8
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3