Anatomy of the Attraction Basins:
Breaking with the Intuition
Leticia Hernando
Intelligent Systems Group, Department of Computer Science and Artificial
Intelligence, University of the Basque Country UPV/EHU, 20018 San Sebastián, Espagne
leticia.hernando@ehu.eus
Alexander Mendiburu
Intelligent Systems Group, Department of Computer Architecture and Technology,
University of the Basque Country UPV/EHU, 20018 San Sebastián, Espagne
alexander.mendiburu@ehu.eus
Jose A. Lozano
Intelligent Systems Group, Department of Computer Science and Artificial
Intelligence, University of the Basque Country UPV/EHU, 20018 San Sebastián,
Spain Basque Center for Applied Mathematics (BCAM), 48009 Bilbao, Espagne
ja.lozano@ehu.eus
https://doi.org/10.1162/evco_a_00227
Abstrait
Solving combinatorial optimization problems efficiently requires the development of
algorithms that consider the specific properties of the problems. In this sense, locale
search algorithms are designed over a neighborhood structure that partially accounts
for these properties. Considering a neighborhood, the space is usually interpreted as a
natural landscape, with valleys and mountains. Under this perception, it is commonly
believed that, if maximizing, the solutions located in the slopes of the same mountain
belong to the same attraction basin, with the peaks of the mountains being the local
optima. Malheureusement, this is a widespread erroneous visualization of a combinatorial
landscape. Ainsi, our aim is to clarify this aspect, providing a detailed analysis of, d'abord,
the existence of plateaus where the local optima are involved, et deuxieme, the proper-
ties that define the topology of the attraction basins, picturing a reliable visualization of
the landscapes. Some of the features explored in this article have never been examined
before. Ainsi, new findings about the structure of the attraction basins are shown. Le
study is focused on instances of permutation-based combinatorial optimization prob-
lems considering the 2-exchange and the insert neighborhoods. As a consequence of
this work, we break away from the extended belief about the anatomy of attraction
basins.
Mots clés
Permutation-based combinatorial optimization problems,
basins, local search, landscape visualization.
local optima, attraction
1
Introduction
Local search algorithms have been one of the most developed metaheuristics used to
solve combinatorial optimization problems (COPs). These algorithms are defined to
work under a neighborhood structure built, on most occasions, by an operator. Là-
fore, their behavior will be conditioned by the properties that this neighborhood im-
poses on the search space, namely the landscape properties. Ainsi, many authors have
already noticed the importance of studying these landscape features in order to predict,
Manuscript received: 18 Novembre 2016; revised: 15 Janvier 2018; accepted: 13 Février 2018.
© 2018 Massachusetts Institute of Technology
Evolutionary Computation 27(3): 435–466
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
in advance, the performance of local search algorithms, or to use them in the develop-
ment of new proposals (Albrecht et al., 2008, 2010; Alyahya and Rowe, 2014; Caruana
and Mullin, 1999; Chicano et al., 2012; Fonlupt et al., 1999; Hernando et al., 2011; Mat-
tfeld and Bierwirth, 1999; Merz, 2004; Merz and Freisleben, 2001; Ochoa et al., 2011,
2014; Prügel-Bennett and Tayarani-Najaran, 2012; Reeves, 1999; Reeves and Aupetit-
Bélaidouni, 2004; Tayarani-Najaran and Prügel-Bennett, 2014, 2015un, 2015b; Tomassini
et coll., 2008; Verel, Ochoa et al., 2011; Watson, 2010; Moser et al., 2016). Some of these
works assume that the topology defined by the neighborhoods in the combinatorial
spaces is analogous to that found in the continuous domain. In the continuous space,
there always exists a ball of radius r > 0 and centered at each of the local optima which
is included in its attraction basin. This intuition has been transferred to the combinato-
rial space. Donc, it is commonly believed that local search algorithms draw paths
in a mountainous landscape, et, depending on the neighborhood, we could find a dif-
ferent number of mountains with different heights and sizes (Hernando et al., 2013b,
2016b; Mattfeld and Bierwirth, 1999; Tayarani-Najaran and Prügel-Bennett, 2014).
Although this thought is widespread across the literature and it has usually been ac-
cepted by the research community, other authors have started to notice a contradiction
with experimental results. Par exemple, in Tomassini et al. (2008), a representation of
the landscape as local optima networks was proposed, c'est, a graph where the nodes
were the local optima and the edges accounted for the probabilities of connecting the
different attraction basins. They showed that the number of edges was extremely large,
c'est, each of the attraction basins connects with almost all of the remaining attraction
basins (Daolio et al., 2010, 2014). This result led them to think of a different landscape pic-
ture than the smooth standard representation of 2D landscapes, where the basins of attraction
are visualized as real mountains. En fait, the first study that warned about this visualiza-
tion of the combinatorial landscape was published in 1999 (Fonlupt et al., 1999). In that
travail, the authors already stated that basins of attraction seem to be highly intertwined, giv-
ing a canyon-like structure to the landscape, rather than a crater-like structure. Nevertheless,
this finding was ignored by those works referring to it (Stützle, 2006; Preux and Talbi,
1999; Angel and Zissimopoulos, 2002; Bouziri et al., 2009). Par exemple, seven years
after that publication, the author in Stützle (2006) contradicted it: Intuitively, the search
landscape can be imagined as a (multi-dimensional) mountainous region with hills, craters, et
valleys. The problem is that even in more recent works, these kinds of declarations are
still found, as in Tayarani-Najaran and Prügel-Bennett (2015b) lequel, for minimization
problems, says: each local optimum has a bowl shape basin of attraction.
As can be observed, different intuitions of the combinatorial landscapes coexist in
the literature. The reason for this is the difficulty in understanding the topology of the
combinatorial spaces. In all these papers, the authors try to provide an interpretation
about the combinatorial landscape, giving insights according to the observed results
collected from landscape features analyses, but without a solid study of the topology of
the space under a specific neighborhood. Precisely, this is the objective of this article: à
examine topological features of the attraction basins of the local optima, in order to pro-
vide a reliable comprehension. Each local optimum has an attraction basin associated;
cependant, it is already known that many different neighboring local optima with the
same fitness could appear in a given instance. Dans ce cas, the local optima belong to a
plateau and we could consider that they share the attraction basin. Ainsi, the study of the
plateaus containing local optima is the starting point for the analysis of the topology of
the attraction basins (Hoos and Stützle, 2004; Watson, 2010). In the literature, the graphs
composed by neighboring solutions with the same fitness value, have been sometimes
known as neutral networks; and when these solutions are local optima, they are called
436
Evolutionary Computation Volume 27, Nombre 3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Anatomy of the Attraction Basins
the local optimum neutral networks. This concept of neutral network emerged in the
literature less than 10 years ago, and it has been analyzed for some problems: the NK
landscapes (Verel, Ochoa et al., 2011), the permutation flowshop problem (Marmion
et coll., 2011b; Daolio et al., 2014), or the traveling salesman problem (Ochoa and Veer-
apen, 2018). Malheureusement, the plateaus containing local optima are not detected by the
common local search algorithms, even though their behavior is highly conditioned by
the presence of these plateaus, as they are trapped inside them. Donc, in the last decade,
some authors identified this situation, and modified common local search algorithms,
such as the hill-climbing algorithm, in order to escape from the plateaus (Sutton et al.,
2010; Marmion et al., 2011un; Tayarani-Najaran and Prügel-Bennett, 2014, 2015b, 2015un;
Prügel-Bennett and Tayarani-Najaran, 2012; Humeau et al., 2013).
The final purpose of this article is, by studying topological features of the attraction
basins, to shed light on the different misunderstandings and contradictions that have
arisen in the last two decades in our research community. We focus on COPs based on
permutations, c'est, those where the search space is the set of permutations of size n.
Particularly, we work with the permutation flowshop scheduling problem (PFSP), le
linear ordering problem (LOP), and the quadratic assignment problem (QAP). D'abord, nous
examine the locally optimal solutions returned by a classical hill-climbing algorithm
with the aim of providing knowledge related to the plateaus. Secondly, we study those
features of the attraction basins that we consider essential in order to understand their
topology: the roundness of the attraction basins, the centrality of the local optima, et
the interior and frontier of the attraction basins. Although the frontier of the attraction
basins has already been explored in previous works (Fonlupt et al., 1999; Tomassini
et coll., 2008; Verel et al., 2008; Ochoa et al., 2014), in this article we take a step forward,
studying the evolution of the neighboring solutions in the same attraction basin with
the increase of the distance to the local optimum. To the best of our knowledge, ce
property, together with the roundness of the attraction basins and the centrality of the
local optima, has never been analyzed before. We include a deep discussion about the
obtained results, emphasizing the importance of the work presented in this article by
giving clues of how to use these discoveries in, Par exemple, the design of efficient local
search algorithms, and pointing out the potential uses these new findings could have
in the combinatorial optimization field. We also present two examples for the graphical
representation of the attraction basins.
The rest of the article is organized as follows. The concepts of local optimum,
plateau, and attraction basin are formally introduced in Section 2. The topological fea-
tures considered in the analysis are explained in Section 3. In Section 4, we carry out
the experiments in order to, d'abord, classify the solutions returned by the hill-climbing
algorithm in terms of plateaus; and secondly, examine the properties of the attraction
basins necessary to understand their topology. Some examples of the visualization of
the anatomy of the attraction basins are shown in Section 5. Enfin, in Section 6, le
conclusions and future work are presented.
2 Definitions
2.1 Neighborhood
A combinatorial optimization problem (COP) consists of finding the optimal solutions
de (from now on, maximizing) a function
F : (cid:2) −→ R
p (cid:3)−→ f (p ),
Evolutionary Computation Volume 27, Nombre 3
437
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
where the search space, (cid:2), is a finite or countable infinite set. Spécifiquement, we work with
instances of permutation-based COPs. Donc, from now on, (cid:2) is the set of permutations of
size n, thus, the search space is of size n!.
We focus on local search algorithms, which are one of the most developed meta-
heuristics used to solve COPs. These algorithms are defined to work under a neighbor-
hood structure. A neighborhood N in a search space (cid:2) is a mapping that assigns, to each
solution σ ∈ (cid:2), a non-empty set of neighboring solutions N (p ):
N : (cid:2) −→ P ((cid:2))\∅
p (cid:3)−→ N (p ),
where P ((cid:2)) is the powerset of (cid:2).
Adding the concept of neighborhood to the instance of a COP, we define a land-
scape as the triple (F, (cid:2), N ), where f is the objective function to optimize (Reidys and
Stadler, 2002). Two examples of the most commonly used neighborhoods in the space of
permutations are given by the 2-exchange and the insert operators (Taillard, 1990; Angel
and Zissimopoulos, 2002; Schiavinotto and Stützle, 2005; Chicano et al., 2012). Given a
permutation σ = (p (1) · · · σ (n)), one swap movement between the i-th and j -th items,
Sj
je (p ), is defined as follows:
je (p ) = Sj
Sj
je (p (1) · · · σ (i − 1)p (je)p (je + 1) · · · σ (j − 1)p (j )p (j + 1) · · · σ (n))
= (p (1) · · · σ (i − 1)p (j )p (je + 1) · · · σ (j − 1)p (je)p (j + 1) · · · σ (n)).
Ainsi, the 2-exchange neighborhood, NS, considers that two solutions are neighbors if one
is generated by swapping two elements of the other:
NS (p ) =
n−1(cid:2)
n(cid:2)
je = 1
j =i+1
Sj
je (p ).
Given a permutation σ = (p (1) · · · σ (n)), the insertion of the i-th item into the j -th po-
sition, for i > j , is defined as follows:
i>j (p ) = I j
I j
i>j (p (1) · · · σ (j − 1)p (j )p (j + 1) · · · σ (i − 1)p (je)p (je + 1) · · · σ (n))
= (p (1) · · · σ (j − 1)p (je)p (j )p (j + 1) · · · σ (i − 1)p (je + 1) · · · σ (n)),
while for i < j :
i
⎭
∪
i=2
j i+1
⎫
⎬
⎭ .
I j
je
Allowing for the equality in the above equation, we have the definition of relaxed
local optimum. In the literature, this is commonly known as local optimum. C'est, un
solution σ ∗ ∈ (cid:2) is a relaxed local optimum, or simply, local optimum if
F (σ ∗
).
F (σ ∗
We define a connecting path L(σ1, σr ) between a solution σ1
) ≥ f (p ), ∀σ ∈ N (σ ∗
).
σr ∈ (cid:2) as a sequence L(σ1, σr ) = (σ1, σ2, . . . , σr ) où
∈ (cid:2) and another solution
σ2
∈ N (σ1), σ3
∈ N (σ2), . . . , σr ∈ N (σr−1).
A plateau is a set of solutions P = {σ1, σ2, . . . , σr } that fulfills (Hoos and Stützle, 2004;
Watson, 2010; Sutton et al., 2010):
(je) ∀σi, σj ∈ P, F (σi ) = f (σj ).
(ii) ∀σi, σj ∈ P, ∃L(σi, σj ) ⊆ P.
(iii) P is maximal, c'est à dire., (cid:15) ∃Q complying (je) et (ii) such that P ⊂ Q.
A plateau P is a local optimal plateau or closed plateau (Hoos and Stützle, 2004; Watson,
le
2010; Sutton et al., 2010) if all the solutions in P are local optima. We denote by P ∗
local optimal plateaus. Ainsi, being P ∗
(cid:2)
a local optimal plateau:
{σ ∗} = P ∗.
σ ∗ ∈P∗
σ ∗ is loc opt.
The plateaus P that contain local optima as well as solutions that are not local optima
are usually known in the literature as benches (Watson, 2010) or as open plateaus (Hoos
and Stützle, 2004; Sutton et al., 2010). Donc, if P is an open plateau:
(cid:2)
σ ∗∈P
σ ∗is loc opt.
{σ ∗} ⊂ P.
Given a plateau P we will denote by O∗
in the plateau:
P the set composed by all the local optima found
O∗
P =
(cid:2)
{σ ∗}.
σ ∗∈P
σ ∗is loc opt.
Enfin, there are also kinds of plateaus that do not contain any local optimum, called
unoptimal plateaus.
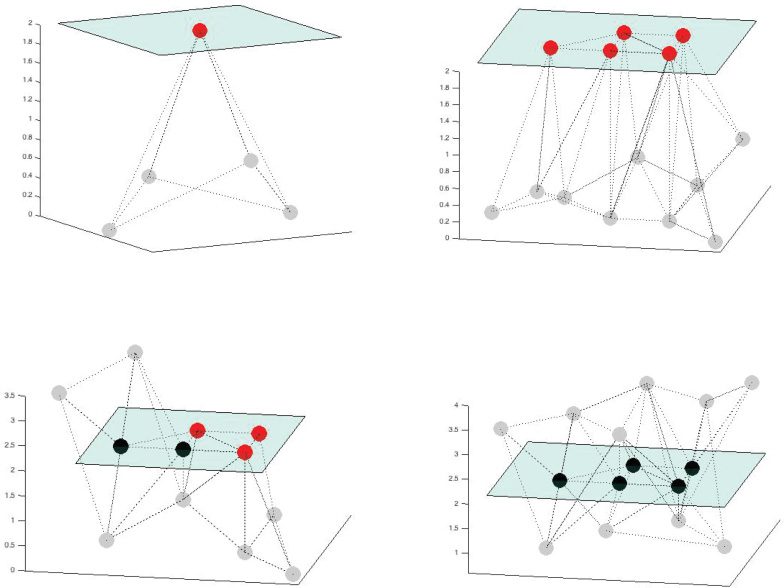
In Figure 1, we represent four different structures found in a figurative combinato-
rial space where the neighboring solutions are joined by an edge. These examples show
a strict local optimum 1(un), a local optimal plateau 1(b), an open plateau 1(c), and an
unoptimal plateau 1(d). The strict and relaxed local optima are in red. Donc, notice that all
the solutions that form the local optimal plateau (1b) are relaxed local optima. Cependant,
in an open plateau (1c), we do find solutions that are not local optima (in black), et
also relaxed local optima. In both cases, 1(b) et 1(c), the red points form the set O∗
P. . Dans
the unoptimal plateaus 1(d), no local optima are found.
It is very important to note that all local optimum σ ∗
will necessarily belong to one,
and only one, of the three following cases:
Evolutionary Computation Volume 27, Nombre 3
439
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
Chiffre 1: Representation of a strict local optimum (un), a local optimal plateau (b), un
open plateau (c), and an unoptimal plateau (d) in a figurative combinatorial landscape
when considering a maximization problem. The nodes represent the solutions of the
search space and they are connected according to a neighborhood. The height indicates
the objective function values. The solutions in red are the local optima, the nonoptimal
solutions that belong to a plateau are in black, while the rest of the solutions are in gray.
1. Be a strict local optimum.
2. Belong to a local optimal plateau.
3. Belong to an open plateau.
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2.3 Attraction Basin of a Local Optimum
, B(σ ∗
The attraction basin of a local optimum σ ∗
), is composed of all the solutions which
lead to the local optimum σ ∗, after applying a greedy local search algorithm to them. Nous
denote by H the operator that associates, to each solution σ , the local optimum obtained
after applying the algorithm. Different definitions could be given for the attraction basin
depending on the nature of the operator H (voir, Par exemple, Verel, Daolio et al., 2011
and Watson, 2010 for stochastic operators). We work with a deterministic H; donc, le
attraction basin of a local optimum, B(σ ∗
), is the set that can be defined in the following
chemin:
(cid:9)
(cid:10)
B(σ ∗
) =
σ ∈ (cid:2) | H(p ) = σ ∗
.
440
Evolutionary Computation Volume 27, Nombre 3
Anatomy of the Attraction Basins
It is also important to define the attraction basin of a plateau. We define this set as
the union of the attraction basins of all the local optima that belong to such a plateau
(Klemm et al., 2014):
(cid:2)
B(P. ) =
B(σ ∗
).
σ ∗∈O∗
P.
Bien sûr, we cannot refer to an attraction basin of an unoptimal plateau, as it does not
contain any local optimum.
This definition of attraction basin of a plateau is consistent with the definitions
found in the literature (Verel, Ochoa et al., 2011; Daolio et al., 2014). In these works,
the plateaus formed by local optima were defined as local optima neutral networks
(LONN). The attraction basin of a LONN was defined as the set of all the solutions
of the search space that belong to the attraction basin of any of the local optima that
compose the LONN.
When two neighboring solutions belong to different attraction basins, it is said that
2 ) as neighboring
the attraction basins are neighbors; c'est, we define B(σ ∗
attraction basins if
1 ) et B(σ ∗
∃σ ∈ B(σ ∗
1 ) and ∃σ (cid:8) ∈ B(σ ∗
2 ) such that σ (cid:8) ∈ N (p ).
In the same way, the attraction basins of two different plateaus, P.
si
1 and P
2, are neighbors
∃σ ∈ B(P.
1) and ∃σ (cid:8) ∈ B(P.
2) such that σ (cid:8) ∈ N (p ).
3 Topology of the Attraction Basins
The attraction basin of a local optimum depends on the algorithm used. En outre,
when using a deterministic algorithm, an important property is derived from the con-
cept of attraction basins of the local optima: they define a partition of (cid:2).
The distance d defined by both the swap and the insert neighborhoods is a metric,
c'est, ∀σ1, σ2, σ3
∈ (cid:2):
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
= σ2,
(je) d(σ1, σ2) = 0 ⇐⇒ σ1
(ii) d(σ1, σ2) = d(σ2, σ1),
(iii) d(σ1, σ3) ≤ d(σ1, σ2) + d(σ2, σ3).
Now, we can study topological features of the attraction basins. Particularly, we focus on
three properties: the roundness of the attraction basins, the centrality of the local optima
within the attraction basins, and the interior and frontier of the attraction basins.
3.1 Roundness of the Attraction Basins
We define the roundness of the attraction basins using the concept of closed ball. A closed
ball Br (π ) of radius r > 0 and centered at a permutation π ∈ (cid:2) est:
Br (π ) = {σ ∈ (cid:2)|d(p, π ) ≤ r}.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Considering the closed ball Br ∗ (σ ∗
d(σi, σ ∗
radius r ∗ = max
σi ∈B(σ ∗ )
) centered at the local optimum σ ∗
and with a
), we say that an attraction basin B(σ ∗
) is round if
B(σ ∗
) = Br ∗ (σ ∗
).
Evolutionary Computation Volume 27, Nombre 3
441
L. Hernando, UN. Mendiburu, and J. UN. Lozano
De même, we define a closed ball Br (P. ) of radius r > 0 and centered at a plateau P
comme:
where dmin(p, P. ) = min
σ ∗∈O∗
P.
Br (P. ) = {σ ∈ (cid:2)|dmin(p, P. ) ≤ r},
d(p, σ ∗
).
Dans ce cas, we consider that the attraction basin of a plateau B(P. ) is round if
B(P. ) = Br ∗ (P. ),
where r ∗ = max
σi ∈B(P. )
dmin(σi, P. ).
3.2 Centrality of the Local Optima
Let us suppose σ ∗
), and let us consider the measure
Dσ ∗ (p ) as the sum of the distances between σ and the rest of the permutations in B(σ ∗
):
(cid:11)
to be a local optimum and σ ∈ B(σ ∗
Dσ ∗ (p ) =
d(σi, p ).
σi ∈B(σ ∗ )
If
σ ∗ = arg min
σi ∈B(σ ∗ )
Dσ ∗ (σi ),
then we say that the local optimum is centered within the attraction basin.
In the case of having a set of local optima belonging to a plateau P, we calculate the
measure D as follows.
If σ ∈ B(P. ) and σ /∈ O∗
P.
DP (p ) = min
σi ∈O∗
P.
d(σi, p ) +
(cid:11)
∈B(P. )
σi
∗
σi /∈O
P.
d(σi, p ),
et
DP (O∗
P. ) =
(cid:11)
∈B(P. )
σi
∗
σi /∈O
P.
min
σj ∈O∗
P.
d(σj , σi ).
As in the previous case, we say that the plateau is centered within the attraction
basin if
∀σ ∈ B(P. ), σ /∈ O∗
P. ,
DP (O∗
P. ) < DP (σ ).
3.3
Interior and Frontier of the Attraction Basins
We differentiate the interior and the frontier of an attraction basin set. The interior of the
attraction basin of a local optimum σ ∗
)), is the subset composed of all the solutions
in B(σ ∗
) which also have all their neighbors in B(σ ∗
, I (B(σ ∗
):
I (B(σ ∗
)) = {σ | σ ∈ B(σ ∗
) ∧ N (σ ) ⊂ B(σ ∗
)}.
, F (B(σ ∗
So, the frontier of the attraction basin of a local optimum σ ∗
)), is composed of all
the solutions in the attraction basin B(σ ∗) that are not located in its interior, F (B(σ ∗)) =
B(σ ∗
) \ I (B(σ ∗
)):
F (B(σ ∗
)}.
Similarly, we define the interior of the attraction basin of a plateau P,
I (B(P )) = {σ | σ ∈ B(P ) ∧ N (σ ) ⊂ B(P )},
)) = {σ | σ ∈ B(σ ∗
) ∧ N (σ ) (cid:15)⊂ B(σ ∗
and the frontier of the attraction basin of a plateau P,
F (B(P )) = {σ | σ ∈ B(P ) ∧ N (σ ) (cid:15)⊂ B(P )}.
442
Evolutionary Computation Volume 27, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
a
_
0
0
2
2
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Anatomy of the Attraction Basins
4
Experiments
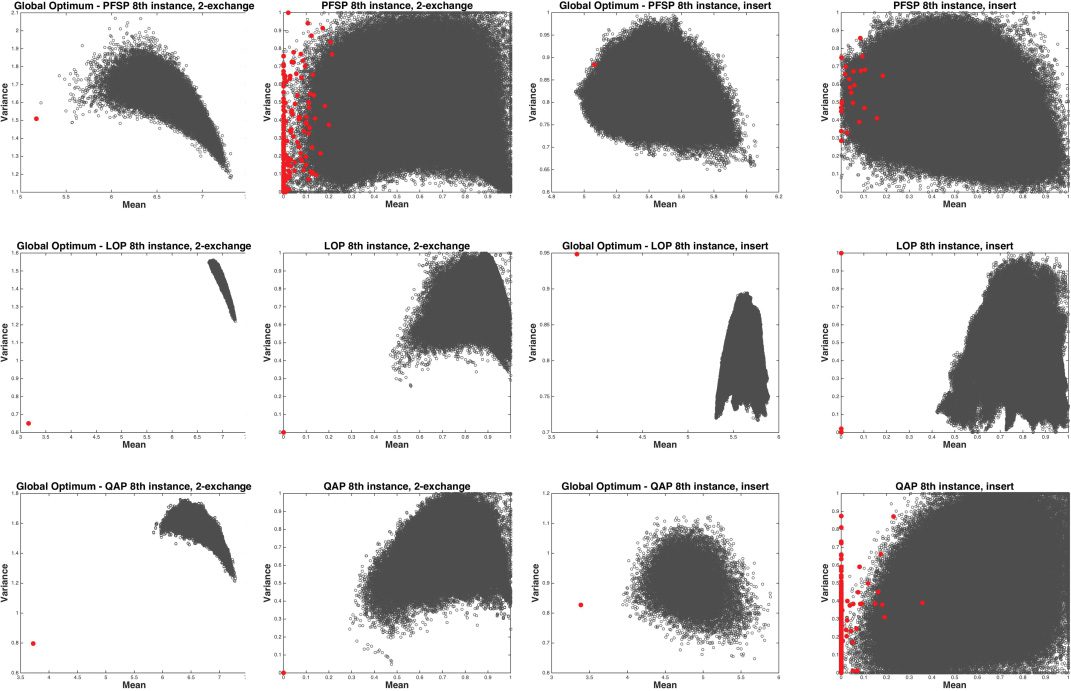
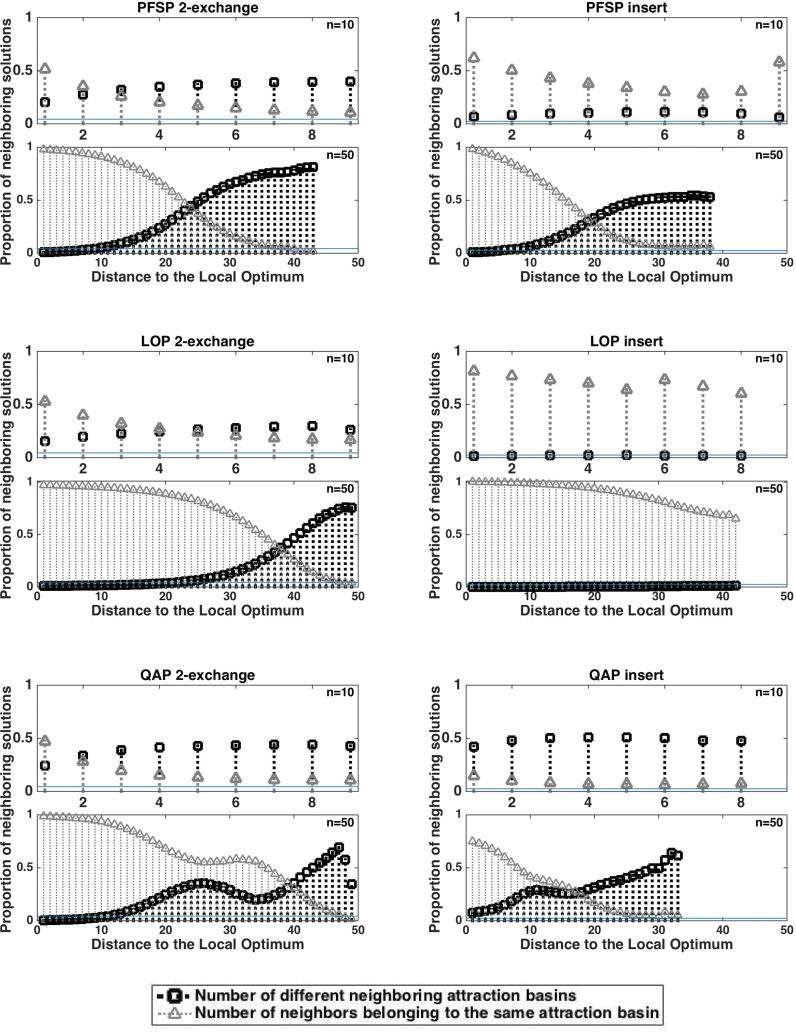
The topological features of the attraction basins described in Section 3 are analyzed in
order to connect the observed results with a comprehension of the structure of the at-
traction basins. This will help us to contradict the commonly found extrapolation from
the continuous domain to the combinatorial space, which is responsible for a visualiza-
tion of the landscape full of mountains and valleys: the assumption that a ball of radius
r > 0 and centered at the local optima is included in their attraction basins. For this pur-
pose, we focus on permutation-based problems, and divide our analysis in two parts:
the study of the type of solution returned by a classical deterministic hill-climbing algo-
rithm in terms of plateaus, and the exploration of the topology of the attraction basins
regarding the roundness, the centrality of the local optima and the interior and frontier
of the attraction basins. D'abord, the experimental design is detailed, and then the results
are shown, followed by a thorough discussion relating them to the topology defined.
4.1
Experimental Design
We work with instances of the permutation flowshop scheduling problem (PFSP), le
linear ordering problem (LOP), and the quadratic assignment problem (QAP), lequel
are known to be NP-hard problems (Garey et al., 1976; Mishra and Sikdar, 2004; Sahni
and Gonzalez, 1976). The flowshop scheduling problem can be stated as follows: là
are b jobs to be scheduled in c machines. A job consists of c operations and the j -th oper-
ation of each job must be processed on machine j for a specific processing time without
interruption. We consider that the jobs are processed in the same order on different ma-
chines. Generally, the objective of the PFSP is to find the order in which the jobs have to
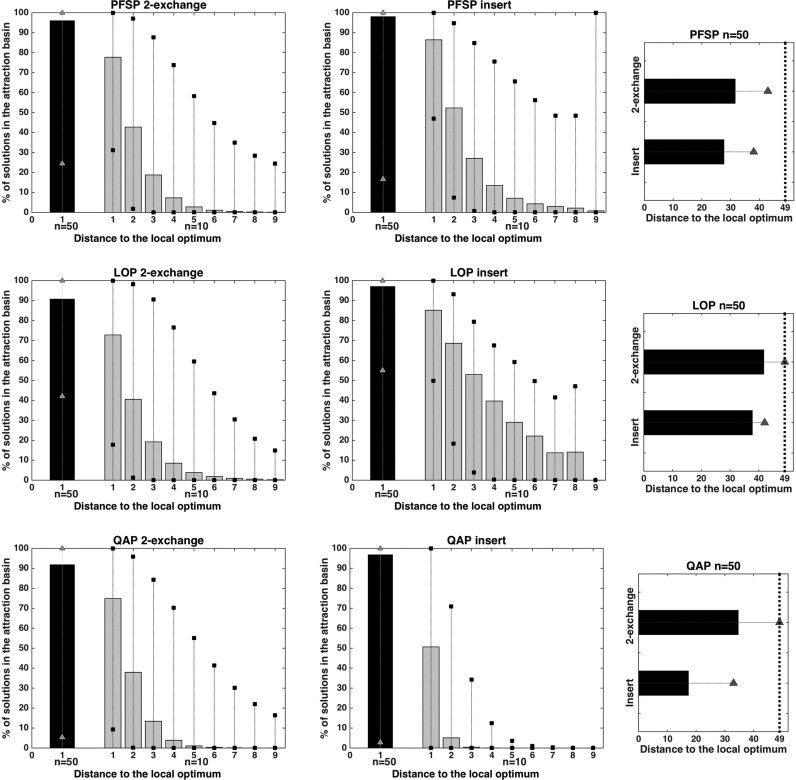
be scheduled on the machines, minimizing the total flow time.
In the LOP, given a matrix B = [bij ]n×n of numerical entries, we have to find a si-
multaneous permutation of the rows and columns of B, such that the sum of the entries
above the main diagonal is maximized (or equivalently, the sum of the entries below
the main diagonal is minimized).
The QAP consists of allocating a set of facilities to a set of locations, with a cost
function associated to the distance and the flow between the facilities. The objective is
to assign each facility to a location such that the total cost is minimized. Spécifiquement, nous
are given two n × n input matrices with real values H = [hij ] and D = [dkl], where hij is
the flow between facility i and facility j , and dkl is the distance between location k and
location l. As PFSP and QAP are minimization problems, they have been transformed
into maximization problems by simply reversing the sign of the cost function.
The solutions of these three problems are coded as permutations of size n, so the
search space is of size n!. We use a deterministic best-improvement local search (voir
Algorithm 1) to solve the instances. It is important to notice that the neighbors are eval-
uated in a specific order, so that, in the case of two neighbors having the same function
valeur, the algorithm will always choose the first encountered. Spécifiquement, for the 2-
exchange, the neighbors are explored swapping the items i and j in ascending order:
the i-th item increases from 1 to n − 1 et, for each value of i, the j -th item goes from
je + 1 to n. For the insert, the neighborhood is evaluated taking the i-th item and insert-
ing it in the j -th position, also in order, with i increasing from 1 to n, and for each value
of i, the j -th item also increases from 1 to n, always considering j (cid:15)= i.
The instances used in the experiments have been taken from three well-known
benchmarks. The PFSP instances were obtained from the Taillard’s benchmark (Tail-
lard, 1993), the LOP instances from the xLOLIB benchmark (Schiavinotto and Stützle,
2005), and the QAP instances from the QAPLIB (Burkard et al., 1997). D'abord, we choose 8
Evolutionary Computation Volume 27, Nombre 3
443
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
instances for each problem (numbered from 1 à 8) for which the number of local optima
and their attraction basins are exhaustively computed according to the 2-exchange (NS)
and the insert (NI ) neighborhoods. C'est, Algorithm 1 is applied to each solution of the
search space, for both neighborhoods separately. As this implies a high computational
coût, the original instances were reduced in order to work with permutations of size
n = 10, so that the experimentation is computationally affordable: |(cid:2)| = 10! ≈ 3.63 · 106.
In the case of the PFSP, we reduce the instances considering 10 jobs and 5 machines.
Secondly, in order to check if those properties observed in the small instances are also
shared by higher dimensions, we work with 4 original instances of each problem of size
n = 50 (50 jobs and 10 machines in the case of the PFSP instances). For these instances,
Algorithm 1 is applied to a sample of initial solutions of size M = 500. Ainsi, a sample of
local optima is obtained. In each run of the algorithm, a sample of solutions belonging to
the attraction basin of each local optimum is also encountered: the initial solution plus
all the solutions found in the path to the local optimum. We analyze the different fea-
tures of the attraction basins of this sample of local optima. Bien sûr, we do not aim to
guarantee that all the different landscapes have the same properties as those observed
in this article.
En résumé, we use 8 + 4 instances for each problem, taking into account the
2-exchange and the insert neighborhoods, c'est, a total of 72 different landscapes
are analyzed. The specific instances used in the experimentation are available in the
website.1
Local Optima and Local Optimal Plateaus
4.2
Algorithm 1 returns a local optimum σ ∗ ∈ (cid:2) such that, by definition, F (σ ∗
F (p ), ∀σ ∈ N (σ ∗
sarily match one, and only one, of the three following options:
). As previously mentioned, this local optimal solution σ ∗
) ≥
will neces-
(je) Be a strict local optimum.
(ii) Belong to a local optimal plateau.
(iii) Belong to an open plateau.
Papers about neutral networks can be found for NK landscapes (Verel, Ochoa et al.,
2011) and PFSP (Marmion et al., 2011b, and Daolio et al., 2014). To the best of our knowl-
bord, there are no analyses about the neutrality carried out for the LOP and the QAP. Dans
the case of PFSP, while Marmion et al. (2011b) and Daolio et al. (2014) used makespan
1http://www.sc.ehu.es/ccwbayes/members/leticia/AnatomyOfAB/Instances.html
444
Evolutionary Computation Volume 27, Nombre 3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Anatomy of the Attraction Basins
as the objective function, our approach focuses on the total flow time. En fait, dans le
literature, the only work analyzing the neutrality for the total flow time is Hernando
et autres. (2017). De plus, in this article, we explicitly present the number and sizes of the
plateaus, distinguishing between the local optimal and the open plateaus, which has
not been reflected in any previous work. Our aim, in this section, is to explore those
plateaus formed by local optima, as a first step in our topological analysis of the basins
of attraction.
We report in Table 1, for the different instances of the problems and the different
neighborhoods, in the columns labeled LO, the number of different solutions output by
Algorithm 1. In the case of the small instances (n = 10), this is the total number of local
optima, while for the larger instances (n = 50), it reflects the number of different solu-
tions obtained after applying Algorithm 1 to the sample of 500 random initial solutions.
Alors, we show in the strict LO, LO plateau, and open plateau columns, (je) the number of
strict local optima, (ii) the number of local optimal plateaus, et (iii) the number of
open plateaus, respectivement. Notice that the unoptimal plateaus are not included in this
analysis because no local optimum belongs to them. These plateaus of the smaller, comme
well as the larger, instances have been calculated starting with each of the observed lo-
cal optima and exploring recursively the neighboring solutions until no more solutions
with the same fitness are found. Notice that the sum of the strict LO, LO plateau, et
open plateau columns is not necessarily the same as the number of LO (more than one
LO can belong to the same plateau). En fait, we add, in parentheses, the average and the
standard deviation of the number of solutions forming the plateaus. Remember that
the local optimal plateaus are composed only of local optima, while the open plateaus
include other nonoptimal solutions. We emphasize in bold, for the smaller instances,
whether the global optimum is a strict local optimum or whether it belongs to a local
optimal plateau. Obviously, the global optima can never belong to an open plateau.
Cependant, in the case of multiple global optima, some of them could be strict local op-
tima while others could form one or more plateaus, meaning that the global optima of
the instance belong to two different classes of local optima: (je) et (ii).
Regarding the results, very different values are obtained for instances of the same
problem. En général, the presence of plateaus is remarkable. The average size of all the
plateaus found in the PFSP instances, under both neighborhoods, is around 2 (with a
low standard deviation). In the smaller LOP instances, for the 2-exchange neighbor-
hood, the number of plateaus is higher than for the insert neighborhood. For the larger
LOP instances, the number of plateaus is high and their size is considerably large. La plupart
of the QAP smaller instances contain a large number of plateaus under both neighbor-
hoods, mais, in general, for the larger instances, except for the Wil50 instance, the pres-
ence of plateaus is small. Enfin, for all the PFSP instances the global optima are strict
local optima. Cependant, in LOP and QAP, strict global optima as well as global optimal
plateaus are found, according to the instance.
En général, the presence of local optima belonging to plateaus is a tangible aspect of
permutation-based combinatorial problems, ou, at least, one should not work with these
problems assuming that they do not exist. One of the main conclusions derived from this
study is that, usually, Algorithm 1 gets trapped inside the plateaus. Although we find
instances with plateaus composed by just two solutions, Algorithm 1 is not designed
to detect and escape from them. Bien sûr, we cannot overlook the fact that some au-
thors have already studied the number and extension of the plateaus. In Marmion et al.
(2011b), the authors concluded that plateaus with local optima are numerous and large
for the PFSP. Cependant, the objective function to minimize considered in that work was
Evolutionary Computation Volume 27, Nombre 3
445
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
t
n
e
r
e
F
F
je
d
e
h
t
,
s
d
o
o
h
r
o
b
h
g
je
e
n
t
r
e
s
n
je
e
h
t
d
n
un
e
g
n
un
h
c
X
e
–
2
e
h
t
g
n
je
r
e
d
je
s
n
o
c
P.
UN
Q
e
h
t
d
n
un
P.,
Ô
L
e
h
t
P.,
S
F
P.
e
h
t
F
o
e
c
n
un
t
s
n
je
h
c
un
e
r
o
F
:
1
e
je
b
un
T
,
)
Ô
L
t
c
je
r
t
s
(
un
m
je
t
p
o
je
un
c
o
je
t
c
je
r
t
s
F
o
r
e
b
m
toi
n
e
h
t
,
s
n
o
je
t
toi
je
o
s
e
s
e
h
t
m
o
r
F
.
d
e
t
r
o
p
e
r
s
je
)
Ô
L
(
s
p
o
t
s
1
m
h
t
je
r
o
g
je
UN
e
h
t
h
c
je
h
w
n
je
s
n
o
je
t
toi
je
o
s
F
o
r
e
b
m
toi
n
D
Ô
Ô
H
R.
Ô
B
H
G
je
E
N
T
R.
E
S
N
je
D
Ô
Ô
H
R.
Ô
B
H
G
je
E
N
E
G
N
UN
H
C
X
E
–
2
/
e
g
un
r
e
v
un
e
h
t
s
e
s
e
h
t
n
e
r
un
p
n
je
g
n
je
t
un
c
je
d
n
je
,
d
e
je
je
un
t
e
d
e
r
un
)
toi
un
e
t
un
je
p
n
e
p
o
(
s
toi
un
e
t
un
je
p
n
e
p
o
d
n
un
,
)
toi
un
e
t
un
je
p
Ô
L
(
s
toi
un
e
t
un
je
p
je
un
m
je
t
p
o
je
un
c
o
je
F
o
r
e
b
m
toi
n
e
h
t
je
un
b
o
je
g
e
h
t
e
r
e
h
w
s
n
o
je
t
toi
je
o
s
F
o
s
e
p
oui
t
e
h
t
,
s
e
c
n
un
t
s
n
je
r
e
je
je
un
m
s
e
h
t
r
o
F
.
s
toi
un
e
t
un
je
p
e
h
t
g
n
je
m
r
o
F
s
n
o
je
t
toi
je
o
s
F
o
r
e
b
m
toi
n
e
h
t
F
o
n
o
je
t
un
je
v
e
d
d
r
un
d
n
un
t
s
.
d
je
o
b
n
je
d
e
z
je
s
un
h
p
m
e
e
r
un
d
n
toi
o
F
e
r
un
un
m
je
t
p
o
.
)
0
0
0
/
0
0
2
(
1
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
2
(
2
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
2
(
1
.
.
)
0
0
0
/
0
0
0
(
0
.
toi
un
e
t
un
je
p
n
e
p
o
toi
un
e
t
un
je
p
Ô
L
.
)
0
0
0
/
0
0
2
(
1
.
.
)
0
0
0
/
0
0
2
(
2
.
.
)
2
1
2
/
0
5
3
(
2
.
.
)
0
0
0
/
0
0
2
(
1
.
.
)
0
0
0
/
0
0
2
(
3
.
.
)
0
0
0
/
0
0
2
(
1
.
.
)
0
0
0
/
0
0
2
(
1
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
4
7
0
/
0
4
2
(
5
1
.
.
)
6
4
0
/
3
1
2
(
3
2
.
.
)
7
9
0
/
3
3
2
(
1
2
.
.
)
9
3
1
/
0
5
2
(
0
2
.
.
)
2
5
0
/
0
2
2
(
1
2
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
4
(
1
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
2
(
2
2
.
.
)
3
4
0
/
9
0
2
(
2
2
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
1
3
0
/
0
1
2
(
2
2
.
.
)
0
0
0
/
0
0
3
(
.
.
)
0
0
0
/
0
0
2
(
.
.
)
0
0
1
/
0
0
3
(
.
1
1
3
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
0
0
/
0
0
5
1
(
.
1
.
)
4
9
3
0
1
2
/
0
0
6
9
9
2
(
4
.
.
)
0
0
0
/
0
0
5
3
7
(
1
.
.
)
0
0
5
4
6
/
6
3
2
2
5
4
1
(
3
0
4
.
.
)
4
8
6
2
4
/
1
9
4
6
8
(
2
2
.
.
)
2
4
2
4
1
/
3
9
9
5
5
(
3
1
1
.
.
)
4
5
5
7
6
/
8
9
7
5
6
1
8
(
5
9
3
.
.
)
3
3
8
9
5
/
6
3
.
2
2
5
8
(
7
9
.
)
5
5
6
9
2
/
8
1
.
2
9
6
(
5
4
4
.
)
3
8
3
0
1
/
4
4
.
2
1
3
(
7
8
2
.
)
7
3
4
5
6
/
2
1
.
0
5
4
4
3
(
5
0
1
t
c
je
r
t
s
Ô
L
2
7
6
6
9
7
2
9
3
3
2
2
6
4
7
5
4
8
5
4
7
5
4
1
1
0
0
0
1
0
0
0
0
0
0
Ô
L
toi
un
e
t
un
je
p
n
e
p
o
toi
un
e
t
un
je
p
Ô
L
t
c
je
r
t
s
Ô
L
Ô
L
3
7
8
8
6
1
1
3
3
4
4
2
0
0
5
0
0
5
0
0
5
0
0
5
1
1
3
2
9
4
)
0
0
.
0
/
0
0
.
0
(
0
)
0
0
.
0
/
0
0
.
2
(
2
)
0
5
.
0
/
5
2
.
2
(
4
)
9
2
.
0
/
8
0
.
2
(
2
1
)
2
8
.
0
/
9
2
.
2
(
4
1
)
0
0
.
0
/
0
0
.
2
(
1
1
)
9
1
.
1
/
1
7
.
2
(
1
2
)
0
5
.
0
/
6
1
.
2
(
9
1
)
0
5
.
0
/
6
1
.
2
(
9
1
)
5
7
.
0
/
6
2
.
2
(
3
2
)
0
0
.
0
/
0
0
.
2
(
1
2
)
9
7
.
0
/
9
3
.
2
(
8
2
)
0
0
.
0
/
0
0
.
0
(
0
)
0
0
.
0
/
0
0
.
2
(
4
)
4
8
.
7
/
8
9
.
7
(
4
4
)
4
5
.
2
/
7
7
.
4
(
1
3
)
0
9
.
4
/
9
9
.
6
(
9
7
)
3
1
.
9
/
1
6
.
0
1
(
9
4
5
1
)
6
3
.
7
9
/
9
7
.
6
7
(
4
3
)
0
0
.
0
/
0
0
0
(
.
)
0
0
.
0
/
0
0
0
(
.
)
0
0
.
0
/
0
0
.
2
(
)
0
0
.
0
/
0
0
.
2
(
)
0
0
.
0
/
0
0
.
2
(
)
0
0
.
0
/
0
0
.
2
(
)
0
0
.
0
/
0
0
.
2
(
)
0
0
.
0
/
0
0
.
2
(
)
0
0
.
0
/
0
0
.
2
(
)
7
1
.
0
/
3
0
.
2
(
)
0
0
.
0
/
0
0
.
2
(
)
3
6
.
0
/
3
2
.
2
(
)
0
0
.
0
/
0
0
.
0
(
)
0
0
.
0
/
0
0
.
0
(
0
0
9
2
6
1
4
1
7
2
4
3
7
1
0
3
0
0
)
0
5
.
0
/
5
2
.
2
(
4
)
4
0
.
1
/
5
7
.
2
(
8
)
3
2
.
1
/
9
8
.
2
(
8
2
)
5
0
.
1
/
1
1
.
3
(
9
)
0
0
.
0
/
0
0
.
5
1
(
2
9
9
3
2
)
5
1
.
1
2
6
0
1
/
1
4
.
5
0
8
3
1
(
2
2
)
0
0
.
0
/
0
0
.
5
3
7
(
1
0
0
5
7
6
4
0
0
5
0
0
4
)
7
7
.
2
0
1
/
4
0
.
0
2
6
8
8
(
3
6
3
)
4
6
.
9
8
/
4
0
.
9
7
5
3
1
(
7
3
1
)
3
1
.
5
2
4
/
6
3
.
9
7
9
9
1
(
9
9
2
)
2
8
.
9
4
2
/
9
7
.
0
4
5
2
2
(
1
0
2
)
9
9
.
7
9
2
/
1
2
.
3
0
0
0
5
(
5
1
3
)
3
3
.
4
0
3
/
1
0
.
8
7
9
5
4
(
5
8
1
)
0
2
.
1
5
3
/
9
7
.
5
6
2
5
6
(
5
2
3
)
4
7
.
5
4
2
/
7
5
.
1
6
5
4
9
(
5
7
1
1
1
2
2
6
3
7
6
1
9
5
4
1
4
9
1
4
7
2
4
5
4
3
4
4
2
6
4
2
4
4
3
1
0
2
1
5
2
2
9
0
0
0
0
0
0
1
1
4
2
8
5
3
8
7
1
1
8
5
1
5
2
2
5
9
2
0
0
5
0
0
5
0
0
5
0
0
5
3
1
4
2
2
1
1
9
2
1
1
7
1
6
2
2
5
3
7
0
0
5
0
0
5
0
0
5
0
0
5
2
5
6
8
1
2
3
4
5
6
7
8
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
0
0
.
0
1
_
0
5
je
un
t
1
0
.
0
1
_
0
5
je
un
t
2
0
.
0
1
_
0
5
je
un
t
3
0
.
0
1
_
0
5
je
un
t
1
2
3
4
5
6
7
8
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
c
e
e
5
7
e
b
–
N
p
n
5
7
e
b
–
N
je
o
5
7
e
b
–
N
t
o
t
5
7
e
b
–
N
P.
S
F
P.
P.
Ô
L
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
446
Evolutionary Computation Volume 27, Nombre 3
D
Ô
Ô
H
R.
Ô
B
H
G
je
E
N
T
R.
E
S
N
je
D
Ô
Ô
H
R.
Ô
B
H
G
je
E
N
E
G
N
UN
H
C
X
E
–
2
.
d
e
toi
n
je
t
n
o
C
:
1
e
je
b
un
T
Anatomy of the Attraction Basins
.
)
0
0
0
/
0
0
2
(
1
.
.
)
0
0
0
/
0
0
2
(
2
.
.
)
0
0
0
/
0
0
0
(
0
.
.
)
0
2
4
/
9
9
3
(
.
6
1
1
.
)
6
6
8
3
1
2
/
1
0
8
0
2
(
6
6
6
2
.
.
)
3
8
3
1
1
4
1
/
7
3
9
4
1
6
(
.
2
4
7
1
.
)
6
5
8
4
5
8
8
/
7
0
1
3
8
0
9
(
.
0
8
5
3
.
)
0
0
0
/
0
0
2
(
9
.
.
)
0
0
0
/
0
0
0
(
0
.
)
0
0
.
0
/
0
0
2
(
6
2
.
.
)
8
4
3
3
1
1
1
/
4
0
2
4
2
4
(
.
2
7
9
.
)
7
2
5
1
7
1
/
1
5
4
8
1
(
4
3
3
1
.
.
)
0
0
0
/
0
0
.
0
(
0
.
)
0
0
0
/
0
0
.
2
(
2
3
.
)
0
0
0
/
0
0
.
2
(
6
.
)
3
4
0
/
4
1
.
2
(
9
9
.
)
8
4
0
/
2
1
.
2
(
4
3
2
.
)
7
3
0
/
9
0
.
2
(
3
6
8
.
)
0
1
1
/
0
5
.
2
(
8
5
8
1
.
)
6
4
1
/
4
7
.
2
(
0
6
0
1
.
)
0
0
0
/
0
0
.
0
(
0
.
)
0
0
0
/
0
0
.
0
(
0
.
)
0
0
0
/
0
0
.
0
(
0
.
)
4
0
1
/
7
4
.
2
(
0
2
1
toi
un
e
t
un
je
p
n
e
p
o
toi
un
e
t
un
je
p
Ô
L
t
c
je
r
t
s
Ô
L
3
1
7
2
4
7
3
4
5
2
7
1
8
8
3
3
2
1
4
6
1
0
9
6
0
1
0
6
5
1
0
9
9
4
8
9
4
0
0
5
4
6
2
Ô
L
3
1
7
2
4
6
4
4
5
7
9
2
2
5
3
5
3
3
4
6
1
4
9
3
5
1
2
1
1
9
0
6
3
2
1
0
0
5
0
0
5
0
0
5
0
0
5
)
0
0
.
0
/
0
0
.
0
(
0
)
0
0
.
0
/
0
0
.
2
(
4
)
0
0
.
0
/
0
0
.
0
(
0
)
9
0
.
1
1
/
4
5
.
7
(
3
6
)
4
2
.
9
/
5
9
.
6
(
2
5
1
)
5
2
.
3
/
5
9
.
3
(
3
2
2
)
6
8
.
5
5
4
4
/
7
5
.
6
1
9
2
(
0
7
.
)
0
0
0
/
0
0
.
0
(
0
)
0
0
.
0
/
0
0
.
2
(
5
.
)
7
6
0
/
0
3
.
2
(
0
1
.
)
0
0
0
/
0
0
.
0
(
.
)
0
0
0
/
0
0
.
0
(
0
0
)
8
5
.
0
/
0
2
.
2
(
5
2
)
0
3
.
5
/
6
7
.
7
(
4
3
)
5
0
.
2
9
9
6
3
/
3
3
.
1
9
5
2
2
(
2
9
1
)
9
9
.
0
1
/
2
9
.
2
1
(
6
2
toi
un
e
t
un
je
p
n
e
p
o
toi
un
e
t
un
je
p
Ô
L
)
0
0
.
0
/
0
0
.
2
(
2
)
0
0
.
0
/
0
0
.
2
(
1
)
0
0
.
0
/
0
0
.
0
(
0
)
3
4
.
8
/
5
6
.
5
(
4
4
2
)
0
0
.
0
/
0
0
.
2
(
)
0
0
.
0
/
0
0
.
0
(
)
0
0
.
0
/
0
0
.
0
(
1
0
0
)
8
0
.
1
/
1
5
.
2
(
2
9
t
c
je
r
t
s
Ô
L
9
1
4
9
8
6
4
7
4
8
8
2
6
9
2
0
0
1
7
4
9
9
4
0
0
5
4
6
1
Ô
L
9
1
8
0
1
5
6
1
4
7
4
6
7
4
8
9
5
2
5
7
4
7
4
0
0
5
0
0
5
0
0
5
0
4
8
1
1
2
3
4
5
6
7
8
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
t
s
n
je
b
0
5
un
p
je
L
un
0
5
je
un
T
b
0
5
je
un
T
0
5
je
je
W
P.
UN
Q
Evolutionary Computation Volume 27, Nombre 3
447
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
Tableau 2: Number of permutations of size 10 at the different distances from a given so-
lution according to the type of neighborhood.
d = 1 d = 2 d = 3
d = 4
d = 5
d = 6
d = 7
d = 8
d = 9
2-exchange
Insert
45
81
870
2521
9450
38281
63273
296326
269325
1100902
723680
1604098
1172700
569794
1026576
16795
362880
1
the makespan, instead of the total flow time, as in this article. According to a recent
travail (Hernando et al., 2017) there is a lower number of local optima sharing the fitness
value when minimizing the total flow time than when minimizing the makespan. Dans-
deed, Tableau 1 shows that, for the PFSP instances, the presence of local optima belonging
to plateaus is not so high.
Once the plateaus are explored, we take into account that those local optima be-
longing to a plateau share the same attraction basin. An attraction basin, thus, will be
the attraction basin of a strict local optima or that of a plateau (optimal or open).
4.3
Topology of the Attraction Basins
From our point of view, the structure of the attraction basins can be characterized by
these principal aspects: roundness of the attraction basins, centrality of the local optima,
and interior and frontier of the attraction basins. We examine these topological features
of the attraction basins of the strict local optima, the open plateaus, and the local optimal
plateaus.
4.3.1 Roundness of the Attraction Basins
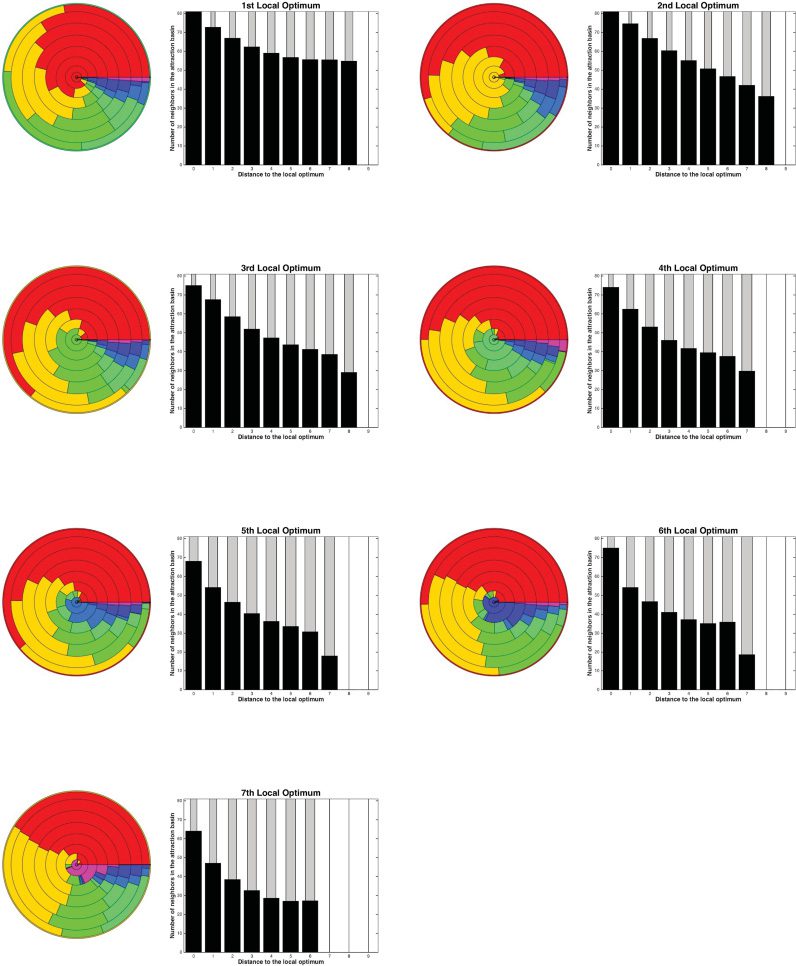
As was explained in Section 3.1, an attraction basin is considered to be round if all the
solutions at distance 1, 2, . . . until a certain distance r from the local optimum or the
plateau are within the attraction basin. We record, for the smaller instances, for each
local optimum, the proportion of solutions belonging to its attraction basin that are at
different distances from it. Just as a reference, in Table 2, we show the total number of
solutions at different distances from any solution in the space of permutations of size
10. Notice that these values differ from the number of solutions at different distances
when referring to a plateau. The distance between one plateau and one solution is the
minimal distance between this solution and all the solutions in the plateau. Par exemple,
if a plateau is formed by two solutions, the number of permutations at distance one is
the sum of the number of the neighbors of both solutions, eliminating repetitions and
both solutions themselves. En outre, in this case, the maximum reachable distance
would be 8. For the larger instances, we take those local optima obtained in the sample
of size 500, et, as it is impossible to check the solutions at all the possible distances
from them, we focus on those at distance 1. Donc, we analyze if the solutions at distance
1 from each of the local optima (or distance 1 from the plateaus) belong to its same
attraction basin. We also record, among the solutions found in the sample for each local
optimum, the maximum distance at which a solution is within the attraction basin.
In Figure 2, the results are plotted distinguishing between problems and neighbor-
hoods. In the x-axis of the figures the distance to the local optimum is indicated and
the y-axis shows the percentage of solutions that belong to their attraction basins. Pour
the smaller instances (bars in gray), the average value obtained in each landscape and
the maximum and minimum percentages found are represented. Those instances of
448
Evolutionary Computation Volume 27, Nombre 3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Anatomy of the Attraction Basins
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2: Average, maximum, and minimum percentage of solutions that are at different
distances from the local optima and that belong to its attraction basin, for the instances
of the (from top to bottom) PFSP, LOP, and QAP, considering the 2-exchange and the
insert neighborhoods. For the instances with n = 10 (bars in gray), the results at all the
possible distances are shown, while for the instances with n = 50 (bars in black), juste
those at distance 1, which is the only computationally affordable in a reasonable time.
The graphs on the right represent the average (and maximum) of the maximal distances
found in the sample obtained for the attraction basins of the instances with n = 50.
the LOP that present just one local optimum under the insert neighborhood have been
removed from Figure 2. The average percentage of solutions in the attraction basin de-
creases with the distance to the local optimum. The maximum and the minimum per-
centage found for a local optimum also decreases with the distance to the local optimum
for the three problems considering the 2-exchange neighborhood. This also happens for
the QAP and the insert neighborhood. Cependant, for the PFSP and LOP under the in-
sert neighborhood, we find that the maximum percentage encountered increases when
Evolutionary Computation Volume 27, Nombre 3
449
L. Hernando, UN. Mendiburu, and J. UN. Lozano
reaching the longest distances. The reason for this phenomenon is that, for the insert
neighborhood, the number of possible solutions decreases quickly at long distances
et, Par exemple, for those strict local optima, there is just 1 possible solution at dis-
tance 9 (see Table 2). Donc, if we find a strict local optimum whose solution at the
maximum distance belongs to its attraction basin, we will find that 100% of the solutions
(just one) at this distance belongs to it, as observed for the PFSP.
Regarding the smaller instances, the average percentage of solutions at distance 1
from the local optima is lower than 100. This means that, on average, we can find neigh-
boring solutions of the local optima that belong to different attraction basins. Obviously,
in all the problems and neighborhoods we find at least one local optimum with all its
neighbors belonging to its own attraction basin: the global optima or the global opti-
mal plateaus. The results obtained for the larger instances (bars in black) confirm this
result. Taking into account the local optima found in the sample, on average, there is
a probability higher than 0 of finding a neighboring solution of the local optima be-
longing to a different attraction basin. In all the scenarios, we find local optima whose
attraction basins contain solutions far from them. In the case of the smaller instances,
solutions at distance 8 ou 9 to the local optima are found in the attraction basins. Pour
the larger instances, in Figure 2 we add a graph showing the average of the maximum
distances from the local optima at which a solution inside the attraction basin has been
trouvé. The maximum distance encountered in all the attraction basins is also included
(the gray triangles). The dashed line indicates the maximum possible distance (49). Ac-
cording to these plots, solutions far from the local optima are also inside their attraction
basins. Notice that the maximum distances presented here are lower bounds of the real
ones, this is because we are exploring just a sample of the solutions of the attraction
basins. Cependant, in this sample for the LOP and QAP using the 2-exchange neighbor-
hood, attraction basins with solutions at the maximum possible distance from the local
optima have already been found.
The percentage of the solutions in an attraction basin is related with the escape rate
analyzed in a number of works, tel que, Merz (2004) and Daolio et al. (2014). The es-
cape rate is a measure that gives the probability of reaching a different attraction basin.
According to all those works, the escape rate increases with the distance to the local op-
tima, that is precisely what can be observed in Figure 2: the decrease of the percentage
of the solutions in the attraction basins means the growth of the percentage of the solu-
tions in different attraction basins. Although examining the roundness of the attraction
basins and delving into the escape rate produce closely related information, we consider
that our perspective is more suitable for giving explicit knowledge about the topology
of the attraction basins and helps in the visualization of the structure of these sets.
En général, Chiffre 2 reveals that, on average, the local optima are located in the fron-
tier of the attraction basins, as they have a number of neighboring solutions belonging
to a different attraction basin. Cependant, on average, we also find solutions at the longest
distances from them that do belong to their attraction basins. This structure clearly dif-
fers from the concept of roundness.
4.3.2 Centrality of the Local Optima
We aim to study the position of the local optima within the attraction basins. For this
but, we focus on the centrality of the local optima inside the attraction basins.
As seen in Section 3.2, the local optima (or the plateaus) are considered to be cen-
tered if they minimize the average distance to the rest of the solutions in the attraction
basin. In order to examine this point, we calculate, for each solution in each attraction
450
Evolutionary Computation Volume 27, Nombre 3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Anatomy of the Attraction Basins
Dσ ∗
|B(σ ∗ )| ou
basin, the previously defined measure D. As computing this experiment for the larger
instances is unaffordable, it has been done just for those smaller instances. For this ex-
periment, we show, as representative cases, one instance of each problem (8th instance
of PFSP, 8th instance of LOP, and 8th instance of QAP) and we report, in Figure 3, le
results obtained for the attraction basins of the global optima as well as the results ob-
tained for all the attraction basins of all the local optima of each of the selected instances.
The figures with the distances of the remaining instances are available at the website.2 In
DP
the x-axis of Figure 3 the average distance, c'est,
|B(P. )| , is indicated, while its
variance is represented in the y-axis. Donc, each point in gray shows the average/variance
of the distances for those solutions that are not local optima, and the points in red rep-
resent the local optima. The three figures in the first and third columns display the
distances for the solutions of the attraction basins of the global optima under the 2-
exchange and the insert neighborhoods, respectivement. In the second and fourth columns,
the distances of the different solutions of each attraction basin have been scaled to the in-
terval [0,1] in order to compare different results belonging to different attraction basins.
Each of these plots shows the scaled average and variance of the distance from each
solution of the search space to the remaining solutions in its same attraction basin. Donc,
a total of 10! points are plotted, highlighting in red those referring to the local optima.
All the plots are very similar for all the problem instances. The global optima have
a really small average distance to the rest of the permutations in their attraction basins.
From those graphs that represent all the solutions of the search space, we can deduce
that not only the global optima, but also all of the local optima of the instance have a
lower average distance than the rest of the solutions of the attraction basins. En fait,
a large proportion of the local optima have their average scaled values equal to zero.
We conclude that the local optima are located close to the barycenter of the attraction
basins, as they have the minimal (or almost the minimal) average distances to the rest
of the solutions: in general, they are almost centered within the attraction basins. Le
large variance observed in some of the local optima (particularly, for the insert neighbor-
hood), corresponds with the behavior observed in Figure 2: not all the solutions close
to the local optima are in their attraction basins, et, at the longest distances, quelques
solutions are found which belong to them.
Interior and Frontier of the Attraction Basins
4.3.3
According to the study about the roundness of the attraction basins (Section 4.3.1), dans
most cases, the local optima are located in the frontier of the attraction basins. Nous de-
velop two different analyses for a deep examination regarding the interior and frontier
of the attraction basins. D'abord, we check whether each solution in the attraction basins
is located in the interior, and for each attraction basin we record the number of neigh-
boring attraction basins. Suivant, we explore the evolution of the number of neighboring
attraction basins and the evolution of the neighboring solutions that share the same
attraction basin, as the distance to the local optimum increases.
je. The interior and the neighboring relations of the attraction basins
In Table 3 we report, for each instance, distinguishing between the 2-exchange
and the insert neighborhoods, the percentage of the solutions found in the attrac-
tion basins that have all their neighboring solutions in their same attraction basin
(interior solutions). For the smaller instances, all the solutions of the search space
are checked, alors que, for the larger instances, the percentages refer to the solutions
2http://www.sc.ehu.es/ccwbayes/members/leticia/AnatomyOfAB/centralityLO.html
Evolutionary Computation Volume 27, Nombre 3
451
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
n
o
je
t
c
un
r
t
t
un
e
h
t
n
je
s
n
o
je
t
toi
je
o
s
e
h
t
F
o
t
s
e
r
e
h
t
o
t
s
e
c
n
un
t
s
je
d
e
h
t
F
o
e
c
n
un
je
r
un
v
d
n
un
e
g
un
r
e
v
un
e
h
t
,
n
je
s
un
b
n
o
je
t
c
un
r
t
t
un
e
h
t
F
o
n
o
je
t
toi
je
o
s
h
c
un
e
r
o
F
:
3
e
r
toi
g
je
F
,
m
o
t
t
o
b
o
t
p
o
t
m
o
r
F
(
P.
UN
Q
e
h
t
F
o
e
c
n
un
t
s
n
je
h
t
8
e
h
t
d
n
un
P.
Ô
L
e
h
t
F
o
e
c
n
un
t
s
n
je
h
t
8
e
h
t
P.,
S
F
P.
e
h
t
F
o
e
c
n
un
t
s
n
je
h
t
8
e
h
t
r
o
F
n
w
o
h
s
e
r
un
n
je
s
un
b
je
un
c
o
je
e
h
t
o
t
je
g
n
d
n
o
p
s
e
r
r
o
c
s
t
je
toi
s
e
r
e
h
T
.
)
oui
je
e
v
je
t
c
e
p
s
e
r
,
t
h
g
je
r
o
t
t
F
e
je
m
o
r
F
(
s
d
o
o
h
r
o
b
h
g
je
e
n
t
r
e
s
n
je
d
n
un
e
g
n
un
h
c
X
e
–
2
e
h
t
g
n
je
s
toi
,
)
oui
je
e
v
je
t
c
e
p
s
e
r
.
oui
un
r
g
n
je
e
r
un
s
n
o
je
t
toi
je
o
s
F
o
t
s
e
r
e
h
t
F
o
e
s
o
h
t
e
je
je
h
w
,
d
e
r
n
je
e
r
un
un
m
je
t
p
o
452
Evolutionary Computation Volume 27, Nombre 3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Anatomy of the Attraction Basins
Tableau 3: Percentage of the number of solutions that fall in the interior of the attraction
basins and, for the smaller instances, the last column shows the average number of
neighboring attraction basins.
strict LO +
LO plateau +
plateau
% in the interior of the
attraction basins
Mean
(Variance) Maximum Minimum
Average number
of neighboring
att. bas.
2-EXCHANGE
PFSP
LOP
QAP
INSERT
PFSP
Inst 1
Inst 2
Inst 3
Inst 4
Inst 5
Inst 6
Inst 7
Inst 8
tai50_10.00
tai50_10.01
tai50_10.02
tai50_10.03
Inst 1
Inst 2
Inst 3
Inst 4
Inst 5
Inst 6
Inst 7
Inst 8
N-be75eec
N-be75np
N-be75oi
N-be75tot
Inst 1
Inst 2
Inst 3
Inst 4
Inst 5
Inst 6
Inst 7
Inst 8
Lipa50b
Tai50a
Tai50b
Wil50
Inst 1
Inst 2
Inst 3
Inst 4
Inst 5
Inst 6
Inst 7
Inst 8
11
24
49
81
111
157
219
294
500
500
500
500
13
24
54
57
81
97
36
23
500
500
500
500
19
103
141
474
440
544
104
218
474
500
500
500
3
7
7
8
13
30
42
24
0.0392 (0.0037)
0.0169 (0.0021)
0.0020 (0.0000)
0.0016 (0.0000)
0.0010 (0.0000)
0.0007 (0.0000)
0.0012 (0.0000)
0.0007 (0.0000)
0.0159 (0.0422)
0.0000 (0.0000)
0.0071 (0.0255)
0.0205 (0.0775)
0.0075 (0.0003)
0.0320 (0.0241)
0.0002 (0.0000)
0.0003 (0.0000)
0.0008 (0.0000)
0.0002 (0.0000)
0.0013 (0.0000)
0.0180 (0.0052)
0.0000 (0.0000)
0.0085 (0.0195)
0.0000 (0.0000)
0.0000 (0.0000)
0.0095 (0.0010)
0.0036 (0.0001)
0.0008 (0.0000)
0.0011 (0.0000)
0.0005 (0.0000)
0.0003 (0.0000)
0.0015 (0.0000)
0.0001 (0.0000)
0.3846 (18.2420)
0.0887 (0.4069)
0.0714 (0.4059)
0.1747 (0.8887)
0.0628 (0.0037)
0.0166 (0.0008)
0.0167 (0.0020)
0.0064 (0.0002)
0.0284 (0.0105)
0.0002 (0.0000)
0.0002 (0.0000)
0.0010 (0.0000)
0.1531
0.2026
0.0387
0.0420
0.0214
0.0231
0.0221
0.0288
2.7027
0.0000
3.5714
5.0000
0.0458
0.7606
0.0026
0.0110
0.0087
0.0117
0.0166
0.3420
0.0000
2.7397
0.0000
0.0000
0.1311
0.0588
0.0288
0.0304
0.0190
0.0180
0.0441
0.0059
67.4419
7.4074
8.4746
11.8644
0.1212
0.0616
0.1171
0.0447
0.3691
0.0024
0.0068
0.0094
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
10.00
23.00
47.76
75.73
106.41
146.82
200.34
260.86
12.00
23.00
51.41
54.04
78.91
89.67
33.83
20.26
18.00
97.07
130.68
398.33
377.24
423.57
91.77
152.19
2.00
6.00
6.00
7.00
12.00
29.00
40.81
23.00
Evolutionary Computation Volume 27, Nombre 3
453
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
strict LO +
LO plateau +
plateau
LOP
tai50_10.00
tai50_10.01
tai50_10.02
tai50_10.03
Inst 1
Inst 2
Inst 3
Inst 4
Inst 5
Inst 6
Inst 7
Inst 8
N-be75eec
N-be75np
N-be75oi
N-be75tot
QAP Inst 1
Inst 2
Inst 3
Inst 4
Inst 5
Inst 6
Inst 7
Inst 8
Lipa50b
Tai50a
Tai50b
Wil50
500
500
500
500
1
1
1
1
3
2
1
5
500
432
500
400
2713
4432
2796
16427
4956
14219
5160
4640
500
500
500
500
Tableau 3: Continued.
% in the interior of the
attraction basins
Mean
(Variance)
0.0000 (0.0000)
0.0000 (0.0000)
0.0045 (0.0103)
0.0096 (0.0232)
100.0000 (0.0000)
100.0000 (0.0000)
100.0000 (0.0000)
100.0000 (0.0000)
0.1612 (0.0052)
0.4072 (0.1448)
100.0000 (0.0000)
0.7944 (3.1556)
0.0524 (0.3991)
2.7516 (37.4291)
0.0305 (0.1204)
0.1546 (1.1971)
0.0000 (0.0000)
0.0002 (0.0000)
0.0001 (0.0000)
0.0009 (0.0001)
0.0001 (0.0000)
0.0005 (0.0001)
0.0000 (0.0000)
0.0000 (0.0000)
0.0000 (0.0000)
0.0000 (0.0000)
0.0000 (0.0000)
0.0000 (0.0000)
Maximum Minimum
0.0000
0.0000
2.2727
2.5641
100.0000
100.0000
100.0000
100.0000
0.2216
0.6763
100.0000
3.9722
10.0000
29.4118
4.6512
16.9811
0.0199
0.0876
0.0606
0.4348
0.0358
0.2283
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
100.0000
100.0000
100.0000
100.0000
0.0818
0.1381
100.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
Average number
of neighboring
att. bas.
—
—
—
—
2.00
1.00
—
3.60
558.08
1167.52
771.59
1453.54
1214.20
1356.76
1180.41
909.66
found in the sample (not only the 500 initial random solutions, but also those
solutions that the algorithm finds in the paths until it reaches the local optima).
The first column in Table 3 shows the sum of the number of strict LO, LO plateau,
and plateau seen in Table 1. In the second column of Table 3, the average per-
centage of the interior solutions with its variance is reported, and the third and
fourth columns provide the maximum and the minimum percentages found for
each of the instances.
En général, the percentages are really small, with the exception of those in-
stances that have just one local optimum, Pour qui, obviously, 100% of the
solutions are located in the interior of the only attraction basin (all of the so-
lutions of the search space are in the same attraction basin). We also find some
high maximum percentages for the QAP larger instances under the 2-exchange
neighborhood and for the LOP larger instances under the insert neighborhood.
Cependant, the average percentages obtained for these instances are very low. Ce
result matches with some previous works where it was found that, for different
optimization problems, most of the solutions were located in the frontier of the
454
Evolutionary Computation Volume 27, Nombre 3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Anatomy of the Attraction Basins
attraction basins (Fonlupt et al., 1999; Tomassini et al., 2008; Verel et al., 2008;
Ochoa et al., 2014).
The fact that there is a really low number of solutions in the interior of the
attraction basins leads us to report in the last column, for the smaller instances,
the average number of neighboring attraction basins. Surprisingly, for most of
the instances of all problems, and considering both neighborhoods, we find that
this average value is really high: close to the total number of local optima. Ba-
sically, we could conclude that, for each pair of attraction basins, we can find
two neighboring solutions belonging to each of them: almost all of the attraction
basins are neighboring attraction basins. This result reveals that all the attraction
basins are intertwined in the search space.
II. Evolution of the neighboring attraction basins with the distance to the local
optima
We still do not know if each of these solutions in the frontier touches just one
or more attraction basins. En outre, we do not know if the distance from
the frontier solution to the local optimum affects this number of neighboring
attraction basins. Donc, in order to take a step forward in the analysis about the
frontier of the attraction basins, we delve into the neighboring relations of the
attraction basins as the distance to the local optima increases.
In this sense, for each solution, we study (je) the number of its neighbors that
belong to its same attraction basin, et (ii) for all those neighbors that do not be-
long to that attraction basin, we record the number of different attraction basins
observed. Notice that, when working with n = 10, each solution can have a max-
imum of 45 et 81 different neighboring attraction basins, for the 2-exchange
and the insert neighborhoods, respectivement (the size of the neighborhood in each
case). In the case of n = 50, this maximum number is 1225 et 2401, respectivement.
In Figure 4, the results are distinguished between problems and neighborhoods.
The results are also separated for the larger and the smaller instances, indicating
n = 10 and n = 50 in each case. In all the graphs, the x-axis indicates the distance
of the solutions in the attraction basins to the local optima. For n = 10, this dis-
tance goes from 1 à 9 (the maximum possible distance for both neighborhoods),
and for n = 50 it goes from 1 à 49. In each graph, the y-axis shows the following:
(je) in gray, the average of the proportion of neighboring solutions that fall in the
same attraction basin.
(ii) in black, the average of the proportion of the number of different neighboring
attraction basins per number of neighboring solutions.
For the three problems a general behavior is observed. The average proportion
of the number of neighbors belonging to the same attraction basin decreases with
the distance to the local optima, while the average proportion of the number of
different neighboring attraction basins increases. C'est, those solutions that are
close to the local optimum have a large proportion of their neighbors inside the
same attraction basin. The solutions that are far from the local optimum have a
small number of neighbors in the same attraction basin. En même temps, le
number of different neighboring attraction basins is large. It seems that if we
take all the solutions of an attraction basin, we will find that the connectivities
with other different attraction basins are higher for those solutions at long dis-
tances from the local optima. The behavior for the LOP instances with the insert
neighborhood is different than in the rest of the landscapes. We could say that in
Evolutionary Computation Volume 27, Nombre 3
455
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4: Average of the proportion of the number of different neighboring attraction
basins and of the proportion of the number of neighbors belonging to the same attrac-
tion basin, according to the distance of the solutions to the local optimum. The differ-
ent graphs show the results for the instances of the PFSP, LOP, and QAP (from top to
bottom), when considering the 2-exchange (gauche) and the insert (droite) neighborhoods.
Inside each of these graphs, the smaller (n = 10) and the larger (n = 50) instances are
distinguished.
456
Evolutionary Computation Volume 27, Nombre 3
Anatomy of the Attraction Basins
this scenario, the attraction basins are less interconnected with each other than
in the others.
We should take into account that the attraction basins are built by the local
search algorithm. It draws paths that start at a certain point and continue from
neighboring to neighboring solutions, ending at the local optimum. Donc,
the starting point has at least one neighbor in the same attraction basin, et le
rest of the points visited across the path have at least two neighbors in the same
attraction basin. In the case of a solution having three or more neighbors be-
longing to the attraction basin, it means that either the paths are not completely
disconnected and they share a number of solutions, or they are so close to each
other that the solutions in one path are neighbors of those of the other paths.
In order to examine this point, we add a blue line in all the graphs of Figure
4. This blue line indicates the proportion of 2 divided by the size of the neigh-
borhood; c'est, 2/45 et 2/81 in the case of n = 10 for the 2-exchange and the
insert neighborhoods, respectivement, et 2/1225 et 2/2401 for n = 50 for the 2-
exchange and the insert neighborhoods, respectivement. Donc, if the gray triangle is
above the blue line, it means that, on average, the solutions have three or more
neighbors in the same attraction basin. For the instances of size n = 10, the blue
line is always below the average proportion of the number of neighbors in the
same attraction basin, even for those solutions at the longest distances. For the
instances of size n = 50, for the insert neighborhood, this average proportion is
also higher than the blue line for all the distances. Considering the 2-exchange
neighborhood, just for those solutions at the longest distances, the average of the
number of neighbors in the same attraction basin is equal to or lower than 2. Un-
der this result, we can assert that the paths drawn by the local search algorithm
are interconnected with each other or, at least, they are close to each other.
4.4 Discussion
The attraction basins can be understood as long intertwined rivers that flow into the dif-
ferent local optima, instead of being mountains in a landscape. En fait, each attraction
basin is composed of several of those rivers ending at the same local optimum, alors que
at the same time, each of them could have different tributaries. De plus, the end of
those rivers can be made up of more than one local optimum that have the same objec-
tive function value, forming a plateau. The local optima or the plateaus composed by
local optima are centered in the attraction basin. Nevertheless, we should be cautious
with this perception, because by understanding the combinatorial optimization land-
scapes as if we were in a 3D natural landscape, we could be misunderstanding the real
anatomy.
Two main conclusions regarding the performance of the algorithms based on lo-
cal search could be derived from this understanding of the combinatorial landscapes.
D'abord, we have seen that the local search is sometimes trapped inside a plateau which
has a better neighboring solution, giving the possibility of reaching a better local op-
timum. Donc, the number and extension of the plateaus containing local optima
should be taken into account when referring to the difficulty of the algorithm for a spe-
cific instance. Secondly, until now, it was believed that the larger an attraction basin,
the further we should go from the local optimum to escape from it and find a differ-
ent one. Cependant, as can be observed in this study, on average, just one movement in
the neighborhood is enough to find a new attraction basin, because, usually, the local
Evolutionary Computation Volume 27, Nombre 3
457
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
optima are located in the frontier of the attraction basins. Obviously, the probability of
finding different attraction basins increases with the distance to the local optimum.
All the information gathered in this article could be used for the design of new
algorithms. Particularly, iterated local search (ILS) algorithms, which are built to escape
from the local optima (Lourenço et al., 2003, 2010). Most of these implementations use
a specific operator in the local search and apply a different operator to escape from
the local optima. Some other authors design ILS algorithms, which escape from the
local optima by applying a large number of movements of the same operator used in
the local search. Nevertheless, with this new knowledge about the attraction basins,
we could find other more simple and effective ways of escaping from the attraction
basins. It just depends on the aim of the researcher: exploitation versus exploration.
D'une part, we know that, on average, once a local optimum is found, just by
checking all the solutions at distance one, we will find at least one solution belonging to
the attraction basin of a different local optimum. En outre, this new local optimum
has a better objective function value than the previous one because that solution has
a neighbor with better fitness than the local optimum, et, donc, the new local
optimum will also have better fitness than the previous one. Dans ce cas, we do not
need to check any acceptance criterion for the new local optimum, as we are sure that
this new local optimum improves the value of the previous one. Cependant, as previously
mentioned, the probability of finding new attraction basins at distance one from the
local optima is lower than at higher distances. That is why, on the other hand, when we
are interested in finding a high number of different attraction basins (exploration), le
results of this article recommend looking among those solutions in the attraction basins
that are far from the local optima. Inside the set of their neighboring solutions, there is a
high probability of finding a large number of different attraction basins. Nevertheless,
in this case, the acceptance criterion should be evaluated, as we do not have information
about the goodness of those new local optima.
The applicability of our results is not limited to the design of algorithms that solve
instances of COPs; en effet, these results are also useful for improving the development
of the study of other features of the landscape. Firstly, having information about the
structure of the attraction basins helps in the estimation of their size, as was seen in
Hernando et al. (2016un). Secondly, this anatomy of the attraction basins can be a use-
ful tool to estimate the number of local optima of the instance, as it is already known
that some of the existing methods to estimate the number of local optima are based on
the distribution of the sizes of the attraction basins (Hernando et al., 2013un). Plus loin-
plus, we can discover from this study those regions of the search space that, with high
probability, contain different local optima or contain solutions belonging to different
attraction basins. This information could somehow be used to estimate the number of
non-observed local optima in the sample.
5 Visualizing the Attraction Basins
We show two examples of the visualization of the attraction basins. D'abord, we choose
a specific instance, and we show, in a more visual way, cependant, all the information
analyzed in the article, in order to provide the reader with an intuition about the con-
nections between the different attraction basins of one instance. Secondly, we choose
a specific attraction basin of an instance, and give a representation by means of a net-
work showing all the paths encountered until the local optimum is reached. We consider
that these two examples help to understand the conclusions collected from the results
obtained in the previous sections. The specific examples presented here have been
458
Evolutionary Computation Volume 27, Nombre 3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Anatomy of the Attraction Basins
chosen as representative cases. These are small but large enough to visualize the stud-
ied features. More examples of similar representations for other different instances and
attraction basins are available at the website.3
5.1
Exemple 1: Interrelation of the Attraction Basins of One Instance
In order to provide an example of how all the attraction basins found in an instance
are interrelated, for each of the 7 local optima of the 2nd PFSP instance under the in-
sert neighborhood, we plot the proportion of the number of solutions at the different
distances from each of the local optima that belong to each of the different attraction
basins. C'est, plots (un)–(g) in Figure 5 show the results obtained for the 1st to the 7th
local optima, respectivement. Notice that, in this instance, all the local optima are strict local
optima. The local optima are sorted according to their objective function value (the 1st
local optimum being the global optimum) and each color refers to the attraction basin
of each of the local optima, maintaining the relation between colors and local optima
dans le 7 plots. Spécifiquement, the proportion in red, yellow, vert, aquamarine, blue, dans-
digo, and purple will refer to the attraction basins from the 1st to the 7th local optima,
respectivement, in all the 7 plots. Without wanting to lose perspective and being aware of
the non-round shape of the attraction basins, we represent them as bullseyes. The cor-
responding local optimum is centered in the bullseye and 9 concentric rings represent
the solutions at the 9 possible distances. Donc, at each of these distances, the proportion of
solutions belonging to the distinct attraction basins are plotted with different colors.
By showing these bullseyes, we provide an intuition on how solutions belonging to
different attraction basins appear while going further from the local optima. Cependant,
all the solutions inside a specific color are not necessarily all together as in the rings
of the bullseyes. C'est, as previously mentioned, the attraction basins are interrelated
with many connectivities appearing among them. Donc, a figure in which all the colors
mixed with each other would be more realistic. Cependant, we found this representation a
bit awkward and, donc, in order to complete this information, we decided to include
a graph accompanying each bullseye. We gather the solutions of each attraction basin
according to their distance to the local optimum. Alors, for each of these solutions, nous
record the number of its neighbors that belong to the same attraction basin. The black
bars represent the average number of the neighboring solutions in the same attraction
basin according to the distance from the local optimum (given by the x-axis). Notice
that the maximum value of the bars is 81, because under the insert neighborhood, ce
is the number of neighboring solutions. The width of the gray bars is proportional to the
average number of different attraction basins found at each distance. According to these
figures, all the local optima of this instance, except the two local optima with highest
fitness, always have neighboring permutations in a different attraction basin. De plus,
for all the local optima (including the global optimum) we find solutions at distance one
that have neighboring solutions belonging to different attraction basins. This means that
paths belonging to other different attraction basins are mixed with them from a distance
of just 1.
5.2
Exemple 2: The Attraction Basin of One Local Optimum
The visualization of an attraction basin is not an easy task. The large number of per-
mutations in the search space and the considerably large number of neighbors for each
solution, together with the non-ordered permutation space, means that any plot in 2D
3http://www.sc.ehu.es/ccwbayes/members/leticia/AnatomyOfAB/visualization.html
Evolutionary Computation Volume 27, Nombre 3
459
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5: The bullseyes represent, for the 1st to the 7th local optimum (pour (un)–(g), respecter-
tivement) the proportion of the number of solutions that belong to the different attraction
basins (plotted in different colors) according to the distance from the local optimum (lo-
cated in the center of the bullseye). For the solutions of each of the attraction basins, le
bars in black show the average proportion of neighbors belonging to the same attraction
basin according to the distance to the local optimum. The width of the bars in gray is
proportional to the number of the different neighboring attraction basins.
460
Evolutionary Computation Volume 27, Nombre 3
Anatomy of the Attraction Basins
Chiffre 6: Visualization of an attraction basin of a local optimal plateau found in the 7th
instance of the PFSP with the 2-exchange neighborhood, considering only the steps of
the algorithm (gauche) and taking into account, as far as possible, the distances between all
the solutions (droite).
or 3D should be interpreted with caution. Ici, we propose a way of visualizing the
attraction basins by means of directed graphs. Each node of the graph represents one
solution belonging to the attraction basin. Edges between nodes indicate that the node
at the end of the edge is the best neighbor of the node at the start of the edge. The color
of the nodes changes with the distance to the local optimum. Particularly, red, yellow,
vert, light blue, dark blue, and purple are used to represent the solutions at distances
0 (the local optima), 1, 2, 3, 4, et 5, respectivement. The size of the nodes and the width of
the edges also decrease as the distance to the local optimum increases.
Chiffre 6 presents two different graphs illustrating the same attraction basin of a
local optimal plateau of the 7th instance of the PFSP when using the 2-exchange neigh-
borhood. Both graphs have been created using the igraph package in the R programming
langue (Csárdi and Nepusz, 2006). Chiffre 6 (gauche) represents this attraction basin con-
sidering the steps that the algorithm takes until it reaches the local optimal plateau (et
not the distances between the solutions). For this purpose, we add the layout_with_kk
option when plotting the graph in R. Dans ce cas, there are two local optima (the nodes
in red) forming the local optimal plateau. This visualization could lead us to think that
the structure defined by an attraction basin is perfectly ordered in the search space and
close to the convexity, roundness and symmetry. Cependant, as previously mentioned, dans
this plot, the distances between each pair of solutions in the attraction basin have not
been considered. De plus, we should point out that the number of edges that each of
the nodes of the graph, and especially the local optima, have is really small compared
with the maximum possible number (45 neighbors). This means that solutions belong-
ing to different attraction basins are mixed, as can be seen in Example 1.
In an attempt to visualize this attraction basin in a more realistic way, we force
the graph to take into account the distances between all the solutions that belong to
the attraction basin (Chiffre 6 (droite)). We use the sammon function also found in R
Evolutionary Computation Volume 27, Nombre 3
461
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
(Venables and Ripley, 2002), which maps a high-dimensional space to a 2D space, trying
to preserve those distances in the high-dimensional space (Sammon, 1969). Bien sûr,
the resulting graph does not fulfill exactly all the distances between each pair of nodes,
because visualizing the permutation space in 2D is impossible. Cependant, it allows us to
observe that the real structure of the attraction basins is more complex than one could
try to imagine, et, bien sûr, much more complex than that shown in Figure 6 (gauche).
The visualization in the 3D space can be found at the website.4
6 Conclusions and Future Work
The landscape of combinatorial problems has been described by many authors as a set
of mountains and valleys, resembling the continuous domain. This widespread idea has
been the basis for the design of algorithms. Cependant, as a few authors already noticed,
some results found for the features of the attraction basins contradict this. Unfortu-
nately, these works have been ignored in practice. Donc, our aim in this article has
been to analyze a number of topological properties of the attraction basins in order to
provide knowledge about their structure and to break with the extended and mistaken
intuition about the anatomy of the attraction basins.
A deep analysis of the features of the attraction basins has been developed. Le
fact of having local optima forming plateaus is a remarkable aspect of the instances of
permutation-based COPs. Ainsi, we usually find that the algorithm gets trapped inside
the plateaus. For this reason, they could be seen as a complexity measure for the in-
stances, ou, at least, the number and extension of plateaus could be a supplement to
the number of local optima when dealing with the difficulty of the instances. It is fun-
damental to take the plateaus into account when analyzing the landscape features or
when proposing a new algorithm. We used this information about plateaus to gather
all the local optima that belong to a plateau, so as to consider that they share the same
attraction basin. It was found that, on average, there are neighboring solutions of the
local optima or of the plateaus that do not belong to their attraction basins. Cependant,
at the same time, there are usually some solutions far from the local optima which still
belong to its attraction basin. This information totally differs from the concept of round-
ness. Cependant, the local optima are located almost centered within the attraction basins.
De plus, not only the local optima but also an incredibly high percentage of the so-
lutions of the attraction basins fall into the frontier. Donc, we could say that the interior
of the attraction basins is almost empty. The attraction basins are neighbors of a large
number of the remaining attraction basins. In this sense, the solutions far from the local
optima and inside their attraction basins present a larger number of neighboring attrac-
tion basins than those solutions nearer to the local optima. En fait, each of the attraction
basins can be seen as a number of long rivers, with tributaries, that flow into the local
optimum (or local optimal plateau). The different rivers are interconnected with each
other or, at least, very close to each other.
The understanding of the landscapes in combinatorial optimization has been one of
the main challenges when developing and improving algorithms. This work not only
breaks with an erroneous extended belief about the attraction basin shapes, mais aussi
provides valuable information for the design of new algorithms based on local search.
Par exemple, this work clearly helps in the development of Iterated Local Search algo-
rithms when looking for an effective way to escape from the local optima. En fait, nous
4http://www.sc.ehu.es/ccwbayes/members/leticia/AnatomyOfAB/visualization/visualizeOneAB
.html
462
Evolutionary Computation Volume 27, Nombre 3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Anatomy of the Attraction Basins
plan to add information about the objective function value of the local optima to our
analysis of the neighboring relations between the attraction basins. In this sense, nous
hope that we will find regularities of the distances to the local optima where they have
more connectivities with other better local optima. De plus, this article also provides
useful knowledge to improve those methods that estimate the number of local optima
or the sizes of the attraction basins.
Remerciements
This work has been partially supported by the Research Groups 2013-2018 (IT-609-13)
programs (Basque Government) and TIN2016-78365R (Spanish Ministry of Economy,
Industry and Competitiveness). Jose A. Lozano is also supported by BERC 2014-2017
and Elkartek programs (Basque government) and Severo Ochoa Program SEV-2013-
0323 (Spanish Ministry of Economy and Competitiveness).
Les références
Albrecht, UN., voie, P., and Steinhofel, K. (2008). Combinatorial landscape analysis for k-SAT in-
stances. In IEEE Congress on Evolutionary Computation, pp. 2498–2504.
Albrecht, UN., voie, P., and Steinhofel, K. (2010). Analysis of local search landscapes for k-SAT
instances. Mathematics in Computer Science, 3(4):465–488.
Alyahya, K., and Rowe, J.. E. (2014). Phase transition and landscape properties of the number
partitioning problem. 14th European Conference on Evolutionary Computation in Combinatorial
Optimisation, pp. 206–217.
Angel, E., and Zissimopoulos, V. (2002). On the hardness of the quadratic assignment problem
with metaheuristics. Journal of Heuristics, 8(4):399–414.
Bouziri, H., Mellouli, K., and Talbi, E.-G. (2009). The k-coloring fitness landscape. Journal of Com-
binatorial Optimization, 21(3):306–329.
Burkard, R.. E., Karisch, S. E., and Rendl, F. (1997). Qaplib—A quadratic assignment problem
library. Journal of Global Optimization, 10(4):391–403.
Caruana, R., and Mullin, M.. (1999). Estimating the number of local minima in big, nasty search
les espaces. In Proceedings of IJCAI-99 Workshop on Statistical Machine Learning for Large-Scale
Optimization.
Chicano, F., Daolio, F., Ochoa, G., Verel, S., Tomassini, M., and Alba, E. (2012). Local optima net-
travaux, landscape autocorrelation and heuristic search performance. In Proceedings of Paral-
lel Problem Solving from Nature, pp. 337–347. Lecture Notes in Computer Science, Vol. 7492.
Springer.
Csárdi, G., and Nepusz, T. (2006). The igraph software package for complex network research.
InterJournal, Complex Systems(1695):1–9.
Daolio, F., Verel, S., Ochoa, G., and Tomassini, M.. (2010). Local optima networks of the quadratic
assignment problem. In IEEE Congress on Evolutionary Computation, pp. 2145–3152.
Daolio, F., Verel, S., Ochoa, G., and Tomassini, M.. (2014). Local optima networks of the permuta-
tion flow-shop problem. In Artificial Evolution, pp. 41–52. Lecture Notes in Computer Science,
Vol. 8752.
Fonlupt, C., Robilliard, D., Preux, P., and Talbi, E.-G. (1999). Fitness landscapes and performance
of meta-heuristics. In Meta-Heuristics: Advances and Trends in Local Search Paradigms for Opti-
mization, pp. 257–268.
Evolutionary Computation Volume 27, Nombre 3
463
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
Garey, M.. R., Johnson, D. S., and Sethi, R.. (1976). The complexity of flowshop and jobshop
scheduling. Mathematics of Operations Research, 1(2):117–129.
Hernando, L., Daolio, F., Veerapen, N., and Ochoa, G. (2017). Local optima networks of the per-
mutation flowshop scheduling problem: Makespan vs. total flow time. In IEEE Congress on
Evolutionary Computation, pp. 1964–1971.
Hernando, L., Mendiburu, UN., and Lozano, J.. UN. (2013un). An evaluation of methods for estimating
the number of local optima in combinatorial optimization problems. Evolutionary Computa-
tion, 21(4):625–658.
Hernando, L., Mendiburu, UN., and Lozano, J.. UN. (2013b). Generating customized landscapes
in permutation-based combinatorial optimization problems. In International Conference on
Learning and Intelligent Optimization, pp. 299–303.
Hernando, L., Mendiburu, UN., and Lozano, J.. UN. (2016un). Estimating attraction basin sizes (pp. 458–
467). Cham: Springer.
Hernando, L., Mendiburu, UN., and Lozano, J.. UN. (2016b). A tunable generator of instances of
permutation-based combinatorial optimization problems. IEEE Transactions on Evolutionary
Computation, 20(2):165–179.
Hernando, L., Pascual, J.. UN., Mendiburu, UN., and Lozano, J.. UN. (2011). A study on the complex-
ity of TSP instances under the 2-exchange neighbor system. In Foundations of Computational
Intelligence, pp. 15–21.
Hoos, H. H., and Stützle, T. (2004). Stochastic local search: Foundations and applications. San Fran-
cisco: Morgan Kaufmann.
Humeau, J., Liefooghe, UN., Talbi, E.-G., and Verel, S. (2013). ParadisEO-MO: From fitness land-
scape analysis to efficient local search algorithms. Journal of Heuristics, 19(6):881–915.
Klemm, K., Qin, J., and Stadler, P.. F. (2014). Geometry and coarse-grained representations of land-
scapes. Recent advances in the theory and application of fitness landscapes. Berlin Heidelberg:
Springer.
Lourenço, H. R., Martine, Ô. C., and Stützle, T. (2003). Iterated local search. Handbook of metaheuris-
tics (pp. 320–353). Boston: Springer.
Lourenço, H. R., Martine, Ô. C., and Stützle, T. (2010). Iterated local search: Framework and appli-
cations. Handbook of metaheuristics (pp. 363–397). Boston: Springer.
Marmion, M.-E., Dhaenens, C., Jourdan, L., Liefooghe, UN., and Verel, S. (2011un). Nils: A neutrality-
based iterated local search and its application to flowshop scheduling. In P. Merz and J.-K.
Hao (Éd.), Evolutionary computation in combinatorial optimization: 11th European Conference
(pp. 191–202) Torino, Italy: Springer Berlin Heidelberg.
Marmion, M.-E., Dhaenens, C., Jourdan, L., Liefooghe, UN., and Verel, S. (2011b). On the neutrality
of flowshop scheduling fitness landscapes. In Learning and Intelligent OptimizatioN Confer-
ence, pp. 238–252.
Mattfeld, D. C., and Bierwirth, C. (1999). A search space analysis of the job shop scheduling prob-
lem. Annals of Operations Research, 86:441–453.
Merz, P.. (2004). Advanced fitness landscape analysis and the performance of memetic algorithms.
Evolutionary Computation, 12(3):303–325.
Merz, P., and Freisleben, B. (2001). Memetic algorithms for the travelling salesman problem. Com-
plex Systems, 13(4):297–345.
Mishra, S., and Sikdar, K. (2004). On approximability of linear ordering and related NP-
optimization problems on graphs. Discrete Applied Mathematics, 136(2-3):249–269.
464
Evolutionary Computation Volume 27, Nombre 3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Anatomy of the Attraction Basins
Moser, JE., Gheorghita, M., and Aleti, UN. (2016). Identifying features of fitness landscapes and re-
lating them to problem difficulty. Evolutionary Computation, 25(3):407–437.
Ochoa, G., and Veerapen, N. (2018). Mapping the global structure of TSP fitness landscapes. Jour-
nal of Heuristics, 24(3):265–294.
Ochoa, G., Verel, S., Daolio, F., and Tomassini, M.. (2011). Clustering of local optima in combina-
torial fitness landscapes. In C. Coello-Coello (Ed.), Learning and intelligent optimization, Vol.
6683, pp. 454–457. Berlin Heidelberg: Springer.
Ochoa, G., Verel, S., Daolio, F., and Tomassini, M.. (2014). Recent advances in the theory and appli-
cation of fitness landscapes. In H. Richter and A. Engelbrecht (Éd.), Emergence, complexity
and computation, Vol. 6, chapter, Local optima networks: A new model of combinatorial fit-
ness landscapes, pp. 233–262. Berlin Heidelber: Springer.
Preux, P., and Talbi, E. G. (1999). Towards hybrid evolutionary algorithms. International Transac-
tions in Operational Research, 6(6):557–570.
Prügel-Bennett, UN., and Tayarani-Najaran, M.. H. (2012). Maximum satisfiability: Anatomy of the
fitness landscape for a hard combinatorial optimization problem. IEEE Transactions on Evo-
lutionary Computation, 16(3):319–338.
Reeves, C., and Aupetit-Bélaidouni, M.. (2004). Estimating the number of solutions for SAT prob-
lems. Parallel Problem Solving from Nature, pp. 101–110. Lecture Notes in Computer Science,
Vol. 3242.
Reeves, C. R.. (1999). Landscapes, operators and heuristic search. Annals of Operations Research,
86:473–490.
Reidys, C. M., and Stadler, P.. F. (2002). Combinatorial landscapes. SIAM Review, 44(1):3–54.
Sahni, S., and Gonzalez, T. (1976). P-complete approximation problems. Journal of the ACM,
23(3):555–565.
Sammon, J.. W. (1969). A nonlinear mapping for data structure analysis. IEEE Transactions on Com-
puters, C-18(5):401–409.
Schiavinotto, T., and Stützle, T. (2005). The Linear Ordering Problem: Instances, search space anal-
ysis and algorithms. Journal of Mathematical Modelling and Algorithms, 3(4):367–402.
Stützle, T. (2006). Iterated local search for the quadratic assignment problem. European Journal of
Operational Research, 174(3):1519–1539.
Sutton, UN. M., Howe, UN. E., and Whitley, L. D. (2010). Directed plateau search for max-k-sat. Dans
Proceedings of SoCS, pp. 90–97.
Taillard, E. (1990). Some efficient heuristic methods for the flow shop sequencing problem. Euro-
pean Journal of Operational Research, 47(1):65–74.
Taillard, E. (1993). Benchmarks for basic scheduling problems. European Journal of Operational Re-
recherche, 64(2):278–285.
Tayarani-Najaran, M.. H., and Prügel-Bennett, UN. (2014). On the landscape of combinatorial opti-
mization problems. IEEE Transactions on Evolutionary Computation, 18(3):420–434.
Tayarani-Najaran, M.. H., and Prügel-Bennett, UN. (2015un). Anatomy of the fitness landscape for
dense graph-colouring problem. Swarm and Evolutionary Computation, 22:47–65.
Tayarani-Najaran, M.. H., and Prügel-Bennett, UN. (2015b). Quadratic assignment problem: A land-
scape analysis. Evolutionary Intelligence, 8(4):165–184.
Tomassini, M., Vérel, S., and Ochoa, G. (2008). Complex-network analysis of combinatorial spaces:
The NK landscape case. Physical Review E, 78(6):66–114.
Evolutionary Computation Volume 27, Nombre 3
465
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
L. Hernando, UN. Mendiburu, and J. UN. Lozano
Venables, W. N., and Ripley, B. D. (2002). Modern applied statistics with S. 4th ed. New York:
Springer.
Verel, S., Daolio, F., Ochoa, G., and Tomassini, M.. (2011). Local optima networks with escape
edges. In International Conference on Artificial Evolution, pp. 10–23.
Verel, S., Ochoa, G., and Tomassini, M.. (2008). The connectivity of nk landscapes’ basins: A net-
work analysis. In Artificial Life XI: Proceedings of the 11th International Conference on the Simu-
lation and Synthesis of Living Systems, pp. 648–655.
Verel, S., Ochoa, G., and Tomassini, M.. (2011). Local optima networks of NK landscapes with
neutrality. IEEE Transactions on Evolutionary Computation, 15(6):783–797.
Watson, J.-P. (2010). An introduction to fitness landscape analysis and cost models for local search.
Handbook of metaheuristics (pp. 599–623). Vol. 146. Berlin: Springer.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
e
d
toi
e
v
c
o
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
2
7
3
4
3
5
1
8
5
8
6
1
2
e
v
c
o
_
un
_
0
0
2
2
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
466
Evolutionary Computation Volume 27, Nombre 3