A Non-Newtonian Fluid Robot
Abstract New types of robots inspired by biological principles of
assembly, locomotion, and behavior have been recently described. Dans ce
work we explored the concept of robots that are based on more
fundamental physical phenomena, such as fluid dynamics, and their
potential capabilities. We report a robot made entirely of non-Newtonian
fluid, driven by shear strains created by spatial patterns of audio waves.
We demonstrate various robotic primitives such as locomotion and
transport of metallic loads—up to 6-fold heavier than the robot
itself—between points on a surface, splitting and merging,
shapeshifting, percolation through gratings, and counting to 3. Nous
also utilized interactions between multiple robots carrying chemical
loads to drive a bulk chemical synthesis reaction. Free of constraints
such as skin or obligatory structural integrity, fluid robots represent a
radically different design that could adapt more easily to unfamiliar,
hostile, or chaotic environments and carry out tasks that neither
living organisms nor conventional machines are capable of.
Guy Hachmon**,†
Noam Mamet**,‡,†
Sapir Sasson**
Tal Barkai**
Nomi Hadar**
Almogit Abu-Horowitz**,‡
Ido Bachelet*,**,‡,§
Bar-Ilan University
Mots clés
Non-Newtonian fluids, robot, fluid
dynamics, biologically inspired robotics
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
1 Introduction
Recent developments in robotics and associated fields such as materials sciences and engineering
have led to a paradigm shift towards unconventional robots inspired by living organisms and their
properties and capabilities [2–5, 7, 8]. Such robots are highly adaptable for tasks in challenging
environnements. Par exemple, soft, solid-state robots fabricated from elastic polymers and devoid of
hard parts or joints could potentially withstand high mechanical loads and survive crushing and
bending forces lethal to conventional machines.
Cependant, the living organisms that inspire these robots are still largely constrained by structural
and functional biological barriers. Par exemple, skins and exoskeletons, which protect the integrity
and chemical composition of organisms, substantially limit their morphological flexibility. De plus,
even organisms devoid of skeleton (Mollusca) tend to adhere to well-defined outlines and shapes,
and while resilient to bending and crushing, they are highly vulnerable to cutting and shearing
forces. These faults could impair the survivability of robots designed to operate in highly dynamic
or hostile environments in which the conditions cannot be predicted a priori. But they could be
addressed by shifting to nonliving matter as the source of inspiration for robots with a radical,
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
* Contact author.
** Faculty of Life Sciences and Institute of Nanotechnology & Advanced Materials, Bar-Ilan University, Ramat Gan 52900, Israel.
† These authors contributed equally to this work.
‡ Current affiliation: Augmanity Labs, Rehovot Science Park, Rehovot, Israel.
§ 8 HaMada Street, Rehovot Science Park, Rehovot 7670308, Israel. E-mail: dogbach@gmail.com
© 2016 Massachusetts Institute of Technology Artificial Life 22: 1–22 (2016) est ce que je:10.1162/ARTL_a_00194
G. Hachmon et al.
A Non-Newtonian Fluid Robot
distinctly non-biological set of behaviors and capabilities. In this work we have focused on fluid
dynamics as a paradigm for this challenge.
Some properties required of a robot, such as motion and the ability to perform mechanical work,
are natural to fluids; others, such as automatic actuation in response to cues, are less trivial. La plupart
importantly, reliable and reproducible control of unbound fluids at high Reynolds numbers is ex-
tremely challenging. The mechanical properties and behavior of Newtonian (or approximately
Newtonian) fluids, such as water under standard conditions, are largely invariant under applied forces
and most other environmental cues. Cependant, in contrast, non-Newtonian fluids exhibit diverse,
peculiar behaviors deriving from the nonlinear relation between fluid deformation rate and shear
stress, which is particular to each system [9]. The physics underlying properties of non-Newtonian
fluids, such as shear thinning or thickening, is still only partly understood [1]. Despite that, comme dans
other fields, incompleteness of theoretic understanding does not prevent successful implementation;
hence, it is possible to assemble specific components to yield a non-Newtonian fluid with the desired
properties in a manner analogous to programming a robot for a specific purpose. In the present study
we designed a non-Newtonian fluid robot and studied its responses in various programming contexts.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
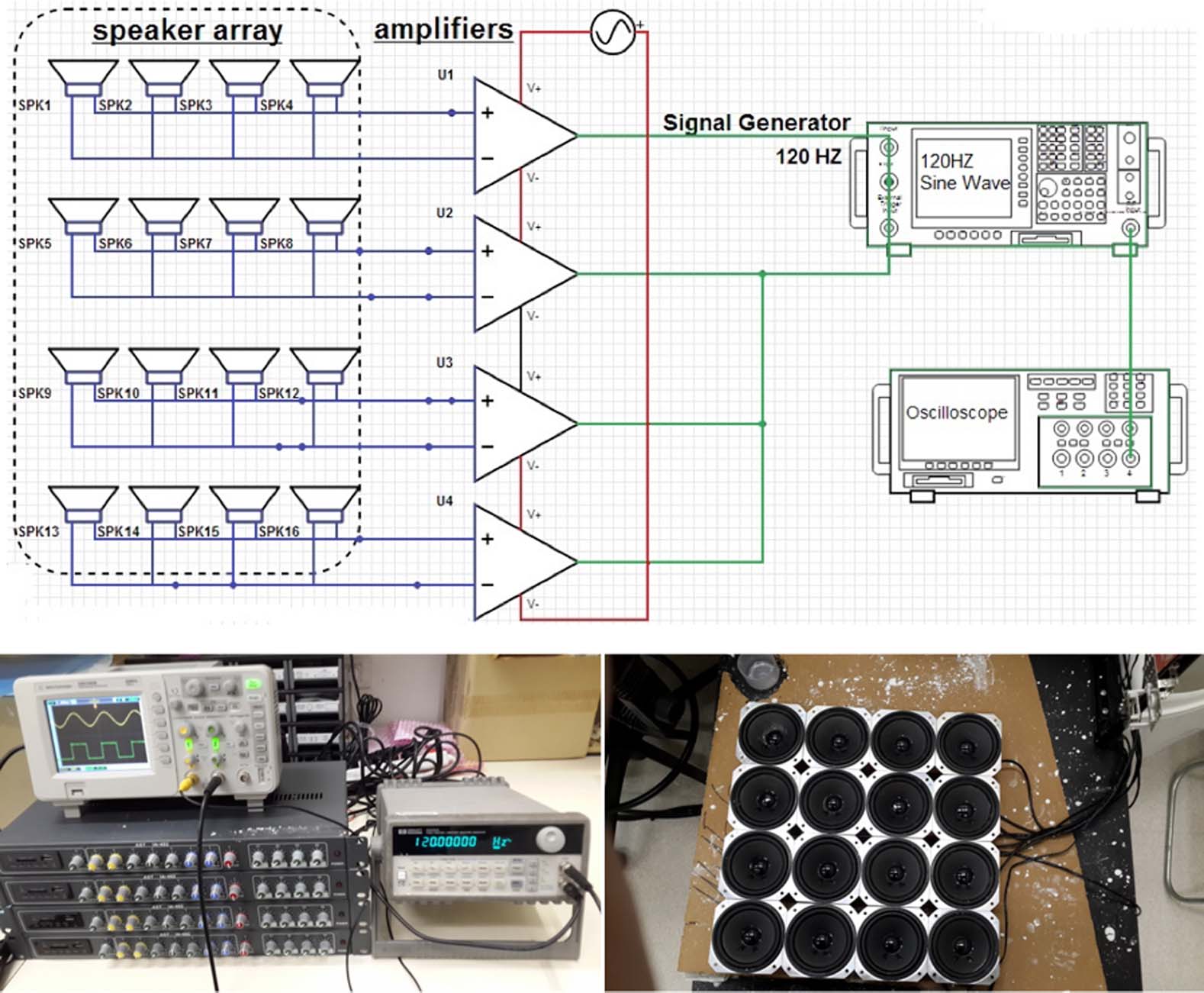
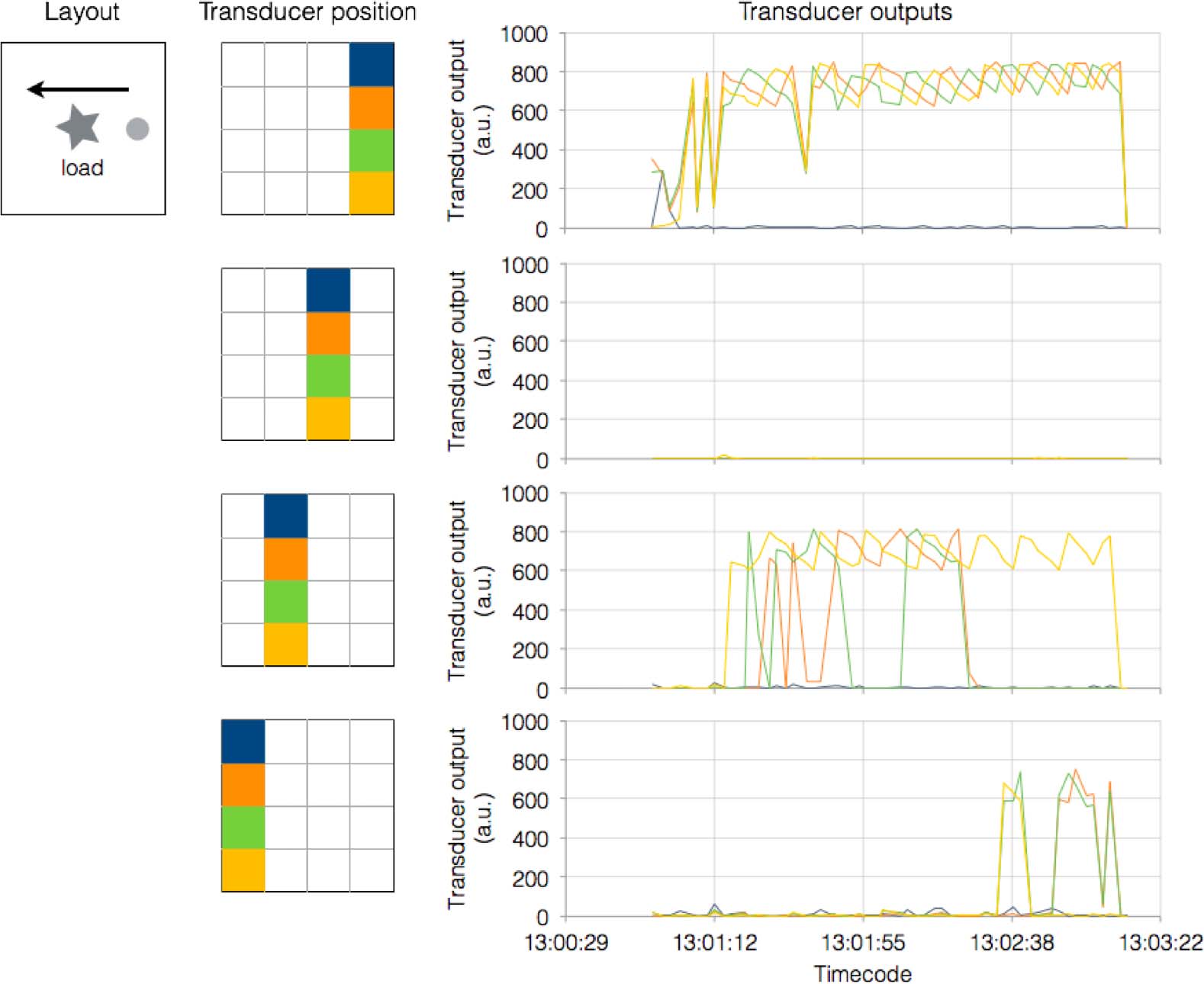
Chiffre 1. Experimental control setup. The signal generator (Hewlett-Packard, 100-MHz max frequency) employed as
source was connected to four amplifier units, each separately controlling four individual transducers/speakers
(specifications to be completed) numbered 1–16. An Agilent oscilloscope was used to visualize sine wave properties.
Bottom left photo shows the signal generator (unit on the right), to which four amplifier units are connected (bottom
racks), and an oscilloscope (unit on top). Bottom right photo shows the 4 × 4 transducer array controlled by the
amplifiers. Three video cameras were mounted around the system, providing X, Oui, and Z axis coverage. Data was
stored in real time on a DVR unit.
2
Artificial Life Volume 22, Nombre 1
G. Hachmon et al.
A Non-Newtonian Fluid Robot
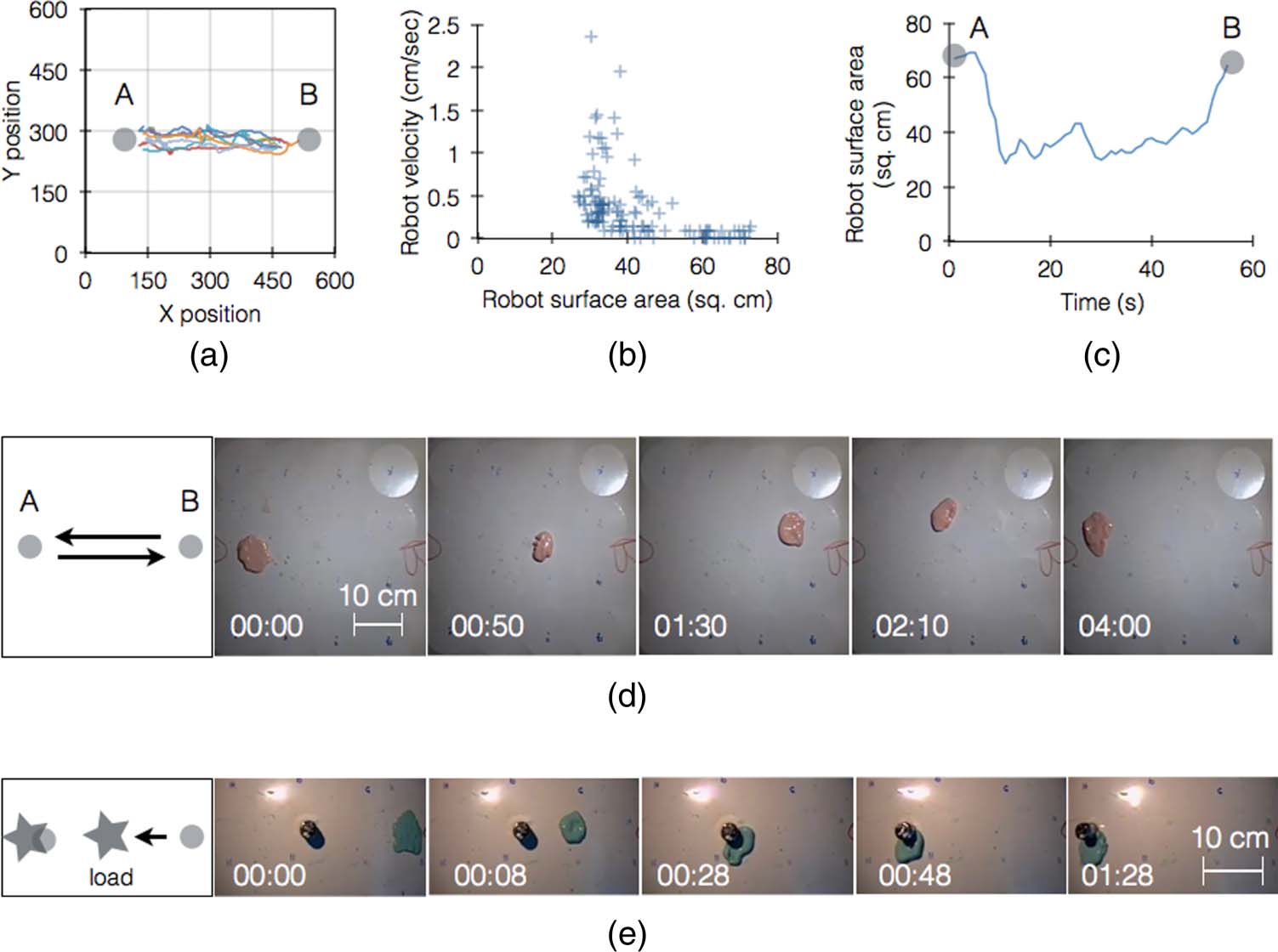
Chiffre 2. Fluid robot moving and carrying load. (un) paths of a fluid robot moving from point A to point B in 10 independent
experiments. X and Y positions are in millimeters. (b) correlation between robot surface area and velocity, deux
parameters dependent on robot strain. Each point represents a second in a typical experiment. (c) robot surface area
(in square centimeters) changes along a path from A to B in a typical experiment. (d) snapshots from a representative
experiment on a fluid robot moving from A to B to A (left panel, schematic; scale bar, 10 cm). (e) snapshots from a
representative experiment on a fluid robot carrying a load (in this case a 100-g metal weight; scale bar, 10 cm).
2 Results
To prove the feasibility of a non-Newtonian fluid robot that can be reliably and reproducibly fab-
ricated and controlled, we examined various fluids with diverse compositions. For our prototype we
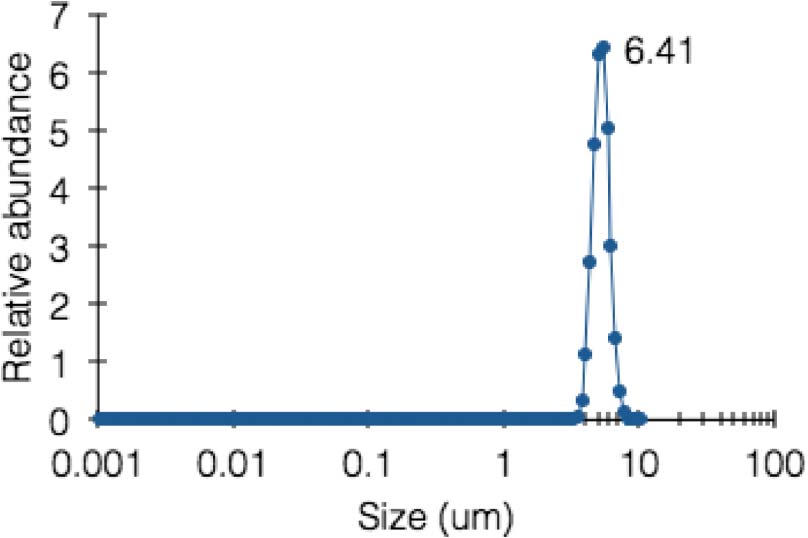
chose a colloidal dispersion of starch microparticles in an aqueous fructose solution (concentration
58% w/v; mean particle diameter 6.41 Am; see Appendix 1), to which shear strains were anisotropically
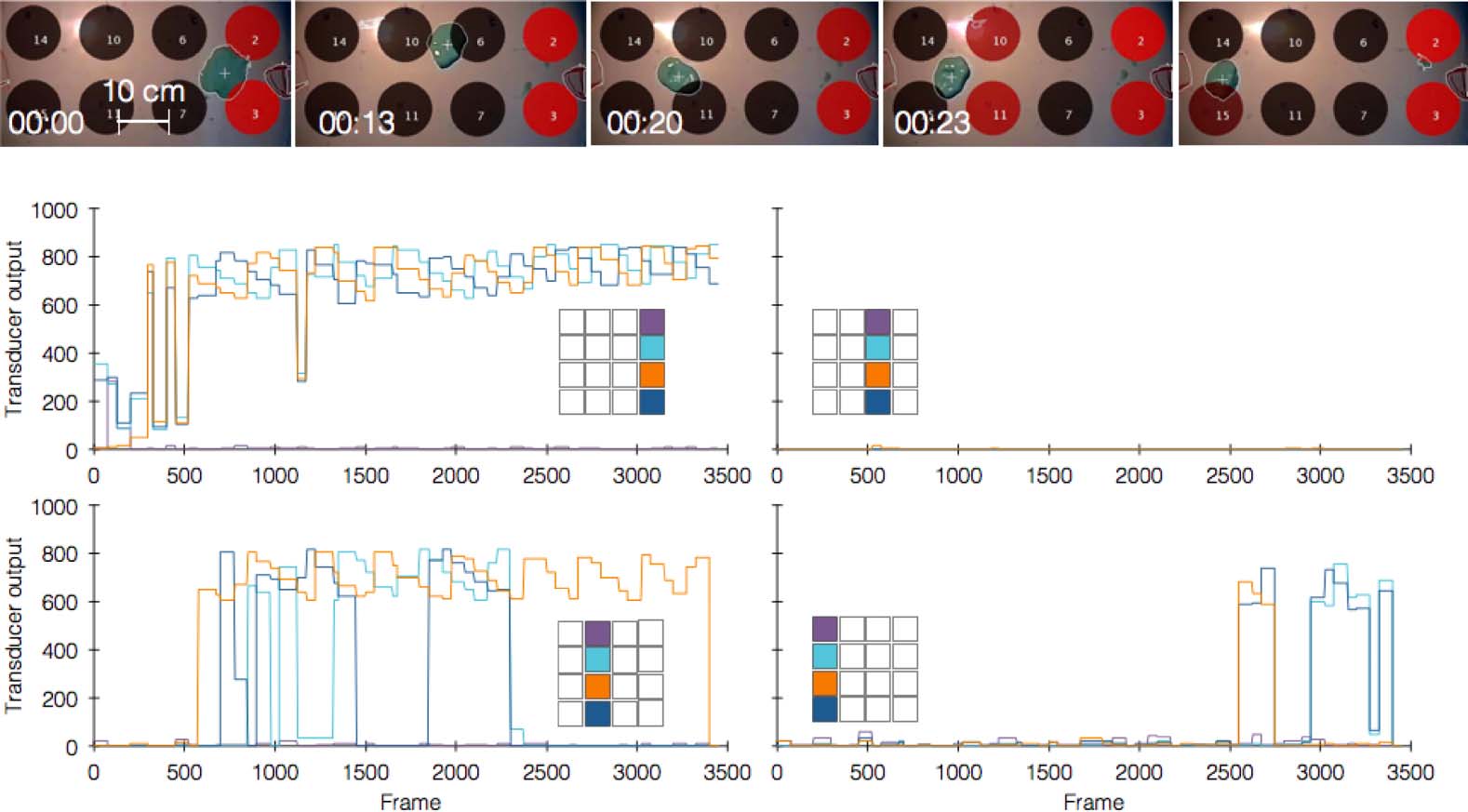
applied through the surface by a 4 × 4 array of individually controlled audio transducers (Chiffre 1). À
construct the control apparatus, the following parts were used: speakers (10-cm diameter, 40 W,
8 V), a Hewlett-Packard 33120A signal generator, 90-W AST 4×25 amplifiers, mini DVR cameras
(25 fps), a digital video recording system, an oscilloscope (Agilent Technologies DSO1052B,
50 MHz, two-channel), and a Sensemode™ voltage sensor and data transceiver. The surface was
made from standard artist canvas sheets (50 cm × 50 cm with wooden frame).
In order to reliably and reproducibly control the fluid robot, we preferred an empirical approach
over simulations, and iteratively sought transducer usage sequences that manipulated the fluid as
desired. We quickly observed that audio waves at specific outputs and frequencies created clearly
visible viscosity gradients within the fluid, which drove the robot in the downhill direction between
arbitrary points on the surface (Figure 2a, Appendix 2, and Videos S1–S3, which can be found at
www.mitpressjournals.org/doi/suppl/10.1162/ARTL_a_00194). At higher velocities produced by
higher strains, the robot was significantly more condensed and rigid (Figure 2b–d; images were
computationally analyzed as described in Appendix 3). Repetitive experiments demonstrated that
Artificial Life Volume 22, Nombre 1
3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
G. Hachmon et al.
A Non-Newtonian Fluid Robot
although the fluid could not be controlled to the extent of identical replication of previous shapes
and trajectories, its statistical behavior was highly reproducible.
The described layout divides a 0.36-m2 area into 16 auxels (audio pixels) de 225 cm2 each. Even at
this low spatial resolution, the fluid robot could be accurately controlled with minimal transducer
utilization. Par exemple, we found that the minimal number of transducers required for driving the
robot along a straight path is two, and that this pair of transducers was sufficient to drive the robot
across the entire surface length (Appendix 5). Smaller auxels and alternative layouts (par exemple., honeycomb
arrayed auxels) could likely allow finer tuning of robot behavior.
Most robots are designed with the ability to do some form of mechanical work. We therefore in-
vestigated the ability of the fluid robot to carry loads that are significantly heavier than itself—in this
case, metal weights. Our initial studies showed clear reduction in the velocity of the robot upon contact
with the target weight (par exemple., depuis 1 cm/s to 0.32 cm/s), indicating that a viscous drag force is created
between the robot and the weight. Our calculations yielded a drag force of 0.07 N, lequel (assuming an
object-to-surface kinetic friction of ≈0.4, and for a robot of the size used here and of the same col-
loidal dispersion) is sufficient to carry objects of ≈176 g—almost 6-fold heavier than the robot itself.
This was confirmed by our measurements, in which the reduction in velocity of the loaded robot is
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
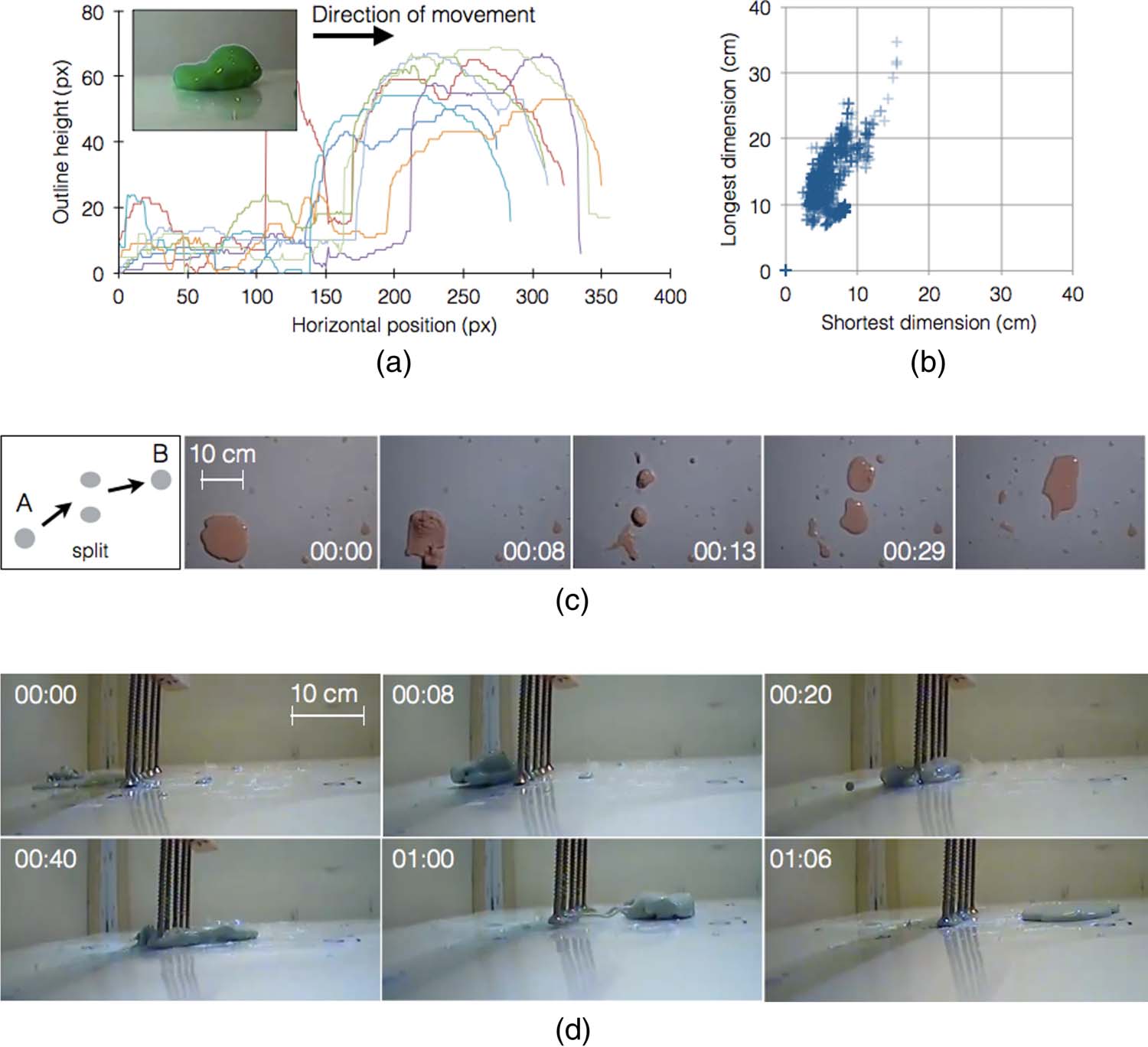
Chiffre 3. Fluid robot shapeshifting, splitting, and percolating. (un) Humps generated in the leading end of robots, shown
depuis 10 overlaid experiments at high-acceleration time points. Inset shows a representative snapshot. (b) Frame-by-
frame change in the fluid robotʼs shape during a typical experiment, measured as the maximal aspect ratio (longest to
shortest robot dimensions). (c) Splitting of the fluid robot into two separate fragments, each controlled independently,
finally merging back to a single robot (scale bar, 10 cm). (d) A representative experiment showing the robot percolating
through a handmade metal grating with a 1-cm gap length (scale bar, 10 cm).
4
Artificial Life Volume 22, Nombre 1
G. Hachmon et al.
A Non-Newtonian Fluid Robot
visible (Figure 2e, Video S4 in the Online Supplement). Although the drag coefficient is not constant,
our measurements were in good agreement with an approximation of the drag equation based on
constant CD (Tableau 2 in Appendix 2). Analysis of robot locomotion using side-mounted cameras re-
vealed a distinct behavior observed in all experiments, involving the robotʼs leading end (head ) assum-
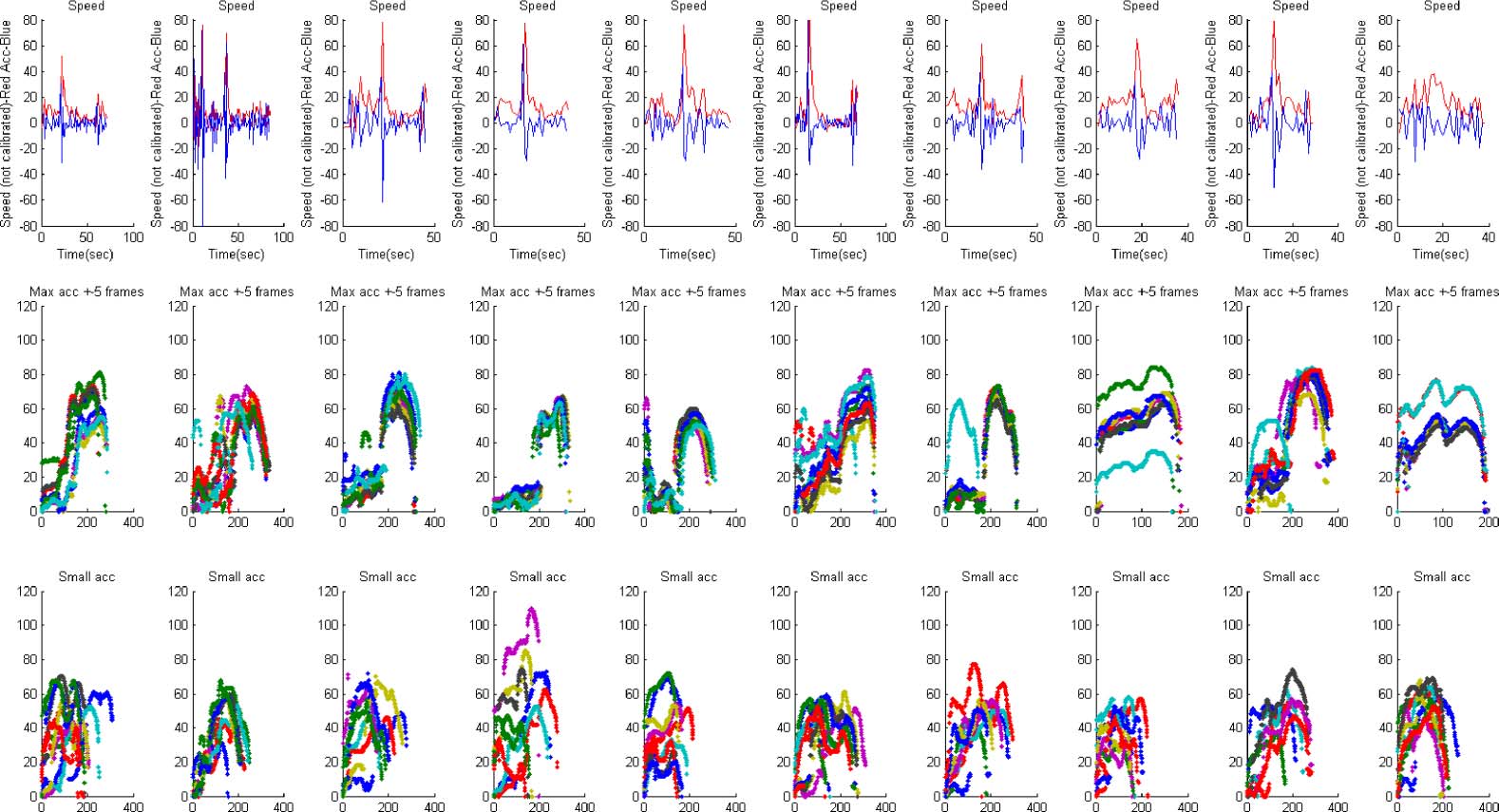
ing a hump shape, sometimes up to 10-fold higher than the robotʼs tail (Figure 3a). Our video analysis
showed that the tail (the rear part relative to the motion vector) remains consistently fluid throughout
the experiment and continuously moves towards the head, which compresses and thickens as a result.
This enables the tail fluid to physically climb on top of the head, creating the hump, which was con-
sequently prominent when acceleration was high (Appendix 2).
A fluid can change shape in ways that are impossible for living organisms, but may be highly
desired in various settings. The morphological diversity of the fluid robot is limited mainly by surface
tension, which depends on volume and composition and could be readily programmed by proper
fluid assembly. The surface tension and thus the volume must be kept within a limited range, robots
beneath it being too rigid and brittle to control, and ones above it too large to maintain integrity; mais
within this range the fluid exhibited remarkable shape flexibility, including changing aspect ratios and
expanding its surface area by a factor of approximately 36 (Figure 3b, Video S5 in the Online Supple-
ment). En outre, the robot can be split by vibration directed perpendicularly at the center of mass into
two or more separate smaller robots, so long as none of them falls beneath the lower volume threshold.
The parts can be controlled individually and be driven to merge to form a single robot again (Figure 3c,
Video S6 in the Online Supplement). De la même manière, the robot can percolate through porous barriers and
gratings (Figure 3d, Videos S7, S8 in the Online Supplement).
We were interested in the possibility of programming the robot to exhibit the equivalents of
computational and logic primitives. One straightforward example is to set the robot to function
as a finite counter, halting or changing behavior when the defined sum has been reached. Dans ce
example the input can be matter directly absorbed by the robot, changing its chemical composition
and subsequently its fluid behavior. To demonstrate this, we used aluminum oxide dough packets as
input bits, and programmed the robot to halt upon absorbing three discrete packets out of four. Ce
was done by assembling a robot that would become too rigid following the assimilation of exactly
three packets (Figure 4a, Video S9 in the Online Supplement). Similar behaviors could be achieved
with robot–robot collisions rather than robot–bit collisions.
This possibility leads to an attractive feature of fluid robotics: the integration of logic and chemistry, un
concept raised previously in microfluidic systems with bubbles functioning as bits that carry chemical
payloads [6]. As a proof-of-concept experiment we chose the carbodiimide-mediated cross-linking of
amine-modified DNA with a protein. In this reaction, the carbodiimide reacts with carboxylic acid
groups in the protein (mainly on the acidic amino acids aspartic acid [Asp/D] and glutamic acid
[Glu/E]), forming an active O-acylisourea intermediate that is then displaced by nucleophilic attack
from the primary amines on the modified DNA strands. The primary amine forms an amide bond with
the original carboxyl group, and a carbodiimide by-product is released as a soluble urea derivative. Three
discrete robots (volume of 10 mL each) carrying the reaction components—protein, amine-modified
DNA, and the crosslinker (1-ethyl-3-(3-dimethylaminopropyl)carbodiimide (EDC), at a 1 : 10 :
5000 molar ratio, respectively—were driven to collide in a stepwise manner, with robot movement pro-
viding constant mixing. The entire experiment was performed at room temperature. Successful synthe-
sis of the product was confirmed by solid-phase flow cytometry and spectrophotometry (Figure 4b).
3 Discussion
Contemporary works in the field of unconventional robotics draw from a wide range of biological
shapes and mechanisms of actuation. While all these robots exhibit peculiar capabilities, more di-
verse than those of conventional ones, they still adhere to the basic physics and architecture of living
bodies, which constrains their behavior. Par exemple, all living systems, from the single cell to com-
plex organisms, have barriers protecting their internal environment from the outer one, tel que
Artificial Life Volume 22, Nombre 1
5
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
G. Hachmon et al.
A Non-Newtonian Fluid Robot
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4. Fluid robot counting and driving chemical synthesis. (un) Snapshots of a fluid robot counting three input bits and
halting. Each input bit (white arrowheads) is an aluminum oxide dough packet. Graph shows the change in robot surface
area (in square centimeters) and the average velocity between bit assimilation events (corresponding to snapshot
timecodes). Counter status is presented in the bottom right corners. Scale bar, 10 cm. (b) A schematic of the
chemical reaction carried out in this experiment (EDC, 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide; green star,
fluorescent dye). Each component is dissolved in a separate robot (R1–R3), and the product is examined by
adsorption onto streptavidin microparticles and solid-phase flow cytometry. Histogram shows samples from R3
before synthesis and from R3 after (mixed with R1 + R2), following precipitation of starch microparticles.
membranes and skins, which crucially limit the shape diversity that a living organism can assume.
De plus, any organism has to maintain its structural integrity to prevent injury or death. Intérêt-
franchement, bio-inspired robots inherit these constraints through their design, and they too must remain
intact in order to remain functional and usually do not change their shape profoundly. This raises the
question whether radically different designs of robots exist that are free of these limits, and could
accordingly carry out tasks that are challenging for more conventional robots.
In this work we report a proof of concept for a reliably and reproducibly controlled robot
based on the properties and behaviors of non-Newtonian fluids. Using non-Newtonian fluids
as the basis of this design was crucial to enable arbitrary control over shape and motion, lequel
was easily obtained by using audio waves created by the user. We describe here a “program” as a
graphic representation of a temporal sequence of transducer outputs leading to a specific behavior
(Appendices 4–5).
Although the physics of non-Newtonian fluids is still not well understood, it is possible to utilize
the known observed behaviors and responses of these fluids in the design of robotic devices. Nous
used an empirical approach to assemble a non-Newtonian fluid with the desired set of properties as
6
Artificial Life Volume 22, Nombre 1
G. Hachmon et al.
A Non-Newtonian Fluid Robot
well as to define control profiles for various tasks. No simulations were used in this process, mais
rather iterative trial and error, in which fluid composition was measured by observed performance in
a process of directed evolution. De la même manière, the control profiles were written after systematic evalua-
tion of how the fluid responds to different spatiotemporal audio patterns. We believe that improved
understanding of non-Newtonian fluids in the near future will simplify this process and enable
reliable prediction of the behavior of specific compositions and their responses to specific audio
wave patterns, and bring this process closer to conventional programming.
Fluid robots could have many interesting applications, and our study raises some interesting di-
rections. Par exemple, it highlights the fascinating possibility of utilizing fluid robots as components
in a large, complex chemical assembly line. À cet égard, further work could produce robots with
specialized functions such as waste removal, affinity chromatography, dialysis from robot to robot,
and more. The surface itself could include regions with heating or cooling, fluid guides and splitters,
and similar topography-based rather than strain-based controls. Fluid robots could find applications
in search and rescue tasks. Par exemple, fluid robots could percolate and drip into areas where ac-
cess is highly limited, such as the debris of collapsed buildings or mines, merging again below to
form a robot that could carry weights and perform work.
Using audio waves to guide the robot on a surface might seem an essential flaw of the system, lim-
iting its potential use to surfaces through which audio waves can be transmitted. Cependant, further stud-
ies could likely extend the current design in many ways. Fluid robots can be controlled by unidirectional
audio beams transmitted from commercially available devices. They can be driven to crawl upwards on
inclined surfaces and climb to higher areas onboard continuous surfaces. The current proof-of-concept
study did not attempt to assemble fluids with additional properties, such as magnetic or charged fluids
which could be controlled by magnetic and electric fields orthogonal to mechanical shear forces. Sur-
laying similar modes of control would likely lead to very elaborate and capable designs.
Enfin, further studies into mechanical devices made of non-Newtonian fluids could elucidate
much of the physics underlying non-Newtonian fluid dynamics, and lead to improved designs with
higher capabilities than the prototype presented here. It would be interesting to design fluid robots
coated with a cell-inspired lipid bilayer, which could provide desired properties such as reducing
water loss by evaporation, hydrophobic or electrostatic repulsion between robots, or even primitive
mechanisms for self–nonself recognition, when two or more populations of robots navigate and
operate in parallel within the same system, avoiding incidental mixing. À cet égard, fluid robots
could show unexpected similarities to primitive life forms.
Remerciements
The authors wish to thank Larisa Zlatin, Sivan Friedman, and all members of the Bachelet lab for
valuable discussions and technical assistance.
Les références
1. Cheng, X., McCoy, J.. H., Israelachvili, J.. N., & Cohen, je. (2011). Imaging the microscopic structure of shear
thinning and thickening colloidal suspensions. Science, 333, 1276–1279.
2. Felton, S., Tolley, M., Demaine, E., Rus, D., & Wood, R.. (2014). A method for building self-folding
machines. Science, 345, 644–646.
3. Laschi, C., Mazzolai, B., Mattoli, V., Cianchetti, M., & Dario, P.. (2009). Design of a biomimetic robotic
octopus arm. Bioinspiration & Biomimetics, 4, 015006.
4. Mame, K. Y., Chirarattananon, P., Fuller, S. B., & Wood, R.. J.. (2013). Controlled flight of a biologically-inspired
insect scale robot. Science, 340, 603–607.
5. Morin, S. UN., Shepherd, R.. F., Kwok, S. W., Stokes, UN. UN., Nemiroski, UN., & Whitesides, G. M.. (2012).
Camouflage and display for soft machines. Science, 337, 828–832.
6. Prakash, M., & Gershenfeld, N. (2007). Microfluidic bubble logic. Science, 315, 832–835.
7. Rubenstein, M., Cornejo, UN., & Nagpal, R.. (2014). Programmable self-assembly in a thousand robot swarm.
Science, 345, 795–799.
Artificial Life Volume 22, Nombre 1
7
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
G. Hachmon et al.
A Non-Newtonian Fluid Robot
8. Shepherd, R.. F., Ilievski, F., Choi, W., Morin, S. UN., Stokes, UN. UN., Mazzeo, UN. D., Chen, X., Wang, M., &
Whitesides, G. M.. (2011). Soft multigait robot. Proceedings of the National Academy of Sciences of the U.S.A.,
108, 20400–20403.
9. Tropea, C., Yarin, UN. L., & Foss, J.. F. (Éd.) (2007). Springer handbook of experimental fluid mechanics.
Berlin: Springer.
Appendix 1: Material Screening
The final assembly protocol for robots was as follows: 58% w/v starch microparticles (Figures 5–6),
7.15% v/v fructose-glucose solution (40% w/v fructose, 27% w/v glucose in DW), 7.15% v/v
color solution (as described below). Color was introduced to enhance robot contrast for video anal-
ysis. See Table 1 and Figure 7.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5. Dynamic light scattering analysis of starch particle size.
Chiffre 6. Zeta potential analysis of starch microparticles. The zeta potential is the electrical potential difference between
the stationary fluid layer on the surface of each particle, and the fluid not adjacent to the particle (the dispersion fluid). Its
value is a measure of the colloidʼs resistance to aggregation, with values between −5 and +5 indicating high tendency to
coagulate and harden. The zeta potential is a significant property of a colloidal fluid, and could be key in future designs
once a quantitative link with the robotʼs performance is defined. Y-axis represents zeta potential values.
8
Artificial Life Volume 22, Nombre 1
UN
r
t
je
F
je
c
je
un
je
L
je
F
e
je
V
o
u
m
e
2
2
,
N
u
m
b
e
r
1
9
Tableau 1. Fluid robot composition screening table. This table lists the main various compositions used in the empirical search for a controllable and reproducible non-Newtonian fluid.
Material sources are entered in parentheses. Stirring included mainly vortexing for several minutes, aided by crushing with a metal spoon when needed.
Particle type
Starch microparticles
(6.4 Am)
Main liquid
Additional liquids
% solid particles
Stirring method
Comments and
observations
Distilled water
7.15% Food coloring
(E-124 / E-143)
7.15% fructose–glucose
mixture (30% glucose,
35% fructose, 35%
distilled water )
33% gouache color (bleu)
7.17% v / v food coloring
(E-124 / E-143)
et 7.15% v / v
fructose–glucose
mixture
58% (40 g per
30 g liquid)
58% (40 g per
30 g liquid)
58% (40 g per
30 g liquid)
58% (40 g per
30 g liquid)
Vortex mixer
and metal spoon
Vortex mixer
and metal spoon
Vortex mixer
This combination fails to
and metal spoon
make NNF.
Vortex mixer
and metal spoon
This combination was
used in the majority
of the experiments,
as it is both stable
and has good visibility
on cameras.
Tap water
7.17% v / v food coloring
(E-124 / E-143)
et 7.15% v / v
fructose–glucose
mixture
Oil from canola seeds
7.17% v / v food coloring
(E-124 / E-143)
et 7.15% v / v
fructose–glucose
mixture
58% (40 g per
30 g liquid)
Vortex mixer
and metal spoon
Liquid behavior differs
from that of DW.
58% (40 g per
30 g liquid)
Vortex mixer
Hydrophobic behavior
and metal spoon
anticipated; cependant,
NNF cannot be created
using these materials.
G
.
H
un
c
h
m
o
n
e
t
un
je
.
UN
N
o
n
–
N
e
w
t
o
n
je
un
n
je
F
u
d
je
R.
o
b
o
t
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1
0
Tableau 1. (a continué )
Particle type
Main liquid
Additional liquids
% solid particles
Stirring method
Comments and
observations
Tomato extract (35% tomato
extract, 63% eau,
2% glucose)
TBE × 1 buffer (Promega)
BupH × 2 buffer (Pierce)
Silica nanoparticles
(200 nm)
PEG (Sigma)
Sea sand
Distilled water
Alumina nanoparticles
(150 nm)
Distilled water
UN
r
t
je
F
je
c
je
un
je
L
je
F
e
je
V
o
u
m
e
2
2
,
N
u
m
b
e
r
1
7.17% v / v food coloring
(E-124 / E-143) et
7.15% v / v fructose–
glucose mixture
7.17% v / v food coloring
(E-124 / E-143) et
7.15% v / v fructose–
glucose mixture
7.17% v / v food coloring
(E-124 / E-143) et
7.15% v / v fructose–
glucose mixture
7.17% v / v food coloring
(E-124 / E-143) et
7.15% v / v fructose–
glucose mixture
7.17% v / v food coloring
(E-124 / E-143) et
7.15% v / v fructose–
glucose mixture
7.17% v / v food coloring
(E-124 / E-143) et
7.15% v / v fructose–
glucose mixture
58% (40 g per
30 g liquid)
Vortex mixer
This extract has pseudoplastic behavior;
and metal spoon
thus anti-dilatant behavior was
expected. Cependant, NNF cannot
be created using these materials.
58% (40 g per
30 g liquid)
Vortex mixer
and metal spoon
58% (40 g per
30 g liquid)
Vortex mixer
Liquid was made for
and metal spoon
synthesis experiment.
58% (40 g per
30 g liquid)
Vortex mixer
and metal spoon
58% (40 g per
30 g liquid)
Vortex mixer
Weak NNF; cannot be
and metal spoon
contrôlé.
58% (40 g per
30 g liquid)
Vortex mixer
and metal spoon
NNF cannot be made with these
materials. Gluey substance was
formed. Was used for bits in
counting experiment (avec
different concentrations).
G
.
H
un
c
h
m
o
n
e
t
un
je
.
UN
N
o
n
–
N
e
w
t
o
n
je
un
n
je
F
u
d
je
R.
o
b
o
t
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
G. Hachmon et al.
A Non-Newtonian Fluid Robot
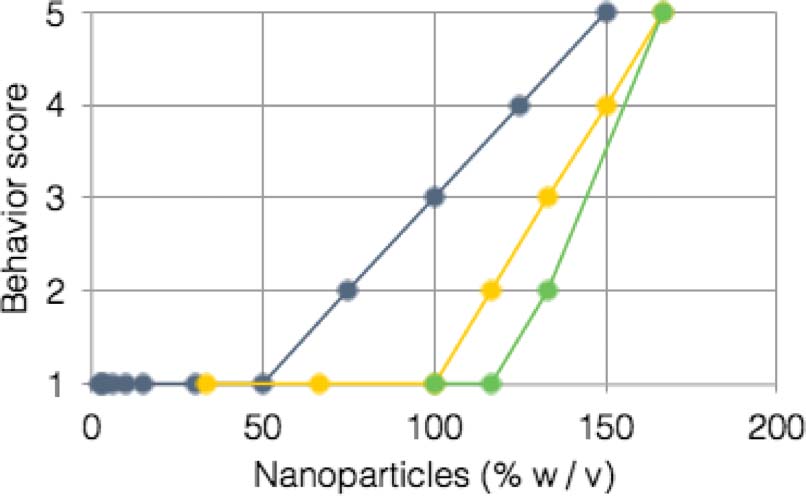
Chiffre 7. Behavior analysis of starch microparticle solutions. A range of aqueous solutions was prepared from starch
microparticles in DW, and the solutions were sheared by vortexing the vessel in a standard vortex at 320 Hz. A score
was given to the fluidʼs behavior based on the measured height of features produced in the fluid: 1, no shear thickening
observed; 2–4, weak (0.5 cm), mild (0.5–1.5 cm), or strong (>1.5 cm) shear thickening; 5, no fluid behavior observed.
This experiment was repeated with various solution volumes (bleu, 200 mL; yellow, 30 mL; vert, 10 mL).
Appendix 2: Additional Movement Data
See Table 2 and Figures 8 et 9.
Appendix 3: Computational Image Analysis
A3.1 Data Acquisition and Basic Analysis
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Video footage was analyzed by a custom-made MATLAB (Mathworks, R2013a) code, which uses
the image-processing toolbox for extracting velocity, area, and path.
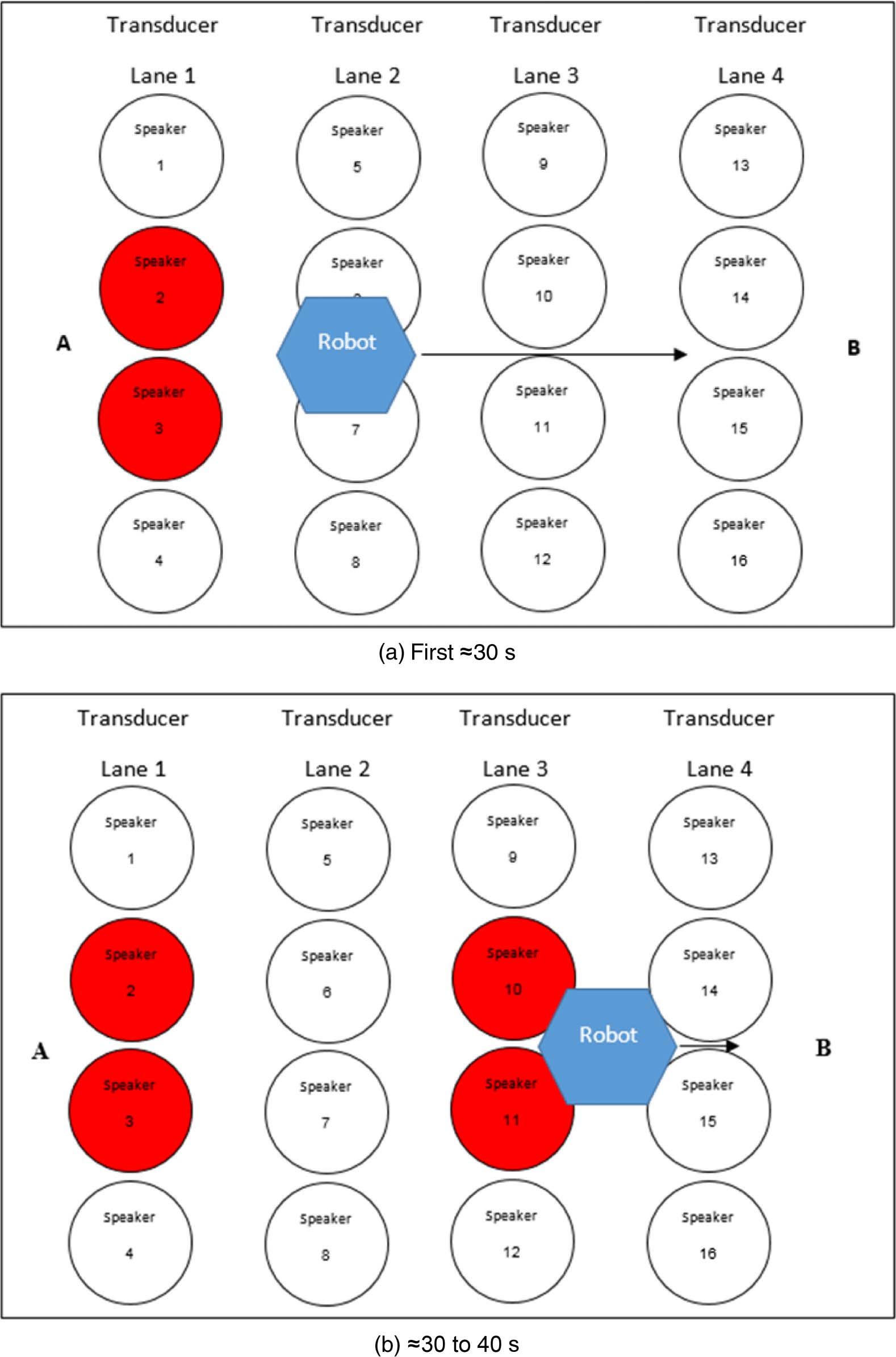
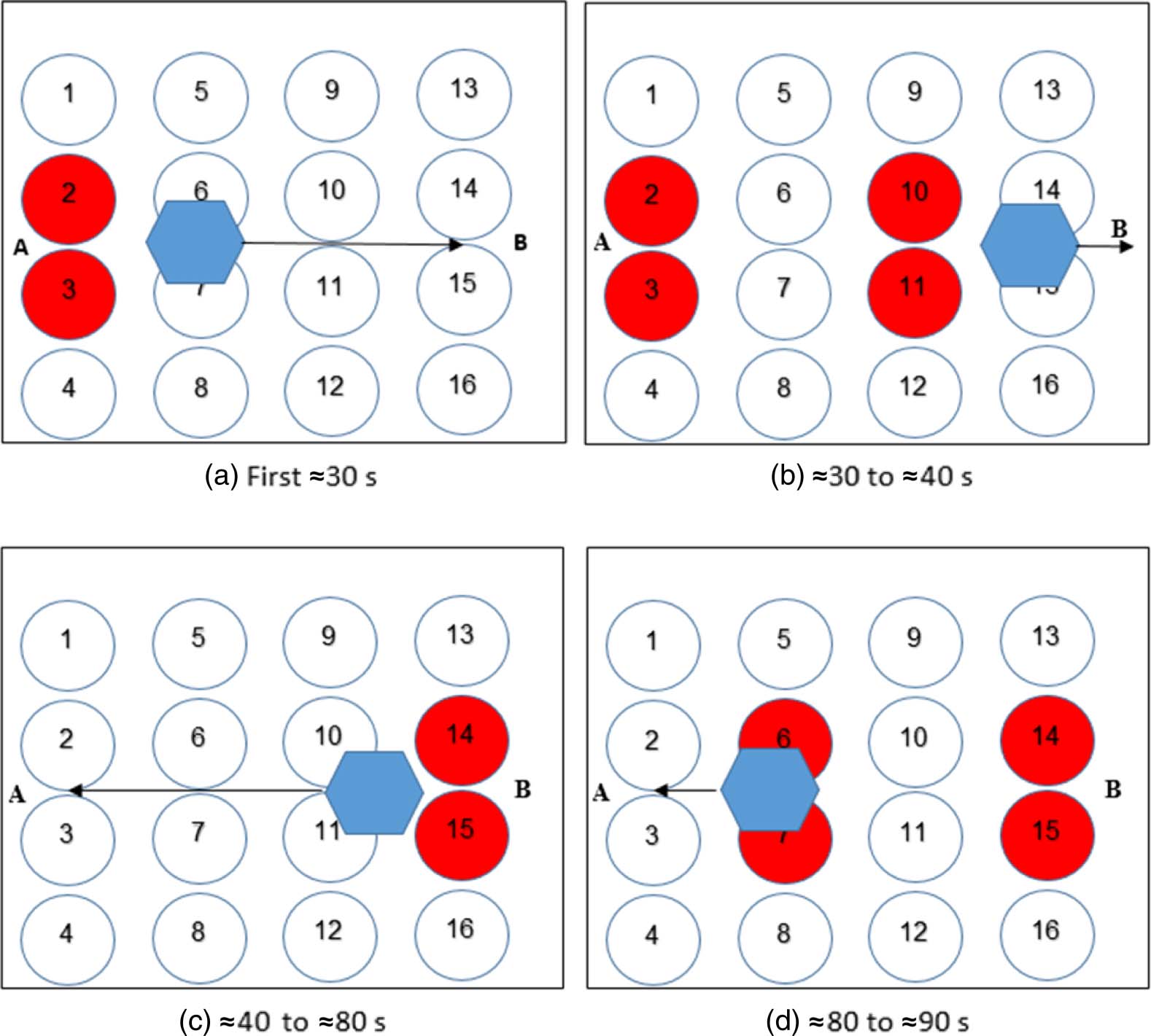
A3.2 Visual Representation of Speaker Activity
Recorded information was integrated graphically into the videos by our code. Each speaker is rep-
resented by a circle in proximity to its original location as it appears in the video. An active speaker
Tableau 2. Load carry measurements.
Weight (g)
Time (s)
5
10
25
50
100
150
200
400
15
23
27
51
63
72
∞
∞
Artificial Life Volume 22, Nombre 1
11
G. Hachmon et al.
A Non-Newtonian Fluid Robot
Chiffre 8. Robot moving between three points not on a direct path.
appears in a red color in a shade related to the speaker intensity. The red shades are divided into
10 levels. Assumed maximal speaker intensity of 900 V; thus every red level represents 90 V. Le
higher the intensity, the stronger the red color.
A3.3 Calculating Aspect Ratio
We used the following algorithm to calculate the aspect ratio of the spot.
initialize max-ratio to 0
set degrees to 1
while degrees is less than or equal to 90, increased by 3
rotate picture at current number of degrees
create a cross in the center of the robot % center was calculated earlier
% the cross is always straight, while the image is rotating
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 9. Robot hump outlines at high versus low acceleration. Summary of 10 independent movement (A to B) experiments.
Each column is an experiment, while the rows are ordered as follows: top, velocity (red) and acceleration (bleu) per frame;
middle, robot outline (pixels) at maximum-acceleration frame ±5 frames (overlaid together ); bottom, robot outline (pixels)
at average-acceleration frame ±5 frames (overlaid together ). Robot hump behavior is clearly shown in middle row samples,
while the behavior is more random in the bottom row samples.
12
Artificial Life Volume 22, Nombre 1
G. Hachmon et al.
A Non-Newtonian Fluid Robot
horizontal-line ←rotated image ∩ horizontal-cross-line
vertical-line ←rotated image ∩ vertical-cross-line
si
vertical-line is longer than horizontal-line
temp ←vertical-line divided by horizontal-line
autre
temp ←horizontal-line divided by vertical-line
end if
si
temp > max-ratio
max-ratio ←temp
end if
degrees ←degrees + 3;
end loop
save max-ratio for current frame
A3.4 Calculating Center, Area, and Velocity
As a preprocessing step before analysis, we converted each frame to a binary image to distinguish
between the spot and the background. After detecting the spot, we were able to use MATLAB
image-processing toolbox built-in functions to find its center and its area in each frame. Those func-
tions get a binary image of an object and return the objectʼs center in a 2D coordinate, and the area
in pixels.
For calculating velocity we sampled two centers from two consecutive seconds and calculated the
Euclidean distance between them. For calculating area per second and center per second we averaged the areas
and the centers, respectivement, obtained for an entire second. This appears in the following pseudocode:
Centers contains spotʼs center (2D coordinate) in each frame
Areas contains spotʼs area (in pixels) in each frame
Set FPS (frames per second) to the frame rate of the video
Set counter to 1
While counter is less than videoʼs number of seconds
% set frames indexes to the start and the end of the current second
% par exemple., if FPS = 25 and counter = 2 then start index = 26 and end index = 50
start-index
end-index
??(counter − 1) * FPS + 1;
??(counter ) * FPS;
% calculate velocity (pixels/sec)
current-coordinate ←Centers[start-index]
next-coordinate
distance
save distance for current second
←Centers[end-index + 1]
←Euclidean distance between current and next coordinates
Artificial Life Volume 22, Nombre 1
13
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
G. Hachmon et al.
A Non-Newtonian Fluid Robot
% calculate average centers
average-center
save average-center for current second
←average of Centers[from start-index to end-index]
% calculate average area
average-area
save average-area for current second
←counter + 1;
counter
←average of Areas[from start-index to end-index]
End loop
Appendix 4: Control Profiles
See Figures 10–12.
Appendix 5: Robot Assembly and Control Protocols
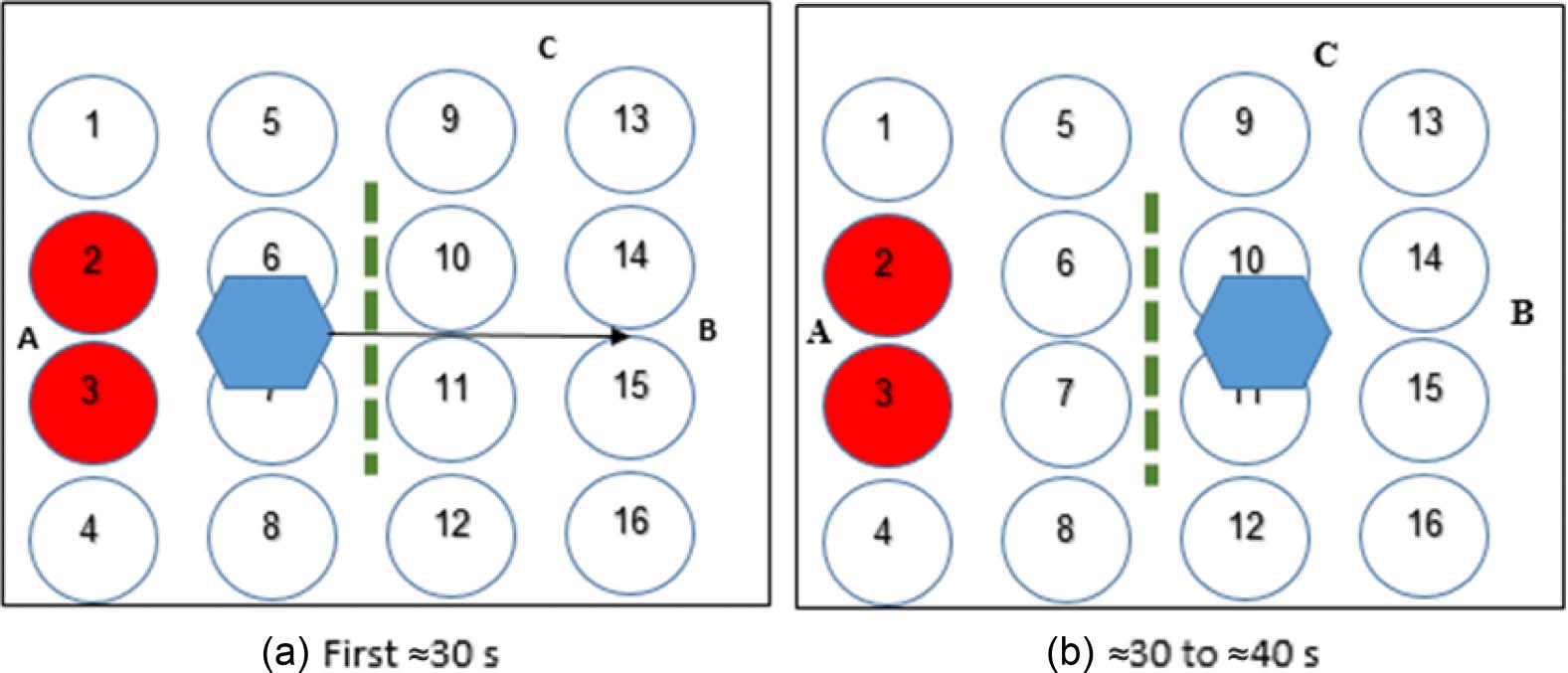
Scheme 1: A→B movement experiments: Voir la figure 13. A robot (30 mL of 58% w/v starch
microparticles, 7.15% v/v E-124 / E-143 coloring, 7.15% v/v fructose–glucose mixture) était
applied onto the speaker surface at point A, yielding a robot ≈10 cm in diameter. Transducers 2 et
3 were activated in pulses for 30 s on average (time changes slightly between experiments) until the
robot reached the third speaker lane. Transducers 10 et 11 were then activated in pulses for a time
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
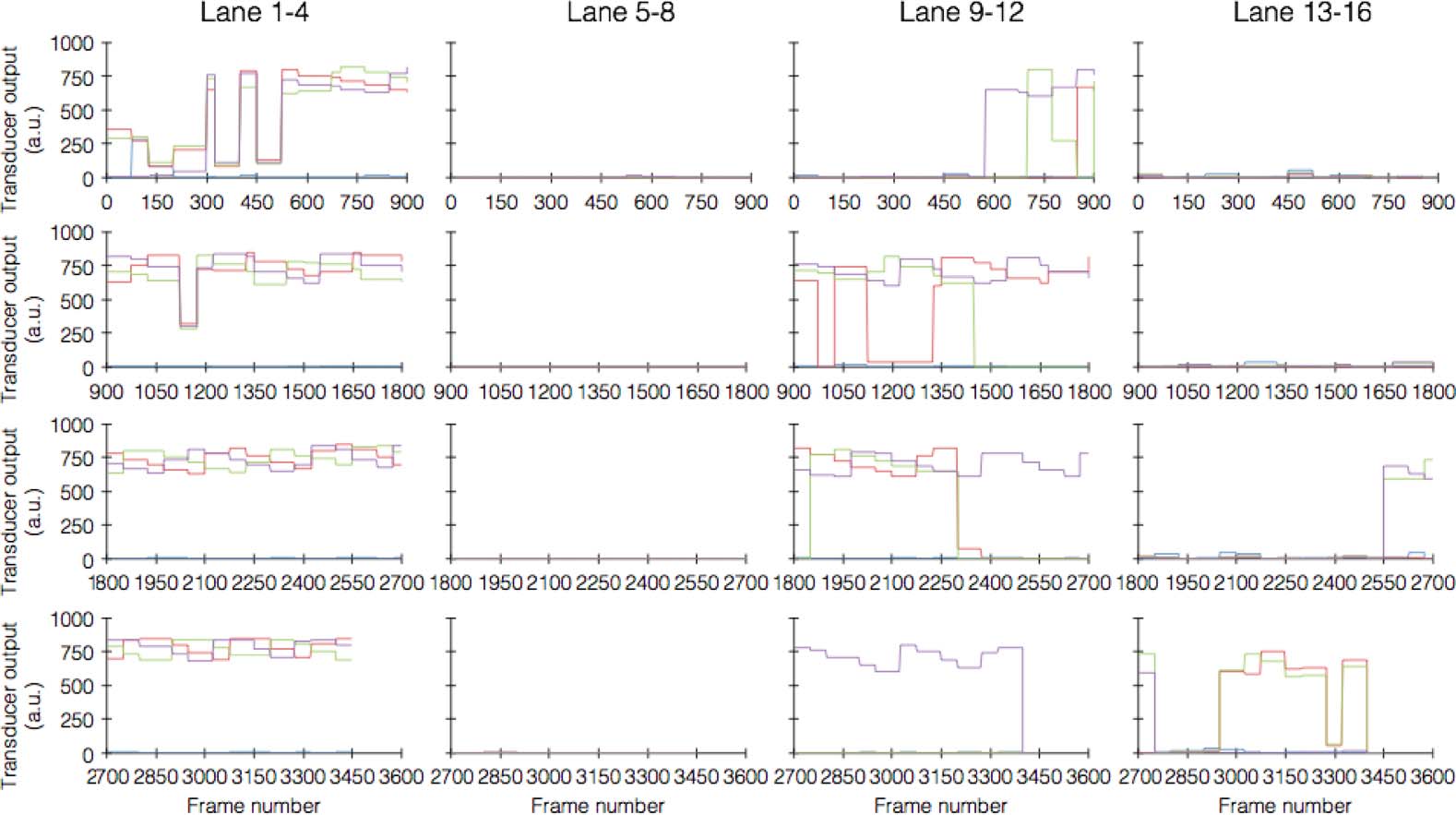
Chiffre 10. Mapping transducer outputs required for driving movement in straight path. Top panels show a robot (dark
vert) driven along a straight path from right to left, while active transducers are shown in red (color brightness
corresponds to output level). Graphs show the output of each transducer lane (colored lane in inset ) along the
course of the experiment, with inset cell color corresponding to transducer position and graph color.
14
Artificial Life Volume 22, Nombre 1
G. Hachmon et al.
A Non-Newtonian Fluid Robot
Chiffre 11. Mapping transducer outputs required for driving movement in straight path. This series of graphs is a zoom-in
on the series in Figure 10, showing enhanced time axis.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 12. Mapping transducer outputs required for carrying load.
Artificial Life Volume 22, Nombre 1
15
G. Hachmon et al.
A Non-Newtonian Fluid Robot
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 13.
16
Artificial Life Volume 22, Nombre 1
G. Hachmon et al.
A Non-Newtonian Fluid Robot
length of 10 s on average up until the robot reached point B. Transducers 2 et 3 were to remain
active all the time.
Scheme 2: A→B→A experiments: Voir la figure 14. As in the A→B experiments, a robot (30 mL of
58% w/v starch microparticles, 7.15% v/v E-124 / E-143 coloring, 7.15% v/v fructose–glucose
mixture) was applied onto the speaker surface at point A, yielding a robot ≈10 cm in diameter.
Transducers 2 et 3 were activated in pulses for 30 s on average (time changes slightly between
experiments) until the robot reached the third speaker lane. Transducers 10 et 11 were then ac-
tivated in pulses for a time length of 10 s on average up until the robot reached point B. At this
indiquer, all transducers were shut off, and transducers 14 et 15 became active for ≈30 s on average.
After the robot reached speaker lane 2, transducers 6 et 7 were activated in the same manner as
before for ≈10 s on average, pushing the robot back to point A.
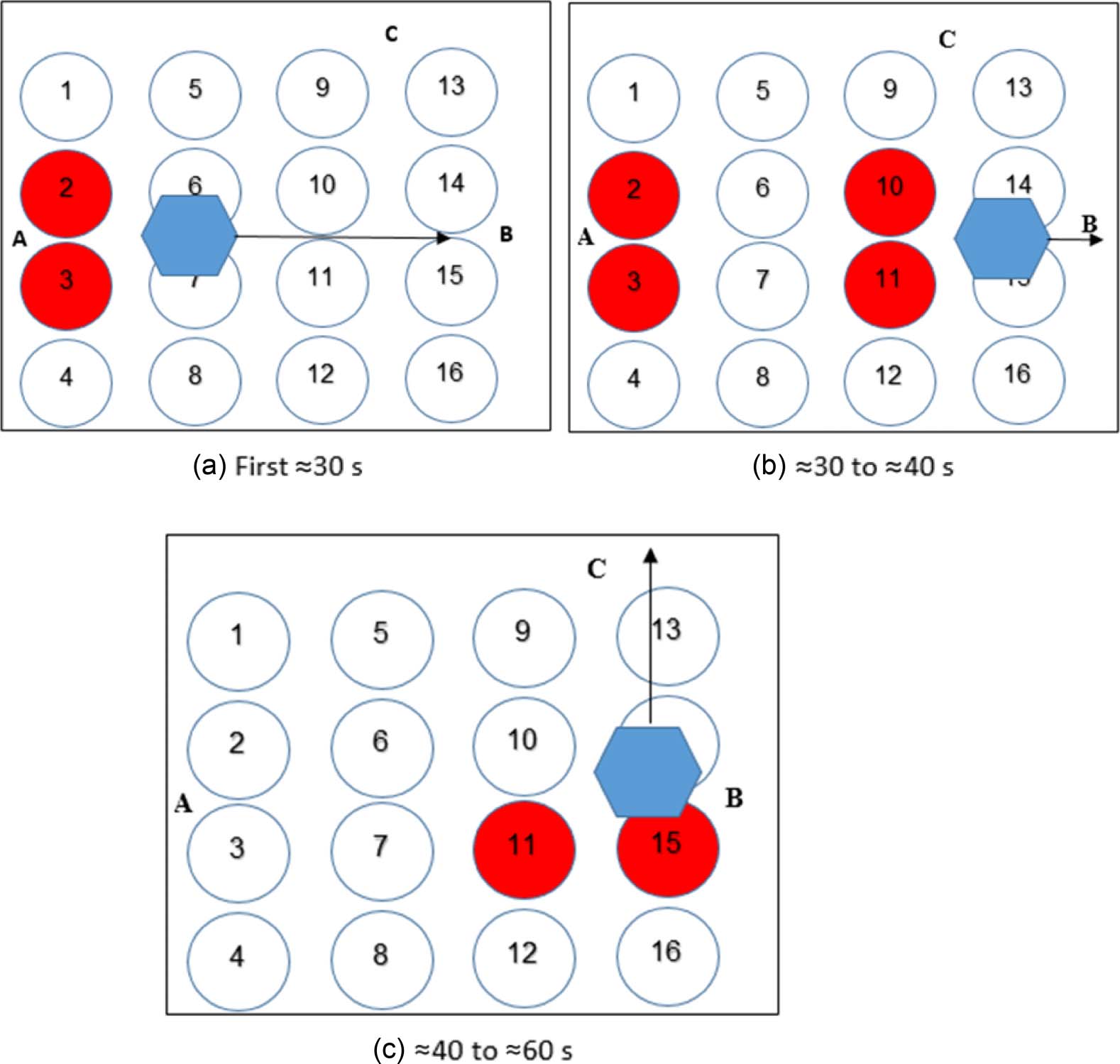
Scheme 3: A→B→C experiments: Voir la figure 15. A robot (30 mL of 58% w/v starch micropar-
ticles, 7.15% v/v E-124 / E-143 coloring, 7.15% v/v fructose–glucose mixture) was applied onto
the speaker surface at point A, yielding a robot ≈10 cm in diameter. Transducers 2 et 3 étaient
activated in pulses for 30 s on average (time changes slightly between experiments) until the robot
reached the third speaker lane. Transducers 10 et 11 were then activated in pulses for a time length
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 14.
Artificial Life Volume 22, Nombre 1
17
G. Hachmon et al.
A Non-Newtonian Fluid Robot
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 15.
de 10 s on average up until the robot reached point B. À ce point, all transducers were shut off,
and transducers 11 et 15 became active for ≈20 s on average up until the robot reached point C.
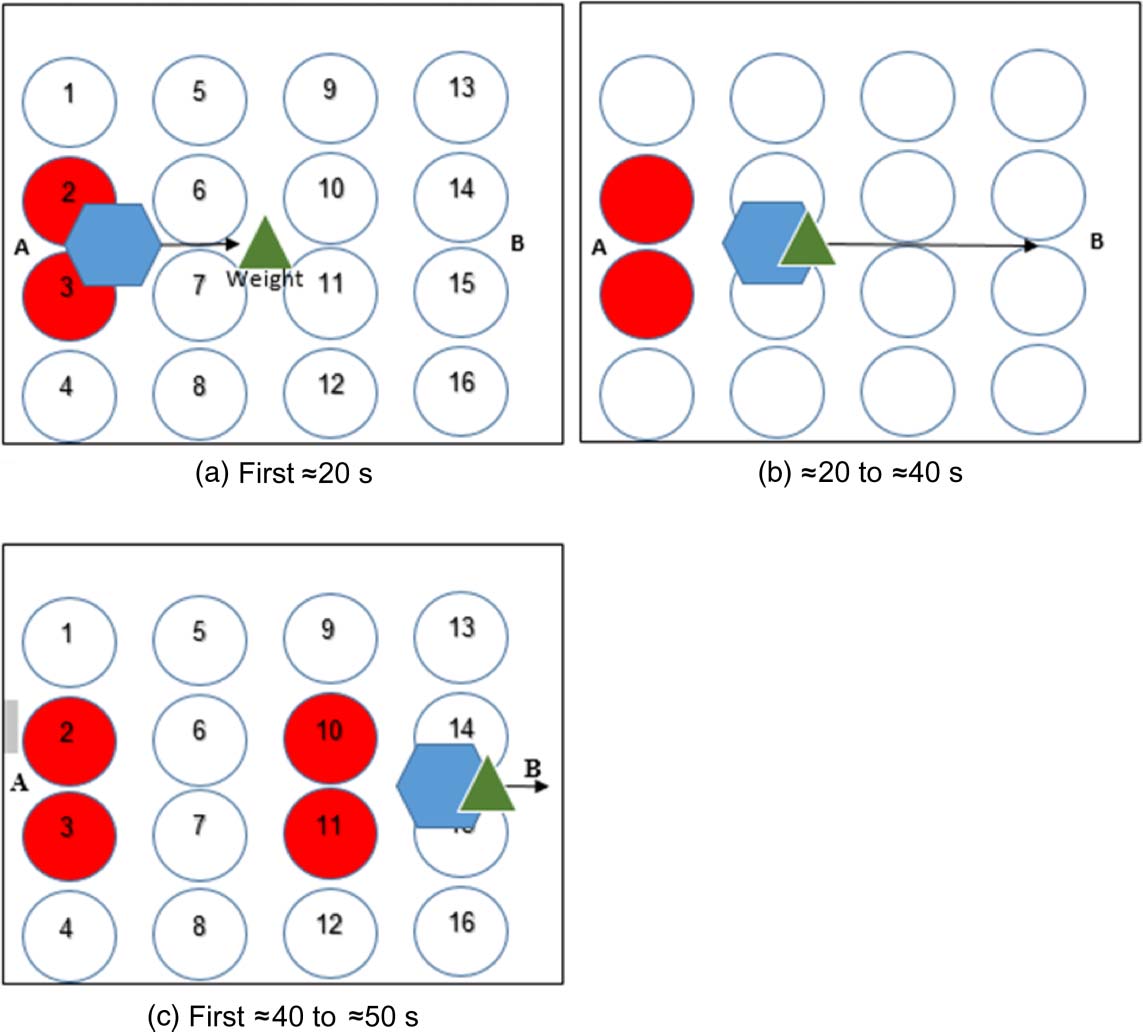
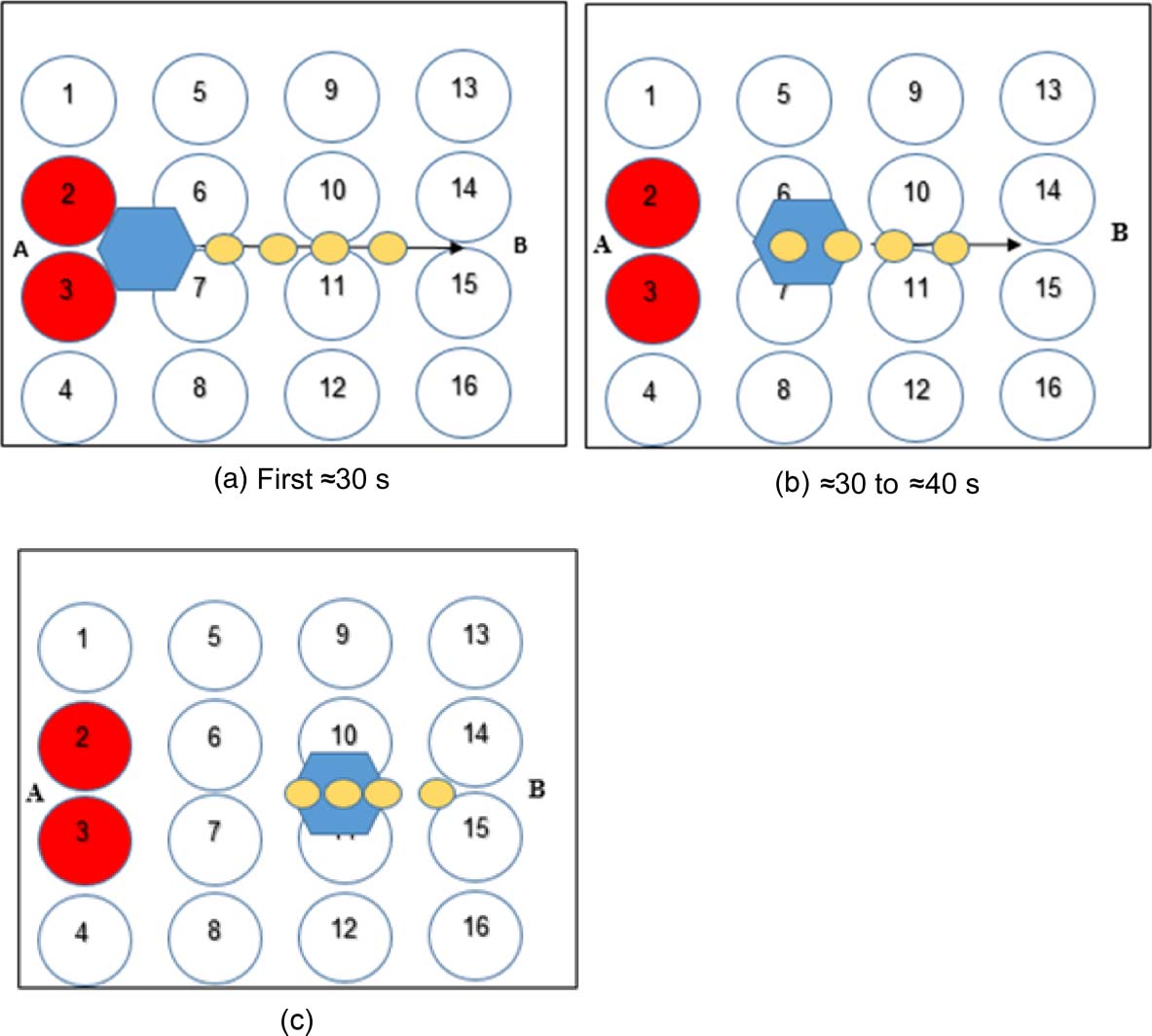
Scheme 4: Load-carrying experiments: Voir la figure 16. A robot (30 mL of 58% w/v starch mi-
croparticles, 7.15% v/v E-124 / E-143 coloring, 7.15% v/v fructose–glucose mixture) was applied
onto the speaker surface at point A, yielding a robot ≈10 cm in diameter. A 100-g weight was placed
upon the surface 10 cm in front of the robot. Transducers 2 et 3 were activated in pulses for ≈20 s
on average (time changes slightly between experiments) until the robot reached and engulfed the
weight. The transducers were kept on for ≈20 s more on average, until reaching line 3. Transducers
10 et 11 were then activated in pulses for a time length of 10 s on average up until the robot
reached point B.
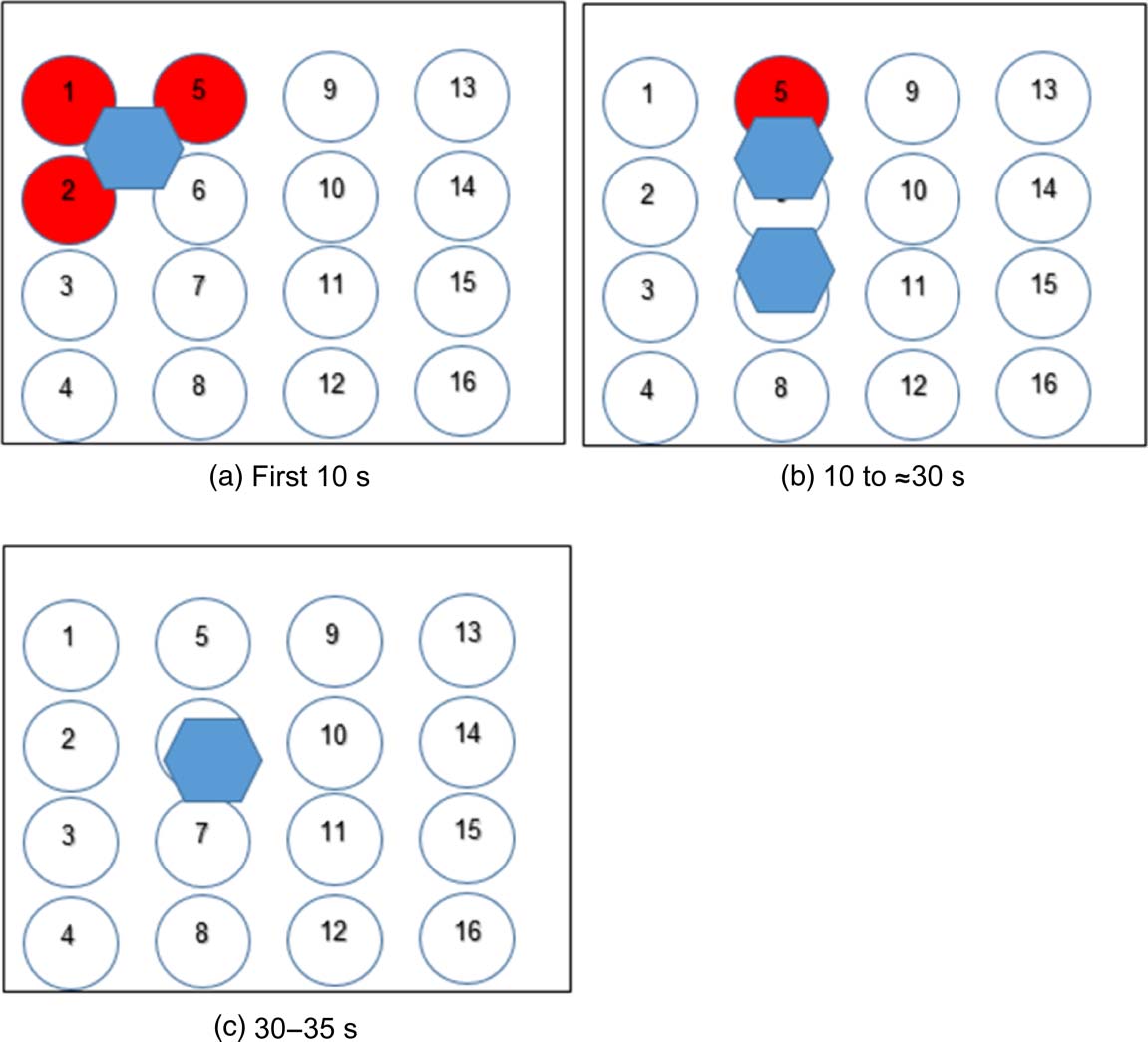
Scheme 5: Splitting and re-merging experiments: Voir la figure 17. A robot (30 mL of 58% w/v
starch microparticles, 7.15% v/v E-124 / E-143 coloring, 7.15% v/v fructose–glucose mixture) était
applied onto the speaker surface between transducers 1, 2, et 5, yielding a robot ≈10 cm in diam-
eter. Transducers 1, 2, et 5 were activated all at once for 10 s until the robot split into two parts.
Transducer 5 was activated in pulses for a time length of 20 s, pushing the closer piece of the robot
into the piece farther away. The two pieces merged back into a single robot.
18
Artificial Life Volume 22, Nombre 1
G. Hachmon et al.
A Non-Newtonian Fluid Robot
Chiffre 16.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 17.
Artificial Life Volume 22, Nombre 1
19
G. Hachmon et al.
A Non-Newtonian Fluid Robot
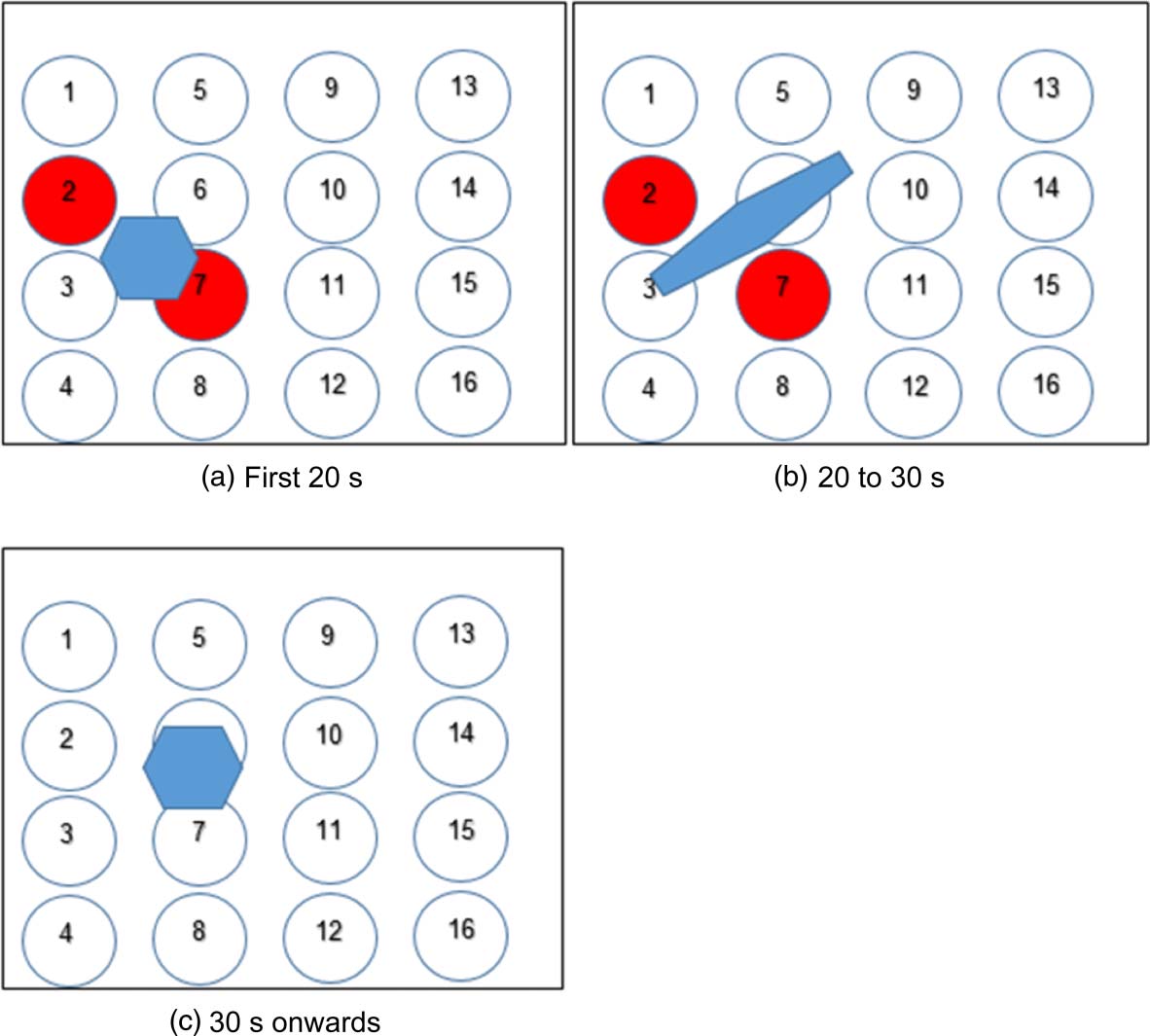
Chiffre 18.
Scheme 6: Shapeshifting experiments: Voir la figure 18. A robot (30 mL of 58% w/v starch micro-
particles, 7.15% v/v E-124 / E-143 coloring, 7.15% v/v fructose–glucose mixture) was applied
onto the speaker surface between transducers 2 et 7, yielding a robot ≈10 cm in diameter. Trans-
ducers 7 et 2 were activated in pulses for 20 s until the robot changed its shape into an elongated
formulaire. The transducers were then shut down, allowing the robot to return to a round shape.
Scheme 7: Counting experiment: Voir la figure 19. As in the A→B experiments, a robot (30 mL of
58% w/v starch microparticles, 7.15% v/v E-124 / E-143 coloring, 7.15% v/v fructose–glucose
mixture) was applied onto the speaker surface at point A, yielding a robot ≈10 cm in diameter. Quatre
alumina bits (10 g of alumina nanoparticles in 10 mL of distilled water each) were placed along the
path from point A to point B. Transducers 2 et 3 were activated in pulses for 100–110 s, pushing
the robot towards point B while collecting the alumina bits on its way. At the third bit, the robot
could not continue its movement.
Scheme 8: Percolation (movement through grating) experiment: Voir la figure 20. A robot (30 mL
de 58% w/v starch microparticles, 7.15% v/v E-124 / E-143 coloring, 7.15% v/v fructose–glucose
mixture) was applied onto the speaker surface at point A, yielding a robot of ≈10 cm in diameter.
Gratings (five bolts 2 cm apart, connected by a wooden board) were placed upon the surface, à propos
10 cm away from the robot. Transducers 2 et 3 were activated in pulses for ≈60 s until the robot
passed through the gratings.
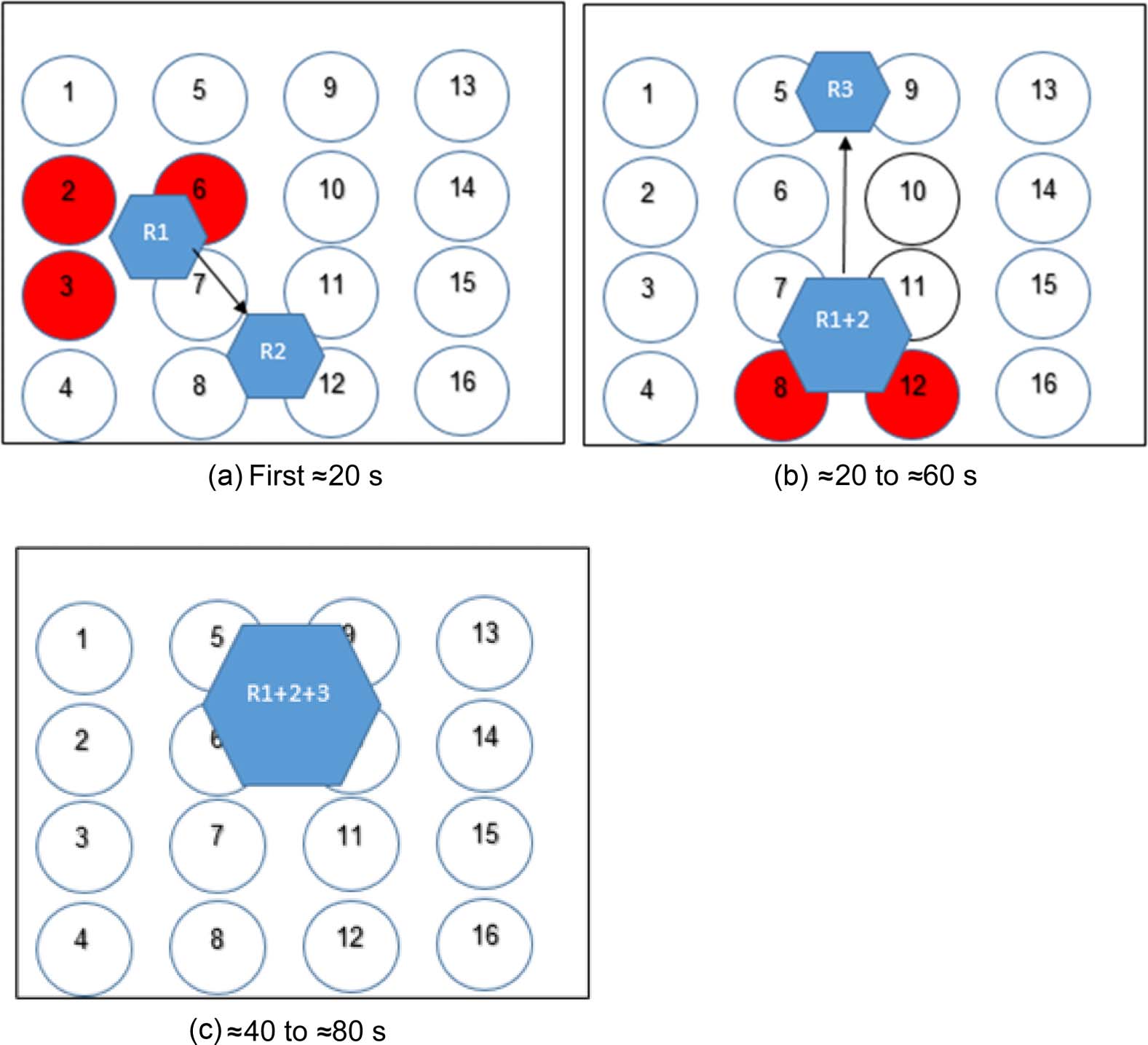
Scheme 9: Chemical synthesis (biosynthesis): Voir la figure 21. As this experiment involved DNA
and proteins, the robot composition was altered slightly. Three robots were made, each mixed with
substances as shown in Table 3. 15 mL of R1 and 15 mL of R2 were applied onto the speaker
surface 15 cm away from each other. Transducers 2 et 3 were activated in pulses for 20 s,
followed by transducer 6. R1 and R2 were then merged into R1+2. Transducers 6 et 7 étaient
activated, thus making R1+2 mix itself. À ce point, 15 mL of R3 was applied onto the surface
between transducers 6 et 10. Transducers 8 et 12 were then activated in pulses for about 15 s,
20
Artificial Life Volume 22, Nombre 1
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
G. Hachmon et al.
A Non-Newtonian Fluid Robot
Chiffre 19.
pushing R1+2 onto R3, making the two robots merge. Transducers 7 et 11 were activated,
allowing the robot to mix for 20 s. A sample of 20 mL was taken from the mixture and run
in a centrifuge at 17,000g for 5 min. The supernatant was collected and mixed with streptavidin
beads for 15 min. This final mixture was then tested with an Accuri BD6 FACS. BupH buffer and
EDC were purchased from Pierce.
Chiffre 20.
Artificial Life Volume 22, Nombre 1
21
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
G. Hachmon et al.
A Non-Newtonian Fluid Robot
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
2
2
1
1
1
6
6
5
4
7
5
un
r
t
je
/
_
un
_
0
0
1
9
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 21.
Tableau 3.
Robot R1
Robot R2
Robot R3
Robot composition 60% w / v starch microparticles,
Loaded substance
20% v / v BupH × 1 buffer,
13% v / v distilled water,
7% v / v E-143
20 mg albumin after DyLight
traitement (performed
according to the
manufacturerʼs instructions)
60% w / v starch microparticles,
20% v / v BupH × 1 buffer,
13% v / v distilled water,
7% v / v E-143
60% w / v starch microparticles,
20% v / v BupH × 1 buffer,
13% v / v distilled water,
7% v / v E-143
200 mg EDC
1 mL 100-AM poly-T ssDNA
0
modified with biotin (3
)
0
and amine (5
)
22
Artificial Life Volume 22, Nombre 1