A Beamformer to Play with
Wall Reflections: Le
Icosahedral Loudspeaker
Franz Zotter,∗ Markus Zaunschirm,∗
Matthias Frank,∗ and Matthias
Kronlachner†
∗Institute of Electronic Music and
Acoustics
University of Music and Performing Arts
Inffeldgasse 10/3
8010 Graz, Autriche
{zotter, zaunschirm, frank}@iem.at
†Automotive Systems GmbH
Harman Becker
Schlesische Str. 135
94315 Straubing, Allemagne
matthias.kronlachner@harman.com
Abstrait: The quote from Pierre Boulez, given as an epigraph to this article, inspired French researchers to start
developing technology for spherical loudspeaker arrays in the 1990s. The hope was to retain the naturalness of sound
sources. Now, a few decades later, one might be able to show that even more can be done: In electroacoustic music,
using the icosahedral loudspeaker array called IKO seems to enable spatial gestures that enrich alien sounds with a
tangible acoustic naturalness.
After a brief discussion of directivity-based composition in computer music, the first part of the article describes the
technical background of the IKO, its usage in a digital audio workstation, and psychoacoustic evidence regarding the
auditory objects the IKO produces. The second part deals with acoustic equations of spherical beamforming, how the
IKO’s loudspeakers are controlled correspondingly, how we deal with excursion limits, and the resulting beam patterns
generated by the IKO.
The loudspeaker “anonymizes” the actual
source. . . . There will be more resemblance,
in a certain way, between amplified piano and
amplified harp, than between amplified and
unamplified piano. One could say that the
instruments have gone through a “rolling mill”
of amplification and have lost some of their
individuality. . . . The composer is left to play
with this phenomenon and to make use of it in
an informed manner.
acoustiques, and were used in his compositions
. . . of Silence (2007), Hist Whist (2009), and most
prominently in the opera Re Orso (2011) with an
eight-loudspeaker column hanging in the middle of
the stage.
A starting point to composing with directivity is
“La Tim ´ee,” a cube housing six loudspeakers utilized
by the researchers at IRCAM in order to give more
naturalness to loudspeaker-based diffusion of sounds
(Causs ´e, Bresciani, and Warusfel 1992; Warusfel,
Derogis, and Causs ´e 1997; Misdariis et al. 2001).
—Boulez 1983
The playback system discussed here, called IKO,
Composing Directivity for Electroacoustic Music
In electroacoustic music, we find the application of
directionality in Marco Stroppa’s music that used
vertically stacked loudspeakers, each of which was
aimed at a different angle. These were called totem
Journal de musique informatique, 41:3, pp. 50–68, Automne 2017
est ce que je:10.1162/COMJ a 00429
c(cid:2) 2017 par le Massachusetts Institute of Technology.
Publié sous Creative Commons
Attribution 3.0 Unported (CC PAR 3.0) Licence.
is a 20-sided, 20-channel loudspeaker system in
the form of the convex regular icosahedron (voir
Chiffre 1). As a compact spherical loudspeaker array,
the IKO provides the technical means to project a
focused sound beam in a freely adjustable direction.
Inside a room, this kind of beam direction can be set
to predominantly excite selected wall reflections,
or combinations of reflections, causing interesting
effects in perceived localization.
Although the beamforming of the IKO is capable
of uniform adjustment to all directions, contiguous
directions are not mapped to contiguous perceived
instructions, as reflection paths of a room are dis-
crete. Toujours, the IKO’s sculptural auditory objects
50
Journal de musique informatique
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
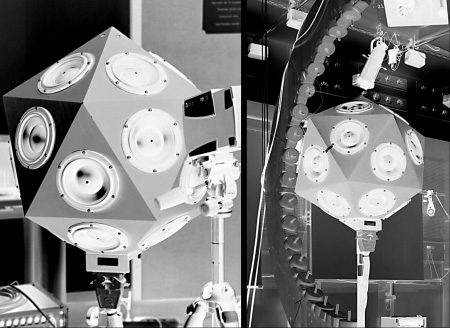
Chiffre 1. The IKO is a
20-sided, 20-channel
loudspeaker array in the
form of an icosahedron. Its
diameter is about 60 cm.
synthesis, what it is built of, how it can be presented
and staged, and which auditory objects can be
expected from the existing perceptual studies.
Technical Background and Literature
Classical beamforming technology aims at focused
emission and reception of waves by arrays of
transducers driven and superimposed with different
weights, delays, or filters. If beamforming only
uses delays or weights, we speak of delay-and-
sum or weight-and-sum beamforming, respectivement,
whereas the most general approach using filters
is called filter-and-sum beamforming (Schelkunoff
1943; Brandstein and Ward 2001). When allowing
filters with gains exceeding the maximum of the
directivity pattern, strong focusing is possible even
with small apertures. This is called superdirective
or supergain beamforming (Bloch, Medhurst, et
Pool 1953; Elko 2000).
Based on the idea of exploiting beamforming
to selectively excite wall reflections as a type of
surround-sound technology, a planar loudspeaker
array at the typical center loudspeaker position
is commercialized in Yamaha’s Sound Bar for
home-cinema applications (Takumai 2006). Dans ce
application, surround and side loudspeakers are
substituted by beams emphasizing suitable wall
reflections.
As an alternative method of creating strongly
focused sound beams, parametric arrays utilize
the nonlinearity of air (Bennett and Blackstock
1975; Croft and Norris 2003). A powerful group
of ultrasound transducers plays an amplitude-
modulated carrier frequency above 35 kHz at a sound
pressure level higher than 120 dB. Its envelope is
demodulated along the propagation path. Le
interpretation as a nonlinear source phenomenon
is called a parametric array. Sugibayashi et al.
(2012) built and evaluated the use of directionally
adjustable ultrasound transducer arrays mounted
on each of the 20 surfaces of an icosahedron to
establish a mixed-reality sound-field synthesis. Ce
intriguing system had to be supplemented, cependant,
by common electrodynamic transducers to support
frequencies below 1 kHz.
Zotter et al.
51
(cf. Sharma 2016) offer an exciting spatialization
technology to composers of electroacoustic mu-
sic, in the broadest sense of the term. The IKO’s
presence on stage offers a scene that is unexpect-
edly pronounced and natural, like that of a human
performer.
We promote the use of variable directivity of
compact spherical loudspeaker arrays in computer
music to create new auditory objects. The first half
of this article is dedicated to the existing software
solutions to working with the IKO, the IKO’s
hardware, its staging, and what is known about the
perception of its sound beams in a room. The second
half provides a deeper understanding of the acoustic
principles behind the IKO’s spherical beamforming,
an approach to stay within excursion limits of
the transducers, and details on how the spherical
beamforming and velocity control of the IKO are
achieved and verified, on the basis of measurements
and a multiple-input, multiple-output (MIMO)
system design.
Part I: Beamforming and the IKO in Practice
The first half of this article deals with a literature
review on beamforming, beamforming applications,
and compact spherical loudspeaker arrays, et
information about the IKO that is relevant for its
practical application—how it is controlled with
plug-ins for a digital audio workstation (DAW), comment
it is virtualized for different rooms using binaural
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The technology utilized for compact spherical
loudspeaker arrays such as the IKO is linear and
superdirective, and is called spherical harmonic
beamforming (cf. Butler and Ehrlich 1977 pour
underwater sound and Warusfel, Derogis, et
Causs ´e 1997 for music). The targeted directional
resolution is uniform and independent of the
beam direction, and the technique is based on
filtering to equalize different attenuations for
spherical harmonics of different orders, quand
radiated to the near or far field (Zotter and Noisternig
2007).
The reasoning behind a variable-directivity
playback device for music (as presented by Causs ´e,
Bresciani, and Warusfel 1992; Warusfel, Derogis, et
Causs ´e 1997; Misdariis et al. 2001) has motivated
other research groups to pursue technical efforts
of establishing and controlling compact spherical
loudspeaker arrays. At Princeton University, arrays
like these have been built for electroacoustic
performances with, par exemple, the Princeton
laptop orchestra (Cook et al. 1998; Trueman et al.
2006). At the University of California, Berkeley,
researchers investigated magnitude-based beam-
pattern control and accuracy limits (Kassakian
and Wessel 2003, 2004; Kassakian 2005, 2006;
Avizienis et al. 2006). Further notable efforts to
build, control, and use arrays such as these have
been undertaken in Austria (Zotter and H ¨oldrich
2007; Zotter and Noisternig 2007; Pomberger 2008;
Zotter, Pomberger, and Schmeder 2008; Zotter 2009;
Kerscher 2010; Zotter and Bank 2012), Allemagne
(Pollow and Behler 2009; Pollow 2014), Brazil and
France (Pasqual 2010; Pasqual, Herzog, and Arruda
2010; Pasqual, Arruda, and Herzog 2010), Israel
(Rafaely and Kaykin 2011; Morgenstern, Zotter,
and Rafaely 2012; Morgenstern, Rafaely, and Zotter
2015), Australia (Miranda, Cabrera, and Stewart
2013), and New Zealand (Poletti, Betlehem, et
Abhayapala 2015).
Other work has been pursued recently in our
present research project Orchestrating Space by
Icosahedral Loudspeaker (OSIL), for which the goal
is to artistically find and define sound sculptures by
composing music with the IKO (Sharma 2016) et à
scientifically investigate these sculptures (Sharma,
Zotter, and Frank 2014; Frank, Sharma, and Zotter
2015; Wendt et al. 2016, 2017; Zaunschirm, Frank,
and Zotter 2016).
Controlling the IKO with DAW Plug-ins
Real-time performances and composition for the
IKO can be controlled from a standard consumer
personal computer, or even a laptop. Le 20 driving
signals for the IKO’s loudspeakers are generated
using a combination of the ambiX and mcfx VST
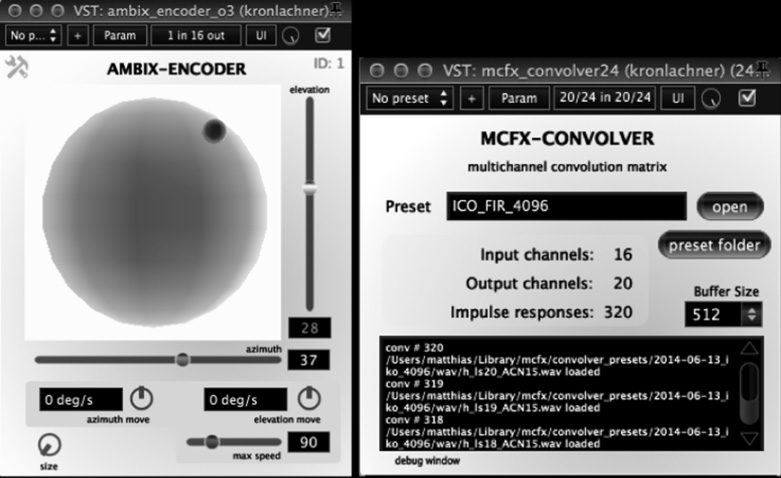
plug-ins (Kronlachner 2014), voir la figure 2. The ambiX
software allows one to create, modify, and decode
higher-order Ambisonics on a DAW. Bien que
Ambisonics is usually associated with loudspeakers
surrounding the audience, the same representation
is deployed to control directional beams radiated
outwards from compact spherical arrays such as the
IKO.
Care has been taken to make the required matrix
convolution efficient, as the IKO’s control system
(voir la figure 3) consists of 320 FIR filters (20 chaînes,
each requiring 16 filters) whose coefficients are
stored as WAV files. The mcfx convolver software
carries out convolutions as nonuniform, partitioned
fast convolutions for low latency and low CPU
load. The filters used by mcfx convolver to connect
each of its inputs to each of its output is specified
in a configuration file. Selecting from different
configuration files allows performance with different
setups—for instance, on a different array or with
a different filter set. To host the ambiX and mcfx
VST plug-ins, DAWs and other music software
environnements, such as Max, AudioMulch, Bidule,
Ardour, and Reaper, must be capable of dealing
with at least 20 chaînes. For the IKO, we mainly
use Reaper because of its support for up to 64
channels per track or bus. En outre, it supports
live performance and improvisation by remote
control using Open Sound Control (OSC). Other
convenient features include the ability to record and
program automations, as well as faster-than-real-
time rendering of finished projects to 20-channel
audio files. Reaper and the plug-ins are available
under Windows, Mac OS, and Wine (Linux).
The signal routing and processing schema is
shown in Figure 3. A playback signal sc(t) et
52
Journal de musique informatique
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2. Screenshots of
VST plug-ins controlling
the IKO. The plug-in
ambix encoder o3 (un)
controls the beam
direction of the IKO for
one input signal by
encoding it to 16
third-order Ambisonic
signals. The plug-in
mcfx convolver24 (b)
generates 20 loudspeaker
signals from the 16
third-order Ambisonic
signals using real-time
convolution.
Chiffre 3. Processing
schema controlling the
IKO’s beamforming. Ce
includes the Ambisonic
bus as the sum of encoded
source signals, feeding the
final MIMO control
système.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2
Chiffre 3
its beam direction θ c(t) are fed into a third-order
Ambisonics encoder as an insert effect (am-
bix encoder o3). The resulting 16 channels are
sent to a master mix. The 20-channel master mix
uses a 20 × 16 fast convolution matrix as an insert
effet (mcfx convolver24), avec 4,096 coefficients at
a sample rate of 44.1 kHz. The resulting 20 signals
feed the amplifiers for the 20 loudspeakers of the
IKO. In the real-time operation of the IKO, CPU
load amounts to 65 percent for ten sources and a
512-sample buffer, using a MacBook Pro 2.53 GHz
Intel Core 2 Duo.
Zotter et al.
53
Chiffre 4. Processing
schema of the virtual IKO
using measured room
impulse responses from
the IKO to the Eigenmike
EM32 and measured
HRIRs.
Chiffre 5. Measurement
setups for loudspeaker
cone velocity and sound
pressure: laser vibrometer
measurement of
voltage-to-loudspeaker
cone-velocity transfer
les fonctions (un) and sound
pressure measurement
with semicircular
microphone array (r =
75 cm) at IEM CUBE, avec
a turntable so that
directivity is measured at
18 × 36 = 648
instructions (b).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5
chi (2007), or smaller arrays such as the prototype
by Kerscher (2010), were not powerful enough for
concert performances. The IKO is constructed of
20 equilateral triangular faces with 34.7-cm-long
outer edges, made from medium density fiberboard,
and cut with a bevel of 20.9◦. Ten of these faces
are glued together in the shape of two pentagonal
pyramids of five triangular faces each. The apexes
of the two pyramids form the upper and lower apex
of the IKO. They are twisted 36◦ with respect to
l'un l'autre, and they are glued to a horizontal belt
of ten faces pointing upward and downward in al-
ternation (cf. Figure 5a). The interior of the IKO is a
The Virtual IKO for Headphones
The virtual IKO (vIKO) by Zaunschirm, Frank,
and Zotter (2016) provides a DAW-based real-time
simulation of the IKO by binaural synthesis to
headphones, optionally head-tracked (voir la figure 4).
It provides a Reaper session with suitable routing
and delivers a collection of presets for the aforemen-
tioned plug-in suites. The presets provided are based
on measurements taken in different rooms using the
IKO as a source and using the Eigenmike EM32 to
capture impulse responses at different listening po-
sitions. The vIKO comes with two exemplary room
responses and, currently, two sets of head-related
impulse responses (HRIRs) measured by the Acous-
tics Research Institute in Vienna. Each of these
sets can be chosen for matrix convolution in the
mcfx convolver plug-in and for binaural rendering
in the ambix binaural plug-in, respectivement. Based
on vIKO, the OSIL Web site (http://iem.at/osil) de-
fers binaural renderings of basic time-variant beam
constructions (called IKO moves) and of musical
pieces.
IKO Hardware
The IKO turned out to perform well in electro-
acoustic concerts thanks to its large and powerful
transducers. Par contre, the transducers described
in the initial technical report by Zotter and Sontac-
54
Journal de musique informatique
Tableau 1. Azimuth and Zenith Angles for IKO Loudspeakers
Loudspeaker Azimuth
Zenith
Loudspeaker Azimuth
Zenith
1
2
3
4
5
6
7
8
9
10
0◦
72◦
144◦
−144◦
−72◦
0◦
72◦
144◦
−144◦
−72◦
142.62◦
142.62◦
142.62◦
142.62◦
142.62◦
100.81◦
100.81◦
100.81◦
100.81◦
100.81◦
11
12
13
14
15
16
17
18
19
20
36◦
108◦
180◦
−108◦
−36◦
36◦
108◦
180◦
−108◦
−36◦
79.19◦
79.19◦
79.19◦
79.19◦
79.19◦
37.38◦
37.38◦
37.38◦
37.38◦
37.38◦
Loudspeaker 1 is next to the cable socket, the sequence runs counterclockwise from
bottom to top.
single unpartitioned volume filled with wool, and it
contains the cabling of the transducers, lequel
is attached to the back of a 42-pin Harting Han
DD industrial socket. In the center of each of the
20 faces, a 6.3-in. Morel CAW-638 transducer is
mounted and can produce an excursion of up to
xmax = ±4.25 mm. The channel indices and angular
coordinates of the loudspeakers are given in Table 1.
The Harting socket on the outside allows one to
attach a cable hanging downwards, which is a
15-m-long bundle of 20 × 1.5-mm2 loudspeaker wire
pairs gathered in a braided sleeving. At the other
fin, the cables are attached to a socket connected
to the 40 banana-jack sockets of a customized
sonible d:24. This is a compact 24-channel ampli-
fier consisting of three rack units with 250 W per
channel.
The prototype of the IKO, developed at the In-
stitute of Electronic Music and Acoustics (IEM)
and described in this article, was used for mea-
surements, experiments, les performances, etc., leading
to a cooperation with the company sonible to
manufacture the IKO and market it commer-
cially (cf. http://iko.sonible.com). This new IKO by
IEM and sonible is redesigned for easier transport
and for easy integration with the MADI/Dante-
capable sonible d:24 multichannel amplifier. Il
uses a newer Morel transducer series ensuring high
performance.
Staging the IKO
The IKO can create auditory objects of high spatial
definition when utilizing first-order reflections of
the walls in the performance space. In current per-
formance practice, two basic staging constellations
are used: one for typical rectangular rooms, and an-
other that uses a concave setup of reflectors behind
the IKO (Sharma 2016; see also Figure 6).
Rectangular rooms are the simplest constellation
in which the IKO is played, preferably between
a corner of the room and the audience. This was
the constellation used, par exemple, in concerts
showcasing IKO held at the International Confer-
ence on Digital Audio Effects (DAFx) dans 2010, à
the Darmstadt International Summer Courses for
New Music in 2014, and in the Media Art Gallery
at the Zagreb Showroom of Contemporary Sound
(Izlog Suvremenog Zvuka) festival in 2015. Ce
arrangement makes it possible to exploit balances
between at least two pronounced reflections from
the walls and the direct sound. The IKO’s distance to
the audience should be at least as far as the distance
to both walls. Rectangular rooms often offer more
effects, such as usable reflections, Par exemple, à
the ceiling, at the floor, or from a more distant side
wall, as well as spatial reverberation effects. Là
est, cependant, some risk depending on the geometry,
wall material, sound material, etc.. It is therefore
Zotter et al.
55
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 6. IKO in the
performance setup in
MUMUTH, Graz, à la
2010 International
Conference on Digital
Audio Effects (un), et en
the ZKM Kubus,
Karlsruhe, à la 2015
InSonic festival (b).
wise to compose pieces that can be adjusted to the
given environment.
Alternativement, concave arrangements of reflectors
behind the IKO were used at a concert in the Signale
Graz festival in 2014 and at the InSonic conference
held at ZKM in 2015 (voir la figure 6), offering a large
set of useful, distinct reflections. We had a similar
performance situation in the French Pavilion at
the Showroom of Contemporary Sound festival in
2015, where the cylindrical wall of the performance
space could be used without modification. Le
concave reflector arrangement behind the IKO
should preferably exhibit a radius of about 5 m to
7 m, and the loudspeaker should be placed in the
symmetry axis of the arrangement at a distance of
à propos 1.5 m to 3 m. The concave setup increases
the number of reflections (stage wall, side walls),
which are otherwise limited, to a plethora of distinct
reflections, available everywhere between the stage
and the side walls. The audience should preferably
be at least about 5 m away from the IKO to allow a
balanced perspective on auditory objects that can be
shaped by the reflections.
At the low-frequency end (less than 100 Hz),
the IKO is omnidirectional and acts as a powerful
subwoofer that is well able to excite large spaces.
In the octave above 100 Hz, beams radiated by the
IKO become directional, so that bass in the octave
au-dessus de 100 Hz can be moved around in the room.
Such sounds are often localized as rotary spacious
zones that are not colocated with the IKO.
Perception of Sound Beams in Rooms
Although it might seem logical that the sound prop-
agation path emphasized the most would appear as
a localized direction in our perception, the prece-
dence effect counteracts this intuition. To study
the perceived localization of directional sources
with variable orientation, our initial studies (Zotter
et autres. 2014; Zotter and Frank 2015) considered a
simulated source with a third-order beam pattern in
a rectangular room. Third-order beam patterns are
composed of all spherical harmonics of the orders
n = 0 . . . 3. Direct and reflected sound were simu-
lated using the image-source method up to first and
second order, which were auralized on 24 Genelec
8020 loudspeakers arranged on a horizontal ring in
an anechoic environment.
The first of these two studies showed that the
orientation of directional sound sources can be
perceived, with a localization that can substantially
deviate from the direct path. It used nine volunteer
listeners who undertook the task of localizing test
signals consisting of bursts of pink noise. Le
localized direction could be modeled (1) by an
extended energy-vector model considering a rough
echo threshold of −0.25 dB/ms (Rakerd, Hartmann,
and Hsu 2000) et (2) by a binaural predictor based
on a model proposed by Werner Lindemann (1986).
The second study, with eleven experienced volun-
teer listeners with normal hearing, was also based on
an auralized source with third-order beam patterns
56
Journal de musique informatique
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
and tested the perceived direction localization for
36 source orientations in 10◦ steps. Each listener
was presented with conditions in individual random
sequence and could respond not only by a single,
primary localization direction, but also by a possible
secondary one. Listeners were asked to respond by
naming integers, based on the even-numbered ticks
visibly attached to the loudspeakers. The primary
direction could be modeled by the aforementioned
extended energy-vector. Secondary directions ap-
peared to be difficult to model and were perceived in
only 24 pour cent de la 36 source orientations using
auralization with direct sound and first-order image-
sources, but in 42 percent with second-order image
sources added, indicating a dependency on later
reflections. Par contre, primary localization direc-
tions were not changed much by second-order image
sources.
Apart from perceived direction, the perceived
distance when using a source with controlled
directivity has also been investigated (Laitinen et al.
2015; Wendt et al. 2016). Wendt and colleagues
described the relation between perceived distance
and beam-pattern control such as beam width (c'est à dire.,
commande) or the angle between a pair of symmetric
third-order beams.
Wendt and coworkers (2017) provided a collection
of formal listening experiments with the physical
IKO’s spherical harmonic beamforming in a real
room. These experiments test (1) the localization of
static beam directions, (2) the localization of time-
variant beam steering using different sounds, et
(3) whether “sculptural” compositional categories
can be distinguished based on spatial impressions,
as opposed to impressions based on monophonic
playback.
From Wendt et al.’s second experiment, nous
can present further results demonstrating that
beamforming from the physical IKO in a physical
room (which is not ideal) is able to influence the
impression of distance in the case of time-varying
beam-pattern control (for details of the acoustical
properties and the exact setup positions of the
experiment, cf. Wendt et al. 2017). Fifteen listeners
with experience in auditing spatial audio, drawn
from IEM’s expert listening panel, took part in the
experiment, in which each listener gave responses
for two listening positions.
The conditions consisted of 5 sec of pink-noise
bursts and a 5-sec, time-varying beam-pattern
control. Subjects were asked to mark the position of
the evoked auditory object in time steps of 0.5 sec,
using ten controllable dots on a graphical interface
showing the layout of both the room and IKO (cf.
Chiffre 7). Each of the dots could be moved by
mouse and flashed at the corresponding moment of
playback. Listeners could repeat the playback until
they were satisfied with the match of their response
and what they perceived.
Binaural renderings using vIKO (Zaunschirm,
Frank, and Zotter 2016) are available online:
http://phaidra.kug.ac.at/o:37710, http://phaidra.kug
.ac.at/o:37712 for the two beam-pattern-control
conditions at position 1, and http://phaidra.kug
.ac.at/o:37711, http://phaidra.kug.ac.at/o:37711 pour
position 2.
Chiffre 7 shows the mean results for each time
step for two beam-pattern control conditions:
(1) left–right amplitude panning from a beam aiming
toward the left to a beam aiming toward the right,
(2) distance panning for beam steering to the back
wall (c'est à dire., direct sound at listening position 1). Le
distance panning gradually changes the order of
the beam pattern from third order to zeroth order
and back again to third order. Distance panning
works more clearly at position 1, but also affects the
perceived location at position 2. The result for left–
right amplitude-panned beam pairs is perceivable
from both listening positions and indicates the
feasibility of lateral distance control for auditory
events created by the IKO.
Part II: Beamformer Theory and Control of the IKO
Based on the technical background provided in
Part I, we now look to a deeper understanding of
the working principles behind beams formed with
compact spherical loudspeaker arrays such as the
IKO. It explains the governing acoustic equations
in general, and for the IKO as a particular case. UN
comprehensive approach is outlined for the design
Zotter et al.
57
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 7. Geometry of the
experiment, montrant le
listening and IKO
positions in our lecture
room for listening
positions 1 (un) et 2 (b).
Dark gray circles indicate
mean localized positions
for distance panning, et
light gray squares the
positions for left-right
panning. Marker size
increases with time.
Chiffre 8. Spherical
harmonic patterns up to
third order (un). Specific
surface vibration patterns
(b) can synthesize
spherical harmonic beam
patterns in the far field
(cap model).
Chiffre 7
Chiffre 8
and verification of the filters required to configure
the DAW plug-ins. A novel limiting criterion is
introduced to safely operate the array by ensuring a
limited loudspeaker excursion. The MIMO system
design presented here is based on laser Doppler
vibrometry measurements. The resulting far-field
beam pattern is examined based on microphone-
array measurements at a finite distance, et le
measured data are extrapolated to the far field to
verify the design.
Beamforming with the IKO
The key to controlling focused sound beams with
the IKO is the ability to control the sound particle
velocity on its surface in the shape of spherical
harmonics; see Figure 8a.
The IKO houses 20 passive loudspeakers that are
mounted into its rigid faces (shown in Figure 1). Être-
cause all loudspeakers of the IKO share one common
enclosure volume, the motion of the loudspeaker
58
Journal de musique informatique
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 9. MIMO synthesis
of spherical harmonic
beam patterns.
Chiffre 10. Surface
vibration patterns on a
sphere are radiated to
sound pressure in the far
field, with frequency
responses depending on
the spherical harmonic
order n. The diagram
shows these responses for a
sphere of the radius R =
28.5 cm. The far-field
sound pressure is
characterized by the
increasingly strong
attenuation of components
of high orders and low
frequencies, yielding (n +
1)th-order high-pass
slopes, cf. Équation 1.
cones is acoustically coupled. Directivity pattern
synthesis requires individual control of the cone mo-
tion, cependant, so that a MIMO crosstalk canceler is
needed. The vibrometry-based identification of the
canceler is described in the section “Measurement
and Control of Loudspeaker Cone Velocity,” see the
rightmost block of the schema in Figure 9.
According to the equations of sound radiation,
any surface velocity vibration pattern in the exact
shape of an individual spherical harmonic (cf.
Figure 8a) propagates to a sound-pressure pattern
of the same shape at any radius. The pattern only
undergoes a radius- and frequency-dependent change
of magnitude and phase, obeying a well-defined
frequency response for each order n of spherical
harmonique (Zotter 2009). In the far field, this is
bn(kR) =
ρc in
(cid:4)(2)
n (kR)
kh
,
(1)
where ρ is the density of air (1.2 kg/m3), c is the
speed of sound (343 m/sec), and i is the imaginary
unit. The wave number k = 2π f/c is defined by the
(cid:4)(2)
n (kR) is the derivative of the nth-
frequency f , and h
order spherical Hankel function of the second kind
that describes radiation for Fourier representations
with a positively signed exponent ei2π f t (Zotter
2009). The effective acoustical radius of the IKO is
R = 28.5 cm.
Complicated surface vibration patterns are
smoothed out as the sound is radiated to the far
field. Par conséquent, signals decoded to high-order
patterns are strongly attenuated, particularly at low
frequencies (voir la figure 10). The remaining low-order
patterns—decoded to the loudspeakers (as seen in
Figure 8b) by the signal processing block in the
Chiffre 10
middle of Figure 9—can be equalized by far-field
radiation control to compensate for the amplitude
and phase changes they undergo when radiated (Zot-
ter and Noisternig 2007; Pomberger 2008; Kerscher
2010). This step consists of single-input, single-
output filters (SISO) and is accomplished by the
leftmost block in Figure 9. This enables one to com-
pose far-field beam patterns out of superimposed
low-order spherical harmonics.
Given a suitable control system achieving the
control of the IKO’s surface velocity and radiation,
the composition of far-field beam patterns in
terms of spherical harmonics works using the
same tools as for arranging sounds in higher-order
Ambisonics, c'est à dire., Ambisonic encoding. Chiffre 11
demonstrates that, for an aiming of a spherical
harmonic beam towards the angle 0◦ on the horizon,
the effort to develop elaborated systems pays off:
Narrower beams can be achieved maintaining a
more consistent shape over a larger frequency
range. Figure 11a shows a beam pattern achieved
by plain max-rE Ambisonic amplitude panning
(Zotter, Pomberger, and Schmeder 2008; see also
Daniel, Rault, and Polack 1998 for details on max-rE
weighting), and Figure 11b displays a system we
designed in 2014 (cf. L ¨osler and Zotter 2015). À
avoid audible distortions due to overload at low
frequencies, this design entailed the necessity of a
low-frequency amendment by crossing over to an
omnidirectional subwoofer mode.
Zotter et al.
59
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 11. Beam pattern of
a horizontal beam, avec
magnitude in dB
(grayscale) over polar angle
and frequency for spherical
harmonic beamforming
with the IKO using
systems with plain max-rE
Ambisonic amplitude
panning (un); a version from
2014 of radiation control
including EQ by ear and
MIMO acoustic crosstalk
cancellation (b); et le
new limited-excursion
design without MIMO
acoustic crosstalk
cancellation but EQ for
the active loudspeaker
velocity (c). Magnitude
levels indicated as levels
of gray (d).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Later in this article, the section “Limiting the
Loudspeaker Cone Excursion” will present our new
design method recognizing excursion as a more
reasonable physical limitation than the white-noise
gain constraint, which we had previously used and
that was adopted from microphone array theory.
Even without a MIMO crosstalk canceler for the
IKO’s loudspeaker cones, this concept achieves
beams that are more focused than in our previous
conception, whose rough equalization by ear obviously
led to a lack of energy above 800 Hz (compare the
graphs in Figures 11b and 11c).
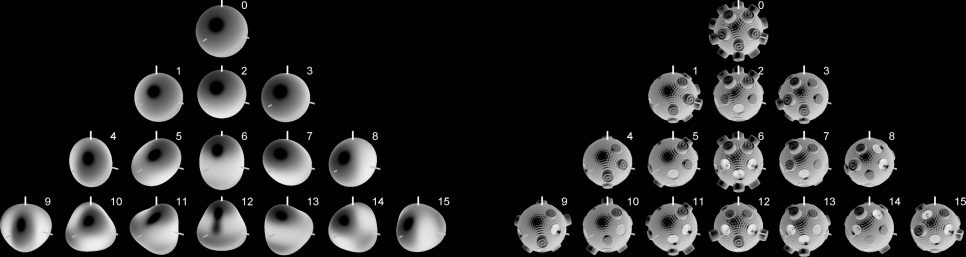
Desired max-rE Beam Patterns
Far-field beam-pattern synthesis by the IKO uses
the same description as the angular amplitude
patterns in higher-order Ambisonics. The max-rE
beam patterns that will be used here turned out
to exhibit sufficiently high side-lobe attenuation
while maintaining a narrow main lobe (Daniel,
Rault, and Polack 1998). On-axis equalized max-rE
beams of the orders i ≤ N are shown in Figure 12
and described in earlier publications (Zotter and
Frank 2012; L ¨osler and Zotter 2015), giving the
equation
N(cid:2)
n(cid:2)
gi(je ) =
n (je) wn,i Ym
Ym
n (θ c),
(2)
m=−n
(cid:7)
Pn
cos
(cid:7)
(cid:8)(cid:8)
137.9◦
i+1.51
(cid:7)
(cid:7)
wn,i =
n=0(2n+1) Pn
cos
137.9◦
i+1.51
n=0
⎧
⎪⎪⎪⎨
⎪⎪⎪⎩
0
(cid:9)
je
(cid:8)(cid:8)
for n ≤ i
elsewhere,
n (je ) are the fully orthonormal spherical
where the Ym
harmonics as depicted in Figure 8, and the Pn(·)
are nth-order Legendre polynomials (cf. Zotter and
Frank 2012). The two direction vectors θ and θ c
denote the observed direction of radiation and
the adjustable beam direction, respectivement. Le
controllable Ambisonics order is considered to be
limited by N, and the weights wn,i are the max-rE
order weights.
The Ambisonic encoding shown in Figure 3
corresponds to the distribution of a single-channel
signal to (N + 1)2 channels using the spherical
n (θ c) evaluated at the beam direction
harmonics Ym
θ c as weights, as suggested by the rightmost term
in Equation 2. The IKO control system has the task
n (je ) et
of representing the two leftmost terms, Ym
60
Journal de musique informatique
Chiffre 12. Spherical
harmonic max-rE beam
patterns of orders i = 0, 1,
2, 3, yielding rotationally
symmetrical directivity
motifs, which could be
drawn as balloon diagrams
in three dimensions. Ici,
the polar diagram shows
semicircular generatrix
curves in alternation on
the interval [0◦, ± 180◦] à
maintain quantitative
legibility.
by the weights vl, is written as
νnm|R = an
L(cid:2)
l=1
n (θ l) vl.
Ym
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
We can stack the (N + 1)2 coefficients of spherical
harmonics νnm|R into a vector νN = [νnm] et le
L loudspeaker velocities of the IKO into another
vector v = [vl]. The an weights, written as vector
aN = [un], and the spherical harmonics up to the
order N sampled at the 20 loudspeakers, written
as matrix YN = [Ym
nm, permit us to express
the matrix equation as νN|R = diag{aN}YN v whose
least-squares inverse
n (θ l)]je
v = YT
N
(cid:15)
(cid:14)−1
(cid:18)
(cid:13)
YNYT
N
(cid:16)(cid:17)
:= DN
diag{aN}−1 νN|R.
yields suitable loudspeaker velocities. Expressed
in its scalar form, with the decoder coefficients
DN = [d(je)
the coefficients νnm|R are
nm], the loudspeaker velocities vl producing
vl =
N(cid:2)
n(cid:2)
n=0
m=−n
d(je)
nm
un
νnm|R..
(3)
Radiation Control
As specified by bn(kR) in the frequency domain
(cf. Équation 1 and Figure 10), the spherical harmonic
coefficient of the surface velocity νnm|R radiates into
the far field, yielding the sound-pressure coefficient
ψnm = bn(kR) νnm|R..
The aim is to control this coefficient to obtain a
far-field beam pattern as in Equation 2
ψnm = Ym
n (θ c) wn,je,
so we invert the equation to obtain
νnm|R.( F , θ c) =
wn,je
bn(kR)
n (θ c).
Ym
wn,je, by achieving the best possible synthesis of all
the controllable (N + 1)2 max-rE -weighted spherical
harmonics in the far field.
The highest controllable order N depends on the
number of loudspeakers L, with L ≥ (N + 1)2. Le
highest-order pattern for the L = 20 of the IKO is
g3(je ) and its synthesis is difficult to accomplish
at low frequencies. Plutôt, reasonable processing
produces a sequence of increasingly focused beam
patterns g0(je), g1(je ), g2(je), g3(je ) over frequency.
Cap Model of Surface Vibration
A unity-gain velocity excited by the loudspeaker
cone sitting at the direction θ l can be modeled as a
spherical cap of the aperture angle α. For a variable
direction of observation, this is expressed as a unit
step function u(θ Tθ l − cos(α/2)). Its contribution to
each spherical harmonic is defined by the transform
(cid:10)
(cid:11)
ν(je)
nm
|R =
u
θ Tθ l − cos
(cid:12)
un
2
n (je ) dθ ,
Ym
(cf. Zotter, Sontacchi, and H ¨oldrich 2007), yielding
ν(je)
nm
|R = an Ym
⎧
⎨
n (θ l),
Pn−1(cos α
an =
⎩
2 ) − cos α
2 Pn(cos α
2 ) n > 0
1 − cos( un
2 )
n = 0.
A weighted superposition of all the IKO’s loud-
speaker cones, assuming their velocities are given
Insertion into Equation 3 yields the loudspeaker
velocities required to produce the desired max-rE
Zotter et al.
61
beam pattern gi(je ), here with i = 0, 1, 2, 3,
v(je)
je ( F , θ c) =
N(cid:2)
n(cid:2)
n=0
m=−n
d(je)
nm
un
wn,je
bn(kR)
n (θ c).
Ym
Chiffre 10 shows that the inverse of bn(kR) peut
require unrealistic bass boosts to compensate for
attenuation of higher orders. For spherical micro-
phone arrays, realistic implementations consider
filtering into successive frequency bands Hi( F ), dans
which only an increasingly focused beam pattern
gi(je ) is synthesized with i = 0, 1, 2, 3 (L ¨osler and Zot-
ter 2015). Summed over these bands, the required
loudspeaker velocities become
vl( F , θ c) =
N(cid:2)
n(cid:2)
N(cid:2)
d(je)
nm
n=0
m=−n
i=0
Hi( F )
un
wn,je
bn(kR)
(cid:16)(cid:17)
(cid:18)
:=Hi,n( F )
(cid:15)
n (θ c). (4)
Ym
corresponding radiation pattern will vanish in the
far field. To exclusively drive excursions producing
audible sounds, economic use of excursion requires
limitation filters of slopes proportional to f n+3,
at least. We define the following filter bank using
zero-phase high- and low-pass filters:
ˆH0( F ) = ( f/ f0)3
1 + ( f/ f0)3
ˆH1( F ) = ( f/ f1)4
1 + ( f/ f1)4
ˆH2( F ) = ( f/ f2)5
1 + ( f/ f2)5
ˆH3( F ) = ( f/ f3)6
1 + ( f/ f3)6
1
1 + ( f/ f1)4
,
1
1 + ( f/ f2)5 ,
1
1 + ( f/ f3)6
,
.
The radiation control filters obtained in this way,
Hi,n( F ), depend on the spherical harmonic order n
and the synthesized beam order i. The question
is how to design the filters Hi( F ) they contain to
comply with physical limitations.
To make these filters complementary in ampli-
tude to an overall high-pass filter
Hsum( F ) = ( f/ f0)3
1 + ( f/ f0)3
,
Limiting the Loudspeaker Cone Excursion
In microphone arrays, white-noise gain limitation
prevents self-noise amplification (L ¨osler and Zotter
2015). For loudspeaker arrays, the limiting relates
instead to a maximum linear transducer excursion
|xl| ≤ xmax. Excursion is defined by integrating
velocity over time. Par conséquent, we formulate the
constraint in the frequency domain
|xl( F , θ c)| ≤ xmax
maximum
je,θ c
using xl( F , θ c) = vl( F , θ c)/i2π f .
The original radiation control filters 1/bn(kR)
exhibit slopes proportional to 1/ f n+1. By the addi-
tional factor 1/i2π f , slopes for unlimited excursion
are proportional to 1/ f n+2. Ainsi, high-pass filters
stabilizing the individual radiation control filters by
enforcing a constant excursion limit must at least be
proportional to f n+2. What is more, whenever such
an excursion limit takes effect, the magnitude of the
they are normalized using
Hi( F ) = ( f/ f0)3
1 + ( f/ f0)3
(cid:9)
ˆHi( F )
N
i=0
ˆHi( F )
.
Inserted into Equation 4, with suitable cut-on
frequencies fi, the filters yield limited excursion
curves as show in Figure 13b, where the excursion
was normalized by the excursion reached at 40 Hz
in omnidirectional radiation mode (dashed line).
Measurement and Control of Loudspeaker
Cone Velocity
This section deals with measuring the voltage-to-
velocity transfer functions of the IKO’s loudspeakers,
including acoustic coupling (crosstalk) entre
active and passive movements of the loudspeaker
cones. The measured matrix is used to design an
equalized and crosstalk-canceled control system
for loudspeaker velocities. The voltage-to-velocity
transfer functions of the 20 loudspeakers were
62
Journal de musique informatique
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 13. Filter bank Hi(F)
and overall response using
suitably chosen cut-on
frequencies [fi]T = [40, 70,
113, 173] Hz (un), et le
resulting limited excursion
normalized at 40 Hz (b).
Chiffre 14. Active
voltage-to-velocity
responses of all 20
loudspeakers (un), et 19
passive responses to
excitation voltages at
loudspeaker 1 out of
T(F) = [tij(F)] (b).
Chiffre 13
Chiffre 14
measured using the exponential sine-sweep method
(Farina 2000) and a laser Doppler vibrometer along
the cone axis, environ 24 cm away from each
loudspeaker (as shown in Figure 5a). All measured
impulse responses were cropped to 4,096 samples
at a 44.1-kHz sample rate. Chiffre 14 shows some
frequency responses.
With the transfer-function matrix in the
frequency domain T, the output velocities
v = [v1, . . . , vL]T caused by the input voltages
u = [u1, . . . , uL]T are calculated as
v = T u.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
by the voltages
u = T−1 v,
and one can insert Equation 4 for beamforming. À
keep the corresponding impulse responses short and
easy to window in the time domain, a regularized
inverse TH(TTH + a tr{TTH}
L
L = 20. The regularization was set to a = 0.1.
je)−1 was used, avec
Le 20 × 20 voltage-to-velocity impulse responses
are available at http://phaidra.kug.ac.at/o:37716.
The frequency dependency is omitted from this
notation to maintain simplicity. Given that T is
invertible, decoupled cone velocities v are controlled
Verification of whether the far-field beam pattern
complies with the desired max-rE beam pattern
Verification by Sound Pressure Measurements
Zotter et al.
63
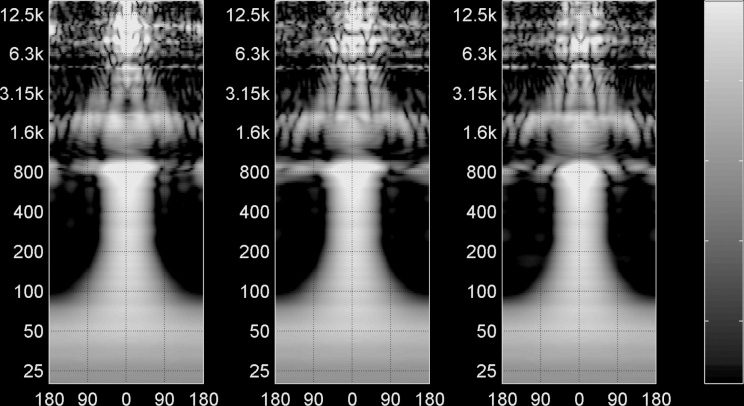
Chiffre 15. Horizontal cuts
through the on-axis
direction of far-field beam
patterns of IKO, using a
MIMO crosstalk canceler
and limited-excursion
radiation control. Using
polar angle and frequency
as axes, the diagrams show
dB values for three beam
instructions: on-axis
direction of loudspeaker 6
(un); direction between
loudspeakers 6, 11, et 15
(b); and directions
between loudspeakers 6
et 11 (c). Magnitude
levels are indicated as
levels of gray (d).
has been achieved by microphone measurements
surrounding the IKO, as shown in Figure 5b (cf. aussi
Zotter and Bank 2012). The impulse responses of the
loudspeaker-to-microphone paths were also mea-
sured using the exponential sine-sweep technique
and windowing to 320 samples. A sine-square fade-
in of 20 samples was used before the first impulse
and an 80-sample fade-out at the very end.
Le 648 × 20 voltage-to-sound-pressure impulse
responses are available at http://phaidra.kug.ac
.at/o:37715.
In the frequency domain, the sound-pressure
sample pj|75 cm received at the jth microphone
due to the driving voltages ul from each of the
loudspeakers is described by the transfer paths gli( F )
of a MIMO system,
pj|75 cm( F ) =
L(cid:2)
l=1
glj( F ) ul.
(5)
The least-square-error inverse
C = (YYT)−1 YT = [c( j)
nm]
of Y = [Ynm(θ j)] (the spherical harmonics sampled at
the microphone positions θ j) permits decomposition
into coefficients of spherical harmonics ψnm|75 cm
up to n ≤ 17 with the given measurement setup.
The far-field sound pressure is calculated from this
decomposition at a desired cross section
pff( F , je ) =
17(cid:2)
n(cid:2)
n=0
m=−n
in+1 Ym
n (je)
k hn(k75 cm)
648(cid:2)
j=1
nm pj|75 cm( F ).
c( j)
Chiffre 15 shows a cross section centered on beams
with different orientations after inserting the IKO
control into Equation 5. The new beam patterns are
more constant and narrow in the range from 150 Hz
à 800 Hz than they were with earlier approaches.
À 200 Hz, the previous approaches in Figure 11
yield beams reaching an attenuation of approx-
imately −6 dB from their maximum at angles
between ±135◦ (Figure 11a), ±60◦ (Figure 11b),
±50◦ (Figure 11c), and the proposed filter design in
Chiffre 15 reaches this value at ±45◦. À 100 Hz,
the proposed design achieves a ±70-degree width
for a −6 dB attenuation from its maximum. Avec
the previous designs, only the design in Figure 11c
achieved focus at all to ±80◦, but it was not able to
maintain the amplitude below 100 Hz.
The new beam patterns in Figure 15 become
roughly omnidirectional below 100 Hz, and above
800 Hz the inherent spatial aliasing counteracts
a smooth beam pattern. A notch around 1 kHz
appears, most probably because of a mismatch of
64
Journal de musique informatique
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
the loudspeaker cone vibration from an ideally rigid
shape. Around the frequencies 1.6 kHz, 5 kHz, et
8 kHz, the IKO seems to lose its directivity. This is
probably caused by modal breakup or interior modes
of the IKO.
Conclusion
We presented the IKO, a new computer music instru-
ment utilizing superdirective spherical harmonic
beamforming to orchestrate the wall reflections in
a room. We could outline its use by free, ready-to-
use DAW plug-ins enabling its spherical harmonic
beamforming in real time, and its use as a virtualized
instrument (vIKO) that is freely available together
with illustrative binaural renderings. We gave a
precise description of our IKO prototype and basic
concert setups that were used in the past.
To describe perceptual aspects of the spherical
harmonic beamforming with the IKO, we reviewed
previous experiments and showed new results
indicating that the IKO allows one to control the
direction as well as the distance impression of the
synthesized sound objects.
We summarized the spherical harmonic beam-
forming theory of compact spherical arrays and
presented a simple way of defining a bank of linear-
phase limitation filters that suppress side lobes in
each of its frequency bands. We were able to outline
constraints that are relevant for compact spherical
loudspeaker arrays, since the more common white-
noise-gain limitations, as applicable to spherical
microphone arrays, become meaningless in this
contexte.
Enfin, we presented a practical study to mea-
sure responses to design an entire multiple-input,
multiple-output control filter set. It is based on laser
Doppler vibrometry measurements for a clean con-
trol of the IKO’s loudspeaker cone velocities, avec
crosstalk cancelled; excursion-limited analytic filter
conception, suppressing side lobes, for radiation con-
trol; and measurements verifying the synthesized
radiation patterns by using far-field extrapolated
measurements with a spherical microphone array.
All measurement data are made available to support
reproducible research.
Remerciements
This work was funded by the Austrian Science
Fund (FWF), project no. AR 328-G21, “Orchestrating
Space by Icosahedral Loudspeaker.” We would like
to thank Computer Music Journal’s anonymous
reviewers and Editor, and Frank Schultz of sonible,
for their valuable comments on our manuscript.
Les références
Avizienis, R., et autres. 2006. “A Compact 120 Independent El-
ement Spherical Loudspeaker Array with Programmable
Radiation Patterns.” In Proceedings of the 120th Audio
Engineering Society Convention. Available online at
www.aes.org/e-lib/browse.cfm?elib=13587 (subscrip-
tion required). Accessed April 2017.
Bennett, M.. B., and D. T. Blackstock. 1975. “Parametric
Array in Air.” Journal of the Acoustical Society of
America 57(3):562–568.
Bloch, UN., R.. Medhurst, et S. Pool. 1953. “A New
Approach to the Design of Super-Directive Aerial
Arrays.” Proceedings of the IEE-Part III: Radio and
Communication Engineering 100(67):303–314.
Boulez, P.. 1983. “L’Acoustique et la musique contempo-
raine: Introduction.” In Revue d’acoustique: Congr `es
international d’acoustique, pp. 213–216.
Brandstein, M., and D. Ward. 2001. Microphone Arrays:
Signal Processing Techniques and Applications. Berlin:
Springer.
Butler, J.. L., et S. L. Ehrlich. 1977. “Superdirective
Spherical Radiator.” Journal of the Acoustical Society
of America 61(6):1427–1431.
Causs ´e, R., J.. Bresciani, and O. Warusfel. 1992. “Radiation
of Musical Instruments and Control of Reproduction
with Loudspeakers.” In Proceedings of the International
Symposium on Musical Acoustics, pp. 67–70.
Cook, P., et autres. 1998. “N>>2: Multi-Speaker Display
Systems for Virtual Reality and Spatial Audio Pro-
jection.” In Proceedings of the International Con-
ference on Auditory Display. Available online at
www.icad.org/Proceedings. Accessed 21 Mars 2017.
Croft, J.. J., and J. Ô. Norris. 2003. “Theory, Histoire, et
the Advancement of Parametric Loudspeakers: A Tech-
nology Overview.” Technical Report 98-10006-1100
Rev. E. San Diego, California: American Technology
Corporation.
Daniel, J., J.-B. Rault, and J.-D. Polack. 1998. “Ambisonics
Encoding of Other Audio Formats for Multiple Listening
Zotter et al.
65
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Conditions.” In Proceedings of the 105th Audio
Engineering Society Convention. Available online at
www.aes.org/e-lib/browse.cfm?elib=8385 (subscription
required). Accessed April 2017.
Elko, G. W. 2000. “Superdirectional Microphone Arrays.”
In J. Benesty and S. L. Gay, éd.. Acoustic Signal
Processing for Telecommunication. Berlin: Kluwer.
Farina, UN. 2000. “Simultaneous Measurement of Im-
pulse Response and Distortion with a Swept-Sine
Technique.” In Proceedings of the 108th Audio En-
gineering Society Convention. Available online at
www.aes.org/e-lib/browse.cfm?elib=10211 (subscrip-
tion required). Accessed April 2017.
Frank, M., G. K. Sharma, and F. Zotter. 2015. "Quoi
We Already Know about Spatialization with Compact
Spherical Arrays as Variable-Directivity Loudspeakers.”
Paper presented at the inSonic Conference, 26–28
Novembre, Karlsruhe, Allemagne. Available online at
iem.kug.ac.at/fileadmin/media/osil/2015 FrankEtAl
inSonic WhatWeAlreadyKnowAboutSpatialization
WithCompactSphericalArraysAsVariabledirectivity
Loudspeakers.pdf. Accessed March 2017.
Kassakian, P.. 2005. “Magnitude Least-Squares Fitting
via Semidefinite Programming with Applications to
Beamforming and Multidimensional Filter Design.”
In Proceedings of the IEEE International Conference
onAcoustics, Speech, and Signal Processing. Avail-
able online at ieeexplore.ieee.org/document/1415644
(subscription required). Accessed May 2017.
Kassakian, P.. 2006. “Convex Approximation with Ap-
plications in Magnitude Filter Design and Beam-
forming.” PhD dissertation, Electrical Engineering
and Computer Science, Université de Californie,
Berkeley. Available online at www2.eecs.berkeley.edu
/Pubs/TechRpts/2006/EECS-2006-64.pdf. Accessed
Mars 2017.
Kassakian, P., and D. Wessel. 2003. “Design of Low-Order
Filters for Radiation Synthesis.” In Proceedings of the
115th Audio Engineering Society Convention. Available
online at www.aes.org/e-lib/browse.cfm?elib=12448
(subscription required). Accessed April 2017.
Kassakian, P., and D. Wessel. 2004. “Characterization of
Spherical Loudspeaker Arrays.” In Proceedings of the
117th Audio Engineering Society Convention. Available
online at www.aes.org/e-lib/browse.cfm?elib=12940
(subscription required). Accessed April 2017.
Kerscher, M.. 2010. Compact Spherical Loudspeaker
Array, Implementation of a System for Variable Sound
Radiation. Saarbr ¨ucken: VDM.
Kronlachner, M.. 2014. “Plug-in Suite for Mastering
the Production and Playback in Surround Sound and
Ambisonics.” Paper presented at the 136th Audio
Engineering Society Convention Student Design Com-
petition, 28 Avril 2014, Berlin. Available online at
www.matthiaskronlachner.com/wp-content/uploads
/2013/01/kronlachner aes studentdesigncompetition
2014.pdf. Accessed March 2017.
Laitinen, M.-V., et autres. 2015. “Controlling the Perceived
Distance of an Auditory Object by Manipulation of
Loudspeaker Directivity.” Journal of the Acoustical
Society of America 137(6):462–468.
Lindemann, W. 1986. “Extension of a Binaural Cross-
Correlation Model by Contralateral Inhibition: je.
Simulation of Lateralization for Stationary Signals.”
Journal of the Acoustical Society of America 80(6):1608–
1622.
L ¨osler, S., and F. Zotter. 2015. “Comprehensive Radial
Filter Design for Practical Higher-Order Ambisonic
Recording.” In Fortschritte der Akustik: Tagungsband
der deutschen Arbeitsgemeinschaft f ¨ur Akustik, pp.
452–455.
Miranda, L., D. Cabrera, and K. Stewart. 2013. “A
Concentric Compact Spherical Microphone and Loud-
speaker Array for Acoustical Measurements.” In
Proceedings of the 135th Audio Engineering Soci-
ety Convention. Available online at www.aes.org
/e-lib/browse.cfm?elib=16986 (subscription required).
Accessed April 2017.
Misdariis, N., et autres. 2001. “Radiation Control on Multi-
Loudspeaker Device: La Tim ´ee.” In Proceedings of
the International Computer Music Conference, pp.
306–309.
Morgenstern, H., B. Rafaely, and F. Zotter. 2015. "Le-
ory and Investigation of Acoustic Multiple-Input
Multiple-Output Systems Based on Spherical Arrays in
a Room.” Journal of the Acoustical Society of America
138(5):2998–3009.
Morgenstern, H., F. Zotter, et B. Rafaely. 2012. “Joint
Spherical Beam Forming for Directional Analysis of
Reflections in Rooms.” Journal of the Acoustical
Society of America 131(4):3207–3207.
Pasqual, UN. M.. 2010. “Sound Directivity Control in a 3-D
Space by a Compact Spherical Loudspeaker Array.”
PhD dissertation, University of Campinas, Faculty of
Mechanical Engineering, Campinas, Brazil.
Pasqual, UN. M., J.. R.. Arruda, and P. Herzog. 2010.
“Application of Acoustic Radiation Modes in the
Directivity Control of a Spherical Loudspeaker Array.”
Acta Acustica United with Acustica 96(1):32–42.
Pasqual, UN. M., P.. Herzog, and J. R.. Arruda. 2010. “Theo-
retical and Experimental Analysis of the Behavior of a
Compact Spherical Loudspeaker Array for Directivity
66
Journal de musique informatique
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Control.” Journal of the Acoustical Society of America
128(6):3478–3488.
Poletti, M.. UN., T. Betlehem, and T. D. Abhayapala. 2015.
“Higher-Order Loudspeakers and Active Compensation
for Improved 2D Sound Field Reproduction in Rooms.”
Journal of the Audio Engineering Society 63(1–2):31–45.
Pollow, M.. 2014. “Directivity Patterns for Room Acousti-
cal Measurements and Simulations.” PhD dissertation,
RWTH-Aachen, Institute of Technical Acoustics.
Pollow, M., and G. K. Behler. 2009. “Variable Directivity
for Platonic Sound Sources Based on Spherical Har-
monics Optimization.” Acta Acustica United with
Acustica 95(6):1082–1092.
Pomberger, H. 2008. “Angular and Radial Directivity
Control for Spherical Loudspeaker Arrays.” Master’s
thesis, University of Music and Performing Arts,
Institute of Electronic Music and Acoustics, Graz,
Autriche.
Rafaely, B., and D. Kaykin. 2011. “Optimal Model-Based
Beamforming and Independent Steering for Spherical
Loudspeaker Arrays.” IEEE Transactions on Audio
Speech and Language Processing 19(7):2234–2238.
Rakerd, B., W. M.. Hartmann, and J. Hsu. 2000. “Echo
Suppression in the Horizontal and Median Sagittal
Planes.” Journal of the Acoustical Society of America
107(2):1061–1064.
Schelkunoff, S. UN. 1943. “A Mathematical Theory of
Linear Arrays.” The Bell System Technical Journal
22(1):80–107.
Sharma, G. K. 2016. “Composing with Sculptural Sound
Phenomena in Computer Music.” PhD dissertation,
University of Music and Performing Arts, Institute of
Electronic Music and Acoustics, Graz, Autriche.
Sharma, G. K., F. Zotter, and M. Frank. 2014. “Or-
chestrating Wall Reflections in Space by Icosahedral
Loudspeaker: Findings from First Artistic Research
Exploration.” In Proceedings of the Joint International
Computer Music Conference and the Sound and Music
Computing Conference, pp. 830–835.
Sugibayashi, Y., et autres. 2012. “Three-Dimensional Acoustic
Sound Field Reproduction Based on Hybrid Combina-
tion of Multiple Parametric Loudspeakers and Electro-
dynamic Subwoofer.” Applied Acoustics 73(12):1282–
1288.
Takumai, S. 2006. “Loudspeaker Array Device and Method
for Setting Sound Beam of Loudspeaker Array Device.”
WIPO patent WO 2,006,001,272 A1, filed 21 Juin 2005,
and granted 5 Janvier 2006.
Trueman, D., et autres. 2006. “PLOrk: The Princeton Laptop
Orchestra, Year 1.” In Proceedings of the International
Computer Music Conference, pp. 443–450.
Warusfel, O., P.. Derogis, et R. Causs ´e. 1997. “Radiation
Synthesis with Digitally Controlled Loudspeakers.”
In Proceedings of the 103rd Audio Engineering So-
ciety Convention. Available online at www.aes.org
/e-lib/browse.cfm?elib=7202 (subscription required).
Accessed April 2017.
Wendt, F., et autres. 2016. “Directivity Patterns Controlling
the Auditory Distance.” In Proceedings of the Interna-
tional Conference on Digital Audio Effects, pp. 295–
300.
Wendt, F., et autres. 2017. “Perception of Spatial Sound
Phenomena Created by the Icosahedral Loudspeaker.”
Journal de musique informatique 41(1):76–88.
Zaunschirm, M., M.. Frank, and F. Zotter. 2016. “An
Interactive Virtual Icosahedral Loudspeaker Ar-
ray.” In Fortschritte der Akustik: Tagungs-CD der
deutschen Arbeitsgemeinschaft f ¨ur Akustik, pp. 1331–
1334.
Zotter, F. 2009. “Analysis and Synthesis of Sound-
Radiation with Spherical Arrays.” PhD dissertation,
University of Music and Performing Arts, Institute of
Electronic Music and Acoustics, Graz, Autriche.
Zotter, F., et B. Bank. 2012. “Geometric Error Estimation
and Compensation in Compact Spherical Loudspeaker
Array Calibration.” In Proceedings of the IEEE Interna-
tional Instrumentation and Measurement Technology
Conference, pp. 2710–2715.
Zotter, F., and M. Frank. 2012. “All-Round Ambisonic Pan-
ning and Decoding.” Journal of the Audio Engineering
Society 60(10):807–820.
Zotter, F., and M. Frank. 2015. “Investigation of Auditory
Objects Caused by Directional Sound Sources in
Rooms.” Acta Physica Polonica A 128(1-UN):5-dix.
Zotter, F., et R. H ¨oldrich. 2007. “Modeling Radi-
ation Synthesis with Spherical Loudspeaker Ar-
rays.” In Proceedings of the International Congress
on Acoustics. Available online at iem.kug.ac.at
/fileadmin/media/iem/altdaten/projekte/publications
/paper/modeling radiation/modeling.pdf. Accessed 21
Mars 2017.
Zotter, F., and M. Noisternig. 2007. “Near- and Far-
Field Beamforming Using Spherical Loudspeaker
Arrays.” In Congress of the Alps Adria Acous-
tics Association. Available online at iem.kug.ac.at
/fileadmin/media/iem/altdaten/projekte/publications
/paper/near/near.pdf. Accessed 21 Mars 2017.
Zotter, F., H. Pomberger, et un. Schmeder. 2008. “Ef-
ficient Directivity Pattern Control for Spherical
Loudspeaker Arrays.” In Proceedings of the Joint
Meeting of the Acoustical Society of America and the
European Acoustics Association. Available online at
Zotter et al.
67
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
iem.kug.ac.at/fileadmin/media/iem/altdaten/projekte
/publications/paper/efficient/efficient.pdf. Accessed
Mars 2017.
Zotter, F., et un. Sontacchi. 2007. “Icosahedral Loud-
speaker Array.” Technical Report IEM Report 39/07.
University of Music and Performing Arts, Institute of
Electronic Music and Acoustics.
Zotter, F., UN. Sontacchi, et R. H ¨oldrich. 2007. “Mod-
eling a Spherical Loudspeaker System as Multipole
Source.” In Fortschritte der Akustik: Tagungsband der
deutschen Arbeitsgemeinschaft f ¨ur Akustik, pp. 221–
222.
Zotter, F., et autres. 2014. “Preliminary Study on the Per-
ception of Orientation-Changing Directional Sound
Sources in Rooms.” In Proceedings of the Forum
Acusticum. Paper presented at the Forum Acusticum,
7–12 September, Krakow, Poland. Available online
at ambisonics.iem.at/Members/zotter/2014 zotter
OrientationDirectionalSource.pdf. Accessed March
2017.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
1
3
5
0
1
8
5
6
4
7
9
/
c
o
m
_
un
_
0
0
4
2
9
p
d
.
j
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
68
Journal de musique informatique