FUNCIÓN DE ENFOQUE:
Topological Neuroscience
Exact topological inference of the resting-state
brain networks in twins
Moo K. Chung1, Hyekyoung Lee2, Alex DiChristofano3, Hernando Ombao4, and Victor Solo5
1University of Wisconsin, Madison, Wisconsin, EE.UU
2Seoul National University, Seoul, Korea
3Washington University, Calle. luis, EE.UU
4King Abdullah University of Science and Technology, Thuwal, Saudi Arabia
5University of New South Wales, Sídney, Australia
Palabras clave: Functional brain networks, Cycles, Betti numbers, Persistent homology, Twin imaging
estudios, Resting-state fMRI
un acceso abierto
diario
ABSTRACTO
A cycle in a brain network is a subset of a connected component with redundant additional
connections. If there are many cycles in a connected component, the connected component
is more densely connected. Whereas the number of connected components represents the
integration of the brain network, the number of cycles represents how strong the integration
es. Sin embargo, it is unclear how to perform statistical inference on the number of cycles in the
brain network. en este estudio, we present a new statistical inference framework for determining
the significance of the number of cycles through the Kolmogorov-Smirnov (KS) distancia,
which was recently introduced to measure the similarity between networks across different
filtration values by using the zeroth Betti number. en este documento, we show how to extend the
method to the first Betti number, which measures the number of cycles. The performance
analysis was conducted using the random network simulations with ground truths. By using a
twin imaging study, which provides biological ground truth, the methods are applied in
determining if the number of cycles is a statistically significant heritable network feature in
the resting-state functional connectivity in 217 twins obtained from the Human Connectome
Proyecto. The MATLAB codes as well as the connectivity matrices used in generating results are
provided at http://www.stat.wisc.edu/~mchung/TDA.
Citación: Chung, M.K., Sotavento, h.,
DiChristofano, A., Ombao, h., & Solo,
V. (2019). Exact topological inference of
the resting-state brain networks in
twins. Neurociencia en red, 3(3),
674–694. https://doi.org/10.1162/
netn_a_00091
DOI:
https://doi.org/10.1162/netn_a_00091
RESUMEN DEL AUTOR
Recibió: 24 Agosto 2018
Aceptado: 23 Abril 2019
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Moo Chung
mkchung@wisc.edu
Editor de manejo:
Paul Expert
Derechos de autor: © 2019
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
en este documento, we propose a new topological distance based on the Kolmogorov- Smirnov (KS)
distance that is adapted for brain networks, and compare them against other topological
network distances including the Gromov-Hausdorff (GH) distances. KS-distance is recently
introduced to measure the similarity between networks across different filtration values by
using the zeroth Betti number, which measures the number of connected components. En esto
paper, we show how to extend the method to the first Betti number, which measures the
number of cycles. The performance analysis was conducted using random network
simulations with ground truths. Using a twin imaging study, which provides biological
ground truth (of network differences), we demonstrate that the KS distances on the zeroth and
first Betti numbers have the ability to determine heritability.
INTRODUCCIÓN
The modular structure and connected components are the fundamental topological features
of a brain network. Brain networks with a higher number of connected components have
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
norte
mi
norte
_
a
_
0
0
0
9
1
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Exact topological inference
Persistent homology:
A topological data analysis technique
for computing topological features at
different spatial resolutions.
many disjointed clusters, and the transfer of information will likely be impeded. Modular struc-
tures are often studied through the Q-modularity in graph theory (Meunier, Lambiotte, Proporcionó,
Ersche, & bullmore, 2009; Hombre nuevo, Barabasi, & vatios, 2006) and the zeroth Betti number in
persistent homology (Carlsson & Memoli, 2008; Carlsson & Mémoli, 2010; Chung, Vilalta-
Gil, Sotavento, Rathouz, Lahey, & Zald, 2017b; Chung, luo, Leow, Adluru, Alexander, Ricardo, &
Goldsmith, 2018b; Sotavento, Chung, & Sotavento, 2014).
Persistent homology provides a coherent framework for obtaining higher order topological
features beyond modular structures (Edelsbrunner & Harer, 2008; Zomorodian & Carlsson,
2005). A brain network can be treated as the 1-skeleton of a simplicial complex, donde el
0-dimensional hole is the connected component, and the 1-dimensional hole is a cycle. El
number of k-dimensional holes is called the k-th Betti number and denoted as β
k (Lee et al.,
2014; Sotavento, Chung, Kang, Choi, kim, & Sotavento, 2018; Petri, Expert, Turkheimer, Carhart-Harris,
Nutt, Hellyer, & Vaccarino, 2014; Sizemore, Giusti, Kahn, Vettel, Betzel, & bassett, 2018). En
este estudio, we will study higher order topological changes of brain networks using cycles. El
cycle structure in networks is important for information propagation, redundancy, and feedback
loops (Lind, González, & Herrmann, 2005). If a cycle exists in the network, information can
be delivered using two different redundant paths and interpreted as redundant connections.
Alternately, it can be viewed as diffusing the spread of information and creating information
bottlenecks (Tarjan, 1972).
Although cycles in a network have been widely studied in graph theory, especially in path anal-
ysis, they are rarely used in brain network analysis (despreciar, 2003; despreciar, Tononi, & Edelman,
2000). Existing graph analysis packages such as Brain Connectivity (http://sites.google.com/
site/bctnet) do not provide any tools related to cycles. Traditionally, cycles are often com-
puted using the brute-force depth-first search algorithm (Tarjan, 1972). In standard graph the-
oretic approaches, graph theory features are measured mainly by determining the difference
in graph theory features such as assortativity, betweenness centrality, small-worldness, y
network homogeneity (bullmore & despreciar, 2009; Rubinov & despreciar, 2010; Rubinov, Knock,
estampar, Micheloyannis, harris, williams, & romper la lanza, 2009; Uddin, Kelly, Biswal, Margulies,
Shehzad, Shaw, Ghaffari, Rotrosen, Adler, Castellanos, & Milham, 2008). Comparison of graph
theory features appears to reveal changes of structural or functional connectivity associated
with different clinical populations (Rubinov & despreciar, 2010). Since weighted brain networks
are difficult to interpret and visualize, they are often turned into binary networks by thresh-
olding edge weights (Él, Chen, & evans, 2008; Wijk, estampar, & Daffertshofer, 2010). Sin embargo,
the thresholds for the edge weights are often chosen arbitrarily and produce results that could
alter the network topology and thus make comparisons difficult. To obtain the proper optimal
threshold where comparisons can be made, the multiple comparison correction over every
possible edge has been proposed (Rubinov et al., 2009; Wijk et al., 2010). Sin embargo, the re-
sulting binary graph is extremely sensitive depending on the chosen p value or threshold value.
Others tried to control the sparsity of edges in the network in obtaining the binary network
(Achard & bullmore, 2007; bassett, 2006; He et al., 2008; Sotavento, Kang, Chung, kim, & Sotavento,
2012; Wijk et al., 2010). Sin embargo, one encounters the problem of thresholding sparse pa-
rameters. Thus existing methods for binarizing weighted networks cannot escape the inherent
problem of arbitrary thresholding.
There is currently no widely accepted criteria for thresholding networks. Instead of trying
to find an optimal threshold that gives rise to a single network that may not be suitable for
comparing clinical populations, cognitive conditions, or different studies, why not use each
network produced from every threshold? Motivated by this simple question, a new multiscale
Neurociencia en red
675
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
norte
mi
norte
_
a
_
0
0
0
9
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Exact topological inference
Graph filtration:
A collection of nested graphs.
Metric space:
A set with a metric defined on the set.
hierarchical network modeling framework based on persistent homology has been proposed
(Cassidy, Rae, & Solo, 2015; Chung, Hanson, Sotavento, Adluru, Alexander, Davidson, & Pollak,
2013; Giusti, Pastalkova, Curto, & Itskov, 2015; Sotavento, Chung, Kang, kim, & Sotavento, 2011a, 2011b;
Lee et al., 2012; Petri, Scolamiero, Donato, & Vaccarino, 2013; Petri et al., 2014; Sizemore,
Giusti, & bassett, 2016; Sizemore et al., 2018; Stolz, Harrington, & Portero, 2017). Persistent
homology, a branch of computational topology (Carlsson & Memoli, 2008; Edelsbrunner &
Harer, 2008; Edelsbrunner, Letscher, & Zomorodian, 2000), provides a more coherent math-
ematical
framework for measuring network distance than the conventional method of
simply taking the difference between graph theoretic features or the norm of the connec-
tivity matrices. Instead of looking at networks at a fixed scale, as is usually done in many
standard brain network analysis, persistent homology observes the changes of topological fea-
tures of the network over multiple resolutions and scales (Edelsbrunner & Harer, 2008; Horak,
Maleti´c, & Rajkovi´c, 2009; Zomorodian & Carlsson, 2005). Al hacerlo, it reveals the most per-
sistent topological features that are robust under noise perturbations. This robustness in perfor-
mance under different scales is needed for most network distances that are parameter and scale
dependent.
In persistent homology–based brain network analysis, instead of analyzing networks at
one fixed threshold that may not be optimal, we build the collection of nested networks
over every possible threshold by using the graph filtration, a persistent homological construct
(Chung et al., 2013; Lee et al., 2011a, 2012). The graph filtration is a threshold-free framework
for analyzing a family of graphs but requires hierarchically building specific nested subgraph
estructuras. The graph filtration shares similarities to the existing multithresholding or multi-
resolution network models that use many different arbitrary thresholds or scales (Achard,
Salvador, Whitcher, Suckling, & bullmore, 2006; He et al., 2008; kim, Adluru, Chung, Okonkwo,
Johnson, Bendlin, & singh, 2015; Lee et al., 2012; Supekar, menón, Frotar, Musen, & Greicius,
2008). Such approaches are mainly used to visually display the dynamic pattern of how graph
theoretic features change over different thresholds, and the pattern of change is rarely quanti-
fied. Persistent homology can be used to quantify such dynamic patterns in a more coherent
mathematical framework. Recientemente, various persistent homological network approaches have
been proposed. In Giusti et al. (2015) and Sizemore et al. (2016, 2018), graph filtration was
developed on cliques. In Petri et al. (2013), weighted clique rank homology was developed.
In Petri et al. (2014), the concept of homological scaffolds was developed and applied to the
resting-state fMRI.
In persistent homology, there are various metrics that have been proposed to measure
similarity and distances, including the bottleneck, Gromov-Hausdorff (GH), and Wasserstein
distances (Chazal, Cohen-Steiner, Guibas, Mémoli, & Oudot, 2009; Kerber, Morozov, & Nigmetov,
2017; Tuzhilin, 2016), the complex vector method (Di Fabio & Ferri, 2015), and the persistence
kernel (Ibanez-Marcelo, Campioni, Manzoni, Santarcangelo, & Petri, 2018a; Ibanez-Marcelo,
Campioni, Phinyomark, Petri, & Santarcangelo, 2018b; Kusano, Hiraoka, & Fukumizu, 2016).
entre ellos, the bottleneck and GH distances are possibly the two most popular distances
that were originally used to measure distance between two metric spaces (Tuzhilin, 2016).
They were later adapted to measure distances in persistent homology, dendrograms (Carlsson &
Memoli, 2008; Carlsson & Mémoli, 2010; Chazal et al., 2009), and brain networks (Lee et al.,
2011b, 2012). The probability distributions of bottleneck and GH-distances are unknown.
De este modo, the statistical inference on them can only be done through resampling techniques such
as permutations (Lee et al., 2012; Sotavento, Kang, Chung, Lim, kim, & Sotavento, 2017), which often
cause serious computational bottlenecks for large-scale networks.
Neurociencia en red
676
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
norte
mi
norte
_
a
_
0
0
0
9
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Exact topological inference
To bypass the computational bottleneck associated with resampling large-scale networks,
the Kolmogorov-Smirnov (KS) distance was introduced (Chung et al., 2013, 1; Lee et al., 2017).
The advantage of using KS-distance is that its gives results that are easier to interpret than those
obtained from less intuitive distances from persistent homology. Furthermore because of its
simplicity in construction, it is possible to determine its probability distribution exactly without
resampling (Chung et al., 2017b). Sin embargo, the KS-distance has been only applied to the num-
ber of connected components β
1 en
graphs and networks. en este documento, for the first time, we show how to extend the KS-distance by
performing statistical inference on β
1. This is achieved by establishing the monotonic property
of the number of cycles over graph filtration. The monotonicity is then used in constructing the
KS-distance for topologically differentiating two networks. Después, the method is applied
to the large-scale resting-state twin fMRI study in determining the heritability of the number of
cycles.
0, and it is unclear how to apply to the number of cycles β
CORRELATION BRAIN NETWORK
The edge weight, which measures the strength of a connection, is usually given by a simi-
larity measure between the observed data on the nodes in brain networks. Various similarity
measures have been proposed. The correlation or mutual information between measurements
for the biological or metabolic network and the frequency of contact between actors for the
social network have been used as edge weights (bassett, Meyer-Lindenberg, Achard, Duke, &
bullmore, 2006; Bien & Tibshirani, 2011; li, Liu, li, Qin, li, Yu, & Jiang, 2009; Mclntosh &
Gonzalez-Lima, 1994; Hombre nuevo & vatios, 1999; Song, Havlin, & Makse, 2005). En particular,
the Pearson correlation has been most widely used as edge weights in functional brain network
modelado.
Consider a weighted graph with node set V = {1, . . . , pag} and edge weights w = (wij)
between nodes i and j. Let xj = (x1j, · · · , xnj)(cid:2) ∈ Rn be n × 1 measurement vector on node
j. Let us center and normalize data xj such that
(cid:4) xj
(cid:4)2= x
(cid:2)
j xj =
norte
∑
yo=1
x2
ij = 1,
norte
∑
yo=1
xij = 0.
(cid:2)
Then we can show that ρ
i xj is the Pearson correlation between xi and xj (Chung,
Hanson, S.M, Davidson, & Pollak, 2015). Note that correlations are invariant under scale and
translations. Naturalmente, we are interested in using correlations or their simple functions such as
ij = x
ρ
ij = x
(cid:2)
i xj
o
ρ
ij = 1 − x
(cid:2)
i xj
as edge weights. Among possible functions of correlations,
wij = (1 − ρ
ij)1/2
(1)
≤ wik + wkj and other metric properties (Chung, Sotavento, Solo,
satisfies triangle inequality wij
Davidson, & Pollak, 2017a). Having metric distances facilitates more mathematically coherent
interpretation of brain networks and offers many nice mathematical properties. With such edge
weight w, X = (V, w) forms a metric space. In the simulation studies in this paper, Ecuación 1
is used as the edge weights.
GRAPH FILTRATION
All topological network distances that will be introduced in later sections are based on filtra-
tions on graphs by thresholding edge weights.
Neurociencia en red
677
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
norte
mi
norte
_
a
_
0
0
0
9
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Exact topological inference
Definición 1 Given weighted network X = (V, w) with positive edge weight w = (wij), el
binary network X(cid:4) = (V, w(cid:4)) is a graph consisting of the node set V and the binary edge
weights w(cid:4) given by
w(cid:4) = (wij,(cid:4)) =
(cid:2)
1
0
if wij > (cid:4);
de lo contrario.
Any edge weight less than or equal to (cid:4) is made into zero while edge weights larger than
(cid:4) are made into one. Lee y otros. (2011b, 1) defines the binary graphs by thresholding above,
eso es, wij,(cid:4) = 1 if wij <= (cid:4), which is consistent with the definition of the Rips filtration.
However, in brain imaging, the higher value of wij indicates stronger connectivity. Thus, we
are thresholding below and leave out stronger connections (Chung et al., 2013, 1).
Note w(cid:4) is the adjacency matrix of X(cid:4), which is a simplicial complex consisting of
0-simplices (nodes) and 1-simplices (edges) (Ghrist, 2008). By increasing the filtration value
(cid:4), we are deleting more edges, so the size of the edge set decreases. Thus, the binary network
satisfies the monotonic subset property
X(cid:4)
0
⊃ X(cid:4)
⊃ X(cid:4)
2
1
⊃ · · ·
for any (cid:4)
0
≤ (cid:4)
≤ (cid:4)
2
1
· · · . Equivalently, we also have
X c
(cid:4)
0
⊂ X c
(cid:4)
1
⊂ X c
(cid:4)
2
⊂ · · · .
The sequence of such nested multiscale graphs is defined as the graph filtration (Lee et al.,
2011b, 1). Note that X
0 is the complete graph and X∞ is the node set V. For a graph with
p nodes, the maximum number of edges is (p2 − p)/2, which is obtained in a complete graph.
If we order the edge weights in increasing order, we have the sorted edge weights:
0 = w(0) < min
j,k
wjk = w(1) < w(2) < · · · < w(q) = max
j,k
wjk,
where q ≤ (p2 − p)/2. The subscript ( ) denotes the order statistic. Hence, we simply construct
the graph filtration at the edge weights
X
0
⊃ Xw(1)
⊃ Xw(2)
⊃ · · · ⊃ Xw(q) .
(2)
The condition of having unique edge weights is not restrictive in practice. Assuming edge
weights to follow some continuous distribution, the probability of any two edges being equal
is zero. The finiteness and uniqueness of the filtration levels over finite graphs are intuitively
clear by themselves and are implicitly assumed in software packages such as javaPlex (Adams,
Tausz, & Vejdemo-Johansson, 2014).
BETTI NUMBERS
In persistent homology, the k-th Betti number is often referred to as the number of k-dimensional
holes (Lee et al., 2014, 1; Petri et al., 2014; Sizemore et al., 2018). In network setting, the 0-th
Betti number is the number of connected components and the 1st Betti number is the number of
cycles. During graph filtration, we can show that β
1 monotonically change. Although it
is not true in general (Bobrowski & Kahle, 2014), on the graph filtration (2), β
1 numbers
have very stable monotonic increases and decreases respectively.
0 and β
0 and β
Network Neuroscience
678
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
Theorem 1 In a graph, Betti numbers β
weights.
0 and β
1 are monotone over graph filtration on edge
Proof. Under graph filtration (2), the edges are deleted one at a time. Since an edge has
only two end points, the deletion of the edge disconnects the graph into at most two. Thus,
the number of connected components (β
0) always increases, and the increase is at most by
one. The Euler characteristic χ of the graph is given by (Adler, Bobrowski, Borman, Subag, &
Weinberger, 2010)
where p and q are the number of nodes and edges respectively. Thus,
χ = β
− β
1 = p − q,
0
β
1 = β
0
− p + q.
Note p is fixed over the filtration but q is decreasing by one while β
Hence, β
1 always decreases and the decrease is at most by one.
0 increases at most by one.
0
− p + q without additional computation. For the computation of β
(Boissonnat, & Teillaud, 2006). Once we compute β
β
Theorem 1 is related to the incremental Betti number computation over a simplical complex
1 number is simply given by
0, it is not necessary to
perform graph filtration for infinitely many possible filtration values. The maximum possible
number of filtration level needed for computing β
0 is one plus the number of unique edge
weights. In the case of trees, β
0 computation is exactly given.
0 number, β
Theorem 2 For tree T = (V, w) with p ≥ 2 nodes and unique positive edge weights
w(1) < w(2) < · · · < w(p−1),
the zeroth Betti number β
0 over graph filtration (2) is given by
β
0(T
0) = 1, β
0(Tw(1) ) = 2,
· · · , β
0(Tw(p−1) ) = p.
The proof is given in Chung et al. (2015). Note a tree with p nodes has p − 1 edges. For a
graph that is not possible, it may not be possible to analytically represent β
0 over a filtration like
Theorem 2. In general, β
0 can be numerically computed using the single linkage dendrogram
(SLD) (Lee et al., 2012), the Dulmage-Mendelsohn decomposition (Chung, Adluru, Dalton,
Alexander, & Davidson, 2011; Pothen & Fan, 1990), or the simplical complex method (Carlsson
& Memoli, 2008; de Silva & Ghrist, 2007; Edelsbrunner, Letscher, & Zomorodian, 2002). In
this study, we computed β
0 over filtration by using the Dulmage-Mendelsohn decomposition.
SINGLE LINKAGE CLUSTERING
The β
0 computation is related to single linkage clustering and dendrogram construction
(Carlsson, 2009; Carlsson, De Silva, & Morozov, 2009; Carlsson, Singh, & Zomorodian, 2009b;
Chowdhury & Mémoli, 2016; Khalid, Kim, Chung, Ye, & Jeon, 2014). In single linkage clus-
tering, the single linkage distance (SLD) sij between the closest nodes in the two disjoint con-
nected components R1 and R2 is given by
sij = min
l∈R1,k∈R2
wlk.
In this study, the square-root of 1 correlation is used as edge weight wkl.
Network Neuroscience
679
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
Permutation test:
Determines the statistical
significance by calculating all
possible values of the test statistic
under all possible rearrangements
of the samples.
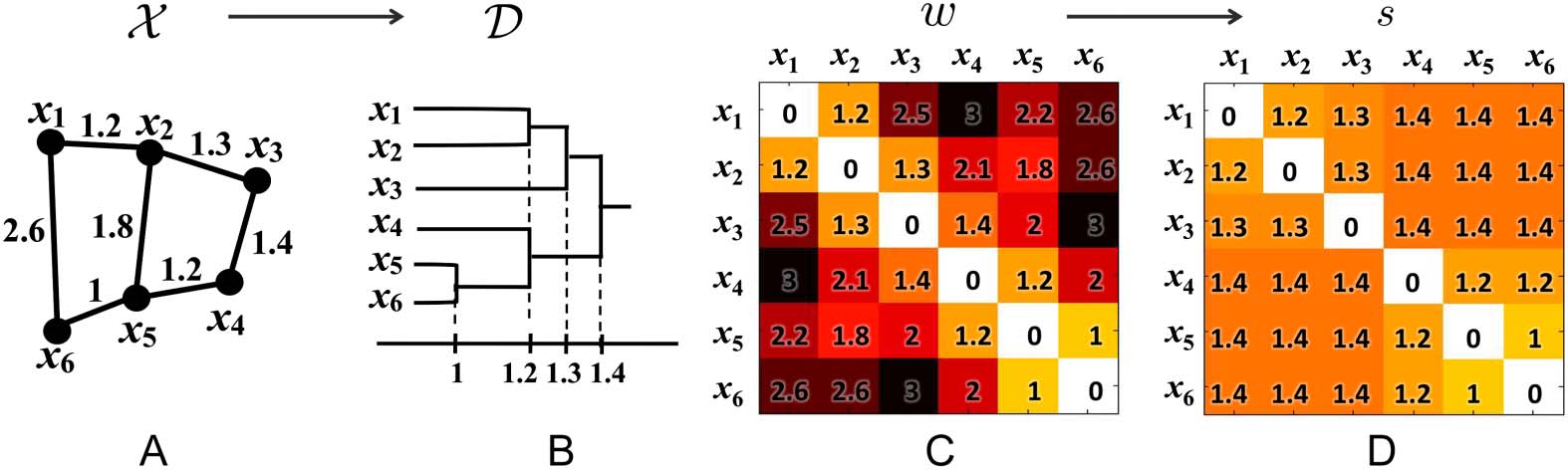
Figure 1.
(A) Toy network, (B) its dendrogram, (C) the distance matrix w based on Euclidean dis-
tance, and (D) the single linkage matrix S. In the case of dendrogram construction, the graph filtration
is done by connecting nodes over increasing edge weights.
Every edge connecting a node in R1 to a node in R2 has the same SLD. The SLD is then used
to construct the single linkage matrix (SLM) S = (sij) (Figure 1). SLM shows how connected
components are merged locally and can be used in constructing a dendrogram over filtration.
If the single linkage distance sij is larger than the current filtration value (cid:4)
k but smaller than the
≤ sij < (cid:4)
k+1, that is, (cid:4)
next filtration value (cid:4)
k+1. Then components R1 and R2 will be con-
k
nected at the next filtration value (cid:4)
k+1. The sequence of how components are merged during
the graph filtration is identical to the sequence of the merging in the dendrogram construction
(Lee et al., 2012). By tracing how each of the connected components are merged, we can com-
pute β
0. In the single linkage clustering, instead of deleting edges, we are connecting nodes
over increasing edge weights.
SLM is an ultrametric, which is a metric space satisfying the stronger triangle inequality
≤ max(sik, skj) (Carlsson & Mémoli, 2010). Thus the dendrogram can be represented as
sij
an ultrametric space D = (V, S), which is again a metric space. In persistent homology, the
Gromov-Hausdorff (GH) distance has been mainly used in quantifying the dendrogram shape
differences (Carlsson & Mémoli, 2010; Chung et al., 2017a; Lee et al., 2011b, 1). The GH-
distance between dendrograms D1 = (V, S1) and D2 = (V, S2) with SLM S1 = (s1
ij) and
S2 = (s2
ij) is given by
DGH(D1, D2) =
1
2
max
∀i,j
|s1
ij
− s2
ij
|.
For the statistical inference on GH-distance, resampling techniques such as jackknife or per-
mutation tests are often used ((Lee et al., 2012), 1). In this study, we will use the permutation
test.
BOTTLENECK DISTANCE
The bottleneck distance is perhaps the most often used distance in persistent homology, al-
though it is rarely used for brain networks. In persistent homology, the topology of underlying
data can be represented by the birth and death of topological features, such as the number of
connected components or cycles (Carlsson, Ishkhanov, De Silva, & Zomorodian, 2008). During
the filtration, these topological features appear and disappear. If a topological feature appears
at the threshold ξ and disappears at τ, it can be encoded into a point, (ξ, τ) (0 ≤ ξ ≤ τ < ∞)
Network Neuroscience
680
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
in R2. If m number of connected components or cycles appear during the filtration of a network
X = (V, w), the homology group can be represented by a point set
P (X ) = {(ξ
1, τ
1), . . . , (ξm, τm)} .
This scatter plot is called a persistence diagram (PD) (Cohen-Steiner, Edelsbrunner, & Harer,
2007).
Given two networks X 1 = (V1, w1) with m features and X 2 = (V2, w2) with n features,
PDs
and
(cid:3)
P (X 1) =
(ξ1
1, τ1
1 ), · · · , (ξ1
m, τ1
m)
(cid:4)
(cid:3)
P (X 2) =
(ξ2
1, τ2
1 ), · · · , (ξ2
n, τ2
n )
(cid:4)
are obtained through the filtration (Lee et al., 2012). The bottleneck distance between the
networks is defined as the bottleneck distance of the corresponding PDs (Cohen-Steiner et al.,
2007):
(cid:5)
DB
P (X 1), P (X 2)
(cid:6)
= infγ
sup
1≤i≤m
(cid:4) t1
i
− γ(t1
i ) (cid:4)∞,
(3)
i = (ξ1
i , τ1
where t1
taken over all possible bijections. If t2
by
i ) ∈ P (X 1) and γ is a bijection from P (X 1) to P (X 2). The infimum is
i ) for some i and j, L∞-norm is given
j ) = γ(t1
j = (ξ2
j , τ2
(cid:4) t1
i
− γ(t1
i ) (cid:4)∞= max
(cid:5)
|ξ1
i
− ξ2
j
|, |τ1
i
− τ2
j
|
(cid:6)
.
Note Equation 3 assumes m = n such that the bijection γ exists. Suppose two networks share
the same node set, that is, V1 = V2, with p nodes and the same number of q unique edge
weights. If the graph filtration is performed on two networks, the number of connected compo-
nents and cycles that appear and disappear during the filtration is p and 1 − p + q, respectively.
Thus, their persistence diagrams always have the same number of points. The bijection γ is de-
termined by the bipartite graph matching algorithm (Cohen-Steiner et al., 2007; Edelsbrunner
& Harer, 2008).
If m (cid:10)= n, there is no one-to-one correspondence between two PDs. Then, auxiliary points
and
(
1 + τ1
ξ1
2
1
,
1 + τ1
ξ1
2
1
), · · · , (
m + τ1
ξ1
m
2
(
1 + τ2
ξ2
2
1
,
ξ2
1 + τ2
2
1
), · · · , (
n + τ2
ξ2
n
2
ξ1
m + τ1
m
2
)
ξ2
n + τ2
n
2
)
,
,
that are orthogonal projections to the diagonal line ξ = τ in P (X 1) and P (X 2) are added to
P (X 2) and P (X 1), respectively, to make the identical number of points in PDs.
The bottleneck distance does not directly measure the distance between two metric spaces
X 1 = (V1, w1) and X 2 = (V2, w2), but measures the distance between their corresponding
persistence diagrams P (X 1) and P (X 1). In practice, the bottleneck distance has been often
used since it is a lower bound on the GH-distance and it is easier to compute (Chazal et al.,
2009). Since the brain regions that form the network nodes are matched across the networks
through predefined parcellations in brain network studies, the GH-distance can be computed
Network Neuroscience
681
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
easily. Thus, in this study, we will only use the GH-distance and not show the result of the
bottleneck distance in the simulation study.
PERMUTATION TEST ON NETWORK DISTANCES
Statistical inference on network distances can be done using resampling techniques such as
the permutation test (Chung et al., 2013; Efron, 1982; Lee et al., 2012). The permutation test
is perhaps the most widely used nonparametric test procedure in the sciences (Chung et al.,
2017b; Nichols & Holmes, 2002; Thompson, Cannon, Narr, van Erp, Poutanen, Huttunen,
Lonnqvist, Standertskjold-Nordenstam, Kaprio, & Khaledy, 2001; Zalesky, Fornito, Harding,
Cocchi, Yücel, Pantelis, & Bullmore, 2010). It is known as the exact test in brain imaging since
the distribution of the test statistic under the null hypothesis can be exactly computed if we
can calculate all possible values of the test statistic under every possible permutation.
Here we explain the permutation test procedure that was used for network distances. The
usual setting in brain imaging applications is a two-sample comparison. Suppose there are m
measurement in Group 1 on node set V of size p. Denote the data matrix as X1
m×p. The edge
weights of Group 1 are given by f (X1) for some function f and the metric space is given by
X 1 = (V, f (X1)). Suppose there are n measurement in Group 2 on the identical node set V.
n×p and the corresponding metric space as X 1 = (V, f (X1)). We test
Denote data matrix as X2
the statistical significance of network distance D(X 1, X 2) under the null hypothesis H0:
H0 : D(X 1, X 2) = 0 vs. H1 : D(X 1, X 2) > 0.
The permutation test is done as follows. Under H0, one can concatenate the data matrices
X = (xij) =
(cid:7)
(cid:8)
X1
X2
(m+n)×p
and then permute the indices of the row vectors of X in the symmetric group of degree m + norte,
eso es, Sm+n (Kondor, Howard, & Jebara, 2007). Denote the i-th permuted data matrix as
Xσ(i) = (xσ(i),j), where σ ∈ Sm+n. Then we split Xσ(i) into submatrices such that
(cid:7)
Xσ(i) =
(cid:8)
,
X1
X2
pag(i)
pag(i)
pag(i) and X2
pag(i) = (V, F (X2
pag(i) are of sizes m × p and n × p respectively. Let X 1
where X1
X 2
across the groups. Then we have distance D(X 1
pag(i), X 2
permutations D(X 1
pag(i))) y
pag(i))) be weighted networks where the rows of the data matrices are permuted
pag(i)) for each permutation. The fraction of
pag(i)) that is larger than D(X 1, X 2) gives the estimate for the p value.
pag(i) = (V, F (X1
pag(i), X 2
Desafortunadamente, generating every possible permutation for whole images is still extremely
time consuming even for a modest sample size. The number of permutations exponentially
aumenta, and it is impractical to generate every possible permutation. In the permutation test,
only a small fraction of possible permutations are generated, and the statistical significance is
computed approximately. In most studies, on the order of 1% of total permutations were often
usado, mainly due to the computational bottleneck of generating permutations (Thompson et al.,
2001; Zalesky et al., 2010). In Zalesky et al. (2010), 5,000 permutations out of possible (27
12) =
17, 383, 860 permutations (2.9%) were used. In Thompson et al. (2001), 1 million permutations
out of (40
20) possible permutations (0.07%) were generated using a super computer. In our study,
Neurociencia en red
682
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
norte
mi
norte
_
a
_
0
0
0
9
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Exact topological inference
Kolmogorov-Smirnov (KS) distancia:
A distance between the empirical
distributions of two samples.
tenemos 131 MZ and 77 DZ twins. The possible number of permutations is (208
77 ). This is a
number so large, we cannot exactly represent it in computing systems such as MATLAB and R.
77 ) is about 1.96 × 1056, which is still astronomically large and beyond the
Even the 1% de (208
computing capability of the most computers. Por otro lado, the proposed KS-distance
method computes for all possible permutations combinatorially and completely bypasses the
computational bottleneck. There is no computational cost involved in the KS-distance and the
computation is done in a few seconds. Además, the method computes p values exactly
and it is not approximate.
KOLMOGOROV-SMIRNOV DISTANCE
Recientemente, the Kolmogorov-Smirnov (KS) distance has been successfully applied in quantifying
the change of β
0 number over graph filtration as a way to quantify brain networks without
thresholding (Chung et al., 2017a, 2017b). The main advantage of the method is that it avoids
using the computationally costly and time consuming permutation test for large-scale net-
obras. en este documento, we show how to apply KS-distance in quantifying the change of the β
number over graph filtration as well.
1
en este estudio, the square root of 1 correlation is used as edge weights. Given two networks
0 y
X 1 = (V, w1) and X 2 = (V, w2), KS distances between X 1 and X 2 for Betti numbers β
b
j are defined as (Chung et al., 2013; Lee et al., 2017):
DKS(X 1, X 2) = sup
(cid:4)≥0
(cid:9)
(cid:9)b
j(X 1
(cid:4) ) − β
j(X 2
(cid:4) )
(cid:9)
(cid:9)
,
j(X i
where β
approximated using the finite number of filtrations:
(cid:4)) is the j-th Betti number for binary network X i
(cid:4). The distance DKS can be discretely
Dq = sup
1≤i≤q
(cid:9)
(cid:9)b
j(X 1
(cid:4)
i
) − β
j(X 2
(cid:4)
i
)
(cid:9)
(cid:9)
.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
norte
mi
norte
_
a
_
0
0
0
9
1
pag
d
.
t
If we choose enough of q such that (cid:4)
j are all the sorted edge weights, entonces
DKS(X 1, X 2) = Dq
(Chung et al., 2017b). This is possible since there are only up to p(p − 1)/2 number of unique
edges in a graph with p nodes and the monotone function increases discretely but not contin-
uously. En la práctica, (cid:4)
j may be chosen uniformly or a divide-and-conquer strategy can be used
to adaptively grid the filtration values. Then the probability distribution of Dq can be computed
exactly by combinatorial means.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
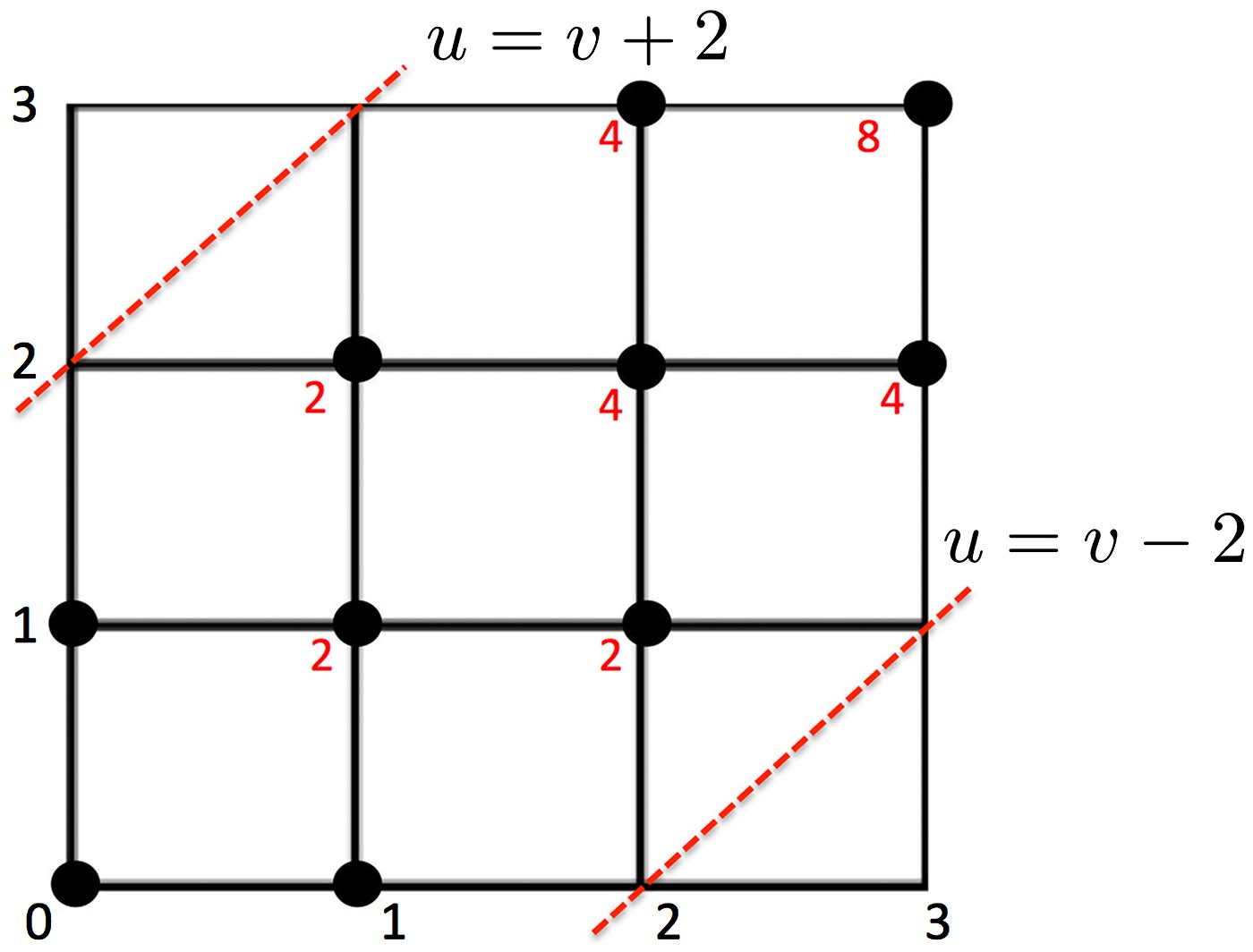
Teorema 3
PAG(Dq ≥ d) = 1 − Aq,q
(2q
q )
,
where Au,v satisfies Au,v = Au−1,v + Au,v−1 with the boundary condition A0,v = Au,0 = 1
within band |u − v| < d and initial condition A0,0 = 0 for u, v ≥ 1.
The proof is given in Chung et al. (2017b).
Network Neuroscience
683
Exact topological inference
Figure 2.
(3,3).
In this example, Au,v is computed within the boundary (dotted red line) from (0,0) to
Example 1 P(D3
left corner A0,0 = 0 and move right or up toward the upper corner
≥ 2) is computed sequentially as follows (Figure 2). We start with the bottom
A1,0 = 1, A0,1 = 1
→ A1,1 = A1,0 + A0,1
→ · · · = · · ·
→ A3,3 = A3,2 + A2,3 = 8.
The probability is then P(D3
3) = 0.6. The computational complexity of the
combinatorial inference is O(q log q) for sorting and O(q2) for computing Aq,q in the grid while
the permutation test requires exponential run time.
≥ 2) = 1 − 8/(6
When q is too large, it may not be possible to represent and compute (2q
q ) in all the digits.
For large q, use the asymptotic probability distribution Dq given by Chung et al. (2017b):
(cid:10)
(cid:11)
lim
q→∞
Dq/
(cid:12)
2q ≥ d
= 2
∞
∑
i=1
(−1)i−1e
−2i2d2
.
(4)
The p value of the test statistic under the null is then computed as
p value = 2e
−d2
o − 2e
−8d2
o + 2e
−18d2
o · · · ,
(cid:11)
where the observed value do is the least integer greater than Dq/
2q in the data.
COMPARISONS
Six network distances (L1, L2, L∞, GH and KS on β
1) were compared in simulation
studies. For the review of various brain network distances, refer to Chung et al. (2017a). We
also used the popular Q-modularity function for community detection in graph theory (Girvan
& Newman, 2002; Meunier et al., 2009; Newman et al., 2006). The difference in Q-modularity
functions was used as the distance measure. The simulations below were independently
0 and β
Network Neuroscience
684
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
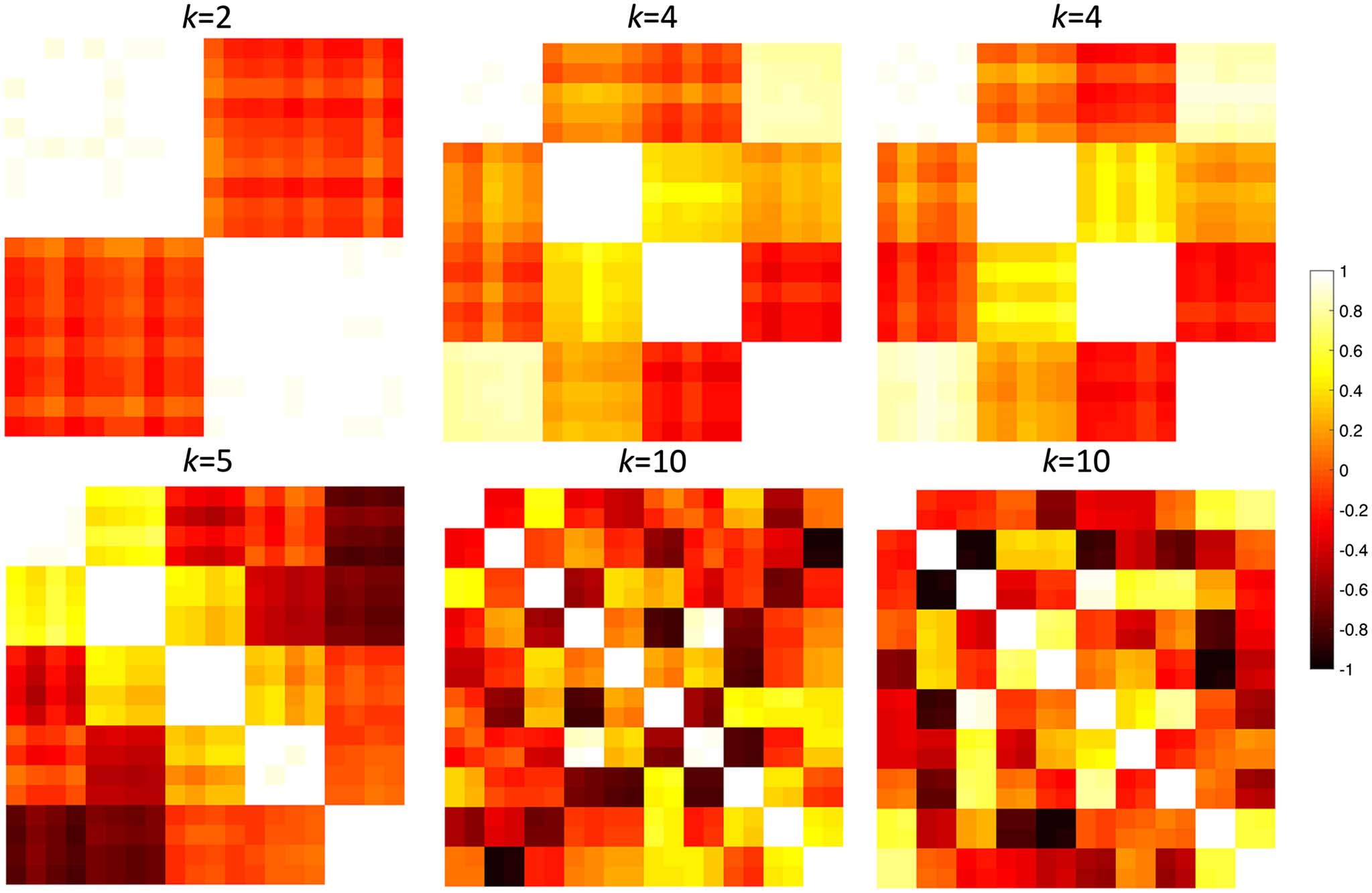
Figure 3. Randomly simulated correlation matrices with different topological structures with k = 2, 4, 5, 10. For k = 4, 10, two different
randomly generated networks are shown.
performed 100 times. We used p = 20, 100, 500 nodes and n = 5 images in each group,
which made it possible for permutations to be exactly (5+5
5 ) = 252 (Figure 3). The small num-
ber of permutations enables us to compare the performance of distances exactly. Through the
simulations, σ = 0.1 was universally used as network variability.
Mixed-effect model:
A model with both fixed and random
effect terms.
(cid:13)
1 − c1
tivariate normal across i, that is, xi
matrix. This gives the correlation matrix C1 = (c1
The data vector xi at node i was simulated as identical and independently distributed mul-
∼ N(0, In) with n by n identity matrix In as the covariance
ij) = (corr(xi, xj)). The edge weights were
ij. The data vector yi at node i that produced node dependency was simu-
given by
lated by adding additional dependency to xi through a hierarchical linear model or mixed-
effect model (Pinehiro & Bates, 2002; Snijders, Spreen, & Zwaagstra, 1995). This is a standard
simulation technique for introducing dependency structures in random simulations. The hier-
archical linear model enables us to explicitly model the data vector at each node and simulate
the amount of dependency between nodes, providing detailed control over the topological
structures in the correlation matrices. Data vector yi at node i will be simulated using xi as
follows.
y1, · · · , yc = x1 + N(0, σ2 In)
yc+1, · · · , y2c = xc+1 + N(0, σ2 In)
...
yc(k−1)+1, · · · , yck = xc(k−1)+1 + N(0, σ2 In)
Network Neuroscience
685
Exact topological inference
Network Neuroscience
This introduces a topological structure of connectedness through statistical dependency. Al-
though we did not try here, a far more complex dependency structure is also possible. In our
simulation c = p/k = 10, 5, 4, 2 and k = p/c = 2, 4, 5, 10 are used (Figure 3). Subsequently,
we have the correlation matrix C2 = (c2
ij) = (corr(yi, yj)) and the subsequent edge weights
(cid:13)
1 − c2
ij.
No Network Difference
It was expected there was no network difference between networks generated using the same
parameters and initial data vectors xi in the above model. For example, Figure 3 shows two
simulated networks generated with the same parameters k = 4, 10. We compared networks
with the same parameter k: 4 vs. 4, 5 vs. 5 and 10 vs. 10. It is expected we should not able to
detect the network differences. The performance results were given in terms of the false posi-
tive error rate computed as the fraction of simulations that gave p value below 0.05 (Table 1).
For all the distances except KS-distance, the permutation test was used. Since there were five
samples in each group, the total number of permutations was (10
5 ) = 272, making the permuta-
tion test exact and the comparisons accurate. All the distances performed very well including
Q-modularity. KS-distance was overly sensitive and was producing up to 7% false positives.
However, for 0.05 level test, it is expected that there is 5% chance of producing false positives.
Thus, KS-distance is producing only 2% above the expected error rate.
The p = 20 simutation might be too small a network to extract topologically distinct
features that are used in topological distances. Thus, we increased the number of nodes to
p = 100 (Table 2). All the network distances except KS-distances performed reasonably well.
KS-distances seem to be overly sensitive to slight topological change in large topological struc-
tures that were present in k = 2, 4, 5 cases. As k increases, KS-distances seem to perform rea-
sonably well.
Network Differences
We generated networks with parameter k = 2, 4, 5, 10 with p = 20 nodes simulation (Figure 3).
Since topological structures were different, the distances are expected to differentiate the net-
works. The performance results were given in terms of the false negative error rate computed
as the fraction of simulations that give p value above 0.05 (Table 1). All the distances including
Q-modularity performed badly, although KS-distance performed the best. Since graph theory
features are not explicitly designed to measure network distances, they do not usually perform
well when there are large topological differences.
We increased the number of nodes to p = 100. All the network distances including
Q-modularity were still performing badly except KS-distances (Table 2). KS-distance on the
Table 1. The p = 20 nodes simulation results given in terms of false positive and negative error
rates.
p = 20
4 vs. 4
5 vs. 5
10 vs. 10
4 vs. 5
2 vs. 4
5 vs. 10
L1
0.00
0.00
0.00
0.63
0.71
0.94
L2
0.00
0.00
0.00
0.40
0.48
0.80
L∞
0.00
0.00
0.00
0.33
0.42
0.78
GH
0.00
0.00
0.00
0.15
0.53
0.72
KS (β
0)
0.04
0.07
0.00
0.27
0.18
0.44
KS (β
1)
0.01
0.01
0.00
0.06
0.00
0.24
Q
0.05
0.06
0.04
0.9
0.95
0.96
686
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
Network Neuroscience
Table 2. The p = 100 nodes simulation results given in terms of false positive and negative error rates.
p = 100
4 vs. 4
5 vs. 5
10 vs. 10
4 vs. 5
2 vs. 4
5 vs. 10
L1
0.00
0.00
0.00
0.51
0.66
0.94
L2
0.00
0.00
0.00
0.37
0.45
0.86
L∞
0.00
0.00
0.00
0.35
0.57
0.79
GH
0.00
0.00
0.00
0.16
0.61
0.72
KS (β
0)
0.26
0.14
0.05
0.11
0.03
0.11
KS (β
1)
0.54
0.43
0.05
0.00
0.00
0.00
Q
0.03
0.05
0.05
0.93
0.91
0.98
number of cycles seems to be the best network distance to use when there are network topol-
ogy differences, although it has tendency to produce false positives when there is no difference.
In terms of computation, distance methods based on the permutation test took about
950 seconds (16 minutes) for 100 nodes, while the KS-like test procedure only took about
20 seconds in a computer. The results given in Tables 1–3 may slightly change if different ran-
dom networks are generated. We also performed the simulation study on the 500 nodes to see
the effect of increased network sizes (Table 3). The proposed KS-distance on both β
1 are
not necessarily performing well in the case of no network differences. Again the KS-distance
is too sensitive and detecting minute network differences. On the other hand, in the case of
actual network differences, the KS-distances are performing exceptionally well compared with
other network differences.
0 and β
APPLICATION
As an application, we show how to apply KS-distances in understanding heritability of brain
networks. Because of their unique relationship, twin imaging studies allow researchers to
examine genetic and environmental influences easily in vivo (Blokland, McMahon, Thompson,
Martin, de Zubicaray, & Wright, 2011; Chiang, McMahon, de Zubicaray, Martin, Hickie, Toga,
Wright, & Thompson, 2011; Glahn, Winkler, Kochunov, Almasy, Duggirala, Carless, Curran,
Olvera, Laird, Smith, Beckmann, Fox, & Blangero, 2010; McKay, Knowles, Winkler, Sprooten,
Kochunov, Olvera, Curran, Kent Jr., Carless, Göring, Dyer, Duggirala, Almasy, Fox, Blangero,
& Glahn, 2014; Smit, Stam, Posthuma, Boomsma, & De Geus, 2008). Monozygotic (MZ) twins
share 100% of genes, whereas dizygotic (DZ) twins share 50% of genes (Chung et al., 2017b).
The difference between MZ and DZ twins measures the degree of genetic and environmental
influence. Twin imaging studies are very useful for understanding the extent to which brain
networks are influenced by genetic factors. This information can then be later used to develop
better ways to prevent and treat disorders and maladaptive behaviors.
Table 3. The p = 500 nodes simulation results given in terms of false positive and negative error
rates.
p = 500
4 vs. 4
5 vs. 5
10 vs. 10
4 vs. 5
2 vs. 4
5 vs. 10
L1
0.04
0.00
0.00
0.20
0.14
0.20
L2
0.05
0.00
0.00
0.20
0.11
0.18
L∞
0.06
0.00
0.00
0.20
0.14
0.19
GH
0.08
0.00
0.00
0.20
0.12
0.16
KS (β
0)
0.20
0.13
0.06
0.11
0.00
0.00
KS (β
1)
0.26
0.20
0.18
0.00
0.00
0.00
Q
0.02
0.02
0.05
0.20
0.17
0.20
687
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
Dataset and Image Preprocessing
We used the resting-state fMRI of 271 twin pairs from the Human Connectome Project
(Van Essen, Ugurbil, Auerbach, Barch, Behrens, Bucholz, Chang, Chen, Corbetta, & Curtiss,
2012). Out of a total 271 twin pairs, we only used genetically confirmed 131 MZ twin pairs
(age 29.3 ± 3.3 years, 56M/75F) and 77 same-sex DZ twin pairs (age 29.1 ± 3.5 years, 30M/47F)
in this study. Since the discrepancy between self-reported and genotype-verified zygosity was
fairly high at 13% of all the available data, 19 MZ and 19 DZ twin pairs that do not have
genotyping were excluded. We additionally excluded 35 twin pairs with missing fMRI data.
◦
fMRI were collected on a customized Siemens 3T Connectome Skyra scanner, using a
gradient-echo-planar imaging (EPI) sequence with multiband factor = 8, TR = 720 ms, TE =
, 104 × 90 (RO×PE) matrix size, 72 slices, and 2-mm isotropic voxels;
33.1 ms, flip angle = 52
1,200 volumes were obtained over a 14 min, 33 sec scanning session. fMRI data has under-
gone spatial and temporal preprocessing including motion and physiological noise removal
(Smith et al., 2013). Using the resting-state fMRI, we employed the Automated Anatomical La-
beling (AAL) brain template to parcellate the brain volume into 116 regions (Tzourio-Mazoyer,
Landeau, Papathanassiou, Crivello, Etard, Delcroix, Mazoyer, & Joliot, 2002). The fMRI were
then averaged across voxels in each brain region for each subject. The averaged fMRI signal
in each parcellation was then temporally smoothed using the cosine series representation as
follows (Chung, Adluru, Lee, Lazar, Lainhart, & Alexander, 2010; Gritsenko, Lindquist, Kirk,
& Chung, 2018).
Given fMRI time series at the i-th parcellation ζ
[0, 1]. Then subtracted its mean over time
time series was represented as
(cid:14)
ζ
1
0
i(t) at time t, we scaled it to fit to unit interval
i(t) dt. Then the resulting scaled and translated
ζ
i(t) =
k
∑
l=0
cli
l(t), t ∈ [0, 1],
ψ
√
l(t) =
0(t) = 1, ψ
2 cos(lπt) were cosine basis functions and cli were coefficients
where ψ
estimated in the least squares fashion. For our study, k = 119 was used such that fMRI were
compressed into 10% of the original data size; k = 119 expansion increased the signal-to-
noise ratio (SNR) as measured by the ratio of variabilities by 81% in average over all 116 brain
regions and 416 subjects, that is, SNR = 1.81. The resulting real-valued Fourier coefficient
vector ci = (c0i, c1i, · · · , cki) was then used to represent the fMRI in each parcellation as 120
features in the spectral domain.
Twin Correlations
The subject level connectivity matrix C = (cij) was computed by correlating 120 features in
the spectral domain. Between i- and j-th parcellations, the connectivity was measured by cor-
relating ci and cj over 120 features, that is, cij = corr(ci, cj). From the individual correlation
matrices C, we computed pairwise twin correlations in each group at the edge level. The result-
ing group level twin correlations matrices CMZ = (cMZ
ij ) are nonsymmetric
cross-correlation matrices. Since there is no preference in the order of twins, we symmetrize
them by
) and CDZ = (cDZ
ij
and
CMZ
← (CMZ + C
(cid:2)
MZ)/2
CDZ
← (CDZ + C
(cid:2)
DZ)/2.
Network Neuroscience
688
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
Heritability index:
A number between 0 and 1 that
measures the amount of genetic
contribution.
Then we are interested in knowing the extent of the genetic influence on resting-state functional
brain network and its statistical significance. For this, we use the widely used ACE genetic
model (Falconer & Mackay, 1995) that mainly uses heritability index (HI), which determines
the amount of variation (in terms of percentage) due to genetic influence in a population. HI is
often estimated using Falconer’s formula (Falconer & Mackay, 1995) as a baseline. MZ twins
share 100% of genes, whereas DZ twins share 50% of genes. Thus, the additive genetic factor
A, the common environmental factor C for each twin type are related as
corr(cMZ
corr(cDZ
) = A + C,
ij
ij ) = A/2 + C,
(5)
(6)
) and corr(cDZ
where corr(cMZ
ij ) are the pairwise correlation within MZ and same-sex DZ twins
at edge between i and j. Solving Equation 5 and Equation 6, we obtain the additive genetic
factor, that is, HI given by
ij
HI = 2(CMZ
− CDZ).
The network differences between MZ and DZ twins are considered as mainly contributed to
heritability and can be used to determine the statistical significance of HI (Chung et al., 2017,
2018). The KS-distance was computed by taking 1 − CMZ and 1 − CDZ as edge weights.
In most brain imaging studies, 5,000–1,000,000 permutations are often used, which puts
the total number of generated permutations to usually less than 0.01 to 1% of all possible per-
mutations. In Zalesky et al. (2010), 5,000 permutations are out of a possible (27
12) = 17, 383, 860
permutations (2.9%) used. In Thompson et al. (2001), for instance, 1 million permutations out
of (40
20) possible permutations (0.07%) were generated using a super computer. In Lee et al.
(2017), 5,000 permutations out of a possible (33
10) = 92, 561, 040 permutations (0.005%) were
used. Since we have 131 MZ and 77 DZ pairs, the total number of possible permutation is
(271
131), which is larger than 1080. Even if we generate only 0.01% of 1080 of all possible permu-
tations, 1076 permutations are still too large for most desktop computers. Thus, we choose the
KS-distance for measuring the network distance. Although the probability distribution of the
KS-distance is actually based on the permutation test but the probability is computed combi-
natorially, bypassing the need for resampling. KS-distance in our study only took a few seconds
to compute the p value.
ij
0 and β
1 in computing KS-distances. Let φ ◦ CMZ = (φ(cMZ
Results
)) and φ ◦ CDZ =
We used β
(φ(cDZ
ij )) for some monotone function φ. Then KS-distance between CMZ and CDZ is
equivalent to KS-distance between 1 − CMZ and 1 − CDZ as well as between φ ◦ (1 − CMZ) and
φ ◦ (1 − CDZ). Thus, we simply built filtrations over CMZ and CDZ and computed KS-distance
without using the square-root of 1 - correlation. We used 101 filtration values between 0 and
1 at 0.01 increment (Figure 4). This gives a reasonably accurate estimate of the maximum
gap in the β
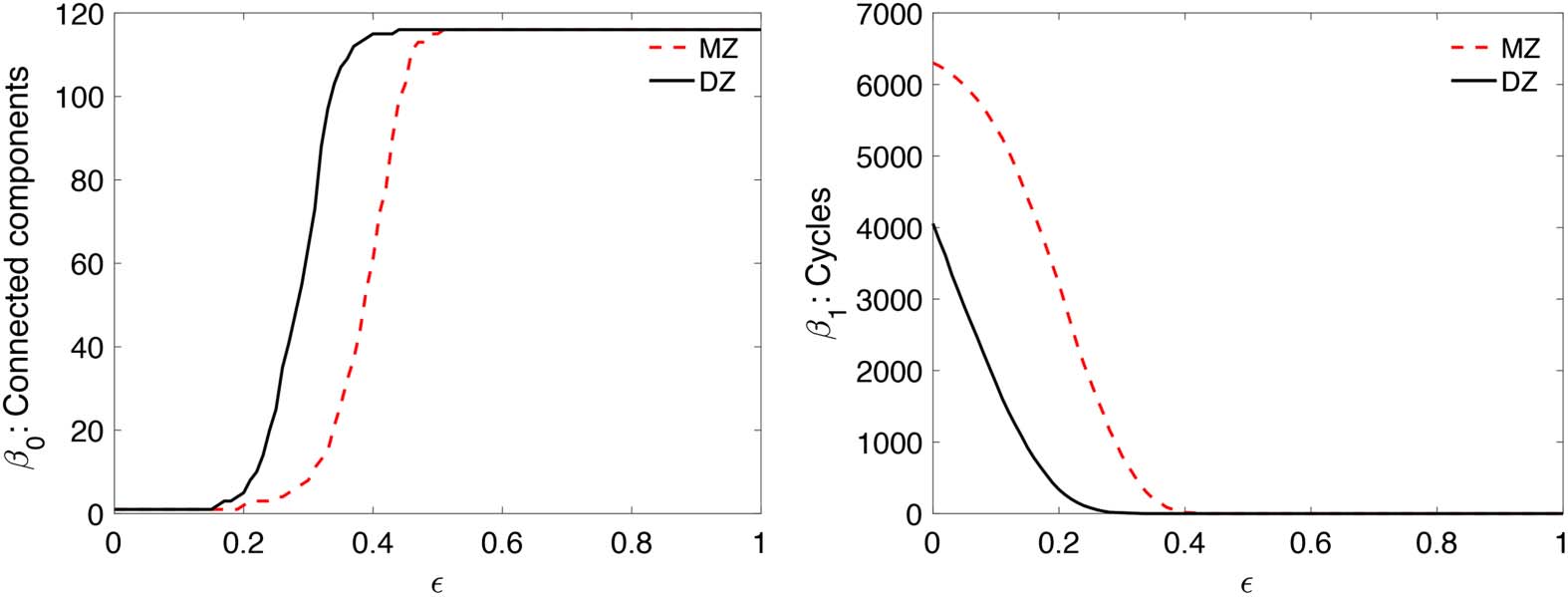
0-plots, the maximum gap is 82, which
1-plots, the maximum gap is 3,647, which gives the
gives the p value smaller than 10
−32. At the same correlation value, MZ twins are more connected than
p value smaller than 10
DZ twins. Also MZ twins have more cycles than DZ twins. Such huge topological differences
are contributed to heritability.
i-plots between the twins (Figure 5). For β
−24. For β
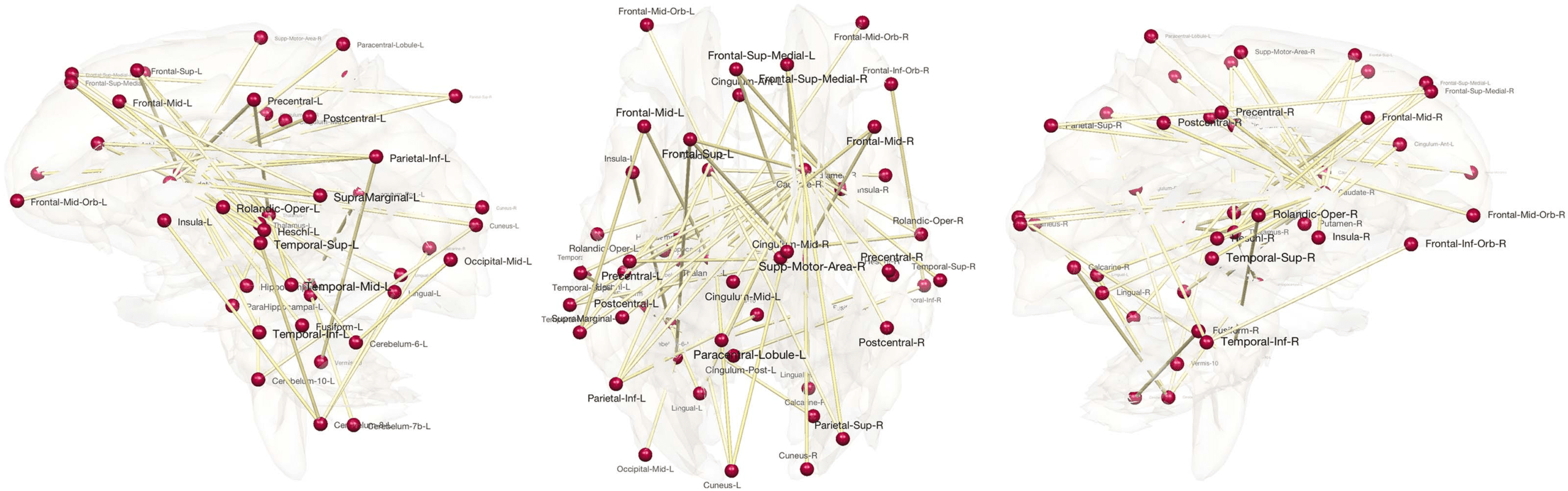
Figure 6, which displays the HI index thresholded at 100% heritability, shows MZ twins far
more similar compared with DZ twins in many connections, suggesting that genes influence
the development of these connections. The most heritable connections include the left frontal
Network Neuroscience
689
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
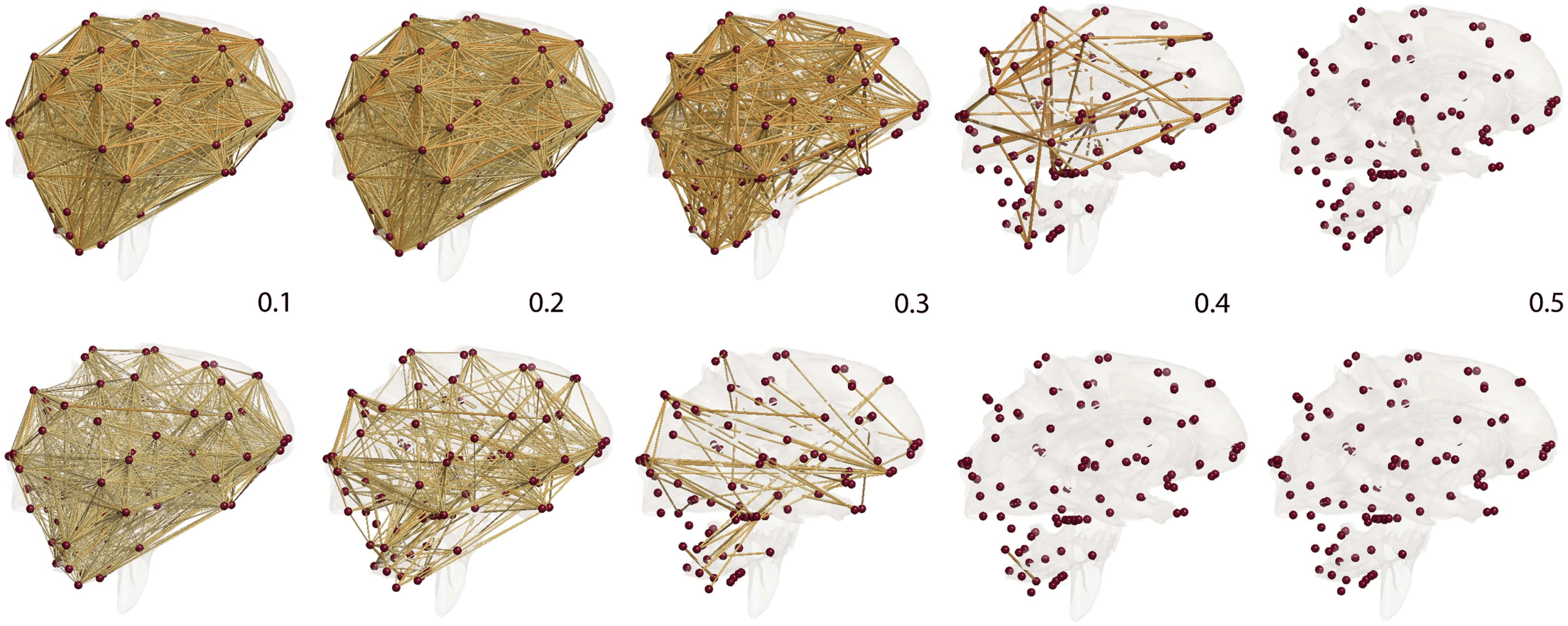
Figure 4. Correlation network filtration thresholded at the indicated correlation values. MZ-twins (top) shows higher correlation connections
compared with DZ-twins (bottom). Such connectivity difference is contributed to heritability.
gyrus, left and right middle frontal gyri, left superior frontal gyrus, left parahippocampal gyrus,
left and right thalami, left and right caudate, and nuclei among many other regions. Most re-
gions overlap with highly heritable regions observed in other twins brain-imaging studies (Fan,
Fossella, Sommer, Wu, & Posner, 2003; Glahn et al., 2010; Gritsenko et al., 2018). Moreover,
the findings here are somewhat consistent with a previous study on diffusion tensor imaging on
twins from our group (Chung, Luo, Adluru, Alexander, Richard, & Goldsmith, 2018a; Chung
et al., 2018b), showing that many regions of both resting-state functional and structural con-
nections are heritable at the same time. The left and right caudate nuclei are identified as the
most heritable hub nodes in our study.
The MATLAB codes for the simulation study as well as the connectivity matrices CMZ and
CDZ used in generating results are given at http://www.stat.wisc.edu/~mchung/TDA.
Betti-plots:
Displays the change of Betti numbers
over filtration values.
Figure 5. Betti-plots showing Betti numbers over correlation (cid:4) as filtration. MZ twins (top) shows
more higher correlation connections and cycles compared with DZ twins (bottom).
Network Neuroscience
690
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
Figure 6. Most highly heritable connections. The connections with 100% heritability are only shown.
DISCUSSION
The Limitation of KS-distances
Currently KS-distance is applied to Betti numbers β
1 separately. It may be possible to
0 and β
construct a new topological distance that uses the combination of both β
1 and come
up with topologically more sensitive distances. One possible approach is to use the convex
i and 0 ≤ α ≤ 1. This is
combination αD0
beyond the scope of this paper and left as a future study.
KS is KS-distance for β
KS + (1 − α)D1
KS, where Di
0 and β
Other Network Distances
The network distances used in this study are not just any other distances but metrics. Since there
are almost infinitely many possible similarity measures and distances we can use in networks,
the performance of the chosen distance is important in discrimination tasks, which we have
shown in simulation studies. The determination of the optimal distance is related to metric
learning, an area of supervised machine learning in which the goal is to learn from data an
optimal similarity function that measures how similar two objects are (Ktena, Parisot, Ferrante,
Rajchl, Lee, Glocker, & Rueckert, 2018; Lowe, 1995). This is left as a future study.
Computational Issues
The total number of permutations in permuting two groups of size q each is (2q
. Even
for small q = 10, more than tens of thousands of permutations are needed for the accurate
approximation of the p value. The main advantage of KS-distance over all other distance mea-
sures is that it avoids numerically performing the permutation test and avoids generating tens of
thousands of permutations. Although the probability distribution of the KS-distance is actually
based on the permutation test, the probability is computed combinatorially. We believe that it
is possible to develop similar theoretical results for other distance measures and come up with
a method for avoiding a resampling-based method for statistical inference.
q ) ∼ 4q√
2πq
ACKNOWLEDGMENTS
We thank Yuan Wang of University of South Carolina, Peter Bebunik of University of
Florida, Bala Krishnamoorthy of Washington State University, Dustin Pluta of University of
Network Neuroscience
691
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
California-Irvine, Alex Leow of University of Illinois-Chicago, and Martin Lindquist of Johns
Hopkins University for valuable discussions. We also thank Andrey Gritsenko and Gregory
Kirk of University of Wisconsin-Madison for logistic support and image preprocessing help.
AUTHOR CONTRIBUTIONS
Moo Chung: Conceptualization; Data curation; Formal analysis; Funding acquisition; Inves-
tigation; Methodology; Project administration; Resources; Software; Supervision; Validation;
Visualization; Writing - Original Draft; Writing - Review & Editing. Hyekyoung Lee: Investi-
gation; Methodology; Validation; Visualization; Writing - Original Draft. Alex DiChristofano:
Investigation. Hernando Ombao: Writing - Review & Editing. Victor Solo: Conceptualization;
Methodology; Writing - Review & Editing.
FUNDING INFORMATION
Moo Chung, National Institutes of Health (http://dx.doi.org/10.13039/100000002), Award
ID: EB022856. Hyekyoung Lee, National Research Foundation of Korea (http://dx.doi.org/
10.13039/501100003725), Award ID: NRF-2016R1D1A1B03935463.
REFERENCES
Achard, S., & Bullmore, E. (2007). Efficiency and cost of economi-
cal brain functional networks. PLoS Computational Biology, 3(2), e17.
Achard, S., Salvador, R., Whitcher, B., Suckling, J., & Bullmore,
E. (2006). A resilient, low-frequency, small-world human brain
functional network with highly connected association cortical
hubs. The Journal of Neuroscience, 26, 63–72.
Adams, H., Tausz, A., & Vejdemo-Johansson, M. (2014). javaPlex: A
research software package for persistent (co) homology. In Math-
ematical Software–icms 2014 (pp. 129–136). Springer.
Adler, R., Bobrowski, O., Borman, M., Subag, E., & Weinberger, S.
(2010). Persistent homology for random fields and complexes. In
Borrowing Strength: Theory Powering Applications–A festschrift for
Lawrence D. Brown (pp. 124–143). Institute of Mathematical Statistics.
Bassett, D. (2006). Small-world brain networks. The Neuroscientist,
12, 512–523.
Bassett, D., Meyer-Lindenberg, A., Achard, S., Duke, T., & Bullmore,
E. (2006). Adaptive reconfiguration of fractal small-world human
brain functional networks. Proceedings of the National Academy
of Sciences, 103, 19518–19523.
Bien, J., & Tibshirani, R. (2011). Hierarchical clustering with proto-
types via minimax linkage. Journal of American Statistical Asso-
ciation, 106, 1075–1084.
Blokland, G., McMahon, K., Thompson, P., Martin, N., de Zubicaray,
G., & Wright, M. (2011). Heritability of working memory brain
activation. The Journal of Neuroscience, 31, 10882–10890.
Bobrowski, O., & Kahle, M. (2014). Topology of random geomet-
ric complexes: A survey. Journal of Applied and Computational
Topology, 1–34.
Boissonnat, J.-D., & Teillaud, M. (Eds.). (2006). Effective computa-
tional geometry for curves and surfaces. Springer.
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Review Neuroscience, 10, 186–98.
Carlsson, G. (2009). Topology and data. Bulletin of the American
Mathematical Society, 46, 255–308.
Carlsson, G., De Silva, V., & Morozov, D. (2009). Zigzag persis-
tent homology and real-valued functions. In Proceedings of the
Twenty-fifth Annual Symposium on Computational Geometry
(pp. 247–256).
Carlsson, G., Ishkhanov, T., De Silva, V., & Zomorodian, A. (2008).
On the local behavior of spaces of natural images. International
Journal of Computer Vision, 76, 1–12.
Carlsson, G., & Memoli, F. (2008). Persistent clustering and a the-
orem of J. Kleinberg. arXiv Preprint arXiv:0808.2241.
Carlsson, G., & Mémoli, F.
(2010). Characterization, stability
and convergence of hierarchical clustering methods. Journal of
Machine Learning Research, 11, 1425–1470.
Carlsson, G., Singh, G., & Zomorodian, A. (2009). Computing mul-
tidimensional persistence. In International Symposium on Algo-
rithms and Computation (pp. 730–739).
Cassidy, B., Rae, C., & Solo, V. (2015). Brain activity: Conditional
dissimilarity and persistent homology. In IEEE 12th International
Symposium on Biomedical Imaging (ISBI) (pp. 1356–1359).
Chazal, F., Cohen-Steiner, D., Guibas, L., Mémoli, F., & Oudot, S.
(2009). Gromov-Hausdorff stable signatures for shapes using per-
sistence. In Computer Graphics Forum (Vol. 28, pp. 1393–1403).
Chiang, M.-C., McMahon, K., de Zubicaray, G., Martin, N., Hickie,
I., Toga, A., . . . Thompson, P. (2011). Genetics of white matter
development: A DTI study of 705 twins and their siblings aged
12 to 29. NeuroImage, 54, 2308–2317.
Chowdhury, S., & Mémoli, F. (2016). Persistent homology of di-
rected networks. In Signals, Systems and Computers, 2016 50th
Asilomar Conference on (pp. 77–81).
Chung, M., Adluru, N., Dalton, K., Alexander, A., & Davidson,
R. (2011). Scalable brain network construction on white matter
fibers. In Proceedings of SPIE (Vol. 7962, p. 79624G).
Chung, M., Adluru, N., Lee, J., Lazar, M., Lainhart, J., & Alexander,
A. (2010). Cosine series representation of 3D curves and its appli-
cation to white matter fiber bundles in diffusion tensor imaging.
Statistics and Its Interface, 3, 69–80.
Network Neuroscience
692
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
Chung, M., Hanson, J., Lee, H., Adluru, N., Alexander, A. L.,
Davidson, R., & Pollak, S. (2013). Persistent homological sparse
network approach to detecting white matter abnormality in mal-
treated children: MRI and DTI multimodal study. MICCAI, Lecture
Notes in Computer Science (LNCS), 8149, 300–307.
Chung, M., Hanson, J., Ye, J., Davidson, R., & Pollak, S. (2015). Persistent
homology in sparse regression and its application to brain mor-
phometry. IEEE Transactions on Medical Imaging, 34, 1928–1939.
Chung, M., Lee, H., Solo, V., Davidson, R., & Pollak, S. (2017a).
International
Topological distances between brain networks.
Workshop on Connectomics in Neuroimaging, Lecture Notes in
Computer Science, 161–170.
Chung, M., Luo, Z., Adluru, A., Alexander, A., Richard, D., &
Goldsmith, H. (2018a). Heritability of hierarchical structural
brain network. International Conference of the IEEE Engineering
in Medicine and Biology Society (EMBC), 554–557.
Chung, M., Luo, Z., Leow, A., Adluru, A., Alexander, A., Richard, D.,
& Goldsmith, H. (2018b). Exact combinatorial inference for brain
images. In International Conference on Medical Image Computing and
Computer-Assisted Intervention (MICCAI) (pp. 629–637).
Chung, M., Vilalta-Gil, V., Lee, H., Rathouz, P., Lahey, B., & Zald,
D. (2017b). Exact topological inference for paired brain networks
via persistent homology. Information Processing in Medical Imag-
ing (IPMI), Lecture Notes in Computer Science (LNCS), 10265,
299–310.
Cohen-Steiner, D., Edelsbrunner, H., & Harer, J. (2007). Stability
of persistence diagrams. Discrete and Computational Geometry,
37, 103–120.
de Silva, V., & Ghrist, R. (2007). Homological sensor networks.
Notices of the American Mathematical Society, 54, 10–17.
Di Fabio, B., & Ferri, M. (2015). Comparing persistence diagrams
through complex vectors. In International Conference on Image
Analysis and Processing (pp. 294–305).
Edelsbrunner, H., & Harer, J. (2008). Persistent homology—a survey.
Contemporary Mathematics, 453, 257–282.
Edelsbrunner, H., Letscher, D., & Zomorodian, A. (2000). Topological
persistence and simplification. In Foundations of Computer Science,
2000. Proceedings. 41st Annual Symposium on (pp. 454–463).
Edelsbrunner, H., Letscher, D., & Zomorodian, A. (2002). Topolog-
ical persistence and simplification. Discrete and Computational
Geometry, 28, 511–533.
Efron, B. (1982). The Jackknife, the Bootstrap and Other Resampling
Plans (Vol. 38). SIAM.
Falconer, D., & Mackay, T. (1995). Introduction to Quantitative
Genetics, (4th ed.). Longman.
Fan, J., Fossella, J., Sommer, T., Wu, Y., & Posner, M. (2003). Map-
ping the genetic variation of executive attention onto brain ac-
tivity. Proceedings of the National Academy of Sciences, 100,
7406–7411.
Ghrist, R. (2008). Barcodes: The persistent topology of data. Bulletin
of the American Mathematical Society, 45, 61–75.
Girvan, M., & Newman, M. (2002). Community structure in social
and biological networks. Proceedings of the National Academy
of Sciences, 99, 7821.
Giusti, C., Pastalkova, E., Curto, C., & Itskov, V. (2015). Clique
topology reveals intrinsic geometric structure in neural correla-
tions. Proceedings of the National Academy of Sciences, 112,
13455–13460.
Glahn, D., Winkler, A., Kochunov, P., Almasy, L., Duggirala, R.,
Carless, M., . . . Blangero, J. (2010). Genetic control over the
resting brain. Proceedings of the National Academy of Sciences,
107, 1223–1228.
Gritsenko, A., Lindquist, M., Kirk, G., & Chung, M. (2018). Hill
climbing optimized twin classification using resting-state func-
tional MRI. arXiv, 1807.00244. Retrieved from https://arxiv.org/
abs/1807.00244
He, Y., Chen, Z., & Evans, A.
insights into
aberrant topological patterns of large-scale cortical networks in
Alzheimer’s disease. Journal of Neuroscience, 28, 4756.
(2008). Structural
Horak, D., Maleti´c, S., & Rajkovi´c, M. (2009). Persistent homology
of complex networks. Journal of Statistical Mechanics: Theory
and Experiment, 2009, P03034.
Ibanez-Marcelo, E., Campioni, L., Manzoni, D., Santarcangelo, E.,
& Petri, G. (2018a). Spectral and topological analysis of the cor-
tical representation of the head position: Does hypnotizability
matter? bioRxiv, 442053.
Ibanez-Marcelo, E., Campioni, L., Phinyomark, A., Petri, G., &
Santarcangelo, E. (2018b). Topology highlights mesoscopic func-
tional equivalence between imagery and perception. bioRxiv,
268383.
Kerber, M., Morozov, D., & Nigmetov, A. (2017). Geometry helps
to compare persistence diagrams. Journal of Experimental Algo-
rithmics, 22.
Khalid, A., Kim, B., Chung, M., Ye, J., & Jeon, D. (2014). Tracing the
evolution of multi-scale functional networks in a mouse model
of depression using persistent brain network homology. Neuro-
Image, 101, 351–363.
Kim, W., Adluru, N., Chung, M., Okonkwo, O.,
Johnson, S.,
Bendlin, B., & Singh, V. (2015). Multi-resolution statistical anal-
ysis of brain connectivity graphs in preclinical Alzheimer’s dis-
ease. NeuroImage, 118, 103–117.
Kondor, R., Howard, A., & Jebara, T. (2007). Multi-object track-
ing with representations of the symmetric group. In Interna-
tional Conference on Artificial Intelligence and Statistics (Aistats)
(Vol. 1, p. 5).
Ktena, S., Parisot, S., Ferrante, E., Rajchl, M., Lee, M., Glocker, B.,
& Rueckert, D. (2018). Metric learning with spectral graph con-
volutions on brain connectivity networks. NeuroImage, 169,
431–442.
Kusano, G., Hiraoka, Y., & Fukumizu, K.
(2016). Persistence
weighted Gaussian kernel for topological data analysis. In Inter-
national Conference on Machine Learning (pp. 2004–2013).
Lee, H., Chung, M. K., Kang, H., & Lee, D. (2014). Hole detection
in metabolic connectivity of Alzheimer’s disease using k-Laplacian.
In International Conference on Medical Image Computing and
Computer-Assisted Intervention (MICCAI), Lecture Notes in
Computer Science (pp. 297–304).
Lee, H., Chung, M., Kang, H., Choi, H., Kim, Y., & Lee, D. (2018).
Abnormal hole detection in brain connectivity by kernel density
of persistence diagram and Hodge Laplacian. In IEEE Interna-
tional Symposium on Biomedical Imaging (ISBI) (p. 20–23).
Lee, H., Chung, M., Kang, H., Kim, B.-N., & Lee, D. (2011a). Com-
puting the shape of brain networks using graph filtration and
Network Neuroscience
693
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Exact topological inference
Gromov-Hausdorff metric. MICCAI, Lecture Notes in Computer
Science, 6892, 302–309.
Lee, H., Chung, M., Kang, H., Kim, B.-N., & Lee, D. (2011b). Dis-
criminative persistent homology of brain networks. In IEEE Inter-
national Symposium on Biomedical Imaging (ISBI) (pp. 841–844).
Lee, H., Kang, H., Chung, M., Kim, B.-N., & Lee, D. (2012). Per-
sistent brain network homology from the perspective of dendro-
gram. IEEE Transactions on Medical Imaging, 31, 2267–2277.
Lee, H., Kang, H., Chung, M., Lim, S., Kim, B.-N., & Lee, D. (2017).
Integrated multimodal network approach to PET and MRI based
on multidimensional persistent homology. Human Brain Map-
ping, 38, 1387–1402.
Li, Y., Liu, Y., Li, J., Qin, W., Li, K., Yu, C., & Jiang, T. (2009). Brain
anatomical network and intelligence. PLoS Computational Biol-
ogy, 5(5), e1000395.
Lind, P., Gonzalez, M., & Herrmann, H. (2005). Cycles and cluster-
ing in bipartite networks. Physical Review E, 72, 056127.
Lowe, D.
(1995). Similarity metric learning for a variable-kernel
classifier. Neural Computation, 7, 72–85.
McKay, D., Knowles, E., Winkler, A., Sprooten, E., Kochunov, P.,
Olvera, R., . . . Glahn, D. (2014). Influence of age, sex and genetic
factors on the human brain. Brain Imaging and Behavior, 8, 143–152.
Mclntosh, A., & Gonzalez-Lima, F. (1994). Structural equation mod-
eling and its application to network analysis in functional brain
imaging. Human Brain Mapping, 2, 2–22.
Meunier, D., Lambiotte, R., Fornito, A., Ersche, K., & Bullmore, E.
(2009). Hierarchical modularity in human brain functional net-
works. Frontiers in Neuroinformatics, 3:37.
Newman, M., Barabasi, A., & Watts, D. (2006). The Structure and
Dynamics of Networks. Princeton University Press.
Newman, M., & Watts, D. (1999). Scaling and percolation in the
small-world network model. Physical Review E, 60, 7332–7342.
Nichols, T., & Holmes, A. (2002). Nonparametric permutation tests
for functional neuroimaging: A primer with examples. Human
Brain Mapping, 15, 1–25.
Petri, G., Expert, P., Turkheimer, F., Carhart-Harris, R., Nutt, D.,
Hellyer, P., & Vaccarino, F. (2014). Homological scaffolds of
brain functional networks. Journal of The Royal Society Interface,
11, 20140873.
Petri, G., Scolamiero, M., Donato, I., & Vaccarino, F. (2013). Topo-
logical strata of weighted complex networks. PloS One, 8, e66506.
Pinehiro, J., & Bates, D. (2002). Mixed Effects Models in S and S-plus
(3rd ed.). Springer.
Pothen, A., & Fan, C. (1990). Computing the block triangular form
of a sparse matrix. ACM Transactions on Mathematical Software
(TOMS), 16, 324.
Rubinov, M., Knock, S. A., Stam, C. J., Micheloyannis, S., Harris,
A. W., Williams, L. M., & Breakspear, M. (2009). Small-world
properties of nonlinear brain activity in schizophrenia. Human
Brain Mapping, 30, 403–416.
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52,
1059–1069.
Sizemore, A., Giusti, C., & Bassett, D. (2016). Classification of
features.
weighted networks through mesoscale homological
Journal of Complex Networks, 5, 245–273.
Sizemore, A., Giusti, C., Kahn, A., Vettel, J., Betzel, R., & Bassett, D.
(2018). Cliques and cavities in the human connectome. Journal
of Computational Neuroscience, 44, 115–145.
Smit, D., Stam, C., Posthuma, D., Boomsma, D., & De Geus, E.
(2008). Heritability of small-world networks in the brain: A graph
theoretical analysis of resting-state EEG functional connectivity.
Human Brain Mapping, 29, 1368–1378.
Smith, S., Beckmann, C., Andersson, J., Auerbach, E., Bijsterbosch,
J., & et. al. (2013). Resting-state fMRI in the Human Connectome
Project. NeuroImage, 80, 144–168.
Snijders, T., Spreen, M., & Zwaagstra, R. (1995). The use of multi-
level modeling for analysing personal networks: Networks of
cocaine users in an urban area. Journal of Quantitative Anthro-
pology, 5, 85–105.
Song, C., Havlin, S., & Makse, H. (2005). Self-similarity of complex
networks. Nature, 433, 392–395.
Sporns, O. (2003). Graph theory methods for the analysis of neural
connectivity patterns. In R. Kötter (Ed.), Neuroscience Databases:
A Practical Guide (pp. 171–185). Boston, MA: Springer US.
Sporns, O., Tononi, G., & Edelman, G. (2000). Theoretical neuro-
anatomy: Relating anatomical and functional connectivity in graphs
and cortical connection matrices. Cerebral Cortex, 10, 127.
Stolz, B., Harrington, H., & Porter, M. (2017). Persistent homology
of time-dependent functional networks constructed from coupled
time series. Chaos: An Interdisciplinary Journal of Nonlinear Sci-
ence, 27, 047410.
Supekar, K., Menon, V., Rubin, D., Musen, M., & Greicius, M.
(2008). Network analysis of intrinsic functional brain connec-
tivity in Alzheimer’s disease. PLoS Computational Biology, 4(6),
e1000100.
Tarjan, R.
(1972). Depth-first search and linear graph algorithms.
SIAM Journal on Computing, 1, 146–160.
Thompson, P., Cannon, T., Narr, K., van Erp, T., Poutanen, V.,
Huttunen, M., . . . Khaledy, M. (2001). Genetic influences on
brain structure. Nature Neuroscience, 4, 1253–1258.
Tuzhilin, A. (2016). Who invented the Gromov-Hausdorff distance?
arXiv preprint arXiv:1612.00728.
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello,
F., Etard, O., Delcroix, N., . . . Joliot, M. (2002). Automated
anatomical labeling of activations in spm using a macroscopic
anatomical parcellations of the MNI MRI single-subject brain.
NeuroImage, 15, 273–289.
Uddin, L., Kelly, A., Biswal, B., Margulies, D., Shehzad, Z., Shaw,
D., . . . Milham, M. (2008). Network homogeneity reveals de-
creased integrity of default-mode network in ADHD. Journal of
Neuroscience Methods, 169, 249–254.
Van Essen, D., Ugurbil, K., Auerbach, E., Barch, D., Behrens, T.,
Bucholz, R., . . . Curtiss, S. (2012). The human connectome proj-
ect: A data acquisition perspective. Neuroimage, 62, 2222–2231.
Wijk, B. C. M., Stam, C. J., & Daffertshofer, A. (2010). Comparing
brain networks of different size and connectivity density using
graph theory. PloS One, 5, e13701.
Zalesky, A., Fornito, A., Harding,
I., Cocchi, L., Yücel, M.,
Pantelis, C., & Bullmore, E. (2010). Whole-brain anatomical
networks: Does the choice of nodes matter? NeuroImage, 50,
970–983.
Zomorodian, A., & Carlsson, G. (2005). Computing persistent ho-
mology. Discrete and Computational Geometry, 33, 249–274.
Network Neuroscience
694
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
6
7
4
1
0
9
2
4
7
7
n
e
n
_
a
_
0
0
0
9
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3