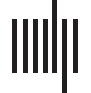FUNCIÓN DE ENFOQUE:
Topological Neuroscience
Topological exploration of artificial neuronal
network dynamics
Jean-Baptiste Bardin
1
, Gard Spreemann
1
1
, and Kathryn Hess
1Laboratory for Topology and Neuroscience, Brain Mind Institute, École Polytechnique Fédérale de Lausanne,
Lausanne, Suiza
Palabras clave: Network dynamics, Topological data analysis, Persistent homology, Artificial neural
network, Spike train, aprendizaje automático
un acceso abierto
diario
ABSTRACTO
One of the paramount challenges in neuroscience is to understand the dynamics of individual
neurons and how they give rise to network dynamics when interconnected. Históricamente,
researchers have resorted to graph theory, Estadísticas, and statistical mechanics to describe the
spatiotemporal structure of such network dynamics. Our novel approach employs tools from
algebraic topology to characterize the global properties of network structure and dynamics.
We propose a method based on persistent homology to automatically classify network
dynamics using topological features of spaces built from various spike train distances. Nosotros
investigate the efficacy of our method by simulating activity in three small artificial neural
networks with different sets of parameters, giving rise to dynamics that can be classified into
four regimes. We then compute three measures of spike train similarity and use persistent
homology to extract topological features that are fundamentally different from those used in
métodos tradicionales. Our results show that a machine learning classifier trained on these
features can accurately predict the regime of the network it was trained on and also
generalize to other networks that were not presented during training. Además, nosotros
demonstrate that using features extracted from multiple spike train distances systematically
improves the performance of our method.
INTRODUCCIÓN
A major objective in neuroscience is to understand how populations of interconnected neurons
perform computations and process information. It is believed that the dynamics of a neuronal
network are indicative of the computations it can perform. Its dynamics are affected by how the
neurons are physically connected and by the activity history of the neurons. Understanding this
spatiotemporal organization of network dynamics is essential for developing a comprehensive
view of brain information-processing mechanisms, the functional connectome. Two neurons
can be considered “functionally connected” if their dynamics are similar or if one appears
highly likely to spike causally after the other. The same notion of functional connectivity can be
considered also on a macroscopic level, where one can study the causal relationships between
regiones del cerebro. The notion can also be formalized for similarly structured systems from outside
of neuroscience. Techniques like the one we present in this paper thus have broad applicability.
Además, it is well-known that certain neuronal systems can play multiple roles, char-
acterized by different patterns of activity. Por ejemplo, neurons in the thalamus have tonic
Citación: Bardin, J.-B., Spreemann, GRAMO.,
& Hesse, k. (2019). Topological
exploration of artificial neuronal
network dynamics. Red
Neurociencia, 3(3), 725–743.
https://doi.org/10.1162/netn_a_00080
DOI:
https://doi.org/10.1162/netn_a_00080
Supporting Information:
https://github.com/JBBardin/
Brunel_AlgebraicTopology
Recibió: 24 Septiembre 2018
Aceptado: 10 Enero 2019
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Kathryn Hess
kathryn.hess@epfl.ch
Editor de manejo:
Giovanni Petri
Derechos de autor: © 2019
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
Topological data analysis (TDA):
Study of data by way of the
algebraic-topological properties
of spaces constructed from
los datos.
Space:
A mathematical object where
notions such as continuity can be
defined. In TDA, data are turned
into spaces, which are then studied.
Persistent homology:
Central tool of TDA that in its
basic form detects connected
componentes, holes, cavities,
and higher-dimensional
voids in data.
or phasic behavior depending on the afferent signals and neuromodulators they receive or on
different phases of the sleep cycle (Weyand et al., 2001). Another example is the hippocampus,
which plays a role both in memory and in navigation. Researchers have also observed distinct
rhythms in EEG recordings in awake and in sleeping rats (Buzsáki, Chen, & Gage, 1990).
An understanding of network dynamics is also of medical importance, as many neurological
disorders are characterized by abnormal global or local activity. During epileptic seizures,
por ejemplo, EEG recordings show an increase in the amplitude of neural oscillations (Pescador
et al., 2005). In Alzheimer’s disease, one observes a shift in the power spectrum toward lower
frequencies and a decrease in the coherence of fast rhythms (jeong, 2004).
Partly because of the clinical importance of neural dynamics, various methods have already
been developed to automatically detect abnormal regimes, for example those related to epilep-
tic seizures (Alkan, Koklukaya, & Subasi, 2005; Kan & Gotman, 2003; Tzallas, Tsipouras, &
fotiadis, 2007). The best ones rely on artificial neural networks. Here we propose a novel
approach using techniques from topological data analysis, a part of applied mathematics.
Traditionally, neuroscientists have analyzed functional networks using pairwise neuron
statistics and graph theory. Such methods often neglect certain global structures that may be
present in the dynamics. The analysis of network dynamics using alternative methods from
topological data analysis has recently enjoyed success (Curto, 2017; Curto & Itskov, 2008;
Dabaghian, Mémoli, Franco, & Carlsson, 2012; Giusti, Pastalkova, Curto, & Itskov, 2015; singh
et al., 2008; Spreemann, Dunn, Botnan, & Baas, 2018). These methods provide information
about connectedness, adjacency, and global structure such as holes (of various dimension) en
a dataset. (The dataset is turned into a mathematical space in a manner detailed in the Meth-
ods section. It is in the context of such a space that the notion of holes arises.) En particular,
persistent homology detects holes or cavities and quantifies how robust these are with respect
to a threshold variable related to the dynamics of the system.
Several interesting properties of neuronal network structure and function have been re-
vealed through these recent developments. Por ejemplo, persistent homology has been ap-
plied to detect and characterize changes in the functional connectome in disorders such as
autism and attention deficit disorder (Sotavento, Chung, Kang, kim, & Sotavento, 2011), in the Parkinson
mouse model (Im et al., 2016), and after injection of a hallucinogenic substance (Petri et al.,
2014). It has also been employed to describe brain function during different tasks, como
multimodal and unimodal speech recognition (Kim y cols., 2015). Además, the homology of
a digital reconstruction of the rat cortical microcircuit revealed that the brain substructure is
nonrandom, that it is substantially different from various other null models, and that its activity
tends to concentrate in areas with greater local organization (Reimann et al., 2017). En el
same article, homology was shown to distinguish the dynamics arising from different stimuli
injected into the digital reconstruction. It is also interesting to note that the mammalian brain
seems to encode topological information, as there are strong indications that the place cells
(O’Keefe & Dostrovsky, 1971) in the hippocampus build a topological, rather than geomet-
ric, representation of the animal’s surroundings (Dabaghian, Brandt, & Franco, 2014). Este último
article also shows how such a map can be encoded by a spiking network of neurons.
To this day, the few articles in which persistent homology has been applied to in vivo (Giusti
et al., 2015; Singh et al., 2008) or synthetic (Spreemann et al., 2018) spike data have all used
spike train (Pearson) correlation as the distance between neurons. The use of correlations re-
quires one to make specific assumptions about neural coding that may not be reasonable or
relevant in all research areas. There exists a wide variety of spike train distances and similarity
Neurociencia en red
726
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
métrica, and the restrictiveness of their assumptions and the kind of information they encode
can vary significantly. As we demonstrate in this paper, the appropriate notion of spike train
distance to use depends on context, and it can also be beneficial to combine several of them.
en este documento, we simulate activity in an artificial network of neurons to generate spiking
data and build weighted graphs based on various spike train similarities. These graphs are then
transformed into topological spaces, which are analyzed using persistent homology. Finalmente,
we extract simple features from topological invariants and use them to train a classifier for
predicting the global network dynamics. These topological features are fundamentally differ-
ent from those that might arise from graph-theoretic or other classical methods, as they take
into account relations within triplets and not just pairs of neurons. The features are also dif-
ferent from other machine learning–suitable ones that have been suggested in the topological
data analysis literature, such as persistence landscapes (Bubenik, 2015), persistence diagram
heat kernels (Reininghaus, Huber, Bauer, & Kwitt, 2015), and persistence-weighted Gaussian
granos (Kusano, Hiraoka, & Fukumizu, 2016).
Our results show that it is possible to perfectly predict network regimes from a few features
extracted from the persistent homology. The trained classifier also predicts with high accuracy
the dynamics of networks other than that on which it was trained. Finalmente, our results illus-
trate the importance of employing several spike train similarities, as the best performance was
achieved using a combination of them.
RESULTADOS
En esta sección, we summarize our work, namely the simulation of network dynamics, el
processing of spike trains, the topological analysis and feature selection, and the classification
método, before presenting our results. A more detailed explanation of the method can be
found in the Methods section.
Simulation of a Downscaled Brunel Network
We consider simulated activity in the Brunel network (Brunel, 2000), a simple and well-studied
in silico model network of sparsely connected excitatory and inhibitory neurons. For compu-
tational reasons, we use a downscaled version of the network as described below.
The Brunel network consists of two homogeneous subpopulations of
The Brunel network.
excitatory (here indexed by E) and inhibitory (indexed by I) neurons modeled by a current-
based leaky integrate-and-fire (LIF) modelo.
Brunel network:
Network of leaky integrate-and-fire
neurons whose parameter space
has four well-studied domains of
highly different dynamics.
Each of the N neurons has a membrane potential Vm(t) whose dynamics are described
by a differential equation. Once the membrane potential reaches a threshold value Vθ, el
neuron sends a spike through its synapses to its postsynaptic neurons, and its potential resets
to a value Vr. The synapses are δ-current synapses, eso es, after a delay D, each presynaptic
spike induces a positive (respectivamente, negative) jump in the membrane potential of the post-
synaptic neurons if the presynaptic neuron is excitatory (respectivamente, inhibitory). The excit-
= 4NI) in accordance with
atory subpopulation is four times larger than the inhibitory one (NE
cortical estimations (Noback, Ruggiero, Demarest, & Strominger, 2007), but their synapses are
relatively weaker. Formalmente, if the excitatory synapses induce an increase of membrane po-
tential of J, the inhibitory ones will induce a decrease of −gJ for some g > 1. Every neuron
receives K inputs coming from a fixed proportion P of the neurons in each subpopulation,
= PNE external excitatory
eso es, K = P(NE
). Además, each neuron receives CE
+ NI
Neurociencia en red
727
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
inputs from an independent Poisson population (of size CEN) with fixed rate νext. The relative
synaptic efficiency (gramo) and the external population rate (νext) are the free parameters with re-
spect to which we study network dynamics, once we have fixed the other model parameters,
in particular J, PAG, y D. We adopt the convention of Brunel’s original article (Brunel, 2000)
and express νext as a multiple of the minimal external rate necessary to trigger spiking in the
neurons without recurrent connections, denoted νθ.
Because computing persistent homology is expensive for large and dense spaces, cual
tend to arise from large and dense networks, the number N of neurons was reduced from 12,500
en (Brunel, 2000) a 2,500. Such a downscaling of the network while N/K is kept constant will
result in an increase in the correlation between the neurons (van Albada, Helias, & Diesmann,
2014), more salient oscillations in the network dynamics (Helias, Tetzlaff, & Diesmann, 2013),
and potentially a loss in the diversity of network dynamics. To prevent these undesirable effects,
a correction to the synaptic strength J was applied, and the external population was modified
according to (Helias et al., 2013). Específicamente, the synaptic strength J was adjusted to keep
JK constant, and the rate of the external population νext was increased. An external inhibitory
population with appropriate rate was also introduced to preserve the mean and variance of
the external inputs. The external rate correction is relevant only when neurons are expected
to show irregular firing, eso es, in the regimes where inhibition dominates (g > 4).
We generated three versions of the Brunel network to validate our method across different
redes.
Versión 1: Relatively sparse connectivity (P = 10%) and fast synaptic transmission (re = 1.5 EM,
J = 0.1 mV).
Versión 2: Denser connectivity (P = 40%), fast and strong synaptic transmission (re = 1.5 EM,
J = 0.2 mV).
Versión 3: Denser connectivity (P = 40%), slow and strong synaptic transmission (re = 3.0 EM,
J = 0.2 mV).
Mesa 1 gives a brief summary of the most important parameters. A complete description of
the final model and parameter sets, following the formalism in the field (Nordlie, Gewaltig, &
Plesser, 2009), can be found in Table 3.
Each network was simulated for 20 s of biological time with 28 differ-
Simulations performed.
ent values of the pairs of free parameters g and vext/vθ. These pairs form a rectangular grid in
the parameter space, with g taking values from 2 a 8 and vext/vθ taking values from 1 a 4.
Mesa 1. Some of the more important parameters in the Brunel network. Mesa 3 gives the full
parameters of the model in the established formalism of the field.
Symbol
NE
NI
CE
CI
j
D
gramo
vext/vθ
Descripción
# excitatory neurons
# inhibitory neurons
# exc. synapses per neuron
# inh. synapses per neuron
Synaptic strength
Synaptic delay
Rel. synaptic efficiency
Rel. external rate
Value(s)
2,000
500
200–800 dep. on network ver.
50–200 dep. on network ver.
0.5–1.0 mV dep. on network ver.
1.5–3.0 ms dep. on network ver.
Free parameter ∈ [2, 8]
Free parameter ∈ [1, 4]
Neurociencia en red
728
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
.
t
Cifra 1. The four regimes produced by the downscaled Brunel network. Each panel shows the
spiking activity (raster plot) de 30 randomly selected neurons (arriba) and the population rate (abajo).
(A) A 100 ms segment of simulation in the synchronous regular regime (SR, g = 2, vext/vθ = 3,
versión 1). (B) A 500 ms segment of simulation in the synchronous irregular regime (SI, g = 5,
vext/vθ = 1, versión 1). (C) A 500 ms piece of simulation in the asynchronous irregular regime
(AI, g = 5, vext/vθ = 2, versión 1). (D) A 500 ms piece of simulation in the alternative regime (Alt,
g = 4, vext/vθ = 2, versión 3).
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Since the network is connected according to a random model, each simulation was repeated
10 times with different network instantiations, resulting in a total of 280 simulations for each
network version. The regimes of Brunel network dynamics are known to be robust (Brunel,
2000), which we also observed in our simulations. We were thus satisfied that 10 instantia-
tions suffice for our further analysis. We recorded the spiking times of all neurons, así como
the overall population firing rate, for all the simulations.
Four distinct activity regimes, como se muestra en la figura 1, were identified by manually inspecting
the simulations and applying the same criteria as in (Brunel, 2000).
SR: A regime characterized by synchronized neurons behaving as high-frequency oscillators,
clustered in a few groups, similar to the synchronous regular regime (Figura 1A).
Neurociencia en red
729
Topological exploration of artificial neuronal network dynamics
SI: A regime characterized by a slow oscillatory global pattern and synchronous irregular
firing of individual neurons (Figura 1B).
AI: A regime characterized by asynchronous irregular firing of individual neurons (Figura 1C).
Alt: A regime characterized by neurons alternating between periods of silence and periods of
rapid firing (Figure 1D).
Note that the Alt regime is not present in the full-size network. This is not an issue for us,
sin embargo, since our goal is to discriminate between different regimes, not to understand the
Brunel network per se.
For each of the three networks, we visually identified the network regime for every pair
of parameters (gramo, vext/vθ) by the same criteria as used in (Brunel, 2000). We believe that
no automated method exists to verify the criteria set out in that paper, but that this visual
identification is quite consistent. The result is shown in Figure 2. The simulations in which
none of the neurons fired were removed from the analysis (40 simulations for versions 2 y
3). Note that the first network (versión 1) does not exhibit the Alt regime, while versions 2 y
3 do not exhibit the AI regime. This issue is addressed in the Methods section concerned with
aprendizaje automático.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Spike Train Similarities
We used three different measures of spike train similarity to compare the recorded neuron
activity in the networks.
One is the widely used Pearson correlation. It is often employed in analyzing spiking data
because it has been shown to encode particular information that is not present in the firing rate
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 2. Diagrams of the different regimes for each version of the Brunel network (A, B, and C cor-
responding to versions 1, 2, y 3 of the network, respectivamente) in the parameter space (vext/vθ, gramo).
The white areas indicate where no neurons fired and no data are available.
Neurociencia en red
730
Topological exploration of artificial neuronal network dynamics
Cifra 3. A pair of spike trains for which Pearson correlation is 0.21, SPIKE-synchronicity is 1.00,
and SPIKE-distance is 0.30.
solo. Por ejemplo, in the auditory cortex of the marmoset, Pearson correlation encodes the
purity of sounds (DeCharms & Merzenich, 1996). It can also be used to infer connectivity or
extract information about network function (cohen & Kohn, 2011). Sin embargo, it is tied to the
correlation population coding hypothesis (Panzeri, Macke, Bruto, & Kayser, 2015), y por lo tanto
may not be relevant to the problem at hand. We therefore also employed two complementary
measures: SPIKE-synchronicity (Kreuz, Chicharro, Houghton, Andrzejak, & Mormann, 2013)
and SPIKE-distance (Kreuz, Mulansky, & Bozanic, 2015). Both are exploratory measures relying
on an adaptive time window to detect cofired spikes and involve a pairwise similarity measure
of spike trains. Conceptually, the size of the window depends on the local firing rate of the
two neurons under consideration. If one of the neurons has a high local firing rate, then the
time window will be short, while if both neurons have low local firing rates, the time window
will be longer. SPIKE-synchronicity is the fraction of cofired spikes according to this adaptive
window, while SPIKE-distance is the average over time of a dissimilarity profile between spike
trains. See Equations 7–13 in (Kreuz et al., 2015) for details.
Cifra 3 shows an example of two very regular spike trains for which the three measures
encode very different relationships.
We computed Pearson correlations by time-binning the spike trains with a 2-ms time win-
dow and a binning error correction, as described in the Methods section. The SPIKE measures
were computed using the Python package PySpike (Mulansky & Kreuz, 2016).
Persistent Homology
In topology, a branch of mathematics, one works with very general objects called spaces.
Spaces have a notion of “nearness,” but in general lack more geometric structure such as
distances or angles, as well as familiar algebraic structure. The unaccustomed reader may still
gain intuition about what is meant by a space by thinking of geometric objects. One should
still keep in mind that the spaces we consider may be defined entirely intrinsically without any
reference to some ambient Euclidean space.
Algebraic topology, entonces, concerns itself with describing a space X in terms of algebraic
invariants that capture global properties of the space. Examples include the Betti numbers,
which can be thought of as the numbers of components and of n-dimensional unfilled cavities
in the space. As these notions can be defined intrinsically, eso es, without any reference to how
the space is embedded in Euclidean space, they are useful in analyzing spaces arising from
abstract data where no such embedding can be constructed in a principled way. We consider
here only the zeroth Betti number b0(X), which is the number of connected components, y
the first Betti number b1(X), which is the number of one-dimensional unfilled loops. En el
special case of graphs — which is not the case we consider — these are precisely the number
of connected components and the number of cycles, respectivamente.
Algebraic topology:
Field of mathematics concerned with
studying (algebraic) properties of
spaces/objects/shapes that are
preserved under continuous
deformations.
Neurociencia en red
731
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
Betti curve:
Simplified summary of persistent
homology counting holes and
cavities across a filtration.
Support vector machine:
Supervised learning algorithm
suitable for use with certain
topological descriptors, como
Betti curves.
Neurociencia en red
The spaces we study here will be built from spiking data, and we are interested in how these
algebraic invariants change as a function of a spike train similarity threshold. We therefore
build a filtration, a multiscale sequence of spaces depending on a threshold, and compute
persistent homology, a multiscale invariant that captures Betti numbers (which are then often
also referred to as Betti curves to reflect their scale-/threshold-dependent nature). Para más detalles,
see the Methods section devoted to the topological analysis. More background information
can be found in the survey (Ghrist, 2008) and its bibliography.
As is common in topological data analysis, we follow the convention that edges with low
weights are to be considered “most important” and enter first in the filtration (see the Methods
section for the definition). The correlation and SPIKE-synchronicity values were transformed
through the function x (cid:3)→ 1 − x so that they range from 0 a 1, con 0 being the value assigned
to a pair of identical spike trains (es decir., we work with dissimilarity measures).
Classifying Network Dynamics
We used the output of persistent homology of the space built from pairwise spike train similar-
ities as an input feature for machine learning in order to discern information about the global
network dynamics. While we did not investigate the matter, it could be that even simpler
features — such as simplex counts across filtrations, or other features based on just counting
local properties — suffice. Such features rely less on the relationships between neurons, y
are sensitive only to the creation (or not) of individual simplices, without considering how
these simplices build greater structures.
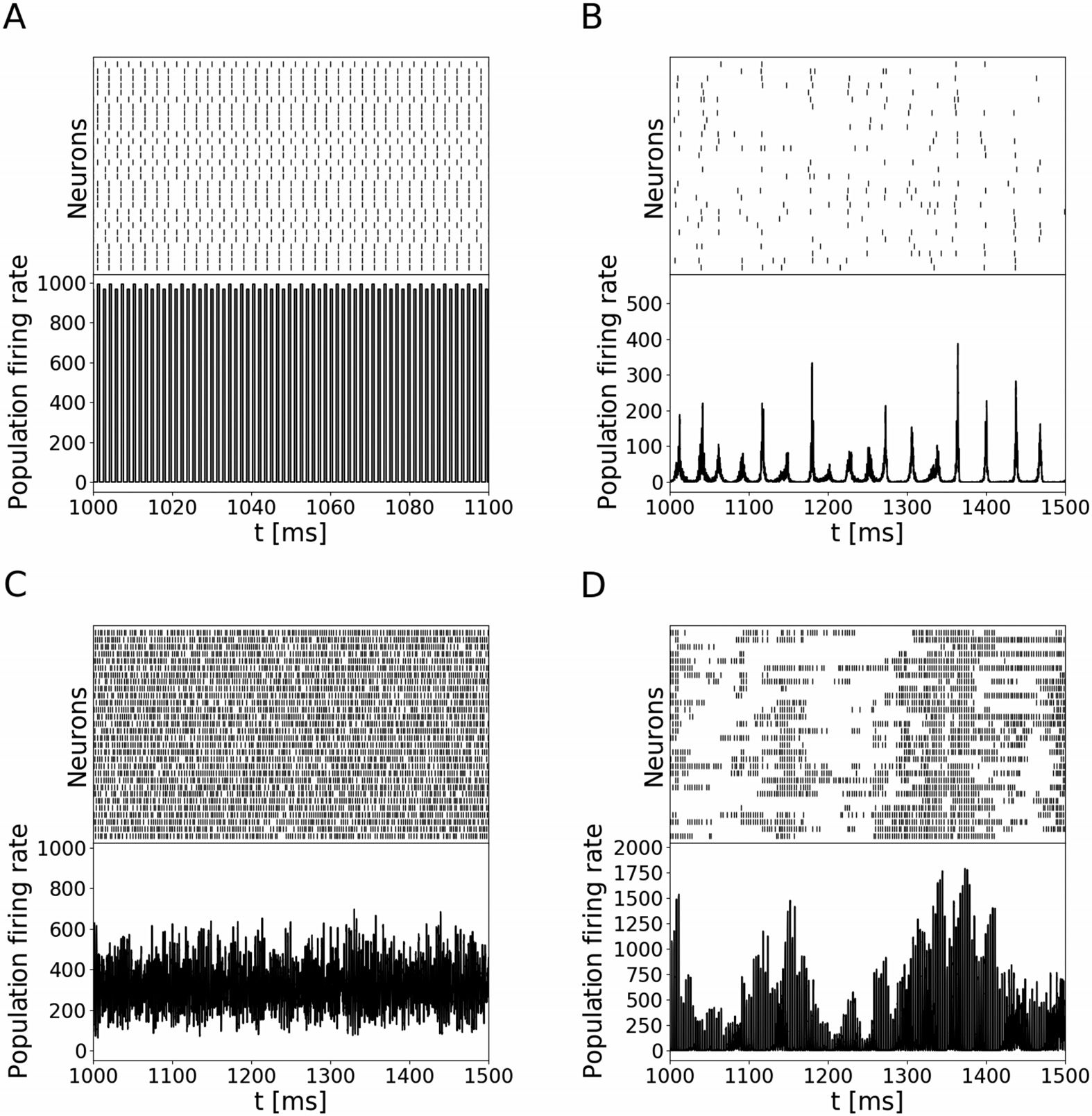
From every filtration, four simple features were extracted:
from the Betti-0 curve, the area under the curve and the filtration value at which it starts
to decrease;
from the Betti-1 curve, the global maximum and the area under the curve.
Como resultado, a total of 12 features were extracted from each simulation (four features per
filtration, three filtrations from the three spike train similarity measures). For some simulations
in the SR regime, all the pairwise similarities attained the maximal value, resulting in a space
with no topological features and a constantly zero Betti-1 curve. The filtration value at which
the curve starts to decrease was defined to be 0 en este caso.
Before doing any classification, potentially good features were selected by plotting all the
features against each other for the samples coming from network version 1. Six features were
selected by visual inspection because they were deemed to produce nonoverlapping clus-
ters. These features are the area under the Betti-0 curve for the three similarity measures, el
area under the Betti-1 curve for correlation and SPIKE-synchronicity, and the maximum of
the Betti-1 curve for the SPIKE-distance. See Figure 4. These features were among the ones
with the highest mutual information in the three networks, although their ranking varied be-
tween the networks. A section under Methods is devoted to the feature selection process; ver
in particular Figure 8.
Four different training sets were used for classification, three of which were composed of
randomly selected samples (90%) coming from a specific network version, while the last set
was the union of the three other sets. For each training set, an L
-regularized support vector
machine (SVM) classifier was trained to identify the different regimes. The classifier was com-
posed of four subclassifiers, each of which had to distinguish one particular regime from the
2
732
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
Cifra 4. Example of three of the features extracted from a filtration: the filtration threshold at
which the Betti-0 curve (izquierda) starts to decrease, the global maximum (rojo) of the Betti-1 curve, y
the area under each curve (gray area).
otros. The final decision was computed in a one-vs-rest manner. The regularizing hyper-
parameter was selected with a tenfold cross-validation.
When assessing the performance of the classifier for network version k using multiclass
exactitud, we validated it on three test sets: one composed of the 10% of the samples from
version k that had not been used for training and two containing all the valid samples from
one of the other network versions. A sample was considered valid if it was labeled with a regime
that was present in the training sets. Por ejemplo, when the classifier trained on version 1 era
tested on version 2, the samples labeled Alt were ignored, since no version 1 networks exhibit
the Alt behavior. The performance accuracy and the numbers of valid samples are reported in
Mesa 2. The trained classifiers all achieved perfect accuracy (100%) on the network version
they were trained on, indicating that the topological features extracted are sufficient to perfectly
discriminate the regimes of the training network. Además, they also generalized well to other
versions, con 94.26% accuracy on average, suggesting that the topological features extracted
are consistent across the three network versions.
Además, we combined all the samples from the three networks and used a 90%-10%
training-testing sample repartition, attaining perfect classification (“All versions” row in Table 2)
Mesa 2. Classification accuracy for each pair of training and testing sets. The training sets were
composed of 90% of the samples coming from a specific network (versión 1, 2, o 3), o 90% de todo
muestras (all versions). The testing sets contained the remaining samples from the network version
that are not used for training, eso es, the remaining 10%. The number of samples in every testing set
is reported in parentheses.
Testing set
Training set
Versión 1
Versión 2
Versión 3
All versions
Ver. 1
100% (28)
97.69% (130)
99.23% (130)
100% (28)
Ver. 2
86.67% (180)
100% (24)
99.17% (240)
100% (24)
Ver. 3
91.18% (170)
93.33% (240)
100% (24)
100% (24)
All ver.
89.68% (378)
95.18% (394)
99.23% (394)
100% (76)
Neurociencia en red
733
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
Cifra 5. Testing accuracy of the classifier trained on samples from version 1 (A), versión 2 (B), versión 3 (C), and all the samples (D).
In each panel, the classification accuracy for the test samples from each network and all the samples together is reported for five sets of
características. “Select” designates the features we visually selected. “Corr,” “sync,” and “dist” designate the features extracted using the correlation,
SPIKE-synchronicity, and SPIKE-distance, respectivamente. “All” designates the set of all the features.
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
t
.
of the four regimes. This provides the complementary information that the Alt and AI regimes
are also distinguishable from one another, since none of the network versions can exhibit both
regimes.
Finalmente, we checked whether the persistent homology-derived features provide complemen-
tary information when based on different similarity measures, and thus whether it can be
advantageous to use several of them together for classification. The same classification ex-
periments were repeated using either all the computed features or only the features coming
from one of the similarity measures. The classifier accuracies were compared with those from
the previous computations (Cifra 5). Although the accuracies obtained using features coming
from a single similarity measure were satisfactory (on average 79.10%, 92.35%, y 80.73%
accuracy for correlation, SPIKE-synchronicity, and SPIKE-distance, respectivamente), better perfor-
mance was consistently attained by a combination of measures. This is consistent with our
expectations, since the similarity measures we use give significantly different orderings of the
pairs of spike trains. Además, selection of potentially good features yields the best results
(94.94% y 96.63% average accuracy with the “all” set and “select” set, respectivamente).
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
DISCUSIÓN
In this paper we analyzed the dynamics of spiking networks of neurons using features de-
rived from persistent homology. We generated three versions of a simple artificial network of
Neurociencia en red
734
Topological exploration of artificial neuronal network dynamics
LIF neurons (a downscaled version of the Brunel network) by modifying connectivity density,
synaptic delay, and synaptic strength. Activity in the networks was then simulated with 28 pares
of the free parameters (external population rate and relative synaptic efficiency values). Across
all the simulations, four regimes of activity were observed based on the pattern of the global
population firing rate and the individual neuron spiking times.
For each simulation, we computed three pairwise spike train similarity measures: Pearson
correlation, SPIKE-synchronicity, and SPIKE-distance. We computed the persistent homology
of the flag complex of the weighted graph coming from each similarity measure and extracted
simple features from the zeroth and first Betti curves. The interesting features were selected by
visual inspection of the sample distribution. Finalmente, an SVM classifier was trained to identify
the dynamics regimes of the simulations.
Our experiments showed that it is possible to perfectly predict the dynamic regime in sim-
ulations coming from the network trained on, and from other networks with a high degree of
exactitud, as long as some samples of the regimes in question were available during training.
We also illustrated the importance of using and combining several similarity measures.
En efecto, SPIKE-synchronicity carries more information, and does so more consistently across
the network versions, than the other two measures, but the best accuracies were consistently
obtained when an ensemble of features selected by visual inspection was used. Además, si
one were to automatically select the features based on a score, we showed that the mutual
information between features and the regime label is a good indicator to consider.
We tested our method in the context of a simple network. It would be interesting to test
it also with more complex networks, with neurons and synapses modeled in greater detail.
Topological features can also be extracted from other types of neural data, such as the popula-
tion firing rate or neuron voltage traces. We consider the examination of how the topological
methods perform in classifying such data as interesting future work.
The present paper does not discuss unsupervised methods. We did perform small exploratory
experiments in which the persistent homologies arising from the spike trains were transformed
into real-valued functions by means of the persistence heat kernel (Reininghaus et al., 2015).
These functions were then considered as points in a metric space of functions, and embedded
in a low-dimensional Euclidean space using multidimensional scaling. While we ultimately
failed at satisfactorily clustering these Euclidean points in an unsupervised way, it is an ap-
proach that may be worth considering in future work. An unsupervised version of our method
may be useful for real-time detection of previously unknown ephemeral regimes of dynamics.
As mentioned, our topological features are simple, but perhaps not the simplest possible. Él
would be interesting to see a comparison between the performance of our features and features
that are merely summaries of local properties, such as the total count of simplices of various
dimensions as a function of the filtration parameter. We suspect that such features pick up too
little of the organizational structure between simplices, and will thus decrease the classifier’s
performance without any significant reduction in computation time.
Here we have illustrated just one concrete use of topological data analysis (TDA) en el
study of network dynamics, but the class of methods should be applicable to a wide vari-
ety of systems from within and without neuroscience. A lo mejor de nuestro conocimiento, allá
have been no previous attempts at applying TDA to automatic detection of regimes in spiking
neural networks, since they are usually identified analytically (Brunel, 2000; Helias et al.,
2013) and can often be discriminated visually. Sin embargo, a topological approach to this task
Neurociencia en red
735
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
may be interesting in recordings of real data, such as EEG or fMRI. One might, Por ejemplo, en-
vestigate the feasibility of solving a more subtle task, such as automatic detection of movement
intention or seizure detection in epileptic patients.
Although great progress has been made in neuroscience since the first recording of a neu-
ron activity in 1928 (Adrian, 1928), a unified model of the brain across its different scales is
still lacking, and many hard challenges have barely been attempted. Recent work has high-
lighted how TDA could help shed new light on both brain structure and dynamics and is a
promising advance towards a more comprehensive understanding of the brain. The method
we have outlined in this paper takes a novel view of one challenge, the automated classifica-
tion of neuronal dynamics, by considering features that are topological in nature. Creemos
that including such features will be of great help in the understanding of both structural and
dynamical aspects of neuronal networks and other similarly structured systems.
While we in this work considered only a very specific system, namely simulated spiking
neuronas, our method should be applicable in a wide variety of settings, both inside and outside
of neuroscience. At its core, the method just requires ways of comparing time series, y eso
may therefore be useful in classifying regimes in general dynamical systems (perhaps coupled
con, or complementing, delay embedding-based methods (Perea & Harer, 2015) En el caso de
smooth time series). Within neuroscience, EEG recordings and fMRI BOLD signals immediately
suggest themselves as data that can be studied in this way.
MÉTODOS
We give here the full details of our computations and expand on the topological constructions
involved in the analysis.
Network Simulations
A complete specification of the three simulated networks following formalism and notation
commonly used in the field (Nordlie et al., 2009) can be found in Table 3.
All the networks were simulated with 28 pairs of parameter values for the relative strength
between inhibition and excitation g (integer values from 2 a 8) and the external population rate
vext/vθ (integer values from 1 a 4). The systems were simulated 10 times for each parameter
pair, for a total of 280 simulations per network. The simulations were performed with the Brian2
simulator (Buen hombre & Brette, 2009), with a time step of 0.01 ms and a total biological time
de 20 s. Because of the downscaling of the network, the synaptic transmission J was increased
compared with that used in (Brunel, 2000) in order to keep CE J constant, and an external
inhibitory population was introduced (Helias et al., 2013) when the spiking of neurons was
expected to be irregular (Brunel, 2000). This external population was modeled by a Poisson
process with rate
as in (Helias et al., 2013). Aquí, pag
loc
is the variance due to local input from recurrent connections in the downscaled network.
The variances can be approximated as
i is the variance of input in the original network and σ
norte
bal
=
p2
i
− σ2
loc
τm J2
ext
− τmνext J
(1 + g2)
2
ext
(cid:2)
p2
i
= C
∗
E J
∗2τm
(cid:2)
(cid:3)(cid:3)
1 + gramo
2γ
νext + ν0
(cid:2)
1 + gramo
2γ
(cid:3)
.
(1)
(2)
(3)
736
Neurociencia en red
p2
loc
= CE J
2τmν0
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
Mesa 3. Description of the neuronal network following the formalism of Nordlie et al. (2009).
A
Populations
Topology
Connectivity
Neuron model
Channel models
Synapse model
Plasticity
Input
Measurements
Model summary
Four: excitatory, inhibitory, excitatory external input, inhibitory external input
–
Random convergent connections with probability P and fixed in-degree of CE = PNE and CI = PNI
Leaky integrate-and-fire, fixed voltage threshold, fixed absolute refractory time (voltage clamp)
–
δ-current inputs
–
Independent fixed-rate Poisson spike trains to all neurons
Spike timing, population firing rate
Elements
Iaf neuron
Iaf neuron
Poisson generator
Poisson generator
Size
NE
NI = γNE = 0.25NE
CE(NE + NI )
CI (NE + NI )
Fuente
mi
I
mi
I
Eext
Iext
Target
mi
mi
I
I
E ∪ I
E ∪ I
Patrón
Random convergent CE → 1, weight J, delay D
Random convergent CE → 1, weight J, delay D
Random convergent CI → 1, weight −gJ, delay D
Random convergent CI → 1, weight −gJ, delay D
Nonoverlapping CE → 1, weight Jext, delay D
Nonoverlapping CI → 1, weight Jext, delay D
Populations
Connectivity
Neuron and synapse model
B
Nombre
mi
I
Eext
Iext
C
Nombre
EE
IE
EI
I I
Extexc
Extinh
D
Nombre
Tipo
Membrane potential
Spiking
mi
Tipo
Poisson generators
˙Vm(t) = −Vm(t) + Rhode Island(t)
– (Brian2)
Leaky integrate-and-fire, δ-synapse
τm
Vm(t) = Vr
I(t) = τm
∑˜t
R
If V(t−) < θ ∧ V(t+) ≥ θ
1. set t
2. emit spike with time-stamp t
ωδ(t − (˜t + D))
∗ = t
∗
if not refractory (t > t
∗ + τrp)
while refractory (t
∗ < t ≤ t ∗ + τrp) Input Description Fixed rate ν, CE + CI generators per neuron, each generator projects to one neuron: if excitation dominates (g ≤ 4): Eext rate = νext, Iext rate = 0 if inhibition dominates (g > 4): Eext rate = νext + norte
bal, Iext rate = ν
Measurement
/gramo
bal
F
Spiking times of all neurons, population firing rate
GRAMO
Parameters
Number of excitatory neurons NE
Number of inhibitory neurons NI
Excitatory synapses per neuron CE
Inhibitory synapses per neuron CI
h
Parameters
Membrane time constant τm/ms
Refractory period τrp/ms
Firing threshold Vθ /mV
Resting potential Vrest/mV
Reset potential Vr /mV
Postsynaptic potential (PSP) amplitude from reccurent connections J/mV
PSP amplitude from external connections Jext/mV:
if excitation dominates (g ≤ 4)
if inhibition dominates (g > 4)
Synaptic delay D/ms
Network parameters
Neuron parameters
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Network configuration
Common
2000
500
–
–
Ver. 1
–
–
200
50
Ver. 2
–
–
800
200
Network configuration
Common
20
2
20
0
10
–
–
–
–
Ver. 1
–
–
–
–
–
0.5
0.5
0.1
1.5
Ver. 2
–
–
–
–
–
1.0
1.0
0.2
1.5
Ver. 3
–
–
800
200
Ver. 3
–
–
–
–
–
1.0
1.0
0.2
3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
t
.
Neurociencia en red
737
Topological exploration of artificial neuronal network dynamics
The parameters for the original network are labeled by an asterisk and differ from their
∗
.
counterpart in the downscaled network by a scaling factor α such that CE
From Equations 2, 3, y 1, we obtain
/α and J = αJ
= C
∗
mi
norte
bal
=
(1/α − α) νext + (1/α − 1) ν0
τm J
(1 + g2)
2
ext
Here ν0 is the stationary frequency of the original population and can be approximated by
(Brunel, 2000):
(4)
(cid:4)
1 + gramo
2γ
(cid:5)
.
ν0 =
νext − νθ
gγ − 1
.
(5)
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological Framework
In algebraic topology, a well-established field of mathematics, one studies topological spaces
by turning them into well-behaved algebraic invariants and deducing properties of the spaces
from those of the algebraic objects. We shall not define any of these concepts precisely here,
but will instead give relevant examples of both. Ver, for example Hatcher (2002) for an intro-
ductory textbook that includes all the details with full precision.
A space will in our context mean a kind of object that is built from certain geometric pieces
by specific rules that reflect the data of the dynamics (or structure) of systems of neurons. Estos
objects are “high-dimensional” in the sense that they can be thought of as inhabiting Rn for
(possibly) very large n, but the way that they do so is of no relevance to the algebraic invariants
we employ here. Además, the Euclidean coordinatization of the space in general contains no
information about the underlying system, so it is therefore to our benefit that the topological
methods ignore it.
A simplicial complex can be thought of as a higher dimensional analog of a graph, con
its constituent building blocks referred to as simplices. In addition to comprising vertices (0-
dimensional pieces, or 0-simplices) and edges (1-dimensional pieces, 1-simplices), a simplicial
complex may have filled triangles (2-simplices), filled tetrahedra (3-simplices), etcétera. Just
as for graphs, the way these simplices fit together is subject to some rules. Primero, a p-simplex is
identified uniquely by a set of p + 1 vertices. We technically impose a global ordering on all
the vertices in the complex and write simplices as tuples respecting this ordering. Segundo,
if a p-simplex σ = (v0, v1, . . . , vp) is present in a simplicial complex K, then its p + 1 boundary
(p − 1)-simplices
(v1, v2, v3, . . . , vp), (v0, v2, v3, . . . , vp), (v0, v1, v2, . . . , vp), . . . , (v0, v1, v2, . . . , vp−1)
are all also required to be present in K. Note that the definition of a boundary and the associated
rule are entirely combinatorial, although they do have a geometric interpretation if we think
of simplices as geometric objects, as illustrated in Figure 6.
Simplicial complexes can encode data and domain-specific knowledge in different ways
depending on the availability of structure and the type of information that is sought. En esto
trabajar, we take as input a choice of spike train similarity and a spike train for each of n neurons
consideró. From this, we build a simplicial complex as follows.
Let G be the complete graph on n vertices (representing the neurons). The edge between
two neurons i and j is assigned a weight w(i, j) equal to the dissimilarity of the corresponding
spike trains. A simplicial complex K is then formed by adding in every possible 2-simplex. Como
a space, this is not very interesting, as there is simply a filled triangle between every triple of
Neurociencia en red
738
Topological exploration of artificial neuronal network dynamics
Filtration:
Multiscale view of topological spaces
built from data, in our case spike
train similarity data.
C
C
Boundary
a
b
a
b
Cifra 6. Left: A simplicial complex consisting of a single 2-simplex ((a, b, C)), three 1-simplices
((a, b), (b, C), y (a, C)), and three 0-simplices ((a), (b), y (C)). Right: The boundary of (a, b, C)
consists of the three 1-simplices and three 0-simplices that one would expect geometrically, donación
geometric meaning to a purely combinatorially defined concept.
neuronas (one says that the space is contractible). The crucial part is that each 2-simplex is given
a weight equal to the maximum of the weights given to its boundary edges, eso es,
w(i, j, k) = max{w(i, j), w(i, k), w(j, k)}.
We then consider a filtration of K, enabling us to study a sequence of thresholded versions
of K. At the start of the filtration, the filtration consists only of the vertices of K. Entonces, como el
threshold increases, 1- and 2-simplices from K appear if their weight is below the threshold,
so as to include into the filtration pieces stemming from ever more dissimilar spike trains. Ver
Cifra 7 for an illustration.
The construction above is applicable to simplices of dimension higher than 2, so even
though we stop at dimension 2 in our analysis, the following description employs generic
dimensions p in order to simplify notation and give the bigger picture.
A basic algebraic invariant that we track as the dissimilarity threshold increases is the Betti
numbers, giving rise to Betti curves for the filtration as a whole. The Betti numbers of a simpli-
cial complex can be defined formally as the dimensions of the homology vector spaces of the
complex, as we now sketch. Define Cp(k) to be the collection of formal binary sums of the
a
γ
b
b
⊂
⊂
⊂
Threshold 0
Threshold α
Threshold β
Threshold γ
a
r
mi
b
metro
tu
norte
i
t
t
mi
B
4
3
2
1
0
Dimension 0
Dimension 1
0
a
b
γ
Filtration threshold (spike train dissimilarity)
Cifra 7. Left: A weighted graph G on four vertices/neurons. Assume that 0 < α < β < γ. Top:
The filtered simplicial complex K built from G. The 0-simplices are drawn in a different way at
threshold 0 to make them more visible. Bottom: The Betti curves of K in dimensions 0 and 1.
Network Neuroscience
739
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
n
e
n
_
a
_
0
0
0
8
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
p-simplices in K. This makes Cp(K) a vector space over the binary numbers, and allows us to
view the boundary as an algebraic operation encoded in a linear map ∂p : Cp(K) → Cp−1(K)
given by
∂p(v0, v1, . . . , vp) = (v1, v2, . . . , vp) + (v0, v2, . . . , vp) + (v0, v1, . . . , vp) + · · · + (v0, v1, . . . , vp−1).
One checks that the application of two consecutive boundary maps always gives zero, that is,
p−1(∂p(σ)) = 0 for every p-simplex σ. This algebraic statement reflects the geometric
that ∂
fact that the boundary of a boundary is empty. A general collection of p-simplices — a sum in
Cp(K) — that has zero boundary is called a p-cycle. Figure 7 shows several examples.
It turns out that p-cycles that are not the boundary of collections of (p + 1)-simplices cor-
respond geometrically to holes (p > 0) or connected components (pag = 0) in the simplicial
complex. Persistent homology, a widely employed construction in topological data analysis,
tracks such holes/components as they appear and disappear across a filtration. The record of
the “life” and “death” of such topological features provides valuable information about the fil-
tration and thus about the underlying data. We do not use all of the data recorded in persistent
homology, but instead just keep track of the number of holes in each dimension as a func-
tion of the filtration. The reason for reducing the data of persistent homology to Betti curves
is in part that the algebraic invariant produced by the former lacks many desirable properties.
The resulting integer-valued functions, called Betti curves, are the features we use for machine
aprendiendo. An example of a Betti curve is given in Figure 7. We emphasize that the features cap-
tured by persistent homology may be much more global in nature than in this small example.
Como ejemplo, the reader is invited to build a torus as a simplicial complex, filter it from one
side to another, and observe what features are captured by persistent homology in dimensions
0, 1, y 2.
Machine Learning
Before doing any machine learning, the features selected were standardized. If a feature was
not computable because there were no corresponding Betti curves, its value was set to 0.
For each version of the network, four training sets were formed, one containing 90% del
samples from a specific network version and a fourth one containing 90% of all the samples,
stratified so that its distribution of the samples was representative of all the samples. Uno
classifier per training set was trained and tested against four test sets: one for each network
versión, using the valid samples not in the training set, and the fourth one containing all the
valid samples not used during training.
2
Support vector machine methods (Cortes & Vapnik, 1995) using a radial basis function ker-
nel with L
-regularization were applied to classify the samples into the four different regimes
(we suspect that a linear classifier would also suffice). The multiclass classification was achieved
by training four subclassifiers with a one-vs-rest decision function. The regularization param-
eter was found by accuracy optimization thanks to tenfold cross-validation.
The performance of the classifiers was assessed using an accuracy score.
Mutual Information
Earlier we mentioned that mutual information between the features we selected by visual in-
spection and the regime labels was relatively high, suggesting that one could use the mu-
tual information score to automatically select features when visual inspection would be time
Neurociencia en red
740
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
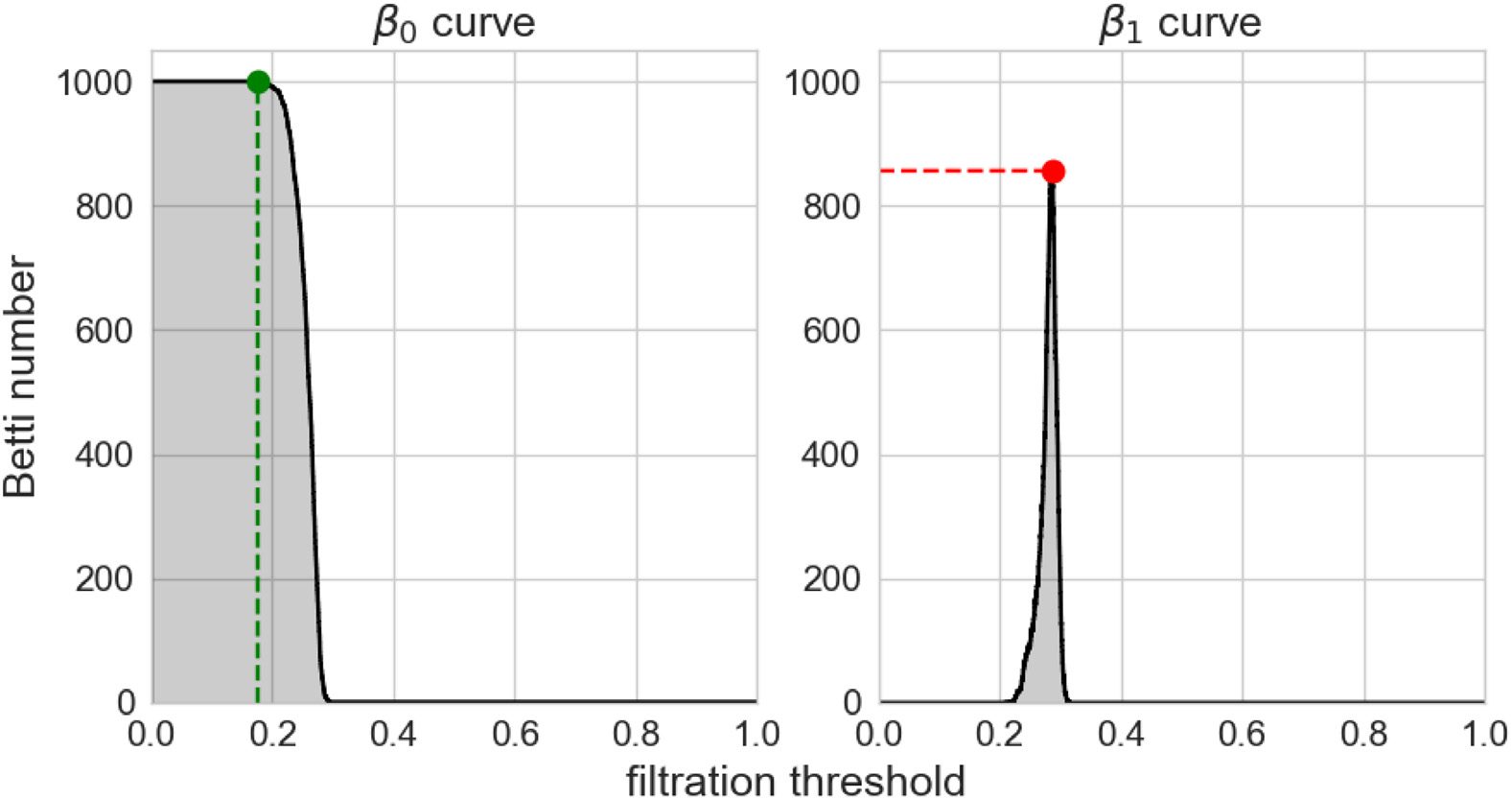
Cifra 8. Mutual information between each feature and the label for the training sets obtained
from the simulations of the different network versions. Features that were selected by visual inspec-
tion are represented with a hashed bar. The peak and AUC labels designate the peak amplitude and
the area under the Betti curve features, respectivamente.
consuming or violate a need for automation or independence from human input. The mutual
information between each feature and the labels for the three datasets is presented in Figure 8,
where one can observe that some features, such as the area under the Betti-0 curve for correla-
tion and SPIKE-distance, have a consistent mutual information score across the three datasets.
This suggests that they are important features that allow the classifier to correctly sample from
other datasets. Además, the area under the curve (AUC) features tend to have a higher score
than the peak amplitude of the Betti curve. This is perhaps natural since the former includes
information from all of the filtration, while the latter includes only one single aspect of it.
EXPRESIONES DE GRATITUD
We thank M.-O. Gewaltig for his insightful discussion about the neural network model used.
We are grateful to the Blue Brain Project (Markram, 2006) for allowing us to use for this
project their computational resources, which are supported by funding from the ETH Domain
and hosted at the Swiss National Supercomputing Center (CSCS).
SUPPORTING INFORMATION
The code for Brunel network simulation, preprocessing before persistent homology computa-
ciones, preprocessing before machine learning, and for the machine learning itself, está disponible en
https://github.com/JBBardin/Brunel_AlgebraicTopology (Bardin, Spreeman, & Hesse, 2018). Ser
aware that the code lacks documentation and is provided as is for reasons of transparency and
reproducibility. The persistent homology computations were performed using Bauer’s Ripser
(Bauer, 2016).
Neurociencia en red
741
Topological exploration of artificial neuronal network dynamics
CONTRIBUCIONES DE AUTOR
Jean-Baptiste Bardin: Análisis formal;
Investigación; Metodología; Software; Validación;
Visualización; Escritura – borrador original; Escritura – revisión & edición. Gard Spreemann: Estafa-
ceptualization; Metodología; Software; Supervisión; Validación; Escritura – borrador original;
Escritura – revisión & edición. Kathryn Hess: Conceptualización; Adquisición de financiación; Proyecto
administración; Supervisión; Escritura – revisión & edición.
INFORMACIÓN DE FINANCIACIÓN
Gard Spreemann, Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen
Forschung (http://dx.doi.org/10.13039/501100001711), Award ID: 200021_172636.
REFERENCIAS
Adrian, mi. D. (1928). The basis of sensation. British Medical Journal,
Ghrist, R. (2008). Barcodes: The persistent topology of data. Boletín
1(4857), 287.
Alkan, A., Koklukaya, MI., & Subasi, A. (2005). Automatic seizure
detection in EEG using logistic regression and artificial neural
network. Journal of Neuroscience Methods, 148(2), 167–176.
Bardin, J.-B., Spreeman, GRAMO., & Hesse, k. (2018). Topological ex-
ploration of neuronal network dynamics, GitHub, https://github.
com/JBBardin/Brunel_AlgebraicTopology
Bauer, Ud.. (2016). Ripser, GitHub, https://github.com/Ripser/ripser
Brunel, norte. (2000). Dynamics of networks of randomly connected
excitatory and inhibitory spiking neurons. Revista de fisiología
París, 94(5–6), 445–463.
Bubenik, PAG. (2015). Statistical topological data analysis using per-
sistence landscapes. The Journal of Machine Learning Research,
16(1), 77–102.
Buzsáki, GRAMO., Chen, l. S., & Gage, F. h. (1990). Spatial organization
of physiological activity in the hippocampal region: relevance
to memory formation.
In J. Storm-Mathisen, h. Zimmer, &
oh. PAG. Ottersen (Editores.), Progress in Brain Research (páginas. 257–268).
Ámsterdam: Elsevier.
cohen, METRO. r., & Kohn, A. (2011). Measuring and interpreting neu-
ronal correlations. Neurociencia de la naturaleza, 14(7), 811–819.
Cortes, C., & Vapnik, V. (1995). Support-vector networks. Machine
Aprendiendo, 20(3), 273–297.
Curto, C. (2017). What can topology tell us about the neural code?
Bulletin of the American Mathematical Society, 54, 63–78.
Curto, C., & Itskov, V. (2008). Cell groups reveal structure of stim-
ulus space. Biología Computacional PLoS, 4(10), e1000205.
Dabaghian, y., Brandt, V. l., & Franco, l. METRO. (2014). Reconceiving
the hippocampal map as a topological template. eVida, 3.
Dabaghian, y., Mémoli, F., Franco, l., & Carlsson, GRAMO. (2012). A topo-
logical paradigm for hippocampal spatial map formation using
persistent homology. Biología Computacional PLoS, 8(8).
DeCharms, R. C., & Merzenich, METRO. METRO. (1996). Primary cortical
representation of sounds by the coordination of action-potential
timing. Naturaleza, 381(6583), 610–613.
Pescador, R. S., Van Emde Boas, w., Blume, w., Elger, C., Genton, PAG.,
Sotavento, PAG., & ángel, j. (2005). Epileptic seizures and epilepsy: Defini-
tions proposed by the international league against epilepsy (ILAE)
and the international bureau for epilepsy (IBE). Epilepsia, 46(4),
470–472.
of the American Mathematical Society, 45(1), 61–75.
Giusti, C., Pastalkova, MI., Curto, C., & Itskov, V. (2015). Clique to-
pology reveals intrinsic geometric structure in neural correla-
ciones. procedimientos de la Academia Nacional de Ciencias, 112(44),
13455–13460.
Buen hombre, D., & Brette, R. (2009). The brian simulator. Fronteras en
Neurociencia, 3, 26.
Hatcher, A.
(2002). Algebraic Topology. Cambridge, United
Kingdom: Prensa de la Universidad de Cambridge.
Helias, METRO., Tetzlaff, T., & Diesmann, METRO.
(2013). Echoes in corre-
lated neural systems. New Journal of Physics, 15, 473.
.
. Sotavento, D. S.
Im, h. J., Hahm, J., Kang, h., Choi, h., Sotavento, h., Hwang, D. w.,
.
(2016). Disrupted brain metabolic connec-
tivity in a 6-OHDA-induced mouse model of Parkinson’s disease
examined using persistent homology-based analysis. Scientific
Informes, 6(Septiembre), 1–11.
jeong, j. (2004). EEG dynamics in patients with Alzheimer’s disease.
Clinical Neurophysiology, 115(7), 1490–1505.
Kan, Y. Ud., & Gotman, j. (2003). Wavelet based automatic seizure
detection in intracerebral electroencephalogram. Clinical Neuro-
physiology, 114(5), 898–908.
kim, h., Hahm, J., Sotavento, h., Kang, MI., Kang, h., & Sotavento, D. S. (2015).
Brain networks engaged in audiovisual integration during speech
perception revealed by persistent homology-based network filtra-
ción. Brain Connectivity, 5(4), 245–258.
Kreuz, T., Chicharro, D., Houghton, C., Andrzejak, R. GRAMO., &
Mormann, F. (2013). Monitoring spike train synchrony. Diario
of Neurophysiology, 109(5), 1457–1472.
Kreuz, T., Mulansky, METRO., & Bozanic, norte. (2015). Spiky: A graphical
user interface for monitoring spike train synchrony. Diario de
Neurofisiología, 113(9), 3432–3445.
Kusano, GRAMO., Hiraoka, y., & Fukumizu, k.
(2016). Persistence
weighted Gaussian kernel for topological data analysis. Proceed-
ings of the 33rd International Conference on Machine Learning,
2004–2013.
Sotavento, h., Chung, METRO. K., Kang, h., kim, B.-N., & Sotavento, D. S. (2011).
Persistent network homology from the perspective of dendro-
gramos. IEEE Transactions in Medical Imaging, 12(2006), 2381.
Markram, h.
(2006). The Blue Brain Project. Reseñas de naturaleza
Neurociencia, 7(2), 153.
Neurociencia en red
742
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topological exploration of artificial neuronal network dynamics
Mulansky, METRO., & Kreuz, t.
(2016). PySpike—A python library for
analyzing spike train synchrony. SoftwareX, 5, 183–189.
Noback, C. r., Ruggiero, D. A., Demarest, R. J., & Strominger,
norte. l. (2007). The human nervous system: Structure and function
(6th ed.). Totowa, Nueva Jersey: Humana Press.
Nordlie, MI., Gewaltig, METRO. o., & Plesser, h. mi. (2009). Towards
reproducible descriptions of neuronal network models. PLoS
Biología Computacional, 5(8).
O’Keefe, J., & Dostrovsky, j. (1971). The hippocampus as a spatial
map: Preliminary evidence from unit activity in the freely-moving
rat. Brain Research, 34(1), 171–175.
Panzeri, S., Macke, j. h., Bruto, J., & Kayser, C. (2015). Neural pop-
ulation coding: Combining insights from microscopic and mass
signals. Tendencias en Ciencias Cognitivas, 19(3), 162–172.
Perea, j. A., & Harer, j. (2015). Sliding windows and persistence:
An application of topological methods to signal analysis. Foun-
dations of Computational Mathematics, 15(3), 799–838.
Petri, GRAMO., Expert, PAG., Turkheimer, F., Carhart-Harris, r., Nutt, D.,
Hellyer, PAG. J., & Vaccarino, F. (2014). Complex brain networks:
Graph theoretical analysis of structural and functional systems.
Journal of the Royal Society Interface.
Reimann, METRO. w., Nolte, METRO., Scolamiero, METRO., Tornero, K., Perin, r.,
(2017). Cliques of neurons
Chindemi, GRAMO., . . . Markram, h.
bound into cavities provide a missing link between structure and
función. Frontiers in Computational Neuroscience, 11, 48.
Reininghaus, J., Huber, S., Bauer, Ud., & Kwitt, R. (2015). A stable
multi-scale kernel for topological machine learning. IEEE Confer-
ence on Computer Vision and Pattern Recognition (CVPR), Junio
7–12, 2015.
singh, GRAMO., Memoli, F., Ishkhanov, T., Sapiro, GRAMO., Carlsson, GRAMO., &
Ringach, D. l. (2008). Topological analysis of population activ-
ity in visual cortex. Revista de visión, 8(8), 1–18.
Spreemann, GRAMO., Dunn, B., Botnan, METRO. B., & Baas, norte. A.
(2018).
Using persistent homology to reveal hidden covariates in sys-
tems governed by the kinetic ising model. Physical Review E,
97, 032313.
Tzallas, A. T., Tsipouras, METRO. GRAMO., & fotiadis, D. I. (2007). Automatic seizure
detection based on time-frequency analysis and artificial neural
redes. Computational Intelligence and Neuroscience, 2007.
van Albada, S. J., Helias, METRO., & Diesmann, METRO. (2014). Scalability
of asynchronous networks is limited by one-to-one mapping be-
tween effective connectivity and correlations. PLoS Computa-
tional Biology.
Weyand, t. GRAMO., Boudreaux, METRO., Guido, w., Tsanov, METRO., Chah, MI.,
(2001). Burst and tonic re-
Wright, NORTE.,
sponse modes in thalamic neurons during sleep and wakefulness.
Revista de neurofisiología, 85(3), 1107–1118.
. Usrey, W.. METRO.
.
.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
3
7
2
5
1
0
9
2
4
2
9
norte
mi
norte
_
a
_
0
0
0
8
0
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Neurociencia en red
743