Evaluación del comportamiento autogenerado: Desenredar
Metacognitive Readout and Error Detection
Tadeusz W. Kononowicz and Virginie van Wassenhove
Abstracto
■ When producing a duration, por ejemplo, by pressing a key
para 1 segundo, the brain relies on self-generated neuronal dynamics
to monitor the “flow of time.” Evidence has suggested that the
brain can also monitor itself monitoring time, the so-called self-
evaluación. How are temporal errors inferred on the basis of
purely internally driven brain dynamics with no external refer-
ence for time? Although studies have shown that participants
can reliably detect temporal errors when generating a duration,
the neural bases underlying the evaluation of this self-generated
temporal behavior are unknown. Theories of psychological
time have also remained silent about such self-evaluation
abilities. We assessed the contributions of an error-detection
mechanism, in which error detection results from the ability
to estimate the latency of motor actions, and of a readout
mechanism, in which errors would result from inferring the
state of a duration representation. Error detection predicts a
V-shape association between neural activity and self-evaluation
at the offset of a produced interval, whereas the readout pre-
dicts a linear association. Aquí, human participants generated
a time interval and evaluated the magnitude of their timing
(primero- and second-order behavioral judgments, respectivamente).
Focusing on the MEG/EEG signatures after the termination of
the self-generated duration, we found several cortical sources
involved in performance monitoring displaying a linear associa-
tion between the power of alpha (α = 8–14 Hz) oscillations and
self-evaluation. Altogether, our results support the readout
hypothesis and indicate that duration representation may be
integrated for the evaluation of self-generated behavior. ■
INTRODUCCIÓN
Metacognition refers to the knowledge gained in intro-
specting one’s cognitive states (Fleming & Dolan, 2012;
Flavell, 1979). Metacognition is often investigated through
the evaluation of confidence on a perceptual decision task;
thereby, a second-order decision (p.ej., confidence rating)
is contingent on a first-order judgment (p.ej., discrimina-
tion of stimuli). Metacognition thus necessitates a meta-
representation of the first-order judgment (Fleming,
Dolan, & Frith, 2012). Aquí, we explored the metarepre-
sentation of endogenous timing, a saber, whether the
mechanisms by which the representation of a duration
can serve temporal metacognition (TMC).
In a seminal study, human participants receiving incor-
rect feedback after their time production showed a neg-
ative evoked brain response (Miltner, Braun, & Coles,
1997; then coined error-related negativity [ERN], now
corresponding to feedback-related negativity). The ob-
served ERN was interpreted as reflecting the difference
between participants’ internal belief about the correct-
ness of their time production and the objective feedback.
These observations suggested the internal representation
Cognitive Neuroimaging Unit, CEA DRF/Joliot, INSERM, Université
Paris-Sud, Université Paris-Saclay, NeuroSpin Center, 91191 Gif/
Yvette, Francia
© 2019 Instituto de Tecnología de Massachusetts
of an intended duration could be studied from the per-
spective of metacognition. Later empirical evidence across
species further hinted at the notion of self-evaluation in
timing: Por ejemplo, seminal work has shown that the
combination of uncertainties of internal representations
and external cues could serve temporal monitoring in
both rats and humans (Balcı, Freestone, & Gallistel,
2009). In a duration discrimination task, rats were de-
scribed to decline the test more often when they were
presented with uncertain stimuli (Foote & Cristal, 2007).
More recently, humans were shown to reliably report their
temporal errors after time reproduction (es decir., the motor
reproduction of a sensory time interval; Akdoğan &
Balcı, 2017) and after their time production (es decir., el
self-generation of a time interval in the absence of
sensory template, Figura 1A; Kononowicz, roger, & camioneta
Wassenhove, 2019). Altogether, these results suggest the
availability of the accuracy and precision of temporal
representation for TMC, yet existing theories of psycho-
logical time have remained silent about the possibility of
introspecting or self-evaluating one’s internal time.
Aquí, we investigated the neural responses after time
production and tested two hypothetical mechanisms,
which could serve the representation of temporal errors
during a time production task. Primero, in the currently
investigated data set, we have recently showed that the
dynamics of beta oscillatory activity (β = 15–40 Hz)
Revista de neurociencia cognitiva 31:11, páginas. 1641–1657
https://doi.org/10.1162/jocn_a_01442
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
/
oh
C
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
oh
C
norte
_
a
_
0
1
4
4
2
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
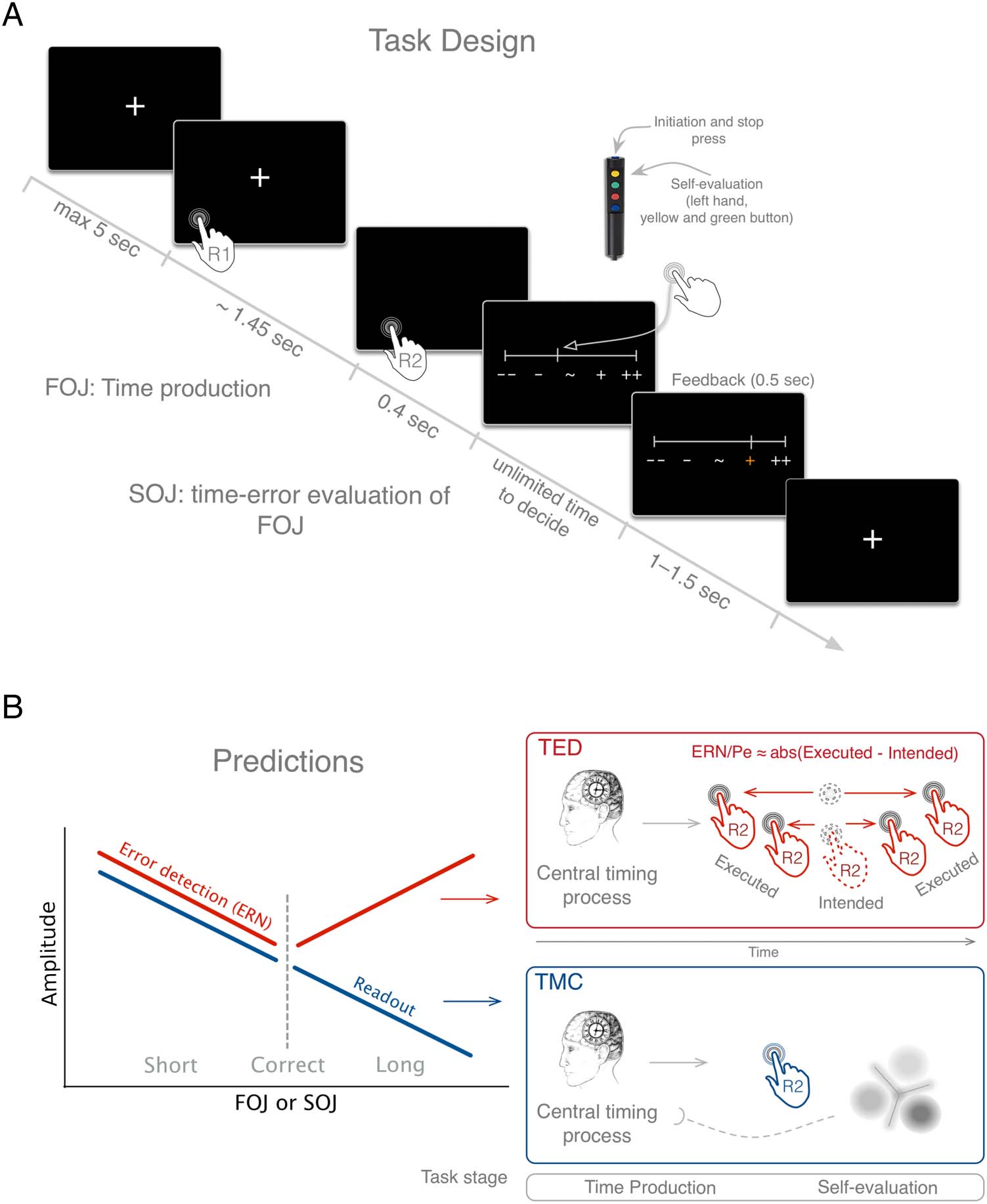
Cifra 1. Experimental
paradigm and predictions.
(A) Time course of one
experimental trial. (B)
Predictions of the TED (rojo)
and temporal metacognitive
readout (TMC; azul) working
hypotheses. According to TED,
the evaluation of a temporal
error arises from the timing
difference between the
intended latency of motor
action execution (dashed hand
as the expected latency of the
motor plan) and the actual
executed action (solid hand
happening anytime before or
after the intended action). Este
temporal residual error would
be captured by the variability of
the ERN/Pe amplitude [ERN/Pe
≈ abs(Executed − Intended)]:
The further away from the
intended latency, the larger the
ERN/Pe irrespective of whether
the act occurred earlier or later
than intended. In the alternative
TMC hypothesis, the evaluation
of the temporal residual error
relies on a metarepresentation
of duration. Contrary to the
TED hypothesis, the TMC
hypothesis proposes the
internal representation of
duration and a readout
mechanism that would actively
infer the state of this internal
timing variable. The TMC would
elicit sustained components,
and a signature of the readout
would show a linear scaling of
the neural response with the
produced duration after the
temporal production (azul
line).
during time production predicted the accuracy of both
the self-generated time intervals and their self-evaluation
(Kononowicz et al., 2019). The observation of a common
cortical signature for first- and second-order temporal
estimates suggested that β power may instantiate the
intended duration (first-order estimate) and serve as a
readable variable for second-order estimation. En otra
palabras, we formulated the TMC hypothesis, which posits
the existence of an internal representation of duration as
a β state–dependent network and a readout mechanism,
which would actively infer the state of this internal timing
variable (Grabot et al., 2019). A temporal metacognitive
readout was predicted to linearly code for the state of
the networks coding the duration at the outset of the
timed interval (Laje & Buonomano, 2013; Cemento, balci,
de Souza, cohen, & holmes, 2011; Ivry & Schlerf,
2008; Karmarkar & Buonomano, 2007). en este estudio,
we thus hypothesize that a neural signature of a internal
duration readout would linearly scale with the produced
duration after the production of a temporal interval
(post-R2). We could not legitimately predict the sign of
the linear scaling, and whether the amplitude of the read-
out signal would increase or decrease with increasingly
produced duration could not be determined a priori.
Under the more classic temporal error detection
(TED) hypothesis, temporal error monitoring would rely
on the monitoring of motor actions with no specific need
for a metarepresentation of duration. The TED hypothe-
sis entails the estimation of a delay between the internally
generated “go” signal and the latency of the actually exe-
cuted action. Por ejemplo, using a simple RT task, Marti,
Sackur, Sigman, and Dehaene (2010) asked participants
to estimate the latency of their RTs on a trial-by-trial ba-
hermana. Participants accurately estimated the latencies of their
1642
Revista de neurociencia cognitiva
Volumen 31, Número 11
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
/
oh
C
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
oh
C
norte
_
a
_
0
1
4
4
2
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
motor actions. In line with TED, participants’ ability to
monitor the timing of their RTs could mediate temporal
error monitoring during a timing task. The self-evaluation
of “too short” productions could be supported by error-
detection mechanisms because of premature respond-
En g, which is known to generate large error responses
during EEG recordings (Scheffers & Coles, 2000).
Similarmente, the brain error responses were previously
reported by Luu, Flaisch, and Tucker (2000), who inves-
tigated the neural correlates of monitoring the latency of
executed actions: In their study, participants performed
an RT task with a deadline response set to the median
RT estimated during a practice block. The feedback could
indicate that the response was on time or too late. Motor
responses that occurred later than the response deadline
elicited larger ERNs than those occurring earlier. Más-
encima, the ERN amplitude increased with increasing
response delays, suggesting a temporal monitoring of the
action latency (Luu et al., 2000). According to TED, el
monitoring of motor action latency could serve temporal
error monitoring and, by analogy to the estimation of the
RT delays (Luu et al., 2000), would likely occur after the
termination of the temporal production (R2). On this
base, we predicted the elicitation of an ERN (cohen,
2014; Gehring, Goss, Coles, Meyer, & Donchin, 1993)
when temporal production was off target. This working
hypothesis was further supported by sensorimotor syn-
chronization tasks in which the ERN amplitude was
found to increase with temporal errors irrespective of
their being early or late ( Jantzen, ratcliff, & Jantzen,
2018). Following the TED hypothesis, a V-shaped pattern
was thus predicted so that the further away time produc-
tions were from the target, the larger the amplitude of the
ERN (Figura 1B). Además, as participants were capable
of TMC in this task (Kononowicz et al., 2019), we predicted
the elicitation of a Pe, an evoked response after the ERN,
which has typically been reported to index the con-
scious evaluation of errors (Nieuwenhuis, Ridderinkhof,
Blom, Band, & Kok, 2001; Falkenstein, Hohnsbein,
Hoormann, & Blanke, 1991) and which takes into account
proprioceptive and reafferent information (Nieuwenhuis
et al., 2001).
En resumen, the TED hypothesis relies on the online
estimation of a motor action, whereas the TMC reads out
the representation of duration. These two working hy-
potheses propose distinct anatomical and dynamical loci
of temporal error monitoring in a time production task.
Aquí, we investigated the neural mechanisms underlying
temporal evaluation with two main working hypotheses:
(i) TED of motor actions (Meckler et al., 2010; Praamstra,
Turgeon, Hesse, Wing, & Perryer, 2003) y (ii) readout of
an internal variable coding for duration (Figura 1B). Para
este, we quantified evoked and oscillatory brain activity
locked to the offset of the produced time interval. We show
how brain activity traces the self-evaluation of temporal
production on a single-trial basis and describe a link be-
tween offset responses and timing signatures (β activity).
MÉTODOS
Participantes
Nineteen right-handed volunteers (11 women, significar
age = 24 años) with no self-reported hearing/vision loss
or neurological pathology were recruited for the exper-
iment and received monetary compensation for their par-
ticipation. Before the experiment, cada participante
provided a written informed consent in accordance with
the Declaration of Helsinki (2008) and the Ethics Com-
mittee on Human Research at Neurospin (Gif-sur-Yvette).
The data of seven participants were excluded from the
analysis because of the absence of anatomical MRI
(aMRI), technical issues with the head positioning system
during MEG acquisition, abnormal artifacts during MEG
recordings, and two participants not having finished the
experimento. These data sets were excluded a priori and
were neither visualized nor inspected. De este modo, the final
sample was composed of 12 Participantes (seven women,
edad media = 24 años). All participants performed six ex-
perimental blocks. One block was removed for two partic-
ipants because of excessive artifacts or lack of conformity
to task requirements.
Stimuli and Procedure
Before the MEG acquisitions, it was explained to par-
ticipants that they were taking part in a time estimation
experimento, and written instructions were provided ex-
plaining all steps of the experimental protocol. In each
trial, participants were first asked to produce a 1.45-sec
time interval and then to rate whether their production
was shorter or longer than the target interval on a linear
escala. After each rating, they received feedback on their
time production (not on their self-evaluation; Figura 1A).
We will refer to the produced time interval as the first-
order temporal judgment (FOJ) and to the self-evaluation
of the first-order judgment as the second-order temporal
judgment (SOJ).
Each trial started with the presentation of a fixation
cross “+” on the screen indicating that participants could
start whenever they decided to (Figura 1A). The intertrial
interval ranged between 1 y 1.5 segundo. Participants initi-
ated their time production with a brief but strong button
press once they felt relaxed and ready to start. Once they
estimated that a 1.45-sec interval had elapsed, they ter-
minated the interval by another brief button press. A
initiate and terminate their time production (FOJ), partícipe-
ipants were asked to press the top button of a Fiber
Optic Response Pad (FORP; Science Plus Group) usando
their right thumb (Figura 1A). The “+” was removed
from the screen during the estimation of the time interval
to avoid any sensory cue or confounding responses in
brain activity related to the FOJ.
After the production of the time interval, Participantes
were asked to self-evaluate their time estimation (segundo-
order judgment; Figura 1A). Para esto, participants were
Kononowicz and van Wassenhove
1643
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
/
oh
C
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
oh
C
norte
_
a
_
0
1
4
4
2
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
provided with a scale displayed on the screen 0.4 sec after
the keypress that terminated the produced time interval.
Participants could move a cursor continuously using the
yellow and green FORP buttons (Figura 1A). Participantes
were instructed to place the cursor according to how
close they thought their FOJ was with respect to the
instructed target interval indicated by the sign “∼”
placed in the middle of the scale. Participants placed
the cursor to indicate whether they considered their
produced time interval to be too short (“− −,” left side
of the scale) or too long (“++,” right side of the scale).
Participants could take as much time as needed to be
accurate in their SOJ.
After the completion of the SOJ, participants received
feedback displayed on a scale identical to the one used
for SOJ. Participants received feedback on all trials in
the first and fourth experimental blocks and on 15% de
the trials in all other blocks (Figura 1A). The row of five
symbols indicated the length of the just-produced FOJ
(Figura 1A). The feedback range was set to the value of
the perceptual threshold estimated on a per-individual
base (mean population threshold = 0.223 segundo, DE =
0.111 segundo). A near-correct FOJ yielded the middle “∼”
symbol to turn green; a too short or too long FOJ turned
the symbols “−“ or “+” orange, respectivamente (Figura 1A);
and a FOJ that exceeded these categories turned the
symbols “− −“ or “++” red. In Blocks 1 y 4, participar-
pants received feedback in all trials; in Blocks 2, 3, 5, y
6, participants received feedback in 15% of randomly
selected trials. From Block 4 en, and unbeknownst to par-
ticipants, the target duration was increased to 1.45 segundo +
individual threshold/2 (mean population duration =
1.56 segundo). This experimental manipulation was outside
the scope of this study and was tackled in another spe-
cific analysis showing the possibility of implicit temporal
recalibration (cf. Kononowicz et al., 2019). De término medio,
the new target duration was 1.56 sec based on the
average threshold. All six blocks were used in the sub-
sequent analyses.
In Blocks 1 y 4, participants had to produce 100
ensayos; in Blocks 2, 3, 5, y 6, participants produced
118 ensayos. Between the experimental blocks, Participantes
were reminded to produce the target duration of 1.45 segundo
as accurately as possible and to maximize the number of
correct trials in each block.
Estimation of Temporal Discrimination Thresholds
The Psychoacoustics toolbox was used to calculate the
temporal discrimination threshold for each participant
(Soranzo & Grassi, 2014) by adapting the available rou-
tine “DurationDiscriminationPureTone” provided in the
toolbox. An adaptive procedure was chosen using a stair-
case method with a two-down one-up rule and stopped
después 12 reversals (Levitt, 1971). For each trial, three iden-
tical tones of 1 kHz were presented to the participants.
One of the tones lasted longer than 1.45 segundo (deviant
tono), whereas the other two tones lasted precisely
1.45 segundo (standard tones). The position of the deviant
tone changed randomly across trials. The task was to identify
the deviant tone and to give its position in the sequence.
Tones were provided by earphones binaurally. The value
of the correct category was set as target duration ± (thresh-
old/3), and the lower and upper limits were set as target
duration ± (2 × individual threshold/3), respectivamente.
These values were used to provide feedback to participants.
Although this method did not provide a direct assessment of
an individual’s temporal production discrimination thresh-
viejo, the link between auditory and motor timing has been
noted (p.ej., Meegan, Aslin, & Jacobs, 2000) and is consid-
ered functionally relevant (p.ej., Zatorre, Chen, & Penhune,
2007).
Simultaneous MEG/EEG Recordings
The experiment was conducted in a dimly lit, standard
magnetically shielded room located at Neurospin (CEA/
DRF) in Gif-sur-Yvette. Participants sat in an armchair
with eyes open looking at a screen used to show visual
stimuli using a projector located outside the magnetically
shielded room. Participants were asked to respond by
pushing a button on a FORP response pad held in their
right hand. Electromagnetic brain activity was recorded
using the whole-head Elekta Neuromag Vector View
306 MEG system (Neuromag Elekta Ltd.) equipped with
102 triple-sensor elements (two orthogonal planar gradi-
ometers and one magnetometer per sensor location)
y el 64 native EEG system using Ag–AgCl electrodes
(EasyCap) with impedances below 15 kΩ. Participants sat
in an upright position. Their head position in the dewar
was measured before each block using four head-position
coils placed over the frontal and mastoid areas. The four
head-position coils and three additional fiducial points
(nasion, left and right preauricular areas) were digitized
for subsequent coregistration with the individual’s aMRI.
MEG and EEG (M/ EEG) recordings were sampled at
1 kHz and band-pass filtered between 0.03 y 330 Hz.
The EOGs (horizontal and vertical eye movements), elec-
trocardiograms, and electromyographics were recorded
simultaneously with MEG. The head position with respect
to the MEG sensors was measured using coils attached to
the scalp. The locations of the coils and EEG electrodes
were digitized with respect to three anatomical landmarks
using a 3-D digitizer (Polhemus). Stimuli were presented
using a PC running Psychtoolbox software (Brainard,
1997) that has been executed in MATLAB environment.
DATA ANALYSIS
M/EEG Data Preprocessing
Signal space separation correction (Taulu & Simola,
2006), head movement compensation, and bad channel
rejection were done using MaxFilter Software (Elekta
1644
Revista de neurociencia cognitiva
Volumen 31, Número 11
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
/
oh
C
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
oh
C
norte
_
a
_
0
1
4
4
2
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Neuromag). Trials containing excessive ocular artifacts,
movement artifacts, amplifier saturation, or SQUID arti-
facts were automatically rejected using rejection criterion
applied on magnetometers (55e−12 T/m) and on EEG
canales (250e−6 V). Trial rejection was performed using
epochs ranging from −0.8 to 2.5 sec after the first press
initiating the time production trial. Eye blinks, heartbeats,
and muscle artifacts were corrected using independent
component analysis (Campana & Sejnowski, 1995) with MNE-
Python. Baseline correction was applied using the mean
value ranging from −0.3 to −0.1 sec before the first
keypress.
Preprocessed M/EEG data were analyzed using MNE-
Python 0.13 (Gramfort et al., 2014) and custom-written
Python code. For the analysis of evoked responses in
the time domain, a low-pass zero-phase lag finite impulse
response filter (40 Hz) was applied to raw M/EEG data.
For time–frequency analyses, raw data were filtered using
a double-pass bandpass finite impulse response filter
(0.8–160 Hz). The high-pass cutoff was added to remove
slow trends, which could lead to instabilities in time–
frequency analyses. To reduce the dimensionality, todo
evoked and time–frequency analyses were performed
on virtual sensor data combining magnetometers and
gradiometers into single MEG sensor types using the
as_type method from MNE-Python 0.13 for gradio-
meters. This procedure largely simplified visualization
and statistical analysis without losing information pro-
vided by all types of MEG sensors (gradiometers and
magnetometers).
M/EEG-aMRI Coregistration
aMRI was used to provide high-resolution structural im-
ages of each individual’s brain. The aMRI was recorded
using a 3-T Siemens Trio MRI scanner. Parameters of
the sequence were as follows: voxel size = 1.0 × 1.0 ×
1.1 mm, acquisition time = 466 segundo, repetition time =
2300 mseg, and echo time = 2.98 mseg. Volumetric
segmentation of participants’ aMRI and cortical surface
reconstruction were performed with the FreeSurfer soft-
mercancía (surfer.nmr.mgh.harvard.edu/). A multiecho FLASH
pulse sequence with two flip angles (5° and 30°) was also
acquired ( Jovicich et al., 2006; Fischl et al., 2004) a
improve coregistration between EEG and aMRI. Estos
procedures were used for group analysis with the MNE
suite software (Gramfort et al., 2014). The coregistra-
tion of the M/EEG data with the individual’s structural
MRI was carried out by realigning the digitized fiducial
points with MRI slices. Using mne_analyze within the
MNE suite, digitized fiducial points were aligned man-
ually with the multimodal markers on the automatically
extracted scalp of the participant. To ensure reliable
coregistration, an iterative refinement procedure was
used to realign all digitized points with the individual’s
scalp.
MEG Source Reconstruction
Individual forward solutions for all source locations
located on the cortical sheet were computed using a
three-layer boundary element model constrained by the
individual’s aMRI. Cortical surfaces extracted with
FreeSurfer were subsampled to 10,242 equally spaced
sources on each hemisphere (3.1 mm between sources).
The noise covariance matrix for each individual was esti-
mated from the baseline activity of all trials and all condi-
ciones. The forward solution, the noise covariance, y
source covariance matrices were used to calculate the dy-
namic SPM estimates (Dale et al., 2000). The inverse
computation was done using a loose orientation con-
straint (loose = 0.4, depth = 0.8) on the radial compo-
nent of the signal. Individuals’ current source estimates
were registered on the FreeSurfer average brain for
surface-based analysis and visualization.
ERF/ERP Analysis
The analyses of MEG evoked-related fields (ERFs) y
EEG potentials (ERPs) focused on the quantification of
the amplitude of slow evoked components using non-
parametric cluster-based permutation tests, cual estafa-
trol for multiple comparisons (Maris & Oostenveld,
2007). The critical cluster value used was 0.05. Este
analysis combined all sensors and electrodes into the
analysis without predefining a particular subset of elec-
trodes or sensors, thus keeping the set of M/EEG data
as similar and consistent as possible. We used a period
ranging from −0.3 to −0.1 sec before the first press as
the baseline.
Time–Frequency Analysis
To analyze the oscillatory power in different frequency
bands using cluster-based permutation, we used discrete
prolate spheroidal sequence tapers with an adaptive time
window of frequency/2 cycles per frequency in 4-msec
steps for frequencies ranging from 3 a 100 Hz, usando
the tfr_multitaper function from MNE-Python. Time
bandwidth for frequency smoothing was set to 2. To re-
ceive the desired frequency smoothing, the time band-
width was divided by the time window defined by the
number of cycles. Por ejemplo, for 10-Hz frequency, tiempo
bandwidth was 2/0.5, resulting in 4-Hz smoothing. Nosotros
used −0.3 to −0.1 sec before the first press as the base-
line. The statistical analyses performed on theta (3–7 Hz),
alfa (8–14 Hz), b (15−40 Hz), and γ (41–100 Hz) bands
used spatiotemporal cluster permutation tests in the
same way as for evoked response analyses.
Cluster-Based Statistical Analysis of M/EEG Data
Cluster-based analyses identified significant clusters of
neighboring electrodes or sensors in the millisecond
Kononowicz and van Wassenhove
1645
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
/
oh
C
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
oh
C
norte
_
a
_
0
1
4
4
2
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
time dimension. To assess the differences between the
experimental conditions as defined by behavioral out-
comes, we ran cluster-based permutation analysis
(Maris & Oostenveld, 2007), as implemented by MNE-
Python by drawing 1,000 samples for the Monte Carlo
approximation and using FieldTrip’s default neighbor
templates. The randomization method identified the
MEG virtual sensors and the EEG electrodes whose statis-
tics exceeded a critical value. Neighboring sensors ex-
ceeding the critical value were considered as belonging
to a significant cluster. The cluster level statistic was de-
fined as the sum of values of a given statistical test in a
given cluster and was compared to a null distribution cre-
ated by randomizing the data between conditions across
multiple participants. The p value was estimated based
on the proportion of the randomizations exceeding the
observed maximum cluster-level test statistic. Only clusters
with corrected p < .05 are reported. For visualization, we
have chosen to plot the MEG sensor or the EEG electrode
of the significant cluster, with the highest statistical power.
For all performed analyses, we used the same window
length (0.4 sec), unless stated otherwise in the Results
section. We used the 0.4-sec window as it was the maximal
window length that could be used post-R2, given the onset
of visual stimulation 0.4 sec after the R2. There was no a
priori reasons to change the window length in subsequent
analyses, hence the same window length was kept for the
analysis of oscillatory power before R2 and post-R1. The
window length was only changed for single-trial analyses
of evoked activity. The latencies of ERP components were
selected at the predicted ERN and Pe latencies (see
Relative contributions of evoked activity and α power to
temporal error monitoring).
Behavioral Data Analysis
The analysis of behavioral data was performed using gen-
eralized additive mixed models (GAMMs; Wood, 2017),
as fully described below in the Single-trial analysis
section, unless stated otherwise in the Results section.
Each model was fitted with participant as a random fac-
tor. For the analysis of metacognitive inference, SOJ was
entered as a linear predictor of FOJ.
Binning Procedure of Behavioral and
Neuroimaging Data
All cluster-based analyses were performed on three con-
ditions defined on the basis of the objective performance
in time production (FOJ: short, correct, long) or the
subjective self-evaluation (SOJ: short, correct, long) sep-
arately for each experimental block. Before the binning,
the behavioral data were z scored on a per-block basis to
keep the trial count even in each category. Computing
these three conditions within a block focused the analysis
on local variations of brain activity as a function of objec-
tive or subjective performance. To overcome limitations
of arbitrary binning and to capitalize on the continuous
performance naturally provided by the time production
and the time self-evaluation tasks, we also used a
single-trial approach, which investigated the interactions
between the first- and second-order terms.
Single-Trial Analysis
To analyze single-trial data, we used GAMMs ( Wood,
2017). We briefly introduce the main advantages and
overall approach of the method. GAMMs are an extension
of the generalized linear regression model in which non-
linear terms can be modeled jointly. They are more flex-
ible than simple linear regression models as there is no
requirement for a nonlinear function to be specified: The
specific shape of the nonlinear function (i.e., smooth) is
determined automatically. Specifically, the nonlinearities
are modeled by so-called basis functions that consist of
several low-level functions (linear, quadratic, etc.). We
have chosen GAMMs as they can estimate the relation-
ship between multiple predictors and the dependent
variable using a nonlinear smooth function. The ap-
propriate degrees of freedom and overfitting concerns
are addressed through cross-validation procedures.
Importantly, interactions between two nonlinear predic-
tors can be modeled as well. In that case, the fitted func-
tion takes a form of a plane consisting of two predictors.
Mathematically, this is accomplished by modeling tensor
product smooths. Here, we used thin plate regression
splines as they seemed most appropriate for large data
sets and flexible fitting ( Wood, 2003). In all presented
analyses, we used a maximum likelihood method for
smooth parameter optimization ( Wood, 2011). GAMM
analyses were performed using the mgcv R package
( Version 1.8.12; Wood, 2009). GAMM results were
plotted using the itsadug R package (Version 1.0.1; van
Rij, Wieling, Baayen, & van Rijn, 2016).
Although not widely used, GAMMs are useful for
modeling EEG data (Tremblay & Newman, 2015). Here,
sensors were not included as fixed effects and the same
model was fitted for every sensor separately. The result-
ing p values were corrected for multiple comparisons
using false discovery rate correction (Genovese, Lazar,
& Nichols, 2002). For plotting purposes, we averaged
the data across significant sensors after false discovery
rate correction and refitted the model. The specifics of
this refitted model can be found in the tables. Besides
typical F and p values, the tables contain the information
on the estimated degrees of freedom (edf ). edf Values
can be interpreted as how much a given variable is
smoothed. Although higher edf values indicate more
complex splines, all tested models showed linear splines
(edf = 1), depicted in the plotted model outcomes in
associated figures.
We fitted the same GAMMs for several neurophysiolog-
ical measurements chosen on the basis of previous liter-
ature. The fitted model contained a random effects term
1646
Journal of Cognitive Neuroscience
Volume 31, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
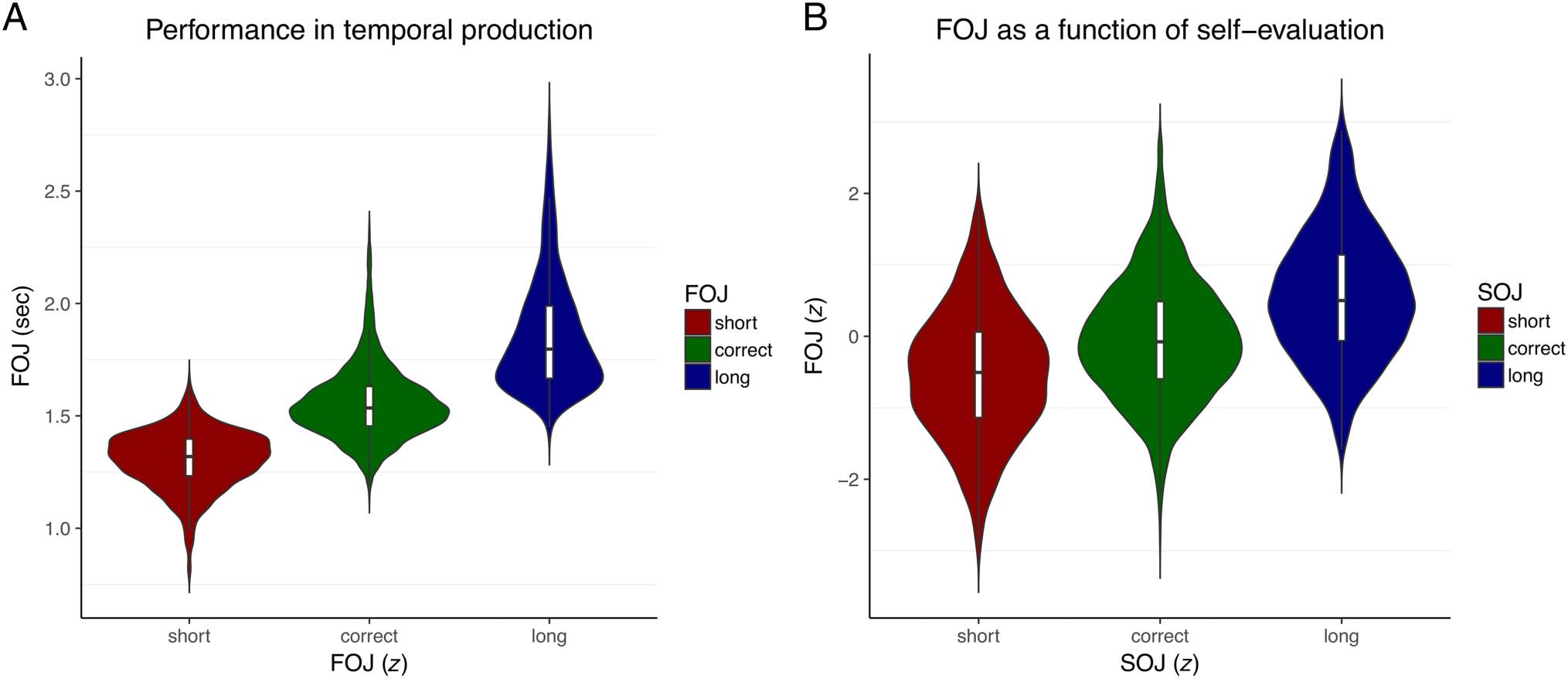
Figure 2. Temporal productions (FOJ) and self-evaluations (SOJ). (A) Participants accurately produced the target duration. The FOJ (first-order
judgments) were clustered on the basis of the z-scored FOJ yielding the short, correct, and long categories. (B) The FOJ increased with increased SOJ
indicating that participants could accurately self-evaluate (SOJ) their produced durations (FOJ).
for participant and fixed effects that were based on
theoretical predictions. Specifically, the full model had
the following specification: μV/T/power ∼ FOJ + SOJ +
SOJ accuracy + FOJ×SOJ + FOJ×SOJ Accuracy. Besides
the random term for participants, the model contained
smooth terms for the first- and second-order judgments,
SOJ accuracy between the first- and second-order judg-
ments, and the interaction term between FOJ and SOJ
accuracy. Notably, FOJ, SOJ, and other predictors were
entered as continuous variables in GAMM analyses as op-
posed to post hoc experimental conditions tested using
cluster permutation, which suffered limitations from
choosing arbitrary split point in the data.
The relative contribution of post-R2 components were
tested similarly to the previous model. The full model
had the following specification: FOJ/SOJ ∼ α power +
ERN + Pe. Besides the random term for participants,
the model contained smooth terms for all three included
predictors. In the model outcomes, higher edf values
(>1) indicate more complex splines. All tested models
showed linear splines (edf = 1), depicted in the plotted
model outcomes in associated figures.
Although GAMMs have built-in regularization proce-
duro (meaning that they are somewhat inherently resis-
tant against multicollinearity), multicollinearity can been
assessed using variance inflation factor (VIF; fmsb R pack-
edad, Versión 0.5.2). Aquí, VIF was assessed for the final
model and consisted in averaging data from multiple sen-
sors collapsed over a particular variable at hand. None of
the VIF values exceeded 1.1, indicating that multicolli-
nearity was unlikely to have had a major influence on
the reported findings. Note that Rogerson (2001) rec-
ommended a maximum VIF value of 5 and the author
of fmsb recommended a value of 10.
Before entering empirical variables in the model, nosotros
calculated normalized values or z scores: Trials in which
a given variable deviated more than 3 z scores were re-
moved from further analysis. This normalization was
computed separately for every MEG sensor and every
EEG electrode. For single-trial analyses of β power in
FOJ, we focused on the maximum power within the
0.4- to 0.8-sec period after the R1, similarly to the ap-
proach taken in Kononowicz et al. (2019). This time win-
dow overlapped with the selected time window that was
used in cluster analyses. For the single-trial analyses of
other brain signatures—that is, alpha power and sus-
tained activity—we focused on the mean values in the
time window of 0.4 sec after or preceding the R2.
RESULTADOS
Participants Track the Signed Magnitude
of Just-Produced Time Intervals
Participants could accurately generate temporal pro-
ductions (FOJ) with estimates centered around 1.5 segundo.
Figure 2A provides the normalized (z score) FOJ as a
function of short, correcto, and long categories defined
according to each individual’s temporal sensitivity (ver
Métodos). To show that participants could accurately
self-evaluate their FOJ, we sorted trials on the basis of
their self-evaluations (SOJ). If FOJ and SOJ were inde-
pendiente, the FOJ sorted as a function of SOJ should
not differ. En cambio, we found the same linear trend when
Kononowicz and van Wassenhove
1647
we sorted FOJ as a function of SOJ (Figura 2B) as when
we sorted FOJ as a function of FOJ (Figura 2A). Este
observation was statistically corroborated using a GAMM
(Wood, 2017) with which we could assess whether SOJs
were predictive of FOJs on a single-trial basis. The model
fits confirmed that participants could correctly evaluate
the signed error magnitude of their FOJ, F(4.0) = 192.5,
edf = 4.0, pag < 10−15; that is, participants could correctly
evaluate whether they were too short or too long and by
how much. These results highlight the main behavioral
effect subtending the question of TMC for subsequent
analyses; complementary behavioral analyses can be
found elsewhere (Kononowicz et al., 2019).
The Outline of Neuroimaging Data Analysis
We first performed a cluster analysis of the evoked and
time–frequency activity, using FOJ and SOJ, which were
binned as factors. We then performed single-trial analyses,
in which FOJs and SOJs were used as continuous predic-
tors. This series of tests was followed by single-trial analyses
using models predictive of FOJs or SOJs to assess the rela-
tive contributions of evoked and oscillatory power activity
within the same statistical model. Using a single-trial ap-
proach, we could thus assess the link between β power (in-
ternal variable coding for duration [Kononowicz et al., 2019;
Wiener, Parikh, Krakow, & Coslett, 2018; Kulashekhar,
Pekkola, Palva, & Palva, 2016; Kononowicz & Van Rijn,
2015]) and the postinterval production signatures (i.e.,
the post-R2 activity). Last, we assessed whether partici-
pants had access to temporal information before the ter-
mination of their temporal production, by analyzing brain
activity locked to R2 during the temporal production.
ERN/Pe is Not Sensitive to the Temporal Dimension
of Motor Action
The ERN and the Pe are seminal electrophysiological
signatures of error monitoring and self-evaluation. The
ERN is characterized by a large negative, and the Pe, a pos-
itive, evoked response occurring 0.1–0.3 sec after an error
( Yeung, Botvinick, & Cohen, 2004; Holroyd & Coles,
2002). The ERN/Pe complex is obtained by subtracting er-
ror trials from correct trials. In our time production task,
incorrect trials could either be too short and too long. The
hypothesis that ERN/Pe could reflect a response selection
error in the temporal domain (e.g., Luu et al., 2000) thus
predicted a V-shaped amplitude pattern so that the further
away the temporal production was from the target
duration, the larger the amplitude of the ERN/Pe would
be. In other words, the larger the error, the larger the
ERN/Pe amplitude irrespective of the sign of the error.
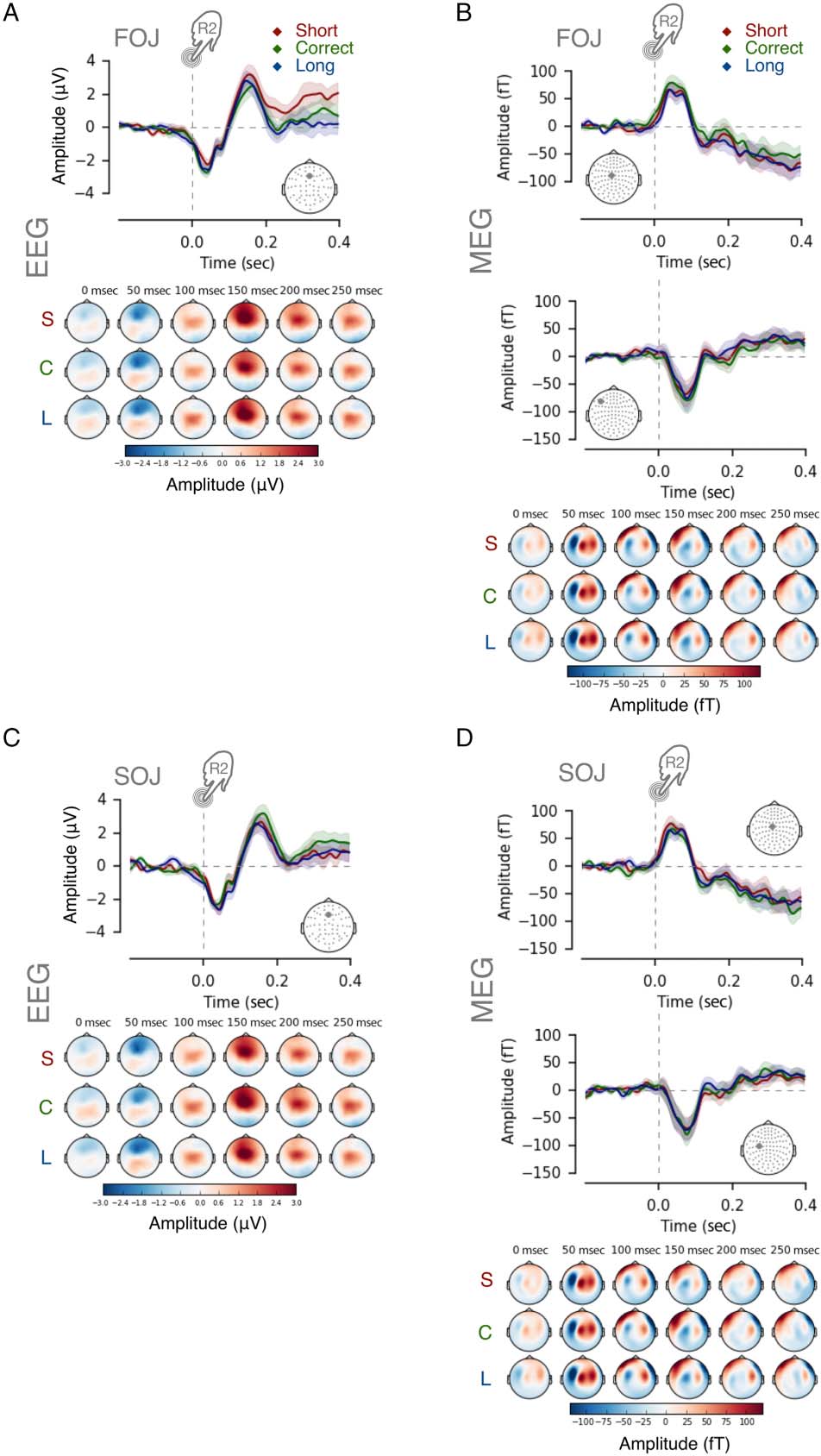
To test this hypothesis, we looked at the evoked
responses after the termination of the temporal produc-
tion, that is, the R2-locked evoked activity. First, we ob-
served a negative component peaking ∼60 msec post-R2,
which seemed characteristic of an early postmovement
activity (Praamstra et al., 2003) in both EEG and MEG
(Figure 3A and C and Figure 3B and D, respectively).
This component was followed by a positive evoked poten-
tial (Pe). To test the possible sensitivity of the presumed
ERN/Pe to temporal error, we used spatiotemporal cluster
permutation tests of EEG and MEG evoked responses. We
first compared the evoked responses after the production
of the time interval (0–0.4 sec post-R2) as a function of
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. No evidence for ERN-like responses. ERPs/ERFs up to 0.4 sec
after the termination of the produced duration (R2). The top displays
the evoked responses as a function of FOJ (A, B), whereas the bottom
displays the data as a function of SOJ (C, D), as indicated by the gray
insets in the top left part of every panel. The evoked responses showed
no significant differences in amplitude or latency as a function of FOJ
or SOJ. Time courses illustrate the evoked responses from the gray EEG
electrode or MEG sensor in the topographical map inset. Colored
topographical maps display the evoked responses for short (S: red),
correct (C: green), and long (L: blue) categories. The EEG time course at
Fz was reported as a function of (A) FOJ and (C) SOJ categories,
respectively. Two MEG sensors are reported as a function of (B) FOJ and
(D) SOJ categories.
1648
Journal of Cognitive Neuroscience
Volume 31, Number 11
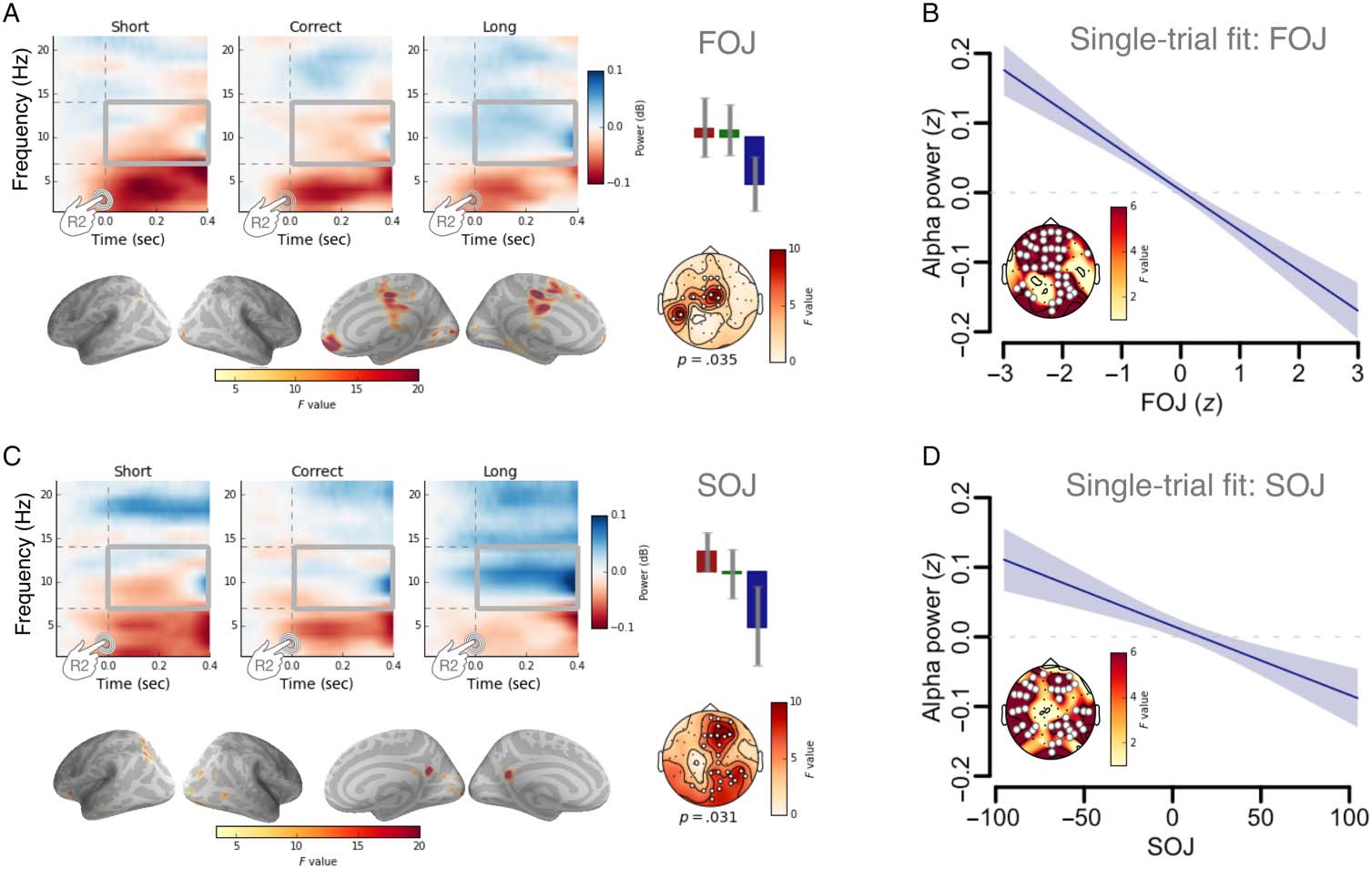
Figure 4. Post-R2 α power
signatures of FOJ and SOJ.
(A) Time–frequency spectra for
one EEG electrode (Cz), with
the highest F value, illustrating
the outcomes of a cluster-based
permutation F test capturing a
decrease of α power (8–14 Hz)
as a function of FOJ categories.
The average α power in the
highlighted time–frequency
window (gray squares)
significantly decreased with
increasing duration production
(bar plot: red indicates short,
green indicates correct, and
blue indicates long). (B) The
single-trial model fit. Post-R2 α
power decreased as a function
of FOJ. Statistical details in
Table 1. (C) Time–frequency
spectra for the Fz EEG electrode
with the largest F value (cluster-
based permutation test). Bar
plot illustrating the average α
power as a function of SOJ categories: α power decreased with increasing SOJ. Source estimates of the α power effect as a function of SOJ
(uncorrected F map; combined M/EEG) implicated medio-central and prefrontal cortices. The strongest source originated from the precuneus.
(D) The single-trial model fit. Post-R2 α power decreased as a function of SOJ. Statistical details in Table 2.
FOJ and SOJ. In Figure 3, the top panels display the data as
a function of FOJ (Figure 3A and B); and the bottom
panels, as a function of SOJ (Figure 3C and D). The
spatiotemporal cluster permutation tests yielded no signif-
icant changes in evoked responses as a function of FOJ
(Figure 3A and B) or SOJ (Figure 3C and D), whether in
EEG (Figure 3A and C; all ps > .1) or in MEG (Figura 3B
y D; all ps > .1).
We next compared the time–frequency activity after
corto, correcto, and long trials (post-R2: 0–0.4 sec). En
the remaining analyses, we solely focused on EEG ac-
actividad, which is more sensitive to activity in midline
structures such as cingulate cortices. Recent work on
cognitive control has suggested a link between ERN
and theta oscillations (i: 3–7 Hz) sharing common mid-
frontal neural generators (Cavanagh & Franco, 2014;
Mesa 1. The Results of Single-Trial GAMM Analysis Based on α Power after the Second Keypress
Parametric Coefficients
Interceptar
Smooth Terms
s(FOJ)
s(SOJ)
s(SOJ accuracy)
de(FOJ × SOJ)
de(FOJ × SOJ Accuracy)
s(partícipe)
Estimate
0.0042
edf
1.0000
1.0000
1.0001
1.0012
1.0009
0.0012
estándar. Error
0.0086
Ref.df
1.0001
1.0001
1.0002
1.0025
1.0018
11.0000
t Value
0.4870
F Value
22.9395
0.3052
0.0775
0.0019
3.9561
0.0000
p Value
.6262
p Value
<.0001*
.5807
.7809
.9650
.0466
.9999
GAMM analysis: R2-locked α power, FOJ cluster, full model
The table displays the results of the model that was based on the data collapsed across the significant sensors, showing the main effect of FOJ, when
the model was fitted on a per-sensor basis. Although FOJ × SOJ Accuracy reached significance level in the refitted model, it was not significant in the
first step where model was assessed for each individual sensor and p values were corrected (see Single-trial analysis).
The asterisk signifies the factors that were significant after false discovery rate correction, applied after the same model was fitted for every sensor
separately.
Kononowicz and van Wassenhove
1649
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Table 2. The Results of Single-Trial GAMM Analysis Based on α Power after the Second Keypress
Parametric Coefficients
Intercept
Smooth Terms
s(SOJ)
s(SOJ accuracy)
ti(FOJ × SOJ)
ti(FOJ × SOJ Accuracy)
s(participant)
Estimate
0.0045
edf
1.0001
1.0032
1.0016
2.1676
0.0012
Std. Error
0.0080
Ref.df
1.0003
1.0064
1.0033
2.6620
11.0000
t Value
0.5651
F Value
12.3827
0.4280
0.2936
2.2540
0.0000
p Value
.5720
p Value
.0004*
.5179
.5888
.1042
.9994
GAMM analysis: R2-locked α power, SOJ cluster, model without FOJ term
The table displays the results of the model that was based on the data collapsed across the significant sensors, showing the main effect of SOJ, when
the model was fitted on a per-sensor basis and the FOJ term has been excluded from the model.
The asterisk signifies the factors that were significant after false discovery rate correction, applied after the same model was fitted for every sensor
separately.
Cohen & Cavanagh, 2011). We thus explored evoked θ
activity from 0 to 0.2 sec post-R2. We constrained the
analysis window from 0.2 to 0.4 sec post-R2 to prevent
capturing spurious evoked activity, which could mask
brain activity specific to the self-evaluation of temporal
error. As for the ERN/Pe, our prediction was that stronger
θ power would indicate larger temporal errors irrespec-
tive of their sign. A cluster permutation test of the θ band
power yielded no significant effect of FOJ or SOJ ( p >
.1). A post hoc spatiotemporal cluster permutation test
showed no significant effects in β (14–40 Hz) or γ
(>40 Hz) frequency ranges as a function of FOJ ( p >
.1) or SOJ ( p > .1). Por eso, we found no evidence for
a V-shaped pattern of the evoked responses as a function
of FOJ or SOJ in the ERN or in a frequency band that
could support the TED hypothesis in this experimental
paradigma.
Postinterval Oscillatory Activity as Readout
While assessing oscillatory activity after the termination
of the time interval, we observed a significant cluster in
the alpha-band power (a: 8–14 Hz) as a function of FOJ
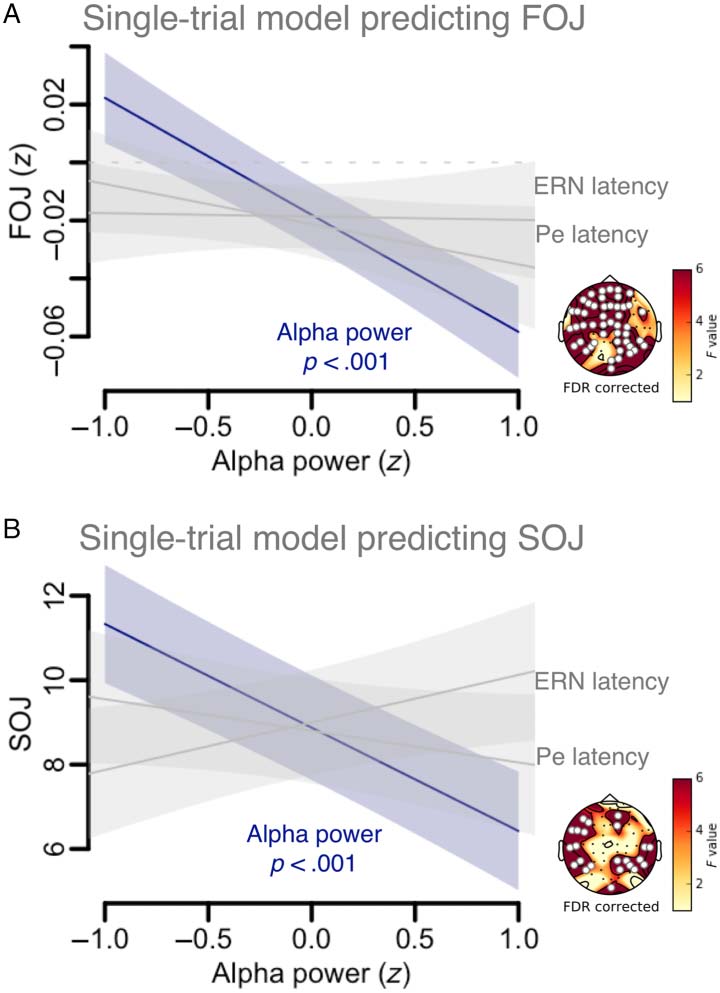
categories (Figura 4A, pag = .035). The main sources of this
effect originated in medial and prefrontal cortices
(Figura 4A, fila inferior). Similarmente, a significant effect
of α power was found as a function of SOJ categories
(Figura 4C, pag = .031). On a given trial, the shorter the
self-evaluation, the larger the α power (Figura 4C).
We tested the possibility of a linear relation between
the observed α power and the behavioral variables using
a single-trial analysis of the normalized mean α power.
The single-trial model used the set of behavioral variables
to predict α power (0–0.4 sec post-R2): Among other pre-
dictors, we used SOJ and FOJ (see Single-trial analysis).
The analysis revealed a consistent pattern across two
factores, one associated with FOJ and the other with
SOJ: The first significant group of electrodes showed a
linear relationship between α power and FOJ (F =
22.9, edf = 1, pag < .0001; Figure 4B, Table 1) so that
shorter trials were associated with a larger α power
(i.e., the shorter the temporal production, the stronger
the α power). Consistent with the topographical scalp dif-
ferences, the neural contributors of α power changes in
FOJ were distinct from those observed in SOJ (Figure 4A
Figure 5. α Power contributes to SOJ and to FOJ. Single-trial statistical
model fit predicting FOJ (A) and SOJ (B) using α power, and evoked
activity amplitude at predicted ERN and Pe latencies. The topographical
map shows the distribution of significant EEG electrodes.
1650
Journal of Cognitive Neuroscience
Volume 31, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
After the end of the temporal production (post-R2),
changes in α power seemed indicative of the signed mag-
nitude difference between the target interval and the pro-
duced time interval. We speculated that a readout activity
would linearly code for the state of the networks related
to duration estimation at the outset of the produced in-
terval. Indeed, the linear trend of α power, together with
distinct generators of FOJ and SOJ effects, appeared in
line with the TMC readout hypothesis. Considering that
an important goal for this work was to compare the pre-
dictions of TED against those of TMC (and not the eval-
uation of TED or TMC per se), we next ran a single-trial
analysis that directly tested the contributions of TED and
TMC.
Relative Contributions of Evoked Activity and α
Power to Temporal Error Monitoring
Considering the hypothetical ERN/Pe predicted by TED
and the α power observed in exploratory analysis, we as-
sessed the relative contribution of evoked and oscillatory
activity to the self-evaluation of a generated duration.
Using a single-trial analysis, we assessed a model in which
FOJ or SOJ was predicted by three factors: evoked activ-
ity at the predicted ERN/Pe latencies and α power. The
associated temporal windows were 0–0.1, 0.1–0.3, and
0–0.4 sec, respectively. These latencies typically predict
the ERN and Pe in the literature, whereas no a priori win-
dow could be defined for oscillatory power. The analysis
revealed that the only contributing factor to FOJ (F =
12.8, edf = 1, p = .0003; Figure 5A) and SOJ (F =
14.1, edf = 1, p = .0004; Figure 5B) was α power. We
thus explored further the notion that a linear scaling with
SOJ may index a readout mechanism during TMC.
β Power Timing Signature Is Consistent with Post-
R2 α Scaling
As previous studies have suggested that β power was
strongly associated with an internal variable coding for
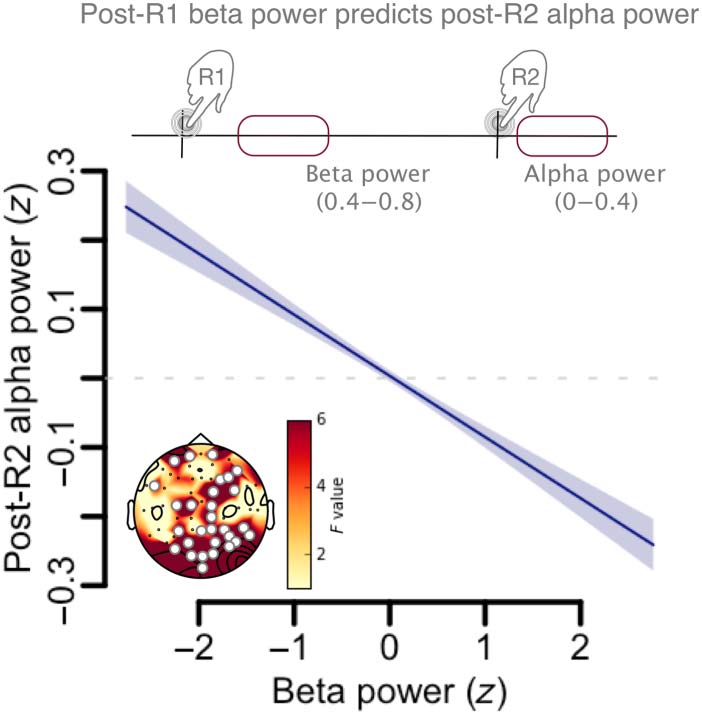
Figure 6. Post-R1 power contributes to post-R2 evaluation. Single-trial
model fit predicting post-R2 α power using the post-R1 power. The
topographical map shows the distribution of significant EEG electrodes.
and C, bottom): Source estimates for the FOJ effect were
found in medial, central, and prefrontal cortices, whereas
those for the SOJ effect were located near the precuneus
cortices.
Considering the anatomical separability of the neural
generators, we refitted the single-trial model without
the FOJ term, which accounted for most of the variance
when the full model was considered (Figure 4B, Table 1).
As SOJ and FOJ were correlated, we expected that remov-
ing the FOJ term would allow to show the SOJ impact
and we hypothesized that this refitted model would show
a different topography than the model including the FOJ
term. This analysis revealed a significant group of elec-
trodes for which α power was linearly predictive of SOJ
(F = 12.4, edf = 1, p = .0004; Figure 4D, Table 2).
Both the analysis using categorical responses (i.e.,
data binning as short/correct/long) and the single-trial
model thus indicated that the FOJ and SOJ effects were
topographically distinct, in agreement with the source
estimations (Figure 4C, bottom).
Table 3. GAMM Analysis: Beta Power Predicting Post-R2 Alpha
Parametric Coefficients
(Intercept)
Smooth Terms
s(β power)
s(participant)
Estimate
0.0034
edf
1.0002
0.0032
Std. Error
0.0079
Ref.df
1.0004
11.0000
t Value
0.4275
F Value
44.5739
0.0000
GAMM analysis: β predicting post-R2 alpha
p Value
.6691
p Value
<.0001*
1.0000
The results of single trial GAMM analysis where β power was tested as a predictor for post-R2 α. The table displays the results for the final model that
was based on the data collapsed across the significant sensors.
The asterisk signifies the factors that were significant after false discovery rate correction, applied after the same model was fitted for every sensor
separately.
Kononowicz and van Wassenhove
1651
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
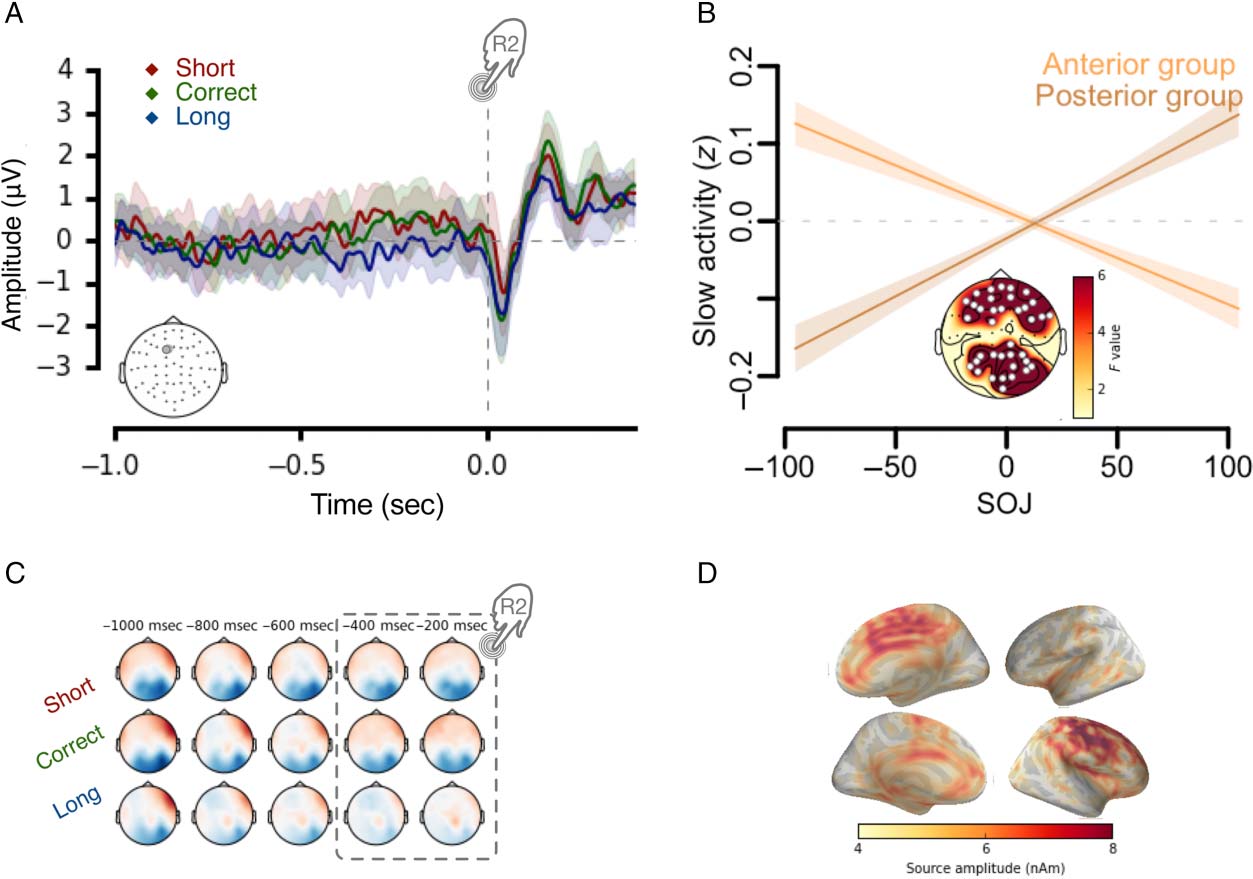
Figure 7. Sustained activity
before R2 indicative of SOJ. (A)
Time courses and topographical
plots of EEG activity 1 sec
before the second keypress as a
function of SOJ. The electrode
location is displayed in the
bottom left corner. (B) Single-
trial model fit. The sustained
brain activity preceding the R2
(−0.4 to 0 sec) predicted SOJ.
The anterior and posterior
clusters were plotted separately
because of reversed polarities of
EEG signals depicted in C.
Statistical details in Tables 3 and
4. (C) Topographical maps
show scalp voltage distribution
1 sec before the R2. (D) Cortical
source estimates collapsed over
all conditions. Motor and
midfrontal regions were the
most likely origins of the
sustained activity.
duration during time estimation (Kononowicz et al.,
2019; Wiener et al., 2018), the post-R2 activity may be
linked to β power during timing. To directly test this
hypothesis, we assessed whether β power after the first
keypress (R1) predicted the postinterval α power. This
analysis showed that β power during temporal produc-
tion (post-R1) was significantly predictive of α power
after temporal production (post-R2) in frontal and poste-
rior sensors (F = 44.6, edf = 1, p < .0001; Figure 6,
Table 3). This effect suggested that β power at the onset
of the temporal production could be used for the post-
interval α modulation (readout). Hence, this obser-
vation supports an interpretation in which the linear
scaling between post-R2 α power and SOJ, as a marker
of self-estimation, relies on an internal variable coding for
duration (β power) during the FOJ.
No Evidence of Self-evaluation before R2
The accurate estimation of signed temporal errors sug-
gested that participants could access their temporal
errors. We thus asked whether such self-evaluation
already started before the completion of the time inter-
val, that is, before R2. Similar to the previous post-R2
analyses, we contrasted evoked activity and α power as
a function of FOJ and SOJ, but this time, from −0.4 to
Table 4. The Results of Single-Trial GAMM Analysis Based on Sustained Activity Preceding the Second Keypress
Parametric Coefficients
Intercept
Smooth Terms
s(FOJ)
s(SOJ)
s(SOJ accuracy)
ti(SOJ × FOJ)
ti(FOJ × SOJ Accuracy)
s(participant)
Estimate
−0.0009
edf
1.0001
1.0002
1.0002
1.0027
1.0089
0.0015
Std. Error
0.0072
Ref.df
1.0001
1.0003
1.0005
1.0055
1.0178
11.0000
t Value
−0.1318
F Value
0.3260
20.5239
1.0091
0.8087
1.3847
0.0000
p Value
.8951
p Value
.5680
<.0001*
.3151
.3700
.2368
.9948
GAMM analysis: R2-locked readiness potential, anterior cluster
The table displays the results for the final model that was based on the data collapsed across the significant sensors, showing the main effect of SOJ,
when the model was fitted on a per-sensor basis. The table depicts the anterior cluster.
The asterisk signifies the factors that were significant after false discovery rate correction, applied after the same model was fitted for every sensor
separately.
1652
Journal of Cognitive Neuroscience
Volume 31, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Table 5. The Results of Single-Trial GAMM Analysis Based on Sustained Activity Preceding the Second Keypress
Parametric Coefficients
(Intercept)
Smooth Terms
s(FOJ)
s(SOJ)
s(SOJ accuracy)
ti(SOJ × FOJ)
ti(FOJ × SOJ Accuracy)
s(participant)
Estimate
−0.0040
edf
1.0000
1.0000
1.0000
2.0365
1.0077
0.0003
Std. Error
0.0074
Ref.df
1.0001
1.0001
1.0001
2.5519
1.0153
11.0000
t Value
−0.5389
F value
0.1091
27.6527
4.4611
1.3882
1.0731
0.0000
p Value
.5900
p Value
.7412
<.0001*
.0347
.2115
.2974
.9815
GAMM analysis: R2-locked readiness potential, posterior cluster
The table displays the results for the final model that was based on the data collapsed across the significant sensors, showing the main effect of SOJ,
when the model was fitted on a per-sensor basis. The table depicts the posterior cluster.
The asterisk signifies the factors that were significant after false discovery rate correction, applied after the same model was fitted for every sensor
separately.
0 sec post-R2 (Figure 7A). First, no significant variation of
α band power was found. Second, a trial-by-trial analysis
revealed a significant effect of SOJ on the amplitude of
evoked activity (Figure 7B): Anterior and posterior clusters
with positive and negative voltages (Figure 7B) covaried
with SOJ such that the positive frontal cluster (F = 20.5,
edf = 1, p < .0001; Figure 7B, Table 4) negatively covaried
with SOJ (Figure 7B and C) and the posterior negative clus-
ter positively covaried with SOJ (F = 27.7, edf = 1, p <
.0001; Figure 7B, Table 5). In line with this bipolar EEG
scalp distribution, and in agreement with previous work
(Figure 7C; Wiener, Turkeltaub, & Coslett, 2010), brain
sources at the origin of this activity were located in the mo-
tor, premotor, and midfrontal cortices (Figure 7D).
As only SOJ covaried with slow evoked activity, we
hypothesized that the sustained activity may reflect an
intrinsic decisional bias affecting self-evaluation, which
would be functionally distinct from the representation
of duration that would involve both FOJ and SOJ. This effect
of SOJ is also in line with the notion that participants have no
access to temporal errors before R2: Although we previously
reported that β power during temporal production pre-
dicted FOJ, whether an agent can act upon that represen-
tation before R2 should be further investigated.
In summary, we identified cortical signatures of self-
evaluation in temporal production. Postinterval α power
was linked to preceding β power, suggesting the evalua-
tion of an internal variable coding for duration as pre-
viously suggested by the accurate representation of
individuals’ temporal uncertainties (Balcı et al., 2009).
DISCUSSION
We assessed two working hypotheses on the neuronal
correlates and mechanisms supporting the evaluation of
self-generated time intervals (TED and TMC), using a task
in which participants produced durations, and evaluated
the signed error magnitude of their time estimates while
being recorded with combined M/EEG. We found no ro-
bust evidence for the generation of an ERN/Pe modulated
as a function of temporal error in this task. However, we
found that α power after R2 negatively correlated with
SOJs and with FOJs. We interpret these findings as evi-
dence in favor of the TMC working hypothesis. In sup-
port of the TMC hypothesis, the initial β power, known
to scale with the duration of a produced time interval in
this task (Kononowicz et al., 2019), predicted the changes
in α power after the produced time interval. Below, we
discuss these interpretations together with the current
shortcomings of our study.
Temporal Metarepresentations
TMC posits the existence of a process that actively infers
the state of duration representation, that is, the meta-
representation of a duration (van Wassenhove, 2009;
Cleeremans, Timmermans, & Pasquali, 2007). What cru-
cially follows is that the metarepresentation of duration
would be specified by neural signatures that would be
anatomically and functionally distinct from the neural
signatures of the duration representation (Lak et al.,
2014). In line with this, the cortical generators for the
post-R2 α power and the post-R1 β power were clearly
distinguishable (Kononowicz et al., 2019), fulfilling the cri-
terion of anatomical separability between the first- and
second-order representations of duration. In addition, both
α and β neural oscillatory activity have typically been as-
cribed different functional roles: α tends to be implicated
in the regulation of a global network (Palva & Palva,
2012), whereas β is implicated in the representation of
Kononowicz and van Wassenhove
1653
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
sensorimotor features (Kilavik, Zaepffel, Brovelli, MacKay, &
Riehle, 2013; Engel & Fries, 2010). Complementary to these
two functional roles, a strong α–β coupling was shown to
monitor the timing precision in this task (Grabot et al., 2019).
Indirect evidence has suggested the existence of meta-
cognitive mechanisms that required either a passive or an
active readout (Fleming & Daw, 2017): A passive sensi-
tivity to the state of the system automatically detects
temporal delays in motor action (in line with the TED hy-
pothesis), or an active process implies a process of infer-
ring of the state of duration representation (in line with
the TMC hypothesis). Here, we suggest that the decrease
in α power after the production of a duration may re-
flect the outcome of an active readout process. This
working hypothesis is also quite testable: If the meta-
cognitive readout is an active process, the absence of
self-evaluation in a task should abolish the post-R2 α
as a function of duration category. One limitation of this
study was that there were no trials in which participants
did not self-evaluate their time production. Fortunately,
previous EEG work assessing time reproduction tasks in
the absence of metacognitive inference (Kononowicz &
Van Rijn; 2015; Figures 4 and 5, bottom) showed no post-R2
α or theta power changes as a function of duration category.
Thus, changes in post-R2 α may only be seen when partic-
ipants are explicitly asked to self-evaluate their temporal
performance. Future experiments should assess under
which conditions self-evaluation is a function of an active
inference or a plausible passive dependency between du-
ration representation and error monitoring variable.
Additional evidence supports the idea that first-order
signals could be read out by second-order areas of brain
regions. For example, the pulvinar neurons have been
shown to encode confidence (second-order variable) inde-
pendently of other areas processing first-order variables
(Komura, Nikkuni, Hirashima, Uetake, & Miyamoto, 2013):
This study suggested that one population of neurons can
read out the activity of neural population encoding primary
sensory variables. Other studies have also suggested that
particular brain regions independently code for first- and
second-order signals (Lak et al., 2014). In humans, similar
notions have been explored: Using TMS, prefrontal areas
have been shown to read out the strength of perceptual
signals in service of confidence judgments (Shekhar &
Rahnev, 2018). In line with these ideas, the mapping be-
tween β power and duration may be realized via networking
through higher-order brain regions. For example, pFC,
implicated in timing (Kim et al., 2017), could monitor sig-
nals in motor cortex (Narayanan & Laubach, 2006) or the
cortico-basal ganglia loop. Indeed, the cortical sources
observed in our study were consistent with the acknowl-
edged role of midline cingulate regions in self-monitoring
(Miyamoto et al., 2017) and error monitoring (Ullsperger,
Fischer, Nigbur, & Endrass, 2014). Moreover, the orbito-
frontal and posterior cingulate were implicated in the
metacognitive performance: The association between FOJ
and α power originated from pFCs and ACC, whereas the
association between SOJ and α power implicated the
precuneus, which has been reported during confidence
judgments (Ye, Zou, Lau, Hu, & Kwok, 2018; De Martino,
Fleming, Garrett, & Dolan, 2013) and error processing
(Menon, Adleman, White, Glover, & Reiss, 2001). Gray matter
volume in precuneus predicts introspective accuracy
(Fleming, Weil, Nagy, Dolan, & Rees, 2010) and meta-
cognitive efficiency in memory (McCurdy et al., 2013).
What Signals Could Be Read Out
Previous studies reported that β power scaled with the
length of produced interval (Kononowicz et al., 2019;
Kononowicz & Van Rijn, 2015) and that the degree of
separation in β power state trajectories predicted individ-
uals’ temporal metacognitive performance (Kononowicz
et al., 2019). If β power conveys information about the
representation of duration, we hypothesized that it could
also serve as a signature for the readout: Congruent with
this, β power predicted the post-R2 α power in our study.
The effects in α power suggest that the monitoring of in-
ternal states could rely on different sources of information
than only β power, and two studies further support this
notion. First, α oscillations have been implicated in per-
formance monitoring when task errors relied more on
the attentional lapses than on the lack of executive con-
trol over the motor system (van Driel, Ridderinkhof, &
Cohen, 2012). Second, participants can monitor their
attentional state, which is indexed by the lateralization pat-
tern of α oscillations (Whitmarsh, Barendregt, Schoffelen, &
Jensen, 2014). The post-R2 α decrease observed here could
also be interpreted as a reorienting of attention after the
generation of durations that were too long. Specifically, in
an attentional gate model of time perception (Zakay &
Block, 1995), long durations would correspond to not
enough attention paid to temporal production, hence
more attention needed for the next trial. However, the
lack of association between α power during the self-
generation of durations and produced duration in this
data set (Kononowicz et al., 2019) and in previous studies
(Kononowicz & Van Rijn, 2015) does not fit well with this
interpretation. Whether α power could contribute to
metacognitive performance in the timing of longer dura-
tions thus remains to be tested. Future studies should
extend the range of tested durations to longer as well as
shorter ones. A better assessment on an extended range
of durations would allow evaluating the relevance of the
current findings to different timing mechanisms (Lewis &
Miall, 2003).
Another open question is why readout-related pro-
cesses and self-monitoring would implicate α oscillations.
When assessing the role of cross-frequency coupling in
this timing task, we found that the coupling strength
between the phase of α oscillations and the power of β
oscillations was indicative of the precision with which
participants produced a duration (Grabot et al., 2019).
This pattern was found during the generation of the
1654
Journal of Cognitive Neuroscience
Volume 31, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
interval. One speculative hypothesis is that the termina-
tion of the interval (R2) may implicate the readout of
the precision maintained in the coupling of β power with
respect to the phase of alpha. This mechanism would be
close to the prediction of oscillatory-based mechanisms in
event timing, which implicate the phase of oscillations in
timing precision (Gallistel, 1990). This, however, remains
an open and very difficult question to address empirically,
one for which a set of dedicated experiments—including
animal work—would be needed.
Why Do Participants Not Correct Temporal Errors
in the Presence of Temporal Information?
Although previous reports suggest that temporal infor-
mation coded by β power is present at the interval onset,
it is not clear when that information is accessible for the
inference of temporal errors: already before or only after
R2? Only SOJ predicted changes in slow evoked activity
before R2. As FOJ did not predict slow evoked activity,
this information did not appear relevant to the termina-
tion of R2, suggesting that slow activity biases SOJ, with-
out FOJ contribution. Together with the post-R2 α power
scaling with FOJ and SOJ, our results suggest that partic-
ipants may only have access to their temporal errors post-
R2. Notably, the notion of readout is not equivalent with
the access to temporal information before R2. However,
it is a viable possibility that the readout process is initial-
ized before the R2, the results of which become accessi-
ble after the R2.
Acknowledgments
This work was supported by an ERC-YStG-263584, an ANR10JCJC-
1904, and an ANR-16-CE37-0004-04 to V. v. W. We thank the mem-
bers of UNIACT and the medical staff at NeuroSpin for their help
in recruiting and scheduling participants. We thank Clémence
Roger for her initial contributions to the study and members of
UNICOG for fruitful discussions. Preliminary results were pre-
sented at Society for Neuroscience (2016).
Reprint requests should be sent to Tadeusz W. Kononowicz,
CEA/DRF NeuroSpin - INSERM Cognitive Neuroimaging Unit,
Bât 145 Point Courrier 156, Gif s/Yvette F-91191, France, or
via e-mail: t.w.kononowicz@icloud.com.
REFERENCES
Akdoğan, B., & Balcı, F. (2017). Are you early or late?: Temporal
error monitoring. Journal of Experimental Psychology:
General, 146, 347–361.
Balcı, F., Freestone, D., & Gallistel, C. R. (2009). Risk
assessment in man and mouse. Proceedings of the National
Academy of Sciences, U.S.A., 106, 2459–2463.
Bell, A. J., & Sejnowski, T. J. (1995). An information-
maximization approach to blind separation and blind
deconvolution. Neural Computation, 7, 1129–1159.
Brainard, D. H. (1997). The psychophysics toolbox. Spatial
Vision, 10, 433–436.
Cavanagh, J. F., & Frank, M. J. (2014). Frontal theta as a mechanism
for cognitive control. Trends in Cognitive Sciences, 18, 414–421.
Cleeremans, A., Timmermans, B., & Pasquali, A. (2007).
Consciousness and metarepresentation: A computational
sketch. Neural Networks, 20, 1032–1039.
Cohen, M. X. (2014). A neural microcircuit for cognitive conflict
detection and signaling. Trends in Neurosciences, 37,
480–490.
Cohen, M. X., & Cavanagh, J. F. (2011). Single-trial regression
elucidates the role of prefrontal theta oscillations in response
conflict. Frontiers in Psychology, 2, 30.
Dale, A. M., Liu, A. K., Fischl, B. R., Buckner, R. L., Belliveau, J. W.,
Lewine, J. D., et al. (2000). Dynamic statistical parametric
mapping: Combining FMRI and MEG for high-resolution
imaging of cortical activity. Neuron, 26, 55–67.
De Martino, B., Fleming, S. M., Garrett, N., & Dolan, R. J.
(2013). Confidence in value-based choice. Nature
Neuroscience, 16, 105–110.
Engel, A. K., & Fries, P. (2010). Beta-band oscillations—
Signaling the status quo? Current Opinion in Neurobiology,
20, 156–165.
Falkenstein, M., Hohnsbein, J., Hoormann, J., & Blanke, L.
(1991). Effects of crossmodal divided attention on late ERP
components. II. Error processing in choice reaction tasks.
Electroencephalography and Clinical Neurophysiology, 78,
447–455.
Foote, A. L., & Crystal, J. D. (2007). Metacognition in the rat.
Current Biology, 17, 551–555.
Flavell, J. H. (1979). Metacognition and cognitive monitoring: A
new area of cognitive–developmental inquiry. American
Psychologist, 34, 906–911.
Fleming, S. M., & Daw, N. D. (2017). Self-evaluation of decision-
making: A general Bayesian framework for metacognitive
computation. Psychological Review, 124, 91–114.
Fleming, S. M., & Dolan, R. J. (2012). The neural basis of
metacognitive ability. Philosophical Transactions of the
Royal Society of London, Series B, Biological Sciences, 367,
1338–1349.
Fleming, S. M., Dolan, R. J., & Frith, C. D. (2012).
Metacognition: Computation, biology and function.
Philosophical Transactions of the Royal Society of London,
Series B, Biological Sciences, 367, 1280–1286.
Fleming, S. M., Weil, R. S., Nagy, Z., Dolan, R. J., & Rees, G.
(2010). Relating introspective accuracy to individual
differences in brain structure. Science, 329, 1541–1543.
Fischl, B., Salat, D. H., van der Kouwe, A. J., Makris, N.,
Ségonne, F., Quinn, B. T., et al. (2004). Sequence-
independent segmentation of magnetic resonance images.
Neuroimage, 23, S69–S84.
Gallistel, C. R. (1990). The organization of learning.
Cambridge, MA: MIT Press.
Gehring, W. J., Goss, B., Coles, M. G. H., Meyer, D. E., &
Donchin, E. (1993). A neural system for error detection and
compensation. Psychological Science, 4, 385–390.
Genovese, C. R., Lazar, N. A., & Nichols, T. (2002).
Thresholding of statistical maps in functional neuroimaging
using the false discovery rate. Neuroimage, 15, 870–878.
Grabot, L., Kononowicz, T. W., La Tour, T. D., Gramfort, A.,
Doyère, V., & van Wassenhove, V. (2019). The strength of
alpha–beta oscillatory coupling predicts motor timing
precision. Journal of Neuroscience, 39, 3277–3291.
Gramfort, A., Luessi, M., Larson, E., Engemann, D. A., Strohmeier,
D., Brodbeck, C., et al. (2014). MNE software for processing
MEG and EEG data. Neuroimage, 86, 446–460.
Holroyd, C. B., & Coles, M. G. (2002). The neural basis of human
error processing: Reinforcement learning, dopamine, and the
error-related negativity. Psychological Review, 109, 679–709.
Ivry, R. B., & Schlerf, J. E. (2008). Dedicated and intrinsic
models of time perception. Trends in Cognitive Sciences, 12,
273–280.
Kononowicz and van Wassenhove
1655
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jantzen, K. J., Ratcliff, B. R., & Jantzen, M. G. (2018). Cortical
networks for correcting errors in sensorimotor
synchronization depend on the direction of asynchrony.
Journal of Motor Behavior, 50, 235–248.
Jovicich, J., Czanner, S., Greve, D., Haley, E., van der Kouwe,
A., Gollub, R., et al. (2006). Reliability in multi-site
structural MRI studies: Effects of gradient non-linearity
correction on phantom and human data. Neuroimage, 30,
436–443.
Karmarkar, U. R., & Buonomano, D. V. (2007). Timing in the
absence of clocks: Encoding time in neural network states.
Neuron, 53, 427–438.
Kilavik, B. E., Zaepffel, M., Brovelli, A., MacKay, W. A., & Riehle, A.
(2013). The ups and downs of β oscillations in sensorimotor
cortex. Experimental Neurology, 245, 15–26.
Kim, Y. C., Han, S. W., Alberico, S. L., Ruggiero, R. N., De Corte,
B., Chen, K. H., et al. (2017). Optogenetic stimulation of
frontal D1 neurons compensates for impaired temporal
control of action in dopamine-depleted mice. Current
Biology, 27, 39–47.
Komura, Y., Nikkuni, A., Hirashima, N., Uetake, T., & Miyamoto,
A. (2013). Responses of pulvinar neurons reflect a subject’s
confidence in visual categorization. Nature Neuroscience,
16, 749–755.
Kononowicz, T. W., Roger, C., & van Wassenhove, V. (2019).
Temporal metacognition as the decoding of self-generated
brain dynamics. Cerebral Cortex, 29, 4366–4380.
Kononowicz, T. W., & van Rijn, H. (2015). Single trial β
oscillations index time estimation. Neuropsychologia, 75,
381–389.
Kulashekhar, S., Pekkola, J., Palva, J. M., & Palva, S. (2016). The
role of cortical beta oscillations in time estimation. Human
Brain Mapping, 37, 3262–3281.
Laje, R., & Buonomano, D. V. (2013). Robust timing and motor
patterns by taming chaos in recurrent neural networks.
Nature Neuroscience, 16, 925–933.
Lak, A., Costa, G. M., Romberg, E., Koulakov, A. A., Mainen,
Z. F., & Kepecs, A. (2014). Orbitofrontal cortex is required
for optimal waiting based on decision confidence.
Neuron, 84, 190–201.
Levitt, H. (1971). Transformed up-down methods in
psychoacoustics. Journal of the Acoustical Society of
America, 49, 467–477.
Lewis, P. A., & Miall, R. C. (2003). Distinct systems for
automatic and cognitively controlled time measurement:
Evidence from neuroimaging. Current Opinion in
Neurobiology, 13, 250–255.
Menon, V., Adleman, N. E., White, C. D., Glover, G. H., & Reiss,
A. L. (2001). Error-related brain activation during a go/nogo
response inhibition task. Human Brain Mapping, 12,
131–143.
Miltner, W. H., Braun, C. H., & Coles, M. G. (1997). Event-
related brain potentials following incorrect feedback in a
time-estimation task: Evidence for a generic neural system for
error detection. Journal of Cognitive Neuroscience, 9,
788–798.
Miyamoto, K., Osada, T., Setsuie, R., Takeda, M., Tamura, K.,
Adachi, Y., et al. (2017). Causal neural network of
metamemory for retrospection in primates. Science, 355,
188–193.
Narayanan, N. S., & Laubach, M. (2006). Top-down control of
motor cortex ensembles by dorsomedial prefrontal cortex.
Neuron, 52, 921–931.
Nieuwenhuis, S., Ridderinkhof, K. R., Blom, J., Band, G. P., &
Kok, A. (2001). Error-related brain potentials are differentially
related to awareness of response errors: Evidence from an
antisaccade task. Psychophysiology, 38, 752–760.
Palva, S., & Palva, J. M. (2012). Discovering oscillatory
interaction networks with M/EEG: Challenges and
breakthroughs. Trends in Cognitive Sciences, 16, 219–230.
Praamstra, P., Turgeon, M., Hesse, C. W., Wing, A. M., &
Perryer, L. (2003). Neurophysiological correlates of error
correction in sensorimotor-synchronization. Neuroimage,
20, 1283–1297.
Rogerson, P. (2001). Statistical methods for geography. Los
Angeles, CA: Sage.
Scheffers, M. K., & Coles, M. G. H. (2000). Performance
monitoring in a confusing world: Error-related brain activity,
judgments of response accuracy, and types of errors. Journal
of Experimental Psychology: Human Perception and
Performance, 26, 141–151.
Shekhar, M., & Rahnev, D. (2018). Distinguishing the roles of
dorsolateral and anterior PFC in visual metacognition.
Journal of Neuroscience, 38, 5078–5087.
Simen, P., Balci, F., de Souza, L., Cohen, J. D., & Holmes, P.
(2011). A model of interval timing by neural integration.
Journal of Neuroscience, 31, 9238–9253.
Soranzo, A., & Grassi, M. (2014). PSYCHOACOUSTICS: A
comprehensive MATLAB toolbox for auditory testing.
Frontiers in Psychology, 5, 712.
Taulu, S., & Simola, J. (2006). Spatiotemporal signal space
separation method for rejecting nearby interference in MEG
measurements. Physics in Medicine and Biology, 51,
1759–1768.
Luu, P., Flaisch, T., & Tucker, D. M. (2000). Medial frontal
Tremblay, A., & Newman, A. J. (2015). Modeling nonlinear
cortex in action monitoring. Journal of Neuroscience, 20,
464–469.
Maris, E., & Oostenveld, R. (2007). Nonparametric statistical
testing of EEG- and MEG-data. Journal of Neuroscience
Methods, 164, 177–190.
Marti, S., Sackur, J., Sigman, M., & Dehaene, S. (2010). Mapping
introspection’s blind spot: Reconstruction of dual-task
phenomenology using quantified introspection. Cognition,
115, 303–313.
McCurdy, L. Y., Maniscalco, B., Metcalfe, J., Liu, K. Y., de Lange,
F. P., & Lau, H. (2013). Anatomical coupling between distinct
metacognitive systems for memory and visual perception.
Journal of Neuroscience, 33, 1897–1906.
Meckler, C., Allain, S., Carbonnell, L., Hasbroucq, T., Burle,
B., & Vidal, F. (2010). Motor inhibition and response
expectancy: A Laplacian ERP study. Biological Psychology,
85, 386–392.
Meegan, D. V., Aslin, R. N., & Jacobs, R. A. (2000). Motor timing
learned without motor training. Nature Neuroscience, 3,
860–862.
relationships in ERP data using mixed-effects regression with
R examples. Psychophysiology, 52, 124–139.
Ullsperger, M., Fischer, A. G., Nigbur, R., & Endrass, T.
(2014). Neural mechanisms and temporal dynamics of
performance monitoring. Trends in Cognitive Sciences, 18,
259–267.
van Driel, J., Ridderinkhof, K. R., & Cohen, M. X. (2012). Not all
errors are alike: Theta and alpha EEG dynamics relate to
differences in error-processing dynamics. Journal of
Neuroscience, 32, 16795–16806.
van Rij, J., Wieling, M., Baayen, R. H., & van Rijn, H. (2016)
Package ‘itsadug’. Retrieved from http://cran.r-project.org/
web/packages/itsadug/itsadug.pdf.
van Wassenhove, V. (2009). Minding time in an amodal
representational space. Philosophical Transactions of the Royal
Society of London, Series B, Biological Sciences, 364, 1815–1830.
Whitmarsh, S., Barendregt, H., Schoffelen, J. M., & Jensen, O.
(2014). Metacognitive awareness of covert somatosensory
attention corresponds to contralateral alpha power.
Neuroimage, 85, 803–809.
1656
Journal of Cognitive Neuroscience
Volume 31, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Wiener, M., Parikh, A., Krakow, A., & Coslett, H. B. (2018). An
intrinsic role of beta oscillations in memory for time
estimation. Scientific Reports, 8, 7992.
Wiener, M., Turkeltaub, P., & Coslett, H. B. (2010). The image of
time: A voxel-wise meta-analysis. Neuroimage, 49, 1728–1740.
Wood, S. N. (2003). Thin plate regression splines. Journal of the
Royal Statistical Society of London, Series B (Statistical
Methodology), 65, 95–114.
Wood, S. N. (2009). Package ‘mgcv’. Retrieved from http://cran.
r-project.org/web/packages/mgcv/mgcv.pdf.
Wood, S. N. (2011). Fast stable restricted maximum
likelihood and marginal likelihood estimation of
semiparametric generalized linear models. Journal of the
Royal Statistical Society, Series B (Statistical
Methodology), 73, 3–36.
Wood, S. N. (2017). Generalized additive models: An
introduction with R. Boca Raton, FL: CRC Press.
Ye, Q., Zou, F., Lau, H., Hu, Y., & Kwok, S. C. (2018). Causal
evidence for mnemonic metacognition in human precuneus.
Journal of Neuroscience, 38, 6379–6387.
Yeung, N., Botvinick, M. M., & Cohen, J. D. (2004). The neural
basis of error detection: Conflict monitoring and the error-
related negativity. Psychological Review, 111, 931–959.
Zakay, D., & Block, R. A. (1995). An attentional-gate model
of prospective time estimation. Time and the dynamic
control of behavior, 167–178.
Zatorre, R. J., Chen, J. L., & Penhune, V. B. (2007). When the
brain plays music: Auditory–motor interactions in music
perception and production. Nature Reviews Neuroscience,
8, 547–558.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
1
1
1
1
6
4
1
1
8
6
0
8
4
2
/
/
j
o
c
n
_
a
_
0
1
4
4
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Kononowicz and van Wassenhove
1657